Последовательное и параллельное соединение конденсаторов (ёмкостей)
Практически ни одно электронное устройство не обходится без конденсатора. Он может стоять на входе или выходе устройства, перед или после некоторых элементов. Применяется последовательное и параллельное соединение конденсаторов. Как и для чего их подключать тем или иным способом и будем обсуждать.
Содержание статьи
Что такое конденсатор и его основные характеристики
Конденсатор — это радиодеталь, которая работает как накопитель электрической энергии. Чтобы понятнее было, как он работает, его можно представить как своего рода небольшой аккумулятор. Обозначается двумя параллельными чёрточками.
Обозначения различных типов конденсаторов на схемах. Чаще всего из строя выходят электролитические конденсаторы, так что стоит запомнить их обозначение
Основная характеристика конденсатора любого типа — ёмкость. Это то количество заряда, которое он в состоянии накопить. Измеряется в Фарадах (сокращенно просто буква F или Ф), а вернее, в более «мелких» единицах:
- микрофарадах — мкФ это 10
- нанофарадах — нФ это 10-9 фарада;
- пикофарадах — пФ это 10-12 фарада.

Вторая важная характеристика — номинальное напряжение. Это то напряжение, при котором гарантирована длительная безотказная работа. Например, 4700 мкФ 35 В, где 35 В — это номинальное напряжение 35 вольт.
У крупных по размеру конденсаторов, ёмкость и напряжение указаны на корпусе
Нельзя ставить конденсатор в цепь с более высоким напряжением чем то, которое на нём указано. В противном случае он быстро выйдет из строя.
Можно использовать конденсаторы на 50 вольт вместо конденсаторов на 25 вольт. Но это порой нецелесообразно, так как те, которые рассчитаны на более высокое напряжение, дороже, да и габариты у них больше.
Что он из себя представляет и как работает
В самом простейшем случае конденсатор состоит из двух токопроводящих пластин (обкладок), разделённых слоем диэлектрика.
Между обкладками находится слой диэлектрика — материала плохо проводящего электрический ток
На пластины подаётся постоянный или переменный ток.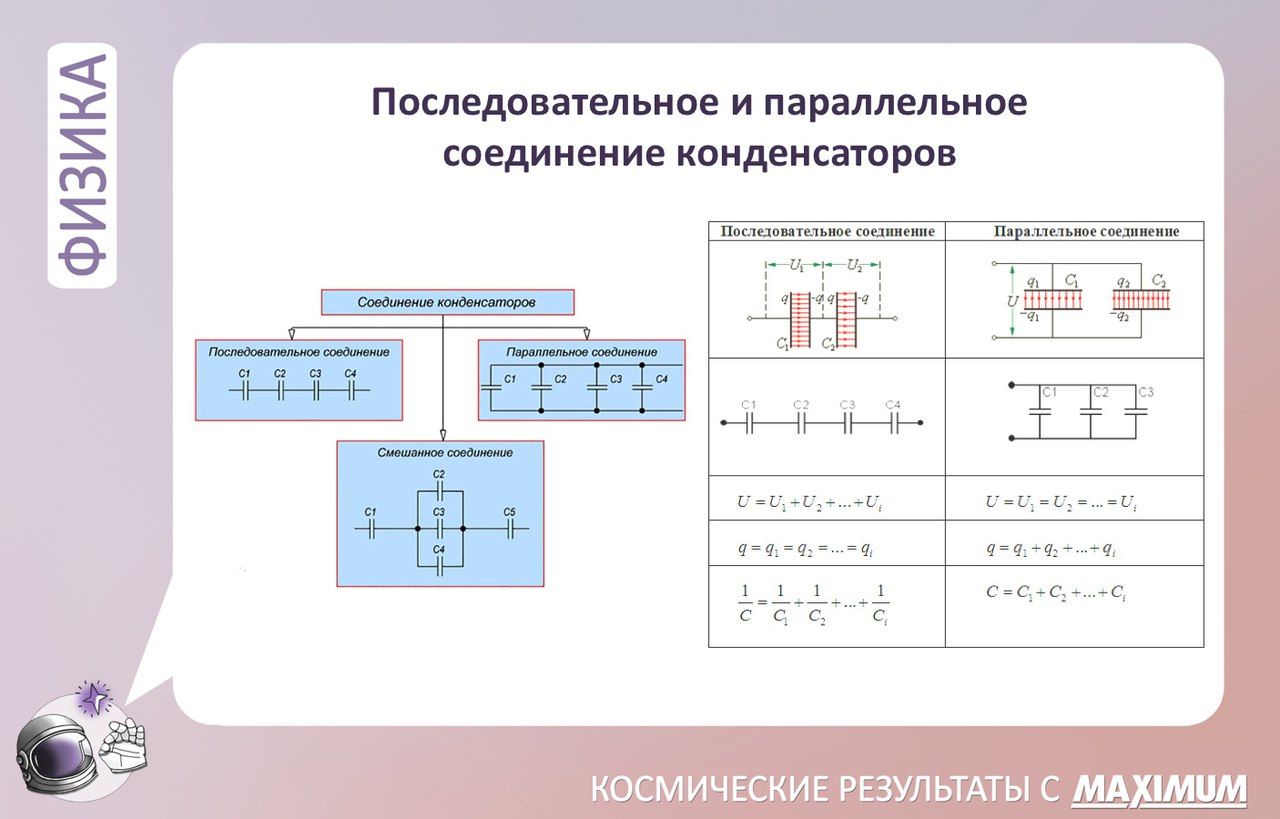 Вначале, пока энергия накапливается, потребление энергии конденсатором высокое. По мере «наполнения» ёмкости оно снижается. Когда заряд набран полностью, токопотребления вообще нет, источник питания как бы отключается. В это время конденсатор сам начинает отдавать накопленный заряд. То есть, он на время становится своеобразным источником питания. Поэтому его и сравнивают с аккумулятором.
Вначале, пока энергия накапливается, потребление энергии конденсатором высокое. По мере «наполнения» ёмкости оно снижается. Когда заряд набран полностью, токопотребления вообще нет, источник питания как бы отключается. В это время конденсатор сам начинает отдавать накопленный заряд. То есть, он на время становится своеобразным источником питания. Поэтому его и сравнивают с аккумулятором.
Где и для чего используются
Как уже говорили, сложно найти схему без конденсаторов. Их применяют для решения самых разных задач:
- Для сглаживания скачков сетевого напряжения. В таком случае их ставят на входе устройств, перед микросхемами, которые требовательны к параметрам питания.
- Для стабилизации выходного напряжения блоков питания. В таком случае надо искать их перед выходом.
- Датчик прикосновения (тач-пады). В таких устройствах оной из «пластин» конденсаторов является человек. Вернее, его палец.
 Наше тело обладает определённой проводимостью. Это и используется в датчиках прикосновения.
Наше тело обладает определённой проводимостью. Это и используется в датчиках прикосновения. - Для задания необходимого ритма работы. Время заряда конденсаторов разной ёмкости отличается. При этом цикл заряд/разряд конденсатора остаётся величиной постоянной. Это и используется в цепях, где надо задавать определённый ритм работы.
- Ячейки памяти. Память компьютеров, телефонов и других устройств — это огромное количество маленьких конденсаторов. Если он заряжен — это единица, разряжен — ноль.
- Есть стартовые конденсаторы, которые помогают «разогнать» двигатель. Они накапливают заряд, потом резко его отдают, создавая требуемый «толчок» для разгона мотора.
- В фотовспышках. Принцип тот же. Сначала накапливается заряд, затем выдаётся, но преобразуется в свет.
Конденсаторы встречаются часто и область их применения широка. Но надо знать как правильно их подключить.
Как подключать конденсаторы
В электротехнике есть два основных вида соединения деталей — параллельное и последовательное. Конденсаторы также можно подключать по любому из указанных способов. Есть ещё особая — мостовая схема. Она имеет собственную область использования.
Конденсаторы также можно подключать по любому из указанных способов. Есть ещё особая — мостовая схема. Она имеет собственную область использования.
В схеме может быть последовательное и параллельное соединение конденсаторов
Параллельное подключение конденсаторов
При параллельном соединении все конденсаторы объединены двумя узлами. Чтобы параллельно подключить конденсаторы, скручиваем попарно их ножки, обжимаем пассатижами, потом пропаиваем. У некоторых конденсаторов большие корпуса (банки), а выводы маленькие. В таком случае используем провода (как на рисунке ниже).
Так физически выглядит параллельное подключение конденсаторов
Если конденсаторы электролитические, следите за полярностью. На них должны стоять «+» или «-«. При их параллельном подключении соединяем одноимённые выводы — плюс к плюсу, минус — к минусу.
Расчёт суммарной ёмкости
При параллельном подключении конденсаторов их номинальная ёмкость складывается. Просто суммируете номиналы всех подключённых элементов, сколько бы их ни было. Два, три, пять, тридцать. Просто складываем. Но следите, чтобы размерность совпадала. Например, складывать будем в микрофарадах. Значит, все значения переводим в микрофарады и только после этого суммируем.
Два, три, пять, тридцать. Просто складываем. Но следите, чтобы размерность совпадала. Например, складывать будем в микрофарадах. Значит, все значения переводим в микрофарады и только после этого суммируем.
Расчёт ёмкости при параллельном подключении конденсаторов
Когда на практике применяют параллельное соединение конденсаторов? Например, тогда, когда надо заменить «пересохший» или сгоревший, а нужного номинала нет и бежать в магазин некогда или нет возможности. В таком случае подбираем из имеющихся в наличии. В сумме они должны дать требуемое значение. Все их проверяем на работоспособность и соединяем по приведенному выше принципу.
Пример расчёта
Например, включили параллельно два конденсатора — 8 мкФ и 12 мкФ. Следуя формуле, их номиналы просто складываем. Получаем 8 мкФ + 12 мкФ = 20 мкФ. Это и будет суммарная ёмкость в данном случае.
Пример расчёта конденсаторов при параллельном подключении
Последовательное соединение
Последовательным называется соединение, когда выход одного элемента соединяется со входом другого. Сравнить можно с вагонами или цепочкой из лампочек. По такому же принципу последовательно соединяют и конденсаторы.
Сравнить можно с вагонами или цепочкой из лампочек. По такому же принципу последовательно соединяют и конденсаторы.
Вот что значит последовательно соединить конденсаторы
При подключении полярных электролитических «кондеров» надо следить за соблюдением полярности. Плюс первого конденсатора подаете на минус второго и так далее. Выстраиваете цепочку.
Существуют неполярные (биполярные) электролитические конденсаторы. При их соединении нет необходимости соблюдать полярность.
Как определить ёмкость последовательно соединенных конденсаторов
При последовательном соединении конденсаторов суммарная ёмкость элементов будет меньше самого маленького номинала в цепочке. То есть, ёмкость последовательно соединённых конденсаторов уменьшается. Это также может пригодиться при ремонте техники — замена конденсатора требуется часто.
Последовательно соединённые конденсаторы
Использовать формулу расчёта приведённую выше не очень удобно, поэтому её обычно используют в преобразованном виде:
Формула расчёта ёмкости при последовательном соединении
Это формула для двух элементов. При увеличении их количества она становится значительно сложнее. Хотя, редко можно встретить больше двух последовательных конденсаторов.
При увеличении их количества она становится значительно сложнее. Хотя, редко можно встретить больше двух последовательных конденсаторов.
Пример расчёта
Какая суммарная ёмкость будет если конденсаторы на 12 мкФ и 8 мкФ соединить последовательно? Считаем: 12*8 / (12+8) = 96 / 20 = 4,8 мкФ. То есть, такая цепочка соответствует номиналу 4,8 мкФ.
Пример расчета ёмкости при последовательном подключении конденсаторов
Как видите, значение меньше чем самый маленький номинал в последовательности. А если подключить таким образом два одинаковых конденсатора, то результат будет вполовину меньше номинала. Например, рассчитаем для двух ёмкостей по 12 мкФ. Получим: 12*12 / (12 + 12) = 144 / 24 = 6 мкФ. Проверим для 8 мкФ. Считаем: 8*8 / (8+8) = 64 / 16 = 4 мкФ. Закономерность подтвердилась. Это правило можно использовать при подборе номинала.
Почему электролитические конденсаторы выходят из строя и что делать
Зачастую, чтобы отремонтировать вышедшую из строя электронную технику, достаточно найти и заменить вздувшиеся конденсаторы.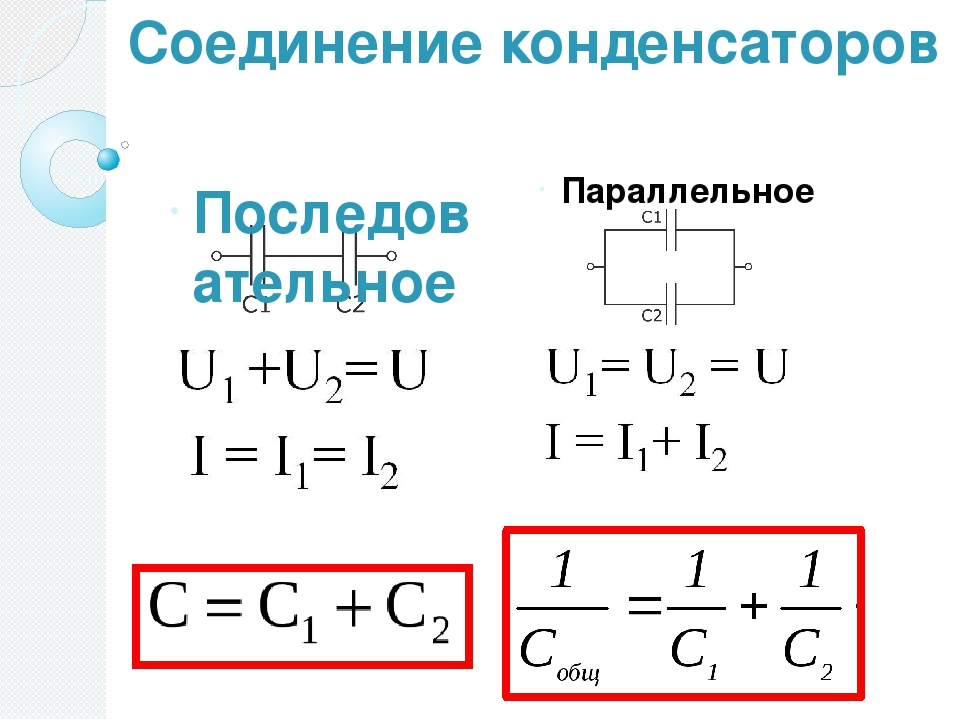
Электролитические конденсаторы имеют специальные насечки на верхушке корпуса, чтобы при выходе из строя избежать взрыва
Высыхает электролит не только во время работы. Даже просто «от времени». Это конструктивная особенность электролитических конденсаторов. Поэтому не стоит ставить выпаянные из старых схем конденсаторы или те, которые несколько лет (или десятков лет) хранятся в мастерской. Лучше купить «свежий», но проверьте дату производства.
Можно ли продлить срок эксплуатации конденсаторов? Можно. Надо улучшить теплоотвод. Чем меньше греется электролит, тем медленнее высыхает. Поэтому не стоит ставить аппаратуру вблизи отопительных приборов.
Для улучшения отвода тепла ставят радиаторы
Второе — надо следить за тем, чтобы хорошо работали кулера. Третье — если рядом стоят детали, которые активно греются во время работы, надо конденсаторы каким-то образом от температуры защитить.
Как подобрать замену
Если часто приходится менять один и тот же конденсатор, его лучше заменить на более «мощный» — той же ёмкости, но на большее напряжение. Например, вместо конденсатора на 25 вольт, поставить конденсатор на 35 вольт. Только надо иметь в виду, что более мощные конденсаторы имеют большие размеры. Не всякая плата позволяет сделать такую замену.
Конденсатор той же ёмкости, но рассчитанный на большее напряжение, имеет больший размер
Можно поставить параллельно несколько конденсаторов с тем же напряжением, подобрав номиналы так, чтобы получить требуемую ёмкость. Что это даст? Лучшую переносимость пульсаций тока, меньший нагрев и, как следствие, более продолжительный срок службы.
Что будет, если поставить конденсатор большей ёмкости?
Часто приходит в голову идея поставить вместо сгоревшего или вздувшегося конденсатор большей ёмкости.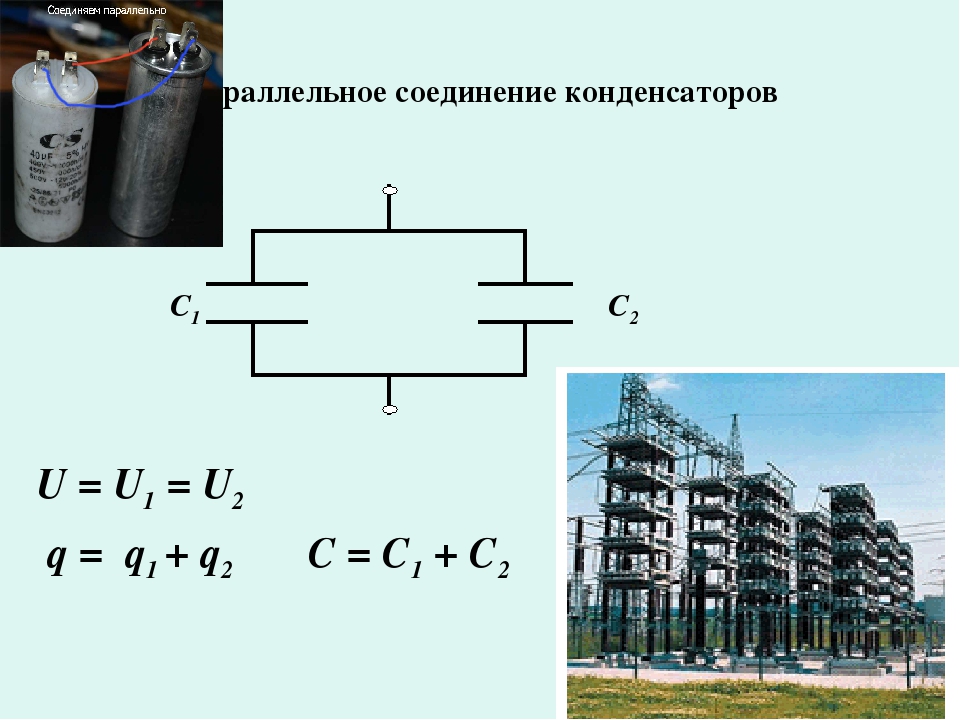 Ведь он должен меньше греться. Так, во всяком случае, кажется. Ёмкость практически никак не связана со степенью нагрева корпуса. И в этом выигрыша не будет.
Ведь он должен меньше греться. Так, во всяком случае, кажется. Ёмкость практически никак не связана со степенью нагрева корпуса. И в этом выигрыша не будет.
Устройство электролитического конденсатора
По нормативным документам отклонение номинала конденсаторов допускается в пределах 20%. Вот на эту цифру можете спокойно ставить больше/меньше. Но это может привести к изменениям в работе устройства. Так что лучше найти «родной» номинал. И учтите, что не всегда можно ставить большую ёмкость. Можно если конденсатор стоит на входе и сглаживает скачки питания. Вот тут большая ёмкость уместна, если для её установки достаточно места. Это точно нельзя делать там, где конденсатор работает как фильтр, отсекающий заданные частоты.
Можно менять на ту же ёмкость, но чуть более высокое напряжение. Это имеет смысл. Но размеры такого конденсатора будут намного больше. Не в любую плату получится его установить. И учтите, что корпус его не должен соприкасаться с другими деталями.
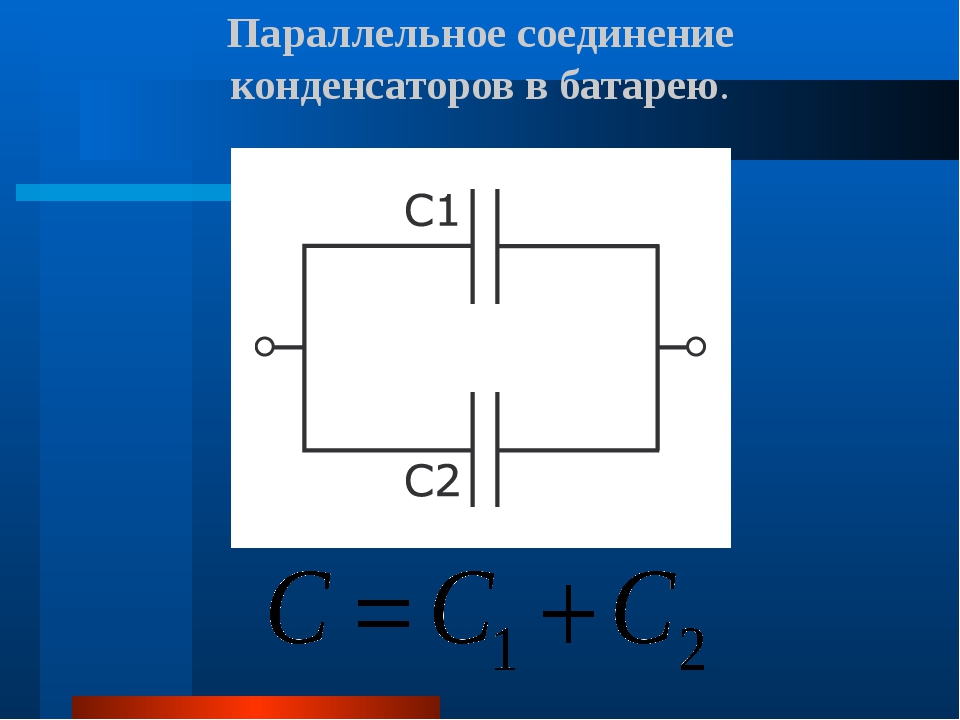
Параллельное соединение конденсаторов | Физика.
 Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко
Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, краткоВ условиях массового применения конденсаторов невозможно организовать изготовление конденсаторов всех возможных значений электроемкости и рабочей разности потенциалов на обкладках. Для получения необходимых параметров стандартные конденсаторы определенным образом соединяют между собой. На практике применяют параллельное, последовательное и смешанное соединение конденсаторов.
| Рис. 4.76. Параллельное соединение конденсаторов |
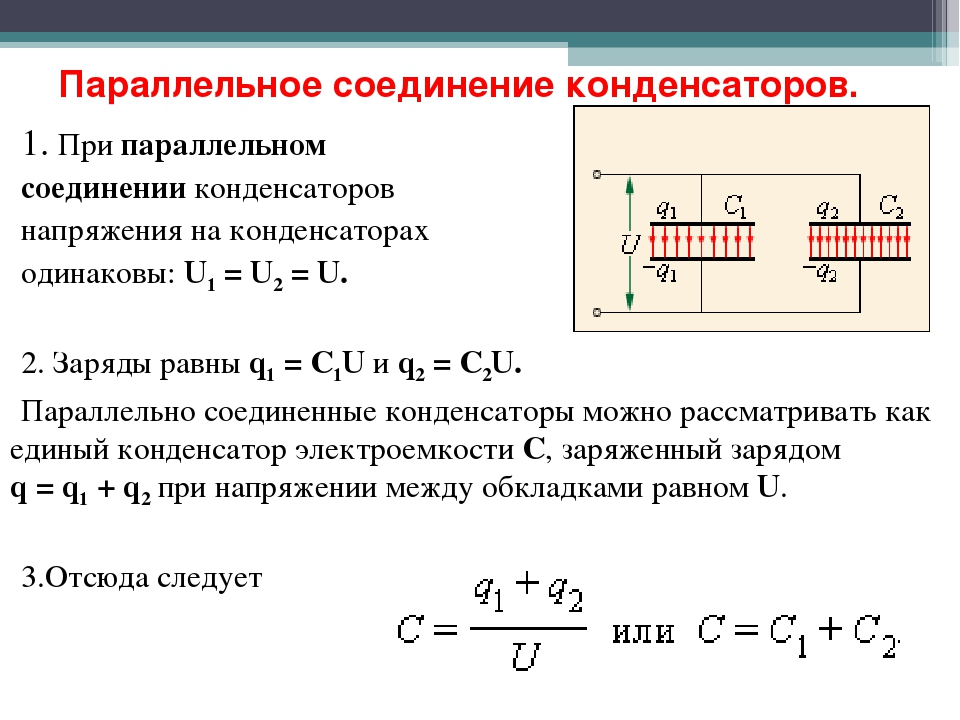
При параллельном соединении конденсаторов все обкладки соединяются в две группы, в каждую из которых входит по одной обкладке каждого конденсатора. На рис. 4.76 изображена схема такого соединения. Каждая группа обкладок имеет одинаковый потенциал.
Если полученную батарею параллельных конденсаторов зарядить, то между обкладками каждого конденсатора будут одинаковые разности потенциалов
Δφ1 = Δφ2 = Δφ3 = … = Δφn.
Общий заряд на пластинах будет равен сумме зарядов каждого конденсатора:
Q = Q1 + Q2 + Q3 + … + Qn.
Учитывая, что Q = CΔφ, получим
CΔφ = C1Δφ + C2Δφ + C3Δφ + … + CnΔφ,
или
C = C1 + C2 + C3 + …+ Cn.
Электроемкость батареи параллельно соединенных конденсаторов равна сумме электроемкостей всех конденсаторов.
| Рис. 4.78. Строение и схема плоского конденсатора с несколькими пластинами |
Если батарея состоит из n конденсаторов емкостью Q каждый, то емкость батареи
C = nC0.
Увеличение емкости при параллельном соединении конденсаторов можно объяснить также тем, что при этом увеличивается площадь пластин, которые имеют одинаковые потенциалы.
Емкость конденсаторов можно увеличить путем их параллельного соединения. Материал с сайта http://worldofschool.ru
Примером параллельного соединения конденсаторов является плоский конденсатор, имеющий n пластин, разделенных диэлектриком (рис. 4.78). Пластины этого конденсатора через одну соединены между собой. Но количество этих конденсаторов всегда на один меньше, чем пластин. Из рис. 4.78, а видно, что шесть пластин образуют пять конденсаторов, соединенных параллельно (рис. 4.78, б). Каждая внутренняя пластина является одновременно обкладкой двух конденсаторов. Поэтому при вычислении электроемкости плоского сложного конденсатора пользуются формулами:
C = (n — 1)C0,
C = (εε0S / d) • (n — 1).
где C — общая электроемкость; Q — электроемкость конденсатора из двух пластин; n — общее количество пластин.
На этой странице материал по темам:Сообщение по физике применение конденсатора
Закон параллельного соединения конденсаторов
Физика параллельное соединение катушки и конденсатора лабораторная работа
Физика -параллельное соединение нескольких конденсаторов
Параллельное соединение конденсатора применяют
С какой целью конденсаторы объединяют в батареи?
Чего достигают, соединяя конденсаторы параллельно?
Чему равна общая электроемкость соединенных параллельно конденсаторов?
Как рассчитать емкость плоского конденсатора из многих пластин?
Физика — 11
• Общая ёмкость цепи, состоящей из последовательно соединенных n конденсаторов одинаковой ёмкости, в n раз меньше ёмкости одного конденсатора:
Cпосл = C
n.
• Напряжение и энергия последовательно соединенных конденсаторов обратно пропорциональны их электрическим ёмкостям:
U = q
C => U1
U2= C2
C1;
W = q2
2C => W1
W2= C2
C1
Параллельное соединение конденсаторов
При параллельном соединении положительно заряженные пластины всех конденсаторов соединяют в одной точке, а отрицательно заряженные пластины в другой точке (d).
• Общий заряд параллельно соединенных конденсаторов равен сумме зарядов отдельных конденсаторов:
q = q1 + q2
• Напряжения на концах параллельно соединенных конденсаторов одинаковы:
U1 = U2 = U
• Общая электроёмкость батареи параллельно соединенных конденсаторов равна сумме электроёмкостей отдельных конденсаторов:
Cпар = C1 + C2.
•Общая электроёмкость n числа параллельно соединенных одинаковых конденсаторов в n раз больше электроёмкости одного конденсатора:
Cпар = nC.
• Электрические заряды и энергии параллельно соединенных конденсаторов прямо пропорциональны их электроёмкостям:
q = UC => q1
q2 = C1
C2;
W= CU2
2 => W1
W2= C1
C2.
Электрическая емкость (страница 1)
Решение:
При перемещении пластины емкость конденсатора в данный момент времени определяется той частью площади пластин, по которой они перекрывают друг друга. В моменты времени t1 и t2 площади
где l=10 см-длина стороны пластины.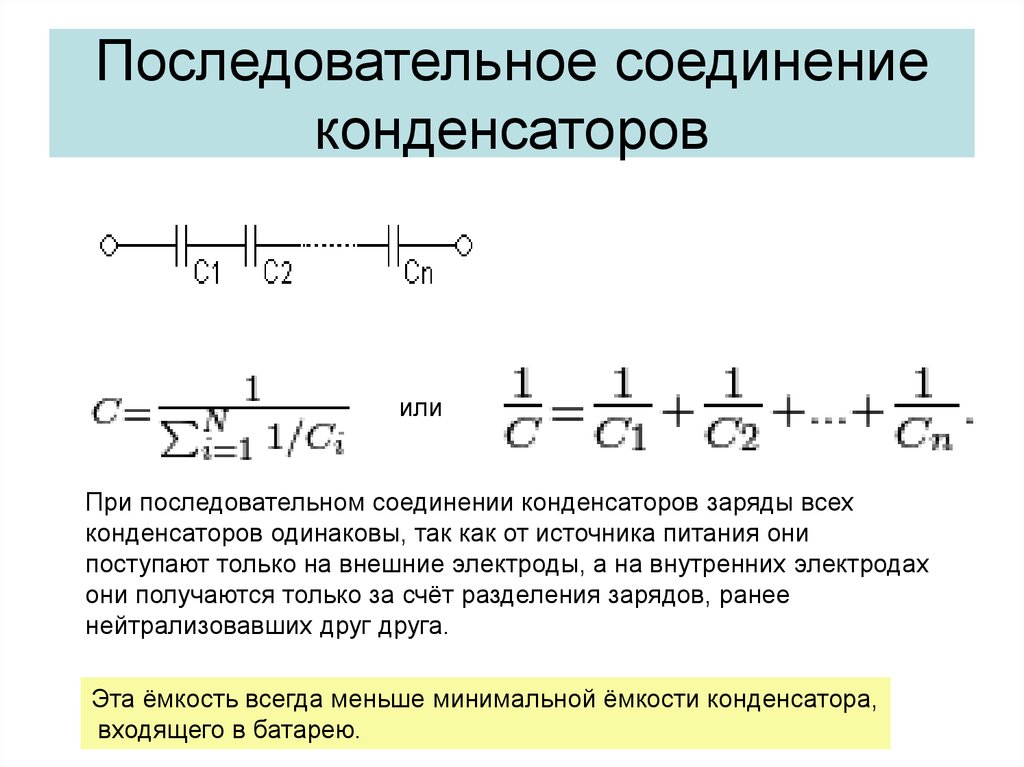 В эти моменты времени конденсатор имеет емкости
В эти моменты времени конденсатор имеет емкости
а заряды на его пластинах
11 Найти заряд, который нужно сообщить двум параллельно соединенным конденсаторам с емкостями C1 = 2 мкФ и С2=1 мкФ, чтобы зарядить их до разности потенциалов V=20кВ.
Решение:
Общий заряд параллельно соединенных конденсаторов
12 Два одинаковых плоских конденсатора соединены параллельно и заряжены до разности потенциалов V0 = 6 В. Найти разность потенциалов V между пластинами конденсаторов, если после отключения конденсаторов от источника тока у одного конденсатора уменьшили расстояние между пластинами вдвое.
Решение:
13 Два конденсатора с емкостями С1 = 1 мкФ и С2 = 2мкФ зарядили до разностей потенциалов V1=20B и V2 = 50 В. Найти разность потенциалов V после соединения — конденсаторов одноименными полосами.
Решение:
14 Конденсатор емкости C1 = 20 мкФ, заряженный до разности потенциалов V1 = 100B, соединили параллельно с заряженным до разности потенциалов V1=40 В конденсатором, емкость которого С2 неизвестна (соединили одноименно заряженные обкладки конденсаторов). Найти емкость С2 второго конденсатора, если разность потенциалов между обкладками конденсаторов после соединения оказалась равной V=80 В.
Решение:
15 Конденсатор емкости С1=4мкФ, заряженный до разности потенциалов V1 = 10B, соединен параллельно с заряженным до разности потенциалов V2 = 20 В конденсатором емкости С2 = 6 мкФ (соединили разноименно заряженные обкладки конденсаторов). Какой заряд окажется на пластинах первого конденсатора после соединения?
Решение:
Заряды конденсаторов до их соединения q1 = C1V1 и q2 = C2V2. После соединения разноименно заряженных обкладок конденсаторов общий заряд q = |q2-q1| = (C1 + C2)V и заряд первого конденсатора где V-разность потенциалов между обкладками конденсаторов после соединения; отсюда
16 Конденсатор, заряженный до разности потенциалов V1 = 20 В, соединили параллельно с заряженным до разности потенциалов V2 = 4 В конденсатором емкости С2 = 33 мкФ (соединили разноименно заряженные обкладки конденсаторов). Найти емкость С1 первого конденсатора, если разность потенциалов между обкладками конденсаторов после их соединения V=2 В.
Решение:
После соединения разноименных обкладок общий заряд q = CV равен разности зарядов q1 = C1V1 и q2 = C2V2 отдельных конденсаторов, где С=С1 + С2 — общая емкость после соединения. Таким образом,
17 Конденсатор емкости С1 = 1 мкФ, заряженный до разности потенциалов V1 = 100B, соединили с конденсатором емкости С2 = 2 мкФ, разность потенциалов V2 на обкладках которого неизвестна (соединили разноименно заряженные обкладки конденсаторов). Найти разность потенциалов V2, если разность потенциалов между обкладками конденсаторов после соединения оказалась равной V=200 В.
Найти разность потенциалов V2, если разность потенциалов между обкладками конденсаторов после соединения оказалась равной V=200 В.
Решение:
До соединения заряды первого и второго конденсаторов
После соединения разноименных обкладок общий заряд
Двойной знак мы здесь поставили потому, что заранее не известно, какой из зарядов, q2 или q1 больше; отсюда
Решение со знаком минус соответствует случаю, когда знаки зарядов на пластинах первого конденсатора после соединения пластин не меняются, а со знаком плюс-случаю, когда эти знаки становятся обратными. Так как в нашем случае , а величина |V2| должна быть всегда положительной, то существует лишь одно решение-со знаком плюс. В результате |V2| = 350 В.
18 Два проводящих шара с радиусами R1 и R2 расположены так, что расстояние между ними во много раз больше радиуса большего шара. На шар радиуса R1 помещен заряд q. Каковы будут заряды на шарах после соединения их проводником, если второй шар не был заряжен? Емкостью проводника, соединяющего шары, пренебречь.
Каковы будут заряды на шарах после соединения их проводником, если второй шар не был заряжен? Емкостью проводника, соединяющего шары, пренебречь.
Решение:
19 Два проводящих шара с радиусами R1 = 8см и R2 = 20 см, находящихся на большом расстоянии друг от друга, имели электрические заряды q1=40 нКл и q2=— 20 нКл. Как перераспределятся заряды, если шары соединить проводником? Емкостью проводника, соединяющего шары, пренебречь.
Решение:
Соединение шаров проводником эквивалентно параллельному соединению конденсаторов. После соединения
20 Два проводящих шара с радиусами R1 = 10см и R2 = 5см, заряженных до потенциалов φ1=20B и φ2=10В, соединяются проводником. Найти поверхностные плотности зарядов на шарах σ1 и σ2 после их соединения. Расстояние между шарами велико по сравнению с их радиусами. Емкостью проводника, соединяющего шары, пренебречь.
Емкостью проводника, соединяющего шары, пренебречь.
Решение:
Заряды на шарах до и после соединения Общий потенциал шаров после соединения определим из условия сохранения заряда
Заряды на первом и втором шарах после соединения
Поверхностные плотности зарядов на шарах
21 Плоский воздушный конденсатор, заряженный до разности потенциалов V0 = 800 В, соединили параллельно с таким же по размерам незаряженным конденсатором, заполненным диэлектриком. Какова диэлектрическая проницаемость e диэлектрика, если после соединения разность потенциалов между пластинами конденсаторов оказалась равной V=100В?
Решение:
22 Найти емкость С трех плоских воздушных конденсаторов, соединенных параллельно. Размеры конденсаторов одинаковы: площадь пластины S=314 см2, расстояние между пластинами d=1 мм. Как изменится емкость трех конденсаторов, если пространство между пластинами одного конденсатора заполнить слюдой (диэлектрическая проницаемость ε1 = 7), а другого — парафином (диэлектрическая проницаемость ε2 = 2)?
Решение:
Емкость трех конденсаторов без диэлектрика При заполнении двух конденсаторов диэлектриками емкость трех конденсаторов
23 В заряженном плоском конденсаторе, отсоединенном от источника тока, напряженность электрического поля равна Е0. Половину пространства между пластинами конденсатора заполнили диэлектриком с диэлектрической проницаемостью ε (толщина диэлектрика равна расстоянию между пластинами). Найти напряженность электрического поля Е в пространстве между пластинами, свободном от диэлектрика.
Половину пространства между пластинами конденсатора заполнили диэлектриком с диэлектрической проницаемостью ε (толщина диэлектрика равна расстоянию между пластинами). Найти напряженность электрического поля Е в пространстве между пластинами, свободном от диэлектрика.
Решение:
Если d-расстояние между пластинами и С0 — емкость конденсатора без диэлектрика, то разность потенциалов между пластинами конденсатора (без диэлектрика) и заряд на пластинах Конденсатор, половина которого заполнена диэлектриком, можно рассматривать как два соединенных параллельно конденсатора (рис. 341), причем один не содержит диэлектрика и имеет емкость а в другом все пространство между пластинами заполнено диэлектриком, и поэтому его емкость Полная емкость конденсатора, половина которого заполнена диэлектриком, При отключенном источнике тока заряд на пластинах сохраняется, поэтому разность потенциалов между пластинами V=q/C, и напряженность электрического поля в пространстве между пластинами, свободном от диэлектрика,
24 Два последовательно соединенных конденсатора с емкостями C1 = 1 мкФ и С2 = 3 мкФ подключены к источнику тока с напряжением V =220 В. Найти напряжение на каждом конденсаторе.
Найти напряжение на каждом конденсаторе.
Решение:
Если V1 и V2 — напряжения на первом и втором конденсаторах, то V= V1 + V2, а заряды на них одинаковы и равны
q=C1V1=C2V2; отсюда
При последовательном соединении конденсаторов на конденсаторе меньшей емкости напряжение больше, чем на конденсаторе большей емкости.
25 Два последовательно соединенных конденсатора с емкостями C1 = 1 мкФ и С2 = 2 мкФ подключены к источнику тока с напряжением V =900 В. Возможна ли работа такой схемы, если напряжение пробоя конденсаторов Vпр = 500 В?
Решение:
Напряжения на первом и втором конденсаторах (см. задачу 24). Работать при указанном в условии задачи напряжении пробоя конденсаторов нельзя, ибо произойдет пробой первого, а затем и второго конденсаторов.
26 Два последовательно соединенных конденсатора подключены к источнику тока с напряжением V= 200 В (рис. 79). Один конденсатор имеет постоянную емкость C1 = 0,5 мкФ, а другой — переменную емкость С2 (от Cmin = 0,05 мкФ до Сmах = 0,5 мкФ). В каких пределах изменяется напряжение на переменном конденсаторе при изменении его емкости от минимальной до максимальной?
79). Один конденсатор имеет постоянную емкость C1 = 0,5 мкФ, а другой — переменную емкость С2 (от Cmin = 0,05 мкФ до Сmах = 0,5 мкФ). В каких пределах изменяется напряжение на переменном конденсаторе при изменении его емкости от минимальной до максимальной?
Решение:
При изменении емкости переменного конденсатора С2 от Cmin до Сmax, напряжение на нем V изменяется в пределах (см. задачу 24)
27 При последовательном соединении трех различных конденсаторов емкость цепи С0 = 1 мкФ, а при параллельном соединении емкость цепи С=11мкФ. Найти емкости конденсаторов С2 и С3, если емкость конденсатора С1 = 2 мкФ.
Решение:
28 При последовательном соединении трех различных конденсаторов емкость цепи С0 = 0,75 мкФ, а при параллельном соединении емкость цепи С = 7 мкФ. Найти емкости конденсаторов С2 и С3 и напряжения на них V2 и V3 (при последовательном соединении), если емкость конденсатора C1 = 3 мкФ, а напряжение на нем V1 = 20B.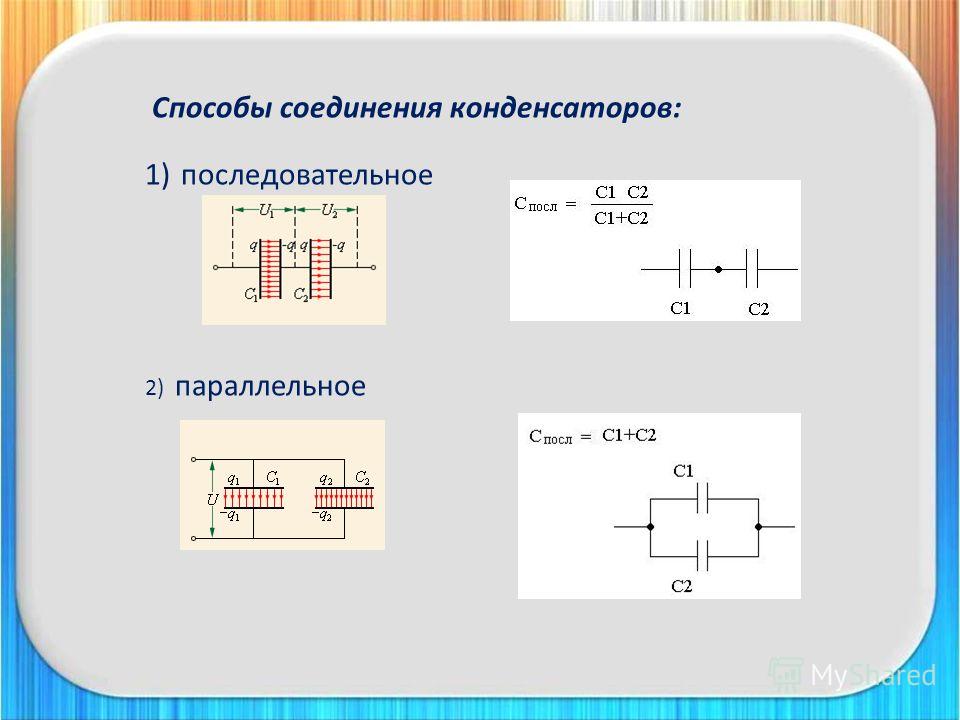
Решение:
При последовательном соединении конденсаторов имеем
при параллельном
Из этих уравнений находим
Согласно теореме Виета С2 и С3 должны быть корнями квадратного уравнения
Решая его, найдем
Заряды на всех конденсаторах при последовательном соединении равны между собой:
29 Три последовательно соединенных конденсатора с емкостями С1 = 100пФ, С2 = 200 пФ, С3 = 500 пФ подключены к источнику тока, который сообщил им заряд q=10нКл. Найти напряжения на конденсаторах V1, V2 и V3, напряжение источника тока V и емкость всех конденсаторов С0.
Решение:
При последовательном соединении конденсаторов заряд каждого конденсатора равен q, поэтому
Напряжение источника тока равно полному напряжению на всех конденсаторах:
Так как при последовательном соединении
то
30 Три последовательно соединенных конденсатора с емкостями С1=0,1мкФ, С2 = 0,25 мкФ и С3 = 0,5 мкФ подключены к источнику тока с напряжением V =32 В. Найти напряжения V1, V2 и V3 на конденсаторах.
Найти напряжения V1, V2 и V3 на конденсаторах.
Решение:
31 Два одинаковых воздушных конденсатора емкости С=100пФ соединены последовательно и подключены к источнику тока с напряжением V= 10 В. Как изменится заряд на конденсаторах, если один из них погрузить в диэлектрик с диэлектрической проницаемостью ε = 2?
Решение:
При последовательном соединении конденсаторов заряды на конденсаторах равны. До погружения одного из них в диэлектрик заряд на каждом конденсаторе
после погружения одного из них в диэлектрик заряды конденсаторов будут
Учитывая, что
Изменение заряда на конденсаторах
32 Два плоских воздушных конденсатора с одинаковыми емкостями соединены последовательно и подключены к источнику тока. Пространство между пластинами одного из конденсаторов заполняют диэлектриком с диэлектрической проницаемостью ε = 9. Во сколько раз изменится напряженность электрического поля Е в этом конденсаторе?
Решение:
Первоначальная напряженность электрического поля в каждом конденсаторе
где d-расстояние между пластинами конденсатора. После заполнения одного конденсатора диэлектриком напряженность электрического поля в нем
После заполнения одного конденсатора диэлектриком напряженность электрического поля в нем
Отношение напряженностей
33 Решить предыдущую задачу для случая, когда конденсаторы после зарядки отключаются от источника тока.
Решение:
После отключения конденсатора от источника тока и заполнения его диэлектриком заряд на нем не изменяется:
Напряженность электрического поля в конденсаторе, заполненном диэлектриком,
Отношение напряженностей
34 Два плоских воздушных конденсатора с одинаковыми емкостями С=10пФ соединены последовательно. Насколько изменится емкость конденсаторов, если пространство между пластинами одного из них заполнить диэлектриком с диэлектрической проницаемостью ε = 2?
Решение:
Изменение емкости соединенных конденсаторов
35 В плоский воздушный конденсатор с площадью обкладок S и расстоянием между ними d введена параллельно обкладкам проводящая пластинка, размеры которой равны размерам обкладок, а ее толщина намного меньше d. Найти емкость конденсатора с проводящей пластинкой, если пластинка расположена на расстоянии l от одной из обкладок конденсатора.
Найти емкость конденсатора с проводящей пластинкой, если пластинка расположена на расстоянии l от одной из обкладок конденсатора.
Решение:
После введения пластинки образовалось два последовательно включенных конденсатора с емкостями
(рис. 342). Их общую емкость определим из соотношения
где С-первоначальная емкость конденсатора. Таким образом, после введения пластинки при любом ее положении С0 = С.
36 В плоский воздушный конденсатор с площадью обкладок S и расстоянием между ними d введена параллельно обкладкам проводящая пластинка, размеры которой равны размерам обкладок, а толщина dп = d/3
Решение:
Введение проводящей пластинки между обкладками конденсатора приводит к образованию двух последовательно включенных конденсаторов с расстояниями между обкладками d1 и d2 и емкостями
(рис.343). Их общую емкость находим из соотношения
При -первоначальная емкость конденсатора.
37 Плоский воздушный конденсатор заряжен до разности потенциалов V0 = 50 В и отключен от источника тока. После этого в конденсатор параллельно обкладкам вносится проводящая пластинка толщины dп= 1 мм. Расстояние между обкладками d=5 мм, площади обкладок и пластинки одинаковы. Найти разность потенциалов V между обкладками конденсатора с проводящей пластинкой.
Решение:
Емкости конденсатора до и после внесения проводящей пластинки толщины dп (см. задачу 36)
Заряд конденсатора, отключенного от источника тока, не изменяется:
отсюда разность потенциалов между обкладками конденсатора после внесения проводящей пластинки
38 В плоский воздушный конденсатор с площадью обкладок S и расстоянием между ними d вводится параллельно обкладкам диэлектрическая пластинка толщины d1<d/ Диэлектрическая проницаемость пластинки равна ε, площади обкладок и пластинки одинаковы и равны S.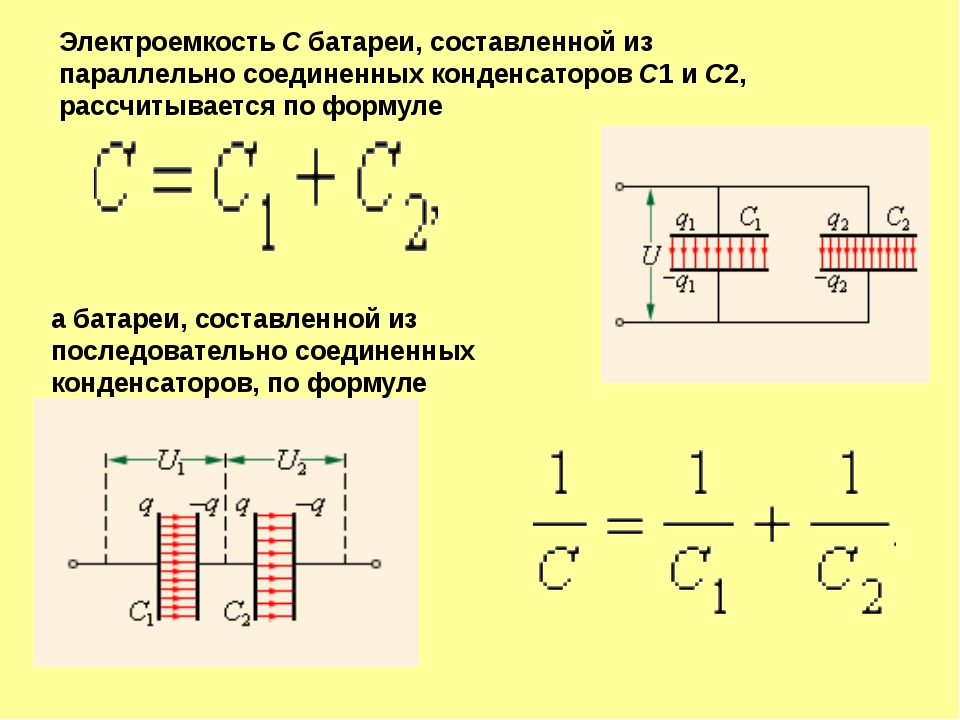 Найти емкость конденсатора с диэлектрической пластинкой.
Найти емкость конденсатора с диэлектрической пластинкой.
Решение:
Смешанное соединение конденсаторов — Мегаобучалка
Встречается смешанное соединение только на различных платах. Для него характерно наличие в одной цепи параллельного и последовательного соединения конденсаторов. При чем смешанное соединение может быть как последовательного, так параллельного характера
Задание
Составить батареи конденсаторов, осуществить параллельное, последовательное и смешанное соединение конденсаторов и определить их емкость.
Приборы и оборудование
1. Конденсаторы: С1 = 10 мкФ+N, С2 = 20 мкФ+2N, С3 = 30 мкФ+4N.
2. Амперметр на.
3. Вольтметр.
4. Генератор тока 1А.
5. Программа Multisim
При проведении лабораторных работ емкость батареи конденсаторов определяется путем измерения ее емкостного сопротивления переменному току.
Экспериментальная часть
1. Соединение конденсаторов последовательно.
Соединение конденсаторов последовательно.
Собрать электрическую цепь (рис. 1.)
Рис. 1.
Установить такое напряжение в цепи, чтобы ток I не превышал 1 А. Емкость батареи конденсаторов определяется формулой
Сэкспер. = Q =1нК
Рассчитать эту же емкость формулой последовательного соединения конденсаторов и сравнить результаты.
2. Соединение конденсаторов параллельно.
Собрать электрическую цепь (рис. 2)
Рис. 2.
Установить напряжение, чтобы I не превышал 1 А. Определить емкость батареи по формуле
Сэкспер. = Q =1нК
Определить эту же емкость по формуле параллельного соединения конденсаторов и
сравнить результаты.
3. Смешанное соединение конденсаторов.
Собрать электрическую цепь (рис. 3.)
Рис. 3.
Установить напряжение, чтобы I не превышал 1 А. Определить емкость батареи по формуле
Определить емкость батареи по формуле
Сэкспер. =
Определить эту же ёмкость по формуле смешанного соединения конденсаторов в батарею.
Расчётная часть
1. Расчёт эквивалентной ёмкости конденсаторов соединённых последовательно.
2. Расчёт эквивалентной ёмкости конденсаторов соединённых параллельно.
3. Расчёт эквивалентной ёмкости конденсаторов соединённых смешано.
4. Рассчитать электрическую энергию заряженного эквивалентного конденсатора
Wэкв.= ;
5. Рассчитать заряд на пластинах конденсатора
Q1=C1U1; Q2=C2U2; Q3=C3U3;
Таблица 1.
| I | U | Сэксп. | Срасч.. | С1 | С2 | С3 | Q1 | Q2 | Q3 | WCэк | |
| A | В | мкФ | мкФ | мкФ | мкФ | мкФ | Кл | Кл | Кл | ||
Соединение конденсаторов
последовательно.
| 10+N | 20+2N | 30+4N | ||||||||
| Соединение конденсаторов параллельно. | |||||||||||
| Смешанное соединение конденсаторов. |
Содержание отчета
1.Соединение конденсаторов последовательно.
Скриншот схемы.
Расчёт ёмкости конденсатора полученной экспериментально. Формулы, единицы измерения
Формулы, единицы измерения
Расчёт ёмкости конденсатора теоретически.
Расчёт электрической энергии заряженного эквивалентного конденсатора.
Расчёт заряд на пластинах конденсатора.
Заполнение таблицы.
2.Соединение конденсаторов параллельно.
Скриншот схемы.
Расчёт ёмкости конденсатора полученной экспериментально. Формулы, единицы измерения
Расчёт ёмкости конденсатора теоретически.
Расчёт электрической энергии заряженного эквивалентного конденсатора.
Расчёт заряд на пластинах конденсатора.
Заполнение таблицы.
3.Смешанное соединение конденсаторов.
Скриншот схемы.
Расчёт ёмкости конденсатора полученной экспериментально. Формулы, единицы измерения
Расчёт теоретической ёмкости конденсатора.
Расчёт электрической энергии заряженного эквивалентного конденсатора.
Расчёт заряд на пластинах конденсатора.
Заполнение таблицы.
Контрольные вопросы
1. Напишите формулу расчета емкости батареи параллельно соединенных конденсаторов.
Напишите формулу расчета емкости батареи параллельно соединенных конденсаторов.
2. Напишите формулу расчета емкости батареи последовательно соединенных конденсаторов.
3. Напишите формулу расчета емкости батареи смешанно соединенных конденсаторов.
4. Назовите типы диэлектриков и раскройте их, применяемых в конденсаторах.
5. Приведите электрические параметры диэлектриков и раскройте их.
6. Опишите характеристики, которыми, кроме емкости обладает конденсатор.
7. Приведите классификацию конденсаторов.
8. Каковы особенности последовательного и параллельного соединения конденсаторов.
9. Когда целесообразно применять метод двух узлов? Каковы особенности метода.
10. Опишите порядок расчёта сложных цепей методом уравнений Кирхгоффа.
Литература
1. Фуфаева Л. И. Электротехника. М., Издательский центр «Академия», 2014.
2. Евдокимов Ф. Е. Теоретические основы электроники. М., Высшая школа, 2012.
М., Высшая школа, 2012.
3. Данилов И. А., Иванов П. М. Общая электротехника с основами электроники. М., Высшая школа, 2013.
Параллельное включение конденсаторов. Соединение конденсаторов Как правильно соединять конденсаторы
В электрических цепях применяются различные способы соединения конденсаторов . Соединение конденсаторов может производиться: последовательно , параллельно и последовательно-параллельно (последнее иногда называют смешанное соединение конденсаторов). Существующие виды соединения конденсаторов показаны на рисунке 1.
Рисунок 1. Способы соединения конденсаторов.
Параллельное соединение конденсаторов.
Если группа конденсаторов включена в цепь таким образом, что к точкам включения непосредственно присоединены пластины всех конденсаторов, то такое соединение называется параллельным соединением конденсаторов (рисунок 2.).
Рисунок 2. Параллельное соединение конденсаторов.
При заряде группы конденсаторов, соединенных параллельно, между пластинами всех конденсаторов будет одна и та же разность потенциалов, так как все они заряжаются от одного и того же источника тока. Общее же количество электричества на всех конденсаторах будет равно сумме количеств электричества, помещающихся на каждом из конденсаторов, так как заряд каждого их конденсаторов происходит независимо от заряда других конденсаторов данной группы. Исходя из этого, всю систему параллельно соединенных конденсаторов можно рассматривать как один эквивалентный (равноценный) конденсатор. Тогда общая емкость конденсаторов при параллельном соединении равна сумме емкостей всех соединенных конденсаторов.
Обозначим суммарную емкость соединенных в батарею конденсаторов буквой Собщ, емкость первого конденсатора С1 емкость второго С2 и емкость третьего С3. Тогда для параллельного соединения конденсаторов будет справедлива следующая формула:
Последний знак + и многоточие указывают на то, что этой формулой можно пользоваться при четырех, пяти и вообще при любом числе конденсаторов.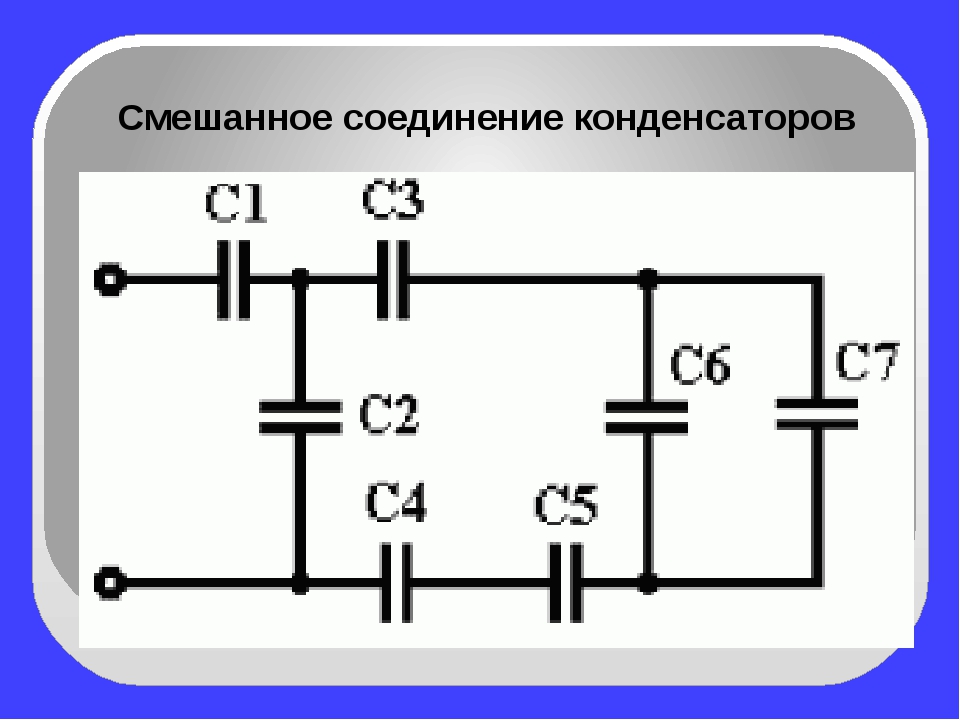
Последовательное соединение конденсаторов.
Если же соединение конденсаторов в батарею производится в виде цепочки и к точкам включения в цепь непосредственно присоединены пластины только первого и последнего конденсаторов, то такое соединение конденсаторов называется последовательным (рисунок 3).
Рисунок 2. Последовательное соединение конденсаторов.
При последовательном соединении все конденсаторы заряжаются одинаковым количеством электричества, так как непосредственно от источника тока заряжаются только крайние пластины (1 и 6), а остальные пластины (2, 3, 4 и 5) заряжаются через влияние. При этом заряд пластины 2 будет равен по величине и противоположен по знаку заряду пластины 1, заряд пластины 3 будет равен по величине и противоположен по знаку заряду пластины 2 и т. д.
Напряжения на различных конденсаторах будут, вообще говоря, различными, так как для заряда одним и тем же количеством электричества конденсаторов различной емкости всегда требуются различные напряжения. Чем меньше емкость конденсатора, тем большее напряжение необходимо для того, чтобы зарядить этот конденсатор требуемым количеством электричества, и наоборот.
Чем меньше емкость конденсатора, тем большее напряжение необходимо для того, чтобы зарядить этот конденсатор требуемым количеством электричества, и наоборот.
Таким образом, при заряде группы конденсаторов, соединенных последовательно, на конденсаторах малой емкости напряжения будут больше, а на конденсаторах большой емкости — меньше.
Аналогично предыдущему случаю можно рассматривать всю группу конденсаторов, соединенных последовательно, как один эквивалентный конденсатор, между пластинами которого существует напряжение, равное сумме напряжений на всех конденсаторах группы, а заряд которого равен заряду любого из конденсаторов группы.
Возьмем самый маленький конденсатор в группе. На нем должно быть самое большое напряжение. Но напряжение на этом конденсаторе составляет только часть общего напряжения, существующего на всей группе конденсаторов. Напряжение на всей группе больше напряжения на конденсаторе, имеющем самую малую емкость. А отсюда непосредственно следует, что общая емкость группы конденсаторов, соединенных последовательно, меньше емкости самого малого конденсатора в группе.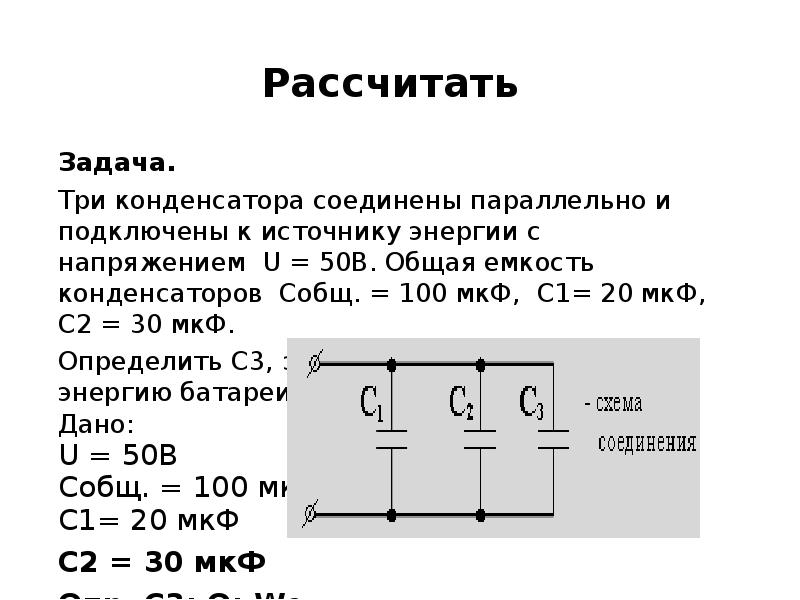
Для вычисления общей емкости при последовательном соединении конденсаторов удобнее всего пользоваться следующей формулой:
Для частного случая двух последовательно соединенных конденсаторов формула для вычисления их общей емкости будет иметь вид:
Последовательно-параллельное (смешанное) соединение конденсаторов
Последовательно-параллельным соединением конденсаторов называется цепь имеющая в своем составе участки, как с параллельным, так и с последовательным соединением конденсаторов.
На рисунке 4 приведен пример участка цепи со смешанным соединением конденсаторов.
Рисунок 4. Последовательно-параллельное соединение конденсаторов.
При расчете общей емкости такого участка цепи с последовательно-параллельным соединением конденсаторов этот участок разбивают на простейшие участки, состоящие только из групп с последовательным или параллельным соединением конденсаторов. Дальше алгоритм расчета имеет вид:
1.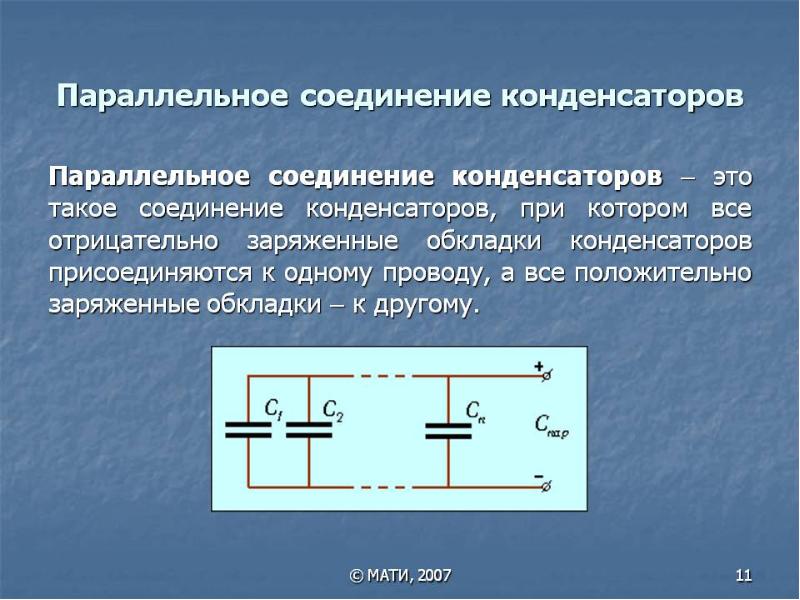 Определяют эквивалентную емкость участков с последовательным соединением конденсаторов.
Определяют эквивалентную емкость участков с последовательным соединением конденсаторов.
2. Если эти участки содержат последовательно соединенные конденсаторы, то сначала вычисляют их емкость.
3. После расчета эквивалентных емкостей конденсаторов перерисовывают схему. Обычно получается цепь из последовательно соединенных эквивалентных конденсаторов.
4. Рассчитывают емкость полученной схемы.
Один из примеров расчета емкости при смешанном соединении конденсаторов приведен на рисунке 5.
Рисунок 5. Пример расчета последовательно-параллельного соединения конденсаторов.
У начинающих электронщиков при сборке любого самодельного устройства могут возникнуть проблемы с соединением конденсатора. Ведь даже у заядлого любителя электроники может не оказаться под рукой конденсатора с нужным номиналом, особенно когда нужно срочно отремонтировать бытовой прибор. Из сложившейся проблемы легко выйти, соединив последовательно или параллельно несколько конденсаторов.
Приготовьте:
- конденсаторы;
- вольтметр;
- провода;
- кусачки.

Для составного конденсатора старайтесь брать однотипные конденсаторы, а если возможно — то с одной партии. Конденсаторы бывают керамические, пленочные, металлобумажные, слюдяные.
У многих начинающих любителей электроники в процессе сборки самодельного устройства возникает вопрос: “Как правильно соединять конденсаторы?”
Казалось бы, зачем это надо, ведь если на принципиальной схеме указано, что в данном месте схемы должен быть установлен конденсатор на 47 микрофарад, значит, берём и ставим необходимый конденсатор. Но, согласитесь, что в мастерской даже заядлого электронщика может не оказаться конденсатора с необходимым номиналом!
Но, согласитесь, что в мастерской даже заядлого электронщика может не оказаться конденсатора с необходимым номиналом!
Похожая ситуация может возникнуть и при ремонте какого-либо прибора. Например, необходим электролитический конденсатор ёмкостью 1000 микрофарад, а под рукой лишь 2 – 3 конденсатора на 470 микрофарад. Ставить конденсатор на 470 микрофарад, вместо положенных 1000? Нет, это допустимо не всегда. Так как же быть? Ехать на радиорынок за несколько десятков километров за одним конденсатором?
Как выйти из сложившейся ситуации? Можно соединить несколько конденсаторов и в результате получить необходимую нам ёмкость. В электронике существует два способа соединения конденсаторов: параллельное и последовательное .
В реальности это выглядит так:
Параллельное соединение
Принципиальная схема параллельного соединения
Последовательное соединение
Принципиальная схема последовательного соединения
Также можно комбинировать параллельное и последовательное соединение конденсаторов. На практике вам вряд ли это пригодиться.
На практике вам вряд ли это пригодиться.
Как рассчитать общую ёмкость соединённых конденсаторов?
Помогут нам в этом несколько простых формул. Не сомневайтесь, если вы будете заниматься электроникой, то эти простые формулы рано или поздно вас выручат.
Общая ёмкость параллельно соединённых конденсаторов:
С 1 – ёмкость первого конденсатора;
С 2 – ёмкость второго конденсатора;
С 3 – ёмкость третьего конденсатора;
С N – ёмкость N -ого конденсатора;
C общ – суммарная ёмкость составного конденсатора.
Как видим, при параллельном соединении ёмкости конденсаторов нужно всего-навсего сложить!
Внимание! Все расчёты необходимо производить в одних единицах. Если рассчитываем ёмкости в микрофарадах, то нужно указывать ёмкость C 1 , C 2 в микрофарадах. Результат также получим в микрофарадах. Это правило стоит соблюдать, иначе ошибки не избежать!
Чтобы не допустить ошибку при переводе микрофарад в пикофарады или нанофарады можно воспользоваться специальной таблицей. В ней указаны приставки, используемые для краткой записи и множители, с помощью которых можно пересчитать значения величин.
Ёмкость двух последовательно соединённых конденсаторов можно рассчитать по другой формуле. Она будет чуть сложнее:
Внимание! Данная формула справедлива только для двух конденсаторов! Для большего количества последовательно включенных конденсаторов потребуется другая формула. Она более запутанная, да и не всегда пригождается .
Или то же самое, но более понятно:
Если вы проведёте несколько расчётов, то увидите, что при последовательном соединении конденсаторов их результирующая ёмкость будет всегда меньше наименьшей ёмкости, включённой в данную цепочку. Что это значить? А это значит, что если соединить последовательно конденсатор ёмкостью 5, 100 и 35 пикофарад, то общая ёмкость составного конденсатора будет меньше 5.
В том случае, если для последовательного соединения применены конденсаторы одинаковой ёмкости, эта громоздкая формула упрощается и принимает вид:
Здесь, вместо буквы M ставиться количество конденсаторов, а C 1 – ёмкость конденсатора.
Стоит также запомнить простое правило:
При последовательном соединении двух конденсаторов с одинаковой ёмкостью результирующая ёмкость будет в два раза меньше ёмкости каждого из конденсаторов.
Таким образом, если вы последовательно соедините два конденсатора, ёмкость каждого из которых 10 нанофарад, то в результате ёмкость составного конденсатора составит 5 нанофарад.
Проверим конденсатор, замерив ёмкость, и на практике подтвердим правильность показанных здесь формул для расчёта.
Возьмём два плёночных конденсатора. Один на 15 нанофарад (0,015 мкф.), другой на 10 нанофарад (0,01 мкф.) Соединим их последовательно. Теперь возьмём мультиметр Victor VC9805+ с функцией измерения ёмкости конденсаторов и замерим суммарную ёмкость двух конденсаторов. Вот что мы получим (см. фото).
Замер ёмкости последовательно соединённых конденсаторов
Ёмкость составного конденсатора составила 6 нанофарад (0,006 мкф.)
А теперь проделаем то же самое, но для параллельного соединения конденсаторов. Проверим результат с помощью тестера (см. фото).
Измерение ёмкости параллельно соединённых конденсаторов
Как видим, при параллельном соединении ёмкость двух конденсаторов сложилась и составляет 25 нанофарад (0,025 мкф.).
Что ещё необходимо знать, чтобы правильно соединить конденсаторы?
Во-первых, не стоит забывать, что кроме ёмкости у конденсаторов есть ещё один немаловажный параметр, как номинальное напряжение.
При последовательном соединении конденсаторов напряжение между ними распределяется обратно пропорционально ёмкостям этих конденсаторов. Поэтому, есть смысл при последовательном соединении применять конденсаторы с номинальным напряжением равным тому, которое должно быть у конденсатора взамен которого мы ставим составной конденсатор.
Если же используются конденсаторы одинаковой ёмкости, то напряжение между ними разделится поровну.
Для электролитических конденсаторов.
При соединении электролитических конденсаторов строго соблюдайте полярность! При параллельном соединении электролитических конденсаторов всегда соединяйте минусовой вывод одного конденсатора с минусовым выводом другого. Плюсовой вывод с плюсовым.
Параллельное соединение электролитических конденсаторов
Схема параллельного соединения
В последовательном соединении электролитических конденсаторов ситуация обратная. Необходимо соединять плюсовой вывод с минусовым. Получается что-то вроде последовательного соединения батареек.
Последовательное соединение электролитических конденсаторов
Также не забывайте про номинальное напряжение. При параллельном соединении каждый из задействованных конденсаторов должен иметь то номинальное напряжение, как если бы мы ставили в схему один конденсатор. То есть если в схему нужно установить конденсатор с номинальным напряжением на 35 вольт и ёмкостью, например, 200 микрофарад, то взамен его можно параллельно соединить два конденсатора на 100 микрофарад и 35 вольт. Если хоть один из этих конденсаторов будет иметь меньшее номинальное напряжение (например, 25 вольт), то он вскоре выйдет из строя.
Желательно, чтобы для составного конденсатора подбирались конденсаторы одного типа (плёночные, керамические, слюдяные, металлобумажные). Лучше будет, если они взяты из одной партии.
Конечно, возможно и смешанное (комбинированное) соединение конденсаторов, но в практике оно не применяется (я не видел ). Расчёт ёмкости смешанного соединения конденсаторов обычно достаётся тем, кто решает задачи по физике и сдаёт экзамены:)
Параллельное и последовательное соединение конденсаторов: ёмкость и сопротивление
Практически все электрические цепи включают в себя емкостные элементы. Соединение конденсаторов между собой выполняют по схемам. Их необходимо знать как при расчетах, так и при выполнении монтажа.
Последовательное соединение
Конденсатор, а в просторечии — «ёмкость», та деталь, без которой не обходится ни одна электрическая или электронная плата. Даже в современных гаджетах он присутствует, правда, уже в измененном виде.
Вспомним, что представляет собой этот радиотехнический элемент. Это накопитель электрических зарядов и энергии, 2 проводящие пластины, между которыми расположен диэлектрик. При прикладывании к пластинам источника постоянного тока через устройство кратковременно потечет ток, и оно зарядится до напряжения источника. Его емкость используют для решения технических задач.
Само это слово произошло задолго до того, как придумали устройство. Термин появился ещё тогда, когда люди считали, что электричество — это что-то типа жидкости, и ею можно наполнить какой-нибудь сосуд. Применительно к конденсатору — он неудачен, т.к. подразумевает, что прибор может вместить только конечное количество электричества. Хотя это и не так, но термин остался неизменным.
Чем больше пластины, и меньше расстояние между ними, тем больше ёмкость конденсатора. Если его обкладки соединить с каким-либо проводником, то через этот проводник произойдет быстрый разряд.
В координатных телефонных станциях с помощью этой особенности происходит обмен сигналами между приборами. Длина импульсов, необходимых для команд, таких как: «соединение линии», «ответ абонента», «отбой», регулируется величиной ёмкости установленных в цепь конденсаторов.
Единица измерения ёмкости — 1 Фарад. Т.к. это большая величина, то пользуются микрофарадами, пикофарадами и нанофарадами, (мкФ, пФ, нФ).
На практике, выполнив последовательное соединение, можно добиться увеличения прикладываемого напряжения. В этом случае поданное напряжение получают 2 внешние обкладки собранной системы, а обкладки, находящиеся внутри, заряжаются с помощью распределения зарядов. К таким приемам прибегают, когда под рукой не оказывается нужных элементов, зато есть детали других номиналов по напряжению.
К участку, имеющему 2 последовательно соединенных конденсатора, рассчитанных на напряжение 125 В, можно подключить питание 250 В.
Если для постоянного тока, конденсатор является препятствием за счет своего диэлектрического промежутка, то с переменным — все иначе. Для токов разных частот, подобно катушкам и резисторам, сопротивление конденсатора будет меняться. Токи высокой частоты он пропускает хорошо, а для их собратьев низкой частоты создает барьер.
У радиолюбителей есть способ — через емкость 220-500 пФ к радиоприемнику подключают вместо антенны сеть освещения напряжением 220 В. Ток с частотой 50 Гц он отфильтрует, а токи высокой частоты пропустит. Это сопротивление конденсаторов легко рассчитать по формуле для емкостного сопротивления:RC =1/6*f*C.
Где:
- Rc — емкостное сопротивление, Ом;
- f — частота тока, Гц;
- C — емкость данного конденсатора, Ф;
- 6 — округленное до целой части число 2π.
Но не только прикладываемое напряжение к цепи можно изменить, пользуясь подобной схемой включения. Так добиваются изменений емкостей при последовательных соединениях. Для легкости запоминания придумали подсказку, что общее значение емкости, полученное при выборе подобной схемы, получается всегда меньше меньшей из двух, включенных в цепочку.
Если так соединить 2 детали одинаковой ёмкости, то их общее значение будет вдвое меньше каждой из них. Расчеты последовательных соединений конденсатора можно выполнить по приведенной ниже формуле:
Собщ = С1*С2/С1+С2,
Пусть С1=110 пФ, а С2=220 пФ, тогда Собщ = 110×220/110+220 = 73 пФ.
Не стоит забывать про простоту и удобство монтажа, а также обеспечение качественной работы собранного устройства или оборудования. В последовательных соединениях у емкостей должен быть 1 производитель. А если детали всей цепочки будут одной партии выпуска, то проблем с эксплуатацией созданной цепи не будет.
Параллельное соединение
Накопители электрического заряда постоянной емкости, различают:
- керамические;
- бумажные;
- слюдяные;
- металлобумажные;
- электролитические конденсаторы.
Их делят на 2 группы: низковольтные и высоковольтные. Применяют их в фильтрах выпрямителей, для связи между низкочастотными участками цепей, в блоках питания различных устройств и т.д.
Конденсаторы переменной ёмкости тоже существуют. Они нашли свое предназначение в настраиваемых колебательных контурах теле- и радиоприемников. Емкость регулируется за счет изменения положения пластин относительно друг друга.
Рассмотрим соединение конденсаторов, когда их выводы соединятся попарно. Подобное включение подходит для 2 или более элементов, рассчитанных на одно и то же напряжение. Номинальное напряжение, которое указано на корпусе детали, превышать нельзя. В противном случае произойдет пробой диэлектрика, и элемент выйдет из строя. Но в цепь, где присутствует напряжение меньше номинального, конденсатор включать можно.
Параллельным включением конденсаторов можно добиться увеличения общей ёмкости. В некоторых устройствах необходимо обеспечить большое накопление электрического заряда. Существующих номиналов не хватает, приходится выполнять параллели и использовать то, что есть под рукой. Определить общую величину полученного соединения просто. Для этого нужно просто сложить величины всех используемых элементов.
Для вычисления емкостей конденсаторов формула имеет вид:
Собщ = С1+С2, где С1 и С2 — емкость соответствующих элементов.
Если С1=20 пФ, а С2=30 пФ, то Собщ = 50 пФ. Деталей в в параллели может быть n-ое количество.
На практике такое соединение находит применение в специальных устройствах, используемых в энергетических системах, и на подстанциях. Их монтируют, зная, как соединить конденсаторы для увеличения емкости, в целые блоки из батарей.
Для того чтобы поддерживать равновесие реактивной мощности как в энергоснабжающих установках, так и в установках энергопотребителей, существует необходимость включать в работу компенсирующие устройства реактивной мощности (УКРМ). Для снижения потерь и регулировки напряжения в сетях при расчетах устройства необходимо знать величины реактивных сопротивлений конденсаторов, используемых в установке.
Случается, что возникает необходимость вычислить по формуле напряжение на конденсаторах. В этом случае будем исходить из того, что С=q/U, т.е. отношение заряда к напряжению. И если величина заряда — q, а ёмкость — C, можем получим искомое число, подставляя значения. Она имеет вид:
U=q/C.
Смешанное соединение
При расчете цепи, представляющей собой совокупность рассмотренных выше комбинаций, поступают так. Сначала ищем в сложной цепи конденсаторы, которые соединены между собой либо параллельно, либо последовательно. Заменив их эквивалентным элементом, получим более простую схему. Потом в новой схеме с участками цепи проводим те же манипуляции. Упрощаем до тех пор, пока не останется только параллельное или последовательное соединение. Их рассчитывать мы уже научились в этой статье.
Параллельно-последовательное соединение применимо для увеличения емкости, батареи или для того, чтобы приложенное напряжение не превышало рабочего напряжения конденсатора.
При параллельном подключении конденсаторов у них одинаковые
При параллельном подключении конденсаторов у них одинаковые
Когда конденсаторы подключены параллельно, имеют ли они одно и то же?
Последовательные конденсаторы имеют одинаковый заряд, а конденсаторы, подключенные параллельно, имеют одинаковое напряжение. Три одинаковых конденсатора соединены последовательно с батареей.
Кстати, при параллельном подключении конденсаторов у них одно и то же?
разница заключается в заряде двух конденсаторов.(Другими словами, конденсаторы, подключенные параллельно, подключены к одним и тем же начальным и конечным точкам входа и выхода, поэтому все они имеют одинаковую разность потенциалов.
Тогда возникает вопрос: что происходит, когда конденсаторы соединяются параллельно?
При параллельном подключении конденсаторов общая емкость складывается из емкостей отдельных конденсаторов. Когда два или более конденсатора соединены параллельно, общая мощность равна мощности одного эквивалентного конденсатора, который имеет сумму площадей якоря отдельных конденсаторов.
Также можно спросить: а параллельно ли конденсаторы имеют одинаковую нагрузку?
Параллельные конденсаторы Параллельно подключенные конденсаторы увеличивают емкость. Параллельное соединение — самый удобный способ увеличить общее накопление электрического заряда. Общее значение напряжения не меняется. На каждом конденсаторе будет одинаковое напряжение.
Что верно для конденсаторов, соединенных параллельно?
(a.) Заряд каждого конденсатора равен заряду соответствующего конденсатора.Разность напряжений на отдельных конденсаторах равна разнице напряжений на соответствующем конденсаторе.
Что делать, если два или более конденсатора подключены параллельно через разность потенциалов?
: два или более конденсатора соединены параллельно через разность потенциалов, разность потенциалов на каждом конденсаторе одинакова. каждый конденсатор несет одинаковое количество заряда. соответствующая емкость комбинации меньше емкости некоторых конденсаторов.
Как рассчитываются параллельные конденсаторы?
Общая ставка Q — это сумма индивидуальных затрат: Q = Q1 + Q2 + Q3. Рисунок 2. (а) Параллельное соединение конденсаторов. Каждый из них подключен непосредственно к источнику напряжения, как если бы он был один, поэтому общая параллельная емкость — это просто сумма отдельных емкостей.
Конденсаторы накапливают больше энергии последовательно или параллельно?
Три конденсатора, соединенные параллельно с другой стороны, имеют падение напряжения V, поэтому общая накопленная энергия составляет 3/2 C V2, что в девять раз больше энергии в трех соединенных последовательно.Чтобы ответить на ваш вопрос, конденсаторы, подключенные параллельно, хранят больше энергии, чем конденсаторы, подключенные последовательно.
Зачем добавлять конденсаторы параллельно?
Когда вы подключаете конденсаторы параллельно, вы в основном подключаете пластины к каждому конденсатору. Таким образом, параллельное соединение двух идентичных конденсаторов существенно увеличивает размер пластин вдвое, что существенно удваивает емкость.
Что является символом мастерства?
Одно и то же напряжение на резисторах, включенных параллельно?
Напряжение на каждом резисторе в параллельной комбинации точно такое же, но ток, протекающий через него, не такой, как он определяется значением его сопротивления и законом Ома.Итак, параллельные цепи — это делители мощности.
Могут ли конденсаторы повышать напряжение?
Ни один конденсатор не увеличивает напряжение. Однако их можно использовать во многих схемах, которые создают более высокое выходное напряжение на входе. Конденсаторы — это запасы энергии. Если вы зарядите два конденсатора параллельно, а затем соедините их последовательно, вы получите удвоенное входное напряжение.
Будет ли напряжение параллельно уменьшаться вдвое?
При параллельном подключении разность электрических потенциалов на каждом резисторе (ΔV) одинакова.При параллельном подключении напряжение на каждой ветви уменьшается по мере увеличения напряжения на батарее. Таким образом, падение напряжения на каждом из этих резисторов одинаковое.
Как рассчитать заряд конденсатора?
Электрический заряд Q, накопленный в конденсаторе (в кулонах, сокращенно C), равен произведению емкости C конденсатора (в фарадах, сокращенно F) и напряжения V (в вольтах, сокращенно V) на нем.
То есть Q = C?
В.
Если, например, C = 33 мкФ и V = 20 В, то Q = (33?
106)?
(20) = 660 ° С.
Когда два конденсатора подключены параллельно к батарее?
Как добавить индукторы параллельно?
Параллельные вспомогательные катушки
Какова эквивалентная емкость двух параллельно соединенных конденсаторов?
Соответствующая емкость для двух конденсаторов, соединенных параллельно, является суммой индивидуальных емкостей. Рисунок 16: Два конденсатора, подключенных последовательно.он общий для всех трех конденсаторов.
Можно ли подключить конденсаторы последовательно?
Конденсаторы серии. Когда конденсаторы подключаются последовательно, это называется последовательным подключением. В случае последовательных конденсаторов общую емкость можно определить путем сложения взаимности отдельных емкостей и суммы взаимных величин.
Что происходит, когда конденсатор подключен к источнику постоянного тока?
Когда конденсаторы переключаются с помощью постоянного напряжения, они заряжаются до значения приложенного напряжения и действуют как буфер и удерживают этот заряд в течение неопределенного периода времени, пока не будет подано напряжение питания.
Как подключить конденсатор?
Что происходит, когда конденсатор подключен к батарее?
Цепь конденсатора. Пластина конденсатора, прикрепленная к отрицательному полюсу батареи, поглощает электроны, генерируемые батареей. Пластина конденсатора, прикрепленная к положительному полюсу батареи, теряет электроны в батарее.
Для чего нужен конденсатор?
При параллельном подключении конденсаторов у них одинаковые3.6 конденсаторов, подключенных последовательно и параллельно — Douglas College Physics 1207
Сводка
- Выведите выражения для полной емкости последовательно и параллельно.
- Обозначение последовательной и параллельной частей в комбинации конденсаторов.
- Рассчитайте эффективную емкость последовательно и параллельно с учетом индивидуальных емкостей.
Несколько конденсаторов могут быть соединены вместе в различных приложениях. Несколько подключений конденсаторов действуют как один эквивалентный конденсатор.Общая емкость этого эквивалентного одиночного конденсатора зависит как от отдельных конденсаторов, так и от способа их подключения. Существует два простых и распространенных типа соединений, которые называются последовательностью и параллельным , для которых мы можем легко вычислить общую емкость. Некоторые более сложные соединения также могут быть связаны с последовательными и параллельными соединениями.
На рис. 1 (а) показано последовательное соединение трех конденсаторов с приложенным напряжением.Как и в случае любого конденсатора, емкость комбинации связана с зарядом и напряжением соотношением C = Q / V.
Обратите внимание на рис. 1, что противоположные заряды величиной Q протекают по обе стороны от первоначально незаряженной комбинации конденсаторов при приложении напряжения В, . Для сохранения заряда необходимо, чтобы на пластинах отдельных конденсаторов создавались заряды одинаковой величины, поскольку заряд разделяется только в этих изначально нейтральных устройствах.Конечным результатом является то, что комбинация напоминает одиночный конденсатор с эффективным разделением пластин больше, чем у отдельных конденсаторов. (См. Рисунок 1 (b).) Чем больше расстояние между пластинами, тем меньше емкость. Общей особенностью последовательного соединения конденсаторов является то, что общая емкость меньше любой из отдельных емкостей.
Рис. 1. (a) Конденсаторы, подключенные последовательно. Величина заряда на каждой пластине — Q .(b) Эквивалентный конденсатор имеет большее расстояние между пластинами d . При последовательном соединении общая емкость меньше, чем у любого из отдельных конденсаторов.Мы можем найти выражение для общей емкости, рассматривая напряжение на отдельных конденсаторах, показанных на рисунке 1. Решение C = Q / V для V дает V = C / Q . Напряжения на отдельных конденсаторах равны. Общее напряжение складывается из отдельных напряжений:
V = V 1 + V 2 + V 3
Теперь, называя общую емкость C серии = C с для последовательной емкости, считайте, что
Вводя выражения для V 1 , V 2 и V 3 , получаем
Отменяя Q s, получаем уравнение для полной емкости в серии C , равное
., где «…» означает, что выражение действительно для любого количества конденсаторов, соединенных последовательно.Выражение этой формы всегда приводит к общей емкости C , которая меньше любой из отдельных емкостей C 1 , C 2 , C 3 , …, как показано в следующем примере.
Общая емкость в серии,
C сОбщая емкость в серии:
Пример 1: Что такое последовательная емкость?
Найдите общую емкость для трех последовательно соединенных конденсаторов, учитывая, что их отдельные емкости равны 1.000, 5.000 и 8.000 мкФ.
Стратегия
Имея данную информацию, общую емкость можно найти, используя уравнение для емкости в серии.
Решение
Ввод заданных емкостей в выражение для дает.
Преобразование для поиска C series или C s урожайности.
Обсуждение
Общая последовательная емкость C с меньше наименьшей индивидуальной емкости, как было обещано.При последовательном соединении конденсаторов сумма меньше деталей. На самом деле это меньше, чем у любого человека. Обратите внимание, что иногда возможно и более удобно решить уравнение, подобное приведенному выше, путем нахождения наименьшего общего знаменателя, который в данном случае (показаны только целочисленные вычисления) равен 40. Таким образом,
, так что
На рис. 2 (а) показано параллельное соединение трех конденсаторов с приложенным напряжением. Здесь общую емкость найти легче, чем в последовательном случае.Чтобы найти эквивалентную общую емкость C параллельно или C p , сначала отметим, что напряжение на каждом конденсаторе составляет В , то же самое, что и у источника, поскольку они подключены напрямую к нему через дирижер. (Проводники являются эквипотенциальными, поэтому напряжение на конденсаторах такое же, как и на источнике напряжения.) Таким образом, конденсаторы имеют такой же заряд, как и при индивидуальном подключении к источнику напряжения.Общая сумма начислений Q — это сумма индивидуальных сборов:
Q = Q 1 + Q 2 + Q 3
Рис. 2. (a) Конденсаторы, включенные параллельно. Каждый из них подключен непосредственно к источнику напряжения, как если бы он был полностью один, поэтому общая параллельная емкость — это просто сумма отдельных емкостей. (b) Эквивалентный конденсатор имеет большую площадь пластины и поэтому может удерживать больше заряда, чем отдельные конденсаторы.Используя соотношение Q = CV , мы видим, что общий заряд составляет Q всего = C p V , а отдельные расходы составляют Q 1 = C 1 V , Q 2 = C 2 V , и Q 3 = C 3 V . Ввод их в предыдущее уравнение дает
Q итого = Q 1 + Q 2 + Q 3
C p V = C 1 V + C 2 V + C 3 V
C p = C 1 + C 2 + C 3
Исключая В из уравнения, мы получаем уравнение для полной емкости параллельно C p :
C p = C 1 + C 2 + C 3 +….
Общая параллельная емкость — это просто сумма отдельных емкостей. (И снова «… » указывает на то, что выражение действительно для любого количества конденсаторов, подключенных параллельно.) Так, например, если конденсаторы в приведенном выше примере были подключены параллельно, их емкость была бы
.C p = C 1 + C 2 + C 3 = 1.000 мкФ + 5.000 мкФ + 8.000 мкФ = 14.000 мкФ
Эквивалентный конденсатор для параллельного соединения имеет значительно большую площадь пластины и, следовательно, большую емкость, как показано на Рисунке 2 (b).
Общая емкость параллельно,
C pОбщая емкость параллельно C p = C 1 + C 2 + C 3 +….
Более сложные соединения конденсаторов иногда могут быть последовательными и параллельными. (См. Рис. 3.) Чтобы найти общую емкость таких комбинаций, мы идентифицируем последовательные и параллельные части, вычисляем их емкости, а затем находим общую.
Рисунок 3. (a) Эта схема содержит как последовательные, так и параллельные соединения конденсаторов. См. Пример 2 для расчета общей емкости цепи. (b) C 1 и C 2 находятся последовательно; их эквивалентная емкость C S меньше, чем у любого из них. (c) Обратите внимание, что C S находится параллельно с C 3 .Таким образом, общая емкость равна сумме C S и C 3 .Смесь последовательной и параллельной емкости
Найдите общую емкость комбинации конденсаторов, показанной на рисунке выше. 3. Предположим, что емкости известны с точностью до трех десятичных знаков.
C p = C 1 + C 2 + C 3 = 1.000 мкФ + 5.000 мкФ + 8.000 мкФ = 14.000 мкФ
C p = C 1 + C 2 + C 3 = 1.000 мкФ + 5.000 мкФ + 8.000 мкФ = 14.000 мкФ
C 1 = 1.000 мкФ, C 2 = 5.000 мкФ и C 3 = 8.000 мкФ. Округлите ответ до трех десятичных знаков.
Стратегия
Чтобы найти общую емкость, мы сначала определяем, какие конденсаторы включены последовательно, а какие — параллельно. Конденсаторы С 1 и С 2 включены последовательно.Их комбинация, Cs на рисунке, параллельна C 3 .
Решение
Поскольку C 1 и C 2 включены последовательно, их общая емкость определяется выражением. Ввод их значений в уравнение дает
Инвертирование дает
Cs = 0,833 мкФ
Эта эквивалентная последовательная емкость подключена параллельно третьему конденсатору; Таким образом, общая сумма составляет
Обсуждение
Этот метод анализа комбинаций конденсаторов по частям, пока не будет получена общая сумма, может быть применен к более крупным комбинациям конденсаторов.
- Суммарная емкость в серии
- Общая емкость параллельно C p = C 1 + C 2 + C 3 +…
- Если схема содержит комбинацию конденсаторов, включенных последовательно и параллельно, определите последовательную и параллельную части, вычислите их емкости, а затем найдите общую сумму.
Концептуальные вопросы
1: Если вы хотите хранить большое количество энергии в конденсаторной батарее, подключите ли вы конденсаторы последовательно или параллельно? Объяснять.
Задачи и упражнения
1: Найдите общую емкость комбинации конденсаторов на рисунке 4.
Рисунок 4. Комбинация последовательного и параллельного подключения конденсаторов.2: Предположим, вам нужна конденсаторная батарея с общей емкостью 0,750 Ф и у вас есть множество конденсаторов 1,50 мФ. Какое наименьшее число вы могли бы связать вместе, чтобы достичь своей цели, и как бы вы их связали?
3: Какую общую емкость можно получить, подключив 5.00 мкФ и конденсатор 8,00 мкФ вместе?
4: Найдите общую емкость комбинации конденсаторов, показанной на рисунке 5.
Рисунок 5. Комбинация последовательного и параллельного подключения конденсаторов.5: Найдите общую емкость комбинации конденсаторов, показанной на рисунке ниже
Рисунок 6. Комбинация последовательного и параллельного подключения конденсаторов.6: Необоснованные результаты
(а) Ан 8.Конденсатор 00 мкФ подключен параллельно другому конденсатору, что дает общую емкость 5,00 мкФ . Какая емкость у второго конденсатора? б) Что неразумного в этом результате? (c) Какие предположения необоснованны или непоследовательны?
Решения
Задачи и упражнения
1: 0,293 мкФ
3: 3,08 мкФ в последовательной комбинации, 13,0 мкФ в параллельной комбинации
4: 2.79 мкФ
6: (a) -3,00 мкФ (b) У вас не может быть отрицательного значения емкости. (c) Предположение, что конденсаторы были подключены параллельно, а не последовательно, было неверным. Параллельное соединение всегда дает большую емкость, в то время как здесь предполагалась меньшая емкость. Это могло произойти, только если конденсаторы подключены последовательно.
Лекция 8
ПОП4 20,49
Два конденсатора емкостью 25 µ F и 5 µ F подключены параллельно с напряжением 100 В на каждом.Какая общая энергия хранится?
A. 150 µ J
Б. 0,150 Дж
С. 150 Дж
D. 150 кДж
Ответ
ПОП4 20,49
Два конденсатора по 25 µ F и 5 µ F подключены последовательно.
Какой Δ В требуется для хранения 0,150 Дж?
А. 22,8 В
Б. 100 В
С. 137 V
D. 268 V
Ответ
klm Walker5e CnEx 21-19
Переключатель на рисунке ниже изначально разомкнут, а конденсатор не заряжен.Если & Escr; = 6,00 В, R = 10,0 Ом и C = 72,0 µ F, какой ток протекает через батарею сразу после включения переключателя?
схемотехнический симулятор
А. 0,432 мА
Б. 0,600 А
С. 0,900 А
D. 1.20 A
Ответ
klm Walker5e CnEx 21-19
Переключатель на рисунке ниже изначально разомкнут, а конденсатор не заряжен. Если & Escr; = 6,00 В, R = 10.0 Ом и C = 72,0 µ F, какой ток течет через батарею долгое время после включения переключателя?
А. 0,432 мА
Б. 0,600 А
С. 0,900 А
D. 1.20 A
Ответ
klm Walker5e Ex 21-17
Если в приведенной ниже схеме C = 24,0 µ F, какова эквивалентная емкость всей цепи?
A. 8.00 µ F
Б. 16.0 µ F
С.36,0 мкм F
D. 72.0 µ F
Ответ
Walker5e 21,61
Два конденсатора, C 1 = C и C 2 = 2 C , подключены к батарее. Конденсатор _____ накапливает больше энергии, когда они подключены к батарее последовательно, а конденсатор _____ накапливает больше энергии, когда они соединяются параллельно с батареей.
А. С 1 … С 1
Б. С 2 … С 1
С. С 1 … С 2
D. C 2 … C 2
Ответ
SJ6 28,33
Батарея была подключена к схеме ниже в течение длительного времени. Какое напряжение на конденсаторе?
А. 2,00 В
Б. 4.00 В
С.6.00 В
D. 8.00 V
Ответ
Б. 0,150 Дж
Д. 268 В
D. 1.20 А
Сразу после включения переключателя конденсатор разряжается и ведет себя как провод. Батарея 6,00 В пропускает 0,600 А тока через каждый из резисторов 10,0 Ом (или, если вы предпочитаете, два резистора, включенных параллельно, имеют эквивалентное сопротивление 5.00 Ом), что дает ток через батарею 1,20 А.
Б. 0,600 А
Через долгое время после включения переключателя конденсатор полностью заряжен и ведет себя как разомкнутая цепь. Батарея на 6,00 В пропускает через левый резистор 10,0 Ом ток 0,600 А.
C. 36.0 µ F
Два последовательно соединенных конденсатора имеют эквивалентную емкость ½ C , и они соединены параллельно с третьим идентичным конденсатором.Следовательно, мы складываем две емкости, чтобы получить эквивалентную емкость 1,50 C или 1,50 × 24,0 µ F = 36,0 µ F.
C. C 1 … C 2
При последовательном соединении два конденсатора имеют одинаковый заряд. Заметив, что U = ½ Q ² / C , вы можете увидеть, что меньший конденсатор C 1 сохраняет больше всего энергии. (Убедитесь сами, что если напряжение АКБ 6.0 V и C = 10,0 µ F, C 1 магазинов 80 µ J и C 2 магазинов 40 µ J.)
При параллельном подключении два конденсатора имеют одинаковое напряжение. Заметив, что U = ½ CV ², вы можете видеть, что больший конденсатор C 2 накапливает больше всего энергии. (Убедитесь сами, что если напряжение батареи составляет 6,0 В и C = 10,0 µ F, C 1 накопитель 180 µ J и C 2 накопитель 360 µ Дж.)
В. 6,00 В
Левая сторона конденсатора находится под более высоким потенциалом.
и параллельные конденсаторы
Последовательные и параллельные конденсаторыПоследовательные и параллельные конденсаторы
Конденсатор — это устройство для хранения разделенного заряда и поэтому накапливается электростатическая потенциальная энергия. Цепи часто содержат более одного конденсатора.
Рассмотрим два конденсатора в параллельно , как показано справа
Когда батарея подключена, электроны будут течь до тех пор, пока потенциал точка A совпадает с потенциалом положительной клеммы аккумулятора и потенциал точки B равен потенциалу отрицательной клеммы аккумулятор.Таким образом, разность потенциалов между обкладками обоих конденсаторов равна V A — V B = V bat . Имеем C 1 = Q 1 / V bat и C 2 = Q 2 / V bat , где Q 1 — заряд конденсатора C 1 , а Q 2 — заряд конденсатора С 2 . Пусть C — эквивалентная емкость двух конденсаторов в параллельно, то есть C = Q / V bat , где Q = Q 1 + Q 2 .Тогда C = (Q 1 + Q 2 ) / V bat = C 1 + C 2 .
Для конденсаторов, включенных параллельно, емкости добавляют.
Для более двух конденсаторов имеем
C = C 1 + C 2 + C 3 + C 4 + ….
Рассмотрим два конденсатора серии , как показано справа.
Пусть Q представляет собой общий заряд на верхней пластине C 1 ,
который затем индуцирует заряд -Q на своей нижней пластине.Заряд на
нижняя пластина C 2 будет -Q, что, в свою очередь, вызывает заряд
+ Q на верхней пластине, как показано.
Пусть V 1 и V 2 представляют разности потенциалов
между обкладками конденсаторов С 1 и С 2 соответственно. потом
V 1 + V 2 = V bat , или (Q / C 1 ) + (Q / C 2 )
= Q / C или (1 / C 1 ) + (1 / C 2 ) = 1 / C. Более двух
конденсаторы последовательно имеем
1 / C = 1 / C 1 + 1 / C 2 + 1 / C 3 + 1 / C 4 +….
где C — эквивалентная емкость двух конденсаторов.
Для конденсаторов, включенных последовательно, величина, обратная их эквивалентная емкость равна сумме обратных величин их индивидуальных емкости.
Проблема:
Какую общую емкость можно получить, подключив 5 мкФ и 8 мкФ конденсатор вместе?
Решение:
- Рассуждение:
Мы можем подключать конденсаторы последовательно или параллельно.
Чтобы получить наибольшую емкость, мы необходимо подключить конденсаторы параллельно.
Чтобы получить наименьшую емкость, мы должны подключить конденсаторы последовательно. - Детали расчета:
Параллельное подключение конденсаторов:
C наибольший = (5 + 8) мкФ = 13 мкФ.
Последовательное соединение конденсаторов.
1 / C наименьшее = (1/5 + 1/8) (мкФ) -1 = 13 / (40 мкФ) = 0,325 / мкФ.
C наименьший = 40/13 мкФ = 3.077 мкФ.
Объяснение урока: конденсаторы, подключенные последовательно и параллельно
В этом объяснении мы узнаем, как рассчитать общую емкость нескольких конденсаторов, соединенных последовательно и параллельно.
Для начала давайте вспомним законы Кирхгофа, которые помогут нам понять эффекты объединения конденсаторов по-разному:
- Ток в переходе равен току из перехода.
- Сумма разностей напряжений в замкнутом контуре равна нулю.
Мы начнем наше обсуждение с рассмотрения конденсаторов, соединенных параллельно, как показано на схеме ниже.
Обратите внимание, что оба конденсатора находятся на своей отдельной ветви этой цепи, и помните, что каждая ветвь в параллельной цепи получает одинаковое напряжение или разность потенциалов. Второй закон Кирхгофа подтверждает это. Таким образом, разность потенциалов на конденсаторе 1, которую мы можем назвать 𝑉, равна разности потенциалов второго конденсатора и разности потенциалов, обеспечиваемой батареей, total.Это общее соотношение математически изложено ниже.
На приведенной выше диаграмме у нас есть два конденсатора, но пунктирное продолжение приведенного ниже уравнения (и других в этом пояснении) подразумевает, что взаимосвязь сохраняется для любого количества конденсаторов, которое мы могли бы захотеть рассмотреть: 𝑉 = 𝑉 = 𝑉 = ⋯ .total
Первый закон Кирхгофа гласит, что ток на входе и выходе из ветви цепи равны. Также помните, что количество заряда, протекающего через ответвление цепи, является произведением тока в ответвлении и времени, в течение которого протекает заряд.Таким образом, когда цепь замкнута и конденсаторы могут заряжаться в течение некоторого времени, заряды на всех конденсаторах (здесь 𝑄 и 𝑄) складываются в общий заряд всей цепи, 𝑄total, как показано ниже: 𝑄 = 𝑄 + 𝑄 + ⋯ .total
Мы уже знаем, что можем связать разность потенциалов и заряд с емкостью, используя уравнение 𝐶 = 𝑄𝑉, которое можно переписать как 𝑄 = 𝐶𝑉.
Применим это к приведенному выше уравнению для заряда, заменив «𝐶𝑉» на «» следующим образом: 𝑄 = 𝐶𝑉 = 𝐶𝑉 + 𝐶𝑉 + ⋯ .totaltotaltotal
Помните, что значения разности потенциалов для всех элементов в параллельной комбинации эквивалентны, поэтому мы можем разделить все это уравнение на разность потенциалов.Это приводит к уравнению, которое мы используем, чтобы связать значение общей емкости со значением каждого конденсатора в параллельной комбинации.
Определение: Общая емкость для параллельной комбинации
Общая емкость для параллельной комбинации конденсаторов определяется как 𝐶 = 𝐶 + 𝐶 + ⋯ .total
В следующих примерах мы попрактикуемся в параллельном соединении конденсаторов.
Пример 1: Параллельное объединение конденсаторов
Схема на схеме содержит два конденсатора, соединенных параллельно.Какова общая емкость цепи?
Ответ
Начнем с того, что вспомним уравнение для конденсаторов, соединенных параллельно: 𝐶 = 𝐶 + 𝐶 + ⋯ .total
Поскольку у нас есть два конденсатора, подключенных параллельно, и мы знаем их значения, мы готовы сложить их, чтобы найти общую емкость цепи: 𝐶 = 35 + 65 = 100.total мкФмкФмкФ
Таким образом, мы обнаружили, что общая емкость этой цепи составляет 100 мкФ.
Пример 2: Параллельное объединение конденсаторов
Схема на схеме содержит два конденсатора, соединенных параллельно.Общая емкость цепи составляет 240 мкФ. Какая емкость 𝐶?
Ответ
Здесь нам нужно определить неизвестное значение емкости 𝐶, и мы можем начать с рассмотрения уравнения для полной емкости параллельной комбинации: 𝐶 = 𝐶 + 𝐶 + ⋯ .total
Таким образом, отдельные значения емкости просто добавляют к общему значению емкости. Подставляя значения, которые нам были даны, уравнение становится 240 = + 135. мкФмкФ
Мы можем найти 𝐶, вычтя 135 мкФ из обеих частей уравнения: 𝐶 = 240−135 = 105.µFµFµF
Таким образом, мы нашли, что емкость 𝐶 равна 105 µF.
Давайте теперь сосредоточимся на последовательном соединении конденсаторов, как показано на схеме ниже.
Напомним, что ток одинаков во всех точках последовательной цепи, что подтверждается первым законом Кирхгофа. Это означает, что последовательно соединенные конденсаторы хранят одинаковые заряды. Таким образом, для комбинации серий 𝑄 = 𝑄 = 𝑄 = ⋯ .total
Из-за второго закона Кирхгофа мы знаем, что сумма разностей потенциалов между элементами в замкнутом контуре равна нулю.Последовательная комбинация представляет собой один большой замкнутый контур, поэтому разность потенциалов на конденсаторах должна в сумме равняться разности потенциалов на батарее. Так, 𝑉 = 𝑉 + 𝑉 + ⋯ .total
Еще раз напомним, что емкость, разность потенциалов и заряд для любого конденсатора даются как 𝐶 = 𝑄𝑉, что можно переформатировать как 𝑉 = 𝑄𝐶.
Мы можем подставить это в приведенное выше уравнение разности потенциалов, чтобы соотношение записывалось как 𝑉 = 𝑄𝐶 = 𝑄𝐶 + 𝑄𝐶 + ⋯ .totaltotaltotal
Мы уже определили, что заряды на всех элементах последовательной цепи эквивалентны, поэтому мы можем разделить все уравнение на заряд.И у нас есть отношение для описания значений емкости в последовательной комбинации.
Определение: Общая емкость для последовательной комбинации
Общая емкость для последовательной комбинации конденсаторов определяется как 1𝐶 = 1𝐶 + 1𝐶 + ⋯ .total
Обратите внимание на обратный характер этого уравнения, что означает, что при последовательном добавлении дополнительных конденсаторов общая емкость уменьшается. Мы рассмотрим эту концепцию в следующих двух примерах.
Пример 3: Объединение конденсаторов в серию
Два конденсатора, 𝐶 и 𝐶, соединены последовательно, где 𝐶> 𝐶.Какое из следующих утверждений правильно связывает общую емкость, total, с 𝐶 и?
- 𝐶 = 𝐶 + 𝐶total
- 𝐶 = (𝐶 + 𝐶) total
- 𝐶 = total
- 𝐶𝐶𝐶total
- total
Ответ
Выбор A может выглядит знакомо, но это уравнение было бы применимо, если бы два конденсатора были добавлены параллельно, а не последовательно. Следовательно, A неверно. Уравнение для полной емкости для двух последовательно соединенных конденсаторов имеет вид 1𝐶 = 1𝐶 + 1𝐶.total
Это уравнение не переупорядочивается и не упрощается до уравнения в B или C, поэтому эти два варианта неверны. Хотя приведенное выше уравнение прямо не указано ни в одном из вариантов ответа, мы можем использовать его для сравнения общего, 𝐶 и размера и определения правильности D или E.
Из-за обратных свойств в приведенном выше уравнении мы можем сказать, что по мере последовательного добавления конденсаторов эквивалентная или общая емкость уменьшается. Таким образом, для последовательной комбинации конденсаторов общая емкость меньше, чем емкость любого одного конденсатора в цепи.Это означает, что «итого» и «итого».
Следовательно, вариант E правильный.
Пример 4: Последовательное объединение конденсаторов
Схема на схеме содержит два конденсатора, соединенных последовательно. Какова общая емкость цепи? Ответить с ближайшим микрофарадом.
Ответ
Мы можем начать с того, что вспомним уравнение, чтобы найти эквивалентную емкость для конденсаторов, соединенных последовательно: 1𝐶 = 1𝐶 + 1𝐶 + ⋯ .total
Теперь давайте подставим значения для двух конденсаторов, показанных выше: 1𝐶 = 1𝐶 + 1𝐶 = 1150 + 1250.totalµFµF
Чтобы сложить дроби в правой части уравнения, мы будем использовать 750 мкФ в качестве наименьшего общего знаменателя: 1𝐶 = 5750 + 3750 = 8750.totalµFµFµF
Теперь мы можем взять обратную или обратную сторону уравнения, чтобы найти окончательное значение 𝐶total: 𝐶 = 7508 = 93,75.total мкФмкФ
Округляя до ближайшего микрофарада, находим, что общая емкость цепи составляет 94 мкФ.
Поскольку мы теперь видели, как добавлять конденсаторы последовательно и параллельно, давайте попробуем оба навыка в следующих примерах.
Пример 5: Последовательное и параллельное объединение конденсаторов
Конденсатор 135 мкФ и конденсатор 264 мкФ можно комбинировать последовательно или параллельно. Найдите отношение общей емкости параллельно к общей емкости последовательно. Ответьте с точностью до двух знаков после запятой.
Ответ
Здесь мы исследуем влияние, которое объединение двух конденсаторов разными способами оказывает на их общую емкость. Мы можем начать с того, что вспомним уравнение для параллельного объединения конденсаторов: 𝐶 = 𝐶 + 𝐶 + ⋯.total
Таким образом, мы можем сказать, прежде чем вставлять какие-либо значения для 𝐶 или, что общая емкость будет больше, чем любое единичное значение емкости любого конденсатора. Теперь, подставив два значения, которые нам даны, мы можем найти общую емкость для параллельной комбинации, которую мы можем назвать 𝐶параллельной: 𝐶 = 135 + 264 = 399.параллельно мкФ мкФ мкФ
Теперь мы можем взглянуть на уравнение для последовательного объединения конденсаторов: 1𝐶 = 1𝐶 + 1𝐶 + ⋯ .total
Мы видим, что общая емкость для последовательной комбинации, которую мы можем назвать серией, будет меньше, чем отдельные значения емкости или.Таким образом, мы можем ожидать, что 𝐶parallel будет больше, чем series, и что соотношение их значений будет больше единицы.
Давайте теперь найдем значение общей емкости в серии: 1𝐶 = 1135 + 1264.seriesµFµF
Переписывая уравнение так, чтобы мы могли складывать дроби, используя наименьший общий знаменатель, мы имеем 1𝐶 = 8811880 + 4511880 = 13311880.seriesµFµFµF
Давайте обратим или перевернем все уравнение для решения 𝐶series, переместив его из знаменателя в числитель: 𝐶 = 11880133 = 89.32.seriesµFµF
Теперь, когда мы знаем 𝐶parallel и 𝐶series, мы можем найти соотношение их значений: 𝐶𝐶 = 39989,32 = 4,4671.parallelseries мкФмкФ
Округляя до двух десятичных знаков, мы находим, что отношение общей емкости параллельно к общей емкости последовательно составляет 4,47.
Пример 6: Последовательное и параллельное объединение конденсаторов
Схема на схеме содержит конденсаторы, соединенные последовательно и параллельно. Какова общая емкость цепи? Дайте ответ с точностью до микрофарада.
Ответ
Здесь у нас есть цепь, содержащая конденсаторы, соединенные последовательно и параллельно. Мы будем работать с этой схемой по частям и обозначать три конденсатора как A, B и C, как показано на схеме ниже.
Конденсаторы A и B соединены последовательно, поэтому давайте сначала определим их эквивалентную емкость. Эта эквивалентная емкость, которую мы можем назвать AB, будет представлять общую емкость среднего провода этой параллельной схемы. Мы можем начать с уравнения для определения общей емкости последовательной комбинации и подставить наши значения для конденсаторов A и B: 1𝐶 = 1𝐶 + 1𝐶 + ⋯ 1𝐶 = 1𝐶 + 1𝐶 = 175 + 155.totalABABµFµF
Наименьший общий знаменатель этих дробей 825 µF: 1𝐶 = 11825 + 15825 = 26825.ABµFµFµF
Теперь мы возьмем обратное или обратное выражение всего уравнения и вычислим значение эквивалентной емкости A и B: 𝐶 = 82526 = 31,73.ABµFµF
Теперь мы можем представить, что схема просто состоит из двух конденсаторов, соединенных параллельно, как показано на диаграмме ниже.
Теперь у нас фактически есть два конденсатора, соединенных параллельно, поэтому мы можем подключить их значения и решить для общей емкости всей цепи: 𝐶 = 𝐶 + 𝐶 + ⋯ всего = 𝐶 + 𝐶 = 31.73 + 35 = 66,73. TotalABCµFµFµF
Округляя до ближайшего микрофарада, находим, что общая емкость этой цепи составляет 67 мкФ.
В заключение резюмируем некоторые важные концепции.
Ключевые моменты
- При параллельном соединении конденсаторов используйте 𝐶 = 𝐶 + 𝐶 + ⋯ total.
- При последовательном соединении конденсаторов используйте 1𝐶 = 1𝐶 + 1𝐶 + ⋯ total.
- Параллельно соединенные конденсаторы имеют одинаковую разность потенциалов.
- Конденсаторы, соединенные последовательно, сохраняют одинаковый заряд.
Физика для науки и техники II
5.7 Параллельное подключение конденсаторов от Office of Academic Technologies на Vimeo.
5.07 Параллельное соединение конденсаторов
Прежде чем мы изучим детали того, как мы подключаем конденсаторы в типичную электрическую цепь, давайте введем некоторые символы, чтобы обозначить некоторые из типичных компонентов электрической цепи.Мы собираемся представить источник питания, который может быть, например, аккумулятором, солнечным элементом или генератором. Которая обеспечивает электрическую потенциальную энергию цепи с этим символом. Большая или длинная линия представляет собой положительный вывод источника питания, а меньший — отрицательный вывод источника питания.
И мы собираемся изобразить направление, в котором заряд получает электрическую потенциальную энергию, стрелкой, которая всегда будет указывать от отрицательной клеммы к положительной клемме источника питания.Мы будем обозначать это как Эпсилон. И это называется стрелкой ЭДС. И мы вернемся к важности этого направления, связанного с этой стрелкой, позже, когда будем изучать Правила Кирхгофа. И, конечно же, мы будем использовать прямые линии, чтобы изобразить провода в электрической цепи.
И следующий компонент, который мы только что представили, — это конденсаторы. И для этого мы будем использовать этот символ для обозначения конденсатора с емкостью C. И мы собираемся использовать этот символ для обозначения переключателя в электрической цепи.А также аналогичным образом это будет представлять собой двухпозиционный переключатель в электрических цепях.
Хорошо. Когда мы смотрим на типы соединений компонентов типичной электрической цепи, мы видим два разных типа соединений. Один из них называется параллельным подключением; другой называется последовательным подключением. В случае параллельного соединения компоненты соединяются друг с другом таким образом, что разность потенциалов на каждом компоненте становится равной другим. А в случае последовательного соединения компоненты подключаются друг за другом, как муфты вагонов поезда на одной и той же железной дороге.И в этом случае разность потенциалов по всей комбинации становится равной сумме разностей потенциалов по каждому компоненту в комбинации.
А теперь рассмотрим эти соединения на примере конденсаторов. Начнем сначала с параллельного включения конденсаторов. В этом случае конденсаторы соединяются друг с другом так, что разность потенциалов на каждом конденсаторе в комбинации или соединении становится равной другому.Таким образом, конденсаторы подключаются параллельно, если к каждому конденсатору приложена одинаковая разность потенциалов.
Пусть C1, C2 и C3 — 3 конденсатора. И мы соединяем эти конденсаторы параллельно таким образом, чтобы приложить одинаковую разность потенциалов к каждому из них, что мы называем параллельным соединением. Если мы подключим концы соединения к клеммам источника питания таким образом, мы увидим, что источник питания будет генерировать V, вольт разности потенциалов. И давайте представим здесь переключатель.А когда мы подключаем переключатель s, положительные заряды, сосредоточенные на положительной клемме источника питания, скажем, здесь батареи, постоянно отталкиваются друг от друга.
Следовательно, как только они найдут этот доступный путь, они будут двигаться по этому пути и придут к этой точке, в которой они увидят три возможных пути для перемещения. И, скажем, если q зарядов поступает с положительного вывода этого источника питания, эти положительные заряды перемещаются по этому пути, и всякий раз, когда они достигают этой точки, где они видят три доступных пути, некоторая их часть будет пройти первый путь и собрать, скажем, левую обкладку конденсатора С1 в качестве заряда q1.И затем некоторая фракция пройдет этот доступный второй путь и снова будет собираться на левой пластине этого конденсатора C2 со значением q2. А затем оставшиеся из них пройдут этот доступный путь и будут собраны через пластину конденсатора емкостью C3 с величиной, скажем, q3.
Точно так же отрицательные заряды отталкиваются друг от друга на отрицательной клемме источника питания, и как только переключатель s замкнется, у нас будет доступный путь для их прохождения по этому пути.А затем некоторая их часть пройдет по этому пути и будет собираться на этом выводе конденсатора C1 как минус q1. Другая фракция пройдет по этому пути и будет собрана здесь как минус q2. А оставшаяся фракция пройдет по этому пути и будет собираться на правой боковой пластине конденсатора C3 как минус q3.
Этот процесс зарядки будет продолжаться до тех пор, пока мы не достигнем достаточно высокого заряда на пластинах этих конденсаторов, чтобы они создавали достаточно сильную силу отталкивания для входящих зарядов.И тогда процесс зарядки остановится, и конденсаторы будут полностью заряжены. Что ж, поскольку основное свойство параллельного соединения таково, что разность потенциалов на каждом компоненте, в данном случае на каждом конденсаторе, становится равной другому, при параллельном подключении мы можем сказать, что если мы называем емкость, или разность потенциалов на C1 как V1 вольт, на C2 как V2 вольт и на C3 как V3 вольт. Первое свойство параллельного подключения становится V1 равно V2, что равно V3.И в этой конкретной схеме все они будут равны любой разности потенциалов, создаваемой источником питания или этой батареей, В вольт.
Прибор, измеряющий разность потенциалов между двумя точками, называется вольтметром. И для этого мы будем использовать этот символ. Вольтметр: устройство, измеряющее разность потенциалов между двумя точками. А чтобы измерить разность потенциалов между двумя точками, мы всегда подключаем вольтметр параллельно этим точкам, представляющим интерес.Другими словами, если вы хотите измерить, например, разность потенциалов между клеммами источника питания, мы подключаем наш вольтметр к интересующим точкам параллельно, вот так, и, следовательно, он измеряет разность потенциалов между этими точками. конец и другой конец.
Следовательно, если вы возьмете вольтметр, подключитесь к этим точкам, он даст нам разность потенциалов между этими двумя точками. Затем мы можем взять их, клеммы вольтметра, и подключить их через комбинацию между этими двумя точками, мы все равно будем считывать вольт, независимо от разности потенциалов, генерируемой этой батареей.А затем, если мы возьмем выводы вольтметра, подключим их к пластинам конденсатора С1, мы снова увидим то же напряжение. И если мы сделаем то же самое с C2, мы снова будем считывать точно такое же напряжение, а на C3 мы будем считывать ту же разность потенциалов. Это первое важное свойство параллельной комбинации состоит в том, что разность потенциалов на каждом конденсаторе в параллельной комбинации или соединении будет равна друг другу. Что ж, это напрямую связано с принципом сохранения энергии, поскольку мы знаем, что потенциал связан с потенциальной энергией, которая является потенциальной энергией на единицу заряда.И когда мы подключаем конденсаторы параллельно в этой форме, мы в основном применяем одинаковую разность потенциалов к каждому конденсатору.
Второе свойство будет связано с принципом сохранения заряда. Когда мы включаем выключатель, это соединение будет получать q заряда от источника питания, от этой батареи, которая генерирует вольт разности потенциалов между ее выводами. Затем эти заряды проходят сюда и видят три доступных пути в этой цепи.Затем некоторая дробь пройдет по этому первому пути, некоторая дробь пройдет по второму пути, а оставшаяся дробь пройдет по третьему пути и сохранится на конденсаторе C1 как q1, на C2 как q2 и на C3 как q3. Таким образом, принцип сохранения заряда гласит, что количество заряда, полученного от этого источника питания, будет равно сумме зарядов, накопленных на пластинах этих конденсаторов. Другими словами, q1 плюс q2 плюс q3 будет равно общему заряду, полученному от источника питания.
Хорошо. Теперь предположим, что мы хотели бы упростить эту схему, просто заменив все эти три конденсатора, которые подключены параллельно, одним конденсатором. Таким образом, этот единственный конденсатор будет выполнять ту же работу, что и эти три при параллельном подключении. В этом случае, заменив эти три одним конденсатором, наша схема упростится до такой формы.
Вот тот же источник питания, вырабатывающий разность потенциалов VV, вот наш переключатель, s, и вот конденсатор, который мы заменяем все эти три.И давайте назовем емкость конденсатора эквивалентом C. Другими словами, эквивалент этих трех конденсаторов в параллельной форме. Что ж, чтобы эта новая схема выполняла ту же работу, что и эти три конденсатора при параллельном подключении, когда мы замыкаем здесь переключатель s, она должна снимать такое же количество заряда q с этого источника питания, с этой батареи. Следовательно, количество заряда, которое будет храниться на месте этого конденсатора, будет таким же, q, которое было получено в предыдущей схеме.
Что ж, если мы вспомним, скажем, свойство три здесь, если мы вспомним определение емкости, она была равна величине заряда, величине заряда, хранящегося на месте конденсатора q, деленному на потенциал разница между пластинами конденсатора. И мы легко можем видеть, что разность потенциалов на пластинах этого конденсатора будет такой же, как у этой батареи. Другими словами, если мы снова подключим наш вольтметр к клеммам этой батареи, мы будем считать V вольт, а затем, если мы снова подключим наш вольтметр параллельно через пластины этого конденсатора, мы будет читать точно такое же напряжение.Таким образом, эквивалент C будет равен q над V.
Что ж, если мы решим для q из этого уравнения, это будет равно C, эквивалентному V, умноженному на V. Точно так же мы можем выразить количество заряда, хранящегося на C1, которое было определено как q1, и которое будет равно a емкость конденсатора C1 умножается на разность потенциалов между пластинами конденсатора C1. Но поскольку V1 было равно V из свойства один, то мы можем выразить это как C1, умноженное на V. Точно так же q2 будет равно C2, умноженному на V2.И снова V2 равно V, что будет равно C2, умноженному на V вольт. И q3 будет равно C3, умноженному на V3, что опять же даст нам, поскольку V3 также равно V вольт, C3 умноженному на V.
Теперь из свойства два, где q равно q1 плюс q2 плюс q3, мы можем выразить q1 через емкость и разность потенциалов как C1, умноженное на V, для q2, C2, умноженное на V, плюс для q3, умноженное на C3. V. Точно так же q можно выразить через эквивалентную емкость и разность потенциалов на одной из пластин этого конденсатора как C, умноженную на эквивалент V.Поскольку напряжение одинаково на каждом члене, мы можем разделить обе части на V. И, следовательно, мы получаем выражение, что эквивалент C равен C1 плюс C2 плюс C3.
Теперь мы можем легко обобщить это соотношение для числа N конденсаторов, подключенных параллельно. Эквивалент C будет равен C1 плюс C2 плюс C3 плюс C sub N. Или, в компактной форме, мы можем записать это как суммирование по I от 1 до N от C sub I. Это соотношение показывает нам, что когда мы подключаем конденсаторы при параллельном подключении эквивалентная емкость цепи становится суммой емкостей каждого отдельного конденсатора в соединении.другими словами, увеличивается общая емкость цепи.
Как подключить конденсаторы параллельно
В C1 = V C2 = V C3 = V AB = 12 В
В приведенной ниже схеме конденсаторы C1, C2 и C3 подключены к каждому другой в параллельном плече между точками A и B, как показано.
В то время как конденсаторы соединены друг с другом параллельно, сумма или сопоставимая емкость, CT в цепи складываются в сумму каждого из конкретных конденсаторов, добавленных вместе.Причина в том, что верхняя пластина конденсатора C1 соединена с верхней пластиной C2, которая прикреплена к верхней пластине C3 и так далее.
То же самое можно наблюдать и на нижних обкладках конденсаторов. Тогда можно рассматривать, как если бы 3 части пластин находились в контакте друг с другом и складывались в одну существенную единую пластину, таким образом увеличивая эффективную площадь пластины в м2.
Учитывая, что емкость C относится к площади пластины (C = ε A / d), емкость, связанная с парой, вероятно, увеличится.Тогда ваша общая величина емкости конденсаторов, подключенных друг к другу параллельно, может быть определена путем совокупного сложения площади пластины. Проще говоря, вся емкость может быть сопоставима с суммой каждой конкретной емкости, соединенной параллельно. Вы могли понять, что общую емкость параллельных конденсаторов можно определить точно так же, как полное сопротивление последовательных резисторов.
Токи (амперы), протекающие через каждый конденсатор и, как все мы заметили в предыдущей статье, имеют отношение к напряжению.В этом случае, применив закон Кирхгофа (KCL) к ранее упомянутой схеме, мы получим
, и это может быть иначе записано как:
Затем мы можем указать полную или сопоставимую схему емкости , C T , чтобы быть суммой каждой отдельной емкости, вместе взятой, давая нам более типичное выражение:
Параллельные конденсаторы Уравнение
При параллельном добавлении взаимно соединенных конденсаторов все они должны быть преобразованы в аналогичные единицы емкости, это может быть мкФ, нФ или пФ.Кроме того, мы можем наблюдать, что ток, протекающий через общее значение емкости, CT не отличается от тока полной цепи, iT
Мы можем дополнительно выделить общую емкость параллельной цепи из общего накопленного кулоновского заряда, используя уравнение Q = CV для заряда обкладок конденсатора. Полный заряд QT, накопленный на всех пластинах, равен сумме удельных накопленных зарядов на каждом конденсаторе, следовательно,
Поскольку напряжение (В) распределяется для параллельно соединенных конденсаторов, вы можете разделить каждую сторону Вышеупомянутая формула через напряжение, выходящее из емкости, и простое сложение друг с другом значений конкретных емкостей дает вам полную емкость CT.Кроме того, это уравнение не основано на количестве конденсаторов, подключенных параллельно в секции, что позволяет вам быть универсальным почти для любого количества N параллельных конденсаторов, подключенных друг к другу.
Конденсаторы в параллельном соединении Пример №1
В результате, используя значения трех конденсаторов из вышеприведенной иллюстрации, мы можем оценить общую сравнительную емкость цепи CT как:
C T = C 1 + C 2 + C 3 = 0.1 мкФ + 0,2 мкФ + 0,3 мкФ = 0,6 мкФ
Один важный момент, который следует учитывать в отношении параллельно соединенных цепей конденсаторов, общая емкость (CT) любых 2 или более конденсаторов, соединенных друг с другом параллельно, оказывается выше значения самого большого конденсатора в группе, поскольку мы складывали значения. Следовательно, на нашей иллюстрации выше CT = 0,6 мкФ, в то время как емкость самого большого конденсатора составляет всего 0,3 мкФ.
Хотя 4, 5, 6 или более конденсаторов соединены друг с другом, общая емкость CT цепи все же будет суммой всех конкретных конденсаторов, соединенных вместе, и, как мы теперь понимаем, общая емкость параллельной цепи неизменно не менее максимальной емкости конденсатора.
Это потому, что мы успешно увеличили общую площадь поверхности пластин. В случае, если мы добьемся этого с помощью пары согласующих конденсаторов, мы теперь удвоили площадь поверхности пластин, что, в свою очередь, увеличивает емкость соединения и так далее.
