Активная мощность формула: Активная мощность | Формулы и расчеты онлайн

Активная мощность трансформатора формула — Морской флот

Простое объяснение с формулами

Активная мощность (P)

Другими словами активную мощность можно назвать: фактическая, настоящая, полезная, реальная мощность. В цепи постоянного тока мощность, питающая нагрузку постоянного тока, определяется как простое произведение напряжения на нагрузке и протекающего тока, то есть

потому что в цепи постоянного тока нет понятия фазового угла между током и напряжением. Другими словами, в цепи постоянного тока нет никакого коэффициента мощности.

Но при синусоидальных сигналах, то есть в цепях переменного тока, ситуация сложнее из-за наличия разности фаз между током и напряжением. Поэтому среднее значение мощности (активная мощность), которая в действительности питает нагрузку, определяется как:

В цепи переменного тока, если она чисто активная (резистивная), формула для мощности та же самая, что и для постоянного тока: P = U I.

Формулы для активной мощности

P = U I – в цепях постоянного тока

P = U I cosθ – в однофазных цепях переменного тока

P = √3 U_L I_L cosθ – в трёхфазных цепях переменного тока

P = √ (S 2 – Q 2 ) или

P =√ (ВА 2 – вар 2 ) или

Активная мощность = √ (Полная мощность 2 – Реактивная мощность 2 ) или

кВт = √ (кВА 2 – квар 2 )

Реактивная мощность (Q)

Также её мощно было бы назвать бесполезной или безваттной мощностью.

Мощность, которая постоянно перетекает туда и обратно между источником и нагрузкой, известна как реактивная (Q).

Реактивной называется мощность, которая потребляется и затем возвращается нагрузкой из-за её реактивных свойств. Единицей измерения активной мощности является ватт, 1 Вт = 1 В х 1 А. Энергия реактивной мощности сначала накапливается, а затем высвобождается в виде магнитного поля или электрического поля в случае, соответственно, индуктивности или конденсатора.

Реактивная мощность определяется, как

и может быть положительной (+Ue) для индуктивной нагрузки и отрицательной (-Ue) для емкостной нагрузки.

Единицей измерения реактивной мощности является вольт-ампер реактивный (вар): 1 вар = 1 В х 1 А. Проще говоря, единица реактивной мощности определяет величину магнитного или электрического поля, произведённого 1 В х 1 А.

Формулы для реактивной мощности

Реактивная мощность = √ (Полная мощность 2 – Активная мощность 2 )

квар = √ (кВА 2 – кВт 2 )

Полная мощность (S)

Полная мощность – это произведение напряжения и тока при игнорировании фазового угла между ними. Вся мощность в сети переменного тока (рассеиваемая и поглощаемая/возвращаемая) является полной.

Комбинация реактивной и активной мощностей называется полной мощностью. Произведение действующего значения напряжения на действующее значение тока в цепи переменного тока называется полной мощностью.

Она является произведением значений напряжения и тока без учёта фазового угла. Единицей измерения полной мощности (S) является ВА, 1 ВА = 1 В х 1 А. Если цепь чисто активная, полная мощность равна активной мощности, а в индуктивной или ёмкостной схеме (при наличии реактивного сопротивления) полная мощность больше активной мощности.

Формула для полной мощности

Полная мощность = √ (Активная мощность 2 + Реактивная мощность 2 )

kUA = √(kW 2 + kUAR 2 )

Следует заметить, что:

• резистор потребляет активную мощность и отдаёт её в форме тепла и света.
• индуктивность потребляет реактивную мощность и отдаёт её в форме магнитного поля.
• конденсатор потребляет реактивную мощность и отдаёт её в форме электрического поля.

Все эти величины тригонометрически соотносятся друг с другом, как показано на рисунке:

Трансформатор является прибором, который призван преобразовывать электроэнергию сети. Эта установка имеет две или больше обмоток. В процессе своей работы трансформаторы могут преобразовать частоту и напряжение тока, а также количество фаз сети.

В ходе выполнения заданных функций наблюдаются потери мощности в трансформаторе. Они влияют на исходную величину электричества, которую выдает на выходе прибор. Что собой представляют потери и КПД трансформатора, будет рассмотрено далее.

Устройство

Трансформатор представляет собой статический прибор. Он работает от электричества. В конструкции при этом отсутствуют подвижные детали. Поэтому рост затрат электроэнергии вследствие механических причин исключены.

При функционировании силовой аппаратуры затраты электроэнергии увеличиваются в нерабочее время. Это связано с ростом активных потерь холостого хода в стали. При этом наблюдается снижение нагрузки номинальной при увеличении энергии реактивного типа. Потери энергии, которые определяются в трансформаторе, относятся к активной мощности. Они появляются в магнитоприводе, на обмотках и прочих составляющих агрегата.

Понятие потерь

При работе установки часть мощности поступает на первичный контур. Она рассеивается в системе. Поэтому поступающая мощность в нагрузку определяется на меньшем уровне. Разница составляет суммарное снижение мощности в трансформаторе.

Существует два вида причин, из-за которых происходит рост потребление энергии оборудованием. На них влияют различные факторы. Их делят на такие виды:

Их следует понимать, дабы иметь возможность снизить электрические потери в силовом трансформаторе.

Магнитные потери

В первом случае потери в стали магнитопривода состоят из вихревых токов и гистериза. Они прямо пропорциональны массе сердечника и его магнитной индукции. Само железо, из которого выполнен магнитопривод, влияет на эту характеристику. Поэтому сердечник изготавливают из электротехнической стали. Пластины делают тонкими. Между ними пролегает слой изоляции.

Также на снижение мощности трансформаторного устройства влияет частота тока. С ее повышением растут и магнитные потери. На этот показатель не влияет изменение нагрузки устройства.

Электрические потери

Снижение мощности может определяться в обмотках при их нагреве током. В сетях на такие затраты приходится 4-7% от общего количества потребляемой энергии. Они зависят от нескольких факторов. К ним относятся:

• Электрическая нагрузка системы.
• Конфигурация внутренних сетей, их длина и размер сечения.
• Режим работы.
• Средневзвешенный коэффициент мощности системы.
• Расположение компенсационных устройств.

Потери мощности в трансформаторах являются величиной переменной. На нее влияет показатель квадрата тока в контурах.

Методика расчета

Потери в трансформаторах можно рассчитать по определенной методике. Для этого потребуется получить ряд исходных характеристик работы трансформатора. Представленная далее методика применяется для двухобмоточных разновидностей. Для измерений потребуется получить следующие данные:

• Номинальный показатель мощности системы (НМ).
• Потери, определяемые при холостом ходе (ХХ) и номинальной нагрузке.
• Потери короткого замыкания (ПКЗ).
• Количество потребленной энергии за определенное количество времени (ПЭ).
• Полное количество отработанных часов за месяц (квартал) (ОЧ).
• Число отработанных часов при номинальном уровне нагрузки (НЧ).

Получив эти данные, измеряют коэффициент мощности (угол cos φ). Если же в системе отсутствует счетчик реактивной мощности, в расчет берется ее компенсация tg φ. Для этого происходит измерение тангенса угла диэлектрических потерь. Это значение переводят в коэффициент мощности.

Формула расчета

Коэффициент нагрузки в представленной методике будет определяться по следующей формуле:

К = Эа/НМ*ОЧ*cos φ, где Эа – количество активной электроэнергии.

Какие потери происходят в трансформаторе в период загрузки, можно просчитать по установленной методике. Для этого применяется формула:

П = ХХ * ОЧ * ПКЗ * К² * НЧ.

Расчет для трехобмоточных трансформаторов

Представленная выше методика применяется для оценки работы двухобмоточных трансформаторов. Для аппаратуры с тремя контурами необходимо учесть еще ряд данных. Они указываются производителем в паспорте.

В расчет включают номинальную мощность каждого контура, а также их потери короткого замыкания. При этом расчет будет производиться по следующей формуле:

Э = ЭСН + ЭНН, где Э – фактическое количество электричества, которое прошло через все контуры; ЭСН – электроэнергия контура среднего напряжения; ЭНН – электроэнергия низкого напряжения.

Пример расчета

Чтобы было проще понять представленную методику, следует рассмотреть расчет на конкретном примере. Например, необходимо определить увеличение потребления энергии в силовом трансформаторе 630 кВА. Исходные данные проще представить в виде таблицы.

Обозначение	Расшифровка	Значение
НН	Номинальное напряжение, кВ	6
Эа	Активная электроэнергия, потребляемая за месяц, кВи*ч	37106
НМ	Номинальная мощность, кВА	630
ПКЗ	Потери короткого замыкания трансформатора, кВт	7,6
ХХ	Потери холостого хода, кВт	1,31
ОЧ	Число отработанных часов под нагрузкой, ч	720
cos φ	Коэффициент мощности	0,9

На основе полученных данных можно произвести расчет. Результат измерения будет следующий:

% потерь составляет 0,001. Их общее число равняется 0,492%.

Измерение полезного действия

При расчете потерь определяется также показатель полезного действия. Он показывает соотношение мощности активного типа на входе и выходе. Этот показатель рассчитывают для замкнутой системы по следующей формуле:

КПД = М1/М2, где М1 и М2 – активная мощность трансформатора, определяемая измерением на входном и исходящем контуре.

Выходной показатель рассчитывается путем умножения номинальной мощности установки на коэффициент мощности (косинус угла j в квадрате). Его учитывают в приведенной выше формуле.

В трансформаторах 630 кВА, 1000 кВА и прочих мощных устройствах показатель КПД может составлять 0,98 или даже 0,99. Он показывает, насколько эффективно работает агрегат. Чем выше КПД, тем экономичнее расходуется электроэнергия. В этом случае затраты электроэнергии при работе оборудования будут минимальными.

Рассмотрев методику расчета потерь мощности трансформатора, короткого замыкания и холостого хода, можно определить экономичность работы аппаратуры, а также ее КПД. Методика расчета предполагает применять особый калькулятор или производить расчет в специальной компьютерной программе.

Многим из нас известна основная единица мощности – Ватт (Вт) или чаще используется его производная киловатт (кВт) и вы привыкли, что эта характеристика у электрооборудования указывается именно в них.

Но если взять трансформатор или приборы, в которых он является основным компонентом, например, стабилизаторы напряжения, вы увидите, что мощность там указана в кВА – киловольт-амперах.

Давайте разберемся, что такое кВА, почему именно в этих единицах измерения указывается мощность трансформатора и как она связана с обычными киловаттами.

Я не буду выкладывать здесь определения из учебников и сыпать физическими терминами, объясню коротко, простыми словами, чтобы было понятно любому.

В первую очередь, вы должны знать, что у некоторых электроприборов, работающих от переменного тока, не вся потребляемая мощность тратится на совершение полезной работы – нагрева, освещения, звучания, вращения и т.д.

Всего существует четыре основных типа нагрузок, которые могут подключаться в частности к трансформатору:

Резистивная

Ярким примером резистивной нагрузки является ТЭН, который нагревается при протекании через него электрического тока.

ТЭН – это обычное сопротивление, ему не важно в какую сторону протекает по нему ток, правило одно, чем сила тока больше, тем больше тепла вырабатывается – соответственно вся мощность тратится на это.

Мощность, которая тратится на резистивной нагрузке называется – активной , как раз она то и измеряется в кВт – киловаттах.

Индуктивная

Знакомым всем примером индуктивной нагрузки является электродвигатель, в нём не весь проходящий электрический ток тратится на вращения. Часть расходуется на создание электромагнитного поля в обмотке или теряется в медном проводнике, эта составляющая мощности называется реактивной .

Реактивная мощность не тратится на совершение работы напрямую, но она необходима для функционирования оборудования.

Кстати, индуктивные электрические плиты, которые так хотят заполучить многие домохозяйки, также используют реактивную мощность, в отличии от обычных электроплит, в которых нагреваются ТЭНы, те чисто резистивные.

Ёмкостная

Еще один пример реактивной составляющей мощности содержит ёмкостная нагрузка, это, например, конденсатор. Принцип работы конденсатора – накапливание и передача энергии, соответственно часть мощности тратится именно на это и напрямую не расходуется на работу оборудования.

Практическаи вся окружающая вас электроника и бытовая техника содержит конденсаторы.

Смешанная

Здесь всё просто, смешенная нагрузка сочетает в себе все представленные выше, активную и реактивные составляющие, большинство бытовых приборов именно такие.

Полная мощность электрооборудования, состоит как из активной мощности, так и из реактивной, и измеряется в кВА – киловольт-амперах . Именно она чаще всего указана в характеристиках трансформатора.

Производители трансформаторов не могут знать, какого типа нагрузка к ним будет подключена и где они будут задействованы, поэтому и указывают полную мощность, для смешенной нагрузки.

Так, если нагрузка трансформатора — это ТЭН, то полная мощность будет равна активной, соответственно значение в кВт = кВА, если же нагрузка будет смешенная, включающая реактивную составляющую, то мощность нагрузки должна учитываться полная.

Будьте внимательны, нередко, на электрооборудовании, например, на электроинструменте, мощность прописана в киловаттах, но кроме того указан коэффициент мощности k. В этом случае, вы должны знать простую формулу:

S (полная мощность)= P (активная мощность)/ k (коэффициент мощности)

Так, например, если мощность перфоратора P = 2,5кВт, а его коэффициент мощности k = 0,9, то полная мощность перфоратора будет равна S=2,5кВт/0,9=2,8 кВА, именно на столько он будет нагружать сеть.

Теперь, я думаю, вам понятно, почему мощность трансформатора измеряют в кВА, а не в кВт – это позволяет учитывать все виды нагрузок, которые могут подключаться к его вторичной обмотке.

Поэтому, обязательно учитывайте полную мощность указываемую в кВА или коэффициент мощности обордования, перед подключением к трансформатору.

Если же у вас еще остались какие-то вопросы – обязательно оставляйте их в комментариях к статье, кроме того, если есть что добавить, нашли неточности или есть, что возразить – также пишите!

Понятие о реактивных и активных мощностях и нагрузках

Главная цель при передаче электроэнергии – повышение эффективности работы сетей. Следовательно, необходимо уменьшение потерь. Основной причиной потерь является реактивная мощность, компенсация которой значительно повышает качество электроэнергии.

Батареи статических конденсаторов

Реактивная мощность вызывает ненужный нагрев проводов, перегружаются электроподстанции. Трансформаторная мощность и кабельные сечения вынужденно подвергаются завышениям, сетевое напряжение снижается.

Понятие о реактивной мощности

Для выяснения, что же такое реактивная мощность, надо определить другие возможные виды мощности. При существовании в контуре активной нагрузки (резистора) происходит потребление исключительно активной мощности, полностью расходуемой на энергопреобразование. Значит, можно сформулировать, что такое активная мощность, – та, при которой ток совершает эффективную работу.

На постоянном токе происходит потребление исключительно активной мощности, рассчитываемой соответственно формуле:

P = U x I.

Измеряется в ваттах (Вт).

В электроцепях с переменным током при наличии активной и реактивной нагрузки мощностной показатель суммируется из двух составных частей: активной и реактивной мощности.

Реактивная нагрузка бывает двух видов:

1. Емкостная (конденсаторы). Характеризуется фазовым опережением тока по сравнению с напряжением;
2. Индуктивная (катушки). Характеризуется фазовым отставанием тока по отношению к напряжению.

Емкостная и индуктивная нагрузка

Если рассмотреть контур с переменным током и подсоединенной активной нагрузкой (обогреватели, чайники, лампочки с накаливающейся спиралью), ток и напряжение будут синфазными, а полная мощность, взятая в определенную временную отсечку, вычисляется путем перемножения показателей напряжения и тока.

Однако когда схема содержит реактивные компоненты, показатели напряжения и тока не будут синфазными, а будут различаться на определенную величину, определяемую углом сдвига «φ». Пользуясь простым языком, говорится, что реактивная нагрузка возвращает столько энергии в электроцепь, сколько потребляет. В результате получится, что для активной мощности потребления показатель будет нулевой. Одновременно по цепи протекает реактивный ток, не выполняющий никакую эффективную работу. Следовательно, потребляется реактивная мощность.

Реактивная мощность – часть энергии, которая позволяет устанавливать электромагнитные поля, требуемые оборудованием переменного тока.

Расчет реактивной мощности ведется по формуле:

Q = U x I x sin φ.

В качестве единицы измерения реактивной мощности служит ВАр (вольтампер реактивный).

Выражение для активной мощности:

P = U x I x cos φ.

Треугольник мощностей

Взаимосвязь активной, реактивной и полной мощности для синусоидального тока переменных значений представляется геометрически тремя сторонами прямоугольного треугольника, называемого треугольником мощностей. Электроцепи переменного тока потребляют две разновидности энергии: активную мощность и реактивную. Кроме того, значение активной мощности никогда не является отрицательным, тогда как для реактивной энергии возможна либо положительная величина (при индуктивной нагрузке), либо отрицательная (при емкостной нагрузке).

Треугольник мощностей

Важно! Из треугольника мощностей видно, что всегда полезно снизить реактивную составляющую, чтобы повысить эффективность системы.

Полная мощность не находится как алгебраическая сумма активного и реактивного мощностного значения, это векторная сумма P и Q. Ее количественное значение вычисляется извлечением квадратного корня из суммы квадратов мощностных показателей: активного и реактивного. Измеряться полная мощность может в ВА (вольтампер) или производных от него: кВА, мВА.

Чтобы была рассчитана полная мощность, необходимо знать разность фаз между синусоидальными значениям U и I.

Коэффициент мощности

Пользуясь геометрически представленной векторной картиной, можно найти отношение сторон треугольника, соответствующих полезной и полной мощности, что будет равно косинусу фи или мощностному коэффициенту:

cos φ = P/S.

Данный коэффициент находит эффективность работы сети.

Количество потребляемых ватт – то же самое, что и количество потребляемых вольтампер при мощностном коэффициенте, равном 1 или 100%.

Важно! Полная мощность тем ближе к показателю активной, чем больше cos φ, или чем меньше угол сдвига синусоидальных величин тока и напряжения.

Если, к примеру, имеется катушка, для которой:

• Р = 80 Вт;
• Q = 130 ВАр;
• тогда S = 152,6 BA как среднеквадратичный показатель;
• cos φ = P/S = 0,52 или 52%

Можно сказать, что катушка требует 130 ВАр полной мощности для выполнения полезной работы 80 Вт.

Коррекция cos φ

Для коррекции cos φ применяется тот факт, что при емкостной и индуктивной нагрузке вектора реактивной энергии располагаются в противофазе. Так как большинство нагрузок является индуктивными, подключив емкость, можно добиться увеличения cos φ.

Принцип компенсации реактивной мощности

Главные потребители реактивной энергии:

1. Трансформаторы. Представляют собой обмотки, имеющие индуктивную связь и посредством магнитных полей преобразуюшие токи и напряжения. Эти аппараты являются основным элементом электросетей, передающих электроэнергию. Особенно увеличиваются потери при работе на холостом ходу и при низкой нагрузке. Широко используются трансформаторы в производстве и в быту;
2. Индукционные печи, в которых расплавляются металлы путем создания в них вихревых токов;
3. Асинхронные двигатели. Крупнейший потребитель реактивной энергии. Вращающий момент в них создается посредством переменного магнитного поля статора;
4. Преобразователи электроэнергии, такие как силовые выпрямители, используемые для питания контактной сети железнодорожного транспорта и другие.

Конденсаторные батареи подсоединяются на электроподстанциях для того, чтобы контролировать напряжение в пределах установленных уровней. Нагрузка меняется в течение дня с утренними и вечерними пиками, а также на протяжении недели, снижаясь в выходные, что изменяет показатели напряжения. Подключением и отключением конденсаторов варьируется его уровень. Это делается от руки и с помощью автоматики.

Как и где измеряют cos φ

Реактивная мощность проверяется по изменению cos φ специальным прибором – фазометром. Его шкала проградуирована в количественных значениях cos φ от нуля до единицы в индуктивном и емкостном секторе. Полностью скомпенсировать негативное влияние индуктивности не удастся, но возможно приближение к желаемому показателю – 0,95 в индуктивной зоне.

Фазометр

Фазометры применяются при работе с установками, способными повлиять на режим работы электросети через регулирование cos φ.

1. Так как при финансовых расчетах за потребленную энергию учитывается и ее реактивная составляющая, то на производствах устанавливаются автоматические компенсаторы на конденсаторах, емкость которых может меняться. В сетях, как правило, используются статические конденсаторы;
2. При регулировании cos φ у синхронных генераторов путем изменения возбуждающего тока необходимо его отслеживать визуально в ручных рабочих режимах;
3. Синхронные компенсаторы, представляющие собой синхронные двигатели, работающие без нагрузки, в режиме перевозбуждения выдают в сеть энергию, которая компенсирует индуктивную составляющую. Для регулирования возбуждающего тока наблюдают за показаниями cos φ по фазометру.

Синхронный компенсатор

Коррекция коэффициента мощности – одна из эффективнейших инвестиций для сокращения затрат на электроэнергию. Одновременно улучшается качество получаемой энергии.

Видео

Оцените статью:

Мгновенная мощность

В отличие от цепей постоянного тока, где мощность в течение определенного промежутка времени остается неизменной, в цепях переменного тока дело обстоит иначе. Так как ток и напряжение постоянно меняют своё значение, то и мощность соответственно будет меняться в каждый момент времени. Такая мощность называется мгновенной.

Мгновенной мощностью p(t) называют произведение приложенного к цепи мгновенного напряжения u(t) на мгновенное значение тока i(t) в этой цепи. 

График мгновенной мощности представлен на рисунке ниже

 

Мощность обозначена заштрихованной областью. Знак мощности зависит от сдвига фаз между током и напряжением. В данном случае в цепи присутствуют только активные сопротивления, которые не создают сдвига фаз, поэтому мощность имеет только положительные значения.

Рассмотрим другой график

На данном графике имеются области отрицательных значений мгновенной мощности. Такой график может соответствовать цепи, в которой присутствуют конденсатор или катушка, причем положительные участки — это мощность, которая пошла в цепь и рассеялась на сопротивлении, либо запаслась в качестве энергии полей конденсаторов или катушек, а отрицательные участки это мощность, которая была возвращена обратно источнику.

Активная мощность

Чтобы понять какое количество энергии потребляет источник, целесообразнее взять среднюю мощность за период. Для этого вернемся к первому графику.

На графике мгновенной мощности выделяют прямоугольник со сторонами T и Pm/2. Часть графика, которая находится выше линии 

Pm/2 точно укладывается в незаштрихованную часть прямоугольника. Таким образом, с помощью линии Pm/2 мы можем определить среднюю мощность за период, которая называется активной мощностью. Активная мощность – это полезная мощность, которая идет на преобразование в другие виды энергии. 

В нашем случае сдвиг фаз равен нулю, поэтому коэффициент мощности равен единице, но в случаях с реактивными элементами нужно этот момент учитывать.

Активная мощность измеряется в ваттах – Вт.

cosφ – коэффициент мощности, который показывает отношение активной мощности к полной мощности. 

 

Реактивная мощность

Реактивная мощность – это энергия, которая периодически циркулирует между источником и приемником. Реактивная мощность возникает потому, что конденсатор и катушка способны накапливать энергию, а затем снова отдавать её в сеть.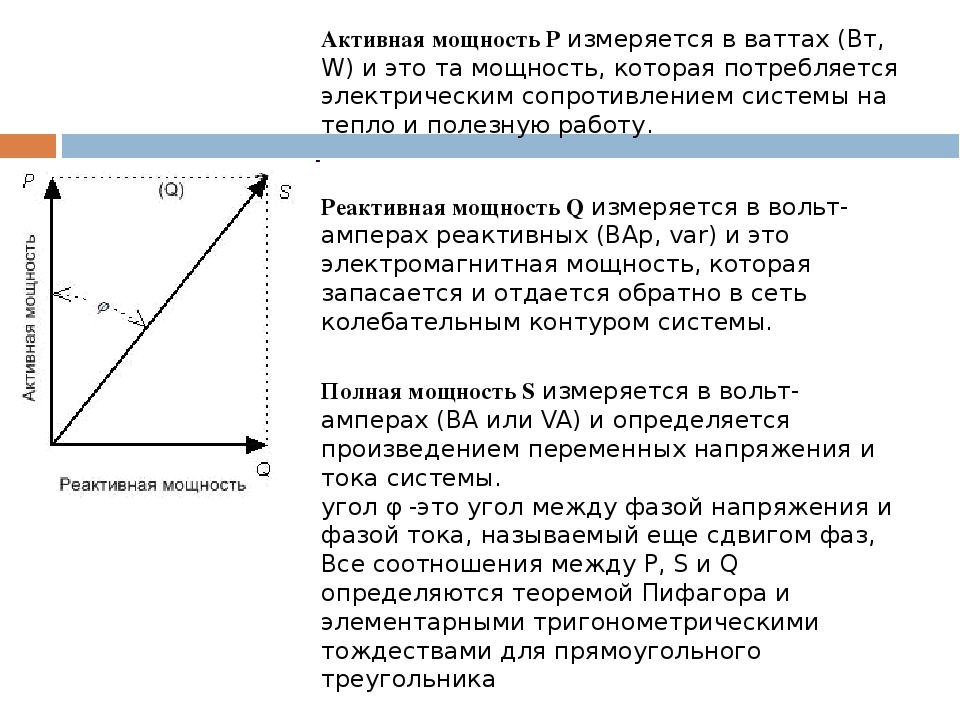

На практике от реактивной мощности зачастую стараются избавиться.

Реактивная мощность измеряется в вольт амперах реактивных – ВАр.

Полная мощность

Полная мощность — это максимальное значение активной мощности.

 

Полная мощность измеряется в вольт-амперах — ВА.

Для наглядного представления существует треугольник мощностей, в котором гипотенузой является полная мощность, а катетами – активная и реактивная составляющие.

 

Читайте также — Последовательная RL-цепь 

Просмотров: 20056

цепи переменного и постоянного тока коэффициент мощности

В статье мы расскажем про мощность в цепи переменного и постоянного тока, а также мгновенную, активную, реактивную и полную мощность, а также что такое коэффициент мощности. Всех их формулы и примеры на нахождение мощности.

Мощность, генерируемая потоком через проводник тока I с напряжением U на его концах, выражается следующей формулой: 

Используя закон Ома, можно определить формулу для мощности с известными сопротивлением и напряжением: 

Аналогично, формула мощности может быть определена в зависимости от сопротивления и тока:

Задачи на нахождение мощности

Задача 1

Напряжение 5 В было измерено на концах резистора 10 Ом. Какая будет мощность? 

Решение:

Применить второе уравнение: Р = 5 ² /10 = 25/10 = 2,5 Вт 

Задача 2

Держатель лампы, несущий опорной мощности P = 21Вт при напряжении U = 12 В для подачи питания накала питания может быть использован со следующим параметры: U = 12В I max= 1А. Какой ток протекает при нормальной работе лампы? 

Решение:

Давайте посчитаем, какой ток протекает при нормальной работе лампы: 

P = U * I 
I = P / U 
I = 21 Вт / 12 В 
I = 1,75 A 

Это означает, что источник питания с заданными параметрами не подходит для питания этой лампы.

Мощность в цепи переменного тока

Мощность в цепи переменного тока в физики и обычной жизни одно из базовых понятий, которое нужно понимать перед началом работы с электроприборами. Далее вы увидите основные формулы мощности и их применение в задачах.

Мгновенная мощность

При рассмотрении энергетических процессов в цепях переменного тока удобно использовать разные типы энергии. Мгновенная мощность равна произведению мгновенных значений тока и напряжения на части цепи:

где: U и I — эффективные значения напряжения и тока, а φ и ω — соответственно разность фаз между током и напряжением и угловой частотой (пульсация).

Активная мощность

Активная мощность характеризуется текущими потерями энергии в течение 1 секунды в активных компонентах цепи (для нагрева, излучения или механических работ). Он измеряется в ваттах и ​​определяется мгновенным значением мощности за период:

Реактивная мощность

Реактивная мощность связана с реактивными сопротивлениями, которые периодически накапливают энергию, а затем возвращают ее источнику, но сами не поглощают энергию.  Единица реактивной мощности вар. Реактивная мощность может быть определена по формуле:

Реактивная мощность положительна при токе, задержанном по отношению к напряжению (φ>0), и отрицательна при токе, который обгоняет напряжение (φ<0).

Если ток действующего значения I протекает через индуктивность L, то: Q = ω*L*I²

Если к конденсатору С приложено напряжение действующего значения U, то: Q = -ω*C*U²

Полная мощность

Полная мощность (кажущаяся) определяется произведением эффективных значений напряжения и тока в сечении провода:

S = I*U

Кажущаяся силовая установка называется ВА (вольтампер). Отношение активной мощности к полной мощности P/S = cosφ называется коэффициентом мощности.

Активная, реактивная и полная мощность связаны друг с другом следующими отношениями:

Задача 3. Рассчитайте угол сдвига фаз цепи, в которой активная мощность составляет 1 кВт, а реактивная мощность — 0,2 кВар.

Решение.

Так мы добрались до конца второго, наверное, самого сложного для понимания руководства по электротехнике. Я не знаю, как это будет принято читателями. Написав это, я должен был решить серьезную дилемму: на самом деле ничего не объясняло простоту и поверхностные вопросы или серьезную трактовку темы. Проблема в том, что последнее возможно только на основе понятий из высшей математики, о которых большинство читателей, вероятно, не имеют ни малейшего понятия. Тем не менее, я должен был быть последовательным. В первой части я использовал элементы высшей математики, поэтому мне пришлось сделать это во второй, хотя я «простил» символический метод описания синусоидальных переменных, но я надеюсь, что те, кто интересуется электротехникой, хотя бы слышали об интегралах, дифференциалах и производных функций. Как я уже писал во введении: вы можете изучать электротехнику только самостоятельно! Это требует прочной основы в области математики, желание и трудолюбие.  Однако это не простая задача, это совсем другая проблема.

Видеоурок по мощности тока

Ниже мы покажем вам простое объяснение по мощности, в котором подведем итоги по данной статье!

Преобразование энергии в электрической цепи. Мгновенная, активная, реактивная и полная мощности синусоидального тока. (Лекция №7)

Передача энергии w по электрической цепи (например, по линии электропередачи), рассеяние энергии, то есть переход электромагнитной энергии в тепловую, а также и другие виды преобразования энергии характеризуются интенсивностью, с которой протекает процесс, то есть тем, сколько энергии передается по линии в единицу времени, сколько энергии рассеивается в единицу времени.

Интенсивность передачи или преобразования энергии называется мощностью р. Сказанному соответствует математическое определение:

.

(1)

Выражение для мгновенного значения мощности в электрических цепях имеет вид:

.

(2)

Приняв начальную фазу напряжения за нуль, а сдвиг фаз между напряжением и током за , получим:

.

(3)

Итак, мгновенная мощность имеет постоянную составляющую и гармоническую составляющую, угловая частота которой в 2 раза больше угловой частоты напряжения и тока.

Когда мгновенная мощность отрицательна, а это имеет место (см. рис. 1), когда u и i разных знаков, т. е. когда направления напряжения и тока в двухполюснике противоположны, энергия возвращается из двухполюсника источнику питания.

Такой возврат энергии источнику происходит за счет того, что энергия периодически запасается в магнитных и электрических полях соответственно индуктивных и емкостных элементов, входящих в состав двухполюсника. Энергия, отдаваемая источником двухполюснику в течение времени t равна .

Среднее за период значение мгновенной мощности называется

активной мощностью .

Принимая во внимание, что , из (3) получим:

.

(4)

Активная мощность, потребляемая пассивным двухполюсником, не может быть отрицательной (иначе двухполюсник будет генерировать энергию), поэтому , т.е. на входе пассивного двухполюсника . Случай Р=0, теоретически возможен для двухполюсника, не имеющего активных сопротивлений, а содержащего только идеальные индуктивные и емкостные элементы.

1. Резистор (идеальное активное сопротивление).

Здесь напряжение и ток (см. рис. 2) совпадают по фазе , поэтому мощность всегда положительна, т.е. резистор потребляет активную мощность

2. Катушка индуктивности (идеальная индуктивность)

При идеальной индуктивности ток отстает от напряжения по фазе на . Поэтому в соответствии с (3) можно записать
.

Участок 1-2: энергия , запасаемая в магнитном поле катушки, нарастает.

Участок 2-3: энергия магнитного поля убывает, возвращаясь в источник.

3. Конденсатор (идеальная емкость)

Аналогичный характер имеют процессы и для идеальной емкости. Здесь . Поэтому из (3) вытекает, что . Таким образом, в катушке индуктивности и конденсаторе активная мощность не потребляется (Р=0), так как в них не происходит необратимого преобразования энергии в другие виды энергии. Здесь происходит только циркуляция энергии: электрическая энергия запасается в магнитном поле катушки или электрическом поле конденсатора на протяжении четверти периода, а на протяжении следующей четверти периода энергия вновь возвращается в сеть.

В силу этого катушку индуктивности и конденсатор называют реактивными элементами, а их сопротивления Х_L и Х_С , в отличие от активного сопротивления R резистора, – реактивными.

Интенсивность обмена энергии принято характеризовать наибольшим значением скорости поступления энергии в магнитное поле катушки или электрическое поле конденсатора, которое называется реактивной мощностью.

В общем случае выражение для реактивной мощности имеет вид:

(5)

Она положительна при отстающем токе (индуктивная нагрузка- ) и отрицательна при опережающем токе (емкостная нагрузка- ). Единицу мощности в применении к измерению реактивной мощности называют вольт-ампер реактивный (ВАр).

В частности для катушки индуктивности имеем:

, так как .

.

Из последнего видно, что реактивная мощность для идеальной катушки индуктивности пропорциональна частоте и максимальному запасу энергии в катушке. Аналогично можно получить для идеального конденсатора:

.

Полная мощность

Помимо понятий активной и реактивной мощностей в электротехнике широко используется понятие полной мощности:

.

(6)

Активная, реактивная и полная мощности связаны следующим соотношением:

.

(7)

Отношение активной мощности к полной называют

коэффициентом мощности. Из приведенных выше соотношений видно, что коэффициент мощности равен косинусу угла сдвига между током и напряжением. Итак,

.

(8)

Комплексная мощность

Активную, реактивную и полную мощности можно определить, пользуясь комплексными изображениями напряжения и тока. Пусть , а . Тогда комплекс полной мощности:

,

(9)

где — комплекс, сопряженный с комплексом .

.

Комплексной мощности можно поставить в соответствие треугольник мощностей (см. рис. 4). Рис. 4 соответствует (активно-индуктивная нагрузка), для которого имеем:

Применение статических конденсаторов для повышения cos

Как уже указывалось, реактивная мощность циркулирует между источником и потребителем. Реактивный ток, не совершая полезной работы, приводит к дополнительным потерям в силовом оборудовании и, следовательно, к завышению его установленной мощности. В этой связи понятно стремление к увеличению в силовых электрических цепях.

Следует указать, что подавляющее большинство потребителей (электродвигатели, электрические печи, другие различные устройства и приборы) как нагрузка носит активно-индуктивный характер.

Если параллельно такой нагрузке (см. рис. 5), включить конденсатор С, то общий ток , как видно из векторной диаграммы (рис. 6), приближается по фазе к напряжению, т.е. увеличивается, а общая величина тока (а следовательно, потери) уменьшается при постоянстве активной мощности . На этом основано применение конденсаторов для повышения .

Какую емкость С нужно взять, чтобы повысить коэффициент мощности от значения до значения ?

Разложим на активную и реактивную составляющие. Ток через конденсатор компенсирует часть реактивной составляющей тока нагрузки :

;

(10)

;

(11)

.

(12)

Из (11) и (12) с учетом (10) имеем

,

но , откуда необходимая для повышения емкость:

.

(13)

Баланс мощностей

Баланс мощностей является следствием закона сохранения энергии и может служить критерием правильности расчета электрической цепи.

а) Постоянный ток

Для любой цепи постоянного тока выполняется соотношение:

(14)

Это уравнение представляет собой математическую форму записи баланса мощностей: суммарная мощность, генерируемая источниками электрической энергии, равна суммарной мощности, потребляемой в цепи.

Следует указать, что в левой части (14) слагаемые имеют знак “+”, поскольку активная мощность рассеивается на резисторах. В правой части (14) сумма слагаемых больше нуля, но отдельные члены здесь могут иметь знак “-”, что говорит о том, что соответствующие источники работают в режиме потребителей энергии (например, заряд аккумулятора).

б) Переменный ток.

Из закона сохранения энергии следует, что сумма всех отдаваемых активных мощностей равна сумме всех потребляемых активных мощностей, т.е.

(15)

В ТОЭ доказывается (вследствие достаточной громоздкости вывода это доказательство опустим), что баланс соблюдается и для реактивных мощностей:

,

(16)

где знак “+” относится к индуктивным элементам , “-” – к емкостным .

Умножив (16) на “j” и сложив полученный результат с (15), придем к аналитическому выражению баланса мощностей в цепях синусоидального тока (без учета взаимной индуктивности):

или

.

Литература

1. Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
2. Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.

Контрольные вопросы и задачи

1. Что такое активная мощность?
2. Что такое реактивная мощность, с какими элементами она связана?
3. Что такое полная мощность?
4. Почему необходимо стремиться к повышению коэффициента мощности ?
5. Критерием чего служит баланс мощностей?
6. К источнику с напряжением подключена активно-индуктивная нагрузка, ток в которой . Определить активную, реактивную и полную мощности.

Ответ: Р=250 Вт; Q=433 ВАр; S=500 ВА.

7. В ветви, содержащей последовательно соединенные резистор R и катушку индуктивности L, ток I=2 A. Напряжение на зажимах ветви U=100 B, а потребляемая мощность Р=120 Вт. Определить сопротивления R и XL элементов ветви.

Ответ: R=30 Ом; XL=40 Ом.

8. Мощность, потребляемая цепью, состоящей из параллельно соединенных конденсатора и резистора, Р=90 Вт. Ток в неразветвленной части цепи I1=5 A, а в ветви с резистором I2=4 A. Определить сопротивления R и XC элементов цепи.

Ответ: R=10 Ом; XС=7,5 Ом.

Реактивная мощность на ощупь, простым языком, без графиков | Электромозг

Сегодня я постараюсь объяснить простым языком, что же такое реактивная мощность электрической энергии.

Активная мощность

Для начала, расскажу про наиболее привычную нам активную мощность, за которую мы, собственно, и платим по счётчику. Эта мощность, потребляемая нагрузкой типа обычного сопротивления. Как правило, это все нагревательные приборы (бойлеры, обычные электроплитки, электро калориферы и т.п.). Потребляемая мощность этих приборов полностью активная. В этих приборах электрическая энергия безвозвратно и полностью преобразуется в другой вид энергии (тепловую и другие).

Активная мощность обозначается буквой P и измеряется в ваттах (Вт).

Величина активной мощности, потребляемой такими приборами считается просто — умножением напряжения в розетке на ток, протекающей в цепи включенного нагревательного прибора:

P = U * I

Тут всё просто. Нагрузка пассивна, постоянна, никаких неожиданностей.

Замечу, что в цепях постоянного тока существует только активная мощность, поскольку значение мгновенной и средней мощности там совпадают.

Реактивная мощность

Если включить в сеть переменного тока не нагревательный прибор, а, например, электромагнит, то помимо активной, в цепи возникает реактивная энергия, которая с частотой переменного тока то потребляется прибором, то возвращается обратно в сеть. Эта энергия переносится от источника к электромагниту и обратно дважды за период, каждую четверть периода меняя направление.

Это происходит из-за того, что при потреблении электроэнергии, например, обмоткой магнита, каждый полупериод в нём происходит временное запасание энергии в магнитном поле катушки, и последующая отдача её назад, из-за чего происходит рассинхронизация синусоид величин напряжения и тока в сети.

Изменения тока в цепи отстаёт от соответствующих синусоидальных изменений напряжения. Такое поведение присуще любой т.н. индуктивной нагрузке (трансформаторы, электродвигатели, дроссели, электромагниты).

Помимо индуктивной нагрузки существует емкостная (различные электронные устройства с конденсаторами, как накопителями энергии, например, в импульсном блоке питания), в которой ток, наоборот, опережает напряжение за счёт временного накопления энергии конденсаторами и последующей отдачи её назад. И в том и в другом случае в цепи помимо активной возникает реактивная энергия.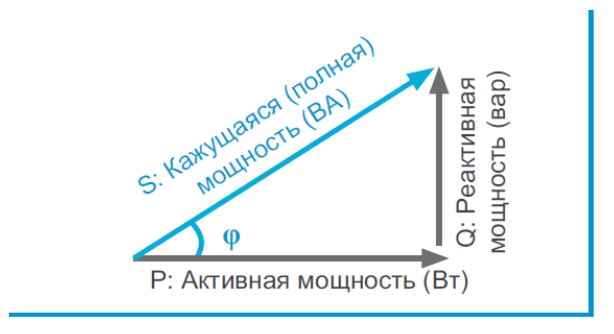

Вред реактивной энергии в электроэнергетике очевиден — она никак не используется, но шляется туда-сюда по проводам, дополнительно нагружая их. Кроме того, при таком «шлянии» эта энергия ещё и частично теряется, преобразуясь в активную энергию при нагреве проводов. Однако в радиотехнике реактивная мощность может быть и полезной (например, в колебательных контурах).

Реактивная мощность обозначается буквой Q и измеряется в вольт-амперах реактивных (вар).

Для вычисления доли реактивной мощности применяется формула:

Q = U * I * sin φ, где:
sin φ — коэффициент мощности, показывающий, какую долю полной мощности составляет реактивная мощность.

Для вычисления активной мощности в сетях с реактивной составляющей применяется формула:

P = U * I * cos φ, где:
cos φ — коэффициент мощности, показывающий, какую долю полной мощности составляет активная мощность.

Коэффициенты мощностей разных приборов обычно указываются в паспортах на них.

Неактивная мощность

Неактивная мощность (пассивная мощность) — это вся мощность кроме активной, т.е. как реактивная мощность, так и мощность любых нелинейных искажений синусоиды, в том числе и мощность колебаний в колебаниях (высших гармоник).

Неактивная мощность обозначается буквой N и измеряется в вольт-амперах реактивных (вар).

Нелинейные искажения могут быть вызваны такой нелинейной нагрузкой, как, например, импульсные блоки питания без корректора коэффициента мощности.

Полная мощность

Полная мощность — эта вся мощность, и активная и неактивная.

Полная мощность обозначается буквой S и измеряется в вольт-амперах (ВА).

Полная мощность равна корню квадратному из суммы квадратов активной и неактивной мощности:

S = √(P² + N²)

В случае линейной (равномерной на протяжении периода) нагрузки полная мощность равна корню квадратному из суммы квадратов активной и реактивной мощности. В этом случае неактивная мощность полностью состоит из реактивной составляющей.

S = √(P² + Q²)

То есть, полная мощность получается не лобовым сложением активной и неактивной частей, а по закону прямоугольного треугольника:

Надеюсь, я немного прояснил данный вопрос.

Если тема всё ещё непонятна, почитайте мою новую статью, где я более тщательно расписал физику процесса.

Ставьте лайки, если статья понравилось. Пишите комментарии.

Делитесь также этой статьёй в социальных сетях (соответствующие кнопочки рядом со статьёй в наличии) и, конечно, подписывайтесь на мой канал! Жду ваших отзывов! Удачи!

Что такое коэффициент мощности?

06 июня 2019

Коэффициент мощности — величина, равная отношению активной мощности P, потребляемой нагрузкой, к ее полной мощности S.

Полная мощность — это произведение действующих значений напряжения и тока:

S=U×I, измеряется в вольт-амперах (ВА).

Активная мощность измеряется в ваттах (Вт) и вычисляется по формуле:

P=U×I×λ, где λ — это коэффициент мощности.

Рассмотрим подробнее, что это такое.

Ранее, когда в основном встречались устройства с нагрузкой линейного типа (т.е. при синусоидальном напряжении нагрузка потребляла синусоидальный же ток), более распространено было понятие cosφ («косинус фи»), учитывающее разность фаз между напряжением и током (см. рис. 1).

Рис. 1. Разность фаз между напряжением и током.

Эта величина при условии линейности нагрузки определялась по той же формуле

cosφ=P/S, или из вида осциллограммы.

Однако если форма тока сильно отличается от синусоиды, такого параметра как cosφ для оценки качества потребляемой электроэнергии не достаточно, т.к. необходимо учитывать гармонический состав потребляемого тока (см. рис. 2).

Рис. 2. Кривая тока современного электронного прибора

Поэтому сейчас энергетики оперируют понятием коэффициент мощности.

Обозначается чаще всего λ («лямбда»), PF (Power Factor) или по старинке cosφ:

THD — Total Harmonic Distortion или КНИ (коэффициент нелинейных искажений) — коэффициент, определяемый отношением действующего значения первой гармоники тока к корню из суммы квадратов высших гармоник.

Математический смысл коэффициента мощности — это отношение интеграла произведения мгновенных значений напряжения и тока к произведению корней интегралов квадратов мгновенных значений тока и напряжения:

Физический смысл в том, что активная мощность (т. е. та, которую показывает ваттметр) не совпадает с полной мощностью, т.е. с произведением показаний вольтметра и амперметра, при отличии формы тока от формы напряжения или при несоответствии их фаз.

На рис. 3 хорошо видно, откуда вообще берется этот коэффициент: мгновенная мощность определяется как произведение мгновенного значения тока на мгновенное значение напряжения.

Рис. 3. Откуда берется коэффициент мощности

Т.е. какую-то часть периода (период Т=0,02 секунды при частоте 50 Гц) ток и напряжение совпадают по «знаку» (выделено синим вдоль оси) и их произведение дает положительную величину, а в остальное время (красным) напряжение, к примеру, больше нуля, а ток — меньше, соответственно их произведение меньше нуля. Активная мощность усредняется по периоду (интегрируется), т. е. в первом приближении алгебраически складываются все значения мощности за период и делятся на величину периода, т.е. будут слагаемые со знаком «+» и со знаком «–», поэтому в итоге сумма получится меньше, чем если бы ток и напряжение совпадали по фазе (см. рис. 4).

Рис. 4. Пример, когда ток и напряжение имеют одинаковую форму и совпадают  по фазе — коэффициент мощности равен 1 (или 100%)

В случае с несинусоидальными токами при синусоидальном напряжении все немного сложнее, но смысл тот же — интеграл произведения тока на напряжение за период всегда меньше произведения действующих значений тока и напряжения. Суть в том, что высшие гармоники (т.е. составляющие тока, частота которых кратна основной частоте тока и напряжения) не создают активной мощности (по причине несовпадения частот с напряжением), но нечетные гармоники (3-я — частота 150 Гц, 5-я — частота 250 Гц, 7-я, 9-я и т. д.) создают полную мощность.

Для полноты информации наглядно поясним, что такое высшие гармоники:

1. Так будет выглядеть осциллограмма тока через обычный резистор 2200 Ом при работе в наших сетях (220 В, 50 Гц):

2. Так будет выглядеть ток с частой 150 Гц (т.е. 3×50 Гц — третья гармоника основной частоты) — синяя кривая. Красным цветом — основная частота или первая гармоника:

3. А так будет выглядеть ток, равный сумме 1-й гармоники и 3-й:

4. А если в составе тока будет много высших гармоник:

Примерно такая ситуация наблюдается в компактных люминесцентных и светодиодных лампах ввиду использования в схемах ЭПРА нелинейных элементов (транзисторы, диоды и т.д.). Это означает, что при тех же значениях активной мощности Р и напряжения U, нагрузочный ток энергосберегающих источников освещения больше, чем у ламп накаливания или галогенных.

Если, например, коэффициент мощности светодиодной лампы равен 0,5, то она потребляет в 2 раза больший ток, чем лампа накаливания той же мощности Р.

Потери мощности на нагрев проводов сети пропорциональны квадрату тока:

Таким образом, при соsφ=0,5 потери мощности в сети больше в 4 раза, чем при соsφ=1. Кроме того, генераторы и трансформаторы будут загружены током в 2 раза больше, и в этом случае требуется примерно в 2 раза большее сечение проводов для обмоток.

Отсюда видно, какое важное значение имеет величина соsφ:

– в электробытовых сетях: квартиры, дачи, частные дома;

– в промышленности: производство с жесткими лимитами электроэнергии;

– в бизнесе: офисы, торговые комплекты, склады;

– а также всюду, где стоит задача минимизировать затраты на электроэнергию.

Почему в нормативных документах требуется повышать коэффициент мощности?

Потому что низкий коэффициент мощности свидетельствует о том, что при низкой потребляемой (и оплачиваемой по времени) активной мощности, ваша нагрузка потребляет бесплатную полную мощность, т.е. фактически вы «гоняете по сетям бесплатный ток», а сетям все равно бесплатный ток или платный — провода греются и даже перегорают, перегружаются трансформаторы и прочее.

Например, известен случай: в одной Подмосковной теплице установили около тысячи КЛЛ на одну сеть — итог: выгорел нулевой провод (по нему при нормальных условиях и линейной нагрузке ток течь не должен вообще).

Поэтому, кстати, стандарты МЭК (стандарт международной электротехнической комиссии) и ГОСТ, соответственно, особенно требовательны к лампам высокой мощности (более 25 Вт).

Shine.ru

Определение реактивной мощности — Руководство по электрическому монтажу

Для большинства электрических нагрузок, таких как двигатели, ток I отстает от напряжения V на угол φ.

Если токи и напряжения являются идеально синусоидальными сигналами , для представления может использоваться векторная диаграмма.

На этой векторной диаграмме вектор тока можно разделить на две составляющие: одна в фазе с вектором напряжения (компонент I _a ), вторая в квадратуре (отставание на 90 градусов) с вектором напряжения (компонент I _r ).См. Рис. L1.

I _a называется активной составляющей тока.

I _r называется реактивной составляющей тока.

Рис. L1 — Векторная диаграмма токов

Предыдущая диаграмма, составленная для токов, также применима к мощности путем умножения каждого тока на общее напряжение V. См. Рис. L2.

Таким образом, мы определяем:

• Полная мощность : S = V x I (кВА)
• Активная мощность : P = V x Ia (кВт)
• Реактивная мощность : Q = V x Ir (квар)

Рис. {2}}

Коэффициент мощности, близкий к единице, означает, что полная мощность S минимальна. Это означает, что мощность электрического оборудования минимальна для передачи данной активной мощности P на нагрузку. Тогда реактивная мощность мала по сравнению с активной. мощность.

Низкое значение коэффициента мощности указывает на противоположное состояние.

Полезные формулы (для сбалансированных и почти сбалансированных нагрузок в 4-проводных системах):

• Активная мощность P (в кВт)
  • Однофазный (1 фаза и нейтраль): P = V.I.cos φ
  • Однофазный (между фазами): P = U.I.cos φ
  • Трехфазный (3 провода или 3 провода + нейтраль): P = √3.U.I.cos φ
• Реактивная мощность Q (в квар)
  • Однофазный (1 фаза и нейтраль): Q = V.I.sin φ
  • Однофазный (между фазами): Q = U.I.sin φ
  • Трехфазный (3 провода или 3 провода + нейтраль): Q = √3.U.I.sin φ
• Полная мощность S (кВА)
  • Однофазный (1 фаза и нейтраль): S = V. Я
  • Однофазный (между фазами): S = U.I
  • Трехфазный (3 провода или 3 провода + нейтраль): S = √3.U.I

где:

В = Напряжение между фазой и нейтралью
U = Напряжение между фазами
I = Линейный ток
φ = Фазовый угол между векторами V и I.

Пример расчета мощности (см. рис. L3)

Рис. L3 — Пример расчета активной и реактивной мощности

Тип цепи		Полная мощность S (кВА)	Активная мощность P (кВт)	Реактивная мощность Q (квар)
Однофазный (фаза и нейтраль)		S = VI	P = VI cos φ	Q = VI sin φ
Однофазный (между фазами)		S = UI	P = UI cos φ	Q = UI sin φ
Пример: нагрузка 5 кВт, cos φ = 0.5		10 кВА	5 кВт	8,7 квар
Трехфазное 3-проводное или 3-проводное + нейтраль		S = 3 {\ displaystyle {\ sqrt {3}}} пользовательского интерфейса	P = 3 {\ displaystyle {\ sqrt {3}}} UI cos φ	Q = 3 {\ displaystyle {\ sqrt {3}}} грех пользовательского интерфейса φ
Пример	Двигатель Pn = 51 кВт	65 кВА	56 кВт	33 квар
	cos φ = 0,86
	ρ = 0. 91 (КПД двигателя)

Расчеты для трехфазного примера, приведенного выше, следующие:

Pn = поставленная мощность на валу = 51 кВт

P = потребляемая активная мощность

P = Pnρ = 510,91 = 56 кВт {\ displaystyle P = {\ frac {Pn} {\ rho}} = {\ frac {51} {0.91}} = 56 \, кВт}

S = полная мощность

S = Pcosφ = 560,86 = 65 кВА {\ displaystyle S = {\ frac {P} {cos \ varphi}} = {\ frac {56} {0.86}} = 65 \, кВА}

Таким образом, при обращении к Рис. L16 или использовании карманного калькулятора значение tan φ, соответствующее cos φ, равному 0.{2}}} = 33 \, квар}

Рис. L4 — Расчетная диаграмма мощности

Истинная, реактивная и полная мощность | Коэффициент мощности

Реактивная мощность

Мы знаем, что реактивные нагрузки, такие как катушки индуктивности и конденсаторы, рассеивают нулевую мощность, но тот факт, что они падают напряжение и потребляют ток, создает обманчивое впечатление, что они на самом деле рассеивают мощность.

Эта «фантомная мощность» называется реактивной мощностью и измеряется в единицах, называемых вольт-ампер-реактивная мощность (VAR), а не в ваттах.

Математическим символом реактивной мощности является (к сожалению) заглавная буква Q.

Истинная сила

Фактическая мощность, используемая или рассеиваемая в цепи, называется истинной мощностью и измеряется в ваттах (как всегда, обозначается заглавной буквой P).

Полная мощность

Комбинация реактивной мощности и истинной мощности называется полной мощностью , и она является произведением напряжения и тока в цепи без учета фазового угла.

Полная мощность измеряется в единицах вольт-ампер (ВА) и обозначается заглавной буквой S.

Расчет реактивной, истинной или полной мощности

Как правило, истинная мощность является функцией рассеивающих элементов схемы, обычно сопротивления (R). Реактивная мощность является функцией реактивного сопротивления цепи (X).

Полная мощность — это функция полного сопротивления цепи (Z). Поскольку для расчета мощности мы имеем дело со скалярными величинами, любые комплексные начальные величины, такие как напряжение, ток и импеданс, должны быть представлены их полярными величинами , а не действительными или мнимыми прямоугольными составляющими.

Например, если я вычисляю истинную мощность по току и сопротивлению, я должен использовать полярную величину тока, а не просто «реальную» или «мнимую» часть тока.

Если я рассчитываю полную мощность по напряжению и импедансу, обе эти ранее комплексные величины должны быть уменьшены до их полярных величин для скалярной арифметики.

Уравнения, использующие скалярные величины

Существует несколько уравнений мощности, связывающих три типа мощности с сопротивлением, реактивным сопротивлением и импедансом (все с использованием скалярных величин):

Обратите внимание, что для расчета истинной и реактивной мощности используются два уравнения каждое.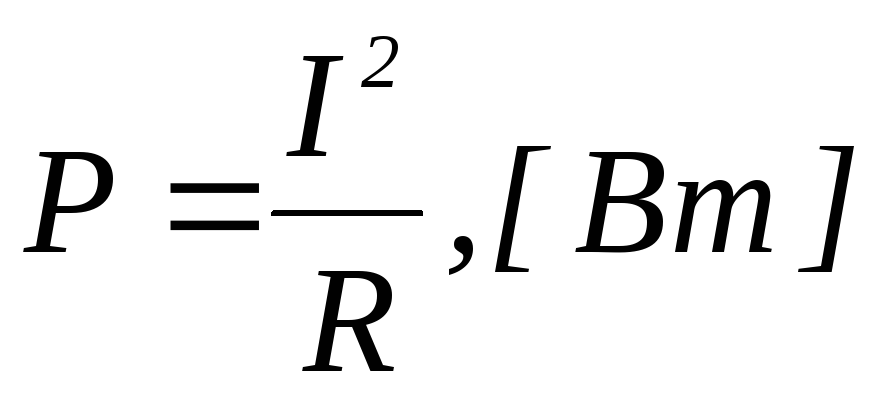

Для расчета полной мощности доступны три уравнения, P = IE подходит только для этой цели .

Изучите следующие схемы и посмотрите, как эти три типа мощности взаимосвязаны: чисто резистивная нагрузка, чисто реактивная нагрузка и резистивная / реактивная нагрузка.

Только резистивная нагрузка

Истинная мощность, реактивная мощность и полная мощность для чисто резистивной нагрузки.

Только реактивная нагрузка

Истинная мощность, реактивная мощность и полная мощность для чисто реактивной нагрузки.

Активная / реактивная нагрузка

Истинная мощность, реактивная мощность и полная мощность для резистивной / реактивной нагрузки.

Треугольник власти

Эти три типа мощности — истинная, реактивная и полная — связаны друг с другом в тригонометрической форме. Мы называем это треугольником мощности : (рисунок ниже).

Треугольник мощности, связывающий полную мощность с реальной мощностью и реактивной мощностью.

Используя законы тригонометрии, мы можем найти длину любой стороны (количество любого типа мощности), учитывая длины двух других сторон или длину одной стороны и угол.

ОБЗОР:

• Мощность, рассеиваемая нагрузкой, обозначается как истинная мощность . Истинная мощность обозначается буквой P и измеряется в ваттах (Вт).
• Мощность, просто потребляемая и возвращаемая нагрузкой из-за ее реактивных свойств, называется реактивной мощностью .Реактивная мощность обозначается буквой Q и измеряется в вольт-амперных реактивных единицах (ВАР).
• Полная мощность в цепи переменного тока, как рассеиваемая, так и поглощаемая / возвращаемая, обозначается как полная мощность , . Полная мощность обозначается буквой S и измеряется в вольт-амперах (ВА).
• Эти три типа мощности тригонометрически связаны друг с другом. В прямоугольном треугольнике P = смежная длина, Q = противоположная длина и S = ​​длина гипотенузы.Противоположный угол равен фазовому углу импеданса цепи (Z).

СВЯЗАННЫЙ РАБОЧИЙ ЛИСТ:

11.2: Истинная, реактивная и полная мощность

Реактивная мощность

Мы знаем, что реактивные нагрузки, такие как катушки индуктивности и конденсаторы, рассеивают нулевую мощность, но тот факт, что они падают напряжение и потребляют ток, создает обманчивое впечатление, что они на самом деле рассеивают мощность. Эта «фантомная мощность» называется реактивной мощностью , и она измеряется в единицах, называемых вольт-ампер-реактивная мощность (ВАР), а не в ваттах.Математическим символом реактивной мощности является (к сожалению) заглавная буква Q.

.

Истинная сила

Фактическое количество мощности, используемой или рассеиваемой в цепи, называется истинной мощностью и измеряется в ваттах (как всегда, обозначается заглавной буквой P).

Полная мощность

Комбинация реактивной мощности и истинной мощности называется кажущейся мощностью , и она является произведением напряжения и тока цепи без учета фазового угла.Полная мощность измеряется в единицах вольт-ампер (ВА) и обозначается заглавной буквой S.

Расчет реактивной, истинной или полной мощности

Как правило, истинная мощность является функцией рассеивающих элементов схемы, обычно сопротивления (R). Реактивная мощность является функцией реактивного сопротивления цепи (X). Полная мощность — это функция полного сопротивления цепи (Z). Поскольку для расчета мощности мы имеем дело со скалярными величинами, любые комплексные начальные величины, такие как напряжение, ток и импеданс, должны быть представлены их полярными величинами , а не действительными или мнимыми прямоугольными составляющими.Например, если я вычисляю истинную мощность по току и сопротивлению, я должен использовать полярную величину для тока, а не просто «реальную» или «мнимую» часть тока. Если я рассчитываю полную мощность по напряжению и импедансу, обе эти ранее комплексные величины должны быть уменьшены до их полярных величин для скалярной арифметики.

Существует несколько уравнений мощности, связывающих три типа мощности с сопротивлением, реактивным сопротивлением и импедансом (все с использованием скалярных величин):

Обратите внимание, что для расчета истинной и реактивной мощности используются два уравнения каждое.Для расчета полной мощности доступны три уравнения, P = IE используется для только для этой цели. Изучите следующие схемы и посмотрите, как эти три типа мощности взаимосвязаны: чисто резистивная нагрузка на рисунке ниже, чисто реактивная нагрузка на рисунке ниже и резистивная / реактивная нагрузка на рисунке ниже.

Только резистивная нагрузка

Истинная мощность, реактивная мощность и полная мощность для чисто резистивной нагрузки.

Только реактивная нагрузка

Истинная мощность, реактивная мощность и полная мощность для чисто реактивной нагрузки.

Активная / реактивная нагрузка

Истинная мощность, реактивная мощность и полная мощность для резистивной / реактивной нагрузки.

Треугольник власти

Эти три типа мощности — истинная, реактивная и полная — связаны друг с другом в тригонометрической форме. Мы называем это треугольником мощности : (рисунок ниже).

Треугольник мощности, связывающий кажущуюся мощность с реальной и реактивной мощностью.

Используя законы тригонометрии, мы можем найти длину любой стороны (количество любого типа мощности), учитывая длины двух других сторон или длину одной стороны и угол.

Обзор

• Мощность, рассеиваемая нагрузкой, обозначается как истинная мощность . Истинная мощность обозначается буквой P и измеряется в ваттах (Вт).
• Мощность, просто поглощаемая и возвращаемая нагрузкой из-за ее реактивных свойств, обозначается как реактивной мощности . Реактивная мощность обозначается буквой Q и измеряется в вольт-амперных реактивных единицах (ВАР).
• Полная мощность в цепи переменного тока, как рассеиваемая, так и поглощаемая / возвращаемая, обозначается как полная мощность . Полная мощность обозначается буквой S и измеряется в вольт-амперах (ВА).
• Эти три типа мощности тригонометрически связаны друг с другом. В прямоугольном треугольнике P = смежная длина, Q = противоположная длина и S = ​​длина гипотенузы.Противоположный угол равен фазовому углу импеданса цепи (Z).

Electric Power Одно- и трехфазная мощность Активная Реактивная кажущаяся

Комплексная мощность

Это очень концептуально и важно для понимания. Чтобы установить выражение для комплексной мощности , мы должны сначала рассмотреть однофазную сеть, напряжение и ток которой могут быть представлены в сложной форме как V.e ^jα и I.e ^jβ . Где α и β — углы, которые составляют вектор напряжения и вектор тока относительно некоторой базовой оси соответственно. Активную мощность и реактивную мощность можно рассчитать, найдя произведение напряжения на сопряжение тока. Это означает, что

Это (α — β) не что иное, как угол между напряжением и током, следовательно, это разность фаз между напряжением. и ток, который обычно обозначается как φ.
Следовательно, приведенное выше уравнение можно переписать как:

Где, P = VIcosφ и Q = VIsinφ.
Эта величина S называется комплексной мощностью .
Величина комплексной мощности i.е. | S | = (P ² + Q ² ) ^½ известна как полная мощность , и ее единица измерения — вольт-ампер. Эта величина является произведением абсолютного значения напряжения и тока. Опять же, абсолютное значение тока напрямую связано с тепловым эффектом согласно закону нагрева Джоуля. Следовательно, номинальные характеристики электрической машины обычно определяются ее полной допустимой мощностью в пределах допустимого температурного предела.
Следует отметить, что в уравнении комплексной мощности член Q [= VIsinφ] положителен, когда φ [= (α — β)] положительно, то есть ток отстает от напряжения, что означает, что нагрузка по своей природе индуктивна. .Снова Q отрицательно, когда φ отрицательно; то есть ток ведет к напряжению, что означает, что нагрузка емкостная.

Однофазное питание

Однофазная система электропередачи практически недоступна, но все же мы должны знать основную концепцию однофазного питания , прежде чем переходить к современной трехфазной системе электроснабжения. Прежде чем переходить к подробностям об однофазном питании, давайте попробуем разобраться в различных параметрах энергосистемы. Три основных параметра системы электроснабжения — это электрическое сопротивление, индуктивность и емкость.

Сопротивление

Сопротивление является неотъемлемым свойством любого материала, благодаря которому он сопротивляется протеканию тока, препятствуя движению электронов через него из-за столкновения с неподвижными атомами. Тепло, выделяемое в результате этого процесса, рассеивается и называется омической потерей мощности. Пока ток протекает через резистор, между напряжением и током не будет разницы фаз, что означает, что ток и напряжение находятся в одной фазе; фазовый угол между ними равен нулю.Если ток I протекает через электрическое сопротивление R в течение t секунд, то общая энергия, потребляемая резистором, равна I ² .R.t. Эта энергия известна как активная энергия , а соответствующая мощность известна как активная мощность .

Индуктивность

Индуктивность — это свойство, благодаря которому индуктор накапливает энергию в магнитном поле в течение положительного полупериода и отдает эту энергию во время отрицательного полупериода однофазного источника питания.Если через катушку с индуктивностью L Генри протекает ток «I», энергия, запасенная в катушке в виде магнитного поля, определяется выражением

. Мощность, связанная с индуктивностью, равна реактивной мощности .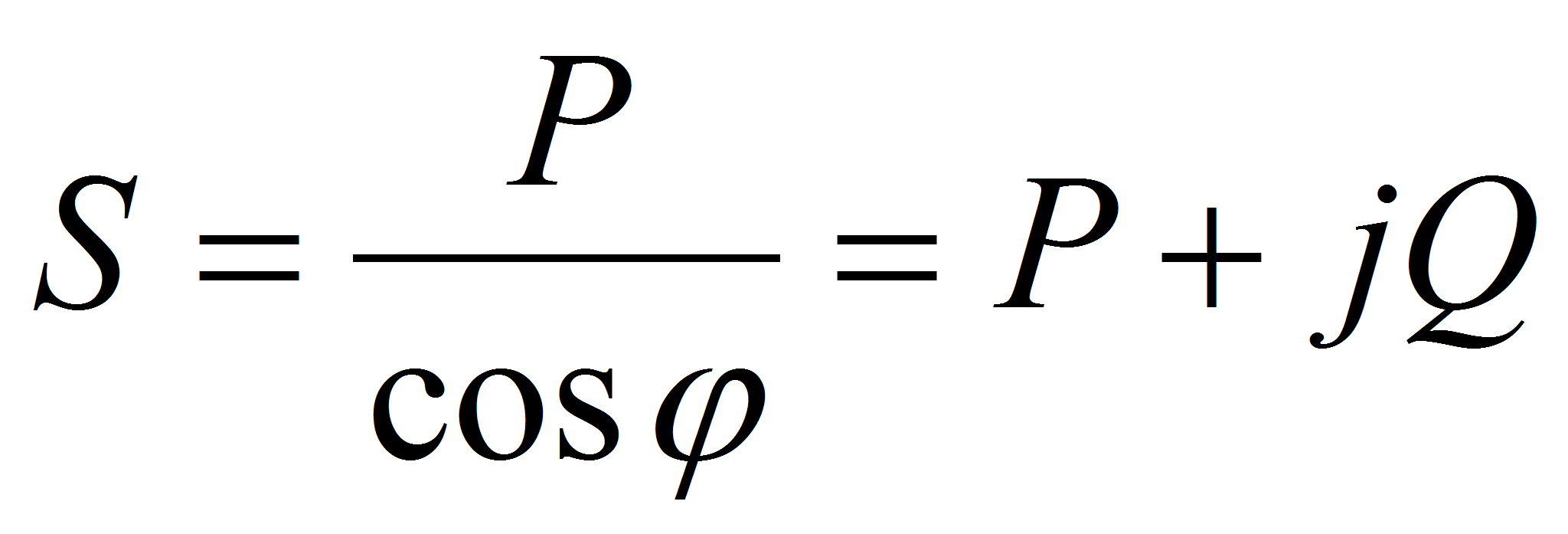

Емкость

Емкость — это свойство, благодаря которому конденсатор накапливает энергию в статическом электрическом поле во время положительного полупериода и отдает во время отрицательного полупериода питания. Энергия, накопленная между двумя параллельными металлическими пластинами с разностью электрических потенциалов V и емкостью между ними C, выражается как

Эта энергия хранится в форме статического электрического поля.Мощность, связанная с конденсатором, также составляет , реактивная мощность .

Активная мощность и реактивная мощность

Рассмотрим однофазную цепь , в которой ток отстает от напряжения на угол φ.
Пусть мгновенная разность электрических потенциалов v = V _m .sinωt
Тогда мгновенный ток может быть выражен как i = I _m . sin (ωt — φ).
Где, V _m и I _m — максимальные значения синусоидально изменяющейся разности электрических потенциалов и тока соответственно.
Мгновенная мощность цепи определяется выражением

Активная мощность

Резистивная мощность

Давайте сначала рассмотрим условие, когда однофазная силовая цепь является полностью резистивной по своей природе, что означает фазовый угол между напряжением и током, т.е. φ = 0 и, следовательно,


Из приведенного выше уравнения ясно, что каким бы ни было значение ωt, значение cos2ωt не может быть больше 1; следовательно, значение p не может быть отрицательным. Значение p всегда положительно независимо от мгновенного направления напряжения v и тока i, это означает, что энергия течет в обычном направлении, т.е.е. от источника к нагрузке, p — это уровень потребления энергии нагрузкой, который называется , активная мощность . Поскольку эта мощность потребляется из-за резистивного эффекта электрической цепи, поэтому иногда ее также называют Resistive Power .

Реактивная мощность

Индуктивная мощность

Теперь рассмотрим ситуацию, когда однофазная силовая цепь полностью индуктивна, что означает, что ток отстает от напряжения на угол φ = + 90 ^o . Положив φ = + 90 ^o


В приведенном выше выражении обнаружено, что мощность течет в альтернативных направлениях.От 0 ^o до 90 ^o он будет иметь отрицательный полупериод, от 90 ^o до 180 ^o он будет иметь положительный полупериод, от 180 ^o до 270 ^o он снова будет иметь отрицательную половину цикл и от 270 ^o до 360 90 483 o он снова будет иметь положительный полупериод. Следовательно, эта мощность является альтернативной по своей природе с частотой, вдвое превышающей частоту питания. Поскольку мощность течет в переменном направлении, то есть от источника к нагрузке в течение одного полупериода и от нагрузки к источнику в следующем полупериоде, среднее значение этой мощности равно нулю.Следовательно, эта сила не делает никакой полезной работы. Эта мощность известна как , реактивная мощность . Поскольку объясненное выше выражение реактивной мощности относится к полностью индуктивной цепи, эта мощность также называется индуктивной мощностью .

Из этого можно сделать вывод, что если цепь является чисто индуктивной, энергия будет накапливаться в виде энергии магнитного поля в течение положительного полупериода и отдаваться в течение отрицательного полупериода и скорости изменения этой энергии, выраженной как реактивной мощности просто индуктивная мощность , и эта мощность будет иметь равный положительный и отрицательный цикл, а чистое значение будет равно нулю.

Емкостная мощность

Давайте теперь рассмотрим, что однофазная силовая цепь полностью емкостная, то есть ток опережает напряжение на 90 ^o , поэтому φ = — 90 ^o .


Следовательно, в выражении емкостной мощности также обнаруживается, что мощность течет в альтернативных направлениях. От 0 ^o до 90 ^o он будет иметь положительный полупериод, от 90 ^o до 180 ^o он будет иметь отрицательный полупериод, от 180 ^o до 270 ^o он будет снова иметь положительную половину цикл и от 270 ^o до 360 90 483 o он снова будет иметь отрицательный полупериод. Таким образом, эта мощность также является альтернативной по своей природе с частотой, вдвое превышающей частоту питания. Следовательно, как индуктивная мощность, емкостная мощность не выполняет никакой полезной работы. Эта мощность также является реактивной мощностью.

Активная составляющая и реактивная составляющая мощности

Уравнение мощности можно переписать как

Это выражение выше имеет две согласные; первая — V _м . I _m .cosφ (1 — cos2ωt), который никогда не становится отрицательным, поскольку значение (1 — cos2ωt) всегда больше или равно нулю, но не может иметь отрицательного значения.

Эта часть уравнения однофазной мощности представляет выражение реактивной мощности, которая также известна как активная мощность или истинная мощность. Среднее значение этой мощности, очевидно, будет иметь какое-то ненулевое значение, мощность физически выполняет некоторую полезную работу, и поэтому эту мощность также называют реальной мощностью или иногда ее называют истинной мощностью. Эта часть уравнения мощности представляет реактивную мощность, которая также известна как активная мощность или истинная мощность.
Второй член V _м .I _m .sinφsin2ωt, который будет иметь отрицательные и положительные циклы. Следовательно, среднее значение этого компонента равно нулю. Этот компонент известен как реактивный компонент, поскольку он перемещается вперед и назад по линии, не выполняя никакой полезной работы.
Как активная мощность , так и реактивная мощность имеют одинаковые размеры в ваттах, но чтобы подчеркнуть тот факт, что реактивная составляющая представляет собой неактивную мощность, она измеряется в вольт-амперах реактивной мощности или коротком VAR.
Однофазное питание относится к распределительной системе, в которой: все напряжения меняются в унисон.Его можно получить просто вращением движущейся катушки в магнитном поле или движением поля вокруг неподвижной катушки. Произведенное таким образом переменное напряжение и переменный ток называют однофазным напряжением и током. Различные типы цепей по-разному реагируют на подачу синусоидального сигнала. Мы рассмотрим все типы цепей по очереди, которые включают только электрическое сопротивление, только емкость и только индуктивность, а также их комбинацию и попытаемся установить уравнение мощности для однофазной цепи .

Уравнение однофазной мощности для чисто резистивной цепи

Давайте рассмотрим расчет мощности однофазной цепи для чисто резистивной цепи. Цепь, состоящая из чистого омического сопротивления, проходит через источник напряжения V, как показано ниже на рисунке.

Где, V (t) = мгновенное напряжение.
В _м = максимальное значение напряжения.
ω = угловая скорость в радианах / секундах.

Согласно закону Ома,

Подставляя значение V (t) в приведенное выше уравнение, мы получаем,

Из уравнений (1.1) и (1.5) видно, что V (t) и I _R синфазны. Таким образом, в случае чистого омического сопротивления нет разницы фаз между напряжением и током, т. е. они находятся в фазе, как показано на рисунке (b).

Мгновенная мощность,

Из уравнения однофазной мощности (1.8) ясно, что мощность состоит из двух членов: одна постоянная часть, то есть

, а другая — колеблющаяся, то есть

Это значение равно нулю для полного цикла. Таким образом, мощность через чисто омический резистор дается как и показано на рис. (C).

Однофазное уравнение мощности для чисто индуктивной цепи

Индуктор является пассивным компонентом. Всякий раз, когда переменный ток проходит через катушку индуктивности, он противодействует протеканию тока через нее, создавая обратную ЭДС. Таким образом, приложенное напряжение, а не падение на нем, должно уравновешивать производимую обратную ЭДС. Схема, состоящая из чистого индуктора, подключенного к источнику синусоидального напряжения V _{действующее значение} , показана на рисунке ниже.

Мы знаем, что напряжение на катушке индуктивности задается как,

Таким образом, из приведенного выше уравнения однофазной мощности видно, что I отстает от V на π / 2 или, другими словами, V ведет к I на π / 2, когда переменный ток проходит через индуктор i. е. I и V не в фазе, как показано на рис. (Е).

Мгновенная мощность определяется как,

Здесь, формула для однофазной мощности состоит только из колеблющегося члена, а значение мощности для полного цикла равно нулю.

Однофазное уравнение мощности для чисто емкостной цепи

Когда переменный ток проходит через конденсатор, он сначала заряжается до максимального значения, а затем разряжается. Напряжение на конденсаторе задается как,


Таким образом, из приведенного выше расчета однофазной мощности I (t) и V (t) ясно видно, что в случае тока конденсатора опережает напряжение на угол π / 2.


Мощность, проходящая через конденсатор, состоит только из колеблющегося члена, а значение мощности для полного цикла равно нулю.

Однофазное уравнение мощности для цепи RL

Чисто омический резистор и катушка индуктивности соединены последовательно ниже, как показано на рис. (G), через источник напряжения V. Тогда падение на R будет V _R = IR и на L будет V _L = IX _L .


Эти падения напряжения показаны в виде треугольника напряжения, как показано на рис. (I).Вектор OA представляет собой падение на R = IR, вектор AD представляет собой падение на L = IX _L , а вектор OD представляет собой результат V _R и V _L .

— полное сопротивление цепи RL.
Из векторной диаграммы видно, что V ведет I и фазовый угол φ определяется как,

Таким образом, мощность состоит из двух членов, одного постоянного члена 0,5 В _м I _м cosφ и другого члена флуктуации 0,5 В _м I _м cos (ωt — φ), значение которого равно нулю для всего цикла.
Таким образом, это единственная постоянная часть, которая влияет на фактическое потребление энергии.
Таким образом, мощность p = VI cos Φ = (среднеквадратичное напряжение × среднеквадратичный ток × cosφ) ватт
Где cosφ называется коэффициентом мощности и определяется выражением,

I можно разделить на две прямоугольные составляющие Icosφ вдоль V и Isinφ перпендикулярно V. Только Icosφ вносит вклад в активную мощность. Таким образом, только VIcosφ называется полностью заполненным компонентом или активным компонентом, а VIsinφ называется безводным компонентом или реактивным компонентом.

Однофазное уравнение мощности для RC-цепи

Мы знаем, что ток в чистой емкости, напряжение на выводах и в чистом омическом сопротивлении синфазны.Таким образом, чистый ток опережает напряжение на угол φ в RC-цепи. Если V = V _m sinωt и I будет I _m sin (ωt + φ).

Мощность такая же, как и в случае цепи R-L. В отличие от схемы R-L коэффициент мощности является ведущим в схеме R-C.

Определение трехфазной мощности

Было обнаружено, что выработка трехфазной мощности более экономична, чем выработка однофазной энергии. В трехфазной системе электроснабжения три формы волны напряжения и тока смещены во времени на 120 ^— в каждом цикле питания.Это значит; каждая форма волны напряжения имеет разность фаз 120 ^o относительно другой формы волны напряжения, и каждая форма волны тока имеет разность фаз 120 ^o относительно другой формы волны тока. Определение трехфазной мощности гласит, что в электрической системе три отдельных однофазных мощности передаются тремя отдельными силовыми цепями. Напряжения этих трех мощностей в идеале находятся на расстоянии 120 90 483 o 90 484 друг от друга по фазе времени. Точно так же токи этих трех мощностей также идеально отстоят друг от друга на 120 ^o .Идеальная трехфазная система питания подразумевает сбалансированную систему.

Трехфазная система считается несбалансированной, когда либо хотя бы одно из трех фазных напряжений не равно другому, либо фазовый угол между этими фазами не совсем равен 120 ^o .

Преимущества трехфазной системы

Есть много причин, по которым эта мощность более предпочтительна, чем однофазная.

1. Уравнение однофазной мощности:
   
   , которое зависит от времени.В то время как уравнение трехфазной мощности — это
   
   , которое является постоянной функцией, не зависящей от времени. Следовательно, однофазное питание пульсирует. Обычно это не влияет на двигатель с низким номиналом, но в двигателе с большим номиналом вызывает чрезмерную вибрацию. Таким образом, трехфазное питание более предпочтительно для силовой нагрузки высокого напряжения.
2. Мощность трехфазной машины в 1,5 раза выше, чем у однофазной машины того же размера.
3. Однофазный асинхронный двигатель не имеет пускового момента, поэтому мы должны предоставить некоторые вспомогательные средства запуска, но трехфазный асинхронный двигатель самозапускается и не требует никаких дополнительных средств.
4. Коэффициент мощности и КПД выше в случае трехфазной системы.

Уравнение трехфазной мощности

Для определения выражения уравнения трехфазной мощности , т.е. для расчета трехфазной мощности , мы должны сначала рассмотреть идеальную ситуацию, когда трехфазная система сбалансирована. Это означает, что напряжение и токи в каждой фазе отличаются от их соседних фаз на 120 ^o , а также амплитуда каждой волны тока одинакова и аналогично амплитуда каждой волны напряжения одинакова. Теперь угловая разница между напряжением и током в каждой фазе трехфазной энергосистемы равна φ.

Тогда напряжение и ток красной фазы будут
соответственно.
Напряжение и ток желтой фазы будут равны —
соответственно.
А напряжение и ток синей фазы будут —
соответственно.
Следовательно, выражение мгновенная мощность в красной фазе —

Аналогично выражение мгновенная мощность в желтой фазе —

Точно так же выражение мгновенная мощность в синей фазе —

Общая трехфазная мощность системы складывается из индивидуальная мощность в каждой фазе —

Приведенное выше выражение мощности показывает, что общая мгновенная мощность постоянна и равна трехкратной реальной мощности на фазу.В случае выражения для однофазной мощности мы обнаружили, что существуют компоненты как реактивной мощности, так и активной мощности, но в случае выражения для трехфазной мощности мгновенная мощность постоянна. Фактически в трехфазной системе реактивная мощность в каждой отдельной фазе не равна нулю, но их сумма в любой момент равна нулю.

Реактивная мощность — это форма магнитной энергии, протекающей в единицу времени в электрической цепи. Его единица измерения — VAR (вольт-ампер, реактивный). Эту мощность нельзя использовать в цепи переменного тока.Однако в электрической цепи постоянного тока он может быть преобразован в тепло, поскольку, когда заряженный конденсатор или индуктор подключается к резистору, энергия, запасенная в элементе, преобразуется в тепло. Наша энергосистема работает от сети переменного тока, и большинство нагрузок, используемых в повседневной жизни, являются индуктивными или емкостными, поэтому реактивная мощность является очень важным понятием с точки зрения электричества.

Коэффициент электрической мощности любого оборудования определяет количество реактивной мощности , которое ему требуется.Это отношение реальной или истинной мощности к полной полной мощности, необходимой электрическому устройству. Эти мощности могут быть определены как,

, где θ — это разность фаз между напряжением и током, а cosθ — коэффициент электрической мощности нагрузки.

Реактивная мощность всегда присутствует в цепи, где есть разность фаз между напряжением и током в этой цепи, например, все наши бытовые нагрузки являются индуктивными. Таким образом, существует разница фаз между напряжением и током, и ток отстает от напряжения на определенный угол во временной области.Индуктивный компонент принимает отстающую реактивную мощность, а емкостной компонент поглощает ведущую реактивную мощность, здесь отстающая реактивная мощность относится к магнитной энергии, а ведущая реактивная мощность относится к электростатической энергии.

В типичной цепи переменного тока, такой как цепь RL (резистивная + индуктивная) или RC-цепь (резистивная + емкостная), реактивная мощность берется из источника питания в течение полупериода и возвращается в источник питания в течение следующего полупериода. Например, мощность, потребляемая для нагрузки RL, определяется как:

V = V _m sinωt, I = I _m sin (ωt — θ)

Здесь Q ₁ sin2ωt — реактивная мощность, которая является средним значением. равен нулю, это означает, что реактивная мощность никогда не используется.

Использование реактивной мощности

В электрической машине для преобразования энергии требуется магнитный домен, чтобы преобразовать ее форму. В электродвигателе необходимая магнитная область создается за счет реактивной мощности, которую он получает от источника питания. Сегодня почти каждой электрической нагрузке требуется реактивная мощность для работы, несмотря на реальную мощность. Даже в электрическом трансформаторе, который является основным блоком энергосистемы, первичный входной ток отстает, так как требуется запаздывающая VAR для намагничивания его сердечника и передачи мощности посредством взаимной индукции.

Реактивная мощность в линиях передачи

В линии передачи электроэнергии поток реактивной мощности в линии определяет напряжение на принимающей стороне. Управление уровнем напряжения на приемном конце очень важно, так как более высокое напряжение может повредить оборудование потребителя и приведет к большим потерям. Во многих случаях мы видим внезапное повышение или падение напряжения из-за молнии или из-за какого-либо сбоя в исправных фазах, и в любом случае происходит повреждение оборудования. Посмотрим, как напряжение зависит от реактивной мощности.
Реактивная мощность принимающей стороны определяется выражением,

Где θ — это угол мощности, который поддерживается на очень низком уровне из-за соображений стабильности, X _l — реактивное сопротивление линии передачи, V _s — напряжение на передающей стороне и V _r — напряжение на приемном конце.
Итак, Q _r становится,

Теперь уравнение формируется как,

Решая, мы получаем,

Математически выражение, данное для реактивной мощности
Примечание: мы не принимали отрицательный знак, поскольку тогда V _r будет становится нулевым, когда Q _r равно нулю, что невозможно.
Пусть Q ₁ будет реактивной мощностью, требуемой нагрузкой на принимающей стороне, а Q ₂ будет источником реактивной мощности от генерирующей или передающей стороны. Тогда Q _r будет (Q ₁ — Q ₂ ).

Случай — 1
Когда подача Q ₂ равна потребности Q ₁ , тогда V _s = V _r , напряжение на принимающей стороне будет равно конечному напряжению отправки, что желательно.

Случай — 2
Когда спрос больше, а предложение меньше, Q _r становится отрицательным.Таким образом, напряжение на принимающей стороне становится меньше, чем на стороне отправки.

Случай — 3
Когда спрос меньше, предложение высокое, Q _r становится положительным. Таким образом, напряжение на принимающей стороне становится больше, чем на стороне отправки, что очень опасно.
Таким образом, мы увидели, как напряжение (и управление его уровнем), которое является основным требованием любой электрической нагрузки; зависит от реактивной мощности. В дневное время потребность в реактивной мощности увеличивается, поэтому происходит провал напряжения.С другой стороны, в утреннее время потребность в реактивной мощности меньше, поэтому происходит повышение уровня напряжения. Для поддержания уровня напряжения необходимо сделать Q ₁ = Q ₂ .

Компенсация реактивной мощности

Как уже обсуждалось, необходимо контролировать как превышение реактивной мощности, так и ее дефицит. Для этого выполняется компенсация с помощью различных устройств. Здесь реактор поглощает избыточную реактивную мощность, тогда как конденсатор обеспечивает компенсацию реактивной мощности в случаях высокого потребления.
Для нагрузок с низким коэффициентом мощности потребность в реактивной мощности очень высока. Следовательно, нам нужно увеличить коэффициент мощности, используя конденсаторную батарею. Это снижает потребность в переменном токе за счет подачи на нагрузку соответствующего количества реактивной мощности. Другие методы включают использование шунтирующего конденсатора, синхронных фазовых модификаторов, трансформатора с переключением ответвлений под нагрузкой и шунтирующего реактора. Синхронный двигатель с перевозбуждением используется в шунте с нагрузкой. Он служит конденсатором и также называется синхронным конденсатором.Шунтирующий реактор используется для снижения коэффициента электрической мощности. В трансформаторах с переключением ответвлений под нагрузкой коэффициент трансформации регулируется соответствующим образом для поддержания желаемого уровня напряжения, поскольку разность напряжений между передающей и принимающей сторонами определяет реактивную мощность.
Математически выражение для реактивной мощности (Q), необходимой для увеличения коэффициента электрической мощности с cosθ ₁ до cosθ ₂ , дается как,

Где, P — фактическая потребляемая мощность нагрузки (в ваттах) .
В случае, если коэффициент электрической мощности должен быть уменьшен с cosθ ₂ до cosθ ₁ , реактивная мощность, которая должна быть поглощена шунтирующим реактором на конце нагрузки, определяется как:

Значения емкости или индуктивности, таким образом, необходимое можно рассчитать с помощью,

Power Triangle Calculator

Треугольник мощности показывает соотношение между реактивной, активной и полной мощностью в цепи переменного тока.

Важные термины

• Реальная мощность (P) — Измеряется в ваттах, определяет мощность, потребляемую резистивной частью цепи.Также известная как истинная или активная мощность, выполняет реальную работу в электрической цепи.
• Реактивная мощность (Q) — Измеренная в ВАХ мощность, потребляемая в цепи переменного тока, которая не выполняет никакой полезной работы, вызванной индукторами и конденсаторами. Реактивная мощность противодействует действию реальной мощности, забирая мощность из цепи для использования в магнитных полях.
• Полная мощность (S) — произведение среднеквадратичного напряжения и действующего тока, протекающего в цепи, содержит активную и реактивную мощность.
• Коэффициент мощности (q) — Отношение активной мощности (P) к полной мощности (S), обычно выражаемое в виде десятичного или процентного значения. Коэффициент мощности определяет фазовый угол между сигналами тока и напряжения. Чем больше фазовый угол, тем больше реактивная мощность.

---

Важные формулы

• Реальная мощность (P) = VIcosq, Вт (Вт)
• Реактивная мощность (Q) = VIsinq, Вольт-амперы, реактивные (VAr)
• Полная мощность (S) = VI, Вольт-амперы (ВА)
• Коэффициент мощности (q) = P / S

• ВА = Вт / cosq
• VA = VAR / sinq
• VAR = VA * sinq
• VAR = W * tanq
• Вт = ВА * cosq
• W = VAR / tanq

• Sin (q) = Противоположно / Гипотенуза = Q / S = VAr / VA
• Cos (q) = Соседний / Гипотенуза = P / S = Вт / ВА = коэффициент мощности, p.f.
• Желто-коричневый (q) = Напротив / Соседний = Q / P = VAr / W

---

Дополнительная литература

Комментарии

Войдите или зарегистрируйтесь, чтобы комментировать.

Что такое коэффициент мощности? | Как рассчитать формулу коэффициента мощности

Как понять коэффициент мощности

Пиво — это активная мощность (кВт) — полезная мощность или жидкое пиво — это энергия, которая выполняет работу.Это то, что вам нужно.

Пена — это реактивная мощность (кВАр) — пена представляет собой потерянную мощность или потерянную мощность. Вырабатываемая энергия не выполняет никакой работы, например выделяет тепло или вибрацию.

Кружка — кажущаяся мощность (кВА) — кружка — это потребляемая мощность или мощность, поставляемая коммунальным предприятием.

Если бы схема была эффективна на 100%, потребность была бы равна доступной мощности. Когда спрос превышает доступную мощность, на энергосистему оказывается нагрузка.Многие коммунальные предприятия добавляют плату за спрос к счетам крупных потребителей, чтобы компенсировать разницу между спросом и предложением (когда предложение ниже спроса). Для большинства коммунальных предприятий потребность рассчитывается на основе средней нагрузки в течение 15–30 минут. Если требования к нагрузке нерегулярны, коммунальное предприятие должно иметь больше резервной мощности, чем если бы требования к нагрузке оставались постоянными.

Пик спроса — это период наибольшего спроса. Перед коммунальными предприятиями стоит задача предоставить мощность, чтобы справиться с пиками нагрузки каждого клиента.Использование энергии в тот момент, когда она пользуется наибольшим спросом, может нарушить общее предложение, если не будет достаточно резервов. Таким образом, коммунальные услуги выставляют счет за пиковый спрос. Для некоторых крупных клиентов коммунальные предприятия могут даже взять самый большой пик и применить его в течение всего расчетного периода.

Коммунальные предприятия применяют надбавки к компаниям с более низким коэффициентом мощности. Издержки более низкой эффективности могут быть очень высокими — сродни вождению автомобиля, потребляющего много бензина. Чем ниже коэффициент мощности, тем менее эффективна схема и выше общие эксплуатационные расходы.Чем выше эксплуатационные расходы, тем выше вероятность того, что коммунальные предприятия накажут клиента за чрезмерную загрузку. В большинстве цепей переменного тока коэффициент мощности никогда не бывает равным единице, потому что на линиях электропередачи всегда присутствует некоторое сопротивление (помехи).

Как рассчитать коэффициент мощности

Для расчета коэффициента мощности вам понадобится анализатор качества электроэнергии или анализатор мощности, который измеряет как рабочую мощность (кВт), так и полную мощность (кВА), а также рассчитывает соотношение кВт / кВА.

Формулу коэффициента мощности можно выразить другими способами:

PF = (Истинная мощность) / (Полная мощность)

OR

PF = W / VA

Где ватты измеряют полезную мощность, а VA измеряют потребляемую мощность.Отношение этих двух значений по существу представляет собой полезную мощность к подаваемой мощности, или:

Как показывает эта диаграмма, коэффициент мощности сравнивает реальную потребляемую мощность с полной мощностью или потребляемой нагрузкой. Мощность, доступная для выполнения работы, называется реальной мощностью. Вы можете избежать штрафов за коэффициент мощности, исправив коэффициент мощности.

Низкий коэффициент мощности означает, что вы используете электроэнергию неэффективно. Это важно для компаний, поскольку может привести к:

• Тепловому повреждению изоляции и других компонентов схемы
• Уменьшению доступной полезной мощности
• Требуемое увеличение размеров проводов и оборудования

Наконец, коэффициент мощности увеличивает общая стоимость системы распределения энергии, поскольку более низкий коэффициент мощности требует более высокого тока для питания нагрузок.

Связанные ресурсы

Мгновенная, средняя, ​​реальная и реактивная мощность

Нападающий

В нескольких последних статьях мы обсудили и разработали некоторые важные концепции линий электропередачи. В прошлый раз мы говорили о протяженных линиях электропередачи. Здесь мы обсуждаем простую, но важную базовую концепцию «Электроэнергия».Это освежит наши знания, прежде чем мы двинемся дальше. Электрическая энергия имеет то же значение, что и механическая энергия, но здесь энергия или энергия, которые нас интересуют, находятся в электрической форме. Мы часто встречаем такие термины, как мгновенная, средняя, ​​полная, действительная, реактивная, полная и комплексная мощность или просто мощность. Что они имеют в виду? как они связаны? Об этом мы поговорим здесь и в следующей статье.

Цепь постоянного тока

Пока наш анализ ограничивается цепью постоянного тока (DC), мощность, потребляемая резистивной нагрузкой, является произведением напряжения на сопротивлении и тока, протекающего через сопротивление. Это действительно просто.

P = V. я

Мощность, потребляемая нагрузкой, является произведением напряжения на нагрузке и тока, потребляемого нагрузкой (рис. A).Или мощность, подаваемая источником постоянного тока (батарея / элемент), является произведением напряжения на элементе и тока, подаваемого элементом. Оба они равны в нашем примере (учитывая идеальную батарею с нулевым внутренним сопротивлением). Закон сохранения энергии подразумевает, что мощность, подаваемая источником, должна быть такой же, как мощность, потребляемая цепью. В случае цепи постоянного тока мгновенная мощность равна средней мощности.

Цепь переменного тока

Что это за мощность, о которой мы говорим при анализе цепей переменного тока.Основная проблема заключается в том, что переменное напряжение и ток синусоидально изменяются со временем. Кроме того, наличие в цепи реактивных элементов, таких как индуктор и конденсатор, сдвигает волну тока относительно волны напряжения (угла сдвига фаз). Мощность — это скорость, с которой энергия потребляется нагрузкой или производится генератором. Будь то цепь постоянного или переменного тока, значение мгновенной мощности получается путем умножения мгновенного напряжения на мгновенный ток.Если в любой момент времени t значения напряжения и тока представлены синусоидальными функциями как

v = V _m sin ωt

i = I _м sin (ωt-φ) V _m и I _m — максимальные значения синусоидального напряжения и тока.Здесь ω = 2 π f
f — частота, а ω — угловая частота вращающихся векторов напряжения или тока. Должно быть понятно, что для энергосистемы f обычно составляет 50 или 60 Гц
φ — разность фаз между напряжением и током.
Как мы уже говорили, мгновенная мощность — это произведение мгновенного напряжения и тока, если мы назовем мгновенную мощность как p, то

p = v.i = V _м sin ωt . I _m sin (ωt-φ)
или p = V _m I _m sin ωt sin (ωt-φ)

Применяя тригонометрическую формулу 2.sin A.sin B = cos (AB) — cos (A + B) получаем

Его можно записать как

Это уравнение мгновенной мощности

. На фиг.8-C нарисованы все три волны, соответствующие v, i и p. Графически мы также можем получить значение мгновенной мощности (p) в любой момент времени t, просто умножив значение тока i и напряжения v в этот конкретный момент t.(Вы можете проверить, что на диаграмме p отрицательно, когда либо v, либо i отрицательно, в противном случае p положительно. См. Точки, где p равно нулю). На графике мы показали горизонтальную ось как угол φ вместо времени t для облегчения визуализации. Должно быть ясно, что оба варианта верны.

Ясно, что мгновенная мощность p состоит из двух членов. Первый член постоянен, потому что для данной нагрузки фазовый угол φ фиксирован.Он не изменится, если не изменится нагрузка. Второй член изменяется во времени синусоидально из-за наличия члена cos (2ωt-φ). Обратите внимание, что мгновенная частота сети в два раза превышает частоту напряжения или тока, поэтому мгновенная мощность в однофазной цепи изменяется синусоидально.

Мгновенная мощность, p = постоянный член + синусоидальный колебательный член.

За один полный период среднее значение колеблющегося члена равно нулю.

Тогда какова средняя мощность в заданное время, скажем, за один период времени волны?

Это постоянный член.

Вот еще один способ думать о средней мощности.
Просто заметьте, что мгновенная мощность на короткое время отрицательна.Для любого временного интервала вы просто найдете общую + ve площадь A + (над горизонтальной осью (синяя линия) и под кривой p) и общую площадь -ve A- (под горизонтальной осью и над кривой p). Чистая площадь получается вычитанием A- из A +. Разделив эту чистую площадь (на интервал времени T _и , мы получим среднюю мощность (P). Вы можете сделать это с помощью расчетов. В конечном итоге вы получите только первый член в приведенной выше формуле для мгновенной мощности p. Еще одним способом легче понять, что формула для мгновенной мощности p имеет постоянный член (V _m .I _m /2) cos φ и другой синусоидальный член (V _m .I _m /2) cos (2 wt — φ). Фактически p — это колебательная мощность, которая колеблется около среднего постоянного члена (V _m .I _m /2) cos φ. Так что средняя мощность
Вышеуказанная формула может быть записана как
здесь,

V и I являются векторным представлением среднеквадратичных значений * синусоид напряжения и тока.Символы | V | и | I | — величины векторов V и I. (См. определение RMS-значения внизу).

Эта формула выше — ваша любимая формула полезной мощности, которая нас больше всего беспокоит. Эта формула средней мощности используется для определения мощности, потребляемой нагрузкой. Ежемесячный счет за электроэнергию дома основан на этой мощности. Инженеры и техники в энергетике или электротехнике просто используют термин мощность вместо средней мощности. Поэтому всякий раз, когда мы просто называем мощность, это означает среднюю мощность.

Конечно, мгновенная мощность колеблется по своей природе. Как мы уже говорили, он колеблется не вокруг горизонтальной оси, а вокруг средней мощности P (голубая горизонтальная линия).

P будет равно нулю, когда cos φ = 0 или φ = 90 градусов, то есть когда фазовый угол между волнами напряжения и тока составляет 90 градусов.Это только тогда, когда нагрузка чисто индуктивная или емкостная. В этом случае второй член остается только в формуле мгновенной мощности.

Из приведенного выше рисунка на некоторое время мощность станет отрицательной, что означает, что нагрузка подает энергию к источнику за этот период. Это связано с наличием в нагрузке реактивного элемента.

Приведенную выше формулу для мгновенной мощности можно записать в другой форме. Эта форма на самом деле является попыткой отличить колеблющуюся реактивную мощность от формулы мгновенной мощности.Переставляя члены в уравнении для мгновенной мощности выше, мы получаем

p = | V | | Я | cos φ (1-cow2ωt) — | V | | Я | sin φ sin2ωt

В этом уравнении первый член | V | | Я | cos φ (1-cow2ωt) колеблется, среднее значение которого | V | | Я | cos φ. Об этой средней мощности мы уже говорили.

Второй член | V | | Я | sin φ sin2ωt, который также является колебательным, но с нулевым средним значением. Максимальное значение этого члена составляет | V | | Я | грех φ. Это так называемая реактивная мощность.Таким образом, реактивная мощность — это максимальное значение колебательной мощности, которая многократно отбирается от источника и снова возвращается к источнику в течение каждого цикла. Таким образом, среднее значение этой реактивной мощности равно нулю.

Средняя мощность P называется реальной мощностью. Иногда ее еще называют активной мощностью.

Активная мощность = P = | V | | Я | cos φ

Обычно записывается как P = VI cos φ. Но следует помнить, что V и I — среднеквадратичные значения напряжения и тока. Например, когда мы говорим однофазный 220 вольт переменного тока, это означает, что действующее значение напряжения составляет 220 вольт (это не максимальное значение синусоиды напряжения)

Реактивная мощность = Q = | V | | Я | sin φ

Реальная мощность измеряется в ваттах, а реактивная мощность — в вар (вольт-ампер-реактивность).В энергетическом секторе эти блоки слишком малы, поэтому реальная мощность измеряется в мегаваттах (МВт), а реактивная мощность — в мегаварах (МВАр). Буква R в конце обозначает реактивную мощность.

Часто студенты и практикующие инженеры не понимают средней мощности (часто называемой просто мощностью). Они думают, что умножая действующее значение напряжения на среднеквадратичный ток, они получают среднеквадратичную мощность. Нет, это неправильно. Нет мощности RMS. RMS мощность не имеет значения или не определена. (Также см. Определение RMS-значения ниже в конце).Это средняя мощность, или реальная мощность, или истинная мощность.

Трехфазная сбалансированная система с питанием

Рассмотрим трехфазную сбалансированную систему. Трехфазная сбалансированная система анализируется с учетом только одной фазы и нейтрали. Это называется поэтапным анализом. Таким образом, приведенный выше анализ для одной фазы верен для сбалансированного трехфазного случая. Пусть здесь суммарная мощность P _t . Тогда мы получаем общую трехфазную мощность как трижды по сравнению с однофазным случаем.

P _t = 3 | V | | Я | cos φ

Следует помнить, что | V | и | Я | — значения для каждой фазы.и φ — фазовый угол нагрузки в пофазном анализе.

Вышеупомянутая формула для сбалансированной трехфазной системы может быть записана как

P _t = √3 | V _l | | I _л | cos φ

В приведенной выше формуле V _l и I _l являются линейным напряжением и током (Рис-D).Это уравнение не зависит от типа подключения трехфазной нагрузки, то есть нагрузки, подключенной по схеме треугольник или звезда. Вы должны знать линейное напряжение, линейный ток и фазовый угол φ, как указано выше. Эта форма очень удобна и часто используется при расчете мощности.

Есть одно основное различие между однофазным и трехфазным питанием. Мгновенная однофазная мощность пульсирует.В сбалансированном трехфазном случае мгновенная мощность каждой фазы пульсирует, но три пульсирующих волны мощности смещены друг от друга на 120 градусов. В любой момент времени сумма этих трех мгновенных волн мощности является постоянной величиной 3 | V | | Я | cos φ. Таким образом, общая мощность, потребляемая в трехфазной сбалансированной системе, не является пульсирующей. Непульсирующая мощность также подразумевает желаемый непульсирующий крутящий момент в случае трехфазных вращающихся машин. В больших трехфазных двигателях это действительно необходимо.

* Действующее значение синусоид переменного тока

Значение переменного напряжения или тока, которое вызывает такой же нагрев (или такую ​​же энергию), который вырабатывается, если вместо переменного тока применяется постоянное напряжение или ток, численно равные действующему значению переменного тока.