Активная реактивная и полная мощности: Понятие активной и реактивной мощности. Что такое активная, реактивная и полная мощность

Понятие активной и реактивной мощности. Что такое активная, реактивная и полная мощность

Мгновенная мощность p произвольного участка цепи, напряжение и ток которого изменяются по законуu =U m sin(t ), i = I m sin(t– ), имеет вид

p = ui= U m sin(t )I m sin(t–  ) = U m I m /2 =

= U i cos — UI cos(2t — ) = (UI cos – UI cos cos2t ) – UI sin sin2t . (1)

Активная мощность цепи переменного тока P определяется как среднее значение мгновенной мощностиp (t ) за период:

так как среднее за период значение гармонической функции равно 0.

Из этого следует, что средняя за период мощность зависит от угла сдвига фаз между напряжением и током и не равна нулю, если участок цепи имеет активное сопротивление. Последнее объясняет ее название активная мощность .

Подчеркнем еще раз, что в активном сопротивлении происходит необратимое преобразование электрической энергии в другие виды энергии, например в тепловую. Активная мощность может быть определена как средняя за период скорость поступления энергии в участок цепи. Активная мощность измеряется в ваттах (Вт).

Реактивная мощность

При расчетах электрических цепей находит широкое применение так называемая реактивная мощность. Она характеризует процессы обмена энергией между реактивными элементами цепи и источниками энергии и численно равна амплитуде переменной составляющей мгновенной мощности цепи. В соответствии с этим реактивная мощность может быть определена из (1) как

Q = UI sin.

В зависимости от знака угла реактивная мощность может быть положительной или отрицательной. Единицу реактивной мощности, чтобы отличить ее от единицы активной, называют не ватт, а вольт-ампер реактивныйвар. Реактивные мощности индуктивного и емкостного элементов равны амплитудам их мгновенных мощностей

p L иp C . С учетом сопротивленийэтих элементов реактивные мощности катушки индуктивности и конденсатора равныQ L =UI =x L I 2 иQ C =UI = x C I 2 , соответственно.

Результирующая реактивная мощность разветвленной электрической цепи находится как алгебраическая сумма реактивных мощностей элементов цепи с учетом их характера (индуктивный или емкостный): Q =Q L –Q С. ЗдесьQ L есть суммарная реактивная мощность всех индуктивных элементов цепи, аQ С представляет собой суммарную реактивную мощность всех емкостных элементов цепи.

Полная мощность

Кроме активной и реактивной мощностей цепь синусоидального тока характеризуется полной мощностью, обозначаемой буквой

S . Под полной мощностью участка понимают максимально возможную активную мощность при заданных напряженииU и токеI . Очевидно, что максимальная активная мощность получается при cos= 1, т. е. при отсутствии сдвига фаз между напряжением и током:

S = UI.

Необходимость во введении этой мощности объясняется тем, что при конструировании электрических устройств, аппаратов, сетей и т. п. их рассчитывают на определенное номинальное напряжение U ном и определенный номинальный токI ном и их произведениеU ном I ном = S ном дает максимально возможную мощность данного устройства (полная мощность S ном указывается в паспорте большинства электрических устройств переменного тока.). Для отличия полной мощности от других мощностей ее единицу измерения называют вольт-ампер и сокращенно обозначают ВА. Полная мощность численно равна амплитуде переменной составляющей мгновенной мощности.

Из приведенных соотношений можно найти связь между различными мощностями:

P = S cos, Q = S sin, S = UI =

и выразить угол сдвига фаз через активную и реактивную мощности:

.

Рассмотрим простой прием, который позволяет найти активную и реактивную мощности участка цепи по комплексным напряжению и току. Он заключается в том, что нужно взять произведение комплексного напряжения и тока, комплексно сопряженного току рассматриваемого участка цепи. Операция комплексного сопряжения состоит в смене знака на противоположный перед мнимой частью комплексного числа либо в смене знака фазы комплексного числа, если число представлено в экспоненциальной форме записи. В результате получим величину, которая называется

полной комплексной мощностью и обозначается. Если
, то для полной комплексной мощности получаем:

Отсюда видно, что активная и реактивная мощности представляют собой вещественную и мнимую части полной комплексной мощности, соответственно. Для облегчения запоминания всех формул, связанных с мощностями, на рис. 7, б (с. 38) построен треугольник мощностей.

Активная и реактивная мощность — потребители электрической энергии на то и потребители, чтобы эту энергию потреблять. Потребителя интересует та энергия, потребление которой идет ему на пользу, эту энергию можно назвать полезной, но в электротехнике ее принято называть активной. Это энергия, которая идет на нагрев помещений, готовку пищи, выработку холода, и превращаемая в механическую энергию (работа электродрелей, перфораторов, электронасосов и пр.).

Кроме активной электроэнергии существует еще и реактивная. Это та часть полной энергии, которая не расходуется на полезную работу. Как понятно из вышесказанного, полная мощность – это активная и реактивная мощность в целом.

В понятиях активная и реактивная мощность сталкиваются противоречивые интересы потребителей электрической энергии и ее поставщиков. Потребителю выгодно платить только за потребленную им полезную электроэнергию, поставщику выгодно получать оплату за сумму активной и реактивной электроэнергии. Можно ли совместить эти кажущиеся противоречивыми требования? Да, если свести количество реактивной электроэнергии к нулю. Рассмотрим, возможно ли подобное, и насколько можно приблизиться к идеалу.

Активная и реактивная мощность

Активная мощность

Существуют потребители электроэнергии, у которых полная и активная мощности совпадают. Это потребители, у которых нагрузка представлена активными сопротивлениями (резисторами). Среди бытовых электроприборов примерами подобной нагрузки являются лампы накаливания, электроплиты, жарочные шкафы и духовки, обогреватели, утюги, паяльники и пр.

Указанная у этих приборов в паспорте, одновременно является активная и реактивная мощность. Это тот случай, когда мощность нагрузки можно определить по известной из школьного курса физики формуле, перемножив ток нагрузки на напряжение в сети. Ток измеряется в амперах (А), напряжение в вольтах (В), мощность в ваттах (Вт). Конфорка электрической плиты в сети с напряжением 220 В при токе в 4,5 А потребляет мощность 4,5 х 220 = 990 (Вт).

Реактивная мощность

Иногда, проходя по улице, можно увидеть, что стекла балконов покрыты изнутри блестящей тонкой пленкой. Эта пленка изъята из бракованных электрических конденсаторов, устанавливаемых с определенными целями на питающих мощных потребителей электрической энергии распределительных подстанциях.

Конденсатор – типичный потребитель реактивной мощности. В отличие от потребителей активной мощности, где главным элементом конструкции является некий проводящий электричество материал (вольфрамовый проводник в лампах накаливания, нихромовая спираль в электроплитке и т.п.). В конденсаторе главный элемент – не проводящий электрический ток (тонкая полимерная пленка или пропитанная маслом бумага).

Реактивная емкостная мощность

Красивые блестящие пленки, что вы видели на балконе – это обкладки конденсатора из токопроводящего тонкого материала. Конденсатор замечателен тем, что он может накапливать электрическую энергию, а затем отдавать ее – своеобразный такой аккумулятор. Если включить конденсатор в сеть постоянного тока, он зарядится кратковременным импульсом тока, а затем ток через него протекать не будет. Вернуть конденсатор в исходное состояние можно, отключив его от источника напряжения и подключив к его обкладкам нагрузку. Некоторое время через нагрузку будет течь электрический ток, и идеальный конденсатор отдает в нагрузку ровно столько электрической энергии, сколько он получил при зарядке.

Подключенная к выводам конденсатора лампочка может на короткое время вспыхнуть, электрический резистор нагреется, а неосторожного человека может «тряхнуть» или даже убить при достаточном напряжении на выводах и запасенном количестве электричества.

Интересная картина получается при подключении конденсатора к источнику переменного электрического напряжения. Поскольку у источника переменного напряжения постоянно меняются полярность и мгновенное значение напряжения (в домашней электросети по закону, близкому к синусоидальному). Конденсатор будет непрерывно заряжаться и разряжаться, через него будет непрерывно протекать переменный ток. Но этот ток не будет совпадать по фазе с напряжением источника переменного напряжения, а будет опережать его на 90°, т.е. на четверть периода.

Это приведет к тому, что суммарно половину периода переменного напряжения конденсатор потребляет энергию из сети, а половину периода отдает, при этом суммарная потребляемая активная электрическая мощность равна нулю. Но, поскольку через конденсатор течет значительный ток, который может быть измерен амперметром, принято говорить, что конденсатор – потребитель реактивной электрической мощности.

Вычисляется реактивная мощность как произведение тока на напряжение, но единица измерения уже не ватт, а вольт-ампер реактивный (ВАр). Так, через подключенный к сети 220 В частотой 50 Гц электрический конденсатор емкостью 4 мкФ течет ток порядка 0,3 А. Это означает, что конденсатор потребляет 0,3 х 220 = 66 (ВАр) реактивной мощности – сравнимо с мощностью средней лампы накаливания, но конденсатор, в отличие от лампы, при этом не светится и не нагревается.

Реактивная индуктивная мощность

Если в конденсаторе ток опережает напряжение, то существуют ли потребители, где ток отстает от напряжения? Да, и такие потребители, в отличие от емкостных потребителей, называются индуктивными, оставаясь при этом потребителями реактивной энергии. Типичная индуктивная электрическая нагрузка – катушка с определенным количеством витков хорошо проводящего провода, намотанного на замкнутый сердечник из специального магнитного материала.

На практике хорошим приближением чисто индуктивной нагрузки является работающий без нагрузки трансформатор (или стабилизатор напряжения с автотрансформатором). Хорошо сконструированный трансформатор на холостом ходу потребляет очень мало активной мощности, потребляя мощность в основном реактивную.

Реальные потребители электрической энергии и полная электрическая мощность

Из рассмотрения особенностей емкостной и индуктивной нагрузки возникает интересный вопрос – что произойдет, если емкостную и индуктивную нагрузку включить одновременно и параллельно. Ввиду их противоположной реакции на приложенное напряжение, эти две реакции начнут компенсировать друг друга. Суммарная нагрузка окажется только емкостной или индуктивной, и в некотором идеальном случае удастся добиться полной компенсации. Выглядеть это будет парадоксально – подключенные амперметры зафиксируют значительные (и равные!) токи через конденсатор и катушку индуктивности, и полное отсутствие тока в объединяющих их общей цепи.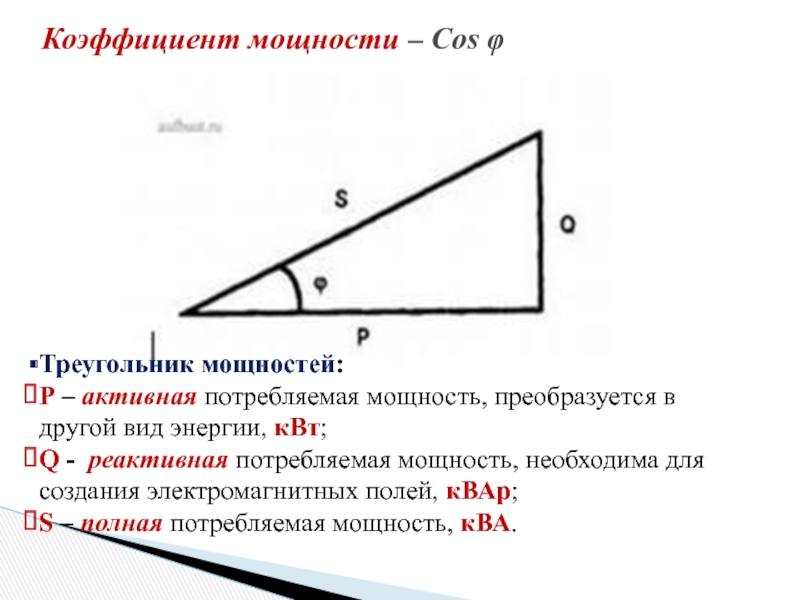 Описанная картина несколько нарушается лишь тем, что не существует идеальных конденсаторов и катушек индуктивности, но подобная идеализация помогает понять суть происходящих процессов.

Вернемся к реальным потребителям электрической энергии. В быту мы пользуемся в основном потребителями чисто активной мощности (примеры приведены выше), и смешанной активно-индуктивной. Это электродрели, перфораторы, электродвигатели холодильников, стиральных машин и прочей бытовой техники. Также к ним относятся электрические трансформаторы источников питания бытовой радиоэлектронной аппаратуры и стабилизаторов напряжения. В случае подобной смешанной нагрузки, помимо активной (полезной) мощности, нагрузка потребляет еще и реактивную мощность, в итоге полная мощность отказывается больше активной мощности. Полная мощность измеряется в вольт-амперах (ВА), и всегда представляет собой произведение тока в нагрузке на напряжение на нагрузке.

Таинственный «косинус фи»

Отношение активной мощности к полной называется в электротехнике «косинусом фи». Обозначается cos φ. Это отношение называется также и коэффициентом мощности. Нетрудно видеть, что для случая чисто активной нагрузки, где полная мощность совпадает с активной, cos φ = 1. Для случаев чисто емкостной или индуктивной нагрузок, где нулю равна активная мощность, cos φ = 0.

В случае смешанной нагрузки значение коэффициента мощности заключается в пределах от 0 до 1. Для бытовой техники обычно в диапазоне 0,5-0,9. В среднем можно считать его равным 0,7, более точное значение указывается в паспорте электроприбора.

За что платим?

И, наконец, самый интересный вопрос – за какой вид энергии платит потребитель. Исходя из того, что реактивная составляющая суммарной энергии не приносит потребителю никакой пользы, при этом долю периода реактивная энергия потребляется, а долю отдается, платить за реактивную мощность незачем. Но бес, как известно, кроется в деталях. Поскольку смешанная нагрузка увеличивает ток в сети, возникают проблемы на электростанциях, где электроэнергия вырабатывается синхронными генераторами, а именно: индуктивная нагрузка «развозбуждает» генератор, и приведение его в прежнее состояние обходится в затраты уже реальной активной мощности на его «довозбуждение».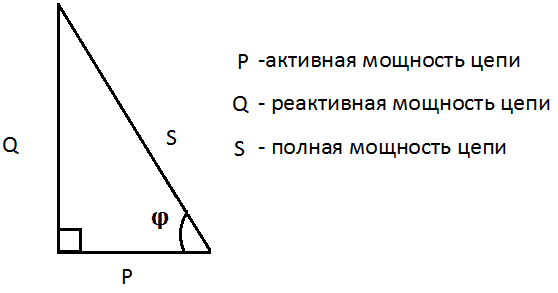

Таким образом, заставить потребителя платить за потребляемую реактивную индуктивную мощность вполне справедливо. Это побуждает потребителя компенсировать реактивную составляющую своей нагрузки, а, поскольку эта составляющая в основном индуктивная, компенсация заключается в подключении конденсаторов наперед рассчитанной емкости.

Потребитель находит возможность платить меньше

Если потребителем оплачивается отдельно потребляемая активная и реактивная мощность. Он готов идти на дополнительные затраты и устанавливать на своем предприятии батареи конденсаторов, включаемые строго по графику в зависимости от средней статистики потребления электроэнергии по часам суток.

Существует также возможность установки на предприятии специальных устройств (компенсаторов реактивной мощности), подключающих конденсаторы автоматически в зависимости от величины и характера потребляемой в данный момент мощности. Эти компенсаторы позволяют поднять значение коэффициента мощности с 0,6 до 0,97, т. е. практически до единицы.

Принято также, что если соотношение потребленной реактивной энергии и общей не превышает 0,15, то корпоративный потребитель от оплаты за реактивную энергию освобождается.

Что же касается индивидуальных потребителей, то, ввиду сравнительно невысокой потребляемой ими мощности, разделять счета на оплату потребляемой электроэнергии на активную и реактивную не принято. Бытовые электрической энергии учитывают лишь активную мощность электрической нагрузки, за нее и выставляется счет на оплату. Т.е. в настоящее время даже не существует технической возможности выставить индивидуальному потребителю счет за потребленную реактивную мощность.

Особых стимулов компенсировать индуктивную составляющую нагрузки у потребителя нет, да это и сложно осуществить технически. Постоянно подключенные конденсаторы при отключении индуктивной нагрузки будут бесполезно нагружать подводящую электропроводку. За электросчетчиком (перед счетчиком тоже, но за то потребитель не платит), что вызовет потребление активной мощности с соответствующим увеличением счета на оплату, а автоматические компенсаторы дороги и вряд ли оправдают затраты на их приобретение.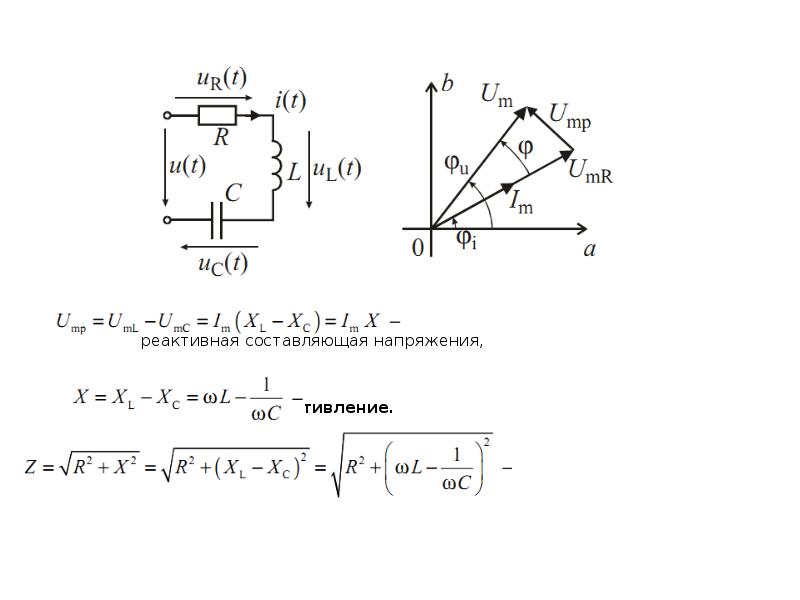

Другое дело, что производитель иногда устанавливает компенсационные конденсаторы на входе потребителей с индуктивной составляющей нагрузки. Эти конденсаторы, при правильном их подборе, несколько снизят потери энергии в подводящих проводах, при этом несколько повысив напряжение на подключенном электроприборе за счет уменьшения падения напряжения на подводящих проводах.

Но, что самое главное, компенсация реактивной энергии у каждого потребителя, от квартиры до огромного предприятия, снизит токи во всех линиях электропитания, от электростанции до квартирного щитка. За счет реактивной составляющей полного тока, что уменьшит потери энергии в линиях и повысит коэффициент полезного действия электросистем.

Чтобы правильно рассчитать нагрузку потребителей по мощности необходимо знать: какие бывают приемники напряжения. Что такое активная, реактивная и линейная нагрузка? Треугольник мощностей. Что такое пусковой ток? Все это разберем по порядку.

К приемникам напряжения относятся все устройства, которые подключаются к источникам напряжения. К ним относятся: электровентилятор, электроплита, стиральная машина, компьютер, телевизор, электродвигатель, бытовой электроинструмент и другие электропотребители.
В цепях переменного тока нагрузки разделяются на активные, реактивные и нелинейные. В цепях постоянного тока деления на типы нагрузок нет.

Активная нагрузка

К устройствам с активной нагрузкой причисляются нагревательные приборы (утюги, электроплиты, лампы накаливания, электрические чайники). Подобные приборы вырабатывают тепло и свет. Они не содержат индуктивности и емкости. Активная нагрузка преобразовывает электроэнергию в свет и тепло.

Реактивная нагрузка содержит емкость и индуктивность. Данные параметры имеют качество собирать энергию, а потом отдавать ее в сеть. Примером может служить электродвигатель, электрическая мясорубка, бытовой инструмент (пылесос, кухонный комбайн). То есть, все устройства, которые содержат электродвигатели.

Треугольник мощностей

Чтобы разобраться с реактивной нагрузкой рассмотрим треугольник мощностей.

где Р – активная мощность, которая измеряется в Ватах и используется для совершения полезной работы;

Q – реактивная, которая измеряется в Варах и используется для создания электромагнитного поля;

S – полная мощность используется для расчета электрических цепей.

Для расчета полной мощности применяем теорему Пифагора: S 2 =P 2 +Q 2 . Или с помощью формулы: S=U*I, где U – это показание напряжения на нагрузке, I — показание амперметра, которое включается последовательно с нагрузкой. В расчетах также используется коэффициент мощности – cosφ. На приборах, которые относятся к реактивной нагрузке, обычно указаны активная мощность и cosφ. С помощью этих параметров также можно получить полную мощность.

Иногда на приборах указывается полная мощность, а cosφ не указан. В этом случае применяется коэффициент 0,7.

Нелинейная нагрузка

Имеет особенность в том, что напряжение и ток не пропорциональны. К нелинейной нагрузке относятся телевизоры, музыкальные центры, настольные электронные часы, компьютеры и его компоненты. Сама нелинейность обусловлена тем, что данное электронное устройство использует импульсные блоки питания. Для подзарядки конденсатора, которые стоят в импульсном блоке питания, достаточно вершины синусоиды.

В остальное время энергию из сети конденсатор не потребляет. В этом случае ток имеет импульсное качество. К чему это все приводит? Это приводит к тому, что синусоида искажается. Но не все электронные устройства работают с искаженной синусоидой. Эта проблема решается за счет применения стабилизаторов двойного преобразования, где сетевое питание преобразуется в постоянное. Затем из постоянного преобразуется в переменное нужной формы и амплитуды.

Пусковой ток

При расчете необходимо учитывать и пусковые токи устройства. Например, сопротивление нити накаливания в лампочке в момент включения в 10 раз меньше, чем в рабочем режиме. Следовательно, пусковой ток этой лампочки в 10 раз больше. Через некоторое время она начнет потреблять ту мощность, которая записана в данных этой лампочки. Поэтому, при включении она перегорает за счет больших пусковых токов.

В радиоэлектронной аппаратуре пока не зарядится конденсатор в блоке питания, также образуется пусковой ток.

В электродвигателях тоже образуется пусковой ток, пока двигатель не наберет номинальные обороты.

В нагревательных приборах пусковой ток образуется, пока спираль не нагреется до дежурной температуры.

Физический аспект процесса и практическое значение использования установок компенсации реактивной мощности

Чтобы понять, что заключает в себе термин «реактивная мощность»,

вспомним определение понятия электрической мощности. Это физическая величина, которая выражает скорость передачи, потребления или генерации электроэнергии в определённое время.

Чем больше уровень мощности, тем большую производительность может иметь электрическая установка в определённую единицу времени. Под термином «мгновенная мощность» понимают произведение силы тока и напряжения за один из моментов на каком-либо участке электроцепи.

Рассмотрим же физический аспект процесса.

Если брать цепи в которых происходит постоянный ток, то там величина средней и мгновенной мощности за определённый отрезок времени являются равными, а реактивной мощности нет. А в цепях где происходит явление переменного тока вышеописанная ситуация имеет место только в том случае, если нагрузка там является чисто активной. Это бывает, например, в таком электроприборе, как электронагреватель. При чисто активной нагрузке в цепи в условиях переменного тока фазы тока и напряжения совпадают и вся мощность отдаётся в нагрузку.

В случае индуктивной нагрузки, как например, в электродвигателях, то у тока происходит отставание по фазе от напряжения, а если она ёмкостная, что имеет случай в разнообразных электроустройствах, тогда ток наоборот, по фазе опережает напряжение. Так как у напряжения и тока нет совпадения по фазе (при реактивной нагрузке), то в нагрузку полная мощность отходит только частично, полностью она могла бы перейти, если сдвиг фаз был бы нулевым, то есть активная нагрузка.

Чем отличаются реактивная и активная мощность

Та часть полной мощности, что передалась в нагрузку в условиях периода переменного тока, носит название активной мощности . Её величина высчитывается в результате произведения значений напряжения и тока на косинус угла сдвига фаз, которые лежат между ними

А та мощность, которая не передалась в нагрузку, и из-за которой произошли потери излучения и нагрева, именуется реактивной мощностью . Её же величина – это произведение значений напряжения и тока на синус угла сдвига фаз, которые лежат между ними.

Следовательно, реактивная мощность – это термин, характеризующий нагрузку . Единица её измерения называется – реактивные вольт амперы, сокращённо вар или var. Но в жизни чаще встречается другая величина измерения – косинус фи, как величины, измеряющей качество электрической установки с аспекта экономии электроэнергии. На самом деле, от величины cos φ , зависит та величина энергии, которая когда подаётся от источника, идёт в нагрузку. Следовательно, вполне возможно пользоваться не очень мощным источником, тогда, соответственно меньшее количество энергии уйдёт в никуда.

Как можно компенсировать реактивную мощность

Как следует из вышесказанного, в случае, когда нагрузка является индуктивной, тогда нужно выполнить её компенсацию, используя конденсаторы, конденсаторов, а емкостную нагрузку следует компенсировать с применением реакторов и дросселей. Таким способом можно поднять косинус фи до достаточных величин в размере 0.7-0.9. Так и выполняется компенсация реактивной мощности .

Чем выгодна компенсация реактивной мощности?

Установки компенсации реактивной мощности могут принести огромную экономическую выгоду. Как гласит статистика, они могут экономить до 50% от счетов за электроэнергию в разных частях РФ. Там где они устанавливаются, деньги потраченные на них, окупаются меньше чем за год.

На стадии проектирования объектов внедрение конденсаторных установок помогает удешевить приобретение кабелей путём уменьшения их сечения. Как пример, автоматическая конденсаторная установка может дать эффект увеличения косинуса фи с 0.6 до 0.97.

Подведём черту:

Как мы поняли, установки по компенсации реактивной мощности помогают существенно экономить финансы, а также увеличивать срок работы оборудования, из-за нижеследующих причин:

1) уменьшается нагрузка на силовые трансформаторы, что повышает их долговечность.

2) Уменьшается уровень нагрузки на кабели и провода, а также можно экономить покупая кабели меньшего сечения.

3) Повышение уровня качества электрической энергии электроприемников.

4) Нет опасности выплаты штрафовых отчислений за снижение cos φ.

5) уменьшается величина высших гармоник в сети.

6) понижается количество расхода электроэнергии.

Напомним ещё раз, что реактивная энергия и мощность понижают итоги работы энергосистемы, из-за того, что загрузка реактивными токами генераторов электростанций ведёт к повышению объёма употребляемого топлива, а также возрастает размер потерь в подводящих сетях и приемниках, и наконец возрастает уровень падения напряжения в сетях.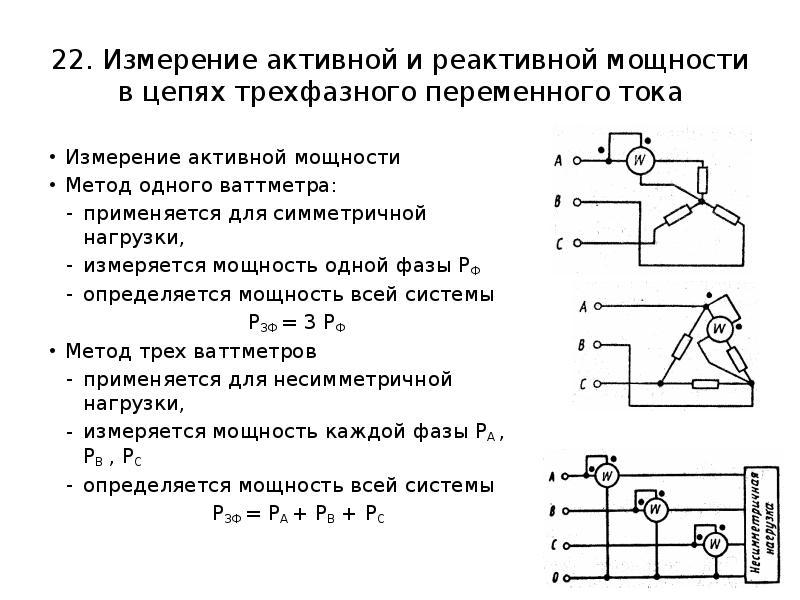

Увидела в интернете энергосберегающие устройства, которые, как я поняла прсто включаются в ближайшую к счетчику розетку. Может кто пользовался? Действительно экономят энергию? И еще пишут, что они повышают качество электроэнергии и таким образом предотвращают порчу электроприборов. Хотелось бы услышать отзывы.

При расчете электрической мощности, потребляемой любым электротехническим или бытовым устройством, обычно учитывается так называемая полная мощность электрического тока, выполняющего определённую работу в цепи данной нагрузки. Под понятием «полная мощность» подразумевается вся та мощность, которая потребляется электроприбором и включает в себя как активную составляющую, так и составляющую реактивную, которая в свою очередь определяется типом используемой в цепи нагрузки. Активная мощность всегда измеряется и указывается в ваттах (Вт), а полная мощность приводится обычно в вольт-амперах (ВА). Различные приборы — потребители электрической энергии могут работать в цепях, имеющих как активную, так и реактивную составляющую электрического тока.

Активная составляющая потребляемой любой нагрузкой мощности электрического тока совершает полезную работу и трансформируется в нужные нам виды энергии (тепловую, световую, звуковую и т.п.). Отдельные электроприборы работают в основном на этой составляющей мощности. Это — лампы накаливания, электроплиты, обогреватели, электропечи, утюги и т.п.
При указанном в паспорте прибора значении активной потребляемой мощности в 1 кВт он будет потреблять от сети полную мощность в 1кВА.

Реактивная составляющая электрического тока возникает только в цепях, содержащих реактивные элементы (индуктивности и ёмкости) и расходуется обычно на бесполезный нагрев проводников, из которых составлена эта цепь. Примером таких реактивных нагрузок являются электродвигатели различного типа, переносные электроинструменты (электродрели, «болгарки», штроборезы и т.п.), а также различная бытовая электронная техника. Полная мощность этих приборов, измеряемая в вольт-амперах, и активная мощность (в ваттах) соотносятся между собой через коэффициент мощности cosφ, который может принимать значение от 0,5 до 0,9.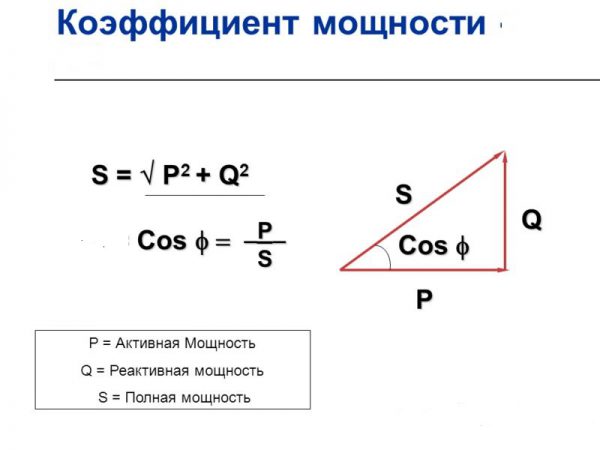 На этих приборах указывается обычно активная мощность в ваттах и значение коэффициента cosφ. Для определения полной потребляемой мощности в ВА, необходимо величину активной мощности (Вт) разделить на коэффициент cosφ.

Пример: если на электродрели указана величина мощности в 600 Вт и cosφ = 0,6, то отсюда следует, что потребляемая инструментом полная мощность составляет 600/0,6=1000 ВА. При отсутствии данных по cosφ можно брать его приблизительное значение, которое для домашнего электроинструмента составляет примерно 0,7.

При рассмотрении вопроса об активной и реактивной составляющих электроэнергии (точнее — её мощности), обычно имеются в виду те явления, которые происходят в цепях переменного тока. Оказалось, что различные нагрузки в цепях переменного тока ведут себя совершенно по-разному. Одни нагрузки используют передаваемую им энергию по прямому назначению (т.е. — для совершения полезной работы), а другой тип нагрузок сначала эту энергию запасает, а потом снова отдаёт её источнику электропитания.

По виду своего поведения в цепях переменного тока, различные потребительские нагрузки делятся на следующие два типа:

1. Активный тип нагрузки поглощает всю получаемую от источника энергию и превращает её в полезную работу (свет от лампы, например), причём форма тока в нагрузке в точности повторяет форму напряжения на ней (сдвиг фаз отсутствует).

2. Реактивный тип нагрузки характеризуется тем, что сначала (в течение некоторого промежутка времени), в нём происходит накопление энергии, поставляемой источником питания. Затем запасённая энергия (в течение определённого промежутка времени) отдаётся обратно в этот источник. К подобным нагрузкам относятся такие элементы электрических цепей, как конденсаторы и катушки индуктивности, а также устройства, содержащие их. При этом в такой нагрузке между напряжением и током присутствует сдвиг фаз, равный 90 градусам. Поскольку основной целью существующих систем электроснабжения является полезная доставка электроэнергии от производителя непосредственно к потребителю (а не перекачивание её туда и обратно) — реактивная составляющая мощности обычно считается вредной характеристикой цепи.

Потери на реактивную составляющую в сети напрямую связаны с величиной рассмотренного выше коэффициента мощности, т.е. чем выше cosφ потребителя, тем меньше будут потери мощности в линии и дешевле обойдётся передача электроэнергии потребителю.
Таким образом, именно коэффициент мощности указывает нам на то, насколько эффективно используется рабочая мощность источника электроэнергии. В целях повышения величины коэффициента мощности (cosφ) во всех видах электрических установок применяются специальные приёмы компенсации реактивной мощности.
Обычно для увеличения коэффициента мощности (за счёт уменьшения сдвига фаз между током и напряжением — угла φ) в действующую сеть включают специальные компенсирующие устройства, представляющие собой вспомогательные генераторы опережающего (емкостного) тока.
Кроме того, очень часто для компенсации потерь, возникающих из-за индуктивной составляющей цепи, в ней используются батареи конденсаторов, подключаемые параллельно рабочей нагрузке и используемые в качестве синхронных компенсаторов.

Реактивная мощность – jelectro.ru

Главная цель при передаче электроэнергии – повышение эффективности работы сетей. Следовательно, необходимо уменьшение потерь. Основной причиной потерь является реактивная мощность, компенсация которой значительно повышает качество электроэнергии.

Батареи статических конденсаторов

Реактивная мощность вызывает ненужный нагрев проводов, перегружаются электроподстанции. Трансформаторная мощность и кабельные сечения вынужденно подвергаются завышениям, сетевое напряжение снижается.

Понятие о реактивной мощности

Для выяснения, что же такое реактивная мощность, надо определить другие возможные виды мощности. При существовании в контуре активной нагрузки (резистора) происходит потребление исключительно активной мощности, полностью расходуемой на энергопреобразование. Значит, можно сформулировать, что такое активная мощность, – та, при которой ток совершает эффективную работу.

На постоянном токе происходит потребление исключительно активной мощности, рассчитываемой соответственно формуле:

P = U x I.

Измеряется в ваттах (Вт).

В электроцепях с переменным током при наличии активной и реактивной нагрузки мощностной показатель суммируется из двух составных частей: активной и реактивной мощности.

Реактивная нагрузка бывает двух видов:

1. Емкостная (конденсаторы). Характеризуется фазовым опережением тока по сравнению с напряжением;
2. Индуктивная (катушки). Характеризуется фазовым отставанием тока по отношению к напряжению.

Емкостная и индуктивная нагрузка

Если рассмотреть контур с переменным током и подсоединенной активной нагрузкой (обогреватели, чайники, лампочки с накаливающейся спиралью), ток и напряжение будут синфазными, а полная мощность, взятая в определенную временную отсечку, вычисляется путем перемножения показателей напряжения и тока.

Однако когда схема содержит реактивные компоненты, показатели напряжения и тока не будут синфазными, а будут различаться на определенную величину, определяемую углом сдвига «φ». Пользуясь простым языком, говорится, что реактивная нагрузка возвращает столько энергии в электроцепь, сколько потребляет. В результате получится, что для активной мощности потребления показатель будет нулевой. Одновременно по цепи протекает реактивный ток, не выполняющий никакую эффективную работу. Следовательно, потребляется реактивная мощность.

Реактивная мощность – часть энергии, которая позволяет устанавливать электромагнитные поля, требуемые оборудованием переменного тока.

Расчет реактивной мощности ведется по формуле:

Q = U x I x sin φ.

В качестве единицы измерения реактивной мощности служит ВАр (вольтампер реактивный).

Выражение для активной мощности:

P = U x I x cos φ.

Треугольник мощностей

Взаимосвязь активной, реактивной и полной мощности для синусоидального тока переменных значений представляется геометрически тремя сторонами прямоугольного треугольника, называемого треугольником мощностей. Электроцепи переменного тока потребляют две разновидности энергии: активную мощность и реактивную. Кроме того, значение активной мощности никогда не является отрицательным, тогда как для реактивной энергии возможна либо положительная величина (при индуктивной нагрузке), либо отрицательная (при емкостной нагрузке).

Треугольник мощностей

Важно! Из треугольника мощностей видно, что всегда полезно снизить реактивную составляющую, чтобы повысить эффективность системы.

Полная мощность не находится как алгебраическая сумма активного и реактивного мощностного значения, это векторная сумма P и Q. Ее количественное значение вычисляется извлечением квадратного корня из суммы квадратов мощностных показателей: активного и реактивного. Измеряться полная мощность может в ВА (вольтампер) или производных от него: кВА, мВА.

Чтобы была рассчитана полная мощность, необходимо знать разность фаз между синусоидальными значениям U и I.

Коэффициент мощности

Пользуясь геометрически представленной векторной картиной, можно найти отношение сторон треугольника, соответствующих полезной и полной мощности, что будет равно косинусу фи или мощностному коэффициенту:

cos φ = P/S.

Данный коэффициент находит эффективность работы сети.

Количество потребляемых ватт – то же самое, что и количество потребляемых вольтампер при мощностном коэффициенте, равном 1 или 100%.

Важно! Полная мощность тем ближе к показателю активной, чем больше cos φ, или чем меньше угол сдвига синусоидальных величин тока и напряжения.

Если, к примеру, имеется катушка, для которой:

• Р = 80 Вт;
• Q = 130 ВАр;
• тогда S = 152,6 BA как среднеквадратичный показатель;
• cos φ = P/S = 0,52 или 52%

Можно сказать, что катушка требует 130 ВАр полной мощности для выполнения полезной работы 80 Вт.

Коррекция cos φ

Для коррекции cos φ применяется тот факт, что при емкостной и индуктивной нагрузке вектора реактивной энергии располагаются в противофазе. Так как большинство нагрузок является индуктивными, подключив емкость, можно добиться увеличения cos φ.

Принцип компенсации реактивной мощности

Главные потребители реактивной энергии:

1. Трансформаторы. Представляют собой обмотки, имеющие индуктивную связь и посредством магнитных полей преобразуюшие токи и напряжения. Эти аппараты являются основным элементом электросетей, передающих электроэнергию. Особенно увеличиваются потери при работе на холостом ходу и при низкой нагрузке. Широко используются трансформаторы в производстве и в быту;
2. Индукционные печи, в которых расплавляются металлы путем создания в них вихревых токов;
3. Асинхронные двигатели. Крупнейший потребитель реактивной энергии. Вращающий момент в них создается посредством переменного магнитного поля статора;
4. Преобразователи электроэнергии, такие как силовые выпрямители, используемые для питания контактной сети железнодорожного транспорта и другие.

Конденсаторные батареи подсоединяются на электроподстанциях для того, чтобы контролировать напряжение в пределах установленных уровней. Нагрузка меняется в течение дня с утренними и вечерними пиками, а также на протяжении недели, снижаясь в выходные, что изменяет показатели напряжения. Подключением и отключением конденсаторов варьируется его уровень. Это делается от руки и с помощью автоматики.

Как и где измеряют cos φ

Реактивная мощность проверяется по изменению cos φ специальным прибором – фазометром. Его шкала проградуирована в количественных значениях cos φ от нуля до единицы в индуктивном и емкостном секторе. Полностью скомпенсировать негативное влияние индуктивности не удастся, но возможно приближение к желаемому показателю – 0,95 в индуктивной зоне.

Фазометр

Фазометры применяются при работе с установками, способными повлиять на режим работы электросети через регулирование cos φ.

1. Так как при финансовых расчетах за потребленную энергию учитывается и ее реактивная составляющая, то на производствах устанавливаются автоматические компенсаторы на конденсаторах, емкость которых может меняться. В сетях, как правило, используются статические конденсаторы;
2. При регулировании cos φ у синхронных генераторов путем изменения возбуждающего тока необходимо его отслеживать визуально в ручных рабочих режимах;
3. Синхронные компенсаторы, представляющие собой синхронные двигатели, работающие без нагрузки, в режиме перевозбуждения выдают в сеть энергию, которая компенсирует индуктивную составляющую. Для регулирования возбуждающего тока наблюдают за показаниями cos φ по фазометру.

Синхронный компенсатор

Коррекция коэффициента мощности – одна из эффективнейших инвестиций для сокращения затрат на электроэнергию. Одновременно улучшается качество получаемой энергии.

Видео

Оцените статью:

Единицы измерения мощности реактивной активной и полной

В электротехнике среди множества определений довольно часто используются такие понятия, как активная, реактивная и полная мощность. Эти параметры напрямую связаны с током и напряжением в замкнутой электрической цепи, когда включены какие-либо потребители. Для проведения вычислений применяются различные формулы, среди которых основной является произведение напряжения и силы тока. Прежде всего это касается постоянного напряжения. Однако в цепях переменного тока мощность разделяется на несколько составляющих, отмеченных выше. Вычисление каждой из них также осуществляется с помощью формул, благодаря которым можно получить точные результаты.

Формулы активной, реактивной и полной мощности

Основной составляющей считается активная мощность. Она представляет собой величину, характеризующую процесс преобразования электрической энергии в другие виды энергии. То есть по-другому является скоростью, с какой потребляется электроэнергия. Именно это значение отображается на электросчетчике и оплачивается потребителями. Вычисление активной мощности выполняется по формуле: P = U x I x cosф.

В отличие от активной, которая относится к той энергии, которая непосредственно потребляется электроприборами и преобразуется в другие виды энергии – тепловую, световую, механическую и т.д., реактивная мощность является своеобразным невидимым помощником. С ее участием создаются электромагнитные поля, потребляемые электродвигателями. Прежде всего она определяет характер нагрузки, и может не только генерироваться, но и потребляться. Расчеты реактивной мощности производятся по формуле: Q = U x I x sinф.

Полной мощностью является величина, состоящая из активной и реактивной составляющих. Именно она обеспечивает потребителям необходимое количество электроэнергии и поддерживает их в рабочем состоянии. Для ее расчетов применяется формула: S = .

Как найти активную, реактивную и полную мощность

Активная мощность относится к энергии, которая необратимо расходуется источником за единицу времени для выполнения потребителем какой-либо полезной работы. В процессе потребления, как уже было отмечено, она преобразуется в другие виды энергии.

В цепи переменного тока значение активной мощности определяется, как средний показатель мгновенной мощности за установленный период времени. Следовательно, среднее значение за этот период будет зависеть от угла сдвига фаз между током и напряжением и не будет равной нулю, при условии присутствия на данном участке цепи активного сопротивления. Последний фактор и определяет название активной мощности. Именно через активное сопротивление электроэнергия необратимо преобразуется в другие виды энергии.

При выполнении расчетов электрических цепей широко используется понятие реактивной мощности. С ее участием происходят такие процессы, как обмен энергией между источниками и реактивными элементами цепи. Данный параметр численно будет равен амплитуде, которой обладает переменная составляющая мгновенной мощности цепи.

Существует определенная зависимость реактивной мощности от знака угла ф, отображенного на рисунке. В связи с этим, она будет иметь положительное или отрицательное значение. В отличие от активной мощности, измеряемой в ваттах, реактивная мощность измеряется в вар – вольт-амперах реактивных. Итоговое значение реактивной мощности в разветвленных электрических цепях представляет собой алгебраическую сумму таких же мощностей у каждого элемента цепи с учетом их индивидуальных характеристик.

Основной составляющей полной мощности является максимально возможная активная мощность при заранее известных токе и напряжении. При этом, cosф равен 1, когда отсутствует сдвиг фаз между током и напряжением. В состав полной мощности входит и реактивная составляющая, что хорошо видно из формулы, представленной выше. Единицей измерения данного параметра служит вольт-ампер (ВА).

Пусть приемник электро­энергии присоединен к источнику синусоидального напряжения u(t) = Usin(ωt) и потребляет синусоидальный ток i(t) = I sin (ωt -φ), сдви­нутый по фазе относительно напряжения на угол φ. U и I – действующие значения. Значение мгновенной мощности на зажимах приемника определяется выражением

p(t) = u(t) ?i(t) = 2UI sin(ωt) sin (ωt -φ) = UI cos φ — UI cos (2ωt -φ)

(5.1)

и является суммой двух величин, одна из которых постоянна во времени, а другая пульсирует с двойной частотой.

Среднее значение p(t) за период Т называется активной мощностью и полностью определяется первым слагаемым уравнения (5.1):

Активная мощность ха­рактеризует энергию, расходуемую необратимо источником в единицу времени на производство полезной работы потребителем. Активная энергия, потребляемая электроприёмниками, преобразуется в другие виды энергии: механическую, тепловую, энергию сжатого воздуха и газа и т. п.

Среднее значение от второго слагаемого мгновенной мощности (1.1) (пульсирует с двойной частотой) за время Т равно нулю, т. е. на ее создание не требуется каких-либо материальных затрат и поэтому она не может совершать полезной ра­боты. Однако ее присутствие указывает, что между источником и приемником происходит обратимый процесс обмена энергией. Это возможно, если имеются элементы, способные накапливать и отдавать электромагнитную энергию – емкость и индуктивность. Эта составляющая характеризует реактивную мощность.

Полную мощность на зажимах приемника в комп­лексной форме можно представить следующим образом:

.

(5.2)

Единица измерения полной мощности S = UI – ВА.

Реактивная мощность – величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями (обменом) энергии между источником и приемником. Для синусоидального тока она равна произведению действующих значений тока I и напряжения U на синус угла сдвига фаз между ними: Q = UI sinφ. Единица измерения – ВАр.

Реактивная мощность не связана с полезной работой ЭП и расходуется только на создание переменных электромагнитных полей в электродвигателях, трансформаторах, аппаратах, линиях и т. д.

Для реактивной мощности приняты такие понятия, как генерация, потребление, передача, потери, баланс. Считается, что если ток отстает по фазе от напряжения (индуктивный характер нагрузки), то реактивная мощ­ность потребляется и имеет положительный знак, а если ток опережает напряжение (емкостный характер нагрузки), то реактивная мощность ге­нерируется и имеет отрицательное значение.

Основными потребителями реактивной мощности на промышленных предприятиях являются асинхронные двигатели (60–65 % общего потреб­ления), трансформаторы (20–25 %), вентильные преобразователи, реакторы, воздушные электрические сети и прочие приемники (10 %).

Передача реактивной мощности загружает электрические сети и установленное в ней оборудование, уменьшая их пропускную способность. Реактивная мощность генерируется синхронными генераторами электростанций, синхронными компенса­торами, синхронными двигателями (регулирование током возбуждения), батареями конденсаторов (БК) и линиями электропередачи.

Реактивная мощность, вырабатываемая емкостью сетей, имеет следующий порядок величин: воздушная линия 20 кВ генерирует 1 кВАр на 1 км трехфазной линии; подземный кабель 20 кВ – 20 кВАр/км; воздушная линия 220 кВ – 150 кВАр/км; подземный кабель 220 кВ – 3 МВАр/км.

Коэффициент мощности и коэффициент реактивной мощности.

Векторное представление величин, характеризующих состояние сети, приводит к представлению реактивной мощности Q вектором, перпендикулярным вектору активной мощности Р (рис. 5.2 ). Их векторная сумма дает полную мощность S.

Рис. 5.1. Треугольник мощностей

Согласно рис. 5.1 и (5.2) следует, что S 2 = Р 2 + Q 2 ; tgφ = Q/P; cosφ = P/S.

Основным нормативным показателем, характе­ризующим реактивную мощность, ранее был коэффициент мощности cosφ. На вводах, питающих промышленное предприятие, средневзвешенное значение этого коэффициента должно было находиться в пределах 0,92–0,95. Однако выбор соотношения P/S в качестве нормативного не дает четкого представления о динамике изменения реального значения реактивной мощности. Например, при изменении коэффициента мощности от 0,95 до 0,94 реактивная мощность изменяется на 10 %, а при изменении этого же коэффициента от 0,99 до 0,98 приращение реактивной мощности составляет уже 42 %. При расчетах удобнее оперировать соотношением tgφ = Q/P, которое называют коэффициентом реактивной мощности.

Предприятиям, у которых присоединенная мощность более 150 кВт (за исключением «бытовых» потребителей), определены предельные значения коэффициента реактивной мощности, потребляемой в часы больших суточных нагрузок электрической сети – с 7 до 23 часов (Приказ Министерства промышленности и энергетики РФ от 22.02.2007 г. № 49 «О порядке расчета значений соотношения потребления активной и реактивной мощности для отдельных энергопринимающих устройств потребителей электрической энергии, применяемых для определения обязательств сторон в договорах об оказании услуг по передаче электрической энергии»).

Предельные значения коэффициентов реактивной мощности (tgφ) нормируются в зависимости от положения точки (напряжения) присоединения потребителя к сети. Для напряжения сети 100 кВ tgφ = 0,5; для сетей 35, 20, 6 кВ – tgφ = 0,4 и для сети 0,4 кВ – tgφ = 0,35.

Введение новых директивных документов по компен­сации реактивной мощности было направлено на повышение эффективности работы всей системы электроснабжения от генераторов энергосистемы до приемников электроэнергии.

С введением коэффициента реактивной мощности стало возможным представлять потери активной мощности через активную или реактивную мощности: Р = (P 2 /U 2 ) R (l + tg 2 φ).

Угол между векторами мощностей Р и S соответствует углу φ между векторами активной составляющей тока I_а и полного тока I, который, в свою очередь, представляет собой векторную сумму активного тока I_а, находящегося в фазе с напряжением, и реактивного тока I_р, находящегося под углом 90° к нему. Это расположение токов является расчетным приемом, связанным с разложением на активную и реактивную мощности, которое можно считать естественным.

Большинство потребителей нуждаются в реактивной мощности, поскольку они функционируют благодаря изменению магнитного поля. Для наиболее употребительных двигателей в нормальном режиме работы можно привести следующие примерные значения tgφ.

Электродвигатели	tgφ	cosφ
Однофазный асинхронный двигатель	1,30–0,90	0,61–0,74
Трехфазный асинхронный двигатель	1,00–0,50	0,70–0,89
Коллекторный двигатель	1,30–1,00	0,61–0,70

В момент пуска двигателей требуется значительное количество реактивной мощности, при этом tgφ = 4–5 (cosφ = 0,2–0,24).

Синхронные машины обладают способностью потреблять или выдавать реактивную мощность в зависимости от степени возбуждения.

В синхронных генераторах и двигателях размеры цепей возбуждения ограничивают возможность поставки реактивной мощности до максимальных значений tgφ = 0,75 (cosφ = 0,8) или до tgφ = 0,5 (cosφ = 0,9) (табл. 5.1).

Синхронные двигатели, выпускаемые отечественной промышленностью, рассчитаны на опережающий коэффициент мощности (cosφ = 0,9) и при номинальной активной нагрузке P_ном и напряжении U_ном могут вырабатывать номинальную реактивную мощность Q_ном ≈ 0,5P_ном.

При недогрузке СД по активной мощности β = P/P_ном 1.

Преимуществом СД, используемым для компенсации реактивной мощности, по сравнению с КБ является возможность плавного регулирования генерируемой реактивной мощности. Недостатком является то, что активные потери на генерирование реактивной мощности для СД больше, чем для КБ.

Дополнительные активные потери в обмотке СД, вызываемые генерируемой реактивной мощностью в пределах изменения cosφ от 1 до 0,9 при номинальной активной мощности СД, равной P_ном, кВт:

где Q_ном – номинальная реактивная мощность СД, кВ Ар; R – сопротивление одной фазы обмотки СД в нагретом состоянии, Ом; U_ном – номинальное напряжение сети, кВ.

В системах электроснабжения промышленных предприятий КБ компенсируют реактивную мощность базисной (основной) части графиков нагрузок, а СД снижают пики нагрузок графика.

Таблица 5.1

Зависимости коэффициента перегрузки по реактивной мощности синхронных двигателей

Серия, номинальное напряжение, частота вращения двига теля	Относительное напряжение на зажимах двигателя U/Uном	Коэффициент перегрузки по реактивной мощности α при коэффициенте загрузки β
0,90	0,80	0,70
СДН, 6 и 10 кВ (для всех частот вращения) СДН, 6 кВ: 600–1000 об/мин 370–500 об/мин 187–300 об/мин 100–167 об/мин СДН, 10 кВ: 1000 об/мин 250–750 об/мин СТД, 6 и 10 кВ, 3000 об/мин СД и СДЗ, 380 В (для всех частот вращения)	0,95 1,00 1,05 1,10 1,10 1,10 1,10 1,10 1,10 0,95 1,00 1,05 1,10 0,95 1,00 1,05 1,10	1,31 1,21 1,06 0,89 0,88 0,86 0,81 0,90 0,86 1,30 1,32 1,12 0,90 1,16 1,15 1,10 0,90	1,39 1,27 1,12 0,94 0,92 0,88 0,85 0,98 0,90 1,42 1,34 1,23 1,08 1,26 1,24 1,18 1,06	1,45 1,33 1,17 0,96 0,94 0,90 0,87 1,00 0,92 1,52 1,43 1,31 1,16 1,36 1,32 1,25 1,15

Синхронные компенсаторы.

Разновидностью СД являются синхронные компенсаторы (СК), которые представляют собой СД без нагрузки на валу. В настоящее время выпускается СК мощностью выше 5000 кВ?Ар. Они имеют ограниченное применение в сетях промышленных предприятий. Для улучшения показателей качества напряжения у мощных ЭП с резкопеременной, ударной нагрузкой (дуговые печи, прокатные станы и т. п.) используются СК.

Статические тиристорные компенсирующие устройства.

В сетях с резкопеременной ударной нагрузкой на напряжении 6–10 кВ рекомендуется применение не конденсаторных батарей, а специальных быстродействующих источников реактивной мощности (ИРМ), которые должны устанавливаться вблизи таких ЭП. Схема ИРМ приведена на рис. 5.2. В ней в качестве регулируемой индуктивности используются индуктивности LR и нерегулируемые ёмкости С1–С3.

Рис. 5.2. Быстродействующие источники реактивной мощности

Регулирование индуктивности осуществляется тиристорными группами VS, управляющие электроды которых подсоединены к схеме управления. Достоинствами статических ИРМ являются отсутствие вращающихся частей, относительная плавность регулирования реактивной мощности, выдаваемой в сеть, возможность трёх- и четырёхкратной перегрузки по реактивной мощности. К недостаткам относится появление высших гармоник, которые могут возникнуть при глубоком регулировании реактивной мощности.

За счет дополнительных потерь мощности в сети, вызванных потреблением реактивной мощности, увеличивается общее потребление электроэнергии. Поэтому снижение перетоков реактивной мощности является одной из основных задач эксплуатации электрических сетей.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Для студента самое главное не сдать экзамен, а вовремя вспомнить про него. 10099 — | 7532 — или читать все.

Простое объяснение с формулами

Активная мощность (P)

Другими словами активную мощность можно назвать: фактическая, настоящая, полезная, реальная мощность. В цепи постоянного тока мощность, питающая нагрузку постоянного тока, определяется как простое произведение напряжения на нагрузке и протекающего тока, то есть

потому что в цепи постоянного тока нет понятия фазового угла между током и напряжением. Другими словами, в цепи постоянного тока нет никакого коэффициента мощности.

Но при синусоидальных сигналах, то есть в цепях переменного тока, ситуация сложнее из-за наличия разности фаз между током и напряжением. Поэтому среднее значение мощности (активная мощность), которая в действительности питает нагрузку, определяется как:

В цепи переменного тока, если она чисто активная (резистивная), формула для мощности та же самая, что и для постоянного тока: P = U I.

Формулы для активной мощности

P = U I — в цепях постоянного тока

P = U I cosθ — в однофазных цепях переменного тока

P = √3 U_L I_L cosθ — в трёхфазных цепях переменного тока

P = √ (S 2 – Q 2 ) или

P =√ (ВА 2 – вар 2 ) или

Активная мощность = √ (Полная мощность 2 – Реактивная мощность 2 ) или

кВт = √ (кВА 2 – квар 2 )

Реактивная мощность (Q)

Также её мощно было бы назвать бесполезной или безваттной мощностью.

Мощность, которая постоянно перетекает туда и обратно между источником и нагрузкой, известна как реактивная (Q).

Реактивной называется мощность, которая потребляется и затем возвращается нагрузкой из-за её реактивных свойств. Единицей измерения активной мощности является ватт, 1 Вт = 1 В х 1 А. Энергия реактивной мощности сначала накапливается, а затем высвобождается в виде магнитного поля или электрического поля в случае, соответственно, индуктивности или конденсатора.

Реактивная мощность определяется, как

и может быть положительной (+Ue) для индуктивной нагрузки и отрицательной (-Ue) для емкостной нагрузки.

Единицей измерения реактивной мощности является вольт-ампер реактивный (вар): 1 вар = 1 В х 1 А. Проще говоря, единица реактивной мощности определяет величину магнитного или электрического поля, произведённого 1 В х 1 А.

Формулы для реактивной мощности

Реактивная мощность = √ (Полная мощность 2 – Активная мощность 2 )

квар = √ (кВА 2 – кВт 2 )

Полная мощность (S)

Полная мощность – это произведение напряжения и тока при игнорировании фазового угла между ними. Вся мощность в сети переменного тока (рассеиваемая и поглощаемая/возвращаемая) является полной.

Комбинация реактивной и активной мощностей называется полной мощностью. Произведение действующего значения напряжения на действующее значение тока в цепи переменного тока называется полной мощностью.

Она является произведением значений напряжения и тока без учёта фазового угла. Единицей измерения полной мощности (S) является ВА, 1 ВА = 1 В х 1 А. Если цепь чисто активная, полная мощность равна активной мощности, а в индуктивной или ёмкостной схеме (при наличии реактивного сопротивления) полная мощность больше активной мощности.

Формула для полной мощности

Полная мощность = √ (Активная мощность 2 + Реактивная мощность 2 )

kUA = √(kW 2 + kUAR 2 )

Следует заметить, что:

• резистор потребляет активную мощность и отдаёт её в форме тепла и света.
• индуктивность потребляет реактивную мощность и отдаёт её в форме магнитного поля.
• конденсатор потребляет реактивную мощность и отдаёт её в форме электрического поля.

Все эти величины тригонометрически соотносятся друг с другом, как показано на рисунке:

активную, реактивную, полную[br] (P, Q, S), а также коэффициент мощности (PF)

Из письма клиента:
Подскажите, ради Бога, почему мощность ИБП указывается в Вольт-Амперах, а не в привычных для всех киловаттах. Это сильно напрягает. Ведь все уже давно привыкли к киловаттам. Да и мощность всех приборов в основном указана в кВт.
Алексей. 21 июнь 2007

 

 

В технических характеристиках любого ИБП указаны полная мощность [кВА] и активная мощность [кВт] – они характеризуют нагрузочную способность ИБП. Пример, см. фотографии ниже:

 

 

Мощность не всех приборов указана в Вт, например:

• Мощность трансформаторов указывается в ВА:
  http://www.mstator.ru/products/sonstige/powertransf (трансформаторы ТП: см приложение)
  http://metz.by/download_files/catalog/transform/tsgl__tszgl__tszglf.pdf (трансформаторы ТСГЛ: см приложение)
• Мощность конденсаторов указывается в Варах:
  http://www.elcod.spb.ru/catalog/k78-39.pdf (конденсаторы K78-39: см приложение)
  http://www.kvar.su/produkciya/25-nizkogo-napraygeniya-vbi (конденсаторы УК: см приложение)
• Примеры других нагрузок — см. приложения ниже.

 

Мощностные характеристики нагрузки можно точно задать одним единственным параметром (активная мощность в Вт) только для случая постоянного тока, так как в цепи постоянного тока существует единственный тип сопротивления – активное сопротивление.

Мощностные характеристики нагрузки для случая переменного тока невозможно точно задать одним единственным параметром, так как в цепи переменного тока существует два разных типа сопротивления – активное и реактивное. Поэтому только два параметра: активная мощность и реактивная мощность точно характеризуют нагрузку.

Принцип действия активного и реактивного сопротивлений совершенно различный. Активное сопротивление – необратимо преобразует электрическую энергию в другие виды энергии (тепловую, световую и т.д.) – примеры: лампа накаливания, электронагреватель (параграф 39, Физика 11 класс В.А. Касьянов М.: Дрофа, 2007).

Реактивное сопротивление – попеременно накапливает энергию затем выдаёт её обратно в сеть – примеры: конденсатор, катушка индуктивности (параграф 40,41, Физика 11 класс В.А. Касьянов М.: Дрофа, 2007).

Дальше в любом учебнике по электротехнике Вы можете прочитать, что активная мощность (рассеиваемая на активном сопротивлении) измеряется в ваттах, а реактивная мощность (циркулирующая через реактивное сопротивление) измеряется в варах; так же для характеристики мощности нагрузки используют ещё два параметра: полную мощность и коэффициент мощности. Все эти 4 параметра:

1. Активная мощность: обозначение P, единица измерения: Ватт
2. Реактивная мощность: обозначение Q, единица измерения: ВАр (Вольт Ампер реактивный)
3. Полная мощность: обозначение S, единица измерения: ВА (Вольт Ампер)
4. Коэффициент мощности: обозначение k или cosФ, единица измерения: безразмерная величина

Эти параметры связаны соотношениями:  S*S=P*P+Q*Q,   cosФ=k=P/S

Также cosФ называется коэффициентом мощности (Power Factor – PF)

Поэтому в электротехнике для характеристики мощности задаются любые два из этих параметров так как остальные могут быть найдены из этих двух.

Например, электромоторы, лампы (разрядные) — в тех. данных указаны P[кВт] и cosФ:
http://www.mez.by/dvigatel/air_table2.shtml (двигатели АИР: см. приложение)
http://www.mscom.ru/katalog.php?num=38 (лампы ДРЛ: см. приложение)
(примеры технических данных разных нагрузок см. приложение ниже)

То же самое и с источниками питания. Их мощность (нагрузочная способность) характеризуется одним параметром для источников питания постоянного тока – активная мощность (Вт), и двумя параметрами для ист. питания переменного тока. Обычно этими двумя параметрами являются полная мощность (ВА) и активная (Вт). См. например параметры ДГУ и ИБП.

Большинство офисной и бытовой техники, активные (реактивное сопротивление отсутствует или мало), поэтому их мощность указывается в Ваттах. В этом случае при расчёте нагрузки используется значение мощности ИБП в Ваттах. Если нагрузкой являются компьютеры с блоками питания (БП) без коррекции входного коэффициента мощности (APFC), лазерный принтер, холодильник, кондиционер, электромотор (например погружной насос или мотор в составе станка), люминисцентные балластные лампы и др. – при расчёте используются все вых. данные ибп: кВА, кВт, перегрузочные характеристики и др.

 

См. учебники по электротехнике, например:

1. Евдокимов Ф. Е. Теоретические основы электротехники. — М.: Издательский центр «Академия», 2004.

2. Немцов М. В. Электротехника и электроника. — М.: Издательский центр «Академия», 2007.

3. Частоедов Л. А. Электротехника. — М.: Высшая школа, 1989.

Так же см. AC power, Power factor, Electrical resistance, Reactance http://en.wikipedia.org
(перевод: http://electron287.narod.ru/pages/page1.html)

 

---

Приложение

 

Пример 1: мощность трансформаторов и автотрансформаторов указывается в ВА (Вольт·Амперах)

Трансформаторы питания номинальной выходной мощностью 25-60 ВА
http://www.mstator.ru/products/sonstige/powertransf (трансформаторы ТП)

 

http://metz.by/download_files/catalog/transform/tsgl__tszgl__tszglf.pdf (трансформаторы ТСГЛ)

 

		АОСН-2-220-82
	Латр 1.25	АОСН-4-220-82
	Латр 2.5	АОСН-8-220-82
		АОСН-20-220
		АОМН-40-220

http://www.gstransformers.com/products/voltage-regulators.html (ЛАТР / лабораторные автотрансформаторы TDGC2)

 

 

Пример 2: мощность конденсаторов указывается в Варах (Вольт·Амперах реактивных)

http://www.elcod.spb.ru/catalog/k78-39.pdf (конденсаторы K78-39)

 

http://www.kvar.su/produkciya/25-nizkogo-napraygeniya-vbi (конденсаторы УК)

 

 

Пример 3: технические данные электромоторов содержат активную мощность (кВт) и cosФ

Для таких нагрузок как электромоторы, лампы (разрядные), компьютерные блоки питания, комбинированные нагрузки и др. — в технических данных указаны P [кВт] и cosФ (активная мощность и коэффициент мощности) или S [кВА] и cosФ (полная мощность и коэффициент мощности).

http://www.mez.by/dvigatel/air_table2.shtml (двигатели АИР)

 

http://www.weiku.com/products/10359463/Stainless_Steel_cutting_machine.html
(комбинированная нагрузка – станок плазменной резки стали / Inverter Plasma cutter LGK160 (IGBT)

 

Технические данные разрядных ламп содержат активную мощность (кВт) и cosФ
http://www.mscom.ru/katalog.php?num=38 (лампы ДРЛ)

 

http://www.silverstonetek.com.tw/product.php?pid=365&area=en (блок питания ПК)

 

 

Дополнение 1

Если нагрузка имеет высокий коэффициент мощности (0.8 … 1.0), то её свойства приближаются к активной нагрузке. Такая нагрузка является идеальной как для сетевой линии, так и для источников электроэнергии, т.к. не порождает реактивных токов и мощностей в системе.

Если нагрузка имеет низкий коэффициент мощности (менее 0.8 … 1.0), то в линии питания циркулируют большие реактивные токи (и мощности). Это паразитное явление приводит к повышению потерь в проводах линии (нагрев и др.), нарушению режима работы источников (генераторов) и трансформаторов сети, а также др. проблемам.

Поэтому во многих странах приняты стандарты нормирующие коэффициент мощности оборудования.

 

Дополнение 2

Оборудование однонагрузочное (например, БП ПК) и многосоставное комбинированное (например, фрезерный промышленный станок, имеющий в составе несколько моторов, ПК, освещение и др.) имеют низкие коэффициенты мощности (менее 0.8) внутренних агрегатов (например, выпрямитель БП ПК или электромотор имеют коэффициент мощности 0.6 .. 0.8). Поэтому в настоящее время большинство оборудования имеет входной блок корректора коэффициента мощности. В этом случае входной коэффициент мощности равен 0.9 … 1.0, что соответствует нормативным стандартам.

 

Дополнение 3. Важное замечание относительно коэффициента мощности ИБП и стабилизаторов напряжения

Нагрузочная способность ИБП и ДГУ нормирована на стандартную промышленную нагрузку (коэффициент мощности 0.8 с индуктивным характером). Например, ИБП 100 кВА / 80 кВт. Это означает, что устройство может питать активную нагрузку максимальной мощности 80 кВт, или смешанную (активно-реактивную) нагрузку максимальной мощности 100 кВА с индуктивным коэффициентом мощности 0.8.

В стабилизаторах напряжения дело обстоит иначе. Для стабилизатора коэффициент мощности нагрузки безразличен. Например, стабилизатор напряжения 100 кВА. Это означает, что устройство может питать активную нагрузку максимальной мощности 100 кВт, или любую другую (чисто активную, чисто реактивную, смешанную) мощностью 100 кВА или 100 кВАр с любым коэффициентом мощности емкостного или индуктивного характера. Обратите внимание, что это справедливо для линейной нагрузки (без высших гармоник тока). При больших гармонических искажениях тока нагрузки (высокий КНИ) выходная мощность стабилизатора снижается.

 

Дополнение 4

Наглядные примеры чистой активной и чистой реактивных нагрузок:

• К сети переменного тока 220 VAC подключена лампа накаливания 100 Вт – везде в цепи есть ток проводимости (через проводники проводов и вольфрамовый волосок лампы). Характеристики нагрузки (лампы): мощность S=P~=100 ВА=100 Вт, PF=1 => вся электрическая мощность активная, а значит она целиком поглащается в лампе и превращается в мощность тепла и света.
• К сети переменного тока 220 VAC подключен неполярный конденсатор 7 мкФ – в цепи проводов есть ток проводимости, внутри конденсатора идёт ток смещения (через диэлектрик). Характеристики нагрузки (конденсатора): мощность S=Q~=100 ВА=100 ВАр, PF=0 => вся электрическая мощность реактивная, а значит она постоянно циркулирует от источника к нагрузке и обратно, опять к нагрузке и т.д.

 

Дополнение 5

Для обозначения преобладающего реактивного сопротивления (индуктивного либо ёмкостного) коэффициенту мощности приписывается знак:

+ (плюс) – если суммарное реактивное сопротивление является индуктивным (пример: PF=+0.5). Фаза тока отстаёт от фазы напряжения на угол Ф.

— (минус) – если суммарное реактивное сопротивление является ёмкостным (пример: PF=-0,5). Фаза тока опережает фазу напряжения на угол Ф.

 

Дополнение 6

В различных областях техники мощность может быть либо полезной, либо паразитной НЕЗАВИСИМО от того активная она или реактивная. Например, необходимо различать активную полезную мощность рассеиваемую на рабочей нагрузке и активную паразитную мощность рассеиваемую в линии электропередачи. Так, например, в электротехнике при расчете активной и реактивной мощностей наиболее часто активная мощность является полезной мощностью, передаваемой в нагрузку и является реальной (не мнимой) величиной. А в электронике при расчёте конденсаторов или расчёте самих линий передач активная мощность является паразитной мощностью, теряемой на разогрев конденсатора (или линии) и является мнимой величиной. Причём, деление на мнимые и немнимые величины производится только для удобства рассчётов. На самом деле, все физические величины конечно реальные.

 

 

Дополнительные вопросы

 

Вопрос 1:
Почему во всех учебниках электротехники при расчете цепей переменного тока используют мнимые числа / величины (например, реактивная мощность, реактивное сопротивление и др.), которые не существуют в реальности?

Ответ:
Да, все отдельные величины в окружающем мире – действительные. В том числе температура, реактивное сопротивление, и т.д. Использование мнимых (комплексных) чисел – это только математический приём, облегчающий вычисления. В результате вычисления получается обязательно действительное число. Пример: реактивная мощность нагрузки (конденсатора) 20кВАр – это реальный поток энергии, то есть реальные Ватты, циркулирующие в цепи источник–нагрузка. Но что бы отличить эти Ватты от Ваттов, безвозвратно поглащаемых нагрузкой, эти «циркулирующие Ватты» решили называть Вольт·Амперами реактивными [6].

Замечание:
Раньше в физике использовались только одиночные величины и при расчете все математические величины соответствовали реальным величинам окружающего мира. Например, расстояние равно скорость умножить на время (S=v*t). Затем с развитием физики, то есть по мере изучения более сложных объектов (свет, волны, переменный электрический ток, атом, космос и др.) появилось такое большое количество физических величин, что рассчитывать каждую в отдельности стало невозможно. Это проблема не только ручного вычисления, но и проблема составления программ для ЭВМ. Для решения данное задачи близкие одиночные величины стали объединять в более сложные (включающие 2 и более одиночных величин), подчиняющиеся известным в математике законам преобразования. Так появились скалярные (одиночные) величины (температура и др.), векторные и комплексные сдвоенные (импеданс и др.), векторные строенные (вектор магнитного поля и др.), и более сложные величины – матрицы и тензоры (тензор диэлектрической проницаемости, тензор Риччи и др.). Для упрощения рассчетов в электротехнике используются следующие мнимые (комплексные) сдвоенные величины:

1. Полное сопротивление (импеданс) Z=R+iX
2. Полная мощность S=P+iQ
3. Диэлектрическая проницаемость e=e’+ie»
4. Магнитная проницаемость m=m’+im»
5. и др.

 

 

Вопрос 2:

На странице http://en.wikipedia.org/wiki/Ac_power показаны S P Q Ф на комплексной, то есть мнимой / несуществующей плоскости. Какое отношение это все имеет к реальности?

 

 

Ответ:
Проводить расчеты с реальными синусоидами сложно, поэтому для упрощения вычислений используют векторное (комплексное) представление как на рис. выше. Но это не значит, что показанные на рисунке S P Q не имеют отношения к реальности. Реальные величины S P Q могут быть представлены в обычном виде, на основе измерений синусоидальных сигналов осциллографом. Величины S P Q Ф I U в цепи переменного тока «источник-нагрузка» зависят от нагрузки. Ниже показан пример [5] реальных синусоидальных сигналов S P Q и Ф для случая нагрузки состоящей из последовательно соединённых активного и реактивного (индуктивного) сопротивлений.

 

 

 

Вопрос 3:
Обычными токовыми клещами и мультиметром измерен ток нагрузки 10 A, и напряжение на нагрузке 225 В. Перемножаем и получаем мощность нагрузки в Вт: 10 A · 225В = 2250 Вт.

Ответ:
Вы получили (рассчитали) полную мощность нагрузки 2250 ВА. Поэтому ваш ответ будет справедлив только, если ваша нагрузка чисто активная, тогда действительно Вольт·Ампер равен Ватту. Для всех других типов нагрузок (например электромотор) – нет. Для измерения всех характеристик любой произвольной нагрузки необходимо использовать анализатор сети, например APPA137:

 

 

 

---

См. дополнительную литературу, например:

 

[1]. Евдокимов Ф. Е. Теоретические основы электротехники. — М.: Издательский центр «Академия», 2004.

[2]. Немцов М. В. Электротехника и электроника. — М.: Издательский центр «Академия», 2007.

[3]. Частоедов Л. А. Электротехника. — М.: Высшая школа, 1989.

[4]. AC power, Power factor, Electrical resistance, Reactance
http://en.wikipedia.org (перевод: http://electron287.narod.ru/pages/page1.html)

[5]. Теория и расчёт трансформаторов малой мощности Ю.Н.Стародубцев / РадиоСофт Москва 2005 г. / rev d25d5r4feb2013

[6]. Международная система единиц, СИ, см напр. ГОСТ 8.417-2002. ЕДИНИЦЫ ВЕЛИЧИН

2.6 Активная, реактивная и полная мощности

Активная мощность – это энергия, которая выделяется в единицу времени в виде теплоты на участке цепи с сопротивлением R

. [Вт].

(2.49)

Реактивная мощность – это энергия, которой обмениваются генератор и приемник.

Под реактивной мощностью Q понимают:

.[Вар]

(2.50)

Если и наоборот –

Полная мощность

[ВА].

(2.51)

Графически связь между мощностями представляют в виде треугольника мощности, у которого два катета Р и Q и гипотенуза S.

Рисунок 2.12 – Треугольник мощностей

Косинус угла сдвига фаз называетсякоэффициентом мощности. Он показывает, какую долю полной мощности составляет активная мощность, а какая доля электроэнергии преобразуется в другие виды энергии. Когда , то это означает, что активная мощность равна полной или сопротивление потребителя только активное.

Коэффициент мощностиважный эксплуатационный параметр электроприемников. Так как

,

(2.52)

то чем выше , тем при меньшем значении тока в цепи происходит преобразование электроэнергии в другие виды энергии, что приводит к уменьшению потерь электроэнергии, ее экономии и снижению стоимости устройств электропередачи.

Повышение коэффициента мощности

Во многих электротехнических устройствах преобладает индуктивная составляющая реактивного тока, т.е. большой положительный угол сдвига фаз φ между напряжением и током, что ухудшает коэффициент мощности. Низкое значение приводит к неполному использованию технических и электротехнологических систем, которые загружаются реактивной (индуктивной) составляющая тока, что приводит к увеличению потерь энергии.

Для увеличения параллельно электротехническому устройству включают батарею конденсаторов. Емкостный (реактивный) ток компенсирует индуктивный ток.

Баланс мощности в цепи синусоидального тока

Баланс мощности заключается в том, что:

1. Алгебраическая сумма активных мощностей всех источников энергии равная арифметической сумме мощностей всех резистивных элементов

(2.53)

2. Алгебраическая сумма реактивных мощностей источников энергии равна разности между арифметическими суммами реактивных мощностей индуктивных элементов и емкостных элементов

(2.54)

Баланс мощностей можно выразить и в комплексной форме: алгебраическая сумма комплексных мощностей источников энергии равна алгебраической сумме комплексных мощностей потребителей энергии

(2.55)

Знаки алгебраических слагаемых источников энергии выбираются по правилу для активных мощностей: знак «+» если направления действия ЭДС совпадает с направлением действия тока и «–», если не совпадают.

2.7 Резонанс в цепях синусоидального тока

В качестве критерия режима «резонанс» в электрических цепях, содержащих катушки индуктивности и конденсаторы, принимается совпадение по фазе тока и напряжения на входных зажимах, т. е. фазовый резонанс.

Если конденсатор зарядить до какого-то напряжения, то его разряд на катушку и повторный заряд имеет колебательный характер. При свободных колебаниях в отсутствии потерь напряжение на обкладках конденсатора меняется во времени по косинусоидальному, а ток в катушке – по синусоидальному законам. В реальном колебательном контуре кроме катушки индуктивности и емкостного элемента должен быть и резистивный элемент.

При подключении колебательного контура к источнику энергии могут возникать резонансные явления. Различают два основных вида резонанса: резонанс напряжений при последовательном соединении контура с источником энергии и резонанс токов – при параллельном соединении.

Резонанс напряжений

Рисунок 2.13 – Последовательный колебательный контур

По закону Ома комплекс тока в контуре будет

(2.56)

где Z – комплексное сопротивление контура, определяемой формулой (2.38).

Полное сопротивление контура и угол сдвига фаз из формул (2.41) и (2.42). Тогда действующее значение тока равно:

(2.57)

Резонанс возникает при равенстве индуктивных и емкостных сопротивлений:

.

(2.58)

При этом начальные фазы тока и напряжения будут равны ,. Полное сопротивление минимально и равно, а действующее значение тока придостигнет максимального значения:

(2.59)

Резонанс напряжений – это режим неразветвленной цепи, при котором ток и напряжение совпадают по фазе, а действующие значения напряжений на индуктивном и емкостном элементах равны, но противоположны по фазе.

Рисунок 2.14 – Векторные диаграммы режимов резонанса напряжений (а)

и резонанса токов (б)

Из условия (2.58) следует, что резонанса можно достичь, изменяя частоту напряжения питания или параметры цепи: индуктивность или емкость. Резонансная угловая частота – частота, при которой наступает резонанс:

.

(2.60)

Отношение напряжения на индуктивном элементе или емкостном элементек напряжению питания при резонансеназывают добротностью контура или коэффициентом резонанса:

(2.61)

Частотные характеристики и резонансные кривые последовательного контура. Изменение частоты ω приводит к изменению параметров контура,

т. е. изменяется его реактивное сопротивление, а также угол . Зависимость от частоты параметров цепи (X_L и X_C) называется частотными характеристиками цепи, а зависимость действующих (или амплитудных) значений тока и напряжения от частоты – резонансными кривыми.

Рисунок 2.15 – Частотные характеристики последовательного контура

Изменение реактивного сопротивления приводит к изменению режима цепи. На рисунке 2.16 показан примерный вид резонансных кривых: тока , напряжений на емкостноми индуктивномэлементах, а также угла φ для цепи с добротностьюQ ≈1,25.

Рисунок 2.16 – Резонансные кривые последовательного контура

Резонансные кривые рисунка 2.17 показывают, что чем выше добротность Q, тем острее резонансная кривая и лучше избирательные свойства цепи, для оценки которых пользуются понятием полосы пропускания, что является разницей верхней и нижней частот . Пересечениес резонансными кривыми и определяет граничные частоты.

Рисунок 2.17 –Резонансные кривые для цепей с различной добротностью

Резонанс токов может возникнуть в цепи, схема которой содержит параллельно соединенные индуктивный, емкостной и резистивный элементы. Резонанс наступает, когда у входной проводимости

(2.62)

равны противоположные по фазе реактивные составляющие токов . Поэтому такой резонанс и называется резонансом токов.

Рисунок 2.18 – Параллельный колебательный контур

При резонансе полная проводимость контура минимальна , и общий ток также минимален

(2.64)

Резонанс токов – это режим участка цепи с параллельными ветвями, при котором сдвиг фаз между напряжением на его выводах и общим током равен нулю. На рисунке 2.19 б приведены резонансные кривые параллельного контура. Точка пересечения кривых исоответствует резонансу токов, при котором.

Рисунок 2.19 – Частотные характеристики (а) и резонансные

кривые (б) параллельного контура

Резонанс напряжений – явление нежелательное, т. к. приводит к перенапряжениям в цепях, которые могут в несколько раз превышать рабочее напряжение установки. Резонанс токов – явление безопасное для установок. Явление резонанса применяется в радиотехнике при настройке контуров на резонансную частоту.

Активная, реактивная и полная мощность

Мгновенная мощность p, потребляемая на данном участке цепи, определяется как произведение мгновенных значений тока i и напряжения u:

. (11)

Из соотношения (11) видно, что мгновенная мощность p, в зависимости от значения синусов, может быть как положительной, так и отрицательной.

Физический смысл положительного значения мгновенной мощности в том, что это мощность, поступающая в цепь от источника (генератора). Под отрицательной мощностью понимают мощность, отдаваемую в цепь и генератору в процессе разрядки конденсатора, а также обусловленную током самоиндукции.

Практический интерес представляет не мгновенная мощность, а так называемая активная мощность, которая определяется как среднее значение мгновенной мощности, потребляемой на данном участке цепи за достаточно большой промежуток времени. Поскольку мгновенная мощность изменяется периодически, то усреднение достаточно провести за один период T = 2/:

. (12)

После преобразования произведения синусов и выполнения интегрирования выражения (12) получим выражение для активной мощности:

. (13)

Для контроля за параметрами электрической цепи используются измерительные приборы, амперметры и вольтметры. Механическое перемещение стрелок, «световых зайчиков» и других элементов, позволяющих регистрировать показание прибора, обусловлено работой тока в течение определенного промежутка времени на участке цепи, где включен прибор. Поэтому измерительные приборы не могут показать мгновенные значения силы тока и напряжения, в том числе и амплитудные их значения.

Показания амперметров и вольтметров в цепи переменного тока соответствуют, так называемым, действующим (эффективным) значениям силы тока I и напряжения U.

Действующим значением силы переменного тока называется сила такого постоянного тока, при протекании которого в том же сопротивлении R за одинаковое время, равное целому числу периодов T, выделяется такая же энергия, как и при протекании переменного тока. Из этого определения следует, что

. (14)

Если сила тока изменяется по гармоническому закону (1), то после подстановки этого выражения в соотношение (14) и интегрирования следует, что

. (15)

Аналогично определяется и действующее значение переменного напряжения

. (16)

Поскольку действующие значения отличаются от амплитудных только постоянным коэффициентом, то для них, на основании, рассмотренной на рисунке 3 векторной диаграммы, можно построить треугольник напряжений (рисунок 5).

К роме того, использование действующих значений позволяет несколько упростить математические соотношения. Так выражение (13) с учетом соотношений (15) и (16) можно записать в виде

. (17)

Из соотношений (13) и (17) следует, что активная мощность P зависит не только от амплитудных или действующих значений силы тока и напряжения, но и от сдвига фаз  между током и напряжением. Максимальное значение мощности, потребляемое данной цепью P_max = IU, характеризует мощность, поступающую в цепь от источника (генератора), называется полной мощностью, обозначается S, и достигается при  = 0, т.е. в случае, когда, согласно соотношению (10), реактивное сопротивление цепи равно нулю.

Следовательно, величина

(18)

показывает, какую часть активная мощность в цепи составляет от полной мощности. Величина cos называется коэффициентом мощности.

Рассмотрим физические процессы, определяющие то, что, в общем случае, коэффициент мощности всегда меньше единицы, т.е. активная мощность всегда меньше полной мощности, поступающей в цепь.

Энергия, поступающая в цепь от источника, расходуется на выделение тепла и энергию магнитного и электрического полей, которые возникают в катушке индуктивности и конденсаторе. Следовательно, полная мощность, поступающая в цепь от источника, может быть представлена следующим образом:

, (19)

где P_R — тепловая мощность, выделяющаяся в резисторе, P_C — скорость изменения энергии электрического поля в конденсаторе, P_L— скорость изменения магнитного поля в катушке индуктивности. Последние две величины можно также рассматривать, как мощности, потребляемые емкостной и индуктивной нагрузками.

Получим в явном виде зависимость введенных мощностей от времени:

, (20)

, (21)

. (22)

С оотношение (20) для мощности, выделяющейся на активном сопротивлении, показывает, что эта величина изменяется во времени с циклической частотой в два раза большей, чем ток и напряжение. График зависимости этой величины от времени представлен на рисунке 6 и показывает, что мощность, потребляемая активной нагрузкой, всегда положительная величина.

Среднее значение этой мощности за период, с учетом связи между напряжениями на рисунке 4 и формул (15) и (16):

.

Следовательно, по физическому смыслу, введенная ранее, активная мощность P представляет собой энергию, которая в виде тепла выделяется в единицу времени на сопротивлении R , т.е. уходит из цепи (поэтому это сопротивление и называется активным). Активная мощность измеряется в ваттах (Вт).

Мощность, потребляемая емкостной и индуктивной нагрузкой, также изменяется в зависимости от времени с циклической частотой в два раза большей, чем ток и напряжение. Но, в отличие от активной мощности, эти величины могут иметь положительные и отрицательные значения, что наглядно представляют графики на рисунке 6.

Рассчитаем средние значения этих мощностей за период:

,

.

Физический смысл равенства нулю среднего значения мощности, потребляемой емкостной нагрузкой за период в том, что, сколько энергии забирается конденсатором из цепи в те доли периода, когда конденсатор заряжается, столько же энергии отдается в цепь при его разрядке.

Аналогичные процессы происходят на участке цепи с соленоидом. Следовательно, в емкостной и индуктивной нагрузках, энергия не уходит из цепи. Дважды за период изменения тока энергия в этих нагрузках забирается и дважды за период отдается обратно в цепь и генератору. Поэтому емкостная и индуктивная нагрузки называются реактивными, и соответственно общее емкостное и индуктивное сопротивление называется реактивным.

Общая мощность, потребляемая реактивной нагрузкой

.

Рассчитаем энергию, потребляемую за четверть периода в емкостной и реактивной нагрузках:

. (23)

Для характеристики меры обменной энергии между реактивной нагрузкой и цепью с генератором вводят понятие реактивной мощности

. (24)

В качестве единицы измерения реактивной мощности используется вольт-ампер реактивный (ВАр).

Соотношение между полной, активной и реактивной мощностями можно также получить из так называемого «треугольника мощностей». Треугольник мощностей, представленный на рисунке 7, получается из треугольника напряжений при умножении всех сторон последнего (рисунок 4) на величину, равную действующему значению силы тока в цепи.

Из треугольника мощностей следует, что

. (25)

Н а практике конструкция, габариты и, следовательно, стоимость различных приборов и устройств определяются не активной или реактивной мощностями, которые зависят от режима работы цепи, а полной мощностью, т.е. действующими значениями тока и напряжения, на которые рассчитано устройство.

Поэтому на корпусах реальных устройств указывается значение полной мощности. Чтобы отличить при расчетах полную мощность от активной и реактивной мощностей, за единицу измерения полной мощности принят Вольт-Ампер (ВА). Распределение полной мощности в цепи, как следует из выше изложенного, зависит от вида нагрузки. Как уже обсуждалось, долю, которую составляет активная мощность от полной мощности, поступающей в сеть, определяет коэффициент мощности, значение которого можно также выразить из треугольника напряжений на рисунке 4:

.

Если в участке цепи имеются только емкостное и индуктивное сопротивления (L  1/(C)  0, R  0), то сдвиг фаз  =  2. Тогда cos = 0 и, несмотря на наличие напряжения и тока в цепи (U  0, I  0), активная мощность P = 0. Поэтому, как обсуждалось выше, сопротивление X_L-X_C= L  1/(C) называется неактивным, или реактивным.

Если нагрузка «чисто индуктивная» (R  0, 1/(C)  0, L  0, tg = + ,  = + /2), то напряжение опережает ток на /2 или по времени на 1/4 периода T. В этом случае коэффициент мощности также равен нулю cos=0. Но проволочные обмотки реальных индуктивных катушек, если они не находятся в сверхпроводящем состоянии, всегда обладают определенным активным сопротивлением R и поэтому сдвиг фаз  в них меньше, чем /2.

Для «чисто емкостной нагрузки» (R  0, L  0, 1/(C)  0, tg = — ,  = — /2) напряжение отстает от тока на /2 и коэффициент мощности также равен нулю.

Если индуктивное и емкостное сопротивления участка цепи одинаковы (L = 1/(C)) или рассматриваемый участок цепи содержит только активное сопротивление (L  0, 1/(C)  0, R  0, tg = 0,  = 0), то напряжение и ток совпадают по фазе, а коэффициент мощности равен cos=1.

Следовательно, коэффициент мощности определяет долю потребляемой мощности в данной цепи.

Остальная часть полной мощности, в виде мощности тока самоиндукции, генерируемого в цепи потребителя, и мощности тока разряда конденсатора, возвращается обратно в цепь и к генератору. Эта мощность теряется, идя на нагревание проводов в линии передач.

Активная реактивная полная мощность. Что такое реактивная мощность и как с ней бороться. Перспективы дальнейшего изучения реактивной энергии, как явления

Мощностные характеристики установки или сети являются основными для большинства известных электрических приборов. Активная мощность (проходящая, потребляема) характеризует часть полной мощности, которая передается за определенный период частоты переменного тока.

Определение

Активная и реактивная мощность может быть только у переменного тока, т. к. характеристики сети (силы тока и напряжения) у постоянного всегда равны. Единица измерений активной мощности Ватт, в то время, как реактивной – реактивный вольтампер и килоВАР (кВАР). Стоит отметить, что как полная, так и активная характеристики могут измеряться в кВт и кВА, это зависит от параметров конкретного устройства и сети. В промышленных цепях чаще всего измеряется в килоВаттах.

Электротехника используется активную составляющую в качестве измерения передачи энергии отдельными электрическими приборами. Рассмотрим, сколько мощности потребляют некоторые из них:

Исходя из всего, сказанного выше, активная мощность – это положительная характеристика конкретной электрической цепи, которая является одним из основных параметров для выбора электрических приборов и контроля расхода электричества.

Обозначение реактивной составляющей:

Это номинальная величина, которая характеризует нагрузки в электрических устройствах при помощи колебаний ЭМП и потери при работе прибора. Иными словами, передаваемая энергия переходит на определенный реактивный преобразователь (это конденсатор, диодный мост и т. д.) и проявляется только в том случае, если система включает в себя эту составляющую.

Расчет

Для выяснения показателя активной мощности, необходимо знать полную мощность, для её вычисления используется следующая формула:

S = U \ I, где U – это напряжение сети, а I – это сила тока сети.

Этот же расчет выполняется при вычислении уровня передачи энергии катушки при симметричном подключении. Схема имеет следующий вид:

Расчет активной мощности учитывает угол сдвига фаз или коэффициент (cos φ), тогда:

S = U * I * cos φ.

Очень важным фактором является то, что эта электрическая величина может быть как положительной, так и отрицательной. Это зависит от того, какие характеристики имеет cos φ. Если у синусоидального тока угол сдвига фаз находится в пределах от 0 до 90 градусов, то активная мощность положительная, если от 0 до -90 – то отрицательная. Правило действительно только для синхронного (синусоидального) тока (применяемого для работы асинхронного двигателя, станочного оборудования).

Также одной из характерных особенностей этой характеристики является то, что в трехфазной цепи (к примеру, трансформатора или генератора), на выходе активный показатель полностью вырабатывается.

Максимальная и активная обозначается P, реактивная мощность – Q.

Из-за того, что реактивная обуславливается движением и энергией магнитного поля, её формула (с учетом угла сдвига фаз) имеет следующий вид:

Q L = U L I = I 2 x L

Для несинусоидального тока очень сложно подобрать стандартные параметры сети. Для определения нужных характеристик с целью вычисления активной и реактивной мощности используются различные измерительные устройства. Это вольтметр, амперметр и прочие. Исходя от уровня нагрузки, подбирается нужная формула.

Из-за того, что реактивная и активная характеристики связаны с полной мощностью, их соотношение (баланс) имеет следующий вид:

S = √P 2 + Q 2 , и все это равняется U*I .

Но если ток проходит непосредственно по реактивному сопротивлению. То потерь в сети не возникает. Это обуславливает индуктивная индуктивная составляющая – С и сопротивление – L. Эти показатели рассчитываются по формулам:

Сопротивление индуктивности: x L = ωL = 2πfL,

Сопротивление емкости: хc = 1/(ωC) = 1/(2πfC).

Для определения соотношения активной и реактивной мощности используется специальный коэффициент. Это очень важный параметр, по которому можно определить, какая часть энергии используется не по назначению или «теряется» при работе устройства.

При наличии в сети активной реактивной составляющей обязательно должен рассчитываться коэффициент мощности. Эта величина не имеет единиц измерения, она характеризует конкретного потребителя тока, если электрическая система содержит реактивные элементы. С помощью этого показателя становится понятным, в каком направлении и как сдвигается энергия относительно напряжения сети. Для этого понадобится диаграмма треугольников напряжений:

К примеру, при наличии конденсатора формула коэффициента имеет следующий вид:

cos φ = r/z = P/S

Для получения максимально точных результатов рекомендуется не округлять полученные данные.

Компенсация

Учитывая, что при резонансе токов реактивная мощность равняется 0:

Q = QL – QC = ULI – UCI

Для того чтобы улучшить качество работы определенного устройства применяются специальные приборы, минимизирующие воздействие потерь на сеть. В частности, это ИБП. В данном приборе не нуждаются электрические потребители со встроенным аккумулятором (к примеру, ноутбуки или портативные устройства), но для большинства остальных источник бесперебойного питания является необходимым.

При установке такого источника можно не только установить негативные последствия потерь, но и уменьшить траты на оплату электричества. Специалисты доказали, что в среднем, ИБП поможет экономить от 20 % до 50 %. Почему это происходит :

Провода меньше нагреваются, это не только положительно влияет на их работу, но и повышает безопасность;

У сигнальных и радиоустройств уменьшаются помехи;

На порядок уменьшаются гармоники в электрической сети.

В некоторых случаях специалисты используют не полноценные ИБП, а специальные компенсирующие конденсаторы. Они подходят для бытового использования, доступны и продаются в каждом электротехническом магазине. Для расчета планируемой и полученной экономии можно использовать все вышеперечисленные формулы.

Реактивная мощность

Электри́ческая мо́щность — физическая величина, характеризующая скорость передачи или преобразования электрической энергии.

Если элемент цепи — резистор c электрическим сопротивлением R , то

Мощность переменного тока

Активная мощность

Среднее за период Т значение мгновенной мощности называется активной мощностью: . В цепях однофазного синусоидального тока , где U и I — действующие значения напряжения и тока , φ — угол сдвига фаз между ними. Для цепей несинусоидального тока электрическая мощность равна сумме соответствующих средних мощностей отдельных гармоник. Активная мощность характеризует скорость необратимого превращения электрической энергии в другие виды энергии (тепловую и электромагнитную). Активная мощность может быть также выражена через силу тока, напряжение и активную составляющую сопротивления цепи r или её проводимость g по формуле . В любой электрической цепи как синусоидального, так и несинусоидального тока активная мощность всей цепи равна сумме активных мощностей отдельных частей цепи, для трёхфазных цепей электрическая мощность определяется как сумма мощностей отдельных фаз. С полной мощностью S активная связана соотношением . Единица активной мощности — ватт (W , Вт ). Для СВЧ электромагнитного сигнала, в линиях передачи, аналогом активной мощности является мощность, поглощаемая нагрузкой.

Реактивная мощность

Реактивная мощность — величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи переменного тока, равна произведению действующих значений напряжения U и тока I , умноженному на синус угла сдвига фаз φ между ними: Q = UI sin φ . Единица реактивной мощности — вольт-ампер реактивный (var , вар ). Реактивная мощность связана с полной мощностью S и активной мощностью Р соотношением: . Реактивная мощность в электрических сетях вызывает дополнительные активные потери (на покрытие которых расходуется энергия на электростанциях) и потери напряжения (ухудшающие условия регулирования напряжения). В некоторых электрических установках реактивная мощность может быть значительно больше активной. Это приводит к появлению больших реактивных токов и вызывает перегрузку источников тока. Для устранения перегрузок и повышения коэффициента мощности электрических установок осуществляется компенсация реактивной мощности. Для СВЧ электромагнитного сигнала, в линиях передачи, аналогом реактивной мощности является мощность, отраженная от нагрузки.

Необходимо отметить, что величина sinφ для значений φ от 0 до плюс 90 ° является положительной величиной. Величина sinφ для значений φ от 0 до минус 90 ° является отрицательной величиной. В соответствии с формулой Q = UI sinφ реактивная мощность может быть отрицательной величиной. Но отрицательное значение мощности нагрузки характеризует нагрузку как генератор энергии. Активное, индуктивное, емкостное сопротивление не могут быть источниками постоянной энергии. Модуль величины Q = UI sinφ приблизительно описывает реальные процессы преобразования энергии в магнитных полях индуктивностей и в электрических полях емкостей. Применение современных электрических измерительных преобразователей на микропроцессорной технике позволяет производить более точную оценку величины энергии возвращаемой от индуктивной и емкостной нагрузки в источник переменного напряжения. Измерительные преобразователи реактивной мощности, использующие формулу Q = UI sinφ , более просты и значительно дешевле измерительных преобразователей на микропроцессорной технике.

Полная мощность

Полная мощность — величина, равная произведению действующих значений периодического электрического тока в цепи I и напряжения U на её зажимах: S = U×I ; связана с активной и реактивной мощностями соотношением: , где Р — активная мощность, Q — реактивная мощность (при индуктивной нагрузке Q > 0 , а при ёмкостной Q ). Единица полной электрической мощности — вольт-ампер (VA , ВА ).

Векторная зависимость между полной, активной и реактивной мощностью выражается формулой:

Измерения

• Для измерения электрической мощности применяются ваттметры и варметры , можно также использовать косвенный метод, с помощью вольтметра и амперметра .
• Для измерения коэффициента реактивной мощности применяют фазометры

Литература

Ссылки

См. также

• Список параметров напряжения и силы электрического тока

Wikimedia Foundation . 2010 .

Смотреть что такое «Реактивная мощность» в других словарях:

реактивная мощность — Величина, равная при синусоидальных электрическом токе и электрическом напряжении произведению действующего значения напряжения на действующее значение тока и на синус сдвига фаз между напряжением и током двухполюсника. [ГОСТ Р 52002 2003]… … Справочник технического переводчика

Электр. мощность в цепи переменного тока, расходуемая на поддержание вызываемых переменным током периодических изменений: 1) магнитного поля при наличии в цепи индуктивности; 2) заряда конденсаторов при наличии конденсаторов и проводов (напр.… … Технический железнодорожный словарь

Величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля. Для синусоидального тока равна произведению действующих тока I и напряжения U на синус угла сдвига фаз между ними: Q =… … Большой Энциклопедический словарь

РЕАКТИВНАЯ МОЩНОСТЬ — величина, характеризующая скорость обмена энергией между генератором переменного тока и магнитным (млн. электрическим) полем цепи, создаваемым электротехническими устройствами (индуктивностью и ёмкостью). Р. м. возникает в цепи при наличии сдвига … Большая политехническая энциклопедия

реактивная мощность — 3.1.5 реактивная мощность (вар): Реактивная мощность сигналов синусоидальной формы какой либо отдельной частоты в однофазной цепи, определяемая как произведение среднеквадратических значений тока и напряжения и синуса фазового угла между ними.… … Словарь-справочник терминов нормативно-технической документации

реактивная мощность — reaktyvioji galia statusas T sritis Standartizacija ir metrologija apibrėžtis Menamoji kompleksinės galios dalis, skaičiuojama pagal formulę Q² = S² – P²; čia Q – reaktyvioji galia, S – pilnutinė galia, P – aktyvioji galia. Matavimo vienetas –… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

реактивная мощность — reaktyvioji galia statusas T sritis fizika atitikmenys: angl. reactive power; wattless power vok. Blindleistung, f; wattlose Leistung, f rus. безваттная мощность, f; реактивная мощность, f pranc. puissance déwatée, f; puissance réactive, f … Fizikos terminų žodynas

Величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля. Для синусоидального тока равна произведению действующих тока I и напряжения U на синус угла сдвига фаз между ними:… … Энциклопедический словарь

реактивная мощность — reaktyvioji galia statusas T sritis automatika atitikmenys: angl. reactive power vok. Blindleistung, f; wattlose Leistung, f rus. реактивная мощность, f pranc. puissance réactive, f … Automatikos terminų žodynas

Величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи переменного тока (См. Переменный ток). Р. м. Q равна произведению действующих значений напряжения U и тока… … Большая советская энциклопедия

Книги

• Электротехника и электроника на судах рыбопромыслового флота , Белов О.А., Парфенкин А.И.. Рассмотрены общие вопросы электротехники и электроники, физические явления, лежащие в основе производства и использования электричества, работы электронных устройств. Приведены примеры…

Содержание:

В электротехнике среди множества определений довольно часто используются такие понятия, как активная, реактивная и полная мощность. Эти параметры напрямую связаны с током и напряжением , когда включены какие-либо потребители. Для проведения вычислений применяются различные формулы, среди которых основной является произведение напряжения и силы тока. Прежде всего это касается постоянного напряжения. Однако в цепях переменного разделяется на несколько составляющих, отмеченных выше. Вычисление каждой из них также осуществляется с помощью формул, благодаря которым можно получить точные результаты.

Формулы активной, реактивной и полной мощности

Основной составляющей считается активная мощность. Она представляет собой величину, характеризующую процесс преобразования электрической энергии в другие виды энергии. То есть по-другому является скоростью, с какой . Именно это значение отображается на электросчетчике и оплачивается потребителями. Вычисление активной мощности выполняется по формуле : P = U x I x cosф.

В отличие от активной, которая относится к той энергии, которая непосредственно потребляется электроприборами и преобразуется в другие виды энергии — тепловую, световую, механическую и т.д., реактивная мощность является своеобразным невидимым помощником. С ее участием создаются электромагнитные поля, потребляемые электродвигателями. Прежде всего она определяет характер нагрузки, и может не только генерироваться, но и потребляться. Расчеты реактивной мощности производятся по формуле : Q = U x I x sinф.

Полной мощностью является величина, состоящая из активной и реактивной составляющих. Именно она обеспечивает потребителям необходимое количество электроэнергии и поддерживает их в рабочем состоянии. Для ее расчетов применяется формула: S = .

Как найти активную, реактивную и полную мощность

Активная мощность относится к энергии, которая необратимо расходуется источником за единицу времени для выполнения потребителем какой-либо полезной работы. В процессе потребления, как уже было отмечено, она преобразуется в другие виды энергии.

В цепи переменного тока значение активной мощности определяется, как средний показатель мгновенной мощности за установленный период времени. Следовательно, среднее значение за этот период будет зависеть от угла сдвига фаз между током и напряжением и не будет равной нулю, при условии присутствия на данном участке цепи активного сопротивления. Последний фактор и определяет название активной мощности. Именно через активное сопротивление электроэнергия необратимо преобразуется в другие виды энергии.

При выполнении расчетов электрических цепей широко используется понятие реактивной мощности. С ее участием происходят такие процессы, как обмен энергией между источниками и реактивными элементами цепи. Данный параметр численно будет равен амплитуде, которой обладает переменная составляющая мгновенной мощности цепи.

Существует определенная зависимость реактивной мощности от знака угла ф, отображенного на рисунке. В связи с этим, она будет иметь положительное или отрицательное значение. В отличие от активной мощности, измеряемой в , реактивная мощность измеряется в вар — вольт-амперах реактивных. Итоговое значение реактивной мощности в разветвленных электрических цепях представляет собой алгебраическую сумму таких же мощностей у каждого элемента цепи с учетом их индивидуальных характеристик.

Основной составляющей полной мощности является максимально возможная активная мощность при заранее известных токе и напряжении. При этом, cosф равен 1, когда отсутствует сдвиг фаз между током и напряжением. В состав полной мощности входит и реактивная составляющая, что хорошо видно из формулы, представленной выше. Единицей измерения данного параметра служит вольт-ампер (ВА).

Главная цель при передаче электроэнергии – повышение эффективности работы сетей. Следовательно, необходимо уменьшение потерь. Основной причиной потерь является реактивная мощность, компенсация которой значительно повышает качество электроэнергии.

Реактивная мощность вызывает ненужный нагрев проводов, перегружаются электроподстанции. Трансформаторная мощность и кабельные сечения вынужденно подвергаются завышениям, сетевое напряжение снижается.

Понятие о реактивной мощности

Для выяснения, что же такое реактивная мощность, надо определить другие возможные виды мощности. При существовании в контуре активной нагрузки (резистора) происходит потребление исключительно активной мощности, полностью расходуемой на энергопреобразование. Значит, можно сформулировать, что такое активная мощность, – та, при которой ток совершает эффективную работу.

На постоянном токе происходит потребление исключительно активной мощности, рассчитываемой соответственно формуле:

Измеряется в ваттах (Вт).

В электроцепях с переменным током при наличии активной и реактивной нагрузки мощностной показатель суммируется из двух составных частей: активной и реактивной мощности.

1. Емкостная (конденсаторы). Характеризуется фазовым опережением тока по сравнению с напряжением;
2. Индуктивная (катушки). Характеризуется фазовым отставанием тока по отношению к напряжению.

Если рассмотреть контур с переменным током и подсоединенной активной нагрузкой (обогреватели, чайники, лампочки с накаливающейся спиралью), ток и напряжение будут синфазными, а полная мощность, взятая в определенную временную отсечку, вычисляется путем перемножения показателей напряжения и тока.

Однако когда схема содержит реактивные компоненты, показатели напряжения и тока не будут синфазными, а будут различаться на определенную величину, определяемую углом сдвига «φ». Пользуясь простым языком, говорится, что реактивная нагрузка возвращает столько энергии в электроцепь, сколько потребляет. В результате получится, что для активной мощности потребления показатель будет нулевой. Одновременно по цепи протекает реактивный ток, не выполняющий никакую эффективную работу. Следовательно, потребляется реактивная мощность.

Реактивная мощность – часть энергии, которая позволяет устанавливать электромагнитные поля, требуемые оборудованием переменного тока.

Расчет реактивной мощности ведется по формуле:

Q = U x I x sin φ.

В качестве единицы измерения реактивной мощности служит ВАр (вольтампер реактивный).

Выражение для активной мощности:

P = U x I x cos φ.

Взаимосвязь активной, реактивной и полной мощности для синусоидального тока переменных значений представляется геометрически тремя сторонами прямоугольного треугольника, называемого треугольником мощностей. Электроцепи переменного тока потребляют две разновидности энергии: активную мощность и реактивную. Кроме того, значение активной мощности никогда не является отрицательным, тогда как для реактивной энергии возможна либо положительная величина (при индуктивной нагрузке), либо отрицательная (при емкостной нагрузке).

Важно! Из треугольника мощностей видно, что всегда полезно снизить реактивную составляющую, чтобы повысить эффективность системы.

Полная мощность не находится как алгебраическая сумма активного и реактивного мощностного значения, это векторная сумма P и Q. Ее количественное значение вычисляется извлечением квадратного корня из суммы квадратов мощностных показателей: активного и реактивного. Измеряться полная мощность может в ВА (вольтампер) или производных от него: кВА, мВА.

Чтобы была рассчитана полная мощность, необходимо знать разность фаз между синусоидальными значениям U и I.

Коэффициент мощности

Пользуясь геометрически представленной векторной картиной, можно найти отношение сторон треугольника, соответствующих полезной и полной мощности, что будет равно косинусу фи или мощностному коэффициенту:

Данный коэффициент находит эффективность работы сети.

Количество потребляемых ватт – то же самое, что и количество потребляемых вольтампер при мощностном коэффициенте, равном 1 или 100%.

Важно! Полная мощность тем ближе к показателю активной, чем больше cos φ, или чем меньше угол сдвига синусоидальных величин тока и напряжения.

Если, к примеру, имеется катушка, для которой:

• Р = 80 Вт;
• Q = 130 ВАр;
• тогда S = 152,6 BA как среднеквадратичный показатель;
• cos φ = P/S = 0,52 или 52%

Можно сказать, что катушка требует 130 ВАр полной мощности для выполнения полезной работы 80 Вт.

Коррекция cos φ

Для коррекции cos φ применяется тот факт, что при емкостной и индуктивной нагрузке вектора реактивной энергии располагаются в противофазе. Так как большинство нагрузок является индуктивными, подключив емкость, можно добиться увеличения cos φ.

Главные потребители реактивной энергии:

1. Трансформаторы. Представляют собой обмотки, имеющие индуктивную связь и посредством магнитных полей преобразуюшие токи и напряжения. Эти аппараты являются основным элементом электросетей, передающих электроэнергию. Особенно увеличиваются потери при работе на холостом ходу и при низкой нагрузке. Широко используются трансформаторы в производстве и в быту;
2. Индукционные печи, в которых расплавляются металлы путем создания в них вихревых токов;
3. Асинхронные двигатели. Крупнейший потребитель реактивной энергии. Вращающий момент в них создается посредством переменного магнитного поля статора;
4. Преобразователи электроэнергии, такие как силовые выпрямители, используемые для питания контактной сети железнодорожного транспорта и другие.

Конденсаторные батареи подсоединяются на электроподстанциях для того, чтобы контролировать напряжение в пределах установленных уровней. Нагрузка меняется в течение дня с утренними и вечерними пиками, а также на протяжении недели, снижаясь в выходные, что изменяет показатели напряжения. Подключением и отключением конденсаторов варьируется его уровень. Это делается от руки и с помощью автоматики.

Как и где измеряют cos φ

Реактивная мощность проверяется по изменению cos φ специальным прибором – фазометром. Его шкала проградуирована в количественных значениях cos φ от нуля до единицы в индуктивном и емкостном секторе. Полностью скомпенсировать негативное влияние индуктивности не удастся, но возможно приближение к желаемому показателю – 0,95 в индуктивной зоне.

Фазометры применяются при работе с установками, способными повлиять на режим работы электросети через регулирование cos φ.

1. Так как при финансовых расчетах за потребленную энергию учитывается и ее реактивная составляющая, то на производствах устанавливаются автоматические компенсаторы на конденсаторах, емкость которых может меняться. В сетях, как правило, используются статические конденсаторы;
2. При регулировании cos φ у синхронных генераторов путем изменения возбуждающего тока необходимо его отслеживать визуально в ручных рабочих режимах;
3. Синхронные компенсаторы, представляющие собой синхронные двигатели, работающие без нагрузки, в режиме перевозбуждения выдают в сеть энергию, которая компенсирует индуктивную составляющую. Для регулирования возбуждающего тока наблюдают за показаниями cos φ по фазометру.

Коррекция коэффициента мощности – одна из эффективнейших инвестиций для сокращения затрат на электроэнергию. Одновременно улучшается качество получаемой энергии.

Видео

Наверняка многие из вас слышали о реактивной электроэнергии. Зная, насколько сложен для понимания этот термин, давайте разберём детально отличия реактивной и активной энергии. Важно осознать тот факт, что реактивную электроэнергию мы можем наблюдать только в переменном токе. Там, где течёт постоянный ток, реактивная энергия не присутствует. Обусловлено это природой появления реактивной энергии .

Через несколько понижающих трансформаторов к потребителю поступает переменный ток, конструкция которых разделяет обмотки низкого и высокого напряжения. То есть получается так, что в трансформаторе отсутствует физический контакт между двумя обмотками, при этом ток всё равно течёт. Объяснить это довольно просто. Электроэнергия всегда передаётся через воздух, который является прекрасным диэлектриком, при помощи электромагнитного поля, составляющая которого – переменное магнитное поле. Оно регулярно пересекает обмотку, появляясь в другой, и не имеет с первой электрического контакта, наводя электродвижущую силу. Коэффициент полезного действия у современных трансформаторов достаточно велик, отсюда потеря электроэнергии сводиться к минимуму, и потому вся мощь переменного тока, который протекает в первичной обмотке, оказывается в цепи вторичной обмотки. Тоже самое происходит в конденсаторе, правда, уже за счёт электрического поля. Ёмкость и индуктивность вместе порождают реактивную энергию. Активная энергия (которой мешает возврат реактивной энергии) преобразовывается в тепловую, механическую и другую.

Реактивная составляющая электрического тока возникает только в цепях, содержащих реактивные элементы (индуктивности и ёмкости) и расходуется обычно на бесполезный нагрев проводников, из которых составлена эта цепь. Примером таких реактивных нагрузок являются электродвигатели различного типа, переносные электроинструменты (электродрели, «болгарки», штроборезы и т.п.), а также различная бытовая электронная техника. Полная мощность этих приборов, измеряемая в вольт-амперах, и активная мощность (в ваттах) соотносятся между собой через коэффициент мощности cosφ, который может принимать значение от 0,5 до 0,9. На этих приборах указывается обычно активная мощность в ваттах и значение коэффициента cosφ. Для определения полной потребляемой мощности в ВА, необходимо величину активной мощности (Вт) разделить на коэффициент cosφ.

Пример : если на электродрели указана величина мощности в 800 Вт и cosφ = 0,8, то отсюда следует, что потребляемая инструментом полная мощность составляет 800/0,8=1000 ВА. При отсутствии данных по cosφ можно брать его приблизительное значение, которое для домашнего электроинструмента составляет примерно 0,7.

Реактивный тип нагрузки характеризуется тем, что сначала, неторое время, в нём происходит накопление энергии, поставляемой источником питания. Затем запасённая энергия отдаётся обратно в этот источник. К подобным нагрузкам относятся такие элементы электрических цепей, как конденсаторы и катушки индуктивности, а также устройства, содержащие их. При этом в такой нагрузке между напряжением и током присутствует сдвиг фаз, равный 90 градусам. Поскольку основной целью существующих систем электроснабжения является полезная доставка электроэнергии от производителя непосредственно к потребителю — реактивная составляющая мощности обычно считается вредной характеристикой цепи.

Для того, чтобы компенсировать противодействие реактивной энергии, применяются специальные устанавливаемые конденсаторы. Это заставляет свести к минимуму появляющееся негативное влияние реактивной энергии. Мы уже отмечали, что реактивная мощность существенно влияет на потерю электрической энергии в сети. Потому получается, что величину той самой негативной энергии приходиться постоянно держать под контролем, и лучший для этого способ – организовать её учёт.

Там, где озабочены этой проблемой (различные промышленные предприятия) довольно часто ставят отдельные специальные приборы, которые ведут учёт не только самой реактивной энергии, но и активной её части. Учёт ведётся в трёхфазных сетях по индуктивной и ёмкостной составляющей. Обычно такие счётчики, это не что иное, как аналого-цифровое устройство, которое преобразует мощность в аналоговый сигнал, который превращается в частоту следования электро-импульсов. Сложив их, мы можем судить о количестве потребляемой энергии. Обычно счётчик сделан из пластмассового корпуса, где установлены 3 трансформатора и блок учёта на печатной плате. На внешней стороне располагается ЖК экран или светодиоды.

Предприятия в настоящее время всё чаще ставят универсальные счётчики учёта электроэнергии, которые измеряют количество как активной, так и реактивной энергии. Более того, такие приборы могут совмещать функции от двух, а иногда и более устройств, что позволяет снижать затраты на обслуживание и позволяет сэкономить во время покупки. Такие устройство способны вычислять реактивную и активную мощность, а также измерять мгновенные значения напряжений. Счётчик фиксирует, каков уровень потребления энергии и показывает всю информацию на дисплее 3-мя сменяющимися кадрами (индуктивная составляющая, ёмкостная составляющая, а также объём активной энергии). Современные модели позволяют передавать данные по ИК цифровому каналу, защищены от магнитных полей, хищения энергии. Более того, мы получаем более точные измерения и малое энергопотребление, что выгодно отличает новые модели от предшественников.

Калькулятор коэффициента мощности

Этот калькулятор коэффициента мощности представляет собой удобный инструмент для анализа переменного тока, протекающего в электрических цепях. Вы, наверное, уже знаете, что вы можете смоделировать постоянный ток (DC) с помощью закона Ома. В случае с переменным током эта задача не так проста, поскольку такие цепи содержат как активную, так и реактивную мощность.

Этот калькулятор поможет вам не только узнать, каковы значения различных типов мощности в цепи, но также предоставит вам формулу коэффициента мощности, которая выражает соотношение между реальной и полной мощностью.

Активная, реактивная и полная мощность

Если вы хотите понять, что такое коэффициент мощности, вам сначала необходимо более глубокое понимание его компонентов: реальной, реактивной и полной мощности.

• Реальная мощность (также называемая истинной или активной мощностью), обозначаемая как P , выполняет реальную работу в электрической цепи и рассеивается на резисторах. Это единственная форма мощности, которая появляется в цепи постоянного тока. В цепи переменного тока значения тока и напряжения не фиксированы — они изменяются синусоидально.Если между этими двумя значениями нет сдвига фазы , то вся переданная мощность активна. Эта мощность измеряется в Вт .

• Реактивная мощность , обозначенная как Q , передается, когда ток и напряжение сдвинуты по фазе на 90 градусов. В таком случае чистая энергия, передаваемая в цепи переменного тока, равна нулю, и реальная мощность не рассеивается. Реактивная мощность никогда не появляется в цепях постоянного тока; в цепях переменного тока он связан с реактивным сопротивлением, создаваемым катушками индуктивности и конденсаторами.Оно измеряется в Вольт-Ампер-реактивное значение (ВАр).

• Полная мощность , обозначенная как S , представляет собой комбинацию активной и реактивной мощностей. Это произведение среднеквадратичных значений напряжения и тока в цепи без учета влияния фазового угла. Это также векторная сумма P и Q. Полная мощность измеряется в Вольт-Ампер (ВА).

Треугольник силы

Поскольку полную мощность можно найти путем векторного сложения реальной и реактивной мощности, вы можете использовать графический метод для представления этих трех значений в форме треугольника, называемого треугольником мощности .

Каждая сторона треугольника представляет собой одну из трех форм мощности, передаваемых в цепи переменного тока. Катеты прямоугольного треугольника представляют собой активную и реактивную мощность, а гипотенуза — полную мощность.

Одним из следствий использования треугольника степеней является то, что вы можете легко установить математическую связь между тремя значениями с помощью теоремы Пифагора:

S² = P² + Q²

Кроме того, угол между реальной мощностью и полной мощностью, обозначенный как φ , представляет собой полное сопротивление угла фазы схемы.

Формула коэффициента мощности

Коэффициент мощности — это соотношение между реальной и полной мощностью в цепи. Если реактивной мощности нет, то коэффициент мощности равен 1. Если, наоборот, активная мощность равна нулю, то полная мощность также равна 0.

Формула коэффициента мощности:

Коэффициент мощности = P / S

Например, коэффициент мощности 0,87 означает, что 87% тока, подаваемого в цепь, выполняет реальную работу.Остальная мощность, а точнее 13%, должна быть предоставлена ​​для компенсации реактивной мощности.

Как рассчитать коэффициент мощности?

Коэффициент мощности также можно рассчитать с помощью треугольника мощности. Используя принципы тригонометрии, вы можете записать это как

P / S = cos φ

Поскольку коэффициент мощности равен отношению реальной мощности к полной,

Коэффициент мощности = cos φ

Это означает, что зная только одно из трех значений — действительную, реактивную или полную мощность — и коэффициент мощности или фазовый угол, вы можете быстро вычислить остальные из этих значений, которые определяют цепь переменного тока.Конечно, вместо того, чтобы вычислять числа вручную, вы можете просто использовать этот калькулятор коэффициента мощности! 🙂

Сопротивление, реактивное сопротивление и импеданс

Три основных компонента цепи переменного тока — это резисторы, конденсаторы и катушки индуктивности. Вы можете использовать этот калькулятор коэффициента мощности не только для описания мощности, передаваемой через каждый из этих компонентов, но и для определения того, что происходит, когда через них проходит электрический ток, а именно, каким сопротивлением, реактивным сопротивлением и импедансом обладают такие элементы.

• Сопротивление , обозначенное как R и выраженное в омах (Ом), является мерой того, насколько проводник (особенно резистор) снижает электрический ток I , протекающий через него. Это значение напрямую связано с реальной мощностью, протекающей в цепи переменного тока. Это соотношение можно записать как P = I²R .

• Реактивное сопротивление , обозначенное как X и также измеренное в омах (Ом), представляет собой инерцию, которая препятствует движению электронов в компоненте схемы.Он присутствует в основном в конденсаторах и катушках индуктивности. Если вы пропустите переменный ток через компонент с высоким реактивным сопротивлением, падение напряжения будет не совпадать по фазе с током на 90 градусов. Реактивное сопротивление связано с реактивной мощностью уравнением Q = I²X .

• Импеданс , обозначенный как Z и измеренный в омах (Ом), является эквивалентом сопротивления в цепях постоянного тока по переменному току. Он присутствует во всех компонентах всех электрических цепей. Его можно рассчитать путем векторного сложения сопротивления (см. Ниже) и реактивного сопротивления или по формуле S = I²Z .

Соотношение между сопротивлением, реактивным сопротивлением и импедансом аналогично треугольнику мощности:

Z² = R² + X²

Идеальные резисторы имеют ненулевое сопротивление, но нулевое реактивное сопротивление. Идеальные катушки индуктивности или конденсаторы имеют нулевое сопротивление, но ненулевое реактивное сопротивление. Все компоненты электрической цепи обладают некоторым сопротивлением.

Познакомьтесь со своим измерителем мощности — что такое реальная, полная и реактивная мощность

Первое — простой вопрос

Верно или нет? Мощность = Напряжение x Ток. Это утверждение верно для систем постоянного тока, но для систем переменного тока есть две основные сложности. Значение тока и напряжения постоянно меняется. Какое значение вы используете? Напряжение и ток могут не совпадать по фазе. Умножение тока и напряжения, когда они не совпадают по фазе, требует регулировки для компенсации фазы. Именно этот фазовый сдвиг заставляет нас определять реальную, полную и реактивную мощность. Этот фазовый сдвиг происходит, когда источник питания питает индуктивную или емкостную нагрузку ». Большинство нагрузок являются индуктивными (двигатели) или резистивными (нагреватели), поэтому сдвиг фаз обычно в одном направлении. Двигатель имеет обмотку. Обмотанный проводник по существу определяет индуктор. Таким образом, обмотка представляет собой сопротивление намотанного провода и индуктивность обмотки.

RMS или эффективное значение

Пиковые значения на кривых переменного напряжения или тока сохраняются лишь на короткое время. Они на самом деле не отражают способность напряжения и тока выполнять работу и поэтому не используются в расчетах мощности.Ученые используют статистический метод для определения эффективных значений. Это называется среднеквадратичным или среднеквадратичным значением. Результатом определения является следующее: Veff / rms = 0,707 x V пик. То же самое относится и к току. СОВЕТ: вы можете разумно предположить, что все напряжения и токи, сообщаемые измерителем мощности, представлены как среднеквадратические или эффективные значения, если не указано иное. . СОВЕТ: Большинство мультиметров сообщают среднеквадратичные значения

Полная мощность

Полная мощность — это мощность, передаваемая источником питания такой нагрузке, как двигатель.Практически во всех реальных ситуациях, когда используется переменный ток, вам необходимо подавать на устройство больше энергии (кажущаяся мощность), чем оно будет работать (реальная мощность). (Векторная) разница между ними представляет работу, проделанную для преодоления индуктивной и Возможности воздействия нагрузки. Полная мощность измеряется в единицах ВА — Вольт-амперы. На самом деле это ватты, но мы используем новое название единицы, чтобы избежать путаницы. Таким образом, когда вы видите VA на листе технических данных, вы можете сделать разумный вывод, что речь идет о кажущейся мощности.Полная мощность рассчитывается: S (общий символ для полной мощности) = Veff / rms x Ieff / rms — однофазный расчет

Коэффициент мощности и фаза

Рассчитан коэффициент мощности: PF = косинус (фазовый угол в радианах) Коэффициент мощности не имеет технических единиц. Значение PF находится в диапазоне от -1 до 0 до 1 (запаздывание — без опережения). Коэффициент мощности резистивной нагрузки (без емкости или индуктивности) равен 1. Индуктивные нагрузки Фаза тока отстает от номинального напряжения — Трансформаторы и двигатели (намотанные проводники) Емкостная нагрузка Фаза тока соответствует типичному напряжению — скрытые кабели, конденсаторные батареи Нет ничего «неправильного» в том, что коэффициент мощности не равен 1,0.

Реальная мощность и реактивная мощность

Думайте о реальной мощности как о полезной мощности — мере того, как много работы выполняется.Единицы измерения реальной мощности — ватты. Реальная мощность рассчитывается по формуле P (действительная) = S (кажущаяся мощность) x pf Реактивная мощность — это (векторная) разница между полной и реальной мощностью. Энергия, используемая для производства реактивной мощности, сохраняется в магнитном / электрическом поле индуктивной нагрузки. В случае емкостной нагрузки магнитное / электрическое поле индуктивной нагрузки создает реактивную мощность. Реактивную мощность нельзя использовать для полезной работы. Реактивная мощность обозначается символом: Q Технические единицы реактивной мощности — VAR — вольт-амперы реактивной мощности.Это также ватты, но мы используем VAR, чтобы знать, что мы говорим о реактивной мощности.

Диаграмма: измерение RMS

Диаграмма: вперед / назад

THD — Общее гармоническое искажение (также называемое искажением)

Проще говоря, THD — это мера искажения, выраженная в%. Если устройству (любому активному устройству, но представьте себе выпрямители, приводы с регулируемой скоростью… как практические примеры) подается синусоида на входе, выход никогда не будет точным 100% воспроизведением входа.Серия гармоник исходной волны искажает исходную форму волны. THD% — это попытка «пронумеровать» степень искажения для сравнения. Число% является несколько спорным, поскольку некоторые гармоники являются более важными, чем другие, и нет никакого взвешивания.

THD (%) = 100 * SQRT [(V22 + V32 + V42 +… + Vn2)] / Vt Где V2, V3 — среднеквадратичные значения каждой гармоники напряжения, а Vt — полное среднеквадратичное выходное напряжение.

Провисание / вздутие или провал / скачок

Продолжительность 0.5 цикл и выше. Провалы напряжения — это наиболее частые нарушения питания. Провалы напряжения могут исходить от электросети. В большинстве случаев провисания возникают внутри здания. Например, в бытовой электропроводке наиболее частой причиной провалов напряжения является пусковой ток, потребляемый двигателями холодильника и кондиционера. Мешки обычно не мешают лампам накаливания или люминесцентному освещению. двигатели или обогреватели. Однако у некоторого электронного оборудования отсутствует достаточный внутренний накопитель энергии, и поэтому оно не может выдерживать провалы напряжения питания.Оборудование может выдерживать очень короткие глубокие провалы или более длинные, но более мелкие провалы.

Пониженное / повышенное напряжение

Перенапряжение — это увеличение действующего напряжения более чем на 110% в течение более одной минуты. Пониженное напряжение — это снижение эффективного напряжения до менее 90% в течение более одной минуты. Будьте осторожны с этим определением, потому что оно имеет тенденцию меняться от поставщика к поставщику.

Переходные напряжения / скачки / скачки

Относится к кратковременным (менее 1 цикла) событиям. Низкочастотные переходные процессы часто называют «переходными процессами при переключении конденсаторов». Высокочастотные переходные процессы часто называют импульсами, пиками или скачками. Они могут быть вызваны включением разряженного конденсатора коррекции коэффициента мощности по линии. Высокочастотные переходные процессы вызваны молнией или отключением индуктивных нагрузок.Типичное время нарастания порядка микросекунды; типичные времена затухания составляют от десятков до сотен микросекунд. Часто затухание представляет собой экспоненциально затухающую форму звонка с частотой примерно 100 кГц. Чрезвычайно быстрые переходные процессы, или EFT, имеют время нарастания и спада в наносекундной области. Они вызываются дуговыми замыканиями, такими как неисправные щетки в двигателях, и быстро гасятся даже несколькими метрами распределительной проводки. Стандартные сетевые фильтры, входящие в комплект почти всего электронного оборудования, устраняют EFT.

Разница между активной и реактивной мощностью (активной и реактивной)

Наиболее важное различие между активной и реактивной мощностью состоит в том, что активная мощность — это реальная мощность, которая используется в цепи, в то время как реактивная мощность колеблется между нагрузкой и источником.

Прежде чем сравнивать активную и реактивную мощность, я хочу объяснить активную и реактивную мощность. Итак, давайте посмотрим на введение активной, реактивной мощности.

Активная мощность:

Активная мощность также называется фактической мощностью, активной мощностью или рабочей мощностью.Это мощность, которая фактически приводит оборудование в действие и выполняет полезную работу. Он измеряется в киловаттах (кВт) или МВт.

Реактивная мощность:

Реактивная мощность — это мощность, необходимая магнитному оборудованию (трансформатору, двигателю и реле) для создания намагничивающего потока. Он течет вперед и назад, что означает, что он движется в обоих направлениях контура.

Реактивная энергия вызывает перегрузку в линиях, трансформаторах и генераторах, не обеспечивая при этом полезной производительности.Однако это записано в счете, поэтому может значительно увеличить общую сумму к оплате. Реактивная мощность измеряется в киловольт-амперах реактивной мощности (кВАр) или в МВАр.

Давайте посмотрим на треугольник мощности, чтобы понять взаимосвязь между активной, реактивной и полной мощностью.

На упомянутом изображении вы можете видеть, что комплексная мощность представляет собой векторную сумму активной и реактивной мощности. Кажущаяся мощность — это величина комплексной мощности. давайте посмотрим на терминологию, которая была использована На изображении

• P => Активная мощность
• Q => Реактивная мощность
• S => Комплексная мощность
• | S | => Полная мощность
• φ => Фаза напряжения относительно тока

Следовательно, следующее выражение, показанное ниже, дает активную, реактивную и полную мощность соответственно.

• Активная мощность P = V x I cosϕ = V I cosϕ
• Реактивная мощность Pr или Q = V x I sinϕ = V I sinϕ
• Комплексная мощность S = P + jQ
• Полная мощность = | S | = √P² + Q²

Теперь я думаю, что мы можем увидеть разницу между активной и реактивной мощностью с помощью диаграммы.

Основа для сравнения	Активная мощность	Реактивная мощность
Определение	Активная мощность — это активная мощность, рассеиваемая в цепи.	Мощность, которая движется вперед и назад между нагрузкой и источником такого типа мощности, известна как реактивная мощность
Формула	P = V x I cosϕ = V I cosϕ	Q = V x I sinϕ = V I sinϕ
Измерительный блок	Вт, кВт, МВт	ВАр, кВАр, МВАр
Представлено	-п.	Q
Причины	Вырабатывает тепло в нагревателе, зажигает лампы и крутящий момент в двигателе.	Измеряет коэффициент мощности цепи.
Измерительный прибор	Ваттметр	VAR-метр

Рекомендуемый пост

О Amlendra

Я инженер-программист встраиваемых систем и корпоративный инструктор. В настоящее время я работаю старшим инженером-программистом в крупнейшей консалтинговой компании по программному обеспечению. Имею опыт работы с различными микроконтроллерами (stm32, LPC, PIC AVR и 8051), драйверами (USB и виртуальный com-порт), POS-устройством (VeriFone) и платежным шлюзом (глобальные и первые данные).

Активная, реактивная и полная мощность

В этом блоге мы поймем концепцию активной, реактивной и полной мощности. Мы также изучим мгновенную мощность. Мы также увидим, как активная, реактивная и полная мощность связаны друг с другом, что объясняется треугольником мощности. Итак, в конце этого блога мы рассмотрим Треугольник власти. Следовательно, в этом блоге есть о чем рассказать. Итак, начнем.

Для инженера-электрика очень важно знать активную, реактивную и полную мощность, потому что этот раздел является одним из строительных блоков энергосистемы.

Активная, реактивная и полная мощность проявляется только в случае цепей переменного тока, а не в случае цепей постоянного тока, потому что все мы знаем, что формы сигналов напряжения и тока синусоидальны в случае цепей переменного тока.

Вот почему мы изучаем активную, реактивную и полную мощность в цепях переменного тока только не в цепях постоянного тока. В цепях постоянного тока мы изучаем мощность постоянного тока.

Прежде чем изучать активную, реактивную и полную мощность, мы должны знать, «что такое мгновенная мощность?»

МГНОВЕННАЯ СИЛА

Мощность, измеряемая в конкретный момент времени, известна как Мгновенная мощность.

(ИЛИ)

Умножение напряжения и тока в определенный момент времени называется мгновенной мощностью.

Чтобы понять концепцию мгновенной мощности, давайте рассмотрим форму волны некоторой цепи, показанной на диаграмме ниже.

В момент t ₁

P ₁ = V ₁ (+ ve) * I ₁ (-ve) = -ve

Мгновенная мощность P ₁ в момент t ₁ отрицательна.

В момент t ₂

P ₂ = V ₂ (+ ve) * I ₂ (+ ve) = + ve

Мгновенная мощность P ₂ в момент t ₂ положительна.

Из приведенного выше примера мы можем сказать, что

• Мгновенная мощность может быть положительной и отрицательной.

Что такое положительная сила и отрицательная сила?

Положительная мощность

Когда мощность течет от источника к нагрузке в цепи, мощность называется Положительная мощность.

Отрицательная мощность

В некоторых ситуациях мощность может течь от нагрузки к источнику. В этом случае мощность известна как отрицательная мощность.

• Отрицательная мощность индуцируется в цепи в случае индуктивной нагрузки, емкостной нагрузки и при наличии некоторых нелинейных устройств, таких как выпрямительный мост.

АКТИВНАЯ МОЩНОСТЬ

Чтобы понять концепцию активной мощности, давайте возьмем пример чисто резистивной цепи.

На принципиальной схеме чисто резистивная нагрузка питается от источника переменного тока с напряжением В, и током в цепи I.

В случае чисто резистивной нагрузки напряжение и ток остаются в одной фазе, как показано на векторной диаграмме. Это означает, что формы сигнала как напряжения, так и тока достигают своего положительного и отрицательного пика одновременно, и обе формы сигнала пересекают нулевое значение в один и тот же момент времени, и это можно проверить на формах сигналов, приведенных ниже.

Теперь мы увидим полярность мгновенной мощности в разные моменты времени.

В момент t ₁

P ₁ = V ₁ (+ ve) * I ₁ (+ ve) = + ve

В момент t ₂

P ₂ = V ₂ (-ve) * I ₂ (-ve) = + ve

Следовательно, в случае чисто резистивной нагрузки мощность всегда положительна в каждый момент времени, что означает, что мощность всегда течет от источника к нагрузке.Этот тип мощности известен как активная мощность .

Свойства активной мощности

• Активная мощность всегда положительная.
• Активная мощность не меняет своего направления, как вы можете видеть на осциллограмме.
• Он всегда перетекает от источника к нагрузке.
• Активная мощность всегда отвечает за полезную работу, например: свет, звук, движение и т. Д.
• Она обозначается буквой «P» и измеряется в «Вт».{\ circ}} \)
• \ (\ Rightarrow P = VI \ quad Watts \) ​​

РЕАКТИВНАЯ МОЩНОСТЬ

Мы поймем концепцию реактивной мощности с помощью чисто индуктивной цепи.

На принципиальной схеме чисто индуктивная нагрузка питается от источника переменного тока с напряжением В, и током в цепи I.

В случае чисто индуктивной нагрузки ток отстает от напряжения питания на 90 ^o , как показано на векторной диаграмме.

Это означает, что форма волны тока достигает своего положительного пика, отрицательного пика и пересекает нулевое значение 90 ^o после формы волны напряжения. Ниже приведены кривые напряжения, тока и мощности для чисто индуктивной нагрузки.

Теперь мы увидим полярность мгновенной мощности в разные моменты времени.

В момент t ₁

P ₁ = V ₁ (+ ve) * I ₁ (-ve) = -ve

В момент t ₂

P ₂ = V ₂ (-ve) * I ₂ (-ve) = + ve

Следовательно, в случае чисто индуктивной нагрузки мощность может быть как положительной, так и отрицательной.Это означает, что мощность идет вперед и назад между источником и нагрузкой точно так же, как маятник, не выполняя никакой полезной работы в системе. Этот тип мощности известен как реактивная мощность .

Теперь давайте посмотрим, что происходит в случае с чисто емкостной нагрузкой .

В случае чисто емкостной нагрузки ток опережает напряжение на 90 ^o , что означает, что форма волны тока достигает своего положительного пика, отрицательного пика и нулевого значения 90 ^o перед формой волны напряжения.Векторная диаграмма и формы сигналов для чисто емкостной нагрузки приведены ниже.

На графике мощности видно, что мощность также является положительной и отрицательной, что означает, что мощность колеблется между источником и нагрузкой без выполнения какой-либо полезной работы. Этот тип мощности известен как реактивная мощность .

Если мы внимательно понаблюдаем за формами колебаний мощности как для чисто индуктивной, так и для чисто емкостной нагрузки, мы обнаружим, что величина положительной и отрицательной мощности абсолютно одинакова.

Следовательно, средняя мощность в случае чисто индуктивной нагрузки и чисто емкостной нагрузки равна нулю.

Почему мощность течет назад и вперед в случае индуктивных и емкостных нагрузок?

Во время положительного полупериода, когда мощность положительная, то есть мощность течет от источника к нагрузке, конденсатор накапливает энергию в виде электрического поля.

Во время отрицательного полупериода электрическое поле конденсатора схлопывается, и вся энергия, накопленная в конденсаторе, отправляется обратно к источнику, и мощность начинает течь от нагрузки к источнику.Следовательно, мы получаем отрицательную мощность.

Аналогичным образом, в случае индуктивной нагрузки, во время положительного полупериода, когда мощность положительная, т.е. мощность течет от источника к нагрузке, индуктор накапливает энергию в виде магнитного поля.

Во время отрицательного полупериода магнитное поле индуктора схлопывается, и вся энергия, накопленная в индукторе, высвобождается и отправляется обратно к источнику, и мощность начинает течь от нагрузки к источнику. {\ circ}} \)

\ (\ Rightarrow Q = VI \ quad VAR \)

ВНЕШНЯЯ МОЩНОСТЬ

Случаи, которые мы видели до сих пор (чисто резистивная, чисто индуктивная и чисто емкостная нагрузка), являются стандартными случаями.

На самом деле, большинство нагрузок, которые мы используем в нашей повседневной жизни (например: электрический вентилятор, электрический утюг, асинхронный двигатель и т. Д.), Представляют собой комбинацию резистивной и индуктивной нагрузки. Некоторые нагрузки также могут представлять собой комбинацию резистивной и емкостной нагрузки, но большинство бытовых и промышленных нагрузок представляют собой смесь резистивной и индуктивной нагрузки.

Общая схема для смеси резистивной и индуктивной нагрузки показана на схеме.

Резистивный компонент потребляет активную мощность, а индуктивный компонент потребляет реактивную мощность.Таким образом, общая мощность, отдаваемая источником, представляет собой комбинацию активной и реактивной мощности, и эта мощность известна как полная мощность .

В случае комбинации резистивной и индуктивной нагрузки, ток отстает от напряжения питания на угол \ (\ phi \), что означает, что форма волны тока достигает своего положительного пика, отрицательного пика и нулевого значения с фазовой задержкой \ (\ phi \) От формы сигнала напряжения.

Векторная диаграмма и формы сигналов для смеси резистивной и индуктивной нагрузки приведены ниже.

На диаграмме формы сигнала мы можем видеть, что мощность бывает положительной и отрицательной из-за наличия активной и реактивной мощности в цепи. Кроме того, величина положительной мощности больше, чем величина отрицательной мощности.

Следовательно, средняя мощность в этом случае не будет равна нулю и, следовательно, мы получим некоторую мощность от системы. Но в этом случае средняя мощность меньше по сравнению со средней мощностью чисто резистивной цепи.

Свойства полной мощности

• Полная мощность — это комбинация активной и реактивной мощности.{2} \)

СИЛОВОЙ ТРЕУГОЛЬНИК

Треугольник мощности — это прямоугольный треугольник, который показывает соотношение между активной, реактивной и полной мощностью.

Основание, нормаль и гипотенуза прямоугольного треугольника обозначают активную, реактивную и полную мощность соответственно.

Чтобы получить треугольник мощности, мы будем использовать векторную диаграмму смеси резистивной и емкостной нагрузки.

В случае сочетания резистивной и емкостной нагрузки ток опережает напряжение питания на некоторый угол \ (\ phi \).Теперь ток можно разделить на две перпендикулярные составляющие, которые равны

• \ (I \ cos {\ phi} \) = Составляющая тока (I), которая находится в фазе с напряжением питания (В).
  • \ (I \ cos {\ phi} \) известен как Активная или ваттная составляющая тока (I)
• \ (I \ sin {\ phi} \) = Компонент тока (I), который на 90 ^o не совпадает по фазе с напряжением питания (В).
  • \ (I \ sin {\ phi} \) известен как Реактивная или безватная составляющая тока (I)

Теперь, чтобы получить треугольник мощности, давайте отдельно нарисуем треугольник тока.{2} \)

Наблюдать за активной, реактивной и полной мощностью

Подробнее

Распределительное устройство и защита

Системы управления и виды систем управления

Поделиться этой записью: в Твиттере на Фейсбуке в Google+

Активная, реактивная и полная мощность в цепях переменного тока

Активная мощность:

Если активное сопротивление (т.е.грамм. нагревательный элемент) подключен к цепи переменного тока, результирующее напряжение и ток совпадают по фазе (синяя и красная кривые на схеме ниже). Умножение связанных пар мгновенных значений напряжения и тока дает мгновенную мощность (зеленая кривая).

Такая кривая мощности всегда положительна, потому что для активного сопротивления напряжение и ток всегда либо положительные, либо отрицательные. Положительная мощность передается от генератора к потребителю.Зеленые зоны отображают выполненную активную работу. Поскольку мощность имеет частоту в два раза превышающую частоту напряжения или тока, не может быть нанесен на график вместе с током и напряжением на нормальной векторной диаграмме.

Мощность переменного тока p ( t ) имеет пиковое значение p ₀ = u ₀ · i ₀ и может быть преобразовано путем приравнивания площадей под кривой в эквивалентную мощность постоянного тока , или активная мощность P .Активная мощность для активного сопротивления составляет половину пиковой мощности, т.е.

Другими словами:

Активная мощность для активного сопротивления является произведением среднеквадратичного напряжения и действующего тока.

Реактивная мощность:

Если чистое реактивное сопротивление, т. Е. Емкостное или индуктивное сопротивление, подключено к цепи переменного тока, сдвиг фазы j между током и напряжением составляет 90 °, ток опережает напряжение в случае емкости и отстает от напряжения в случай индуктивности (как показано на диаграмме ниже).Кривая мощности здесь симметрична относительно оси времени, так что положительная и отрицательная (серые) области компенсируют друг друга, и в целом активная мощность не потребляется. Отрицательные значения означают, что мощность возвращается от потребителя к генератору. В течение одного периода энергия дважды возвращается от катушки (потребителя) к генератору. Общая энергия постоянно колеблется между генератором и потребителем. Это приводит к чистому потреблению реактивной мощности индуктивного или емкостного характера в зависимости от используемого компонента.Реактивная мощность обозначается Q и выражается в единицах Var .

Полная мощность:

Если нагрузка, включающая компоненты активного и реактивного сопротивления, подключена к переменному напряжению, возникают компоненты активной и реактивной мощности. Схема ниже демонстрирует это в случае индуктивной нагрузки, ток и напряжение которой сдвинуты по фазе на 60 °. Кривая мощности здесь в основном расположена выше оси времени.Серые области частично компенсируют друг друга и представляют компонент реактивной мощности, а зеленые области представляют активную мощность (или выполненную активную работу).

Умножение измеренных значений напряжения и сдвинутого по фазе тока дает здесь полную мощность S , которая выражается в вольт-амперах (ВА):

Кажущаяся мощность — это , а не , мера преобразования электрической энергии в цепи, вместо этого она служит просто вычисляемой переменной, состоящей из активной и реактивной мощности.Соответственно, активная мощность P , показанная измерителем мощности (ваттметром) при наличии фазового сдвига между током и напряжением, всегда меньше, чем кажущаяся мощность S , вычисленная из среднеквадратичных значений тока и напряжения.

Активная, реактивная и полная мощность

Активная мощность

Фактическая мощность, используемая или рассеиваемая в цепи, называется истинной мощностью, или активной мощностью, или реальной мощностью. Он измеряется в ваттах (Вт), киловаттах (кВт) или МВт.Обозначается заглавной буквой P.

.

Видно, что мощность расходуется только на сопротивление.

Реактивная мощность

Реактивные нагрузки, такие как катушки индуктивности , и конденсаторы , рассеивают или потребляют нулевую мощность, однако тот факт, что они падают напряжение и потребляют ток, создает обманчивое впечатление, что они фактически рассеивают мощность. Эта « фантомная или фиктивная мощность » называется реактивной мощностью . Реактивная мощность измеряется в киловольт-амперах реактивной мощности (кВАр) или в МВАр.

Реактивная мощность не выполняет никакой полезной работы в цепи. Чистая катушка индуктивности и чистый конденсатор не потребляют никакой энергии, поскольку в течение полупериода, какая бы мощность ни принималась от источника этими компонентами, та же самая мощность возвращается к источнику.

Полная мощность

Произведение среднеквадратичного значения напряжения и тока известно как кажущаяся мощность . Эта мощность измеряется в кВА или МВА.

или

Комбинация реактивной мощности и истинной мощности называется полной мощностью .

Комплексная мощность

Комплексная сумма активной мощности (P) и реактивной мощности (Q) известна как комплексная мощность, которую можно выразить как S = P + jQ и измерить в единицах реактивной мощности вольт-ампер (обычно в кВАр).

Это также может быть выражено как S = VI *, где «I *» — это сопряжение комплексного тока I. Этот ток «I» протекает через реактивную нагрузку Z, вызванную напряжением.

Следовательно,

Истинная мощность = напряжение x ток в фазе с напряжением
Реактивная мощность = напряжение x ток в фазе с напряжением

Векторная диаграмма индуктивной цепи представлена ​​на рис.1.

Рис. 1 Векторная диаграмма для индуктивной цепи

Векторная диаграмма для емкостной цепи показана на рис. 2.

Рис. 2 Векторная диаграмма для емкостной цепи

Если взять за эталон напряжение V, то ток I отстает от напряжения V на рис. 1 и опережает напряжение на рис. 2 на угол коэффициента мощности θ соответственно. Ток I делится на две составляющие

I Cosθ в фазе с напряжением V
I Sinθ не совпадает по фазе на 90 ° с напряжением V

Следовательно, следующее выражение, показанное ниже, дает активную, реактивную и полную мощность соответственно

Активная мощность

P = V x I cosθ = V I cosθ

Реактивная мощность

Q = V x I sinθ = V I sinθ

Полная мощность

S = V x I = VI

Активная составляющая тока

Составляющая тока, которая находится в фазе с напряжением цепи и вносит вклад в активную или истинную мощность схемы, называется активной составляющей или составляющей полной мощности, или синфазной составляющей тока.

Реактивная составляющая тока

Составляющая тока, которая находится в квадратуре или на 90 ° сдвинута по фазе к напряжению схемы и вносит вклад в реактивную мощность схемы, называется реактивной составляющей тока.

Треугольник силы

Истинная, реактивная и полная мощности связаны друг с другом в тригонометрической форме как треугольник мощности .

Мощность

— активная энергия, реактивная энергия или просто энергия?

Могу ли я сказать, что, используя активную мощность, я могу оценить потребление активной энергии двигателем, или что активная энергия не является широко используемым термином, особенно в промышленной среде?

Истинная мощность — это фактическое потребление / преобразование энергии, поэтому нет необходимости оценивать его, если вы это уже знаете.Активная или истинная энергия, при условии, что это действительные термины, будет просто количеством энергии, которое должно быть преобразовано в неэлектрическую энергию, а активная / истинная мощность — это скорость преобразования.

Если я могу использовать вышеупомянутый термин, нормально ли, если я вообще не рассматриваю реактивную энергию? Имеет ли смысл говорить о реактивной энергии?

Я подозреваю, что это сильно зависит от того, что вы делаете. Если это не имеет отношения к вашей задаче, да, вы можете проигнорировать это, но если вы обычно спрашиваете, можете ли вы игнорировать коэффициент мощности или что-то в этом роде, ответ — нет.

Что мы обычно имеем в виду, когда говорим об электроэнергии на заводе?

Когда мы говорим об электроэнергии на заводе или в любой другой системе, мы имеем в виду потенциальную энергию, доступную из-за разницы напряжений, которая вызывает протекание тока для выполнения задач, электрических по своей природе или нет.

Мы имеем в виду сумму активной мощности в кВтч?

кВтч, или тысяча ватт-часов, относится к потреблению / преобразованию энергии, которую они производят, умножая скорость преобразования энергии (показатель мощности) на период, в течение которого энергия преобразуется, поэтому цифра в кВтч выражает количество используемой или доступной энергии.

Или мы используем полную мощность для расчета энергии в этом случае?

Хммм, я думаю, вы можете быть очень не уверены в том, что в первую очередь означают мощность и энергия. Прежде чем продолжить, я хотел бы отметить, что непонятно, о чем вы говорите. Используем ли мы , какое значение полной мощности в , каким образом , чтобы вычислить какое значение энергии? На большинство ваших вопросов также трудно ответить, поэтому я добавлю следующее:

Хмммм… Хорошо, я думаю, небольшое разъяснение может исправить ситуацию для вас.

Истинная мощность — это мощность, которая фактически «используется» (преобразуется в какую-либо другую форму энергии и удаляется из схемы в виде тепла, кинетической энергии и т. Д.).

Реактивная мощность — это мощность, которая накапливается в реакторах (катушках индуктивности и конденсаторах) и позже возвращается в схему. Хотя эта мощность сама по себе не используется схемой, она может способствовать потере тепла, так как увеличивает ток в отдельных частях схемы, поскольку он «звенит» взад и вперед между реакторами.

Полная мощность — это мощность, которая появляется, когда вы просто измеряете цепь без выделения реактивной части мощности. Какой-то модный парень понял, что взаимосвязь между этими фигурами может быть выражена с помощью математики, связанной со сторонами треугольника, как вы видите здесь:

Реактивная энергия, во всяком случае, будет энергией, запасенной реакторами в цепи, и ее скорость передачи / накопления, вероятно, будет реактивной мощностью.

Надеюсь, это поможет.

.