Активная мощность. Единица измерения — ватт (w, Вт).
Среднее за период T значение мгновенной мощности называется активной мощностью: В цепях однофазного синусоидального токагдеU и I — среднеквадратичные значения напряжения и тока, φ — угол сдвига фаз между ними.
Реактивная мощность. Единица измерения — вольт-ампер реактивный (var, вар)
Реактивная мощность — величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи синусоидального переменного тока, равна произведению среднеквадратичных значений напряжения U и тока I, умноженному на синус угла сдвига фаз φ между ними: (если ток отстаёт от напряжения, сдвиг фаз считается положительным, если опережает — отрицательным). Реактивная мощность связана с полной мощностьюS и активной мощностью Р соотношением: .
Коэффициент мощности — безразмерная физическая величина, характеризующая потребителя переменного электрического тока с точки зрения наличия в нагрузке реактивной составляющей. Коэффициент мощности показывает, насколько сдвигается по фазе переменный ток, протекающий через нагрузку, относительно приложенного к ней напряжения.
26
studfiles.net
Активная, реактивная, полная мощность и коэффициент мощности
Мощностные характеристики нагрузки можно точно задать одним единственным параметром (активная мощность в Вт) только для случая постоянного тока, так как в цепи постоянного тока существует единственный тип сопротивления – активное сопротивление.Мощностные характеристики нагрузки для случая переменного тока невозможно точно задать одним единственным параметром, так как в цепи переменного тока существует два разных типа сопротивления – активное и реактивное. Поэтому только два параметра: активная мощность (это полезная мощность, отбираемая нагрузкой, в том числе и ИБП, из электросети и преобразуемая в энергию любого иного вида (механическую, тепловую, электрическую, электромагнитную и др.) и реактивная мощность ( это мощность или поток энергии, циркулирующий через реактивное сопротивление электрической цепи (емкостное или индуктивное).
Рассеяния энергии на реактивных элементах не происходит, так как полученная ими энергия от источника и энергия и возвращенная обратно в сеть в течение периода эквивалентны. Считается, что в большинстве случаев реактивная энергия (мощность), циркулирующая в электрической цепи, является паразитной и приводит к нежелательному разогреву проводников, а также к перегреву и ухудшению режимов работы прочих устройств сети, как генерирующих электричество, так и его потребителей.) точно характеризуют нагрузку.
Принцип действия активного и реактивного сопротивлений совершенно различный. Активное сопротивление – необратимо преобразует электрическую энергию в другие виды энергии (тепловую, световую и т.д.) – примеры: лампа накаливания, электронагреватель (параграф 39, Физика 11 класс В.А. Касьянов М.: Дрофа, 2007). Реактивное сопротивление – попеременно накапливает энергию затем выдаёт её обратно в сеть – примеры: конденсатор, катушка индуктивности (параграф 40,41, Физика 11 класс В.А. Касьянов М.: Дрофа, 2007).
Дальше в любом учебнике по электротехнике Вы можете прочитать, что активная мощность (рассеиваемая на активном сопротивлении) измеряется в ваттах, а реактивная мощность (циркулирующая через реактивное сопротивление) измеряется в варах; так же для характеристики мощности нагрузки используют ещё два параметра: полную мощность и коэффициент мощности.
Все эти 4 параметра:
- Активная мощность: обозначение P, единица измерения: Ватт
- Реактивная мощность: обозначение Q, единица измерения: ВАр (Вольт Ампер реактивный)
- Полная мощность:обозначение S, единица измерения: ВА (Вольт Ампер)
- Коэффициент мощности: обозначение k или cosФ, единица измерения: безразмерная величина
Также cosФ называется коэффициентом мощности (Power Factor – PF)
Поэтому в электротехнике для характеристики мощности задаются любые два из этих параметров так как остальные могут быть найдены из этих двух.
То же самое и с источниками питания. Их мощность (нагрузочная способность) характеризуется одним параметром для источников питания постоянного тока – активная мощность (Вт), и двумя параметрами для ист. питания переменного тока. Обычно этими двумя параметрами являются полная мощность (ВА) и активная (Вт). См. например параметры ДГУ и ИБП.
Большинство офисной и бытовой техники, активные (реактивное сопротивление отсутствует или мало), поэтому их мощность указывается в Ваттах. В этом случае при расчёте нагрузки используется значение мощности ИБП в Ваттах. Если нагрузкой являются компьютеры с блоками питания (БП) без коррекции входного коэффициента мощности (APFC), лазерный принтер, холодильник, кондиционер, электромотор (например погружной насос или мотор в составе станка), люминисцентные балластные лампы и др. – при расчёте используются все вых. данные ибп: кВА, кВт, перегрузочные характеристики и др.
Нагрузочная способность ИБП и ДГУ нормирована на стандартную промышленную нагрузку (коэффициент мощности 0.8 с индуктивным характером). Например, ИБП 100 кВА / 80 кВт. Это означает, что устройство может питать активную нагрузку максимальной мощности 80 кВт, или смешанную (активно-реактивную) нагрузку максимальной мощности 100 кВА с индуктивным коэффициентом мощности 0.8. В стабилизаторах напряжения дело обстоит иначе.
Для стабилизатора напряжения коэффициент мощности нагрузки безразличен. Например, стабилизатор напряжения 100 кВА. Это означает, что устройство может питать активную нагрузку максимальной мощности 100 кВт, или любую другую (чисто активную, чисто реактивную, смешанную) мощностью 100 кВА или 100 кВАр с любым коэффициентом мощности емкостного или индуктивного характера. Обратите внимание, что это справедливо для линейной нагрузки (без высших гармоник тока). При больших гармонических искажениях тока нагрузки (высокий КНИ) выходная мощность стабилизатора снижается.
stabhouse.ru
активная, реактивная, полная (P, Q, S), коэффициент мощности (PF)
Из письма клиента:
Подскажите, ради Бога, почему мощность ИБП указывается в Вольт-Амперах, а не в привычных для всех киловаттах. Это сильно напрягает. Ведь все уже давно привыкли к киловаттам. Да и мощность всех приборов в основном указана в кВт.
Алексей. 21 июнь 2007
В технических характеристиках любого ИБП указаны полная мощность [кВА] и активная мощность [кВт] – они характеризуют нагрузочную способность ИБП. Пример, см. фотографии ниже:
 |
 |
Мощность не всех приборов указана в Вт, например:
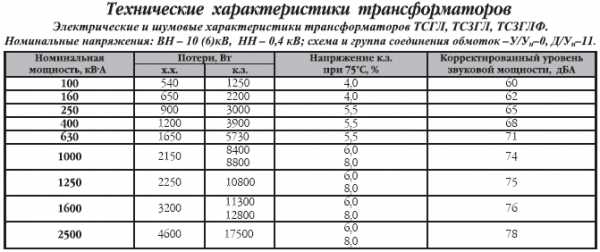
- Мощность трансформаторов указывается в ВА:
http://www.mstator.ru/products/sonstige/powertransf (трансформаторы ТП: см приложение)
http://metz.by/download_files/catalog/transform/tsgl__tszgl__tszglf.pdf (трансформаторы ТСГЛ: см приложение) - Мощность конденсаторов указывается в Варах:
http://www.elcod.spb.ru/catalog/k78-39.pdf (конденсаторы K78-39: см приложение)
http://www.kvar.su/produkciya/25-nizkogo-napraygeniya-vbi (конденсаторы УК: см приложение) - Примеры других нагрузок — см. приложения ниже.
Мощностные характеристики нагрузки можно точно задать одним единственным параметром (активная мощность в Вт) только для случая постоянного тока, так как в цепи постоянного тока существует единственный тип сопротивления – активное сопротивление.
Мощностные характеристики нагрузки для случая переменного тока невозможно точно задать одним единственным параметром, так как в цепи переменного тока существует два разных типа сопротивления – активное и реактивное. Поэтому только два параметра: активная мощность и реактивная мощность точно характеризуют нагрузку.
Принцип действия активного и реактивного сопротивлений совершенно различный. Активное сопротивление – необратимо преобразует электрическую энергию в другие виды энергии (тепловую, световую и т.д.) – примеры: лампа накаливания, электронагреватель (параграф 39, Физика 11 класс В.А. Касьянов М.: Дрофа, 2007).
Реактивное сопротивление – попеременно накапливает энергию затем выдаёт её обратно в сеть – примеры: конденсатор, катушка индуктивности (параграф 40,41, Физика 11 класс В.А. Касьянов М.: Дрофа, 2007).
Дальше в любом учебнике по электротехнике Вы можете прочитать, что активная мощность (рассеиваемая на активном сопротивлении) измеряется в ваттах, а реактивная мощность (циркулирующая через реактивное сопротивление) измеряется в варах; так же для характеристики мощности нагрузки используют ещё два параметра: полную мощность и коэффициент мощности. Все эти 4 параметра:
- Активная мощность: обозначение P, единица измерения: Ватт
- Реактивная мощность: обозначение Q, единица измерения: ВАр (Вольт Ампер реактивный)
- Полная мощность: обозначение S, единица измерения: ВА (Вольт Ампер)
- Коэффициент мощности: обозначение k или cosФ, единица измерения: безразмерная величина
Эти параметры связаны соотношениями: S*S=P*P+Q*Q, cosФ=k=P/S
Также cosФ называется коэффициентом мощности (Power Factor – PF)
Поэтому в электротехнике для характеристики мощности задаются любые два из этих параметров так как остальные могут быть найдены из этих двух.
Например, электромоторы, лампы (разрядные) — в тех. данных указаны P[кВт] и cosФ:
http://www.mez.by/dvigatel/air_table2.shtml (двигатели АИР: см. приложение)
http://www.mscom.ru/katalog.php?num=38 (лампы ДРЛ: см. приложение)
(примеры технических данных разных нагрузок см. приложение ниже)
То же самое и с источниками питания. Их мощность (нагрузочная способность) характеризуется одним параметром для источников питания постоянного тока – активная мощность (Вт), и двумя параметрами для ист. питания переменного тока. Обычно этими двумя параметрами являются полная мощность (ВА) и активная (Вт). См. например параметры ДГУ и ИБП.
Большинство офисной и бытовой техники, активные (реактивное сопротивление отсутствует или мало), поэтому их мощность указывается в Ваттах. В этом случае при расчёте нагрузки используется значение мощности ИБП в Ваттах. Если нагрузкой являются компьютеры с блоками питания (БП) без коррекции входного коэффициента мощности (APFC), лазерный принтер, холодильник, кондиционер, электромотор (например погружной насос или мотор в составе станка), люминисцентные балластные лампы и др. – при расчёте используются все вых. данные ибп: кВА, кВт, перегрузочные характеристики и др.
См. учебники по электротехнике, например:
1. Евдокимов Ф. Е. Теоретические основы электротехники. — М.: Издательский центр «Академия», 2004.
2. Немцов М. В. Электротехника и электроника. — М.: Издательский центр «Академия», 2007.
3. Частоедов Л. А. Электротехника. — М.: Высшая школа, 1989.
Так же см. AC power, Power factor, Electrical resistance, Reactance http://en.wikipedia.org
(перевод: http://electron287.narod.ru/pages/page1.html)
Приложение
Пример 1: мощность трансформаторов и автотрансформаторов указывается в ВА (Вольт·Амперах)
Трансформаторы питания номинальной выходной мощностью 25-60 ВА
http://www.mstator.ru/products/sonstige/powertransf (трансформаторы ТП)
|
|
http://metz.by/download_files/catalog/transform/tsgl__tszgl__tszglf.pdf (трансформаторы ТСГЛ)
|
|
|
| АОСН-2-220-82 | |
| Латр 1.25 | АОСН-4-220-82 |
| Латр 2.5 | АОСН-8-220-82 |
| АОСН-20-220 | |
| АОМН-40-220 | |
http://www.gstransformers.com/products/voltage-regulators.html (ЛАТР / лабораторные автотрансформаторы TDGC2)
Пример 2: мощность конденсаторов указывается в Варах (Вольт·Амперах реактивных)
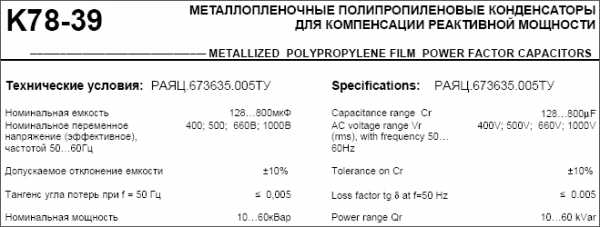 |
http://www.elcod.spb.ru/catalog/k78-39.pdf (конденсаторы K78-39)
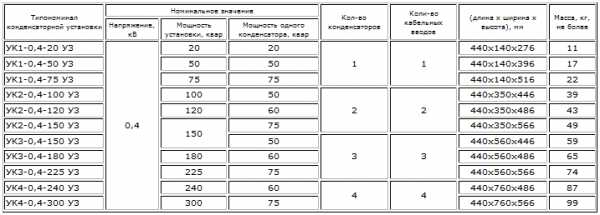 |
http://www.kvar.su/produkciya/25-nizkogo-napraygeniya-vbi (конденсаторы УК)
Пример 3: технические данные электромоторов содержат активную мощность (кВт) и cosФ
Для таких нагрузок как электромоторы, лампы (разрядные), компьютерные блоки питания, комбинированные нагрузки и др. — в технических данных указаны P [кВт] и cosФ (активная мощность и коэффициент мощности) или S [кВА] и cosФ (полная мощность и коэффициент мощности).
http://www.mez.by/dvigatel/air_table2.shtml (двигатели АИР)
 |
http://www.weiku.com/products/10359463/Stainless_Steel_cutting_machine.html
(комбинированная нагрузка – станок плазменной резки стали / Inverter Plasma cutter LGK160 (IGBT)
Технические данные разрядных ламп содержат активную мощность (кВт) и cosФ
http://www.mscom.ru/katalog.php?num=38 (лампы ДРЛ)
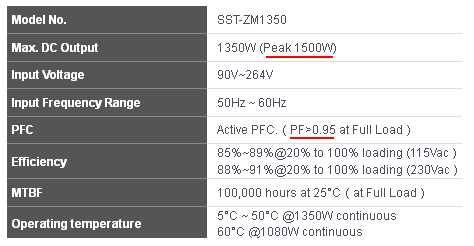 |
http://www.silverstonetek.com.tw/product.php?pid=365&area=en (блок питания ПК)
Дополнение 1
Если нагрузка имеет высокий коэффициент мощности (0.8 … 1.0), то её свойства приближаются к активной нагрузке. Такая нагрузка является идеальной как для сетевой линии, так и для источников электроэнергии, т.к. не порождает реактивных токов и мощностей в системе.
Если нагрузка имеет низкий коэффициент мощности (менее 0.8 … 1.0), то в линии питания циркулируют большие реактивные токи (и мощности). Это паразитное явление приводит к повышению потерь в проводах линии (нагрев и др.), нарушению режима работы источников (генераторов) и трансформаторов сети, а также др. проблемам.
Поэтому во многих странах приняты стандарты нормирующие коэффициент мощности оборудования.
Дополнение 2
Оборудование однонагрузочное (например, БП ПК) и многосоставное комбинированное (например, фрезерный промышленный станок, имеющий в составе несколько моторов, ПК, освещение и др.) имеют низкие коэффициенты мощности (менее 0.8) внутренних агрегатов (например, выпрямитель БП ПК или электромотор имеют коэффициент мощности 0.6 .. 0.8). Поэтому в настоящее время большинство оборудования имеет входной блок корректора коэффициента мощности. В этом случае входной коэффициент мощности равен 0.9 … 1.0, что соответствует нормативным стандартам.
Дополнение 3. Важное замечание относительно коэффициента мощности ИБП и стабилизаторов напряжения
Нагрузочная способность ИБП и ДГУ нормирована на стандартную промышленную нагрузку (коэффициент мощности 0.8 с индуктивным характером). Например, ИБП 100 кВА / 80 кВт. Это означает, что устройство может питать активную нагрузку максимальной мощности 80 кВт, или смешанную (активно-реактивную) нагрузку максимальной мощности 100 кВА с индуктивным коэффициентом мощности 0.8.
В стабилизаторах напряжения дело обстоит иначе. Для стабилизатора коэффициент мощности нагрузки безразличен. Например, стабилизатор напряжения 100 кВА. Это означает, что устройство может питать активную нагрузку максимальной мощности 100 кВт, или любую другую (чисто активную, чисто реактивную, смешанную) мощностью 100 кВА или 100 кВАр с любым коэффициентом мощности емкостного или индуктивного характера. Обратите внимание, что это справедливо для линейной нагрузки (без высших гармоник тока). При больших гармонических искажениях тока нагрузки (высокий КНИ) выходная мощность стабилизатора снижается.
Дополнение 4
Наглядные примеры чистой активной и чистой реактивных нагрузок:
- К сети переменного тока 220 VAC подключена лампа накаливания 100 Вт – везде в цепи есть ток проводимости (через проводники проводов и вольфрамовый волосок лампы). Характеристики нагрузки (лампы): мощность S=P~=100 ВА=100 Вт, PF=1 => вся электрическая мощность активная, а значит она целиком поглащается в лампе и превращается в мощность тепла и света.
- К сети переменного тока 220 VAC подключен неполярный конденсатор 7 мкФ – в цепи проводов есть ток проводимости, внутри конденсатора идёт ток смещения (через диэлектрик). Характеристики нагрузки (конденсатора): мощность S=Q~=100 ВА=100 ВАр, PF=0 => вся электрическая мощность реактивная, а значит она постоянно циркулирует от источника к нагрузке и обратно, опять к нагрузке и т.д.
Дополнение 5
Для обозначения преобладающего реактивного сопротивления (индуктивного либо ёмкостного) коэффициенту мощности приписывается знак:
+ (плюс) – если суммарное реактивное сопротивление является индуктивным (пример: PF=+0.5). Фаза тока отстаёт от фазы напряжения на угол Ф.
— (минус) – если суммарное реактивное сопротивление является ёмкостным (пример: PF=-0,5). Фаза тока опережает фазу напряжения на угол Ф.
Дополнение 6
В различных областях техники мощность может быть либо полезной, либо паразитной НЕЗАВИСИМО от того активная она или реактивная. Например, необходимо различать активную полезную мощность рассеиваемую на рабочей нагрузке и активную паразитную мощность рассеиваемую в линии электропередачи. Так, например, в электротехнике при расчете активной и реактивной мощностей наиболее часто активная мощность является полезной мощностью, передаваемой в нагрузку и является реальной (не мнимой) величиной. А в электронике при расчёте конденсаторов или расчёте самих линий передач активная мощность является паразитной мощностью, теряемой на разогрев конденсатора (или линии) и является мнимой величиной. Причём, деление на мнимые и немнимые величины производится только для удобства рассчётов. На самом деле, все физические величины конечно реальные.
Дополнительные вопросы
Вопрос 1:
Почему во всех учебниках электротехники при расчете цепей переменного тока используют мнимые числа / величины (например, реактивная мощность, реактивное сопротивление и др.), которые не существуют в реальности?
Ответ:
Да, все отдельные величины в окружающем мире – действительные. В том числе температура, реактивное сопротивление, и т.д. Использование мнимых (комплексных) чисел – это только математический приём, облегчающий вычисления. В результате вычисления получается обязательно действительное число. Пример: реактивная мощность нагрузки (конденсатора) 20кВАр – это реальный поток энергии, то есть реальные Ватты, циркулирующие в цепи источник–нагрузка. Но что бы отличить эти Ватты от Ваттов, безвозвратно поглащаемых нагрузкой, эти «циркулирующие Ватты» решили называть Вольт·Амперами реактивными [6].
Замечание:
Раньше в физике использовались только одиночные величины и при расчете все математические величины соответствовали реальным величинам окружающего мира. Например, расстояние равно скорость умножить на время (S=v*t). Затем с развитием физики, то есть по мере изучения более сложных объектов (свет, волны, переменный электрический ток, атом, космос и др.) появилось такое большое количество физических величин, что рассчитывать каждую в отдельности стало невозможно. Это проблема не только ручного вычисления, но и проблема составления программ для ЭВМ. Для решения данное задачи близкие одиночные величины стали объединять в более сложные (включающие 2 и более одиночных величин), подчиняющиеся известным в математике законам преобразования. Так появились скалярные (одиночные) величины (температура и др.), векторные и комплексные сдвоенные (импеданс и др.), векторные строенные (вектор магнитного поля и др.), и более сложные величины – матрицы и тензоры (тензор диэлектрической проницаемости, тензор Риччи и др.). Для упрощения рассчетов в электротехнике используются следующие мнимые (комплексные) сдвоенные величины:
- Полное сопротивление (импеданс) Z=R+iX
- Полная мощность S=P+iQ
- Диэлектрическая проницаемость e=e’+ie»
- Магнитная проницаемость m=m’+im»
- и др.
Вопрос 2:
На странице http://en.wikipedia.org/wiki/Ac_power показаны S P Q Ф на комплексной, то есть мнимой / несуществующей плоскости. Какое отношение это все имеет к реальности?
Ответ:
Проводить расчеты с реальными синусоидами сложно, поэтому для упрощения вычислений используют векторное (комплексное) представление как на рис. выше. Но это не значит, что показанные на рисунке S P Q не имеют отношения к реальности. Реальные величины S P Q могут быть представлены в обычном виде, на основе измерений синусоидальных сигналов осциллографом. Величины S P Q Ф I U в цепи переменного тока «источник-нагрузка» зависят от нагрузки. Ниже показан пример [5] реальных синусоидальных сигналов S P Q и Ф для случая нагрузки состоящей из последовательно соединённых активного и реактивного (индуктивного) сопротивлений.
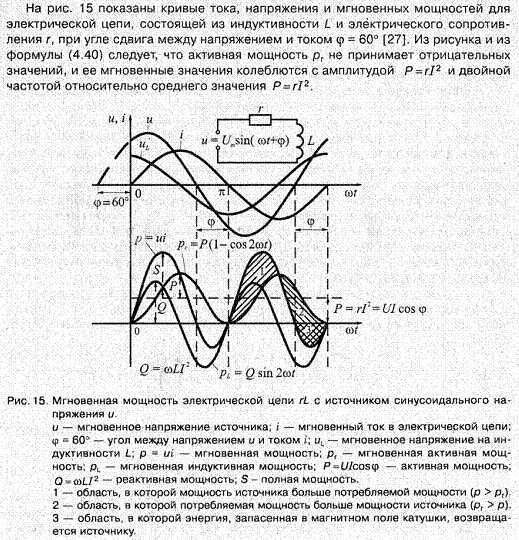 |
Вопрос 3:
Обычными токовыми клещами и мультиметром измерен ток нагрузки 10 A, и напряжение на нагрузке 225 В. Перемножаем и получаем мощность нагрузки в Вт: 10 A · 225В = 2250 Вт.
Ответ:
Вы получили (рассчитали) полную мощность нагрузки 2250 ВА. Поэтому ваш ответ будет справедлив только, если ваша нагрузка чисто активная, тогда действительно Вольт·Ампер равен Ватту. Для всех других типов нагрузок (например электромотор) – нет. Для измерения всех характеристик любой произвольной нагрузки необходимо использовать анализатор сети, например APPA137:
 |
См. дополнительную литературу, например:
[1]. Евдокимов Ф. Е. Теоретические основы электротехники. — М.: Издательский центр «Академия», 2004.
[2]. Немцов М. В. Электротехника и электроника. — М.: Издательский центр «Академия», 2007.
[3]. Частоедов Л. А. Электротехника. — М.: Высшая школа, 1989.
[4]. AC power, Power factor, Electrical resistance, Reactance
http://en.wikipedia.org (перевод: http://electron287.narod.ru/pages/page1.html)
[5]. Теория и расчёт трансформаторов малой мощности Ю.Н.Стародубцев / РадиоСофт Москва 2005 г. / rev d25d5r4feb2013
[6]. Международная система единиц, СИ, см напр. ГОСТ 8.417-2002. ЕДИНИЦЫ ВЕЛИЧИН
www.380v.ru
Реактивной мощности измерение
Спасибо за интерес, проявленный к нашей Компании
Реактивной мощности измерение
Отправить другу
Измерение реактивной мощности осуществляется с помощью специального прибора варметра, также можно определить косвенным методом с помощью ряда приборов вольтметра, амперметра, фазометра.
Реактивная мощность — величина, характеризующая нагрузки, создаваемые в электрооборудование изменениями энергии электромагнитного поля в цепях переменного тока:
Q = UIsin φ
Единица измерения реактивной мощности — вольт-ампер реактивный (вар).. Реактивная мощность в электрических сетях вызывает дополнительные активные потери и падение напряжения. В электра установках специального назначения (индукционные печи) реактивная мощность значительно больше активной. Это приводит к увеличению реактивной составляющей тока и вызывает перегрузку источников электроснабжения. Для устранения перегрузок и повышения мощности коэффициента электрических установок осуществляется компенсация реактивной мощности.
НЕОБХОДИМА КОНСУЛЬТАЦИЯ?
Чтобы правильно определить необходимое значение мощности установки компенсации реактивной мощности надо произвести измерения в электросети.
Применение современных электрических измерительных приборов на микропроцессорной технике позволяет производить более точную оценку величины энергии в сети.
Анализатор качества энергии и параметров сети потребителей является универсальной измерительной системой, предназначенной для измерения, хранения в памяти и контроля электрических параметров в электросетях с низким и средним напряжением. Измерение осуществляется в однофазных и трёхфазных сетях. Одним из главных достоинств анализатора качества энергии и параметров сети потребителей являются высокая точность измерений, компактные размеры и возможность измерения гармоник тока и напряжения в сети. Один анализатор качества энергии и параметров сети потребителей совмещает в себе 13 различных измерительных приборов: амперметр, вольтметр, ваттметр, измерители реактивной и полной мощности, коэффициента мощности cos φ, частотомер, анализатор гармоник тока и напряжения, счётчики активной, реактивной и полной потребляемой электроэнергии. Трёхфазная электронная измерительная система прибора измеряет и оцифровывает действующие значения напряжения и тока в трёхфазной сети с частотой 50/60 Гц. Прибор производит 2 измерения в течение секунды. Из полученных значений микропроцессором высчитываются электрические параметры. Максимальные, минимальные значения параметров и программные данные сохраняются в памяти. Выбранные измеряемые значения, а также данные о перебоях в сети записываются в буферную память с указанием даты и времени. После чего данную информацию можно просмотреть и проанализировать на мониторе компьютера или распечатать на принтере.
НЕОБХОДИМА КОНСУЛЬТАЦИЯ?
Возврат к списку
www.nucon.ru
В чем физический смысл активной, реактивной и полной мощностей? Назовите единицы измерения?
⇐ ПредыдущаяСтр 4 из 4
Активная мощность потребляется в активных сопротивлениях, и, в конечном итоге, за счет нее выполняется механическая работа или происходит нагревание резисторов. Реактивная мощность-эта та мощность, которая попросту «болтается в проводах». Она не потребляется активно цепью, но системы передачи оказываются ею загруженными.
Пусть приемник электроэнергии присоединен к источнику синусоидального напряжения u(t) = Usin(ωt) и потребляет синусоидальный ток i(t) = I sin (ωt -φ), сдвинутый по фазе относительно напряжения на угол φ. U и I – действующие значения. Значение мгновенной мощности на зажимах приемника определяется выражением
| p(t) = u(t) ∙i(t) = 2UI sin(ωt) sin (ωt -φ) = UI cos φ — UI cos (2ωt -φ) | (5.1) |
и является суммой двух величин, одна из которых постоянна во времени, а другая пульсирует с двойной частотой.
Среднее значение p(t) за период Т называется активной мощностью и полностью определяется первым слагаемым уравнения (5.1):
Активная мощность характеризует энергию, расходуемую необратимо источником в единицу времени на производство полезной работы потребителем. Активная энергия, потребляемая электроприёмниками, преобразуется в другие виды энергии: механическую, тепловую, энергию сжатого воздуха и
газа и т. п.
Среднее значение от второго слагаемого мгновенной мощности (1.1) (пульсирует с двойной частотой) за время Т равно нулю, т. е. на ее создание не требуется каких-либо материальных затрат и поэтому она не может совершать полезной работы. Однако ее присутствие указывает, что между источником и приемником происходит обратимый процесс обмена энергией. Это возможно, если имеются элементы, способные накапливать и отдавать электромагнитную энергию – емкость и индуктивность. Эта составляющая характеризует реактивную мощность.
Полную мощность на зажимах приемника в комплексной форме можно представить следующим образом:
| . | (5.2) |
Единица измерения полной мощности S = UI – ВА.
Реактивная мощность – величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями (обменом) энергии между источником и приемником. Для синусоидального тока она равна произведению действующих значений тока I и напряжения U на синус угла сдвига фаз между ними: Q = UI sinφ. Единица измерения – В∙Ар.
Реактивная мощность не связана с полезной работой ЭП и расходуется только на создание переменных электромагнитных полей в электродвигателях, трансформаторах, аппаратах, линиях и т. д.
Для реактивной мощности приняты такие понятия, как генерация, потребление, передача, потери, баланс. Считается, что если ток отстает по фазе от напряжения (индуктивный характер нагрузки), то реактивная мощность потребляется и имеет положительный знак, а если ток опережает напряжение (емкостный характер нагрузки), то реактивная мощность генерируется и имеет отрицательное значение.
Основными потребителями реактивной мощности на промышленных предприятиях являются асинхронные двигатели (60–65 % общего потребления), трансформаторы (20–25 %), вентильные преобразователи, реакторы, воздушные электрические сети и прочие приемники (10 %).
Передача реактивной мощности загружает электрические сети и установленное в ней оборудование, уменьшая их пропускную способность. Реактивная мощность генерируется синхронными генераторами электростанций, синхронными компенсаторами, синхронными двигателями (регулирование током возбуждения), батареями конденсаторов (БК) и линиями электропередачи.
Реактивная мощность, вырабатываемая емкостью сетей, имеет следующий порядок величин: воздушная линия 20 кВ генерирует 1 кВ∙Ар на 1 км трехфазной линии; подземный кабель 20 кВ – 20 кВ∙Ар/км; воздушная линия 220 кВ – 150 кВ∙Ар/км; подземный кабель 220 кВ – 3 МВ∙Ар/км.
Коэффициент мощности и коэффициент реактивной мощности.Векторное представление величин, характеризующих состояние сети, приводит к представлению реактивной мощности Q вектором, перпендикулярным вектору активной мощности Р (рис. 5.2 ). Их векторная сумма дает полную мощность S.
Рис. 5.1. Треугольник мощностей
Согласно рис. 5.1 и (5.2) следует, что S2 = Р2 + Q2; tgφ = Q/P; cosφ = P/S.
Основным нормативным показателем, характеризующим реактивную мощность, ранее был коэффициент мощности cosφ. На вводах, питающих промышленное предприятие, средневзвешенное значение этого коэффициента должно было находиться в пределах 0,92–0,95. Однако выбор соотношения P/S в качестве нормативного не дает четкого представления о динамике изменения реального значения реактивной мощности. Например, при изменении коэффициента мощности от 0,95 до 0,94 реактивная мощность изменяется на 10 %, а при изменении этого же коэффициента от 0,99 до 0,98 приращение реактивной мощности составляет уже 42 %. При расчетах удобнее оперировать соотношением tgφ = Q/P, которое называют коэффициентом реактивной мощности.
Предприятиям, у которых присоединенная мощность более 150 кВт (за исключением «бытовых» потребителей), определены предельные значения коэффициента реактивной мощности, потребляемой в часы больших суточных нагрузок электрической сети – с 7 до 23 часов (Приказ Министерства промышленности и энергетики РФ от 22.02.2007 г. № 49 «О порядке расчета значений соотношения потребления активной и реактивной мощности для отдельных энергопринимающих устройств потребителей электрической энергии, применяемых для определения обязательств сторон в договорах об оказании услуг по передаче электрической энергии»).
Контрольные вопросы лаб. работы № 2
Законы Кирхгофа.
Для формулировки законов Кирхгофа, в электрической цепи выделяются узлы — точки соединения трёх и более проводников и контуры — замкнутые пути из проводников. При этом каждый проводник может входить в несколько контуров.
В этом случае законы формулируются следующим образом.
Первый закон гласит, что суммарный ток, втекающий в любой узел цепи, равен нулю. Иными словами, сколько тока втекает в узел, столько из него и вытекает. Данный закон следует из закона сохранения заряда. Если цепь содержит p узлов, то она описывается p − 1 уравнениями токов.
Второй закон гласит, что суммарное напряжение по любому замкнутому контуру цепи, равно сумме ЭДС, которые в нём находятся. Если в контуре нет ЭДС, то суммарное напряжение равно нулю. Иными словами, при обходе цепи по контуру, потенциал, изменяясь, возвращается к исходному значению. Если цепь содержит m ветвей, то она описывается m − (p − 1) уравнениями напряжений.
Законы Кирхгофа –правила, которые показывают, как соотносятся токи и напряжения в электрических цепях. Эти правила были сформулированы Густавом Кирхгофом в 1845 году. В литературе часто называют законами Кирхгофа, но это не верно, так как они не являются законами природы, а были выведены из третьего уравнения Максвелла при неизменном магнитном поле. Но все же, первое более привычное для них название, поэтому и мы будет их называть, как это принято в литературе – законы Кирхгофа.
Первый закон Кирхгофа – сумма токов сходящихся в узле равна нулю.
Давайте разбираться. Узел это точка, соединяющая ветви. Ветвью называется участок цепи между узлами. На рисунке видно, что ток i входит в узел, а из узла выходят токи i1 и i2. Составляем выражение по первому закона Кирхгофа, учитывая, что токи, входящие в узел имеют знак плюс, а токи, исходящие из узла имеют знак минус i-i1-i2=0. Ток i как бы растекается на два тока поменьше и равен сумме токов i1 и i2 i=i1+i2. Но если бы, например, ток i2 входил в узел, тогда бы ток I определялся как i=i1-i2. Важно учитывать знаки при составлении уравнения.
Первый закон Кирхгофа это следствие закона сохранения электричества: заряд, приходящий к узлу за некоторый промежуток времени, равен заряду, уходящему за этот же интервал времени от узла, т.е. электрический заряд в узле не накапливается и не исчезает.
Второй закон Кирхгофа – алгебраическая сумма ЭДС, действующая в замкнутом контуре, равна алгебраической сумме падений напряжения в этом контуре.
Напряжение выражено как произведение тока на сопротивление (по закону Ома).
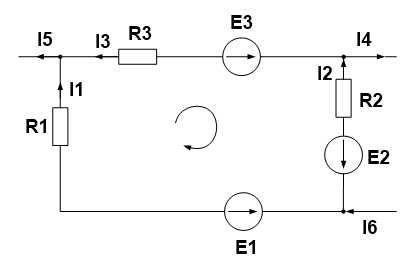
В этом законе тоже существуют свои правила по применению. Для начала нужно задать стрелкой направление обхода контура. Затем просуммировать ЭДС и напряжения соответственно, беря со знаком плюс, если величина совпадает с направлением обхода и минус, если не совпадает. Составим уравнение по второму закону Кирхгофа, для нашей схемы. Смотрим на нашу стрелку, E2 и Е3 совпадают с ней по направлению, значит знак плюс, а Е1 направлено в противоположную сторону, значит знак минус. Теперь смотрим на напряжения, ток I1 совпадает по направлению со стрелкой, а токи I2 и I3 направлены противоположно. Следовательно:
-E1+E2+E3=I1R1-I2R2-I3R3
На основании законов Кирхгофа составлены методы анализа цепей переменного синусоидального тока. Метод контурных токов – метод основанный на применении второго закона Кирхгофа и метод узловых потенциалов основанный на применении первого закона Кирхгофа.
Рекомендуемые страницы:
lektsia.com
В чем физический смысл активной, реактивной и полной мощностей? Назовите единицы измерения? Единица измерения активной мощности
В чем физический смысл активной, реактивной и полной мощностей? Назовите единицы измерения?
⇐ ПредыдущаяСтр 4 из 4Активная мощность потребляется в активных сопротивлениях, и, в конечном итоге, за счет нее выполняется механическая работа или происходит нагревание резисторов. Реактивная мощность-эта та мощность, которая попросту «болтается в проводах». Она не потребляется активно цепью, но системы передачи оказываются ею загруженными.
Пусть приемник электроэнергии присоединен к источнику синусоидального напряжения u(t) = Usin(ωt) и потребляет синусоидальный ток i(t) = I sin (ωt -φ), сдвинутый по фазе относительно напряжения на угол φ. U и I – действующие значения. Значение мгновенной мощности на зажимах приемника определяется выражением
| p(t) = u(t) ∙i(t) = 2UI sin(ωt) sin (ωt -φ) = UI cos φ — UI cos (2ωt -φ) | (5.1) |
и является суммой двух величин, одна из которых постоянна во времени, а другая пульсирует с двойной частотой.
Среднее значение p(t) за период Т называется активной мощностью и полностью определяется первым слагаемым уравнения (5.1):
Активная мощность характеризует энергию, расходуемую необратимо источником в единицу времени на производство полезной работы потребителем. Активная энергия, потребляемая электроприёмниками, преобразуется в другие виды энергии: механическую, тепловую, энергию сжатого воздуха и
газа и т. п.
Среднее значение от второго слагаемого мгновенной мощности (1.1) (пульсирует с двойной частотой) за время Т равно нулю, т. е. на ее создание не требуется каких-либо материальных затрат и поэтому она не может совершать полезной работы. Однако ее присутствие указывает, что между источником и приемником происходит обратимый процесс обмена энергией. Это возможно, если имеются элементы, способные накапливать и отдавать электромагнитную энергию – емкость и индуктивность. Эта составляющая характеризует реактивную мощность.
Полную мощность на зажимах приемника в комплексной форме можно представить следующим образом:
| . | (5.2) |
Единица измерения полной мощности S = UI – ВА.
Реактивная мощность – величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями (обменом) энергии между источником и приемником. Для синусоидального тока она равна произведению действующих значений тока I и напряжения U на синус угла сдвига фаз между ними: Q = UI sinφ. Единица измерения – В∙Ар.
Реактивная мощность не связана с полезной работой ЭП и расходуется только на создание переменных электромагнитных полей в электродвигателях, трансформаторах, аппаратах, линиях и т. д.
Для реактивной мощности приняты такие понятия, как генерация, потребление, передача, потери, баланс. Считается, что если ток отстает по фазе от напряжения (индуктивный характер нагрузки), то реактивная мощность потребляется и имеет положительный знак, а если ток опережает напряжение (емкостный характер нагрузки), то реактивная мощность генерируется и имеет отрицательное значение.
Основными потребителями реактивной мощности на промышленных предприятиях являются асинхронные двигатели (60–65 % общего потребления), трансформаторы (20–25 %), вентильные преобразователи, реакторы, воздушные электрические сети и прочие приемники (10 %).
Передача реактивной мощности загружает электрические сети и установленное в ней оборудование, уменьшая их пропускную способность. Реактивная мощность генерируется синхронными генераторами электростанций, синхронными компенсаторами, синхронными двигателями (регулирование током возбуждения), батареями конденсаторов (БК) и линиями электропередачи.
Реактивная мощность, вырабатываемая емкостью сетей, имеет следующий порядок величин: воздушная линия 20 кВ генерирует 1 кВ∙Ар на 1 км трехфазной линии; подземный кабель 20 кВ – 20 кВ∙Ар/км; воздушная линия 220 кВ – 150 кВ∙Ар/км; подземный кабель 220 кВ – 3 МВ∙Ар/км.
Коэффициент мощности и коэффициент реактивной мощности.Векторное представление величин, характеризующих состояние сети, приводит к представлению реактивной мощности Q вектором, перпендикулярным вектору активной мощности Р (рис. 5.2 ). Их векторная сумма дает полную мощность S.
Рис. 5.1. Треугольник мощностей
Согласно рис. 5.1 и (5.2) следует, что S2 = Р2 + Q2; tgφ = Q/P; cosφ = P/S.
Основным нормативным показателем, характеризующим реактивную мощность, ранее был коэффициент мощности cosφ. На вводах, питающих промышленное предприятие, средневзвешенное значение этого коэффициен
10i5.ru
Мощность в цепях синусоидального тока. Активная, реактивная, полная и комплексная. Единицы измерения.
Поиск ЛекцийМожно считать, что мощность в цепи переменного тока выражается комплексным числом таким, что активная мощность является его действительной частью, реактивная мощность — мнимой частью, полная мощность — модулем, а угол φ (сдвиг фаз) — аргументом. Для такой модели оказываются справедливыми все выписанные ниже соотношения.
Активная мощность
Среднее за период значение мгновенной мощности называется активной мощностью: . В цепях однофазного синусоидального тока , где и — действующие значения напряжения и тока, φ — угол сдвига фаз между ними. Активная мощность может быть также выражена через силу тока, напряжение и активную составляющую сопротивления цепи r или её проводимость g по формуле . В любой электрической цепи как синусоидального, так и несинусоидального тока активная мощность всей цепи равна сумме активных мощностей отдельных частей цепи. С полной мощностью S активная связана соотношением . Единица активной мощности — ватт (W, Вт).
Реактивная мощность
Реактивная мощность — величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи синусоидального переменного тока, равна произведению действующих значений напряжения U и тока I, умноженному на синус угла сдвига фаз φ между ними: (если ток отстаёт от напряжения, сдвиг фаз считается положительным, если опережает — отрицательным). Единица реактивной мощности — вольт-ампер реактивный (var, вар).Реактивная мощность связана с полной мощностью S и активной мощностью Р соотношением: .
Необходимо отметить, что величина sin φ для значений φ от 0 до плюс 90° является положительной величиной. Величина sin φ для значений φ от 0 до —90° является отрицательной величиной. В соответствии с формулой Q = UI sin φ реактивная мощность может быть как положительной величиной (если нагрузка имеет активно-индуктивный характер), так и отрицательной (если нагрузка имеет активно-ёмкостный характер).
Полная мощность
Полная мощность — величина, равная произведению действующих значений периодического электрического тока I в цепи и напряжения U на её зажимах: S = U×I; связана с активной и реактивной мощностями соотношением: , где Р — активная мощность, Q — реактивная мощность (при индуктивной нагрузке Q > 0, а при ёмкостной Q < 0). Единица полной электрической мощности — вольт-ампер (V*A, В*А).
Векторная зависимость между полной, активной и реактивной мощностью выражается формулой:
Нелинейные цепи постоянного тока. Понятие статического и дифференциального сопротивления нелинейного элемента. Последовательное соединение линейного и нелинейного элемента.
Нелинейные свойства таких цепей определяет наличие в них нелинейных резисторов.
В связи с отсутствием у нелинейных резисторов прямой пропорциональности между напряжением и током их нельзя охарактеризовать одним параметром (одним значением ). Соотношение между этими величинами в общем случае зависит не только от их мгновенных значений, но и от производных и интегралов по времени.
Параметры нелинейных резисторов
В зависимости от условий работы нелинейного резистора и характера задачи различают статическое, дифференциальное и динамическое сопротивления.
Если нелинейный элемент является безинерционным, то он характеризуется первыми двумя из перечисленных параметров.
Статическое сопротивление равно отношению напряжения на резистивном элементе к протекающему через него току. В частности для точки 1 ВАХ на рис. 1
.
Под дифференциальным сопротивлением понимается отношение бесконечно малого приращения напряжения к соответствующему приращению тока
.
Следует отметить, что у неуправляемого нелинейного резистора всегда, а может принимать и отрицательные значения (участок 2-3 ВАХ на рис. 1).
В случае инерционного нелинейного резистора вводится понятие динамического сопротивления
,
определяемого по динамической ВАХ. В зависимости от скорости изменения переменной, например тока, может меняться не только величина, но и знак .
16. Законы коммутации. Классический метод анализа переходных процессов. Свободный и принужденный процессы.
Переходный процесс – процесс, происходящий в системе после изменения её состояния, и связанный с перераспределением энергии. Коммутация – изменение состояния в электрических цепях.
Законы коммутации:
ТОК в катушке индуктивности скачком измениться не может. iL(0 − ) = iL(0) = iL(0 + )
НАПРЯЖЕНИЕ на конденсаторе не может измениться скачком. uC(0 − ) = uC(0) = uC(0 + )
Этапы расчета переходного процесса в цепи классическим методом:
1.Найти независимые начальные условия, то есть, напряжения на ёмкостях и токи на индуктивностях в момент начала переходного процесса.
2.Далее необходимо составить систему уравнений на основе законов Кирхгофа, Ома, электромагнитной индукции и т.д., описывающих состояние цепи после коммутации, и исключением переменных получить одно дифференциальное уравнение, в общем случае неоднородное относительно искомого тока i или напряжения u. Для простых цепей получается дифференциальное уравнение первого или второго порядка, в котором в качестве искомой величины выбирают либо ток в индуктивном элементе, либо напряжение на емкостном элементе.
3.Далее следует составить общее решение полученного неоднородного дифференциального уравнения цепи в виде суммы частного решения неоднородного дифференциального уравнения и общего решения соответствующего однородного дифференциального уравнения.
4.Наконец, в общем решении следует найти постоянные интегрирования из начальных условий, т. е. условий в цепи в начальный момент времени после коммутации.
Математическим обоснованием разложения переходного процесса в цепи на принужденный и свободный является известное положение высшей математики: общий интеграл линейного неоднородного дифференциального уравнения равен сумме частного решения неоднородного уравнения и полного решения однородного уравнения. Последнее должно содержать постоянные интегрирования, число которых равно порядку этого дифференциального уравнения. В применении к электрическим цепям определенное частное решение неоднородного уравнения выражает собой принужденный режим, а полное решение однородного уравнения — свободный режим. Переходный процесс в целом выражается общим решением линейного неоднородного дифференциального уравнения, следовательно, суммой принужденной и свободной составляющих.
Заряд конденсатора через сопротивление. Разряд конденсатора через сопротивление. Переходные процессы в RL-цепи (подключение к источнику постоянного напряжения, закорачивание катушки с током, скачкообразное увеличение сопротивления).
Рекомендуемые страницы:
Поиск по сайту
poisk-ru.ru