Закон Ома для полной цепи переменного тока. | |
Если в цепи переменного тока имеются нагрузки разных типов, то закон Ома выполняется только для максимальных (амплитудных) и действующих значений тока и напряжения. В этом случае: — полное сопротивление переменному току. | |
Учитывая, что отношение напряжения к силе тока – это сопротивление, и подставляя конкретные выражения для соответствующих сопротивлений, получим: . | |
Сдвиг фаз в цепи переменного тока определяется характером нагрузки: или . |
|
Мощность в цепи переменного тока. | |
Активной мощностью переменного тока называется средняя за период мощность необратимых преобразований в цепи переменного тока (преобразование энергии электрического тока во внутреннюю энергию): | |
или, переходя к действующим значениям, . | |
Величина наз. коэффициентом мощности. При малом коэффициенте мощности потребляется лишь малая часть мощности, вырабатываемой генератором. Остальная часть мощности периодически перекачивается от генератора к потребителю и обратно и рассеивается в линиях электропередач. | коэффициент мощности |
Резонанс в электрической цепи. | |
Резонанс в электрической цепи — явление резкого возрастания амплитуды вынужденных колебаний тока при приближении частоты внешнего напряжения (эдс) и собственной частоты колебательного контура. |
|
Из выражения для полного сопротивления переменному току видим, что сопротивление будет минимальным (сила тока при заданном напряжении – максимальной) при условии или .
| |
Следовательно, — т.е. частота изменения внешнего напряжения равна собственной частоте колебаний в контуре. | |
Амплитуды колебаний напряжения на индуктивности и емкости будут равны
и — т.е. они равны по величине и противоположны по фазе (напряжение на индуктивности опережает по фазе напряжение на емкости на p). |
|
Следовательно, . |
|
Полное падение напряжения в контуре равно падению напряжения на активном сопротивлении. |
|
При этом если величина , то напряжения на емкостной и индуктивной нагрузках могут оказаться много больше внешнего напряжения (эдс генератора)! | |
На рисунке представлена зависимость тока в колебательном контуре от частоты при значениях R, где R1<R2<R3. | |
В параллельном контуре при малых активных сопротивлениях R1 и R2 токи в параллельных ветвях противоположны по фазе. Тогда, согласно правилу Кирхгофа . | |
В случае резонанса . |
|
Применение: одно из основных применений резонанса в электрической цепи – настройка радио и телевизионных приемников на частоту передающей станции. Необходимо учитывать резонансные явления, когда в цепи, не рассчитанной на работу в условиях резонанса, возникают чрезмерно большие токи или напряжения (расплавление проводов, пробой изоляции и т.д.). |
|
Явления резонанса в цепях переменного тока
Электрическим резонансом называется явление совпадения частоты источника переменного тока с частотой собственных свободных колебаний электрической цепи. Электрические колебания возникают в цепи, которая включает в себя индуктивность и емкость.
Изначально емкость заряжается до начального напряжения Uн, после чего ее замыкают на индуктивность, в результате чего в цепи возникает постепенно увеличивающийся ток i. Сила тока возрастает постепенно, так как ее увеличению препятствует э. д. с. самоиндукции. При увеличении силы тока в магнитном поле индуктивности L накапливается энергия.
Ток достигает максимального значения, после чего уменьшается постепенно, так как его уменьшению препятствует э. д. с. самоиндукции. Она поддерживает ток, благодаря чему конденсатор перезаряжается в обратном направлении.
В случае, когда в колебательном контуре нет потерь, перезарядка емкости продолжается до тех пор, пока емкость не зарядится до первоначального напряжения Uн. Резонанс возникает в цепи, когда цепь подключена к внешнему источнику, а частота этого источника ? равна частоте ?0.
Существуют два основных вида резонанса: резонанс напряжений, который возникает при последовательном соединении реактивных элементов, и резонанс токов — при параллельном соединении.
Резонанс напряжений происходит в неразветвленной цепи переменного тока, которая содержит источник энергии, индуктивность L, емкость С и активное сопротивление R. Когда активное сопротивление цепи R мало, при резонансе сила тока быстро увеличивается, и при этом возрастают напряжения на емкости и индуктивности. Добротностью электрического контура называется величина Q = ? / R.
На практике в устройствах резонанс напряжений является не- желательным явлением, которое связано с возникновением перенапряжений.
Положительное действие резонанса проявляется в радиотехнике, проволочной телефонии, в автоматике и т. п. Резонанс токов возникает при параллельном соединении источника и колебательного контура. Данное явление происходит при условии, что bC = bL, когда I = Ug и cos? = 1. Токи в каждой из реактивных ветвей пропорциональны одному и тому же напряжению и поэтому при резонансе равны:
IC = UbC = IL = UbL.
В реальных цепях не существует катушек, которые обладают индуктивностью и не обладают активным сопротивлением, что относится и к емкости.
Резонанс в цепи переменного тока
Давайте с вами вспомним, что вывести закон Ома для участка цепи переменного тока, содержащего резистор, катушку индуктивности, конденсатор и источник переменного напряжения нам помогла векторная диаграмма амплитуд напряжений на резисторе, конденсаторе и катушке.
Мы показали, что амплитуда приложенного напряжения должна быть равна геометрической сумме этих амплитуд. Угол между амплитудами приложенного напряжения и силы тока определяет разность фаз между силой тока и напряжением. Тангенс этого угла, как видно из рисунка, равен отношению разности амплитуд напряжений на катушке и конденсаторе к амплитуде напряжения на активном сопротивлении:
Используя закон Ома для участка цепи нетрудно показать, что этот же угол определяется отношением реактивного сопротивления к активному:
А средняя мощность, выделяемая в цепи на активном сопротивлении, будет определяться выражением, представленном на экране:
Здесь cos φ0 — это коэффициент
мощности. Являясь безразмерной физической величиной, он характеризует
потребителя переменного электрического тока с точки зрения наличия в нагрузке
реактивной составляющей, и показывает, насколько сдвигается по фазе переменный
ток, протекающий через нагрузку, относительно приложенного к ней напряжения.
Являясь безразмерной физической величиной, он характеризует
потребителя переменного электрического тока с точки зрения наличия в нагрузке
реактивной составляющей, и показывает, насколько сдвигается по фазе переменный
ток, протекающий через нагрузку, относительно приложенного к ней напряжения.
Из последних двух формул следует, что если реактивное сопротивление цепи равно нулю, то уравнение для мощности примет привычный для нас вид:
В этом случае в цепи выделяется максимальная мощность — наступает явление резонанса.
Резонансом в электрическом колебательном контуре называется явление резкого возрастания амплитуды вынужденных колебаний силы тока или напряжения при совпадении частоты внешнего переменного напряжения с собственной частотой колебательного контура:
Рассмотрим это явление более подробно. Для начала представим
себе, что мы раскачиваем маятник, действуя на него периодически изменяющейся
силой. В этом случае маятник будет совершать колебания не самостоятельно, не
свободно, а под действием периодической внешней силы. Такие колебания маятника,
как мы помним, называются вынужденными колебаниями
Такие колебания маятника,
как мы помним, называются вынужденными колебаниями
В электрических колебательных контурах также могут происходить вынужденные электромагнитные колебания. Если в каком-либо колебательном контуре, состоящем из катушки индуктивности и конденсатора, всё время действует генератор переменного тока, то ЭДС генератора будет вызывать в этом контуре переменный электрический ток, частота которого будет равна частоте колебаний ЭДС генератора.
Частота этих вынужденных колебаний в общем случае не совпадает с частотой собственных колебании контура:
Когда собственная частота колебательного контура далека от частоты ЭДС, действующей в контуре, общее сопротивление контура велико и ток в нём незначителен. Однако если в такой цепи подобрать ёмкость конденсатора и индуктивность катушки так, чтобы их сопротивления оказались равными, то разность фаз между колебаниями силы тока и напряжения станет равным нулю, то есть изменения тока и напряжения будут происходить синфазно:
Таким образом, условием возникновения резонанса в колебательном контуре является равенство частоты внешнего подаваемого на контур напряжения частоте собственных колебаний контура:
Эту частоту называют резонансной.
При этом условии полное сопротивление контура становится наименьшим и равным активному сопротивлению, а амплитуда силы тока при данном напряжении принимает наибольшее значение. В этом случае амплитуда напряжения на активном сопротивлении равна амплитуде внешнего напряжения, приложенного к участку цепи (U0r = U0), а напряжения на катушке индуктивности и конденсаторе одинаковы по модулю и противоположны по фазе:
Обратите внимание на то, что амплитудные значения резонансных напряжений на катушке и конденсаторе равны между собой, и они могут значительно превышать амплитуду приложенного напряжения:
Это явление называется резонансом напряжений. При этом чем меньше активное сопротивление контура, тем сильнее ток в контуре и круче резонансная кривая. Такой случай принято называть острым резонансом.
Контур, обладающим острым резонансом, очень чувствителен к колебаниям
резонансной частоты. Это широко используется в радио- и электротехнике
для усиления колебаний напряжения какой-либо определённой частоты.
Это широко используется в радио- и электротехнике
для усиления колебаний напряжения какой-либо определённой частоты.
Так, например, радиоволны от различных передающих станций возбуждают в антенне радиоприёмника переменные токи различных частот, так как каждая передающая радиостанция работает на своей частоте. С антенной индуктивно связан колебательный контур, в катушке которого возникают вынужденные колебания силы тока и напряжения. Но только при резонансе из колебаний различных частот, возбуждаемых в антенне, контур выделяет только те, частота которых равна его собственной частоте. Настройка контура на нужную частоту обычно осуществляется путём изменения ёмкости конденсатора.
Теперь давайте рассмотрим участок цепи переменного тока, содержащий параллельно включённые конденсатор и катушку индуктивности.
Предположим, что активное сопротивление цепи настолько мало, что им можно пренебречь. Пусть к данной цепи приложено переменное напряжение, изменяющееся по закону синуса:
Тогда
ток, проходящей в ветви с ёмкостным сопротивлением, будет опережать по фазе
приложенное напряжение на π/2. А проходящей в ветви с индуктивным
сопротивлением — отставать по фазе на π/2 от приложенного напряжения:
А проходящей в ветви с индуктивным
сопротивлением — отставать по фазе на π/2 от приложенного напряжения:
Таким образом, разность фаз токов в двух ветвях равна π, то есть колебания токов в ветвях противоположны по фазе. Амплитуда же тока во внешней цепи равна модулю разности амплитуд сил токов обеих ветвей:
Если частота колебаний в контуре будет равна резонансной частоте, то амплитудные значения сил токов в ветвях будут равны, и амплитуда силы тока во внешней цепи станет равной нулю.
Конечно же, если учесть наличие активного сопротивления, то разность фаз не будет равна π, как и не будет равно нулю амплитудное значение силы тока во внешней цепи. Но оно примет наименьшее возможное значение. При этом амплитуды сил токов в ветвях могут значительно превышать амплитуду тока во внешней цепи.
Явление резкого уменьшения амплитуды силы тока во внешней
цепи, питающей параллельно включённые конденсатор и катушку индуктивности, при
приближении частоты приложенного напряжения к резонансной частоте называется
резонансом токов (или параллельным резонансом).
Это явление используется в резонансных усилителях, позволяющих выделять одно определённое колебание из сигнала сложной формы, а также в индукционных печах, чтобы сила тока в подводящих проводах была гораздо меньше силы тока в катушке.
Для закрепления нового материала давайте решим с вами такую задачу. Контур, состоящий из конденсатора ёмкостью 507 мкФ, катушки индуктивностью 20 мГн и резистора сопротивлением 100 Ом включили последовательно в сеть переменного тока с частотой 50 Гц и напряжением 220 В. Определите силу тока в цепи, сдвиг фаз между напряжением и силой тока, а также резонансную частоту контура.
Понятие резонанса напряжений в электрических цепях переменного тока
Резонанс в электрической цепи возникает при резком увеличении амплитуды стационарных колебаний при совпадении частоты внешнего воздействия с определенной резонансной частотой системы. Это происходит тогда, когда два элемента противоположного характера компенсируют эффект друг друга в цепи.
Резонанс токов и напряжений
RLC-цепьСхема RLC – это электрическая цепь с последовательно или параллельно соединенными элементами:
- резистора,
- индуктора,
- конденсатора.
Название RLC связано с тем, что эти буквы являются обычными символами электрических элементов: сопротивления, индуктивности и емкости.
Векторная диаграмма последовательной RLC-цепи представлена в одном из трех вариантов:
- индуктивном,
- емкостном,
- активном.
В последнем варианте при нулевом сдвиге фаз, равенстве индуктивного и емкостного сопротивлений возникает резонанс напряжений.
Электрический резонансВ природе бывают резонанс токов и резонанс напряжений. Наблюдаются они в цепи с параллельным и последовательным соединением элементов R, L и С. Резонансная частота одинакова для обеих цепей, она находится из условия противоположности сопротивлений реактивных элементов и вычисляется по нижеследующей формуле.
Резонансная частота
Векторные диаграммы практически идентичны, только сигналы отличаются. В последовательном контуре резонируют напряжения, в параллельном – ток. Но если отступиться от резонансной частоты такая симметрия естественно нарушится. В первом случае сопротивление возрастет, во втором – уменьшится.
Резонанс напряжений, достигающих максимальной амплитуды
На картинке ниже представлена векторная диаграмма цепи последовательного контура, где:
- I – вектор общего тока;
- Ul – опережает I на 900;
- UС – отстает от I на 900;
- UR – синфазно I.
Из трех векторов напряжения (Ul, UС, UR) два первых взаимно компенсируют друг друга. Они между собой:
- противоположны по направлению,
- равны по амплитуде,
- отличаются по фазе на пи.
Получается, что напряжение по второму закону Кирхгофа приложено только к резистору. В этот момент:
- импеданс последовательного контура на резонансной частоте минимален и равен просто R;
- так как сопротивление цепи минимальное, то соответственно ток по амплитуде максимальный;
- также приблизительно максимальны напряжения на индуктивности и на емкости.

Если рассматривать отдельно последовательный контур LC, то он даёт нулевое сопротивление на резонансной частоте:
ZL = -ZC
Резонанс напряжений в цепи переменного тока
Важно! Когда установился гармонический режим c резонансной частотой, в контуре происходит следующее: источник обеспечивает установившуюся амплитуду колебаний; мощность источника расходуется лишь на нагрев резистора.
Резонанс токов через реактивные элементы
Диаграмма параллельного контура на той же частоте. Поскольку все элементы соединены параллельно, то диаграмму лучше начать строить с общего напряжения.
- U – вектор общего тока;
- Ic – опережает U на 900;
- IU – отстает от U на 900;
- Ток в резисторе (IR) синфазен общему напряжению.
Поскольку сопротивления реактивности по модулю равны, то и амплитуды токов Ic и Iu:
- одинаковы;
- достигают максимальной амплитуды.

Получается, что по первому закону Кирхгофа IR равен току источника. Другими словами, ток источника течет только через резистор.
Если рассматривать отдельно параллельный контур LC, то на резонансной частоте его сопротивление бесконечно большое:
ZL = ZC.
Когда установится гармонический режим c резонансной частотой, в контуре происходит следующее:
- источник обеспечивает установившуюся амплитуду колебаний;
- мощность источника тока расходуется лишь на пополнение потерь в активном сопротивлении.
Резонанс токов
Двойственность RLC-контуровТаким образом, можно сделать сравнительный вывод:
- У последовательной RLC цепи импеданс минимален на резонансной частоте и равен активному сопротивлению контура;
- У параллельной RLC цепи импеданс максимален на резонансной частоте и равен так называемому сопротивлению утечки, фактически тоже активному сопротивлению контура.

Для того чтобы предуготовить условия для резонанса тока или напряжения, требуется проверить электрическую цепь с целью предопределения ее комплексного сопротивления или проводимости. Помимо этого, её мнимую часть необходимо приравнять к нулю.
Для информации. Напряжения в последовательной цепи ведут себя очень похоже токам параллельной цепи на резонансной частоте, в этом проявляется двойственность RLC-контуров.
Резонанс в цепи переменного тока
Применение резонансного явленияХорошим примером применения резонансного явления может служить электрический резонансный трансформатор, разработанный изобретателем Николой Тесла ещё в 1891 году. Тесла проводил эксперименты с различными конфигурациями, состоящими в сочетании из двух, а иногда трех резонансных электрических цепей.
Для информации. Термин «катушки Теслы» применяются к ряду высоковольтных резонансных трансформаторов. Устройства используются для получения высокого напряжения, низкого тока, высокой частоты переменного тока.
В то время как обычный трансформатор предназначен для эффективной передачи энергии с первичной на вторичную обмотку, резонансный трансформатор предназначен для временного хранения электрической энергии. Устройство управляет воздушным сердечником резонансно настроенного трансформатора для получения высоких напряжений при малых токах. Каждая обмотка имеет емкость и функционирует как резонансный контур.
Чтобы произвести наибольшее выходное напряжение, первичный и вторичный контуры настроены в резонанс друг с другом. Оригинальные схемы изобретателя применяются как простые разрядники для возбуждения колебаний с помощью настроенных трансформаторов. В более сложных конструкциях используют транзисторные или тиристорные выключатели.
Для информации. Трансформатор Теслы основан на использовании резонансных стоячих электромагнитных волн в катушках. Своеобразный дизайн катушки продиктован необходимостью достигнуть низкого уровня резистивных потерь энергии (высокая добротность) на высоких частотах, что приводит к увеличению вторичных напряжений.
Резонанс в электрической цепи
Электрический резонанс – одно из самых распространенных в мире физических явлений, без которого не было бы TV, диагностических мед. аппаратов. Одни из самых полезных видов резонанса в электрической цепи – это резонанс токов и резонанс напряжений.
Видео Оцените статью:Резонанс напряжений и резонанс токов
В физике резонансом называется явление, при котором в колебательном контуре частота свободных колебаний совпадает с частотой вынужденных колебаний. В электричестве аналогом колебательного контура служит цепь, состоящая из сопротивления, ёмкости и индуктивности. В зависимости от того как они соединены различают резонанс напряжений и резонанс токов.
Резонанс напряжений
Резонанс напряжений возникает в последовательной RLC-цепи.
Условием возникновения резонанса является равенство частоты источника питания резонансной частоте w=wр, а следовательно и индуктивного и емкостного сопротивлений xL=xC. Так как они противоположны по знаку, то в результате реактивное сопротивление будет равно нулю. Напряжения на катушке UL и на конденсаторе UC будет противоположны по фазе и компенсировать друг друга. Полное сопротивление цепи при этом будет равно активному сопротивлению R, что в свою очередь вызывает увеличение тока в цепи, а следовательно и напряжение на элементах.
При резонансе напряжения UC и UL могут быть намного больше, чем напряжение источника, что опасно для цепи.
С увеличением частоты сопротивление катушки увеличивается, а конденсатора уменьшается. В момент времени, когда частота источника будет равна резонансной, они будут равны, а полное сопротивление цепи Z будет наименьшим. Следовательно, ток в цепи будет максимальным.
Из условия равенства индуктивного и емкостного сопротивлений найдем резонансную частоту
Исходя из записанного уравнения, можно сделать вывод, что резонанса в колебательном контуре можно добиться изменением частоты тока источника (частота вынужденных колебаний) или изменением параметров катушки L и конденсатора C.
Следует знать, что в последовательной RLC-цепи, обмен энергией между катушкой и конденсатором осуществляется через источник питания.
Резонанс токов
Резонанс токов возникает в цепи с параллельно соединёнными катушкой резистором и конденсатором.
Условием возникновения резонанса токов является равенство частоты источника резонансной частоте w=wр, следовательно проводимости BL=BC. То есть при резонансе токов, ёмкостная и индуктивная проводимости равны.
Для наглядности графика, на время отвлечёмся от проводимости и перейдём к сопротивлению. При увеличении частоты полное сопротивление цепи растёт, а ток уменьшается. В момент, когда частота равна резонансной, сопротивление Z максимально, следовательно, ток в цепи принимает наименьшее значение и равен активной составляющей.
Выразим резонансную частоту
Как видно из выражения, резонансная частота определяется, как и в случае с резонансом напряжений.
Явление резонанса может носить как положительный, так и отрицательный характер. Например, любой радиоприемник имеет в своей основе колебательный контур, который с помощью изменения индуктивности или емкости настраивают на нужную радиоволну. С другой стороны, явление резонанса может привести к скачкам напряжения или тока в цепи, что в свою очередь приводит к аварии.
Резонанс в электрической цепи
Начнём с основных определений.
Определение 1
Резонанс — это явление, при котором частота колебаний какой-либо системы увеличивается колебаниями внешней силы.
Вынужденные колебания, источником которых является внешняя сила, увеличивают даже те колебания, амплитуда которых имеет довольно небольшие значения. Максимальный резонанс с наибольшей амплитудой возможен именно при совпадении частот внешнего воздействия и рассматриваемой системы.
Примером резонанса является раскачивание моста ротой солдат. Частота шага солдат, являющаяся по отношению к мосту примером вынужденных колебаний, при этом синхронизирована и может совпасть с собственной частотой колебаний моста. В результате мост может разрушиться.
Электрический резонанс в физике считается одним из распространенных в мире физических явлений, без которого было бы невозможным, например, телевидение и диагностика с помощью медицинских аппаратов.
Одними из наиболее полезных видов резонанса в электрической цепи являются:
- резонанс токов;
- резонанс напряжений.
Возникновение резонанса в электрической цепи
Замечание 1
Возникновению резонанса в электрической цепи способствует резкое увеличение амплитуды стационарных собственных колебаний системы при условии совпадения частоты внешней стороны воздействия и соответствующей колебательной резонансной частоты системы.
Схема $RLC$ представляет электрическую цепь с соединенными последовательным или параллельным образом элементами (резистора, индуктора, конденсатора). Название $RLC$ состоит из простых символов электрических элементов: сопротивления, емкости, индуктивности.
Векторная диаграмма последовательной $RLC$-цепи представлена в одной из трех вариаций:
Готовые работы на аналогичную тему
- емкостной;
- активной;
- индуктивной.
В последней вариации резонанс напряжений возникает при условии нулевого сдвига фаз, и совпадении значений индуктивного и емкостного сопротивлений.
Резонанс напряжений
При последовательном соединении активного элемента $r$, емкостного $С$ и индуктивного $L$ в цепях переменного тока может возникать такое физическое явление, как резонанс напряжений. Колебания источника напряжения в этом случае будут равны по частоте колебаниям контура. При этом известна как полезность (например, в радиотехнике) этого явления, так и негативные последствия (для электрических установок большой мощности), например, при резком скачке напряжения в системах возможно возникновение неисправности или даже пожара.2L}$
Частота $w_0$ считается резонансной. При условии неизменности в цепи и напряжения, и активного сопротивления $r$, сила тока при резонансе напряжения в ней окажется максимальной и равной:
$\frac{U}{r}$
Это предполагает полную независимость силы тока от реактивного сопротивления цепи. В ситуации, когда реактивные сопротивления $XC = XL$ по своему значению будут превосходить активное сопротивление $r$, на зажимах катушки и конденсатора появится напряжение, существенно превосходящее напряжение на зажимах цепи.
Кратность превышения на зажимах емкостного и индуктивного элемента напряжения по отношению к сети определяется выражением:
$Q = \frac{U_c0}{U}$
Величина $Q$ характеризует резонансные свойства контура, называясь при этом добротностью контура. Также резонансные свойства характеризуются величиной $\frac{1}{Q}$, то есть — затуханием контура.
Резонанс токов через реактивные элементы
Резонанс токов появляется в электроцепях цепях переменного тока при условии параллельного соединения ветвей с разнохарактерными реактивными сопротивлениями. В резонансном режиме токов реактивная индуктивная проводимость цепи будет равнозначной ее собственной реактивной емкостной проводимости, т.е. $BL = BC$.
Колебания контура, частота которых имеет определённое значение, в данном случае совпадают по частоте с источником напряжения.
Простейшей электроцепью, в которой мы наблюдаем резонанс токов, считается цепь с параллельным соединением конденсатора с катушкой индуктивности.
Поскольку сопротивления реактивности равнозначны по модулю, амплитуды токов $I_c$ и $I_u$ будут одинаковыми и смогут достигать максимальной амплитуды. На основании первого закона Кирхгофа $IR$ равен току источника. Ток источника, иными словами, протекает только через резистор. При рассмотрении отдельного параллельного контура $LC$, на резонансной частоте его сопротивление оказывается бесконечно большим: $ZL = ZC$. При установлении гармонического режима с резонансной частотой, в контуре наблюдается обеспечение источником установившейся определенной амплитуды колебаний, а мощность источника тока при этом расходуется исключительно на пополнение потерь в активном сопротивлении.
Таким образом, у последовательной $RLC$ цепи импеданс оказывается минимальным на резонансной частоте и равным активному сопротивлению контура. В то же время, у параллельной $RLC$ цепи импеданс максимальный на резонансной частоте и считается равным сопротивлению утечки, фактически также активному сопротивлению контура. С целью обеспечения условий для резонанса силы тока или напряжения, требуется проверка электрической цепи для предопределения ее комплексного сопротивления или проводимости. Помимо этого, её мнимая часть должна приравниваться к нулю.
Применение явления резонанса
Хороший пример использования резонансного явления представляет электрический резонансный трансформатор, разработанный Николой Тесла ещё в 1891 году. Ученый проводил эксперименты на разных конфигурациях, состоящих в сочетании из двух, а зачастую и трех резонансных электроцепей.
Замечание 2
Термин «катушки Теслы» применяют к высоковольтным резонансным трансформаторам. Устройства используют при получении высокого напряжения, частоты переменного тока. Обычный трансформатор необходим для эффективной передачи энергии с первичной на вторичную обмотку, резонансный используется для временного хранения электроэнергии.
Устройство отвечает за управление воздушным сердечником настроенного резонансно трансформатора с целью получения высоких напряжений при малых значениях силы токов. Каждая обмотка обладает емкостью и функционирует в качестве резонансного контура. Для произведения наибольшего выходного напряжения первичный и вторичный контуры настраивают в резонанс друг с другом.
физический смысл и применение, формулы и способы расчета
Физическое явление параллельного резонанса широко применяется в радиоэлектронике. Для построения колебательных контуров, состоящих из активного и реактивного сопротивлений, следует собрать цепь из сопротивления, емкости, а также индуктивности. Для этого необходимо разобраться в назначении резонанса, нахождении сопротивления радиокомпонентов, его основном применении в радиотехнике, а также условии его возникновения.
Общие сведения
Электрическим сопротивлением проводника является свойство проводить электрический ток. Для построения и расчета колебательного контура необходимо знать способы нахождения активного и реактивного сопротивлений. Сопротивление для цепей, питающихся от переменного тока (ЦПТ), бывает следующих видов: активное, реактивное и полное.
Активным сопротивлением ® является обыкновенный резистор. Реактивное состоит из следующих типов нагрузки: индуктивное и емкостное. Индуктивное (Xl) — сопротивление катушки индуктивности в цепи переменного тока, а емкостное (Xc) определяется наличием емкости в цепи (конденсатора).
При сложении активного и реактивного сопротивлений получается полное сопротивление участка электрической цепи, которое обозначается литерой Z.
Активное сопротивление
Активным сопротивлением в ЦПТ называется наличие любой нереактивной нагрузки. Его можно рассчитать следующими способами: при помощи измерения величины сопротивления и расчетным методом. Для измерения R применяется прибор, который называется омметром. Омметр входит в состав комбинированных приборов измерения электрических величин, которые называются мультиметрами. Он подключается параллельно нагрузке, причем для проведения измерений следует выключить электрическую цепь, поскольку наличие тока приведет прибор к выходу из строя.
Существует еще один способ, который является расчетным, однако он требует знаний в области физики. При вычислении величины R следует произвести измерения силы тока и напряжения, а точнее, их амплитудных значений (Uм и Iм соответственно). Это возможно сделать при помощи соответствующих приборов.
Для измерения величины напряжения применяется вольтметр, а силу тока можно измерить при помощи амперметра. Кроме того, эти приборы измеряют только действующие значения напряжения (Uд) и силы тока (Iд). Для расчета амплитудных значений следует воспользоваться следующими формулами:
- Uм = Uд * sqrt (2).
- Iм = Iд * sqrt (2).
Для расчета R, которое можно найти, используя закон Ома для участка цепи (Iм = Uм / R): R = Uм / Iм. Воспользовавшись соотношениями зависимостей амплитудных значений от действующих, возможно рассчитать R: R = Uд * sqrt (2) / Iд * sqrt (2) = Uд / Iд. На практике применяют способ измерения сопротивления омметром.
Другие виды нагрузок
При наличии в ЦПТ катушки индуктивности возникает Xl, которую необходимо только рассчитывать. Индуктивное сопротивление рассчитывается по формуле, для которой необходимы циклическая частота (w) и индуктивность катушки (L): Xl = w * L.
Циклическая частота рассчитывается по следующей формуле, для которой необходимо только знать частоту переменного тока (f) и число ПИ (3,1416): w = 2 * 3,1416 * f. Индуктивность катушки рассчитывается, исходя из значений диаметра катушки (D в мм), числа витков (n) и длины намотки (l): L = (sqr (D/10) * sqr (n)) / (4,5 * D + 10 * l). Если подставить в формулу расчета индуктивного сопротивления все соотношения, то получается: Xl = 2 * 3,1416 * f * (sqr (D/10) * sqr (n)) / (4,5 * D + 10 * l).
Если в ЦПТ присутствует конденсатор с емкостью C, то добавляется еще и емкостное сопротивление — Xl, которое рассчитывается по следующей формуле: Xc = 1 / (w * C) = 1 / (2 * 3,1416 * f * C). Полное сопротивление в ЦПТ обозначается литерой Z и рассчитывается по формуле: Z = sqrt [sqr® +sqr (Xс — Xl)]. Если подставить в формулу полного сопротивления соотношения, по которым находятся R, Xl и Xc, то получается следующая формула: Z = sqrt [sqr (Uд / Iд) +sqr ((1 / (2 * 3,1416 * f * C)) — (2 * 3,1416 * f * (sqr (D/10) * sqr (n)) / (4,5 * D + 10 * l))]. Для упрощения вычисления можно рассчитать отдельно значения R, Xc и Xl.
Понятие о резонансе
Резонанс в цепи переменного тока происходит при образовании резонансной частоты, при которой некоторые сопротивления компенсируют друг друга. Основными признаками резонанса являются:
- Совпадения по фазе U и I в цепи.
- Значение активного и полного сопротивлений совпадают: Z = R.
- Сила тока является максимальной.
- Падение величины U на R равно U, которое приложено к контуру LC.
- Выполняется равенство падений U на индуктивности и емкости, а также противоположность по фазе и больше приложенного напряжения: Ul > U, Ul = I * Xl = I * Xc и U = I * R.
В последнем случае коэффициент усиления по напряжению рассчитываются следующим способом: Ku = Ul / U = sqrt (L/C) / R = p / R. Этот коэффициент называется добротностью контура и обозначается литерой Q. Волновое сопротивление контура обозначается p, которое вычисляется по формуле: p = sqrt (L/C).
Резонанс в ЦПТ бывает двух видов: последовательный и параллельный. Для последовательного резонанса условием является минимальное сопротивление и нулевая фаза. В основном он применяется в схемах с реактивными составляющими L и C. При параллельном типе резонанса происходит равенство емкостных и индуктивных сопротивлений, которые компенсируют друг друга. Этот тип соединения должен постоянно быть равен расчетной величине. Он получил широкое применение, благодаря резкому минимуму импеданса. Импеданс — полное сопротивление в цепи переменного тока, который обозначается Z.
Контур является схемой, в которой подключены параллельно или последовательно следующие элементы: резистор, катушка индуктивности и конденсатор.
Эта схема образует осциллятор для тока с гармонической составляющей. Наличие сопротивления в схеме приводит к затуханию и уменьшает резонансную пиковую частоту.
Во всей силовой радиоэлектронике применяются колебательные контуры. Примером его является силовой трансформатор. Кроме того, контур используется для настройки телевизоров, согласования антенн. Возможно применение в качестве полосового и режекторного фильтров, которые применяются в датчиках для распределения низких и высоких частот. Эффект резонанса применяется и в медицине при микротоковой терапии, и при проведении биорезонансной диагностики.
Случаи для тока и напряжения
В радиоэлектронике применяется резонанс напряжений и токов. Они отличаются друг от друга и применяются в определенных случаях. Резонанс напряжений возникает при последовательном соединении в RLC-цепи (схема 1):
Схема 1 — Последовательное соединение элементов.
Основным условием возникновения резонанса является равенство частот источника питания и колебательного контура. Кроме того, Xc = Xl, они являются противоположными величинами (по знаку) и равны 0. Напряжения Uc и Ul противоположны по фазам и компенсируют друг друга, следовательно, Z = R. В результате этого происходит увеличение тока, так как при уменьшении сопротивления по закону Ома происходит увеличение I. Вырастает не только I, но и значения U на элементах схемы. При резонансе значения напряжений на конденсаторе и катушке индуктивности могут быть больше относительно напряжения источника питания.
При увеличении частоты значение Xl увеличивается, а Xc — уменьшается. При равенстве частот резонансной и источника питания значение Z будет уменьшаться. Резонансная частота находится по формуле: w = sqrt (1 / (L * C)). Резонанс в ЦПТ зависит от следующих величин: частоты источника питания — f, параметров L и C. Обмен электрической энергией осуществляется между катушкой и конденсатором через источник питания.
Резонанс токов в цепи переменного тока возникает при параллельном включении активных и реактивных нагрузок. На схеме 2 изображен контур с параллельным соединением:
Схема 2 — Параллельное соединение в RLC-контуре.
В этом случае резонанс возникает при равенстве частот источника питания и резонансной, а также равенства проводимостей конденсатора (Bc) и катушки (Bl). Проводимость — величина, обратная сопротивлению. При увеличении частоты источника питания происходит рост полного сопротивления, при котором ток уменьшается. В результате этого, ток уменьшается и равняется активной составляющей. Для определения резонансной частоты следует воспользоваться алгоритмом нахождения этой величины:
- Удельные проводимости для резистора, катушки индуктивности и конденсатора: G = 1 / R, Bl = 1 / (w * L) и Bc = w * C соответственно.
- 1 / (w * L) = w * C.
- Резонансная частота вычисляется по формуле: w = sqrt (1 / (L * C)).
Явление резонанса может привести к выходу из строя элементов схемы, приборов или устройств. Для того чтобы избежать этого, необходимо производить точные расчеты колебательных контуров.
Расчет параллельного контура
Необходимо сделать параллельный контур, частота резонанса которого равна 1,5 МГц. Для его изготовления нужно осуществить расчет, исходя из которого возможно будет его изготовить. Рассчитывать контур следует точно, поскольку любая неточность может привести к негативным последствиям. Основной задачей является расчет нужных индуктивности катушки и емкости конденсатора. Расчет осуществляется по следующему алгоритму:
- Вычислить необходимую индуктивность в мкГн при заданной емкости и частоте: L = sqr (159,12 / f) / C.
- Рассчитать количество витков (n) и диаметр каркаса (d в мм) катушки: n = 32 * sqrt (L / d).
Пусть С = 2000 пФ, тогда L = sqr (159,12 / 2) / 2000 = 5,6 мкГн. Количество витков для катушки с d = 3 мм: n = 32 * sqr (5,6 / 3) = 112.
Этот метод является приближенным, поскольку не учитывается межвитковое пространство катушки. Радиолюбители часто применяют уже готовые катушки, имеющие длину 15 мм с диаметром d = 3 мм. Вычислить можно, используя другую формулу: n = 8,5 * sqrt (L) = 8,5 * 2,3664 = 21.
Таким образом, явление резонанса применяется при построении различной радиоаппаратуры и требует выполнения верных расчетов, поскольку даже при незначительных ошибках могут выйти из строя дорогостоящие детали.
Резонансв цепи переменного тока — University Physics Volume 2
Цели обучения
К концу раздела вы сможете:
- Определите пиковую резонансную угловую частоту переменного тока для цепи RLC
- Объясните ширину кривой зависимости средней мощности от угловой частоты и ее значение, используя такие термины, как полоса пропускания и коэффициент качества
В последовательной цепи RLC (рисунок), амплитуда тока, из (рисунок),
Если мы можем изменять частоту генератора переменного тока, сохраняя при этом постоянную амплитуду его выходного напряжения, то ток изменится соответствующим образом.График зависимости показан на (Рисунок).
На резонансной частоте цепи RLC амплитуда тока находится на максимальном значении.В «Колебаниях» мы встретили похожий график, на котором амплитуда затухающего гармонического осциллятора была построена в зависимости от угловой частоты синусоидальной движущей силы (см. «Принудительные колебания»). Это сходство — больше, чем просто совпадение, как было показано ранее применением правила петли Кирхгофа к схеме (рисунок).Это дает
или
, где мы заменили dq (t) / dt на и (t). Сравнение (Рисунок) и, из «Колебаний», «Затухающие колебания» для затухающего гармонического движения ясно демонстрирует, что управляемая последовательная цепь RLC является электрическим аналогом управляемого затухающего гармонического генератора.
Резонансная частота цепи RLC — это частота, на которой амплитуда тока максимальна, и цепь будет колебаться, если не будет управляться источником напряжения.При осмотре это соответствует угловой частоте, при которой импеданс Z на (Рисунок) является минимальным, или когда
и
Это резонансная угловая частота контура. Подставляя в (Рисунок), (Рисунок) и (Рисунок), мы находим, что при резонансе
Следовательно, в резонансе цепь RLC является чисто резистивной, с приложенной ЭДС и током в фазе.
Что происходит с мощностью при резонансе? (Рисунок) показывает, как средняя мощность, передаваемая от генератора переменного тока комбинации RLC , изменяется в зависимости от частоты.Кроме того, достигает максимума, когда значение Z , которое зависит от частоты, является минимальным, то есть когда Таким образом, при резонансе средняя выходная мощность источника в последовательной цепи RLC является максимальной. Из (Рисунок) это максимум
(рисунок) — типичный график зависимости максимальной выходной мощности. Ширина полосы резонансного пика определяется как диапазон угловых частот, в котором средняя мощность превышает половину максимального значения. Резкость пика описывается безразмерной величиной, известной как добротность Q схема.По определению
где — резонансная угловая частота. Высокое значение Q указывает на резкий пик резонанса. Мы можем дать Q по параметрам схемы как
Как и ток, средняя мощность, передаваемая от генератора переменного тока к цепи RLC , достигает пика на резонансной частоте.
Резонансные цепи обычно используются для пропуска или отклонения выбранных частотных диапазонов. Это делается путем регулировки значения одного из элементов и, следовательно, «настройки» схемы на определенную резонансную частоту.Например, в радиоприемнике приемник настраивается на желаемую станцию путем регулировки резонансной частоты его схемы в соответствии с частотой станции. Если схема настройки имеет высокое значение Q , она будет иметь небольшую полосу пропускания, поэтому сигналы от других станций на частотах, даже немного отличающихся от резонансной частоты, сталкиваются с высоким импедансом и не проходят через схему. Сотовые телефоны работают аналогичным образом, передавая сигналы с частотой около 1 ГГц, которые настраиваются цепью индуктивности и конденсатора.Одним из наиболее распространенных применений конденсаторов является их использование в цепях синхронизации переменного тока, основанное на достижении резонансной частоты. Металлоискатель также использует сдвиг резонансной частоты при обнаружении металлов ((Рисунок)).
Когда металлоискатель приближается к куску металла, самоиндукция одной из его катушек изменяется. Это вызывает сдвиг резонансной частоты цепи, содержащей катушку. Этот сдвиг фиксируется схемой и передается дайверу через наушники.(кредит: модификация работы Эрика Липпмана, ВМС США)
Резонанс в цепи серии RLC (a) Какова резонансная частота цепи (рисунок)? (b) Если генератор переменного тока настроен на эту частоту без изменения амплитуды выходного напряжения, какова амплитуда тока?
СтратегияРезонансная частота для цепи RLC рассчитывается по (рисунок), которая получается из баланса между реактивными сопротивлениями конденсатора и катушки индуктивности. {- 3} \ phantom {\ rule {0.{2} \ phantom {\ rule {0.2em} {0ex}} \ text {Hz} \ text {.} \ Hfill \ end {array} *** Сообщение об ошибке: В преамбуле выравнивания вставлен пропущенный #. начальный текст: $ \ begin {array} {} Не указан $ вставлен. начальный текст: $ \ begin {array} {} \\ \\ \ hfill {f} _ Не указан $ вставлен. начальный текст: $ \ begin {array} {} \\ \\ \ hfill {f} _ {0} & Вкладка «Дополнительное выравнивание» изменена на \ cr. начальный текст: $ \ begin {array} {} \\ \\ \ hfill {f} _ {0} & Не указан $ вставлен. начальный текст: … ay} {} \\ \\ \ hfill {f} _ {0} & = \ frac {1} {2 \ pi} Extra}, или забытый $.начальный текст: … ay} {} \\ \\ \ hfill {f} _ {0} & = \ frac {1} {2 \ pi} Ошибка пакета inputenc: символ Юникода × (U + 00D7) начальный текст: … \ phantom {\ rule {0.2em} {0ex}} \ text {F} \ right)} Ошибка пакета inputenc: символ Юникода × (U + 00D7) начальный текст: … \ phantom {\ rule {0.2em} {0ex}} \ text {F} \ right)} Отсутствует} вставлено. начальный текст: … le {0.2em} {0ex}} \ text {F} \ right)}} \ hfill \\ &
Значение Если бы цепь не была настроена на резонансную частоту, нам потребовалось бы полное сопротивление всей цепи для расчета тока.
Проверьте свое понимание Что происходит с резонансной частотой последовательной цепи RLC , когда следующие величины увеличиваются в 4 раза: (а) емкость, (б) самоиндукция и (в) сопротивление?
а. вдвое; б. вдвое; c. тот же
Проверьте свое понимание Резонансная угловая частота цепи серии RLC равна. Источник переменного тока, работающий на этой частоте, передает в цепь среднюю мощность в.Сопротивление цепи: Напишите выражение для ЭДС источника.
Сводка
- На резонансной частоте индуктивное реактивное сопротивление равно емкостному реактивному сопротивлению.
- График зависимости средней мощности от угловой частоты для цепи RLC имеет пик, расположенный на резонансной частоте; резкость или ширина пика называется полосой пропускания.
- Полоса пропускания связана с безразмерной величиной, называемой коэффициентом качества.Высокое значение добротности — это острый или узкий пик.
Проблемы
(a) Рассчитайте резонансную угловую частоту последовательной цепи RLC , для которой, и (b) Если R изменится на, что произойдет с резонансной угловой частотой?
Резонансная частота последовательной цепи RLC равна. Если самоиндукция в цепи составляет 5,0 мГн, какова ее емкость?
(a) Какова резонансная частота цепи серии RLC с, и? (б) Какое сопротивление цепи при резонансе?
Для последовательной цепи RLC ,, и (a) Если к цепи подключен источник переменного тока переменной частоты, на какой частоте максимальная мощность рассеивается в резисторе? б) Каков коэффициент качества схемы?
Источник переменного тока с амплитудой напряжения 100 В и переменной частотой f управляет последовательной цепью RLC с, и (a) График зависимости тока через резистор от частоты f .(b) Используйте график, чтобы определить резонансную частоту контура.
(a) Какова резонансная частота последовательно соединенных резистора, конденсатора и катушки индуктивности, если, и? (b) Если эта комбинация подключена к источнику 100 В, работающему на резонансной частоте, какова выходная мощность источника? (c) Что такое Q схемы? (d) Какова полоса пропускания цепи?
а. 50 Гц; б. 50 Вт; c. 6,32; d. 50 рад / с
Предположим, катушка имеет собственную индуктивность 20.0 H и сопротивление. Какая (а) емкость и (б) сопротивление должны быть соединены последовательно с катушкой, чтобы создать цепь с резонансной частотой 100 Гц и Q равной 10?
Генератор переменного тока подключен к устройству, внутренние схемы которого неизвестны. Мы знаем только ток и напряжение вне устройства, как показано ниже. Что вы можете сделать на основании предоставленной информации об электрической природе устройства и его потребляемой мощности?
Реактивное сопротивление конденсатора больше, чем реактивное сопротивление катушки индуктивности, потому что ток опережает напряжение.Потребляемая мощность 30 Вт.
Глоссарий
- полоса пропускания
- диапазон угловых частот, в которых средняя мощность больше половины максимального значения средней мощности
- добротность
- безразмерная величина, описывающая резкость пика полосы пропускания; высокая добротность — острый или узкий резонансный пик
- резонансная частота
- частота, при которой амплитуда тока максимальна, и цепь будет колебаться, если не будет управляться источником напряжения
12.5 Резонанс в цепи переменного тока — Введение в электричество, магнетизм и схемы
ЗАДАЧИ ОБУЧЕНИЯ
К концу раздела вы сможете:
- Определите пиковую резонансную угловую частоту переменного тока для цепи RLC
- Объясните ширину кривой зависимости средней мощности от угловой частоты и ее значение, используя такие термины, как полоса пропускания и коэффициент качества
В последовательной цепи, показанной на рисунке 12.3.1, амплитуда тока определяется уравнением 12.3,2,
(12.5.1)
Если мы можем изменять частоту генератора переменного тока, сохраняя при этом постоянную амплитуду его выходного напряжения, то ток изменится соответствующим образом. График зависимости показан на рисунке 12.5.1.
(рисунок 12.5.1)
Рисунок 12.5.1 На резонансной частоте цепи амплитуда тока имеет максимальное значение.Рисунок 12.5.1 имеет вид, аналогичный графику изменения амплитуды затухающего гармонического осциллятора в зависимости от угловой частоты синусоидальной движущей силы.Это сходство — больше, чем просто совпадение, как показывает применение правила петли Кирхгофа к схеме на рис. 12.3.1. Это дает
(12.5.2)
или
, где мы заменили уравнение 12.5.2, имеет общую форму дифференциального уравнения для затухающего гармонического движения, демонстрируя, что управляемая последовательная цепь является электрическим аналогом управляемого затухающего гармонического генератора.
Резонансная частота цепи — это частота, на которой амплитуда тока максимальна, и цепь будет колебаться, если не будет управляться источником напряжения.При осмотре это соответствует угловой частоте, при которой полное сопротивление в уравнении 12.5.1 является минимальным, или когда
и
(12.5.3)
Это резонансная угловая частота контура. Подставляя ω0ω0 в уравнения 12.3.1, 12.3.2 и 12.3.3, мы находим, что при резонансе
Следовательно, в резонансе цепь является чисто резистивной, с приложенной ЭДС и током в фазе.
Что происходит с мощностью при резонансе? Уравнение 12.4.3 говорит нам, как средняя мощность, передаваемая от генератора переменного тока к комбинации, изменяется в зависимости от частоты. Кроме того, достигает максимума, когда, зависящее от частоты, является минимумом, то есть когда и Таким образом, при резонансе средняя выходная мощность источника в последовательной цепи является максимальной. Из уравнения 12.4.3 этот максимум составляет
.Рисунок 12.5.2 представляет собой типичный график зависимости максимальной выходной мощности.Ширина полосы резонансного пика определяется как диапазон угловых частот, в котором средняя мощность превышает половину максимального значения. Резкость пика описывается безразмерной величиной, известной как коэффициент качества схема. По определению
(12.5.4)
где — резонансная угловая частота. Высокий уровень указывает на резкий пик резонанса. В параметрах схемы мы можем дать
(12.5.5)
(рисунок 12.5.2)
Рисунок 12.5.2 Как и в случае с током, средняя мощность, передаваемая от генератора переменного тока в цепь, достигает пика на резонансной частоте.Резонансные цепи обычно используются для пропуска или отклонения выбранных частотных диапазонов. Это делается путем регулировки значения одного из элементов и, следовательно, «настройки» схемы на определенную резонансную частоту. Например, в радиоприемнике приемник настраивается на желаемую станцию путем регулировки резонансной частоты его схемы в соответствии с частотой станции.Если схема настройки имеет высокий уровень, она будет иметь небольшую полосу пропускания, поэтому сигналы от других станций на частотах, даже немного отличающихся от резонансной частоты, сталкиваются с высоким импедансом и не проходят через схему. Сотовые телефоны работают аналогичным образом, передавая сигналы от окружающих, которые настраиваются цепью индуктивности и конденсатора. Одним из наиболее распространенных применений конденсаторов является их использование в цепях синхронизации переменного тока, основанное на достижении резонансной частоты. Металлоискатель также использует сдвиг резонансной частоты при обнаружении металлов (Рисунок 12.5.3).
(рисунок 12.5.3)
Рисунок 12.5.3 Когда металлоискатель приближается к куску металла, самоиндукция одной из его катушек изменяется. Это вызывает сдвиг резонансной частоты цепи, содержащей катушку. Этот сдвиг фиксируется схемой и передается дайверу через наушники.ПРИМЕР 12.5.1
Резонанс в последовательной цепи
(а) Какова резонансная частота цепи из Примера 12.2.1? (b) Если генератор переменного тока настроен на эту частоту без изменения амплитуды выходного напряжения, какова амплитуда тока?
Стратегия
Резонансная частота цепи рассчитывается по уравнению 12.5.3, которое получается из баланса между реактивными сопротивлениями конденсатора и катушки индуктивности. Поскольку цепь находится в резонансе, сопротивление равно сопротивлению резистора. Затем максимальный ток рассчитывается делением напряжения на сопротивление.
Решение
а.Резонансная частота находится из уравнения 12.5.3:
.г. В резонансе сопротивление цепи чисто резистивное, а амплитуда тока равна
.Значение
Если бы цепь не была настроена на резонансную частоту, нам потребовалось бы полное сопротивление всей цепи для расчета тока.
ПРИМЕР 12.5.2
Передача мощности
в цепи серии
RLC при резонансе(а) Какова резонансная угловая частота контура с и? (b) Если на эту частоту установлен источник переменного тока постоянной амплитуды, какова средняя мощность, передаваемая в цепь? (c) Определите полосу пропускания этой цепи.
Стратегия
Резонансная угловая частота рассчитывается по уравнению 12.5.3. Средняя мощность рассчитывается на основе действующего напряжения и сопротивления в цепи. Добротность рассчитывается по уравнению 12.5.5, зная резонансную частоту. Полоса пропускания рассчитывается по уравнению 12.5.4 и с учетом коэффициента качества.
Решение
а. Резонансная угловая частота
г. На этой частоте средняя мощность, передаваемая в цепь, является максимальной.Это
г. Добротность схемы
Затем находим для пропускной способности
Значение
Если требуется более узкая полоса пропускания, могут помочь более низкое сопротивление или более высокая индуктивность. Однако более низкое сопротивление увеличивает мощность, передаваемую в схему, что может быть нежелательным, в зависимости от максимальной мощности, которая может быть передана.
ПРОВЕРЬТЕ ПОНИМАНИЕ 12.6
ПРОВЕРЬТЕ ПОНИМАНИЕ 12.7
Что происходит с резонансной частотой последовательной цепи, когда следующие величины увеличиваются в раз: (а) емкость, (б) самоиндукция и (в) сопротивление?
ПРОВЕРЬТЕ ПОНИМАНИЕ 12.8
Резонансная угловая частота последовательной цепи: Источник переменного тока, работающий на этой частоте, передает в цепь среднюю мощность в. Сопротивление цепи: Напишите выражение для ЭДС источника.
Candela Citations
Лицензионный контент CC, особая атрибуция
- Загрузите бесплатно по адресу http://cnx.org/contents/[email protected]. Получено с : http://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
Резонансные цепи используются для избирательного реагирования на сигналы заданной частоты при одновременном различении сигналов разных частот.Если характеристика схемы имеет более узкий пик около выбранной частоты, мы говорим, что схема имеет более высокую «избирательность». «Фактор качества» Q, как описано ниже, является мерой этой селективности, и мы говорим о схеме, имеющей «высокую добротность», если она является более узкоселективной.
Поскольку эта ширина оказывается равной Δω = R / L, значение Q также можно выразить как Q — это обычно используемый параметр в электронике, значения которого обычно находятся в диапазоне от Q = 10 до 100 для схемных приложений. | Index AC Circuits Reference |
Видео с вопросом: Резонанс в цепях переменного тока
Расшифровка стенограммы
Схема состоит из резистора, конденсатор и катушка индуктивности, все из которых включены последовательно. Источник переменного напряжения подключен к цепи, и генерируется переменный ток.Как резонансная частота схему изменить, если индуктивность индуктора увеличится? (а) Резонансная частота уменьшается. (б) Резонансная частота увеличивается. (c) Резонансная частота не изменение.
Нам задают вопрос о резонансная частота цепи переменного тока. В частности, для последовательной цепи с резистором, конденсатором и катушкой индуктивности вопрос спрашивает нас, что произойдет если индуктивность индуктора увеличена.Вот схема нашего схема. У нас есть переменное напряжение источник, резистор сопротивления 𝑅, индуктор индуктивности и конденсатор емкости 𝐶. Мы будем использовать символ 𝜔 для угловая частота источника напряжения.
Напомним, что резонанс будет в эта схема, когда разница между индуктивным и емкостным сопротивлениями, что , полное реактивное сопротивление равно нулю.Другими словами, резонанс — это когда индуктивное и емкостное сопротивления равны. У нас также есть формулы, которые связать угловую частоту с реактивным сопротивлением, поскольку индуктивное реактивное сопротивление — это угловая частота умножить на индуктивность и емкостное реактивное сопротивление, разделенное на угловую частоту, умноженное на емкость. Если мы приравняем эти выражения, как будет истинным на резонансной частоте, мы получим, что ничто равно единице делится на ноль, где ноль — резонансная угловая частота.
Если решить это равенство относительно 𝜔 ноль, мы находим, что резонансная угловая частота равна единице, деленной на корень квадратный из индуктивности индуктора, умноженной на емкость конденсатор. Эта формула связывает резонансные частота к индуктивности, поэтому давайте воспользуемся этим, чтобы ответить на наш вопрос. По мере увеличения индуктивности квадратный корень из индуктивности, умноженной на емкость, увеличивается. Итак, знаменатель нашей дроби становится больше, что означает, что значение общей доли становится больше меньше.Но значение этой дроби просто резонансная частота. Так как индуктивность индуктор увеличивается, резонансная частота уменьшается. Интересно, что из нашего формула, что резонансная частота также уменьшится, если мы увеличим емкость конденсатора. Но если мы изменим сопротивление резистора, резонансная частота не изменится.
Резонанс в цепях RLC
Резонанс — это тенденция системы к колебаниям с большей амплитудой на одних частотах, чем на других.Частоты, при которых амплитуда отклика является относительным максимумом, известны как резонансные частоты системы. Чтобы изучить резонанс в цепи RLC, как показано ниже, мы можем увидеть, как цепь ведет себя в зависимости от частоты источника управляющего напряжения. 2}} $,
, где I rms и V rms — действующие значения тока и напряжения, соответственно .Реактивные сопротивления изменяются в зависимости от частоты $ \ nu $, при этом X L большое на высоких частотах и X C большое на низких частотах, определяемое как:
$ X_L = 2 \ pi \ nu L, X_C = \ frac {1} {2 \ pi \ nu C} $.
При некоторой промежуточной частоте $ \ nu_0 $ реактивные сопротивления будут равны и уравновешены, давая Z = R — это минимальное значение для импеданса, а максимальное значение для I действующее значение . Мы можем получить выражение для $ \ nu_0 $, взяв X L = X C . Подстановка определений X L и X C дает:
$ \ nu_0 = \ frac {1} {2 \ pi \ sqrt {LC}} $.
$ \ nu_0 $ — резонансная частота последовательного контура RLC. Это также собственная частота, на которой цепь будет колебаться, если не будет управляться источником напряжения. При $ \ nu_0 $ влияние катушки индуктивности и конденсатора компенсируется, так что Z = R, а I среднеквадратичное значение является максимальным. Резонанс в цепях переменного тока аналогичен механическому резонансу, где резонанс определяется как вынужденные колебания (в данном случае вызванные источником напряжения) на собственной частоте системы.
Приемник в радиостанции представляет собой схему RLC, которая лучше всего генерирует колебания на своем $ \ nu_0 $.Переменный конденсатор часто используется для регулировки резонансной частоты, чтобы получить желаемую частоту и отклонить другие. представляет собой график зависимости тока от частоты, иллюстрирующий резонансный пик I rms при $ \ nu_0 = f_0 $. Две кривые относятся к двум разным схемам, которые различаются только величиной сопротивления в них. Пик ниже и шире для цепи с более высоким сопротивлением. Таким образом, цепи с более высоким сопротивлением не резонируют так сильно, и они не будут такими избирательными, например, в радиоприемнике.
Зависимость тока от частоты
График зависимости тока от частоты для двух цепей серии RLC, различающихся только величиной сопротивления. Оба имеют резонанс при f0, но для более высокого сопротивления он ниже и шире. Источник управляющего переменного напряжения имеет фиксированную амплитуду V0.
Цепи переменного тока серииRLC | Физика
Цели обучения
К концу этого раздела вы сможете:
- Рассчитайте полное сопротивление, фазовый угол, резонансную частоту, мощность, коэффициент мощности, напряжение и / или ток в последовательной цепи RLC.
- Нарисуйте принципиальную схему последовательной цепи RLC.
- Объясните значение резонансной частоты.
Когда один в цепи переменного тока, все катушки индуктивности, конденсаторы и резисторы препятствуют току. Как они себя ведут, когда все три встречаются вместе? Интересно, что их индивидуальные сопротивления в Ом не складываются просто так. Поскольку катушки индуктивности и конденсаторы ведут себя противоположным образом, они частично полностью нейтрализуют влияние друг друга. На рисунке 1 показана последовательная цепь RLC с источником переменного напряжения, поведение которой является предметом этого раздела.Суть анализа цепи RLC — это частотная зависимость X L и X C , а также влияние, которое они оказывают на фазу зависимости напряжения от тока (установлено в предыдущий раздел). Это приводит к частотной зависимости схемы с важными «резонансными» характеристиками, которые лежат в основе многих приложений, таких как радиотюнеры.
Рисунок 1. Последовательная цепь RLC с источником переменного напряжения.
Комбинированный эффект сопротивления R , индуктивного реактивного сопротивления X L и емкостного реактивного сопротивления X C определяется как импеданс , аналог сопротивления переменного тока в цепи постоянного тока. Ток, напряжение и импеданс в цепи RLC связаны версией закона Ома для переменного тока:
[латекс] {I} _ {0} = \ frac {{V} _ {0}} {Z} \ text {или} {I} _ {\ text {rms}} = \ frac {{V} _ {\ text {rms}}} {Z} \\ [/ latex].
Здесь I 0 — пиковый ток, В 0 — пиковое напряжение источника и Z — полное сопротивление цепи. Единицы измерения импеданса — омы, и его влияние на схему такое, как и следовало ожидать: чем больше импеданс, тем меньше ток. Чтобы получить выражение для Z в терминах R , X L и X C , мы теперь рассмотрим, как напряжения на различных компонентах связаны с источником. Напряжение.Эти напряжения обозначены как В R , В L и В C на рисунке 1. Для сохранения заряда ток должен быть одинаковым в каждой части цепи. всегда, так что мы можем сказать, что токи в R , L и C равны и синфазны. Но из предыдущего раздела мы знаем, что напряжение на катушке индуктивности В L опережает ток на одну четверть цикла, напряжение на конденсаторе В C следует за током на единицу. -четвертый цикл, и напряжение на резисторе В R точно совпадает по фазе с током.На рисунке 2 показаны эти отношения на одном графике, а также показано общее напряжение вокруг цепи В = В R + В L + В C , где все четыре напряжения — мгновенные значения. Согласно правилу петли Кирхгофа, полное напряжение вокруг цепи В, также является напряжением источника. {2}} \\ [/ latex],
, который является сопротивлением цепи переменного тока серии RLC .Для схем без резистора принять R = 0; для тех, у кого нет индуктора, возьмите X L = 0; а для тех, у кого нет конденсатора, возьмем X C = 0.
Рис. 2. На этом графике показана зависимость напряжений в цепи RLC от тока. Напряжения на элементах схемы в сумме равняются напряжению источника, которое, как видно, не совпадает по фазе с током.
Пример 1.Расчет импеданса и тока
Последовательная цепь RLC имеет резистор 40,0 Ом, индуктивность 3,00 мГн и конденсатор 5,00 мкФ. (a) Найдите полное сопротивление цепи при 60,0 Гц и 10,0 кГц, отметив, что эти частоты и значения для L и C такие же, как в Примере 1 и Примере 2 из раздела Реактивное, индуктивное и емкостное. (b) Если источник напряжения имеет В действующее значение = 120 В, что будет I среднеквадратичное значение на каждой частоте?
СтратегияДля каждой частоты мы используем [latex] Z = \ sqrt {{R} ^ {2} + \ left ({X} _ {L} — {X} _ {C} \ right) ^ {2}} \ \ [/ latex], чтобы найти импеданс, а затем закон Ома, чтобы найти ток. { 2}} \\ & = & \ sqrt {\ left (40.{2}} \\ & = & 190 \ text {} \ Omega \ text {at} 10.0 \ text {кГц} \ end {array} \\ [/ latex]
Обсуждение для (а)В обоих случаях результат почти такой же, как и наибольшее значение, и импеданс определенно не является суммой отдельных значений. Ясно, что X L доминирует на высокой частоте, а X C доминирует на низкой частоте.
Решение для (b)Текущее значение I среднеквадратичное значение можно найти, используя версию закона Ома по переменному току в уравнении I среднеквадратичное значение = В среднеквадратичное значение / Z :
[латекс] {I} _ {\ text {rms}} = \ frac {{V} _ {\ text {rms}}} {Z} = \ frac {120 \ text {V}} {531 \ text { } \ Omega} = 0.226 \ text {A} \\ [/ latex] при 60,0 Гц
Наконец, на частоте 10,0 кГц мы находим
[латекс] {I} _ {\ text {rms}} = \ frac {{V} _ {\ text {rms}}} {Z} = \ frac {120 \ text {V}} {190 \ text { } \ Omega} = 0,633 \ text {A} \\ [/ latex] при 10,0 кГц
Обсуждение для (а)Ток при 60,0 Гц такой же (с точностью до трех цифр), найденный для одного только конденсатора в Примере 2 из раздела «Реактивное сопротивление, индуктивность и емкость». Конденсатор преобладает на низкой частоте. Ток на частоте 10,0 кГц лишь немного отличается от того, который был обнаружен для одного индуктора в Примере 1 из раздела «Реактивное сопротивление, индуктивный и емкостной».{2}}} \\ [/ latex]
Реактивные сопротивления изменяются в зависимости от частоты: X L большое на высоких частотах и X C большое на низких частотах, как мы видели в трех предыдущих примерах. На некоторой промежуточной частоте f 0 реактивные сопротивления будут равны и уравновешены, давая Z = R — это минимальное значение для импеданса и максимальное значение для I rms результаты .Мы можем получить выражение для f 0 , взяв
X L = X C .
Замена определений X L и X C ,
[латекс] 2 \ pi f_ {0} L = \ frac {1} {2 \ pi f_ {0} C} \\ [/ latex].
Решение этого выражения для f 0 дает
[латекс] {f} _ {0} = \ frac {1} {2 \ pi \ sqrt {LC}} \\ [/ latex],
, где f 0 — резонансная частота последовательной цепи RLC .Это также собственная частота , , при которой цепь будет колебаться, если не будет управляться источником напряжения. При f 0 влияние катушки индуктивности и конденсатора компенсируется, так что Z = R и I среднеквадратичное значение является максимальным.
Резонанс в цепях переменного тока аналогичен механическому резонансу, где резонанс определяется как вынужденное колебание — в данном случае вызванное источником напряжения — на собственной частоте системы.Приемник в радиоприемнике представляет собой схему RLC , которая лучше всего колеблется на ее f 0 . Переменный конденсатор часто используется для настройки f 0 , чтобы получить желаемую частоту и отклонить другие. Фиг.3 представляет собой график зависимости тока от частоты, иллюстрирующий резонансный пик в I среднеквадратичное значение при f 0 . Две кривые относятся к двум разным схемам, которые различаются только величиной сопротивления в них.Пик ниже и шире для цепи с более высоким сопротивлением. Таким образом, цепь с более высоким сопротивлением не так сильно резонирует и, например, не будет такой избирательной в радиоприемнике.
Рис. 3. График зависимости тока от частоты для двух последовательных цепей RLC, различающихся только величиной сопротивления. Оба имеют резонанс при f 0 , но для более высокого сопротивления он ниже и шире. Источник управляющего переменного напряжения имеет фиксированную амплитуду В 0 .
Пример 2. Расчет резонансной частоты и тока
Для той же последовательной цепи RLC , имеющей резистор 40,0 Ом, индуктивность 3,00 мГн и конденсатор 5,00 мкФ: (a) Найдите резонансную частоту. (b) Рассчитайте I среднеквадратичное значение при резонансе, если В среднеквадратичное значение равно 120 В.
Стратегия
Резонансная частота находится с помощью выражения в [latex] {f} _ {0} = \ frac {1} {2 \ pi \ sqrt {LC}} \\ [/ latex].{-6} \ text {F} \ right)}} = 1,30 \ text {кГц} \ end {array} \\ [/ latex]
Обсуждение для (а)Мы видим, что резонансная частота находится между 60,0 Гц и 10,0 кГц, двумя частотами, выбранными в предыдущих примерах. Этого и следовало ожидать, поскольку конденсатор преобладает на низкой частоте, а катушка индуктивности — на высокой. Их эффекты такие же на этой промежуточной частоте.
Решение для (b)Ток определяется законом Ома.В резонансе два реактивных сопротивления равны и компенсируются, так что полное сопротивление равно только сопротивлению. Таким образом,
[латекс] {I} _ {\ text {rms}} = \ frac {{V} _ {\ text {rms}}} {Z} = \ frac {120 \ text {V}} {40.0 \ text { } \ Omega} = 3,00 \ text {A} \\ [/ latex].
Обсуждение для (б)В резонансе ток больше, чем на более высоких и низких частотах, рассмотренных для той же цепи в предыдущем примере.
Питание в цепях переменного тока серии
RLCЕсли ток изменяется с частотой в цепи RLC , то мощность, подаваемая на нее, также зависит от частоты.Но средняя мощность — это не просто ток, умноженный на напряжение, как в чисто резистивных цепях. Как видно на рисунке 2, напряжение и ток в цепи RLC не совпадают по фазе. Существует фазовый угол ϕ между напряжением источника В и током I , который можно найти из
[латекс] \ cos \ varphi = \ frac {R} {Z} \\ [/ latex]
Например, на резонансной частоте или в чисто резистивной цепи Z = R , так что [latex] \ text {cos} \ varphi = 1 \\ [/ latex].Это означает, что ϕ = 0º и что напряжение и ток синфазны, как и ожидалось для резисторов. На других частотах средняя мощность меньше, чем на резонансе. Причина в том, что напряжение и ток не совпадают по фазе, а также потому, что I действующее значение ниже. Тот факт, что напряжение и ток источника не совпадают по фазе, влияет на мощность, подаваемую в цепь. Можно показать, что средняя мощность составляет
[латекс] {P} _ {\ text {ave}} = {I} _ {\ text {rms}} {V} _ {\ text {rms}} \ cos \ varphi \\ [/ latex],
Таким образом, cos ϕ называется коэффициентом мощности , который может находиться в диапазоне от 0 до 1.Например, при разработке эффективного двигателя желательны коэффициенты мощности, близкие к 1. На резонансной частоте cos ϕ = 1.
Пример 3. Расчет коэффициента мощности и мощности
Для той же последовательной цепи RLC , имеющей резистор 40,0 Ом, индуктор 3,00 мГн, конденсатор 5,00 мкФ и источник напряжения с В действующее значение 120 В: (a) Рассчитайте коэффициент мощности и фазу угол для f = 60,0 Гц. (б) Какая средняя мощность при 50.0 Гц? (c) Найдите среднюю мощность на резонансной частоте цепи.
Стратегия и решение для (а)Коэффициент мощности при 60,0 Гц находится из
.[латекс] \ cos \ varphi = \ frac {R} {Z} \\ [/ latex].
Мы знаем, что Z = 531 Ом из Пример 1: Расчет импеданса и тока , так что
[латекс] \ cos \ varphi = \ frac {40.0 \ text {} \ Omega} {531 \ text {} \ Omega} = 0,0753 \ text {at} 60.0 \ text {Hz} \\ [/ latex].
Это небольшое значение указывает на то, что напряжение и ток значительно не совпадают по фазе.{-1} 0,0753 = \ text {85,7º} \ text {at} 60,0 \ text {Hz} \\ [/ latex].
Обсуждение для (а)Фазовый угол близок к 90 °, что согласуется с тем фактом, что конденсатор доминирует в цепи на этой низкой частоте (чистая цепь RC имеет напряжение и ток, сдвинутые по фазе на 90 °).
Стратегия и решение для (b)Средняя мощность при 60,0 Гц —
P ср. = I среднеквадратичное значение В среднеквадратичное значение cos ϕ .
I среднеквадратичное значение оказалось равным 0,226 А в Пример 1: Расчет импеданса и тока . Ввод известных значений дает
P средн. = (0,226 A) (120 В) (0,0753) = 2,04 Вт при 60,0 Гц.
Стратегия и решение для (c)На резонансной частоте мы знаем, что cos ϕ = 1, и I среднеквадратичное значение оказалось равным 6,00 A в Пример 3: Расчет резонансной частоты и тока .Таким образом, P ave = (3,00 A) (120 В) (1) = 360 Вт при резонансе (1,30 кГц)
ОбсуждениеКак ток, так и коэффициент мощности больше в резонансе, производя значительно большую мощность, чем на высоких и низких частотах.
Мощность, подаваемая в цепь переменного тока серии RLC , рассеивается только за счет сопротивления. Катушка индуктивности и конденсатор имеют входную и выходную энергию, но не рассеивают ее из схемы. Скорее они передают энергию туда и обратно друг другу, а резистор рассеивает именно то, что источник напряжения вводит в цепь.Это предполагает отсутствие значительного электромагнитного излучения от катушки индуктивности и конденсатора, например радиоволн. Такое излучение может происходить и даже быть желательным, как мы увидим в следующей главе об электромагнитном излучении, но оно также может быть подавлено, как в случае в этой главе. Схема аналогична колесу автомобиля, движущегося по рифленой дороге, как показано на рисунке 4. Ровные неровности дороги аналогичны источнику напряжения, приводящему колесо в движение вверх и вниз. Амортизатор аналогичен демпфирующему сопротивлению и ограничивающему амплитуду колебаний.Энергия внутри системы перемещается между кинетической (аналогично максимальному току и энергии, запасенной в индукторе) и потенциальной энергией, запасенной в автомобильной пружине (аналогично отсутствию тока и энергии, запасенной в электрическом поле конденсатора). Амплитуда движения колес максимальна, если неровности дороги встречаются с резонансной частотой.
Рис. 4. Вынужденное, но демпфированное движение колеса на автомобильной пружине аналогично цепи переменного тока серии RLC .Амортизатор гасит движение и рассеивает энергию, аналогично сопротивлению в цепи RLC . Масса и пружина определяют резонансную частоту.
Чистая цепь LC с незначительным сопротивлением колеблется на f 0 , той же резонансной частоте, что и цепь RLC . Он может служить эталоном частоты или схемой часов — например, в цифровых наручных часах. При очень маленьком сопротивлении требуется лишь очень небольшая подводимая энергия для поддержания колебаний.Схема аналогична автомобилю без амортизаторов. Как только он начинает колебаться, он некоторое время продолжает работать на своей собственной частоте. На рисунке 5 показана аналогия между цепью LC и грузом на пружине.
Рис. 5. LC-контур аналогичен массе, колеблющейся на пружине без трения и без движущей силы. Энергия движется вперед и назад между катушкой индуктивности и конденсатором, точно так же, как она движется от кинетической к потенциальной в системе масса-пружина.
Исследования PhET: комплект для конструирования цепей (AC + DC), виртуальная лабораторияСоздавайте цепи с конденсаторами, катушками индуктивности, резисторами и источниками переменного или постоянного напряжения и проверяйте их с помощью лабораторных инструментов, таких как вольтметры и амперметры.
Щелкните, чтобы загрузить симуляцию. Запускать на Java.
Сводка раздела
- Аналогом сопротивления переменного тока является сопротивление Z , комбинированное действие резисторов, катушек индуктивности и конденсаторов, определяемое версией закона Ома для переменного тока:
[латекс] {I} _ {0} = \ frac {{V} _ {0}} {Z} \ text {или} {I} _ {\ text {rms}} = \ frac {{V} _ {\ text {rms}}} {Z} \\ [/ latex],
, где I o — пиковый ток, а В o — пиковое напряжение источника.{2}} \\ [/ латекс].
- Резонансная частота f 0 , при которой X L = X C , составляет
[латекс] {f} _ {0} = \ frac {1} {2 \ pi \ sqrt {LC}} \\ [/ latex]
- В цепи переменного тока существует фазовый угол ϕ между напряжением источника В и током I , который можно найти из
[латекс] \ text {cos} \ varphi = \ frac {R} {Z} \\ [/ latex],
- ϕ = 0º для чисто резистивной цепи или цепи RLC в резонансе.
- Средняя мощность, подаваемая в цепь RLC , зависит от фазового угла и определяется выражением
[латекс] {P} _ {\ text {ave}} = {I} _ {\ text {rms}} {V} _ {\ text {rms}} \ cos \ varphi \\ [/ latex],
cos ϕ называется коэффициентом мощности, который находится в диапазоне от 0 до 1.
Концептуальные вопросы
1. Зависит ли резонансная частота цепи переменного тока от пикового напряжения источника переменного тока? Объясните, почему да или почему нет.
2. Предположим, у вас есть двигатель с коэффициентом мощности значительно меньше 1.Объясните, почему было бы лучше улучшить коэффициент мощности как метод улучшения выходной мощности двигателя, чем увеличивать входное напряжение.
Задачи и упражнения
1. Схема RL состоит из резистора 40,0 Ом и катушки индуктивности 3,00 мГн. (a) Найдите его полное сопротивление Z при 60,0 Гц и 10,0 кГц. (b) Сравните эти значения Z со значениями, найденными в Пример 1: Расчет импеданса и тока , в котором также был конденсатор.
2. Схема RC состоит из резистора 40,0 Ом и конденсатора 5,00 мкФ. (а) Найдите его полное сопротивление при 60,0 Гц и 10,0 кГц. (b) Сравните эти значения Z со значениями, найденными в Пример 1: Расчет импеданса и тока , в котором также была катушка индуктивности.
3. Цепь LC состоит из катушки индуктивности 3,00 мГн и конденсатора 5,00 мкФ. (а) Найдите его полное сопротивление при 60,0 Гц и 10,0 кГц. (b) Сравните эти значения Z со значениями, найденными в Пример 1: Расчет импеданса и тока , в котором также был резистор.
4. Какова резонансная частота индуктора 0,500 мГн, подключенного к конденсатору 40,0 мкФ?
5. Для приема AM-радио вам нужна цепь RLC , которая может резонировать на любой частоте от 500 до 1650 кГц. Это достигается с помощью фиксированной катушки индуктивности 1,00 мкГн, подключенной к конденсатору переменной емкости. Какой диапазон емкости нужен?
6. Предположим, у вас есть запас индукторов от 1,00 нГн до 10,0Гн и конденсаторов от 1.От 00 пФ до 0,100 F. Каков диапазон резонансных частот, который может быть достигнут при сочетании одной катушки индуктивности и одного конденсатора?
7. Какая емкость необходима для получения резонансной частоты 1,00 ГГц при использовании катушки индуктивности 8,00 нГн?
8. Какая индуктивность необходима для получения резонансной частоты 60,0 Гц при использовании конденсатора 2,00 мкФ?
9. Самая низкая частота в диапазоне FM-радио — 88,0 МГц. (а) Какая индуктивность необходима для создания этой резонансной частоты, если она подключена к 2.Конденсатор 50 пФ? (b) Конденсатор регулируемый, что позволяет регулировать резонансную частоту до 108 МГц. Какой должна быть емкость на этой частоте?
10. Последовательная цепь RLC имеет резистор 2,50 Ом, индуктивность 100 мкГн и конденсатор 80,0 мкФ. (A) Найдите полное сопротивление цепи при 120 Гц. (b) Найдите полное сопротивление цепи на частоте 5,00 кГц. (c) Если источник напряжения имеет В среднеквадратичное значение = 5,60 В, что будет I среднеквадратичное значение на каждой частоте? (г) Какова резонансная частота контура? (e) Что такое I среднеквадратичное значение при резонансе?
11.Последовательная цепь RLC имеет резистор 1,00 кОм, индуктивность 150 мкГн и конденсатор 25,0 нФ. (а) Найдите полное сопротивление цепи при 500 Гц. (b) Найдите полное сопротивление цепи на частоте 7,50 кГц. (c) Если источник напряжения имеет В действующее значение = 408 В, что будет I среднеквадратичное значение на каждой частоте? (г) Какова резонансная частота контура? (e) Что такое I среднеквадратичное значение при резонансе?
12. Цепь серии RLC имеет 2.Резистор 50 Ом, катушка индуктивности 100 мкГн и конденсатор 80,0 мкФ. (a) Найдите коэффициент мощности при f = 120 Гц. (б) Каков фазовый угол при 120 Гц? (c) Какая средняя мощность при 120 Гц? (d) Найдите среднюю мощность на резонансной частоте цепи.
13. Последовательная цепь RLC имеет резистор 1,00 кОм, индуктивность 150 мкГн и конденсатор 25,0 нФ. (a) Найдите коэффициент мощности при f = 7,50 Гц. б) Каков фазовый угол на этой частоте? (c) Какая средняя мощность на этой частоте? (d) Найдите среднюю мощность на резонансной частоте цепи.
14. {2}} \\ [/ latex]
- резонансная частота:
- частота, при которой полное сопротивление в цепи минимально, а также частота, с которой цепь будет колебаться, если не будет управляться источником напряжения; рассчитывается по [latex] {f} _ {0} = \ frac {1} {2 \ pi \ sqrt {\ text {LC}}} \\ [/ latex]
- фазовый угол:
- обозначается как ϕ , величина, на которую напряжение и ток не совпадают по фазе друг с другом в цепи
- Коэффициент мощности:
- — величина, на которую мощность, передаваемая в цепи, меньше теоретического максимума цепи из-за того, что напряжение и ток не совпадают по фазе; рассчитывается по cos ϕ
Избранные решения проблем и упражнения
1.(a) 40,02 Ом при 60,0 Гц, 193 Ом при 10,0 кГц (b) При 60 Гц, с конденсатором, Z = 531 Ом, что в 13 раз больше, чем без конденсатора. Конденсатор имеет большое значение на низких частотах. На 10 кГц, с конденсатором Z = 190 Ом, примерно так же, как без конденсатора. Конденсатор оказывает меньшее влияние на высоких частотах.
3. (a) 529 Ом при 60,0 Гц, 185 Ом при 10,0 кГц (b) Эти значения близки к значениям, полученным в Пример 1: Расчет импеданса и тока , поскольку на низкой частоте преобладает конденсатор, а на высокой — индуктор доминирует.Таким образом, в обоих случаях резистор вносит небольшой вклад в общий импеданс.
5. От 9,30 нФ до 101 нФ
7. 3,17 пФ
9. (а) 1,31 мкГн (б) 1,66 пФ
11. (a) 12,8 кОм (b) 1,31 кОм (c) 31,9 мА при 500 Гц, 312 мА при 7,50 кГц (d) 82,2 кГц (e) 0,408 A
13. (а) 0,159 (б) 80,9 ° (в) 26,4 Вт (г) 166 Вт
15. 16.0 Вт
Резонанс в цепи переменного тока — Физический ключ
Явление резонанса также имеет место в электрических цепях, подобное механическому резонансу, который мы обсуждали в «Механике».Механический резонанс возник, когда частота движущей силы была равна собственной частоте колебательной системы.
Здесь мы достигаем электрического резонанса в последовательной цепи RLC. Вы знаете тот факт, что если частота возбуждения равна собственной частоте, возникает явление резонанса. Какая собственная частота в цепи RLC? Мы видели в LC-цепи, что ток сам по себе колеблется с определенной частотой, и мы называем эту частоту собственной частотой.
Здесь у нас есть частота возбуждения, и мы убеждаемся, что частота возбуждения равна собственной частоте (без сопротивления) с присутствующим сопротивлением для получения резонанса. Мы знаем, что как индуктивное, так и емкостное сопротивление зависят от частоты, то есть $ X_L = L \ omega $ и $ X_C = 1 / C \ omega $.
Индуктивное реактивное сопротивление увеличивается, а емкостное реактивное сопротивление уменьшается с увеличением частоты. Для данной индуктивности и емкости индуктивное и емкостное реактивные сопротивления равны на частоте, называемой резонансной частотой, и эта резонансная частота равна собственной частоте.2} $. Когда $ X_L = X_C $, $ Z = R $, и это то же самое, что нет конденсатора и катушки индуктивности!
В резонансе $ X_L = X_C $, то есть $ \ omega_0 \, L = 1 / \ omega_0 \, C $, и это дает $ \ omega_0 = 1 / \ sqrt {LC} $, и это угловая частота колебательный ток в LC-цепи. Это показывает, что частота без демпфирования является собственной частотой или резонансной частотой. Частота с демпфированием называется демпфированной частотой или иногда называется демпфированной собственной частотой .
Когда частота возбуждения равна собственной частоте, явление резонанса имеет место при минимальном импедансе, и, следовательно, ток максимален на резонансной частоте. На рисунке 1 показаны пики тока при резонансе в цепях серии RLC.
Рисунок 1 Пик тока при резонансе. Пик разный для разного сопротивления.Кривые $ a $, $ b $ и $ c $ имеют разные пики тока при резонансе. Это потому, что каждая кривая предназначена для разного значения сопротивления.{\ circ} $. В резонансе два напряжения равны и противоположны, и они компенсируют друг друга. Следовательно, в резонансе цепь ведет себя так, как будто нет катушки индуктивности и конденсатора, и напряжение источника появляется только через сопротивление.
Мы также можем изменить частоту, изменив индуктивность или емкость.



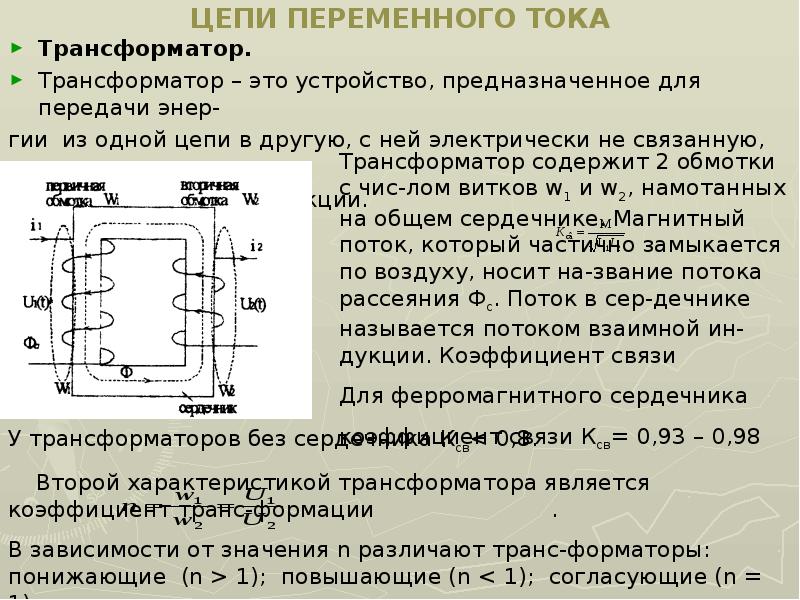 Амплитуда установившихся колебаний тока будет определяться уравнением . В этом и состоит смысл явления резонанса.
Амплитуда установившихся колебаний тока будет определяться уравнением . В этом и состоит смысл явления резонанса. Резкое уменьшение амплитуды силы тока во внешней цепи, питающей параллельно соединенные емкостное и индуктивное сопротивления при приближении частоты внешнего напряжения к собственной частоте колебательного контура наз.
Резкое уменьшение амплитуды силы тока во внешней цепи, питающей параллельно соединенные емкостное и индуктивное сопротивления при приближении частоты внешнего напряжения к собственной частоте колебательного контура наз.