Этих данных недостаточно для решения задачи.
Последовательное соединение показано на рисунке
Общая емкость любого количества последовательно соединенных конденсаторов определяется по формуле
Величина, обратная эквивалентной (общей) емкости последовательно соединенных конденсаторов, равна сумме величин, обратных емкостям этих конденсаторов.
Из формулы следует, что эквивалентная (общая) емкость всегда меньше емкости любого из последовательно соединенных конденсаторов т. е. меньше наименьшей емкости, входящей в данное соединение.
Первый частный случай
Если последовательно соединены только два конденсатора, то их общую емкость можно быстро определить по формуле
Второй частный случай
Если последовательно соединено любое количество конденсаторов одинаковых емкостей, то их общую емкость можно быстро вычислить, разделив емкость одного конденсатора на их количество.
Если батарею из последовательно соединенных конденсаторов присоединить к какому-либо участку цепи, то напряжение, приложенное к батарее последовательно соединенных конденсаторов, равно сумме напряжений на этих конденсаторах U = U1+U2+U3
По величине эти напряжения не равны между собой:
Напряжения между последовательно соединенными конденсаторами распределяются обратно пропорционально емкостям этих конденсаторов.
В частном случае, если емкости последовательно соединенных конденсаторов одинаковы, то и напряжения на этих конденсаторах равны между собой.
Последовательное соединение конденсаторов применяется в тех случаях, когда имеющиеся конденсаторы рассчитаны на более низкое, чем предусмотрено в данной схеме, напряжение, а также для образования емкостных делителей напряжения.
Пример. Определить эквивалентную емкость двух последовательно соединенных конденсаторов
Последовательное соединение конденсаторов – батарея, образованная цепочкой конденсаторов. Отсутствует ветвление, выход одного элемента подключается к входу следующего.
Отсутствует ветвление, выход одного элемента подключается к входу следующего.
Физические процессы при последовательном соединении
При последовательном соединении конденсаторов заряд каждого равноценен. Обусловлено природным принципом равновесия. С источником соединены только крайние обкладки, другие заряжаются путем перераспределения меж ними зарядов. Используя равенство, находим:
q = q1 = q2 = U1 C1 = U2 C2, откуда запишем:
Напряжения меж конденсаторами распределяются обратно пропорционально номинальным емкостям. В сумме оба составляют вольтаж питающей сети. При разряде конструкция способна отдать заряд q вне зависимости от того, сколько конденсаторов включено последовательно. Емкость батареи найдем из формулы:
C = q/u = q/(U1 + U2), подставляя выражения, приведенные выше, приводя к общему знаменателю:
Вычисление общей емкости батареи
При последовательном соединении конденсаторов в батарею складываются величины, обратные номинальным емкостям. Приводя последнее выражение к общему знаменателю, переворачивая дроби, получаем:
Приводя последнее выражение к общему знаменателю, переворачивая дроби, получаем:
Выражение используется для нахождения емкости батареи. Если конденсаторов более двух, формула усложняется. Для нахождения ответа номиналы перемножаются меж собой, выходит числитель дроби. В знаменатель ставят попарные произведения двух номиналов, перебирая комбинации. Практически иногда удобнее вести вычисление через обратные величины. Полученным результатом разделить единицу.
Соединение последовательное конденсаторов
Формула сильно упрощается, если номиналы батареи одинаковы. Требуется просто цифру поделить общим числом элементов, получая результирующее значение. Напряжение распределится равномерно, следовательно, достаточно номинал питающей сети разбить поровну на общее число. При питании аккумулятором 12 вольт, 4-х емкостях, на каждой упадет 3 вольта.
Одно упрощение сделаем для случая, когда номиналы равны, одна емкость включена переменная, чтобы подстраивать результат. Тогда максимальное напряжение каждого элемента удастся приближенно найти, разделив вольтаж источника уменьшенным на единицу количеством. Получится результат с заведомым запасом. Что касается переменной емкости, требования намного жёстче. В идеале рабочее значение перекрывает вольтаж источника.
Получится результат с заведомым запасом. Что касается переменной емкости, требования намного жёстче. В идеале рабочее значение перекрывает вольтаж источника.
Необходимость в последовательном соединении
На первый взгляд идея соединения конденсаторов батареей последовательным образом покажется лишенной смысла. Первое преимущество очевидно: падают требования к максимальному напряжению обкладок. Больше рабочий вольтаж, дороже изделие. Подобным образом мир видит радиолюбитель, владеющий рядом низковольтных конденсаторов, желающий применить железо составной частью высоковольтной цепи.
Рассчитывая по приведенным выше формулам действующие напряжения элементом, можно легко решить поставленную задачу. Рассмотрим для пущей наглядности пример:
Пусть установлены аккумулятор напряжением 12 вольт, три емкости номиналами 1, 2 и 4 нФ. Найдем напряжение при последовательном соединении элементов батареей.
Для нахождения трех неизвестных потрудитесь составить равное количество уравнения. Известно из курса высшей математики. Результат будет выглядеть следующим образом:
Известно из курса высшей математики. Результат будет выглядеть следующим образом:
- U1 + U2 + U3 = 12;
- U1/U2 = 2/1 = 2, откуда запишем: U1 = 2U2;
- U2/U3 = 4/2 = 2, откуда видно: U2 = 2U
Не сложно заметить, последние два выражения подставим первому, выразив 12 вольт через вольтаж третьего конденсатора. Получится следующее:
4U3 + 2U3 + U3 = 12, откуда находим, напряжение третьего конденсатора составляет 12/7 = 1,714 вольта, U2 – 3,43 вольта, U1 – 6,86 вольта. Сумма чисел дает 12, каждое меньше напряжения питающего аккумулятора. Причем тем больше разница, чем меньший номинал у соседей. Из этого правила следует: в последовательном соединении конденсаторы низкой емкости показывают большее рабочее напряжение. Найдем для определенности номинал составленной батареи, заодно проиллюстрируем формулу, поскольку выше описана чисто словесно:
С = С1С2С3/(С1С2 + С2С3 + С1С3) = 8/(2 + 8 + 4) = 8/14 = 571 пФ.
Результирующий номинал меньше каждого конденсатора, составляющего последовательное соединение. Из правила видно: максимальное влияние на суммарную емкость оказывает меньший. Следовательно, при необходимости подстройки полного номинала батареи должен быть переменный конденсатор. В противном случае поворот винта не окажет большого влияния на конечный результат.
Из правила видно: максимальное влияние на суммарную емкость оказывает меньший. Следовательно, при необходимости подстройки полного номинала батареи должен быть переменный конденсатор. В противном случае поворот винта не окажет большого влияния на конечный результат.
Видим очередной подводный камень: после подстройки распределение напряжений по конденсаторам изменится. Просчитайте крайние случаи, дабы вольтаж не превысил рабочее значение для составляющих батарею элементов.
Программные пакеты исследования электрических цепей
Помимо онлайн- калькуляторов расчета последовательного соединения конденсаторов присутствуют и инструменты помощнее. Большой минус общедоступных средств объясняется нежеланием сайтов проверять программный код, значит, содержат ошибки. Плохо, если одна емкость выйдет из строя, сломленная процессом испытаний неправильно собранной схемы. Не единственный недостаток. Иногда схемы гораздо сложнее, разобраться комплексно невозможно.
В отдельных приборах встречаются фильтры высокой частоты, использующие конденсатор, включенные каскадами. Тогда на схеме помимо замыкания через резистор на землю образуется последовательное соединение емкостей. Обычно не применяют формулу, показанную выше. Принято считать, каждый каскад фильтра существует отдельно, результат прохождения сигнала описывается амплитудно-частотной характеристикой. Графиком, показывающим, как сильно обрежет на выходе спектральную составляющую сигнала.
Желающим провести ориентировочные расчеты рекомендуется ознакомиться с программным пакетом персонального компьютера Electronics Workbench. Конструктив выполнен по английским стандартам, потрудитесь учитывать нюанс: обозначение резисторов на электрической схеме изломанным зигзагом. Номиналы, названия элементов будут изложены на иностранный манер. Не мешает пользоваться оболочкой, предоставляющей оператору гору источников питания различного толка.
И главное – Electronics Workbench позволит задать контрольные точки на каждой, в режиме реального времени посмотреть напряжение, ток, спектр, форму сигнала. Полагается дополнить проект амперметром, вольтметром, прочими аналогичного толка приборами.
Полагается дополнить проект амперметром, вольтметром, прочими аналогичного толка приборами.
При помощи такого программного пакета смоделируете ситуацию, посмотрите, сколько падает напряжения на элементе батареи. Уберегает от громоздких расчетов, намного ускоряя процесс проектирования схемы. Одновременно исключаются ошибки. Легко и просто становится добавлять, удалять конденсаторы с немедленной оценкой результата.
Рабочий пример
Скрин показывает рабочий стол Electronics Workbench 5.12 с собранной электрической схемой последовательного соединения конденсаторов. Каждый емкостью 1 мкФ, одинаковые элементы взяты для целей демонстрации. Чтобы каждый мог без труда проверить правильность.
Последовательная батарея конденсаторов
Обратим вначале внимание на источник. Переменное напряжение частотой 60 Гц. В стране разработчика действует иной стандарт, нежели российские. Рекомендуется правой кнопкой мыши щелкнуть источник, посетить свойства, выставить:
- Частоту (frequency) 50 Гц вместо 60 Гц.

- Действующее значение напряжения (voltage) 220 вольт вместо 120.
- Фазу (phase – имитация реактивности) взять согласно своим нуждам.
Для буквоедов будет полезно полистать свойства элементов цепи. У источника вольны задать допустимое отклонение напряжения (voltage tolerance) в процентах. Достаточно добавить один резистор размером 1 кОм, цепь становится фильтром верхних частот. Рекомендуется не упрощать действия. Поставить правильно знак заземления, убедиться: схема полностью тривиальна. В противном случае результаты заставят надолго поломать голову.
Проиллюстрированный скрином фильтр верхних частот обнаруживает подъем амплитудно-частотной характеристики в районе 1 кГц. При нахождении полосы пропускания необходимо учесть: вертикальная шкала логарифмическая. Посему срез на уровне 70% максимума не соответствует семи десятым высоты пологой части пика. Заядлым любителям будет интересна фазочастотная характеристика, в окне расположенная снизу.
Тот и другой график строятся из меню Analysis раздел AC Frequency. А еще тут… Fourier. Доступно посмотреть спектр выходного сигнала. В нашем случае не будет ничего интересного, поскольку собрали унылый пассивный фильтр, колебание на входе гармоническое. Гораздо интереснее наблюдать спектр импульсного сигнала.
А еще тут… Fourier. Доступно посмотреть спектр выходного сигнала. В нашем случае не будет ничего интересного, поскольку собрали унылый пассивный фильтр, колебание на входе гармоническое. Гораздо интереснее наблюдать спектр импульсного сигнала.
Раздел Transient показывает отклик на подачу фронта питающего напряжения. На графике фактически представлен процесс заряда батареи, откуда найдем постоянную времени по уровню 0,7 максимума. Тонкости понятны желающим собрать сглаживающий фильтр амплитудного детектора. Как видно из графика, значение составляет 250 мкс. Параметр определяется из окна следующим образом:
- Считается, за три постоянные времени цепи заряд конденсаторов, разряд производится приблизительно на 95%.
- Легко заметить, точка находится в районе 800 мкс.
- Следует разделить значение на три, получится постоянная времени батареи последовательно соединенных конденсаторов.
По-другому постоянная времени вычисляется произведением сопротивления на общую емкость батареи.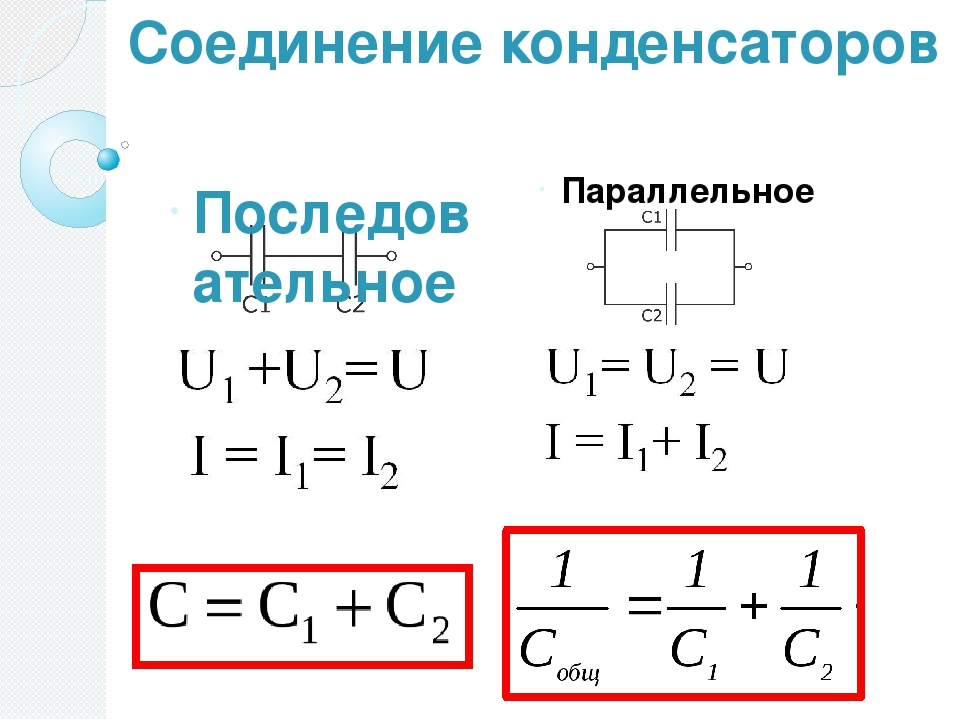 Пользуясь приведенными выше формулами, вычислим: С = 1 мкФ / 4 = 250 нФ. Осталось умножить значение на 1000 Ом, получится 250 мкс. Программный пакет Electronics Workbench 5.12 при умелом использовании высвобождает уйму свободного времени.
Пользуясь приведенными выше формулами, вычислим: С = 1 мкФ / 4 = 250 нФ. Осталось умножить значение на 1000 Ом, получится 250 мкс. Программный пакет Electronics Workbench 5.12 при умелом использовании высвобождает уйму свободного времени.
Раздобыть программный пакет расчета электрики
В интернете бытует мнение: автором Electronics Workbench выступает дочерняя компания корпорации National Instruments, разрабатывающая программное обеспечение. Неправда. Из окна авторских прав упомянутого приложения видно: разработка выполнена отделом Interactive Image Technologies.
Вышеозначенное подразделение обрело самостоятельность в 1995 году. Отдел направленно занимался рекламными и обучающими материалами. Electronics Workbench разработан для целей обучения студентов Канады. Потом программный продукт распространился всемирно, с некоторых пор именуется Multisim.
Обновленный программный продукт продают официальные дилеры, перечень представлен официальным сайтом компании National Instruments: russia. ni.com/contact. На момент исследования счастливчиками, получившими право купить ПО не выезжая за город, назовем жителей Москвы, Санкт-Петербурга. Удачи решившимся связаться с официальными представителями, в Multisim добавлены новые фишки:
ni.com/contact. На момент исследования счастливчиками, получившими право купить ПО не выезжая за город, назовем жителей Москвы, Санкт-Петербурга. Удачи решившимся связаться с официальными представителями, в Multisim добавлены новые фишки:
- Более 36000 схемных элементов.
- Возможность разработки печатных плат на основе собранной электрической схемы.
- Продвинутые опции анализа вместо убогости, демонстрируемой скринам, версии 20-летней давности.
Батарея из двух последовательно соединенных конденсаторов
Последовательное соединение показано на рисунке
Общая емкость любого количества последовательно соединенных конденсаторов определяется по формуле
Величина, обратная эквивалентной (общей) емкости последовательно соединенных конденсаторов, равна сумме величин, обратных емкостям этих конденсаторов.
Из формулы следует, что эквивалентная (общая) емкость всегда меньше емкости любого из последовательно соединенных конденсаторов т.
Первый частный случай
Если последовательно соединены только два конденсатора, то их общую емкость можно быстро определить по формуле
Второй частный случай
Если последовательно соединено любое количество конденсаторов одинаковых емкостей, то их общую емкость можно быстро вычислить, разделив емкость одного конденсатора на их количество.
Если батарею из последовательно соединенных конденсаторов присоединить к какому-либо участку цепи, то напряжение, приложенное к батарее последовательно соединенных конденсаторов, равно сумме напряжений на этих конденсаторах U = U1+U2+U3
По величине эти напряжения не равны между собой:
Напряжения между последовательно соединенными конденсаторами распределяются обратно пропорционально емкостям этих конденсаторов.
В частном случае, если емкости последовательно соединенных конденсаторов одинаковы, то и напряжения на этих конденсаторах равны между собой.
Последовательное соединение конденсаторов применяется в тех случаях, когда имеющиеся конденсаторы рассчитаны на более низкое, чем предусмотрено в данной схеме, напряжение, а также для образования емкостных делителей напряжения.
Пример. Определить эквивалентную емкость двух последовательно соединенных конденсаторов
Последовательное соединение показано на рисунке
Общая емкость любого количества последовательно соединенных конденсаторов определяется по формуле
Величина, обратная эквивалентной (общей) емкости последовательно соединенных конденсаторов, равна сумме величин, обратных емкостям этих конденсаторов.
Из формулы следует, что эквивалентная (общая) емкость всегда меньше емкости любого из последовательно соединенных конденсаторов т. е. меньше наименьшей емкости, входящей в данное соединение.
е. меньше наименьшей емкости, входящей в данное соединение.
Первый частный случай
Если последовательно соединены только два конденсатора, то их общую емкость можно быстро определить по формуле
Второй частный случай
Если последовательно соединено любое количество конденсаторов одинаковых емкостей, то их общую емкость можно быстро вычислить, разделив емкость одного конденсатора на их количество.
Если батарею из последовательно соединенных конденсаторов присоединить к какому-либо участку цепи, то напряжение, приложенное к батарее последовательно соединенных конденсаторов, равно сумме напряжений на этих конденсаторах
U = U1+U2+U3По величине эти напряжения не равны между собой:
Напряжения между последовательно соединенными конденсаторами распределяются обратно пропорционально емкостям этих конденсаторов.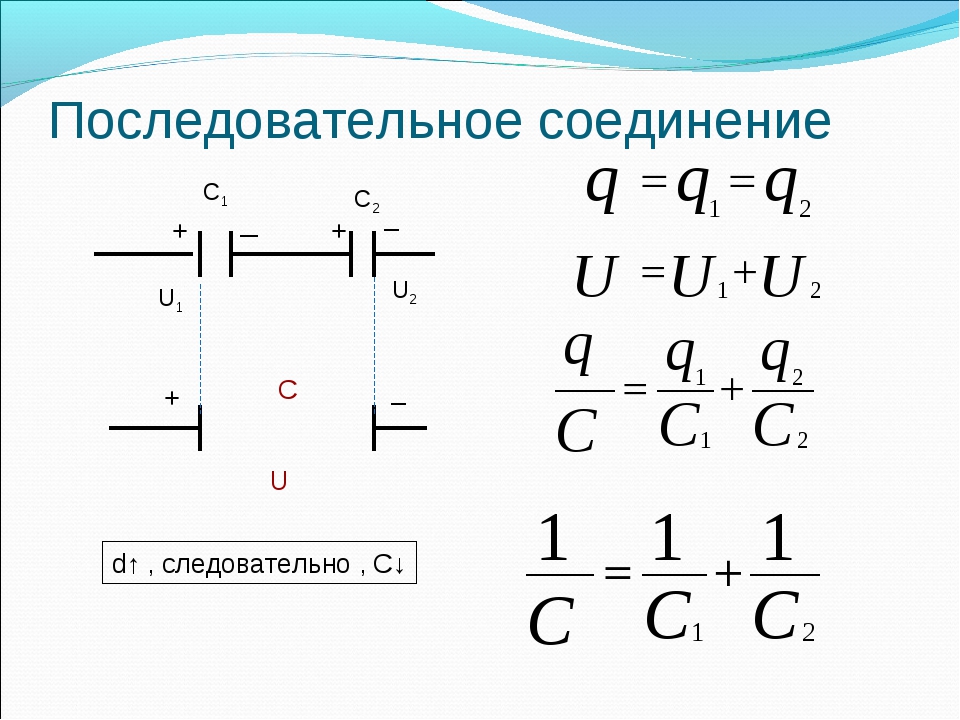
В частном случае, если емкости последовательно соединенных конденсаторов одинаковы, то и напряжения на этих конденсаторах равны между собой.
Последовательное соединение конденсаторов применяется в тех случаях, когда имеющиеся конденсаторы рассчитаны на более низкое, чем предусмотрено в данной схеме, напряжение, а также для образования емкостных делителей напряжения.
Пример. Определить эквивалентную емкость двух последовательно соединенных конденсаторов
Для достижения нужной емкости или при напряжении, превышающем номинальное напряжение, конденсаторы, могут соединяться последовательно или параллельно. Любое же сложное соединение состоит из нескольких комбинаций последовательного и параллельного соединений.
Последовательное соединение конденсаторов
При последовательном соединении, конденсаторы подключены таким образом, что только первый и последний конденсатор подключены к источнику ЭДС/тока одной из своих пластин.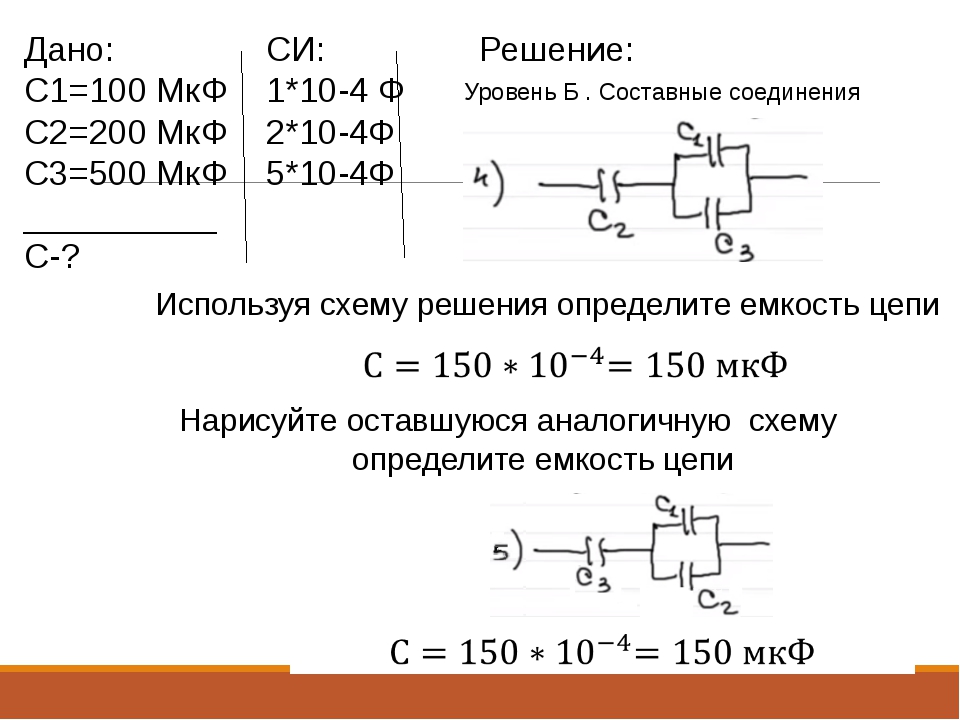 Заряд одинаков на всех пластинах, но внешние заряжаются от источника, а внутренние образуются только за счет разделения зарядов ранее нейтрализовавших друг друга. При этом заряд конденсаторов в батарее меньше, чем, если бы каждый конденсатор подключался бы отдельно. Следовательно, и общая емкость батареи конденсаторов меньше.
Заряд одинаков на всех пластинах, но внешние заряжаются от источника, а внутренние образуются только за счет разделения зарядов ранее нейтрализовавших друг друга. При этом заряд конденсаторов в батарее меньше, чем, если бы каждый конденсатор подключался бы отдельно. Следовательно, и общая емкость батареи конденсаторов меньше.
Напряжение на данном участке цепи соотносятся следующим образом:
Зная, что напряжение конденсатора можно представить через заряд и емкость, запишем:
Сократив выражение на Q, получим знакомую формулу:
Откуда эквивалентная емкость батареи конденсаторов соединенных последовательно:
Параллельное соединение конденсаторов
При параллельном соединении конденсаторов напряжение на обкладках одинаковое, а заряды разные.
Величина общего заряда полученного конденсаторами, равна сумме зарядов всех параллельно подключенных конденсаторов. В случае батареи из двух конденсаторов:
Так как заряд конденсатора
А напряжения на каждом из конденсаторов равны, получаем следующее выражение для эквивалентной емкости двух параллельно соединенных конденсаторов
Пример 1
Какова результирующая емкость 4 конденсаторов включенных последовательно и параллельно, если известно что С1 = 10 мкФ, C2 = 2 мкФ, C3 = 5 мкФ, а C4 = 1 мкФ?
При последовательном соединении общая емкость равна:
При параллельном соединении общая емкость равна:
Пример 2
Определить результирующую емкость группы конденсаторов подключенных последовательно-параллельно, если известно, что С1 = 7 мкФ, С2 = 2 мкФ, С3 = 1 мкФ.
Сначала найдем общую емкость параллельного участка цепи:
Затем найдем общую емкость для всей цепи:
По сути, расчет общей емкости конденсаторов схож с расчетом общего сопротивления цепи в случае с последовательным или параллельным соединением, но при этом, зеркально противоположен.
Батарея из двух последовательно соединенных конденсаторов электроемкостью
Условие задачи:
Батарея из двух последовательно соединенных конденсаторов электроемкостью 300 и 500 пФ заряжена до разности потенциалов 12 кВ. Определить разность потенциалов на первом конденсаторе.
Задача №6.4.25 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(C_1=300\) пФ, \(C_2=500\) пФ, \(U=12\) кВ, \(U_1-?\)
Решение задачи:
Для начала запишем формулу электроемкости и выразим из этой формулы заряд \(q\):
\[C = \frac{q}{U}\]
\[q = CU\;\;\;\;(1)\]
Пусть \(U_1\) – разность потенциалов между обкладками первого конденсатора, а \(U_2\) – разность потенциалов между обкладками второго. Известно, что при последовательном соединении конденсаторов заряд на их обкладках одинаковый, а общее напряжение равно сумме напряжений на каждом из конденсаторов. Учитывая все написанное и пользуясь формулой (1), мы получим такую систему:
\[\left\{ \begin{gathered}
{C_1}{U_1} = {C_2}{U_2} \hfill \\
U = {U_1} + {U_2} \hfill \\
\end{gathered} \right.\]
Из верхнего равенства системы выразим разность потенциалов \(U_2\):
\[{U_2} = {U_1}\frac{{{C_1}}}{{{C_2}}}\]
Полученное выражение подставим в нижнее равенство системы:
\[U = {U_1} + {U_1}\frac{{{C_1}}}{{{C_2}}}\]
\[U = {U_1}\frac{{{C_1} + {C_2}}}{{{C_2}}}\]
Откуда искомая разность потенциалов на первом конденсаторе \(U_1\) равна:
\[{U_1} = \frac{{U{C_2}}}{{{C_1} + {C_2}}}\]
Задача решена в общем виде, нам остается только посчитать ответ, для чего подставим данные задачи в полученную формулу, не забыв при этом перевести их в систему СИ:
\[{U_1} = \frac{{12 \cdot {{10}^3} \cdot 500 \cdot {{10}^{ – 12}}}}{{300 \cdot {{10}^{ – 12}} + 500 \cdot {{10}^{ – 12}}}} = 7500\;В\]
Ответ: 7500 В.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
способы, правила, формулы. Вычисление падений напряжения на конденсаторах
Конденсаторы, как и резисторы, можно соединять последовательно и параллельно. Рассмотрим соединение конденсаторов: для чего применяются каждая из схем, и их итоговые характеристики.
Эта схема – самая распространенная. В ней обкладки конденсаторов соединяются между собой, образуя эквивалентную емкость, равную сумме соединяемых емкостей.
При параллельном соединении электролитических конденсаторов необходимо, чтобы между собой соединялись выводы одной полярности.
Особенность такого соединения – одинаковое напряжение на всех соединяемых конденсаторах . Номинальное напряжение группы параллельно соединенных конденсаторов равно рабочему напряжению конденсатора группы, у которого оно минимально.
Токи через конденсаторы группы протекают разные: через конденсатор с большей емкостью потечет больший ток.
На практике параллельное соединение применяется для получения емкости нужной величины, когда она выходит за границы диапазона, выпускаемого промышленностью, или не укладываются в стандартный ряд емкостей. В системах регулирования коэффициента мощности (cos ϕ) изменение емкости происходит за счет автоматического подключения или отключения конденсаторов в параллель.
При последовательном соединении обкладки конденсатором соединяются друг к другу, образуя цепочку. Крайние обкладки подключаются к источнику, а ток по всем конденсаторам группы потечет одинаковый.
Эквивалентная емкость последовательно соединенных конденсаторов ограничена самой маленькой емкостью в группе. Объясняется это тем, что как только она полностью зарядится, ток прекратится. Подсчитать общую емкость двух последовательно соединенных конденсаторов можно по формуле
Но применение последовательного соединения для получения нестандартных номиналов емкостей не так распространено, как параллельного.
При последовательном соединении напряжение источника питания распределяется между конденсаторами группы. Это позволяет получить батарею конденсаторов, рассчитанную на большее напряжение , чем номинальное напряжение входящих в нее компонентов. Так из дешевых и небольших по размерам конденсаторов изготавливаются блоки, выдерживающие высокие напряжения.
Еще одна область применения последовательного соединения конденсаторов связана с перераспределением напряжений между ними. Если емкости одинаковы, напряжение делится пополам, если нет – на конденсаторе большей емкости напряжение получается большим. Устройство, работающее на этом принципе, называют емкостным делителем напряжения .
Смешанное соединение конденсаторов
Такие схемы существуют, но в устройствах специального назначения, требующие высокой точности получения величины емкости, а также для их точной настройки.
1 мФ = 0,001 Ф. 1 мкФ = 0,000001 = 10⁻⁶ Ф. 1 нФ = 0,000000001 = 10⁻⁹ Ф. 1 пФ = 0,000000000001 = 10⁻¹² Ф.
В соответствии со вторым правилом Кирхгофа, падения напряжения V₁ , V₂ and V₃ на каждом из конденсаторов в группе из трех соединенных последовательно конденсаторов в общем случае различные и общая разность потенциалов V равна их сумме:
По определению емкости и с учетом того, что заряд Q группы последовательно соединенных конденсаторов является общим для всех конденсаторов, эквивалентная емкость C eq всех трех конденсаторов, соединенных последовательно, определяется как
Для группы из n соединенных последовательно конденсаторов эквивалентная емкость C eq равна величине, обратной сумме величин, обратных емкостям отдельных конденсаторов:
Эта формула для C eq и используется для расчетов в этом калькуляторе. Например, общая емкость соединенных последовательно трех конденсаторов емкостью 10, 15 and 20 мкФ будет равна 4,62 мкФ:
Если конденсаторов только два, то их общая емкость определяется по формуле
Если имеется n соединенных последовательно конденсаторов с емкостью C , их эквивалентная емкость равна
Отметим, что для расчета общей емкости нескольких соединенных последовательно конденсаторов используется та же формула, что и для расчета общего сопротивления параллельно соединенных резисторов .
Отметим также, что общая емкость группы из любого количества последовательно соединенных конденсаторов всегда будет меньше, чем емкость самого маленького конденсатора, а добавление конденсаторов в группу всегда приводит к уменьшению емкости.
Отдельного упоминания заслуживает падение напряжения на каждом конденсаторе в группе последовательно соединенных конденсаторов. Если все конденсаторы в группе имеют одинаковую номинальную емкость, падение напряжения на них скорее всего будет разным, так как конденсаторы в реальности будут иметь разную емкость и разный ток утечки. На конденсаторе с наименьшей емкостью будет наибольшее падение напряжения и, таким образом, он будет самым слабым звеном этой цепи.
Для получения более равномерного распределения напряжений параллельно конденсаторам включают выравнивающие резисторы. Эти резисторы работают как делители напряжения, уменьшающие разброс напряжений на отдельных конденсаторах. Но даже с этими резисторами все равно для последовательного включения следует выбирать конденсаторы с большим запасом по рабочему напряжению.
Если несколько конденсаторов соединены параллельно , разность потенциалов V на группе конденсаторов равна разности потенциалов соединительных проводов группы. Общий заряд Q разделяется между конденсаторами и если их емкости различны, то заряды на отдельных конденсаторах Q₁ , Q₂ and Q₃ тоже будут различными. Общий заряд определяется как
У многих начинающих любителей электроники в процессе сборки самодельного устройства возникает вопрос: “Как правильно соединять конденсаторы?”
Казалось бы, зачем это надо, ведь если на принципиальной схеме указано, что в данном месте схемы должен быть установлен конденсатор на 47 микрофарад, значит, берём и ставим. Но, согласитесь, что в мастерской даже заядлого электронщика может не оказаться конденсатора с необходимым номиналом!
Похожая ситуация может возникнуть и при ремонте какого-либо прибора. Например, необходим электролитический конденсатор ёмкостью 1000 микрофарад, а под рукой лишь два-три на 470 микрофарад. Ставить 470 микрофарад, вместо положенных 1000? Нет, это допустимо не всегда. Так как же быть? Ехать на радиорынок за несколько десятков километров и покупать недостающую деталь?
Как выйти из сложившейся ситуации? Можно соединить несколько конденсаторов и в результате получить необходимую нам ёмкость. В электронике существует два способа соединения конденсаторов: параллельное и последовательное .
В реальности это выглядит так:
Параллельное соединение
Принципиальная схема параллельного соединения
Последовательное соединение
Принципиальная схема последовательного соединения
Также можно комбинировать параллельное и последовательное соединение. Но на практике вам вряд ли это пригодиться.
Как рассчитать общую ёмкость соединённых конденсаторов?
Помогут нам в этом несколько простых формул. Не сомневайтесь, если вы будете заниматься электроникой, то эти простые формулы рано или поздно вас выручат.
Общая ёмкость параллельно соединённых конденсаторов:
С 1 – ёмкость первого;
С 2 – ёмкость второго;
С 3 – ёмкость третьего;
С N – ёмкость N -ого конденсатора;
C общ – суммарная ёмкость составного конденсатора.
Как видим, при параллельном соединении ёмкости нужно всего-навсего сложить!
Внимание! Все расчёты необходимо производить в одних единицах. Если выполняем расчёты в микрофарадах, то нужно указывать ёмкость C 1 , C 2 в микрофарадах. Результат также получим в микрофарадах. Это правило стоит соблюдать, иначе ошибки не избежать!
Чтобы не допустить ошибку при переводе микрофарад в пикофарады, а нанофарад в микрофарады, необходимо знать сокращённую запись численных величин. Также в этом вам поможет таблица. В ней указаны приставки, используемые для краткой записи и множители, с помощью которых можно производить пересчёт. Подробнее об этом читайте .
Ёмкость двух последовательно соединённых конденсаторов можно рассчитать по другой формуле. Она будет чуть сложнее:
Внимание! Данная формула справедлива только для двух конденсаторов! Если их больше, то потребуется другая формула. Она более запутанная, да и на деле не всегда пригождается .
Или то же самое, но более понятно:
Если вы проведёте несколько расчётов, то увидите, что при последовательном соединении результирующая ёмкость будет всегда меньше наименьшей, включённой в данную цепочку. Что это значить? А это значит, что если соединить последовательно конденсаторы ёмкостью 5, 100 и 35 пикофарад, то общая ёмкость будет меньше 5.
В том случае, если для последовательного соединения применены конденсаторы одинаковой ёмкости, эта громоздкая формула волшебным образом упрощается и принимает вид:
Здесь, вместо буквы M ставиться количество конденсаторов, а C 1 – его ёмкость.
Стоит также запомнить простое правило:
При последовательном соединении двух конденсаторов с одинаковой ёмкостью результирующая ёмкость будет в два раза меньше ёмкости каждого из них.
Таким образом, если вы последовательно соедините два конденсатора, ёмкость каждого из которых 10 нанофарад, то в результате она составит 5 нанофарад.
Не будем пускать слов по ветру, а проверим конденсатор , замерив ёмкость, и на практике подтвердим правильность показанных здесь формул.
Возьмём два плёночных конденсатора. Один на 15 нанофарад (0,015 мкф.),а другой на 10 нанофарад (0,01 мкф.) Соединим их последовательно. Теперь возьмём мультиметр Victor VC9805+ и замерим суммарную ёмкость двух конденсаторов. Вот что мы получим (см. фото).
Замер ёмкости при последовательном соединении
Ёмкость составного конденсатора составила 6 нанофарад (0,006 мкф.)
А теперь проделаем то же самое, но для параллельного соединения. Проверим результат с помощью того же тестера (см. фото).
Измерение ёмкости при параллельном соединении
Как видим, при параллельном соединении ёмкость двух конденсаторов сложилась и составляет 25 нанофарад (0,025 мкф.).
Что ещё необходимо знать, чтобы правильно соединять конденсаторы?
Во-первых, не стоит забывать, что есть ещё один немаловажный параметр, как номинальное напряжение.
При последовательном соединении конденсаторов напряжение между ними распределяется обратно пропорционально их ёмкостям. Поэтому, есть смысл при последовательном соединении применять конденсаторы с номинальным напряжением равным тому, которое имеет конденсатор, взамен которого мы ставим составной.
Если же используются конденсаторы с одинаковой ёмкостью, то напряжение между ними разделится поровну.
Для электролитических конденсаторов.
Последовательное соединение электролитов
Схема последовательного соединения
Также не забывайте про номинальное напряжение. При параллельном соединении каждый из задействованных конденсаторов должен иметь то номинальное напряжение, как если бы мы ставили в схему один конденсатор. То есть если в схему нужно установить конденсатор с номинальным напряжением на 35 вольт и ёмкостью, например, 200 микрофарад, то взамен его можно параллельно соединить два конденсатора на 100 микрофарад и 35 вольт. Если хоть один из них будет иметь меньшее номинальное напряжение (например, 25 вольт), то он вскоре выйдет из строя.
Желательно, чтобы для составного конденсатора подбирались конденсаторы одного типа (плёночные, керамические, слюдяные, металлобумажные). Лучше всего будет, если они взяты из одной партии, так как в таком случае разброс параметров у них будет небольшой.
Конечно, возможно и смешанное (комбинированное) соединение, но в практике оно не применяется (я не видел ). Расчёт ёмкости при смешанном соединении обычно достаётся тем, кто решает задачи по физике или сдаёт экзамены:)
Тем же, кто не на шутку увлёкся электроникой непременно надо знать, как правильно соединять резисторы и рассчитывать их общее сопротивление!
Для достижения нужной емкости или при напряжении, превышающем номинальное напряжение, конденсаторы , могут соединяться последовательно или параллельно. Любое же сложное соединение состоит из нескольких комбинаций последовательного и параллельного соединений.
При последовательном соединении, конденсаторы подключены таким образом, что только первый и последний конденсатор подключены к источнику ЭДС/тока одной из своих пластин. Заряд одинаков на всех пластинах, но внешние заряжаются от источника, а внутренние образуются только за счет разделения зарядов ранее нейтрализовавших друг друга. При этом заряд конденсаторов в батарее меньше, чем, если бы каждый конденсатор подключался бы отдельно. Следовательно, и общая емкость батареи конденсаторов меньше.
Напряжение на данном участке цепи соотносятся следующим образом:
Зная, что напряжение конденсатора можно представить через заряд и емкость, запишем:
Сократив выражение на Q, получим знакомую формулу:
Откуда эквивалентная емкость батареи конденсаторов соединенных последовательно:
При параллельном соединении конденсаторов напряжение на обкладках одинаковое, а заряды разные.
Величина общего заряда полученного конденсаторами, равна сумме зарядов всех параллельно подключенных конденсаторов. В случае батареи из двух конденсаторов:
Так как заряд конденсатора
А напряжения на каждом из конденсаторов равны, получаем следующее выражение для эквивалентной емкости двух параллельно соединенных конденсаторов
Пример 1
Какова результирующая емкость 4 конденсаторов включенных последовательно и параллельно, если известно что С 1 = 10 мкФ, C 2 = 2 мкФ, C 3 = 5 мкФ, а C 4 = 1 мкФ?
При последовательном соединении общая емкость равна:
При параллельном соединении общая емкость равна:
Пример 2
Определить результирующую емкость группы конденсаторов подключенных последовательно-параллельно, если известно, что С 1 = 7 мкФ, С 2 = 2 мкФ, С 3 = 1 мкФ.
Рис.2 U=U 1 =U 2 =U 3
Общий заряд Q всех конденсаторов
Общая емкость С, или емкость батареи, параллельно включенных конденсаторов равна сумме емкостей этих конденсаторов.
Параллельное подключение конденсатора к группе других включенных конденсаторов увеличивает общую емкость батареи этих конденсаторов. Следовательно, параллельное соединение конденсаторов применяется для увеличения емкости.
4)Если параллельно включены т одинаковых конденсаторов емкостью С´ каждый, то общая (эквивалентная) емкость батареи этих конденсаторов может быть определена выражением
Последовательное соединение конденсаторов
Рис.3
На обкладках последовательно соединенных конденсаторов, подключенных к источнику постоянного тока с напряжением U , появятся заряды одинаковые по величине с противоположными знаками.
Напряжение на конденсаторах распределяется обратно пропорционально емкостям конденсаторов:
Обратная величина общей емкости последовательно соединенных конденсаторов равна сумме обратных величин емкостей этих конденсаторов.
При последовательном включении двух конденсаторов их общая емкость определяется следующим выражением:
Если в цепь включены последовательно п одинаковых конденсаторов емкостью С каждый, то общая емкость этих конденсаторов:
Из (14) видно, что, чем больше конденсаторов п соединено последовательно, тем меньше будет их общая емкость С, т. е. последовательное включение конденсаторов приводит к уменьшению общей емкости батареи конденсаторов.
На практике может оказаться, что допустимое рабочее напряжение U p конденсатора меньше напряжения, на которое необходимо подключить конденсатор. Если этот конденсатор подключить на такое напряжение, то он выйдет из строя, так как будет пробит диэлектрик. Если же последовательно включить несколько конденсаторов, то напряжение распределится между ними и на каждом конденсаторе напряжение окажется меньше его допустимого рабочего U p . Следовательно, последовательное соединение конденсаторов применяют для того, чтобы напряжение на каждом конденсаторе не превышало его рабочего напряжения U p .
Смешанное соединение конденсаторов
Смешанное соединение (последовательно-параллельное) конденсаторов применяют тогда, когда необходимо увеличить емкость и рабочее напряжение батареи конденсаторов.
Рассмотрим смешанное соединение конденсаторов на нижеприведенных примерах.
Энергия конденсаторов
где Q — заряд конденсатора или конденсаторов, к которым приложено напряжение U ; С — электрическая емкость конденсатора или батареи соединенных конденсаторов, к которой приложено напряжение U .
Таким образом, конденсаторы служат для накопления и сохранения электрического поля и его энергии.
15. Дайте определение понятиям трех лучевая звезда и треугольник сопротивлений. Запишите формулы для преобразования трех лучевой звезды сопротивлений в треугольник сопротивлений и наоборот. Преобразуйте схему к двум узлам (Рисунок 5)
Рисунок 5- Схема электрическая
6.СХЕМЫ ЗАМЕЩЕНИЯ
Для облегчения расчета составляется схема замещения электрической цепи, т. е. схема, отображающая свойства цепи при определенных условиях.
На схеме замещения изображают все элементы, влиянием которых на результат расчета нельзя пренебречь, и указывают также электрические соединения между ними, которые имеются в цепи.
1.Схемы замещения элементов электрических цепей
На расчетных схемах источник энергии можно представить ЭДС без внутреннего сопротивления, если это сопротивление мало по сравнению с сопротивлением приемника (рис. 3.13,6).
Приr= 0 внутреннее падение напряженияUо = 0, поэтомунапряжение на зажимах источника при любом токе равно
ЭДС: U = E = const.
В некоторых случаях источник электрической энергии на расчетной схеме заменяют другой (эквивалентной) схемой (рис. 3.14, а), где вместо ЭДСЕ источник характеризуется его током короткого замыканияI K , а вместо внутреннего сопротивления в расчет вводится внутренняя проводимостьg =1/ r .
Возможность такой замены можно доказать, разделив равенство (3.1) на r:
U / r = E / r — I ,
где U / r = Io -некоторый ток, равный отношению напряжения на зажимах источника к внутреннему сопротивлению;E / r = I K — ток короткого замыкания источника;
Вводя новые обозначения, получим равенство I K = Io + I , которому удовлетворяет эквивалентная схема рис. 3.14,а.
В этом случае при любой величине напряжения на зажимах; источника его ток остается равным току короткого замыкания (рис. 3.14,6):
Источник с неизменным током, не зависящим от внешнего сопротивления, называют источником тока.
Один и тот же источник электрической энергии может быть заменен в расчетной схеме источником ЭДС или источником тока.
Последовательно соединенный конденсатор — Большая Энциклопедия Нефти и Газа, статья, страница 4
Последовательно соединенный конденсатор
Cтраница 4
Напряжение к сегнето-электрику подводится через последовательно соединенный конденсатор С0 большой ( по сравнению с Сх) емкости. Напряжение, возникающее на конденсаторе С0, подается на вертикально отклоняющие пластины осциллографа. [46]
Величина, обратная эквивалентной емкости последовательно соединенных конденсаторов, равна сумме величин, обратных емкостям этих конденсаторов. Из формулы ( 1 — 26) следует, что эквивалентная емкость меньше емкости любого из последовательно соединенных конденсаторов. [47]
В практической схеме каждый из последовательно соединенных конденсаторов шунтирован резистором. Резисторы, с одной стороны, обеспечивают выравнивание напряжений на конденсаторах, а с другой стороны, выполняют роль дополнительной нагрузки и гарантируют разряд конденсаторов при отключении источника от сети. [48]
Почему при расчете емкости батареи последовательно соединенных конденсаторов оговаривалось условие, чтобы они предварительно не были заряжены. [50]
Задача 7.1. Батарею из двух последовательно соединенных конденсаторов, электроемкости которых равны Сг — 4 мкФ и С2 6 мкФ, зарядили до разности потенциалов Ду 2 кВ и отключили от источника напряжения. На сколько уменьшится энергия батареи, если одноименно заряженные обкладки конденсаторов соединить параллельно. [51]
При разомкнутых выходных зажимах заряды последовательно соединенных конденсаторов одинаковы. В каждой параллельной ветви, очевидно, заряды конденсаторов также равны между собой, так как эти ветви одинаковы. [52]
Величина, обратная емкости батареи последовательно соединенных конденсаторов, равна сумме величин, обратных емкостям отдельных конденсаторов этой батареи. [53]
Задача III.4. Батарея из двух последовательно соединенных конденсаторов ( емкостью 2 и 4 мкФ) заряжена до напряжения 1200 В. Отключив конденсаторы от источника и друг от друга, их соединяют параллельно. Какие заряды и напряжения были и установятся на конденсаторах. Чему равна работа разряда. [54]
Эквивалентная емкость Ci — всех последовательно соединенных конденсаторов имеет напряжение nU0 и обычно называется емкостью генератора в ударе. Индуктивность LJ представляет собой сумму индуктив-ностей отдельных элементов импульсного генератора и зависит от его конструктивного выполнения. Сопротивление Ri I1RR равно сумме успокоительных Сопротивлений, предназначенных успокаивать ( демпфировать) колебания в цепи разряда. Сопротивление R2 соответствует разрядному сопротивлению Rv, которое включается на выходе ГИН для регулирования длины волны. Фронтовое сопротивление Rq, включается для регулирования длины фронта волны. Индуктивность L2 складывается из индуктивности, регулирующей форму импульса, и индуктивности испытуемого объекта. Суммарная емкость С2 включает в себя емкость испытуемого объекта, емкости на землю проводов за промежутком ИП0, емкость измерительных устройств ( шаров, делителей напряжения) и разрядную емкость Ср, служащую для регулирования длины фронта волны. [55]
Верхний продукт конденсируется в двух последовательно соединенных конденсаторах трубчатого типа. Корпусы конденсаторов выполнены из биметаллического листа со слоем моиель-метал-ла, а трубные пучки — из адмиралтейского сплава. Конденсированный верхний продукт подается по стальной трубе в сепаратор, где бензин отделяется от воды, направляемой в канализацию. На дренажной трубе установлен рН — метр. В сепараторе газ также отделяется от бензина и выпускается наверх, в газовую систему завода. [56]
Уравнение (3.21) формально соответствует модели двух последовательно соединенных конденсаторов с емкостями С § 2 и С. [57]
Если к точкам А к В последовательно соединенных конденсаторов подвести заряды q, то вследствие электростатической индукции на обкладках конденсаторов появятся равные и противоположные до знаку заряды 71729з — ( 7 — Ри этом пластинки соседних конденсаторов, соединенные между собой проводником, имеют одинаковый потенциал. [58]
Конденсаторный делитель напряжения представляет собой несколько последовательно соединенных конденсаторов. [60]
Страницы: 1 2 3 4 5
Общая емкость двух последовательно соединенных конденсаторов 160 пФ. Определить емкость
Два проводника соединены последовательно и подключены к источнику тока.Напряжение на первом проводнике 60 В, на втором — 20 В. Сравните сопротивлениеR … 1 первого проводника с сопротивлением R 2 второго проводника.1)R 1 = R 2 2)R 1 = 3R 2 3)R 2 = 3R 1 4) R 1 = 4R 2
Помогите решить! Два одинаковых металлических шарика находятся на расстоянии 50 см друг от друга. Заряд одного шарика в два раза больше заряда другого … . Шарики привели в соприкосновение и развели на некоторое расстояние. Найдите это расстояние если сила взаимодействия уменьшилась в 2 раза.
Помогите! Даю 10 баллов Яблоко массой 180 г свободно падает с ветки яблони на высоте 1,4 м на землю. Какой будет кинетическая энергия яблока перед уда … ром о землю? Чему равна его скорость перед ударом? Н (Принять g = 9. 8 кг) Ответ (округли до десятых): v=… м/с Eк=… Дж
Срочно помогите пожалуйста!!
Тема «КПД простых механизмов» КЕЙС №1 Изобретатель Иванов Сергей Павлович утверждал, что он создал простейший механизм для поднятия грузов с КПД = 110 … %. Защищая свою разработку, он заявил, что бесполезную работу, которая тратилась на нагревание трущихся деталей при подъёме, он исключил. Для этого обычные тросы он заменил на шёлковые, которые постоянно увлажнялись за счет смачивания их водой. Его оппонентами стали мастер цеха и экономист завода, которые доказали, что его изобретение не продумано серьёзно и требует доработки. Вопросы к кейсу — Какие аргументы могли выдвинуть мастер цеха и экономист? — Есть ли физические неточности в тексте?
Какие частицы находятся в плазме при низких температурах
Помогите прошу! Яблоко массой 180 г свободно падает с ветки яблони на высоте 1,4 м на землю. Какой будет кинетическая энергия яблока перед ударом о зе … млю? Чему равна его скорость перед ударом? Н (Принять g = 9. 8 кг) Ответ (округли до десятых): v=… м/с Eк=… Дж
Определите центр массы тела неправильной формы. Можно взять ЛЮБОЕ тело, только подробно распишите решение.
1. Кинематика. Свойства механического движения. Типы движения 2. Динамика. Законы классической механики 3. Законы сохранения в механике. 4. Основны … е принципы молекулярно-кинетической теории. 5. Основные уравнения молекулярно-кинетической теории идеального газа. 6. Термодинамические параметры. 7. Уравнение состояния. Газовые законы. Изопроцессы 8. Испарение и конденсация. Насыщенный пар и его свойства. Влажность 9. Тепловые двигатели и их эффективность. Цикл Карно 10. Поверхность. пол. Поверхностное натяжение. Инфекционное заболевание. Капиллярные явления 11. Свойства твердых тел. Кристаллы 12. Механические свойства твердых тел. Сублимация и десублимация 13. Внутренняя энергия идеального газа. Измерение внутренней энергии 14. Первый закон термодинамики. Применение первого закона термодинамики к различным тепловым процессам 15. Необратимость процессов в природе. Концепция второго начала термодинамики 16. Электрический заряд. Закон сохранения электрического заряда. Закон Кулона 17. Электрическое поле. Напряженность электрического поля. Принцип суперпозиции электрических полей 18. Потенциал. Разность потенциалов электрического поля. Связь между напряжением и потенциалом 19. Проводники и диэлектрики в электрическом поле. 20. Электрическая мощность. Конденсатор. Энергия электрического поля 21. Электрический ток, сила тока. Электродвижущая сила 22. Законы Ома. Сопротивление проводника. Собственный барьер 23. Электрическая цепь с проводниками, включенными последовательно и параллельно. 24. Разветвление цепи. Правила Кирхгофа 25. Работа и мощность электрического тока. Закон Джоуля-Ленца 26. Электрический ток в металлах. 27. Электрический ток в электролитах. Законы электролиза 28. Электропроводность газов. Зависимая и независимая категория 29. Электрический ток в вакууме. Термоэлектронная эмиссия 30. Электропроводность полупроводников и ее температурная зависимость.
1. Кинематика. Свойства механического движения. Типы движения 2. Динамика. Законы классической механики 3. Законы сохранения в механике. 4. Основны … е принципы молекулярно-кинетической теории. 5. Основные уравнения молекулярно-кинетической теории идеального газа. 6. Термодинамические параметры. 7. Уравнение состояния. Газовые законы. Изопроцессы 8. Испарение и конденсация. Насыщенный пар и его свойства. Влажность 9. Тепловые двигатели и их эффективность. Цикл Карно 10. Поверхность. пол. Поверхностное натяжение. Инфекционное заболевание. Капиллярные явления 11. Свойства твердых тел. Кристаллы 12. Механические свойства твердых тел. Сублимация и десублимация 13. Внутренняя энергия идеального газа. Измерение внутренней энергии 14. Первый закон термодинамики. Применение первого закона термодинамики к различным тепловым процессам 15. Необратимость процессов в природе. Концепция второго начала термодинамики 16. Электрический заряд. Закон сохранения электрического заряда. Закон Кулона 17. Электрическое поле. Напряженность электрического поля. Принцип суперпозиции электрических полей 18. Потенциал. Разность потенциалов электрического поля. Связь между напряжением и потенциалом 19. Проводники и диэлектрики в электрическом поле. 20. Электрическая мощность. Конденсатор. Энергия электрического поля 21. Электрический ток, сила тока. Электродвижущая сила 22. Законы Ома. Сопротивление проводника. Собственный барьер 23. Электрическая цепь с проводниками, включенными последовательно и параллельно. 24. Разветвление цепи. Правила Кирхгофа 25. Работа и мощность электрического тока. Закон Джоуля-Ленца 26. Электрический ток в металлах. 27. Электрический ток в электролитах. Законы электролиза 28. Электропроводность газов. Зависимая и независимая категория 29. Электрический ток в вакууме. Термоэлектронная эмиссия 30. Электропроводность полупроводников и ее температурная зависимость. 31. Магнитное поле. Магнитная индукция. Ампер эксперименты. Мощность в амперах 32. Сила Лоренца. Движение заряженных частиц в магнитном поле. 33. Магнитные свойства веществ. Температура Кюри 34. Электромагнитная индукция. Закон электромагнитной индукции. Правило Ленца 35. Явление самоиндукции. Индуктивность. Энергия магнитного поля 36. Свободные и непроизвольные электромагнитные колебания. Сходства между механическими и электромагнитными колебаниями 37. Уравнения и графики гармонических колебаний. 38. Генератор переменного тока. Мгновенные, максимальные и фактические значения ЭДС, напряжения, тока 39. Активное и реактивное сопротивление в цепи переменного тока. Индуктивное сопротивление в цепи переменного тока. Емкостное сопротивление в цепи переменного тока 40. Закон Ома для полной цепи переменного тока. Мощность в цепи переменного тока 41. Резонанс напряжений в электрической цепи. 42. Трансформатор. Производство, передача и использование электроэнергии 43. Циркуляция энергии в замкнутом колебательном контуре. 44. Распространение механических волн. Излучение и прием электромагнитных волн 45. Радиосвязь. Модуляция и обнаружение. Распространение радиоволн. Радар. Цифровая технология 46. Принцип Гюйгенса. Закон отражения света. Закон преломления света 47. Электромагнитная природа света. Скорость света. Световая дисперсия 48. Интерференция света. Дифракция света 49. Визуализация в системе линз, формула тонкой линзы. 50. Оптические инструменты. Глаз как оптическая система 51. Постулаты теории относительности. Преобразования Лоренца 52. Виды излучения. Спектры. Инфракрасные и ультрафиолетовые лучи. Рентгеновские лучи 53. Формула Планка. Фотон. Фотоэффект 54. Эксперименты Резерфорда по рассеянию альфа-частиц. 55. Естественная радиоактивность. Закон радиоактивного распада 56. Радиационная защита. Ядерного реактора 57. Ядерная энергия. Термоядерная реакция 58. Основные достижения, актуальные проблемы и этапы развития нанотехнологий. Наноматериалы 59. Мир звезд. Теория большого взрыва. Основные этапы мировой эволюции 60. Космическое будущее человечества и освоение космоса.
Как набрать емкость конденсаторами — Инженер ПТО
Как правильно соединять конденсаторы?
У многих начинающих любителей электроники в процессе сборки самодельного устройства возникает вопрос: “Как правильно соединять конденсаторы?”
Казалось бы, зачем это надо, ведь если на принципиальной схеме указано, что в данном месте схемы должен быть установлен конденсатор на 47 микрофарад, значит, берём и ставим. Но, согласитесь, что в мастерской даже заядлого электронщика может не оказаться конденсатора с необходимым номиналом!
Похожая ситуация может возникнуть и при ремонте какого-либо прибора. Например, необходим электролитический конденсатор ёмкостью 1000 микрофарад, а под рукой лишь два-три на 470 микрофарад. Ставить 470 микрофарад, вместо положенных 1000? Нет, это допустимо не всегда. Так как же быть? Ехать на радиорынок за несколько десятков километров и покупать недостающую деталь?
Как выйти из сложившейся ситуации? Можно соединить несколько конденсаторов и в результате получить необходимую нам ёмкость. В электронике существует два способа соединения конденсаторов: параллельное и последовательное.
В реальности это выглядит так:
Параллельное соединение
Принципиальная схема параллельного соединения
Последовательное соединение
Принципиальная схема последовательного соединения
Также можно комбинировать параллельное и последовательное соединение. Но на практике вам вряд ли это пригодиться.
Как рассчитать общую ёмкость соединённых конденсаторов?
Помогут нам в этом несколько простых формул. Не сомневайтесь, если вы будете заниматься электроникой, то эти простые формулы рано или поздно вас выручат.
Общая ёмкость параллельно соединённых конденсаторов:
С1 – ёмкость первого;
С2 – ёмкость второго;
С3 – ёмкость третьего;
СN – ёмкость N-ого конденсатора;
Cобщ – суммарная ёмкость составного конденсатора.
Как видим, при параллельном соединении ёмкости нужно всего-навсего сложить!
Внимание! Все расчёты необходимо производить в одних единицах. Если выполняем расчёты в микрофарадах, то нужно указывать ёмкость C1, C2 в микрофарадах. Результат также получим в микрофарадах. Это правило стоит соблюдать, иначе ошибки не избежать!
Чтобы не допустить ошибку при переводе микрофарад в пикофарады, а нанофарад в микрофарады, необходимо знать сокращённую запись численных величин. Также в этом вам поможет таблица. В ней указаны приставки, используемые для краткой записи и множители, с помощью которых можно производить пересчёт. Подробнее об этом читайте здесь.
Ёмкость двух последовательно соединённых конденсаторов можно рассчитать по другой формуле. Она будет чуть сложнее:
Внимание! Данная формула справедлива только для двух конденсаторов! Если их больше, то потребуется другая формула. Она более запутанная, да и на деле не всегда пригождается .
Или то же самое, но более понятно:
Если вы проведёте несколько расчётов, то увидите, что при последовательном соединении результирующая ёмкость будет всегда меньше наименьшей, включённой в данную цепочку. Что это значить? А это значит, что если соединить последовательно конденсаторы ёмкостью 5, 100 и 35 пикофарад, то общая ёмкость будет меньше 5.
В том случае, если для последовательного соединения применены конденсаторы одинаковой ёмкости, эта громоздкая формула волшебным образом упрощается и принимает вид:
Здесь, вместо буквы M ставиться количество конденсаторов, а C1 – его ёмкость.
Стоит также запомнить простое правило:
При последовательном соединении двух конденсаторов с одинаковой ёмкостью результирующая ёмкость будет в два раза меньше ёмкости каждого из них.
Таким образом, если вы последовательно соедините два конденсатора, ёмкость каждого из которых 10 нанофарад, то в результате она составит 5 нанофарад.
Не будем пускать слов по ветру, а проверим конденсатор, замерив ёмкость, и на практике подтвердим правильность показанных здесь формул.
Возьмём два плёночных конденсатора. Один на 15 нанофарад (0,015 мкф.),а другой на 10 нанофарад (0,01 мкф.) Соединим их последовательно. Теперь возьмём мультиметр Victor VC9805+ и замерим суммарную ёмкость двух конденсаторов. Вот что мы получим (см. фото).
Замер ёмкости при последовательном соединении
Ёмкость составного конденсатора составила 6 нанофарад (0,006 мкф.)
А теперь проделаем то же самое, но для параллельного соединения. Проверим результат с помощью того же тестера (см. фото).
Измерение ёмкости при параллельном соединении
Как видим, при параллельном соединении ёмкость двух конденсаторов сложилась и составляет 25 нанофарад (0,025 мкф.).
Что ещё необходимо знать, чтобы правильно соединять конденсаторы?
Во-первых, не стоит забывать, что есть ещё один немаловажный параметр, как номинальное напряжение.
При последовательном соединении конденсаторов напряжение между ними распределяется обратно пропорционально их ёмкостям. Поэтому, есть смысл при последовательном соединении применять конденсаторы с номинальным напряжением равным тому, которое имеет конденсатор, взамен которого мы ставим составной.
Если же используются конденсаторы с одинаковой ёмкостью, то напряжение между ними разделится поровну.
Для электролитических конденсаторов.
При соединении электролитических конденсаторов (электролитов) строго соблюдайте полярность! При параллельном соединении всегда подключайте минусовой вывод одного конденсатора к минусовому выводу другого,а плюсовой вывод с плюсовым.
Параллельное соединение электролитов
Схема параллельного соединения
В последовательном соединении электролитов ситуация обратная. Необходимо подключать плюсовой вывод к минусовому. Получается что-то вроде последовательного соединения батареек.
Последовательное соединение электролитов
Схема последовательного соединения
Также не забывайте про номинальное напряжение. При параллельном соединении каждый из задействованных конденсаторов должен иметь то номинальное напряжение, как если бы мы ставили в схему один конденсатор. То есть если в схему нужно установить конденсатор с номинальным напряжением на 35 вольт и ёмкостью, например, 200 микрофарад, то взамен его можно параллельно соединить два конденсатора на 100 микрофарад и 35 вольт. Если хоть один из них будет иметь меньшее номинальное напряжение (например, 25 вольт), то он вскоре выйдет из строя.
Желательно, чтобы для составного конденсатора подбирались конденсаторы одного типа (плёночные, керамические, слюдяные, металлобумажные). Лучше всего будет, если они взяты из одной партии, так как в таком случае разброс параметров у них будет небольшой.
Конечно, возможно и смешанное (комбинированное) соединение, но в практике оно не применяется (я не видел ). Расчёт ёмкости при смешанном соединении обычно достаётся тем, кто решает задачи по физике или сдаёт экзамены 🙂
Тем же, кто не на шутку увлёкся электроникой непременно надо знать, как правильно соединять резисторы и рассчитывать их общее сопротивление!
Вопрос о том, как соединить конденсаторы может возникнуть у любого человека, интересующегося электроникой и пайкой. Чаще всего, необходимость в этом возникает в случаях отсутствия под рукой устройства подходящего номинала при сборке или ремонте какого-либо прибора.
К примеру, человеку нужно отремонтировать устройство, заменив в нем электролитический конденсатор ёмкостью 1000 микрофарад или больше, на руках подходящие по номиналу детали отсутствуют, но есть несколько изделий с меньшими параметрами. В этом случае есть три варианта выхода из сложившейся ситуации:
- Поставить вместо конденсатора на 1000 микрофарад устройство с меньшим номиналом.
- Поехать в ближайший магазин или радио-рынок для покупки подходящего варианта.
- Соединить несколько элементов вместе для получения необходимой ёмкости.
От установки радиоэлемента меньшего номинала лучше отказаться, так как подобные эксперименты не всегда заканчиваются успешно. Можно съездить на рынок или в магазин, но это требует немало времени. Потому в сложившейся ситуации чаще соединяют несколько конденсаторов и получают необходимую емкость.
Параллельное соединение конденсаторов
Параллельная схема подключения конденсаторов предполагает соединение в две группы всех обкладок приборов. В одну группу соединяются первые выводы, а в другую группу – вторые выводы. На рисунке ниже представлен пример.
Конденсаторы, соединенные параллельно между собой, подключаются к одному источнику напряжения, поэтому на них существует две точки напряжения или разности потенциалов. Следует учитывать, что на всех выводах подключенных параллельно конденсаторов напряжение будет иметь одинаковую величину.
Параллельная схема образует из элементов единую ёмкость, величина которой равняется сумме ёмкостей всех подключенных в группу конденсаторов. При этом через конденсаторы в процессе работы устройства будет протекать ток разной величины. Параметры проходящего через изделия тока зависят от индивидуальной ёмкости устройства. Чем выше ёмкость, тем больший по величине ток пройдет через него. Формула, характеризующее параллельное соединение, имеет следующий вид:
Параллельная схема чаще всего используется в быту, она позволяет собрать необходимую ёмкость из любого числа отдельных, различных по номиналу элементов.
Последовательное соединение конденсаторов
Схема последовательного подключения представляет собой цепочку, в которой первая обкладка конденсатора соединяется со второй обкладкой предыдущего устройства, а вторая обкладка – с первой обкладкой следующего прибора. Первый вывод первого конденсатора и второй вывод последней детали в цепи соединяются с источником электрического тока, благодаря чему между ними осуществляется перераспределение электрических зарядов. Все промежуточные обкладки имеют одинаковые по величине заряды, чередующиеся по знаку.
На рисунке ниже представлен пример последовательного подключения.
Через соединенные в группу конденсаторы протекает ток одинаковой величины. Общая мощность ограничивается площадью обкладок устройства с наименьшим номиналом, так как после зарядки наименьшего по ёмкости устройства, вся цепь перестанет пропускать ток.
Несмотря на явные недостатки, данный способ обеспечивает увеличение изоляции между отдельными обкладками до суммы расстояний между выводами на всех последовательно соединенных конденсаторах. То есть, при последовательном соединении двух элементов с рабочим напряжением 200 В, изоляция между их выводами сможет выдерживать напряжение до 1000 В. Ёмкость по формуле:
Данный способ позволяет получить эквивалент меньшего по ёмкости конденсатора в группе, способной работать при высоких напряжениях. Всего этого можно достичь путем покупки одного единственного элемента подходящего номинала, потому на практике последовательные соединения практически не встречаются.
Эта формула актуальна для расчета общей ёмкости цепи последовательно соединенных двух конденсаторов. Для определения общей ёмкости цепи с большим числом приборов необходимо воспользоваться формулой:
Смешанная схема
Пример смешанной схемы подключения представлен ниже.
Чтобы определить общую ёмкость нескольких устройств, всю схему необходимо разделить на имеющиеся группы последовательного и параллельного соединения и рассчитать параметры ёмкости для каждой из них.
На практике данный способ встречаются на различных платах, с которыми приходиться работать радиолюбителям.
В электрических цепях применяются различные способы соединения конденсаторов. Соединение конденсаторов может производиться: последовательно, параллельно и последовательно-параллельно (последнее иногда называют смешанное соединение конденсаторов). Существующие виды соединения конденсаторов показаны на рисунке 1.
Рисунок 1. Способы соединения конденсаторов.
Параллельное соединение конденсаторов.
Если группа конденсаторов включена в цепь таким образом, что к точкам включения непосредственно присоединены пластины всех конденсаторов, то такое соединение называется параллельным соединением конденсаторов (рисунок 2.).
Рисунок 2. Параллельное соединение конденсаторов.
При заряде группы конденсаторов, соединенных параллельно, между пластинами всех конденсаторов будет одна и та же разность потенциалов, так как все они заряжаются от одного и того же источника тока. Общее же количество электричества на всех конденсаторах будет равно сумме количеств электричества, помещающихся на каждом из конденсаторов, так как заряд каждого их конденсаторов происходит независимо от заряда других конденсаторов данной группы. Исходя из этого, всю систему параллельно соединенных конденсаторов можно рассматривать как один эквивалентный (равноценный) конденсатор. Тогда общая емкость конденсаторов при параллельном соединении равна сумме емкостей всех соединенных конденсаторов.
Обозначим суммарную емкость соединенных в батарею конденсаторов буквой Собщ, емкость первого конденсатора С1 емкость второго С2 и емкость третьего С3. Тогда для параллельного соединения конденсаторов будет справедлива следующая формула:
Последний знак + и многоточие указывают на то, что этой формулой можно пользоваться при четырех, пяти и вообще при любом числе конденсаторов.
Последовательное соединение конденсаторов.
Если же соединение конденсаторов в батарею производится в виде цепочки и к точкам включения в цепь непосредственно присоединены пластины только первого и последнего конденсаторов, то такое соединение конденсаторов называется последовательным (рисунок 3).
Рисунок 2. Последовательное соединение конденсаторов.
При последовательном соединении все конденсаторы заряжаются одинаковым количеством электричества, так как непосредственно от источника тока заряжаются только крайние пластины (1 и 6), а остальные пластины (2, 3, 4 и 5) заряжаются через влияние. При этом заряд пластины 2 будет равен по величине и противоположен по знаку заряду пластины 1, заряд пластины 3 будет равен по величине и противоположен по знаку заряду пластины 2 и т. д.
Напряжения на различных конденсаторах будут, вообще говоря, различными, так как для заряда одним и тем же количеством электричества конденсаторов различной емкости всегда требуются различные напряжения. Чем меньше емкость конденсатора, тем большее напряжение необходимо для того, чтобы зарядить этот конденсатор требуемым количеством электричества, и наоборот.
Таким образом, при заряде группы конденсаторов, соединенных последовательно, на конденсаторах малой емкости напряжения будут больше, а на конденсаторах большой емкости — меньше.
Аналогично предыдущему случаю можно рассматривать всю группу конденсаторов, соединенных последовательно, как один эквивалентный конденсатор, между пластинами которого существует напряжение, равное сумме напряжений на всех конденсаторах группы, а заряд которого равен заряду любого из конденсаторов группы.
Возьмем самый маленький конденсатор в группе. На нем должно быть самое большое напряжение. Но напряжение на этом конденсаторе составляет только часть общего напряжения, существующего на всей группе конденсаторов. Напряжение на всей группе больше напряжения на конденсаторе, имеющем самую малую емкость. А отсюда непосредственно следует, что общая емкость группы конденсаторов, соединенных последовательно, меньше емкости самого малого конденсатора в группе.
Для вычисления общей емкости при последовательном соединении конденсаторов удобнее всего пользоваться следующей формулой:
Для частного случая двух последовательно соединенных конденсаторов формула для вычисления их общей емкости будет иметь вид:
Последовательно-параллельное (смешанное) соединение конденсаторов
Последовательно-параллельным соединением конденсаторов называется цепь имеющая в своем составе участки, как с параллельным, так и с последовательным соединением конденсаторов.
На рисунке 4 приведен пример участка цепи со смешанным соединением конденсаторов.
Рисунок 4. Последовательно-параллельное соединение конденсаторов.
При расчете общей емкости такого участка цепи с последовательно-параллельным соединением конденсаторов этот участок разбивают на простейшие участки, состоящие только из групп с последовательным или параллельным соединением конденсаторов. Дальше алгоритм расчета имеет вид:
1. Определяют эквивалентную емкость участков с последовательным соединением конденсаторов.
2. Если эти участки содержат последовательно соединенные конденсаторы, то сначала вычисляют их емкость.
3. После расчета эквивалентных емкостей конденсаторов перерисовывают схему. Обычно получается цепь из последовательно соединенных эквивалентных конденсаторов.
4. Рассчитывают емкость полученной схемы.
Один из примеров расчета емкости при смешанном соединении конденсаторов приведен на рисунке 5.
Рисунок 5. Пример расчета последовательно-параллельного соединения конденсаторов.
Подробнее о расчетах соединения конденсаторов можно узнать в мультимедийном учебнике по основам электротехники и электроники:
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Лекция 8
POP4 20,49
Два конденсатора емкостью 25 µ Ф и 5 µ Ф подключены параллельно с 100 В на каждом.
Какая общая энергия хранится?
A. 150 µ J
Б. 0,150 Дж
С. 150 Дж
D. 150 кДж
Ответ
POP4 20,49
Два конденсатора по 25 µ Ф и 5 µ Ф подключены последовательно.
Что Δ В требуется для хранения 0.150 Дж?
А. 22,8 В
Б. 100 В
С. 137 V
D. 268 V
Ответ
klm Walker5e CnEx 21-19
Переключатель на рисунке ниже изначально разомкнут, а конденсатор не заряжен. Если & Escr; = 6,00 В, R = 10,0 Ом и C = 72,0 µ F, какой ток протекает через батарею сразу после включения переключателя?
схемотехнический симулятор
А. 0,432 мА
Б.0,600 А
С. 0,900 А
D. 1.20 A
Ответ
klm Walker5e CnEx 21-19
Переключатель на рисунке ниже изначально разомкнут, а конденсатор не заряжен. Если & Escr; = 6,00 В, R = 10,0 Ом и C = 72,0 µ F, какой ток течет через батарею через долгое время после включения переключателя?
А. 0,432 мА
Б. 0,600 А
С. 0,900 А
D. 1.20 A
Ответ
klm Walker5e Ex 21-17
Если C = 24.0 µ F в схеме ниже, какова эквивалентная емкость всей цепи?
A. 8.00 µ F
В. 16.0 µ F
С. 36,0 µ F
D. 72.0 µ F
Ответ
Walker5e 21.61
Два конденсатора, C 1 = C и C 2 = 2 C , подключены к батарее. Конденсатор _____ накапливает больше энергии, когда они подключены к батарее последовательно, а конденсатор _____ накапливает больше энергии, когда они соединяются параллельно с батареей.
А. С 1 … С 1
Б. С 2 … С 1
С. С 1 … С 2
D. C 2 … C 2
Ответ
SJ6 28,33
Батарея была подключена к указанной ниже цепи в течение длительного времени. Какое напряжение на конденсаторе?
А.2,00 В
Б. 4.00 В
В. 6.00 В
D. 8.00 V
Ответ
Б. 0,150 Дж
Д. 268 В
D. 1.20 А
Сразу после включения переключателя конденсатор разряжается и ведет себя как провод. Батарея 6,00 В пропускает 0,600 А тока через каждый из резисторов 10,0 Ом (или, если вы предпочитаете, два резистора, включенных параллельно, имеют эквивалентное сопротивление 5.00 Ом), что дает ток через батарею 1,20 А.
Б. 0,600 А
Через долгое время после включения переключателя конденсатор полностью заряжен и ведет себя как разомкнутая цепь. Батарея на 6,00 В пропускает 0,600 А через левый резистор 10,0 Ом.
C. 36.0 µ F
Два последовательно соединенных конденсатора имеют эквивалентную емкость ½ C , и они соединены параллельно с третьим идентичным конденсатором.Следовательно, мы складываем две емкости, чтобы получить эквивалентную емкость 1,50 C или 1,50 × 24,0 µ F = 36,0 µ F.
C. C 1 … C 2
При последовательном соединении два конденсатора имеют одинаковый заряд. Заметив, что U = ½ Q ² / C , вы можете увидеть, что меньший конденсатор C 1 сохраняет больше всего энергии. (Убедитесь сами, что если напряжение АКБ 6.0 В и C = 10,0 µ F, C 1 накопителей 80 µ J и C 2 накоплений 40 µ Дж.)
При параллельном подключении два конденсатора имеют одинаковое напряжение. Заметив, что U = ½ CV ², вы можете увидеть, что больший конденсатор C 2 накапливает больше всего энергии. (Убедитесь сами, что если напряжение батареи составляет 6,0 В и C = 10,0 µ F, C 1 хранит 180 µ Дж и C 2 хранит 360 µ Дж.)
В. 6,00 В
Левая сторона конденсатора находится под более высоким потенциалом.
и параллельный калькулятор емкости Apogeeweb
Часто задаваемые вопросы
1. Как рассчитать параллельную емкость?
Общее значение емкости конденсаторов, соединенных параллельно, фактически вычисляется путем сложения площадей пластин. Другими словами, общая емкость равна сумме всех отдельных емкостей, включенных параллельно.
2. Как отличить последовательный конденсатор от параллельного?
Когда разность потенциалов на пластинах одинакова, они параллельны. Когда ток через них равен, они включены последовательно.
3. Зачем нужно последовательно включать конденсаторы?
Причина, по которой вы можете соединять конденсаторы последовательно, заключается в том, чтобы увеличить эффективное управление напряжением цепи. Конденсаторы имеют номинальное напряжение пробоя, превышение которого значительно увеличивает вероятность отказа.Два одинаковых конденсатора будут иметь половину напряжения на каждом.
4. Последовательные или параллельные конденсаторы накапливают больше энергии?
Энергия, запасенная в конденсаторе, является функцией напряжения на конденсаторе. Напряжение будет выше, когда они подключены параллельно, поэтому при параллельном подключении сохраняется больше энергии.
5. Какова основная функция конденсатора?
Конденсатор — это электронный компонент, который накапливает и выделяет электричество в цепи. Он также пропускает переменный ток, не пропуская постоянный ток.Конденсатор является неотъемлемой частью электронного оборудования и поэтому почти всегда используется в электронных схемах.
6. В чем разница между последовательным и параллельным подключением?
В последовательной цепи сумма напряжений, потребляемых каждым отдельным сопротивлением, равна напряжению источника. Компоненты, соединенные параллельно, соединяются несколькими путями, так что ток может разделяться; одинаковое напряжение приложено к каждому компоненту.
7. Почему последовательно подключенные конденсаторы уменьшают емкость?
Полное сопротивление двух последовательно соединенных конденсаторов равно сумме индивидуальных сопротивлений двух конденсаторов.Поскольку импеданс пропорционален обратной величине емкости, больший импеданс последовательной цепи означает меньшую емкость.
8. Что произойдет, если резистор и конденсатор соединить параллельно?
Когда резисторы и конденсаторы смешиваются вместе в параллельных цепях (так же, как в последовательных цепях), общий импеданс будет иметь фазовый угол где-то между 0 ° и -90 °. Ток в цепи будет иметь фазовый угол от 0 ° до + 90 °.
9.Как узнать, включен ли последовательный конденсатор параллельно?
Если у каждого конденсатора ОБЕ клеммы подключены к ОБЕИМ клеммам других, то они включены параллельно. Если у каждого конденсатора только одна клемма, подключенная к одной клемме другого конденсатора, они подключены последовательно.
10. Почему последовательно подключенные конденсаторы уменьшают емкость?
Полное сопротивление двух последовательно соединенных конденсаторов равно сумме индивидуальных сопротивлений двух конденсаторов. Поскольку импеданс пропорционален обратной величине емкости, больший импеданс последовательной цепи означает меньшую емкость.
11. Как соединить параллельно конденсаторы и резисторы?
Детальная операция начинается с 1:42.
12. Почему мы используем конденсаторы в цепях постоянного тока?
При использовании в цепи постоянного или постоянного тока конденсатор заряжается до напряжения питания, но блокирует прохождение тока через него, потому что диэлектрик конденсатора непроводящий и в основном является изолятором.
13. Преобразует ли конденсатор переменный ток в постоянный?
Конденсатор не может самостоятельно преобразовывать переменный ток в постоянный, но хороший синхронизированный переключатель, который пропускает выбранные пики и отклоняет части формы волны переменного тока, сделает это.
14. Что произойдет, если конденсатор подключен к постоянному току?
Когда конденсаторы подключаются к источнику постоянного напряжения постоянного тока, они становятся заряженными до значения приложенного напряжения, действуя как устройства временного хранения и сохраняя или удерживая этот заряд неопределенно долго, пока присутствует напряжение питания.
15. Есть ли у конденсаторов положительная и отрицательная сторона?
Большинство электролитических конденсаторов поляризованного типа, то есть напряжение, подключенное к клеммам конденсатора, должно иметь правильную полярность, т.е.е. положительное на положительное и отрицательное на отрицательное.
16. Как решить проблемы, связанные с подключением конденсаторов последовательно и параллельно?
Видео ниже показывает, как рассчитать емкость в последовательной и параллельной цепи, а также дает лабораторный пример, демонстрирующий математические действия.
Серия Подключение конденсаторов
На рис. 1 (а) показано, что два конденсатора соединены последовательно. Для каждого конденсатора он имеет одинаковый ток, а соотношение тока и напряжения соответствует
.«
(а) (б)
Рисунок 1.Последовательное соединение
Итак, два конденсатора соединены последовательно, эквивалентная емкость составляет
Эквивалентная схема показана на рисунке 1 (б). Когда конденсаторы соединены последовательно, напряжение на каждом конденсаторе соответствует
Параллельное соединение конденсаторов
На рис. 2 (а) показано, что два конденсатора подключены параллельно. Для каждого конденсатора оно имеет одинаковое напряжение, а соотношение тока и напряжения соответствует
.Рисунок 2.Cicuit параллельных конденсаторов
Два конденсатора соединены параллельно, эквивалентная емкость
Эквивалентная схема показана на рисунке 2 (б). Когда конденсаторы соединены параллельно, ток на каждом конденсаторе соответствует
Разница между последовательными конденсаторами и параллельными конденсаторами
При последовательном соединении конденсаторов емкость уменьшается (для расчета общей емкости после последовательного соединения см. Метод параллельного подключения резисторов), а выдерживаемое напряжение увеличивается.
Конденсаторы подключаются параллельно, емкость увеличивается (добавление каждой емкости), а выдерживаемое напряжение наименьшее. Последовательный конденсатор: чем больше число последовательно, тем меньше емкость, но выше выдерживаемое напряжение. Отношение емкости: 1 / C = 1 / C1 + 1 / C2 + 1 / C3 Параллельная емкость: чем больше параллельное соединение, тем больше емкость, но выдерживаемое напряжение не изменилось, отношение емкости: C = C1 + C2 + C3
См. Более подробную информацию о конденсаторах, включенных последовательно и параллельно.Кликните сюда!
Конденсаторы комбинированные
В некоторых цепях конденсаторы соединены последовательно и параллельно. Чтобы определить, например, общий заряд, накопленный набором конденсаторов, мы должны найти единственную эквивалентную емкость набора. Это делается путем идентификации пары конденсаторов в наборе, которые включены последовательно или параллельно друг другу, замены этой пары эквивалентным конденсатором (тем самым уменьшая количество конденсаторов на один) и повторения до тех пор, пока у нас не останется один. конденсатор, который является эквивалентом набора.
Возьмем, к примеру, ситуацию выше. Четыре конденсатора имеют следующие значения:
C 1 = C 2 = 90 пФ.
C 3 = 45 пФ
C 4 = 120 пФ
Какова разность потенциалов на каждом конденсаторе? Сколько заряда у каждого конденсатора?
Чтобы решить эту проблему, нам нужно найти эквивалентную емкость набора конденсаторов. Первый шаг — перерисовать схему так, чтобы C 1 был нарисован вертикально — это делает более очевидным, что идет параллельно или последовательно.
Теперь сократите цепь с 4 конденсаторов до 1.
Шаг 1 — C 2 и C 3 идут последовательно. Замените эту пару одним конденсатором C 23 :
1 / C 23 = 1 / C 2 + 1 / C 3 = 1/90 + 1/45 = 3/90.
Следовательно, C 23 = 90/3 = 30 пФ.
Шаг 2 — C 1 и C 23 работают параллельно. Замените эту пару одним конденсатором C 123 = 90 + 30 = 120 пФ.
Шаг 3 — C 4 и C 123 идут последовательно. Замените эту пару одним конденсатором C eq :
1 / C экв. = 1 / C 4 + 1 / C 123 = 1/120 + 1/120 = 2/120
C экв = 120/2 = 60 пФ
Шаг 4 — Определите заряд на C eq .
Q = C экв ΔV = 60 пФ * 12 В = 720 пКл.
Теперь нам нужно расширить схему до четырех исходных конденсаторов и определить заряд и разность потенциалов на каждом из них по мере продвижения.
Шаг 1 — C eq представляет C 4 и C 123 последовательно. Последовательные конденсаторы имеют одинаковый заряд, но разделяют разность потенциалов.
Q 4 = Q 123 = 720 пКл.
Конденсаторы одинаковые, поэтому на каждый из них подается по 6 вольт.
Шаг 2 — C 123 представляет C 1 и C 23 параллельно. Параллельно подключенные устройства имеют одинаковую разность потенциалов (в данном случае 6 В).
Q 1 = C 1 * 6 = 540 пКл.
Q 23 = C 23 * 6 = 180 пКл.
Они добавляют к 720 пКл, как и должно быть.
Шаг 3 — C 23 представляет последовательно C 2 и C 3 .
Q 2 = Q 3 = 180 пКл.
ΔV 2 = Q 2 / C 2 = 180/90 = 2 вольта.
ΔV 3 = Q 3 / C 3 = 180/45 = 4 В.
Они добавляют к 6 вольт, как должны.
Шаг 4. Хороший способ проверить согласованность — пометить потенциал в разных точках. Выберите некоторую точку в качестве ориентира (скажем, 0 В на отрицательном полюсе батареи) и пометьте другие точки, относящиеся к ней. Убедитесь, что разность потенциалов на конденсаторах соответствует этим значениям потенциала.
Последовательные конденсаторы — Основные вопросы и ответы по электротехнике
Этот набор вопросов и ответов с множественным выбором (MCQ) по базовой электротехнике посвящен «последовательным конденсаторам».
1. Какова общая емкость при последовательном соединении двух конденсаторов C1 и C2?
a) (C1 + C2) / C1C2
b) 1 / C1 + 1 / C2
c) C1C2 / (C1 + C2)
d) C1 + C2
Посмотреть ответ
Ответ: c
Пояснение: когда конденсаторы при последовательном соединении эквивалентная емкость составляет:
1 / Ctotal = 1 / C1 + 1 / C2, следовательно, Ctotal = C1C2 / (C1 + C2).
2. N конденсаторов емкостью C соединены последовательно, рассчитайте эквивалентную емкость.
a) C / N
b) C
c) CN
d) N / C
Посмотреть ответ
Ответ: d
Пояснение: При последовательном соединении конденсаторов эквивалентная емкость составляет:
1 / Ctotal = 1 / C + 1 / C + 1 / C + ……..N раз.
1 / Ctotal = N / C.
Cобщ. = C / N.
3. При последовательном соединении конденсаторов эквивалентная емкость составляет ___________ каждой отдельной емкости.
a) Более
b) Менее
c) Равно
d) Предоставлено недостаточно данных
Просмотреть ответ
Ответ: b
Пояснение: При последовательном соединении конденсаторов эквивалентная емкость составляет:
1 / Ctotal = 1 / С1 + 1 / С2. Поскольку мы находим величину, обратную сумме обратных величин, эквивалентная емкость меньше отдельных значений емкости.
4. Какая эквивалентная емкость?
a) 1,5F
b) 0,667F
c) 2,45F
d) 2,75F
Просмотреть ответ
Ответ: b
Пояснение: При последовательном соединении конденсаторов
1 / C всего = 1 / C1 + 1 / C2 = 1/2 + 1 = 3/2
C итого = 2/3 = 0,667 F.
5. При последовательном соединении конденсаторов ___________ не меняется.
a) Напряжение на каждом конденсаторе
b) Заряд
c) Емкость
d) Сопротивление
Просмотр ответа
Ответ: b
Объяснение: Когда конденсаторы соединены последовательно, заряд остается прежним, поскольку существует такая же величина протекающего тока в каждом конденсаторе.
6. Когда конденсаторы соединены последовательно _______________ Разные
a) Напряжение на каждом конденсаторе
b) Заряд
c) Емкость
d) Сопротивление
Посмотреть ответ
Ответ: a
Пояснение: Когда конденсаторы соединены последовательно, напряжение меняется, потому что падение напряжения на каждом конденсаторе отличается.
7. Четыре конденсатора 10Ф подключены последовательно, рассчитайте эквивалентную емкость.
а) 1,5F
б) 2,5F
в) 3.5F
d) 0,5F
Посмотреть ответ
Ответ: b
Объяснение: При последовательном соединении конденсаторов
1 / C всего = 1 / C1 + 1 / C2 + 1 / C3 + 1 / C4 = 1 / 10 + 1/10 + 1/10 + 1/10 = 4 / 10F.
C всего = 10/4 = 2,5F.
8. Рассчитайте заряд в цепи.
a) 66.67C
b) 20.34C
c) 25.45C
d) 30.45C
Просмотр ответа
Ответ: a
Объяснение: При последовательном соединении конденсаторов эквивалентная емкость составляет:
1 / C всего = 1 / C1 + 1 / C2 = 1/2 + 1 = 3/2
C всего = 2/3 F
Q = CV = (2/3) * 100 = 200/3 C = 66.67C.
9. Рассчитайте напряжение на конденсаторе 1Ф.
a) 33,33 В
b) 66,67 В
c) 56,56 В
d) 23,43 В
Просмотр ответа
Ответ: b
Пояснение: При последовательном соединении конденсаторов
1 / C всего = 1 / C1 + 1 / C2 = 1/2 + 1 = 3/2
Q = CV = (2/3) * 100 = 66,67 ° C.
В на конденсаторе 1F = 66,67 / 1 = 66,67 В.
10. Рассчитайте напряжение на конденсаторе 2F.
а) 33,33 В
б) 66,67 В
в) 56.56V
d) 23,43V
Посмотреть ответ
Ответ: a
Объяснение: При последовательном соединении конденсаторов
1 / C всего = 1 / C1 + 1 / C2 = 1/2 + 1 = 3/2
Q = CV = (2/3) * 100 = 66,67 С.
В на конденсаторе 2F = 66,67 / 2 = 33,33 В.
Серия Sanfoundry Global Education & Learning — Основы электротехники.
Чтобы практиковаться во всех областях базовой электротехники, представляет собой полный набор из 1000+ вопросов и ответов с несколькими вариантами ответов .
Примите участие в конкурсе сертификации Sanfoundry, чтобы получить бесплатную Почетную грамоту. Присоединяйтесь к нашим социальным сетям ниже и будьте в курсе последних конкурсов, видео, стажировок и вакансий!
Физика для науки и техники II
Пример из отдела академических технологий на Vimeo.
Пример подключения конденсаторов
Давайте рассмотрим пример, связанный с подключением конденсаторов.Предположим, что у нас есть цепь с источником питания, который генерирует разность потенциалов v вольт, подключенную к конденсатору c 1. Скажем, таким образом c 2, c 3, c 4 и c5. Допустим, у нас есть еще один конденсатор с емкостью c 6. Мы хотели бы вычислить эквивалентную емкость этой схемы.
Приведем числовые значения этих конденсаторов. Скажем, c 1 равно 1 мкФ, c 2 равно 2 мкФ, а c 3 равно 2 мкФ. c 4 равно 3 мкФ, а c 5 равно 5 мкФ.Наконец, c 6 равно 1 мкФ. Когда мы смотрим на нашу схему, мы сразу понимаем, что c 3, c 4 и c 5, эти три, соединены параллельно. Таким образом, эквивалент этой параллельной комбинации подключается последовательно к c 1, c 2 и c6. Решая эти типы проблем или анализируя эти типы схем, мы можем продолжить и вычислить эквивалентную емкость соединений конденсаторов внутри схемы, и на каждом этапе мы перерисовываем схему.
Сначала давайте посчитаем эквивалентную емкость этой параллельной комбинации.Другими словами, просто выньте этот блок и замените его эквивалентной емкостью. По мере того, как мы это делаем, давайте перерисуем схему. Тогда наша схема будет равна c 1 здесь, c 2 здесь, а вот эквивалент этой параллельной комбинации, и давайте назовем эту схему c эквивалентом 1 и продолжим, c 6 здесь. Все они теперь соединены последовательно. Поскольку эти три c 3, c 4 и c 5 соединены параллельно, мы можем мгновенно вычислить их эквивалентную емкость для параллельного подключения, эквивалент c — это непосредственно сумма емкостей каждого конденсатора, поэтому эквивалент c равен c 3 плюс c 4 плюс c 5.Следовательно, эквивалент C 1 будет равен c 3 равен 2 микрофарадам, плюс c 4 равен 3 микрофарадам, плюс c 5 равен 5 микрофарадам, поэтому эквивалент c будет равен 10 микрофарадам.
После того, как мы определим c эквивалент 1, теперь мы можем легко продолжить и вычислить эквивалентную емкость этих четырех конденсаторов, которые соединены последовательно. Мы знаем, что для последовательного соединения величина, обратная эквивалентной емкости, равна сумме обратных величин каждой емкости в комбинации.Поэтому мы заменим все эти четыре на одну, и это будет полная эквивалентная емкость этой схемы. Наша последняя упрощенная схема примет эту форму.
1 по сравнению с эквивалентом c, следовательно, будет равно 1 по сравнению с эквивалентом c 1 плюс 1 по сравнению с c 2 плюс 1 по сравнению с эквивалентом c 1 плюс 1 вместо c 6. Если мы подставим числовые значения, 1 вместо эквивалента c будет равно c равно 1 микрофараду, а c 2 составляет 2 микрофарада, поэтому у нас 1 больше 1 плюс 1 больше 2 плюс 1 больше c эквивалентно 1 и это 10 микрофарад, 1 больше 10, плюс c 6 и c 6 были равны 1 микрофараду, поэтому 1 больше 1.
Если у нас есть общий знаменатель, это будет 10, поэтому мы умножим это на 10, это на 5, числитель и знаменатель, это будет умножено на 1, и это будет снова умножено на 10, чтобы получить общий знаменатель. Следовательно, эквивалент 1 по c будет равен 10 плюс 5 плюс 1 плюс 10, деленный на 10. Таким образом, эквивалент 1 по c будет равен 10, 20, 25, 26 по 10 и отсюда, решение для эквивалента c, что мы возьмем обратное, у нас будет 10 на 26, или мы можем упростить это как 5 на 13 микрофарад как эквивалентную емкость этой схемы.
Емкостьпоследовательно | Электрический потенциал и электрическое поле
Несколько конденсаторов могут быть соединены вместе в различных приложениях. Несколько подключений конденсаторов действуют как один эквивалентный конденсатор. Общая емкость этого эквивалентного одиночного конденсатора зависит как от отдельных конденсаторов, так и от способа их подключения. Существует два простых и распространенных типа соединений, называемых серии и параллельно , для которых мы можем легко вычислить общую емкость.Некоторые более сложные соединения также могут быть связаны с комбинациями последовательного и параллельного.
Емкость в серии
На этом рисунке (а) показано последовательное соединение трех конденсаторов с приложенным напряжением. Как и в случае любого конденсатора, емкость комбинации связана с зарядом и напряжением соотношением \ (C = \ cfrac {Q} {V} \).
Обратите внимание на этот рисунок, что противоположные заряды величины \ (Q \) текут по обе стороны от первоначально незаряженной комбинации конденсаторов при приложении напряжения \ (V \).Для сохранения заряда необходимо, чтобы на пластинах отдельных конденсаторов создавались заряды одинаковой величины, поскольку заряд разделяется только в этих изначально нейтральных устройствах. Конечным результатом является то, что комбинация напоминает одиночный конденсатор с эффективным разделением пластин больше, чем у отдельных конденсаторов. (См. Этот рисунок (b).) Чем больше расстояние между пластинами, тем меньше емкость. Общей особенностью последовательного соединения конденсаторов является то, что общая емкость меньше любой из отдельных емкостей.
(а) Конденсаторы, подключенные последовательно. Величина заряда на каждой пластине равна \ (Q \). (b) Эквивалентный конденсатор имеет большее расстояние между пластинами \ (d \). Последовательные соединения производят общую емкость, которая меньше, чем у любого из отдельных конденсаторов.
Мы можем найти выражение для общей емкости, рассматривая напряжение на отдельных конденсаторах, показанных на этом рисунке. Решение \ (C = \ cfrac {Q} {V} \) для \ (V \) дает \ (V = \ cfrac {Q} {C} \). Таким образом, напряжения на отдельных конденсаторах равны \ ({V} _ {1} = \ cfrac {Q} {{C} _ {1}} \), \ ({V} _ {2} = \ cfrac {Q} {{C} _ {2}} \) и \ ({V} _ {3} = \ cfrac {Q} {{C} _ {3}} \).Общее напряжение — это сумма отдельных напряжений:
\ (V = {V} _ {1} + {V} _ {2} + {V} _ {3}. \)
Теперь, подсчитав общее емкость \ ({C} _ {\ text {S}} \) для последовательной емкости, примите во внимание, что
\ (V = \ cfrac {Q} {{C} _ {\ text {S}}} = {V} _ {1} + {V} _ {2} + {V} _ {3}. \)
Ввод выражений для \ ({V} _ {1} \), \ ({V} _ {2} \) и \ ({V} _ {3} \), получаем
\ (\ cfrac {Q} {{C} _ {\ text {S}}} = \ cfrac {Q} {{C} _ {1}} + \ cfrac {Q} {{C} _ {2}} + \ cfrac {Q} {{C} _ {3}}. \)
Отменяя \ (Q \) s, мы получим уравнение для полной емкости в серии \ ({C} _ {\ text {S}} \) равной
\ (\ cfrac {1} {{C} _ {\ text {S}}} = \ cfrac {1} {{C} _ {1}} + \ cfrac {1} {{C} _ {2}} + \ cfrac {1} {{C} _ {3}} + \ text {.} \ text {.} \ text {.}, \)
где «…» указывает, что выражение действительно для любого количества конденсаторов, соединенных последовательно. Выражение этой формы всегда приводит к общей емкости \ ({C} _ {\ text {S}} \), которая меньше любой из отдельных емкостей \ ({C} _ {1} \), \ ({ C} _ {2} \),…, как показано в следующем примере.
Общая последовательная емкость, \ ({C} _ {\ text {s}} \)
Общая последовательная емкость: \ (\ cfrac {1} {{C} _ {\ text {S}}} = \ cfrac {1} {{C} _ {1}} + \ cfrac {1} {{C} _ {2}} + \ cfrac {1} {{C} _ {3}} + \ text {.} \ text {.} \ text {.} \)
Пример: какова последовательная емкость?
Найдите общую емкость для трех последовательно соединенных конденсаторов, учитывая, что их отдельные емкости составляют 1.000, 5.000 и 8.000 \ (\ text {µF} \).
Стратегия
Имея данную информацию, общую емкость можно найти, используя уравнение для емкости в серии.
Решение
Ввод заданных емкостей в выражение для \ (\ cfrac {1} {{C} _ {\ text {S}}} \) дает \ (\ cfrac {1} {{C} _ {S}} = \ cfrac {1} {{C} _ {1}} + \ cfrac {1} {{C} _ {2}} + \ cfrac {1} {{C} _ {3}} \ ).
FFF \ (\ cfrac {1} {{C} _ {\ text {S}}} = \ cfrac {1} {1 \ text {.} \ Text {000 мкФ}} + \ cfrac {1} { 5 \ text {.} \ Text {000 мкФ}} + \ cfrac {1} {8 \ text {.} \ Text {000 мкФ}} = \ cfrac {1 \ text {.} \ Text {325}} { \ text {µF}} \)
Инвертирование для поиска \ ({C} _ {\ text {S}} \) дает \ (\) F \ ({C} _ {\ text {S}} = \ cfrac {\ text {µF}} {1 \ text {.} \ text {325}} = 0 \ text {.} \ text {755 µF} \).
Обсуждение
Общая последовательная емкость \ ({C} _ {\ text {s}} \) меньше наименьшей индивидуальной емкости, как и обещали. При последовательном соединении конденсаторов сумма меньше деталей.На самом деле это меньше, чем у любого человека. Обратите внимание, что иногда возможно и более удобно решить уравнение, подобное приведенному выше, путем нахождения наименьшего общего знаменателя, который в данном случае (показаны только целочисленные вычисления) равен 40. Таким образом,
FFFF \ (\ cfrac { 1} {{C} _ {\ text {S}}} = \ cfrac {\ text {40}} {\ text {40 мкФ}} + \ cfrac {8} {\ text {40 мкФ}} + \ cfrac {5} {\ text {40 мкФ}} = \ cfrac {\ text {53}} {\ text {40 мкФ}}, \)
, так что
FF \ ({C} _ {\ text {S }} = \ cfrac {\ text {40 мкФ}} {\ text {53}} = 0 \ text {.} \ text {755 мкФ}. \)
Онлайн-расчет емкости последовательного соединения конденсатора
Калькуляторы и формулы для расчета последовательного включения конденсатора
Последовательное соединение конденсатора
Когда конденсаторы соединены последовательно, полный ток протекает через все конденсаторы.
Расчет последовательного включения конденсаторов
Чтобы рассчитать емкость, введите значения отдельных конденсаторов, разделенных точкой с колонкой.
Пример: 3.3; 12; 22
Экспоненты не допускаются. Вместо этого введите значения в подходящей единице измерения. Если вы введете все значения в нано-фарадах, результат также отобразится в нано-фарадах.
|
Формулы для расчета общей мощности
Общая емкость последовательного соединения рассчитывается с использованием обратной величины отдельных конденсаторов.Отдельные обратные значения добавляются для расчета общей емкости. Итак, формула для трех последовательно соединенных конденсаторов:
\ (\ displaystyle \ frac {1} {C_ {ges}} = \ frac {1} {C_1} + \ frac {1} {C_2} + \ frac {1} {C_3} \)
Следующая формула может использоваться для расчета общей емкости двух последовательно соединенных конденсаторов.
\ (\ Displaystyle C_ {ges} = \ гидроразрыва {C_1 · C_2} {C_1 + C_2} \)
|
.
