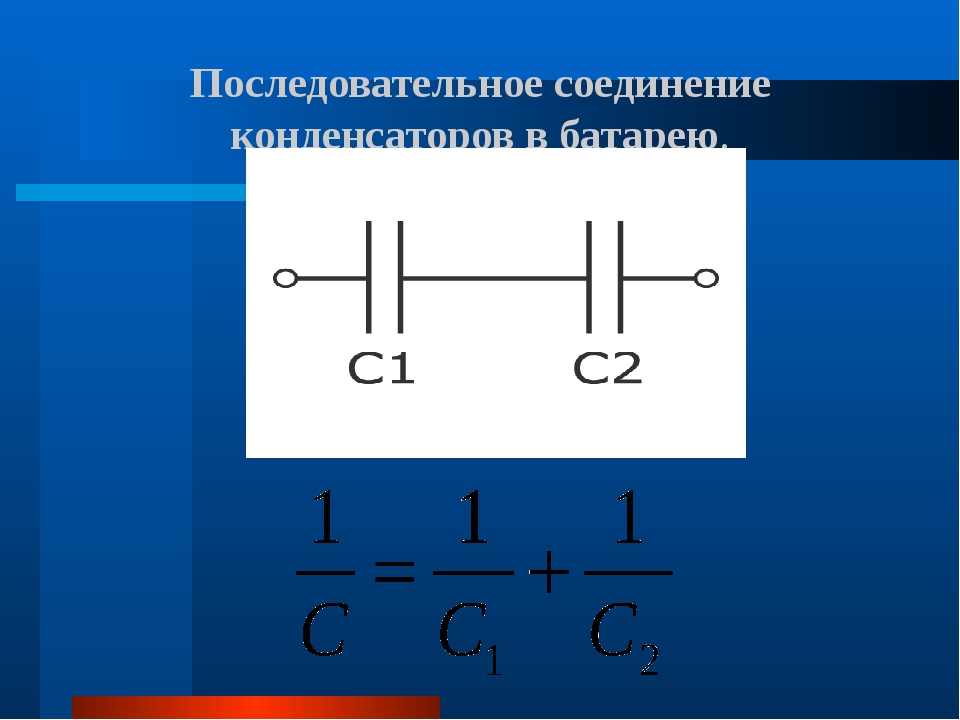
Последовательное и параллельное соединение конденсаторов
Последовательное и параллельное соединение конденсаторов применяют в зависимости от поставленной цели. При последовательном соединении конденсаторов уменьшается общая емкость и увеличивается общее напряжение конденсаторов.
Емкость набора при последовательном соединении конденсаторов будет вычисляться по формуле:
| 1 | = | 1 | + | 1 | + | 1 |  .. | |
| C | C1 | C2 | C3 |
А общее напряжение будет равняться сумме напряжений всех конденсаторов.
Например: мы имеем три конденсатора по 30 мкФ x 100 В каждый. При их последовательном соединении общий конденсатор будет иметь следующие данные: 10 мкФ x 300 В.
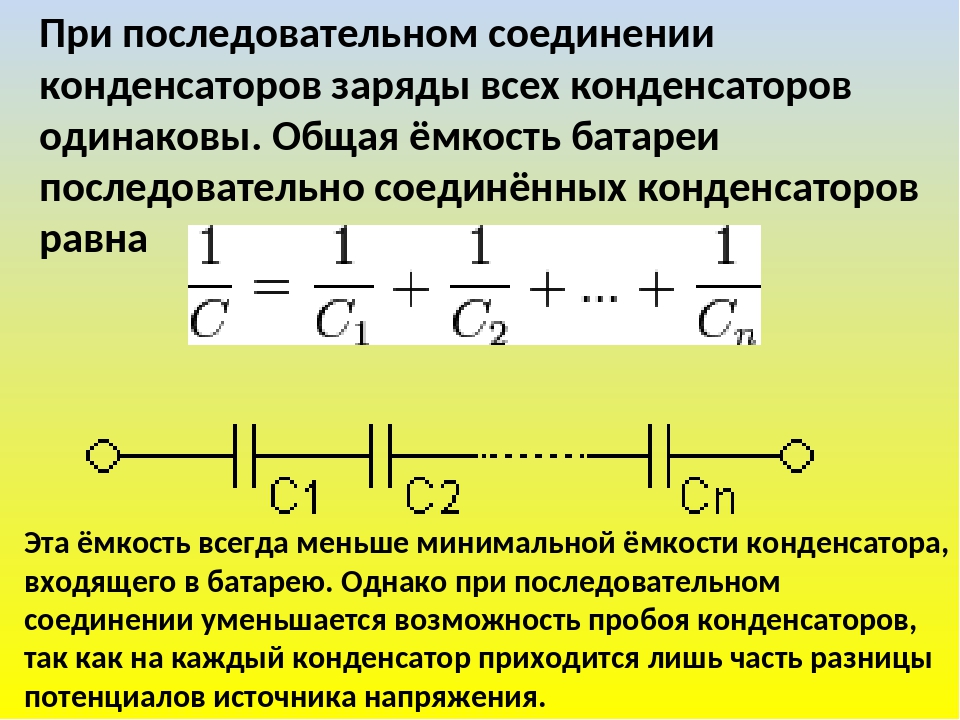
При параллельном соединении общая емкость конденсаторов складывается, а допустимое напряжение всего набора будет равно напряжению конденсатора, имеющего самое низкое значение допустимого напряжения из всего набора.
C = C1 + C2 + C3 + C4 + …Например: мы имеем три конденсатора 30 мкФ x 100 В, соединённые параллельно. Параметры всего набора конденсаторов в этом случае будут следующие: 90 мкФ x 100 В.
Соединение более двух конденсаторов последовательно редко встречается в реальных схемах.
Хотя для увеличения общего напряжения такой набор может встретиться в высоковольтных источниках питания. А вот в низковольтных источниках довольно часто встречается параллельное соединение нескольких конденсаторов для сглаживания пульсаций после выпрямления при больших токах потребления.
Обратите внимание, формулы вычисления емкости последовательного и параллельного соединения конденсаторов в точности обратны формулам вычисления сопротивления при последовательном и параллельном соединении резисторов.
15. Соединение конденсаторов (параллельное и последовательное)
Помимо показанного на рис. 60 и 61, а также на рис. 62, а параллельного соединения конденсаторов, при котором соединены между собой все положительные и все отрицательные обкладки, иногда соединяют конденсаторы последовательно, т. е. так, чтобы отрицательная обкладка
Рис.
62. Соединение конденсаторов: а)
параллельное; б) последовательное
первого конденсатора была соединена с положительной обкладкой второго, отрицательная обкладка второго — с положительной обкладкой третьего и т. д. (рис. 62, б). В случае параллельного соединения все конденсаторы заряжаются до одной и той же разности потенциалов U, но заряды на них могут быть различными. Если емкости их равны С1, С2,…, Сn, то соответствующие заряды будут
Общий заряд на всех конденсаторах
и, следовательно, емкость всей системы конденсаторов (35.1)
Итак,
емкость группы параллельно соединенных
конденсаторов равна сумме емкостей
отдельных конденсаторов. В случае
последовательно соединенных конденсаторов
(рис. 62, б) одинаковы заряды на всех
конденсаторах. Действительно, если мы
поместим, например, заряд +q на левую
обкладку первого конденсатора, то
вследствие индукции на правой его
обкладке возникнет заряд —q, а на левой
обкладке второго конденсатора — заряд
+q. Наличие этого заряда на левой обкладке
второго конденсатора опять-таки
вследствие индукции создает на правой
его обкладке заряд —q, а на левой обкладке
третьего конденсатора — заряд +q и т.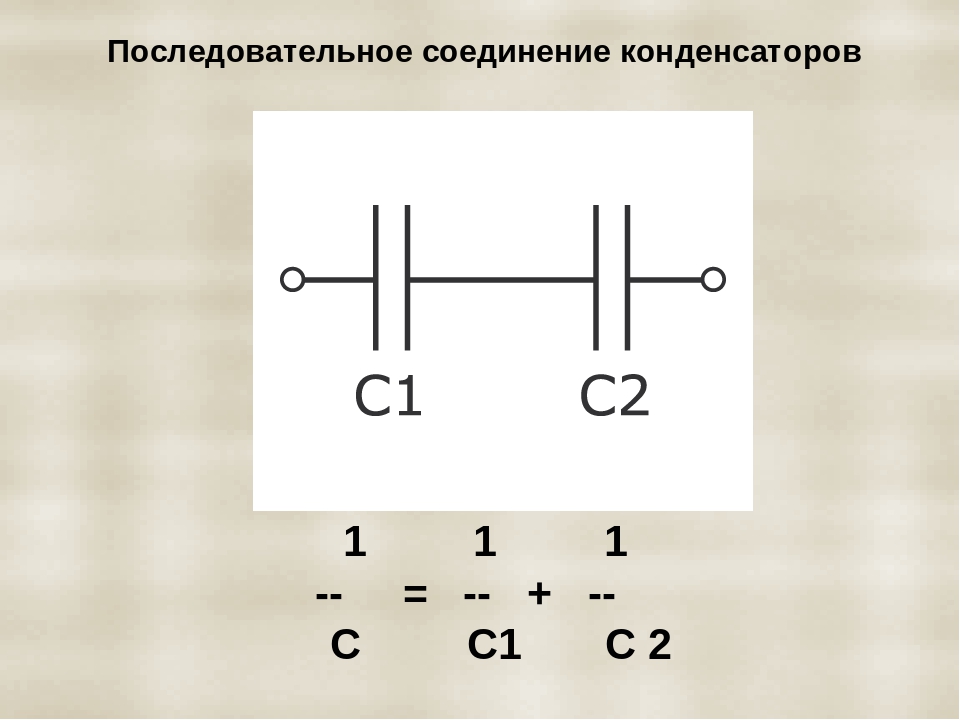
где Сi — емкость одного конденсатора. Суммарное напряжение между крайними (свободными) обкладками всей группы конденсаторов
Следовательно, емкость всей системы конденсаторов определяется выражением (35.2)
Из этой формулы видно, что емкость группы последовательно соединенных конденсаторов всегда меньше емкости каждого из этих конденсаторов в отдельности.
16. Энергия электрического поля и её объёмная плотность.
Энергия электрического поля. Энергию заряженного конденсатора можно выразить через величины, характеризующие электрическое поле в зазоре между обкладками. Сделаем это на примере плоского конденсатора. Подстановка выражения для емкости в формулу для энергии конденсатора дает
Частное U / d равно
напряженности поля в зазоре;
произведение S·d представляет
собой объем V,
занимаемый полем.
Следовательно,
Если поле однородно (что имеет место в плоском конденсаторе при расстоянии dмного меньшем, чем линейные размеры обкладок), то заключенная в нем энергия распределяется в пространстве с постоянной плотностью w. Тогда объемная плотность энергии электрического поля равна
C учетом соотношения можно записать
В изотропном диэлектрике направления векторов D и E совпадают и .Подставим выражение , получим
Первое слагаемое в этом выражении совпадает с плотностью энергии поля в вакууме. Второе слагаемое представляет собой энергию, затрачиваемую на поляризацию диэлектрика. Покажем это на примере неполярного диэлектрика. Поляризация неполярного диэлектрика заключается в том, что заряды, входящие в состав молекул, смещаются из своих положений под действием электрического поляЕ. В расчете на единицу объема диэлектрика работа, затрачиваемая на смещение зарядов qi на величину dri, составляет
Выражение в скобках есть дипольный момент единицы объема или поляризованность диэлектрика
Следовательно, .Вектор P связан с вектором E соотношением . Подставив это выражение в формулу для работы, получим
Проведя интегрирование, определим работу, затрачиваемую на поляризацию единицы объема диэлектрика
.
Зная плотность энергии поля в каждой точке, можно найти энергию поля, заключенного в любом объеме V. Для этого нужно вычислить интеграл:
17. Постоянный электрический ток, его характеристики и условия существования. Закон Ома для однородного участка цепи (интегральная и дифференциальная формы)
Для существования постоянного электрического тока необходимо наличие свободных заряженных частиц и наличие источника тока. в котором осуществляется преобразование какого-либо вида энергии в энергию электрического поля.
Источник
тока —
устройство, в котором осуществляется
преобразование какого-либо вида энергии
в энергию электрического поля. В источнике
тока на заряженные частицы в замкнутой
цепи действуют сторонние силы.
Электродвижущей силой источника тока называют отношение работы сторонних сил к величине положительного заряда, переносимого от отрицательного полюса источника тока к положительному.
Сила тока — скалярная физическая величина, равная отношению заряда, прошедшего через проводник, ко времени, за которое этот заряд прошел.
где I — сила тока, q — величина заряда (количество электричества), t — время прохождения заряда.
Плотность
тока —
векторная физическая величина, равная
отношению силы тока к площади поперечного
сечения проводника.
где j -плотность тока, S — площадь сечения проводника.
Направление вектора плотности тока совпадает с направлением движения положительно заряженных частиц.
Напряжение — скалярная физическая величина, равная отношению полной работе кулоновских и сторонних сил при перемещении положительного заряда на участке к значению этого заряда.
где A — полная работа сторонних и кулоновских сил, q — электрический заряд.
Электрическое сопротивление — физическая величина, характеризующая электрические свойства участка цепи.
где ρ — удельное сопротивление проводника, l — длина участка проводника, S — площадь поперечного сечения проводника.
Проводимостью называется величина, обратная сопротивлению
где G — проводимость.
Закон Ома для однородного участка цепи.
Сила тока в однородном участке цепи прямо пропорциональна напряжению при постоянном сопротивлении участка и обратно пропорциональна сопротивлению участка при постоянном напряжении.
где U — напряжение на участке, R — сопротивление участка.
Закон Ома для однородного участка цепи, все точки которого имеют одинаковую температуру, выражается формулой (в современных обозначениях):
В таком виде формула закона Ома справедлива только для проводников конечной длины, так как входящие в это выражение величины I и U измеряются приборами, включенными на этом участке.
,
где представляет
собой суммарное сопротивление участка
цепи, первый интеграл в правой части —
разность потенциалов на
концах участка, а второй интеграл
определяет ЭДС ,
действующую на участке цепи.
Таким
образом.
Эквивалентная ёмкость конденсаторов
| Эквивалентная ёмкость конденсаторов при последовательном соединении |
| Альтернативное отображение |
| Эквивалентная ёмкость конденсаторов при паралельном соединении |
| Альтернативное отображение |
Последовательное соединение
Написав бот, расчета размерностей Система единиц измерения онлайн теперь начнем осваивать такую многогранную и сложную область как электротехника.
И первое, что нам пригодится, это расчет эквивалентных характеристик основных электрических элементов( ёмкость, индуктивность, сопротивление).
Хотелось бы напомнить, что ёмкости некоторых типовых конструкций мы уже умеем рассчитывать Ёмкость конденсатора онлайн
Сами по себе формулы очень просты, но нюанс состоит в том, как нам точно посчитать ёмкость двух последовательно соединенных конденсаторов если один из конденсаторов имеет ёмкость 10 пФ, а второй 250нФ.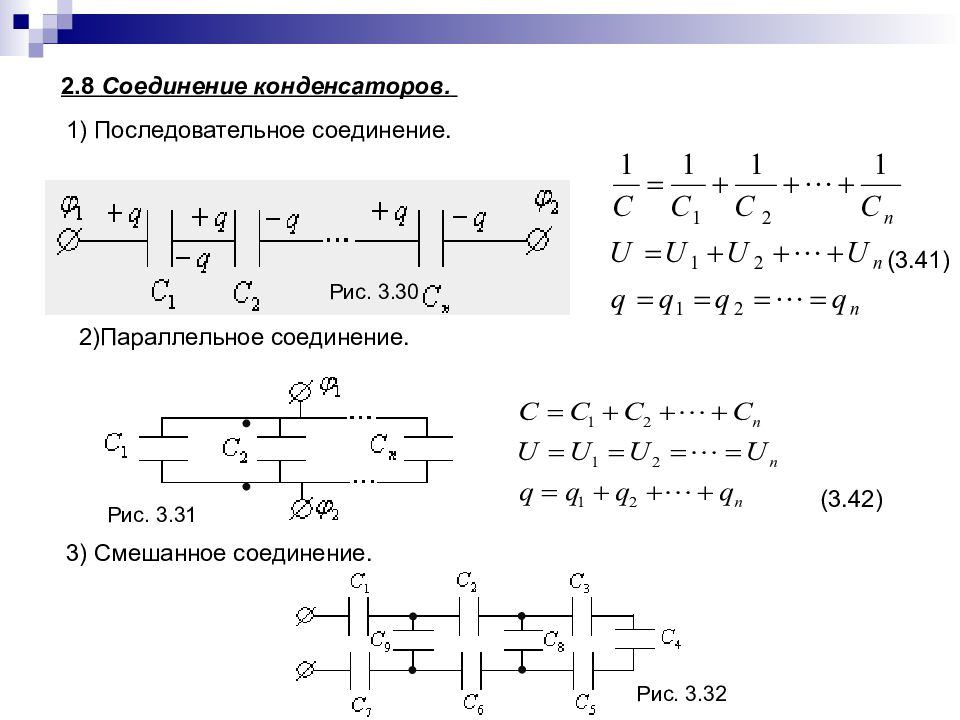
Размерность показывает что они различаются в 1000 раз. Можно конечно все перевести в абсолютные значения, но это при большом количестве конденсаторов способствует возникновению ошибок.
Итак, последовательное соединение конденсаторов имеет следующий вид
И формула расчета эквивалентной ёмкости выглядит так
Паралельное СОЕДИНЕНИЕ
Последовательное соединение нескольних конденсаторов выглядит так, как показано на рисунке
А формула становится до безобразия простой и наглядной
Синтаксис
Он очень прост
calc_e список емкостей с размерностями через запятую.
В ответе мы получим эквививалентное значение ёмкости при последовательном и паралельных соединениях.
Важное замечание: размерности нужно писать на русском языке. Для пользователей сайта, не знающих русский язык, можем по запросу добавить обработку англоязычных наименований приставок и размерностей.
Это не сложно.
Примеры
Рассчитать ёмкость трех конденсаторов следующих номиналов: 10 пФ, 0.2нФ и 344мФ
В запросе так и пишем calc_e 10пФ,0.2нФ,344мФ
Ответ не заставит себя долго ждать и выглядит вот так
| Эквивалентная ёмкость конденсаторов при паралельном соединении |
|
9.5238095235459пикофарад |
| Альтернативное отображение |
| Эквивалентная ёмкость конденсаторов при последовательном соединении |
|
344.00000021милифарад |
| Альтернативное отображение |
Удачи в расчетах!
- Эквивалентное сопротивление онлайн >>
При последовательном соединении конденсаторов результирующая емкость С всегда _ наименьшей емкости, используемой в батарее
По теории _, электрические явления определяются мгновенным взаимодействием зарядов на любых расстояниях
(*ответ*) дальнодействия
близкодействия
среднедействия
краткодействия
Поместим проводник во внешнее электростатическое поле; на заряды проводника будет действовать электростатическое поле, в результате чего они начнут
(*ответ*) перемещаться
группироваться
видоизменяться
поляризоваться
перезаряжаться
конденсироваться
Потенциал — физическая величина, определяемая _ по перемещению единичного положительного заряда при удалении его из заданной точки поля в бесконечность
(*ответ*) работой
энергией
силой
эквипотенциальной работой
работой линий напряженности
Потенциалом ионизации φи называется разность потенциалов, которую должен пройти электрон в ускоряющем электрическом поле, чтобы увеличение его _ было равно работе ионизации
(*ответ*) энергии
ЭДС
излучения
спина
заряда
силового поля
Поток вектора смещения электростатического поля в диэлектрике сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности _ электрических зарядов
(*ответ*) свободных
однородных
изотропных
неоднородных
анизотропных
При внесении диэлектриков во внешнее электрическое поле в любом макроскопически малом его объеме Δ V возникает отличный от нуля результирующий электрический момент диэлектрика, т.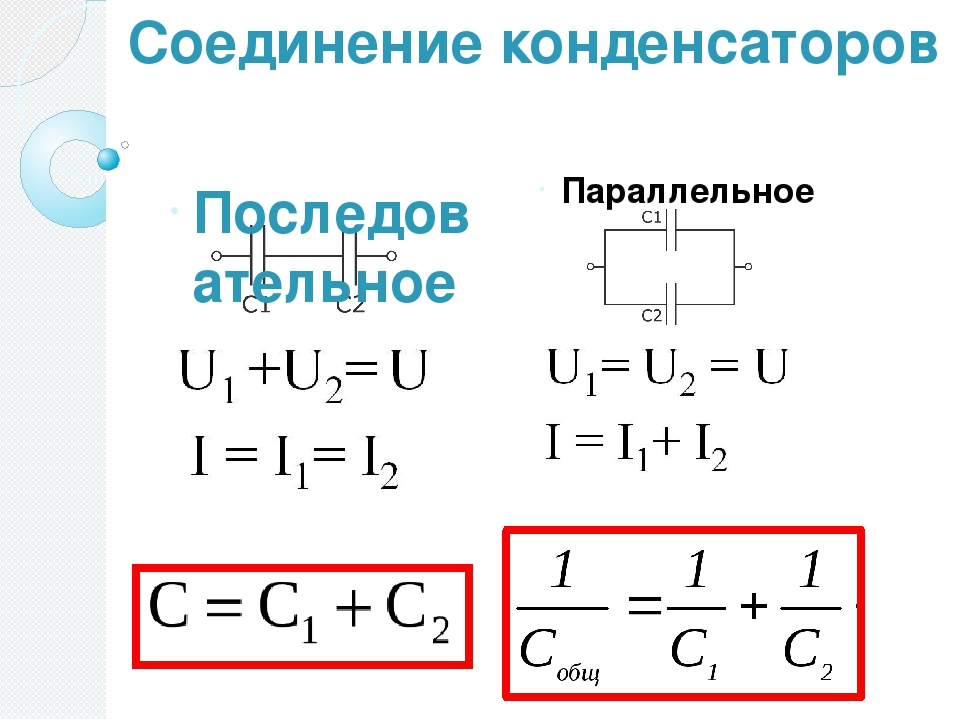
е.
(*ответ*) происходит поляризация диэлектрика
происходит электрическое смещение диэлектрика
возникает взаимодействие параллельных токов в диэлектрике
возникает вихревое электрическое поле в диэлектрике
возникает магнитный поток в диэлектрике
При наложении внешнего электрического поля на металлический проводник, кроме теплового движения электронов, возникает их упорядоченное движение, т.е. возникает
(*ответ*) электрический ток
напряжение
электродвижущая сила
сторонняя сила
При наложении на ионный кристалл электрического поля происходит относительное смещение подрешетки положительных ионов вдоль поля, а отрицательных — против поля, приводящее к возникновению _ моментов
(*ответ*) дипольных
магнитных
электромагнитных
силовых
полярных
вихревых
При последовательном соединении конденсаторов результирующая емкость С всегда _ наименьшей емкости, используемой в батарее
(*ответ*) меньше
больше
равна
отлична от
В электрических цепях и схемах используются различные методы соединения конденсаторов. Соединение конденсаторов может быть последовательным, параллельным и последовательно-параллельным (смешанное соединение конденсаторов). Если подключение емкостей в батарею осуществляется в виде цепочки и к точкам включения в цепь присоединены пластины только первого и последнего конденсаторов, то такое соединение называется последовательным . При последовательном соединение конденсаторов они заряжаются одинаковым количеством электричества, хотя от источника тока заряжаются только две крайние пластины, а остальные пластины заряжаются через влияние электрического поля. Но если говорить точнее, напряжения на различных емкостных элементах будут отличаться, так как для заряда одним и тем же количеством электричества при различной номинальной емкости всегда необходимы различные напряжения. Чем нижее емкость конденсатора, тем больший уровень напряжение требуется для того, чтобы зарядить радиокомпонент необходимым количеством электричества, и наоборот. Таким образом, при заряде группы емкостей, соединенных последовательно, на конденсаторах малой емкости напряжения будут выше, а на элементах большой емкости — ниже. Рассмотрим всю группу емкостей соединенных последовательно, как одну эквивалентную емкость, между пластинами которой существует какой-то уровень напряжения, равный сумме напряжений на всех элементах группы, а заряд которого равен заряду любого компонента из данной группы. Если более пристально рассмотреть самый меньший номинал емкос |
Смешанное соединение конденсаторов
21) видно, что при последовательном соединении электроемкость батареи оказывается меньше самой маленькой из электроемкостей отдельных конденсаторов .
15.33. Такой способ соединения дает экономию в материале, так как заряды располагаются с обеих сторон обкладок конденсаторов (кроме двух крайних обкладок).
При этом заряд пластины 2 будет равен по номиналу, но противоположен по знаку заряду пластины 1, заряд пластины 3 будет равен заряду пластины 2, но также будет противоположной полярности и т. д.
Как рассчитать емкость в последовательной и параллельной цепях?
Есть две комбинации конденсаторов: последовательная и параллельная цепи. В последовательных цепях общая емкость меньше наименьшего значения емкости из-за увеличения эффективного расстояния между пластинами. В параллельных цепях общая емкость складывается из отдельных емкостей.
, когда конденсаторы соединены последовательно, общая емкость меньше наименьшего значения емкости, потому что эффективное расстояние между пластинами увеличивается.Расчет общей последовательной емкости аналогичен расчету общего сопротивления параллельных резисторов.
Комбинация этого типа имеет следующие характеристики:
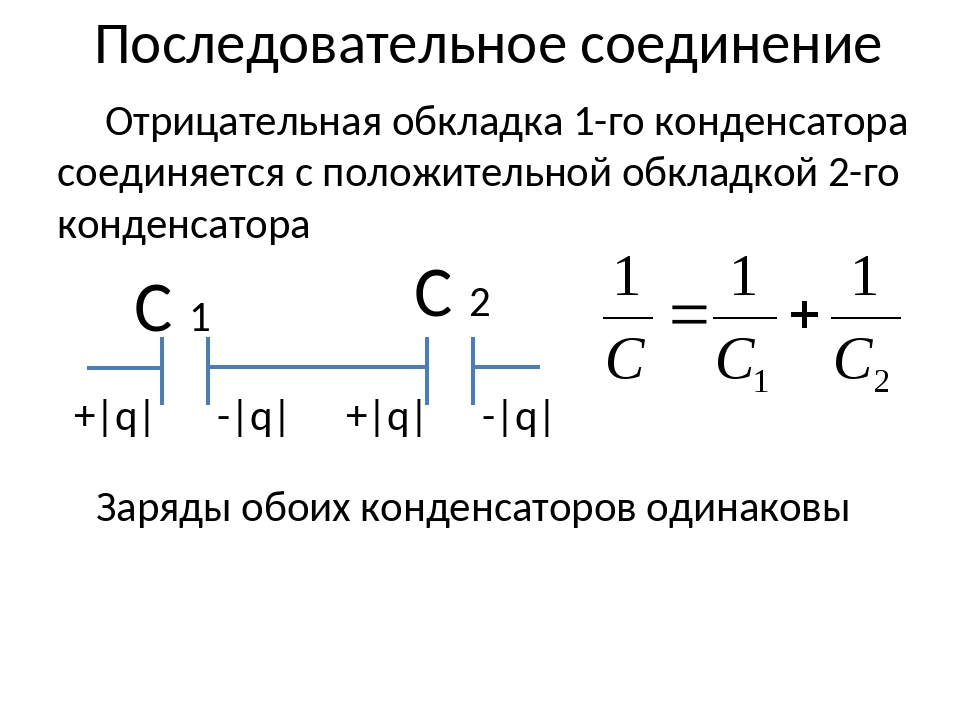
- Каждый конденсатор имеет одинаковый заряд. Если батарея подает заряд + Q на левую пластину конденсатора C1 из-за индукции, на его правой пластине индуцируется заряд -Q, а на левой пластине конденсатора C2 — заряд + Q т.
е.
е. Q = Q 1 + Q 2 + Q 3
2 : Разность потенциалов на каждом конденсаторе разная из-за разных значений емкостей.
3 : Напряжение батареи было разделено между различными конденсаторами, поэтому
В = В 1 + В 2 + В 3
= Q / C 1 + Q / C 2 + Q / C 3
= Q [1 / C 1 + 1 / C 2 + 1 / C 3 ]
V / Q = [1 / C 1 + 1 / C 2 +1 / C 3 ]
4: Эквивалентная емкость
, мы можем заменить последовательную комбинацию конденсаторов одним эквивалентным конденсатором емкостью C eq i.e,
1 / C eq = 1 / C 1 + 1 / C 2 + 1 / C 3
Формула для общей емкости в параллельной цепи
При параллельном подключении конденсаторов общая емкость является суммой отдельных емкостей, поскольку эффективная площадь пластины увеличивается.
Расчет общей параллельной емкости аналогичен расчету общего последовательного сопротивления.
На приведенном выше рисунке левая пластина каждого конденсатора соединена с положительной клеммой батареи проводящим проводом.Таким же образом правая пластина каждого конденсатора подключается к отрицательному выводу батареи. Такая комбинация имеет следующие характеристики.
- Каждый конденсатор, подключенный к батарее с напряжением V, имеет такую же разность потенциалов, как:
В = В 1 + В 2 + В 3
2. Развиваемое напряжение на пластинах каждого конденсатора будет отличаться из-за разной емкости.
3. Общий заряд Q, обеспечиваемый батареей, делится между различными конденсаторами.Следовательно:
Q = Q 1 + Q 2 + Q 3
Или Q = C 1 V + C 2 V + C 3 V
Q = V (C 1 + C 2 + C 3 )
Q / V = C 1 + C 2 + C 3
4.
Мы можем заменить параллельную комбинацию конденсаторов одним эквивалентным конденсатором, имеющим емкость C eq , так что
C eq = C 1 + C 2 + C 3
В случае n конденсаторов, подключенных параллельно, эквивалентная емкость определяется по формуле:
C eq = C 1 + C 2 + C 3 + …… + C n
5.Эквивалентная емкость параллельной комбинации конденсаторов больше любой из отдельных емкостей.
Смотрите также видео
и емкость — материалы исследования для IIT JEE
- Полный курс физики — 11 класс
ПРЕДЛАГАЕМАЯ ЦЕНА: Rs.
2 968- Просмотр подробностей
2 968
Что такое конденсатор?
Конденсатор, также известный как Электрический конденсатор , представляет собой двухконтактный электрический компонент, который имеет способность или емкость для хранения энергии в виде электрического заряда .Конденсаторы обычно предназначены для усиления и увеличения эффекта емкости, учитывая размер и форму конденсатора. Емкость хранения варьируется от небольшой емкости до большой емкости.
Конденсаторы
Емкость в физике
Способность конденсатора накапливать энергию в виде электрического заряда известна как Емкость .
Другими словами, емкость , можно описать как способность конденсатора накапливать, и она измеряется в фарадах .
Для примера , если мы подключим конденсатор к 9-вольтовой батарее и измерим, что он хранит 9 кулонов заряда, его емкость будет равна 1 фараду
Конструкция конденсатора
Большинство конденсаторов обычно содержит два электрических проводника, поверхность которых разделена диэлектриком или между металлическими пластинами .
Проводники могут быть в форме электролита, тонкой пленки, спеченного металла и т. Д.
Конструкция конденсатора
Роль непроводящего диэлектрика в конденсаторе
Непроводящий диэлектрик используется для увеличения емкости конденсатора для зарядки. В качестве диэлектрика в конденсаторе обычно используются следующие материалы:
Слюда
Пленка полиэтиленовая
Стекло
Бумага
Керамика
Добавление конденсаторов
Конденсаторы можно добавить двумя способами
Либо в серийном
или параллельно
В серии
Конденсатор С 1 и С 2 соединены последовательно.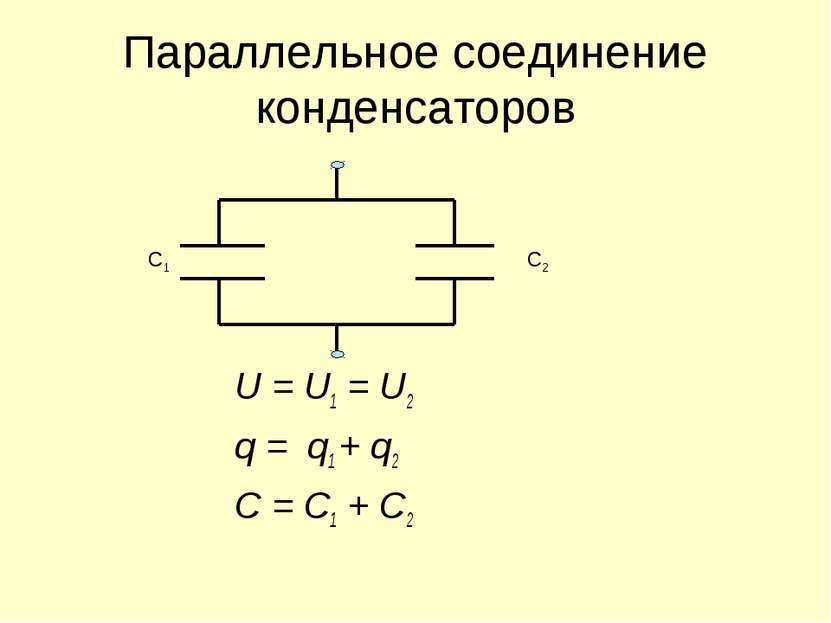
Когда конденсаторы подключаются последовательно, общая емкость, которая составляет C, всего , меньше любой емкости конденсатора.
конденсаторы, включенные последовательно
Емкость конденсатора, соединенного последовательно, можно рассчитать как:
Параллельно
Конденсатор С 1 и С 2 соединены параллельно. Когда конденсаторы подключены параллельно, общая емкость, которая составляет C, всего , равна любой емкости конденсатора
.Конденсатор, подключенный параллельно
Емкость конденсатора, подключенного параллельно, можно рассчитать как:
Параллельные емкости
C всего = C 1 + C 2 +….С н
Номинал конденсатора
Значение емкости двух разных конденсаторов может быть совершенно одинаковым, а номинальное напряжение двух конденсаторов различается.
Давайте возьмем два конденсатора, один с малым номинальным напряжением, а другой с высоким номинальным напряжением, тогда, если конденсатор меньшего номинального напряжения будет заменен конденсатором с более высоким номинальным напряжением, повышенное напряжение может повредить меньший конденсатор.
Общее рабочее напряжение постоянного тока конденсатора указано на конденсаторе и составляет 10 В, 16 В, 25 В, 35 В, 50 В, 63 В, 100 В, 160 В, 250 В, 400 В и 1000 В. .
Рис. 1.5 Номинальное напряжение постоянного тока на конденсаторе
Свойства или характеристики конденсатора
Свойства или характеристики конденсаторов могут отличаться друг от друга. Немного характеристик конденсаторов:
Номинальная емкость, (C): Это свойство конденсатора является важным из всех свойств конденсаторов.Он измеряется в пикофарадах (пФ), нанофарадах (нФ) или микрофарадах (мкФ) и печатается на корпусе конденсатора в виде числа или текста.
Рабочее напряжение, (WV): Общее количество постоянного (DC) или переменного (AC) тока, приложенного к конденсатору без каких-либо сбоев в течение всего срока службы конденсатора. Это указанное выше количество можно определить через рабочее напряжение.
Допуск, (±%): Точно так же, как номинальное напряжение, конденсатор также имеет допуски, которые варьируются от плюсового до минусового значения либо в пикофарадах (± пФ) для конденсаторов малой емкости, как правило, менее 100 пФ, либо в процентах (±%) для конденсаторов более высокой емкости обычно выше 100 пФ.
Ток утечки: Конденсаторы Ток утечки — это небольшой постоянный ток, протекающий в области наноампер (нА). Ток утечки — это результат того, что электроны физически проходят через диэлектрическую среду, вокруг ее краев или между выводами и со временем полностью разряжают конденсатор, если напряжение питания снимается.
Суперконденсатор
Суперконденсатор, также известный как электрический двухслойный конденсатор (EDLC), Supercap , Ultracapacitor или Goldcap имеет гораздо более высокое значение емкости по сравнению с другими конденсаторами, но с более низкими пределами напряжения
Классификация суперконденсаторов
Параллельный пластинчатый конденсатор
Конденсатор, состоящий из диэлектрика и электрода, известен как конденсатор с параллельными пластинами.
Используются две параллельные проводящие пластины (электроды) и промежуточная среда из диэлектрика . Значение емкости зависит от материала или среды между двумя пластинами
— это общая площадь двух пластин, а d — расстояние между пластинами.
Емкость параллельного пластинчатого конденсатора
C воздух = ε 0 A / d
C med = Kε 0 A / d
Здесь A — это общая площадь двух пластин, а d — это расстояние между пластинами.
Влияние диэлектрика на емкость конденсатора
Фарадей дал эту теорию, то есть , если пространство между двумя электродами заполнено диэлектриком, емкость конденсатора будет увеличена на .
Если все пространство заполнено диэлектриком, которому не осталось места, то емкость конденсатора будет увеличена на К.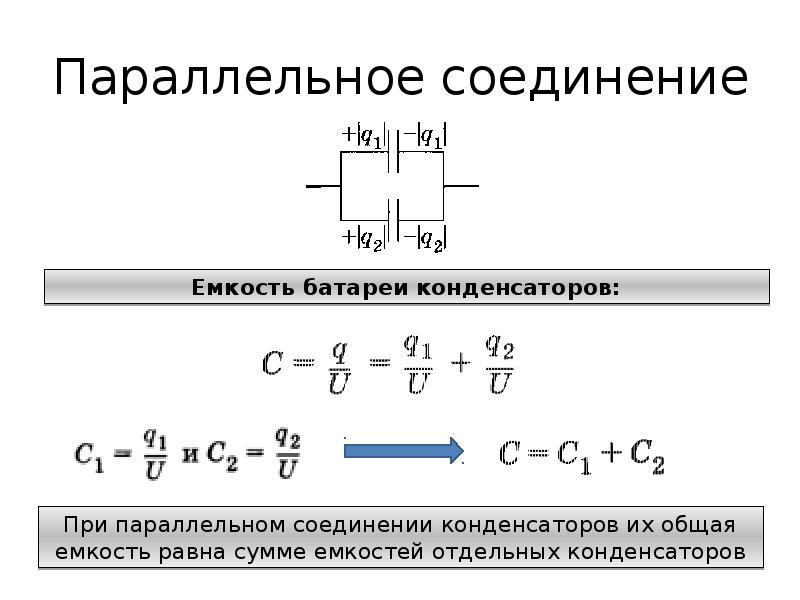
, и здесь К известна как диэлектрическая постоянная .
Влияние диэлектрика на конденсатор
Проба
Рассмотрим следующую схему
Диэлектрик между двумя конденсаторами
E = E o — E p
Электрическое поле E o во внешней области диэлектрика будет нулевым.Теперь уравнение разности потенциалов между двумя пластинами равно
V = o (d-t) + Et
Но E o = E r или K
Следовательно, E = E o / k
Так
V = E o (d-t) + E o t / k
V = E или [d-t + t / k]
Как известно
E o = σ / ε 0
= Q / A ε 0
V = Q / A ε 0 [d — t + t / k]
Емкость конденсатора:
C = Q / V
= A ε 0 / (d — t + t / k)
= A / d — t (1-1 / K)
, то есть , C = A / d-t (1-1 / k)
Итак, C> C o
Ясно, что доказано, что если диэлектрическую пластину поместить в пластины конденсатора, то его емкость увеличится на некоторую величину.
Энергия, накопленная в конденсаторе
Работа, выполняемая по перемещению положительного заряда от отрицательного проводника к положительному проводнику против сил отталкивания, известна как энергия , накопленная в конденсаторе .
Это может быть , вычисленное как:
Числовой
(добавление конденсаторов)
- Ниже приведена схема последовательно подключенных конденсаторов .
Рассчитать общую емкость?
Взяв значения трех конденсаторов, мы можем рассчитать общую емкость C T для трех последовательно соединенных конденсаторов как:
Общая емкость,
C T = C 1 + C 2 = 47 нФ + 47 нФ = 94 нФ или 0,094 мкФ
Общая емкость,
C T = C 1 + C 2 = 470 нФ + 1 мкФ
, следовательно, C T = 470 нФ + 1000 нФ = 1470 нФ или 1.
47 мкФ
Таким образом, общая или эквивалентная емкость C T электрической цепи, содержащей два или более конденсаторов , подключенных параллельно , представляет собой сумму всех индивидуальных емкостей, сложенных вместе по мере увеличения эффективной площади пластин.
(относится к конденсатору с параллельными пластинами)
Конденсатор с параллельными пластинами состоит из двух металлических пластин, каждая площадью A = 150 см 2 , разделенных вакуумным зазором d = 0.60 толщиной см. Какая емкость у этого устройства? Какая разность потенциалов должна быть приложена между пластинами, если конденсатор должен удерживать заряд величиной Q = 1,00 × 10 -3 мкКл на каждой пластине?
Емкость определяется как
Разность напряжений между пластинами и величина заряда Q, накопленного на каждой пластине, связаны соотношением C = Q / V.
Следовательно, если Q = 1,00 X 10 -3
, затем
(Относится к энергии, запасенной в конденсаторе)
Заполненный воздухом конденсатор с параллельными пластинами имеет емкость пФ.С помощью аккумуляторной батареи к пластинам, которые находятся на расстоянии см, прикладывается потенциал 100 В. Какая энергия хранится в конденсаторе? Предположим, что аккумулятор отключен, и пластины перемещаются, пока они не окажутся на расстоянии см. Какая сейчас энергия хранится в конденсаторе? Вместо этого предположим, что аккумулятор остается подключенным, и пластины снова перемещаются, пока они не окажутся на расстоянии см. Какая энергия в этом случае хранится в конденсаторе?
Начальная энергия, запасенная в конденсаторе, составляет
Когда расстояние между пластинами увеличивается вдвое, емкость конденсатора уменьшается вдвое до пФ.
Если аккумулятор отключен, то этот процесс происходит при постоянном заряде Q. Таким образом, это следует из формулы
, что энергия, запасенная в конденсаторе, удваивается. Таким образом, новая энергия составляет 5,0 x 10 -8 Дж. Между прочим, повышенная энергия конденсатора объясняется работой, совершаемой при разрыве пластин конденсатора (поскольку эти пластины заряжены противоположно, они притягиваются друг к другу.
Если аккумулятор оставить подключенным, то емкость все равно уменьшится вдвое, но теперь процесс происходит при постоянном напряжении В .Из формулы
следует, что энергия, запасенная в конденсаторе, уменьшена вдвое. Итак, новая энергия составляет 1,25 x 10 -8 Дж. Между прочим, энергия, потерянная конденсатором, передается батарее (фактически, она идет на повторную зарядку батареи). Точно так же работа, выполняемая по разъединению пластин, также возлагается на аккумулятор.
Другие показания
Конденсаторы и емкость
Особенности курса
- 101 Видеолекция
- Примечания к редакции
- Документы за предыдущий год
- Ментальная карта
- Планировщик обучения
- Решения NCERT
- Обсуждение Форум
- Тестовая бумага с видео-решением
Емкостное реактивное сопротивление
— Как найти последовательные и параллельные конденсаторы
Найдите емкостное реактивное сопротивление цепи с последовательными или параллельными конденсаторами, используя этот простой двухэтапный процесс.
Шаг 1: Найдите общую емкость цепи
Предположим, у нас есть три конденсатора, 12 Ф, 20 Ф и 30 Ф, подключенных к источнику с частотой 60 Гц. Каково полное емкостное реактивное сопротивление (X C ) при последовательном или параллельном подключении?
1А. Для конденсаторов серии
Когда конденсаторы соединены последовательно, общая емкость меньше, чем любая из отдельных емкостей последовательных конденсаторов.Если два или более конденсатора соединены последовательно, общий эффект будет таким, как у одиночного (эквивалентного) конденсатора, имеющего суммарное расстояние между пластинами отдельных конденсаторов.
Конденсаторы серии Пример:
1/12 = 0,083, 1/20 = 0,050, 1/30 = 0,033
0,083 + 0,050 + 0,033 = 0,166
1 / 0,163 = 6,02 мкФ
Примечание: математические расчеты упрощены для целей иллюстрации.
Для более точных чисел воспользуйтесь калькулятором.
1Б. Для параллельных конденсаторов
При параллельном подключении конденсаторов общая емкость представляет собой сумму емкостей отдельных конденсаторов. Если два или более конденсатора соединены параллельно, общий эффект будет таким, как у одного эквивалентного конденсатора, имеющего сумму площадей пластин отдельных конденсаторов.
Параллельные конденсаторы Пример:
12 + 20 + 30 = 62 мкФ
Шаг 2: Найдите емкостное сопротивление
Как и сопротивление, реактивное сопротивление измеряется в Ом, но ему присваивается символ X, чтобы отличить его от чисто резистивного значения R, и, поскольку рассматриваемый компонент является конденсатором, реактивное сопротивление конденсатора называется емкостным реактивным сопротивлением (X C ) который измеряется в Ом.
Поскольку конденсаторы заряжаются и разряжаются пропорционально скорости изменения напряжения на них, чем быстрее изменяется напряжение, тем больше тока протекает.
Точно так же, чем медленнее изменяется напряжение, тем меньше будет протекать ток. Это означает, что реактивное сопротивление конденсатора переменного тока «обратно пропорционально» частоте источника питания.
X C — емкостное реактивное сопротивление в омах, f — частота в герцах, а C — емкость переменного тока в фарадах. Очень важно перевести наш пример из микрофарад в фарады, чтобы получить правильный результат!
1 мкФ = 0,000001 F
Серия 60 Гц Пример:
6,02 мкФ = 0,000006 Ф (упрощенно)
2 х 3,14 х 60 х 0,000006 = 0,0022608
1 / 0,0022608 = 442,32 Ом
60 Гц Параллельный Пример:
62 мкФ = 0,000062 F
2 х 3.14 х 60 х 0,000062 = 0,0233616
1 / 0,0233616 = 42,805 Ом
Теперь посмотрим, что произойдет при изменении частоты на 400 Гц :
Серия 400 Гц Пример:
2 х 3,14 х 400 х 0,000006 = 0,015072
1 / 0,015072 = 66,34 Ом
Параллельный 400 Гц Пример:
2 х 3,14 х 400 х 0,000062 = 0,155744
1 / 0,155744 = 6,42 Ом
Полезные ссылки
на комментарий.