Энергия катушки формула: 44 — энергия катушки индуктивности • 31415.ru

Самоиндукция. Энергия магнитного поля.

Определение 1

Самоиндукция – это значимый частный случай электромагнитной индукции, когда магнитный поток, изменяясь и вызывая ЭДС индукции, создается током в самом контуре.

В случае, когда ток рассматриваемого контура по каким-либо причинам изменен, то имеет место изменение и магнитного поля этого тока, а значит и собственного магнитного потока, проходящего через контур. В контуре создается ЭДС самоиндукции, создавая препятствие для изменений тока в контуре (по правилу Ленца).

Собственный магнитный поток Φ, который проходит через контур или катушку с током, является пропорциональным силе тока I: Φ=LI.

Определение 2

Коэффициент пропорциональности L в формуле Φ=LI есть коэффициент самоиндукции или индуктивность катушки. Единица индуктивности в СИ носит название генри (Гн). Индуктивность контура или катушки равна 1 Гн, когда при силе постоянного тока 1 А собственный поток составляет 1 Вб: 1 Гн=1 Вб1 А.

Расчет индуктивности

Пример 1

Для наглядности произведем расчет индуктивности длинного соленоида, который имеет N витков, площадь сечения S и длину l. Соленоид – это цилиндрическая катушка индуктивности, у которой длина много больше диаметра. Магнитное поле соленоида задается формулой:

B=μ0nI,

где I является обозначением тока в соленоиде, n = Ne указывает число витков на единицу длины соленоида.

Магнитный поток внутри катушки соленоида, проходящий через все N витков, составляет:

Φ=B·S·N=μ0n2Sl

Таким образом, индуктивность соленоида будет выражена формулой:

L=μ0n2S·l=μ0n2V,

где V=Sl – объем соленоида, содержащий магнитное поле.

Результат, который мы получили, не берет в расчет краевых эффектов, а значит он является приближенно верным лишь для катушек достаточной длины. Когда соленоид заполнен веществом, имеющим магнитную проницаемость μ, при заданном токе

I индукция магнитного поля будет возрастать по модулю в μ раз, а значит и индуктивность катушки с сердечником тоже получит увеличение в μ раз:

Lμ=μ·L=μ0·μ·n2·V.

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание Определение 3

ЭДС самоиндукции, которая возникает в катушке при постоянном значении индуктивности, в соответствии с законом Фарадея записывается в виде формулы:

δинд=δL=-∆Φ∆t=-L∆I∆t.

ЭДС самоиндукции является прямо пропорциональной индуктивности катушки и скорости изменения силы тока в ней.

Магнитное поле выступает носителем энергии. Так же, как заряженный конденсатор обладает запасом электрической энергии, катушка, по виткам которой проходит ток, обладает запасом магнитной энергии. Включив электрическую лампу параллельно катушке с большой индуктивностью в электрическую цепь постоянного тока, при размыкании ключа будем наблюдать короткую вспышку лампы (рис. 1.21.1). Ток в цепи появится под влиянием ЭДС самоиндукции. Источником энергии, которая будет выделяться в этом процессе электрической цепью, будет служить магнитное поле катушки.

Рисунок 1.21.1. Магнитная энергия катушки. В момент размыкания ключа K лампа ярко вспыхнет.

Закон сохранения энергии позволяет говорить, что вся энергия, составляющая запас катушки, будет выделена в виде джоулева тепла. Обозначим как Rполное сопротивление цепи, тогда за время Δt будет выделено количество теплоты ΔQ=I2·R·Δt.

Ток в цепи составляет:

I=δLR=-LR∆I∆t

Выражение для ΔQ можем записать так:

∆Q=-L·I·∆I=-Φ(I)∆I

В данной записи ΔI < 0; значение тока в цепи постепенно снижается от изначального I0 до нуля. Полное количество теплоты, которое выделится в цепи, возможно получить, осуществив действие интегрирования в пределах от I0 до 0. Тогда получим:

Q=LI022

Графический вывод формулы

Существует возможность получить записанную формулу, используя графический метод. Для этого отобразим на графике зависимость магнитного потока Φ(I) от тока I (рис. 1.21.2). Полное количество выделившейся теплоты, которое равно изначальному запасу энергии магнитного поля, определится как площадь получившегося на рис. 1.21.2 треугольника:

Рисунок 1.21.2. Вычисление энергии магнитного поля.

В итоге формула энергии Wм магнитного поля катушки с индуктивностью L, создаваемого током I, будет записана в виде формулы:

Wм=ΦI2=LI22=Φ22L

Используем выражение, которое мы получили, для энергии катушки к длинному соленоиду с магнитным сердечником. Применяя указанные выше формулы для коэффициента самоиндукции Lμ соленоида и для магнитного поля

B, создаваемого током I, получим запись:

Wм=μ0·μ·n2·I22V=B22μ0·μV

В этой формуле V является объемом соленоида. Полученное выражение демонстрирует нам, что магнитная энергия имеет локализацию не в витках катушки, по которым проходит ток, а распределена по всему объему, в котором возникло магнитное поле.

Определение 4

Объёмная плотность магнитной энергии – это физическая величина, которая равна энергии магнитного поля в единице объема: Wм=B22μ·μ.

В свое время Максвелл продемонстрировал, что указанная формула (в нашем случае выведенная для длинного соленоида) верна для любых магнитных полей.

Электричество и магнетизм

Обратимся снова к процессу замыкания цепи на рис. 8.33-1. Умножая правую и левую части уравнения (8.23) на , получим

(8.29)

Левая часть уравнения (8.29) выражает работу, совершаемую источником тока за время . В правой части первое слагаемое есть величина работы, расходуемой на выделение джоулева тепла в проводнике. Ясно, что перед нами — уравнение закона сохранения энергии в рассматриваемой цепи. Каков же смысл второго слагаемого? Оно связано с катушкой, о чем свидетельствует множитель L, и представляет собой работу, затраченную на преодоление противодействия ЭДС самоиндукции. Куда же девается эта работа? В процессе замыкания цепи в катушкой создается магнитное поле.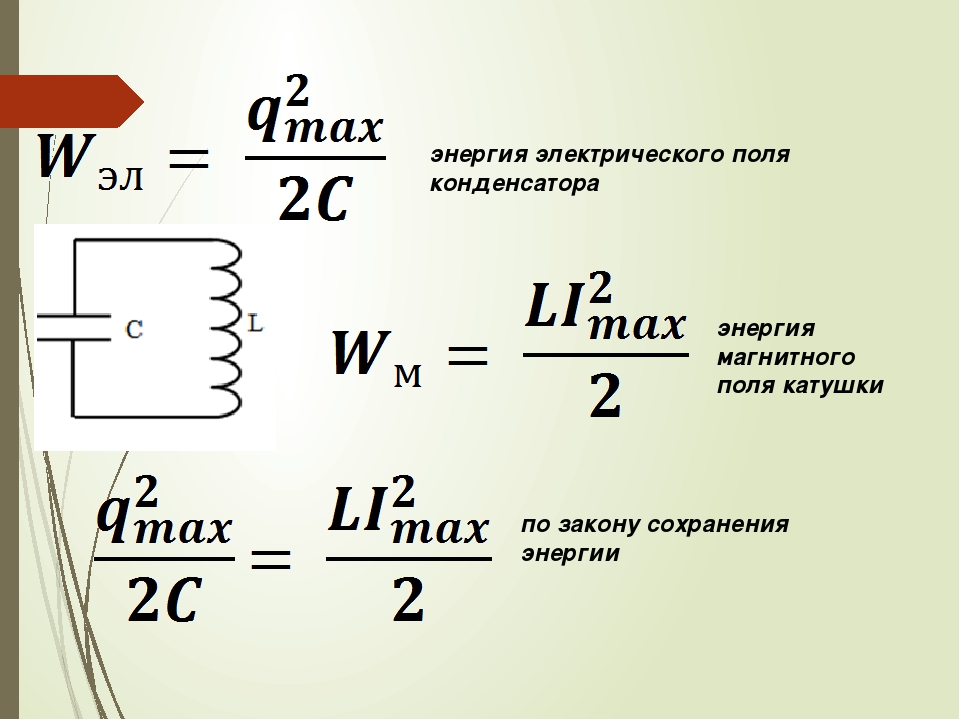

Значит, указанная работа аккумулируется именно в катушке как запасенная в ней энергия её магнитного поля. Ток возрастает от нуля до некого установившегося значения I. Поэтому полная энергия поля катушки равна 

(8.30)

Поскольку

этот же результат можно записать в формах

(8.31)

Эти формулы очень похожи на выражения для энергии конденсатора как функции его заряда или разности потенциалов на обкладках. Мы помним, что их можно привести к виду, где явно выделен объем конденсатора. Это позволило нам связать плотность энергии электрического поля с его напряженностью.

Выполним аналогичную программу и для магнитного поля, используя в качестве «катушки» достаточно длинный соленоид. 

Индуктивность соленоида дается выражением (8.21)

Магнитная индукция в соленоиде определяется по формуле (7.18)

Выразим плотность числа витков в соленоиде через магнитное поле в нем

и подставим в выражение для индуктивности соленоида. Получим

Наконец, подставим это выражение в формулу (17.28) для энергии поля в катушке 

(8.32)

Мы достигли своей цели: параметры соленоида, с которого мы начали, не присутствуют в этой формуле. Мы все выразили через магнитную индукцию поля, и энергия в катушке оказалась пропорциональной ее объему.

Отсюда следует выражение для плотности энергии магнитного поля (неважно, чем и как созданного)

(8.33)

Вспоминая связь напряженности магнитного поля с магнитной индукцией

находим эквивалентные представления для плотности энергии магнитного поля:

(8.34)

Для магнитного поля в вакууме следует положить во всех этих формулах . Нетрудно заметить сходство (8.34) с аналогичными формулами (3.35), (3.36) для электрического поля (рис. 8.36, рис. 8.37).

Рис. 8.36. Мощное магнитное поле Солнца производит выбросы плазмы

Рис. 8.37. Мощное магнитное поле нейтронной звезды 

Пример. Сравнить энергии, содержащиеся в объеме 1 л, если он пронизан: 1) однородным электрическим полем с напряженностью Е = 100 кВ/м; 2) однородным магнитным полем с индукцией В = 1 Тл.

Решение. Энергия электрического поля равна

Энергия магнитного поля равна

Оба указанных поля считаются достаточно сильными, но могут быть созданы без особых проблем. Задача демонстрирует, что практически выгоднее накапливать энергию в магнитном поле: в данном примере отношение энергий равно

Катушка индуктивности. Описание, характеристики, формула расчета

Катушка индуктивности является пассивным компонентом электронных схем, основное предназначение которой является сохранение энергии в виде магнитного поля. Свойство катушки индуктивности чем-то схоже с конденсатором, который хранит энергию в виде электрического поля.

Тестер транзисторов / ESR-метр / генератор

Многофункциональный прибор для проверки транзисторов, диодов, тиристоров…

Индуктивность (измеряется в Генри) — это эффект возникновения магнитного поля вокруг проводника с током. Ток, протекающий через катушку индуктивности, создает магнитное поле, которое имеет связь с электродвижущей силой (ЭДС) оказывающее противодействие приложенному напряжению.

Возникающая противодействующая сила (ЭДС) противостоит изменению переменного напряжения и силе тока в катушке индуктивности. Это свойство индуктивной катушки называется индуктивным сопротивлением. Следует отметить, что индуктивное сопротивление находится в противофазе к емкостному реактивному сопротивлению конденсатора в цепи переменного тока. Путем увеличения числа витков можно повысить индуктивность самой катушки.

Накопленная энергия в индуктивности

Как известно магнитное поле обладает энергией. Аналогично тому, как в полностью заряженном конденсаторе существует запас электрической энергии, в индуктивной катушке, по обмотке которой течет ток, тоже существует запас — только уже магнитной энергии.

Энергия, запасенная в катушке индуктивности равна затраченной энергии необходимой для обеспечения протекания тока I в противодействии ЭДС. Величина запасенной энергии в индуктивности можно рассчитать по следующей формуле:

где L — индуктивность, I — ток, протекающий через катушку индуктивности.

Гидравлическая модель

Работу катушки индуктивности можно сравнить с работой гидротурбины в потоке воды. Поток воды, направленный сквозь еще не раскрученную турбину, будет ощущать сопротивление до того момента, пока турбина полностью не раскрутится.

Далее турбина, имеющая определенную степень инерции, вращаясь в равномерном потоке, практически не оказывая влияния на скорость течения воды. В случае же если данный поток резко остановить, то турбина по инерции все еще будет вращаться, создавая движение воды. И чем выше инерция данной турбины, тем больше она будет оказывать сопротивление изменению потока.

Также и индуктивная катушка сопротивляется изменению электрического тока протекающего через неё.

Индуктивность в электрических цепях

В то время как конденсатор оказывает сопротивление изменению переменного напряжения, индуктивность же сопротивляется переменному тока. Идеальная индуктивность не будет оказывать сопротивление постоянному току, однако, в реальности все индуктивные катушки сами по себе обладают определенным сопротивлением.

В целом, отношение между изменяющимися во времени напряжением V(t) проходящим через катушку с индуктивностью L и изменяющимся во времени током I(t), проходящим через нее можно представить в виде дифференциального уравнения следующего вида:

Когда переменный синусоидальной ток (АС) протекает через катушку индуктивности, возникает синусоидальное переменное напряжение (ЭДС). Амплитуда ЭДС зависит от амплитуды тока и частоте синусоиды, которую можно выразить следующим уравнением:

где ω является угловой частотой резонансной частоты F:

Причем, фаза тока отстает от напряжения на 90 градусов.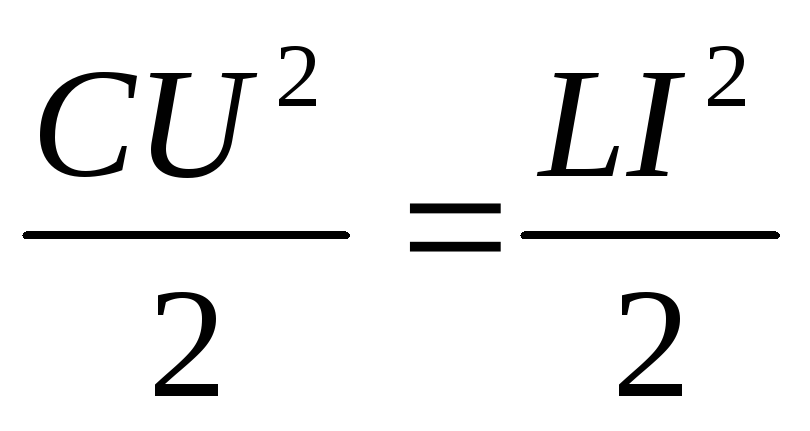 В конденсаторе же все наоборот, там ток опережает напряжение на 90 градусов. Когда индуктивная катушка соединена с конденсатором (последовательно либо параллельно), то образуется LC цепь, работающая на определенной резонансной частоте.

 Индуктивное сопротивление ХL определяется по формуле:

где ХL — индуктивное сопротивление, ω — угловая частота, F — частота в герцах, и L индуктивность в генри.

Индуктивное сопротивление — это положительная составляющая импеданса. Оно измеряется в омах. Импеданс катушки индуктивности (индуктивное сопротивление) вычисляется по формуле:

Схемы соединения катушек индуктивностей

Параллельное соединение индуктивностей

Напряжение на каждой из катушек индуктивностей, соединенных параллельно, одинаково. Эквивалентную (общую) индуктивность параллельно соединенных катушек можно определить по формуле:

Последовательное соединение индуктивностей

Ток, протекающий через катушки индуктивности соединенных последовательно, одинаков, но напряжение на каждой катушке индуктивности отличается. Сумма разностей потенциалов (напряжений) равна общему напряжению. Общая индуктивность последовательно соединенных катушек можно высчитать по формуле:

Эти уравнения справедливы при условии, что магнитное поле каждой из катушек не оказывает влияние на соседние катушки.

Добротность катушки индуктивности

На практике катушка индуктивности имеет последовательное сопротивление, созданное медной обмоткой самой катушки. Это последовательное сопротивление преобразует протекающий через катушку электрический ток  в тепло, что приводит к потере качества индукции, то есть добротности. Добротность является отношением индуктивности к сопротивлению.

Добротность катушки индуктивности может быть найдена через следующую формулу:

 где R является собственным сопротивлением обмотки.

Катушка индуктивности. Формула индуктивности

Базовая формула индуктивности катушки:

• L = индуктивность в генри
• μ 0 = проницаемость свободного пространства = 4π × 10 -7 Гн / м
• μ г = относительная проницаемость материала сердечника
• N = число витков
• A = Площадь поперечного сечения катушки в квадратных метрах (м 2 )
• l = длина катушки в метрах (м)

Индуктивность прямого проводника:

• L = индуктивность в нГн
• l = длина проводника
• d = диаметр проводника в тех же единицах, что и l

Индуктивность катушки с воздушным сердечником:

• L = индуктивность в мкГн
• r = внешний радиус катушки
• l = длина катушки
• N = число витков

Индуктивность многослойной катушки с воздушным сердечником:

• L = индуктивность в мкГн
• r = средний радиус катушки
• l = длина катушки
• N = число витков
• d = глубина катушки

Индуктивность плоской катушки:

• L = индуктивность в мкГн
• r = средний радиус катушки
• N = число витков
• d = глубина катушки

Конструкция катушки индуктивности

Катушка индуктивности представляет собой обмотку из проводящего материала, как правило, медной проволоки, намотанной вокруг либо железосодержащего сердечника, либо вообще без сердечника.

Применение в качестве сердечника материалов с высокой магнитной проницаемостью, более высокой чем воздух, способствует удержанию магнитного поля вблизи катушки, тем самым увеличивая ее индуктивность. Индуктивные катушки бывают разных форм и размеров.

Большинство изготавливаются путем намотки эмалированного медного провода поверх ферритового сердечника.

Некоторые индуктивные катушки имеют регулируемый сердечник, при помощи которого обеспечивается изменение индуктивности.

Миниатюрные катушки могут быть вытравлены непосредственно на печатной плате в виде спирали. Индуктивности с малым значением могут быть расположены в микросхемах с использованием тех же технологических процессов, которые используются при создании транзисторов.

Применение катушек индуктивности

Индуктивности широко используются в аналоговых схемах и схемах обработки сигналов. Они в сочетании с конденсаторами и другими радиокомпонентами образуют специальные схемы, которые могут усилить или отфильтровать сигналы определенной частоты.

Катушки индуктивности получили широкое применение начиная от больших катушек индуктивности, таких как дроссели в источниках питания, которые в сочетании с конденсаторами фильтра устраняют остаточные помехи и другие колебания на выходе источника питания, и до столь малых индуктивностей, которые располагаются внутри интегральных микросхем.

Две (или более) катушки индуктивности, которые соединены единым магнитным потоком, образуют трансформатор, являющимся основным компонентом схем работающих с электрической сетью электроснабжения. Эффективность трансформатора возрастает с увеличением частоты напряжения.

По этой причине, в самолетах используется переменное напряжение с частотой 400 герц вместо обычных 50 или 60 герц, что в свою очередь позволяет значительно сэкономить на массе используемых трансформаторов в электроснабжении самолета.

Так же индуктивности используются в качестве устройства для хранения энергии в импульсных стабилизаторах напряжения, в высоковольтных электрических системах передачи электроэнергии для преднамеренного снижения системного напряжения или ограничения ток короткого замыкания.

Блок питания 0…30 В / 3A

Набор для сборки регулируемого блока питания…

Свободные электромагниные колебания в контуре, катушка, конденсатор, сохранение энергии. Курсы по физике

Тестирование онлайн

• Электромагнитные колебания. Основные понятия

• Электромагнитные колебания

Свободные электромагнитные колебания

Рассмотрим электрическую цепь, состоящую из катушки индуктивностью L и конденсатора электроемкостью C. Если предварительно зарядить конденсатор (рис. a), то получим колебательный контур (рис. б).

1) В начальный момент времени конденсатор имеет максимальный заряд, обладает максимальной энергией W_C.

2) В следующий момент времени конденсатор начинает разряжаться. В цепи появляется ток. По мере разрядки конденсатора ток в цепи и в катушке нарастает. Из-за явления самоиндукции это происходит не мгновенно.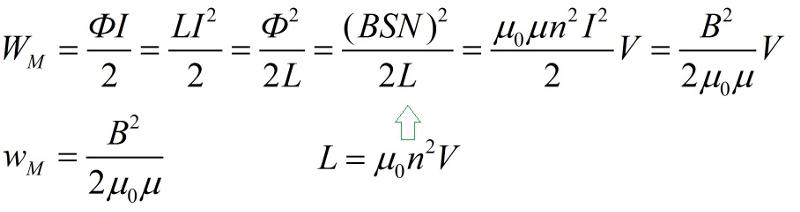 Энергия катушки W_L становится максимальной.

3) Электрические заряды вновь накапливаются на конденсаторе, но обкладка конденсатора, первоначально заряженная положительно, будет заряжена отрицательно. Энергия конденсатора максимальная.

4) Конденсатор разряжается, но ток протекает уже в обратном направлении.

Этот процесс будет повторяться снова и снова. Возникнут электромагнитные колебания. Если отсутствуют потери (R=0), то сила тока, заряд и напряжение со временем изменяются по гармоническому закону.

Период колебаний. Формула Томсона

Наименьший промежуток времени, в течение которого происходит переход зарядов с одной обкладки конденсатора на другую и обратно, называется периодом свободных электромагнитных колебаний.

Энергия колебательного контура

Если пренебречь потерями (R=0), то полная энергия колебательного контура остается постоянной. Выполняется закон сохранения энергии.

Мгновенное значение силы тока в катушке

Мгновенное значение ЭДС самоиндукции

Что делает катушка индуктивности в цепи.

Накопленная энергия в индуктивности

Сегодня нами будет рассмотрена катушка индуктивности в цепи переменного тока, узнаем, в чем бы была разница, если бы цепь питалась от постоянного тока, а также много интересных особенностей этого простого, но очень важного радиоэлемента.

Для начала давайте определим назначение этой детали, а также основные понятия и термины, связанные с ней.

Что такое катушка индуктивности

Катушка индуктивности – это радиоэлемент, применяющийся в разных схемах для следующего:

• Сглаживание биений;
• Подавление помех;
• Ограничение переменного тока;
• Накопление энергии и прочее.

Представляет собой данный элемент спиральную, винтовую или винтоспиральную катушку, сделанную из изолированного проводника. Деталь обладает относительно малой емкостью и малым активным сопротивлением, при этом у него имеет высокая индуктивность, то есть способность возникновения ЭДС (электродвижущей силы) в проводнике, при протекании в цепи электрического тока.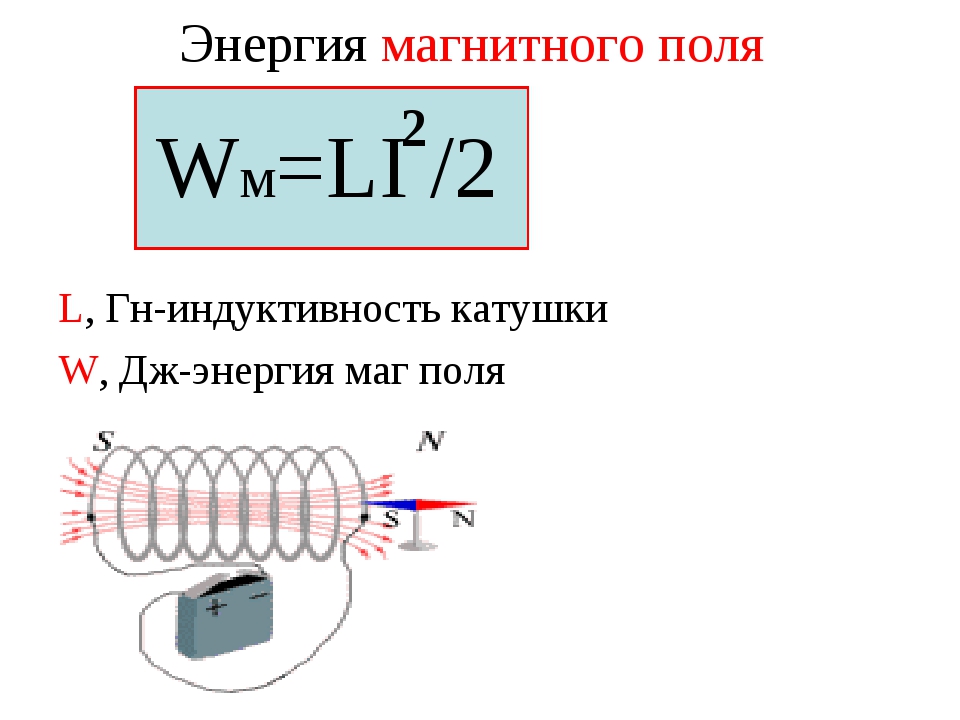

• Катушка индуктивности, в зависимости от места и цели применения может иметь и другие названия. Например, если элемент используется для изоляции по высокой частоте в разных частях схемы, накоплении энергии магнитного поля сердечника, сглаживания пульсаций и подавления помех, катушку называют дросселем либо реактором (второе название употребляется редко).
• Если говорить про силовую электротехнику, то там устоялось название ректор – его применяют при необходимости ограничения тока, например, если произошло замыкание на ЛЭП.

• Бывают также и цилиндрические катушки индуктивности, называемые соленоидами. Длина такого цилиндра в несколько раз превышает его диаметр.

Интересно знать! Магнитное поле внутри соленоида однородно. Данное магнитное поле может выполнять механическую работу, втягивая ферритовый сердечник.

• Применяются катушки индуктивности и в электромагнитных реле, где их называют обмоткой реле.
• Устанавливаются подобные элементы и в индукционные нагреватели – тут их называют нагревательными индукторами.

• Также можно услышать термины вроде индукционного накопителя или накопительного дросселя, если речь идет об устройствах импульсной стабилизации напряжения.

Конструкционные особенности

Конструкционно катушка индуктивности представляет собой намотанную по спирали или винтом изолированную одножильный или многожильный проводник (чаще, лакированная медная проволока), вокруг диэлектрического сердечника (каркаса). Форма сердечника может быть круглой, тороидальной, прямоугольной, квадратной. Материалы, применяемые для сердечника, имеют магнитную проницаемость выше, чем у воздуха, что дополнительно удерживает магнитное поле возле катушки, а значит, увеличивается и индуктивность.

Существуют и катушки, вовсе не имеющие сердечника, или же он является регулируемым, что позволяет менять индуктивность детали.

Намотка проводника может быть как однослойной, ее еще называют рядовой с шагом, или многослойной (применяются названия универсал, внавал, рядовая). Расстояние между витками называется шагом.

Применение

Используются катушки в схемах обработки сигналов и аналоговых схемах. В сочетании с конденсаторами и прочими радиокомпонентами могут формировать участки схем, которые усиливают или отфильтровывают определенные сигналы.

Широко применяются дроссели в источниках питания, где они вместе с конденсаторами фильтра призваны устранить остаточные помехи и прочие колебания, возникающие на выходе.

Если две катушки соединить одним магнитным полем, то получится трансформатор – устройство, способное передавать электричество от одной части цепи к другой, за счет электромагнитной индукции, попутно меняя величину напряжения.

Для справки! Трансформаторы способны функционировать только с переменным током.

Основные характеристики катушек индуктивности

Прежде чем разбираться с тем, как ведет себя ток, проходя в цепи через катушку индуктивности, давайте сначала узнаем главные характеристики этого элемента.

• Прежде всего, нас интересует индуктивность – значение, численно выражающаяся соотношением потока магнитного поля, которое создается протекающим током, к силе этого самого тока. Измеряется этот параметр в Генри (Гн).
• Если говорить более простым языком, то это явление можно описать так. При протекании тока через катушку индуктивности создается электромагнитное поле, которое напрямую связано с ЭДС, которая оказывает противодействие изменению переменного напряжения, то есть в цепи возникает ток, который течет в обратном направлении основному.
• Измерение силы тока на катушке индуктивности и переменного напряжения, противостоят данной силе, точнее наоборот. Это свойство элемента называется индуктивным сопротивлением, которое находится в противофазе реактивному емкостному сопротивлению конденсатора, включенному в цепь переменного тока.

Рассмотрим цепь, содержащую в себе катушку индуктивности , и предположим, что активное сопротивление цепи, включая провод катушки, настолько мало, что им можно пренебречь.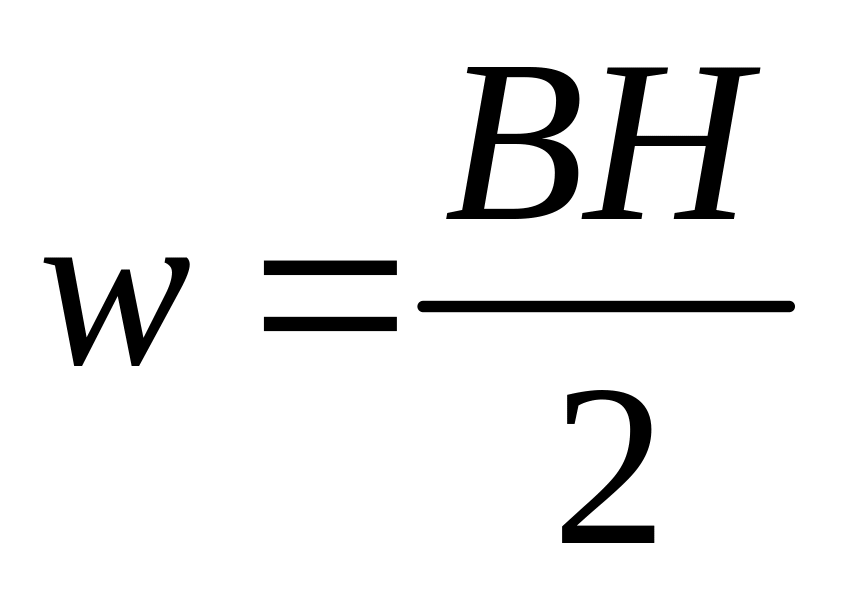 В этом случае подключение катушки к источнику постоянного тока вызвало бы его короткое замыкание, при котором, как известно, сила тока в цепи оказалась бы очень большой.

Иначе обстоит дело, когда катушка присоединена к источнику переменного тока. Короткого замыкания в этом случае не происходит. Это говорит о том. что катушка индуктивности оказывает сопротивление проходящему по ней переменному току .

Каков характер этого сопротивления и чем оно обусловливается?

Чтобы ответить ил этот вопрос, вспомним . Всякое изменение тока в катушке вызывает появление в ней ЭДС самоиндукции, препятствующей изменению тока. Величина ЭДС самоиндукции прямо пропорциональна и скорости изменения тока в ней. Но так как непрерывно изменяется, то непрерывно возникающая в катушке ЭДС самоиндукции создает сопротивление переменному току.

Для уяснения процессов, происходящих в с катушкой индуктивности, обратимся к графику. На рисунке 1 построены кривые линии, характеризующие соответственно тик в цепи, напряжение на катушке и возникающую в ней ЭДС самоиндукции. Убедимся в правильности произведенных па рисунке построений.

С момента t = 0, т. е. с начального момента наблюдения за током, он начал быстро возрастать, но по мере приближения к своему максимальному значению скорость нарастания тока уменьшалась. В момент, когда ток достиг максимальной величины, скорость его изменения на мгновение стала равной нулю, т. е. прекратилось изменение тока. Затем ток начал сначала медленно, а потом быстро убывать и по истечении второй четверти периода уменьшился до нуля. Скорость же изменения тока за эту четверть периода, возрастая от пуля, достигла наибольшей величины тогда, когда ток станет равным нулю.

Рисунок 2. Характер изменений тока во времени в зависимости от величины тока

Из построений на рисунке 2 видно, что при переходе кривой тока через ось времени увеличение тока за небольшой отрезок времени t больше, чем за этот же отрезок времени, когда кривая тока достигает своей вершины.

Следовательно, скорость изменения тока уменьшается по мере увеличения тока и увеличивается по мере его уменьшения, независимо от направления тока в цепи.

Очевидно, и ЭДС самоиндукции в катушке должна быть наибольшей тогда, когда скорость изменения тока наибольшая, и уменьшаться до нуля, когда прекращается его изменение. Действительно, на графике кривая ЭДС самоиндукции e L за первую четверть периода, начиная от максимального значения, упала до нуля (см. рис. 1).

На протяжении следующей четверти периода ток от максимального значения уменьшался до нуля, однако скорость его изменения постепенно возрастала и была наибольшей в момент, когда ток стал равным нулю. Соответственно и ЭДС самоиндукции за время этой четверти периода, появившись вновь в катушке, постепенно возрастала и оказалась максимальной к моменту, когда ток стал равным нулю.

Однако направление свое ЭДС самоиндукции изменила на обратное, так как возрастание тока в первой четверти периода сменилось во второй четверти его убыванием.

Продолжив дальше построение кривой ЭДС самоиндукции, мы убеждаемся в том, что за период изменения тока в катушке и ЭДС самоиндукции совершит в ней полный период своего изменения. Направление ее определяется : при возрастании тока ЭДС самоиндукции будет направлена против тока (первая и третья четверти периода), а при убывании тока, наоборот, совпадать с ним по направлению (вторая и четвертая четверти периода).

Таким образом, ЭДС самоиндукции, вызываемая самим переменным током, препятствует его возрастанию и, наоборот, поддерживает его при убывании .

Обратимся теперь к графику напряжения на катушке (см. рис. 1). На этом графике синусоида напряжения на зажимах катушки изображена равной и противоположной синусоиде ЭДС самоиндукции. Следовательно, напряжение на зажимах катушки в любой момент времени равно и противоположно ЭДС самоиндукции, возникающей в ней. Напряжение это создается генератором переменного тока и идет на то, чтобы погасить действие в цепи ЭДС самоиндукции.

Таким образом, в катушке индуктивности, включенной в цепь переменного тока, создается сопротивление прохождению тока. Но так как такое сопротивление вызывается в конечном счете индуктивностью катушки , то и называется оно индуктивным сопротивлением.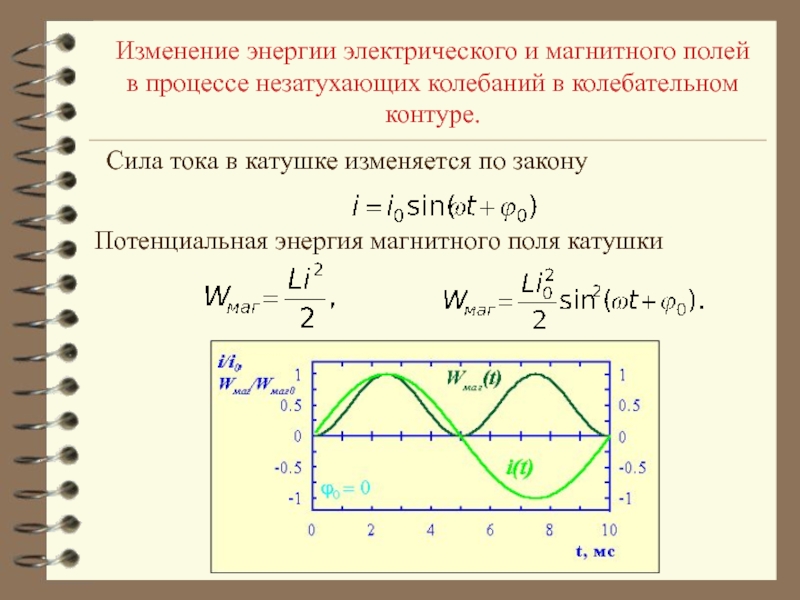

Индуктивное сопротивление обозначается через X L и измеряется, как и активное сопротивление, в омах.

Индуктивное сопротивление цепи тем больше, чем больше , питающего цепь, и чем больше индуктивность цепи. Следовательно, индуктивное сопротивление цепи прямо пропорционально частоте тока и индуктивности цепи; определяется оно по формуле XL = ω L, где ω — круговая частота, определяемая произведением 2π f . — индуктивность цепи в гн.

Для цепи переменного тока, содержащей индуктивное сопротивление, звучит так: величина тока прямо пропорциональна напряжению и обратно пропорциональна индуктивному сопротивлению цеп и , т. е. I = U / X L , где I и U — действующие значения тока и напряжения, а X L — индуктивное сопротивление цепи.

Рассматривая графики изменения тока в катушке. ЭДС самоиндукции и напряжения на ее зажимах, мы обратили внимание на то, что изменение этих в еличин не совпадает по времени. Иначе говоря, синусоиды тока, напряжения и ЭДС самоиндукции оказались для рассматриваемой нами цепи сдвинутыми по времени одна относительно другой. В технике переменных токов такое явление принято называть сдвигом фаз .

Если же две переменные величины изменяются по одному и тому же закону (в нашем случае по синусоидальному) с одинаковыми периодами, одновременно достигают своего максимального значения как в прямом, так и в обратном направлении, а также одновременно уменьшаются до нуля, то такие переменные величины имеют одинаковые фазы или, как говорят, совпадают по фазе.

В качестве примера на рисунке 3 приведены совпадающие по фазе кривые изменения тока и напряжения. Такое совпадение фаз мы всегда наблюдаем в цепи переменного тока, состоящей только из активного сопротивления.

В том случае, когда цепь содержит индуктивное сопротивление, фазы тока и напряжения, как это видно из рис. 1 не совпадают, т. е. имеется сдвиг фаз между этими переменными величинами. Кривая тока в этом случае как бы отстает от кривой напряжения на четверть периода.

Следовательно, при включении катушки индуктивности в цепь переменного тока в цепи появляется сдвиг фаз между током и напряжением, причем ток отстает по фазе от напряжения на четверть периода . Это значит, что максимум тока наступает через четверть периода после того, как наступил максимум напряжения.

ЭДС же самоиндукции находится в противофазе с напряжением на катушке, отставая, в свою очередь, от тока на четверть периода. При этом период изменения тока, напряжения, а также и ЭДС самоиндукции не меняется и остается равным периоду изменения напряжения генератора, питающего цепь. Сохраняется также и синусоидальный характер изменения этих величин.

Когда же цепь не содержит активного сопротивления (мы условно считаем его равным нулю), а состоит лишь из индуктивного сопротивления катушки, энергия источника тока расходуется не на нагрев проводов, а только на создание ЭДС самоиндукции, т. е. она превращается в энергию магнитного поля. Однако переменный ток непрерывно изменяется как по величине, так и по направлению, а следовательно, и катушки непрерывно изменяется в такт с изменением тока. В первую четверть периода, когда ток возрастает, цепь получает энергию от источника тока и запасает ее в магнитном поле катушки. Но как только ток, достигнув своего максимума, начинает убывать, он поддерживается за счет энергии, запасенной в магнитном поле катушки посредством ЭДС самоиндукции.

Таким образом, источник тока, отдав в течение первой четверти периода часть своей энергии в цепь, в течение второй четверти получает ее обратно от катушки, выполняющей при этом роль своеобразного источника тока. Иначе говоря, цепь переменного тока, содержащая только индуктивное сопротивление, не потребляет энергии : в данном случае происходит колебание энергии между источником и цепью. Активное же сопротивление, наоборот, поглощает в себе всю энергию, сообщенную ему источником тока.

Говорят, что катушка индуктивности, в противоположность омическому сопротивлению, не активна по отношению к источнику переменного тока, т. е. реактивна . Поэтому индуктивное сопротивление катушки называют также реактивным сопротивлением .

» говорится, что при включении и при всяком изменении тока в электрической цепи вследствие пересечения проводника своим же собственным магнитным полем в нем возникает индуктированная электродвижущая сила (ЭДС).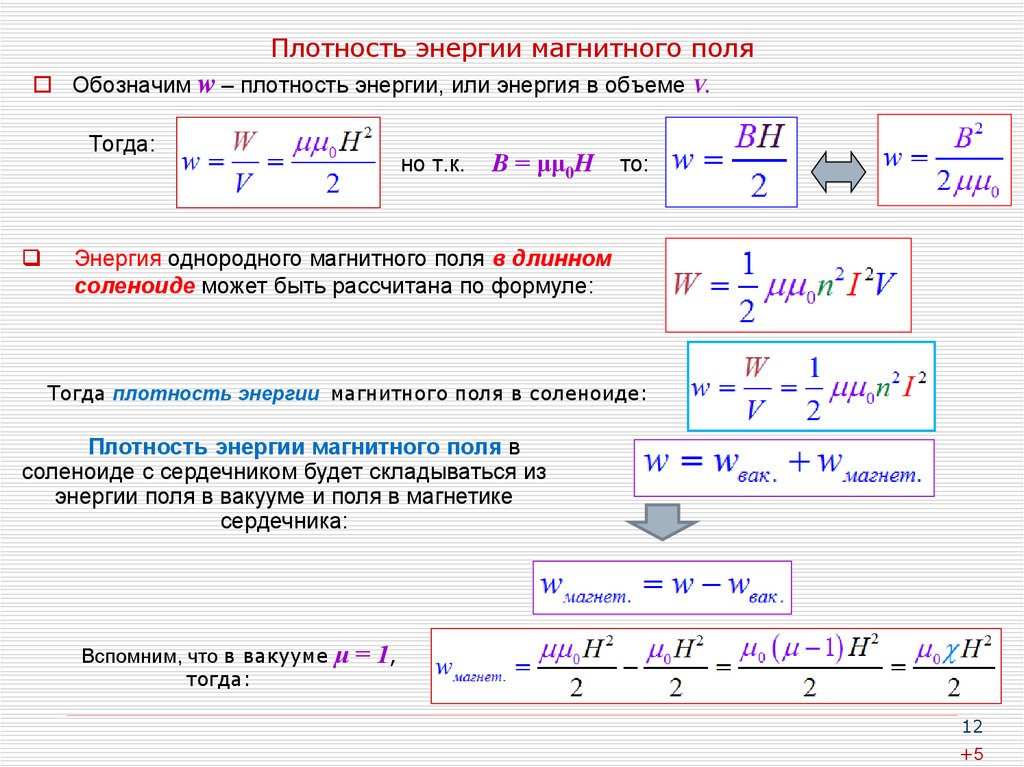 Эту ЭДС мы назвали ЭДС самоиндукции. ЭДС самоиндукции имеет реактивный характер. Так, например, при увеличении тока в цепи ЭДС самоиндукции будет направлена против ЭДС источника напряжения, и поэтому ток в электрической цепи не может установиться сразу. И, наоборот, при уменьшении тока в цепи индуктируется ЭДС самоиндукции такого направления, что, мешая току исчезать, она поддерживает этот убывающий ток.

Рисунок 1. Цепь переменного тока, содержащая индуктивность

Как нам уже известно, ЭДС самоиндукции зависит от скорости изменения тока в цепи и от индуктивности этой цепи (числа витков, наличия стальных сердечников).

В цепи переменного тока ЭДС самоиндукции возникает непрерывно, так как ток в цепи непрерывно изменяется.

На рисунке 1 представлена схема цепи переменного тока, содержащей катушку с индуктивностью L без стального сердечника. Для простоты будем считать сначала, что активное сопротивление катушки очень мало и им можно пренебречь.

Рассмотрим внимательнее изменение переменного тока за время одного периода. На рисунке 2 показана кривая изменения переменного тока. Первая половина периода разбита на мелкие одинаковые части.

Рисунок 2. Определение скорости изменения переменного тока

За промежуток времени 0 — 1 величина тока изменилась от нуля до 1 — 1 ’. Прирост величины тока за это время равен а .

За время, обозначенное отрезком 1 — 2 , мгновенная величина выросла до 2 — 2 ’, причем прирост величины тока равен б .

В течение времени, обозначенного отрезком 2 — 3 , ток увеличивается до 3 — 3 ’, прирост тока показывает отрезок в и так далее.

Так, с течением времени переменный ток возрастет до максимума (при 90°). Но, как видно из чертежа, прирост тока делается все меньше и меньше, пока, наконец, при максимальном значении тока этот прирост не станет равным нулю.

При дальнейшем изменении тока от максимума до нуля убыль величины тока становится все больше и больше, пока, наконец, около нулевого значения ток, изменяясь с наибольшей скоростью, не исчезнет, но тут же появляется вновь, протекая в обратном направлении.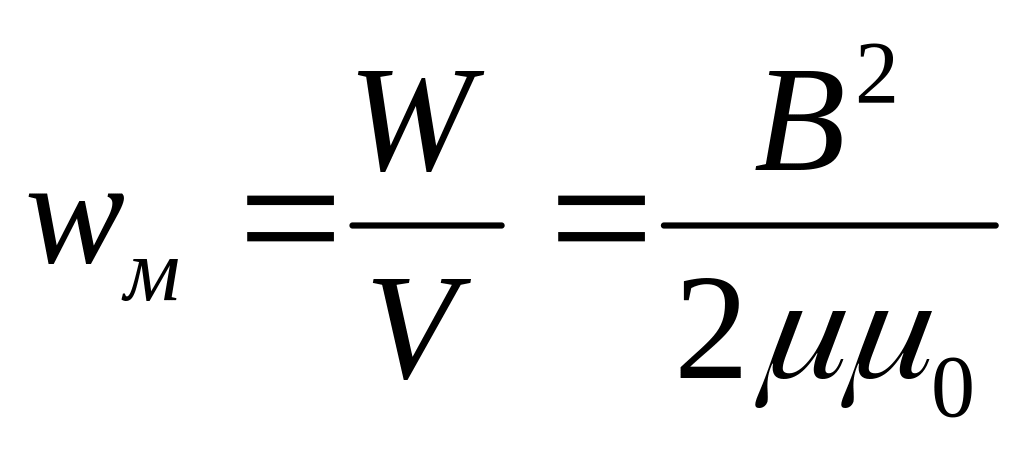

Рассматривая изменение тока в течение периода, мы видим, что с наибольшей скоростью изменяется ток около своих нулевых значений. Около максимальных значений скорость изменения тока падает, а при максимальном значении тока прирост его равен нулю. Таким образом, переменный ток меняется не только по величине и направлению, но также и по скорости своего изменения. Переменный ток, проходя по виткам катушки, создает переменное магнитное поле. Магнитные линии этого поля, пересекая витки своей же катушки, индуктируют в них ЭДС самоиндукции.

На рисунке 3 кривая i показывает изменение переменного тока в катушке. Как было уже указано, величина ЭДС самоиндукции зависит от скорости изменения тока и от индуктивности катушки. Но так как индуктивность катушки в нашем случае остается без изменения, ЭДС самоиндукции будет зависеть только от скорости изменения тока. Выше было показано, что наибольшая скорость изменения тока имеет место около нулевых значений тока. Следовательно, наибольшее изменение ЭДС самоиндукции имеет те же моменты.

Рисунок 3. ЭДС самоиндукции в катушке, включенной в цепь переменного тока

В момент а ток резко и быстро увеличивается от нуля, а поэтому, как следует из вышеприведенной формулы, ЭДС самоиндукции (кривая e L ) имеет отрицательное максимальное значение. Так как ток увеличивается, то ЭДС самоиндукции по правилу Ленца должна препятствовать изменению (здесь увеличению) тока. Поэтому ЭДС самоиндукции при возрастании тока будет иметь направление, обратное току (положение б ), что следует также из указанной формулы. Скорость изменения тока по мере приближения его к максимуму уменьшается. Поэтому ЭДС самоиндукции также уменьшается, пока, наконец, при максимуме тока, когда изменения его будут равны нулю, она не станет равной нулю (положение в ).

Переменный ток, достигнув максимума, начинает убывать. По правилу Ленца ЭДС самоиндукции будет мешать току убывать и, направленная уже в сторону протекания тока, будет его поддерживать (положение г ).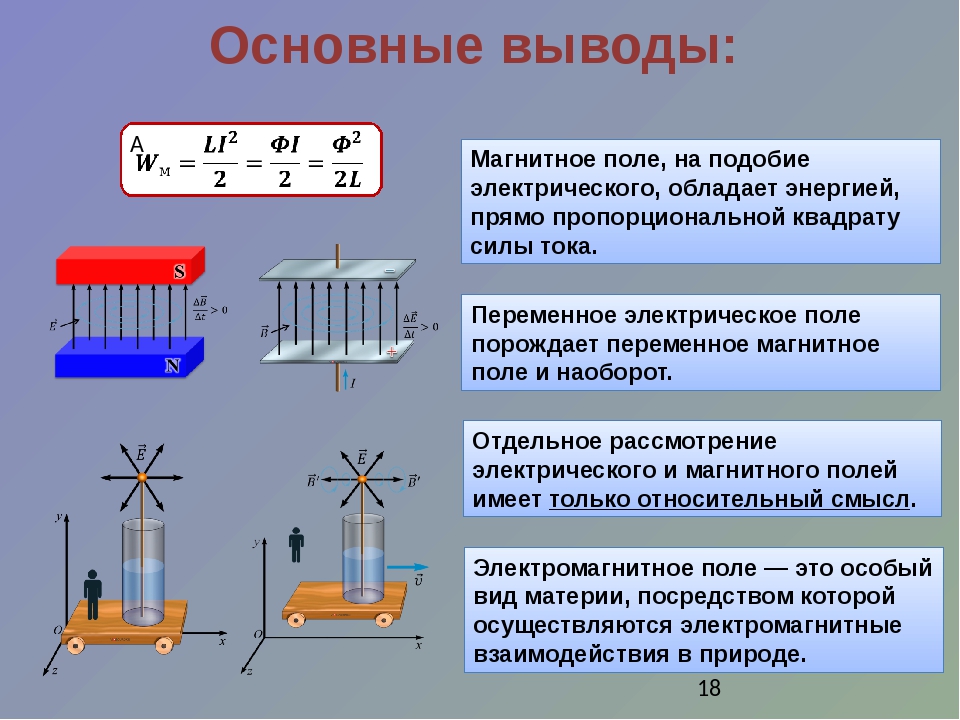

При дальнейшем изменении переменный ток быстро убывает до нуля. Резкое уменьшение тока в катушке повлечет за собой также быстрое уменьшение магнитного поля и в результате пересечения магнитными линиями витков катушки в них будет индуктироваться наибольшая ЭДС самоиндукции (положение д ).

Рисунок 4. Ток в катушке опережает ЭДС самоиндукции по фазе на 90°

Во вторую половину периода изменения тока картина повторяется и снова при возрастании тока ЭДС самоиндукции будет мешать ему, имея направление, обратное току (положение е ).

При убывании тока ЭДС самоиндукции, имея направление в сторону тока, будет поддерживать его, не давая ему исчезнуть сразу (положение з ).

На рисунке видно, что ЭДС самоиндукции отстает по фазе от тока на 90° или на ¼ периода. Так как магнитный поток совпадает по фазе с током, то можно сказать, что ЭДС, наводимая магнитным потоком, отстает от него по фазе на 90° или на ¼ периода.

Нам уже известно, что две синусоиды, сдвинутые одна относительно другой на 90°, можно изобразить векторами, расположенными под углом 90° (рисунок 4).

Так как ЭДС самоиндукции в цепях переменного тока непрерывно противодействует изменениям тока, то, чтобы дать возможность току протекать по виткам катушки, напряжение сети должно уравновешивать ЭДС самоиндукции. Иными словами, напряжение сети в каждый момент времени должно быть равно и противоположно ЭДС самоиндукции.

Рисунок 5. Приложенное к катушке напряжение сети опережает ток на 90° и противоположно ЭДС самоиндукции

Вектор напряжения сети, равный и противоположный ЭДС самоиндукции e L , мы обозначим через U (рисунок 5). Только при условии, что к зажимам катушки будет приложено напряжение сети, равное и противоположное ЭДС самоиндукции, и, стало быть, это напряжение сети U уравновесит ЭДС самоиндукции e L , по катушке сможет проходить переменный ток I .

Но в этом случае напряжение сети U будет опережать по фазе ток I на 90°.

Таким образом, в цепях переменного тока ЭДС самоиндукции, возникая непрерывно, вызывает сдвиг фаз между током и напряжением. Возвращаясь к рисунку 3, мы видим, что ток i по катушке будет проходить и тогда, когда напряжение сети (кривая u L ) равно нулю (положение в ), и даже тогда, когда напряжение сети направлено в сторону, обратную току (положение г и з ).

Итак отметим, что в цепи переменного тока, когда ЭДС самоиндукции отсутствует, напряжение сети и ток совпадают по фазе. Индуктивная же нагрузка в цепях переменного тока (обмотки электродвигателей и генераторов, обмотки трансформаторов, индуктивные катушки) всегда вызывает сдвиг фаз между током и напряжением.

Можно показать, что скорость изменения тока пропорциональна угловой частоте ω. Следовательно, действующее значение ЭДС самоиндукции e L может быть найдено по формуле:

e L = ω × L × I = 2 × π × f × L × I .

Как было отмечено выше, напряжение, приложенное к зажимам цепи, содержащей индуктивность, в каждый момент времени должно быть по величине равно ЭДС самоиндукции:

u L = e L .

u L = 2 × π × f × L × I .

Обозначая 2 × π × f × L = x L , получим

u L = x L × I .

Формула закона Ома для цепи переменного тока, содержащего индуктивность, будет такова:

Величина x L называется индуктивным сопротивлением цепи , или реактивным сопротивлением индуктивности , и измеряется в омах. Таким образом, реактивное индуктивное сопротивление представляет собой своеобразное препятствие, которое оказывает цепь изменениям тока в ней. Оно равно произведению индуктивности на угловую частоту. Формула индуктивного сопротивления имеет вид:

x L = ω × L .

Индуктивное сопротивление проводника зависит от частоты переменного тока и индуктивности проводника. Поэтому индуктивное сопротивление катушки, включаемой в цепь токов различной частоты, будет различным. Например, если имеется катушка индуктивностью 0,05 Гн, то путем расчета индуктивного сопротивления выяснится, что в цепи частотой 50 Гц ее индуктивное сопротивление будет:

x L1 = 2 × π × f 1 × L = 2 × 3,14 × 50 × 0,05 = 15,7 Ом,

а в цепи тока частотой 400 Гц

x L2 = 2 × π × f 2 × L = 2 × 3,14 × 400 × 0,05 = 125,6 Ом.

Та часть напряжения сети, которая идет на преодоление (уравновешивание) ЭДС самоиндукции, называется индуктивным падением напряжения или реактивной слагающей напряжения .

u L = x L × I .

Рассмотрим теперь, какая мощность потребляется от источника переменного напряжения, если к его зажимам подключена индуктивность.

Рисунок 6. Кривые мгновенных значений напряжения, тока и мощности для цепи, содержащей индуктивность

На рисунке 6 даны кривые мгновенных значений напряжения, тока и мощности для этого случая. Мгновенное значение мощности равно произведению мгновенных значений напряжения и тока:

p = u × i .

Из чертежа видно, что если u и i имеют одинаковые знаки, то кривая p положительная и располагается выше оси ωt . Если же u и i имеют разные знаки, то кривая p отрицательна и располагается ниже оси ωt .

В первую четверть периода ток, а в месте с ним и магнитный поток катушки увеличиваются. Катушка забирает из сети мощность. Площадь, заключенная между кривой p и осью ωt , есть работа (энергия) электрического тока. За первую четверть периода энергия, забираемая из сети, идет на создание магнитного поля вокруг витков катушки (мощность положительная). Количество энергии, запасаемое в магнитном поле за время роста тока, можно определить по формуле:

За вторую четверть периода ток убывает. ЭДС самоиндукции, которая в первую четверть периода стремилась помешать возрастанию тока, теперь, когда ток начинает уменьшаться, будет мешать ему уменьшаться. Сама катушка становится как бы генератором электрической энергии. Она возвращает в сеть энергию, запасенную в ее магнитном поле. Мощность отрицательна, и на рисунке 6 кривая p располагается ниже оси ωt .

За вторую половину периода явление повторяется. Таким образом, между источником переменного напряжения и катушкой, содержащей индуктивность, происходит обмен мощностью. В течение первой и третьей четвертей периода мощность поглощается катушкой, в течение второй и четвертой мощность возвращается источнику.

В этом случае, в среднем, расхода мощности не будет, несмотря на то, что на зажимах цепи есть напряжение U и в цепи протекает ток I .

Тот же результат мы получим, если вычислим среднюю или активную мощность по формуле, приведенной выше:

P = U × I × cos φ .

В нашем случае между напряжением и током существует сдвиг фаз, равный 90°, и cos φ = 90° = 0.

Поэтому активная мощность также равна нулю, то есть расхода мощности нет.

Как ведет себя катушка индуктивности в цепи постоянного и переменного тока?

Катушка индуктивности в цепи постоянного тока

Итак, для этого опыта нам понадобится блок питания , который выдает постоянное напряжение, лампочка накаливания и собственно сама катушка индуктивности.

Чтобы сделать катушку индуктивности с хорошей индуктивностью, нам надо взять ферритовый сердечник:

Намотать на него лакированного медного провода и зачистить выводы:

Замеряем индуктивность нашей катушки с помощью LC метра :

132 микрогенри.

Теперь собираем все это вот по такой схеме:

где

L — катушка индуктивности

La — лампочка накаливания на напряжение 12 Вольт

Bat — блок питания, с выставленным напряжением 12 Вольт

Лампочка засветилась!

Как вы помните из , конденсатор у нас не пропускал постоянный электрический ток:

Делаем вывод: постоянный электрический ток почти беспрепятственно течет через катушку индуктивности. Сопротивлением обладает только сам провод, из которого намотана катушка.

Катушка индуктивности в цепи переменного тока

Для того, чтобы узнать, как ведет себя катушка индуктивности в цепи переменного тока, нам понадобится , генератор частоты , собственно сама катушка индуктивности и резистор на 100 Ом. Чем больше сопротивление, тем меньше будет проседать напряжение с моего генератора частоты, поэтому я взял резистор на 100 Ом.Он у меня будет в качестве шунта. Падение напряжения на этом резисторе будет зависеть от тока, протекающего через него

Собираем все это дело по такой схеме:

Получилось как то так:

Сразу договоримся, что у нас первый канал будет красным цветом, а второй канал — желтым. Следовательно, красная синусоида — это частота, которую нам выдает генератор частоты, а желтая синусоида — это сигнал, который снимается с резистора.

Мы с вами узнали, что при нулевой частоте (постоянный ток), катушка почти беспрепятственно пропускает через себя электрический ток. В нашем опыте мы будем подавать с генератора частоты синусоидальный сигнал с разной частотой и смотреть, меняется ли напряжение на резисторе.

Опыт N1

Для начала подаем сигнал с частотой в 1 Килогерц.

Давайте разберемся, что есть что. В зеленой рамочке я вывел автоматические замеры, которые делает осциллограф

Красный кружок с цифрой «1» — это замеры «красного»канала. Как мы видим, F (частота) =1 Килогерц, а Ма (амплитуда) = 1,96 Вольт. Ну грубо скажем 2 Вольта. Смотрим на кружочек с цифрой «2». F =1 Килогерц, а Ма =1,96 Вольт. То есть можно сказать, что сигнал на выходе точно такой же, как и на входе.

Увеличиваем частоту до 10 Килогерц

Амплитуда не уменьшилась.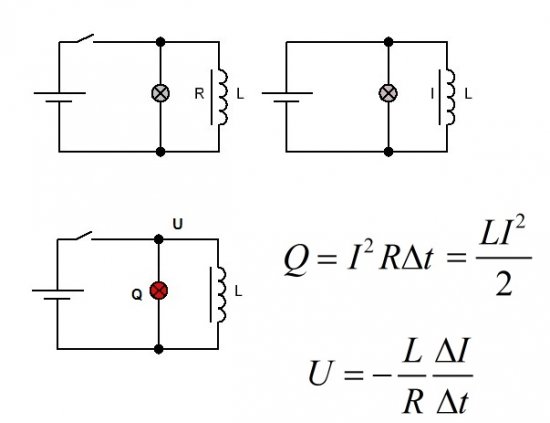 Сигнал какой есть, такой и остался.

Увеличиваем до 100 Килогерц

Заметили разницу? Амплитуда желтого сигнала стала меньше, да еще и график желтого сигнала сдвигается вправо, то есть запаздывает, или научным языком, появляется . Красный сигнал никуда не сдвигается, запаздывает именно желтый. Это имейте ввиду.

Сдвиг фаз — это разность между начальными фазами двух измеряемых величин . В данном случае напряжения. Для того, чтобы произвести замер сдвига фаз, должно быть условие, что у этих сигналов одна и та же частота . Амплитуда может быть любой. Ниже на рисунке приведен этот самый сдвиг фаз или, как еще его называют, разность фаз :

Увеличиваем частоту до 200 Килогерц

На частоте 200 Килогерц амплитуда упала вдвое, да и разность фаз стала больше.

Увеличиваем частоту до 300 Килогерц.

Амплитуда желтого сигнала упала уже до 720 милливольт. Разность фаз стала еще больше.

Увеличиваем частоту до 500 Килогерц

Амплитуда уменьшилась до 480 милливольт.

Добавляем еще частоту до 1 Мегагерц

Амплитуда желтого канала стала 280 милливольт.

Ну и добавляем частоту до предела, который позволяет выдать генератор частоты: 2 Мегагерца

Амплитуда «желтого» сигнала стала настолько маленькой, что мне пришлось ее даже увеличить в 5 раз.

И можно сказать, что сдвиг фаз стал почти 90 градусов или π/2.

Но станет ли сдвиг фаз больше, чем 90 градусов, если подать очень-очень большую частоту? Эксперименты говорят, что нет. Если сказать просто, то при бесконечной частоте сдвиг фаз будет равняться 90 градусов. Если совместить наши графики на бесконечной частоте, то можно увидеть примерно вот такой рисунок:

Так какой вывод можно сделать?

С увеличением частоты сопротивление катушки растет, а также увеличивается сдвиг фаз. И чем больше частота, тем больше будет сдвиг фазы, но не более, чем 90 градусов.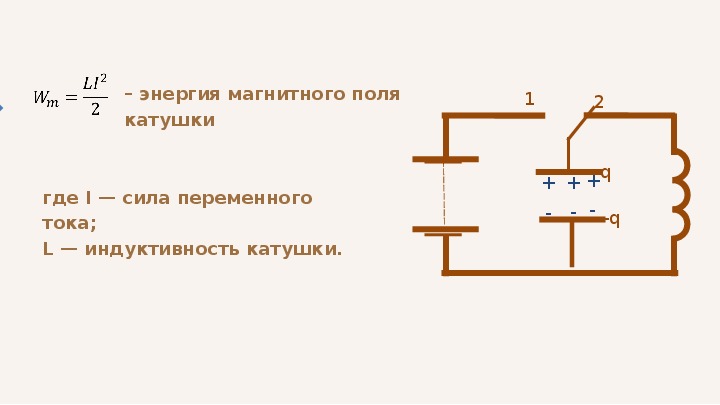

Опыт N2

Давайте же уменьшим индуктивность катушки. Прогоним еще раз по тем же самым частотам. Я убрал половину витков и сделал витки на край феррита, тем самым уменьшил индуктивность до 33 микрогенри.

Итак, прогоняем все по тем же значениям частоты

При частоте в 1 Килогерц у нас значение почти не изменилось.

10 Килогерц

Здесь тоже ничего не изменилось.

100 Килогерц

Тоже почти ничего не изменилось, кроме того, что желтый сигнал стал тихонько сдвигаться.

200 Килогерц

Здесь уже видим, что амплитуда на желтом сигнале начинает проседать и сдвиг фаз наращивает обороты.

300 Килогерц

Сдвиг фаз стал больше и амплитуда просела еще больше

500 Килогерц

Сдвиг стал еще больше и амплитуда желтого сигнала тоже просела.

1 Мегагерц

Амплитуда желтого сигнала падает, сдвиг фаз прибавляется. 😉

2 Мегагерца, предел моего генератор частоты

Сдвиг фаз стал почти равен 90 градусов, а амплитуда стала даже меньше, чем пол Вольта.

Обратите внимание на амплитуду в Вольтах на тех же самых частотах. В первом случае у нас индуктивность была больше, чем во втором случае, но амплитуда желтого сигнала во втором случае больше, чем в первом.

Отсюда вывод напрашивается сам собой:

При уменьшении индуктивности, сопротивление катушки индуктивности также уменьшается.

Реактивное сопротивление катушки индуктивности

С помощью нехитрых умозаключений, физиками была выведена формула:

где

Х L — катушки, Ом

П — постоянная и равна приблизительно 3,14

F — частота, Гц

L — индуктивность, Гн

В данном опыте мы с вами получили (ФНЧ). Как вы видели сами, на низких частотах катушка индуктивности почти не оказывает сопротивление напряжению, следовательно амплитуда и мощность на выходе такого фильтра будет почти такой же, как и на входе.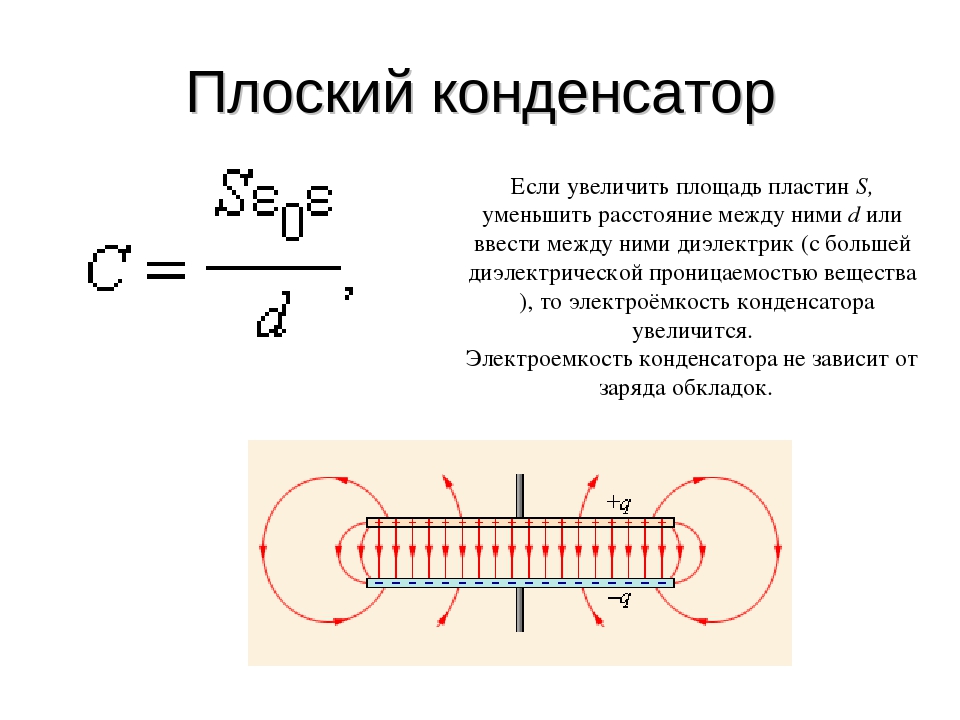 Но с увеличением частоты у нас амплитуда гасится. Применив такой фильтр на динамик, можно с уверенностью сказать, что будет усиливаться только бас, то есть низкая частота звука.

Заключение

Постоянный ток протекает через катушку индуктивности без каких-либо проблем. Сопротивлением обладает только сам провод, из которого намотана катушка.

Сопротивление катушки зависит от частоты протекающего через нее тока и выражается формулой:

Катушка индуктивности – электронный компонент, представляющий собой винтовую либо спиральную конструкцию, выполненную с применением изолированного проводника. Основным свойством катушки индуктивности, как понятно из названия – индуктивность. Индуктивность – это свойство преобразовать энергию электрического тока в энергию магнитного поля. Величина индуктивности для цилиндрической или кольцевой катушки равна

Где ψ — потокосцепление, µ0 = 4π*10-7 – магнитная постоянная, N – количество витков, S – площадь поперечного сечения катушки.

Также катушке индуктивности присущи такие свойства как небольшая ёмкость и малое активное сопротивление, а идеальная катушка и вовсе их лишена. Применение данного электронного компонента отмечается практически повсеместно в электротехнических устройствах. Цели применения различны:

Подавление помех в электрической цепи;
— сглаживание уровня пульсаций;
— накопление энергетического потенциала;
— ограничение токов переменной частоты;
— построение резонансных колебательных контуров;
— фильтрация частот в цепях прохождения электрического сигнала;
— формирование области магнитного поля;
— построение линий задержек, датчиков и т.д.

Энергия магнитного поля катушки индуктивности

Электрический ток способствует накоплению энергии в магнитном поле катушки. Если отключить подачу электричества, накопленная энергия будет возвращена в электрическую цепь. Значение напряжения при этом в цепи катушки возрастает многократно. Величина запасаемой энергии в магнитном поле равна примерно тому значению работы, которое необходимо получить, чтобы обеспечить появление необходимой силы тока в цепи. Значение энергии, запасаемой катушкой индуктивности можно рассчитать с помощью формулы.

Реактивное сопротивление

При протекании переменного тока , катушка обладает кроме активного, еще и реактивным сопротивлением, которое находится по формуле

По формуле видно, что в отличие от конденсатора , у катушки с увеличением частоты, реактивное сопротивление растет, это свойство применяется в фильтрах частот.

При построении векторных диаграмм важно помнить, что в катушке, напряжения опережает ток на 90 градусов.

Добротность катушки

Еще одним важным свойством катушки является добротность. Добротность показывает отношение реактивного сопротивления катушки к активному.

Чем выше добротность катушки, тем она ближе к идеальной, то есть она обладает только главным своим свойством – индуктивностью.

Конструкции катушек индуктивности

Конструктивно катушки индуктивности могут быть представлены в разном исполнении. Например, в исполнении однослойной или многослойной намотки проводника. При этом намотка провода может выполняться на диэлектрических каркасах разных форм: круглых, квадратных, прямоугольных. Нередко практикуется изготовление бескаркасных катушек. Широко применяется методика изготовления катушек тороидального типа.

Индуктивность катушки можно изменять, добавляя в конструкцию катушки ферромагнитный сердечник. Внедрение сердечников отражается на подавлении помех. Поэтому практически все дроссели, предназначенные для подавления высокочастотных помех, как правило, имеют ферродиэлектрические сердечники, изготовленные на основе феррита, флюкстрола, ферроксона, карбонильного железа. Низкочастотные помехи хорошо сглаживаются катушками на пермалоевых сердечниках или на сердечниках из электротехнической стали.

Самоиндукция. Индуктивность. Энергия магнитного поля.

    

 Самоиндукция — является важным частным случаем электромагнитной индукции, когда изменяющийся магнитный поток, вызывающий ЭДС индукции, создается током в самом контуре. Если ток в рассматриваемом контуре по каким-то причинам изменяется, то изменяется и магнитное поле этого тока, а, следовательно, и собственный магнитный поток, пронизывающий контур. В контуре возникает ЭДС самоиндукции, которая согласно правилу Ленца препятствует изменению тока в контуре.
     Явление самоиндукции подобно явлению инерции. Так же, как в механике нельзя мгновенно остановить движущееся тело, так и ток не может мгновенно приобрести определенное значение за счет явления самоиндукции. Если в цепь, состоящую из двух параллельно подключенных к источнику тока одинаковых ламп, последовательно со второй лампой включить катушку, то при замыкании цепи первая лампа загорается практически сразу, а вторая с заметным запаздыванием.

При размыкании цепи сила тока быстро уменьшается, и возникающая ЭДС самоиндукции препятствует уменьшению магнитного потока. При этом индуцированный ток направлен так же, как и исходный. ЭДС самоиндукции может во многом раз превысить внешнюю ЭДС. Поэтому электрические лампочки очень часто перегорают при выключении света.

Собственный магнитный поток Φ, пронизывающий контур или катушку с током, пропорционален силе тока I:  Коэффициент пропорциональности L в этой формуле называется коэффициентом самоиндукции или индуктивностью катушки. Единица индуктивности в СИ называетсягенри (Гн). Индуктивность контура или катушки равна 1 Гн, если при силе постоянного тока 1 А собственный поток равен 1 Вб: 

1 Гн = 1 Вб / 1 А.

В качестве примера рассчитаем индуктивность длинного соленоида, имеющего N витков, площадь сечения S и длину l. Магнитное поле соленоида определяется формулой 

где I – ток в соленоиде, n = N / e – число витков на единицу длины соленоида.

Магнитный поток, пронизывающий все N витков соленоида, равен 

Φ = B S N = μ0 n2 S l I.

Следовательно, индуктивность соленоида равна 

L = μ0 n2 S l = μ0 n2 V,

где V = Sl – объем соленоида, в котором сосредоточено магнитное поле. Полученный результат не учитывает краевых эффектов, поэтому он приближенно справедлив только для достаточно длинных катушек. Если соленоид заполнен веществом с магнитной проницаемостью μ, то при заданном токе I индукция магнитного поля возрастает по модулю в μ раз, поэтому индуктивность катушки с сердечником также увеличивается в μ раз: 

Lμ = μ L = μ0 μ n2 V.

ЭДС самоиндукции, возникающая в катушке с постоянным значением индуктивности, согласно закона Фарадея равна 

ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в ней.

Магнитное поле обладает энергией.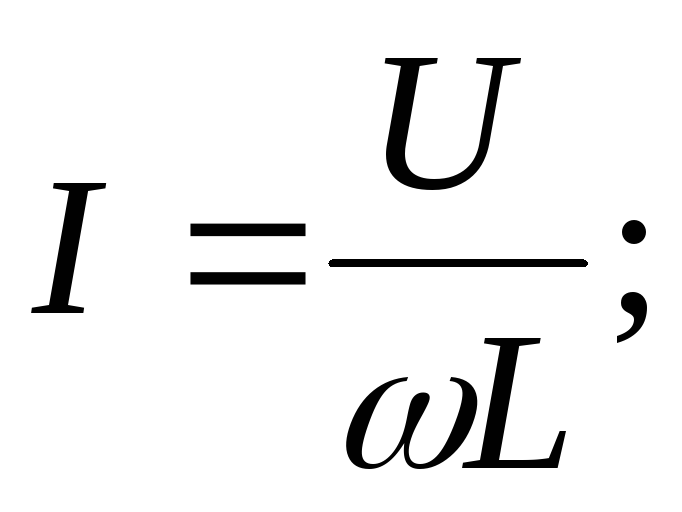 Подобно тому, как в заряженном конденсаторе имеется запас электрической энергии, в катушке, по виткам которой протекает ток, имеется запас магнитной энергии. Если включить электрическую лампу параллельно катушке с большой индуктивностью в электрическую цепь постоянного тока, то при размыкании ключа наблюдается кратковременная вспышка лампы. Ток в цепи возникает под действием ЭДС самоиндукции. Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки.

Магнитная энергия катушки. При размыкании ключа K лампа ярко вспыхивает

Из закона сохранения энергии следует, что вся энергия, запасенная в катушке, выделится в виде джоулева тепла. Если обозначить через R полное сопротивление цепи, то за время Δt выделится количество теплоты ΔQ = I² R Δt.

Ток в цепи равен 

Выражение для ΔQ можно записать в виде 

ΔQ = –L I ΔI = –Φ (I) ΔI.

В этом выражении ΔI < 0; ток в цепи постепенно убывает от первоначального значения I₀ до нуля. Полное количество теплоты, выделившейся в цепи, можно получить, выполнив операцию интегрирования в пределах от I₀ до 0. Это дает 

Эту формулу можно получить графическим методом, изобразив на графике зависимость магнитного потока Φ (I) от тока I  Полное количество выделившейся теплоты, равное первоначальному запасу энергии магнитного поля, определяется площадью изображенного  треугольника.

Вычисление энергии магнитного поля

Таким образом, энергия W_м магнитного поля катушки с индуктивностью L, создаваемого током I, равна 

???Вопросы

1. В чем заключается явление самоиндукции?
2. В каких опытах можно наблюдать это явление?
3. Дайте определение индуктивности? В каких единицах СИ она измеряется?
4. Как вычислить энергию магнитного поля катушки с током?

Домашнее задание упр. №25

Колебательный контур. LCR, LC — контур. Катушка индуктивности, конденсатор Формула Томсона Энергия

Колебательный контур – электрическая цепь, состоящая из последовательно соединённых конденсатора с ёмкостью

, катушки с индуктивностью и электрического сопротивления .

Идеальный колебательный контур — цепь, состоящая только из катушки индуктивности (не имеющей собственного сопротивления) и конденсатора (

-контур). Тогда в такой системе поддерживаются незатухающие электромагнитные колебания силы тока в цепи, напряжения на конденсаторе и заряда конденсатора. Давайте разберём контур и подумаем, откуда возникают колебания. Пусть изначально заряженный конденсатор помещён в описываемую нами цепь.

Рис. 1. Колебательный контур

В начальный момент времени весь заряд сосредоточен на конденсаторе, на катушке тока нет (рис. 1.1). Т.к. на обкладках конденсатора внешнего поля тоже нет, то электроны с обкладок начинают «уходить» в цепь (заряд на конденсаторе начинает уменьшаться). При этом (за счёт освобождённых электронов) возрастает ток в цепи. Направление тока, в данном случае, от плюса к минусу (впрочем, как и всегда), и конденсатор представляет собой источник переменного тока для данной системы. Однако при росте тока на катушке, вследствие явления электромагнитной индукции, возникает обратный индукционный ток (

). Направление индукционного тока, согласно правилу Ленца, должно нивелировать (уменьшать) рост основного тока. Когда заряд конденсатора станет равным нулю (весь заряд стечёт), сила индукционного тока в катушке станет максимальной (рис. 1.2).

Однако текущий заряд в цепи пропасть не может (закон сохранения заряда), тогда этот заряд, ушедший с одной обкладки через цепь, оказался на другой обкладке. Таким образом, происходит перезарядка конденсатора в обратную сторону (рис. 1.3). Индукционный ток на катушке уменьшается до нуля, т.к. изменение магнитного потока также стремится к нулю.

При полной зарядке конденсатора электроны начинают двигаться в обратную сторону, т.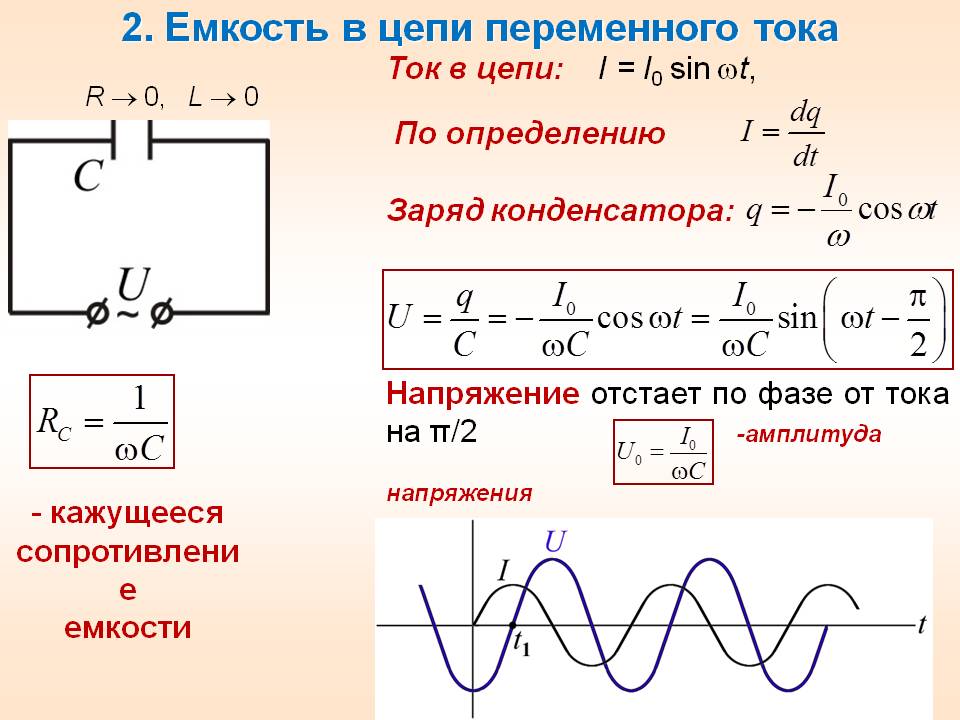 е. происходит разрядка конденсатора в обратную сторону и возникает ток, доходящий до своего максимума при полной разрядке конденсатора (рис. 1.4).

Дальнейшая обратная зарядка конденсатора приводит в систему в положение на рисунке 1.1. Такое поведение системы повторяется сколь угодно долго. Таким образом, мы получаем колебание различных параметров системы: тока в катушке, заряд на конденсаторе, напряжение на конденсаторе. В случае идеальности контура и проводов (отсутствие собственного сопротивления), эти колебания — гармонические.

Для математического описания этих параметров этой системы (в первую очередь, периода электромагнитных колебаний) вводится рассчитанная до нас формула Томсона:

(1)

Неидеальным контуром является всё тот же идеальный контур, который мы рассмотрели, с одним небольшим включением: с наличием сопротивления

(-контур). Данное сопротивление может быть как сопротивлением катушки (она не идеальна), так и сопротивлением проводящих проводов. Общая логика возникновения колебаний в неидеальном контуре аналогична той, что и в идеальном. Отличие только в самих колебаниях. В случае наличия сопротивления, часть энергии будет рассеиваться в окружающую среду — сопротивление будет нагреваться, тогда энергия колебательного контура будет уменьшаться и сами колебания станут затухающими.

Для работы с контурами в школе используется только общая энергетическая логика. В данном случае, считаем, что полная энергия системы в начале сосредоточена на конденсаторе и/или катушке, и описывается:

 

(2)

(3)

Для идеального контура полная энергия системы остаётся постоянной:

(4)

• где
  • — полная энергия колебательной системы.

Для неидеального контура часть начальной энергии переходит в тепло, что можно описать законом Джоуля-Ленца. Тогда энергетические превращения в таком контуре можно описать:

(5)

Вывод: работа с контурами достаточно сложна.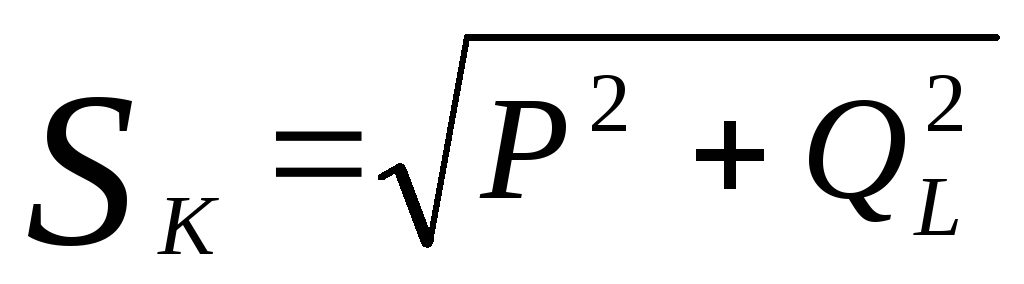 Чаще всего это работа со схемами, в которых присутствуют ключи. Энергетически рассмотреть переход из начального состояния в конечное практически невозможно, тогда стоит работать с начальным и конечным положением системы. Определяем вид контура (идеальный/неидеальный) и рассмотреть энергию системы в обоих случаях. Далее, используя (4) или (5), получаем уравнение, которое можно решать.

Поделиться ссылкой:

Калькулятор накопления энергии индуктора

Вам интересно, на что способен этот калькулятор накопления энергии индуктора? Что ж, он оценивает энергию, запасенную в индукторе, когда через него проходит электрический ток . Мы также приводим уравнение для магнитной энергии в соленоиде и откуда взялось это уравнение для энергии. Далее по тексту вы также найдете полезную информацию о том, как это явление используется на практике.

Магнитная энергия, запасенная в катушке, формула

Предполагая, что у нас есть электрическая цепь, содержащая источник питания и соленоид с индуктивностью L , мы можем записать уравнение магнитной энергии E , хранящейся в индукторе, как:

E = 1/2 * L * I² ,

, где I — ток, протекающий по проводу.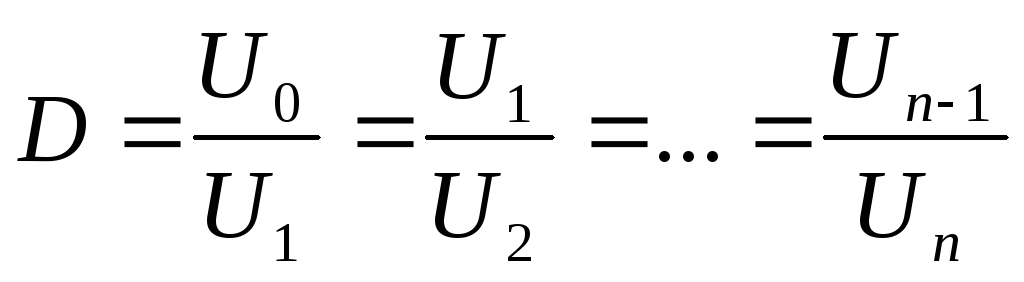

Другими словами, мы можем сказать, что эта энергия равна работе, совершаемой источником энергии для создания такого магнитного поля.

Как мы видим, энергия, запасенная в катушке индуктивности, зависит от тока второй мощности. Это говорит нам о том, что соленоид предотвращает внезапный скачок тока в цепи, и именно по этой причине мы можем видеть искру при отключении некоторых электронных устройств.

Как пользоваться калькулятором накопления энергии индуктора?

Допустим, у нас есть цепь, содержащая источник питания и катушку индуктивности L = 20 мкГн .Мы ищем энергию, запасенную в катушке индуктивности, когда мы пропускаем через систему постоянный ток I = 300 мА .

1. Если вы не хотите портить единицы измерения, давайте запишем все значения в экспоненциальном представлении: L = 2 · 10⁻⁵ H , I = 3 · 10⁻¹ A
2. Используйте формулу для магнитной энергии в соленоиде: E = 1/2 * 2 · 10⁻⁵ H * (3 · 10⁻¹ A) ² = 9 · 10⁻⁷ J
3. Энергия, запасенная в катушке индуктивности, также может быть записана как E = 0. 9 мкДж или 900 нДж
4. Вы всегда можете использовать этот калькулятор накопления энергии индуктора, чтобы убедиться, что ваш результат верен!

Иногда нам может потребоваться больше энергии для нашего приложения. Единственное, что мы можем сделать, — это увеличить индуктивность, добавив материал с высокой магнитной проницаемостью, например ферромагнитные сердечники.

Применение магнитных накопителей энергии

Одно из основных применений этой накопленной магнитной энергии — в LC-цепях (содержащих как индуктивность, так и емкость).В этих случаях энергия, запасенная в катушке индуктивности, преобразуется в электрическую энергию конденсатора и наоборот. Система может быть настроена на отправку и прием радиосигналов, когда колебания тока достигают резонансной частоты радиоволн.

Катушки индуктивности

также широко используются в трансформаторах, которые изменяют амплитуду напряжения от одной цепи к другой. Магнитная энергия от одной катушки переносится на вторую через мягкую ферромагнитную среду. Благодаря этому у нас есть удобный и безопасный доступ к электричеству в наших городах и домах.

Магнитные поля и новый взгляд на Максвелла

Энергия, запасенная в магнитном поле

В индукторе энергия хранится в магнитном поле.

Цели обучения

Опишите поведение индуктора при изменении тока и выразите энергию, запасенную в магнитном поле, в форме уравнения

Основные выводы

Ключевые моменты

• Формула для энергии, запасенной в магнитном поле, E = 1/2 LI ² .2} {2 \ mu} [/ латекс].

Ключевые термины

• индуктор : Устройство или компонент схемы, который демонстрирует значительную самоиндукцию; устройство, которое хранит энергию в магнитном поле.

Когда по проводнику проходит ток, создается магнитное поле, окружающее проводник. Результирующий магнитный поток пропорционален току. Если ток изменяется, изменение магнитного потока пропорционально скорости изменения тока во времени с помощью коэффициента, называемого индуктивностью (L).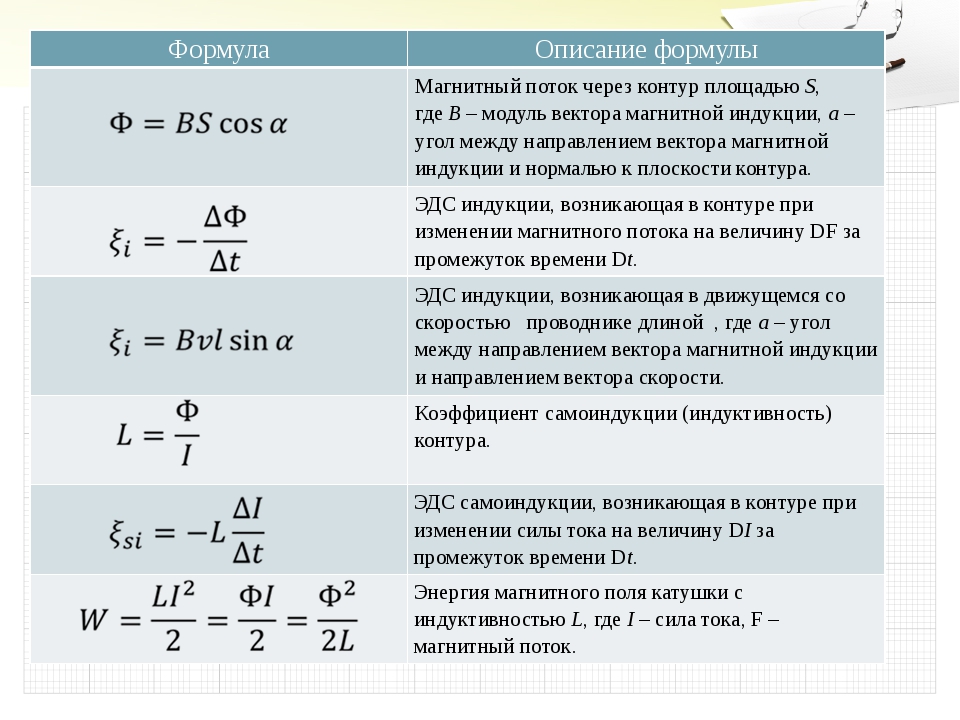 Поскольку природа не терпит быстрых изменений, создаваемое в проводнике напряжение (электродвижущая сила , , ЭДС ) противодействует изменению тока, которое также пропорционально изменению магнитного потока. Таким образом, индукторы противодействуют изменению тока, создавая напряжение, которое, в свою очередь, создает ток, противодействующий изменению магнитного потока; напряжение пропорционально изменению тока.

Энергия, накопленная в индукторе

Из-за энергосбережения энергия, необходимая для управления исходным током, должна иметь выход.2 [/ латекс]

(уравнение 1), где L — индуктивность в единицах Генри, а I — ток в единицах Ампера.

Энергия, запасенная в магнитном поле

Рассмотрим Рис. 1, пример соленоида (ℓ: длина, N: количество витков, I: ток, A: площадь поперечного сечения), который работает как индуктор. Из уравнения. 1, энергия, запасенная в магнитном поле, создаваемом соленоидом, составляет:

Магнитное поле, создаваемое соленоидом : Магнитное поле, создаваемое соленоидом (вид в разрезе), описываемое с помощью силовых линий.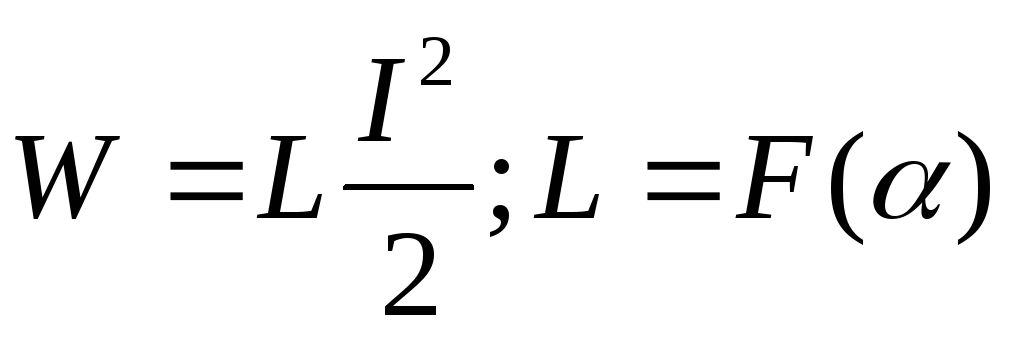 2} {2 \ mu} [/ латекс].

Предсказания Максвелла и подтверждение Герца

Предсказание Максвелла об электромагнитной силе было подтверждено Герцем, который генерировал и обнаруживал электромагнитные волны.

Цели обучения

Объясните, как Герц

подтвердил предсказание Максвелла об электромагнитной силе.

Основные выводы

Ключевые моменты

• Максвелл предсказал, что электрические и магнитные силы связаны.
Уравнения
• Максвелла предсказывают, что независимо от длины волны и частоты каждая световая волна имеет одинаковую структуру.
• Hertz смог экспериментально подтвердить уравнение Максвелла, генерируя и обнаруживая определенные типы электромагнитных волн в лаборатории.

Ключевые термины

• электрическое поле : область пространства вокруг заряженной частицы или между двумя напряжениями; он воздействует на заряженные объекты поблизости.
• магнитное поле : Состояние в пространстве вокруг магнита или электрического тока, в котором существует обнаруживаемая магнитная сила и где присутствуют два магнитных полюса.
• электродвижущая сила : (ЭДС) — напряжение, генерируемое батареей или магнитной силой в соответствии с законом Фарадея. Она измеряется в вольтах, а не в ньютонах, и поэтому на самом деле не является силой.

Предсказания Максвелла и подтверждение Герца

Объединив работы физиков, включая Эрстеда, Кулона, Гаусса и Фарадея, и добавив свои собственные идеи, Джеймс Клерк Максвелл разработал полную и всеобъемлющую теорию, показывающую, что электрические и магнитные силы не разделены, а представляют собой разные формы одного и того же: электромагнитная сила.В 1865 году он сделал это в форме четырех уравнений, которые утверждали следующее:

1. Линии электрического поля берут начало на положительных зарядах и оканчиваются на отрицательных зарядах, а электрическое поле определяется как сила, приходящаяся на единицу заряда испытательного заряда. Сила силы связана с электрической постоянной ε ₀ , также известной как диэлектрическая проницаемость свободного пространства.
2. Линии магнитного поля непрерывны, не имеют ни начала, ни конца. О существовании магнитных монополей не известно.
3. Изменяющееся магнитное поле индуцирует электродвижущую силу (ЭДС) и, следовательно, электрическое поле. Направление ЭДС противодействует изменению.
4. Магнитные поля создаются движущимися зарядами или изменяющимися электрическими полями.

Уравнения Максвелла предсказывают, что независимо от длины и частоты волны все световые волны имеют одинаковую структуру. Это означает, что уравнения Максвелла предсказывали существование радио- и рентгеновских волн, хотя на самом деле они еще не были обнаружены.

Доказательство уравнений Максвелла

Известные уравнения Максвелла, простые и гениальные по своей проницательности, по-прежнему трудно доказать. Поскольку изменяющиеся электрические поля создают относительно слабые магнитные поля, их было нелегко обнаружить во время гипотезы Максвелла.

Только в 1888 году предсказание Максвелла прошло серьезную проверку, когда Генрих Герц сгенерировал и обнаружил определенные типы электромагнитных волн в лаборатории.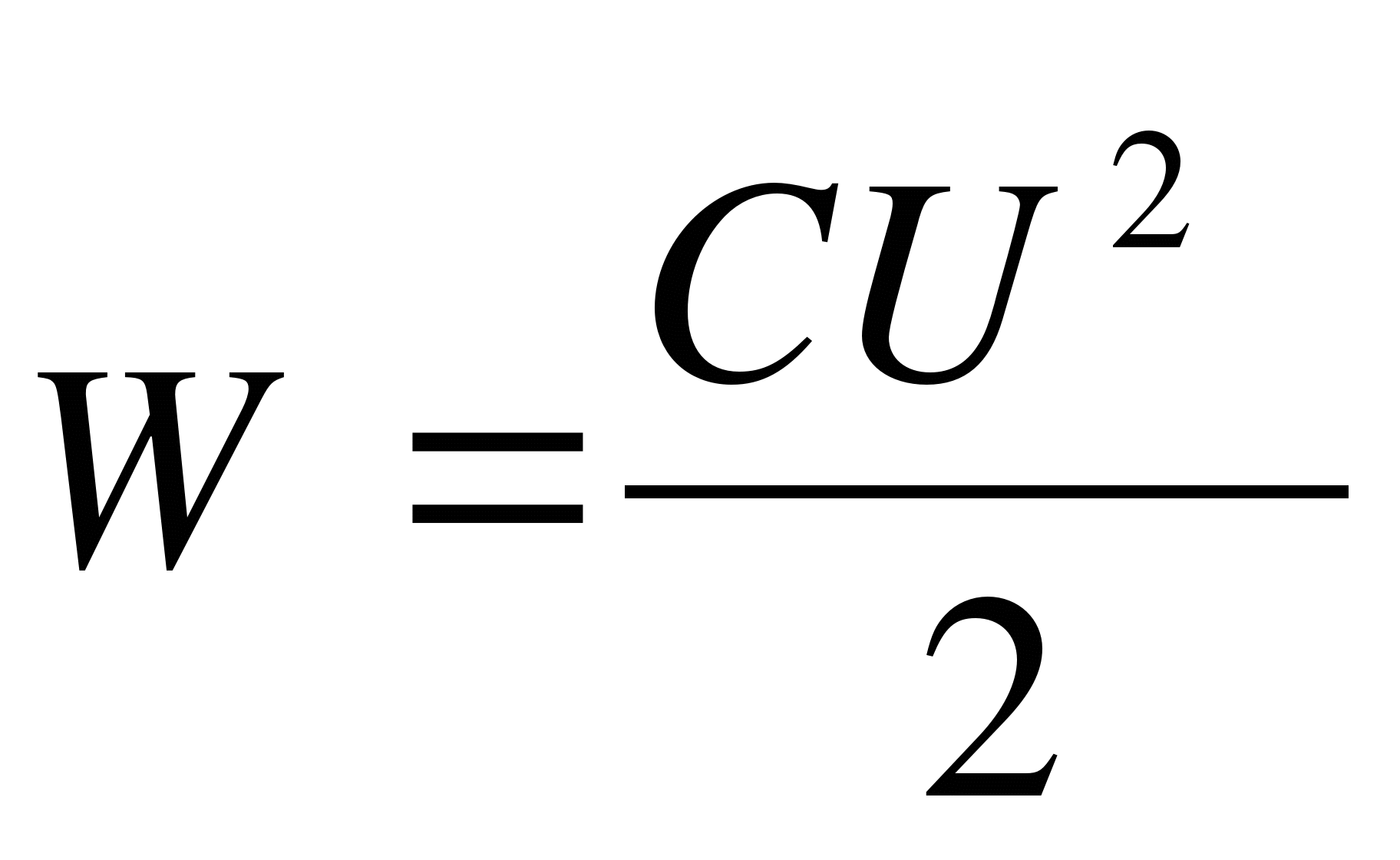 Он провел серию экспериментов, которые не только подтвердили существование электромагнитных волн, но и подтвердили, что они движутся со скоростью света.

Герц использовал цепь переменного тока RLC (резистор-индуктор-конденсатор), которая резонирует на известной частоте, и подключила ее к проволочной петле, как показано на рисунке. Высокое напряжение, индуцированное через зазор в петле, вызывало искры, которые были видимым свидетельством наличия тока. в цепи, и это помогло генерировать электромагнитные волны. Через всю лабораторию Герц подключил еще один контур к другому контуру RLC, который можно было настроить (как циферблат на радио) на ту же резонансную частоту, что и первый, и, таким образом, можно было заставить принимать электромагнитные волны.В этой петле также имелся зазор, в котором возникали искры, что давало твердое свидетельство приема электромагнитных волн.

Аппарат, используемый Герцем : Аппарат, использованный Герцем в 1887 году для генерации и обнаружения электромагнитных волн. Схема RLC, подключенная к первому контуру, вызвала искры через разрыв в проводном контуре и генерировала электромагнитные волны. Искры в щели во второй петле, расположенной напротив лаборатории, свидетельствовали о том, что волны были приняты.

EM Wave : Распространение электромагнитной волны, предсказанное Максвеллом и подтвержденное Герцем.

энергии в индукторе

энергии в индукторе
следующий: Схема Up: индуктивность Предыдущий: Самоиндуктивность

Энергия, накопленная в индукторе Предположим, что индуктор индуктивности подключен к источник переменного постоянного напряжения. Электропитание регулируется таким образом, чтобы увеличить ток, протекающий через индуктор от нуля до некоторого конечного значения.Поскольку ток через индуктор нарастает, ЭДС генерируется, что препятствует увеличению тока. Ясно, что работа должна быть сделано против этой ЭДС источником напряжения, чтобы установить ток в катушке индуктивности. Работа, совершаемая источником напряжения во время временной интервал

(247)

Здесь, — мгновенная скорость, с которой источник напряжения выполняет работу. Чтобы найти общую работу, проделанную для установления конечного тока в индуктора, мы должны интегрировать приведенное выше выражение.Таким образом,

(248)

давая

(249)

Эта энергия фактически хранится в магнитном поле, создаваемом током протекает через индуктор. В чистом индукторе энергия накапливается без потери, и возвращается в остальную часть цепи, когда ток через катушка индуктивности снижается, и связанное с ней магнитное поле разрушается.

Рассмотрим простой соленоид. Уравнения (244), (246) и (249) можно объединить, чтобы получить

(250)

что сводится к

(251)

Это представляет собой энергию, запасенную в магнитном поле соленоида. Однако объем заполненного полем сердечника соленоида составляет, поэтому магнитная плотность энергии ( i.е. , энергия на единицу объема) внутри соленоид есть, или

(252)

Оказывается, это довольно общий результат. Таким образом, мы можем вычислить энергосодержание любого магнитного поля за счет разделения пространства на маленькие кубики (в каждом из которых магнитное поле приблизительно однородно), применяя приведенная выше формула, чтобы найти содержание энергии каждого куба, и суммируя полученные таким образом энергии, чтобы найти полную энергию.

Когда электрическое и магнитное поля существуют вместе в пространстве, уравнения. (122) и (252) можно объединить, чтобы получить выражение для общая энергия, накопленная в комбинированном полей на единицу объема:

(253)

---

следующий: Схема Up: индуктивность Предыдущий: Самоиндуктивность

Ричард Фицпатрик 2007-07-14

Энергия в магнитном поле — Университетская физика, том 2

Цели обучения

К концу этого раздела вы сможете:

• Объясните, как можно накапливать энергию в магнитном поле
• Выведите уравнение для энергии, запасенной в коаксиальном кабеле, с учетом плотности магнитной энергии.

Энергия конденсатора хранится в электрическом поле между его пластинами. Точно так же индуктор может накапливать энергию, но в своем магнитном поле. Эту энергию можно найти, интегрировав плотность магнитной энергии,

больше соответствующего объема. Чтобы понять, откуда взялась эта формула, давайте рассмотрим длинный цилиндрический соленоид из предыдущего раздела. Опять же, используя приближение бесконечного соленоида, мы можем предположить, что магнитное поле по существу постоянное и задается везде внутри соленоида. Таким образом, энергия, запасенная в соленоиде, или плотность магнитной энергии, умноженная на объем, эквивалентна

При замене (Рисунок) это становится

Хотя это уравнение получено для частного случая, оно дает энергию, запасенную в магнитном поле любой индуктивности .Мы можем убедиться в этом, рассмотрев произвольную катушку индуктивности, через которую проходит изменяющийся ток. В любой момент величина наведенной ЭДС такова, что мощность, потребляемая катушкой индуктивности, равна

.

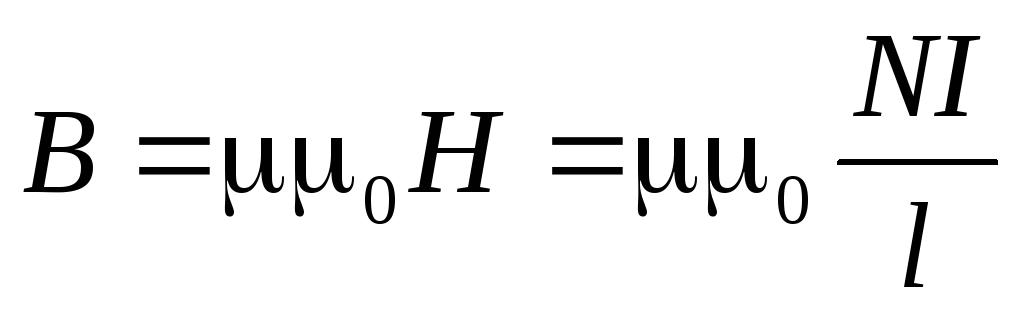
Полная энергия, запасенная в магнитном поле, когда ток увеличивается от 0 до 90 333 I в интервале времени от 0 до 90 333 t , может быть определена путем интегрирования этого выражения:

Самоиндуктивность коаксиального кабеля (рисунок) показывает две длинные концентрические цилиндрические оболочки радиусов и. Как обсуждалось в разделе «Емкость по емкости», эта конфигурация представляет собой упрощенное представление коаксиального кабеля.Емкость на единицу длины кабеля уже рассчитана. Теперь (а) определите магнитную энергию, запасенную на единицу длины коаксиального кабеля, и (б) используйте этот результат, чтобы найти самоиндуктивность на единицу длины кабеля.

(a) Коаксиальный кабель здесь представлен двумя полыми концентрическими цилиндрическими проводниками, по которым электрический ток течет в противоположных направлениях. (b) Магнитное поле между проводниками можно найти, применив закон Ампера к пунктирной траектории.(c) Цилиндрическая оболочка используется для определения магнитной энергии, запасенной на длине х кабеля.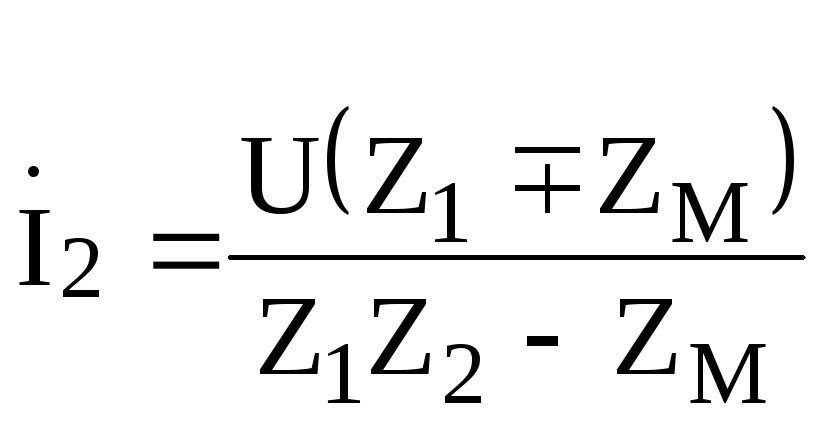

Стратегия Магнитное поле внутри и снаружи коаксиального кабеля определяется законом Ампера. Основываясь на этом магнитном поле, мы можем использовать (рисунок) для расчета плотности энергии магнитного поля. Магнитная энергия рассчитывается как интеграл плотности магнитной энергии, умноженный на дифференциальный объем по цилиндрической оболочке. После того, как интегрирование выполнено, у нас есть закрытое решение для части (а).На основании этого результата и (рисунок) определяется самоиндукция на единицу длины.

Решение

1. Мы определяем магнитное поле между проводниками, применяя закон Ампера к пунктирной круговой траектории, показанной на (Рисунок) (b). Из-за цилиндрической симметрии постоянно вдоль пути, а
   

   
   Это дает нам
   

   
   В области за пределами кабеля аналогичное применение закона Ампера показывает, что, поскольку чистый ток не пересекает область, ограниченную круговой траекторией, этот аргумент также справедлив, когда это происходит в области внутри внутреннего цилиндра.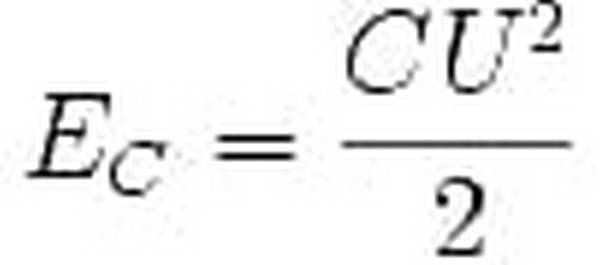 Таким образом, вся магнитная энергия кабеля сохраняется между двумя проводниками. Поскольку плотность энергии магнитного поля равна
   

   
   энергия, запасенная в цилиндрической оболочке с внутренним радиусом r , внешним радиусом и длиной l (см. Часть (c) рисунка) составляет
   

   
   Таким образом, полная энергия магнитного поля на длине l кабеля составляет
   

   
   , а энергия на единицу длины равна.

2. Из (Рисунок),
   

   
   , где L — собственная индуктивность коаксиального кабеля на длине 90 333 l .Приравнивая предыдущие два уравнения, находим, что самоиндукция на единицу длины кабеля составляет
   

Значение Индуктивность на единицу длины зависит только от внутреннего и внешнего радиусов, как видно из результата. Чтобы увеличить индуктивность, мы могли либо увеличить внешний радиус, либо уменьшить внутренний радиус.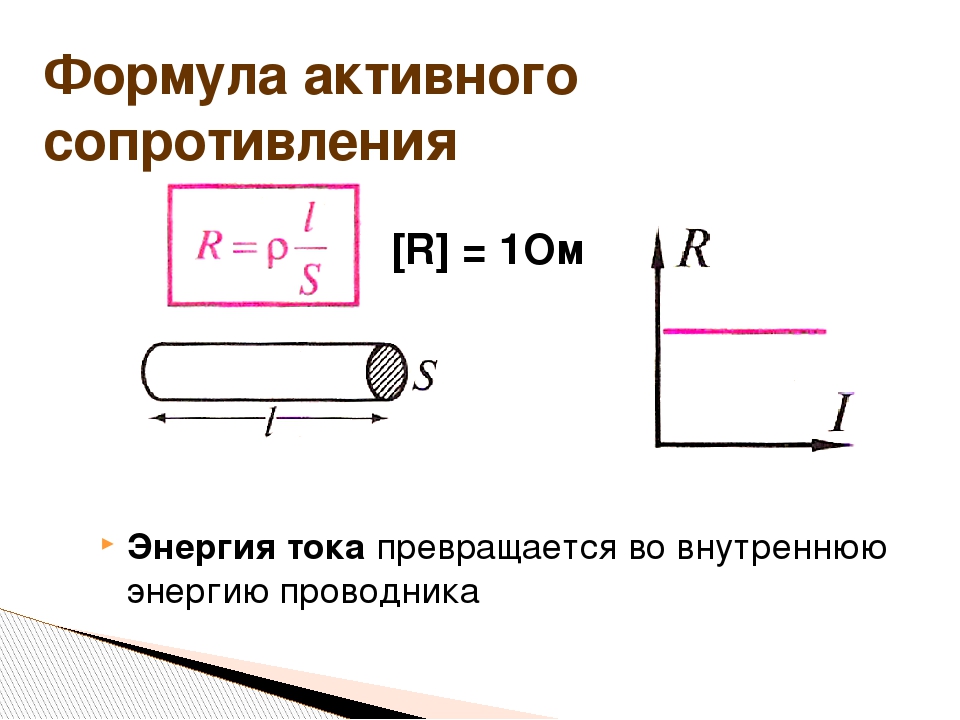 В пределе, когда два радиуса становятся равными, индуктивность стремится к нулю. В этом пределе нет коаксиального кабеля. Кроме того, магнитная энергия на единицу длины из части (а) пропорциональна квадрату тока.

Проверьте свое понимание Сколько энергии хранится в катушке индуктивности (рисунок) после того, как ток достигнет максимального значения?

Сводка

• Энергия, запасенная в катушке индуктивности U , составляет
  
• Собственная индуктивность на единицу длины коаксиального кабеля составляет
  

Концептуальные вопросы

Шоу, у которого есть единицы энергии.

Проблемы

В данный момент ток 0.20 А протекает через катушку с проволокой, энергия, запасенная в ее магнитном поле, равна. Какова собственная индуктивность катушки?

Предположим, что прямоугольный тороид имеет 2000 обмоток и самоиндукцию 0,040 Гн. Если, то какой ток течет через прямоугольный тороид, когда энергия в его магнитном поле равна

?

Соленоид A плотно намотан, в то время как соленоид B имеет обмотки, равномерно распределенные с зазором, равным диаметру провода.В остальном соленоиды идентичны. Определите соотношение энергий, накопленных на единицу длины этих соленоидов, когда через каждый из них протекает одинаковый ток.

Катушка индуктивности 10 Гн проводит ток 20 А. Сколько льда может быть растоплено за счет энергии, накопленной в магнитном поле индуктора? ( Совет : используйте значение льда.)

Катушка с самоиндуктивностью 3,0 Гн и сопротивлением 1 м3 проводит постоянный ток 2,0 А. а) Какая энергия хранится в магнитном поле катушки? (б) Какая энергия в секунду рассеивается на сопротивлении катушки?

А ток 1.2 А протекает по коаксиальному кабелю, внешний радиус которого в пять раз превышает его внутренний радиус. Какая энергия магнитного поля хранится в кабеле длиной 3,0 м?

Глоссарий

плотность магнитной энергии

энергии, запасенной на единицу объема в магнитном поле

Дайте выражение энергии, запасенной в индуктивности, класс 12, физика CBSE

Подсказка: Чтобы найти выражение энергии, запасенной в катушке индуктивности или в катушке индуктивности, несущей ток, вспомните формулу для ЭДС, генерируемой в катушке индуктивности.Затем используйте это значение ЭДС, чтобы найти выражение для скорости выполненной работы, и, используя это значение, найдите выражение для выполненной работы.

Полный ответ:
Нас просят найти энергию, запасенную в катушке индуктивности, по которой проходит ток. Предположим, что к катушке индуктивности или катушке индуктивности с индуктивностью \ [L \] применяется ток, при котором ток через катушку индуктивности возрастает от нуля. до максимального значения \ [I \]. 2} \]
Эта энергия сохраняется в магнитном поле, создаваемом в индукторе из-за протекания тока.2} \].

Примечание: Помните, что одна из функций индуктора — накапливать электрическую энергию. Есть еще один компонент, называемый конденсатором. Конденсатор хранит энергию в электрическом поле, тогда как индуктор хранит энергию в магнитном поле, студенты иногда путаются между этими двумя компонентами.

Расчет конструкции катушки и индуктивности

На этой странице вы узнаете, как создать свою собственную катушку, сделанную своими руками. Я сделал это для изготовления катушек для хрустальные радиоприемники и Катушки Тесла, но он работает с любой катушкой цилиндрической формы.Это также полезно, если вы собираетесь использовать свою катушку в Танк LC резонансный схема.

Предусмотрен калькулятор индуктивности. ниже, чтобы упростить задачу.

Намотка катушки вручную.

Индуктивность — это часто то, чего вы пытаетесь достичь при разработке катушки. то есть вы знаете нужную индуктивность, и теперь вам нужно спроектировать катушку который будет иметь эту индуктивность.

Индуктивность

Катушки имеют свойство, называемое индуктивностью. Что такое индуктивность? Когда электрический ток изменяется при прохождении через провод катушки, он создает изменяющееся магнитное поле, которое индуцирует (производит) напряжение или ЭДС (электродвижущая сила) в проводе, который противостоит течению. Это называется индукцией и индуктивностью. — величина, определяющая способность катушки индуцировать это напряжение. Символ индуктивности — Генри, а единица измерения — H.Вот мы на самом деле говоря о катушке, индуцирующей напряжение в себе, что является самоиндукцией, но мы просто скажем индукция.

Магнитное поле вокруг катушки.

Параметры для формулы индуктивности

Одна формула для индуктивности выглядит следующим образом:

Где:

• L = индуктивность
• u _r = относительная проницаемость материала сердечника (воздух = 1)
• витков = количество витков на катушке
• площадь = площадь поперечного сечения жилы в квадратных метрах *, включая часть катушки, как показано на схеме
• длина = длина бухты в метрах *

* Калькулятор индуктивности ниже также принимает дюймы, а также сантиметры и миллиметры, и переводит их в метры за вас.

Как сказано выше, μ _r является относительной магнитной проницаемость для всего, что вы используете для сердечника катушки, цилиндр, на который вы наматываете провод. Это греческая буква мю, μ, хотя часто для удобства используется буква u, например u _r . Если это полая картонная или пластиковая трубка, то картонная или пластиковая считается воздухом, и вы можете использовать 1. Такие материалы, как железо и феррит, имеют более высокие относительные проницаемости в сотнях и тысячах.Для железного сердечника приблизительное число — 100, хотя оно действительно варьируется. в зависимости от сплава. То же самое и с ферритом, который может иметь ценность где-то от 20 до 5000, но если вы не знаете, что использовать, тогда 1000 — грубый компромисс. Поскольку он умножается на остальную часть формулы, это означает использование этих материалы дадут более высокое значение индуктивности. Ядра для кристаллического радио катушки иногда бывают пластиковыми или картонными и, следовательно, представляют собой катушки с воздушным сердечником, а иногда это ферритовый сердечник.Сердечники для вторичной обмотки Тесла катушки обычно пластиковые, а меньшие могут быть картонными, и поэтому считаются катушками с воздушным сердечником.

И если вы не знакомы с обозначениями 1.26×10 ^-6 , это просто другой способ записи 0.00000126.

Область включает часть катушки, как показано на схеме выше. Если площадь рассчитывается с использованием радиуса, включите радиус сердцевины. плюс радиус проволоки. При расчете площади по диаметру затем включите диаметр сердечника плюс диаметр проволоки.Обратите внимание, что при выполнении расчетов для катушки с очень тонкой проволокой, как в случае кристалл радио и катушка Тесла, показанная выше (например, 24 калибра / AWG) тогда размер провода, вероятно, будет незначительным по сравнению с область жилы, и обычно можно не обращать внимания на провод.

Калькулятор индуктивности

Вот калькулятор индуктивности, который использует приведенную выше формулу. Диаграмма выше можно использовать в качестве руководства для некоторых параметров.

Видео — Как разработать катушку с удельной индуктивностью

В этом видео я подробно объясняю формулу индукции. а также привести пример и поговорить о других факторах, таких как емкость катушки, частота и связь.

Transformer Formula

Трансформатор — это электрическое устройство, которое позволяет увеличивать или уменьшать напряжение в электрической цепи переменного тока, сохраняя при этом мощность. Мощность, которая поступает в оборудование, в случае идеального трансформатора равна мощности, получаемой на выходе. Реальные машины имеют небольшой процент потерь. Это устройство, которое преобразует переменную электрическую энергию определенного уровня напряжения в переменную энергию другого уровня напряжения на основе явления электромагнитной индукции.Он состоит из двух катушек из проводящего материала, намотанных на замкнутое ядро ​​из ферромагнитного материала, но электрически изолированных друг от друга. Единственная связь между катушками — это общий магнитный поток, установленный в сердечнике. Катушки называются первичными и вторичными в соответствии с входом или выходом рассматриваемой системы соответственно.

Значение мощности для электрической цепи — это значение напряжения, равное значению силы тока. Как и в случае с трансформатором, значение мощности первичной обмотки такое же, как и мощность вторичной обмотки:

входное напряжение первичной катушки * входной ток первичной катушки = выходное напряжение вторичной катушки * выходной ток вторичной катушки.

Уравнение записано

Мы также можем рассчитать выходное напряжение трансформатора, если мы знаем входное напряжение и количество витков (катушек) на первичной и вторичной катушках, используя приведенное ниже уравнение;

входное напряжение на первичной обмотке / выходное напряжение на вторичной обмотке = количество витков провода на первичной обмотке / количество витков провода на вторичной обмотке

Уравнение записано

имеем:

В _p = входное напряжение на первичной обмотке.

В _с = входное напряжение на вторичной обмотке.

I _p = входной ток первичной обмотки.

I _с = входной ток вторичной обмотки.

n _p = количество витков провода на первичной обмотке.

n _s = количество витков провода на вторичной катушке.

Trasnformer Вопросы:

1) У нас есть трансформатор с током в первичной катушке 10 А и входным напряжением в первичной катушке 120 В, если напряжение на выходе вторичной катушки 50 В, рассчитайте ток на выходе вторичная обмотка.

Ответ: Поскольку мы хотим определить выходной ток во вторичной катушке, мы используем первое уравнение

, →,

= 2,4 * 10 А = 24 А.

I _с = 24 А.

2) Имеем трансформатор с выходным током на вторичной катушке 30 А и входным током на первичной катушке 2000 витков 6 А, определяем количество витков на вторичной катушке.

Ответ: Мы будем использовать два уравнения: первое уравнение для определения выходного напряжения на вторичной катушке и второе уравнение для определения количества витков на вторичной катушке.