Формула делителя напряжения: Онлайн-калькулятор делителя напряжения на резисторах — Мир Антенн

Содержание

Делитель напряжения: теория и принцип действия

Делитель напряжения позволяет получить меньшее напряжение из большего, напряжение может быть как постоянным, так и переменным.

Рис. 1. Схема простейшего делителя напряжения

Простейшая схема делителя напряжения содержит минимум два сопротивления. Если величины сопротивлений одинаковы, то согласно закону Ома, на выходе делителя будет получено напряжение, в два раза меньшее, чем на входе, так как падение напряжений на резисторах будет одинаковым. Для других случаев величина падения напряжений на резисторах делителя определяется по формулам

U_R1 = I*R1; U_R2 = I*R2 (1)

где U_R1, U_R2 — падения напряжения на резисторах R1 и R2 соответственно, I — ток в цепи. В схемах делителей выходное напряжение обычно снимают с нижнего по схеме резистора.

Сумма падений напряжений U_R1, U_R2 на резисторах равна напряжению источника питания.

Ток в цепи будет равен напряжению источника питания, делённому на сумму сопротивлений резисторов R1 и R2:

I = U_пит / (R1 + R2) (2)

Рассмотрим практическую схему делителя постоянного напряжения (рис.2)

Рис. 2. Делитель постоянного напряжения.

Ток, протекающий в этой схеме, согласно формуле (2) будет равен

I = 10 / (10000+40000) = 0,0002 А = 0,2 мА.

Тогда согласно формуле (1) падение напряжения на резисторах делителя напряжения будет равно:

U_R1 = 0,0002*10000 = 2 В;
U_R2 = 0,0002*40000 = 8 В.

Если из формулы (1) вывести ток:

I = U_R1 / R1 (3)

И подставить его значение в формулу (2), то получится универсальная формула для расчёта делителя напряжения:

U_R1 / R1 = U_пит / (R1 + R2)

Откуда

U_R1 = U_пит

* R1 / (R1 + R2) (4)

Подставляя значения напряжения и сопротивлений в формулу (4), получим величину напряжения на резисторе R1:

U_R1 = 10 * 10000 / (10000+40000) = 2 В,

и на резисторе R2:

U_R2 = 10 * 40000 / (10000+40000) = 8 В.

Делитель напряжения с реактивными элементами в цепи переменного тока

В вышеприведённой схеме делителя напряжения (рис. 2) были использованы активные элементы — резисторы, и питание схемы осуществлялось постоянным напряжением (хотя схему можно питать и переменным током). Делитель напряжения может содержать так же и реактивные компоненты (конденсаторы, катушки индуктивности), но в этом случае для нормальной работы потребуется питание синусоидальным током (рис. 3).

Рис. 3. Ёмкостный делитель напряжения в цепи переменного тока.

Изображённый на рисунке 3 ёмкостный делитель напряжения работает аналогично резистивному делителю, но рассчитывается несколько иначе, поскольку реактивное сопротивление конденсаторов обратно пропорционально их ёмкости:

R_c = 1/(2 * π * f * C)

Здесь R_c — реактивное сопротивление конденсатора;
π — число Пи = 3,14159…;
f — частота синусоидального напряжения, Гц;
C — ёмкость конденсатора, Фарад.

То есть чем больше ёмкость конденсатора, тем меньше его сопротивление, и следовательно в схеме делителя напряжения на конденсаторе с большей ёмкостью падение напряжения будет меньше, чем на конденсаторе с меньшей ёмкостью. Следовательно, формула (4) для ёмкостного делителя напряжения примет следующий вид:

U_С1 = U_пит * С2 / (С1 + С2) (5)

U_С1 = 10 * 40*10^-9 / (10*10^-9+40*10^-9) = 8 В,
U_С2 = 10 * 10*10^-9 / (10*10^-9+40*10

-9) = 2 В.

Индуктивный делитель напряжения (рис. 4.) так же как и ёмкостный требует для своей работы синусоидальное питающее напряжение.

Рис. 4. Индуктивный делитель напряжения в цепи переменного тока.

Поскольку реактивное сопротивление катушки индуктивности в цепи переменного тока пропорционально номиналу катушки:

R_L = 2 * π * f * L

Здесь R_c — реактивное сопротивление катушки индуктивности;
π — число Пи = 3,14159. ..;
f — частота синусоидального напряжения, Гц;
L — индуктивность катушки, Генри.

То следовательно и формула для расчёта индуктивного делителя напряжения будет точно такой же, как и формула для расчёта резистивного делителя напряжения (4), где вместо сопротивлений будут использоваться индуктивности:

U_L1 = U_пит * L1 / (L1 + L2) (6)

Подставив в эту формулу параметры элементов из рисунка 4, получим:

U_L1 = 10 * 10*10^-6 / (10*10^-6+40*10^-6) = 2 В,
U_L2 = 10 * 40*10^-6 / (10*10^-6+40*10^-6) = 8 В.

В заключении следует отметить, что во всех расчётах величина нагрузки была принята равной бесконечности, поэтому полученные значения верны при работе рассмотренных делителей на сопротивление нагрузки, во много раз большее, чем величина собственных сопротивлений.

BACK

напряжения на резисторе и после

При разработке печатных плат для электронного оборудования специалистам часто приходится выполнять расчет делителя. С виду простая схема помогает уменьшить выходное напряжение, необходимое для питания отдельных элементов цепи. Такая компоновка является базовой для электроники. В основу изучения принципа действия входят два момента: схематическое исполнение и формула для вычисления параметров работы делителя.

Что такое делитель напряжения

Схематическое исполнение понижающего устройства представляет собой последовательную цепь, состоящую из двух резистивных элементов. Суммарные значения сопротивлений позволяют уменьшить входящее напряжение до необходимых параметров на выходе. Между собой они связаны передаточным коэффициентом, находящимся в интервале от 0 до 1, включая границы (0<=aplha<=1).

Общее представление делителя напряжения

Существует несколько вариантов схематического исполнения приборов, но все они обладают одним и тем же функционалом — понижать вольтаж для потребителей, однако ток на всех полюсах остается одинаковым. Два последовательных участка цепи называют плечами. Нижнее плечо находится между центральной точкой и нулевым потенциалом. Именно здесь необходимо снимать показатели работы схемы. Другое плечо является верхним.

Простая схема на резисторах

В зависимости от расположения резисторов, различают линейные и нелинейные схемы делителей. Первый вариант используют для создания разности потенциалов и вольтажа в нескольких точках рабочих узлов. Понижение входного напряжения определяется по линейному закону.

Дополнительная информация! Понижающие узлы применяют для постоянного и переменного тока. Структурное исполнение обоих отличается друг от друга, поскольку в некоторых случаях требует включение дополнительных фильтров для подавления помех и шумов.

В нелинейных схемах разница определяется по передаточному коэффициенту. Такие устройства активно применяют в потенциометрах. Здесь учитывают присутствие активного и реактивного сопротивления, включая нелинейные и токовые нагрузки.

Принцип работы делителя напряжения

В состав простейшей понижающей схемы всегда входит не меньше одного резистора.

Если элементы обладают одинаковыми коэффициентами сопротивляемости электронов, то на выходе вольтаж понизится в два раза. Для каждого узла понижение рассчитывается по закону Ома.

Внимание! Сумма пониженных величин в каждой точке равна общему вольтажу источника питания.

Схема с несколькими резисторами

Резисторы используют в принципиальных схемах с источником питания постоянного тока. В цепях переменного напряжения присутствует еще и реактивное сопротивление, куда входят конденсаторы, индуктивные катушки и другие элементы с электромагнитными полями.

В цепях с синусоидальным током в качестве резистивного элемента выступает конденсатор или катушка. Их называют емкостными. Расчет ведется уже по другой формуле, так как емкость конденсаторов обратно пропорциональна их реактивному сопротивлению. Для вычисления резистивной составляющей необходимо учитывать постоянное число ПИ, частоту синусоидального тока (Гц) и емкость (Фарад). Таким образом получается, что с увеличением емкости падает сопротивление и наоборот.

Кроме конденсаторов, в качестве реактивных компонентов также могут выступать индуктивные катушки, которые могут присутствовать в платах переменного тока. Коэффициент реактивного сопротивления обмоток также прямо пропорционален их номинальным значениям. Для вычислений также необходимо постоянное число ПИ, частота переменного магнитного поля (Гц) и индуктивность (Генри).

Делитель на индукционных катушках

Внимание! В описании выше токовая нагрузка равна бесконечности, поэтому все значения верны только при полученных показателях делителя на сопротивления нагрузки. Они в несколько раз больше внутреннего.

Формула для расчета делителя напряжения

Начинающие радиолюбители часто задаются главным вопросом, как правильно рассчитать напряжение после резистора. Для этого необходимо знать, какой ток пойдет по цепи. В простейших схемах постоянного тока его вычисляют по линейному закону Ома. Формула расчета выглядит U=I*R, где:

U — напряжение, В;
I — ток, А;

В цепях с синусоидальным током, где присутствует реактивное сопротивление катушки или конденсатора, формула выглядит как R=1/(2*pi*f*L) и R=1/(2*pi*f*C) соответственно.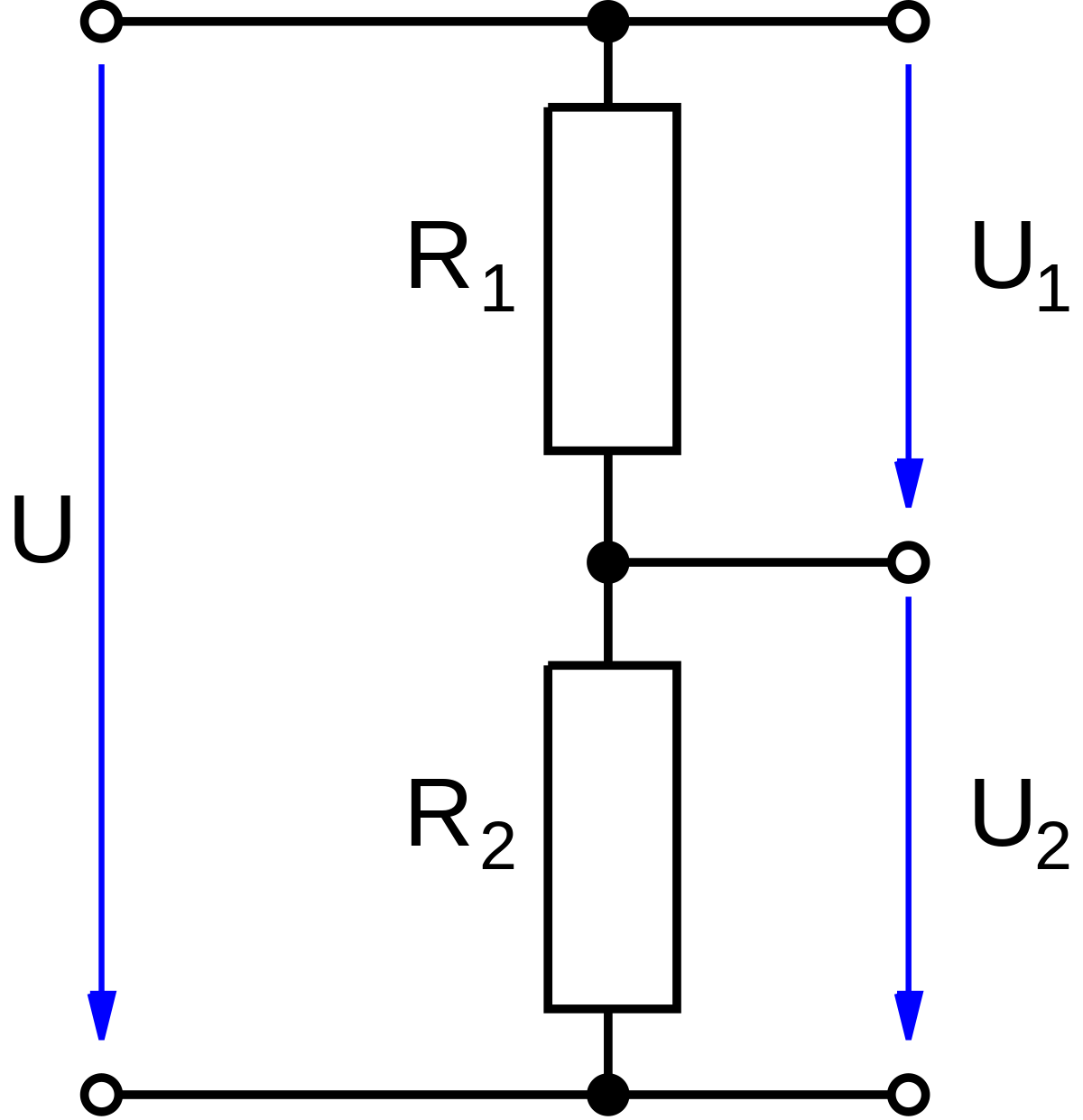 В формуле использованы показатели:

График зависимости показателей от сопротивления

R — реактивное сопротивление;
R — сопротивление, Ом.
pi — постоянное число Пи, равное 3,14;
f — частота, Гц;
L — индуктивность катушки, Генри;
C — емкость конденсатора, Фарад.

Получив в расчетах внутреннюю резистивность элементов, далее можно воспользоваться линейной формулой для вычисления выходного значения.

На резисторе

В схеме делителя всегда участвует не меньше двух узлов нагрузки. Их коэффициенты могут быть равны другу, но и отличаться. Поэтому порой возникает необходимость получить номинал выходного вольтажа для каждого из них. Для этого используют всем известную формулу закона Ома: U=I*R.

После резистора

Для расчета показателя после резистора необходимо учитывать номиналы обоих элементов, так как они работают совместно друг с другом. Применив закон Ома, получается следующая формула: Uвых=Uпит*R1/(R1+R2), где:

Uвых — вольтаж на выходе, В;
Uпит — входной вольтаж, В;
R1 — первый узел, Ом;
R2 — второй узел, Ом.

Падение потенциалов за резистором рассчитывают для каждого узла в отдельности. То есть для второго элемента формула будет выглядеть так: Uвых=Uпит*R2/(R1+R2).

Делитель позволяет разработчикам получить несколько номинальных значений выходного напряжения от одного питающего источника. По этой причине схема получила широкое применение в электронике как в понижающих блоках питания, так и в качестве интегрированного узла электроцепи.

Делитель напряжения

2.7. Делитель напряжения

Достаточно часто в некоторых участках схемы необходимо иметь величину напряжения меньше, чем напряжение источника питания. В этом случае можно использовать делитель напряжения на резисторах (рис. 2.5а). Изменяя соотношение между величинами сопротивлений R₁ и R₂, на выходе делителя можно получить любое значение напряжения, но не более входного. Выходное напряжение делителя при бесконечно большом сопротивлении нагрузки можно рассчитать по формуле

(2.14)

Для объяснения принципа работы электронных схем необходимо хорошо представлять работу делителя напряжения на резисторах. Можно выделить три задачи, которые необходимо быстро решать при рассмотрении принципа работы электронных устройств, содержащих делитель напряжения:

1. Как и почему изменяется выходное напряжение делителя, если входное напряжение не изменяется (постоянное напряжение или переменное напряжение с неизменяющейся со временем амплитудой), сопротивление резистора R₂ не изменяется, а сопротивление резистора R₁ увеличивается (уменьшается)?

2. Как и почему изменяется выходное напряжение делителя, если входное напряжение не изменяется (постоянное напряжение или переменное напряжение с неизменяющейся со временем амплитудой), сопротивление резистора R₁ не изменяется, а сопротивление резистора R₂ увеличивается (уменьшается)?

3. Как и почему изменяется выходное напряжение делителя, если сопротивления резисторов R₁, R₂ не изменяются, а входное напряжение увеличивается (уменьшается)?

Для всех трех задач дать ответ на поставленный вопрос можно, проанализировав формулу (2.14) для определения выходного напряжения делителя. Решить указанные задачи можно и другим способом.

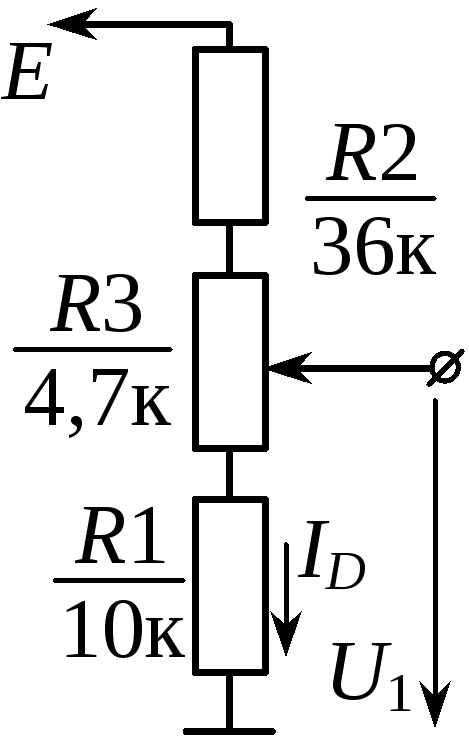
В первой задаче для определения изменения выходного напряжения воспользуемся формулой U_вых=I_д×R₂. Так как сопротивление резистора R₂ неизменно, то для ответа на вопрос задачи достаточно выяснить, как будет изменяться ток I_д при увеличении (уменьшении) сопротивления резистора R₁. При увеличении сопротивления резистора R₁ общее сопротивление последовательно соединенных резисторов R₁ и R₂будет увеличиваться и при неизменном входном напряжении делителя будет уменьшаться ток делителя I_д_{(по закону Ома для участка цепи). Уменьшение тока делителя при
неизменном сопротивлении резистора R₂ приведет к уменьшению
выходного напряжения.}

При уменьшении сопротивления резистора R₁ сила тока в цепи увеличивается и увеличивается выходное напряжение.

Во второй задаче при увеличении сопротивления резистора R₂ общее сопротивление цепи увеличится, следовательно, при неизменном входном напряжении сила тока в цепи уменьшится. Использовать формулу U_вых=I_д×R₂ для определения изменения выходного напряжения нельзя, так как в этом случае сила тока I_д уменьшается, а сопротивление R₂ увеличивается. Поэтому определим сначала, как изменится напряжение U₁: U₁=I_д×R₁. Поскольку сила тока I_д_{уменьшается, а сопротивление R₁ не изменяется, то
напряжение U₁ уменьшится. Входное напряжение равно сумме
напряжений на резисторах R₁ и R₂:
U_вх= U₁+U_вых. Поскольку входное
напряжение не изменяется, то при уменьшении напряжения на первом резисторе
выходное напряжение (напряжение на втором резисторе) увеличивается. Таким
образом, при увеличении сопротивления того резистора делителя, с которого
снимается выходное напряжение, выходное напряжение увеличивается, и
наоборот.}

В третьей задаче при увеличении (уменьшении) входного напряжения выходное напряжение делителя увеличивается (уменьшается), поскольку увеличивается (уменьшается) сила тока I_д.

Сопротивления резисторов делителя при конечном значении сопротивления нагрузки (рис. 2.5 б, в) можно рассчитать по формулам:

где U_вх и U_вых_{— входное и выходное напряжение делителя, а I_д_{и I_н — ток делителя и ток
нагрузки.}}

Делители напряжения рекомендуется использовать при малой силе тока нагрузки и небольших ее колебаниях.

В качестве делителя можно использовать потенциометры, в которых плавно изменяется отношение входного и выходного напряжений (рис.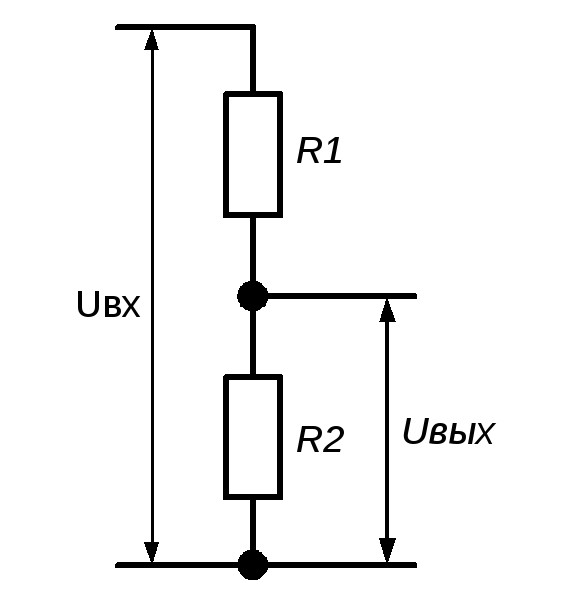 2.5 в). При регулировках в цепях постоянного напряжения дополнительно к делителю напряжения на переменном резисторе широко используют усилитель тока на биполярном транзисторе (рис. 2.5 г). Такая схема подключения нагрузки позволяет получить существенно больший ток при тех же значениях выходного напряжения. Транзистор VT1 желательно взять составным, так как такой транзистор имеет большой коэффициент усиления по току.

Иногда требуется очень точно и плавно регулировать выходное напряжение делителя. Такую задачу можно решить, используя одну из двух схем делителя, приведенных на рисунке 2.6. Если в схеме рисунка 2.6а сопротивление резистора R3 существенно больше сопротивления резистора R4, то резистором R2 осуществляют грубую регулировку выходного напряжения, а резистором R1 – точную. В схеме рисунка 2.6 б сопротивление резистора R1 выбирают меньше сопротивления резистора R2 и резистором R2 выходное напряжение регулируют грубо, а резистором R1 – точно.

1. Делители напряжения | 5. Схемы делителей и законы Кирхгофа | Часть1

1. Делители напряжения

Делители напряжения

Давайте проанализируем простую последовательную цепь и определим напряжения на каждом из ее резисторов:

Зная сопротивления каждого из резисторов, мы можем вычислить общее сопротивление цепи (которое для последовательной цепи будет равно сумме отдельных сопротивлений):

Теперь, используя закон Ома (I = U/R), определяем общую силу тока, которая будет одинакова на всех компонентах нашей последовательной цепи:

И наконец, зная общую силу тока (2 миллиампера), давайте рассчитаем напряжение на каждом из резисторов:

Из этой таблицы видно, что напряжения на резисторах пропорциональны их сопротивлениям (учитывая, что сила тока через все резисторы одинакова). Заметьте, напряжение на резисторе R₂ в два раза больше напряжения на резисторе R₁, так же как и сопротивление R₂ в два раза больше сопротивления R₁.

Если мы изменим общее напряжение цепи, то увидим, что эта пропорциональность сохранится:

Несмотря на увеличение напряжение источника питания, напряжение на резисторе R2 по прежнему в два раза больше напряжения на резисторе R1.

Произведя несколько подобных наблюдений становится очевидным, что напряжение на каждом из резисторов составляет фиксированную пропорцию от общего напряжения. Например, при напряжении батареи 45 вольт, напряжение на резисторе R₁ составляло 10 вольт. Когда напряжение батареи было увеличено до 180 вольт (в 4 раза), напряжение на резисторе R1 так же увеличилось в 4 раза (с 10 до 40 вольт). Как видите, соотношение между напряжением на резисторе R₁ и общим напряжением не изменилось:

Соотношения других напряжений с увеличением напряжения питания так же не изменятся:

Из за способности последовательной цепи пропорционально распределять общее напряжение по резистивным компонентам, ее часто называют делителем напряжения. Немного поколдовав с математикой, можно получить формулу для определения напряжения на любом резисторе, имея только значения сопротивлений отдельных резисторов, общего напряжения и общего сопротивления:

Полученная нами формула известна как формула делителя напряжения, с ее помощью легче рассчитывать напряжения последовательной цепи, чем производить аналогичные расчеты с использованием закона Ома.

Используя эту формулу можно повторно проанализировать приведенную выше схему, и определить ее напряжения произведя меньшее количество действий:

Делители напряжения нашли широкое применение в схемах измерительных приборов, где определенные комбинации соединенных последовательно резисторов используются для «деления» напряжения на нужные пропорции, необходимые для измерения разных величин того же напряжения.

Одним из устройств, часто используемых в качестве делителя напряжения, является потенциометр. Потенциометр представляет собой проводник с большим омическим сопротивлением (резистор), снабженный скользящим контактом:

Условное обозначение потенциометра представляет собой вертикальный символ резистора с примыкающей к нему стрелкой — скользящим контактом. Если скользящий контакт переместить ближе к контакту 1, то сопротивление между ними будет меньше, чем сопротивление между скользящим контактом и контактом 2. Если скользящий контакт переместить ближе к контакту 2, то эффект будет противоположным. Сопротивление между контактами 1 и 2 будет постоянным, независимо от положения скользящего контакта:

На рисунке ниже показана конструкция двух типов потенциометров, роторного и линейного:

Некоторые линейные потенциометры приводятся в действие посредством прямолинейного движения рычага или слайд-кнопки. Другие, как тот, который изображен на рисунке — посредством отвертки, для более точной настройки. Такие потенциометры называют еще «подстроечными». Следует отметить, что не у всех линейных потенциометров назначение выводов соответствует показанным на рисунке. У некоторых, вывод скользящего контакта находится посередине, между выводами конечных контактов.

На следующей фотографии изображен реальный ротационный потенциометр с открытыми для просмотра скользящим контактом и резистивным элементом. Рукоятка этого потенциометра повернута таким образом, что его скользящий контакт почти касается левого вывода резистивного элемента:

А здесь показан тот же самый потенциометр, но его скользящий контакт повернут против часовой стрелки в другую сторону:

Если постоянное напряжение приложить к контактам резистивного элемента потенциометра, то скользящий контакт выступит в роли своеобразного «крана», с помощью которого можно регулировать величину этого напряжения на выходе прибора:

По аналогии с фиксированным делителем напряжения, пропорциональность деленного потенциометром напряжения является исключительно функцией сопротивления, а не приложенного напряжения. Иными словами, если ручкой потенциометра установить его скользящий контакт строго посередине резистивного элемента, то на выходе мы получим ровно половину от приложенного напряжения, независимо от его величины. Можно сказать, что потенциометр функционирует как регулируемый делитель напряжения, в котором пропорциональность деленного напряжения устанавливается положением скользящего контакта.

Такая функция потенциометра очень полезна для получения регулируемого напряжения от фиксированного источника, например батареи. Если собранная вами схема требует напряжение, которое меньше напряжения имеющейся батареи, то вы можете подключить к этой батарее выводы резистивного элемента потенциометра, и ручкой «выставить» нужное напряжение между скользящим контактом и одним из конечных контактов:

Такое применение потенциометра при проектировании электрических схем пользуется большой популярностью.

На следующей фотографии показаны небольшие потенциометры, которые обычно применяются в бытовых электроприборах и различных радиолюбительских схемах:

Самый левый и самый правый потенциометры могут устанавливаться непосредственно на макетную или печатную плату. Средние устройства предназначены для установки на плоскую панель, со схемой они соединяются при помощи проводов.

Ниже показаны специализированные потенциометры:

Делитель напряжения / делитель разности потенциалов. Формула, номограмма для расчетов. Таблица делителя напряжения.

Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Физический справочник / / Электрические и магнитные величины / / Понятия и формулы для электричества и магнетизма. / / Делитель напряжения / делитель разности потенциалов. Формула, номограмма для расчетов. Таблица делителя напряжения.

Делитель напряжения / делитель разности потенциалов. Формула, номограмма для расчетов. Таблица делителя напряжения.

U_out= U_inR₂/ (R₁ + R₂)
где
U_out = выходное напряжение (В,V)

R = сопротивление (Ом,Ohms, Ω)

U_in = входное напряжение (В,V)

Выходное напряжение стандартного делителя напряжений = делителя разностей потенциалов:

* Источник — в основном — www.engineeringtoolbox.com (классный сайт)

Поиск в инженерном справочнике DPVA. Введите свой запрос:

Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста.
Вложите в письмо ссылку на страницу с ошибкой, пожалуйста.

Коды баннеров проекта DPVA.ru
Начинка: KJR Publisiers

Консультации и техническая
поддержка сайта: Zavarka Team

Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator

Решение задач и курсовых по электротехнике Сайт Электротехника и электроника на «пять»

Схема резистивного делителя напряжения:

(1)

Простейший резистивный делитель напряжения представляет собой два последовательно включённых резистора R₁ и R₂, подключённых к источнику напряжения U. Поскольку резисторы соединены последовательно, то ток через них будет одинаков в соответствии с Первым законом Кирхгофа. Падение напряжения (уменьшение потенциала при перемещении заряда от одной точки цепи до другой её точки) на каждом резисторе согласно закону Ома будет пропорционально сопротивлению (ток, как было установлено ранее, одинаков):

U=I·R;

Для каждого резистора:

U₁=I·R₁

U₂=I·R₂

Разделив выражение для U₁ на выражение для U₂ в итоге получаем:

U₁/U₂=R₁/R₂;

Таким образом, отношение напряжений U₁ и U₂ в точности равно отношению сопротивлений R₁ и R₂.

Используя равенство

U=U₁+U₂

Получим формулу, связывающую выходное(U₂) и входное(U) напряжение делителя:

U₂=U·R₂/(R₂+R₁)

Следует обратить внимание, что сопротивление нагрузки делителя напряжения должно быть много больше собственного сопротивления делителя, так, чтобы в расчетах этим сопротивлением, включенным параллельно R₂ можно было бы пренебречь. Для выбора конкретных значений сопротивлений на практике, как правило, достаточно следовать следующему алгоритму. Сначала необходимо определить величину тока делителя, работающего при отключенной нагрузке. Этот ток должен быть значительно больше тока (обычно принимают превышение от 10 раз по величине), потребляемого нагрузкой, но, однако, при этом указанный ток не должен создавать излишнюю нагрузку на источник напряжения . Исходя из величины тока, по закону Ома определяют значение суммарного сопротивления R=R₁+R₂. Остается только взять конкретные значения сопротивлений из стандартного ряда, отношение величин которых близко́ требуемому отношению напряжений, а сумма величин близка расчетной. При расчете реального делителя необходимо учитывать температурный коэффициент сопротивления, допуски на номинальные значения сопротивлений, диапазон изменения входного напряжения и возможные изменения свойств нагрузки делителя, а также максимальную рассеиваемую мощность резисторов — она должна превышать выделяемую на них мощность P=I²·(R₁+R₂), где I — ток источника при отключенной нагрузке (в этом случае через резисторы течет максимально возможный ток) .

Делитель напряжения — это… Что такое Делитель напряжения?

Дели́тель напряже́ния — устройство, в котором входное и выходное напряжение связаны коэффициентом передачи .^[1]

В качестве делителя напряжения обычно применяют регулируемые сопротивления (потенциометры). Можно представить как два участка цепи, называемые плечами, сумма напряжений на которых равна входному напряжению. Плечо между нулевым потенциалом и средней точкой называют нижним, а другое — верхним. Различают линейные и нелинейные делители напряжения. В линейных выходное напряжение изменяется по линейному закону в зависимости от входного. Такие делители используются для задания потенциалов и рабочих напряжений в различных точках электронных схем. В нелинейных делителях выходное напряжение зависит от коэффициента нелинейно. Нелинейные делители напряжения применяются в функциональных потенциометрах.^[1] Сопротивление может быть как активным, так и реактивным.

Резистивный делитель напряжения

Схема простейшего резистивного делителя напряжения

Простейший резистивный делитель напряжения представляет собой два последовательно включённых резистора и , подключённых к источнику напряжения . Поскольку резисторы соединены последовательно, то ток через них будет одинаков в соответствии с Первым правилом Кирхгофа. Падение напряжения на каждом резисторе согласно закону Ома будет пропорционально сопротивлению (ток, как было установлено ранее, одинаков):

Для каждого резистора:

Разделив выражение для на выражение для в итоге получаем:
Таким образом, отношение напряжений и в точности равно отношению сопротивлений и .
Используя равенство
, в котором , а
И, выражая из него соотношение для тока:

Получим формулу, связывающую выходное ( ) и входное ( ) напряжение делителя:

Следует обратить внимание, что сопротивление нагрузки делителя напряжения должно быть много больше собственного сопротивления делителя, так, чтобы в расчетах этим сопротивлением, включенным параллельно можно было бы пренебречь. Для выбора конкретных значений сопротивлений на практике, как правило, достаточно следовать следующему алгоритму. Сначала необходимо определить величину тока делителя, работающего при отключенной нагрузке. Этот ток должен быть значительно больше тока (обычно принимают превышение от 10 раз по величине), потребляемого нагрузкой, но, однако, при этом указанный ток не должен создавать излишнюю нагрузку на источник напряжения . Исходя из величины тока, по закону Ома определяют значение суммарного сопротивления . Остается только взять конкретные значения сопротивлений из стандартного ряда, отношение величин которых близко́ требуемому отношению напряжений, а сумма величин близка расчетной. При расчете реального делителя необходимо учитывать температурный коэффициент сопротивления, допуски на номинальные значения сопротивлений, диапазон изменения входного напряжения и возможные изменения свойств нагрузки делителя, а также максимальную рассеиваемую мощность резисторов — она должна превышать выделяемую на них мощность , где — ток источника при отключенной нагрузке (в этом случае через резисторы течет максимально возможный ток) .

Применение

Делитель напряжения имеет важное значение в схемотехнике. В качестве реактивного делителя напряжения как пример можно привести простейший электрический фильтр, а в качестве нелинейного — параметрический стабилизатор напряжения.

Делители напряжения использовались как электромеханическое запоминающее устройство в АВМ. В таких устройствах запоминаемым величинам соответствуют углы поворота реостатов. Подобные устройства могут неограниченное время хранить информацию.^[1]

Усилитель напряжения

Делитель напряжения может использоваться для усиления входного напряжения — это возможно, если , а — отрицательно, например как на участке вольт-амперной характеристики туннельного диода^{[источник не указан 213 дней]}

Ограничения в применении резистивных делителей напряжения

Номинал сопротивлений делителя должен быть в 100 — 1000 раз меньше, чем номинальное сопротивление нагрузки.

Малые значения сопротивлений, являющихся делителем напряжения, приводят к возникновению больших токов в делителе. Снижается КПД схемы из-за нагрева сопротивлений.

Резистивный делитель напряжения нельзя использовать для подключения мощных электрических приборов: электрические машины, нагревательные элементы.

Нормативно-техническая документация

ГОСТ 11282-93 (МЭК 524-75) — Резистивные делители напряжения постоянного тока

Примечания

↑ ¹ ² ³ Словарь по кибернетике / Под редакцией академика В. С. Михалевича. — 2-е. — Киев: Главная редакция Украинской Советской Энциклопедии имени М. П. Бажана, 1989. — 751 с. — (С48). — 50 000 экз. — ISBN 5-88500-008-5

Ссылки

Делители напряжения — схемы, уравнения и приложения

Делитель напряжения, также известный как делитель потенциала, представляет собой очень распространенную простую схему, которая используется для преобразования большого напряжения в малое напряжение. Из этой статьи вы узнаете о:

Что такое делитель напряжения?
Схемы делителя напряжения
Уравнение / формула делителя напряжения
Применение делителей напряжения

Что такое делитель напряжения?

Пассивная линейная схема, вырабатывающая выходное напряжение, составляющее часть входного напряжения.
Он уменьшает входное напряжение до меньшего напряжения в зависимости от соотношения двух резисторов путем распределения входного напряжения между компонентами делителя.
Часто используется для подачи напряжения, отличного от имеющегося в наличии аккумулятора или источника питания.
Выходное напряжение делителя напряжения зависит от сопротивления входящей нагрузки.

Схема делителя напряжения

Схема делителя напряжения обычно выглядит так в схеме с последовательностью из 2 резисторов.

R1 = резистор, ближайший к входному напряжению (Vin)
R2 = резистор, ближайший к земле
В _вход = входное напряжение
В _выход = выходное напряжение на R2, которое является разделенным напряжением (1/4 от входное напряжение)

Формула / уравнение делителя напряжения

Уравнение для определения выходного напряжения цепи делителя:

R2 / R1 + R2 = Ratio определяет масштабный коэффициент уменьшенного напряжения.

Например,
V _в = 100, R ₁ = 20, R ₂ = 10

С помощью калькулятора получите:

Правило делителя напряжения

Правило деления напряжения гласит: Напряжение, разделенное между двумя последовательными резисторами, прямо пропорционально их сопротивлению.
Это означает, что ваша схема может иметь более 2 резисторов!
Формула правила делителя напряжения:

Пример уравнения правила делителя напряжения:

Закон Ома

Теперь мы можем использовать закон Ома для расчета напряжения, протекающего через каждый резистор:

Уравнение для закона Ома = E = IR
- E = Ток на каждом резисторе
- I = Ток цепи
- R = Сопротивление

	R1	R2	R3	Всего
E (В)	5	10	15	30
I (А)	2.5 м	2,5	2,5 м	2,5 м
R (Ом)	2K	4K	6K	12K

Таким образом, ток на каждом резисторе составляет 5 В, 10 В и 15 В. соответственно!

Упрощенные уравнения

Если вы решаете для R1,

Если вы решаете для R2,

Применение делителей напряжения

Цепи делителей напряжения

очень распространены и используются во многих приложениях.Вот несколько примеров того, где находится схема делителя напряжения:

Потенциометр

Потенциометр — это пассивный электронный компонент с функцией скольжения или вращения, который действует как регулируемый делитель напряжения.
Входное напряжение подается по всей длине потенциометра, а выходное напряжение (падение напряжения) регулируется фиксированным и скользящим контактом потенциометра.
Существует два типа потенциометров
- Поворотные потенциометры (поворотная ручка)
- Линейный потенциометр (ползунок)
Компания Seeed предлагает оба типа!

Grove — Потенциометр скольжения

Как это работает?
- Ручной стеклоочиститель, который перемещается, касается резистивной полосы материала.Когда он перемещается ближе к клемме 1 и дальше от клеммы 2, сопротивление уменьшается до клеммы 1, в то время как сопротивление увеличивается на клемме 2, и наоборот.
Потенциометр полезен для получения переменного напряжения от источника постоянного напряжения. Он может подключать внешние клеммы потенциометра к источнику напряжения и контролировать необходимое напряжение между потенциометром и одной из внешних клемм вашей цепи.
Потенциометр Grove — Slide включает линейный переменный резистор с максимальным сопротивлением 10 кОм.При перемещении ползунка выходное напряжение будет варьироваться от 0 В до применяемого вами Vcc.
Он подключается к другим модулям Grove через стандартный 4-контактный кабель Grove.
Ниже приведено изображение принципиальной схемы потенциометра:

Он имеет множество целей, например, он может быть регулируемым резистором, автономным, делителем напряжения с Arduino или даже устройством интерфейса человека (HID), что означает, что его можно использовать для управления автомобилем!
Некоторые проекты, которые вы можете выполнять с помощью Grove — Slide Potentiometer, похожи на создание собственного Beatbox или Boombox с Arduino!

Grove — Датчик угла поворота (P)

Датчик угла поворота Grove-Rotary (P) способен выдавать аналоговый выходной сигнал от 0 до Vcc (5 В постоянного тока с Seeeduino) на разъеме D1.
Со значением сопротивления 10 кОм идеально подходит для использования с Arduino.
Он поддерживается на всех платформах MCU, таких как Arduino, Raspberry Pi, BeagleBone, Wio, а также LinkIt ONE.
Один из проектов, который вы можете сделать с этим потенциометром, — это использовать его для управления яркостью светодиодов.

Использование Arduino для управления яркостью светодиода с помощью датчика угла поворота Grove (P)

Grove — Делитель напряжения

Grove — Делитель напряжения предоставляет интерфейс для измерения внешнего напряжения, который устраняет необходимость подключения сопротивления к входному интерфейсу.
С помощью дискового переключателя вы можете легко выбрать коэффициент усиления напряжения, что упрощает его использование.

Чтение резистивных датчиков

Большинство датчиков представляют собой простые резистивные устройства, такие как наш Grove — инфракрасный датчик отражения. Однако большинство из них могут считывать только напряжение, но не сопротивление.
Добавив в схему еще один резистор, мы можем создать делитель напряжения вместе с датчиком.
Поскольку мы можем проверить выход делителя напряжения, теперь мы можем рассчитать величину сопротивления датчика.
Пример схемы показан ниже, где R2 — резистивный датчик:

Например, резистивный датчик представляет собой датчик температуры Grove, который представляет собой термистор с сопротивлением комнатной температуры 350 Ом, где сопротивление R1 фиксировано на 350 Ом
Использование уравнения делителя напряжения:

Температура	Vin (фиксированная)	R2	R1	R2 / (R1 + R2)	Vout
Холодная	5V	300 Ом	350 Ом	0 .46	2,3 В
Комнатная температура	5 В	350 Ом	350 Ом	0,5	2,5 В
Горячий	5 В	400 Ом	350 Ом	0,53	2,65 В

Переключатели уровня

Что происходит, когда встречаются датчик и микроконтроллер с двумя разными напряжениями? Без выравнивания напряжения, например, напрямую связав микроконтроллер с логическим выходом 5 В с микроконтроллером 3.Входной датчик 3 В может вызвать повреждение цепи 3,3 В.
Вот где главный герой: делитель напряжения спасает положение, действуя как переключатель уровня, который соединяет две цепи, использующие разные рабочие напряжения.
Делитель напряжения может помочь снизить напряжение с микроконтроллера (например, с 5 В до 3,3 В), чтобы избежать повреждения датчика, что делает его безопасным для обращения с датчиком.
Обратите внимание, что делитель напряжения может работать только в одном направлении: понижать напряжение, но не повышать.
Вот таблица комбинаций резисторов для понижения часто встречающихся напряжений:

Комбинация резисторов	Напряжения, которые необходимо выровнять
4,7 кОм и 3,9 кОм	9 В до 5 В
3,6 кОм и 9,1 кОм	от 12В до 3,3В
от 3,3 кОм и 5,7 кОм	от 9В до 3,3В

Обратите внимание, что не рекомендуется использовать делитель напряжения для понижения уровня большой нагрузки, такой как 12В. до 5 В, поскольку они не предназначены для подачи такого питания на нагрузку, как с такой нагрузкой, это может расплавить резистор.(Вместо этого вы можете использовать регуляторы напряжения, такие как наш регулируемый преобразователь постоянного и постоянного тока (1,25 В — 35 В и 3 А)

Резюме

Обладая всеми знаниями делителя напряжения в ваших руках, вы можете превратить любое напряжение в меньшее, как фокусник! Хотите проверить свои навыки, создав свой собственный проект делителя напряжения? Вот несколько идей для проектов, которые помогут вам начать использовать потенциометр и Arduino для создания битбокса или бумбокса на нашей вики-странице: Grove — Slide Potentiometer Wiki

Следите за нами и ставьте лайки:

Продолжить чтение

Что такое делитель напряжения?

Делитель напряжения представляет собой простую схему, которая может понижать напряжение.Он распределяет входное напряжение между компонентами схемы. Лучшим примером делителя напряжения являются два последовательно соединенных резистора, при этом входное напряжение прикладывается к паре резисторов, а выходное напряжение снимается в точке между ними. Он используется для создания разных уровней напряжения от общего источника напряжения, но с одинаковым током для всех компонентов в последовательной цепи.

Схема делителя напряжения

Падение напряжения и входное напряжение

Падение напряжения на R2 — это выходное напряжение, а также разделенное напряжение в цепи.Делитель напряжения относительно земли создается путем последовательного соединения двух резисторов. Входное напряжение прикладывается к последовательным сопротивлениям R ₁ и R ₂, а выходное напряжение — на R ₂. Отсюда следует, что то же самое значение электрического тока, протекающего через каждый резистивный элемент цепи, некуда больше деваться. Таким образом обеспечивается падение напряжения IxR на каждом резистивном элементе.

Имея напряжение питания, мы можем применить закон Кирхгофа и закон Ома, чтобы найти падение напряжения на каждом резисторе, рассчитанное исходя из общего тока, протекающего через них.

Используя KVL (закон Кирхгофа),

С законом Ома,

Используя два приведенных выше уравнения, вы получите:

Уравнения делителя напряжения

В делителе напряжения выходное напряжение всегда уменьшает входное напряжение и ток, протекающий через последовательную сеть, которые можно рассчитать по закону Ома, I = V / R. Поскольку ток общий для обоих резисторов, ток на них одинаков.Мы можем рассчитать падение напряжения на резисторе R ₂, используя следующее уравнение:

Из приведенного выше уравнения вы можете решить падение напряжения на R ₂:

Аналогично, для резистора R ₁ можно использовать уравнение:

Тогда при решении падения напряжения на R1:

Пример задачи

Рассчитайте падение напряжения, возникающее на каждом резисторе, и сколько тока будет протекать через резистор 30 Ом, подключенный последовательно с резистором 50 Ом, когда напряжение питания на последовательной комбинации составляет 10 вольт постоянного тока.

Расчет сопротивления

Рассчитайте общее сопротивление в цепи и просто сложите все это, поскольку резисторы включены последовательно.

Общее сопротивление позволит вам рассчитать ток, протекающий в резисторах.

Используя приведенные выше уравнения, можно рассчитать падение напряжения на резисторах.

Делитель напряжения и правило 10%

Вы должны знать подаваемое напряжение и сопротивление нагрузки при создании делителя напряжения для конкретной нагрузки.Делитель напряжения должен иметь только 10% тока утечки — ток, непрерывно потребляемый от источника напряжения, чтобы уменьшить влияние изменений нагрузки или обеспечить падение напряжения на резисторе. Это означает, что ток, проходящий через нагрузку, в десять раз больше тока, проходящего через нижнюю часть делителя напряжения на землю.

Например:

Этот делитель напряжения должен обеспечивать напряжение 25 В и ток 910 мА на нагрузку от источника напряжения 100 В.

Расчет R1 и R2

Определите размер резистора, используемого в цепи делителя напряжения, используя 10% эмпирическое правило. Ток в резисторе делителя должен составлять примерно 10% тока нагрузки. Этот ток, который не проходит ни через одно из устройств нагрузки, называется током утечки.

Сначала определите требования к нагрузке и доступный источник напряжения.

Затем найдите истекающий ток, применив правило 10%.

После получения тока утечки теперь можно рассчитать сопротивление кровотока на R1.

Затем найдите общий ток, сложив ток нагрузки и утечки.

Теперь по рассчитанным значениям вы можете найти значение R2.

Теперь вы можете перерисовать схему делителя напряжения, следуя правилу 10%.

Обратите внимание, что на первом рисунке значение сопротивления параллельной сети всегда меньше, чем значение наименьшего резистора в сети, поскольку нагрузка, подключенная между точкой B и землей, образует параллельную сеть нагрузки и резистора R1.

Лестница напряжения

Лестница напряжения — это схема, состоящая из нескольких последовательно включенных резисторов, с напряжением, подаваемым на всю сеть резисторов. На каждом резисторе в сети падение напряжения выше, чем на предыдущем. Поскольку резисторы в лестнице включены последовательно, ток везде одинаковый. Чтобы получить его значение, вам следует разделить общее напряжение на общее сопротивление. Падение напряжения на каждом резисторе можно рассчитать, умножив общий ток на номинал каждого резистора.Напряжение относительно земли в любом узле может быть определено как сумма напряжений, падающих на каждый резистор между этим узлом и землей.

Лестничная схема напряжения

Делитель напряжения Формула

Делитель напряжения — это конфигурация электрической цепи, которая вырабатывает выходное напряжение, составляющее часть входного напряжения, разделяя напряжение источника между одним или несколькими последовательными сопротивлениями.

Предположим, у вас есть источник напряжения (входное напряжение), подключенный последовательно с n импедансами.Чтобы узнать выходное напряжение по общему импедансу, используется закон Ома:

выходное напряжение = (общий импеданс / сумма от первого до n-го импеданса цепи) * входное напряжение.

Уравнение записано

У нас:

В _выход = выходное напряжение.

Z _i = общий импеданс.

= сумма от первого до n-го импеданса цепи.

В _в = входное напряжение.

Формула делителя напряжения Вопросы.

1) У нас есть цепь с двумя резисторами, первый 3 Ом и второй 5 Ом, подключенные последовательно, напряжение источника имеет значение 12 В, рассчитайте напряжение деления после первого сопротивления.

Ответ:

Прежде всего следует отметить, что это схема резистивного делителя, поэтому значения импедансов совпадают со значениями сопротивлений. Импеданс Z _и принимает значение 3 Ом.Теперь добавим импедансы цепи, чтобы получить делитель напряжения, это

= 3 Ом + 5 Ом = 8 Ом.

Затем мы делим значение второго импеданса на сумму импедансов и умножаем его на значение входного напряжения, чтобы получить делитель напряжения,

В _выход = (5 Ом / 8 Ом) * 12 В = 0,625 * 12 В = 7,824 В

В _выход = 7,824 В.

2) Рассчитайте делитель напряжения для двух последовательно соединенных конденсаторов, имеющих значения емкости 10 мкФ и 22 мкФ соответственно.Здесь напряжение в цепи составляет 10 В при частоте 40 Гц.

Ответ:

Прежде всего необходимо получить значение импеданса каждого конденсатора.

Z = 1 / (2 * π * f * C)

Z ₁ = 1 / (2 * π * 40 Гц * 10 * 10 ^-6 F) = 400 Ом.

Z ₂ = 1 / (2 * π * 40 Гц * 22 * 10 ^-6 F) = 180 Ом.

Затем,

В _выход = = 10 В = 0,31 * 10 В = 3,1 В

В _выход = 3.1 V.

Как работает эта простая формула

Делитель напряжения — это схема, которая делит напряжение между двумя резисторами. Вы всегда будете видеть это как в простых, так и в сложных схемах.

Это очень полезно знать!

Если вы знаете, как это работает, гораздо легче увидеть, как работают схемы. И это позволит вам рассчитать напряжения во многих разных точках цепи, что часто необходимо для понимания этого.

Формула делителя напряжения

Должен признать, что я больше использовал свой практический опыт построения схем, чем теорию электроники, которую я изучил в университете.Но эта формула — одна из немногих формул для электроники, которую я использую регулярно.

Используется для определения выходного напряжения, когда у вас есть два резистора, подключенных следующим образом:

Формула для расчета выходного напряжения:

Я рекомендую вам запомнить эту формулу. Часто пригодится. Или добавьте в закладки этот калькулятор делителя напряжения, если предпочитаете простой способ;)

Где найти делитель напряжения?

Один из примеров схемы делителя напряжения — для аналоговых датчиков.Например, термистор — это датчик температуры. Он изменяет свое сопротивление в зависимости от температуры. Если вы подключите его с резистором известного номинала в схеме делителя напряжения, вы получите напряжение, зависящее от температуры:

Или можно комбинировать известный резистор с фоторезистором . Фоторезистор изменяет сопротивление в зависимости от количества обнаруживаемого света. Таким образом, у вас есть схема, которая увеличивает или уменьшает напряжение в зависимости от света.

Вы можете подключить выход любой из этих схем к компаратору, чтобы проверить, что оно выше или ниже определенного напряжения.Тогда сделайте что-нибудь исходя из этого. Например, если температура выше 40 градусов, включите вентилятор.

Или подключитесь к аналоговому выводу Arduino или микроконтроллера и сделайте с ним крутые штуки. Может, включить свет, если фотоэлемент показывает, что темно?

Пример расчета: разные значения резистора

Допустим, у нас есть следующие значения:

Используя формулу выше, мы получаем

Пример расчета: одинаковые значения резисторов

Теперь предположим, что R1 и R2 имеют одинаковое значение.

Используя формулу выше, мы получаем

Это означает, что когда два резистора имеют одинаковое значение, выход всегда равен половине входного.

Можно ли использовать делитель напряжения в качестве источника питания?

Если у вас есть цепь, которая требует 4,5 В, можно ли использовать делитель напряжения с двумя резисторами по 500 Ом, чтобы получить 4,5 В от батареи 9 В?

К сожалению, это не так просто.

Любая цепь, которую вы хотите запитать, будет иметь внутреннее сопротивление.Таким образом, с точки зрения делителя напряжения, любую схему, которую вы подключаете к выходу напряжения, можно рассматривать как резистор (R _{НАГРУЗКА}), подключенный параллельно с R2.

Если внутреннее сопротивление цепи (R _{НАГРУЗКА}) также составляет 500 Ом, что произойдет?

Теперь R2 из формулы делителя напряжения становится параллельным сопротивлением R2 и R _{НАГРУЗКА}. А это всего 250 Ом. Если вы поместите это в формулу делителя напряжения, вы получите выходное напряжение 3 В вместо 4.5V ты хотел.

Для источника питания вы хотите, чтобы напряжение оставалось на выбранном уровне, независимо от того, имеет ли цепь, которую вы подключаете, высокое или низкое внутреннее сопротивление. Вот почему делитель напряжения обычно не используется в источниках питания.

Вместо этого нужно использовать регулятор напряжения.

Вопросы?

Какие у вас вопросы по делителю напряжения? Дайте мне знать в разделе комментариев ниже.

Делители напряжения | Книга Ultimate Electronics

Ultimate Electronics: практическое проектирование и анализ схем

Чрезвычайно распространенная конфигурация резисторов 2+.Приближения, рекомендации по проектированию. Пример светодиодного регулятора тока. Читать 22 мин

Делители напряжения — это просто определенные комбинации резисторов, последовательно подключенных к идеальным источникам напряжения и тока.

В то время как математика решения этих схем была рассмотрена в предыдущих разделах, делители напряжения заслужили свое собственное название, потому что они появляются достаточно часто, чтобы быть полезным сокращением при анализе многих более крупных схем. (Поскольку более сложные подсхемы могут быть аппроксимированы как один резистор, этот термин и методы также могут применяться в более широком смысле, помимо резисторов.Мы начнем с идеального случая, рассмотрим неидеальный случай, а затем покажем, когда приближения полезны при проектировании и анализе.

Когда вы видите, как опытный инженер-электрик бросает быстрый взгляд на аналоговую схему и быстро определяет, что происходит, он, скорее всего, делает приближения делителя напряжения в своей голове — иногда даже не осознавая этого!

Идеальный делитель напряжения состоит из двух последовательно соединенных резисторов. Физически это иногда реализуется в виде потенциометра, который разделяет один физический резистор на два с физически подвижным проводящим центральным контактом.Но чаще всего это два дискретных постоянных резистора.

Когда на пару подается напряжение, выходное напряжение составляет некоторую часть входного напряжения:

Exercise Щелкните, чтобы открыть и смоделировать схему выше. Измените сопротивления и посмотрите, как изменяется выходное напряжение в ответ.

Это можно увидеть, используя закон Кирхгофа плюс закон Ома, чтобы записать сумму разностей напряжений вокруг контура:

vin-iR1-iR2 = 0вин = i (R1 + R2) vinR1 + R2 = i

Теперь мы можем записать закон Ома для R2, vout = iR2 (поскольку другой конец R2 заземлен), и подставляем в наше выражение для тока контура i выше:

vout = vin (R2R1 + R2)

Для удобства вытащим дробь f , коэффициент делителя напряжения :

f = R2R1 + R2

где vout = vin⋅f .Поскольку сопротивления не могут быть отрицательными, 0≤f≤1 .

Есть несколько особых случаев, о которых следует подумать:

В относительно частом частном случае двух равных сопротивлений R1 = R2 , отношение f = 12 .
Если R1≫R2 отношение f → 0 .
Если R1≪R2 отношение f → 1 .

Эти приближения невероятно полезны, и более подробные версии разработаны в разделе «Алгебраические приближения».

Делитель напряжения всегда выдает уменьшенную версию входного напряжения.Вот пример с делителем напряжения, управляемым синусоидой от функционального генератора:

Exercise Щелкните, чтобы открыть и смоделировать схему выше и посмотреть на взаимосвязь между входными и выходными сигналами.

Поскольку делитель напряжения выводит масштабированную мультипликативно версию входного сигнала, если мы возьмем логарифм обеих сторон (по любому основанию), мы обнаружим, что коэффициент делителя напряжения превращается в аддитивную константу:

vout = vin⋅flog (vout) = журнал (vin) + журнал (f)

As f≤1 , всегда будет так, что log (f) ≤0 .

Вот пример с функциональным генератором, управляющим делителем напряжения, где мы отображаем напряжения в логарифмической шкале:

Exercise Щелкните, чтобы открыть и смоделировать схему выше. Обратите внимание, как в логарифмическом масштабе две кривые кажутся просто сдвинутыми по вертикали на постоянное смещение. В разделе «Advanced Graphing» измените его обратно на линейный масштаб, чтобы увидеть исходный сигнал.

В этом примере мы особо позаботились о том, чтобы наш входной сигнал оставался строго положительным, но вы также можете применить ту же логику к амплитуде сигнала, который со временем становится как положительным, так и отрицательным.В этом случае делитель напряжения производит сдвиг амплитудного графика в частотной области:

Exercise Щелкните, чтобы открыть и смоделировать схему выше.

При запуске этого моделирования графики входного и выходного напряжений с уровнем −6 дБ. сдвиг между входной и выходной амплитудой. Это −6 дБ потому что амплитуда напряжения уменьшается вдвое. См. Дополнительные сведения в разделах «Порядок величины», «Логарифмические шкалы» и «Децибелы».

Делители напряжения могут быть выполнены с N резисторы серии N − 1 узлы между ними.Пока нет тока, входящего или выходящего из цепи делителя напряжения, с точки зрения любого конкретного ответвления, резисторы «вверху» можно объединить в один, а резисторы «внизу» можно объединить в другой.

Это упрощает создание большого количества соотношений напряжений для одного входа. Например:

Exercise Щелкните, чтобы открыть и смоделировать схему выше.

На схеме выше используются пять последовательно соединенных резисторов. Он превращает 12-вольтный вход в четыре разных выхода, которые могут быть полезны в блоке питания компьютера.

Поскольку это последовательная цепь, существует только один ток, и его легко определить, рассматривая последовательно включенные резисторы:

итотал = vin∑R

Падение напряжения на любом резисторе будет равно:

Δvn = Rn⋅итотал

и доля полного падения напряжения на любом резисторе Rn это:

fn = Δvnvinfn = Rn⋅itotalvinfn = (Rnvin) (vin∑R) fn = Rn∑R

Дробное падение напряжения на одном резисторе — это просто отношение его сопротивления к сумме всех сопротивлений.

Для пяти последовательно соединенных выше резисторов мы можем рассчитать напряжения на каждом узле (относительно земли), посмотрев на отношение сопротивления «ниже» этого узла (то есть между этим узлом и землей) к общему сопротивлению цепи. В этом примере с узлами и резисторами, как указано выше:

vA = (Δv1) = vin (f1) vB = (Δv1 + Δv2) = vin (f1 + f2) vC = (Δv1 + Δv2 + Δv3) = vin (f1 + f2 + f3) vD = (Δv1 + Δv2 + Δv3 + Δv4) = vin (f1 + f2 + f3 + f4)

Когда мы разработаем решение для схемы выше:

vA = vin (R1R1 + R2 + R3 + R4 + R5) = 2.5 VvB = vin (R1 + R2R1 + R2 + R3 + R4 + R5) = 3,3 VvC = vin (R1 + R2 + R3R1 + R2 + R3 + R4 + R5) = 5,0 VvD = vin (R1 + R2 + R3 + R4R1 + R2 + R3 + R4 + R5) = 9,0 В

Конечно, для решения проблем мы выбрали определенные значения, которые было легко вычислить вручную: вы могли заметить, что мы выбрали vin = 12 В. и ∑R = 12 кОм так что итотал = 1 мА .

Как мы увидим позже, схемы этого типа не очень энергоэффективны и не могут обеспечивать большой ток. Однако это был бы один из потенциально действенных способов превратить одно опорное напряжение в ряд других пропорциональных опорных напряжений, которые затем можно было бы использовать как часть контура обратной связи в конструкции эффективного импульсного источника питания.

Один из распространенных способов решения проблем — это заметить, когда резисторы в делителе напряжения являются целыми числами, кратными друг другу.

Например, если R1 = 100 Ом, R2 = 300 Ом , то есть соотношение 3: 1. Всякий раз, когда соотношение 3: 1, независимо от фактических значений, мы будем иметь f = R2R1 + R2 = 34. .

Это также помогает в дизайне. Если вы пытаетесь достичь известной доли напряжения f которое вы можете выразить в виде дроби целых чисел, тогда вы можете быстро вычислить необходимое соотношение сопротивлений.

Например, если вы пытаетесь попасть, f = 0,4 = 25 , вы можете найти значения резисторов, где R2 = 2x, R1 = 3x для любого значения x , так что R2R1 = 23 . (Продолжайте читать ниже, чтобы узнать, как мы выбираем x !)

В некоторых ситуациях прототипирования, если целые числа в числителе и знаменателе достаточно малы, вы можете просто использовать пять равных резисторов, соединяя два последовательно, чтобы сформировать R2. и три последовательно для R1 .

Когда мы включаем источник управляющего напряжения, мы можем включить рассмотрение того, что происходит, когда мы смотрим на промежуточный вывод делителя напряжения, чтобы найти эквивалентную схему Тевенина:

Напряжение холостого хода — это просто напряжение, которое мы измеряем на этих клеммах без протекания внешнего тока, которое является всего лишь дробным входным напряжением, которое мы вычислили выше:

Veq = vout, без нагрузки = vin (R2R1 + R2)

Как только мы начнем позволять току течь извне к этим клеммам и от них, измеренное напряжение изменится.Как описано в разделе Thevenin, мы можем вставить источник тестового тока и установить все независимые источники на ноль, чтобы вычислить эквивалентное сопротивление:

Отсюда ясно, что эквивалентное сопротивление равно сопротивлению двух резисторов, включенных параллельно:

Req = R1 // R2 = R1R2R1 + R2

Таким образом, двухрезисторный делитель напряжения имеет вид однорезисторной схемы замещения Тевенина:

Мы только что преобразовали двухрезисторный делитель напряжения в однорезисторную эквивалентную схему Тевенина, которая имеет идентичное поведение кривой вольт-амперной характеристики по отношению к некоторой внешней подключенной нагрузке.Но когда у нас есть эквивалентная схема Тевенина, часто самое полезное, что с ней делать, — это подключить ее к какой-либо внешней нагрузке. Если эта нагрузка представляет собой резистор, то мы только что сформировали новый делитель напряжения .

Например, мы могли бы взять схему с тремя резисторами слева и рассмотреть R1 и R2 как делитель напряжения, а затем заменить их их эквивалентом Тевенина:

Exercise Щелкните, чтобы открыть и смоделировать схему выше.

Вы должны запустить моделирование, чтобы убедиться, что R3 имеет одинаковый ток, протекающий через него в обоих случаях.

Замена делителя напряжения его эквивалентом Тевенина может сама по себе сформировать новый делитель напряжения, что также может быть решено таким же образом. Это отличный метод решения проблем.

Эквивалентный пример Thevenin, приведенный выше, особенно полезен, потому что он поднимает концепцию нагрузки : что происходит, когда текущая «нагрузка» снимается с среднего вывода делителя напряжения?

В приведенной выше математике идеального делителя напряжения мы вычислили выходное напряжение как функцию входного напряжения vin и коэффициент делителя напряжения f = R2R1 + R2 Только.Но этот расчет предполагал, что тот же ток i протекала через оба резистора R1 и R2.

В нагруженном делителе напряжения это не так: есть некоторый внешний ток i3 извлекается из середины делителя напряжения:

В результате, если i3 ≠ 0 , то у нас также будет i1 ≠ i2 . Это нарушает фундаментальное предположение, сделанное нами ранее для идеальных делителей напряжения.

Обратите внимание, что ни схема, ни уравнения «не знают», что R3 является внешней нагрузкой, а R2 — частью исходного делителя напряжения.Оба резистора подключены к одной и той же паре узлов, и математические расчеты будут одинаковыми, если мы поменяем имена, которые мы даем. Тем не менее, проведя границу, отделяющую внутреннее от внешнего, и подумав об этом таким образом, делители напряжения под нагрузкой становятся полезными для проектирования и анализа схем, как мы увидим ниже.

Теперь, когда мы применяем наши правила для решения цепных систем, у нас есть разные значения тока в разных ветвях цепи. Наше уравнение закона тока Кирхгофа плюс два наших уравнения закона Ома образуют следующую систему из трех уравнений:

i1 = i2 + i3vin-vout = i1R1vout = i2R2

Мы хотим решить эту систему для одного выражения vout как функция от vin, R1, R2 и i3 .(Мы решили лечить i3 в качестве независимой переменной, поэтому мы можем видеть влияние тока нагрузки напрямую, а не связывать его с напряжением через сопротивление R3 .) Поучительно решать эту проблему вручную, так что вы можете увидеть, как подход Solving Circuit Systems дает тот же ответ, что и подход Тевенина, описанный выше, поэтому, пожалуйста, возьмите лист бумаги и следуйте инструкциям.

Сначала мы перегруппируем несколько уравнений, взяв i2 = i1 − i3 из первого уравнения и подставив его в третье, чтобы получить:

vout = (i1 − i3) R2

Мы также возьмем второе уравнение и разделим обе части на R1. :

i1 = vin-voutR1

Мы можем объединить эти два, заменив i1 :

vout = (vin-voutR1-i3) R2

Отсюда нам просто нужно заняться алгеброй.Раздайте R2 :

vout = (vin − vout) (R2R1) −i3R2

Забрать ваут условия в левой части:

vout (1 + R2R1) = vin (R2R1) −i3R2

Заменить (1 + R2R1) = (R1 + R2R1) :

vout (R1 + R2R1) = vin (R2R1) −i3R2

И разделите, чтобы изолировать вау :

vout = vin (R2R1) (R1R1 + R2) −i3R2 (R1R1 + R2) vout = vin (R2R1 + R2) −i3 (R1R2R1 + R2)

Это уравнение описывает выходное напряжение нагруженного делителя напряжения.

Посмотрите внимательно на коэффициенты при вин и i3 :

Коэффициент при вин , (R2R1 + R2) , это просто коэффициент делителя напряжения f мы нашли ранее в ненагруженном ящике.Если i3 = 0 , затем разделитель разгружается, и общее уравнение упрощается, чтобы быть таким же, как мы нашли в начале этого раздела.
Коэффициент для i3 равно (R1R2R1 + R2) = R1 // R2 , параллельно сопротивления двух резисторов! (Да, параллельно — хотя R1 и R2 кажутся в делителе напряжения серии !) Это тот же противоречивый результат, который мы только что нашли в разделе «Эквивалент Тевенина» выше.

Этот пример показывает, что возможность решить схему из KCL и KVL может потребовать некоторой алгебраической работы, но это всегда работает и всегда дает правильный ответ.Если вы не уверены, правильно ли применяете эквивалентный процесс Thevenin, вы всегда можете вставить тестовый источник тока i3 и приступайте к решению схемы вручную.

Что такое интуиция за током нагрузки в нагруженном делителе напряжения, вызывающим падение напряжения, пропорциональное параллельному сопротивлению R1 и R2, которые (без учета нагрузки) кажутся последовательными?

Быстрый способ запомнить это — рассмотреть крайние случаи и работать в обратном направлении.

С одной стороны, рассмотрим R1 = 0 или R2 = 0 (но не оба сразу). В этом случае выходное напряжение вообще не изменится с i3. . Нулевое сопротивление параллельно с ненулевым сопротивлением всегда равно нулевому эквивалентному сопротивлению. В этом случае нагрузка напрямую подключена (с нулевым сопротивлением) к одному концу источника напряжения.

Вот как упрощается нагруженный делитель напряжения при крайнем нулевом сопротивлении:

С другой стороны, рассмотрим R1 = ∞ или R2 = ∞ (но не оба сразу).В этом случае делитель напряжения отключен с одной стороны. Бесконечное сопротивление параллельно с конечным сопротивлением всегда равно конечному сопротивлению.

(Для параллельных сопротивлений помните, что полное сопротивление всегда на меньше , чем наименьшее отдельных сопротивлений. Или, что эквивалентно, общая проводимость всегда на больше , чем наибольшая отдельных проводимостей.)

Вот как упрощается нагруженный делитель напряжения на пределе бесконечного сопротивления:

Уравнение идеального делителя напряжения правильно сводится к этим случаям, если падение напряжения из-за нагрузки пропорционально параллельному сопротивлению R1 // R2 .

А как насчет случая посередине, где оба сопротивления конечны? Один из способов подумать об этом заключается в том, что небольшое увеличение тока нагрузки i3 имеет двойной эффект: увеличение i1 и уменьшая i2 . Фактически ни один из двух токов i1 или i2 нужно изменить на полную величину изменения i3 , потому что они буквально разделяют разницу (с противоположным знаком, но это просто вопрос маркировки токов):

Δi1 − Δi2 = Δi3

Например, если R1 = R2 , то они разделят разницу поровну: Δi1 = 12Δi3 , причем Δi2 = −12Δi3 .Поскольку величина изменения тока через каждый резистор меньше, его изменение напряжения также меньше, просто из-за закона Ома.

На этой иллюстрации показано, как ток нагрузки делится поровну обоими резисторами делителя напряжения, когда R1 = R2. :

Мы можем смоделировать этот эффект численно:

Exercise Щелкните, чтобы открыть и смоделировать схему выше. Обратите внимание, что наклон отдельных токов для R1 и R2 составляет половину крутизны, чем для испытательного тока.Измените сопротивление и посмотрите, как изменится поведение в ответ.

На практике загружены практически все реальные делители напряжения: что-то будет подключено к среднему выводу, так что промежуточная точка будет полезной — иначе мы бы просто использовали один резистор или вообще не использовали!

Однако, как видно из уравнения нагруженного делителя напряжения, математика для определения vout значительно усложняется, когда мы вводим ток нагрузки i3 .Было бы неплохо знать, когда это возможно, и небезопасно приблизительно рассчитывать делитель напряжения как приблизительно без нагрузки.

Ответ приходит из рассмотрения дополнительного падения напряжения из-за нагрузки как члена ошибки аппроксимации verr :

vout = vin (R2R1 + R2) −i3 (R1R2R1 + R2) vout = vout, идеально + verr

Если сосредоточиться только на термине ошибки:

verr = −i3 (R1R2R1 + R2) verr = −i3 (R1 // R2)

Если нам известна максимальная величина тока нагрузки | i3, max | , и мы можем определить максимальную ошибку напряжения | verr, max | мы готовы терпеть, тогда мы можем ограничить (R1 // R2) :

| i3, max | (R1 // R2) ≤ | verr, max | (R1 // R2) ≤ | verr, max || i3, max |

Если наша допустимая погрешность напряжения мала, сопротивление также должно быть небольшим.Если допустимый ток нагрузки велик, это также приведет к уменьшению сопротивления. Определение этого в терминах максимальных допусков означает, что даже если фактический ток нагрузки меняется, пока он меньше, чем максимальный ток нагрузки, на который мы рассчитали, мы можем быть уверены, что наш делитель напряжения по-прежнему будет в пределах наших проектных ограничений.

Это невероятно полезно на практике, потому что это означает, что нам не нужно проектировать всю систему сразу. Приближения позволяют нам разделить большую проектную проблему на ряд более мелких, где мы можем решать одну часть за раз. У этого есть два преимущества:

Более быстрое время проектирования. Часто бывает проще решить две маленькие подзадачи, чем одну большую.
Более надежная работа. Решение, которое мы достигаем путем декомпозиции нашей системы на модули с границами ошибок, может быть более терпимым к непреднамеренной дисперсии компонентов, потому что оно уже было разработано с учетом рассчитанных границ ошибок. Напротив, оптимизированное решение «все сразу» может быть неожиданно хрупким, когда какой-либо компонент на 5% отличается от желаемого значения.(Этот риск хрупкости особенно велик, когда мы начинаем добавлять какие-либо нелинейные элементы схемы, такие как транзисторы и усилители.)

Давайте рассмотрим типичный пример проектной задачи, когда мы должны спроектировать делитель напряжения как часть более крупной схемы.

Мы разработаем контроллер постоянного тока для светодиода (Light Emitting Diode), в котором мы хотим убедиться, что светодиод потребляет не более 20 мА тока, чтобы предотвратить его выгорание. Варианты изготовления означают, что мы не знаем точное напряжение светодиода, при котором будет возникать напряжение, поэтому нам необходимо управление светодиодами на основе тока, даже если у нас есть регулируемое напряжение в качестве источника питания.

При сохранении деталей для следующей главы, один из способов создать практический источник тока — это использовать BJT (Biploar Junction Transistor) с резистором для обратной связи. Нам нужно закрепить один вывод (базу) этого транзистора на 1,7 В, а у нас есть блок питания на 5 В. Для этого мы можем использовать делитель напряжения:

Мы разделили схему на три основных элемента: источник напряжения и делитель напряжения (V1, R1 и R2), транзисторный источник тока (Q1 и RE) и нагрузку, которой мы пытаемся управлять (D1 ).

Теперь нам нужно найти неизвестные резисторы R1 и R2, чтобы установить соответствующее напряжение смещения базы для нашего транзистора. На самом деле делитель напряжения загружен, что требует гораздо больше информации для расчета точного базового напряжения. В соответствии с приведенным выше уравнением для нагруженного делителя напряжения нам также необходимо знать базовый ток, и это быстро усложнится, поскольку это циклически зависит от сопротивлений R1 и R2, а также от свойств самих транзисторов и светодиода. Сложность вычислений растет экспоненциально!

Вместо этого давайте сделаем предположение, что мы можем рассматривать делитель напряжения R1 и R2 как приблизительно без нагрузки и довольно просто найти желаемое выходное напряжение.Если делитель напряжения не нагружен:

voutvin = f = R2R1 + R2f (R1 + R2) = R2fR1 = R2 (1 − f) R2R1 = f1 − fR2R1 = voutvin1 − voutvinR2R1 = voutvin − vout

так что если мы знаем vin = 5 В и vout = 1,7 В , то:

R2R1 = 1,75–1,7R2R1 = 0,52

Сделав предположение, что мы можем решить делитель напряжения как ненагруженный, мы быстро решили для отношения R2R1 .

Это показывает нам относительных сопротивлений двух резисторов в делителе напряжения, чтобы получить желаемое напряжение.Однако мы еще не установили их абсолютное значение : мы могли бы выбрать (R1 = 10 Ом, R2 = 5,2 Ом) или (R1 = 1 МОм, R2 = 520 кОм) и оба будут соответствовать нашему требованию по соотношению.

Выбор места для фиксации этих абсолютных значений имеет практические инженерные компромиссы в обоих крайних случаях:

Если сопротивление слишком мало: сам делитель напряжения потребляет большой ток (i = 5 VR1 + R2 ) и мощности (P = (5 В) 2R1 + R2 ). Это расточительно: это увеличивает наши требования к источнику питания или разряжает нашу батарею быстрее, и мы должны начать думать о тепловыделении резистора и температурных коэффициентах, а также о физических ожогах пользователей, прикоснувшись к этим горячим резисторам!
Если сопротивление слишком велико: , то ошибка напряжения из-за нагрузки | verr | = i3 (R1 // R2) будет неприемлемо большим, и мы не получим ожидаемое заданное значение напряжения.

Как выбрать?

У нас есть инженерный компромисс между потребляемой мощностью и точностью. Это типичный инженерный компромисс, на который должен пойти дизайнер. Правильный подход к проектированию будет заключаться в том, чтобы поставить некоторые разумные границы на желаемый уровень точности и убедиться, что это дает разумный результат в энергопотреблении.

Допустим, мы хотим, чтобы желаемое напряжение было в пределах 5% от проектного целевого значения. Эта цифра в 5% может показаться произвольной.Разумный способ выбрать бюджет ошибки — рассмотреть значения на разных порядках величины с обеих сторон: 50%, очевидно, слишком большая ошибка практически во всех обстоятельствах; 10%, вероятно, было бы хорошо, если бы мы действительно не заботились о точности; 1% или 0,5% потребует от нас более точной информации о других компонентах нашей системы, таких как светодиоды и сами транзисторы, не говоря уже о резисторах, точность которых обычно составляет всего 1% или 5%. 5% приятно посередине! (Это часто используемая отправная точка для достижения цели дизайна, если у вас нет причин выбрать иное.)

Выбор 5% в качестве максимально допустимой погрешности напряжения позволяет нам сказать:

vout = 1,7 В ± 5% vout = 1,7 В ± 85 мВ | verr | ≤85 мВ

Из вышесказанного мы знаем, что для нагруженного делителя напряжения | verr | = i3 (R1 // R2) . Мы еще не рассматривали биполярные переходные транзисторы, такие как Q1, но пока просто предположим, что базовый ток (который равен i3 ) — малая часть тока нагрузки (коллектора) iL , вероятно, между 100≤iLi3≤200 — т.е. базовый ток, вероятно, будет составлять от 0,5% до 1% от тока нашего светодиода.

Это очень грубое предположение плюс знание того, что желаемый ток нагрузки светодиода iL = 20 мА. , объедините, чтобы позволить нам поставить максимум на i3 :

i3≤iL100i3≤20 мА 100i3≤200 мкА

Это устанавливает максимальный предел значений сопротивления:

i3 (R1 // R2) ≤85 мВ (R1 // R2) ≤85 мВ 200 мкА (R1 // R2) ≤425 Ом

Теперь мы знаем, что хотим, чтобы параллельное сопротивление R1 и R2 было не более 425 Ом. .

Мы снова воспользуемся другим приближением (обратите внимание: добавляем больше ошибок, за пределами наших ранее установленных границ!) И помним, что если два резистора имеют очень разные значения, мы можем приблизить их параллельное сопротивление как примерно меньшее сопротивление.Наше соотношение R2R1 = 0,52 не достаточно большой, чтобы это было правдой, но он достаточно хорош для решения «обратной стороны конверта» и позволяет нам быстро выбрать некоторые общие значения резисторов, зная, что мы ищем примерно соотношение два к одному. где меньшее значение составляет примерно 400 Ом. ориентировочно:

R1 = 910 Ом R2 = 470 Ом

Это дешевые и распространенные номиналы резисторов, и мы получаем:

(R1 // R2) = R1R2R1 + R2 = 310 Ом R2R1 = 0,516

Это соответствует нашему ограничению погрешности напряжения и почти в точности соответствует нашему желаемому соотношению.Это достаточно близко, чтобы другие допуски (например, отдельные резисторы и транзисторы) преобладали в общей ошибке.

Вот наша последняя схема управления током светодиода с R1 и R2 на месте:

Exercise Щелкните, чтобы открыть и смоделировать схему выше. Запустите моделирование постоянного тока и посмотрите, как регулируется ток светодиода, равный примерно 20 мА. Вы также увидите расчетную рассеиваемую мощность на резисторах делителя напряжения P (R1) + P (R2). .

Насколько чувствительна эта схема к выбранным нами конкретным значениям R1 и R2? Что, если мы сохраним соотношение f = R2R1 = 0.52 , но выбрать разные (как большие, так и меньшие) номиналы резисторов? Режим DC Sweep симулятора позволяет нам быстро ответить на этот вопрос. Сначала мы определяем свободную переменную параметра x , а затем позвольте двум сопротивлениям масштабироваться вместе с ним:

R1 = xR2 = 0,52x

Вот симуляция, показывающая ток светодиода с различными значениями x :

Exercise Щелкните, чтобы открыть и смоделировать схему выше. Запустите DC Sweep по параметру x и посмотрите, как изменяется ток светодиода, когда мы регулируем сопротивление на много порядков величины.

Обратите внимание, как точка, которую мы выбрали выше, x = 910 , находится прямо перед «коленом» — визуально почти кусочно-линейным изменением поведения на кривой — где производительность начинает быстро ухудшаться. Мы построили график с использованием логарифмической шкалы для параметра, чтобы вы могли увидеть эффект замены сопротивлений на многие порядки величины. Прокрутите вниз, чтобы увидеть график рассеивания тепла резистором, так как это то, что мы обычно стараемся минимизировать. Симуляторы контуров позволяют быстро увидеть этот эффект «колена», а не рассчитывать его по множеству точек.

Выбирая точку чуть ближе к устойчивой стороне колена, мы получаем желаемое стабильное поведение при минимальном потреблении энергии.

Мы можем использовать симулятор, чтобы посмотреть, правильно ли работает схема, если разные значения компонентов различаются. Можно ожидать расхождения в значениях светодиода, транзистора и всех резисторов. Мы также можем ожидать некоторых отклонений в напряжении источника питания.

В каждом случае мы можем использовать режим моделирования DC Sweep для изменения компонента.

Вот что происходит, когда транзистор становится сильнее или слабее:

Exercise Щелкните, чтобы открыть и смоделировать схему выше. Ток светодиода не сильно зависит от характеристик транзистора.

А вот что происходит, когда индикатор немного отличается:

Exercise Щелкните, чтобы открыть и смоделировать схему выше. Ток светодиода также не сильно зависит от его параметров — мы разработали хороший регулятор тока!

Мы также можем использовать DC Sweep для изменения двух разных параметров.Например, предположим, что и R1, и R2 имеют 5% диапазонов допуска:

Exercise Щелкните, чтобы открыть и смоделировать схему выше. Ток светодиода нанесен на график для различных комбинаций значений R1 и R2.

В этом случае мы видим примерно +/- 10% общего диапазона токов светодиодов, что соответствует объединенным ошибкам наших двух отдельных допусков +/- 5%.

В производстве мы хотели бы проверить все углы нашего процесса — все наши крайние допуски для всех наших компонентов — в любом случае убедиться, что схема по-прежнему работает достаточно хорошо.Если этого не произойдет, нам придется перепроектировать или спроектировать схему, используя компоненты с более жесткими допусками, что может увеличить стоимость.

Если у вас есть N параметры компонента с полями допуска, которые теоретически могут составлять 2N углы проверять! На практике мы используем нашу инженерную интуицию для поиска наиболее потенциально проблемных, и мы проектируем наши схемы так, чтобы они были надежными по конструкции, как указано выше.

Один из распространенных случаев использования делителя напряжения — измерение неизвестного значения сопротивления.Например, мы можем использовать фиксированное значение сопротивления R1 и неизвестное значение R2, которое мы хотим определить. (R2 может быть, например, резистором, зависящим от температуры или света.)

В этом случае мы можем измерить выходное напряжение делителя напряжения vout (например, с помощью мультиметра или аналого-цифрового преобразователя) и выразить это как долю известного приложенного напряжения vin . Затем мы решаем уравнение идеального делителя напряжения для неизвестного сопротивления следующим образом:

voutvin = f = R2R1 + R2fR1 + fR2 = R2fR1 = (1 − f) R2R2 = R1 (f1 − f)

Если мы знаем R1 , и мы можем измерить f , затем вычисляя R2 просто.

Exercise Щелкните, чтобы открыть и смоделировать схему выше. Развертка по постоянному току меняет R2. График настроен так, чтобы показать отношение f на верхнем графике, а затем использует приведенное выше уравнение для обратного вычисления значения R2 от измеренных напряжений.

Вернитесь к содержанию, чтобы продолжить. Скоро появятся новые разделы!

Роббинс, Майкл Ф. Ultimate Electronics: Практическое проектирование и анализ схем. CircuitLab, Inc., 2021, ultimateelectronicsbook.com. Доступно. (Авторское право © CircuitLab, Inc., 2021)

Калькулятор правила делителя напряжения

— Примеры и приложения VDR

Цепь делителя напряжения

— Правило делителя напряжения Калькулятор «VDR», примеры и приложения

Цепь делителя напряжения

В цепи делителя напряжения используются резисторы для снижения напряжения, и самая распространенная схема, применяемая в электронике. Делитель напряжения можно использовать для многих вещей, например, для создания цепи регулировки громкости или генерации опорного напряжения и многого другого.Делители напряжения также используются в аналоговых схемах для получения выходов переменного напряжения. Эта схема отлично работает как с переменным, так и с постоянным входным напряжением, при этом это значение входного напряжения преобразуется в другое значение напряжения.

Примечание: Значение выходного напряжения схемы делителя напряжения всегда меньше значения входного напряжения.

В схеме делителя напряжения выходное напряжение всегда зависит от пропорции величины сопротивления. Например, если вы взяли два резистора равного номинала, вы получите на выходе ровно половину входного напряжения.

Электрическая эквивалентная схема делителя напряжения приведена ниже:

Как вы можете видеть, схема делителя напряжения состоит из двух последовательно соединенных резисторов с отводом напряжения между ними. Входное напряжение подается на резисторы R ₁ и R ₂. Следовательно, мы можем наблюдать, что выходное напряжение — это падение напряжения на резисторе R ₂. Напряжение на R ₁ и R ₂ будет равно значению входного напряжения, приложенного к цепи делителя напряжения.

Формула Уравнение делителя напряжения для определения значения выходного напряжения будет выражена как:

Где,

В _дюймов = Входное напряжение
В _выход = Выходное напряжение
R ₁ = Резистор, подключенный к источнику
R ₂ = Резистор, подключенный к земле

Связанные сообщения:

Доказательство формулы делителя напряжения

Теперь мы объясним вам математическое объяснение приведенной выше формулы.Итак, согласно закону Ома, разность потенциалов на идеальном проводнике будет равна току, протекающему по нему.

V = IR

Где, V, I и R — напряжение, ток и сопротивление соответственно.

Таким образом, напряжение на вышеуказанной цепи будет равно произведению тока в цепи на полное сопротивление.

Общее сопротивление цепи в цепи делителя напряжения составляет

R _T = R ₁ + R ₂

Vin = IR _T

Vin = I (R ₁ + R ₂)

При решении,

I = V _in / (R ₁ + R ₂)

Здесь выходное напряжение снимается через сопротивление R ₂, поэтому V _{на выходе} будет выражаться как:

В _выход = IR ₂

Теперь поместите значение I из приведенного выше уравнения:

Теперь мы объясним вам, как работает делитель напряжения и как вы можно даже найти значение сопротивления, чтобы получить желаемое значение напряжения.

Напряжение Делитель Схема — пример

Как показано выше, схема делителя напряжения состоит из двух резисторов (R ₁ и R ₂), и выход будет проходить через резистор Р ₂. Единственное, о чем нужно позаботиться, — это номинальная мощность резисторов. Потому что, если мы не выберем правильную номинальную мощность резистора, резисторы будут перегреваться или также могут сгореть. Вы можете рассчитать номинальную мощность, если знаете значение I (в зависимости от нагрузки), используя уравнение степенного закона (P = VI).

Вещи, необходимые для разработки схемы делителя напряжения:

Резисторы (10 кОм, 47 кОм)
Входное питание (9 В)
Макетная плата
Мультиметр (для измерения)

Теперь мы продемонстрирует вам выход схемы делителя напряжения практически и теоретически.

Здесь в эту схему мы подключили входное напряжение 9 В и резисторы R ₁ и R ₂ (47 кОм и 10 кОм соответственно). Снимая с мультиметра выход схемы делителя напряжения, получаем 1.49В .

Теперь мы рассчитаем выходное напряжение вышеуказанной схемы теоретически,

Здесь, V _в = 9 В, R ₁ = 47 кОм и R ₂ = 10 кОм

Итак, используя Уравнение делителя напряжения

У нас есть

В _{на выходе} = (9 × 10) / (47 + 10)

В _{на выходе} = 1,5789

Следовательно, вы можете увидеть разницу Между практическим и теоретическим значением, потому что напряжение батареи не совсем 9 В.Кроме того, вы можете найти номинал резистора в соответствии с желаемым выходным напряжением, используя приведенную выше формулу.

Связанные сообщения:

Калькулятор правил делителя напряжения

Вы также можете использовать калькулятор делителя напряжения для расчета выходного значения делителя напряжения или даже значения резисторов в соответствии с желаемыми входными и выходными значениями.

Введите любые три из следующих значений и нажмите кнопку «Рассчитать». Результат отобразит требуемое значение.

Примечание: формулы и уравнения для этого калькулятора приведены ниже (после калькулятора). Также не забывайте делиться и предлагать своим друзьям. Кроме того, если вы хотите увидеть другие электрические и электронные калькуляторы в прямом эфире в нашем блоге, укажите это в поле для комментариев ниже. Благодарю.

Формула для VDR Calculator

V _OUT = V _IN x (R ₂ / (R ₁ + R ₂))

Где

V _IN = Входное напряжение питания
R ₁ + R ₂ = Значения резисторов
V _OUT = Выходное напряжение

Связанные сообщения:

Преимущества и недостатки делителя напряжения Схема

Имеются некоторые преимущества и недостатки схемы делителя напряжения, которые указаны ниже:

Преимущества схемы делителя напряжения

Простой и удобный метод измерения высокого напряжения (до 100 кВ)
Простой метод измерения напряжения смещение уровня.
Помогает установить выходное напряжение регуляторов (например, LM317)

Недостатки схемы делителя напряжения

Неэффективно использовать для источников питания.
Резисторы делителей напряжения вносят небольшие потери мощности.
Иногда сопротивление вольтметра влияет на соотношение резисторов.

Применение схемы делителя напряжения
Теперь, как мы знаем, существует ряд применений схемы делителя напряжения.Некоторые из приложений упомянуты ниже:
Потенциометры
Потенциометр — это трехконтактный переменный резистор, с его помощью можно разработать регулируемый делитель напряжения. Если вы будете использовать только два контакта потенциометра (один должен быть регулируемым), он будет работать как реостат. Но если вы используете все клеммы и пропускаете выход через регулируемый вывод, здесь он работает как делитель напряжения.
Точно так же потенциометры имеют много применений, они также используются в джойстиках и для создания опорного напряжения.
Считывание резистивных датчиков
Большинство датчиков представляют собой просто резистивные устройства, такие как LDR (светозависимый резистор), сопротивление которого изменяется в зависимости от интенсивности падающего на него света. Подобно LDR, существует ряд датчиков, которые делают то же самое в отношении сопротивления, таких как датчик изгиба, датчик силы и термисторы.
Здесь схема делителя напряжения используется для расчета сопротивления датчика. Заменив резистор R ₂ (согласно принципиальной схеме) на резистивный датчик, мы можем рассчитать его сопротивление по следующей формуле:
R ₂ = (В _из x R ₁) / (Vin — Vout)
Где R ₂ — резистивный датчик
Сдвиг уровня
При взаимодействии с микроконтроллером не все датчики работают при стандартном значении напряжения (5 В), есть несколько датчиков который работает при относительно низком напряжении.Здесь возникает проблема смещения уровня, поэтому для снижения напряжения интерфейса мы используем схемы делителя напряжения, чтобы получить определенное напряжение.
Измерение высокого напряжения
Когда трудно измерить значение высокого напряжения, снова применяется делитель напряжения. Делитель напряжения уменьшает очень высокое напряжение, поэтому его легко измерить с помощью вольтметров.
Проще говоря, высокое напряжение подается на вход делителя напряжения, а его выход (установлен ниже, чем макс.диапазон) измеряется вольтметром. В вольтметрах специально разработаны зонды с высоковольтным резистором, чтобы выдерживать приходящее высокое входное напряжение и получать точные результаты при измерении высокого напряжения. Используя эту схему делителя напряжения, мы можем измерить напряжение до 100 кВ. Схема конденсаторного делителя используется для измерения значения напряжения более 100 кВ.
Связанное сообщение: Калькулятор параллельного резистора
Делитель напряжения для переменного источника питания
Предположим, у нас есть батарея 9 В, и вам нужно значение выходного напряжения от 1 В до 8 В.Как упоминалось выше, регулируя потенциометр, подключенный к батарее 9 В, мы можем получить выходное напряжение от 1 В до 8 В.
Подключите аккумулятор в соответствии со схемой ниже:
Примечание: Использование схемы делителя напряжения для источника питания может вызвать эффект нагрузки . Кроме того, это неэффективный способ управления напряжением питания, поскольку мощность рассеивается в резисторе R ₁ без полезного усиления.
Таким образом, потенциометр может выдавать переменное выходное напряжение.
Теперь предположим, что вам нужно фиксированное напряжение питания для любого конкретного устройства или контроллера, что вы будете делать? Для этого вам нужно точное значение резистора вместо потенциометра, чтобы получить желаемый выход.
Например, нам нужен выход 5 В от батареи 9 В (без учета тока нагрузочного резистора)
Переставив формулу делителя напряжения, вы можете найти значения резистора, который вам нужен для любого конкретного выходного значения.
Во-первых, вы должны выбрать значение входного напряжения и любое значение резистора (R ₁ или R ₂).Итак, если вы зафиксировали значение ₁ рэнд и теперь вам нужно найти значение ₂ рэнд, используйте следующую формулу:
Если вы зафиксировали значение ₂ рэнд и вам нужно найдите значение R ₁, затем используйте приведенную ниже формулу:
Здесь мне нужно 5 В на выходе из входного напряжения 9 В,
Итак,
В _в = 9 В
В _{на выходе} = 5V
R ₁ = 8k (постоянный резистор)
R ₂ =?
Используя формулу для R ₂
Имеем,
R ₂ = (5 x 8) / (9-5)
R ₂ = 40/4
R ₂ = 10
Следовательно, если вы возьмете ₂ рэндов 10 кОм и ₁ 8 кОм с входным напряжением 9 В, выходное напряжение будет равно 5 В.
Похожие сообщения:
Делитель напряжения (делитель потенциала) и делитель тока
Делитель напряжения и Делитель тока — это наиболее распространенные правила, применяемые в практической электронике. Как вы знаете, в схеме есть два типа комбинаций: последовательное и параллельное соединение. Параллельные схемы также известны как схемы делителей тока, потому что в этих схемах ток делится через каждый резистор. В то время как последовательные цепи известны как схемы делителей напряжения, потому что здесь напряжение делится на все резисторы. Правило деления напряжения и правило деления тока необходимо для понимания напряжения и тока, протекающих через каждый резистор. Эти правила разделения используются в большинстве распространенных электронных устройств.
Схема делителя напряжения
Чтобы пропустить ток через электрический проводник, необходимо приложить электродвижущую силу. Когда мы говорим, что ток «I» проходит через резистор «R», из этого логически следует, что сила, действующая на резистор R.Эта сила известна как разность потенциалов или падение напряжения на резисторе R. Точно так же, если мы рассмотрим любую часть электрической цепи, три величины, то есть напряжение, ток и сопротивление, объединяются.
Как мы узнали, последовательная схема называется схемой делителя напряжения. Это схема, которая делит напряжение на мелкие части. Итак, с источником питания и двумя резисторами мы можем сделать простую схему делителя напряжения. Здесь нам нужно соединить два резистора последовательно, а затем подать источник напряжения на последовательную цепь.
Схема делителя напряжения
В этом случае подключаются резистор R1 на 5 Ом и резистор R2 с сопротивлением 10 Ом. Напряжения V _out1 и V _out2 делятся между резисторами R1 и R2. Их можно рассчитать с помощью простого уравнения деления напряжения.
Где R _x — это резистор, на котором нам нужно найти напряжение, а R _total — полное сопротивление (R1 + R2) в цепи.Его можно просто рассчитать, сложив их все, поскольку они соединены последовательно. Таким образом, в данной схеме значения напряжения на каждом резисторе равны
.
Следовательно, напряжение на R1 составляет 4 В, а напряжение на R2 — 8 В. Таким образом, здесь напряжение делится в цепи между резисторами. Следовательно, это называется схемой делителя напряжения.
Делители напряжения
используются во многих приложениях, но они широко используются во всех типах переменных резисторов. Возьмем пример потенциометра.Потенциометр — это переменный резистор, который можно использовать для создания регулируемого делителя напряжения. Потенциометр имеет три клеммы, две клеммы подключены к концам резистора, а средняя клемма подключена к дворнику. У него одно сопротивление. Два внешних контакта подключены к источнику напряжения, а средний вывод действует как делитель напряжения.
Цепь делителя тока
Делитель тока — это цепь, которая делит ток на мелкие части.Как мы узнали, параллельные цепи представляют собой схему делителя тока. Таким образом, с источником питания и двумя параллельными резисторами мы можем сделать простую схему делителя тока. Как и в схеме делителя тока, здесь нам нужно соединить два резистора параллельно, а затем подать источник тока через параллельную цепь.
Цепь делителя тока
«I ₁» и «I ₂» — это ток, разделенный между резисторами R1 и R2. Их можно рассчитать с помощью простого уравнения деления тока.
«I _n» — это требуемый ток, протекающий через резистор R _n. R _eq — эквивалентное сопротивление параллельных резисторов.
Эквивалентное сопротивление (R _eq) равно
Таким образом, ток, протекающий через резисторы R1 и R2, будет равен
.
Здесь резисторы одинакового номинала, поэтому ток через каждый резистор будет делиться ровно пополам.

Делитель напряжения: теория и принцип действия

Делитель напряжения с реактивными элементами в цепи переменного тока

BACK

напряжения на резисторе и после

Что такое делитель напряжения

Принцип работы делителя напряжения

Формула для расчета делителя напряжения

На резисторе

После резистора

Делитель напряжения

1. Делители напряжения | 5. Схемы делителей и законы Кирхгофа | Часть1

1. Делители напряжения

Делитель напряжения / делитель разности потенциалов. Формула, номограмма для расчетов. Таблица делителя напряжения.

Делитель напряжения / делитель разности потенциалов. Формула, номограмма для расчетов. Таблица делителя напряжения.

Решение задач и курсовых по электротехнике Сайт Электротехника и электроника на «пять»

Делитель напряжения — это… Что такое Делитель напряжения?

Резистивный делитель напряжения

Применение

Усилитель напряжения

Ограничения в применении резистивных делителей напряжения

Нормативно-техническая документация

Примечания

Ссылки

Делители напряжения — схемы, уравнения и приложения

Что такое делитель напряжения?

Схема делителя напряжения

Формула / уравнение делителя напряжения

Правило делителя напряжения

Закон Ома

Упрощенные уравнения

Применение делителей напряжения

Потенциометр

Grove — Потенциометр скольжения

Grove — Датчик угла поворота (P)

Grove — Делитель напряжения

Чтение резистивных датчиков

Переключатели уровня

Резюме

Продолжить чтение

Что такое делитель напряжения?

Падение напряжения и входное напряжение

Уравнения делителя напряжения

Пример задачи

Расчет сопротивления

Расчет R1 и R2

Делитель напряжения Формула

Как работает эта простая формула

Формула делителя напряжения

Где найти делитель напряжения?

Пример расчета: разные значения резистора

Пример расчета: одинаковые значения резисторов

Можно ли использовать делитель напряжения в качестве источника питания?

Вопросы?

Делители напряжения | Книга Ultimate Electronics

— Примеры и приложения VDR

— Правило делителя напряжения Калькулятор «VDR», примеры и приложения

Цепь делителя напряжения

Преимущества и недостатки делителя напряжения Схема

Делитель напряжения (делитель потенциала) и делитель тока

Схема делителя напряжения

Цепь делителя тока

Читайте также

Что делать, если грудничок не спит днем: советы по налаживанию режима сна

Антигистаминные препараты для новорожденных: лечение и профилактика аллергии у грудничков

Методика «Цветоник» М. Лазарева для музыкального развития детей

Добавить комментарий Отменить ответ