Формула параллельного сопротивления: Формула расчета сопротивления при параллельном соединении резистора

При проектировании электрических схем возникает необходимость использования последовательного и параллельного соединений резисторов. Соединения применяются также и при ремонтах электрооборудования, поскольку в некоторых ситуациях невозможно найти эквивалентный номинал резистора. Выполнить расчет просто, и справиться с этой операцией может каждый.

Типы проводников

Проводимость веществом электрического тока связана с наличием в нем свободных носителей заряда. Их количество определяется по электронной конфигурации. Для этого необходима химическая формула вещества, при помощи которой можно вычислить их общее число. Значение для каждого элемента берется из периодической системы Дмитрия Ивановича Менделеева.

Электрический ток — упорядоченное движение свободных носителей заряда, на которые воздействует электромагнитное поле. При протекании тока по веществу происходит взаимодействие потока заряженных частиц с узлами кристаллической решетки, при этом часть кинетической энергии частицы превращается в тепловую энергию. Иными словами, частица «ударяется» об атом, а затем снова продолжает движение, набирая скорость под действием электромагнитного поля.

Процесс взаимодействия частиц с узлами кристаллической решетки называется электрической проводимостью или сопротивлением материала. Единицей измерения является Ом, а определить его можно при помощи омметра или расчитать. Согласно свойству проводимости, вещества можно разделить на 3 группы:

1. Проводники (все металлы, ионизированный газ и электролитические растворы).
2. Полупроводники (Si, Ge, GaAs, InP и InSb).
3. Непроводники (диэлектрики или изоляторы).

Проводники всегда проводят электрический ток, поскольку содержат в своем атомарном строении свободные электроны, анионы, катионы и ионы. Полупроводники проводят электричество только при определенных условиях, которые влияют на наличие или отсутствие свободных электронов и дырок. К факторам, влияющим на проводимость, относятся следующие: температура, освещенность и т. д. Диэлектрики вообще не проводят электричество, поскольку в их структуре вообще отсутствуют свободные носители заряда. При выполнении расчетов каждый радиолюбитель должен знать зависимость сопротивления от некоторых физических величин.

Зависимость сопротивления

Значение электропроводимости зависит от нескольких факторов, которые необходимо учитывать при расчетах, изготовлении элементов резистивной нагрузки (резисторов), ремонте и проектировании устройств. К этим факторам необходимо отнести следующие:

1. Температура окружающей среды и материала.
2. Электрические величины.
3. Геометрические свойства вещества.
4. Тип материала, из которого изготовлен проводник (полупроводник).

К электрическим величинам можно отнести разность потенциалов (напряжение), электродвижущую силу (ЭДС) и силу тока. Геометрией проводника является его длина и площадь поперечного сечения.

Электрические величины

Зависимость величины электропроводимости от параметров электричества определяется законом Ома. Существует две формулировки: одна — для участка, а другая — для полной цепи. В первом случае соотношение определяются, исходя из значений силы тока (I) и напряжения (U) простой формулой: I = U / R. Из соотношения видна прямо пропорциональная зависимость тока от величины напряжения, а также обратно пропорциональная от сопротивления. Можно выразить R: R = U / I.

Для расчета электропроводимости всего участка следует воспользоваться соотношением между ЭДС (e), силой тока (i), а также внутренним сопротивлением источника питания (Rвн): i = e / (R+Rвн). В этом случае величина R вычисляется по формуле: R = (e / i) — Rвн. Однако при выполнении расчетов необходимо учитывать также геометрические параметры и тип проводника, поскольку они могут существенно повлиять на вычисления.

Тип и геометрические параметры

Свойство вещества к проводимости электричества определяется структурой кристаллической решетки, а также количеством свободных носителей. Исходя из этого, тип вещества является ключевым фактором, который определяет величину электропроводимости. В науке коэффициент, определяющий тип вещества, обозначается литерой «р» и называется удельным сопротивлением. Его значение для различных материалов (при температуре +20 градусов по Цельсию) можно найти в специальных таблицах.

Иногда для удобства расчетов используется обратная величина, которая называется удельной проводимостью (σ). Она связана с удельным сопротивлением следующим соотношением: p = 1 / σ. Площадь поперечного сечения (S) влияет на электрическое сопротивление. С физической точки зрения, зависимость можно понять следующим образом: при малом сечении происходят более частые взаимодействия частиц электрического тока с узлами кристаллической решетки. Поперечное сечение можно вычислить по специальному алгоритму:

1. Измерение геометрических параметров проводника (диаметр или длину сторон) при помощи штангенциркуля.
2. Визуально определить форму материала.
3. Вычислить площадь поперечного сечения по формуле, найденной в справочнике или интернете.

В случае когда проводник имеет сложную структуру, необходимо вычислить величину S одного элемента, а затем умножить результат на количество элементов, входящих в его состав. Например, если провод является многожильным, то следует вычислить S для одной жилы. После этого нужно умножить, полученную величину S, на количество жил. Зависимость R от вышеперечисленных величин можно записать в виде соотношения: R = p * L / S. Литера «L» является длиной проводника. Однако для получения точных расчетов необходимо учитывать температурные показатели внешней среды и проводника.

Температурные показатели

Существует доказательство зависимости удельного сопротивления материала от температуры, основанное на физическом эксперименте. Для проведения опыта нужно собрать электрическую цепь, состоящую из следующих элементов: источника питания, нихромовой спирали, соединительных проводов амперметра и вольтметра. Приборы нужны для измерения значений силы тока и напряжения соответственно. При протекании электричества происходит нагревание нихромовой пружины. По мере ее нагревания, показания амперметра уменьшаются. При этом происходит существенное падение напряжения на участке цепи, о котором свидетельствуют показания вольтметра.

В радиотехнике уменьшение величины напряжение называется просадкой или падением. Формула зависимости р от температуры имеет следующий вид: p = p0 * [1 + a * (t — 20)]. Значение p0 — удельное сопротивление материала, взятого из таблицы, а литера «t» — температура проводника.

Температурный коэффициент «а» принимает следующие значения: для металлов — a>0, а для электролитических растворов — a<0. Для получения формулы, определяющей все зависимости, необходимо подставить все соотношения в общую формулу зависимости R от типа материала, температуры, длины и сечения: R = p0 * [1 + a * (t — 20)] * L / S. Формулы используются только для расчетов и изготовления резисторов. Для быстрого измерения величины сопротивления применяется омметр.

Объединение резистивных радиокомпонентов

Для получения необходимого номинала сопротивления применяются два типа соединения резисторов: параллельное и последовательное. Если их соединить параллельно, то нужно два вывода одного резистора подключить к двум выводам другого. Если соединение является последовательным, то один вывод резистора соединяется с одним выводом другого резистора. Соединения используются для получения необходимых номиналов сопротивлений, а также для увеличения рассеивания мощности тока, протекающего по цепи.

Каждое из соединений обладает определенными характеристиками. Кроме того, последовательно или параллельно могут объединяться несколько резисторов. Соединения также могут быть смешанными, т. е. применяться оба типа объединения радиокомпонентов.

Параллельное соединение

При параллельном подключении значение напряжения на всех резисторах одинаковое, а сила тока — обратно пропорциональна их общему сопротивлению. В интернете web-разработчики создали для расчета величины общего сопротивления параллельного соединения резисторов онлайн-калькулятор.

Рассчитывается общее сопротивление при параллельном соединении по формуле: 1 / Rобщ = (1 / R1) + (1 / R2) + …+ (1 / Rn). Если выполнить математические преобразования и привести к общему знаменателю, то получится удобная формула параллельного соединения для расчета Rобщ. Она имеет следующий вид: Rобщ = (R1 * R2 * … * Rn) / (R1 + R2 + … + Rn). Если необходимо рассчитать величину Rобщ только для двух радиокомпонентов, то формула параллельного сопротивления имеет следующий вид: Rобщ = (R1 * R2) / (R1 + R2).

При ремонте или проектировании схемы устройства возникает задача объединения нескольких резистивных элементов для получения конкретной величины сопротивления. Например, значение Rобщ для определенной цепочки элементов равно 8 Ом, которое получено при расчетах. Перед радиолюбителем стоит задача, какие нужно подобрать номиналы для получения нужного значения (в стандартном ряду резисторов отсутствует радиокомпонент с номиналом в 8 Ом, а только 7,5 и 8,2). В этом случае нужно найти сопротивление при параллельном соединении резистивных элементов. Посчитать значение Rобщ для двух элементов можно следующим образом:

1. Номинал резистора в 16 Ом подойдет.
2. Подставить в формулу: R = (16 * 16) / (16 + 16) = 256 / 32 = 8 (Ом).

В некоторых случаях следует потратить больше времени на подбор необходимых номиналов. Можно применять не только два, но и три элемента. Сила тока вычисляется с использованием первого закона Кирхгофа. Формулировка закона следующая: общее значение тока, входящего и протекающего по цепи, равен выходному его значению. Величина силы тока для цепи, состоящей из двух резисторов (параллельное соединение) рассчитывается по такому алгоритму:

1. Ток, протекающий через R1 и R2: I1 = U / R1 и I2 = U / R2 соответственно.
2. Общий ток — сложение токов на резисторах: Iобщ = I1 + I2.

Например, если цепь состоит из 2 резисторов, соединенных параллельно, с номиналами в 16 и 7,5 Ом. Они запитаны от источника питания напряжением в 12 В. Значение силы тока на первом резисторе вычисляется следующим способом: I1 = 12 / 16 = 0,75 (А). На втором резисторе ток будет равен: I2 = 12 / 7,5 = 1,6 (А). Общий ток определяется по закону Кирхгофа: I = I1 + I2 = 1,6 + 0,75 = 2,35 (А).

Последовательное подключение

Последовательное включение резисторов также применяется в радиотехнике. Методы нахождения общего сопротивления, напряжения и тока отличаются от параллельного подключения. Основные правила соединения следующие:

1. Ток не изменяется на участке цепи.
2. Общее напряжение равно сумме падений напряжений на каждом резисторе.
3. Rобщ = R1 + R2 + … + Rn.

Пример задачи следующий: цепочка, состоящая из 2 резисторов (16 и 7,5 Ом), питается от источника напряжением 12 В и током в 0,5 А. Необходимо рассчитать электрические параметры для каждого элемента. Порядок расчета следующий:

1. I = I1 = I2 = 0,5 (А).
2. Rобщ = R1 + R2 = 16 + 7,5 = 23,5 (Ом).
3. Падения напряжения: U1 = I * R1 = 0,5 * 16 = 8 (В) и U2 = I * R2 = 0,5 * 7,5 = 3,75 (В).

Не всегда выполняется равенство напряжений (12 В не равно 8 + 3,75 = 11,75 В), поскольку при этом расчете не учитывается сопротивление соединительных проводов. Если схема является сложной, и в ней встречается два типа соединений, то нужно выполнять расчеты по участкам. В первую очередь, рассчитать для параллельного соединения, а затем для последовательного.

Таким образом, параллельное и последовательное соединения резисторов применяются для получения более точных значений сопротивлений, а также при отсутствии необходимого номинала радиокомпонента при проектировании или ремонте устройств.

Последовательное и параллельное соединение резисторов.

Как я и обещал в статье про переменные резисторы (ссылка), сегодня речь пойдет о возможных способах соединения, в частности о последовательном соединении резисторов и о параллельном.

Последовательное соединение резисторов.

Давайте начнем с рассмотрения цепей, элементы которой соединены последовательно. И хоть мы и будем рассматривать только резисторы в качестве элементов цепи в данной статье, но правила, касающиеся напряжений и токов при разных соединениях будут справедливы и для других элементов. Итак, первая цепь, которую мы будем разбирать выглядит следующим образом:

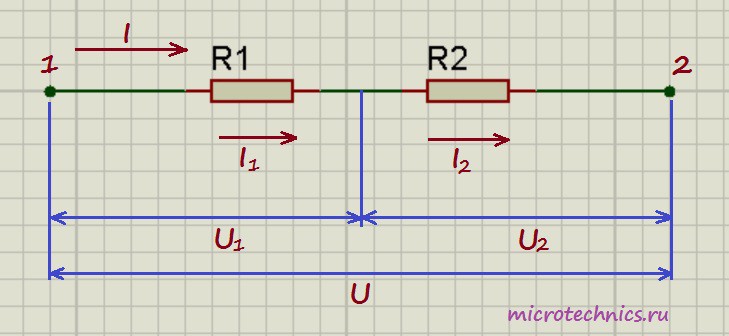
Здесь у нас классический случай последовательного соединения – два последовательно включенных резистора. Но не будем забегать вперед и рассчитывать общее сопротивление цепи, а для начала рассмотрим все напряжения и токи. Итак, первое правило заключается в том, что протекающие по всем проводникам токи при последовательном соединении равны между собой:

I = I_1 = I_2

А для определения общего напряжения при последовательном соединении, напряжения на отдельных элементах необходимо просуммировать:

U = U_1 + U_2

В то же время, по закону Ома для напряжений, сопротивлений и токов в данной цепи справедливы следующие соотношения:

U_1 = I_1R_1 = IR_1

U_2 = I_2R_2 = IR_2

Тогда для вычисления общего напряжения можно будет использовать следующее выражение:

U = U_1 + U_2 = IR_2 + IR_2 = I(R_1 + R_2)

Но для общего напряжение также справедлив закон Ома:

U = IR_0

Здесь R_0 – это общее сопротивление цепи, которое исходя из двух формул для общего напряжения равно:

R_0 = R_1 + R_2

Таким образом, при последовательном соединении резисторов общее сопротивление цепи будет равно сумме сопротивлений всех проводников.

Например для следующей цепи:

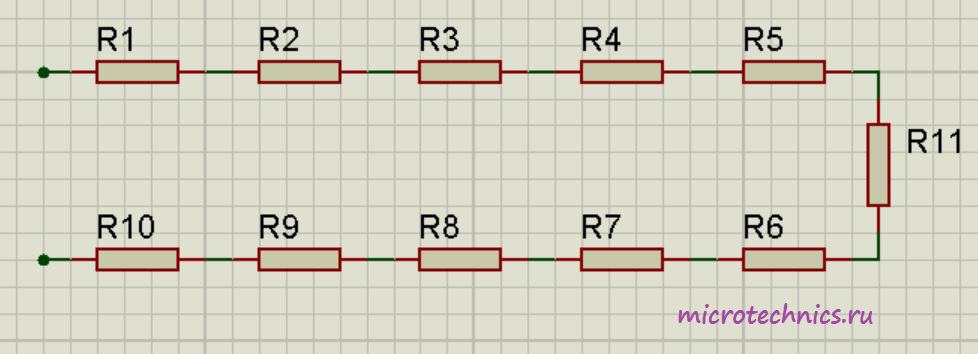
Общее сопротивление будет равно:

R_0 = R_1 + R_2 + R_3 + R_4 + R_5 + R_6 + R_7 + R_8 + R_9 + R_{10}

Количество элементов значения не имеет, правило, по которому мы определяем общее сопротивление будем работать в любом случае 🙂 А если при последовательном  соединении все сопротивления равны (R_1 = R_2 = … = R), то общее сопротивление цепи составит:

R_0 = nR

В данной формуле n равно количеству элементов цепи. С последовательным соединением резисторов мы разобрались, давайте перейдем к параллельному.

Параллельное соединение резисторов.

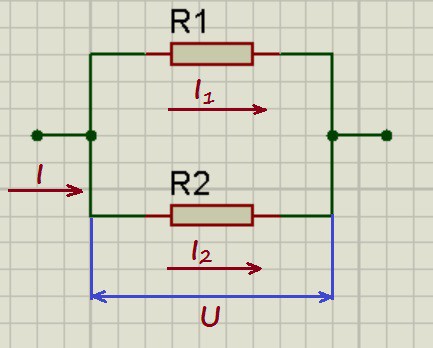
При параллельном соединении напряжения на проводниках равны:

U_1 = U_2 = U

А для токов справедливо следующее выражение:

I = I_1 + I_2

То есть общий ток разветвляется на две составляющие, а его значение равно сумме всех составляющих. По закону Ома:

I_1 = \frac{U_1}{R_1} = \frac{U}{R_1}

I_2 = \frac{U_2}{R_2} = \frac{U}{R_2}

Подставим эти выражения в формулу общего тока:

I = \frac{U}{R_1} + \frac{U}{R_2} = U\medspace (\frac{1}{R1} + \frac{1}{R2})

А по закону Ома ток:

I = \frac{U}{R_0}

Приравниваем эти выражения и получаем формулу для общего сопротивления цепи:

\frac{1}{R_0} = \frac{1}{R_1} + \frac{1}{R_2}

Данную формулу можно записать и несколько иначе:

R_0 = \frac{R_1R_2}{R_1 + R_2}

Таким образом, при параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.

Аналогичная ситуация будет наблюдаться и при большем количестве проводников, соединенных параллельно:

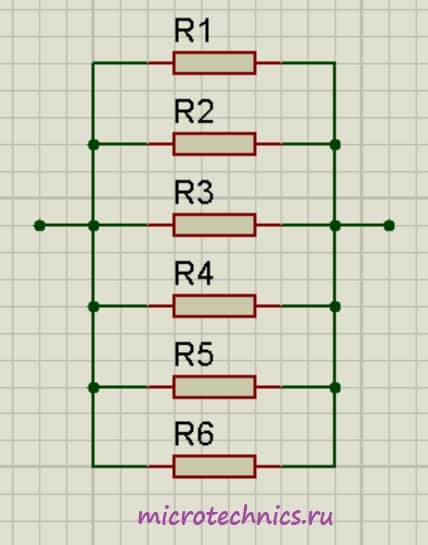
\frac{1}{R_0} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \frac{1}{R_4} + \frac{1}{R_5} + \frac{1}{R_6}

Смешанное соединение резисторов.

Помимо параллельного и последовательного соединений резисторов существует еще смешанное соединение. Из названия уже понятно, что при таком соединении в цепи присутствуют резисторы, соединенные как параллельно, так и последовательно. Вот пример такой цепи:

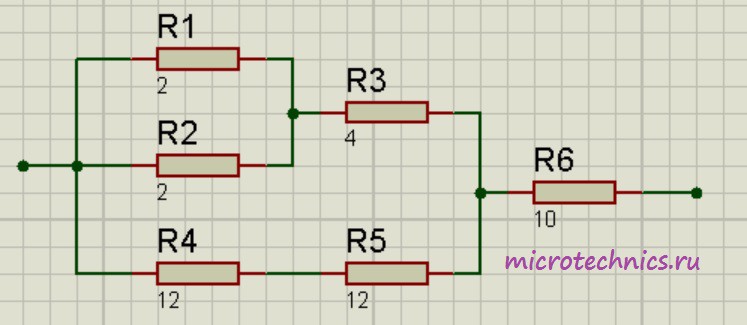
Давайте рассчитаем общее сопротивление цепи. Начнем с резисторов R_1 и R_2 – они соединены параллельно. Мы можем рассчитать общее сопротивление для этих резисторов и заменить их в схеме одним единственным резистором R_{1-2}:

R_{1-2} = \frac{R1\cdot R2}{R1 + R2} = 1

Теперь у нас образовались две группы последовательно соединенных резисторов:

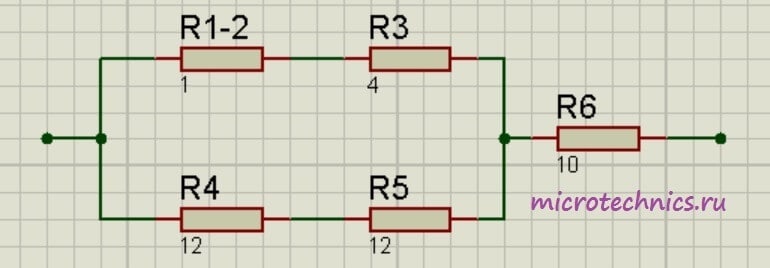
Заменим эти две группы двумя резисторами, сопротивление которых равно:

R_{1-2-3} = R_{1-2} + R_3 = 5

R_{4-5} = R_4 + R_5 = 24

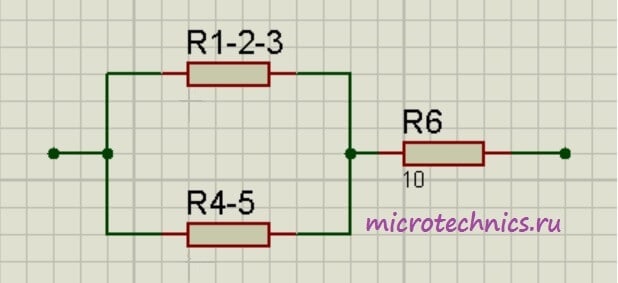
Как видите, схема стала уже совсем простой 🙂 Заменим группу параллельно соединенных резисторов R_{1-2-3} и R_{4-5}  одним резистором R_{1-2-3-4-5}:

R_{1-2-3-4-5}\enspace = \frac{R_{1-2-3}\medspace\cdot R_{4-5}}{R_{1-2-3} + R_{4-5}} = \frac{5\cdot24}{5 + 24} = 4.14

И в итоге у нас на схеме осталось только два резистора соединенных последовательно:

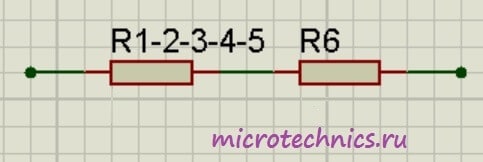
Общее сопротивление цепи получилось равным:

R_0 = R_{1-2-3-4-5}\medspace +\medspace R_6 = 4.14 + 10 = 14.14

Таким вот образом достаточно большая схема свелась к простейшему последовательному соединению двух резисторов!

Тут стоит отметить, что некоторые схемы невозможно так просто преобразовать и определить общее сопротивление – для таких схем нужно использовать правила Кирхгофа, о которых мы обязательно поговорим в будущих статьях. А сегодняшняя статья на этом подошла к концу, до скорых встреч на нашем сайте!

как подключить резистор в цепь

Резистор — это прибор, который обладает устойчивым, стабильным показателем сопротивления. Это помогает производить регулировку параметров на любом участке схемы. В этой статье говорится о том, как подключить резистор в цепь и какие методы для этого существуют. Также продемонстрированы несколько простых, но полезных схем, которые могут пригодиться при работе с электрикой.

Что такое соединение резисторов

Подключение приборов различными методами помогает получить нужное число мощности одной единицы цепи. Есть три основных метода подключения прибора — последовательное, параллельное и смешанное. Ниже подробно рассказано о каждом из них.

Как выглядят резисторы

Внимание! Для работы необходимо использовать только качественные приборы, на которые действует гарантия.

Как подключить резистор в цепь

Для сборки составного устройства необходимо соединить несколько элементов одним из основных методов и таким образом получить нужный номинальный показатель. В практике это используется очень часто. Навыки правильного подключения устройств и расчета их общего сопротивления используются мастерами для ремонта проводки или радиолюбителями при сборке устройства. В интернете можно найти много схем с различным видом подключения. Ниже описано какое соединение резисторов называется параллельным.

Параллельное соединение резисторов схема

Параллельно

Параллельное — это одно из двух типов электрических соединений, когда два вывода единственного устройства соединены с соответствующими выводами других элементов. Очень часто их могут соединять последовательно или параллельно, чтобы сделать более усложненные электрические схемы.

При этом виде соединения напряжение на всех устройствах будет равным, а проходящий через них ток — пропорционален их сопротивлению.

Такой вариант подключения один из простых, очень часто именно его рекомендуют использовать тем, кто не имеет опыта работы с электрикой.

Последовательно

Формула расчета достаточно легкая. Общее сопротивление при параллельном соединении формула:

Rобщ. = R1+R2+R3+…+Rn.

Сопротивление двух и более параллельно соединенных резисторов указано как Rобщ.

Последовательный способ подключения

Остальные элементы указываются как R, R2, R3 и так далее.

Обратите внимание! Используя последовательное соединение, необходимо запомнить один важный нюанс. Из общего количества компонентов, соединённых последовательным методом, основную роль занимает тот, у которого самое высокое сопротивление.

Как это понять? Для примера, если необходимо соединить три устройства, номинал которых будет равняться 1, 10 и 100 Ом, то в итоге получится составной на 111 Ом.

Смешанный тип подключения

Если исключить прибор на 100 Ом, то все сопротивление схемы резко снизится до 11 Ом. А если исключить, например, на 1 Ом, то показатель получится уже 110 Ом. В итоге устройства с небольшим сопротивлениями в последовательной цепочке почти не влияют на все показатели.

Какая мощность тока при последовательном и параллельном соединении

При соединении устройств последовательным методом ток будет проходить через каждое сопротивление. Показатель тока в любом месте цепочки будет равным. Это правило определяется при помощи закона Ома. Если суммировать все показатели в цепи, получится такое выражение:

Образец цепи

R = 200+100+51+39 = 390 Ом.

Напряжение на схеме равняется 100 В, по правилу Ома сила тока будет выражаться:

I = U/R = 100/390 = 0,256 A.

Теперь с помощью этих уравнений можно посчитать мощность при последовательном подключении, используя это выражение:

P = I2 x R = 0,2562×390 = 25,55 Вт.

При параллельном соединении все основания нужно подсоединить к одному узлу цепи, а концы — к другому. В таком варианте получается разветвление тока, и он будет проходить по каждому узлу. По правилу Ома, сила тока будет обратно пропорциональна всем имеющимся устройствам, а показатель напряжения везде одинаковый.

При смешанном подключении используются свойства обоих видов соединений.

Закон Ома для участка цепи

Как правильно рассчитать сопротивление

Для выбора и установки элементов в цепь нужно заранее просчитать номинал и мощность составных частей.

Применяют для этого правило Ома для участка цепи, чтобы рассчитать сопротивление, выражение выглядит так:

R = U/I.

U — будет напряжением на выводах компонента.

I — показатель тока на участке цепи.

Это выражение используется для токов постоянного направления.

Если трудно самостоятельно рассчитать этот показатель, то существуют специальные онлайн-калькуляторы. Туда необходимо вставить имеющиеся значения и можно получить результат за секунды. Но поскольку закон Ома изучается еще в школе, то не составит проблем провести вычисления самостоятельно.

Внимание! Если нет опыта в работе с электрикой, желательно не выполнять ремонт проводки самостоятельно, потому что при неправильной работе может случиться короткое замыкание, что чревато возникновением пожара. Также необходимо помнить, что при работе с проводкой нужно полностью обесточить сеть.

Подключение для светодиодов

В заключении необходимо отметить, что подключать резисторы можно тремя способами: параллельно, последовательно и смешанно. Для тех, кто не имеет особых навыков работы с электрикой, рекомендуется выбирать последовательный метод соединения.

параллельного резисторного калькулятора R1 + R2 = эквивалентный резистор R сопротивление цепи в эквиваленте суммарный резистор искатель легко сделать контрейлер = параллельный Параллельный резисторный калькулятор R1 + R2 = эквивалентный резистор R сопротивление цепи в эквиваленте суммарный резистор искатель легко сделать контрейлер = параллель — sengpielaudio Sengpiel Berlin

R всего

Формула: R всего = R1 × R2 / (R1 + R2)

Пожалуйста, введите два значения резистора , будет рассчитано третье значение параллельной цепи.
Вы даже можете ввести общее сопротивление R _всего и одно известное сопротивление R ₁ или R ₂ .

Формула (уравнение) для расчета двух сопротивлений R ₁ и R ₂ , соединенных параллельно:

Расчет необходимого параллельного резистора R ₂ , когда R ₁ и полное сопротивление R _всего дается:

Решение по формуле R итого = ( R 1 × R 2 ) / ( R 1 + R 2 ) для R 1 : Первый шаг — очистить все дроби, умножив на самое низкое значение . общий знаменатель, то есть R т × R 1 × R 2 … так мы получаем: 1/ R всего = 1/ R 1 + 1/ R 2 R всего × R 1 × R 2 [1/ R всего = 1/ R 1 + 1/ R 2 ] R 1 × R 2 = R всего × R 2 + R всего × R 1 , затем соберите члены с R 1 и решить R 1 × R 2 — R всего × R 1 = R всего × R 2 R 1 ( R 2 — R всего ) = R 2 × R всего Последний шаг: R 1 = R 2 × R всего / ( R 2 — R всего ) или: R 2 = R 1 × R всего / ( R 1 — R всего )

Примечание: Этот калькулятор также может решать другие математические задачи.Расчет резисторов параллельно составляет
точно так же, как расчеты, необходимые для параллельных индукторов или последовательно соединенных конденсаторов.

Два резистора параллельно и полученное суммарное сопротивление: два одинаковых значения, также покажите уравнение, что результаты всегда наполовину. Это облегчает, когда проектирование схем или прототипирование. С заглавными буквами он всегда двойной, потом опять заглавные буквы просто просто сложить параллельно.

• Поисковые сопротивления R ₁ и R ₂ , когда известно целевое сопротивление (эквивалентное сопротивление) •

Расчет: резисторные пары — обратный инженерный калькулятор
Поиск R ₁ и R ₂ с известным сопротивлением цели

● Рассчитать много резисторов параллельно ●

Этот калькулятор определяет сопротивление от до 10 резисторов параллельно . Введите сопротивления в поля ниже и, когда все значения были введены, нажмите на кнопку «Рассчитать», и результат появится в поле под этой кнопкой. В качестве теста, если мы введем сопротивления 4, 6 и 12 Ом, ответ должен быть 2 Ом. Примечание: очистка полей вручную не сбрасывает сохраненные значения. Используйте «сброс».

закон Ома — калькулятор и формулы

Два резистора параллельно и полученное суммарное сопротивление
Сопротивление в диапазоне от 1 Ом до 100 Ом

R2	R1
	1	1.5	2,2	3,3	4,7	6,8	10	15	22	33	47	68
1	0,5	0,6	0.69	0,77	0,83	0,87	0,91	0,93	0,95	0,97	0,98	0,99
1,5	0,6	0,75	0,89	1,03	1,14	1,22	1,30	1,36	1,40	1.43	1,45	1,46
2,2	0,69	0,89	1,1	1,32	1,50	1,66	1,82	1,92	2,0	2,06	2,10	2,13
3,3	0,77	1.03	1,32	1,65	1,94	2,22	2,48	2,70	2,87	3,00	3,08	3,14
4,7	0,83	1,14	1,50	1,94	2,35	2,78	3,20	3,58	3.87	4,12	4,27	4,39
6,8	0,87	1,22	1,66	2,22	2,78	3,40	4,05	4,68	5,19	5,64	5,94	6,18
10	0.91	1,30	1,82	2,48	3,20	4,05	5,0	6,0	6,9	7,7	8,3	8,7
15	0,93	1,36	1,92	2,70	3,58	4,68	6,0	7.50	8,9	10,3	11,4	12,2
22	0,95	1,40	2,00	2,87	3,87	5,19	6,9	8,9	11,0	13,2	15.0	16,6
33	0.97	1,43	2,06	3,0	4,12	5,64	7,7	10,3	13,2	16,5	19,4	22,2
47	0,98	1,45	2,1	3,08	4,27	5,94	8,3	11.4	15,0	19,4	23,5	27,8
68	0,99	1,46	2,13	3,14	4,39	6,18	8,7	12,2	16,6	22,2	27,8	34,0

Примечание: Этот калькулятор также может решать другие математические задачи.Расчет резисторов параллельно составляет
точно так же, как расчеты, необходимые для параллельных индукторов или последовательно соединенных конденсаторов.

Мощность, рассеиваемая в резисторе: P = В × I , P = В 2 / R , P = I 2 × R .

Примечание: Для последовательно включенных резисторов ток для каждого резистора равен , и для параллельных резисторов напряжение одинаково для каждого резистора.

,

параллельный калькулятор сопротивления — дюймовый калькулятор

Рассчитайте общее сопротивление в омах резисторов, которые включены параллельно, введя значение каждого ниже.

Хотите рассчитать резисторы последовательно?

Как рассчитать резисторы параллельно

Резистор — это устройство, которое добавляет сопротивление в электрическую цепь. Сопротивление измеряется в омах (Ω), и это также показатель, используемый этим калькулятором.

Когда резисторы добавляются параллельно в цепи, они соединяются в тех же точках, что и друг с другом, таким образом, есть несколько путей, которые может пройти напряжение.Из-за этого, обратная величина каждого значения сопротивления должна быть сложена вместе, чтобы найти полное сопротивление цепи.

Параллельный резистор Формула

Когда несколько резисторов добавляются в цепь параллельно, общее сопротивление может быть найдено с помощью этой формулы.

1R _T = 1R ₁ + 1R ₂ + 1R ₃ +… + 1R _n

Таким образом, обратная величина полного сопротивления резисторов, соединенных параллельно, является суммой обратной величины каждого сопротивления.

Схема, показывающая цепь с 3 резисторами, соединенными параллельно.

Например, , давайте найдем полное сопротивление цепи с параллельно подключенными резисторами 200 Ом, 400 Ом и 500 Ом.

1R _T = 1200 Ом + 1400 Ом + 1500 Ом
1R _T = 0,005 + 0,0025 + 0,002
1R _T = 0,0095
R _T = 1 ÷ 0,0095
R _T = 105,263 Ω

,Серия

и параллельные резисторы

• Изучив этот раздел, вы сможете:
• Рассчитать значения полного сопротивления в последовательных сетях сопротивления.
• Используйте соответствующие формулы для расчета сопротивления в параллельных сетях сопротивления.
• • Взаимный от суммы взаимных.
• • Товар сверх суммы.
• Рассчитать значения полного сопротивления в последовательных / параллельных сетях.

Расчеты в последовательных и параллельных резисторных сетях

Компоненты, включая резисторы в цепи, могут быть соединены вместе двумя способами:

В СЕРИИ, так что через все компоненты протекает один и тот же ток, но для каждого из них может существовать разная разность потенциалов (напряжение).

В ПАРАЛЛЕЛЬНОМ, так что одинаковая разность потенциалов (напряжение) существует во всех компонентах, но каждый компонент может нести различный ток.

Рис. 4.2.1 Резисторы в серии

Рис. 4.2.2 Параллельные резисторы

В любом случае (для резисторов) общее сопротивление этой части цепи, содержащей резисторы, можно рассчитать, используя методы, описанные ниже.

Способность рассчитать комбинированное (общее) значение резисторов таким способом позволяет легко вычислять неизвестные значения сопротивления, тока и напряжения для довольно сложных цепей, используя относительно простые методы.Это очень полезно для поиска неисправностей.

ПЕРЕД ПОЛУЧЕНИЕМ ДАЛЕЕ, ПРАКТИКА С ИСПОЛЬЗОВАНИЕМ ФОРМУЛ ДЛЯ РАСЧЕТА ВСЕГО ЗНАЧЕНИЯ СЕРИИ И ПАРАЛЛЕЛЬНЫХ РЕЗИСТОРОВ.

Для резисторов в серии:

Полное сопротивление двух или более резисторов, соединенных последовательно , дается простым сложением отдельных значений резисторов, чтобы найти общую сумму (R _TOT ):

Для резисторов параллельно:

Для расчета полного сопротивления цепи с параллельными резисторами можно использовать следующую формулу.

Обратите внимание, однако, что эта формула НЕ дает вам полное сопротивление R _TOT . Это дает вам Взаимное R _TOT или:

Это совсем другое значение — и НЕ является полным сопротивлением. Это 1 делится на R _TOT . Чтобы получить правильное значение для R _TOT (которое будет равно 1 / R _TOT , то есть R _TOT /1, просто нажмите ответную клавишу на вашем калькуляторе (отмечено 1 / x или x-1) ,

Еще один способ расчета параллельных цепей.

Общее сопротивление двух резисторов в параллельном соединении , которое не связано с взаимными ответами, определяется как:

Эта формула часто упоминается как «Продукт над суммой».

Он рассчитывает только два резистора параллельно? Ну да, но это не большая проблема. Если имеется более двух параллельных резисторов, просто выберите два из них и определите общее сопротивление для этих двух — затем используйте это общее значение, как если бы это был один резистор, и создайте другую пару с третьим резистором.Отрабатывайте новый итог и так далее, пока не включите все параллельные резисторы в эту конкретную сеть.

О, еще одна вещь, которую нужно помнить о продукте над суммой, см. Скобки вокруг суммы (нижняя часть) формулы? Это означает, что вы должны решить это, прежде чем использовать его, чтобы разделить продукт (верхняя часть) на. Если вы этого не сделаете, ваш ответ будет неверным.

Звучит сложно? Не совсем, это просто вопрос повторения, и на практике вы не часто сталкиваетесь со многими параллельными сетями с более чем двумя резисторами.Тем не менее, какая формула вы выбираете, зависит от вас, взаимных или переоценки продукта.

Советы

по взаимному методу

Если вы используете Взаимный метод для параллельных цепей, НЕ ЗАБУДЬТЕ, когда вы добавили ответные сигналы отдельных резисторов — Вы должны снова найти ответные сигналы.1 / R1 + 1 / R2 + 1 / R3 = 1 / R _TOT и чтобы найти R _TOT вы должны найти обратную величину 1 / R _TOT .

Упрощающие схемы

Для комбинированных последовательных и параллельных цепей сначала определите участок цепи (последовательный или параллельный).Затем заново нарисуйте схему, заменив участок, сопротивление которого вы нашли, одним резистором. Теперь у вас есть упрощенная схема, в которой можно найти R _TOT .

Вы можете использовать формулу «продукт сверх суммы»:

Для цепей с более чем двумя параллельными резисторами, просто отработайте два параллельных резистора одновременно, используя формулу произведения по сумме, а затем заново проведите схему, заменив два резистора одним резистором, значение которого представляет собой объединенное сопротивление двух ,

Теперь вы можете использовать ваше первое объединенное значение как один резистор со следующим параллельным резистором и так далее. Таким образом, можно рассчитать большое количество параллельных резисторов, используя произведение на сумму.

Когда все параллельные резисторы имеют одинаковое значение.

Если подключено несколько идентичных параллельных резисторов, общее сопротивление будет значением резистора, умноженным на величину, обратную количеству резисторов.

, т. Е. Два параллельных резистора 12 кОм имеют суммарное сопротивление

12K x 1/2 = 6K

Три параллельных резистора 12K имеют суммарное сопротивление

12K x 1/3 = 4K и т. Д.

Проверка вашего ответа

Суммарное значение любого количества параллельных резисторов всегда будет МЕНЬШЕ, чем значение наименьшего отдельного резистора в сети. Используйте этот факт, чтобы проверить свои ответы.

серии и параллельные комбинированные

Попробуйте несколько расчетов на основе последовательных и параллельных резисторных сетей. Для этого вам просто нужно использовать информацию на этой странице и страницу «Советы по расчету резисторов». Вас просят определить общее сопротивление для каждой цепи.Вы можете выбрать, какую формулу использовать

Вы также можете найти помощь по математике, загрузив нашу бесплатную брошюру Maths Tips.

Прежде чем начать, подумайте об этих нескольких советах. Они облегчат проблемы, если вы будете внимательно следить за ними.

1. Отработайте ответы, используя карандаш и бумагу; перерисовать схему, над которой вы работаете.

2. Конечно, ответ — это не просто число, это будет определенное количество Ом, не забудьте указать правильную единицу измерения (например,грамм. Ω, KΩ или MΩ) или ваш ответ не имеет смысла.

3. Когда вы вводите значения в свой калькулятор, преобразуйте все значения KΩ или MΩ в Ом, используя клавишу EXP. Если вы проскользнете сюда, это даст действительно глупые ответы, тысячи раз слишком большие или слишком маленькие.

Итак, теперь вы прочитали эти инструкции, вы готовы начать. Вот способ решить типичную проблему на бумаге, чтобы (с практикой) вы не запутались.

Серия

и пример параллельной цепи.

Хорошо, хорошо, что стоит вспомнить, так почему бы не попробовать некоторые практические вопросы в модуле 4.5 резисторов по нахождению полного сопротивления некоторых резисторных сетей?

,

Серии & Параллельные Резисторы | Расчеты Формулы

Описание способа последовательного и параллельного размещения резисторов для получения других значений сопротивления.

---

Сопротивление Учебник включает в себя:
Что такое сопротивление Закон Ома удельное сопротивление Таблица удельного сопротивления для обычных материалов Температурный коэффициент сопротивления Электрическая проводимость Последовательные и параллельные резисторы Таблица параллельных резисторов Параллельный калькулятор резисторов

---

Резисторы

могут быть размещены во многих конфигурациях в электрической или электронной цепи.

В некоторых случаях резисторы могут быть расположены последовательно, тогда как в других они могут быть расположены параллельно.

Когда они размещены в этих конфигурациях, важно иметь возможность рассчитать общее сопротивление. Этого легко добиться, если использовать правильные формулы — существуют простые формулы как для последовательных, так и для параллельных резисторов.

Резисторы в серии

Если резисторы размещены последовательно, то общее сопротивление — это просто сумма отдельных резисторов.

Резисторы в серии

Это можно выразить математически следующим образом:

RTOTAL знак равно р 1 + р 2 + р 3 + , , , , , ,

В качестве примера, если три резистора, имеющие значения 1 кОм, 2 кОм и 3 кОм, расположены последовательно, то общее сопротивление составляет 1 + 2 + 3 кОм = 6 кОм.

Резисторы параллельно

Если резисторы расположены параллельно, они делят ток, и ситуацию немного сложнее вычислить, но все же довольно легко.

1 RTOTAL знак равно 1 R1 + 1 R2 + 1 R3 + , , , , , ,

Пример
Для примера, если есть три резистора параллельно со значениями 1 кОм, 2 кОм и 3 кОм, тогда можно рассчитать общее значение комбинации:

1 / R Итого = 1/1000 + 1/2000 + 1/3000

1 / R Итого = 1/1000 + 1/2000 + 1/3000

1 / R Итого = 6/6000 + 3/6000 + 2/6000

1 / R Итого = 11/6000

R Итого = 6000/11 Ом или 545 Ом

Корпус только двух параллельных резисторов

Иногда это может быть довольно утомительным для расчета.К счастью, когда параллельно работают только два резистора, формула упрощается до:

р общее количество знак равно р 1 р 2 р 1 + р 2

Эта формула действительно упрощает расчет стоимости двух резисторов параллельно.

Более основные понятия:
Напряжение Текущий сопротивление емкость Мощность трансформеры РЧ шум Децибел, дБ Q, добротность
Возврат в меню основных понятий., ,

.