Главная » Разное » Формула расчета индуктивного сопротивления: Расчёт индуктивного и ёмкостного сопротивления

Формула расчета индуктивного сопротивления: Расчёт индуктивного и ёмкостного сопротивления

| – Комментировать

Содержание

Формула индуктивного сопротивления

При включении катушки индуктивности в цепь переменного тока, под действием непрерывно изменяющегося напряжения происходят изменения этого тока. В свою очередь, эти изменения вызывают генерацию магнитного поля, которое периодический возрастает или убывает. Под его влиянием в катушке индуцируется встречное напряжение, препятствующее изменениям тока. Таким образом, протекание тока происходит под непрерывным противодействием, получившим название индуктивного сопротивления.

От чего зависит индуктивное сопротивление

Данная величина связана напрямую с частотой приложенного напряжения (f) и значением индуктивности (L). Формула индуктивного сопротивления будет выглядеть следующим образом: XL = 2πfL. Прямая пропорциональная зависимость, в случае необходимости, позволяет путем преобразования основной формулы вычислить частоту или значение индуктивности.

Под действием переменного тока, проходящего по проводнику, вокруг этого проводника образуется переменное магнитное поле. Действие этого поля приводит к наведению в проводнике электродвижущей силы обратного направления, известной еще как ЭДС самоиндукции. Противодействие или сопротивление ЭДС переменному току получило название реактивного индуктивного сопротивления.

Данная величина зависит от многих факторов. В первую очередь на нее оказывает влияние как значение тока не только в собственном проводнике, но и в соседних проводах. То есть увеличение сопротивления и потока рассеяния происходит по мере увеличения расстояния между фазными проводами. Одновременно снижается воздействие соседних проводов.

Существует такое понятие, как погонное индуктивное сопротивление, которое вычисляется по формуле: X0 = ω x (4,61g x (Dср/Rпр) + 0,5μ) x 10-4 = X0’ + X0’’, в которой ω является угловой частотой, μ – магнитной проницаемостью, Dср – среднегеометрическим расстоянием между фазами ЛЭП, а Rпр – радиусом провода.

Величины X0’ и X0’’ представляют собой две составные части погонного индуктивного сопротивления. Первая из них X0’ представляет собой внешнее индуктивное сопротивление, зависящее только от внешнего магнитного поля и размеров ЛЭП. Другая величина – X0’’ является внутренним сопротивлением, зависящим от внутреннего магнитного поля и магнитной проницаемости μ.

На линиях электропередачи высокого напряжения от 330 кВ и более, проходящие фазы расщепляются на несколько отдельных проводов. Например, при напряжении 330 кВ фаза разделяется на два провода, что позволяет снизить индуктивное сопротивление примерно на 19%. Три провода используются при напряжении 500 кВ – индуктивное сопротивление удается снизить на 28%. Напряжение 750 кВ допускает разделение фаз на 4-6 проводников, что способствует снижению сопротивления примерно на 33%.

Погонное индуктивное сопротивление имеет величину в зависимости от радиуса провода и совершенно не зависит от сечения. Если радиус проводника будет увеличиваться, то значение погонного индуктивного сопротивления будет соответственно уменьшаться. Существенное влияние оказывают проводники, расположенные рядом.

Индуктивное сопротивление в цепи переменного тока

Одной из основных характеристик электрических цепей является сопротивление, которое может быть активным и реактивным. Типичными представителями активного сопротивления считаются обычные потребители – лампы, накаливания, резисторы, нагревательные спирали и другие элементы, в которых электрический ток совершает полезную работу.

К реактивному относятся индуктивное и емкостное сопротивления, находящиеся в промежуточных преобразователях электроэнергии – индуктивных катушках и конденсаторах. Эти параметры в обязательном порядке учитываются при выполнении различных расчетов. Например, для определения общего сопротивления участка цепи, складываются активная и реактивная составляющие. Сложение осуществляется геометрическим, то есть, векторным способом, путем построения прямоугольного треугольника. В нем оба катета являются обоими сопротивлениями, а гипотенуза – полным. Длина каждого катета соответствует действующему значению того или иного сопротивления.

В качестве примера можно рассмотреть характер индуктивного сопротивления в простейшей цепи переменного тока. В нее входит источник питания, обладающий ЭДС (Е), резистор, как активная составляющая (R) и катушка, обладающая индуктивностью (L). Возникновение индуктивного сопротивления происходит под действием ЭДС самоиндукции (Еси) в катушечных витках. Индуктивное сопротивление увеличивается в соответствии с ростом индуктивности цепи и значения тока, протекающего по контуру.

Таким образом, закон Ома для такой цепи переменного тока будет выглядеть в виде формулы: Е + Еси = I x R. Далее с помощью этой же формулы можно определить значение самоиндукции: Еси = -L x Iпр, где Iпр является производной тока от времени. Знак «минус» означает противоположное направление Еси по отношению к изменяющемуся значению тока. Поскольку в цепи переменного тока подобные изменения происходят постоянно, наблюдается существенное противодействие или сопротивление со стороны Еси.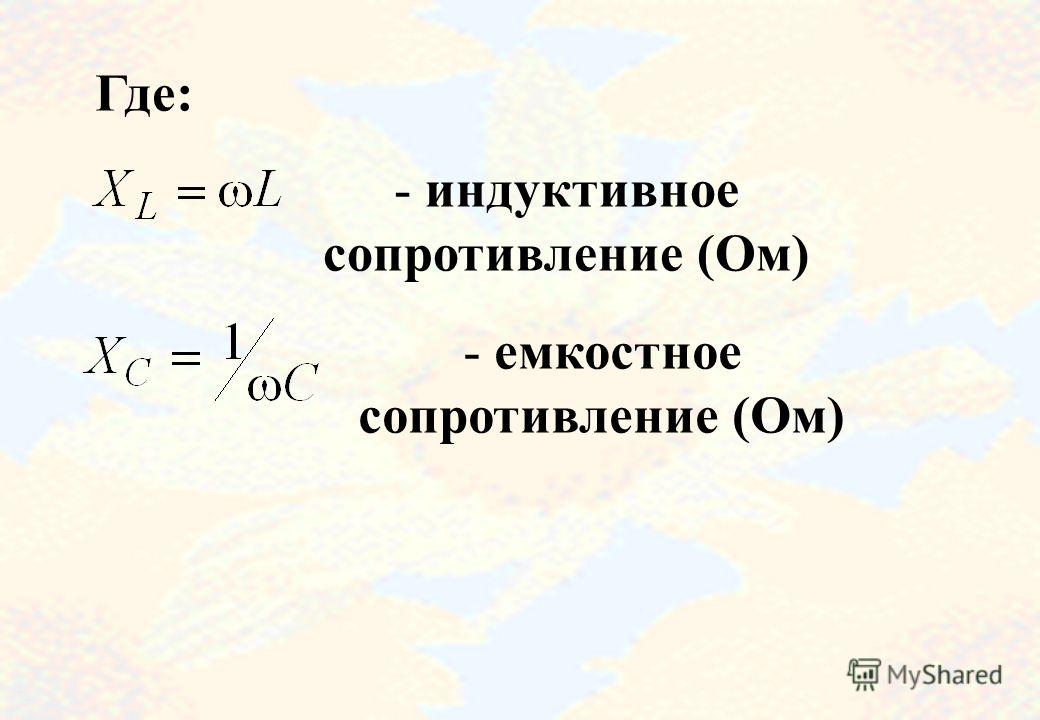 При постоянном токе данная зависимость отсутствует и все попытки подключения катушки в такую цепь привели бы к обычному короткому замыканию.

Для преодоления ЭДС самоиндукции, на выводах катушки источником питания должна создаваться такая разность потенциалов, чтобы она могла хотя-бы минимально компенсировать сопротивление Еси (Uкат = -Еси). Поскольку увеличение переменного тока в цепи приводит к возрастанию магнитного поля, происходит генерация вихревого поля, которое и вызывает рост противоположного тока в индуктивности. В результате, между током и напряжением происходит смещение фаз.

Индуктивное сопротивление катушки

Катушка индуктивности относится к категории пассивных компонентов, используемых в электронных схемах. Она способна сохранять электроэнергию, превращая ее в магнитное поле. В этом и состоит ее основная функция. Катушка индуктивности по своим характеристиками и свойствам напоминает конденсатор, сохраняющий энергию в виде электрического поля.

Индуктивность, измеряемая в Генри, заключается в появлении вокруг проводника с током магнитного поля. В свою очередь, связано с электродвижущей силой, которая противодействует приложенному переменному напряжению и силе тока в катушке. Данное свойство и есть индуктивное сопротивление, находящееся в противофазе с емкостным сопротивлением конденсатора. Индуктивность катушки возможно повысить за счет увеличения количества витков.

Для того чтобы выяснить, чему равно индуктивное сопротивление катушки, следует помнить, что оно, в первую очередь, противодействует переменному току. Как показывает практика, каждая индуктивная катушка сама по себе имеет определенное сопротивление.

Прохождение переменного синусоидального тока через катушку, приводит к возникновению переменного синусоидального напряжения или ЭДС. В результате, возникает индуктивное сопротивление, определяемое формулой: XL = ωL = 2πFL, в которой ω является угловой частотой, F – частотой в герцах, L – индуктивностью в генри.

Расчет индуктивного сопротивления — Энциклопедия по машиностроению XXL

При проектировании токовых нагревателей самую сложную задачу представляет собой расчет индуктивных сопротивлений и конструирование токоподводов с минимальными потерями. КПД нагревателя тем выше, чем меньшую долю составляет сопротивление токоподводов от общего сопротивления цепи нагревателя.  [c.82]

Это позволяет при вычислении волнового сопротивления тела в сверхзвуковом потоке применять тот же метод разложения в тригонометрические ряды, что при расчете индуктивного сопротивления крыла конечного размаха по теории несущей линии.  [c.330]


Расчет индуктивного сопротивления  [c.
64]

Наряду с разработкой теории крыла бесконечного размаха почти одновременно были предприняты шаги для построения методов расчета обтекания крыла конечного размаха. Общее представление о схеме схода вихрей с такого крыла содержалось уже в трактате Ф. Ланчестера а применительно к расчету винтов — у Н. Е. Жуковского. Попытки разработать соответствующую теорию крыла конечного размаха были предприняты примерно в одном и том же направлении Л. Прандтлем и С. А. Чаплыгиным. Однако Чаплыгин, получив ряд важных результатов для расчета индуктивного сопротивления крыла, прекратил свою работу в этой области и ничего  [c.289]

Методика расчета индуктивного сопротивления трансформатора с полностью разнесенными обмотками разработана достаточно подробно.  [c.228]

При расчете индуктивного сопротивления трансформаторов с нормальной геометрией,  [c.229]

На фиг. 146 представлена схема вторичной цепи сварочной машины, для которой требуется определить общее сопротивление.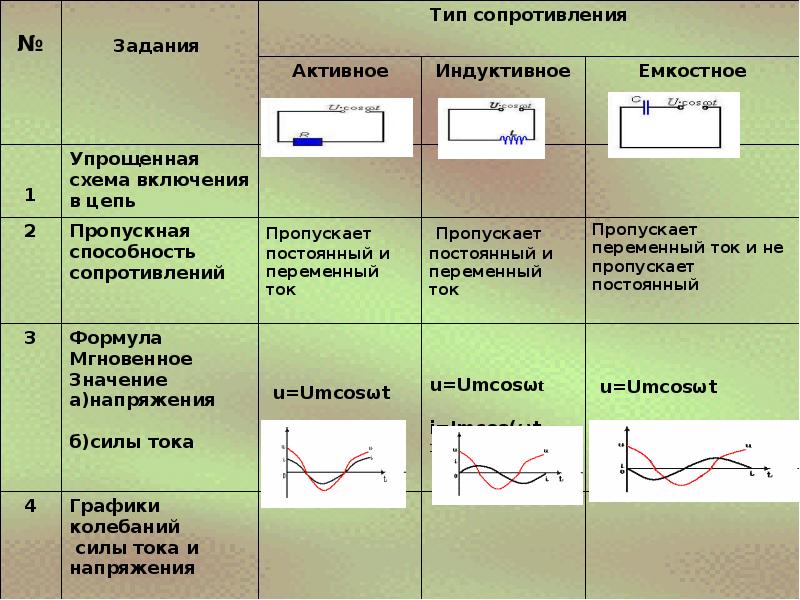

Для расчета индуктивного сопротивления найдем по формз ле (71) индуктивность прямоугольной рамки площадью 70 X 20 сл1.  [c.211]

Влияние формы крыла в плане на аэродинамические характеристики можно оценить по величине коэффициента 8, который используется в расчетах индуктивного сопротивления -  [c.69]

I, меньшей Хл/4. Их эквивалентная схема представляет собой последовательную индуктивность, шунтированную небольшими емкостями С/2, возникающими вследствие резкого изменения ширины центрального проводника. Часто при расчете индуктивного сопротивления ими можно пренебречь.  [c.96]

Например, в быстрых расчетных моделях СГ средней и малой мощности можно выделить следующие типовые блоки 1) расчет геометрии активных частей 2) расчет обмоточных данных 3) расчет ненасыщенных параметров (активных и индуктивных сопротивлений) 4) расчет магнитной цепи в установившемся режиме 5) расчет насыщенных параметров 6) расчет потерь и КПД  

[c. 124]

Расчеты, произведенные для крыльев с различной формой в плане, показали, что коэффициент индуктивного сопротивления следует определять по следующей формуле  [c.224]

Теория проходных и, главным образом, накладных катушек при их взаимодействии с различными материалами обычно сводится к анализу составляющих сопротивления эквивалентного витка. Конечно, датчик в виде витка на практике не применяется. Кроме того, экспериментальное подтверждение теории в этом случае вызывает огромные трудности из-за малой добротности, и индуктивности витка, а также значительных потерь в подводящих проводах. Однако это один из наиболее простых путей для получения важных для практики положений. При расчете индуктивности катушек используют понятие массивного эквивалентного витка. Считают, что  

[c.22]


Выясним влияние индуктивности полос контура на значение его z . Для этого проведем расчет импульсного сопротивления этого контура без учета искровых процессов в грунте (г) по импульсным коэффициентам протяженного заземлителя (см. рис. 4-2), рассматривая контур как две параллельные полосы с вертикальными электродами и пренебрегая их взаимным влиянием из-за большого расстояния между ними.  [c.133]

При приближенном расчете импульсного сопротивления искусственного заземлителя подстанции (без учета искровых процессов в земле) схемой замещения заземлителя является эквивалентный проводник длиной I с индуктивностью, равной индуктивности (/п- -1) параллельных полос заземлителя, и проводимостью, соответствующей полному стационарному сопротивлению искусственного заземлителя подстанции в грозовой сезон. При этом индуктивностью полос сетки другого (перпендикулярного) направления пренебрегаем.  

[c.212]

Развитие теории винтокрылых аппаратов на ранней стадии шло двумя раздельными путями, которые слились в 1920-х годах. (Термины импульсная теория и теория элемента лопасти имели тогда смысл, несколько отличный от современного, и в ранних работах означали отдельные и представлявшиеся независимыми методы исследования работы воздушного винта.) Ключевым фактором была идея индуктивного сопротивления, которую гидродинамики в первых десятилетиях XX в. еще разрабатывали и для крыльев, и для вращающихся лопастей. Прежде чем стал возможен достаточно точный расчет нагрузок несущего винта, необходимо было полностью выяснить смысл индуктивного сопротивления, т. е. сопротивления, неизбежного при создании подъемной силы крыла конечного размаха, и связать это сопротивление со скоростями, индуцируемыми на крыле следом.  

[c.60]

Для расчета величины индуктивного сопротивления удобнее исключить профильное сопротивление, которое направлено вдоль истинного потока.  [c.61]

Увеличение скоса потока при уменьшении удлинения должно привести и к соответствующему возрастанию индуктивного сопротивления (рис. 2.19). При расчетах это учитывается величиной показателя индуктивности А, который при дозвуковых скоростях обратно пропорционален удлинению крыла  [c.83]

Таким образом, индуктивное сопротивление при сверхзвуковом обтекании значительно слабее уменьшается при увеличении удлинения, чем при дозвуковом обтекании (это видно из сравнения рис. 3.12 и 3.09). Вот почему для приближенных расчетов при сверхзвуковом обтекании можно пользоваться формулой (2.16), не учитывающей влияния удлинения.  

[c.85]

Для выбора мощности высокочастотного оборудования и элементов сварочного устройства нужно производить расчет активного и индуктивного сопротивлений кондуктора и индуктора, а также мощности, требуемой для разогрева кромок до сварочной температуры. Необходим также расчет параметров свариваемых кромок.  [c.45]

Методика расчета параметров кромок для идеализированного случая, когда зазор между кромками или магнитопроводами и кромками весьма мал по сравнению с толщиной кромок, приведена в работе [6]. Рассчитанные по этой методике активное и индуктивное сопротивления значительно выше экспериментальных, а мощность, необходимая для сварки, значительно ниже, чем на практике.  

[c.45]

Активное и индуктивное Хкр.вн сопротивления кромок определяются по методике, изложенной в п. 8. Однако при расчете охватывающего индуктора значение индуктивного сопротивления кромок Хкр, вн необходимо уточнить, используя формулу кр.вн = /(1/ вн Кто), где Ято = [2щo n rJr ) — —сопротивление магнитному потоку на участке между наружной поверхностью заготовки радиусом и окружностью радиусом (см. рис. 33, а). Если наружный магнитопровод не используется, принимается 2,4/-з, Сопротивление необходимо вычесть, иначе окажется, что магнитное сопротивление промежутка (наружный магнитопровод — отрезок окружности, соединяющий наружные углы кромок) будет учтено дважды — при определении Хкр и Хз.  [c.79]

Скорость г 1, с которой поверхность раздела опускается вниз после удара, примем для простоты постоянной, т.

е., согласно сказанному по поводу формулы (94), поставим задачу об отыскании минимального индуктивного сопротивления. Эта скорость равна удвоенной индуктивной скорости ю (см. приближенный расчет, сделанный на стр. 285 для случая, изображенного на рис. 165). Связь между циркуляцией Г на поверхности раздела и скоростью ТО1 определяется однозначно из второй краевой задачи теории потенциала, а именно, циркуляция Г пропорциональна скорости гсг. Из соображений о размерностях можно принять, что  [c.289]


При использовании переменного тока в дуговых печах (что обычно имеет место в промышленной практике) напряжение на электродах изменяется во времени по величине и по знаку. Полярность электродов будет меняться в соответствии с частотой тока, и один и тот же электрод будет являться то катодом, то анодом. При прохождении значения напряжения через нуль дуга должна гаснуть. Непрерывное горение дуги переменного тока может поддерживаться при введении в цепь индуктивного сопротивления.
Расчеты показывают, что для того, чтобы обеспечить непрерывное горение дуги, значение угла сдвига фаз между напряжением и током ф должно удовлетворять условию os ф [c.250]

В такой постановке эта задача очень трудна, если не сводить ее к определенным более простым частным практическим случаям. Вообще она будет иметь два аспекта 1) нахождение условий, при которых индуктивное сопротивление системы было бы минимальным, и 2) расчет аэродинамических характеристик некоторой заданной комплексной системы.  [c.415]

Батарею конденсаторов большой емкости (из расчета 100 мкф на 1 а максимальной силы тока сварочной цепи) и индуктивного сопротивления.  [c.426]

Из уравнения равновесия моста легко вывести формулу для расчета индуктивности и сопротивления образца  

[c.269]

По величинам а, -б, в, /»б и Гв рассчитываются магнитные характеристики образца. При расчете принимают, что измерения проводятся в области начальной проницаемости, когда сопротивление потерь мало по сравнению с индуктивным сопротивлением образца.  [c.278]

Полный расчет индуктора должен включать далее определение параметров активного сопротивления первичной и вторичной цепей, толщины катушки, индуктивного сопротивления первичной и вторичной цепей, величины полного сопротивления и коэффициента мощности, допустимой силы тока в индукторной обмотке.  [c.315]

В такой постановке расчет дает только индуктивное сопротивление системы. Активную мощность в проводнике можно найти, рассчитав тангенциальную напряженность магнитного поля Н( на его поверхности, по формуле  [c.65]

Во втором случае, характерном для многих нагревательных и закалочных индукторов, магнитопровод имеет П-образную форму (рис. 2.16). Обмотка, расположенная в пазу, может иметь один или несколько слоев. Электромагнитные процессы в пазу мало связаны с процессами в остальном пространстве системы, и целесообразно использовать полную схему замещения, считая х внутренним индуктивным сопротивлением обмотки в пазу, а Xs2 — сопротивлением остальной части системы, Хв = х .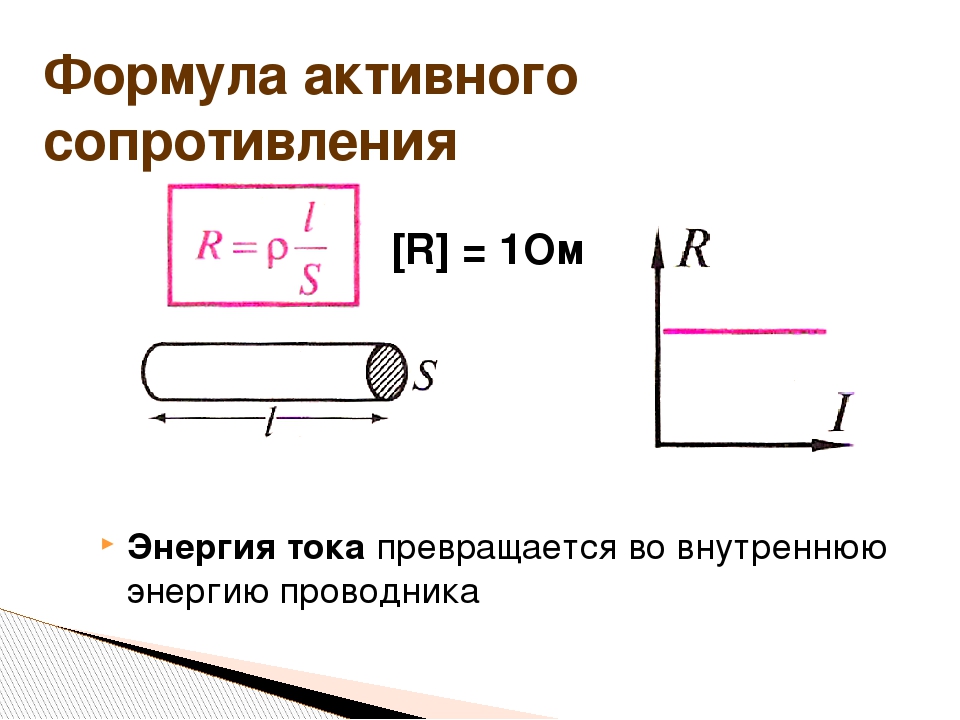 Границей раздела полей является поверхность с диаметром, равным внутреннему диаметру О полюсов магнитопровода. Параметры индуктора вне паза рассчитываются по обычной методике общего потока, причем вместо длины обмотки I следует брать ширину паза /п. Коэффициент Кь определяется по рис. 2.14 при О = Ц >/1. Ширина полюса с , как показал анализ, слабо влияет на результаты расчета. Подробнее этот вопрос рассмотрен далее для плоских индукторов.  [c.78]

Таким образом были заложены основы аэродинамики крыла бесконечного размаха. Почти одновременно с разработкой этой теории были предприняты исследования в теории крыла конечного размаха. Одной из первых работ, в которой для построения течения около крыла использовалась вихревая схема, был трактат Ф, Ланчестера, опубликованный в 1907 г. [43]. В 1910 г. Чаплыгин предложил вихревую схему крыла, а в 1913 г. на основе замены крыла П-образным вихрем дал метод расчета индуктивного сопротивления крыла. Аналогичная идея была использована Л. Прапдтлем, опубликовавшим теорию несущей линии [44], пригодную для расчета индуктивного сопротивления крыла достаточно большого удлинения. Ему же принадлежат важные для последующего развития аэродинамики результаты в теории пограничного слоя (1904 г.), в том числе объяснение сопротивления формы при обтекании тела с отрывом пограничного слоя от его поверхности [45].  [c.288]

Самой интересной является аналогия между внешним сопротивлением и индуктивным сопротивлением обратного замыкания, которое тоже обозначено х на схемах замещения индуктора в 6-1. Это сопротивление при расчете индуктора находится на основании предположения, что внешнее магнитное поле индуктора с загрузкой подобно полю пустого индуктора. Справедливость такого предположения доказана экспериментально. Очевидно, справедливо и аналогичное утверждение внешнее (краевое) электрическое поле конденсатора с загрузксй подобно полю пустого конденсатора. Отсюда сразу следует способ расчета  [c. 164]

Альсиферовые и карбонильные сердечники изготавливаются из высокодисперсных ферромагнитных частиц, которые изолируются полистироловой или бакелитовой смолой эта масса затем прессуется в сердечники нужной формы. Расчет индуктивности катушек с ферритовыми и другими магнитодиэлектрическими сердечниками весьма сложен. Уменьшение магнитного сопротивления может быть учтено с помощью так называемой катушечной эффективной магнитной проницаемости, представляющей собой отношение индуктивности катушки с сердечником к индуктивности той же катушки без сердечника.  [c.15]

Расчет сопротивления петли фаза — ноль в установках низкого напряжения с ааземленной нейтралью. Основная формула для расчета с учетом индуктивного сопротивления петли  [c.745]

На основании упрощенного представления о вторичных течениях в решетках как о парном вихре, рядом авторов для расчета вторичных потерь были предложены эмпирические формулы, аналогичные формуле индуктивного сопротивления крыла конечной длины. Так, например, Хоуэлл [112] для расчета коэффициента сопротивления компрессорных решеток с лопатками длины /г рекомендует нолуэмпирическую формулу  [c.445]

Эта формула описывает, основные закономерности изменения аэродинамических характеристик винта на висении и имеет приемлемую точность, если при расчете индуктивной мощности взять подходящую величину коэффициента k, а при расчете профильной мощности — подходящую величину среднего коэффициента сопротивления График зависимости коэффициента мощности от коэффициента силы тяги (или зависимости Ср/а от Ст/а) называют полярой несущего винта. Поляра идеального винта (профильная мощность равна нулю, индуктивная мощность минимальна, и, следовательно, коэффициент соверщенст-ва М равен 1) задается уравнением p = rVV2- Реальная поляра расположена выще идеальной из-за наличия профильных потерь и поднимается с увеличением Ст быстрее вследствие того, что индуктивные затраты больще. Примеры поляр несущего винта на висении приведены в разд. 2.6.9. Указанной выще формуле коэффициента мощности соответствует следующее выражение коэффициента соверщенства  [c.68]


Произвольный несущий ви-нт с любыми распределениями хорд и профилей лопасти, а также с любой круткой требует более обстоятельного анализа. Такой анализ-должен быть применим не только к обычным, но и к экстремальным режимам полета, в том числе режимам больщих нагрузок и больщих скоростей. Мощности, затрачиваемые на набор высоты и вредное сопротивление, можно определить точно, предполагая, что угол наклона траектории полета и вредное сопротивление известны (т. е. предполагая, что ориентацию винта можно точно найти из условий равновесия сил и моментов, действующих на вертолет). Таким образом, уточнение аэродинамического расчета вертолета достигается в основном посредством уточнения расчета индуктивной и профильной мощностей. Имеем  [c.287]
Рис.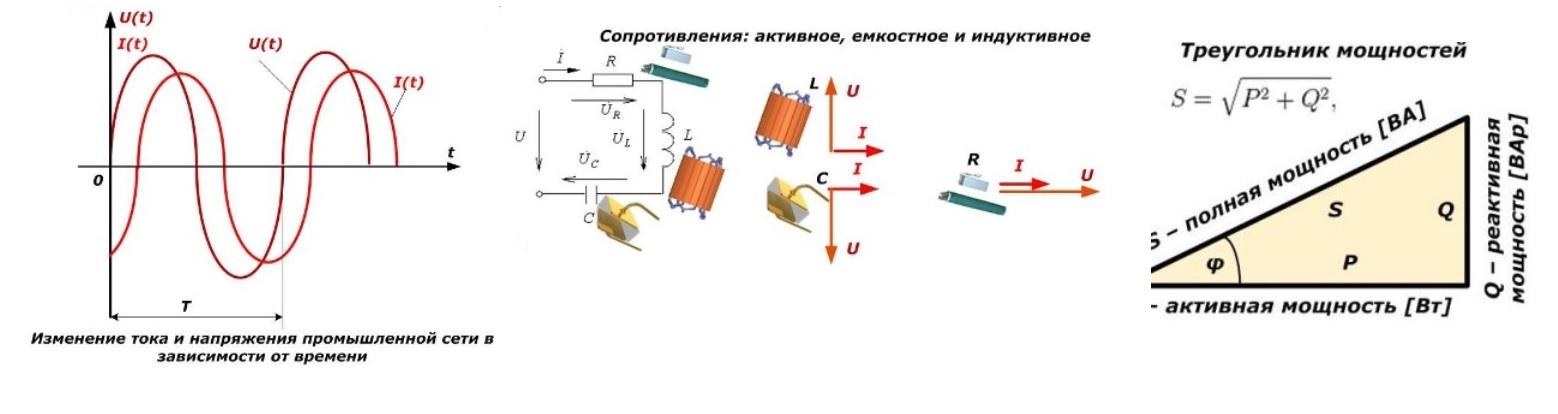 20. График для расчета актноного и внутреннего индуктивного сопротивлений цилиндрических заготовок из ферромагнитных и парамагнитных материалов
Выбор и расчет основных параметров процесса и оборудования. Активное и внутреннее индуктивное сопротивление заготовок цилиндрической формы из ферромагнитных и парамагнитных материалов определяют по рис. 20. Для заготовок из ферромагнитных материалов в виде прямоугольников, равнобоких уголков, тавров, двутавров можно пользоваться этими же графиками, если аргумент Tq/zo заменить отношением 231Пг , где S, П н Го — соответственно площадь и периметр поперечного сечения, радиус заготовки Zq = Д — глубина проникновения тока в металл (см. табл. 2).  [c.268]

Особенность высокочастотного зажигания состоит в том, что с увеличением частоты инициирующего сигнала напряжение, при котором возникает пробой, уменьшается и при некоторой частоте достигает минимума, далее с увеличением частоты напряжение про- боя снова возрастает [6]. При коротких разрядных промежутках (не более нескольких сантиметров) минимум напряжения пробоя приходится на область частот 10—20 МГц. При длинных промежутках минимум смещается к частоте в 1 МГц и ниже [7]. Это может быть объяснено тем, что с повышением частоты инициирующий сигнал все больше шунтируется распределенной емкостью длинной газоразрядной трубки. Кроме того, с ростом частоты следует учитывать необходимость повышения инициирующего напряжения для компенсации дополнительно возникающих потерь энергии сигнала. Так, например, с увеличением частоты часть инициирующего напряжения может падать на индуктивном сопротивлении подводящих проводов,. С повышением частоты растут также потери инициирующего сигнала на электромагнитное излучение. Мощность этого излучения пропорциональна току, квадрату частоты, квадрату длины проводов и зависит от магнитной и диэлектрической проницаемостей среды. Из расчетов видно, что при частоте 10 МГц и длине проводов 10 м потери на излучение достигают 807о, ири 1 МГц — 20%, при 0,1 МГц —2%.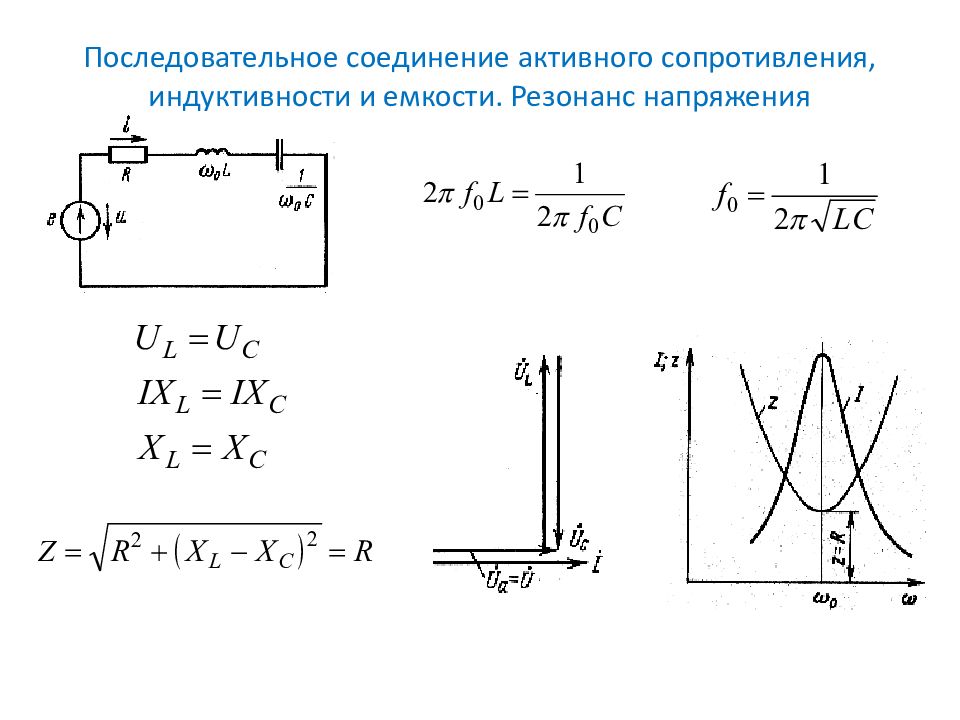  [c.6]

Здесь плотность распределения зарядов более неравномерная, на периферии она выше в 8,5 раз. Поэтому на частотах свыше 50 Гц начинается радиальное движение частиц электрореологического заполнителя в дроссельных каналах. Причем, в отличие от обычных реологических заполнителей, эпюры скоростей в каналах не будут соответствовать параболическому закону. На частотах свыше 100 Гц скорость частиц электрореологического заполнителя в пристеночной области будет даже выше, чем на осевой линии. Это свидетельствует о том, что на высоких частотах динамическая жесткость гидроопоры имеет тенденцию к понижению и, следовательно, к возрастанию диссипации энергии внешнего вибросигнала. При расчетах вязкостного сопротивления движению рабочей жидкости на частотах свыше 100 Гц необходимо произвести оценку влияния внутреннего индуктивного сопротивления.  [c.107]

При любом г /й или /d.индуктивного сопротивлений кромок может быть проведен по мето-дике, указанной в работе [6].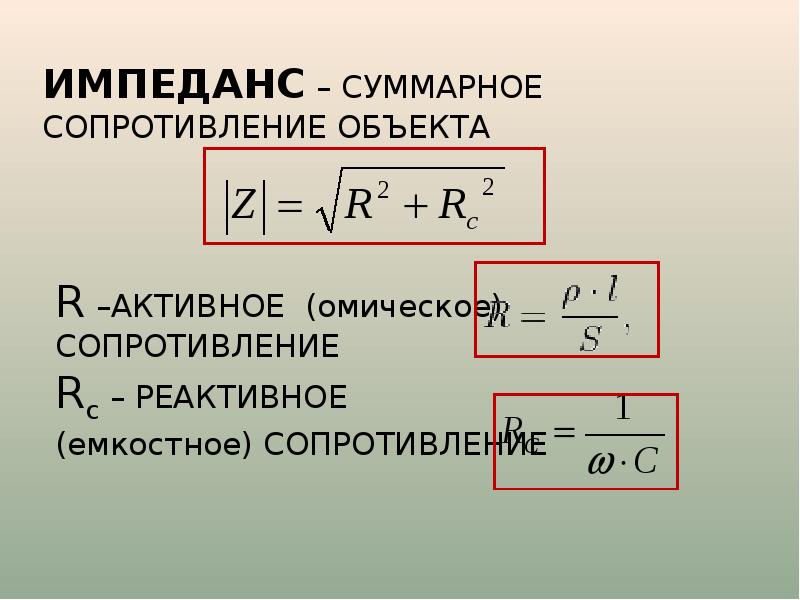 20  [c.69]

Так же как и в генераторе Г2-Б э. д. с. в обмотках статора генератора Г271 индуктируется за счет пересечения витков катушек магнитным полем вращающегося ротора. Однако в отличие от генератора Г2-Б обмоточные данные и индуктивность фазных катушек генератора Г271 подобраны с таким расчетом, чтобы обеспечить самоограничение тока, отдаваемого генератором. При 5000 об1мин индуктивное сопротивление обмоток статора возрастет настолько, что отдаваемая им сила тока не может превысить 30 а.  [c.101]

К работам по теории крыла конечного размаха тесно примыкают исследования взаимодействия несущих поверхностей с телами вращения (интерференция). А. А. Дородницыным (1944) было предложено решение задачи об определении несущих свойств системы, состоящей из крыла большого удлинения и тонкого длинного фюзеляжа. Крыло заменялось несущей линией (пронизывающей фюзеляж) с переменной по размаху циркуляцией и сходящими с нее свободными вихрями, а фюзеляж — соответствующими особенностями, расположенными на оси.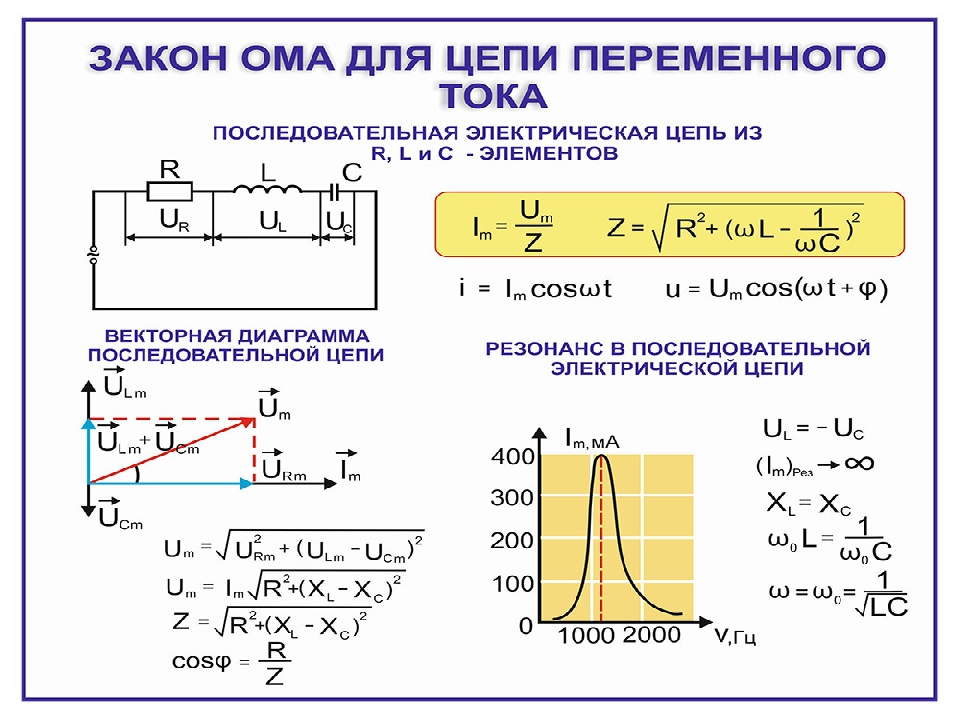 В. Ф. Лебедев (1958) обобщил метод А. А. Дородницына на случай стреловидного крыла и крыла малого удлинения с тонким фюзеляжем. В работе А. А. Никольского (1957) предложено правило расчета подъемной силы а индуктивного сопротивления и рассмотрены некоторые задачи оптимизации системы крыло — фюзеляж в случае, когда крыло мало возмущает осесимметричный поток вокруг фюзеляжа. Вихревые линии, сходящие с крыла, при этом криволинейны и расположены вдоль линий тока исходного осесимметричного потока около изолированного фюзеляжа. А. И. Го-лубинский (1961) разработал метод решения задачи для обтекания крыла с бесконечно длинным цилиндрическим фюзеляжем. При этом для крыла использовалась теория несущей поверхности, а на поверхности фюзеляжа удовлетворялись граничные условия и путем разложения в ряды с помощью цилиндрических функций решалась соответствующая краевая задача. Расчет и опыты показали, что если диаметр фюзеляжа сравним с размахом крыла, то аэродинамическая сила, возникающая вследствйе интерференции, получается того же порядка, что и сила, действующая на изолированные консоли крыла. 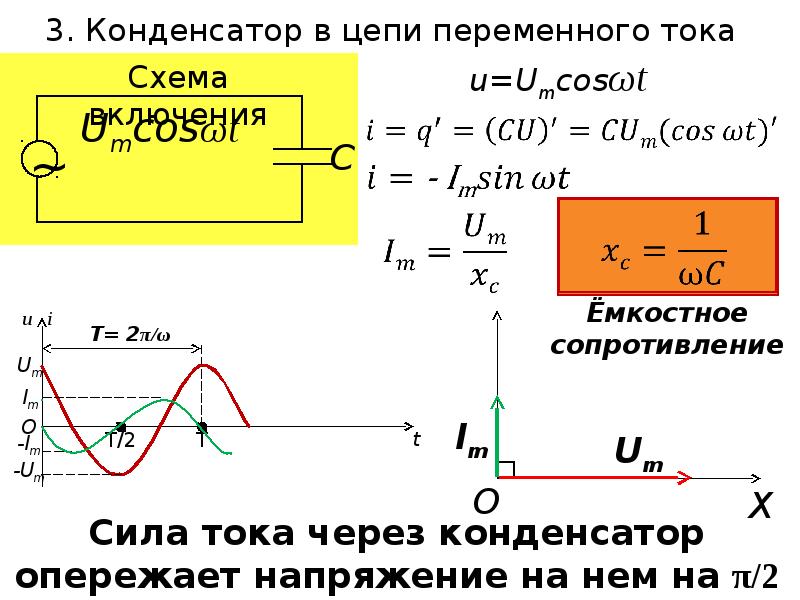 [c.97]

Индуктивное сопротивление катушки — Основы электроники

Так как самоиндукция препятствует всякому резкому изменению силы тока в цепи, то, следовательно, она представляет собой для переменного тока особого рода сопротивление, называемое индуктивным сопротивлением.

Чисто индуктивное сопротивление отличается от обычного (омического) сопротивления тем, что при прохождении через него переменного тока в нем не происходит потери мощности.

Под чисто индуктивным сопротивлением мы понимаем сопротивление, оказываемое переменному току катушкой, проводник которой не обладает вовсе омическим сопротивлением. В действительности же всякая катушка обладает некоторым омическим сопротивлением. Но если это сопротивление невелико по сравнению с индуктивным сопро¬тивлением, то им можно пренебречь.

При этом наблюдается следующее явление: в течение одной четверти периода, когда ток возрастает, магнитное поле потребляет энергию из цепи, а в течение следующей четверти периода, когда ток убывает, возвращает ее в цепь. Следовательно, в среднем за период в индуктивном сопротивлении мощность не затрачивается. Поэтому индуктивное сопротивление называется реактивным (прежде его неправильно называли безваттным).

Индуктивное сопротивление одной и той же катушки будет различным для токов различных частот. Чем выше частота переменного тока, тем большую роль играет индуктивность и тем больше будет индуктивное сопротивление данной катушки. Наоборот, чем ниже частота тока, тем индуктивное сопротивление катушки меньше. При частоте, равной нулю (установившийся постоянный ток), индуктивное сопротивление тоже равно нулю.

 Рисунок 1. Зависимость индуктивного сопротивления катушки от частоты переменного тока. Реактивное сопротивление катушки возрастает с увеличением часторы тока.

Индуктивное сопротивление обозначается буквой XL и измеряется в омах.

Подсчет индуктивного сопротивления катушки для переменного тока данной частоты производится по формуле

XL=2π• f •L

где XL — индуктивное сопротивление в ом; f—частота переменного тока в гц; L — индуктивность катушки в гн

Как известно, величину 2π• f называют круговой частотой и обозначают буквой ω (омега). Поэтому приведенная выше формула может быть представлена так:

XL=ω•L

Отсюда следует, что для постоянного тока (ω = 0) индуктивное сопротивление равно нулю. Поэтому, когда, нужно пропустить по какой-либо цепи постоянный ток, задержав в то же время переменный, то в цепь включают последовательно катушку индуктивности.

Для преграждения пути токам низких звуковых частот ставят катушки с железным сердечником, так называемые дроссели низкой частоты, а для более высоких радиочастот — без железного сердечника, которые носят название дросселей высокой частоты.

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Похожие материалы:

Добавить комментарий

Расчёт реактивного сопротивления

Реактивное сопротивление – электрическое сопротивление переменному току, обусловленное передачей энергии магнитным полем в индуктивностях или электрическим полем в конденсаторах.

Элементы, обладающие реактивным сопротивлением, называют реактивными.

Реактивное сопротивление катушки индуктивности.

При протекании переменного тока I в катушке, магнитное поле создаёт в её витках ЭДС, которая препятствует изменению тока.
При увеличении тока, ЭДС отрицательна и препятствует нарастанию тока, при уменьшении — положительна и препятствует его убыванию, оказывая таким образом сопротивление изменению тока на протяжении всего периода.

В результате созданного противодействия, на выводах катушки индуктивности в противофазе формируется напряжение U, подавляющее ЭДС, равное ей по амплитуде и противоположное по знаку.

При прохождении тока через нуль, амплитуда ЭДС достигает максимального значения, что образует расхождение во времени тока и напряжения в 1/4 периода.

Если приложить к выводам катушки индуктивности напряжение U, ток не может начаться мгновенно по причине противодействия ЭДС, равного -U, поэтому ток в индуктивности всегда будет отставать от напряжения на угол 90°. Сдвиг при отстающем токе называют положительным.

Запишем выражение мгновенного значения напряжения u исходя из ЭДС (ε), которая пропорциональна индуктивности L и скорости изменения тока: u = -ε = L(di/dt).
Отсюда выразим синусоидальный ток .

Интегралом функции sin(t) будет -соs(t), либо равная ей функция sin(t-π/2).
Дифференциал dt функции sin(ωt) выйдет из под знака интеграла множителем 1/ω.
В результате получим выражение мгновенного значения тока со сдвигом от функции напряжения на угол π/2 (90°).
Для среднеквадратичных значений U и I в таком случае можно записать .

В итоге имеем зависимость синусоидального тока от напряжения согласно Закону Ома, где в знаменателе вместо R выражение ωL, которое и является реактивным сопротивлением:

Реактивное сопротивлениие индуктивностей называют индуктивным.

Реактивное сопротивление конденсатора.

Электрический ток в конденсаторе представляет собой часть или совокупность процессов его заряда и разряда – накопления и отдачи энергии электрическим полем между его обкладками.

В цепи переменного тока, конденсатор будет заряжаться до определённого максимального значения, пока ток не сменит направление на противоположное. Следовательно, в моменты амплитудного значения напряжения на конденсаторе, ток в нём будет равен нулю. Таким образом, напряжение на конденсаторе и ток всегда будут иметь расхождение во времени в четверть периода.

В результате ток в цепи будет ограничен падением напряжения на конденсаторе, что создаёт реактивное сопротивление переменному току, обратно-пропорциональное скорости изменения тока (частоте) и ёмкости конденсатора.

Если приложить к конденсатору напряжение U, мгновенно начнётся ток от максимального значения, далее уменьшаясь до нуля. В это время напряжение на его выводах будет расти от нуля до максимума. Следовательно, напряжение на обкладках конденсатора по фазе отстаёт от тока на угол 90 °. Такой сдвиг фаз называют отрицательным.

Ток в конденсаторе является производной функцией его заряда i = dQ/dt = C(du/dt).
Производной от sin(t) будет cos(t) либо равная ей функция sin(t+π/2).
Тогда для синусоидального напряжения u = Uampsin(ωt) запишем выражение мгновенного значения тока следующим образом:

i = UampωCsin(ωt+π/2).

Отсюда выразим соотношение среднеквадратичных значений .

Закон Ома подсказывает, что 1/ωC есть не что иное, как реактивное сопротивление для синусоидального тока:

Реактивное сопротивление конденсатора в технической литературе часто называют ёмкостным. Может применяться, например, в организации ёмкостных делителей в цепях переменного тока.


Калькулятор расчёта реактивного сопротивления

Необходимо вписать значения и кликнуть мышкой в таблице.
При переключении множителей автоматически происходит пересчёт результата.

Расчитать реактивное сопротивление ёмкости или индуктивности:

Реактивное сопротивление ёмкости
XC = 1 /(2πƒC)

Реактивное сопротивление индуктивности
XL = 2πƒL

Расчитать ёмкость и индуктивность от сопротивления:

Расчёт ёмкости: C = 1 /(2πƒXC)

Расчёт индуктивности: L = XL /(2πƒ)


Похожие страницы с расчётами:

Расcчитать импеданс.

Расcчитать частоту резонанса колебательного контура LC.

Расcчитать реактивную мощность и компенсацию.

что это такое и от чего зависит

В радиотехнике часто приходится сталкиваться с индуктивным сопротивлением. Его источником являются катушки. Они представляют собой двухполюсник, намотанный медным эмалированным проводом (обычно это ПЭТВ) на ферритовый или железный сердечник. Подобные детали встречаются в широком перечне оборудования: от древних советских радиоприёмников до материнских плат ПК последних моделей.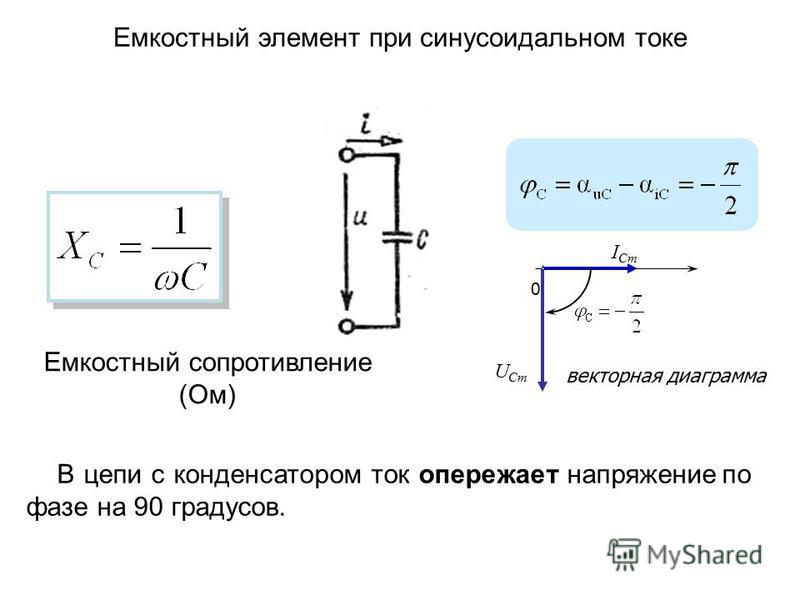

Катушки индуктивности

Формулы, зависимости и виды индуктивности

Электрическая индуктивность L – это величина, равная коэффициенту пропорциональности между током I, протекающим в замкнутом контуре, и создаваемым им магнитным потоком, иначе называемым потокосцеплением Y:

Y = LI.

Если к выводам катушки на некоторое время приложить напряжение, то в ней начнёт протекать ток I и формироваться магнитное поле. Чем меньше индуктивность L, тем быстрее протекает данный процесс. В итоге рассматриваемый двухполюсник накопит некоторое количество потенциальной энергии. При отключении питания он будет стремиться её вернуть. В результате на выводах катушки образуется ЭДС самоиндукции E, которая многократно превышает изначально приложенное напряжение. Подобная технология ранее использовалась в магнето систем зажигания ДВС, а сейчас широко встречается в повышающих DC-DC преобразователях.

Формула ЭДС самоиндукции, здесь t – это время, в течение которого ток I уменьшится до нуля

Простой DC-DC повышающий преобразователь

Катушка (она же – дроссель) – это радиодеталь с ярко выраженной индуктивностью, ведь именно для этого её и создавали. Однако подобным свойством обладают в принципе все элементы. Например, конденсатор, резистор, кабель, просто кусок провода и даже тело человек также имеют некоторую индуктивность. В расчетах ВЧ схем это обязательно принимается во внимание.

Важно! Проводя измерение индуктивности специализированным прибором, стоит помнить, что нельзя держаться руками за оба его вывода. В противном случае показания могут измениться и будут неверными. Вызвано это включением в измеряемую цепь тела человека с его собственной индуктивностью.

Сопротивление катушки переменному току

Гораздо интереснее дела обстоят с индуктивностью в контуре переменного тока. Любая катушка содержит в себе две составляющие сопротивления:

  1. Активную;
  2. Индуктивную.

При постоянном токе учитывается только первый фактор, а при переменном – оба. Формула индуктивного сопротивления XL катушки имеет следующий вид:

XL = 2pfL,

где:

  • p = 3. 14;
  • f – частота переменного тока, Гц;
  • L – индуктивность катушки, Гн.

Полное сопротивление катушки Z, называемое импедансом, определяется, исходя из активной R и индуктивной XL составляющих.

Импеданс катушки

Важно! Если катушка установлена в печатную плату, то для проверки её следует отпаять. В таком случае индуктивность будет измеряться независимо от других компонентов, что существенно повысит точность показаний прибора.

Расчёт индуктивного сопротивления катушки

Любая индуктивность, в т.ч. катушка, оказывает переменному току некоторое сопротивление. Как его рассчитать, было описано выше. Из формулы XL=2pfL видно, что сопротивление дросселя в первую очередь зависит от частоты протекающего по нему тока и его индуктивности. При этом с обоими параметрами связь прямо пропорциональная.

Частота – это характеристика внешней среды, индуктивность катушки зависит от ряда её геометрических свойств:

L=u0urN2S/l,

где:

  • u0 – магнитная проницаемость вакуума — 4p*10-7 Гн/м;
  • ur – относительная проницаемость сердечника;
  • N – количество витков дросселя;
  • S – его поперечное сечение в м2;
  • l – длина катушки в метрах.

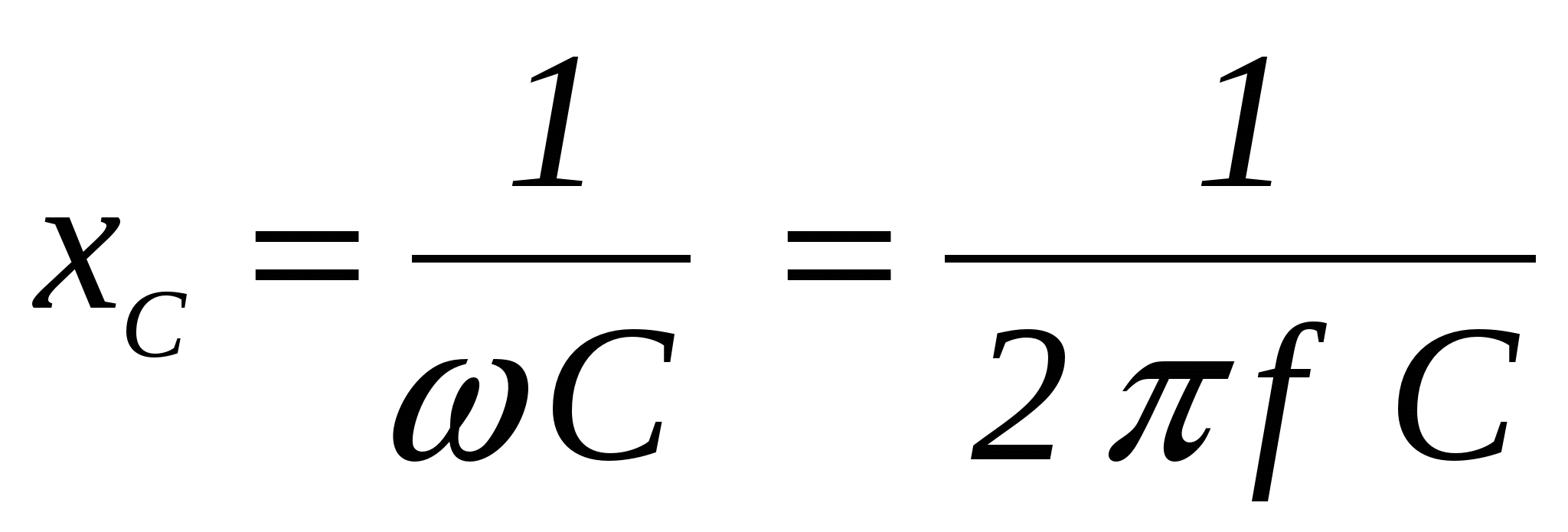
Располагая вышеописанными формулами и информацией о материале и размерах катушки, можно достаточно точно прикинуть её индуктивное сопротивление без каких-либо измерительных приборов.

Дополнительная информация. Некоторые цифровые мультиметры имеют режим замера индуктивности. Подобная функция встречается редко, однако иногда оказывается очень полезной. Поэтому при выборе прибора стоит обратить внимание на то, способен ли он измерять индуктивность.

Где применяется катушка (дроссель, индуктивность)

Дроссели имеют примитивную конструкцию: просто намотанный витками на каком-либо сердечнике проводник. В то же время в таком приборе нечему ломаться. Также у дросселей широчайший функционал и десятки применений. Из всего этого следует, что в какой бы точке города ни находился человек, в радиусе 1 км от него всегда будут тысячи катушек индуктивности, настолько они распространены.

Катушка как электромагнит

Самое простое применение катушки – это электромагнит. С подобным применением каждый сталкивается, заходя в подъезд. Сила, удерживающая дверь на месте и препятствующая несанкционированному доступу чужака, берётся из электромагнита. Он находится сверху.

Электрический ток, проходя по виткам катушки, создаёт вокруг неё переменное электромагнитное поле. Оно возбуждает в металлическом «бруске», расположенном на двери, вихревые токи, которые так же создают магнитное поле. В результате получаются два управляемых магнита. Они притягиваются друг к другу. Тем самым дверь надёжно удерживается на месте.

Другое применение электромагнитов в быту – индукционные плиты. Катушка наводит в металлической посуде переменный высокочастотный ток. Он, в свою очередь, своим тепловым действием разогревает кастрюлю. В промышленности нечто подобное используется для разогрева и плавки металлов. Только в таком случае применяются на порядки более высокие мощности и другие частоты тока.

Индукционный нагрев металла

Индуктивность как фильтр

Импульсные блоки питания, электрические двигатели и диммеры для регулировки яркости ламп накаливания выбрасывают в сеть большое количество искажений и помех. Вызвано это неравномерностью потребляемого тока. Для борьбы с подобными сетевыми шумами применяются специальные фильтры на основе конденсаторов и дросселей.

Данный узел представляет собой небольшую катушку из медного эмалированного провода диаметром 0,2-2 мм. Обмотка наматывается на ферритовый сердечник. Чаще всего он изготовлен в форме кольца, немного реже встречаются так называемые «гантельки».

Подобные фильтры имеются в компьютерных блоках питания, компактных люминесцентных лампах (иногда не ставят, экономят), на выходах сварочных инверторов.

Также фильтр может быть звуковым. Его задача – срезать определённый диапазон частот. Индуктивные свойства этого прибора таковы, что он хорошо проводит низкие частоты, а высокие – приглушает. Поэтому дроссели используют для того, чтобы до динамиков дошёл только бас. По факту ослаблено будут слышны и другие частоты. Для более эффективной работы фильтра нужны дополнительные детали: конденсаторы и операционные усилители.

Самодельный звуковой фильтр

Катушка как источник ЭДС

Китайская промышленность удивила школьников 2000-х новой игрушкой – вечным фонариком. Его не нужно было заряжать. Фонарик работал от катушки индуктивности, около которой под действием движения рук перемещался магнит. Он наводил в обмотке переменную ЭДС, которая питала осветительный прибор.

Подобное явление объясняется законом электромагнитной индукции.  Если проводник (рамка) находится в переменном электромагнитном поле, то в нём начинает наводиться электродвижущая сила. Иными словами, появляется напряжение.

Закон этот совсем неигрушечный, ведь он используется в работе генераторов на подавляющем большинстве электростанций, в том числе любые ТЭЦ, ГЭС, АЭС и ветряки. По подобному принципу работают динамомашины, питающие фары велотранспорта.

Принцип работы генератора

Две катушки – трансформатор

Ещё одно распространённое применение – это электрический трансформатор. Конструктивно он состоит из двух и более катушек, расположенных на одном железном или ферритовом сердечнике. Подобный агрегат работает только с переменным напряжением. Если на первичную обмотку подать ток, то он создаст в сердечнике магнитный поток. Он, в свою очередь, наведёт ЭДС во вторичной обмотке. Напряжения во входной и выходной катушках прямо зависят от количества их витков.

Таким образом, можно трансформировать 220 В из розетки в 12 В, необходимых для питания небольшой стереосистемы, или преобразовать 10 000 вольт в 220 для передачи от подстанции к жилым домам. Подобным методом можно добиться и повышения напряжения, т.е. превратить 12 В обратно в 220.

Устройство трансформатора

Катушка индуктивности — элемент колебательного контура

Сейчас это уже редкость, но раньше для подстройки нужной радиостанции использовали колебательный контур. Он состоит из двух элементов, включенных параллельно: катушки индуктивности и переменного конденсатора. Работая в паре, они способны выделить из множества окружающих сигналов именно тот, который требуется. При попадании на антенну приёмника нужной частоты электромагнитных волн колебательный контур входит в резонанс. Процесс сопровождается лавинообразным увеличением ЭДС. Частота, на которой это происходит, зависит от индуктивности катушки и ёмкости конденсатора.

Катушка индуктивности – дроссель ДРЛ ламп

Несмотря на то, что освещение улиц и промышленных предприятий стремительно переходит на LED светильники, по СНГ всё ещё осталось огромное количество мест, где используются устаревшие дуговые ртутные люминесцентные лампы типа ДРЛ. Более всего они распространены в мелких городах и на второстепенных улицах. Их можно узнать по характерному холодно-белому свету и долгому розжигу.

ДРЛ лампы не способны работать без пускорегулирующего дросселя. Он обладает высоким индуктивным сопротивлением и призван ограничить пусковой ток осветительного прибора. Дроссели для ламп подбираются, исходя из их мощности. Наиболее распространённые номиналы – 250, 400 и 1000 Вт. Информация о мощности указывается на самом дросселе. Там же можно найти схемы включения.

Из вышесказанного можно подчеркнуть, что катушка индуктивности является консервативным и давно освоенным на практике электронным компонентом. Однако спрос на его применение по-прежнему не спадает. Поэтому знания, необходимые для расчета катушек и их правильного включения, необходимы каждому специалисту, имеющему дело с электроникой.

Видео

Емкостное сопротивление конденсатора формула расчёта и последовательность соединения в цепи

Емкостное сопротивление конденсатора – величина, измеряемая в омах, создается непосредственно самим конденсатором, который включен в любую цепь. Оно должно иметь большую величину, то есть быть большим. Если на них происходит подача переменного тока, в устройстве происходят процессы заряда и последующего разряда. Последнее происходит по требованию цепи. При включении электрического тока, напряжение будет равно 0. Само устройство при этом начнет заряжаться, следовательно его величина напряжения постепенно растет. В случае необходимости, при достижении максимального заряда, произойдет разряд конденсатора.

В статье, посвященной теме расчета сопротивления конденсатора, приведена вся информация о процессе, как происходит заряд-разряд. В качестве бонуса есть интересный материал по теме, который можно скачать, и видеоролик в конце статьи.

Формула сопротивления конденсаторов.

Формула сопротивления

Формула ёмкостного сопротивления выводится следующим образом:

  • Вначале следует вычислить угловую частоту. Для этого частоту протекающего по цепи тока (в герцах) необходимо умножить на удвоенное число «пи».
  • Затем полученное число следует перемножить на ёмкость конденсатора в фарадах.

Чтобы получить значение ёмкостного сопротивления в омах, следует разделить единицу на число, полученное после умножения угловой частоты на ёмкость. Из этой формулы вытекает, что чем больше ёмкость конденсатора или частота переменного тока, тем меньше его сопротивление. Когда частота будет равна нулю (постоянный ток), ёмкостное сопротивление станет бесконечно большим. Конденсатор очень большой ёмкости будет проводить ток в широком диапазоне частот.

Формула сопротивления.

Применение на практике

Свойства конденсатора используются при конструировании различных фильтров. Действие ёмкостного сопротивления в этом случае зависит от способа подключения детали:

  • Если он присоединён параллельно нагрузке, то получится фильтр, задерживающий высокие частоты. С их ростом падает сопротивление конденсатора. Соответственно, нагрузка на высоких частотах шунтируется сильнее, чем на низких.
  • Если деталь подключена последовательно с нагрузкой, то получится фильтр, задерживающий низкие частоты. Эта схема также не пропускает постоянное напряжение.
  • Ещё одна область применения — отделение переменной составляющей от постоянной. Например, в оконечных каскадах усилителей звуковой частоты. Чем выше ёмкость, тем более низкую частоту способен воспроизвести подключённый громкоговоритель.

В фильтрах электропитания, наряду с ёмкостным сопротивлением, используется также свойство накопления и отдачи заряда. В момент повышения нагрузки заряженная ёмкость фильтра разряжается, отдавая дополнительную энергию. Она также осуществляет подавление пульсаций и прочих паразитных сигналов, пропуская их через себя и замыкая на общий провод. Таким образом, обеспечивается сглаживание и поддержание напряжения на нагрузке в заданных пределах, и устранение нежелательных междукаскадных связей, вызывающих нестабильную работу.

Измерение сопротивления конденсаторов.

Характеристики прибора

Важнейшей характеристикой накопительного прибора является ёмкость. От неё зависит время заряда при подключении устройства к источнику тока. Время разряда напрямую связано со значением сопротивления нагрузки: чем оно выше, тем быстрее происходит процесс отдачи накопленной энергии. Определяется эта ёмкость следующим выражением:

C = E*Eo*S / d, где E — относительная диэлектрическая проницаемость среды (справочная величина), S — площадь пластин, d — расстояние между ними. Кроме ёмкости конденсатор характеризуется рядом параметров, такими как:

  • удельная ёмкость — определяет отношение величины ёмкости к массе диэлектрика;
  • рабочее напряжение — номинальное значение, которое может выдержать устройство при подаче его на обкладки элемента;
  • температурная стабильность — интервал, в котором ёмкость конденсатора практически не изменяется;
  • сопротивление изоляции — характеризуется саморазрядом устройства и определяется током утечки;
  • эквивалентное сопротивление — состоит из потерь, образуемых на выводах прибора и слое диэлектрика;
  • абсорбция — процесс возникновения разности потенциалов на обкладках после разряда устройства до нуля;
  • ёмкостное сопротивление — уменьшение проводимости при подаче переменного тока;
  • полярность — из-за физических свойств материала, используемого при изготовлении, конденсатор сможет правильно работать, только если к обкладкам приложен потенциал с определённым знаком;
  • эквивалентная индуктивность — паразитный параметр, появляющийся на контактах устройства и превращающий конденсатор в колебательный контур.

Таблицы максимальных значений емкости конденсаторов.

Импеданс элемента

Общее сопротивление конденсатора (импеданс) переменному сигналу складывается из трёх составляющих: ёмкостного, резистивного и индуктивного сопротивления. Все эти величины при конструировании схем, содержащих накопительный элемент, необходимо учитывать. В ином случае в электрической цепи, при соответствующей обвязке, конденсатор может вести себя как дроссель и находится в резонансе.

Из всех трёх величин наиболее значимой является ёмкостное сопротивление конденсатора, но при определённых обстоятельствах индуктивное тоже оказывает влияние. Часто при расчётах паразитные значения вроде индуктивности или активного сопротивления принимаются ничтожно малыми, а конденсатор в этом случае называется идеальным.

Полное сопротивление элемента выражается в формуле Z = (R2 + (Xl-Xc) 2 ) ½, где

  • Xl — индуктивность;
  • Xс — ёмкость;
  • R — активная составляющая.

Последняя возникает из-за появления электродвижущей силы (ЭДС) самоиндукции. Непостоянство тока приводит к изменению магнитного потока, поддерживающего ток ЭДС самоиндукции постоянным. Это значение определяется индуктивностью L и частотой протекающих зарядов W. Xl = wL = 2*p*f*L. Xc — ёмкостное сопротивление, зависящее от ёмкости накопителя C и частоты тока f. Xc = 1/wC = ½*p*f*C, где w — круговая частота.

Материал в тему: все о переменном конденсаторе.

Разница между ёмкостным и индуктивным значениями называется реактивным сопротивлением конденсатора: X = Xl-Xc. По формулам можно увидеть, что при увеличении частоты f сигнала начинает преобладать индуктивное значение, при уменьшении — ёмкостное. Поэтому если:

  • X > 0, в элементе проявляются индуктивные свойства;
  • X = 0, в ёмкости присутствует только активная величина;
  • X < 0, в элементе проявляется ёмкостное сопротивление.

Активное сопротивление R связывается с потерями мощности, превращением её электрической энергии в тепловую. Реактивное – с обменом энергии между переменным током и электромагнитным полем. Таким образом, полное сопротивление можно найти, используя формулу Z = R +j*X, где j — мнимая единица.

Импеданс элемента.

Пример расчёта

Ёмкостное и индуктивное сопротивления относятся к реактивным, то есть таким, которые не потребляют мощности. Поэтому закон Ома для участка схемы с ёмкостью имеет вид I = U/Xc, где ток и напряжение обозначают действующие значения. Именно из-за этого конденсаторы используются в цепях для разделения не только постоянных и переменных токов, но и низкой и высокой частот. При этом чем ёмкость будет ниже, тем более высокой частоты сможет пройти ток. Если же последовательно с конденсатором включено активное сопротивление, то общий импеданс цепи находится как Z = (R 2 +Xc 2 ) ½.

Практическое применение формул можно рассмотреть при решении задачи. Пусть имеется RC цепочка, состоящая из ёмкости C = 1 мкФ и сопротивления R = 5 кОм. Необходимо найти импеданс этого участка и ток цепи, если частота сигнала равна f = 50 Гц, а амплитуда U = 50 В.

Стоит почитать: все об электролитических конденсаторах.

В первую очередь понадобится определить сопротивление конденсатора в цепи переменного тока для заданной частоты. Подставив данные в формулу, получим, что для частоты 50 Гц сопротивление будет

Xc = 1/ (2*p*F*C) = 1/ (2*3,14*50*1* 10 −6 ) = 3,2 кОм.

По закону Ома можно найти ток: I = U /Xc = 50 /3200 = 15,7 мА.

Напряжение берётся изменяемым по закону синуса, поэтому: U (t) = U * sin (2*p*f*t) = 50*sin (314*t). Соответственно, ток будет I (t) = 15,7* 10 −3 + sin (314*t+p/2). Используя полученные результаты, можно построить график тока и напряжения при этой частоте. Общее сопротивление участка цепи находим как Z = (50002+32002)½ = 5 936 Ом =5,9 кОм.

Таким образом, подсчитать полное сопротивление на любом участке цепи несложно. При этом можно воспользоваться и так называемыми онлайн-калькуляторами, куда вводят начальные данные, такие как частота и ёмкость, а все расчёты выполняются автоматически. Это удобно, так как нет необходимости запоминать формулы и вероятность ошибки при этом стремится к нулю.

Свойства ёмкостей

Основное свойство состоит в их способности накапливать и отдавать электрический заряд. Оба этих процесса происходят не мгновенно, а за вполне определённый период, который поддаётся расчету. Данное свойство используется для создания различных времязадающих RC цепей. Если зарядить конденсатор до некоторого значения, то время его разряда через резистор R будет зависеть от ёмкости C. RC цепь Ещё одно распространённое свойство конденсаторов – это возможность ограничивать переменный ток. Вызвана она реактивом этих элементов. Ёмкость, включенная в цепь переменного тока, ограничивает его до значения I = 2pfCU.

Свойства ёмкостей.

Здесь U – напряжение источника питания. Дополнительная информация. Ёмкость, подключенная параллельно с катушкой, имеющей индуктивный характер сопротивления, называется колебательным контуром. Данная цепь обладает высокой амплитудой колебаний на резонансной частоте. Она применяется для выделения из множества окружающих радиосигналов именно того, на который требуется настроить приём.

Сопротивление – это одна их характеристик конденсатора, подключенного к цепи переменного тока. Понимание процессов, происходящих с этим элементом в подобных схемах, существенно расширяет сферу его использования. Реактивное сопротивление конденсаторов учитывается как в простых бытовых электроприборах, так и в сложной вычислительной технике.

Резистор обладает активным (омическим) сопротивлением. Катушка индуктивности и конденсатор обладают реактивным сопротивлением. В цепи переменного тока на конденсаторе ток опережает напряжение на 90 градусов, а на катушке ток отстает от напряжения на 90 градусов. Сопротивление катушки вычисляется по формуле. Сопротивление конденсатора вычисляется по формуле:

Расчет сопротивления.

В цепи переменного тока на идеальном реактивном сопротивлении не выделяется мощность.

Z = R + i X , где Z – импеданс, R – величина активного сопротивления , X – величина реактивного сопротивления, i – мнимая единица . В зависимости от величины X какого-либо элемента электрической цепи, говорят о трёх случаях:

  • X > 0 – элемент проявляет свойства индуктивности .
  • X = 0 – элемент имеет чисто активное сопротивление .
  • X < 0 – элемент проявляет ёмкостные свойства.

Величина реактивного сопротивления может быть выражена через величины индуктивного и ёмкостного сопротивлений.

Индуктивное сопротивление (X L ) обусловлено возникновением ЭДС самоиндукции . Электрический ток создает магнитное поле. Изменение тока, и как следствие изменение магнитного поля, вызывает ЭДС самоиндукции, которая препятствует изменению тока. Величина индуктивного сопротивления зависит от индуктивности элемента и частоты протекающего тока. Ёмкостное сопротивление (X C ). Величина ёмкостного сопротивления зависит от ёмкости элемента С и также частоты протекающего тока.

Заключение

В данной статье были рассмотрены основные вопросы расчета сопротивления конденсаторов.  Больше информации можно найти в скачиваемой версии учебника по электромеханике “Что такое конденсаторы”

В нашей группе ВК можно задавать вопросы и получать на них подробные ответы от профессиональных электронщиков. Чтобы подписаться на группу, вам необходимо будет перейти по следующей ссылке: https://vk.com/electroinfonet. В завершение статьи хочу выразить благодарность источникам, откуда мы черпали информацию:

www.amperof.ru

www.eduspb.com

www.beasthackerz.ru

www.electroandi.ru

www.websor.ru

Предыдущая

КонденсаторыСколько стоят керамические конденсаторы?

Следующая

КонденсаторыЧто такое ионистор?

Определение активных и индуктивных сопротивлений проводов

Доброго времени суток. В данной статье речь пойдет о расчете активных и индуктивных сопротивлений для воздушных и кабельных линий из цветных металлов, таких как медь и алюминий. Данные расчеты обычно приходится выполнять, когда нужно выполнить расчет токов короткого замыкания в распределительных сетях.

Определение активного сопротивления проводов

Активное сопротивлении проводов проще всего определять по справочным данным, составленным на основании ГОСТ 839-80 – «Провода неизолированные для воздушных линий электропередач» таблицы 1 – 4. Данные таблицы вы сможете найти непосредственно в самом ГОСТ, приведу лишь не которые.

Пользоваться всеми известными формулами по определению активного сопротивления — не рекомендуется [Л1. с.18],связано это с тем, что действительное сечение отличается от номинального сечения, провода выпускались в разное время, по разным ГОСТ и ТУ и величины удельной проводимости (ρ) и удельного сопротивления (γ) у них разные:

где:

  • γ – значение удельной проводимости для медных и алюминиевых проводов при температуре 20 °С принимается: для медных проводов – 53 м/Ом*мм2; для алюминиевых проводов – 31,7 м/Ом*мм2;
  • s – номинальное сечение провода(кабеля),мм2;
  • l – длина линии, м;
  • ρ – значение удельного сопротивления принимается: для медных проводов — 0,017-0,018 Ом*мм2/м; для алюминиевых проводов – 0,026 — 0,028 Ом*мм2/м, см. таблицу 1.14 [Л2. с.30].

Активные сопротивления стальных проводов математическому расчету не поддаются. Поэтому рекомендую для определения активного сопротивления использовать приложения П23 – П25 [Л1. с.80,81].

Определение индуктивного сопротивления проводов

Индуктивное сопротивление воздушных линий для стандартной частоты f = 50 Гц и относительной магнитной проницаемости для цветных металлов µ = 1, определяется по известной всем формуле [Л1.с.19]:

где:

  • Dср. – среднее геометрическое расстояние между проводами, мм;
  • dр – расчетный диаметр провода (мм2), определяется по ГОСТ 839-80, таблицы 1 -4;

Среднее геометрическое расстояние между проводами определяется по формуле [Л1.с.19]:

где:

  • D1-2 — расстояние между проводами первой и второй фазы;
  • D2-3 — расстояние между проводами второй и третей фазой;
  • D1-3 — расстояние между первой и третей фазой.

Данные значения определяются по чертежам опор линий электропередачи.

Для упрощения расчетов индуктивного сопротивления проводов рекомендуется использовать приложения П28-П31 [Л1.с.83-85], предварительно определив значение Dср.

Если же нужно выполнить приближенный расчет, то можно использовать в расчетах средние значения сопротивлений:

  • для линий 0,4 – 10 кВ х = 0,3 Ом/км;
  • для линий 35 кВ х = 0,4 Ом/км;
  • для стальных проводов использовать приложение П6 [Л1.с.70];

Индуктивное сопротивление кабелей рассчитать довольно сложно, из-за различной их конструкции. Поэтому активные и индуктивные сопротивления кабелей рекомендуется принимать по справочникам, приложение П7 [Л1.с.70].

Если же нужно выполнить приближенный расчет, можно принять индуктивные сопротивления:

  • для кабелей сечением 16 – 240 мм2 х = 0,06 Ом/км для напряжения до 1000 В;
  • для кабелей сечением 16 – 240 мм2 х = 0,08 Ом/км для напряжения 6 – 10 кВ;
  • для проводов проложенных на роликах х = 0,20 Ом/км;
  • для проводов проложенных на изоляторах х = 0,25 Ом/км;

Литература:

1. Расчет токов короткого замыкания в электросетях 0,4-35 кВ, Голубев М.Л. 1980 г.
2. Справочная книга электрика. Григорьева В.И. 2004 г.

Всего наилучшего! До новых встреч на сайте Raschet.info.

Поделиться в социальных сетях

Реактивное сопротивление, индуктивное и емкостное | Физика II

Цели обучения

К концу этого раздела вы сможете:

  • Зависимость напряжения и тока от времени в простых индуктивных, емкостных и резистивных цепях.
  • Рассчитайте индуктивное и емкостное сопротивление.
  • Рассчитывайте ток и / или напряжение в простых индуктивных, емкостных и резистивных цепях.

Многие цепи также содержат конденсаторы и катушки индуктивности в дополнение к резисторам и источнику переменного напряжения.Мы видели, как конденсаторы и катушки индуктивности реагируют на постоянное напряжение при его включении и выключении. Теперь мы исследуем, как катушки индуктивности и конденсаторы реагируют на синусоидальное переменное напряжение.

Катушки индуктивности и индуктивное сопротивление

Предположим, индуктор подключен непосредственно к источнику переменного напряжения, как показано на рисунке 1. Разумно предположить, что сопротивление пренебрежимо мало, поскольку на практике мы можем сделать сопротивление индуктора настолько малым, что оно окажет незначительное влияние на схему.Также показан график зависимости напряжения и тока от времени.

Рис. 1. (a) Источник переменного напряжения, включенный последовательно с катушкой индуктивности, имеющей незначительное сопротивление. (б) График зависимости тока и напряжения на катушке индуктивности от времени.

График на Рисунке 1 (b) начинается с максимального напряжения. Обратите внимание, что ток начинается с нуля и повышается до своего пика после напряжения, которое им управляет, точно так же, как это было в случае, когда напряжение постоянного тока было включено в предыдущем разделе.Когда напряжение становится отрицательным в точке а, ток начинает уменьшаться; оно становится нулевым в точке b, где напряжение является самым отрицательным. Затем ток становится отрицательным, снова вслед за напряжением. Напряжение становится положительным в точке c и начинает делать ток менее отрицательным. В точке d ток проходит через ноль, когда напряжение достигает своего положительного пика, чтобы начать следующий цикл. Кратко это поведение можно описать следующим образом:

Напряжение переменного тока в индукторе

Когда на катушку индуктивности подается синусоидальное напряжение, оно опережает ток на одну четверть цикла или на фазовый угол 90º.

Ток отстает от напряжения, поскольку индукторы препятствуют изменению тока. Изменение тока индуцирует обратную ЭДС В = — L (Δ I / Δ t ). Это считается эффективным сопротивлением катушки индуктивности переменному току. Среднеквадратичный ток I через катушку индуктивности L определяется версией закона Ома:

[латекс] I = \ frac {V} {{X} _ {L}} \\ [/ latex],

, где В, — среднеквадратичное значение напряжения на катушке индуктивности, а X L определяется как

.

[латекс] {X} _ {L} = 2 \ pi {fL} \\ [/ латекс],

с f частота источника переменного напряжения в герцах (анализ схемы с использованием правила петли Кирхгофа и вычислений фактически дает это выражение). X L называется индуктивным реактивным сопротивлением , потому что катушка индуктивности препятствует прохождению тока. X L имеет единицы измерения Ом (1 Гн = 1 Ом с, так что частота, умноженная на индуктивность, имеет единицы (циклы / с) (Ом ⋅ с) = Ом)), что соответствует его роли в качестве эффективное сопротивление. Имеет смысл, что X L пропорционально L , поскольку чем больше индукция, тем больше его сопротивление изменению.Также разумно, что X L пропорционально частоте f , поскольку большая частота означает большее изменение тока. То есть Δ I / Δ t является большим для больших частот (большие f , маленькие Δ t ). Чем больше изменение, тем больше сопротивление катушки индуктивности.

Пример 1. Расчет индуктивного сопротивления, а затем тока

(a) Рассчитайте индуктивное сопротивление 3.Индуктор 00 мГн при подаче переменного напряжения 60,0 Гц и 10,0 кГц. (b) Каков среднеквадратичный ток на каждой частоте, если приложенное действующее напряжение составляет 120 В?

Стратегия

Индуктивное реактивное сопротивление находится непосредственно из выражения X L = 2πf L . Как только X L было найдено на каждой частоте, закон Ома, как указано в уравнении I = В / X L , может быть использован для определения тока на каждой частоте.

Решение для (а)

Ввод частоты и индуктивности в уравнение X L = 2πf L дает

X L = 2πf L = 6,28 (60,0 / с) (3,00 мГн) = 1,13 Ом при 60 Гц.

Аналогично, на 10 кГц,

X L = 2πf L = 6,28 (1,00 × 10 4 / с) (3,00 мГн) = 188 Ом при 10 кГц.

Решение для (b)

Среднеквадратичное значение тока теперь определяется с использованием версии закона Ома в уравнении I = В / X L , при условии, что приложенное действующее напряжение составляет 120 В.Для первой частоты это дает

[латекс] I = \ frac {V} {{X} _ {L}} = \ frac {120 \ text {V}} {1.13 \ text {} \ Omega} = 106 \ text {A at} 60 \ текст {Hz} \\ [/ latex].

Аналогично, на 10 кГц,

[латекс] I = \ frac {V} {{X} _ {L}} = \ frac {120 \ text {V}} {188 \ text {} \ Omega} = 0,637 \ text {A at} 10 \ текст {кГц} \\ [/ latex].

Обсуждение

Катушка индуктивности по-разному реагирует на двух разных частотах. На более высокой частоте его реактивное сопротивление велико, а ток невелик, что соответствует тому, как катушка индуктивности препятствует быстрому изменению.Таким образом, наиболее затруднены высокие частоты. Индукторы могут использоваться для фильтрации высоких частот; например, большую катушку индуктивности можно включить последовательно с системой воспроизведения звука или последовательно с вашим домашним компьютером, чтобы уменьшить высокочастотный звук, выводимый из ваших динамиков или высокочастотные всплески мощности на ваш компьютер.

Обратите внимание, что, хотя сопротивлением в рассматриваемой цепи можно пренебречь, переменный ток не очень велик, потому что индуктивное реактивное сопротивление препятствует его протеканию.С переменным током нет времени, чтобы ток стал слишком большим.

Конденсаторы и емкостное сопротивление

Рассмотрим конденсатор, подключенный непосредственно к источнику переменного напряжения, как показано на рисунке 2. Сопротивление такой цепи можно сделать настолько малым, что оно окажет незначительное влияние по сравнению с конденсатором, поэтому мы можем предположить, что сопротивление незначительно. Напряжение на конденсаторе и ток показаны на рисунке как функции времени.

Рисунок 2.(а) Источник переменного напряжения, включенный последовательно с конденсатором С, имеющим незначительное сопротивление. (б) График зависимости тока и напряжения на конденсаторе от времени.

График на Рисунке 2 начинается с максимального напряжения на конденсаторе. В этот момент ток равен нулю, потому что конденсатор полностью заряжен и останавливает поток. Затем напряжение падает, а ток становится отрицательным по мере разряда конденсатора. В точке а конденсатор полностью разряжен (на нем Q = 0 ) и напряжение на нем равно нулю.Ток остается отрицательным между точками a и b, вызывая обратное напряжение на конденсаторе. Это завершается в точке b, где ток равен нулю, а напряжение имеет самое отрицательное значение. Ток становится положительным после точки b, нейтрализуя заряд конденсатора и доводя напряжение до нуля в точке c, что позволяет току достичь своего максимума. Между точками c и d ток падает до нуля, когда напряжение достигает своего пика, и процесс начинает повторяться. На протяжении всего цикла напряжение соответствует тому, что делает ток, на четверть цикла:

Напряжение переменного тока в конденсаторе

Когда на конденсатор подается синусоидальное напряжение, оно следует за током на одну четверть цикла или на фазовый угол 90º.

Конденсатор влияет на ток, имея возможность полностью его остановить, когда он полностью заряжен. Поскольку применяется переменное напряжение, возникает среднеквадратичный ток, но он ограничивается конденсатором. Это считается эффективным сопротивлением конденсатора переменному току, поэтому среднеквадратичный ток I в цепи, содержащей только конденсатор C , определяется другой версией закона Ома как

.

[латекс] I = \ frac {V} {{X} _ {C}} \\ [/ latex],

, где В, — среднеквадратичное значение напряжения, а X C определяется (Как и в случае с X L , это выражение для X C является результатом анализа цепи используя правила и исчисление Кирхгофа) равным

[латекс] {X} _ {C} = \ frac {1} {2 \ pi fC} \\ [/ latex],

, где X C называется емкостным реактивным сопротивлением , потому что конденсатор препятствует прохождению тока. X C имеет единицы измерения Ом (проверка оставлена ​​в качестве упражнения для читателя). X C обратно пропорциональна емкости C ; Чем больше конденсатор, тем больший заряд он может накапливать и тем больше может протекать ток. Она также обратно пропорциональна частоте f ; чем выше частота, тем меньше времени остается для полной зарядки конденсатора, и поэтому он меньше препятствует току.

Пример 2. Расчет емкостного реактивного сопротивления, а затем тока

(a) Рассчитайте емкостное реактивное сопротивление конденсатора 5,00 мФ при приложении переменного напряжения 60,0 Гц и 10,0 кГц. (b) Каков среднеквадратичный ток, если приложенное действующее напряжение составляет 120 В?

Стратегия

Емкостное реактивное сопротивление находится непосредственно из выражения в [latex] {X} _ {C} = \ frac {1} {2 \ pi fC} \\ [/ latex]. После того, как X C было обнаружено на каждой частоте, закон Ома, сформулированный как I = В, / X C , можно использовать для определения тока на каждой частоте.

Решение для (а)

Ввод частоты и емкости в [латекс] {X} _ {C} = \ frac {1} {2 \ pi fC} \\ [/ latex], дает

[латекс] \ begin {array} {lll} {X} _ {C} & = & \ frac {1} {2 \ pi fC} \\ & = & \ frac {1} {6.28 \ left (60.0 / \ text {s} \ right) \ left (5.00 \ text {} \ mu \ text {F} \ right)} = 531 \ text {} \ Omega \ text {at} 60 \ text {Hz} \ end {массив }\\[/латекс].

Аналогично, на 10 кГц,

[латекс] \ begin {array} {lll} {X} _ {C} & = & \ frac {1} {2 \ pi fC} = \ frac {1} {6.{4} / \ text {s} \ right) \ left (5,00 \ mu \ text {F} \ right)} \\ & = & 3,18 \ text {} \ Omega \ text {at} 10 \ text {кГц} \ end {array} \\ [/ latex].

Решение для (b)

Среднеквадратичное значение тока теперь определяется с использованием версии закона Ома в I = В / X C , учитывая приложенное действующее напряжение 120 В. Для первой частоты это дает

[латекс] I = \ frac {V} {{X} _ {C}} = \ frac {120 \ text {V}} {531 \ text {} \ Omega} = 0,226 \ text {A at} 60 \ текст {Hz} \\ [/ latex].

Аналогично, на 10 кГц,

[латекс] I = \ frac {V} {{X} _ {C}} = \ frac {120 \ text {V}} {3.18 \ text {} \ Omega} = 3.37 \ text {A at} 10 \ текст {Hz} \\ [/ latex].

Обсуждение

Конденсатор очень по-разному реагирует на двух разных частотах, а индуктор реагирует прямо противоположным образом. На более высокой частоте его реактивное сопротивление мало, а ток велик. Конденсаторы одобряют изменения, тогда как индукторы противодействуют изменениям. Конденсаторы больше всего препятствуют низким частотам, так как низкая частота позволяет им успеть зарядиться и остановить ток.Конденсаторы можно использовать для фильтрации низких частот. Например, конденсатор, включенный последовательно с системой воспроизведения звука, избавляет ее от гула 60 Гц.

Хотя конденсатор в основном представляет собой разомкнутую цепь, в цепи с напряжением переменного тока, приложенным к конденсатору, присутствует среднеквадратичный ток. Это связано с тем, что напряжение постоянно меняет направление, заряжая и разряжая конденсатор. Если частота стремится к нулю (постоянный ток), X C стремится к бесконечности, и ток равен нулю, когда конденсатор заряжен.На очень высоких частотах реактивное сопротивление конденсатора стремится к нулю — он имеет незначительное реактивное сопротивление и не препятствует току (действует как простой провод). Конденсаторы оказывают противоположное влияние на цепи переменного тока, чем индукторы .

Резисторы в цепи переменного тока

В качестве напоминания рассмотрим Рисунок 3, на котором показано напряжение переменного тока, приложенное к резистору, и график зависимости напряжения и тока от времени. Напряжение и ток равны точно в фазе в резисторе.Отсутствует частотная зависимость поведения простого сопротивления в цепи:

Рис. 3. (a) Источник переменного напряжения, включенный последовательно с резистором. (b) График зависимости тока и напряжения на резисторе от времени, показывающий, что они точно совпадают по фазе.

Напряжение переменного тока в резисторе

Когда на резистор подается синусоидальное напряжение, напряжение точно совпадает по фазе с током — они имеют фазовый угол 0 °.

Сводка раздела

  • Для катушек индуктивности в цепях переменного тока мы обнаруживаем, что когда на индуктор подается синусоидальное напряжение, оно опережает ток на одну четверть цикла или на фазовый угол 90 °.
  • Противодействие катушки индуктивности изменению тока выражается как сопротивление переменному току.
  • Закон Ома для катушки индуктивности

    [латекс] I = \ frac {V} {{X} _ {L}} \\ [/ latex],

    , где В, — среднеквадратичное значение напряжения на катушке индуктивности.

  • X L определяется как индуктивное реактивное сопротивление, определяемое по формуле

    [латекс] {X} _ {L} = 2 \ pi fL \\ [/ латекс],

    с f частота источника переменного напряжения в герцах.

  • Индуктивное реактивное сопротивление X L выражается в единицах Ом и имеет наибольшее значение на высоких частотах.
  • Для конденсаторов мы обнаруживаем, что когда на конденсатор подается синусоидальное напряжение, напряжение следует за током на одну четверть цикла или на фазовый угол 90º.
  • Поскольку конденсатор может останавливать ток при полной зарядке, он ограничивает ток и предлагает другую форму сопротивления переменному току; Закон Ома для конденсатора

    [латекс] I = \ frac {V} {{X} _ {C}} \\ [/ latex],

    , где В, — среднеквадратичное значение напряжения на конденсаторе.

  • X C определяется как емкостное реактивное сопротивление, определяемое по формуле

    [латекс] {X} _ {C} = \ frac {1} {2 \ pi fC} \\ [/ latex].

  • X C имеет единицы измерения Ом и имеет наибольшее значение на низких частотах.

Концептуальные вопросы

1. Пресбиакузис — это возрастная потеря слуха, которая постепенно влияет на высокие частоты. Усилитель слухового аппарата предназначен для равномерного усиления всех частот. Чтобы отрегулировать его мощность на пресбиакузис, включите ли вы конденсатор последовательно или параллельно динамику слухового аппарата? Объяснять.

2. Будете ли вы использовать большую индуктивность или большую емкость последовательно с системой для фильтрации низких частот, таких как гул 100 Гц в звуковой системе? Объяснять.

3. Высокочастотный шум в сети переменного тока может повредить компьютеры. Использует ли съемный блок, предназначенный для предотвращения этого повреждения, большую индуктивность или большую емкость (последовательно с компьютером) для фильтрации таких высоких частот? Объяснять.

4. Зависит ли индуктивность от тока, частоты или и того, и другого? А как насчет индуктивного сопротивления?

5. Объясните, почему конденсатор на рисунке 4 (a) действует как фильтр низких частот между двумя цепями, тогда как конденсатор на рисунке 4 (b) действует как фильтр высоких частот.

Рисунок 4. Конденсаторы и катушки индуктивности. Конденсатор с высокой и низкой частотой.

6. Если конденсаторы на Рисунке 4 заменить катушками индуктивности, что будет действовать как фильтр низких частот, а какой — как фильтр высоких частот?

Задачи и упражнения

1. На какой частоте индуктор 30,0 мГн будет иметь реактивное сопротивление 100 Ом?

2. Какое значение индуктивности следует использовать, если требуется реактивное сопротивление 20,0 кОм при частоте 500 Гц?

3.Какую емкость следует использовать для получения реактивного сопротивления 2,00 МОм при 60,0 Гц?

4. На какой частоте конденсатор 80,0 мФ будет иметь реактивное сопротивление 0,250 Ом?

5. (a) Найдите ток через катушку индуктивности 0,500 H, подключенную к источнику переменного тока 60,0 Гц, 480 В. (б) Каким будет ток на частоте 100 кГц?

6. (a) Какой ток протекает, когда источник переменного тока 60,0 Гц, 480 В подключен к конденсатору 0,250 мкФ? (b) Каким будет ток на частоте 25,0 кГц?

7. А 20.Источник 0 кГц, 16,0 В, подключенный к катушке индуктивности, производит ток 2,00 А. Что такое индуктивность?

8. Источник 20,0 Гц, 16,0 В вырабатывает ток 2,00 мА при подключении к конденсатору. Какая емкость?

9. (a) Катушка индуктивности, предназначенная для фильтрации высокочастотного шума от энергии, подаваемой на персональный компьютер, включается последовательно с компьютером. Какая минимальная индуктивность должна обеспечивать реактивное сопротивление 2,00 кОм для шума 15,0 кГц? (б) Каково его реактивное сопротивление при 60?0 Гц?

10. Конденсатор на рисунке 4 (а) предназначен для фильтрации низкочастотных сигналов, препятствуя их передаче между цепями. (а) Какая емкость необходима для создания реактивного сопротивления 100 кОм при частоте 120 Гц? (б) Каким было бы его реактивное сопротивление на частоте 1,00 МГц? (c) Обсудите значение ваших ответов на (a) и (b).

11. Конденсатор на Рисунке 4 (b) будет фильтровать высокочастотные сигналы, замыкая их на землю / землю. (a) Какая емкость необходима для получения реактивного сопротивления [латекса] \ text {10.0 м \ Omega} [/ latex] для сигнала 5,00 кГц? (б) Каким будет его реактивное сопротивление при 3,00 Гц? (c) Обсудите значение ваших ответов на (a) и (b).

12. Необоснованные результаты При регистрации напряжений, обусловленных мозговой активностью (ЭЭГ), сигнал 10,0 мВ с частотой 0,500 Гц подается на конденсатор, создавая ток 100 мА. Сопротивление незначительное. а) Какая емкость? б) Что неразумного в этом результате? (c) Какое предположение или предпосылка ответственны?

13. Создайте свою проблему Рассмотрите возможность использования индуктора последовательно с компьютером, работающим от электричества 60 Гц. Постройте задачу, в которой вы вычисляете относительное снижение напряжения входящего высокочастотного шума по сравнению с напряжением 60 Гц. Среди вещей, которые следует учитывать, — допустимое последовательное реактивное сопротивление катушки индуктивности для мощности 60 Гц и вероятные частоты шума, проходящего через линии электропередач.

Глоссарий

индуктивное реактивное сопротивление:
противодействие катушки индуктивности изменению тока; рассчитывается по X L = 2π fL
емкостное реактивное сопротивление:
сопротивление конденсатора изменению тока; рассчитывается по [latex] {X} _ {C} = \ frac {1} {2 \ pi fC} \\ [/ latex]

Избранные решения проблем и упражнения

1.531 Гц

3. 1,33 нФ

5. (а) 2,55 А (б) 1,53 мА

7. 63,7 мкГн

9. (а) 21,2 мГн (б) 8,00 Ом

Формула вывода и векторная диаграмма

Катушка индуктивности обычно представляет собой катушку с проволокой. Когда ток проходит через эту катушку, создается электрическое поле. Таким образом, поле будет индуцировано. Наведенное поле зависит от количества витков, а это индуктивность. Катушка индуктивности из-за своей индуктивности сопротивляется протеканию переменного тока.Согласно закону Ленца, индуктор будет сопротивляться изменению тока. Реактивное сопротивление определяется как сопротивление, оказываемое переменным токам только конденсаторами и катушками индуктивности. Обычно реактивное сопротивление обозначается X, частота — f, индуктивность — L, а емкость — C. Индуктивное реактивное сопротивление зависит от частоты. Расчет этого можно сделать с помощью простых формул.

Что такое индуктивное реактивное сопротивление?

Индуктивное реактивное сопротивление определяется как эффект, благодаря которому уменьшается протекание переменного тока в катушке индуктивности.Любой переменный ток или изменяющийся ток будут затруднены из-за связанной с ним индуктивности.

Дроссели и индукторы — это в основном петли из проволоки или катушек, которые наматываются на какой-то ферромагнитный материал или вокруг полого трубчатого формирователя для увеличения их индуктивного значения, называемого индуктивностью. Когда напряжение подается на клеммы индуктора, индукторы накапливают энергию в виде магнитного поля. Напряжение обратной ЭДС катушки индуктивности пропорционально скорости изменения тока, протекающего через нее.

Индуктивное реактивное сопротивление

Если мы начнем исследовать или наблюдать самоиндуктивность и эффекты, возникающие в цепи, то мы легко сможем узнать причину этого индуктивного реактивного сопротивления. Чтобы определить это в простой форме, это похоже на противостояние текущему потоку.

Когда на катушку индуктивности подается напряжение переменного тока, протекание тока будет отличаться от того, когда на нее подается напряжение постоянного тока. Разность фаз между сигналами напряжения и тока создается синусоидальным источником питания.Как частота формы волны, так и индуктивность катушки определяют противодействие протеканию тока в обмотках катушки в цепи переменного тока.

Сопротивление переменного тока определяет противодействие протеканию тока через катушку в цепи переменного тока и обычно известно как полное сопротивление (Z) цепи. Чтобы отличить сопротивление постоянному току от сопротивления переменного тока, сопротивление всегда ассоциируется с цепями постоянного тока, и общий термин, используемый для этого, — реактивное сопротивление. Значение реактивного сопротивления измеряется в омах, как и сопротивление.Чтобы узнать разницу между значением реактивного сопротивления и значением сопротивления, значение реактивного сопротивления обозначается символом «X».

Поскольку мы фокусируемся на компонентной катушке индуктивности, реактивное сопротивление катушки индуктивности называется индуктивным реактивным сопротивлением. Чтобы упростить его в другой форме, его можно определить как электрическое сопротивление индуктора при использовании в цепи переменного тока. Обозначение индуктивного реактивного сопротивления — XL.

Формула индуктивного реактивного сопротивления

Индуктивное реактивное сопротивление можно рассчитать по следующей формуле.Индуктивное реактивное сопротивление — это произведение удвоенного числа пи, индуктивности катушки и частоты переменного тока. Таким образом, формула может быть обозначена как

XL = 2πfL

Где XL — индуктивное реактивное сопротивление, измеряемое в омах

f — частота переменного тока источника питания в герцах

L — индуктивность стоимость катушки в генри.

Из этой формулы индуктивного реактивного сопротивления мы можем четко знать, что индуктивное реактивное сопротивление будет увеличиваться при увеличении частоты или индуктивности.Индуктивное реактивное сопротивление достигает бесконечности, когда частота приближается к бесконечности, и это действует как разомкнутый контур. Точно так же он приближается к нулю, когда частота уменьшается до нуля, и это действует как короткое замыкание. он четко определяет, что частота и индуктивное сопротивление прямо пропорциональны.

Идеальный индуктор — это индуктор, который имеет только индуктивность, но не имеет сопротивления и емкости. Хотя идеальных катушек индуктивности не существует. Чтобы определить формулы и расчеты, представим себе размещение идеального индуктора.Если к идеальной катушке индуктивности приложена синусоида, реактивное сопротивление препятствует прохождению тока и подчиняется закону сопротивления

XL = V / I

«XL» — индуктивное реактивное сопротивление в омах

«I» — ток в амперах

«V» — это напряжение в вольтах.

В зависимости индуктивного сопротивления от частоты, поскольку мы четко знаем, что частота прямо пропорциональна частоте. Таким образом, мы можем видеть, что катушка индуктивности имеет нулевое реактивное сопротивление при постоянном токе, а катушка индуктивности имеет бесконечное реактивное сопротивление на высоких частотах.

Вывод формулы индуктивного реактивного сопротивления

Синусоидальный переменный

Напряжение V = Vmsinwt

Обратная ЭДС индукция, e = Ldi / dt

e = v

Ldi / dt = Vmsinwt

Diwt с обеих сторон

∫ di = ∫Vm / L sinwtdt

I = Vm / wL sin (wt-π / 2)

При wt = π sin (wt-π / 2) = 1

Im = Vm / wL

Vm / Im = wL

W = 2πf

Индуктивное реактивное сопротивление XL = Vm / Im = 2πfL

Подача переменного тока через последовательную цепь LR

В основном мы рассматриваем чисто индуктивную катушку, но каждый раз, рассматривая чисто индуктивную катушку, Это невозможно, но соленоиды будут иметь определенное сопротивление, неважно, насколько маленьким оно было связано с витками катушки используемого провода.Так что мы можем рассматривать эту простую катушку, поскольку это сопротивление последовательно с индуктивностью.

Сопротивление «R» и индуктивность «L» присутствуют в цепи переменного тока, а напряжение V будет векторной суммой VL и VR. Фазовый угол цепи определяется новым фазовым углом между током и напряжением и дается греческим символом фи.

Векторная диаграмма результирующего напряжения

Здесь линия OB — это опорный горизонтальный ток, OA — это напряжение на резистивной составляющей, находящееся в фазе с током, OC представляет собой индуктивное напряжение, которое находится на 90 градусов впереди тока, OD даст результирующее напряжение питания.

Векторная диаграмма результирующего напряжения

V = действующее значение приложенного напряжения

I = действующее значение последовательного тока

VR = падение напряжения IR на сопротивлении, которое находится в фазе с током

VL = падение напряжения на индуктивности который ведет ток под углом 90 градусов

Фазовый угол

Когда две или более индуктивных катушки соединены последовательно, в противном случае одна катушка при последовательном соединении со многими неиндуктивными сопротивлениями, общее сопротивление резистивных элементов будет равно R1 + R2 + R3 , так далее.это даст общее значение сопротивления для цепи.

Фазовый угол

Что касается реактивного сопротивления, полное реактивное сопротивление индуктивных элементов равно X1 + X2 + X3 и т. Д. И дает значение полного реактивного сопротивления цепи.

Разница между индуктивностью и реактивным сопротивлением включает

  • Реактивное сопротивление — это влияние индуктивности на заданной частоте.
  • Индуктивность определяется как физическое свойство проводника или катушки. Единицы измерения — генри, и это не зависит от частоты сигнала в компоненте.
  • Что касается реактивного сопротивления, оно зависит от частоты сигнала.

Это полное описание индуктивного реактивного сопротивления, его формула, единицы измерения и размеры. Вот вопрос, в чем разница между реактивным сопротивлением и емкостью.

Интернет-курсов PDH. PDH для профессиональных инженеров. ПДХ Инжиниринг.

«Мне нравится широта ваших курсов по HVAC; не только экологичность или экономия энергии

курсов. «

Russell Bailey, P.E.

Нью-Йорк

«Это укрепило мои текущие знания и научило меня еще нескольким новым вещам.

, чтобы познакомить меня с новыми источниками

информации.»

Стивен Дедак, П.Е.

Нью-Джерси

«Материал был очень информативным и организованным. Я многому научился, и они были

.

очень быстро отвечает на вопросы.

Это было на высшем уровне. Будет использовать

снова. Спасибо. «

Blair Hayward, P.E.

Альберта, Канада

«Простой в использовании сайт.Хорошо организовано. Я действительно буду снова пользоваться вашими услугами.

проеду по вашей компании

имя другим на работе. «

Roy Pfleiderer, P.E.

Нью-Йорк

«Справочные материалы были превосходными, а курс был очень информативным, особенно потому, что я думал, что я уже знаком.

с подробной информацией о Канзасе

Городская авария Хаятт.»

Майкл Морган, P.E.

Техас

«Мне очень нравится ваша бизнес-модель. Мне нравится просматривать текст перед покупкой. Я нашел класс

.

информативно и полезно

в моей работе ».

Вильям Сенкевич, П.Е.

Флорида

«У вас большой выбор курсов, а статьи очень информативны.Вы

— лучшее, что я нашел ».

Russell Smith, P.E.

Пенсильвания

«Я считаю, что такой подход позволяет работающему инженеру легко зарабатывать PDH, давая время на просмотр

материал «

Jesus Sierra, P.E.

Калифорния

«Спасибо, что позволили мне просмотреть неправильные ответы.На самом деле

человек узнает больше

от отказов »

John Scondras, P.E.

Пенсильвания

«Курс составлен хорошо, и использование тематических исследований является эффективным.

способ обучения »

Джек Лундберг, P.E.

Висконсин

«Я очень впечатлен тем, как вы представляете курсы; i.е., позволяя

студент для ознакомления с курсом

материалов до оплаты и

получение викторины. «

Арвин Свангер, П.Е.

Вирджиния

«Спасибо за то, что вы предложили все эти замечательные курсы. Я определенно выучил и

получил огромное удовольствие «.

Мехди Рахими, П.Е.

Нью-Йорк

«Я очень доволен предлагаемыми курсами, качеством материалов и простотой поиска.

на связи

курсов.»

Уильям Валериоти, P.E.

Техас

«Этот материал в значительной степени оправдал мои ожидания. По курсу было легко следовать. Фотографии в основном обеспечивали хорошее наглядное представление о

.

обсуждаемых тем ».

Майкл Райан, P.E.

Пенсильвания

«Именно то, что я искал. Потребовался 1 балл по этике, и я нашел его здесь.»

Джеральд Нотт, П.Е.

Нью-Джерси

«Это был мой первый онлайн-опыт получения необходимых мне кредитов PDH. Это было

информативно, выгодно и экономично.

Я очень рекомендую

всем инженерам. »

Джеймс Шурелл, P.E.

Огайо

«Я понимаю, что вопросы относятся к« реальному миру »и имеют отношение к моей практике, и

не на основе какой-то неясной раздел

законов, которые не применяются

— «нормальная» практика.»

Марк Каноник, П.Е.

Нью-Йорк

«Отличный опыт! Я многому научился, чтобы перенести его на свой медицинский прибор.

организация «

Иван Харлан, П.Е.

Теннесси

«Материалы курса имели хорошее содержание, не слишком математическое, с хорошим акцентом на практическое применение технологий».

Юджин Бойл, П.E.

Калифорния

«Это был очень приятный опыт. Тема была интересной и хорошо изложенной,

а онлайн-формат был очень

Доступно и просто

использовать. Большое спасибо. «

Патрисия Адамс, P.E.

Канзас

«Отличный способ добиться соответствия требованиям PE Continuing Education в рамках ограничений по времени лицензиата.»

Joseph Frissora, P.E.

Нью-Джерси

«Должен признаться, я действительно многому научился. Помогает иметь распечатанный тест во время

обзор текстового материала. Я

также оценил просмотр

фактических случаев предоставлено.

Жаклин Брукс, П.Е.

Флорида

«Документ» Общие ошибки ADA при проектировании объектов «очень полезен.Модель

испытание потребовало исследования в

документ но ответы были

в наличии «

Гарольд Катлер, П.Е.

Массачусетс

«Я эффективно использовал свое время. Спасибо за широкий выбор вариантов.

в транспортной инженерии, что мне нужно

для выполнения требований

Сертификат ВОМ.»

Джозеф Гилрой, П.Е.

Иллинойс

«Очень удобный и доступный способ заработать CEU для моих требований PG в Делавэре».

Ричард Роадс, P.E.

Мэриленд

«Я многому научился с защитным заземлением. Пока все курсы, которые я прошел, были отличными.

Надеюсь увидеть больше 40%

курсов со скидкой.»

Кристина Николас, П.Е.

Нью-Йорк

«Только что сдал экзамен по радиологическим стандартам и с нетерпением жду возможности сдать дополнительный

курсов. Процесс прост, и

намного эффективнее, чем

в пути «.

Деннис Мейер, P.E.

Айдахо

«Услуги, предоставляемые CEDengineering, очень полезны для Professional

Инженеры получат блоки PDH

в любое время.Очень удобно ».

Пол Абелла, P.E.

Аризона

«Пока все отлично! Поскольку я постоянно работаю матерью двоих детей, у меня мало

время искать где

получить мои кредиты от. «

Кристен Фаррелл, P.E.

Висконсин

«Это было очень познавательно и познавательно.Легко для понимания с иллюстрациями

и графики; определенно делает это

легче поглотить все

теорий. «

Виктор Окампо, P.Eng.

Альберта, Канада

«Хороший обзор принципов работы с полупроводниками. Мне понравилось пройти курс по

.

мой собственный темп во время моего утром

до метро

на работу.»

Клиффорд Гринблатт, П.Е.

Мэриленд

«Просто найти интересные курсы, скачать документы и взять

викторина. Я бы очень рекомендовал

вам на любой PE нужно

CE единиц. «

Марк Хардкасл, П.Е.

Миссури

«Очень хороший выбор тем из многих областей техники.»

Randall Dreiling, P.E.

Миссури

«Я заново узнал то, что забыл. Я также рад оказать финансовую помощь

по ваш промо-адрес который

сниженная цена

на 40%. «

Конрадо Казем, П.E.

Теннесси

«Отличный курс по разумной цене. Воспользуюсь вашими услугами в будущем».

Charles Fleischer, P.E.

Нью-Йорк

«Это был хороший тест и фактически подтвердил, что я прочитал профессиональную этику

кодов и Нью-Мексико

правил. «

Брун Гильберт, П.E.

Калифорния

«Мне очень понравились занятия. Они стоили потраченного времени и усилий».

Дэвид Рейнольдс, P.E.

Канзас

«Очень доволен качеством тестовых документов. Буду использовать CEDengineerng

.

при необходимости дополнительно

сертификация. «

Томас Каппеллин, П.E.

Иллинойс

«У меня истек срок действия курса, но вы все же выполнили свое обязательство и дали

мне то, за что я заплатил — много

оценено! «

Джефф Ханслик, P.E.

Оклахома

«CEDengineering предлагает удобные, экономичные и актуальные курсы.

для инженера »

Майк Зайдл, П.E.

Небраска

«Курс был по разумной цене, материал был кратким, а

хорошо организовано. «

Glen Schwartz, P.E.

Нью-Джерси

«Вопросы подходили для уроков, а материал урока —

.

хороший справочный материал

для деревянного дизайна. «

Брайан Адамс, П.E.

Миннесота

«Отлично, я смог получить полезные рекомендации по простому телефонному звонку.»

Роберт Велнер, П.Е.

Нью-Йорк

«У меня был большой опыт работы в прибрежном строительстве — проектирование

Building курс и

очень рекомендую .»

Денис Солано, P.E.

Флорида

«Очень понятный, хорошо организованный веб-сайт. Материалы курса этики Нью-Джерси были очень хорошими

хорошо подготовлены. »

Юджин Брэкбилл, P.E.

Коннектикут

«Очень хороший опыт. Мне нравится возможность загружать учебные материалы на

.

обзор везде и

всякий раз, когда.»

Тим Чиддикс, P.E.

Колорадо

«Отлично! Поддерживаю широкий выбор тем на выбор».

Уильям Бараттино, P.E.

Вирджиния

«Процесс прямой, без всякой ерунды. Хороший опыт».

Тайрон Бааш, П.E.

Иллинойс

«Вопросы на экзамене были зондирующими и продемонстрировали понимание

материала. Полная

и комплексное. »

Майкл Тобин, P.E.

Аризона

«Это мой второй курс, и мне понравилось то, что мне предлагали курс

поможет по моей линии

работ.»

Рики Хефлин, P.E.

Оклахома

«Очень быстро и легко ориентироваться. Я определенно буду использовать этот сайт снова».

Анджела Уотсон, П.Е.

Монтана

«Легко выполнить. Никакой путаницы при подходе к сдаче теста или записи сертификата».

Кеннет Пейдж, П.E.

Мэриленд

«Это был отличный источник информации о солнечном нагреве воды. Информативный

и отличный освежитель ».

Луан Мане, П.Е.

Conneticut

«Мне нравится подход к регистрации и возможность читать материалы в автономном режиме, а затем

Вернуться, чтобы пройти викторину «

Алекс Млсна, П.E.

Индиана

«Я оценил объем информации, предоставленной для класса. Я знаю

это вся информация, которую я могу

использование в реальных жизненных ситуациях »

Натали Дерингер, P.E.

Южная Дакота

«Обзорные материалы и образец теста были достаточно подробными, чтобы позволить мне

успешно завершено

курс.»

Ира Бродский, П.Е.

Нью-Джерси

«Веб-сайт прост в использовании, вы можете скачать материал для изучения, а потом вернуться

и пройдите викторину. Очень

удобно и на моем

собственный график «

Майкл Гладд, P.E.

Грузия

«Спасибо за хорошие курсы на протяжении многих лет.»

Деннис Фундзак, П.Е.

Огайо

«Очень легко зарегистрироваться, получить доступ к курсу, пройти тест и распечатать PDH

сертификат. Спасибо за создание

процесс простой. »

Фред Шейбе, P.E.

Висконсин

«Положительный опыт.Быстро нашел курс, который соответствовал моим потребностям, и закончил

один час PDH в

один час. «

Стив Торкильдсон, P.E.

Южная Каролина

«Мне понравилось загружать документы для проверки содержания

и пригодность, до

имея заплатить за

материал .»

Ричард Вимеленберг, P.E.

Мэриленд

«Это хорошее напоминание об ЭЭ для инженеров, не занимающихся электричеством».

Дуглас Стаффорд, П.Е.

Техас

«Всегда есть возможности для улучшения, но я ничего не могу придумать в вашем

.

процесс, который требует

улучшение.»

Thomas Stalcup, P.E.

Арканзас

«Мне очень нравится удобство участия в онлайн-викторине и получение сразу

сертификат. «

Марлен Делани, П.Е.

Иллинойс

«Учебные модули CEDengineering — это очень удобный способ доступа к информации по номеру

.

много разные технические зоны за пределами

своя специализация без

приходится путешествовать.»

Гектор Герреро, П.Е.

Грузия

ИСКРЫ: Расчет реактивного сопротивления

Расчет реактивного сопротивления


f = 4,4 кГц R = 220 Ом
L = 3,6 мГн C = 0,48 мкФ

Рисунок 1. Пример цепи RLC

Току в цепи могут препятствовать три типа компонентов схемы:

  • Резисторы: вносят сопротивления , R (в Ом)
  • Катушки индуктивности: вносят индуктивного сопротивления , X L (в омах)
  • Конденсаторы: вносят емкостное реактивное сопротивление , X C (в Ом)

Вот формулы для расчета последних двух выше: X L и X C .Обратите внимание, что оба зависят от частоты переменного тока, f :

и

, где f — частота в Герц (или -1 сек), L — индуктивность в Генри и C — емкость в фарад . Вы редко встретите индуктивность величиной 1 Генри или емкость 1 фарад, вместо этого вы будете иметь дело с такими префиксами, как милли-, микро- и даже пико-.

Индуктивное сопротивление

Например, рассмотрим схему, показанную на рисунке 1. Воспользуемся формулой для X L для расчета реактивного сопротивления катушки индуктивности. Преобразование префиксов в научное представление может помочь избежать ошибок. Примечание что f = 4,4 кГц = 4,4 x 10 3 Гц и L = 3,6 м H = 3,6 x 10 −3 H

Вы могли заметить, что произведение килограмм (или 10 3 ) и милли- (или 10 −3 ) дает: 10 3 ⋅ 10 −3 = 1.Это упрощает расчет: X L = 2π ⋅ 4,4 ⋅ 3,6 = 100 Ом (округлено).

Емкостное реактивное сопротивление

Аналогично, мы можем использовать формулу для X C , чтобы вычислить реактивное сопротивление конденсатора. Опять же, преобразование в научная запись, f = 4,4 Икс 10 3 Гц и C = 0,48 мкФ = 4,8 x 10 −7 ф.

Опять же, если вы будете осторожны с префиксами, вы заметите, что продукт кило- (или 10 3 ) и микро- (или 10 −6 ) дает 10 3 ⋅ 10 −6 = 10 −3 , или 1/1000.Тогда X C = 1000 / (2π ⋅ 4,4 ⋅ 0,48) = 75 Ом (округлено).

Эти электрические блоки определены таким образом, что их продукция и коэффициенты работают до Ом:

и

Определение, символ, формула и вывод

Одним из известных законов, связанных с электричеством, является «Закон Ома». Закон Ома дает эмпирическое соотношение, которое описывает проводимость различных электропроводящих материалов.Согласно этому закону, ток, протекающий в проводнике, прямо пропорционален напряжению на проводнике, а сопротивление является константой пропорциональности. Здесь единицами измерения тока являются амперы, единицы напряжения — вольты, а единицы сопротивления — омы. В физике этот закон обычно также используется для обозначения различных обобщений закона, например, в векторной форме в электромагнетизме. Точно так же при работе с индукторами переменного тока используется закон сопротивления, где сопротивление называется «индуктивным реактивным сопротивлением», а не «сопротивлением».


Что такое индуктивное сопротивление?

Когда напряжение подается на катушку индуктивности, в цепи индуктивности индуцируется ток. Однако этот ток не генерируется мгновенно, а нарастает с большой скоростью, определяемой самоиндуцированными значениями индуктивности. Индуцированный ток ограничивается резистивными элементами, присутствующими в обмотках катушки индуктивности. Здесь величина сопротивления зависит от отношения приложенного напряжения к индуцированному току, как указано в Законе Ома.

На рисунке ниже показана цепь индуктивности, используемая для расчета индуктивного сопротивления.


Inductive-Reactance

Однако, когда индуктор подключен к цепи переменного тока, протекание тока ведет себя иначе. Здесь используется синусоидальный источник питания. Следовательно, возникает разность фаз между формой волны напряжения и тока. Теперь, когда для катушки индуктивности используется источник переменного тока, помимо индуктивности катушки ток также должен встречать сопротивление со стороны частоты формы волны переменного тока. Это сопротивление, с которым сталкивается ток в катушке индуктивности при включении в цепь переменного тока, называется «индуктивным сопротивлением».

Разница между индуктивностью и реактивным сопротивлением

Индуктивность — это способность материала индуцировать в нем напряжение при изменении тока внутри него. Символ индуктивности — «L». В то время как реактивное сопротивление — это свойство электрических материалов, которое препятствует изменению тока. Единицами реактивного сопротивления являются «Ом», и оно обозначается символом «X», чтобы отличить его от нормального сопротивления.

Реактивное сопротивление работает аналогично электрическому сопротивлению, но, в отличие от сопротивления, реактивное сопротивление не рассеивает мощность в виде тепла.Скорее он сохраняет энергию в виде значения реактивного сопротивления и возвращает ее в схему. Идеальный индуктор имеет нулевое сопротивление, тогда как идеальный резистор имеет нулевое реактивное сопротивление.


Вывод формулы индуктивного реактивного сопротивления

Индуктивное реактивное сопротивление — это термин, относящийся к цепям переменного тока. Он препятствует протеканию тока в цепях переменного тока. В индуктивной цепи переменного тока из-за разности фаз форма волны тока «ЗАСТАВЛЯЕТ» форму волны приложенного напряжения на 90 градусов. Т.е. если форма волны напряжения находится под углом 0 градусов, форма волны тока будет под углом -90 градусов.

В индуктивной цепи катушка индуктивности подключается к источнику переменного напряжения. Самоиндуцированная ЭДС в катушке индуктивности увеличивается и уменьшается с увеличением и уменьшением частоты напряжения питания. Самоиндуцированная ЭДС прямо пропорциональна скорости изменения тока в катушке индуктивности. Наибольшая скорость изменения происходит, когда форма волны напряжения питания переходит от положительного полупериода к отрицательному полупериоду или наоборот.

В индуктивной цепи ток отстает от напряжения.Итак, если напряжение равно 0 градусов, тогда ток будет на -90 градусов по отношению к напряжению. Следовательно, когда рассматриваются синусоидальные формы волны, форма волны напряжения V L может быть классифицирована как синусоидальная волна, а форма волны тока I L — как отрицательная косинусоидальная волна.

Таким образом, ток в точке можно определить как:

I L = I max . sin (ωt — 90 0 ), φω в радианах и t в секундах

Соотношение напряжения и тока в индуктивной цепи дает значение индуктивного реактивного сопротивления X L

Таким образом, X L = V L / I L Ом = ωL = 2πfL Ом

Здесь L — индуктивность, f — частота, а 2πf = ω

Из этого вывода видно, что индуктивное реактивное сопротивление прямо пропорционально к частоте f и индуктивности L индуктора.С увеличением частоты напряжения или индуктивности катушки общее реактивное сопротивление цепи увеличивается. Когда частота увеличивается до бесконечности, индуктивное реактивное сопротивление также увеличивается до бесконечности, действуя аналогично разомкнутой цепи. При падении частоты до нуля индуктивное реактивное сопротивление также уменьшается до нуля, действуя аналогично короткому замыканию.

Символ

Индуктивное реактивное сопротивление — это сопротивление, с которым сталкивается ток, протекающий в катушке индуктивности при подаче переменного напряжения.Его единицы аналогичны единицам сопротивления. Обозначение индуктивного реактивного сопротивления — «X L ». Поскольку ток отстает на 90 градусов относительно индуктора напряжения, имея значение для любой из величин, можно легко вычислить другое. Если напряжение известно, то по отрицательному смещению формы волны напряжения на 90 градусов можно получить форму волны тока.

Пример

Рассмотрим пример расчета индуктивного реактивного сопротивления.

Катушка индуктивности с индуктивностью 200 мГн и нулевым сопротивлением подключена к источнику напряжения 150 В.Частота подачи напряжения 60 Гц. Рассчитайте индуктивное реактивное сопротивление и ток, протекающий через катушку индуктивности

Индуктивное реактивное сопротивление

X L = 2πfL

= 2π × 50 × 0,20

= 76,08 Ом

Ток

84 I L L 900 V L / X L

= 150 / 76,08

= 1,97 A

В электрических и электронных схемах термин «реактивное сопротивление» обычно используется в цепях индуктивности и конденсатора.Увеличение значения реактивного сопротивления в этих цепях приводит к уменьшению тока в них. Индуктивное реактивное сопротивление приводит к тому, что напряжение и ток не совпадают по фазе. В электроэнергетических системах это ограничит мощность линий электропередачи переменного тока. Хотя в таких ситуациях ток все еще течет, линии электропередачи нагреваются и не будет эффективной передачи энергии. Итак, важно контролировать индуктивное сопротивление цепей. Какова разница фаз между сигналами напряжения и тока в цепи индуктивности?

Индуктивное и емкостное сопротивление | Определение и формула

В основном, в цепях переменного тока можно найти три типа элементов.Их можно разделить на резистивные, индуктивные и емкостные. Значение сопротивления не зависит от частоты, но значение как индуктивной цепи, так и емкостной цепи зависит от частоты напряжения.

Если цепь содержит только резистивных элементов , значение тока в цепи переменного тока можно рассчитать по соотношению

\ [I = \ frac {V} {R} \]

где R — сопротивление ( Ом). В чисто резистивной цепи ток находится в фазе с приложенным напряжением.

Рисунок 1: Фазорная диаграмма для чисто резистивной цепи

Если цепь содержит только индуктивных элементов , значение тока может быть определено соотношением

\ [I = \ frac {V} {\ omega L} \]

Где

В — вольты (перем. Ток)

ω = 2πf (рад / с)

L — индуктивность (Гн)

В чисто индуктивной цепи ток отстает от приложенного напряжения на 90 ° на векторной диаграмме V – I.

Рисунок 2: Фазорная диаграмма для чисто индуктивной цепи

Если цепь содержит только емкостных элементов , значение тока может быть определено соотношением

\ [I = V \ omega C \]

Где C — емкость (F).На векторной диаграмме V – I для чисто емкостной цепи ток опережает приложенное напряжение на 90 °.

Рисунок 3: Фазорная диаграмма для чисто емкостной цепи

Вышеупомянутые отношения напряжения и тока интересны и представляют ценность. Будет обнаружено, что при вычислении напряжений и токов, которые имеют смесь этих элементов, концепция импеданса будет иметь очень практическое применение.

По сути, импеданс переменного тока — это комплексное (не скалярное) отношение вольт к амперам в цепи переменного тока.Импеданс представляет собой способность цепи переменного тока сопротивляться прохождению тока. Импеданс — это также отношение двух векторов, но это не вектор. Это комплексное число, соединяющее один вектор с другим. Выраженное как «Z», импеданс может быть выражен математически как

\ [\ underline {Z} = \ frac {\ underline {V}} {\ underline {I}} \]

ПРИМЕЧАНИЕ : подчеркнутая переменная, поскольку «$ \ underline {Z} $» означает, что переменная является векторной величиной, а не скалярной величиной. Однако практика подчеркивания переменных для обозначения векторной величины не соблюдается строго.В большинстве случаев подразумевается, что указанная переменная является векторной величиной и не обязательно подчеркнута.

Чаще всего подчеркивание служит напоминанием о том, что переменная является векторной величиной. Переменная, обозначенная как абсолютное значение, как | Z |, конкретно указывает, что переменная является скалярной величиной, и ее не следует путать с векторной величиной.

Для чисто резистивной цепи Z R = R, где R — значение сопротивления в омах. {1} / {} _ {j \ omega C} \]

Формула индуктивного реактивного сопротивления

Считайте, что синусоидальный ток протекает в чистой индуктивности, как показано на следующем рис.то есть

$ i = {{I} _ {m}} \ sin \ left (wt \ right) $

Поскольку синусоидальная волна тока постоянно меняется, катушка вырабатывает противоэдс, равную

$ {{V} _ {L}} = L \ frac {di} {dt} $

Напряжение на катушке индуктивности пропорционально крутизне синусоидальной волны тока и, следовательно, является косинусоидальной волной, поскольку показано на рис.

Таким образом, в чисто индуктивной цепи ток отстает от напряжения на фазовый угол 90 °. Теперь подставляя уравнение для тока в уравнение для напряжения катушки индуктивности, мы находим, что

\ [{{V} _ {L}} = L \ frac {di} {dt} = L \ frac {d \ left ({{ I} _ {m}} sinwt \ right)} {dt} = {{I} _ {m}} wL \ cos \ left (wt \ right) \]

Величина I m ωL — максимальное значение напряжения на катушке индуктивности (это происходит при t = 0)

\ [\ begin {matrix} {{V} _ {m}} = {{\ operatorname {I}} _ {m}} \ omega L & {} & \ left (1 \ right) \\\ end {matrix} \]

Величина ωL называется индуктивным реактивным сопротивлением и является мерой сопротивления переменному току.Индуктивное реактивное сопротивление измеряется в Ом. Обозначение X L используется для обозначения индуктивного сопротивления.

$ {{X} _ {L}} = wL = 2 \ pi fL $

Поскольку максимальные значения уравнения (1) связаны с эффективными значениями, мы можем написать

$ {{V} _ { L}} = {{I} _ {L}} {{X} _ {L}} $

Чистая индуктивность не может рассеивать мощность. Напротив, индуктивность накапливает и выделяет энергию в виде магнитного поля. Индуктивная реактивная мощность равна произведению V L I L .{2} {{X} _ {L}} $

Пример индуктивного реактивного сопротивления

Напряжение на индукторе 1 Гн составляет e = 10sin200t. каково выражение мгновенного тока?

Решение

$ {{X} _ {L}} = \ omega L = 200 * 1 = 200 ~ \ Omega $

$ {{I} _ {m}} = \ frac {{{V } _ {m}}} {{{X} _ {L}}} = \ frac {10} {200} = 0,05 ~ A $

По индуктивности я отстает от e на 90 градусов, поэтому мы можем написать выражение для мгновенного тока как:

$ i = {{I} _ {m}} \ sin \ left (wt — {{90} ^ {{} ^ \ circ}} \ right) = 0.\ circ}} \ right) $

Формула емкостного реактивного сопротивления

Рассмотрим чистый конденсатор, подключенный к синусоидальному переменному напряжению, как показано на следующем рисунке.

Напряжение на конденсаторе

$ v = {{V} _ {m}} \ sin \ left (wt \ right) $

В то время как мгновенный ток, протекающий через конденсатор, равен

\ [i = C \ frac {dV} {dt} \]

Это выражение показывает, что ток пропорционален наклону кривой напряжения. В этом случае ток пропорционален наклону синусоидальной волны.Фактически, наклон синусоидальной волны представляет собой косинусоидальную волну, как показано на рисунке. Следовательно, в чисто емкостной цепи ток опережает напряжение на угол 90 °.

Теперь подставляем синусоидальное выражение для напряжения в уравнение тока. Получаем

\ [i = C \ frac {d \ left ({{V} _ {m}} \ sin \ left (wt \ right) \ right)} {dt} = wC {{V} _ {m }} \ cos \ left (wt \ right) \]

$ i = wC {{V} _ {m}} \ cos \ left (wt \ right) ~~~~~ \ text {} \ cdots \ text {} ~~ \ left (2 \ right) $

Из уравнения (2) определяется максимальный ток;

\ [\ begin {matrix} {{\ operatorname {I}} _ {m}} = \ omega C {{V} _ {m}} & {} & at \ text {} t = 0 \\\ end {matrix} \]

или

\ [\ frac {{{V} _ {m}}} {{{I} _ {m}}} = \ frac {1} {wC} \]

Величина 1 / ωC называется емкостным реактивным сопротивлением, измеряется в омах и обозначается как Xc.{-6}}} = 79,5 ~ \ Omega \]

$ {{I} _ {C}} = \ frac {{{V} _ {C}}} {{{X} _ {C}}} = \ frac {10} {79.5} = 0,126 ~

австралийских долларов

(b):

$ {{Q} _ {C}} = {{V} _ {C}} {{I} _ {C} } = 10 * 0,126 = 1,26 ~ vars $

Комбинированное сопротивление и реактивность

На практике большинство схем содержат смесь резистивных компонентов вместе с реактивными компонентами, которые могут быть индуктивными или емкостными. Для анализа этих типов цепей особенно полезным инструментом оказывается использование импеданса. Как указывалось ранее, полное сопротивление цепи, независимо от природы компонентов, может быть описано соотношением

\ [Z = \ frac {V} {I} \]

Рисунок 8: Диаграмма импеданса

В схеме, содержащей как резистивные, так и реактивные элементы, полное сопротивление в комплексной плоскости можно описать общей зависимостью, изображенной на рис. 8 , где в прямоугольной форме

\ [Z = R + jX \]

R — резистивная составляющая импеданса (Ом)

X — реактивная составляющая импеданса (Ом)

Расчет индуктивного реактивного сопротивления

  • Изучив этот раздел, вы сможете описать:
  • • Расчеты индуктивного сопротивления.
  • • Многоступенчатые расчеты.

Для расчетов на основе индуктивного реактивного сопротивления вам сначала нужно подумать об информации о реактивном сопротивлении и сопротивлении во введении к этому модулю, чтобы узнать о различиях между реактивным сопротивлением и сопротивлением. Для расчетов вы можете выбрать, какую формулу использовать для индуктивного реактивного сопротивления: 2πƒL или ωL, но чаще используется 2πƒL (одна из причин состоит в том, что в научных калькуляторах в большинстве случаев есть клавиша π, но нет клавиши ω!).

Помните, что некоторые проблемы, которые вам, возможно, придется решить, не обязательно имеют очевидное решение, например, простой расчет реактивного сопротивления компонента. Например, если вас просят рассчитать напряжение питания, необходимое для создания определенного тока, протекающего через компонент, или напряжение на компоненте, могут потребоваться два или более шагов, используя ответ из одного расчета, чтобы предоставить информацию для второго расчета до достижения окончательный ответ.

Перед тем, как начать, подумайте о следующих советах, они облегчат решение, если вы будете внимательно им следовать.

1. Разработайте ответы с помощью карандаша и бумаги; перерисуйте схему, над которой работаете.

2. Перечислите элементы информации, которую вам дают, и то, что вам нужно найти для своего ответа. Это поможет вам решить, можно ли найти ответ за один шаг или вам понадобится промежуточный ответ.

3. После того, как вы перечислили информацию на шаге 2 (выше), вам нужно будет решить, какую соответствующую формулу (или формулы) использовать. Запишите и это.

4. Конечно, ответ — это не просто число. Если вы рассчитываете X L , это будет определенное количество Ом, не забудьте указать правильные единицы измерения (например, Ω, KΩ или MΩ) или ваше ответ бессмысленный.

5. Когда вы вводите значения в калькулятор, преобразуйте все значения KΩ или MΩ в Ом с помощью клавиши EXP. Если вы здесь ошибетесь, то получите действительно глупые ответы, в тысячи раз слишком большие или слишком маленькие.

Все эти шаги сначала кажутся довольно утомительными, но войдите в привычку, и они упростят ваши вычисления, потому что вы будете следовать знакомому методу.Они также будут более надежными, потому что, когда вам нужно выполнить многоэтапные расчеты, вам нужно быть организованным. Так легко ошибиться на полпути в тренировке, потому что вы забыли, где именно вы находитесь в расчетах. Однако если вы выписали каждую проблему, это позволит вам вернуться назад и посмотреть, где вы ошиблись, и не повторять одни и те же ошибки. См. Рабочий пример ниже.

Зачем тратить время на все эти хлопоты, когда в Интернете есть множество калькуляторов, которые сделают расчеты за вас?

Многие электронные и сетевые калькуляторы превосходны, просто введите данные и нажмите, чтобы получить ответ.Но вам все равно нужно инстинктивно знать, какую формулу использовать, когда и почему. Чтобы быть достаточно знакомым, чтобы делать это хорошо, вам необходимо знать, как работают различные формулы. Лучший способ сделать это — начать с решения некоторых проблем вручную, тогда вы обнаружите, что многие из калькуляторов, предлагаемых на веб-сайтах, гораздо более полезны.

Чтобы помочь вам на правильном пути, почему бы не загрузить нашу брошюру «Подсказки по математике», в которой показано, как использовать калькулятор с показателями степени и инженерной нотацией, чтобы работать с этими единицами и каждый раз получать правильный ответ.

Нет научного калькулятора? Буклет «Подсказки по математике» объясняет, что вам нужно (и что вам не нужно, чтобы не тратить деньги без надобности). Если вы не хотите покупать научный калькулятор, вы всегда можете получить его бесплатно на сайте www.calculator.org/download.html. Пользователи ПК могут попробовать Calc98.

Какой бы калькулятор вы ни выбрали, помните, что вам следует прочитать инструкции, чтобы ознакомиться с методами работы, которые вам следует использовать, поскольку они различаются от калькулятора к калькулятору.

Хорошо, теперь вы прочитали эти инструкции, и вы готовы к работе. Вот способ решить типичную проблему на бумаге, чтобы (с практикой) вы не запутались.

Пример рабочего реактивного сопротивления.

Вопрос:

Рассчитайте напряжение питания (V S ), необходимое для протекания тока 10 мА через катушку индуктивности 15 мГн при частоте питания 400 Гц.

1. Нарисуйте схему и перечислите значения:

L = 15 мГн

ƒ = 400 Гц

I = 10 мА

2.Перечислите необходимые формулы.

Напряжение питания В S = IX L

Индуктивное реактивное сопротивление X L = 2ΠƒL

3. Рассчитать X L

X L = 2Π x 400 x 15exp -3 = 37,7 Ом

4. Используйте X L для расчета V S

V S = IX L = 10exp -3 x 37,7 = 0,377

5. Дайте ответ в соответствующей форме (используйте кнопку калькулятора ENG для преобразования между В, мВ, мкВ и т. Д.чтобы числовой ответ оставался от 1 до 999)

Ответ: V

S = 377 мВ

Примечание. При ответе на подобные проблемы обычно округляйте все десятичные дроби до двух знаков после запятой. Если вы используете Calc98 для своих расчетов, вам необходимо установить в меню View> Option> Display значение Engineering (в разделе «Decimal»), и было бы неплохо, пока вы находитесь в этом меню, выбрать 2 из раскрывающегося списка Decimals. поле для установки количества цифр после десятичного разряда.Это округлит ваш ответ до двух знаков после запятой, что является достаточно точным для большинства случаев, и не даст вам получить глупые ответы, такие как 75.666666666667, что было бы слишком точным для большинства целей.

.

Читайте также

Что делать, если грудничок не спит днем: советы по налаживанию режима сна

Антигистаминные препараты для новорожденных: лечение и профилактика аллергии у грудничков

Методика «Цветоник» М. Лазарева для музыкального развития детей

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *