Формула резонанса частоты: Электротехника: Резонансная частота.

Электротехника: Резонансная частота.

 Параллельный колебательный контур (рисунок 1) или последовательный колебательный контур (рисунок 2) могут использоваться в генераторах синусоидальных колебаний. Если в одной из этих схем зарядить конденсатор то он будет разряжаться заряжая катушку индуктивности, катушка разряжаясь будет заряжать конденсатор, этот процесс будет повторяться с определённым периодом T. Период это время одного колебания. Частота колебаний это величина обратная периоду. Разделив единицу на численное значение периода получим  численное значение частоты. Рисунок 1 —  Параллельный колебательный контур

Рисунок 2 —  Последовательный колебательный контур  

 Частота возникших колебаний называется собственной частотой колебаний контура для контуров изображённых на рисунках выше эта частота равна резонансной частоте этих контуров. Резонансная частота контура зависит от индуктивности L и ёмкости C её элементов, для колебательного контура (последовательного или параллельного) её можно найти по формуле:
Где L-индуктивность катушки контура, C-ёмкость конденсатора контура.
Если на параллельный или последовательный колебательный контур подавать переменное синусоидальное напряжение и изменять его частоту то будут меняться реактивные сопротивления элементов контура, если частота увеличивается то сопротивление конденсатора уменьшается а сопротивление катушки увеличивается и наоборот: если частота уменьшается то сопротивление конденсатора увеличивается а сопротивление катушки уменьшается, очевидно что есть такая частота при которой сопротивление катушки и конденсатора равны эта частота и есть резонансная. Сопротивление параллельного колебательного контура при этой частоте будет наибольшим (по сравнению с сопротивлениями этого контура при других частотах) а сопротивление последовательного колебательного контура при такой частоте будет наименьшим. Эти свойства контуров используют для построения фильтров например в полосно-пропускающем фильтре последовательно с нагрузкой ставиться последовательный контур и при подаче на это соединение (нагрузки и контура) переменного напряжения с резонансной частотой ток в нагрузке будет максимальным при других частотах ток будет меньше. Резонанс в параллельном контуре называют — резонансом токов, резонанс в последовательном контуре — резонансом напряжений. Можно простым способом определить каким будет сопротивление контура при резонансной частоте: например допустим что на параллельный колебательный контур подаётся постоянный ток, постоянный ток можно считать частным случаем переменного короче говоря постоянный ток это переменный с наименьшей возможной частотой, известно что при постоянном токе катушка действует как перемычка следовательно сопротивление контура будет равно нулю если резонансная частота не бесконечно мала (т.е. не постоянный ток) и сопротивление есть то оно больше нуля (т.е. сопротивления при постоянном токе) следовательно сопротивление параллельного колебательного контура на резонансной частоте максимальное а у последовательного контура наоборот. Зная то что конденсатор постоянный ток не пропускает, можно аналогично определить каким д.б. сопротивление последовательного контура на резонансной частоте. Выведем формулу для расчёта резонансной частоты зная то что при резонансе реактивные сопротивления элементов (катушки и конденсатора) контура равны:

Для расчёта резонансной частоты и периода колебаний колебательного контура с катушкой и конденсатором можно воспользоваться программой:

Резонанс | Формулы и расчеты онлайн

При заданных возмущающей силе F_{max. возм} и коэффициенте трения β амплитуда Y_m является функцией только угловой частоты возмущающей силы.

На рисунке показана зависимость Y_m от ω (резонансная кривая). Параметром служит коэффициент затухания δ.

При ω ≈ ω₀ она достигает особенно большого значения (резонанс).

При самых малых значениях δ величина Y_m резко возрастает.

Если δ > 0, то в случае резонанса ω < ω₀; величина Y_max.ст представляет собой статическое отклонение системы под действием постоянной силы Y_max.возм (ω = 0).

Для определения резонансной частоты необходимо найти максимум функции Ym = Ym(ω) и приравнять первую производную нулю; тогда, если

ωрез	резонансная частота, при которой амплитуда максимальна,	радиан/сек
ω0	частота собственных незатухающих колебаний системы,	радиан/сек
m	масса колебательной системы,	кг
β	коэффициентом вязкого трения,	кг/сек
δ	коэффициентом затухания,	радиан/сек

Частота резонанса

\[ ω_{рез} = \sqrt[-1. 2} \]

Условие отсутствия резонанса

\[ δ ≥   \frac{ω_{0}}{\sqrt{2}} \]

Амплитуда резонанса

Чтобы найти величину амплитуды в резонансном случае, нужно подставить формулу (1) в формулу отклонения при вынужденных колебаниях.

Если

Ymax.рез	резонансная амплитуда колебаний системы,	метр
Fmax.возм	максимальное значение возмущающей силы,	Ньютон
m	масса колебательной системы,	кг
ωрез	резонансная частота, при которой амплитуда максимальна,	радиан/сек
ω0	частота собственных незатухающих колебаний системы,	радиан/сек
ω	частота колебаний системы с затуханием,	радиан/сек
β	коэффициентом вязкого трения,	кг/сек
δ	коэффициентом затухания,	радиан/сек

то имеем

\[ Y_m = \frac[-2. 2} } } \]

\[ Y_m = \frac{F_{max.возм}}{βω} \]

\[ Y_m = \frac{F_{max.возм}}{2δmω} \]

Согласно формуле, разность фаз α также зависит от частоты возмущающей силы. Параметром служит коэффициент δ.

На рисунке представлена зависимость α от частоты.

Независимо от величины затухания при ω = ω₀ разность фаз составляет

\[ α = 90° \]

Резонанс

играет большую роль в технике и в повседневной жизни. В большинстве механических устройств под действием внешних периодических сил могут возникать колебания. При резонансе происходит нарастание амплитуды колебаний, и это может привести к разрушениям («резонансная катастрофа»). В случае вращательного движения резонансную частоту называют критическим числом оборотов.

Резонанс	стр. 556

в цепи переменного тока и напряжения

Многие люди, изучая электронику и все, что с ней связано, сталкиваются с таким понятием как резонанс токов.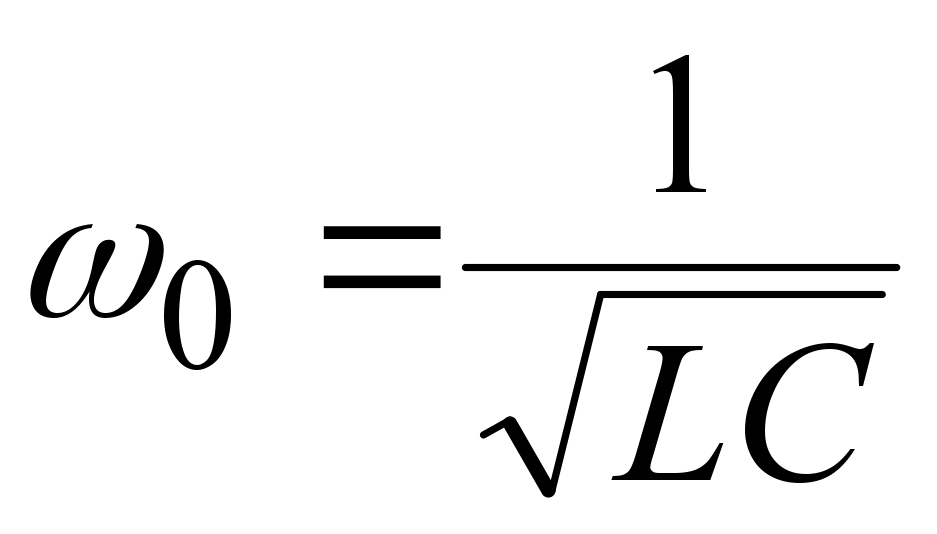 Что оно собой представляет, при каких условиях возникает резонанс токов, как используется и как его правильно подсчитать? Об этом далее.

Что это такое

Резонанс токов — разновидность состояния электрической цепи, когда общий вид токовых показателей совпадает по фазам уровню напряжения, а мощность реактивного вида равна нулю или же она представлена в активном виде.

. Резонанс токов

Этот вариант развития событий характерен для переменного тока и имеет не только положительные свойства, но и некоторые нежелательные последствия. Так, благодаря резонансу работает радиотехника, автоматика и проволочная телефония, но в то же время возникают перенапряжения и сбои в работе электрической системы.

Определение из учебного пособия

При каких условиях возникает

Условием того, чтобы возникло это явление, является равные показатели проводниковой частоты, где BL=BC. То есть емкостная с индуктивной проводимостью должна быть равна. Только тогда подобное явление резонанса токов наблюдается в электрической цепи.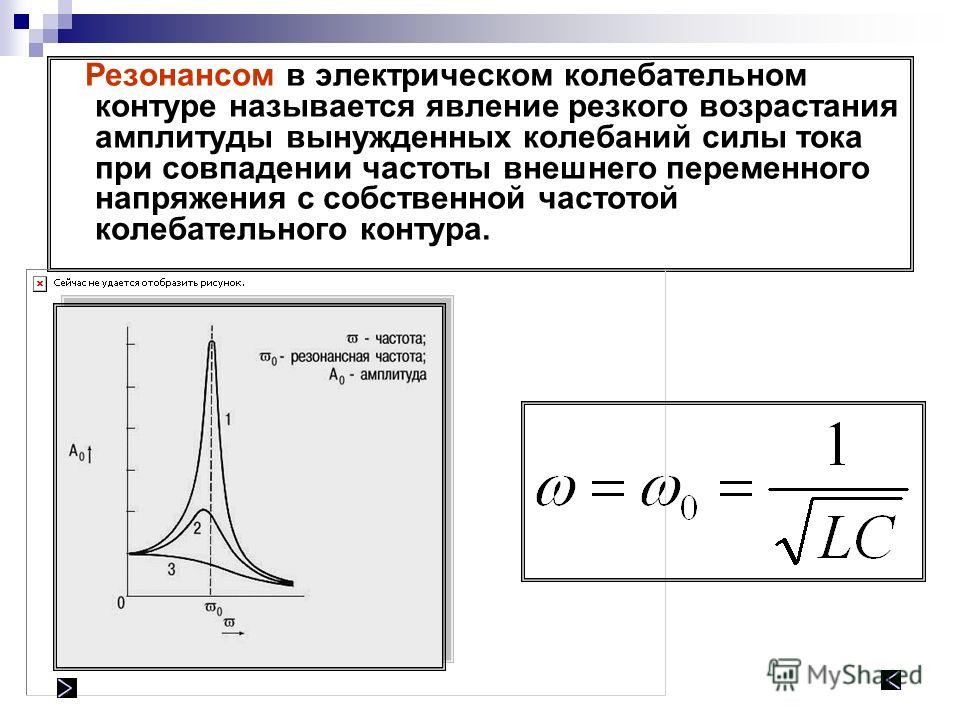 Он при этом может быть как положительным, так и отрицательным. В любом радиоприемнике есть колебательный контур, который из-за индуктивного или емкостного изменения, настраивается на нужный сигнал радиоволны. В другом случае, это ведет к тому, что появляются скачки напряжения или ток в цепи и появляется аварийная ситуация.

В условиях лаборатории, он возникает во время, когда изменяется емкость и не изменяется индуктивность катушки L. В таком случае формула выглядит как Bc=C

При каких условиях возникает

Как используется

Резонансные токи используются сегодня в некоторых фильтрующих системах, радиотехнике, электричестве, радиостанциях, асинхронных двигателях, высокоточных электрических сварных установках, колебательных генераторных электрических контурах и высокочастотных приборах. Нередко, когда они применяются, чтобы снизить генераторную нагрузку.

Обратите внимание! Простейшая цепь, где наблюдаются они, это параллельного вида колебательный контур. Такие контуры используются в современном промышленном индукционном котловом оборудовании и улучшают показатели КПД.

Сфера применения

Принцип действия

Токовый резонанс можно заметить во внутренней поверхности электрической цепи, которая имеет параллельное катушечное, резисторное и конденсаторное подсоединение. Главный принцип того, как работает стандартный аппарат, не сложен в понимании.

Когда включается электрическое питание, внутри конденсаторной установки накапливается заряд до номинального напряжения. В этом время отключается питающий источник и замыкается цепь в контур. Этот момент сопровождается переносом разряда на часть катушки. Далее показатели тока, которые проходят по катушке, генерируют магнитное поле. Создается электродвижущая самостоятельная индукционная сила по направлению встречному току. При полном конденсаторном разряде максимально увеличиваются токовые показатели. Объем энергии становится магнитным индукционным полем. В результате данный цикл повторяется, и катушечное поле преобразовывается в конденсаторный заряд.

Принцип работы

Как правильно рассчитать

Токовый резонанс очень важно правильно рассчитать, если есть параллельное соединение, предотвращающая появление помех около системы. Для правильного расчета необходимо понять, какие показатели мощности в электросети. Средняя стандартная мощность, рассеивающаяся при резонансном контуре, выражается при помощи среднеквадратичных токовых показателей и напряжения. При резонансе мощностный коэффициент равен единице и формула имеет вид, как на картинке.

Формула расчета

Чтобы правильно определить нулевой импеданс, понадобиться воспользоваться стандартной формулой, которая дана ниже.

Формула резонансных кривых

Что касается аппроксимирования резонанса колебательных частот, это можно выяснить по следующей формуле.

Расчет колебательного контура

Обратите внимание! Для получения максимально точных данных по приведенным формулам, округлять данные не нужно. Благодаря этому получится грамотный расчет, который приведет к достойной экономии переменного тока, если речь идет о подсчете в целях снижения счетов.

В целом, резонанс токов — это то, что происходит в части параллельного колебательного контура, в случае его подключения к источнику напряжения, частота какого может совпадать с контурной. Возникает при условиях, когда цепь, имеющая параллельное соединение резисторной катушки и конденсатора, равна проводимости BL=BC. Правильно сделать весь необходимый подсчет можно по специальной формуле или, прибегая к использованию специальных измерительных инструментов в виде мультиметра.

Линии передачи и объемные резонаторы

В рассматриваемом случае уравнения Максвелла (1.33) и (1.39) из пособия 1 можно переписать в виде:

и (2. 5)

Выражая в (2.4) вектор Е1 через Н1 или, наоборот, вектор Н1через Е1 получаем:

(2.6)

Слева в (2.6) стоит квадрат резонансной угловой частоты объемного резонатора, а справа — всегда положительная величина, равная отношению двух объемных интегралов. Численное значение каждого из этих интегралов зависит от формы объема V0 и его размеров, а также от характера подынтегральной функции. Поэтому резонансная частота резонатора зависит от структуры полей в резонаторе, его формы и размеров.

Структура полей в резонаторе, как и в направляющих системах, определяется путем решения уравнений Максвелла при определенных граничных условиях на поверхности, окружающей объем V0. В случае закрытых резонаторов без потерь задача сводится к решению трехмерного векторного волнового уравнения:

(2.7)

при граничном условии (1. 108) из пособия 1:

(2.8)

где S — внутренняя поверхность металлической оболочки резонатора, а — орт нормали к этой поверхности.

Можно доказать, что уравнение (2.7) при граничном условии (2.8), как и аналогичные уравнения теории направляющих систем, имеет бесконечное число различных решений, каждому из которых, согласно (2.6), соответствует определенное значение резонансной угловой частоты, т.е. объемные резонаторы, в отличие от обычных контуров из сосредоточенных элементов, резонируют не на одной частоте, а на бесконечном множестве дискретных частот . То колебание, которому при данных размерах резонатора соответствует минимальная резонансная частота ω01, называют низшим колебанием. Отметим, что каждой резонансной частоте соответствует определенная структура электромагнитного поля в резонаторе.

Не исключено, что в объемном резонаторе резонансные частоты двух или большего числа колебаний с различной структурой полей совпадут. Обладающие этим свойством колебания принято называть вырожденными.

Наряду с резонансной угловой частотой вводят понятия резонансной, или собственной, длины волны и резонансной (собственной) частоты

Амплитудно-частотная характеристика. Резонанс — Студопедия

ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ

Уравнение вынужденных колебаний

Рассмотрим реальную колебательную систему – пружинный маятник. Свободные колебания груза описываются уравнением (9.10):

,

где: β = r/(2m) – коэффициент затухания,

 − собственная частота,

r – сопротивление среды,

m – масса груза,

k – жёсткость пружины.

И пусть на шарик начинает действовать внешняя периодическая сила

F (t)= F₀ cos ωt,                                      (10.1)

где ω – частота этого воздействия, F₀  — амплитуда силы. Частота ω внешней силы может принимать произвольные значения, никак не связана с собственной частотой ω₀, которая является параметром самой колебательной системы. Внешней силой (10.1) может быть, например, воздушный поток. Тогда уравнение движения груза (второй закон Ньютона) будет иметь вид:

m = ∑F_x= F_{тр. х} + F_{упр. х} + F_{внеш. х} = −r − kx + F₀ cos ωt

или:

m + r + kx = F₀ cos ωt,

или, как и в разд (9.8),

.                                 (10.2)

Уравнение (10.2) называется уравнением вынужденных колебаний груза. Без специальных методов процедура решения уравнения (10.2) весьма громоздка, и ею мы заниматься не будем.

Если груз начинает движение под действием силы (10.1) из состояния покоя, то сначала он раскачиваться и его амплитуда Х будет расти. Этот этап «раскачки» называется переходным процессом (рис. 10.1). Затем амплитуда колебаний устанавливается определённой величины, зависящей от параметров системы r, m, k и от частоты ω и амплитуды F₀  внешней силы. Наступает установившийся синусоидальный процесс вынужденных колебаний:

х(t) = Х sin(ωt + φ),

где Х = Х(ω, F₀, m, r, k) – амплитуда установившихся колебаний, φ − начальная фаза.

Замечание 1. Частота вынужденных колебаний ω всегда устанавливается равной частоте внешней силы, какова бы ни была собственная частота ω₀.

Замечание 2. Теоретически переходный процесс длится бесконечно долго, экспоненциально приближаясь к установившемуся, но реально полагают, что он практически заканчивается за время порядка 3τ, где τ = 1/β – время релаксации (разд. 9.8), когда амплитуда Х достигает примерно 95% от своего установившегося значения при t →∞ (рис. 10.1).

Амплитудно-частотная характеристика. Резонанс

При заданных параметрах m, k и r колебательной системы и среды амплитуда установившихся колебаний Х зависит от частоты ω внешней силы.

Определение. Зависимость Х(ω) называется амплитудно-частотной характеристикой колебательной системы.

Формула зависимости Х(ω) достаточно сложна. Графический вид этой зависимости показан на рис. 10.2. На этом рисунке Х(0) – это отклонения груза под действием постоянной силы F₀. При частоте внешнего воздействия ω→∞ отклонение груза стремится к нулю. При частоте ω = ω₀ амплитуда колебаний достигает максимума и в Q раз превышает значение Х(0), где Q – добротность колебательной системы. Это явление называется резонансом в колебательной системе, а соответствующая частота ω = ω₀ называется резонансной (ω_рез).

При резонансе амплитуда колебаний может достигать очень больших значений, что может привести к разрушению колебательной системы. Так например, при добротности Q = 100 постоянная сила, дающая смещение в колебательной системе всего на 1 мм, при резонансе приведёт к смещению в 100 мм. Поэтому резонанс в механических системах (мостах, машинах, высоких мачтах и других конструкциях) весьма опасен и его стараются избегать различными методами. Иногда резонанс можно наблюдать в дрожании оконных стёкол, когда недалеко от дома проезжает какая-нибудь тяжёлая машина и в ней частота работающего двигателя совпадает с резонансной частотой оконного стекла.

 

Вынужденные колебания. Резонанс. Резонансная частота. — КиберПедия

Лекция 12

Колебательное движение

Вопросы

1. Затухающие колебания.

2. Вынужденные колебания. Резонанс.

Затухающие колебания

Во всякой реальной колебательной системе имеются силы сопротивления, действие которых уменьшает энергию системы. Если убыль энергии не восполняется за счет работы внешних сил, то колебания будут затухать. Сила сопротивления пропорциональна величине скорости:

, (1)

r— постоянная величина, называемая коэффициентом сопротивления среды.

Уравнение второго закона Ньютона

, . (2)

Это дифференциальное уравнение описывает затухающие колебания системы,b-коэффициент затухания.

Общее решение уравнения (2) ищем в виде: (3)(2) (3)

;

;

;(4)

,(5)

, (6)

При незначительном сопротивлении среды (b² << ) период колебаний практически равенТ₀ = 2p/w₀. С ростом коэффициента затухания период колебаний увеличивается, а при движение становится апериодическим, система возвращается в положение равновесия.

Физический смысл коэффициента затухания:

. (7)

Коэффициент затуханияобратно пропорционален по величине времени релаксации (времени затухания) t, за которое амплитуда уменьшается в е = 2,72 раз.

Отношение амплитуд, соответствующих моментам времени, отличающимся на период

. (8)

называетсядекрементом затухания,а его логарифм-логарифмическим декрементом затухания:

. (9)

Важной характеристикой колебательной системы, совершающей свободные затухающие колебания, является добротностьQ. Этот параметр определяется как число N полных колебаний, совершаемых системой за время затухания τ, умноженное на π:

(10)

Понятие добротности имеет глубокий энергетический смысл. Можно определить добротность Q колебательной системы следующим энергетическим соотношением:

Таким образом, добротность характеризует относительную убыль энергии колебательной системы из-за наличия трения на интервале времени, равном одному периоду колебаний.

2. Вынужденные колебания. Резонанс

Пусть колебательная система подвергается действию внешней вынуждающей силы, изменяющейся со временем по гармоническому закону:

F_x = F₀sinWt . (11)

В этом случае уравнение второго закона Ньютона имеет вид:

. ,f₀ = F₀/m(12)

Общее решение равно сумме решения однородного уравнения и частного решения неоднородного уравнения

, (13)

(13) (12)

,(14)

Если частота W внешней силы приближается к собственной частоте ω₀, возникает резкое возрастание амплитуды вынужденных колебаний. Это явление называется резонансом. Зависимость амплитудыВ вынужден­ных колебаний от частоты W вынуж­дающей силы называется резонансной характеристикой или резонансной кривой.

Нахождение резонансной частоты и амплитуды

.(15)

(15) (14)(16)

В отсутствие трения (b = 0) амплитуда вынужденных колебаний при резонансе должна неограниченно возрастать. В реальных условиях амплитуда установившихся вынужденных колебаний определяется условием: работа внешней силы в течение периода колебаний должна равняться потерям механической энергии за то же время из-за трения. Чем меньше трение (т. е. чем выше добротность Q колебательной системы), тем больше амплитуда вынужденных колебаний при резонансе.

Явление резонанса может явиться причиной разрушения мостов, зданий и других сооружений, если собственные частоты их колебаний совпадут с частотой периодически действующей силы, возникшей, например, из-за вращения несбалансированного мотора.

Рис. 4

Вынужденные колебания – это незатухающие колебания. Существуют системы, в которых незатухающие колебания возникают не за счет периодического внешнего воздействия, а в результате имеющейся у таких систем способности самой регулировать поступление энергии от постоянного источника. Такие системы называются автоколеба­тель­ными, а процесс незатухающих колебаний в таких системах – автоколебаниями. В автоколе­бательной системе можно выделить три характерных элемента – колебательная система, источник энергии и устройство обратной связи между колебательной системой и источником.

Глава 2. Механические колебания и волны Волны

2.6. Механические волны

Если в каком-нибудь месте твердой, жидкой или газообразной среды возбуждены колебания частиц, то вследствие взаимодействия атомов и молекул среды колебания начинают передаваться от одной точки к другой с конечной скоростью. Процесс распространения колебаний в среде называется волной.

Механические волны бывают разных видов. Если при распространении волны частицы среды испытывают смещение в направлении, перпендикулярном направлению распространения, такая волна называется поперечной. Примером волны такого рода могут служить волны, бегущие по натянутому резиновому жгуту (рис. 2.6.1) или по струне.

Если смещение частиц среды происходит в направлении распространения волны, такая волна называется продольной. Волны в упругом стержне (рис. 2.6.2) или звуковые волны в газе являются примерами таких волн.

Волны на поверхности жидкости имеют как поперечную, так и продольную компоненты.

Как в поперечных, так и в продольных волнах не происходит переноса вещества в направлении распространения волны. В процессе распространения частицы среды лишь совершают колебания около положений равновесия. Однако волны переносят энергию колебаний от одной точки среды к другой.

Рисунок 2.6.1. Распространение поперечного волнового импульса по натянутому резиновому жгуту.

 

Рисунок 2.6.2. Распространение продольного волнового импульса по упругому стержню.

Характерной особенностью механических волн является то, что они распространяются в материальных средах (твердых, жидких или газообразных). Существуют волны, которые способны распространяться и в пустоте (например, световые волны). Для механических волн обязательно нужна среда, обладающая способностью запасать кинетическую и потенциальную энергию. Следовательно, среда должна обладать инертными и упругими свойствами. В реальных средах эти свойства распределены по всему объему. Так, например, любой малый элемент твердого тела обладает массой и упругостью. В простейшей одномерной моделитвердое тело можно представить как совокупность шариков и пружинок (рис. 2.6.3).

Рисунок 2.6.3. Простейшая одномерная модель твердого тела.

В этой модели инертные и упругие свойства разделены. Шарики обладают массой m, а пружинки – жесткостью k. С помощью такой простой модели можно описать распространение продольных и поперечных волн в твердом теле. В продольных волнах шарики испытывают смещения вдоль цепочки, а пружинки растягиваются или сжимаются. Такая деформация называется деформацией растяжения или сжатия (см. §1.12). В жидкостях или газах деформация такого рода сопровождается уплотнением или разрежением.

Вынужденные колебания

ОПРЕДЕЛЕНИЕ

Вынужденные колебания – это колебания, происходящие под действием внешней периодически действующей силы.

В отличие от свободных колебаний, когда система получает энергию лишь один раз (при выведении системы из состояния равновесия), в случае вынужденных колебаний система поглощает эту энергию от источника внешней периодической силы непрерывно. Эта энергия восполняет потери, расходуемые на преодоление трения, и потому полная энергия колебательной системыno-прежнему остается неизменной.

Вынужденные колебания в отличие от свободных могут происходить с любой частотой. Частота вынужденных колебаний совпадает с частотой внешней силы, действующей на колебательную систему. Таким образом, частота вынужденных колебаний определяется не свойствами самой системы, а частотой внешнего воздействия.

Примерами вынужденных колебаний являются колебания детских качелей, колебания иглы в швейной машине, поршня в цилиндре автомобильного двигателя, рессор автомобиля, движущегося по неровной дороге и т.д.

Резонанс

ОПРЕДЕЛЕНИЕ

Резонанс – это явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к собственной частоте колебательной системы.

Резонанс возникает из-за того, что привнешняя сила, действуя в такт со свободными колебаниями, все время имеет одинаковое направление со скоростью колеблющегося тела и совершает положительную работу: энергия колеблющегося тела увеличивается, и амплитуда его колебаний становится большой. Если же внешняя сила действует «не в такт», то эта силы попеременно совершает то отрицательную, то положительную работу и вследствие этого энергия системы меняется незначительно.

На рис.1 показана зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы. Видно, что эта амплитуда достигает максимума при определенном значении частоты, т.е. при, где собственная частота колебательной системы. Кривые 1 и 2 отличаются величиной силы трения. При малом трении (кривая 1) резонансная кривая имеет резкий максимум, при большей силе трения (кривая 2) такого резкого максимума нет.

Механические колебания

Примеры решения задач

ПРИМЕР 1

Задание	На конец пружины горизонтального маятника, груз которого имеет массу 1 кг, действует переменная сила, частота колебаний которой равна 16 Гц. Будет ли при этом наблюдаться резонанс, если жесткость пружины 400 Н/м.
Решение	Определим собственную частоту колебательной системы по формуле:   Гц Так как частота внешней силы не равна собственной частоте системы, явление резонанса наблюдаться не будет.
Ответ	Явление резонанса наблюдаться не будет.

ПРИМЕР 2

Задание	Маленький шарик подвешен на нити длиной 1 м к потолку вагона. При какой скорости вагона шарик будет особенной сильно колебаться под действием ударов колес о стыки рельсов? Длина рельса 12,5 м.
Решение	Шарик совершает вынужденные колебания с частотой , равной частоте ударов колес о стыки рельсов:   Если размеры шарика малы по сравнению с длиной нити, то систему можно считать математическим маятником, собственная частота колебаний которого:   амплитуда вынужденных незатухающих колебаний максимальна в случае резонанса, т.е. когда . Таким образом можно записать:   откуда скорость вагона:   Ускорение свободного падениям/с Вычислим:
Ответ	Скорость вагона, при которой колебания шарика будут максимальны, равна 6,2 м/с.

Резонанс

 

Как амплитуда установившихся вынужденных колебаний зависит от частоты внешней силы?
При увеличении частоты внешней силы амплитуда колебаний постепенно возрастает.
Она достигает максимума, когда частота вынужденных колебаний становится равной частоте внешней периодически действующей силы.
При дальнейшем увеличении частоты амплитуда установившихся колебаний уменьшается.

Резкое возрастание амплитуды вынужденных колебаний при совпадении частоты изменения внешней силы, действующей на систему, с частотой ее свободных колебаний называется резонансом.

Почему возникает резонанс?

При резонансе внешняя сила действует в такт со свободными колебаниями.
Ее направление совпадает с направлением скорости мммаятника, поэтому эта сила совершает только положительную работу.
При установившихся колебаниях положительная работа внешней силы равна по модулю отрицательной работе силы сопротивления.

Большое влияние на резонанс оказывает трение в системе.
Чем меньше коэффициент трения, тем больше амплитуда установившихся колебаний.

Изменение амплитуды вынужденных колебаний в зависимости от трения:

кривая 1 — минимальное трение,
кривая 3 — максимальное трение.
Возрастание амплитуды вынужденных колебаний при резонансе выражено тем отчетливее, чем меньше трение в системе.
При малом трении резонанс «острый», а при большом «тупой».

Согласно закону сохранения энергии вызвать в системе колебания с большой амплитудой при небольшой внешней силе можно только за продолжительное время.
Если трение велико, то амплитуда колебаний будет небольшой, и для установления колебаний не потребуется много времени.

 

Автоколебания

Как было показано в § 5.5, незатухающие колебания могут под­держиваться в системе даже при наличии сил сопротивления, если на систему периодически оказывается внешнее воздействие (вы­нужденные колебания). Это внешнее воздействие не зависит от са­мой колеблющейся системы, в то время как амплитуда и частота вынужденных колебаний зависят от этого внешнего воздействия.

Однако существуют и такие колебательные системы, которые сами регулируют периодическое восполнение растраченной энер­гии и поэтому могут колебаться длительное время.

Незатухающие колебания, существующие в какой-либо сис­теме с затуханием при отсутствии переменного внешнего воз­действия, называются автоколебаниями, а сами системы — автоколебательными.

Амплитуда и частота автоколебаний зависят от свойств самой автоколебательной системы, в отличие от вынужденных колеба­ний они не определяются внешними воздействиями.

Во многих случаях автоколебательные системы можно пред­ставить тремя основными элементами: 1) собственно колебатель­ная система; 2) источник энергии; 3) регулятор поступления энер­гии в собственно колебательную систему. Колебательная система каналом обратной связи (рис. 5.19) воздействует на регулятор, информируя регулятор о состоянии этой системы.

Классическим примером механической автоколебательной сис­темы являются часы, в которых маятник или баланс являются ко­лебательной системой, пружина или поднятая гиря — источником энергии, а анкер — регулятором поступления энергии от источни­ка в колебательную систему.

Многие биологические системы (сердце, легкие и др.) являют­ся автоколебательными. Характерный пример электромагнитной автоколебательной системы — генераторы электромагнитных ко­лебаний

 

 

Вынужденные колебания. Резонанс. Резонансная частота.

 

 

Вынужденные колебания. Резонанс

Для того чтобы система совершала незатухающие колебания, необходимо извне восполнять потери энергии колебаний на трение. Для того, чтобы энергия колебаний системы не убывала обычно вводят силу, периодически воздействующую на систему (такую силу будем называть вынуждающей, а колебания вынужденными).

ОПРЕДЕЛЕНИЕ: вынужденными называются такие колебания, которые возникают в колебательной системе под действием внешней периодически изменяющейся силы.

Эта сила, как правило, выполняет двоякую роль:

— во-первых, она раскачивает систему и сообщает ей определенный запас энергии;

— во-вторых, она периодически восполняет потери энергии (расход энергии) на преодоление сил сопротивления и трения.

Пусть вынуждающая сила изменяется со временем по закону:

.

Составим уравнение движения для системы, колеблющейся под воздействием такой силы. Предполагаем, что на систему также действует квазиупругая сила и сила сопротивления среды (что справедливо в предположении малости колебаний).

Тогда уравнение движения системы будет иметь вид:

или .

Проведя подстановки , , – собственная частота колебаний системы, получим неоднородное линейной дифференциальное уравнение 2^го порядка:

.

Из теории дифференциальных уравнений известно, что общее решение неоднородного уравнения равно сумме общего решения однородного уравнения и частного решения неоднородного уравнения.

Общее решение однородного уравнения известно:

,

где ; a₀ и a – произвольные const.

Далее предположим, что частное (не содержащее произвольных констант) решение неоднородного уравнения имеет вид:

.

С помощью векторной диаграммы можно убедиться, что такое предположение справедливо, а также определить значения “a” и “j”.

Амплитуда колебаний определяется следующим выражением:

.

Значение “j”, которое представляет собой величину отставания по фазе вынужденного колебания от обусловившей его вынуждающей силы , также определяется из векторной диаграммы и составляет:

.

Окончательно, частное решение неоднородного уравнения примет вид:

(8.18)

Эта функция в сумме с

(8.19)

дает общее решение неоднородного дифференциального уравнения, описывающего поведение системы при вынужденных колебаниях. Слагаемое (8.19) играет заметную роль в начальной стадии процесса, при так называемом установлении колебаний (рис. 8.10).

С течением времени из-за экспоненциального множителя роль второго слагаемого (8.19) все больше уменьшается, и попрошествии достаточного времени им можно пренебречь, сохраняя в решении лишь слагаемое (8.18).

Таким образом, функция (8.18) описывает установившиеся вынужденные колебания. Они представляют собой гармонические колебания с частотой равной частоте вынуждающей силы. Амплитуда вынужденных колебаний пропорциональна амплитуде вынуждающей силы. Для данной колебательной системы (определенных w₀ и b) амплитуда зависит от частоты вынуждающей силы. Вынужденные колебания отстают по фазе от вынуждающей силы, причем величина отставания “j” также зависит от частоты вынуждающей силы.

Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы приводит к тому, что при некоторой определенной для данной системы частоте амплитуда колебаний достигает максимального значения. Колебательная система оказывается особенно отзывчивой на действие вынуждающей силы при этой частоте. Это явление называется резонансом, а соответствующая частота – резонансной частотой.

ОПРЕДЕЛЕНИЕ: явление, при котором наблюдается резкое возрастание амплитуды вынужденных колебаний, называется резонансом.

Резонансная частота определяется из условия максимума для амплитуды вынужденных колебаний:

. (8.20)

Тогда, подставив это значение в выражение для амплитуды, получим:

. (8.21)

При отсутствии сопротивления среды амплитуда колебаний при резонансе обращалась бы в бесконечность; резонансная частота при тех же условиях (b = 0) совпадает с собственной частотой колебаний.

Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы (или, что то же самое, от частоты колебаний) можно представить графически (рис. 8.11). Отдельные кривые соответствуют различным значениям “b”. Чем меньше “b”, тем выше и правее лежит максимум данной кривой (см. выражение для w_рез.). При очень большом затухании резонанс не наблюдается – с увеличением частоты амплитуда вынужденных колебаний монотонно убывает (нижняя кривая на рис. 8.11).

Совокупность представленных графиков, соответствующих различным значениям b, называется резонансными кривыми.

Замечанияпо поводу резонансных кривых:

При стремлении w®0 все кривые приходят к одному, отличному от нуля значению, равному . Это значение представляет собой смещение из положения равновесия, которое получает система под действием постоянной силы F₀.

При w®¥ все кривые асимптотически стремятся к нулю, т.к. при большой частоте сила так быстро изменяет свое направление, что система не успевает заметно сместится из положения равновесия.

Чем меньше b, тем сильнее изменяется с частотой амплитуда вблизи резонанса, тем «острее» максимум.

Примеры:

С явлением резонанса приходится считаться при конструировании машин, механизмов и сооружений (мосты, самолеты, корабли и т.п.).

Явление резонанса часто оказывается полезным, особенно в акустике и радиотехнике.

Лекция 12

Колебательное движение

Вопросы

1. Затухающие колебания.

2. Вынужденные колебания. Резонанс.

Затухающие колебания

Во всякой реальной колебательной системе имеются силы сопротивления, действие которых уменьшает энергию системы. Если убыль энергии не восполняется за счет работы внешних сил, то колебания будут затухать. Сила сопротивления пропорциональна величине скорости:

, (1)

r— постоянная величина, называемая коэффициентом сопротивления среды.

Уравнение второго закона Ньютона

, . (2)

Это дифференциальное уравнение описывает затухающие колебания системы,b-коэффициент затухания.

Общее решение уравнения (2) ищем в виде: (3)(2) (3)

;

;

;(4)

,(5)

, (6)

При незначительном сопротивлении среды (b² << ) период колебаний практически равенТ₀ = 2p/w₀. С ростом коэффициента затухания период колебаний увеличивается, а при движение становится апериодическим, система возвращается в положение равновесия.

Физический смысл коэффициента затухания:

. (7)

Коэффициент затуханияобратно пропорционален по величине времени релаксации (времени затухания) t, за которое амплитуда уменьшается в е = 2,72 раз.

Отношение амплитуд, соответствующих моментам времени, отличающимся на период

. (8)

называетсядекрементом затухания,а его логарифм-логарифмическим декрементом затухания:

. (9)

Важной характеристикой колебательной системы, совершающей свободные затухающие колебания, является добротностьQ. Этот параметр определяется как число N полных колебаний, совершаемых системой за время затухания τ, умноженное на π:

(10)

Понятие добротности имеет глубокий энергетический смысл. Можно определить добротность Q колебательной системы следующим энергетическим соотношением:

Таким образом, добротность характеризует относительную убыль энергии колебательной системы из-за наличия трения на интервале времени, равном одному периоду колебаний.

2. Вынужденные колебания. Резонанс

Пусть колебательная система подвергается действию внешней вынуждающей силы, изменяющейся со временем по гармоническому закону:

F_x = F₀sinWt . (11)

В этом случае уравнение второго закона Ньютона имеет вид:

. ,f₀ = F₀/m(12)

Общее решение равно сумме решения однородного уравнения и частного решения неоднородного уравнения

, (13)

(13) (12)

,(14)

Если частота W внешней силы приближается к собственной частоте ω₀, возникает резкое возрастание амплитуды вынужденных колебаний. Это явление называется резонансом. Зависимость амплитудыВ вынужден­ных колебаний от частоты W вынуж­дающей силы называется резонансной характеристикой или резонансной кривой.

Нахождение резонансной частоты и амплитуды

.(15)

(15) (14)(16)

В отсутствие трения (b = 0) амплитуда вынужденных колебаний при резонансе должна неограниченно возрастать. В реальных условиях амплитуда установившихся вынужденных колебаний определяется условием: работа внешней силы в течение периода колебаний должна равняться потерям механической энергии за то же время из-за трения. Чем меньше трение (т. е. чем выше добротность Q колебательной системы), тем больше амплитуда вынужденных колебаний при резонансе.

Явление резонанса может явиться причиной разрушения мостов, зданий и других сооружений, если собственные частоты их колебаний совпадут с частотой периодически действующей силы, возникшей, например, из-за вращения несбалансированного мотора.

Рис. 4

Вынужденные колебания – это незатухающие колебания. Существуют системы, в которых незатухающие колебания возникают не за счет периодического внешнего воздействия, а в результате имеющейся у таких систем способности самой регулировать поступление энергии от постоянного источника. Такие системы называются автоколеба­тель­ными, а процесс незатухающих колебаний в таких системах – автоколебаниями. В автоколе­бательной системе можно выделить три характерных элемента – колебательная система, источник энергии и устройство обратной связи между колебательной системой и источником.

Глава 2. Механические колебания и волны Волны

2.6. Механические волны

Если в каком-нибудь месте твердой, жидкой или газообразной среды возбуждены колебания частиц, то вследствие взаимодействия атомов и молекул среды колебания начинают передаваться от одной точки к другой с конечной скоростью. Процесс распространения колебаний в среде называется волной.

Механические волны бывают разных видов. Если при распространении волны частицы среды испытывают смещение в направлении, перпендикулярном направлению распространения, такая волна называется поперечной. Примером волны такого рода могут служить волны, бегущие по натянутому резиновому жгуту (рис. 2.6.1) или по струне.

Если смещение частиц среды происходит в направлении распространения волны, такая волна называется продольной. Волны в упругом стержне (рис. 2.6.2) или звуковые волны в газе являются примерами таких волн.

Волны на поверхности жидкости имеют как поперечную, так и продольную компоненты.

Как в поперечных, так и в продольных волнах не происходит переноса вещества в направлении распространения волны. В процессе распространения частицы среды лишь совершают колебания около положений равновесия. Однако волны переносят энергию колебаний от одной точки среды к другой.

Рисунок 2.6.1. Распространение поперечного волнового импульса по натянутому резиновому жгуту.

 

Рисунок 2.6.2. Распространение продольного волнового импульса по упругому стержню.

Характерной особенностью механических волн является то, что они распространяются в материальных средах (твердых, жидких или газообразных). Существуют волны, которые способны распространяться и в пустоте (например, световые волны). Для механических волн обязательно нужна среда, обладающая способностью запасать кинетическую и потенциальную энергию. Следовательно, среда должна обладать инертными и упругими свойствами. В ре



Формула частоты

Частота — это количество циклов в единице времени. «Циклы» могут быть движениями чего-либо с периодическим движением, таких как пружина, маятник, что-то вращающееся или волна. Частота равна 1, деленному на период, который представляет собой время, необходимое для одного цикла.

Производной единицей измерения частоты в системе СИ является герц, названный в честь Генриха Рудольфа Герца (символ hz). Один Гц — это один цикл в секунду.

f = частота, количество циклов в единицу времени

T = период, время, необходимое для одного цикла

N = количество циклов

t = количество времени

Частотная формула Вопросы:

1) Длинный маятник занимает 5.00 с для завершения одного цикла вперед-назад. Какая частота движения маятника?

Ответ: Для завершения одного цикла маятнику требуется 5,00 с , поэтому это его период T. Частоту можно найти с помощью уравнения:

f = 0,20 цикла / с

частота маятника 0,20 цикл / с . Единицы циклов / с часто обозначаются как «Герцы» с символом «Гц». Итак, частота этого маятника также может быть указана как 0.20 Гц.

2) Тахометр в автомобиле измеряет количество оборотов шин в минуту (обороты и циклы — это одно и то же). Автомобиль движется с постоянной скоростью, а тахометр показывает 2400 оборотов в минуту. Какова частота вращения шин, измеренная в циклах в секунду? Какой период в секундах?

Ответ: Количество циклов (оборотов), которое необходимо учитывать, составляет 2400 . Это количество циклов, которые происходят за одну минуту, что равно 60 секундам.Итак, частоту можно найти с помощью уравнения:

f = 40 циклов / с

Частота вращения шин составляет 40 циклов / с , что также можно записать как 40 Гц. Чтобы найти период из этого, измените уравнение, которое связывает период и частоту:

T = 0,025 с

Период вращения шин составляет 0,025 секунд.

Справочные и учебные пособия по боеприпасам

Армейские руководства по боеприпасам, базовая математика, боеприпасы, публикации по боеприпасам, идентификация боеприпасов, безопасность мест хранения журналов, операции по хранению боеприпасов, операции по получению боеприпасов, операции по складированию боеприпасов, операции по транспортировке боеприпасов, техническое обслуживание боеприпасов, точки поставки боеприпасов, аварийное уничтожение , Обычные боеприпасы

Интегрированное издательское дело

Армейские боеприпасы

MM0099A-Основы математики

mm0142a-Введение в область боеприпасов

мм0143a-Публикации боеприпасов

mm0145a-Идентификация боеприпасов

Mm0148a-Площадки для хранения журналов

Mm0149a-Безопасность зоны хранения журналов

Mm0150a-Место для хранения журналов Количество — расстояние и совместимость

mm0151a-Склад боеприпасов

mm0152a-Операции приема боеприпасов

mm0154a-Операции по складированию боеприпасов

мм0156a-Отгрузка боеприпасов Транспортные операции

мм0159a — Исследование неисправностей обычных боеприпасов

MM0160A-Обслуживание боеприпасов

MM0163A-Пункт поставки боеприпасов ASP Количество — расстояние и совместимость

MM0164A-Выбор места поставки боеприпасов ASP

MM0165A-Аварийное уничтожение обычных боеприпасов

MM0166A-Создание мест складирования обычных боеприпасов

MM0167A — Выявление неисправности обычных боеприпасов и сообщение о них

mm0168a-Оценка операций по хранению обычных боеприпасов, часть 1

mm0170a-Оценка операций по хранению обычных боеприпасов, часть III

Mm0176a-Оценка операций по отгрузке и выдаче обычных боеприпасов

мм0308-Введение в электричество

Mm03097-Введение в электронику

мм 03119-Электронные трубки

мм 03206-Основы связи

мм 03219-AM Радиопередатчики

Mm03229-AM Радиоприемники

Mm03236-FM Радиопередатчики

мм03246-FM радиоприемники

мм 03276-частотный синтез

mm0396a-Устранение неполадок Ремонт ANUXC-7 на уровне блока

Mm03989-Установка и использование облегченного цифрового факса ANUXC-7

Mm04108-Принципы телефона на местной батарее

MM04118-Устранение неисправностей и окончательное тестирование телефона TA-312PT MOS 29N

MM04268-Поиск и устранение неисправностей и окончательное тестирование телефонного аппарата TA-236FT

Mm04409-Калибровочные операции

мм04557-потенциометрические измерители

MM04567-DC Низкочастотные измерения температуры

мм 04620-Модель 5345A Система измерения частоты и времени

MM0474-Измерения мощности

MM0478 — Измерения размеров

мм0479-Измерение массы

мм 0483-Термометрия

MM04868-Принципы механических и электромеханических измерений

Mm04990-Армейская калибровочная система

MM0651A-Торговая практика и безопасность

Mm07047-Основное электричество, часть II

MM0812A-Очистка приборов ночного видения

мм 2600-Обращение с боеприпасами и обозначение знаков пожарной и химической опасности

мм2603a-Требования к совместимости боеприпасов и количеству-дистанционному хранению

мм2604a-Проверка и обслуживание боеприпасов

MM36707-Проверка транспортных средств, используемых для перевозки боеприпасов

мм36715-Проверка железнодорожных вагонов, милванов с боеприпасами и авиаперевозок

мм3676a-Inspecting Обычные боеприпасы Часть II

мм36798-Осмотр буксира GM и его контейнера

мм 36808-Проверка остатков

мм 36827-Проверка базовой нагрузки агрегата

мм36867-Проверка боеприпасов, хранящихся на судах

мм46106-Обезвреживание боеприпасов

мм 46178-Ведение публикаций в блоке

мм 46188-Боеприпасы и отчеты

мм 46198-Подготовка плана хранения

мм 46218-Проверка состояния складских помещений и помещений

мм 46248-Планирование операций по утилизации боеприпасов

мм 4631a-Division Ammunition Office Operations

MM4632A-Расчет разрешенных уровней боеприпасов

MM46399-Контроль выбора акций для выпуска

MM46409-Контроль передачи документации

Mm46469-Управление учебными информационными системами управления боеприпасами Отчеты ТАМИС

MM46739-Проверка объекта по обслуживанию боеприпасов

MM46749-Выбор и использование чертежей для хранения и выгрузки

MM46759-Чертежи выбора и использования боеприпасов

MM4676A-Проект СОП по операциям наблюдения

MM4812-Ночной прицел АНТАС-4А

MM5000-Цепи синхронизации

мм 5004-уровневый радар, регулировка источника питания и центрального тока, а также синхронизация точной развертки

мм 50058-Радиолокационный передатчик

Mm50078-Регулировка PPI, IFF и Precision Display, а также контроль задержки PPI

Mm50129-Устранение неисправностей облегченной доплеровской навигации

мм 50248-Прямая поддержка обслуживания пеленгатора

MM50398-Устранение неполадок и ремонт системы управления коммуникациями

ММ50447-У.С. Армейский авиационный центр

Резонанс полости

Одночастотный объемный резонанс предполагает параллель с одночастотной резонансной частотой груза на пружине. Фактически, термин «акустическая масса» иногда используется в связи с такими колебаниями. Размышление о резонансе полости как о колеблющейся массе воздуха может дать некоторое представление о том, почему физические свойства полости так же влияют на резонансную частоту.Вы можете визуализировать процесс нагнетания лишнего воздуха в полость для создания избыточного давления. Это избыточное давление представляет собой накопленную энергию аналогично поднятию груза на пружине выше ее положения равновесия. Если отверстие в полости больше, избыточный воздух может выходить быстрее, чтобы снизить давление до атмосферного, и это приводит к более высокой резонансной частоте полости. Чем длиннее шейка полости, тем больше сопротивление потоку избыточного воздуха и резонансная частота понижается.Если объем полости увеличивается, то для создания заданного избыточного давления требуется большая избыточная масса воздуха, и, следовательно, для сброса этого избыточного давления требуется больше времени. У большей полости будет более низкая резонансная частота. Опять визуализируя массу на пружине, мы знаем, что если мы поднимем ее из состояния равновесия и позволим ей упасть, она не остановится, когда достигнет этой точки равновесия, а перескочит ее и начнет колебаться относительно равновесия, потому что работа, которую мы проделали. чтобы поднять массу, вложите энергию в упругую систему.Точно так же, когда мы проделали работу по увеличению давления в полости, мы дали ей энергию, и когда воздух вырвется наружу, он выйдет за пределы равновесия (атмосферное давление) и создаст небольшой вакуум в полости. Эта упругая система создает резонанс полости, но она сильно демпфирована и не будет продолжать колебаться, как груз на пружине.

Указатель Волновые концепции Резонансные концепции

Микроволны101 | Саморезонансная частота

Щелкните здесь, чтобы перейти на нашу главную страницу с сосредоточенными элементами

Щелкните здесь, чтобы перейти на нашу страницу по математике конденсаторов

Щелкните здесь, чтобы перейти на нашу страницу по математике индуктивности

Щелкните здесь, чтобы перейти на нашу страницу по проектированию косой тройки с сосредоточенными элементами

Когда вы указываете или покупаете элементы с сосредоточенными параметрами, такие как катушки индуктивности и конденсаторы (особенно устройства для поверхностного монтажа), вы сталкиваетесь с термином «собственная резонансная частота».Что это означает? Это хорошая вещь? Как вы это моделируете?

Многие вещи в природе обладают саморезонансом. Это не означает, что они колеблются сами по себе, это просто означает, что когда они возбуждаются приложенной энергией, они стремятся к резонансу на определенных частотах. Если вы возбудите реальный конденсатор или катушку индуктивности с функцией скачка напряжения, возникнут переходные колебания на собственной резонансной частоте, но они быстро затихнут из-за паразитного сопротивления.Вы можете увидеть это явление на осциллографе: когда вы подаете импульс напряжения на компонент, он «звенит» на короткое время. Кто-нибудь может прислать нам снимок этого прицела?

Модель индуктора

Модель индуктивности с сосредоточенными параметрами, представленная ниже, имеет индуктивность и SRF в качестве входов, и она вычисляет паразитный параллельный конденсатор, вызывающий резонанс. В формулу для C1 встроен коэффициент 1000, так что единицы получаются правильными. В микроволновых печах мы стараемся придерживаться пикофарад, ГГц и нано-Генри.

На графиках ниже показано значение индуктивности 51 нГн при SRF 2,3 ГГц. Возникает саморезонанс, деталь выглядит почти как разомкнутая цепь, что может быть очень желательно в зависимости от применения (подумайте о «тройнике смещения»). Обратите внимание, что R2 в модели учитывает сопротивление детали постоянному току (также указывается производителем или легко измеряется точным измерителем постоянного тока). Резистор R1 является частью модели, уменьшающей коэффициент отражения при резонансе; ни одна настоящая деталь никогда не достигает идеального разомкнутого контура.

Модель конденсатора

Модель ниже фактически имеет два резонанса. Первый SRF — это последовательный резонанс, при котором индуктор L1 и конденсатор C1 компенсируют друг друга, и получается близкое к короткому замыканию. Вы никогда не получите настоящего короткого замыкания из-за эквивалентного последовательного сопротивления «ESR», которое учитывается в R1. Второй резонанс — это параллельный резонанс емкости C2 со структурой. Обычно это нежелательно, конденсатор выглядит близко к разомкнутой цепи.

На графике ниже мы проанализировали ограничение на 51 пФ с SRF 2.3 ГГц.

На этой странице более подробно обсуждается моделирование собственной резонансной частоты, где мы покажем вам, как спроектировать тройник смещения с сосредоточенными элементами (также новинка октября 2011 года!)

Coil32 — Частота собственного резонанса

На заре Эры Радио было обнаружено, что спиральный индуктор не идеальный индуктор. На определенной частоте он находится в режиме резонанса даже при отсутствии внешней емкости, а выше этой частоты сопротивление катушки является емкостным.Для объяснения этого явления предполагается, что в дополнение к самоиндукции реальная катушка имеет собственную емкость (предположительно между соседними витками) и катушка представлена ​​как модель сосредоточенных элементов RLC, где L — индуктивность, C — собственная емкость, а R учитывает различные потери в катушке. Такая модель имеет только одну резонансную частоту, называемую частотой собственного резонанса катушки (SRF). Эта модель стала классической моделью настоящей катушки во всех учебниках.

Поскольку катушка в большинстве практических применений работает на частотах намного ниже SRF, целью разработчика является обеспечение этого условия.Большинство инженеров с этой целью пытались уменьшить эту «межвитковую паразитную емкость». В случае, если катушка работает на частотах, близких к SRF, как, например, в спиральном резонаторе или катушках Тесла, RLC-модель дает неверные результаты, но в таких случаях были разработаны альтернативные алгоритмы расчета, и все конструкторы остались довольны и не совсем перебирал в уме причины таких несоответствий.

В век цифровых технологий появились приложения, дающие возможность моделировать любые высокочастотные устройства с высокой степенью точности, так называемые электромагнитные симуляторы.Существуют мощные пакеты, такие как CST Studio, HFSS и многие другие. Проверим однослойную спиральную катушку в HFSS. В первой модели поместите катушку на идеально проводящую поверхность и возбудите ее через сосредоточенный порт с внутренним сопротивлением 50 МОм. Второй конец катушки заземлен. Моделирование будет выполнено в режиме «HFSS Design» с использованием метода конечных элементов. Вторую катушку мы моделируем методом «Design HFSS-IE» с использованием метода моментов. Мы возбуждаем катушку короткими выводами от того же порта с сосредоточенными параметрами.Поскольку в этой модели катушка не заземлена, первый резонанс — это полуволновой резонанс.
В ходе исследования мы получили графики импеданса на выводах источника в зависимости от частоты. Графики показывают, что спиральная катушка имеет много резонансов. Из этого следует, что катушка не представляет собой одиночную LC-цепь с ее самоиндукцией и паразитной собственной емкостью в виде сосредоточенных элементов, а является линией передачи с распределенными параметрами. Тот факт, что линия передачи состоит из одного провода, не должен сбивать с толку.Вы знаете, что явление резонанса наблюдается даже в одном проводе, это пример диполя. Существование волновых явлений в проводах свидетельствует о том, что электромагнитное взаимодействие распространяется с конечной скоростью. И катушка в этом отношении недалеко от диполя, потому что, несмотря на малые размеры, длина провода, на который она наматывается, имеет размеры, сопоставимые с длиной волны. Саморезонансную частоту диполя довольно легко определить, зная его длину. Для катушки все не так просто.

---

В учебниках по электродинамике можно найти описание работы спиральных волноводов с поверхностными электромагнитными (ЭМ) волнами, распространяющимися по спиральному проводу. Такие волноводы используются в качестве замедляющих структур в спиральных антеннах и лампах бегущей волны. В таких волноводах длина витка и шаг намотки сравнимы с длиной волны, фазовая скорость волны вдоль оси винтового волновода намного меньше скорости света, и его применение в качестве замедляющей структуры основан на этом.

[1]

Относительная фазовая скорость волны вдоль оси такого волновода зависит только от геометрии спирали и не зависит от частоты, поскольку ЭМ-волна почти распространяется только вдоль проволоки спирали.

---

В катушке длина каждого витка, длина обмотки и шаг намотки намного меньше длины волны.В этом случае, помимо основной моды вдоль проволоки, существуют более высокие моды непосредственно вдоль оси спирали. Другими словами, ЭМ волна распространяется не только по длине провода, но и часть ее «перескакивает с витка на виток». Относительная фазовая скорость по оси катушки определяется следующим приближенным выражением:

[2]

где:

• λ ₀ — длина волны рабочей частоты в свободном пространстве
• D , p — диаметр и шаг намотки
• c — скорость света

Как видно из формулы, скорость зависит от диаметра катушки, шага намотки и длины волны.По сути, катушка — это тот же спиральный волновод с медленными волнами, но он работает в другом режиме.
Из-за наличия мод электромагнитной волны высокого порядка частота первого резонанса катушки всегда выше, чем частота, рассчитанная по длине провода. По этой причине высокочастотные резонансы не кратны первому и друг другу.
Короткие катушки имеют последующие резонансы, которые отделены от первой по частоте намного выше, что вы можете видеть в результатах моделирования HFSS: на частотах намного ниже первой резонансной частоты пространственная задержка намного меньше, чем период колебаний ЭМ поле.Поле вокруг катушки представляет собой статическое поле соленоида, и скоростью распространения волны вдоль его оси можно пренебречь. В этом случае модель RLC с сосредоточенными параметрами будет полностью рабочей и точно отображает поведение катушки. Стоит только помнить, что паразитная собственная емкость — это не статическая емкость между витками. Катушки всех трех моделей работают в этом режиме в диапазоне SW и ниже. Однако частота первого резонанса начинает проявлять волновые эффекты, связанные с ограниченной скоростью передачи электромагнитной связи, и катушку следует рассматривать только как спиральный волновод.В этом случае RLC-модель неверна. Более того, это приводит к неправильному пониманию механизма резонансных явлений в катушке.
Катушка как набор RLC-элементов с сосредоточенными параметрами и катушка как цепь с распределенными параметрами — это две разные модели реальной катушки. Первая модель основана на предположении, что плотность тока во всех витках одинакова, поэтому она ограничена и применима только на низких частотах, вторая является полной и применимой на любой частоте.

Особо хочу отметить следующее обстоятельство.На низких частотах, где, как мы видели, справедлива модель RLC, можно предположить, что индуктивность и собственная емкость катушки не зависят от частоты и определяются только геометрией обмотки. Это хорошо известный факт, зафиксированный, например, в формуле Нагаока. Но на самом деле параметры винтовой линии передачи зависят от частоты. Не просто v _ax , а емкость и индуктивность на единицу длины. Только на низких частотах эта зависимость незначительна, однако на частотах, близких к первому резонансу, значения индуктивности и собственной емкости катушки начинают заметно «плыть» по частоте.В конце концов, мы сталкиваемся с ситуацией, когда эти значения, измеренные или рассчитанные на низкой частоте, не подходят для расчета собственной резонансной частоты по формуле Томсона. Расчет даст неверный результат! Поэтому для расчета резонансной частоты катушки необходимо использовать более сложный численный метод из [1]. Во-вторых, любой объект рядом с катушкой, в том числе измерительный зонд, влияет на параметры линии передачи. В этом случае частота собственного резонанса сдвинута с фактического значения для «свободной» катушки.

Если разработчику необходимо создать катушку с минимальными размерами и максимальной собственной резонансной частотой, то наилучшая обмотка будет с расстоянием между витками, равным диаметру провода, и с отношением l / D ≈ 1. .1,5. На практике следует придерживаться следующих простых правил: если общая длина провода катушки меньше четверти длины волны на самой высокой рабочей частоте, катушка будет работать ниже своего первого резонанса.

Артикул:

1. САМОРЕЗОНАНС И САМОЕМКОСТЬ СОЛЕНОИДНЫХ КАТУШЕК — применимая теория, модели и методы расчета.Автор: Дэвид Найт1 (G3YNH)
2. САМОРЕЗОНАНС В КАТУШКАХ и миф о собственной емкости. Автор: Алан Пейн (G3RBJ),
3. Радиочастотные катушки, спиральные резонаторы и увеличение напряжения когерентными пространственными модами. К.Л. Corum и J.F. Corum

Саморезонанс индуктора

[Analog Devices Wiki]

Цель:

Целью этой лабораторной работы является измерение собственной резонансной частоты катушки индуктивности и определение паразитной емкости на основе измеренных данных.

Фон:

Индукторы, входящие в комплект деталей, как и все неидеальные электрические компоненты, несовершенны. Схема на рисунке 1 показывает наиболее распространенную простую модель реальной катушки индуктивности. В дополнение к желаемой индуктивности L реальный компонент также имеет потери (смоделированные как последовательное сопротивление, показанное на схеме как R) и параллельную паразитную емкость, показанную как C. Чем меньше сопротивление , т.е. близко к 0 Ом и тем меньше емкость мкл.е. близко к 0 F, тем более идеальным становится индуктор.

Рисунок 1, Трехэлементная модель индуктора LRC

Межобмоточная емкость и частота саморезонанса

Классическое описание C состоит в том, что он представляет собой распределенную межвитковую емкость катушки индуктивности (между витками и сердечником и т. Д.). На некоторой частоте, «собственной резонансной частоте» или SRF, эта межвитковая емкость образует параллельный резонанс с индуктивностью L, и катушка индуктивности становится настроенным контуром.

Трехэлементная модель LRC в зависимости от частоты

На частотах ниже Частоты Саморезонирования модель кажется индуктивной; на частотах выше SRF он кажется емкостным, а на SRF — резистивным, поскольку индуктивное и емкостное реактивное сопротивление равны по величине, но противоположны по знаку и, таким образом, сокращаются.

На SRF катушки индуктивности выполняются все следующие условия:
• Входное сопротивление находится на пике.
• Фазовый угол входного импеданса равен нулю, переход от положительного (индуктивного) к отрицательному (емкостный).
• Поскольку фазовый угол равен нулю, Q равно нулю.
• Эффективная индуктивность равна нулю, поскольку отрицательное емкостное реактивное сопротивление (X _C = 1 / jωC) просто нейтрализует положительное индуктивное реактивное сопротивление (X _L = jωL).
• 2-портовые вносимые потери (S21 дБ, ) являются максимальными, что соответствует минимуму на графике зависимости частоты от S21 дБ .
• 2-портовая фаза (угол S21) равна нулю, переходя от отрицательной на более низких частотах к положительной на более высоких частотах.

Следующее уравнение показывает, как SRF связана с индуктивностью и емкостью в цепи модели индуктора.

в Гц

где:
L — индуктивность по Генри
C _p — паразитная емкость в Фарадах

Из этого уравнения ясно, что увеличение индуктивности или емкости снижает измеряемую SRF. Уменьшение индуктивности или емкости увеличивает SRF.

Предварительное моделирование трехэлементного индуктора LRC модели

Схема на рисунке 2 показывает схему имитационного испытания для трехэлементной модели индуктора LRC.L, R и C _P используются для моделирования индуктора. V1 является идеальным источником испытательного напряжения переменного тока, а резистор RS служит сопротивлением источника для V1. CL и RL являются компонентами нагрузки с CL, равным типичной входной емкости входного канала осциллографа ADALM2000. RL либо устанавливается равным RS, либо может иметь более высокое значение, например входное сопротивление 1 МОм канала осциллографа.

Рисунок 2 Схема моделирования

Вы должны смоделировать схему, показанную на рисунке 2, перед построением реальной испытательной схемы индуктора.

Два моделирования частотной развертки были запущены от 10 кГц до 10 МГц в качестве примера индуктора 1 мГн, L, с C _P , установленным на 15 пФ, и R, установленным на 100 мОм. Красная кривая соответствует RL, равному 200 Ом, что и RS. Амплитуда, наблюдаемая в точке RL, имеет резкий спад на частоте собственного резонанса, когда полное сопротивление катушки индуктивности является максимальным. Синяя кривая соответствует RL, равному 1 МОм на входе осциллографа. Снова мы видим резкий нуль, когда импеданс максимален. Мы также видим резкий пик амплитуды, наблюдаемый в RL примерно на октаву ниже метки.Этот пик возникает, когда сопротивления источника и нагрузки не совпадают.

Рисунок 3, Результаты моделирования Красная кривая RL = 200 Ом, синяя кривая RL = 1 Мега Ом

Материалы:

Модуль активного обучения ADALM2000
Макетная плата без пайки и комплект перемычек
Индуктор 1–1 мГн
Катушки индуктивности другого номинала
Резисторы 2–200 Ом (могут быть изготовлены из 21 последовательно соединенных резисторов 100 Ом)

Направление:

Соберите испытательную схему индуктора, как показано на рисунке 4, на беспаечной макетной плате.Зеленые квадраты указывают, где подключить ADALM2000 AWG и каналы осциллографа.

Рисунок 4, Схема испытания индуктора

Настройка оборудования:

Подключения к выходу ADALM2000 AWG и входам канала осциллографа обозначены зелеными прямоугольниками на рисунке 4. Ваш комплект деталей должен содержать несколько индукторов с разными номиналами. Вставьте каждую катушку индуктивности по одной в вашу испытательную цепь.

Рисунок 5 Соединения макетной платы цепи испытания индуктора

Процедура:

Откройте программный инструмент сетевого анализатора из окна Scopy.Настройте развертку для запуска на частоте 100 кГц и остановки на частоте 30 МГц . Установите амплитуду на 1 В и смещение на ноль вольт. По шкале Боде установите верхнюю величину на 40 дБ и нижнюю на -60 дБ . Установите верхнюю часть фазы на 180 ° и нижнюю на -180 °. В области каналов нажмите на использовать канал 1 как ссылку. Установите количество шагов на 100.

Выполните одиночную развертку для каждого индуктора в вашем комплекте деталей. Вы должны увидеть графики зависимости амплитуды и фазы от частоты, которые очень похожи на результаты моделирования.Обязательно экспортируйте данные в файл .csv для дальнейшего анализа в Excel или Matlab.

Рисунок 6 Scopy Shot, L = 100 мкГн, RL = 200 Ом

Рисунок 7 Scopy Shot, L = 100 мкГн, RL = 1 МОм

Вопросы:

Используйте формулу для собственного резонанса, чтобы вычислить значение межвитковой паразитной емкости каждой из ваших катушек индуктивности.