Формулы расчета резонансной частоты колебательного контура
Для генерации высокочастотных волн часто применяются схемы на основе колебательного контура. Подобрав параметры элементов цепи, можно производить частоты свыше 500 МГц. Схемы используются в ВЧ-генераторах, высокочастотном нагреве, телевизионных и радиоприемниках.
Колебательный контур
Колебательный контур
Колебательный контур – это последовательное или параллельное соединение индуктивных и конденсаторных элементов, генерирующих электромагнитные колебания любой заданной частоты. Оба компонента схемы способны хранить энергию.
Когда существует разность потенциалов на конденсаторных пластинах, он сохраняет энергию электрического поля. Аналогично энергия сохраняется в магнитном поле индуктивной катушки.
Работа колебательного контура
Когда первоначально конденсатор подключается к источнику постоянного тока, на нем возникает разность потенциалов. Одна пластина имеет избыток электронов и заряжена отрицательно, другая – недостаток электронов и заряжена положительно.
Что будет, если в цепь включить индуктивную катушку:
- При замыкании контакта, соединяющего электроцепь, конденсатор начинает разряжаться через катушку индуктивности. Накопленная им энергия электрического поля снижается;
- Ток, протекающий через катушку L, индуцирует ЭДС, противостоящую потоку электронов. Из-за этого скорость нарастания тока медленная. В катушке создается магнитное поле, которое начинает накапливать свою энергию. После полного разряда конденсатора поток электронов через катушку уменьшается до нуля. Электростатическая энергия, накопленная в конденсаторе, преобразуется в энергию магнитного поля катушки;
- Когда конденсатор разряжен, магнитное поле начинает постепенно разрушаться, но, согласно закону Ленца, индукционный ток катушки способствует заряду конденсатора с противоположной полярностью. Энергия, связанная с магнитным полем, снова превращается в электростатическую;
Важно! В идеальном случае, когда нет потерь на L и С, конденсатор зарядился бы до первоначального значения с противоположным знаком.
- После того, как уменьшающееся магнитное поле перезарядило конденсатор, он снова начинает разряжаться с потоком тока обратной направленности, а МП опять нарастает.
Последовательность зарядки и разрядки продолжается, то есть процесс преобразования электростатической энергии в магнитную и наоборот периодически повторяется, подобно маятнику, у которого потенциальная энергия циклически превращается в кинетическую и обратно.
Непрерывный процесс зарядки и разрядки приводит к меняющему направление движению электронов или к колебательному току.
Обмен энергией между L и С будет продолжаться бесконечно, если отсутствуют потери. Часть энергии теряется, рассеиваясь в виде тепла на проводах катушки, соединительных проводниках, из-за тока утечки конденсатора, электромагнитного излучения. Поэтому колебания будут затухающими.
Затухающие колебания
Резонанс
Если схема с конденсатором, катушкой и резистором возбуждается напряжением, постоянно меняющимся во времени с определенной частотой, то также изменяются реактивные сопротивления: индуктивное и емкостное. Амплитуда и частота выходного сигнала будет изменяться по сравнению с входным.
Амплитуда и частота выходного сигнала будет изменяться по сравнению с входным.
Индуктивное сопротивление прямо пропорционально частоте:
X(L) = 2π x f x L,
а емкостное сопротивление обратно пропорционально этому показателю:
X(C) = 1/(2π x f x C).
Важно! На более низких частотах индуктивное сопротивление незначительное, а емкостное будет высоким и сможет создавать практически разомкнутый контур. На высоких частотах картина обратная.
При конкретной комбинации конденсатора и катушки схема становится резонансной, или настроенной, имеющей частоту колебаний, при которой индуктивное сопротивление идентично емкостному. И они компенсируют друг друга.
Следовательно, в цепи остается исключительно активное сопротивление, противостоящее протекающему току. Созданные условия получили наименование резонанса колебательного контура. Фазовый сдвиг между током и напряжением отсутствует.
Резонанс LC-цепи
Для расчета резонансной частоты колебательного контура учитывается следующее условие:
X(L) = X(C).
Следовательно, 2π x f x L = 1/(2πx f x C).
Отсюда получается формула резонансной частоты:
f = 1/(2π x √(L x C)).
Расчет резонансной частоты, индуктивности и емкости можно сделать на онлайн калькуляторе, подставив конкретные значения.
Скорость, с которой рассеивается энергия от LC-схемы, должна быть такой же, как энергия, подаваемая на схему. Устойчивые, или незатухающие, колебания производятся электронными схемами генераторов.
LC-цепи используются либо для генерации сигналов на определенной частоте, либо для выделения частотного сигнала из более сложного. Они являются ключевыми компонентами многих электронных устройств, в частности радиооборудования, используемого в генераторах, фильтрах, тюнерах и частотных микшерах.
Видео
Оцените статью:Формулы расчета резонансной частоты колебательного контура: амплитуда резонанса
Галилео Галилей, исследуя маятники и музыкальные струны, описал явление, которое впоследствии стали называть резонансом. Оно проявляется не только в акустике, но и в механике, электронике, оптике и астрофизике. Резонансный эффект имеет как положительные, так и отрицательные воздействия на колебательные системы.
Оно проявляется не только в акустике, но и в механике, электронике, оптике и астрофизике. Резонансный эффект имеет как положительные, так и отрицательные воздействия на колебательные системы.
Резонанс
Эффект резонанса
Ярким примером механического класса резонаторов является пружинный маятник. Профессор из технологического Массачусетского института (в Америке), В. Левин, акцентирует внимание своих студентов на то, что резонанс (resonance) – это эффект, сопряжённый с увеличением амплитуды. Для демонстрации явления используется установка. Она состоит из следующих компонентов:
- электродвигатель;
- механизм, превращающий вращение в возвратно-поступательное движение;
- ЛАТР – лабораторный автотрансформатор;
- медная пружина из проволоки с набором грузиков;
- направляющая для пружины.
Направление колебания пружины – вертикальное. Вращение вала мотора заставляет пружину совершать колебания. С помощью автотрансформатора присутствует возможность регулировать напряжение. Регулировка позволяет варьировать частоту вращения вала и колебаний маятника. При изменении частоты вращения вала амплитуда возвратно-поступательного движения остаётся неизменной.
Регулировка позволяет варьировать частоту вращения вала и колебаний маятника. При изменении частоты вращения вала амплитуда возвратно-поступательного движения остаётся неизменной.
Перед опытом замеряется удлинение медной пружины под действием грузиков (для оценки резонансной частоты пружины). Изменение скорости вращения вала заставляет амплитуду колебания конца пружины с грузом изменяться. Амплитуда увеличивается и на 1-м герце частоты становится максимальной (~30 см).
Важно! При дальнейшем увеличении скорости вращения вала амплитуда конца пружины начинает уменьшаться. Это означает, что resonance пройден. Если уменьшать напряжение, а с ним и частоту вращения двигателя, снова можно наблюдать эффект resonance колебания пружины.
Пружинный маятник
Добротность пружины Q определяется как отношение амплитуды колебания пружины Aпр к амплитуде колебания вынуждающей силы Aвс. В этом случае Q = Aпр/Aвс = 30/5 = 6, где Aвс = 5.
Определение колебательного контура
Резонансные явления, отмеченные в электротехнике, ярко выражены в схемах колебательных контуров (КК). Подобные конструкции представляют собой элементарные системы, способные осуществлять свободные колебания электромагнитной природы. Сам КК в цепи состоит из следующих элементов:
Подобные конструкции представляют собой элементарные системы, способные осуществлять свободные колебания электромагнитной природы. Сам КК в цепи состоит из следующих элементов:
- конденсатора;
- катушки индуктивности;
- источника тока.
Внимание! Выводы элементов схемы могут соединяться друг с другом параллельно или последовательно. Все зависит от того, какого результата нужно добиться от резонанса в КК.
Подключение к цепи индуктивной катушки
Включение в ёмкостную цепь катушки индуктивности сразу превращает её в КК. В зависимости от схемы подключения, различают два вида КК 1 класса: параллельный и последовательный.
Параллельный КК
В данной схеме конденсатор С соединён с катушкой L параллельно. Если заряженный конденсатор присоединить к катушке, то энергия, запасённая в нём, передастся ей. Через индуктивную катушку L потечёт ток, вызывая электродвижущую силу (ЭДС).
ЭДС самоиндукции L будет направлена на снижение тока в параллельной цепи. Ток, созданный этой ЭДС, и ток разряда ёмкости сначала одинаковы, а их суммарное значение равно нулю. Конденсатор передаст свою энергию Ec в катушку и полностью разрядится. Индуктивность, получив максимальную магнитную энергию EL, начнёт заряжать ёмкость напряжением уже другой полярности. Когда вся энергия из индуктивности перейдёт в ёмкость, конденсатор будет полностью заряжен. В цепи появляются колебания, такой контур называется колебательным.
Ток, созданный этой ЭДС, и ток разряда ёмкости сначала одинаковы, а их суммарное значение равно нулю. Конденсатор передаст свою энергию Ec в катушку и полностью разрядится. Индуктивность, получив максимальную магнитную энергию EL, начнёт заряжать ёмкость напряжением уже другой полярности. Когда вся энергия из индуктивности перейдёт в ёмкость, конденсатор будет полностью заряжен. В цепи появляются колебания, такой контур называется колебательным.
Параллельный КК
К сведению. Если бы в такой цепи отсутствовали потери, то такие колебания никогда не стали затухать. На практике, продолжительность процесса зависит от потери энергии. Чем больше потери, тем меньше длительность колебаний.
Параллельное соединение C и L вызывает резонанс токов. Это значит, что токи, проходящие через C и L, выше по значению, чем ток через сам контур, в конкретное число раз. Это число носит название добротности Q. Оба тока (емкостной и индуктивный) остаются внутри цепи, потому что они находятся в противофазе, и происходит их обоюдная компенсация.
Стоит отметить! На fрез величина R КК устремляется к бесконечности.
Последовательный КК
В этой схеме соединены последовательно друг с другом катушка и конденсатор.
Последовательный КК
В такой схеме происходит resonance напряжений, R контура устремляется к нулю в случае образования резонансной частоты (fрез). Это позволяет использовать подобную систему резонанса в качестве фильтра.
Резонансная частота
При подаче на два КК (параллельного и последовательного) переменного напряжения с изменяющейся частотой их реактивные сопротивления C и L будут меняться. Изменения происходят следующим образом:
- с увеличением f – ёмкостное сопротивление уменьшается, а индуктивное увеличивается;
- с уменьшением f – ёмкостное сопротивление увеличивается, а индуктивное уменьшается.
Частота, при которой реактивные сопротивления обоих элементов контура равны, называется резонансной.
Важно! При fрез сопротивление параллельного КК будет максимальным, а последовательного КК – минимальным.
Резонансная частота формула, которой имеет вид:
fрез = 1/2π*√L*C,
где:
- L – индуктивность, Гн;
- C – ёмкость, Ф.
Подставляя известные значения ёмкости и индуктивности в формулу резонансной частоты колебательного контура любой конфигурации, можно рассчитать этот параметр.
Для определения периода колебаний КК и частоты резонанса можно воспользоваться онлайн калькулятором на соответствующем портале в сети. Профессиональная программа имеет несложный интерфейс.
Пример интерфейса онлайн калькулятора LC-контура
Применение колебательных контуров
Подробный расчет колебательного контура позволяет точно подбирать величину необходимых элементов КК. Это позволяет использовать их в схемах электроники в виде:
- частотных фильтров – в радиоприёмниках, генераторах сигналов, преобразователях и выпрямителях;
- колебательных контуров – для выделения и настройки на определённую частоту станции вещания;
- силовых resonance-фильтров – для формирования напряжения синусоидальной формы.

На самолётах гражданской авиации КК применяется в блоках регулировки частоты генераторов.
Условие отсутствия резонанса
Для того чтобы возник резонанс формула которого для тока равна ω0*C = 1/ ω0*L, необходимо выполнения этого равенства. Существуют условия для невозможности появления этого эффекта, а именно:
- отсутствие у системы собственных колебаний;
- невозможность совпадения частоты внешнего воздействия с собственной частотой системы.
Амплитуда резонанса
В КК при подаче переменного напряжения от внешнего источника наблюдаются два вида резонанса и резкое увеличение двух видов амплитуды: амплитуды тока и амплитуды напряжения.
Амплитуда тока
Амплитуда тока резко возрастает при резонансе напряжений в последовательном контуре (последовательный резонанс). Источник переменной ЭДС включён в цепь, где нагрузкой служат последовательно включённые элементы L и С.
В этом случае в цепь входят сопротивления: активное r и реактивное x, равное:
x = xL – xC.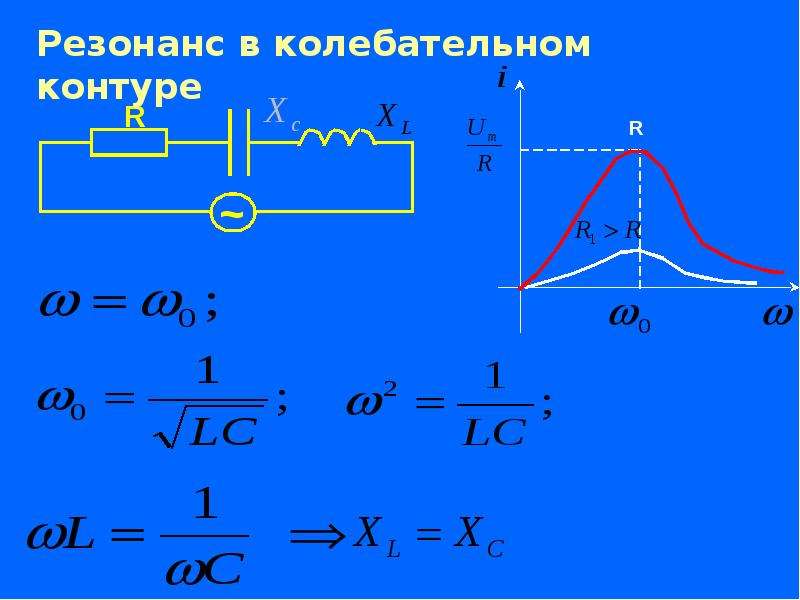
Так как для внутренних колебаний xL и xC равны, то для тока, поступающего от генератора, при резонансе (когда частоты совпадают) эти значения тоже одинаковы. Поэтому x = 0. В итоге полное сопротивление цепи будет состоять только из небольшого активного сопротивления. Ток при этом получается максимальным.
Схема (а) и резонансные кривые (б) для резонанса напряжений
Амплитуда напряжения
Резонанс токов (параллельный резонанс) является условием резкого возрастания амплитуды напряжения. Источник ЭДС подключается вне контура и нагружен параллельно соединёнными элементами L и С. В этом случае на эффект резонанса влияет внутреннее сопротивление генератора. Амплитуда напряжения на контуре максимальна при малом отличии напряжения контура от напряжения генератора. Это возможно при малом Ri.
Внимание! Изменение частоты генератора меняет ток, а амплитуда напряжения на контуре не отстаёт по величине от напряжения на генераторе. Если, U = Е — I*Ri, где Е – ЭДС, I – ток, то при малом Ri U = Е.
Схема (а) и резонансные кривые (б) для резонанса токов
Формула для определения расчётной резонансной частоты для разных колебательных систем различается по входящим в неё параметрам. Несмотря на все различия, суть остаётся неизменной: эффект резонанса наступает тогда, когда частота внутренних колебаний системы и внешних воздействий становятся равны друг другу.
Видео
Расчёт частоты резонанса колебательного контура
Колебательный контур — электрическая цепь, в которой могут возникать колебания с частотой, определяемой параметрами цепи. Простейший колебательный контур состоит из конденсатора и катушки индуктивности, соединенных параллельно или последовательно.
— Конденсатор C – реактивный элемент. Обладает способностью накапливать и отдавать электрическую энергию.
— Катушка индуктивности L – реактивный элемент. Обладает способностью накапливать и отдавать магнитную энергию.
Рассмотрим, как возникают и поддерживаются свободные электрические колебания в параллельном контуре LC.
Основные свойства индуктивности
— Ток, протекающий в катушке индуктивности, создаёт магнитное поле с энергией .
— Изменение тока в катушке вызывает изменение магнитного потока в её витках, создавая в них ЭДС, препятствующую изменению тока и магнитного потока.
Природа электромагнитных колебаний в контуре
Период свободных колебаний контура LC можно описать следующим образом:
Если конденсатор ёмкостью C заряжен до напряжения U, потенциальная энергия его заряда составит.
Если параллельно заряженному конденсатору подключить катушку индуктивности L, в цепи пойдёт ток разряда конденсатора, создавая магнитное поле в катушке.
Внешний магнитный поток создаст ЭДС в направлении противоположном току в катушке, что будет препятствовать нарастанию тока в каждом витке, поэтому конденсатор разрядится не мгновенно, а через время t1,
которое определяется индуктивностью катушки и ёмкостью конденсатора из расчёта t1 = .
По истечении времени t1, когда конденсатор разрядится до нуля, ток в катушке и магнитная энергия будут максимальны.
Накопленная катушкой магнитная энергия в этот момент составит.
В идеальном рассмотрении, при полном отсутствии потерь в контуре, EC будет равна EL.
Таким образом, электрическая энергия конденсатора перейдёт в магнитную энергию катушки.
Далее изменение (уменьшение от максимума) магнитного потока накопленной энергии катушки будет создавать в ней ЭДС,
которая продолжит ток в том же направлении и начнётся процесс заряда конденсатора индукционным током. Уменьшаясь от максимума до нуля в течении времени t2 = t1, он перезарядит конденсатор от нулевого до максимального отрицательного значения (-U).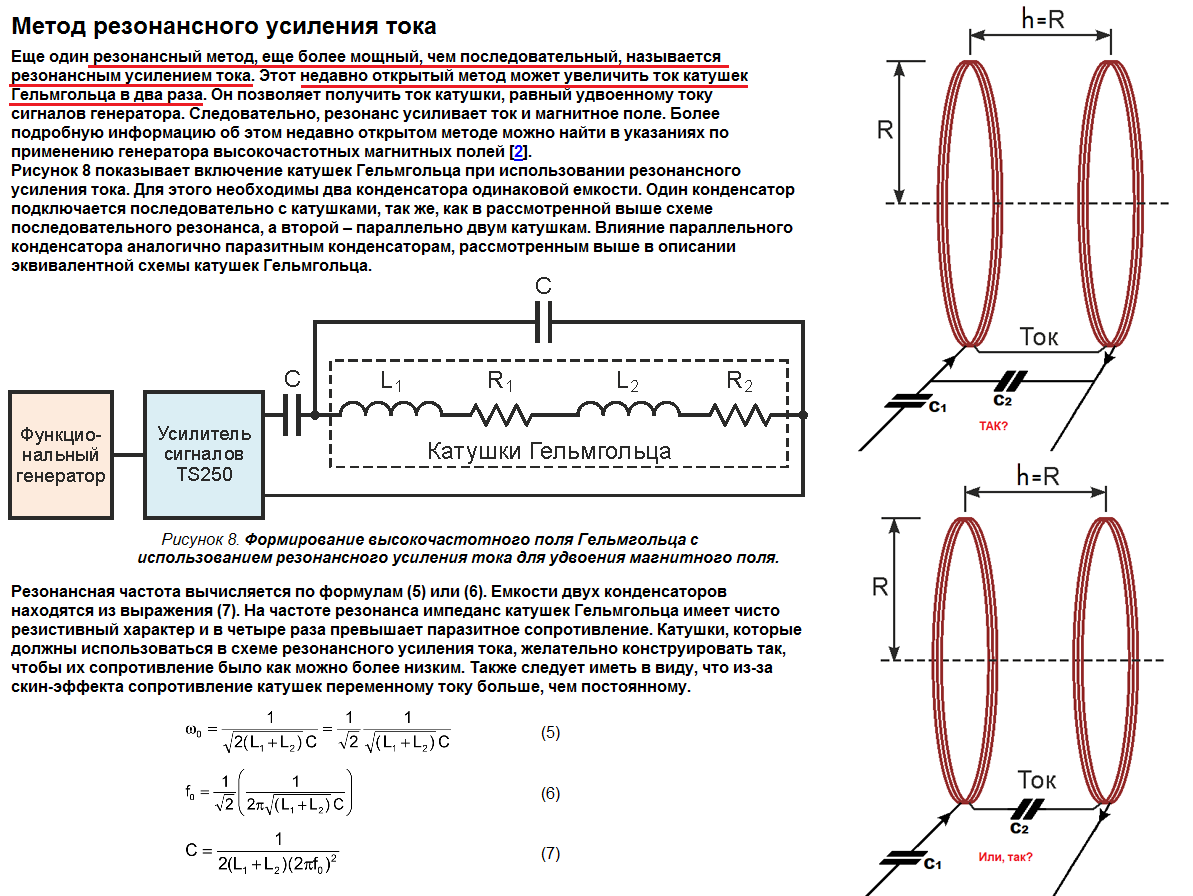
Так магнитная энергия катушки перейдёт в электрическую энергию конденсатора.
Описанные интервалы t1 и t2 составят половину периода полного колебания в контуре.
Во второй половине процессы аналогичны, только конденсатор будет разряжаться от отрицательного значения, а ток и магнитный поток сменят направление.
Магнитная энергия вновь будет накапливаться в катушке в течении времени t3, сменив полярность полюсов.
В течении заключительного этапа колебания (t4), накопленная магнитная энергия катушки зарядит конденсатор до первоначального значения U (в случае отсутствия потерь) и процесс колебания повторится.
В реальности, при наличии потерь энергии на активном сопротивлении проводников,
фазовых и магнитных потерь, колебания будут затухающими по амплитуде.
Время t1 + t2 + t3 + t4 составит период колебаний .
Частота свободных колебаний контура ƒ = 1 / T
Частота свободных колебаний является частотой резонанса контура, на которой реактивное сопротивление индуктивности XL=2πfL равно реактивному сопротивлению ёмкости XC=1/(2πfC).
Расчёт частоты резонанса
LC-контура:Предлагается простой онлайн-калькулятор для расчёта резонансной частоты колебательного контура.
Необходимо вписать значения и кликнуть мышкой в таблице.
При переключении множителей автоматически происходит пересчёт результата.
Расчёт частоты:
Частота резонанса колебательного контура LC. |
Расчёт ёмкости:
Ёмкость для колебательного контура LC |
Расчёт индуктивности:
Индуктивность для колебательного контура LC |
Похожие страницы с расчётами:
Рассчитать импеданс.
Рассчитать реактивное сопротивление.
Рассчитать реактивную мощность и компенсацию.
формула индуктивности катушки и резонансной частоты
Любая колебательная система характеризуется собственной частотой. Если на систему периодически воздействовать извне, и частота воздействия будет совпадать с внутренней периодичностью возмущения силового поля материи, то можно наблюдать резкое увеличение амплитуды колебаний. Данное явление является резонансом. Для ремонта и конструирования радиотехнических устройств необходимо уметь производить расчет резонансных частот колебательных контуров.
Что такое колебательный контур
Колебательный контур это несколько элементов в любой электрической цепи, емкость и индуктивность, которых соединены параллельно или последовательно. Для нормального функционирования колебательного контура в цепи необходим источник энергии.
Параллельный контур колебанийПри параллельном или последовательном соединениях элементов, входящих в состав электрической цепи, та или иная замкнутая проводниковая система получает одноимённое название. Явление резонанса в обоих случаях, возникает аналогичным образом, только в случае параллельного колебательного контура этот показатель относится к силе тока, а в случае с последовательным – возникает предельная частотность мгновенного изменения напряжений.
Как работает контур колебаний
Работа контура колебаний основана на циклическом преобразовании энергии индуктивности в качественный показатель эффективности конденсатора и наоборот. Допустим, что конденсатор полностью заряжен и энергия, запасенная в нем, максимальна. При подключении его к катушке индуктивности, он начинает разряжаться. При этом, через индуктивность начинает протекать ток, вызывающий появление ЭДС самоиндукции, направленную на уменьшение протекающего тока. Это означает, что начинается процесс перезарядки конденсатора. В тот момент, когда энергия прибора становится равной нулю, та же величина для катушки максимальна.
Далее, энергия индуктивности снижается, расходуясь на заряд емкости с противоположной полярностью. После уменьшения показателя коэффициента самоиндукции до нуля, на конденсаторе она опять имеет максимальное значение.
Процессы в системеВажно! В идеальном случае, данный процесс способен протекать бесконечно. В реальных устройствах колебание затухает со скоростью, пропорциональной потерям в цепи проводников.
Вне зависимости от величины энергии, наличия потерь, частота колебаний постоянна и зависит только от значений параметров коэффициента самоиндукции и емкости. Данная величина называется резонансной. Формула резонанса учитывает значение величины емкости и индуктивности контура колебаний.
ОсциллограммаПри воздействии на электрическую цепь с катушкой внешним сигналом с частотой, равной резонансной, амплитуда изменения положения частиц резко возрастает. Резонанс отсутствует при несовпадении частот. Из-за предельных значений электрическую цепь с катушкой индуктивности часто называют резонансной.
Потери в цепи с катушкой индуктивности (потери в диэлектрике конденсатора, сопротивление самого устройства, соединительных проводов) ограничивают величину предельных изменений направления частиц. В следствие этого, введена характеристика электроцепи, именуемая добротностью. Добротность обратно пропорциональна предельной величине потерь.
Зависимость предельной частоты от добротностиВажно! Снижение добротности приводит к тому, что предел изменения направлений наступает не только на основной частоте, но и на некотором приближении к ней, то есть, в некоторой полосе частот, где резонансное значение находится посередине. Чем выше добротность, тем более узкой становится полоса частот.
Формула индуктивности
Расчет резонанса колебательного контура производится на основании значений емкости и индуктивности. Как правило, емкость конденсатора является постоянной величиной, за исключением случаев использования переменных устройств в перестраиваемых электроцепях. Коэффициент самоиндукции катушки зависит от многих факторов:
- Количество и расположение витков обмотки;
- Наличие или отсутствие сердечника;
- Материал сердечника.
Общей формулы для определения индуктивности катушки колебательного контура не существует. Для расчетов используют формулы, соответствующие форме катушки. К сожалению, все формулы определения качественной величины электрической цепи с подсоединённой к ней катушкой индуктивности позволяют производить только приблизительные расчеты.
Приборы индуктивности различных типовВажно! Для того, чтобы получить катушку с заданными параметрами, приходится принимать дополнительные меры, например, производить подстройку коэффициента самоиндукции путем изменения длины сердечника или корректировки расстояния между витками в однорядных катушках.
Формула резонансной частоты
Формула резонансной частоты колебательного контура не зависит от его типа, а также от метода подключения – последовательного или параллельного. Выглядит она следующим образом:
f0=1/(2∙π∙√L∙C),
где f0 – частота резонанса
Как видно из формулы, для получения заданной частоты резонанса, существует бесконечное количество пар емкостей и индуктивностей. На деле, от выбранного соотношения параметров зависит также и добротность.
Как правильно рассчитать частоту контура колебаний
Для последовательного колебательного контура добротность растет с увеличением значения индуктивности. Таким образом, при расчетах элементов, следует учитывать величину добротности. Также, необходимо иметь в виду, что емкости конденсаторов выбираются из стандартного ряда значений, и на этом основании изготавливается катушка индуктивности.
Явление резонанса позволяет использовать колебательные контуры в качестве частотно зависимых цепей и в элементах фильтров. Радиоприемные устройства наиболее широко используют избирательные свойства колебательных систем. Если вместо емкости использовать кварцевый резонатор, то можно получить электрическую цепь с катушкой индуктивности, обладающей очень высокой добротностью. Такие схемы широко используются в задающих генераторах, где требуется высокая точность для определения периода изменения направления частиц.
2.4.3 Методика расчета резонансных характеристик. Кривые подвода-отвода
В пункте 2.4.2 был приведен приближенный метод решения уравнения движения зонда в произвольном потенциале. Как было показано резонансные характеристики системы зонд-образец имеет следующий вид:
(1)
(2)
Однако уравнения (1,2) связывают амплитуду, фазу и частоту вынуждающей силы в неявной форме. Для того, чтобы облегчить расчет резонансных характеристик рассмотрим следующую методику. Выразим в (1) обратную зависимость частоты вынуждающей силы от амплитуды колебаний. Проделывая не сложные выкладки, получим:
(3)
Выражение (3) описывает две ветви АЧХ системы, при этом знак «+» соответствует ветви , а знак «-» – ветви . Здесь введено новое обозначение . Но теперь, несмотря на наличие двух ветвей вместо одной, зависимость частоты от амплитуды колебаний имеет явную форму. Далее, используя выражение (2), получим полные резонансные характеристики системы:
(4)
(5)
где амплитуда колебаний выступает как параметр, который пробегает значения в интервале .
Обе ветви сшиваются в точке с максимальной амплитудой колебаний (резонанс) . Данному значению амплитуды колебаний соответствует частота вынуждающей силы . Таким образом, резонансная частота системы при расстоянии зонд-образец равном .
Теперь можно записать, как изменяется резонансная частота системы при изменении расстояния зонд образец. Вспоминая значение вспомогательной функции (см. (9) пункта 2.4.2), получим для относительного сдвига резонансной частоты:
(6)
Таким образом, зависимость изменения резонансной частоты колебаний кантилевера при отводе его от образца содержит информацию о виде потенциала взаимодействия.
Если же амплитуда колебаний мала, т.е. , то выражение (6) можно переписать в виде:
(7)
где введено обозначение сила взаимодействия между зондом и образцом. Вспоминая теорию малых колебаний кантилевера в поле силы , сдвиг резонансной частоты в том случае в точности совпадает с выражением (7).
Для нахождения зависимости изменения амплитуды колебаний при отводе зонда от образца будем считать, что кантилевер возбуждается на частоте равной его собственной резонансной частоте при отсутствии взаимодействия зонд-образец, т.е. и, соответственно, . Исходя из вида АЧХ системы, легко получить, что в этом случае для амплитуды колебаний должно выполняться:
(8)
Выражение (8) можно записать в виде , которое задает вид зависимости амплитуды колебаний от расстояния зонд-образец. При этом в некоторых случаях (в зависимости от вида потенциала взаимодействия и расстояния зонд-образец) решение (8) неоднозначно, что соответствует случаю одновременного существования нескольких режимов колебаний с различной амплитудой и, соответственно, фазой, т.к. из (2) фаза колебаний является однозначной функцией от амплитуды.
Рассмотрим, что произойдет в случае малости колебаний. Как уже было показано в случае со сдвигом резонансной частоты колебаний, в этом случае выполняется:
(9)
Подставляя (9) в выражение (8), получим
(10)
Если вертикальный градиент силы взаимодействия зонд-образец мал (сила слабо меняется на амплитуде колебаний), то относительное изменение амплитуды можно выразить в виде:
(11)
Сравнив полученное выражение с изменением амплитуды, вычисленным в теории малых колебаний, легко убедиться, что обе теории дают полностью идентичные ответы.
Теперь рассмотрим сдвиг фазы колебаний, которые происходит при отводе зонда от поверхности образца. Как и в случае с амплитудой будет считать, что . С учетом (2) получим
(12)
Используя условие малости колебаний (9) выражение (12) преобразуется к виду:
(13)
который опять в точности соответствует выведенному в теории малых колебаний.
Выводы.
- Предложен метод расчета резонасных характеристик системы зонд-образец при произвольной амплитуде вынуждающей силы. Он позволяет в явной форме вычислить частоту и фазу колебаний, соответствующие определенной амплитуде колебаний. При этом отпадает необходимость решать неявную нелинейную систему уравнений (1, 2).
- Из вида резонансных характеристик системы выведены зависимости амплитуды, резонасной частоты и фазы колебаний при подводе-отводе зонда от образца.
- Показано, что в пределе малых амплитуд , теория возмущений дает результаты полностью идентичные полученным в теории малых колебаний кантилевера.
Основные элементы колебательного контура. Резонансная частота: формула
Колебательный контур
электрическая цепь, содержащая катушку индуктивности и конденсатор, в которой могут возбуждаться электрические колебания. Если в некоторый момент времени зарядить конденсатор до напряжения V 0 , то энергия, сосредоточенная в электрическом поле конденсатора, равна Е с = , где С — ёмкость конденсатора. При разрядке конденсатора в катушке потечёт ток I , который будет возрастать до тех пор, пока конденсатор полностью не разрядится. В этот момент электрическая энергия К. к. E c = 0, а магнитная, сосредоточенная в катушке, E L =L — индуктивность катушки, I 0 — максимальное значение тока. Затем ток в катушке начинает падать, а напряжение на конденсаторе возрастать по абсолютной величине, но с противоположным знаком. Спустя некоторое время ток через индуктивность прекратится, а конденсатор зарядится до напряжения — V 0 . Энергия К. к. вновь сосредоточится в заряженном конденсаторе. Далее процесс повторяется, но с противоположным направлением тока. Напряжение на обкладках конденсатора меняется по закону V = V 0 cos ω 0 t, а ток в катушке индуктивности I = I 0 sin ω 0 t , т. е. в К. к. возбуждаются собственные гармонические колебания напряжения и тока с частотой ω 0 = 2 π/T 0 , где T 0 — период собственных колебаний, равный T 0 = 2π
В реальных К. к., однако, часть энергии теряется. Она тратится на нагрев проводов катушки, обладающих активным сопротивлением, на излучение электромагнитных волн в окружающее пространство и потери в диэлектриках (см. Диэлектрические потери), что приводит к затуханию колебаний. Амплитуда колебаний постепенно уменьшается, так что напряжение на обкладках конденсатора меняется уже по закону: V=V 0 e -δt cosωt, где коэффициент δ = R/2L — показатель (коэффициент) затухания, а ω = — частота затухающих колебаний. Т. о., потери приводят к изменению не только амплитуды колебаний, но и их периода Т = 2 π/ω. Качество К. к. обычно характеризуют его добротностью Q определяет число колебаний, которое совершит К. к. после однократной зарядки его конденсатора, прежде чем амплитуда колебаний уменьшится в е раз (е — основание натуральных логарифмов).
Если включить в К. к. генератор с переменной эдс: U = U 0 cosΩt (), то в К. к. возникнет сложное колебание, являющееся суммой его собственных колебаний с частотой ω 0 и вынужденных с частотой Ω. Через некоторое время после включения генератора собственные колебания в контуре затухнут и останутся только вынужденные. Амплитуда этих стационарных вынужденных колебаний определяется соотношением
Т. е. зависит не только от амплитуды внешней эдс U 0 , но и от её частоты Ω. Зависимость амплитуды колебаний в К. к.
от частоты внешней эдс называется резонансной характеристикой контура. Резкое увеличение амплитуды имеет место при значениях Ω, близких к собственной частоте ω 0 К. к. При Ω = ω 0 амплитуда колебаний V makc в Q раз превышает амплитуду внешней эдс U. Т. к. обычно 10 Q 100, то К. к. позволяет выделить из множества колебаний те, частоты которых близки к ω 0 . Именно это свойство (избирательность) К. к. используется на практике. Область (полоса) частот ΔΩ вблизи ω 0 , в пределах которой амплитуда колебаний в К. к. меняется мало, зависит от его добротности Q. Численно Q равно отношению частоты ω 0 собственных колебаний к ширине полосы частот ΔΩ.
Для повышения избирательности К. к. необходимо увеличивать Q. Однако рост добротности сопровождается увеличением времени установления колебаний в К. к. Изменения амплитуды колебаний в контуре с высокой добротностью не успевают следовать за быстрыми изменениями амплитуды внешней эдс. Требование высокой избирательности К. к. противоречит требованию передачи быстро изменяющихся сигналов. Поэтому, например, в усилителях телевизионных сигналов искусственно снижают добротность К. к. Часто используются схемы с двумя или несколькими связанными между собой К. к. Такие системы при правильно подобранных связях обладают почти прямоугольной резонансной кривой (пунктир).
Кроме описанных линейных К. к. с постоянными L и С, применяются нелинейные К. к., параметры которых L или С зависят от амплитуды колебаний. Например, если в катушку индуктивности К. к. вставлен железный сердечник, то намагниченность железа, а с ним и индуктивность L катушки меняется с изменением тока, текущего через неё. Период колебания в таком К. к. зависит от амплитуды, поэтому резонансная кривая приобретает наклон, а при больших амплитудах становится неоднозначной (). В последнем случае имеют место скачки амплитуды при плавном изменении частоты Ω внешней эдс. Нелинейные эффекты проявляются тем сильнее, чем меньше потери в К. к. В К. к. с низкой добротностью нелинейность вообще не сказывается на характере резонансной кривой.
Лит.: Стрелков С. П.. Введение в теорию колебаний, М. — Л., 1951.
В. Н. Парыгин.
Рис. 2. Колебательный контур с источником переменной эдс U =U 0 cos Ωt.
Рис. 3. Резонансная кривая колебательного контура: ω 0 — частота собственных колебаний; Ω — частота вынужденных колебаний; ΔΩ — полоса частот вблизи ω 0 , на границах которой амплитуда колебаний V = 0,7 V makc . Пунктир — резонансная кривая двух связанных контуров.
Большая советская энциклопедия. — М.: Советская энциклопедия . 1969-1978 .
Колебательный контур представляет собой простую электрическую цепь, состоящую из катушки индуктивности и емкости конденсатор. В такой схеме могут возникать колебания тока или напряжения. Резонансная частота таких колебаний определяется по формуле Томсона.
Эта разновидность LC колебательного контура (КК) простейший пример резонансной колебательной цепи. Состоит из последовательно соединенных катушки индуктивности и емкости. При протекание через такую схему переменного тока, величина его определяется по : I = U / Х Σ , где Х Σ — сумма реактивных сопротивлений катушки индуктивности и емкости.
Напомню зависимости реактивного сопротивления емкости и индуктивности от частоты напряжения их формулы выглядят вот так:
Из формул хорошо видно, что с ростом частоты, реактивное сопротивление индуктивности увеличивается. В отличии от катушки, у конденсатора при увеличении частоты, реактивное сопротивление снижается. На рисунке ниже приведены графические зависимости реактивных сопротивлений катушки индуктивности X L и емкости Х C от циклической частоты омега ω , и график зависимости ω от их алгебраической суммы Х Σ . График показывает зависимость от частоты общего реактивного сопротивления последовательного колебательного контура состоящего из конденсатора и индуктивности.
Из графика хорошо видно, что на определенной частоте ω=ω р , реактивные сопротивления индуктивности и емкости совпадают по значению, но противоположны по знаку, а общее сопротивление цепи равно нулю. На этой частоте в контуре будет протекать максимально возможный ток, ограниченный только омическими потерями в индуктивности (т.е. активным сопротивлением катушки) и внутренним активным сопротивлением источника тока. Эту частоту, при которой происходит это явление называют частотой резонанса. Кроме того из графика можно сделать следующий вывод: на частотах, ниже резонансной частоты реактивное сопротивление последовательного КК имеет емкостной фактор, а на более высоких частотах носит индуктивный характер. Резонансная частоты, может быть найдена при помощи формулы Томсона, которая легко выводится из формул реактивных сопротивлений обоих компонентов КК, приравняв их реактивные сопротивления:
На рисунке ниже, отобразим эквивалентную схему последовательного резонансного контура с учетом активных омических потерь R , при идеальном источнике тока гармонического напряжения с определенной амплитудой U . Полное сопротивление, или его еще называют импедансом схемы вычисляется: Z = √(R 2 +X Σ 2) , где X Σ = ω L-1/ωC . На частоте резонанса, когда обои реактивные сопротивления X L = ωL и Х С = 1/ωС равны по модулю, X Σ стремится к нулю и носит только активный характер, а ток в схеме вычисляется отношением амплитуды напряжения источника тока к сопротивлению потерь по закону Ома: I= U/R . При этом на катушке и емкости, в которых имеется запас реактивных составляющих энергии, падает одинаковое значение напряжения, т.е U L = U С = IX L = IX С .
На любой частоте, кроме резонансной, напряжения на индуктивности и емкости отличаются — они зависят от амплитуды тока в схеме и номиналами модулей реактивных сопротивлений X L и X С .Поэтому резонанс в последовательном колебательном контуре называют резонансом напряжений .
Очень важными характеристиками КК также являются его волновое сопротивление ρ и добротность КК Q . Волновым сопротивлением ρ считают величину реактивного сопротивления обоих компонентов (L,C) на резонансной частоте: ρ = Х L = Х C при ω =ω р . Волновое сопротивление можно рассчитать по следующей формуле: ρ = √(L/C) . Волновое сопротивление ρ считается количественной мерой оценки энергии, сохраненными реактивными компонентами контура — W L = (LI 2)/2 и W C =(CU 2)/2 . Отношение энергии, сохраненными реактивными элементами КК, к энергии резистивных потерь за период называют добротностью Q КК. Добротность колебательного контура — величина, определяющая амплитуду и ширину амплитудно частотной характеристики резонанса и говорящая о том, во сколько раз сохраненной энергии в КК больше, чем потери энергии за единичный период колебаний. Добротность кроме того учитывает и активного сопротивление R . Для последовательного КК в RLC цепях, в котором все три пассивных компонента соединены последовательно, добротность вычисляется по выражению:
где R , L и C — сопротивление, индуктивность и ёмкость резонансной цепи КК.
Величину, обратную добротности d = 1 / Q физики назвали затуханием КК. Для определения добротности обычно применяют выражение Q = ρ / R , где R -сопротивление омических потерь КК, характеризующее мощность активных потерь КК Р = I 2 R . Добротность большинства колебательных контуров варьируется от нескольких единиц до сотни и выше. Добротность таких колебательных систем, как пьезоэлектрические или может быть нескольких тысяч и даже больше.
Частотные свойства КК обычно оценивают с помощью АЧХ, при этом сами схемы рассматривают как четырёхполюсники. На рисунках ниже отображены элементарные четырехполюсники, содержащие последовательный КК и АЧХ этих цепей. По оси Х графиков отложен коэффициент передачи схемы по напряжению К, или отношение выходного напряжения к входному.
Для пассивных схем (не имеющих усилительных элементов и источников энергии), величина К никогда не выше единицы. Сопротивление переменному току, будет минимально при резонансной частоте. Тогда коэффициент передачи стремится к единице. На частотах, отличных от резонансной, сопротивление КК переменному току велико и коэффициент передачи будет близок к нулевым значениям.
При резонансе источник входного сигнала практически замкнут накоротко низким сопротивлением КК, поэтому коэффициент передачи падает почти до нуля. Наоборот, при частотах входного воздействия, отстоящих от резонансной, коэффициент стремится к единице. Свойство КК изменять коэффициент передачи на частотах, около резонансных, широко применяется в радиолюбительской практике, когда необходимо выделить сигнал с требуемой частотой из множества подобных, но на других частотах. Так, в любом радиоприемнике при помощи КК выполняется настройка на частоту требуемой радиостанции. Свойство выделять из множества частот только одну называют селективностью. При этом интенсивность изменения коэффициента передачи при настройке частоты воздействия от резонанса описывают полосой пропускания. За нее берется диапазон частот, в диапазонах которого уменьшение (увеличение) коэффициента передачи относительно его значения на резонансной частоте, не выше 0,7 (дБ).
Пунктирными линиями на рисунках обозначены АЧХ подобных цепей, КК которых имеют такие же резонансы, но обладающие меньшей добротностью. Как видим из графиков, при этом увеличивается полоса пропускания и уменьшается ее селективность.
В данной цепи параллельно соединены два реактивных элемента с разным уровнем реактивности. На рисунке ниже рассмотрены графические зависимости реактивных проводимостей индуктивности B L = 1/ωL и емкости конденсатора В C = -ωC , а также общей проводимости В Σ . И в этом колебательном контуре, имеется резонансная частота на которой реактивные сопротивления обоих компонентов одинаковы. Это говорит о том, что на этой частоте параллельный КК обладает огромным сопротивлением переменному току.
Сопротивление реального параллельного КК (с потерями), разумеется, не стремится к бесконечности — оно тем ниже, чем выше омическое сопротивление потерь в контуре, т.е снижается прямо пропорционально уменьшению добротности.
Рассмотрим простейшую цепь, состоящую из источника гармонических колебаний и параллельного КК. Если, собственная частота колебаний генератора (источника напряжения) совпадает с резонансной частотой контура, то индуктивная и емкостная ветви оказывают одинаковое сопротивление переменному току, и токи в ветвях будут совершенно одинаковыми. Поэтому уверенно скажем, что в этой схеме имеет место резонанс токов . Реактивности обоих компонентов вполне успешно компенсируют друг друга, и сопротивление КК протекающему току становится полностью активным (имеет только резистивную составляющую). Величина этого сопротивления, вычисляется произведением добротности КК на характеристическое сопротивление R экв = Q·ρ . На других частотах сопротивление параллельного КК падает и приобретает реактивный характер на более низких индуктивный, а на более высоких — емкостной.
Рассмотрим, зависимость коэффициентов передачи четырехполюсников от частоты в данном случае.
Четырехполюсник, на частоте резонанса представляет собой достаточно большое сопротивление протекающему переменному току, поэтому при ω=ω р его коэффициент передачи стремится к нулю (и это даже с учетом реальных омических потерь). На прочих частотах, отличных от резонансной, сопротивление КК будет падать, а коэффициент передачи четырехполюсника — увеличиваться. Для четырехполюсника второго варианта, ситуация будет диаметрально противоположной — на резонансной частоте КК будет оказывать очень большое сопротивление, т.е коэффициент передачи будет максимален и стремится к единице). При существенном отличии частоты от резонансной, источник сигнала, окажется практически зашунтированным, а коэффициент передачи будет стремится к нулю.
Предположим нам нужно изготовить параллельный КК, с частотой резонанса 1 МГц. Осуществим предварительный упрощенный расчет такого КК. То есть, вычислим необходимые значения емкости и индуктивности. Воспользуемся упрощенной формулой:
L=(159,1/F) 2 / C где:L индуктивность катушки в мкГн; С емкость конденсатора в пФ; F резонансная частота в МГц
Зададимся частотой в 1 МГц и емкостью 1000 пФ. Получим:
L=(159,1/1) 2 /1000 = 25 мкГн
Таким образом если в нашей радиолюбительской самоделки используется КК на частоту 1 МГц, то нам необходимо взять емкость на 1000 пФ и индуктивность на 25 мкГн. Конденсатор достаточно легко подобрать, а вот индуктивность ИМХО проще изготовить самостоятельно.
Для этого рассчитаем число витков для катушки без сердечника
N=32 *v(L/D) где:N необходимое число витков; L заданная индуктивность в мкГн; D диаметр каркаса катушки.
Предположим, диаметр каркаса 5 мм, тогда:
N=32*v(25/5) = 72 витка
Данная формула считается приближенной, она совершенно не учитывает собственную межвитковую емкость индуктивности. Формула служит для предварительного расчета параметров катушки, которые затем подстраиваются при регулировке контура в устройстве.
В радиолюбительской практике очень часто применяются катушки с подстроечным сердечником из феррита, обладающие длиной 12-14 мм и диаметром 2,5 — 3 мм. Такие сердечники, активно используются в колебательных контурах приемников.
Практический расчет последовательного или параллельного LC контура.
Доброго дня уважаемые радиолюбители!
Сегодня мы с вами рассмотрим порядок расчета LC контура .
Некоторые из вас могут спросить, а на черта нам это нужно? Ну, во-первых, лишние знания никогда не помешают, а во-вторых, бывают в жизни моменты, когда вам знание этих расчетов может понадобиться. К примеру, очень многие начинающие радиолюбители (естественно, в основном молодые), увлекаются сборкой так называемых “жучков” – устройств позволяющих на расстоянии прослушивать что-нибудь. Конечно я уверен, что это делается без всяких нехороших (даже грязных) мыслей подслушать кого-нибудь, а в благих целях. Например устанавливают “жучок” в комнате с малышом, а на радиовещательный приемник прослушивают не проснулся ли он. Все схемы “радиожучков” работают на определенной частоте, но что делать, когда эта частота вас не устраивает. Вот тут вам придет на помощь знание нижеприведенной статьи.
LC колебательные контура применяются практически в любой аппаратуре, работающей на радиочастотах. Как известно из курса физики, колебательный контур состоит из катушки индуктивности и конденсатора (емкости), которые могут быть включены параллельно (параллельный контур ) или последовательно (последовательный контур ), как на рис.1:
Реактивные сопротивления индуктивности и емкости, как известно, зависят от частоты переменного тока. При увеличении частоты реактивное сопротивление индуктивности растет, а емкости – падает. При уменьшении частоты, наоборот, индуктивное сопротивление падает, а емкостное – растет. Таким образом, для каждого контура есть некоторая частота резонанса, на которой индуктивное и емкостное сопротивления оказываются равными. В момент резонанса резко увеличивается амплитуда переменного напряжения на параллельном контуре или резко увеличивается амплитуда тока на последовательном контуре. На рис.2 показан график зависимости напряжения на параллельном контуре или тока на последовательном контуре от частоты:
На частоте резонанса эти величины имеют максимальное значение. А полоса пропускания контура определяется на уровне 0,7 от максимальной амплитуды, которая есть на частоте резонанса.
Теперь перейдем к практике. Предположим нам нужно сделать параллельный контур, имеющий резонанс на частоте 1 МГц. Прежде всего нужно сделать предварительный расчет такого контура. То есть, определить необходимую емкость конденсатора и индуктивность катушки. Для предварительного расчета есть упрощенная формула:
L=(159,1/F) 2 /C где:
L – индуктивность катушки в мкГн;
С – емкость конденсатора в пФ;
F – частота в МГц
Зададимся частотой 1 МГц и емкостью, к примеру, 1000 пФ. Получим:
L=(159,1/1) 2 /1000 = 25 мкГн
Таким образом, если мы захотим контур на частоту 1 МГц, то нужен конденсатор на 1000 пФ и индуктивность на 25 мкГн. Конденсатор можно подобрать, а вот индуктивность нужно сделать самостоятельно.
N=32 *√(L/D) где:
N – требуемое число витков;
L – заданная индуктивность в мкГн;
D – диаметр каркаса в мм, на котором предполагается намотать катушку.
Предположим, диаметр каркаса – 5 мм, тогда:
N=32*√(25/5) = 72 витка.
Данная формула является приближенной, она не учитывает собственную межвитковую емкость катушки. Формула служит для предварительного вычисления параметров катушки, которые затем настраиваются при настройке контура.
В радиолюбительской практике чаще используются катушки с подстроечными сердечниками из феррита, имеющими длину 12-14 мм и диаметр 2,5 – 3 мм. Такие сердечники, например, применяются в контурах телевизоров и приемников. Для предварительного расчета числа витков для такого сердечника есть другая приближенная формула:
N=8,5*√L , подставляем значения для нашего контура N=8,5*√25 = 43 витка . То есть, в таком случае на потребуется намотать на катушку 43 витка провода.
Последовательный колебательный контур — это цепь, состоящая их катушки индуктивности и конденсатора, которые соединяются последовательно. На схемах идеальный последовательный колебательный контур обозначается вот так:
Реальный колебательный контур имеет сопротивление потерь катушки и конденсатора. Это суммарное суммарное сопротивление потерь обозначается буквой R. В результате, реальный последовательный колебательный контур будет иметь такой вид:
R — это суммарное сопротивление потерь катушки и конденсатора
L — собственно сама индуктивность катушки
С — собственно сама емкость конденсатора
Колебательный контур и генератор частоты
Давайте проведем классический эксперимент, который есть в каждом учебнике по электронике. Для этого соберем вот такую схему:
Генератор у нас будет выдавать синус.
Для того, чтобы снять осциллограмму через последовательный колебательный контур, мы подключим в схему шунтовый резистор с малым сопротивлением в 0,5 Ом и с него уже будем снимать напряжение. То есть в данном случае мы шунт используем для наблюдения силы тока в цепи.
А вот и сама схема в реальности:
Слева-направо: шунтовый резистор, катушка индуктивности и конденсатор. Как вы уже поняли, сопротивление R — это суммарное сопротивление потерь катушки и конденсатора, так как нет идеальных радиоэлементов. Оно «прячется» внутри катушки и конденсатора, поэтому в реальной схеме отдельным радиоэлементом мы его не увидим.
Теперь нам осталось подцепить эту схему к генератору частоты и осциллографу , и прогнать по некоторым частотам, снимая осциллограмму с шунта U ш , а также снимая осциллограмму с самого генератора U ГЕН .
С шунта мы будем снимать напряжение , которое у нас отображает поведение силы тока в цепи, а с генератора собственно сам сигнал генератора. Давайте прогоним нашу схемку по некоторым частотам и глянем что есть что.
Влияние частоты на сопротивление колебательного контура
Итак, погнали. В схеме я взял конденсатор на 1мкФ и катушку индуктивности на 1 мГн. На генераторе настраиваю синус размахом в 4 Вольта. Вспоминаем правило: если в цепи соединение радиоэлементов идет последовательно друг за другом, значит, через них течет одинаковая сила тока.
Красная осциллограмма — это напряжение с генератора частоты, а желтая осциллограмма — отображение силы тока через напряжение на шунтовом резисторе.
Частота 200 Герц с копейками:
Как мы видим, при такой частоте ток в этой цепи есть, но очень слабый
Добавляем частоту. 600 Герц с копейками
Здесь мы уже отчетливо видим, что сила тока возросла, а также видим, что осциллограмма силы тока опережает напряжение. Попахивает конденсатора.
Добавляем частоту. 2 Килогерца
Сила тока стала еще больше.
3 Килогерца
Сила тока увеличилась. Заметьте также, что сдвиг фаз стал уменьшаться.
4,25 Килогерц
Осциллограммы почти уже сливаются в одну. Сдвиг фаз между напряжением и силой тока становится почти незаметным.
И вот на какой-то частоте у нас сила тока стала максимальной, а сдвиг фаз стал равен нулю. Запомните этот момент. Для нас он будет очень важен.
Еще совсем недавно ток опережал напряжение, а сейчас уже стал запаздывать после того, как выровнялся с ним по фазе. Так как ток уже отстает от напряжения, здесь уже попахивает реактивным сопротивлением катушки индуктивности.
Увеличиваем частоту еще больше
Сила тока начинает падать, а сдвиг фаз увеличивается.
22 Килогерца
74 Килогерца
Как вы видите, с увеличением частоты, сдвиг приближается к 90 градусов, а сила тока становится все меньше и меньше.
Резонанс
Давайте подробнее рассмотрим тот самый момент, когда сдвиг фаз был равен нулю и сила тока, проходящая через последовательный колебательный, контур была максимальна:
Это явление носит название резонанса .
Как вы помните, если у нас сопротивление становится малым, а в данном случае сопротивления потерь катушки и конденсатора очень маленькие, то в цепи начинает течь большая сила тока согласно закону Ома : I=U/R . Если генератор мощный, то напряжение на нем не меняется, а сопротивление становится пренебрежимо малым и вуаля! Ток растет как грибы после дождя, что мы и увидели, посмотрев на желтую осциллограмму при резонансе.
Формула Томсона
Если при резонансе у нас реактивное сопротивление катушки равняется реактивному сопротивлению конденсатора X L =X C , то можно уравнять их реактивные сопротивления и уже отсюда вычислить частоту, на которой произошел резонанс. Итак, реактивное сопротивление катушки у нас выражается формулой:
Реактивное сопротивление конденсатора вычисляется по формуле:
Приравниваем обе части и вычисляем отсюда F :
В данном случае мы получили формулу резонансной частоты . Это формула по другому называется формулой Томсона , как вы поняли, в честь ученого, который ее вывел.
Давайте по формуле Томсона посчитаем резонансную частоту нашего последовательного колебательного контура. Для этого я буду использовать свой RLC-транзисторметр .
Замеряем индуктивность катушки:
И замеряем нашу емкость:
Высчитываем по формуле нашу резонансную частоту:
У меня получилось 5, 09 Килогерц.
С помощью регулировки частоты и осциллографа я поймал резонанс на частоте 4,78 Килогерц (написано в нижнем левом углу)
Спишем погрешность в 200 с копейками Герц на погрешность измерений приборов. Как вы видите, формула Томпсона работает.
Резонанс напряжений
Давайте возьмем другие параметры катушки и конденсатора и посмотрим, что у нас происходит на самих радиоэлементах. Нам ведь надо досконально все выяснить;-). Беру катушку индуктивности с индуктивностью в 22 микрогенри:
и конденсатор в 1000 пФ
Итак, чтобы поймать резонанс, я не буду в схему добавлять . Поступлю более хитрее.
Так как мой генератор частоты китайский и маломощный, то при резонансе у нас в цепи остается только активное сопротивление потерь R. В сумме получается все равно маленькое значение сопротивления, поэтому ток при резонансе достигает максимальных значений. В результате этого, на внутреннем сопротивлении генератора частоты падает приличное напряжение и выдаваемая амплитуда частоты генератора падает. Я буду ловить минимальное значение этой амплитуды. Следовательно это и будет резонанс колебательного контура. Перегружать генератор — это не есть хорошо, но что не сделаешь ради науки!
Ну что же, приступим;-). Давайте сначала посчитаем резонансную частоту по формуле Томсона. Для этого я открываю онлайн калькулятор на просторах интернета и быстренько высчитываю эту частоту. У меня получилось 1,073 Мегагерц.
Ловлю резонанс на генераторе частоты по его минимальным значениям амплитуды. Получилось как-то вот так:
Размах амплитуды 4 Вольта
Хотя на генераторе частоты размах более 17 Вольт! Вот так вот сильно просело напряжение. И как видите, резонансная частота получилась чуток другая, чем расчетная: 1,109 Мегагерц.
Теперь небольшой прикол;-)
Вот этот сигнал мы подаем на наш последовательный колебательный контур:
Как видите, мой генератор не в силах выдать большую силу тока в колебательный контур на резонансной частоте, поэтому сигнал получился даже чуть искаженным на пиках.
Ну а теперь самое интересное. Давайте замеряем падение напряжения на конденсаторе и катушке на резонансной частоте. То есть это будет выглядеть вот так:
Смотрим напряжение на конденсаторе:
Размах амплитуды 20 Вольт (5х4)! Откуда? Ведь подавали мы на колебательный контур синус с частотой в 2 Вольта!
Ладно, может с осциллографом что-то произошло?. Давайте замеряем напряжение на катушке:
Народ! Халява!!! Подали 2 Вольта с генератора, а получили 20 Вольт и на катушке и на конденсаторе! Выигрыш энергии в 10 раз! Успевай только снимать энергию или с конденсатора или с катушки!
Ну ладно раз такое дело… беру лампочку от мопеда на 12 Вольт и цепляю ее к конденсатору или катушке. Лампочке ведь вроде как по-барабану на какой частоте работать и какой ток кушать. Выставляю амплитуду, чтобы на катушке или конденсаторе было где то Вольт 20 так как среднеквадратичное напряжение будет где-то Вольт 14, и цепляю поочередно к ним лампочку:
Как видите — полный ноль. Лампочка гореть не собирается, так что побрейтесь фанаты халявной энергии). Вы ведь не забыли, что мощность определяется произведением силы тока на напряжение? Напряжения вроде как-бы хватает, а вот силы тока — увы! Поэтому последовательный колебательный контур носит также название узкополосного (резонансного) усилителя напряжения , а не мощности!
Давайте обобщим, что у нас получилось в этих опытах.
При резонансе напряжение на катушке и на конденсаторе оказались намного больше, чем то, которое мы подавали на колебательный контур. В данном случае у нас получилось в 10 раз больше. Почему же напряжение на катушке при резонансе равняется напряжению на конденсаторе. Это легко объясняется. Так как в последовательном колебательном контуре катушка и кондер идут друг за другом, следовательно, в цепи протекает одна и та же сила тока.
При резонансе реактивное сопротивление катушки равняется реактивному сопротивлению конденсатора. Получаем по правилу шунта, что на катушке у нас падает напряжение U L = IX L , а на конденсаторе U C = IX C . А так как при резонансе у нас X L = X C , то получаем что U L = U C , ток ведь в цепи один и тот же;-). Поэтому резонанс в последовательном колебательном контуре называют также резонансом напряжений , так как напряжение на катушке на резонансной частоте равняется напряжению на конденсаторе .
Добротность
Ну раз уж мы начали задвигать тему колебательных контуров, поэтому мы не можем обойти стороной такой параметр, как добротность колебательного контура. Так как мы уже провели некоторые опыты, то нам будет проще определить добротность, исходя из амплитуды напряжений. Добротность обозначается буквой Q и вычисляется по первой простой формуле:
Давайте посчитаем добротность в нашем случае.
Так как цена деления одного квадратика по вертикали 2 Вольта, следовательно, амплитуда сигнала генератора частоты 2 Вольта.
А это то, что мы имеем на зажимах конденсатора или катушки. Здесь цена деления одного квадратика по вертикали 5 Вольт. Считаем квадратики и умножаем. 5х4=20 Вольт.
Считаем по формуле добротности:
Q=20/2=10 . В принципе немного и не мало. Пойдет. Вот так вот на практике можно найти добротность.
Есть также вторая формула для вычисления добротности.
где
R — сопротивление потерь в контуре, Ом
L — индуктивность, Генри
С — емкость, Фарад
Зная добротность, можно легко найти сопротивление потерь R последовательного колебательного контура.
Также хочу добавить пару слов о добротности. Добротность контура — это качественный показатель колебательного контура. В основном его стараются всегда увеличить различными всевозможными способами. Если взглянуть на формулу выше, то можно понять, для того, чтобы увеличить добротность, нам надо как-то уменьшить сопротивление потерь колебательного контура. Львиная доля потерь относится к катушке индуктивности, так как она уже конструктивно имеет большие потери. Она намотана из провода и в большинстве случаев имеет сердечник. На высоких частотах в проводе начинает проявляться скин-эффект, который еще больше вносит потери в контур.
Резюме
Последовательный колебательный контур состоит из катушки индуктивности и конденсатора, соединенных последовательно.
На какой-то частоте реактивное сопротивление катушки становится равным реактивному сопротивлению конденсатора и в цепи последовательного колебательного контура наступает такое явление, как резонанс .
При резонансе реактивные сопротивления катушки и конденсатора хоть и равны по модулю, но противоположны по знаку, поэтому они вычитается и в сумме дают ноль. В цепи остается только активное сопротивление потерь R.
При резонансе сила тока в цепи становится максимальной, так как сопротивление потерь катушки и конденсатора R в сумме дают малое значение.
При резонансе напряжение на катушке равняется напряжению на конденсаторе и превышает напряжение на генераторе.
Коэффициент, показывающий во сколько раз напряжение на катушке либо на конденсаторе превышает напряжение на генераторе, называется добротностью Q последовательного колебательного контура и показывает качественную оценку колебательного контура. В основном стараются сделать Q как можно больше.
На низких частотах колебательный контур имеет емкостную составляющую тока до резонанса, а после резонанса — индуктивную составляющую тока.
Сегодня нас интересует простейший колебательный контур , его принцип работы и применение.
За полезной информацией по другим темам переходите на наш телеграм-канал .
Колебания – процесс, повторяющийся во времени, характеризуется изменением параметров системы около точки равновесия.
Первое, что приходит на ум — это механические колебания математического или пружинного маятников. Но ведь колебания бывают и электромагнитными.
По определению колебательный контур (или – это электрическая цепь, в которой происходят свободные электромагнитные колебания.
Такой контур представляет собой электрическую цепь, состоящую из катушки индуктивностью L и конденсатора емкостью C . Соединены эти два элемента могут быть лишь двумя способами — последовательно и параллельно. Покажем на рисунке ниже изображение и схему простейшего колебательного контура.
Кстати! Для всех наших читателей сейчас действует скидка 10% на .
Кстати! Для всех наших читателей сейчас действует скидка 10% на .
Принцип действия колебательного контура
Давайте рассмотрим пример, когда сначала мы заряжаем конденсатор и замыкаем цепь. После этого в цепи начинает течь синусоидальный электрический ток. Конденсатор разряжается через катушку. В катушке при протекании через нее тока возникает ЭДС самоиндукции , направленная в сторону, противоположную току конденсатора.
Разрядившись окончательно, конденсатор благодаря энергии ЭДС катушки, которая в этот момент будет максимальна, начнет заряжаться вновь, но только в обратной полярности.
Колебания, которые происходят в контуре – свободные затухающие колебания. То есть без дополнительной подачи энергии колебания в любом реальном колебательном контуре рано или поздно прекратятся, как и любые колебания в природе.
Это обусловлено тем, что контур состоит из реальных материалов (конденсатор, катушка, провода), обладающих таким свойством, как электрическое сопротивление, и потери энергии в реальном колебательном контуре неизбежны. В противном случае это нехитрое устройство могло бы стать вечным двигателем , существование которого, как известно, невозможно.
Еще одна важная характеристика – добротность Q . Добротность определяет амплитуду резонанса и показывает, во сколько раз запасы энергии в контуре превышают потери энергии за один период колебаний. Чем выше добротность системы, тем медленнее будут затухать колебания.
Резонанс LC-контура
Электромагнитные колебания в происходят с определенной частотой, которая называется резонансной Подробнее про – в нашей отдельной статье. Частоту колебаний можно менять, варьируя такие параметры контура, как емкость конденсатора C , индуктивность катушки L , сопротивление резистора R (для LCR-контура ).
Применение колебательного контура
Колебательный контур широко применяется на практике. На его основе строятся частотные фильтры, без него не обходится ни один радиоприемник или генератор сигналов определенной частоты.
Если вы не знаете, как подступиться к расчету LC-контура или на это совершенно нет времени, обратитесь в профессиональный студенческий сервис . Качественная и быстрая помощь в решении любых задач не заставит себя ждать!
Расчёт первой резонансной частоты и первого резонансного коэффициента звукопог лощения материала МР Текст научной статьи по специальности «Химические науки»
УДК 621.396
РАСЧЁТ ПЕРВОЙ РЕЗОНАНСНОЙ ЧАСТОТЫ
И ПЕРВОГО РЕЗОНАНСНОГО КОЭФФИЦИЕНТА ЗВУКОПОГЛОЩЕНИЯ
МАТЕРИАЛА МР
© 2009 Е. А. Изжеуров1, М. В. Дегтярев1, Цзян Хунюань2, У Гочи2
Самарский государственный аэрокосмический университет 2Харбинский политехнический университет г. Харбин, Китай
Материал МР является однородным упругим пористым материалом, обладает газопроницаемостью, поэтому относится к пористым звукопоглощающим материалам. Можно выражать звукопоглощающее свойство материала МР первой резонансной частотой f и первым резонансным коэффициентом звукопоглощения ar. Чтобы вывести уравнение приближённого расчёта первой резонансной частоты материала МР предполагается распространение звуковой волны в материале МР без затухания. В работе получено уравнение расчёта первой резонансной частоты материала МР в функции cos, из которой графическим способом получена первая резонансная частота. После сравнения значений первой резонансной частоты, полеченных в результате решения формулы со значениями, полученными методом длинных линий, сделан вывод о большей точности нового метода.
Материал МР, коэффициент звукопоглощения, акустический импеданс, резонанс, резонансная частота
Первая резонансная частота и первый резонансный коэффициент звукопоглощения пористого звукопоглощающего материала являются важными параметрами, выражающими звукопоглощающие свойства пористо -го материала. Поэтому по структурным свойствам и формулам расчёта акустических параметров материала МР соответственно выведены формулы расчёта первой резонансной частоты и первого резонансного коэффициента звукопоглощения материала МР. Результаты исследования являются теоретической основой изучения способности шумопоглощения материала МР.
1 Расчёт первой резонансной частоты материала МР
Основными параметрами звукопоглощающих свойств материала МР являются коэффициенты звукопоглощения а0 и акустический импеданс 2$, которые характеризуют звукопоглощающие свойства. Кривая звукопоглощающего свойства материала МР аналогична кривым других пористых звуко -поглощающих материалов: с увеличением
частоты коэффициент звукопоглощения возрастает, возникают первая резонансная частота /г и первый резонансный коэффициент звукопоглощения аГ. Свыше резонансной частоты /г величина коэффициента звукопоглощения находится между максимумом и минимумом, и с увеличением частоты коэффициент звукопоглощения стремится к по -стоянному Поэтому можно выражать звуко -поглощающее свойство материала МР первой резонансной частотой и первым резонансным коэффициентом звукопоглощения.
На практике материал МР расположен на жесткой стенке или с воздушным зазором. Метод расположенного на определённом расстоянии от жесткой стенки МР может улучшить низкочастотное поглощение. Структурные параметры материала МР, толщина воздушного зазора I и частота / обусловливают звукопоглощающие свойства материала МР. = — jW cos D. (1)
Волновой импеданс материала МР ра-
вен
s
(2)
где р0с0 — волновой импеданс воздуха, % -структурный фактор материала, имеющий вид [7]
X = X
0.68
exp 10.25(1 _ s) _ 1
I sd 0
+1
где xw является фактором от 1 до 4/3 и с увеличением частоты падает.
Из формулы (1) видно, что резонанс возникает, когда А = (2n+1) p /2. Из условия непрерывности импеданса на границе слоя материала МР и воздушного зазора, при том, что А] — половина фазового угла комплексного коэффициента отражения на границе в материале со стороны зазора в сумме с
(2Pf4x / С)h имеет в результате (2n+1)p/2,
получаем уравнение расчёта первой резо-нансной частоты материала МР, где с0 — ско-рость звука в воздухе:
hX = cosf Р ^ • (3)
2p f i cos I —— Ц +
1 + оШ I со Если правая и левая части уравнения (3) равны у, то первая резонансная частота материала МР получается графическим решением (рис. 1). На рис. 1 величина абсциссы
первой точки пересечения двух кривых является величиной первой резонансной частоты /г материала МР. Сравниваем первую резонансную частоту, полученную графическим решением, с первой резонансной частотой, измеренной методом длинных линий. Результаты сравнения приведены в табл .1.
Рис. 1. Расчёт первой резонансной частоты материала МР графическим методом
Таблица 1- Сравнение расчётных значений первой резонансной частоты материала МР с измеренными значениями
Структурные параметры Расчётные значения Измеренные значения
/=0.81, d=0.1mm, h=20mm l=0mm 3300 3400
l=20mm 1600 1700
l=50mm 950 1000
l=100mm 600 630
/*=0.81, d=0.2mm, h=20mm l=50mm 1000 1100
/=0.6, d=0.2mm, h=10mm l=20mm 1800 1700
Из табл. 1 видно, что значения первой резонансной частоты материала МР, полученные путём решения уравнением (3), более точны. Поэтому этот метод является лучшим методом расчёта первой резонансной частоты материала МР.
2 Расчёт первого резонансного коэффициента звукопоглощения МР
В общем случае акустический импеданс является комплексной величиной, на-
пример Хц = X+уУ. Резонанс возникает, когда мнимая часть составляющей акустического импеданса равна нулю, следовательно, ко -эффициент звукопоглощения является резонансным максимумом. Результаты экспериментальных исследований показывают, что резонансный максимум коэффициента звукопоглощения материала МР главным образом зависит от структурных параметров, а воздушный зазор в меньшей степени влияет на него. Поэтому при одинаковых структурных параметрах максимум первого резонансного коэффициента звукопоглощения материала МР, расположенного на жесткой стенке, приближенно равен максимуму первого резонансного коэффициента звукопоглощения материала МР, расположенного с воздушным зазором.
Чтобы исследовать звукопоглощающие свойства материала МР, нужны волновой импеданс Ж и постоянная распространения у, которые полностью определяют акустическое поведение материала, и в общем случае являются комплексными величинами, зависящими от частоты и структурных свойств материала. Акустический импеданс материала МР, расположенного на жесткой стенке, имеет вид
Хц = Ж соШ ук. (4)
На комплексной плоскости зависимость соШ ук от частоты выглядит как логарифмическая спираль, которая с увеличением частоты стремится к единице. Когда мнимая часть равна нулю, значение соШ ук находится между 0 и 1. Так как мнимая часть волнового импеданса Ж материала МР меньше вещественной части, то мнимая часть акустического импеданса приближается к нулю, когда соШ ук становится вещественной величиной, возникает резонанс. Поэтому значение акустического импеданса приближено равно произведению вещественной части волнового импеданса и вещественной части соШ ук.
Волновой импеданс Ж материала МР записывается в виде [8]
W =
о
153(l — о)2 kh 2о3 d 2®
(5)
где р0 — плотность воздуха, ц — вязкость воздуха, а — угловая частота, к — модуль упругости материала.
Согласно формуле (5) вещественная часть Жх волнового импеданса Ж будет равна
W =
A WЛ2 + B2
(6)
где
Л = 13ХРо р0 +
198. 2о3 d2 k®
(7)
Полагаем далее постоянную распространения у = а + у/, где а — коэффициент затухания, / — волновое число. Из формулы (7) получаем коэффициент затухания а:
a =
®
2 E
\D(2CF + DE)
C
(8)
coth yh можно записать [6]:
,/ .ч, sinh3ah — jsin26h /пч
coth yh = coth (a + jb)h =————-—. (9)
cosh 2ah — cos 2fih
Из формулы (9) и предыдущего анализа видно, что резонанс звукопоглощения материала МР возникает при 2j0h = ж. Тогда формула (9) примет вид
cothyh = sinh3ah = exp(2ah)- exp(-lah) . (10) cosh3ah + 1 exp(2ah) + exp(- 2ah) + 2
Анализ результатов расчётных и экспериментальных исследований коэффициента затухания материала МР показывает, что результат расчёта меньше экспериментальных данных в области высоких частот. Это объясняется тем, что резонансы возникают в
2
порах материала, а теоретическая модель не учитывает часть затухания резонанса пор. Поэтому нужно делать поправку для формулы (10). Вставляем поправочный коэффициент 5 в формулу (10), тогда значение соШ ук лучше совпадает с действительным значением. Так из формулы (10), при возникновении первого резонанса для материала МР, акустический импеданс равен:
= X :
exp(2ah)- exp(- 10ah) IA W A2 + B2 ,(11)
exp(2ah) + exp(- 0.4ah) + 2 v 2
а формула расчёта первого резонансного ко -эффициента звукопоглощения материала МР будет следующей:
4 X
«г =
(X +1)2′
(12)
Подстановка формулы (11) в (12) дает первый резонансный коэффициент звукопоглощения материала МР. Результаты расчёта и измерения первого резонансного коэффициента звукопоглощения материала МР приведены в табл. 2.
Таблица 2. Сравнение расчётных значений первого резонансного коэффициента звукопоглощения материала МР с измеренными значениями
Структурные параметры Расчётные значения Измеренные значения
P=0.81, d=0.1mm, h=20mm P=0.81, d=0.1mm, h=30mm P=0.81, d=0.2mm, h=20mm P=0.62, d=0.1mm, h=20mm P=0.6, d=0.2mm, h=20mm 0.92 0.94
0.95 0.97
0.68 0.70
0.80 0.82
0.99 0.97
Из табл. 2 видно, что расчётные значения первого резонансного коэффициента звукопоглощения материала МР более точны. Поэтому этот метод может считаться точным методом расчёта первого резонансного ко -эффициента звукопоглощения материала МР.
Вывод
1. Выведено уравнение расчёта первой резонансной частоты материала МР в функ-
ции cos, учитывающее распространение колебаний без затухания в пористом материале. При графическом решении результаты расчёта первой резонансной частоты достаточно точные. Видно, что теоретический метод расчёта первой резонансной частоты материала МР более практичен и точен.
2. Выведена формула расчёта первого резонансного коэффициента звукопоглощения материала МР по теоретическим формулам расчёта акустических параметров материала МР. Причём, учитывая влияние затухания резонанса пор материала, для coth gh сделана поправка. Результаты расчёта первого резонансного коэффициента звуко-поглощения более точны. Результаты расчёта позволяют сказать, что формула расчёта первого резонансного коэффициента звуко -поглощения материала МР достаточно точно и полно учитывает влияние на неё многих факторов.
Библиографический список
1. ZHANG Qiang, WANG Huaming, HU Zhangwei. Analysis for helicopter noise signal based on wavelet transform. Acta Acustica(\n Chinese), 2001; 26(5): р.450—454.
2. Gerard A., Berry A., Masson P. Control of tonal noise from subsonic axial fan. Part 2: active control simulations and experiments in free field. Journal of Sound and Vibration, 2005; 288(4-5): р.1077—1104.
3. Audi M S. Optimum attenuation of gas turbine noise by acoustical corner treatment. Applied Acoustics, 1992; 35(4): р.283—295.
4. Tam C K W, Pastouchenko N N, Schlinker R H. Noise source distribution in supersonic jets. Journal of Sound and Vibration, 2006; 291(1-2): р.192—201.
5. Изжеуров, Е. А. Формирование элементов конструкций гидродинамического тракта энергетических установок из упругого пористого материала МР,/ Е. А. Изжеуров.. М.: Машиностроение. 2001
6. C. Zwikker, C. W. Kosten. Sound absorbing materials. Beijing: Science press, 1960.
7. JIANG Hongyuan, WU Guoqi, Izzheurov E A. Research on sound absorption performance of metal rubber material. Acta Acustica(ln Chinese), 2008.
8. JIANG Hongyuan, WU Guoqi, Izzheurov E A. Theoretical calculation and experiment study on the acoustic parameters of metal rubber material. Acta Acustica(ln Chinese), 2007; 32(6): р.542—546.
References
1. ZHANG Qiang, WANG Huaming, HU Zhangwei. Analysis for helicopter noise signal based on wavelet transform. Acta Acustica(In Chinese), 2001; 26(5): p.450—454.
2. Gerard A., Berry A., Masson R Control of tonal noise from subsonic axial fan. Part 2: active control simulations and experiments in free field. Journal of Sound and Vibration, 2005; 288(4-5): p.1077—1104.
3. Audi M S. Optimum attenuation of gas turbine noise by acoustical corner treatment. Applied Acoustics, 1992; 35(4): p.283—295.
4. Tam C K W, Pastouchenko N N, Schlinker R H. Noise source distribution in supersonic jets. Journal of Sound and Vibration, 2006; 291(1-2): p.192—201.
5. Izzheurov E.A. The forming of hydro-gas tract construction elements made from material MR. Moscow. Machinesindustry. 2001.
6. C. Zwikker, C. W. Kosten. Sound absorbing materials. Beijing: Science press, 1960.
7. JIANG Hongyuan, WU Guoqi, Izzheurov E A. Research on sound absorption performance of metal rubber material. Acta Acustica (In Chinese), 2008.
8. JIANG Hongyuan, WU Guoqi, Izzheurov E A. Theoretical calculation and experiment study on the acoustic parameters of metal rubber material. Acta Acustica(In Chinese), 2007; 32(6): p.542—546.
CALCULATION OF THE FIRST RESONANT FREQUENCY AND THE FIRST RESONANT FACTOR OF A SOUND ABSORPTION OF MATERIAL М R
© 2009 E. A. Izzheurrov1, M. V. Degtyarev1, Jiang Hongyuan 2, Wu Guoqi2
1Samara State Aerospace University 2Kharbin Polytechnic University
It is possible to express sound-proof property of material МR (MR) by the first resonant frequency (FRF) and by the first resonant factor of a sound absorption аg. In work the equation of calculation of the FRF of МR in function of cos, from which the graphic way receives the FRF is received. After comparison of values of the FRF treated as a result of the decision of the formula with values, received by a method of long lines, it is drawn a conclusion on greater accuracy of new method. Considering influence of attenuation of a resonance of pores, for coth yh the amendment is made. As a result of the decision of two equations are received the first resonant factor of a sound absorption аg. After comparison with the measured values аg, it is drawn a conclusion on accuracy of calculation information.
Material MR, factor of a sound absorption, sound-proof property, aqoustik impedance, resonance, resonant frequency
Информация об авторах
Изжеуров Евгений Александрович, доктор технических наук, профессор Самарского государственного аэрокосмического университета. E-mail: [email protected]. Область научных интересов: перспективные материалы, теплопередающие конструкции энергетических установок, звукопоглощение пористых материалов.
Дегтярёв Михаил Владимирович — аспирант Самарского государственного аэрокосмического университета. E-mail: [email protected]. Область научных интересов: перспективные материалы в авиа-, ракето- и двигателестроении, в медицинской технике и нефтегазовой промышленности.
Цзян Хунюань, профессор кафедры деталей машин Харбинского политехнического университета, г. Харбин, Китайская Народная Республика. Тел. 1086-451-6418028. Область научных интересов: звукопоглощение пористых материалов.
У Гочи, докторант кафедры деталей машин Харбинского политехнического университета, г. Харбин, Китайская Народная Республика. Область научных интересов: звукопоглощение пористых материалов.
Izzheurrov Evgeny Aleksandrovich, doctor of science, professor of the Samara State Aerospace University. E-mail: [email protected]. Area of research: sealing made of MR material.
Degtyarev Michael Vladimirovich, postgraduate of the Samara State Aerospace University. E-mail: [email protected]. Area of research: sealing made of MR material.
Jiang Hongyuan, professor of Kharbin Polytechnic University. Phone: 1086-451-6418028. Area of research: sealing made of MR material.
Wu Guoqi, postgraduate of Kharbin Polytechnic University. Area of research: sealing made of MR material.
Калькулятор резонансной частотыдля LC-контура
Если вы хотите рассчитать резонансную частоту LC-контура, не смотрите дальше — этот калькулятор резонансной частоты — инструмент для вас. Введите индуктивность и емкость, и вы сразу же найдете резонансную и угловую частоту. Мы также предлагаем некоторую теорию, поскольку это может быть удобно — ниже вы узнаете, как рассчитать резонансную частоту, а также дадим краткое определение того, что такое резонансная частота на самом деле.
Если вас интересуют электронные схемы, вы, вероятно, хотели бы знать, как получить некоторую долю входного напряжения — наш калькулятор делителя напряжения просто необходим для этой задачи.
Что такое контур LC (контур резервуара)?
LC-контур (также называемый резонансным контуром, резервуарным контуром или настроенным контуром) представляет собой идеализированный контур RLC с нулевым сопротивлением. Он содержит только катушку индуктивности и конденсатор в параллельной или последовательной конфигурации:
| Параллельный LC-контур | Цепь LC серии
Tank обычно используются в качестве генераторов сигналов и полосовых фильтров — это означает, что они выбирают сигнал определенной частоты из более сложного сигнала.Они широко применяются в электронике — LC-схемы можно найти в усилителях, генераторах, тюнерах, радиопередатчиках и приемниках. Цепи LC и RC могут использоваться для фильтрации сигнала путем блокировки определенных частот.
Что такое резонансная частота?
Резонансная частота — это естественная незатухающая частота системы. Если мы применяем резонансную частоту, тогда колебания становятся максимальной амплитудой, и даже относительно небольшие силы могут создавать большие амплитуды.Однако, если выбрана любая другая частота, этот сигнал ослабляется. Есть много разных типов резонансов, например
- механический и акустический,
- электрика,
- оптический,
- орбитальный,
- молекулярный.
Для LC-контуров резонансная частота определяется емкостью C и импедансом L.
Как рассчитать резонансную частоту?
Следующая формула описывает взаимосвязь в цепи LC:
f = 1 / (2 * π * √ (L * C))
Где:
-
f— резонансная частота -
L— индуктивность цепи -
C— емкость цепи
Откуда взялась эта формула? Резонанс в LC-цепи возникает, когда индуктивное сопротивление катушки индуктивности становится равным емкостному сопротивлению конденсатора.Итак:
-
xL = 2 * π * f * L -
xC = 1 / (2 * π * f * C)
Тогда, преобразовав уравнение, находим:
-
xL = xC -
2 * π * f * L = 1 / (2 * π * f * C)
так: -
f² = 1 / (4 * π² * L * C)
и наконец: -
f = 1 / (2 * π * √ (L * C))
Также угловая частота может быть вычислена по следующей известной формуле:
ω = 2 * π * f
Как пользоваться вычислителем резонансной частоты
С помощью нашего инструмента прогулка по парку:
- Введите значение конденсатора .Например, у нас емкость равна 1 мкФ.
- Тип индуктивности . Наша индуктивность в нашей LC-цепи равна 0,18 мГн.
- Вычислитель резонансной частоты сделал свое дело! Мы быстро выяснили, что такое резонансная частота: 11,863 кГц. Если вы хотите также проверить угловую частоту, просто нажмите кнопку расширенного режима
, и результат появится внизу.
Калькулятор резонансной частоты - гибкий инструмент, поэтому, как обычно, вы можете ввести любые две переменные, и недостающая переменная будет вычислена мгновенно.
Калькулятор резонансной частоты | LC Calculator
Этот калькулятор резонансной частоты использует значения емкости (C) и индуктивности (L) LC-контура (также известного как резонансный контур, резервуарный контур или настроенный контур) для определения его резонансной частоты (f).
Вы можете использовать калькулятор в три простых шага:
- Введите любые два параметра для резонансного контура.
- Выберите единицы измерения, которые вы хотите использовать.
- Нажмите «Рассчитать», и калькулятор резонансной частоты вычислит третий недостающий параметр.
Ссылка
В области электроники LC-цепь используется либо для генерации сигналов с определенной частотой, либо для выбора одного сигнала из более сложного сигнала с определенной частотой. LC-схемы играют фундаментальную роль в работе многих электронных устройств, включая радиооборудование, и используются в таких схемах, как фильтры, генераторы, тюнеры и смесители частот.
LC-контуры состоят из двух соединенных между собой электронных компонентов: индуктора (L) и конденсатора (C).
Когда L и C размещены параллельно или последовательно, они имеют резонансную частоту. Эта резонансная частота представлена следующим уравнением:
f = 1 / (2π √LC)
Где: f - резонансная частота в герцах (Гц), L - индуктивность в генри (H ), C - емкость в фарадах (F), π - константа (3,141592654…)
Пример расчета резонансной частоты
Допустим, мы хотим определить резонансную частоту LC-контура с индуктором емкостью 3 мГн и конденсатор емкостью 3 мкФ.(-6)))
f = 1677,64 Гц ≈ 1,678 кГц.
Формулы
В этом калькуляторе резонансной частоты используются следующие формулы:
f = 1 / (2π √LC) Резонансная частота [Гц]
L = 1 / (4π 2 f 2 C) Индуктивность [H]
C = 1 / (4π 2 f 2 L) Емкость [F]
Вас также может заинтересовать наш бесплатный калькулятор кроссовера
RLC Resonant Frequency Calculator [Series / Parallel ] • Электрические калькуляторы Org
Вычислитель резонансной частотыRLC используется для расчета резонансной частоты последовательных / параллельных цепей.Он также рассчитывает последовательный и параллельный коэффициент демпфирования.
RLC Резонансная частота Формула
RLC Резонанс - это особая частота, на которой резонирует электрическая цепь. Значение частоты RLC определяется индуктивностью и емкостью цепи. Резонанс возникает как в последовательной, так и в параллельной цепях. Хотя основная формула для расчета серий и резонансной частоты одинакова, тем не менее, существуют определенные различия, которые определяют резонансную частоту.
Резонансная частота серииРезонанс последовательной цепи возникает, когда индуктивное реактивное сопротивление в точности равно емкостному реактивному сопротивлению. Однако необходимым условием является разность фаз в 180 градусов, при которой они должны компенсировать друг друга. Последовательный резонансный контур имеет минимальное сопротивление при резонансе. Последовательный резонансный контур и его формула:
Частота параллельного резонанса
Параллельная резонансная частота чаще встречается в электронных схемах, но не менее сложна.Мы можем определить параллельный резонанс как условие нулевой разности фаз или единичного коэффициента мощности. Параллельный резонансный контур имеет максимальное сопротивление.
Коэффициент демпфирования
Коэффициент демпфирования цепи определяется как отношение ширины полосы пропускания к центральной частоте. Коэффициент демпфирования схемы определяет частоту полосы пропускания. Более высокий коэффициент демпфирования означает более широкую полосу пропускания, а более низкий коэффициент демпфирования означает, что полоса пропускания будет ниже.Коэффициент демпфирования последовательной цепи напрямую связан с сопротивлением по формуле:
В то время как коэффициент параллельного демпфирования обратно пропорционален сопротивлению:
Практическое применение
Практически последовательные и параллельные RLC и LC резонансные цепи используются в приложениях электронного проектирования и моделирования схем.
Проектирование схем фильтров
Частотные фильтры, такие как фильтры нижних и верхних частот, полосовые и полосовые фильтры, используют в своей конструкции концепции полосовой и резонансной частоты.
Настройка аналоговой магнитолы
Настройка аналогового радиоприемника выполняется с помощью переменного конденсатора с параллельными пластинами, значение которого изменяется для настройки радиоприемника на частоты, поступающие от радиоприемника.
Пример числовых задач
Пример № 1: Последовательный резонансный контур имеет индуктивность 50 мГн и емкость 20 мкФ, которые подключаются к резистору 10 кОм. Найдите резонансную частоту и коэффициент затухания.
Решение:
Приведенные значения: L = 50 мГн и C = 20 мкФ
Из формулы:
= 1 / (50 * 0.001 * 20 * 0,000001) = 1000 Гц или 1 кГц
Коэффициент демпфирования серииможно рассчитать по формуле:
= (5 кОм) √ ((20 * 0,000001) / (50 * 0,001) = 100
Пример № 2: Параллельный резонансный контур имеет резистор 1 МОм, конденсатор 20 пФ и катушку индуктивности 500 мкГн. Найдите резонансную частоту и коэффициент параллельного демпфирования.
Решение:
Приведенные значения: L = 500 мкГн, C = 20 пФ
из
= 1 / √ (500 мкГн * 20 пФ) = 10 МГц
Для расчета параллельного демпфирования используйте уравнение:
= 1 / (2 * 1 МОм) √ (500 мкГн / 20 пФ)
Частота резонанса- обзор
Влияние уровней насыщения кислородом на сигналы ядерного магнитного резонанса
Частота ЯМР ядер с ненулевым спином пропорциональна ядерному гиромагнитному отношению и силе локального поля, испытываемого ядром.Таким образом, изменения в распределении поля внутри и вокруг эритроцитов влияют на несколько параметров ЯМР, включая резонансную частоту и времена релаксации ЯМР. Эти два параметра будут обсуждаться отдельно в следующих нескольких абзацах. Обсуждение будет сосредоточено на ядрах водорода, наиболее часто изучаемых ядерных частицах в биомедицинских ЯМР и МРТ. Большая часть сигналов ЯМР водорода от живых организмов исходит от несвязанной воды, которая присутствует в высокой молярной концентрации во многих тканях, включая кровь.Высокая концентрация, большое гиромагнитное отношение и высокое содержание изотопов значительно увеличивают чувствительность ЯМР-обнаружения водорода, что позволяет получать МР-изображения живых организмов с высоким разрешением.
Локальное микроскопическое поле, которое испытывает ядро в однородной среде с заданной восприимчивостью χ , погруженное во внешнее приложенное поле B 0 isBL − B0 = Ds − 23χ − χ0B0, где D - размагничивающий фактор зависит от геометрии образца, а 2/3 - геометрический фактор сферы, нарисованной вокруг ядра.Эту конструкцию обычно называют «сферой Лоренца», условной сферической вакуумной полостью, окружающей ядро, что объясняет тот факт, что в атомном масштабе среда не может быть представлена как континуум. Интересно отметить, что для сферического образца D s = 2/3 и резонансная частота не зависит от изменений χ . Для эритроцитов геометрия далека от сферической, и следует ожидать сдвига резонансной частоты для молекул воды в суспензии эритроцитов при изменении восприимчивости клеток.Действительно, разница в 0,33 ppm в резонансной частоте ядер водорода в оксигенированной и деоксигенированной крови человека была измерена Thulburn и его коллегами в экспериментах, проведенных in vitro в сильных магнитных полях. Чтобы рассчитать влияние чувствительности на сигналы ЯМР в такой сложной среде, как кровь, необходимо уточнить теоретические основы.
В однородном материале фактический размер сферы Лоренца явно не появляется в расчетах.Однако кровь очень неоднородна, гемоглобин разделен на дискретные единицы (эритроциты), встроенные в плазму. Количественный расчет сдвига линии ЯМР протонов в крови требует немного более сложной конструкции, чтобы учесть различные масштабы характерной длины вкладов в локальное поле, обусловленных удаленными эритроцитами и гемоглобином. Сначала рисуется сфера Лоренца вокруг ядра достаточного размера, чтобы содержать большое количество эритроцитов, так что вклады в локальное поле от удаленных источников вокруг сферы плавно меняются.Поле, которое испытывает ядро в центре сферы, равно BL = B0 + Ds − 23χbloodB0 + Bi, где B i обозначает вклады в локальное поле от источников внутри сферы, а χ кровь восприимчивость крови (сфера велика в клеточном масштабе, а внешняя среда выглядит как континуум). χ кровь зависит от относительного объема, занятого эритроцитами V rbc (т. Е. Гематокрит): χblood = Vrbc × χrbc + Vrbc − 1χpl Для оценки B i нарисована сфера Лоренца, меньше клетки, но большая в молекулярном масштабе.Если эта сфера полностью находится внутри внутриклеточного пространства: Bi = Drbc − 23χrbc − χplB0
Для сложной формы эритроцитов геометрический фактор D rbc должен быть оценен численно с помощью процедур, аналогичных тем, которые используются для расчета распределение поля, показанное на рисунке 3, и зависит от ориентации ячейки по отношению к внешнему магнитному полю. В сильных полях, используемых Тулберном и его сотрудниками, эритроциты полностью ориентированы в конфигурации с минимальной энергией, и D rbc = 0.75.
Используя эту конструкцию, можно рассчитать относительные изменения в локальном поле, испытываемые ядрами, для компартментов плазмы и эритроцитов: ΔBpl / B0 = Ds − 23VrbcΔχrbcΔBrbc / B0 = Ds − 23VrbcΔχrbc + Drbc − 23Δχrbc
быстро рассеиваютсявнутри и вне клетки и динамически усреднять все распределение поля в типичной шкале времени ЯМР. В этом режиме быстрого обмена сигнал ЯМР состоит из узкого резонанса, центральная частота которого отражает среднее поле, испытываемое ядром.Таким образом, резонансный сдвиг для ядер водорода молекулы воды в крови пропорционален среднему значению изменений локального поля во внутри- и внеклеточной среде, взвешенных по относительным размерам водных компартментов (0,3 и 0,7 для эритроцитов и эритроцитов). плазма соответственно).
Для изменения внутриклеточной магнитной восприимчивости Δ χ rbc = 2,5 × 10 −6 , что соответствует разнице между оксигенированными и деоксигенированными эритроцитами, и для цилиндрического образца крови с гематокритом 40% эти расчеты предсказывают сдвиг водородного резонанса на 0.3 ppm, что близко к сдвигу, измеренному Thulburn и соавторами при аналогичных условиях. Приведенная выше теоретическая оценка показывает, что этот сдвиг можно почти полностью объяснить изменениями магнитной восприимчивости крови, а не прямым взаимодействием молекул воды с парамагнитными центрами.
Сдвиг резонансной частоты - не единственное и не самое сильное влияние магнитных свойств крови, зависящих от оксигенации, на параметры ЯМР. Быстрая диффузия молекул воды в градиентах поля внутри и снаружи клеток, а также вблизи небольших капилляров способствует необратимой потере фазовой когерентности ядерной спиновой системы.Характерное время этого процесса называется временем спин-спиновой релаксации, или T 2 . Для более крупных кровеносных сосудов несоответствие восприимчивости крови и окружающей ткани приводит к градиентам магнитного поля в большем масштабе, чем тот, который измеряется при диффузии молекул воды. Частично обратимая дефазировка спинов, вызванная этими более протяженными в пространстве градиентами, регулируется постоянной времени, называемой T2 *.
Оба механизма релаксации более эффективны в присутствии более сильных градиентов, а T 2 и T2 * короче в деоксигенированной крови.Важно отметить, что изменения оксигенации крови не только влияют на время ЯМР-релаксации ядерных спинов в крови, но и в окружающей ткани. Сосудистая сеть сильно структурирована, мельчайшие капилляры имеют диаметр всего несколько микрон и разделены несколькими десятками микрон. Следовательно, изменение оксигенации крови влияет на время релаксации большого количества спинов как во внутри-, так и во внесосудистом отделах, а времена релаксации ЯМР более чувствительны, чем относительно небольшой сдвиг резонансной частоты, к изменениям уровней оксигенации крови.МР-изображения могут быть сенсибилизированы к T 2 и T2 * с помощью соответствующих последовательностей радиочастотных импульсов, тем самым используя эритроциты в качестве эндогенного источника контраста. Применение этих методов для отображения паттернов мозговой активности обсуждается в следующем разделе.
Частота механического резонанса и как ее анализировать
В какой-то момент своей карьеры системные инженеры, вероятно, столкнутся с ситуацией, когда резонансная реакция системы вызывает проблемы с движением и / или слышимое раздражение.Этот резонанс или вибрация нежелательны и могут привести к значительному снижению производительности. Например, фрезерный станок с ЧПУ (который обычно имеет высокую резонансную частоту из-за высокой жесткости) [1] будет дрожать вокруг желаемой траектории фрезерования при возбуждении резонансной частоты. Другой пример - фармацевтический инструмент для работы с жидкостью, в котором возникают неожиданные вибрации, вызывающие перемешивание транспортируемого жидкого раствора. В этой статье будет рассмотрено, почему присутствуют резонансы и какие инструменты можно использовать для их анализа.
Почему механические системы демонстрируют резонансную частоту?
Первым шагом в ответе на этот вопрос является создание модели механической системы. Для определения положения массы с учетом трения и податливости требуется, чтобы модель была системой одного или нескольких дифференциальных уравнений 2-го порядка (или выше). Чтобы найти решение, а также упростить анализ поведения, нерешенные уравнения временной области преобразуются в s-область с помощью преобразования Лапласа .Это облегчает создание передаточной функции системного уровня, которую также называют «характеристическим уравнением».
Знаменатель передаточной функции содержит переменные состояния порядка n. Значения s (действительные и / или мнимые), где знаменатель равен нулю, называются корнями знаменателя, которые называются «полюсами». Числитель может быть константой или содержать переменные состояния порядка n, аналогичные знаменателю. Значения s (действительные и / или мнимые), где числитель равен нулю, называются корнями числителя, которые называются «нулями».Если числитель постоянный, то нулей нет. Эта информация может быть использована для формулирования решения модели во временной области. Однако используемый здесь частотный анализ будет ограничен s-областью для простоты вычислений.
Полюса и нули очень полезны для определения поведения и стабильности. Например, критерии устойчивости диктуют, что порядок знаменателя (количества полюсов) не должен быть меньше порядка числителя (количества нулей). Кроме того, действительная часть доминирующих полюсов должна быть отрицательной (левая часть s-плоскости), чтобы система считалась стабильной.Полюса будут использоваться здесь для объяснения существования резонансной частоты.
Инерциальные системы имеют резонансную частоту, которая существует из-за внутренних свойств. Однако система должна быть более сложной, чем инерция чисто твердого тела, иначе ее характеристическое уравнение будет иметь только полюсы в нуле. Другие члены в характеристическом уравнении, которые могут быть такими же простыми, как член податливости (пружина), будут вводить ненулевые частотные составляющие (корни с мнимыми частями) в характеристическое уравнение.Чисто инерциальные системы будут иметь полюса на нуле и, следовательно, не будут показывать резонансную частоту.
«Твердое тело» - это просто академическая конструкция, которой не существует в реальном мире, поэтому даже простые инерционные системы могут демонстрировать механическую резонансную частоту, когда к ним добавляются пружинные элементы (податливость) и / или демпфирующие компоненты (вязкое трение). модель. Некоторые системы достаточно демпфированы, чтобы подавить резонансную частоту. В этом случае резонансная частота все еще существует (мнимая часть корней), но она едва заметна, так как действительные части корней доминируют в отклике.
Демонстрационная установка
Система, используемая в этой демонстрации (рис. 1), представляет собой массу в верхней части металлической линейки, которая действует как пружина. Нижняя часть пружины прикреплена к ступени линейного двигателя. Для простоты будет анализироваться только движение в направлении линейного двигателя. Движение м 2 будет рассматриваться как линейное, что является допустимым приближением для малых углов. Это упрощение все еще актуально в контексте описания источника резонансной частоты.Кроме того, измеряется только положение двигателя, м 1 .
Модель содержит коэффициент демпфирования системы, b s , который передает силу, пропорциональную скорости и противоположную направлению движения. Это свойство обычно называется «вязким трением» и представляет собой любые фрикционные свойства, пропорциональные скорости. Сила, прикладываемая к системе магнитным полем двигателя, регулируется путем изменения тока в обмотках двигателя.
Рисунок 1 - Демонстрационная система
Отклик положения м 1 на силу, действующую на эту систему, выражается следующим образом:
(Уравнение 1) - получено из реакции на скорость кручения в ссылке 1
Обратите внимание, что член слева от правой части уравнения - это «несвязанный» отклик. Если пружина имеет бесконечную жесткость, крайний правый член равен единице, а две массы жестко прикреплены и действуют как одна масса.В этом случае есть только полюса на нуле и, следовательно, нет резонансной частоты.
Член справа вводит корни с мнимыми компонентами, тем самым создавая потенциал для частотной характеристики. Для случая, когда b s равно нулю, корни этого члена становятся:
(ур. 2)
Введение умеренного демпфирующего члена ( 0,1K s s <0,6K s / w n ) [2], вводит реальный компонент в корни и перемещает их так, что резонансная частота немного меньше собственной незатухающей частоты.Более сильный демпфирующий член ( b s <0,6K s / w n ) [2] еще больше уменьшит резонансную частоту, но отклик на частоте будет ослаблен и окажет небольшое влияние. В этом случае преобладают настоящие части корней.
Из-за нуля в числителе эта модель также будет показывать «антирезонансную» частоту. Это можно наблюдать как уменьшение отклика при заданном антирезонансе. Системы со связанными массами, подобные анализируемой здесь, будут содержать антирезонансную частоту чуть ниже резонансной частоты.
За пределами резонансной частоты отклик больше, чем у системы, в которой массы жестко связаны. В последнем случае вибрация создает больше всего проблем [1].
Экспериментальное определение резонансной частоты
Использование в качестве определения резонансной частоты «частота, на которой система будет демонстрировать локализованный максимальный отклик» означает, что эксперимент может быть проведен в системе, где отклик как функция частоты измеряется.
Один инструмент, называемый частотной разверткой, вводит в систему сигнал переменной частоты. Ввод частоты начинается с предварительно определенного значения и непрерывно изменяется до тех пор, пока не будет достигнуто заданное максимальное значение. Большинство механических систем имеют резонансные частоты в сотни герц или ниже. Если резонансная частота значительна, она обычно производит слышимый звук, который может воспринимать слушатель.
Аналогичный, но более точный инструмент, график Боде, анализирует усиление и фазу отклика и генерирует график в частотной области.Чтобы упростить вычисления на цифровом процессоре, дискретизируется набор дискретных частот, а результаты обрабатываются с помощью БПФ (быстрого преобразования Фурье).
Это видео на YouTube демонстрирует использование различных инструментов в Pro-Motion® для определения резонансной частоты системы на Рисунке 1:
Метод № 1: Расчет на основе трассировки фактического положения реакции на возмущение.
В систему введено нарушение.Функция Pro-Motion SCOPE используется для отслеживания реакции положения на м 1 . Резонансная частота - это величина, обратная периоду времени между одним пиком и другим. Из видео видно, что период довольно близок к 100 мс. Это соответствует резонансной частоте 10 Гц.
Метод № 2: развертка по частоте используется для перехода от низкой к высокой частоте.
На систему действует синусоидальная сила (через магнитное поле двигателя).Колебания системы наблюдаются визуально (или на слух). Отмечается частота локального максимума отклика. Из метода №1 уже известна приблизительная резонансная частота. Однако, если система быстро установится в ответ на введенный «импульс» метода № 1, то данных для определения резонансной частоты может не хватить. Непрерывное возмущение, вводимое методом № 2, предоставит больше данных в этом отношении, поскольку система никогда не успокаивается.
Как видно на видео, амплитуда колебаний фактического положения начинает увеличиваться около 5.2-секундная отметка (11 Гц). Частота продолжает увеличиваться до 14 Гц, и отклик гаснет после прохождения резонансной частоты. Затем развертка меняет направление и перемещается с 14 Гц на 10,5 Гц и остается там. Как и ожидалось, амплитуда отклика увеличивается по мере приближения к резонансной частоте.
Метод № 3: Создается диаграмма Боде системы, охватывающая тот же диапазон частот.
И снова на систему действует синусоидальная сила.На этот раз реакция положения по отношению к приложенной силе используется для расчета усиления и фазы отклика. В этом случае пользователю не нужно полагаться на визуальные или звуковые подсказки. Пользователь может анализировать данные усиления, чтобы найти локальный максимум и частоту, связанную с этим максимумом. Для более детального анализа числовые данные могут быть перенесены в электронную таблицу и проанализированы.
Рис. 2: Данные об усилении Боде в виде электронной таблицы.
Рисунок 2 демонстрирует более точное определение резонансной частоты (10.6 Гц). Антирезонансная частота также может наблюдаться на рисунке 2 примерно на уровне 10,1 Гц.
В конце дня…
Поскольку никакая инерциальная система не содержит истинных масс «твердого тела», все механические системы имеют ненулевую резонансную частоту. Возбуждение резонансной частоты ухудшит работу системы как с точки зрения кратковременной точности, так и с точки зрения долгосрочного технического обслуживания.
Продемонстрированы три метода экспериментального определения резонансной частоты.Метод №1 обеспечил результат в пределах 10%, но этот метод был ограничен системами, которые имеют недостаточно затухающий отклик на импульс. Метод № 2, который полагается на визуальные и звуковые подсказки, дал эквивалентную точность и работает как в системах с избыточным, так и с недостаточным демпфированием. Метод № 3 предоставил наиболее подробную информацию о частотной характеристике системы. Значительно улучшена точность оценки резонансной частоты. Кроме того, этот метод также позволил идентифицировать антирезонансную частоту.
Артикул:
1 Г. Эллис, Лекарства от механического резонанса в промышленных сервосистемах
2 Дж. Д’Аццо и К. Хупис, Анализ и проектирование линейных систем управления: традиционные и современные, McGraw-Hill, Inc., 1995, стр. 292-293.
Продукты PMD, поддерживающие серводвигатели
PMD производит ИС, которые обеспечивают расширенное управление движением щеточных и бесщеточных двигателей постоянного тока более двадцати пяти лет. С тех пор мы также встраивали эти ИС в модули plug and play и платы управления движением.Несмотря на разную упаковку, все эти продукты управляются C-Motion, простым в использовании языком управления движением PMD и идеально подходят для использования в медицинских, лабораторных, полупроводниковых, роботизированных и промышленных приложениях управления движением.
Программное обеспечение для анализа движения Pro-Motion
Pro-Motion - это простая в использовании программа для упражнений и анализа движения PMD на базе Windows. Он предлагает готовые возможности, которыми сможет поделиться вся ваша команда разработчиков. Пошаговый мастер настройки осей позволяет разработчикам быстро и легко настраивать контур положения, контур тока и параметры управляющего двигателя с ориентацией на поле.Опытные пользователи могут получить доступ к полному пакету анализа движения с генерацией графиков Боде и автонастройкой.
Подробнее >>ИС серии MC58113
ИС серии MC58113 являются частью популярного семейства микросхем Magellan Motion Control от PMD и обеспечивают расширенное управление положением для шаговых двигателей, BLDC и щеточных двигателей постоянного тока. Стандартные функции включают автонастройку, профилирование s-образной кривой, FOC (полевое управление), управление сигналом переключения высокого / низкого уровня, прямой энкодер, ввод импульсов и направления и многое другое.ИС семейства MC58113, используемые для автоматизации лабораторий, управления насосами, систем наведения или универсальной автоматизации, являются идеальным решением для вашей следующей конструкции машины.
Подробнее >>Цифровые приводы ION
Цифровые приводы ION объединяют одноосную микросхему Magellan и сверхэффективный цифровой усилитель в компактном прочном корпусе. В дополнение к расширенному управлению серводвигателем, ION обеспечивают перемещение от точки к точке с S-образной кривой, управление питанием i2T, загружаемый код пользователя и ряд функций безопасности, включая обнаружение перегрузки по току, перенапряжения и перегрева.ION - это простые в использовании устройства plug and play, которые мгновенно запускают ваше приложение.
Подробнее >>Платы управления движением Prodigy
Платы Prodigy® / CME Machine-Controller обеспечивают высокопроизводительное управление движением для медицинских, научных, автоматических, промышленных и робототехнических приложений. Доступные в конфигурациях с 1, 2, 3 и 4 осями, эти платы поддерживают щеточные двигатели постоянного тока, бесщеточные двигатели постоянного тока и шаговые двигатели и позволяют загружать и запускать написанный пользователем код на языке C непосредственно на плате.Машинный контроллер Prodigy / CME имеет встроенные усилители Atlas , которые устраняют необходимость во внешних усилителях. Для построения полностью функционирующей системы требуется только один высоковольтный источник питания, двигатели и кабели. Опции хост-интерфейса включают Ethernet UDP и TCP, CANbus, RS-232 и RS-485.
Подробнее >>Вас также может заинтересовать:
Резонансная частота f0, онлайн калькулятор
Калькулятор и формулы для расчета резонансной частоты ЖК-резонатора
Расчет резонансной частоты LC
На этой странице вы можете рассчитать резонансную частоту, индуктивность катушки или емкость конденсатора в колебательном контуре.Чтобы вычислить третье, необходимо знать два значения.
Формулы резонансной частоты
В следующем описании показан расчет резонансных частот LC-резонансного контура. В теоретических системах без демпфирования резонансная частота равна незатухающей собственной частоте \ ({\ displaystyle f_ {0}} \).
В демпфированных системах частота с максимальной амплитудой всегда меньше незатухающей собственной частоты.2 · C} \)
|
Формула и вывод резонансной частоты
Формула резонансной частоты для последовательного и параллельного резонансного контура, состоящего из резистора, индуктора и конденсатора, различается.В этой статье мы рассмотрим формулу резонансной частоты для последовательного, а также параллельного резонансного контура и их вывод. Мы также обсудим метод определения резонансной частоты для любой данной цепи с помощью некоторых примеров.
Формула резонансной частоты - последовательная резонансная цепьФормула для резонансной частоты для последовательного резонансного контура задается как
f = 1 / 2π√ (LC)
Деривация:Рассмотрим последовательное соединение R, L и C.Это последовательное соединение возбуждается источником переменного тока.
Давайте сначала вычислим полное сопротивление Z цепи.
Z = R + jωL - j / ωC
= R + j (ωL - 1 / ωC)
В условиях резонанса цепь является чисто резистивной. Это означает, что мнимая часть импеданса Z будет равна нулю в условиях резонанса или на резонансной частоте. Вы всегда должны помнить об этом при вычислении резонансной частоты для данной цепи.
Это означает, что
(ωL - 1 / ωC) = 0
ωL = 1 / ωC
ω 2 = 1 / (LC)
ω = 1 / (ЖК)
As, мы знаем, что
ω = 1 / 2πf
Следовательно, f = 1 / 2πω
Резонансная частота (f 0 ) для цепи последовательного резонанса,
Обратите внимание, что рисовать векторную диаграмму не нужно. Вам нужно только найти импеданс и сделать мнимую часть импеданса равной нулю, чтобы найти резонансную частоту данной цепи.Мы применим ту же технику и для параллельного резонансного контура.
Формула резонансной частоты - параллельная резонансная цепьФормула для резонансной частоты для параллельного резонансного контура имеет вид,
Деривация:Давайте рассмотрим параллельный резонансный контур, как показано ниже. Наша цель - найти формулу резонансной частоты для этой цепи.
Опять же, прежде всего, мы найдем импеданс Z цепи.
Приравнивая мнимую часть нулю, получаем
⇒ - (ωL 2 ) / C + L / (ωC 2 ) - R 2 / (ωC) = 0
⇒ -ω 2 L 2 C + L - R 2 C = 0
⇒ ω 2 L 2 C = L - R 2 C
⇒ ω 2 = 1 / (LC) - R 2 / L 2
Так как, ω = 1 / 2πf
Резонансная частота f 0
Итак, насколько просто найти значение резонансной частоты? Не правда ли? Давайте решим какой-нибудь пример, чтобы лучше понять.
Пример:Найдите резонансную частоту для цепи, показанной на рисунке ниже.
Значения R L , L, R и C равны 1 Ом, 1 Генри, 0,5 Фарада и 1 Ом соответственно.
Решение:
Как уже говорилось, сначала мы найдем импеданс, а затем приравняем мнимую часть Z к нулю, чтобы получить значение резонансной частоты. Но давайте будем немного резче. Поскольку схема представляет собой параллельное соединение элементов, для простоты вычислений лучше найти полную проводимость Y, а не импеданс.
Y = 1 / R + jωC + 1 / (R L + jωL)
= 1 / R + jωC + (R L - jωL) / (R L 2 + ω 2 L 2 )
Мнимая часть Y
= ωC - ωL / (R L 2 + ω 2 L 2 )
Чтобы получить резонансную частоту, сделайте мнимую часть полной проводимости равной нулю.
ωC - ωL / (R L 2 + ω 2 L 2 ) = 0
(правый левый 2 + ω 2 левый 2 ) = аккредитив
ω 2 = (1 / LC) - (R L 2 / L 2 )
Теперь поместите значение C, L и R L
ω 2 = 1
ω = 1 рад / сек. (Отв.
