Параллельная схема: характеристики, преимущества и недостатки
Параллельное соединение проводников
Параллельным соединением проводников называется такое соединение, когда начала всех проводников соединены в одну точку, а концы проводников – в другую точку (рисунок 4). Начало цепи присоединяется к одному полюсу источника напряжения, а конец цепи – к другому полюсу.
| Рисунок 4. Схема параллельного соединения проводников |
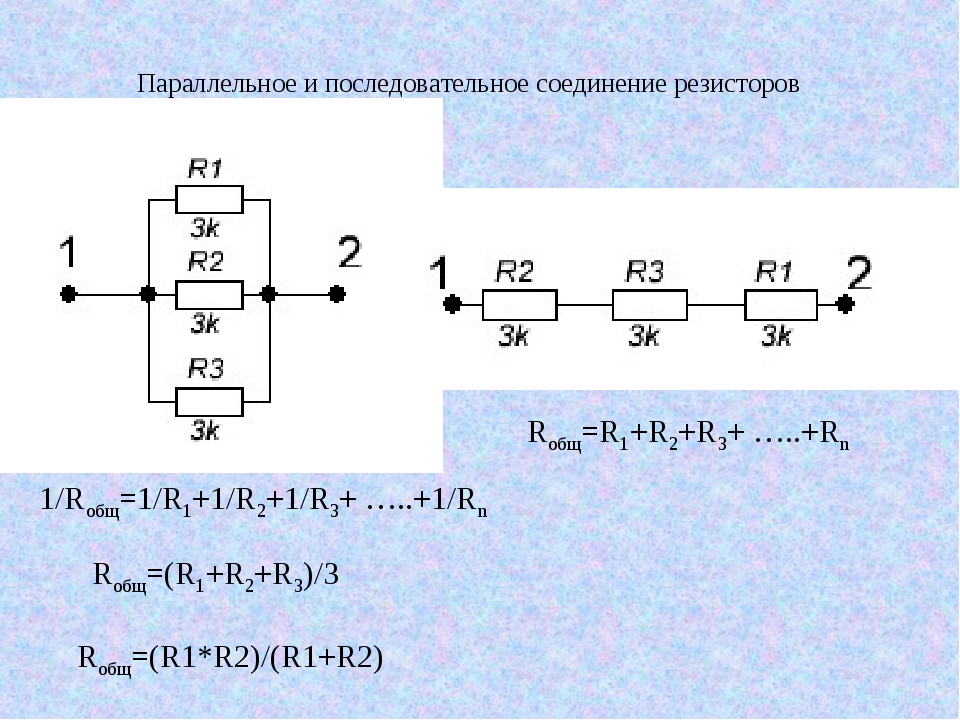
Из рисунка видно, что при параллельном соединении проводников для прохождения тока имеется несколько путей. Ток, протекая к точке разветвления А, растекается далее по трем сопротивлениям и равен сумме токов, уходящих от этой точки:
I = I1 + I2 + I3.
Если токи, приходящие к точке разветвления, считать положительными, а уходящие – отрицательными, то для точки разветвления можно написать:
то есть алгебраическая сумма токов для любой узловой точки цепи всегда равна нулю.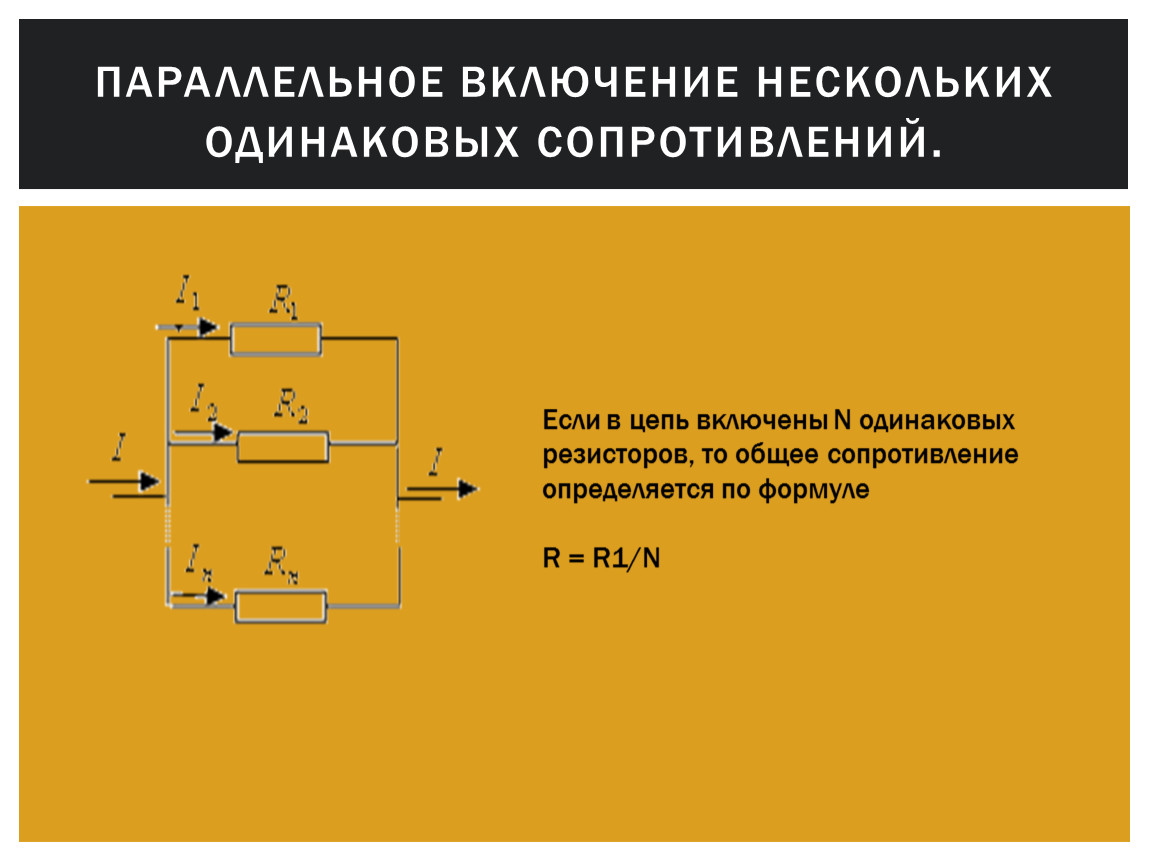 Это соотношение, связывающее токи в любой точке разветвления цепи, называется первым законом Кирхгофа. Определение первого закона Кирхгофа может звучать и в другой формулировке, а именно: сумма токов втекающих в узел электрической цепи равна сумме токов вытекающих из этого узла.
Это соотношение, связывающее токи в любой точке разветвления цепи, называется первым законом Кирхгофа. Определение первого закона Кирхгофа может звучать и в другой формулировке, а именно: сумма токов втекающих в узел электрической цепи равна сумме токов вытекающих из этого узла.
Видео 2. Первый закон Кирхгофа
Обычно при расчете электрических цепей направление токов в ветвях, присоединенных к какой либо точке разветвления, неизвестны. Поэтому для возможности самой записи уравнения первого закона Кирхгофа нужно перед началом расчета цепи произвольно выбрать так называемые положительные направления токов во всех ее ветвях и обозначить их стрелками на схеме.
Пользуясь законом Ома, можно вывести формулу для подсчета общего сопротивления при параллельном соединении потребителей.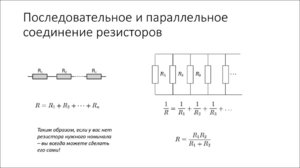
Общий ток, приходящий к точке А, равен:
Токи в каждой из ветвей имеют значения:
По формуле первого закона Кирхгофа
I = I1 + I2 + I3
или
Вынося U в правой части равенства за скобки, получим:
Сокращая обе части равенства на U, получим формулу подсчета общей проводимости:
или
g = g1 + g2 + g3.
Таким образом, при параллельном соединении увеличивается не сопротивление, а проводимость.
Пример 3. Определить общее сопротивление трех параллельно включенных сопротивлений, если r1 = 2 Ом, r2 = 3 Ом, r3 = 4 Ом.
откуда
Пример 4. Пять сопротивлений 20, 30 ,15, 40 и 60 Ом включены параллельно в сеть. Определить общее сопротивление:
откуда
Следует заметить, что при подсчете общего сопротивления разветвления оно получается всегда меньше, чем самое меньшее сопротивление, входящее в разветвление.
Если сопротивления, включенные параллельно, равны между собой, то общее сопротивление r цепи равно сопротивлению одной ветви r1, деленному на число ветвей n:
Пример 5.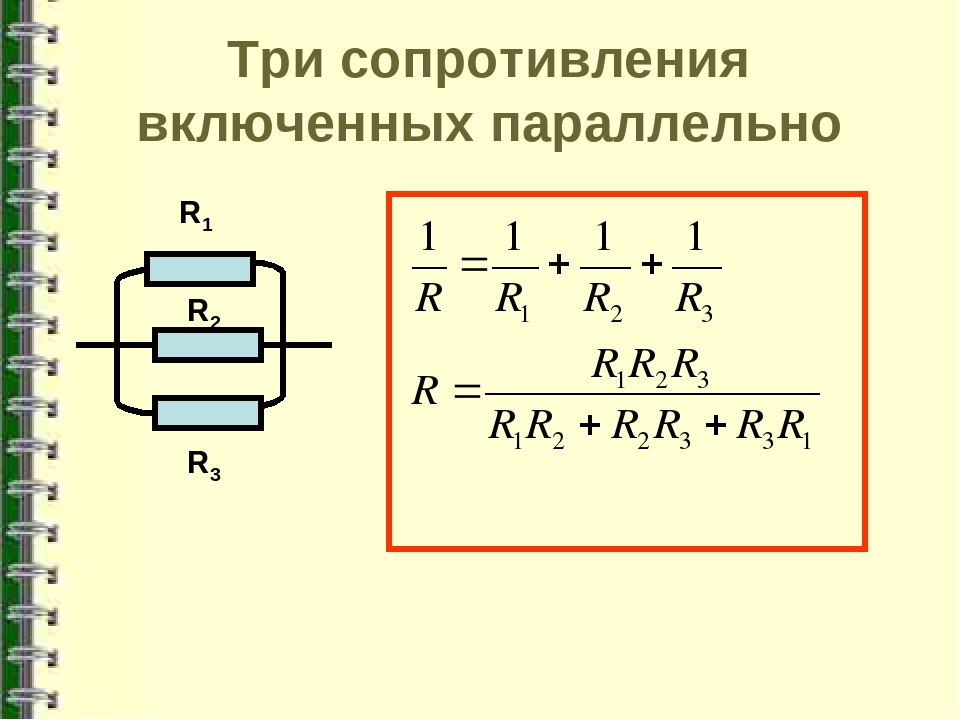 Определить общее сопротивление четырех параллельно включенных сопротивлений по 20 Ом каждое:
Определить общее сопротивление четырех параллельно включенных сопротивлений по 20 Ом каждое:
Для проверки попробуем найти сопротивление разветвления по формуле:
откуда
Как видим, ответ получается тот же.
Пример 6. Пусть требуется определить токи в каждой ветви при параллельном их соединении, изображенном на рисунке 5, а.
| Рисунок 5. К примеру 6 |
Найдем общее сопротивление цепи:
откуда
Теперь все разветвления мы можем изобразить упрощенно как одно сопротивление (рисунок 5, б).
Падение напряжения на участке между точками А и Б будет:
U = I × r = 22 × 1,09 = 24 В.
Возвращаясь снова к рисунку 5, а видим, что все три сопротивления окажутся под напряжением 24 В, так как они включены между точками А и Б.
Рассматривая первую ветвь разветвления с сопротивлением r1, мы видим, что напряжение на этом участке 24 В, сопротивление участка 2 Ом. По закону Ома для участка цепи ток на этом участке будет:
Ток второй ветви
Ток третьей ветви
Проверим по первому закону Кирхгофа
I = I1 + I2 + I3 = 12 + 6 + 4 = 22 А.
Следовательно, задача решена верно.
Обратим внимание на то, как распределяются токи в ветвях нашего параллельного соединения. Первая ветвь: r1 = 2 Ом, I1 = 12 А
Вторая ветвь: r2 = 4 Ом, I2 = 6 А. Третья ветвь: r3 = 6 Ом, I3 = 4 А
Первая ветвь: r1 = 2 Ом, I1 = 12 А. Вторая ветвь: r2 = 4 Ом, I2 = 6 А. Третья ветвь: r3 = 6 Ом, I3 = 4 А.
Как видим, сопротивление первой ветви в два раза меньше сопротивление второй ветви, а ток первой ветви в два раза больше тока второй ветви. Сопротивление третьей ветви в три раза больше сопротивления первой ветви, а ток третьей ветви в три раза меньше тока первой ветви. Отсюда можно сделать вывод, что токи в ветвях при параллельном соединении распределяются обратно пропорционально сопротивлениям этих ветвей. Таким образом, по ветви с большим сопротивлением потечет ток меньший, чем по ветви с малым сопротивлением.
Для двух параллельных ветвей можно также, конечно, пользоваться данной выше формулой.
Однако общее сопротивление проводника при параллельном соединении в этом случае легче подсчитать по формуле:
или окончательно:
Последовательное соединение ламп накаливания.
Последовательное соединение ламп накаливания в домашнем быту используется редко. В свое время я подключал две лампы последовательно у себя в подъезде, но это был единичный случай.
Тут ситуация была такая, что подъездная лампа перегорала с периодичностью в один месяц, и надо было что-то делать.
Обычно, в таких случаях лампу включают через диод, чтобы она питалась пониженным напряжением 110В и долго служила. Вариант проверенный, но при этом сама лампа мерцает, да и светит в полнакала.
Когда же стоят две последовательно, то они так же питаются пониженным напряжением 110В, не мерцают, долго служат, светят и потребляют энергии как одна. Причем их можно развести по разным углам помещения, что тоже плюс.Но повторюсь – это редкий случай.
Посмотрите на рисунок ниже. Здесь изображены две схемы последовательного соединения ламп накаливания.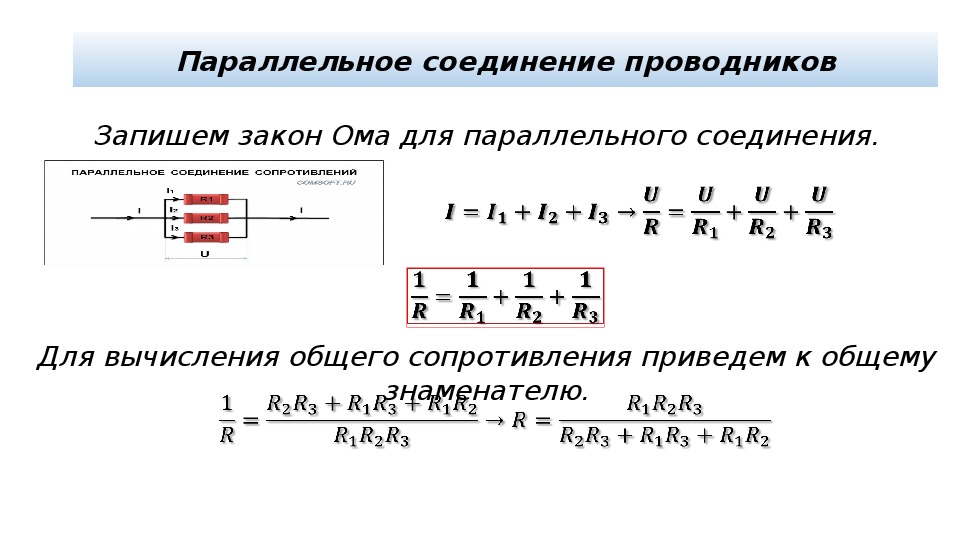 В верхней части рисунка показана принципиальная схема, а в нижней части – монтажная. Причем для лучшего восприятия, монтажная схема показана с реальным изображением ламп и двужильного провода.
В верхней части рисунка показана принципиальная схема, а в нижней части – монтажная. Причем для лучшего восприятия, монтажная схема показана с реальным изображением ламп и двужильного провода.
Здесь в линии коричневого цвета, лампы HL1 и HL2 соединены последовательно – одна за другой. Поэтому такое соединение называют последовательным.
Если подать напряжение питания 220В на концы L и N, то загорятся обе лампы, но гореть они будут не в полную силу, а в половину накала. Так как сопротивление нитей ламп рассчитано на питающее напряжение 220В, и когда они стоят в цепи последовательно, одна за другой, то за счет добавления сопротивления нити накала следующей лампы, общее сопротивление цепи будет увеличиваться, а значит, для следующей лампы напряжение всегда будет меньше согласно закону Ома.
Поэтому при последовательном соединении двух ламп напряжение 220В будет делиться пополам, и составит 110В для каждой.
На следующем рисунке показаны три лампы соединенные последовательно.
На этой схеме напряжение на каждой лампе составит около 73 Вольт, так как будет делиться уже между тремя лампами.
Так же примером последовательного соединения могут служить новогодние гирлянды. Здесь из миниатюрных лампочек с низким питанием создается одна лампа на напряжение 220В.
Например, берем лампочки, рассчитанные на 6,3 Вольта и делим их на 220 Вольт. Получается 35 штук. То есть, чтобы сделать одну лампу на напряжение 220В, нам нужно соединить последовательно 35 штук с напряжением питания 6,3 Вольта.
P.S. Так как напряжение в сети не постоянно, то расчет лучше производить исходя из 245 – 250 Вольт.
Как Вы знаете, у гирлянд есть один недостаток. Перегорает одна из ламп, например, канала зеленого цвета, значит, не горит канал зеленого цвета. Тогда мы идем на базар, покупаем лампочки зеленого цвета, а потом дома по одной вынимаем, вставляем новую, и пока не заработает канал, перебираем его весь.
Вывод:
Недостатком последовательного соединения является то, что если выйдет из строя хоть одна из ламп, гореть не будут все, так как нарушается электрическая цепь.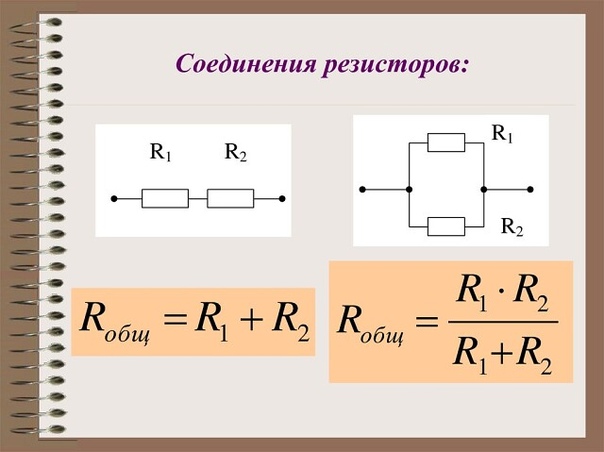
А вторым недостатком, как Вы уже догадались, является слабое свечение. Поэтому последовательное соединение ламп накаливания на напряжение 220В в домашних условиях практически не применяется.
Первый закон Кирхгофа
Как я уже упоминал, законы Кирхгофа вместе с законом Ома являются основными при анализе и расчётах электрических цепей. Закон Ома был подробно рассмотрен в двух предыдущих статьях, теперь настала очередь для законов Кирхгофа. Их всего два, первый описывает соотношения токов в электрических цепях, а второй – соотношение ЭДС и напряжениями в контуре. Начнём с первого.
Первый закон Кирхгофа гласит, что алгебраическая сумма токов в узле равна нулю. Описывается это следующим выражением
где ∑ — обозначает алгебраическую сумму.
Слово «алгебраическая» означает, что токи необходимо брать с учётом знака, то есть направления втекания. Таким образом, всем токам, которые втекают в узел, присваивается положительный знак, а которые вытекают из узла – соответственно отрицательный.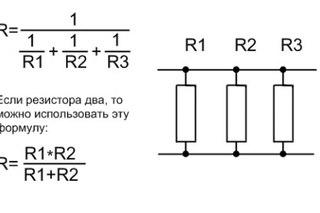 Рисунок ниже иллюстрирует первый закон Кирхгофа
Рисунок ниже иллюстрирует первый закон Кирхгофа
На рисунке изображен узел, в который со стороны сопротивления R1 втекает ток, а со стороны сопротивлений R2, R3, R4 соответственно вытекает ток, тогда уравнение токов для данного участка цепи будет иметь вид
Первый закон Кирхгофа применяется не только к узлам, но и к любому контуру или части электрической цепи. Например, когда я говорил о параллельном соединении приемников энергии, где сумма токов через R1, R2 и R3 равна втекающему току I.
Примеры использования
- Батареи гальванических элементов или аккумуляторов, в которых отдельные химические источники тока соединены последовательно (для увеличения напряжения) или параллельно (для увеличения тока).
- Регулировка мощности электрического устройства, состоящего из нескольких одинаковых потребителей электроэнергии, путём их переключения с параллельного на последовательное соединение. Таким способом регулируется мощность конфорки электрической плиты, состоящей из нескольких спиралей; мощность (скорость движения) электровоза, имеющего несколько тяговых двигателей.
- Делитель напряжения
- Балласт
- Шунт
Какой способ лучше?
Метод «шлейфов» не слишком удобен только тем, что любой потребитель по цепи зависит от предыдущего. Например, если произойдёт обрыв провода на второй розетке, то третья и четвёртая также останутся без напряжения. Но при этом нельзя не выделить экономию проводника при начальном монтаже электропроводки.
Рисунок 3: Комбинированное соединение розеток
К тому же, «шлейфом» очень удобно проводить линии, когда необходимо минимизировать количество штроб в стенах. А делают это при монтаже проводки по полу или потолку, в специальной гофрированной трубе. Тогда остаётся провести только основные штробы к розеткам и между ними.
Вывод: прокладка электропроводки «шлейфом» удобна и экономична, не занимает много времени в процессе монтажа, имеет длительный эксплуатационный срок и совсем незначительные недостатки, которые можно оставить без внимания.
Последовательное соединение ламп накаливания.

Последовательное соединение ламп накаливания в домашнем быту используется редко. В свое время я подключал две лампы последовательно у себя в подъезде, но это был единичный случай.
Тут ситуация была такая, что подъездная лампа перегорала с периодичностью в один месяц, и надо было что-то делать.
Обычно, в таких случаях лампу включают через диод, чтобы она питалась пониженным напряжением 110В и долго служила. Вариант проверенный, но при этом сама лампа мерцает, да и светит в полнакала.
Когда же стоят две последовательно, то они так же питаются пониженным напряжением 110В, не мерцают, долго служат, светят и потребляют энергии как одна. Причем их можно развести по разным углам помещения, что тоже плюс.Но повторюсь – это редкий случай.
Посмотрите на рисунок ниже. Здесь изображены две схемы последовательного соединения ламп накаливания. В верхней части рисунка показана принципиальная схема, а в нижней части – монтажная. Причем для лучшего восприятия, монтажная схема показана с реальным изображением ламп и двужильного провода.
Здесь в линии коричневого цвета, лампы HL1 и HL2 соединены последовательно – одна за другой. Поэтому такое соединение называют последовательным.
Если подать напряжение питания 220В на концы L и N, то загорятся обе лампы, но гореть они будут не в полную силу, а в половину накала. Так как сопротивление нитей ламп рассчитано на питающее напряжение 220В, и когда они стоят в цепи последовательно, одна за другой, то за счет добавления сопротивления нити накала следующей лампы, общее сопротивление цепи будет увеличиваться, а значит, для следующей лампы напряжение всегда будет меньше согласно закону Ома.
Поэтому при последовательном соединении двух ламп напряжение 220В будет делиться пополам, и составит 110В для каждой.
На следующем рисунке показаны три лампы соединенные последовательно.
На этой схеме напряжение на каждой лампе составит около 73 Вольт, так как будет делиться уже между тремя лампами.
Так же примером последовательного соединения могут служить новогодние гирлянды.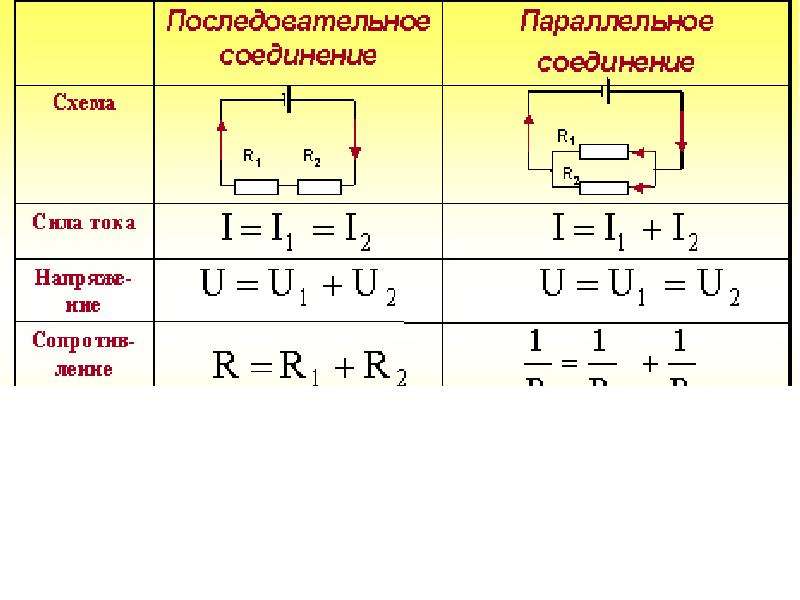 Здесь из миниатюрных лампочек с низким питанием создается одна лампа на напряжение 220В.
Здесь из миниатюрных лампочек с низким питанием создается одна лампа на напряжение 220В.
Например, берем лампочки, рассчитанные на 6,3 Вольта и делим их на 220 Вольт. Получается 35 штук. То есть, чтобы сделать одну лампу на напряжение 220В, нам нужно соединить последовательно 35 штук с напряжением питания 6,3 Вольта.
P.S. Так как напряжение в сети не постоянно, то расчет лучше производить исходя из 245 – 250 Вольт.
Как Вы знаете, у гирлянд есть один недостаток. Перегорает одна из ламп, например, канала зеленого цвета, значит, не горит канал зеленого цвета. Тогда мы идем на базар, покупаем лампочки зеленого цвета, а потом дома по одной вынимаем, вставляем новую, и пока не заработает канал, перебираем его весь.
Вывод:
Недостатком последовательного соединения является то, что если выйдет из строя хоть одна из ламп, гореть не будут все, так как нарушается электрическая цепь.
А вторым недостатком, как Вы уже догадались, является слабое свечение. Поэтому последовательное соединение ламп накаливания на напряжение 220В в домашних условиях практически не применяется.
Поэтому последовательное соединение ламп накаливания на напряжение 220В в домашних условиях практически не применяется.
Как выглядит формула Георга Ома
Примером такого типа подключения резисторов может быть соединение цепи потребителей электроэнергии в многоквартирном доме. Так, светодиоды, отопительный радиатор, микроволновка и другие приборы установлены в цепи параллельно.
Вольтметр, который подключают в цепь, будет показывать напряжение на всех резисторах. Тогда оно везде будет равным и формулу можно записать как:
U1 = U2 = U.
Схема параллельного соединения
Когда образуются ветви при подключении, то часть общего напряжения проходит через первый резистор, а часть — через второй и так далее. Поэтому при таком виде соединения резисторов Fтока в неразветвлённой точке будет равняться суммарной Fтока в отдельных резисторах и записывается как:
I = I1 + I2.
Расчет силы тока при помощи закона Ома записывается как:
I = U/R;
I1 = U1/R1;
I2 = U2/R2.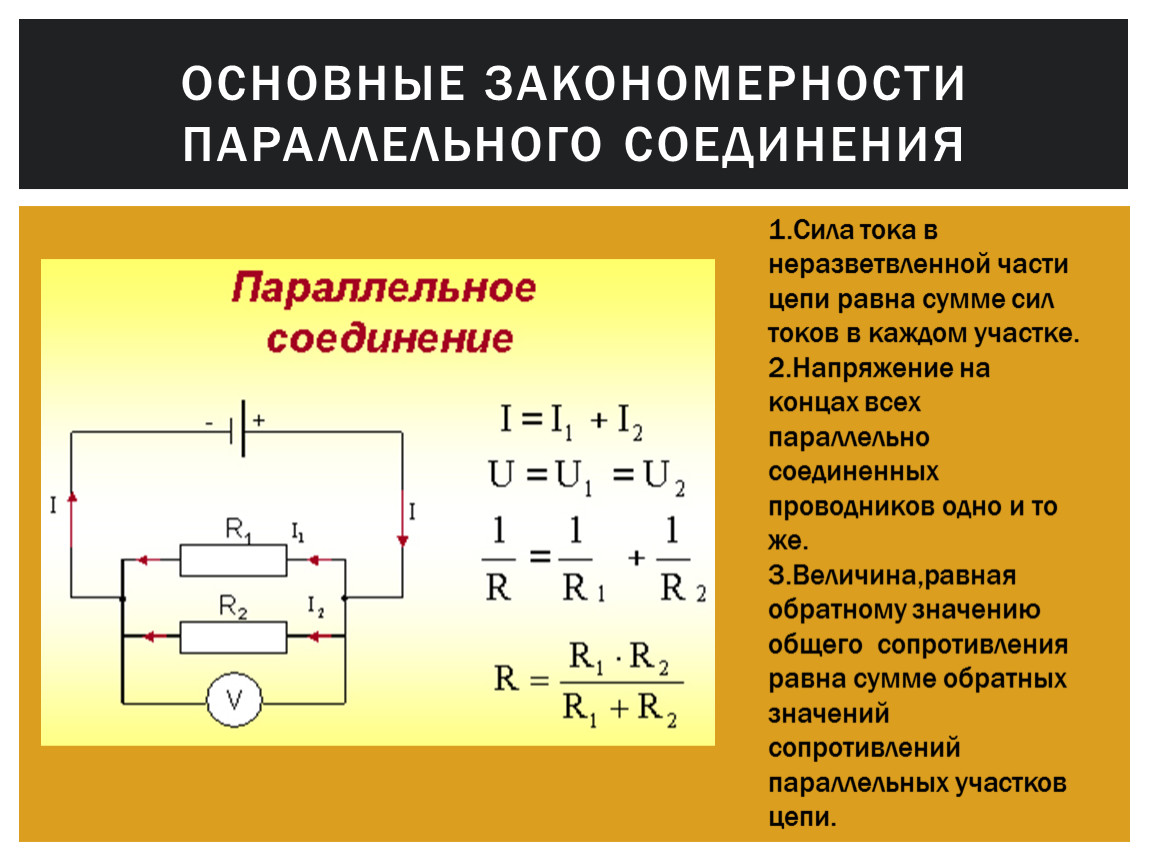
Из формулы следует:
U/R = U1/R1 + U2/R2;
U = U1 = U2;
1/R = 1/R1 + 1/R2.
Дословно правило звучит так: число, обратное общему сопротивлению при параллельном подключении, будет суммарно равно числу обратного сопротивления.
Зависимость сопротивления
Значение электропроводимости зависит от нескольких факторов, которые необходимо учитывать при расчетах, изготовлении элементов резистивной нагрузки (резисторов), ремонте и проектировании устройств. К этим факторам необходимо отнести следующие:
- Температура окружающей среды и материала.
- Электрические величины.
- Геометрические свойства вещества.
- Тип материала, из которого изготовлен проводник (полупроводник).
Электрические величины
Зависимость величины электропроводимости от параметров электричества определяется законом Ома. Существует две формулировки: одна — для участка, а другая — для полной цепи. В первом случае соотношение определяются, исходя из значений силы тока (I) и напряжения (U) простой формулой: I = U / R. Из соотношения видна прямо пропорциональная зависимость тока от величины напряжения, а также обратно пропорциональная от сопротивления. Можно выразить R: R = U / I.
Существует две формулировки: одна — для участка, а другая — для полной цепи. В первом случае соотношение определяются, исходя из значений силы тока (I) и напряжения (U) простой формулой: I = U / R. Из соотношения видна прямо пропорциональная зависимость тока от величины напряжения, а также обратно пропорциональная от сопротивления. Можно выразить R: R = U / I.
Для расчета электропроводимости всего участка следует воспользоваться соотношением между ЭДС (e), силой тока (i), а также внутренним сопротивлением источника питания (Rвн): i = e / (R+Rвн). В этом случае величина R вычисляется по формуле: R = (e / i) — Rвн. Однако при выполнении расчетов необходимо учитывать также геометрические параметры и тип проводника, поскольку они могут существенно повлиять на вычисления.
Тип и геометрические параметры
Свойство вещества к проводимости электричества определяется структурой кристаллической решетки, а также количеством свободных носителей. Исходя из этого, тип вещества является ключевым фактором, который определяет величину электропроводимости.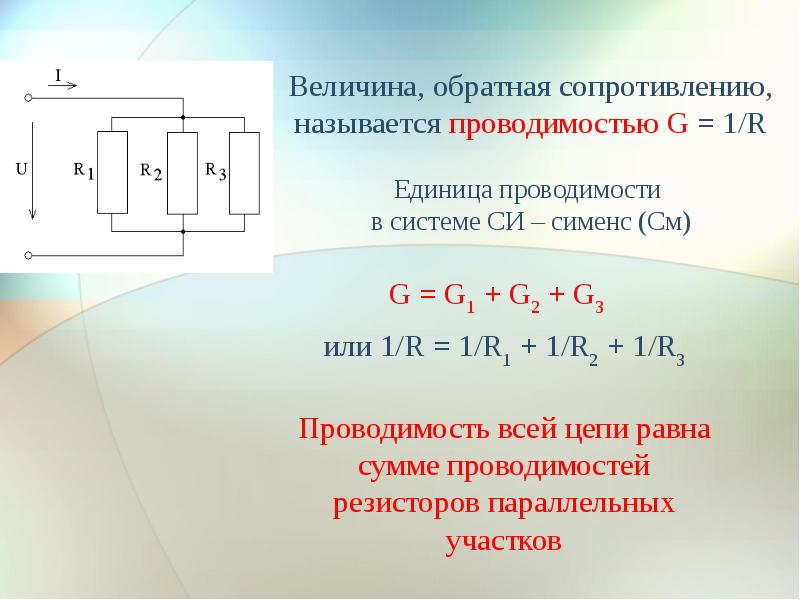 В науке коэффициент, определяющий тип вещества, обозначается литерой «р» и называется удельным сопротивлением. Его значение для различных материалов (при температуре +20 градусов по Цельсию) можно найти в специальных таблицах.
В науке коэффициент, определяющий тип вещества, обозначается литерой «р» и называется удельным сопротивлением. Его значение для различных материалов (при температуре +20 градусов по Цельсию) можно найти в специальных таблицах.
Иногда для удобства расчетов используется обратная величина, которая называется удельной проводимостью (σ). Она связана с удельным сопротивлением следующим соотношением: p = 1 / σ. Площадь поперечного сечения (S) влияет на электрическое сопротивление. С физической точки зрения, зависимость можно понять следующим образом: при малом сечении происходят более частые взаимодействия частиц электрического тока с узлами кристаллической решетки. Поперечное сечение можно вычислить по специальному алгоритму:
- Измерение геометрических параметров проводника (диаметр или длину сторон) при помощи штангенциркуля.
- Визуально определить форму материала.
- Вычислить площадь поперечного сечения по формуле, найденной в справочнике или интернете.
В случае когда проводник имеет сложную структуру, необходимо вычислить величину S одного элемента, а затем умножить результат на количество элементов, входящих в его состав. Например, если провод является многожильным, то следует вычислить S для одной жилы. После этого нужно умножить, полученную величину S, на количество жил. Зависимость R от вышеперечисленных величин можно записать в виде соотношения: R = p * L / S. Литера «L» является длиной проводника. Однако для получения точных расчетов необходимо учитывать температурные показатели внешней среды и проводника.
Температурные показатели
Существует доказательство зависимости удельного сопротивления материала от температуры, основанное на физическом эксперименте. Для проведения опыта нужно собрать электрическую цепь, состоящую из следующих элементов: источника питания, нихромовой спирали, соединительных проводов амперметра и вольтметра. Приборы нужны для измерения значений силы тока и напряжения соответственно. При протекании электричества происходит нагревание нихромовой пружины. По мере ее нагревания, показания амперметра уменьшаются. При этом происходит существенное падение напряжения на участке цепи, о котором свидетельствуют показания вольтметра.
В радиотехнике уменьшение величины напряжение называется просадкой или падением. Формула зависимости р от температуры имеет следующий вид: p = p0 * . Значение p0 — удельное сопротивление материала, взятого из таблицы, а литера «t» — температура проводника.
Температурный коэффициент «а» принимает следующие значения: для металлов — a>0, а для электролитических растворов — a<0. Для получения формулы, определяющей все зависимости, необходимо подставить все соотношения в общую формулу зависимости R от типа материала, температуры, длины и сечения: R = p0 * * L / S. Формулы используются только для расчетов и изготовления резисторов. Для быстрого измерения величины сопротивления применяется омметр.
Формула параллельного соединения резисторов
Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:
Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:
Пример №1
При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.
Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:
Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:
Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.
Пример расчета №2
Найти общее сопротивление R из трех параллельно соединенных резисторов:
Общее сопротивление R рассчитывается по формуле:
Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.
Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.
Как рассчитать сложные схемы соединения резисторов
Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).
Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:
В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:
Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.
Ток, протекающий в цепи параллельно соединенных резисторах
Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.
Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).
Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .
Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».
- Таким образом, протекающий общий ток в цепи можно определить как:
- I = I1 + I2
- Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:
- Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА
- Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА
- Таким образом, общий ток будет равен:
- I = 0,545 мА + 0,255 мА = 0,8 мА
- Это также можно проверить, используя закон Ома:
- I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)
- где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)
- И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.
Параллельное соединение резисторов — онлайн калькулятор
Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:
Подведем итог
Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.
Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.
Последовательное соединение источников питания
Теперь давайте представим вот такую ситуацию. Что будет, если в нашей обрезанной водобашне полной воды добавим еще одну такую же сверху полную воды? Схематически это будет выглядеть примерно вот так:
Как вы думаете, уменьшится давление на землю, или увеличится? Понятное дело, что увеличится! Да еще и ровно в два раза! Почему так произошло? Уровень воды стал выше, следовательно, давление на дно увеличилось.
Если “минус” одной батарейки соединить с “плюсом” другой батарейки, то их общее напряжение суммируется.
Полностью заряженная батарейка будет выглядеть как башня, полностью залитая водой с учетом того, что работает насос автоматической подачи воды. По аналогии, насос – это ЭДС.
Наполовину разряженная батарейка будет уже выглядеть примерно вот так:
Можно сказать, насос уже не справляется.
Батарейка посаженная в “ноль” будет выглядеть вот так:
Насос автоматической подачи воды сломался.
Естественно, что если вы соедините полностью заряженную и наполовину дохлую батарейку последовательно, то их общее напряжение будет выглядеть примерно вот так:
Давайте все это продемонстрируем на практике. Итак, у нас есть 2 литий-ионных аккумулятора. Я их пометил цифрами 1 и 2. С плюса каждого аккумулятора я вывел красный провод, а с минуса – черный.
Давайте замеряем напряжение аккумулятора под №1 с помощью мультиметра. Как это сделать, я еще писал в статье Как измерить ток и напряжение мультиметром.
На первом аккумуляторе у нас напряжение 3,66 Вольт. Это типичное значение литий-ионного аккумулятора.
Таким же способом замеряем напряжение на аккумуляторе №2
О, как совпало). Те же самые 3,66 Вольт.
Для того, чтобы соединить последовательно эти аккумуляторы, нам надо сделать что-то подобное:
Также как и в башнях, нам надо соединить основание одной башни с верхушкой другой башни. В источниках питания, типа аккумуляторов или батареек, нам надо соединить минус одной батарейки с плюсом другой. Так мы и сделаем. Соединяем плюс одной батарейки с минусом другой и получаем… сумму напряжений каждой батарейки! Как вы помните, на первой батарейке у нас было напряжение 3,66 В, на второй тоже 3,66 В. 3,66+3,6=7,32 В.
Мультиметр показывает 7,33 В. 0,01В спишем на погрешность измерений.
Это свойство прокатывает не только с двумя аккумуляторами, но также с их бесконечным множеством. Думаю, не стоит говорить, что если выставить в ряд штук 100 таких аккумуляторов, соединить последовательно и коснуться крайних полюсов голыми руками, то все это может завершиться даже летальным исходом.
Оцените статью:формула расчета общего сопротивления. Примеры параллельного соединения проводников
Резистор — это элемент электрической схемы, который обладает сопротивлением электрическому току. Классифицируют два типа резисторов: постоянные и переменные (подстроечные). При моделировании той или иной электрической схемы, а также при ремонте электронных изделий, возникает необходимость использовать резистор определенного номинала. Хотя и существует множество различных номиналов постоянных резисторов, в данный момент под рукой может не оказаться требуемого, либо резистора с таким номиналом не существует. Чтобы выйти из такой ситуации, можно использовать как последовательное так и параллельное соединение резисторов. О том, как правильно произвести расчет и подбор различных номиналов сопротивлений, будет рассказано в этой статье.
Последовательное соединение резисторов — это самая элементарная схема сборки радиодеталей, оно применяется для увеличения общего сопротивления цепи. При последовательном соединении, сопротивление используемых резисторов просто складывается, а вот при параллельном соединении необходимо производить расчет по нижеописанным формулам. Параллельное соединение необходимо для снижения результирующего сопротивления, а также для увеличения мощности, несколько параллельно подключенных резисторов имеют большую мощность, чем у одного.
На фотографии можно увидеть параллельное подключение резисторов.
Ниже представлена принципиальная схема параллельного соединения резисторов.
Общее номинальное сопротивление необходимо рассчитывать по следующей схеме:
R(общ)=1/(1/R1+1/R2+1/R3+1/R n).
R1, R2, R3 и Rn — параллельно подключенные резисторы.
Когда параллельное соединение резисторов состоит всего из двух элементов, в таком случае общее номинальное сопротивление можно высчитать по следующей формуле:
R(общ)=R1*R2/R1+R2.
R(общ) — общее сопротивление;
R1, R2 — параллельно подключенные резисторы.
В радиотехнике существует следующее правило: если параллельное подключение резисторов состоит из элементов одного номинала, то результирующее сопротивление можно высчитать, разделив номинал резистора на количество соединенных резисторов:
R(общ) — общее сопротивление;
R — номинал параллельно подключенного резистора;
N — количество соединенных элементов.
Важно учитывать, что при параллельном соединении результирующее сопротивление всегда будет ниже, чем сопротивление самого малого по номиналу резистора.
Приведем практический пример: возьмем три резистора, со следующими значениями номинального сопротивления: 100 Ом, 150 Ом и 30 Ом. Проведем расчет общего сопротивления, по первой формуле:
R(общ)=1/(1/100+1/150+1/30)=1/(0,01+0,007+0,03)=1/0,047=21,28Ом.
После расчета формулы мы видим, что параллельное соединение резисторов, состоящее из трех элементов, с наименьшим номиналом 30 Ом, в результате дает общее сопротивление в электрической цепи 21,28 Ом, что ниже наименьшего номинального сопротивления в цепи почти на 30 процентов.
Параллельное соединение резисторов чаще всего используют в тех случаях, когда необходимо получить сопротивление с большей мощностью. В таком случае необходимо взять резисторы одинаковой мощности и с одинаковым сопротивлением. Результирующая мощность в таком случае рассчитывается путем умножения мощности одного элемента сопротивления на общее количество параллельно подключенных резисторов в цепи.
Например: пять резисторов с номиналом в 100 Ом и с мощностью 1 Вт в каждом, подключенные параллельно, имеют общее сопротивление 20 Ом и мощность 5 Вт.
При последовательном подключении тех же резисторов (мощность так же складывается), получим результирующую мощность 5 Вт, общее сопротивление составит 500 Ом.
Проверим справедливость показанных здесь формул на простом эксперименте.
Возьмём два резистора МЛТ-2 на 3 и 47 Ом и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.
Замер общего сопротивления при последовательном соединении
Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.
Измерение сопротивления при параллельном соединении
Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:
При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.
Что ещё нужно учитывать при соединении резисторов?
Во-первых, обязательно учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом и мощностью 1 Вт . Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?
Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим
Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.
Подробнее о мощности рассеивания резистора читайте .
Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.
На практике нередко встречается задача нахождения сопротивления проводников и резисторов при различных способах соединения. В статье рассмотрено, как рассчитывается сопротивление при параллельном соединении проводников и некоторые другие технические вопросы.
Сопротивление проводника
Все проводники имеют свойство препятствовать течению электрического тока, его принято называть электрическим сопротивлением R, оно измеряется в омах. Это основное свойство проводниковых материалов.
Для ведения электротехнических расчётов применяется удельное сопротивление — ρ Ом·м/мм 2 . Все металлы — хорошие проводники, наибольшее применение получили медь и алюминий, гораздо реже применяется железо. Лучший проводник — серебро, оно применяется в электротехнической и электронной промышленности. Широко распространены сплавы с высоким
При расчёте сопротивления используется известная из школьного курса физики формула:
R = ρ · l/S, S — площадь сечения; l — длина.
Если взять два проводника, то их сопротивление при параллельном соединении станет меньше из-за увеличения общего сечения.
и нагрев проводника
Для практических расчётов режимов работы проводников применяется понятие плотности тока — δ А/мм 2 , она вычисляется по формуле:
δ = I/S, I — ток, S — сечение.
Ток, проходя по проводнику, нагревает его. Чем больше δ, тем сильнее нагревается проводник. Для проводов и кабелей разработаны нормы допустимой плотности, которые приводятся в Для проводников нагревательных устройств существуют свои нормы плотности тока.
Если плотность δ выше допустимой, может произойти разрушение проводника, например, при перегреве кабеля у него разрушается изоляция.
Правилами регламентируется производить расчёт проводников на нагрев.
Способы соединения проводников
Любой проводник гораздо удобнее изображать на схемах как электрическое сопротивление R, тогда их легко читать и анализировать. Существует всего три способа соединения сопротивлений. Первый способ самый простой — последовательное соединение.
На фото видно, что полное сопротивление равно: R = R 1 + R 2 + R 3 .
Второй способ более сложный — параллельное соединение. Расчёт сопротивления при параллельном соединении выполняется поэтапно. Рассчитывается полная проводимость G = 1/R, а затем полное сопротивление R = 1/G.
Можно поступить и по-другому, прежде рассчитать общее сопротивление при R1 и R2, после этого повторить операцию и найти R.
Третий способ соединения наиболее сложный — смешанное соединение, то есть присутствуют все рассмотренные варианты. Схема приведена на фото.
Для расчёта этой схемы её следует упростить, для этого заменяют резисторы R2 и R3 одним R2,3. Получается несложная схема.
R2,3,4 = R2,3 · R4/(R2,3 + R4).
Схема становится ещё проще, в ней остаются резисторы, имеющие последовательное соединение. В более сложных ситуациях используется этот же метод преобразования.
Виды проводников
В электронной технике, при производстве проводники представляют собою тонкие полоски медной фольги. Ввиду малой длины сопротивление у них незначительно, им во многих случаях можно пренебречь. Для этих проводников сопротивление при параллельном соединении уменьшается вследствие увеличения сечения.
Большой раздел проводников представляют обмоточные провода. Они выпускаются разных диаметров — от 0,02 до 5,6 миллиметра. Для мощных трансформаторов и электродвигателей выпускаются медные шинки прямоугольного сечения. Иногда при ремонте заменяют провод большого диаметра на несколько параллельно соединённых меньшего размера.
Особый раздел проводников представляют провода и кабели, промышленность предоставляет широчайший выбор марок для самых различных нужд. Нередко приходится заменять один кабель на несколько, меньшего сечения. Причины этого бывают самые различные, например, кабель сечением 240 мм 2 очень трудно прокладывать по трассе с крутыми изгибами. Его заменяют на 2×120 мм 2 , и проблема решена.
Расчёт проводов на нагрев
Проводник нагревается протекающим током, если его температура превысит допустимую, наступает разрушение изоляции. ПУЭ предусматривает расчёт проводников на нагрев, исходными данными для него являются сила тока и условия внешней среды, в которой проложен проводник. По этим данным из таблиц в ПУЭ выбирается рекомендуемое проводника сечение (провода или кабеля).
На практике встречаются ситуации, когда нагрузка на действующий кабель сильно возросла. Существует два выхода ‒ заменить кабель на другой, это бывает дорого, или параллельно ему проложить ещё один, чтобы разгрузить основной кабель. В этом случае сопротивление проводника при параллельном соединении уменьшается, следовательно падает выделение тепла.
Чтобы правильно выбрать сечение второго кабеля, пользуются таблицами ПУЭ, важно при этом не ошибиться с определением его рабочего тока. В этой ситуации охлаждение кабелей будет даже лучше, чем у одного. Рекомендуется рассчитать сопротивление при двух кабелей, чтобы точнее определить их тепловыделение.
Расчёт проводников на потерю напряжения
При расположении потребителя R н на большом расстоянии L от источника энергии U 1 возникает довольно большое падение напряжения на проводах линии. К потребителю R н поступает напряжение U 2 значительно ниже начального U 1 . Практически в качестве нагрузки выступает различное электрооборудование, подключаемое к линии параллельно.
Для решения проблемы производят расчет сопротивления при параллельном соединении всего оборудования, так находится сопротивление нагрузки R н. Далее следует определить сопротивление проводов линии.
R л = ρ · 2L/S,
Здесь S — сечение провода линии, мм 2 .
Параллельное соединение резисторов. При параллельном соединении резисторов нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви (рис. 26, а). Заменяя
лампы резисторами с сопротивлениями R1, R2, R3, получим схему, показанную на рис. 26, б.
При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Поэтому согласно закону Ома:
I 1 =U/R 1 ; I 2 =U/R 2 ; I 3 =U/R 3 .
Ток в неразветвленной части цепи согласно первому закону Кирхгофа I = I 1 +I 2 +I 3 , или
I = U / R 1 + U / R 2 + U / R 3 = U (1/R 1 + 1/R 2 + 1/R 3) = U / R эк (23)
Следовательно, эквивалентное сопротивление рассматриваемой цепи при параллельном соединении трех резисторов определяется формулой
1/R эк = 1/R 1 + 1/R 2 + 1/R 3 (24)
Вводя в формулу (24) вместо значений 1/R эк, 1/R 1 , 1/R 2 и 1/R 3 соответствующие проводимости G эк, G 1 , G 2 и G 3 , получим: эквивалентная проводимость параллельной цепи равна сумме проводимостей параллельно соединенных резисторов :
G эк = G 1 + G 2 +G 3 (25)
Таким образом, при увеличении числа параллельно включаемых резисторов результирующая проводимость электрической цепи увеличивается, а результирующее сопротивление уменьшается.
Из приведенных формул следует, что токи распределяются между параллельными ветвями обратно пропорционально их электрическим сопротивлениям или прямо пропорционально их проводимостям. Например, при трех ветвях
I 1: I 2: I 3 = 1/R 1: 1/R 2: 1/R 3 = G 1 + G 2 + G 3 (26)
В этом отношении имеет место полная аналогия между распределением токов по отдельным ветвям и распределением потоков воды по трубам.
Приведенные формулы дают возможность определить эквивалентное сопротивление цепи для различных конкретных случаев. Например, при двух параллельно включенных резисторах результирующее сопротивление цепи
R эк =R 1 R 2 /(R 1 +R 2)
при трех параллельно включенных резисторах
R эк =R 1 R 2 R 3 /(R 1 R 2 +R 2 R 3 +R 1 R 3)
При параллельном соединении нескольких, например n, резисторов с одинаковым сопротивлением R1 результирующее сопротивление цепи Rэк будет в n раз меньше сопротивления R1, т.е.
R эк = R1 / n (27)
Проходящий по каждой ветви ток I1, в этом случае будет в п раз меньше общего тока:
I1 = I / n
При параллельном соединении приемников, все они находятся под одним и тем же напряжением, и режим работы каждого из них не зависит от остальных. Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются включенными. Поэтому параллельное соединение имеет существенные преимущества перед последовательным, вследствие чего оно получило наиболее широкое распространение. В частности, электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, всегда включают параллельно.
На электровозах постоянного тока и некоторых тепловозах тяговые двигатели в процессе регулирования скорости движения нужно включать под различные напряжения, поэтому они в процессе разгона переключаются с последовательного соединения на параллельное.
Возьмем три постоянных сопротивления R1, R2 и R3 и включим их в цепь так, чтобы конец первого сопротивления R1 был соединен с началом второго сопротивления R 2, конец второго — с началом третьего R 3, а к началу первого сопротивления и к концу третьего подведем проводники от источника тока (рис. 1 ).
Такое соединение сопротивлений называется последовательным. Очевидно, что ток в такой цепи будет во всех ее точках один и тот же.
Рис 1
Как определить общее сопротивление цепи, если все включенные в нее последовательно сопротивления мы уже знаем? Используя положение, что напряжение U на зажимах источника тока равно сумме падений напряжений на участках цепи, мы можем написать:
U = U1 + U2 + U3
где
U1 = IR1 U2 = IR2 и U3 = IR3
или
IR = IR1 + IR2 + IR3
Вынеся в правой части равенства I за скобки, получим IR = I(R1 + R2 + R3) .
Поделив теперь обе части равенства на I , будем окончательно иметь R = R1 + R2 + R3
Таким образом, мы пришли к выводу, что при последовательном соединении сопротивлений общее сопротивление всей цепи равно сумме сопротивлений отдельных участков.
Проверим этот вывод на следующем примере. Возьмем три постоянных сопротивления, величины которых известны (например, R1 == 10 Ом, R 2 = 20 Ом и R 3 = 50 Ом). Соединим их последовательно (рис. 2 ) и подключим к источнику тока, ЭДС которого равна 60 В ( пренебрегаем).
Рис. 2. Пример последовательного соединения трех сопротивлений
Подсчитаем, какие показания должны дать приборы, включенные, как показано на схеме, если замкнуть цепь. Определим внешнее сопротивление цепи: R = 10 + 20 + 50 = 80 Ом.
Найдем ток в цепи : 60 / 80 = 0 ,75 А
Зная ток в цепи и сопротивления ее участков, определим падение напряжения на каждое участке цепи U 1 = 0,75х 10 = 7,5 В, U 2 = 0,75 х 20=15 В, U3 = 0,75 х 50 = 37,5 В.
Зная падение напряжений на участках, определим общее падение напряжения во внешней цепи, т. е. напряжение на зажимах источника тока U = 7,5+15 + 37,5 = 60 В.
Мы получили таким образом, что U = 60 В, т. е. несуществующее равенство ЭДС источника тока и его напряжения. Объясняется это тем, что мы пренебрегли внутренним сопротивлением источника тока.
Замкнув теперь ключ выключатель К, можно убедиться по приборам, что наши подсчеты примерно верны.
Возьмем два постоянных сопротивления R1 и R2 и соединим их так, чтобы начала этих сопротивлений были включены в одну общую точку а, а концы — в другую общую точку б. Соединив затем точки а и б с источником тока, получим замкнутую электрическую цепь. Такое соединение сопротивлений называется параллельным соединением.
Рис 3. Параллельное соединение сопротивлений
Проследим течение тока в этой цепи. От положительного полюса источника тока по соединительному проводнику ток дойдет до точки а. В точке а он разветвится, так как здесь сама цепь разветвляется на две отдельные ветви: первую ветвь с сопротивлением R1 и вторую — с сопротивлением R2. Обозначим токи в этих ветвях соответственно через I1 и I 2. Каждый из этих токов пойдет по своей ветви до точки б. В этой точке произойдет слияние токов в один общий ток, который и придет к отрицательному полюсу источника тока.
Таким образом, при параллельном соединении сопротивлений получается разветвленная цепь. Посмотрим, какое же будет соотношение между токами в составленной нами цепи.
Включим амперметр между положительным полюсом источника тока (+) и точкой а и заметим его показания. Включив затем амперметр (показанный «а рисунке пунктиром) в провод, соединяющий точку б с отрицательным полюсом источника тока (-), заметим, что прибор покажет ту же величину силы тока.
Значит, до ее разветвления (до точки а) равна силе тока после разветвления цепи (после точки б).
Будем теперь включать амперметр поочередно в каждую ветвь цепи, запоминая показания прибора. Пусть в первой ветви амперметр покажет силу тока I1 , а во второй — I 2. Сложив эти два показания амперметра, мы получим суммарный ток, по величине равный току I до разветвления (до точки а).
Следовательно, сила тока, протекающего до точки разветвления, равна сумме сил токов, утекающих от этой точки. I = I1 + I2 Выражая это формулой, получим
Это соотношение, имеющее большое практическое значение, носит название закона разветвленной цепи .
Рассмотрим теперь, каково будет соотношение между токами в ветвях.
Включим между точками а и б вольтметр и посмотрим, что он нам покажет. Во-первых, вольтметр покажет напряжение источника тока, так как он подключен, как это видно из рис. 3 , непосредственно к зажимам источника тока. Во-вторых, вольтметр покажет падения напряжений U1 и U2 на сопротивлениях R1 и R2, так как он соединен с началом и концом каждого сопротивления.
Следовательно, при параллельном соединении сопротивлений напряжение на зажимах источника тока равно падению напряжения на каждом сопротивлении.
Это дает нам право написать, что U = U1 = U2 ,
где U — напряжение на зажимах источника тока; U1 — падение напряжения на сопротивлении R1 , U2 — падение напряжения на сопротивлении R2. Вспомним, что падение напряжения на участке цепи численно равно произведению силы тока, протекающего через этот участок, на сопротивление участка U = IR .
Поэтому для каждой ветви можно написать: U1 = I1R1 и U2 = I2R2 , но так как U1 = U2, то и I1R1 = I2R2 .
Применяя к этому выражению правило пропорции, получим I1/ I2 = U2 / U1
т. е. ток в первой ветви будет во столько раз больше (или меньше) тока во второй ветви, во сколько раз сопротивление первой ветви меньше (или больше) сопротивления второй ветви.
Итак, мы пришли к важному выводу, заключающемуся в том, что при параллельном соединении сопротивлений общий ток цепи разветвляется на токи, обратно пропорциональные величинам сопротивлении параллельных ветвей.
Иначе говоря, чем больше сопротивление ветви, тем меньший ток потечет через нее, и, наоборот, чем меньше сопротивление ветви, тем больший ток потечет через эту ветвь.
Убедимся в правильности этой зависимости на следующем примере. Соберем схему, состоящую из двух параллельно соединенных сопротивлений R1 и R 2, подключенных к источнику тока. Пусть R1 = 10 Ом, R2 = 20 Ом и U = 3 В.
Подсчитаем сначала, что покажет нам амперметр, включенный в каждую ветвь:
I1 = U / R1 = 3 / 10 = 0 ,3 А = 300 мА
I 2 = U / R 2 = 3 / 20 = 0,15 А = 150 мА
Общий ток в цепи I = I1 +I2 = 300 + 150 = 450 мА
Проделанный нами расчет подтверждает, что при параллельном соединении сопротивлений ток в цепи разветвляется обратно пропорционально сопротивлениям.
Действительно, R1 == 10 Ом вдвое меньше R 2 = 20 Ом, при этом I1 = 300 мА вдвое больше I2 = 150 мА. Общий ток в цепи I = 450 мА разветвился на две части так, что большая его часть (I1 = 300 мА) пошла через меньшее сопротивление (R1 = 10 Ом), а меньшая часть (R2 = 150 мА) -через большее сопротивление (R 2 = 20 Ом).
Такое разветвление тока в параллельных ветвях сходно с течением жидкости по трубам. Представьте себе трубу А, которая в каком-то месте разветвляется на две трубы Б и В различного диаметра (рис. 4). Так как диаметр трубы Б больше диаметра трубок В, то через трубу Б в одно и то же время пройдет больше воды, чем через трубу В, которая оказывает потоку воды большее сопротивление.
Рис. 4
Рассмотрим теперь, чему будет равно общее сопротивление внешней цепи, состоящей из двух параллельно соединенных сопротивлений.
Под этим общим сопротивлением внешней цепи надо понимать такое сопротивление, которым можно было бы заменить при данном напряжении цепи оба параллельно включенных сопротивления, не изменяя при этом тока до разветвления. Такое сопротивление называется эквивалентным сопротивлением.
Вернемся к цепи, показанной на рис. 3, и посмотрим, чему будет равно эквивалентное сопротивление двух параллельно соединенных сопротивлений. Применяя к этой цепи закон Ома, мы можем написать: I = U/R , где I — ток во внешней цепи (до точки разветвления), U — напряжение внешней цепи, R — сопротивление внешней цепи, т. е. эквивалентное сопротивление.
Точно так же для каждой ветви I1 = U1 / R1
, I2 = U2 / R2
, где I1
и I
2 — токи в ветвях; U1
и U2 — напряжение на ветвях; R1
и R2
— сопротивления ветвей.
По закону разветвленной цепи: I = I1 + I2
Подставляя значения токов, получим U / R = U1 / R1 + U2 / R2
Так как при параллельном соединении U = U1 = U2 , то можем написать U / R = U / R1 + U / R2
Вынеся U в правой части равенства за скобки, получим U / R = U (1 / R1 + 1 / R2 )
Разделив теперь обе части равенства на U , будем окончательно иметь 1 / R = 1 / R1 + 1 / R2
Помня, что проводимостью называется величина, обратная сопротивлению , мы можем сказать, что в полученной формуле 1 / R — проводимость внешней цепи; 1 / R1 проводимость первой ветви; 1 / R2- проводимость второй ветви.
На основании этой формулы делаем вывод: при параллельном соединении проводимость внешней цепи равна сумме проводимостей отдельных ветвей.
Следовательно, чтобы определить эквивалентное сопротивление включенных параллельно сопротивлений, надо определить проводимость цепи и взять величину, ей обратную.
Из формулы также следует, что проводимость цепи больше проводимости каждой ветви, а это значит, что эквивалентное сопротивление внешней цепи меньше наименьшего из включенных параллельно сопротивлений.
Рассматривая случай параллельного соединения сопротивлений, мы взяли наиболее простую цепь, состоящую из двух ветвей. Однако на практике могут встретиться случаи, когда цепь состоит из трех и более параллельных ветвей. Как же поступать в этих случаях?
Оказывается, все полученные нами соотношения остаются справедливыми и для цепи, состоящей из любого числа параллельно соединенных сопротивлений.
Чтобы убедиться в этом, рассмотрим следующий пример.
Возьмем три сопротивления R1 = 10 Ом, R2
= 20 Ом и R3
= 60 Ом и соединим их параллельно. Определим эквивалентное сопротивление цепи (рис. 5
).
Рис. 5. Цепь с тремя параллельно соединенными сопротивлениями
Применяя для этой цепи формулу 1 / R = 1 / R1 + 1 / R2 , можем написать 1 / R = 1 / R1 + 1 / R2 + 1 / R3 и, подставляя известные величины, получим 1 / R = 1 / 10 + 1 / 20 + 1 / 60
Сложим эта дроби: 1/R = 10 / 60 = 1 / 6, т. е.. проводимость цепи 1 / R = 1 / 6 Следовательно, эквивалентное сопротивление R = 6 Ом.
Таким образом, эквивалентное сопротивление меньше наименьшего из включенных параллельно в цепь сопротивлений , т. е. меньше сопротивления R1.
Посмотрим теперь, действительно ли это сопротивление является эквивалентным, т. е. таким, которое могло бы заменить включенные параллельно сопротивления в 10, 20 и 60 Ом, не изменяя при этом силы тока до разветвления цепи.
Допустим, что напряжение внешней цепи, а следовательно, и напряжение на сопротивлениях R1, R2, R3 равно 12 В. Тогда сила токов в ветвях будет: I1 = U/R1 = 12 / 10 = 1 ,2 А I 2 = U/R 2 = 12 / 20 = 1 ,6 А I 3 = U/R1 = 12 / 60 = 0,2 А
Общий ток в цепи получим, пользуясь формулой I = I1 + I2 + I3 =1,2 + 0,6 + 0,2 = 2 А.
Проверим по формуле закона Ома, получится ли в цепи ток силой 2 А, если вместо трех параллельно включенных известных нам сопротивлений включено одно эквивалентное им сопротивление 6 Ом.
I = U / R = 12 / 6 = 2 А
Как видим, найденное нами сопротивление R = 6 Ом действительно является для данной цепи эквивалентным.
В этом можно убедиться и на измерительных приборах, если собрать схему с взятыми нами сопротивлениями, измерить ток во внешней цепи (до разветвления), затем заменить параллельно включенные сопротивления одним сопротивлением 6 Ом и снова измерить ток. Показания амперметра и в том и в другом случае будут примерно одинаковыми.
На практике могут встретиться также параллельные соединения, для которых рассчитать эквивалентное сопротивление можно проще, т. е. не определяя предварительно проводимостей, сразу найти сопротивление.
Например, если соединены параллельно два сопротивления R1 и R2 , то формулу 1 / R = 1 / R1 + 1 / R2 можно преобразовать так: 1/R = (R2 + R1) / R1 R2 и, решая равенство относительно R, получить R = R1 х R2 / (R1 + R2 ), т. е. при параллельном соединении двух сопротивлений эквивалентное сопротивление цепи равно произведению включенных параллельно сопротивлений, деленному на их сумму.
Формула расчёта общего сопротивления при параллельном соединении
Из закона Ома и первого и второго правил Кирхгофа следует:
При параллельном соединении величина обратная полному сопротивлению, равна сумме величин, обратных сопротивлений ветвей.
При параллельном соединении полное сопротивление цепи меньше самого малого из сопротивлений ветвей.
Поскольку 1/R = G, т.е. проводимость, то
при параллельном соединении электрические проводимости отдельных ветвей складываются
Параллельное соединение двух сопротивлений
При параллельном соединении двух сопротивлений формула (1) упрощается
Параллельное соединение двух сопротивлений
При параллельном соединении двух сопротивлений формула (1) упрощается
Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы.
Схема параллельного соединения резисторов показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:
Формула параллельного соединения резисторов
Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:
Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:
Параллельное соединение резисторов — расчет
Пример №1
При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.
Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:
Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:
Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.
Пример расчета №2
Найти общее сопротивление R из трех параллельно соединенных резисторов:
Общее сопротивление R рассчитывается по формуле:
Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.
Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.
Как рассчитать сложные схемы соединения резисторов
Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:
Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).
Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:
В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:
Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.
Ток, протекающий в цепи параллельно соединенных резисторах
Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.
Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).
Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .
Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».
Таким образом, протекающий общий ток в цепи можно определить как:
Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:
Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА
Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА
Таким образом, общий ток будет равен:
I = 0,545 мА + 0,255 мА = 0,8 мА
Это также можно проверить, используя закон Ома:
I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)
где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)
И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.
Параллельное соединение резисторов — онлайн калькулятор
Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:
Подведем итог
Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.
Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.
Как правильно соединять резисторы?
О том, как соединять конденсаторы и рассчитывать их общую ёмкость уже рассказывалось на страницах сайта. А как соединять резисторы и посчитать их общее сопротивление? Именно об этом и будет рассказано в этой статье.
Резисторы есть в любой электронной схеме, причём их номинальное сопротивление может отличаться не в 2 – 3 раза, а в десятки и сотни раз. Так в схеме можно найти резистор на 1 Ом, и тут же неподалёку на 1000 Ом (1 кОм)!
Поэтому при сборке схемы либо ремонте электронного прибора может потребоваться резистор с определённым номинальным сопротивлением, а под рукой такого нет. В результате быстро найти подходящий резистор с нужным номиналом не всегда удаётся. Это обстоятельство тормозит процесс сборки схемы или ремонта. Выходом из такой ситуации может быть применение составного резистора.
Для того чтобы собрать составной резистор нужно соединить несколько резисторов параллельно или последовательно и тем самым получить нужное нам номинальное сопротивление. На практике это пригождается постоянно. Знания о правильном соединении резисторов и расчёте их общего сопротивления выручают и ремонтников, восстанавливающих неисправную электронику, и радиолюбителей, занятых сборкой своего электронного устройства.
Последовательное соединение резисторов.
В жизни последовательное соединение резисторов имеет вид:
Последовательно соединённые резисторы серии МЛТ
Принципиальная схема последовательного соединения выглядит так:
На схеме видно, что мы заменяем один резистор на несколько, общее сопротивление которых равно тому, который нам необходим.
Подсчитать общее сопротивление при последовательном соединении очень просто. Нужно сложить все номинальные сопротивления резисторов входящих в эту цепь. Взгляните на формулу.
Общее номинальное сопротивление составного резистора обозначено как Rобщ.
Номинальные сопротивления резисторов включённых в цепь обозначаются как R1, R2, R3,…RN.
Применяя последовательное соединение, стоит помнить одно простое правило:
Из всех резисторов, соединённых последовательно главную роль играет тот, у которого самое большое сопротивление. Именно он в значительной степени влияет на общее сопротивление.
Так, например, если мы соединяем три резистора, номинал которых равен 1, 10 и 100 Ом, то в результате мы получим составной на 111 Ом. Если убрать резистор на 100 Ом, то общее сопротивление цепочки резко уменьшиться до 11 Ом! А если убрать, к примеру, резистор на 10 Ом, то сопротивление будет уже 101 Ом. Как видим, резисторы с малыми сопротивлениями в последовательной цепи практически не влияют на общее сопротивление.
Параллельное соединение резисторов.
Можно соединять резисторы и параллельно:
Два резистора МЛТ-2, соединённых параллельно
Принципиальная схема параллельного соединения выглядит следующим образом:
Для того чтобы подсчитать общее сопротивление нескольких параллельно соединённых резисторов понадобиться знание формулы. Выглядит она вот так:
Эту формулу можно существенно упростить, если применять только два резистора. В таком случае формула примет вид:
Есть несколько простых правил, позволяющих без предварительного расчёта узнать, каково должно быть сопротивление двух резисторов, чтобы при их параллельном соединении получить то, которое требуется.
Если параллельно соединены два резистора с одинаковым сопротивлением, то общее сопротивление этих резисторов будет ровно в два раза меньше, чем сопротивление каждого из резисторов, входящих в эту цепочку.
Это правило исходит из простой формулы для расчёта общего сопротивления параллельной цепи, состоящей из резисторов одного номинала. Она очень проста. Нужно разделить номинальное сопротивление одного из резисторов на общее их количество:
Здесь R1 – номинальное сопротивление резистора. N – количество резисторов с одинаковым номинальным сопротивлением.
Ознакомившись с приведёнными формулами, вы скажите, что все они справедливы для расчёта ёмкости параллельно и последовательно соединённых конденсаторов. Да, только в отношении конденсаторов всё действует с точностью до «наоборот”. Узнать подробнее о соединении конденсаторов можно здесь.
Проверим справедливость показанных здесь формул на простом эксперименте.
Возьмём два резистора МЛТ-2 на 3 и 47 Ом и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.
Замер общего сопротивления при последовательном соединении
Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.
Измерение сопротивления при параллельном соединении
Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:
При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.
Что ещё нужно учитывать при соединении резисторов?
Во-первых, обязательно учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом и мощностью 1 Вт. Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?
Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А), а сопротивление каждого из них равно 50 Ом, тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт. В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт.
Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.
Подробнее о мощности рассеивания резистора читайте тут.
Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.
Калькулятор соединения резисторов онлайн. Параллельное соединение резисторов
В каждой электрической схеме присутствует резистор, имеющий сопротивление электрическому току. Резисторы бывают двух типов: постоянные и переменные. Во время разработки любой электрической схемы и ремонта электронных изделий часто приходится применять резистор, обладающий необходимым номиналом.
Несмотря на то что для резисторов предусмотрены различные номиналы , может случиться так, что не будет возможности найти необходимый или же вообще ни один элемент не сможет обеспечить требуемый показатель.
Решением этой проблемы может стать применение последовательного и параллельного соединения. Ознакомившись с этой статьей, вы узнаете об особенностях выполнения расчета и подбора различных номиналов сопротивлений.
Параллельное соединение: общая информация
Часто при изготовлении какого-либо устройства используют резисторы, которые соединяются в соответствии с последовательной схемой. Эффект от применения такого варианта сборки сводится к увеличению общего сопротивления цепи. Для данного варианта соединения элементов создаваемое ими сопротивление рассчитывается как сумма номиналов. Если же сборка деталей выполняется по параллельной схеме, то здесь потребуется рассчитать сопротивление , используя нижеописанные формулы.
К схеме параллельного соединения прибегают в ситуации, когда стоит задача по снижению суммарного сопротивления, а, помимо этого, увеличения мощности для группы элементов, подключенных по параллельной схеме, которое должно быть больше, чем при их отдельном подключении.
Расчет сопротивления
В случае подключения деталей друг с другом, с применением параллельной схемы для расчета суммарного сопротивления, будет использоваться следующая формула:
R(общ)=1/(1/R1+1/R2+1/R3+1/Rn).
- R1- R3 и Rn – резисторы, подсоединенные по параллельной схеме.
Причем, если цепь создается на основе только двух элементов, то для определения суммарного номинального сопротивления следует использовать такую формулу:
R(общ)=R1*R2/R1+R2.
- R(общ) – суммарное сопротивление;
- R1 и R2 – резисторы, подсоединенные по параллельной схеме.
Видео: Пример расчёта сопротивления
Универсальная схема расчетаПрименительно к радиотехнике следует уделить внимание одному важному правилу: если подключаемые друг к другу элементы по параллельной схеме имеют одинаковый показатель , то для расчета суммарного номинала необходимо общее значение разделить на число подключенных узлов:
- R(общ) – суммарное значение сопротивления;
- R – номинал резистора, подсоединенного по параллельной схеме;
- n – число подключенных узлов.
Особое внимание следует обратить на то, что конечный показатель сопротивления в случае использования параллельной схемы подключения обязательно будет меньше по сравнению с номиналом любого элемента, подключаемого в цепь.
Пример расчёта
Для большей наглядности можно рассмотреть следующий пример: допустим, у нас есть три резистора, чьи номиналы соответственно равны 100, 150 и 30 Ом. Если воспользоваться первой формулой для определения общего номинала, то получим следующее:
R(общ)=1/(1/100+1/150+1/30)=
1/(0,01+0,007+0,03)=1/0,047=21,28Ом.
Если выполнить несложные расчеты, то можно получить следующее: для цепи, включающей в себя три детали, где наименьший показатель сопротивления составляет 30 Ом, результирующее значение номинала будет равно 21,28 Ом. Этот показатель будет меньше минимального значения номинала в цепи практически на 30%.
Важные нюансы
Обычно для резисторов параллельное соединение применяется тогда, когда стоит задача по созданию сопротивления большей мощности. Для ее решения потребуются резисторы, которые должны иметь равные показатели сопротивления и мощности. При таком варианте определить общую мощность можно следующим образом : мощность одного элемента необходимо перемножить с суммарным числом всех резисторов, из которых состоит цепь, подсоединенных друг с другом в соответствии с параллельной схемой.
Скажем, если нами будут использоваться пять резисторов, чей номинал составляет 100 Ом, а мощность каждого равна 1 Вт, которые присоединены друг к другу в соответствии с параллельной схемой, то суммарный показатель сопротивления будет равен 20 Ом, а мощность составит 5 Вт.
Если взять те же резисторы, но подсоединить их в соответствии с последовательной схемой, то конечная мощность составит 5 Вт, а суммарный номинал будет равен 500 Ом.
Видео: Правильное подключение светодиодов
Параллельная схема подключения резисторов очень востребована по той причине, что часто возникает задача по созданию такого номинала, которого невозможно добиться при помощи простого параллельного соединения. При этом процедура расчета этого параметра отличается достаточной сложностью , где необходимо учитывать разные параметры.
Здесь важная роль отводится не только количеству подключаемых элементов, но и рабочим параметрам резисторов — прежде всего, сопротивлению и мощности. Если один из подключаемых элементов будет иметь неподходящий показатель, то это не позволит эффективно решить задачу по созданию требуемого номинала в цепи.
Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую или параллельно для того, чтобы создать более сложные электронные схемы.
Схема параллельного соединения показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:
Формула параллельного соединения резисторов
Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:
Ток, протекающий через отдельно взятый резистор, согласно , можно найти по формуле:
Параллельное соединение резисторов — расчет
Пример №1
При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.
Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:
Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:
Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.
Пример расчета №2
Найти общее сопротивление R из трех параллельно соединенных резисторов:
Общее сопротивление R рассчитывается по формуле:
Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.
Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.
Как рассчитать сложные схемы соединения резисторов
Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:
Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).
Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:
В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:
Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.
Ток, протекающий в цепи параллельно соединенных резисторах
Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.
Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).
Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов (I1 и I2) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .
Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».
Таким образом, протекающий общий ток в цепи можно определить как:
Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:
Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА
Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА
Таким образом, общий ток будет равен:
I = 0,545 мА + 0,255 мА = 0,8 мА
Это также можно проверить, используя закон Ома:
I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)
где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)
И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать .
Параллельное соединение резисторов — онлайн калькулятор
Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:
Подведем итог
Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.
Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.
1 мОм = 0,001 Ом. 1 кОм = 1 000 = 10³ Ом. 1 МОм = 1 000 000 = 10⁶ Ом.
Эквивалентное сопротивление R eq группы параллельно соединенных резисторов является величиной, обратной сумме величин, обратно пропорциональных сопротивлениям этих резисторов.
Иными словами, проводимость G параллельно соединенных резисторов равна сумме проводимостей этих резисторов:
Эта формула для R eq и используется в данном калькуляторе для расчетов. Например, общее сопротивление трех резисторов 10, 15 и 20 ом, соединенных параллельно, равно 4.62 Ом:
Если параллельно соединены только два резистора, формула упрощается:
Если имеется n соединенных параллельно одинаковых резисторов R , то их эквивалентное сопротивление будет равно
Отметим, что общее сопротивление группы из любого количества соединенных параллельно резисторов всегда будет меньше, чем наименьшее сопротивление резистора в группе и добавление нового резистора всегда приведет к уменьшению эквивалентного сопротивления.
Отметим также, что все резисторы, соединенные параллельно находятся под одним и тем же напряжением. Однако токи, протекающие через отдельные резисторы, отличаются и зависят от их сопротивления. Общий ток через группу резисторов равен сумме токов в отдельных резисторах.
При соединении нескольких резисторов параллельно всегда нужно учитывать их допуски и рассеиваемую мощность.
Примеры применения параллельного соединения резисторов
Одним из примеров параллельного соединения резисторов является шунт в приборе для измерения токов, которые слишком велики для того, чтобы быть напрямую измеренными прибором, предназначенным для измерения небольших токов или напряжений. Для измерения тока параллельно гальванометру или электронному прибору, измеряющему напряжение, подключается резистор с очень маленьким точно известным сопротивлением, изготовленный из материала со стабильными характеристиками. Этот резистор называется шунтом. Измеряемый ток протекает через шунт. В результате на нем падает небольшое напряжение, которое и измеряется вольтметром. Поскольку падение напряжения пропорционально току, протекающему через шунт с известным и точным сопротивлением, вольтметр, подключенный параллельно шунту, можно проградуировать непосредственно в единицах тока (амперах).
Параллельные и последовательные схемы часто используются для получения точного сопротивления или если резистора с требуемым сопротивлением нет или он слишком дорог, если его приобретать в небольших количествах для массового производства . Например, если устройство содержит много резисторов по 20 кОм и необходим только один резистор 10 кОм. Конечно, несложно найти резистор на 10 кОм. Однако для массового производства иногда бывает лучше поставить два резистора на 20 кОм параллельно, чтобы получить необходимые 10 кОм. Это приведет к снижению себестоимости печатной платы, так как будет снижена оптовая цена компонентов, а также стоимость монтажа, так как будет уменьшено количество типоразмеров элементов, которые должен установить на плату автомат установки компонентов.
Проверим справедливость показанных здесь формул на простом эксперименте.
Возьмём два резистора МЛТ-2 на 3 и 47 Ом и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.
Замер общего сопротивления при последовательном соединении
Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.
Измерение сопротивления при параллельном соединении
Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:
При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.
Что ещё нужно учитывать при соединении резисторов?
Во-первых, обязательно учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом и мощностью 1 Вт . Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?
Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А ), а сопротивление каждого из них равно 50 Ом , тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт . В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт .
Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.
Подробнее о мощности рассеивания резистора читайте .
Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.
Параллельное соединение резисторов, наряду с последовательным, является основным способом соединения элементов в электрической цепи. Во втором варианте все элементы установлены последовательно: конец одного элемента соединен с началом следующего. В такой схеме сила тока на всех элементах одинаковая, а падение напряжений зависит от сопротивления каждого элемента. В последовательном соединении есть два узла. К одному подсоединены начала всех элементов, а ко второму их концы. Условно для постоянного тока можно обозначить их как плюс и минус, а для переменного как фазу и ноль. Благодаря своим особенностям находит широкое применение в электрических схемах, в том числе и со смешанным соединением. Свойства одинаковы для постоянного и переменного тока.
Расчет общего сопротивления при параллельном соединении резисторов
В отличие от последовательного соединения, где для нахождения общего сопротивления достаточно сложить значение каждого элемента, для параллельного то же самое будет справедливо для проводимости. А так как она обратно пропорциональна сопротивлению, получим формулу, представленную вместе со схемой на следующем рисунке:
Необходимо отметить одну важную особенность расчета параллельного соединения резисторов: общее значение будет всегда меньше, чем самое маленькое из них. Для резисторов справедливо как для постоянного, так и для переменного тока. Катушки и конденсаторы имеют свои особенности.
Сила тока и напряжение
При расчете параллельного сопротивления резисторов необходимо знать, как рассчитать напряжение и силу тока. В этом случае нам поможет закон Ома, определяющий связь между сопротивлением, силой тока и напряжением.
Исходя из первой формулировки закона Кирхгофа, получим, что сумма сходящихся в одном узле токов равна нулю. Направление выбираем по направлению протекания тока. Таким образом, положительным направлением для первого узла можно считать входящий ток от источника питания. А отрицательными будут отходящие из каждого резистора. Для второго узла картина противоположна. Исходя из формулировки закона, получим, что суммарный ток равен сумме токов, проходящих через каждый параллельно соединенный резистор.
Итоговое напряжение же определяется по второму закону Кирхгофа. Оно одинаково для каждого резистора и равно общему. Эта особенность используется для подключения розеток и освещения в квартирах.
Пример расчета
В качестве первого примера приведем расчет сопротивления при параллельном соединении одинаковых резисторов. Сила тока, протекающая через них, будет одинаковой. Пример расчета сопротивления выглядит так:
По этому примеру прекрасно видно, что общее сопротивление ниже в два раза, чем каждое из них. Это соответствует тому, что суммарная сила тока в два раза выше, чем у одного. А также прекрасно соотносится с увеличением проводимости в два раза.
Второй пример
Рассмотрим пример параллельного соединения трех резисторов. Для расчета используем стандартную формулу:
Похожим образом рассчитываются схемы с большим количеством параллельно соединенных резисторов.
Пример смешанного соединения
Для смешанного соединения, например, представленного ниже, расчет будет производиться в несколько этапов.
Для начала последовательные элементы можно условно заменить одним резистором, обладающим сопротивлением, равным сумме двух заменяемых. Далее общее сопротивление считаем тем же способом, что и для предыдущего примера. Данный метод подойдет и для других более сложных схем. Последовательно упрощая схему, можно получить необходимое значение.
Например, если вместо резистора R3 будут подключены два параллельных, потребуется сначала рассчитать их сопротивление, заменив их эквивалентным. А далее то же самое, что и в примере выше.
Применение параллельной схемы
Параллельное соединение резисторов находит свое применение во многих случаях. Последовательное подключение увеличивает сопротивление, а для нашего случая оно уменьшится. Например, для электрической цепи требуется сопротивление в 5 Ом, но есть только резисторы на 10 Ом и выше. Из первого примера мы знаем, что можно получить в два раза меньшее значение сопротивления, если установить два одинаковых резистора параллельно друг другу.
Уменьшить сопротивление можно еще больше, например, если две пары параллельно соединенных резисторов соединить параллельно относительно друг друга. Можно уменьшить сопротивление еще в два раза, если резисторы имеют одинаковое сопротивление. Комбинируя с последовательным соединением, можно получить любое значение.
Второй пример — это использование параллельного подключения для освещения и розеток в квартирах. Благодаря такому подключению напряжение на каждом элементе не будет зависеть от их количества и будет одинаковым.
Еще один пример использования параллельного подключения — это защитное заземление электрооборудования. Например, если человек касается металлического корпуса прибора, на который произойдет пробой, получится параллельное соединения его и защитного проводника. Первым узлом будет место прикосновения, а вторым нулевая точка трансформатора. По проводнику и человеку будет течь разный ток. Величину сопротивления последнего принимают за 1000 Ом, хотя реальное значение зачастую гораздо больше. Если бы не было заземления, весь ток, протекающий в схеме, пошел бы через человека, так как он был бы единственным проводником.
Параллельное соединение может использоваться и для батарей. Напряжение при этом остается прежним, однако в два раза возрастает их емкость.
Итог
При подключении резисторов параллельно, напряжение на них будет одинаковым, а ток равен сумме протекающих через каждый резистор. Проводимость будет ровняться сумме каждого. От этого и получается необычная формула суммарного сопротивления резисторов.
Необходимо учитывать при расчете параллельного соединения резисторов то, что итоговое сопротивление будет всегда меньше самого маленького. Это также можно объяснить суммированием проводимости резисторов. Последняя будет возрастать при добавлении новых элементов, соответственно и проводимость будет уменьшаться.
Как отличается параллельное и последовательное соединение резисторов?
Большое разнообразие схем основано на двух видах соединений – последовательное параллельное. Для каждого типа существуют свои собственные законы и принципы. Именно это и позволяет создавать устройства с самыми различными техническими параметрами, в том числе и резисторы. Что же такое резистор?
Резистор – радиодеталь, созданная для контроля напряжения и тока в цепи, увеличивая либо понижая его. Резисторы могут быть двух видов – постоянные и переменные. Так, например, светодиоды требуют для себя совсем небольшого тока. Для этого в электрическую цепочку перед светодиодом устанавливается резистор, который обеспечивает необходимое напряжение для работы последнего.
В статье подробны рассмотрены все аспекты последовательного и параллельного подключения резисторов. Бонусом к статье являются видеоролик и детальная информационная статья на рассматриваемую тему.
Последовательное подключение
Начнем с последовательного соединения. По этой схеме каждый резистор подключается с другим только в одной точке, их может быть в цепи 2, 3 и больше. Обозначим сопротивления: R1, R2, R3 и напряжение источника в цепи Uц. При подключении источника питания в ней начнет протекать ток Iц. В цепи с последовательным соединением ток протекает по всем резисторам один за другим.
Поскольку ток течет через все резисторы их сопротивления и ток суммируется, Iц = I1+I2+I3, Rц = R1 +R2 + R3, чем больше отдельно взятое сопротивление, тем тяжелее электронам преодолевать участок цепи. Мощность резисторов при последовательном и параллельном соединении рассчитывается по разным формулам. В последовательных цепях — складываем, в параллельных — это обратно пропорциональная величина.
Последовательное соединение характеризуется тем, что элементы идут друг за другом. Конец одного подключается к началу другого. При подключении полученной цепочки к источнику тока получается кольцо.
Теоретическая часть
Последовательное соединение характерно тем, что через все элементы протекает ток одинаковой силы. То есть, если цепочка состоит из двух резисторов R1 и R2 (как на рисунке ниже), то ток протекающий через каждое из них и любую другую часть цепи будет одинаковой (I = I1 = I2). Суммарное сопротивление всей цепи последовательно соединенных резисторов считается как сумма сопротивлений всех ее элементов. То есть, номиналы складывают. R = R1 + R2 — это и есть формула расчета сопротивления при последовательном соединении резисторов. Если элементов больше двух, будет просто больше слагаемых. Еще одно свойство последовательного соединения — на каждом элементе напряжение отличается. Ток в цепи одинаковый, а напряжение на резисторе зависит от его номинала.
Последовательное подключение.
Примеры расчета
Давайте рассмотрим пример. Цепь представлена на рисунке выше. Есть источник тока и два сопротивления. Пусть R1=1,2 кОм, R2= 800 Ом, а ток в цепи 2 А. По закону Ома U = I * R. Подставляем наши значения:
- U1 = R1 * I = 1200 Ом * 2 А = 2400 В;
- U2 = R2 * I = 800 Ом * 2А = 1600 В.
Общее напряжение цепи считается как сумма напряжений на резисторах: U = U1 + U2 = 2400 В + 1600 В = 4000 В. Полученную цифру можно проверить. Для этого найдем суммарное сопротивление цепи и умножим его на ток. R = R1 + R2 = 1200 Ом + 800 Ом = 2000 Ом.
Если подставить в формулу напряжения при последовательном соединении сопротивлений, получаем: U = R * I = 2000 Ом * 2 А = 4000 В. Получаем, что общее напряжение данной цепи 4000 В.
А теперь посмотрите на схему. На первом вольтметре (возле резистора R1) показания будут 2400 В, на втором — 1600 В. При этом напряжение источника питания — 4000 В. Последовательное соединение – это соединение двух или более резисторов в форме цепи, в которой каждый отдельный резистор соединяется с другим отдельным резистором только в одной точке.
Материал по теме: Как проверить варистор мультиметром.
Общее сопротивление R
общПри таком соединении, через все резисторы проходит один и тот же электрический ток. Чем больше элементов на данном участке электрической цепи, тем «труднее» току протекать через него. Следовательно, при последовательном соединении резисторов их общее сопротивление увеличивается, и оно равно сумме всех сопротивлений.
Параллельное соединение резисторов
Параллельное соединение – это соединение, при котором резисторы соединяются между собой обоими контактами. В результате к одной точке (электрическому узлу) может быть присоединено несколько резисторов.
Параллельное подключение резисторов.
Общее сопротивление R
общПри таком соединении, через каждый резистор потечет отдельный ток. Сила данного тока будет обратно пропорциональна сопротивлению резистора. В результате общая проводимость такого участка электрической цепи увеличивается, а общее сопротивление в свою очередь уменьшается. Таким образом, при параллельном подсоединении резисторов с разным сопротивлением, общее сопротивление будет всегда меньше значения самого маленького отдельного резистора. Если посмотреть на изображение параллельного соединения, заметно, что ко всем элементам прилагается одинаковое напряжение.
То есть, при параллельном соединении резисторов, на каждом из них будет одинаковое напряжение U = U1 = U2 = U3. Получается, что ток разделяется на несколько «ручейков». То есть, при параллельном соединении резисторов сила тока, протекающего через каждый из элементов, отличается. I = I1+I2+I3. И зависит сила тока (согласно тому же закону Ома) от сопротивления каждого участка цепи. В случае с параллельным соединением резисторов — от их номинала.
Предлагаем также почитать интересный материал про малоизвестные факты о двигателях постоянного тока в другой нашей статье.
Схема параллельного соединения
Общее сопротивление участка цепи при таком соединении становится ниже. Его высчитывают по формуле: 1/R = 1/R1 + 1/R + 1/R3+. Такая форма хоть и понятна, но неудобна. Формула расчета сопротивления параллельно подключенных резисторов получается тем сложнее, чем больше элементов соединены параллельно. Но больше двух-трех редко кто объединяет, так что на практике достаточно знать только две формулы приведенные ниже.
Если подставить значения в эти формулы, то заметим, что результат будет меньше, чем сопротивление резистора с наименьшим номиналом. Это стоит запомнить: результирующее сопротивление включенных параллельно резисторов будет ниже самого маленького номинала. Давайте сначала рассчитаем параллельное соединение двух резисторов разного номинала и посмотрим что получится.
Соединили параллельно 150 Ом и 100 Ом. Считаем результирующее: 150*100 / (150+100) = 15000/250 = 60 Ом. Если соединить 150 Ом и 50 Ом, получим: 150*50 / (150+50) = 7500 / 200 = 37,5 Ом. Как видим, в обоих случаях результат оказывается меньше чем самый низкий номинал соединенных деталей. Этим и пользуются, если в наличии нет сопротивления небольшого номинала. Проблема только в том, что подбирать сложновато: надо каждый раз считать используя калькулятор.
Как высчитывать сопротивление составных резисторов
Возможно, вам будет проще, если знать, что соединив два одинаковых резистора параллельно, получим результат в два раза меньше. Например, соединив параллельно два резистора по 100 Ом получим составное сопротивление 50 Ом. Проверим? Считаем: 100*100 / (100+100) = 10000 / 200 = 50 Ом. При соединении параллельно трех резисторов, считать приходится больше, так как формула сложнее.
Если подключить параллельно 150 Ом, 100 Ом и 50 Ом, результирующее будет 27,3 Ом. Попробуем с более низкими номиналами. Если параллельно включены 20 Ом, 15 Ом и 10 Ом. Получим результирующее сопротивление 4,61 Ом. Вот вам подтверждение правила. Суммарное сопротивление параллельно соединенных резисторов меньше чем самый низкий номинал.
Параллельное соединение резисторов
Параллельное соединение резисторов это соединение, в котором начала всех резисторов соединены в одну общую точку (А), а концы в другую общую точку. При этом по каждому резистору течет свой ток. При параллельном соединении при протекании тока из точки А в точку Б, он имеет несколько путей. Таким образом, увеличение числа параллельно соединенных резисторов ведет к увеличению путей протекания тока, то есть к уменьшению противодействия протеканию тока. А это значит, чем большее количество резисторов соединить параллельно, тем меньше станет значение общего сопротивления такого участка цепи. Общее сопротивление параллельно соединенных резисторов определяется следующим отношением: 1/Rобщ= 1/R1+1/R2+1/R3+…+1/Rn.
Формулы расчета параллельного и последовательного подключения.
Следует отметить, что здесь действует правило «меньше – меньшего». Это означает, что общее сопротивление всегда будет меньше сопротивления любого параллельно включенного резистора. Общее сопротивление для двух параллельно соединенных резисторов рассчитывается по следующей формуле: Rобщ= R1*R2/R1+R2.
Если имеет место два параллельно соединенных резистора с одинаковыми сопротивлениями, то их общее сопротивление будет равно половине сопротивления одного из них. Параллельное соединение резисторов. При параллельном соединении резисторов нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви.
Заменяя лампы резисторами с сопротивлениями R1, R2, R3, При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Поэтому согласно закону Ома: I1=U/R1; I2=U/R2; I3=U/R3.
Ток в неразветвленной части цепи согласно первому закону Кирхгофа I = I1+I2+I3, или I = U / R1 + U / R2 + U / R3 = U (1/R1 + 1/R2 + 1/R3) = U / Rэк . Следовательно, эквивалентное сопротивление рассматриваемой цепи при параллельном соединении трех резисторов определяется формулой 1/Rэк = 1/R1 + 1/R2 + 1/R3. Вводя в формулу (24) вместо значений 1/Rэк, 1/R1, 1/R2 и 1/R3 соответствующие проводимости Gэк, G1, G2 и G3, получим: эквивалентная проводимость параллельной цепи равна сумме проводимостей параллельно соединенных резисторов:
Gэк = G1+ G2 +G3 (25)
Таким образом, при увеличении числа параллельно включаемых резисторов результирующая проводимость электрической цепи увеличивается, а результирующее сопротивление уменьшается. Из приведенных формул следует, что токи распределяются между параллельными ветвями обратно пропорционально их электрическим сопротивлениям или прямо пропорционально их проводимостям. Например, при трех ветвях I1 : I2 : I3 = 1/R1 : 1/R2 : 1/R3 = G1 + G2 + G3.
В этом отношении имеет место полная аналогия между распределением токов по отдельным ветвям и распределением потоков воды по трубам. Приведенные формулы дают возможность определить эквивалентное сопротивление цепи для различных конкретных случаев. Например, при двух параллельно включенных резисторах результирующее сопротивление цепи – Rэк=R1R2/(R1+R2) при трех параллельно включенных резисторах Rэк=R1R2R3/(R1R2+R2R3+R1R3).
При параллельном соединении нескольких, например n, резисторов с одинаковым сопротивлением R1 результирующее сопротивление цепи Rэк будет в n раз меньше сопротивления R1, т.е.
Rэк = R1 / n.
Проходящий по каждой ветви ток I1, в этом случае будет в п раз меньше общего тока: I1 = I / n. При параллельном соединении приемников, все они находятся под одним и тем же напряжением, и режим работы каждого из них не зависит от остальных. Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются включенными.
Поэтому параллельное соединение имеет существенные преимущества перед последовательным, вследствие чего оно получило наиболее широкое распространение. В частности, электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, всегда включают параллельно.
На электровозах постоянного тока и некоторых тепловозах тяговые двигатели в процессе регулирования скорости движения нужно включать под различные напряжения, поэтому они в процессе разгона переключаются с последовательного соединения на параллельное.
Более подробную информацию можно узнать, прочитав файл по данной теме “Расчет мощности резисторов”. Всю новую информацию по этой и многим другим темам, вы сможете найти в группе. Подписывайтесь на нашу группу в социальной сети «Вконтакте».
Для этого вам необходимо будет перейти по следующей ссылке https://vk.com/electroinfonet. Также в группе можно задавать вопросы и получать на них подробные ответы от профи. В завершение объемной статьи хочу выразить благодарность источникам, откуда мы черпали информацию:
www.elektroznatok.ru
www.themechanic.ru
www.electrono.ru
www.hightolow.ru
www.sxemotehnika.ru
ПредыдущаяРезисторыКак рассчитать резистор для светодиода?
СледующаяРезисторыЧто такое фоторезистор?
Выведите формулы последовательного и параллельного соединений сопротивлений
Рисунок 1.9.4.Цепи, подобные изображенной на рис. 1.9.4, а также цепи с разветвлениями, содержащие несколько источников, рассчитываются с помощью правил Кирхгофа.
Параллельное и последовательное соединение проводников
Элементы цепи могут быть подключены двумя способами:
Проиллюстрируем данные подключения на примере двух резисторов (рис. 1). Помним о том, что соединительные провода не имеют сопротивления (являются идеальными).
- последовательное соединение проводников
Рис. 1. Последовательное соединение проводников
Просмотрим движение электронов по ABC. Т.к. электроны «потеряться» или «задержаться» нигде внутри проводника не могут, при последовательном подключении элементов сила тока, проходящая через каждый из проводников, одинакова.
С точки зрения логики, отдельно взятый электрон нужно «протащить» между точками АB, а потом между точками BC. «Протащить» — это, фактически значит, совершить работу по переносу заряда (за нас это делает электрическое поле):
- где
- — работа по переносу заряда,
- — переносимый заряд,
- , — потенциалы конечной и начальной точки переноса заряда.
Нами ранее уже было введено понятие напряжения:
- где
- — напряжение (разность потенциалов) между точками 2 и 1,
- , — потенциалы соответствующих точек.
Тогда, используя (2) и рисунок 1, проанализируем напряжения. Пусть:
- — напряжение (разность потенциалов) между точками С и А,
- — напряжение (разность потенциалов) между точками В и А,
- — напряжение (разность потенциалов) между точками С и В.
Подставим (4) и (5) в (3):
Таким образом, напряжение в последовательной цепи равно сумме напряжений на каждом из элементов.
Рис. 2. Последовательное соединение проводников (общее сопротивление)
Часть задач школьной физики касается поиска общего сопротивления участка цепи, логика такого поиска: найти такое сопротивление, которым можно заменить цепь, чтобы параметры напряжения и силы тока остались неизменными (рис. 2). Пусть по цепи течёт ток , т.к. соединение последовательное, ток на каждом из элементов одинаков, тогда, используя закон Ома для участка цепи:
Подставим (7) — (9) в (6):
Или, сократив на :
Обобщив данное выражение на любое количество последовательно соединённых сопротивлений, получим:
- где
- — общее (полное) сопротивление цепи элементов, соединённых последовательно,
- — сумма последовательно соединённых сопротивлений.
- параллельное соединение проводников
Рис. 3. Параллельное соединение проводников
Ток, подходящий в точку А ( ), разделяется на два потока: , текущий через сопротивление и , текущий через сопротивление . В точке В оба этих тока складываются в изначальной ток (т.к. электроны не могут «потеряться»), тогда:
Напряжения на каждом из элементов одинаково, т.к. сопротивления и подключены к одним и тем же точкам А и В, а напряжение, по сути, есть разность потенциалов между точками.
Рис. 4. Параллельное соединение проводников (общее сопротивление)
Поищем общее сопротивление такого соединения. Пусть разность потенциалов (напряжение) между точками А и В — . Тогда, исходя из закона Ома для участка цепи:
Подставим (12)-(14) в (11):
Обобщив данное выражение на любое количество параллельно соединённых сопротивлений, получим:
- где
- — общее (полное) сопротивление цепи элементов, соединённых параллельно,
- — обратная сумма параллельно соединённых сопротивлений.
Для цепи из двух сопротивлений:
Вывод: в задачах, в которых присутствует цепь, необходимо рассмотреть, какое конкретно соединение рассматривается, а потом использовать соответствующую логику рассуждений:
- для последовательного соединения
- ток в каждом элементе постоянен ,
- напряжение во всей цепи есть сумма напряжений на каждом из элементов ,
- полное сопротивление цепи есть сумма сопротивлений каждого из элементов .
- для параллельного соединения
- ток во всей цепи есть сумма токов на каждом элементе ,
- напряжение на каждом элементе постоянно
- обратное значение полного сопротивление равно сумме обратных сопротивлений каждого из элементов .
Последовательное и параллельное соединение резисторов.
Как я и обещал в статье про переменные резисторы (ссылка), сегодня речь пойдет о возможных способах соединения резисторов, в частности о последовательном соединении и о параллельном.
Последовательное соединение резисторов.
Давайте начнем с рассмотрения цепей, элементы которой соединены последовательно. И хоть мы и будем рассматривать только резисторы в качестве элементов цепи в данной статье, но правила, касающиеся напряжений и токов при разных соединениях будут справедливы и для других элементов. Итак, первая цепь, которую мы будем разбирать выглядит следующим образом:
Здесь у нас классический случай последовательного соединения – два последовательно включенных резистора. Но не будем забегать вперед и рассчитывать общее сопротивление цепи, а для начала рассмотрим все напряжения и токи. Итак, первое правило заключается в том, что протекающие по всем проводникам токи при последовательном соединении равны между собой:
А для определения общего напряжения при последовательном соединении, напряжения на отдельных элементах необходимо просуммировать:
В то же время, по закону Ома для напряжений, сопротивлений и токов в данной цепи справедливы следующие соотношения:
Тогда для вычисления общего напряжения можно будет использовать следующее выражение:
Но для общего напряжение также справедлив закон Ома:
Здесь
– это общее сопротивление цепи, которое исходя из двух формул для общего напряжения равно:Таким образом, при последовательном соединении резисторов общее сопротивление цепи будет равно сумме сопротивлений всех проводников.
Например для следующей цепи:
Общее сопротивление будет равно:
Количество элементов значения не имеет, правило, по которому мы определяем общее сопротивление будем работать в любом случае А если при последовательном соединении все сопротивления равны (
), то общее сопротивление цепи составит:в данной формуле равно количеству элементов цепи.С последовательным соединением резисторов мы разобрались, давайте перейдем к параллельному.
Параллельное соединение резисторов.
При параллельном соединении напряжения на проводниках равны:
А для токов справедливо следующее выражение:
То есть общий ток разветвляется на две составляющие, а его значение равно сумме всех составляющих. По закону Ома:
Подставим эти выражения в формулу общего тока:
А по закону Ома ток:
Приравниваем эти выражения и получаем формулу для общего сопротивления цепи:
Данную формулу можно записать и несколько иначе:
Таким образом, при параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
Аналогичная ситуация будет наблюдаться и при большем количестве проводников, соединенных параллельно:
Смешанное соединение резисторов.
Помимо параллельного и последовательного соединений резисторов существует еще смешанное соединение. Из названия уже понятно, что при таком соединении в цепи присутствуют резисторы, соединенные как параллельно, так и последовательно. Вот пример такой цепи:
Давайте рассчитаем общее сопротивление цепи. Начнем с резисторов
и – они соединены параллельно. Мы можем рассчитать общее сопротивление для этих резисторов и заменить их в схеме одним единственным резистором :Теперь у нас образовались две группы последовательно соединенных резисторов:
Заменим эти две группы двумя резисторами, сопротивление которых равно:
Как видите, схема стала уже совсем простой ) Заменим группу параллельно соединенных резисторов
и одним резистором :И в итоге у нас на схеме осталось только два резистора соединенных последовательно:
Общее сопротивление цепи получилось равным:
Таким вот образом достаточно большая схема свелась к простейшему последовательному соединению двух резисторов
Тут стоит отметить, что некоторые схемы невозможно так просто преобразовать и определить общее сопротивление – для таких схем нужно использовать правила Кирхгофа, о которых мы обязательно поговорим в будущих статьях. А сегодняшняя статья на этом подошла к концу, до скорых встреч на нашем сайте!
Последовательное и параллельное соединение сопротивлений
Последовательное соединение сопротивлений
Возьмем три постоянных сопротивления R1, R2 и R3 и включим их в цепь так, чтобы конец первого сопротивления R1 был соединен с началом второго сопротивления R 2, конец второго — с началом третьего R 3, а к началу первого сопротивления и к концу третьего подведем проводники от источника тока (рис. 1 ).
Такое соединение сопротивлений называется последовательным. Очевидно, что ток в такой цепи будет во всех ее точках один и тот же.
Рис 1 . Последовательное соединение сопротивлений
Как определить общее сопротивление цепи, если все включенные в нее последовательно сопротивления мы уже знаем? Используя положение, что напряжение U на зажимах источника тока равно сумме падений напряжений на участках цепи, мы можем написать:
U1 = IR1 U2 = IR2 и U3 = IR3
IR = IR1 + IR2 + IR3
Вынеся в правой части равенства I за скобки, получим IR = I(R1 + R2 + R3) .
Поделив теперь обе части равенства на I , будем окончательно иметь R = R1 + R2 + R3
Таким образом, мы пришли к выводу, что при последовательном соединении сопротивлений общее сопротивление всей цепи равно сумме сопротивлений отдельных участков.
Проверим этот вывод на следующем примере. Возьмем три постоянных сопротивления, величины которых известны (например, R1 == 10 Ом, R 2 = 20 Ом и R 3 = 50 Ом). Соединим их последовательно (рис. 2 ) и подключим к источнику тока, ЭДС которого равна 60 В (внутренним сопротивлением источника тока пренебрегаем).
Рис. 2. Пример последовательного соединения трех сопротивлений
Подсчитаем, какие показания должны дать приборы, включенные, как показано на схеме, если замкнуть цепь. Определим внешнее сопротивление цепи: R = 10 + 20 + 50 = 80 Ом.
Найдем ток в цепи по закону Ома: 60 / 80 = 0 ,75 А
Зная ток в цепи и сопротивления ее участков, определим падение напряжения на каждое участке цепи U 1 = 0,75 х 10 = 7,5 В, U 2 = 0,75 х 20=15 В, U3 = 0,75 х 50 = 37,5 В.
Зная падение напряжений на участках, определим общее падение напряжения во внешней цепи, т. е. напряжение на зажимах источника тока U = 7,5+15 + 37,5 = 60 В.
Мы получили таким образом, что U = 60 В, т. е. несуществующее равенство ЭДС источника тока и его напряжения. Объясняется это тем, что мы пренебрегли внутренним сопротивлением источника тока.
Замкнув теперь ключ выключатель К, можно убедиться по приборам, что наши подсчеты примерно верны.
Параллельное соединение сопротивлений
Возьмем два постоянных сопротивления R1 и R2 и соединим их так, чтобы начала этих сопротивлений были включены в одну общую точку а, а концы — в другую общую точку б. Соединив затем точки а и б с источником тока, получим замкнутую электрическую цепь. Такое соединение сопротивлений называется параллельным соединением.
Рис 3. Параллельное соединение сопротивлений
Проследим течение тока в этой цепи. От положительного полюса источника тока по соединительному проводнику ток дойдет до точки а. В точке а он разветвится, так как здесь сама цепь разветвляется на две отдельные ветви: первую ветвь с сопротивлением R1 и вторую — с сопротивлением R2. Обозначим токи в этих ветвях соответственно через I1 и I 2. Каждый из этих токов пойдет по своей ветви до точки б. В этой точке произойдет слияние токов в один общий ток, который и придет к отрицательному полюсу источника тока.
Таким образом, при параллельном соединении сопротивлений получается разветвленная цепь. Посмотрим, какое же будет соотношение между токами в составленной нами цепи.
Включим амперметр между положительным полюсом источника тока (+) и точкой а и заметим его показания. Включив затем амперметр (показанный «а рисунке пунктиром) в провод, соединяющий точку б с отрицательным полюсом источника тока (—), заметим, что прибор покажет ту же величину силы тока.
Значит, сила тока в цепи до ее разветвления (до точки а) равна силе тока после разветвления цепи (после точки б).
Будем теперь включать амперметр поочередно в каждую ветвь цепи, запоминая показания прибора. Пусть в первой ветви амперметр покажет силу тока I1 , а во второй — I 2. Сложив эти два показания амперметра, мы получим суммарный ток, по величине равный току I до разветвления (до точки а).
Следовательно, сила тока, протекающего до точки разветвления, равна сумме сил токов, утекающих от этой точки. I = I1 + I2 Выражая это формулой, получим
Это соотношение, имеющее большое практическое значение, носит название закона разветвленной цепи .
Рассмотрим теперь, каково будет соотношение между токами в ветвях.
Включим между точками а и б вольтметр и посмотрим, что он нам покажет. Во-первых, вольтметр покажет напряжение источника тока, так как он подключен, как это видно из рис. 3 , непосредственно к зажимам источника тока. Во-вторых, вольтметр покажет падения напряжений U1 и U2 на сопротивлениях R 1 и R2, так как он соединен с началом и концом каждого сопротивления.
Следовательно, при параллельном соединении сопротивлений напряжение на зажимах источника тока равно падению напряжения на каждом сопротивлении.
Это дает нам право написать, что U = U1 = U2 ,
где U — напряжение на зажимах источника тока; U 1 — падение напряжения на сопротивлении R 1 , U2 — падение напряжения на сопротивлении R2. Вспомним, что падение напряжения на участке цепи численно равно произведению силы тока, протекающего через этот участок, на сопротивление участка U = IR .
Поэтому для каждой ветви можно написать: U1 = I1R1 и U2 = I2R2 , но так как U 1 = U2, то и I1R1 = I2R2 .
Применяя к этому выражению правило пропорции, получим I1/ I2 = U2 / U1 т. е. ток в первой ветви будет во столько раз больше (или меньше) тока во второй ветви, во сколько раз сопротивление первой ветви меньше (или больше) сопротивления второй ветви.
Итак, мы пришли к важному выводу, заключающемуся в том, что при параллельном соединении сопротивлений общий ток цепи разветвляется на токи, обратно пропорциональные величинам сопротивлении параллельных ветвей. Иначе говоря, чем больше сопротивление ветви, тем меньший ток потечет через нее, и, наоборот, чем меньше сопротивление ветви, тем больший ток потечет через эту ветвь.
Убедимся в правильности этой зависимости на следующем примере. Соберем схему, состоящую из двух параллельно соединенных сопротивлений R1 и R 2, подключенных к источнику тока. Пусть R1 = 10 Ом, R2 = 20 Ом и U = 3 В.
Подсчитаем сначала, что покажет нам амперметр, включенный в каждую ветвь:
I1 = U / R1 = 3 / 10 = 0 ,3 А = 300 мА
I 2 = U / R 2 = 3 / 20 = 0,15 А = 150 мА
Общий ток в цепи I = I1 + I2 = 300 + 150 = 450 мА
Проделанный нами расчет подтверждает, что при параллельном соединении сопротивлений ток в цепи разветвляется обратно пропорционально сопротивлениям.
Действительно, R1 == 10 Ом вдвое меньше R 2 = 20 Ом, при этом I1 = 300 мА вдвое больше I2 = 150 мА. Общий ток в цепи I = 450 мА разветвился на две части так, что большая его часть ( I1 = 300 мА) пошла через меньшее сопротивление ( R1 = 10 Ом), а меньшая часть ( R2 = 150 мА) — через большее сопротивление ( R 2 = 20 Ом).
Такое разветвление тока в параллельных ветвях сходно с течением жидкости по трубам. Представьте себе трубу А, которая в каком-то месте разветвляется на две трубы Б и В различного диаметра (рис. 4). Так как диаметр трубы Б больше диаметра трубок В, то через трубу Б в одно и то же время пройдет больше воды, чем через трубу В, которая оказывает потоку воды большее сопротивление.
Рис. 4 . Через тонкую трубу в один и тот же промежуток времени пройдет воды меньше, чем через толстую
Рассмотрим теперь, чему будет равно общее сопротивление внешней цепи, состоящей из двух параллельно соединенных сопротивлений.
Под этим общим сопротивлением внешней цепи надо понимать такое сопротивление, которым можно было бы заменить при данном напряжении цепи оба параллельно включенных сопротивления, не изменяя при этом тока до разветвления. Такое сопротивление называется эквивалентным сопротивлением.
Вернемся к цепи, показанной на рис. 3, и посмотрим, чему будет равно эквивалентное сопротивление двух параллельно соединенных сопротивлений. Применяя к этой цепи закон Ома, мы можем написать: I = U/R , где I — ток во внешней цепи (до точки разветвления), U — напряжение внешней цепи, R — сопротивление внешней цепи, т. е. эквивалентное сопротивление.
Точно так же для каждой ветви I1 = U1 / R1 , I2 = U2 / R2 , где I1 и I 2 — токи в ветвях; U 1 и U2 — напряжение на ветвях; R1 и R2 — сопротивления ветвей.
По закону разветвленной цепи: I = I1 + I2
Подставляя значения токов, получим U / R = U1 / R1 + U2 / R2
Так как при параллельном соединении U = U1 = U2 , то можем написать U / R = U / R1 + U / R2
Вынеся U в правой части равенства за скобки, получим U / R = U (1 / R1 + 1 / R2 )
Разделив теперь обе части равенства на U , будем окончательно иметь 1 / R = 1 / R1 + 1 / R2
Помня, что проводимостью называется величина, обратная сопротивлению , мы можем сказать, что в полученной формуле 1 / R — проводимость внешней цепи; 1 / R1 проводимость первой ветви; 1 / R2- проводимость второй ветви.
На основании этой формулы делаем вывод: при параллельном соединении проводимость внешней цепи равна сумме проводимостей отдельных ветвей.
Следовательно, чтобы определить эквивалентное сопротивление включенных параллельно сопротивлений, надо определить проводимость цепи и взять величину, ей обратную.
Из формулы также следует, что проводимость цепи больше проводимости каждой ветви, а это значит, что эквивалентное сопротивление внешней цепи меньше наименьшего из включенных параллельно сопротивлений.
Рассматривая случай параллельного соединения сопротивлений, мы взяли наиболее простую цепь, состоящую из двух ветвей. Однако на практике могут встретиться случаи, когда цепь состоит из трех и более параллельных ветвей. Как же поступать в этих случаях?
Оказывается, все полученные нами соотношения остаются справедливыми и для цепи, состоящей из любого числа параллельно соединенных сопротивлений.
Чтобы убедиться в этом, рассмотрим следующий пример.
Возьмем три сопротивления R1 = 10 Ом, R2 = 20 Ом и R3 = 60 Ом и соединим их параллельно. Определим эквивалентное сопротивление цепи (рис. 5 ).
Рис. 5. Цепь с тремя параллельно соединенными сопротивлениями
Применяя для этой цепи формулу 1 / R = 1 / R1 + 1 / R2 , можем написать 1 / R = 1 / R1 + 1 / R2 + 1 / R3 и, подставляя известные величины, получим 1 / R = 1 / 10 + 1 / 20 + 1 / 60
Сложим эта дроби: 1/R = 10 / 60 = 1 / 6, т. е.. проводимость цепи 1 / R = 1 / 6 Следовательно, эквивалентное сопротивление R = 6 Ом.
Таким образом, эквивалентное сопротивление меньше наименьшего из включенных параллельно в цепь сопротивлений , т. е. меньше сопротивления R1.
Посмотрим теперь, действительно ли это сопротивление является эквивалентным, т. е. таким, которое могло бы заменить включенные параллельно сопротивления в 10, 20 и 60 Ом, не изменяя при этом силы тока до разветвления цепи.
Допустим, что напряжение внешней цепи, а следовательно, и напряжение на сопротивлениях R1, R2, R3 равно 12 В. Тогда сила токов в ветвях будет: I1 = U/R1 = 12 / 10 = 1 ,2 А I 2 = U/R 2 = 12 / 20 = 1 ,6 А I 3 = U/R1 = 12 / 60 = 0, 2 А
Общий ток в цепи получим, пользуясь формулой I = I1 + I2 + I3 = 1,2 + 0,6 + 0,2 = 2 А.
Проверим по формуле закона Ома, получится ли в цепи ток силой 2 А, если вместо трех параллельно включенных известных нам сопротивлений включено одно эквивалентное им сопротивление 6 Ом.
I = U / R = 12 / 6 = 2 А
Как видим, найденное нами сопротивление R = 6 Ом действительно является для данной цепи эквивалентным.
В этом можно убедиться и на измерительных приборах, если собрать схему с взятыми нами сопротивлениями, измерить ток во внешней цепи (до разветвления), затем заменить параллельно включенные сопротивления одним сопротивлением 6 Ом и снова измерить ток. Показания амперметра и в том и в другом случае будут примерно одинаковыми.
На практике могут встретиться также параллельные соединения, для которых рассчитать эквивалентное сопротивление можно проще, т. е. не определяя предварительно проводимостей, сразу найти сопротивление.
Например, если соединены параллельно два сопротивления R1 и R2 , то формулу 1 / R = 1 / R1 + 1 / R2 можно преобразовать так: 1/R = (R2 + R1) / R1 R2 и, решая равенство относительно R, получить R = R1 х R2 / ( R1 + R2 ), т. е. при параллельном соединении двух сопротивлений эквивалентное сопротивление цепи равно произведению включенных параллельно сопротивлений, деленному на их сумму.
Оценка статьи:
Загрузка…Выведите формулы последовательного и параллельного соединений сопротивлений Ссылка на основную публикацию wpDiscuzAdblockdetector
Напряжение при параллельном соединении резисторов. Сопротивление при параллельном соединении: формула расчета
При решении задач принято преобразовывать схему, так, чтобы она была как можно проще. Для этого применяют эквивалентные преобразования. Эквивалентными называют такие преобразования части схемы электрической цепи, при которых токи и напряжения в не преобразованной её части остаются неизменными.
Существует четыре основных вида соединения проводников: последовательное, параллельное, смешанное и мостовое.
Последовательное соединение
Последовательное соединение – это такое соединение, при котором сила тока на всем участке цепи одинакова. Ярким примером последовательного соединения является старая елочная гирлянда. Там лампочки подключены последовательно, друг за другом. Теперь представьте, одна лампочка перегорает, цепь нарушена и остальные лампочки гаснут. Выход из строя одного элемента, ведет за собой отключение всех остальных, это является существенным недостатком последовательного соединения.
При последовательном соединении сопротивления элементов суммируются.
Параллельное соединение
Параллельное соединение – это соединение, при котором напряжение на концах участка цепи одинаково. Параллельное соединение наиболее распространено, в основном потому, что все элементы находятся под одним напряжением, сила тока распределена по-разному и при выходе одного из элементов все остальные продолжают свою работу.
При параллельном соединении эквивалентное сопротивление находится как:
В случае двух параллельно соединенных резисторов
В случае трех параллельно подключенных резисторов:
Смешанное соединение
Смешанное соединение – соединение, которое является совокупностью последовательных и параллельных соединений. Для нахождения эквивалентного сопротивления нужно, “свернуть” схему поочередным преобразованием параллельных и последовательных участков цепи.
Сначала найдем эквивалентное сопротивление для параллельного участка цепи, а затем прибавим к нему оставшееся сопротивление R 3 . Следует понимать, что после преобразования эквивалентное сопротивление R 1 R 2 и резистор R 3 , соединены последовательно.
Итак, остается самое интересное и самое сложное соединение проводников.
Мостовая схема
Мостовая схема соединения представлена на рисунке ниже.
Для того чтобы свернуть мостовую схему, один из треугольников моста, заменяют эквивалентной звездой.
И находят сопротивления R 1 , R 2 и R 3 .
Последовательное соединение – это соединение двух или более резисторов в форме цепи, в которой каждый отдельный резистор соединяется с другим отдельным резистором только в одной точке.
Параллельное соединение – это соединение, при котором резисторы соединяются между собой обоими контактами. В результате к одной точке (электрическому узлу) может быть присоединено несколько резисторов.
2) Общее сопротивление R общ
При таком соединении, через все резисторы проходит один и тот же электрический ток. Чем больше элементов на данном участке электрической цепи, тем «труднее» току протекать через него. Следовательно, при последовательном соединении резисторов их общее сопротивление увеличивается, и оно равно сумме всех сопротивлений.
Общее сопротивление R общ
При таком соединении, через каждый резистор потечет отдельный ток. Сила данного тока будет обратно пропорциональна сопротивлению резистора. В результате общая проводимость такого участка электрической цепи увеличивается, а общее сопротивление в свою очередь уменьшается.
Таким образом, при параллельном подсоединении резисторов с разным сопротивлением, общее сопротивление будет всегда меньше значения самого маленького отдельного резистора.
Формула эквивалентного общего сопротивления при параллельном соединении резисторов:
Для двух одинаковых резисторов общее сопротивление будет равно половине одного отдельного резистора:
Соответственно, для n одинаковых резисторов общее сопротивление будет равно значению одного резистора, разделенного на n.
3)Электропроводность, электрическая проводимость, проводимость, способность тела пропускать электрический ток под воздействием электрического поля, а также физическая величина, количественно характеризующая эту способность. Тела, проводящие электрический ток, называются проводниками, в отличие от изоляторов.. .
Основная единица измерения сопротивления — Ом. Удельная проводимость — величина обратная сопротивлению, она измеряется в Сименсах, ранее назывшихся mho. Применительно к сыпучим веществам удобнее говорить об особой проводимости, обычно называемой удельной проводимостью.
Удельная проводимость — это проводимость, измеренная между противоположными сторонами куба вещества со стороной 1 см. Единицей данного типа измерений является Сименс/см. При измерении проводимости воды чаще используются более точные мкС/см (микросименс) и мС/см (миллисименс) .
Соответствующие единицы измерения сопротивления (или удельного сопротивления) — Ом/см, МегаОм/см и килоОм/см. При измерении сверхчистой воды чаще используют МегаОм/см, так как это дает более точные результаты. Сопротивление менее чистой воды, как например, водопроводной, измеряют в килоОм/см.
4) Общее сопротивление при последовательном соединении равно сумме сопротивлений Rсумм=R1+R2+R3…
Ток через все сопротивления протекает один (I). Поэтому ток вычисляешь как Отношение напряжения источника U к Rсумм.
Мощность
P=U*I или P=I*I*R (так как U=I*R).
P1=I*I*R1
P2=I*I*R2
P3=I*I*R3
5) мощность электрического тока в цепи, состоящей из параллельно соединенных участков,
равна сумме мощностей на отдельных участках:
При параллельном соединении каждая лампа подсоединяется на своё номинальное напряжение 220 В. при этом в каждой лампе появляется свой номинальный ток, обеспечивающий заданное свечение в соответствии с номинальной мощностью. мощность зависит от сопротивления нити накаливания. чем больше сопротивление нити, тем меньше ток и соответственно меньше номинальная мощность.
при последовательном соединении ток идёт один и тот же в каждой лампе. а напряжение распределяется в зависимости от доли сопротивления каждой лампы по отношению к сопротивлению всей цепи.
для цепи из двух ламп общее напряжение делится.
напряжение на лампе 40 Вт будет 220Х60:(40+60)=132; В.
напряжение на лампе 60 Вт будет 220Х40:(40+60)=80; В.
Параллельным соединением сопротивлений называется такое соединение, когда начала сопротивлений соединены в одну общую точку, а концы — в другую.
Для параллельного соединения сопротивлений характерны следующие свойства:
Напряжения на зажимах всех сопротивлений одинаковы:
U 1 = U 2 = U 3 = U;
— проводимость всех параллельно соединённых сопротивлений равна сумме проводимостей отдельных сопротивлений:
1/R = 1/R 1 + 1/R 2 + 1/R 3 = R 1 R 2 + R 1 R 3 + R 2 R 3 /R 1 R 2 R 3 ,
где R — эквивалентное (равнодействующее) сопротивление трёх сопротивлений (в данном случае R 1 , R 2 и R 3).
Чтобы получить сопротивление такой цепи, надо перевернуть дробь, определяющую величину её проводимости. Следовательно, сопротивление параллельного разветвления из трёх резисторов:
R = R 1 R 2 R 3 /R 1 R 2 + R 2 R 3 + R 1 R 3 .
Эквивалентным сопротивлением называется такое сопротивление, которым можно заменить несколько сопротивлений (включенных параллельно или последовательно), не изменяя величины тока в цепи.
Чтобы найти эквивалентное сопротивление при параллельном соединении, необходимо сложить проводимости всех отдельных участков, т.е. найти общую проводимость. Величина, обратная общей проводимости, и является общим сопротивлением.
При параллельном соединении эквивалентная проводимость равна сумме проводимостей отдельных ветвей, следовательно, эквивалентное сопротивление в этом случае всегда меньше наименьшего из параллельно включенных сопротивлений.
На практике могут быть случаи, когда цепь состоит из более, чем трёх параллельных ветвей. Все полученные соотношения остаются справедливыми и для цепей, состоящих из любого числа параллельно соединённых резисторов.
Найдём эквивалентное сопротивление двух параллельно включенных сопротивлений R 1 и R 2 (см. рис.). Проводимость первой ветви равна 1/R 1 , проводимость второй ветви — 1/R 2 . Общая проводимость:
1/R = 1/R 1 + 1/R 2 .
Приведём к общему знаменателю:
1/R = R 2 + R 1 /R 1 R 2 ,
отсюда эквивалентное сопротивление
R = R 1 R 2 /R 1 + R 2 .
Эта формула и служит для расчётов общего сопротивления цепи, состоящей из двух параллельно включенных сопротивлений.
Таким образом, эквивалентное сопротивление двух параллельно включенных сопротивлений равно произведению этих сопротивлений, делённому на их сумму.
При параллельном соединении n равных сопротивлений R1 эквивалентное сопротивление их будет в n раз меньше, т.е.
R = R 1 /n.
На схеме, изображённой на последнем рисунке, включено пять сопротивлений R 1 по 30 Ом каждое. Следовательно, общее сопротивление R будет
R = R 1 /5 = 30/5 = 6 Ом.
Можно сказать, что сумма токов, подходящих к узловой точке А (на первом рисунке), равна сумме токов, от неё отходящих:
I = I 1 + I 2 + I 3 .
Рассмотрим, как происходит разветвление тока в цепях с сопротивлениями R 1 и R 2 (второй рисунок). Так как напряжение на зажимах этих сопротивлений одинаково, то
U = I 1 R 1 и U = I 2 R 2 .
Левые части этих равенств одинаковы, следовательно, равны и правые части:
I 1 R 1 = I 2 R 2 ,
или
I 1 /I 2 = R 2 /R 1 ,
т.е. ток при параллельном соединении сопротивлений разветвляется обратно пропорционально сопротивлениям ветвей (или прямо пропорционально их проводимостям). Чем больше сопротивление ветви, тем меньше ток в ней, и наоборот.
Таким образом, из нескольких одинаковых резисторов можно получить общий резистор с бОльшей мощностью рассеивания.
При параллельном соединении неодинаковых резисторов в наиболее высокоомном резисторе выделяется наибольшая мощность.
Пример 1. Имеются два сопротивления, включенных параллельно. Сопротивление R 1 = 25 Ом, а R 2 = 50 Ом. Определить общее сопротивление цепи R общ.
Решение. Rобщ = R 1 R 2 /R 1 + R 2 = 25 x 50 / 25 + 50 ≈ 16, 6 Ом.
Пример 2. В ламповом усилителе имеются три лампы, нити накала которых включены параллельно. Ток накала первой лампы I 1 = 1 ампер, второй I 2 = 1, 5 ампера и третьей I 3 = 2, 5 ампера. Определить общий ток цепи накала ламп усилителя I общ.
Решение. I общ = I 1 + I 2 + I 3 = 1 + 1, 5 + 2, 5 = 5 ампер.
Параллельное соединение резисторов часто встречается в радиотехнической аппаратуре. Два или более резисторов включается параллельно в тех случаях, когда ток в цепи слишком большой и может вызвать чрезмерный нагрев резистора.
Примером параллельного соединения потребителей электрической энергии может служить включение электрических ламп обычной осветительной сети, которые соединяются параллельно. Достоинство параллельного соединения потребителей заключается в том, что выключение одного из них не влияет на работу других.
Параллельное соединение резисторов. При параллельном соединении резисторов нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви (рис. 26, а). Заменяя
лампы резисторами с сопротивлениями R1, R2, R3, получим схему, показанную на рис. 26, б.
При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Поэтому согласно закону Ома:
I 1 =U/R 1 ; I 2 =U/R 2 ; I 3 =U/R 3 .
Ток в неразветвленной части цепи согласно первому закону Кирхгофа I = I 1 +I 2 +I 3 , или
I = U / R 1 + U / R 2 + U / R 3 = U (1/R 1 + 1/R 2 + 1/R 3) = U / R эк (23)
Следовательно, эквивалентное сопротивление рассматриваемой цепи при параллельном соединении трех резисторов определяется формулой
1/R эк = 1/R 1 + 1/R 2 + 1/R 3 (24)
Вводя в формулу (24) вместо значений 1/R эк, 1/R 1 , 1/R 2 и 1/R 3 соответствующие проводимости G эк, G 1 , G 2 и G 3 , получим: эквивалентная проводимость параллельной цепи равна сумме проводимостей параллельно соединенных резисторов :
G эк = G 1 + G 2 +G 3 (25)
Таким образом, при увеличении числа параллельно включаемых резисторов результирующая проводимость электрической цепи увеличивается, а результирующее сопротивление уменьшается.
Из приведенных формул следует, что токи распределяются между параллельными ветвями обратно пропорционально их электрическим сопротивлениям или прямо пропорционально их проводимостям. Например, при трех ветвях
I 1: I 2: I 3 = 1/R 1: 1/R 2: 1/R 3 = G 1 + G 2 + G 3 (26)
В этом отношении имеет место полная аналогия между распределением токов по отдельным ветвям и распределением потоков воды по трубам.
Приведенные формулы дают возможность определить эквивалентное сопротивление цепи для различных конкретных случаев. Например, при двух параллельно включенных резисторах результирующее сопротивление цепи
R эк =R 1 R 2 /(R 1 +R 2)
при трех параллельно включенных резисторах
R эк =R 1 R 2 R 3 /(R 1 R 2 +R 2 R 3 +R 1 R 3)
При параллельном соединении нескольких, например n, резисторов с одинаковым сопротивлением R1 результирующее сопротивление цепи Rэк будет в n раз меньше сопротивления R1, т.е.
R эк = R1 / n (27)
Проходящий по каждой ветви ток I1, в этом случае будет в п раз меньше общего тока:
I1 = I / n (28)
При параллельном соединении приемников, все они находятся под одним и тем же напряжением, и режим работы каждого из них не зависит от остальных. Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются включенными. Поэтому параллельное соединение имеет существенные преимущества перед последовательным, вследствие чего оно получило наиболее широкое распространение. В частности, электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, всегда включают параллельно.
На электровозах постоянного тока и некоторых тепловозах тяговые двигатели в процессе регулирования скорости движения нужно включать под различные напряжения, поэтому они в процессе разгона переключаются с последовательного соединения на параллельное.
Соединение разными способами позволяет получить необходимую величину сопротивления и одного эквивалентного резистора. Всего существует три способы соединения резисторов – последовательное, параллельное и смешанное.
Последовательное соединение резисторовПоследовательное соединение резисторов предполагает использование двух и более радиоэлектронных элемента. Конец предыдущего элемента соединяется с началом последующего и так далее. При последовательном соединении сопротивления и мощности рассеивания всех резисторов складываются.
Рассмотрим следующий пример. Соединим последовательно четыре резистора, каждый имеет R = 1 кОм и мощность рассеивания P = 0,25 Вт .
Rобщ = R1 + R2 + R3 + R4 = 1кОм + 1кОм + 1кОм + 1кОм = 4 кОм.
Pобщ = P1 + P2 + P3 + P4 = 0,25 Вт + 0,25 Вт + 0,25 Вт + 0,25 Вт = 1 Вт.
Таким образом, получается один эквивалентный или общий резистор, имеющий следующие параметры:
Rобщ = 4 кОм; Pобщи = 1 Вт .
В последовательной цепи электрической ток протекает одной и той же величины, поэтому электроны на протяжении всего пути неизбежно наталкиваются на все препятствия в виде сопротивлений. С каждым препятствием уменьшается число свободных зарядов, что приводит к снижению силы электрического тока.
При параллельном соединении резисторов увеличивается количество путей для перемещения свободных зарядов, то есть электронов, из одного участка пути к другому. Поэтому при параллельном соединении резисторов их суммарное (общее, эквивалентное) сопротивление всегда ниже наименьшего сопротивления из всех резисторов.
Величина, обратная сопротивлению называется проводимостью. Проводимость измеряется в сименсах [См] и обозначается большей латинской буквой G .
G = 1/R = 1/Ом = См
Поэтому при выполнении различных подсчетов в электрических цепях, имеющих параллельное соединение, пользуются проводимостью.
Если сопротивления всех параллельно соединенных резисторов равны, то для определения общего Rобщ достаточно R одного из них разделить на их общее количество:
Если R1 = R2 = R3 = R4 = R , то
Rобщ = R/4.
Например, каждый из четырех резисторов имеет R = 10 кОм , тогда
Rобщ = 10 кОм/4 = 2,5 кОм .
Мощности рассеивания суммируются также, как и при последовательном соединении.
Смешанное соединение резисторовСмешанное соединение резисторов представляет собой комбинации последовательных и параллельных соединений. В принципе любую даже самую сложную электрическую цепь, состоящую из источников питания, диодов, и других радиоэлектронных элементов в конкретный момент времени можно заменить резисторами и источниками напряжения, параметры которых изменяются с каждым последующим моментом времени. Для примера изобразим схему, имеющую несколько соединений.
Серияи параллельные резисторы
- Изучив этот раздел, вы сможете:
- Рассчитайте значения общего сопротивления в цепях с последовательным сопротивлением.
- Используйте соответствующие формулы для расчета сопротивления в цепях с параллельным сопротивлением.
- • Вычисление суммы обратных величин.
- • Произведение над суммой.
- Рассчитайте значения общего сопротивления в последовательных / параллельных сетях.
Расчеты в последовательно- и параллельных резисторных цепях
Компоненты, включая резисторы в цепи, могут быть соединены вместе двумя способами:
ПОСЛЕДОВАТЕЛЬНО, так что один и тот же ток течет через все компоненты, но на каждом из них может существовать разная разность потенциалов (напряжение).
ПАРАЛЛЕЛЬНО, так что одинаковая разность потенциалов (напряжение) существует на всех компонентах, но каждый компонент может проводить разный ток.
Рис. 4.2.1 Резисторы серии
Рис. 4.2.2 Параллельные резисторы
В любом случае (для резисторов) общее сопротивление той части цепи, которая содержит резисторы, может быть рассчитано с использованием методов, описанных ниже.
Возможность рассчитать суммарное (общее) значение резисторов таким способом позволяет легко вычислить неизвестные значения сопротивления, тока и напряжения для довольно сложных цепей, используя относительно простые методы.Это очень полезно при поиске неисправностей.
ПЕРЕД ДАЛЬНЕЙШЕЙ ДАЛЬНОСТЬЮ ПОПРОБУЙТЕ ИСПОЛЬЗОВАНИЕ ФОРМУЛ ДЛЯ РАСЧЕТА ОБЩИХ ЗНАЧЕНИЙ СЕРИИ И ПАРАЛЛЕЛЬНЫХ РЕЗИСТОРОВ.
Для резисторов в серии:
Общее сопротивление двух или более резисторов, подключенных последовательно , определяется простым сложением индивидуальных значений резисторов, чтобы найти общую сумму (R TOT ):
Для резисторов, включенных параллельно:
Для расчета общего сопротивления цепи, в которой используются параллельные резисторы, можно использовать следующую формулу.
Обратите внимание, однако, что эта формула НЕ дает вам общего сопротивления R TOT . Это дает вам ВЗАИМОДЕЙСТВИЕ R TOT или:
Это совсем другое значение — и НЕ является полным сопротивлением. Он делится на 1, деленный на TOT . Чтобы получить правильное значение для TOT рэндов (которое будет обратным 1/ TOT , т. Е. TOT /1, просто нажмите соответствующую клавишу на вашем калькуляторе (отмеченную 1 / x или x-1) .
Другой способ расчета параллельных цепей.
Суммарное сопротивление двух резисторов, включенных параллельно , которое не включает обратные, определяется по формуле:
Эту формулу часто называют «произведение над суммой».
Он рассчитывает только ДВА резистора параллельно? Ну да, но это не большая проблема. Если имеется более двух параллельных резисторов, просто выберите два из них и определите общее сопротивление для этих двух — затем используйте это общее сопротивление, как если бы это был один резистор, и составьте еще одну пару с третьим резистором.Определите новую сумму и так далее, пока вы не включите все параллельные резисторы в этой конкретной сети.
О, еще одна вещь, которую следует помнить о произведении над суммой, видите скобки вокруг суммы (нижняя часть) формулы? Это означает, что вы должны решить это, прежде чем использовать его для разделения продукта (верхняя часть) на. Если вы этого не сделаете, ваш ответ будет неправильным.
Звучит сложно? Не совсем, это просто вопрос повторения, и на практике вы не часто встречаетесь с множеством параллельных сетей с гораздо более чем двумя резисторами.Тем не менее, какую формулу вы выберете, зависит от вас, взаимная или сумма продукта.
подсказки
Использование обратного метода
Если вы используете МЕТОД ВЗАИМОДЕЙСТВИЯ для параллельных цепей, НЕ ЗАБУДЬТЕ, когда вы добавили обратные величины отдельных резисторов — вы должны снова найти обратную величину 1 / R1 + 1 / R2 + 1 / R3 = 1 / R TOT , а чтобы найти R TOT , вы должны найти обратное 1 / R TOT .
Упрощающие схемы
Для комбинированных последовательных и параллельных цепей сначала определите участок цепи (последовательный или параллельный).Затем перерисуйте схему, заменив участок, сопротивление которого вы нашли, одним резистором. Теперь у вас есть упрощенная схема, по которой можно найти R TOT .
Вы можете использовать формулу «произведение на сумму»:
Для цепей с более чем двумя параллельными резисторами просто определите два параллельных резистора одновременно, используя формулу произведения на сумму, а затем перерисуйте схему, заменив два резистора одним резистором, значение которого является объединенным сопротивлением двух .
Теперь вы можете использовать ваше первое комбинированное значение в качестве единственного резистора со следующим параллельным резистором и так далее. Таким образом, можно выработать большое количество параллельных резисторов с использованием произведения на сумму.
Когда все параллельные резисторы одинакового номинала.
Если несколько одинаковых параллельных резисторов подключены, общее сопротивление будет равно величине резистора, умноженной на обратную величину количества резисторов.
, т. Е. Два параллельных резистора 12 кОм имеют общее сопротивление
12K x 1/2 = 6K
Три параллельно включенных резистора 12 кОм имеют общее сопротивление
12K x 1/3 = 4K и т. Д.
Проверяю ответ
Суммарное значение любого количества параллельных резисторов всегда будет МЕНЬШЕ, чем значение наименьшего отдельного резистора в сети. Используйте этот факт, чтобы проверить свои ответы.
Серияи параллельная комбинация
Попробуйте несколько вычислений, основанных на последовательной и параллельной цепях резисторов. Для этого вам просто нужно использовать информацию на этой странице и на странице «Советы по расчету резисторов». Вас просят вычислить общее сопротивление для каждой цепи.Вы можете выбрать, какую формулу использовать
Вы также можете получить помощь по математике, загрузив нашу бесплатную брошюру «Советы по математике».
Прежде чем начать, подумайте над этими несколькими советами. Они упростят задачу, если вы будете внимательно им следовать.
1. Разработайте ответы с помощью карандаша и бумаги; перерисуйте схему, над которой работаете.
2. Конечно, ответ будет не просто числом, это будет определенное количество Ом, не забудьте указать правильную единицу (например,грамм. Ω, KΩ или MΩ) или ваш ответ не имеет смысла.
3. Когда вы вводите значения в калькулятор, преобразуйте все значения KΩ или MΩ в Ом с помощью клавиши EXP. Если вы здесь ошибетесь, то получите действительно глупые ответы, в тысячи раз слишком большие или слишком маленькие.
Итак, вы прочитали эти инструкции и готовы приступить к работе. Вот способ решить типичную проблему на бумаге, чтобы (со временем) вы не запутались.
Пример последовательной и параллельной цепи.
Хорошо, есть что вспомнить, так почему бы не попробовать несколько практических вопросов в модуле резисторов 4.5 по определению общего сопротивления некоторых цепей резисторов?
Цепь параллельных резисторови простая схема делителя тока
Формула для параллельного резистора будет нашим основным фокусом здесь. После обсуждения последовательного резистора и делителя напряжения давайте узнаем о параллельных резисторах и делении тока. Параллельный резистор относится к одному из пассивных элементов.
Вы узнаете, включены ли резисторы параллельно или последовательно, просто по их клеммному соединению. Мы называем резисторы подключенными параллельно, если их выводы соединены вместе, соответственно, от резистора к резистору.
Определение параллельной цепиЭтот параллельный резистор отличается от последовательного резистора, в котором есть только один прямой путь, проходящий через резисторы. В параллельном резисторе будет много путей от головы к голове и от хвоста к хвосту.Исходя из этого термина, параллельный резистор используется как делитель тока, а последовательный резистор — как делитель напряжения.
Поскольку ток разделяется на несколько путей или ответвлений, ток для каждой ветви может отличаться друг от друга. Но падение напряжения на каждом резисторе будет одинаковым для каждого другого. Отсюда следует, что для резисторов, включенных параллельно, они могут иметь разный ток через каждый из них, но всегда иметь одинаковое падение напряжения на каждом из них.
Зачем нам нужно изучать формулу для параллельного резистора? Вы должны знать, прочитав этот пост, пока не закончите.
Определение параллельных резисторов — это резистивная схема, в которой резисторы подключены вместе к одним и тем же узлам и образуют более одного пути тока, подключенного к одному источнику напряжения. Если вы все еще не понимаете, как мы делаем параллельную резистивную схему, мы можем найти ее ниже.
Схема параллельной цепиВ приведенном ниже примере показан простой параллельный резистор в цепи. Мы используем три резистора R 1 , R 2 и R 3 .Из объяснения выше, падение напряжения на резисторах при параллельном подключении будет одинаковым для друг друга и равным источнику напряжения.
Следовательно,
Все три резистора соединены между собой между A и B.
В отличие от последовательных резистивных цепей, где эквивалентное сопротивление является суммой всех резисторов, параллельный резистор рассчитывается по-другому. Мы используем величину, обратную сопротивлению (1 / R) для каждого сложенного резистора.
Формула для параллельного резистораКак мы уже упоминали выше, эквивалентное сопротивление параллельных резисторов является суммой, обратной величине каждого резистора. Если резисторы, соединенные параллельно, имеют одинаковое значение, это будет очень просто.
Как мы уже упоминали выше, мы можем посмотреть на пример ниже:
Если два резистора, подключенных параллельно, имеют одинаковое сопротивление, то эквивалентное сопротивление, R T — это половина сопротивления одного резистора. резистор.Следовательно, эквивалентное сопротивление двух параллельно включенных резисторов, если они имеют одинаковое сопротивление, равно R / 2. Если параллельно подключено три резистора, эквивалентное сопротивление будет R / 3 и так далее.
Помимо последовательных резисторов, этот тип цепи является наиболее распространенным типом электрических цепей. Для анализа схемы параллельного резистора мы можем использовать тот же метод для последовательного резистора, используя законы Кирхгофа и закон Ома.
Рассмотрим схему на рисунке (1),
Рисунок 1.Параллельное соединениерезисторов, при котором два резистора соединены параллельно и, следовательно, имеют одинаковое напряжение на них.
Из закона Ома
(1)
Применение KCL в узле a дает полный ток i как
(2)
Подставляя уравнение (1) в (2), мы получаем
(3)
, где R eq — эквивалентное сопротивление резисторов, включенных параллельно:
(4)
или
(5)
Следовательно,
Эквивалентное сопротивление двух параллельных резисторов равно произведение их сопротивлений, деленное на их сумму.
Выше приведено простейшее уравнение параллельного резистора, которое мы можем использовать каждый раз, когда оно нам нужно.
Следует отметить, что уравнение (5) работает только для двух параллельно подключенных резисторов.
Мы можем расширить уравнение параллельного резистора в уравнении (4) до общего случая цепи с N резисторами, включенными параллельно. Эквивалентное сопротивление составляет
(6)
Обратите внимание, что R eq всегда меньше, чем сопротивление наименьшего резистора при параллельном подключении.Если R 1 = R 2 =… = R N = R , то
(7)
Например, если 4 резистора с сопротивлением 100 Ом подключены параллельно, их эквивалентное сопротивление составляет 25 Ом.
Имейте в виду, что,
Формула проводимости для параллельной цепиЭквивалентное сопротивление параллельных резисторов всегда меньше, чем сопротивление наименьшего резистора, подключенного к этой сети. Следовательно, эквивалентное сопротивление RT будет уменьшаться каждый раз, когда у нас есть дополнительные параллельные резисторы.
Из-за этого простого, но сложного уравнения параллельного резистора для эквивалентного сопротивления мы узнаем о новом значении, известном как проводимость (G), измеренном в Сименсах (S). Проводимость обратно пропорциональна сопротивлению, где G = 1 / R. После того, как мы получим проводимость, мы преобразуем ее обратно обратно, чтобы получить эквивалентное сопротивление R T параллельных резисторов.
При параллельном подключении резисторов легче использовать проводимость, чем сопротивление.
Из уравнения (6) эквивалентная проводимость резисторов N равна
(8)
где:
Уравнение (8) утверждает:
Эквивалентная проводимость резисторов, подключенных параллельно, является суммой их индивидуальная проводимость.
Это означает, что мы можем перерисовать рисунок (1) на (2), где мы заменим сопротивления на проводимости.
Эквивалентные проводимости параллельных резисторов получаются таким же образом, как эквивалентные сопротивления последовательных резисторов.
Напротив, эквивалентные проводимости последовательных резисторов получаются таким же образом, как эквивалентные сопротивления параллельных резисторов.
Рисунок 2. Эквивалентное сопротивление или проводимостьСледовательно, эквивалентная проводимость G eq последовательно соединенных резисторов N составляет
(9)
Учитывая полный ток i, входящий в узел a на рисунке. (1) с одинаковые значения напряжения, получаем
(10)
Мы определяем параллельные резисторы как резисторы, соединенные между собой между одними и теми же двумя точками.Сам параллельный резистор имеет различные схемы.
Как найти ток в параллельной цепиПоскольку ток в параллельной цепи зависит от ее сопротивления, теперь мы узнаем, как найти ток в параллельной цепи. Токи I 1 , I 2 ,…, I n , входящие в параллельный путь резисторов, зависят от сопротивления этой ветви. Полный ток, I T , представляет собой сумму токов в параллельных ветвях.Если сопротивление между ветвями равно, то токи также будут разделены поровну.
Если R 1 = R 2 , то I 1 = I 2 = 0,5 I T . Это означает, что общий ток I T делится поровну на две ветви. Если сопротивление R 1 отличается от сопротивления R 2 , тогда нам нужно рассчитать I 1 и I 2 по-разному.Даже если напряжения на ветвях равны, ток может отличаться по закону Ома.
Для примера параллельной схемы давайте посмотрим на схему ниже и попытаемся найти все токи,
Поскольку R 1 и R 2 имеют разные значения, тогда токи I 1 и I 2 гарантированно имеют разные значения. Помните один из законов Кирхгофа?
Текущие законы Кирхгофа гласят:
Общий ток, выходящий из узла, равен току, входящему в тот же самый узел.
Следовательно,
Полный ток в цепи может быть выражен как:
После этого мы будем использовать закон Ома для расчета тока, поступающего в каждую ветвь через резисторы. I 1 — это входящий ток R 1 , а I 2 — текущий вход R 2 . Источник напряжения В с имеет 12 В, и мы получаем:
И получаем полный ток,
Чтобы прояснить это, мы используем закон Ома для вычисления I T из В. с и R T .
Общее сопротивление R T составляет
Тогда полный ток I T равен
Следовательно, это проясняет наши расчеты.
Мы заключаем, что
Комбинируя уравнения. (1) и (10) мы получаем уравнение текущего делителя.
(11)
, который показывает, что полный ток i распределяется между резисторами обратно пропорционально их сопротивлениям.
Это известно как принцип деления тока , а схема на рисунке (1) известна как делитель тока .
Обратите внимание, что больший ток проходит через меньшее сопротивление.
Рисунок 3. Короткое замыкание и разрыв в параллельном соединенииПредположим, что один из резисторов на рисунке (1) равен нулю, скажем, R 2 = 0; поэтому R 2 — это короткое замыкание, как видно на рисунке. (3a).
Из уравнения.(11), R 2 = 0 означает, что i 1 = 0, i 2 = i . Это означает, что весь ток i обходит R 1 и протекает через короткое замыкание R 2 = 0, путь с наименьшим сопротивлением.
При коротком замыкании цепи, как показано на рисунке (3a), обратите внимание, что:
- Эквивалентное сопротивление R экв. = 0
- Весь ток протекает через короткое замыкание.
Для другого крайнего примера, где R 2 = ∞, то есть R 2 — это разомкнутая цепь, как видно на рисунке. (3b).
Ток по-прежнему течет по пути с наименьшим сопротивлением, R 1 .
Уравнение (11) преобразуется в
(12)
В общем, если делитель тока имеет N проводников, параллельных току источника i , N -й проводник будет иметь ток
(13)
Очень удобно комбинировать резисторы последовательно и параллельно в одно эквивалентное сопротивление R eq .
Такое эквивалентное сопротивление должно иметь те же значения тока и напряжения, что и исходная сеть на выводе.
Примеры параллельного резистора Давайте рассмотрим приведенный ниже пример для лучшего понимания
Найдите R eq для схемы на рисунке. (4)
6 Ом и 3 Ом в параллельно
1 Ом и 5 Ом последовательно
2 Ом и 2 Ом последовательно
6 Ом и 4 Ом параллельно
Три резистора последовательно
Резисторы в Формула параллельности
В электрических цепях часто можно заменить группу резисторов одним эквивалентным резистором.Эквивалентное сопротивление ряда резисторов, включенных параллельно, можно найти с помощью обратной величины сопротивления 1 / R. Обратная величина эквивалентного сопротивления равна сумме обратных величин каждого сопротивления. Единицей измерения сопротивления является Ом (Ом), который равен Вольт на Ампер (1 Ом = 1 В / А). Также распространены более крупные резисторы с сопротивлением килоом (1 кОм = 10 3 Ом) или мегаом (1 МОм = 10 6 Ом).
R eq = эквивалентное сопротивление (Ом или более единицы)
R 1 = сопротивление первого резистора (Ом)
R 2 = сопротивление второго резистора (Ом)
R 3 = сопротивление третьего резистора (Ом)
Параллельные резисторы Вопросы по формуле:
1) Какое эквивалентное сопротивление 1000 кОм и 250 Ом.Резистор 0 кОм подключен параллельно?
Ответ: Оба сопротивления выражены в килоомах, поэтому нет необходимости изменять их единицы. Эквивалентное сопротивление можно найти в кОм по формуле:
Последний шаг — инвертировать значения с обеих сторон формулы, чтобы найти эквивалентное сопротивление:
R экв = 200,0 кОм
Эквивалентное сопротивление 1000 кОм и 250.Параллельно подключенные резисторы 0 кОм составляют 200,0 кОм.
2) Три резистора включены параллельно в электрическую цепь. Их сопротивления составляют 400 Ом, 40,0 кОм и 4,00 МОм. Какое эквивалентное сопротивление?
Ответ: Три значения сопротивления выражены в разных единицах измерения. Первым шагом к нахождению эквивалентного сопротивления является преобразование их в общую единицу. Два значения можно преобразовать в ту же единицу, что и третье. В этом решении все значения будут преобразованы в Ом.
Если R 1 = 400 Ом, R 2 = 40,0 кОм и R 3 = 4,00 МОм, то:
R 2 = 40,0 кОм
R 2 = 40000 Ом
Стоимость 3 рэнд составляет:
R 3 = 4,00 МОм
R 3 = 4000000 Ом
Эквивалентное сопротивление можно найти в Ом по формуле:
.Последний шаг — инвертировать значения с обеих сторон формулы, чтобы найти эквивалентное сопротивление:
Эквивалентное сопротивление 400 Ом, 40.Сопротивление резисторов 0 кОм и 4,00 МОм, включенных параллельно, составляет примерно 396 Ом.
Серияи параллельная — AP Physics 1
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или несколько ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
резисторов, включенных последовательно и параллельно | Комбинации резисторов
Результаты обучения
- Рассчитайте общее сопротивление различных комбинаций резисторов i.е., последовательно, параллельно и последовательно-параллельно.
- Покажите, как резисторы используются в качестве делителей напряжения и тока.
- Рассчитайте сопротивление и значение мощности для последовательного резистора, понижающего напряжение.
Отдельные резисторы могут быть соединены вместе последовательно, параллельно или в комбинации как последовательно, так и параллельно. Это приводит к более сложной схеме, полное сопротивление которой представляет собой комбинацию отдельных резисторов.
Комбинация резисторов серии
Для подключения резисторов серии , они соединяются конец к концу вместе в одну линию, как показано на рис. 1 .Характеристики последовательно соединенных резисторов можно резюмировать следующим образом:
- Общее сопротивление цепи ( R T ) увеличивается, если дополнительные резисторы соединены последовательно, и уменьшается, если резисторы удалены.
- Чтобы определить общее сопротивление цепи, просто найдите сумму отдельных сопротивлений нагрузок.
- В этом примере, если резисторы имеют маркировку R 1 , R 2 и R 3 , то общее сопротивление R T рассчитывается по формуле
Рисунок 1 Резисторы, подключенные последовательно.
ПРИМЕР 1
Проблема: Три резистора, R 1 (4 Ом), R 2 (50 Ом) и R 3 (75 Ом) подключены последовательно, как показано на Рисунок 2 . Определите значение общего сопротивления комбинированной цепи.
Рисунок 2 Схема для примера 1.
Решение:
Резисторы, соединенные последовательно, используются как делители напряжения , , как показано на схеме , рис. 3 .Делители напряжения широко используются в схемах, где один источник напряжения должен обеспечивать несколько разных значений напряжения для разных частей схемы.
Характеристики схемы последовательного делителя напряжения можно резюмировать следующим образом:
- Через каждый резистор протекает одинаковое количество тока.
- Входное напряжение делится пропорционально между последовательно соединенными резисторами.
- Падение напряжения на резисторе в последовательной цепи прямо пропорционально сопротивлению резистора.
- Чем выше значение сопротивления, тем больше падение напряжения.
Рисунок 3 Схема делителя напряжения.
Для схемы делителя напряжения падение напряжения на каждом резисторе обычно является фактором, который необходимо определить. Падение напряжения на любом резисторе пропорционально отношению его сопротивления к общему сопротивлению цепи.
Формула делителя напряжения позволяет рассчитать падение напряжения на любом из последовательно подключенных резисторов без необходимости сначала рассчитывать значение тока цепи.Заявлено в виде формулы:
ПРИМЕР 2
Резисторы R 1 (5 кОм), R 2 (3 кОм) и R 3 (2 кОм) ) соединены последовательно, образуя делитель напряжения, как показано на Рисунок 4 . Если на схему подается входное напряжение 9 вольт, рассчитайте значение падения напряжения на каждом из резисторов, используя формулу делителя напряжения.
Рисунок 4 Схема для примера 2.
Решение:
ПРИМЕР 3
У вас есть источник на 120 В и вы хотите использовать последовательно понижающий резистор в сочетании с контрольной лампой 6 В при 150 мА для индикации подачи питания ( Рисунок 5 ). Определите значение сопротивления падения серии и требуемую мощность.
Рисунок 5 Схема для примера 3.
Решение:
Параллельная комбинация резисторовРезисторы подключаются параллельно путем соединения их бок о бок друг напротив друга, как показано на Рисунок 6 .Обратите внимание, что два конца резисторов подключены к одним и тем же двум точкам.
Характеристики параллельно соединенных резисторов можно резюмировать следующим образом:
- Общее сопротивление (R T ) сформированной цепи на меньше , чем сопротивление самого низкого значения сопротивления, присутствующего в любой из ветвей.
- Каждый резистор обеспечивает отдельный параллельный путь для прохождения тока.
- Если у вас есть несколько резисторов одинакового номинала, подключенных параллельно, то общее сопротивление легче всего найти, разделив общее значение сопротивления на количество подключенных резисторов.Для трех резисторов по 150 Ом, включенных параллельно, общее сопротивление составляет
Рисунок 6 Сопротивление , подключенных параллельно.
Чтобы найти полное сопротивление двух неравных значений резисторов, соединенных параллельно (очень распространенное использование), используется формула произведения на сумму. Эта формула:
ПРИМЕР 4
Проблема: Резистор сопротивлением 60 Ом подключен параллельно с резистором 40 Ом, как показано на рис. 7 .Определите значение общего комбинированного сопротивления двух компонентов, используя формулу «произведение на сумму».
Рисунок 7 Схема для примера 4.
Решение:
Формула произведения на сумму лучше всего работает для двух резисторов, включенных параллельно. Если параллельно подключено более двух резисторов, использование становится труднее и менее практичным. Для более чем двух резисторов разных номиналов, соединенных параллельно, используется общая формула для полного сопротивления параллельной цепи.Эта формула:
ПРИМЕР 5
Проблема: Три резистора, R 1 (120 Ом), R 2 (60 Ом) и R 3 ( 40 Ом) подключены параллельно, как показано на Рисунок 8 . Определите значение общего сопротивления комбинированной цепи.
Рисунок 8 Цепь для примера 5.
Решение:
Параллельные резистивные цепи можно рассматривать как делители тока , потому что ток разделяется или делится между различными резисторами, как показано на рисунке 9 .
Характеристики схемы параллельного делителя тока можно резюмировать следующим образом:
- Ток, протекающий через каждый резистор ответвления, обратно пропорционален его значению сопротивления.
- Чем меньше значение сопротивления, тем больше ток, и наоборот.
- Резисторы с одинаковым сопротивлением будут пропускать через них одинаковое количество тока.
- Формула, описывающая делитель тока, аналогична формуле для делителя напряжения и может быть выражена следующим образом:
Рисунок 9 Схема делителя тока.
ПРИМЕР 6
Проблема: Резисторы R 1 R 2 и R 3 (2 Ом, 3 Ом и 6 Ом соответственно) подключены параллельно, как показано на Рисунок 10 . Используйте формулу делителя тока, чтобы вычислить значение тока, протекающего через каждый из нагрузочных резисторов, если общий ток, протекающий в цепи, составляет 10 ампер.
Рисунок 10 Схема для примера 6.
Решение:
ПРИМЕР 7
Проблема: При параллельном подключении дополнительных нагрузок общее сопротивление цепи уменьшается. Для цепи, показанной на рис. 11 , определите полное сопротивление цепи при каждом из следующих рабочих условий:
- Переключатели 1 и 2 замкнуты.
- Переключатели 1, 2 и 3 замкнуты.
Рисунок 11 Схема для примера 7.
Решение:
Последовательно-параллельная комбинация резисторовКомбинированные резистивные цепи, также известные как последовательно-параллельные резистивные цепи , объединяют резисторы последовательно с резисторами, включенными параллельно, как показано на рисунке 12 .
Правила, регулирующие эти цепи, такие же, как и правила, разработанные для последовательных и параллельных цепей. Сначала определяется сопротивление совокупного полного сопротивления параллельной части.Затем общее сопротивление параллельной части добавляется к любому последовательному сопротивлению, чтобы найти общее сопротивление последовательно-параллельной комбинированной цепи.
Рисунок 12 Последовательно-параллельное соединение резисторов.
ПРИМЕР 8
Проблема: Резистор 9 Ом, R 1 , и резистор 60 Ом, R 2 , подключены параллельно друг другу и последовательно с резистор 40 Ом, R 3 , как показано на Рисунок 13 .Определите общее сопротивление этой последовательно-параллельной комбинации резисторов.
Рисунок 13 Цепь для примера 8.
Решение:
ПРИМЕР 9
Проблема: Показания сопротивления можно использовать для проверки цепей на наличие неисправностей. Как определено в предыдущем примере, нормальное полное сопротивление этой последовательно-параллельной схемы цепи , рис. 14, составляет 60 Ом.
- Найдите новое значение R T , если резистор R 1 будет поврежден разомкнут , в то время как значения сопротивления R 2 и R 3 останутся тем же.
- Аналогичным образом найдите новое значение R T , если резистор R 3 будет поврежден закорочен , в то время как значения сопротивления R 1 и R 2 останутся такой же.
Рисунок 14 Цепь для примера 9.
Решение:
- При разомкнутом отказе R 1 цепь будет состоять из R 3 последовательно с R 2 и всего сопротивление будет:
- При замкнутом коротком замыкании R 3 цепь будет состоять из R 1 , включенных параллельно с R 2 , а общее сопротивление будет:
Вопросы для обзора
- Рассчитайте общее сопротивление для каждой из следующих цепей резисторов:
- Последовательная цепь: R1 = 40 Ом, R2 = 75 Ом
- Параллельная цепь: R1 = 200 Ом, R2 = 200 Ом, R3 = 200 Ом
- Последовательная цепь: R1 = 2000 Ом, R2 = 6000 Ом, R3 = 2200 Ом
- Параллельная цепь: R1 = 14 Ом, R2 = 32 Ом
- Последовательная цепь: R1 = 4700 Ом, R2 = 800 Ом, R3 = 200 Ом
- Параллельная цепь: R1 = 60 Ом, R2 = 30 Ом, R3 = 15 Ом
9 0003 Резисторы R 1 , R 2 и R 3 (50 Ом, 30 Ом и 20 Ом соответственно) подключены последовательно через приложенное напряжение 200 В, чтобы сформировать делитель напряжения.Используя формулу делителя напряжения, рассчитайте напряжения E 1 , E 2 и E 3 . - Суммарный ток на два параллельно соединенных резистора составляет 3 А. Сопротивление резистора R 1 составляет 10 Ом, а сопротивление R 2 равно 40 Ом. Используя формулу делителя тока, рассчитайте токи I 1 и I 2 .
- Резистор 5 Ом, R 1 , и резистор 20 Ом, R 2 , подключены параллельно друг другу и последовательно с резистором 6 Ом, R 3 .Вычислите полное сопротивление этой последовательно-параллельной цепи.
- Вам даны три резистора по 100 Ом, которые нужно соединить вместе. Опишите три возможные конфигурации цепей и вычислите их значения общего сопротивления.
Контрольные вопросы — ответы
- (a) 115 Ом, (b) 66,7 Ом, (c) 10 200 Ом, (d) 9,74 Ом, (e) 5700 Ом, (f) 8,57 Ом
- E 1 = 100 В, E 2 = 60 В, E 3 = 40 В
- I 1 = 2.4 A, I 2 = 0,6 A
- 10 Ом
- Три резистора по 100 Ом, подключенных последовательно, общее сопротивление 300 Ом. Три резистора по 100 Ом, подключенные параллельно, общее сопротивление 33,3 Ом. Два резистора 100 Ом, подключенные параллельно, а затем последовательно соединенные с резистором 100 Ом, общее сопротивление 150 Ом.
19.3 Параллельные схемы — Физика
Задачи обучения раздела
К концу этого раздела вы сможете делать следующее:
- Расшифровка принципиальных схем с параллельными резисторами
- Расчет эквивалентного сопротивления комбинаций резисторов, содержащих последовательные и параллельные резисторы
Поддержка учителей
Поддержка учителей
Цели обучения в этом разделе помогут вашим ученикам овладеть следующими стандартами:
- (5) Научные концепции.Студент знает природу сил в физическом мире. Ожидается, что студент:
- (ж) дизайн. построить и рассчитать в терминах сквозного тока, разности потенциалов, сопротивления и мощности, используемой элементами электрической цепи, соединенными как в последовательной, так и в параллельной комбинациях.
Кроме того, лабораторное руководство по физике в средней школе рассматривает содержание этого раздела лаборатории под названием «Схемы», а также следующие стандарты:
- (5) Учащийся знает природу сил в физическом мире.Ожидается, что студент:
- (F) проектировать, конструировать и рассчитывать в терминах сквозного тока, разности потенциалов, сопротивления и мощности, используемой элементами электрической цепи, соединенными как в последовательной, так и в параллельной комбинациях.
Раздел Ключевые термины
Параллельные резисторы
В предыдущем разделе мы узнали, что последовательно включенные резисторы — это резисторы, которые подключаются друг за другом. Если вместо этого мы объединим резисторы, подключив их рядом друг с другом, как показано на рисунке 19.16, то говорят, что резисторы подключены параллельно . Резисторы включены параллельно, когда оба конца каждого резистора соединены непосредственно вместе.
Обратите внимание, что верхние части резисторов подключены к одному проводу, поэтому напряжение на верхушках каждого резистора одинаково. Точно так же все нижние части резисторов подключены к одному и тому же проводу, поэтому напряжение на нижней стороне каждого резистора одинаково. Это означает, что падение напряжения на каждом резисторе одинаковое.В этом случае падение напряжения соответствует номинальному напряжению батареи В, , потому что верхний и нижний провода подключаются к положительной и отрицательной клеммам батареи соответственно.
Хотя падение напряжения на каждом резисторе одинаково, мы не можем сказать то же самое для тока, протекающего через каждый резистор. Таким образом, I1, I2 и I3I1, I2 и I3 не обязательно одинаковы, потому что резисторы R1, R2 и R3R1, R2 и R3 не обязательно имеют одинаковое сопротивление.
Обратите внимание, что три резистора на рисунке 19.16 обеспечивают три разных пути, по которым может течь ток. Это означает, что эквивалентное сопротивление для этих трех резисторов должно быть меньше наименьшего из трех резисторов. Чтобы понять это, представьте, что наименьший резистор — это единственный путь, по которому может течь ток. Теперь добавьте альтернативные пути, подключив другие резисторы параллельно. Поскольку у тока больше путей, общее сопротивление (то есть эквивалентное сопротивление) будет уменьшаться. Следовательно, эквивалентное сопротивление должно быть меньше наименьшего сопротивления параллельных резисторов.
Рисунок 19.16 На левой принципиальной схеме показаны три резистора, включенных параллельно. Напряжение В батареи приложено ко всем трем резисторам. Токи, протекающие через каждую ветвь, не обязательно равны. На правой принципиальной схеме показано эквивалентное сопротивление, заменяющее три параллельных резистора.
Teacher Support
Teacher Support
Подчеркните, что напряжение на каждом параллельном резисторе одинаковое, а ток может отличаться; то же самое будет, если пара резисторов будет иметь одинаковое сопротивление.
Чтобы найти эквивалентное сопротивление RequivRequiv трех резисторов R1, R2 и R3R1, R2 и R3, мы применим закон Ома к каждому резистору. Поскольку падение напряжения на каждом резисторе составляет В , мы получаем
V = I1R1, V = I2R2, V = I3R3V = I1R1, V = I2R2, V = I3R319,21
или
I1 = VR1, I2 = VR2, I3 = VR3. I1 = VR1, I2 = VR2, I3 = VR3.19,22
Из сохранения заряда мы также знаем, что три тока I1, I2 и I3I1, I2 и I3 должны складываться, чтобы получить ток I , который проходит через батарею.Если бы это было не так, ток должен был бы таинственным образом создаваться или разрушаться где-то в цепи, что физически невозможно. Таким образом, имеем
Я = I1 + I2 + I3. I = I1 + I2 + I3.19,23
Вставка выражений для I1, I2 и I3I1, I2 и I3 в это уравнение дает
I = VR1 + VR2 + VR3 = V (1R1 + 1R2 + 1R3) I = VR1 + VR2 + VR3 = V (1R1 + 1R2 + 1R3)19,24
или
V = I (11 / R1 + 1 / R2 + 1 / R3). V = I (11 / R1 + 1 / R2 + 1 / R3).19,25
Эта формула представляет собой закон Ома, где множитель в скобках представляет собой эквивалентное сопротивление.
V = I (11 / R1 + 1 / R2 + 1 / R3) = IRэкв. V = I (11 / R1 + 1 / R2 + 1 / R3) = IRequiv.19,26
Таким образом, эквивалентное сопротивление для трех параллельно включенных резисторов составляет
Требование = 11 / R1 + 1 / R2 + 1 / R3. Требование = 11 / R1 + 1 / R2 + 1 / R3.19,27
Та же самая логика работает для любого количества резисторов, включенных параллельно, поэтому общая форма уравнения, которая дает эквивалентное сопротивление резисторов Н , подключенных параллельно, составляет
Требование = 11 / R1 + 1 / R2 + ⋯ + 1 / RN. Требование = 11 / R1 + 1 / R2 + ⋯ + 1 / RN.19,28
Рабочий пример
Найдите ток через параллельные резисторы
Три схемы ниже эквивалентны.Если номинальное напряжение батареи Vbattery = 3VVbattery = 3V, каково эквивалентное сопротивление цепи и какой ток проходит через цепь?
Стратегия
Три резистора подключены параллельно, и падение напряжения на них составляет В АКБ . Таким образом, мы можем применить уравнение для эквивалентного сопротивления резисторов, включенных параллельно, которое принимает вид
Требование = 11 / R1 + 1 / R2 + 1 / R3. Требование = 11 / R1 + 1 / R2 + 1 / R3.19,29
Схема с эквивалентным сопротивлением показана ниже.Как только мы узнаем эквивалентное сопротивление, мы можем использовать закон Ома, чтобы найти ток в цепи.
Решение
Вставка заданных значений сопротивления в уравнение эквивалентного сопротивления дает
Требуемое = 11 / R1 + 1 / R2 + 1 / R3 = 11/10 Ом + 1/25 Ом + 1/15 Ом = 4,84 Ом Требуемое = 11 / R1 + 1 / R2 + 1 / R3 = 11/10 Ом + 1/25 Ом + 1/15 Ом = 4,84 Ом.19,30
Таким образом, ток в цепи равен
V = IRI = VR = 3 В 4,84 Ом = 0,62 А. V = IRI = VR = 3 В 4,84 Ом = 0,62 А.19,31
Обсуждение
Хотя 0.62 А протекает через всю цепь, обратите внимание, что этот ток не проходит через каждый резистор. Однако, поскольку электрический заряд должен сохраняться в цепи, сумма токов, проходящих через каждую ветвь цепи, должна составлять ток, проходящий через батарею. Другими словами, мы не можем волшебным образом создать заряд где-нибудь в цепи и добавить этот новый заряд к току. Давайте проверим это рассуждение, используя закон Ома, чтобы найти ток через каждый резистор.
I1 = VR1 = 3 В 10 Ом = 0.30AI2 = VR2 = 3V25Ω = 0.12AI3 = VR3 = 3V15Ω = 0.20AI1 = VR1 = 3V10Ω = 0.30AI2 = VR2 = 3V25Ω = 0.12AI3 = VR3 = 3V15Ω = 0.20A19,32
Как и ожидалось, эти токи в сумме дают 0,62 A, который представляет собой обнаруженный полный ток, проходящий через эквивалентный резистор. Также обратите внимание, что наименьший резистор имеет наибольший ток, протекающий через него, и наоборот.
Рабочий пример
Рассуждения с параллельными резисторами
Без каких-либо расчетов, каково эквивалентное сопротивление трех одинаковых резисторов R , включенных параллельно?
Стратегия
Три идентичных резистора R , включенных параллельно, образуют три идентичных пути, по которым может течь ток.Таким образом, току протекать через эти резисторы в три раза легче, чем через один из них.
Решение
Если протекать через три одинаковых резистора R в три раза легче, чем через один из них, эквивалентное сопротивление должно быть втрое меньше: R /3.
Обсуждение
Давайте проверим наши рассуждения, вычислив эквивалентное сопротивление трех одинаковых резисторов R , включенных параллельно.Уравнение эквивалентного сопротивления параллельно включенных резисторов дает
Требуется = 11 / R + 1 / R + 1 / R = 13 / R = R3. Требуется = 11 / R + 1 / R + 1 / R = 13 / R = R3.19,33
Таким образом, наши рассуждения были правильными. В общем, когда доступно больше путей, по которым может течь ток, эквивалентное сопротивление уменьшается. Например, если у нас есть идентичные резисторы R параллельно, эквивалентное сопротивление будет R /10.
Практические задачи
10.Три резистора 10, 20 и 30 Ом подключены параллельно.Какое эквивалентное сопротивление?
- Эквивалентное сопротивление 5,5 Ом
- Эквивалентное сопротивление 60 Ом
- Эквивалентное сопротивление 6 × 103 Ом
- Эквивалентное сопротивление 6 × 104 Ом
Если падение напряжения на 5 \ text {-V} происходит на R_1, а R_1 подключен параллельно к R_2, каково падение напряжения на R_2?
- Падение напряжения на 0 \, \ text {V}.
- Падение напряжения на 2.5 \, \ text {V}.
- Падение напряжения на нем 5 \, \ text {V}.
- Падение напряжения на нем 10 \, \ text {V}.
Сопротивления параллельно и последовательно
Более сложные соединения резисторов иногда представляют собой просто комбинации последовательного и параллельного. Комбинации последовательных и параллельных резисторов могут быть уменьшены до одного эквивалентного сопротивления с помощью техники, показанной на рисунке 19.17. Различные части идентифицируются как последовательные или параллельные, уменьшаются до их эквивалентов и далее уменьшаются до тех пор, пока не останется единственное сопротивление.Процесс более трудоемкий, чем трудный.
Рисунок 19.17 Эта комбинация из семи резисторов имеет как последовательные, так и параллельные части. Каждое из них идентифицируется и приводится к эквивалентному сопротивлению, а затем уменьшается до тех пор, пока не будет достигнуто единичное эквивалентное сопротивление.
Поддержка учителей
Поддержка учителей
Предупреждение о неправильном представлении
У студентов может возникнуть соблазн немедленно сложить R1R1 и R7R7 вместе, потому что они кажутся последовательными.Обратите внимание, что R1R1 включен последовательно с параллельной комбинацией R7R7 и всех резисторов справа от R7R7. Таким образом, перед добавлением к R1R1 необходимо найти эквивалентное сопротивление этой параллельной комбинации.
Поддержка учителей
Поддержка учителей
Рассмотрите этот пример вместе с учащимися, чтобы убедиться, что они понимают сокращение, которое происходит на каждом этапе.
Давайте проработаем четыре шага на рисунке 19.17, чтобы уменьшить семь резисторов до одного эквивалентного резистора.Чтобы не отвлекать внимание от алгебры, предположим, что каждый резистор имеет сопротивление 10 Ом. На шаге 1 мы уменьшаем два набора параллельных резисторов, обведенных синей пунктирной петлей. Верхний набор имеет три резистора, включенных параллельно, и будет уменьшен до одного эквивалентного резистора RP1RP1. Нижний набор имеет два резистора, включенных параллельно, и будет уменьшен до одного эквивалентного резистора RP2RP2. Используя уравнение эквивалентного сопротивления параллельно включенных резисторов, получаем
RP1 = 11 / R2 + 1 / R3 + 1 / R4 = 11 / 10Ω + 1 / 10Ω + 1 / 10Ω = 103Ω RP2 = 11 / R5 + 1 / R6 = 11 / 10Ω + 1 / 10Ω = 5Ω.RP1 = 11 / R2 + 1 / R3 + 1 / R4 = 11 / 10Ω + 1 / 10Ω + 1 / 10Ω = 103Ω RP2 = 11 / R5 + 1 / R6 = 11 / 10Ω + 1 / 10Ω = 5Ω.19,34
Эти два эквивалентных сопротивления обведены красной пунктирной петлей после шага 1. Они включены последовательно, поэтому мы можем использовать уравнение для эквивалентного сопротивления последовательно включенных резисторов, чтобы уменьшить их до одного эквивалентного сопротивления RS1RS1. Это делается на шаге 2, в результате получается
RS1 = RP1 + RP2 = 103 Ом + 5 Ом = 253 Ом. RS1 = RP1 + RP2 = 103 Ом + 5 Ом = 253 Ом.19,35
Эквивалентный резистор RS1RS1 появляется в зеленой пунктирной петле после шага 2.Этот резистор включен параллельно резистору R7R7, поэтому пара может быть заменена эквивалентным резистором RP3RP3, который равен
. RP3 = 11 / RS1 + 1 / R7 = 13 / 25Ω + 1 / 10Ω = 5011Ω. RP3 = 11 / RS1 + 1 / R7 = 13 / 25Ω + 1 / 10Ω = 5011Ω.19,36
Это делается на шаге 3. Резистор RP3RP3 включен последовательно с резистором R1R1, как показано в фиолетовой пунктирной петле после шага 3. Эти два резистора объединяются на последнем шаге, чтобы сформировать окончательный эквивалент резистора RequivRequiv, что составляет
Requiv = R1 + RP3 = 10 Ом + 5011 Ом = 16011 Ом.Requiv = R1 + RP3 = 10 Ом + 5011 Ом = 16011 Ом.19,37
Таким образом, вся комбинация из семи резисторов может быть заменена одним резистором с сопротивлением около 14,5 Ом.
Это была большая работа, и вы можете спросить, зачем мы ее делаем. Для нас важно знать эквивалентное сопротивление всей цепи, чтобы мы могли рассчитать ток, протекающий по цепи. Закон Ома говорит нам, что ток, протекающий по цепи, зависит от сопротивления цепи и напряжения в цепи.Но чтобы узнать силу тока, мы должны сначала узнать эквивалентное сопротивление.
Вот общий подход к поиску эквивалентного резистора для любой произвольной комбинации резисторов:
- Определите группу резисторов, которые включены только параллельно или только последовательно.
- Для резисторов, включенных последовательно, используйте уравнение для эквивалентного сопротивления резисторов, подключенных последовательно, чтобы уменьшить их до одного эквивалентного сопротивления. Для резисторов, подключенных параллельно, используйте уравнение для эквивалентного сопротивления резисторов, подключенных параллельно, чтобы уменьшить их до одного эквивалентного сопротивления.
- Нарисуйте новую принципиальную схему с резисторами из шага 1, замененными их эквивалентными резисторами.
- Если в цепи осталось более одного резистора, вернитесь к шагу 1 и повторите. В противном случае все готово.
Развлечение по физике
Робот
Роботы захватывают наше коллективное воображение уже более века. Теперь мечта о создании умных машин для выполнения нашей грязной работы, а иногда и просто для того, чтобы составить нам компанию, становится реальностью. Робототехника стала огромной областью исследований и разработок, некоторые технологии уже коммерциализированы.Подумайте, например, о небольших автономных пылесосах.
На рис. 19.18 показаны лишь некоторые из множества различных форм, которые могут принимать роботы. Самые продвинутые роботы-гуманоиды могут ходить, наливать напитки и даже танцевать (хотя и не очень изящно). Другие роботы вдохновлены биологией, например, собачий робот , показанный на средней фотографии рис. 19.18. Этот робот может нести сотни фунтов груза по пересеченной местности. Фотография справа на рис. 19.18 показывает внутреннюю работу блока M, , разработанного Массачусетским технологическим институтом.Эти простые на вид блоки содержат инерционные колеса и электромагниты, которые позволяют им вращаться, переворачиваться в воздух и соединяться друг с другом в самых разных формах. Обмениваясь беспроводной связью между собой, они самостоятельно собираются в различные формы, такие как столы, стулья и, возможно, когда-нибудь даже здания.
Все роботы включают в себя огромное количество физики и инженерии. Простое наливание напитка было освоено роботами совсем недавно, после более 30 лет исследований и разработок! Баланс и выбор времени, которые мы, люди, считаем само собой разумеющимися, на самом деле являются очень сложной задачей, требующей отличного баланса, ловкости и обратной связи.Чтобы справиться с этим, требуются датчики для обнаружения баланса, вычислительная мощность для анализа данных и передачи соответствующих компенсирующих действий, а также соединения и приводы для выполнения требуемых действий.
Помимо определения силы тяжести или ускорения, роботы могут содержать несколько различных датчиков для обнаружения света, звука, температуры, запаха, вкуса и т. Д. Все эти устройства основаны на физических принципах, которые вы изучаете в этом тексте. Например, оптика, используемая для машинного зрения, аналогична оптике, используемой в ваших цифровых камерах: пиксельные полупроводниковые детекторы, в которых свет преобразуется в электрические сигналы.Для определения температуры можно использовать простые термисторы, которые представляют собой резисторы, сопротивление которых изменяется в зависимости от температуры.
Строить робота сегодня намного проще, чем несколько лет назад. Многие компании сейчас предлагают комплекты для сборки роботов. Они варьируются по сложности, от чего-то подходящего для младших школьников до чего-то, что бросает вызов лучшим профессиональным инженерам. Если интересно, вы можете легко найти их в Интернете и начать создавать своего собственного робота уже сегодня.
Рис. 19.18 Роботы бывают разных форм и размеров, от классического типа гуманоид до собачьих роботов до небольших кубиков, которые самостоятельно собираются для выполнения различных задач.
Watch Physics
Параллельные резисторы
В этом видео лектор обсуждает простую схему с параллельной батареей и парой резисторов. Он подчеркивает, что электроны текут в направлении, противоположном положительному току, а также использует тот факт, что напряжение одинаково во всех точках идеального провода.Вывод очень похож на то, что делается в этом тексте, но лектор хорошо его проходит, объясняя каждый шаг.
Проверка захвата
Верно или неверно. На принципиальной схеме мы можем предположить, что напряжение одинаково в каждой точке данного провода.
- ложь
- правда
Watch Physics
Последовательные и параллельные резисторы
В этом видео показано, как рассчитать эквивалентное сопротивление цепи, содержащей резисторы, включенные параллельно и последовательно.Лектор использует тот же подход, что и описанный выше, для поиска эквивалентного сопротивления.
Проверка захвата
Представьте, что N одинаковых резисторов соединены параллельно. Каждый резистор имеет сопротивление R . Какое эквивалентное сопротивление для этой группы параллельных резисторов?
- Эквивалентное сопротивление ( R ) N .
- Эквивалентное сопротивление — NR.
- Эквивалентное сопротивление RN.РН.
- Эквивалентное сопротивление — NR.NR.
Рабочий пример
Найдите ток через схему комплексного резистора
Батарея в цепи ниже имеет номинальное напряжение 10 В. Какой ток течет по цепи и в каком направлении?
Стратегия
Примените стратегию поиска эквивалентного сопротивления, чтобы заменить все резисторы одним эквивалентным сопротивлением, затем используйте закон Ома, чтобы найти ток через эквивалентный резистор.
Решение
Комбинацию резисторов R4R4 и R5R5 можно уменьшить до эквивалентного сопротивления
RP1 = 11 / R4 + 1 / R5 = 11/45 Ом + 1/60 Ом = 25,71 Ом R. RP1 = 11 / R4 + 1 / R5 = 11/45 Ом + 1/60 Ом = 25,71 Ом R.19,38
Замена R4R4 и R5R5 с этим эквивалентным сопротивлением дает схему ниже.
Теперь мы заменим два верхних резистора R2R2 и R3R3 эквивалентным резистором RS1RS1 и два нижних резистора RP1RP1 и R6R6 их эквивалентным резистором RS2RS2.Эти резисторы включены последовательно, поэтому мы складываем их вместе, чтобы найти эквивалентное сопротивление.
RS1 = R2 + R3 = 50 Ом + 30 Ом = 80 Ом RS2 = RP1 + R6 = 25,71 Ом + 20 Ом = 45,71 Ом RS1 = R2 + R3 = 50 Ом + 30 Ом = 80 Ом RS2 = RP1 + R6 = 25,71 Ом + 20 Ом = 45,71 Ом19,39
Замена соответствующих резисторов на их эквивалентные резисторы дает схему, приведенную ниже.
Теперь замените два резистора RS1 и RS2RS1 и RS2, которые включены параллельно, на их эквивалентные резисторы RP2RP2. Сопротивление RP2RP2 —
RP2 = 11 / RS1 + 1 / RS2 = 11 / 80Ω + 1/45.71 Ом = 29,09 Ом. RP2 = 11 / RS1 + 1 / RS2 = 11/80 Ом + 1 / 45,71 Ом = 29,09 Ом.19,40
Обновление принципиальной схемы путем замены RS1 и RS2 RS1 и RS2 с этим эквивалентным сопротивлением дает схему ниже.
Наконец, мы объединяем резисторы R1 и RP2R1 и RP2, которые включены последовательно. Эквивалентное сопротивление: RS3 = R1 + RP2 = 75 Ом + 29,09 Ом = 104,09 Ом. RS3 = R1 + RP2 = 75 Ом + 29,09 Ом = 104,09 Ом. Окончательная схема показана ниже.
Теперь мы используем закон Ома, чтобы найти ток в цепи.
V = IRS3I = VRS3 = 10V104.09Ω = 0,096AV = IRS3I = VRS3 = 10V 104,09Ω = 0,096A19,41
Ток идет от положительной клеммы батареи к отрицательной клемме батареи, поэтому в этой цепи он течет по часовой стрелке.
Обсуждение
Этот расчет может показаться довольно длинным, но, немного попрактиковавшись, вы сможете объединить несколько этапов. Также обратите внимание, что при вычислении учитывались лишние значащие цифры. Только в конце окончательный результат был округлен до двух значащих цифр.
Рабочий пример
Странные электрические схемы
Иногда вы можете встретить принципиальные схемы, которые нарисованы не очень аккуратно, например, схему, показанную ниже.Эта принципиальная схема больше похожа на то, как настоящая схема может появиться на лабораторном столе. Каково эквивалентное сопротивление резисторов на этой диаграмме, если каждый резистор имеет сопротивление 10 Ом и номинальное напряжение батареи 12 В.
Стратегия
Давайте перерисуем эту принципиальную схему, чтобы было понятнее. Затем мы применим описанную выше стратегию для расчета эквивалентного сопротивления.
Решение
Чтобы перерисовать диаграмму, рассмотрите рисунок ниже.В верхней схеме синие резисторы образуют путь от положительной клеммы батареи к отрицательной. Параллельно с этой цепью расположены красные резисторы, которые составляют еще один путь от положительной к отрицательной клемме батареи. Синий и красный пути показаны более четко на нижней принципиальной схеме. Обратите внимание, что как на верхней, так и на нижней схемах синий и красный пути соединяют положительную клемму аккумулятора с отрицательной клеммой аккумулятора.
Теперь легче увидеть, что R1 и R2R1 и R2 подключены параллельно, а параллельная комбинация находится последовательно с R4R4. Эта комбинация, в свою очередь, параллельна последовательной комбинации R3 и R5R3 и R5. Сначала мы вычисляем синюю ветвь, которая содержит R1, R2 и R4R1, R2 и R4. Эквивалентное сопротивление
Rblue = 11 / R1 + 1 / R2 + R4 = 11 / 10Ω + 1 / 10Ω + 10Ω = 15Ω. Rblue = 11 / R1 + 1 / R2 + R4 = 11 / 10Ω + 1 / 10Ω + 10Ω = 15Ω.19,42
где мы показываем вклад параллельной комбинации резисторов и последовательной комбинации резисторов.Теперь рассчитаем эквивалентное сопротивление красной ветви, которое составляет
Rred = R3 + R5 = 10 Ом + 10 Ом = 20 Ом. Rred = R3 + R5 = 10 Ом + 10 Ом = 20 Ом.19,43
Если вставить эти эквивалентные резисторы в схему, получится схема, показанная ниже.
Эти два резистора включены параллельно, поэтому их можно заменить одним эквивалентным резистором с сопротивлением
Requiv = 11 / Rblue + 1 / Rred = 11 / 15Ω + 1 / 20Ω = 8,6Ω. Requiv = 11 / Rblue + 1 / Rred = 11 / 15Ω + 1 / 20Ω = 8.6Ω.19,44
Окончательная эквивалентная схема показана ниже.
Обсуждение
Найти эквивалентное сопротивление было проще благодаря понятной принципиальной схеме. Вот почему мы стараемся делать четкие принципиальные схемы, где резисторы, включенные параллельно, выстроены параллельно друг другу и в одном и том же горизонтальном положении на схеме.
Теперь мы можем использовать закон Ома, чтобы найти ток, проходящий через каждую ветвь этой цепи. Рассмотрим принципиальную схему с RblueRblue и RredRred. Напряжение на каждой из этих ветвей составляет 12 В (т.е.е. номинальное напряжение аккумулятора). Ток в синей ветке —
Iblue = VRblue = 12В15Ω = 0,80A Синий = VRblue = 12V15Ω = 0,80A.19,45
Ток через красную ветвь
Ired = VRred = 12 В20 Ом = 0,60 А. Ired = VRred = 12 В 20 Ом = 0,60 А.19,46
Ток, протекающий через батарею, должен быть суммой этих двух токов (вы понимаете, почему?), Или 1,4 А.
Практические задачи
12.Какова формула эквивалентного сопротивления двух параллельных резисторов с сопротивлением R 1 и R 2 ?
- Эквивалентное сопротивление двух параллельных резисторов Reqv = R1 + R2 Reqv = R1 + R2
- Эквивалентное сопротивление двух параллельных резисторов Reqv = R1 × R2Reqv = R1 × R2
- Эквивалентное сопротивление двух параллельных резисторов Reqv = R1-R2Reqv = R1-R2
- Эквивалентное сопротивление двух параллельных резисторов Reqv = 11 / R1 + 1 / R2Reqv = 11 / R1 + 1 / R2
Рисунок 19.19
Какое эквивалентное сопротивление для двух показанных резисторов?
- Эквивалентное сопротивление 20 Ом
- Эквивалентное сопротивление 21 Ом
- Эквивалентное сопротивление 90 Ом
- Эквивалентное сопротивление 1,925 Ом
Проверьте свое понимание
14.Падение напряжения на параллельных резисторах ________.
- то же для всех резисторов
- больше для больших резисторов На
- меньше для резисторов большего размера
- больше для меньших резисторов
Рассмотрим схему из параллельных резисторов. Наименьший резистор — 25 Ом. Каков верхний предел эквивалентного сопротивления?
- Верхний предел эквивалентного сопротивления составляет 2,5 Ом.
- Верхний предел эквивалентного сопротивления составляет 25 Ом.
- Верхний предел эквивалентного сопротивления составляет 100 Ом.
- Нет верхнего предела.
резисторов, подключенных параллельно | Формула эквивалентного сопротивления
ВведениеДва резистора считаются подключенными параллельно, если оба вывода резистора подключены к каждому соответствующему выводу другого резистора.В сети параллельных резисторов ток может проходить по нескольким путям, в отличие от сети с последовательными резисторами, поскольку существует несколько путей для прохождения тока. Следовательно, параллельные резистивные цепи являются делителями тока.
Параллельные резисторыЕсли два или более резистора подключены параллельно, то разность потенциалов на каждом резисторе одинакова. При параллельном соединении резисторы подключаются к одним и тем же узлам. Это можно определить по наличию более чем одного пути прохождения тока.Например, приведенная ниже схема представляет собой параллельное соединение резисторов. Разность потенциалов на резисторе R1 такая же, как и на резисторе R2, который равен потенциалу питания V AB .
Если V AB — это приложенный потенциал, тогда
V R1 = V R2 = V AB
В следующей схеме резисторы R1, R2 и R3 подключены параллельно комбинация.
Здесь потенциал питания V AB между точками A и B.Поскольку резисторы R1, R2 и R3 соединены параллельно, разность потенциалов на каждом резисторе такая же, как у источника питания. Следовательно, V AB = V R1 = V R2 = V R3 .
Где
В R1 — потенциал на резисторе R1.
В R2 — это потенциал на резисторе R2.
В R3 — потенциал на резисторе R3.
Но ток, протекающий через эти три резистора, разный.Если I — это ток, покидающий узел A, то он имеет три пути, чтобы достичь узла B. Ток, протекающий через каждый резистор, зависит от его сопротивления. Следовательно, в случае параллельных резистивных цепей ток во всех резисторах неодинаков. Если I1 — это ток, протекающий через резистор R1, I2 — это ток, протекающий через резистор R2, а I3 — это ток, протекающий через резистор R3, тогда токи I, I1, I2 и I3 могут быть связаны с помощью закона тока Кирхгофа. . Согласно закону Кирхгофа о токах, «сумма токов, входящих в узел, равна сумме токов, выходящих из узла.
Следовательно,
I = I1 + I2 + I3.
Формула эквивалентного сопротивленияЛюбое количество резисторов, включенных в параллельную комбинацию, можно заменить одним резистором с сопротивлением, равным эквивалентному сопротивлению резисторов параллельной комбинации.
Было установлено, что напряжение на каждом резисторе в параллельной комбинации одинаково, а общий ток равен сумме отдельных токов. Рассмотрим следующую схему.
Здесь I = I1 + I2 + I3
I1 = V / R1
I2 = V / R2
I3 = V / R3
Если R T — полное сопротивление цепи, то
I = V / R T
Следовательно, V / R T = V / R 1 + V / R 2 + V / R 3
1 / R T = 1 / R 1 + 1 / R 2 + 1 / R 3
Если R eq является эквивалентным сопротивлением цепи, то оно рассчитывается путем сложения обратных значений отдельных сопротивлений (1 / R).Обратная величина этой алгебраической суммы даст эквивалентное сопротивление. Уравнение эквивалентного сопротивления R eq показано ниже для параллельной резистивной цепи из n резисторов.
(1 / R экв ) = (1 / R1) + (1 / R2) + (1 / R3) + ……… + (1 / Rn)
Из приведенного выше уравнения можно сделать вывод, что эквивалентное сопротивление резисторов, соединенных параллельно, всегда меньше, чем сопротивление самого маленького резистора.
Если два резистора подключены параллельно, то эквивалентное сопротивление будет
(1 / R eq ) = (1 / R1) + (1 / R2)
R EQ = R 1 * R 1 / (R 1 + R 2 )
Если два резистора равного сопротивления R соединены параллельно, то эквивалентное сопротивление комбинации будет R / 2.
Аналогичным образом, если три резистора равного сопротивления R соединены в параллельной комбинации, тогда эквивалентное сопротивление комбинации будет R / 3.
Параллельное соединение резисторов дает значение проводимости. Проводимость — это величина, обратная сопротивлению. Обычно он обозначается символом G. Единицы проводимости — Сименс, представленные символом S. Ранее единицами проводимости были Mho (℧), что означает обратное написание Ом, а символ — перевернутое представление Ω.
Несмотря на то, что параллельные резисторы подключены между двумя узлами, представление этого подключения может иметь любую из следующих форм.
Все вышеупомянутые комбинации представляют собой параллельные резистивные схемы, и все правила параллельных резисторов применимы и к вышеупомянутым комбинациям.
Расчет токаТок в каждой ветви параллельной резистивной цепи отличается от другой. Поскольку напряжение на каждом резисторе одинаково, ток, протекающий через каждый резистор, зависит от сопротивления этого резистора.Следовательно, если значение сопротивления в одной ветви отличается от другой, тогда ток в этих ветвях будет другим. Величину этого тока можно определить с помощью закона Ома.
Рассмотрим параллельную сеть из двух резисторов с напряжением питания V между двумя точками A и B.
Пусть I будет полным током в следующей цепи.
Пусть ток, протекающий через резистор R 1 , равен I R1 , а ток, протекающий через резистор R 2 , равен I R2 .
Тогда, согласно закону Кирхгофа, «полный ток, входящий в цепь, равен току, выходящему из цепи».
Если I T — это полный ток, тогда
I T = I R1 + I R2
Поскольку падение напряжения на каждом резисторе одинаково
I R1 = V / R 1
And I R2 = V / R 2
Если рассматривается параллельная резистивная цепь, состоящая из n резисторов, то общий ток в цепи составляет
I Total = I R1 + Я R2 +….+ I Rn
Если последовательные резистивные цепи называются цепями делителя напряжения, то аналогично параллельные резистивные цепи называются цепями делителя тока.
Если рассматривается параллельная резистивная цепь из n резисторов с разным сопротивлением, то можно иметь n разных путей для протекания тока и n разных значений тока через эти пути. Резисторы в параллельной комбинации можно менять местами, не влияя на общий ток и эквивалентное сопротивление.
Пример параллельного подключения резисторов- Рассмотрим следующую схему, в которой четыре резистора R1, R2, R3 и R4 подключены параллельно.
Значения сопротивления каждого резистора:
R1 = 10 Ом
R2 = 20 Ом
R3 = 30 Ом
R4 = 40 Ом
Напряжение питания V = 24 В
Полный ток в схеме можно рассчитать двумя способами.
Первый метод — вычислить отдельные токи, протекающие через каждый резистор.
Если I1 — это ток, протекающий через резистор R1, то согласно закону Ома
I1 = V / R 1 = 24/10 = 2,4 А
Аналогично, если I2 — это ток, протекающий через резистор R2, то согласно по закону Ома
I2 = V / R 2 = 24/20 = 1,2 A
Если I3 — это ток, протекающий через резистор R3, то по закону Ома
I3 = V / R 3 = 24 / 30 = 0,8 А
А если I4 — ток, протекающий через резистор R4, то по закону Ома
I4 = V / R 4 = 24/40 = 0.6 A
Если I ИТОГО — это полный ток в цепи, то, согласно закону Кирхгофа,
I ИТОГО = I1 + I2 + I3 + I4 = 2,4 + 1,2 + 0,8 + 0,6 = 5A
Второй метод расчета тока — это определение эквивалентного сопротивления цепи.
Эквивалентное сопротивление цепи
1 / R EQ = (1 / R 1 ) + (1 / R 2 ) + (1 / R 3 ) + (1 / R 4 )
1 / R EQ = (1/10) + (1/20) + (1/30) + (1/40)
R EQ = 1/2.083 = 4,8 Ом
Этот единственный резистор можно использовать для замены всех резисторов в параллельной комбинации.
∴ I ИТОГО = V / R EQ = 24 / 4,8 = 5A.
Рассмотрим следующую схему, в которой три резистора R1, R2 и R3 соединены параллельно.
Ток, протекающий через R1, равен I1 = 6A
Ток, протекающий через R2, равен I2 = 4A
Ток, протекающий через R3, равен I3 = 2A
В параллельных резистивных цепях напряжение на каждом резисторе одинаковое и равно напряжению питания.
Здесь напряжение питания V = 12 В.
Если V1 — это напряжение на резисторе R1, V2 — это напряжение на резисторе R2, а V3 — это напряжение на резисторе R3, тогда
V = V1 = V2 = V3 = 12В
Тогда по закону Ома
R1 = V 1 / I 1
R1 = 12/6
R1 = 2 Ом
R2 = V 2 / I 2
R2 = 12/4
R2 = 3 Ом
R3 = V 3 / I 3
R3 = 12/2
R3 = 6 Ом
ПримененияКонцепция резисторов в parallel используется при анализе мостовой схемы Уитстона.
