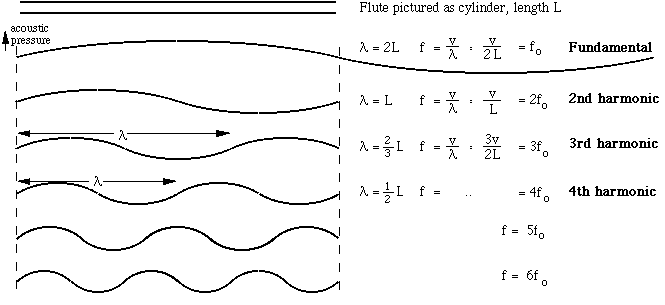Гармоника частоты: Гармонический — Harmonic — qaz.wiki — Мир Антенн

Содержание

Гармонический — Harmonic — qaz.wiki

Эта статья о составляющих периодических сигналов. Для использования в других целях, см Гармоника (значения) . В узлах колеблющейся струны являются гармоники. Два разных обозначения естественных гармоник на виолончели. Сначала как звучащий (чаще), затем как прикосновенный (легче читать с листа).

Гармоника является любым членом гармонического ряда . Этот термин используется в различных дисциплинах, включая музыку, физику, акустику , электронную передачу энергии, радиотехнику и другие области. Обычно он применяется к повторяющимся сигналам, например синусоидальным волнам. Гармоника такой волны — это волна с частотой, которая является положительным целым числом, кратным частоте исходной волны, известной как основная частота . Исходная волнатакже называется 1-й гармоникой, следующие гармоники известны как высшие гармоники. Поскольку все гармоники периодичны на основной частоте, сумма гармоник также периодична на этой частоте. Например, если основная частота равна 50 Гц , это обычная частота источника питания переменного тока, частоты первых трех высших гармоник составляют 100 Гц (2-я гармоника), 150 Гц (3-я гармоника), 200 Гц (4-я гармоника) и любые дополнительные волн с этими частотами является периодическим с частотой 50 Гц.

В n- ^й характеристической моде для n > 1 узлы не будут вибрировать. Например, 3-я характеристическая мода будет иметь узлы на L и L , где L — длина строки. Фактически, каждая n- ^я характеристическая мода, для n, не кратного 3, не будет иметь узлов в этих точках. Эти и другие характерные режимы будут вибрировать в положениях L и L . Если игрок мягко коснется одной из этих позиций, то другие характерные режимы будут подавлены. Тональные гармоники из этих других характеристических режимов также будут подавлены. Следовательно, тональные гармоники из
n- ^ых характеристических режимов, где n кратно 3, будут относите

Bard — Справка по программе

Начальные сведения о звуковых волнах

Алфавитный указатель:

Гармоника — это синусоидальное колебание:

График показывает, как изменяется воздушное давление на барабанную перепонку слушателя: вверх и вниз по дуге, периодически. Воздух давит то сильнее, то слабее. Сила воздействия совсем невелика, и колебания происходят очень быстро: сотни и тысячи толчков каждую секунду. Такие периодические колебания мы воспринимаем как звук.

Сложение двух разных гармоник дает колебание более сложной формы:

Сумма трех гармоник — еще сложнее, а естественные, природные звуки и звуки музыкальных инструментов складываются из большого количества гармоник, и в сумме может получиться что-нибудь вроде этого:

В такой сумме может быть неопределенно много гармоник, но среди них заметный (на слух) вклад вносят лишь некоторые, самые сильные (самые громкие). Поэтому при анализе разумно ограничивать число гармоник сотнями, может быть, тысячами. Набор гармоник, выделенных из звукового колебания — это спектр. Выглядит он примерно так (по горизонтали — частота, по вертикали — амплитуда гармоники):

Каждая гармоника характеризуется тремя параметрами: амплитудой, частотой и фазой.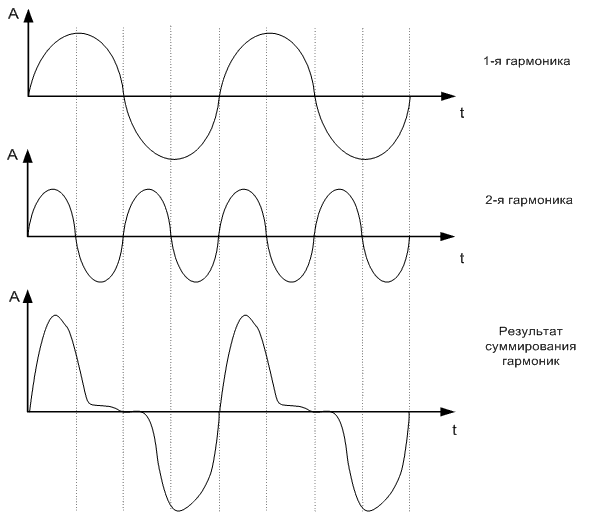

Амплитуда — это размах колебаний. Чем размах больше, тем сильнее воздействие на барабанную перепонку, и тем громче звук, который мы слышим. Амплитуда может измеряться несколькими способами:

Из этих единиц первие три более наглядны, когда смотришь график колебаний. А децибелы ближе к тому, как это воспринимается на слух. Если принять за 0 дБ максимальную громкость в обычных компьютерных наушниках, то -30 дБ — это примерно такой уровень громкости, который едва можно расслышать при регуляторе громкости, выведенном на максимум. При равномерном изменении амплитуды от 0 до -30 дБ, субъективно (на слух) громкость тоже изменяется равномерно, хотя на самом деле — по экспоненте. Это особенность физиологии слуха (закон Фехнера).

Частота колебаний — второй параметр гармоники. Частота показывает, сколько толчков давления воздуха происходит за одну секунду. Как обычно, частота измеряется в Герцах (Гц) или килогерцах (кГц).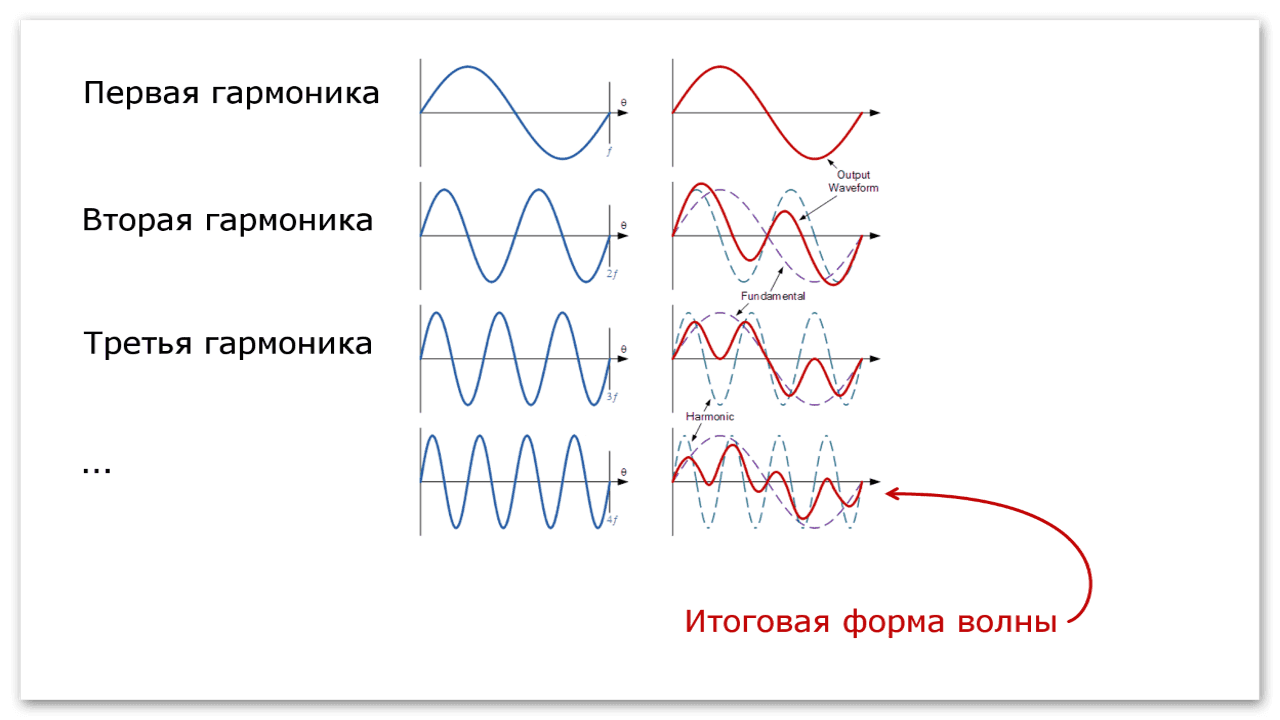 кГц = 1000 Гц.

Человек может услышать гармоники с частотой от 20 Гц до 20 кГц (могут быть небольшие индивидуальные отличия). Этот диапазон называется «звуковым». Все, что ниже — это «инфразвук», все, что выше — «ультразвук». Ультразвук и инфразвук человек не слышит по крайней мере как звуки. Если инфразвук или ультразвук имеет очень большую мощность (громкость), то он может оказывать физическое воздействие на организм. К сожалению, трудно найти достоверные материалы об эффектах такого воздействия, а легенд на эту тему ходит очень много. Кроме того, инфразвуковые или ультразвуковые колебания могут вызывать вторичные колебания каких-нибудь предметов уже в звуковом диапазоне (какое-нибудь дребезжание), и тогда эти вторичные колебания будут слышны.

Большие частоты воспринимаются как «высокие», «тонкие» звуки. Выше 10 кГц — писк, свист. Маленькие частоты воспринимаются как «низкие», «басовые» звуки, рокот. Обычные частоты гармоник мужского голоса — ниже, женского — выше, детского — еще выше.

Кроме частоты, могут применяться другие единицы измерения, которые однозначно связаны с частотой — это период колебаний и высота.

Период колебаний (T) — это просто величина, обратная к частоте (f):

T = 1/ f

Высота связана с музыкальной записью, нотами. Высота может быть вычислена по формулам:

f = 440.0 * 2^{(12 V + N — 57) / 12}

— где f — частота, V — номер октавы от 0 до 9, N — номер ноты от 0 до 11. Можно выполнить и обратное преобразование из частоты в номер ноты и октавы:

12 V + N = 12 * log_₂(f / 440.0) + 57

Понятно, что для произвольно заданной частоты f может не найтись целых чисел V, N. Тогда говорят об отклонении частоты от ближайшей ноты.

Для понимания многих аспектов работы со звуком знание музыкальных нот необязательно.

Достаточно, понимания, что октава и нота — это два числа, два номера, которые по формуле дают частоту. В музыке каждая нота и октава имеют собственное уникальное название, но при вычислениях удобнее работать с номерами.

Обратите внимание, что и здесь равномерное повышение номера ноты вызывает экспоненциальный рост частоты. Это также связано с биологией слуха. При равномерном изменении ноты высота повышается приблизительно равномерно, если судить субъективно, на слух.

При увеличении номера ноты на 1 частота увеличивается в Q = (2^1/12) раз. Такое увеличение частоты в Q раз называется «повышением на полутон«, а уменьшение в Q раз — «понижением на полутон». Изменение частоты в x раз соотвествует изменению высоты на log_{_Q}

x полутонов.

Таким образом, полутон — это относительная единица изменения частоты, т.е. она показывает не величину частоты в герцах, а соотношение между двумя частотами. 12-кратное изменение частоты в Q раз дает в сумме 2-кратное изменение частоты. Изменение частоты в 2 раза называют изменением на одну октаву. Обратите внимание, что словом «октава» называют и номер для вычисления частот, и относительную единицу измерения частоты.

И есть еще две единицы измерения: тон (2 полутона) и цент (1/100 полутона).

Единица	Величина
Октава	2
Тон	2^1/6
Полутон	2^1/12
Цент	2^1/1200

Фаза — это смещение колебаний во времени (третий и последний параметр гармоники).

Фаза может измеряться в градусах или радианах. В зависимости от фазы смещается нулевой отсчет на графике. Для задания гармоники достаточно указать фазу от -180 до +180 градусов, поскольку при значениях, выходящих за этот диапазон, график гармоники повторяется.

Также нередко «фазой» называют разного рода задержки по времени, и тогда ее измеряют в секундах или миллисекундах. Такого рода задержки по-разному воспринимаются на слух, но здесь уже восприятие примерно соответствует времени, а не логарифмам или степеням. То есть, для восприятия фазы закон Фехнера не работает.

В целом график одной гармоники можно выразить формулой:

p(t) = A sin(2 π f + φ)

— где t — время, p — давление воздуха, f — частота, φ — фаза, A — амплитуда.

Обертон

Несколько гармоник с кратными частотами f, 2f, 3f, 4f,… субъективно воспринимаются как единый звук, как звучание одного инструмента. Тогда первая гармоника (f) — называется основной (или базовой) гармоникой, а остальные — «обертонами» (2f — первый обертон, 3f — второй обертон и так далее). Иногда основную гармонику называют нулевым обертоном.

Тембр

Тембр — это набор гармоник из записи звучания какого-нибудь инструмента. Если тембр состоит из одной гармоники, то звук кажется чистым, но «бедным». Такой тембр имеют гудки в телефонной трубке. Если есть много гармоник, звук более «сочный». Если все гармоники близки по частоте к основной частоте и обертонам (то есть, как бы сгруппированы вокруг них), то такой звук воспринимается, как «нота» определенной высоты, и из таких звуков может образоваться музыка, мелодия. Если гармоники разбросаны хаотично, то такой тембр характерен для ударных инструментов, шумов, шорохов. Из таких тембров нельзя создать полноценную мелодию, можно только задать ее ритмический рисунок.

Дискретизация

Для обработки на компьютере звуковые колебания подвергаются дискретизации. Это значит, что функция, представляющая звуковую волну, строится по точкам, которые идут с некоторым шагом:

Шаги очень маленькие — тысячи раз в секунду. Частота этих шагов называется частотой дискретизации. Для единообразия принято несколько стандартных частот дискретизации: 8000, 11025, 22050, 44100, 48000 и 96000 Гц. Из них наиболее распространенная — 44100.

Преобразование Фурье

Для того, чтобы получить спектр звукового колебания, существуют разные методы, и самый распространенный среди них — преобразование Фурье. В комьютерной технике для него применяется конкретный алгоритм, именуемый «быстрым дискретным преобразованием Фурье», сокращенно БПФ или ДПФ (Fast Fourier Transformation = FFT).

Представьте себе, что мы подвергли дискретизации некоторый фрагмент звуковой волны. Пусть частота дискретизации равна S, и в результате дискретизации получено N точек функции, представляющей волну. Теперь представьте себе набор частот, идущих с равным интервалом:

0, S/N, 2S/N, 3S/N … kS/N… (N-1)S/N

k — номер частоты БПФ.

Теперь можно легко представить себе, что делает преобразование Фурье. Оно рассчитывает «отклик» каждой из этих частот. Если в спектре исходного сигнала есть частота kS/N, то частота с номером k «откликнется», а остальные останутся нулевыми. Но так бывает редко. Обычно частоты в спектре исходного сигнала попадают в интервал между соседними частотами БПФ. Например, если частота попадает в интервал между kS/N и (k+1)S/N, то «отклик» будет в основном в частотах с номерами k, k+1 и (значительно меньше) рядом с ними:

На рисунке выше вертикальными зелеными линиями показана величина «отклика» частот БПФ, а пунктиром — частота в исходном сигнале. Таким образом БПФ позволяет, если и не вычислить спектр исходного сигнала в точности, то хотя бы получить о нем более-менее наглядное представление.

Частоту в исходном сигнале назвают истинной частотой. Эффект, при котором истинная частота представлена в спектре БПФ группой близких частот, — эффектом размазывания или рассеяния. Дополнительные ухищрения помогают его уменьшить, а иногда и вовсе устранить.

Гармоника • ru.knowledgr.com

Гармоника волны — составляющая частота сигнала, который является целым числом, многократным из фундаментальной частоты, т.е. если фундаментальная частота — f, у гармоники есть частоты 2f, 3f, 4f… и т.д. У гармоники есть собственность, что они все периодические в фундаментальной частоте, поэтому сумма гармоники также периодическая в той частоте. Гармонические частоты равномерно распределены шириной фундаментальной частоты и могут быть найдены, неоднократно добавляя ту частоту. Например, если фундаментальная частота (первая гармоника) составляет 25 Гц, частоты следующей гармоники: 50 Гц (2-я гармоника), 75 Гц (3-я гармоника), 100 Гц (4-я гармоника) и т.д.

Особенности

Много генераторов, включая человеческий голос, наклоненную скрипичную струну, или звезду переменной цефеиды, более или менее периодические, и так составленные из гармоники, также известной как гармоника partials.

Большинство пассивных генераторов, таких как щипнувшая последовательность гитары или пораженная кожа барабана или пораженный звонок, естественно колеблется в не один, но несколько частот, известных как partials. Когда генератор длинный и тонкий, такой как последовательность гитары или колонка воздуха в трубе, многие partials — сеть магазинов целого числа фундаментальной частоты; их называют гармоникой. Звуки, сделанные длинными, тонкими генераторами, по большей части устроены гармонично, и эти звуки, как обычно полагают, музыкально приятны. Partials, частоты которых не сеть магазинов целого числа фундаментального, упоминаются как негармоничный partials. Инструменты, такие как тарелки, фортепьяно и щипнувшее пиццикато последовательностей создают негармоничные звуки.

Нетренированное человеческое ухо, как правило, не чувствует гармонику как отдельные примечания. Скорее музыкальное письмо, написанное многих гармонично связанных частот, воспринято как один звук, качество или тембр того звука, являющегося результатом относительных преимуществ отдельных гармонических частот. У колоколов есть более ясно заметный inharmonics, чем большинство инструментов. Старинные поющие чаши известны за свое уникальное качество производства многократной гармоники partials или мультиакустики.

Гармоника и подтекст

Обертон — любая частота выше, чем фундаментальное. Трудное отношение между подтекстом и гармоникой в музыке часто приводит к тому, что они были используемыми синонимично в строго музыкальном контексте, но они посчитаны, по-другому приведя к некоторому возможному беспорядку. Эта диаграмма демонстрирует, как они посчитаны:

Во многих музыкальных инструментах возможно играть верхнюю гармонику без фундаментального присутствующего примечания. В простом случае (например, рекордер) это имеет эффект того, чтобы заставлять примечание повыситься в подаче октавой; но в более сложных случаях получены много других изменений подачи. В некоторых случаях это также изменяет тембр примечания. Это — часть нормального метода получения более высоких примечаний в духовых инструментах, где это называют, раздувая. Расширенный метод игры мультиакустики также производит гармонику. На струнных инструментах возможно произвести очень чистые звучащие примечания, названные гармоникой или флажолетами струнниками, у которых есть жуткое качество, а также находиться высоким в подаче. Гармоника может использоваться, чтобы проверить в унисоне настройку последовательностей, которые не настроены на унисон. Например, слегка перебирая узел, найденный на полпути вниз, самая высокая последовательность виолончели производит ту же самую подачу как слегка перебирающий узел 1/3 пути вниз вторая по высоте последовательность. Поскольку человеческий голос видит, что Обертон поет, который использует гармонику.

В то время как верно, что в электронном виде у произведенных периодических тонов (например, прямоугольные волны или другие несинусоидальные волны) есть «гармоника», которая является сетью магазинов целого числа фундаментальной частоты, у практических инструментов все нет этой особенности. Например, более высокая «гармоника»’ примечаний фортепьяно не является истинной гармоникой, но является «подтекстом» и может быть очень острой, т.е. более высокая частота, чем данный чистым гармоническим рядом. Это особенно верно для инструментов кроме струнного или меди/деревянных духовых инструментов, например, ксилофон, барабаны, колокола и т.д., где не у всего подтекста есть простое отношение целого числа с фундаментальной частотой.

Фундаментальная частота — аналог периода периодического явления.

Гармоника на струнных инструментах

Следующая таблица показывает пункты остановки на струнном инструменте, такие как гитара (гармоника гитары), в котором нежное касание последовательности вызовет его в гармонический способ, когда вибрируется. Гармоника последовательности (тоны флажолета) описана как наличие «подобного флейте, серебристого качества, которое может быть очень эффективно как специальный цвет», когда используется и услышано в гармоническом сочетании. Необычно столкнуться с естественной гармоникой выше, чем пятое частичное на любом струнном инструменте кроме контрабаса вследствие его намного более длинных последовательностей.

Стол

Искусственная гармоника

Хотя гармоника чаще всего используется на открытых последовательностях, иногда счет будет призывать к искусственной гармонике, произведенной, играя обертон на остановленной последовательности. Как исполнительный метод, это достигнуто при помощи двух пальцев на грифе, первое, чтобы сократить последовательность к желаемому фундаментальному, со вторым касанием узла, соответствующего соответствующей гармонике.

Другая информация

Гармонику можно или использовать или рассмотреть как основание просто систем интонации. Композитор Арнольд Дреиблатт в состоянии произвести различную гармонику на единственной последовательности его измененного контрабаса, немного изменяя его уникальный метод поклона на полпути между ударом и поклоном последовательностей. Композитор Лоуренс Болл использует гармонику, чтобы произвести музыку в электронном виде.

См. также

Гармоника (электроэнергия)

Электронный тюнер

Гармонический генератор

Зажмите гармонику

Пифагореец, настраивающийся

Масштаб гармоники

Сферическая гармоника

Протянутая октава

Выявите гармонику

Внешние ссылки

Гармоника, partials и подтекст от фундаментальной частоты

Обсуждение этюдов и примечания скрипки Скиаррино выпускает

что это и чем они опасны

В идеальном случае в электрической сети должно быть переменное напряжение, которое изменяется по синусоидальному закону с частотой 50 Гц (50 раз в секунду), если речь идет об отечественных сетях. На практике дело обстоит иначе – напряжение далеко от синусоидальной формы, оно искажено, не только по фронтам, но и по всей длине наполнено различными всплесками и помехами. Данное явление называется гармоники в электрических сетях. В этой статье мы подробнее рассмотрим, что это такое и чем опасны гармоники для оборудования, подключенного к сети.

Определение гармоник

График сигнала, который изменяется по синусоидальному закону, имеет вид:

Но это значительно отличается от реальной формы напряжения в электрической сети:

Эти зазубрины и всплески и вызваны гармониками. Мы попытаемся рассказать об этом явлении простыми словами. Изображенный выше график можно представить как сумму сигналов различной частоты и величины. Если всё это сложить, то в результате получится именно такой сигнал. Пример и результат сложения сигналов изображен на графике ниже:

Гармоники различают по номерам, где первая гармоника — это та составляющая, у которой самая большая величина. Однако такое описание слишком кратко. Поэтому давайте приведем формулу определения величины гармоники. Это возможно при гармоническом анализе и разложении в ряд Фурье:

Из этой формулы можно выделить и величины частот и фаз гармонических составляющих электрической сети и любого другого синусоидального сигнала.

Источники помех

К источникам помех можно отнести целый ряд оборудования, начиная от бытовых приборов, заканчивая мощными промышленными электрическими машинами. Для начала давайте кратко рассмотрим причины их возникновения.

Гармоники в электрической сети переменного тока возникают из-за особенностей электрооборудования, например из-за нелинейности их характеристик, или характера потребления тока.

Например, в трёхфазных сетях в магнитопроводах трансформаторов длины магнитных путей средних и крайних фаз различаются почти в 2 раза, поэтому и токи их намагничивания различаются до полутора раз. Отсюда возникают гармоники в трёхфазных сетях.

Другой источник помех в электротехнике — это электродвигатели, как трёхфазные синхронные и асинхронные, так и однофазные, в том числе и универсальные коллекторные двигатели. Последний тип двигателей используется в большей части бытовой техники, например:

стиральные машины;
кухонные комбайны;
дрели, болгарки, перфораторы и пр.

В результате работы импульсных блоков питания возникают высокочастотные гармоники (помехи) в электрической сети. Чтобы понять как они образуются, нужно иметь сведения об их внутреннем устройстве. Это связано с тем, что ток первичной обмотки ИБП отличается от непрерывного, он протекает только тогда, когда открыт силовой полупроводниковый ключ. А последний открывается и закрывается с частотой выше 20 кГц.

Интересно: Рабочая частота некоторых современных импульсных блоков питания достигает 150 кГц.

Для уменьшения этих гармоник используют фильтры электромагнитных помех, например, синфазный дроссель и конденсаторы. Для улучшения графика потребления тока относительно питающего однофазного напряжения используют активные корректоры коэффициента мощности (рус. ККМ, англ. PFC).

Такие блоки питания установлены в:

светодиодных лампах;
ЭПРА для люминесцентных ламп;
компьютерные блоки питания;
современные зарядные устройства для мобильных телефонов;
телевизоры и прочая техника.

Также к этим источникам питания можно отнести и преобразователи частоты.

Для измерения гармоник в сети можно использовать многофункциональные измерительные приборы от компании EKF. Помимо гармоник, данные приборы могут измерять такие параметры сети, как ток, частота, напряжение, активная, реактивная и полная мощность, а также коэффициенты мощности и частоты. Кроме того, мнофункциональные измерители дают возможность управления, анализа и оптимизации работы энергетического оборудования, систем и промышленных цепей. Они достаточно легко монтируются и могут настраиваться под любой трансформатор тока. Подробнее о многофункциональных измерительных приборах вы можете узнать, перейдя по ссылке: https://ekfgroup.com/catalog/pribory-izmeritelnye/mnogofunkcionalnye-izmeriteli.

Последствия гармонических помех

Наличие гармоник в электрической сети переменного тока вызывает определенные проблемы. Среди них – повышенный нагрев электродвигателей и питающих проводов. Последствия влияния гармоник – это вибрация двигателей. Дальнейшие последствия могут быть различными – начиная от ускоренного износа подшипников ротора двигателя, заканчивая пробоем на корпус обмоток от повышенного нагрева.

В электрике встречаются ложные срабатывания коммутационной и защитной аппаратуры – автоматических выключателей, контакторов и магнитных пускателей. В звуковой аппаратуре и технике для связи из-за гармоник возникают помехи. С ними борются аналогично – установкой фильтров электромагнитных помех.

На видео ниже рассказывается, что такое гармоники и интергармоники в электросети:

В заключение хотелось бы отметить, что гармоники в электрических сетях в принципе не несут никакой пользы. Они лишь вызывают неисправности, ложные срабатывания коммутационной аппаратуры и прочие проявления нестабильности в работе. Это может нести не только неудобства в эксплуатации, но и экономические проблемы, убытки и аварийные ситуации, которые могут быть опасны для жизни.

Материалы по теме:

Гармоники, основная частота, тон

Звуки в реальном мире редко бывают чистыми. В данном случае «чистота» имеет точное значение: чистый тон — это энергия на одной частоте. Инженеры называют это синусоидальной волной (sine wave), поскольку график ее давления зависимости от времени является математической функцией «синус». Помните нашу воображаемую гитарную струну, колеблющуюся на одной высоте тона? Для заданной струны и натяжения высота тона определяется тем, какого размера волна укладывается в точности от одного закрепленного конца до другого. Частота этого тона называется основной частотой (fundamental frequency). Но струны гитары могут гнуться и перегибаться посредине, поэтому множество более коротких волн с более высокой частотой могут также укладываться точно от края до края. Они называются гармониками (harmonic), и они с математической точностью кратны основной частоте. На рисунке показаны основная гармоника вместе с гармониками с частотами в два и в четыре раза большими, чем основная. Поскольку основная частота и гармоники высших порядков могут возникать одновременно, они заставляют колеблющуюся струну описывать сложные, постоянно меняющиеся кривые. Вы можете увидеть их на осциллографе, который отображает изменение напряжения во времени. (Обычно вы будете использовать микрофон для преобразования изменяющегося давления воздуха в электрическое напряжение для осциллографа. Но поскольку мы обсуждаем воображаемую струну, я использовал компьютерную программу для того, чтобы создать эту волну). На втором рисунке показана фотография осциллографа, на который подана комбинация гармоник с первого рисунка.

А — это основная гармоника, измеренная от одного пика сжатия до следующего.
В — это вторая гармоника. Мы видим их ровно две штуки на одну фундаментальную волну, что значит, что ее частота в точности в два раза выше. Обратите внимание, как пики сжатия А и В складываются вместе в начале волны.
С — это четвертая гармоника с частотой в точности в четыре раза больше фундаментальной.

Минимумы давления (т. е. максимумы разрежения) всех трех волн накладываются в точке X. Они складываются вместе и дают в итоге точку низшего напряжения во всей волне. Теоретически не существует предела того, как много гармоник высшего порядка может существовать для заданной основной гармоники (хотя вы можете и не услышать выше какой-то из них). В этом примере я показал только четные гармоники, в звуках из реального мира могут быть также и нечетные. Вдобавок я приводил гармоники, имеющие одинаковую силу. Но для реальных гармоник их сила определяется механическими свойствами колеблющегося элемента, резонансами в музыкальном инструменте и даже тем, за какое место вы его ущипнули или по какому месту ударили. Сила каждой гармоники меняется со временем. Поэтому классическая гитара, электрогитара и ученическая гитара — все звучат по-разному при извлечении одной и той же ноты. Трек включает в себя два звука: чистый тон на 200Гц и он же с добавлением всего двух гармоник на частотах 400Гц. и 800Гц. Это очень простой звук, Вы должны услышать разницу. Первый тон будет звучать электронно. Второй скорей похож на звук органа

автор: Джей Роуз

длительность: 0мин.11сек.
объем: 178 Кб

все статьи в разделе «Теория звукозаписи»:

История звукозаписи
Что такое звук?
Аналого-цифровое преобразование
Чем цифровая запись лучше аналоговой?
Форматы передачи цифровых звуковых данных
Моно и стерео запись звука
Основные проблемы звучания
Гармоники

Что такое гармоники или обертона

В этой статье я хочу рассказать о том, что такое гармоники или обертона.

Любой музыкальный звук состоит из основного тона и дополнительных гармоник (обертонов).

Основной тон – это основа звука, отправная точка строения обертонов. Мы воспринимаем именно этот тон с точки зрения его высотности.

Гармоники – это производные основного тона. Причем, кратные производные.

Это значит, что если основной тон ноты «до» малой октавы имеет частоту приблизительно 130 Гц, то его обертона будут иметь частоту 260 Гц, 390 Гц, 520 Гц и т.д. То есть все эти гармоники можно разделить на 130 и получится целое число. Поэтому говорят вторая гармоника, третья гармоника и т.д. За счет этих гармоник и формируется окраска звука. Мы не можем воспринимать каждую гармонику разрозненно. Мы лишь слышим результат сочетания гармоник с основным тоном.

Основной тон всегда лежит ниже гармоник и является более громким, что и определяет его выраженность.

Гармоники – это основа окраски звука. Любой инструмент имеет свой неповторимый тембр, порождённый гармониками. Поэтому мы и слышим различия в звучании фортепиано, гитары и саксофона. Всё дело в гармониках.

Что такое гармоники

Для того чтобы наглядно продемонстрировать вам гармоники, я проведу один простой эксперимент. Для этого мне понадобятся синтезатор Sylenth2 в комплексе с плагином iZotope Ozone 4. C помощью синтезатора я буду генерировать различные звуки и анализировать результаты используя анализатор спектра в iZotope Ozone 4.

Итак, приступим!

1. Выберу пустой пресет, включу один осциллятор, выберу синусоидальную форму волны и сгенерирую звук ноты «Ля» большой октавы.

Как видно из скриншота, я сгенерировал основной тон ноты «Ля» 110 Гц. Кроме него никаких гармоник в сигнале нет.

2. Изменю форму волны на пилообразную.

Из скриншота видно, что у основного тона ноты «Ля» появились гармоники кратные 110.

3. Теперь выберу какой-нибудь пресет. Например, 44. LD Cello.

На скриншоте отчётливо видно, что тембр этого звука сформирован большим количеством дополнительных обертонов.

Из всего вышесказанного следует, что гармоники являются неотъемлемой составляющей любого звука. Без наличия обертонов музыка бы потеряла всю свою колоритность. Все инструменты звучали бы одинаково и примитивно.

Благодаря гармоникам мы имеем огромную палитру разнообразных тембров. Их число бесконечно велико. Это даёт возможность музыкантам и саунд продюсерам постоянно экспериментировать и синтезировать новые более интересные и насыщенные тембры.

В этой статье я рассказал о том, что такое гармоники.

Если есть вопросы, задавайте их в комментариях.

Понравилась статья? Поделись с друзьями.

4.6 Гармоники серии II: гармоники, интервалы и инструменты

Названия различных интервалов и то, как они написаны на нотоносце, в основном являются результатом долгой истории развития музыкальной нотации и теории. Но сами интервалы — то, как звучат ноты — не являются случайностью истории. Как и октавы, другие интервалы также производятся гармоническим рядом. Напомним, что частоты любых двух высот, разнесенных на октаву, имеют соотношение 2: 1.(См. «Гармонический ряд I», чтобы рассмотреть это.) Любой другой интервал, о котором говорят музыканты, также можно описать как имеющий определенное соотношение частот. Чтобы найти эти отношения, посмотрите на гармонический ряд, записанный в общепринятых обозначениях.

Рисунок 4.53. Гармонический ряд, записанный в виде нот

Посмотрите на третью гармонику на рисунке 4.53. Его частота в три раза больше частоты первой гармоники (соотношение 3: 1). Помните, что частота второй гармоники в два раза больше частоты первой гармоники (соотношение 2: 1).Другими словами, есть две волны высшей C для каждой волны низшей C и три волны третьей гармоники G для каждой волны основной гармоники. Таким образом, соотношение частот второй гармоники к третьей составляет 2: 3. (Другими словами, две волны C на каждые три из G.) Из гармонического ряда, показанного выше, вы можете видеть, что интервал между этими двумя нотами составляет идеальную квинту. Соотношение частот всех идеальных квинт — 2: 3.

Упражнение 4.6.1. (Перейти к решению)

Интервал между четвертой и шестой гармониками (соотношение частот 4: 6) также является пятой. Вы можете это объяснить?
Какие еще гармоники имеют пятый интервал?
Какие гармоники имеют интервал четвертой?
Какое соотношение частот для интервала четверти?

Запись

Если вы внимательно изучили приведенный выше гармонический ряд, то, возможно, заметили, что некоторые ноты, написанные для получения одного и того же интервала, имеют разные соотношения частот.Например, интервал между седьмой и восьмой гармониками является основной секундой, как и интервалы между 8 и 9, между 9 и 10 и между 10 и 11. Но 7: 8, 8: 9, 9:10, и 10:11, хотя они довольно близки, не совсем то же самое. Фактически, современная западная музыка использует систему настройки равной темперации, которая делит октаву на двенадцать нот, которые находятся на равном расстоянии друг от друга. (У них одинаковое соотношение частот, в отличие от полушагов в гармоническом ряду.) Положительный аспект равной темперации (и причина, по которой она используется) заключается в том, что инструмент будет одинаково настроен во всех тональностях.Отрицательный аспект заключается в том, что это означает, что все интервалы, кроме октав, немного расстроены относительно фактического гармонического ряда. Для получения дополнительной информации о равномерном темпераменте см. «Системы настройки». Интересно, что музыканты имеют тенденцию возвращаться к истинным гармоникам, когда это возможно (другими словами, когда легко настроить каждую ноту). Например, хоровая группа a capella или ансамбль духовых инструментов может петь или играть безупречные четверти и квинты, «сжатые» мажорные трети и «расширенные» минорные трети, а также половину и целые шаги слегка различающихся размеров.

Гармонический ряд особенно важен для медных духовых инструментов. Пианист или ксилофонист получает только одну ноту из каждой клавиши. Струнный исполнитель, которому нужна другая нота из струны, крепко держит струну в другом месте. По сути, это делает вибрирующую струну новой длины с новой основой.

Но медник, не меняя длины инструмента, получает разные ноты, фактически играя на гармониках инструмента.Деревянные духовые инструменты тоже делают это, хотя и не в такой степени. Большинство деревянных духовых инструментов могут иметь две разные октавы с практически одинаковой аппликатурой; нижняя октава является основой столба воздуха внутри инструмента при этой аппликатуре. Верхняя октава — первая гармоника.

Запись

В некоторых деревянных духовых инструментах, таких как кларнет, верхняя «октава» может фактически быть третьей гармоникой, а не второй, что усложняет аппликатуру этих инструментов. См. «Стоячие волны» и «Духовые инструменты» для объяснения этого явления.

Это медные инструменты, которые позволяют извлекать разные ноты из трубки одинаковой длины. Звучание духовых инструментов начинается с вибраций губ музыканта. Вибрируя губами с разной скоростью, игрок может заставить звучать гармонику столба воздуха вместо основной. Таким образом, горностай может сыграть любую ноту в гармонической последовательности инструмента, которая попадает в диапазон музыканта. Сравните эти хорошо известные звуковые сигналы с гармоническим рядом выше.

Рисунок 4.54. Горн звонит

Несмотря на то, что рожок ограничен тем, что может воспроизводить только одну гармоническую серию, он все же может воспроизводить многие известные мелодии.

На протяжении веков все медные духовые инструменты были бесклапанными. Духовой инструмент мог играть только ноты одного гармонического ряда. (Важным исключением был тромбон и его родственники, которые могут легко изменять длину и гармонический ряд с помощью слайда.) Верхние октавы ряда, где ноты расположены достаточно близко друг к другу, чтобы сыграть интересную мелодию, часто было трудно играть , и некоторые гармоники звучат совершенно не в гармонии с ушами, ожидающими такого же темперамента.Решение этих проблем, когда латунные клапаны были усовершенствованы, заключалось в добавлении к прибору нескольких клапанов; трех обычно достаточно. Каждый клапан открывает дополнительную длину трубки, что делает инструмент немного длиннее и делает доступным совершенно новую серию гармоник. Обычно один клапан дает гармонический ряд на полшага ниже, чем бесклапанный ввод; другой, на целую ступеньку ниже; а третий — на полторы ступеньки ниже. Клапаны также можно использовать в комбинации, делая доступными еще больше гармонических последовательностей.Таким образом, медный инструмент с клапаном может найти в удобной середине своего диапазона (его средний регистр ) комбинацию клапанов, которая даст разумно настроенную версию для каждой ноты хроматической гаммы. (Подробнее об истории клапанной латуни см. История валторны. Подробнее о том, как и почему создаются гармоники в духовых инструментах, см. «Стоячие волны» и «Духовые инструменты»)

Запись

Тромбоны до сих пор используют слайд вместо клапанов, чтобы сделать свой инструмент длиннее.Но основной принцип все тот же. В каждой «позиции» слайда инструмент получает новый гармонический ряд. Ноты между позициями не являются частью хроматической гаммы, поэтому они обычно используются только для специальных эффектов, таких как глиссандо (скользящие ноты).

Рисунок 4.55. Серии гармоник с перекрытием в духовых инструментах

Эти гармонические серии предназначены для медного инструмента с основной гармоникой «C», когда не используются никакие клапаны, например, для трубы C.Помните, что для каждой основной гармоники существует целый ряд гармоник, и любая нота может быть основной. Вам просто нужно найти латунную трубку подходящей длины. Таким образом, труба или туба могут получить один гармонический ряд без использования клапанов, другой на полшага ниже, используя один клапан, другой — на целую ступень ниже, используя другой клапан, и так далее. К тому времени, когда будут использованы все комбинации клапанов, есть способ получить настроенную версию каждой ноты, которая им нужна.

Упражнение 4.6.2. (Перейти к решению)

Запишите ряд гармоник для прибора выше, когда и первый, и второй клапаны открыты. (Вы можете использовать этот PDF-файл, если вам нужна нотная бумага для нотоносцев.) Какие новые ноты добавлены в средний диапазон инструмента? Какие-нибудь заметки все еще отсутствуют?

Запись

Валторна имеет репутацию «сложного» инструмента для игры. Это тоже из-за гармонического ряда. Большинство медных духовых инструментов играют в первых нескольких октавах гармонического ряда, где ноты расположены дальше друг от друга, и требуется довольно большая разница во рту и губах (амбушюр, произносится как AHM-buh-sher), чтобы получить другую ноту.Диапазон валторны выше в гармоническом ряду, где ноты расположены ближе друг к другу. Таким образом, очень небольшие различия во рту и губах могут означать, что выходит неправильная гармония.

Игра гармоник на струнных

Струнные исполнители также используют гармоники, хотя и не так много, как медные. Гармоники на струнных имеют очень отличный тембр от обычных струнных звуков. Они дают более тихий, тонкий, более похожий на колокольчик тон и обычно используются как своего рода особый эффект, привлекающий ухо.

Обычно струнный исполнитель держит струну очень плотно. Это укорачивает длину колеблющейся части струны, фактически делая (временно) более короткую колеблющуюся струну, которая имеет свой собственный полный набор гармоник.

Чтобы «сыграть гармонику», вместо этого нужно очень, очень легко касаться струны. Длина строки не меняется. Вместо этого легкое прикосновение мешает всем вибрациям, у которых нет узла в этом месте.

Рисунок 4.56.Струнные гармоники

Более тонкий и тихий звук «играющих гармоник» вызван тем фактом, что большая часть гармонического ряда отсутствует в звуке, что, конечно, влияет на тембр. Легкое прикосновение к струне в большинстве мест приведет к отсутствию звука. Этот метод хорошо работает только в тех местах на струне, где основная гармоника (одна из более длинных и громких гармоник с нижним номером) имеет узел. Некоторые исполнители на струнах могут получить больше гармоник, удерживая струну в одном месте и слегка касаясь ее в другом месте, но это продвинутая техника.

Управление шумом гироскопа с помощью фильтров Static Notch и Dynamic Harmonic Notch — документация Copter

Как уже говорилось, управление вибрацией в установках автопилота ArduPilot чрезвычайно важно для обеспечения предсказуемого управления летательным аппаратом. Обычно в установках используется механическое демпфирование вибрации для устранения наиболее сильной вибрации. Тем не менее, механическое демпфирование может быть ограничено, и для удаления дополнительных шумов необходимо использовать программную фильтрацию. Для автопилота вибрационный шум выглядит как любое другое нарушение (например,г. ветер), который автопилот должен компенсировать, чтобы управлять самолетом. ArduPilot использует программный фильтр нижних частот, чтобы удалить большую часть этого оставшегося вибрационного шума, однако фильтрация имеет нежелательный побочный эффект — она удаляет всего , включая информацию о положении и управлении самолетом. Таким образом, хотя агрессивная фильтрация может устранить шум, она также может снизить управляемость и скорость реакции самолета. Эта проблема становится особенно острой на вертолетах с очень высоким уровнем вибрационного шума на гармониках скорости несущего винта и на небольших, мощных вертолетах с низким уровнем естественного механического демпфирования, которые требуют большего контроля.

Для мультикоптеров практически все вибрации исходят от двигателей, и, что важно, об этом источнике шума известно довольно много, так как большая часть его связана с частотой вращения двигателя. Для вертолетов колебания связаны со скоростью ротора. Таким образом, теоретически возможно построить программный фильтр, который нацелен на только этого шума, оставив всю полезную информацию гироскопа в покое. Это то, что делает режекторный фильтр — он нацелен на узкую полосу частот.

ArduPilot поддерживает два разных режекторных фильтра — статический режекторный фильтр, который может быть установлен на фиксированную частоту, и динамический режекторный фильтр, который может быть нацелен на диапазон, связанный с частотой вращения двигателя для двигателей мультикоптеров или скоростью ротора для вертолетов.

С введением динамической режекторной фильтрации необходимость в статической режекторной фильтрации снижается, хотя она может быть полезна при нацеливании на определенные резонансные частоты (например, кадра). Поэтому сначала рассмотрим динамическую фильтрацию.

Настройка

Предполетная подготовка

ArduPilot позволяет выбрать механизм, используемый для управления частотой режекции гармоник. По умолчанию этот механизм основан на дросселировании, так как он будет работать на всех коптерах / квадроциклах. Однако для коптеров с датчиком частоты вращения или поддержкой телеметрии BLHeli ESC настройка может быть радикально проще:

Установите INS_HNTCH_MODE = 2, чтобы использовать датчик частоты вращения для установки частоты режекции гармоник. В основном это используется в вертолетах
Установите INS_HNTCH_MODE = 3, чтобы использовать поддержку телеметрии BLHeli ESC для установки частоты гармонической режекции.Для этого необходимо, чтобы ваши ESC были правильно настроены для поддержки телеметрии BLHeli через последовательный порт
Набор INS_HNTCH_REF = 1, чтобы установить гармоническое опорное режекторное значение, которое для ESC телеметрии, как правило означает отсутствие масштабирования

Установка на основе дроссельной заслонки

Если у вас нет телеметрии ESC, то установка на основе дроссельной заслонки, как правило, подходит.

Установите INS_HNTCH_MODE = 1, чтобы использовать оценку на основе дроссельной заслонки для установки частоты гармонической режекции.

Чтобы настроить динамический режекторный фильтр на основе дроссельной заслонки, важно установить базовый уровень, который идентифицирует шум двигателя на уровне парящего газа.Для этого необходимо использовать пробоотборник серии

Полетный и послеполетный анализ

Выполните полет в режиме зависания не менее 30 с в удержании высоты и загрузите журналы данных.
Откройте Планировщик миссий, нажмите Ctrl-F, нажмите кнопку FFT, нажмите «новый журнал DF» и выберите файл журнала .bin, загруженный выше

На графике должно быть возможно определить значительный пик шума, который соответствует частоте вращения двигателя. На меньшем коптере это, вероятно, будет около 200 Гц, а на более крупном коптере / квадрокоптере 100 Гц или около того.Вот пример 5-дюймового квадроцикла:

В том же журнале откройте его обычным способом в планировщике миссий и нанесите на график значение газа. На основании этого определите среднее значение дроссельной заслонки при зависании.
Также можно использовать MOT_HOVER_LEARN = 2 в Copter и считывать значение MOT_THST_HOVER или Q_M_HOVER_LEARN = 2 в QuadPlane и считывать значение Q_M_THST_HOVER
Это дает вам частоту парящего двигателя hover_freq и значение тяги hover_thrust

Конфигурация гармонической режекции

Установите INS_HNTCH_ENABLE = 1, чтобы включить гармонический режектор
Набор INS_HNTCH_REF = hover_thrust , чтобы установить опорное значение гармоники режекторных
Установите INS_HNTCH_FREQ = hover_freq , чтобы установить опорную частоту гармонической режекции
Установите INS_HNTCH_BW = hover_freq /2, чтобы установить полосу пропускания гармонической режекции

Пост-конфигурация полета и анализ после полета

Выполните аналогичный полет и таким же образом проанализируйте журналы флэш-памяти.На этот раз вы должны увидеть значительно меньше шума и, что более важно, ослабление пика шума двигателя. Если пик не кажется ослабленным, вы можете поэкспериментировать с увеличением полосы пропускания и ослаблением метки. Однако чем шире выемка, тем большую задержку она вносит в управление самолетом, поэтому это может быть контрпродуктивным.

Вот пример того же 5-дюймового четырехугольника с настроенной гармонической режекцией:

Масштабирование частоты режекции

Режектор гармоник предназначен для согласования с частотой шума двигателя при ее изменении путем интерпретации значения дроссельной заслонки.Частота увеличивается от частоты наведения и никогда не будет ниже этой частоты. Тем не менее, в динамическом полете во время промывки двигателя часто встречаются довольно низкие частоты двигателя. Чтобы решить эту проблему, можно изменить значение ref для масштабирования с более низкой частоты.

Сначала выполните длительный динамический полет, используя текущие настройки и постфильтровое пакетное ведение журнала. Изучите БПФ и посмотрите, насколько пик шума двигателя простирается ниже частоты зависания.Используйте эту частоту — min_freq — в качестве нижней границы масштабирования. Затем, чтобы рассчитать обновленное значение задания газа, используйте:

INS_HNTCH_REF = hover_thrust * SQUAREROOT ( min_freq / hover_freq )

Традиционная установка для вертолета

Выполните разделы «Предполетная настройка» и «Полетный и послеполетный анализ» описанной выше настройки мультикоптера. Однако для анализа после полета просто постройте БПФ. С помощью БПФ вы должны увидеть всплески частоты вращения вашего ротора в Гц (об / мин / 60) и гармоники этой частоты.На изображении ниже частота вращения ротора составляет 25 Гц. Обратите внимание, что следующие два самых больших всплеска происходят при 50 Гц и 100 Гц.

В большинстве случаев только частота вращения ротора, вторая гармоника и 4-я гармоника.

Статическая гармоническая режекция

Если датчик частоты вращения отсутствует, опорная частота гармонической режекции будет установлена и не изменится. Если скорость вращения ротора в оборотах в минуту в зависимости от настроек губернатора ESC или губернатора внутреннего RSC известно, то это значение преобразуется в Гц будет использоваться для установки гармоник опорного надреза частоты.Итак, вот настройки для статической гармонической режекции. Обратите внимание, что параметр INS_HNTCH_REF установлен в ноль для статической гармонической режекции.

Установите INS_HNTCH_ENABLE = 1, чтобы включить гармонический режектор
Набор INS_HNTCH_REF = 0 для задания опорного гармонического режекторного значения для статической гармонической выемки
Установите INS_HNTCH_FREQ = Скорость ротора в Гц, чтобы установить опорную частоту гармонической режекции.
Установите INS_HNTCH_BW = 10, чтобы установить полосу пропускания гармонических искажений
Установите INS_HNTCH_HMNCS = 11, чтобы установить 1-ю, 2-ю и 4-ю гармоники.

Dynamic Harmonic Notch

Если датчик частоты вращения настроен на число оборотов 1, опорная частота гармонической режекции может быть установлена динамически с помощью датчика числа оборотов 1.Гармоники параметр частоты опорного надреза, INS_HNTCH_FREQ, используется для обозначения самой низкой скорости вращения ротора, для которой датчик частоты вращения должен быть использован, чтобы динамически устанавливать гармоническую опорную частоту надреза. Рекомендуется установить его на половину регулируемой скорости ротора.

Во-первых, убедитесь, что данные об / мин 1 действительны и масштабированы по скорости ротора с помощью параметра RPM_SCALING. Затем установите для параметра INS_HNTCH_REF значение 1, что позволит динамическую настройку гармонической режекции.Функция гармонической метки автоматически масштабирует данные датчика частоты вращения до Гц. Если по какой-то причине датчик частоты вращения не может быть настроен на скорость ротора, то параметр INS_HNTCH_REF может использоваться для масштабирования данных датчика частоты вращения. Например, предположим, что датчик числа оборотов измерял число оборотов двигателя, которое было настроено на 10: 1 относительно числа оборотов ротора. Тогда параметр INS_HNTCH_REF будет установлен на 0,1 для масштабирования данных датчика частоты вращения для частоты вращения ротора. Итак, вот настройки для динамической гармонической режекции.

Установите INS_HNTCH_ENABLE = 1, чтобы включить гармонический режектор
Набор INS_HNTCH_REF = 1, чтобы установить гармоническую опорную режекторный значение данных датчика оборотов в минуту.Данные датчика частоты вращения автоматически масштабируются до Гц.
Установите INS_HNTCH_FREQ = половина регулируемой скорости ротора в Гц, чтобы установить нижнюю границу опорная частота динамической гармонической режекции.
Установите INS_HNTCH_BW = 10, чтобы установить полосу пропускания гармонических искажений
Установите INS_HNTCH_HMNCS = 11, чтобы установить 1-ю, 2-ю и 4-ю гармоники.

Проверка эффективности гармонической режекции

После настройки режекции гармоник влияние на данные управляющего сигнала можно проверить с помощью инструкций для полетного анализа после конфигурации и послеполетного анализа в разделе настройки мультикоптера выше.

Статическая выемка

В дополнение к подавлению гармоник также можно настроить независимый статический режекторный фильтр. Вы можете сделать это, когда у вас есть значительный резонанс рамы или пропеллера при определенном значении газа. Анализ идентичен анализу для гармонической метки, но на этот раз проведите анализ после настройки гармонической метки, чтобы вы могли видеть любую остаточную вибрацию.

Установите INS_NOTCH_ENABLE = 1 для включения статической метки
Установите INS_NOTCH_FREQ = резонансный пик в Гц, чтобы установить центральную частоту режекции.
Установите INS_NOTCH_BW = полосу пропускания, разумное значение по умолчанию — половина центральной частоты
Установите INS_NOTCH_ATT = затухание надреза, большее затухание сделает надрез глубже и уже

Гармоники

, часть 1 — Введение в гармоники и BLE

2 марта 2018 г. Автор: Чарли Келлерман

Добро пожаловать в первую часть блога, состоящего из двух частей, представленного вам командой Punch Through! Мы надеемся, что этот раздел из двух частей поможет познакомить читателей с темой, в которой Punch Through лучше всех.Этот пост в блоге призван помочь вам лучше понять, что такое гармоники, откуда они берутся, как они соотносятся с Bluetooth Low Energy (BLE) и как заставить их исчезнуть, чтобы вы могли снова мечтать о радугах и единорогах, пока ваш продукт делает вам $ тесто $. Определение будущих проблем и знание того, куда обратиться за помощью, — важнейший путь к успеху, и Punch Through здесь, чтобы помочь!

Вот обзор тем, которые будут затронуты в каждой публикации из двух частей:

Гармоники, часть 1 (эта часть) — Введение в гармоники и BLE

Что такое паразитные гармонические излучения и почему они могут быть плохими? Назад к основам

Гармоники, часть 2 — Определение источника гармоник

Как генерируются гармоники и как их ослабить? Немного более технического

Это сообщение в блоге зовет ваше имя, если:

Вы слышали термины «гармонические», «паразитные» или «выбросы», которые используются в электронной промышленности, и задаетесь вопросом, о чем они.
Гармоническая эмиссия когда-то вызывала у вас кошмары из-за продукта BLE, который вы разрабатывали.
Вы никогда в жизни не слышали об этом и просто жаждете знаний — не волнуйтесь, мы рассмотрим основы гармоник и BLE, чтобы вы ушли сытым.

Приступим!

Что такое электромагнитное поле?

Устройства Bluetooth, помимо другой электроники, использующей такие технологии, как Wi-Fi, сотовая связь и GPS, обмениваются данными по беспроводной сети.Все эти устройства обеспечивают беспроводную связь, используя свойства электромагнитного (ЭМ) излучения электрических проводников, описанные старым добрым Джеймсом Клерком Максвеллом:

Рисунок 1

Когда электрический заряд прикладывается к проводнику, такому как провод, и ток течет по проводнику, он всегда создает электрическое поле и магнитное поле . Когда эти два поля объединяются, они называются полем EM .Электромагнитное поле распространяется в пространстве в виде волн, как свет. Фактически, видимый свет — это просто еще один класс электромагнитных волн, которые составляют лишь небольшую часть всего электромагнитного спектра. Спектр состоит из всех электромагнитных полей на всех длинах волн — длины волн видимого света на намного короче радиоволн (примерно в 10 000 раз короче, чем ваша обычная длина волны связи 2,4 ГГц). Волнистые диаграммы на рисунках 2 и 3 изображают электромагнитное поле, движущееся в пространстве:

Рисунок 2 Рисунок 3
Рискуя отправить вас в глубокую темную кроличью нору, пытаясь обернуть ваш мозг вокруг квантовой физики, следует упомянуть, что электромагнитное поле проходит через пространство в форме фотонов.Фотоны — это частицы с нулевым зарядом и нулевой массой, которые движутся со скоростью света. Еще больше — и мозги превращаются в кашу, так что оставим все как есть.
Другими примерами электромагнитных волн, о которых вы, возможно, слышали, но не можете видеть своими глазами, являются рентгеновские лучи, ультрафиолетовые лучи, инфракрасные лучи и, наконец, что не менее важно: вышеупомянутые «радиоволны». Обратите внимание на разбивку электромагнитного спектра на рис. 4 по длинам волн, частотам и общепринятым названиям групп волн. Обратите внимание, что частота обратно пропорциональна длине волны:
λ [длина волны] = c [скорость света] / ƒ [частота]
Рисунок 4
[Изображение любезно предоставлено обсерваторией ALMA]
Различные радиотехнологии обычно работают на разных радиочастотах (RF) — Bluetooth работает на 2.4 ГГц (гигагерцы), Wi-Fi на частоте 2,4 или 5 ГГц, GPS обычно составляет 1575,42 МГц (мегагерцы), а сотовые устройства могут работать на многих разных частотах в диапазоне от 700 МГц до 2,6 ГГц в зависимости от вашего региона, мобильного телефона оператор связи и поддержка устройства.
В целях данного обсуждения мы сосредоточимся на радиостанциях Bluetooth Low Energy (BLE) и их рабочей частоте 2,4 ГГц или длине волны примерно 5 дюймов.
Как насчет побочного излучения?
Радиоволновая часть ЭМ спектра представляет ценность.Достаточно ценный до такой степени, что государственные органы жестко регулируют его использование. Федеральная комиссия по связи (FCC) является версией этого типа вышибалы для США. Если вы используете часть электромагнитного спектра (намеренно или непреднамеренно) до точки, где она заслуживает их расследования, они найдут вас и отключат. Они разделили электромагнитный спектр радиоволн на множество участков, некоторые из которых более слабо регулируются, чем другие. Один из наиболее слабо регулируемых участков спектра находится на 2.4 ГГц. Вот почему многие беспроводные устройства бытовой электроники работают на частоте 2,4 ГГц: устройства BLE, маршрутизаторы Wi-Fi, устройство открывания гаражных ворот и даже старый беспроводной телефон в вашем доме.
Радиостанции
BLE работают на частоте 2,4 ГГц, а точнее, где-то между 2,402 ГГц и 2,480 ГГц в любой момент времени. Этот частотный диапазон разделен на 40 «каналов» в случае BLE. В случае Wi-Fi, который может работать в том же частотном диапазоне, он делится только на три «более широких» канала. На рисунке 5 показано очень распространенное и полезное изображение распределения частот BLE и Wi-Fi.Частоты рекламных каналов BLE были специально разработаны для существования между тремя каналами Wi-Fi. Когда два устройства BLE находятся в беспроводном соединении друг с другом, они постоянно «переключаются» между оставшимися 37 каналами, разговаривая друг с другом. Такое переключение каналов помогает избежать помех, создаваемых соседним устройством Wi-Fi, использующим один из трех более широких каналов, или другими соседними устройствами BLE.
Рисунок 5
На этом этапе мы установили, что устройства BLE намеренно создают электромагнитное излучение на любой частоте от 2 до 2.402 ГГц и 2,480 ГГц, и FCC не хочет, чтобы устройства BLE создавали электромагнитное излучение где-либо за пределами этого диапазона частот.
A побочное излучение классифицируется как любое электромагнитное излучение на частоте, которая не излучается намеренно, особенно в контексте электроники, которая намеренно излучает одну или несколько частот. FCC требует, чтобы вся электроника проходила испытания, чтобы гарантировать, что они не излучают электромагнитные волны чрезмерной интенсивности на всех частотах, кроме тех, которые излучаются преднамеренно — это известно как испытание на электромагнитную совместимость (ЭМС) .На рисунке 6 показан такой тест беспроводного устройства, работающего на заданной частоте и полосе пропускания. Частоты начала / конца доменов, помеченных как внеполосные (OoB) излучения , являются функцией ширины полосы сигнала. Домены, обозначенные как , побочные излучения непрерывно выходят за края изображения. Например, если ширина полосы сигнала составляет ƒ _BW, , то в типичных случаях область внеполосных излучений начинается с ƒ ₀ +/- 0,5 * ƒ _BW , а область побочных излучений начинается с ƒ ₀ +/- 2.5 * ƒ _BW . Если уровень мощности в любом из этих доменов превышает предел мощности домена, ваше устройство не пройдет тест, и его необходимо исправить, прежде чем его можно будет использовать.
Рисунок 6
А гармоническое побочное излучение?
Побочные излучения — это любое электромагнитное излучение, которое генерируется электронным устройством, когда электронное устройство не генерирует электромагнитное излучение намеренно. Гармоническое побочное излучение — это просто особый тип побочного излучения.В контексте нормативной сертификации — например, FCC — это обычно применяется к беспроводной электронике, которая намеренно генерирует электромагнитное излучение на одной или нескольких частотах. Гармоника представляет собой любое целое число, кратное одной частоте — эту частоту обычно называют основной частотой или иногда первой гармоникой . Таким образом, ваша основная частота ( ƒ ₀ ) гармоник будет:
1 ^st гармоника = 1 x ƒ ₀ = основная частота
2 ^nd гармоника = 2 x ƒ ₀
n ^th гармоника = nx ƒ ₀
По частоте vs.график мощности, основная частота ƒ ₀ с гармониками до 6-й гармоники будет выглядеть примерно так, как показано на рисунке 7. Обратите внимание, что есть и другие негармонические побочные излучения, но они вполне могут быть гармоники, возникающие из какой-то другой основной частоты.
Рисунок 7
Но чем вредны побочные излучения?
Давайте начнем с утверждения, что не все побочные излучения являются «плохими». Иногда основная частота на самом деле является намеренно созданной гармоникой некоторой более низкой частоты.Эти «уловки» обычно используются при проектировании радиочастот.
Однако в контексте нежелательных побочных излучений они плохи. Эти побочные излучения существуют всегда, но они не всегда могут быть основным PITA.
По мнению FCC, они не хотят, чтобы электронные устройства излишне переполняли электромагнитный спектр непреднамеренно созданным электромагнитным излучением. Если электронный продукт генерирует слишком много электромагнитного излучения на некоторой непреднамеренной частоте, он может воздействовать по беспроводной сети или создавать помехи другому электронному продукту, намеренно использующему ту же частоту.FCC установила определенные ограничения для всех частот спектра, чтобы избежать этого типа помех и загрязнения электромагнитного спектра. Устройство радиочастотных помех (которое является незаконным в Соединенных Штатах) является примером электронного устройства, которое злонамеренно использует электромагнитные помехи, генерируя высокие уровни электромагнитного излучения на определенной частоте или в широком диапазоне частот для снижения производительности ближайших беспроводных сетей. электроника.
В глазах разработчика беспроводной электроники побочные излучения могут вызвать головную боль, кроме непрохождения нормативного тестирования — конечно, образно говоря, если они не вызывают у вас достаточного стресса.Иногда побочные излучения, генерируемые беспроводной электроникой, недостаточно серьезны, чтобы превышать пределы, установленные FCC, но они все же существуют. И если они существуют на нужной частоте, в нужное время и с нужной интенсивностью, они могут начать «заглушать» электронный приемник, эффективно делая его менее чувствительным к низким уровням сигнала. По сути, это тот же эффект, который устройство подавления оказывает на бедную беззащитную жертву радиосвязи, и его обычно называют «защитой приемника», «самоглушением», «самоинтерференцией» или «самозатуханием» (возможно, наиболее подходящим вариантом). по сравнению со стрельбой себе в ногу).На рисунке 8 показан этот сценарий самозатухания. Не вдаваясь в подробности, потери на трассе в свободном пространстве (FSPL) — это просто, сколько мощности теряется между источником сигнала и приемником сигнала из-за расстояния, на которое сигнал проходит по воздуху; с увеличением расстояния потери мощности увеличиваются. В крайнем левом углу, смотрящая на рождественскую елку, изображена антенна «для проверки излучения», а антенна «устройства» радиоэлектроники показана слева. «Зашумленная ИС» излучает нежелательные излучения с уровнем мощности -70 дБмВт.Зашумленная ИС намного ближе к антенне устройства, чем тестовая антенна, таким образом, излучение -70 дБмВт от зашумленной ИС ослабляется воздухом только на 10 дБ по сравнению с ослаблением 60 дБ в направлении более удаленной тестовой антенны. Уровень мощности шума, принимаемый испытательной антенной, составляет -70 дБм минус 60 дБ = -130 дБм, что меньше предела излучения FCC в -100 дБм, поэтому электроника проходит испытание FCC на излучение. Уровень мощности шума, принимаемый антенной устройства, составляет -70 дБм минус 10 дБ = -80 дБм.Это плохо для радиоприемника, поскольку в идеальных условиях он способен обнаруживать сигналы связи вплоть до очень небольшого уровня мощности -110 дБмВт. Однако, поскольку радиостанция принимает уровень шума -80 дБмВт, он больше не может обнаруживать сигналы связи ниже -80 дБмВт. Иначе говоря, чувствительность радиоприемника -110 дБмВт подавляется на 30 дБ, и теперь эффективная чувствительность приемника составляет -80 дБмВт.
Рисунок 8
Непреднамеренный радиатор vs.преднамеренный радиатор
Как упоминалось ранее, побочное излучение — это просто электромагнитное излучение, которое не создается намеренно электронным устройством, особенно электроникой, которая «намеренно излучает» определенные частоты. Большинство современных электронных устройств подпадают под одну из следующих категорий, определенных FCC: «непреднамеренные излучатели» и «преднамеренные излучатели». Преднамеренные излучатели — это упомянутые электронные устройства, которые намеренно излучают определенные частоты, такие как устройства BLE.И наоборот, непреднамеренные излучатели — это «все» другие электронные устройства, которые намеренно не генерируют электромагнитную энергию для целей беспроводной связи. Конечно, есть исключения, когда электроника не попадает ни в одну из этих двух категорий или на нее не распространяются правила, установленные для устройств из этих категорий, но мы проигнорируем их в данном обсуждении.
FCC требует, чтобы «вся» электроника проходила тестирование, определенное для категории непреднамеренных радиаторов. Основной тест для электроники, попадающей в эту категорию, измеряет паразитные излучения в диапазоне от 30 до 1000 МГц.Эти тесты обычно включают несколько единиц специального (т.е. дорогостоящего) оборудования для измерения выбросов электронного устройства или испытываемого оборудования (EUT):
Тестовая антенна (логопериодическая или рупорная) для приема побочных излучений, исходящих от испытуемого электронного оборудования (EUT) — эта тестовая антенна обычно размещается на расстоянии 3 или 10 метров от EUT:
Рисунок 9
Анализатор спектра для измерения мощности паразитных излучений, улавливаемых испытательной антенной:
Рисунок 10
[Изображение любезно предоставлено Rohde & Schwarz]
Малошумящий усилитель (LNA) для усиления слабой РЧ-энергии, улавливаемой испытательной антенной, чтобы анализатор спектра мог фактически обнаружить РЧ-энергию, исходящую от EUT:
Рисунок 11
[Изображение предоставлено Kuhne electronic]
Большая безэховая комната с радиочастотным излучением, изолированная от внешних радиоволн — это, по сути, комната с металлическими потолками, стенами и полом с материалом на стенах, который поглощает радиочастотную энергию.Эту комнату потенциально можно заменить большим открытым полем в сельской местности (вдали от любых источников радиочастотной энергии, таких как вышки сотовой связи и бытовая электроника).
Рисунок 12
Во время этих испытаний необходимо измерить выбросы от EUT под всеми углами в одной плоскости. Иначе говоря, выбросы следует измерять, пока EUT медленно вращается на 360˚. Обычно это делается путем помещения EUT на медленно вращающийся поднос. В качестве альтернативы вы можете сделать это вручную, выполнив измерение, слегка повернув EUT вручную, сделав еще одно измерение и повторяя его, пока не будут измерены все 360˚.Не идеально. Затем, по-прежнему направляя испытательную антенну на EUT, поверните антенну на 90 ° и снова начните вращение EUT на 360 °. http://i.imgur.com/RGz3IET.gifv
EUT должно постоянно работать в активном состоянии, пока этот тест сканирует непреднамеренные излучения; Если электроника содержит радиомодуль, который может намеренно генерировать электромагнитное излучение, он должен быть установлен в режим «только прием», когда он не передает электромагнитную энергию. Иногда уровень мощности побочных излучений vs.частота выглядит довольно «тихой» и скучной, как график, показанный на Рисунке 13. Когда это происходит, основная линия тренда кривой является «минимальным уровнем шума» измерительного оборудования — фоновым шумом. Даже при отсутствии EUT в испытательной камере испытательное оборудование будет измерять этот минимальный уровень шума.
Рисунок 13
Хотя часто, даже когда дизайн создается с особым вниманием к контролю электромагнитного излучения, он выглядит так, как это 2spooky4me , но все еще выходит за пределы ограничений FCC:
Рисунок 14
В дополнение к испытаниям на непреднамеренное излучение радиатора, FCC требует, чтобы электроника преднамеренного радиатора подвергалась дальнейшим испытаниям, определенным специально для их предполагаемой частоты работы.Основной тест, который нас интересует в этом обсуждении, — это сканирование преднамеренного побочного излучения излучателя, в то время как EUT непрерывно излучает РЧ-мощность на предполагаемой частоте передачи.
В случае BLE, который может передавать по любому из 40 каналов от 2,402 ГГц до 2,480 ГГц, FCC требует, чтобы сканирование преднамеренных побочных излучений выполнялось три отдельных раза, в то время как ваше устройство настроено на непрерывную передачу на канале с самой низкой частотой (2,402 ГГц), канал средней частоты (2.440 ГГц) и канал с самой высокой частотой (2,480 ГГц). Наиболее частый отказ в этом тесте происходит из-за того, что паразитные гармонические излучения, упомянутые ранее (2 ^-я, 3 ^-я,… n ^-я гармоники основной передачи 2,4 ГГц), являются слишком высокими. На Рисунке 15 показано, как может выглядеть обычное тестовое сканирование (превышающее ограничения FCC). Обратите внимание, что основная частота 2,44 ГГц выше линии предела побочных излучений, и это нормально, потому что ограничение не применяется к основной частоте.Гармоники 2 ^и и 3 появляются на частотах 4,88 ГГц и 7,32 ГГц, но ниже допустимых пределов.
Рисунок 15
До следующего раза…
Весь процесс тестирования ЭМС, требуемый FCC (и регулирующими органами в странах, кроме США), может быть очень обременительным для людей, проходящих его первые несколько раз, даже если их продукт проходит все тесты безупречно. Punch Through готов помочь на любом этапе процесса! Мы успешно помогли многим нашим клиентам начать поставки своих продуктов, помогая им устранять серьезные проблемы с EMC — подробнее об этом — во второй части этого сообщения в блоге!
Продолжите с Гармоники Часть 2 — Определение источника гармоники!
Хотите узнать больше?
Мы группа инженеров, которые любят учиться и преподавать.Если вам интересно узнать больше о нас, о том, как мы работаем и почему мы делаем то, что делаем, зацените нас!
границ | Интерпретации частотного анализа нейронного увлечения: периодичность, основная частота и гармоники
Введение
Корковая активность, измеренная с помощью электроэнцефалографии (ЭЭГ), магнитоэнцефалографии (МЭГ) или регистрации потенциала местного поля (LFP), может синхронизироваться с ритмом сенсорного стимула.Например, когда интенсивность звука, например чистого тона, колеблется на заданной частоте ( f Гц), часто наблюдается нейронная реакция на этой частоте ( f Гц), которую называют слуховой. устойчивый ответ (aSSR; Galambos et al., 1981; Ross et al., 2000; Wang et al., 2012). Точно так же, когда яркость зрительного стимула, например пятна Габора, колеблется на уровне f Гц, также может наблюдаться нервный ответ на f Гц, который называется устойчивым визуальным вызванным ответом (SSVEP; Norcia и другие., 2015). В последнее время низкочастотное (<3 Гц) нейронное вовлечение также наблюдалось для абстрактных свойств стимула, таких как ритмы музыкальных ударов и языковых составляющих (Buiatti et al., 2009; Nozaradan et al., 2011; Ding et al., 2016) и во время обработки естественной речи или фильмов (Ding and Simon, 2012; Zion Golumbic et al., 2013; Koskinen, Seppä, 2014; Lankinen et al., 2014). Была высказана гипотеза, что низкочастотная нейронная синхронизация со стимулом обеспечивает механизм избирательного внимания и временной интеграции информации (Schroeder et al., 2008; Шредер и Лакатос, 2009; Giraud and Poeppel, 2012), и важен для анализа временной структуры речи и музыки (Nozaradan et al., 2011; Ding et al., 2016).
Нейронное вовлечение в ритмы стимула часто анализируется в частотной области, тогда как традиционные нейрофизиологические реакции, например, реакции, связанные с событием, обычно анализируются во временной области. Таким образом, некоторые измерения в частотной области могут показаться неинтуитивными для исследователей, в основном использующих методы анализа во временной области.Например, когда ритм стимула находится на частоте f Гц, нейронные реакции часто можно наблюдать не только при f , но и на его гармониках, то есть на 2 f , 3 f , 4 f и т. Д. Гармоники могут дать дополнительное представление о лежащих в основе механизмах нейронного кодирования (O’connell et al., 2015), но их интерпретация непроста. В этой статье мы объясняем, как эти гармоники связаны с сигналами во временной области. Мы ограничиваем метод анализа частотной области дискретным преобразованием Фурье (ДПФ), наиболее классическим методом анализа частотной области.Мы подробно рассмотрим, как свойства сигнала представлены в призме ДПФ, и не будем обсуждать, является ли ДПФ лучшим методом для представления конкретного сигнала.
Статья организована следующим образом: сначала мы представляем примеры, которые описывают взаимосвязь между периодичностью сигнала во временной области и спектром сигнала. Поскольку остается спорным вопрос о том, отражает ли экспериментально наблюдаемое нейронное отслеживание таких низкочастотных ритмов стимулов последовательность связанных с событием ответов или надлежащее вовлечение нейронных осцилляторов (Ding and Simon, 2014; Keitel et al., 2014). Мы также описываем, как интерпретировать спектр мощности серии реакций, связанных с событием. Эти обсуждения основаны исключительно на интуитивных примерах, избегая более формальной математической обработки (формальную трактовку см., Например, Oppenheim et al., 1989). Глоссарий представлен в таблице 1.
Таблица 1. Таблица глоссария .
Периодичность сигнала и спектр Фурье
Здесь мы будем рассматривать сигнал с периодом T .Другими словами, сигнал повторяется каждые T секунды. Преобразование Фурье анализирует частотный состав сигнала, разлагая его на синусоиды на разных частотах. Сигнал с периодом T повторяется со скоростью f ₀ = 1/ T , что называется основной частотой сигнала. Обычно интуитивно понятно, что спектр Фурье такого сигнала показывает сильную мощность при f ₀. Другими словами, сигнал хорошо объясняется синусоидой на частоте f ₀.Иногда ответ на f ₀ может быть единственным компонентом в спектре Фурье, указывая на то, что сигнал является синусоидой. Рисунок 1 иллюстрирует это состояние.
Рис. 1. Синусоида с частотой 1 Гц. В спектре мощность сигнала концентрируется на частоте 1 Гц. Здесь мы сосредотачиваемся только на форме волны нервного отклика, а не на ее масштабе. Следовательно, амплитуда измеряется произвольной единицей (а.е.).
Синусоиды, конечно, являются математическими абстракциями, и в реальном мире очень немногие сигналы являются точно синусоидальными.Когда сигнал отклоняется от синусоиды, его спектр Фурье будет иметь мощность не только f ₀, но также кратно f ₀, например, 2 f ₀, 3 f ₀, 4 f ₀ и т. Д. На рисунке 2 показано одно из таких условий, при котором короткий двухфазный сигнал длительностью 200 мс повторяется каждые 1 с. На этой иллюстрации двухфазный сигнал представляет собой один цикл синусоиды 5 Гц, в то время как сигнал повторяется с частотой 1 Гц (т.е.е., f ₀ = 1 Гц). Спектр мощности этого сигнала распространяется на несколько частот, например, f ₀, 2 f ₀, 3 f ₀, 4 f ₀… Самая сильная мощность в спектр Фурье появляется при 4 f ₀ вместо f ₀. Этот сигнал можно рассматривать как грубое моделирование последовательности переходных реакций, связанных с событием.
Рисунок 2.Один цикл синусоиды 5 Гц, повторяющийся каждые 1 с. Спектр сигнала показывает мощность на нескольких частотах, как на основной частоте, т. Е. 1 Гц, так и на гармониках, т. Е. Кратных 1 Гц. Наибольшая мощность проявляется на 4-й гармонике, а не на основной частоте.
На рисунке 2 показано, что сигнал с периодом T может иметь разброс мощности по f ₀ и его гармоникам. Далее мы показываем дополнительный пример, в котором нет мощности даже при f ₀.В этом примере (рис. 3) синусоида с частотой 10 Гц модулируется по амплитуде с частотой 1 Гц. Амплитудная модуляция включает произведение двух сигналов. Быстрый сигнал называется несущей, а медленный — огибающей. В общем, огибающая отражает колебания мощности сигнала во времени. На рисунке 3 модулированный сигнал представляет собой произведение синусоиды с частотой 20 Гц и синусоиды с частотой 1 Гц. Амплитудно-модулированный сигнал имеет период 1 с, как видно из его формы волны. Тем не менее, спектр Фурье не показывает мощности на частоте 1 Гц.В этом примере сигнал огибающей является синусоидой, если сигнал не является синусоидой, дополнительные отклики будут видны при 20 ± 2 Гц, 20 ± 3 Гц… поверх откликов на 20 Гц и 20 ± 1 Гц.
Рис. 3. Синусоида с частотой 20 Гц, модулированная по амплитуде с частотой 1 Гц. Пунктирная черная кривая показывает огибающую, а серая кривая показывает форму волны. Огибающая 1 Гц накладывает четкий ритм в 1 Гц на то, как мощность сигнала колеблется во времени. Однако спектр модулированного сигнала показывает не мощность на частоте 1 Гц, а мощность на частоте 20 Гц и 20 ± 1 Гц.
Пример на рисунке 3 также представляет более общие случаи, в которых периодичность сигнала возникает в области модуляции, то есть в огибающей сигнала. На рисунке 4 несущая представляет собой белый шум с ограниченной полосой частот между 70 и 200 Гц, в то время как сигнал огибающей остается синусоидой 1 Гц. Визуальный осмотр формы сигнала позволяет предположить наличие сильного ритма с частотой 1 Гц, в то время как в спектре не может быть обнаружено никакой информации с частотой 1 Гц. В этом случае кажущаяся периодичность 1 Гц существует только в огибающей сигнала и может быть обнаружена только после извлечения самого сигнала огибающей.Фурье-анализ огибающей сводится к условию, показанному на рисунке 1. Этот пример можно рассматривать как моделирование нейронной активности с высоким уровнем гамма-излучения, отслеживающей ритм с частотой 1 Гц. Огибающая сигнала может быть извлечена либо явно с помощью, например, преобразования Гильберта, либо неявно с помощью частотно-временного анализа, такого как краткосрочное преобразование Фурье (STFT) или вейвлет-преобразование. Одна интерпретация спектрограммы, полученной с помощью STFT или вейвлет-анализа, состоит в том, что входной сигнал фильтруется в узкие полосы частот, и в каждой полосе выделяется огибающая мощности сигнала (Vaidyanathan, 1990).Следовательно, периодичность в области модуляции может быть выявлена путем анализа динамики STFT или вейвлет-спектрограммы.
Рис. 4. Широкополосный шум от 70 до 200 Гц модулируется по амплитуде с частотой 1 Гц. Пунктирная черная кривая показывает огибающую, а серая кривая показывает форму волны. Огибающая 1 Гц накладывает четкий ритм в 1 Гц на то, как мощность сигнала колеблется во времени. Однако спектр модулированного сигнала не показывает мощности на частоте 1 Гц.
Таким образом, мы показываем здесь, что если период сигнала составляет T , спектр ДПФ сигнала может показывать мощность на f ₀ и его гармонически связанных частот.Важно отметить, что мощность при f ₀ может быть не самой высокой (Рисунок 2) и может даже не существовать (Рисунок 3). Более того, даже когда сигнал является периодическим, он может демонстрировать регулярность более высокого порядка, включая периодичность в его огибающей (рисунок 4).
Факторы, влияющие на мощность на частоте гармоник
В предыдущем разделе показано, что нейронный сигнал, повторяющийся каждые T секунд, представлен в частотной области гармонически связанными частотами на f ₀, 2 f ₀, 3 f ₀, 4 f ₀… В этом разделе мы более подробно обсудим, какие факторы определяют мощность на каждой частоте.Периодический сигнал полностью характеризуется одним циклом. На рис. 5 показан анализ Фурье периодического сигнала (включая несколько циклов) и анализ Фурье одного цикла. Все ненулевые значения в спектре периодического сигнала захватываются спектром одного цикла. Спектр периодического сигнала можно получить, вставив нули в спектр одного цикла. Спектр периодического сигнала может иметь ненулевые значения только на основной частоте и ее гармониках, а спектр одного цикла принимает значения только на этих частотах.Как правило, ненулевые значения в спектре периодического сигнала определяются формой волны одного цикла, в то время как частоты, на которых спектр показывает ненулевые значения, определяются его периодом. Другими словами, спектр одного цикла представляет собой спектральную огибающую спектра периодического сигнала.
Рис. 5. Связь между спектром периодического сигнала и спектром одного цикла. (A) Форма волны и спектр одного цикла сигнала, которые можно рассматривать как имитацию реакции, связанной с событием.Измерение сигнала длится 1 с, тогда как сигнал колеблется всего около 300 мс. Когда измерение сигнала составляет 1 с, в спектре отображаются только дискретные значения с частотой 1 Гц и его гармоники, отмеченные крестиком. Однако обычно дискретные значения соединяют в виде кривой, показанной пунктирной кривой. (B) Когда сигнал в (A) повторяется каждые 1 с, создается периодический сигнал. На рисунке показано 3-секундное измерение периодического сигнала, которое включает три цикла сигнала.Спектр этого сигнала показывает дискретные значения на 1/3 Гц и его гармоники. Однако мощность равна нулю на частотах, которые не являются гармониками 1 Гц, то есть основной частотой сигнала. Спектр в (A) воспроизводится в (B) красным цветом. Понятно, что спектр в (A) является огибающей спектра сигнала в (B) .
На основании анализа выше, когда форма волны одного цикла содержит «быстрые» колебания или «резкие» края, сигнал будет иметь большую мощность на высокочастотных гармониках.Здесь «быстрые» колебания означают колебания на частотах, намного превышающих основную частоту периодического сигнала (рисунок 3). «Острые» края означают, что края нарастают / затухают быстрее относительно того, насколько быстро синусоида на f ₀ нарастает или затухает. Мощность периодического сигнала будет концентрироваться на f ₀, только если частота стимула соответствует спектральному резонансу, т. Е. Временным масштабам, ответа в одном цикле стимула (подробности см. В следующем разделе и на рисунке 6) .Следовательно, нейронный пик на f ₀ Гц в спектре Фурье не только указывает на повторение нейронной формы волны на f ₀ Гц, но также указывает, что повторяющаяся форма волны примерно представляет собой цикл f ₀ Гц синусоида.
Рис. 6. Ответ, связанный с событием, повторяется с разной частотой. Рисунки на левой панели показывают форму волны отклика, а рисунки на правой панели показывают спектр отклика.На рисунках левой панели каждая красная точка обозначает сенсорное событие. (A) Отдельный ответ, связанный с событием, мощность которого концентрируется в тета-диапазоне (4–8 Гц). (B) Ответы на сенсорные события, повторяющиеся с разной скоростью. Когда частота стимулов намного ниже тета-диапазона, например, при 1 Гц, существует небольшое перекрытие между ответами на различные сенсорные события. В спектре мощность отклика мала и распределена по ряду гармонически связанных частот.Когда стимул находится в пределах тета-диапазона, например, 4 и 6 Гц, ответы на различные сенсорные события перекрываются. В спектре наблюдается сильный отклик на основной частоте ритма стимула, а также на второй гармонике, если она попадает в диапазон резонансных частот реакции, связанной с событием. Если частота стимула очень высока, четкая реакция появляется только в начале стимула.
Фурье-анализ серии ответов, связанных с событием
В этом разделе мы описываем представление в частотной области периодического нейронного отклика, состоящего из серии дискретных устойчивых откликов, связанных с событием.В частности, сенсорный стимул представляет собой последовательность периодически происходящих событий, и каждое событие моделируется как импульс, который можно рассматривать как приближение короткого звукового сигнала или короткой вспышки света. Мы предполагаем, что, когда нейронная реакция достигает устойчивого состояния, реакция, связанная с событием, на каждое сенсорное событие идентична (неизменность во времени), а измеренная нейронная реакция является линейной суперпозицией различных реакций, связанных с событием (линейность). При этих предположениях нейронная сеть, генерирующая измеренный нейронный отклик, может быть смоделирована линейной инвариантной во времени системой (Oppenheim et al., 1989). Из этого следует, что внутренние свойства нейронной сети полностью характеризуются импульсной реакцией, то есть реакцией, связанной с событием.
Согласно линейной инвариантной во времени теории, каждый цикл нейронной реакции, то есть реакции, связанной с событием, является свойством нейронной системы, а периодичность — свойством стимула. Если реакция, связанная с событием, снижается до исходного уровня в течение каждого цикла стимула, спектральная огибающая периодической нейронной реакции определяется спектром реакции, связанной с событием (рис. 5).Этот вывод, однако, также верен, если реакция, связанная с событием, не возвращается к исходному уровню при появлении следующего стимула по причинам, которые не будут уточняться. Кроме того, линейная модель неизменной во времени системы также применима к апериодическим стимулам и к постоянно меняющимся стимулам. В этой статье, однако, рассматривается только реакция на периодические сенсорные сигналы.
На рисунке 6 мы проиллюстрировали, как спектр отдельного события, связанного с событием, и частота повторения стимула совместно определяют спектр нейронных ответов согласно теории линейных систем, не зависящих от времени.В этом примере мы предполагаем, что реакция, связанная с событием, имеет наибольшую мощность в тета-диапазоне (4–8 Гц), а стимул представляет собой последовательность импульсов, то есть очень короткие сенсорные события. Произвольно выбирается диапазон резонансных частот нейронной системы, т. Е. Тета-диапазон. Когда частота стимула ниже диапазона резонансных частот, отклик слабый и показывает мощность на высокочастотных гармониках (например, условие 1 Гц на рисунке 6B). Когда частота стимула находится в пределах диапазона резонансных частот, сильная реакция наблюдается при f ₀, а также частоты гармоник, попадающие в диапазон резонансных частот (например,g., условия 4 и 6 Гц на рисунке 6B). Наконец, если частота стимула выше диапазона резонансных частот, реакция в установившемся режиме будет очень слабой (например, условие 12 Гц на рисунке 6B). Следовательно, если сильное нейронное увлечение наблюдается на f ₀, а не на какой-либо гармонической частоте, это указывает на то, что f ₀ находится в диапазоне резонансной частоты, а 2 f ₀ находится за пределами этого диапазона. спектр.
Что требует дополнительного объяснения, так это то, почему ответ такой слабый на любой частоте, когда скорость стимула низкая (рис. 6А).Когда частота стимула ниже диапазона резонансной частоты, нейронная система без труда реагирует на каждое событие стимула. Причина слабого отклика двоякая. Во-первых, ответ отклоняется от базовой линии только в течение короткого периода времени после каждого стимулирующего события, что делает общую мощность ответа, то есть мощность, суммированную во времени, очень низкой. Во-вторых, мощность в частотной области распределяется по нескольким частотам гармоник, что делает отклик на каждой отдельной частоте еще слабее.
В приведенном выше обсуждении мы рассматриваем только нейронные реакции на последовательность кратковременных сенсорных событий. Тем не менее многие сенсорные стимулы, такие как речь и музыка, постоянно меняются. Как нейронная активность следует за постоянно меняющимся стимулом, все еще остается нерешенным вопросом исследования (см. Обзор в Ding and Simon, 2014). Одна из гипотез состоит в том, что реакция все еще запускается дискретными сенсорными или перцептивными событиями, например, акустическими границами или началом слога / предложения, и в этом случае вышеупомянутое обсуждение все еще актуально.Другая гипотеза, однако, заключается в том, что реакция постоянно следует за стимулом. Согласно этой гипотезе, для линейной системы, не зависящей от времени, ответ — это непрерывно изменяющаяся характеристика стимула, связанная с реакцией, связанной с событием. Если характеристика стимула изменяется плавно, например, синусоидально, его мощность будет концентрироваться на основной частоте. В этом случае мощность отклика также будет сосредоточена на основной частоте, и любой отклик на частотах гармоник будет отражать нелинейную нейронную обработку.
Интерпретация низкочастотного нейронного вовлечения
Когда ответ показывает сильную мощность при f ₀, это указывает на «базовые» колебания в течение каждого периода стимула. Например, когда f ₀ ниже 1 Гц и сильный нейронный отклик наблюдается на f ₀, это указывает на медленный дрейф «базовой линии» отклика во временном интервале, сравнимом с продолжительностью цикл стимулов. Если ответ является «локальным», то есть длится более короткое время, чем цикл стимула, он вряд ли может способствовать нейронному отслеживанию на основной частоте (рисунок 6, условие 1 Гц).Например, слуховой вызванный ответ со средней задержкой длится менее 100 мс. Если этот ответ повторяется каждые 1 с, он вряд ли может способствовать увлечению нейронов частотой 1 Гц. Очень низкочастотное (например, <1 Гц) нейронное отслеживание указывает на длительные и медленно меняющиеся реакции. Фактически, его основная особенность - медленность низкочастотного увлечения. Ключевая гипотеза относительно низкочастотного нейронного вовлечения заключается в том, что нейронный ответ не возвращается к исходному уровню, когда приходит следующий стимул, и этот «дрейф базовой линии» обеспечивает контекст для обработки следующего стимула (Schroeder et al., 2008; Шредер и Лакатос, 2009).
Низкочастотное нейронное вовлечение во время обработки речи, музыки и слуха
Низкочастотное нейронное увлечение часто наблюдается во время обработки речи и музыки. При прослушивании речевых материалов на уровне дискурса вовлечение нейронов достоверно наблюдается в дельта-диапазоне (> 4 Гц), включая частотный диапазон около или ниже 1 Гц (Ding and Simon, 2012; Zion Golumbic et al., 2013; Koskinen and Seppä, 2014; Lankinen et al., 2014).Далее показано, что нейронное вовлечение в дельта-полосу отражает не только нейронное кодирование акустических характеристик, но также нейронное кодирование синтаксических структур (Ding et al., 2016). Подобное нейронное увлечение дельта-полосы наблюдается во время обработки музыки. В частности, было показано, что нейронная активность может следовать ритму музыкального ритма и метра (Nozaradan et al., 2011, 2012; Sturm et al., 2014; Tierney, Kraus, 2014). Эти результаты предполагают, что низкочастотное нейронное вовлечение может играть роль в разборе временной структуры речи и музыки, формируя фрагменты фразового уровня.
С другой стороны, хотя очень низкочастотное нейронное вовлечение надежно наблюдается при обработке речи и музыки, это вовсе не универсальное явление при обработке произвольных слуховых стимулов, даже с очень низкочастотным акустическим ритмом (Lakatos et al., 2013; Doelling, Poeppel, 2015). Например, в исследовании, проведенном Lakatos et al. (2013) тонкие точки появляются каждые 1,5 с. Только временные слуховые вызванные ответы, то есть комплекс P1-N1-P2, видны после каждого тонального сигнала во время пассивного прослушивания.Однако, когда субъекты выполняют задачу по обнаружению выбросов, возникает медленный дрейф базовой линии в течение 1,5-секундного периода стимула (у здоровых субъектов, но не у пациентов с шизофренией). В качестве другого примера, Доеллинг и Поппель (2015) изучали нейронные реакции на музыку в очень медленном темпе, в некоторых случаях ниже 1 Гц. Нейронные реакции музыкантов улавливаются темпом данной пьесы, в то время как нейронные реакции музыкантов проявляются только в гармониках с темпом. Оба примера показывают, что очень медленное нейронное вовлечение (> 1 Гц) не является естественным следствием сенсорных вызванных реакций и возникает только в результате выполнения задачи или опыта.
Медленные реакции, связанные с событиями, такие как компоненты N400, P3 и P600, действительно могут способствовать очень низкочастотному нейронному увлечению около 1 Гц или ниже. Обычно трудно отделить эти медленные, связанные с событием реакции от низкочастотного нейронного вовлечения, просто основываясь на спектре / форме волны ответа (O’connell et al., 2012). Тем не менее парадигма нейронного вовлечения не требует изолировать реакцию на отдельное событие и, следовательно, обеспечивает более гибкую исследовательскую парадигму.Более того, очень низкочастотное нейронное вовлечение наблюдалось в первичных сенсорных областях, которые не рассматривались как генераторы ответов, связанных с длительными латентными событиями (Lakatos et al., 2008, 2009). Чтобы показать, что увлеченная активность отличается от классической реакции, связанной с событием с длительной задержкой, можно использовать другой подход, чтобы показать, что они обладают различными функциональными свойствами (Ding et al., 2016).
Следовательно, низкочастотное нейронное вовлечение на основной частоте ритма стимула обычно подразумевает медленные колебания формы волны нейронного ответа, что можно рассматривать как медленный дрейф «базовой линии» ответа в каждом цикле стимула.Нейронная активность, которая колеблется со скоростью, намного превышающей ритм стимула, и переходные нейронные реакции, которые затухают в течение небольшой части периода стимула, сильнее отражаются гармоническими частотами в спектре. Когда низкочастотное нервное вовлечение возникает на основной частоте ритма стимула, это указывает на то, что влияние предыдущих стимулов не исчезает, когда приходит следующий стимул. Другими словами, предыдущие стимулы задают (нейронный) контекст, в котором будет обрабатываться новый стимул.
В итоге, низкочастотное нейронное вовлечение означает, что либо нейрогенераторы обладают медленной внутренней динамикой, либо нейронная система непрерывно отслеживает определенные плавно изменяющиеся свойства стимула. Маловероятно, что очень низкочастотное нейронное вовлечение (например, <1 Гц) состоит из серии переходных реакций, вызванных дискретными сенсорными / перцептивными событиями.
Взносы авторов
ND задумал исследование. HZ и ND провели моделирование. Статью написали HZ, LM, DP и ND.
Финансирование
Работа поддержана Национальным фондом естественных наук Китая 31500873 (ND), Фондом фундаментальных исследований для центральных университетов (ND), Китайским фондом естественных наук провинции Чжэцзян LR16C0
(ND) и грантом 2R01DC05660 (DP) Национальных институтов здравоохранения США.
Заявление о конфликте интересов
Авторы заявляют, что исследование проводилось в отсутствие каких-либо коммерческих или финансовых отношений, которые могли бы быть истолкованы как потенциальный конфликт интересов.
Сноски
На рисунке 5B мы рассматриваем только три цикла периодического сигнала, и поэтому два нуля вставлены между любыми двумя частотами, разрешенными на рисунке 5A (то есть частотами, обозначенными x на рисунке 5A). В общем, если сигнал содержит N цикла, N -1 точек будет вставлено между любыми двумя частотами, разрешенными на рисунке 5A. Если сигнал действительно периодический и бесконечен по длительности, спектр будет непрерывным и равен нулю на любой частоте, кроме частот, разрешенных на рисунке 5A.
Для линейных систем, не зависящих от времени, нейронная реакция — это стимул, свертывающий реакцию, связанную с событием. Преобразование Фурье свертки двух сигналов является продуктом преобразования Фурье каждого сигнала. В качестве стимула здесь рассматривается периодическая последовательность импульсов. Преобразование Фурье последовательности импульсов также является последовательностью импульсов. Спектр последовательности импульсов отличен от нуля только при 0, f ₀, 2 f ₀, 3 f ₀… и возьмем то же ненулевое значение при 0, f ₀ , 2 f ₀, 3 f ₀….Преобразование Фурье периодического нейронного отклика является продуктом спектра реакции, связанной с событием, и последовательности импульсов в спектральной области. Следовательно, спектр реакции, связанной с событием, является огибающей спектра периодической реакции.
Список литературы
Буйатти, М., Пенья, М., Дехане-Ламбертц, Г. (2009). Исследование нейронных коррелятов вычисления непрерывной речи с частотно-маркированными нейроэлектрическими ответами. Neuroimage 44, 509–551.DOI: 10.1016 / j.neuroimage.2008.09.015
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Дин Н., Меллони Л., Чжан Х., Тиан X. и Поппель Д. (2016). Корковое отслеживание иерархических языковых структур в связной речи. Нат. Neurosci. 19, 158–164. DOI: 10.1038 / nn.4186
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Динг, Н., Саймон, Дж. З. (2012). Нейронное кодирование непрерывной речи в слуховой коре при монофоническом и дихотическом слушании. J. Neurophysiol. 107, 78–89. DOI: 10.1152 / jn.00297.2011
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Доеллинг, К. Б., Поппель, Д. (2015). Корковое увлечение музыкой и ее модуляция с помощью опыта. Proc. Natl. Акад. Sci. U S A 112, E6233 – E6242. DOI: 10.1073 / pnas.1508431112
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Галамбос Р., Макейг С. и Талмахофф П. Дж. (1981). Слуховой потенциал 40 Гц, зарегистрированный на коже черепа человека. Proc. Natl. Акад. Sci. U S A 78, 2643–2647. DOI: 10.1073 / pnas.78.4.2643
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Жиро, А.-Л., Поппель, Д. (2012). Корковые колебания и обработка речи: новые вычислительные принципы и операции. Нат. Neurosci. 15, 511–517. DOI: 10.1038 / nn.3063
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Кейтель К., Куигли К. и Рухнау П. (2014). Стимулируемые колебания мозга в альфа-диапазоне: захват собственных ритмов или частотно-следящая реакция? Дж.Neurosci. 34, 10137–10140. DOI: 10.1523 / JNEUROSCI.1904-14.2014
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Лакатос, П., Кармос, Г., Мехта, А. Д., Ульберт, И., и Шредер, К. Э. (2008). Удержание нейронных колебаний как механизм отбора внимания. Наука 320, 110–113. DOI: 10.1126 / science.1154735
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Лакатос, П., Мусаккия, Г., О’Коннел, М.Н., Фальшер А. Ю., Джавитт Д. К. и Шредер К. Э. (2013). Механизм спектрально-временного фильтра слухового избирательного внимания. Нейрон 77, 750–761. DOI: 10.1016 / j.neuron.2012.11.034
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Лакатос П., О’Коннелл М. Н., Барчак А., Миллс А., Джавитт Д. К. и Шредер К. Э. (2009). Ведущее значение: надрамодальный контроль внимания за нейрофизиологическим контекстом. Нейрон 64, 419–430.DOI: 10.1016 / j.neuron.2009.10.014
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Ланкинен, К., Саари, Дж., Хари, Р., и Коскинен, М. (2014). Межпредметная согласованность сигналов МЭГ коры головного мозга во время просмотра фильмов. Neuroimage 92, 217–224. DOI: 10.1016 / j.neuroimage.2014.02.004
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Норча, А.М., Аппельбаум, Л.Г., Алес, Дж. М., Коттеро, Б. Р., Россион, Б. (2015). Устойчивый визуальный вызванный потенциал в исследованиях зрения: обзор. J. Vis. 15: 4. DOI: 10.1167 / 15.6.4
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Nozaradan, S., Peretz, I., Missal, M., and Mouraux, A. (2011). Пометка вовлечения нейронов в биение и измерение. J. Neurosci. 31, 10234–10240. DOI: 10.1523 / jneurosci.0411-11.2011
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Nozaradan, S., Peretz, I., and Mouraux, A. (2012). Избирательное вовлечение нейронов в ритм и метр, встроенные в музыкальный ритм. J. Neurosci. 32, 17572–17581. DOI: 10.1523 / jneurosci.3203-12.2012
PubMed Аннотация | CrossRef Полный текст | Google Scholar
О’Коннелл, М. Н., Барчак, А., Росс, Д., Макгиннис, Т., Шредер, К. Э., и Лакатос, П. (2015). Многоуровневый захват связанных нейрональных колебаний в первичной слуховой коре. Фронт. Гм. Neurosci. 9: 655. DOI: 10.3389 / fnhum.2015.00655
PubMed Аннотация | CrossRef Полный текст | Google Scholar
О’Коннелл, Р.Г., Докри П. М., Келли С. П. (2012). Супрамодальный сигнал от накопления к привязке, который определяет перцепционные решения у людей. Нат. Neurosci. 15, 1729–1735. DOI: 10.1038 / nn.3248
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Оппенгейм, А. В., Шафер, Р. В., и Бак, Дж. Р. (1989). Обработка сигналов в дискретном времени . Река Аппер Сэдл, Нью-Джерси: Prentice-Hall, Inc.
Google Scholar
Росс, Б., Боргманн, К., Драганова, Р., Робертс, Л. Е., и Пантев, К. (2000). Высокоточное магнитоэнцефалографическое исследование устойчивых звуковых реакций человека на амплитудно-модулированные тона. J. Acoust. Soc. Am. 108, 679–691. DOI: 10.1121 / 1.429600
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Шредер К. Э., Лакатос П., Кадзикава Ю., Партан С. и Пьюс А. (2008). Нейрональные колебания и визуальное усиление речи. Trends Cogn. Sci. 12, 106–113.DOI: 10.1016 / j.tics.2008.01.002
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Штурм, И., Бланкерц, Б., Потес, К., Шальк, Г., Курио, Г. (2014). Высокая гамма-активность ЭКоГ выявляет отчетливые корковые репрезентации отрывков текстов, гармонические и тембровые изменения в рок-песне. Фронт. Гм. Neurosci. 8: 798. DOI: 10.3389 / fnhum.2014.00798
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Вайдьянатан, П.П. (1990). Многоскоростные цифровые фильтры, банки фильтров, многофазные сети и приложения: учебное пособие. Proc. IEEE 78, 56–93. DOI: 10.1109 / 5.52200
CrossRef Полный текст | Google Scholar
Ван Ю., Дин Н., Ахмар Н., Сян Дж., Поппель Д. и Саймон Дж. З. (2012). Чувствительность к скорости временной модуляции и спектральной полосе пропускания в слуховой системе человека: данные МЭГ. J. Neurophysiol. 107, 2033–2041. DOI: 10.1152 / jn.00310.2011
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Сион Голумбик, Э.М., Динг, Н., Бикель, С., Лакатос, П., Шевон, К. А., Макханн, Г. М. и др. (2013). Механизмы избирательного нейронного слежения за речью присутствующих на «коктейльной вечеринке». Нейрон 77, 980–991. DOI: 10.1016 / j.neuron.2012.12.037
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Артикул: серия гармоник
Артикул: серия гармоник
teoria.com использует файлы cookie. Используя наш сайт, вы соглашаетесь на использование файлов cookie. Прочтите нашу политику конфиденциальности для получения дополнительной информации.Закрыть
Когда мы слышим звук, издаваемый музыкальным инструментом, мы на самом деле слышим множество звуков, которые образуют гармонический ряд. В семнадцатом веке француз Жозеф Совер (1653-1716) и англичанин Томас Пиго (1657-1686) отметили, что струны колеблются по частям — явление, объясняющее, почему одна струна производит такое множество звуков.
На видео ниже показан спектральный анализ C на две октавы ниже среднего C (C2):
Примечания:
Мы написали ноты, соответствующие первым 16 гармоникам серии.Очевидно, что за этими первыми гармониками следует много гармоник.
Первая гармоника или основная гармоника не обязательно является самой сильной гармоникой.
Баланс между гармониками постоянно меняется. В сочетании с огромным количеством гармоник это объясняет трудности, с которыми мы сталкиваемся при синтезе звуков.
Важность гармонического ряда
Гармонический ряд определяет многие из наших интервалов. Ниже перечислены октава, пятая, четвертая, мажорная треть и минорная седьмая:
.
Мы можем вычислить математическое соотношение (или размер), разделив частоты нот.Здесь мы используем частоту некоторых гармоник для вычисления размера интервалов:
Интервал Коэффициент От гармоник
Октава 130/65 = 2 1 и 2
Пятый 195/130 = 1,5 2 и 3
Четвертый 260/195 = 1.33 3 и 4
Главный третий 325/260 = 1,25 4 и 5
Малый седьмой 455/260 = 1,75 4 и 7
Интересно, что мы можем вычислить значения, используя номера гармоник:
Интервал Коэффициент От гармоник
Октава 2/1 = 2 1 и 2
Пятый 3/2 = 1.5 2 и 3
Четвертый 4/3 = 1,33 3 и 4
Главный третий 5/4 = 1,25 4 и 5
Малый седьмой 7/4 = 1,75 4 и 7
Расчет частот
Математические соотношения могут использоваться для расчета частоты нот.Из A 440 мы вычисляем частоту C #, E и G:
А C # (мажорная треть) E (идеальная квинта) G (второстепенный седьмой)
440 440 х 1,25 = 550 440 х 1,5 = 660 440 x 1,75 = 770
Если разделить на математическое соотношение, мы получим убывающие интервалы. Здесь мы вычисляем частоту F, большую треть ниже A:
Твит Подписывайтесь на @teoriaEng
Частота гармоники — Большая химическая энциклопедия
Введем безразмерные координаты изгиба qr = t / XrPr anti qc = tAcPc, где Xt = (kT -r) = PrOir, Xc = sJ kcPc) = Pc nc.где cor и fOc — частоты гармоник для чистых транс- и цис-изгибных колебаний соответственно. После интегрирования по 0 мы получаем эффективный гамильтониан H = Ho + H, который используется в пертурбативной обработке эффекта R-T и спин-орбитальной связи. Его поверхность нулевого порядка состоит из … [Pg.534]
Расчет колебаний — это первый шаг анализа колебаний. Он включает в себя трудоемкий этап оценки матрицы Гессе (вторых производных энергии по отношению к декартовым координатам атомов) и ее диагонализацию для определения нормальных мод и частот гармоник.Для методов SCF матрица Гессе оценивается конечной разностью аналитических градиентов, поэтому требуемое время быстро растет с размером системы. [Стр.124]
Чрезмерное заживление магнитных сердечников в результате гармонических частот из-за гистерезиса и потерь на вихревые токи (уравнения (1.I2) и (1.13)). [Pg.506]
Таким образом, номинальные характеристики конденсаторного блока будут изменяться пропорционально квадрату эффективного гармонического напряжения и прямо пропорционально частоте гармоники. Однако это повышение кВАр не будет способствовать улучшению системы p.f. а только от перегрузки самих конденсаторов. [Pg.734]
Для гармоники порядка n и гармонической частоты nf реактивное сопротивление гармоники станет … [Pg.734]
Схема фильтра представляет собой комбинацию конденсатора и последовательного реактивного сопротивления, настроенного на определенную частоту гармоники ( последовательный резонанс), чтобы предложить ему наименьшее сопротивление на этой частоте и, следовательно, отфильтровать его. Сказать. для пятой гармоники, = … [Pg.735]
Это параллельные резонансные L-C цепи, настроенные так, чтобы обеспечить высокий импеданс для определенной частоты гармоники… [Pg.735]
Следует убедиться, что ни при каких условиях нарушения в системе цепь фильтра не станет емкостной, когда она приближается к резонансу. Для этого схемы фильтров могут быть настроены на немного меньшую, чем определенная частота гармоник. Это сделает L и, следовательно, Xl всегда выше, чем Xc, поскольку … [Pg.745]
Наконец, частоты гармоник получаются на уровне HF / 6-31G и равномерно масштабируются с помощью общепринятого коэффициента 0,8929. Это учитывает вклад Больцмана в колебательные моды.[Pg.323]
Таблица 11.13. Зависимость частот ВЧ гармоник h3O (см) от базисных экспериментальных значений: 3943 см, 3832 см и 1649 см …
Обработка MP2 восстанавливает большую часть эффекта корреляции, и результаты CCSD (T) с базисными наборами cc-pVQZ хорошо согласуются с экспериментальными значениями. Остающиеся расхождения в 9 см, 13 см и 10 см в основном связаны с несоответствием базового набора, как показывают результаты MP2 / cc-pV5Z.Значения MP2 неплохо согласуются с экспериментальными частотами гармоник, но, конечно, все же завышают экспериментальные фундаментальные из-за ангармонизма. По этой причине расчетные частоты гармоник MP2 часто масштабируются на 0,97 для сравнения с экспериментальными результатами. … [Pg.272]
h3O CCSD (T) частоты гармоник как функция базиса (только валентные электроны) … [Pg.273]
Таблица 11.16 Частоты гармоник h3O MP2 (cm функция базиса установить (все электроны) «) как a…
Для сравнения с экспериментальными частотами (которые обязательно являются ангармоническими) обычно нет смысла улучшать теоретический уровень выше MP2 с базисным набором типа TZ (2df, 2pd), если константы ангармоничности не рассчитываются явно. Хотя ангармонизм можно приблизительно учесть путем масштабирования частот гармоник на 0,97, оставшиеся ошибки в константах гармонической силы на этом уровне обычно меньше, чем соответствующие ошибки из-за вариаций ангармонизма.[Стр.273]
Частоты гармоник, вычисленные с помощью различных функционалов ДПФ, как функция базового набора, показаны в таблицах 11.17-11.19. Сходимость как функция базисного набора аналогична наблюдаемой для метода HF. Функционал B3PW91 снова показывает лучшую производительность. С базисным набором cc-pV5Z отклонения от экспериментальных частот гармоник составляют всего 0 см, 9 см и 17 см, что существенно лучше, чем у … [Pg.273]
Таблица 11.17 h3O наивысшая частота гармоники ( см] DFT функционалы экспериментальное значение 3943 см «…
Таблица 11.23. Базис cc-pVTZ. Частоты гармоник для 0 3 с … [Pg.288]
Вышеупомянутое рассмотрение сделало некоторые предположения, такие как частоты гармоник и достаточно малый энергетический интервал между уровнями вращения. Если требуется более подробное рассмотрение, суммирование статистических сумм должно выполняться явно. Многие молекулы также имеют внутреннее вращение с довольно маленькими препятствиями, вышесказанное предполагается, что они описываются простыми гармоническими колебаниями, что может быть плохим приближением.Расчет уровней энергии для тормозного ротора несколько сложен и выполняется редко. Если барьер очень низкий, движение можно рассматривать как свободный ротор, и в этом случае он вносит постоянный фактор RT в энтальпию и R / 2 в энтропию. [Pg.306]
Частоты субгармоник (т.е. меньшие, чем фактическая частота вращения вала) являются основным инструментом оценки для подшипников с жидкостной пленкой, и за ними следует внимательно следить. Абсолютно необходимо узкополосное окно, охватывающее весь диапазон частотных составляющих вибрации между электронным шумом и скоростью движения.[Pg.711]
Вертикальный Механический люфт в вертикальной плоскости генерирует ряд гармонических и полугармонических частотных составляющих. Рисунок 44.37 представляет собой простой пример сигнатуры вертикального механического ослабления. [Pg.737]
Внутреннее (т. Е. Пеленг) и несоосность смещения также возбуждают вторую (2x) гармоническую частоту. За один полный оборот вал создает две высокие точки. Эти две высокие точки создают составляющие первой (lx) и второй гармоники (2x).[Pg.738]
Угловое смещение может принимать различные формы сигнатуры и вызывает возбуждение основных (lx) и вторичных (2x) компонентов. Он может возбуждать частоту третьей (3x) гармоники в зависимости от фактического соотношения фаз углового смещения. Это также создает сильную осевую вибрацию. [Pg.738]
В большинстве случаев этот режим отказа также возбуждает частоту третьей (3х) гармоники и создает сильную осевую вибрацию. В зависимости от серьезности нестабильности и конструкции машины, нестабильность процесса также может создавать различные формы колебаний вала.В свою очередь, это возбуждает компоненты радиальной вибрации lx, 2x и 3x. [Pg.740]
Фридли (F4) расширил теоретический анализ Харта и МакКлюра и включил члены возмущения второго порядка. Его анализ показывает, что линейный отклик зоны горения (то есть акустическая проводимость) существенно не изменяется за счет включения членов возмущения второго порядка. Однако члены возмущения второго порядка предсказывают изменения в скорости горения топлива (т.е. переход от линейного к нелинейному поведению) в соответствии с экспериментальными наблюдениями.Анализ, включающий члены второго порядка, также показывает, что колебания частоты второй гармоники камеры сгорания могут стать важными.

Интервал	Коэффициент	От гармоник
Октава	130/65 = 2	1 и 2
Пятый	195/130 = 1,5	2 и 3
Четвертый	260/195 = 1.33	3 и 4
Главный третий	325/260 = 1,25	4 и 5
Малый седьмой	455/260 = 1,75	4 и 7

Интервал	Коэффициент	От гармоник
Октава	2/1 = 2	1 и 2
Пятый	3/2 = 1.5	2 и 3
Четвертый	4/3 = 1,33	3 и 4
Главный третий	5/4 = 1,25	4 и 5
Малый седьмой	7/4 = 1,75	4 и 7

А	C # (мажорная треть)	E (идеальная квинта)	G (второстепенный седьмой)
440	440 х 1,25 = 550	440 х 1,5 = 660	440 x 1,75 = 770

Гармонический — Harmonic — qaz.wiki

Bard — Справка по программе

Гармоника • ru.knowledgr.com

Особенности

Гармоника и подтекст

Гармоника на струнных инструментах

Стол

Искусственная гармоника

Другая информация

См. также

Внешние ссылки

что это и чем они опасны

Определение гармоник

Источники помех

Последствия гармонических помех

Гармоники, основная частота, тон

Что такое гармоники или обертона

Что такое гармоники

Понравилась статья? Поделись с друзьями.

Читайте также:

4.6 Гармоники серии II: гармоники, интервалы и инструменты

Игра гармоник на струнных

Управление шумом гироскопа с помощью фильтров Static Notch и Dynamic Harmonic Notch — документация Copter

Настройка

Предполетная подготовка

Установка на основе дроссельной заслонки

Полетный и послеполетный анализ

Конфигурация гармонической режекции

Пост-конфигурация полета и анализ после полета

Масштабирование частоты режекции

Традиционная установка для вертолета

Статическая гармоническая режекция

Dynamic Harmonic Notch

Проверка эффективности гармонической режекции

Статическая выемка

, часть 1 — Введение в гармоники и BLE

Гармоники, часть 1 (эта часть) — Введение в гармоники и BLE

Гармоники, часть 2 — Определение источника гармоник

Это сообщение в блоге зовет ваше имя, если:

Что такое электромагнитное поле?

Как насчет побочного излучения?

А гармоническое побочное излучение?

Но чем вредны побочные излучения?

Непреднамеренный радиатор vs.преднамеренный радиатор

До следующего раза…

Хотите узнать больше?

границ | Интерпретации частотного анализа нейронного увлечения: периодичность, основная частота и гармоники

Введение

Периодичность сигнала и спектр Фурье

Факторы, влияющие на мощность на частоте гармоник

Фурье-анализ серии ответов, связанных с событием

Интерпретация низкочастотного нейронного вовлечения

Низкочастотное нейронное вовлечение во время обработки речи, музыки и слуха

Взносы авторов

Финансирование

Заявление о конфликте интересов

Сноски

Список литературы

Артикул: серия гармоник

Важность гармонического ряда

Расчет частот

Частота гармоники — Большая химическая энциклопедия

Читайте также

Что делать, если грудничок не спит днем: советы по налаживанию режима сна

Антигистаминные препараты для новорожденных: лечение и профилактика аллергии у грудничков

Методика «Цветоник» М. Лазарева для музыкального развития детей

Добавить комментарий Отменить ответ