РАДИОТЕХНИЧЕСКИЕ РАСЧЕТЫ
силовой трансформатор радиотехнические расчеты радио калькулятор
РАДИОТЕХНИЧЕСКИЕ РАСЧЕТЫ
Во время конструирования радиолюбителю приходится производить массу расчетов. Один из самых трудоемких - расчет колебательного контура. Рассмотрим методику такого расчета.
Как и при любом расчете нам нужны будут
исходные данные. Предположим, нам нужно
рассчитать частоту колебательного контура
для фиксированных значений емкости
конденсатора и индуктивности катушки.
Допустим, емкость конденсатора равна 10
пикофарадам, индуктивность катушки — 10
микрогенри. По формуле (1 (А)) определяем
частоту. Она равна 15900 килогерц (то есть 15,9
Мегагерца). При расчете индуктивности
катушки при известных частоте настройки
и емкости контура используем формулу 1(В).
Статья из журнала «Радио» для упрощенного расчета колебательного контура лежит здесь. Номограмму по расчету числа витков и размера катушек можно скачать по этой ссылке. Обе статьи в формате DjVu — программу для их чтения можно скачать здесь.
Емкости конденсаторов и сопротивления резисторов имеют стандартный числовой ряд, но иногда требуются нестандартные значения. Как можно выйти из такого положения? Можно взять несколько, например, резисторов и соединить их так, чтобы получить нужное значение.
Пользуясь формулой (2) можно рассчитать
величину, которую мы получим в результате
параллельного (а), либо последовательного (b)
соединения резисторов. При
последовательном соединении резисторов их
номиналы складываются между собой.
Параллельное соединение позволяет
получить результирующее сопротивление
всегда меньшее, чем номинал наименьшего из
соединяемых резисторов.
Соединение конденсаторов:
При последовательном соединении конденсаторов (формула 3(b)) результирующая емкость будет всегда меньше емкости наименьшего из соединяемых конденсаторов. При параллельном соединении (3(a)) результирующая емкость будет равна сумме емкостей конденсаторов.
При работе на переменном токе иногда приходится рассчитывать реактивные сопротивления катушек индуктивности и конденсаторов.
Реактивное сопротивление катушки можно определить, пользуясь формулой (4), сопротивление конденсатора на переменном токе можно вычислить при помощи формулы (5):
В обоих формулах «Pi» — это всем
известная математическая константа «Пи»,
равная (округленно) 3,14.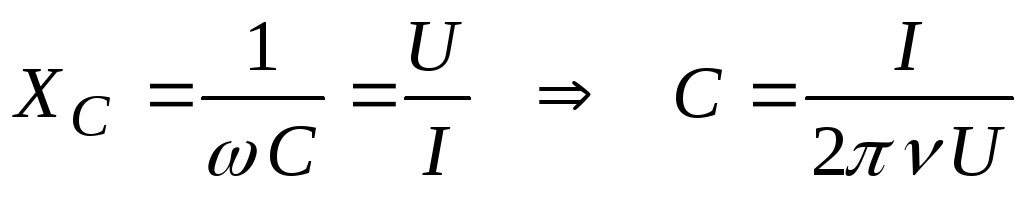
В заключении хотелось бы обратить ваше внимание на сноски в формулах. Для того, чтобы получить истинное значение при расчетах не забывайте использовать нужные величины!
В дальнейшем мы с вами рассмотрим формулы расчета катушек индуктивности с сердечником и без сердечника.
Индуктивность, емкость и сопротивление в цепи переменного тока.
Рассмотрим электрическую цепь, состоящую из сопротивления R, катушки индуктивностиL, и конденсатора емкостьюC, к которым приложена внешняя ЭДС, изменяющаяся со временемε(t). Согласно закону Ома для данной цепи можно записать:
(8)
где I– сила тока,
R– сопротивление, ,(o– максимальное значение внешней ЭДС,ω– частота колебаний),Учитывая, что и, выражение (8) можно записать в виде:
. (9)
(9)
Это дифференциальное уравнение второго порядка описывает вынужденные колебания с учетом сопротивления. Решая это уравнение, получаем выражение для амплитудного значения силы тока:
(10)
Выражение (10) можно рассматривать как закон Ома для переменного тока.
В этом случае
– полное сопротивление цепи переменного тока,R– омическое сопротивление,ωL– индуктивное
4
сопротивление, – емкостное сопротивление, величину– часто называют реактивным сопротивлением. В случае если в цепи переменного тока отсутствует либо катушка индуктивности, либо конденсатор, выражение (10) упрощается, т.к. в этом случае либоRL=ωL, либо равны нулю.
Схема установки
Рассмотрим электрическую цепь, собранную согласно рис.2, где P
ползунковый реостат;
L– соленоид с омическим
cопротивлением R;
А – амперметр,
V– вольтметр, К – ключ.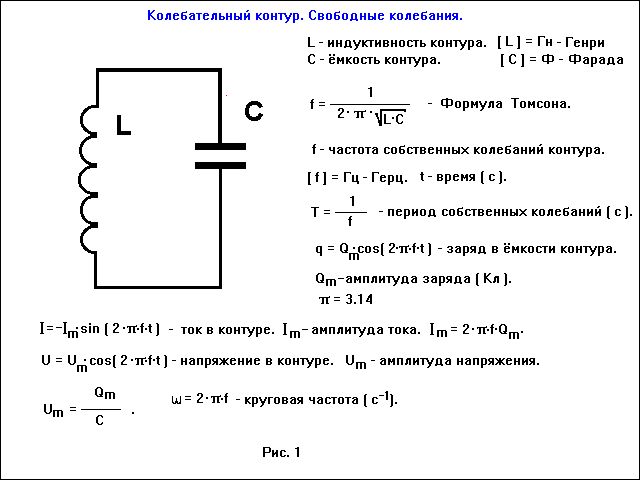
Для нахождения неизвестного значения индуктивности Lможно использовать закон Ома для участка цепиab:, (11)
где I0 иU0 – амплитудные значения силы тока и напряжения на участкеab,R– омическое сопротивление соленоида,RL=ωLиндуктивное сопротивление соленоида. Приборы переменного тока измеряют эффективные значения силы тока и напряжения, которые связаны с амплитудными значениями следующим образом:
и
(под эффективным значением, например, силы переменного тока, понимают такую величину постоянного тока, который в омическом сопротивлении выделяет ту же мощность, что и переменный ток). Учитывая вышесказанное, формулу (11) можно записать в следующем виде:
(12)
Найдя с помощью приборов Iэф. иUэф. Можно определить полное сопротивление участка цепиab:
5
Так как , то зная омическое сопротивлениеR, можно найти индуктивность соленоидаL:
(14)
Здесь
= 6,2850 Гц = 314 Гц.
Порядок выполнения работы
Собрать цепь по схеме рис.2.
Определить цену деления амперметра и вольтметра.
Вынув сердечник из катушки, включить ключ «К».
Изменяя ползунковым реостатом ток в цепи, измерить Iэф. иUэф. Измерения выполнить для пяти значений токов и напряжений. Результаты измерений занести в таблицу 1.
Примечание.Амперметр и вольтметр регистрируют эффективные значения тока и напряжения Iэф.и
Uэф..Таблица 1.
№ | Iэф А | Uэф В | Z Ом | L Гн | Lср. Гн | ΔL Гн | ΔLср. Гн | |
1. | ||||||||
2. | ||||||||
3. | ||||||||
4. | ||||||||
5. | ||||||||
Омическое сопротивлениеR= | = | |||||||
Занести в таблицу 1 и таблицу 2 значение сопротивления соленоида R.

Вставить ферромагнитный сердечник в катушку. Измерить Uэфпри заданном преподавателем значенииIэф.
Выдвигая сердечник из катушки каждый раз на 2 см и поддерживая ползунковым реостатом заданное значение Iэф, найти соответствующие значенияUэффдо полного удаления сердечника из катушки. Результаты измерений занести в таблицу 2.
6
Таблица 2.
№ | Iэф. | l см | Uэф. В | Z Ом | L Гн |
1. | 16 | ||||
2. | 14 | ||||
3. | 12 | ||||
4. | 10 | ||||
5. | 8 | ||||
6. | 6 | ||||
7. | 4 | ||||
8. | 2 | ||||
9. | 0 | ||||
Омическое сопротивлениеR= | = | ||||
Примечание:l(см) – часть сердечника, находящаяся в катушке.
Обработка результатов измерений
Пользуясь формулой (13), рассчитать полное сопротивление для каждого измерения и данные занести в таблицу 1.
Рассчитать значения индуктивности соленоида по формуле (14) для каждого измерения и данные занести в таблицу 1.
Рассчитать среднее значение индуктивности соленоида , абсолютные погрешности измерения , среднюю абсолютную погрешность , и относительную погрешность .
 Все рассчитанные величины записать в
таблицу 1.
Все рассчитанные величины записать в
таблицу 1.Повторить расчеты, указанные в п. 1 и 2, используя данные таблицы 2.
Построить график зависимости индуктивности соленоида Lот глубины погруженияlсердечника в катушку.
7
Глава 24. Электромагнитные колебания и волны
Электрическая цепь, состоящая из катушки индуктивности и конденсатора (см. рисунок), называется колебательным контуром. В этой цепи могут происходить своеобразные электрические колебания. Пусть, например, в начальный момент времени мы заряжаем пластины конденсатора положительным и отрицательным зарядами, а затем разрешим зарядам двигаться. Если бы катушка отсутствовала, конденсатор начал бы разряжаться, в цепи на короткое время возник электрический ток, и заряды пропали бы. Здесь же происходит следующее. Сначала благодаря самоиндукции катушка препятствует увеличению тока, а затем, когда ток начинает убывать, препятствует его уменьшению, т. е. поддерживает ток. В результате ЭДС самоиндукции заряжает конденсатор с обратной полярностью: та пластина, которая изначально была заряжена положительно, приобретает отрицательный заряд, вторая — положительный. Если при этом не происходит потерь электрической энергии (в случае малого сопротивления элементов контура), то величина этих зарядов будет такая же, как величина первоначальных зарядов пластин конденсатора. В дальнейшем движение процесс перемещения зарядов будет повторяться. Таким образом, движение зарядов в контуре представляет собой колебательный процесс.
е. поддерживает ток. В результате ЭДС самоиндукции заряжает конденсатор с обратной полярностью: та пластина, которая изначально была заряжена положительно, приобретает отрицательный заряд, вторая — положительный. Если при этом не происходит потерь электрической энергии (в случае малого сопротивления элементов контура), то величина этих зарядов будет такая же, как величина первоначальных зарядов пластин конденсатора. В дальнейшем движение процесс перемещения зарядов будет повторяться. Таким образом, движение зарядов в контуре представляет собой колебательный процесс.
Для решения задач ЕГЭ, посвященных электромагнитным колебаниям, нужно запомнить ряд фактов и формул, касающихся колебательного контура. Во-первых, нужно знать формулу для периода колебаний в контуре. Во-вторых, уметь применять к колебательному контуру закон сохранения энергии. И, наконец (хотя такие задачи встречаются редко), уметь использовать зависимости силы тока через катушку и напряжения на конденсаторе от времени
Период электромагнитных колебаний в колебательном контуре определяется соотношением:
(24. |
где — емкость конденсатора, — индуктивность катушки.
При электромагнитных колебаниях энергия колебательного контура складывается из энергии конденсатора и энергии тока в катушке:
(24.2) |
где и — заряд на конденсаторе и сила тока в катушке в этот момент времени, и — емкость конденсатора и индуктивность катушки. Если электрическое сопротивление элементов контура мало, то электрическая энергия контура (24.2) остается практически неизменной, несмотря на то, что заряд конденсатора и ток в катушке изменяются с течением времени. Из формулы (24.4) следует, что при электрических колебаниях в контуре происходят превращения энергии: в те моменты времени, когда ток в катушке равен нулю, вся энергия контура сводится к энергии конденсатора. В те моменты времени, когда равен нулю заряд конденсатора, энергия контура сводится к энергии магнитного поля в катушке.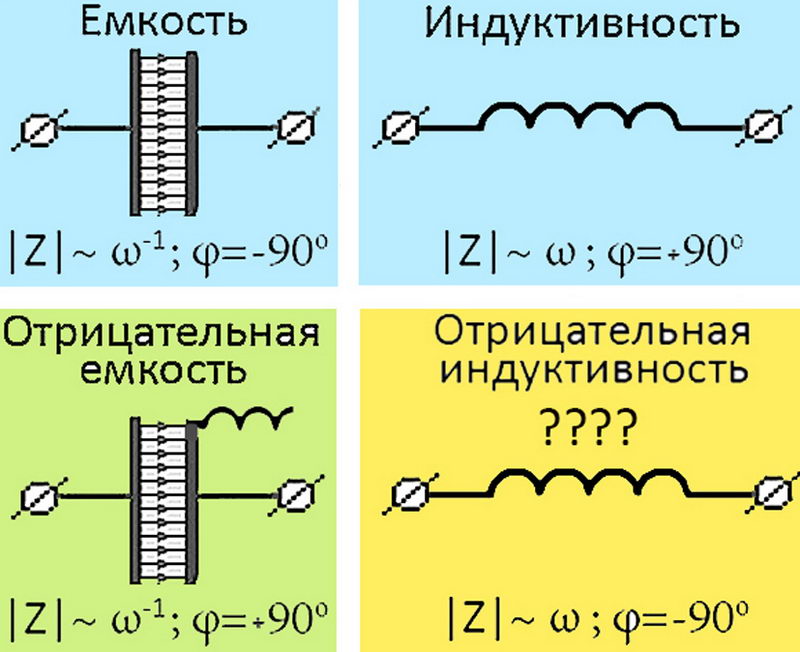 Очевидно, в эти моменты времени заряд конденсатора или ток в катушке достигают своих максимальных (амплитудных) значений.
Очевидно, в эти моменты времени заряд конденсатора или ток в катушке достигают своих максимальных (амплитудных) значений.
При электромагнитных колебаниях в контуре заряд конденсатора изменяется с течением времени по гармоническому закону:
(24.3) |
где — амплитуда колебаний заряда на конденсаторе, — циклическая (или круговая) частота колебаний, — начальная фаза. Циклическая частота колебаний связана с периодом по формуле
(24.4) |
стандартной для любых гармонических колебаний. Поскольку сила тока в катушке представляет собой производную заряда конденсатора по времени, из формулы (24.4) можно найти зависимость силы тока в катушке от времени
(24.5) |
В ЕГЭ по физике часто предлагаются задачи на электромагнитные волны. Необходимый для решения этих задач минимум знаний включает в себя понимание основных свойств электромагнитной волны и знание шкалы электромагнитных волн. Сформулируем кратко эти факты и принципы.
Необходимый для решения этих задач минимум знаний включает в себя понимание основных свойств электромагнитной волны и знание шкалы электромагнитных волн. Сформулируем кратко эти факты и принципы.
Согласно законам электромагнитного поля переменное магнитное поле порождает поле электрическое, переменное электрическое поле порождает поле магнитное. Поэтому если одно из полей (например, электрическое) начнет меняться, возникнет второе поле (магнитное), которое затем снова порождает первое (электрическое), затем снова второе (магнитное) и т.д. Процесс взаимного превращения друг в друга электрического и магнитного полей, который может распространяться в пространстве, называется электромагнитной волной. Опыт показывает, что направления, в которых колеблются векторы напряженности электрического и индукции магнитного поля в электромагнитной волне перпендикулярны направлению ее распространения. Это означает, что электромагнитные волны являются поперечными. В теории электромагнитного поля Максвелла доказывается, что электромагнитная волна создается (излучается) электрическими зарядами при их движении с ускорением. В частности, источником электромагнитной волны является колебательный контур.
В частности, источником электромагнитной волны является колебательный контур.
Длина электромагнитной волны , ее частота (или период ) и скорость распространения связаны соотношением, которое справедливо для любой волны (см. также формулу (11.6)):
(24.6) |
Электромагнитные волны в вакууме распространяются со скоростью = 3 • 108 м/с, в среде скорость электромагнитных волн меньше, чем в вакууме, причем эта скорость зависит от частоты волны. Такое явление называется дисперсией волн. Электромагнитной волне присущи все свойства волн, распространяющихся в упругих средах: интерференция, дифракция, для нее справедлив принцип Гюйгенса. Единственное, что отличает электромагнитную волну, это то, что для ее распространения не нужна среда — электромагнитная волна может распространяться и в вакууме.
В природе наблюдаются электромагнитные волны с сильно отличающимися друг от друга частотами, и обладающие благодаря этому существенно различными свойствами (несмотря на одинаковую физическую природу). Классификация свойств электромагнитных волн в зависимости от их частоты (или длины волны) называется шкалой электромагнитных волн. Дадим краткий обзор этой шкалы.
Классификация свойств электромагнитных волн в зависимости от их частоты (или длины волны) называется шкалой электромагнитных волн. Дадим краткий обзор этой шкалы.
Электромагнитные волны с частотой меньшей 105 Гц (т.е. с длиной волны, большей нескольких километров) называются низкочастотными электромагнитными волнами. Излучают волны такого диапазона большинство бытовых электрических приборов.
Волны с частотой от 105 до 1012 Гц называются радиоволнами. Этим волнам отвечают длины волн в вакууме от нескольких километров до нескольких миллиметров. Эти волны применяются для радиосвязи, телевидения, радиолокации, сотовых телефонов. Источниками излучения таких волн являются заряженные частицы, движущиеся в электромагнитных полях. Радиоволны излучаются также свободными электронами металла, которые совершают колебания в колебательном контуре.
Область шкалы электромагнитных волн с частотами, лежащими в интервале 1012 — 4,3 • 1014 Гц (и длинами волн от нескольких миллиметров до 760 нм) называется инфракрасным излучением (или инфракрасными лучами). Источником такого излучения служат молекулы нагретого вещества. Человек излучает инфракрасные волны с длиной волны 5 — 10 мкм.
Источником такого излучения служат молекулы нагретого вещества. Человек излучает инфракрасные волны с длиной волны 5 — 10 мкм.
Электромагнитное излучение в интервале частот 4,3 • 1014 — 7,7 • 1014 Гц (или длин волн 760 — 390 нм) воспринимается человеческим глазом как свет и называется видимым светом. Волны различных частот внутри этого диапазона воспринимаются глазом, как имеющие различный цвет. Волна с самой маленькой частотой из видимого диапазона 4,3 • 1014 воспринимается как красная, с самой большой частотой внутри видимого диапазона 7,7 • 1014 Гц — как фиолетовая. Видимый свет излучается при переходе электронов в атомах, молекулами твердых тел, нагретых до 1000 °С и более.
Волны с частотой 7,7 • 1014 — 1017 Гц (длина волны от 390 до 1 нм) принято называть ультрафиолетовым излучением. Ультрафиолетовое излучение имеет выраженное биологическое действие: оно способно убивать ряд микроорганизмов, способно вызвать усиление пигментации человеческой кожи (загар), при избыточном облучении в отдельных случаях может способствовать развитию онкологических заболеваний (рак кожи). Ультрафиолетовые лучи содержатся в излучении Солнца, в лабораториях создаются специальными газоразрядными (кварцевыми) лампами.
Ультрафиолетовые лучи содержатся в излучении Солнца, в лабораториях создаются специальными газоразрядными (кварцевыми) лампами.
За областью ультрафиолетового излучения лежит область рентгеновских лучей (частота 1017 — 1019 Гц, длина волны от 1 до 0,01 нм). Эти волны излучаются при торможении в веществе заряженных частиц, разогнанных напряжением 1000 В и более. Обладают способностью проходить сквозь толстые слои вещества, непрозрачного для видимого света или ультрафиолетового излучения. Благодаря этому свойству рентгеновские лучи широко используются в медицине для диагностики переломов костей и ряда заболеваний. Рентгеновские лучи оказывают губительное действие на биологические ткани. Благодаря этому свойству их можно использовать для лечения онкологических заболеваний, хотя при избыточном облучении они смертельно опасны для человека, вызывая целый ряд нарушений в организме. Из-за очень малой длины волны волновые свойства рентгеновского излучения (интерференцию и дифракцию) можно обнаружить только на структурах, сравнимых с размерами атомов.
Гамма-излучением (-излучением) называют электромагнитные волны с частотой, большей, чем 1020 Гц (или длиной волны, меньшей 0,01 нм). Возникают такие волны в ядерных процессах. Особенностью -излучения является его ярко выраженные корпускулярные свойства (т.е. это излучение ведет себя как поток частиц). Поэтому о -излучении часто говорят как о потоке -частиц.
В задаче 24.1.1 для установления соответствия между единицами измерений используем формулу (24.1), из которой следует, что период колебаний в контуре с конденсатором емкостью 1 Ф и индуктивностью 1 Гн равен секунд (ответ 1).
Из графика, данного в задаче 24.1.2, заключаем, что период электромагнитных колебаний в контуре составляет 4 мс (ответ 3).
По формуле (24.1) находим период колебаний в контуре, данном в задаче 24.1.3: (ответ 4). Отметим, что согласно шкале электромагнитных волн такой контур излучает волны длинноволнового радиодиапазона.
Периодом колебания называется время одного полного колебания. Это значит, что если в начальный момент времени конденсатор заряжен максимальным зарядом (задача 24.1.4), то через половину периода конденсатор будет также заряжен максимальным зарядом, но с обратной полярностью (та пластина, которая изначально была заряжена положительно, будет заряжена отрицательно). А максимальный в контуре ток будет достигаться между этими двумя моментами, т.е. через четверть периода (ответ 2).
Если увеличить индуктивность катушки в четыре раза (задача 24.1.5), то согласно формуле (24.1) период колебаний в контуре возрастет в два раза, а частота уменьшится в два раза (ответ 2).
Согласно формуле (24.1) при увеличении емкости конденсатора в четыре раза (задача 24.1.6) период колебаний в контуре увеличивается в два раза (ответ 1).
При замыкании ключа (задача 24.1.7) в контуре вместо одного конденсатора будут работать два таких же конденсатора, соединенных параллельно (см. рисунок). А поскольку при параллельном соединении конденсаторов их емкости складываются, то замыкание ключа приводит к двукратному увеличению емкости контура. Поэтому из формулы (24.1) заключаем, что период колебаний увеличивается в раз (ответ 3).
Пусть заряд на конденсаторе совершает колебания с циклической частотой (задача 24.1.8). Тогда согласно формулам (24.3)-(24.5) с той же частотой будет совершать колебаний ток в катушке. Это значит, что зависимость тока от времени может быть представлена в виде . Отсюда находим зависимость энергии магнитного поля катушки от времени
Из этой формулы следует, что энергия магнитного поля в катушке совершает колебания с удвоенной частотой, и, значит, с периодом, вдвое меньшим периода колебания заряда и тока (ответ 1).
В задаче 24.1.9 используем закон сохранения энергии для колебательного контура. Из формулы (24.2) следует, что для амплитудных значений напряжения на конденсаторе и тока в катушке справедливо соотношение
(здесь в отличие от (24.2) использовано другое выражение для энергии конденсатора). Или А (ответ 2).
В задаче 24.1.10 удобно использовать закон сохранения энергии в виде (24.2). Имеем
где и — амплитудные значения заряда конденсатора и тока в катушке. Из этой формулы с использованием соотношения (24.1) для периода колебаний в контуре находим амплитудное значение тока
ответ 3.
Радиоволны — электромагнитные волны с определенными частотами. Поэтому скорость их распространения в вакууме равна скорости распространения любых электромагнитных волн, и в частности, рентгеновских. Эта скорость — скорость света (задача 24.2.1 — ответ 1).
Как указывалось ранее, заряженные частицы излучают электромагнитные волны при движении с ускорением. Поэтому волна не излучается только при равномерном и прямолинейном движении (задача 24.2.2 — ответ 1).
Электромагнитная волна — это особым образом изменяющиеся в пространстве и времени и поддерживающие друг друга электрическое и магнитное поля. Поэтому правильный ответ в задаче 24.2.3 — 2.
Из данного в условии задачи 24.2.4 графика следует, что период данной волны — = 4 мкс. Поэтому из формулы (24.6) получаем м (ответ 1).
В задаче 24.2.5 по формуле (24.6) находим
(ответ 4).
С антенной приемника электромагнитных волн связан колебательный контур. Электрическое поле волны действует на свободные электроны в контуре и заставляет их совершать колебания. Если частота волны совпадает с собственной частотой электромагнитных колебаний, амплитуда колебаний в контуре возрастает (резонанс) и может быть зарегистрирована. Поэтому для приема электромагнитной волны частота собственных колебаний в контуре должна быть близка к частоте этой волны (контур должен быть настроен на частоту волны). Поэтому если контур нужно перенастроить с волны длиной 100 м на волну длиной 25 м (задача 24.2.6), собственная частота электромагнитных колебаний в контуре должна быть увеличена в 4 раза. Для этого согласно формулам (24.1), (24.4) емкость конденсатора следует уменьшить в 16 раз (ответ 4).
Согласно шкале электромагнитных волн (см. введение к настоящей главе), максимальной длиной из перечисленных в условии задачи 24.2.7 электромагнитных волн обладает излучение антенны радиопередатчика (ответ 4).
Среди перечисленных в задаче 24.2.8 электромагнитных волн максимальной частотой обладает рентгеновское излучение (ответ 2).
Электромагнитная волна является поперечной. Это значит, что векторы напряженности электрического поля и индукции магнитного поля в волне в любой момент времени направлены перпендикулярно направлению распространения волны. Поэтому при распространении волны в направлении оси (задача 24.2.9), вектор напряженности электрического поля направлен перпендикулярно этой оси. Следовательно, обязательно равна нулю его проекция на ось = 0 (ответ 3).
Скорость распространения электромагнитной волны — есть индивидуальная характеристика каждой среды. Поэтому при переходе электромагнитной волны из одной среду в другую (или из вакуума в среду) скорость электромагнитной волны изменяется. А что можно сказать о двух других параметрах волны, входящих в формулу (24.6), — длине волны и частоте . Будут ли они изменяться при переходе волны из одной среды в другую (задача 24.2.10)? Очевидно, что частота волны не изменяется при переходе из одной среды в другую. Действительно, волна это колебательный процесс, в котором переменное электромагнитное поле в одной среде создает и поддерживает поле в другой среде благодаря именно этим изменениям. Поэтому периоды этих периодических процессов (а значит и частоты) в одной и другой среде должны совпадать (ответ 3). А поскольку скорость волны в разных средах разная, то из проведенных рассуждений и формулы (24.6) следует, что длина волны при ее переходе из одной среды в другую — изменяется.
Колебательный контур. LCR, LC — контур. Катушка индуктивности, конденсатор Формула Томсона Энергия
Колебательный контур – электрическая цепь, состоящая из последовательно соединённых конденсатора с ёмкостью
, катушки с индуктивностью и электрического сопротивления .Идеальный колебательный контур — цепь, состоящая только из катушки индуктивности (не имеющей собственного сопротивления) и конденсатора (
-контур). Тогда в такой системе поддерживаются незатухающие электромагнитные колебания силы тока в цепи, напряжения на конденсаторе и заряда конденсатора. Давайте разберём контур и подумаем, откуда возникают колебания. Пусть изначально заряженный конденсатор помещён в описываемую нами цепь.Рис. 1. Колебательный контур
В начальный момент времени весь заряд сосредоточен на конденсаторе, на катушке тока нет (рис. 1.1). Т.к. на обкладках конденсатора внешнего поля тоже нет, то электроны с обкладок начинают «уходить» в цепь (заряд на конденсаторе начинает уменьшаться). При этом (за счёт освобождённых электронов) возрастает ток в цепи. Направление тока, в данном случае, от плюса к минусу (впрочем, как и всегда), и конденсатор представляет собой источник переменного тока для данной системы. Однако при росте тока на катушке, вследствие явления электромагнитной индукции, возникает обратный индукционный ток (
). Направление индукционного тока, согласно правилу Ленца, должно нивелировать (уменьшать) рост основного тока. Когда заряд конденсатора станет равным нулю (весь заряд стечёт), сила индукционного тока в катушке станет максимальной (рис. 1.2).Однако текущий заряд в цепи пропасть не может (закон сохранения заряда), тогда этот заряд, ушедший с одной обкладки через цепь, оказался на другой обкладке. Таким образом, происходит перезарядка конденсатора в обратную сторону (рис. 1.3). Индукционный ток на катушке уменьшается до нуля, т.к. изменение магнитного потока также стремится к нулю.
При полной зарядке конденсатора электроны начинают двигаться в обратную сторону, т.е. происходит разрядка конденсатора в обратную сторону и возникает ток, доходящий до своего максимума при полной разрядке конденсатора (рис. 1.4).
Дальнейшая обратная зарядка конденсатора приводит в систему в положение на рисунке 1.1. Такое поведение системы повторяется сколь угодно долго. Таким образом, мы получаем колебание различных параметров системы: тока в катушке, заряд на конденсаторе, напряжение на конденсаторе. В случае идеальности контура и проводов (отсутствие собственного сопротивления), эти колебания — гармонические.
Для математического описания этих параметров этой системы (в первую очередь, периода электромагнитных колебаний) вводится рассчитанная до нас формула Томсона:
(1)Неидеальным контуром является всё тот же идеальный контур, который мы рассмотрели, с одним небольшим включением: с наличием сопротивления
(-контур). Данное сопротивление может быть как сопротивлением катушки (она не идеальна), так и сопротивлением проводящих проводов. Общая логика возникновения колебаний в неидеальном контуре аналогична той, что и в идеальном. Отличие только в самих колебаниях. В случае наличия сопротивления, часть энергии будет рассеиваться в окружающую среду — сопротивление будет нагреваться, тогда энергия колебательного контура будет уменьшаться и сами колебания станут затухающими.Для работы с контурами в школе используется только общая энергетическая логика. В данном случае, считаем, что полная энергия системы в начале сосредоточена на конденсаторе и/или катушке, и описывается:
(2) (3)
Для идеального контура полная энергия системы остаётся постоянной:
(4)- где
- — полная энергия колебательной системы.
Для неидеального контура часть начальной энергии переходит в тепло, что можно описать законом Джоуля-Ленца. Тогда энергетические превращения в таком контуре можно описать:
(5)Вывод: работа с контурами достаточно сложна. Чаще всего это работа со схемами, в которых присутствуют ключи. Энергетически рассмотреть переход из начального состояния в конечное практически невозможно, тогда стоит работать с начальным и конечным положением системы. Определяем вид контура (идеальный/неидеальный) и рассмотреть энергию системы в обоих случаях. Далее, используя (4) или (5), получаем уравнение, которое можно решать.
Поделиться ссылкой:
Измерение частоты, индуктивности и ёмкости в электрических цепях
Измерение частоты, индуктивности и ёмкости в электрических цепях.
Измерение индуктивности и ёмкости.
Обычно измерение параметров линейных компонентов (индуктивности и емкости) производят на высокой частоте резонансным методом. Он основан на том, что зависимость резонансной частоты колебательного контура от его параметров определяется формулой fo = 1/(2πx LC).
Определив резонансную частоту контура и зная значение эталонного компонента (конденсатора или индуктивности), можно определить значение другого.
Рис. 9.10. Измерение фазовых сдвигов:
А — двухканальным осциллографом; б — методом эллипса; в — компенсационным методом
Приборы для таких измерений получили название куметров, так как они позволяют определять добротность колебательного контура Q, которая равна отношению напряжения на конденсаторе к напряжению на входе контура.
Куметр включает генератор высокой частоты, образцовый градуированный в значениях емкости конденсатор и клеммы подключения измеряемой катушки индуктивности
или конденсатора. Для измерения индуктивности катушки Lx ее подключают к выводам кат и настройкой генератора высокой частоты добиваются явления последовательного резонанса. Его находят по показанию электронного вольтметра, подключенного к эталонному конденсатору. Формула LX = 1 / (4π2 · F · C0) где F — частота, C0 — ёмкость образцового конденсатора, позволяет по известным значениям емкости эталонного конденсатора и резонансной частоте определить величину индуктивности катушки. Напряжение высокочастотного сигнала генератора обычно фиксировано, что позволяет шкалу измерительного электронного вольтметра отградуировать непосредственно в значениях добротности Q.
Для измерения емкости конденсатор подключают к выводам схемы конденсатора, а к выводам кат эталонную катушку индуктивности. При вычислении емкости конденсатора необходимо учесть, что параллельно ему подключен эталонный конденсатор, величину емкости которого необходимо вычесть из полученного значения суммарной емкости. Указанные методы измерения значений емкости и индуктивности применимы только для малых величин, но именно такие методы используются в высокочастотных цепях различной аппаратуры.
Приборы непосредственной оценки и сравнения
К измерительным приборам непосредственной оценки значения измеряемой емкости относятся микрофарадметры, действие которых базируется на зависимости тока или напряжения в цепи переменного тока от значения включенной в нее измеряемой емкости. Значение емкости определяют по шкале стрелочного измерителя.
Более широко для измерения параметров конденсаторов и индуктивностей применяют уравновешенные мосты переменного тока, позволяющие получить малую погрешность измерения (до 1 %). Питание моста осуществляется от генераторов, работающих на фиксированной частоте 400—1000 Гц. В качестве индикаторов применяют выпрямительные или электронные милливольтметры, а также осциллографические индикаторы.
Измерение производят балансированием моста в результате попеременной подстройки двух его плеч. Отсчет показаний берется по лимбам рукояток тех плеч, которыми сбалансирован мост.
В качестве примера рассмотрим измерительные мосты, являющиеся основой измерителя индуктивности ЕЗ-3 (рис. 1) и измерителя емкости Е8-3 (рис. 2).
Рис. 1. Схема моста для измерения индуктивности
Рис. 2. Схема моста для измерения емкости с малыми (а) и большими (б) потерями
При балансе моста (рис. 1) индуктивность катушки и ее добротность определяют по формулам Lx = R1R2C2; Qx = wR1C1.
При балансе мостов (рис. 2) измеряемая емкость и сопротивление потерь определяют по формулам
Измерение емкости и индуктивности методом амперметра-вольметра
Для измерения малых емкостей (не более 0,01 — 0,05 мкФ) и высокочастотных катушек индуктивности в диапазоне их рабочих частот широко используют резонансные методы Резонансная схема обычно включает в себя генератор высокой частоты, индуктивно или через емкость связанный с измерительным LС-контуром. В качестве индикаторов резонанса применяют чувствительные высокочастотные приборы, реагирующие на ток или напряжение.
Методом амперметра-вольтметра измеряют сравнительно большие емкости и индуктивности при питании измерительной схемы от источника низкой частоты 50 — 1000 Гц. Для измерения можно воспользоваться схемами рис. 3.
Рисунок 3. Схемы измерения больших (а) и малых (б) сопротивлений переменному току
По показаниям приборов полное сопротивление
где
из этих выражений можно определить
Когда можно пренебречь активными потерями в конденсаторе или катушке индуктивности, используют схему рис. 4. В этом случае
Рис. 4. Схемы измерения больших (а) и малых (б) сопротивлений методом амперметра — вольтметра
Измерение взаимной индуктивности двух катушек
Измерение взаимной индуктивности двух катушек можно произвести по методу амперметра-вольтметра (рис. 5) и методу последовательно соединенных катушек.
Рис. 5. Измерение взаимной индуктивности по методу амперметра-вольтметра
Значение взаимной индуктивности при измерении по методу амперметра-вольтметра
При измерении по второму методу замеряют индуктивности двух последовательно соединенных катушек при согласном LI и встречном LII включении катушек. Взаимоиндуктивность вычисляется по формуле
Измерение индуктивности может быть произведено одним из описанных ранее методов.
Измерение частоты переменного тока
Частоту переменного тока измеряют частотомерами. Обычно применяют резонансные электромагнитные или ферродинамические приборы.
Электромагнитный резонансный частотомер имеет электромагнит 2 (рис. 344, а), в поле которого расположены стальной якорь 1 и соединенный с ним стальной брусок 5. Этот брусок укреплен на упругих пружинах 4 и на нем размещен ряд гибких стальных пластинок 3, площадь поперечного сечения которых подобрана таким образом, что каждая следующая пластинка имеет частоту собственных колебаний на 0,5 Гц больше, чем предыдущая.
Рис. 344. Устройство электромагнитного резонансного частотомера
Рис. 345. Принципиальная схема ферродинамического частотомера .
Свободные концы пластинок введены в прорезь, имеющуюся на шкале прибора. Катушка электромагнита присоединена к сети переменного тока так же, как и катушка вольтметра.
При прохождении по катушке переменного тока электромагнит создает магнитное поле, пульсирующее с частотой изменения тока. Находящийся в этом поле якорь 1 также начнет совершать колебательные движения и вызывать колебания связанных с ним пластинок 3.
Колебания пластинок обычно бывают настолько незначительными, что они не могут быть замечены глазом.
Однако, если частота собственных колебаний какой-либо пластинки совпадает с частотой изменения переменного тока, т. е. с частотой колебаний якоря, то наступит явление механического резонанса, при котором эта пластинка начнет колебаться с большой амплитудой. Белый квадратик на ее конце превращается при этом в белую полоску (рис. 344,б), против которой по шкале можно отсчитывать измеряемую частоту. Значительно слабее колеблются две пластинки, колебания же всех остальных пластинок обычно совершенно незаметны для глаза.
Ферродинамический частотомер (рис. 345) представляет собой логометр ферродинамической системы. Катушки логометра соединяются в две параллельные цепи, которые подключаются к двум точкам а и б, между которыми действует напряжение переменного тока U (так же, как и вольтметры). Последовательно с неподвижной 3 и одной из подвижных 1 катушек включены катушка индуктивности L и конденсатор С, а последовательно с другой подвижной катушкой 2 — резистор с сопротивлением R (могут быть и другие комбинации R, L и С). Поэтому ток I1 в первой параллельной ветви зависит от частоты f, а ток I2 во второй цепи не зависит от f.
В результате при изменении частоты f будут изменяться ток I1 и положение подвижной части логометра до тех пор, пока не наступит равновесие моментов М1 и М2, создаваемых его катушками. Показания такого прибора будут зависеть от частоты f.
Непосредственное измерение частоты производят частотомерами, в основу которых положены различные методы измерения в зависимости от диапазона измеряемых частот и требуемой точности измерения. Наиболее распространенными методами измерения частоты являются:
Метод перезаряда конденсатора за каждый период измеряемой частоты. Среднее значение тока перезаряда пропорционально частоте и измеряется магнитоэлектрическим амперметром, шкала которого проградуирована в единицах частоты. Выпускают конденсаторные частотомеры с пределом измерения 10 Гц — 1 МГц и погрешностью измерения +2%.
Резонансный метод, основанный на явлении электрического резонанса в контуре с подстраиваемыми элементами в резонанс с измеряемой частотой. Измеряемая частота определяется по шкале механизма подстройки. Метод применяется на частотах более 50 кГц. Погрешность измерения можно уменьшить до сотых долей процента.
Метод сравнения измеряемой частоты с эталонной. Электрические колебания неизвестной и образцовой частот смешиваются таким образом, чтобы возникли биения некоторой частоты. При частоте биений, равной нулю, измеряемая частота равна образцовой. Смешение частот осуществляют гетеродинным способом (способ нулевых биений) или осциллографическим.
При последнем способе применяют осциллограф с отключенным генератором внутренней развертки. Напряжение образцовой частоты подают на вход усилителя горизонтальной развертки, а напряжение неизвестной частоты — на вход усилителя вертикального отклонения.
Изменяя образцовую частоту, получают неподвижную или медленно меняющуюся фигуру Лиссажу. Форма фигуры зависит от соотношения частот, амплитуд и фазового сдвига между напряжениями, подаваемыми на отклоняющие пластины осциллографа.
Если мысленно пересечь фигуру по вертикали и горизонтали, то отношение числа пересечений по вертикали m к числу пересечений по горизонтали n равно при неподвижной фигуре отношению измеряемой fх и образцовой fобр частот.
При равенстве частот фигура представляет собой наклонную прямую, эллипс или окружность.
Частота вращения фигуры будет точно соответствовать разности df между частотами fx’ и fx, где fx’ = fобр (m / n) и, следовательно, fx = fобр (m / n) + df. Точность способа определяется в основном погрешностью задания образцовой частоты и определения величины df.
Другой способ измерения частоты методом сравнения — с использованием осциллографа, имеющего калиброванное значение длительности развертки либо встроенный генератор калиброванных меток.
Зная длительность развертки осциллографа, и подсчитав, сколько периодов измеряемой частоты укладывается на выбранной длине центрального участка экрана осциллографа, имеющего наиболее линейную развертку, можно легко определить частоту. Если в осциллографе имеются калибрационные метки, то, зная временной интервал между метками и подсчитав их число на один или несколько периодов измеряемой частоты, определяют длительность периода.
Другим способом является подсчет периодов сигнала измеряемой частоты за фиксированное время, например, за 1 секунду.
Практическая работа № 10
DOC / 30.5 Кб
Онлайн расчет сопротивления конденсатора Xc и индуктивности Xl переменному току | hardware
Удобные методы онлайн-расчета сопротивления емкости C и индуктивности L переменному току с частотой F.
[Xc — сопротивление конденсатора переменному току]
Формула для расчета: Xc = 1/(2*pi*F*C), где Xc — сопротивление конденсатора переменному току в Омах, F — частота в Герцах, C — емкость в Фарадах. В таблице ниже расчет ведется по той же формуле, но в более удобных единицах — Гц, мкФ, Ом. В качестве исходных параметров можно использовать числа с плавающей запятой (запятая указывается в виде точки).
[Xl — сопротивление индуктивности переменному току]
Формула для расчета: Xl = 2*pi*F*L, где Xl — сопротивление индуктивности переменному току в Омах, F — частота в Герцах, L — индуктивность в Генри. В таблице ниже расчет ведется по той же формуле, но в более удобных единицах — Гц, мкГн, Ом. В качестве исходных параметров можно использовать числа с плавающей запятой (запятая указывается в виде точки).
[Общие замечания по использованию калькуляторов]
1. 1 микрофарад (мкф) = 1000000 пикофарад (пФ). 1 фарад (Ф) = 1000000 микрофарад (мкФ) = 1012 пикофарад (пФ).
2. Десятичные значения с точкой нужно вводить с точкой, а не с запятой, иначе скрипт будет выдавать «infinity». Например, емкость 50 пФ следует ввести как 0.00005.
[Ссылки]
1. Микрофарад, Электрическая ёмкость site:convertworld.com. Очень удобный калькулятор для преобразования физических величин.
2. Расчёт резонансной частоты колебательного контура.
3. Расчет начальной магнитной проницаемости ферритовых колец по пробной обмотке.
4. Расчет дросселей на резисторах МЛТ.
формула расчета. Измерение индуктивности. Индуктивность контура
Кто в школе не изучал физику? Для кого-то она была интересна и понятна, а кто-то корпел над учебниками, пытаясь выучить наизусть сложные понятия. Но каждый из нас запомнил, что мир основан на физических знаниях. Сегодня мы поговорим о таких понятиях, как индуктивность тока, индуктивность контура, и узнаем, какие бывают конденсаторы и что такое соленоид.
Электрическая цепь и индуктивность
Индуктивность служит для характеристики магнитных свойств электрической цепи. Ее определяют как коэффициент пропорциональности между текущим электрическим током и магнитным потоком в замкнутом контуре. Поток создается этим током через поверхность контура. Еще одно определение гласит, что индуктивность является параметром электрической цепи и определяет ЭДС самоиндукции. Термин применяется для указания элемента цепи и приходится характеристикой эффекта самоиндукции, который был открыт Д. Генри и М. Фарадеем независимо друг от друга. Индуктивность связана с формой, размером контура и значением магнитной проницаемости окружающей среды. В единице измерения СИ эта величина измеряется в генри и обозначается как L.
Самоиндукция и измерение индуктивности
Индуктивностью называется величина, которая равна отношению магнитного потока, проходящего по всем виткам контура к силе тока:
Индуктивность контура находится в зависимости от формы, размеров контура и от магнитных свойств среды, в которой он находится. Если в замкнутом контуре протекает электрический ток, то возникает изменяющееся магнитное поле. Это впоследствии приведет к возникновению ЭДС. Рождение индукционного тока в замкнутом контуре носит название «самоиндукция». По правилу Ленца величина не дает изменяться току в контуре. Если обнаруживается самоиндукция, то можно применять электрическую цепь, в которой параллельно включены резистор и катушка с железным сердечником. Последовательно с ними подсоединены и электрические лампы. В этом случае сопротивление резистора равно сопротивлению на постоянном токе катушки. Результатом будет яркое горение ламп. Явление самоиндукции занимает одно из главных мест в радиотехнике и электротехнике.
Как найти индуктивность
Формула, которая является простейшей для нахождения величины, следующая:
где F – магнитный поток, I – ток в контуре.
Через индуктивность можно выразить ЭДС самоиндукции:
Из формулы напрашивается вывод о численном равенстве индукции с ЭДС, которое возникает в контуре при изменении силы тока на один амперметр за одну секунду.
Переменная индуктивность дает возможность найти и энергию магнитного поля:
«Катушка ниток»
Катушка индуктивности представляет собой намотанную изолированную медную проволоку на твердое основание. Что касается изоляции, то выбор материала широк – это и лак, и проводная изоляция, и ткань. Величина магнитного потока зависит от площади цилиндра. Если увеличить ток в катушке, то магнитное поле будет становиться все больше и наоборот.
Если подать электрический ток на катушку, то в ней возникнет напряжение, противоположное напряжению тока, но оно внезапно исчезает. Такого рода напряжение называется электродвижущей силой самоиндукции. В момент включения напряжения на катушку сила тока меняет свое значение от 0 до некоего числа. Напряжение в этот момент тоже меняет значение, согласно закону Ома:
где I характеризует силу тока, U – показывает напряжение, R – сопротивление катушки.
Еще одной особенной чертой катушки является следующий факт: если разомкнуть цепь «катушка – источник тока», то ЭДС добавится к напряжению. Ток тоже вначале вырастет, а потом пойдет на спад. Отсюда вытекает первый закон коммутации, в котором говорится, что сила тока в катушке индуктивности мгновенно не меняется.
Катушку можно разделить на два вида:
- С магнитным наконечником. В роли материала сердца выступают ферриты и железо. Сердечники служат для повышения индуктивности.
- С немагнитным. Используются в случаях, когда индуктивность не больше пяти миллиГенри.
Устройства различаются и по внешнему виду, и внутреннему строению. В зависимости от таких параметров находится индуктивность катушки. Формула в каждом случае разная. Например, для однослойной катушки индуктивность будет равна:
- L = 10µ0ΠN2R2 : 9R + 10l.
А вот уже для многослойной другая формула:
- L= µ0N2R2 :2Π(6R + 9l + 10w).
Основные выводы, связанные с работой катушек:
- На цилиндрическом феррите самая большая индуктивность возникает в середине.
- Для получения максимальной индуктивности необходимо близко наматывать витки на катушку.
- Индуктивность тем меньше, чем меньше количество витков.
- В тороидальном сердечнике расстояние между витками не играет роли катушки.
- Значение индуктивности зависит от «витков в квадрате».
- Если последовательно соединить индуктивности, то их общее значение равно сумме индуктивностей.
- При параллельном соединении нужно следить, чтобы индуктивности были разнесены на плате. В противном случае их показания будут неправильными за счет взаимного влияния магнитных полей.
Соленоид
Под этим понятием понимается цилиндрическая обмотка из провода, который может быть намотан в один или несколько слоев. Длина цилиндра значительно больше диаметра. За счет такой особенности при подаче электрического тока в полости соленоида рождается магнитное поле. Скорость изменения магнитного потока пропорциональна изменению тока. Индуктивность соленоида в этом случае рассчитывается следующим образом:
Еще эту разновидность катушек называют электромеханическим исполнительным механизмом с втягиваемым сердечником. В данном случае соленоид снабжается внешним ферромагнитным магнитопроводом – ярмом.
В наше время устройство может соединять в себе гидравлику и электронику. На этой основе созданы четыре модели:
- Первая способна контролировать линейное давление.
- Вторая модель отличается от других принудительным управлением блокировки муфты в гидротрансформаторах.
- Третья модель содержит в своем составе регуляторы давления, отвечающие за работу переключения скоростей.
- Четвертая управляется гидравлическим способом или клапанами.
Необходимые формулы для расчетов
Чтобы найти индуктивность соленоида, формула применяется следующая:
где µ0 показывает магнитную проницаемость вакуума, n – это число витков, V – объем соленоида.
Также провести расчет индуктивности соленоида можно и с помощью еще одной формулы:
где S – это площадь поперечного сечения, а l – длина соленоида.
Чтобы найти индуктивность соленоида, формула применяется любая, которая подходит по решению к данной задаче.
Работа на постоянном и переменном токе
Магнитное поле, которое создается внутри катушки, направлено вдоль оси, и равно:
где µ0 – это магнитная проницаемость вакуума, n – это число витков, а I – значение тока.
Когда ток движется по соленоиду, то катушка запасает энергию, которая равна работе, необходимая для установления тока. Чтобы вычислить в этом случае индуктивность, формула используется следующая:
где L показывает значение индуктивности, а E – запасающую энергию.
ЭДС самоиндукции возникает при изменении тока в соленоиде.
В случае работы на переменном токе появляется переменное магнитное поле. Направление силы притяжения может изменяться, а может оставаться неизменным. Первый случай возникает при использовании соленоида как электромагнита. А второй, когда якорь сделан из магнитомягкого материала. Соленоид на переменном токе имеет комплексное сопротивление, в которое включаются сопротивление обмотки и ее индуктивность.
Самое распространенное применение соленоидов первого типа (постоянного тока) — это в роли поступательного силового электропривода. Сила зависит от строения сердечника и корпуса. Примерами использования являются работа ножниц при отрезании чеков в кассовых аппаратах, клапаны в двигателях и гидравлических системах, язычки замков. Соленоиды второго типа применяются как индукторы для индукционного нагрева в тигельных печах.
Колебательные контуры
Простейшей резонансной цепью является последовательный колебательный контур, состоящий из включенных катушек индуктивности и конденсатора, через которые протекает переменный ток. Чтобы определить индуктивность катушки, формула используется следующая:
где XL показывает реактивное сопротивление катушки, а W — круговая частота.
Если используется реактивное сопротивление конденсатора, то формула будет выглядеть следующим образом:
Xc = 1 : W х C.
Важными характеристиками колебательного контура являются резонансная частота, волновое сопротивление и добротность контура. Первая характеризует частоту, где сопротивление контура имеет активный характер. Вторая показывает, как проходит реактивное сопротивление на резонансной частоте между такими величинами, как емкость и индуктивность колебательного контура. Третья характеристика определяет амплитуду и ширину амплитудно-частотных характеристик (АЧХ) резонанса и показывает размеры запаса энергии в контуре по сравнению с потерями энергии за один период колебаний. В технике частотные свойства цепей оцениваются при помощи АЧХ. В этом случае цепь рассматривается как четырехполюсник. При изображении графиков используется значение коэффициента передачи цепи по напряжению (К). Эта величина показывает отношение выходного напряжения к входному. Для цепей, которые не содержат источников энергии и различных усилительных элементов, значение коэффициента не больше единицы. Оно стремится к нулю, когда на частотах, отличающихся от резонансной, сопротивление контура имеет высокое значение. Если же величина сопротивления минимальна, то коэффициент близок к единице.
При параллельном колебательном контуре включены два реактивных элемента с разной силой реактивности. Использование такого вида контура подразумевает знание, что при параллельном включении элементов нужно складывать только их проводимости, но не сопротивления. На резонансной частоте суммарная проводимость контура равна нулю, что говорит о бесконечно большом сопротивлении переменному току. Для контура, в котором параллельно включены емкость (C), сопротивление (R) и индуктивность, формула, объединяющая их и добротность (Q), следующая:
При работе параллельного контура за один период колебаний дважды происходит энергетический обмен между конденсатором и катушкой. В этом случае появляется контурный ток, который значительно больше значения тока во внешней цепи.
Работа конденсатора
Устройство представляет собой двухполюсник малой проводимости и с переменным или постоянным значением емкости. Когда конденсатор не заряжен, сопротивление его близко к нулю, в противном случае оно равно бесконечности. Если источник тока отсоединить от данного элемента, то он становится этим источником до своей разрядки. Использование конденсатора в электронике заключается в роли фильтров, которые удаляют помехи. Данное устройство в блоках питания на силовых цепях применяются для подпитки системы при больших нагрузках. Это основано на способности элемента пропускать переменную составляющую, но непостоянный ток. Чем выше частота составляющей, тем меньше у конденсатора сопротивление. В результате через конденсатор глушатся все помехи, которые идут поверх постоянного напряжения.
Сопротивление элемента зависит от емкости. Исходя из этого, правильнее будет ставить конденсаторы с различным объемом, чтобы улавливать разного рода помехи. Благодаря способности устройства пропускать постоянный ток только в период заряда его используют как времязадающий элемент в генераторах или как формирующее звено импульса.
Конденсаторы бывают многих типов. В основном используется классификация по типу диэлектрика, так как этот параметр определяет стабильность емкости, сопротивление изоляции и так далее. Систематизация по данной величине следующая:
- Конденсаторы с газообразным диэлектриком.
- Вакуумные.
- С жидким диэлектриком.
- С твердым неорганическим диэлектриком.
- С твердым органическим диэлектриком.
- Твердотельные.
- Электролитические.
Существует классификация конденсаторов по назначению (общий или специальный), по характеру защиты от внешних факторов (защищенные и незащищенные, изолированные и неизолированные, уплотненные и герметизированные), по технике монтажа (для навесного, печатного, поверхностного, с выводами под винт, с защелкивающимися выводами). Также устройства можно различить по способности к изменению емкости:
- Постоянные конденсаторы, то есть у которых емкость остается всегда постоянной.
- Подстроечные. У них емкость не меняется при работе аппаратуры, но можно ее регулировать разово или периодически.
- Переменные. Это конденсаторы, которые допускают в процессе функционирования аппаратуры изменение ее емкости.
Индуктивность и конденсатор
Токоведущие элементы устройства способны создавать его собственную индуктивность. Это такие конструктивные части, как кладки, соединительные шины, токоотводы, выводы и предохранители. Можно создать дополнительную индуктивность конденсатора путем присоединения шин. Режим работы электрической цепи зависит от индуктивности, емкости и активного сопротивления. Формула расчета индуктивности, которая возникает при приближении к резонансной частоте, следующая:
где Ce определяет эффективную емкость конденсатора, C показывает действительную емкость, f – это частота, L – индуктивность.
Значение индуктивности всегда должно учитываться при работе с силовыми конденсаторами. Для импульсных конденсаторов наиболее важна величина собственной индуктивности. Их разряд приходится на индуктивный контур и имеет два вида – апериодический и колебательный.
Индуктивность в конденсаторе находится в зависимости от схемы соединения элементов в нем. Например, при параллельном соединении секций и шин эта величина равна сумме индуктивностей пакета главных шин и выводов. Чтобы найти такого рода индуктивность, формула следующая:
где Lk показывает индуктивность устройства, Lp –пакета, Lm – главных шин, а Lb – индуктивность выводов.
Если при параллельном соединении ток шины меняется по ее длине, то тогда эквивалентная индуктивность определяется так:
- Lk = Lc : n + µ0 l х d : (3b) + Lb,
где l – длина шин, b – ее ширина, а d – расстояние между шинами.
Чтобы снизить индуктивность устройства, необходимо токоведущие части конденсатора расположить так, чтобы взаимно компенсировались их магнитные поля. Иными словами, токоведущие части с одинаковым движением тока нужно удалять друг от друга как можно дальше, а с противоположным направлением сближать. При совмещении токоотводов с уменьшением толщины диэлектрика можно снизить индуктивность секции. Этого можно достигнуть еще путем деления одной секции с большим объемом на несколько с более мелкой емкостью.
Реактивное сопротивление, индуктивное и емкостное | Физика II
Цели обучения
К концу этого раздела вы сможете:
- Зависимость напряжения и тока от времени в простых индуктивных, емкостных и резистивных цепях.
- Рассчитайте индуктивное и емкостное сопротивление.
- Рассчитывайте ток и / или напряжение в простых индуктивных, емкостных и резистивных цепях.
Многие цепи также содержат конденсаторы и катушки индуктивности в дополнение к резисторам и источнику переменного напряжения.Мы видели, как конденсаторы и катушки индуктивности реагируют на постоянное напряжение при его включении и выключении. Теперь мы исследуем, как катушки индуктивности и конденсаторы реагируют на синусоидальное переменное напряжение.
Катушки индуктивности и индуктивное сопротивление
Предположим, что индуктор подключен непосредственно к источнику переменного напряжения, как показано на рисунке 1. Разумно предположить, что сопротивление пренебрежимо мало, поскольку на практике мы можем сделать сопротивление индуктора настолько малым, что оно окажет незначительное влияние на схему.Также показан график зависимости напряжения и тока от времени.
Рис. 1. (a) Источник переменного напряжения, включенный последовательно с катушкой индуктивности, имеющей незначительное сопротивление. (б) График зависимости тока и напряжения на катушке индуктивности от времени.
График на Рисунке 1 (b) начинается с максимального напряжения. Обратите внимание, что ток начинается с нуля и достигает своего пика после напряжения, которое им управляет, точно так же, как это было в случае, когда напряжение постоянного тока было включено в предыдущем разделе.Когда напряжение становится отрицательным в точке а, ток начинает уменьшаться; оно становится нулевым в точке b, где напряжение является самым отрицательным. Затем ток становится отрицательным, снова вслед за напряжением. Напряжение становится положительным в точке c и начинает делать ток менее отрицательным. В точке d ток проходит через ноль, когда напряжение достигает своего положительного пика, чтобы начать следующий цикл. Кратко это поведение можно описать следующим образом:
Напряжение переменного тока в индуктореКогда на катушку индуктивности подается синусоидальное напряжение, оно опережает ток на одну четверть цикла или на фазовый угол 90º.
Ток отстает от напряжения, поскольку индукторы препятствуют изменению тока. Изменение тока индуцирует обратную ЭДС В = — L (Δ I / Δ t ). Это считается эффективным сопротивлением катушки индуктивности переменному току. Среднеквадратичный ток I через катушку индуктивности L определяется версией закона Ома:
[латекс] I = \ frac {V} {{X} _ {L}} \\ [/ latex],
, где В, — среднеквадратичное значение напряжения на катушке индуктивности, а X L определяется как
.[латекс] {X} _ {L} = 2 \ pi {fL} \\ [/ латекс],
с f частота источника переменного напряжения в герцах (анализ схемы с использованием правила петли Кирхгофа и вычислений фактически дает это выражение). X L называется индуктивным реактивным сопротивлением , потому что катушка индуктивности препятствует прохождению тока. X L имеет единицы измерения Ом (1 Гн = 1 Ом с, так что частота, умноженная на индуктивность, имеет единицы (циклы / с) (Ом ⋅ с) = Ом)), что соответствует его роли в качестве эффективное сопротивление. Имеет смысл, что X L пропорционально L , поскольку чем больше индукция, тем больше его сопротивление изменению.Также разумно, что X L пропорционально частоте f , поскольку большая частота означает большее изменение тока. То есть Δ I / Δ t является большим для больших частот (большие f , маленькие Δ t ). Чем больше изменение, тем больше сопротивление катушки индуктивности.
Пример 1. Расчет индуктивного сопротивления, а затем тока
(a) Рассчитайте индуктивное сопротивление 3.Индуктор 00 мГн при подаче переменного напряжения 60,0 Гц и 10,0 кГц. (b) Каков среднеквадратичный ток на каждой частоте, если приложенное действующее напряжение составляет 120 В?
СтратегияИндуктивное реактивное сопротивление находится непосредственно из выражения X L = 2πf L . Как только X L было найдено на каждой частоте, закон Ома, как указано в уравнении I = В / X L , может быть использован для определения тока на каждой частоте.
Решение для (а)Ввод частоты и индуктивности в уравнение X L = 2πf L дает
X L = 2πf L = 6,28 (60,0 / с) (3,00 мГн) = 1,13 Ом при 60 Гц.
Аналогично, на 10 кГц,
X L = 2πf L = 6,28 (1,00 × 10 4 / с) (3,00 мГн) = 188 Ом при 10 кГц.
Решение для (b)Среднеквадратичное значение тока теперь определяется с использованием версии закона Ома в уравнении I = В / X L , при условии, что приложенное действующее напряжение составляет 120 В.Для первой частоты это дает
[латекс] I = \ frac {V} {{X} _ {L}} = \ frac {120 \ text {V}} {1.13 \ text {} \ Omega} = 106 \ text {A at} 60 \ текст {Hz} \\ [/ latex].
Аналогично, на 10 кГц,
[латекс] I = \ frac {V} {{X} _ {L}} = \ frac {120 \ text {V}} {188 \ text {} \ Omega} = 0,637 \ text {A at} 10 \ текст {кГц} \\ [/ latex].
ОбсуждениеКатушка индуктивности по-разному реагирует на двух разных частотах. На более высокой частоте его реактивное сопротивление велико, а ток невелик, что соответствует тому, как катушка индуктивности препятствует быстрому изменению.Таким образом, наиболее затруднены высокие частоты. Индукторы могут использоваться для фильтрации высоких частот; например, большую катушку индуктивности можно включить последовательно с системой воспроизведения звука или последовательно с вашим домашним компьютером, чтобы уменьшить высокочастотный звук, выводимый из ваших динамиков или высокочастотные всплески мощности на ваш компьютер.
Обратите внимание, что, хотя сопротивлением в рассматриваемой цепи можно пренебречь, переменный ток не очень велик, поскольку индуктивное реактивное сопротивление препятствует его протеканию.С переменным током нет времени, чтобы ток стал слишком большим.
Конденсаторы и емкостное сопротивление
Рассмотрим конденсатор, подключенный непосредственно к источнику переменного напряжения, как показано на рисунке 2. Сопротивление такой цепи можно сделать настолько малым, что оно окажет незначительное влияние по сравнению с конденсатором, поэтому мы можем предположить, что сопротивление незначительно. Напряжение на конденсаторе и ток показаны на рисунке как функции времени.
Рисунок 2.(а) Источник переменного напряжения, включенный последовательно с конденсатором С, имеющим незначительное сопротивление. (б) График зависимости тока и напряжения на конденсаторе от времени.
График на Рисунке 2 начинается с максимального напряжения на конденсаторе. В этот момент ток равен нулю, потому что конденсатор полностью заряжен и останавливает поток. Затем напряжение падает, и ток становится отрицательным по мере разряда конденсатора. В точке а конденсатор полностью разряжен (на нем Q = 0 ) и напряжение на нем равно нулю.Ток остается отрицательным между точками a и b, вызывая обратное напряжение на конденсаторе. Это завершается в точке b, где ток равен нулю, а напряжение имеет самое отрицательное значение. Ток становится положительным после точки b, нейтрализуя заряд конденсатора и доводя напряжение до нуля в точке c, что позволяет току достичь своего максимума. Между точками c и d ток падает до нуля, когда напряжение достигает своего пика, и процесс начинает повторяться. На протяжении всего цикла напряжение соответствует тому, что делает ток, на четверть цикла:
Напряжение переменного тока в конденсатореКогда на конденсатор подается синусоидальное напряжение, оно следует за током на одну четверть цикла или на фазовый угол 90º.
Конденсатор влияет на ток, имея возможность полностью его отключить, когда он полностью заряжен. Поскольку применяется переменное напряжение, возникает среднеквадратичный ток, но он ограничивается конденсатором. Это считается эффективным сопротивлением конденсатора переменному току, поэтому среднеквадратичный ток I в цепи, содержащей только конденсатор C , определяется другой версией закона Ома как
.[латекс] I = \ frac {V} {{X} _ {C}} \\ [/ latex],
, где В, — среднеквадратичное значение напряжения, а X C определяется (Как и в случае с X L , это выражение для X C является результатом анализа цепи используя правила и исчисление Кирхгофа) равным
[латекс] {X} _ {C} = \ frac {1} {2 \ pi fC} \\ [/ latex],
, где X C называется емкостным реактивным сопротивлением , потому что конденсатор препятствует прохождению тока. X C имеет единицы измерения Ом (проверка оставлена в качестве упражнения для читателя). X C обратно пропорциональна емкости C ; Чем больше конденсатор, тем больший заряд он может накапливать и тем больше может протекать ток. Она также обратно пропорциональна частоте f ; чем выше частота, тем меньше времени остается для полной зарядки конденсатора, и поэтому он меньше препятствует току.
Пример 2. Расчет емкостного реактивного сопротивления, а затем тока
(a) Рассчитайте емкостное реактивное сопротивление конденсатора 5,00 мФ при приложении переменного напряжения 60,0 Гц и 10,0 кГц. (b) Каков среднеквадратичный ток, если приложенное действующее напряжение составляет 120 В?
СтратегияЕмкостное реактивное сопротивление находится непосредственно из выражения в [latex] {X} _ {C} = \ frac {1} {2 \ pi fC} \\ [/ latex]. После того, как X C было обнаружено на каждой частоте, закон Ома, сформулированный как I = В, / X C , можно использовать для определения тока на каждой частоте.
Решение для (а)Ввод частоты и емкости в [латекс] {X} _ {C} = \ frac {1} {2 \ pi fC} \\ [/ latex] дает
[латекс] \ begin {array} {lll} {X} _ {C} & = & \ frac {1} {2 \ pi fC} \\ & = & \ frac {1} {6.28 \ left (60.0 / \ text {s} \ right) \ left (5.00 \ text {} \ mu \ text {F} \ right)} = 531 \ text {} \ Omega \ text {at} 60 \ text {Hz} \ end {массив }\\[/латекс].
Аналогично, на 10 кГц,
[латекс] \ begin {array} {lll} {X} _ {C} & = & \ frac {1} {2 \ pi fC} = \ frac {1} {6.{4} / \ text {s} \ right) \ left (5,00 \ mu \ text {F} \ right)} \\ & = & 3,18 \ text {} \ Omega \ text {at} 10 \ text {кГц} \ end {array} \\ [/ latex].
Решение для (b)Среднеквадратичное значение тока теперь определяется с использованием версии закона Ома в I = В / X C , учитывая приложенное действующее напряжение 120 В. Для первой частоты это дает
[латекс] I = \ frac {V} {{X} _ {C}} = \ frac {120 \ text {V}} {531 \ text {} \ Omega} = 0,226 \ text {A at} 60 \ текст {Hz} \\ [/ latex].
Аналогично, на 10 кГц,
[латекс] I = \ frac {V} {{X} _ {C}} = \ frac {120 \ text {V}} {3.18 \ text {} \ Omega} = 3.37 \ text {A at} 10 \ текст {Hz} \\ [/ latex].
ОбсуждениеКонденсатор очень по-разному реагирует на двух разных частотах, а индуктор реагирует прямо противоположным образом. На более высокой частоте его реактивное сопротивление мало, а ток велик. Конденсаторы одобряют изменения, а индукторы — противодействуют. Конденсаторы больше всего препятствуют низким частотам, поскольку низкая частота позволяет им успеть зарядиться и остановить ток.Конденсаторы можно использовать для фильтрации низких частот. Например, конденсатор, включенный последовательно с системой воспроизведения звука, избавляет ее от гула 60 Гц.
Хотя конденсатор в основном представляет собой разомкнутую цепь, в цепи с напряжением переменного тока, приложенным к конденсатору, присутствует среднеквадратичный ток. Это связано с тем, что напряжение постоянно меняет направление, заряжая и разряжая конденсатор. Если частота стремится к нулю (постоянный ток), X C стремится к бесконечности, и ток равен нулю, когда конденсатор заряжен.На очень высоких частотах реактивное сопротивление конденсатора стремится к нулю — он имеет незначительное реактивное сопротивление и не препятствует току (он действует как простой провод). Конденсаторы имеют противоположное влияние на цепи переменного тока, чем индукторы .
Резисторы в цепи переменного тока
В качестве напоминания рассмотрим Рисунок 3, на котором показано напряжение переменного тока, приложенное к резистору, и график зависимости напряжения и тока от времени. Напряжение и ток равны точно в фазе в резисторе.Отсутствует частотная зависимость поведения простого сопротивления в цепи:
Рис. 3. (a) Источник переменного напряжения, включенный последовательно с резистором. (b) График зависимости тока и напряжения на резисторе от времени, показывающий, что они точно совпадают по фазе.
Напряжение переменного тока в резистореКогда на резистор подается синусоидальное напряжение, напряжение точно совпадает по фазе с током — они имеют фазовый угол 0 °.
Сводка раздела
- Для катушек индуктивности в цепях переменного тока мы обнаруживаем, что когда на индуктор подается синусоидальное напряжение, оно опережает ток на одну четверть цикла или на фазовый угол 90 °.
- Противодействие катушки индуктивности изменению тока выражается как сопротивление переменному току.
- Закон Ома для катушки индуктивности
[латекс] I = \ frac {V} {{X} _ {L}} \\ [/ latex],
, где В, — среднеквадратичное значение напряжения на катушке индуктивности.
- X L определяется как индуктивное реактивное сопротивление, определяемое по формуле
[латекс] {X} _ {L} = 2 \ pi fL \\ [/ латекс],
с f частота источника переменного напряжения в герцах.
- Индуктивное реактивное сопротивление X L выражается в единицах Ом и имеет наибольшее значение на высоких частотах.
- Для конденсаторов мы обнаруживаем, что когда на конденсатор подается синусоидальное напряжение, напряжение следует за током на одну четверть цикла или на фазовый угол 90º.
- Поскольку конденсатор может останавливать ток при полной зарядке, он ограничивает ток и предлагает другую форму сопротивления переменному току; Закон Ома для конденсатора
[латекс] I = \ frac {V} {{X} _ {C}} \\ [/ latex],
, где В, — среднеквадратичное значение напряжения на конденсаторе.
- X C определяется как емкостное реактивное сопротивление, определяемое по формуле
[латекс] {X} _ {C} = \ frac {1} {2 \ pi fC} \\ [/ latex].
- X C имеет единицы измерения Ом и имеет наибольшее значение на низких частотах.
Концептуальные вопросы
1. Пресбиакузис — это возрастная потеря слуха, которая постепенно влияет на высокие частоты. Усилитель слухового аппарата предназначен для равномерного усиления всех частот. Чтобы отрегулировать его мощность на пресбиакузис, включите ли вы конденсатор последовательно или параллельно динамику слухового аппарата? Объяснять.
2. Будете ли вы использовать большую индуктивность или большую емкость последовательно с системой для фильтрации низких частот, таких как гул 100 Гц в звуковой системе? Объяснять.
3. Высокочастотный шум в сети переменного тока может повредить компьютеры. Использует ли съемный блок, предназначенный для предотвращения этого повреждения, большую индуктивность или большую емкость (последовательно с компьютером) для фильтрации таких высоких частот? Объяснять.
4. Зависит ли индуктивность от тока, частоты или и того, и другого? А как насчет индуктивного сопротивления?
5. Объясните, почему конденсатор на рисунке 4 (а) действует как фильтр низких частот между двумя цепями, тогда как конденсатор на рисунке 4 (b) действует как фильтр высоких частот.
Рисунок 4. Конденсаторы и катушки индуктивности. Конденсатор с высокой и низкой частотой.
6. Если конденсаторы на рис. 4 заменить катушками индуктивности, что будет действовать как фильтр низких частот, а какой — как фильтр высоких частот?
Задачи и упражнения
1. На какой частоте индуктор 30,0 мГн будет иметь реактивное сопротивление 100 Ом?
2. Какое значение индуктивности следует использовать, если требуется реактивное сопротивление 20,0 кОм при частоте 500 Гц?
3.Какую емкость следует использовать для получения реактивного сопротивления 2,00 МОм при 60,0 Гц?
4. На какой частоте конденсатор 80,0 мФ будет иметь реактивное сопротивление 0,250 Ом?
5. (a) Найдите ток через катушку индуктивности 0,500 H, подключенную к источнику переменного тока 60,0 Гц, 480 В. (б) Каким будет ток на частоте 100 кГц?
6. (a) Какой ток течет, когда источник переменного тока 60,0 Гц, 480 В подключен к конденсатору 0,250 мкФ? (b) Каким будет ток на частоте 25,0 кГц?
7. А 20.Источник 0 кГц, 16,0 В, подключенный к катушке индуктивности, вырабатывает ток 2,00 А. Что такое индуктивность?
8. Источник 20,0 Гц, 16,0 В вырабатывает ток 2,00 мА при подключении к конденсатору. Какая емкость?
9. (a) Катушка индуктивности, предназначенная для фильтрации высокочастотного шума от энергии, подаваемой на персональный компьютер, включается последовательно с компьютером. Какая минимальная индуктивность должна обеспечивать реактивное сопротивление 2,00 кОм для шума 15,0 кГц? (б) Каково его реактивное сопротивление при 60?0 Гц?
10. Конденсатор на рисунке 4 (а) предназначен для фильтрации низкочастотных сигналов, препятствуя их передаче между цепями. (а) Какая емкость необходима для создания реактивного сопротивления 100 кОм при частоте 120 Гц? (b) Каким будет его реактивное сопротивление на частоте 1,00 МГц? (c) Обсудите значение ваших ответов на (a) и (b).
11. Конденсатор на Рисунке 4 (b) будет фильтровать высокочастотные сигналы, замыкая их на землю / землю. (a) Какая емкость необходима для получения реактивного сопротивления [латекса] \ text {10.0 м \ Omega} [/ latex] для сигнала 5,00 кГц? (б) Каким будет его реактивное сопротивление при 3,00 Гц? (c) Обсудите значение ваших ответов на (a) и (b).
12. Необоснованные результаты При регистрации напряжений, обусловленных мозговой активностью (ЭЭГ), сигнал 10,0 мВ с частотой 0,500 Гц подается на конденсатор, создавая ток 100 мА. Сопротивление незначительное. а) Какая емкость? б) Что неразумного в этом результате? (c) Какое предположение или предпосылка ответственны?
13. Создайте свою проблему Рассмотрите возможность использования индуктора последовательно с компьютером, работающим от электричества 60 Гц. Постройте задачу, в которой вы вычисляете относительное снижение напряжения входящего высокочастотного шума по сравнению с напряжением 60 Гц. Среди вещей, которые следует учитывать, — допустимое последовательное реактивное сопротивление катушки индуктивности для мощности 60 Гц и вероятные частоты шума, проходящего через линии электропередач.
Глоссарий
- индуктивное реактивное сопротивление:
- противодействие катушки индуктивности изменению тока; рассчитывается по X L = 2π fL
- емкостное реактивное сопротивление:
- сопротивление конденсатора изменению тока; рассчитывается по [latex] {X} _ {C} = \ frac {1} {2 \ pi fC} \\ [/ latex]
Избранные решения проблем и упражнения
1.531 Гц
3. 1,33 нФ
5. (а) 2,55 А (б) 1,53 мА
7. 63,7 мкГн
9. (а) 21,2 мГн (б) 8,00 Ом
Видео с вопросом: Определение емкости в цепи LC
Стенограмма видеозаписи
Цепь в тюнере AM в автомобильной стереосистеме использует катушку с индуктивностью 2,5 миллигенри и переменный конденсатор. Если собственная частота цепи должна регулироваться в диапазоне от 540 до 1600 килогерц, вещательном диапазоне AM, какой диапазон емкости требуется?
Мы можем назвать индуктивность в этой цепи, 2.5 миллигенри, заглавная. Мы будем называть нижнюю границу диапазона частот, 540 килогерц, 𝑓 суб. А верхний предел диапазона, 1600 килогерц, мы назовем 𝑓 меньше двух. Мы хотим найти диапазон значений емкости, который позволит передавать этот частотный диапазон. Мы назовем нижний конец этого диапазона 𝑐 второстепенным, а верхний — вторым. Если мы определим эти два значения емкости по отдельности, то мы узнаем диапазон.
Мы можем начать с напоминания о соотношении между частотой, емкостью и индуктивностью в-цепи.В этом типе цепи частота заряда при его движении по цепи равна единице более чем в два раза корню квадратному из индуктивности цепи, умноженной на ее емкость.
В этом соотношении мы хотим найти не частоту 𝑓, а емкость. Таким образом, мы можем перестроить его алгебраически, чтобы сделать это. Мы находим, что емкость равна единице из четырех 𝜋 в квадрате, умноженном на квадрат частоты, умноженный на индуктивность.
Это означает, что если мы хотим найти суб-один, нижний предел нашего диапазона емкости, мы можем сделать это, подставив наше значение для индуктивности our и наше 𝑓 суб-значение для частоты.Когда мы это сделаем, указав нашу частоту в герцах, а индуктивность в генри, мы готовы вычислить единицу на нашем калькуляторе. Мы находим, что до двух значащих цифр 𝑐 к югу от единицы составляет 3,5 умножить на 10 до отрицательной 11-й фарад. Это нижний предел диапазона наших значений емкости.
Теперь мы переходим к решению для 𝑐 sub two, верхнего диапазона значения емкости. Для этого мы можем использовать то же уравнение, что и для 𝑐 sub. Но мы просто меняем частоту и меняем индекс на sub two.Сделав это изменение, мы затем вводим эти значения в наш калькулятор и находим, что 𝑐 два равно 4,0 умножить на 10 до отрицательной 12-й фарады. Эти значения 𝑐 один и два позволят нам вести вещание в диапазоне частот AM.
онлайн-курсов PDH. PDH для профессиональных инженеров. ПДХ Инжиниринг.
«Мне нравится широта ваших курсов по HVAC; не только экологичность или экономия энергии
курсов. «
Рассел Бейли, П.E.
Нью-Йорк
«Он укрепил мои текущие знания и научил меня еще нескольким новым вещам.
, чтобы познакомить меня с новыми источниками
информации.
Стивен Дедак, П.Е.
Нью-Джерси
«Материал был очень информативным и организованным. Я многому научился, и они были
.очень быстро отвечает на вопросы.
Это было на высшем уровне. Будет использовать
снова. Спасибо. «
Blair Hayward, P.E.
Альберта, Канада
«Простой в использовании веб-сайт. Хорошо организованный. Я действительно воспользуюсь вашими услугами снова.
проеду по вашей компании
имя другим на работе. «
Roy Pfleiderer, P.E.
Нью-Йорк
«Справочные материалы были превосходными, и курс был очень информативным, особенно потому, что я думал, что я уже знаком.
с деталями Канзас
Городская авария Хаятт.»
Майкл Морган, P.E.
Техас
«Мне очень нравится ваша бизнес-модель. Мне нравится просматривать текст перед покупкой. Я нашел класс
.информативно и полезно
в моей работе ».
Вильям Сенкевич, П.Е.
Флорида
«У вас большой выбор курсов, а статьи очень информативны.Вы
— лучшее, что я нашел ».
Russell Smith, P.E.
Пенсильвания
«Я считаю, что такой подход позволяет работающему инженеру легко зарабатывать PDH, давая время на просмотр
материал «
Jesus Sierra, P.E.
Калифорния
«Спасибо, что позволили мне просмотреть неправильные ответы.На самом деле
человек узнает больше
от отказов »
John Scondras, P.E.
Пенсильвания
«Курс составлен хорошо, и использование тематических исследований является эффективным.
способ обучения »
Джек Лундберг, P.E.
Висконсин
«Я очень впечатлен тем, как вы представляете курсы; i.е., позволяя
студент для ознакомления с курсом
материалов до оплаты и
получение викторины. «
Арвин Свангер, П.Е.
Вирджиния
«Спасибо за то, что вы предложили все эти замечательные курсы. Я определенно выучил и Получил огромное удовольствие «. Мехди Рахими, П.Е. Нью-Йорк «Я очень доволен предлагаемыми курсами, качеством материалов и простотой поиска. на связи курсов.» Уильям Валериоти, P.E. Техас «Этот материал в значительной степени оправдал мои ожидания. По курсу было легко следовать. Фотографии в основном обеспечивали хорошее наглядное представление о обсуждаемых тем ». Майкл Райан, P.E. Пенсильвания «Именно то, что я искал. Потребовался 1 балл по этике, и я нашел его здесь.» Джеральд Нотт, П.Е. Нью-Джерси «Это был мой первый онлайн-опыт получения необходимых мне кредитов PDH. Это было информативно, выгодно и экономично. Я очень рекомендую всем инженерам. » Джеймс Шурелл, P.E. Огайо «Я понимаю, что вопросы относятся к« реальному миру »и имеют отношение к моей практике, и не на основе какой-то неясной раздел законов, которые не применяются — «нормальная» практика.» Марк Каноник, П.Е. Нью-Йорк «Отличный опыт! Я многому научился, чтобы перенести его на свой медицинский прибор. организация « Иван Харлан, П.Е. Теннесси «Материалы курса имели хорошее содержание, не слишком математическое, с хорошим акцентом на практическое применение технологий». Юджин Бойл, П.E. Калифорния «Это был очень приятный опыт. Тема была интересной и хорошо изложенной, а онлайн-формат был очень Доступно и просто использовать. Большое спасибо. « Патрисия Адамс, P.E. Канзас «Отличный способ добиться соответствия требованиям PE Continuing Education в рамках ограничений по времени лицензиата.» Joseph Frissora, P.E. Нью-Джерси «Должен признаться, я действительно многому научился. Помогает иметь распечатанный тест во время обзор текстового материала. Я также оценил просмотр фактических случаев предоставлено. Жаклин Брукс, П.Е. Флорида «Документ» Общие ошибки ADA при проектировании объектов «очень полезен.Модель испытание потребовало исследования в документ но ответы были в наличии « Гарольд Катлер, П.Е. Массачусетс «Я эффективно использовал свое время. Спасибо за широкий выбор вариантов. в транспортной инженерии, что мне нужно для выполнения требований Сертификат ВОМ.» Джозеф Гилрой, П.Е. Иллинойс «Очень удобный и доступный способ заработать CEU для моих требований PG в Делавэре». Ричард Роудс, P.E. Мэриленд «Я многому научился с защитным заземлением. Пока все курсы, которые я прошел, были отличными. Надеюсь увидеть больше 40% курсов со скидкой.» Кристина Николас, П.Е. Нью-Йорк «Только что сдал экзамен по радиологическим стандартам и с нетерпением жду возможности сдать дополнительный курсов. Процесс прост, и намного эффективнее, чем в пути «. Деннис Мейер, P.E. Айдахо «Услуги, предоставляемые CEDengineering, очень полезны для Professional Инженеры получат блоки PDH в любое время.Очень удобно ». Пол Абелла, P.E. Аризона «Пока все отлично! Поскольку я постоянно работаю матерью двоих детей, у меня мало время искать где получить мои кредиты от. « Кристен Фаррелл, P.E. Висконсин «Это было очень познавательно и познавательно.Легко для понимания с иллюстрациями и графики; определенно делает это проще поглотить все теорий. « Виктор Окампо, P.Eng. Альберта, Канада «Хороший обзор принципов работы с полупроводниками. Мне понравилось пройти курс по мой собственный темп во время моего утром до метро на работу.» Клиффорд Гринблатт, П.Е. Мэриленд «Просто найти интересные курсы, скачать документы и взять викторина. Я бы очень рекомендовал вам на любой PE нужно CE единиц. « Марк Хардкасл, П.Е. Миссури «Очень хороший выбор тем из многих областей техники.» Randall Dreiling, P.E. Миссури «Я заново узнал то, что забыл. Я также рад оказать финансовую помощь по ваш промо-адрес который сниженная цена на 40%. « Конрадо Казем, П.E. Теннесси «Отличный курс по разумной цене. Воспользуюсь вашими услугами в будущем». Charles Fleischer, P.E. Нью-Йорк «Это был хороший тест и фактически подтвердил, что я прочитал профессиональную этику кодов и Нью-Мексико правил. « Брун Гильберт, П.E. Калифорния «Мне очень понравились занятия. Они стоили потраченного времени и усилий». Дэвид Рейнольдс, P.E. Канзас «Очень доволен качеством тестовых документов. Буду использовать CEDengineerng при необходимости дополнительно сертификация. « Томас Каппеллин, П.E. Иллинойс «У меня истек срок действия курса, но вы все же выполнили свое обязательство и дали мне то, за что я заплатил — много оценено! « Джефф Ханслик, P.E. Оклахома «CEDengineering предлагает удобные, экономичные и актуальные курсы. для инженера » Майк Зайдл, П.E. Небраска «Курс был по разумной цене, материал был кратким, а хорошо организовано. « Glen Schwartz, P.E. Нью-Джерси «Вопросы подходили для уроков, а материал урока — хороший справочный материал для деревянного дизайна. « Брайан Адамс, П.E. Миннесота «Отлично, я смог получить полезные рекомендации по простому телефонному звонку.» Роберт Велнер, P.E. Нью-Йорк «У меня был большой опыт работы в прибрежном строительстве — проектирование Building курс и очень рекомендую .» Денис Солано, P.E. Флорида «Очень понятный, хорошо организованный веб-сайт. Материалы курса этики Нью-Джерси были очень хорошими хорошо подготовлены. » Юджин Брэкбилл, P.E. Коннектикут «Очень хороший опыт. Мне нравится возможность загружать учебные материалы на обзор везде и всякий раз, когда.» Тим Чиддикс, P.E. Колорадо «Отлично! Поддерживаю широкий выбор тем на выбор». Уильям Бараттино, P.E. Вирджиния «Процесс прямой, без всякой ерунды. Хороший опыт». Тайрон Бааш, П.E. Иллинойс «Вопросы на экзамене были зондирующими и продемонстрировали понимание материала. Полная и комплексное. » Майкл Тобин, P.E. Аризона «Это мой второй курс, и мне понравилось то, что мне предлагали курс поможет по моей линии работ.» Рики Хефлин, P.E. Оклахома «Очень быстро и легко ориентироваться. Я определенно буду использовать этот сайт снова». Анджела Уотсон, П.Е. Монтана «Легко выполнить. Никакой путаницы при подходе к сдаче теста или записи сертификата». Кеннет Пейдж, П.E. Мэриленд «Это был отличный источник информации о солнечном нагреве воды. Информативный и отличный освежитель ». Луан Мане, П.Е. Conneticut «Мне нравится подход, когда я подписываюсь и могу читать материалы в автономном режиме, а затем Вернуться, чтобы пройти викторину « Алекс Млсна, П.E. Индиана «Я оценил объем информации, предоставленной для класса. Я знаю это вся информация, которую я могу использование в реальных жизненных ситуациях. » Натали Дерингер, P.E. Южная Дакота «Обзорные материалы и образец теста были достаточно подробными, чтобы позволить мне успешно завершено курс.» Ира Бродский, П.Е. Нью-Джерси «Веб-сайт прост в использовании, вы можете скачать материал для изучения, а потом вернуться и пройдите викторину. Очень удобно и на моем собственный график « Майкл Гладд, P.E. Грузия «Спасибо за хорошие курсы на протяжении многих лет.» Деннис Фундзак, П.Е. Огайо «Очень легко зарегистрироваться, получить доступ к курсу, пройти тест и распечатать PDH сертификат. Спасибо за создание процесс простой ». Фред Шейбе, P.E. Висконсин «Положительный опыт.Быстро нашел курс, который соответствовал моим потребностям, и прошел один час PDH в один час. « Стив Торкильдсон, P.E. Южная Каролина «Мне понравилась возможность скачать документы для проверки содержания и пригодность, до имея заплатить за материал .» Ричард Вимеленберг, P.E. Мэриленд «Это хорошее напоминание об ЭЭ для инженеров, не занимающихся электричеством». Дуглас Стаффорд, П.Е. Техас «Всегда есть возможности для улучшения, но я ничего не могу придумать в вашем процесс, который требует улучшение.» Thomas Stalcup, P.E. Арканзас «Мне очень нравится удобство участия в онлайн-викторине и получение сразу сертификат. « Марлен Делани, П.Е. Иллинойс «Учебные модули CEDengineering — это очень удобный способ доступа к информации по номеру много разные технические зоны за пределами своя специализация без приходится путешествовать.» Гектор Герреро, П.Е. Грузия В большинстве лабораторий имеется достаточный запас цифровых мультиметров для измерения сопротивления постоянному току, но когда
речь идет об измерении индуктивности, емкости и импеданса, это не всегда
легко найти измеритель LCR. LCR работают, подавая на устройство напряжение переменного тока.
при испытании, и измеряя результирующий ток, как по амплитуде, так и по
фаза относительно сигнала переменного напряжения.Емкостный импеданс будет иметь
форма волны тока, которая опережает форму волны напряжения. Индуктивный импеданс будет
имеют форму волны тока, которая отстает от формы волны напряжения. К счастью, если
у вас есть осциллограф и генератор функций в вашей лаборатории, вы можете использовать
аналогичный метод для измерения многочастотного импеданса с хорошим
полученные результаты. Этот подход также может быть адаптирован для использования в качестве учебной лаборатории.
упражнение. Импеданс — это полное сопротивление току в
цепь переменного тока. Он состоит из сопротивления (реального) и реактивного сопротивления.
(мнимая) и обычно представлена в сложных обозначениях как Z = R + jX ,
где R — сопротивление, а X — реактивное сопротивление. Реальные компоненты состоят из проводов, соединений,
проводники и диэлектрические материалы. Эти элементы вместе составляют
характеристики импеданса компонента, и это полное сопротивление изменяется в зависимости от
частота тестового сигнала и уровень напряжения, наличие напряжения смещения постоянного тока
или текущие и окружающие факторы, такие как рабочие температуры или
высота.Из этих возможных влияний частота тестового сигнала часто оказывается определяющей.
наиболее значимый фактор. В отличие от идеальных компонентов, настоящие компоненты не являются чисто
индуктивный или емкостной. Все компоненты имеют последовательное сопротивление, которое
Параметр R в его импедансе. Но у них также есть несколько участников
реактивное сопротивление. Например, конденсатор имеет последовательную индуктивность, которая становится больше
проявляется на высоких частотах. Когда мы измеряем реальный конденсатор, серия
индуктивность (ESL) будет влиять на показания емкости, но мы не сможем
измерять его как отдельный, самостоятельный компонент. Метод I-V, описанный в этом примечании по применению, просто
один из многих методов измерения импеданса. Другие включают мостовой метод.
и резонансный метод. Метод I-V использует значение напряжения и тока на
тестируемое устройство (DUT) для расчета неизвестного импеданса, Z x . Текущий
измеряется путем измерения падения напряжения на прецизионном резисторе последовательно
с тестируемым устройством, как показано на рисунке 2.Уравнение 1 показывает, как можно использовать схему.
найти Z x .
Уравнение 1: В этом документе мы будем использовать Tektronix AFG2021.
произвольный / функциональный генератор и осциллограф Tektronix серии MDO4000 для выполнения
измерение. Полоса пропускания AFG2021 в 20 МГц хорошо подходит для этого.
измерение. Точность усиления постоянного тока MDO4000 составляет 2% при настройке 1 мВ / дел.
1,5% при других вертикальных настройках. Как вы можете видеть в уравнении 1,
Точность измерения напряжения осциллографом является наиболее важным фактором в
общая точность теста. На основании уравнения 1 теоретическая точность этого
метод измерения должен составлять около 4% при настройке MDO4000 1 мВ / дел и 3%
при других настройках. Так как частота дискретизации осциллографа очень велика.
выше, чем частота стимулов, используемых в этих тестах, ошибка
вклад фазовых измерений будет незначительным. В следующих двух примерах представлены конденсатор / индуктор /
Измерение ESR с помощью осциллографа и функционального генератора. Для этого применения большинство осциллографов и функций
генераторы дадут приемлемые результаты, так как тестовые частоты ниже
100 кГц. Однако мы воспользуемся статистикой измерений на MDO4000.
Серии в этом примере. Установите испытательную схему, как показано на рисунке 3. Примечание.
что R ESR и
C связаны с тестируемым керамическим конденсатором, и что R fg — это выходное сопротивление 50 Ом.
генератор функций. Установите функциональный генератор на выход 1,9 В.
амплитуда, синусоида 100 Гц.Вы можете использовать ручку AFG2021 или клавиатуру для
установить напряжение и частоту. Отрегулируйте настройку вертикального масштаба
осциллографа, чтобы использовать как можно большую часть дисплея — используя как можно больше
диапазон, насколько это возможно, вы улучшите точность своего напряжения
измерения. Используйте осциллограф для проверки узлов A1 и A2. Рисунок 4
показывает результирующую форму волны. Выберите средний режим сбора данных осциллографа.
и установите количество средних значений на 128. Это уменьшит влияние случайных
шум по вашим измерениям.Настройте осциллограф на измерение канала 1
частота, фаза между каналом 2 и каналом 1, амплитуда канала 1 и
амплитуда канала 2, как показано на рисунке 4. Если ваш осциллограф предлагает
статистику измерений, такую как серия MDO4000, запишите средние значения для вашего
расчеты. В противном случае запишите самые последние значения. Из измерительной установки мы знаем: Из измерений, выполненных на осциллографе и показанных
на рисунке 4: Обратите внимание, что в узле A1 напряжение имеет фазовый угол 0 °,
то есть он находится в фазе с выходом функционального генератора. На А2 напряжение равно
сдвинуты вперед на фазовый угол θ. Полное сопротивление тестируемого конденсатора можно найти
используя уравнение 1. Импеданс можно выразить в полярной форме, где
величина определяется уравнением 2. Угол импеданса определяется вычитанием двух
углы: Для теста в нашем примере мы можем использовать уравнение 2
и уравнение 3, чтобы найти величину и угол импеданса
конденсатор тестируемый: Теперь мы можем преобразовать импеданс в прямоугольную форму.
найти сопротивление и емкость. Используя приведенные выше уравнения, мы можем решить для ESR и
Емкость ИУ: Используя уравнение 4 и уравнение 5, мы можем рассчитать СОЭ
и емкость для тестируемого конденсатора: пользователя
Область применения / FG пользователя
USB VNA пользователя
LCR пользователя
Область применения / FG пользователя
USB VNA пользователя
LCR Частота емкость
(мкФ) емкость
(мкФ) емкость
(мкФ) СОЭ (Ом) СОЭ (Ом) СОЭ (Ом) 10 Гц 10.3 10,4 НЕТ 28,3 32,8 Н / Д 30 Гц 10,1 10,4 НЕТ 9,1 7,8 НЕТ 100 Гц 9.8 10,3 10,22 2,4 3,2 2,3 300 Гц 9,8 10,1 НЕТ 0,7 1,1 НЕТ 1 кГц 9.7 9,8 9,96 0,3 0,3 0,21 В таблице 1 сравниваются результаты, полученные с помощью осциллографа.
и генератор функций для результатов, достигаемых с помощью недорогого ВАЦ и
традиционный измеритель LCR.Измеритель LCR, используемый в этом случае, поддерживает только тест
частоты 100 Гц и 1 кГц, которые являются общими частотами тестирования компонентов.
Вы заметите, что эти три метода достаточно хорошо коррелируют. Значения пассивных компонентов указаны с особым
частоту, и измерители LCR часто имеют более одной тестовой частоты для
эта причина. В таблице 1 показаны результаты с использованием осциллографа / функции.
комбинация генераторов на пяти разных частотах. Вы можете увидеть эффект
паразитная индуктивность в испытательной цепи при увеличении испытательной частоты —
измеренная емкость падает с увеличением испытательной частоты.См. Раздел о
«Диапазон измерения» для получения дополнительной информации о тестовых частотах. Для достижения наилучших результатов вам необходимо сохранить значение
прецизионного резистора (R ref )
достаточно низкий, чтобы дать значительную волну напряжения в узле A2. Резистор
также должно быть больше 50 Ом, иначе выходное сопротивление функционального генератора
будет учитываться при измерении. Схема и процедура проверки практически идентичны
те, которые использовались для проверки конденсатора в Примере 1. Используйте функциональный генератор для вывода 1,9 В.
амплитуда синусоиды 10 кГц. Сигнал подается на опорный резистор и
испытуемый индуктор. Используйте осциллограф для проверки узлов A1 и A2. Рисунок 6
показаны две результирующие формы волны. Выберите средний режим сбора данных осциллографа.
и установите количество средних значений на 128. Это уменьшит влияние случайных
шум по вашим измерениям.Настройте осциллограф на измерение канала 1
частота, фаза между каналом 2 и каналом 1, амплитуда канала 1 и
амплитуда канала 2, как показано на рисунке 6. Если ваш осциллограф предлагает
статистику измерений, такую как серия MDO4000, запишите средние значения для вашего
расчеты. В противном случае запишите самые последние значения. Из измерительной установки мы знаем: Из измерений, выполненных на осциллографе и показанных
на рисунке 6: Обратите внимание, что в узле A1 напряжение имеет фазовый угол 0 °,
то есть он находится в фазе с выходом функционального генератора. На А2 напряжение равно
сдвинуты вперед на фазовый угол θ. Мы можем использовать те же уравнения для расчета импеданса
ИУ, которое мы использовали для измерения конденсатора в примере 1. Импеданс может
быть выраженным в полярной форме, где величина и угол импеданса равны
предоставлено: Теперь мы можем преобразовать в прямоугольную форму
сопротивление, чтобы найти сопротивление и индуктивность Используя приведенные выше уравнения, мы можем решить для ESR и
Индуктивность ИУ: Используя уравнения 6 и 7, мы можем рассчитать СОЭ
и индуктивность для испытуемой катушки индуктивности: пользователя
Область применения / FG через USB
ВНА по LCR пользователя
Область применения / FG через USB
ВНА по LCR Частота индуктивность
(мГн) индуктивность
(мГн) индуктивность
(мГн) СОЭ (Ом) СОЭ (Ом) СОЭ (Ом) 10 Гц 12 10.3 НЕТ 20,5 20,8 Н / Д 100 Гц 10,1 10,4 10,31 20,6 20,9 20,9 1 кГц 10,3 10.2 10,1 20,5 22 21,5 10 кГц 10 9,8 9,76 29,8 31,5 29,4 Опять же, в таблице 2 сравниваются достигнутые результаты с
осциллографа и генератора функций для результатов, достигаемых с помощью недорогого ВАЦ и
традиционный измеритель LCR.Эти три метода хорошо коррелируют. Таблица 2 также показывает результаты, полученные с помощью осциллографа /
комбинация функционального генератора на четырех разных частотах. См. Раздел
в разделе «Диапазон измерений» для получения дополнительной информации о тестовых частотах. Еще раз, вам, возможно, придется поэкспериментировать со стоимостью рэнд (ref ), чтобы получить наилучшее
полученные результаты. Существуют практические ограничения на частоту стимула и
значения конденсатора или индуктора ИУ для этого метода измерения импеданса. Рисунок 7 — это блок емкости / частоты. Если емкость
значение и частота тестирования указаны в рамке, тогда вы сможете
измерить это. В заштрихованной области точность измерения будет около 3%,
а за пределами заштрихованной области точность падает примерно до 5%.Эти неопределенности
предположим, что вы позаботились о том, чтобы использовать весь экран осциллографа,
усреднено 128 периодов сигналов и использовано среднее значение
амплитуды и фазы для выполнения расчетов. Аналогичный блок индуктивности / частоты показан на рисунке.
8 для испытания индуктора. Если в вашей лаборатории нет измерителя LCR или вы
хочу продемонстрировать поведение конденсаторов и катушек индуктивности при синусоидальном
стимула, осциллографа и генератора функций могут помочь вам сделать простой,
прозрачное измерение импеданса.Вы можете рассчитывать на емкость и индуктивность
значения с погрешностью 3% -5%. Чтобы воспользоваться этим методом, вы
нужен только функциональный генератор с хорошим диапазоном частот и амплитуд,
осциллограф с хорошими характеристиками и функциями, которые мы обсуждали, несколько
прецизионные резисторы, а также калькулятор или электронную таблицу. The Photon превосходно ответил на этот вопрос, но я чувствую, что есть некоторая важная информация, которой следует поделиться, и она будет интересна некоторым читателям или самому человеку, задающему вопрос. ВНИМАНИЕ !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! Во-первых, добавлю, что катушки индуктивности тоже могут накапливать емкостной заряд. Это известное явление, которое можно ярко проявить, намотав бифилярную катушку и подключив КОНЕЦ провода A к НАЧАЛУ провода B (проводка СЕРИИ). Соединяя их последовательно, вы фактически получаете один очень длинный кусок провода, в котором каждый провод примыкает к другому витку, напряжение которого составляет 50% разницы от общего напряжения на катушке индуктивности. Это было ясно объяснено в патенте Николы Теслы «Катушка для электромагнитов».Его патентный рисунок показывает блинную катушку, но эффект работает на ВСЕХ катушках. Расположив провода рядом друг с другом, вы можете усилить электростатическое поле между проводами. И да, если вы проведете эксперимент правильно, вы можете зарядить индуктор и заставить его накапливать энергию, а затем разрядить энергию позже. Но даже в обычной катушке с прямой обмоткой заряд и емкостное поле все еще присутствуют — они настолько смехотворно малы, что их обычно игнорируют. Однако это становится очевидным на высоких частотах, если вы измеряете добротность катушки.Расстояние между витками радиокатушки увеличивает добротность, поскольку снижает емкостную напряженность поля между обмотками. Более того, существует заметная разница между магнитным полем индуктора и емкостным зарядом, которая делает их более разными, чем думает большинство людей, и их действительно не следует сравнивать напрямую. Читайте дальше … Если вы попытаетесь разрядить конденсатор, заряженный 12 В, в другой конденсатор, заряженный 12 В, ничего не произойдет, потому что энергии уравновешиваются.С другой стороны, если вы попытаетесь разрядить индуктор, заряженный током, идущим от источника 12 вольт, в конденсатор на 12 вольт, индуктор фактически перезарядит целевой конденсатор до некоторого уровня выше его начальных 12 вольт. Насколько высоко он поднимется, будет напрямую зависеть от магнитного потока в катушке индуктивности и емкости конденсатора. Если емкость очень мала, напряжение может быть повышено до в зависимости от других условий цепи. Чтобы поэкспериментировать с основами этого поведения, вам просто понадобится диод и немного сообразительности, чтобы зарядить конденсатор от катушки, не позволяя ему немедленно разрядиться в обратном направлении. Фактически, именно это явление является единственной причиной, по которой контуры резервуара вообще могут функционировать. Если бы у индуктора не было возможности перезарядить свою цель, цепи танка никогда не работали бы. В баковой цепи конденсатор полностью разряжается через катушку индуктивности, пока не достигнет напряжения практически 0. Если бы не заряженная катушка индуктивности, все движения в цепи остановились бы в этой точке. Но вместо этого магнитное поле индуктора теперь действует как накачка заряда и вынуждает конденсатор в отрицательную область намного дальше нуля.После того, как индуктор завершает разряд, весь процесс меняется на противоположный. С этим поведением можно делать и другие более интересные вещи, помимо примитивных контуров танков. Теперь давайте исследуем взаимную индуктивность обмоток статора и ротора. Сначала мы исследуем матрицу взаимной индуктивности Lsr. Это связано с величиной магнитного потока, который создается обмотками ротора и связывает обмотки статора.Взаимная индуктивность состоит из девяти компонентов: (4,19) Lsr = [LasarLasbrLascrLbsarLbsbrLbscrLcsarLcsbrLcscr] В качестве примера рассмотрим взаимную индуктивность Lasar, которая представляет отношение потока, связывающего поток в статоре с обмоткой ротора, как . ar ток в обмотке, создающий магнитный поток. Если обмотка ротора вращается со скоростью ωr, относительное положение θr между двумя обмотками будет меняться со временем. Таким образом, взаимная индуктивность изменяется синусоидально относительно угла смещения θr ротора, как показано на рис.4.6. Рисунок 4.6. Взаимоиндуктивность между статором как обмотка и ротором и обмоткой . Учитывая соотношение витков между двумя обмотками, Lasar определяется как (4.20) Lasar = Lmr (NsNr) cosθr = Lms (NrNs) cosθr (θr = ∫ωrdt) Аналогично, даны другие взаимные индуктивности по (4,21) Лазар = Lbsbr = Lcscr = (NrNs) Lmscosθr (4,22) Lasbr = Lbscr = Lcsar = (NrNs) Lmscos (θr + 2π3) (4,23) Lascr = Lbsarr = Lcsbr = Lmscos (θr − 2π3) С этими индуктивностями матрица взаимной индуктивности Lsr равна (4.24) Lsr = [LasarLasbrLascrLbsarLbsbrLbscrLcsarLcsbrLcscr] = nLms [cosθrcos (θr + 2π3) cos (θr − 2π3) cos (θr − 2π3) cosθrcos (θr + 2π3) cosθ 9r (9r000) θr5000) cosθ3 (9) θr + 2πθ3. Из уравнения. (4.24), мы легко можем видеть, что взаимные индуктивности являются функцией положения ротора и, таким образом, изменяются во времени, за исключением состояния покоя. Следовательно, изменяющиеся во времени коэффициенты появятся в уравнениях напряжения статора по формулам. (4.2) — (4.4). Потоковая связь обмоток статора по формулам. (4.14) и (4.24) дается формулой (4.25) λabcs = Lsiabcs + Lsriabcr = [Lls + Lms − Lms2 − Lms2 − Lms2Lls + Lms − Lms2 − Lms2 − Lms2Lls + Lms] [iasibsics] + nLms [cosθrcos (θr + 2π3) cos (θr − 2πr3) cos (θr − 2πr3) cos (θr − 2πr3) cos −2π3) cosθrcos (θr + 2π3) cos (θr + 2π3) cos (θr − 2π3) cosθr] [iaribricr] Затем исследуем взаимную индуктивность Lrs. Это связано с величиной магнитного потока, который создается обмотками статора и связывает обмотки ротора. Эта взаимная индуктивность Lrs равна транспонированной Lrs как (4,26) Lrs = LsrT = [LarasLarbsLarcsLbrasLbrbsLbrcsLcrasLcrbsLcrcs] = nLms [cosθrcos (θr − 2π3) cos (θr θr + 2πr3) cos (θr θ3) cosθ (θr) 2π3) cos (θr − 2π3) cos (θr + 2π3) cosθr] Как и Lsr, взаимная индуктивность Lrs также изменяется во времени, за исключением состояния покоя.Следовательно, изменяющиеся во времени коэффициенты появятся в уравнениях напряжения обмоток ротора. Потоковая связь обмоток ротора по формулам. (4.18) и (4.26) задается формулами (4.27) λabcr = Lriabcr + Lrsiabcs = [Lls + n2Lms − n2Lms2 − n2Lms2 − Lms2Lls + n2Lms − n2Lms2 − n2Lms2 − n2Lms2Lls + iLarLms] [cosθ (θr − 2π3) cos (θr + 2π3) cos (θr + 2π3) cosθrcos (θr − 2π3) cos (θr − 2π3) cos (θr + 2π3) cosθr] [iasibsics] Наконец, из формул. (4.25) и (4.27), общие потокосцепления асинхронного двигателя равны Путем замены этих потоковых связей в уравнения. (4.2) — (4.7) уравнения напряжения асинхронного двигателя завершаются. Вам приходило в голову, что если рост тока в катушке приводит к обратной ЭДС, которая противодействует увеличению тока, ток не может мгновенно измениться в цепи, содержащей индуктивность. Это правильно. (Напомним также, что разность потенциалов в цепи не может мгновенно измениться в цепи, содержащей емкость.Если подумать, вряд ли емкость или индуктивность какой-либо цепи может быть точно равна нулю; любая реальная цепь должна иметь некоторую емкость и индуктивность, даже если они очень малы.) Рассмотрим схему на рисунке X.9. Батарея ЭДС \ (Е \) включена последовательно с сопротивлением и индуктивностью. (Катушка, соленоид или любой индуктор в целом будут иметь как индуктивность, так и сопротивление, поэтому \ (R \) и \ (L \) на рисунке могут принадлежать к одному элементу.) Мы должны быть очень осторожны с подписывает в дальнейшем. \ (\ text {РИСУНОК X.9} \) Когда цепь замкнута (например, переключателем), ток течет в показанном направлении. стрелкой, которая также указывает направление увеличения тока. ЭДС \ (L \ dot I \) индуцируется в направлении, противоположном \ (\ dot I \). Таким образом, закон Ома или, если хотите, второе правило Кирхгофа, примененное к схеме (внимательно следите за знаками): \ [E = IR -L \ dot I = 0. \ Label {10.12.1} \] Отсюда: \ [\ label {10.{-1} \)) своего конечного значения за время \ (L / R \). На рисунке X.10 ток показан в единицах \ (E / R \), а время — в единицах \ (L / R \). Вы должны проверить, что \ (L / R \), который называется постоянной времени схемы, имеет размерность времени. \ (\ text {РИСУНОК X.10} \) Вот задача, которая даст вам практический опыт в пропускании тока через катушку индуктивности, применении правил Кирхгофа и решении дифференциальных уравнений. Аналогичная проблема с конденсатором описана в главе 5, раздел 5.19. В приведенной выше схеме, когда переключатель разомкнут, \ (I_1 = I_2 = E / (2 R) \ text {и} I_3 = 0 \). Спустя долгое время после того, как переключатель замкнут и достигнут установившийся ток, \ (I_1 \) будет \ (2E / (3R) \), а \ (I_2 \ text {и} I_3 \) будет каждый \ (E / ( 3R) \). Но мы хотим исследовать, что происходит в короткий момент, когда ток меняется. Применяем правила Кирхгофа: \ [\ label {10.12.4} E = I_1R + I_2R \] \ [\ label {10.12.5} I_3R + L \ dot I_3 -I_2R = 0 \] \ [\ label {10.12.6} I_1 = I_2 + I_3, \] [Получение знака \ (L \ точка I_3 \) прямо в уравнении \ ref {10.12.5} важно. Думайте о катушке индуктивности как о батарее ЭДС \ (L \ dot I_3 \), ориентированной следующим образом:.] Удалите \ (I_1 \ text {и} I_2 \), чтобы получить единственное уравнение в \ (I_3 \). \ [\ label {10.12.7} \ frac {dI_3} {dt} + \ frac {3R} {2L} I_3 = \ frac {E} {2L}. \] Это имеет форму \ ( \ frac {dy} {dx} + ay = b \), и тем, кто имеет опыт работы с дифференциальными уравнениями, не составит труда прийти к решению \ [\ label {10.{- \ frac {3Rt} {2L}} \ right) \] Таким образом, \ (I_1 \) переходит от начального \ (\ frac {E} {2R} \ text {к окончательному} \ frac {2E} {3R } \). \ (I_2 \) идет от начального \ (\ frac {E} {2R} \ text {до finally} \ frac {E} {3R} \). \ (I_3 \) изменяется от начального нуля до конечного \ (\ frac {E} {3R} \). Измерение емкости и индуктивности с помощью осциллографа и функционального генератора
Что такое импеданс?
Методы измерения импеданса
Теоретическая точность
Тестовый пример
Использованное оборудование:
Пример 1: керамический конденсатор 10 мкФ
Таблица 1. Пример 1 сравнительная таблица. LCR
в руководстве указано, что точность составляет 0,05%, а в руководстве по USB VNA указано, что это
2% точность. Пример 2: индуктор 10 мГн
Рисунок 6. Формы напряжения и измерения
взяты в узлах A1 и A2.
Таблица 2. Сравнительная таблица примера 2. Рисунок 7.
Емкость / частота
коробка. Рисунок 8.Индуктивность / частота
коробка. Диапазон измерения
Заключение
Катушка индуктивности эквивалент заряда конденсатора
— обзор
4.1.3 Индуктивность между обмотками статора и ротора
10.12: Рост тока в цепи, содержащей индуктивность

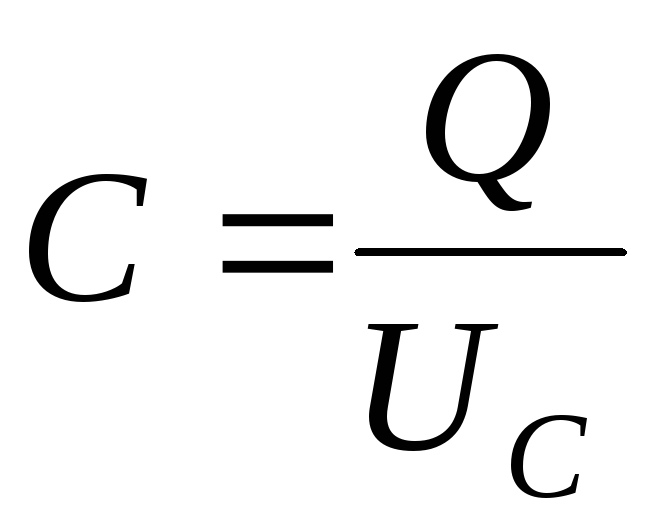


 1)
1)