Индуктивность катушки формула через частоту – Катушка индуктивности. Описание, характеристики, формула расчета

Расчёт частоты резонанса колебательного контура

Колебательный контур — электрическая цепь, в которой могут возникать колебания с частотой, определяемой параметрами цепи.

Простейший колебательный контур состоит из конденсатора и катушки индуктивности, соединенных параллельно или последовательно.

— Конденсатор C – реактивный элемент. Обладает способностью накапливать и отдавать электрическую энергию.
— Катушка индуктивности L – реактивный элемент. Обладает способностью накапливать и отдавать магнитную энергию.

Свободные электрические колебания в параллельном контуре.

Основные свойства индуктивности:

— Ток, протекающий в катушке индуктивности, создаёт магнитное поле с энергией .
— Изменение тока в катушке вызывает изменение магнитного потока в её витках, создавая в них ЭДС, препятствующую изменению тока и магнитного потока.

Период свободных колебаний контура LC можно описать следующим образом:

Если конденсатор ёмкостью C заряжен до напряжения

U, потенциальная энергия его заряда составит.
Если параллельно заряженному конденсатору подключить катушку индуктивности L, в цепи пойдёт ток его разряда, создавая магнитное поле в катушке.

Магнитный поток, увеличиваясь от нуля, создаст ЭДС в направлении противоположном току в катушке, что будет препятствовать нарастанию тока в цепи, поэтому конденсатор разрядится не мгновенно, а через время t₁, которое определяется индуктивностью катушки и ёмкостью конденсатора из расчёта t₁ = .
По истечении времени t₁, когда конденсатор разрядится до нуля, ток в катушке и магнитная энергия будут максимальны.
Накопленная катушкой магнитная энергия в этот момент составит.
В идеальном рассмотрении, при полном отсутствии потерь в контуре, E_C будет равна E_L. Таким образом, электрическая энергия конденсатора перейдёт в магнитную энергию катушки.

Изменение (уменьшение) магнитного потока накопленной энергии катушки создаст в ней ЭДС, которая продолжит ток в том же направлении и начнётся процесс заряда конденсатора индукционным током. Уменьшаясь от максимума до нуля в течении времени

t₂ = t₁, он перезарядит конденсатор от нуля до максимального отрицательного значения (-U).
Так магнитная энергия катушки перейдёт в электрическую энергию конденсатора.

Описанные интервалы t₁ и t₂ составят половину периода полного колебания в контуре.
Во второй половине процессы аналогичны, только конденсатор будет разряжаться от отрицательного значения, а ток и магнитный поток сменят направление. Магнитная энергия вновь будет накапливаться в катушке в течении времени t₃, сменив полярность полюсов.

В течении заключительного этапа колебания (t₄), накопленная магнитная энергия катушки зарядит конденсатор до первоначального значения

U (в случае отсутствия потерь) и процесс колебания повторится.

В реальности, при наличии потерь энергии на активном сопротивлении проводников, фазовых и магнитных потерь, колебания будут затухающими по амплитуде.
Время t₁ + t₂ + t₃ + t₄ составит период колебаний .
Частота свободных колебаний контура ƒ = 1 / T

Частота свободных колебаний является частотой резонанса контура, на которой реактивное сопротивление индуктивности X_L=2πfL равно реактивному сопротивлению ёмкости X_C=1/(2πfC).

---

Расчёт частоты резонанса LC-контура:

Предлагается простой онлайн-калькулятор для расчёта резонансной частоты колебательного контура.

Необходимо вписать значения и кликнуть мышкой в таблице.
При переключении множителей автоматически происходит пересчёт результата.

Частота резонанса колебательного контура LC. ƒ = 1/(2π√(LC))

Расчёт ёмкости:

Ёмкость для колебательного контура LC C = 1/(4𲃲L)

Расчёт индуктивности:

Индуктивность для колебательного контура LC L = 1/(4𲃲C)

---

Похожие страницы с расчётами:

Рассчитать импеданс.
Рассчитать реактивное сопротивление.
Рассчитать реактивную мощность и компенсацию.

tel-spb.ru

Индуктивное сопротивление катушки — Основы электроники

Так как самоиндукция препятствует всякому резкому изменению силы тока в цепи, то, следовательно, она представляет собой для переменного тока особого рода сопротивление, называемое индуктивным сопротивлением.

Чисто индуктивное сопротивление отличается от обычного (омического) сопротивления тем, что при прохождении через него переменного тока в нем не происходит потери мощности.

Под чисто индуктивным сопротивлением

мы понимаем сопротивление, оказываемое переменному току катушкой, проводник которой не обладает вовсе омическим сопротивлением. В действительности же всякая катушка обладает некоторым омическим сопротивлением. Но если это сопротивление невелико по сравнению с индуктивным сопро¬тивлением, то им можно пренебречь.

При этом наблюдается следующее явление: в течение одной четверти периода, когда ток возрастает, магнитное поле потребляет энергию из цепи, а в течение следующей четверти периода, когда ток убывает, возвращает ее в цепь. Следовательно, в среднем за период в индуктивном сопротивлении мощность не затрачивается. Поэтому индуктивное сопротивление называется реактивным (прежде его неправильно называли безваттным).

Индуктивное сопротивление одной и той же катушки будет различным для токов различных частот. Чем выше частота переменного тока, тем большую роль играет индуктивность и тем больше будет индуктивное сопротивление данной катушки. Наоборот, чем ниже частота тока, тем индуктивное сопротивление катушки меньше. При частоте, равной нулю (установившийся постоянный ток), индуктивное сопротивление тоже равно нулю.

 Рисунок 1. Зависимость индуктивного сопротивления катушки от частоты переменного тока. Реактивное сопротивление катушки возрастает с увеличением часторы тока.

Индуктивное сопротивление обозначается буквой X_L и измеряется в омах.

Подсчет индуктивного сопротивления катушки для переменного тока данной частоты производится по формуле

X_L=2π• f •L

где X_L — индуктивное сопротивление в ом; f—частота переменного тока в гц; L — индуктивность катушки в гн

Как известно, величину 2π• f называют круговой частотой и обозначают буквой ω (омега). Поэтому приведенная выше формула может быть представлена так:

X

L=ω•L

Отсюда следует, что для постоянного тока (ω = 0) индуктивное сопротивление равно нулю. Поэтому, когда, нужно пропустить по какой-либо цепи постоянный ток, задержав в то же время переменный, то в цепь включают последовательно катушку индуктивности.

Для преграждения пути токам низких звуковых частот ставят катушки с железным сердечником, так называемые дроссели низкой частоты, а для более высоких радиочастот — без железного сердечника, которые носят название дросселей высокой частоты.

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Похожие материалы:

Добавить комментарий

www.sxemotehnika.ru

Лабораторная работа № 2.07 определение индуктивности катушки

Цель работы

Целью данной работы является изучение явления электромагнитной индукции и его законов, измерение индуктивности катушки, исследование зависимости индуктивности катушки от силы тока, протекающего по ее обмотке, а также индуктивности катушки, ее полного и индуктивного сопротивлений от частоты переменного тока.

Краткая теория.

Всякий контур, по которому течет ток, пронизывается магнитным полем, созданным этим током. Если сила тока в контуре меняется, то изменяется и сцепленный с контуром магнитный поток, поэтому вследствие явления электромагнитной индукции в контуре возникает ЭДС. Возникновение ЭДС в контуре при изменении силы тока в нем называется самоиндукцией. В соответствии с законом Фарадея величина ЭДС индукции пропорциональна скорости изменения магнитного потока, пронизывающего контур, то есть,

(2.07.1)

Магнитный поток, создаваемый током, протекающим в контуре, называется потоком самоиндукции

_s. Поток самоиндукции пропорционален индукции магнитного поля, создаваемого этим током, которая, в свою очередь, пропорциональна величине силы тока в контуре. Поэтому магнитный поток самоиндукции пропорционален величине силы тока

, (2.07.2)

где L – индуктивность контура.

Индуктивность контура – это скалярная физическая величина, характеризующая способность контура создавать поток самоиндукции и зависящая от его формы, размеров и магнитной проницаемости среды. Из (2.07.2) следует, что индуктивность контура измеряется величиной магнитного потока, сцепленного с контуром, при силе тока в нем равной 1 А. За единицу измерения индуктивности в системе СИ принимается 1 Гн – это индуктивность такого контура, с которым сцеплен магнитный поток в 1 Вб при силе тока в контуре, равной 1 А.

При неизменной индуктивности закон Фарадея для самоиндукции выглядит следующим образом:

(2.07.3)

т. е. ЭДС самоиндукции пропорциональна скорости изменения силы тока в контуре. В соответствии с законом Фарадея можно дать другое определение индуктивности. Индуктивность определяется величиной ЭДС, возникающей в контуре, при изменении в нем силы тока на 1 А за 1 с. Тогда, согласно (2.07.3), 1 Гн – это индуктивность такого контура, в котором индуцируется ЭДС, равная 1 В, при изменении в нем силы тока на 1 А за 1 с. Знак минус в формуле (2.07.3) отражает правило Ленца, согласно которому самоиндукция противодействует всякому изменению силы тока в контуре и представляет собой аналогию с инерцией в механике.

В электрической цепи наличие индуктивности приводит к возникновению добавочного индуктивного сопротивления катушки переменному току

, (2.07.4)

где  – частота переменного тока.

Модуль полного сопротивления Z катушки переменному току определяется по закону Ома

(2.07.5)

где U и I – эффективные значения напряжения и силы тока в катушке.

Полное сопротивление катушки Z складывается из сопротивления катушки в цепи постоянного тока R (омического или активного сопротивления) и индуктивного сопротивления X_L в соответствии с формулой:

. (2.07.6)

или, подставив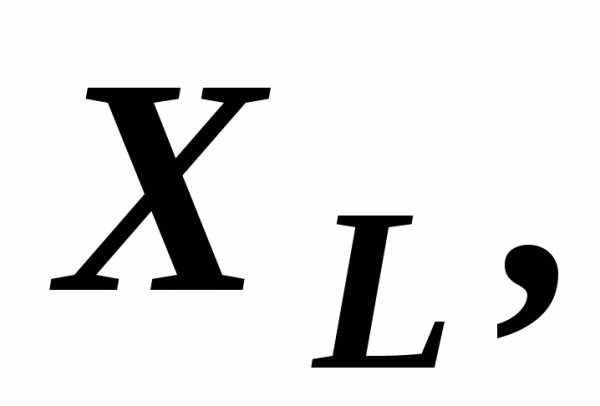

(2.07.7)

из которого можно выразить индуктивность катушки L

(2.07.8)

Соотношение (2.07.8) лежит в основе опыта по определению индуктивности. Для того, чтобы определить индуктивность, необходимо измерить частоту переменного тока, действующее значение силы переменного тока, протекающего через катушку, действующее значения напряжения на катушке и омическое сопротивление катушки.

Индуктивность длинного соленоида с сердечником может быть рассчитана по формуле

, (2.07.9)

где  – магнитная проницаемость сердечника; – магнитная постоянная;n – число витков, приходящихся на единицу длины катушки; V – объем катушки.

Измеряя индуктивность катушки, можно определять магнитную проницаемость материала, из которого изготовлен сердечник. В частности, таким способом можно определять магнитную проницаемость горных пород. Определив индуктивность катушки с сердечником из исследуемой породы L_с и без сердечника L₀, по отношению этих индуктивностей L_С/L₀ определяют . Определение магнитной проницаемости горных пород и минералов необходимо для изучения вопросов, связанных с установлением качества железных руд и железистых пород, магнитным обогащением полезных ископаемых, с разведкой рудных тел, исследованием трещиноватости массива горных пород.

Выполнение работы

Необходимые приборы: лабораторный стенд, внутри которого смонтированы все элементы схемы; генератор периодических сигналов; цифровой вольтметр. Рабочая схема опыта показана на рис. 18 и на панели стенда.

studfiles.net

Катушка индуктивности

Катушка индуктивности – электронный компонент, представляющий собой винтовую либо спиральную конструкцию, выполненную с применением изолированного проводника.  Основным свойством катушки индуктивности, как понятно из названия – индуктивность. Индуктивность – это свойство преобразовать энергию электрического тока в энергию магнитного поля. Величина индуктивности для цилиндрической или кольцевой катушки равна 

Где  ψ — потокосцепление, µ0 = 4π*10-7 – магнитная постоянная, N – количество витков, S – площадь поперечного сечения катушки.

Также катушке индуктивности присущи такие свойства как небольшая ёмкость и малое активное сопротивление, а идеальная катушка и вовсе их лишена. Применение данного электронного компонента отмечается практически повсеместно в электротехнических устройствах. Цели применения различны:

— подавление помех в электрической цепи;
— сглаживание уровня пульсаций;
— накопление энергетического потенциала;
— ограничение токов переменной частоты;
— построение резонансных колебательных контуров;
— фильтрация частот в цепях прохождения электрического сигнала;
— формирование области магнитного поля;
— построение линий задержек, датчиков и т.д.

Энергия магнитного поля катушки индуктивности

Электрический ток способствует накоплению энергии в магнитном поле катушки. Если отключить подачу электричества, накопленная энергия будет возвращена в электрическую цепь. Значение напряжения при этом в цепи катушки возрастает многократно. Величина запасаемой энергии в магнитном поле равна примерно тому значению работы, которое необходимо получить, чтобы обеспечить появление необходимой силы тока в цепи. Значение энергии, запасаемой катушкой индуктивности можно рассчитать с помощью формулы.

 

Реактивное сопротивление

При протекании переменного тока, катушка обладает кроме активного, еще и реактивным сопротивлением, которое находится по формуле 

По формуле видно, что в отличие от конденсатора, у катушки с увеличением частоты, реактивное сопротивление растет, это свойство применяется в фильтрах частот.

При построении векторных диаграмм важно помнить, что в катушке, напряжения опережает ток на 90 градусов.

Добротность катушки

Еще одним важным свойством катушки является добротность. Добротность показывает отношение реактивного сопротивления катушки к активному. 

Чем выше добротность катушки, тем она ближе к идеальной, то есть она обладает только главным своим свойством – индуктивностью.

Конструкции катушек индуктивности

Конструктивно катушки индуктивности могут быть представлены в разном исполнении. Например, в исполнении однослойной или многослойной намотки проводника. При этом намотка провода может выполняться на диэлектрических каркасах разных форм: круглых, квадратных, прямоугольных. Нередко практикуется изготовление бескаркасных катушек. Широко применяется методика изготовления катушек тороидального типа. 

Витки проводника, как правило, наматываются плотно один к одному. Однако в некоторых случаях намотка производится с шагом. Подобная методика отмечается, к примеру, когда изготавливаются высокочастотные дроссели. Намотка провода с шагом способствует снижению образования паразитной ёмкости, так же как и намотка, выполненная отдельными секциями. 

Индуктивность катушки можно изменять,  добавляя в конструкцию катушки ферромагнитный сердечник. Внедрение сердечников отражается на подавлении помех. Поэтому практически все дроссели, предназначенные для подавления высокочастотных помех, как правило, имеют ферродиэлектрические сердечники, изготовленные на основе феррита, флюкстрола, ферроксона, карбонильного железа. Низкочастотные помехи хорошо сглаживаются катушками на пермалоевых сердечниках или на сердечниках из электротехнической стали.

Просмотров:

electroandi.ru

взаимная индуктивность, закон Неймана, собственная индуктивность, катушка индуктивности

В статье мы рассмотрим понятие индуктивности, что такое катушка индуктивности, подробно разберем закон Неймана или по-другому «взаимная индуктивность», покажем все на примере с формулами.

Взаимная индуктивность, формула Неймана

Предположим, что у нас есть две проводящие петли, петля номер один, взаимодействующая с ней, и петля номер два, вызывающая в ней магнитный поток, используя равенство индукции магнитного поля и определение индукции магнитного поля через векторный потенциал магнитного поля и изменив в этом потоке интеграл на поверхности, ограниченный замкнутым контуром, на интеграл по контуру, затем:

(1)

Из магнитостатики векторный магнитный потенциал магнитного поля из первой петли определяется как:

(2)

Если подставить формулу для векторного магнитного потенциала (2) в формулу для магнитного потока, ограниченного каким-либо произвольным контуром (1), то:

(3)

Очевидно, что формула (3) после перестановки круговых интегралов в одно место, эквивалентна:

(4)

Здесь R — расстояние друг от друга: dl(1) от dl(2)

Формула (4) может быть сохранена в виде разделения константы M ₁₂ , тогда:

(5)

где

(6)

Формула для размера взаимной индукции (6) является симметричной из-за регулировки dl(1) от dl(2), то есть взаимная индукция после этого изменения не меняется, она симметрична. Очевидно, что она не зависит от времени. Значение M_12 в формуле (6) это формула Неймана . Если подставить формулу (5) в интегральную формулу Фарадея для первого цикла, аналогично и для второго цикла, то тогда закономерность взаимной индукции второй петли относительно первой петли для электродвижущей силы для двух петель выражаются в формулах:

(7)(8)

Мы видим, что закономерности для электромагнитной силы одинаковы, но они зависят от изменений длительности электрического тока во втором контуре (формула (7) ) или в первом контуре (формула (8)).

Собственная индуктивность

Здесь мы будем иметь дело только с одним контуром, который магнитно взаимодействует с самим собой.

Закон Фарадея и собственная индукция

Мы должны иметь дело с индуктивностью, когда одна и та же цепь взаимодействует с одной и той же цепью магнетизмом, то есть это особый случай взаимной индуктивности. Мы записываем формулу для этой ситуации:

Ф = L*I (9)

Тогда формула для электромагнитной силы возникает после подстановки формулы (9) в закон Фарадея:

(10)

Формула для L такая же, как формула Неймана (6) , используется только двойное интегрирование по одному и тому же периметру, то есть геометрия применяется только к одной цепи.

Собственная энергия магнитной системы

Сила, создаваемая против ЭДС в индуктивности собственной цепи, зависит от электродвижущей силы, вызванной самоиндукцией, если ток течет в ней, и от того, что ее работа выполняется против электромагнитной силы ЭДС в единицу времени, равна:

(11)

Используя определение электродвижущей силы, обусловленной собственной индуктивностью (10), которая вытекает из закона индуктивности Фарадея, мы спрашиваем себя, что работа выполнялась системой, когда ток в системе с индуктивностью L от I равен нулю до некоторой ненулевой величины, поэтому мы приходим к выводу:

(12)

Работа, выполненная против ЭДС в системе индуктивности L, после переписывания окончательного применения (12), выражается:

(13)

Это не зависит от того, как долго протекает ток, а зависит только от геометрии системы и тока, протекающего в нашей цепи, которая взаимодействует сама с собой в результате действия магнитного поля.

Катушка индуктивности (дроссель)

Далее мы поговорим о катушке индуктивности и способе измерения индуктивности.

Определение и теория катушек индуктивности

Катушка индуктивности (дроссель) — катушка из свёрнутого изолированного проводника, обладающая значительной индуктивностью при относительно малой ёмкости и малом активном сопротивлении, способная накапливать электромагнитную энергию в собственном магнитном поле. Обозначается – L. Внешний вид может быть различным, но если вы её мотаете самостоятельно, то будет выглядеть как-то так:

Величина индуктивности измеряется в Генри [Гн].

1 Генри – очень большая величина, поэтому применяемые в технике катушки индуктивности имеют величины: микрогенри – 10^-6 (мкГн) и миллигенри – 10^-3 (мГн).

Процессы, происходящие в катушке индуктивности (далее — индуктивности) на временном графике при подключении индуктивности к источнику прямоугольного однополярного сигнала, показаны на рисунке.

Из рисунка сбоку видно, реакция индуктивности на воздействие электрического тока абсолютно противоположно реакции конденсатора (ёмкости). В момент подачи прямоугольного импульса источника тока (красный), ток индуктивности (фиолетовый) сначала равен нулю и с изменением времени увеличивается по экспоненте – индуктивность накапливает энергию, в начальный момент её внутреннее сопротивление максимально. Напряжение на выводах индуктивности (зелёный) наоборот сначала максимально, но потом по мере накопления энергии уменьшается по экспоненте до нуля. При пропадании входного импульса, так как индуктивность — элемент инерционный, напряжение на выводах индуктивности резко изменив полярность сначала максимально, а ток продолжает течь в том же направлении, уменьшаясь при этом по экспоненте – запасённая в индуктивности энергия иссякает. Напряжение из отрицательной области так же по экспоненте стремится к нулю. Скорость изменения напряжения и тока зависит от значения индуктивности. Чем больше индуктивность, тем медленнее они изменяются (экспонента более вытянута по времени). Напряжение и ток на нагрузочном резисторе ведут себя одинаково, и изображены на временном графике оранжевым цветом. Если сравнить с конденсатором — полная противоположность. Взаимосвязь тока и напряжения в индуктивности так же описывается законом Ома, с учётом реактивного сопротивления индуктивности.

Фактически, мы рассмотрели «четырёхполюсник» состоящий из катушки индуктивности и резистора, который называют интегрирующей цепочкой.

Интегрирующая цепочка чаще всего применяется для формирования пилообразных импульсов в любой радио аппаратуре и временной (ударение на «о») задержки прямоугольных импульсов. Чтобы, Вам было понятнее, интегрирующая цепочка и получение пилообразного импульса изображены на следующем рисунке. Для получения последнего, используется наиболее прямолинейный участок интегрированного импульса — его начало, и «обрезается» по времени или по амплитуде (порогу).

Для задержки импульсов используют пороговое устройство. По достижении амплитуды сигнала прошедшего через интегрирующую цепочку определённого значения (порога), пороговое устройство пропускает входной сигнал на выход. После чего, сигнал усиливается усилителем до необходимой величины. В целях уменьшения размеров (исключения громоздкости), схемы формирования пилообразных импульсов, и схемы задержки импульсов эффективнее делать на интегрирующей цепочке состоящей из резистора и конденсатора.

Кроме функции преобразования прямоугольных импульсов, интегрирующая цепочка может применяться в качестве фильтра низких частот (ФНЧ). Индуктивность – инертный элемент. Если к дросселю с большим значением индуктивности приложить переменное напряжение высокой частоты, в силу своей инертности, индуктивность будет не способной пропустить через себя ток, ведь индуктивности сначала надо будет запастись энергией в собственном сердечнике, а потом отдавать эту энергию. Свойство индуктивности сопротивляться переменному электрическому току называют реактивным сопротивлением индуктивности, которое используется при конструировании частотных фильтров и колебательных контуров. Реактивное сопротивление индуктивности обозначается X_L или Z_L и измеряется в Омах. Реактивное сопротивление индуктивности связано с частотой тока выражением:

Из формулы видно, что реактивное сопротивление индуктивности прямо пропорционально частоте. Другими словами, чем выше частота, тем больше реактивное сопротивление индуктивности.

Теперь представьте, что интегрирующая цепь, это – описанный на сайте делитель напряжения, где вместо первого резистора выступает индуктивность. А мы из формулы теперь знаем, что индуктивность легко пропускает низкие частоты – его сопротивление минимально и плохо пропускает высокие частоты – его сопротивление максимально. Не изменяя текста повторюсь: В радиоэлектронике, когда рассчитывают частотные фильтры, то считают характеристикой фильтра – частоту среза, которая определяется как значение частоты сигнала, на котором амплитуда выходного сигнала уменьшается (затухает) до значения 0,7 от входного сигнала. Чтобы было понятнее, изображу это на рисунке.

То, что изображено, называется амплитудно-частотной характеристикой, или сокращённо — АЧХ. Для фильтра высоких частот соответствует АЧХ фиолетового цвета, и частота среза равная значению f₂.

Зная, как рассчитывается делитель напряжения и реактивное сопротивление индуктивности на определённой частоте, Вы элементарно можете рассчитать простейший г-образный фильтр низкой частоты на катушке индуктивности (дросселе) и резисторе.

Если в интегрирующей цепочке поменять местами индуктивность и резистор, то мы получим – дифференцирующую цепочку. Все процессы в дифференцирующей цепочке происходят точно так же, как и в интегрирующей. Временные графики, показанные на первом рисунке абсолютно справедливы для дифференцирующей цепочки. Отличие заключается в том, что выходным элементом является не резистор, а катушка индуктивности.

Как описывалось в статье про конденсатор: если дифференцирующая цепочка – это фильтр высоких частот, то интегрирующая цепочка – это фильтр низких частот (ФНЧ). И рассчитывается он так же, через делитель напряжения. Для фильтра низких частот соответствует АЧХ на рисунке — оранжевого цвета, и частота среза равная значению f₁.

Cледует добавить, частотные фильтры, выполненные на катушках индуктивности и резисторах, так же, как и на конденсаторах и резисторах имеют пологую амплитудно-частотную характеристику. Другими словами у таких фильтров слабо выражен частотный срез. Более качественный срез, имеют фильтры состоящие из конденсаторов и катушек индуктивности (дросселей), но об этом в следующей статье.

Способ измерения индуктивности

Наверняка прочитав данную статью, грамотный читатель подумает: «Хм, теория это конечно хорошо, но как измерить руками значение индуктивности на практике?». Однажды этим вопросом задался и я, и собрал простую схему для проверки индуктивностей.

meanders.ru

Как рассчитать сердечник и витки самодельных катушек индуктивности

Катушки индуктивности предназначены для фильтрации токов высокой частоты. Они устанавливаются в колебательных контурах и используются для других целей в электрических и электронных схемах. Готовое устройство заводского изготовления надёжнее в работе, но дороже, чем изготовленное своими руками. Кроме того, не всегда удаётся приобрести элемент с необходимыми характеристиками. В этом случае расчёт катушки  индуктивности и само устройство можно сделать самостоятельно.

Устройство катушки индуктивности

Конструкция катушки

Каркас устройства изготавливается из диэлектрика. Это может быть тонкий (нефольгированный) гетинакс, текстолит, а на тороидальных сердечниках –просто обмотка из лакоткани или аналогичного материала.

Обмотка выполняется из одножильного или многожильного изолированного провода.

Внутрь обмотки вставляется сердечник. Он изготавливается из железа, трансформаторной стали, феррита и других материалов. Он может быть замкнутым, тороидальным (бублик), квадратным или незамкнутым (стержень). Выбор материала зависит от условий работы: частоты, магнитного потока и других параметров.

Кроме того, есть приборы, в которых сердечник отсутствует. Они характеризуются большой линейностью импеданса, но при намотке тороидальной формы обладают паразитной ёмкостью.

Расчет параметров катушки индуктивности

Протекающий по проводу электрический ток создаёт вокруг него электромагнитное поле. Соотношение величины поля к силе тока называется индуктивностью. Если провод свернуть кольцом или намотать на каркас, то получится катушка индуктивности. Её параметры рассчитывают по определённым формулам.

Расчёт индуктивности прямого провода

Индуктивность прямого стержня – 1-2мкГн на метр. Она зависит от его диаметра. Точнее можно рассчитать по формуле:

L=0.2l(logl/d-1), где:

• d – диаметр провода,
• l – длина провода.

Эти величины нужно измерять в метрах (м). При этом результат будет иметь размерность микрогенри (мкГн). Вместо натурального логарифма ln допустимо использовать десятичный lg, который в 2,3 раза меньше.

Предположим, что какая-то деталь подключена проводами длиной 4 см и диаметром 0,4 мм. Произведя при помощи калькулятора расчет по выше приведённой формуле, получаем, что индуктивность каждого из этих проводов составит (округлённо) 0,03 мкГн, а двух – 0,06 мкГн.

Ёмкость монтажа составляет порядка 4,5пФ. При этом резонансная частота получившегося контура составит 300 МГц. Это диапазон УКВ.

Важно! Поэтому при монтаже устройств, работающих в частотах УКВ, длину выводов деталей нужно делать минимальной.

Расчёт однослойной намотки

Для увеличения индуктивности провод сворачивается кольцом. Величина магнитного потока внутри кольца выше примерно в три раза. Рассчитать её можно при помощи следующего выражения:

L = 0,27D(ln8D/d-2), где D – диаметр кольца, измеренный в метрах.

При увеличении количества витков индуктивность продолжает расти. При этом индукция отдельных витков влияет на соседние, поэтому получившиеся параметры пропорциональны не количеству витков N, а их квадрату.

Однослойная намотка

Дроссель с сердечником

Параметры обмотки, намотанной на каркас, диаметром намного меньше длины рассчитывается по формуле:

L=*0*N2*S.

Она справедлива для устройства большой длины или большого тора.

Размерность в ней дана в метрах (м) и генри (Гн). Здесь:

• 0 = 4•10-7 Гн/м – магнитная константа,
• S = D2/4 – площадь поперечного сечения обмотки, магнитная проницаемость магнитопровода, которая меньше проницаемости самого материала и учитывает длину сердечника; в разомкнутой конструкции она намного меньше, чем у материала.

Например, если стержень антенны изготовить из феррита с проницаемостью 600 (марки 600НН), то у получившегося изделия она будет равна 150. При отсутствии магнитного сердечника = 1.

Для того чтобы использовать это выражение для расчёта обмоток, намотанных на тороидальном сердечнике, его необходимо измерять по средней линии «бублика». При расчёте обмоток, намотанных на железе Ш-образной формы без воздушного зазора, длину пути магнитного потока измеряют по средней линии сердечника.

Катушка с Ш-образным сердечником

В расчёте диаметр провода не учитывается, поэтому в низкочастотных конструкциях сечение провода выбирается по таблицам, исходя из допустимого нагрева проводника.

В высокочастотных устройствах, так же как и в остальных, стремятся свести омическое сопротивление к минимуму для достижения максимальной добротности прибора. Простое повышение сечения провода не помогает. Это приводит к необходимости наматывать обмотку в несколько слоёв. Но ток ВЧ идёт преимущественно по поверхности, что приводит к увеличению сопротивления. Добротность в высокочастотных элементах растёт вместе с увеличением всех размеров: длины и диаметров обмотки и провода.

Максимальная добротность получается в короткой обмотке большого диаметра, с соотношением диаметр/длина, равным 2,5. Параметры такого устройства вычисляются по формуле:

L=0.08D2N2/(3D+9b+10c).

В этой формуле все параметры измеряются в сантиметрах (см), а результат получается в микрогенри (мкГн).

По этой формуле рассчитывается также плоская катушка. Диаметр «D» измеряется по среднему витку, а длина «l» по ширине:

l=Dmax-Dmin.

Плоская катушка

Многослойная намотка

Многослойная намотка без сердечника вычисляется по формуле:

L=0.08D2N2/(3D+9b+10c).

Размеры здесь измеряются в сантиметрах (см), а результат получается в микрогенри (мкГн).

Добротность такого устройства зависит от способа намотки:

• обычная плотная намотка – самая плохая, не более 30-50;
• внавал и универсал;
• «сотовая».

Многослойная катушка

Для увеличения добротности при частоте до 10 мГц вместо обычного, одножильного провода, можно взять литцендрат или посеребренный проводник.

Справка. Литцендрат – это провод, скрученный из большого количества тонких изолированных друг от друга жил.

Литцендрат имеет большую поверхность, по сравнению с одножильным проводником того же сечения, поэтому на высоких частотах его сопротивление ниже.

Использование сердечника в высокочастотных устройствах повышает индуктивность и добротность катушки. Особенно большой эффект даёт использование замкнутых сердечников. При этом добротность дросселя зависит не от активного сопротивления провода, а от проницаемости магнитопровода. Рассчитывается такой прибор по обычным формулам для низкочастотных устройств.

Сделать катушку или дроссель можно самостоятельно. Перед тем, как её изготавливать, необходимо рассчитать индуктивность катушки по формулам или при помощи онлайн-калькулятора.

Видео

Оцените статью:

elquanta.ru