Катушка индуктивности является пассивным компонентом электронных схем, основное предназначение которой является сохранение энергии в виде магнитного поля. Свойство катушки индуктивности чем-то схоже с конденсатором, который хранит энергию в виде электрического поля.
Индуктивность (измеряется в Генри) — это эффект возникновения магнитного поля вокруг проводника с током. Ток, протекающий через катушку индуктивности, создает магнитное поле, которое имеет связь с электродвижущей силой (ЭДС) оказывающее противодействие приложенному напряжению.
Возникающая противодействующая сила (ЭДС) противостоит изменению переменного напряжения и силе тока в катушке индуктивности. Это свойство индуктивной катушки называется индуктивным сопротивлением. Следует отметить, что индуктивное сопротивление находится в противофазе к емкостному реактивному сопротивлению конденсатора в цепи переменного тока. Путем увеличения числа витков можно повысить индуктивность самой катушки.
Накопленная энергия в индуктивности
Как известно магнитное поле обладает энергией. Аналогично тому, как в полностью заряженном конденсаторе существует запас электрической энергии, в индуктивной катушке, по обмотке которой течет ток, тоже существует запас — только уже магнитной энергии.
Энергия, запасенная в катушке индуктивности равна затраченной энергии необходимой для обеспечения протекания тока I в противодействии ЭДС. Величина запасенной энергии в индуктивности можно рассчитать по следующей формуле:
где L — индуктивность, I — ток, протекающий через катушку индуктивности.
Гидравлическая модель
Работу катушки индуктивности можно сравнить с работой гидротурбины в потоке воды. Поток воды, направленный сквозь еще не раскрученную турбину, будет ощущать сопротивление до того момента, пока турбина полностью не раскрутится.
Далее турбина, имеющая определенную степень инерции, вращаясь в равномерном потоке, практически не оказывая влияния на скорость течения воды. В случае же если данный поток резко остановить, то турбина по инерции все еще будет вращаться, создавая движение воды. И чем выше инерция данной турбины, тем больше она будет оказывать сопротивление изменению потока.
Также и индуктивная катушка сопротивляется изменению электрического тока протекающего через неё.
Индуктивность в электрических цепях
В то время как конденсатор оказывает сопротивление изменению переменного напряжения, индуктивность же сопротивляется переменному тока. Идеальная индуктивность не будет оказывать сопротивление постоянному току, однако, в реальности все индуктивные катушки сами по себе обладают определенным сопротивлением.
В целом, отношение между изменяющимися во времени напряжением V(t) проходящим через катушку с индуктивностью L и изменяющимся во времени током I(t), проходящим через нее можно представить в виде дифференциального уравнения следующего вида:
Когда переменный синусоидальной ток (АС) протекает через катушку индуктивности, возникает синусоидальное переменное напряжение (ЭДС). Амплитуда ЭДС зависит от амплитуды тока и частоте синусоиды, которую можно выразить следующим уравнением:
где ω является угловой частотой резонансной частоты F:
Причем, фаза тока отстает от напряжения на 90 градусов. В конденсаторе же все наоборот, там ток опережает напряжение на 90 градусов. Когда индуктивная катушка соединена с конденсатором (последовательно либо параллельно), то образуется LC цепь, работающая на определенной резонансной частоте.
Индуктивное сопротивление ХL определяется по формуле:
где ХL — индуктивное сопротивление, ω — угловая частота, F — частота в герцах, и L индуктивность в генри.
Индуктивное сопротивление — это положительная составляющая импеданса. Оно измеряется в омах. Импеданс катушки индуктивности (индуктивное сопротивление) вычисляется по формуле:
Схемы соединения катушек индуктивностей
Параллельное соединение индуктивностей
Напряжение на каждой из катушек индуктивностей, соединенных параллельно, одинаково. Эквивалентную (общую) индуктивность параллельно соединенных катушек можно определить по формуле:
Последовательное соединение индуктивностей
Ток, протекающий через катушки индуктивности соединенных последовательно, одинаков, но напряжение на каждой катушке индуктивности отличается. Сумма разностей потенциалов (напряжений) равна общему напряжению. Общая индуктивность последовательно соединенных катушек можно высчитать по формуле:
Эти уравнения справедливы при условии, что магнитное поле каждой из катушек не оказывает влияние на соседние катушки.
Добротность катушки индуктивности
На практике катушка индуктивности имеет последовательное сопротивление, созданное медной обмоткой самой катушки. Это последовательное сопротивление преобразует протекающий через катушку электрический ток в тепло, что приводит к потере качества индукции, то есть добротности. Добротность является отношением индуктивности к сопротивлению.
Добротность катушки индуктивности может быть найдена через следующую формулу:
где R является собственным сопротивлением обмотки.
Катушка индуктивности. Формула индуктивности
Базовая формула индуктивности катушки:
- L = индуктивность в генри
- μ 0 = проницаемость свободного пространства = 4π × 10 -7 Гн / м
- μ г = относительная проницаемость материала сердечника
- N = число витков
- A = Площадь поперечного сечения катушки в квадратных метрах (м 2 )
- l = длина катушки в метрах (м)
Индуктивность прямого проводника:
- L = индуктивность в нГн
- l = длина проводника
- d = диаметр проводника в тех же единицах, что и l
Индуктивность катушки с воздушным сердечником:
- L = индуктивность в мкГн
- r = внешний радиус катушки
- l = длина катушки
- N = число витков
Индуктивность многослойной катушки с воздушным сердечником:
- L = индуктивность в мкГн
- r = средний радиус катушки
- l = длина катушки
- N = число витков
- d = глубина катушки
Индуктивность плоской катушки:
- L = индуктивность в мкГн
- r = средний радиус катушки
- N = число витков
- d = глубина катушки
Конструкция катушки индуктивности
Катушка индуктивности представляет собой обмотку из проводящего материала, как правило, медной проволоки, намотанной вокруг либо железосодержащего сердечника, либо вообще без сердечника.
Применение в качестве сердечника материалов с высокой магнитной проницаемостью, более высокой чем воздух, способствует удержанию магнитного поля вблизи катушки, тем самым увеличивая ее индуктивность. Индуктивные катушки бывают разных форм и размеров.
Большинство изготавливаются путем намотки эмалированного медного провода поверх ферритового сердечника.
Некоторые индуктивные катушки имеют регулируемый сердечник, при помощи которого обеспечивается изменение индуктивности.
Миниатюрные катушки могут быть вытравлены непосредственно на печатной плате в виде спирали. Индуктивности с малым значением могут быть расположены в микросхемах с использованием тех же технологических процессов, которые используются при создании транзисторов.
Применение катушек индуктивности
Индуктивности широко используются в аналоговых схемах и схемах обработки сигналов. Они в сочетании с конденсаторами и другими радиокомпонентами образуют специальные схемы, которые могут усилить или отфильтровать сигналы определенной частоты.
Катушки индуктивности получили широкое применение начиная от больших катушек индуктивности, таких как дроссели в источниках питания, которые в сочетании с конденсаторами фильтра устраняют остаточные помехи и другие колебания на выходе источника питания, и до столь малых индуктивностей, которые располагаются внутри интегральных микросхем.
Две (или более) катушки индуктивности, которые соединены единым магнитным потоком, образуют трансформатор, являющимся основным компонентом схем работающих с электрической сетью электроснабжения. Эффективность трансформатора возрастает с увеличением частоты напряжения.
По этой причине, в самолетах используется переменное напряжение с частотой 400 герц вместо обычных 50 или 60 герц, что в свою очередь позволяет значительно сэкономить на массе используемых трансформаторов в электроснабжении самолета.
Так же индуктивности используются в качестве устройства для хранения энергии в импульсных стабилизаторах напряжения, в высоковольтных электрических системах передачи электроэнергии для преднамеренного снижения системного напряжения или ограничения ток короткого замыкания.
Расчёт индуктивности. Часть 2 | HomeElectronics
Всем доброго времени суток. Сегодняшняя статья является продолжением предыдущей. Здесь продолжим рассматривать расчёт индуктивностей индуктивных элементов без сердечников. В прошлой статье я рассказал, как рассчитать индуктивность прямого провода и провода свёрнутого в кольцо (виток), в данной статье будем рассчитывать индуктивность круговых катушек, то есть поперечный профиль, которых представляет собой окружности.
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Виды катушек индуктивности
Круговые катушки индуктивности являются, наверное, самыми распространёнными. В тоже время из-за разнообразия их форм существует некоторая трудность в расчёте индуктивности. Для некоторого упрощения расчёта катушки индуктивности делятся на несколько видов. Рассмотрим основные конструктивные особенности круговых катушек индуктивности
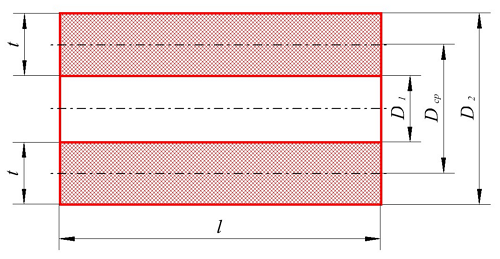
Расчёт индуктивности катушки.
Для расчёта индуктивности круговой катушки необходимо знать следующие размеры:
D1 – внутренний диаметр, D2 – внешний диаметр, Dср – средний диаметр, l – длина катушки (аксиальный размер), t – толщина обмотки (радиальный размер), где t можно вычислить
Поэтому, в зависимости от соотношения между этими размерами различают следующие катушки индуктивности:
если l > Dср – длинная катушка,
если l < Dср – короткая катушка,
если l << Dср – очень короткая катушка,
если l = 0 – плоская катушка,
если t ≈ Dср – толстая катушка,
если t << Dср – тонкая катушка,
если t = 0 – соленоид.
Особенности расчёта катушек индуктивности
Кроме конструктивных параметров, на индуктивность влияет также параметры обмоточного провода (диаметр, толщина изоляции, шаг намотки), хотя в большинстве случаев влияние их незначительно, но в некоторых случаях, например, при большом шаге намотки их следует учитывать. Поэтому общая индуктивность катушки можно представить следующим выражением
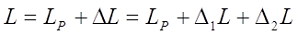
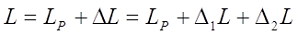
где LР – расчётная индуктивность;
∆L – поправка на «изоляцию», ∆L = ∆1L + ∆2L;
∆1L – поправка учитывающая влияние индуктивности витков;
∆2L – поправка учитывающая влияние взаимной индуктивности витков.
В большинстве случаев, например, при плотной намотке «виток к витку» поправка ∆L составляет несколько процентов от расчётной индуктивности LР, поэтому если нет необходимости в точном значении общей индуктивности L, поправку на изоляцию ∆L можно не учитывать.
Особенности расчёта круговых катушек индуктивности состоят в следующем:
1. При определении расчётной индуктивности LP, средний диаметр принимается равным среднему диаметру реальной катушки;
2. Длина намотки l и толщина намотки t принимается равными шагу обмотки (p – шаг по длине катушки, q – шаг по толщине намотки) умноженному на количество слоёв ω в том или ином направлении
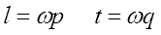
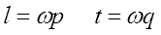
3. Если у катушки в каком-либо направлении (по длине намотки l или по толщине намотки t) имеется только один ряд (или слой), то в этом направлении размер l или t можно принять равным нулю, то есть расчёт ведётся как для соленоида или плоской катушки.
4. В некоторых случаях, при большом диаметре провода или шаге намотки у однослойных катушках размер l или t принимается равным диаметру голого провода d.
5. Так как величина поправки на взаимную индуктивность ∆2L в несколько раз меньше, чем поправка на индуктивность витков ∆1L, то при расчётах можно учитывать только ∆1L.
Приступим к расчётным выражениям, в начале рассчитаем простейшие круговые катушки – соленоид и плоскую катушку.
Расчёт индуктивности соленоида
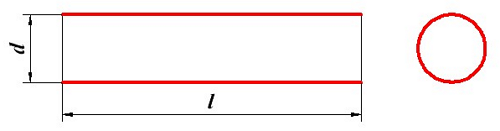
Определение индуктивности соленоида, d – диаметр соленоида, l – длина соленоида.
Соленоид представляет собой катушку, намотанную на каркас в один слой, поэтому толщину слоя можно принять равной нулю t = 0, а расчётная формула индуктивности будет иметь вид
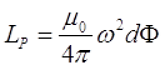
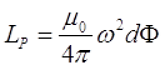
где μ0 – магнитная постоянная, μ0 = 4π•10-7 Гн/м;
ω – число витков соленоида;
d – диаметр соленоида, м;
Φ – коэффициент, который зависит от отношения α = l/D;
l – длина соленоида, м;
Поправочный коэффициент Φ зависит от отношения длины соленоида l к его диаметру d
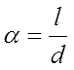
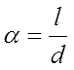
Для длинного соленоида, то есть α > 0,75, поправочный коэффициент составит
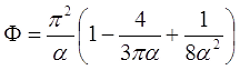
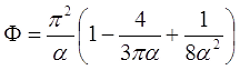
Для короткого соленоида, то есть α < 0,75, поправочный коэффициент составит
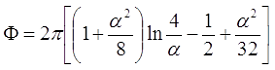
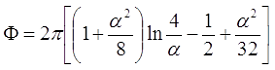
Пример. Необходимо рассчитать соленоид диаметром d = 1 см и длиной l = 5 см, который имеет ω = 75 витков.
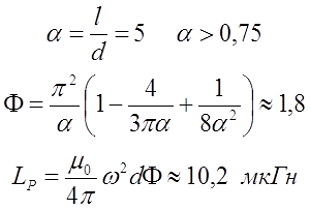
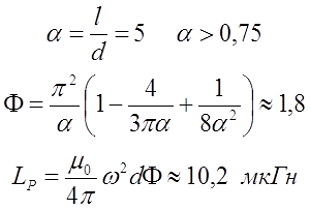
Стоит отметить, что формула расчёта соленоида подходит для большинства однослойных катушек с точностью в несколько процентов.
Индуктивность плоской катушки
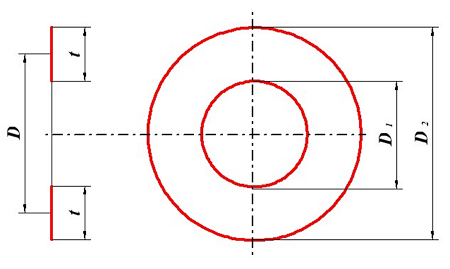
Определение индуктивности плоской катушки, D1 – внутренний диаметр, D2 – внешний диаметр, D – средний диаметр, t – толщина намотки.
В данном случае в качестве плоской катушки представлена идеализированная катушка, длина намотки которой приняли равной нулю l = 0, тогда индуктивность такой катушки можно вычислить по следующей формуле
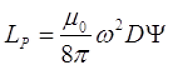
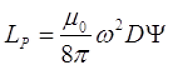
где μ0 – магнитная постоянная, μ0 = 4π•10-7 Гн/м;
ω – число витков соленоида;
D – средний диаметр катушки, м;
Ψ – коэффициент, который зависит от отношения ρ = t/D;
t – толщина намотки катушки.
Коэффициент Ψ зависит от соотношения толщины намотки t и среднего диаметра катушки D
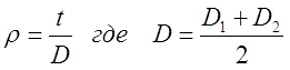
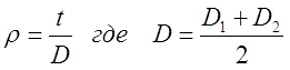
При небольшой толщине намотки, когда ρ < 0,5
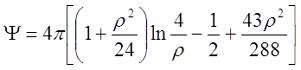
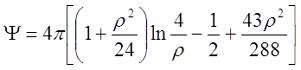
При большой толщине намотки, когда ρ > 0,5
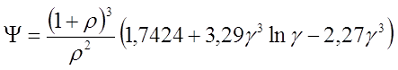
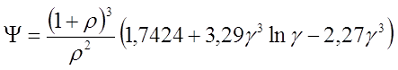
где γ – коэффициент учитывающий соотношение внешнего и внутреннего диаметров обмотки катушки
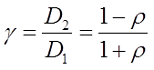
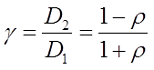
Пример. Рассчитаем плоскую катушку со средним диаметром D = 5 см и толщиной намотки t = 1 см, состоящую из ω = 20 витков.
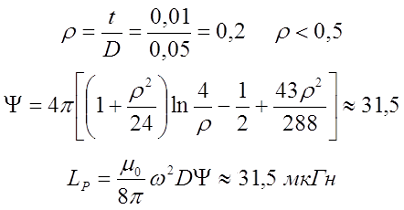
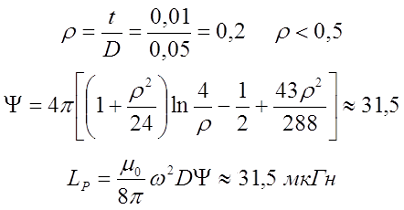
Выражения для индуктивности тонкой катушки позволяют рассчитать индуктивность и большинства катушек с малой длиной и большой толщиной обмоток.
Индуктивность круговой катушки прямоугольного сечения
Теперь перейдём от идеализированных катушек к реальным, которые в своем сечении представляют собой прямоугольник
Индуктивность прямоугольной катушки.
Катушку прямоугольного сечения можно представить в виде соленоида с ненулевой толщиной обмотки t ≠ 0, либо в виде плоской катушки с ненулевой длиной l ≠ 0, поэтому рассчитать необходимую катушку можно либо как соленоид, либо как плоскую катушку, а затем внести поправку.
Таким образом, индуктивность прямоугольной катушки можно вычислить по следующей формуле
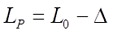
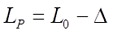
где L0 – индуктивность идеальной катушки (соленоида или плоской катушки) в зависимости от α = l/Dcp;
l – длина катушки, м;
Dcp – средний диаметр катушки, м;
∆ — поправка на форму катушки.
В принципе реальную катушку индуктивности, в зависимости от отношения длины намотки l к среднему диаметру Dcp, можно разделить на несколько типов:
1. Длинная катушка, у которой α > 0,75.
2. Короткая катушка, имеющая α < 0,75 и γ < 1.
3. Очень короткая катушка, имеет α << 1 и γ > 1.
где
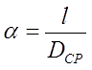
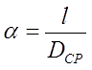
Рассмотрим каждый случай по отдельности.
Индуктивность длинной катушки
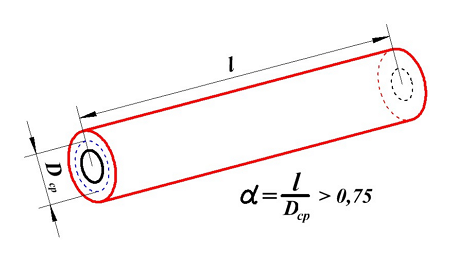
Длинная катушка.
Для длинной катушки (α > 0,75) величина L0 рассчитывается также как для длинного соленоида, где l – длина соленоида, Dcp – средний диаметр соленоида, а значение поправки ∆ вычисляется по следующему выражению
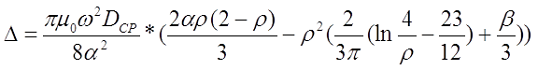
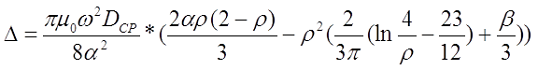
где α – коэффициент, учитывающий отношение длины катушки l к её среднему диаметру DCP;
γ – коэффициент, учитывающий отношение толщины намотки t к длине намотки l;
ρ – коэффициент, учитывающий отношение толщины намотки t к её среднему диаметру DCP.
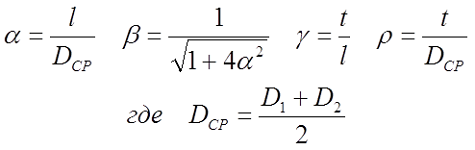
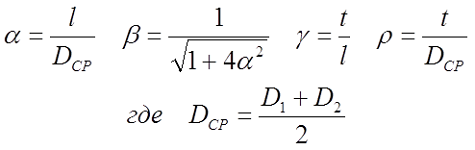
где D1 – внутренний диаметр, D2 – внешний диаметр.
Пример. Рассчитаем индуктивность катушки длиной l = 10 см, средним диаметром DCP = 2 см, количеством витков ω = 100 и толщиной намотки t = 5 мм.
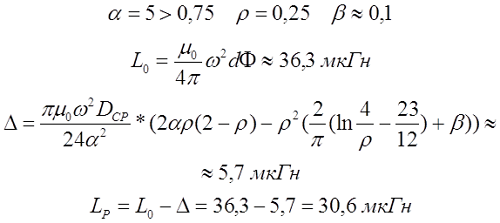
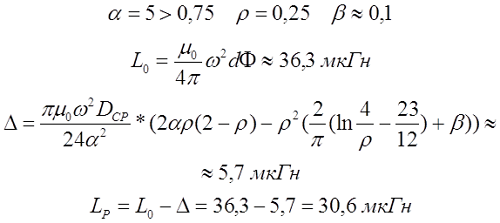
Индуктивность короткой катушки
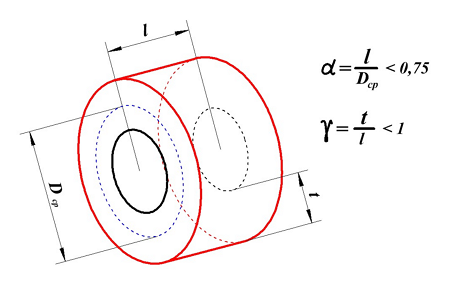
Короткая катушка.
Для короткой катушки (α < 0,75, t < l) величина L0 рассчитывается также как для короткого соленоида, где l – длина соленоида, DСР – средний диаметр соленоида, а значение поправки ∆ вычисляется по следующему выражению
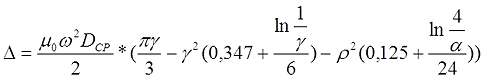
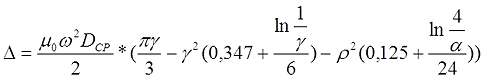
где α – коэффициент, учитывающий отношение длины катушки l к её среднему диаметру DCP;
γ – коэффициент, учитывающий отношение толщины намотки t к длине намотки l;
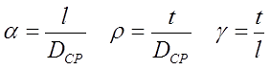
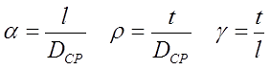
Пример. Рассчитаем индуктивность катушки длиной l = 1 см, средним диаметром DСР = 2 см, толщиной намотки t = 5 мм, количеством витков ω = 50.
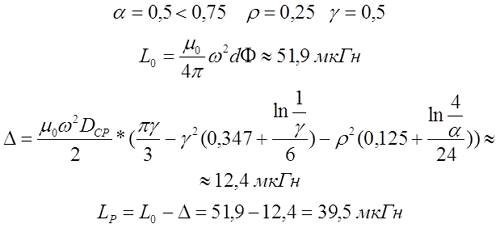
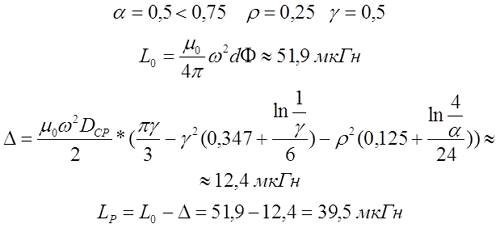
Индуктивность очень короткой катушки
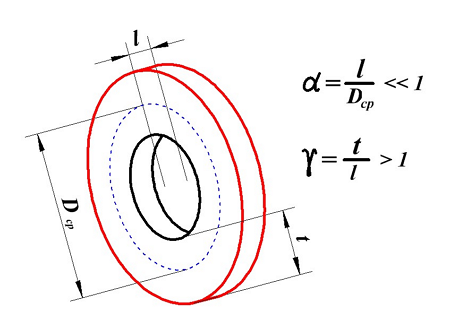
Очень короткая катушка.
Для очень короткой катушки (α << 1, t > l) величина L0 рассчитывается также как для плоской катушки, где t – толщина намотки, Dcp – средний диаметр катушки, а значение поправки ∆ вычисляется по следующему выражению
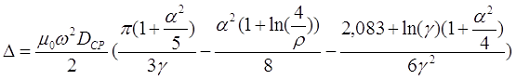
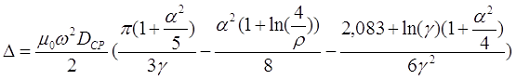
где α – коэффициент, учитывающий отношение длины катушки l к её среднему диаметру DCP;
γ – коэффициент, учитывающий отношение толщины намотки t к длине намотки l, γ < 1;
ρ – коэффициент, учитывающий отношение толщины намотки t к её среднему диаметру DCP.
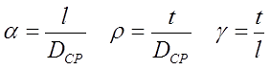
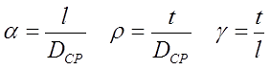
Пример. Рассчитаем индуктивность катушки длиной l = 5 мм, средним диаметром DCP = 7 см, намотка толщиной t = 1 см, количество витков ω = 150.
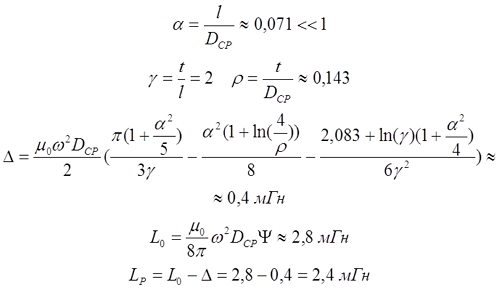
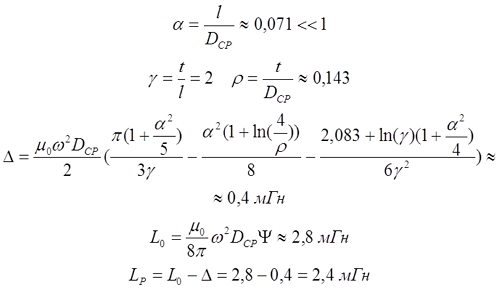
Расчёт поправки на собственную индуктивность витков
Как я писал в начале статьи, полная индуктивность катушки L состоит из расчётной индуктивности LP и поправки на изоляцию ∆L, которая в свои очередь состоит из поправки на собственную индуктивность витков ∆1L и поправки на взаимную индуктивность витков ∆2L
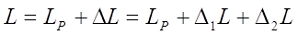
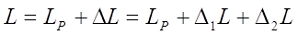
Данные поправки зависят от взаимного расположения витков в катушке. Для провода круглого сечения возможны следующие варианты заполнения катушки
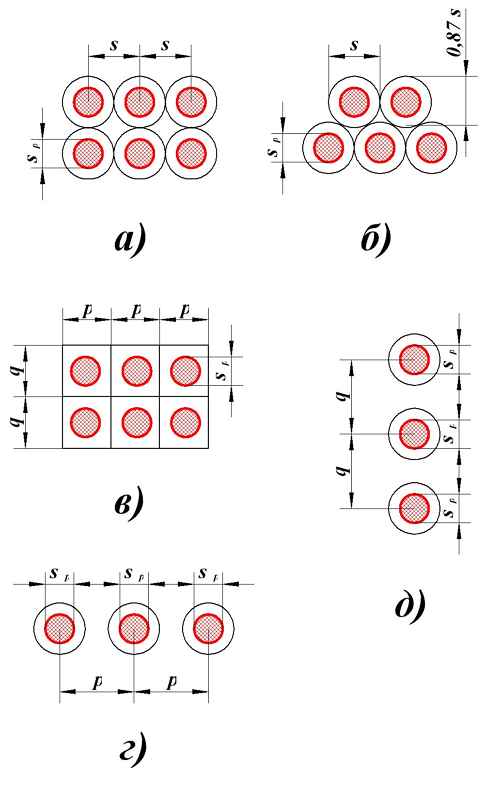
Расположение провода круглого сечения в катушке индуктивности. s – диаметр провода с изоляцией, sp – диаметр голого провода (без изоляции), p – шаг намотки по длине катушки, q – шаг намотки по толщине катушки.
В общем случае поправка на собственную индуктивность витков рассчитывается по следующему выражению
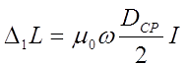
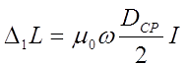
где μ0 – магнитная постоянная, μ0 = 4π•10-7 Гн/м;
ω – число витков соленоида;
DСР – средний диаметр катушки, м;
I – коэффициент, зависящий от расположения витков катушки.
Коэффициент I определяется в зависимости от расположения провода, варианты которого изображены на рисунке выше.
Для варианта а), провод намотан с небольшим коэффициентом заполнения
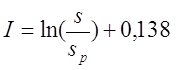
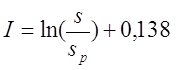
где s – диаметр провода с изоляцией, sp – диаметр голого провода (без изоляции).
Для варианта б), провод намотан с большим коэффициентом заполнения
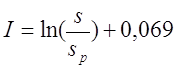
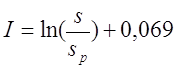
где s – диаметр провода с изоляцией, sp – диаметр голого провода (без изоляции).
Для варианта в), провод намотан с шагом p по длине катушки и с шагом q по толщине катушки
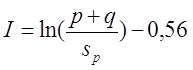
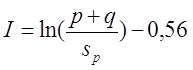
где s – диаметр провода с изоляцией, sp – диаметр голого провода (без изоляции).
Для варианта г), провод намотан в один слой по длине катушки с шагом p. В зависимости от способа вычисления расчётной индуктивности LP
— если при вычислении расчётной индуктивности LP толщина намотки t принята равной диаметру голого провода sP, то коэффициент I будет равен
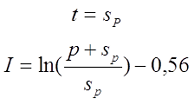
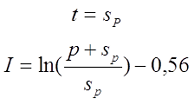
— если при вычислении расчётной индуктивности LP толщина намотки t принята равной нулю (расcчитывалась как соленоид), то коэффициент I будет равен
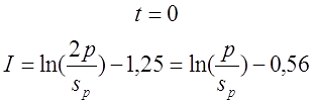
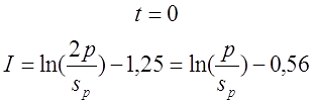
где p – шаг намотки по длине катушки, sp – диаметр голого провода (без изоляции).
Для варианта д), провод намотан в один слой по толщине намотки с шагом q, также возможно два случая
— если при вычислении расчётной индуктивности LP длина намотки l принята равной диаметру голого провода sP, то коэффициент I будет равен
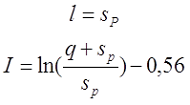
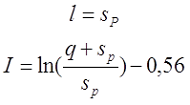
— если при вычислении расчётной индуктивности LP длина намотки l принята равной нулю (рассчитывалась как плоская катушка), то коэффициент I будет равен
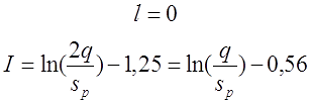
как найти число витков в катушке, формула
Катушка индуктивности является спиральным или винтовым проводником, который преобразовывает энергию электрополя в магнитное поле. Каково более полное определение этого элемента электроцепи, как сделать расчёт катушки индуктивности и что влияет на ее индуктивность? Об этом далее.
Описание устройства
Катушка индуктивности бывает винтовой, спиральной или винтоспиральной, имеющей свернутый изолированный проводник, который обладает значительным показателем индукции при малой емкости с активным сопротивлением. Как следствие, ток протекает через источник тока со значительной инерционностью.
Главный компонент электроцепиОбратите внимание! Применяется, чтобы подавлять помехи, сглаживать биения, накапливать энергию, ограничивать переменный ток или резонансный/частотно-избирательный контур цепи.
Стоит указать, что ее применение разнообразно. Называется она дросселем, вариометром, соленоидом и токоограничивающим реактором. При этом основные технические характеристики варьируются. Могут отличаться силой тока, сопротивлением потерь, добротностью, емкостью и температурным добротным коэффициентом.
Полное определение из физикиФакторы, влияющие на индукцию
Влияет на индукцию число проводниковых витков, площадь поперечного сечения, длина и материалы. Благодаря увеличению витков повышается индукция и наоборот. Что касается сечения, чем больше источник, тем больше показатель. Также чем больше магнитный вид проницаемости, тем больше индуктивный показатель.
Факторы, влияющие на преобразование энергии в магнитное полеРасчет
Вычислить число витков, зная конструкцию, можно по формуле нахождения энергии и ее магнитного поля W = LI2/2, где L является индукцией, I — силой тока. Витки находятся из формулы L/d, где d является проводным диаметром. Стоит указать, что есть специальный калькулятор, в который нужно только подставить необходимые параметры. При этом можно определить, однослойный или многослойный проводник.
С сердечником
Стоит отметить, что со стержнем, намоткой, обмоткой индукция вычисляется через замкнутый магнитный поток индуктивных элементов, в то время как без него учитывается поток, который пронизывает только проводник с токовой энергией. Расчитывая индуктивность подобных элементов, необходимо учесть размеры и материал центральной части. Обобщенно можно представить формулу схематично. При этом требуется взять в расчет источник с сопротивлением магнитной цепи, абсолютной магнитной проницаемостью вещества, площадью поперечного сердечникового сечения и длиной средней силовой линии. Зная это, можно посчитать индукцию. Стоит учитывать погрешность. Она будет равна 25%.
Расчет индуктивности катушки с сердечникомБез сердечника
Стоит указать, что без ферритового, геометрического и цилиндрического сердечника с мощным каркасом источник имеет небольшую индукцию, а с ним она повышается. Это связано с тем, что имеется материальная магнитная проницаемость. Форма бывает разная. Есть броневой, стержневой и тороидальный материал.
Обратите внимание! Рассчитать можно, используя метод эллиптических максвелловских интегралов и специальную онлайн программу.
Расчет индуктивности без сердечникаКатушка — незаменимый компонент любой электросети, который имеет вид скрученного или обвивающего элемента с проводником. Влияет на ее индукцию число проводных витков, площадь сечения, длина и материал сердечника. Отыскать количество витков и посчитать индуктивность с сердечником и без него несложно, главное — руководствоваться приведенными выше рекомендациями.
Что такое катушка индуктивности
Что вы себе представляете под словом “катушка” ? Ну… это, наверное, какая-нибудь “фиговинка”, на которой намотаны нитки, леска, веревка, да что угодно! Катушка индуктивности представляет из себя точь-в-точь то же самое, но вместо нитки, лески или чего-нибудь еще там намотана обыкновенная медная проволока в изоляции.
Изоляция может быть из бесцветного лака, из ПВХ-изоляции и даже из матерчатой. Тут фишка такая, что хоть и провода в катушке индуктивности очень плотно прилегают к друг другу, они все равно изолированы друг от друга. Если будете мотать катушки индуктивности своими руками, ни в коем случае не вздумайте брать обычный медный голый провод!
Индуктивность
Любая катушка индуктивности обладает индуктивностью. Индуктивность катушки измеряется в Генри (Гн), обозначается буковкой L и замеряется с помощью LC – метра.
Что такое индуктивность? Если через провод пропустить электрический ток, то он вокруг себя создаст магнитное поле:
где
В – магнитное поле, Вб
I – сила тока, А
А давайте возьмем и намотаем в спиральку этот провод и подадим на его концы напряжение
И у нас получится вот такая картина с магнитными силовыми линиями:
Грубо говоря, чем больше линий магнитного поля пересекут площадь этого соленоида, в нашем случае площадь цилиндра, тем больше будет магнитный поток (Ф). Так как через катушку течет электрический ток, значит, через нее проходит ток с Силой тока (I), а коэффициент между магнитным потоком и силой тока называется индуктивностью и вычисляется по формуле:
С научной же точки зрения, индуктивность – это способность извлекать энергию из источника электрического тока и сохранять ее в виде магнитного поля. Если ток в катушке увеличивается, магнитное поле вокруг катушки расширяется, а если ток уменьшается , то магнитное поле сжимается.
Самоиндукция
Катушка индуктивности обладает также очень интересным свойством. При подаче на катушку постоянного напряжения, в катушке возникает на короткий промежуток времени противоположное напряжение.
Это противоположное напряжение называется ЭДС самоиндукции. Эта ЭДС зависит от значения индуктивности катушки. Поэтому, в момент подачи напряжения на катушку сила тока в течение долей секунд плавно меняет свое значение от 0 до некоторого значения, потому что напряжение, в момент подачи электрического тока, также меняет свое значение от ноля и до установившегося значения. Согласно Закону Ома:
где
I – сила тока в катушке , А
U – напряжение в катушке, В
R – сопротивление катушки, Ом
Как мы видим по формуле, напряжение меняется от нуля и до напряжения, подаваемого в катушку, следовательно и ток тоже будет меняться от нуля и до какого то значения. Сопротивление катушки для постоянного тока также постоянное.
И второй феномен в катушке индуктивности заключается в том, что если мы разомкнем цепь катушка индуктивности – источник тока, то у нас ЭДС самоиндукции будет суммироваться к напряжению, которое мы уже подали на катушку.
То есть как только мы разрываем цепь, на катушке напряжение в этот момент может быть в разы больше, чем было до размыкания цепи, а сила тока в цепи катушки будет тихонько падать, так как ЭДС самоиндукции будет поддерживать убывающее напряжение.
Сделаем первые выводы о работе катушки индуктивности при подаче на нее постоянного тока. При подаче на катушку электрического тока, сила тока будет плавно увеличиваться, а при снятии электрического тока с катушки, сила тока будет плавно убывать до нуля. Короче говоря, сила тока в катушке мгновенно измениться не может.
Типы катушек индуктивности
Катушки индуктивности делятся в основном на два класса: с магнитным и немагнитным сердечником. Снизу на фото катушка с немагнитным сердечником.
Но где у нее сердечник? Воздух – это немагнитный сердечник :-). Такие катушки также могут быть намотаны на какой-нибудь цилиндрической бумажной трубочке. Индуктивность катушек с немагнитным сердечником используется, когда индуктивность не превышает 5 миллигенри.
А вот катушки индуктивности с сердечником:
В основном используют сердечники из феррита и железных пластин. Сердечники повышают индуктивность катушек в разы. Сердечники в виде кольца (тороидальные) позволяют получить большую индуктивность, нежели просто сердечники из цилиндра.
Для катушек средней индуктивности используются ферритовые сердечники:
Катушки с большой индуктивностью делают как трансформатор с железным сердечником, но с одной обмоткой, в отличие от трансформатора.
Дроссель
Также есть особый вид катушек индуктивностей. Это так называемые дроссели. Дроссель – это катушка индуктивности, задача которой состоит в том, чтобы создать в цепи большое сопротивление для переменного тока, чтобы подавить токи высоких частот.
Постоянный ток через дроссель проходит без проблем. Почему это происходит, можете прочитать в этой статье. Обычно дроссели включаются в цепях питания усилительных устройств. Дроссели предназначены для защиты источников питания от попадания в них высокочастотных сигналов (ВЧ-сигналов). На низких частотах (НЧ) они используются в фильтрах цепей питания и обычно имеют металлические или ферритовые сердечники. Ниже на фото силовые дроссели:
Также существует еще один особый вид дросселей – это сдвоенный дроссель. Он представляет из себя две встречно намотанных катушки индуктивности. За счет встречной намотки и взаимной индукции он более эффективен. Сдвоенные дроссели получили широкое распространение в качестве входных фильтров блоков питания, а также в звуковой технике.
Что влияет на индуктивность?
От каких факторов зависит индуктивность катушки? Давайте проведем несколько опытов. Я намотал катушку с немагнитным сердечником. Ее индуктивность настолько мала, что LC – метр мне показывает ноль.
Имеется ферритовый сердечник
Начинаю вводить катушку в сердечник на самый край
LC-метр показывает 21 микрогенри.
Ввожу катушку на середину феррита
35 микрогенри. Уже лучше.
Продолжаю вводить катушку на правый край феррита
20 микрогенри. Делаем вывод, самая большая индуктивность на цилиндрическом феррите возникает в его середине. Поэтому, если будете мотать на цилиндрике, старайтесь мотать в середине феррита. Это свойство используется для плавного изменения индуктивности в переменных катушках индуктивности:
где
1 – это каркас катушки
2 – это витки катушки
3 – сердечник, у которого сверху пазик под маленькую отвертку. Вкручивая или выкручивая сердечник, мы тем самым изменяем индуктивность катушки.
Экспериментируем дальше. Давайте попробуем сжимать и разжимать витки катушки. Для начала ставим ее в середину и начинаем сжимать витки
Индуктивность стала почти 50 микрогенри!
А давайте-ка попробуем расправим витки по всему ферриту
13 микрогенри. Делаем вывод: для максимальной индуктивности мотать катушку надо “виток к витку”.
Убавим витки катушки в два раза. Было 24 витка, стало 12.
Совсем маленькая индуктивность. Убавил количество витков в 2 раза, индуктивность уменьшилась в 10 раз. Вывод: чем меньше количество витков – тем меньше индуктивность и наоборот. Индуктивность меняется не прямолинейно виткам.
Давайте поэкспериментируем с ферритовым кольцом.
Замеряем индуктивность
15 микрогенри
Отдалим витки катушки друг от друга
Замеряем снова
Хм, также 15 микрогенри. Делаем вывод: расстояние от витка до витка не играет никакой роли в катушке индуктивности тороидального исполнения.
Мотнем побольше витков. Было 3 витка, стало 9.
Замеряем
Офигеть! Увеличил количество витков в 3 раза, а индуктивность увеличилась в 12 раз! Вывод: индуктивность меняется не прямолинейно виткам.
Если верить формулам для расчета индуктивностей, индуктивность зависит от “витков в квадрате”. Эти формулы я здесь выкладывать не буду, потому как не вижу надобности. Скажу только, что индуктивность зависит еще от таких параметров, как сердечник (из какого материала он сделан), площадь поперечного сечения сердечника, длина катушки.
Обозначение на схемах
Последовательное и параллельное соединение катушек индуктивности
При последовательном соединении индуктивностей, их общая индуктивность будет равняться сумме индуктивностей.
А при параллельном соединении получаем вот так:
При соединении индуктивностей должно выполняться правило, чтобы они были пространственно разнесены на плате. Это связано с тем, что при близком расположении друг друга их магнитные поля будут влиять с друг другом, и поэтому показания индуктивностей будут неверны. Не ставьте на одну железную ось две и более тороидальных катушек. Это может привести к неправильным показаниям общей индуктивности.
Резюме
Катушка индуктивности играет в электронике очень большую роль, особенно в приемопередающей аппаратуре. На катушках индуктивности строятся также различные фильтры для электронной радиоаппаратуры, а в электротехнике ее используют также в качестве ограничителя скачка силы тока.
Ребята из Паяльника забабахали очень неплохой видос про катушку индуктивности. Советую посмотреть в обязательном порядке:
Расчет индуктивности катушек: формула :: SYL.ru
У каждого из нас бывали проблемы с предметами в школе. У кого-то были проблемы с химией, у кого-то — с физикой. Но даже если с этими предметами у вас всё всегда было хорошо, вы наверняка не помните всех тем, что вам давали в школе. Одной из таких тем является электромагнетизм в целом и расчёт индуктивности катушек в частности.
Для начала окунёмся немного в историю такого явления, как магнетизм.
История
Магнетизм начинает свою историю ещё с Древнего Китая и Древней Греции. Открытый в Китае магнитный железняк использовался тогда в качестве стрелки компаса, указывающей на север. Есть упоминания, что китайский император использовал его во время битвы.
Однако вплоть до 1820 года магнетизм рассматривался лишь как явление. Всё его практическое применение было заключено в указании стрелки компаса на север. Однако в 1820 году Эрстед провёл свой опыт с магнитной стрелкой, показывающий влияние электрического поля на магнит. Этот опыт послужил толчком для некоторых учёных, взявшихся за это всерьёз, чтобы разработать теорию магнитного поля.
Спустя всего 11 лет, в 1831 году, Фарадей открыл закон электромагнитной индукции и ввёл в обиход физиков понятие «магнитное поле». Именно этот закон послужил основой для создания катушек индуктивности, о которых сегодня и пойдёт речь.
А прежде чем приступить к рассмотрению самого устройства этих катушек, освежим в голове понятие магнитного поля.
Магнитное поле
Это словосочетание знакомо нам со школьной скамьи. Но многие уже забыли о том, что оно означает. Хотя каждый из нас помнит, что магнитное поле способно воздействовать на предметы, притягивая или отталкивая их. Но, помимо этого, у него есть и другие особенности: например, магнитное поле может воздействовать на электрически заряженные объекты, а это значит, что электричество и магнетизм тесно связаны между собой, и одно явление может плавно перетекать в другое. Учёные поняли это достаточно давно и поэтому стали называть все эти процессы вместе одним словом — «электромагнитные явления». На самом деле электромагнетизм — довольно интересная и ещё не до конца изученная область физики. Она очень обширна, и те знания, что мы можем здесь изложить вам, — это очень малая часть того, что известно человечеству о магнетизме сегодня.
А сейчас перейдём непосредственно к предмету нашей статьи. Следующий раздел будет посвящён рассмотрению непосредственно устройства катушки индуктивности.
Что такое катушка индуктивности?
Мы сталкиваемся с этими предметами постоянно, но вряд ли придаём им какое-то особое значение. Это для нас обыденность. На самом деле катушки индуктивности встречаются сегодня практически в каждом приборе, но наиболее яркий пример их использования — трансформаторы. Если вы думаете, что трансформаторы бывают только на энергетических подстанциях, то вы сильно ошибаетесь: ваше зарядное устройство от ноутбука или смартфона — тоже своего рода трансформатор, только меньшего размера, чем те, что используются на электростанциях и распределительных подстанциях.
Любая катушка индуктивности состоит из сердечника и обмотки. Сердечник представляет собой стержень из диэлектрического или ферромагнитного материала, на который наматывается обмотка. Последняя делается чаще всего из медной проволоки. Количество витков обмотки напрямую связано с величиной магнитной индукции полученной катушки.
Теперь, прежде чем рассмотреть расчет индуктивности катушек и формулы, необходимые для него, поговорим о том, какие параметры и свойства мы будем вычислять.
Какие параметры есть у катушки?
Катушка обладает несколькими физическими характеристиками, отражающими её качество и пригодность для той или иной работы. Одной из них является индуктивность. Она численно равна отношению потока магнитного поля, создаваемого катушкой, к величине этого тока. Индуктивность измеряется в Генри (Гн) и в большинстве случаев принимает значения от единиц микрогенри до десятков Генри.
Индуктивность является, пожалуй, самым важным параметром катушки. Поэтому неудивительно, что большинство людей даже не думают о том, что существуют другие величины, способные описывать поведение катушки и отражать её пригодность для того или иного применения.
При выборе катушки индуктивности профессионалы также обращают внимание на сопротивление потерь. Как можно понять из этого словосочетания, оно отражает величину потерь электроэнергии, происходящих вследствие паразитных эффектов, таких как, например, нагревание проводов, происходящее по закону Джоуля-Ленца. Нетрудно понять, что чем ниже это значение для катушки, тем она лучше.
Ещё один параметр, который необходимо учитывать, — добротность контура. Она тесно связана с предыдущим параметром и представляет собой отношение реактивного сопротивления к активному (сопротивлению потерь). Соответственно, чем выше добротность — тем лучше. Её повышение достигается за счёт выбора оптимального диаметра провода, материала и диаметра сердечника, числа обмоток.
Сейчас рассмотрим подробнее самый важный и наиболее волнующий нас параметр — индуктивность катушки.
Немного больше про индуктивность
Мы уже разобрали это понятие, и теперь осталось поговорить о нём немного подробнее. Зачем? Нам ведь предстоит расчет индуктивности катушек, а значит, необходимо понимать, что это такое и зачем нам её рассчитывать.
Катушка индуктивности предназначена для создания магнитного поля, а значит, имеет параметры, которые описывают его силу. Таким параметром является магнитный поток. Но разные катушки имеют разные потери при прохождении через них тока и, соответственно, разный КПД. В зависимости от диаметра проводов и количества витков катушка может давать разное по величине магнитное поле. Значит, необходимо ввести такую величину, которая бы отражала зависимость между величиной магнитного потока и силой тока, пропускаемой через катушку. Таким параметром и является индуктивность.
Зачем нужен расчёт индуктивности?
Катушек разных видов в мире достаточно много. Они отличаются между собой свойствами, а значит, и применениями. Одни используются в трансформаторах, другие, соленоиды, выполняют роль электромагнитов большой силы. Кроме этих, применений у катушек индуктивности найдётся предостаточно. И для всех них необходимы разные типы катушек. Они отличаются по своим свойствам. Но большую часть этих свойств можно объединить с помощью понятия индуктивности.
Мы уже близко подошли к объяснению того, что включает в себя формула расчета индуктивности катушки. Но стоит оговориться, что речь пойдёт не о «формуле», а о «формулах», так как все катушки можно разделить на несколько больших групп, для каждой из которых своя отдельная формула.
Виды катушек
По функциональности различают контурные катушки, находящие применение в радиофизике, катушки связи, используемые в трансформаторах, и вариометры, то есть катушки, показатели которых можно варьировать изменением взаимного расположения катушек.
Также существует такой вид катушек, как дроссели. Внутри этого класса также есть деление на обычные и сдвоенные. Они имеют высокое сопротивление переменному току и очень низкое — постоянному, благодаря чему могут служить хорошим фильтром, пропускающим постоянный ток и задерживающим переменный. Сдвоенные дроссели отличаются большей эффективностью при больших токах и частотах по сравнению с обычными.
Формулы расчёта
Пришла пора нам перейти к основной теме статьи. Начнём мы с того, что расскажем о том, как произвести расчет индуктивности катушки без сердечника. Это самый простой вид расчёта. Но тут тоже есть свои тонкости. Возьмём, для простоты, катушку, обмотка которой лежит одним слоем. Для неё справедлив расчет однослойной катушки индуктивности:
L=D2*n2/(45D+100l).
Здесь L — индуктивность, D — диаметр катушки в сантиметрах, n — число витков, l — длина намотки в сантиметрах. Однослойная катушка предполагает то, что толщина намотки будет не больше одного слоя, а значит, для неё справедлив расчет плоской катушки индуктивности. В целом большинство формул для расчётов индуктивностей очень похожи: существенные различия только в коэффициентах при переменных в числителе и знаменателе. Самым простым тут является расчет индуктивности катушки без сердечника.
Представляет интерес также формула расчета индуктивности катушки с большим числом витков:
L=0,08*D2*n2/(3*D+9*b+10*c).
Здесь b — ширина провода, c — его высота. Такая формула эффективна для того, чтобы произвести расчет многослойной катушки индуктивности. Применяется она на практике чуть менее часто, чем та, о которой пойдёт речь ниже.
Самым актуальным, пожалуй, будет расчет индуктивности катушки с сердечником. Есть специальная формула, которая показывает, что эта индуктивность определяется материалом, из которого сделан сердечник, а точнее — его магнитной проницаемостью. Выглядит эта формула так:
L=m*m0*n2*S/l,
где m — магнитная проницаемость материала сердечника, m0 — магнитная постоянная (она равна 12,56·10-7 Гн/м), S — площадь поперечного сечения катушки, l — длина намотки.
Расчет витков катушки индуктивности производится очень просто: это число намотанных на сердечник слоёв проводника.
Мы разобрались с формулами, а теперь немного о том, где же конкретно эти формулы и расчёты могут нам пригодиться.
Практическое применение
Эти формулы имеют очень широкое применение ввиду повсеместного распространения катушек индуктивности. Как мы уже выяснили, бывают разные виды катушек, каждый из которых соответствует своему применению. В связи с этим становится необходимым как-то разделять их по характеристикам, ведь для каждой отрасли необходима своя определённая индуктивность и добротность.
В основном расчет индуктивности катушек применяется на производстве и в электротехнике. Каждый радиолюбитель должен знать, как производить расчет индуктивности, иначе как ему определить, какая катушка из огромного множества подойдёт для его цели, а какая — нет.
Вам интересно?
Сегодня очень много учёных, интересующихся магнетизмом и магнитными явлениями. Они изучают как магнитную, так и электрическую стороны веществ, пытаясь выявить закономерности и синтезировать мощные магниты с определёнными нужными свойствами: например, с высокой температурой плавления или сверхпроводимостью. Все эти материалы могут быть использованы в огромном количестве отраслей.
Приведём пример с аэрокосмической отраслью: перспективными для дальних межзвёздных перелётов являются ракеты с ионными двигателями, которые создают тягу посредством выброса ионизированного газа из сопла. Сила толчка в таком двигателе зависит от температуры газа и скорости его движения. Соответственно, чтобы придать газу максимальную силу для разгона, нам требуется очень сильный магнит, разгоняющий заряженные частицы и к тому же имеющий очень высокую температуру плавления для того, чтобы не расплавиться при выходе газов из сопла.
Заключение
Знание никогда не бывает лишним и всегда где-нибудь, да пригодится. Теперь, если вам попадётся программа расчета индуктивности катушки, вы без труда сможете сказать, почему там именно такие формулы и какие переменные в них что означают. Эта статья предназначена лишь для вашего ознакомления, и если вы хотите знать больше, стоит почитать специализированную литературу (благо за много лет изучения магнитных явлений её накопилось очень много).
Coil32 — Одиночный круглый виток
- Информация о материале
- Просмотров: 9321
Расчет индуктивности одиночного круглого витка
Индуктивность, реализованная в виде простой петли провода, другими словами в виде одного витка, чаще всего применяется в диапазоне метровых волн. Ввиду отсутствия эффекта близости, имеет довольно высокую добротность, зависящую от диаметра провода и небольшую собственную емкость.
Одновитковую петлю можно рассчитывать численными методами по уравнению Д.К.Максвелла:
где:
- E(k) — полный эллиптический интеграл первого рода
- K(k) — полный эллиптический интеграл второго рода
- r = D/2 — радиус петли (м)
- a = d/2 — радиус поперечного сечения провода, половина диаметра (м)
, а параметр k рассчитывается следующим образом:
Однако в программе Coil32 расчет катушки ведется по простой эмпирической формуле, которую впервые вывел в 1946 году F.W.Grover. Применять более сложные алгоритмы расчета в этом случае не имеет смысла, т.к. точность расчета вполне достаточна для практических целей, при D/d > 5 около 1%. Численный алгоритм расчета в программе основан на методе последовательных приближений, до достижения заданной индуктивности. При расчете по заданной индуктивности максимально возможный диаметр петли принят за 10 м. Если при расчете получается бóльшая величина, программа выдает сообщение: «Катушка не может быть реализована». В таком случае необходимо выбрать другую форму катушки, например — однослойную.
Формула расчета:
- L— индуктивность (мкГн)
- D— диаметр витка (мм)
- d— диаметр провода (мм)
Диаметр петли считается от центра до центра провода.
Вперед…
Добавить комментарийПомогите решить / разобраться (Ф)
EUgeneUS в [url=/post1354947.html#p1354947]сообщении #1354947[/url] писал(а):
Подскажите, как получают квадратичную зависимость?
Примерно, как Вы и написали.
Важно понимать вот что: квадратичная зависимость получается при некоторой идеализации — 100% магнитосцеплении. То есть 100% магнитного потока от одного любого витка проходят через каждый другой виток.
Да конечно, коэффициент связи идеальных контуров, у меня равен 1. Просто я пытался понять логику получения квадратичной зависимости от числа витков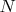 
.
— 18.11.2018, 15:13 —
realeugene в [url=/post1354964.html#p1354964]сообщении #1354964[/url] писал(а):
Это взаимоиндукция идеальных витков?
Нет, если вы рассматриваете индуктивность одной катушки целиком. У вас один общий контур, а не два контура. В котором ни один виток сам по себе не является замкнутым контуром. Поэтому, на мой взгляд, про взаимоиндукцию витков тут лучше не рассуждать.Можно ли аналог катушки, составить из идеальных несвязных (общим током) контуров расположенных на близком расстоянии друг от друга?
Если да, то получаем взаимоиндукцию и эффект квадратичной зависимости общей индуктивности от числа контуров (витков).
— 18.11.2018, 15:33 —
EUgeneUS в [url=/post1354957.html#p1354957]сообщении #1354957[/url] писал(а):
Kiev
Если Вы проследите ход Ваших рассуждений\вычислений, то увидите, что используется (явно или не явно) условие: магнитный поток от одного витка полностью проходит через каждый другой виток. В реальном мире
а) это может выполняться приближенно, и с хорошей точностью — тогда зависимость индуктивности от количества витков можно считать квадратичной.
б) для некоторых геометрий катушек это может выполняться приближенно, но характер зависимости остается квадратичным, например, для «толстой катушки».
в) для некоторых геометрий катушек может приводить к неточной формуле для индуктивности. Например, если мы смотаем провод в соленоид, то его индуктивность будет пропорциональная количеству витков в квадрате, а значит квадрату длины провода. Далее начинаем вытягивать соленоид в прямой провод, а у прямого провода зависимость индуктивности от длины уже не квадратичная.
Да я взял 100%-й коэффициент связи витков по полю, то есть бесконечно близко их сблизил (наложил), при этом сказал что токи не суммируются (ток последовательный, как и в катушке).
Мне главное было понять, логику происхождения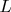 
~ 
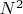в идеальном случае.
— 18.11.2018, 15:55 —
Простое объяснение зависимости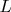 
~ 
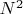
У изолированных витков с током есть только — самоиндукция.
У связных (в катушку) витков появляется и взаимоиндукция.
И сумма Самоиндукций и Взаимоиндукций даёт .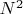
В отличии от суммы Самоиндукций которые дают только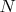 
.
Калькулятор индуктивности катушки
Чтобы рассчитать индуктивность однослойной катушки с воздушным сердечником:1. Выберите единицы измерения (дюймы или сантиметры).
2. Введите число витков (обмоток).
3. Введите диаметр катушки (диаметр формы + диаметр проволоки — см. Схему).
4. Введите длину катушки (расстояние от первой до последней обмотки — см. Схему).
5. Нажмите Рассчитать .
дюймов
сантиметров
Однослойная катушка
Многослойная, многорядная катушка
Многослойная однорядная катушка
(Следующая формула индуктивности требует единиц в дюймах.)
Обороты
Введите количество ходов.
Диаметр
Введите диаметр катушки.
Длина
Введите длину катушки.
Глубина
Введите глубину катушки.
Результат:
Ссылка: Руководство АРРЛ по радиосвязи 2017
См. Также: Калькулятор обмотки тороидальной катушки
Французская версия
,Coil32 — Как рассчитать индуктивность?
- Подробнее
- Хиты: 7331
Как рассчитать индуктивность? — 5,0 из 5 основанный на 2 отзыва
Мы можем использовать различные методы для расчета индуктивности, используя численные методы или формулы справочника.Их условно можно разделить на три уровня — высокий, средний и низкий уровень.
Высокий уровень предполагает использование программ, имеющих общее название — электромагнитные тренажеры. Например, Comsol Multisystems с радиочастотным модулем, Ansys HFSS и т. Д. Их работа основана на дифференциальных уравнениях Максвелла для электромагнитного поля, обеспечивающего граничные условия. Преимущества
: точный расчет индуктивности и других параметров катушки с любой геометрией намотки в любом диапазоне частот.
Недостатки: эти программы довольно сложны и требуют предварительного обучения, требуют больших вычислительных ресурсов, расчет занимает много времени. Может использоваться для профессиональной работы, или если индуктор используется на частоте саморезонанса или выше.
Средний уровень основан на упрощенной модели индуктора, представленной J.C.Maxwell. Преимущества
: приемлемая точность расчетов для радиолюбителей, возможность использования в простых программах, низкие требования к вычислительной мощности компьютера.
Недостатки: менее точные расчеты, чем высокий уровень; расчет невозможен для любой геометрии обмотки и может быть только в диапазоне частот, который не превышает 60-70% собственной резонансной частоты (или, скорее, 1-резонанса) катушки.
Низкий уровень основан на простых формулах справочника. Эти формулы основаны на упрощении формул среднего уровня или на основе набора измерений реальных катушек.
Преимущества: простой расчет, нетребовательный к ресурсам компьютера
Недостатки: формулы работают только с ограниченной геометрией обмотки и на частотах, намного меньших частоты саморезонанса.
Подробнее о расчете среднего уровня, который использует Col32 … Великий физик Дж. К. Максвелл показал в конце XIX века в своей знаменитой работе — «Трактат об электричестве и магнетизме». что взаимная индуктивность между двумя бесконечно тонкими круглыми коаксиальными проводниками может быть рассчитана следующим образом: 
Где 
- М — взаимная индуктивность;
- r1, r2 — радиусы двух круговых нитей;
- x — расстояние между центрами окружностей, ограниченных этими нитями;
- K, E — эллиптические интегралы первого и второго рода;
Численный метод расчета формулы Максвелла сводится к численным методам решения эллиптических интегралов.
С помощью уравнения Максвелла можно рассчитать индуктивность однослойной, многослойной или плоской катушки и взаимную индуктивность двух отдельных катушек. Ошибки, связанные с приближением коаксиальных круговых нитей (фактически мы имеем дело с спиралью круглой проволоки), могут быть уменьшены за счет дополнительных исправлений.
,Электромагнитная индукция возникает, когда магнитный поток в движении относительно одиночного проводника или катушки индуцирует эдс в проводнике или катушке. Поскольку рост или уменьшение тока через катушку генерирует изменяющийся поток, ЭДС индуцируется в катушке собственным изменением тока. Тот же эффект может вызвать ЭДС в соседней катушке. Уровень ЭДС, индуцируемой в каждом случае, зависит от самоиндуктивности катушки или от взаимной индуктивности между двумя катушками.Во всех случаях полярность индуцированной ЭДС такова, что она противостоит первоначальному изменению, которое вызвало ЭДС.
Компоненты, называемые индукторами или дросселями, имеют заданные значения индуктивности. Индукторы могут работать последовательно или параллельно. Даже самый короткий из проводников имеет индуктивность. Это обычно нежелательное количество и называется паразитной индуктивностью.
Самоиндуктивность
Индуктивность катушки и проводника
Было показано, что ЭДС индуцируется в проводнике, движущемся через магнитное поле, и что рост тока в катушке может индуцировать ЭДС в другом магнитном поле. спаренная катушка.Катушка также может индуцировать напряжение при изменении уровня тока. Это явление известно как самоиндуктивность, и принцип показан на рисунке 1.
Рис.1: Катушка с током и ее площадь поперечного сечения
Магнитный поток, растущий наружу вокруг витков катушки обрезает (или замазывает) другую катушку, поворачивает и индуцирует эдс в катушке
Катушка и ее площадь поперечного сечения показаны на рисунке 1, хвостовые части стрелок и точки указывают направления тока в каждом витке.Каждый виток катушки имеет поток вокруг него, создаваемый током, протекающим через катушку. Однако для удобства на рисунке показан рост потока только за один оборот катушки. Видно, что с ростом тока поток расширяется наружу и обрезает (или закрашивает) другие витки. Это вызывает токи, которые индуцируются на других витках, и направление индуцированных токов таково, что они создают поток, который противодействует потоку, вызывающему их.
Помня, что ток через катушку заставляет поток расти вокруг всех витков одновременно, видно, что поток с каждого витка индуцирует ток, который противостоит ему в каждом втором витке.
Чтобы установить противоположные потоки, индуцированный ток в катушке должен быть противоположен току, протекающему через катушку от внешнего источника питания. Индуцированный ток, конечно, является результатом индуцированной ЭДС. Таким образом, видно, что самоиндуктивность катушки устанавливает индуцированную эдс, которая противостоит внешней эдс, которая пропускает ток через катушку. Поскольку эта индуцированная ЭДС противоположна напряжению питания, ее обычно называют противо-ЭДС или противо-ЭДС .Противо-ЭДС возникает только тогда, когда ток катушки растет или уменьшается. Когда ток достигает постоянного уровня, поток больше не меняется и противоэдс не генерируется.
Даже один проводник обладает собственной индуктивностью. На рисунке 2 показано, что при увеличении тока в проводнике поток может расти наружу от центра проводника. Этот поток перерезает другие части проводника и вызывает противоэдс.
Рис.2: поперечное сечение проводника
Рост тока внутри проводника вызывает эдс в других частях проводника.
На рисунке 3 показана полярность противо-ЭДС, индуцированной в катушке, для данной полярности напряжения питания. На рисунке 3 (а) переключатель замкнут, и ток I начинает расти с нуля. Полярность противо-ЭДС (e L ) такова, что она противодействует росту I, следовательно, она последовательно противостоит напряжению питания. Когда выключатель размыкается (рисунок 3 (б)), ток имеет тенденцию падать до нуля. Но теперь полярность e L такова, что она противодействует снижению I.это последовательное соединение с напряжением питания. Фактически, e L может вызвать искрение на клеммах переключателя, поскольку это зависит от индуктивности катушки.
Рис.3: Индуцированная полярность эдс
Противо-ЭДС, индуцированная в катушке, всегда противодействует увеличению или уменьшению тока.
Единицей индуктивности СИ является Генри (H).
Индуктивность цепи равна единице Генри, когда эдс 1 В индуцируется током, изменяющимся со скоростью 1 А / с.
Таким образом, соотношение между индуктивностью, наведенным напряжением и скоростью изменения тока:
\ [\ begin {matrix} L = \ frac {{{e} _ {L}}} {{\ Delta i} / {\ Delta t} \;} & {} & \ left (1 \ right) \\\ end {matrix} \]
Где L — индуктивность по Генри, e L — индуцированная противо-ЭДС в вольтах и скорость изменения тока в А / с. перед e L иногда включается отрицательный знак, чтобы показать, что наведенная эдс противоположна приложенной эдс.Когда е , L = 1 В и = 1 А / с, L = 1Н. Если скорость изменения тока составляет 2 А / с и e L, = 1 В, индуктивность равна 0,5 H.
Катушка, имеющая определенную индуктивность, обычно называется индуктором или дросселем. Обратите внимание на графические символы для индуктора, показанного на рисунке 3.
Формула самоиндукции
Выражение индуктивности может быть получено с учетом размеров катушки и числа витков [см. Рисунок 4].
Рис.4: Число витков в катушке
Индуктивность катушки зависит от числа витков, а также от изменения потока и тока.
Из уравнения (2):
\ [\ begin {matrix} {{e} _ {L}} = N \ frac {\ Delta \ phi} {\ Delta t} & {} & \ left ( 2 \ right) \\\ end {matrix} \]
Подстановка для e L в уравнение (1) дает
\ [L = N \ frac {{\ Delta \ phi} / {\ Delta t} \ ;} {{\ Delta i} / {\ Delta t} \;} \]
или
\ [\ begin {matrix} L = N \ frac {\ Delta \ phi} {\ Delta i} & {} & \ left (3 \ right) \\\ end {matrix} \]
Также,
\ [\ phi = B \ times A \]
И
$ B = {{\ mu} _ {o }} \ times {{\ mu} _ {r}} \ times H = {{\ mu} _ {o}} \ times {{\ mu} _ {r}} \ times \ frac {IN} {l} $
Следовательно,
$ \ phi = {{\ mu} _ {o}} \ times {{\ mu} _ {r}} \ times IN \ times \ frac {A} {l} $
с I — максимальный уровень тока, он также представляет изменение тока (∆i) от нуля до максимального уровня.{A} / {} _ {l} & {} & \ left (4 \ right) \\\ end {matrix} \]
Обратите внимание, что, как показано на рисунке 5, индуктивность пропорциональна сечению площадь катушки и до квадрата числа витков. Он также обратно пропорционален длине катушки. Поэтому максимальная индуктивность достигается с короткой катушкой, которая имеет большую площадь поперечного сечения и большое количество витков.
Рис.5: Размеры катушки
Индуктивность катушки можно рассчитать по ее размерам и проницаемости сердечника.
Уравнение (4) теперь позволяет рассчитать индуктивность катушки известных размеров. Альтернативно, это может использоваться, чтобы определить требуемые размеры для катушки, чтобы иметь данную индуктивность. Однако его не так легко применить к катушкам с железной сердцевиной, потому что проницаемость ферромагнитного материала изменяется при изменении плотности потока. Следовательно, индуктивность катушки с железной сердцевиной постоянно изменяется по мере увеличения и уменьшения тока катушки.
Неиндуктивная катушка
Во многих случаях желательно иметь неиндуктивную катушку; например, прецизионные резисторы обычно не индуктивные.Чтобы создать такую катушку, обмотка состоит из двух параллельных проводников, как показано на рисунке 6. Каждый виток катушки имеет смежный виток, несущий ток в противоположном направлении. Магнитные поля, создаваемые соседними витками, компенсируют друг друга. Следовательно, противо-ЭДС не генерируется, и катушка не индуктивная.
Рис.6: Неиндуктивная катушка
Пример с самоиндуктивностью
Соленоид с 900 витками имеет общий поток 1,33 X 10 -7 Wb через сердечник, когда ток катушки составляет 100 мА.{-3}}} = 1,6 мВ \]
Взаимная индуктивность
Когда поток от одной катушки обрезает другую соседнюю (или магнитно-связанную) катушку, во второй катушке индуцируется эдс. Следуя закону Ленца, ЭДС, индуцированная во второй катушке, создает поток, который противодействует исходному потоку от первой катушки. Таким образом, индуцированная ЭДС снова является противо-ЭДС, и в этом случае индуктивный эффект называется взаимной индуктивностью. На рисунке 7 показаны графические символы, используемые для катушек с взаимной индуктивностью, также называемых связанными катушками.
Рис.7: Графические символы для катушек с воздушной и железной сердцевиной
Как и в случае собственной индуктивности, взаимная индуктивность измеряется в Генри (H) .
Формула взаимной индуктивности
Две катушки имеют взаимную индуктивность 1Н, когда в одной катушке индуцируется эдс 1 В при изменении тока со скоростью 1 А / с в другой катушке.
Это определение порождает уравнение, связывающее взаимную индуктивность с наведенным напряжением и скорость изменения тока:
\ [\ begin {matrix} M = \ frac {{{e} _ {L}}} {{ \ Delta i} / {\ Delta t} \;} & {} & \ left (5 \ right) \\\ end {matrix} \]
Где M — взаимная индуктивность в Генри, e L — это ЭДС в вольтах индуцируется во вторичной катушке и представляет собой скорость изменения тока в первичной катушке в А / с.
Катушка, через которую пропускается ток от внешнего источника, называется первичной, а катушка, на которую наведена ЭДС, называется вторичной.
Уравнение для эдс, индуцированной во вторичной катушке, можно записать в виде:
\ [\ begin {matrix} {{e} _ {L}} = {{N} _ {s}} \ frac {\ Delta \ phi} {\ Delta t} & {} & \ left (6 \ right) \\\ end {matrix} \]
Здесь ∆ϕ — полное изменение связи флюса со вторичной обмоткой, N с, — это число витков во вторичной обмотке, а ∆t — время, необходимое для изменения потока.
Подстановка для e L из уравнения (6) в уравнение (5) дает
\ [M = {{N} _ {s}} \ frac {{\ Delta \ phi} / {\ Delta t} \ ;} {{\ Delta i} / {\ Delta t} \;} \]
Следовательно,
\ [\ begin {matrix} M = {{N} _ {s}} \ frac {\ Delta \ phi } {\ Delta i} & {} & \ left (7 \ right) \\\ end {matrix} \]
Рисунок 8 (a) иллюстрирует тот факт, что, когда две катушки намотаны на один ферромагнитный сердечник, эффективно весь поток, создаваемый первичной катушкой, связан со вторичной катушкой.Однако, когда катушки имеют воздушную сердцевину, только часть потока от первичной обмотки может соединиться с вторичной обмоткой [см. Рисунок 8 (b)]. В зависимости от того, сколько первичного потока перерезает вторичную, катушки могут быть классифицированы как слабо связанные или тесно связанные. Один из способов обеспечения надежного сцепления показан на рисунке 8 (с), где каждый виток вторичной обмотки идет рядом с одним витком первичной обмотки. Катушки, намотанные таким образом, называются бифилярными.
Рис.8: Связи магнитного потока в первичной и вторичной обмотках
Величина магнитного потока от первичной обмотки, которая связана со вторичной обмоткой, зависит от того, насколько тесно связаны обмотки. Коэффициент сцепления определяет связь.
Количество потоков, соединяющих первичную и вторичную, также определяется в терминах коэффициента связи, k. Если все первичные потоки соединяются с вторичными, коэффициент связи равен 1. Когда только 50% первичного потока соединяется с вторичной катушкой, коэффициент связи равен 0.5. Таким образом,
\ [k = \ frac {flux \ text {} связывает \ text {} между \ text {} primary \ text {} и \ text {} \ sec ondary} {total \ text {} fluxproduced \ text {} by \ text {} primary} \]
Возвращаясь к уравнению (7). Когда ∆ϕ — полное изменение потока в первичной катушке, поток, связывающий с вторичной обмоткой, равен k∆ϕ. Следовательно, уравнение для M
\ [\ begin {matrix} M = k {{N} _ {s}} \ frac {\ Delta \ phi} {\ Delta i} & {} & \ left (8 \ right) ) \\\ end {matrix} \]
Также, заменив $ \ Delta \ phi = {{\ mu} _ {o}} \ times {{\ mu} _ {r}} \ times \ Delta i \ раз N \ times \ frac {A} {l} $ в уравнение (8) дает
\ [M = \ frac {k {{N} _ {s}}} {\ Delta i} \ times {{\ mu } _ {o}} \ times {{\ mu} _ {r}} \ times \ Delta i \ times {{N} _ {p}} \ times \ frac {A} {l} \]
или
\ [\ begin {matrix} M = k \ times {{N} _ {p}} \ times {{N} _ {s}} \ times {{\ mu} _ {o}} \ times {{\ mu} _ {r}} \ times \ frac {A} {l} & {} & \ left (9 \ right) \\\ end {matrix} \]
Каждая рассматриваемая обмотка обладает собственной индуктивностью, которая может рассчитываться по уравнению (4).{2}} $
или
\ [\ begin {matrix} \ sqrt {{{L} _ {1}} \ times {{L} _ {2}}} = {{N} _ {p} } \ times {{N} _ {s}} \ times {{\ mu} _ {o}} \ times {{\ mu} _ {r}} \ times \ frac {A} {l} & {} & \ left (10 \ right) \\\ end {matrix} \]
Сравнивая уравнения 9 и 10, видно, что
\ [\ begin {matrix} M = k \ sqrt {{{L} _ { 1}} \ times {{L} _ {2}}} & {} & \ left (11 \ right) \\\ end {matrix} \]
Пример взаимной индуктивности
Две одинаковые катушки намотаны на железный сердечник в форме кольца, который имеет относительную проницаемость 500.{-2}}} \ cong 9.42mH \\\ end {align} \]
Поскольку катушки намотаны на одно и то же железное ядро, k = 1. Уравнение (11):
$ M = k \ sqrt {{{L} _ {1}} \ times {{L} _ {2}}} = \ sqrt {9,42 \ times 9,42} = 9,42 мГн $
.Индуктивность катушки зависит от ее геометрических характеристик, количества витков и способа намотки катушки. Чем больше диаметр, длина и большее количество витков обмотки, тем больше ее индуктивность.
Если катушка плотно намотана, поверните на виток, то у нее будет больше индуктивности, чем на катушке, не намотанной плотно, с зазорами между витками. Иногда вам нужно намотать катушку с заданной геометрией, и у вас нет проволоки с необходимым диаметром, тогда, если вы используете более толстую проволоку, вам следует немного увеличить число витков, а если вы используете более тонкую проволоку, требуется уменьшить ее. витков катушки, чтобы получить требуемую индуктивность.
Все вышеперечисленные соображения относятся к обмоткам без ферритовых сердечников.
Индуктивность однослойных катушек на цилиндрических формах обмоток можно рассчитать по формуле:
L = ( D /10) 2 * n 2 /(4.5* D + 10 * l ) (1)
где
L — индуктивность катушки, мкГн;
D — диаметр рулона (диаметр первого), мм;
л, — длина рулона, мм;
n — число витков обмоток.
В расчете может быть две задачи:
А. Приведена геометрия катушки, найдите индуктивность;
В. Дается индуктивность катушки, рассчитывается количество витков и диаметр провода.
В случае «А» приведены все данные, легко найти индуктивность.
Пример 1. Рассчитаем индуктивность катушки, показанной на рисунке выше. Поместите значения в формулу 1:
L = (18/10) 2 * 20 2 / (4.5 * 18 + 10 * 20) = 4,6 мкГн
Во втором случае диаметр катушки и длина раны известны. Длина намотки зависит от количества витков и диаметра проволоки. Поэтому рекомендуется рассчитывать в этом порядке. Исходя из геометрических соображений, определяем размер витка, диаметр и длину раны, а затем подсчитываем количество витков по формуле:
n = 10 * (5 * L * (0,9 * D + 2 * l )) 1/2 / D (2)
После того, как вы нашли число витков, определите диаметр провода с изоляцией по формуле:
d = l / n (3)
где
d — диаметр проволоки, мм;
л — длина намотки, мм;
n — число оборотов.
Пример 2. Нам необходимо изготовить катушку диаметром 10 мм и длиной обмотки 20 мм, катушка должна иметь индуктивность 0,8 мкГн. Обмотка имеет один слой, поворот к повороту.
Положим значения в формулу 2, получим:
n = 10 * (5 * 0,8 * (0,9 * 10 + 2 * 20)) 1/2 /10 = 14
Диаметр проволоки: d, = 20/14 = 1,43 мм,
Для намотки катушки проволокой меньшего диаметра необходимо разместить полученные расчетным путем 14 витков по всей длине катушки (20 мм) с равными интервалами между витками (шаг намотки).Индуктивность катушки будет на 1-2% меньше номинальной величины, это следует учитывать при изготовлении этих катушек. Чтобы намотать катушку более толстым проводом, чем 1,43 мм, новый расчет следует проводить с увеличенным диаметром или длиной обмотки катушки. Вам также может понадобиться увеличить как диаметр, так и длину одновременно, пока не получите желаемые размеры катушки для данной индуктивности.
Следует отметить, что приведенная выше формула предназначена для расчета катушек с длиной намотки l, равной или равной половине диаметра.Если длина обмотки меньше половины диаметра обмотки D /2, более точные результаты можно получить, используя следующие формулы:
L = (D /10) 2 * n 2 / ((4 D +11 l )) (4)
и
n = (10 L * (4 D +11 l )) 1/2 / D (5)
Ссылка: «300 практических советов»
,