Расчёт индуктивности. Часть 2 | HomeElectronics
Всем доброго времени суток. Сегодняшняя статья является продолжением предыдущей. Здесь продолжим рассматривать расчёт индуктивностей индуктивных элементов без сердечников. В прошлой статье я рассказал, как рассчитать индуктивность прямого провода и провода свёрнутого в кольцо (виток), в данной статье будем рассчитывать индуктивность круговых катушек, то есть поперечный профиль, которых представляет собой окружности.
Виды катушек индуктивности
Круговые катушки индуктивности являются, наверное, самыми распространёнными. В тоже время из-за разнообразия их форм существует некоторая трудность в расчёте индуктивности. Для некоторого упрощения расчёта катушки индуктивности делятся на несколько видов. Рассмотрим основные конструктивные особенности круговых катушек индуктивности

Расчёт индуктивности катушки.
Для расчёта индуктивности круговой катушки необходимо знать следующие размеры:
D1 – внутренний диаметр, D2 – внешний диаметр, Dср – средний диаметр, l – длина катушки (аксиальный размер), t – толщина обмотки (радиальный размер), где t можно вычислить
Поэтому, в зависимости от соотношения между этими размерами различают следующие катушки индуктивности:
если l > Dср – длинная катушка,
если l < Dср – короткая катушка,
если l << Dср – очень короткая катушка,
если l = 0 – плоская катушка,
если t ≈ Dср – толстая катушка,
если t << Dср – тонкая катушка,
если t = 0 – соленоид.
Особенности расчёта катушек индуктивности
Кроме конструктивных параметров, на индуктивность влияет также параметры обмоточного провода (диаметр, толщина изоляции, шаг намотки), хотя в большинстве случаев влияние их незначительно, но в некоторых случаях, например, при большом шаге намотки их следует учитывать. Поэтому общая индуктивность катушки можно представить следующим выражением
где LР – расчётная индуктивность;
∆L – поправка на «изоляцию», ∆L = ∆1L + ∆2L;
∆1L – поправка учитывающая влияние индуктивности витков;
∆2L – поправка учитывающая влияние взаимной индуктивности витков.
В большинстве случаев, например, при плотной намотке «виток к витку» поправка ∆L составляет несколько процентов от расчётной индуктивности LР, поэтому если нет необходимости в точном значении общей индуктивности L, поправку на изоляцию ∆L можно не учитывать.
Особенности расчёта круговых катушек индуктивности состоят в следующем:
1. При определении расчётной индуктивности LP, средний диаметр принимается равным среднему диаметру реальной катушки;
2. Длина намотки l и толщина намотки t принимается равными шагу обмотки (p – шаг по длине катушки, q – шаг по толщине намотки) умноженному на количество слоёв ω в том или ином направлении
3. Если у катушки в каком-либо направлении (по длине намотки l или по толщине намотки t) имеется только один ряд (или слой), то в этом направлении размер l или t можно принять равным нулю, то есть расчёт ведётся как для соленоида или плоской катушки.
4. В некоторых случаях, при большом диаметре провода или шаге намотки у однослойных катушках размер l или t принимается равным диаметру голого провода d.
5. Так как величина поправки на взаимную индуктивность ∆2L в несколько раз меньше, чем поправка на индуктивность витков ∆1L, то при расчётах можно учитывать только ∆1L.
Приступим к расчётным выражениям, в начале рассчитаем простейшие круговые катушки – соленоид и плоскую катушку.
Расчёт индуктивности соленоида
Определение индуктивности соленоида, d – диаметр соленоида, l – длина соленоида.
Соленоид представляет собой катушку, намотанную на каркас в один слой, поэтому толщину слоя можно принять равной нулю t = 0, а расчётная формула индуктивности будет иметь вид
где μ0 – магнитная постоянная, μ0 = 4π•10-7 Гн/м;
ω – число витков соленоида;
d – диаметр соленоида, м;
Φ – коэффициент, который зависит от отношения α = l/D;
l – длина соленоида, м;
Поправочный коэффициент Φ зависит от отношения длины соленоида l к его диаметру d
Для длинного соленоида, то есть α > 0,75, поправочный коэффициент составит
Для короткого соленоида, то есть α < 0,75, поправочный коэффициент составит
Пример. Необходимо рассчитать соленоид диаметром d = 1 см и длиной l = 5 см, который имеет ω = 75 витков.
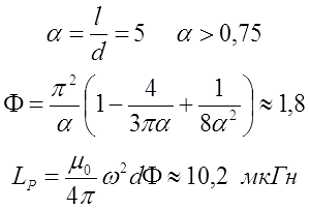
Стоит отметить, что формула расчёта соленоида подходит для большинства однослойных катушек с точностью в несколько процентов.
Индуктивность плоской катушки

Определение индуктивности плоской катушки, D1 – внутренний диаметр, D2 – внешний диаметр, D – средний диаметр, t – толщина намотки.
В данном случае в качестве плоской катушки представлена идеализированная катушка, длина намотки которой приняли равной нулю l = 0, тогда индуктивность такой катушки можно вычислить по следующей формуле
где μ0 – магнитная постоянная, μ0 = 4π•10-7 Гн/м;
ω – число витков соленоида;
D – средний диаметр катушки, м;
Ψ – коэффициент, который зависит от отношения ρ = t/D;
t – толщина намотки катушки.
Коэффициент Ψ зависит от соотношения толщины намотки t и среднего диаметра катушки D
При небольшой толщине намотки, когда ρ < 0,5
При большой толщине намотки, когда ρ > 0,5
где γ – коэффициент учитывающий соотношение внешнего и внутреннего диаметров обмотки катушки
Пример. Рассчитаем плоскую катушку со средним диаметром D = 5 см и толщиной намотки t = 1 см, состоящую из ω = 20 витков.
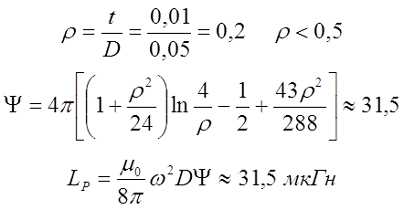
Выражения для индуктивности тонкой катушки позволяют рассчитать индуктивность и большинства катушек с малой длиной и большой толщиной обмоток.
Индуктивность круговой катушки прямоугольного сечения
Теперь перейдём от идеализированных катушек к реальным, которые в своем сечении представляют собой прямоугольник

Индуктивность прямоугольной катушки.
Катушку прямоугольного сечения можно представить в виде соленоида с ненулевой толщиной обмотки t ≠ 0, либо в виде плоской катушки с ненулевой длиной l ≠ 0, поэтому рассчитать необходимую катушку можно либо как соленоид, либо как плоскую катушку, а затем внести поправку.
Таким образом, индуктивность прямоугольной катушки можно вычислить по следующей формуле
где L0 – индуктивность идеальной катушки (соленоида или плоской катушки) в зависимости от α = l/Dcp;
l – длина катушки, м;
Dcp – средний диаметр катушки, м;
∆ — поправка на форму катушки.
В принципе реальную катушку индуктивности, в зависимости от отношения длины намотки l к среднему диаметру Dcp, можно разделить на несколько типов:
1. Длинная катушка, у которой α > 0,75.
2. Короткая катушка, имеющая α < 0,75 и γ < 1.
3. Очень короткая катушка, имеет α << 1 и γ > 1.
где
Рассмотрим каждый случай по отдельности.
Индуктивность длинной катушки
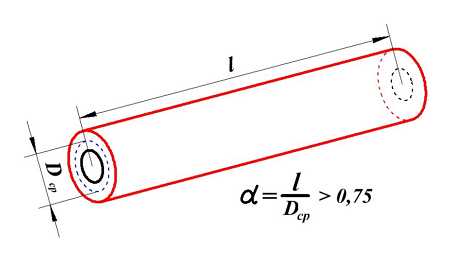
Длинная катушка.
Для длинной катушки (α > 0,75) величина L0 рассчитывается также как для длинного соленоида, где l – длина соленоида, D cp – средний диаметр соленоида, а значение поправки ∆ вычисляется по следующему выражению
где α – коэффициент, учитывающий отношение длины катушки l к её среднему диаметру DCP;
γ – коэффициент, учитывающий отношение толщины намотки t к длине намотки l;
ρ – коэффициент, учитывающий отношение толщины намотки t к её среднему диаметру DCP.
где D1 – внутренний диаметр, D2 – внешний диаметр.
Пример. Рассчитаем индуктивность катушки длиной l = 10 см, средним диаметром DCP = 2 см, количеством витков ω = 100 и толщиной намотки t = 5 мм.
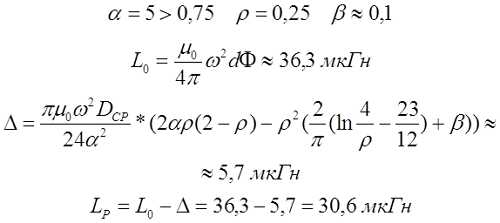
Индуктивность короткой катушки
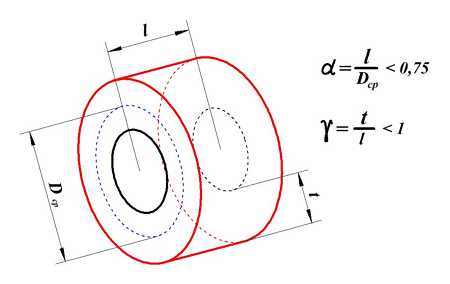
Короткая катушка.
Для короткой катушки (α < 0,75, t < l) величина L
где α – коэффициент, учитывающий отношение длины катушки l к её среднему диаметру DCP;
γ – коэффициент, учитывающий отношение толщины намотки t к длине намотки l;
Пример. Рассчитаем индуктивность катушки длиной l = 1 см, средним диаметром DСР = 2 см, толщиной намотки t = 5 мм, количеством витков ω = 50.
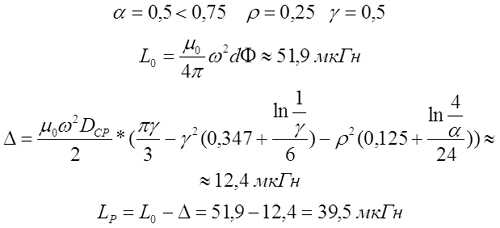
Индуктивность очень короткой катушки
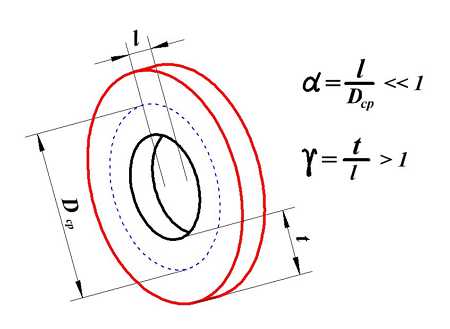
Очень короткая катушка.
Для очень короткой катушки (α << 1, t > l) величина L0 рассчитывается также как для плоской катушки, где t – толщина намотки, Dcp – средний диаметр катушки, а значение поправки ∆ вычисляется по следующему выражению
где α – коэффициент, учитывающий отношение длины катушки l к её среднему диаметру DCP;
γ – коэффициент, учитывающий отношение толщины намотки t к длине намотки l, γ < 1;
ρ – коэффициент, учитывающий отношение толщины намотки t к её среднему диаметру DCP.
Пример. Рассчитаем индуктивность катушки длиной l = 5 мм, средним диаметром DCP = 7 см, намотка толщиной t = 1 см, количество витков ω = 150.

Расчёт поправки на собственную индуктивность витков
Как я писал в начале статьи, полная индуктивность катушки L состоит из расчётной индуктивности LP и поправки на изоляцию ∆L, которая в свои очередь состоит из поправки на собственную индуктивность витков ∆1L и поправки на взаимную индуктивность витков ∆2L
Данные поправки зависят от взаимного расположения витков в катушке. Для провода круглого сечения возможны следующие варианты заполнения катушки

Расположение провода круглого сечения в катушке индуктивности. s – диаметр провода с изоляцией, sp – диаметр голого провода (без изоляции), p – шаг намотки по длине катушки, q – шаг намотки по толщине катушки.
В общем случае поправка на собственную индуктивность витков рассчитывается по следующему выражению
где μ0 – магнитная постоянная, μ0 = 4π•10-7 Гн/м;
ω – число витков соленоида;
DСР – средний диаметр катушки, м;
I – коэффициент, зависящий от расположения витков катушки.
Коэффициент I определяется в зависимости от расположения провода, варианты которого изображены на рисунке выше.
Для варианта а), провод намотан с небольшим коэффициентом заполнения
где s – диаметр провода с изоляцией, sp – диаметр голого провода (без изоляции).
Для варианта б), провод намотан с большим коэффициентом заполнения
где s – диаметр провода с изоляцией, sp – диаметр голого провода (без изоляции).
Для варианта в), провод намотан с шагом p по длине катушки и с шагом q по толщине катушки
где s – диаметр провода с изоляцией, sp – диаметр голого провода (без изоляции).
Для варианта г), провод намотан в один слой по длине катушки с шагом p. В зависимости от способа вычисления расчётной индуктивности LP
— если при вычислении расчётной индуктивности LP толщина намотки t принята равной диаметру голого провода sP, то коэффициент I будет равен
— если при вычислении расчётной индуктивности LP толщина намотки t принята равной нулю (расcчитывалась как соленоид), то коэффициент I будет равен
где p – шаг намотки по длине катушки, sp – диаметр голого провода (без изоляции).
Для варианта д), провод намотан в один слой по толщине намотки с шагом q, также возможно два случая
— если при вычислении расчётной индуктивности LP длина намотки l принята равной диаметру голого провода sP, то коэффициент I будет равен
— если при вычислении расчётной индуктивности LP длина намотки l принята равной нулю (рассчитывалась как плоская катушка), то коэффициент I будет равен
где q – шаг намотки по толщине катушки, sp – диаметр голого провода (без изоляции).
Расчёт поправки на взаимную индуктивность витков
В общем случае поправка на взаимную индуктивность витков ∆2L катушки определяется выражением
где μ0 – магнитная постоянная, μ0 = 4π•10-7 Гн/м;
ω – число витков соленоида;
DСР – средний диаметр катушки, м;
J – коэффициент, зависящий формы катушки и от числа витков катушки.
1. Для катушки выполненной в один слой по длине катушки (соленоид):
а) при определении расчётной индуктивности LP толщина намотки t принята равной шагу намотки р, то коэффициент J составит
где ω – количество витков катушки.
б) при определении расчётной индуктивности LP толщина намотки t принята равной нулю (рассчитывается как соленоид), то коэффициент J составит
где ω – количество витков катушки.
2. Для катушки, выполненной в один слой по толщине намотки (плоская катушка):
а) при определении расчётной индуктивности LP длина катушки l принята равной шагу намотки р, то коэффициент J составит
где ω – количество витков катушки.
б) при определении расчётной индуктивности LP длина катушки l принята равной нулю (рассчитывается как плоская катушка), то коэффициент J составит
где ω – количество витков катушки.
На сегодня всё. В следующей статье я закончу с индуктивными элементами без сердечников.
Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.
Скажи спасибо автору нажми на кнопку социальной сети
www.electronicsblog.ru
3. Факторы, влияющие на индуктивность катушки | 14. Катушки индуктивности | Часть1
3. Факторы, влияющие на индуктивность катушки
Факторы, влияющие на индуктивность катушки
На индуктивность катушки оказывают влияние следующие основные факторы:
Число витков провода в катушке: При прочих равных условиях, увеличение числа витков приводит к увеличению индуктивности; уменьшение числа витков приводит к уменьшению индуктивности.
Пояснение: чем больше количество витков, тем больше будет магнитодвижущая сила для заданной величины тока.
Площадь поперечного сечения катушки: При прочих равных условиях, катушка с большей площадью поперечного сечения будет иметь большую индуктивность; а катушка с меньшей площадью поперечного сечения — меньшую индуктивность.
Пояснение: Катушка с большей площадью поперечного сечения оказывает меньшее сопротивление формированию магнитного потока для заданной величины магнитодвижущей силы.
Длина катушки: При прочих равных условиях, чем больше длина катушки, тем меньше ее индуктивность; чем меньше длина катушки, тем больше ее индуктивность.
Пояснение: Чем больше длина катушки, тем большее сопротивление она оказывает формированию магнитного потока для заданной величины магнитодвижущей силы.
Материал сердечника: При прочих равных условиях, чем больше магнитная проницаемость сердечника, вокруг которого намотана катушка, тем больше индуктивность; чем меньше магнитная проницаемость сердечника — тем меньше индуктивность.
Пояснение: Материал сердечника с большей магнитной проницаемостью способствует формированию большего магнитного потока для заданной величины магнитодвижущей силы.
Приблизительное значение индуктивности любой катушки можно найти по следующей формуле:
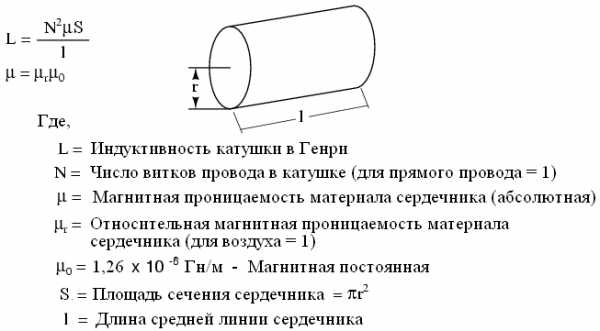
Следует понимать, что данная формула дает только приблизительные цифры. Одной из причин такого положения дел является изменение величины магнитной проницаемости при изменении напряженности магнитного поля (вспомните нелинейность кривой В/Н для разных материалов). Очевидно, если проницаемость (µ) в уравнении будет непостоянна, то и индуктивность (L) также будет в некоторой степени непостоянна. Если гистерезис материала сердечника будет существенным, то это непременно отразится на индуктивности катушки. Разработчики катушек индуктивности пытаются минимизировать эти эффекты, проектируя сердечник таким образом, чтобы его намагниченность никогда не приближалась к уровням насыщения, и катушка работала в более линейной части кривой B/H.
Если катушку сделать таким образом, что любой из вышеперечисленных факторов у нее можно механически изменить, то получится катушка с регулируемой величиной индуктивности или вариометр. Наиболее часто встречаются вариометры, индуктивность которых регулируется количеством витков или положением сердечника (который перемещается внутри катушки). Пример вариометра с изменяемым количеством витков можно увидеть на следующей фотографии:

Это устройство использует подвижные медные контакты, которые подключаются к катушке в различных точках ее длины. Подобные катушки, имеющие воздушный сердечник, применялись в разработке самых первых радиоприемных устройств.
Катушка с фиксированными значениями индуктивности, показанная на следующей фотографии, представляет собой еще одно раритетное устройство, использовавшееся в первых радиостанциях. Здесь вы можете увидеть несколько витков относительно толстого провода, а так же соединительные выводы:

А это еще одна катушка индуктивности, так же предназначенная для радиостанций. Для большей жесткости ее провод намотан на керамический каркас:

Многие катушки индуктивности обладают небольшими размерами, что позволяет монтировать их непосредственно на печатные платы. Посмотрев внимательно на следующую фотографию, можно увидеть две расположенные рядом катушки:

Две катушки индуктивности расположены справа в центре этой платы и имеют обозначения L1 и L2. В непосредственной близости от них находятся резистор R3 и конденсатор С16. Показанные на плате катушки называются «торроидальными», так как их провод намотан вокруг сердечника, имеющего форму тора.
Как резисторы и конденсаторы, катушки индуктивности могут выполняться в корпусе для поверхностного монтажа (SMD). На следующей фотографии представлено несколько таких катушек:

Две индуктивности здесь расположены справа в центре платы. Они представляют собой маленькие черные чипы с номером «100», а над одной из них можно увидеть обозначение L5.
www.radiomexanik.spb.ru
Каталог радиолюбительских схем. Как произвести расчет катушек индуктивности (однослойных, цилиндрических без сердечника).
Каталог радиолюбительских схем. Как произвести расчет катушек индуктивности (однослойных, цилиндрических без сердечника).Как произвести расчет катушек индуктивности (однослойных, цилиндрических без сердечника)
Индуктивность катушки зависит от ее геометрических размеров, числа витков и способа намотки катушки. Чем больше диаметр, длина намотки и число витков катушки, тем больше ее индуктивность.
Если катушка наматывается плотно виток к витку, то индуктивность ее будет больше по сравнению с катушкой, намотанной неплотно, с промежутками между витками. Когда требуется намотать катушку по заданным размерам и нет провода нужного диаметра, то при намотке ее более толстым проводом надо несколько увеличить, а тонким — уменьшить число витков катушки, чтобы получить необходимую индуктивность.
Все приведенные выше соображения справедливы при намотке катушек без ферритовых сердечников.
Расчет однослойных цилиндрических катушек производится по формуле
где L — индуктивность катушки, мкГн; D — диаметр катушки, см; l — длина намотки катушки, см; n—число витков катушки.
При расчете катушки могут встретиться два случая:
а) по заданным геометрическим размерам необходимо определить индуктивность катушки;
б) при известной индуктивности определить число витков и диаметр провода катушки.
В первом случае все исходные данные, входящие в формулу, известны, и расчет не представляет затруднений.
Пример. Определим индуктивность катушки, изображенной на рис. 97; для этого подставим в формулу все необходимые величины:
Во втором случае известны диаметр катушки и длина намотки, которая, в свою очередь, зависит от числа витков и диаметра провода. Поэтому расчет рекомендуется вести в следующей последовательности. Исходя из конструктивных соображений определяют размеры катушки, диаметр и
длину намотки, а затем рассчитывают число витков по формуле
После того как будет найдено число витков, определяют диаметр провода с изоляцией по формуле
где d— диаметр провода, мм, l — длина обмотки, мм, п — число витков.
Пример. Нужно изготовить катушку диаметром 1 см при длине намотки 2 см, имеющую индуктивность 0,8 мкГн. Намотка рядовая виток к витку.
Подставив в последнюю формулу заданные величины,
получим:
Диаметр провода
Если эту катушку наматывать проводом меньшего диаметра, то нужно полученные расчетным путем 14 витков разместить по всей длине катушки (20 мм) с равными промежутками между витками, т. е. с шагом намотки. Индуктивность данной катушки будет на 1—2% меньше номинальной, что следует учитывать при изготовлении таких катушек. При намотке в случае необходимости более толстым проводом, чем 1,43 мм, следует сделать новый расчет, увеличив диаметр или длину намотки катушки. Возможно, также придется увеличить и то и другое одновременно, пока не будут получены необходимые габариты катушки, соответствующие заданной индуктивности.
Следует заметить, что по приведенным выше формулам рекомендуется рассчитывать такие катушки, у которых длина намотки l равна или больше половины диаметра. Если же длина намотки меньше половины диаметра D/2 , то более точные результаты можно получить по формулам
В.Г.Бастанов, «300 практических советов»
irls.narod.ru
Расчет индуктивности
Контрольная работа
по курсу «Компоненты электронной техники»
Тема: «Расчет индуктивности».
Методы расчета индуктивностей
Индуктивностью (коэффициентом самоиндукции) называют коэффициент пропорциональности между током и возбуждаемым им потокосцеплением. Если речь идет об отношении потокосцепления одного из двух контуров в силе обусловливающего его тока в другом контуре, то говорят о взаимной индуктивности (коэффициенте взаимной индуктивности).
Поскольку индуктивность, как это следует из определения, зависит от распределения тока в проводниках, при ее расчете надо учитывать влияние частоты. Под низкой частотой понимается такая, при которой можно пренебречь неравномерностью распределения тока по сечениям проводов; длина электромагнитной волны при этом значительно больше линейных размеров сечения. Под весьма высокой частотой понимают частоту, длина волны которой значительно меньше размеров поперечного сечения провода; при этом ток можно считать сосредоточенным в поверхностном слое нулевой толщины. Высокие частоты занимают промежуточное положение.
С практической точки зрения целесообразно рассмотреть отдельно методы расчета индуктивности воздушных контуров, катушек с замкнутыми сердечниками и катушек с сердечниками, имеющими воздушный зазор.
Воздушные контуры
Под воздушными контурами подразумевают такую систему проводов, для которых магнитная проницаемость равна проницаемости окружающей среды. Расчет в общем случае сводится к следующему. Задаваясь токами в рассматриваемых контурах, разбивают каждый из токов на элементарные нити и на основе закона Био-Савара определяют индуктивность в выбранной точке поля. По ее значению находят поток, сцепляющийся с какой-нибудь нитью тока, затем вычисляют полный магнитный поток, сцепляющийся с рассматриваемым контуром и определяемый соответствующим током.
Если справедливо предположение, что ток распределен равномерно по сечению или по поверхности провода, применяют вариант метода, заключающийся в следующем. Поток, сцепляющийся с какой-нибудь нитью тока, выражают как сумму потоков взаимной индукции, создаваемых другими нитями, причем суммирование должно быть распространено на все нити данного контура при вычислении взаимной индуктивности. При этом получают выражения, содержащие в явном виде указания на необходимые математические операции.
Таким образом, имеем
; ; ,где L и M – собственная и взаимная индуктивности; di – нити тока; dl – элементы длины нитей; Ө — угол между элементами; μ0 – магнитная постоянная.
Сложность расчетов приводит к тому, что выше приведенным методом определяют индуктивность либо проводов простой формы, либо участков, составляющих сложные контуры. В последнем случае индуктивность контура состоит из суммы индуктивностей всех участков и двойной суммы взаимной индуктивности между участками, т.е.
(k ≠ i),где n – число участков.
Получение расчетных соотношений для индуктивности возможно на основе и иных соображений. По определению индуктивность
,где I – ток; Ψ – обусловленное им потокосцепление; ω – число витков; G – некоторая величина, являющаяся функцией геометрических размеров системы и имеющая размерность магнитной проводимости.
Если частные потоки сцепляются со всеми витками, то для расчета индуктивности берется проводимость пространства, в котором рассматривается суммарный поток.
Расчет индуктивностей катушек выполняют по одному из двух методов суммирования или массивного витка. Метод суммирования, заключающийся в учете частичных собственных и взаимных индуктивностей отдельных витков, не имеет явных преимуществ и применяется довольно редко (главным образом для численных расчетов катушек сложной формы). Методом массивного витка сравнивают индуктивность рассматриваемой катушки с индуктивностью массивного витка, имеющего такую же форму и размеры, при этом предполагая, что коэффициент заполнения равен единице. Таким образом, находят расчетную индуктивность, к которой затем вычисляют поправки на изоляцию.
Катушки с замкнутыми магнитопроводами (сердечниками). Расчет индуктивности катушек в магнитопроводах замкнутой формы осуществляют по общим соотношениям для магнитных цепей. В конечном своем виде эти соотношения отличаются от результатов, полученных для воздушных катушек, наличием множителя, учитывающего свойства сердечника и равного его магнитной проницаемости.
Для получения практических формул принимают, как правило, что весь магнитный поток проходит через магнитопровод (без утечек и рассеивания), а средняя магнитная силовая линия пронизывает центры масс поперечных сечений магнитной цепи (т. е. совпадает со средней линией магнитопровода). Исключением являются особые случаи, например катушки на сердечниках тороидальной формы с неполной обмоткой.
Если для какой — либо цепи возможно интегральное определение формализованной магнитной проводимости (или сопротивления), для вычисления индуктивности можно использовать формулу
,связывающую индуктивность с магнитным сопротивлением RM , в виде
,где SM — площадь поперечного сечения магнитопровода;lM — длина средней магнитной силовой линии; μa — абсолютная магнитная проницаемость материала сердечника.
Катушки с сердечниками, имеющими воздушный зазор
Для магнитопроводов с большим воздушным зазором необходимо учитывать отклонение распределения поля в зазоре от идеализированного. При этом магнитные сопротивления для основного потока и потока рассеивания становятся соизмеримыми, и расчетные формулы существенно усложняются.
Поэтому для таких катушек применяют различные приближенные методы, основанные либо на аппроксимации картины поля простыми геометрическими фигурами, либо на выборе так называемых расчетных полюсов, либо на использовании картин плоскопараллельных полей.
На практике удобно применять метод эквивалентного зазора, позволяющий использовать все формулы для сердечников с малыми зазорами. При этом эквивалентным зазором называют такой, который имеет ту же проводимость, что и реальный, а геометрия его определяется сечением полюсов магнитопровода и некоторой эквивалентной длиной. Эквивалентную длину находят из условия равенства проводимости на основе аппроксимации возможных путей потока.
Применительно к элементам радиоэлектронных цепей случай больших зазоров встречается сравнительно редко (исключение – катушки на стержневых сердечниках), и большая точность расчетов при этом не требуется. Индуктивность катушек на стержневых сердечниках определяют с помощью магнитной проницаемости тела (сердечника), выражаемой через коэффициент размагничивания. В этом случае коэффициент размагничивания равен проводимости (формально введенной) окружающего сердечник пространства при условии, что весь поток проходит через торцы сердечника.
Если известен для данного сердечника коэффициент размагничивания, то индуктивность катушки легко найти путем рассмотрения магнитной цепи, состоящей из двух участков с известными магнитными сопротивлениями.
В тех случаях, когда для расчетов используют коэффициент размагничивания, в формулы вместо μr подставляют μ0 (относительную магнитную проницаемость сердечника)
,где N – коэффициент размагничивания.
Основная сложность заключается в определении коэффициентов размагничивания, зависящих в общем случае от геометрических размеров сердечника, магнитных свойств материала сердечника и характера распределения намагничивающего поля катушки.
Индуктивность воздушных катушек и тел специальной формы
Рассмотрим формулы для расчета индуктивности элементов, для которых магнитная проницаемость равна проницаемости окружающего пространства. Под общим названием «тела специальной формы» объединены элементы, не являющиеся катушками в собственном смысле, но входящие в состав цепей РЭА (провода, электро
mirznanii.com
Электротехника: Расчёт индуктивности однослойной катушки.
На рисунке 1 представлена однослойная катушка: имеющая круглое сечение, не имеющая сердечника (магнитная проницаемость равна единице), длинной l=0.01м, диаметром d=0.01м, числом витков w=3: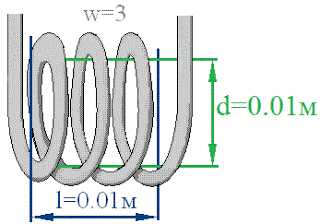
Рисунок 1 — Катушка
Индуктивность — это коэффициент связывающий ток (силу тока) I протекающий по виткам катушки и её потокосцепление, математически это можно представить в виде формулы (1):
Из (1) можно выразить индуктивность:
В знаменателе формулы (3) длинна l.
Подставим (3) в (2) и получим формулу для расчёта индуктивности, для данного случая:
Так как сечение круглое и известен диаметр d то площадь можно найти по формуле:
Диаметр берется средний.
Подставим найденную площадь S; известные: число витков w, длину l, магнитную проницаемость материала сердечника, магнитную проницаемость вакуума в (4) и найдем индуктивность для нашего примера (рисунок 1):
Если страница открыта в Internet Explorer то для работы программы может понадобиться «разрешить заблокированное содержимое».
Если число слоёв катушки не велико (несколько слоёв) а диаметр провода мал по отношению к её размерам то можно воспользоваться формулой (4) и получить приближенный результат. Необходимо учитывать что форма катушки может быть такой что результат расчёта её индуктивности по формуле (4) может быть очень неточным.
electe.blogspot.com
