Индуктивность проводника формула: Индуктивность проводника — Основы электроники

Расчёт индуктивности. Часть 1 | HomeElectronics

Всем доброго времени суток! В прошлой статье я рассказывал о таком явлении как электромагнитная индукция и ЭДС возникающая при самоиндукции и взаимной индукции. Устройства, в основе которых лежат данные явления и процессы, называются индуктивными элементами (катушки колебательных контуров, трансформаторы, дроссели, реакторы). В качестве одного из основных параметров данных элементов выступает индуктивность L(также имеет название коэффициента самоиндукции). О том, как рассчитать данный параметр пойдёт речь в данной статье.

Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.

Методы расчёта индуктивностей

Индуктивностью (обозначается L) или коэффициентом самоиндукции называется коэффициент пропорциональности между потокосцеплением (обозначается Ψ­_L) и электрическим током, который возбуждает данное потокосцепление.

В простых случаях индуктивность можно рассчитать, применяя формулы для вычисления магнитной индукции

B₀ (закон Био-Савара-Лапласа), магнитного потока Φ и потокосцепления Ψ­_L

где S – площадь поверхности ограниченная контуром, который создает магнитную индукцию;

n – количество контуров с током, которые пронизывает магнитный поток.

Однако это в идеальном случае, в реальности говоря о токе I, который протекает по проводнику, необходимо отметить, что его распределение по сечению проводника не всегда равномерно, вследствие возникновения скин-эффекта при переменном токе. В результате этого эффекта плотность электрического тока распределяется неравномерно, происходит её уменьшение от внешнего слоя проводника к его центру. Уменьшение плотности тока также происходит неравномерно и зависит от частоты переменного тока. Для оценки скин-эффекта ввели понятие толщины скин-слоя ∆, которая показывает, на каком расстоянии от поверхности проводника плотность тока падает в е = 2,718 раз. Толщину скин-слоя можно вычислить по выражению

где δ – глубина проникновения переменного тока или толщина скин-слоя;

μ – магнитная проницаемость вещества;

γ – удельная электрическая проводимость материала проводника;

ω – круговая частота переменного тока, ω = 2πf.

Поэтому непосредственный способ вычисления индуктивности практически не применяется.

На практике применяется выражения для индуктивности, выведенные с некоторыми допущениями, погрешности вычисления индуктивности по этим выражениями составляет порядка нескольких процентов.

Так как индуктивные элементы довольно разнообразны, их можно разделить на три группы:

индуктивные элементы без сердечников;

индуктивные элементы с замкнутыми сердечниками;

индуктивные элементы с сердечниками, имеющие воздушный зазор.

Самые простые по конструкции являются индуктивные элементы без сердечников, поэтому рассмотрим их в первую очередь. Простейшим из таких элементов является прямой провод.

Индуктивность прямолинейного провода круглого сечения

При расчёте индуктивности необходимо разделять индуктивность на постоянном токе и индуктивность на высокой частоте. Под высокой частотой следует понимать такую частоту, на которой толщина скин-слоя меньше размеров поперечного сечения провода. В случае если толщина скин-слоя больше поперечных размеров провода, то можно вести расчёт для постоянного тока.

Определение индуктивности прямого провода. l – это длина проводника, d = 2r – диаметр проводника.

В случае постоянного тока или тока низкой частоты индуктивность составит

где μ₀ – магнитная постоянная, μ

0 = 4π•10^-7 Гн/м;

l – длина провода, м;

d – диаметр провода, м.

Как я уже говорил, на величину индуктивности влияет частота переменного тока, поэтому в случае необходимости рассчитать индуктивность на любой частоте применяется следующее выражение

где ξ – коэффициент, вносящий поправку на распространение переменного тока по сечению провода. Данный коэффициент зависит от величины k*r, где

d = 2r – диаметр поперечного сечения провода, м.

где ω – угловая частота переменного тока, ω = 2πf;

μ₀ – магнитная постоянная, μ₀ = 4π•10^-7 Гн/м;

γ – удельная проводимость вещества проводника.

Тогда если k*r < 3, то

если k*r > 3, то

где

Пример. Необходимо рассчитать индуктивность прямолинейного провода круглого сечения из меди (γ = 5,81*10⁷ См/м) диаметром d = 2 мм и длиной l = 4 м, при постоянном токе и токе частотой f = 50 кГц.

На постоянном токе

На частоте 50 кГц

Индуктивность кругового кольца круглого сечения

Теперь рассмотрим, какова будет индуктивность если провод свернуть в кольцо. Такой индуктивный элемент будет иметь вид

Определение индуктивности кругового витка. D – диаметр кольца (витка), d – диаметр провода, из которого сделано кольцо (виток).

При этом его индуктивность можно вычислить по следующему выражению

для  постоянного тока

где R – радиус витка, м, R = D/2;

r – радиус провода, м, r = d/2;

μ₀ – магнитная постоянная, μ₀ = 4π•10^-7 Гн/м.

Так же как и для проводника существует выражение для индуктивности кругового витка на любой частоте

где ξ – коэффициент, вносящий поправку на распространение переменного тока по сечению провода.

Определяется также как и для прямого проводника.

Пример. В качестве примера рассчитаем индуктивность такого же провода, как и в первом примере, только свёрнутом в кольцо. В этом случае диаметр провода d = 2 мм, а диаметр кольца D = l/π = 4/3,142 ≈ 1,273 м, провод выполнен из меди (γ = 5,81*10⁷ См/м).

Для постоянного тока индуктивность составит

На частоте 50 кГц

В следующей части я продолжу рассмотрение расчётов индуктивности для различных индуктивных элементов.

Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.

Глава 23. Закон электромагнитной индукции

Если в магнитном поле находится замкнутый проводящий контур, не содержащий источников тока, то при изменении магнитного поля в контуре возникает электрический ток. Это явление называется электромагнитной индукцией. Появление тока свидетельствует о возникновении в контуре электрического поля, которое может обеспечить замкнутое движение электрических зарядов или, другими словами, о возникновении ЭДС.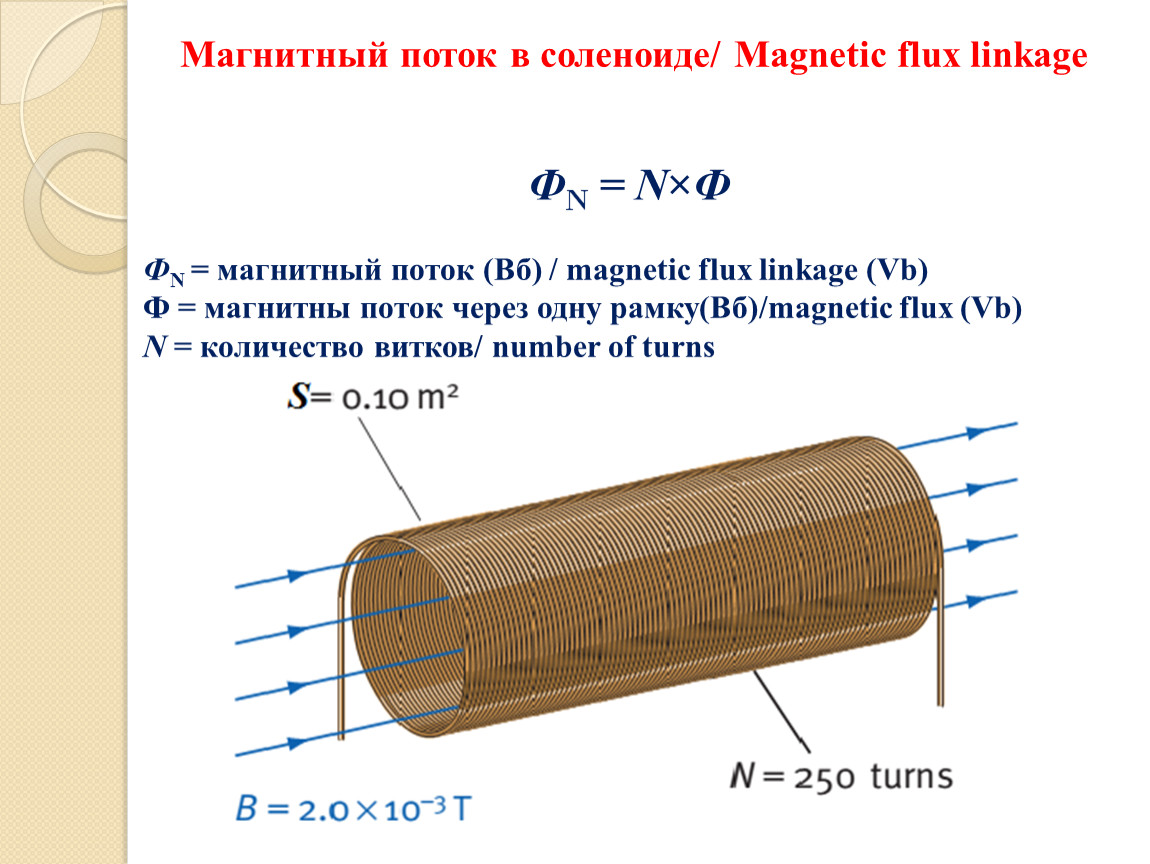

Электрическое поле, которое возникает при изменении поля магнитного и работа которого при перемещении зарядов по замкнутому контуру не равна нулю, имеет замкнутые силовые линии и называется вихревым.

Для количественного описания электромагнитной индукции вводится понятие магнитного потока (или потока вектора магнитной индукции) через замкнутый контур. Для плоского контура, расположенного в однородном магнитном поле (а только такие ситуации и могут встретиться школьникам на едином государственном экзамене), магнитный поток определяется как

(23.1)

где — индукция поля, — площадь контура, — угол между вектором индукции и нормалью (перпендикуляром) к плоскости контура (см. рисунок; перпендикуляр к плоскости контура показан пунктиром). Единицей магнитного потока в международной системе единиц измерений СИ является Вебер (Вб), который определяется как магнитный поток через контур площади 1 м² однородного магнитного поля с индукцией 1 Тл, перпендикулярной плоскости контура.

Величина ЭДС индукции , возникающая в контуре при изменении магнитного потока через этот контур, равна скорости изменения магнитного потока

(23.2)

Здесь — изменение магнитного потока через контур за малый интервал времени . Важным свойством закона электромагнитной индукции (23.2) является его универсальность по отношению к причинам изменения магнитного потока: магнитный поток через контур может меняться из-за изменения индукции магнитного поля, изменения площади контура или изменения угла между вектором индукции и нормалью, что происходит при вращении контура в поле. Во всех этих случаях по закону (23.2) в контуре будет возникать ЭДС индукции и индукционный ток.

Знак минус в формуле (23.2) «отвечает» за направление тока, возникающего в результате электромагнитной индукции (правило Ленца). Однако понять на языке закона (23.2), к какому направлению индукционного тока приведет этот знак при том или ином изменении магнитного потока через контур, не так-то просто. Но достаточно легко запомнить результат: индукционный ток будет направлен таким образом, что созданное им магнитное поле будет «стремиться» компенсировать то изменение внешнего магнитного поля, которое этот ток и породило. Например, при увеличении потока внешнего магнитного поля через контур в нем возникнет индукционный ток, магнитное поле которого будет направлено противоположно внешнему магнитному полю так, чтобы уменьшить внешнее поле и сохранить, таким образом, первоначальную величину магнитного поля. При уменьшении потока поля через контур поле индукционного тока будет направлено так же, как и внешнее магнитное поле.

Если в контуре с током ток в силу каких-то причин изменяется, то изменяется и магнитный поток через контур того магнитного поля, которое создано самим этим током. Тогда по закону (23.2) в контуре должна возникать ЭДС индукции. Явление возникновения ЭДС индукции в некоторой электрической цепи в результате изменения тока в самой этой цепи называется самоиндукцией. Для нахождения ЭДС самоиндукции в некоторой электрической цепи необходимо вычислить поток магнитного поля, создаваемого этой цепью через нее саму. Такое вычисление представляет собой сложную проблему из-за неоднородности магнитного поля. Однако одно свойство этого потока является очевидным. Поскольку магнитное поле, создаваемого током в цепи, пропорционально величине тока, то и магнитный поток собственного поля через цепь пропорционален току в этой цепи

(23.3)

где — сила тока в цепи, — коэффициент пропорциональности, который характеризует «геометрию» цепи, но не зависит от тока в ней и называется индуктивностью этой цепи. Единицей индуктивности в международной системе единиц СИ является Генри (Гн). 1 Гн определяется как индуктивность такого контура, поток индукции собственного магнитного поля через который равен 1 Вб при силе тока в нем 1 А. С учетом определения индуктивности (23. 3) из закона электромагнитной индукции (23.2) получаем для ЭДС самоиндукции

(23.4)

Благодаря явлению самоиндукции ток в любой электрической цепи обладает определенной «инерционностью» и, следовательно, энергией. Действительно, для создания тока в контуре необходимо совершить работу по преодолению ЭДС самоиндукции. Энергия контура с током и равна этой работе. Необходимо запомнить формулу для энергии контура с током

(23.5)

где — индуктивность контура, — сила тока в нем.

Явление электромагнитной индукции широко применяется в технике. На нем основано создание электрического тока в электрических генераторах и электростанциях. Благодаря закону электромагнитной индукции происходит преобразование механических колебаний в электрические в микрофонах. На основе закона электромагнитной индукции работает, в частности, электрическая цепь, которая называется колебательным контуром (см. следующую главу), и которая является основой любой радиопередающей или радиопринимающей техники.

Рассмотрим теперь задачи.

Из перечисленных в задаче 23.1.1 явлений только одно есть следствие закона электромагнитной индукции — появление тока в кольце при проведении сквозь него постоянного магнита (ответ 3). Все остальное — результат магнитного взаимодействия токов.

Как указывалось во введении к настоящей главе, явление электромагнитной индукции лежит в основе работы генератора переменного тока (задача 23.1.2), т.е. прибора, создающего переменный ток, заданной частоты (ответ 2).

Индукция магнитного поля, создаваемого постоянным магнитом, уменьшается с увеличением расстояния до него. Поэтому при приближении магнита к кольцу (задача 23.1.3) поток индукции магнитного поля магнита через кольцо изменяется, и в кольце возникает индукционный ток. Очевидно, это будет происходить при приближении магнита к кольцу и северным, и южным полюсом. А вот направление индукционного тока в этих случаях будет различным. Это связано с тем, что при приближении магнита к кольцу разными полюсами, поле в плоскости кольца в одном случае будет направлено противоположно полю в другом. Поэтому для компенсации этих изменений внешнего поля магнитное поле индукционного тока должно быть в этих случаях направлено по-разному. Поэтому и направления индукционных токов в кольце будут противоположными (ответ 4).

Для возникновения ЭДС индукции в кольце необходимо, чтобы менялся магнитный поток через кольцо. А поскольку магнитная индукция поля магнита зависит от расстояния до него, то в рассматриваемом в задаче 23.1.4 случае поток через кольцо будет меняться, в кольце возникнет индукционный ток (ответ 1).

При вращении рамки 1 (задача 23.1.5) угол между линиями магнитной индукции (а, значит, и вектором индукции) и плоскостью рамки в любой момент времени равен нулю. Следовательно, магнитный поток через рамку 1 не изменяется (см. формулу (23.1)), и индукционный ток в ней не возникает. В рамке 2 индукционный ток возникнет: в положении показанном на рисунке, магнитный поток через нее равен нулю, когда рамка повернется на четверть оборота — будет равен , где — индукция, — площадь рамки. Еще через четверть оборота поток снова будет равен нулю и т.д. Поэтому поток магнитной индукции через рамку 2 изменяется в процессе ее вращения, следовательно, в ней возникает индукционный ток (ответ 2).

В задаче 23.1.6 индукционный ток возникает только в случае 2 (ответ 2). Действительно, в случае 1 рамка при движении остается на одном и том же расстоянии от проводника, и, следовательно, магнитное поле, созданное этим проводником в плоскости рамки, не изменяется. При удалении рамки от проводника магнитная индукция поля проводника в области рамки изменяется, меняется магнитный поток через рамку, и возникает индукционный ток

В законе электромагнитной индукции утверждается, что индукционный ток в кольце будет течь в такие моменты времени, когда изменяется магнитный поток через это кольцо. Поэтому пока магнит покоится около кольца (задача 23.1.7) индукционный ток в кольце течь не будет. Поэтому правильный ответ в этой задаче — 2.

Согласно закону электромагнитной индукции (23.2) ЭДС индукции в рамке определяется скоростью изменения магнитного потока через нее. А поскольку по условию задачи 23.1.8 индукция магнитного поля в области рамки изменяется равномерно, скорость ее изменения постоянна, величина ЭДС индукции не изменяется в процессе проведения опыта (ответ 3).

В задаче 23.1.9 ЭДС индукции, возникающая в рамке во втором случае, вчетверо больше ЭДС индукции, возникающей в первом (ответ 4). Это связано с четырехкратным увеличением площади рамки и, соответственно, магнитного потока через нее во втором случае.

В задаче 23.1.10 во втором случае в два раза увеличивается скорость изменения магнитного потока (индукция поля меняется на ту же величину, но за вдвое меньшее время). Поэтому ЭДС электромагнитной индукции, возникающая в рамке во втором случае, в два раза больше, чем в первом (ответ 1).

При увеличении тока в замкнутом проводнике в два раза (задача 23.2.1), величина индукции магнитного поля возрастет в каждой точке пространства в два раза, не изменившись по направлению. Поэтому ровно в два раза изменится магнитный поток через любую малую площадку и, соответственно, и весь проводник (ответ 1). А вот отношение магнитного потока через проводник к току в этом проводнике, которое и представляет собой индуктивность проводника , при этом не изменится (задача 23.2.2 — ответ 3).

Используя формулу (23.3) находим в задаче 32.2.3 Гн (ответ 4).

Связь между единицами измерений магнитного потока, магнитной индукции и индуктивности (задача 23.2.4) следует из определения индуктивности (23.3): единица магнитного потока (Вб) равна произведению единицы тока (А) на единицу индуктивности (Гн) — ответ 3.

Согласно формуле (23.5) при двукратном увеличении индуктивности катушки и двукратном уменьшении тока в ней (задача 23.2.5) энергия магнитного поля катушки уменьшится в 2 раза (ответ 2).

Когда рамка вращается в однородном магнитном поле, магнитный поток через рамку меняется из-за изменения угла между перпендикуляром к плоскости рамки и вектором индукции магнитного поля. А поскольку и в первом и втором случае в задаче 23.2.6 этот угол меняется по одному и тому же закону (по условию частота вращения рамок одинакова), то ЭДС индукции меняются по одному и тому же закону, и, следовательно, отношение амплитудных значений ЭДС индукции в рамках равно единице (ответ 2).

Магнитное поле, создаваемое проводником с током в области рамки (задача 23.2.7), направлено «от нас» (см. решение задач главы 22). Величина индукции поля провода в области рамки при ее удалении от провода будет уменьшаться. Поэтому индукционный ток в рамке должен создать магнитное поле, направленное внутри рамки «от нас». Используя теперь правило буравчика для нахождения направления магнитной индукции, заключаем, что индукционный ток в рамке будет направлен по часовой стрелке (ответ 1).

При увеличении тока в проводе будет возрастать созданное им магнитное поле и в рамке возникнет индукционный ток (задача 23.2.8). В результате возникнет взаимодействие индукционного тока в рамке и тока в проводнике. Чтобы найти направление этого взаимодействия (притяжение или отталкивание) можно найти направление индукционного тока, а затем по формуле Ампера силу взаимодействия рамки с проводом. Но можно поступить и по-другому, используя правило Ленца. Все индукционные явления должны иметь такое направление, чтобы компенсировать вызывающую их причину. А поскольку причина — увеличение тока в рамке, сила взаимодействия индукционного тока и провода должна стремиться уменьшить магнитный поток поля провода через рамку. А поскольку магнитная индукция поля провода убывает с увеличением расстояния до него, то эта сила будет отталкивать рамку от провода (ответ 2). Если бы ток в проводе убывал, то рамка притягивалась бы к проводу.

Задача 23.2.9 также связана с направлением индукционных явлений и правилом Ленца. При приближении магнита к проводящему кольцу в нем возникнет индукционный ток, причем направление его будет таким, чтобы компенсировать вызывающую его причину. А поскольку эта причина — приближение магнита, кольцо будет отталкиваться от него (ответ 2). Если магнит отодвигать от кольца, то по тем же причинам возникло бы притяжение кольца к магниту.

Задача 23.2.10 — единственная вычислительная задача в этой главе. Для нахождения ЭДС индукции нужно найти изменение магнитного потока через контур . Это можно сделать так. Пусть в некоторый момент времени перемычка находилась в положении, показанном на рисунке, и пусть прошел малый интервал времени . За этот интервал времени перемычка переместится на величину . Это приведет к увеличению площади контура на величину . Поэтому изменение магнитного потока через контур будет равно , а величина ЭДС индукции (ответ 4).

Магнетизм — Физика — Теория, тесты, формулы и задачи

Оглавление:

 

Основные теоретические сведения

Сила Ампера

К оглавлению…

Заряженные тела способны создавать кроме электрического еще один вид поля. Если заряды движутся, то в пространстве вокруг них создается особый вид материи, называемый магнитным полем. Следовательно, электрический ток, представляющий собой упорядоченное движение зарядов, тоже создает магнитное поле. Как и электрическое поле, магнитное поле не ограничено в пространстве, распространяется очень быстро, но все же с конечной скоростью. Его можно обнаружить только по действию на движущиеся заряженные тела (и, как следствие, токи).

Для описания магнитного поля необходимо ввести силовую характеристику поля, аналогичную вектору напряженности E электрического поля. Такой характеристикой является вектор B магнитной индукции. В системе единиц СИ за единицу магнитной индукции принят 1 Тесла (Тл). Если в магнитное поле с индукцией B поместить проводник длиной l с током I, то на него будет действовать сила, называемая силой Ампера, которая вычисляется по формуле:

где: В – индукция магнитного поля, I – сила тока в проводнике, l – его длина. Сила Ампера направлена перпендикулярно вектору магнитной индукции и направлению тока, текущего по проводнику. 

Для определения направления силы Ампера обычно используют правило «Левой руки»: если расположить левую руку так, чтобы линии индукции входили в ладонь, а вытянутые пальцы были направлены вдоль тока, то отведенный большой палец укажет направление силы Ампера, действующей на проводник (см. рисунок).

Если угол α между направлениями вектора магнитной индукции и тока в проводнике отличен от 90°, то для определения направления силы Ампера надо взять составляющую магнитного поля, которая перпендикулярна направлению тока. Решать задачи этой темы нужно так же как и в динамике или статике, т.е. расписав силы по осям координат или складывая силы по правилам сложения векторов.

Момент сил, действующих на рамку с током

Пусть рамка с током находится в магнитном поле, причём плоскость рамки перпендикулярна полю. Силы Ампера будут сжимать рамку, а их равнодействующая будет равна нулю. Если поменять направление тока, то силы Ампера поменяют своё направление, и рамка будет не сжиматься, а растягиваться. Если линии магнитной индукции лежат в плоскости рамки, то возникает вращательный момент сил Ампера. Вращательный момент сил Ампера равен:

где: S — площадь рамки, α — угол между нормалью к рамке и вектором магнитной индукции (нормаль — вектор, перпендикулярный плоскости рамки), N – количество витков, B – индукция магнитного поля, I – сила тока в рамке.

 

Сила Лоренца

К оглавлению…

Сила Ампера, действующая на отрезок проводника длиной Δl с силой тока I, находящийся в магнитном поле B может быть выражена через силы, действующие на отдельные носители заряда. Эти силы называют силами Лоренца. Сила Лоренца, действующая на частицу с зарядом q в магнитном поле B, двигающуюся со скоростью v, вычисляется по следующей формуле:

Угол α в этом выражении равен углу между скоростью и вектором магнитной индукции. Направление силы Лоренца, действующей на положительно заряженную частицу, так же, как и направление силы Ампера, может быть найдено по правилу левой руки или по правилу буравчика (как и сила Ампера). Вектор магнитной индукции нужно мысленно воткнуть в ладонь левой руки, четыре сомкнутых пальца направить по скорости движения заряженной частицы, а отогнутый большой палец покажет направление силы Лоренца. Если частица имеет отрицательный заряд, то направление силы Лоренца, найденное по правилу левой руки, надо будет заменить на противоположное.

Сила Лоренца направлена перпендикулярно векторам скорости и индукции магнитного поля. При движении заряженной частицы в магнитном поле сила Лоренца работы не совершает. Поэтому модуль вектора скорости при движении частицы не изменяется. Если заряженная частица движется в однородном магнитном поле под действием силы Лоренца, а ее скорость лежит в плоскости, перпендикулярной вектору индукции магнитного поля, то частица будет двигаться по окружности, радиус которой можно вычислить по следующей формуле:

Сила Лоренца в этом случае играет роль центростремительной силы. Период обращения частицы в однородном магнитном поле равен:

Последнее выражение показывает, что для заряженных частиц заданной массы m период обращения (а значит и частота, и угловая скорость) не зависит от скорости (следовательно, и от кинетической энергии) и радиуса траектории R.

 

Теория о магнитном поле

К оглавлению…

Магнитное взаимодействие токов

Если по двум параллельным проводам идёт ток в одном направлении, то они притягиваются; если в противоположных направлениях, то отталкиваются. Закономерности этого явления были экспериментально установлены Ампером. Взаимодействие токов вызывается их магнитными полями: магнитное поле одного тока действует силой Ампера на другой ток и наоборот. Опыты показали, что модуль силы, действующей на отрезок длиной Δl каждого из проводников, прямо пропорционален силам тока I₁ и I₂ в проводниках, длине отрезка Δl и обратно пропорционален расстоянию R между ними:

где: μ₀ – постоянная величина, которую называют магнитной постоянной. Введение магнитной постоянной в СИ упрощает запись ряда формул. Ее численное значение равно:

μ₀ = 4π·10^–7 H/A² ≈ 1,26·10^–6 H/A².

Сравнивая приведенное только что выражение для силы взаимодействия двух проводников с током и выражение для силы Ампера нетрудно получить выражение для индукции магнитного поля создаваемого каждым из прямолинейных проводников с током на расстоянии R от него:

где: μ – магнитная проницаемость вещества (об этом чуть ниже). Если ток протекает по круговому витку, то в центре витка индукция магнитного поля определяется по формуле:

Силовыми линиями магнитного поля называют линии, по касательным к которым располагаются магнитные стрелки. Магнитной стрелкой называют длинный и тонкий магнит, его полюса точечны. Подвешенная на нити магнитная стрелка всегда поворачивается в одну сторону. При этом один её конец направлен в сторону севера, второй — на юг. Отсюда название полюсов: северный (N) и южный (S). Магниты всегда имеют два полюса: северный (обозначается синим цветом или буквой N) и южный (красным цветом или буквой S). Магниты взаимодействуют так же, как и заряды: одноименные полюса отталкиваются, а разноименные – притягиваются. Невозможно получить магнит с одним полюсом. Даже если магнит разломать, то у каждой части будет по два разных полюса.

Вектор магнитной индукции

Вектор магнитной индукции — векторная физическая величина, являющаяся характеристикой магнитного поля, численно равная силе, действующей на элемент тока в 1 А и длиной 1 м, если направление силовой линии перпендикулярно проводнику. Обозначается В, единица измерения — 1 Тесла. 1 Тл — очень большая величина, поэтому в реальных магнитных полях магнитную индукцию измеряют в мТл.

Вектор магнитной индукции направлен по касательной к силовым линиям, т.е. совпадает с направлением северного полюса магнитной стрелки, помещённой в данное магнитное поле. Направление вектора магнитной индукции не совпадает с направлением силы, действующей на проводник, поэтому силовые линии магнитного поля, строго говоря, силовыми не являются.

Силовая линия магнитного поля постоянных магнитов направлена по отношению к самим магнитам так, как показано на рисунке:

В случае магнитного поля электрического тока для определения направления силовых линий используют правило «Правой руки»: если взять проводник в правую руку так, чтобы большой палец был направлен по току, то четыре пальца, обхватывающие проводник, показывают направление силовых линий вокруг проводника:

В случае прямого тока линии магнитной индукции — окружности, плоскости которых перпендикулярны току. Вектора магнитной индукции направлены по касательной к окружности.

Соленоид — намотанный на цилиндрическую поверхность проводник, по которому течёт электрический ток I. Магнитное поле соленоида подобно полю прямого постоянного магнита. Внутри соленоида длиной l и количеством витков N создается однородное магнитное поле с индукцией (его направление также определяется правилом правой руки):

Линии магнитного поля имеют вид замкнутых линий — это общее свойство всех магнитных линий. Такое поле называют вихревым. В случае постоянных магнитов линии не оканчиваются на поверхности, а проникают внутрь магнита и замыкаются внутри. Это различие электрического и магнитного полей объясняется тем, что, в отличие от электрических, магнитных зарядов не существует.

Магнитные свойства вещества

Все вещества обладают магнитными свойствами. Магнитные свойства вещества характеризуются относительной магнитной проницаемостью μ, для которой верно следующее:

Данная формула выражает соответствие вектора магнитной индукции поля в вакууме и в данной среде. В отличие от электрического, при магнитном взаимодействии в среде можно наблюдать и усиление, и ослабление взаимодействия по сравнению с вакуумом, у которого магнитная проницаемость μ = 1. У диамагнетиков магнитная проницаемость μ немного меньше единицы. Примеры: вода, азот, серебро, медь, золото. Эти вещества несколько ослабляют магнитное поле. Парамагнетики — кислород, платина, магний — несколько усиливают поле, имея μ немного больше единицы. У ферромагнетиков — железо, никель, кобальт — μ >> 1. Например, у железа μ ≈ 25000.

 

Магнитный поток. Электромагнитная индукция

К оглавлению…

Явление электромагнитной индукции было открыто выдающимся английским физиком М.Фарадеем в 1831 году. Оно заключается в возникновении электрического тока в замкнутом проводящем контуре при изменении во времени магнитного потока, пронизывающего контур. Магнитным потоком Φ через площадь S контура называют величину:

где: B – модуль вектора магнитной индукции, α – угол между вектором магнитной индукции B и нормалью (перпендикуляром) к плоскости контура, S – площадь контура, N – количество витком в контуре. Единица магнитного потока в системе СИ называется Вебером (Вб).

Фарадей экспериментально установил, что при изменении магнитного потока в проводящем контуре возникает ЭДС индукции ε_инд, равная скорости изменения магнитного потока через поверхность, ограниченную контуром, взятой со знаком минус:

Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум возможным причинам.

1. Магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле. Возникновение ЭДС индукции объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.
2. Вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре.

При решении задач важно сразу определить за счет чего меняется магнитный поток. Возможно три варианта:

1. Меняется магнитное поле.
2. Меняется площадь контура.
3. Меняется ориентация рамки относительно поля.

При этом при решении задач обычно считают ЭДС по модулю. Обратим внимание также внимание на один частный случай, в котором происходит явление электромагнитной индукции. Итак, максимальное значение ЭДС индукции в контуре состоящем из N витков, площадью S, вращающемся с угловой скоростью ω в магнитном поле с индукцией В:

 

Движение проводника в магнитном поле

К оглавлению…

При движении проводника длиной l в магнитном поле B со скоростью v на его концах возникает разность потенциалов, вызванная действием силы Лоренца на свободные электроны в проводнике. Эту разность потенциалов (строго говоря, ЭДС) находят по формуле:

где: α — угол, который измеряется между направлением скорости и вектора магнитной индукции. В неподвижных частях контура ЭДС не возникает.

Если стержень длиной L вращается в магнитном поле В вокруг одного из своих концов с угловой скоростью ω, то на его концах возникнет разность потенциалов (ЭДС), которую можно рассчитать по формуле:

 

Индуктивность. Самоиндукция. Энергия магнитного поля

К оглавлению…

Самоиндукция является важным частным случаем электромагнитной индукции, когда изменяющийся магнитный поток, вызывающий ЭДС индукции, создается током в самом контуре. Если ток в рассматриваемом контуре по каким-то причинам изменяется, то изменяется и магнитное поле этого тока, а, следовательно, и собственный магнитный поток, пронизывающий контур. В контуре возникает ЭДС самоиндукции, которая согласно правилу Ленца препятствует изменению тока в контуре. Собственный магнитный поток Φ, пронизывающий контур или катушку с током, пропорционален силе тока I:

Коэффициент пропорциональности L в этой формуле называется коэффициентом самоиндукции или индуктивностью катушки. Единица индуктивности в СИ называется Генри (Гн).

Запомните: индуктивность контура не зависит ни от магнитного потока, ни от силы тока в нем, а определяется только формой и размерами контура, а также свойствами окружающей среды. Поэтому при изменении силы тока в контуре индуктивность остается неизменной. Индуктивность катушки можно рассчитать по формуле:

где: n — концентрация витков на единицу длины катушки:

ЭДС самоиндукции, возникающая в катушке с постоянным значением индуктивности, согласно формуле Фарадея равна:

Итак ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в ней.

Магнитное поле обладает энергией. Подобно тому, как в заряженном конденсаторе имеется запас электрической энергии, в катушке, по виткам которой протекает ток, имеется запас магнитной энергии. Энергия W_м магнитного поля катушки с индуктивностью L, создаваемого током I, может быть рассчитана по одной из формул (они следуют друг из друга с учётом формулы Φ = LI):

Соотнеся формулу для энергии магнитного поля катушки с её геометрическими размерами можно получить формулу для объемной плотности энергии магнитного поля (или энергии единицы объёма):

 

Правило Ленца

К оглавлению…

Инерция – явление, происходящее и в механике (при разгоне автомобиля мы отклоняемся назад, противодействуя увеличению скорости, а при торможении отклоняемся вперёд, противодействуя уменьшению скорости), и в молекулярной физике (при нагревании жидкости увеличивается скорость испарения, самые быстрые молекулы покидают жидкость, уменьшая скорость нагревания) и так далее. В электромагнетизме инерция проявляется в противодействии изменению магнитного потока, пронизывающего контур. Если магнитный поток нарастает, то возникающий в контуре индукционный ток направлен так, чтобы препятствовать нарастанию магнитного потока, а если магнитный поток убывает, то возникающий в контуре индукционный ток направлен так, чтобы препятствовать убыванию магнитного потока.

Правило Ленца для определения направления индукционного тока: возникающий в контуре индукционный ток имеет такое направление, что создаваемое им магнитное поле препятствует изменению магнитного потока, которое вызывало этот ток.

Самоиндукция. Индуктивность. Энергия магнитного поля тока

Самоиндукция. Индуктивность. Энергия магнитного поля тока

Подробности

Просмотров: 621

Самоиндукция

Каждый проводник, по которому протекает эл.ток, находится в собственном магнитном поле.

При изменении силы тока в проводнике меняется м.поле, т.е. изменяется магнитный поток, создаваемый этим током. Изменение магнитного потока ведет в возникновению вихревого эл.поля и в цепи появляется ЭДС индукции.

Это явление называется самоиндукцией.

Самоиндукция — явление возникновения ЭДС индукции в эл.цепи в результате изменения силы тока.
Возникающая при этом ЭДС называется ЭДС самоиндукции

Проявление явления самоиндукции

Замыкание цепи

При замыкании в эл.цепи нарастает ток, что вызывает в катушке увеличение магнитного потока, возникает вихревое эл.поле, направленное против тока, т.е. в катушке возникает ЭДС самоиндукции, препятствующая нарастанию тока в цепи (вихревое поле тормозит электроны).
В результате Л1 загорается позже, чем Л2.

Размыкание цепи

При размыкании эл.цепи ток убывает, возникает уменьшение м.потока в катушке, возникает вихревое эл.поле, направленное как ток (стремящееся сохранить прежнюю силу тока) , т.е. в катушке возникает ЭДС самоиндукции, поддерживающая ток в цепи.
В результате Л при выключении ярко вспыхивает.

Вывод:

в электротехнике явление самоиндукции проявляется при замыкании цепи (электрический ток нарастает постепенно) и при размыкании цепи (электрический ток пропадает не сразу).

ИНДУКТИВНОСТЬ

От чего зависит ЭДС самоиндукции?

Электрический ток создает собственное магнитное поле. Магнитный поток через контур пропорционален индукции магнитного поля (Ф ~ B), индукция пропорциональна силе тока в проводнике
(B ~ I), следовательно магнитный поток пропорционален силе тока (Ф ~ I).
ЭДС самоиндукции зависит от скорости изменения силы тока в эл.цепи, от свойств проводника (размеров и формы) и от относительной магнитной проницаемости среды, в которой находится проводник.
Физическая величина, показывающая зависимость ЭДС самоиндукции от размеров и формы проводника и от среды, в которой находится проводник, называется коэффициентом самоиндукции или индуктивностью.

Индуктивность — физическая величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1Ампер за 1 секунду.
Также индуктивность можно рассчитать по формуле:

где Ф — магнитный поток через контур, I — сила тока в контуре.

Единицы измерения индуктивности в системе СИ:

Индуктивность катушки зависит от:
числа витков, размеров и формы катушки и от относительной магнитной проницаемости среды ( возможен сердечник).

ЭДС САМОИНДУКЦИИ

ЭДС самоиндукции препятствует нарастанию силы тока при включении цепи и убыванию силы тока при размыкании цепи.

ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ ТОКА

Вокруг проводника с током существует магнитное поле, которое обладает энергией.
Откуда она берется? Источник тока, включенный в эл.цепь, обладает запасом энергии.
В момент замыкания эл.цепи источник тока расходует часть своей энергии на преодоление действия возникающей ЭДС самоиндукции. Эта часть энергии, называемая собственной энергией тока, и идет на образование магнитного поля.

Энергия магнитного поля равна собственной энергии тока.
Собственная энергия тока численно равна работе, которую должен совершить источник тока для преодоления ЭДС самоиндукции, чтобы создать ток в цепи.

Энергия магнитного поля, созданного током, прямо пропорциональна квадрату силы тока.
Куда пропадает энергия магнитного поля после прекращения тока? — выделяется ( при размыкании цепи с достаточно большой силой тока возможно возникновение искры или дуги)

ВОПРОСЫ К ПРОВЕРОЧНОЙ РАБОТЕ

по теме «Электромагнитная индукция»

1. Перечислить 6 способов получения индукционного тока.
2. Явление электромагнитной индукции (определение).
3. Правило Ленца.
4. Магнитный поток ( определение, чертеж, формула, входящие величины, их ед. измерения).
5. Закон электромагнитной индукции (определение, формула).
6. Свойства вихревого электрического поля.
7. ЭДС индукции проводника, движущегося в однородном магнитном поле ( причина появления, чертеж, формула, входящие величины, их ед. измерения).
8. Самоиндукция (кратко проявление в электротехнике, определение).
9. ЭДС самоиндукции (ее действие и формула).
10. Индуктивность (определение, формулы, ед. измерения).
11. Энергия магнитного поля тока (формула, откуда появляется энергия м. поля тока, куда пропадает при прекращении тока).

Электромагнитное поле — Класс!ная физика

Взаимодействие токов. Магнитное поле. Вектор магнитной индукции. Сила Ампера — Действие магнитного поля на движущийся заряд.Магнитные свойства вещества — Явление электромагнитной индукции. Магнитный поток. Направление индукционного тока. Правило Ленца — ЭДС электромагнитной индукции. Вихревое электрическое поле — ЭДС индукции в движущихся проводниках
— Самоиндукция. Индуктивность. Энергия магнитного поля. Вопросы к пр/работе

Явление самоиндукции — определение, формулы, примеры

Магнитный поток

Прежде чем говорить об электромагнитной индукции и самоиндукции, нам нужно определить сущность магнитного потока.

Представьте, что вы взяли в руки обруч и вышли на улицу в ливень. Потоки воды будут проходить через обруч.

Если держать обруч горизонтально, то через него пройдет много воды. А если начать его поворачивать — уже меньше, потому что он расположен не под прямым углом к вертикали.

Теперь давайте поставим обруч вертикально — ни одной капли не пройдет сквозь него (если ветер не подует, конечно).

Магнитный поток очень похож на поток воды, проходящей через обруч, только считаем мы величину прошедшего через площадь магнитного поля, а не дождя.

Магнитным потоком через площадь ​S​ контура называют скалярную физическую величину, равную произведению:

• модуля вектора магнитной индукции ​B​,
• площади поверхности ​S​, которую пронизывает поток,
• и косинуса угла ​α​ между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности).

Магнитный поток Ф — магнитный поток [Вб] B — магнитная индукция [Тл] S — площадь пронизываемой поверхности [м2] n — вектор нормали (перпендикуляр к поверхности) [-]

Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.

В зависимости от угла ​α магнитный поток может быть положительным (α < 90°) или отрицательным (α > 90°). Если α = 90°, то магнитный поток равен 0.

Изменить магнитный поток можно, меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).

В случае неоднородного магнитного поля и неплоского контура магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.

Электромагнитная индукция

Электромагнитная индукция — явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.

Явление электромагнитной индукции открыл Майкл Фарадей в ходе серии опытов.

Опыт раз. На одну непроводящую основу намотали две катушки таким образом, что витки одной катушки были расположены между витками второй. Витки первой катушки были замкнуты на гальванометр, а второй — подключены к источнику тока.

При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.

Опыт два. Первую катушку подключили к источнику тока, а вторую — к гальванометру. При этом вторая катушка перемещалась относительно первой. При приближении или удалении катушки фиксировался ток.

Опыт три. Катушку замкнули на гальванометр, а магнит передвигали относительно катушки.

Вот что показали эти опыты:

1. Индукционный ток возникает только при изменении линий магнитной индукции.


2. Направление тока различается при увеличении числа линий и при их уменьшении.


3. Сила индукционного тока зависит от скорости изменения магнитного потока. При этом как само поле может изменяться, так и контур может перемещаться в неоднородном магнитном поле.

Почему возникает индукционный ток?

Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна электродвижущей силе (ЭДС).

Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.

Самоиндукция

Представим себе любую электрическую цепь, параметры которой можно менять. Если мы изменим силу тока в этой цепи — например, подкрутим реостат или подключим другой источник тока — произойдет изменение магнитного поля. В результате этого изменения в цепи возникнет дополнительный индукционный ток за счет электромагнитной индукции, о которой мы говорили выше. Такое явление называется самоиндукцией, а возникающий при этом ток — током самоиндукции.

Формула магнитного потока для самоиндукции Ф = LI Ф — собственный магнитный поток [Вб] L — индуктивность контура [Гн] I — сила тока в контуре [А]

Самоиндукция — это возникновение в проводящем контуре ЭДС, создаваемой вследствие изменения силы тока в самом контуре.

Самоиндукция чем-то напоминает инерцию: как в механике нельзя мгновенно остановить движущееся тело, так и ток не может мгновенно приобрести определенное значение за счет самоиндукции.

Представим цепь, состоящую из двух одинаковых ламп, параллельно подключенных к источнику тока. Если мы последовательно со второй лампой включим в эту цепь катушку, то при замыкании цепи произойдет следующее:

• первая лампа загорится практически сразу,
• вторая лампа загорится с заметным запаздыванием.

При размыкании цепи сила тока быстро уменьшается, и возникающая ЭДС самоиндукции препятствует уменьшению магнитного потока. При этом индуцированный ток направлен так же, как и исходный. ЭДС самоиндукции может во многом раз превысить внешнюю ЭДС. Поэтому электрические лампочки так часто перегорают при отключении света.

ЭДС самоиндукции ξis — ЭДС самоиндукции [В] ΔФ/Δt — скорость изменения магнитного потока [Вб/с] ΔI/Δt — скорость изменения силы тока в контуре [А/с] L — индуктивность [Гн]

Знак минуса в формуле закона электромагнитной индукции указывает на то, что ЭДС индукции препятствует изменению магнитного потока, который вызывает ЭДС. При решении расчетных задач знак минуса не учитывается.

Индуктивность

Индуктивность — это способность накапливать магнитное поле. Она характеризует способность проводника сопротивляться электрическому току. Проще всего это делать с помощью катушки, потому что катушка состоит из витков, которые представляют собой контуры. Вспомните про магнитный поток и обруч под дождем — в контуре создается магнитный поток. Где поток, там и электромагнитная индукция.

Индуктивность контура зависит от его формы и размеров, от магнитных свойств окружающей среды и не зависит от силы тока в контуре.

Можно ли увеличивать индуктивность катушки?

Конечно! Можно увеличить число витков, например. Или поместить в центр катушки железный сердечник.

Как работает катушка

Вокруг каждого проводника, по которому протекает ток, образуется магнитное поле. Если поместить проводник в переменное поле — в нем возникнет ток.

Магнитные поля каждого витка катушки складываются. Поэтому вокруг катушки, по которой протекает ток, возникает сильное магнитное поле. При изменении силы тока в катушке будет изменяться и магнитный поток вокруг нее.

Задачка раз

На рисунке приведен график зависимости силы тока от времени в электрической цепи, индуктивность которой 1 мГн. Определите модуль ЭДС самоиндукции в интервале времени от 15 до 20 с. Ответ выразите в мкВ.

Решение

За время от 15 до 20 с сила тока изменилась от 20 до 0 мА. Модуль ЭДС самоиндукции равен:

Ответ: модуль ЭДС самоиндукции с 15 до 20 секунд равен 4 мкВ.

Задачка два

По проволочной катушке протекает постоянный электрический ток силой 2 А. При этом поток вектора магнитной индукции через контур, ограниченный витками катушки, равен 4 мВб. Электрический ток какой силы должен протекать по катушке для того, чтобы поток вектора магнитной индукции через указанный контур был равен 6 мВб?

Решение

При протекании тока через катушку индуктивности возникает магнитный поток, численно равный Ф = LI.

Отсюда индуктивность катушки равна:

Тогда для достижения значений потока вектора магнитной индукции в 6 мВб ток будет равен:

Ответ: для достижения значений потока вектора магнитной индукции в 6 мВб необходим ток в 3 А.

Как рассчитать индуктивность электрического кабеля ~ Изучение электротехники

Пользовательский поиск

Индуктивность L на жилу трехжильного кабеля или трех одножильных кабелей состоит из двух частей, а именно самоиндукции проводника и взаимной индуктивности с другими жилами.

Формула для расчета индуктивности кабеля:

$ L = K + 0.2Log_e {\ frac {2S} {d}} $ (Гм / км)

Где:
L = Индуктивность кабеля в (Гм / км)

K = постоянная, относящаяся к формированию проводника (см. Таблицу ниже)

S = осевое расстояние между проводниками внутри кабеля (мм) или осевое расстояние между

Жилы трилистной группы одножильных кабелей (мм) или

= 1.26-кратное расстояние между фазами для плоского формирования трех одножильных кабелей (мм)

d = диаметр жилы или для фигурных конструкций диаметр эквивалентного круглого

проводник (мм)

Для двухжильных, трехжильных и четырехжильных кабелей индуктивность, полученную по формуле, следует умножить на 1,02, если жилы круглой или секторной формы, и на 0,97 для 3-жильных овальных проводников.

Типичные значения K для различных многожильных проводников (при 50 Гц)

Количество проводов в проводнике	К
3	0.0778
9	0,0642
7	0,0554
37	0,0528
61 и старше	0,0514
1 (сплошной)	0,0500
Полый проводник, канал 12 мм	0.0383

Калькулятор собственной индуктивности провода

Обзор калькулятора собственной индуктивности провода

Обычно мы ассоциируем индуктивность с петлей или катушкой с проволокой. Однако даже прямой кусок проволоки или ваш электрод имеет некоторую самоиндукцию. Этот инструмент используется для расчета индуктивности отрезка провода с учетом его диаметра и длины. В большинстве случаев самоиндукция провода игнорируется.Потому что индуктивность очень мала, чтобы существенно повлиять на схему. Однако по мере того, как частота увеличивается в микроволновом диапазоне, даже индуктивность коротких отрезков провода может иметь значительное влияние.

Формула для калькулятора собственной индуктивности провода

Где

Для этого расчета единицы измерения диаметра и длины указаны в см.
Проницаемость ( µ ) принята равной 1,0.
Приведенное выше уравнение взято из «Расчетов индуктивности» Ф.W. Grover

Примечание. Узнайте, что такое собственная индуктивность, из следующего видео:

Самоиндуктивность индукторов и катушек

Люди тоже спрашивают (Q&A)

1. Что означает самоиндукция?
Определения самоиндукции
Самоиндукция: Самоиндукция определяется как явление, при котором изменение электрического тока в цепи вызывает индуцированную электродвижущую силу в той же цепи.

2. Какова собственная индуктивность прямого провода?
ноль
Поскольку в прямом проводе нет замкнутых контуров, собственная индуктивность равна нулю.

3. Что такое собственная индуктивность L?
В электрической цепи, когда ЭДС индуцируется в той же цепи, в которой изменяется ток, этот эффект называется самоиндукцией (L), но иногда его обычно называют обратной ЭДС, поскольку ее полярность противоположна приложенное напряжение.

4. Где используется собственная индуктивность?
Применения самоиндукции включают следующее.
Цепи настройки
Дроссели, используемые в качестве реле
Датчики
Ферритовые шарики
Накопление энергии в устройстве
Дроссели
Асинхронные двигатели
Фильтры

5.В чем разница между самоиндукцией и самоиндукцией?
Самоиндукция — это явление, при котором изменение электрического тока в катушке вызывает наведенную ЭДС в самой катушке. … Самоиндукция катушки определяется как отношение самоиндуцированной ЭДС к скорости изменения тока в катушке.

6. Что такое самоиндукция и ее единицы?
S.I., единицей самоиндукции является Генри. то есть 1 Генри = 1 виток Вебера / Ампер. или 1 Генри = 1 Вольт / ампер / секунду.Самоиндукция катушки составляет 1 Генри, когда изменение тока через катушку со скоростью 1 ампер / сек индуцирует в катушке ЭДС в 1 вольт.

myCableEngineering.com> Индуктивность и реактивность

Индуктивность кабеля состоит из двух частей:

1. самоиндукция проводника
2. взаимная индуктивность между проводниками

Справочник по электрическим кабелям

BICC

Справочник BICC по электрическим кабелям, дайте формулу для индуктивности как:

L = (К + 0.2ln2Sd) × 10−6

где:
L — индуктивность кабеля, Hm ^-1
K — постоянная образования жилы
S — осевое расстояние между проводниками в кабеле, мм
— осевое расстояние между кондукторами в трилистнике, мм
— 1,26 x шаг плоских пластовых жил, мм
d — диаметр кондуктора, мм

Для 2-, 3- или 4-жильных круглых или секторных кабелей умножьте указанное выше на 1,02, чтобы получить индуктивность.Умножьте на 0,97 для трехжильных овальных проводников.

Типичные значения K

Количество жил в жиле	К
1 (сплошной)	0,0500
3	0,0778
7	0,0642
19	0,0554
37	0.0528
61 и более	0,0514

Реактивное сопротивление

Реактивное сопротивление проводника определяется по формуле:

.

Х = 2πfL

где:

X — реактивное сопротивление в Ом · м — ¹
L i — реактивное сопротивление в Н · м ^-1

CENELEC CLC / TR 50480

Уравнения для индуктивности приведены в CENELEC CLC / TR 50480 «Определение площади поперечного сечения проводов и выбор защитных устройств».

Трехстрочный или межстрочный:

Линия на нейтраль:

где:
x — реактивное сопротивление на метр жилы, мОм м ^-1
X _c — реактивное сопротивление жилы, мОм
X _cN —
X _cPE —
X _cPEN —

МЭК 60909

См. Импеданс

Индуктивность линии передачи — двухпроводная линия, трехфазная симметричная линия и трехфазная несимметричная линия

В средних и длинных линиях передачи индуктивность (реактивное сопротивление) более эффективно, чем сопротивление.Ток в линии передачи взаимодействует с другим параметром, то есть с индуктивностью. Мы знаем, что когда ток течет по проводнику, создается магнитный поток. При изменении тока в проводнике изменяется и количество линий потока, и в нем индуцируется ЭДС (закон Фарадея). Эта наведенная ЭДС представлена ​​параметром, известным как индуктивность.

Флюсовая связь с проводником состоит из двух частей: внутреннего и внешнего.Внутренний поток возникает из-за протекания тока в проводнике. Внешний поток, создаваемый вокруг проводника, возникает из-за его собственного тока, а ток других проводников проходит вокруг него. Полная индуктивность проводника определяется расчетом внутреннего и внешнего магнитного потока.

Индуктивность двухпроводной линии

Считается однофазной линией, состоящей из двух проводов (фаза и нейтраль) a и b равного радиуса r. Они расположены на расстоянии D метров.Сечения проводов показаны на схеме ниже.

Пусть ток течет в проводниках противоположного направления, так что один становится обратным путем для другого.

Потоковые связи проводника «а» задаются формулой

Здесь,

I _a = + I
I _b = -I
D _aa = r ’
D _ab = D

Подставляя эти значения в уравнение выше

Точно так же потокосцепление с проводником «b» будет

Индуктивность проводника «а»

Аналогично индуктивность проводника «b»

Индуктивность на провод

Индуктивность обоих проводников определяется по формуле

.

Индуктивность отдельного проводника составляет половину общей индуктивности двухпроводной линии.

Индуктивность симметричной трехфазной линии

В симметричной трехфазной линии все проводники расположены в углах равностороннего треугольника. Такое расположение проводов также называют равносторонним шагом. Это показано на схеме ниже

Пусть расстояние между проводниками равно D, а радиус каждого проводника r. Потоковые связи проводников и задаются уравнением:

В данном случае

Для трехпроводной системы алгебраическая сумма токов в проводниках равна нулю.

Таким образом, уравнение потока становится

Используя формулу Индуктивность проводника, «а» равно

.

Индуктивность проводников b и c также будет такой же, как у проводников a. Индуктивность трехфазной линии равна двухпроводной линии.

Индуктивность несимметричной трехфазной линии

Трехфазная линия считается несимметричной, если ее проводники расположены на разных расстояниях. Такое расположение жил наиболее распространено на практике из-за их дешевизны и удобства в конструкции и конструкции .

Рассмотрим трехфазную несимметричную линию с разным расстоянием между проводниками, радиус каждого проводника равен r. Это показано на схеме ниже

Потоковая связь в «а» выражается формулой

Потоковая связь в проводнике «a» из-за «b» определяется формулой

Потоковая связь в проводнике «a» из-за «c» определяется по

Среднее значение потокосцепления «а» составляет

Т.к. для уравновешенных условий

По формуле

Средняя индуктивность фазы а составляет

Аналогично

Таким образом, установлено, что значения индуктивности для трех фаз уравниваются транспозициями.

7.14: Индуктивность коаксиальной структуры

Давайте теперь определим индуктивность коаксиальной структуры, показанной на рисунке \ (\ PageIndex {1} \). Индуктивность этой структуры представляет интерес по ряду причин, в частности, для определения характеристического импеданса коаксиальной линии передачи, как описано в разделе 3.10.

Рисунок \ (\ PageIndex {1} \): Определение индуктивности коаксиальной линии.

Для наших настоящих целей мы можем смоделировать структуру, как показано на рисунке \ (\ PageIndex {1} \).Эта модель состоит из двух концентрических идеально проводящих цилиндров радиусов \ (a \) и \ (b \), разделенных однородным материалом с проницаемостью \ (\ mu \). Чтобы облегчить анализ, разместим ось \ (+ z \) вдоль общей оси концентрических цилиндров, чтобы цилиндры можно было описать как поверхности \ (\ rho = a \) и \ (\ rho = b \ ).

Ниже мы найдем индуктивность, приняв ток \ (I \) на внутреннем проводнике и интегрируя по результирующему магнитному полю, чтобы получить магнитный поток \ (\ Phi \) между проводниками.Затем индуктивность может быть определена как отношение потока отклика к току источника.

Прежде чем мы начнем, обратите внимание, что вывод, который мы собираемся сделать, аналогичен выводу емкости коаксиальной структуры, рассмотренному в разделе 5.24. Читателю может быть полезно ознакомиться с этим разделом, прежде чем пытаться сделать это.

Первый шаг — найти магнитное поле внутри конструкции. Это относительно просто, если мы можем пренебречь краевыми полями, поскольку тогда внутреннее поле можно считать постоянным по отношению к \ (z \).Этот анализ также применим к случаю, когда длина \ (l \) относится к одному короткому участку гораздо более длинной конструкции; в этом случае мы получим индуктивность на длину , а не полную индуктивность конструкции. Обратите внимание, что последнее — именно то, что нам нужно для модели эквивалентной схемы с сосредоточенными элементами (раздел 3.4).

Чтобы определить индуктивность, мы используем определение: \ [L \ треугольник \ frac {\ Phi} {I} \ label {m0125_eIndDef} \] Ток \ (I \), текущий в направлении \ (+ z \) на внутренний проводник создает магнитное поле внутри коаксиальной структуры.Напряженность магнитного поля для этого сценария была определена в разделе 7.5, где мы нашли \ [{\ bf H} = \ hat {\ phi} \ frac {I} {2 \ pi \ rho} ~~, ~~ a \ le \ rho \ le b \] Читатель должен заметить, что в этом разделе мы рассматривали просто линию тока; не коаксиальная структура. Итак, на каком основании мы утверждаем, что поле внутри коаксиальной структуры одинаково? Это следствие закона Ампера (раздел 7.14): \ [\ oint _ {\ mathcal C} {\ bf H} \ cdot d {\ bf l} = I_ {encl} \] Если в этой новой задаче мы укажем то же круговой путь \ (\ mathcal {C} \) с радиусом больше \ (a \) и меньше \ (b \), тогда заключенный ток будет просто \ (I \).Наличие внешнего проводника не меняет радиальную симметрию проблемы, и больше ничего не остается, что могло бы изменить исход. Это стоит отметить для справки в будущем:

Магнитное поле внутри коаксиальной структуры, состоящей из концентрических проводников, несущих ток \ (I \), идентично магнитному полю линейного тока \ (I \) в свободном пространстве.

Нам понадобится плотность магнитного потока (\ ({\ bf B} \)) в отличие от \ ({\ bf H} \), чтобы получить магнитный поток.Это просто, поскольку они связаны проницаемостью среды; т.е. \ ({\ bf B} = \ mu {\ bf H} \). Таким образом: \ [{\ bf B} = \ hat {\ phi} \ frac {\ mu I} {2 \ pi \ rho} ~~, ~~ a \ le \ rho \ le b \]

Затем мы получаем \ (\ Phi \) путем интегрирования по плотности магнитного потока \ [\ Phi = \ int _ {\ mathcal S} {{\ bf B} \ cdot d {\ bf s}} \] где \ ( \ mathcal {S} \) — это любая открытая поверхность, через которую должны проходить все силовые линии магнитного поля внутри конструкции. Так как это может быть любая такая поверхность, мы можем также выбрать самую простую.{b} \ frac {d \ rho} {\ rho} \ right) \\
& = \ frac {\ mu I l} {2 \ pi} \ ln \ left (\ frac {b} {a} \ right )
\ конец {выровнено}

Заключение: \ [L \ треугольник \ frac {\ Phi} {I} = \ frac {\ left (\ mu Il / 2 \ pi \ right) \ ln \ left (b / a \ right)} {I} \] Обратите внимание, что множители \ (I \) в числителе и знаменателе сокращаются, оставляя: \ [\ boxed {L = \ frac {\ mu l} {2 \ pi} \ ln \ left (\ frac {b} {a} \ right)} \] Обратите внимание, что это размерно правильный, имея единицы H. Также обратите внимание, что это выражение зависит только от материалов (через \ (\ mu \)) и геометрии (через \ (l \), \ (a \) и \ (b \)).Примечательно, что , а не , зависит от тока, что подразумевает нелинейное поведение.

Чтобы восстановить соединение с параметрами модели линии передачи с сосредоточенными элементами (разделы 3.4 и 3.10), мы просто разделим на \ (l \), чтобы получить параметр длины на единицу: \ [\ boxed {L ‘= \ frac { \ mu} {2 \ pi} \ ln \ left (\ frac {b} {a} \ right)} \ label {m0125_eLp} \], который имеет ожидаемые единицы H / m.

Пример \ (\ PageIndex {1} \): Индуктивность коаксиального кабеля RG-59

Коаксиальный кабель

RG-59 состоит из внутреннего проводника радиусом \ (0.292 \) мм, внешний проводник с радиусом \ (1.855 \) мм и полиэтиленовый (немагнитный диэлектрик) промежуточный материал. Оцените индуктивность на длину RG-59.

Решение

Из постановки задачи, \ (a = 0,292 \) мм, \ (b = 1,855 \) мм и \ (\ mu \ cong \ mu_0 \), поскольку промежуточный материал немагнитен. Используя уравнение \ ref {m0125_eLp}, мы находим \ (L ‘\ cong 370 \) nH / m.

Авторы и ссылки

Вычисление индуктивности прямого провода

Иногда возникает вопрос, можете ли вы вычислить индуктивность одиночного прямого провода.На этот, казалось бы, простой вопрос на самом деле нет ответа, и он дает нам возможность поговорить об очень интересном моменте при решении уравнений Максвелла. Любой, кто работает в области вычислительной электромагнетизма, должен понимать эту ключевую концепцию, поскольку она поможет вам правильно создавать и интерпретировать модели, включающие магнитные поля.

Какова индуктивность одиночного прямого провода?

Прежде чем мы перейдем к этой концепции, давайте еще раз рассмотрим вопрос: какова индуктивность одиночного прямого провода? Чтобы решить эту проблему, мы рассмотрим определение индуктивности, основанное на энергии:

Индуктивность, L , определяется в терминах тока, I , протекающего через систему, и Вт _м , плотность магнитной энергии пропорциональна B ² .Магнитное поле B существует внутри и снаружи провода. Внутри проволоки он линейно увеличивается кнаружи от центральной линии, а за пределами проволоки опускается как 1/ r , где r — радиус. Итак, чтобы вычислить магнитное поле и распределение магнитной энергии, мы строим модель, основанную на уравнениях Максвелла, в данном случае на Законе Ампера. Источник тока подается на один конец провода, а другой конец заземлен. Плотность тангенциального магнитного потока ограничена нулем на внешних границах модели.

Мы можем построить эту модель в COMSOL Multiphysics, используя физический интерфейс Magnetic and Electric Fields модуля AC / DC, который будет определять электрические поля и токи в проводе, а также магнитные поля в проводе и окружающей среде. воздух. Граничное условие Клемма возбудит конструкцию и автоматически вычислит индуктивность, используя приведенную выше формулу. Граничное условие Заземление на другом конце провода обеспечивает сток тока, а граничное условие Магнитная изоляция устанавливает плотность тангенциального магнитного потока равной нулю.

Теперь поля бесконечно распространяются вокруг провода, но плотность магнитной энергии падает как 1/ r ² , поэтому мы можем подумать, что достаточно изучить увеличивающиеся радиусы нашей области моделирования, и что индуктивность будет сходятся. Однако, если мы попробуем это сделать, индуктивность как функция радиуса будет выглядеть так:

С увеличением радиуса увеличивается и индуктивность. Независимо от того, насколько большой мы делаем область моделирования, индуктивность для этой модели прямого провода не сходится!

Не только решение для индуктивности

Все выглядит довольно мрачно, если мы даже не можем правильно вычислить этот простой случай, верно? На самом деле, мы не просто вычисляем индуктивность провода в этой модели.Вы всегда рассчитываете для индуктивности системы, которая должна включать текущий обратный путь. Основные уравнения Максвелла сформулированы в предположении, что ток (электронов) не может быть ни создан, ни разрушен . Фактически, граничные условия Magnetic Insulation обеспечивают этот обратный путь тока. Мы можем увидеть это, нанеся ток в объемах, а также поверхностные токи:

Красные стрелки на рисунке выше показывают, что ток течет по проводу, а также течет по граничным условиям Magnetic Insulation как поверхностный ток.Граничное условие Magnetic Insulation можно рассматривать как представление материала с бесконечной проводимостью, по которому может беспрепятственно течь ток. Путь тока на приведенном выше рисунке — , соленоидальный , что означает, что ток течет по замкнутому пути. Существует токопроводящий путь не только от клеммы к граничным условиям заземления через провод, но также от граничного условия заземления обратно к клеммам вдоль границ.

Соленоидный тракт

Ключевым моментом здесь является концепция соленоидального пути для тока.Всякий раз, когда вы настраиваете какую-либо модель магнитного поля, вы должны убедиться, что ток может течь по замкнутому контуру. У вас нет выбора: этого требуют уравнения Максвелла. Вы также должны знать, что этот текущий путь возврата повлияет на результаты. В приведенной выше модели мы не только вычисляем индуктивность из-за тока, протекающего по проводу, мы также учитываем влияние тока, протекающего обратно вдоль граничных условий магнитной изоляции.

При настройке любого типа модели магнитного поля вы должны смоделировать полный путь соленоидального тока, а индуктивность, которую вы вычисляете по такой модели, представляет собой всю токовую петлю.

Вот почему вы не можете вычислить индуктивность одиночного прямого провода!

Конечно, пока система, которую вы анализируете, является соленоидальной, с током, протекающим по петле, вы можете правильно вычислить индуктивность.

Дополнительная литература

Чтобы увидеть примеры, которые вычисляют взаимную индуктивность между кольцевыми витками провода и сравнивают с аналитическими решениями, см .:

Формула индуктивности

для прямоугольных плоских спиральных индукторов с прямоугольным поперечным сечением проводника

Дж.Чен и Дж. Дж. Лиу, Спиральные индукторы на кристалле для ВЧ-приложений: обзор, Journal of Semiconductor Technology and Science, vol. 4, вып. 3, 149-167, 2004.

Д. Парет, RFID и приложения для бесконтактных смарт-карт, John Wiley & Sons, Ltd, Западный Суссекс, 2005 г.

Смотреть статью

Д. Парет, Конструкции антенн для устройств NFC, ISTE Ltd, Лондон, 2016.

Смотреть статью

р.А. Потирайло, К. Сурман, С. Го, Й. Ли, Т. Сивавек и В. Г. Моррис, Разработка датчиков радиочастотной идентификации на основе органических электронных чувствительных материалов для избирательного обнаружения токсичных паров, Журнал прикладной физики. , т. 106, 124902-1 — 124902-6, 2009.

Смотреть статью

Дж. М. Парк, К. Б. Ли и К. Х. Бэк, Устройство и метод беспроводной зарядки, Патент США US 9,590,446 B2, 2017.

С.Панчал, С. Стеген, ан Дж. Лу, Обзор статической и динамической беспроводной системы зарядки электромобилей, «Инженерная наука и технологии», международный журнал, вып. 21, нет. 5, 922-937, 2018.

Смотреть статью

T. P. Theodoulidis и E. E. Kriezis, Оценка импеданса прямоугольных катушек для вихретокового тестирования плоских сред, Ndt & E International, vol. 35, нет. 6, 407-414, 2002.

Смотреть статью

р.Дж. Дитчберн и С. К. Берк, Плоские прямоугольные спиральные катушки в вихретоковом неразрушающем контроле, Ndt & E International, vol. 38, нет. 8, 690-700, 2005.

Смотреть статью

Х. М. Теплица, Проектирование плоских прямоугольных микроэлектронных индукторов, IEEE Trans. по деталям, гибридам и упаковке, т. 10, вып. 2, 101-109, 1974.

Смотреть статью

Х. А. Эбишер, Сравнительное исследование аналитических формул индуктивности для квадратных плоских спиральных индукторов, Advanced Electromagnetics, vol.7, вып. 5, 3-48, 2018.

Смотреть статью

Дж. Кролс, П. Кингет, Дж. Кранинкс и М. Стейарт, Аналитическая модель плоских индукторов на низколегированных кремниевых подложках для проектирования высокочастотных аналоговых сигналов до 3 ГГц, Симпозиум IEEE по схемам СБИС, Гонолулу, Дайджест технических Статьи, 28-29, 1996.

С. С. Джаяраман, В. Ванукуру, Д. Наир и А. Чакра-Ворти, Масштабируемая, широкополосная и физическая модель для встроенных в кристалл прямоугольных спиральных индукторов, IEEE Trans.по магнетике, т. 55, нет. 9, 8402006, 2019.

Смотреть статью

С. С. Мохан, Проектирование, моделирование и оптимизация схем индуктивности и трансформатора на кристалле, Ph.D. диссертация, Dept. Elect. Англ. Стэнфордский университет, Калифорния, США, 2000 г.

http://cc.ee.nchu.edu.tw/~aiclab/public_htm/VCO/Theses/1999mohan.pdf

Х. А. Эбишер, Формула индуктивности для квадратных плоских спиральных индукторов с прямоугольным поперечным сечением проводника, Advanced Electromagnetics, vol.8, вып. 4, 80-88, 2019.

Смотреть статью

Х. А. Эбишер и Б. Эбишер, Улучшенные формулы для индуктивности прямых проводов, Усовершенствованная электромагнетизм, т. 3, вып. 1, 31-43, 2014.

Смотреть статью

М. Камон, М. Дж. Цук и Дж. К. Уайт, FASTHENRY: трехмерная программа извлечения индуктивности с многополюсным ускорением, IEEE Trans. по теории и технике микроволнового излучения, т. 42, нет. 9, 1750-1758, 1994.

Смотреть статью

W. M. Haynes, Th. Дж. Бруно и Д. Р. Лиде, Справочник CRC по химии и физике, 95-е изд., Интернет-версия 2015, стр. 12-41, 2015.

К. Р. Пол, Индуктивность, John Wiley & Sons, Хобокен, штат Нью-Джерси, 2010 г.

Э. Б. Роза, Самостоятельная и взаимная индуктивность линейных проводников, Бюллетень Бюро стандартов, т. 4, вып. 2, 301-344, Вашингтон, 1908.

Смотреть статью

Ф.W. Grover, Inductance Calculations: Working For-Mulas and Tables, Dover Publications, New York, 2004, впервые опубликовано D. Van Nostrand Co., New York, 1946.

Э. Б. Роза, Расчет самоиндукции однослойных катушек, Бюллетень Бюро стандартов, т. 2, вып. 2, 161–187, Вашингтон, 1906.

Смотреть статью

Х. А. Эбишер и Х. Фридли, Аналитическое приближение для индуктивности кругло-цилиндрических двухпроводных линий передачи с эффектом близости, Advanced Electromagnetics, vol.