Как формулируется закон ома для полной цепи: Полный закон Ома для полной цепи. Формула закона Ома. « ЭлектроХобби

Закон Ома для полной цепи

Зако́н Ома — это физический закон, определяющий связь между напряжением, силой тока и сопротивлением проводника в электрической цепи. Назван в честь его первооткрывателя Георга Ома. Суть закона проста: сила тока в проводнике прямо пропорциональна напряжению между концами проводника, если при прохождении тока свойства проводника не изменяются. Следует также иметь в виду, что закон Ома является фундаментальным и может быть применён к любой физической системе, в которой действуют потоки частиц или полей, преодолевающие сопротивление. Его можно применять для расчёта гидравлических, пневматических, магнитных, электрических, световых, тепловых потоков и т. д., также, как и Правила Кирхгофа, однако, такое приложение этого закона используется крайне редко в рамках узко специализированных расчётов.

Закон Ома формулируется так: Сила тока в однородном участке цепи прямо пропорциональна напряжению, приложенному к участку, и обратно пропорциональна характеристике участка, которую называют электрическим сопротивлением этого участка.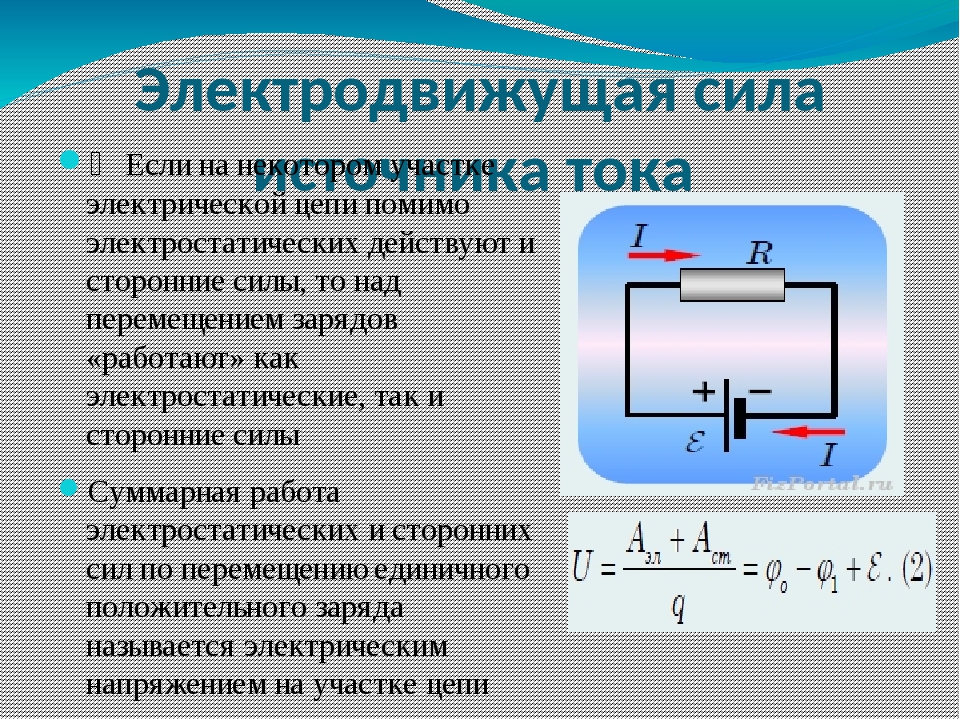

Ток, А	Напряжение, В	Сопротивление, Ом	Мощность, Вт
I	U	R	P

История закона Ома

Георг Ом, проводя эксперименты с проводником, установил, что сила тока I в проводнике пропорциональна напряжению U, приложенному к его концам:

,

или

.

Коэффициент пропорциональности назвали электропроводностью, а величину принято именовать электрическим сопротивлением проводника.

Закон Ома был открыт в 1827 году.

Закон Ома в интегральной форме

Схема, иллюстрирующая три составляющие закона Ома

Диаграмма, помогающая запомнить закон Ома. Нужно закрыть искомую величину, и два других символа дадут формулу для ее вычисления

Закон Ома для участка электрической цепи имеет вид:

U = RI

где:

• U — напряжение или разность потенциалов,
• I — сила тока,
• R — сопротивление.

Закон Ома также применяется ко всей цепи, но в несколько изменённой форме:

,

где:

Закон Ома в дифференциальной форме

Сопротивление R зависит как от материала, по которому течёт ток, так и от геометрических размеров проводника. Полезно переписать закон Ома в так называемой дифференциальной форме, в которой зависимость от геометрических размеров исчезает, и тогда закон Ома описывает исключительно электропроводящие свойства материала. Для изотропных материалов имеем:

где:

Все величины, входящие в это уравнение, являются функциями координат и, в общем случае, времени. Если материал анизотропен, то направления векторов плотности тока и напряжённости могут не совпадать. В этом случае удельная проводимость является тензором ранга (1, 1).

Раздел физики, изучающий течение электрического тока в различных средах, называется электродинамикой сплошных сред.

Закон Ома для переменного тока

Если цепь содержит не только активные, но и реактивные компоненты (ёмкости, индуктивности), а ток является синусоидальным с циклической частотой ω, то закон Ома обобщается; величины, входящие в него, становятся комплексными:

где:

• U = U₀e^iωt — напряжение или разность потенциалов,
• I — сила тока,
• Z = Re^—iδ — комплексное сопротивление (импеданс),
• R = (R_a²+R_r²)^1/2 — полное сопротивление,
• R_r = ωL — 1/ωC — реактивное сопротивление (разность индуктивного и емкостного),
• R_а — активное (омическое) сопротивление, не зависящее от частоты,
• δ = —arctg R_r/R_a — сдвиг фаз между напряжением и силой тока.

При этом переход от комплексных переменных в значениях тока и напряжения к действительным (измеряемым) значениям может быть произведен взятием действительной или мнимой части (но во всех элементах цепи одной и той же!) комплексных значений этих величин. Соответственно, обратный переход строится для, к примеру, U = U₀sin(ωt + φ) подбором такой , что . Тогда все значения токов и напряжений в схеме надо считать как

Если ток изменяется во времени, но не является синусоидальным (и даже периодическим), то его можно представить как сумму синусоидальных Фурье-компонент. Для линейных цепей можно считать компоненты фурье-разложения тока действующими независимо.

Также необходимо отметить, что закон Ома является лишь простейшим приближением для описания зависимости тока от разности потенциалов и для некоторых структур справедлив лишь в узком диапазоне значений. Для описания более сложных (нелинейных) систем, когда зависимостью сопротивления от силы тока нельзя пренебречь, принято обсуждать вольт-амперную характеристику.

Отклонения от закона Ома наблюдаются также в случаях, когда скорость изменения электрического поля настолько велика, что нельзя пренебрегать инерционностью носителей заряда.

Объяснение закона Ома

Закон Ома можно просто объяснить при помощи теории Друде

См. также

Wikimedia Foundation. 2010.

Закон Ома для полной цепи: определение для замкнутого участка

Одним из принципов электротехники является закон Ома для полной цепи. Используя установленную учёным закономерность, можно вычислить сопротивление электрической цепи или источника тока, рассчитать электродвижущую силу (ЭДС). Практическое же применение полученным при расчёте данным велико. Это подбор шунтирующих и предохранительных элементов, вычисление необходимой мощности используемых деталей, согласование электронных узлов.

История открытия

Зависимость между током, напряжением и сопротивлением в электрической цепи была установлена опытным путём в 1827 году. Занимаясь исследованиями электричества, Георг Симон Ом проводил ряд экспериментов над проводниками, изучая их проводимость, и в частности, подключая последовательно к источнику энергии тонкие проводники, выполненные из различных материалов. Изменяя их длину, он получал определённую силу тока. Им было установлено, что на результаты экспериментов влияет источник электрической энергии, сопротивление которого оказывалось выше, чем у используемых в опытах проводников.

По совету своего наставника Поггендорфа Ом собрал термоэлектрическую батарею, отказавшись от использования химических элементов, применив вместо них открытую Зеебеком термопару медь-висмут. Для измерения параметров цепи им использовались крутильные весы, с магнитной стрелкой сконструированные Кулоном.

На основании своих исследований физик-экспериментатор пришёл к выводу, что отклонение стрелки зависит от определённой силы, названной силой тока. Когда стрелка отклонялась, Ом закручивал весы таким образом, чтобы она возвращалась в своё начальное положение. Угол, на который закручивалась нить, он считал пропорциональной силе тока. Изменяя условия, Ом вывел математическую зависимость, составив уравнение. Выглядело оно следующим образом: Х = а/b + x, где за Х принималась сила, отклоняющая магнитную стрелку, за а — длина исследуемого образца, а b+x обозначали интенсивность и считались постоянной величиной.

В 1862 году в журнале «Физика и химия» публикуется статья Ома под названием «Определение закона, по которому металлы проводят контактное электричество». Результаты его исследований не производят впечатления на других ученых, и его выводы остаются незамеченными. Ом продолжает эксперименты, выясняя, что электричество можно рассмотреть наподобие теплового потока. Подобно разнице температур, благодаря которой совершается тепловое движение, некой величиной можно описать движение электрического заряда. Так он вводит понятие ЭДС.

Открытие Ома было принято учёным миром уже после его смерти. Существенный вклад в это внесли русские учёные Ленц и Якоби. В 1842 году Лондонское Королевское общество наградило физика золотой медалью, а закон, открытый им, был назван его именем.

Понятие тока и напряжения

Закономерность учёного

устанавливает зависимость между собой трёх электрических величин: тока, напряжения и сопротивления. Поэтому для того чтобы разобраться в сути закона Ома для полной электрической цепи, необходимо понимать, что же из себя они представляют.

В любом теле существуют свободные элементарные частички, обладающие определённым количеством энергии — зарядом. Если тело находится в спокойном состоянии, то есть на него не оказывается никакого воздействия, то происходит их хаотичное перемещение. Если же к телу приложено электрическое поле, то их перемещение становится упорядоченным, и они начинают передвигаться в одну сторону.

Такое направленное движение называют электрическим током. Мерой его служит сила тока, скалярная величина, определяемая отношением количества зарядов прошедших через поперечное сечение проводника за единицу времени: I = dq/dt. За единицу измерения силы тока принят ампер.

Если направление перемещения зарядов остаётся неизменным, то движение тока считается постоянным, а если изменяется — переменным. Возникновение тока возможно только в замкнутой цепи. Для того чтобы заряд переместился, приложенное поле должно выполнить работу. То есть затратить какую-то энергию для перемещения заряда с одной точки в другую. Если принять, что в начальном положении частичка обладает нулевым зарядом, то тогда переместившись, она уже будет иметь другое его значение. Разность между этими величинами называется разностью потенциалов или напряжением.

Для поддержания силы тока в полной цепи необходим источник, постоянно воздействующий на свободные заряды и поддерживающий разности потенциалов на различных участках цепи. Величина силы, которая действует на цепь, называется ЭДС. Физически она представляет собой отношение работы, затрачиваемой на передвижение заряда от одного своего полюса к другому, к значению заряда: E = A/q. Измеряется ЭДС, так же как и напряжение, в вольтах.

При перемещении заряд из-за особенностей строения кристаллической решётки вещества, он сталкивается с различными дефектами и примесями. В результате этого происходит частичное рассеивание его потенциала, а скорость движения замедляется. Потеря энергии характеризуется электрической величиной-сопротивлением. Другими словами, сопротивление — это величина, препятствующая прохождению тока.

Импеданс цепи

Немецкий физик, проводя эксперименты, смог обнаружить зависимость между током и напряжением. Их связь определялась через постоянную величину, которая после была названа сопротивлением. Так, формула закона Ома для полной цепи может быть записана в виде выражения:

I = E/Z, где:

• I — сила тока цепи;
• E — электродвижущая сила, приложенная к цепи;
• Z — постоянная величина (полное сопротивление).

Полное сопротивление (импеданс) электрической цепи важный параметр, определяющий силу тока и полезную мощность. Состоит она из нескольких составляющих: внутреннего сопротивления источника тока и сопротивления элементов, из которых состоит схема.

Поэтому в отличие от участка цепи, где берётся во внимание только сопротивление проводников, закон для всей цепи учитывает и электрическое сопротивление источника тока. В то же время характер происхождения сопротивления может носить как активную составляющую, так и реактивную, учитывающуюся для переменного тока.

Активная составляющая

Такое сопротивление называется активным, так как оно забирает на себя часть мощности, поступающей от источника питания. Эта забираемая энергия, проходя через проводник, превращается в тепло. При этом можно обнаружить, что если проводник подключить к переменному источнику сигнала, то его сопротивление будет немного больше.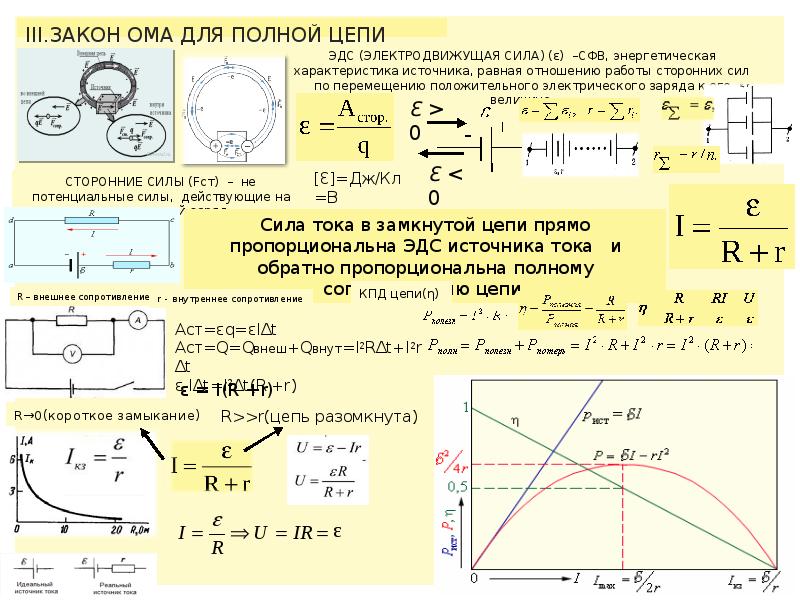 Связано это с тем, что индуцируемая ЭДС в материале в любой его точке неодинаковая. Ближе к центру она будет больше, чем у поверхности. То есть при переменном сигнале как бы происходит уменьшение полезного сечения проводника.

Сопротивление зависит от физических параметров материала. Математически это может быть описано выражением: R = p*L/S, где L — длина проводника, S — поперечное сечение, p — удельное сопротивление (табличное значение). Активное сопротивление слабо зависит от частоты сигнала, но при его увеличении возрастает.

Отличительной чертой элемента, обладающего активным сопротивлением, будет совпадение по фазе, протекающего через него тока и напряжения. Поэтому вычисляться оно по формуле: R = U/I.

Реактивное сопротивление

Индуктивное сопротивление связано с ЭДС самоиндукции. При протекании через элемент, обладающий индуктивностью, переменного тока, возникает магнитное поле, создающее ЭДС. Эта сила противодействует внешнему полю и препятствует его распространению. Затрачиваемая энергия увеличивает мощность магнитного поля. Как только ток уменьшается, значение магнитного поля начинает тоже снижаться, индуцируя ток самоиндукции. Его направление совпадает с убывающим током. В результате энергия, отобранная магнитным полем, начинает отдаваться обратно в цепь. То есть фактически, в отличие от активного сопротивления, потерь энергии не возникает.

Величина индуктивного сопротивления находится по формуле X L = 2 p * f * L, где: f — частота сигнала, L — значение индуктивности. Напряжение, приложенное к индуктивности и ток, поступающий от источника энергии, сдвинуты относительно друг друга по фазе на 90^{, при этом ток отстаёт от напряжения.}

Ёмкостное же сопротивление обусловлено возникновением электродвижущей силы. При прохождении через ёмкость энергия, поступающая от источника питания должна преодолеть ёмкостное сопротивление, затрачивая часть мощности для её заряда. Но как только подаваемый сигнал изменит знак, весь накопленный заряд ёмкостью начнёт возвращаться в цепь, увеличивая энергию электрического поля.

Другими словами, ёмкость становится источником ЭДС. Ёмкостное сопротивление описывается выражением: X c = 1/ (2 p * f * C), где: C — величина ёмкости. При таком роде сопротивления ток будет опережать напряжение по фазе на 90^.

Таким образом, реактивное сопротивление зависит от частоты сигнала. Общий же импеданс определяется не как сумма всех сопротивлений, а по формуле Z = (R²+ X l²+ X c²)^½.

Суть закона

Общепринятая формулировка закона Ома гласит, что сила тока в полной цепи прямо пропорциональна электродвижущей силе источника, делённой на общее сопротивление всех элементов замкнутой цепи. Классическая формула закона Ома для цепи постоянного тока выглядит следующим образом:

I = E /(r+R), где:

• R — сопротивление внешней части цепи, Ом;
• r — внутренний импеданс источника энергии.

В замкнутой схеме ток течёт от источника энергии, протекает через различные элементы, последовательно или параллельно подключённые к нему, и возвращается обратно. Изучая открытие Ома можно сформулировать основной физический принцип, на котором строится электротехника. Заключается он в том, что чем больше ЭДС, тем большей энергией будут обладать носители заряда, а значит и их скорость перемещения будет больше. При увеличении сопротивления в цепи скорость движения, а значит, и энергия носителей заряда уменьшается, соответственно снижается и ток.

Величина ЭДС зависит от характеристик источника энергии, а сопротивление от физических параметров материала и температуры. Значение активного сопротивления не может быть изменено увеличением направленного движения частиц или напряжения, но при этом реактивная составляющая зависит от частоты сигнала.

Поэтому закон Ома для полного участка цепи переменного тока и учитывает индуктивную и ёмкостную составляющую, причём как источника питания, так и самой цепи.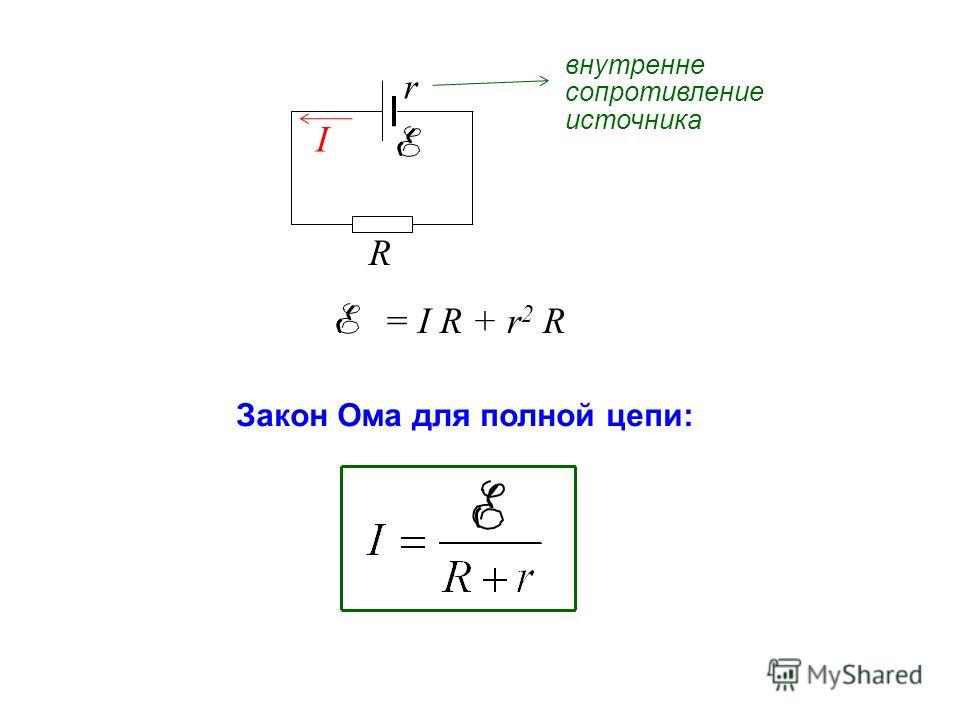 Описывается математически он формулой: I = Um /Z, где:

• Um — ЭДС источника питания;
• Z — импеданс всей замкнутой цепи: Z = (R²+(wL — 1/wC)²)^½.

То есть для переменного тока закон будет описываться выражением вида:

I = Um/ (R2+(wL -1/wC)2)½.

Однако следует понимать, что в формуле используются амплитудные значения величин, а не мгновенные.

Дифференциальное уравнение

Так как сопротивление зависит не только от физических свойств материала, но и от его геометрических параметров, часто последнее при использовании закона Ома исключается из формулы. Открытие учёного, учитывающее только электропроводящие свойства, записывают в так называемой дифференциальной форме.

Такая формула имеет вид: J = σ*E, где:

• J — плотность, характеризующая силу электричества протекающего через единицу площади;
• σ — удельная проводимость, величина обратная удельному сопротивлению;
• E — напряжённость поля, определяется в определённой точке как отношение силы действующей на неподвижный заряд к его величине.

Составляющие уравнения представляются в виде функции координат и времени. Удельная проводимость выражается в виде единичной матрицы. Поэтому закон можно представить формулой:

Таким образом, закон Ома для замкнутой цепи практически ничем не отличается от его формулировки для неполной схемы, лишь только дополнительно учитывает внутреннее сопротивление источника ЭДС. При этом его формулировка не изменяется.

Закон Ома для участка цепи | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко

Закон Ома для однородного участка элект­рической цепи кажется до­вольно простым: сила тока в однородном участке цепи прямо пропорциональна на­пряжению на концах этого участка и об­ратно пропорциональна его сопротивлению:

I = U / R,

где I —сила тока в участке цепи; U — на­пряжение на этом участке; R — сопротив­ление участка.

После известных опытов Эрстеда, Ам­пера, Фарадея возник вопрос: как зависит ток от рода и характеристик источника то­ка, от природы и характеристик провод­ника, в котором существует ток. Попытки установить такую зависимость удались лишь в 1826—1827 гг. немецкому физику, учи­телю математики и физики Георгу Симону Ому (1787—1854). Он разработал установку, в которой в значительной степени можно было устранить внешние влияния на ис­точник тока, исследуемые проводники и т. п. Следует также иметь в виду: для многих ве­ществ, которые проводят электрический ток, закон Ома вообще не выполняется (полу­проводники, электролиты). Металлические же проводники при нагревании увеличи­вают свое сопротивление.

Ом (Ohm) Георг Симон (1787—1854) — немецкий физик, учитель математики и физики, член-корреспондент Берлин­ской АН (1839). С 1833 г. профессор и с 1839 г. ректор Нюрнбергской высшей по­литехнической школы, в 1849—1852 гг. — профессор Мюнхенского университе­та. Открыл законы, названные его име­нем, для однородного участка цепи и для полной цепи, ввел понятие элект­родвижущей силы, падения напряже­ния, электрической проводимости. В 1830 г. произвел первые измерения электродвижущей силы источника тока.

В формулу закона Ома для однородного участка цепи входит напряжение U, которое измеряется работой, выполняемой при пе­ренесении заряда в одну единицу в данном участке цепи:

U = A / q,

где A — работа в джоулях (Дж), заряд q — в кулонах (Кл), а на­пряжение U — в вольтах (В).

Из формулы для закона Ома можно лег­ко определить значение сопротивления для участка цепи:

R = U / I.

Если напряжение определено в вольтах, а сила тока — в амперах, то значение со­противления получается в омах (Ом):

Ом = В/А.

На практике часто используются меньшие или большие единицы для измерения сопро­тивления: миллиом (1мОм = 10 Ом), килоом (1кОм = 10³ Ом), мегаом (1МОм = 10⁶ Ом) и т. п. Материал с сайта http://worldofschool.ru

Закон Ома для однородного участка цепи можно выразить через плотность тока и на­пряженность электрического поля в нем. В самом деле, с одной стороны, I = jS, а с дру­гой — I = (φ₁ — φ₂) / R = —Δφ / R. Если имеем однородный проводник, то и напряженность элект­рического поля в нем будет одинаковой и равной E = —Δφ / l. Вместо R подставляем его значение ρ • l / S и получаем:

j = —Δφ / ρl = (-1 / ρ) • (Δφ / l) = (1 / ρ) • E = σE.

Учитывая, что плотность тока j̅ и напряженность поля E̅ — величины векторные, имеем закон Ома в наиболее общем виде:

j̅ = σ͞E.

Это — одно из важнейших уравнений электродинамики, оно справедливо в любой точке электрического поля.

На этой странице материал по темам:

• Доклад по теме элементы электроцепи. закон ома для участка цепи

• Реферат по физике закон ома для участка цепи

• Шпаргалка «закон ома для однородного участка линейной цепи»

• Закон ома для неоднородного участка цепи реферат

• Краткий конспект участка земли закон ома

Вопросы по этому материалу:

• Какие электрические величины и как объединяет между собой за­кон Ома для однородного участка цепи?

• Что такое электрическое напряжение?

• Как определяется сопротивление проводников?

• Как формулируется закон Ома для каждой точки проводника с током, который объединяет такие электрические величины: плотность тока, удельные сопротивление или электропроводимость вещества проводника и напряженность электрического поля в данной точке проводника?

Закон ома для полной цепи простыми словами.

Закона ома и применение его на практике

Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже

Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.

Размещено на http://www.allbest.ru/

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ

Кафедра естественнонаучных дисциплин

Реферат

Закон Ома

Выполнил:

Иванов М. А.

Введение

1. Общий вид закона Ома

2. История открытия закона Ома, краткая биография ученого

3. Виды законов Ома

4. Первые исследования сопротивления проводников

5. Электрические измерения

Заключение

Литература, другие источники информации

Введение

Явления, связанные с электричеством были замечены в древнем Китае, Индии и древней Греции за несколько столетий до начала нашей эры. Около 600 года до н. э., как гласят сохранившиеся предания, древнегреческому философу Фалесу Милетскому было известно свойство янтаря, натертого об шерсть, притягивать легкие предметы. Кстати словом “ электрон” древние греки называли янтарь. От него же пошло и слово “электричество”. Но греки всего лишь наблюдали явления электричества, но не могли объяснить.

XIX век был полон открытий связанных с электричеством. Одно открытие порождало целую цепь открытий в течении нескольких десятилетий. Электричество из предмета исследования начало превращаться в предмет потребления. Началось его широкое внедрение в различные области производства. Были изобретены и созданы электрические двигатели, генераторы, телефон, телеграф, радио. Начинается внедрение электричества в медицину.

Напряжение, сила тока и сопротивление — физические величины, характеризующие явления, происходящие в электрических цепях. Эти величины связаны между собой. Эту связь впервые изучил немецкий физик 0м. Закон Ома был открыт в 1826 .

1. Общий вид закона Ома

Закон Ома звучит так: Сила тока на участке цепи прямо пропорциональна напряжению на этом участке (при заданном сопротивлении) и обратно пропорциональна сопротивлению участка (при заданном напряжении): I = U / R, из формулы следует, что U = IЧR и R = U / I. Так как сопротивление данного проводника не зависит ни от напряжения, ни от силы тока, то последнюю формулу надо читать так: сопротивление данного проводника равно отношению напряжения на его концах к силе протекающего по нему тока. В электрических цепях чаще всего проводники (потребители электрической энергии) соединяются последовательно (например, лампочки в елочных гирляндах) и параллельно (например, домашние электроприборы).

При последовательном соединении сила тока в обоих проводниках (лампочках) одинакова: I = I1 = I2, напряжение на концах рассматриваемого участка цепи складывается из напряжения на первой и второй лампочках: U = U1 + U2. Общее сопротивление участка равно сумме сопротивлений лампочек R = R1 + R2.

При параллельном соединении резисторов напряжение на участке цепи и на концах резисторов одинаково: U = U1 = U2. сила тока в неразветвленной части цепи равна сумме сил токов в отдельных резисторах: I = I1 + I2. Общее сопротивление участка меньше сопротивления каждого резистора.

Если сопротивления резисторов одинаковы (R1 = R2) то общее сопротивление участка Если в цепь включено параллельно три и более резисторов, то общее сопротивление может быть —

найдено по формуле: 1/R = 1/R1 + 1/R2 + … + 1/RN. Параллельно соединяются сетевые потребители, которые рассчитаны на напряжение, равное напряжению сети.

Итак, Закон Ома устанавливает зависимость между силой тока I в проводнике и разностью потенциалов (напряжением) U между двумя фиксированными точками (сечениями) этого проводника:

Коэффициент пропорциональности R , зависящий от геометрических и электрических свойств проводника и от температуры, называется омическим сопротивлением или просто сопротивлением данного участка проводника.

2. История открытия закона Ома, краткая биография ученого

Георг Симон Ом родился 16 марта 1787 года в Эрлангене, в семье потомственного слесаря. После окончания школы Георг поступил в городскую гимназию. Гимназия Эрлангена курировалась университетом. Занятия в гимназии вели четыре профессора. Георг, закончив гимназию, весной 1805 года приступил к изучению математики, физики и философии на философском факультете Эрлангенского университета.

Проучившись три семестра, он принял приглашение занять место учителя математики в частной школе швейцарского городка Готтштадта.

В 1811 году он возвращается в Эрланген, заканчивает университет и получает степень доктора философии. Сразу же по окончании университета ему была предложена должность приват-доцента кафедры математики этого же университета.

В 1812 году Ом был назначен учителем математики и физики школы в Бамберге. В 1817 году он публикует свою первую печатную работу, посвященную методике преподавания «Наиболее оптимальный вариант преподавания геометрии в подготовительных классах». Ом занялся исследованиями электричества. В основу своего электроизмерительного прибора Ом заложил конструкцию крутильных весов Кулона. Результаты своих исследований Ом оформил в виде статьи под названием «Предварительное сообщение о законе, по которому металлы проводят контактное электричество». Статья была опубликована в 1825 году в «Журнале физики и химии», издаваемом Швейггером. Однако выражение, найденное и опубликованное Омом, оказалось неверным, что стало одной из причин его длительного непризнания. Приняв все меры предосторожности, заранее устранив все предполагаемые источники ошибок, Ом приступил к новым измерениям.

Появляется в свет его знаменитая статья «Определение закона, по которому металлы проводят контактное электричество, вместе с наброском теории вольтаического аппарата и мультипликатора Швейггера», вышедшая в 1826 году в «Журнале физики и химии».

В мае 1827 года «Теоретические исследования электрических цепей» объемом в 245 страниц, в которых содержались теперь уже теоретические рассуждения Ома по электрическим цепям. В этой работе ученый предложил характеризовать электрические свойства проводника его сопротивлением и ввел этот термин в научный обиход. Ом нашел более простую формулу для закона участка электрической цепи, не содержащего ЭДС: «Величина тока в гальванической цепи прямо пропорциональна сумме всех напряжений и обратно пропорциональна сумме приведенных длин. При этом общая приведенная длина определяется как сумма всех отдельных приведенных длин для однородных участков, имеющих различную проводимость и различное поперечное сечение».

В 1829 году появляется его статья «Экспериментальное исследование работы электромагнитного мультипликатора», в которой были заложены основы теории электроизмерительных приборов. Здесь же Ом предложил единицу сопротивления, в качестве которой он выбрал сопротивление медной проволоки длиной 1 фут и поперечным сечением в 1 квадратную линию.

В 1830 году появляется новое исследование Ома «Попытка создания приближенной теории униполярной проводимости». Только в 1841 году работа Ома была переведена на английский язык, в 1847 году — на итальянский, в 1860 году — на французский.

16 февраля 1833 года, через семь лет после выхода из печати статьи, в которой было опубликовано его открытие, Ому предложили место профессора физики во вновь организованной политехнической школе Нюрнберга. Ученый приступает к исследованиям в области акустики. Результаты своих акустических исследований Ом сформулировал в виде закона, получившего впоследствии название акустического закона Ома.

Раньше всех из зарубежных ученых закон Ома признали русские физики Ленц и Якоби. Они помогли и его международному признанию. При участии русских физиков, 5 мая 1842 года Лондонское Королевское общество наградило Ома золотой медалью и избрало своим членом.

В 1845 году его избирают действительным членом Баварской академии наук. В 1849 году ученого приглашают в Мюнхенский университет на должность экстраординарного профессора. В этом же году он назначается хранителем государственного собрания физико-математических приборов с одновременным чтением лекций по физике и математике. В 1852 году Ом получил должность ординарного профессора. Ом скончался 6 июля 1854 года. В 1881 году на электротехническом съезде в Париже ученые единогласно утвердили название единицы сопротивления — 1 Ом.

3. Виды законов Ома

Существует несколько видов закона Ома.

Закон Ома для однородного участка цепи (не содержащего источника тока): сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника:

Закон Ома для полной цепи — сила тока в цепи пропорциональна действующей в цепи ЭДС и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника.

где I — сила тока

E — электродвижущая сила

R — внешнее сопротивление цепи (т.е. сопротивление той

части цепи, которая находится за пределами источника ЭДС)

ЭДС — работа сторонних сил (т.е. сил неэлектрического происхождения) по перемещению заряда в цепи отнесенная к величине этого заряда.

Единицы измерения:

ЭДС — вольты

Ток — амперы

Сопротивления (R и r) — омы

Применяя основной закон электрической цепи (закон Ома), можно объяснить многие природные явления, которые на первый взгляд кажутся загадочными и парадоксальными. Например, всем известно, что любой контакт человека с электрическими проводами, находящимися под напряжением, является смертельно опасным. Всего лишь одно прикосновение к оборвавшемуся проводу высоковольтной линии способно убить электрическим током человека или животное. Но в то же время, мы постоянно видим, как птицы спокойно усаживаются на высоковольтные провода электропередач, и ничто не угрожает жизни этих живых существ. Тогда как же найти объяснение такому парадоксу?

А объясняется подобное явление довольно просто, если представить, что находящаяся на электрическом проводе птица — это один из участков электрической сети, сопротивление второго значительно превышает сопротивление другого участка той же цепи (то есть небольшого промежутка между лапками птицы). Следовательно, сила электрического тока, воздействующая на первый участок цепи, то есть на тело птицы, будет совершенно безопасной для неё. Однако полная безопасность гарантирована ей только при соприкосновении с участком высоковольтного провода.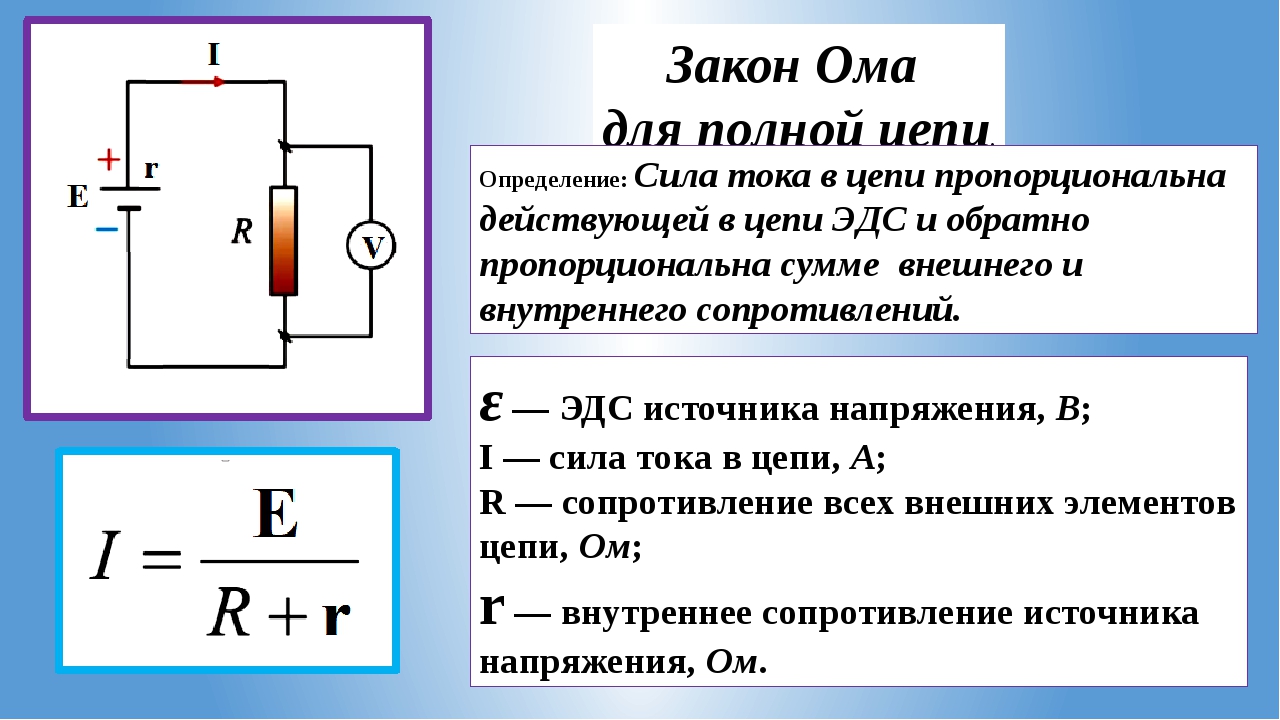 Но стоит только птице, усевшейся на линию электропередач, задеть крылом или клювом провод или какой-либо предмет, находящийся вблизи от провода (например, телеграфный столб), то птица неминуемо погибнет. Ведь столб непосредственно связан с землёй, и поток электрических зарядов, переходя на тело птицы, способен мгновенно убить её, стремительно двигаясь по направлению к земле. К сожалению, по этой причине в городах гибнет немало птиц.

Для защиты пернатых от губительного воздействия электричества зарубежными учеными были разработаны специальные устройства — насесты для птиц, изолированные от электрического тока. Такие приспособления размещали на высоковольтных линиях электропередач. Птицы, усаживаясь на изолированный насест, могут без всякого риска для жизни прикасаться клювом, крыльями или хвостом к проводам, столбам или кронштейнам. Наибольшим сопротивлением обладает поверхность верхнего, так называемого рогового слоя кожи человека. Сопротивление сухой и неповреждённой кожи может достигать 40 000 — 100 000 Ом. Роговой слой кожи очень незначителен, всего 0,05 — 0,2 мм. и легко пробивается напряжением 250 В. При этом сопротивление уменьшается в сто раз и падает тем скорее, чем дольше действует на тело человека ток. Резко, до 800 — 1000 Ом, уменьшают сопротивление тела человека повышенная потливость кожного покрова, переутомление, нервное возбуждение, опьянение. Этим объясняется, что порой даже небольшое напряжение может вызвать поражение электрическим током. Если, например, сопротивление тела человека равно 700 Ом, то опасным будет напряжение всего в 35 В. Именно поэтому, например, специалисты-электрики даже при работе с напряжением 36 В применяют изолирующие защитные средства — резиновые перчатки или инструмент с изолированными ручками.

Закон Ома выглядит настолько просто, что трудности, которые пришлось преодолеть при его установлении, упускают из виду и забывают. Закон Ома нелегко проверить, и его нельзя рассматривать как очевидную истину; действительно, для многих материалов он не выполняется.

В чем же все-таки заключаются эти трудности? Разве нельзя проверить, что дает изменение числа элементов вольтова столба, определяя ток при разном числе элементов?

Дело в том, что, когда мы берем разное число элементов, мы меняем всю цепь, т.к. дополнительные элементы имеют и дополнительное сопротивление. Поэтому необходимо найти способ изменять напряжение, не меняя самой батареи. Кроме того, разный по величине ток нагревает проволоку до развой температуры, и этот эффект тоже может влиять на силу тока. Ом (1787—1854) преодолел эти трудности, воспользовавшись явлением термоэлектричества, которое открыл Зеебек (1770—1831) в 1822 г.

Таким образом, Ом показал, что ток пропорционален напряжению и обратно пропорционален полному сопротивлению цепи. Это был простой результат для сложного эксперимента. Так по крайней мере должно казаться нам сейчас.

Современники Ома, в особенности его соотечественники, полагали иначе: возможно, именно простота закона Ома вызывала у них подозрение. Ом столкнулся с затруднениями в cлужебной карьере, испытывал нужду; особенно угнетало Ома то, что не признавались его труды. К чести Великобритании, и в особенности Королевского общества, нужно сказать, что работа Ома получила там заслуженное признание. Ом входит в число тех великих людей, имена которых часто встречаются написанными с маленькой буквы: название «ом» было присвоено единице сопротивления.

4. Первые исследования сопротивления проводников

Что такое проводник? Это чисто пассивная составная часть электрической цепи, отвечали первые исследователи. Заниматься его исследованием — значит попросту ломать себе голову над ненужными загадками, т.к. только источник тока представляет собой активный элемент.

Такой взгляд на вещи объясняет нам, почему ученые, по крайней мере до 1840 г., почти не проявляли интереса к тем немногим работам, которые проводились в этом направлении.

Так, на втором съезде итальянских ученых, состоявшемся в Турине в 1840 г. (первый собирался в Пизе в 1839 г. и приобрел даже некое политическое значение), выступая в прениях по докладу, представленному Марианини, Де ла Рив утверждал, что проводимость большинства жидкостей не является абсолютной, «а скорее относительной и изменяется с изменением силы тока». А ведь закон Ома был опубликован за 15 лет до этого!

Среди тех немногих ученых, которые первыми стали заниматься вопросом проводимости проводников после изобретения гальванометра, был Стефано Марианини (1790—1866).

К своему открытию он пришел случайно, изучая напряжение батарей. Он заметил, что с увеличением числа элементов вольтова столба электромагнитное воздействие на стрелку не увеличивается заметным образом. Это заставило Марианини сразу же подумать, что каждый вольтов элемент представляет собой препятствие для прохождения тока. Он делал опыты с парами «активными» и «неактивными» (т. е. состоящими из двух медных пластинок, разделенных влажной прокладкой) и опытным путем нашел отношение, в котором современный читатель узнает частный случай закона Ома, когда сопротивление внешней цепи не принимается во внимание, как это и было в опыте Марианини.

Георг Симон Ом (1789—1854) признавал заслуги Марианини, хотя его труды и не оказали Ому непосредственной помощи в работе. Ом вдохновлялся в своих исследованиях работой («Аналитическая теория тепла», Париж, 1822 г.) Жана Батиста Фурье (1768—1830)—одной из самых значительных научных работ всех времен, очень быстро получившей известность и высокую оценку среди математиков и физиков того времени. Ому пришла мысль, что механизм «теплового потока», о котором говорит Фурье, можно уподобить электрическому току в проводнике. И подобно тому как в теории Фурье тепловой поток между двумя телами или между двумя точками одного и того же тела объясняется разницей температур, точно так же Ом объясняет разницей «электроскопических сил» в двух точках проводника возникновение электрического тока между ними.

Придерживаясь такой аналогии, Ом начал свои экспериментальные исследования с определения относительных величин проводимости различных проводников. Применив метод, который стал теперь классическим, он подключал последовательно между двумя точками цепи тонкие проводники из различных материалов одинакового диаметра и изменял их длину так, чтобы получалась определенная величина тока. Первые результаты, которые ему удалось получить, сегодня кажутся довольно скромными. закон ом электрический гальванометр

Историки поражаются, например, тем, что по измерениям Ома серебро обладает меньшей проводимостью, чем медь и золото, и снисходительно принимают данное впоследствии самим Омом объяснение, согласно которому опыт проводился с серебряной проволокой, покрытой слоем масла, и это вводило в заблуждение относительно точного значения диаметра.

В то время имелось множество источников ошибок при проведении опытов (недостаточная чистота металлов, трудность калибровки проволоки, трудность точных измерений и т. п.). Важнейшим же источником ошибок была поляризация батарей. Постоянные (химические) элементы тогда еще не были известны, так что за время, необходимое для измерений, электродвижущая сила элемента существенно менялась. Именно эти причины, вызывавшие ошибки, привели к тому, что Ом на основании своих опытов пришел к логарифмическому закону зависимости силы тока от сопротивления проводника, включенного между двумя точками цепи. После опубликования первой статьи Ома Поггендорф посоветовал ему отказаться от химических элементов и воспользоваться лучше термопарой медь — висмут, незадолго до этого введенной Зеебеком.

Ом прислушался к этому совету и повторил свои опыты, собрав установку с термоэлектрической батареей, во внешнюю цепь которой включались последовательно восемь медных проволок одинакового диаметра, но разной длины. Силу тока он измерял с помощью своего рода крутильных весов, образуемых магнитной стрелкой, подвешенной на металлической нити. Когда ток, параллельный стрелке, отклонял ее, Ом закручивал нить, на которой она была подвешена, пока стрелка не оказывалась в своем обычном положении;

сила тока считалась пропорциональной углу, на который закручивалась нить. Ом пришел к выводу, что результаты опытов, проведенных с восемью различными проволоками, «могут быть выражены очень хорошо уравнением

где X означает интенсивность магнитного действия проводника, длина которого равна х, а а и b — константы, зависящие соответственно от возбуждающей силы и от сопротивления остальных частей цепи».

Условия опыта менялись: заменялись сопротивления и термоэлектрические пары, но результаты все равно сводились к приведенной выше формуле, которая очень просто переходит в известную нам, если X заменить силой тока, a —электродвижущей силой и b+x,—общим сопротивлением цепи.

Получив эту формулу, Ом пользуется ею для изучения действия мультипликатора Швейггера на отклонение стрелки и для изучения тока, который проходит во внешней цепи батареи элементов, в зависимости от того, как они соединены — последовательно или параллельно. Таким образом он объясняет (как это делается теперь в учебниках), чем определяется внешний ток батареи,— вопрос, который был довольно темным для первых исследователей. Ом надеялся, что его экспериментальные работы откроют ему путь в университет, чего он так желал. Однако статьи прошли незамеченными. Тогда он оставил место преподавателя в кельнской гимназии и отправился в Берлин, чтобы теоретически осмыслить полученные результаты. В 1827 г. в Берлине он опубликовал свой главный труд «Die galvanische Kette, mathe-matisch bearbeitet» («Гальваническая цепь, разработанная математически»).

Эта теория, при разработке которой он вдохновлялся, как мы уже указывали, аналитической теорией теплоты Фурье, вводит понятия и точные определения электродвижущей силы, или «электроскопической силы», как ее называет Ом, электропроводности (Starke der Leitung) и силы тока. Выразив выведенный им закон в дифференциальной форме, приводимой современными авторами, Ом записывает его и в конечных величинах для частных случаев конкретных электрических цепей, из которых особенно важна термоэлектрическая цепь. Исходя из этого, он формулирует известные законы изменения электрического напряжения вдоль цепи.

Но теоретические исследования Ома также остались незамеченными, а если кто-нибудь и писал о них, то лишь для того, чтобы, высмеять «болезненную фантазию, единственной целью которой является стремление принизить достоинство природы». И лишь лет десять спустя его гениальные работы постепенно начали пользоваться должным признанием: в

Германии их оценили Поггендорф и Фехнер, в России — Ленц, в Англии — Уитстон, в Америке — Генри, в Италии — Маттеуччи.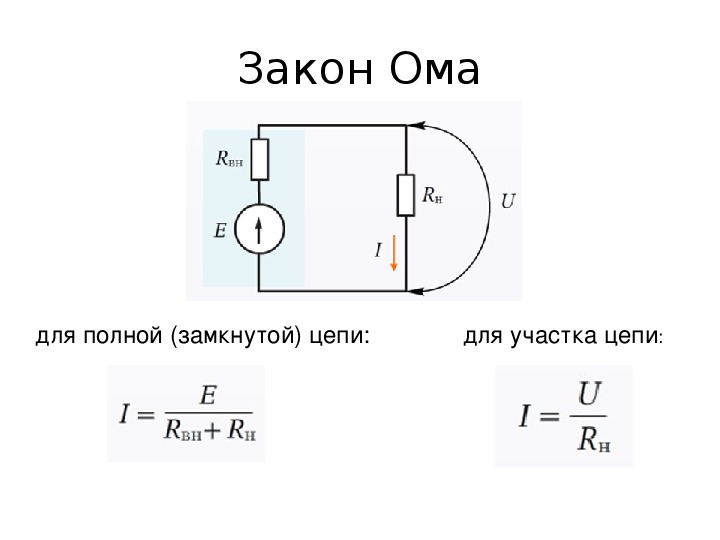

Одновременно с опытами Ома во Франции проводил свои опыты А. Беккерель, а в Англии — Барлоу. Опыты первого особенно замечательны введением дифференциального гальванометра с двойной обмоткой рамки и применением «нулевого» метода измерения. Опыты же Барлоу стоит упомянуть потому, что они экспериментально подтвердили постоянство силы тока во всей цепи. Этот вывод был проверен и распространен на внутренний ток батареи Фехнером в 1831 г., обобщен в 1851 г. Рудольфом Кольраушем

(180Э—1858) на жидкие проводники, а затем еще раз подтвержден тщательными опытами Густава Нидмана (1826—1899).

5. Электрические измерения

Беккерель применил дифференциальный гальванометр для сравнения электрических сопротивлений. На основе проведенных им исследований он сформулировал известный закон зависимости сопротивления проводника от его длины и сечения. Эти работы были продолжены Пуйе и описаны им в последующих изданиях его известных «Elements de

physique experimentale» («Основы экспериментальной физики»), первое издание которых появилось в 1827 г. Сопротивления определялись методом сравнения.

Уже в 1825 г. Марианини показал, что в разветвляющихся цепях электрический ток распределяется по всем проводникам независимо от того, из какого материала они сделаны, вопреки утверждению Вольты, который полагал, что если одна ветвь цепи образуется металлическим проводником, а остальные — жидкими, то весь ток должен проходить по металлическому проводнику. Араго и Пуйе популяризировали во Франции наблюдения Марианини. Не зная еще закона Ома, Пуйе в 1837 г. воспользовался этими наблюдениями и законами Беккереля, чтобы показать, что проводимость цепи, эквивалентной двум

разветвленным цепям, равна сумме проводимостей обеих цепей. Этой работой Пуйе положил начало изучению разветвленных цепей. Пуйе установил для них целый ряд терминов,

которые живы и до сих пор, и некоторые частные законы, обобщенные Кирхгофом в 1845 г. в его известных «принципах»..

Самый большой толчок для проведения электрических измерений, и в частности измерений сопротивления, был дан возросшими потребностями техники, и в первую очередь проблемами, возникшими с появлением электрического телеграфа. Впервые мысль об использовании электричества для передачи сигналов на расстояние родилась еще в XVIII веке. Вольта описал проект телеграфа, а Ампер еще в 1820 г. предлагал использовать электромагнитные явления для передачи сигналов. Идея Ампера была подхвачена многими учеными и техниками: в 1833 г. Гаусс и Вебер построили в Геттингене простейшую телеграфную линию, соединявшую астрономическую обсерваторию и физическую лабораторию. Но практическое применение телеграф получил благодаря американцу Самуэлу Морзе (1791—1872), которому в 1832 г. пришла удачная мысль создать телеграфный алфавит, состоящий всего из двух знаков. После многочисленных попыток Морзе в 1835 г. наконец удалось построить частным образом первую грубую модель телеграфа в Нью-Йоркском университете. В 1839 г. была проведена экспериментальная

линия между Вашингтоном и Балтиморой, а в 1844 г. возникла организованная Морзе первая американская компания по коммерческой эксплуатации нового изобретения. Это было также первое практическое применение результатов научных изысканий в области электричества.

В Англии изучением и усовершенствованием телеграфа занялся Чарльз Уитстон (1802—1875), бывший мастер по изготовлению музыкальных инструментов. Понимая важность

измерений сопротивления, Уитстон стал искать наиболее простые и точные методы таких измерений. Бывший в то время в ходу метод сравнения, как мы видели, давал ненадежные результаты, главным образом из-за отсутствия стабильных источников питания. Уже в 1840 г. Уитстон нашел способ измерения сопротивления независимо от постоянства электродвижущей силы и показал свое устройство Якоби. Однако статья, в которой это устройство описано и которую вполне можно назвать первой работой в области электротехники, появилась лишь в 1843 г. В этой статье дано описание знаменитого «мостика», названного затем в честь Уитстона. Фактически такое устройство было описано —

еще в 1833 г. Гюнтером Кристи и независимо от него в 1840 г. Марианини; оба они предлагали метод сведения к нулю, но их теоретические объяснения, при которых не учитывался закон Ома, оставляли желать лучшего.

Уитстон же был поклонником Ома и очень хорошо знал его закон, так что данная им теория «мостика Уитстона» ничем не отличается от приводимой сейчас в учебниках. Кроме того, Уитстон, чтобы можно было быстро и удобно изменять сопротивление одной стороны мостика для получения нулевой силы тока в гальванометре, включенном в диагональное плечо мостика, сконструировал три типа реостатов (само это слово было предложено им по

аналогии с «реофором», введенным Ампером, в подражание которому Пекле ввел также термин «реометр»). Первый тип реостата с подвижной скобкой, применяемый и сейчас, был создан Уитстоном по аналогии со схожим приспособлением, применявшимся Якоби в 1841 г. Второй тип реостата имел вид деревянного цилиндра, вокруг которого была намотана часть подключенного в цепь провода, который легко перематывался с деревянного цилиндра на бронзовый. Третий тип реостата был похож на «магазин сопротивлений», который Эрнст

Вернер Сименс (1816—1892), ученый и промышленник, в 1860 г. улучшил и широко распространил. «Мостик Уитстона» дал возможность измерять электродвижущие силы и сопротивления.

Создание подводного телеграфа, пожалуй, еще более, нежели воздушного телеграфа, потребовало разработки методов электрических измерений. Опыты с подводным телеграфом начались еще в 1837 г., и одной из первых проблем, которую предстояло разрешить, было определение скорости распространения тока. Еще в 1834 г. Уитстон с помощью вращающихся зеркал, о чем мы уже упоминали в гл. 8, произвел первые измерения этой скорости, но полученные им результаты противоречили результатам Латимера Кларка, а последние в свою очередь не соответствовали более поздним исследованиям других ученых.

В 1855 г. Уильям Томсон (получивший впоследствии титул лорда Кельвина) объяснил причину всех этих расхождений. Согласно Томсону, скорость тока в проводнике не имеет определенной величины. Подобно тому как скорость распространения тепла в стержне зависит от материала, так и скорость тока в проводнике зависит от произведения его сопротивления на электрическую емкость. Следуя этой своей теории, которая в»»его времена

подверглась ожесточенной критике, Томсон занялся проблемами, связанными с подводным телеграфом.

Первый трансатлантический кабель, соединивший Англию и Америку, функционировал около месяца, но затем испортился. Томсон рассчитал новый кабель, провел многочисленные измерения сопротивления и емкости, придумал новые передающие аппараты, из коих следует упомянуть астатический отражательный гальванометр, замененный «сифонным регистратором» его же изобретения. Наконец, в 1866 г. новый трансатлантический кабель успешно вступил в действие. Созданию этого первого большого электротехнического сооружения сопутствовала разработка системы единиц электрических и магнитных измерений.

Основа электромагнитной метрики была заложена Карлом Фридрихом Гауссом (1777—1855) в его знаменитой статье «Intensitas vis magneticae terrestris ad mensuram absolutam revocata» («Величина силы земного магнетизма в абсолютных мерах»), опубликованной в 1832 г. Гаусс заметил, что различные магнитные единицы измерения несоотносимы между

собой, по крайней мере в большей своей части, и поэтому предложил систему абсолютных единиц, основанную на трех основных единицах механики: секунде (единице времени), миллиметре (единице длины) и миллиграмме (единице массы). Через них он выразил все остальные физические единицы и придумал ряд измерительных приборов, в частности магнетометр для измерения в абсолютных единицах земного магнетизма. Работу Гаусса продолжил Вебер, который построил много собственных приборов и приборов, задуманных еще Гауссом. Постепенно, особенно благодаря работам Максвелла, проводившимся в созданной Британской ассоциацией специальной комиссии по измерениям, которая издавала ежегодные отчеты с 1861 по 1867 г., возникла идея создать единые системы мер, в частности систему электромагнитных и электростатических мер.

Мысли о создании таких абсолютных систем единиц были подробно изложены в историческом отчете за 1873 г. второй комиссии Британской ассоциации. Созванный в Париже в 1881 г. Международный конгресс впервые установил международные единицы измерения, присвоив каждой из них название в честь какого-нибудь великого физика. Большая часть этих названий сохраняется до сих пор: вольт, ом, ампер, джоуль и т. д. После

многих перипетий в 1935 г. была введена международная система Джорджи, или MKSQ, которая принимает за основные единицы метр, килограмм-массу, секунду и ом.

С «системами» единиц связаны «формулы размерностей», примененные впервые Фурье в его аналитической теории тепла (1822 г.) и распространенные Максвеллом, которым и установлены применяемые в них обозначения. Метрология прошлого века, основывавшаяся на стремлении объяснить все явления с помощью механических моделей, придавала большое значение формулам размерностей, в которых она хотела видеть не больше и не меньше как ключ к тайнам природы. При этом выдвигался ряд утверждений почти догматического характера. Так, чуть ли не обязательным догматом было требование, чтобы основных величин было непременно три. Но к концу века начали понимать, что формулы размерностей — это чистая условность, вследствие чего интерес к теориям размерностей стал постепенно падать.

Заключение

О значении исследований Ома хорошо сказал профессор физики Мюнхенского университета Е. Ломмель при открытии памятника ученому в 1895 году:

«Открытие Ома было ярким факелом, осветившим ту область электричества, которая до него была окутана мраком. Ом указал единственно правильный путь через непроходимый лес непонятных фактов. Замечательные успехи в развитии электротехники, за которыми мы с удивлением наблюдали в последние десятилетия, могли быть достигнуты только на основе открытия Ома. Лишь тот в состоянии господствовать над силами природы и управлять ими, кто сумеет разгадать законы природы, Ом вырвал у природы так долго скрываемую ею тайну и передал ее в руки современников».

Список используемых источников

Дорфман Я. Г. Всемирная история физики . М., 1979 Ом Г. Определение закона, по которому металлы проводят контактное электричество.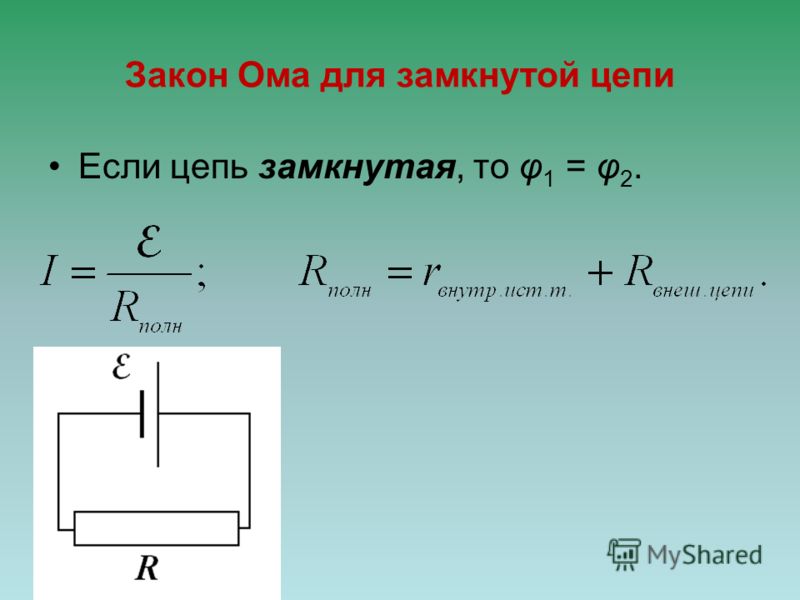 — В кн.: Классики физической науки. М., 1989

Энциклопедия Сто человек. Которые изменили мир. Ом.

Прохоров А. М. Физический энциклопедический словарь, М., 1983

Орир Дж. Физика , т. 2. М., 1981

Джанколи Д. Физика , т. 2. М., 1989

http://www.portal-slovo.ru/

http://www.polarcom.ru/~vvtsv/s_doc9c.html)

Размещено на Allbest.ru

Подобные документы

История открытия Исааком Ньютоном «Закона всемирного тяготения», события, предшествующие данному открытию. Суть и границы применения закона. Формулировка законов Кеплера и их применение к движению планет, их естественных и искусственных спутников.

презентация , добавлен 25.07.2010


Изучение движения тела под действием постоянной силы. Уравнение гармонического осциллятора. Описание колебания математического маятника. Движение планет вокруг Солнца. Решение дифференциального уравнения. Применение закона Кеплера, второго закона Ньютона.

реферат , добавлен 24. 08.2015


История открытия закона всемирного тяготения. Иоган Кеплер как один из первооткрывателей закона движения планет вокруг солнца. Сущность и особенности эксперимента Кавендиша. Анализ теории силы взаимного притяжения. Основные границы применимости закона.

презентация , добавлен 29.03.2011


Изучение «Закона Архимеда», проведение опытов по определению архимедовой силы. Вывод формул для нахождения массы вытесненной жидкости и расчета плотности. Применение «Закона Архимеда» для жидкостей и газов. Методическая разработка урока по данной теме.

конспект урока , добавлен 27.09.2010


Биографические сведения о Ньютоне — великом английском физике, математике и астрономе, его труды. Исследования и открытия ученого, эксперименты по оптике и теории цвета. Первый вывод Ньютоном скорости звука в газе, основанный на законе Бойля-Мариотта.

презентация , добавлен 26.08.2015


Изучение причины магнитной аномалии. Методы определения горизонтальной составляющей напряженности магнитного поля Земли. Применение закона Био-Савара-Лапласа. Определение причины поворота стрелки после подачи напряжения на катушку тангенс–гальванометра.

контрольная работа , добавлен 25.06.2015


Описание основных законов Ньютона. Характеристика первого закона о сохранении телом состояния покоя или равномерного движения при скомпенсированных действиях на него других тел. Принципы закона ускорения тела. Особенности инерционных систем отсчета.

презентация , добавлен 16.12.2014


Законы движения планет Кеплера, их краткая характеристика. История открытия Закона всемирного тяготения И. Ньютоном. Попытки создания модели Вселенной. Движение тел под действием силы тяжести. Гравитационные силы притяжения. Искусственные спутники Земли.

реферат , добавлен 25.07.2010


Проверка справедливости соотношений при параллельном соединении резисторов и первого закона Кирхгофа. Особенности сопротивления приемников. Методика расчета напряжения и тока для различных соединений.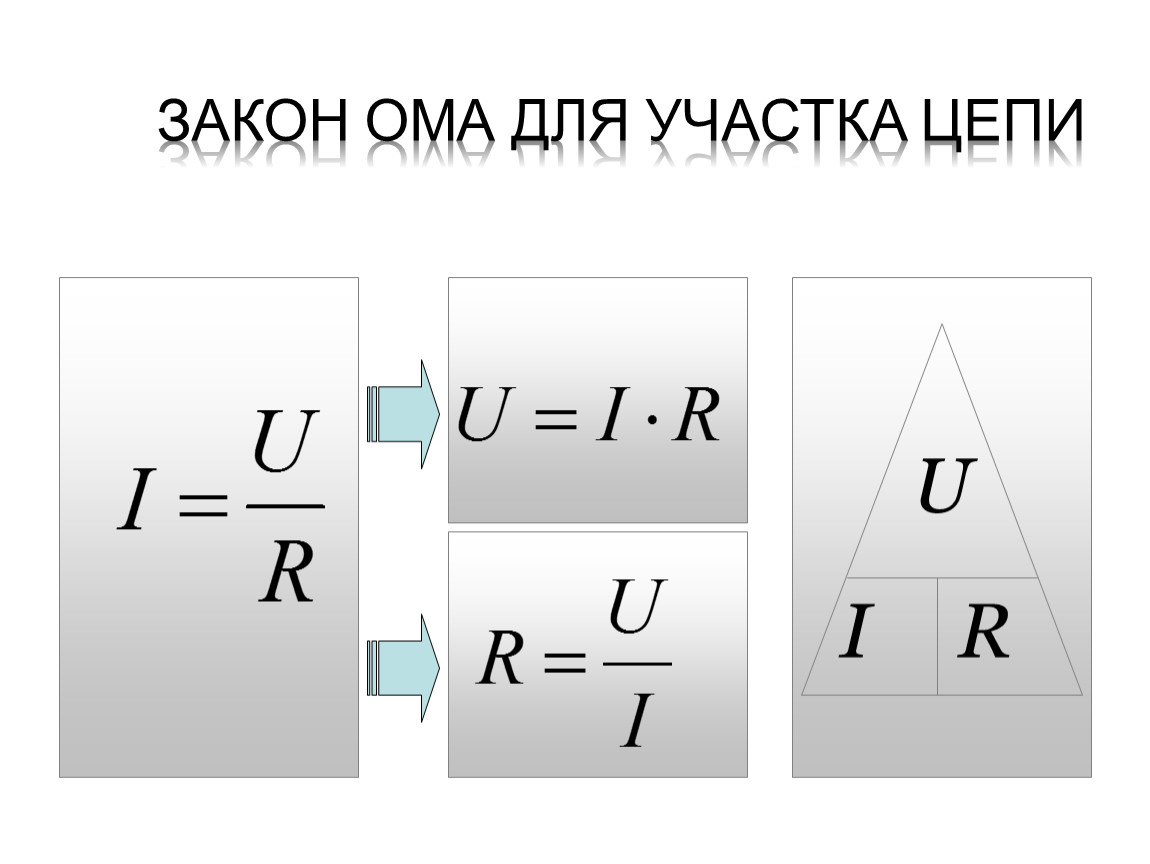 Сущность закона Ома для участка и для всей цепи.

лабораторная работа , добавлен 12.01.2010


Фундаментальные взаимодействия в природе. Взаимодействие электрических зарядов. Свойства электрического заряда. Закон сохранения электрического заряда. Формулировка закона Кулона. Векторная форма и физический смысл закона Кулона. Принцип суперпозиции.

Закон Ома для участка цепи: сила тока I на участке электрической цепи прямо пропорциональна напряжению U на концах участка и обратно пропорциональна его сопротивлению R.

Формула закона: I =. Отсюда запишем формулыU = IR и R = .

Рис.1. Участок цепи Рис.2. Полная цепь

Закон Ома для полной цепи: сила тока I полной электрической цепи равнаЭДС (электродвижущей силе) источника тока Е , деленной на полное сопротивление цепи (R + r). Полное сопротивление цепи равно сумме сопротивлений внешней цепи R и внутреннего r источника тока.Формула закона I =
. На рис. 1 и 2 приведены схемы электрических цепей.

3. Последовательное и параллельное соединение проводников

Проводники в электрических цепях могут соединяться последовательно и параллельно . Смешанное соединение сочетает оба эти соединения.

Сопротивление,при включении которого вместо всех других проводников, находящихся между двумя точками цепи, ток и напряжение остаются неизменными, называют эквивалентным сопротивлением этих проводников.

Последовательное соединение

Последовательным называется соединение, при котором каждый проводник соединяется только с одним предыдущим и одним последующим проводниками.

Как следует из первого правила Кирхгофа , при последовательном соединении проводников сила электрического тока, протекающего по всем проводникам, одинакова (на основании закона сохранения заряда).

1. При последовательном соединении проводников (рис. 1) сила тока во всех проводниках одинакова: I 1 = I 2 = I 3 = I

Рис. 1.Последовательное соединение двух проводников.

2. Согласно закону Ома, напряженияU 1 иU 2 на проводниках равны U 1 = IR 1 , U 2 = IR 2 , U 3 = IR 3 .

Напряжение при последовательном соединении проводников равно сумме напряжений на отдельных участках (проводниках) электрической цепи.

U = U 1 + U 2 + U 3

Позакону Ома, напряжения U 1, U 2 на проводниках равныU 1 = IR 1 , U 2 = IR 2 , В соответствии вторым правилом Кирхгофа напряжение на всем участке:

U = U 1 + U 2 = IR 1 + IR 2 = I(R 1 + R 2 )= I·R. Получаем: R = R 1 + R 2

Общее напряжение U на проводниках равно сумме напряжений U 1 , U 2 , U 3 равно: U = U 1 + U 2 + U 3 = I · (R 1 + R 2 + R 3 ) = IR

где R ЭКВ – эквивалентное сопротивление всей цепи. Отсюда: R ЭКВ = R 1 + R 2 + R 3

При последовательном соединении эквивалентное сопротивление цепи равно сумме сопротивлений отдельных участков цепи: R ЭКВ = R 1 + R 2 + R 3 +…

Этот результат справедлив для любого числа последовательно соединенных проводников.

Из закона Омаследует: при равенстве сил тока при последовательном соединении:

I = , I = . Отсюда = или =, т. е. напряжения на отдельных участках цепи прямо пропорциональны сопротивлениям участков.

При последовательном соединении n одинаковых проводников общее напряжение равно произведению напряжению одного U 1 на их количество n :

U ПОСЛЕД = n · U 1 . Аналогично для сопротивлений: R ПОСЛЕД = n · R 1

При размыкании цепи одного из последовательно соединенных потребителей ток исчезает во всей цепи, поэтому последовательное соединение на практике не всегда удобно.

Соединенный проводами с различными электроприборами и потребителями электри-ческой энергии, образует электрическую цепь.

Электрическую цепь принято изображать с помощью схем, в которых элементы электрической цепи (сопротивления , источники тока, включатели, лампы, при-боры и т. д.) обозначены специальными значками.

Направление тока в цепи — это направление от положи-тельного полюса источника тока к отрицательному. Это пра-вило было установлено в XIX в. и с тех пор соблюдается. Перемещение реальных зарядов может не совпадать с ус-ловным направлением тока. Так, в металлах носителями тока являются отрицательно заряжен-ные электроны, и движутся они от отрицательного полюса к положительному, т. е. в обратном направлении. В электролитах реальное перемещение зарядов может совпадать или быть противоположным направлению тока, в зависимости от того, какие ионы являются носителями заря-да — положительные или отрицательные.

Включение элементов в электрическую цепь может быть последовательным или параллельным .

Закон Ома для полной цепи.

Рассмотрим электрическую цепь, состоящую из источника тока и ре-зистора R .

Закон Ома для полной цепи устанавливает связь между силой тока в цепи, ЭДС и полным сопротивлением цепи, состоя-щим из внешнего сопротивления R и внутреннего сопротивления источ-ника тока r .

Работа сторонних сил A ст источника тока, согласно определению ЭДС (ɛ ) равна A ст = ɛq , где q — заряд , перемещенный ЭДС. Согласно определе-нию тока q = It , где t — время, в течение которого переносился заряд. Отсюда имеем:

A ст = ɛ It .

Тепло, выделяемое при совершении работы в цепи, согласно закону Джоуля — Ленца , равно:

Q = I 2 Rt + I 2 rt .

Согласно закону сохранения энергии А = Q . Приравнивая (A ст = ɛ It ) и (Q = I 2 Rt + I 2 rt ), получим:

ɛ = IR + Ir.

Закон Ома для замкнутой цепи обычно записывается в виде:

.

Сила тока в полной цепи равна отношению ЭДС цепи к ее полному сопротивлению.

Если цепь содержит несколько последовательно соединенных ис-точников с ЭДС ɛ 1 , ɛ 2 , ɛ 3 и т. д., то полная ЭДС цепи равна алгебраической сумме ЭДС отдельных источников. Знак ЭДС источника определяется по отношению к направлению обхода контура, который выбирается произвольно, например, на рисунке ниже — против часовой стрелки.

Сторонние силы внутри источника совершают при этом по-ложительную работу . И наоборот, для цепи справедливо следующее уравнение:

ɛ = ɛ 1 + ɛ 2 + ɛ 3 = | ɛ 1 | — | ɛ 2 | -| ɛ 3 | .

В соответствии с сила тока положительна при положительной ЭДС — направление тока во внешней цепи совпадает с направлением обхода контура. Полное сопротивление цепи с несколькими источниками равно сумме внешнего и внутренних сопротивлений всех источников ЭДС, например, для рисунка выше:

R n = R + r 1 + r 2 + r 3 .

Закон Ома часто называют основным законом электричества. Открывший его в 1826 г. известный немецкий физик Георг Симон Ом установил зависимость между основными физическими величинами электрической цепи – сопротивлением, напряжением и силой тока.

Электрическая цепь

Чтобы лучше понять смысл закона Ома, нужно представлять, как устроена электрическая цепь.

Что же такое электрическая цепь? Это путь, который проходят электрически заряженные частицы (электроны) в электрической схеме.

Чтобы в электрической цепи существовал ток, необходимо наличие в ней устройства, которое создавало бы и поддерживало разность потенциалов на участках цепи за счёт сил неэлектрического происхождения. Такое устройство называется источником постоянного тока , а силы — сторонними силами .

Электрическую цепь, в которой находится источник тока, называют полной электрической цепью . Источник тока в такой цепи выполняет примерно такую же функцию, что и насос, перекачивающий жидкость в замкнутой гидравлической системе.

Простейшая замкнутая электрическая цепь состоит из одного источника и одного потребителя электрической энергии, соединённых между собой проводниками.

Параметры электрической цепи

Свой знаменитый закон Ом вывел экспериментальным путём.

Проведём несложный опыт.

Соберём электрическую цепь, в которой источником тока будет аккумулятор, а прибором для измерения тока – последовательно включенный в цепь амперметр. Нагрузкой служит спираль из проволоки. Напряжение будем измерять с помощью вольтметра, включенного параллельно спирали. Замкнём с помощью ключа электрическую цепь и запишем показания приборов.

Подключим к первому аккумулятору второй с точно таким же параметрами. Снова замкнём цепь. Приборы покажут, что и сила тока, и напряжение увеличились в 2 раза.

Если к 2 аккумуляторам добавить ещё один такой же, сила тока увеличится втрое, напряжение тоже утроится.

Вывод очевиден: сила тока в проводнике прямо пропорциональна напряжению, приложенному к концам проводника .

В нашем опыте величина сопротивления оставалась постоянной. Мы меняли лишь величину тока и напряжения на участке проводника. Оставим лишь один аккумулятор. Но в качестве нагрузки будем использовать спирали из разных материалов. Их сопротивления отличаются. Поочерёдно подключая их, также запишем показания приборов. Мы увидим, что здесь всё наоборот. Чем больше величина сопротивления, тем меньше сила тока. Сила тока в цепи обратно пропорциональна сопротивлению .

Итак, наш опыт позволил нам установить зависимость силы тока от величины напряжения и сопротивления.

Конечно, опыт Ома был другим. В те времена не существовало амперметров, и, чтобы измерить силу тока, Ом использовал крутильные весы Кулона. Источником тока служил элемент Вольта из цинка и меди, которые находились в растворе соляной кислоты. Медные проволоки помещались в чашки со ртутью. Туда же подводились концы проводов от источника тока. Проволоки были одинакового сечения, но разной длины. За счёт этого менялась величина сопротивления. Поочерёдно включая в цепь различные проволоки, наблюдали за углом поворота магнитной стрелки в крутильных весах. Собственно, измерялась не сама сила тока, а изменение магнитного действия тока за счёт включения в цепь проволок различного сопротивления. Ом называл это «потерей силы».

Но так или иначе эксперименты учёного позволили ему вывести свой знаменитый закон.

Георг Симон Ом

Закон Ома для полной цепи

Между тем, формула, выведенная самим Омом, выглядела так:

Это не что иное, как формула закона Ома для полной электрической цепи: « Сила тока в цепи пропорциональна действующей в цепи ЭДС и обратно пропорциональна сумме сопротивлений внешней цепи и внутреннего сопротивления источника ».

В опытах Ома величина Х показывала изменение величины тока. В современной формуле ей соответствует сила тока I , протекающего в цепи. Величина а характеризовала свойства источника напряжения, что соответствует современному обозначению электродвижущей силы (ЭДС) ε . Значение величины l зависело от длины проводников, соединявших элементы электрической цепи. Эта величина являлась аналогией сопротивления внешней электрической цепи R . Параметр b характеризовал свойства всей установки, на которой проводился опыт. В современной обозначении это r – внутреннее сопротивление источника тока.

Как выводится современная формула закона Ома для полной цепи?

ЭДС источника равна сумме падений напряжений на внешней цепи (U ) и на самом источнике (U 1 ).

ε = U + U 1 .

Из закона Ома I = U / R следует, что U = I · R , а U 1 = I · r .

Подставив эти выражения в предыдущее, получим:

ε = I · R + I · r = I · (R + r) , откуда

По закону Ома напряжение во внешней цепи равно произведению силы тока на сопротивление. U = I · R . Оно всегда меньше, чем ЭДС источника. Разница равна величине U 1 = I · r .

Что происходит при работе батарейки или аккумулятора? По мере того, как разряжается батарейка, растёт её внутренне сопротивление. Следовательно, увеличивается U 1 и уменьшается U .

Полный закон Ома превращается в закон Ома для участка цепи, если убрать из него параметры источника.

Короткое замыкание

А что произойдёт, если сопротивление внешней цепи вдруг станет равно нулю? В повседневной жизни мы можем наблюдать это, если, например, повреждается электрическая изоляция проводов, и они замыкаются между собой. Возникает явление, которое называется коротким замыканием . Ток, называемый током короткого замыкания , будет чрезвычайно большим. При этом выделится большое количество теплоты, которое может привести к пожару. Чтобы этого не случилось, в цепи ставят устройства, называемые предохранителями. Они устроены так, что способны разорвать электрическую цепь в момент короткого замыкания.

Закон Ома для переменного тока

В цепи переменного напряжения кроме обычного активного сопротивления встречается реактивное сопротивление (ёмкости, индуктивности).

Для таких цепей U = I · Z , где Z — полное сопротивление, включающее в себя активную и реактивную составляющие.

Но большим реактивным сопротивлением обладают мощные электрические машины и силовые установки. В бытовых приборах, окружающих нас, реактивная составляющая настолько мала, что её можно не учитывать, а для расчётов использовать простую форму записи закона Ома:

I = U / R

Мощность и закон Ома

Ом не только установил зависимость между напряжением, током и сопротивлением электрической цепи, но и вывел уравнение для определения мощности:

P = U · I = I 2 · R

Как видим, чем больше ток или напряжение, тем больше мощность . Так как проводник или резистор не является полезной нагрузкой, то мощность, которая приходится на него, считается мощностью потерь. Она идёт на нагревание проводника. И чем больше сопротивление такого проводника, тем больше теряется на нём мощности. Чтобы уменьшить потери от нагревания, в цепи используют проводники с меньшим сопротивлением. Так делают, например, в мощных звуковых установках.

Вместо эпилога

Небольшая подсказка для тех, кто путается и не может запомнить формулу закона Ома.

Разделим треугольник на 3 части. Причём, каким образом мы это сделаем, совершенно неважно. Впишем в каждую из них величины, входящие в закон Ома — так, как показано на рисунке.

Закроем величину, которую нужно найти. Если оставшиеся величины находятся на одном уровне, то их нужно перемножить. Если же они располагаются на разных уровнях, то величину, расположенную выше, необходимо разделить на нижнюю.

Закон Ома широко применяется на практике при проектировании электрических сетей в производстве и в быту.

Закон Ома был открыт немецким физиком Георгом Омом в 1826 году и с тех пор начал широко применяться в электротехнической области в теории и на практике. Он выражается известной формулой, с посредством которой можно выполнить расчеты практически любой электрической цепи. Тем не менее, закон Ома для переменного тока имеет свои особенности и отличия от подключений с постоянным током, определяемые наличием реактивных элементов. Чтобы понять суть его работы, нужно пройти по всей цепочке, от простого к сложному, начиная с отдельного участка электрической цепи.

Закон ома для участка цепи

Закон Ома считается рабочим для различных вариантов электрических цепей. Более всего он известен по формуле I = U/R, применяемой в отношении отдельного отрезка цепи постоянного или переменного тока.

В ней присутствуют такие определения, как сила тока (I), измеряемая в амперах, напряжение (U), измеряемое в вольтах и сопротивление (R), измеряемое в Омах.

Широко распространенное определение этой формулы выражается известным понятием: сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению на конкретном отрезке цепи. Если увеличивается напряжение, то возрастает и сила тока, а рост сопротивления, наоборот, снижает ток. Сопротивление на этом отрезке может состоять не только из одного, но и из нескольких элементов, соединенных между собой .

Формулу закона Ома для постоянного тока можно легко запомнить с помощью специального треугольника, изображенного на общем рисунке. Он разделяется на три секции, в каждой из которых помещен отдельно взятый параметр. Такая подсказка дает возможность легко и быстро найти нужное значение. Искомый показатель закрывается пальцем, а действия с оставшимися выполняются в зависимости от их положения относительно друг друга.

Если они расположены на одном уровне, то их нужно перемножить, а если на разных — верхний параметр делится на нижний. Данный способ поможет избежать путаницы в расчетах начинающим электротехникам.

Закон ома для полной цепи

Между отрезком и целой цепью существуют определенные различия. В качестве участка или отрезка рассматривается часть общей схемы, расположенная в самом источнике тока или напряжения. Она состоит из одного или нескольких элементов, соединенных с источником тока разными способами.

Система полной цепи представляет собой общую схему, состоящую из нескольких цепочек, включающую в себя батареи, разные виды нагрузок и соединяющие их провода. Она также работает по закону Ома и широко используется в практической деятельности, в том числе и для переменного тока.

Принцип действия закона Ома в полной цепи постоянного тока можно наглядно увидеть при выполнении несложного опыта. Как показывает рисунок, для этого потребуется источник тока с напряжением U на его электродах, любое постоянное сопротивление R и соединительные провода. В качестве сопротивления можно взять обычную лампу накаливания. Через ее нить будет протекать ток, создаваемый электронами, перемещающимися внутри металлического проводника, в соответствии с формулой I = U/R.

Система общей цепи будет состоять из внешнего участка, включающего в себя сопротивление, соединительные проводки и контакты батареи, и внутреннего отрезка, расположенного между электродами источника тока. По внутреннему участку также будет протекать ток, образованный ионами с положительными и отрицательными зарядами. Катод и анод станут накапливать заряды с плюсом и минусом, после чего среди них возникнет .

Полноценное движение ионов будет затруднено внутренним сопротивлением батареи r, ограничивающим выход тока в наружную цепь, и понижающим его мощность до определенного предела. Следовательно, ток в общей цепи проходит в пределах внутреннего и внешнего контуров, поочередно преодолевая общее сопротивление отрезков (R+r). На размеры силы тока влияет такое понятие, как электродвижущая сила — ЭДС, прилагаемая к электродам, обозначенная символом Е.

Значение ЭДС возможно измерить на выводах батареи с использованием вольтметра при отключенном внешнем контуре. После подключения нагрузки на вольтметре появится наличие напряжения U. Таким образом, при отключенной нагрузке U = E, в при подключении внешнего контура U

ЭДС дает толчок движению зарядов в полной цепи и определяет силу тока I = E/(R+r). Данная формула отражает закон Ома для полной электрической цепи постоянного тока. В ней хорошо просматриваются признаки внутреннего и наружного контуров. В случае отключения нагрузки внутри батареи все равно будут двигаться заряженные частицы. Это явление называется током саморазряда, приводящее к ненужному расходу металлических частиц катода.

Под действием внутренней энергии источника питания сопротивление вызывает нагрев и его дальнейшее рассеивание снаружи элемента. Постепенно заряд батареи полностью исчезает без остатка.

Закон ома для цепи переменного тока

Для цепей переменного тока закон Ома будет выглядеть иначе. Если взять за основу формулу I = U/R, то кроме активного сопротивления R, в нее добавляются индуктивное XL и емкостное ХС сопротивления, относящиеся к реактивным. Подобные электрические схемы применяются значительно чаще, чем подключения с одним лишь активным сопротивлением и позволяют рассчитать любые варианты.

Сюда же включается параметр ω, представляющий собой циклическую частоту сети. Ее значение определяется формулой ω = 2πf, в которой f является частотой этой сети (Гц). При постоянном токе эта частота будет равной нулю, а емкость примет бесконечное значение. В данном случае электрическая цепь постоянного тока окажется разорванной, то есть реактивного сопротивления нет.

Цепь переменного тока ничем не отличается от постоянного, за исключением источника напряжения. Общая формула остается такой же, но при добавлении реактивных элементов ее содержание полностью изменится. Параметр f уже не будет нулевым, что указывает на присутствие реактивного сопротивления. Оно тоже оказывает влияние на ток, протекающий в контуре и вызывает резонанс. Для обозначения полного сопротивления контура используется символ Z.

Отмеченная величина не будет равной активному сопротивлению, то есть Z ≠ R. Закон Ома для переменного тока теперь будет выглядеть в виде формулы I = U/Z. Знание этих особенностей и правильное использование формул, помогут избежать неправильного решения электротехнических задач и предотвратить выход из строя отдельных элементов контура.

Военно-техническая подготовка

1.2. Постоянный ток

1.2.1. Законы Ома.

Закон Ома — эмпирический физический закон, определяющий связь электродвижущей силы источника или электрического напряжения с силой тока и сопротивлением проводника.

В своей оригинальной форме он был записан его автором в виде :

,

где X — показания гальванометра, т.е в современных обозначениях сила тока I ;

a — величина, характеризующая свойства источника напряжения, постоянная в широких пределах и не зависящая от величины тока, то есть в современной терминологии электродвижущая сила (ЭДС) ;

l — величина, определяемая длиной соединяющих проводов, чему в современных представлениях соответствует сопротивление внешней цепи R ;

b — параметр, характеризующий свойства всей установки, в котором сейчас можно усмотреть учёт внутреннего сопротивления источника тока r .

В таком случае в современных терминах и в соответствии с предложенной автором записи формулировка Ома (1) выражает

Закон Ома для полной цепи :

,

где ε — ЭДС источника напряжения;

I — сила тока в цепи;

R — сопротивление всех внешних элементов цепи;

r — внутреннее сопротивление источника напряжения.

Из закона Ома для полной цепи вытекают следствия:

• При r<<R сила тока в цепи обратно пропорциональна её сопротивлению. А сам источник в ряде случаев может быть назван источником напряжения
• При r>>R сила тока от свойств внешней цепи (от величины нагрузки) не зависит. И источник может быть назван источником тока.

Часто выражение

,

где есть напряжение, или падение напряжения (или, что то же, разность потенциалов между началом и концом участка проводника), тоже называют «Законом Ома».

Таким образом, электродвижущая сила в замкнутой цепи, по которой течёт ток в соответствии с (2) и (3) равняется:

,

То есть сумма падений напряжения на внутреннем сопротивлении источника тока и на внешней цепи равна ЭДС источника. Последний член в этом равенстве специалисты называют «напряжением на зажимах», поскольку именно его показывает вольтметр, измеряющий напряжение источника между началом и концом присоединённой к нему замкнутой цепи. В таком случае оно всегда меньше ЭДС.

К другой записи формулы (3), а именно:

,

применима другая формулировка:

<<

Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи.

>>

Выражение (5) можно переписать в виде:

,

где коэффициент пропорциональности G назван проводимость или электропроводность. Изначально единицей измерения проводимости был «обратный Ом» — Mо, в Международной системе единиц (СИ) единицей измерения проводимости является сименс (русское обозначение: См; международное: S ), величина которого равна обратному Ому.

Рис 1. Схема, иллюстрирующая три составляющие закона Ома.

Рис 2. Диаграмма, помогающая запомнить закон Ома. Нужно закрыть искомую величину, и два других символа дадут формулу для её вычисления

1.2.2. Правила Кирхгофа.

Правила Кирхгофа (часто, в литературе, называются не совсем корректно Законы Кирхгофа, название «Правила» корректнее потому, что эти правила не являются фундаментальными законами природы, а вытекают из фундаментальных законов сохранения заряда и безвихревости электростатического поля) — соотношения, которые выполняются между токами и напряжениями на участках любой электрической цепи. Правила Кирхгофа позволяют рассчитывать любые электрические цепи постоянного, переменного и квазистационарного(«почти стационарного») тока.

Для формулировки правил Кирхгофа вводятся понятия узел , ветвь и контур электрической цепи.

Ветвью называют любой двухполюсник, входящий в цепь.

Узлом называют точку соединения трех и более ветвей.

Контур — замкнутый цикл из ветвей. Термин замкнутый цикл означает, что, начав с некоторого узла цепи и однократно пройдя по нескольким ветвям и узлам, можно вернуться в исходный узел. Ветви и узлы, проходимые при таком обходе, принято называть принадлежащими данному контуру. При этом нужно иметь в виду, что ветвь и узел могут принадлежать одновременно нескольким контурам.

В терминах данных определений правила Кирхгофа формулируются следующим образом.

Первое правило .

Первое правило Кирхгофа гласит, что алгебраическая сумма токов в каждом узле любой цепи равна нулю. При этом направленный к узлу ток принято считать положительным, а направленный от узла — отрицательным: Алгебраическая сумма токов, направленных к узлу равна сумме направленных от узла.

.

Иными словами, сколько тока втекает в узел, столько из него и вытекает. Это правило следует из фундаментального закона сохранения заряда.

Второе правило .

Второе правило Кирхгофа (правило напряжений Кирхгофа) гласит, что алгебраическая сумма падений напряжений на всех ветвях, принадлежащих любому замкнутому контуру цепи, равна алгебраической сумме ЭДС ветвей этого контура. Если в контуре нет источников ЭДС (идеализированных генераторов напряжения), то суммарное падение напряжений равно нулю:

для постоянных напряжений:

для переменных напряжений:

Это правило вытекает из 3-го уравнения Максвелла, в частном случае стационарного магнитного поля.

Иными словами, при полном обходе контура потенциал, изменяясь, возвращается к исходному значению. Частным случаем второго правила для цепи, состоящей из одного контура, является закон Ома для этой цепи. При составлении уравнения напряжений для контура нужно выбрать положительное направление обхода контура. При этом падение напряжения на ветви считают положительным, если направление обхода данной ветви совпадает с ранее выбранным направлением тока ветви, и отрицательным — в противном случае.

Правила Кирхгофа справедливы для линейных и нелинейных линеаризованных цепей при любом характере изменения во времени токов и напряжений.

Особенности составления уравнений для расчёта токов и напряжений .

Если цепь содержит p узлов, то она описывается p — 1 уравнениями токов. Это правило может применяться и для других физических явлений (к примеру, система трубопроводов жидкости или газа с насосами), где выполняется закон сохранения частиц среды и потока этих частиц.

Если цепь содержит m ветвей, из которых содержат источники тока ветви в количестве m i , то она описывается m – m i – ( p — 1) уравнениями напряжений.

• Правила Кирхгофа, записанные для p — 1 узлов или m – ( p — 1) контуров цепи, дают полную систему линейных уравнений, которая позволяет найти все токи и все напряжения.
• Перед тем, как составить уравнения, нужно произвольно выбрать:
• положительные направления токов в ветвях и обозначить их на схеме, при этом не обязательно следить, чтобы в узле направления токов были и втекающими, и вытекающими, окончательное решение системы уравнений всё равно даст правильные знаки токов узла;
• положительные направления обхода контуров для составления уравнений по второму закону, с целью единообразия рекомендуется для всех контуров положительные направления обхода выбирать одинаковыми (напр.: по часовой стрелке).
• Если направление тока совпадает с направлением обхода контура (которое выбирается произвольно), падение напряжения считается положительным, в противном случае — отрицательным.
• При записи линейно независимых уравнений по второму правилу Кирхгофа стремятся, чтобы в каждый новый контур, для которого составляют уравнение, входила хотя бы одна новая ветвь, не вошедшая в предыдущие контуры, для которых уже записаны уравнения по второму закону ( достаточное, но не необходимое условие ).

Рис 3. Сколько тока втекает в узел, столько из него и вытекает. i2 + i3 = i1 + i4

Рис 4. На этом рисунке для каждой ветви обозначен протекающий по ней ток (буквой «I») и напряжение между соединяемыми ею узлами (буквой «U»).

1.4. Законы Ома и Кирхгофа

1.4. Законы Ома и Кирхгофа

Закон Ома для всей цепи выражает соотношение между электродвижущей силой (ЭДС), сопротивлением и током. Согласно этому закону ток в замкнутой цепи равен ЭДС источника деленной на сопротивление всей цепи:

 

,                                                  (1.19)

где I – ток, протекающий по цепи;

E – ЭДС, генератора, подключенного к электрической цепи;

Rг – сопротивление генератора;

Rц – сопротивление цепи.

Закон Ома для участка цепи. Ток на участке цепи прямо пропорционален напряжению между началом и концом  участка и обратно пропорционален сопротивлению участка. Аналитически закон выражается в следующем виде:

,                                                                  (1.20)

где I – ток, протекающий на участке цепи;

R – сопротивление участка цепи;

U – напряжение на участке цепи.

Обобщенный закон Ома. Сила тока  в контуре цепи прямо пропорциональна алгебраической сумме ЭДС всех источников цепи и обратно пропорциональна арифметической сумме всех активных сопротивлений цепи.

,                                                          (1.21)

где m и n – количество источников и резисторов в контуре цепи.

При алгебраическом суммировании со знаком “плюс” берутся те ЭДС, направление которых совпадает с направлением тока, а со знаком “минус”– те ЭДС, направление которых не совпадает с направлением тока.

Первый закон Кирхгофа. Электрические цепи подразделяют на неразветвленные и разветвленные. На рис. 1.10 представлена простейшая разветвленная цепь.

Рис. 1.10 Схема разветвленной цепи.

Разветвленной называется такая электрическая цепь, в которой ток от какого-либо источника может идти по различным путям и, в которой, следовательно, имеются точки, где сходятся два и более проводников. Эти точки называютузлами. Токи, текущие к узлу считаются имеющими один знак, а от узла – другой.

Учитывая это правило для схемы, изображенной на рис. 1.11,а можно записать

или.

Для цепи, имеющей n ветвей, сходящихся в одном узле, имеем:

,                                                          (1.22)

т.е. алгебраическая сумма токов ветвей, сходящихся в любом узле, равна

нулю.

Рис. 1.11 Схема поясняющая законы Кирхгофа.

Физически первый закон Кирхгофа означает, что движение зарядов в цепи происходит так, что ни в одном из узлов они не скапливаются.

Второй закон Кирхгофа устанавливает связь между ЭДС, токами и сопротивлениями в любом замкнутом контуре, который можно выделить в рассматриваемой цепи.

В соответствии со вторым законом Кирхгофа алгебраическая сумма ЭДС, действующих в любом контуре разветвленной электрической цепи, равна алгебраической сумме падений напряжений на всех сопротивлениях контура

,                                                  (1.23)

Рассмотрим электрическую цепь, изображенную на рис. 1.11,б. Обозначим стрелкой направление обхода контура. При составлении уравнений будем брать со знаком “плюс” те ЭДС и падения напряжений, направления которых совпадают с направлением обхода контура и со знаком “минус” те, которые направлены против обхода. Для цепи, изображенной на рис. 1.11,б второй закон Кирхгофа запишется в следующем виде:

.

Закон ома для полной замкнутой цепи формула. Закон Ома для полной электрической цепи. Закон Ома для параллельной и последовательной цепи

Нельзя организовать циркуляцию заряда по замкнутому контуру под действием только электростатической силы. Для переноса заряда в область высокого потенциала (2-b -1) придётся использовать силы неэлектростатической природы . Такие силы получили название сторонних сил. В качестве сторонних сил могут выступать любые силы кроме электростатических. Приборы, в которых на электрические заряды действуют сторонние силы, называются источниками тока. В аккумуляторах, например, сторонние силы возникают в результате химической реакции взаимодействия электродов с электролитом, в генераторах сторонними являются силы, действующие на заряды, движущиеся в магнитном поле и т.д. Именно в источниках тока благодаря работе сторонних сил создаётся генерируемая энергия, которая затем расходуется в электрической цепи.

Работа, которую совершают сторонние силы при перемещении единичного положительного заряда — одна из основных характеристик источника, его электродвижущая сила e:

Поле сторонних сил, также как и электростатическое поле, характеризуется вектором напряжённости :

Электродвижущая сила источника равна работе, совершаемой сторонними силами при перемещении единичного положительного заряда по замкнутому контуру.

На участке цепи 1-а-2 движение носителей заряда происходит под действием только электростатической силы = q . Такие участки называются однородными.

Участок замкнутого контура, где наряду с электростатической силой действуют и сторонние силы, называют неоднородным.

Можно показать, что на однородном участке цепи средняя скорость направленного движения носителей заряда пропорциональна действующей на них силе. Для этого достаточно сравнить формулы, полученные на прошлой лекции: = (6.3) и = l

Пропорциональность скорости силе, а плотности тока — напряжённости сохранится и в случае неоднородного участка цепи. Но теперь напряжённость поля равна сумме напряжённостей электростатического поля и поля сторонних сил : .

Это уравнение закона Ома в локальной дифференциальной форме для неоднородного участка цепи.

Теперь перейдём к закону Ома для неоднородного участка цепи в интегральной форме.

Для замкнутого контура уравнение закона Ома несколько видоизменяется, так как разность потенциалов в этом случае равна нулю: .

В законе Ома для замкнутой цепи (7.8) R — полное сопротивление контура, складывающееся из внешнего сопротивления цепи R 0 и внутреннего сопротивления источника r: R = R 0 + r.

12) Закон Джоуля-Ленца в дифференциальной форме и интегральной форме.

Пусть на участке электрической цепи протекает постоянный ток I . Напряжение U на концах этого участка численно равно работе, совершаемой электрическими силами при перемещении единичного положительного заряда по этому участку. Это следует из определения напряжения.

Отсюда работа A = q  × U . За время t по участку будет перенесён заряд q = I  × t и при этом будет совершена работа: A = q  × U = U  × I  × t .

Это выражение работы электрического тока справедливо для любых проводников.

Работа, совершаемая в единицу времени — мощность электрического тока: .

Работа электрического тока (6.14) может затрачиваться на нагревание проводника, совершение механической работы (электродвигатель) и на химическое действие тока при его течении через электролит (электролиз).

Если химическое действие и механическая работа при течении тока не производятся, то вся работа электрического тока расходуется только на нагревание проводника: Q = A = U  × I  × t = I 2  × R  × t . (6.15)

Закон о тепловом эффекте электрического тока (6.15) был экспериментально установлен независимо английским учёным Д. Джоулем и русским академиком Э.Х. Ленцем. Формула (6.15) — математическая запись закона Джоуля-Ленца в интегральной форме , позволяющая вычислить количество теплоты, выделяющейся в проводнике.

.

Перед нами закон Джоуля-Ленца в дифференциальной форме .

Учитывая, что i = lE = , это выражение можно записать ещё и так:

Правила Кирхгофа.

Рассмотренные нами законы постоянного тока позволяют рассчитать токи в сложных разветвлённых электрических цепях. Эти расчёты упрощаются, если пользоваться правилами Кирхгофа.

Правил Кирхгофа два: правило токов и правило напряжений .

Правило токов относится к узлам цепи, то есть, к таким точкам схемы, где сходятся не менее трёх проводников (рис. 7.4.). Правило токов гласит: алгебраическая сумма токов в узле равняется нулю:

При составлении соответствующего уравнения, токи, втекающие в узел, берутся со знаком плюс, а покидающие его — со знаком минус. Это первое правило Кирхгофа является следствием уравнения непрерывности (см. (6.7)) или закона сохранения электрического заряда.

Правило напряжений относится к любому замкнутому контуру разветвлённой цепи.

Правило напряжений формулируется так: в любом замкнутом контуре алгебраическая сумма падений напряжения равна алгебраической сумме э.д.с., встречающихся в этом контуре:

При составлении уравнения второго правила Кирхгофа задаются направлением обхода.

Токи, совпадающие с направлением обхода, берутся со знаком плюс, токи противоположного направления — со знаком минус Э.д.с. источника берётся со знаком плюс, если он создаёт ток, совпадающий с направлением обхода. В противном случае э.д.с. отрицательна.

Содержание:

Каждый специалист, ремонтирующий и обслуживающий электроустановки, должен хорошо знать и применять на практике закон Ома для замкнутой цепи. Это действительно так, поскольку закономерности, открытые немецким физиком Георгом Омом, лежат в основе всей электротехники. Данный закон стал весомым вкладом в дальнейшее развитие научных знаний в области электричества.

Физические свойства закона Ома

Прямая взаимосвязь между силой тока, напряжением, подведенным к сети, и была обнаружена Омом в 1826 году. В дальнейшем, понятие напряжения было заменено на более точный термин — электродвижущую силу (ЭДС). После теоретического обоснования этой зависимости был выведен закон для замкнутой цепи. Его важной особенностью считается обязательное отсутствие какого-либо внешнего возмущения. Поэтому стандартные формулировки потеряют свою актуальность, если, например, поместить проводник в переменное магнитное поле.

Для экспериментов по выводу закона использовалась простейшая схема, состоящая из источника питания, обладающего ЭДС и подключенных к нему двух выводов, соединенных с резистором. В проводнике начинают в определенном направлении перемещаться элементарные частицы, несущие заряд. Таким образом, представляется в виде отношения ЭДС к общему сопротивлению всей цепи: I = E/R.

В представленной формуле Е — является электродвижущей силой, измеряемой в вольтах, I — сила тока в амперах, а R выступает в роли электрического сопротивления резистора, измеряемого в омах. При этом, учитываются все составляющие сопротивления и при расчетах используется их суммарное значение. Они включают сопротивление самого резистора, проводника (r) и источника питания (r0). Окончательно формула будет выглядеть так: I = E/(R+r+r0). Если значение внутреннего сопротивления источника тока r0 превышает сумму R+r, то в этом случае отсутствует зависимость силы тока от характеристик подключенной нагрузки, а источник ЭДС исполняет роль источника тока. Когда r0 ниже суммы R+r, получается обратная пропорция тока с суммарным внешним сопротивлением, а напряжение поступает за счет источника питания.

Закон Ома для выполнения расчетов

Точные расчеты требуют учета всех потерь напряжения, в том числе и в местах соединений. Для определения электродвижущей силы на выводах источника тока замеряется разность потенциалов при разомкнутой цепи, когда нагрузка полностью отключена. В этом случае применяется не только закон Ома для замкнутой цепи, но и закон, действующий . Данный участок считается однородным, поскольку здесь принимается в расчет только разность потенциалов, без учета ЭДС. Это дает возможность рассчитать каждый элемент электрической цепи по формуле I=U/R, в которой U является разностью потенциалов или напряжением, измеряемым в вольтах.

Замеры выполняются с помощью вольтметра при подключении щупов к выводам нагрузки или сопротивления. Полученное значение напряжения будет всегда ниже электродвижущей силы. Это наиболее распространенная формула, позволяющая найти любую составляющую при наличии двух известных.

Закон Ома для замкнутой цепи имеет много общего с законом, выведенным для магнитной цепи. В этой системе проводник выполнен в виде замкнутого магнитопровода. В качестве источника выступает обмотка катушки по виткам которой протекает электрический ток. Появляющийся магнитный поток (Ф) замыкается на магнитопровод и начинает циркулировать по контуру. Он находится в непосредственной зависимости от магнитодвижущей силы и сопротивления материала, через который проходит. Данное явление выражено формулой Ф=F/Rm, в которой F представляет собой магнитодвижущую силу, а Rm служит сопротивлением, вызывающим затухание.

Как рассчитать цепи

Соединенный проводами с различными электроприборами и потребителями электри-ческой энергии, образует электрическую цепь.

Электрическую цепь принято изображать с помощью схем, в которых элементы электрической цепи (сопротивления , источники тока, включатели, лампы, при-боры и т. д.) обозначены специальными значками.

Направление тока в цепи — это направление от положи-тельного полюса источника тока к отрицательному. Это пра-вило было установлено в XIX в. и с тех пор соблюдается. Перемещение реальных зарядов может не совпадать с ус-ловным направлением тока. Так, в металлах носителями тока являются отрицательно заряжен-ные электроны, и движутся они от отрицательного полюса к положительному, т. е. в обратном направлении. В электролитах реальное перемещение зарядов может совпадать или быть противоположным направлению тока, в зависимости от того, какие ионы являются носителями заря-да — положительные или отрицательные.

Включение элементов в электрическую цепь может быть последовательным или параллельным .

Закон Ома для полной цепи.

Рассмотрим электрическую цепь, состоящую из источника тока и ре-зистора R .

Закон Ома для полной цепи устанавливает связь между силой тока в цепи, ЭДС и полным сопротивлением цепи, состоя-щим из внешнего сопротивления R и внутреннего сопротивления источ-ника тока r .

Работа сторонних сил A ст источника тока, согласно определению ЭДС (ɛ ) равна A ст = ɛq , где q — заряд , перемещенный ЭДС. Согласно определе-нию тока q = It , где t — время, в течение которого переносился заряд. Отсюда имеем:

A ст = ɛ It .

Тепло, выделяемое при совершении работы в цепи, согласно закону Джоуля — Ленца , равно:

Q = I 2 Rt + I 2 rt .

Согласно закону сохранения энергии А = Q . Приравнивая (A ст = ɛ It ) и (Q = I 2 Rt + I 2 rt ), получим:

ɛ = IR + Ir.

Закон Ома для замкнутой цепи обычно записывается в виде:

.

Сила тока в полной цепи равна отношению ЭДС цепи к ее полному сопротивлению.

Если цепь содержит несколько последовательно соединенных ис-точников с ЭДС ɛ 1 , ɛ 2 , ɛ 3 и т. д., то полная ЭДС цепи равна алгебраической сумме ЭДС отдельных источников. Знак ЭДС источника определяется по отношению к направлению обхода контура, который выбирается произвольно, например, на рисунке ниже — против часовой стрелки.

Сторонние силы внутри источника совершают при этом по-ложительную работу . И наоборот, для цепи справедливо следующее уравнение:

ɛ = ɛ 1 + ɛ 2 + ɛ 3 = | ɛ 1 | — | ɛ 2 | -| ɛ 3 | .

В соответствии с сила тока положительна при положительной ЭДС — направление тока во внешней цепи совпадает с направлением обхода контура. Полное сопротивление цепи с несколькими источниками равно сумме внешнего и внутренних сопротивлений всех источников ЭДС, например, для рисунка выше:

R n = R + r 1 + r 2 + r 3 .

Рассмотрим простейшую замкнутую цепь, состоящую из источника (гальванического элемента, аккумулятора или генератора)

и резистора сопротивлением (рис. 161). Источник тока имеет и сопротивление Сопротивление источника часто называют внутренним сопротивлением в отличие от внешнего сопротивления цепи. В генераторе это сопротивление обмоток, а в гальваническом элементе — сопротивление раствора электролита и электродов

Закон Ома для замкнутой цепи связывает силу тока в цепи, ЭДС и полное сопротивление цепи. Эта связь может быть установлена теоретически, если использовать закон сохранения энергии и закон Джоуля — Ленца (9.17).

Пусть за время через поперечное сечение проводника пройдет заряд Тогда работу сторонних сил по перемещению заряда можно записать так: Согласно определению силы тока Поэтому

При совершении этой работы на внутреннем и внешнем участках цепи, сопротивления которых и выделяется некоторое количество теплоты. По закону Джоуля — Ленца оно равно:

Согласно закону сохранения энергии Приравнивая (9.20) и (9.21), получим:

Произведение силы тока на сопротивление участка цепи часто называют падением напряжения на этом участке. Таким образом, ЭДС равна сумме падений напряжений на внутреннем и внешнем участках замкнутой цепи.

Обычно закон Ома для замкнутой цепи записывают в форме:

Сила тока в замкнутой цепи равна отношению ЭДС цепи к ее полному сопротивлению.

Сила тока зависит от трех величин: сопротивлений и внешнего и внутреннего участков цепи. Внутреннее сопротивление источника тока не оказывает заметного влияния на силу тока, если оно мало по сравнению с сопротивлением внешней части цепи При этом напряжение на зажимах источника приблизительно равно

Но при коротком замыкании сила тока в цепи определяется именно внутренним сопротивлением источника и может при электродвижущей силе в несколько вольт быть очень большой, если мало (например, у аккумулятора Ом). Провода могут расплавиться, а сам источник — выйти из строя.

Если цепь содержит несколько последовательно соединенных элементов с то полная ЭДС цепи равна алгебраической сумме ЭДС отдельных элементов. Для определения знака ЭДС любого источника нужно вначале условиться относительно выбора положительного направления обхода контура. На рисунке 162 положительным (произвольно) считает направление обхода против часовой стрелки.

Если при обходе цепи переходят от отрицательного полюса источника к положительному, то Сторонние силы внутри источника совершают при этом положительную работу. Если же при обходе цепи переходят от положительного полюса источника к отрицательному, ЭДС будет отрицательной. Сторонние силы внутри источника совершают отрицательную работу. Так, для цепи, изображенной на рисунке 162:

Если то согласно (9.23) сила тока т. е. направление тока совпадает с направлением обхода контура. При наоборот, направление тока противоположно направлению обхода контура. Полное сопротивление цепи равно сумме всех сопротивлений:

При параллельном соединении гальванических элементов с одинаковыми ЭДС (или других источников) ЭДС батареи равна ЭДС одного из элементов (рис. 163). Внутреннее же сопротивление батареи рассчитывают по обычному правилу параллельного соединения проводников. Для цепи, изображенной на рисунке 163, согласно закону Ома для замкнутой цепи сила тока определяется следующей формулой:

1. Почему электрическое поле заряженных частиц (кулоновское поле) не способно поддерживать постоянный электрический ток в цепи? 2. Что называют сторонними силами? 3. Что называют электродвижущей силой?

4. Сформулируйте закон Ома для замкнутой цепи. 5. От чего зависит знак ЭДС в законе Ома для замкнутой цепи?

Закон ома для замкнутой цепи говорит о том что. Величина тока в замкнутой цепи, которая состоит из источника тока обладающего внутренним сопротивлением, а также внешним нагрузочным сопротивлением. Будет равна отношению электродвижущей силы источника к сумме внешнего и внутреннего сопротивлений.

Формула 1 — Закон Ома для замкнутой цепи

Где R Сопротивление внешней цепи измеряется в Омах

r внутреннее сопротивление источника тока также измеряется в Омах

I Сила тока в цепи. Измеряется в Амперах

E Электродвижущая сила источника тока измеряется в Вольтах

Иногда возникают ситуации, когда необходимо найти силу тока в цепи, но при этом напряжение на ее концах не задано. Но всё же известно сопротивление цепи и электродвижущая сила источника тока. Применить в этом случае закон Ома для участка цепи невозможно.

В этом случае применяют закон Ома для замкнутой цепи. Для пояснения принципа действия этого закона проведем опыт. Для этого нам понадобится источник тока реостат вольтметр и амперметр.

Для начала построим цепь, состоящую из источника тока реостата и амперметра. Перед началом эксперимента реостат выведем в максимальное положение. После включения в цепи появится ток, который можно наблюдать по амперметру. Двигая ползунок реостата увидим, что при изменении внешнего сопротивления цепи изменяется ток.

Рисунок 1 — измерение тока в цепи

Далее оставив на реостате определённое сопротивление, подключим параллельно источнику тока еще один такой же. И мы увидим, что ток в цепи увеличится. Казалось бы, оба источника имеют одно и то же напряжение сопротивление внешней цепи не изменилось, почему же увеличился ток.

Произошло это по тому, что уменьшилось внутренне сопротивление источника тока. А поскольку в замкнутой цепи оно включено последовательно с внешним сопротивлением и источником тока. То это внутренне сопротивление также участвует в формировании тока в цепи.

Формула 2 — закон Ома для замкнутой цепи с n количеством параллельно включенных источников тока.

Исходя из выше сказанного, можно заключить, что в реальной замкнутой электрической цепи величина тока не способна возрасти бесконечно при возникновении короткого замыкания в источнике тока, так как эту величину ограничивает внутренне сопротивление источника тока.

Facebook

Twitter

Вконтакте

Google+

Обслуживание Закон

Ома для простых электрических цепей, Рон Куртус

SfC Home> Физика> Электричество>

Рона Куртуса (от 23 октября 2019 г.)

Закон Ома является наиболее фундаментальной формулой для простых электрических цепей . Он утверждает, что электрический ток, проходящий через проводник, прямо пропорционален разности потенциалов на проводнике. Впервые он был сформулирован в 1827 году немецким физиком Георгом Омом во время экспериментов по изучению того, насколько хорошо металлы проводят электричество.

Закон

Ома лучше всего демонстрируется в простой электрической цепи постоянного тока. Хотя это также относится к цепям переменного тока, необходимо учитывать другие возможные переменные.

Связь между током, напряжением и сопротивлением в цепи позволяет вычислить одну переменную, если вы используете значения двух других.

Вопросы, которые могут у вас возникнуть:

• Что означают параметры в уравнении?
• Какая конфигурация схемы?
• Как применить закон Ома?

Этот урок ответит на эти вопросы.Полезный инструмент: Конвертация единиц

---

---

Уравнение

Закон

Ома показывает взаимосвязь между напряжением, током и сопротивлением в простой электрической цепи. Самая простая форма уравнения:

В = ИК

где:

• V — напряжение в вольтах ( V )
• I — ток в амперах или амперах ( A )
• R — сопротивление в Ом ( Ом, — греческая буква Омега)

Таким образом, если вы знаете ток и сопротивление, вы можете использовать формулу для определения напряжения.

Используя алгебру, вы можете изменить порядок переменных в соответствии со своими потребностями. Например, если вы знаете напряжение и сопротивление и хотите найти ток, вы можете использовать:

I = V / R

Или, если вы знаете напряжение и ток и хотите найти сопротивление, вы можете использовать:

R = V / I

Конфигурация

Простая электрическая цепь состоит из металлических проводов, идущих к источнику питания и от него, а также источника сопротивления, такого как резисторы или электрическая лампочка, соединенных последовательно с источником.Типичным источником питания является батарея постоянного тока, хотя также может применяться генератор постоянного или переменного тока.

Примечание : Если цепь переменного тока включает в себя такие компоненты, как конденсаторы или катушки индуктивности, закон Ома не применяется.

Простая цепь постоянного тока

Используя уравнение

Важность закона Ома заключается в том, что, если вы знаете значение двух переменных в уравнении, вы можете определить третью. Вы можете измерить любой из параметров с помощью вольтметра.Большинство вольтметров или мультиметров измеряют напряжение, ток и сопротивление как переменного, так и постоянного тока.

Найти напряжение

Если вам известны ток и сопротивление, вы можете найти напряжение из В = I R . Например, если ток I = 0,2 А и сопротивление R = 1000 Ом , то

В = 0,2 А * 1000 Ом = 200 В

Найти текущий

Если вы знаете напряжение и сопротивление, вы можете использовать алгебру, чтобы изменить уравнение на I = V / R , чтобы найти ток.Например, если В = 110 В и R = 22000 Ом , то

I = 110 В / 22000 Ом = 0,005 А

Найдите сопротивление

Если вы знаете напряжение и ток, вы можете использовать алгебру, чтобы изменить уравнение на R = V / I , чтобы найти сопротивление. Если В = 220 В и I = 5 А , то

R = 220 В / 5 A = 44 Ом

Сводка

Закон Ома — это уравнение V = I R , которое показывает взаимосвязь между напряжением, током и сопротивлением в простой электрической цепи.Он может применяться как к цепям переменного, так и к постоянному току.

---

Будьте полны решимости сделать все возможное

---

Ресурсы и ссылки

Полномочия Рона Куртуса

Сайты

Немного истории об Ом — Краткая история

Закон Ома — Объяснение, включая калькулятор закона Ома

Основные электрические законы — Включает теорию схем

Формулы электрических цепей — Уравнения высокого уровня для решения проблем

Электроэнергетические ресурсы постоянного и переменного тока

Физические ресурсы

Книги

Научитесь электричеству и электронике Стэна Гибилиско; Макгроу-Хилл; (2001) 34 доллара.95 — Руководство для профессионалов, любителей и техников, желающих изучить цепи переменного и постоянного тока

---

Вопросы и комментарии

Есть ли у вас какие-либо вопросы, комментарии или мнения по этой теме? Если да, отправьте свой отзыв по электронной почте. Я постараюсь вернуться к вам как можно скорее.

---

Поделиться страницей

Нажмите кнопку, чтобы добавить эту страницу в закладки или поделиться ею через Twitter, Facebook, электронную почту или другие службы:

---

Студенты и исследователи

Веб-адрес этой страницы:
www.school-for-champions.com/science/
electric_ohms_law.htm

Пожалуйста, включите его в качестве ссылки на свой веб-сайт или в качестве ссылки в своем отчете, документе или тезисе.

Авторские права © Ограничения

---

Где ты сейчас?

Школа чемпионов

Физические темы

Закон Ома для простых электрических цепей

---

Закон Ома 101: его формула, история и применение

Электрический ток, который питает вентиляторы и чайники в наших домах, регулируется законом Ома, фундаментальным правилом электрического потока, которое было дано Георгом Омом в 1827 году.Широкую применимость этого закона можно понять по тому факту, что, несмотря на то, что он был сформулирован почти 200 лет назад, он по-прежнему актуален сегодня и имеет значение почти для всех нас в нашей повседневной жизни.

Включаете ли вы обогреватель в комнате или настраиваете утюг на режим хлопка, закон Ома — это то, что позволяет вам достичь желаемого потока тока для ваших конкретных нужд. В мире физики этот закон считается важным и важным способом определения силы электрического тока, протекающего через проводник.

Что такое закон Ома? Треугольник

Ома Источник: PNG Kit

Закон Ома объясняет взаимосвязь между током, напряжением и сопротивлением. Он утверждает, что при постоянной температуре и физических условиях количество электрического тока (I), проходящего через металлический проводник в цепи, прямо пропорционально напряжению (V). Ом выразил это открытие в форме простого уравнения, описывающего взаимосвязь напряжения, тока и сопротивления:

В ∝ I

В = IR

I = V / R или R = V / I

Здесь V = напряжение (вольты),

I = ток (ампер)

и R = сопротивление (Ом)

Этот закон легко понять по аналогии с наблюдением за потоком. воды через трубу.Чем больше давление воды, тем больше воды будет выходить из трубы. Точно так же при заданном значении сопротивления, когда к проводнику приложено большее напряжение, будет течь больше тока. Закон Ома также означает, что, если мы знаем значения любых двух: напряжения, тока или сопротивления в цепи, мы можем определить третье.

Получение закона Ома из модели Друде Модель Друде. Источник: Rafaelgarcia / Wikimedia Commons

В 1900 году Пол Друде предложил модель Друде, которая упрощает объяснение движения электронов в твердом теле, например в металле.Модель использовала классическую механику, чтобы рассматривать твердое тело как фиксированный массив ядер в «море» несвязанных электронов, и кинетическую теорию газов, чтобы оценить скорость дрейфа.

Друде использовал следующую формулу для расчета средней скорости дрейфа электронов и аппроксимации проводимости ряда невалентных металлов:

p = −eEτ

Здесь p = средний импульс

−e = заряд электрона

τ = среднее время между

Плотность тока оказалась прямо пропорциональной электрическому полю, так как и плотность тока, и импульс были пропорциональны скорости дрейфа.Применив закон Ома к своей модели движения электронов, Друде смог построить модели, предсказывающие электронные транспортные свойства металлов.

История закона Ома

Источник: BerndGehrmann / Wikimedia Commons

В 1827 году закон Ома был представлен в книге Георга Ома «Гальваническая цепь, математически вычисленная », но, несмотря на то, что он был настолько фундаментальным для физики электричества, этот закон не был не был хорошо принят другими учеными и критиками в то время. Тогдашний министр образования Германии посчитал открытия Георга Ома ересью и сказал, что «…. физик, исповедующий такие ереси, был недостоин преподавать науку ».

В последующие годы Ом жил в бедности, частным образом обучая в Берлине, пока в 1833 году не стал директором Политехнической школы Нюрнберга. Лондонское королевское общество признало важность его открытия и наградило его медалью Копли. В следующем году они приняли его в члены.

В 1849 году, всего за 5 лет до его смерти, мечта всей жизни Ома осуществилась, когда ему вручили Профессор экспериментальной физики Мюнхенского университета.

Закон Ома получил широкое признание, и, помимо науки об электричестве, он также оказался полезным при проектировании телеграфных систем по сравнению с предыдущим законом, данным Питером Барлоу, который ранее ошибочно заключил, что величина тока была пропорциональна площади поперечного сечения проводника.

Даже современные теории, определяющие электромагнетизм и электрические цепи, согласуются с законом Ома. Удивительно, но закон работает даже на атомарном уровне; электрический ток через кремниевые провода, состоящие из 5 атомов, все еще течет согласно соотношению, заданному в законе Ома.

Последние тенденции

Законы, выведенные Георгом Омом, до сих пор являются предметом дискуссий и экспериментов среди ученых всего мира. Каждый год проводится множество исследований, основанных либо на принципах Ома, либо в попытках избежать их воздействия.

В 2019 году исследователи из Калифорнийского университета в Беркли провели эксперимент по улучшению ионной проводимости в литий-ионных батареях. В этом эксперименте была предложена обновленная версия закона Ома для анализа силы тока через бинарные электролиты, в котором для управления током использовался постоянный потенциал.

Этот эксперимент проводился в рамках попытки усовершенствовать технологию литий-ионных аккумуляторов, которая питает нынешнее поколение электромобилей, ноутбуков, смартфонов, аэрокосмических устройств и даже некоторых технологий военного уровня.

В мае 2020 года еще один такой интересный эксперимент провела группа ученых из Окинавского института науки и технологий аспирантуры (OIST).

В то время как закон Ома предполагает, что, когда сопротивление поровну разделено между двумя путями, электроны делятся поровну по одним и тем же путям, отдел квантовой динамики в OIST провел эксперименты, чтобы найти любое отклонение в движении электронов, когда они находятся в жидкости, а не в жидкости. твердая среда.

Эксперименты, проведенные учеными из отдела квантовой динамики, позволили выявить некоторые интересные детали, касающиеся поведения риплополяронов (электронов, захваченных в тяжелой жидкости), и обнаружили, что в определенных ситуациях движение электронов следовало за сохранением импульса, а не за движением Ома. Закон.

Интересные факты о законе Ома

Источник: T_Tide / Pixabay

Применение закона Ома (на основе V = IR) ограничено цепями только с постоянным током (DC) и не работает при наличии переменного тока (AC) протекает по контуру.

Этот закон также связан с конструкцией и функционированием современных электронных устройств, таких как смартфоны, ноутбуки и зарядные устройства, работающие от постоянного тока. Это позволяет инженерам рассчитать достаточный запас энергии через эти устройства.

Единица сопротивления названа Ом (Ом) в честь Георга Ома в честь его вклада в области физики.

Считается, что этот популярный закон физики впервые открыл английский физик Генри Кавендиш, который никогда не публиковал свои научные открытия по электрическому току.Позже, когда Ом проводил собственное исследование связи между напряжением и током, он натолкнулся на аналогичные открытия и опубликовал закон под своим именем.

Амперметр постоянного тока, используемый для измерения значения постоянного тока на любом устройстве постоянного тока, также следует этому закону.

Предохранители и резисторы, которые препятствуют прохождению электрического тока и служат в качестве предохранительных компонентов в электронных приборах, работают в соответствии с формулами, указанными в законе Ома.

Георг Ом — MagLab

Георг Симон Ом имел скромные корни и большую часть своей жизни боролся с финансами, но сегодня немецкий физик хорошо известен своей формулировкой закона, называемого законом Ома, описывающего математическую связь между электрическим током, сопротивлением и напряжением.

Закон

Ома гласит, что постоянный ток ( I ), протекающий через материал с заданным сопротивлением, прямо пропорционален приложенному напряжению ( В, ) и обратно пропорционален сопротивлению ( R ). Закон обычно выражается как I = V / R . Большинство материалов, но не все, подчиняются закону Ома. Те, которые этого не делают, обычно описываются как безомные проводники . В слегка измененной форме закон Ома может быть распространен на цепи переменного тока, а также на магнитные цепи.

Ом родился 16 марта 1789 года в Эрлангене, Бавария (ныне часть Германии), сын слесаря. Первоначально он получил образование у своего отца, который обладал значительными знаниями по множеству предметов, несмотря на отсутствие у него формального образования, а затем поступил в гимназию Эрлангена. К тому времени, когда он начал учиться в Университете Эрлангена в 1805 году, Ом обладал прекрасным пониманием высшей математики. Тем не менее, он не уделял достаточно времени своему образованию, чтобы доставить удовольствие отцу, предпочитая принимать участие в различных развлечениях, а не заниматься своими книгами.Из-за отцовского недовольства Ом бросил школу после трех семестров и переехал в Швейцарию, где стал учителем математики.

Ом больше не учился в университете, но в свободное время изучал труды выдающихся математиков. В 1809 году он решил оставить свой преподавательский пост и заняться частным репетитором, продолжая при этом свое собственное обучение. В конце концов он повторно поступил в Университет Эрлангена, получив докторскую степень через год. После выпуска Ом начал читать лекции в своей альма-матер.Но он был недоволен этой позицией, которая плохо оплачивалась, поскольку он был бы на большинстве преподавательских должностей, которые он занимал на протяжении всей своей жизни. Он ушел в отставку через несколько семестров и занял другую должность в Бамберге.

Пытаясь улучшить свои перспективы, Ом написал учебник по геометрии и начал экспериментальную работу, которая, как он надеялся, приведет к созданию трактатов, которые можно будет опубликовать. Положительный прием текста геометрии привел к тому, что ему предложили преподавать в школе в Кельне. Физическая лаборатория там предоставила Ому пространство и инструменты, необходимые для проведения исследований электричества и магнетизма, явлений, которые интенсивно исследовались в начале 1820-х годов после открытия Гансом Кристианом Эрстедом их взаимосвязи.Работа Ома в конечном итоге привела к его публикации Die galvanische Kette, Mathematisch Bearbeitet (Гальваническая цепь, исследованная математически) в 1827 году. Трактат содержал отчет о его электромагнитных теориях и включал все компоненты закона Ома.

В отличие от большинства немецких ученых того времени, Ом использовал математический подход при рассмотрении электричества и магнетизма. Это могло быть частично причиной того, что трактат вначале был плохо принят многими его современниками.За годы, прошедшие после публикации, положение Ома среди коллег-ученых постепенно улучшилось, особенно в других странах. Наконец, в 1840-х он обрел успех, которого стремился к большей части своей жизни. В 1841 году он получил престижную медаль Копли от Королевского общества Англии, а в следующем году был удостоен чести иностранного членства в той же ассоциации. Вскоре последовало дополнительное членство в других научных организациях. Возможно, наиболее значимым для Ома было его назначение профессором Мюнхенского университета в 1849 году, которое, наконец, положило конец его долгому потоку переходов на неудовлетворительные преподавательские должности.Незадолго до смерти он был удостоен кафедры физики в университете, что стало последним показателем значительного успеха Ома.

В наше время имя Ома настолько знакомо, что трудно поверить в трудности, с которыми он столкнулся при жизни. Помимо закона Ома, его имя связано с международной единицей электрического сопротивления. В цепи присутствует сопротивление в один Ом, когда один вольт генерирует один ампер тока.

Ом, Джордж Саймон

Закон Ома был разработан Георгом Симоном Омом (1787-1854). Хотя он обнаружил один из самые фундаментальные законы тока электричества, он был практически игнорировали большую часть своей жизни ученые в его собственной стране. В 1827 году Георг Симон Ом открыл некоторые законы, относящиеся к сила тока в проводе. Ом обнаружил, что электричество действует как вода в трубе.

Ом обнаружил, что ток в цепи прямо пропорционально электрическому давлению и обратно сопротивлению проводников.

Закон Ома — одна из самых важных вещей, которые вы будете использовать на протяжении всей вашей электротехнической карьеры. Это математический инструмент, который очень полезен при определении неизвестный фактор напряжения, тока или сопротивления в электрическом цепь, в которой два других фактора неизвестны.

Это простой закон, который устанавливает взаимосвязь между напряжением, ток и сопротивление в математическом уравнении. В электрическом термины, напряжение обозначается буквой «Е» (электродвижущая сила) Ток буквой «I» (интенсивность) и сопротивление буквой «R» .

Формула Ома не может работать должным образом, если не заданы все значения. выражается в правильных единицах измерения:

НАПРЯЖЕНИЕ выражается в ВОЛЬТАХ
ТОК выражается в АМПЕРАХ
СОПРОТИВЛЕНИЕ выражается в ОМ

---

Рабочая тетрадь с вопросами и Ответы

Также в наличии: Закон Ома был разработан по: Георг Симон Ом

Главная | FAQs | Каталог | Почта Заказ | Политика возврата Код , электрические классы Inc.
7449 Citrus Avenue
Winter Park, FL 32792 Тел: (407) 671-0020 или Бесплатный номер 1-800-642-2633
Факс: (407) 671-6497 Электронная почта: [email protected]
Для комментариев и предложений, щелкните конверт

Авторские права , Электротехнические классы по Кодексу Тома Генри Inc.

Как записан закон Ома для участка цепи. Закон Ома для полной цепи

Закон Ома для полной цепи — это эмпирический (полученный из эксперимента) закон, который устанавливает взаимосвязь между мощностью тока, электродвижущей силой (ЭДС) и внешним и внутренним сопротивлением в цепи.

При проведении реальных исследований электрических характеристик цепей постоянного тока необходимо учитывать сопротивление самого источника тока.Таким образом, в физике это переход от идеального источника тока к реальному источнику тока, имеющему собственное сопротивление (см. Рис. 1).

Рис. 1. Изображение идеального и реального источников тока

Учет источника тока с собственным сопротивлением обязывает использовать закон Ома для всей цепи.

Мы формулируем закон Ома для всей цепи так (см. Рис. 2): Ток в полной цепи прямо пропорционален ЭДС и обратно пропорционален общему сопротивлению цепи, где полное сопротивление понимается как сумма внешних и внутренних сопротивлений.

Рис. 2. Схема закона Ома для полной цепи.

• R — внешнее сопротивление [ОМ];
• р — сопротивление источника ЭДС (внутреннего) [ОМ];
• I — сила тока [А];
• ε- EDC источника тока [B].

Рассмотрим несколько задач по этой теме. Задания закона Ома для полной цепочки, как правило, ставят ученикам 10-й класс, чтобы они лучше усвоили указанную тему.

И.Определите силу тока в цепи с помощью лампочки сопротивлением 2,4 Ом, источником тока которой 10 В и внутренним сопротивлением 0,1 Ом.

По определению закона Ома для всей цепи ток равен:

II. Определите внутреннее сопротивление источника тока с ЭДС 52 В. Если известно, что при подключении этого источника к цепи с сопротивлением 10 Ом, амперметр показывает значение 5 А.

Запишем закон Ома для полной цепи и выразим из него внутреннее сопротивление:

III.Однажды школьник спросил учителя физики: «Почему садится батарейка?» Как грамотно ответить на этот вопрос?

Мы уже знаем, что у реального источника есть собственное сопротивление, которое возникает либо из-за сопротивления растворов электролитов для гальванических элементов и аккумуляторов, либо из-за сопротивления проводников для генераторов. По закону Ома для полной цепочки:

следовательно, ток в цепи может уменьшаться либо из-за уменьшения ЭДС, либо из-за увеличения внутреннего сопротивления.Величина ЭДС возле АКБ практически постоянная. Следовательно, ток в цепи уменьшается за счет увеличения внутреннего сопротивления. Итак, «батарейка» садится, так как ее внутреннее сопротивление увеличивается.

Закон Ома для участка цепочки: ток Мощность I. Расположение на электрической цепи Прямо пропорционально напряжению U. На концах площадки и обратно пропорционально ее сопротивлению р.

Формула закона: I. =. Отсюда пишем формулу U. = IR. и R =. .

Рис.1. Цепочка сюжетов Рис.2. Полная цепь

Закон Ома для полной цепи: ток Power I. Полная электрическая цепь РАВИДЫ (электрическая мощность) источник тока E. делится на полное сопротивление цепи ( R + R). Полное сопротивление цепи равно сумме сопротивлений внешней цепи Р. и внутренней Р. Источник тока. Формула закона I =.
. На рис. 1 и 2 — схемы электрических цепей.

3. Последовательное и параллельное соединение проводов

Проводники в электрических цепях можно подключать последовательно и параллельно .Смешанное соединение объединяет оба этих соединения.

Сопротивление, при включении которого вместо всех остальных проводников, расположенных между двумя точками цепи, ток и напряжение остаются неизменными, называется эквивалентным сопротивлением этих проводников.

Последовательное соединение

Постоянно называемое соединение, в котором каждый проводник соединяется только с одним предыдущим и одним последующим проводниками.

Как следует из первых правил Кирхгофа При последовательном соединении проводников мощность электрического тока, протекающего по всем проводникам, одинакова (исходя из закона экономии заряда).

1. При последовательном подключении проводников (рис. 1) мощность тока во всех проводниках одинакова: I. 1 = I. 2 = I. 3 = I.

Рис. 1. Выборочное соединение двух проводов.

2. По закону Ома напряжение U. 1 и U. 2 На жилах равны У. 1 = IR. 1 , г. U. 2 = IR. 2 , г. U. 3 = IR. 3 .

Напряжение при последовательном соединении проводов равно величине напряжений в отдельных участках (проводниках) электрической цепи.

U. = U. 1 + U. 2 + U. 3

Обзор Ом, напряжение U. 1, U. 2 на жилах равны У. 1 = IR. 1 , г. U. 2 = IR. 2 , г. В соответствии со вторым правилом Кирхгофа, напряжение на всей площадке:

U. = U. 1 + U. 2 = IR. 1 + IR. 2 знак равно I (р. 1 + р. 2 ) = Ир. Получаем: р. = р. 1 + р. 2

Общее напряжение U. На жилах, равных сумме напряжений У. 1 , г. U. 2 , U. 3 равно: U. = U. 1 + U. 2 + U. 3 = I. · ( р. 1 + р. 2 + р. 3 ) = IR.

где р. Эк. — эквивалент Сопротивление всей цепи.Отсюда: р. Эк. = р. 1 + р. 2 + р. 3

При последовательном включении эквивалентное сопротивление цепи равно сумме сопротивлений отдельных участков цепи : R. Эк. = р. 1 + р. 2 + р. 3 +…

Этот результат является удовлетворительным для любого числа последовательно соединенных проводников.

Из закона, омассы: при равенстве тока для последовательного подключения:

I. = , г. I. = .Отсюда знак равно или = , т.е. напряжения в отдельных участках цепи прямо пропорциональны сопротивлению участков.

При последовательном подключении н. одинаковых проводника общим напряжением, равным напряжению одного U 1 по их количеству п. :

U. ПОСЛЕ РОЖДЕНИЯ = н. · U. 1 . Аналогично сопротивлению : р. ПОСЛЕ РОЖДЕНИЯ знак равно н. · р. 1

При размыкании цепи одного из последовательно подключенных потребителей ток пропадает во всей цепи, поэтому последовательное включение на практике не всегда удобно.

Невозможно услышать электрический ток и опасное напряжение (кроме жужжания высоковольтных линий и электроустановок).Токовые части, находящиеся под напряжением, внешне ничем не отличаются.

Невозможно распознать их и по запаху, и по высоким температурам в стандартных режимах эксплуатации, они не отличаются. Но мы превращаемся в бесшумную и тихую розетку пылесоса, щелкаем выключателем — и энергия словно берется из ниоткуда, сама по себе материализуя шум и сжатие внутри бытового прибора.

Опять же, если воткнуть в разъемы разъемов два гвоздя и взять их, то буквально все ваше тело ощутит реальность и объективность существования электрического тока.Делать это настоятельно не рекомендуется. Но примеры с пылесосом и гвоздями ясно демонстрируют нам, что изучение и понимание основных законов электротехники способствует безопасности при обращении с электричеством потребителей, а также устраняет суеверные предрассудки, связанные с электрическим током и напряжением.

Итак, рассмотрим один, наиболее ценный закон электротехники, который полезно знать. И постарайтесь сделать это в максимально популярной форме.

Закон Ома

1.Дифференциальная форма записи Закона Ома

Самый важный закон электротехники — это, конечно же, закон Ома . О его существовании знают даже люди, не имеющие отношения к электротехнике. А между тем вопрос «Знаете ли вы закон Ома?» В технических вузах — ловушка для укоренившегося и заносчивого Щолярова. Товарищ, конечно, отвечает, что закон Ома знает отлично, а потом просят привести этот закон в дифференциальную форму.Получается, что стипендиат или первокурсник еще учатся и учатся.

Однако дифференциальная форма записи Закона Ома на практике практически не применима. Он отражает зависимость между плотностью тока и напряженностью поля:

где G — проводимость цепи; Е — сила электрического тока.

Все это попытки выразить электрический ток с учетом только физических свойств материала проводника, без учета его геометрических параметров (длины, диаметра и т.п.).Дифференциальная форма записи закона Ома — чистая теория, знания о ней вообще не требуются.

2. Интегральная форма записи закона Ома для участка цепи

Прочие виды деятельности — это неотъемлемая форма записи. Также у нее есть несколько разновидностей. Самый популярный из них — закон Ома для участка цепочки: i = u / r

Другими словами, ток в области цепи всегда тем выше, чем больше напряжение приложено к этому участку и тем меньше сопротивление этой области.

Этот «вид» Закона Ома просто обязателен для запоминания всем, кому хоть иногда приходится иметь дело с электричеством. К счастью, зависимость довольно проста. Ведь напряжение в сети можно считать неизменным. Для розетки он равен 220 вольт. Следовательно, получается, что ток в цепи зависит только от сопротивления цепи, подключенной к розетке. Хеза — это простая мораль: этому сопротивлению нужно следовать.

Короткие замыкания, которые у всех на слуху происходят именно из-за низкого сопротивления внешней цепи.Предположим, что из-за неправильного соединения проводов фазный и нулевой провод в ответвительной коробке были напрямую соединены между собой. Тогда сопротивление участка цепи резко уменьшится почти до нуля, а также резко возрастет ток до очень большого значения. Если разводка правильная, сработает автоматический выключатель, а если нет, или он неисправен или неправильно, провод не справится с повышенным током, нагревается, плавится и может стать причиной пожара.

Но бывает, что включенные в розетку устройства, проработавшие далеко не один час, становятся причиной короткого замыкания.Типичный случай — вентилятор, обмотки двигателя которого перегрелись из-за подрыва лопастей. Изоляция обмоток двигателя не рассчитана на серьезный нагрев, быстро приходит в негодность. В результате возникают аварийные короткие замыкания, которые снижают сопротивление, а также в соответствии с законом Ома приводят к увеличению тока.

Повышенный ток, в свою очередь, приводит к полному износу изоляции обмоток, и не происходит интерсенсона, а, скорее всего, происходит полное короткое замыкание.Ток идет в дополнение к обмоткам, сразу от фазы в нулевом проводе. Правда, все сказанное может произойти только с совершенно простым и дешевым вентилятором, не оснащенным термозащитой.

Закон Ома для переменного тока

Следует отметить, что приведенная выше запись закона Ома описывает участок цепи постоянного напряжения. В сетях переменного напряжения имеется дополнительное реактивное сопротивление, а общее сопротивление принимает значение квадратного корня из суммы квадратов активного и реактивного сопротивления.

Закон Ома для участка цепи переменного тока принимает вид: I = U / Z ,

где Z — полное сопротивление цепи.

Но большое реактивное сопротивление характерно, прежде всего, для мощных электрических машин и силовой преобразовательной техники. Бытовое электрическое сопротивление Бытовые приборы и лампы почти полностью активны. Поэтому в повседневной жизни для расчетов можно использовать простейшую форму записи закона Ома: I = U / R.

3.Интегральная форма записи для полной цепочки

Если существует форма записи закона для участка цепи, то для полной цепи действует закон Ом: i = E / (R + R) .

Здесь R — внутреннее сопротивление источника ЭДС сети, а R — полное сопротивление самой цепи.

На физическую модель Чтобы проиллюстрировать этот подвид Закона Ома, необязательно ходить — это бортовая электрическая сеть Автомобиль, аккумулятор в котором является источником EDC.Невозможно предположить, что сопротивление накопления равно абсолютному нулю, поэтому даже при прямом замыкании между его выводами (отсутствие сопротивления R) ток будет расти не до бесконечности, а просто до большого значения. Однако этого высокого значения, конечно же, достаточно, чтобы вызвать оплавление проводов и возгорание автомобиля. Поэтому электрические цепи автомобилей защищают от короткого замыкания с помощью предохранителей.

Такой защиты может оказаться недостаточно, если произойдет замыкание блока предохранителей относительно аккумулятора или если один из предохранителей полностью заменен на кусок.медная проволока. Тогда спасение только в одном — нужно как можно быстрее разорвать цепочку, закинув «массу», то есть минусовую клемму.

4. Интегральная форма записи закона Ома для участка цепи, содержащей источник ЭЦП

Следует отметить, что существует еще одна разновидность закона Ома — для участка цепочки, содержащей источник ЭДС:

Здесь u — разность потенциалов в начале и в конце рассматриваемой области.Знак перед значением EDS зависит от его направления относительно напряжения. Воспользуйтесь законом Омала для участка схемы, который часто учитывается при определении параметров цепи, когда часть схемы недоступна для детального изучения и нас не интересует. Предположим, это скрыто в деталях тела предметов. Остальная схема имеет источник EDC и элементы с известным сопротивлением. Затем, измерив напряжение на входе неизвестного участка цепи, можно рассчитать ток, а затем — и сопротивление неизвестного элемента.

выводы

Таким образом, мы видим, что «простой» закон Омы не так прост, как кому-то может показаться. Зная все формы интегральной записи законов Ома, можно понять и легко запомнить многие требования электробезопасности, а также обрести уверенность в обращении с электричеством.

Физический закон, определяющий связь (или электрическое напряжение) с током, протекающим в проводнике, и сопротивлением проводника.Установлен Георгом Омом в 1826 году и назван в его честь.

Закон Ома для переменного тока

Приведенные выше соображения относительно свойств электрической цепи при использовании источника (генератора) с переменной во времени ЭДС остаются справедливыми. Особое внимание уделяется только учету специфических свойств потребителя, приводящих к расхождению достижения напряжения и тока его максимальных значений, то есть учет фазового сдвига.

Если ток синусоидальный с циклической частотой Ω (\ DisplayStyle \ Omega), а в цепи есть не только активные, но и реактивные компоненты (емкости, индуктивность), то закон Ома является обобщенным; Включенные в него значения становятся исчерпывающими:

U = я ⋅ Z (\ displaystyle \ mathbb (u) = \ mathbb (i) \ cdot z)

• U = U. 0 e. и. ω т. — напряжение или разность потенциалов,
• I. — сила тока
• Z = Re. — и. Δ — интегральное сопротивление (электрическое сопротивление),
• пр. = √ пр. 2 + пр. 2 — полное сопротивление,
• R R. = ω L. — 1 / (Ω C. ) — реактивное сопротивление (индуктивная и емкостная разность),
• р А. — активное (омическое) сопротивление, не зависящее от частоты,
• Δ = — arctg ( R R. / R A. ) — фазовый сдвиг между напряжением и силой тока.

В этом случае переход от комплексных переменных в текущих значениях и напряжении к действительным (измеренным) значениям может производиться по действительной или мнимой части (но во всех элементах цепочки одинаково!) Комплексные значения этих величин. Соответственно обратный переход строится, например, для U = u 0 sin \ u2061 (ω t + φ) (\ displaystyle u = u_ (0) \ sin (\ Omega T + \ Varphi) ) Выбор таких U = u 0 E i (ω t + φ), (\ displaystyle \ mathbb (u) = u_ (0) e ^ (i (\ omega t + \ varphi)) ),) то, что IM \ u2061 U = U.(\ DisplayStyle \ Operatorname (IM) \ MathBB (U) = U.) Тогда все значения тока и напряжения в схеме следует рассматривать как F = im \ f (\ displaystyle f = \ OperatorName (im) \ mathbb (f))

Здравствуйте, уважаемые читатели сайта «Заметки электрика» ..

Сегодня открываю новый раздел на сайте под названием.

В этом разделе я постараюсь объяснить вопросы электротехники в наглядной и простой форме. Сразу скажу, что далеко углубляться в теоретические знания мы не будем, но с основами познакомимся в достаточном порядке.

Первое, с чем я хочу вас познакомить, это закон Ома для участка цепи. Это главный закон, который нужно знать каждому.

Знание этого закона позволит нам беспрепятственно и безошибочно определять значения силы тока, напряжения (разности потенциалов) и сопротивления на участке цепи.

Кто такой ОМ? Немного истории

Закон Ома открыл известный немецкий физик Георг Симон Ом в 1826 году.Вот так он выглядел.

Не буду рассказывать всю биографию Георга Ома. Подробнее об этом вы можете узнать на других ресурсах.

Скажу только самое главное.

Его именем назван самый основной закон электротехники, который мы активно применяем в сложных расчетах при проектировании, производстве и в быту.

Закон Ома для однородного участка цепи выглядит так:

I — величина тока, протекающего через участок цепи (измеряется в амперах)

U — значение напряжения на участке цепи (в вольтах)

R — сопротивление участка цепи (измерено в Омах)

Если формулу объяснить словами, то окажется, что ток пропорционален напряжению и обратно пропорционален сопротивлению участка цепи.

Проведем эксперимент

Чтобы понять формулу не на словах, а на самом деле, необходимо собрать следующую схему:

Цель этой статьи — наглядно показать, как использовать закон Ома для участка цепи. Поэтому я собрал эту схему на своем рабочем стенде. Смотрите ниже, как это выглядит.

С помощью управляющей клавиши (элемента) можно выбрать либо постоянное напряжение, либо переменное напряжение на выходе.В нашем случае используется постоянное напряжение. Уровень напряжения меняю с помощью лабораторного автотрансформатора (ПОЗЖЕ).

В нашем эксперименте я буду использовать напряжение на участке цепи, равное 220 (В). За контролем напряжения на выходе следит вольтметр.

Теперь мы полностью готовы провести собственный эксперимент и проверить закон Омы в реальности.

Ниже я приведу 3 примера. В каждом примере мы определим желаемое значение двумя способами: с помощью формулы и практическим способом.

Пример №1.

В первом примере нам нужно найти ток (i) в цепи, зная размер источника постоянного напряжения и сопротивление светодиодной лампочки.

Напряжение источника постоянного напряжения U = 220 (В) . Сопротивление светодиодной лампочки равно R = 40740 (ОМ) .

С помощью формулы находим ток в цепи:

I = u / r = 220/40740 = 0.0054 (а)

Подключаем светодиодную лампочку, включенную в режим амперметра, и измеряем ток в цепи.

На дисплее мультиметра отображается ток цепи. Его значение составляет 5,4 (мА) или 0,0054 (а), что соответствует току, найденному по формуле.

Пример №2.

Во втором примере нам нужно найти напряжение (U) участка цепи, зная величину тока в цепи и значение сопротивления светодиодной лампочки.

I = 0,0054 (а)

R = 40740 (ОМ)

С помощью формулы находим напряжение участка цепи:

U = I * R = 0,0054 * 40740 = 219,9 (B) = 220 (B)

А теперь практически проверяем полученный результат.

Подключить параллельно светодиодную лампочку мультиметра, включенного в режим вольтметра, и измерить напряжение.

На дисплее мультиметра отображается измеренное значение напряжения. Его значение составляет 220 (В), что соответствует напряжению, найденному с помощью формулы закона OMA для участка цепи.

Пример №3.

В третьем примере нам нужно найти сопротивление (R) участка цепи, зная значение тока в цепи и значение напряжения участка цепи.

I = 0,0054 (а)

U = 220 (В)

Снова воспользуемся формулой и находим сопротивление участка цепи:

R = U / I = 220/0.0054 = 40740,7 (ОМ)

А теперь практически проверяем полученный результат.

Измеряем сопротивление светодиодной лампочки с помощью или мультиметром.

Полученное значение составили R = 40740 (ОМ) Что соответствует найденному по формуле сопротивлению.

Как легко запомнить закон Ома для участка цепочки !!!

Чтобы не запутаться и легко запомнить формулу, можно воспользоваться небольшой подсказкой, которую вы можете сделать самостоятельно.

Нарисуйте треугольник и введите в него параметры электрической цепи, как показано на рисунке ниже. У вас должно получиться вот так.

Как им пользоваться?

Использовать треугольник-наконечник очень легко и просто. Закройте пальцем параметр цепочки, который хотите найти.

Если параметры, оставшиеся в треугольнике, расположены на одном уровне, то их необходимо умножить.

Если оставшиеся в треугольнике параметры находятся на разных уровнях, то необходимо разделить верхний параметр на нижний.

С помощью наконечников-треугольников вы не запутаетесь в формуле. Но лучше выучить ее как таблицу умножения.

выводы

В конце статьи сделаю вывод.

Электрический ток — это направленный поток электронов из точки с потенциалом минус в точку A с потенциалом плюс. И чем выше разность потенциалов между этими точками, тем больше электронов перемещается из точки в точку A, i.е. Ток в цепи увеличится при условии, что сопротивление цепи останется неизменным.

Но сопротивление лампочки противодействует прохождению электрического тока. И чем больше сопротивление в цепи (последовательное соединение нескольких лампочек), тем меньше будет ток в цепи, при постоянном напряжении сети.

П.С. Тут в интернете нашел забавную, но поясняющую карикатуру на тему закона Ома для схемы сайта.

3.4: Закон Ома (снова) — Workforce LibreTexts

Принцип «текущее убивает» по существу верен. Это электрический ток, который сжигает ткани, замораживает мышцы и вызывает фибрилляцию сердца. Однако электрический ток не возникает сам по себе: должно быть доступное напряжение, чтобы заставить электроны проходить через жертву. Тело человека также оказывает сопротивление току, что необходимо учитывать.

Принимая закон Ома для напряжения, тока и сопротивления и выражая его через ток для заданных напряжения и сопротивления, мы получаем следующее уравнение:

Величина тока, протекающего через тело, равна величине напряжения, приложенного между двумя точками этого тела, деленному на электрическое сопротивление, оказываемое телом между этими двумя точками.Очевидно, что чем больше напряжения доступно, чтобы заставить электроны течь, тем легче они будут проходить через любое заданное сопротивление. Следовательно, опасность высокого напряжения: высокое напряжение означает возможность протекания через ваше тело большого количества тока, который может повредить или убить вас. И наоборот, чем большее сопротивление тело оказывает току, тем медленнее электроны будут течь при любом заданном напряжении. Насколько опасно напряжение, зависит от того, какое полное сопротивление в цепи препятствует потоку электронов.

Сопротивление тела не является фиксированной величиной. Это варьируется от человека к человеку и время от времени. Существует даже метод измерения содержания жира в организме, основанный на измерении электрического сопротивления между пальцами рук и ног. Различное процентное содержание жира в организме дает разное сопротивление: всего одна переменная, влияющая на электрическое сопротивление в организме человека. Чтобы методика работала точно, человек должен регулировать потребление жидкости за несколько часов до теста, что указывает на то, что гидратация тела является еще одним фактором, влияющим на электрическое сопротивление тела.

Сопротивление тела также зависит от того, как происходит контакт с кожей: от руки к руке, от руки к ноге, от ступни к ступне, от руки к локтю и т. Д.? Пот, богатый солями и минералами, является отличным проводником электричества, будучи жидкостью. То же самое и с кровью с таким же высоким содержанием проводящих химикатов. Таким образом, контакт с проводом потной рукой или открытой раной будет оказывать гораздо меньшее сопротивление току, чем контакт с чистой сухой кожей.

Измеряя электрическое сопротивление чувствительным измерителем, я измеряю сопротивление примерно 1 миллион Ом (1 МОм) двумя руками, держась за металлические щупы измерителя между пальцами.Измеритель показывает меньшее сопротивление, когда я сильно сжимаю щупы, и большее сопротивление, когда я держу их слабо. Я сижу за компьютером и печатаю эти слова, мои руки чистые и сухие. Если бы я работал в жаркой, грязной промышленной среде, сопротивление между моими руками, вероятно, было бы намного меньше, представляя меньшее сопротивление смертельному току и большую угрозу поражения электрическим током.

А какой ток вреден? Ответ на этот вопрос также зависит от нескольких факторов.Химический состав тела человека оказывает значительное влияние на то, как электрический ток влияет на человека. Некоторые люди очень чувствительны к току, испытывая непроизвольное сокращение мышц из-за ударов статического электричества. Другие могут получить большие искры от разряда статического электричества и почти не почувствовать его, не говоря уже о мышечном спазме. Несмотря на эти различия, с помощью тестов были разработаны приблизительные руководящие принципы, которые показывают, что для проявления вредных эффектов требуется очень небольшой ток (опять же, информацию об источнике этих данных см. В конце главы).Все текущие значения даны в миллиамперах (миллиампер равен 1/1000 ампер):

Таблица воздействия электричества на тело

«Гц» означает единицу герц , меру того, насколько быстро изменяется переменный ток, мера, также известная как частота . Таким образом, столбец цифр, обозначенный «60 Гц переменного тока», относится к току, который изменяется с частотой 60 циклов (1 цикл = период времени, когда электроны текут в одном направлении, а затем в другом) в секунду.Последний столбец, обозначенный «10 кГц переменного тока», относится к переменному току, который совершает десять тысяч (10 000) возвратно-поступательных циклов каждую секунду.

Имейте в виду, что эти цифры являются приблизительными, поскольку люди с разным химическим составом тела могут реагировать по-разному. Было высказано предположение, что ток через грудную клетку всего 17 мА переменного тока достаточно, чтобы вызвать фибрилляцию у человека при определенных условиях. Большинство наших данных относительно индуцированной фибрилляции получены в результате испытаний на животных.Очевидно, что проводить тесты индуцированной фибрилляции желудочков на людях непрактично, поэтому имеющиеся данные отрывочны. О, и если вам интересно, я понятия не имею, почему женщины, как правило, более восприимчивы к электрическому току, чем мужчины!

Предположим, я положил обе руки на клеммы источника переменного напряжения с частотой 60 Гц (60 циклов, или чередование назад и вперед, в секунду). Сколько напряжения потребуется в этом чистом, сухом состоянии кожи, чтобы произвести ток в 20 миллиампер (достаточно, чтобы я не мог отпустить источник напряжения)? Мы можем использовать закон Ома (E = IR), чтобы определить это: необходимо ли в этом чистом, сухом состоянии кожи производить ток в 20 миллиампер (достаточно, чтобы я не мог отпустить источник напряжения)? Мы можем использовать закон Ома (E = IR), чтобы определить это:

E = IR

E = (20 мА) (1 МОм)

E = 20 000 вольт или 20 кВ

Имейте в виду, что это «лучший случай» (чистая, сухая кожа) с точки зрения электробезопасности, и что это значение напряжения представляет собой величину, необходимую для индукции столбняка.Чтобы вызвать болезненный шок, потребуется гораздо меньше! Также имейте в виду, что физиологические эффекты любой конкретной силы тока могут значительно отличаться от человека к человеку, и что эти расчеты являются приблизительными оценками только .

Обрызгав пальцы водой, чтобы имитировать пот, я смог измерить сопротивление рук в руках всего 17 000 Ом (17 кОм). Имейте в виду, что это касается только одного пальца каждой руки, касающегося тонкой металлической проволоки. Пересчитав напряжение, необходимое для возникновения тока в 20 мА, мы получим эту цифру:

E = IR

E = (20 мА) (17 кОм)

E = 340 вольт

В этих реальных условиях потребуется всего 340 вольт потенциала от одной моей руки к другой, чтобы вызвать ток 20 миллиампер.Тем не менее, все же возможно получить смертельный удар от меньшего напряжения, чем это. При условии значительно более низкого показателя сопротивления тела, увеличенного за счет контакта с кольцом (полоса золота, обернутая по окружности пальца, составляет отличную точку контакта для поражения электрическим током) или полного контакта с большим металлическим предметом, таким как труба или металл рукояткой инструмента сопротивление корпуса может упасть до 1000 Ом (1 кОм), что приведет к тому, что даже более низкое напряжение будет представлять потенциальную опасность:

E = IR

E = (20 мА) (1 кОм)

E = 20 вольт

Обратите внимание, что в этом состоянии 20 вольт достаточно, чтобы вызвать ток в 20 миллиампер через человека: достаточно, чтобы вызвать столбняк.Помните, было высказано предположение, что сила тока всего 17 миллиампер может вызвать фибрилляцию желудочков (сердца). При сопротивлении рукопашной в 1000 Ом для создания этого опасного состояния потребуется всего 17 вольт:

E = IR

E = (17 мА) (1 кОм)

E = 17 вольт

Семнадцать вольт — это не очень много для электрических систем. Конечно, это «наихудший» сценарий с напряжением переменного тока 60 Гц и отличной проводимостью тела, но он действительно показывает, насколько низкое напряжение может представлять серьезную угрозу при определенных условиях.

Условия, необходимые для создания сопротивления тела 1000 Ом, также не должны быть такими экстремальными, как то, что было представлено (потная кожа при контакте с золотым кольцом). Сопротивление тела может уменьшаться при приложении напряжения (особенно если столбняк заставляет пострадавшего крепче держать проводник), так что при постоянном напряжении удар может усилиться после первого контакта. То, что начинается как легкий шок — ровно настолько, чтобы «заморозить» жертву, чтобы она не могла отпустить ее, может перерасти в нечто достаточно серьезное, чтобы убить ее, поскольку сопротивление их тела уменьшается, а сила тока соответственно увеличивается.

Research предоставило приблизительный набор цифр для электрического сопротивления точек контакта человека в различных условиях (информацию об источнике этих данных см. В конце главы):

• Провод, касающийся пальцем: от 40 000 Ом до 1 000 000 Ом в сухом состоянии, от 4 000 Ом до 15 000 Ом во влажном состоянии.
• Провод, удерживаемый рукой: от 15 000 Ом до 50 000 Ом в сухом состоянии, от 3 000 Ом до 5 000 Ом во влажном состоянии.
• Металлические плоскогубцы, удерживаемые вручную: от 5000 Ом до 10 000 Ом в сухом состоянии, от 1000 Ом до 3000 Ом во влажном состоянии.
• Контакт ладонью: от 3000 Ом до 8000 Ом в сухом состоянии, от 1000 Ом до 2000 Ом во влажном состоянии.
• 1,5-дюймовая металлическая труба, удерживаемая одной рукой: от 1000 Ом до 3000 Ом в сухом состоянии, от 500 Ом до 1500 Ом во влажном состоянии.
• 1,5-дюймовая металлическая труба, захватываемая двумя руками: от 500 Ом до 1500 кОм в сухом состоянии, от 250 Ом до 750 Ом во влажном состоянии.
• Рука, погруженная в проводящую жидкость: от 200 Ом до 500 Ом.
• Опора, погруженная в проводящую жидкость: от 100 Ом до 300 Ом.

Обратите внимание на значения сопротивления для двух условий с металлической трубой диаметром 1,5 дюйма. Сопротивление, измеренное при захвате трубы двумя руками, составляет ровно половину сопротивления, когда одна рука держит трубу.

Двумя руками площадь соприкосновения с телом вдвое больше, чем с одной рукой. Это важный урок: электрическое сопротивление между любыми контактирующими объектами уменьшается с увеличением площади контакта при прочих равных условиях. Когда две руки держат трубку, электроны имеют два параллельных путей, по которым они проходят от трубки к телу (или наоборот).

Как мы увидим в более поздней главе, параллельных цепей всегда приводят к меньшему общему сопротивлению, чем любой отдельный путь, рассматриваемый отдельно.

В промышленности 30 вольт обычно считается консервативным пороговым значением для опасного напряжения. Осторожный человек должен рассматривать любое напряжение выше 30 вольт как опасное, не полагаясь на нормальное сопротивление тела для защиты от поражения электрическим током. При этом, по-прежнему, держать руки в чистоте и сухости и снимать все металлические украшения при работе с электричеством — это отличная идея. Даже при более низком напряжении металлические украшения могут представлять опасность, поскольку проводят ток, достаточный для ожога кожи, при контакте между двумя точками в цепи.Металлические кольца, в частности, были причиной более чем нескольких ожогов пальцев из-за замыкания между точками в низковольтной и сильноточной цепи.

Кроме того, напряжение ниже 30 может быть опасным, если его достаточно, чтобы вызвать неприятное ощущение, которое может привести к рывку и случайному контакту с более высоким напряжением или другой опасностью. Я вспоминаю, как однажды жарким летним днем ​​работал над автомобилем. На мне были шорты, моя голая нога касалась хромового бампера автомобиля, когда я затягивал контакты аккумулятора.Когда я прикоснулся металлическим ключом к положительной (незаземленной) стороне 12-вольтовой батареи, я почувствовал покалывание в том месте, где моя нога касалась бампера. Сочетание плотного контакта с металлом и моей вспотевшей кожи позволило почувствовать шок всего лишь при напряжении 12 вольт.

К счастью, ничего страшного не произошло, но если бы двигатель работал и удар ощущался в моей руке, а не в ноге, я мог бы рефлекторно толкнуть руку на пути вращающегося вентилятора или уронить металлический ключ на клеммы аккумулятора ( генерирует больших величин тока через гаечный ключ с большим количеством сопутствующих искр).Это иллюстрирует еще один важный урок, касающийся электробезопасности; этот электрический ток сам по себе может быть косвенной причиной травмы, заставляя вас подпрыгивать или спазмировать части вашего тела в опасную для вас сторону.

Ток, проходящий через человеческое тело, имеет значение, насколько он опасен. Ток будет влиять на все мышцы, находящиеся на его пути, а поскольку мышцы сердца и легких (диафрагмы), вероятно, являются наиболее важными для выживания, пути удара, проходящие через грудную клетку, являются наиболее опасными.Это делает путь электрического тока из рук в руки очень вероятным способом получения травм и летального исхода.

Во избежание подобных ситуаций рекомендуется работать с цепями под напряжением, находящимися под напряжением, только одной рукой, а вторую руку держать в кармане, чтобы случайно ни к чему не прикоснуться. Конечно, всегда безопаснее работать в цепи, когда она отключена, но это не всегда практично или возможно. При работе одной рукой обычно предпочитают правую руку левой по двум причинам: большинство людей правши (что обеспечивает дополнительную координацию при работе), а сердце обычно находится слева от центра в грудной полости.

Для левшей этот совет может быть не лучшим. Если такой человек недостаточно скоординирован с правой рукой, он может подвергнуть себя большей опасности, используя ту руку, с которой ему меньше всего комфортно, даже если электрический ток, протекающий через эту руку, может представлять большую опасность для его сердца. Относительная опасность между сотрясением одной рукой или другой, вероятно, меньше, чем опасность работы с менее чем оптимальной координацией, поэтому выбор руки для работы лучше всего оставить на усмотрение человека.

Лучшая защита от ударов цепи под напряжением — это сопротивление, а сопротивление может быть добавлено к телу с помощью изолированных инструментов, перчаток, обуви и другого снаряжения. Ток в цепи является функцией доступного напряжения, деленного на общего сопротивления на пути потока. Как мы рассмотрим более подробно позже в этой книге, сопротивления имеют аддитивный эффект, когда они сложены так, что электроны могут двигаться только по одному пути:

Теперь мы рассмотрим эквивалентную схему для человека в изолированных перчатках и ботинках:

Поскольку электрический ток должен проходить через ботинок и тело и перчатку, чтобы замкнуть цепь обратно к батарее, общая сумма ( сумма ) этих сопротивлений противодействует потоку электронов в большей степени, чем любое другое. сопротивлений рассматривается индивидуально.

Безопасность — одна из причин, по которой электрические провода обычно покрывают пластиковой или резиновой изоляцией: чтобы значительно увеличить сопротивление между проводником и тем, кто или что-либо может с ним контактировать. К сожалению, было бы непомерно дорого заключать проводники линии электропередачи в достаточную изоляцию, чтобы обеспечить безопасность в случае случайного контакта, поэтому безопасность поддерживается за счет того, что эти линии держатся достаточно далеко вне досягаемости, чтобы никто не мог случайно прикоснуться к ним.

Обзор

• Вред для тела зависит от силы электрического тока.Более высокое напряжение позволяет производить более высокие и опасные токи. Сопротивление противостоит току, поэтому высокое сопротивление является хорошей защитой от ударов.
• Обычно считается, что любое напряжение выше 30 может создавать опасные ударные токи.
• Металлические украшения определенно плохо носить при работе с электрическими цепями. Кольца, ремешки для часов, ожерелья, браслеты и другие подобные украшения обеспечивают отличный электрический контакт с вашим телом и сами могут проводить ток, достаточный для возникновения ожогов кожи даже при низком напряжении.
• Низкое напряжение все еще может быть опасным, даже если оно слишком низкое, чтобы напрямую вызвать поражение электрическим током. Их может быть достаточно, чтобы напугать жертву, заставив ее отпрянуть и коснуться чего-то более опасного в непосредственной близости.
• Когда необходимо работать с «живым» контуром, лучше всего выполнять работу одной рукой, чтобы предотвратить смертельный путь электрического тока из рук в руки (через грудную клетку).

Пример закона Ома

Аронс А. (1999) Индуктивное и дедуктивное обучение концепциям и теориям: использование исторической основы

.В: Труды конференции по истории, философии и преподаванию естественных наук, Университет

Калгари, стр. 49–63

Барлоу П. (1825 г.) О законах электромагнитного действия в зависимости от длины и размеров проводника

. проволока и др. Edinb Philos J 12: 105–114

Бауман Р.П. (1980) Гидравлические модели элементов электрических цепей. Phys Teacher 18 (5): 378–380

Беккерель AC (1823a) Du de

´

veloppement de l’e

´

lectricite

´

par le contact deux portions d’une me

ˆ

me metal,

dans un etat suf samment ine

´

gal de temperature и т. Д.Annales de Chimie et de Physique 23: 135–154

Беккерель AC (1823b) Описание

´

лекций, которые являются развитием подвески, развлекают химические действия.

Annales de Chimie et de Physique 23: 244–258

Becquerel AC (1826) Du pouvoir conducteur de l’e

´

lectricite

´

dans les me

´ 9000 l’intensite

´

de la force

e

´

lectrodynamique и т. д.Annales de Chimie et de Physique 32: 420–430

Beiser A, Krauskopf K (1964) Введение в физику и химию. McGraw-Hill Books, Нью-Йорк

Boutet de Monvel B (1863) Cours de Physique. L. Hachette, Paris, стр. 515–516

Buster S (1995) Использование исторического подхода во избежание неправильных представлений учащихся об электричестве

. В: Finley F et al (eds) Proceedings of the третьей международной конференции по истории, философии и науке

.Университет Миннесоты, Миннеаполис, Миннесота, стр. 170–175

Кэмпбелл Н. (1957) Основы науки. Dover Publications, New York

Cavendish H (1771) Попытка объяснить некоторые из основных явлений электричества с помощью упругой жидкости

. Philos Trans R Soc Lond 61: 584–677

Chappuis J, Berget A (1891) Lec¸ons de Physique ge

´

ne

´

rale, 3 vols. Gauthier-Villars, Paris, Version 2, p. 147

Children JG (1809) Отчет о некоторых экспериментах, проведенных с целью определения наиболее передового метода построения гальванических аппаратов для целей химических исследований.J Natur

Philos, Chem Arts 24: 150–155

Christie SH (1833) Бейкерская лекция. Экспериментальное определение законов магнитоэлектрической

индукции в разных массах одного и того же металла и ее интенсивности в разные металлы. Philos Trans R

Soc Lond 123: 95–142

Cohen R (1976) Физические науки. Холт, Райнхарт и Уинстон, Нью-Йорк и др.

Коэн Р и др. (1983) Разница потенциалов и ток в простых электрических цепях: исследование концепций студентов

.Am J Phys 51 (5): 407–412

Камминг Дж. (1822a) О связи гальванизма и магнетизма. Trans Camb Philos Soc 1: 269–279

Камминг Дж. (1822b) Применение магнетизма как меры электричества. Trans Camb Philos Soc

1: 281–286

Катбертсон Дж. (1804) Письмо, сообщающее о важном и любопытном отличительном свойстве между гальваническими и электрическими жидкостями

. J Nat Philos Chem Arts 8 (97–8): 205–206

Daguin P (1863) Cours de Physique e

´

le

´

mentaire.E. Privat, Тулуза; Ф. Танду, Париж

Дэви Х. (1821a) О магнитных явлениях, порождаемых электричеством. Philos Trans R Soc Lond 111: 7–19

Дэви Х. (1821b) Дальнейшие исследования магнитных явлений, производимых электричеством; с некоторыми новыми экспериментами

по свойствам наэлектризованных тел в их отношении к проводящей мощности и температуре. Philos Trans R Soc Lond 111: 425–439

Driver R et al (1994) Осмысление вторичной науки: исследование детских идей.Рутледж, Лондон

Дафф А. (1925) Физический колледж. Longmans, Green and Co, Нью-Йорк,

Dupin J, Johsua S (1989) Аналогии и «моделирующие аналогии» в обучении: некоторые примеры в области базового электричества

. Sci Edu 73 (2): 207–224

Элдридж Дж. (1940) Физика колледжа, 2-е изд. Wiley & Sons, Нью-Йорк

Fechner GT (1831) Massbestimmungen u

¨

ber die galvanische Kette, FA Brockhaus, Leipzig

Gavarret J (1858) Traite

´

d’e лектрицит

×

, 2 тт.Victor Masson, Paris, vol 2

Giere R (1988) Объяснение науки: когнитивный подход. University of Chicago Press, Chicago

Giere R (1999) Наука без законов. University of Chicago Press, Chicago, p 90

Gilbert LW (1820) Untersuchungen u

¨

ber die Einwirkungdes geschlossenen galvanische-lectrischen Kreises

auf die Magnetnadel. Annalen der Physik 66: 331–391

Холлидей Д., Резник Р. (1978) Физика, части 1 и 2 вместе, 3-е изд.Wiley, New York и др., Стр. 682

Гарвардский проект по физике (1975) Текст проекта по физике. Холт, Райнхарт и Уинстон, Нью-Йорк, Блок 4, стр. 55

Иона М. (1979) Обучение электрическому сопротивлению. Учитель физики 17 (5): 299–305

Якоби М. Х. (1837) О применении электромагнетизма к движению машин. In: Taylor R

(ed) Scienti ‑ Memoirs, vol 1. Taylor, London, pp 503–531

Jacobi MH (1839) Ueber das chemische und das magnetische-гальванометр. Annalen der Physik 48: 26–57

Jamin J (1866) Cours de Physique de l’E

´

cole Polytechnique, 3 vols.