Как найти среднюю мощность формула: A. Мощность — PhysBook

A. Мощность — PhysBook

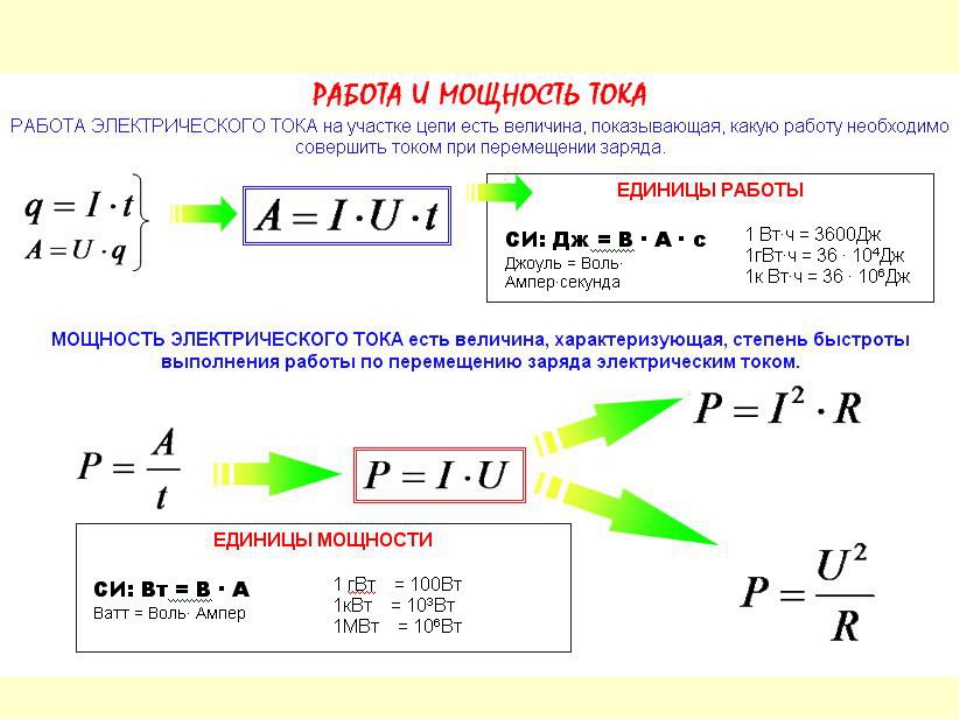
Мощность

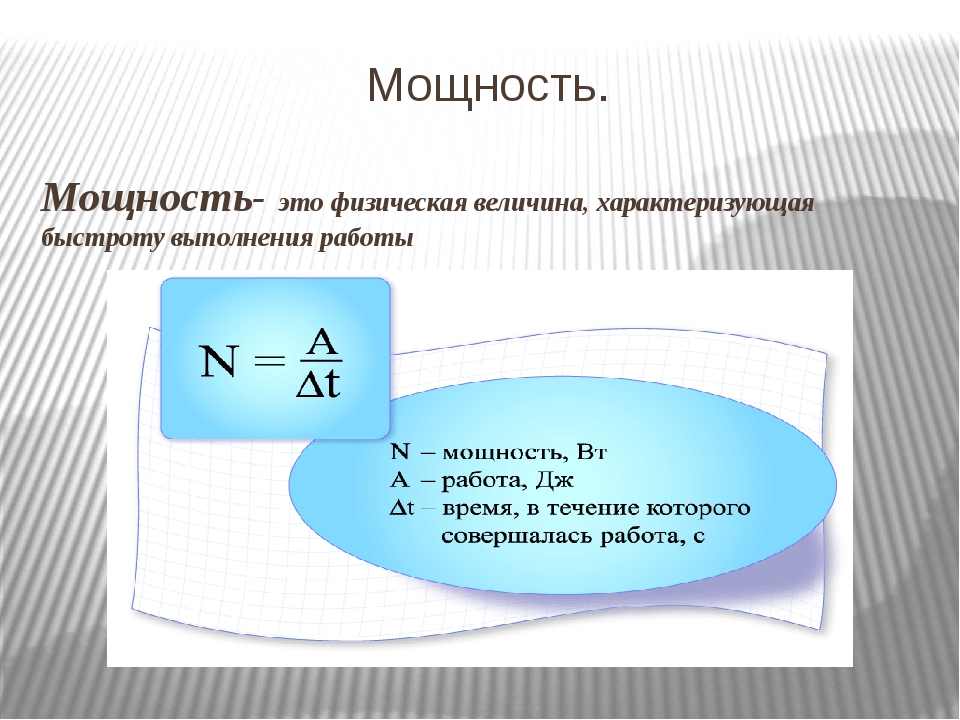
Различные машины и механизмы, выполняющие одинаковую работу, могут отличаться мощностью. Мощность характеризует быстроту совершения работы. Очевидно, что чем меньшее время требуется для выполнения данной работы, тем эффективнее работает машина, механизм и др.

При движении любого тела на него в общем случае действует несколько сил. Каждая сила совершает работу, и, следовательно, для каждой силы мы можем вычислить мощность.

Средняя мощность силы — скалярная физическая величина Ν, равная отношению работы А, совершаемой силой, к промежутку времени Δt, в течение которого она совершается:

\(~N = \frac{A}{\Delta t}.\)

В СИ единицей мощности является ватт (Вт).

Если тело движется прямолинейно и на него действует постоянная сила, то она совершает работу \(~A = F \Delta r \cos \alpha\). Поэтому мощность этой силы

\(~N = \frac{F \Delta r \cos \alpha}{\Delta t} = F \upsilon \cos \alpha = F_{\upsilon} \cdot \upsilon. \)

где F_υ — проекция силы на направление движения.

По этой формуле можно рассчитывать и среднюю, и мгновенную мощности, подставляя значения средней \(~\mathcal h \upsilon \mathcal i\) или мгновенной υ скорости.

Мгновенная мощность — это мощность силы в данный момент времени.

\(~N_m = \lim_{\Delta t \to 0} \frac{A}{\Delta t} = A’ .\)

Любой двигатель или механизм предназначены для выполнения определенной механической работы, которую называют полезной работой A_p. Но любой машине приходится совершать большую работу, так как вследствие действия сил трения часть подводимой к машине энергии не может быть преобразована в механическую работу. Поэтому эффективность работы машины характеризуют коэффициентом полезного действия η (КПД).

Коэффициент полезного действия η — это отношение полезной работы

A_p, совершенной машиной, ко всей затраченной работе A_z (подведенной энергии W):

\(~\eta = \frac{A_p}{A_z} = \frac{A_p}{W} = \frac{N_p}{N_z},\)

где N_p, N_z — полезная и затраченная мощности соответственно. КПД обычно выражают в процентах.

Литература

Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 63-64.

Коэффициент мощности, формула и примеры

Определение и формула коэффициента мощности

Средняя мощность переменного электрического тока , выражаемая через действующие значения силы тока (I) и напряжение (U) равна:

   

где — действующее (эффективное) значение силы тока, — амплитуда силы тока, — действующее (эффективное) значение напряжения, — амплитуда напряжения.

Коэффициент мощности используют для характеристики потребителя переменного тока как реактивную составляющую нагрузки. Величина этого коэффициента отражает сдвиг фазы () переменного тока, который течет через нагрузку, по отношению к приложенному к нагрузке напряжению. Из выражения (1) видно, что по величине коэффициент мощности равен косинусу от этого сдвига. Если сила тока отстает от напряжения, то сдвиг фаз считают большим нуля, если обгоняет, то

Практическое значение коэффициента мощности

На практике коэффициент мощности стараются сделать максимально большим. Так как при малом для выделения в цепи необходимой мощности надо пропускать ток большой силы, а это приводит к большим потерям в подводящих проводах (см. закон Джоуля — Ленца).

Коэффициент мощности учитывают при проектировании электрических сетей. Если коэффициент мощности является низким, это приводит к росту части потерь электрической энергии в общей сумме потерь. Для увеличения данного коэффициента применяют компенсирующие устройства.

Ошибки при расчетах коэффициента мощности ведут к повышенному потреблению электрической энергии и уменьшению коэффициента полезного действия оборудования.

Коэффициент мощности измеряют фазометром.

Способы расчета коэффициента мощности

Коэффициент мощности рассчитывают как отношение активной мощности (P) к полной мощности (S)

   

где — реактивная мощность.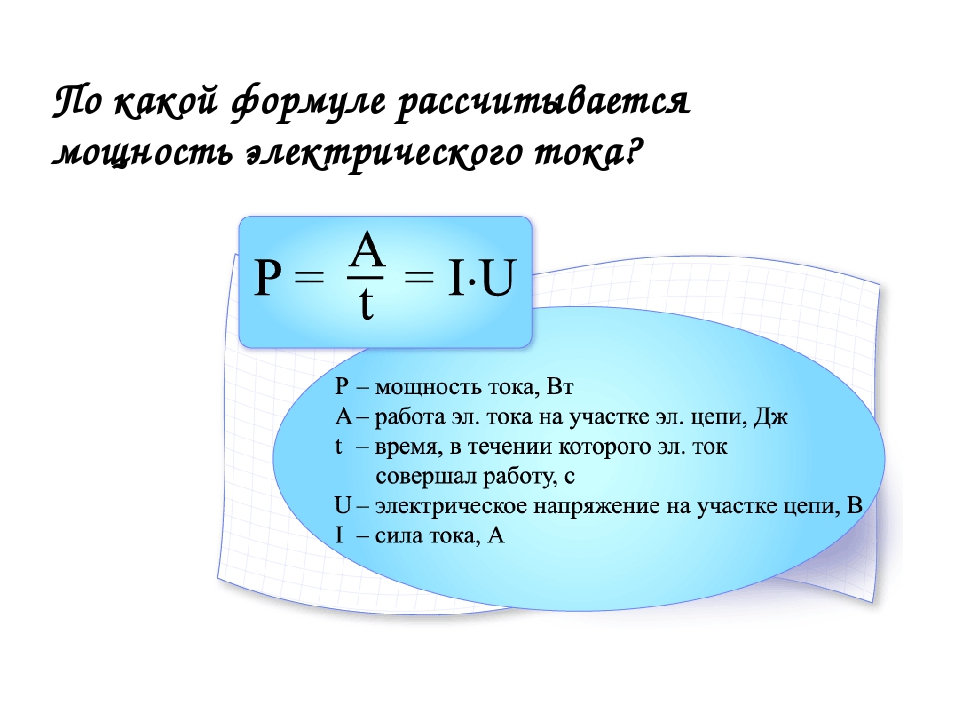

Коэффициент мощности для трехфазного асинхронного двигателя вычисляют при помощи формулы:

   

Коэффициент мощности можно определить, используя, например треугольник сопротивлений (рис.1а) или треугольник мощностей (рис.1b).

Треугольники на рис. 1(a и b) подобны, так как из стороны пропорциональны.

Единицы измерения

Коэффициент мощности — безразмерная физическая величина.

Примеры решения задач

Формула полезной мощности в физике

Определение и формула полезной мощности

Определение

Мощность — это физическая величина, которую использует как основную характеристику любого устройства, которое применяют для совершения работы. Полезная мощность может быть использована для выполнения поставленной задачи.

Отношение работы ($\Delta A$) к промежутку времени за которое она выполнена ($\Delta t$) называют средней мощностью ($\left\langle P\right\rangle $) за это время:

\[\left\langle P\right\rangle =\frac{\Delta A}{\Delta t}\left(1\right). \]

Мгновенной мощностью или чаще просто мощностью называют предел отношения (1) при $\Delta t\to 0$:

\[P={\mathop{\lim }_{\Delta t\to 0} \frac{\Delta A}{\Delta t}\ }=A'(t)\left(2\right).\]

Приняв во внимание, что:

\[\Delta A=\overline{F}\cdot \Delta \overline{r\ }\left(3\right),\]

где $\Delta \overline{r\ }$ — перемещение тела под действием силы $\overline{F}$, в выражении (2) имеем:

\[P={\mathop{\lim }_{\Delta t\to 0} \left(\frac{\overline{F}\cdot \Delta \overline{r\ }}{\Delta t}\right)\ }=\overline{F}{\mathop{\lim }_{\Delta t\to 0} \left(\frac{\Delta \overline{r\ }}{\Delta t}\right)=\ }\overline{F}\cdot \overline{v}\left(4\right),\]

где $\ \overline{v}-$ мгновенная скорость.

Коэффициент полезного действия

При выполнении необходимой (полезной) работы, например, механической, приходится выполнять работу большую по величине, так как в реальности существуют силы сопротивления и часть энергии подвержена диссипации (рассеиванию). Эффективность совершения работы определяется при помощи коэффициента полезного действия ($\eta $), при этом:

\[\eta =\frac{P_p}{P}\left(5\right),\]

где $P_p$ — полезная мощность; $P$ — затраченная мощность.

Из выражения (5) следует, что полезная мощность может быть найдена как:

\[P_p=\eta P\ \left(6\right).\]

Формула полезной мощности источника тока

Пусть электрическая цепь состоит из источника тока, имеющего сопротивление $r$ и нагрузки (сопротивление $R$). Мощность источника найдем как:

\[P=?I\ \left(7\right),\]

где $?$ — ЭДС источника тока; $I$ — сила тока. При этом $P$ — полная мощность цепи.

Обозначим $U$ — напряжение на внешнем уча

формула, мгновенный и средний расчет силы.

Термин «мощность» в физике имеет специфический смысл. Механическая работа может выполняться с различной скоростью. А механическая мощность обозначает, как быстро совершается эта работа. Способность правильно измерить мощность имеет важное значение для использования энергетических ресурсов.

Физический смысл мощности

Разные виды мощности

Для формулы механической мощности применяется следующее выражение:

N = ΔA/Δt.

В числителе формулы затраченная работа, в знаменателе – временной промежуток ее совершения. Это отношение и называется мощностью.

Существует три величины, которыми можно выразить мощность: мгновенная, средняя и пиковая:

1. Мгновенная мощность – мощностной показатель, измеренный в данный момент времени. Если рассмотреть уравнение для мощности N = ΔA/Δt , то мгновенная мощность представляет собой ту, которая берется в чрезвычайно малый промежуток времени Δt. Если имеется построенная графическая зависимость мощности от времени, то мгновенная мощность – это просто считываемое с графика значение в любой взятый момент времени. Другая запись выражения для мгновенной мощности:

N = dA/dt.

2. Средняя мощность – мощностная величина, измеренная за относительно большой временной отрезок Δt;
3. Пиковая мощность – максимальное значение, которое мгновенная мощность может иметь в конкретной системе в течение определенного временного промежутка. Стереосистемы и двигатели автомобилей – примеры устройств, способных обеспечить максимальную мощность, намного выше их средней номинальной мощности. Однако поддерживать эту мощностную величину можно в течение короткого времени. Хотя для эксплуатационных характеристик устройств она может быть более важной, чем средняя мощность.

Важно! Дифференциальная форма уравнения N = dA/dt универсальна. Если механическая работа выполняется равномерно в течение времени t, то средняя мощность будет равна мгновенной.

Из общего уравнения получается запись:

N = A/t,

где A будет общая работа за заданное время t. Тогда при равномерной работе вычисленный показатель равен мгновенной мощности, а при неравномерной –средней.

Формулы для механической мощности

В каких единицах измеряют мощность

Стандартной единицей для измерения мощности служит Ватт (Вт), названный в честь шотландского изобретателя и промышленника Джеймса Ватта. Согласно формуле, Вт = Дж/с.

Существует еще одна единица мощности, до сих пор широко используемая, –  лошадиная сила (л. с.).

Интересно. Термин «лошадиная сила» берет свое начало в 17-м веке, когда лошадей использовали для поднятия груза из шахты. Одна л. с. равна мощности для поднятия 75 кг на 1 м за 1 с. Это эквивалентно 735,5 Вт.

Мощность силы

Уравнение для мощности соединяет выполненную работу и время. Поскольку известно, что работа выполняется силами, а силы могут перемещать объекты, можно получить другое выражение для мгновенной мощности:

1. Работа, проделанная силой при перемещении:

A = F x S x cos φ.

2. Если поставить А в универсальную формулу для N, определяется мощность силы:

N = (F x S x cos φ)/t = F x V x cos φ, так как V = S/t.

3. Если сила параллельна скорости частицы, то формула принимает вид:

N = F x V.

Мощность вращающихся объектов

Процессы, связанные с вращением объектов, могут быть описаны аналогичными уравнениями. Эквивалентом силы для вращения является крутящий момент М, эквивалент скорости V – угловая скорость ω.

Если заменить соответствующие величины, то получается формула:

N = M x ω.

M = F x r, где r – радиус вращения.

Для расчета мощности вала, вращающегося против силы, применяется формула:

N = 2π x M x n,

где n – скорость в об/с (n = ω/2π).

Отсюда получается то же упрощенное выражение:

N = M x ω.

Таким образом, двигатель может достичь высокой мощности либо при высокой скорости, либо, обладая большим крутящим моментом. Если угловая скорость ω равна нулю, то мощность тоже равна нулю, независимо от крутящего момента.

Видео

Оцените статью:

ФИЗИКА: Задачи на механическую мощность

Задачи на механическую мощность
с решениями

Формулы, используемые на уроках «Задачи на механическую мощность».

Название величины	Обозначение	Единица измерения	Формула
Работа	A	Дж	A = Nt, А = mgh, A = Fs
Мощность	N	Вт	N = A / t
Время	t	с	t = А / N
Постоянная	g ≈ 10 Н/кг	Н/кг

---

---

---

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

---

Задача № 1.  Действуя силой 80 Н, человек поднимает из колодца глубиной 10 м ведро воды за 20 с. Какую мощность развивает при этом человек?

---

Задача № 2.  Мощность тягового электродвигателя троллейбуса равна 86 кВт. Какую работу может совершить двигатель за 2 ч?

---

Задача № 3.  Какую мощность развивает альпинист массой 80 кг, поднявшийся на высоту 500 м за 2 ч?

---

Задача № 4.  Человек, поднимающий ведро воды из колодца за 15 с, развивает мощность 0,16 кВт. Какую работу он при этом совершает?

---

Задача № 5.  Какую мощность развивает двигатель мотороллера, движущегося со скоростью 57,6 км/ч при силе тяги 245 Н?

---

Задача № 6.  Для выборки кошелькового невода неводовыборочная машина с электрическим приводом развивает мощность, равную 2 кВт. За сколько времени она выберет невод длиной 500 м при силе тяги 5 кН?

---

Задача № 7.  Мощность подъемного крана 10 кВт. Им можно равномерно поднять груз массой 2 т за 0,5 мин. Какую работу произведет в этом случае кран? На какую высоту переместит он груз?

---

 

Краткая теория для решения задачи на механическую мощность

 

---

Конспект урока «Задачи на механическую мощность с решениями».

Следующая тема: «Задачи на простые механизмы».

 

Как получить среднее значение с помощью формул Excel

Примеры показывают, как усреднить ячейки Excel с числами, текстом, пробелами, или ячейки на основе определенных критериев. Используйте СРЕДНИЙ, СРЕДНИЙ, СРЕДНИЙ или функции AVERAGEIFS, или TRIMMEAN для среднего, исключающего выбросы.

средних ячеек с числами — СРЕДНЕЕ

Функция СРЕДНЕЕ будет усреднять ячейки, содержащие числа.это синтаксис:
= СРЕДНЕЕ (значение1 , значение2, . .. значение30).
Аргументы (например, значение1) могут быть ссылками на ячейки или типизированными значениями. в формулу СРЕДНЕГО.

В следующем примере функции AVERAGE используется один аргумент — ссылка в ячейки A1: A5.

1. Введите данные образца в свой рабочий лист
2. В ячейке A7 введите формулу СРЕДНЕГО, чтобы усреднить числа в столбец A: = СРЕДНЕЕ (A1: A5)

3. Нажмите клавишу Enter, чтобы заполнить формулу.
4. Результатом будет 21,83, среднее значение ячеек, содержащих числа.
   Ячейка A1 не включается в среднее значение, поскольку она содержит текст, а пустая ячейка C3 игнорируется.

Примечание : Поскольку даты хранятся в виде чисел, функция СРЕДНИЙ будет включать любые ячейки, содержащие даты.

ячеек среднего значения с данными — AVERAGEA

Функция СРЗНАЧ будет усреднять непустые ячейки. это синтаксис:
= СРЗНАЧ (значение1 , значение2, … значение30).
Аргументы (например, значение1) могут быть ссылками на ячейки или типизированными значениями. в формулу. В следующем примере используется один аргумент — ссылка в ячейки A1: A5.

1. Введите данные образца в свой рабочий лист
2. В ячейке A7 введите формулу AVERAGEA, чтобы усреднить числа в столбец A: = СРЕДНЕЕ (A1: A5)

3. Нажмите клавишу Enter, чтобы заполнить формулу.
4. Результатом будет 16,38, среднее значение ячеек, содержащих данные. Ячейка A1 содержит текст, который рассматривается как ноль, и ячейка A3 не включен в среднее значение, потому что он пуст.

Примечание : AVERAGEA будет включать ячейки с формулами, включая те, которые выглядят пустыми, потому что они оцениваются как «», например = ЕСЛИ (B2 = «», «», B2).

Среднее количество ячеек, соответствующих критериям — AVERAGEIF

Точное соответствие критерию

. В Excel — средние значения ячеек, соответствующих определенному критерию.В этом примере усредняются только количества для заказов Pen.

1. Выберите ячейку, в которой вы хотите увидеть среднее значение (ячейка A12 в этом примере)
2. Введите знак равенства (=), чтобы начать формулу
3. Тип: AVERAGEIF (
4. Выберите ячейки, содержащие значения для проверки критерия. В этом примере будут проверяться ячейки A1: A10
5. Введите запятую для разделения аргументов
6. Введите критерий.В этом примере вы проверяете текст, поэтому введите слово в двойных кавычках: «Pen»
   Примечание: верхний и нижний регистр обрабатываются одинаково
   
7. Введите запятую для разделения аргументов
8. Выберите ячейки, содержащие значения для усреднения. В этом примере ячейки B1: B10 содержат значения
9. Введите закрывающую скобку
   Заполненная формула: = СРЗНАЧЕСЛИ (A1: A10, «Pen», B1: B10)
10. Нажмите клавишу Enter, чтобы завершить ввод
11. Результат будет 9.25, среднее количество строк, содержащих «Ручка»

Критерий соответствия в строке

В Excel средние ячейки в строках, которые содержат критерий как часть содержимого ячейки. В этом примере все Pen, Gel Pen и Pencil заказы будут усреднены, так как содержат строку «ручка».

1. Выберите ячейку, в которой вы хотите увидеть среднее значение (ячейка A12 в этом примере)
2. Введите знак равенства (=), чтобы начать формулу
3. Тип: AVERAGEIF (
4. Выберите ячейки, содержащие значения для проверки критерия. В этом примере будут проверяться ячейки A1: A10
5. Введите запятую для разделения аргументов
6. Введите критерий. В этом примере вы проверяете текст, поэтому введите слово в двойных кавычках с одной или несколькими звездочками (*) подстановочные знаки: «* Pen *»
   Примечание: верхний и нижний регистр обрабатываются одинаково
   
7. Введите запятую для разделения аргументов
8. Выберите ячейки, содержащие значения для усреднения.В этом примере ячейки B1: B10 содержат значения
9. Введите закрывающую скобку
   Заполненная формула: = СРЗНАЧЕСЛИ (A1: A10, «* Pen *», B1: B10)
10. Нажмите клавишу Enter, чтобы завершить ввод
11. Результатом будет 8,83, среднее значение строк, содержащих строка «Pen» в столбце A

Примечание : вместо того, чтобы вводить критерий в формуле, вы можете относятся к ячейке. Например, формула на шаге 7 выше может быть изменено на:
= СРЕДНЕЛИ (A1: A10, «*» & B12 & «*», B1: B10)
, если в ячейке B12 был текст — pen .

Критерий и оператор

Вы можете использовать оператор с критерием. В этом примере только строки, в которых количество больше или равно десяти, будут усреднены.

1. Выберите ячейку, в которой вы хотите увидеть среднее значение (ячейка A12 в этом примере)
2. Введите знак равенства (=), чтобы начать формулу
3. Тип: AVERAGEIF (
4. Выберите ячейки, содержащие значения для проверки критерия.В этом примере будут проверяться ячейки B1: B10
5. Введите запятую для разделения аргументов
6. Введите критерий. В этом примере вы проверяете строки где количество больше или равно 10. Оператор> = используется перед числом, и весь критерий заключен в двойных кавычках: «> = 10»
   Примечание.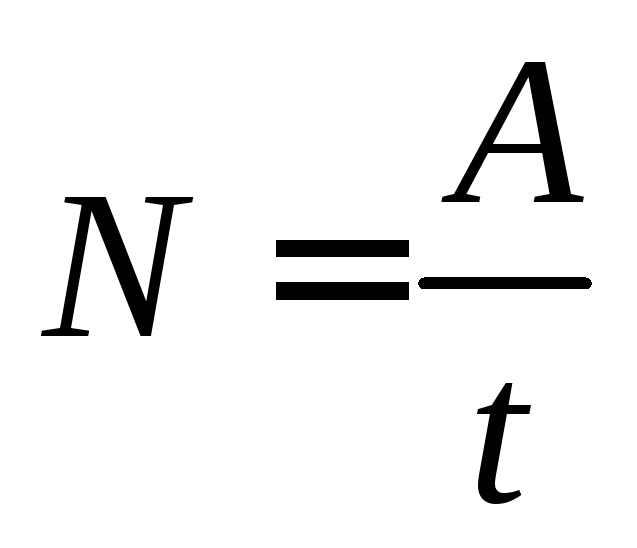 Несмотря на то, что это числовой критерий, он должен заключаться в в двойных кавычках.
   
7. Тип закрывающей скобки
8. Заполненная формула:
   = СРЕДНЕЛИ (B1: B10, «> = 10»)
   
9. Нажмите клавишу Enter, чтобы завершить ввод

Примечание : вместо того, чтобы вводить критерий в формуле, вы можете относятся к ячейке. Например, формула на шаге 8 выше может быть изменено на:
= СРЗНАЧЕСЛИ (B1: B10, «> =» & B12)
, если ячейка B12 содержала число — 10 .

Средние ячейки для нескольких критериев — СРЕДНЕНОМН

Соответствие нескольким критериям

В Excel 2007 и более поздних версиях можно использовать функцию СРЗНАЧЕСЛИМН. для усреднения строк, соответствующих двум или более критериям.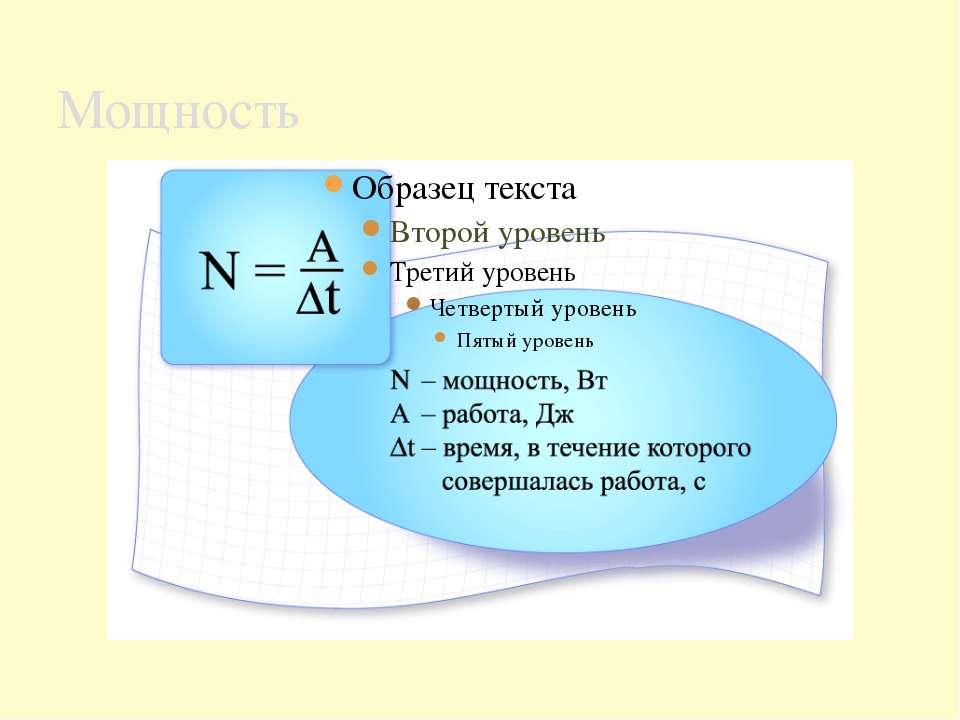 Только в этом примере строки, где элемент — «Ручка», а количество больше будет усреднено не менее десяти.

Критерии введены в ячейки D3 и E3.Мы будем ссылаться на эти ячейки в формуле вместо ввода значений в формулу.

1. Выберите ячейку, в которой вы хотите увидеть итог
2. Введите знак равенства (=), чтобы начать формулу
3. Тип: AVERAGEIFS (
4. Выберите ячейки, содержащие значения для усреднения. В этом примере ячейки B2: B10 будет усреднено
5. Чтобы начать следующий аргумент, введите запятую
6. Выберите ячейки, содержащие значения, которые нужно проверить на критерий.В этом примере будут проверяться ячейки A2: A10
7. Введите запятую и щелкните ячейку D3, которая содержит первый критерий, «Ручка»
8. Чтобы начать следующий набор критериев, введите запятую
9. Выберите ячейки, содержащие значения для проверки второго критерий. В этом примере будут проверяться ячейки B2: B10
10. Введите запятую и оператор для второго критерия: «> = »
    Примечание. Оператор заключен в двойные кавычки.
    
11. Введите амперсанд (&) и щелкните ячейку E3, содержащую минимальное количество для усредненных ячеек — 10.
12. Чтобы начать следующий аргумент, введите запятую
13. Выберите ячейки, содержащие значения для проверки второго критерий. В этом примере будут проверяться ячейки B2: B10
14. Отделка закрывающей скобкой 🙂
15. Заполненная формула показана ниже.
    
16. Нажмите клавишу Enter, чтобы завершить ввод

Заполненная формула:

= СРЕДНИЙ РАЗМН (B2: B10, A2: A10, D3, B2: B10, «> =» & E3)

Примечание : вместо того, чтобы ссылаться на ячейки для критериев, вы можно ввести их в формулу. Вот та же формула с набранным критерии:

= СРЕДНЕНОМН (B2: B10, A2: A10, «Pen», B2: B10, «> = 10»)

средних строк в отфильтрованном списке — ИТОГО

После фильтрации строк в списке можно использовать функцию ПРОМЕЖУТОЧНЫЙ ИТОГ. чтобы усреднить видимые строки.

1. Примените к столу автофильтр. Здесь есть инструкции — Основы автофильтра
2. Отфильтруйте хотя бы один из столбцов в таблице. В этом примере первый столбец отфильтрован для связующих.
3. Выберите ячейку непосредственно под столбцом, для которого нужно суммировать.
4. Нажмите кнопку «Автосумма» на вкладке «Главная» ленты или в формулах. таб.
   • Если вы хотите, чтобы функция ПРОМЕЖУТОЧНЫЙ ИТОГ в ячейке, отличной от один прямо под отфильтрованным списком, вы можете ввести формулу, вместо использования кнопки Автосумма.
5. Будет автоматически вставлена ​​формула ПРОМЕЖУТОЧНЫЙ ИТОГ, видимые ячейки в столбце

• Первый аргумент функции ПРОМЕЖУТОЧНЫЙ ИТОГ — это номер функции, который определяет, как следует рассчитывать числа. По умолчанию равно 9, что говорит Excel о суммировании чисел.
• Можно использовать другие номера функций, например, 1 для СРЕДНЕГО или 2 для COUNT.

Чтобы усреднить все непустые ячейки в столбце D, выберите 1 — СРЕДНИЙ из раскрывающегося списка функций в качестве первого аргумента:
= ПРОМЕЖУТОЧНЫЙ ИТОГ (1, D2: D10)

Проверить диапазон ячеек для усреднения и исправить диапазон адрес, если необходимо.

Нажмите клавишу Enter, чтобы завершить ввод формулы.

Примечание : в функции «Промежуточный итог» вместо этого можно использовать 101 of 1:
= SUBTOTAL (101, D2: D10)
для строк промежуточных итогов, которые были вручную скрыты, а также отфильтрованы ряды.

Видео: усеченное среднее с функцией TRIMMEAN

Чтобы исключить определенный процент выпадающих данных из среднего, вы можете использовать функцию Excel TRIMMEAN. Посмотрите это видео, чтобы узнать, как для настройки формулы, а письменные инструкции находятся под видео.

Усеченное среднее с функцией TRIMMEAN

Чтобы исключить выпадающие данные из среднего, вы можете использовать TRIMMEAN функция.Эта функция исключает определенный процент точек данных сверху и снизу набора данных, затем возвращает среднее значение (среднее значение) остальных точек данных.

ПРИМЕЧАНИЕ : В этом примере количества отсортированы по возрастанию. порядок, чтобы было легче увидеть верхние и нижние числа. Числа НЕ нужно сортировать, чтобы функция TRIMMEAN могла рассчитывать правильно.

Функция TRIMMEAN

Для функции TRIMMEAN требуется 2 аргумента: TRIMMEAN (массив, процент)

В этом примере

• значения для массива находятся в ячейках B2: B21
• обрезка процентов вводится в ячейку E3 как 25% (или 0. 25)

Чтобы вычислить усеченное среднее, введите эту формулу в ячейку E4 ::

= TRIMMEAN (B2: B21, E3)

Результат TRIMMEAN (53.06) отличается от среднего (51.95), который показан в ячейке E5.

Как работает TRIMMEAN

В этом примере 20 значений, а процент обрезки равен 25%.

Чтобы вычислить, сколько чисел нужно обрезать,

• значения подсчитываются, затем умножаются на процент обрезки (е.г. 20 * 0,25 = 5
• Это число делится на 2, чтобы получить число для обрезки на каждом конец (например, 5/2 = 2,5)
• Чтобы удалить равное количество точек данных на каждом конце, число округляется до ближайшего целого числа (например, INT (2.5) = 2)

Итак, в этом примере верхние 2 (86,97) и нижние 2 (3,4) точки данных не будут включены в среднее значение, рассчитываемое TRIMMEAN.

Функция СРЗНАЧ, используемая в этом примере для ячеек B4: B19, возвращает тот же результат, что и функция TRIMMEAN, с процентом обрезки 25%.

Скачать бесплатную рабочую тетрадь

Чтобы увидеть формулы и тестовые данные, используемые в этом примере, вы можете скачать Средние функции образец файла. Файл в формате xlsx (Excel 2007 и новее. версии).

Учебные пособия по функциям Excel

Суммарные функции

Функция VLOOKUP

Функции ИНДЕКС / ПОИСКПОЗ

Функции подсчета

КОСВЕННАЯ функция

Не пропустите наши советы по Excel

Не пропустите мои последние советы и видео по Excel! Нажмите OK, чтобы получать мой еженедельный информационный бюллетень с советами по Excel и ссылками на другие новости и ресурсы Excel.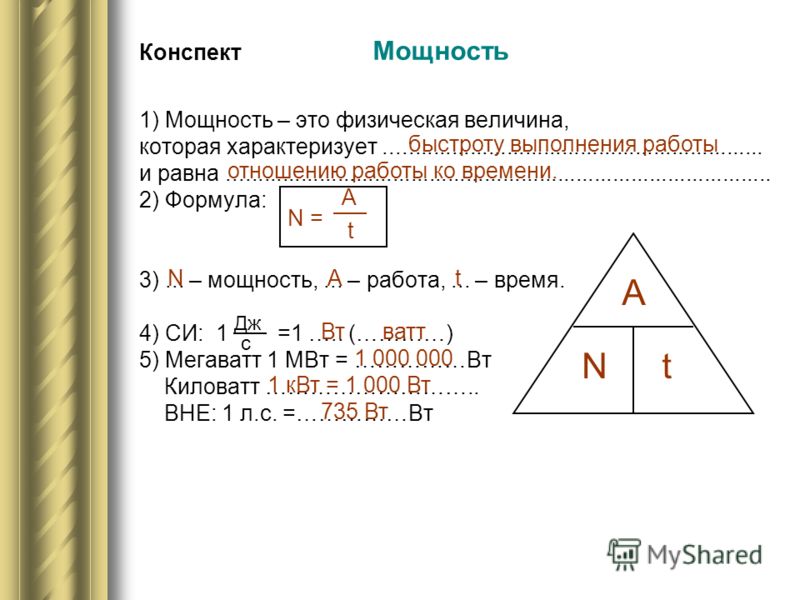

Как использовать функцию СРЕДНЕЕ в Excel

Функция СРЕДНЕЕ вычисляет среднее значение чисел, предоставленных в качестве аргументов. Чтобы вычислить среднее значение, Excel суммирует все числовые значения и делит их на количество числовых значений. Это поведение можно воспроизвести с помощью функций СУММ и СЧЁТ, например:

 
 = СУММ (A1: A5) / COUNT (A1: A5) // расчет среднего вручную 

AVERAGE может обрабатывать до 255 отдельных аргументов, которые могут включать числа, ссылки на ячейки, диапазоны, массивы и константы.

Функция СРЕДНИЙ автоматически игнорирует текстовые значения и пустые ячейки. Однако включены нулевые (0) значения. Вы можете игнорировать нулевые (0) значения и / или применять определенные критерии с помощью функции СРЗНАЧЕСЛИМН, как описано ниже.

Функция AVERAGE игнорирует логические значения и числа, введенные в виде текста. Если вам нужно включить эти значения в среднее значение, см. Функцию СРЗНАЧ.

Если значения, заданные для AVERAGE, содержат ошибки, AVERAGE возвращает ошибку.Вы можете использовать функцию АГРЕГАТ, чтобы игнорировать ошибки.

Базовое использование

Типичный способ использования функции СРЕДНИЙ — указать диапазон, как показано ниже. Скопированная формула в F3:

.

В каждой новой строке AVERAGE вычисляет среднее значение оценок каждого человека.

Пустые ячейки

Функция СРЕДНИЙ автоматически игнорирует пустые ячейки. На приведенном ниже экране обратите внимание, что ячейка C4 пуста, а AVERAGE просто игнорирует ее и вычисляет среднее значение только с B4 и D4:

Однако обратите внимание, что нулевое (0) значение в C5 включено в среднее значение , поскольку это допустимое числовое значение.Чтобы исключить нулевые значения, используйте вместо этого СРЗНАЧЕСЛИ или СРЗНАЧЕСЛИ. В приведенном ниже примере AVERAGEIF используется для исключения нулевых значений. Как и функция СРЗНАЧ, СРЗНАЧ автоматически исключает пустую ячейку.

Смешанные аргументы

Номера, предоставленные для СРЕДНЕГО, могут быть смесью ссылок и констант:

Среднее с критериями

Чтобы вычислить среднее значение с критериями, используйте СРЕДНЕЛИ или СРЕДНЕЛИМН.В приведенном ниже примере СРЗНАЧЕСЛИМН используется для расчета среднего балла для красных и синих групп:

Функция СРЗНАЧЕСЛИМН также может применять несколько критериев.

Средняя верхняя 3

Комбинируя функцию СРЕДНЕЕ с функцией НАИБОЛЬШИЙ, вы можете вычислить среднее из n верхних значений. В приведенном ниже примере формула в столбце I вычисляет среднее значение трех лучших результатов тестов в каждой строке:

Подробное объяснение здесь.

Средневзвешенное значение

Чтобы вычислить средневзвешенное значение , вам нужно использовать функцию СУММПРОИЗВ, как показано ниже:

Прочтите полное объяснение здесь.

Банкноты

1. AVERAGE автоматически игнорирует пустые ячейки и ячейки с текстовыми значениями.
2. СРЕДНИЙ включает нулевые значения. Используйте AVERAGEIF или AVERAGEIFS, чтобы игнорировать нулевые значения.
3. Аргументы могут быть предоставлены как константы, диапазоны, именованные диапазоны или ссылки на ячейки.
4. AVERAGE может обрабатывать до 255 общих аргументов.
5. Чтобы увидеть быстрое среднее значение без формулы , вы можете использовать строку состояния.

Формула средней скорости и вопросы

Среднее значение в основном определяется как сумма наблюдений, деленная на количество наблюдений. Принимая во внимание раздел «Количественные способности» любого конкурсного экзамена, из этой главы задаются 1-2 вопроса. Это не трудная глава, если вы знаете приемы, позволяющие решить вопрос за очень короткое время.

Чтобы лучше понять концепцию, давайте попробуем задать несколько вопросов.

Вопросы 1: Каким будет среднее значение для следующего набора терминов: 23, 25, 27, 29 и 31?

Решение: Мы знаем, что среднее значение — это средний член, когда количество членов нечетное, но перед этим давайте посмотрим, является ли оно A. P. или нет.

Поскольку существует разница между двумя последовательными терминами, среднее значение будет принято как средний член, т.е. 27.

Вопрос 2: Найдите среднее значение следующих членов: 22, 23, 24, 25, 26 и 27.

Решение: Выше мы обсуждали, что если количество членов четное, то среднее значение будет средним из двух средних членов.

Итак, среднее здесь будет (24 + 25) / 2 = 49/2 = 24,5

Обязательно читать средние статьи

Вопрос 3: Средний вес класса из 24 учеников составляет 36 лет. Если также учитывать вес учителя, средний вес увеличивается на 1 кг. Какой вес у учителя?

Решение: Мы знаем, что в случае увеличения среднего,

Возраст нового члена = Предыдущее среднее + (Увеличение среднего X Количество членов, включая нового члена)
Следовательно,
Возраст нового члена = 36 + (1 × 25)
Возраст нового члена = 36 + 25 = 61

Вопрос 4: Найдите среднее значение первых 30 натуральных чисел.

Решение: Сумма первых n натуральных чисел = n (n + 1) / 2
Следовательно, Среднее значение = (30 (30 + 1)) / (2 * 30)
= (30 * 31) / (2 * 31) = 15,5

Вопрос 5: У продавца есть продажа рупий. 6435, рупий. 6927, рупий. 6855, рупий. 7230 и рупий. 6562 в течение 5 месяцев подряд. Сколько продаж он должен иметь на шестом месяце, чтобы он получил среднюю продажу рупий. 6500?

Решение: Общая продажа за 5 месяцев = 6435 + 6927 + 6855 + 7230 + 6562 = 34009
Требуемая продажа = 6500 * 6 = 39000
Продажа требуется в течение 6 ^-го месяцев, так что среднее значение составляет 6500 = 39000–34009 = 4991

рупий Пройдите этот тест, чтобы проверить свое понимание темы: средние значения.

Вопрос 6: Средний возраст учителя и шести учеников — 12 лет, который уменьшается на 5 лет, если не учитывать возраст учителя. Какого возраста учитель?

Решение: Общий возраст шести учеников и учителя = 12 * 7 = 84
Новое среднее значение при исключении учителя = 7
Таким образом, общий возраст шести учеников = 6 * 7 = 42
Следовательно, возраст учителя = 84 — 42 = 42

Вопрос 7: 19 человек отправились в гостиницу на совместный обед. 13 из них потратили на ужин по 79 рупий каждый, а остальные потратили на 4 рупия больше, чем средние расходы всех 19. Какую общую приблизительную сумму они потратили?

Решение: Предположим, что «×» — это средние расходы 19 человек.
Тогда 19 × = 13 * 79 + 6 (× + 4)
13 × = 1051
× ≅81 (примерно, как и в вопросе, запрашиваются приблизительные деньги)
Таким образом, общие расходы = 81 * 19 = 1539

рупий

Вопрос 8: Средние оценки 13 студентов 40.Средняя оценка первых 7 учеников — 42, а у последних семи — 35. Найдите оценки 7-го ученика.

Решение: Сумма оценок 13 учеников = 13 * 40 = 520 Оценки первых 7 учеников = 7 * 42 = 294
Оценки последних 7 учеников = 7 * 35 = 245
Оценки 7 ^-го учеников = (294 +245) — 520 = 19

Вопрос 9: Аман имеет определенное среднее значение для 9 иннингов в десятом иннинге; он набирает 100 пробежек, тем самым увеличивая свой средний результат на 8 пробежек. Его новое среднее значение —

.

Решение: Пусть его общее среднее значение b «×»
Его общее количество пробежек за 9 иннингов будет 9 ×
Новый тотал; 9x + 100 = 10 (× + 8)
× = 20
Следовательно, новое среднее значение = 20 + 8 = 28

Вопрос 10: Средний вес 5 мужчин уменьшается на 3 кг, когда один из них весом 150 кг заменяется другим человеком. Этот новый человек снова заменяется другим человеком, вес которого на 30 кг ниже, чем у человека, которого он заменил. Каково общее изменение среднего значения из-за двойного изменения?

Решение: Второй человек весит 135 кг, а третий — 105 кг.
Следовательно, чистый результат — падение на 45 на 5 человек.
Таким образом, общее падение составляет 9 кг.

Вопрос 11: Расстояние между двумя станциями A и B составляет 778 км. Поезд преодолевает путь от A до B со скоростью 84 км / час и возвращается обратно в A с постоянной скоростью 56 км / час. Узнать среднюю скорость поезда за весь путь?

Решение: Требуемая средняя скорость = 2xy / (x + y)
(2 * 84 * 56) / (84 + 56) = 67,2 км / ч

Ключевое обучение

• Мы научились определять новое среднее значение при замене, добавлении или удалении человека в группе.
• Концепция средней скорости, когда расстояние постоянное, а скорости разные, находит прямое применение в концепции времени, скорости и расстояния.

Среднее ускорение

: определение, формула, примеры и многое другое

В этой статье вы узнаете, что мы подразумеваем под средним ускорением при описании движения частицы.

Мы увидим определение и формулу для среднего ускорения, а также примеры, показывающие, как использовать формулу на практике.

Мы также обсудим другие важные вещи, например, как найти среднее ускорение по графику скорости и времени .

Определение и формула для среднего ускорения

Рассмотрим частицу, которая движется по прямой линии:

Частица на оси x.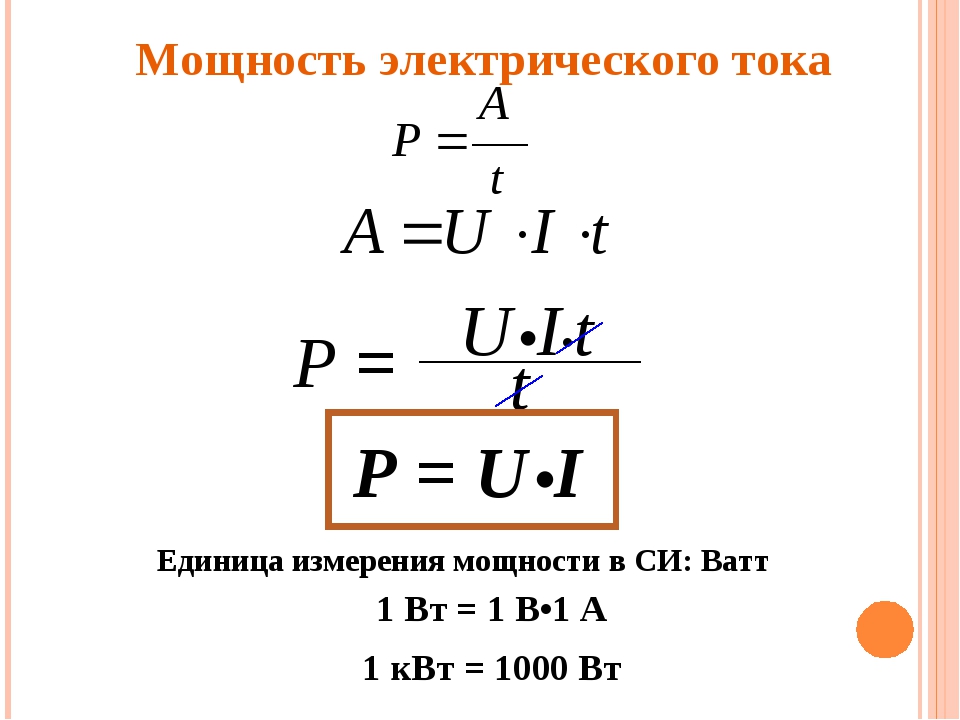 XO

Если в момент t ₁ частица имеет скорость v ₁ и в следующий момент t ₂ он имеет скорость v ₂ , мы указываем изменение скорости между t ₁ и t ₂ , т.е.е., v ₂ — v ₁ , с Δv (дельта-v):

Также мы указываем интервал времени между t ₁ и t ₂ , т.е. t ₂ — t ₁ , с Δt (delta-t):

Среднее ускорение a ₁₂ , которое частица имеет между моментом t ₁ и моментом t ₂ , определяется как отношение изменения скорости между t ₁ и t ₂ , т.е. v ₂ — v ₁ , на интервал времени между t ₁ и t ₂ , т.е.е., т ₂ — т ₁ .

Следовательно, формула для среднего ускорения :

a 12 =	v 2 — v 1	=	Δv
	t —		Δt

Другими словами, среднее ускорение a за интервал времени Δt равно изменению скорости Δv, которое происходит в течение этого интервала времени, деленному на сам интервал времени:

Таким образом, среднее ускорение — средняя скорость изменения скорости .

Единица среднего ускорения

Поскольку среднее ускорение — это отношение скорости ко времени, единица измерения среднего ускорения в системе СИ составляет метров в секунду в секунду ((м / с) / с) или, проще говоря, метров в секунду в квадрате. (м / с ² ).

Средняя скорость и среднее ускорение

Разница между средней скоростью и средним ускорением состоит в том, что средняя скорость — это средняя скорость изменения положения, тогда как среднее ускорение — это средняя скорость изменения скорости:

v 12 =	x 2 — x 1	=	Δx
	t 2 — t 1		Δt

906 907 907 903 907 907 903 907 207 — v ₁

=	Δv
	t 2 — t 1	Δt

Пример: Среднее ускорение автомобиля с

до

км / км ч в 4. 75 с. Какое среднее ускорение у машины?

Предположим, что момент, когда автомобиль начинает ускоряться, равен 0, и обозначим его как t ₁ . Итак, скорость v ₁ в момент t ₁ равна 0.

Мы знаем, что в следующий момент t ₂ автомобиль достигает скорости 100 км / ч. Итак, скорость v ₂ в момент t ₂ равна 100 км / ч.

Кроме того, поскольку время между t ₁ и t ₂ равно 4.75 с, а t ₁ равно нулю, отсюда следует, что t ₂ равно 4,75 с.

t ₂ = 4,75 с, v ₂ = 100 км / ч

Мы хотим найти среднее ускорение между t ₁ и t ₂ , которое мы обозначим как ₁₂ .

Среднее ускорение a ₁₂ между моментом t ₁ и моментом t ₂ равно отношению изменения скорости, которое происходит между t ₁ и t ₂ , к интервалу времени. между t ₁ и t ₂ :

a 12 =	v 2 — v 1	=	100 км / ч — 0	=	100 h
	t 2 — t 1		4. 75 с — 0		4,75 с

Прежде чем мы сможем завершить расчет, нам нужно преобразовать 100 км / ч в м / с.

Чтобы преобразовать км / ч в м / с, мы разделим число на 3,6.

Итак, 100 км / ч, выраженное в м / с:

Теперь мы можем завершить расчет среднего ускорения:

a 12 =	27,8 м / с	= 5,85 м / с 2
	4,75 с

Таким образом, среднее ускорение автомобиля равно 5.85 м / с ² .

Пример: Среднее ускорение поезда

Поезд, первоначально находящийся в неподвижном состоянии, достигает скорости 40 км / ч за 13 с. Затем он дополнительно увеличивает свою скорость на 35 км / ч за 25 с. Рассчитайте среднее ускорение поезда за первые 13 с, среднее ускорение за следующие 25 с и общее среднее ускорение.

Предположим, что момент, когда поезд начинает ускоряться, равен 0, и обозначим его как t ₁ . Итак, скорость v ₁ в момент t ₁ равна 0.

В следующий момент t ₂ поезд достигает скорости 40 км / ч. Итак, скорость v ₂ в момент t ₂ составляет 40 км / ч.

Время, которое проходит между моментом t ₁ и моментом t ₂ , составляет 13 с, а поскольку t ₁ равно нулю, отсюда следует, что t ₂ равно 13 с.

В момент t ₃ , через 25 с после t ₂ , поезд увеличил свою скорость на 35 км / ч. Таким образом, в момент t ₃ поезд имеет скорость v ₃ , которая на 35 км / ч больше, чем v ₂ .

v ₃ — v ₂ = 35 км / ч

t ₃ — t ₂ = 25 с

Наша задача — рассчитать среднее ускорение поезда за первые 13 с, которое начинаются в t ₁ и заканчиваются в t ₂ , следующие 25 с, которые начинаются в t ₂ и заканчиваются в t ₃ , и общее среднее ускорение, т.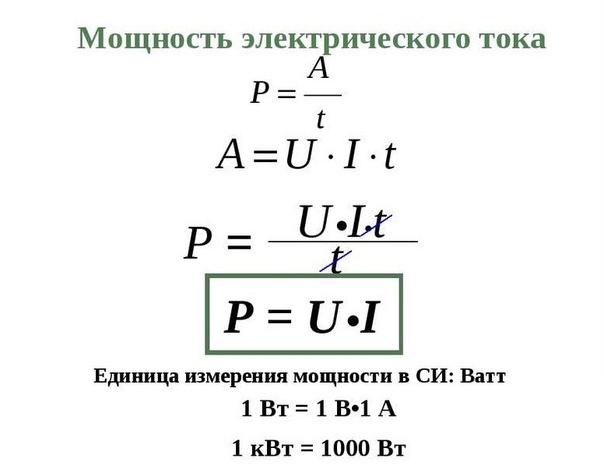 е. среднее ускорение с момента начала t ₁ до конечного момента t ₃ .

Начнем с вычисления среднего ускорения a ₁₂ между t ₁ и t ₂ :

a 12 =	v 2 — v 1	24 =	=	=	40 км / ч — 0	=	40 км / ч
	t 2 — t 1						13 с — 0	13 с

40 км / ч =	40	м / с = 11 м / с
	3.6

a 12 =	11 м / с	= 0,85 м / с 2
	13 с

Далее, давайте вычислим среднее ускорение 6 между _{23 t 2 и t 3 :}

a 23 =	v 3 — v 2	=	35 км / ч
	6 t 3 2		25 с

35 км / ч =	35	м / с = 9. 7 м / с
	3,6

0 24 25 с Последнее, но не менее 907 , найдем среднее ускорение a ₁₃ между t ₁ и t ₃ :

a 23 =	9,7 м / с	= 0,39 м / с 2

a 13 =	v 3 — v 1
	t 3 3 90-663 t 1

Как мы можем определить, что такое v ₃ — v ₁ ?

Если мы посмотрим на ось v, которая показывает скорость поезда в разные моменты времени, мы увидим, что изменение скорости v ₃ — v ₁ равно сумме v ₂ — v ₁ и v ₃ — v ₂ :

Ось v, где изменение скорости v3 — v1 рассматривается как сумма изменения скорости v2 — v1 и изменения скорости v3 — v2 .vO1v2v3v3v − 1v2v − 1v3v − 2v

v ₃ — v ₁ = (v ₂ — v ₁ ) + (v ₃ — v ₂ )

v _{— 3 906 1} = 40 км / ч + 35 км / ч

v ₃ — v ₁ = 75 км / ч

Имея это в виду, нетрудно увидеть, что интервал времени t ₃ — t ₁ равно t ₂ — t ₁ и t ₃ — t ₂ :

t ₃ — t ₁ = (t ₂ — t ₁ ) + (t ₃ — t ₂ )

t ₃ — t ₁ = 13 с + 25 с

t ₃ — t ₁ = 38 с

Таким образом, среднее ускорение a ₁₃ составляет

75 км / ч =	75	м / с = 21 м / с
	3. 6

a 13 =	21 м / с	= 0,55 м / с 2
	38 с

Обратите внимание, что хотя в некоторых случаях общее среднее ускорение 13 может быть равно среднему арифметическому среднего ускорения a ₁₂ и среднего ускорения ₂₃ , вам не следует делать это предположение при решении проблемы.

В самом деле, для поезда это не так, как мы можем видеть, вычислив среднее арифметическое ₁₂ и ₂₃ :

a 12 + a 23	=	0.85 м / с 2 + 0,39 м / с 2	= 0,62 м / с 2
2		2

Еще раз не предполагайте, что среднее ускорение для всего равно среднему арифметическому средних ускорений деталей.

Знак среднего ускорения

Поскольку среднее ускорение равно отношению изменения скорости к интервалу времени

, а интервал времени Δt всегда положителен, следует, что знаком среднего ускорения a является такой же, как и знак изменения скорости Δv.

Изменение скорости Δv может быть положительным, отрицательным или нулевым, в зависимости от того, увеличила ли частица свою скорость, уменьшила скорость или закончила с той же скоростью, с которой она начала.

Следовательно, среднее ускорение a может быть положительным, отрицательным или нулевым:

Пример: Среднее ускорение лифта

Лифт ускоряется из состояния покоя в течение 9,35 с, пока не достигнет скорости 7,83 м / с. Затем он продолжает двигаться с постоянной скоростью.Наконец, когда лифт приближается к месту назначения, он замедляется на 12,5 с, пока не остановится. Найдите среднее ускорение лифта для фазы ускорения, для фазы замедления и от момента начала разгона до момента его замедления до остановки.

Считаем момент, когда лифт начинает ускоряться, равным 0 и обозначим его как t ₁ . Таким образом, скорость v ₁ в момент t ₁ равна 0.

В следующий момент t ₂ ,9. Через 35 с после t ₁ лифт достигает скорости 7,83 м / с. Следовательно, скорость v ₂ в момент t ₂ равна 7,83 м / с.

Поскольку t ₁ равно нулю, t ₂ равно 9,35 с.

t ₂ = 9,35 с, v ₂ = 7,83 м / с

Лифт поддерживает постоянную скорость в течение некоторого времени, а затем в какой-то момент t ₃ начинает замедляться.

Скорость v ₃ , которую лифт имеет в момент t ₃ , совпадает со скоростью в момент t ₂ , т.е.е., 7,83 м / с.

t ₃ = неизвестно

v ₃ = 7,83 м / с

Наконец, в момент t ₄ , через 12,5 с после t ₃ , лифт останавливается.

Скорость v ₄ , которую лифт имеет при остановке, равна 0.

Нам нужно найти среднее ускорение лифта для фазы ускорения, которая начинается в t ₁ и заканчивается в t ₂ , фаза замедления, которая начинается в t ₃ и заканчивается в t ₄ , и с момента начала разгона лифта до момента его замедления до остановки, т. е.е., от момента t ₁ до момента t ₄ .

Давайте начнем с определения среднего ускорения a ₁₂ между t ₁ и t ₂ :

м / с — 0

a 12 =	v 2 — v 1	= 7,83 23	=	7,83 м / с	= 0,837 м / с 2
	т 2 — t 1			9,35 с — 0		9.35 с

Затем давайте найдем среднее ускорение a ₃₄ между t ₃ и t ₄ :

=

a 34 =	v 4 — v 3 64	0 — 7,83 м / с	=	−7,83 м / с	= −0,626 м / с 2
	t 4 — t 3	907 12,5 с 907,5 s

В заключение найдем среднее ускорение a ₁₄ между t ₁ и t ₄ :

=

a 14 =	v 4 — v 1 64	0-0	=	0	= 0
	t 4 — t 1	t 4 — t 1		1 4

Таким образом, элевато r имеет положительное среднее ускорение (0.837 м / с ² ) для фазы ускорения, отрицательное среднее ускорение (-0,626 м / с ² ) для фазы замедления и нулевое среднее ускорение с момента начала ускорения до момента его замедления до останавливается.

Графики зависимости скорости от времени и среднего ускорения

График зависимости скорости от времени показывает, как скорость частицы изменяется во времени.

Вот пример:

График зависимости скорости от времени; скорость в момент времени 0 равна 0, затем становится положительной и, наконец, в какой-то момент через 9 секунд она возвращается к 0.v20t (s) 897654321O (м / с) 100806040

Как найти среднее ускорение из графика зависимости скорости от времени

График зависимости скорости от времени позволяет нам определить скорость частицы в любой момент.

Например, на графике зависимости скорости от времени, показанном выше, в момент времени t = 4 с частица имеет скорость v = 60 м / с:

График зависимости скорости от времени; через 4 секунды скорость составляет 60 метров в секунду. v20100806040t (s) 897654321O (m / s)

Итак, график зависимости скорости от времени дает нам достаточно информации, чтобы найти среднее ускорение частицы за любой промежуток времени.

Например, мы можем найти среднее ускорение между 4 и 8 секундами из приведенного выше графика зависимости скорости от времени, выполнив следующие 3 простых шага:

1. Посмотрите на график и определите скорость v ₁ , которую имеет частица. в момент t ₁ = 4 с.
2. Посмотрите на график и определите скорость v ₂ , которую имеет частица в момент t ₂ = 8 с.
3. Рассчитайте среднее ускорение, разделив изменение скорости v ₂ — v ₁ на интервал времени t ₂ — t ₁ .

Начнем с шагов 1 и 2:

График зависимости скорости от времени; через 4 секунды скорость составляет 60 метров в секунду; за 8 секунд скорость составляет 80 метров в секунду. v20100806040t (s) 897654321O (м / с)

t ₁ = 4 с, v ₁ = 60 м / с

t ₂ = 8 с, v ₂ = 80 м / с

Затем на шаге 3 мы вычисляем среднее ускорение:

a 12 =	v 2 — v 1	=	80 м / с — 60 м / с	=	20 м / с	= 5 м / с 2
	т 2 — t 1		8 с — 4 с		4 с

Среднее ускорение как наклон секущей линии к графику зависимости скорости от времени

Рассмотрим график зависимости скорости от времени, который показывает, как скорость частицы менялась с течением времени:

График зависимости скорости от времени; скорость в момент времени 0 равна 0, затем становится положительной и, наконец, возвращается к 0.vtO

Теперь давайте возьмем момент t ₁ , в который частица имеет скорость v ₁ , и последующий момент t ₂ , в который частица имеет скорость v ₂ :

График зависимости скорости от времени; в момент t1 скорость равна v1, а в последующий момент t2 она равна v2.vtO1t2tvv12

Посмотрев на график, мы можем увидеть, что изменение скорости v ₂ — v ₁ = Δv является вертикальным расстояние между точками, соответствующими t ₁ и t ₂ на графике:

График зависимости скорости от времени; изменение скорости Δv обозначается как расстояние по вертикали между точками t1 и t2 на графике.vtO1t2tΔvvv12

Мы также можем видеть, что интервал времени t ₂ — t ₁ = Δt — это горизонтальное расстояние между точками, соответствующими t ₁ и t ₂ на графике:

График зависимости скорости от времени; интервал времени Δt обозначен как горизонтальное расстояние между точками t1 и t2 на графике. vtO1t2tΔvΔtvv12

Теперь давайте изобразим секущую линию, которая проходит через точки t ₁ и t ₂ на графике:

Скорость график против времени; секущая линия, проходящая через точки t1 и t2 на графике.vtO1t2tΔvΔtvv12

Отношение Δv к Δt — это отношение вертикального изменения к горизонтальному изменению между двумя точками на секущей линии. Итак, это отношение равно наклону m секущей линии:

Мы также знаем, что это отношение равно среднему ускорению между t ₁ и t ₂ :

Отсюда следует, что наклон m отрезка Секущая линия равна среднему ускорению a:

Следовательно, среднее ускорение между моментом t ₁ и моментом t ₂ равно наклону секущей линии, которая проходит через точки t ₁ и t ₂ на графике зависимости скорости от времени.

Как определить знак среднего ускорения по графику зависимости скорости от времени

Определить знак среднего ускорения по графику зависимости скорости от времени оказывается довольно просто.

Давайте вернемся к тому же графику зависимости скорости от времени, что и выше, и рассмотрим момент t ₁ , в который частица имеет скорость v ₁ , и последующий момент t ₂ , в котором частица имеет скорость v _{. 2} :

График зависимости скорости от времени; в момент t1 скорость равна v1; в момент t2 скорость равна v2; Указаны Δv и Δt.vtO1t2tΔvΔtvv12

Затем представим секущую линию, которая проходит через точки t ₁ и t ₂ на графике зависимости скорости от времени, и назовем θ углом, который она образует с положительной осью t:

График зависимости скорости от времени ; угол θ, который секущая линия, проходящая через точки t1 и t2 на графике, составляет с положительной осью t. vtO1t2tΔvΔtθvv12

Чтобы определить, является ли среднее ускорение между t ₁ и t ₂ положительным, отрицательным, или ноль, все, что нам нужно сделать, это посмотреть на знак угла θ:

1. График зависимости скорости от времени; угол θ, который секущая образует с положительной осью t, положительный.vtO1t2tΔvΔtθvv12
2. График зависимости скорости от времени; угол θ, который секущая линия образует с положительной осью t, отрицателен. vtO1t2tΔvΔtθvv12
3. График зависимости скорости от времени; секущая линия представляет собой горизонтальную линию. vtO1t2tvv12 =

Таким образом, знак среднего ускорения между моментом t ₁ и моментом t ₂ такой же, как и у угла θ, который проходит секущая линия через точки t ₁ и t ₂ на графике зависимости скорости от времени, составляет с положительной осью t.

Изменение скорости и интервал времени, выраженный в терминах среднего ускорения

Есть много случаев, когда мы могли бы захотеть выразить изменение скорости Δv или интервал времени Δt через среднее ускорение a.

Мы можем легко это сделать, сначала вспомнив, что среднее ускорение a за интервал времени Δt равно отношению изменения скорости Δv, которое происходит во время Δt, к самому Δt:

Затем мы можем решить эту уравнение для изменения скорости Δv:

Мы должны понимать это следующим образом: изменение скорости Δv, которое происходит в интервале времени Δt, равно среднему ускорению a для этого интервала времени, умноженному на сам интервал времени .

Мы также можем решить указанное выше уравнение для интервала времени Δt:

Мы должны понимать это так: интервал времени Δt равен изменению скорости Δv, которое происходит в течение этого интервала времени, деленному на среднее значение. ускорение a за этот промежуток времени.

Пример: Среднее ускорение ракеты

После старта ракета достигает скорости 1645 км / ч со средним ускорением 5,870 м / с ² . Затем ракета продолжает разгоняться 91.85 с, до выключения главного двигателя, со средним ускорением 20,32 м / с ² . Каково среднее ускорение ракеты с момента ее запуска до момента остановки главного двигателя?

Давайте рассмотрим момент, когда ракета собирается взлететь, как 0 и обозначим его как t ₁ . Таким образом, скорость v ₁ в момент t ₁ равна 0.

В следующий момент t ₂ ракета движется со скоростью 1645 км / ч.Итак, скорость v ₂ в момент t ₂ равна 1645 км / ч.

Момент t ₂ неизвестен. Однако мы знаем, что среднее ускорение между t ₁ и t ₂ составляет 5,870 м / с ² .

t ₂ = неизвестно, v ₂ = 1645 км / ч

a ₁₂ = 5,870 м / с ²

Затем, в момент t ₃ , 91,85 с после t ₂ , главный двигатель ракеты выключен.

Скорость v ₃ в момент t ₃ неизвестна. Однако мы знаем, что среднее ускорение между t ₂ и t ₃ составляет 20,32 м / с ² .

t ₃ = неизвестно, v ₃ = неизвестно

t ₃ — t ₂ = 91,85 с

a ₂₃ = 20,32 м / с ²

Наша работа сейчас рассчитать среднее ускорение ракеты с момента ее запуска до момента остановки главного двигателя, т.е.е., от момента t ₁ до момента t ₃ .

Среднее ускорение a ₁₃ между t ₁ и t ₃ равно

a 13 =	v 3 — v 1
	t 1

Начнем с определения того, что такое v ₃ — v ₁ .

В примере поезда мы уже видели, что изменение скорости v ₃ — v ₁ равно сумме v ₂ — v ₁ и v ₃ — v ₂ :

по оси v, где изменение скорости v3 — v1 рассматривается как сумма изменения скорости v2 — v1 и изменения скорости v3 — v2.vO1v2v3v3v − 1v2v − 1v3v − 2v

v ₃ — v ₁ = (v ₂ — v ₁ ) + (v ₃ — v ₂ )

Найти v не сложно ₂ — v ₁ , поскольку известны как v ₁ , так и v ₂ :

v ₂ — v ₁ = 1645 км / ч — 0

v ₂ — v ₁ = 1645 км / ч

А как насчет v ₃ — v ₂ ?

Мы знаем v ₂ , но не знаем v ₃ .

Итак, мы знаем интервал времени между t ₂ и t ₃ , а также среднее ускорение между t ₂ и t ₃ :

t ₃ — t ₂ = 91,85 с

a ₂₃ = 20,32 м / с ²

А поскольку среднее ускорение между t ₂ и t ₃ выражается как

a 23 =	v 3 — v 2
	t 3 — t 2

Если известны как ₂₃ , так и t ₃ — t ₂ , мы можем найти значение v ₃ — v ₂ :

v ₃ — v ₂ = a ₂₃ (t ₃ — t ₂ )

v ₃ — v ₂ = (20.32 м / с ² ) (91,85 с)

v ₃ — v ₂ = 1866 м / с

Теперь, когда известно v ₃ — v ₂ , мы можем вычислить значение v ₃ — v ₁ :

v ₃ — v ₁ = (v ₂ — v ₁ ) + (v ₃ — v ₂ )

v ₃ — v ₁ = 1645 км / ч + 1866 м / с

1645 км / ч =	1645	м / с = 456.9 м / с
	3,6

v ₃ — v ₁ = 456,9 м / с + 1866 м / с

v ₃ — v ₁ = 2323 м / с

Итак, мы определили, что такое v ₃ — v ₁ .

Далее найдем t ₃ — t ₁ .

t ₃ — t ₁ равно сумме t ₂ — t ₁ и t ₃ — t ₂ :

t ₃ — t ₁ = ( t ₂ — t ₁ ) + (t ₃ — t ₂ )

Мы знаем, что t ₃ — t ₂ это:

Но мы не знаем, что t ₂ — т ₁ есть.

Мы знаем только t ₁ , но не t ₂ .

Однако мы знаем изменение скорости между t ₁ и t ₂ , а также среднее ускорение между t ₁ и t ₂ :

v ₂ — v ₁ = 1645 км / ч = 456,9 м / с

a ₁₂ = 5,870 м / с ²

А поскольку среднее ускорение между t ₁ и t ₂ выражается как

a 12 =	v 2 — v 1
	t 2 — t 1

Где и ₁₂ и v ₂ — v ₁ известны, мы можем найти значение t ₂ — t ₁ :

(t ₂ — t ₁ ) a ₁₂ = v ₂ — v ₁

t 2 — t 1 =	v 2 — v 1
	а 12

т 2 — т 1 =	456.9 м / с
	5,870 м / с 2

t ₂ — t ₁ = 77,84 с

Зная, что такое t ₂ — t ₁ , мы можем вычислить t ₃ — t ₁ :

t ₃ — t ₁ = (t ₂ — t ₁ ) + (t ₃ — t ₂ )

t ₃ — t ₁ = 77,84 с + 91,85 с

t ₃ — t ₁ = 169.69 с

Теперь, когда мы знаем как v ₃ — v ₁ и t ₃ — t ₁ , мы можем наконец вычислить среднее ускорение a ₁₃ :

a 13 =	v 3 — v 1
	t 3 — t 1

2 2

a 13 =	2323 м / с	=	м / с
	169.69 с

Следовательно, среднее ускорение ракеты с момента ее взлета до момента остановки главного двигателя составляет 13,69 м / с ² .

Сводка

• Среднее ускорение a между моментом t ₁ и моментом t ₂ определяется как отношение изменения скорости v ₂ — v ₁ к интервалу времени t ₂ — t ₁ :

  a =	v 2 — v 1	=	Δv
  t 2 — t 9023		9024 9024 t

• Единица измерения среднего ускорения в системе СИ — это метры в секунду в секунду ((м / с) / с) или, проще говоря, метры в секунду в квадрате (м / с ² ).

• Знак среднего ускорения a совпадает со знаком изменения скорости Δv.

• Среднее ускорение между моментом t ₁ и моментом t ₂ равно наклону секущей линии, которая проходит через точки t ₁ и t ₂ на график зависимости скорости от времени.

  Знак среднего ускорения совпадает со знаком угла θ, который секущая линия составляет с положительной осью t.

• Изменение скорости Δv, которое происходит в течение интервала времени Δt, равно среднему ускорению a для этого интервала времени, умноженному на сам интервал времени:

• Интервал времени Δt равно изменению скорости Δv, которое происходит в течение этого интервала времени, деленному на среднее ускорение a для этого интервала времени:

Упражнения

# 1

Когда ракета запускается, она достигает скорости 4140 км / ч всего за 95.0 с. Вычислите среднее ускорение, которое ракета имеет в течение первых 95,0 с после запуска.

Показать решение

Решение

12,1 м / с ²

Как найти решение

t ₁ = 0, v ₁ = 0

t ₂ = 95,0 s, v ₂ = 4140 км / ч

a ₁₂ =?

₁

a 12 =	v 2 — v 1	=	4140 км / ч — 0	=	4140 км / ч
	t
t	95.0 с — 0	95,0 с

4140 км / ч =	4140	м / с = 1150 м / с
	3,6

6 12 1150 м / с	= 12,1 м / с 2
		95,0 с

# 2

Автомобиль разгоняется до скорости 81,0 км / ч из состояния покоя за 5,60 с. Он продолжает ускоряться еще 3,80 с, в результате чего его скорость увеличивается на 17.0 км / ч. Каковы средние ускорения автомобиля с момента начала разгона до момента, когда он достигнет скорости 81,0 км / ч, за интервал времени, в течение которого он увеличивает свою скорость на 17,0 км / ч, и с момента старта до достижения его конечная скорость?

Показать решение

Решение

4,02 м / с ² ; 1,24 м / с ² ; 2,89 м / с ²

Как прийти к решению

t ₁ = 0, v ₁ = 0

t ₂ = 5.60 с, v ₂ = 81,0 км / ч

t ₃ — t ₂ = 3,80 с, v ₃ — v ₂ = 17,0 км / ч

a ₁₂ =?, a ₂₃ =?, a ₁₃ =?

₁

a 12 =	v 2 — v 1	=	81,0 км / ч — 0	=	81,0 км / ч
	т
т	5,60 с — 0	5.60 с

81,0 км / ч =	81,0	м / с = 22,5 м / с
	3,6

907 227 227 227 22 = 4,02 м / с ²

a 12 =
	5,60 с

a 23 =

v 3 — v 2

=

7 907 907 907 907 907 907

7 3 — т 2

3.80 с

17,0 км / ч =	17,0	м / с = 4,72 м / с
	3,6

907 4,724 4,7 = 1,24 м / с ²

a 23 =
	3,80 с

a 13 =	v 3 — v 1
	t 906

v ₃ — v ₁ = (v ₂ — v ₁ ) + (v ₃ — v ₂ )

v ₃ — v ₁ = 81.0 км / ч + 17,0 км / ч

v ₃ — v ₁ = 98,0 км / ч

t ₃ — t ₁ = (t ₂ — t ₁ ) + ( t ₃ — t ₂ )

t ₃ — t ₁ = 5,60 с + 3,80 с

t ₃ — t ₁ = 9,40 с

a 13 9063	v 3 — v 1	=	98,0 км / ч
	t 3 — t 1		9.40 с

98,0 км / ч =	98,0	м / с = 27,2 м / с
	3,6

907 24 27 27 27 = 2,89 м / с ²

a 13 =
	9,40 с

# 3

Поезд отправляется со станции и разгоняется до скорости 85,0 км / ч за 30,0 с. Некоторое время он продолжает двигаться с постоянной скоростью. Затем, когда поезд приближается к станции назначения, он тормозит и успешно останавливается после 39.0 с. Найдите средние ускорения поезда для фазы ускорения, для фазы торможения и от момента начала ускорения до момента остановки.

Показать решение

Решение

0,787 м / с ² ; −0,605 м / с ² ; 0

Как прийти к решению

t ₁ = 0, v ₁ = 0

t ₂ = 30,0 с, v ₂ = 85,0 км / ч

t ₃ = неизвестно, v ₃ = 85.0 км / ч

t ₄ — t ₃ = 39,0 с, v ₄ = 0

a ₁₂ =?, A ₃₄ =?, A ₁₄ =?

_{906 906 906 1}

a 12 =	v 2 — v 1	=	85,0 км / ч — 0	=	85,0 км / ч
	т
30,0 с — 0	30,0 с

85,0 км / ч =	85.0	м / с = 23,6 м / с
	3,6

30,0 907 907

a 12 =	23,6 м / с	= 0,787 м / с 2

907 34 — т ₃

a 34 =	v 4 — v 3	=	0 — 85,0 км / ч	=	−85,0 км / ч
39,0 с	39.0 с

−85,0 км / ч =	−85,0	м / с = −23,6 м / с
	3,6

,623 / с

a 34 −	= −0,605 м / с 2
		39,0 с

# # #

В спринте у бегуна среднее ускорение 3.12 м / с ² за первые 2,40 с. После этого она продолжает ускоряться и дополнительно увеличивает свою скорость на 5,31 м / с при среднем ускорении 1,85 м / с ² . Рассчитайте среднее ускорение бегуна за весь период ускорения.

Показать решение

Решение

2,43 м / с ²

Как найти решение

t ₁ = 0, v ₁ = 0

t ₂ = 2,40 s, v ₂ = неизвестно, a ₁₂ = 3.12 м / с ²

t ₃ = неизвестно, v ₃ — v ₂ = 5,31 м / с, a ₂₃ = 1,85 м / с ²

a ₁₃ = ?

a 14 =	v 4 — v 1	=	=	0	= 0
	t 4 — t 1			t 4 — t 1		t 4 — t 1

a 13 =	v 3 — v 1
	t 3 — t 1

v _{3 906 164 — v 906 2} — v ₁ ) + (v ₃ — v ₂ )

v ₃ — v ₂ = 5.31 м / с

t ₂ — t ₁ = 2,40 с — 0 = 2,40 с

a ₁₂ = 3,12 м / с ²

a 12 =	v 2 — v 1
	t 2 — t 1

v ₂ — v ₁ = a ₁₂ (t ₂ — t _{) 9}

v ₂ — v ₁ = (3,12 м / с ² ) (2,40 с)

v ₂ — v ₁ = 7.49 м / с

v ₃ — v ₁ = (v ₂ — v ₁ ) + (v ₃ — v ₂ )

v ₃ — v ₁ = 7,49 м / с + 5,31 м / с

v ₃ — v ₁ = 12,80 м / с

t ₃ — t ₁ = (t ₂ — t ₁ ) + (t ₃ — t ₂ )

t ₂ — t ₁ = 2,40 с

v ₃ — v ₂ = 5.31 м / с

a ₂₃ = 1,85 м / с ²

a 23 =	v 3 — v 2
	t 64 — t 906 264 — t

(t ₃ — t ₂ ) a ₂₃ = v ₃ — v ₂

3 907 v — v ₂

t 3 — t 2 =
	a 23

t 3 — t 2 =

5. Читайте также Что делать, если грудничок не спит днем: советы по налаживанию режима сна Антигистаминные препараты для новорожденных: лечение и профилактика аллергии у грудничков Методика «Цветоник» М. Лазарева для музыкального развития детей Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт