Функции: понятие функция и аргумент, функциональная зависимость
Если две переменные величины находятся между собой в такой зависимости, что каждому значению одной переменной соответствует строго определённое значение другой, то первая величина называется аргументом, а вторая его функцией.
Функция – это зависимая переменная величина. Аргумент – это независимая переменная. Зависимость функции от аргумента называется функциональной зависимостью.
Если нужно указать на тот факт, что y функция от x, не акцентируя внимания на то, в какой именно зависимости находится функция от аргумента, то пишут просто:
y = f(x),
где f (начальная буква слова function – функция) заменяет слово функция
, y – это функция, а x – аргумент.
Иногда, чтобы показать, что y зависит от x, пишут просто:
y(x
Обратите внимание, что вместо y и x могут использоваться любые другие буквы.
Значение y, соответствующее заданному значению x, называют значением функции. Все значения, которые принимает аргумент, образуют область определения функции. Все значения, которые принимает зависимая переменная, образуют множество значений функции. Для функции f приняты следующие обозначения:
D(f) – область определения функции
(множество значений аргумента).
E(f) – множество значений функции.
f(x0) – значение функции в точке x0.
Пример. Возьмём формулу нахождения расстояния по скорости и времени:
S = vt
Где S – это расстояние, v – скорость, а t – время. Если взять скорость, равную 50 км/ч, то каждому неотрицательному значению t будет соответствовать строго определённое значение S:
| t (ч) | 1 | 1,5 | 2 | 2,5 | 3 |
|---|---|---|---|---|---|
| S (км) | 50 | 75 | 100 | 125 | 150 |
Следовательно, S является функцией от t – S(t)
, область определения функции – D(S) ⩾ 0, так как время не может быть отрицательным, но при этом можно не затратить времени вообще, если не двигаться, в этом случае t = 0. Значение этой функции в точке t0 можно обозначить в виде S(t0), то есть записать таблицу со значениями в таком виде:
S(1) = 50, S(1,5) = 75, S(2) = 100, S(2,5) = 125, S(3) = 150
Нахождение области определения и области значений числовой функции
Тема: Числовые функции
Урок: Нахождение области определения и области значений числовой функции
Понятие функции одно из важнейших в математике. Именно функции описывают реальную жизнь: полет ракеты или самолета, движение поезда, изменение прибыли предприятия и т.д. Свойства функции связывают воедино, казалось бы, разрозненные методы решения уравнений, неравенств, систем.
Функцией называется закон 
, по которому каждому элементу 
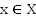ставится в соответствие единственный элемент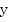 
Множество всех допустимых значений аргумента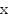 
называется областью определения функции и обозначается 
.
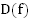Область определения функции – важнейшая характеристика функции. Если при задании функции множество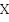 
не задано, то область определения считается естественной, т.е. совпадающей с областью определения выражения 
.
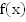Множество всех значений, которые принимает зависимая переменная, называют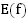 
.
Смысл выражения «область значений функции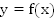 
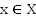, , есть множество 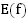» состоит в следующем:
1. Любому элементу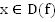 
соответствует единственный элемент 
2. Любое значение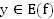 
достигается хотя бы при одном значении 
.
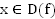interneturok.ru
Определение, понятие, свойства и значение функций в алгебре
Одним из основных понятий в математике, если не самым основным, является понятие функции. Для понимания этого термина, его значения, смысла и необходимости, обратимся к следующему примеру:…
Вконтакте
Google+
Мой мир
| Сколько времени находится в пути автомобиль? | Сколько километров автомобиль проехал? |
| 1 ч | 80 км |
| 2 ч | 160 км |
| 3 ч | 240 км |
| 4 часа | 320 км |
| 5 часов | 400 км |
Нам были известны всего две величины: скорость автомобиля и время, которое он находился в пути. Взглянув на таблицу, можно понять, что между временем, которое находился автомобиль в пути, и пройденным им расстоянием есть чёткая зависимость — каждый час автомобиль проезжает на 80 километров больше. Что ж, давайте немного приблизимся к алгебре и введём две переменные: y и x.Y — это наше расстояние, а x — время пути. Составим уравнение: y = 80 * x. Теперь вместо x подставим время:
- Y = 80 * 1. Получается 80 — значение расстояния, которое автомобиль пройдёт за 1 час.
- Теперь вместо x подставим 2. Получается: y = 80 * 2 = 160. Это значение расстояния, которое пройдёт автомобиль при условии, что он будет ехать 2 часа.
Теперь введём следующую запись: y(x). Эта запись означает зависимость первой переменной от второй, а наше окончательное уравнение для движения автомобиля будет выглядеть следующим образом: y(x)=80x. Y в алгебре принято называть функцией, а x — аргументом.
Это интересно: какой вектор называется разностью двух векторов?
Смысл
Пользуясь приведённым примером, мы чётко и ясно можем понять, что определение функции — это зависимость одной переменной от другой.Очень важно понимать, что y = 80 * x — не единственная зависимость. Стоит нам лишь изменить скорость
автомобиля, то все ý при тех же значениях аргумента будут совсем другие. Кроме того, существует огромное множество зависимостей, которые могут иметь другой вид.Способы задания
Всего в математике существует три способа задания функции:
- «Формульный способ». С помощью формулы мы всегда можем определить ý. Допустим, что у нас есть зависимость y = 5x + 1. Чтобы найти все y, нам просто нужно подставить вместо x любое число, например: если x = 0, y = 1, если x = 5, y = 26. В этой функции мы можем принимать любые значения аргумента, но если нам встретится следующая зависимость: y = √x, то мы сможем взять за x все числа, кроме отрицательных, так как число под корнем не может быть с минусом.
- Табличный способ задания также очень сильно распространён. Мы уже встречались с таблицей, когда приводили пример про автомобиль. Для того чтобы составить таблицу, необходимо всего лишь найти несколько значений y при нескольких значениях аргумента.
- Графический способ задания. Когда только начинают знакомятся с функциями, обязательно вводят такое понятие, как график. Давайте рассмотрим, что же он из себя представляет.
Перед вами координатная плоскость — основа для графика. Она состоит из вертикальной оси Y — оси значений, и из горизонтальной оси X — аргумента. У координатной плоскости обязательно есть начало отсчёта, которая обозначается нулём, и единичный отрезок (в данном примере единичный отрезок равен одной клетке).
На координатной плоскости мы можем взять любой единичный отрезок. Например, если нам удобно, значение одной клетки будет ни 1, а 100. Следовательно, две клетки — 200 и так далее. Здесь мы можем построить любой график и, соответственно, увидеть любую зависимость.
На координатной плоскости мы видим график 2x — 1. Графиком является прямая. Как же определить зависимость? Давайте приметим любое значение аргумента, например, 0. Когда x = 0, значение равно 1, что чётко видно на графике. Когда аргумент = -1, значение также равно -1.
Свойства
В алгебре есть невообразимое количество свойств функции, но основными и действительно важными являются лишь некоторые.
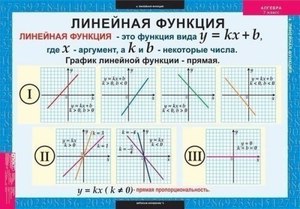
«Область определения». Это понятие очень простое: оно подразумевает собой абсолютно все числа, которые может принимать переменная x. Например, в функции y = x — 2, переменная x может принимать все значения, то есть от минус бесконечности до плюс бесконечности. Другое дело, например, такая функция: y = √x. Так как под корнем не может стоять отрицательное число, допустимыми значениями аргумента могут быть все числа от нуля до плюс бесконечности.- Если область определения все значения аргумента, то следующее свойство функции, называемое «область значений» — это все значения, которые может принимать переменная y. Поскольку значения функции зависимы от аргумента, то тут ничего выдумывать не надо, а просто вычислять.
- «Ограниченность» определить очень просто: если в рассматриваемой функции существует максимальное или минимальное значение y, то мы говорим, что функция будет называться ограниченной либо сверху, либо снизу.
- «Непрерывность» —тоже очень простое свойство. Например, зависимость ý = 2x — 1, которую мы уже рассматривали, непрерывна, так как её график нигде не прерывается. Если же в какой-либо функции график будет прерываться, можно говорить, что она прерывается на определённом промежутке.
- «Выпуклость» также присуща не всем графикам. У линейной зависимости её быть не может, поскольку это прямая и она не может быть выпуклой. А, например, парабола может быть выпуклой либо вверх, либо вниз.
- Нули функции — это пересечение с осями. То есть, если нам необходимо описать данное свойство, нужно будет найти, в каком месте график пересекается с осью абсцисс и в каком месте с осью ординат.
Подводя итог, мы можем сказать, что функция — это важнейшее понятие в математике, ведь, по сути, ею можно описать любые процессы.
obrazovanie.guru
« Основные свойства функции. » – Яндекс.Знатоки
К основным свойствам функции относятся:
- Четность и нечетность функции
Функция называется четной, если
– область определения функции симметрична относительно нуля
– для любого х из области определения f(-x) = f(x)
!https://ykl-shk.azureedge.net//goods/ymk/algebra/work3/theory/5/image003.gif
График четной функции симметричен относительно оси 0y
Функция называется нечетной, если
– область определения функции симметрична относительно нуля
– для любого х из области определения f(-x) = –f(x)
!https://ykl-shk.azureedge.net//goods/ymk/algebra/work3/theory/5/image004.gif
График нечетной функции симметричен относительно начала координат.
2.Периодичность
Функция f(x) называется периодической с периодом !https://ykl-shk.azureedge.net//goods/ymk/algebra/work3/theory/5/image005.gif, если для любого х из области определения f(x) = f(x+Т) = f(x-Т).
!https://ykl-shk.azureedge.net//goods/ymk/algebra/work3/theory/5/image006.gif
График периодической функции состоит из неограниченно повторяющихся одинаковых фрагментов.
- Монотонность (возрастание, убывание)
Функция f(x) возрастает на множестве Р , если для любых x1 и x2 из этого множества, таких, что x1 < x2 выполнено неравенство f(x1)< f(x2).
!https://ykl-shk.azureedge.net//goods/ymk/algebra/work3/theory/5/image011.gif
Функция f(x) убывает на множестве Р , если для любых x1 и x2 из этого множества, таких, что x1 < x2 выполнено неравенство f(x1) > f(x2).
!https://ykl-shk.azureedge.net//goods/ymk/algebra/work3/theory/5/image013.gif
- Экстремумы
Точка Хmax называется точкой максимума функции f(x) , если для всех х из некоторой окрестности Хmax , выполнено неравенство f(х)!https://ykl-shk.azureedge.net//goods/ymk/algebra/work3/theory/5/image014.gif f(Xmax).
Значение Ymax=f(Xmax) называется максимумом этой функции.
!https://ykl-shk.azureedge.net//goods/ymk/algebra/work3/theory/5/image015.gif
Хmax – точка максимума
Уmax – максимум
Точка Хmin называется точкой минимума функции f(x) , если для всех х из некоторой окрестности Хmin , выполнено неравенство f(х)!https://ykl-shk.azureedge.net//goods/ymk/algebra/work3/theory/5/image016.gif f(Xmin).
Значение Ymin=f(Xmin) называется минимумом этой функции.
!https://ykl-shk.azureedge.net//goods/ymk/algebra/work3/theory/5/image017.gif
Xmin – точка минимума
Ymin – минимум
Xmin, Хmax – точки экстремума
Ymin, Уmax – экстремумы.
- Нули функции
Нулем функции y = f(x) называется такое значение аргумента х , при котором функция обращается в нуль: f(x) = 0.
!https://ykl-shk.azureedge.net//goods/ymk/algebra/work3/theory/5/image018.gif
Х1,Х2,Х3 – нули функции y = f(x).
yandex.ru
| Символ (TeX) | Символ (Unicode) | Название | Значение | Пример |
|---|---|---|---|---|
| Произношение | ||||
| Раздел математики | ||||
| ⇒ → ⊃ | Импликация, следование | означает «если верно, то также верно». (→ может использоваться вместо ⇒ или для обозначения функции, см. ниже.) (⊃ может использоваться вместо ⇒, или для обозначения надмножества, см. ниже.). | верно, но неверно (так как также является решением). | |
| «влечёт» или «если…, то» | ||||
| везде | ||||
| ⇔ | Равносильность | означает « верно тогда и только тогда, когда верно». | ||
| «если и только если» или «равносильно» | ||||
| везде | ||||
| ∧ | Конъюнкция | истинно тогда и только тогда, когда и оба истинны. | , если — натуральное число. | |
| «и» | ||||
| Математическая логика | ||||
| ∨ | Дизъюнкция | истинно, когда хотя бы одно из условий и истинно. | , если — натуральное число. | |
| «или» | ||||
| Математическая логика | ||||
| ¬ | Отрицание | истинно тогда и только тогда, когда ложно . | ||
| «не» | ||||
| Математическая логика | ||||
| ∀ | Квантор всеобщности | обозначает « верно для всех ». | ||
| «Для любых», «Для всех» | ||||
| Математическая логика | ||||
| ∃ | Квантор существования | означает «существует хотя бы один такой, что верно » | (подходит число 5) | |
| «существует» | ||||
| Математическая логика | ||||
| = | Равенство | обозначает « и обозначают одно и то же значение». | 1 + 2 = 6 − 3 | |
| «равно» | ||||
| везде | ||||
| := :⇔ | Определение | означает « по определению равен ». означает « по определению равносильно » | (Гиперболический косинус) (Исключающее или) | |
| «равно/равносильно по определению» | ||||
| везде | ||||
| { , } | Множество элементов | означает множество, элементами которого являются , и . | (множество натуральных чисел) | |
| «Множество…» | ||||
| Теория множеств | ||||
| { | } { : } | Множество элементов, удовлетворяющих условию | означает множество всех таких, что верно . | ||
| «Множество всех… таких, что верно…» | ||||
| Теория множеств | ||||
| ∅ {} | Пустое множество | и означают множество, не содержащее ни одного элемента. | ||
| «Пустое множество» | ||||
| Теория множеств | ||||
| ∈ ∉ | Принадлежность/непринадлежность к множеству | означает « является элементом множества » означает « не является элементом множества » | ||
| «принадлежит», «из» «не принадлежит» | ||||
| Теория множеств | ||||
| ⊆ ⊂ | Подмножество | означает «каждый элемент из также является элементом из ». обычно означает то же, что и . Однако некоторые авторы используют , чтобы показать строгое включение (то есть ). | ||
| «является подмножеством», «включено в» | ||||
| Теория множеств | ||||
| ⊇ ⊃ | Надмножество | означает «каждый элемент из также является элементом из ». обычно означает то же, что и . Однако некоторые авторы используют , чтобы показать строгое включение (то есть ). | ||
| «является надмножеством», «включает в себя» | ||||
| Теория множеств | ||||
| ⊊ | Собственное подмножество | означает и . | ||
| «является собственным подмножеством», «строго включается в» | ||||
| Теория множеств | ||||
| ⊋ | Собственное надмножество | означает и . | ||
| «является собственным надмножеством», «строго включает в себя» | ||||
| Теория множеств | ||||
| ∪ | Объединение | означает множество элементов, принадлежащих или (или обоим сразу). | ||
| «Объединение … и …», «…, объединённое с …» | ||||
| Теория множеств | ||||
| ⋂ | Пересечение | означает множество элементов, принадлежащих и , и . | ||
| «Пересечение … и … », «…, пересечённое с …» | ||||
| Теория множеств | ||||
| \ | Разность множеств | означает множество элементов, принадлежащих , но не принадлежащих . | ||
| «разность … и … », «минус», «… без …» | ||||
| Теория множеств | ||||
| → | Функция | означает функцию с областью определения и областью прибытия (областью значений) . | Функция , определённая как | |
| «из … в», | ||||
| везде | ||||
| ↦ | Отображение | означает, что образом после применения функции будет . | Функцию, определённую как , можно записать так: | |
| «отображается в» | ||||
| везде | ||||
| N или ℕ | Натуральные числа | означает множество или реже (в зависимости от ситуации). | ||
| «Эн» | ||||
| Числа | ||||
| Z или ℤ | Целые числа | означает множество | ||
| «Зед» | ||||
| Числа | ||||
| Q или ℚ | Рациональные числа | означает | ||
| «Ку» | ||||
| Числа | ||||
| R или ℝ | Вещественные числа, или действительные числа | означает множество всех пределов последовательностей из | ( — комплексное число: ) | |
| «Эр» | ||||
| Числа | ||||
| C или ℂ | Комплексные числа | означает множество | ||
| «Це» | ||||
| Числа | ||||
| < > | Сравнение | обозначает, что строго меньше . означает, что строго больше . | ||
| «меньше чем», «больше чем» | ||||
| Отношение порядка | ||||
| ≤ или ⩽ ≥ или ⩾ | Сравнение | означает, что меньше или равен . означает, что больше или равен . | ||
| «меньше или равно»; «больше или равно» | ||||
| Отношение порядка | ||||
| ≈ | Приблизительное равенство | с точностью до означает, что 2,718 отличается от не больше чем на . | с точностью до . | |
| «приблизительно равно» | ||||
| Числа | ||||
| √ | Арифметический квадратный корень | означает неотрицательное действительное число, которое в квадрате даёт . | ||
| «Корень квадратный из …» | ||||
| Числа | ||||
| ∞ | Бесконечность | и суть элементы расширенного множества действительных чисел. Эти символы обозначают числа, меньшее/большее всех действительных чисел. | ||
| «Плюс/минус бесконечность» | ||||
| Числа | ||||
| | | | Модуль числа (абсолютное значение), модуль комплексного числа или мощность множества | обозначает абсолютную величину . обозначает мощность множества и равняется, если конечно, числу элементов . | ||
| «Модуль»; «Мощность» | ||||
| Числа и Теория множеств | ||||
| ∑ | Сумма, сумма ряда | означает «сумма , где принимает значения от 1 до », то есть . означает сумму ряда, состоящего из . | ||
| «Сумма … по … от … до …» | ||||
| Арифметика, Математический анализ | ||||
| ∏ | Произведение | означает «произведение для всех от 1 до », то есть | ||
| «Произведение … по … от … до …» | ||||
| Арифметика | ||||
| ! | Факториал | означает «произведение всех натуральных чисел от 1 до включительно, то есть | ||
| « факториал» | ||||
| Комбинаторика | ||||
| ∫ | Интеграл | означает «интеграл от до функции от по переменной ». | ||
| «Интеграл (от … до …) функции … по (или d)…» | ||||
| Математический анализ | ||||
| df/dx f'(x) | Производная | или означает «(первая) производная функции от по переменной ». | ||
| «Производная … по …» | ||||
| Математический анализ | ||||
| Производная -го порядка | или (во втором случае если — фиксированное число, то оно пишется римскими цифрами) означает «-я производная функции от по переменной ». | |||
| «-я производная … по …» | ||||
| Математический анализ |
dic.academic.ru
Понятие функции | Алгебра
Понятие функции в математике — одно из основных. Выражает зависимость одних переменных величин от других.
Определение.
Функция — это соответствие между двумя множествами, при котором каждому элементу одного множества соответствует единственный элемент другого множества.
Пусть каждому числу x из множества значений D поставлено в соответствие число y из множества значений E.
«Поставлено в соответствие» — значит, указан определённый способ (правило), по которому для каждого x∈D находят y∈E. (∈ — знак принадлежности. Запись x∈D читают «икс принадлежит дэ»).
Чаще всего этот способ обозначают как y=f(x). Для обозначения функции применяют и другие буквы: y=g(x), s=f(t) и т.д.
Если функция задана соответствием y=f(x), переменная x называется независимой переменной или аргументом, y — зависимой переменной или функцией.
Множество значений D, которые может принимать x, называется областью определения функции.
Множество значений E, которые может принимать y, называется областью значений функции.
Функцию можно задать несколькими способами:
— аналитическим (с помощью формулы),
— графическим,
— табличным,
— описанием с помощью словесной формулировки).
Функции, в которых значения аргумента и значения функции — числа, называются числовыми функциями. В курсе алгебры изучаются, в основном, числовые функции.
Примеры функций.
1) При движении автомобиля с постоянной скоростью пройденный путь является функцией от времени .
Например, если автомобиль движется с постоянной скоростью 60 км/ч, зависимость пути от времени можно задать формулой s=60t, где s — пройденный путь (в километрах), t — время (в часах).
2) Периметр квадрата является функцией от его стороны.
Зависимость периметра от стороны квадрата можно задать формулой P=4a, где P — периметр, a — длина стороны.
www.algebraclass.ru
| Символ (TeX) | Символ (Unicode) | Название | Значение | Пример |
|---|---|---|---|---|
| Произношение | ||||
| Раздел математики | ||||
| $ \Rightarrow\, $ | ⇒ | Импликация, следование | $ A \Rightarrow B\, $ означает «если $ A $ верно, то $ B $ также верно». Иногда вместо него используют $ \rightarrow\, $. | $ x = 2 \Rightarrow x^2 = 4\, $ верно, но $ x^2 = 4 \Rightarrow x = 2\, $ неверно (так как $ x=-2 $ также является решением). |
| «влечёт» или «если…, то» | ||||
| везде | ||||
| $ \Leftrightarrow $ | ⇔ | Равносильность | $ A \Leftrightarrow B $ означает «$ A $ верно тогда и только тогда, когда $ B $ верно». | $ x + 5 = y + 2 \Leftrightarrow x + 3 = y\, $ |
| «если и только если» или «равносильно | ||||
| везде | ||||
| $ \wedge $ | ∧ | Конъюнкция | $ A \wedge B $ истинно тогда и только тогда, когда $ A $ и $ B $ оба истинны. | $ (n>2)\wedge (n<4)\Leftrightarrow (n=3) $, если $ n $ — натуральное число. |
| «и» | ||||
| Математическая логика | ||||
| $ \vee $ | ∨ | Дизъюнкция | $ A\vee B $ истинно, когда хотя бы одно из условий $ A $ и $ B $ истинно. | $ (n\leqslant 2)\vee (n\geqslant 4)\Leftrightarrow n\ne 3 $, если $ n $ — натуральное число. |
| «или» | ||||
| Математическая логика | ||||
| $ \neg $ | ¬ | Отрицание | $ \neg A $ истинно тогда и только тогда, когда ложно $ A $. | $ \neg (A\wedge B)\Leftrightarrow (\neg A)\vee (\neg B) $ $ x\notin S\Leftrightarrow \neg(x\in S) $ |
| «не» | ||||
| Математическая логика | ||||
| $ \forall $ | ∀ | Квантор всеобщности | $ \forall x, P(x) $ обозначает «$ P(x) $ верно для всех $ x $». | $ \forall n\in \mathbb N,\;n^2\geqslant n $ |
| «Для любых», «Для всех» | ||||
| Математическая логика | ||||
| $ \exists $ | ∃ | Квантор существования | $ \exists x,\;P(x) $ означает «существует хотя бы один $ x $ такой, что верно $ P(x) $» | $ \exists n\in \mathbb N,\;n+5=2n $ (подходит число 5) |
| «существует» | ||||
| Математическая логика | ||||
| $ =\, $ | = | Равенство | $ x=y $ обозначает «$ x $ и $ y $ обозначают один и тот же объект». | 1 + 2 = 6 − 3 |
| «равно» | ||||
| везде | ||||
| $ := $ $ :\Leftrightarrow $ $ \stackrel{\rm{def}}{=} $ | := :⇔ | Определение | $ x := y $ означает «$ x $ по определению равен $ y $». $ P :\Leftrightarrow Q $ означает «$ P $ по определению равносильно $ Q $» | $ {\rm ch} (x) := {1\over 2}\left(e^x+e^{-x}\right) $ (Гиперболический косинус) $ A \oplus B :\Leftrightarrow (A\vee B)\wedge \neg (A\wedge B) $ (Исключающее или) |
| «равно/равносильно по определению» | ||||
| везде | ||||
| $ \{ ,\} $ | { , } | Множество элементов | $ \{a,\;b,\;c\} $ означает множество, элементами которого являются $ a $, $ b $ и $ c $. | $ \mathbb N = \{0,\;1,\;2,\;\ldots \} $ (множество натуральных чисел) |
| «Множество…» | ||||
| Теория множеств | ||||
| $ \{ | \} $ $ \{ : \} $ | { | } { : } | Множество элементов, удовлетворяющих условию | $ \{x\,|\,P(x)\} $ означает множество всех $ x $ таких, что верно $ P(x) $. | $ \{n\in \mathbb N\,|\,n^2<20\} = \{0,\;1,\;2,\;3,\;4\} $ |
| «Множество всех… таких, что верно…» | ||||
| Теория множеств | ||||
| $ \varnothing $ $ \{\} $ | ∅ {} | Пустое множество | $ \{\} $ и $ \varnothing $ означают множество, не содержащее ни одного элемента. | $ \{n\in \mathbb N\,|\,1<n^2<4\} = \varnothing $ |
| «Пустое множество» | ||||
| Теория множеств | ||||
| $ \in $ $ \notin $ | ∈ ∉ | Принадлежность/непринадлежность к множеству | $ a\in S $ означает «$ a $ является элементом множества $ S $» $ a\notin S $ означает «$ a $ не является элементом $ S $» | $ 2\in \mathbb N $ $ {1\over 2}\notin \mathbb N $ |
| «принадлежит», «из» «не принадлежит» | ||||
| Теория множеств | ||||
| $ \subseteq $ $ \subset $ | ⊆ ⊂ | Подмножество | $ A\subseteq B $ означает «каждый элемент из $ A $ также являестя элементом из $ B $». $ A\subset B $ обычно означает то же, что и $ A\subseteq B $. Однако некоторые авторы используют $ \subset $, чтобы показать строгое включение |
vlab.wikia.org