Как посчитать напряжение в цепи: «Как рассчитать напряжение в цепи?» – Яндекс.Кью

Расчет простых цепей постоянного тока

В электротехнике принято считать, что простая цепь – это цепь, которая сводится к цепи с одним источником и одним эквивалентным сопротивлением. Свернуть цепь можно с помощью эквивалентных преобразований последовательного, параллельного и смешанного соединений. Исключением служат цепи, содержащие более сложные соединения звездой и треугольником. Расчет цепей постоянного тока производится с помощью закона Ома и Кирхгофа.  

Пример 1

  Два резистора подключены к источнику постоянного напряжения 50 В, с внутренним сопротивлением r= 0,5 Ом. Сопротивления резисторов  R₁ = 20 и R₂ = 32 Ом. Определить ток в цепи и напряжения на резисторах.

 

Так как резисторы подключены последовательно, эквивалентное сопротивление будет равно их сумме.

Зная его, воспользуемся законом Ома для полной цепи, чтобы найти ток в цепи. 

Теперь зная ток в цепи, можно определить падения напряжений на каждом из резисторов. 

Проверить правильность решения можно несколькими способами. Например, с помощью закона Кирхгофа, который гласит, что сумма ЭДС в контуре равна сумме напряжений в нем. 

Но с помощью закона Кирхгофа удобно проверять простые цепи, имеющие один контур. Более удобным способом проверки является баланс мощностей.

В цепи должен соблюдаться баланс мощностей, то есть энергия отданная источниками должна быть равна энергии полученной приемниками. 

Мощность источника определяется как произведение ЭДС на ток, а мощность полученная приемником как произведение падения напряжения на ток.

Преимущество проверки балансом мощностей в том, что не нужно составлять сложных громоздких уравнений на основании законов Кирхгофа, достаточно знать ЭДС, напряжения и токи в цепи.

Пример 2

  Общий ток цепи, содержащей два соединенных параллельно резистора R₁=70 Ом и R₂=90 Ом, равен 500 мА. Определить токи в каждом из резисторов.

Два последовательно соединенных резистора ничто иное, как делитель тока. Определить токи, протекающие через каждый резистор можно с помощью формулы делителя, при этом напряжение в цепи нам не нужно знать, потребуется лишь общий ток и сопротивления резисторов. 

Токи в резисторах 

В данном случае удобно проверить задачу с помощью первого закона Кирхгофа, согласно которому сумма токов сходящихся, в узле равна нулю.

Если у вас возникли затруднения, прочтите статью законы Кирхгофа.

Если вы не помните формулу делителя тока, то можно решить задачу другим способом. Для этого необходимо найти напряжение в цепи, которое будет общим для обоих резисторов, так как соединение параллельное. Для того чтобы его найти, нужно сначала рассчитать сопротивление цепи 

А затем напряжение 

Зная напряжения, найдем токи, протекающие через резисторы 

Как видите, токи получились теми же.

Пример 3

  В электрической цепи, изображенной на схеме R₁=50 Ом, R

₂=180 Ом, R₃=220 Ом. Найти мощность, выделяемую на резисторе R₁, ток через резистор R₂, напряжение на резисторе R₃, если известно, что напряжение на зажимах цепи 100 В.

 

Чтобы рассчитать мощность постоянного тока, выделяемую на резисторе R₁, необходимо определить ток I₁, который является общим для всей цепи. Зная напряжение на зажимах и эквивалентное сопротивление цепи, можно его найти.

Эквивалентное сопротивление и ток в цепи 

Отсюда мощность, выделяемая на R₁ 

Ток I₂ определим с помощью формулы делителя тока, учитывая, что ток I₁ для этого делителя является общим 

Так как, напряжение при параллельном соединении резисторов одинаковое, найдем U₃, как напряжение на резисторе R₂ 

Таким образом производится расчет простых цепей постоянного тока.

Просмотров: 68046

чему равно напряжение, как найти сопротивление нагрузки

В наши дни электричество играет в жизни человека очень большую роль, в следствие чего базовые знания в области физики и электротехники нужны практически каждому. Напряжение является одной из главных физических величин, которая позволяет объяснить теорию возникновения электрического поля и методы подбора оптимального сечения кабеля для применения его в повседневной жизни.

Что такое напряжение в сети электричества.

Напряжение – это физическая величина, которая характеризует электрическое поле. Иными словами, оно показывает, какую работу оно совершает при перемещении одного положительного заряда на определённое расстояние.

Показатель напряжения на вольтметре

За единицу напряжения в международной системе принимается такой показатель на концах проводника, при котором заряд в 1 Кл совершает работу в 1 Дж для перемещения его по этому проводнику. Общепринятой единицей измерения напряжения считается 1 В – Вольт.

Важно! Работа измеряется в Джоулях, заряды в Кулонах, а напряжение в Вольтах, следовательно, 1 Вольт равняется 1 Джоулю, деленному на 1 Кулон.

Чему равно напряжение.

Напряжение напрямую связано с работой тока, зарядом и сопротивлением.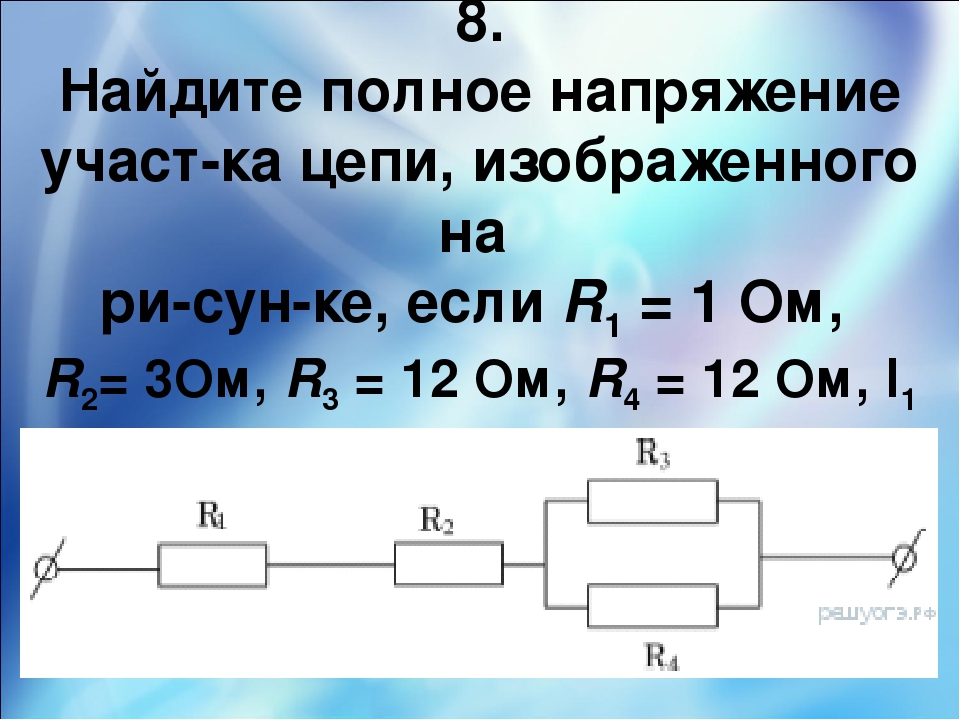 Чтобы измерить напряжение непосредственно в электрической цепи, к ней нужно подключить вольтметр. Он присоединяется к цепи параллельно, в отличие от амперметра, который подключается последовательно. Зажимы измерительного прибора крепятся к тем точкам, между которыми нужно вычислить напряжение. Чтобы он правильно показал значение, нужно включить цепь. На схемах вольтметр обозначается буквой V, обведенной в кружок.

Изображение вольтметра и электрической цепи

Напряжение обозначается латинской [U], а измеряется в [В]. Оно равно работе, которое совершает поле при перемещении единичного заряда. Формула напряжения тока – это U = A/q, где A – работа тока, q – заряд, а U – само напряжение.

Обратите внимание! В отличие от магнитного поля, где заряды неподвижны, в электрическом поле они находятся в постоянном движении.

Электрическое поле

Формула закона Ома

Свои опыты Ом направлял на изучение такой физической величины, как сопротивление, в результате чего в 1826 году он стал автором закона, который не потерял совей актуальность вплоть до сегодняшнего дня. Из своих опытов Ом вывел, что в различных цепях сила тока может возрастать с различной скоростью, и происходит это по мере увеличения напряжения.

Также, Ом сделал вывод, что каждый проводник обладает индивидуальными свойствами проводимости.

Сопротивление обозначается заглавной латинской [R] и измеряется в Омах. Сопротивление – физическая величина, характеризующая свойства проводника оказывать влияние на идущий по нему ток. Оно прямо пропорционально напряжению  в сети и обратно пропорционально  силе тока. В виде формулы данный закон можно записать как R = U/I, где U – напряжение, а I – сила тока. 1 Ом равняется 1 Вольту, деленному на 1 Ампер.

Запомните! Реостат – прибор, обеспечивающий возможность изменять сопротивление. Прежде всего, он влияет на показатель R в цепи, а, следовательно, на 2 другие величины, описанные в законе Ома. Силу тока может помочь определить амперметр.

Ползунковый реостат

Из формулы закона Ома можно вывести практически любую зависимость, связанную с электричеством.

Также, существует понятие удельного сопротивления проводника – физической величины, которая демонстрирует, каким сопротивлением будет обладать проводник из определенного вещества. Обозначается эта величина буквой ρ и через неё можно также найти сопротивление в цепи как произведению удельного сопротивления и длины проводника, деленного на площадь его поперечного сечения.

Важно! В виде формулы нахождение сопротивления через удельное сопротивление выглядит так: R = ρ*(l/S), где l – длина проводника, а S – площадь поперечного сечения.

Физический смысл удельного сопротивления показывает, какое влияние будет оказывать проводник длиной в 1 м с площадью поперечного сечения в 1 квадратный мм, изготовленный из определенного вещества. Измеряется в Омах, умноженных на метр: [ρ] = [Ом*м].

Ом и формула

Как найти сопротивление нагрузки

Сопротивление нагрузки обозначается латинскими буквами Rn или Rн. По сути, это является тем же сопротивлением участка цепи и вычисляется также по формулам закона Ома.

Нагрузка обозначается символами, которые на электрической схеме изображаются в виде крестиков в кружке – лампочкой; то есть двигатель, лампа, конкретный прибор и т. д.

Каждая нагрузка имеет своё собственное сопротивление. Например, если к сети подключена одна лампочка, то сопротивление нагрузки – показатель этого единственного прибора в цепи. Если к цепи подключено несколько нагрузок, то сопротивление считается суммарно для каждой из них.

Сопротивление нагрузки вычисляется в соответствии с законом Ома, то есть Rn = U/I. Если к сети подключено несколько нагрузок, то оно будет рассчитываться следующим образом: сначала находится сопротивление каждой отдельной «лампочки». Далее Rn вычисляется в зависимости от того, какой тип подключения в цепи: последовательное или параллельное. При параллельном 1/R = 1/R1 + 1/R2 + 1/Rn, где n –количество подключенных приборов. Если же соединение последовательное, общее R равно сумме всех R цепи.

Последовательное/параллельное соединения

Как найти с помощью формулы напряжение

Людей, интересующихся электричеством и физикой, всегда волнует вопрос, как найти напряжения, если известны другие характеристики. Его можно найти через многие формулы: в соответствии с законом Ома, через работу тока, путём сложения всех напряжений в электрической цепи и практическим способом – с помощью вольтметра. Как вычислить показатель с помощью последнего способа было описано выше.

Важно! В цепях с последовательным соединением общее напряжение – сумма значений каждой нагрузки. При параллельном соединении общее напряжение равно значению каждой лампочки, у которых оно также эквивалентно.

Измерение напряжения

По каким формулам вычисляется напряжение через работу и сама сила тока, рассказывают на уроках физики, так как эти величины считаются базовыми. Работа тока равна произведению напряжения и заряда: A = U*q. Также, из этой формулы выводится A = U*I*t, так как заряд – произведение силы тока и времени. Из них следует, что U = A/q или U = A/(I*t). Кроме того, одной из основных является формула напряжения, выведенная из закона Ома: U = R/I.

Важно! Определить напряжение можно и через мощность электрического тока. Мощность [P] равна A/t, и, так как A = U*I*t, конечная формула выглядит, как P = (U*I*t)/t. Здесь t сократится, и останется P = U*I, из которой следует, что U = P/I.

Как найти силу тока через сопротивление и напряжение

Сила тока обозначается латинскими [I] или [Y], и она зависит от количества заряда, перенесенного от одного полюса к другому за определенный промежуток времени, т.е. I = q/t. Измеряется сила тока в амперах, а узнать её значение в цепи можно при помощи амперметра.

Мужчина считает силу тока

Существуют формулы определения силы тока через напряжение и сопротивление. В первом случае произведение силы тока на время равняется работе, деленной на напряжение: I*t = A/U, во втором – по закону Ома, I = U/R. Через мощность сила будет равняться P/U.

При последовательном соединении, сила тока одинакова на всех участках цепи, следовательно, равна общему значению в цепи. В противоположном случае сила электрического тока равняется сумме силы тока всех нагрузок.

Таким образом, существует огромное множество формул для нахождения силы тока, напряжения и сопротивления. Они всегда могут пригодиться для теории, а на практике всегда помогут специальные приборы – амперметр и вольтметр.

Закон Ома для участка цепи. Закон Джоуля — Ленца. Работа и мощность электрического тока. Виды соединения проводников.

Количество теплоты, выделившееся при прохождении электрического тока по проводнику, прямо пропорционально квадрату силы тока, сопротивлению проводника и времени, в течение которого шел ток:

Последовательное соединение. 1. Сила тока во всех последовательно соединенных участках цепи одинакова: I1=I2=I3=…=In=… 2. Напряжение в цепи, состоящей из нескольких последовательно соединенных участков, равно сумме напряжений на каждом участке: U=U1+U2+…+Un+… 3. Сопротивление цепи, состоящей из нескольких последовательно соединенных участков, равно сумме сопротивлений каждого участка: R=R1+R2+…+Rn+… Если все сопротивления в цепи одинаковы, то: R=R1. N При последовательном соединении общее сопротивление увеличивается (больше большего).

Параллельное соединение. 1. Сила тока в неразветвленном участке цепи равна сумме сил токов во всех параллельно соединенных участках. I=I1+I2+…+In+…

2. Напряжение на всех параллельно соединенных участках цепи одинаково:     U1=U2=U3=…=Un=…  3. При параллельном соединении проводников проводимости складываются (складываются величины, обратные сопротивлению): Если все сопротивления в цепи одинаковы, то:  При параллельном соединении общее сопротивление уменьшается (меньше меньшего).

4. Работа электрического тока в цепи, состоящей из последовательно соединенных участков, равна сумме работ на отдельных участках: A=A1+A2+…+An+…   т.к.  A=I2Rt=I2(R1+R2+…+Rn+…)t. 5. Мощность электрического тока в цепи, состоящей из последовательно соединенных участков, равна сумме мощностей на отдельных участках: P=P1+P2+…+Pn+…   6. Т.к. силы тока во всех участках одинаковы, то:       U1:U2:…:Un:…  = R1:R2:…:Rn:… Для двух резисторов:  — чем больше сопротивление, тем больше напряжение.

4. Работа электрического тока в цепи, состоящей из параллельно соединенных участков, равна сумме работ на отдельных участках: A=A1+A2+…+An+…    т.к.     .   5. Мощность электрического тока в цепи, состоящей из параллельно соединенных участков, равна сумме мощностей на отдельных участках: P=P1+P2+…+Pn+…   6. Т.к. напряжения на всех участках одинаковы, то: I1R1= I2R2=…= I3R3=… Для двух резисторов:  — чем больше сопротивление, тем меньше сила тока.

Формула напряжения тока. Как найти, вычислить электрическое напряжение.

 

 

 

Тема: как рассчитать величину напряжения зная ток, сопротивление, мощность.

 

Как известно у электрического напряжения должна быть своя мера, которая изначально соответствует той величине, что рассчитана для питания того или иного электротехнического устройства. Превышение или снижение величины этого напряжения питания негативно влияет на электрическую технику, вплоть до полного выхода ее из строя. А что такое напряжение? Это разность электрических потенциалов. То есть, если для простоты понимания его сравнить с водой, то это примерно будет соответствовать давлению. По научному электрическое напряжение — это физическая величина, показывающая, какую работу совершает на данном участке ток при перемещении по этому участку единичного заряда.

 

Наиболее распространенной формулой напряжения тока является та, в которой имеются три основные электрические величины, а именно это само напряжение, ток и сопротивление. Ну, а формула эта известна под названием закона Ома (нахождение электрического напряжения, разности потенциалов).

 

 

Звучит эта формула следующим образом — электрическое напряжение равно произведению силы тока на сопротивление. Напомню, в электротехнике для различных физических величин существуют свои единицы измерения. Единицей измерения напряжения является «Вольт» (в честь ученого Алессандро Вольта, который открыл это явление). Единица измерения силы тока — «Ампер», и сопротивления — «Ом». В итоге мы имеем — электрическое напряжение в 1 вольт будет равно 1 ампер умноженный на 1 ом.

 

 

 

 

Помимо этого второй наиболее используемой формулой напряжения тока является та, в которой это самое напряжение можно найти зная электрическую мощность и силу тока.

 

 

Звучит эта формула следующим образом — электрическое напряжение равно отношению мощности к силе тока (чтобы найти напряжение нужно мощность разделить на ток). Сама же мощность находится путем перемножения тока на напряжение. Ну, и чтобы найти силу тока нужно мощность разделить на напряжение. Все предельно просто. Единицей измерения электрической мощности является «Ватт». Следовательно 1 вольт будет равен 1 ватт деленный на 1 ампер.

 

Ну, а теперь приведу более научную формулу электрического напряжения, которая содержит в себе «работу» и «заряды».

 

 

В этой формуле показывается отношение совершаемой работы по перемещению электрического заряда. На практике же данная формула вам вряд ли понадобится. Наиболее встречаемой будет та, которая содержит в себе ток, сопротивление и мощность (то есть первые две формулы). Но, хочу предупредить, что она будет верна лишь для случая применения активных сопротивлений. То есть, когда расчеты производятся для электрической цепи, у которой имеется сопротивления в виде обычных резисторов, нагревателей (со спиралью нихрома), лампочек накаливания и так далее, то приведенная формула будет работать. В случае использования реактивного сопротивления (наличии в цепи индуктивности или емкости) нужна будет другая формула напряжения тока, которая учитывает также частоту напряжения, индуктивность, емкость.

 

P.S. Формула закона Ома является фундаментальной, и именно по ней всегда можно найти одну неизвестную величину из двух известных (ток, напряжение, сопротивление). На практике закон ома будет применяться очень часто, так что его просто необходимо знать наизусть каждому электрику и электронику.

 

Закон Ома (страница 1)

Применение закона Ома к расчету линейных электрических цепей постоянного тока

1. Найти ток ветви (рисунок 3), если: U=10 В, Е=20 В, R=5 Ом.

Решение:

Так как все схемы рисунка 3 представляют собой активные ветви, то для определения токов в них используем закон Ома обобщенный закон Ома. Рассмотрим рисунок 3 а: направление ЭДС совпадает с произвольно выбранным условно положительным направлением тока, следовательно, в формуле обобщенного закона Ома величина ЭДС учитывается со знаком «плюс». Направление напряжения не совпадает с направлением тока, и в формуле обобщенного закона Ома величина напряжения учитывается со знаком «минус»;

Аналогично определяются токи в схемах б, в, г рисунка 3:

2. Найти напряжение между зажимами нетвей (рисунок 4).

Решение:

Участок цепи, изображенный на рисунке 4 а содержит источник ЭДС, т.е. является активным, поэтому воспользуемся обобщенным законом Ома:

откуда выразим напряжение на зажимах:

Аналогично определяются напряжения на зажимах участков, изображенных на рисунках 4 б и 4 в.

3. Определить неизвестные потенциалы точек участка цени (рисунок 5).

Решение:
Для схемы рисунка 5 а запишем обобщенный закон Ома:

откуда выразим напряжение на зажимах ветви:

Если представить напряжение как разность потенциалов:

тогда при известных параметрах цепи, токе и потенциале определим потенциал :

Эту же задачу можно решить другим способом. Напряжение на зажимах источника ЭДС , без учета внутреннего сопротивления источника, по величине равно и направлено от точки с большим потенциалом (точка С) к точке с меньшим потенциалом (точка b):

и тогда, зная потенциал , определим потенциал точки С:

Потенциал точки d больше потенциала точки С на величину падения напряжения на сопротивлении R:

тогда

Потенциал точки а определяем с учетом направления напряжения на зажимах источника ЭДС . Напряжение направлено от точки с большим потенциалом (точка d) к точке с меньшим потенциалом (точка а):

откуда следует, что

или

Рассмотрим решение задачи для схемы рисунка 5 б. При известном потенциале точки С, параметрах элементов и токе, определим потенциалы крайних точек участка цепи . Напряжение на участке b — с, выраженное через разность потенциалов, определим по закону Ома:

откуда следует

Напряжение на участке с — а, равное по величине Е, направлено от точки с большим потенциалом к точке с меньшим потенциалом:

4. В цепи (рисунок 6) известны величины сопротивлений резистивных элементов: , входное напряжение U=100 В и мощность, выделяемая на резистивном элементе с сопротивлением . Определить величину сопротивления резистора .

Решение:
Согласно закону Джоуля-Ленца, мощность на резистивном элементе определяется:

или, согласно закону Ома:

По известному значению мощности на резистивном элементе и величине сопротивления этого элемента определим ток в ветви:

По закону Ома напряжение на зажимах определится:

тогда величина сопротивления резистивного элемента:

5. Определить показания вольтметров цепи (рисунок 7), если .

Решение:
Ток в цепи определим по закону Ома:

Вольтметр показывает напряжение на источнике ЭДС Е:

Вольтметры показывают величину падения напряжения на резистивных элементах :

Вольтметр , показывает напряжение на участке 2 — 1 , которое определим как алгебраическую сумма напряжений :

6. Ток симметричной цепи (рисунок 8) , внутреннее сопротивлении источника ЭДС . Определить ЭДС Е и мощность источника энергии.

Решение:
Напряжение на зажимах 1 — 2 определим по закону Ома для пассивной ветви:

Величину ЭДС источника энергии определим из выражения закона Ома для активной ветви:

Мощность, развиваемая источником энергии, определится:

Расчеты напряжения, силы, сопротивления, нагрузки электрического тока

Современная структура общества такова, что на бытовом и промышленном уровне повсеместно используется электроэнергия. Генераторные установки, вырабатывающие электроэнергию, преобразующие подстанции работают для того, чтобы передать ее потребителям на бытовые электрические приборы и промышленные электроустановки.

Общая схема передачи электроэнергии потребителям с учетом мощностей

Что такое мощность электроэнергии

В электросетях, по которым передается энергия, существует ряд основных параметров, которые обязательно учитываются при проектировании и эксплуатации электроустановок.

Одним из таких показателей является электрическая мощность, под этим подразумевается способность электроустановки генерировать, передавать или преобразовывать определенную величину электроэнергии за определенный период времени. Преобразованием считается процесс изменения электрической энергии в тепло, механические движения или другой вид энергии. Чтобы сделать расчет мощности, надо знать, как минимум, величины тока, напряжения и ряда других параметров.

Расчет тока и напряжения, мощности иногда не делают, а измеряют параметры на месте. Но такая возможность не всегда предоставляется. Надо знать, как рассчитать мощность, когда цепь обесточена, при проектировании электроустановок, уметь пользоваться таблицей законов Ома и рассчитать силу тока по известным значениям параметров. Рассчитывать мощность нагрузки и ток нагрузки приходится для того, чтобы правильно выбрать сечение проводов в цепи, величину тока срабатывания для защитных автоматов и других нужд.

Законы Ома наглядно показывают, как посчитать ток по мощности и напряжению

Физический смысл электрической мощности в цепях переменного и постоянного тока одинаковый, но от условий нагрузки в цепи мощность может выражаться разными соотношениями. Для стандартизации закономерности явлений вводится понятие мгновенное значение, что указывает на зависимость скорости преобразований электроэнергии от фактора времени.

Электрическая мощность – это величина, выражающая скорость преобразования энергии электричества в другой вид энергии, обозначается буквой «Р».

Мгновенное значение электрической мощности

Определение – электрическая мощность тесно связана с другими параметрами цепи, током и напряжением, при изменении величины одного из них изменяются другие. Поэтому показания мощности фиксируются в короткий промежуток времени – ∆t.

Напряжение в данном случае обозначают буквой «U» – это выражает разность потенциалов зарядов, перемещенных электрическим полем из одной точки в другую за промежуток времени ∆t.

Сила тока обозначается буквой «I» – это поток, переносимый магнитным полем зарядов, другими словами заряд, перенесенный во временной интервал ∆t.

Исходя из этих определений, просматривается пропорциональная зависимость между этими параметрами:

Р = UxI.

При расчетах можно учитывать зависимость мощности от сопротивления нагрузки «R». По законам Ома для участка цепи с постоянным током мощность выражается как:

Р = I2xR или P = U2|R.

Если поставить в схему питания амперметр и вольтметр, то не придется думать, как вычислить силу тока.

Обратите внимание! Амперметр ставится последовательно в цепь по отношению к сопротивлению нагрузки, а вольтметр – параллельно.

В качестве источника питания используется аккумулятор, как нагрузка установлен прожектор. В данном случае не делается расчет силы тока, параллельно нагрузке подключен вольтметр, для измерения напряжения в Вольтах. Амперметр подключается последовательно для измерения тока в Амперах. Зная показания напряжения и тока по формулам, показанным выше, легко рассчитывается мощность.

Для участков цепи с переменным током формулы расчетов сложнее – необходимо учитывать характер нагрузки.

Расчеты мощности для электроцепей переменного тока

Переменный ток и напряжение имеют синусоидальный вид, при различных нагрузках происходит смещение фазы между ними на определенный угол. По этой причине направление тока иногда может быть противоположным, от нагрузки к источнику питания. Это бывает в электродвигателях, когда обмотка начинает генерировать энергию, это негативно сказывается на эффективности работы оборудования, снижается мощность. При большом количестве потребителей в электросети характер нагрузки имеет смешанный вид, в идеале выделяют три типа нагрузки:

• Активная нагрузка, ее представляют такие электроприборы, как лампы накаливания, нагревательные тэны, спиральные электроплиты;
• Емкостная нагрузка – это конденсаторы в оборудовании различного назначения;
• Индуктивная нагрузка представлена катушками в электродвигателях, обмотках электромагнитов, дросселями и трансформаторами, другими приборами, где ток протекает через обмотки.

Емкостные и индуктивные виды выделяют как реактивную энергию в электросетях. Зная вид нагрузки, расчет потребляемой мощности делается точнее.

Расчет мощности в цепи с активной нагрузкой

Это классический случай в однофазной сети 220 В, в качестве нагрузки можно использовать обычные резисторы. Мощность рассчитывается как произведение действующих значений тока и напряжения, умноженное на соsϕ. В данном случае ϕ – угол смещения между фазами тока и напряжения.

Р = UI cos ϕ

График зависимости мощности по току и напряжению при активной нагрузке

Из графика можно узнать, что колебания тока и напряжения одинаковы по частоте и фазе, мощность всегда положительная с частотой в два раза больше.

Активная электрическая мощность характеризует процесс преобразования в сетях с переменным током энергии в тепло, механические движения, излучение света, в любой вид другой энергии. Измеряется активная нагрузка в Вт, кВт.

Расчет реактивной мощности

Как найти мощность в цепях с индуктивной и емкостной нагрузками? Это делается аналогичным образом. Расчет потребляемой мощности, как и в случае с активной нагрузкой, означает, что действующие напряжение и ток перемножаются, и результат умножается на sin ϕ. Где ϕ – угол сдвига фаз тока и напряжения.

Р = UI sin ϕ

Диаграмма, показывающая взаимосвязь параметров цепи при индуктивной нагрузке

График показывает, что мощность может принимать отрицательные значения, в этот момент энергия отдается в сторону источника питания, фактически она бесполезна и расходуется на нагрев.

Реактивная составляющая энергии характеризует работу нагрузки в виде электронного оборудования, электротехнических схем, моторов с наличием емкостной и индуктивной нагрузки. Единица измерения реактивной мощности при подсчете измеряется в Вар, это (Вольт-Ампер реактивный), обозначается буквой «Q».

Треугольник, отображающий отношение мощностей в сети

Зависимость мощности в цепи переменного тока от реактивной и активной составляющих с учетом угла сдвига фаз хорошо отображается на диаграмме, которую называют треугольником мощностей.

Формула расчета полной мощности обозначается буквой «S»

В этом случае учитывается полный импеданс рассчитываемой мощности электрического тока (комплексное сопротивление нагрузки). Тем, кому вычислением заниматься сложно даже на калькуляторе, можно воспользоваться онлайн калькуляторами на сайте https://www.fxyz.ru с вычислением мощности в цепях с различной нагрузкой. Вычисляется все мгновенно, достаточно заполнить таблицу с исходными параметрами. Когда такой калькулятор под рукой, я вычислю быстро нужные мне параметры.

Видео

Оцените статью:

Онлайн калькулятор закона Ома для участка цепи

Рад приветствовать тебя, дорогой читатель, в этой первой статье моего блога! Ее я посвятил самому основному закону, который должен хорошо понимать современный человек, работающий с электричеством.

Мой онлайн калькулятор закона Ома создан для участка цепи. Он значительно облегчает электротехнические расчеты в домашней проводке, подходит для цепей переменного и постоянного тока.

Им просто пользоваться: прочти правила ввода данных и работай!

Содержание статьи

Правила работы на калькуляторе

В быту нас интересуют, как правило, четыре взаимосвязанных характеристики электричества:

1. напряжение;
2. ток;
3. сопротивление;
4. или мощность.

Если тебе известны две величины, входящие в закон Ома (U, R, I), то вводи их в соответствующие строки, а оставшийся параметр и мощность будут вычислены автоматически.

Будь внимательным, чтобы не допустить ошибки.

Все значения надо заполнять в одной размерности: амперы, вольты, омы, ватты без использования обозначений дольности или кратности.

Осуществить переход к ним тебе поможет наглядная таблица.

Онлайн калькулятор закона Ома

Простые примеры расчета

Бытовая сеть переменного тока

Пример №1. Проверка ТЭНа.

В стиральную машину встроен трубчатый электронагреватель 1,25 кВт на 220 вольт. Требуется проверить его исправность замером сопротивления.
По мощности рассчитываем ток и сопротивление.

I = 1250 / 220 = 5,68 А; R = 220 / 5,68 = 38,7 Ом.

Проверяем расчет сопротивления калькулятором по току и напряжению. Данные совпали. Можно приступать к электрическим замерам.

Пример №2. Проверка сопротивления двигателя

Допустим, что мы купили моющий пылесос на 1,6 киловатта для уборки помещений. Нас интересует ток его потребления и сопротивление электрического двигателя в рабочем состоянии. Считаем ток:

I = 1600 / 220 = 7,3 А.

Вводим в графы калькулятора напряжение 220 вольт и ток 7,3 ампера. Запускаем расчет. Автоматически получим данные:

• сопротивление двигателя — 30,1 Ома;
• мощность 1600 ватт.

Цепи постоянного тока

Рассчитаем сопротивление нити накала галогенной лампочки на 55 ватт, установленной в фаре автомобиля на 12 вольт.

Считаем ток:

I = 55 / 12 = 4,6 А.

Вводим в калькулятор 12 вольт и 4,6 ампера. Он вычисляет:

• сопротивление 2,6 ома.
• мощность 5 ватт.

Здесь обращаю внимание на то, что если замерить сопротивление в холодном состоянии мультиметром, то оно будет значительно ниже.

Это свойство металлов позволяет создавать простые и относительно дешевые лампы накаливания без сложной пускорегулирующей аппаратуры, необходимой для светодиодных и люминесцентных светильников.

Другими словами: изменение сопротивления вольфрама при нагреве до раскаленного состояния ограничивает возрастание тока через него. Но в холодном состоянии металла происходит бросок тока. От него нить может перегореть.

Для продления ресурса работы подобных лампочек используют схему постепенной, плавной подачи напряжения от нуля до номинальной величины.

В качестве простых, но надежных устройств для автомобиля часто используется релейная схема ограничения тока, работающая ступенчато.

При включении выключателя SA сопротивление резистора R ограничивает бросок тока через холодную нить накала. Когда же она разогреется, то за счет изменения падения напряжения на лампе HL1 электромагнит с обмоткой реле KL1 поставит свой контакт на удержание.

Он зашунтирует резистор, чем выведет его из работы. Через нить накала станет протекать номинальный ток схемы.

Полезная информация для начинающего электрика

Как использовать закон Ома на практике

Почти два столетия назад в далеком 1827 году своими экспериментами Георг Ом выявил закономерность между основными характеристиками электричества.

Он изучил и опубликовал влияние сопротивления участка цепи на величину тока, возникающего под действием напряжения. Ее удобно представлять наглядной картинкой.

Любую работу всегда создает трудяга электрический ток. Он вращает ротор электрического двигателя, вызывает свечение электрической лампочки, сваривает или режет металлы, выполняет другие действия.

Поэтому ему необходимо создать оптимальные условия: величина электрического тока должна поддерживаться на номинальном уровне. Она зависит от:

1. значения приложенного к цепи напряжения;
2. сопротивления среды, по которой движется ток.

Здесь напряжение, как разность потенциалов приложенной энергии, является той силой, которая создает электрический ток.

Если напряжения не будет, то никакой полезной работы от подключённой электрической схемы не произойдёт из-за отсутствия тока. Эта ситуация часто встречается при обрыве, обломе или отгорании питающего провода.

Сопротивление же решает обратную для напряжения задачу. При очень большой величине оно так ограничивает ток, что он не способен совершить никакой работы. Этот режим применяется у хороших диэлектриков.

Примеры из жизни

№1: выключатель освещения разрывает цепь электрических проводов, по которым напряжение добирается до лампочки.

Между контактами образуется воздушный зазор. Он отличный изолятор, исключающий движение тока по осветительному прибору.

№2: клеммы розетки, как источника напряжения, замкнули между собой без сопротивления короткой проволокой. В этой ситуации создается короткое замыкание.

Ток КЗ способен сжечь электропроводку, вызвать пожар в квартире. Поэтому от таких ситуаций существует только одно спасение: использование защит, способных максимально быстро отключить питающее напряжение.

Для бытовой сети это функция автоматических выключателей или предохранителей, о работе которых я буду рассказывать в других статьях.

Используя сопротивление, следует понимать, что оно, само по себе, не вечно: обладая резервом противостояния приложенной энергии, оно может его израсходовать, не справиться со своей задачей и сгореть.

Поэтому для сопротивления вводится понятие мощности рассеивания, которая надежно отводится во внешнюю среду. Если тепловая энергия, развиваемая прохождением тока, превышает эту величину, то сопротивление сгорает.

Напряжение и сопротивление в комплексе формируют электрические процессы. Онлайн калькулятор закона Ома позволяет оптимально рассчитать величину тока, необходимую для совершения полезной работы.

Что такое участок цепи

Рассмотрим самую простую электрическую схему, состоящую из батарейки, лампочки и проводов. В ней циркулирует электрический ток.

Представленная схема или полная цепь состоит из двух контуров:

1. Внутреннего источника напряжения.
2. Внешнего участка: лампочки с подключенными проводами.

Те процессы, которые происходят внутри батарейки, нас интересуют в основном как познавательные. Их мы можем только ухудшить при неправильной эксплуатации.

Например, приходящая в квартиру электрическая энергия от трансформаторной подстанции нам не подвластна. Мы ей просто пользуемся. От неисправностей и аварийных режимов нас защищают автоматические выключатели, УЗО, реле РКН, ограничители перенапряжения или УЗИП, другие современные модули защит.

Внешний же, подключенный к источнику напряжения контур, является участком цепи, в котором мы, используя закон Ома, совершаем полезную для себя работу.

Как использовать треугольник закона Ома

Простое мнемоническое правило представлено тремя составляющими в виде частей треугольника. Оно позволяет легко запомнить взаимосвязи между током, сопротивлением и напряжением.

Вверху всегда стоит напряжение. Ток и сопротивление снизу. Когда вычисляем какую-то одну величину по двум другим, то ее изымаем из треугольника и выполняем арифметическое действие: деление или умножение.

Шпаргалка электрика для новичков

Треугольник закона Ома легко запоминается, но он не позволяет учитывать мощность потребления электроприбора. Этот четвертый параметр, важный для любого домашнего электрика, всегда надо учитывать. .

На всех бытовых электрических приборах указывают мощность потребления электрической энергии в ваттах или киловаттах. Ее формулы, совместно с предыдущими величинами, можно брать со следующей картинки.

Такая шпаргалка электрика позволяет делать простые вычисления в уме или на бумаге. Формулы из нее заложены в алгоритм, по которому работает мой онлайн калькулятор закона Ома.

Предлагаю провести одинаковые вычисления обоими методами и сравнить полученные результаты. Если вдруг найдете расхождения, то укажите в комментариях. Это будет ваша помощь моему проекту.

Я постарался кратко и просто рассказать о принципах работы закона Ома применительно к задачам, решаемым домашним мастером. Считаю, что это достаточно и не рассматриваю закон Ома для полной цепи в обычной форме, комплексных числах, или ином виде.

Если же вы хотите просмотреть видеоурок по этой теме, то воспользуйтесь материалами владельца Физика-Закон Ома.

Возможно, у вас остались вопросы о работе калькулятора? Задавайте. Я на них отвечу. Воспользуйтесь разделом комментариев.

Напоследок напоминаю, что у вас сейчас самое благоприятное время поделиться этим материалом с друзьями в соц сетях и подписаться на рассылку сайта. Тогда вы сможете своевременно получать информацию о новых публикуемых статьях.

Цепи простой серии

| Последовательные и параллельные схемы

На этой странице мы изложим три принципа, которые вы должны понимать в отношении последовательных цепей:

1. Ток : величина тока одинакова для любого компонента в последовательной цепи.
2. Сопротивление : Общее сопротивление любой последовательной цепи равно сумме отдельных сопротивлений.
3. Напряжение : напряжение питания в последовательной цепи равно сумме отдельных падений напряжения.

Давайте взглянем на несколько примеров последовательных цепей, демонстрирующих эти принципы.

Начнем с последовательной схемы, состоящей из трех резисторов и одной батареи:

Первый принцип, который нужно понять о последовательных схемах, заключается в следующем:

Величина тока в последовательной цепи одинакова для любого компонента в цепи.

Это связано с тем, что в последовательной цепи существует только один путь прохождения тока.Поскольку электрический заряд проходит через проводники, как шарики в трубке, скорость потока (скорость мрамора) в любой точке цепи (трубки) в любой конкретный момент времени должна быть одинаковой.

Использование закона Ома в последовательных цепях

По расположению 9-вольтовой батареи мы можем сказать, что ток в этой цепи будет течь по часовой стрелке от точки 1 к 2, к 3 к 4 и обратно к 1. Однако у нас есть один источник напряжение и три сопротивления. Как мы можем использовать здесь закон Ома?

Важная оговорка к закону Ома заключается в том, что все величины (напряжение, ток, сопротивление и мощность) должны относиться друг к другу в терминах одних и тех же двух точек в цепи.Мы можем увидеть эту концепцию в действии на примере схемы с одним резистором ниже.

Использование закона Ома в простой цепи с одним резистором

В схеме с одной батареей и одним резистором мы можем легко вычислить любое количество, потому что все они относятся к одним и тем же двум точкам в цепи:

Поскольку точки 1 и 2 соединены вместе проводом с незначительным сопротивлением, как и точки 3 и 4, мы можем сказать, что точка 1 электрически является общей с точкой 2, а точка 3 электрически общей с точкой 4.Поскольку мы знаем, что у нас есть 9 вольт электродвижущей силы между точками 1 и 4 (непосредственно через батарею), и поскольку точка 2 является общей для точки 1, а точка 3 — общей для точки 4, мы также должны иметь 9 вольт между точками 2 и 3. (прямо через резистор).

Следовательно, мы можем применить закон Ома (I = E / R) к току через резистор, потому что мы знаем напряжение (E) на резисторе и сопротивление (R) этого резистора. Все термины (E, I, R) относятся к одним и тем же двум точкам в цепи, к одному и тому же резистору, поэтому мы можем безоговорочно использовать формулу закона Ома.

Использование закона Ома в схемах с несколькими резисторами

В схемах, содержащих более одного резистора, мы должны соблюдать осторожность при применении закона Ома. В приведенном ниже примере схемы с тремя резисторами мы знаем, что у нас есть 9 вольт между точками 1 и 4, что является величиной электродвижущей силы, управляющей током через последовательную комбинацию R ₁ , R ₂ и R _{. 3} . Однако мы не можем взять значение 9 вольт и разделить его на 3 кОм, 10 кОм или 5 кОм, чтобы попытаться найти значение тока, потому что мы не знаем, какое напряжение есть на любом из этих резисторов по отдельности.

Цифра 9 вольт — это всего величин для всей цепи, тогда как цифры 3 кОм, 10 кОм и 5 кОм представляют собой отдельных величин для отдельных резисторов. Если бы мы включили цифру для общего напряжения в уравнение закона Ома с цифрой для отдельного сопротивления, результат не будет точно соответствовать какой-либо величине в реальной цепи.

Для R ₁ закон Ома будет связывать величину напряжения на R ₁ с током через R ₁ , учитывая сопротивление R ₁ , 3 кОм:

Но, поскольку мы не знаем напряжение на R ₁ (только полное напряжение, подаваемое батареей на комбинацию из трех последовательно соединенных резисторов), и мы не знаем ток через R ₁ , мы можем ‘ t делать какие-либо расчеты по любой из формул.То же самое касается R ₂ и R ₃ : мы можем применять уравнения закона Ома тогда и только тогда, когда все члены представляют свои соответствующие величины между одними и теми же двумя точками в цепи.

Итак, что мы можем сделать? Нам известно напряжение источника (9 вольт), приложенное к последовательной комбинации R ₁ , R ₂ и R ₃ , и мы знаем сопротивление каждого резистора, но поскольку эти величины не входят в В том же контексте мы не можем использовать закон Ома для определения тока в цепи.Если бы мы только знали, каково общее сопротивление для цепи: тогда мы могли бы вычислить общий ток с нашей цифрой для общего напряжения (I = E / R).

Объединение нескольких резисторов в эквивалентный общий резистор

Это подводит нас ко второму принципу последовательной схемы:

Общее сопротивление любой последовательной цепи равно сумме отдельных сопротивлений.

Это должно иметь интуитивный смысл: чем больше последовательно подключенных резисторов, через которые должен протекать ток, тем труднее будет протекать ток.

В примере задачи у нас были последовательно подключены резисторы 3 кОм, 10 кОм и 5 кОм, что дало нам общее сопротивление 18 кОм:

По сути, мы вычислили эквивалентное сопротивление для R ₁ , R ₂ и R ₃ вместе взятых. Зная это, мы могли бы перерисовать схему с одним эквивалентным резистором, представляющим последовательную комбинацию R ₁ , R ₂ и R ₃ :

.

Расчет тока цепи по закону Ома

Теперь у нас есть вся необходимая информация для расчета тока цепи, потому что у нас есть напряжение между точками 1 и 4 (9 вольт) и сопротивление между точками 1 и 4 (18 кОм):

Расчет напряжений компонентов по закону Ома

Зная, что ток одинаков во всех компонентах последовательной цепи (и мы только что определили ток через батарею), мы можем вернуться к нашей исходной принципиальной схеме и отметить ток через каждый компонент:

Теперь, когда мы знаем величину тока, протекающего через каждый резистор, мы можем использовать закон Ома для определения падения напряжения на каждом из них (применяя закон Ома в его надлежащем контексте):

Обратите внимание на падение напряжения на каждом резисторе и на то, как падает сумма напряжений (1.5 + 5 + 2,5) равно напряжению аккумулятора (питания): 9 вольт.

Это третий принцип последовательных цепей:

Напряжение питания в последовательной цепи равно сумме отдельных падений напряжения.

Анализ простых последовательных цепей с помощью «табличного метода» и закона Ома

Однако метод, который мы только что использовали для анализа этой простой последовательной схемы, можно упростить для лучшего понимания. Используя таблицу для перечисления всех напряжений, токов и сопротивлений в цепи, становится очень легко увидеть, какие из этих величин могут быть правильно связаны в любом уравнении закона Ома:

Правило с такой таблицей — применять закон Ома только к значениям в каждом вертикальном столбце.Например, E _R1 только с I _R1 и R ₁ ; E _R2 только с I _R2 и R ₂ ; и т.д. Вы начинаете свой анализ с заполнения тех элементов таблицы, которые даны вам с самого начала:

Как вы можете видеть из расположения данных, мы не можем подать 9 вольт ET (полное напряжение) ни на одно из сопротивлений (R ₁ , R ₂ или R ₃ ) ни при каких условиях. Формула закона Ома, потому что они находятся в разных столбцах.Напряжение батареи 9 В составляет , а не , приложенное непосредственно к R ₁ , ₂ R или ₃ R. Однако мы можем использовать наши «правила» для последовательных цепей, чтобы заполнить пустые места в горизонтальном ряду. В этом случае мы можем использовать правило ряда сопротивлений для определения общего сопротивления из суммы отдельных сопротивлений:

Теперь, когда значение общего сопротивления вставлено в крайний правый столбец («Всего»), мы можем применить закон Ома I = E / R к общему напряжению и общему сопротивлению, чтобы получить общий ток 500 мкА:

Затем, зная, что ток распределяется поровну между всеми компонентами последовательной цепи (еще одно «правило» для последовательных цепей), мы можем ввести токи для каждого резистора из только что рассчитанного значения тока:

Наконец, мы можем использовать закон Ома для определения падения напряжения на каждом резисторе, по столбцу за раз:

Проверка расчетов с помощью компьютерного анализа (SPICE)

Ради удовольствия, мы можем использовать компьютер для автоматического анализа этой самой схемы.Это будет хороший способ проверить наши расчеты, а также познакомиться с компьютерным анализом. Во-первых, мы должны описать схему компьютеру в формате, распознаваемом программным обеспечением.

Программа SPICE, которую мы будем использовать, требует, чтобы все электрически уникальные точки в цепи были пронумерованы, а размещение компонентов понималось по тому, какие из этих пронумерованных точек или «узлов» они разделяют. Для ясности я пронумеровал четыре угла схемы в нашем примере с 1 по 4. SPICE, однако, требует, чтобы где-то в схеме был нулевой узел, поэтому я перерисую схему, немного изменив схему нумерации:

Все, что я здесь сделал, это перенумеровал нижний левый угол цепи 0 вместо 4.Теперь я могу ввести несколько строк текста в компьютерный файл, описывающий схему в терминах, понятных SPICE, вместе с парой дополнительных строк кода, предписывающих программе отображать данные о напряжении и токе для нашего удовольствия от просмотра. Этот компьютерный файл известен как список цепей в терминологии SPICE:

последовательная цепь
v1 1 0
r1 1 2 3к
r2 2 3 10к
r3 3 0 5k
.dc v1 9 9 1
.print dc v (1,2) v (2,3) v (3,0)
.конец
 

Теперь все, что мне нужно сделать, это запустить программу SPICE для обработки списка соединений и вывода результатов:

версия 1	в (1,2)	в (2,3)	в (3)	я (v1)
9.000E + 00	1.500E + 00	5.000E + 00	2.500E + 00	-5.000E-04

Эта распечатка сообщает нам, что напряжение аккумулятора составляет 9 вольт, а падение напряжения на R ₁ , R ₂ и R ₃ составляет 1,5 В, 5 В и 2,5 В соответственно. Падения напряжения на любом компоненте в SPICE обозначаются номерами узлов, между которыми находится компонент, поэтому v (1,2) относится к напряжению между узлами 1 и 2 в цепи, которые являются точками, между которыми находится R ₁ . .

Порядок номеров узлов важен: когда SPICE выводит число для v (1,2), он учитывает полярность так же, как если бы мы держали вольтметр с красным измерительным проводом на узле 1 и черным измерительным проводом на узел 2. У нас также есть дисплей, показывающий ток (хотя и с отрицательным значением) на уровне 0,5 мА или 500 мкА. Итак, наш математический анализ был подтвержден компьютером. Эта цифра отображается как отрицательное число в анализе SPICE из-за необычного способа обработки текущих вычислений SPICE.

Таким образом, последовательная цепь определяется как имеющая только один путь, по которому может течь ток. Из этого определения следуют три правила последовательных цепей: все компоненты имеют одинаковый ток; сопротивления складываются, чтобы равняться большему общему сопротивлению; а падение напряжения в сумме равняется большему общему напряжению. Все эти правила находят корень в определении последовательной цепи. Если вы полностью понимаете это определение, то правила — не что иное, как сноски к определению.

ОБЗОР:

• Компоненты в последовательной цепи имеют одинаковый ток: I _Всего = I ₁ = I ₂ =.. . Я _n
• Общее сопротивление в последовательной цепи равно сумме отдельных сопротивлений: RTotal = R ₁ + R ₂ +. . . Р _н
• Общее напряжение в последовательной цепи равно сумме отдельных падений напряжения E _Всего = E ₁ + E ₂ +. . . En

Попробуйте наш Калькулятор закона Ома в разделе Инструменты .

СВЯЗАННЫЕ РАБОЧИЕ ЛИСТЫ:

простых параллельных схем | Последовательные и параллельные схемы

На этой странице мы изложим три принципа, которые вы должны понимать в отношении параллельных цепей:

1. Напряжение: Напряжение одинаково на всех компонентах в параллельной цепи.
2. Ток: Полный ток цепи равен сумме токов отдельных ответвлений.
3. Сопротивление: Отдельные сопротивления уменьшают , чтобы равняться меньшему общему сопротивлению, вместо прибавляют , чтобы получить общее.

Давайте взглянем на несколько примеров параллельных цепей, демонстрирующих эти принципы.

Начнем с параллельной схемы, состоящей из трех резисторов и одной батареи:

Напряжение в параллельных цепях

Первый принцип для понимания параллельных цепей заключается в том, что напряжение одинаково на всех компонентах в цепи . Это связано с тем, что в параллельной цепи есть только два набора электрически общих точек, и напряжение, измеренное между наборами общих точек, всегда должно быть одинаковым в любой момент времени.

Следовательно, в приведенной выше схеме напряжение на R ₁ равно напряжению на R ₂ , которое равно напряжению на R ₃ , которое равно напряжению на батарее.

Это равенство напряжений можно представить в другой таблице для наших начальных значений:

Применение закона Ома для простых параллельных схем

Как и в случае с последовательными цепями, применимо то же предостережение для закона Ома: значения напряжения, тока и сопротивления должны быть в одном контексте, чтобы вычисления работали правильно.

Однако в приведенном выше примере схемы мы можем немедленно применить закон Ома к каждому резистору, чтобы найти его ток, потому что мы знаем напряжение на каждом резисторе (9 вольт) и сопротивление каждого резистора:

На данный момент мы все еще не знаем, каков полный ток или полное сопротивление для этой параллельной цепи, поэтому мы не можем применить закон Ома к крайнему правому столбцу («Всего»). Однако, если мы внимательно подумаем о том, что происходит, должно стать очевидным, что общий ток должен равняться сумме всех токов отдельных резисторов («ответвлений»):

По мере того, как полный ток выходит из положительной (+) клеммы батареи в точке 1 и проходит через цепь, часть потока разделяется в точке 2, чтобы пройти через R ₁ , еще часть разделяется в точке 3, чтобы пройти через R ₂ , а оставшаяся часть идет через R ₃ .Подобно реке, разветвляющейся на несколько более мелких ручьев, общий расход всех потоков должен равняться расходу всей реки.

То же самое происходит, когда токи через R ₁ , R ₂ и R ₃ соединяются, чтобы течь обратно к отрицательной клемме батареи (-) в направлении точки 8: ток из точки 7 до точки 8 должно равняться сумме токов (ответвлений) через R ₁ , R ₂ и R ₃ .

Это второй принцип параллельных цепей: полный ток цепи равен сумме токов отдельных ветвей .

Используя этот принцип, мы можем заполнить место ИТ на нашем столе суммой I _R1 , I _R2 и I _R3 :

Как рассчитать полное сопротивление в параллельных цепях

Наконец, применив закон Ома к крайнему правому столбцу («Всего»), мы можем вычислить полное сопротивление цепи:

Уравнение сопротивления в параллельных цепях

Обратите внимание на кое-что очень важное. Общее сопротивление цепи составляет всего 625 Ом: на меньше , чем у любого из отдельных резисторов.В последовательной цепи, где полное сопротивление было суммой отдельных сопротивлений, общее сопротивление должно было быть на больше, чем , чем у любого из резисторов по отдельности.

Здесь, в параллельной цепи, верно обратное: мы говорим, что отдельных сопротивлений уменьшают , а не прибавляют , чтобы получить общее .

Этот принцип завершает нашу триаду «правил» для параллельных цепей, точно так же, как было обнаружено, что у последовательных цепей есть три правила для напряжения, тока и сопротивления.

Математически соотношение между общим сопротивлением и отдельными сопротивлениями в параллельной цепи выглядит следующим образом:

Как изменить схемы нумерации параллельных цепей для SPICE

Та же самая основная форма уравнения работает для любого числа резисторов, соединенных вместе параллельно, просто добавьте столько членов 1 / R к знаменателю дроби, сколько необходимо для размещения всех параллельных резисторов в цепи.

Как и в случае с последовательной схемой, мы можем использовать компьютерный анализ для перепроверки наших расчетов.Во-первых, конечно, мы должны описать нашу примерную схему компьютеру в понятных ему терминах. Я начну с рисования схемы:

И снова мы обнаруживаем, что исходная схема нумерации, используемая для идентификации точек в цепи, должна быть изменена в интересах SPICE.

В SPICE все электрически общие точки должны иметь одинаковые номера узлов. Вот как SPICE узнает, что с чем связано и как.

В простой параллельной схеме все точки электрически являются общими в одном из двух наборов точек.В нашей примерной схеме провод, соединяющий верхние части всех компонентов, будет иметь один номер узла, а провод, соединяющий низ компонентов, будет иметь другой номер.

Оставаясь верным соглашению о включении нуля в качестве номера узла, я выбираю числа 0 и 1:

Пример, подобный этому, делает обоснование номеров узлов в SPICE довольно ясным для понимания. Поскольку все компоненты имеют общие наборы чисел, компьютер «знает», что все они подключены параллельно друг другу.

Чтобы отобразить токи ответвлений в SPICE, нам нужно вставить источники нулевого напряжения последовательно (последовательно) с каждым резистором, а затем привязать наши измерения тока к этим источникам.

По какой-то причине создатели программы SPICE сделали так, чтобы ток мог быть рассчитан только с по источника напряжения. Это несколько раздражающее требование программы моделирования SPICE. После добавления каждого из этих «фиктивных» источников напряжения необходимо создать несколько новых номеров узлов, чтобы подключить их к соответствующим резисторам ответвления:

Как проверить результаты компьютерного анализа

Все фиктивные источники напряжения настроены на 0 вольт, чтобы не влиять на работу схемы.

Файл описания схемы или список цепей выглядит так:

Параллельная схема
 v1 1 0
 r1 2 0 10к
 r2 3 0 2k
 r3 4 0 1k
 vr1 1 2 постоянного тока 0
 vr2 1 3 постоянного тока 0
 vr3 1 4 постоянного тока 0
 .dc v1 9 9 1
 .print dc v (2,0) v (3,0) v (4,0)
 .print dc i (vr1) i (vr2) i (vr3)
 .конец
 

Запустив компьютерный анализ, мы получили следующие результаты (я снабдил распечатку описательными этикетками):

версия 1	в (2)	в (3)	в (4)
9.000E + 00	9.000E + 00	9.000E + 00	9.000E + 00
аккумулятор	Напряжение R1	R2 напряжение	R3 напряжение

Напряжение

версия 1	я (vr1)	я (vr2)	я (vr3)
9.000E + 00	9.000E-04	4.500E-03	9.000E-03
аккумулятор	R1 ток	R2 текущий	R3 ток

Напряжение

Эти значения действительно совпадают со значениями, вычисленными ранее по закону Ома: 0.9 мА для I _R1 , 4,5 мА для I _R2 и 9 мА для I _R3 . При параллельном подключении, естественно, все резисторы имеют одинаковое падение напряжения на них (9 вольт, как у батареи).

Три правила параллельных цепей

Таким образом, параллельная цепь определяется как цепь, в которой все компоненты подключены между одним и тем же набором электрически общих точек. Другими словами, все компоненты подключены друг к другу через клеммы.Из этого определения следуют три правила параллельных цепей:

• Все компоненты имеют одинаковое напряжение.
• Сопротивления уменьшаются до меньшего общего сопротивления.
• Токи ответвления в сумме равняются большему общему току.

Как и в случае с последовательными цепями, все эти правила находят корень в определении параллельной цепи. Если вы полностью понимаете это определение, то правила — не что иное, как сноски к определению.

ОБЗОР:

• Компоненты в параллельной цепи имеют одинаковое напряжение: E _Всего = E ₁ = E ₂ =. . . E _n
• Общее сопротивление в параллельной цепи на меньше , чем любое из отдельных сопротивлений: R _Всего = 1 / (1 / R ₁ + 1 / R ₂ + … 1 / R _n )
• Общий ток в параллельной цепи равен сумме токов отдельных ветвей: I _Всего = I ₁ + I ₂ +.. . Я _№ .

СВЯЗАННЫЕ РАБОЧИЕ ЛИСТЫ:

Практический рабочий лист цепей постоянного тока серии

с рабочим листом ответов

Позвольте электронам сами дать вам ответы на ваши собственные «практические проблемы»!

Примечания:

По моему опыту, студентам требуется много практики с анализом цепей, чтобы стать профессионалом. С этой целью инструкторы обычно предоставляют своим ученикам множество практических задач, над которыми нужно работать, и дают ученикам ответы, с которыми они могут проверить свою работу.Хотя такой подход позволяет студентам овладеть теорией схем, он не дает им полноценного образования.

Студентам нужна не только математическая практика. Им также нужны настоящие практические схемы построения схем и использование испытательного оборудования. Итак, я предлагаю следующий альтернативный подход: учащиеся должны построить свои собственные «практические задачи» с реальными компонентами и попытаться математически предсказать различные значения напряжения и тока. Таким образом, математическая теория «оживает», и учащиеся получают практические навыки, которых они не приобрели бы, просто решая уравнения.

Еще одна причина для использования этого метода практики — научить студентов научному методу : процессу проверки гипотезы (в данном случае математических предсказаний) путем проведения реального эксперимента. Студенты также разовьют реальные навыки поиска и устранения неисправностей, поскольку они время от времени допускают ошибки при построении схемы.

Выделите несколько минут времени со своим классом, чтобы ознакомиться с некоторыми «правилами» построения схем, прежде чем они начнутся. Обсудите эти проблемы со своими учениками в той же сократической манере, в которой вы обычно обсуждаете вопросы рабочего листа, вместо того, чтобы просто говорить им, что они должны и не должны делать.Я никогда не перестаю удивляться тому, насколько плохо студенты понимают инструкции, представленные в типичном формате лекции (монолог инструктора)!

Примечание для тех инструкторов, которые могут жаловаться на «потраченное впустую» время, необходимое ученикам для построения реальных схем вместо того, чтобы просто математически анализировать теоретические схемы:

Какова цель студентов, посещающих ваш курс?

Если ваши ученики будут работать с реальными схемами, им следует по возможности учиться на реальных схемах.Если ваша цель — обучить физиков-теоретиков, то во что бы то ни стало придерживайтесь абстрактного анализа! Но большинство из нас планируют, чтобы наши ученики что-то делали в реальном мире с образованием, которое мы им даем. «Потраченное впустую» время, потраченное на создание реальных схем, принесет огромные дивиденды, когда им придет время применить свои знания для решения практических задач.

Кроме того, если студенты создают свои собственные практические задачи, они учатся выполнять первичных исследований , тем самым давая им возможность продолжить свое образование в области электрики / электроники в автономном режиме.

В большинстве наук реалистичные эксперименты намного сложнее и дороже, чем электрические схемы. Профессора ядерной физики, биологии, геологии и химии хотели бы, чтобы их студенты применяли передовую математику в реальных экспериментах, не представляющих опасности для безопасности и стоивших меньше, чем учебник. Они не могут, но вы можете. Воспользуйтесь удобством, присущим вашей науке, и заставьте своих учеников практиковать математику на множестве реальных схем!

Схемы серии

(часть 1) — Видеолекция по схемам

В начале четвертой главы мы упоминали, что собираемся рассмотреть четыре основных способа построения схем, и первый метод, который мы собираемся рассмотреть, и самый простой — это последовательные схемы.

Техническому специалисту важно разбираться в последовательных схемах. Последовательная схема характеризуется как имеющая только один путь для прохождения тока, поэтому здесь у нас есть источник ЭДС и подключенный компонент, так как здесь внизу у нас есть источник напряжения и компонент, подключенный, в данном случае лампочка, но в обоих В этих случаях существует только один путь для прохождения тока. Есть только один способ протекания тока, нет альтернативных путей, есть только один путь, и это делает его последовательной схемой.

Компоненты серии

соединены таким образом, что существует только один путь для прохождения тока без каких-либо ответвлений в цепи.

Цепи серии

Если каждый электрон, который покидает отрицательный вывод источника питания, имеет только один путь для прохождения тока, тогда схема представляет собой последовательную цепь, и в этом случае вы видите здесь отрицательную сторону этого… и положительную… каждый проходящий электрон имеет только один путь для тока, поэтому мы будем называть его последовательной схемой.В последовательной цепи, поскольку существует только один путь для прохождения тока, через каждый компонент протекает тот же ток, что и через всю цепь. Это важный аспект последовательной цепи. Поскольку существует только один путь для прохождения тока, то это тот же ток, который проходит через R2, R3 и R1, то есть такая же величина. Это похоже на то, как мы говорили об этой гидравлической системе и о том, что в гидравлической системе есть насос, и если это контур, то такое же количество жидкости, которое проходит через него, проходит через это, и это была аналогия с гидравлическим насосом, который мы говорилось в предыдущих уроках.

Теперь, вот эта конкретная схема, у меня есть вопрос по вышеуказанным последовательным схемам … ну, это, очевидно, последовательная схема … в этом случае мы начинаем с нашего источника напряжения, ток входит и проходит через все … ток от источник идет от R2, но теперь у нас есть то, что мы называем разветвлением, и это будет параллельная схема, поэтому схема будет проходить через эту ветвь резисторов здесь, а затем вернуться через эту схему. Это уже не действительно последовательная схема.Это последовательная схема, но здесь есть параллельная ветвь, и позже в этой главе мы рассмотрим параллельные схемы.

Интуитивные отношения

Цепи серии

, этот раздел называется интуитивными отношениями, а интуитивные отношения — это вещи, которые просто имеют смысл, а в последовательных цепях есть некоторые вещи, которые просто интуитивно понятны для последовательной цепи, и в вашем тексте будет немного обсуждения. каждый из них, если неясно, как я это преодолел.Во-первых, все токи в последовательной цепи равны, весь ток через эту конкретную цепь будет одинаковым. Общее сопротивление больше любого сопротивления. Возможно, это очевидно, но общее сопротивление всех компонентов будет больше, чем какое-либо одно сопротивление. Аналогично, общая мощность больше, чем рассеиваемая мощность любого одного компонента, поэтому общая рассеиваемая мощность этой схемы будет больше, чем рассеиваемая мощность любого отдельного компонента. Падение большего сопротивления приводит к большему падению напряжения.Это может быть не так очевидно, но если мы вспомним, что напряжения … помните, мы говорили о том, что такое напряжение с точки зрения закона Ома? Мы сказали, что напряжение равно I, умноженному на R, теперь помните, что у нас одинаковый ток, протекающий по всей цепи, поэтому мы говорим, что ток будет таким, мы просто покажем плоскую стрелку, показывающую горизонтальную, плоское соотношение не изменится. Если сопротивление увеличивается, то падение напряжения на этом компоненте будет увеличиваться, и поэтому у нас здесь три компонента, это самые большие 30 кОм, поэтому это будет самое большое падение напряжения, основанное на формуле, согласно которой ток, умноженный на сопротивление, равен напряжению, и, поскольку это имеет самое большое сопротивление и все токи равны, падение здесь будет самым большим.

Наконец, последнее интуитивное соотношение, полное напряжение больше, чем напряжение любого компонента, поэтому общее напряжение в этом случае составляет 120 вольт, и оно будет больше, чем падение любого отдельного напряжения, и эти отношения называются интуитивными отношениями для последовательных цепей. схемы.

Математические отношения

Математические соотношения, в последовательной цепи существуют следующие соотношения в отношении текущего напряжения и сопротивления. Первый, у нас есть что-то здесь, называемое IA, в этом случае A имеет отношение к приложенному току, ток, который выходит из нашего источника питания, равен тому, который проходит через R1, R2 и R3, и математически это то, что состояния.Сопротивление, в данном случае RT — это полное сопротивление. В этом случае общее сопротивление всех компонентов будет равно R1 + R2 + R3. Затем у нас есть VT для напряжения, и снова это общее напряжение, в данном случае 120 вольт, но оно будет равно падению напряжения на R1, R2 и R3. Приложенное напряжение в замкнутом контуре равно сумме падений составляющих напряжения. Это важное соотношение известно как закон напряжения Кирхгофа.

Полярность падений напряжения

Когда через резистор протекает ток, на этом резисторе возникает соответствующее падение напряжения.Точка, где ток входит в резистор, является отрицательной, а точка выхода тока будет положительной. Итак, у нас есть источник питания, он подает ток, ток течет в этом направлении, и обратите внимание, что здесь мы находимся на отрицательной клемме, но первая точка здесь, где мы вводим компонент, полярность будет отрицательной, а затем другая сторона будет положительной. Когда мы будем моделировать наши схемы, вы сможете использовать вольтметр, чтобы измерить это и подтвердить, что это действительно так.Полярность здесь будет минус к положительному, минус к положительному, минус к положительному. Это имеет смысл, если вы думаете, что у вас есть батарея, и у вас есть только один компонент, вот этот компонент, и батарея имеет положительную или отрицательную полярность, что полярность в компоненте будет такой же; положительное будет на положительной стороне, отрицательное — на отрицательной. В любом случае, точка, где ток входит в компонент, будет отрицательной стороной компонента.

Замкнутые уравнения

Следующая процедура может использоваться для создания уравнения с обратной связью для описания последовательной цепи.В этом есть два шага. Во-первых, обозначьте полярность падений напряжения и источников, так что здесь у нас есть полярность, мы сделали это ранее нормально, положительный к минусу, а затем минус к положительному минусу к положительному минусу к положительному. Начните с любой точки схемы и запишите напряжения, указывающие полярность, по мере продвижения по петле в любом направлении. Помните, что полярность падения напряжения определяется направлением тока. Наконец, переместитесь по контуру и запишите напряжения на выходных концах компонентов.

Закон Кирхгофа о напряжении

Мы можем это сделать… перейдем к следующему слайду; на следующем слайде немного больше места. На самом деле мы применяем закон напряжения Кирхгофа, и другой способ сформулировать этот закон состоит в том, что алгебраическая сумма всех падений напряжения и всех источников напряжения в любом замкнутом контуре равна нулю. Вы можете сделать это, суммируя полярность каждого компонента в зависимости от того, где этот ток входит в компоненты. Мы смотрим на это и думаем, что ток течет в этом направлении, и мы собираемся оценить полярность на основе того, где ток входит в этот конкретный компонент.Давайте начнем с этого момента. Полярность, при которой ток поступает в источник питания, положительная, поэтому мы начинаем со 120, а затем собираемся суммировать на основе того, где ток входит в компонент. Мы начинаем здесь с положительного значения, затем мы входим в этот компонент, и у нас есть знак «минус», поэтому мы идем -60 и продолжаем примерно до -40, а затем продолжаем примерно до -20. Если мы сложим эти значения, сумма будет равна нулю. Это то, о чем мы упоминали на предыдущем слайде, что сумма всех напряжений по кругу будет равна нулю, и это еще один способ сформулировать закон Кирхгофа.Если бы вы были обычным человеком и хотели бы пойти в другом направлении, вы могли бы сделать это с тем же успехом, но вы должны быть последовательны, если собираетесь это делать. Если мы скажем, что положительные силы движутся в этом направлении, тогда мы начнем с этого момента, и мы начнем с -120, идущим в этом направлении, + 20, +40, а затем +60, но снова сумма будет равна нулю.

Теперь я предлагаю вам прочитать текст по этой конкретной теме, и есть несколько симуляций схем, которые вы можете сделать в multisim, чтобы подтвердить это, и вам нужно иметь возможность войти в симуляцию и подключить мультиметр и фактически измерить их. падает и убедитесь сами, что это так и закон Кирхгофа имеет смысл.Если вы алгебраически просуммируете все значения в последовательной схеме, сумма будет равна нулю.

Мы рассмотрели здесь закон напряжения Кирхгофа при решении уравнения замкнутого контура, мы рассмотрели полярность и падение напряжения, мы рассмотрели математические зависимости, мы рассмотрели некоторые интуитивно понятные взаимосвязи между последовательными цепями и мы посмотрели, что такое последовательная цепь. и что не является последовательной схемой. На этом мы завершаем наш раздел, посвященный последовательным схемам.

Видеолекции, созданные Тимом Фигенбаумом в Общественном колледже Северного Сиэтла.

Как рассчитать выходное напряжение

Обновлено 8 декабря 2020 г.

Пол Меслер

Закон Ома — важная математическая формула, которую электрики и физики используют для определения определенных измерений в данной цепи. Формула:

В = I \ раз R

, где V — напряжение, измеренное в вольтах, I — величина тока, измеренная в амперах, а R — сопротивление, измеренное в омах. Резисторы препятствуют прохождению потока электронов в цепи и, в зависимости от их материала, обладают большим сопротивлением, чем другие.Напряжение в цепи — не что иное, как «источник электрического потенциала» внутри этой цепи.

Цепь в серии

Определите общую силу тока в цепи. Если у вас была цепь, и вы обнаружили, что она пропускает общий ток 6 ампер, вы должны использовать это значение в качестве силы тока в цепи. Помните, что в цепи общая сила тока везде одинакова.

Определите общее количество сопротивлений в цепи. Вы измеряете сопротивление в омах, которое выражается греческой буквой омега.Если вы измеряете, что в этой цепи есть резистор с сопротивлением 3 Ом, а другой — с сопротивлением 2 Ом, это означает, что общее сопротивление цепи составляет 5 Ом.

Найдите выходное напряжение, умножив силу тока на общее количество сопротивлений в цепи. В приведенных выше примерах мы знаем, что сила тока составляет 6 ампер, а общее сопротивление — 5 Ом. Следовательно, выходное напряжение для этой схемы:

В = I \ times R = 6 \ times 5 = 30 \ text {volts}

Параллельные цепи

Определите общий ток в цепи.Как и в последовательной цепи, ток или сила тока везде одинаковы. Используя тот же пример, мы скажем, что общая сила тока составляет 6 ампер.

Найдите полное сопротивление в цепи. Общее сопротивление в параллельной цепи отличается от последовательной цепи. В последовательной цепи мы получаем общее сопротивление, просто добавляя каждое отдельное сопротивление в цепи; однако в параллельной цепи нам нужно найти полное сопротивление по формуле:

R_ {tot} = \ frac {1} {\ frac {1} {R_1} + \ frac {1} {R_2} + … + \ frac {1} {R_n}}

То есть единица, деленная на сумму обратных величин всех резисторов в параллельной цепи. На том же примере скажем, что резисторы имеют сопротивление 2 Ом и 3 Ом. Следовательно, полное сопротивление в этой параллельной серии составляет:

R_ {tot} = \ frac {1} {\ frac {1} {2} + \ frac {1} {3}} = 1,2 \ text {ohms}

Найдите напряжение так же, как вы нашли напряжение в последовательной цепи. Мы знаем, что общая сила тока для цепи составляет 6 ампер, а полное сопротивление — 1.2 Ом. Следовательно, общее выходное напряжение для этой параллельной цепи составляет:

В = I \ times R = 6 \ times 1.2 = 7.2 \ text {volts}

Напряжение в последовательной цепи

Напряжение в последовательной цепи

Напряжение, падающее на резисторе в цепи, состоящей из одного резистора и источника напряжения, представляет собой полное напряжение в цепи и равно приложенному напряжению.Общее напряжение в последовательной цепи, состоящей из более чем одного резистора, также равно приложенному напряжению, но состоит из суммы падений напряжения отдельных резисторов. В любой последовательной схеме сумма падений напряжения на резисторе должна равняться напряжению источника. Это утверждение может быть подтверждено исследованием схемы, показанной на рисунке 3-17. В этой цепи потенциал источника (E _T ) в 20 вольт падает на последовательную цепь, состоящую из двух резисторов сопротивлением 5 Ом. Общее сопротивление цепи (R _T ) равно сумме двух отдельных сопротивлений или 10 Ом.Используя закон Ома, ток в цепи можно рассчитать следующим образом:

Рисунок 3-17. — Расчет отдельных падений напряжения в последовательной цепи.

Поскольку известно, что сопротивление резисторов составляет 5 Ом, а ток через резисторы равен 2 амперам, падение напряжения на резисторах может быть рассчитано. Таким образом, напряжение (E ₁ ) на R ₁ составляет:

. Осмотрев цепь, вы можете увидеть, что R ₂ имеет такое же омическое значение, что и R ₁ , и пропускает тот же ток.Падение напряжения на R ₂ также равно 10 вольт. Если сложить эти два падения по 10 вольт, общее падение составит 20 вольт, что в точности равно приложенному напряжению. Для последовательной схемы тогда:

E _T = E ₁ = E ₂ + E ₃ =. . . E _n

Пример: последовательная цепь состоит из трех резисторов, имеющих номиналы 20 Ом, 30 Ом и 50 Ом соответственно. Найдите приложенное напряжение, если ток через резистор 30 Ом равен 2 ампера.(Аббревиатура amp обычно используется для обозначения ампер.)

Для решения проблемы сначала рисуется принципиальная схема и маркируется (рис. 3-18).

Рисунок 3-18. — Решение для приложенного напряжения в последовательной цепи.

Подстановка:

ПРИМЕЧАНИЕ. При использовании закона Ома величины для уравнения ДОЛЖНЫ быть взяты из ОДНОЙ части схемы. В приведенном выше примере напряжение на R ₂ было вычислено с использованием тока через R ₂ и сопротивления R ₂ .

Величина падения напряжения на резисторе определяется приложенным напряжением и пропорционально сопротивлению цепи. Падения напряжения, возникающие в последовательной цепи, прямо пропорциональны сопротивлениям. Это результат того, что через каждый резистор протекает одинаковый ток — чем больше сопротивление резистора, тем больше падение напряжения на нем.

Последовательная цепь, состоящая из трех резисторов, имеет ток 3 ампера. Если R ₁ = 20 Ом, R ₂ = 60 Ом и R ₃ = 80 Ом, каковы (а) полное сопротивление и (b) напряжение источника цепи?

Какое напряжение падает на каждом резисторе цепи, описанной в вопросе 17?

Если бы ток был увеличен до 4 ампер, каким было бы падение напряжения на каждом резисторе в цепи, описанной в вопросе 17?

Что нужно сделать со схемой, описанной в вопросе 17, чтобы увеличить ток до 4 ампер?

Ток и напряжение

• Изучив этот раздел, вы сможете:
• Опишите распределение электрических потенциалов (напряжений) и токов в электрических цепях.
• • Последовательные резистивные цепи.
• • Параллельные резистивные цепи.
• Рассчитайте распределение напряжений в резистивном делителе потенциала.

Ток и напряжение в резисторных цепях

В поисках неизвестного

Помимо определения сопротивления, закон Ома может использоваться для расчета напряжений и токов в резистивных цепях. Перед тем, как попробовать это, было бы неплохо взглянуть на некоторые основные факты о сетях резисторов.

Рис.4.0.1 Простая последовательная схема

Рис.4.0.2 Простая параллельная схема

В простой цепи СЕРИИ , показанной на рис. 4.0.1, одинаковый ток течет через все компоненты. Однако каждый компонент будет иметь разное НАПРЯЖЕНИЕ (p.d.) на нем. Сумма этих отдельных напряжений (V _R1 + V _R2 + V _R3 и т. Д.) В последовательной цепи равна напряжению питания (ЭДС).

Однако в простой схеме ПАРАЛЛЕЛЬНАЯ ЦЕПЬ , показанной на рис. 4.0.2, одинаковое напряжение присутствует на всех компонентах, но через каждый компонент может протекать разный ТОК. Сумма этих отдельных составляющих токов в параллельной цепи равна току питания. (I _S = I _R1 + I _R2 + I _R3 и т. Д.)

Правило разделителя потенциала

Рис. 4.0.3 Делитель потенциала

Если два или более резистора соединены последовательно через потенциал (например,грамм. Напряжение питания), напряжение на каждом резисторе будет пропорционально сопротивлению этого резистора. V _R1 ∝ R ₁ и V _R2 ∝ _R1 и т. Д.

Чтобы рассчитать напряжение на любом резисторе в делителе потенциала, умножьте напряжение питания (E) на пропорцию этого резистора к общему сопротивлению всех резисторов.

Например, если R ₂ вдвое больше, чем R ₁ , то напряжение на R ₂ будет вдвое больше, чем на R ₁ .Следовательно, напряжение на R ₁ будет составлять одну треть напряжения питания (E), а напряжение на R ₂ будет составлять две трети напряжения питания (E). Таким образом, если напряжение питания и значения резистора известны, то напряжение на каждом резисторе может быть вычислено с помощью ПРОПОРЦИИ, и как только напряжение на каждом резисторе известно, можно рассчитать напряжение в любой точке цепи.

Используя эти несколько фактов, можно получить огромное количество информации о токах и напряжениях в цепи, если известны значения сопротивлений цепи.Попробуйте сами с помощью нашей викторины на странице «Сетевые расчеты модуля» 4.6 «Резисторы и схемы».

.