Как рассчитать индуктивность катушек с замкнутыми сердечниками?
Всем доброго времени суток. В прошлых статьях (часть 1, часть 2, часть 3) я рассказал о расчёте индуктивности индуктивных элементов без сердечников. Однако их применение ограниченно, вследствие, больших габаритных размеров. Поэтому для увеличения индуктивности и уменьшения размеров и улучшения других показателей индуктивные элементы устанавливают на сердечники из материалов с различными магнитными свойствами.
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Особенности расчёта индуктивных элементов с сердечниками
В отличие от индуктивных элементов без сердечников, при расчёте которых учитывался магнитный поток пронизывающий только проводник с током, магнитный поток индуктивных элементов с сердечниками практически полностью замыкается на сердечники. Поэтому при расчёте индуктивности таких элементов необходимо учитывать размеры сердечника и материал, из которого он изготовлен, то есть его магнитную проницаемость.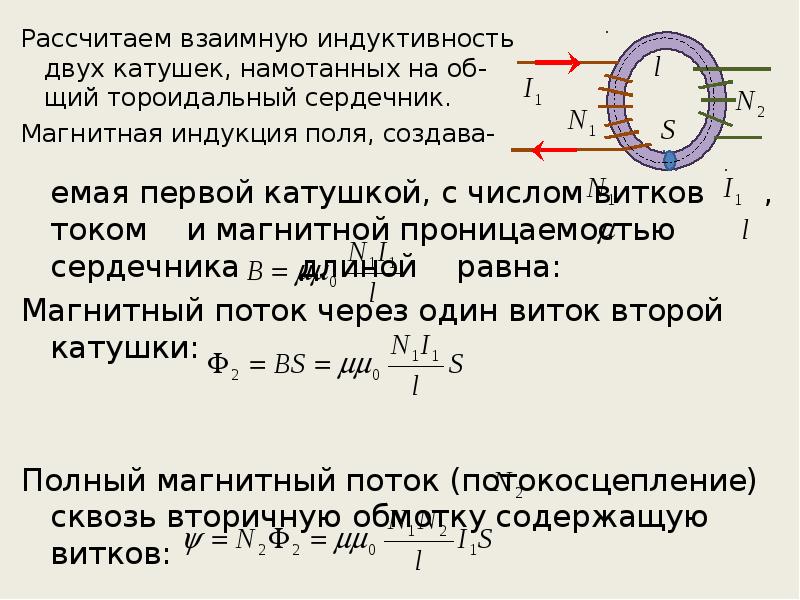
Обобщённую формулу для расчёта индуктивных элементов с сердечниками можно выразит с помощью следующего выражения
где ω – количество витков катушки,
RM – сопротивление магнитной цепи,
μа – абсолютная магнитная проницаемость вещества, из которого изготовлен сердечник,
SM – площадь поперечного сечения сердечника,
lM – длина средней магнитной силовой линии,
Таким образом, зная размеры сердечника можно достаточно просто вычислить индуктивность. Однако в связи с такой простотой выражения и разбросом магнитной проницаемости материала сердечника, погрешность в расчёте индуктивности составит 25 %.
Для сердечников, имеющих сложную конструктивную конфигурацию, вводится понятие эффективных (эквивалентных) размеров, которые учитывают особенности формы сердечников: эффективный путь магнитной линии l e и эффективная площадь поперечного сечения Se сердечника.
Тогда индуктивность катушки с сердечником будет вычисляться по формуле
где ω – количество витков катушки,
μ0 – магнитная постоянная, μ0 = 4π*10-7,
μr – относительная магнитная проницаемость вещества,
Se – эффективная площадь поперечного сечения сердечника,
le – эффективный путь магнитной линии сердечника.
Таким образом, расчёт индуктивности индуктивных элементов с сердечниками сводится к нахождению эффективных размеров сердечника. Для упрощения нахождения данных размеров сердечника ввели вспомогательные величины, называемые постоянные сердечников:
С1 – первая постоянная сердечника, которая равна сумме отношений длины однородных по сечению участков сердечника к поперечного сечения сердечника, измеряется в мм
С2 – вторая постоянная сердечника, которая равна сумме отношений длин однородных по сечению участков сердечника к квадрату своего сечения, измеряется в мм-3;
где N – количество разнородных участков сердечника,
lN – длина N – го участка сердечника,
SN – площадь N – го участка сердечника.
Тогда величины Se и le определятся из следующих выражений
Кроме индуктивности с помощью постоянных С1 и С2 определяют эффективный объём Ve, который требуется для определения параметоров силовых индуктивных элементов – трансформаторов и дросселей. Если же есть необходимость рассчитать только индуктивность L, то используют только постоянную С1 по следующему выражению
где ω – количество витков катушки,
μ0 – магнитная постоянная, μ0 = 4π*10-7,
μr – относительная магнитная проницаемость вещества,
С1 – первая постоянная сердечника, которая равна сумме отношений длины однородных по сечению участков сердечника к поперечного сечения сердечника.
Несмотря на довольно сложные формулировки и формулы, вычисление индуктивности по ним достаточно простое.
Выпускается достаточно много типов сердечников, которые обладают различными конструктивными особенностями и свойствами, рассмотрим некоторые из них.
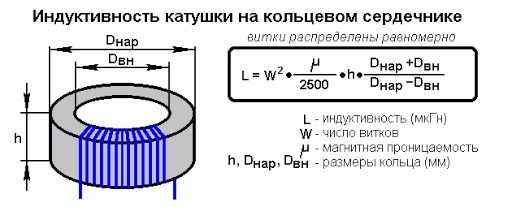
Расчёт катушки с тороидальным сердечником
Тороидальные (кольцевые) сердечники, благодаря своей простоте изготовления находят широкое применение в различных импульсных трансформаторах, фильтрах и дросселях и обеспечивают небольшую потребляемую мощность при минимальных потерях.
Тороидальный сердечник.
Для расчёта индуктивности достаточно знать три конструктивных параметра такого магнитопровода: D
Расчёт эффективных параметров сердечника, как сказано выше, основан на двух величинах С1 и С2, которые составляют
где he – эффективная высота сердечника,
D1 – внешний диаметр сердечника,
D2 – внутренний диаметр сердечника.
Расчёт эффективной высоты he сердечника зависит от конструктивных особенностей.
Расчёт эквивалентной высоты тороидального сердечника: прямоугольное сечение (вверху) и трапецеидальное сечение (снизу).
Рассмотрим несколько случаев:
а) прямоугольное поперечное сечение с острыми кромками
б) прямоугольное поперечное сечение со скруглёнными кромками и радиусом скругления r s
в) трапецеидальное поперечное сечение с острыми кромками
г) трапецеидальное поперечное сечение со скруглёнными кромками
Пример. В качестве примера рассчитаем индуктивность тороидальной катушки, имеющий ω = 50 витков, намотанных на равномерно на магнитопровод со следующими размерами D1 = 20 мм, D2 = 10 мм, h = 7 мм, сечение магнитопровода прямоугольное со скруглёнными кромками, радиус скругления rs = 0,5 мм, относительная магнитная проницаемость материала сердечника μr = 1000.
Так как рассчитываем только индуктивность, то в расчёте коэффициента С2 нет необходимости
Расчёт катушки с П–образным сердечником прямоугольного сечения
В отличие от тороидальных сердечников, П – образные сердечники выполняются разборными и состоят из двух частей.
Существует две модификации таких сердечников: состоящие из двух П – образных частей и из П – образной и прямоугольной замыкающей пластины.
Такие сердечники применяются в импульсных трансформаторах и трансформаторах строчной развертки и, обладая большой магнитной проницаемостью, обеспечивают малую потребляемую мощность.
П-образный сердечник с прямоугольным сечением: из двух П-образных частей (слева) и П-образной части с замыкающей прямоугольной пластиной (справа).
Для расчёта параметров сердечника рассмотрим сечение замкнутого П-образного сердечника
Сечение П-образного прямоугольного сердечника.
Данный сердечник состоит из нескольких участков l1, l2, l3, l4, l5 имеющих различное сечение S1, S2, S3, S4, S5,. Тогда коэффициенты С1 и С2 составят
Неизвестные величины можно найти следующим образом
Пример.
Необходимо рассчитать индуктивность обмотки трансформатора, выполненного на П-образном сердечнике фирмы Epcos типа UU93/152/16, выполненного из двух П-образных половинок, материал сердечника N87 μr = 1950, количество витков ω = 150.
Сердечник Epcos U93/76/16.
Таким образом, расчётные параметры сердечника составят
Таким образом коэффициент С1 и индуктивность L составят
Расчёт катушки с П-образным сердечником круглого сечения
Кроме П-образных катушек с прямоугольным сечение, широко применяются П-образные катушки с круговым сечением. Они также состоят из двух П-образных частей
П-образный сердечник с круговым сечением.
Для расчёта рассмотрим сечение замкнутого сердечника состоящего из двух пловинок.
Сечение П-образного сердечника с круговым сечением.
Аналогично сердечнику с прямоугольным сечением выделим пять участков длины сердечника с различным сечением и расчёт соответственно тоже.
Пример. В качестве примера рассчитаем индуктивность катушки, выполненной на сердечнике. Сердечник из двух частей типа SDMR 40 UY20 (μr = 2500), количество витков ω = 60.
Сердечник типа SDMR 40 UY20.
Параметры сердечника для расчёта составят
Таким образом коэффициент С1 и индуктивность L составят
На сегодня всё. Продолжение смотри в следующей статье.
Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.
Inductance Calculator
Inductance Calculator
Расчет катушки индуктивности
Расчет однослойной воздушной катушки индуктивности
Расчет дросселя без сердечника
Расчетная формула:
Индуктивность
в мкГн = R2 * N2 / (
25.
4*R + 22.9*L )
R = радиус катушки по центру провода (см) N = количество витков в катушке (может быть не целым числом) L = длина катушки (см) — возможна намотка не виток к витку, а с зазором. |
результат конечно приблизителен!
|
Реклама недорогих радиодеталей почтой:
А вот
результаты измерения реальных катушек
с помощью Вы можете
проверить по этим таблицам результат
расчета. Максимальная добротность достигается при намотке с зазором между витками равными диаметру провода!
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Все катушки мотались медным
эмалевым обмоточным проводом 0.6 мм.
29
см провод 0.6 ммРасчет индукторов, дросселей, катушек индуктивности методом численного моделирования FEM
Расчет индукторов, дросселей, катушек индуктивности методом численного моделирования FEM.
Современный подход к разработке сложной электронной и электротехнической продукции предполагает точное проектирование силовых элементов схемы. С ростом мощностей разрабатываемого оборудования, цена ошибок и неточностей в расчетах растет в геометрической прогрессии. А особенно это становится заметно, когда разрабатывается уникальное оборудование.
Безусловно, существует масса литературы по расчету и проектированию трансформаторов, дросселей, катушек индуктивности с сердечником и без сердечника, где рассмотрены большинство стандартных применений.
Для студентов, которые только начинают заниматься электроникой и электротехникой, я всегда рекомендовал замечательную книгу —
Семенов Б.Ю. Силовая электроника: от простого к сложному. 2005г.
Ясное и понятное изложение для начинающих.
Далее, по расчету катушек индуктивности, есть не менее полезная книга-
Калантаров П.Л., Цейтлин Л.А. Расчет индуктивностей. 1986г.
По расчету трансформаторов напряжения (тока) и дросселей существует масса литературы.
Приводить их нет смысла. Интернет велик. Все можно найти.
Особняком стоят книги по расчету, разработке и конструированию индукторов для технологий индукционного нагрева.
Тут Слухоцкого А.Е. вне конкуренции. Хотя, в последнее время, появилось достаточно много статей и книг, где подробно и более глубоко рассмотрены проблемы проектирования индукторов для конкретных видов технологий индукционного нагрева ТВЧ.
Для простейших случаев существует множество on-line калькуляторов, которые позволяют прикинуть или даже рассчитать простые варианты катушек индуктивности, дросселей, трансформаторов.
Например, очень хорошая программа Coil32. Сайт — http://coil32.narod.ru/
Позволяет определить основные параметры катушек индуктивности различной формы.
Для простейшего расчета трансформаторов, например, калькулятор радиолюбителя.
Сайт — http://www.
radioamcalc.narod.ru/
Но все это расчеты для устройств, в лучшем случае, до 1кВт.
Дальше начинается своя специфика. Особенно если эти устройства работают на частотах выше нескольких десяток кГц.
В мощных высокочастотных дросселях, катушках индуктивности, индукторах, трансформаторах существенно возрастают потери от поверхностных эффектов протекания тока. Высокочастотный ток может легко концентрироваться и перегревать локальные участки силового устройства.
На высокой частоте существенно возрастает сложность точного расчета потерь мощности в магнитопроводе и обмоточном проводе или шинах. Существенно увеличивается влияние на потери многослойность катушки. Учет влияния зазора в магнитопроводе также становится достаточно сложной задачей.
Использование программ численного моделирования FEM позволяет решить большинство технических вопросов, возникающих при расчете и проектировании индукторов, дросселей, катушек индуктивности, трансформаторов, шиносборок и т.
д., а также существенно повысить точность расчета и провести оптимизацию проектируемого устройства в кратчайшие сроки во многих случаях без создания натурального макета, что особенно важно для мощных и дорогих устройств.
Несколько слов хотел сказать о индукционных водонагревателях.
Индукционные водонагреватели, индукционные котлы, индукционные парогенераторы – это технически сложные устройства, требующие особенно тщательной проработки и проектирования индукционной системы. В качестве источника питания обычно используется промышленная частота 50Гц с напряжением 220В или 380В.
Основной проблемой при проектировании индукционных водонагревателей является оптимальное конфигурировании индуцирующей обмотки. Т. е. проектирование геометрии обмотки, числа витков, сечения провода. Необходимо учитывать, что индукционная система имеет cosφ существенно отличный от 1. Поэтому, без установки дополнительного конденсатора, параллельно обмотки, от сети будет потребляться дополнительный реактивный ток.
Выбор и расчет требуемого компенсирующего конденсатора является обязательным требованием для получения максимального КПД водонагревательного устройства. Также многие путают электрический и тепловой КПД нагревательного устройства. Тепловой КПД для таких устройств действительно может составлять почти 100%.
Принцип работы индукционного котла показан на рисунках:
Одной из лучших программ FEM моделирования электротехнических устройств является программа Jmag-Designer. Сайт — http://www.jmag-international.com/
Несколько примеров расчетов и моделирования индукторв для разных технологий:
1. Расчет и моделирование индукционной системы тигель-индуктор-магнитопровод.
Определение параметров индукционной системы, КПД, распределение тока в индукторе, определение потерь в магнитопроводе.
2. Расчет и моделирование процесса нагрева шестерни в индукторе под закалку.
Решалась совместная электромагнитная и тепловая задача.
В результате моделирования были определены параметры индукционной системы, КПД, требуемая мощность, частота и время нагрева под закалку.
3. Ресчет и моделирование нагрева шейки коленчатого вала под закалку.
Решалась электромагнитная и тепловая задача в 3D с вращением нагреваемой детали (коленчатого вала).
В результате моделирования определены параметры индукционной системы, КПД, требуемая мощность и время нагрева под закалку.
4. Еще один вариант расчета и моделирования шейки коленчатого вала под закалку.
Вращение детали присутствует.
Несколько примеров расчетов катушек индуктивности и трансформаторов:
— Трансформатор тока.
Частота около 100кГц. Сердечник феррит 2500НМС1. Обмотка задана, как FEM Coil с распределенными витками по геометрии заданной области.
Задается в параметрах число витков и общее сопротивление обмотки.
Моделировалось распределение тока в медной шине и магнитной индукциии в магнитопроводе. Проверялось отсутствие насыщения магнитопровода для различных режимов работы трансформатора тока. Оптимизировалассь конструкция трансформатора тока для ВЧ применений.
— Расчет и моделирование трехфазного трансформатора с кожухом.
На рисунке справа показана расчетная схема и схема включения обмоток и нагрузки трансформатора.
Определялся КПД трансформатра (потери в обмотках, сердечнике, кожухе) и рассеяние в различных режимах работы.
— Расчет, моделирование и анализ потерь в трансформаторе с плоскими обмотками.
Оценивалось распределение потерь в сердечнике и обмотках трансформатора.
Электромагнитный расчет и оптимизация планарных катушек на печатных платах
Планарные катушки используются в самых различных устройствах — от датчиков артериального давления до платежных карт. Они располагаются на печатных платах и хорошо подходят для создания взаимных индуктивных связей, особенно при ограниченном пространстве. При проектировании таких катушек важно точно рассчитать как индуктивность, так и активное сопротивление, так как эти факторы играют ключевую роль в производительности устройства. Для эффективного описания катушек на плоскости инженеры могут использовать технологию задания многослойных оболочек (layered shell), доступную в пакете COMSOL®.
Планарные катушки: преимущества и примеры использования
Планарные катушки названы так из-за того, что все их части (витки) находятся практически на одной плоскости (т. е. они почти плоские). Они занимают намного меньше места, чем другие индукторы, и поэтому подходят для любых практических приложений с ограничениями по размерам, что очень актуально, к примеру, в микроэлектромеханических системах (МЭМС) или в имплантированных медицинских устройствах, например, сердечных насосах. Такие катушки могут изготавливаться как на жестких, так и на упругих подложках, и следовательно могут быть интегрированы как на классические печатные платы, так и на элементы для т.н. гибкой электроники. Планарные катушки также могут изготавливаться серийно, что является экономически выгодным.
Благодаря этим качествам, планарные катушки находят применение в различных областях, в основном, в высокочастотных приложениях. Некоторые примеры использования:
- Дистанционный мониторинг состояния здоровья (например, датчики кровяного давления)
- Беспроводная передача энергии (например, носимые/имплантируемые медицинские устройства)
- Радиочастотная идентификация (например, платежные карты)
- Индукционный нагрев (например, индукционные варочные панели)
Планарные катушки могут использоваться на печатных платах в портативных устройствах типа фитнес-трекеров.
В контексте разработки и проектирования планарных катушек наиболее важные характеристики — это индуктивность и сопротивление. Последнее определенно должно быть очень низким (в идеальном случае нулевым), так как любое сопротивление уменьшает эффективность катушки. Индуктивность, напротив, для эффективной связи с другими системами должна быть высокой. Определение сопротивления и индуктивности может являться достаточно сложной задачей, так как необходимо учитывать материал катушки, количество витков, связь между электрическими и магнитными полями.
Инженеры могут получить данные о сопротивлении и индуктивности планарных катушек на печатных платах численно, используя возможности модуля AC/DC для электромагнитных расчетов, являющегося расширением пакета COMSOL Multiphysics. Это модуль содержит в числе прочих физический интерфейс Electric Currents, Layered Shell (Электрические токи в многослойных оболочках), который позволяет эффективно описывать и моделировать в т.
ч. конструкции плоских катушек. В качестве примера давайте рассмотрим простую модель планарной катушки.
Представление планарной катушки как многослойной оболочки с помощью модуля AC/DC
Модель представляет собой медную катушку, размещенную на печатной плате. Катушка содержит три витка, два межслойных соединения (перемычки), два контакта-терминала, один из которых служит источником тока, а второй заземлён. Ток с терминала начинает течь по верхнему слою. Затем он переходит по соединительной перемычке (via) на нижний слой, далее – по нему под витками, обратно на верхний слой по второй перемычке (via), и, наконец, проходит по всем виткам к контакту заземления. Протекая по катушке, ток индуцирует магнитное поле, причем отношение тока к магнитному полю как раз определяет индуктивность.
Геометрия планарной катушки, цветом на изображении показано распределение электрического потенциала.
Так как медная катушка является очень тонкой (толщина 0.1 мм, длина и ширина 0.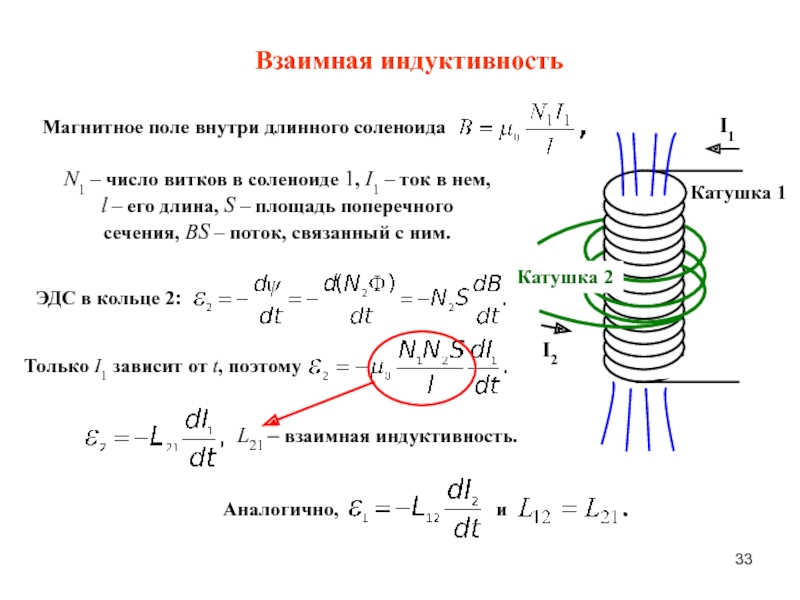
5 мм), её предпочтительней моделировать в качестве граничного, а не объёмного компонента. Для того, чтобы описать топологию катушки в плоскости можно воспользоваться функционалом физического интерфейса Electric Currents, Layered Shell, который доступен с версии 5.4 программного обеспечения COMSOL®. К тому же, данный интерфейс можно использовать совместно с физическим интерфейсом Magnetic Fields (Магнитные поля), что позволит провести анализ растекания токов, генерации магнитных полей и, следовательно, вычислить не только сопротивление, но и индуктивность катушки. Процесс такого совместного расчета будет состоять из двух этапов:
- В рамках физического интерфейса Electric Currents, Layered Shell проводится расчёт как сосредоточенного сопротивления, так и поверхностной плотности тока в области катушки. Собственно данный интерфейс и предназначен для решения закона сохранения тока, протекающего по двумерному слою.
- Физический интерфейс Magnetic Fields затем использует рассчитанную в интерфейсе Electric Currents, Layered Shell поверхностную плотность тока для расчёта распределения магнитного поля вокруг катушки.
Не смотря на то, что конкретно этот пример довольно простой, вы можете использовать точно такой же подход для других более сложных геометрий и постановок. Чтобы узнать все детали и настройки выполненные при моделировании, ознакомьтесь с учебным примером Planar PCB Coil. По ссылке вы найдёте pdf-файл с пошаговыми инструкциями по сборке. А если у вас есть действующая лицензия, то сможете скачать и соответствующий MPH-файл модели.
Визуализация результатов электромагнитного расчета
После проведения расчета в результатах автоматически сгенерируются дефолтные графики с наиболее характерными визуализациями и величинами. В данной модели выведены графики распределения электрического потенциала (показан выше), а также магнитного поля, которое создаётся током, протекающим по катушке (показано ниже). В дополнение к графическим результатам, также можно рассчитать числовые выражения, в т.ч. на основе классических формул. В нашем случае, проведен расчет сопротивления и индуктивности.
Для рассмотренной конструкции индуктивность равна 0.06 мкГн, а сопротивление — 21.6 мОм.
Распределение магнитной индукции вокруг катушки (цветом) и плотность тока (стрелки).
В данном примере мы продемонстрировали преимущества использования технологии по заданию многослойных оболочек в модуле AC/DC. С её помощью легко реализовать модель планарной катушки и определить сосредоточенные параметры — сопротивление и индуктивность. Используя расчетные данные, инженеры могут проводить оптимизацию топологий катушек для определенных сфер применения, например, добавляя больше витков для увеличения индуктивности. Результаты расчета предсказывают увеличение индуктивности с 0.06 мкГн до 0.11 мкГн при добавлении 4го витка.
Сравнение сопротивления и индуктивности для катушек с тремя и четырьмя витками. Визуализация распределения магнитной индукции приведена для случая четырёхвитковой катушки.
Дальнейшие шаги
Поработайте самостоятельно с рассмотренным примером расчета планарной катушки на печатной плате.
По нажатию на кнопку вы перейдете в Библиотеку моделей и приложений (Application Gallery,), в которой сможете загрузить MPH-файл и документацию к рассмотренной модели.
Дополнительные материалы
Вычисление матриц индуктивностей и импеданса в Maxwell 2D/3D
При проектировании катушек индуктивности, трансформаторов, дросселей, реакторов и т.д. одними из наиболее важных величин для расчетов являются индуктивности, активное и реактивное сопротивление обмоток. Аналитически легко считаются обмотки правильных форм при отсутствии нелинейных материалов, в противном случае расчёт сильно усложняется.
В данной статье кратко описан процесс расчёта 11 слойной обмотки токоограничивающего реактора с применением численных методов, реализованных в програмном обеспечении ANSYS Maxwell 2D/3D для электромагнитных расчетов. Имея исходные данные о геометрии обмотки, реально измерянные величины сопротивлений и индуктивностей (X=0.35Ом, L=1.113mH), проведем расчет электромагнитного поля, созданного током обмотки, для определения применения данного програмного продукта для решения задач такого класса, только значительно усложненных.2) и представлена в виде:
Для упрощения получения искомой величины в программе предусмотрены удобные элементы постпроцессора, где мы задаем число витков слоев обмоток и компонуем их нужным образом, в результате имеем более наглядное решение:
Используя текущее разбиение модели на конечные элементы, проводим гармонический анализ реактора на частоте 50Гц, в результате которого нам доступны результаты вычисления матрицы сопротивления, откуда X=0.36Ом.
Полученные результаты с погрешностью около 1% демонстрируют хорошее понимание постановки задачи, задание граничных условий и постпроцессорной обработки. Нет никаких сложностей, чтобы ввести в модель нелинейный магнитопровод, тем самым для анализа представлен 3х фазный реактор, необходимо рассчитать те же параметры.
В рассматриваемом случае индуктивность пропроциональна точке на кривои намагничивания магнитомягкого материала, поэтому в качестве возбуждения исползуются мгновенные значения тока в каждой фазе реактора.
Inductance phaseA phaseB PhaseC
phaseA 1.5145 -0.00011395 -3.29E-05
phaseB -0.00011395 1.5187 -0.00011423
PhaseC -3.29E-05 -0.00011423 1.5159
После расчета нам доступны все величины поля в скалярных и векорных графиках.
Использование инструмента матриц вычисления индуктивности и импеданса может использоваться не только для получения абсолютных значений, но и передана в виде схемы замещения в SIMPLORER для исследования реактора в прототипе будующей рабочей схемы. Так же по желанию пользователя может быть вычислена не только явная, но и дифференциальная индуктивность.
Расчет катушек индуктивности | Микросхема
Крайне полезная программа для любого радиолюбителя. Позволяет в считанные секунды подсчитать индуктивность любой катушки, контура или отрезка провода. Нередко на схемах можно увидеть катушки и рядом с ними надпись, обозначающую её индуктивность (Гн — Генри, 1 Гн=109 см). Но часто количество витков и размеры катушки не указывают. Так вот, с помощью данной программы можно быстро подобрать необходимое количество витков на уже имеющийся каркас катушки или любой сердечник. Все возможности показаны на картинках ниже.
В первое низпадающее меню входят следующие виды расчетов: “Предельная нагрузка провода”, “Отрезок круглого провода”, “Отрезок провода прямоугольного сечения”, “Одиночный круглый виток”, “Тонкопленочный круглый виток”, “Тонкопленочный квадратный виток”.
Во втором меню можно подсчитать следующие виды катушек: “Однослойная круглого сечения”, “Однослойная квадратного сечения”, “Многослойная цилиндрическая короткая”, “Плоская круглая спиральная”, “Плоская квадратная спиральная”, “Тороидальная однослойная квадратного сечения”, “Тороидальная однослойная круглого сечения”, “Тороидальная многослойная”.
В третьем пункте только катушки на ферритах: “Катушка на тороидальном ферромагнитном сердечнике прямоугольной формы с плотной намоткой”, “Катушка на П-, Ш-образном ферромагнитном замкнутом сердечнике”, “Катушка в броневом цилиндрическом сердечнике”. И ещё приведу пример работы программы. По радиусу, длине катушки и количеству витков легко расчитывается индуктивность. Главное смотрите единицы измерения.
Скачать
Огромное спасибо автору Струкову И.В.
Обсуждайте в социальных сетях и микроблогах
Метки: справка
Радиолюбителей интересуют электрические схемы:
Расчет количества витков в катушке
Электронное ухо
Катушка индуктивности и индуктивность — формулы и уравнения
Формулы и уравнения для индуктивности и индуктивности
Следующие формулы и уравнения можно использовать для расчета индуктивности и связанных с ней величин для различных форм индукторов, как показано ниже.
Индуктивность индуктора:Индуктивность индуктора по основной формуле индуктора:
Напряжение на индукторе: Ток индуктора: 9000- V — напряжение на катушке индуктивности
- L — индуктивность катушки индуктивности в Генри
- Di / dt — мгновенная скорость изменения тока через катушку индуктивности.
- i от до = ток в момент времени t = 0.
Индуктивное реактивное сопротивление — это сопротивление индуктора переменному току переменного тока, которое зависит от его частоты f и измеряется в Ом только как сопротивление. Индуктивное реактивное сопротивление рассчитывается по формуле:
X L = ωL = 2π f L
Где
- X L — индуктивное сопротивление
- f — приложенная частота
- L — Индуктивность в Генри
Эффективность катушки индуктивности известна как коэффициент качества и измеряется следующим образом:
QF = X L / ESR
Где
- X L — индуктивное реактивное сопротивление
- ESR — эквивалентное последовательное сопротивление цепи.
Это обратный коэффициенту качества и показывает рассеиваемую мощность внутри индуктора и определяется по формуле:
DF = tan δ = ESR / X L
Где
- DF — коэффициент рассеяния.
- δ — угол между Виктором емкостного реактивного сопротивления и отрицательной осью.
- X C — емкостное реактивное сопротивление
- ESR — эквивалентное последовательное сопротивление цепи.
Энергия E, запасенная в индукторе, определяется по формуле:
E = ½ Li 2
Где
- E — энергия в джоулях
- L — индуктивность в Генри
- i — ток в амперах
Связанные сообщения:
Средняя мощность индуктораСредняя мощность индуктора определяется по формуле:
P av = Li 2 / 2t
Где
- t = время в секундах.
Как и конденсатор, индуктор требует постоянной времени до 5 для полной зарядки или разрядки, в течение этого времени ток можно рассчитать по:
Во время зарядки:Мгновенный ток индуктора во время зарядки определяется по формуле:
Во время разряда:Ток во время разряда в любой момент времени t определяется по формуле:
Где
- I C — ток индуктора
- I 0 — ток в момент времени t = 0
- t — время, прошедшее после подачи тока.
- τ = L / R — постоянная времени цепи RL
Связанные сообщения:
Формулы индуктивности Индуктивность спиральной катушки «Формула Уиллера»Где:
- L — индуктивность
- R — радиус
- n — количество витков
- h — высота
Где:
- OR — крайний радиус в дюймах
- IR — внутренний радиус в дюймах
Где:
- θ — угол вне конуса (предположим, что θ ≈ 15 ° )
Связанные формулы и уравнения Сообщения:
Индуктивность — Гипертекст по физике
Обсуждение
введение
Готов? Вот так.
Пуск с соленоидом. Пропустите через него ток, и вы получите электромагнит. Поле внутри задается формулой…
| B = μ 0 nI = μ 0 | N | I |
| ℓ |
В то же время соленоид — это еще и устройство для улавливания магнитного потока.
Φ B = NBA
Статическая ситуация, безусловно, достаточно интересна, но когда дело доходит до потока, то, что нас действительно волнует, — это скорость изменения во времени.Это то, что дает нам электромагнитную индукцию или индуцированную электродвижущую силу, или как вы хотите это называть. Эта ситуация описывается законом Фарадея.
Давайте снова рассмотрим эти уравнения, но с изменяющимся во времени поворотом. Соленоид с изменяющимся током, проходящим через него, будет генерировать изменяющееся магнитное поле.
| дБ | = мк 0 | N | dI | |
| дт | ℓ | дт |
Это изменяющееся магнитное поле затем улавливается тем самым соленоидом, который его создал.Захваченное поле называется потоком, а изменяющийся поток генерирует ЭДС — в данном случае самоиндуцированную или обратную ЭДС.
| ℰ = — | d Φ B | = — N | ⎛ ⎜ ⎝ | мкм 0 | N | dI | ⎞ ⎟ ⎠ | А | |
| дт | ℓ | дт |
Немного изменив порядок вещей, мы получим это уравнение…
| ℰ = — | мкм 0 AN 2 | dI | |
| ℓ | дт |
, который может показаться не таким уж большим, пока вы не поймете, что члены первой дроби в значительной степени определяются геометрией соленоида.Если бы мы выбрали другую конфигурацию проводов, произошло бы то же самое.
Самоиндуцированная ЭДС в цепи прямо пропорциональна скорости изменения тока во времени ( dI / dt ), умноженной на константу ( L ). Эта постоянная называется индуктивностью (или, точнее, самоиндуктивностью ) и определяется геометрией схемы (или, чаще, геометрией отдельных элементов схемы).Например, индуктивность соленоида (как определено выше) определяется формулой…
Символ L для обозначения индуктивности был выбран в честь Генриха Ленца (1804–1865), чья новаторская работа в области электромагнитной индукции сыграла важную роль в развитии окончательной теории. Если вы помните, Закон Ленца гласит, что индуцированный ток в цепи всегда действует таким образом, чтобы противодействовать изменению, которое в первую очередь его вызвало. Это наблюдение является причиной того, почему во всех версиях закона Фарадея стоит знак минус.Ленц поставил нам знак минус, и мы его чествуем символом L .
Индуктивность лучше всего определяется по ее роли в уравнении, полученном из закона индукции Фарадея. Некоторым это не нравится, и они предпочитают определения, написанные в форме простого предложения субъект-глагол-объект.
На английском языке мы бы прочитали это как «самоиндукция ( L ) — это отношение обратной ЭДС () к скорости изменения тока, производящего ее ( dI / dt ).«Как я уже сказал, мне не очень нравится такое определение, но оно помогает нам определить подходящие единицы.
| ⎡ ⎢ ⎣ | H = | В | = | Дж / К | = | (кг · м 2 / с 2 ) / (A · с) | = | кг м 2 | ⎤ ⎥ ⎦ |
| А / с | п / с | п / с | A 2 с 2 |
Единицей индуктивности является генри , названный в честь Джозефа Генри (1797–1878), американского ученого, который открыл электромагнитную индукцию независимо и примерно в то же время, что и Майкл Фарадей (1791–1867) в Англии.Первым свои открытия опубликовал Фарадей, поэтому ему заслуга в большей степени. Генри также открыл самоиндукцию и взаимную индуктивность (которые будут описаны позже в этом разделе) и изобрел электромеханическое реле (которое легло в основу телеграфа). Схема с собственной индуктивностью в один генри будет испытывать противоэдс в один вольт, когда ток изменяется со скоростью один ампер в секунду.
Индуктивность — это что-то. Индуктивность — это сопротивление элемента схемы изменениям тока.Индуктивность в цепи — это аналог массы в механической системе.
| ⇕ | |||||
| |||||
| ⇕ | |||||
детектор индуктивной петли
Движение на некоторых перекрестках контролируется с помощью индуктивных петлевых детекторов (ILD).ILD — это петля из проводящего провода, проложенная всего на несколько сантиметров ниже тротуара. Когда автомобиль проходит через поле, он действует как проводник, изменяя индуктивность контура. Изменение индуктивности контура указывает на наличие автомобиля наверху. Затем эту информацию можно использовать для активации сигналов светофора, отслеживания транспортного потока или автоматического цитирования.
примеров
Индуктивностьзависит от геометрии
соленоид ( A площадь поперечного сечения, N количество витков, длина ℓ, n количество витков на длину)
| Φ B | = N | B | А | ||
| Φ B | = N | мкм 0 NI | А | ||
| ℓ | |||||
| Φ B | = | мкм 0 AN 2 | I | ||
| ℓ | |||||
| d Φ B | = | мкм 0 AN 2 | dI | ||
| дт | ℓ | дт | |||
| L | = | мкм 0 AN 2 | = | мкм 0 Aℓn 2 | |
| ℓ |
коаксиальных проводников ( a внутренний радиус, b внешний радиус, ℓ длина)
| Φ B | = | ⌠ ⌡ | B | · | d A | ||||
| б | б | ||||||||
| Φ B | = | ⌠ ⌡ | мкм 0 I | ℓ др | = | мкм 0 Iℓ | ⌠ ⌡ | др | |
| 2π r | 2π | r | |||||||
| a | a | ||||||||
| Φ B | = | мкм 0 ℓ | пер. | ⎛ ⎜ ⎝ | a | ⎞ ⎟ ⎠ | I | ||
| 2π | б | ||||||||
| d Φ B | = | мкм 0 ℓ | пер. | ⎛ ⎜ ⎝ | a | ⎞ ⎟ ⎠ | dI | ||
| дт | 2π | б | дт | ||||||
| L | = | мкм 0 ℓ | пер. | ⎛ ⎜ ⎝ | a | ⎞ ⎟ ⎠ | |||
| 2π | б | ||||||||
тороид ( A площадь поперечного сечения, R радиус вращения, N количество витков)
| Φ B | = | N | B | А | |
| Φ B | ≈ | N | мкм 0 NI | А | |
| 2π R | |||||
| Φ B | ≈ | N | мкм 0 NA | I | |
| 2π R | |||||
| d Φ B | ≈ | мкм 0 AN 2 | dI | ||
| дт | 2π R | дт | |||
| L | ≈ | мкм 0 AN 2 | |||
| 2π R | |||||
прямоугольная петля ( w ширина, h высота, a радиус провода )
| Φ B | = | N | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Φ B | = | N |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Φ B | = | 2 | мкм 0 N 2 | ⎡ ⎢ ⎣ | y ln | ⎛ ⎜ ⎝ | x | ⎞ ⎟ ⎠ | + | x дюймов | ⎛ ⎜ ⎝ | y | ⎞ ⎟ ⎠ | ⎤ ⎥ ⎦ | I | |||||||||||||||||||||||||||||||||||||||||||||||||
| 2π | a | a | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| d Φ B | = | мкм 0 N 2 | ⎡ ⎢ ⎣ | y ln | ⎛ ⎜ ⎝ | x | ⎞ ⎟ ⎠ | + | x дюймов | ⎛ ⎜ ⎝ | y | ⎞ ⎟ ⎠ | ⎤ ⎥ ⎦ | dI | ||||||||||||||||||||||||||||||||||||||||||||||||||
| дт | π | a | a | дт | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| L | = | мкм 0 N 2 | ⎡ ⎢ ⎣ | y ln | ⎛ ⎜ ⎝ | x | ⎞ ⎟ ⎠ | + | x дюймов | ⎛ ⎜ ⎝ | y | ⎞ ⎟ ⎠ | ⎤ ⎥ ⎦ | |||||||||||||||||||||||||||||||||||||||||||||||||||
| π | a | a | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Эта формула не совсем работает, поскольку она игнорирует краевые эффекты.Вы можете найти точную формулу (а также скрипты, которые будут рассчитывать индуктивность для вас) в Интернете на нескольких веб-сайтах по электротехнике.
Импеданс индуктора — Индуктивное реактивное сопротивление — Индуктивность
Импеданс индуктора и импеданс конденсатора являются частными случаями общего представления импеданса. Импеданс катушки индуктивности (также называемый индуктивностью или индуктивным реактивным сопротивлением) является мерой сопротивления изменению электрического тока в этом компоненте.
В целом можно резюмировать, что индуктор пропускает сигналы низких частот (включая сигналы 0 Гц) и блокирует сигналы высоких частот.
Формула импеданса катушки индуктивности: Z = jLw, где:
- Z: импеданс в омах
- j: оператор для мнимых чисел. (мнимая единица)
- L: значение индуктора в Генри (H)
- w: равно 2π.f, где буква f представляет частоту сигнала, подаваемого на индуктор.(Единица частоты — Герцы).
Импеданс индуктора (индуктивное реактивное сопротивление).
Обычно индукторы используются в цепях с частотой сигналов, отличной от нуля (0 Гц).
Из формулы импеданса катушки индуктивности видно, что импеданс пропорционален частоте. Это означает, что если частота равна нулю (0 Гц), полное сопротивление равно нулю.
Теперь, если полное сопротивление равно нулю, напряжение на выводах индуктора также равно нулю. (V = 0 вольт) и короткое замыкание в катушке индуктивности.В этом случае ток свободно течет до максимально возможного значения.
Полное сопротивление имеет общую формулу: Z = V / I (действующее значение напряжения / среднеквадратичное значение тока). Эта формула похожа на закон Ома, который применяется к резисторам, но в этом случае он используется для сигналов переменного тока.
Оператор «j».
Причина, по которой этот оператор используется в электронике, заключается в том, что существует разность фаз между напряжением и током в индукторах. Эта разность фаз составляет 90 ° или π / 2. и напряжение опережает ток на 90 °.(90 градусов). Частота переменного напряжения и переменного тока в катушке индуктивности одинакова.
Разность фаз между напряжением и током в катушке индуктивности
Оператор «j» не используется с резисторами, поскольку нет разности фаз между напряжением и током. Другими словами, напряжение и ток в резисторе синфазны.
Вт (угловая частота).
Значение w напрямую зависит от f (частоты) и измеряется в радианах / сек.(w = 2.π.f)
Например, для частоты 300 Гц w = 2.π.f = 2 x (3,1416) x 300 = 1884,96 рад / сек.
Как рассчитать индуктивность индуктора?
Для расчета индуктивности катушки индуктивности используется формула Z = wL.
Пример 1:
Как получить импеданс индуктора 25 мГн при 300 Гц.
Z = 2 x π x 300 Гц x 25 мГн = 2 x (3,1416) x 300 x 0,025 = 47,124 Ом
Пример 2:
Как получить импеданс индуктора 25 мГн при 50 Гц?
Z = 2 x π x 300 Гц x 25 мГн = 2 x (3.1416) x 50 x 0,025 = 7,854 Ом.
Из двух предыдущих примеров, где величина индуктивности одинакова (25 мА), видно, что сопротивление выше для более высоких частот. Можно резюмировать, что катушка индуктивности пропускает низкочастотные сигналы (низкое сопротивление) и блокирует высокочастотные сигналы (высокое сопротивление).
Пример 3:
Как получить импеданс индуктора 12 мГн при 60 Гц?
Z = 2 x π x 60 Гц x 12 мГн = 2 x 3.1416 x 60 x 0,012 = 4,524 Ом.
Индуктивность
- Изучив этот раздел, вы сможете описать:
- • Единица индуктивности.
- • Факторы, влияющие на индуктивность.
- • Напряжение и ЭДС.
- • Самоиндукция.
- • Задний э.м. и его эффекты.
Индуктивность
Ток, генерируемый в проводнике изменяющимся магнитным полем, пропорционален скорости изменения магнитного поля.Этот эффект называется ИНДУКТИВНОСТЬЮ и обозначается символом L. Он измеряется в единицах, называемых генри (H), названных в честь американского физика Джозефа Генри (1797-1878). Один генри — это величина индуктивности, необходимая для создания ЭДС в 1 вольт в проводнике, когда ток в проводнике изменяется со скоростью 1 ампер в секунду. Генри — довольно большая единица измерения для использования в электронике, чаще всего используются миллигенри (мГн) и микрогенри (мкГн). Эти единицы описывают одну тысячную и одну миллионную генри соответственно.
Несмотря на то, что генри обозначается символом (заглавной) H, в имени генри применяется к единице индуктивности строчная буква h. Форма множественного числа генри может быть генри или генри; Американский национальный институт стандартов и технологий рекомендует использовать в публикациях США генри.
Факторы, влияющие на индуктивность.
Величина индуктивности в катушке индуктивности зависит от:
- а. Количество витков провода в индукторе.
- г.Материал сердечника.
- г. Форма и размер сердечника.
- г. Форма, размер и расположение проволоки, из которой состоят катушки.
Поскольку индуктивность (в генри) зависит от множества переменных величин, ее довольно сложно рассчитать точно; были разработаны многочисленные формулы, учитывающие различные особенности конструкции. Также в этих формулах часто необходимо использовать специальные константы и таблицы данных преобразования для работы с необходимой степенью точности.Использование компьютерных программ и систем автоматизированного проектирования несколько облегчило ситуацию. Однако внешние эффекты, вызванные другими компонентами и проводкой рядом с индуктором, также могут повлиять на его значение индуктивности после его сборки в цепь, поэтому, когда требуется точное значение индуктивности, одним из подходов является расчет приблизительного значения и разработка индуктор так, чтобы он был регулируемым.
Типичная формула для приближения значения индуктивности катушки индуктивности приведена ниже.Эта конкретная версия предназначена для расчета индуктивности «соленоида, намотанного одним слоем витков бесконечно тонкой ленты, а не проволоки, и с равномерно и близко расположенными витками».
Рис. 3.2.1 Миниатюрный индуктор переменного тока.
Где:
- L — индуктивность в генри.
- d — диаметр рулона в метрах.
- n — количество витков в катушке.
- l — длина змеевика в метрах.
Для катушек, не соответствующих точно указанным выше спецификациям, должны быть включены дополнительные факторы. На рис. 3.2.1 показан один из способов получения достаточно точной индуктивности, используемый в некоторых ВЧ и ВЧ схемах. Миниатюрная катушка индуктивности намотана на пластмассовый каркас, в который достаточно ввинчен ферритовый (железная пыль) сердечник, чтобы обеспечить сердечник с нужной индуктивностью.
Напряжение и э.д.с.
Напряжение , индуцированное в проводнике, называется e.м.ф. (электродвижущая сила), потому что ее источником является изменяющееся магнитное поле вокруг проводника и вне его. Любое внешнее напряжение (в том числе создаваемое внешней батареей или источником питания) называется э.д.с., в то время как напряжение (разность потенциалов или п.о.) на внутреннем компоненте в цепи называется напряжением.
Задний э.м.
Противоэдс (также называемая противоэдс) — это ЭДС, создаваемая на индукторе изменяющимся магнитным потоком вокруг проводника, вызванная изменением тока в индукторе.Его значение можно рассчитать по формуле:
Где:
- E — наведенная обратная ЭДС. в вольтах
- L — индуктивность катушки в генри.
- ΔI — изменение тока в амперах.
- Δt — время, необходимое для изменения тока, в секундах.
Примечания:
Δ (греч. D — дельта) обозначает различие или изменение собственности.
Таким образом, формула описывает обратную ЭДС в зависимости от индуктивности (в генри), умноженной на скорость изменения тока (в амперах в секунду).
Знак минус перед L указывает на то, что полярность наведенной обратной ЭДС будет обратной по сравнению с изменяющимся напряжением на проводнике, которое первоначально вызвало изменение тока и, как следствие, изменение магнитного поля.
Помните, что при работе с практическими значениями милли или микрогенри все значения, используемые в формуле, должны быть преобразованы в стандартные значения генри-ампер и секунд, как описано в нашем буклете «Советы по математике».
Пример
Поскольку величина обратной ЭДС зависит от скорости изменения тока, она будет наибольшей, когда произойдет самое быстрое изменение.Например, скорость изменения чрезвычайно высока, когда ток через катушку индуктивности отключается; тогда изменение может быть от максимума до нуля всего за несколько миллисекунд.
Представьте, что индуктор на 200 мГн, подключенный к источнику питания 9 В, пропускает ток 2 ампера. Когда ток отключается, он падает до нуля через 10 мсек. Какой будет обратная ЭДС, генерируемая на катушке?
E = 200 мГн x 2 А / 10 мс
или
E = 200 x 10 -3 x 2/10 x 10 -3
= 40 вольт
Значит, обратная ЭДС, возникающая при выключении, более чем в 4 раза превышает напряжение питания!
Эти высоковольтные импульсы, возникающие при выключении индуктивного компонента, такого как двигатель или катушка реле, могут потенциально вызвать повреждение выходного транзистора или интегральной схемы, переключающей устройство.Поэтому существенная защита обеспечивается включением диода в выходной каскад, как показано на рис. 3.2.2 и 3.2.3
Задняя защита от ЭДС
Рис. 3.2.2 Задняя э.д.с. Защитный диод.
Защитный диод на рис. 3.2.2, подключенный к катушке индуктивности, обычно имеет обратное смещение, так как напряжение на его катоде, подключенном к шине питания + V, будет более положительным, чем его анод на коллекторе транзистора. Однако при выключении на индукторе появляется большой всплеск напряжения противоположной полярности из-за схлопывающегося магнитного поля.Во время этого скачка напряжения коллектор транзистора может находиться под более высоким потенциалом, чем питание, за исключением того, что если это произойдет, диод станет смещенным в прямом направлении и предотвратит повышение напряжения коллектора выше, чем на шине питания.
Рис. 3.2.3 Защитные диоды в ULN2803.
На рис. 3.2.3 показан популярный I.C. (ULN2803) для переключения индуктивных нагрузок. Выходы восьми инвертирующих усилителей защищены диодом, общие катоды которого подключены к положительной шине питания + V на выводе 10.
Самоиндукция
Принцип работы самоиндукции зависит от двух взаимосвязанных действий, происходящих одновременно, и от каждого из этих действий в зависимости от другого.
Действие 1.
Любой проводник, в котором изменяется ток, создает вокруг себя изменяющееся магнитное поле.
Действие 2.
Любой проводник в ИЗМЕНЯЕМОМ магнитном поле будет иметь изменяющуюся ЭДС, наведенную в него.Величина этой наведенной ЭДС и величина индуцированного тока, который она производит в проводнике, будут зависеть от скорости изменения магнитного поля; чем быстрее изменяется поток поля, тем больше будет наведенная ЭДС. и его последующий ток.
Эффект индукции эдс самим собой индуктором называется самоиндукцией (но часто его называют просто индукцией). Когда катушка индуктивности индуцирует ЭДС в отдельную соседнюю катушку индуктивности, это называется взаимной индукцией и является свойством, используемым трансформаторами.
Изменяющееся магнитное поле, создаваемое вокруг проводника изменяющимся током в проводнике, вызывает изменение ЭДС в этом проводнике. Эта изменяющаяся ЭДС, в свою очередь, создает переменный ток, текущий в направлении, противоположном исходному току. Таким образом, изменения в этом токе противодействуют изменениям в исходном токе.
Таким образом, действие 2 ограничивает изменения, происходящие из-за действия 1. Если исходный ток увеличивается, индуцированный ток замедляет скорость увеличения.Точно так же, если исходный ток уменьшается, индуцированный ток замедляет скорость уменьшения. Общий результат этого — уменьшение амплитуды переменного тока через катушку индуктивности и, таким образом, уменьшение амплитуды переменного напряжения на катушке индуктивности.
Поскольку сила магнитного поля, создаваемого исходным током, зависит от скорости (скорости) изменения тока, индуктор уменьшает поток переменного тока (AC) больше на высоких частотах, чем на низких.Этот ограничивающий эффект, создаваемый наведенной ЭДС, будет сильнее на более высоких частотах, потому что на высоких частотах ток и, следовательно, поток изменяются быстрее. Этот эффект получил название «Индуктивное реактивное сопротивление».
Индуктивное реактивное сопротивление.
Реактивное сопротивление препятствует прохождению переменного тока. Как и сопротивление, оно измеряется в Ом, но поскольку сопротивление имеет одно и то же значение на любой частоте, а сопротивление переменному току в индукторах зависит от частоты, его нельзя назвать сопротивлением.Вместо этого он называется Reactance (X). Конденсаторы также обладают свойством реактивного сопротивления, но они по-разному реагируют на частоту, поэтому существует два типа реактивного сопротивления; индукторы имеют индуктивное реактивное сопротивление (X L ), а конденсаторы — емкостное реактивное сопротивление (X C ).
Метод расчета значения индуктивности подвесных индукторов MEMS с кремниевыми подложками
Подвесные индукторы MEMS состояли из медных проводов в воздушном слое, кремниевой подложки (диэлектрический слой) и земли (слой идеального проводника).Для подвесного индуктора MEMS ширина w и толщина t проводов были порядка 10 мкм, а длина проводов была порядка 100 мкм. При частоте 10 ГГц длина волны составляла 3 см. Таким образом, длина, ширина и толщина проводов индуктора были намного меньше длины волны. Провода индуктора рассматривались как серия электрических диполей.
2.1. Расчет значения индуктивности подвесного индуктора, состоящего из одного провода
Схема подвесного индуктора MEMS, состоящего из одного провода, показана на, а рассматриваемая геометрия показана на.
Схема подвесного индуктора микроэлектромеханической системы (МЭМС), состоящего из одного провода.
Геометрия проволоки на высоте d над подложкой.
Как показано, медный провод расположен на высоте d над кремниевой подложкой. Длина провода a, толщина подложки l. В области 0 (z> 0) обозначен слой воздуха над подложкой, область 1 (-l≤z≤0) указывает кремниевую подложку, а область 2 (z <−l) указывает землю.Диэлектрическая проницаемость, магнитная проницаемость и проводимость области i выражаются как εi, μi, σi in.
В цилиндрических координатах интегральные выражения компонентов электромагнитного поля в области 0, обусловленные горизонтальным электрическим диполем в (0, 0, d), могут быть выражены как:
E0ρ (ρ, φ, z) = −ωμ0Idl4πk02cosφ [Fρ0 (ρ, z − d) −Fρ0 (ρ, z + d) + Fρ1 (ρ, z + d) + Fρ2 (ρ, z + d)]
(1)
E0φ (ρ, φ, z) = ωμ0Idl4πk02sinφ [Fφ0 (ρ, z − d) −Fφ0 (ρ, z + d) + Fφ1 (ρ, z + d) + Fφ2 (ρ, z + d)]
(2)
E0z (ρ, φ, z) = iωμ0Idl4πk02cosφ [Fz0 (ρ, z − d) −Fz0 (ρ, z + d) + Fz1 (ρ, z + d)]
(3)
B0ρ (ρ, φ , z) = — μ0Idl4πsinφ [Gρ0 (ρ, z − d) −Gρ0 (ρ, z + d) + Gρ1 (ρ, z + d) + Gρ2 (ρ, z + d)]
(4)
B0φ (ρ, φ, z) = — μ0Idl4πcosφ [Gφ0 (ρ, z − d) −Gφ0 (ρ, z + d) + Gφ1 (ρ, z + d) + Gφ2 (ρ, z + d)]
(5)
B0z (ρ, φ, z) = iμ0Idl4πsinφ [Gz0 (ρ, z − d) −Gz0 (ρ, z + d) + Gz2 (ρ, z + d)]
(6)
где ki — волновое число в области i , а ki можно вычислить, используя:
Fm0 (ρ, z − d) и Gm0 (ρ, z − d) ( m = ρ, φ, z) — прямые волны электрического диполя, Fm0 (ρ, z + d) и Gm0 (ρ, z + d) ( м = ρ, φ, z) являются идеальными отраженными волнами.Fm1 (ρ, z + d) и Gm1 (ρ, z + d) ( m = ρ, φ, z) — волны электрического типа. Fm2 (ρ, z + d) и Gm2 (ρ, z + d) ( м = ρ, φ, z) — волны магнитного типа.
Индуктивность провода складывается из внутренней и внешней индуктивностей. Внешняя индуктивность рассчитывается с использованием внешнего магнитного потока. Только плотность магнитного потока вдоль направления, перпендикулярного плоскости подложки (вдоль оси z in), выраженная как B0z, вносит вклад в магнитный поток.В цилиндрических координатах B0z из-за горизонтального электрического диполя в точке (0, 0, d) может быть выражено как [18]:
B0z (ρ, φ, z) = iμ0Idl4πsinφ {- (ρr1) (k0r1 + ir12) eik0r1 + (ρr2) (k0r2 + ir22) eik0r2 + 2π∑jλjB * 2tanγ1B * lp ′ (λjB *) · eiγ0B * (z + d) · h2 (1) (λjB * ρ) −2k021πk0ρ · eik0r2 · −4 π2ρi · T · exp (−ik0ρ2 (z + dρ + iT) 2) · erfc (−ik0ρ2 (z + dρ + iT) 2)]}
(8)
Четыре члена в скобках уравнения (8) указывают прямую волну, идеально отраженную волну, захваченную поверхностную волну магнитного типа и боковую волну магнитного типа электрического диполя соответственно.Захваченная поверхностная волна магнитного типа не существует, когда k12 − k02l <π2. В данном исследовании диэлектрическая проницаемость и проницаемость воздуха равны ε0 = 8,85 × 10–12 Ф / м и μ0 = 4π × 10–7 Гн / м, диэлектрическая проницаемость и магнитная проницаемость кремния равны ε1 = 11,9 × 8,85 × 10– 12 Ф / м и μ1 = μ0 = 4π × 10-7 Гн / м. Поскольку толщина подложки составляет порядка 100 мкм, даже когда частота достигает 10 ГГц, можно рассчитать, что k12-k02l составляет всего лишь порядка 0,1. Таким образом, в данной работе можно не учитывать захваченную поверхностную волну магнитного типа.
В уравнении (8) r1 — это расстояние между электрическим диполем источника в (0, 0, d) и точкой поля, а r2 — расстояние между точкой поля и диполем идеального изображения в (0, 0, −d). T может быть выражено как:
T = k12 − k02k0tank12 − k02l
(9)
Функция ошибок «erfc» определяется как [20]:
erfc (x) = — ∫x∞e − t2dt
(10)
а также
erfc (x) ≈1πxe − x (1−12x + 34×2 +…)
(11)
Уравнение (8) можно переписать в форме в прямоугольной системе координат как:
B0z (x, y, z) = iμ0Idl4π · yρ · {- (ρr1) (k0r1 + ir12) eik0r1 + (ρr2) (k0r2 + ir22) eik0r2−2k021πk0ρ · eik0r2 · [πk0ρ − π2eiπ4 · iT · exp (−ikρ0 + 2) 2) · erfc (−ik0ρ2 (z + dρ + iT) 2)]}
(12)
куда
а также
показывает вертикальный вид рассматриваемой геометрии.
Вертикальный вид рассматриваемой геометрии.
В соответствии с уравнением (12) на плоскости (x, y, d) плотность магнитного потока B0z из-за провода длиной a может быть выражена как:
B0z (x, y, d) = ∫0aiμ0I4π · Yρ · {- (ρr1) (k0r1 + ir12) eik0r1 + (ρr2) (k0r2 + ir22) eik0r2−2k021πk0ρ · eik0r2 · [πk0ρ − π2eiπ4 · T · exp (−ik0ρ2 (2dρ + iTc) 2 -) ik0ρ2 (2dρ + iT) 2)]} dx0
(16)
куда
а также
r2 = (x − x0) 2 + y2 + 4d2
(19)
Внешний магнитный поток, создаваемый проводом, может быть выражен как:
Ψ = ∫w2∞∫0aB0zdxdy
(20)
Внешнюю индуктивность подвесного индуктора, состоящего из одного провода, можно рассчитать по формуле:
Внутреннюю индуктивность можно рассчитать с помощью уравнения (22) [21]:
где a, w, t — длина, ширина и толщина провода.γ — проводимость материала проволоки. В данном исследовании материал проволоки был медным. ϑ — коэффициент, связанный с w / t, а ϑ можно получить с помощью справочной таблицы.
Тогда значение индуктивности подвешенного индуктора, состоящего из одного провода, можно рассчитать по формуле (23):
2.2. Расчет значения индуктивности подвесного индуктора, состоящего из одной прямоугольной катушки
Схема подвесного индуктора MEMS, состоящего из одной прямоугольной катушки, показана на рис.Высота подвеса катушки d. Длина и ширина прямоугольной катушки равны a1 и a2 соответственно. Прямоугольная катушка состоит из четырех сегментов провода, и плотность магнитного потока на плоскости (x, y, d), обусловленная каждым сегментом провода, также может быть рассчитана с помощью уравнения (16).
Схема подвесного индуктора MEMS, состоящего из одной прямоугольной катушки.
Таким образом, магнитный поток в области, ограниченной прямоугольной катушкой, можно выразить как:
Ψcoil = 2 × (∫w2a2 − w2∫w2a1 − w2B0z1dxdy + ∫w2a1 − w2∫w2a2 − w2B0z2dxdy (24)
где B0z1 и B0z2 — плотность магнитного потока, обусловленная отрезком провода, а длина равна a1 и a2 соответственно.
Тогда внешняя индуктивность подвешенного индуктора, состоящего из одной прямоугольной катушки, может быть рассчитана по формуле:
Внутренняя индуктивность каждого сегмента провода также может быть рассчитана с использованием (22). Внутренняя индуктивность прямоугольной катушки может быть выражена как:
Li = 2 × (a1wtμ02ωγϑ + a2wtμ02ωγϑ)
(26)
Сумма внешней индуктивности и внутренней индуктивности представляет собой значение индуктивности подвешенного индуктора, состоящего из одиночная прямоугольная катушка.
Микроволны101 | Математика индуктивности
Щелкните здесь, чтобы перейти на страницу с основной индуктивностью
В марте 2016 года наши друзья из Keysight Technologies предоставили нам видео о том, как моделировать спиральные индукторы. Спасибо, Keysight!
Ниже приведен индекс нашего математического обсуждения индукторов:
Индуктивное сопротивление
Индуктивность ЛЭП (отдельная страница)
Индуктивность соленоида
Дроссель спиральный (проволочный)
Спиральные индукторы на подложке (Новинка марта 2016!)
Индуктивность тороида
Индуктивность Wirebond (теперь на отдельной странице)
Индуктивность воздушного моста (отдельная страница)
Индуктивность через отверстие (отдельная страница)
Индуктивность проводов (отдельная страница)
Сопротивление катушек индуктивности постоянному току и ВЧ
Резонансы
Индуктивное сопротивление
Воспользуйтесь нашим калькулятором реактивного сопротивления, если вам интересна эта тема!
Хорошо известное уравнение для индуктивного реактивного сопротивления показано ниже.Обратите внимание, что индуктивное реактивное сопротивление положительное, полярность противоположная емкостному. На диаграмме Смита это означает, что последовательная индуктивность имеет тенденцию изменять коэффициент отражения по часовой стрелке.
Более полезная форма уравнения индуктивного реактивного сопротивления приведена ниже, где частота выражается в ГГц, а индуктивность — в наногенри. К счастью, все эти десятичные знаки просто отменяют друг друга!
Индуктивность соленоида
Соленоид цилиндрической формы, намотанный проволокой для создания индуктивности.Он может иметь один слой обмоток или многослойный, и он может использовать воздушный сердечник или сердечник с высокой магнитной проницаемостью для увеличения индуктивности. Самыми полезными (читай, «наивысшей добротностью») соленоидами для микроволновых приложений являются миниатюрные однослойные индукторы с воздушным сердечником. Рисунок ниже предоставлен Себастьяном. Большое спасибо!
Классическая формула однослойной индуктивности (воздушный сердечник) называется формулой Уиллера, которая восходит к временам радиоэфира 1920-х годов:
где:
L = индуктивность в микро-Генри (не нано-Генри!)
N = количество витков провода
R = радиус катушки в дюймах
H = высота катушки в дюймах
Вот оно в пересчете на D, диаметр катушки:
(Эта формула исправлена 9 апреля 2006 г. благодаря KB!)
ФормулаУиллера не учитывает диаметр проволоки и расстояние между витками.В формуле Уиллера витки касаются друг друга, но предполагается, что некоторая изоляция предотвращает короткое замыкание. На практике необходимо некоторое расстояние между витками, чтобы уменьшить межвитковую емкость и увеличить рабочую частоту. Посмотрим правде в глаза, Уиллера не интересовала точность нано-катушек Генри для микроволнового оборудования.
Предположительно более точный метод расчета индуктивности однослойных индукторов с воздушным сердечником для микроволновых компонентов можно найти на веб-сайте Microwave Components Incorporated:
где:
L = индуктивность в нано-Генри
N = количество витков провода
D = внутренний диаметр катушки (дюймы)
D1 = диаметр неизолированного провода (дюймы)
S = расстояние между витками (дюймы)
Используя формулу MCI, применительно к проводу 47 калибра (1.Диаметр неизолированного провода 2 мил) и расстояние между витками 0,5 мил, оборачивая витки вокруг штифтовых тисков 20 мил, можно получить следующие значения для воздушной катушки:
1 оборот = 2 нГн
2 оборота = 5 нГн
3 оборота = 8 нГн
4 оборота = 12 нГн
5 оборотов = 16 нГн
6 оборотов = 20 нГн
7 оборотов = 25 нГн
8 оборотов = 30 нГн
9 оборотов = 35 нГн
10 оборотов = 40 нГн
Щелкните здесь, чтобы перейти к нашей таблице калибра проводов в США (AWG).
Дроссель спиральный (проволочный)
Эта формула и рисунок также были предоставлены Себастьяном (единицы также являются микро-Генри): Мы должны признать, что мы лично не проверяли точность некоторых формул на этой странице по сравнению с измеренными данными.Также обратите внимание, что любая модель индуктора, не учитывающая паразитную емкость и сопротивление, будет иметь ограниченную точность на микроволновых частотах.
Катушки индуктивности спиральные на подложке
Спиральные индукторы часто используются в конструкциях MIC, MMIC и RFIC, особенно ниже 18 ГГц. Катушки индуктивности могут быть прямоугольными или круглыми, если вы умеете их моделировать. Модель спирального индуктора с сосредоточенными элементами может иметь множество элементов конденсатора и резистора, чтобы учесть все паразиты, которые делают ее все менее и менее идеальной по мере увеличения частоты.Для моделирования индуктора требуются хорошие извлеченные данные об одном или нескольких значениях индуктивности, что приводит к масштабируемой модели, позволяющей прогнозировать характеристики произвольных значений индуктивности, требуемых вашей конструкцией.
Хотите немного более практического описания того, как моделировать спиральные индукторы? Посмотрите это видео на ТОЧНО ЭТОМ. Франц Сишка из SisConsult проведет вас через полную модель спирального индуктора с сосредоточенными элементами, включая скин-эффекты, вихревые токи подложки и соединение с металлическим экраном 1.Программа Keysight для определения характеристик и анализа интегральных схем (IC-CAP) используется для согласования двух примеров измерений. Элементы настраиваются вручную с последующей оптимизацией. Предоставляются методы проверки модели, и файлы с примерами могут быть загружены.
Индуктивность тороида
Тороид похож на соленоид, но имеет форму пончика. Еще не все!
Сопротивление индукторов постоянному току и ВЧ
Вычислить сопротивление спирального индуктора постоянному току просто, и разработчики часто не обращают на него внимания, пока не построят схему усилителя, и деталь не смещается правильно на первой итерации.Вам нужно знать сопротивление листа вашей металлизации в Ом на квадрат и вычислить количество квадратов в катушке индуктивности. Количество квадратов — это общая длина (если вы ее размотали), деленная на ширину, и может легко исчисляться сотнями для большой катушки индуктивности.
При вычислении радиочастотного сопротивления вам, возможно, придется учитывать эффект глубины скин-слоя.
Модель, показанная ниже, является классической моделью спиральных индукторов. Вычислить элементы не так просто, как вы могли бы надеяться.
Резонансы индуктора
Еще впереди!
энергии в индукторе
энергии в индуктореследующий: Схема Up: индуктивность Предыдущий: Самоиндуктивность
Энергия, накопленная в индукторе Предположим, что индуктор индуктивности подключен к переменное напряжение постоянного тока. Электропитание регулируется таким образом, чтобы увеличить ток, протекающий через индуктор от нуля до некоторого конечного значения.Поскольку ток через индуктор нарастает, ЭДС генерируется, что препятствует увеличению тока. Ясно, что работа должна быть сделано против этой ЭДС источником напряжения, чтобы установить ток в катушке индуктивности. Работа, выполняемая источником напряжения во время временной интервал
| (247) |
Здесь, — мгновенная скорость, с которой источник напряжения выполняет работу. Чтобы найти общую работу, проделанную для установления конечного тока в индуктора, мы должны интегрировать приведенное выше выражение.Таким образом,
| (248) |
давая
| (249) |
Эта энергия фактически хранится в магнитном поле, создаваемом током протекает через индуктор. В чистом индукторе энергия накапливается без потери, и возвращается в остальную часть цепи, когда ток через катушка индуктивности снижается, и связанное с ней магнитное поле разрушается.
Рассмотрим простой соленоид.
Уравнения (244), (246) и (249) можно объединить, чтобы получить
| (250) |
что сводится к
| (251) |
Это представляет собой энергию, запасенную в магнитном поле соленоида. Однако объем заполненного полем сердечника соленоида составляет, поэтому магнитная плотность энергии ( i.е. , энергия на единицу объема) внутри соленоид есть, или
| (252) |
Оказывается, это довольно общий результат. Таким образом, мы можем вычислить энергосодержание любого магнитного поля путем разделения пространства на маленькие кубики (в каждом из которых магнитное поле приблизительно однородно), применяя приведенная выше формула, чтобы найти содержание энергии каждого куба, и суммируя полученные таким образом энергии, чтобы найти полную энергию.
Когда электрическое и магнитное поля существуют вместе в пространстве, уравнения. (122) и
(252) можно объединить, чтобы получить выражение для
общая энергия, накопленная в комбинированном
полей на единицу объема:
| (253) |
следующий: Схема Up: индуктивность Предыдущий: Самоиндуктивность Ричард Фицпатрик 2007-07-14 .