Как рассчитать индуктивность трансформатора: что это, как рассчитать, формулы и примеры — Мир Антенн

Содержание

что это, как рассчитать, формулы и примеры

Трансформатор, как элемент радиотехники и электротехники, работает на основе электромагнитной индукции. Говоря об индуктивности трансформатора, имеют в виду индуктивность обмоток и взаимоиндукцию между ними.

Каждая из обмоток представляет некоторое количество витков провода, намотанных на ферромагнитный сердечник, то есть обыкновенную катушку индуктивности.

Трудность в определении параметров катушки заключается в том, что они изменяются в зависимости от нескольких параметров и их сочетания:

токи в обмотках;
уровень намагниченности магнитопровода;
магнитные характеристики сердечника;
взаимодействие между соседними обмотками;
наличия постоянной составляющей тока.

Конструкция и принцип действия силового трансформатора

В основе конструкции любого трансформатора находятся следующие элементы:

Сердечник из ферромагнитного материала.

Первичная и вторичные обмотки. В случае автотрансформатора одна обмотка выполняет обе функции.

В сетях переменного тока промышленной частоты (50 или 60Гц) в качестве ферромагнитного материала используется сталь, обработанная по специальной технологии. На высоких частотах часто делаются трансформаторы без сердечника, поскольку для нормальной работы достаточно взаимосвязи межу катушками.

Принцип работы:

в первичной обмотке, подключенной в цепь питания, создается переменное электрическое поле;
под действием поля первичной катушки в сердечнике создается переменное магнитное поле;
в силу электромагнитной индукции во всех обмотках наблюдается ЭДС индукции.

ЭДС индукции в первичной обмотке направлена противоположно поданному напряжению, поэтому они взаимно компенсируются. В результате, при отсутствии нагрузки через первичную обмотку протекает сравнительно небольшой ток холостого хода.

Наличие тока вторичной цепи аналогично вызывает дополнительный магнитный поток, а он – ЭДС самоиндукции в первичное катушке. В результате компенсация первичного напряжения снижается и растет ток в первичной цепи.

Физическое понятие индуктивности обмоток

Индуктивность представляет собой коэффициент пропорциональности между током, создаваемым замкнутым электрическим контуром, и магнитным потоком, который создается этим контуром.

Более понятной формулировкой будет та, которая говорит о величине ЭДС самоиндукции в замкнутом контуре, которая возникает при изменении силы тока за единицу времени. То есть, понятие индуктивности справедливо для изменяющегося тока.

При постоянном токе говорить об индуктивности бессмысленно.

В идеальном трансформаторе все электромагнитное поле, создаваемое обмотками, замкнуто в магнитном сердечнике. В реальных конструкциях существует поле рассеяния, величина которого зависит от способа выполнения катушки и конструктивных особенностей сердечника. Чем больше толщина намотки, тем большая часть электромагнитного поля замыкается вне магнитопровода.

Этому способствует также качество сборки магнитопровода. Зазоры между пластинами способствуют резкому увеличению рассеивания. В связи с этим наилучшими свойствами обладают О-образные сердечники.

Формулы и измерение

Формулы для расчета индуктивности катушек довольно сложны и имеет различный вид для различных типов исполнения обмоток:

линейный проводник;
одновитковая катушка;
плоская катушка;
соленоидальная обмотка;
тороидальная форма.

Наибольшие сложности возникают при расчетах многовитковых многослойных катушек, то есть тех, которые составляют обмотку трансформаторов.

В подавляющем большинстве случаев точный расчет невозможен, поэтому приходится использовать примерные данные и уточнять их после проведения измерений.

Формулы для расчета индуктивности трансформатора основаны на расчетах соленоида:

L=µ_{µN²S/l, где}

µ0 – магнитная постоянная;

µ – магнитная проницаемость сердечника;

N – количество витков;

S – площадь одного витка;

l – длина обмотки.

Для измерения индуктивности существует несколько методик и приборов, созданных на их основе. В большинстве случаев измерение производится путем вычислений индуктивного сопротивления катушки при подаче образцового напряжения заданной частоты и измеренного значения тока через обмотку.

В специализированных приборах вычисления производятся автоматически, и пользователь только считывает показания шкалы прибора, выраженные в единицах индуктивности – Гн, мГн или мкГн.

Как измерить в домашних условиях

Приборы для непосредственного измерения индуктивности имеют высокую стоимость и редко используются в домашних условиях. С приемлемой точностью результаты можно получить, используя обычные приборы для измерения переменного тока: амперметр и вольтметр. Также необходим омметр.

Порядок действий следующий:

При помощи омметра определяют активное сопротивление обмотки R.
Подключают трансформатор последовательно с амперметром в сеть.
Параллельно обмотке подключают вольтметр.
По показаниям приборов определяют полное сопротивление трансформатора: Z=U/I
Индуктивное сопротивление находят, вычитая из полного сопротивления активное: X_L=Z-R
Индуктивность определяется по формуле: L=X_L/(2πf), где π – число пи 3.14, f – частота измерений.

Как правило, активное сопротивление намотки значительно (на несколько порядков) меньше индуктивного, поэтому можно его не учитывать. Именно поэтому, включение трансформатора в цепь постоянного напряжения вызывает короткое замыкание. Ток обмотки при этом будет ограничиваться только активным сопротивлением.

Пример расчета

К примеру, требуется рассчитать индуктивность первичной обмотки трансформатора питания. Путем измерений определено:

Сопротивление обмотки 3 Ом.
Напряжение сети 220 В.
Частота питающего напряжения 50 Гц.
Ток холостого хода 05 А.

Полное сопротивление:

Z=U/I=220/0.05=4400 Ом

Активное сопротивление меньше полного в 10000 раз и его можно не учитывать.

Определяем индуктивность:

L=X_L/(2πf) =4400/ (2∙3.14∙50) =14 Гн.

Индуктивность трансформатора

Итак, явление взаимной индукции используется в широко распространенных устройствах – трансформаторах.

Трансформатор был изобретен Яблочковым, русским ученым, в 1876 г. для раздельного питания отдельных электрических источников света (свечи Яблочкова).

Рассчитаем взаимную индуктивность двух катушек и , намотанных на общий сердечник (рис. 5.5).

Когда в первой катушке идет ток , в сердечнике возникает магнитная индукция и магнитный поток Ф через поперечное сечение S.

Рис. 5.5.

Магнитное поле тороида можно рассчитать по формуле

Через вторую обмотку проходит полный магнитный поток ,

сцепленный со второй обмоткой:

здесь – потокосцепление, которое можно найти по формуле:

По определению, взаимная индуктивность двух катушек равна:

К первичной обмотке подключена переменная ЭДС . По закону Ома ток в этой цепи будет определяться алгебраической суммой внешней ЭДС и ЭДС индукции.

где – сопротивление обмотки.

– делают малым (медные провода) и . Тогда

Во второй обмотке, по аналогии, , отсюда

(5.4.1)

Если пренебречь потерями, т.е. предположить, что , то

(5.4.2)

Коэффициент трансформации будет равен:

Онлайн расчет трансформатора за 6 простых шагов

Ремонт современных электрических приборов и изготовление самодельных конструкций часто связаны с блоками питания, пускозарядными и другими устройствами, использующими трансформаторное преобразование энергии. Их состояние надо уметь анализировать и оценивать.

Считаю, что вам поможет выполнить расчет трансформатора онлайн калькулятор, работающий по подготовленному алгоритму, или старый проверенный дедовский метод с формулами, требующий вдумчивого отношения. Испытайте оба способа, используйте лучший.

Содержание статьи

Сразу заостряю ваше внимание на том вопросе, что приводимые методики не способны точно учесть магнитные свойства сердечника, который может быть выполнен из разных сортов электротехнических стали.

Поэтому реальные электрические характеристики собранного трансформатора могут отличаться на сколько-то вольт или число ампер от полученного расчетного значения. На практике это обычно не критично, но, всегда может быть откорректировано изменением числа количества в одной из обмоток.

Поперечное сечение магнитопровода передает первичную энергию магнитным потоком во вторичную обмотку. Обладая определенным магнитным сопротивлением, оно ограничивает процесс трансформации.

От формы, материала и сечения сердечника зависит мощность, которую можно преобразовывать и нормально передавать во вторичную цепь.

Как пользоваться онлайн калькулятором для расчета трансформатора пошагово

Подготовка исходных данных за 6 простых шагов

Шаг №1. Указание формы сердечника и его поперечного сечения

Лучшим распределением магнитного потока обладают сердечники, набранные из Ш-образных пластин. Кольцевая форма из П-образных составляющих деталей обладает большим сопротивлением.

Для проведения расчета надо указать форму сердечника по виду пластины (кликом по точке) и его измеренные линейные размеры:

Ширину пластины под катушкой с обмоткой.
Толщину набранного пакета.

Вставьте эти данные в соответствующие ячейки таблицы.

Шаг №2. Выбор напряжений

Трансформатор создается как повышающей, понижающей (что в принципе обратимо) или разделительной конструкцией. В любом случае вам необходимо указать, какие напряжения вам нужны на его первичной и вторичной обмотке в вольтах.

Заполните указанные ячейки.

Шаг №3. Частота сигнала переменного тока

По умолчанию выставлена стандартная величина бытовой сети 50 герц. При необходимости ее нужно изменить на требуемую по другому расчету. Но, для высокочастотных трансформаторов, используемых в импульсных блоках питания, эта методика не предназначена.

Их создают из других материалов сердечника и рассчитывают иными способами.

Шаг №4. Коэффициент полезного действия

У обычных моделей сухих трансформаторов КПД зависит от приложенной электрической мощности и вычисляется усредненным значением.

Но, вы можете откорректировать его значение вручную.

Шаг №5. Магнитная индуктивность

Параметр определяет зависимость магнитного потока от геометрических размеров и формы проводника, по которому протекает ток.

По умолчанию для расчета трансформаторов принят усредненный параметр в 1,3 тесла. Его можно корректировать.

Шаг №6. Плотность тока

Термин используется для выбора провода обмотки по условиям эксплуатации. Среднее значение для меди принято 3,5 ампера на квадратный миллиметр поперечного сечения.

Для работы трансформатора в условиях повышенного нагрева его следует уменьшить. При принудительном охлаждении или пониженных нагрузках допустимо увеличить. Однако 3,5 А/мм кв вполне подходит для бытовых устройств.

Выполнение онлайн расчета трансформатора

После заполнения ячеек с исходными данными нажимаете на кнопку «Рассчитать». Программа автоматически обрабатывает введенные данные и показывает результаты расчета таблицей.

Как рассчитать силовой трансформатор по формулам за 5 этапов

Привожу упрощенную методику, которой пользуюсь уже несколько десятков лет для создания и проверки самодельных трансформаторных устройств из железа неизвестной марки по мощности нагрузки.

По ней мне практически всегда получалось намотать схему с первой попытки. Очень редко приходилось добавлять или уменьшать некоторое количество витков.

Этап №1. Как мощность сухого трансформатора влияет на форму и поперечное сечение магнитопровода

В основу расчета положено среднее соотношение коэффициента полезного действия ŋ, как отношение электрической мощности S2, преобразованной во вторичной обмотке к приложенной полной S1 в первичной.

ŋ = S1 / S2

Потери мощности во вторичной обмотке оценивают по статистической таблице.

Мощность трансформатора, ватты	Коэффициент полезного действия ŋ
15÷50	0,50÷0,80
50÷150	0,80÷0,90
150÷300	0,90÷0,93
300÷1000	0,93÷0,95
>1000	0.95÷0,98

Электрическая мощность устройства определяется произведением номинального тока, протекающего по первичной обмотке в амперах, на напряжение бытовой проводки в вольтах.

Она преобразуется в магнитную энергию, протекающую по сердечнику, полноценно распределяясь в нем в зависимости от формы распределения потоков:

для кольцевой фигуры из П-образных пластин площадь поперечного сечения под катушкой магнитопровода рассчитывается как Qc=√S1;
у сердечника из Ш-образных пластин Qc=0,7√S1.

Таким образом, первый этап расчета позволяет: зная необходимую величину первичной или вторичной мощности подобрать магнитопровод по форме и поперечному сечению сердечника;или по габаритам имеющегося магнитопровода оценить электрические мощности, которые сможет пропускать проектируемый трансформатор.

Этап №2. Особенности вычисления коэффициента трансформации и токов внутри обмоток

Силовой трансформатор создается для преобразования электрической энергии одной величины напряжения в другое, например, U1=220 вольт на входе и U2=24 V — на выходе.

Коэффициент трансформации в приведенном примере записывается как выражение 220/24 или дробь с первичной величиной напряжения в числителе, а вторичной — знаменателе. Он же позволяет определить соотношение числа витков между обмотками.

n = W1 / W2

Коэффициент трансформации трансформатора

На первом этапе мы уже определили электрические мощности каждой обмотки. По ним и величине напряжения необходимо рассчитать силу электрического тока I=S/U внутри любой катушки.

Этап №3. Как вычислить диаметры медного провода для каждой обмотки

При определении поперечного сечения проводника катушки используется эмпирическое выражение, учитывающее, что плотность тока лежит в пределах 1,8÷3 ампера на квадратный миллиметр.

Величину тока в амперах для каждой обмотки мы определили на предыдущем шаге.

Теперь просто извлекаем из нее квадратный корень и умножаем на коэффициент 0,8. Полученное число записываем в миллиметрах. Это расчетный диаметр провода для катушки.

Он подобран с учетом выделения допустимого тепла из-за протекающего по нему тока. Если место в окне сердечника позволяет, то диаметр можно немного увеличить. Тогда эти обмотки будут лучше приспособлены к тепловым нагрузкам.

Когда даже при плотной намотке все витки провода не вмещаются в окне магнитопровода, то его поперечное сечение допустимо чуть уменьшить. Но, такой трансформатор следует использовать для кратковременной работы и последующего охлаждения.

При выборе диаметра провода добиваются оптимального соотношения между его нагревом при эксплуатации и габаритами свободного пространства внутри сердечника, позволяющими разместить все обмотки.

Этап №4. Определение числа витков обмоток по характеристикам электротехнической стали: важные моменты

Вычисление основано на использовании магнитных свойств железа сердечника. Промышленные трансформаторы собираются из разных сортов электротехнической стали, подбираемые под конкретные условия работы. Они рассчитываются по сложным, индивидуальным алгоритмам.

Домашнему мастеру достаются магнитопроводы неизвестной марки, определить электротехнические характеристики которой ему практически не реально. Поэтому формулы учитывают усредненные параметры, которые не сложно откорректировать при наладке.

Для расчета вводится эмпирический коэффициент ω’. Он учитывает величину напряжения в вольтах, которое наводится в одном витке катушки и связан с поперечным сечением магнитопровода Qc (см кв).

ω’=45/Qc (виток/вольт)

В первичной обмотке число витков вычислим, как W1= ω’∙U1, а во вторичной — W2= ω’∙U2.

Этап №5. Учет свободного места внутри окна магнитопровода

На этом шаге требуется прикинуть: войдут ли все обмотки в свободное пространство окна сердечника с учетом габаритов катушки.

Для этого допускаем, что провод имеет сечение не круглое, а квадрата со стороной одного диаметра. Тогда при совершенно идеальной плотной укладке он займет площадь, равную произведению единичного сечения на количество витков.

Увеличиваем эту площадь процентов на 30, ибо так идеально намотать витки не получится. Это будет место внутри полостей катушки, а она еще займет определенное пространство.

Далее сравниваем полученные площади для катушек каждой обмотки с окном магнитопровода и делаем выводы.

Второй способ оценки — мотать витки «на удачу». Им можно пользоваться, если новая конструкция перематывается проводом со старых рабочих катушек на том же сердечнике.

4 практических совета по наладке и сборке трансформатора: личный опыт

Сборка магнитопровода

Степень сжатия пластин влияет на шумы, издаваемые железом сердечника при вибрациях от протекающего по нему магнитного потока.

Одновременно не плотное прилегание железа с воздушными зазорами увеличивает магнитное сопротивление, вызывает дополнительные потери энергии.

Если для стягивания пластин используются металлические шпильки, то их надо изолировать от железа сердечника бумажными вставками и картонными шайбами.

Иначе по этому креплению возникнет искусственно созданный короткозамкнутый виток. В нем станет наводиться дополнительная ЭДС, значительно снижающая коэффициент полезного действия.

Состояние изоляции крепежных болтов относительно железа сердечника проверяют мегаомметром с напряжением от 1000 вольт. Показание должно быть не менее 0,5 Мом.

Расчет провода по плотности тока

Оптимальные размеры трансформатора играют важную роль для устройств, работающих при экстремальных нагрузках.

Для питающей обмотки, подключенной к бытовой проводке лучше выбирать плотность тока из расчета 2 А/мм кв, а для остальных — 2,5.

Способы намотки витков

Быстрая навивка на станке «внавал» занимает повышенный объем и нормально работает при относительно небольших диаметрах провода.

Качественную укладку обеспечивает намотка плотными витками один возле другого с расположением их рядами и прокладкой ровными слоями изоляции из конденсаторной бумаги, лакоткани, других материалов.

Хорошо подходят для создания диэлектрического слоя целлофановые (не из полиэтилена) ленты. Можно резать их от упаковок сигарет. Отлично справляется с задачами слоя изоляции кулинарная пленка для запекания мясных продуктов и выпечек.

Она же придает красивый вид внешнему покрытию катушки, одновременно обеспечивая ее защиту от механических повреждений.

Обмотки сварочных и пускозарядных устройств, работающие в экстремальных условиях с высокими нагрузками, желательно дополнительно пропитывать между рядами слоями силикатного клея (жидкое стекло).

Ему требуется дать время, чтобы засох. После этого наматывают очередной слой, что значительно удлиняет сроки сборки. Зато созданный по такой технологии трансформатор хорошо выдерживает высокие температурные нагрузки без создания межвитковых замыканий.

Как вариант такой защиты работает пропитка рядов провода разогретым воском, но, жидкое стекло обладает лучшей изоляцией.

Когда длины провода не хватает для всей обмотки, то его соединяют. Подключение следует делать не внутри катушки, а снаружи. Это позволит регулировать выходное напряжение и силу тока.

Замер тока на холостом ходу трансформатора

Мощные сварочные аппараты требуют точного подбора объема пластин и количества витков под рабочее напряжение, что взаимосвязано.

Выполнить качественную наладку позволяет замер тока холостого хода при оптимальной величине напряжения на входной обмотке питания.

Его значение должно укладываться в предел 100÷150 миллиампер из расчета на каждые 100 ватт приложенной мощности для трансформаторных изделий длительного включения. Когда используется режим кратковременной работы с частыми остановками, то его можно увеличить до 400÷500 мА.

Выполняя расчет трансформатора онлайн калькулятором или проверку его вычислений дедовскими формулами, вам придется собирать всю конструкцию в железе и проводах. При первых сборках своими руками можно наделать много досадных ошибок.

Чтобы их избежать рекомендую посмотреть видеоролик владельца Юность Ru. Он очень подробно и понятно объясняет технологию сборки и расчета. Под видео расположено много полезных комментариев, с которыми тоже следует ознакомиться.

Если заметите в ролике некоторые моменты, которые немного отличаются от моих рекомендаций, то можете задавать вопросы в комментариях. Обязательно обсудим.

Индуктивности обмоток трансформатора и электромагнитное рассеяние

Дата публикации: 29 июля 2013.
Категория: Трансформаторы.

Индуктивности обмоток

В трансформаторах со стальным магнитопроводом магнитная проницаемость стали µ во время цикла перемагничивания непостоянна. Поэтому в течение этого цикла непостоянны также собственные L и взаимные М индуктивности обмоток трансформатора. В результате такого непостоянства µ при подключении трансформатора к сети с синусоидальным напряжем в его намагничивающем токе i₀ возникают высшие гармоники (смотрите статью «Явления, возникающие при намагничивании магнитопроводов трансформаторов»).

Рисунок 1. Магнитные потоки трансформатора при одностороннем намагничивании (i₁ ≠ 0, i₂ = 0)

При работе трансформатора на ток i₀ накладывается ток нагрузки, по отношению к которому ток i₀ и, в особенности, его высшие гармоники малы. Поэтому при исследовании режимов работы трансформатора указанными гармониками можно пренебречь и учитывать только основную гармонику тока i₀. Это равносильно допущению, что во время цикла перемагничивания µ, L и M постоянны. Влияние насыщения магнитопровода при этом можно учесть, принимая в расчет при разных режимах работы трансформатора, при разных амплитудах потока магнитопровода, значения µ, L и M для данного режима работы. В соответствии с изложенным будем полагать, что µ, L и M постоянны.

Рассмотрим индуктивности и индуктивные сопротивления обмоток, обусловленные магнитным потоком магнитопровода Ф_с, все силовые линии которого полностью замыкаются по замкнутому магнитопроводу и поэтому сцепляются со всеми витками первичной и вторичной обмоток (рисунок 1).

Пусть поток Ф_с создается током первичной обмотки i₁, когда ток вторичной обмотки i₂ = 0. Значения Ф_с и i₁ могут быть известны, например, из данных расчета магнитной цепи или из опыта. Тогда собственная индуктивность первичной обмотки от потока в магнитопроводе

L_с1 = w₁ × Ф_с / i₁.

(1)

Величину L_с1 можно выразить также через магнитное сопротивление магнитопровода

(2)

где l_k, S_k и µ_k соответственно означают длину, площадь сечения и магнитную проницаемость k-го участка магнитной цепи. При этом

Ф_c = F₁ / R_µc = w₁× i₁ / R_µc.

(3)

и после подстановки этого значения Ф_с в выражение (1) получим

Отметим, что значение R_µc также может быть определено по данным расчета магнитной цепи или из данных опыта по соотношению (3).

Аналогично индуктивность вторичной обмотки от потока магнитопровода

а взаимная индуктивность первичной и вторичной обмоток от потока магнитопровода

M_с = w₁ × w₂ / R_µс

(6)

Картина магнитного поля, замыкающегося целиком по магнитопроводу, одинакова независимо от того, какой из обмоток это поле создается. Поэтому и магнитное сопротивление потоку Ф_с одинаково для поля обеих обмоток и в равенства (4), (5) и (6) входит одинаковая величина R_µс. Вследствие этого также

(7)

Кроме потока Ф_с, ток первичной обмотки i₁ создает также поток Ф_в1 (рисунок 1), силовые линии которого замыкаются частично по воздуху или через трансформаторное масло. Потокосцеплениям Ψ_в1 и Ψ_в12 этого потока с первичной и вторичной обмотками соответствует собственная индуктивность первичной обмотки

L_в1 = Ψ_в1 / i₁

и взаимная индуктивность двух обмоток

M_в12 = Ψ_в12 / i₁.

Точно так же при питании вторичной обмотки током i₂ создается поток Ф_в2, замыкающийся частично по воздуху. Потокосцеплениям Ψ_в2 и Ψ_в21 этого потока с вторичной и первичной обмотками соответствует собственная индуктивность вторичной обмотки

L_в2 = Ψ_в2 / i₂

и взаимная индуктивность двух обмоток

M_в21 = Ψ_в21 / i₂.

При этом, согласно принципу взаимности,

M_в12 = M_в21 = M_в

Поля потоков Ф_в1 и Ф_в2 имеют гораздо более сложный характер, чем поле потока Ф_с. Отдельные магнитные линии этих потоков сцепляются с неполными и разными числами витков первичной и вторичной обмоток. Поэтому в отличие от L_с2 [смотрите соотношение (7)]

(8)

Полные собственные индуктивности первичной и вторичной обмоток

L₁₁ = L_с1 + L_в1; L₂₂ = L_с2 + L_в2,

(9)

и полная взаимная индуктивность

Первые слагаемые равенств (9) и (10) значительно больше вторых, так как потоки через воздух относительно малы.

Понятие об электромагнитном рассеянии

Полнота электромагнитной связи двух индуктивно связанных цепей характеризуется коэффициентом связи этих цепей

(11)

Как известно из курса теоретических основ электротехники, в реальных условиях всегда c < 1.

Если бы в трансформаторе отсутствовали потоки Ф_в1 и Ф_в2, замыкающиеся по воздуху, то L₁₁ = L_c1, L₂₂ = L_c2, M = M_c, и в этом случае в соответствии с равенствами (4), (5), (6) и (11)

Таким образом, неполнота электромагнитной связи в трансформаторе, выражаемая неравенством c < 1, обусловлена наличием потоков Ф_в1 и Ф_в2 или, точнее, неодинаковым их сцеплением с обеими обмотками. Условие c = 1 было бы достигнуто только в том случае, если бы удалось полностью совместить первичную и вторичную обмотки, что фактически невозможно.
Явление неполной электромагнитной связи называется электромагнитным рассеянием.

Наряду с соотношением (11) целесообразно ввести в рассмотрение коэффициент электромагнитного рассеяния

(12)

Чем меньше c и чем больше σ, тем больше рассеяние.

Ввиду того что явление рассеяния обусловлено неодинаковостью или неполнотой сцепления потоков Ф_в1 и Ф_в2, проходящих по воздуху, с обеими обмотками, эти потоки называют часто также потоками рассеяния, однако это название до некоторой степени условно, так как потоки Ф_в1 и Ф_в2 обусловливают также явление взаимной индукции, поскольку M_в ≠ 0. Степень неполноты электромагнитной связи, или величина электромагнитного рассеяния, оказывает большое влияние на многие технические показатели и характеристики трансформаторов и вращающихся электрических машин.

В трансформаторах с ферромагнитным магнитопроводом потоки Ф_в1 и Ф_в2 относительно малы.

Поэтому электромагнитная связь в трансформаторах чрезвычайно высока, а рассеяние мало.

В силовых трансформаторах, например, c = 0,998 – 0,9995 и соответственно σ = 0,001 – 0,004.

Вследствие этого значение σ, определяемое по формуле (12), представляет собой разность весьма близких величин и вычисление σ по этой формуле связано с очень большими погрешностями, так как L₁₁, L₂₂ и M в практических устройствах не могут быть рассчитаны или определены из опыта с достаточной степенью точности. Поэтому возникает необходимость в непосредственном определении параметров, характеризующих электромагнитное рассеяние.

Источник: Вольдек А. И., «Электрические машины. Учебник для технических учебных заведений» – 3-е издание, переработанное – Ленинград: Энергия, 1978 – 832с.

О трансформаторе импульсном замолвите слово / Хабр Несмотря не то, что не так давно проскакивали довольно неплохо написанные статьи о расчете трансформатора импульсного источника питания, я предложу вашему вниманию свою методику, и не просто голую методику, а максимально прозрачное описание принципов, в ней использующихся.

Картинок не будет, будет около 18 несложных формул и много текста. Всех желающих приобщиться прошу на борт.

Я хочу поведать вам о том, как расчитать такого хитрого зверя, как импульсный трансформатор обратноходового источника питания. Обратноходовик, или FlyBack — это, наверное, самая популярная топология импульсного преобразователя. По моему мнению, в ИИП есть два очень важных и тонких момента — это трансформатор и петля обратной связи. В данной статье я хочу показать один из возможных наборов несложных математических уравнений, решая которые мы можем получить данные вполне реального трансформатора для флайбэка.

В интернете, в различных авторских статьях, или в AppNotes различных производетелей, можно найти различные методики расчета, которые зачастую максимально «сжаты», так, что из формул совершенно не понятно, как они получается. Я хочу сделать упор не на точность, а на максимальную наглядность и прозрачность производимых расчетов, так чтобы вы поняли, «почему так».

Далее постараюсь писать кратко и емко, так, чтобы вы смогли сесть и посчитать сразу после прочтения статьи. Эпюры напряжений и токов в обратноходовом источнике рисовать не буду, считаю, что вы достаточно подготовлены для того, что бы такие термины, как «индуктивность рассеяния», «отраженное напряжение», «пиковое значение тока через силовой ключ», «размагничивание магнитопровода» вам понятны.

Итак, считать будем трансформатор обратноходового источника питания, без корректора коэфициента мощности, как наиболее распространенный, да и «расчётка» моя пока только под него заточена.

Отдельно сделаю примечание, что подразумевается т.н. квазирезонансный режим работы преобразователя, когда накачка энергии в трансформатор начинается сразу после полного размагничивания магнитопровода. Т.е. т.н. «коэффициент безразрывности тока» =1, т.е. как только вся энергия вытекла через вторичную обмотку(и рассеялась в снабберной цепи), сразу включаем ключ и накачиваем снова. Такой режим в последнее время очень популярен в обратноходовых источниках питания, т.к. позволяет чуток поднять КПД.

Заранее оговорюсь — нижеприведенная методика весьма груба, но она «железобетонно» работает, многократно проверена на реальных трансформаторах в реальных источниках питания.

Для начала скачайте расчетку, откройте, пробегитесь глазами. В нее уже «вбиты» значения для расчета трансформатора источника питания, с выходной мощностью 100Вт.

Расчетка: к сожалению, по какой-то неведомой мне причине, публичная ссылка не отображается.
Возможно публикация публичных ссылок противоречит правилам. Надеюсь на то, что модераторы услышат этот крик души и снизошлют на меня персональную настройку фильтра, а пока можете переписать в Эксель, или маткад, все нижеприводимые формулы и получить годный результат.

Итак, поехали. Для того, чтобы начать расчет нам потребуется задаться несколькими исходными параметрами (все они выделены зеленым цветом в расчетке), а именно:

1. Выходная мощность источника питания для которого делаем трансформатор (POUTmax).
2. Выходное напряжение источника (Uout)(1).
3. Выходное напряжение служебной обмотки (Ubias)(2).
4. Минимальное напряжение питающей сети (UACmin)(3).
5. Максимальное напряжение в сети (UACmax)(3).
6. Уровень пульсаций на фильтрующем конденсаторе сетевого выпрямителя (Urpl)(4).
7. Ожидаемый КПД трансформатора (берите 0,85 и не прогадаете) (ŋ).
8. Частота работы преобразователя (5).
9. Пиковое значение тока протекающего через ключ коммутирующий первичную обмотку (ILPRpeak) (6).

(1) Если выходные напряжения достаточно низкие- учитывайте прямое падение напряжения на диоде.
(2) В подавляющем большинстве конструкций источников питания, требуется третья обмотка, от которой будет питаться управляющая микросхема.
(3) Всегда берите с запасом, т.е. если указан диапазон 180-264, берите от 160 до 280.
(4) Этот параметр зачастую можно только угадать, берите 10% от постоянной составляющей на нем и не ошибетесь, по факту полученного рабочего прототипа «подрихтуете» расчет.
(5) Частота к преобразователях с ожиданием размагничивания сердечника- плавающая, берем «с потолка» такую, которую хотим получить при полной нагрузке.
(6) Я надеюсь вы в курсе, что форма тока треугольная, что коммутирует ключ, что такое ключ и т.п.

Итак, первая формула:
Начнем с определения индуктивности первичной обмотки, Lpr.

Lpr=(1000×2×POUTmax)/(ŋ×F×ILPRpeak^2 )     	(1)

Для упрощения я выкину КПД, и множитель 1000, который нужен только для приведения результата к микроГенри от Генри, получится нижеследующее уравнение:

Lpr=(2×POUTmax)/(F×ILPRpeak^2 )     		(1.1)

На первый взгляд совершенно непонятно как так получается. Давайте попробуем ее преобразовать. Перенеся множители справа-налево, получим.

(Lpr×ILPRpeak^2)/2=POUTmax/F       (1.2)

Преобразуем правую часть, получим:

(Lpr×ILPRpeak^2)/2=POUTmax×T	(1.3)

Итак, в левой части у нас энергия содержащаяся в индуктивности (учебник физики, если не понятно). В правой части имеем мощность которая расходуется за период работы преобразователя. Т.е. энергия запасенная в индуктивности первичной обмотки (на этапе накачки, от начала периода до размыкания ключа) равна мощности передаваемой в нагрузку за весь период T (от начала накачки, до полного исчерпания энергии в трансформаторе и начала нового импульса).

В установившемся режиме то, что закачали в трансформатор из сети, должно равняться тому, что слили в нагрузку. Т.е. все рассуждения предполагают, что наш источник уже работает, а не стартует.

Оставим-же пока эту формулу (1), мы потом воспользуемся ею в расчётке, я лишь хотел продемонстрировать как она так получается.
Теперь о параметрах. Присмотримся к формуле. Зафиксировав (выбрав на свое усмотрение) три из четырех неизвестных, мы можем получить значение четвертой.

Мощность (POUTmax), мы уже задали.

Частота, ее можно просто выбрать по своему желанию. Не мудрствуя лукаво тыкнем скажем 50кГц и не проиграем. Лезть за 150кГц не стоит, так как потери на переключение станут неоправданно высокими, да еще скинэффект, не нужно это нам во флайбэке.

Пиковое значение тока через первичную обмотку, и одновременно ключ- ILPRPeak, это параметр на нервах которого мы будем играть. Выбирая его значение ILPRPeak, мы изменяем Lpr, а вместе с ней еще много чего другого. В моей расчетке будем менять ILPRpeak и наблюдать за другими ячейками таблицы, в которых будут находится результаты других формул. Опять-же, ближе к реальности, для 100Вт источника можно задаться для начала ILPRpeak= 3…4A.

Просто попробуйте подставить в ячейку различные числа, и вы увидите, как изменятся другие производные параметры. В частности, выбирая пиковый ток «первички», мы смотрим на «отраженное» напряжение, и исходим из соображений наличествующих у нас ключей. Так же этот параметр влияет на пиковое значение тока «вторички», что тоже важно, ибо во флайбэках токи имеют форму прямоугольного треугольника, и пиковые значения в разы превышают действующие, т.е. если ток нагрузки 5А, то пиковое может быть и 50, ориентируйтесь на наличествующие диоды и потери в меди обмотки.

Вторая формула:

UDCmin=UACmin×1.41-Urpl     	(2)

Тут упрощать нечего, думаю понятно, что мы получаем самое худшее значение постоянного напряжения, с учетом просадки на буферном конденсаторе, что стоит за сетевым выпрямителем, или за ККМ.

Ton=(Lpr×ILPRpeak)/UDCmin    	(3)

В формуле (3) мы вычисляем, сколько времени должен быть открыт ключ, чтоб ток в индуктивности, при приложении к ней нашего самого худшего UDCmin вырос от нуля до желаемого ILPRpeak.

T=1/F×1000  		(4)

Частотой мы задались ранее, период посчитали в (4). На 1000 умножаем потому, что желаемую частоту мы записали в кГц а не в 1000-х Герц.

Toff=T-Ton    	(5)

Оставшаяся часть периода, которая будет посвящена передаче энергии в нагрузку, вычисляется по формуле (5).

Q=Toff/Ton    (6)

Максимальный коэффициент заполнения для худшего напряжения в сети и максимальной просадки на фильтрующем конденсаторе вычисляем в (6).

Urv=UDCmin×Ton/Toff    	(7)

«Отраженное» напряжение. Наш трансформатор, хоть и обратноходовый, но таки трансформатор, а значит коэффициент трансформации к нему так-же применим. Если на нашей вторичной обмотке во время протекания тока через выпрямительный диод, апряжение (например) 12.7В, то через соотношение количества витков это напряжение трансформируется в первичную обмотку (ведь магнитный поток «омывает» одновременно все обмотки).

Формула (7), немного хитрая, попробуем ее «раскрутить». Получим:

UDCmin×Ton=Urv×Toff 		(7.1)

(7.1) Демонстрирует один очень важный момент, называемый в народе «равенство вольт*секундных интервалов». Возможно справедливость утверждения (7.1) не очевидна, или не сразу понятна, пока используем полученное с помощью (7) численное значение как есть, в его правомерности не сомневайтесь.

UVTmax=UACmax×1.41+Urv 	(8)

Надеюсь вы хорошо понимаете, что на обратном ходу, первичная обмотка, для постоянного напряжения, что на фильтрующем конденсаторе- просто кусок проволоки, т.е. если наш фильтрующий конденсатор все еще заряжен до 310В, то при разомкнутом силовом ключе, протекании тока через вторичную обмотку, постоянка попросту «проходит» через первичку и прикладывается к ключу, но вместе с ней, к ключу добавляется еще отраженное напряжение. И самое печальное, что оно суммируется с постоянкой. И это без учета выброса от индуктивности рассеяния, имейте это ввиду, в расчетке данное обстоятельство специально выделено красным шрифтом.

Тогда (8) показывает, какое напряжение будет приложено к силовому ключу на обратном ходу. Можно сразу прибавить к максимальному напряжению, на которое расчитан ключ, еще сверху вольт этак 200 и не ошибетесь. Макетирование покажет реальную амплитуду выброса напряжения порожденного индуктивностью рассеяния.

Теперь можем посчитать коэффициент трансформации трансформатора, например таким образом:

Kfb=Uout/Urv 	(9)

Я называю этот коэффициент трансформации «обратным», т.к. считается он задом наперед. Теперь классический коэффициент трансформации, который можно получить:

K=1/Kfb 	(10)

Далее посчитаем максимальное напряжение, которое будет приложено к выпрямительному диоду на прямом ходу преобразователя. Думаю вы хорошо понимаете, что оно будет складываться из напряжения на фильтрующем конденсаторе нагрузки, которое в рабочем режиме, можно считать постоянным, и трансформированного, через коэффициент трансформации, напряжения приложенного к первичной обмотке.

UVDmax=Uout+(VACmax×1.41)/K  	(11)

И не забываем, что выбросы от паразитных индуктивностей обмоток трансформатора, действуют и на диод в т.ч. Если речь идет о источниках с высокими выходными напряжениями, берите запас по напряжению минимум 200В. Для низковольтных, как минимум 1.5, и внимательно смотрите осциллографом на выпрямитель.

Далее.

Lsec=Lpr/K^2   (12)

Из (12) получаем индуктивность вторичной обмотки трансформатора. Правило которое используется в формуле гласит, что «индуктивности обмоток трансформатора соотносятся как квадраты их витков», т.к. выражение можно представить как:

Lsec/Lpr=N2^2/N1^2   (12.1)  ( N2^2/N1^2 =K^2)

Далее посчитаем пиковый ток вторичной обмотки. Готовьтесь получить тут достаточно большие цифры, потому, что это «обратноход», и ток у него во «вторичке» — треугольный, и пиковое значение может быть ощутимо больше тока нагрузки.

ILSECpeak=√(1000×2×POUTmax)/(F×ŋ×Lsec) 	(13)

Данная формула преобразуется точно также как и первая формула для ILPRpeak.

ILSECrms=ILSECpeak√(1-Q)/3 	(14)

В (14) вычисляется действующее значение тока через вторичную обмотку трансформатора. Обяснить почему корень из (1-Q)/3 я не могу, вероятно это можно объяснить построив эпюры и прибегнув к геометрии. Тут же прикинем и действующее значение тока первичной обмотки.

ILPRrms=ILPRmax√Q/3 	(15)

Итак, индуктивности, токи, частоты посчитали. А как выбрать магнитопровод, спросите вы, как расчитать немагнитный зазор? Для начала мы его «прикинем», основываясь на своем жизненном опыте, а «загнав» его параметры в расчетку, поглядев посчитанную индукцию, можно выбрать другой магнитопровод. Вот захотелось мне источник мощностью 100Вт, с выходным напряжением 12В. Беру я «с потолка» магнитопровод типоразмера PQ2620.

Из его Datasheet выписываю Ae, предполагаемый зазор, и Коэффициент индуктивности для данного зазора (в даташитах Epcos, часто приводится таблица со стандартными зазорами для данного магнитопровода, и значениях Al и эквивалентной проницаемости). Если-же данных о коэфициенте Al для желаемого вами зазора, нет, придется его(зазор) изготовить, намотать пробные 100 витков, и посчитать по простой формуле Al=√(L/N^2), где L- измеренное значение индуктивности на сердечнике с пропиленным вами зазором, N — количество витков, что вы набросали(рекомендую мотать пробных 100 витков).

Объяснять что Такое Ae, G, и Al не буду, предполагая, что вы и сами знаете, зачем нужен зазор в магнитопроводе, и что такое Al. Также в расчетку можно вписать эквивалентную проницаемость сердечника с зазором, но она там не используется, чисто для красоты). В формуле (16) считаем необходимое количество витков.

Npr=√Lpr/Al 	(16)

Один из самых важных параметров для трансформатора- пиковое значение потока магнитной индукции.

B=(Lpr×ILPRpeak)/(Npr×Ae) 	(17)

Превышать значение 0,3 я категорически не рекомендую, а 0,4 это уже катастрофа. Так совпало, что данный магнитопровод вроде как вполне подходит под наши нужды. Индукция меньше 0,3Тл, так и хочется его заложить под наши нужды. К сожалению, расчетка не содержит формул для расчета заполненности окна магнитопровода медью, поэтому дать по ней окончательный вердикт — нельзя.

Если же индукция больше 0,3Тл, можем или выбрать более крупный магнитопровод, или увеличить зазор. Увеличив зазор мы получим уже другое значение Al и соотв. значение потока индукции.

Вообще, жизненный опыт показывает, что лучше не лезть в зазоры более 1.5мм., ибо им свойственны свои паразитные явления, такие как выпучивание линий магнитного поля, разогрев витков находящихся вблизи зазора, до температур, при которых им может настать «хана», короче от 0.2мм до 1.5мм. Меньше 0.2- температурное расширение материала может существенно изменить параметры трансформатора. Больше 1.5мм — написал выше.

Выбирая магнитопровод, а именно сравнивая различные модели, только по поперечному сечению керна (Ae), можно упустить из виду то, что длина магнитной линии тоже влияет на Al при том-же сечении, и зазоре.

Например магнитопровод PQ2620 имеет площадь сечения керна 122мм.кв, а ETD34 только 97мм.кв., но длины магнитных линий этих магнитопроводов различны, и через ETD34 можно так-же успешно прокачать 100Вт, как и через PQ2620. Я к тому, что берите и подставляйте в расчетку все феррриты, что находятся вблизи тех размеров, что, как вам кажется, могут прокачать желаемую мощность.
После расчета магнитной индукции в расчетке идет расчет количества витков вторичной обмотки и вспомогательной обмотки, на них специально останавливаться не буду, методология та-же, что и ранее.

Я надеюсь написанное выше будет вам полезно. Разработка ИИП это огромный пласт прикладной науки, и сия «расчетка» лишь маленький листик одного из талмудов, в котором собран весь опыт человечества, но она крайне полезна в прикладном плане, для разработки простеньких «флайбэков».

Моя «расчетка» (а на самом деле не моя, а унаследованная от идейного вдохновителя) довольно примитивный инструмент, поэтому я могу порекомендовать использовать сборник программ Владимира Денисенко, что легко находятся через поисковик. Тех, кто «рубит» в «силовой» теме, и имеет что сказать- вэлкам в коменты. Любая критика приветствуется!

Что непонятно — спрашивайте, я дополню статью более детальными объяснениями.

Расчёт и изготовление трансформатора для импульсного блока питания

«Как-то лет в 12 нашёл я старый трансформатор, слегка перемотал его и включил.
Энергосистема опознала нового радиотехника и приветливо моргнула всем домом.
Вот так я и начал изучать силовую электронику».

А тем временем традиционные линейные источники питания на силовых трансформаторах всё чаще стали вытесняться своими импульсными коллегами.
При этом, что бы там не говорили авторитетные товарищи про многочисленные технические достоинства импульсных преобразователей, плюс у них только один — массогабаритные показатели. Всё остальное — сплошной минус.
Однако этот единственный плюс оказался настолько жирным, что заслонил собой все многочисленные минусы, особенно в тех замесах, когда к электроустройствам не предъявляется каких-либо жёстких требований.

Наиболее популярными среди радиолюбителей стали сетевые источники питания, собранные на микросхемах IR2153 и IR2155, которые представляют из себя самотактируемые высоковольтные драйверы, позволяющие получать полумостовые импульсные блоки питания мощностью до 1,5 кВт с минимальной обвязкой.
И если сердце импульсного блока питания колотится внутри готовой буржуйской микросхемы, то главным, ответственным за электрохозяйство среди остальных наружных образований, безусловно, является правильно выполненный трансформатор.

Для наших высокотоковых дел лучше всего применять трансформаторы с тороидальным магнитопроводом. В сравнении с другими сердечниками они имеют меньший вес и габариты, а также отличаются лучшими условиями охлаждения обмоток и повышенным КПД.
Но самое главное — при равномерном распределении обмоток по периметру сердечника практически отсутствует магнитное поле рассеяния, что в большинстве случаев отметает потребность в тщательном экранировании трансформаторов.

По сути дела, умных статей в сети на предмет расчёта импульсных трансформаторов великое множество, с картинками, формулами, таблицами и прочими авторитетными причиндалами. Наблюдаются в свободном доступе и многочисленные онлайн-калькуляторы на интересующую нас тематику.

И снизошла б на нас благодать неземная, кабы вся полученная информация сложилась в наших любознательных головах в единое большое целое.
Да вот, что-то не получается. Ништяк обламывается из-за того, что следуя этими различным компетентным источникам, мы устойчиво получаем на выходе и различные результаты.

Вот и гуляют по сети идентичные радиолюбительские схемы импульсных блоков питания на IR2153 с идентичными заявленными характеристиками, трансформаторами на одних и тех же кольцах, но радикально не идентичным количеством витков первичных обмоток трансформаторов.
А когда эти различия выражаются многими разами, то возникает желание «что-то подправить в консерватории». Объясняется это желание просто — существенной зависимостью КПД устройства от значения индуктивности, на которую нагружены ключевые транзисторы преобразователя. А в качестве этой индуктивности как раз и выступает первичная обмотка импульсного трансформатора.

А для лучшего восприятия сказанного, приведу типовую схему источника питания на IR2153, не обременённую ни устройством защиты, ни какими-либо другими излишествами.

Рис.1

Схема проверена временем и многочисленными опытами изрядно пощипанных током, неустрашимых радиолюбителей, так что не работать в ней — просто нечему.

Ну и наконец, переходим к расчёту импульсного трансформатора.

Мотать его будем на бюджетных низкочастотных ферритовых кольцах отечественного производителя 2000НМ или импортных — EPCOS N87, а для начала определимся с габаритной мощностью тороидального ферритового магнитопровода.

Концепция выбора габаритной мощности с запасом в 10% от максимальной мощности в нагрузке, заложенная в режимы автоматического подбора сердечника в большинстве калькуляторов, хотя и не противоречит теоретическим расчётам, учитывающим высокий КПД импульсного трансформатора, но всё же наводит на грустную мысль о ненадлежащей надёжности и возможной скорой кончине полученного моточного изделия.
Куда мне ближе трактовка этого параметра, описанная в литературе: P_габ>1,25×Р_н .

Расчёты поведём исходя из частоты работы преобразователя IR2153, равной 50 кГц. Почему именно такой?
Не ниже, потому что такой выбор частоты позволяет нам уложиться в достаточно компактные размеры ферритового сердечника, и при этом гарантирует полное отсутствие сигналов комбинационных частот ниже 30 кГц при работе девайса в составе качественной звуковоспроизводящей аппаратуры.
А не выше, потому что мы пилоты… А феррит у нас низкочастотный и может почахнуть и ответить значительным снижением магнитной проницаемости при частотах свыше 60-70 кГц. Не забываем, что сигнал, на выходах ключей имеет форму меандра и совокупная амплитуда гармоник, с частотами в 3-9 раз превышающими основную, имеет весьма ощутимую величину.

Параметры первичной обмотки трансформатора рассчитаем при помощи программы Lite-CalcIT, позволяющей, на мой взгляд, вполне адекватно оценить как размер сердечника, так и количество витков первичной обмотки.
Результаты сведём в таблицу.

Мощность блока питания, Вт	Размеры кольца, мм ; (габаритная мощность, Вт)	Количество витков первичной обмотки	Индуктивность обмотки, мГн
25	R 20×12×6 2000НМ (33,8 Вт) R 22,1×13,7×6,35 №87 (51,5 Вт)	208 (d=0,25мм) 152 (d=0,25мм)	51,9 30,9
50	R 22,1×13,7×12,5 №87 (100,1 Вт) R 22,1×13,7×7,9 №87 (63,9 Вт) R 27×18×6 2000НМ (85,3 Вт)	78 (d=0,35мм) 122 (d=0,35мм) 185 (d=0,35мм)	15,9 24,8 32,8
100	R 28×16×9 2000НМ (136 Вт) R 32,0×20,0×6,0 №27 (141 Вт)	93 (d=0,5мм) 139 (d=0,5мм)	17,0 19,3
200	R 28×16×18 2000НМ (268 Вт) R 29,5×19,0×14,9 №87 (297 Вт) R 30,5×20,0×12,5 №87 (265 Вт) R 34,0×20,5×10,0 №87 (294 Вт) R 34,0×20,5×12,5 №87 (371 Вт) R 38×24×7 2000НМ (278 Вт)	47 (d=0,7мм) 52 (d=0,7мм) 62 (d=0,7мм) 61 (d=0,7мм) 49 (d=0,7мм) 102 (d=0,7мм)	8,7 7,8 8,9 8,3 6,7 13,2
400	R 36,0×23,0×15,0 №87 (552 Вт) R 38×24×14 2000НМ (565 Вт) R 40×25×11 2000НМ (500 Вт)	42 (d=1,0мм) 51 (d=1,0мм) 61 (d=1,0мм)	5,2 6,6 7,6
800	R 40×25×22 2000НМ (998 Вт) R 45×28×16 2000НМ (1036 Вт) R 45×28×24 2000НМ (1580 Вт)	31 (d=1,6мм) 37 (d=1,6мм) 25 (d=1,6мм)	3.9 4,1 2,8
1500	R 50,0×30,0×20,0 №87 (1907 Вт) R 58,3×32,0×18,0 №87 (2570 Вт)	21 (d=2×1,5мм) 18 (d=2×1,5мм)	2,0 1,5

Как следует мотать первичную обмотку трансформатора?

Рис. 2 а) б) в) г) д)

Если используются кольца 2000НМ отечественного производителя, то для начала — посредством наждачной бумаги скругляем наружные острые грани до состояния, приведённого на Рис.2 а).

Далее на кольцо следует намотать термостойкую изоляционную прокладку (Рис.2 б). В качестве изоляционного материала можно выбрать лакоткань, стеклолакоткань, киперную ленту, или сантехническую фторопластовую ленту.

Для буржуйских колец фирмы EPCOS первые два пункта практической ценности не имеют.

Настало время намотать однослойную обмотку «виток к витку» (Рис.2 в). Обмотка должна быть равномерно распределена по периметру магнитопровода — это важно!

Если в закромах радиолюбительского хозяйства не завалялся обмоточный провод необходимого диаметра, то обмотку можно намотать сразу в два, или несколько проводов меньшего диаметра (Рис.2 г). Не забываем, что зависимость тока от диаметра квадратичная и если, к примеру, нам надо заменить провод диаметром 1мм, то это будет не два провода по 0,5мм, а четыре (или два провода по 0,7мм).

Ну и для завершения первичного процесса поверх первичной обмотки трансформатора наматываем межобмоточную прокладку — пару слоёв лакоткани или другой изолирующей ленты (Рис.2 д).

А вот теперь мы плавно переходим к выполнению второй части упражнения.
Казалось бы, расчёты количества витков вторичной обмотки импульсного трансформатора настолько банальны и очевидны, что, как говаривал товарищ Мамин-Сибиряк — «яйца выеденного не стоят».
Да только вот опять — не складываются куличики в пирамидку, потому как далеко не каждый источник информации радует ожидаемым результатом. Поэтому для начала приведём формулу зависимости выходного напряжения от соотношения количества витков обмоток:
W1 (Uвх — Uдм1)/2 — Uнас ,
W2 (Uвых+Uдм2)
где Uвх — значение выпрямленного напряжения сети, равное 1,41×220≈310В,
Uдм1 — падение напряжения на входном диодном мосте ≈ 1В,
Uдм2 — падение напряжения на выходном диодном мосте ≈ 1В,
Uнас — напряжение насыщения на ключевом транзисторе ≈ 1,6В.
Подставив значения, получаем конечную формулу W2 = W1×(Uвых+1)/153.
Это формула верна для случаев, когда мы хотим получить расчётное значение выходного напряжения на холостом ходу.
Если же данный параметр нас интересует при максимальном токе нагрузки, то практика показывает, что количество витков вторичной обмотки следует увеличить на 10%.

Теперь, что касается диаметра провода вторичной обмотки трансформатора. Диаметр этот достаточно просто вычисляется по формуле:
D = 1,13×√ I / J,
где I — ток обмотки, а J — параметр плотности тока, напрямую зависящий от мощности трансформатора и принимающий для кольцевых сердечников значения:
≈4,5 для мощностей до 50Вт; ≈4 для 50-150Вт; ≈3,25 для 150-300Вт и ≈2,75 для 300-1000Вт.

И в завершении приведу незамысловатый калькулятор для расчёта параметров вторичной обмотки импульсного трансформатора.

Точно так же, как и в случае с первичной обмоткой — вторичная должна быть как можно более равномерно распределена по периметру магнитопровода.

Количество вторичных обмоток ограничено только размерами магнитопровода. При этом суммарная величина снимаемых с обмоток мощностей не должна превышать расчётную мощность трансформатора.

При необходимости поиметь двуполярный источник питания, обе обмотки следует мотать одновременно, затем присовокупить начало одной обмотки к концу другой, а уже потом направить это соединение, в зависимости от личных пристрастий — к земле, средней точке, общей шине, корпусу, или совсем на худой конец — к GND-у.

Ну что ж, с трансформатором определились, пора озадачиться полным джентльменским набором настоящего мужчины — плавками с меховым гульфиком, а главное, непосредственно импульсным блоком питания, оснащённым такими значимыми прибамбасами, как устройства мягкого пуска и защиты от токовых перегрузок и КЗ.
Всё это хозяйство подробно опишем на странице Ссылка на страницу.

Расчет трансформатора для обратноходового импульсного источника питания (Flyback)Популярность обратноходовых источников питания (ОИП, Flyback) последнее время сильно возросла в связи с простотой и дешевизной этого схемного решения – на рынке можно часто встретить интегральные схемы, включающие в себя практически всю высоковольтную часть такого источника, пользователю остается только подключить трансформатор и собрать низковольтную часть по стандартным схемам. Для расчета трансформаторов также имеется большое количество программного обеспечения – начиная от универсальных программ и заканчивая специализированным ПО производителей интегральных схем.

Сегодня же я хочу поговорить о ручном расчете импульсного трансформатора. «Зачем это нужно?», может спросить читатель. Во-первых, ручной расчет трансформатора подразумевает полное понимание процессов, происходящих в источнике питания, чего зачастую не происходит, если начинающий радиолюбитель рассчитывает трансформатор в специальном ПО. Во-вторых, ручной расчет позволяет выбирать оптимальные параметры функционирования источника (и иметь представление, какой параметр в какую сторону надо изменить для достижения заданного результата) еще на этапе разработки.

Итак, начнем. Структурная схема ОИП представлена на рис. 1. Он состоит из следующих основных функциональных узлов: ключ Sw, трансформатор Т1, выпрямитель выходного напряжения VD1 и C2, фильтр высокочастотных помех С1 и снаббер Snb.

Рис. 1

Работает такой источник следующим образом (см. упрощенные графики на рис. 2): в начальный момент времени t0 ключ Sw открывается, подавая входное напряжение Uin на первичную обмотку трансформатора Т1. В это время напряжение на нижнем выводе обмотки I (точка а) равно нулю (относительно отрицательного провода входного напряжения), в обмотке I начинает линейно нарастать ток, а на обмотке II появляется напряжение, пропорциональное коэффициенту трансформации Т1 (UoutInv). Но полярность этого напряжения оказывается отрицательной (на верхнем по схеме выводе обмотки II, точка b), поэтому диод VD1 закрыт и напряжение на выходной конденсатор С2 не проходит. За промежуток Ton (от t0 до t1) ток через обмотку I линейно нарастает до значения Imax, и энергия запасается внутри трансформатора Т1 в виде магнитного поля.

Рис. 2

В момент времени t1 ключ Sw резко закрывается, ток через обмотку I прекращается и в ней возникает ЭДС самоиндукции, направленная так, чтобы продолжить прекратившийся ток. В этот момент обмотка I сама становится источником напряжения. Так получается потому, что энергия в катушке индуктивности запасается в виде тока (на самом деле, в виде магнитного поля, но он пропорционален току через катушку, поэтому формула энергии в катушке A = LI²/2), но по закону сохранения энергии она не может исчезнуть бесследно, она должна куда-то перейти. Следовательно, ток в катушке не может прекратиться мгновенно, поэтому катушка сама становится источником напряжения, причем любой амплитуды (!) – такой, чтобы обеспечить сразу после закрытия ключа продолжение того же самого тока Imax. Это является первой важной особенностью катушки индуктивности, которую следует запомнить – при резком прекращении тока в катушке, она становится источником напряжения любой амплитуды, пытаясь поддержать прекратившийся в ней ток, как по направлению, так и по амплитуде. Какой же именно «любой» амплитуды? Достаточно большой, чтобы, например, вывести из строя высоковольтный ключ или образовать искру в свече зажигания автомобиля (да, в зажигании автомобиля использует именно это свойство катушек индуктивности).

Все, что описано выше так и происходило бы, если бы обмотка I была единственной обмоткой трансформатора Т1. Но в нем еще есть обмотка II, индуктивно связанная с I. Поэтому, в момент времени t1 в ней тоже возникает ЭДС, направленная так, что в точке b оказывается плюс по отношению к земле. Эта ЭДС открывает диод VD1 и начинает заряжать конденсатор C2 током I2max. Т.е. заряд конденсатора C2 и передача энергии в нагрузку происходит в тот момент времени, когда ключ Sw закрыт. Именно поэтому источники питания, построенные по такому принципу, называют обратноходовыми – потому что в них нет прямой передачи энергии из высоковольтной части в низковольтную, энергия сначала запасается в трансформаторе, а потом отдается потребителю.

В интервал времени от t1 до t2 линейно спадающий от I2max до 0 ток I2 вторичной обмотки поддерживает магнитное поле внутри катушки в соответствии с законом сохранения энергии и не дает напряжению на первичной обмотке (т.к. они индуктивно связаны) вырасти до неконтролируемого значения. Напряжение на обмотке I в этот момент становится равно напряжению выхода, умноженному на коэффициент трансформации Т1. Однако, полярность этого напряжения такова, что оно складывается с входным напряжением Uin и прикладывается к закрытому ключу Sw. Т.е. на закрытый ключ Sw прикладывается напряжение больше входного! Это также является важной особенностью ОИП, которую следует запомнить.

В момент времени t2 энергия, запасенная в трансформаторе Т1 заканчивается, диод VD1 закрывается, напряжение в точке b становится равным нулю, в точке a – входному напряжению питания, и все процессы в схеме прекращаются до момента t3, когда весь цикл повторяется с самого начала. При этом, в интервалах времени t0-t1 и t2-t4 питание нагрузки осуществляется исключительно за счет энергии, запасенной выходным конденсатором С2.

Описанный режим работы ОИП называется режимом разрывных токов – т.е. за интервал Toff (t1-t3) вся энергия, запасенная в трансформаторе Т1 передается в нагрузку, поэтому, в момент t3 ток через первичную обмотку I начинает нарастать с нуля. Существует также режим неразрывных токов, когда на момент t3 некоторая часть энергии еще продолжает находиться в трансформаторе Т1, и ток через обмотку I в момент t3 начинается не с нулевого значения. Данный режим имеет свои особенности, преимущества и недостатки, о которых мы поговорим в следующий раз.

Итак, какими основными особенностями обладает ОИП в режиме разрывных токов? Выпишем основные пункты:

Передача энергии от источника к потребителю в ОИП не идет напрямую, энергия сначала запасается в трансформаторе, а затем передается в нагрузку. Это однозначно определяет фазировку первичной и вторичной обмоток, а также заставляет использовать только однополупериодный выпрямитель на выходе блока. Также отсюда следует неявный вывод 2, который, как показала моя личная практика, к сожалению, не до конца понимают даже достаточно опытные конструкторы блоков питания.
Максимальная мощность, которую может выдать ОИП в нагрузку, кроме всего прочего, ограничена максимальным количеством энергии, которую может запасти трансформатор! А это, в свою очередь, определяется конструктивными особенностями сердечника и не зависит от обмоток и количества их витков (ниже в статье я рассмотрю данный «парадокс» отдельно и приведу математические доказательства). Эта особенность ограничивает применение ОИП там, где нужны большие выходные мощности.
Низковольтная цепь ОИП состоит из диода, конденсатора и, возможно, дополнительных фильтрующих элементов. Однако, в ОИП первым всегда стоит диод, затем идет конденсатор и никак иначе.
В установившемся режиме работы ОИП количество энергии, полученное первичной обмоткой I трансформатора Т1 за время Ton равно (без учета потерь) количеству энергии, отданному обмоткой II за время Toff. Поскольку скорость приема или отдачи энергии катушкой определяется напряжением на ней, то зависимость между напряжением «заряда» и «разряда» определяется именно интервалами Toff и Ton. Т.е., по сути, в самом сложном режиме работы блока Duty cycle (коэффициент заполнения, D), равный Ton/(Ton + Toff) определяет отношение обратного напряжения на обмотке I к напряжению питания Uin. Этот пункт будет пояснен подробнее ниже.
По закону сохранения энергии, ток I2max, отдаваемый обмоткой II в нагрузку в момент времени t1 численно равен току Imax, только что протекавшему в первичной обмотке, умноженному на отношение количества витков в обмотке I к количеству витков в обмотке II (пояснение ниже).
Импульсное значение тока I2max значительно превышает средний выходной ток блока питания (в 2.5 и более раз), поэтому на выпрямительном диоде VD1 может рассеиваться значительная мощность. Именно эта особенность ограничивает применение ОИП там, где нужны большие выходные токи.
То же самое (высокое импульсное значение тока) относится и к вторичной обмотке II.
Обратное напряжение на диоде VD1 в несколько раз выше выходного напряжения. Это происходит из-за того, что обычно обратное напряжение на первичной обмотке (которое является прямым для диода) выбирается в несколько раз ниже входного, поэтому входное (которое является обратным для диода) после трансформации оказывается в несколько раз выше выходного.

Пояснение к п. 4. Из физики мы помним формулу для катушки индуктивности:

U(t) = L*(dI(t)/dt),

которая означает, что напряжение на катушке прямо пропорционально ее индуктивности, умноженной на скорость изменения тока в ней. Что это нам дает? Прежде всего, то, что если мы прикладываем к катушке постоянное напряжение U, то скорость изменения тока в ней постоянна. Это позволяет переписать формулу для постоянного напряжения без дифференциалов:

U = L*(ΔI/Δt),

и именно в соответствии с этой формулой графики тока на рис. 2 прямые. Далее, если мы прикладываем напряжение Uin к катушке на время Ton, ток в ней возрастет до значения

Imax = Uin*Ton/L

Теперь мы хотим (в самом нагруженном режиме работы), чтобы вся энергия катушки, которую мы только что набрали, была передана в нагрузку за интервал Toff, т.е. на момент t3 ток в катушке должен упасть до нуля. Здесь для упрощения представим, что мы как подаем, так и снимаем напряжение/ток с одной и той же катушки I, позже я объясню, почему такое допущение возможно. Посчитаем, на какое напряжение мы можем «разряжать» катушку, чтобы ток в момент t3 достиг нуля:

Udis = L*Imax/Toff,

Подставляем и упрощаем:

Udis = L*Uin*Ton/(L*Toff) = Uin*Ton/Toff

Т.е. напряжение, на которое мы должны «разряжать» катушку в моменты закрытия ключа Sw зависит только от входного напряжения и интервалов «заряда»-«разряда». Вспомним формулу коэффициента заполнения D:

D = Ton/(Ton + Toff),

таким образом:

Udis = Uin*D/(1 – D)

Но, напряжение, на которое мы «разряжаем» катушку – это и есть то обратное напряжение, которое возникает в первичной обмотке в моменты закрытия ключа. Т.е. мы получили, что оно зависит только от входного напряжения и коэффициента заполнения D и определяется формулой:

Uinv = Uin*D/(1 – D)

При работе в реальных условиях значение коэффициента заполнения D будет меняться в зависимости от входного напряжения и нагрузки блока питания. Свое максимальное значение D будет принимать при минимальном входном напряжении и максимальной выходной мощности — этот режим работы считается самым сложным, и данное максимальное значение D и задается при проектировании блока. Что будет в те моменты, когда входное напряжение блока будет выше или нагрузка будет неполной? D будет принимать меньшие значения, т.к. от более высокого напряжения энергия быстрее «запасется» в первичной обмотке, или же (в случае меньшей нагрузки) надо просто «запасать» меньшее количество энергии. В любом случае, обратное напряжение на первичной обмотке будет всегда одинаковым, т.к. оно жестко связано с выходным напряжением, а то, в свою очередь, стабилизируется схемой. Итак, максимальное обратное напряжение на ключе равно:

Usw = Umax + Umin*D/(1 – D)

Это важный момент при проектировании ОИП, т.к. обычно максимальное обратное напряжение на ключе является исходным параметром, т.е. максимальный коэффициент заполнения D также является исходной величиной. На практике обычно применяют следующие максимальные значения D: 25% (1/4), 33% (1/3) и реже 50% (1/2). Как вы понимаете, в последнем случае максимальное обратное напряжение на ключе будет равно удвоенному минимальному входному напряжению, что усложняет выбор полупроводникового прибора. Более низкие максимальные значения D, в свою очередь, снижают максимальную мощность при том же токе Imax, затрудняют процесс управления ключом Sw и снижают стабильность работы блока.

Почему же здесь мы применили допущение, что мы как подаем энергию, так и снимаем ее с первичной обмотки I, и что будет в реальности, когда снимается энергия с катушки II? То же самое. Напряжение на выводах любой обмотки трансформатора пропорционально скорости изменения магнитного поля в сердечнике (а поле пропорционально току, поэтому напряжение пропорционально скорости изменения тока). Поэтому не важно, с какой обмотки мы будем снимать энергию, если мы будем делать это с одной и той же скоростью, магнитное поле в трансформаторе будет уменьшаться одинаково, а на выводах первичной обмотки будет одно и то же напряжение. Но на какое напряжение надо «разряжать» вторичную обмотку, чтобы снятие энергии происходило с той же самой скоростью? Для этого сначала рассмотрим ток во вторичной обмотке.

Пояснение к п. 5. Пусть обмотка I имеет N1 витков, в то время как обмотка II – N2. Магнитное поле создается током, проходящим через каждый виток катушки, т.е. оно пропорционально произведению I*N. Тогда, получаем Imax*N1 = I2max*N2 (исходя из того, что обе обмотки намотаны в абсолютно одинаковых условиях), отсюда начальный ток вторичной обмотки:

I2max = Imax*N1/N2

Итак, ток во вторичной обмотке будет в N1/N2 раз выше, чем в первичной. Но на какое напряжение мы должны «разряжать» вторичную обмотку, чтобы к моменту t3 потратить всю энергию, запасенную в трансформаторе? Очевидно, что делать это мы должны с точно такой же скоростью; т.е. в каждый отдельный момент времени трансформатор будет терять одно и то же значение энергии dA(t). Но в первом случае dA(t) = Udis*I1(t)*dt (получено из A = W*T, W = U*I), а теперь это будет dA(t) = Uout*I2(t)*dt. Приравняем эти две функции:

Uout *I2(t) = Udis*I1(t), следовательно, в самом начале «разряда» моментальные мощности разряда должны быть равны:

Uout*I2max = Udis*Imax,

Uout = Udis*Imax/I2max = Udis*Imax/(Imax*N1/N2) = Udis*N2/N1

Т.е. для того, чтобы потратить всю энергию трансформатора к моменту t3, мы должны «разряжать» вторичную обмотку II на напряжение Udis*N2/N1, при этом ток разрядки будет линейно падать от Imax*N1/N2 до нуля. Таким образом, мы установили связь между выходным напряжением блока, количеством витков в обмотках и обратным напряжением на первичной обмотке трансформатора.

На этом сугубо теоретическая часть заканчивается, и мы можем перейти к практике. Первый вопрос, который, скорее всего, возникает на данный момент у читателя – это с чего вообще начать разработку ОИП? Ниже я приведу рекомендованную последовательность шагов. Начнем с ситуации, когда трансформатор планируется изготовить полностью самостоятельно (на него нет жестких ограничений).

Определяем выходные напряжения и токи источника питания.
Увеличиваем выходные напряжения на величину, падающую на выпрямительных диодах (VD1). Лучше всего воспользоваться справочной информацией, но в первом приближении можно брать 1В для обычных кремниевых диодов и 0.3В для диодов Шоттки. Особую точность следует соблюдать, когда ОИП имеет несколько выходных обмоток с разным напряжением, т.к. стабилизовать напряжение возможно только на одной из них.
Считаем суммарную выходную мощность трансформатора.
Считаем расчетную входную мощность блока как Pin = Pout/0.8 (здесь берется КПД блока 80%).
Определяем частоту преобразования F. Обычно выбирается частота от 20КГц до 150КГц. Частоты ниже 20КГц могут быть слышны человеческому уху (блок будет «пищать»), частоты выше 150КГц накладывают более серьезные ограничения на элементную базу, также увеличиваются потери на переключение полупроводников (ключа и диодов). Увеличение частоты преобразования позволяет уменьшить габариты трансформатора, наиболее распространенный диапазон частот для ОИП: от 66 до 100 Кгц.
Вычисляем максимальное входное напряжение, от которого нам придется работать. Обычно оно вычисляется как выпрямленное напряжение сети +20%, т.е. Umax = Uсети*1.7 (391В для сети 230В). На это напряжение также должен быть рассчитан конденсатор входного фильтра (не менее 400В в данном случае).
Вычисляем минимальное входное напряжение, от которого нам придется работать. Обычно вычисляется как минимальное допустимое рабочее напряжение -20%, минус просадка напряжения на фильтрующем конденсаторе за полупериод входного напряжения. Для сети 230В и емкости конденсатора входного фильтра из расчета не менее 1мкф на 1 ватт нагрузки, можно брать (в среднем) значение Umin = 220В. Если представить, что напряжение на конденсаторе вообще не просаживается от одного полупериода входного напряжения до другого, то Umin можно взять 260В.
Определяем коэффициент заполнения D исходя из максимально допустимого обратного напряжения на ключе (считается по формуле Uinv = Umax + Umin*D/(1 – D)).
Рассчитываем количество энергии, которую необходимо передать во вторичную обмотку за один импульс: Aimp = Рin*1s/F = Рin/F.
Решаем систему уравнений для самого тяжелого режима работы: A = LImax²/2, Umin = LImax*F/D, получаем L = Umin²*D²/(2*Aimp*F²), Imax = Umin*D/(L*F) – это будет требуемая индуктивность первичной обмотки и максимальный ток, протекающий через нее.
Исходя из полученного Imax выбираем ключ.
Если Imax получился несколько больше, чем может обеспечить имеющийся (выбранный) ключ, меняем исходные параметры – увеличиваем D (насколько возможно исходя из допустимого обратного напряжения ключа), увеличиваем емкость фильтрующего конденсатора, чтобы поднять Umin. На первый взгляд может показаться удивительным, но максимальный ток в первичной обмотке не зависит от частоты – если всё подставить в формулы, получим Imax = 2*Pin/(Umin*D). Исходя из этой формулы, можно было рассчитать максимальный ток и на этапе 8 (сразу после выбора D), но там было бы сложно объяснить, откуда взялся такой расчет.
Если значение Imax все равно оказывается больше допустимого и увеличить его никак нельзя, следует рассмотреть конструкцию ОИП в режиме неразрывных токов.
Исходя из требуемой индуктивности первичной обмотки и максимального тока в ней, выбираем сердечник трансформатора, рассчитываем необходимый зазор и количество витков первичной обмотки (формулы будут ниже в статье).
По формуле N2 = Uout*N1*(1 – D)/(Umin*D) рассчитываем количество витков вторичной обмотки.
Определяем среднеквадратичное значение токов в обмотках трансформатора по формуле Irms = Imax*SQRT(D/3), исходя из которых рассчитываем диаметр провода, необходимого для намотки. Чаще всего в импульсных источниках питания применяется плотность тока от 2 до 5 А/мм².
Мотаем трансформатор по всем правилам намотки трансформаторов для ОИП.
Для того, чтобы убедиться в правильности намотки, измеряем индуктивность первичной обмотки.

Теперь немного рассмотрим сам трансформатор и его конструкцию. Традиционно для импульсных источников питания трансформатор изготавливается на каком-либо сердечнике, выполненном из материала с высокой магнитной проницаемостью. Это позволяет при том же самом количестве витков обмоток сильно увеличить их индуктивность, т.е. сократить количество витков для достижения заданной индуктивности, и, следовательно, уменьшить габариты намотки. Однако, применение сердечника добавляет и недостатки – за счет магнитного гистерезиса в сердечнике теряется некоторая часть энергии, сердечник нагревается, причем потери в сердечнике растут с увеличением частоты (еще одна причина, из-за которой нельзя сильно повышать частоту преобразования). Также добавление сердечника вносит новое, ранее нигде не озвучиваемое ограничение – максимально допустимую плотность потока магнитной индукции Bmax. На практике это проявляется в том, что если увеличивать ток через обмотку, в определенный момент времени, когда ток достигнет определенного максимального значения, сердечник войдет в насыщение и дальнейшее увеличение тока не будет вызывать такое же как раньше увеличение магнитного потока. Это, в свою очередь, приведет к тому, что «относительная индуктивность» обмотки резко упадет, что вызовет еще более быстрое нарастание тока через нее. На практике, если не предусмотреть защиту ключа Sw ОИП от входа сердечника в насыщение, ключ просто сгорит от перегрузки по току. Поэтому во всех схемах ОИП, за исключением простейших блокинг-генераторов, применяется контроль тока через ключ Sw и досрочное закрытие ключа при достижении максимально допустимого тока через первичную обмотку.

Насколько же велико это максимальное значение плотности потока магнитной индукции? Для наиболее распространенного материала сердечников – феррита – оно считается равным 0.3Т. Это – среднее значение, оно может отличаться для каждого конкретного материала, поэтому здесь неплохо обратиться к справочнику. Также, оно зависит от температуры сердечника и, как вы, наверное, уже догадались, падает с ее увеличением. Если вы проектируете ОИП, предназначенный для работы в экстремальных условиях, где температура сердечника может доходить до 125 градусов, уменьшайте Bmax до 0.2Т.

Основная формула, которой вам придется пользоваться при расчете трансформаторов – это индуктивность обмотки по ее габаритам:

L = (μ0*μe*Se*N²)/le, где

μ0 – абсолютная магнитная проницаемость вакуума, 4πе-7,
μe – эффективная магнитная проницаемость сердечника,
Se – эффективная площадь сечения магнитопровода, м².
N – количество витков
le – длина средней магнитной линии сердечника, м

Плотность потока магнитной индукции в сердечнике:

B = (μ0*μe*I*N)/le, где

I – ток через обмотку, А

Таким образом, исходя из максимальной допустимой плотности потока магнитной индукции, максимально допустимый ток для обмотки будет равен:

Imax = (Bmax*le)/(μ0*μe*N)

А теперь еще один очень важный момент – на практике, если подставить реальные данные трансформатора в вышеприведенные формулы, окажется, что максимально допустимый ток в первичной обмотке оказывается в несколько раз меньше того, который нам нужен! Т.е. сердечник будет введен в насыщения еще до того, как мы сможем «вкачать» в него требуемую энергию Aimp. Так что же делать, не увеличивать же габариты трансформатора до неприличных значений?

Нет. Надо вводить в сердечник немагнитный зазор! Введение немагнитного зазора сильно снижает эффективную магнитную проницаемость сердечника, позволяя пропускать через обмотки значительно больший ток. Но, как вы понимаете, это потребует большего числа витков для достижения требуемой индуктивности обмотки.

Рассмотрим формулы для сердечника с зазором. Эффективная магнитная проницаемость сердечника с зазором:

μe = le/g, где

g – суммарная толщина зазора, м.

Следует отметить, что данная формула справедлива только если получаемая μe много меньше исходной магнитной проницаемости (несколько раз), а g много меньше размеров поперечного сечения сердечника. Итак, рассмотрим формулу индуктивности обмотки на сердечнике с зазором:

L = (μ0*Se*N²)/g

Формула от введения зазора стала только проще. Максимально допустимый ток через обмотку:

Imax = (Bmax*g)/(μ0*N)

Ну и последняя формула, которую можно вывести и самостоятельно. Размер зазора для заданного тока:

g = (I*μ0*N)/Bmax

А теперь сделаем интересный вывод. Как вы помните, энергия, запасенная в катушке, выражается формулой A = LI²/2. Так какую максимальную энергию можно запасти в каком-то абстрактном сердечнике? Подставим данные в формулы.

Amax = (μ0*Se*N²)*(Bmax*g) ²/((μ0*N) ²*2g) = Se*g*Bmax²/2μ0

Сейчас вы можете удивиться, но максимальная энергия, которую можно запасти в сердечнике, не зависит от того, какие обмотки на нем намотаны! Но это и логично, ведь энергия выражается в магнитном поле, а обмотки лишь позволяют его менять в ту или другую сторону! Количество витков в обмотках определяет только скорость, с которой магнитная индукция может достигнуть своего максимального значения при данном подведенном напряжении, но это максимальное значение определяется только конструкцией сердечника!

Данный вывод имеет огромное значение при проектировании ОИП на унифицированных сердечниках. Если перед вами стоит именно такая задача, то, прежде всего, вам необходимо рассчитать, какое максимальное количество энергии способен «впитать» выбранный сердечник за один импульс, чтобы понять, подходит ли он для вашей мощности блока. Как вы понимаете, в этом случае максимальную мощность блока можно повысить только за счет повышения частоты преобразования – чем чаще мы будем перекачивать энергию Amax от входа на выход, тем большую мощность блока в результате сможем получить.

Также, из полученной формулы видно, что количество энергии, которое может «уместиться» в сердечнике прямо пропорционально немагнитному зазору! Это позволяет использовать маленькие сердечники на больших мощностях за счет увеличения зазора в них. Ограничением теперь будет только физические размеры – увеличение зазора вызывает уменьшение магнитной проницаемости, что требует большее количество витков.

А теперь вернемся к структурной схеме ОИП на рис. 1. В ней остались два блока, о которых я ничего не сказал – это конденсатор С1 и снаббер Snb.

Назначение конденсатора С1 – заземление выходной части блока по высоким частотам. Дело в том, что любой трансформатор, даже намотанный по всем правилам с экранами, имеет какую-то межобмоточную емкость. Прямоугольное высокочастотное напряжение огромной амплитуды из точки а проходит через эту емкость в выходные цепи блока. Конденсатор С1, имеющий емкость намного больше емкости трансформатора Т1, заземляет выход блока по высоким частотам. Значение емкости этого конденсатора в ОИП чаще всего выбирают в районе 2нф, напряжение – около киловольта. Если предполагается жесткое заземление выхода блока (например, используется только розетка с заземлением), С1 можно не ставить.

Необходимость в Снаббере Snb также вытекает из неидеальности трансформатора Т1, но уже совсем другого рода. Не смотря на то, что обмотки I и II индуктивно связаны между собой, эта связь не составляет 100%. В схемотехнике ОИП принято говорить, что обмотка I представляет собой две части, соединенные последовательно, где первая полностью индуктивно связана с обмоткой II, а вторая – полностью изолирована от нее. Эту вторую часть обмотки I называют «индуктивностью рассеяния».

Когда в момент t1 ток в первичной обмотке (обоих частях ее) резко прекращается, индуктивность рассеяния также пытается его продолжить. А так, как она не связана ни с какой другой обмоткой, она генерирует высоковольтный импульс, прикладываемый к закрытому ключу Sw. Энергия этого импульса во много раз меньше полезной энергии Aimp (чем лучше трансформатор, тем она меньше вообще), но и ее может оказаться достаточно, чтобы повредить ключ (в случае с биполярным транзистором, например, ее вполне хватит для лавинного пробоя). Для защиты ключа от этого импульса, он гасится на специальном схемном решении.

Рис. 3

Самый простой вариант – RCD снаббер, выполненный из диода, конденсатора и резистора (см. рис. 3). Обратное напряжение, возникающее на обмотке I, открывает диод VD и начинает заряжать конденсатор С. В результате, вся энергия импульса передается в конденсатор. В перерывах между импульсами конденсатор разряжается через резистор R. Т.е. энергия, снимаемая с индуктивности рассеяния, превращается в конечном счете в тепло на резисторе R, поэтому мощность этого резистора должна быть значительной (достигает единиц ватт). Преимуществом снаббера можно считать его схемную простоту, и то, что часть энергии из конденсатора С можно выкачать обратно в трансформатор Т применяя медленный диод VD, но эти процессы уже несколько сложней нашей простой статьи. Основным же недостатком снаббера является то, что на нем падает и полезная мощность! Ведь рабочее обратное напряжение первичной обмотки Vinv также заряжает конденсатор до этого значения, т.е. полезная мощность Uinv²/R теряется впустую.

Схемным решением, лишенным этого недостатка является супрессор. Он представляет собой последовательно соединенный быстрый диод VD1 и мощный и быстрый стабилитрон VD2. Когда индуктивность рассеяния генерирует свой высоковольтный импульс, он открывает диод VD1, пробивает стабилитрон VD2 и энергия импульса рассеивается на нем. Стабилитрон VD2 выбирается с большим напряжением пробоя, чем обратное напряжение Uinv, поэтому он не рассеивает полезной мощности блока. К недостаткам супрессора можно отнести более высокий уровень электромагнитных помех, связанный с резким открытием и закрытием полупроводниковых приборов.

Что будет, если этот высоковольтный импульс не погасить ничем? В случае биполярного ключа, скорее всего, в нем возникнет лавинный пробой и блок питания перейдет в режим кипятильника. Современные же полевые транзисторы устойчивы к лавинному пробою и позволяют рассеивать некоторое количество энергии на стоке (это описано в документации), поэтому такой транзистор может работать и без снаббера или супрессора – его роль будет выполнять сам транзистор. Более того, я встречал некоторые дешевые китайские блоки питания, в которых так и было сделано. Однако, я настоятельно не рекомендую такой режим работы, т.к. он дополнительно снижает надежность блока. Супрессорный диод (стабилитрон) стоит очень дешево и рассчитан на колоссальные импульсные мощности (600W, 1.5KW), так почему бы не применять его по назначению?

Также из вышеописанного следует еще один вывод. Независимо от того, решили ли вы применять снаббер или супрессор, обратное напряжение на закрытом ключе будет еще выше, чем рабочее рассчитанное значение Usw! Это следует иметь в виду при выборе ключа.

Обычно современные ключевые транзисторы и микросхемы имеют допустимое обратное напряжение 600 – 800 вольт. При Umax = 391В, Umin = 220В, обратное напряжение на ключе Usw будет иметь следующие значения (в зависимости от D): D = 25%, Usw = 464B; D = 33%, Usw = 501B; D = 50%, Usw = 611B. Это означает, что для ключей с максимальным обратным напряжением 600В следует выбирать только D = 33% или меньше. Для ключей с обратным напряжением 700В можно выбирать D = 50%.

Ну и в завершении статьи приведу простой пример расчета ОИП. Допустим, мы хотим сделать простой блок питания, позволяющий получить на своем выходе 12В 1А. Рассчитаем его по пунктам:

Выход блока – 12В 1А.
До выходного диода (будем применять обычный кремниевый) должно быть 13В.
Выходная мощность трансформатора – 13Вт.
Расчетная входная мощность блока Pin = 13/0.8 = 16Вт.
F = 100 КГц.
Umax = 391В.
Umin = 220В (емкость конденсатора входного фильтра – 22мкф).
D = 33%, Uinv = 110В, Usw = 501В. Будем ориентироваться на ключи с обратным напряжением 600В.
Aimp = 16/100000 = 1.6e-4Дж = 160мкДж.
L = 1.65е-3Гн = 1.65мГн, Imax = 0.44А
Производим выбор сердечника, расчет параметров намотки и зазора.

А теперь, для сравнения рассчитаем тот же ОИП для случая, когда допустимое напряжение сети может быть в интервале 85-230В. В чем будут отличия?

Umax = 391B
Umin = 85B (емкость конденсатора фильтра надо будет увеличить до 47мкф)
D = 60%, Uinv = 128В, Usw = 519В, Будем ориентироваться на ключи с обратным напряжением 600В.
Aimp = 16/100000 = 1.6e-4Дж = 160мкДж.
L = 813мкГн, Imax = 0.63А

Заметьте, что параметры максимального тока через ключ изменились не столь значительно — с 0.44А до 0.63А, индуктивность упала в два раза, однако диапазон допустимых входных напряжений расширился очень существенно. В этом заключается еще одно преимущество ОИП — легкость в создании источников питания, работающих от широкого диапазона входных напряжений.

Возможно, в данной статье не до конца рассмотрены все нюансы построения ОИП, однако ее объем и так получился больше, чем планировалось. Но тем не менее, я надеюсь, что она сможет помочь начинающим радиолюбителям понять принципы и самостоятельно создавать обратноходовые источники питания.

Конструкция трансформатора и индуктора — Switchcraft

Максимальный поток в сердечнике рассчитывается следующим образом:

\ [\ Phi = B \ cdot A = 1,3 \ cdot 0,00135 = 0,00176 Wb \]

Максимальное изменение потока в сердечнике однако является двойным, так как ядро может быть намагничено в обоих направлениях, то есть: \ (0.00352 Wb \).

Число оборотов, необходимое для получения этого потока, определяется следующим образом:

\ begin {уравнение *}
N = \ frac {V \ cdot t} {\ Phi}
\ end {уравнение *}

где \ ( V \) — среднее напряжение, приложенное к обмотке.{\ pi} \]

\ (\ cos (0) = 1 \) и \ (\ cos (\ pi) = -1 \), следовательно:

\ [V_ {avg} = \ frac {2 V_p } {\ pi} \]

Для нашего примера среднее напряжение вычисляется как:

\ [V_ {avg} = \ frac {2 \ cdot 230 \ cdot \ sqrt {2}} {\ pi} = 207 V \]

Требуемое число витков вычисляется следующим образом:

\ [N = \ frac {207 \ cdot 0.01} {0.00352} = 588 \]

Следовательно, в пересчете на среднеквадратичное значение мы имеем 0,39 вольт на виток, или 2,56 витка на вольт. Для второстепенного необходимое число оборотов затем просто рассчитывается умножением 2.56 желаемым напряжением.

Например если требуемое вторичное напряжение равно \ (18 \; В \) (которое может подходить для линейного регулируемого источника питания 12 В), требуемое количество витков будет:

\ begin {уравнение *}
2,56 \ cdot 18 = 46
\ end {уравнение *}

Мощность питания

Вычислить мощность не так просто, как вычислить необходимое количество оборотов. Однако для небольших трансформаторов обычно безопасно делать некоторые предположения на основе опыта. Одним из таких предположений является то, что эффективность составляет 90%, т.е.2} {R} = \ frac {230 \ cdot 0,05} {8.59} = 15,4 Вт \]

Номинальная входная мощность трансформатора рассчитывается следующим образом:

\ [P = \ frac {15.4} {0.1} = 154 Вт \]

Примечание о постоянном токе

Постоянный ток в трансформаторе обычно не очень хорошая вещь. Он будет , а не , который будет вносить вклад в мощность, передаваемую трансформатором, но он будет способствовать магнитному потоку в сердечнике. Это означает, что ядро будет ближе к насыщению. Если трансформатор рассчитан на насыщение без постоянного тока, он будет насыщаться.

Если вы хотите иметь постоянный ток в трансформаторе, вы должны применять те же конструктивные ограничения, что и при проектировании индуктора, предназначенного для постоянного тока. Обычно это означает добавление воздушного зазора к сердечнику, чтобы уменьшить эффективную проницаемость.

Индуктивность — это параметр любой электрической сети, характеризующий ее способность противостоять изменению тока.

\ begin {уравнение}
\ text {EMF} = -L \ frac {\ mathrm {d} i} {\ mathrm {d} t} \ Rightarrow L = — \ text {EMF} \ frac {\ mathrm { d} t} {\ mathrm {d} i}
\ end {уравнение}

Накопитель энергии

Накопитель энергии в трансформаторах обычно нежелателен, однако часто он является основной целью индуктора.2
\ end {уравнение}

Где \ (I \) — ток намагничивания. То есть при расчете запаса энергии в трансформаторе он будет меньше общего тока.

Коэффициент качества

Коэффициент качества индуктора описывает устройство по отношению к идеальному компоненту. Это имеет особое значение в радиочастотных приложениях.

Коэффициент качества дросселя определяется следующим образом:

\ begin {уравнение}
Q_L = \ frac {X_L} {R_L} = \ frac {2 \ pi f L} {R_L}
\ end {уравнение}

Следовательно, добротность зависит от частоты, под которой используется индуктор.2 \) площадь поперечного сечения. Лучший способ увеличить мощность — это уменьшить индуктивность и, следовательно, увеличить ток в сердечнике. Помните, что мощность зависит от текущего квадрата.

При введении воздушной щели в магнитный сердечник эффективная проницаемость уменьшится, и, следовательно, значение \ (A_L \) — также уменьшится.

Энергия, накопленная в сердечнике, может быть извлечена второй обмоткой на том же сердечнике, что и в топологии с обратной связью. В качестве альтернативы его можно использовать, подключив индуктор к другой цепи после ее зарядки, как в топологиях с понижением / повышением.

Тороиды

Тороидальные сердечники можно разделить на две основные категории, в зависимости от материала, из которого они изготовлены. Ферритовые и железные порошковые сердечники.

Феррит обладает самой высокой проницаемостью, но он не подходит для высоких частот. Кроме того, как мы видели, высокая проницаемость не всегда является преимуществом.

Полезный веб-сайт со спецификациями для различных тороидальных сердечников находится по адресу: http://toroids.info/

Как уже упоминалось ранее, плотность потока должна быть ограничена во избежание насыщения сердечника.Для ферритовых тороидальных сердечников это накладывает ограничение:

\ begin {уравнение}
\ frac {V} {2 f NA} \ le 0.3
\ end {уравнение}

где \ (N \) — число витков обмотки и \ (A \) — площадь поперечного сечения ядра.

формула индуктивности с несколькими решенными примерами

- Классы
  Класс 1 — 3
  Класс 4 — 5
  Класс 6 — 10
  Класс 11 — 12
- КОНКУРСЫ
  BBS
  000000000000 Книги
  NCERT Книги для 5 класса
  NCERT Книги Класс 6
  NCERT Книги для 7 класса
  NCERT Книги для 8 класса
  NCERT Книги для 9 класса
  NCERT Книги для 10 класса
  NCERT Книги для 11 класса
  NCERT Книги для 12-го класса
  NCERT Exemplar
  NCERT Exemplar Class 8
  NCERT Exemplar Class 9
  NCERT Exemplar Class 10
  NCERT Exemplar Class 11
  NCERT Exemplar Class 12
  9000al Aggar Agard Agard Agard Agard Agulis Class 12
  Решения RS Aggarwal класса 10
  Решения RS Aggarwal класса 11
  Решения RS Aggarwal класса 10
  90 003 Решения RS Aggarwal Class 9
  Решения RS Aggarwal Class 8
  Решения RS Aggarwal Class 7
  Решения RS Aggarwal Class 6
  Решения RD Sharma
  Решения RD Sharma класса 9
  Решения RD Sharma Class 7 Решения RD Sharma Class 8
  Решения RD Sharma Class 9
  Решения RD Sharma Class 10
  Решения RD Sharma Class 11
  Решения RD Sharma Class 12
  ФИЗИКА
  Механика
  000000 Электромагнетизм
  ХИМИЯ
  Органическая химия
  Неорганическая химия
  Периодическая таблица
  МАТС
  Теорема Пифагора
  Отношения и функции
  Последовательности и серии
  Таблицы умножения
  Детерминанты и матрицы
  Прибыль и убыток
  Полиномиальные уравнения
  Делительные дроби
  000 ФОРМУЛЫ
  Математические формулы
  Алгебровые формулы
  Тригонометрические формулы
  Геометрические формулы
  КАЛЬКУЛЯТОРЫ
  Математические калькуляторы
  S000
  S0003
  Pегипс Класс 6
  Образцы документов CBSE для класса 7
  Образцы документов CBSE для класса 8
  Образцы документов CBSE для класса 9
  Образцы документов CBSE для класса 10
  Образцы документов CBSE для класса 11
  Образец образца CBSE pers for Class 12
  CBSE Документ с вопросами о предыдущем году
  CBSE Документы за предыдущий год Class 10
  CBSE Вопросы за предыдущий год Class 12
  HC Verma Solutions
  HC Verma Solutions Класс 11 Физика
  Решения HC Verma Class 12 Physics
  Решения Lakhmir Singh
  Решения Lakhmir Singh Class 9
  Решения Lakhmir Singh Class 10
  Решения Lakhmir Singh Class 8
  Примечания
  CBSE
  Notes
  CBSE Класс 7 Примечания CBSE
  Класс 8 Примечания CBSE
  Класс 9 Примечания CBSE
  Класс 10 Примечания CBSE
  Класс 11 Примечания CBSE
  Класс 12 Примечания CBSE
  Примечания пересмотра
  CBSE Редакция
  CBSE
  CBSE Class 10 Примечания к пересмотру
  CBSE Class 11 Примечания к пересмотру 9000 4
  Замечания по пересмотру CBSE класса 12
  Дополнительные вопросы CBSE
  Дополнительные вопросы CBSE 8 класса
  Дополнительные вопросы CBSE 8 по естественным наукам
  CBSE 9 класса Дополнительные вопросы
  CBSE 9 дополнительных вопросов по науке CBSE
  9000 Класс 10 Дополнительные вопросы по математике
  CBSE Класс 10 Дополнительные вопросы по науке
  Класс CBSE
  Класс 3
  Класс 4
  Класс 5
  Класс 6
  Класс 7
  Класс 8
  Класс 9
  Класс 10
  Класс 11
  Класс 12
  Решения для учебников
- Решения NCERT
  Решения NCERT для класса 11
  Решения NCERT для физики класса 11
  Решения NCERT для класса 11 Химия
  Решения для класса 11 Биология
  NCERT Решения для класса 11 Математика
  9 0003 NCERT Solutions Class 11 Бухгалтерия
  NCERT Solutions Class 11 Бизнес исследования
  NCERT Solutions Class 11 Экономика
  NCERT Solutions Class 11 Статистика
  NCERT Solutions Class 11 Коммерция
  NCERT Solutions для класса 12
  NCERT Solutions для Класс 12 Физика
  Решения NCERT для 12 класса Химия
  Решения NCERT для 12 класса Биология
  Решения NCERT для 12 класса Математика
  Решения NCERT Класс 12 Бухгалтерский учет
  Решения NCERT Класс 12 Бизнес исследования
  Решения NCERT Класс 12 Экономика
  NCERT Solutions Class 12 Бухгалтерский учет Часть 1
  NCERT Solutions Class 12 Бухгалтерский учет Часть 2
  NCERT Solutions Class 12 Микроэкономика
  NCERT Solutions Class 12 Коммерция
  NCERT Solutions Class 12 Макроэкономика
  NCERT Solutions Для Класс 4
  Решения NCERT для класса 4 Maths
  Решения NCERT для класса 4 EVS
  Решения NCERT для класса 5
  Решения NCERT для класса 5
  Решения NCERT для класса 5 EVS
  Решения NCERT для класса 6
  Решения NCERT для класса 6 Математика
  Решения NCERT для класса 6 Наука
  Решения NCERT для класса 6 Общественные науки
  Решения NCERT для класса 6 Английский
  Решения NCERT для класса 7
  Решения NCERT для класса 7 Математика
  NCERT Решения для 7 классов науки

,
Понимание Индуктивности »Электроника Примечания
Понимание основ индуктивности позволяет более эффективно использовать индукторы и трансформаторы.
Индуктивность и трансформатор Учебник включает в себя:
Индуктивность Символы Закон Ленца Собственная индуктивность Расчеты индуктивного сопротивления Теория индуктивного сопротивления Индуктивность проводов и катушек трансформеры
Индуктивность является ключевым параметром в электрических и электронных цепях.Подобно сопротивлению и емкости, это основное электрическое измерение, которое в той или иной степени влияет на все цепи.
Индуктивность используется во многих областях электрических и электронных систем и цепей. Компоненты могут иметь различные формы и могут называться различными именами: катушки, катушки индуктивности, дроссели, трансформаторы. , , Каждый из них также может иметь множество различных вариантов: с сердечниками и без сердечников, а материалы сердечника могут быть разных типов.
Понимание индуктивности и различных форм и форматов индукторов и трансформаторов помогает понять, что происходит в электрических и электронных цепях.

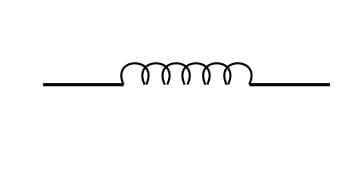
Термин индуктивность был введен Оливером Хевисайдом в 1886 году. Обычно используют символ L для индукторов, показанных на принципиальных схемах, и индуктивность в уравнениях после физика Генриха Ленца.
Основы индуктивности
Индуктивность — это способность индуктора накапливать энергию, и она делает это в магнитном поле, которое создается потоком электрического тока.
Энергия требуется для установки магнитного поля, и эта энергия должна высвобождаться при падении поля.
В результате магнитного поля, связанного с протеканием тока, индукторы генерируют противоположное напряжение, пропорциональное скорости изменения тока в цепи.
Индуктивность вызвана магнитным полем, создаваемым электрическими токами, протекающими внутри электрической цепи. Обычно катушки из проволоки используются в качестве катушки, увеличивающей связь магнитного поля и увеличивающей эффект.
Существует два способа использования индуктивности:
Самоиндуктивность: Самоиндуктивность — это свойство цепи, часто катушки, при которой изменение тока вызывает изменение напряжения в этой цепи из-за магнитного эффекта, вызванного протеканием тока.Можно видеть, что самоиндуктивность относится к одной цепи — другими словами, это индуктивность, обычно внутри одной катушки. Этот эффект используется в одиночных катушках или дросселях.
Взаимная индуктивность: Взаимная индуктивность — это индуктивный эффект, когда изменение тока в одной цепи вызывает изменение напряжения на второй цепи в результате воздействия магнитного поля, связывающего обе цепи. Этот эффект используется в трансформаторах.
Определение единицы индуктивности
При обозначении индуктора на принципиальной схеме или в уравнении обычно используется символ «L».На принципиальных схемах индукторы обычно пронумерованы, L1, L2 и т. Д.
Единицей индуктивности СИ является Генри, H, который можно определить с точки зрения скорости изменения тока и напряжения.
Определение Генри:
Индуктивность цепи составляет один Генри, если скорость изменения тока в цепи составляет один ампер в секунду, и это приводит к электродвижущей силе в один вольт.
Один генри равен 1 Wb / A.
Индуктивность — что происходит
Когда ток протекает внутри проводника, будь то прямой или в форме катушки, вокруг него создается магнитное поле, и это влияет на то, как ток накапливается после замыкания цепи.
С точки зрения влияния индуктивности и электрической цепи, это помогает взглянуть на то, как работает схема, сначала для постоянного тока, а затем для переменного тока. Хотя они следуют одним и тем же законам и дают одинаковые результаты, это помогает объяснению, пример постоянного тока проще, и тогда это объяснение может быть использовано в качестве основы для случая переменного тока.
Постоянный ток: По мере замыкания цепи начинает течь ток.Когда ток увеличивается до своего постоянного значения, магнитное поле, которое он создает, накапливается до его окончательной формы. Когда это происходит, магнитное поле изменяется, поэтому оно индуцирует напряжение обратно в саму катушку, как и следовало ожидать в соответствии с законом Ленца.
Индуктор в цепи с аккумулятором и резистором Постоянная времени Т в секундах цепи, которая будет включать в себя значение индуктивности L Генри и соответствующее сопротивление цепи, R Ом, может быть рассчитана как L / R.T — это время, когда ток I ампер поднимается до 0,63 от своего окончательного значения установившегося состояния V / R. Энергия, запасенная в магнитном поле, составляет 1/2 л I ².
Увеличение тока при установлении постоянного напряжения на индуктивности Когда ток отключен, это означает, что сопротивление цепи резко возрастает до бесконечности. Это означает, что отношение L / R становится очень маленьким, а магнитное поле падает очень быстро. Это представляет собой большое изменение в магнитном поле, и, соответственно, индуктивность пытается поддерживать ток, и обратная ЭДС устанавливается для противодействия этому, возникающему из энергии, запасенной в магнитном поле.Напряжения означают, что искры могут появиться на контакте переключателя, особенно когда контакт оборван. Это приводит к точечным контактам и износу любых механических переключателей. В электронных схемах эта обратная ЭДС может разрушить полупроводниковые устройства, и поэтому часто используются способы уменьшения этой обратной ЭДС.
Переменный ток: В случае переменного тока, проходящего через индуктор, используются те же основные принципы, но, поскольку форма сигнала является повторяющейся, мы склонны смотреть на то, как индуктор реагирует немного по-другому, так как это удобнее.
По своей природе переменная форма волны постоянно меняется. Это означает, что результирующее магнитное поле всегда будет изменяться, и всегда будет создаваться индуцированная обратная ЭДС. Результатом этого является то, что индуктор препятствует протеканию переменного тока через него в результате индуктивности. Это в дополнение к сопротивлению, вызванному но омическим сопротивлением провода.
Это означает, что если омическое сопротивление индуктора низкое, он будет пропускать постоянный ток, постоянный ток с небольшими потерями, но он может представлять высокий импеданс для любого высокочастотного сигнала.Эта характеристика индуктора может использоваться для обеспечения того, чтобы любые высокочастотные сигналы не проходили через индуктор.
Еще одним аспектом индуктивности является то, что реактивное сопротивление индуктора и конденсатора может действовать вместе в цепи, чтобы нейтрализовать друг друга. Это называется резонансом и широко используется в полосовых фильтрах.
Индуктивность проводов и катушек
Прямые провода и катушки имеют индуктивность. Обычно катушки используются для катушек индуктивности, потому что связывание магнитного поля между различными витками катушки увеличивает индуктивность и позволяет удерживать провод в меньшем объеме.
Для большинства низкочастотных применений индуктивность прямого провода можно игнорировать, но по мере увеличения частоты в области ОВЧ и за ее пределами индуктивность самого провода может стать значительной, и соединения должны быть короткими, чтобы минимизировать эффекты ,
Имеются расчеты
, позволяющие достаточно точно рассчитать индуктивность проводов, но индуктивность катушек немного сложнее и зависит от множества факторов, включая форму катушки и постоянство материала внутри и вокруг катушки. ,
Индуктивность является ключевым аспектом проводов и катушек. Индуктивность является незаменимой характеристикой, которая может быть использована для многих целей.
Более основные понятия:
Напряжение Текущий сопротивление емкость Мощность трансформеры РЧ шум Децибел, дБ Q, добротность
Возврат в меню основных понятий. , ,
.
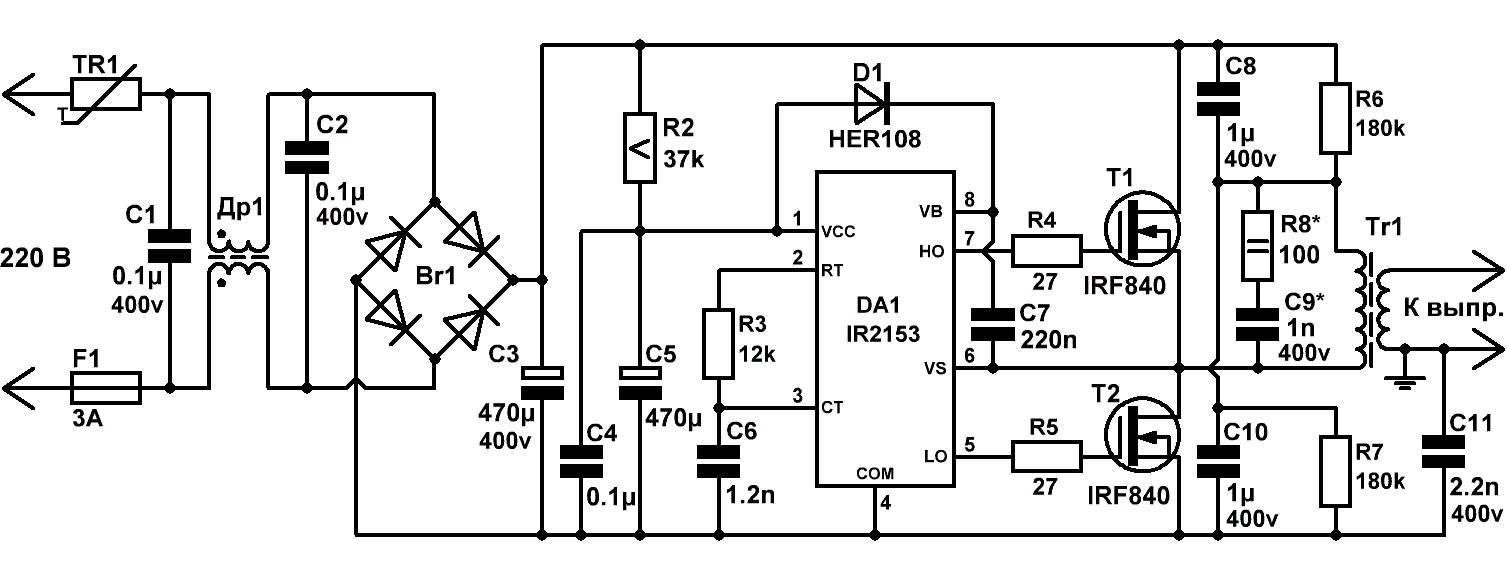
Рубрика: Рубрика:Разное