Как рассчитать индуктивность трансформатора: РАСЧЕТ ИНДУКТИВНОСТЕЙ ОБМОТОК ТРАНСФОРМАТОРА, ОБУСЛОВЛЕННЫХ МАГНИТНЫМИ ПОТОКАМИ В ВОЗДУХЕ

Как я могу рассчитать индуктивность первичной обмотки трансформатора с учетом конкретной нагрузки на вторичной обмотке?

Индуктивность в первичной обмотке трансформатора уменьшается с увеличением нагрузки на вторичной обмотке.

Нет, это не так. Может показаться, что это так (потому что при нагрузке ваш трансформатор потребляет больше тока в первичной обмотке), но просто представьте, что нагрузка, которую вы кладете на вторичную (скажем, 1: 1), была приложена к первичной обмотке — ток в нагрузке будет то же самое (соотношение 1: 1) и малый ток, который поступает в первичную обмотку трансформатора (при отсутствии нагрузки), все равно будет поступать в первичную (этот малый ток является индуктивностью возбуждения и остается неповрежденным при различных условиях нагрузки).

Если ваше отношение было (скажем) 10: 1, и вы подключили резистор 10 Ом на вторичной обмотке, это эквивалентно подключению 10 Ом x ( N п N S ) 2 ( N п N S ) 2 резистор на первичном то есть 1000 Ом. Np и Ns являются первичными и вторичными витками, а ваша эквивалентная первичная нагрузка является квадратом отношения витков.

При «эквивалентной» нагрузке, подключенной к первичной обмотке, индуктивность трансформатора может «казаться» измененной, но она все еще там и параллельно с «эквивалентной» нагрузкой.

РЕДАКТИРОВАТЬ Я добавляю картинку ниже, показывающую трансформатор 1: 1 с обмотками 10 мГн каждая. На вторичной обмотке установлен конденсатор емкостью 2,53 мкФ, а на первичной обмотке 10 В R M S 10 В р M S при 1 кГц: —

Вывод, добавление нагрузки любого описания не влияет на первичную индуктивность намагничивания трансформатора. Если вы поместите индуктор на вторичную обмотку, вы можете подумать, что индуктивность первичной обмотки уменьшилась, но фактически добавленная индуктивность вторичной обмотки становится параллельной неизменной индуктивности намагничивания первичной обмотки.

Расчет силовых трансформаторов при произвольных законах изменения напряжения и тока

Расчету трансформаторов посвящено много работ, например [1–5]. В данной статье представлен подход к их расчету,
основанный на обеспечении:

• заданного нагрева магнитопровода (МП) при намагничивании его переменным напряжением произвольной формы и нагрева обмоток рабочим током произвольной формы;

• получения заданной индуктивности рассеивания, то есть получения заданного значения напряжения короткого замыкания или заданной длительности фронта импульса.

Первый подход хорошо зарекомендовал себя при расчете дросселей с магнитопроводом при произвольной форме тока [6]. Созданная теория подтверждалась результатами статистической обработки значений удельной энергии промышленных дросселей, которая выявила зависимость удельной энергии дросселя как степень 1/7 от значения самой энергии в широких пределах изменения энергий от долей до тысяч джоулей.

Далее не рассматривается расчет «строчных» трансформаторов, которые по виду выполняемых функций являются двухобмоточными дросселями.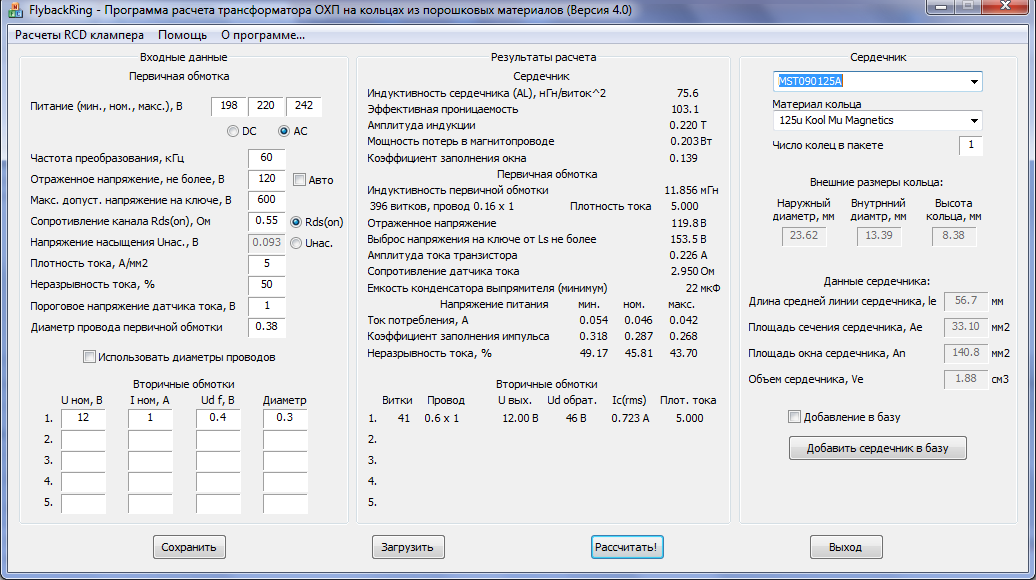

В трансформаторе закон изменения индукции задается напряжением, в дросселе — током. Другими словами, сердечник трансформатора намагничивается напряжением, а дросселя — током. Можно выделить несколько типичных несинусоидальных режимов работы трансформатора.

1. Минимальное и максимальное значения напряжения близки по абсолютному значению, но имеют противоположные знаки
   (рис. 1а). Имеет место режим переменного тока.

2. Минимальное и максимальное значения напряжения намного отличаются друг от друга, например,
   одно равно 5–10% другого (рис. 1б). Время действия положительного и отрицательного напряжения сильно отличаются.
   

   Режим принято называть импульсным. Разность между максимальным и минимальным значением индукции называют перепадом ΔB
   (иногда размахом), а половину этого значения — амплитудой переменной составляющей B_m.

В обоих режимах постоянная составляющая индуктированного напряжения равна нулю.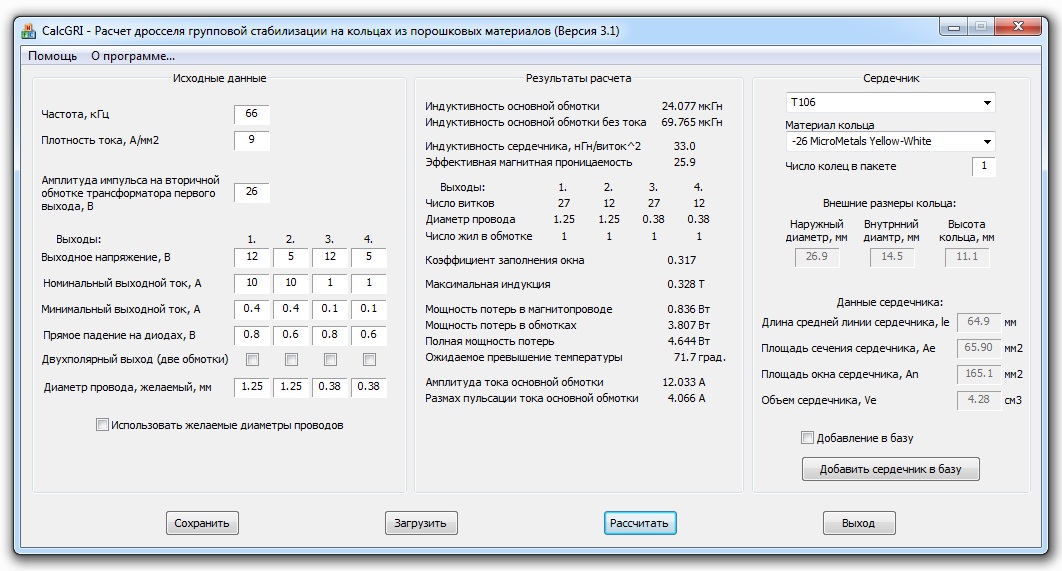 В противном случае индукция в магнитопроводе стала бы непрерывно нарастать.

Дроссель и трансформатор состоят из одинаковых частей: магнитопровода и обмоток. Задачей конструктивного расчета трансформатора и дросселя является определение основных геометрических размеров магнитопровода, числа витков обмоток, сечения проводов обмоток, а для дросселя — еще и определение размеров воздушного зазора.

Исходными данными для расчета трансформатора являются:

1. Закон изменения напряжения u(t) и тока i(t) с заданными параметрами: средним
   значением напряжения U_ср, эффективным значением тока I или амплитудой I_m
   и коэффициентом амплитуды импульса k_a = I_m/I, а также скважностью импульсов
   ν = τ_и/T (рис. 1б).

2. L_s — индуктивность рассеивания, или напряжение короткого замыкания u_к,
   или τ_s = L_s/R_н — постоянная времени, где R_н — сопротивление нагрузки
   трансформатора.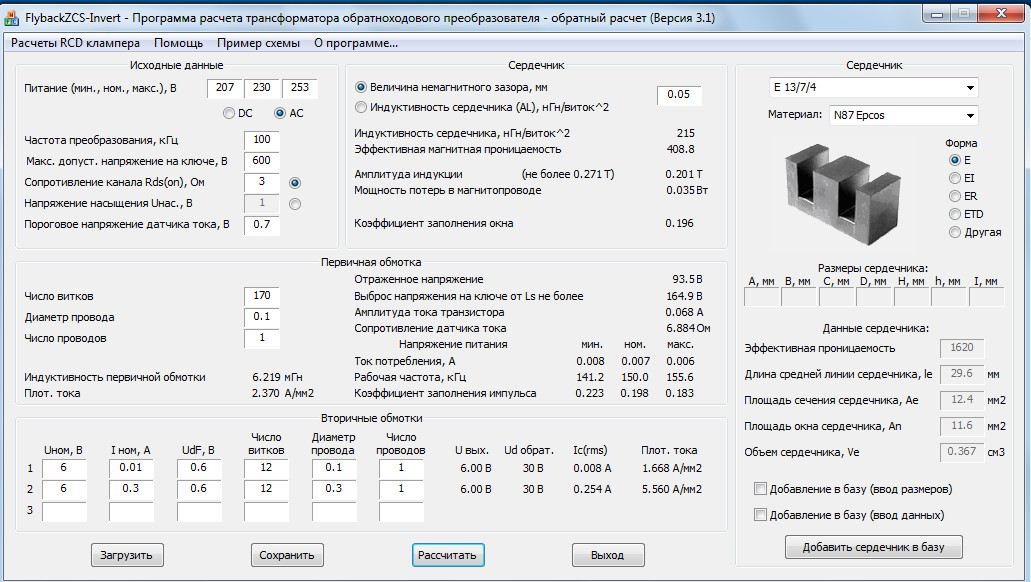

Если трансформатор работает совместно с формирующей линией, то при вычислении постоянной времени сопротивление

нагрузки должно быть удвоено, так как сопротивление нагрузки и, как правило, равное ему волновое сопротивление
линии включены последовательно с индуктивностью рассеивания трансформатора.

Далее будут рассмотрены броневые и стержневые типы трансформаторов. Самые плохие условия охлаждения, ввиду закрытости
магни-топровода катушками, имеет стержневой тип с катушками на обоих стержнях. Стержневой тип трансформатора с двумя
катушками эквивалентен тороидальному трансформатору. Удельные потери для этих магнитопроводов, как правило, должны
составлять 3–5 Вт/кг, а для остальных — 7–10 Вт/кг.

Предварительно по принятому значению удельных потерь в магнитопроводе при известном законе изменения индукции
определяют допустимую амплитуду переменной составляющей индукции В_mc или перепад индукции
ΔB_и.

Рассмотрим выбор и расчет режима работы магнитопроводов.

Самым простым является выбор рабочей индукции для работы на очень низких частотах — 10–20 Гц.
В этом случае могут быть применены шихтованные или витые магнитопро-воды из обычных трансформаторных
сталей с толщиной листа или ленты 0,3–0,5 мм. Для импульсных трансформаторов перепад индукций может
быть близким к значению 2В_s. Для обеспечения такого режима должно быть применено смещение рабочей
точки на кривой намагничивания путем подмагничивания МП постоянным током.

На частотах в десятки и сотни герц должен быть проведен традиционный выбор материалов и режимов работы.

На частотах несколько десятков килогерц потери в МП являются определяющими в выборе марки и толщины магнитного
материала. На этих частотах вихревые потери можно регулировать выбором толщины материала. Особо тонкими выпускаются

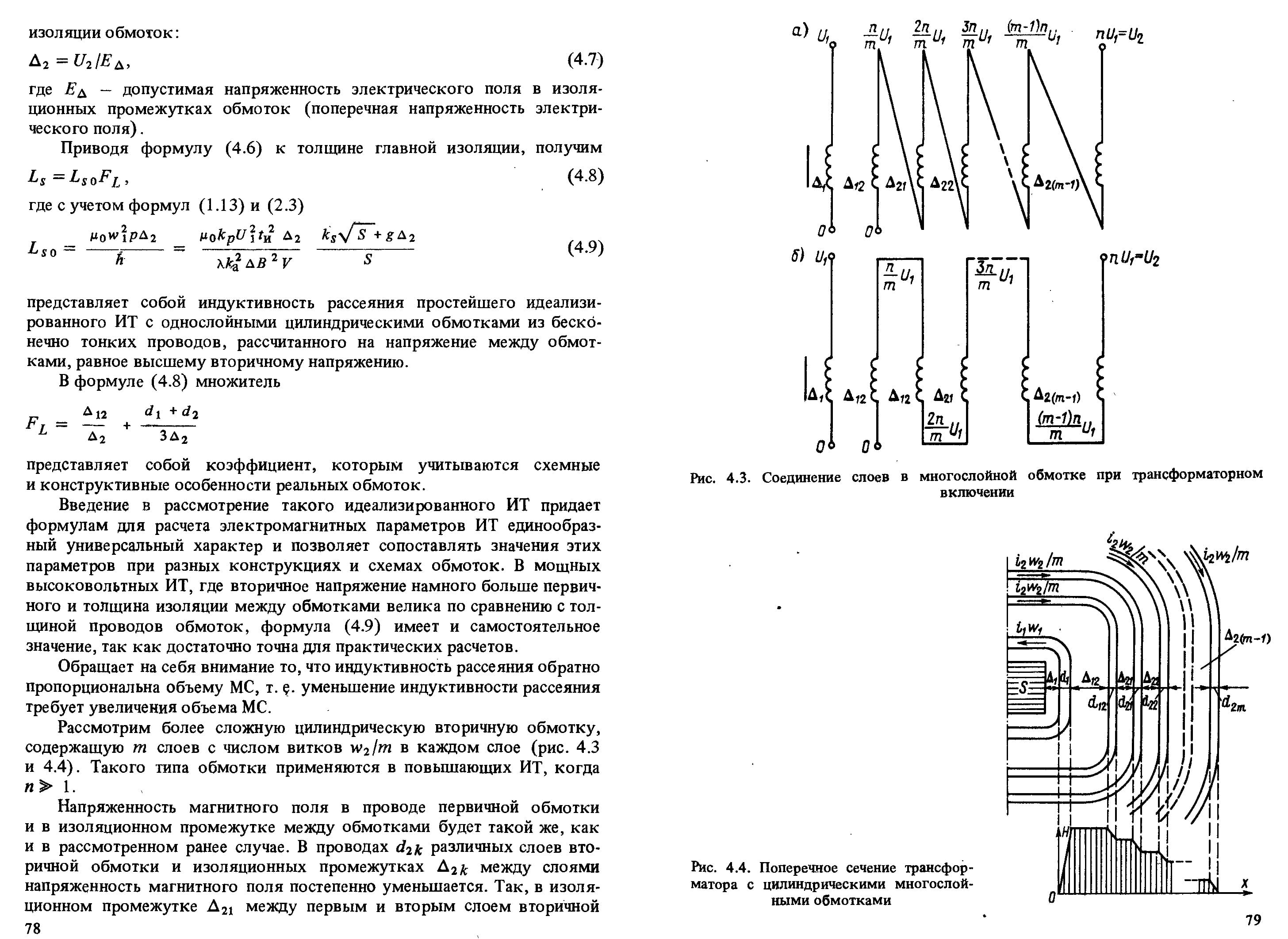ленты из пермаллоев (толщиной 10–20 мк) и аморфные или нанокристаллические материалы (25 мк). Гистерезисные потери
не зависят от толщины материала, а на высоких частотах становятся определяющими. Необходимо выбирать материалы с
узкой петлей гистерезиса или с высокой начальной магнитной проницаемостью. Здесь МП из аморфных сплавов практически
не имеют преимуществ по сравнению с МП из высоколегированных сплавов (пермаллоев).

Радикальный способ снижения потерь — это уменьшение рабочего значения индукции вплоть до десятых долей тесла.
Повышенное значение индукции насыщения материала часто оказывается невостребованным. При малом значении индукции
размеры магнитопровода и трансформатора сильно возрастают.

Для повышения индукции и уменьшения размеров трансформатора может быть применен интенсивный обдув или масляное

охлаждение, повышающие теплосъем с поверхностей в 1,5-2 раза. Ферритовые сердечники при естественном охлаждении
позволяют работать с индукцией 0,3-0,4 Тл.

Выше 10-15 кГц — область работы ферри-товых сердечников или обычных сплавов с очень низкими значениями рабочей
индукции или принудительным охлаждением. К сожалению, изготовление ферритовых сердечников больших размеров связано
с технологическими трудностями. Выбор рабочей индукции производится расчетным путем или по графикам справочных
материалов [7, 8].

Объективным способом контроля качества расчета является экспериментальная проверка теплового режима магнитопровода
при выбранной рабочей индукции на опытном сердечнике или его модели. На сердечник наматывается контрольная обмотка
из тонкого провода с числом витков, обеспечивающим выбранное значение индукции при известной амплитуде импульса

контрольного генератора w=U_г × τ_и/(s × ΔВ_и).

Такой генератор имеет небольшую мощность, так как обеспечивает намагничивание сердечника только на холостом ходу.
Те участки сердечника, на которых будет располагаться обмотка, могут быть закрыты теплоизоляционным материалом.

Пример результатов проверки приведен на графиках (рис. 2). Выбором магнитного материала и величины рабочей индукции заканчивается первый этап расчета трансформатора.

В последующих выводах принято допущение, что тепловой режим магнитопровода не влияет на тепловой режим катушки. При тепловом расчете магнитопровода и катушек не должны учитываться поверхности их соприкосновения.

Второй этап — расчет обмоток. За основную переменную величину принимаем сечение магнитопровода (первая строка таблицы).

Сечение — единственный геометрический параметр, входящий в формулу закона электромагнитной индукции. Закон инвариантен
по отношению к форме сечения. Через сечение при выбранной конфигурации трансформатора могут быть определены все
остальные размеры трансформатора, например, короткая сторона сечения a=0,5×s^1/2 (вторая строка таблицы), длинная
сторона в=2а, высота окна h=4,6а, длина средней силовой линии l_c=(4,6+4,6+2+2+3,14)×а=k₂×s^1/2
(третья строка таблицы), длина витка l_м=k₄×s^1/2 , сечение окна
s_ок=k₆×s. При вычислении площади охлаждения катушек участки поверхности,
соприкасающиеся с маг-нитопроводом, исключены из общей площади охлаждения.

В таблице приведены данные об отношении открытой для охлаждения поверхности магнитопровода к его объему (k₁₂),
определяющие допустимые удельные потери в сердечнике Вт·м/кг.

Выбор в качестве аргумента сечения s удобен тем, что после определения основных геометрических размеров трансформатора
стержень с прямоугольным сечением может быть заменен стержнем любой формы (например, круглым, ступенчатым) с
равновеликим сечением при сохранении основных электрических параметров трансформатора. В таблице представлен ряд
типовых конструкций трансформаторов броневого и стержневого типов. Два первых — броневые с квадратным и прямоугольным
сечением магнитопровода, два следующих — стержневые с квадратным и прямоугольным сечением магнитопровода с катушками
на каждом стержне, и два последних — тоже стержневые с катушкой на одном стержне.

Проблема рассматривается без учета нелинейности вебер-амперных характеристик и при предположении, что в обмотках
отсутствуют дополнительные каналы охлаждения.

Напряжение, индукция, сечение магнитопровода и число витков связаны законом электромагнитной индукции:

• при переменном напряжении:

  отсюда может быть найдено число витков:

• при синусоидальном напряжении:

• при импульсном напряжении:

  где ΔB_и=2B_mc — перепад индукций, B_mc — максимальное
  значение индукции в материале сердечника.

Видно, что при произвольном законе изменения напряжения роль импульса намагничивания играет среднее значение
напряжения за ту часть периода, в которой напряжение выше (или ниже) нуля; эффективное значение тока вычисляется
за целый период. Импульсный режим отличается от периодического, в первую очередь, наличием скважности, отличием
амплитуд и длительностей положительной и отрицательной частей кривой напряжения.

Умножая левую и правую части первых уравнений при переменном режиме на I, а при импульсном режиме на I_и,
с учетом того, что I=I_m/k_a√v и T=1/f, получим:

• при переменном напряжении:

• при синусоидальном напряжении:

• при импульсном напряжении:

Покажем, что МДС (Iw)1 катушек каждого магнитопровода имеет некоторое предельное значение, ограниченное
нагревом катушек. Пусть в окне сердечника площадью s_ок размещается w витков обмотки, коэффициент заполнения
окна проводниковым материалом k_м=0,35, тогда активное сопротивление обмотки:

где l_м1 — средняя длина одного витка обмотки, ρ=1,85 × 10^–8 Ом·м — удельное
сопротивление медного провода.

Для того чтобы сопротивление обмотки и выделяющаяся мощность не увеличивались с ростом рабочей частоты (кГц)
трансформатора, его обмотки должны быть намотаны проводом типа литцендрат. Жила провода литцендрат состоит из
многих изолированных проводников. Диаметр одного проводника (мм) не должен превышать значения [9]:

Мощность, выделяемая в катушке и рассеиваемая ее поверхностью:

где s_охл — поверхность охлаждения обмотки, то есть поверхность обмотки за исключением частей,
обращенных к стержню; q=650 Вт/м2 — допустимая плотность теплового потока при превышении температуры
поверхности обмотки над окружающим воздухом на 55 °С.

Для уменьшения индуктивности рассеивания (см. далее) бывает целесообразно при заданной площади окна снизить
толщину намотки, то есть занять обмоткой лишь часть ширины окна. Эта же задача возникает при необходимости
разместить в окне высоковольтную изоляцию первичной или вторичной обмотки.

Введем параметр ß

Предельная МДС зависит от геометрических размеров катушки, коэффициента теплоотдачи с ее поверхности,
удельного сопротивления провода и коэффициента использования ширины окна.

Поверхность охлаждения, площадь окна, площадь сечения сердечника, средняя длина витка для выбранной
формы сердечника могут быть выражены через сечение зазора s, и поэтому

для распространенных геометрических форм магнитопроводов приведены в таблице (при расчетах предполагается
использование системы СИ).

В каждой катушке стержня трансформатора имеется минимум две обмотки, их магнитодвижущие силы равны:
(Iw)₁=(Iw)₂=(Iw)_пред/2. С учетом этого уравнения (3) и (4) примут вид:

• при переменном напряжении:
• при синусоидальном напряжении:
• при импульсном напряжении:

Это первая группа формул для определения сечения магнитопровода проектируемого трансформатора. Затем могут
быть определены остальные размеры, например, короткая сторона сечения магнитопровода a=√s при
квадратной или a=√(s/2) при прямоугольной форме сечения, высота окна h=4a и т. д.

Обратим внимание, что исходными данными для расчета трансформатора на переменном токе являются среднее напряжение
за полпериода и эффективный ток обмоток без учета фазы их взаимного расположения во времени. Другими словами,
размеры трансформатора зависят не от передаваемой активной мощности, а от полной или кажущейся мощности S.

Однако если производить расчет трансформатора исходя только из условий охлаждения, то может оказаться, что
индуктивность рассеивания L_s обмоток будет очень большой, что приведет к недопустимо большому падению напряжения
u_к при синусоидальном режиме работы трансформатора, искажению формы кривой при другом законе изменения напряжения
или к недопустимо большой длительности фронта τ_s/τ_и в импульсном режиме.

Значение индуктивности рассеивания L_s пропорционально площади сечения катушек трансформатора в плоскости,
перпендикулярной оси катушек, и обратно пропорционально их длине. Если одна обмотка короче другой, то индуктивность
рассеивания резко возрастает, поэтому длины обмоток должны совпадать. При малом числе витков для выполнения этого
условия секции с малым числом витков должны быть повторены необходимое число раз, а затем соединены параллельно.
Эффективная площадь рассеивания s_s представляет сумму третьей части от площади сечения обмоток и полной площади
сечения зазора между обмотками. Если обмотки занимают не всю ширину окна, то:

Значения коэффициента k_Ls приведены в таблице.

У стержневого трансформатора с двумя катушками длина катушек вдвое больше, чем у трансформаторов остальных видов,
а их толщина вдвое меньше. Индуктивность рассеивания получается примерно в 4 раза меньше, чем у других видов.
Она сопоставима с индуктивностью рассеивания трансформатора, выполненного на тороидальном сердечнике с обмоткой,
расположенной не по всей длине средней силовой линии МП (из-за необходимости выполнить выводы от нижней обмотки).
Однако, если на высоких частотах из-за плохого охлаждения сердечника придется вдвое снизить индукцию, то потребуется
вдвое увеличивать число витков, в четыре раза возрастет индуктивность рассеивания. Преимущества тороидальной конструкции
полностью теряются.

Подставим в формулу (12) значения витков (1) и (2) для обоих режимов и получим:

• при переменном напряжении
• при импульсном напряжении

Мы получили вторую пару формул для определения размеров трансформатора. Она определяет размеры трансформатора при
любой форме кривой напряжения. Предполагается, что известно значение индуктивности рассеивания и напряжение той
обмотки, относительно которой определяется эта индуктивность.

Если значение L_s неизвестно, то размеры могут быть определены через относительные величины: напряжение короткого
замыкания для синусоидального режима (понятие напряжение короткого замыкания существует только для синусоидального
режима, когда существует величина — круговая частота ω=2πf) или относительную длительность фронта импульса для
импульсного режима.

Умножим левую и правую части уравнения (13) для синусоидального режима на I, а для импульсного режима
(15) — на I_и и после несложных преобразований получим:

• при синусоидальном напряжении
• при импульсном напряжении

где u_к=100ω>L_sI/U — напряжение короткого замыкания в %, а
для импульсного режима τ_s/τ_и — относительная длительность фронта импульса.

Таким образом, мы получили третью пару формул для определения площади сечения магнитопровода.

Если известны L_s и u_к или τ_s/τ_и,
то вторая и третья группы формул дают одинаковый результат. Из найденных по (9-11) сечения s₁
и по (14, 16-18) сечения s₂ должно быть выбрано большее по величине,
и с ним проведены расчеты остальных геометрических параметров, чисел витков и др. Однако, если сечение,
найденное из (14, 16-18), окажется много больше сечения, полученного из (9-11) с учетом только тепловой
нагрузки трансформатора (через k_Iw),, то должен быть произведен повторный расчет с β s^20/21 ≡ s¹) значение р может быть принято равным отношению полученных на первом шаге
сечений s₁/s₂.

Тепловыделение внутри обмоток трансформатора, поверхность охлаждения и принятая допустимая температура поверхности
катушек определяют максимально допустимую плотность тока в проводах обмоток:

Значения коэффициента k_Δ также приведены в таблице.

С учетом найденных соотношений могут быть определены объемы меди обмотки и стали сердечника.

Зная плотность меди и стали, предполагая массу конструктивных элементов (10%), найдем массу этих частей и
общую массу трансформатора, кг:

Значения коэффициентов k_g , k_g и k_g приведены в таблице.

В формулу для определения общей массы трансформатора m_Т (21) может быть подставлено
значение сечения из (9). Получим выражение для вычисления массы трансформатора без учета влияния индуктивности
рассеивания:

Используя формулу (17), найдем выражение для массы через полную мощность и напряжение короткого замыкания:

Используя формулу (18), определим массу трансформатора при одновременном задании энергии импульса и постоянной времени цепи нагрузки:

Значения коэффициентов k_gSu=k_gWz приведены в таблице.

При анализе этих коэффициентов видно, что если проектировать трансформатор с одинаковым уровнем индукции
(если позволяют условия охлаждения МП), то самым легким является стержневой трансформатор с прямоугольным
сечением магнитопровода.

Порядок применения формул для инженерных расчетов покажем на примерах.

Пример 1

Требуется спроектировать трансформатор, работающий от генератора напряжения прямоугольной формы («меандр») с
амплитудой 375 В. Ток нагрузки в виде резонансного контура обуславливает синусоидальную форму тока с эффективным
значением I=I_m/(k_a√v) = 43 А, рабочая частота 15 кГц, индуктивность рассеивания
должна составлять 9,5 мкГн.

Высокая рабочая частота заставляет сразу обраться к применению ферритового магнитопровода. Коэффициент заполнения
материалом сердечника k_c=1. В соответствии с приведенным на рис. 2 графиком выбираем уровень рабочей индукции
B_cm=0,22 Тл.

Выбираем магнитопровод стержневого типа с прямоугольным сечением. Рассчитываем сечение магнитопровода без учета
требований к напряжению короткого замыкания по (9), первоначально с Β=1.

Теперь с учетом требований к индуктивности рассеивания рассчитаем по (16):

Очевидно, трансформатор должен быть выполнен на магнитопроводе с большим сечением — 8,6 см2. По найденному сечению
могут быть определены остальные размеры трансформатора. Например, а=0,71√s=0,02 м,
высота окна h=4a=0,08м; ширина окна 1,6а=0,032м; площадь окна 0,0026 м² и т. д.
Число витков рассчитываем по формуле (1):

Плотность тока вычисляем по формуле (19):

Сечение провода 43/2,9 = 14,8 мм2, или иначе:

Диаметр составляющих литцендрат проводников по (6) составит 1/√15 = 0,26 мм.

Число витков и сечение другой обмотки будут отличаться в коэффициент трансформации раз.

Масса трансформатора составит m_Т= k_gs((β+1)/2)s^3/2,
m_Т=1,40×10⁵×1×(8,6×10⁴)3/2 = 3,5 кг.

Пример 2

Требуется рассчитать трансформатор, работающий совместно с формирующей линией, импульсным напряжением 40 кВ,
током 300 А (импульсная мощность 12 МВт), длительностью импульса 360 мкс, длительностью фронта t_ф = 10% и частотой
повторения импульсов 1 Гц.

Скважность импульсов 1/0,00036 = 2780. Трансформатор, работающий на активную нагрузку без формирующей линии,
будет иметь постоянную времени фронта вдвое больше — 20%. Длительность фронта — 360×0,2 = 72 мкс = 3τ_s.
Постоянная времени фронта трансформатора тs составит 72/3=24 мкс. При этом сопротивление нагрузки
R_н=40 000/300=133 Ом, и индуктивность рассеивания L_s=τ_sR_н=24×133 = 3200 мкГ.

Расчет начинаем с выбора режима работы магнитного материала сердечника. При частоте повторения 1 Гц можно использовать
любой магнитомягкий материал — листовую трансформаторную сталь. Максимальное значение индукции может
быть ΔВ_и=2B_s=2,4 Тл.

Выбираем стержневой магнитопровод с квадратным (круглым, ступенчатым) сечением стержня с двумя катушками.

Рассчитываем сечение магнитопровода по энергии импульса без учета требований к длительности фронта (11)
первоначально β=1.

Теперь по энергии импульса с учетом требований к длительности фронта (18) находим s:

Масса трансформатора с сечением 255·10^–4 м² составит в соответствии с (21):

Редкие импульсы не могут сильно нагреть обмотки, поэтому первое сечение и магнитопровод получаются небольшими.
Второе большое сечение является следствием требований, связанных с длительностью фронта, то есть с индуктивностью
рассеивания. Два полученных сечения отличаются примерно в пять раз. Можно в 2-3 раза уменьшить толщину обмотки.
Проведем расчет по тем же формулам (11) и (18) при β=0,4:

Дальнейшие вычисления необходимо производить с этим значением сечения, например, масса трансформатора будет не 1006 кг, а:

Значение В может быть еще уменьшено.

Пример 3

Оценим размеры трансформатора с прямоугольной формой кривых рабочего напряжения и тока (меандр) 50 В, ток 1 А (эфф.) для работы на частоте 50 кГц.

Предполагаем применение ферритового броневого магнитопровода (Ш-образного) с индукцией 200 мТл.

По формуле (9) находим необходимое сечение магнитопровода: 0,31 см² = 31 мм².

По формуле (22) его массу: 0,012 кг =12 г и т. д.

Далее могут быть проанализированы другие варианты конструкций, иные соотношения размеров с целью проведения уточнений при той или иной оптимизации (по массе, объему, стоимости, введению каналов охлаждения и т. п.).

Расчет по разработанным формулам типовых, выпускаемых промышленностью рядов трансформаторов серии ТН, ОСМ дает совпадение расчетных параметров с фактическими.

Одинаково успешный расчет и малых, и больших трансформаторов при различных законах изменения напряжения и тока указывает на фундаментальность приведенной теории расчета.

Литература

1. Тихомиров П. М. Расчет трансформаторов. М.: Госэнергоиздат, 1953.

2. Ицхоки Я. С. Импульсная техника. М.: Советское радио, 1949.

3. Булгаков Н. И. Расчет трансформаторов. М.: Госэнергоиздат, 1950.

4. Ицхоки Я. С. Импульсные устройства. М.: Советское радио, 1959.

5. Черкашин Ю. С. Определение условий эквивалентности электрических режимов мощных силовых и импульсных трансформаторов // Электричество. 1966. № 5.

6. Черкашин Ю. С. Расчет дросселей с маг-нитопроводом при произвольной форме тока // Силовая электроника. 2008. № 3.

7. Черкашин Ю. С. Процесс и энергия намагничивания листового магнитопровода при прямоугольном напряжении // Электричество. 1978. № 6.

8. Бабин С. В., Карасев В. В., Филиппов Ф. Е. Характеристики магнитопроводов трансформаторов тока при одновременном воздействии постоянного и переменного магнитного поля // Электротехническая промышленность. 1981. Вып. 6.

9. Черкашин Ю. С. Проектирование катушек индуктивности для мощных радиотехнических устройств // Радиотехника. 1986. № 6.

Индуктивности обмоток трансформатора и электромагнитное рассеяние

Дата публикации: 29 июля 2013.
Категория: Статьи.

Индуктивности обмоток

В трансформаторах со стальным магнитопроводом магнитная проницаемость стали µ во время цикла перемагничивания непостоянна. Поэтому в течение этого цикла непостоянны также собственные L и взаимные М индуктивности обмоток трансформатора. В результате такого непостоянства µ при подключении трансформатора к сети с синусоидальным напряжем в его намагничивающем токе i₀ возникают высшие гармоники (смотрите статью «Явления, возникающие при намагничивании магнитопроводов трансформаторов»).

Рисунок 1. Магнитные потоки трансформатора при одностороннем намагничивании (i1 ≠ 0, i2 = 0)

При работе трансформатора на ток i₀ накладывается ток нагрузки, по отношению к которому ток i₀ и, в особенности, его высшие гармоники малы. Поэтому при исследовании режимов работы трансформатора указанными гармониками можно пренебречь и учитывать только основную гармонику тока i₀. Это равносильно допущению, что во время цикла перемагничивания µ, L и M постоянны. Влияние насыщения магнитопровода при этом можно учесть, принимая в расчет при разных режимах работы трансформатора, при разных амплитудах потока магнитопровода, значения µ, L и M для данного режима работы. В соответствии с изложенным будем полагать, что µ, L и M постоянны.

Рассмотрим индуктивности и индуктивные сопротивления обмоток, обусловленные магнитным потоком магнитопровода Ф_с, все силовые линии которого полностью замыкаются по замкнутому магнитопроводу и поэтому сцепляются со всеми витками первичной и вторичной обмоток (рисунок 1).

Пусть поток Ф_с создается током первичной обмотки i₁, когда ток вторичной обмотки i₂ = 0. Значения Ф_с и i₁ могут быть известны, например, из данных расчета магнитной цепи или из опыта. Тогда собственная индуктивность первичной обмотки от потока в магнитопроводе

Lс1 = w1 × Фс / i1.

(1)

Величину L_с1 можно выразить также через магнитное сопротивление магнитопровода

(2)

где l_k, S_k и µ_k соответственно означают длину, площадь сечения и магнитную проницаемость k-го участка магнитной цепи. При этом

Фc = F1 / Rµc = w1× i1 / Rµc.

(3)

и после подстановки этого значения Ф_с в выражение (1) получим

Отметим, что значение R_µc также может быть определено по данным расчета магнитной цепи или из данных опыта по соотношению (3).

Аналогично индуктивность вторичной обмотки от потока магнитопровода

а взаимная индуктивность первичной и вторичной обмоток от потока магнитопровода

Mс = w1 × w2 / Rµс

(6)

Картина магнитного поля, замыкающегося целиком по магнитопроводу, одинакова независимо от того, какой из обмоток это поле создается. Поэтому и магнитное сопротивление потоку Ф_с одинаково для поля обеих обмоток и в равенства (4), (5) и (6) входит одинаковая величина R_µс. Вследствие этого также

(7)

Кроме потока Ф_с, ток первичной обмотки i₁ создает также поток Ф_в1 (рисунок 1), силовые линии которого замыкаются частично по воздуху или через трансформаторное масло. Потокосцеплениям Ψ_в1 и Ψ_в12 этого потока с первичной и вторичной обмотками соответствует собственная индуктивность первичной обмотки

L_в1 = Ψ_в1 / i₁

и взаимная индуктивность двух обмоток

M_в12 = Ψ_в12 / i₁.

Точно так же при питании вторичной обмотки током i₂ создается поток Ф_в2, замыкающийся частично по воздуху. Потокосцеплениям Ψ_в2 и Ψ_в21 этого потока с вторичной и первичной обмотками соответствует собственная индуктивность вторичной обмотки

L_в2 = Ψ_в2 / i₂

и взаимная индуктивность двух обмоток

M_в21 = Ψ_в21 / i₂.

При этом, согласно принципу взаимности,

M_в12 = M_в21 = M_в

Поля потоков Ф_в1 и Ф_в2 имеют гораздо более сложный характер, чем поле потока Ф_с. Отдельные магнитные линии этих потоков сцепляются с неполными и разными числами витков первичной и вторичной обмоток. Поэтому в отличие от L_с2 [смотрите соотношение (7)]

(8)

Полные собственные индуктивности первичной и вторичной обмоток

L11 = Lс1 + Lв1; L22 = Lс2 + Lв2,

(9)

и полная взаимная индуктивность

Первые слагаемые равенств (9) и (10) значительно больше вторых, так как потоки через воздух относительно малы.

Понятие об электромагнитном рассеянии

Полнота электромагнитной связи двух индуктивно связанных цепей характеризуется коэффициентом связи этих цепей

(11)

Как известно из курса теоретических основ электротехники, в реальных условиях всегда c < 1.

Если бы в трансформаторе отсутствовали потоки Ф_в1 и Ф_в2, замыкающиеся по воздуху, то L₁₁ = L_c1, L₂₂ = L_c2, M = M_c, и в этом случае в соответствии с равенствами (4), (5), (6) и (11)

Таким образом, неполнота электромагнитной связи в трансформаторе, выражаемая неравенством c < 1, обусловлена наличием потоков Ф_в1 и Ф_в2 или, точнее, неодинаковым их сцеплением с обеими обмотками. Условие c = 1 было бы достигнуто только в том случае, если бы удалось полностью совместить первичную и вторичную обмотки, что фактически невозможно.
Явление неполной электромагнитной связи называется электромагнитным рассеянием.

Наряду с соотношением (11) целесообразно ввести в рассмотрение коэффициент электромагнитного рассеяния

(12)

Чем меньше c и чем больше σ, тем больше рассеяние.

Ввиду того что явление рассеяния обусловлено неодинаковостью или неполнотой сцепления потоков Ф_в1 и Ф_в2, проходящих по воздуху, с обеими обмотками, эти потоки называют часто также потоками рассеяния, однако это название до некоторой степени условно, так как потоки Ф_в1 и Ф_в2 обусловливают также явление взаимной индукции, поскольку M_в ≠ 0. Степень неполноты электромагнитной связи, или величина электромагнитного рассеяния, оказывает большое влияние на многие технические показатели и характеристики трансформаторов и вращающихся электрических машин.

В трансформаторах с ферромагнитным магнитопроводом потоки Ф_в1 и Ф_в2 относительно малы.

Поэтому электромагнитная связь в трансформаторах чрезвычайно высока, а рассеяние мало.

В силовых трансформаторах, например, c = 0,998 – 0,9995 и соответственно σ = 0,001 – 0,004.

Вследствие этого значение σ, определяемое по формуле (12), представляет собой разность весьма близких величин и вычисление σ по этой формуле связано с очень большими погрешностями, так как L₁₁, L₂₂ и M в практических устройствах не могут быть рассчитаны или определены из опыта с достаточной степенью точности. Поэтому возникает необходимость в непосредственном определении параметров, характеризующих электромагнитное рассеяние.

Источник: Вольдек А. И., «Электрические машины. Учебник для технических учебных заведений» – 3-е издание, переработанное – Ленинград: Энергия, 1978 – 832с.

Методы определения индуктивности рассеяния обмоток силового трансформатора Текст научной статьи по специальности «Электротехника, электронная техника, информационные технологии»

Г.М. МИХЕЕВ, В.М. ШЕВЦОВ, Т.Г. ИВАНОВА

МЕТОДЫ ОПРЕДЕЛЕНИЯ ИНДУКТИВНОСТИ РАССЕЯНИЯ ОБМОТОК СИЛОВОГО ТРАНСФОРМАТОРА

Ключевые слова: диагностика, силовой трансформатор, регулятор напряжения под нагрузкой, индуктивность рассеяния.

Разработан уточненный метод определения индуктивности рассеяния обмоток силовых трансформаторов. Дано сравнение предложенного метода с известными в настоящее время расчетными методами.

G.M. MIKHEEV, V.M. CHEVSOV, T.G. IVANOVA METHOD FOR DEFINITION STRAY INDUCTION OF HIGH-VOLTAGE TRANSFORMER WINDING

Key words: diagnostic, transformer, tap on-load, stray induction.

For definition stray induction high-voltage of transformer winding a new method is developed. The proposed method is compared with the known conventional methods.

Магнитные потоки рассеяния наряду с потоками намагничивания играют важную роль в силовом трансформаторе, так как они участвуют непосредственно в основном процессе преобразования электромагнитной энергии. На схемных моделях трансформаторов принято их наличие отражать линейной индуктивностью рассеяния LCT.

В аварийных режимах индуктивность рассеяния ограничивает уровни токов коротких замыканий и интенсивность нагрева обмоток, способствует уменьшению электродинамических усилий, благодаря чему снижается вероятность повреждения силового трансформатора при коротких замыканиях, как внутренних, так и сквозных. С другой стороны, с индуктивностью рассеяния связаны добавочные потери в элементах конструкции трансформатора, что уменьшает его полезную мощность, к.п.д. и напряжение на вторичных обмотках и обуславливает потребление реактивной мощности.

Известен расчетный метод определения индуктивности рассеяния обмоток силовых трансформаторов по заданным конструктивным параметрам [5]. Например, для концентрических обмоток индуктивность рассеяния определяется по формуле:

La = Lia + L2C =ц0W12 [a 12 + j, (1)

где La — суммарная величина индуктивности рассеяния обмоток; L1a — индуктивность рассеяния высоковольтной обмотки; L2a — индуктивность рассеяния низковольтной обмотки, приведенной к высоковольтной, при этом L 2a = k L2a; L2a — индуктивность рассеяния низковольтной обмотки; k — коэффициент трансформации; /и0 — постоянная магнитная проницаемость среды; W1 — число витков высоковольтной обмотки; Dcp — средний диаметр двух обмоток; kR — коэффициент Роговского; l — высота обмоток; a12 — расстояние между обмотками; a1 — ширина высоковольтной обмотки; a2 — ширина низковольтной обмотки.

Данный расчет значений индуктивности рассеяния трансформатора является приближенным, кроме того, затруднительно определение этого параметра в

отдельности для каждой его обмотки, так как нельзя установить точную границу разделов магнитных линий, сцепляющихся с разными обмотками. Другим недостатком способа является присутствие некоторых допущений: равенство числа витков первичной и вторичной обмоток, диапазон коэффициентов Роговского от 0,93 до 0,98, что не позволяет выбрать его с высокой точностью.

Существует более простой экспериментальный способ определения индуктивности рассеяния трансформатора [1-3,5] из опыта короткого замыкания с использованием паспортных данных (ик%), а также известных параметров трансформатора — номинального напряжения (ин) и тока (7н) по формуле:

. (2)

° 1н -ю-100

Однако и в этом случае индуктивность рассеяния определяется приближенно как суммарная индуктивность двух обмоток трансформатора, а точность расчета также не высока, так как в формуле расчета используется полное сопротивление, пренебрегается активными сопротивлениями обмоток и индуктивностью намагничивания.

Можно предложить более точный метод определения индуктивности рассеяния силового трансформатора на основе обработки цифровых осциллограмм (цифрограм). В работе [4] показано, что в режиме осциллографирования токов контактной системы регулятора напряжения под нагрузкой (РПН) благодаря симметричной подаче постоянного тока по всем трем фазам высоковольтной обмотки силового трансформатора (при этом низковольтная обмотка разомкнута и находится в режиме холостого хода) все три фазных магнитодвижущих силы одинаковы по величине и направлены встречно, вследствие чего возбуждаемые магнитные потоки являются в основном потоками рассеяния.

В этом режиме магнитные потоки (рис. 1) отдельных фаз будут замыкаться каждый через свой магнитный стержень, воздушно-масляное пространство, стальной корпус трансформатора и не сцепляются с обмотками других фаз.

Каждая коммутируемая фаза высоковольтной обмотки силового трансформатора с достаточной точностью может быть представлена схемой замещения как активно-индуктивная Л£-цепь, например фаза Л-Ы (рис. 2, а).

Аналитическая модель процесса переключения высоковольтной обмотки описывается в этом случае дифференциальным уравнением первого порядка:

Ч I)+£ •

где Ь1а — индуктивность рассеяния высоковольтной обмотки; Яц — активное сопротивление цепь.

Реальный процесс переключения положений Ъ-с-С переключающего устройства иллюстрируется кривой переходного тока і(ґ), состоящей из трех интервалов (Ъ-с), — исходного, (с-С) — спадающего и (сі-/) — нарастающего тока [6].

Спадающий участок переходного тока соответствует интервалу времени, когда включен в последовательной коммутируемой цепи токоограничивающий резистор. Постоянные времени переходных процессов в режиме переключения ответвлений обмотки определяются только индуктивностью рассеяния и активными сопротивлениями элементов цепей. Значения активных сопротивлений обмоток силового трансформатора обычно могут быть определены с высокой точностью,

Рис. 1. Схема осциллографирования токов контактной системы РПН типа РНТА-35/200 ИДТ — измерительные датчики тока; ИНПТ — источник напряжения постоянного тока; ЧК — четырехпроводный кабель; ЦО — цифровой осциллограф

так как они содержатся в паспорте или измеряются в эксплуатации обычными стандартными методами, причем значения приводятся затем к одной и той же температуре. Поскольку индуктивность рассеяния высоковольтной обмотки (£1ст) на порядок меньше полной индуктивности каждой из фаз обмотки, переходные процессы в этом режиме протекают достаточно быстро, причем удается на осциллограмме токов четко зафиксировать моменты переключения контактов быстродействующего переключающего устройства с помощью цифрового регистратора. На интервалах спадающего (е-ф) и нарастающего (<3-/) тока (см.ехр(-ґ/т):

/■(О = /уст + А • ехр(—/т),

где А — постоянная интегрирования, т — постоянная времени коммутируемой цепи, определяемая по формуле:

т L\a/Яц- >

где Яц — общее активное сопротивление коммутируемой цепи.

а б

Рис. 2. Эквивалентная электрическая схема для расчета индуктивности рассеяния высоковольтной обмотки силового трансформатора (а), где 1 — схема замещения цепи одной фазы высоковольтной обмотки силового трансформатора; 2 — источник напряжения постоянного тока;

3 — упрощенный вид контактной системы контактора РПН; А — вывод фазы А высоковольтной обмотки, N — вывод нейтрали трансформатора и соответствующая форма кривой переходного тока контактной системы регулятора напряжения под нагрузкой (б)

Если взять любое мгновенное значение тока і1 в некоторый момент времени і1 на спадающем участке (с-с1) и ввести местное время, то легко находится А:

і і (0) = /уСТ + А,

откуда

А = /уст — іі(0).1а / Яц

Затем определяется индуктивность рассеяния высоковольтной обмотки:

Ll<з т • Яц.

Таким образом, реальное значение индуктивности рассеяния высоковольтной обмотки фазы легко рассчитывается без решения сложных трансцендентных уравнений и с высокой степенью точности.

Определение индуктивности рассеяния этим расчетным методом выполняется в несколько этапов. На первых трех этапах определяют искомый параметр на спадающем участке кривой тока, как минимум, в трех точках.

Для этого на начальном участке (с-ф спадающей кривой переходного тока /\ выбирают произвольно (несколько ниже от установившегося значения до переключения регулятора напряжения под нагрузкой) и по нему находится время 1\ на кривой (см.; Е — эдс источника напряжения постоянного тока; Яц — суммарное активное сопротивление элементов в цепи высоковольтной обмотки; Я0 — внутренне сопротивление источника напряжения постоянного тока; Я0бм.отв.(-) — активное сопротивление обмотки трансформатора на ответвлении до переключения переключающего устройства; Яобм.отв.(+) -активное сопротивление обмотки трансформатора на переключаемом ответвлении; Я\ — активное сопротивление обмотки одного ответвления; Яобм отв.(+) = Яобм отв.(-) + Я\; Ятор. — активное сопротивление токоограничивающего резистора РПН; е — основание натурального логарифма; 1уст. — установившееся значение тока в цепи обмотки трансформатора на спадающем участке; Зная значение /2, по кривой тока осциллограммы, полученной экспериментальным путем с помощью цифрового регистратора, находят Ь. Далее определяется постоянная времени переходного процесса (т):

т = t2 — Ь.

Таким образом, постоянная времени переходного процесса т определяется как разность времен, полученных между двумя значениями переходного тока, первое значение из которых выбирается произвольно, а второе значение переменной составляющей тока определяется по формуле (3) через время т. лобм.отв.(+) 1,03

ч Ч = 1 уст + Ае Т , А 2,12 1,59 1,39

. 1 уст(е -1)+ А А е 1,43 1,24 1,16

ґ2, мс 12,98 19,66 23,6

т = ґ2 — ґь мс 8,98 9,66 9,6

І<т1 = т -Яс, мГн 104,17 112,05 109,17

Lamid, мГН 109,1

Математическая обработка данных экспериментальной кривой осцилло-графирования работы контактной системы РПН и расчет индуктивности рассеяния высоковольтной обмотки данного трансформатора показывают, что равняется 109 мГн.

Для сравнения приведем расчет значений индуктивности рассеяния этого же трансформатора другими способами, например, по формуле (1) при следующих его параметрах обмотки: Ж1 =841 — число витков высоковольтной обмотки; Дср = 871,5 мм; =0,95; I =1818 мм; а12 =90 мм; а1 =141 мм;

а2=157 мм.

Подставляя эти выражения в формулу (1), находим, что полная индуктивность рассеяния первичной и приведенной вторичной обмоток одной фазы трансформатора Ьа составляет 240 мГн.

Обычно считается, что индуктивность высоковольтной обмотки составляет приближенно половину индуктивности рассеяния трансформатора. В нашем случае индуктивность рассеяния высоковольтной обмотки Ь1а тогда составит 120 мГн.

Важно отметить, что, пользуясь значениями индуктивности рассеяния высоковольтной обмотки, полученными предложенным способом (L1a=109 мГн), можно определить более точно индуктивность рассеяния и низковольтной обмотки. L72a=La — L1a = 240 — 109= 131 мГн.

Далее определим индуктивность рассеяния этого же трансформатора другим известным способом согласно [2] для конкретных параметров данного трансформатора:

UH = 110 кВ, 1н = 200,8 A, Uk=10,56 %.

La = U ■ %’U ■ = 10’56-110000 = 184 мГн.

1н -ю -100 200,8-314-100

Определим индуктивность рассеяния низковольтной обмотки L2a :

L72a=La — L1a = 184 — 109= 75 мГн.

Меньшие значения индуктивностей рассеяния трансформатора, определенные по второму известному способу по сравнению с первым, можно объяснить шунтирующим влиянием индуктивности намагничивания.

Таким образом, предложенный способ определения индуктивности рассеяния высоковольтной обмотки трансформатора дополняет известные приближенные методы, дает более точное значение и позволяет рассчитать отдельно значения индуктивностей как высоковольтной, так и низковольтной обмоток.

Литература

1. Васютинский С.Б. Вопросы теории и расчета трансформаторов / С.Б. Васютинский. Л.: Энергия, 1970. С. 432.

2. Вольдек А.И. Электрические машины: учебник для студентов высш. техн. учеб. заведений. 2-е изд., перераб. и доп. /А.И. Вольдек. Л.: Энергия, 1974. С. 840.

3. Копылов И.П. Электрические машины: учеб. для вузов. 4-е изд., испр. / И.П. Копылов. М.: Высш. школа, 2004. С. 607.

4. Пат. № 2290653 Российская Федерация, МПК G01R 29/20. Способ оценки в силовых трехфазных трансформаторах параметров процесса переключения контактов контактора быстродействующего регулятора под нагрузкой без его вскрытия и устройство для его осуществления / Ю.А. Федоров, Г.М. Михеев, В.М. Шевцов, С.Н. Баталыгин; заявитель и патентообладатель авторы; заявл. 20.12.2004; опубл. 27.12.2006. Бюл. № 36.

5. Петров Г.Н. Электрические машины: в 3 ч. Ч.1. Введение. Трансформаторы: учебник для вузов / Г.Н. Петров. М.: Энергия, 1974. С. 240.

6. Положительное решение от 17 июня 2009 года о выдаче патента РФ на изобретение по заявке №2008114112/28(015429). Способ определения индуктивности рассеяния трехфазной высоковольтной обмотки силового трансформатора / Г.М. Михеев, В.М. Шевцов, С.Н. Баталы-гин, Иванова Т.Г., Ю.А. Федоров.

МИХЕЕВ ГЕОРГИЙ МИХАИЛОВИЧ — кандидат технических наук, доцент кафед-

ры электроснабжения промышленных предприятий, Чувашский государственный уни-

верситет, Россия, Чебоксары ([email protected]).

MIKHEEV GEORGIY MIKHAYLOVICH — candidate of technical sciences, associate professor of department of electrical supply of the industrial enterprises, Chuvash State University, Russia, Cheboksary.

ШЕВЦОВ ВИКТОР МИТРОФАНОВИЧ — кандидат технических наук, доцент кафедры теоретических основ электротехники, релейной защиты и автоматики, Чувашский государственный университет, Россия, Чебоксары ([email protected]).

CHEVSOV VIKTOR MITROFANONICH — candidate of technical sciences, assistant professor, Chuvache State University, Russian, Cheboksary.

ИВАНОВА ТАТЬЯНА ГЕОРГИЕВНА — инженер электротехнической службы ООО «Инженерный центр», Россия, Чебоксары ([email protected]).

IVANOVA TATYANA GEORGIEVNA — engineer, Open Company «Engineering centre», Russia, Cheboksary.

Power Electronics • Просмотр темы

Maikl писал(а):

В паспортах на силовые трансформаторы завод-изготовитель указывает потери на ХХ и напряжение КЗ. Принято считать, что потери на ХХ это потери в «железе» транса, а потери при КЗ — потери в обмоточном проводе (потери в меди) обмоток.
На рис.3 в.у. статьи приведён опыт КЗ. Далее приводится расчёт по определению Ls и конечным итогом является вывод коэффициента связи между обмотками.

Трансформатор достаточно сложное электротехническое устройство и может быть описан бесконечным количеством параметров. По понятным причинам производитель не может и не должен указывать все эти параметры, а поэтому указывает только те, которые особенно важны потребителю при использовании трансформатора. В промышленных сетях много внимания уделяется энергетической эффективности электротехнического оборудования и поэтому в числе основных указываются именно эти параметры.
В данном случае нас интересует не эффективность трансформатора, а его корректное моделирование в SPICE симуляторе. И вот здесь мы встречаемся с необходимостью определения параметра К-коэффициент связи. Данный параметр не указывается производителями трансформатора, и тем более не известен, если трансформатор сделан своими ручками. Поэтому возникает проблема его экспериментального определения. Так как, в наших применениях, К имеет значения очень близкие к 1, то измерить его непосредственно практически невозможно. Поэтому в статье предлагается методика определения коэффициента связи К через индуктивности рассеяния Ls и намагничивания L1 трансформатора.

Maikl писал(а):

Может я что-то «не догоняю», но в модели (рис.3) в директиве уже указан Ксв., а посему, определение Ls первички и вторички, а через них обратно к Ксв., ИМХО, «притянут за уши».

Модель на рис.3 используется для проверки правильности выбранного значения К.

Maikl писал(а):

1.Есть ли необходимость указывать в модели Ls первички и вторички, если Ксв. реально измерен и внесён в директиву?

Достаточно указать корректное значение коэффициента связи.

Maikl писал(а):

2.Как понимаю, желательно, определение Ксв. проводить при малом сигнале, чтобы не вогнать сердечник в насыщение и на предполагаемой рабочей частоте проектируемого девайса. Прав ли?

Коэффициент связи является элементом линейной (идеальной) модели трансформатора и поэтому должен измеряться в условиях исключающих насыщение сердечника трансформатора. Однако это условие весьма легко выполнить. Вернее проще выполнить, чем нарушить, т.к. очень трудно, в процессе эксперимента, насытить сердечник трансформатора, если одна из его обмоток закорочена.

Maikl писал(а):

3.По большому счёту Ксв., ИМХО, можно найти экспериментально и вычислить другим путём, не зная индуктивности обмоток первички и вторички. Прав ли?

Коэффициент связи определяется индуктивностями рассеяния и намагничивания трансформатора. По сути это коэффициент передачи индуктивного делителя напряжения, состоящего из индуктивности рассеяния и намагничивания. В Статьях лежит статья Назначение параметров модели трансформатора в Spice симуляторах, где более подробно расписан смысл коэффициента связи.

Страница не найдена — Время электроники

Кажется мы ничего не нашли. Может быть вам помогут ссылки ниже или поик?

Архивы

Архивы Выберите месяц Июнь 2021 Май 2021 Апрель 2021 Март 2021 Февраль 2021 Январь 2021 Декабрь 2020 Ноябрь 2020 Октябрь 2020 Сентябрь 2020 Август 2020 Июль 2020 Июнь 2020 Май 2020 Апрель 2020 Март 2020 Февраль 2020 Январь 2020 Декабрь 2019 Ноябрь 2019 Октябрь 2019 Сентябрь 2019 Август 2019 Июль 2019 Июнь 2019 Май 2019 Апрель 2019 Март 2019 Февраль 2019 Январь 2019 Декабрь 2018 Ноябрь 2018 Октябрь 2018 Сентябрь 2018 Август 2018 Июль 2018 Июнь 2018 Май 2018 Апрель 2018 Март 2018 Февраль 2018 Январь 2018 Декабрь 2017 Ноябрь 2017 Октябрь 2017 Сентябрь 2017 Август 2017 Июль 2017 Июнь 2017 Май 2017 Апрель 2017 Март 2017 Февраль 2017 Январь 2017 Декабрь 2016 Ноябрь 2016 Октябрь 2016 Сентябрь 2016 Август 2016 Июль 2016 Июнь 2016 Май 2016 Апрель 2016 Март 2016 Февраль 2016 Январь 2016 Декабрь 2015 Ноябрь 2015 Октябрь 2015 Сентябрь 2015 Август 2015 Июль 2015 Июнь 2015 Май 2015 Апрель 2015 Март 2015 Февраль 2015 Январь 2015 Декабрь 2014 Ноябрь 2014 Октябрь 2014 Сентябрь 2014 Август 2014 Июль 2014 Июнь 2014 Май 2014 Апрель 2014 Март 2014 Февраль 2014 Январь 2014 Декабрь 2013 Ноябрь 2013 Октябрь 2013 Сентябрь 2013 Август 2013 Июль 2013 Июнь 2013 Май 2013 Апрель 2013 Март 2013 Февраль 2013 Январь 2013 Декабрь 2012 Ноябрь 2012 Октябрь 2012 Сентябрь 2012 Август 2012 Июль 2012 Июнь 2012 Май 2012 Апрель 2012 Март 2012 Февраль 2012 Январь 2012 Декабрь 2011 Ноябрь 2011 Октябрь 2011 Сентябрь 2011 Август 2011 Июль 2011 Июнь 2011 Май 2011 Апрель 2011 Март 2011 Февраль 2011 Январь 2011 Декабрь 2010 Ноябрь 2010 Октябрь 2010 Сентябрь 2010 Август 2010 Июль 2010 Июнь 2010 Май 2010 Апрель 2010 Март 2010 Февраль 2010 Январь 2010 Декабрь 2009 Ноябрь 2009 Октябрь 2009 Сентябрь 2009 Август 2009 Июль 2009 Июнь 2009 Май 2009 Апрель 2009 Март 2009 Февраль 2009 Январь 2009 Декабрь 2008 Ноябрь 2008 Апрель 2008 Март 2008 Февраль 2008 Январь 2008 Декабрь 2007 Ноябрь 2007 Октябрь 2007 Сентябрь 2007

Определение длины воздушного зазора в сердечнике для дросселей и трансформаторов — Компоненты и технологии

Введение

Расчет сердечников дросселей и трансформаторов — этой темы, наверное, не удавалось
избежать тем, кто начинал работу в области
электроники. За прошедшие годы автору
приходилось рассчитывать десятки дросселей и трансформаторов различной частоты
и мощности, от единиц ватт до сотен киловатт, притом, что нужны были они, вначале,
в одном экземпляре.

Сегодняшняя действительность показывает, что среди методов расчета существует мода. В электротехнических расчетах вместо традиционных методов превалируют нечеткая
логика, нейронные сети, вейвлет-преобразование, резольвента Лагранжа и т. д. Хотя использование простых соображений, подобных такому «мощность сетевого трансформатора, в ваттах, равняется квадрату сечения
его сердечника, в сантиметрах» дает приемлемый, в большинстве случаев, результат, полезно убедиться в справедливости, разобраться в генезисе приведенной фразы и определить диапазон ее применимости. Поэтому
автору импонируют результаты расчетов,
пусть проведенные с помощью сложнейших
алгоритмов, как в программах схемотехнического моделирования, но доведенные до
инженерного уровня.

Лучшие источники научно-технической
информации — не те книги, которые сейчас
издаются в отличном оформлении, а подчас
невзрачные, но под редакцией И. В. Антика,
имя которого стало синонимом качественного издания. Остаются полезными переводные книги зарубежных издательств, например, «Искусство схемотехники», или были
еще книги Воениздата, которые писали, наверное, лучшие специалисты страны. В большинстве новых книг отражено состояние техники 20–30-летней давности. Сегодня издается масса печатных ведомственных изданий,
например, вузовских сборников научных трудов, которые изначально рассчитаны для публикации работ студентов и аспирантов. Они
представляют интерес только для авторов.
Оперативный источник информации—научно-технические журналы, в частности, журнал «Компоненты и технологии», необходимый каждому практическому специалисту…

Стальной сердечник в катушках индуктивности применяется очень широко: в трансформаторах источников питания промышленной частоты и трансформаторах повышенной частоты, выходных трансформаторах
усилителей звуковой частоты, дросселях
фильтров, в катушках зажигания автомобильных, авиационных двигателей, контакторах, реле и других электромагнитных элементах радиоэлектронной аппаратуры.

В катушках индуктивности стальной сердечник с большим значением индукции насыщения используется для увеличения индуктивности. Однако наличие сердечника
придает катушке нелинейные свойства, которые ограничивают диапазон ее эффективного применения. В случае, когда через катушку протекает чрезмерно большой ток,
магнитный материал сердечника насыщается. Насыщение сердечника дросселя может
привести к повышению потерь в материале
сердечника. При насыщении сердечника его
относительная магнитная проницаемость
уменьшается, что приводит к уменьшению
индуктивности катушки.

В этих случаях сердечник катушки выполняют с воздушным зазором на пути магнитного потока катушки индуктивности. Это позволяет исключить насыщение сердечника, уменьшить потери мощности в нем, увеличить ток
катушки и обеспечить ряд других преимуществ.
Аналитический расчет воздушного зазора сердечника представляет нелегкую задачу, вследствие ненадежности исходных данных о магнитных свойствах стальных сердечников; таблицы изобилуют неточностями. Допуск на
величину исходных данных от производителей магнитных материалов обычно составляет ±10%. Для использования в практике инженерных расчетов катушки с сердечником
такая точность допустима, но аддитивная погрешность исходных данных возрастает.

Исследование магнитных свойств катушек
индуктивности с ферромагнитными сердечниками и диэлектрическим зазором стало эффективным лишь с применением PSpice-моделей и использующих эти модели программ
схемотехнического моделирования, например Micro-Cap [1, 2]. Программы схемотехнического моделирования позволяют с необходимой точностью определить все необходимые параметры катушек индуктивности
и магнитные параметры сердечника [3–7].
Причем магнитные параметры можно определять в различных координатах, в том числе и комбинированных.

Определение параметров

PSpice-модели сердечника

Для определения PSpice-параметров модели
сердечника используем программу Model 7.0.0,
приложение кMicro-Cap 7. Создание модели
стального сердечника основывается на оптимизации уравнения Джилса-Атертона (Jiles-Atherton), описывающего его магнитные
свойства, при инициализации исходных данных, установленных по умолчанию, и введенных данных для расчетных точек кривой
намагничивания [8]. Данные кривой намагничивания используются для расчета безгистерезисной кривой, построенной на основе
гиперболического котангенса.

Различные трансформаторные стали насыщаются при величине плотности потока
магнитной индукции примерно 1 Тл, насыщение всех ферритовых материалов происходит при величине примерно 400×10–3 Тл.
После инициализации расчета происходит
оптимизация решения уравнения ДжилсаАтертона и определяется ошибка аппроксимации кривой намагничивания.

На рис. 1 приведена кривая намагничивания стали Э42 (B vs H) и рассчитанные PSpice-параметры модели (Model Parameters) стального сердечника. Рассчитанная ошибка моделирования (Error) составляет 3,2%. Ошибка
моделирования характеризует «гладкость»
полученной кривой, любые «выпадающие»
исходные данные увеличивают ошибку.

Рис. 1. Исходные данные, кривая намагничивания и параметры PSpice-модели стального сердечника

При создании модели сердечника (core) ей
присваивается имя Part (только на латинице)
и указываются особенности, затем в таблице
(B vs H, Region) вводятся тройки чисел — Н,
В и область их существования. Величина Н
вводится в эрстедах (Oersteds), а величина
В — в гауссах (Gauss), область указывается
как 1, 2 или 3 квадрант (B vs H).

На рис. 1 показана кривая намагничивания
для сердечника, выполненного из ленты
стальной электротехнической, холоднокатанной, анизотропной (ГОСТ 21.427.4-78) отечественного производства.

При создании модели (табл. 1) нелинейного магнитного сердечника определяются следующие параметры — MS, ALPHA, A, C и K.
Заметим, что в параметрах модели используют смешанные MKS- или SI-единицы (A/м)
и CGS-единицы (см и см²).

Таблица 1. Определяемые параметры
PSpice-модели сердечника

Наименование	Параметр	Единицы измерения	По умолчанию
MS	Индукция насыщения	A/м	400×10–3
A	Параметр формы безгистерезисной кривой намагничивания	A/м	25
C	Постоянная упругого смещения доменных границ	–	0,001
K	Постоянная подвижности доменов	–	25
ALPHA	Параметр магнитной связи доменов. В Micro-Cap 9 не поддерживается	–	2×10–5

Кривая намагничивания сердечника игнорирует геометрические параметры конкретного сердечника— площадь, длину магнитной линии и величину зазора в сердечнике,
устанавливая их по умолчанию согласно таблице 2. Названные PSpice-параметры модели — AREA, PATH и GAP — вводятся при
использовании в программе схемотехнического моделирования конкретного сердечника.

Таблица 2. Геометрические параметры
PSpice-модели сердечника

Наимено вание	Параметр	По умолчанию
AREA	Площадь поперечного сечения сердечника	1 см2
PATH	Средняя длина магнитного пути	1 см
GAP	Длина воздушного зазора	0 см

Далее приведены полученные нами PSpice-описания модели кольцевого ферритового
и «стального» сердечников для катушек индуктивности аппаратуры радиоэлектронного назначения:

• Модель кольцевого сердечника с размерами 25×10×6 мм из феррита марки 3C85,
  без зазора: .MODEL E25_10_6_3C85 CORE
  (A=22.691 AREA=.395 C=.10603 K=19.399
  MS=378.470000E+03 PATH=4.9).
• Модель стального сердечника из Ст.42 с зазором 0,2 см: .MODEL CORE (A=462.714
  AREA=4 C=0.00287197 K=0.00292649
  MS=1.38139e+006 PATH=20 GAP=0.2).

Параметр GAP — длина воздушного зазора сердечника — определяется при расчетах
схемотехнической модели как модельный параметр и поэтому может изменяться с заданным шагом.

Полученные модели используются при схемотехническом моделировании совместно со
Spice-описанием генератора тока синусоидальных колебаний (I generator), график тока которого показан на рис. 2 слева. Справа
показана панель задания параметров генератора. В генераторе тока задается величина
амплитуды постоянной и переменной составляющей, частота и ряд других параметров,
указанных на панели.

Рис. 2. Панель задания параметров генератора синусоидального тока

На рис. 3 приведен пример использования
модели «стального» сердечника для определения параметров катушки индуктивности L1.
Для катушки индуктивности с магнитным
сердечником К1 при схемотехническом моделировании указывается количество витков.
Коэффициент связи (COUPLING), а также
все параметры модели сердечника могут варьироваться в установленных пределах с заданным шагом расчета.

Рис. 3. Схемотехническая модель сердечника (вверху) и его кривые намагничивания
при различной величине воздушного зазора

Из рис. 3 следует, что «большой» воздушный зазор в модели линеаризирует магнитные параметры сердечника и катушки индуктивности.

Определение длины

воздушного зазора в сердечнике

Когда по обмотке дросселя или первичной
обмотке трансформатора низкой частоты,
кроме переменной составляющей, протекает еще и постоянный ток, то индуктивность
обмотки уменьшается. Чтобы избавиться
от этого явления, в сердечнике делают воздушный зазор, длина которого зависит от
размеров сердечника, индуктивности обмотки и силы постоянного тока, проходящего
по обмотке.

Зазор в сердечнике дросселя играет исключительно важную роль. На рис. 4 приведен
эскиз сердечника с эквивалентным объемом,
равным длине средней линии магнитного поля (см), умноженной на площадь его сечения
(см²). Пусть по катушке с начальной индуктивностью L = 20 Гн протекает постоянный
ток I = 60 мА.

Рис. 4. Эскиз сердечника магнитопровода
с воздушным зазором

Кривая, приведенная на рис. 5, дает возможность определить длину воздушного зазора в миллиметрах в зависимости от величины L×I²/V: где L — индуктивность обмотки дросселя или трансформатора, Гн; I — сила
постоянного тока, проходящего по обмотке, А; V — объем железного сердечника, см³.
По графику рис. 5 находим величину δ, которая после умножения на длину магнитного пути сердечника определяет необходимую
величину воздушного зазора стального сердечника в миллиметрах.

Рис. 5. Номограмма для определения зазора
в сердечнике

Так как задана индуктивность первичной
обмотки трансформатора L = 20 Гн, сила постоянного тока — 60 мА, а объем железного
сердечника — 40 см³ и длина магнитного пути — 10 см, определим промежуточную величину:

L×I ²/V = 10×3600×10^–6/40 = 9×10^–4.

Исходя из графика рис. 5, определяем величину δ = 20×10^–3. Длина воздушного зазора стального сердечника, изображенного на
рис. 4, должна быть равна 20×10^–3×10 = 0,2 мм.
Таким образом, в сердечнике необходим воздушный зазор по 0,1 мм с каждой стороны.
Согласно [9] такой же зазор необходим для
катушки с индуктивностью 40 Гн, при токе
подмагничивания 30 мА, объеме сердечника
80 см² и длине магнитного пути 20 см.

Моделирование показывает, что индуктивность катушки с введением рассчитанного зазора изменяется незначительно. Использование номограммы удобно для разработчиков
радиоаппаратуры, если не применять схемотехническое моделирование. Для силовых
трансформаторов и дросселей [10, 11] построение подобных номограмм нецелесообразно, так как устройства силовой электроники,
как правило, требуют моделирования дросселя как составной части электрической схемы силового устройства [12–15].

Литература

1. Разевиг В. Д. Схемотехническое моделирование с помощью Micro-CAP 7. М.: Горячая линия–Телеком, 2003.
2. Колпаков А. САПР схемотехнического моделирования. Практика и психология разработки //
   Электронные компоненты. 2008. № 5.
3. Валиуллина З., Зинин Ю. Схемотехническое моделирование силовых дросселей для тиристорных преобразователей повышенной частоты //
   Силовая электроника. 2007. № 1.
4. Валиуллина З., Зинин Ю. Проектирование тиристорного инверторно-индукторного закалочного комплекса с выходным трансформатором //
   Силовая электроника. 2007. № 3.
5. Валиуллина З. Егоров А., Есаулов А., Зинин Ю.
   Исследование средствами схемотехнического моделирования нелинейного дросселя переменного тока в составе тиристорного высокочастотного инвертора // Силовая электроника. 2008. № 2.
6. Валиуллина З., Есаулов А., Егоров А., Зинин Ю.
   Особенности проектирования силовых выпрямителей в качестве источников постоянного тока для тиристорных преобразователей повышенной частоты // Силовая электроника. 2008. № 3.
7. Болотовский Ю., Таназлы Г. Опыт моделирования
   систем силовой электроники в среде OrCAD 9.2 //
   Силовая электроника. 2008. № 3.
8. Новиков А. А., Амелин С. А. Экспериментальное
   исследование параметров модели перемагничивания ферромагнетиков Джилса-Атертона //
   Электричество. 1995. № 9.
9. Определение длины зазора в сердечниках дросселей и трансформаторов // С.М. Радиофронт.
   1940. № 5–6.
10. Шапиро С. В., Зинин Ю. М., Иванов А. В.
    Системы управления с тиристорными преобразователями частоты для электротехнологии.
    М.: Энергоатомиздат, 1989.
11. Шапиро С. В. Резольвента Лагранжа и ее применение в электромеханике. М.: Энергоатомиздат, 2008.
12. Зинин Ю. М. Анализ интервала восстановления управляемости тиристора в несимметричном инверторе // Электричество. 2006. № 10.
13. Зинин Ю. М. Анализ гармоник выходного тока тиристорных полирезонансных инверторов // Электричество. 2008. № 8.
14. Зинин Ю. Проектирование малогабаритного
    тиристорного преобразователя повышенной
    частоты для индукционной плавки металлов. //
    Силовая электроника. 2009. № 1.
15. Кук Р. Л., Лавлес Д. Л., Руднев В. И. Согласование с нагрузкой в современных системах индукционного нагрева // Силовая электроника.
    2007. № 2.

Конструкция трансформатора и индуктора — Switchcraft

Максимальный поток в сердечнике затем рассчитывается как:

\ [\ Phi = B \ cdot A = 1,3 \ cdot 0,00135 = 0,00176 Вт \]

Максимальное изменение потока в сердечнике однако является двойным, так как сердечник может быть намагничен в обоих направлениях, то есть: \ (0,00352 Вт \).

Число витков, необходимых для получения этого потока, определяется как:

\ begin {уравнение *}
N = \ frac {V \ cdot t} {\ Phi}
\ end {уравнение *}

Где \ ( V \) — среднее напряжение, приложенное к обмотке.{\ pi} \]

\ (\ cos (0) = 1 \) и \ (\ cos (\ pi) = -1 \), следовательно:

\ [V_ {avg} = \ frac {2 V_p } {\ pi} \]

Для нашего примера среднее напряжение вычисляется как:

\ [V_ {avg} = \ frac {2 \ cdot 230 \ cdot \ sqrt {2}} {\ pi} = 207 V \]

Требуемое количество витков рассчитывается как:

\ [N = \ frac {207 \ cdot 0,01} {0,00352} = 588 \]

Следовательно, выраженное в единицах среднеквадратичного значения, мы имеем 0,39 вольт на оборот, или 2,56 витка на вольт. Для вторичной обмотки необходимое количество витков затем просто вычисляется путем умножения на 2.56 на желаемое напряжение.

Например, если требуемое вторичное напряжение равно \ (18 \; В \) (что может быть подходящим для линейного регулируемого источника питания 12 В), необходимое количество витков будет:

\ begin {уравнение *}
2,56 \ cdot 18 = 46
\ end {формула *}

Допустимая мощность

Вычислить мощность не так просто, как вычислить необходимое количество витков. Однако для небольших трансформаторов обычно безопасно делать некоторые предположения, основанные на опыте. Одно из таких предположений — эффективность 90%, т.е.2} {R} = \ frac {230 \ cdot 0.05} {8.59} = 15.4W \]

Затем номинальная входная мощность трансформатора рассчитывается как:

\ [P = \ frac {15.4} {0.1} = 154 Вт \]

Примечание о постоянном токе

Постоянный ток в трансформаторе обычно не очень хорошо. Он будет вносить вклад в мощность, передаваемую трансформатором, не , а , но он будет вносить вклад в магнитный поток в сердечнике. Это означает, что ядро ​​будет ближе к насыщению. Если трансформатор предназначен для работы на границе насыщения без постоянного тока, он будет насыщаться.

Если вы намереваетесь иметь постоянный ток в трансформаторе, вы должны применить те же конструктивные ограничения, что и при проектировании индуктора, предназначенного для постоянного тока. Обычно это означает добавление к сердцевине воздушного зазора для уменьшения эффективной проницаемости.

Индуктивность — это параметр любой электрической сети, характеризующий ее способность сопротивляться изменению тока.

\ begin {уравнение}
\ text {EMF} = -L \ frac {\ mathrm {d} i} {\ mathrm {d} t} \ Rightarrow L = — \ text {EMF} \ frac {\ mathrm { d} t} {\ mathrm {d} i}
\ end {формула}

Накопление энергии

Накопление энергии обычно нежелательно в трансформаторах, однако часто это основная цель индуктора.2
\ end {формула}

Где \ (I \) — ток намагничивания. Т.е. при вычислении накопителя энергии в трансформаторе он будет меньше полного тока.

Добротность

Добротность индуктора описывает устройство по отношению к идеальному компоненту. Это особенно важно в радиочастотных приложениях.

Добротность катушки индуктивности определяется по формуле:

\ begin {уравнение}
Q_L = \ frac {X_L} {R_L} = \ frac {2 \ pi f L} {R_L}
\ end {уравнение}

Следовательно, добротность зависит от частоты, при которой используется индуктор.2 \) площадь поперечного сечения. Лучший способ увеличить мощность — уменьшить индуктивность и, следовательно, увеличить ток в сердечнике. Помните, что мощность зависит от тока в квадрате.

При введении воздушного зазора в магнитопроводе эффективная проницаемость будет уменьшаться, и, следовательно, значение \ (A_L \) также будет уменьшаться.

Энергия, запасенная в сердечнике, может быть извлечена второй обмоткой на том же сердечнике, как в топологии обратного хода. В качестве альтернативы его можно использовать, подключив катушку индуктивности к другой цепи после ее зарядки, как в топологиях понижающего / повышающего напряжения.

Тороиды

Тороидальные сердечники можно разделить на две основные категории в зависимости от материала, из которого они изготовлены. Сердечники из феррита и железного порошка.

Феррит имеет самую высокую проницаемость, но он не подходит для высоких частот. Кроме того, как мы видели, высокая проницаемость не всегда является преимуществом.

Полезный веб-сайт со спецификациями для различных тороидальных сердечников находится по адресу: http://toroids.info/

Как упоминалось ранее, плотность потока должна быть ограничена, чтобы избежать насыщения сердечника.Для ферритовых тороидальных сердечников это накладывает ограничение:

\ begin {уравнение}
\ frac {V} {2 f NA} \ le 0.3
\ end {уравнение}

Где \ (N \) — количество витков обмотки. , \ (A \) — площадь поперечного сечения сердечника.

Как я могу рассчитать индуктивность первичной обмотки трансформатора с учетом конкретной нагрузки на вторичной обмотке?

Я не согласен с интерпретацией Энди aka. Математика верна, но интерпретация этой математики нефизическая и явно не может быть верной.

Это должно быть самоочевидным: если вы подключаете что-то через вторичную обмотку, это не волшебным образом появляется в двух местах одновременно, чтобы быть и через первичную обмотку. Простая, на первый взгляд очевидная реальность состоит в том, что все, что связано с вторичной обмоткой, на самом деле подключается только к вторичной обмотке. Сказать, что это параллельно первичному, полезно как теоретическая эквивалентность, но не как истинное физическое описание того, что на самом деле происходит. Да, числа работают так же, как если бы нагрузка была параллельно с основной, но это не значит, что на самом деле — это .

Очевидно, что нагрузка не параллельна первичной, потому что она не подключена параллельно первичной. Это так просто. Можно притвориться, что математика позволяет это допустить, но это всего лишь теоретическая выдумка, не имеющая отношения к тому, что на самом деле происходит физически.

Вот что на самом деле происходит физически :

Во-первых, нам нужно рассмотреть, почему у катушек индуктивности вообще есть реактивное сопротивление. Их реактивное сопротивление в конечном итоге является результатом самоиндукции .Изменение тока вызывает изменение магнитного поля. Что делают меняющиеся магнитные поля? Они индуцируют напряжение согласно закону индукции Фарадея.

Тот факт, что индуктор является источником этого изменяющегося магнитного поля, не заставляет это изменяющееся поле перестать вести себя как изменяющееся магнитное поле. Любой изменяющийся магнитный поток через данную катушку индуктивности индуцирует на ней напряжение — даже если сам индуктор является источником этого изменяющегося потока.

Это означает, что реактивное сопротивление катушек индуктивности обусловлено накопленной ими энергией в их магнитном поле.Если ток через катушку индуктивности увеличивается, это вызывает увеличение магнитного потока, которое индуцирует напряжение через катушку индуктивности, противоположное знаку изменения напряжения. Таким образом, если напряжение увеличивается, это противоположное напряжение будет иметь противоположную полярность, что приведет к падению напряжения на катушке индуктивности.

Все падения напряжения связаны с сопротивлением. Импеданс представляет собой то, что поглощает энергию — оно может быть диссипативным (навсегда покидает цепь), что мы называем сопротивлением, или вместо этого оно может быть связано с накоплением энергии, которое мы называем реактивным сопротивлением.

В этом случае падение напряжения дает энергию для увеличения магнитного поля. Точно так же, когда ток падает, энергия, запасенная в этом поле, возвращается обратно в катушку индуктивности по мере уменьшения магнитного потока, вызывая напряжение, которое снова противодействует изменению напряжения — так что теперь катушка индуктивности действует как источник напряжения при схлопывании потока.

Здесь важно понимать, что именно это напряжение, или ЭДС , возникающее из-за собственной самоиндукции индуктора, в конечном итоге является причиной реактивного сопротивления катушки индуктивности.Чем быстрее вы пытаетесь изменить магнитный поток, тем больше будет эта обратная ЭДС из-за самоиндукции, ограничивая скорость, с которой ток может расти и падать, и, таким образом, все больше и больше уменьшая пиковый ток для переменного тока по мере увеличения частоты. . Это верно для любой составляющей переменного тока и происходит даже при смещении постоянного тока (так называемый пульсирующий ток).

Итак, импеданс катушки индуктивности не является строго результатом ее индуктивности , а скорее обратной ЭДС, которая возникает из-за этой индуктивности.

В конкретном случае изолированной одиночной катушки индуктивности это зависит только от индуктивности.

В случае трансформатора (или любой схемы связанных индукторов) это уже не так. Это связано с тем, что обратная ЭДС через данную обмотку больше не зависит только от индуктивности этой обмотки. Ток через другие обмотки также приводит к магнитному потоку. Это отражается обратно в первичную обмотку как напряжение / ЭДС, но эта ЭДС противодействует собственной обратной ЭДС первичной обмотки из-за ее самоиндукции.Другими словами, поток от тока через вторичную обмотку действует, чтобы противодействовать потоку от тока через первичную обмотку.

Это известно как взаимная индуктивность . Лучший способ визуализировать это — энергия, которая передается посредством изменения магнитного потока, а не сохраняется.

Отношения довольно простые.

Обратная ЭДС, возникающая на первичной обмотке, равна:

\ $ V_ {p} = L_ {p} * \ frac {di_ {p}} {dt} — M * \ frac {di_ {s}} {dt} \ $

Где Vp — это ЭДС в первичной обмотке, ip — первичный ток, is — вторичный ток, а M — взаимная индуктивность.

Когда вторичная обмотка разомкнута, взаимная индуктивность не действует, и вся ожидаемая обратная ЭДС появляется на первичной обмотке, препятствуя изменению тока. Однако, когда вторичная обмотка загружена, это вызывает уменьшение обратной ЭДС в первичной обмотке. Он активно противодействует некоторой самоиндукции первичной обмотки, и, как мы поняли из ранее, это в основном источник индуктивного реактивного сопротивления.

Таким образом, индуктивность одной из обмоток никогда не изменяется, но реактивное сопротивление связанных катушек индуктивности зависит от тока через другую, а не только от тока через саму .Таким образом, реактивное сопротивление первичной обмотки падает по мере увеличения нагрузки вторичной обмотки, потому что ток вторичной обмотки противодействует некоторому потоку первичной обмотки, ограничивая индуцированную обратную ЭДС и, таким образом, основной источник реактивного сопротивления первичной обмотки.

Когда вы измеряете индуктивность первичной обмотки, большинство измерителей фактически измеряют реактивное сопротивление, измеряя ток на известной частоте или измеряя резонансную частоту, образованную резервуаром LC известной емкости и испытуемой катушкой индуктивности.Резонансная частота в конечном итоге является результатом частоты, на которой импедансы самые низкие. В любом случае, вы действительно измеряете импеданс, и измеритель рассчитывает индуктивность на его основе. Это работает только в том случае, если нет связанных индукторов или если они все имеют разомкнутую цепь. В противном случае эти методы измерения индуктивности больше не действуют. Вам нужно будет одновременно измерить взаимную индуктивность и другие токи обмотки, чтобы правильно определить истинную индуктивность любой конкретной обмотки.

Трансформаторы Часть 1

Трансформаторы Часть 1 Верх

Продукты Elliott Sound

Руководство по трансформаторам для начинающих — часть 1

© 2001 — Род Эллиотт
Страница опубликована и обновлена ​​в ноябре 2018 г.

---

Указатель статей
Основной указатель

---

Содержание — Часть 1

---

Предисловие

Одна вещь, которая явно сбивает с толку многих, — это идея плотности потока внутри сердечника трансформатора.Хотя это более подробно рассматривается в Разделе 2, важно, чтобы информация из этого раздела запоминалась на каждом этапе чтения этой статьи. Для любого силового трансформатора максимальная плотность магнитного потока в сердечнике достигается при простое трансформатора. Повторюсь, это очень важно …

Для любого силового трансформатора максимальная магнитная индукция достигается, когда трансформатор находится в режиме ожидания.

Идея противоречит интуиции, она даже почти не имеет смысла.Как бы то ни было, это факт, и его отсутствие разрушит ваше понимание трансформаторов. На холостом ходу обратная ЭДС трансформатора почти точно компенсирует приложенное напряжение. Небольшой ток, который течет, поддерживает плотность потока на максимально допустимом значении и представляет потери в стали (см. Раздел 2). Поскольку ток отводится от вторичной обмотки, поток немного падает. Причина этого кроется в конечном сопротивлении обмотки и в законе Ома.

Неважно, что вы понимаете причины этого с самого начала, но — это , важно помнить, что для любого силового трансформатора максимальная плотность потока достигается, когда трансформатор находится в режиме ожидания .Пожалуйста, не забывай об этом.

В другом месте в сети вы найдете утверждения о том, что максимальная мощность, доступная от трансформатора, ограничена насыщением сердечника — это чушь, полная ложь и необходимо игнорировать , иначе вы никогда не поймете, правильно, трансформаторы! Информация, представленная здесь, является точной и правильной, и любой, кто утверждает иное, неправильный! Это может показаться резким, но, тем не менее, это правда.

Еще нужно задуматься об индуктивности трансформатора. Принято считать, что трансформатор представляет собой индуктивную нагрузку, но … это справедливо только при отсутствии нагрузки или при очень небольшой нагрузке . Когда трансформатор нагружен до номинальной мощности резистивной нагрузкой, индуктивная составляющая незначительна. Когда любой трансформатор подает что-либо от 5% до 100% от его полного тока нагрузки, индуктивная составляющая подавляется током нагрузки, и фазовый угол (Φ) между первичным напряжением и током минимален.Более подробно все это объясняется ниже.

---

‘Окружной ток’ (добавлено в июле 2020 г.)

Существует некоторая путаница из-за статьи в Википедии, в которой обсуждаются тороидальные трансформаторы (по состоянию на июль 2020 г.). Почти все, что нужно знать, исключено, но есть продолжительная дискуссия об «окружном токе». Во-первых, я не отрицаю, что он существует, но я знаю из многолетнего опыта (наряду с множеством измерений), что это неактуально для 99,9% пользователей.Мне кажется, что страница была взломана кем-то, кто либо хочет показать, насколько он умен, либо просто хочет продвинуть эту конкретную тему по неизвестным причинам.

Стоит отметить, что ссылки, представленные в статье Википедии, (в основном) бесполезны, и некоторые из них возвращают вас на страницу, где цитируется ссылка. Довольно много людей очень недовольны страницей, и один участник описал ее как «как руководство IBM; полное совершенно правильной, но совершенно бесполезной информации».

Все трансформаторы имеют некоторую «утечку» магнитного потока, и думать иначе… неразумно. Важно то, вызывает ли утечка флюса какие-либо проблемы с разумной компоновкой. Ответ на этот вопрос — «нет». Прокладка даже кабеля динамика через тороидальный трансформатор обычно вызывает «гудение» в динамике (из-за нелинейного тока намагничивания), но это не то, как люди подключают усилители. Точно так же следует избегать прокладки проводов постоянного тока поверх (или в непосредственной близости от) любого трансформатора .Утечка магнитного потока и / или окружной ток вызывают мало проблем для любого, кто понимает, что периферия любого трансформатора электрически враждебна. Единственное корректирующее действие, необходимое для тороидального трансформатора, — это поддержание «безопасного» расстояния, которое обычно должно быть не более 25 мм. Если проводка находится на таком расстоянии (или более), помехи обычно незначительны.

Чтобы доказать (по крайней мере, самому себе), что я не ошибаюсь, я использовал тороидальный трансформатор на 300 ВА и исследовал его во всех направлениях с помощью одного петлевого детектора, усиленного в 1000 раз (да, 60 дБ).Я слушал результат через усилитель и динамик. Как и ожидалось, наибольший поток утечки наблюдается в местах выхода выводов, поскольку при выводе выводов из обмоток возникает разрыв. Петля зонда должна быть в пределах 10 мм или около того от обмоток, чтобы обнаружить что-либо существенное. Выталкивание петли зонда внутрь отверстия в середине трансформатора дало самые высокие показания, но это пространство всегда используется только для монтажного болта.

Я не показывал формы сигналов и амплитуду и не пытался измерить ток, который может возникнуть в контуре с низким сопротивлением.Я этого не делал по одной простой причине — нет точки . Мы, , знаем, что будет утечка магнитного потока и / или «окружной ток», но нам все равно. Это ничего не меняет, и мы все можем продолжать использовать тороидальные трансформаторы, как если бы этих вещей не существовало. Это может быть важно для некоторых коммутационных приложений, где сложно полностью окружить сердечник обмотками, и могут быть другие приложения, где это важно. На блоки питания аудиосистемы это никак не влияет!

---

Введение

Эта статья посвящена трансформаторам, используемым в типичных электронных проектах, источниках питания и т.п., а не , не распространяется на большие трансформаторы, используемые на подстанциях и в электросети в целом (кроме проходных), хотя обсуждаемые факторы также применимы к этим гораздо более крупным трансформаторам. В машиностроении трансформатор — одна из самых эффективных машин, которые есть в нашем распоряжении, но те, которые используются для распределения и промышленности, являются (большим) шагом вперед по сравнению с теми, с которыми мы обычно работаем.

Основы, которые позволяют нам использовать электромагнетизм, были открыты только в 1824 году, когда датский физик Ганс Эрстед обнаружил, что ток, протекающий по проводу, отклоняет стрелку компаса.Через несколько лет после этого было обнаружено, что движущееся магнитное поле индуцирует ток в проводе. От этой, казалось бы, базовой концепции, область электромагнетизма выросла до такой степени, что общество в том виде, в каком мы его знаем, не существовало бы без множества машин, использующих эти открытия.

Принципы магнитной индукции охватываются законом Фарадея, названным в честь Майкла Фарадея, британского ученого, который впервые количественно оценил вовлеченные процессы (1831 г.). Основные принципы были независимо открыты Джозефом Генри (в честь которого названа единица индуктивности) в 1832 году.«Закон индукции» Фарадея описывает способ, которым (нестатическое) магнитное поле индуцирует ток в проводе, и, наоборот, как ток в проводе создает магнитное поле. Трансформаторы основаны на принципе постоянно меняющегося магнитного поля (создаваемого первичной обмоткой), которое взаимодействует со вторичной обмоткой, генерируя переменное напряжение (и ток при нагрузке) во вторичной обмотке. Экспериментальные данные Фарадея были преобразованы в уравнения Джеймсом Клерком Максвеллом и добавлены и расширены Оливером Хевисайдом.Эмиль Ленц сформулировал концепцию «обратной ЭДС» (электродвижущей силы), где полярность тока в проводе (или обмотке) создает магнитное поле, которое противодействует магнитному полю, приложенному к обмотке (1834).

Все эти концепции важны, но, к счастью, полное понимание различных законов и формул не является необходимым для понимания того, как работает трансформатор. Я говорю «к счастью», потому что многие вычисления обширны и трудны для большинства нематематиков.Большинство из них даже не является обязательным при проектировании трансформаторов, тем более что существует множество практических правил, которые обычно применяются на этапе проектирования, что упрощает процесс.

---

Когда вы просматриваете эту статью, вас могут простить за восклицание: «Это для новичков? — этот человек сошел с ума. Я говорю вам, что сумасшедший!» Вероятно, это справедливый комментарий, но трансформаторы не просты, и нет простого способа предоставить всю информацию, которая вам нужна, чтобы правильно их понять.Здесь есть разделы, которые, вероятно, идут немного глубже, чем я изначально предполагал, но были слишком интересны, чтобы их не учитывать. Хотя это может не выглядеть так, информация здесь упрощена. Это не учебник по теории магнитного поля или глубокое обсуждение плотности потока и того, как она рассчитывается. Эти темы не являются обязательными для понимания того, как работает трансформатор или что с ним можно делать.

Есть части этой статьи, которые вы можете пропустить, но я предлагаю вам прочитать их полностью, если сможете.Полное понимание того, в какой степени вы можете спроектировать свой собственный трансформатор, не является целью, но большая часть информации, по крайней мере, интересна и расширит ваши общие знания в области электроники.

Для тех, кто хочет погрузиться глубже, Раздел 2 делает именно это. Рекомендуется к прочтению даже новичкам, поскольку о трансформаторах можно многое узнать, несмотря на их кажущуюся простоту.

Трансформаторы необходимы для всего современного электронного оборудования, и очень мало устройств, которые их не используют.Каждый тип трансформатора имеет определенное применение, и редко бывает, что трансформатор, предназначенный для одного применения, может использоваться для другой (совершенно другой) цели. Это не значит, что «переориентация» невозможна, но вы должны знать, что вы делаете, и какие риски могут вас поджидать, чтобы вызвать горе.

Прежде чем приступить к описанию различных типов, необходимо понять основную теорию. Все трансформаторы используют один и тот же основной принцип, и меняются только самые мелкие детали. Трансформатор работает по принципу магнитной связи для передачи энергии от одной стороны (обмотки) к другой.

Трансформаторы

двунаправленные и будут работать независимо от того, где подключен вход. Они могут работать не так хорошо, как в противном случае, но базовая функциональность не изменилась. Идеальный трансформатор не нагружает источник питания (питает первичную обмотку), если нет нагрузки на вторичную обмотку — в реальных компонентах есть потери, так что это не совсем так, но это предположение можно использовать в качестве основы для понимания.

Силовые трансформаторы указаны в вольт-амперах (ВА).Использование ваттов бесполезно, так как полностью реактивная нагрузка не рассеивает мощность, но все же есть вольты и амперы. Это продукт реального напряжения и тока, который важен — ваттметр может указывать на то, что в нагрузке мало или совсем нет реальной мощности, но трансформатор все еще подает напряжение и ток и нагревается из-за внутренних потери независимо от мощности.

Сердечники трансформатора имеют указанную проницаемость, которая является мерой того, насколько хорошо они «проводят» магнитное поле.Магнетизм будет придерживаться пути наименьшего сопротивления и останется в ядре с высокой проницаемостью с небольшой утечкой. Чем ниже проницаемость, тем больше утечка потока из активной зоны (это, конечно, грубое упрощение, но достаточно хорошо, чтобы дать начальное объяснение этого термина).

Трансформатор может быть изготовлен с использованием различных материалов в качестве сердечника (магнитного пути). К ним относятся …

• Air — обеспечивает наименьшую связь, но идеально подходит для высоких частот (особенно RF).Проницаемость 1.
• Железо — неправильное название, поскольку все трансформаторы с сердечником из железа являются стальными с различными добавками для улучшения магнитных свойств. Начальная проницаемость обычно около 500 и выше.
• Порошковое железо — стальные магнитные частицы, сформированные в сердечник, скрепленные связующим веществом и обожженные при высокой температуре для создания керамический материал с очень хорошими свойствами на средних и высоких частотах (более 1 МГц). Особенно подходит для приложений, где есть значительная составляющая постоянного тока в обмотке или при очень большой мощности.Начальная проницаемость обычно составляет 40-90.
• Феррит — магнитная керамика, обычно использующая экзотические магнитные материалы для получения чрезвычайно высокой проницаемости и отличных высоких частот. производительность (от 50 кГц до более 1 МГц). Для разных областей применения доступен удивительный диапазон различных составов. Начальная проницаемость примерно от 500 до 9000 и более.

Проницаемость указана выше как «начальная проницаемость» — фактическая проницаемость материалов керна, отличных от воздуха (записывается как µ i).Это параметр «слабого сигнала», и он почти всегда уменьшается при значительных уровнях магнитного потока. Фактические характеристики ( эффективная проницаемость — µ e) зависят от материала и напряженности поля, и здесь они не рассматриваются. См. Термины и определения (от Hitachi Metals), если вам нужны более полные объяснения.

Технически порошковое железо и ферриты классифицируются как мягкие (см. Ниже) ферриты, но они имеют очень разные характеристики, даже в пределах одного «семейства».Обычно они не подходят для работы на низких частотах, за исключением низких уровней. Ферриты часто используются в качестве трансформаторов сигналов (например, изолирующих трансформаторов для телекоммуникаций или других приложений с малыми сигналами), где высокая магнитная проницаемость делает их идеальным выбором для небольших размеров и высокой индуктивности.

Материалы сердечника обычно классифицируются как «мягкие» — это не имеет ничего общего с их физическими свойствами (все они от твердого до очень твердого), но указывает на их способность сохранять магнетизм (остаточную намагниченность).Магнитно-мягкий материал имеет низкую намагничиваемость и его трудно намагнитить. Твердые магнитные материалы используются для «постоянных» магнитов, и они обладают очень высокой остаточной намагниченностью, то есть сохраняют очень большую часть исходного магнитного поля, которое было наведено в них во время производства.

Во всех импульсных источниках питания используются ферритовые трансформаторы, поскольку обычные пластинки нельзя сделать достаточно тонкими, чтобы предотвратить огромные потери в сердечнике. Для любого основного материала существует множество ограничений.Для низкочастотных источников питания кремнистая сталь с ориентированной зеренной структурой (около 4% кремния) является наиболее распространенной, так как она имеет очень высокую магнитную индукцию до насыщения. Большинство других материалов уступают в этом отношении, что является одной из основных причин, по которым этот материал до сих пор так распространен. К специализированным материалам относятся MuMetal (он же µMetal, Mu-Metal и т. Д.) И Permalloy, и это материалы сердечника (и магнитного экранирования) с очень высокой проницаемостью.

Выше показан небольшой образец некоторых трансформаторов (не в масштабе).Тороидальный трансформатор и трансформатор E-I имеют одинаковую номинальную мощность, а также показан небольшой набор небольших трансформаторов и вставной блок (настенный трансформатор, стенная бородавка и т. Д.).

---

1. Магнетизм и индукторы

Трансформатор состоит из двух (или более) катушек индуктивности, имеющих общий магнитный путь. Любые две катушки индуктивности, размещенные достаточно близко друг к другу, будут работать как трансформатор, и чем теснее они соединены магнитным полем, тем более эффективными они становятся.Вот почему пассивные кроссоверные сети громкоговорителей должны иметь индукторы, ориентированные по-разному, чтобы они не работали как трансформатор.

Когда изменяющееся магнитное поле находится вблизи катушки с проволокой (индуктора), в катушке индуцируется напряжение, соответствующее приложенному магнитному полю. Статическое магнитное поле не действует и не генерирует электрическую мощность. Те же принципы применимы к генераторам, генераторам переменного тока, электродвигателям и громкоговорителям, хотя это действительно была бы очень длинная статья, если бы я охватил все существующие устройства магнитного поля.

Когда электрический ток проходит через катушку с проволокой, создается магнитное поле — это работает с переменным или постоянным током, но с постоянным током магнитное поле, очевидно, статично. По этой причине трансформаторы не могут использоваться напрямую с постоянным током, потому что, хотя магнитное поле существует, оно должно быть изменено на , чтобы вызвать напряжение в другой катушке. Статическое магнитное поле не может производить выходное напряжение / ток.

Попробуйте этот эксперимент. Возьмите катушку с проводом (для этого подойдет кроссоверная катушка громкоговорителя) и магнит.Подключите мультиметр (желательно аналоговый) к катушке и установите диапазон на наиболее чувствительный диапазон тока на измерителе. По мере того, как вы перемещаете магнит к катушке или от нее, вы увидите ток, показанный отклонением стрелки измерителя. При повороте магнита в одну сторону сила тока будет положительной, а в другую — отрицательной. Чем выше индуктивность катушки и чем сильнее магнит (и / или чем ближе он к катушке), тем больше будет индуцированный ток.

Двигайте магнит медленно, и сила тока будет меньше, чем при быстром перемещении.Оставьте его неподвижным, и ток вообще не будет, независимо от того, насколько близко может быть магнит. Это принцип магнитной индукции, и он применим ко всем катушкам (действительно, ко всем кускам провода, хотя катушка усиливает эффект).

Если вы теперь возьмете пригоршню гвоздей и поместите их через центр катушки, вы увидите, что ток увеличился во много раз — магнитное поле теперь более сконцентрировано, потому что стальные гвозди образуют лучший магнитный путь (более высокая проницаемость) чем воздух.

Легкость, с которой любой материал может переносить магнитное поле, называется проницаемостью (или, точнее, начальной проницаемостью , ), и разные материалы имеют разные проницаемости. Некоторые из них оптимизированы особым образом для конкретных требований — например, сердечники, используемые для трансформатора импульсного источника питания, сильно отличаются от сердечников, используемых для обычных сетевых трансформаторов 50/60 Гц.

Проницаемость сердечников трансформаторов сильно различается в зависимости от материала и применяемой обработки.Проницаемость воздуха равна 1, и большинство традиционных кернов имеют гораздо более высокую (т.е.> 1) проницаемость. Пара заметных исключений — это алюминий и латунь, которые иногда используются для уменьшения индуктивности катушек с воздушным сердечником в радиочастотной (RF) работе. Это гораздо реже, чем ферритовый сердечник, который увеличивает индуктивность и используется для настройки многих ВЧ трансформаторов.

Помимо проницаемости, магнитопроводы (за исключением воздуха) обладают максимальным магнитным потоком, с которым они могут работать без насыщения.В этом контексте насыщение означает то же самое, что и в большинстве других: когда полотенце пропитано, оно не может больше удерживать воду, а когда магнитный сердечник насыщен, он не может больше переносить магнитный поток. В этот момент магнитное поле больше не меняется, поэтому ток в обмотке не индуцируется.

Вероятно, вам не удастся пропитать ногти магнитом, так как между двумя полюсными наконечниками очень большой воздушный зазор. Это означает, что сердечник всегда сможет поддерживать магнитный поток, но эффективность также намного ниже, поскольку магнитная цепь разомкнута.Почти все трансформаторы, которые вы увидите, имеют полностью замкнутую магнитную цепь, чтобы гарантировать, что как можно большая часть наведенного на сердечник магнетизма пройдет через обмотку (и).

В некоторых случаях крошечный воздушный зазор будет оставлен намеренно, и это делается обычно, когда трансформатор или катушка должны выдерживать значительную составляющую постоянного тока, а также переменного тока. Об этом вкратце рассказывается ниже, но больше по этому поводу во втором разделе статьи.

Рисунок 1.1 — Основные принципы работы трансформатора

На Рисунке 1.1 показаны основы всех трансформаторов. Катушка (первичная) подключена к источнику переменного напряжения — обычно это сеть для силовых трансформаторов. Поток, наведенный в сердечник, передается во вторичную обмотку, в обмотке индуцируется напряжение, и через нагрузку создается ток.

На схеме также показаны различные части трансформатора. Это простой трансформатор с двумя обмотками. Первичная обмотка (обозначенная как таковая при проектировании) будет индуцировать магнитное поле в сердечнике в соответствии с током, создаваемым приложенным напряжением переменного тока.Магнитное поле концентрируется сердечником, и почти все оно также проходит через обмотки вторичной обмотки, где индуцируется напряжение. Сердечник в этом случае типичен для конструкции трансформатора «C-Core», где первичная и вторичная обмотки иногда разделены. Более распространенным является «традиционный» тип E-I (ee-eye), который, хотя и несколько не в моде, в наши дни все еще широко используется. Это показано ниже.

Величина напряжения во вторичной обмотке определяется по очень простой формуле, которая определяет отношение витков (N) компонента — это традиционно рассчитывается путем деления витков вторичной обмотки на витки первичной обмотки…

1.1.1 N = Ц / Тп

Tp — это просто количество витков провода, составляющего первичную обмотку, а Ts — количество витков вторичной обмотки. Трансформатор с 500 витками на первичной обмотке и 50 витками на вторичной имеет отношение витков 1:10 (т.е. 1/10 или 0,1)

1.1.2 Vs = Vp × N

В большинстве случаев вы никогда не узнаете количество витков, но, конечно, мы можем просто перевернуть формулу, чтобы соотношение витков можно было вывести из первичного и вторичного напряжений…

1.1.3 N = Vs / Vp

Если напряжение 230 В (естественно, переменного тока) приложено к первичной обмотке, мы ожидаем 23 В на вторичной обмотке, и это действительно то, что будет измеряться. У трансформатора есть дополнительная полезная функция — «трансформируется» не только напряжение, но и ток.

1.1.4 Is = Ip / N

Если в приведенном выше примере из вторичной обмотки потребляется ток 10 А, то логически в первичной обмотке будет измеряться ток 1 А — напряжение снижается, но увеличивается ток.Так было бы, если бы трансформатор был на 100% эффективен, но даже эта самая эффективная «машина», которая у нас есть, к сожалению, никогда не будет идеальной. В результате при потреблении 10 А от вторичной обмотки напряжение будет меньше, чем 23 В, которые были у нас без нагрузки. Это мера регулирования трансформатора, и большая часть падения напряжения происходит из-за сопротивления обмотки.

При использовании больших трансформаторов для национальной энергосистемы, КПД трансформаторов обычно превышает 95%, а некоторых достигает 98% (или даже больше).

Меньшие трансформаторы всегда будут иметь более низкий КПД, но блоки, обычно используемые в усилителях мощности, могут иметь КПД до 90% для больших размеров. Причины потери мощности станут ясны (я надеюсь) по мере нашего продвижения. Пока что для простоты будем считать трансформатор «идеальным» (т.е. без потерь).

Рисунок 1.2 — Ламинирование E-I

Обычный набор для ламинирования E-I все еще широко используется, и стоит упомянуть несколько важных моментов.Центральная ножка всегда в два раза больше ширины внешних ножек для сохранения площади поперечного сечения. Точно так же ламинация «I» и «задняя часть» буквы E имеют такую ​​же ширину (или иногда немного больше) ширины внешних ножек. Окно обмотки — это место, где живут медные обмотки, и в хорошо спроектированном трансформаторе оно будет почти полностью заполнено. Это максимизирует количество меди и снижает резистивные потери, поскольку обмотки имеют максимально возможную толщину.

См. Раздел 2, чтобы узнать, как определяются размеры пластин E и I.Это обычно называют ламинированием без царапин и практически исключает любые потери материала.

---

2. Терминология магнитного сердечника

Этот список далеко не полный, но его будет достаточно, чтобы вы начали или отпугнули. Я включил символы и единицы только трех из приведенных ниже записей, так как большинство из них не представляют особого интереса.

Коэрцитивная сила — это напряженность поля, которая должна применяться для уменьшения (или coerce ) остаточного потока до нуля.Материалы с высокой коэрцитивной силой (например, те, которые используются для постоянных магнитов) называются твердыми . Материалы с низкой коэрцитивной силой (используемые для трансформаторов) называются soft .

Эффективная площадь — сердечника — это площадь поперечного сечения центральной ветви для пластин E-I или общая площадь для тороида. Обычно это соответствует физическим размерам сердечника, но поскольку поток может распределяться неравномерно, производитель может указать значение, которое отражает это.

Эффективная длина — сердечника — это расстояние, которое магнитный поток проходит при замыкании цепи. Обычно это близко соответствует среднему физическому размеру сердечника, но поскольку поток имеет тенденцию концентрироваться на внутренних углах пути, производитель может указать значение эффективной длины.

Плотность потока — (символ; B, единица; тесла (Т)) — это просто общий поток, деленный на эффективную площадь магнитной цепи, через которую он течет.

Магнитопровод — в идеальном индукторе магнитный поток, создаваемый одним витком, будет заключаться во всех остальных витках. Настоящие катушки приближаются к этому идеалу, когда другие размеры катушки малы по сравнению с ее диаметром или если подходящий сердечник направляет поток через обмотки.

Магнитодвижущая сила — MMF можно рассматривать как магнитный эквивалент электродвижущей силы. Это произведение тока, протекающего в катушке, и количества витков, составляющих катушку.

Напряженность магнитного поля — (обозначение: H, единица измерения; амперметры (A m ^-1 )), когда ток течет в проводнике, он всегда сопровождается магнитным полем. Сила или интенсивность этого поля пропорциональна величине тока и обратно пропорциональна расстоянию от проводника (отсюда и надстрочный индекс -1).

Магнитный поток — (символ:; единица измерения: Webers (Wb)) мы относимся к магнетизму в терминах силовых линий или магнитных линий, которые являются мерой общей величины магнетизма.

Проницаемость — (символ; µ, единицы: генри на метр (Hm ^-1 ) определяется как отношение плотности потока к напряженности поля и определяется типом материала в магнитном поле, т. Е. Сердечником Сам материал. Большинство ссылок на проницаемость на самом деле относится к «относительной проницаемости», поскольку проницаемость почти всех материалов изменяется в зависимости от напряженности поля (и в большинстве случаев также от температуры).

Remanence — (или остаток) — это плотность магнитного потока, которая остается в магнитном материале, когда внешнее приложенное поле удаляется.Трансформаторы требуют минимально возможной остаточной намагниченности, в то время как постоянные магниты требуют высокой остаточной намагниченности.

Насыщенность — точка, в которой ядро ​​больше не может принимать больше потока. Когда это происходит, первичный ток трансформатора ограничивается только любым последовательным сопротивлением (например, внешним сопротивлением и сопротивлением обмотки). Насыщение сердечника ограничивает пиковое входное напряжение переменного тока для заданного числа витков первичной обмотки. Начало насыщения обычно довольно постепенное, но может быть очень резким для некоторых материалов с высокой проницаемостью.

Я упоминаю их здесь для полноты картины, но их реальная важность не обсуждается далее в этом разделе. В разделе 2 этой статьи снова рассматриваются термины, и их важность несколько увеличивается в контексте.

---

3. Как работает трансформатор

Идеальный трансформатор без нагрузки практически не потребляет ток из сети, поскольку это просто большая индуктивность. Весь принцип работы основан на индуцированном магнитном потоке, который не только создает напряжение (и ток) во вторичной обмотке, но также и в первичной! Именно эта характеристика позволяет любой катушке индуктивности функционировать должным образом, а напряжение, генерируемое в первичной обмотке, называется «обратной ЭДС» (электродвижущая сила).Величина этого напряжения такова, что оно почти равно (и составляет , фактически, в той же фазе, что и) приложенной ЭДС.

Хотя для определения внутреннего генерируемого напряжения можно выполнить простой расчет, это бессмысленно, поскольку его нельзя изменить. Для синусоидальной формы волны ток через катушку индуктивности отстает от напряжения на 90 градусов. Поскольку наведенный ток отстает на 90 градусов, внутреннее генерируемое напряжение снова смещается на назад на на 90 °, поэтому оно находится в фазе с входным напряжением.Для простоты представьте себе катушку индуктивности или трансформатор (без нагрузки) с приложенным напряжением 230 В. Чтобы эффективная обратная ЭДС сопротивлялась полному приложенному напряжению переменного тока (как и должно), фактическая величина наведенного напряжения (обратная ЭДС) составляет чуть менее 230 В. Выходное напряжение трансформатора всегда совпадает по фазе с приложенным напряжением (в пределах нескольких тысячных градуса).

Например … первичная обмотка трансформатора, работающая на входе 230 В, потребляет 15 мА из сети на холостом ходу и имеет сопротивление постоянному току 2 Ом.Обратной ЭДС должно быть достаточно, чтобы ограничить ток через сопротивление 2 Ом до 15 мА, поэтому будет достаточно близко к 229,97 В (30 мВ на 2 Ом составляет 15 мА). В реальных трансформаторах есть дополнительные сложности, которые увеличивают общий ток (в частности, потери в стали и / или частичное насыщение), но принцип не сильно изменился.

Если все это слишком сбивает с толку, не беспокойтесь об этом. Если вы не собираетесь посвятить свою карьеру проектированию трансформаторов, эта информация на самом деле мало полезна для вас, поскольку вы ограничены «реальными» характеристиками компонентов, которые вы покупаете — внутреннее устройство не имеет большого значения.Даже если вы посвятите свою жизнь дизайну трансформеров, эта информация по большей части останется просто любопытством, поскольку вы все еще мало что можете с этим поделать.

Когда вы подключаете нагрузку к выходной (вторичной) обмотке, через нагрузку проходит ток, который отражается через трансформатор на первичную обмотку. В результате первичная обмотка теперь должна потреблять больше тока из сети. Возможно, несколько интригующе то, что чем больше тока потребляется из вторичной обмотки, исходный фазовый сдвиг тока на 90 ° становится все меньше и меньше по мере того, как трансформатор приближается к полной мощности.Коэффициент мощности ненагруженного трансформатора очень низкий, что означает, что, хотя есть вольты и амперы, но есть относительно небольшая мощность. Коэффициент мощности улучшается с увеличением нагрузки и при полной нагрузке будет близок к единице (идеал).

Однако это зависит от нагрузки — нелинейная нагрузка на вторичной обмотке трансформатора отражает нелинейную нагрузку на сеть.

Теперь можно рассмотреть еще один интересный факт о трансформаторах.

Мы будем использовать тот же пример, что и выше.Первичная обмотка 230 В потребляет 1 А, а вторичная 23 В подает 10 А. Таким образом, согласно закону Ома, сопротивление нагрузки (импеданс) составляет 23/10 = 2,3 Ом. Полное сопротивление первичной обмотки должно составлять 230/1 = 230 Ом. Это соотношение 100: 1, а соотношение оборотов всего 10: 1 — что происходит?

Коэффициент импеданса трансформатора равен квадрату отношения витков …

3.1.1 Z = N²

Трансформаторы

обычно проектируются в зависимости от требуемой мощности, и это определяет размер сердечника для данного материала сердечника.Исходя из этого, можно определить необходимое число витков на вольт, исходя из максимальной плотности магнитного потока, которую может выдержать материал сердечника. Опять же, это сильно зависит от материалов сердечника.

Можно применить эмпирическое правило, согласно которому площадь сердечника для «стандартных» (если действительно существует) стальных пластин (в квадратных сантиметрах) равна квадратному корню из мощности. Таким образом, трансформатору на 625 ВА потребуется сердечник (как минимум) 25 кв. См, если предположить, что проницаемость сердечника составляет около 500, что довольно типично для стандартных пластин трансформатора.Это также предполагает, что материал сердечника не будет насыщаться с плотностью потока, необходимой для получения этой мощности.

Следующим шагом является вычисление количества витков на вольт первичной обмотки. Это зависит от частоты, но для трансформатора с частотой 50 Гц количество витков на вольт (приблизительно) составляет 45, деленное на площадь сердечника (в квадратных сантиметрах). Для трансформатора на 60 Гц требуется меньше витков, и число витков на вольт будет около 38 на площадь жилы. Материалы сердечника с более высокими эксплуатационными характеристиками могут допускать более высокую плотность магнитного потока, поэтому возможно меньшее количество витков на вольт, что увеличивает общую эффективность и регулирование.Эти расчеты необходимо производить с осторожностью, иначе трансформатор перегреется без нагрузки.

Для трансформатора 625 ВА вам потребуется около 432 витков для первичной обмотки 230 В, хотя на практике это может быть меньше этого значения. Кремнистые стали с ориентированной структурой, используемые в трансформаторах более высокого качества, часто допускают более высокий общий магнитный поток на единицу площади, и потребуется меньше витков.

Вы можете определить количество витков на вольт любого трансформатора (по причинам, которые станут яснее по мере дальнейшего развития), добавив ровно 10 витков тонкого «провода звонка» или аналогичного изолированного провода к тестируемому трансформатору, намотанному поверх существующих обмоток.При питании от правильного номинального напряжения питания измерьте напряжение на созданной вами дополнительной обмотке. Разделите количество витков (10) на измеренное напряжение, чтобы получить число витков на вольт для этого трансформатора. Например, если вы измеряете 5 В, трансформатор имеет 2 витка / вольт.

Итак, какая вам польза от этого на земле? Что ж, вы можете быть удивлены тем, что вы можете сделать с этими знаниями. Предположим на мгновение, что у вас есть трансформатор для усилителя мощности приличного размера. Вторичное напряжение составляет 35-0-35 В, что слишком велико для питания цепи предусилителя или даже его источника питания, но вы сможете сделать это с помощью одной обмотки 16 В.Обычно используется другой трансформатор, но вы также можете добавить дополнительную обмотку самостоятельно. С тороидальными трансформаторами это почти слишком просто, но с другими может быть вообще невозможно. Если трансформатор использует (скажем) 2 витка на вольт, всего 32 дополнительных витка провода звонка (или эмалированного медного провода) обеспечат 16 В при типичных 100 мА или около того, которые вам понадобятся. Добавьте 10% запаса, и у вас останется только 36 витков, и это можно будет сделать за несколько минут. Убедитесь, что дополнительная обмотка надежно закреплена лентой хорошего качества (настоятельно рекомендуется использовать каптон, если вы можете его достать).Не используйте , а не , обычную электротехническую ленту — она ​​не рассчитана на температуру, при которой трансформаторы могут работать при постоянной нагрузке.

ПРИМЕЧАНИЕ: Убедитесь, что нет никакой возможности дополнительного короткого замыкания обмотки между витками — это вызовет эффектный выход дыма из изоляции, и вы можете повредить сам трансформатор.

---

3.1 Насыщение ядра

Ток намагничивания, указанный или измеренный для любого трансформатора, обычно представляет собой комбинацию истинного тока намагничивания (который обычно очень низкий) и тока насыщения, который может составлять до половины расчетного тока полной нагрузки для небольших трансформаторов.Любой трансформатор с сердечником (кремнистая сталь, феррит и т. Д.) Перейдет в насыщение, если первичное напряжение холостого хода будет увеличено достаточно сильно. Это более подробно рассматривается в Части 2, Разделе 12.1.

Насыщение сердечника достигается, когда пиковое входное напряжение является достаточным для достижения сердечником максимального номинального магнитного потока. Когда плотность потока слишком высока, сердечник больше не может принимать больше и насыщается. Форма волны насыщения показана в Разделе 2, и хотя вы можете увидеть указанный «ток намагничивания» трансформатора, это почти всегда первичный ток холостого хода, включая ток насыщения .

Нереалистично ожидать, что какой-либо сетевой трансформатор останется значительно ниже насыщения на всех рабочих уровнях. Это потребовало бы, чтобы ядро ​​было намного больше и дороже, чем обычно. Когда плотность потока сердечника превышает примерно 1,4 Тесла (кремнистая сталь), он начинает насыщаться. Когда сердечник на полностью насыщен, на он больше не существует, и ток ограничивается только сопротивлением цепи. Это недопустимо, но частичное насыщение на холостом ходу является обычным явлением, и это увеличивает кажущийся ток намагничивания.

Для трансформаторов, используемых в аудиосистеме (выходные трансформаторы вентилей, микрофонные или «линейные» трансформаторы и т. Д.), Сердечник должен работать при всех возможных напряжениях и частотах значительно ниже насыщения, чтобы предотвратить серьезные искажения. Для силовых трансформаторов характерно небольшое насыщение без нагрузки. Хотя это увеличивает ток холостого хода (и температуру) трансформатора, это также позволяет немного лучше регулировать, поскольку используется меньше витков, что снижает сопротивление обмотки.

Насыщение — сложный процесс, который не совсем понятен большинству любителей (и даже некоторым профессионалам).Степень допустимой насыщенности зависит от предполагаемого использования и допустимого искажения. При уменьшении частоты трансформатор будет больше насыщаться, если входное напряжение остается неизменным. Например, силовой трансформатор, рассчитанный на работу с частотой 60 Гц, обычно сильно насыщается на частоте 50 Гц, даже если напряжение правильное. Нормальная работа может быть восстановлена ​​только в том случае, если входное напряжение уменьшается в том же соотношении, что и частота — от 60 Гц до 50 Гц составляет 17%, поэтому входное напряжение также должно быть уменьшено на 17%, чтобы получить расчетный ток «намагничивания».

---

4. Интересные факты о трансформаторах

Как обсуждалось выше, отношение импеданса — это квадрат отношения витков, но это только одна из многих интересных особенностей трансформаторов … (ну, и , в любом случае, думают, что они интересны).

Например, можно подумать, что увеличение числа витков приведет к увеличению плотности потока, поскольку больше витков вносят вклад в магнитное поле. На самом деле, верно обратное, и при том же входном напряжении увеличение числа витков приведет к уменьшению плотности потока и наоборот.Это нелогично, пока вы не поймете, что увеличение числа витков увеличивает индуктивность и, следовательно, уменьшает ток через обмотку.

Я уже упоминал, что коэффициент мощности (и фазовый сдвиг) изменяется в зависимости от нагрузки, и это (хотя и довольно интересно) не имеет для большинства из нас никаких реальных последствий.

Когда мы потребляем ток от вторичной обмотки, возникает очень интересное явление. Поскольку первичный ток увеличивается для питания нагрузки, мы ожидаем, что магнитный поток в сердечнике также увеличится (больше ампер, то же количество витков, больше потока).На самом деле плотность потока уменьшается! В идеальном трансформаторе без потерь в меди магнитный поток останется прежним — дополнительный ток питает только вторичную обмотку. В реальном трансформаторе, когда ток увеличивается, потери увеличиваются пропорционально, и первичное напряжение немного меньше (из-за сопротивления меди), поэтому магнитный поток при полной нагрузке на ниже, чем на , чем при отсутствии нагрузки. Об этом стоит немного пошуметь, так как это широко неправильно понимается. Хотя это уже было указано в начале, это настолько важно, что я повторю это еще раз…

Плотность магнитного потока в трансформаторе максимальна на холостом ходу, и уменьшается при увеличении нагрузки.

Когда вы испытываете трансформатор без нагрузки, первичный ток возникает исключительно из-за тока намагничивания и дополнительного тока, вызванного частичным насыщением (почти все сетевые трансформаторы покажут некоторые свидетельства тока насыщения — см. Часть 2, Раздел 12.1). Предположим, что трансформатор работает от 230 В на первичной обмотке и имеет сопротивление первичной обмотки 10 Ом.Если мы теперь подключим нагрузку к вторичной обмотке, которая вызывает повышение первичного тока до 1 А, эффективное первичное напряжение уменьшится на 10 В (10 Ом × 1 А), поэтому оно упадет до 220 В. Плотность потока уменьшается пропорционально, и при более низком уровне эффективного напряжения плотность потока должна быть ниже , когда ток отводится от вторичной обмотки.

Плотность потока от вторичной обмотки не влияет, потому что любой дополнительный поток, создаваемый током нагрузки, равен, но противоположен потоку, вызванному первичным током, потому что направление тока противоположно (правило правой руки Флеминга).Это (IMO) «периферийная» тема, и она объясняет, почему вторичный ток не увеличивает плотность потока. Настоящая причина того, что магнитная индукция падает на , связана исключительно с сопротивлением обмотки. Трансформатор, использующий «сверхпроводники» (нулевое сопротивление) для первичной и вторичной обмоток, будет поддерживать одинаковый магнитный поток независимо от тока нагрузки.

---

4,1 Индуктивность

Также важно понимать еще один интересный факт о сетевом трансформаторе . Мы склонны полагать, что индуктивность важна — в конце концов, это то, что мешает трансформатору потреблять 10 А или более из сети на холостом ходу.На самом деле индуктивность обычно не является параметром конструкции, а просто результатом правильного расчета числа витков на вольт. Индуктивность также является туманной цифрой, и ее значение составляет , а не , постоянное, но изменяется (или, по крайней мере, кажется, что меняется) в зависимости от условий. Когда у вас есть нужное количество витков первичной обмотки, индуктивность в значительной степени заботится о себе. Быстрый расчет продемонстрирует, что я имею в виду.

Предположим, тороидальный трансформатор на 600 ВА с измеренной индуктивностью 52 Гн при 50 Гц.Формула для индуктивности говорит нам, что ток намагничивания будет …

I _mag = В / (2 × π × f × L)
I _mag = 230 / (2 × π × 50 × 52) = 14 мА

Однако, когда этот трансформатор испытывается (см. Часть 2 — Ток намагничивания), фактически измеренный ток намагничивания составляет 42 мА — в 3 раза выше ожидаемого. Это происходит потому, что сердечник частично насыщен, а не , а не , потому что индуктивность ниже измеренной или рассчитанной.При работе при (намного) более низком напряжении, когда ток намагничивания не искажается (что означает, что нет насыщения сердечника вообще), ток намагничивания подчиняется формуле, показанной выше. Без насыщения сердечника ток определяется индуктивностью, напряжением и частотой, как и в любой катушке индуктивности. Однако трансформаторы (большинство) не являются индукторами как таковые !

Примечание: Для многих других трансформаторов индуктивность является параметром конструкции (и очень важным).Это относится к трансформаторам, используемым в импульсных источниках питания, или к аудио трансформаторам и другим, где критична низкочастотная характеристика. Это только с трансформаторами частоты сети (50 или 60 Гц), где мы действительно не заботимся об индуктивности, при условии, что ток намагничивания является ощутимым. «Разумность» определяется тем, как и где используется трансмиссия, и чего хотел достичь дизайнер. Здесь нет никаких «правил» — если он работает, как требуется (и согласно проектной спецификации), остается при приемлемой температуре, надежен и безопасен, то это все, что имеет значение.

Вот почему производители редко (если вообще когда-либо) указывают индуктивность трансформаторов сетевой частоты. Вместо этого (и если вам повезет) они могут сказать ток намагничивания без нагрузки при номинальном напряжении и частоте. Большинство даже не удосуживаются рассказать вам об этом. В конце концов, вы все равно ничего не можете с этим поделать.

В предисловии я упомянул, что трансформатор не является индуктивным при работе с номинальной нагрузкой. Если мы представим тот же самый трансформатор, описанный выше (индуктивность 52H), он будет потреблять 14 мА индуктивного тока на холостом ходу (без учета насыщения).Ток будет отставать от напряжения на 90 °, а коэффициент мощности, определяемый cos (Φ), равен cos (90) = 0. Если вторичная обмотка загружена так, что первичный ток нагрузки составляет всего 14 мА (общий ток теперь составляет 20 мА , , а не 28 мА, как вы могли предположить), фазовый угол падает до 45 °, а коэффициент мощности увеличивается до cos (45) = 0,707 — при токе нагрузки всего 14 мА !

Если нагрузка такова, что первичный ток составляет около 5% или более номинального значения трансформатора (около 130 мА для трансформатора на 600 ВА), фазовый сдвиг составляет всего несколько градусов (около 5.6 °), а коэффициент мощности близок к единице (0,995 для обсуждаемого гипотетического трансформатора). Однако (и это важно) первичный ток является почти идеальным воспроизведением вторичного тока, и если вторичный ток является нелинейным, первичный ток также является нелинейным. Выпрямительные и конденсаторные нагрузки, которые используются почти во всех линейных источниках питания, имеют низкий коэффициент мощности, но это из-за нелинейности , а не индуктивности .

Итак, для обычных сетевых трансформаторов индуктивность не является частью спецификации и может считаться «случайной».Он должен существовать, чтобы ограничить ток холостого хода до разумно разумного значения, но большая часть тока намагничивания возникает из-за частичного насыщения. Большинство сетевых трансформаторов необходимо испытывать при напряжении значительно ниже заданного входного напряжения сети, чтобы можно было измерить индуктивность. Типичный трансформатор 230 В должен быть измерен при напряжении не более 50-100 В, чтобы получить фактическую индуктивность.

Измерив индуктивность первичной обмотки, вы быстро обнаруживаете, что эти данные бесполезны — вы ничего не можете с ними поделать, и это не поможет вам понять ни на йоту.Отчасти это связано с тем простым фактом, что он меняется. Поскольку плотность потока внутри сердечника изменяется, также изменяется и измеренная индуктивность, так что это действительно бессмысленный параметр в более широкой схеме вещей. Трансформаторы предназначены для получения требуемых напряжения и тока на вторичной обмотке, а процесс проектирования основан на количестве витков первичной обмотки, необходимых для получения ощутимого тока холостого хода («намагничивания»).

Это в значительной степени балансирующее действие. Для данного размера сердечника более высокий ток намагничивания является результатом использования меньшего количества витков на первичной обмотке, и это улучшает регулирование, поскольку провод может быть больше.Однако, если ток холостого хода слишком высок, трансформатор будет перегреваться из-за насыщения сердечника из-за высокого первичного тока. Трансформатор , который никогда не работает на холостом ходу , может быть спроектирован так, чтобы быть намного меньше, чем в противном случае.

Если мы предположим, что трансформатор для конкретного применения должен обеспечивать хорошее регулирование и что он всегда работает только при полной нагрузке, нет причин делать сердечник настолько большим, насколько это было бы необходимо в противном случае. Мы также можем использовать меньше витков и уменьшить резистивные потери.Современные трансформаторы для микроволновых печей попадают в эту категорию — если они работают без нагрузки, ток намагничивания может быть настолько высоким, что трансформатор может перегреться и выйти из строя, но при нормальной работе (питание магнетрона) они идеально подходят для этой работы. Большинство из них также охлаждаются вентилятором, что позволяет им быть еще меньше!

Когда трансформатор работает только с полной нагрузкой, ток намагничивания больше не является важным фактором, и количество необходимых витков основывается на эффективном напряжении на обмотке при полной нагрузке.Трансформатор мощностью 1 кВт обычно может иметь сопротивление первичной обмотки от 1,0 до 1,2 Ом, но если его можно уменьшить, потери в меди также уменьшатся. При 1 кВт первичный ток составляет 4,35 А, и это снизит напряжение, воспринимаемое трансформатором, возможно, на 5–6 В RMS. Вместо того, чтобы разрабатывать трансформатор для приятного низкого тока намагничивания при 230 В, его можно спроектировать для несколько более высокого тока намагничивания при 225 В — один только ток намагничивания может составлять 1 или 2 А, а может быть и больше.

Попытка измерить индуктивность такого трансформатора — пустая трата времени.Вы сможете измерить это, но чтение не имеет значения. Еще более традиционные сетевые трансформаторы находятся в той же лодке — индуктивность (возможно, с натяжкой) можно считать « показателем качества », но единственное, что действительно имеет значение, — это общий ток намагничивания, включая эффекты частичного насыщения. Не думайте ни на минуту, что обычные сетевые трансформаторы не насыщаются — каждый трансформатор, который я когда-либо измерял, потребляет ток в 2-5 раз больше, чем вы ожидаете, основываясь только на одной индуктивности.Конечно, при нормальном рабочем напряжении они неразделимы.

Коэффициент индуктивности любого трансформатора (между первичной и вторичной обмотками) — это квадрат отношения витков. Трансформатор, рассчитанный на сеть 230 В с измеренным выходным напряжением 23 В без нагрузки (полная нагрузка 20 В), имеет коэффициент трансформации 10: 1 (230: 23). Если вы измеряете индуктивность первичной обмотки (скажем) 30 Гн, индуктивность вторичной обмотки составляет 300 мГн. Это тоже бесполезно, но может пригодиться, если вы хотите использовать трансформатор в обратном направлении, например, с генератором и усилителем мощности.

---

4.2 Взаимная индуктивность

Одна из вещей, которая имеет тенденцию вызывать путаницу, связана с тем, как трансформатор «знает», что кто-то пытается получить ток из вторичной обмотки, поэтому первичный ток может быть увеличен пропорционально. Это связано с взаимной индуктивностью (также известной как взаимная связь или просто коэффициент связи) между обмотками. Когда две или более обмоток используют одну и ту же магнитную цепь, они связаны магнитным потоком. В идеальном трансформаторе эта связь равна единице, что означает, что любое возмущение на одной обмотке напрямую связано с другой (конечно, с учетом коэффициента трансформации).

Если связь равна единице, обмотки действуют как единое целое. Электрическое разделение (изоляция) не имеет значения, поэтому попытка получения тока из вторичной обмотки ничем не отличается от получения тока из первичной обмотки — две обмотки соединены вместе и неразделимы. Конечно, настоящие трансформаторы не идеальны, но (что может удивить) это лишь немного меняет ситуацию. Это ключ к работе трансформатора, но (несмотря на его большое значение) он мало влияет на конструкцию трансформатора.Это также то, что вы не можете изменить — трансформатор такой, какой он есть, а параметры можно изменить только во время разработки.

Индуктивность утечки уменьшает взаимную индуктивность, предотвращая единичную связь. Однако в преобразователях частоты это практически ничего не меняет. Даже «обычные» трансформаторы (с ламинированием E-I) имеют сравнительно низкую индуктивность рассеяния (по сравнению с индуктивностью первичной обмотки), а тороидальные трансформаторы имеют очень низкую индуктивность рассеяния . Любой поток, который «просачивается» из сердечника, не может проходить через две обмотки одинаково, что снижает эффективный поток во вторичной обмотке и уменьшает связь между ними.

Связь такова, что если вы управляете сетевым трансформатором от генератора сигналов с низким импедансом, все, что находится на вторичной обмотке, отражается обратно в первичную. Если нагрузка представляет собой конденсатор, первичная обмотка будет казаться емкостной (опережающий коэффициент мощности). Когда нагрузка представляет собой резистор, первичная обмотка кажется резистивной. Первичная обмотка будет индуктивной только , если нагрузка — индуктор. Чтобы провести этот тест (который нетрудно сделать), ток, потребляемый от вторичной обмотки, должен быть как минимум в 10 раз (а предпочтительно в 100 раз) больше, чем ток намагничивания (ток холостого хода из-за индуктивности первичной обмотки трансформатора.

Например, если трансформатор имеет индуктивность первичной обмотки (при низком напряжении) 100 Гн, ток намагничивания будет около 390 мкА при 50 Гц. Вам необходимо потреблять не менее 39 мА от вторичной обмотки, и этого достаточно, чтобы напряжение и ток в первичной обмотке находились в пределах менее одного градуса друг от друга. Если вы теперь подключите конденсатор, который потребляет такой же ток (это необходимо рассчитать на основе напряжения и частоты), первичная обмотка окажется полностью емкостной.

Это аспект взаимной связи, который редко объясняется, но понимание этой простой концепции означает, что вы можете избежать целой кучи довольно утомительной математики, которая на самом деле не поможет вам понять задействованные принципы.Как знают постоянные читатели, я не буду приводить подробных формул, если они никому не помогут понять, как что-то работает. Это показательный пример. Использование формулы почти ничего не покажет, но если вы запустите тест для себя, вы поймете, как это работает.

---

4,3 Импеданс

Трансформатор не имеет определенного импеданса. Вы можете извиниться за то, что думаете иначе, но это потому, что некоторые трансформаторы предназначены для выходных каскадов ламповых усилителей или для номинальных сигнальных линий 600 Ом (например).Для выходного трансформатора отношения импеданса определяются для согласования анодного сопротивления / импеданса конкретных выходных клапанов и преобразуются в импеданс, подходящий для громкоговорителя. В этой роли важна индуктивность первичной обмотки , потому что она должна быть достаточно высокой, чтобы обеспечить хорошее соединение между лампами и динамиками на самой низкой интересующей частоте.

Это кратко рассматривается в этом разделе и более подробно рассматривается в разделе 2.Хотя индуктивность важна, еще более важно обеспечить, чтобы сердечник оставался вдали от даже частичного насыщения на самых низких частотах. Вот почему хорошие выходные трансформаторы такие большие и дорогие. Однако важно понимать, что, хотя трансформатор разработан и рекламируется как (например) 6 кОм P-P: 8 Ом, это не означает, что сам трансформатор имеет такие импедансы. означает, что означает, что при питании от источника 6 кОм (пара выходных клапанов) выходное сопротивление будет таким, что максимальная мощность будет подаваться на нагрузку 8 Ом.

Точно такой же трансформатор может питаться от источника 3 кОм и выдавать максимальную мощность на нагрузку 4 Ом. Он также работает с более высоким импедансом источника, но тогда индуктивность может быть недостаточно большой для обеспечения хорошего воспроизведения низких частот. Требуемая индуктивность определяется импедансом источника и самой низкой интересующей частотой — обычно 40 Гц для многих ламповых усилителей. Итак, используя приведенный пример, можно определить индуктивность и частоту -3 дБ …

L = Z / (2 × π × f _{-3 дБ} ) (где Z — импеданс источника, а f _{-3 дБ} — частота -3 дБ)
L = 6k / (2 × π × 40) = 24H

Как должно быть очевидно, по мере увеличения импеданса источника требуется большая индуктивность для той же частоты -3 дБ.Это также требует, чтобы поток в сердечнике оставался значительно ниже насыщения. Даже небольшая насыщенность вызывает грубые искажения. Некоторые утверждают, что это искажение не так нежелательно, как можно было бы представить, потому что оно спадает с увеличением частоты. Однако, если низкая и высокая частота передаются одновременно, более высокая частота также будет искажена — как только ядро ​​начинает насыщаться, искажаются все частоты, присутствующие в то время, а не только частота, вызывающая насыщение.

---

5. Примеры использования трансформатора

Это лишь краткое описание множества применений трансформаторов. В этом разделе я отказался от источников питания с переключаемым режимом и представлю только наиболее распространенные линейные приложения. Применение источников питания более полно описано в Разделе 2, а также в статье Проектирование линейных источников питания.

Было бы невозможно охватить все аспекты трансформаторов и их использования, поскольку они очень разнообразны и используются во многих разных вещах.Компьютерные сетевые карты, модемы, усилители мощности и микроволновые печи, автомобильные и морские системы зажигания, катушки Тесла и фонокорректоры с подвижной катушкой, распределение мощности от электростанции до вашего дома … разнообразие скромного трансформера (ну, может, не так уж и скромно).

---

5.1 — Выходной каскад двухтактного клапана

Трансформаторы используются не только в источниках питания, но и в других областях.Почти все ламповые усилители мощности используют трансформатор для выходного каскада, который преобразует высокий импеданс анодов в импеданс громкоговорителя, а также обеспечивает подачу напряжения на выходные клапаны. Здесь не было показано никаких смещений или других компонентов поддержки — для получения дополнительной информации см. Как работают усилители. Еще одна ссылка на ступени клапана находится в разделе «Клапаны».

Рисунок 5.1 — Выходной каскад двухтактного клапана

Рисунок 5.1 показывает, как это работает. Работа первичной обмотки может поначалу вас удивить, но это вполне соответствует всей теории. Показанное напряжение питания составляет 500 В, и мы предполагаем, что клапан может включаться достаточно сильно, чтобы уменьшить его до нуля поочередно на каждом конце обмотки. В действительности это не так, потому что клапаны не имеют достаточно низкого внутреннего импеданса, но это упрощает объяснение.

Ни один из клапанов не будет потреблять значительный ток без сигнала, и потребляемая величина не намагничивает сердечник.Причина проста — через каждую секцию первичной обмотки проходит равный ток, но фактически в противоположных направлениях. Магнитное поле, создаваемое одной половиной обмотки, компенсируется магнитным полем второй половины, оставляя чистый установившийся магнитный поток равным нулю.

Когда клапан V1 полностью включается, напряжение на его конце обмотки снижается до нуля, а напряжение на аноде V2 составляет 1000 вольт. Так должно быть, иначе теория трансформаторов развалилась.Первичная обмотка работает как «автотрансформатор». Аналогичным образом, когда V1 выключается, а V2 включается, ситуация меняется на противоположную. Вы вполне можете спросить, зачем вообще нужны 2 клапана? Казалось бы, напряжение от одного клапана вполне способно качнуть напряжение из одной крайности в другую.

Это не так. Поскольку клапан может только включаться, он сможет подавать ток только на половину формы волны. В двухтактной конструкции класса A каждый клапан обычно пропускает 1/2 максимального пикового тока, необходимого на холостом ходу, и полный пиковый ток при включении на максимум до искажения (другой клапан выключен).В случае двухтактной конструкции насыщение сердечника отсутствует из-за постоянного тока (который, как и раньше, компенсируется), поэтому, хотя необходимы два клапана, трансформатор будет меньше и будет иметь гораздо лучшие характеристики. Для несимметричных усилителей класса A требуется очень большой сердечник с воздушным зазором для предотвращения насыщения. Это резко снижает производительность трансформатора, увеличивает искажения и ухудшает низкочастотную характеристику из-за более низкой индуктивности. Также могут отрицательно сказаться высокие частоты, потому что воздушный зазор заставляет часть магнитного потока «просачиваться» из сердечника.Это одна из причин возникновения индуктивности рассеяния (более подробно рассматривается в разделе 2).

Стоит отметить, что эффективный размах размаха по всей первичной обмотке трансформатора составляет 2000 В. Когда V1 полностью включен, он имеет нулевое напряжение (только для нашего примера) на пластине, а V2 имеет напряжение на пластине 1000 В. V1 и V2 имеют одинаковые пики напряжения, но они сдвинуты по фазе на 180 градусов. Таким образом, полное напряжение на трансформаторе является суммой двух напряжений. С точки зрения переменного тока линию питания B + можно рассматривать как нулевое напряжение (помните, что она будет шунтироваться с большой емкостью).

Среднеквадратичное значение напряжения (с учетом синусоиды и игнорирования потерь) легко вычисляется по стандартной формуле …

5.1.1 В (размах) = В (размах) / 2

Чтобы получить пиковое значение от пика к пику, затем …

5.1.2 Vrms = Vp / √2

Чтобы найти среднеквадратичное значение.

В этом случае размах напряжения составляет 2000 В, поэтому от пика до 1000 В. Среднеквадратичное значение составляет 707 В.

---

5.2 Выход на несимметричный триод (SET)

Рисунок 5.2 показано базовое устройство выходного каскада усилителя SET. Полный постоянный ток должен протекать через первичную обмотку трансформатора, и, как обсуждалось выше, в сердечнике должен быть воздушный зазор, чтобы предотвратить насыщение. Поскольку воздушный зазор снижает эффективность магнитного пути, сердечник должен быть значительно больше, чем в противном случае.

Рисунок 5.2 — Выходной каскад на несимметричном триоде

Сердечник работает только с одной полярностью потока, которая меняется в зависимости от сигнала.Можно подумать, что одно только это уменьшит искажения, поскольку поток никогда не пересекает нулевую точку, но это не так. По-прежнему необходимо, чтобы поток изменял направление, и характеристики магнитных материалов указывают на то, что сопротивление изменению (а не абсолютная полярность магнитного поля) является доминирующим фактором. Клапан (и первичная обмотка трансформатора) теперь должны пропускать ток, равный пиковому переменному току, требуемому нагрузкой — конечно, в зависимости от коэффициента трансформации.

Максимальное отрицательное колебание (клапан включен) удвоит этот ток и снизится почти до нуля при выключении клапана (положительное колебание). Когда ток уменьшается ниже среднего постоянного (покоящегося) тока, напряжение на трансформаторе увеличивается в противоположной полярности — отсюда и тот факт, что напряжение на пластине превышает напряжение питания. Это одна из областей, где трансформатор на самом деле является катушкой индуктивности , а работа схемы зависит от накопленного «заряда» катушки индуктивности.Вторичная обмотка просто передает напряжение на нагрузку.

Для той же выходной мощности клапан в несимметричной цепи должен быть значительно больше, чем требуется для двухтактной схемы, из-за более высокого рассеяния, необходимого для дополнительного тока. Есть также много других проблем с этой схемой — в частности, высокие искажения и сравнительно высокий выходной импеданс.

Не менее важная проблема заключается в том, что преимущество дополнительного размаха напряжения при использовании трансформатора с центральным ответвлением теперь утрачено, поэтому максимальное эффективное среднеквадратичное напряжение, которое может быть разработано, составляет 353 В — значительное падение первичного переменного напряжения (опять же без учета потерь, это ровно половина).Это означает, что нагрузка клапана выше при том же импедансе динамика, потому что коэффициент трансформации меньше, поэтому мы снова получаем меньшую мощность.

Постоянные читатели знают, что я считаю «НАБОР» мерзостью. Заявленные преимущества в основном видны (или ухом) смотрящего и не выдерживают ни малейшей проверки.

---

5.3 Приложения линейного уровня Трансформаторы

также используются для «линейных» приложений с низким энергопотреблением, как правило, для симметричных микрофонных входов и линейных выходных каскадов.Трансформатор не имеет себе равных для реальных симметричных схем, поскольку вход или выход действительно плавающий и не требует заземления. Это означает, что синфазные сигналы (то есть любой сигнал, общий для обоих сигнальных проводов) почти полностью отклоняются.

На рис. 5.3 показан симметричный вход трансформатора, преобразующийся в несимметричный. Сигнал усиливается и снова отправляется на выходной трансформатор для распределения в виде сбалансированного сигнала. «Усилитель», как правило, представляет собой микшерный пульт и принимает сигналы микрофонного или линейного уровня в качестве входа (идущие от сцены к зоне микширования), а конечный микшированный выход отправляется обратно на сцену для основного (передний дома) усилители громкой связи и колонки.От микрофона до микшера и обратно к основным усилителям может быть более 100 метров кабеля, и при этом практически не будет слышен какой-либо шум.

Рисунок 5.3 — Симметричный микрофонный и линейный выходы

Телефонная система раньше полностью зависела от трансформаторов для передачи сигнала от АТС (или центрального офиса в США) на оборудование в помещении клиента (CPE). Телефонный коммутатор, используемый в офисах, оборудовании (PABX — Private Automatic Branch Exchange, или PBX для США) по-прежнему использует трансформаторы почти для всех входящих цепей, будь то аналоговые или цифровые.

Принцип в точности такой же, как и для показанного выше аудиоприложения, за исключением того, что для телефонных цепей обычно присутствует постоянное напряжение для питания CPE (в случае домашнего телефона) и для обеспечения некоторой базовой сигнализации. В современных схемах PABX используются трансформаторы с ферритовым сердечником и схема развязки постоянного тока, чтобы гарантировать, что постоянный ток не протекает через обмотки трансформатора, поскольку это ухудшает характеристики так же, как и выходной трансформатор для усилителя мощности SET. (Обратите внимание, что многие абонентские цепи теперь управляются через специально изготовленные ИС, которые исключают трансформатор.)

Аудиоприложения для трансформаторов в симметричных схемах пришли из телекоммуникационной отрасли, где впервые были придуманы эти концепции. Телефонная линия может иметь длину 4 км и более и не экранирована, поэтому метод устранения гудения и шума был необходим. Сегодня существуют десятки (сотни?) Миллионов трансформаторов, используемых для соединений Ethernet LAN, и розетки RJ45 доступны со встроенными трансформаторами.

---

6. Безопасность

Безопасность является основным соображением для любого силового трансформатора (а в случае телекоммуникаций — изолирующих трансформаторов), и электрический контакт между первичной и вторичной обмотками не должен допускаться при любых реальных условиях неисправности .Во всех странах есть стандарты безопасности, которые применяются к трансформаторам, где важна электрическая изоляция, и если есть какие-либо сомнения в безопасности трансформатора для конкретной цели, убедитесь, что вы убедитесь, что трансформатор соответствует соответствующему стандарту (-ам). Рассмотрение всех возможных стандартов и вопросов соответствия выходит за рамки данной статьи, поэтому я оставлю это вам — и вашему поставщику.

Многие силовые трансформаторы оснащены внутренним предохранителем, работающим только на один раз, который размыкает цепь в случае превышения заданной температуры.Эта температура выбрана в качестве максимальной безопасной температуры обмоток перед тем, как изоляция расплавится или сломается, поэтому в случае неисправности плавкий предохранитель сработает до того, как будет повреждена изоляция, и компонент станет потенциально опасным. Это также помогает предотвратить риск пожара (и нет, это не предназначено для юмора — мой друг сгорел дотла из-за неисправного силового трансформатора в видеомагнитофоне — как было определено следователями по пожару.Правдивая история!). См. Рис. 6.1 (ниже) в качестве примера того, насколько плохо может быть, если трансформатор не защищен.

После размыкания плавкого предохранителя трансформатор необходимо выбросить, так как обычно невозможно получить доступ к предохранителю для его замены. Это не так глупо, как может показаться, поскольку термическое разрушение перегретой изоляции невозможно предсказать, и трансформатор может быть небезопасным, если его все еще можно использовать.

Есть трансформаторы, которые спроектированы так, чтобы быть «изначально безопасными», и у них обычно есть обмотки на отдельных участках сердечника, а не в физическом контакте друг с другом.Если сердечник соединен с заземлением с электрической безопасностью (что обычно является обязательным), никакой метод отказа (включая полное расплавление) в первичной обмотке не позволит сетевому напряжению появиться на вторичной. Боковые обмотки являются следующими по безопасности, и хотя первичная и вторичная обмотки находятся на одной катушке, используемый материал выбран так, чтобы выдерживать высокие температуры и обеспечивать разделение обмоток. Тороидальные сердечники и другие трансформаторы с концентрической намоткой являются наименее безопасными, поскольку единственное разделение между первичной и вторичной обмотками — это довольно тонкий слой изоляции.Это одна из причин того, что термопредохранители часто используются с тороидами. Обратите внимание, что любой трансформатор, классифицированный как «безопасный по своей природе», обычно должен соответствовать очень строгим условиям утверждения в большинстве стран.

Рисунок 6.1 — Расплавление трансформатора

На рис. 6.1 показан трансформатор, который я снял с ремонтных работ. Это полный расплав, и остатки пластиковой шпульки видны достаточно четко. В любой цепи чрезвычайно важно защитить пользователя от контакта с сетью, если это произойдет.В этом случае бобина расплавилась от обмоток, капала на основание оборудования и в целом создавала большой беспорядок. Несмотря на все это, не было электрического соединения между первичной и вторичной обмотками или пластинами. Это был хорошо сделанный трансформатор (он вышел из строя из-за большой продолжительной перегрузки, а не из-за отказа самого трансформатора).

Надлежащее защитное заземление — единственный реальный способ гарантировать, что катастрофический отказ трансформатора (как показано на рисунке) не приведет к подаче напряжения на шасси — не все трансформаторы созданы равными с точки зрения безопасности.Правильный предохранитель гарантирует, что предохранитель перегорит — надеюсь, с до электробезопасность будет нарушена. Тепловой предохранитель не позволил бы ситуации стать настолько плохой, как показано на рисунке, но трансформатор был бы так же мертв.

---

7. Шум

Трансформаторы шумят. Это не только электрический шум, который создается опасной формой волны тока через обмотки, диоды и конденсаторы фильтра, но и реальный слышимый шум. Одним из источников является вибрация обмотки из-за движения провода из-за магнитного поля и тока, протекающего по проводникам.Этого следует избегать любой ценой, поскольку постоянная вибрация в конечном итоге приведет к износу изоляции, короткому замыканию обмоток и выходу трансформатора из строя. К счастью, это довольно необычно, но иногда случается (и случается).

Большая часть шума исходит от пластин или другого материала сердечника, который сжимается под воздействием сильного магнитного поля. Это называется магнитострикцией и происходит в большей или меньшей степени со всеми магнитными материалами. Стетоскоп проверит источник шума, и нет ничего или почти ничего, что могло бы его остановить.Упругая установка предотвратит акустическое усиление большей части шума шасси, и, как правило, шум будет хуже без нагрузки. В некоторых случаях трансформатор может быть рассчитан на 60 Гц, но используется на 50 Гц. В этом случае плотность потока, вероятно, превысит максимально допустимую для сердечника (который насыщается), и трансформатор станет намного горячее, чем должен, и почти наверняка будет намного более шумным. Тороидальные трансформаторы обычно намного тише, чем ламинированные EI (т.е.е. обычные) типы.

Большинство (все?) Трансформаторов, разработанных специально для 60 Гц, в конечном итоге выйдут из строя в сети 50 Гц из-за перегрева. Обратное неверно, и трансформаторы на 50 Гц могут вполне безопасно работать на 60 Гц.

Еще одна проблема с пластинами E-I заключается в том, что они могут быть недостаточно хорошо скреплены друг с другом, и это, в частности, позволяет внешним пластинам вибрировать. Обычные трансформаторы более высокого качества обычно пропитывают лаком (иногда под вакуумом) и запекают в умеренной печи до готовности…. ой, то есть до полного высыхания лака. Это связывает пластинки и обмотки вместе, предотвращая шум, а также делая трансформатор более устойчивым к повреждениям водой или другими загрязнениями и / или в условиях высокой влажности (например, в тропиках).

---

Щелкните любой из вышеперечисленных разделов, чтобы просмотреть остальные разделы этой серии. Как вы, наверное, заметили, трансформаторы все-таки не так просты.

---

Список литературы

Эти ссылки являются общими для обоих разделов статьи, хотя большинство из них относится только к разделу 2.Во время составления этих статей было исследовано бесчисленное количество различных веб-страниц, и хотя некоторые из них были интересными, большинство из них использовались минимально. Из тех, кого я действительно помню (сложная задача сама по себе, учитывая огромное количество поисков, которые мне приходилось делать), я должен поблагодарить следующие веб-страницы (в алфавитном порядке) …

• Амидон
• Школа ATDL (Армия США)
• Трансформеры Jensen
• Корпорация Mitchell Electronics
• Томи Энгдал — (ePanorama.нетто)

Я рекомендую статью «История трансформатора», хотя и не используется в качестве справочной. Он не технический, но дает некоторое представление о разработке трансформаторов в том виде, в каком мы их знаем.

Кроме того, я использовал различные другие ссылки, но, в частности (в порядке полезности) …

---

Следующие (слегка отредактированные) определения взяты из Единицы измерения

Авторские права на сайт «Единицы измерения» принадлежат Рассу Роулетту и Университету Северной Каролины в Чапел-Хилл.
(Определения использованы с разрешения автора.)

Тесла (Тл) — плотность потока (или напряженность поля) для магнитных полей (также называемая магнитной индукцией). Напряженность магнитного поля можно измерить, поместив в поле проводник с током. Магнитное поле оказывает на проводник силу, которая зависит от силы тока и длины проводника. Один Тесла определяется как напряженность поля, создающая один Ньютон силы на ампер тока на метр проводника.Эквивалентно, одна тесла представляет собой плотность магнитного потока, равную одному Веберу на квадратный метр площади. Поле в один тесла достаточно велико: самые сильные поля, доступные в лабораториях, составляют около 20 тесла, а плотность магнитного потока Земли на ее поверхности составляет около 50 микротесла (мкТл). Одна Тесла равна 10000 Гс. Tesla, определенная в 1958 году, названа в честь Николы Теслы (1856-1943), чья работа в области электромагнитной индукции привела к появлению первых практических генераторов и двигателей, использующих переменный ток (к большому раздражению Эдисона, который утверждал, что постоянный ток был « более безопасным »). .

Weber (Wb) — магнитный поток. «Поток» — это скорость (в единицу времени), с которой что-то пересекает поверхность, перпендикулярную потоку. В случае магнитного поля магнитный поток через перпендикулярную поверхность является произведением плотности магнитного потока в теслах и площади поверхности в квадратных метрах. Если переменное магнитное поле проходит перпендикулярно круговой петле из проводящего материала (один виток), изменение поля индуцирует электрический потенциал в петле.Если поток изменяется с постоянной скоростью один Вебер в секунду, индуцированный потенциал составляет один вольт. Это означает, что численно поток в веберах равен потенциалу в вольтах, который был бы создан путем равномерного сжатия поля до нуля за одну секунду. Один Вебер — это поток, индуцированный таким образом током, изменяющимся с постоянной скоростью один ампер в секунду. Единица посвящена немецкому физику Вильгельму Эдуарду Веберу (1804–1891), одному из первых исследователей магнетизма.

---

---

Основной индекс
Указатель статей

Уведомление об авторских правах. Эта статья, включая, но не ограничиваясь, весь текст и диаграммы, является интеллектуальной собственностью Рода Эллиотта и защищена авторским правом © 2001. Воспроизведение или повторная публикация любыми способами, электронными, механическими или электромеханическими, строго запрещены. в соответствии с международными законами об авторском праве. Автор (Род Эллиотт) предоставляет читателю право использовать эту информацию только для личного использования, а также разрешает сделать одну (1) копию для справки. Коммерческое использование запрещено без письменного разрешения Рода Эллиотта.

Страница создана и авторские права © 17 марта 2001 г. / обновлено 25 июня 2005 г. / ноя 2018 — незначительные обновления, удалены мертвые ссылки. / Ноя 2018 — добавлена ​​взаимная индуктивность.

Индуктивность | Физика II

Индукция — это процесс, при котором ЭДС индуцируется изменением магнитного потока. До сих пор обсуждалось множество примеров, некоторые из которых более эффективны, чем другие. Трансформаторы, например, спроектированы так, чтобы быть особенно эффективными при наведении желаемого напряжения и тока с очень небольшими потерями энергии в другие формы.Есть ли полезная физическая величина, связанная с тем, насколько «эффективно» данное устройство? Ответ положительный, и эта физическая величина называется , индуктивность . Взаимная индуктивность — это влияние закона индукции Фарадея для одного устройства на другое, например, первичная катушка, при передаче энергии вторичной обмотке в трансформаторе. См. Рис. 1, где простые катушки индуцируют ЭДС друг в друге.

Рис. 1. Эти катушки могут вызывать ЭДС друг в друге, как неэффективный трансформатор.Их взаимная индуктивность M указывает на эффективность связи между ними. Здесь видно, что изменение тока в катушке 1 вызывает ЭДС в катушке 2. (Обратите внимание, что « E ₂ индуцированный» представляет наведенную ЭДС в катушке 2.)

Во многих случаях, когда геометрия устройств фиксирована, магнитный поток изменяется за счет изменения тока. Поэтому мы сконцентрируемся на скорости изменения тока Δ I / Δ t как причине индукции. Изменение тока I ₁ в одном устройстве, катушка 1 на рисунке, индуцирует ЭДС ₂ в другом.Мы выражаем это в форме уравнения как

[латекс] {\ text {emf}} _ {2} = — M \ frac {\ Delta {I} _ {1}} {\ Delta t} \\ [/ latex],

, где M определяется как взаимная индуктивность между двумя устройствами. Знак минус является выражением закона Ленца. Чем больше взаимная индуктивность M , тем эффективнее связь. Например, катушки на Рисунке 1 имеют небольшой размер M по сравнению с катушками трансформатора на Рисунке 3 от Transformers. Единицами измерения для M являются (В с) / A = Ом ⋅ с, который назван henry (H) в честь Джозефа Генри.То есть 1 H = 1 Ω⋅s. Природа здесь симметрична. Если мы изменим ток I ₂ в катушке 2, мы индуцируем ЭДС ₁ в катушке 1, что равно

[латекс] {\ text {emf}} _ {1} = — M \ frac {\ Delta {I} _ {2}} {\ Delta t} \\ [/ latex],

, где M то же, что и для обратного процесса. Трансформаторы работают в обратном направлении с такой же эффективностью или взаимной индуктивностью M . Большая взаимная индуктивность M может быть или нежелательна.Мы хотим, чтобы трансформатор имел большую взаимную индуктивность. Но такой прибор, как электрическая сушилка для одежды, может вызвать опасную ЭДС на корпусе, если взаимная индуктивность между его катушками и корпусом велика. Один из способов уменьшить взаимную индуктивность M состоит в том, чтобы намотать катушки противотоком для подавления создаваемого магнитного поля. (См. Рисунок 2.)

Рис. 2. Нагревательные катушки электрической сушилки для одежды могут быть намотаны в противоположную сторону, так что их магнитные поля нейтрализуют друг друга, что значительно снижает взаимную индуктивность по сравнению с корпусом сушилки.

Самоиндукция , действие закона индукции Фарадея устройства на самого себя, также существует. Когда, например, увеличивается ток через катушку, магнитное поле и магнитный поток также увеличиваются, вызывая противоэдс, как того требует закон Ленца. И наоборот, если ток уменьшается, индуцируется ЭДС, которая препятствует уменьшению. Большинство устройств имеют фиксированную геометрию, поэтому изменение магнитного потока полностью связано с изменением тока Δ I через устройство.Индуцированная ЭДС связана с физической геометрией устройства и скоростью изменения тока. Выдается

[латекс] \ text {emf} = — L \ frac {\ Delta I} {\ Delta t} [/ latex],

, где L — собственная индуктивность устройства. Устройство, которое демонстрирует значительную самоиндукцию, называется индуктором и обозначено символом на рисунке 3.

Рисунок 3.

Знак минус является выражением закона Ленца, означающего, что ЭДС препятствует изменению тока.Единицами самоиндукции является генри (Гн), как и для взаимной индуктивности. Чем больше самоиндукция L устройства, тем сильнее оно сопротивляется любому изменению тока через него. Например, большая катушка с множеством витков и железным сердечником имеет большой L и не позволит току быстро меняться. Чтобы избежать этого эффекта, необходимо добиться небольшого размера L , например, за счет встречной намотки катушек, как показано на рисунке 2. Катушка индуктивности 1 H — это большая катушка индуктивности. Чтобы проиллюстрировать это, рассмотрим устройство с L = 1.0 H, через который протекает ток 10 A. Что произойдет, если мы попытаемся быстро отключить ток, возможно, всего за 1,0 мс? ЭДС, заданная как ЭДС = — L (Δ I / Δ t ), будет препятствовать изменению. Таким образом, ЭДС будет индуцирована ЭДС = — L (Δ I / Δ t ) = (1,0 H) [(10 A) / (1,0 мс)] = 10 000 В. Положительный знак означает, что это большое напряжение идет в том же направлении, что и ток, противодействуя его уменьшению. Такие большие ЭДС могут вызвать дуги, повредить коммутационное оборудование, и поэтому может потребоваться более медленное изменение тока.Есть применение для такого большого наведенного напряжения. Во вспышках камеры используются батарея, два индуктора, которые работают как трансформатор, и система переключения или генератор для создания больших напряжений. (Помните, что нам нужно изменяющееся магнитное поле, вызванное изменяющимся током, чтобы вызвать напряжение в другой катушке.) Система генератора будет делать это много раз, когда напряжение батареи повышается до более чем тысячи вольт. (Вы можете услышать пронзительный свист трансформатора во время зарядки конденсатора.) Конденсатор сохраняет высокое напряжение для последующего использования при питании вспышки. (См. Рисунок 4.)

Рис. 4. Благодаря быстрому переключению катушки индуктивности можно использовать батареи 1,5 В для индукции ЭДС в несколько тысяч вольт. Это напряжение можно использовать для хранения заряда в конденсаторе для последующего использования, например, в насадке для вспышки камеры.

Можно рассчитать L для индуктора, учитывая его геометрию (размер и форму) и зная создаваемое магнитное поле. В большинстве случаев это сложно из-за сложности создаваемого поля.Таким образом, в этом тексте индуктивность L обычно является заданной величиной. Единственным исключением является соленоид, потому что он имеет очень однородное поле внутри, почти нулевое поле снаружи и простую форму. Поучительно вывести уравнение для его индуктивности. Начнем с того, что наведенная ЭДС определяется законом индукции Фарадея как ЭДС = — Н (Δ Φ / Δ t ) и, по определению самоиндукции, как ЭДС = — L . (Δ I / Δ т ).Приравнивая эти доходности к

[латекс] \ text {emf} = — N \ frac {\ Delta \ Phi} {\ Delta t} = — L \ frac {\ Delta I} {\ Delta t} \\ [/ latex]

Решение для L дает

[латекс] L = N \ frac {\ Delta \ Phi} {\ Delta I} \\ [/ latex]

Это уравнение для самоиндукции L устройства всегда верно. Это означает, что самоиндукция L зависит от того, насколько эффективен ток для создания магнитного потока; чем эффективнее, тем больше Δ Φ / Δ I .Давайте воспользуемся этим последним уравнением, чтобы найти выражение для индуктивности соленоида. Поскольку площадь A соленоида является фиксированной, изменение магнитного потока составляет Δ Φ = Δ ( B A ) = A Δ B . Чтобы найти Δ B , заметим, что магнитное поле соленоида определяется выражением [латекс] B = {\ mu} _ {0} {nI} = {\ mu} _ {0} \ frac {NI} { \ ell} \\ [/ латекс]. (Здесь n = N / , где N — количество катушек, а ℓ — длина соленоида.{2} A} {\ ell} \ text {(соленоид)} \\ [/ latex].

Это самоиндукция соленоида с площадью поперечного сечения A, и длиной ℓ . Обратите внимание, что индуктивность зависит только от физических характеристик соленоида, в соответствии с его определением.

Пример 1. Расчет самоиндукции соленоида среднего размера

Рассчитайте самоиндукцию соленоида длиной 10,0 см и диаметром 4,00 см, который имеет 200 катушек.

Стратегия

Это простое применение [латекса] L = \ frac {{\ mu} _ {0} {N} ^ {2} A} {\ ell} \\ [/ latex], поскольку все величины в уравнении, кроме L известны. {2} \ влево (1.{2} \ right)} {0.100 \ text {m}} \\ & = & 0.632 \ text {mH} \ end {array} \\ [/ latex].

Обсуждение

Этот соленоид среднего размера. Его индуктивность около миллигенри также считается умеренной.

Одно из распространенных применений индуктивности используется в светофорах, которые могут определить, когда автомобили ждут на перекрестке. Электрическая цепь с индуктором размещается на дороге под местом остановки ожидающей машины. Кузов автомобиля увеличивает индуктивность, и схема изменяется, посылая сигнал на светофор, чтобы изменить цвет.Точно так же металлоискатели, используемые для безопасности аэропортов, используют ту же технику. Катушка или индуктор в корпусе металлоискателя действует как передатчик и как приемник. Импульсный сигнал в катушке передатчика вызывает сигнал в приемнике. На самоиндукцию цепи влияет любой металлический предмет на пути. Такие детекторы могут быть настроены на чувствительность, а также могут указывать приблизительное местонахождение обнаруженного на человеке металла. (Но они не смогут обнаружить пластиковую взрывчатку, подобную той, которая была обнаружена на «бомбардировщике в нижнем белье.”) См. Рисунок 5.

Рис. 5. Знакомые ворота безопасности в аэропорту могут не только обнаруживать металлы, но и указывать их приблизительную высоту над полом. (Источник: Alexbuirds, Wikimedia Commons)

Как рассчитать обмотку трансформатора

Обновлено 28 декабря 2020 г.

Автор S. Hussain Ather

Если вы когда-нибудь задумывались, как дома и здания используют электроэнергию от электростанций, вы должны узнать о трансформаторах в силовых распределительные сети, которые преобразуют токи высокого напряжения в те, которые вы используете в бытовых приборах.Эти трансформаторы имеют простую конструкцию для большинства типов трансформаторов, но могут сильно различаться по степени изменения входного напряжения в зависимости от конструкции.

Формула обмотки трансформатора

Трансформаторы, которые используются в системах распределения электроэнергии, имеют простую конструкцию, в которой в различных областях используются катушки, намотанные на магнитный сердечник.

Эти катушки с проводом принимают входящий ток и изменяют напряжение в соответствии с коэффициентом поворота трансформатора , который равен

\ frac {N_P} {N_S} = \ frac {V_P} {V_S}

для числа обмотки первичной обмотки и вторичной обмотки N _p и N _s соответственно, а напряжение первичной обмотки и вторичной обмотки V _p и V _s соответственно.

Эта формула обмотки трансформатора сообщает вам долю, на которую трансформатор изменяет входящее напряжение, и что напряжение обмоток катушки прямо пропорционально количеству обмоток самих катушек.

Имейте в виду, что, хотя эта формула называется «отношением», на самом деле это дробь, а не соотношение. Например, если у вас есть одна обмотка первичной обмотки и четыре обмотки вторичной обмотки трансформатора, это будет соответствовать доле 1/4, что означает, что трансформатор снижает напряжение на величину 1/4.Но соотношение 1: 4 означает, что для одного из чего-то есть четыре из чего-то другого, что не всегда означает то же самое, что и дробь.

Трансформаторы могут повышать или понижать напряжение и известны как повышающие трансформаторы , или понижающие трансформаторы , , в зависимости от того, какое действие они выполняют. Это означает, что коэффициент трансформации трансформатора всегда будет положительным, но может быть больше единицы для повышающих трансформаторов или меньше единицы для понижающих трансформаторов.

Формула обмотки трансформатора верна только тогда, когда углы первичной и вторичной обмоток совпадают по фазе друг с другом. Это означает, что для данного источника питания переменного тока (AC), который переключается вперед и назад между прямым и обратным током, ток в первичной и вторичной обмотках синхронизируется друг с другом во время этого динамического процесса.

Могут быть трансформаторы с коэффициентом трансформации 1, которые не изменяют напряжение, а вместо этого используются для разделения различных цепей друг от друга или для небольшого изменения сопротивления цепи.

Калькулятор конструкции трансформатора

Вы можете понять свойства трансформаторов, чтобы определить, что калькулятор конструкции трансформатора будет учитывать в качестве метода определения того, как сконструировать трансформаторы.

Хотя первичная и вторичная обмотки трансформатора отделены друг от друга, первичная обмотка индуцирует ток во вторичных обмотках с помощью метода индуктивности. Когда источник питания переменного тока подается через первичные обмотки, ток течет по виткам и создает магнитное поле с помощью метода, называемого взаимной индуктивностью.

Формула обмотки трансформатора и магнетизм

Магнитное поле описывает, в каком направлении и насколько сильный магнетизм будет действовать на движущуюся заряженную частицу. Максимальное значение этого поля составляет dΦ / dt , скорость изменения магнитного потока Φ за небольшой промежуток времени.

Поток — это измерение того, сколько магнитного поля проходит через определенную площадь поверхности, например прямоугольную. В трансформаторе силовые линии магнитного поля направляются наружу от магнитной катушки, вокруг которой намотаны провода.

Магнитный поток связывает обе обмотки вместе, а сила магнитного поля зависит от силы тока и количества обмоток. Это может дать нам калькулятор конструкции трансформатора , который учитывает эти свойства.

Закон индуктивности Фарадея, который описывает, как магнитные поля индуцируются в материалах, диктует, что напряжение любой из обмоток индуцирует

либо для первичной обмотки, либо для вторичной обмотки. Обычно это называется наведенной электродвижущей силой ( ЭДС ).

Если бы вы измерили изменение магнитного потока за небольшой период времени, вы могли бы получить значение dΦ / dt и использовать его для вычисления эдс . Общая формула для магнитного потока:

\ Phi = BA | cos {\ theta}

для магнитного поля B , площадь поверхности плоскости в поле A и угол между магнитным полем линии и направление, перпендикулярное площади θ .

Вы можете учесть геометрию обмоток вокруг магнитного сердечника трансформатора, чтобы измерить поток, аскат

для источника переменного тока, где ω — угловая частота ( 2πf для частоты f ) и Φ _макс. — это максимальный поток.В этом случае частота f относится к количеству волн, которые проходят через заданное место каждую секунду. Инженеры также называют произведение тока на количество витков обмотки « ампер-витков », что является мерой силы намагничивания катушки.

Примеры калькулятора обмотки трансформатора

Если вы хотите сравнить экспериментальные результаты того, как обмотки трансформаторов влияют на их использование, вы можете сравнить наблюдаемые экспериментальные свойства с характеристиками калькулятора обмоток трансформатора.

Компания-разработчик программного обеспечения Micro Digital предлагает онлайн-калькулятор обмотки трансформатора для расчета стандартного калибра проводов (SWG) или американского калибра проводов (AWG). Это позволяет инженерам изготавливать провода соответствующей толщины, чтобы они могли нести заряды, необходимые для их целей. Калькулятор оборотов трансформатора подскажет вам индивидуальное напряжение на каждом витке обмотки.

Другие калькуляторы, такие как калькулятор от компании-производителя Flex-Core, позволяют рассчитать размер провода для различных практических применений, если вы вводите номинальную нагрузку, номинальный вторичный ток, длину провода между трансформатором тока и измерителем и входную нагрузку. метра.

Трансформатор тока создает напряжение переменного тока во вторичной обмотке, пропорциональное току в первичной обмотке. Эти трансформаторы снижают токи высокого напряжения до более низких значений, используя простой метод контроля фактического электрического тока. Нагрузка — это сопротивление самого измерительного прибора пропускаемому через него току.

Hyperphysics предлагает онлайн-интерфейс расчета мощности трансформатора, который позволяет использовать его в качестве калькулятора конструкции трансформатора или в качестве калькулятора сопротивления трансформатора.Чтобы использовать его, вам необходимо ввести частоту напряжения питания, индуктивность первичной обмотки, индуктивность вторичной обмотки, количество катушек первичной обмотки, количество катушек вторичной обмотки, вторичное напряжение, сопротивление первичной обмотки, сопротивление вторичной обмотки, сопротивление нагрузки вторичной обмотки и взаимная индуктивность.

Взаимная индуктивность M учитывает влияние изменения нагрузки на вторичную обмотку на ток через первичную обмотку с ЭДС:

ЭДС = -M \ frac {\ Delta I_1} {\ Delta t }

для изменения тока через первичную обмотку ΔI ₁ и изменения во времени Δt .

Любой онлайн-калькулятор обмотки трансформатора делает предположения о самом трансформаторе. Убедитесь, что вы знаете, как каждый веб-сайт рассчитывает заявленные ценности, чтобы вы могли понять теорию и принципы, лежащие в основе трансформаторов в целом. Насколько они близки к формуле обмотки трансформатора, вытекающей из физики трансформатора, зависит от этих свойств.

Первичная индуктивность — обзор

1.

Первая стадия работы : Первая стадия определяется временем включения t _на переключателя S ₁ и показана на Рис. .6.8A (i). На первом этапе работы преобразователя ток в обоих индукторах для 0 < t < t _на можно определить как:

(6,38) iL1 = i + (v1rL1) t

(6,39) iL2 = — i + (v1rL2) t

, где iL1, i’L2 — ток, протекающий в катушке индуктивности L ₁ и L ₂ , v _{1 r} — абсолютное значение синусоидального входного напряжения ( v _1r = | v _s | = V _s | sin ωt |), i — ток, который существует в обоих индукторах L ₁ и L ₂ после диода D ₅ перестает проводить, как показано на рис.6.8C и D.

2.

Второй этап операции : Этот этап продолжается до тех пор, пока i _{L 1} не станет отрицательным для i _{L 2} и отображается на рис. 6.8A (ii). На этом этапе преобразователя SEPIC переключатель выключен, а диод D ₅ горит в течение t _до раз. Токи индуктора iL1 и iL2 для, t _на < t < t _don задаются как:

(6.40) iL1 = i + (v1rL1) dTs− (vDCnL1) t

(6.41) iL2 = −i + (v1rL2) dTs− (vDCnL2) t

, где d — скважность переключателя, равная t _на / T _с и T _с — период переключения.

Продолжительность включения (ddon) выходного диода D ₅ связана с продолжительностью включения переключателя в соответствии со следующим соотношением:

(6,42) ddond = v1rv’DC

Время включения диода D ₅ вычисляется из отношения продолжительности включения по формуле.(6.42) как:

(6.43) tdon = ddonTs = (ndTsvDC) v1r

Ур. (6.43) дополнительно упрощается заменой значения v _{1 r} , время включения диода D ₅ дается как:

(6.44) tdon = (ndTsM) | sin (ωt) |

, где M — пиковое значение входного напряжения v _DC / V _s .

3.

Третий этап работы : Эта стадия свободного хода длится до начала нового периода переключения и показана на рис.6.8A (iii). На этом этапе работы ни переключатель « S ₁ », ни выходной диод « D ₅ » не работают. Время выключения переключателя и выходного диода определяется как:

(6,45) toff = (TS − ​​ton − tdon)

4.

Расчет критического параметра проводимости : Критический параметр проводимости является решающим фактором в Прерывистый режим работы преобразователя SEPIC по току проводимости. Пиковое значение тока ( i _pk ), протекающего в диоде D ₅ , определяется как:

(6.46) ipk = v1rdTSnLeq

, где L _eq — эквивалентная индуктивность, ( L ₁ L ₂ ) / ( L ₁ + L 2).

Средний ток диода в период переключения определяется как:

(6.47) iavg = (ipktdon2TS) = (vS2d2TSsin2 (ωt) 2LeqVDC)

Для половины периода линии этот средний ток задается как:

( 6.48) Iavg = vS2d2TS4LeqvDC

Входной ток рассчитывается с учетом входной мощности, равной выходной мощности.

(6,49) vSiS = vDCiavg

Используя уравнения. (6.47) и (6.49) входной ток рассчитывается как:

(6.50) iS = (vSd2Ts2Leq) = Issin (ωt)

, где I _с — эквивалентный ток источника ( В _с d ² T _s ) / (2 L _экв ).

Для успешной работы преобразователя SEPIC в режиме прерывистого тока должны выполняться следующие неравенства:

(6.51) ton + tdon

(6.52) d | {1+ (nM) sin (ωt)} | <1

Для наихудших условий ωt = 90 градусов для работы в DCM коэффициент заполнения задается как:

(6.53) d <{MM + n}

Средний выходной ток определяется как:

(6.54) iavg = vDCR

Для режима работы с прерывистым током, приравнивая уравнения. (6.48) и (6.54) скважность должна удовлетворять следующему равенству:

(6.55) d = 2MKa

В предыдущем уравнении параметр проводимости ( K _a ) преобразователя SEPIC PFP задан как :

(6.56) Ka = 2LeqRTs

Критическое значение K _a , для работы SEPIC PFP в DCM, можно получить, приравняв уравнения. (6.53) и (6.55) он должен удовлетворять следующему критерию:

(6.57) Kacrit <12 (M + n) 2

При выборе подходящего значения параметра проводимости преобразователя SEPIC эквивалентная индуктивность L _{уравнение} получается из уравнения. (6.56) как:

(6.58) Leq = RTsKa2

Значения L ₁ и L ₂ рассчитываются на основе процентной пульсации ( r ) входного тока, а Пиковое значение пульсации входного тока определяется как:

(6.59) irip = v1rdTsL1

Его максимальное значение возникает для ωt = 90 градусов и задается как:

(6.60) irip = vsdTsL1

Следовательно, L ₁ может быть получено с учетом указанной максимальной пульсации тока и L’2 из полученного таким образом значения L ₁ и эквивалентной индуктивности как:

(6,61) L1 = vsdTsirip

(6,62) L2 = L1Leq (L1 − Leq)

После получения расчетного значения индуктивности L ₁ и L ₂ промежуточный конденсатор C ₁ выбирается с учетом того факта, что при работе DCM напряжение на конденсаторе C ₁ подвергается двум конфликтующим ограничениям а именно, почти постоянное значение в течение периода переключения и следование профилю входного напряжения в течение периода линии.На рис. 6.7 показана емкость « C ₁ », подключенная к первичной обмотке трансформатора. Значение C ₁ рассчитывается как:

(6,63) C1 = 2ωar2 (L1 + L2)

Резонансная угловая частота ( ω _ar ) преобразователя выбрана так, чтобы ω < ω _ar < ω _s .

Где ω — угловая частота сетевого напряжения, а ω _s — угловая рабочая частота переключателя ( S ₁ ).

5.

Выбор выходного емкостного фильтра постоянного тока : Значение выходной емкости выбирается согласно формуле. (6.34), полученное ранее для преобразователя AC-DC Cuk.

Калькулятор идеального трансформатора

Калькулятор идеального трансформатора — это простой инструмент, который помогает решить вопрос: как работает трансформатор? Вы когда-нибудь задумывались, как электрический ток из высоковольтных линий электропередач превращается в привычные 110 (или 220 В) в розетке? Вот что делают электрические трансформаторы.Текст ниже объясняет работу трансформаторов. Прочитав его, вы также узнаете о специальных типах трансформаторов, таких как трансформатор тока и трансформатор напряжения.

Как работает трансформатор?

Трансформатор — это, по сути, две катушки, первичная и вторичная, которые расположены рядом друг с другом. Переменный ток, проходящий через первичную катушку, создает переменное магнитное поле. Это магнитное поле индуцирует разность напряжений, электродвижущую силу, во вторичной катушке.Вы можете узнать больше о проверке индуктивности с помощью калькулятора индуктивности соленоида. Возвращаясь к трансформатору , по существу, магнитное поле передает энергию от одной цепи к другой . Если вы удивлены, что магнитное поле может передавать энергию, вы можете проверить калькулятор плотности энергии полей.

В идеализированной картине мы пренебрегаем всеми потенциальными потерями и предполагаем, что все магнитное поле от первичной катушки проходит через вторичную катушку.Тогда единственное, что имеет значение, — это соотношение количества обмоток между первичной и вторичной обмотками . Это связано с тем, что сила магнитного поля зависит от количества обмоток в первичной катушке. Количество витков вторичной обмотки определяет силу электродвижущей силы.

Калькулятор идеального трансформатора

Идеальное уравнение трансформатора связывает первичное и вторичное напряжение,

Vs = Vp * Ns / Np ,

где

• Vs [V] — напряжение на вторичной катушке
• Vp [V] — напряжение на первичной обмотке,
• Ns — количество витков первичной обмотки,
• Np — количество витков вторичной обмотки,

Есть второе уравнение, которое связывает первичный и вторичный токи,

Is = Ip * Np / Ns ,

где

• Is [A] — ток на вторичной обмотке,
• Ip [A] — ток в первичной обмотке.

Поучительно видеть, что электрическая мощность в первичной обмотке и вторичной обмотке одинакова

P = Ip * Vp = Is * Vs .

Это знак сохранения энергии. В реальном трансформаторе из-за потерь мощность на вторичной обмотке всегда будет меньше, чем мощность на первичной обмотке.

Трансформатор тока

Трансформаторы тока используются для точного измерения тока. В трансформаторах тока вторичных обмоток больше, чем первичных.Следовательно, вторичный ток меньше первичного. Таким образом, мы можем контролировать или измерять большие токи, используя только стандартные малоточные измерительные устройства. Обычно мы подключаем трансформатор тока последовательно.

Трансформатор напряжения

Трансформаторы напряжения подключаются параллельно, и их обычная роль заключается в понижении напряжения. Пониженное напряжение полезно для работы бытовых предметов. Также, как и в случае с трансформаторами тока, он позволяет стандартным измерительным устройствам контролировать линии высокого напряжения.