Как увеличить индуктивность катушки: 3. Факторы, влияющие на индуктивность катушки | 14. Катушки индуктивности | Часть1

3. Факторы, влияющие на индуктивность катушки | 14. Катушки индуктивности | Часть1

3. Факторы, влияющие на индуктивность катушки

Факторы, влияющие на индуктивность катушки

На индуктивность катушки оказывают влияние следующие основные факторы:

Число витков провода в катушке: При прочих равных условиях, увеличение числа витков приводит к увеличению индуктивности; уменьшение числа витков приводит к уменьшению индуктивности.

Пояснение: чем больше количество витков, тем больше будет магнитодвижущая сила для заданной величины тока.

 

 

Площадь поперечного сечения катушки: При прочих равных условиях, катушка с большей площадью поперечного сечения будет иметь большую индуктивность; а катушка с меньшей площадью поперечного сечения — меньшую индуктивность.

Пояснение: Катушка с большей площадью поперечного сечения оказывает меньшее сопротивление формированию магнитного потока для заданной величины магнитодвижущей силы.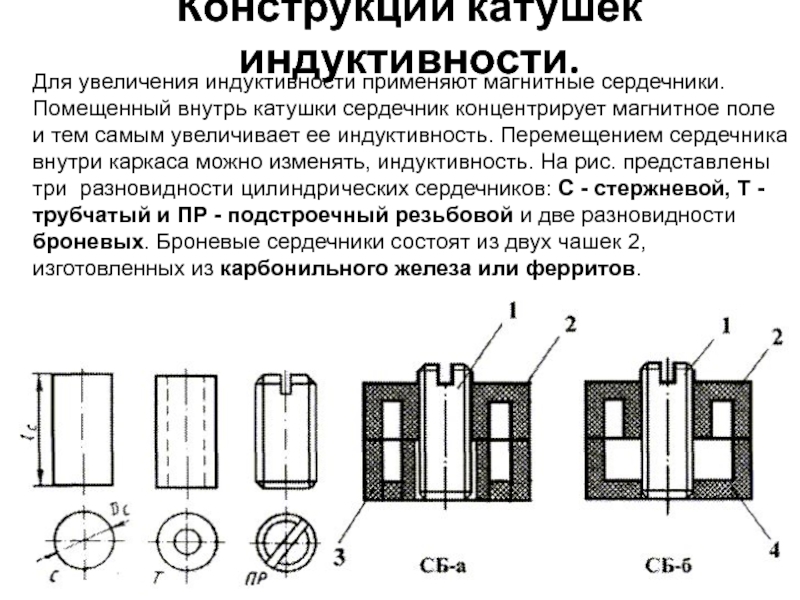

 

 

Длина катушки: При прочих равных условиях, чем больше длина катушки, тем меньше ее индуктивность; чем меньше длина катушки, тем больше ее индуктивность.

Пояснение: Чем больше длина катушки, тем большее сопротивление она оказывает формированию магнитного потока для заданной величины магнитодвижущей силы.

 

 

Материал сердечника: При прочих равных условиях, чем больше магнитная проницаемость сердечника, вокруг которого намотана катушка, тем больше индуктивность; чем меньше магнитная проницаемость сердечника — тем меньше индуктивность.

Пояснение: Материал сердечника с большей магнитной проницаемостью способствует формированию большего магнитного потока для заданной величины магнитодвижущей силы.

 

 

Приблизительное значение индуктивности любой катушки можно найти по следующей формуле:

 

 

Следует понимать, что данная формула дает только приблизительные цифры. Одной из причин такого положения дел является изменение величины магнитной проницаемости при изменении напряженности магнитного поля (вспомните нелинейность кривой В/Н для разных материалов). Очевидно, если проницаемость (µ) в уравнении будет непостоянна, то и индуктивность (L) также будет в некоторой степени непостоянна. Если гистерезис материала сердечника будет существенным, то это непременно отразится на индуктивности катушки. Разработчики катушек индуктивности пытаются минимизировать эти эффекты, проектируя сердечник таким образом, чтобы его намагниченность никогда не приближалась к уровням насыщения, и катушка работала в более линейной части кривой B/H.

Если катушку сделать таким образом, что любой из вышеперечисленных факторов у нее можно механически изменить, то получится катушка с регулируемой величиной индуктивности или вариометр. Наиболее часто встречаются вариометры, индуктивность которых регулируется количеством витков или  положением сердечника (который перемещается внутри катушки). Пример вариометра с изменяемым количеством витков можно увидеть на следующей фотографии:

 

 

Это устройство использует подвижные медные контакты, которые подключаются к катушке в различных точках ее длины. Подобные катушки, имеющие воздушный сердечник, применялись в разработке самых первых радиоприемных устройств.

Катушка с фиксированными значениями индуктивности, показанная на следующей фотографии, представляет собой еще одно раритетное устройство, использовавшееся в первых радиостанциях. Здесь вы можете увидеть несколько витков относительно толстого провода, а так же соединительные выводы:

 

 

А это еще одна катушка индуктивности, так же предназначенная для радиостанций. Для большей жесткости ее провод намотан на керамический каркас:

 

 

Многие катушки индуктивности обладают небольшими размерами, что позволяет монтировать их непосредственно на печатные платы. Посмотрев внимательно на следующую фотографию, можно увидеть две расположенные рядом катушки:

 

 

Две катушки индуктивности расположены справа в центре этой платы и имеют обозначения L₁ и L₂. В непосредственной близости от них находятся резистор R₃ и конденсатор С₁₆. Показанные на плате катушки называются «торроидальными», так как их провод намотан вокруг сердечника, имеющего форму тора.

Как резисторы и конденсаторы, катушки индуктивности могут выполняться в корпусе для поверхностного монтажа (SMD). На следующей фотографии представлено несколько таких катушек:

 

 

Две индуктивности здесь расположены справа в центре платы. Они представляют собой маленькие черные чипы с номером «100», а над одной из них можно увидеть обозначение L₅.

Как увеличить индуктивность катушки

Индуктивность катушки зависит от целого ряда ее конструктивных особенностей. К ним относятся число витков, диаметр, вид сердечника, его расположение и др. Для того чтобы индуктивность изменилась, достаточно соответствующих образом изменить хотя бы один из этих параметров.

Домотайте к катушке дополнительные витки. Это увеличит индуктивностьпри неизменных параметрах ее остальных конструктивных элементов, а у вариометра (катушки с подвижным сердечником) — сместит оба предела изменения индуктивности (верхний и нижний) в сторону увеличения. При намотке дополнительных витков может оказаться, что они не помещаются на каркасе. Не поддавайтесь соблазну использовать более тонкий провод, чем тот, что использован в катушке первоначально, чтобы не вызвать нагрев обмотки протекающим по ней током.

К катушке, не имеющей сердечника, добавьте таковой. Но помните, что он должен быть выполнен из такого материала, в котором рабочей частоте катушки не возникает потерь на вихревые токи. Для электромагнита, работающего на постоянном токе, подойдет сплошной стальной сердечник, для 50-герцового трансформатора — сердечник, набранный из оксидированных листов стали, в более высокочастотных катушках придется использовать сердечники из ферритов различных марок.

Помните, что даже при одном и том же количестве витков и прочих равных параметрах катушка большего диаметра будет иметь и большую индуктивность. Понятно, однако, что провода для ее изготовления потребуется больше.

Феррит выпускается с различной магнитной проницаемостью. Замените один ферритовый сердечник в катушке на другой, у которого значение этого параметра выше, и ее индуктивность увеличится. Но при этом уменьшится граничная частота, на которой такая катушка сможет работать без возникновения заметных потерь в сердечнике.

Существуют катушки, снабженные специальными механизмами для перемещения сердечника. Для того чтобы увеличить индуктивность в этом случае, вдвиньте сердечник внутрь каркаса.

Замкнутый магнитопровод при прочих равных условиях обеспечивает большую индуктивность, чем разомкнутый. Но старайтесь не применять такое решение в трансформаторах и дросселях, работающих при наличии постоянной составляющей. Она способна подмагничивать и насыщать замкнутый сердечник, тем самым, наоборот, вызывая снижение индуктивности катушки.

Увеличение — индуктивность — катушка

Увеличение — индуктивность — катушка

Cтраница 1

Увеличение индуктивности катушки достигается ввертыванием сердечника в ее каркас, а уменьшение-вывертыванием его.  [2]

Для увеличения индуктивности катушек их обмотки располагают на замкнутом сердечнике из ферромагнитного материала, обладающего высокой магнитной проницаемостью. Так как магнитная проницаемость ферромагнитных материалов зависит от магнитной индукции, то индуктивность катушек с ферромагнитными сердечниками не является величиной постоянной, а зависит от тока в обмотке катушки или соответственно от напряжения на ее зажимах. Кроме того, необходимо считаться с наличием потерь в таких катушках, связанных с магнитным гистерезисом и вихревыми токами.  [3]

Для увеличения индуктивности катушек обмотку их располагают на замкнутом стальном сердечнике; обычно эти сердечники изготовляют из листовой электротехнической стали.  [4]

Для увеличения индуктивности катушек обмотку их располагают на замкнутом стальном сердечнике; обычно эти сердечники изготовляют из листовой электротехнической стали. Индуктивность этих катушек не остается постоянной величиной, а зависит от величины тока в обмотке катушки.  [5]

При увеличении индуктивности катушки время перехода из точки А в точку В возрастает, переходный процесс протекает медленнее.  [6]

В целях увеличения индуктивности катушек, уменьшения их физических размеров, а также достижения других качеств витки катушек наматываются на магнитопроводы различной конструкции, изготовленные из ферромагнитных сплавов или ферритов с различными магнитными свойствами.  [7]

На нагрев ферромагнитных сердечников, применяемых для увеличения индуктивности катушек, за счет магнитного гистерезиса и вихревых токов ( токов Фуко), возникающих в сердечниках.  [8]

Применение сердечников из ферромагнитных материалов приводит к увеличению индуктивности катушек, уменьшению их габаритных размеров, увеличению добротности и возможности их подстройки. Изменение индуктивности катушек производится изменением числа витков, изменением коэффициента взаимоиндукции, использованием магнитного сердечника.  [9]

Преимуществом шунтовых заградителей является возможность обеспечения большого запирающего сопротивления за счет увеличения индуктивности катушки, так как через последнюю не протекает рабочий ток линии.  [10]

Однако это требует одновременного увеличения диаметра витков, что в свою очередь приводит к увеличению индуктивности катушки. Поэтому подобное решение может быть использовано только в длинноволновой части метрового диапазона.

 [12]

Если же вблизи катушки поместить ферромагнитный металл, к этим двум явлениям добавляется еще два: некоторое увеличение индуктивности катушки из-за уменьшения магнитного сопротивления и значительное возрастание активных потерь с ростом частоты питающего тока.  [13]

Второй этап процесса срабатывания реле ( этап движения) характеризуется уменьшением зазора между сердечником и движущимся якорем, что приводит к увеличению индуктивности катушки реле.  [14]

Применение для ослабления радиопомех, создаваемых контактными устройствами, индуктивно-емкостного Г — образного фильтра, хотя и обеспечивает отсутствие паразитного резонанса на низких частотах, в большинстве случаев нецелесообразно, так как повышение его эффективности осуществляется обычно посредством

увеличения индуктивности катушек и приводит к увеличению входного сопротивления, а следовательно, и напряжения радиопомех на входе фильтра. Этот способ дает относительно меньший выигрыш в коэффициенте эффективности фильтра.  [15]

Страницы:      1    2

Сердечники катушек индуктивности — выбор материала и формы

Автор: Mark A. Swihart, Менеджер отдела прикладной техники Magnetics Inc, отделение Spang&Co. Питтсбург, Пенсильвания, США.

Резюме: Внимательное рассмотрение характеристик силовых катушек индуктивности часто является ключевым фактором успешного конструирования компактных и экономичных преобразователей с высоким к.п.д. Во многих вариантах применения катушек индуктивности порошковые сердечники обладают явными преимуществами в сравнении с сердечниками, изготовленными из других материалов – таких, как ферриты или стальные ламинаты. В распоряжении разработчика имеется множество вариантов выбора материала и формы порошкового сердечника, каждый из которых является выбором компромисса по таким характеристикам, как величина потерь, стоимость, габариты и простота намотки.

Кроме того, при изменении критериев конструирования изменяется комбинация преимуществ и недостатков каждого из материалов для порошкового сердечника. Понимание этих преимуществ и недостатков необходимо для осуществления правильного выбора.

Катушка индуктивности является устройством, фильтрующим ток. Создавая препятствия прохождению тока, фильтрующая катушка индуктивности фактически накапливает электрическую энергию по мере того, как переменный ток нарастает в каждом цикле, и высвобождает данную энергию, когда ток спадает до минимума. В силовых катушках индуктивности требуется наличие воздушного зазора внутри конструкции сердечника. Назначение воздушного зазора состоит в накапливании энергии и в предотвращении насыщения сердечника при нахождении его под нагрузкой. В иной формулировке, назначение воздушного зазора состоит в том, чтобы уменьшать и регулировать эффективную магнитную проницаемость магнитной конструкции. Поскольку μ = B/H, то уменьшение μ означает увеличение H (то есть, рост электрического тока), который поддерживается при уровне B, меньшем максимально допустимого значения магнитной индукции (B_sat), являющегося внутренней (природной) характеристикой заданного магнитного материала.

Существует общее ограничение, связанное с узкими пределами изменений индукции насыщения Bsat. Физика мягких магнитных материалов такова, что значение B_sat материалов, доступных на современном рынке, составляет примерно от 0,3T до 1,8T. В наиболее экзотичном имеющемся материале, каковым является сплав кобальта – железа – ванадия (супермендюр), это значение достигает 2,2T. Более высокие значения не существуют.

Воздушный зазор в силовых катушках индуктивности может быть распределенным или дискретным. Распределенные зазоры создаются в порошковых сердечниках. На микроскопическом уровне, гранулы порошка магнитного сплава отделяются одна от другой посредством изоляции связующим веществом или посредством высокотемпературной изоляции покрытия каждой гранулы. (Это не относится к уровню магнитных доменов; домены имеют размеры намного меньше размеров гранул порошкового сердечника). Распределение зазора по всей конструкции порошкового сердечника служит двум основным целям: (1) устраняются недостатки конструкции с дискретным зазором, каковыми являются резкое насыщение, краевые потери и электромагнитные помехи (EMI), и (2) регулируются потери от вихревых токов до такой степени, при которой сплавы с повышенным значением B_sat могут быть использованы на относительно высоких частотах, несмотря на относительно низкое значение объемного удельного сопротивления в сплаве.

Дискретные зазоры используются главным образом в ферритовых сердечниках. Основным функциональным преимуществом феррита являются низкие потери по переменному току в сердечниках при работе на высокой частоте, что объясняется более высоким удельным сопротивлением в керамическом материале по сравнению с металлическими сплавами. Ферриты находятся на нижнем конце существующей области значений B_sat, и они существенно смещаются в сторону дальнейшего понижения B_sat при повышении температуры. Конструкция с дискретным зазором приводит к созданию катушки индуктивности, в которой достигается точка резкого насыщения и при этом требуется большая габаритная высота в конструкции. Дискретные зазоры приводят также к получению катушек индуктивности, которые уязвимы к потерям от вихревых токов в обмотке вследствие краевого эффекта и имеют тенденцию к генерации электромагнитных помех (EMI). Дискретные зазоры используются также в аморфных и нанокристаллических ленточных сердечниках с ориентацией потока вдоль волокна, имеющих улучшенные показатели потерь по переменному току в сравнении с порошковыми сердечниками, но зачастую более дорогостоящих.

Разработчик катушки индуктивности должен выполнять требования по накапливанию энергии (величине индуктивности) и одновременно учитывать требования к суммарным потерям, рабочему объему, стоимости, электромагнитным помехам, температурным характеристикам, надежности и устойчивости к отказам.

Во многих случаях порошковые сердечники обладают явными преимуществами. При этом разработчик имеет множество вариантов выбора среди имеющихся порошковых сердечников.

Сердечники MPP (из мо-пермаллоевого (Molypermalloy) порошка) представляют собой тороидальные сердечники с распределенным воздушным зазором, изготавливаемые из порошкового материала, являющегося сплавом никеля, железа и молибдена. MPP обеспечивает самые низкие потери в сердечнике по сравнению с другими материалами для порошкового сердечника, но сердечники из данного сплава являются при этом самыми дорогостоящими ввиду высоких затрат на технологическую обработку и по причине 80-процентного содержания никеля в сплаве. Тороидальные сердечники из MPP выпускаются с наружными диаметрами от 3,5 мм до 125 мм.

Сердечники High Flux представляют собой тороидальные сердечники с распределенным воздушным зазором, изготавливаемые из порошкового материала, являющегося сплавом никеля с железом. Сплав High Flux содержит 50% никеля, по затратам на технологическую обработку сравним с MPP и по цене обычно выигрывает по сравнению с MPP примерно 5% – 25%. High Flux характеризуется более высокими потерями в сердечнике, нежели MPP и Kool Mμ, но благодаря своему повышенному значению B_sat сплав High Flux имеет оптимальное соотношение между магнитной проницаемостью и силой подмагничивания. Иными словами, повышенное значение B_sat трансформируется в оптимальную стабильность (самый низкий уровень сдвига) катушки индуктивности в условиях сильного подмагничивания постоянным током или при высоких пиковых значениях переменного тока. Как и сердечники из MPP, сердечники из сплава High Flux не получили широкого распространения в каких-либо геометрических формах, кроме тороидов.

Сердечники Kool Mμ®, или «сендаст», представляют собой сердечники с распределенным воздушным зазором, изготавливаемые из порошкового материала, являющегося сплавом железа, алюминия и кремния.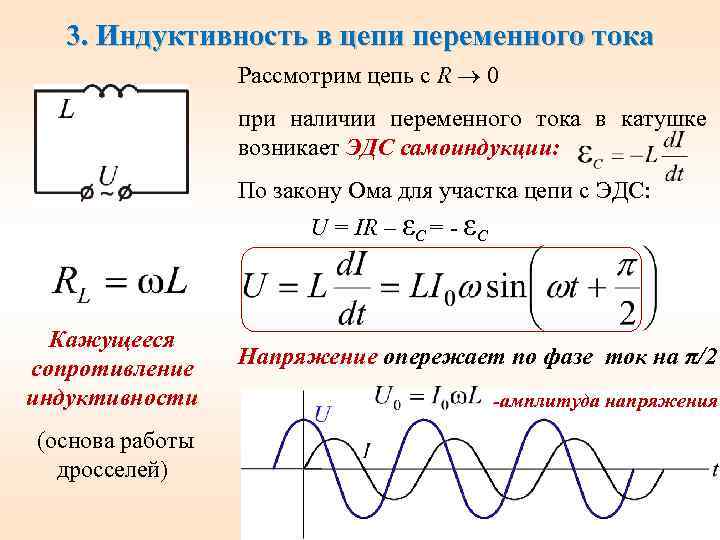 По характеристикам подмагничивания постоянным током материал Kool Mμ сравним с MPP. Отсутствие никеля в формуле сплава делает Kool Mμ намного более экономичным, чем MPP. Основной недостаток Kool Mμ состоит в том, что данный сплав имеет более высокие потери по переменному току, нежели MPP. Этот сплав призван служить практичной альтернативой в случаях, когда порошковое железо имеет слишком высокие потери (в типовых случаях при умеренных или высоких значениях частоты) и при этом использование MPP является слишком дорогостоящим. Сердечники из Kool Mμ выпускаются не только в форме тороидов, но и в виде E-сердечников, что позволяет в максимально возможной степени снизить затраты на намотку.

В таблице 1 приведены сравнительные данные о свойствах различных материалов для сердечников.

	MPP	High Flux	Kool Mμ	Железный порошок
Проницаемость	14 — 550	14 — 160	26 — 125	10 — 100
Насыщение (Bsat)	0,7 T	1,5 T	1,0 T	1,2 — 1,4 T
Максимальная температура (°C)	200	200	200
Потери в сердечнике по переменному току	Самые низкие	Высокие	Низкие	Самые высокие (и переменные)
Форма сердечника	Тороид	Тороид	Тороид, E-сердечник	Тороид, E-сердечник, другие формы

Сердечники из железного порошка имеют более высокие внутренние потери (потери в сердечнике), чем сердечники из MPP, High Flux или Kool Mμ, но обычно являются менее дорогостоящими. Железный порошок часто является оптимальным выбором для силовых катушек индуктивности, в которых не требуется максимально высокий к.п.д. и миниатюрные размеры, но критичным показателем является цена; этот выбор может быть оптимальным также при работе на очень низкой частоте или с очень малой амплитудой пульсаций переменного тока (что означает очень слабый магнитный поток от переменного тока и соответственно низкие потери по переменному току). Большинство сердечников из железного порошка содержит связующее вещество для изоляции между гранулами, и это вещество уязвимо к пробоям при работе с высокими температурами в течение длительного времени, поэтому разработчику может понадобиться учет кривых теплового старения для выбираемого железного порошка. Значения плотности штамповки (то есть, прижимных усилий сжатия) для железных порошков являются умеренно высокими, поэтому данные материалы обеспечивают возможность широкого разнообразия геометрических форм, включая тороидальные сердечники, E-сердечники, броневые сердечники, U-сердечники и стержневые сердечники. Для сердечников с очень сильными токами, но без необходимости работы на высоких частотах, крупногабаритный E-сердечник, U-сердечник или броневой сердечник из порошкового железа может оказаться единственным практически приемлемым вариантом.

Ферритовые сердечники с зазором являются альтернативой порошковым сердечникам при выборе вариантов конструирования. Как видно из рисунка 1, порошковые материалы насыщаются постепенно и при этом сохраняют полезную предсказуемую индуктивность даже при существенном нарастании тока нагрузки. Ферритовый сердечник с зазором сохраняет значение индуктивности, приближенное к значению при отсутствии подмагничивания, пока не происходит насыщение, при котором наблюдается резкое спадание индуктивности. При создании конструкций с ферритами для работы на повышенных температурах необходимо учитывать ряд дополнительных факторов. Как видно из рис. 2, мощность потока индукции любого силового феррита существенно уменьшается при повышении температуры; в то же время, мощность потока индукции порошковых сердечников фактически не зависит от температуры.

Кривая плавного насыщения порошкового сердечника отражает существенные преимущества для конструирования: (1) рабочая точка в основной части кривой (80% — 50%), позволяющая повысить степень компактности конструкции; (2) минимальный сдвиг при изменении температуры; (3) малая чувствительность к изменениям кривой как в части температуры, так и в части допусков на материал; (4) природная устойчивость к отказам; (5) естественные колебания индуктивности – высокое значение L при низкой нагрузке, регулируемая индуктивность при высокой нагрузке. Другие преимущества порошковых сердечников в сравнении с ферритовыми сердечниками состоят в том, что порошковые сердечники не уязвимы к краевым потерям и к EMI-эффектам в зазоре и имеют более высокие значения внутренней B_sat.

Рисунок 1. Кривые подмагничивания постоянным током для феррита и Kool Mμ.

Рисунок 2. Кривая насыщения для силового феррита.

Возможными вариантами применения катушки индуктивности, в частности, являются:

1. Компактная катушка индуктивности цепи постоянного тока (DC) с малыми пульсациями переменного тока (конструкция с ограниченным размером окна)
2. Крупногабаритная катушка индуктивности цепи постоянного тока (конструкция с ограничением насыщения)
3. Катушка индуктивности с сильным переменным током (конструкция с ограничением потерь в сердечнике)

Каждый из трех вариантов характеризуется специфическими требованиями к конструкции. В компактной катушке индуктивности цепи постоянного тока ограничительный фактор определяется в большей степени доступным размером окна сердечника, нежели площадью поперечного сечения сердечника. Окно сердечника должно быть достаточно большим для того, чтобы расположить в нем количество витков провода, достаточное для получения требуемой индуктивности. В крупногабаритной катушке индуктивности цепи постоянного тока ограничительным фактором часто является точка насыщения сердечника. Сердечник должен иметь достаточно крупные габариты и достаточно малую магнитную проницаемость, чтобы избежать насыщения (или смещения величины индуктивности ниже минимального требуемого уровня). Эти факторы требуют увеличения числа витков и длины медных проводов, что вызывает проблему в виде потерь в проводах. Основным ограничительным фактором для катушки индуктивности с сильным переменным током являются потери в сердечнике. Поскольку потери в сердечнике зависят от колебаний потока, создаваемого переменным током, а не уровнем индукции, создаваемой постоянным током, потери в сердечнике становятся доминирующим фактором, определяющим выбор конструкции.

Ниже приведены в качестве примера требования, которым должна отвечать типовая конструкция.

Постоянный ток (IDC)	500 мА (не более)
Требуемая индуктивность (Lmin)	100 мкГ
Пульсации переменного тока (Iac)	50 мА (пиковый размах)
Частота (f)	100 кГц

Для конструирования катушки с данными характеристиками компания Magnetics использует программное обеспечение Inductor Design Using Powder Cores (Конструирование катушки индуктивности с использованием порошковых сердечников). В данной программе реализуется алгоритм конструирования, имеющий целью определение минимально возможных габаритов модуля для заданных входных параметров (значений тока, индуктивности, частоты и др.). Программа определяет размер требуемого сердечника, исходя из необходимой величины энергетического показателя в виде произведения, получаемого умножением индуктивности при полной нагрузке на квадрат пикового значения тока (постоянного тока с приращением на пульсацию переменного тока), проходящего через катушку индуктивности. Увеличение значений индуктивности и силы тока подразумевают увеличение габаритов сердечника. Программы выполнялись с вводом указанных выше исходных значений конструирования, а материал сердечника выбирался вручную для каждого из типов сердечников, указанных ниже в таблице 2. Число витков, коэффициент плотности намотки провода, габариты намотки, величина потерь и рост температуры были определены по выходным данным выполняемых программ.

	MPP	High Flux	Kool Mμ, торидальные сердечники	Kool Mμ, E-сердечники
Номер компонента	55025-A2	58278-A2	77280-A7	K1808E090
Проницаемость	300	160	125	90
Габариты сердечника (дюймы)	0,335 x 0,150	0,405 x 0,150	0,405 x 0,150	0,77 x 0,65 x 0,19
AL (нГ/виток²)	124	68	53	69
Число витков	32	41	48	39
Коэффициент плотности намотки провода	37%	31%	37%	14%
Габариты обмотки (дюймы)	0,375 x 0,209	0,448 x 0,209	0,455 x 0,209	0,77 x 0,65 x 0,644
Потери в сердечнике (мВт)	2,0	0,7	0,7	0,5
Потери в проводе (мВт)	24,2	33,3	40,0	83,0
Суммарные потери (мВт)	26,2	34,0	40,7	83,5
Рост температуры (°C)	6,1	6,0	6,9	4,3

В каждом случае программы определяли самое высокое значение магнитной проницаемости из числа значений, имеющихся для выбранного материала. С учетом относительно слабого тока, любое уменьшение магнитной проницаемости выбранного материала не приводит к оптимизации индуктивности при пиковой нагрузке; в этих условиях больше теряется ввиду уменьшения индуктивности при отсутствии нагрузки, нежели приобретается за счет оптимизации кривой спадания силы подмагничивания постоянным током. Потери в сердечнике и рост температуры не являются важными влияющими факторами в катушке индуктивности данного типа вследствие низкой магнитной индукции по переменному току в сердечнике. Например, в сердечнике High Flux сила намагничивания H определяется по закону Ампера следующим образом:

H (эрстеды) = .4 (π) (N) (I)/L_e, где:

N — число витков
I — ток в амперах
L_e — длина линии магнитной индукции сердечника в см.

Сердечник 58278-A2 имеет длину линии магнитной индукции, равную 2,18 см, поэтому сила намагничивания постоянным током равняется:

H = .4 (π) (41) (0,5)/(2,18) = 11,8 эрстед

Процент начальной магнитной проницаемости, или значение «спадания», можно определить по данным, публикуемым в справочнике Magnetics по порошковым сердечникам (см. рис. 3).

Рисунок 3. Кривая спадания подмагничивания постоянным током для High Flux.

Кривая проницаемости 160 для High Flux показывает, что магнитная проницаемость при силе подмагничивании постоянным током, равной 11,8 эрстедам, равняется примерно 90% начального значения этой проницаемости. Эта рабочая точка является консервативной рабочей точкой для данного материала, но возможности конструирования ограничиваются в большей степени не уровнем насыщения сердечника, а площадью окна сердечника. Коэффициент заполнения окна для катушки данного типа равняется 37%, что приближается к типовому предельному значению для тороидальных сердечников. Усилия по уменьшению габаритов сердечника с целью получения преимуществ от имеющейся мощности магнитной индукции приводят к нереалистичным значениям коэффициента заполнения окна, равным 50% и более.

Как видно из приводимых данных, тороидальный сердечник MPP обеспечивает получение наиболее компактной и эффективной конструкции вследствие того, что данный материал доступен для использования с более высоким значением магнитной проницаемости (300μ), чем другие материалы. Это трансформируется в более высокое значение коэффициента одновитковой индуктивности (A_L) при заданном размере сердечника, что позволяет снижать габариты используемого сердечника. Компромиссным фактором является ускоренное спадание силы намагничивания постоянным током. Тороидальный сердечник Kool Mμ является привлекательным в основном благодаря существенным преимуществам в цене. Выбираемый E-сердечник из материала Kool Mμ является самым «миниатюрным» из числа сердечников, имеющихся в настоящее время, и имеет избыточные габариты для рассматриваемого здесь набора требований.

Типовыми требованиями к катушкам данного типа являются:

Постоянный ток (IDC)	20 А (не более)
Требуемая индуктивность (Lmin)	100 мкГ (минимум)
Пульсации переменного тока (Iac)	1 А (пиковый размах)
Частота (f)	100 кГц
Максимальный рост температуры (°C)	40°C

В таблице 3 приведены применимые данные конструирования, полученные на выходе программы для данного случая.

	MPP	High Flux	Kool Mμ, торидальные сердечники	Kool Mμ, E-сердечники
Номер компонента	55868-A2	58867-A2	77868-A7	K5528E040
Проницаемость	26	60	26	40
Габариты сердечника (дюймы)	3,108 x 0,545	3,108 x 0,545	3,108 x 0,545	2,19 x 2,20 x 0,81
AL (нГ/виток²)	30	68	30	157
Число витков	62	45	70	30
Коэффициент плотности намотки провода	24%	18%	27%	72%
Габариты обмотки (дюймы)	3,657 x 0,884	3,514 x 0,884	3,720 x 1,053	2,19 x 2,20 x 1,98
Потери в сердечнике (мВт)	116	230	182	290
Потери в проводе (мВт)	14371	9780	16959	5489
Суммарные потери (мВт)	14487	10010	17141	5779
Рост температуры (°C)	35,3	27,4	37,7	22,4

Для катушки данного типа необходимо выбирать сердечники с пониженной магнитной проницаемостью и с большим поперечным сечением, чтобы избежать насыщения при высоком уровне подмагничивания постоянным током.

Сердечник 58867-A2 имеет длину линии магнитной индукции, равную 20 см, поэтому сила намагничивания H равняется:

H = 0,4 (π) (45) (20)/(20) = 56,5 эрстед

Кривая для материала High Flux с магнитной проницаемостью 60 на рисунке 3 показывает, что магнитная проницаемость составляет примерно 83% своего начального значения при силе подмагничивания постоянным током, равной 56,5 эрстедам, что соответствует безопасной рабочей точке. Критичным параметром является в данном случае не коэффициент плотности намотки провода, а рост температуры вследствие потерь в меди. Последующие итерации при конструировании должны быть направлены на увеличение диаметра провода или на использование многожильного провода для уменьшения плотности тока с целью снижения потерь в меди, что достигается ценой повышения плотности намотки. Из приводимых данных можно видеть, что High Flux обеспечивает конструирование тороидальных сердечников с меньшим ростом температур, нежели другие материалы. Высокая индкуция насыщения данного материала и улучшенные характеристики подмагничивания постоянным током позволяют выбирать сердечники с повышенной магнитной проницаемостью и увеличенным значением A_L, что позволяет уменьшить число витков и сократить потери в меди. И в этом случае потери в сердечнике малы следствие относительно слабого потока подмагничивания переменным током в сердечнике.

Конструкция E-сердечника из материала Kool Mμ превосходит аналоги в части потерь благодаря тому, что поперечное сечение E-сердечника (и значение A_L) намного превышают аналогичные показатели тороидальных сердечников. Это позволяет уменьшить и существенно сократить потери в меди. E-сердечник имеет относительно малую площадь окна, что подразумевает повышенный коэффициент плотности намотки (72%), но это достижимо в конструкциях с бобинной намоткой. Для E-сердечников допускается вариант с намоткой фольги. Недостаток состоит в том, что суммарная высота E-сердечника с готовой обмоткой примерно в 2 раза превышает аналогичную высоту в других конструкциях.

Типовыми требованиями к катушкам индуктивности переменного тока являются:

Постоянный ток (IDC)	4 А (номинал)
Требуемая индуктивность (Lmin)	100 мкГ (минимум)
Пульсации переменного тока (Iac)	8 А (пиковый размах)
Частота (f)	100 кГц
Максимальный рост температуры (°C)	35°C

В отличие от малых и крупногабаритных катушек индуктивности постоянного тока, рассмотренных в двух предыдущих примерах, генерация тепла, сопутствующая потерям в сердечнике, в катушке индуктивности переменного тока достаточно велика для того, чтобы являться первичным ограничительным фактором при выборе конструкции. Варианты выбора конструкции ограничиваются ростом температуры вследствие потерь в сердечнике, или целевым показателем к.п.д. В таблице 4 приведены значения характеристик для данного примера.

	MPP	High Flux	Kool Mμ, тороидальные сердечники	Kool Mμ, E-сердечники
Номер компонента	55440-A2	58441-A2	77191-A7	K4020E026
Проницаемость	26	14	26	26
Габариты сердечника (дюймы)	1,875 x 0,745	1,875 x 0,745	2,285 x 0,635	1,71 x 1,67 x 0,61
AL (нГ/виток²)	59	32	60	80
Число витков	42	57	43	37
Коэффициент плотности намотки провода	12%	16%	10%	23%
Габариты обмотки (дюймы)	1,982 x 0,843	2,019x 0,940	2,375 x 0,733	1,71 x 1,67 x 1,53
Потери в сердечнике (мВт)	2947	3316	4110	3255
Потери в проводе (мВт)	1722	2352	1836	2212
Суммарные потери (мВт)	4669	5668	5946	5467
Рост температуры (°C)	31,7	34,9	32,1	31,8

Для определения потерь в сердечнике необходимо вычислить колебания потока подмагничивания переменным током в сердечнике. Поток подмагничивания постоянным током не вызывает потерь в сердечнике. Первым шагом расчета является вычисление силы намагничивания H по закону Ампера с использованием размаха значений переменного тока (в данном случае пиковый размах составляет 8 А). Для сердечника 58441-A2 из материала High Flux длина линии магнитной индукции равняется 10,74 см.

H = 0.4 (π) (57) (8)/(10.74) = 53,4 эрстед

Изменение плотности потока можно определить путем приложения данного результата к нормальной кривой намагничивания из справочника (см. рис. 4).

Рисунок 4. Кривые намагничивания при высокой плотности потока намагничивания.

Диапазон изменения силы намагничивания составляет от 0 эрстед до 53,4 эрстед. В случае материала с магнитной проницаемостью 14 это трансформируется в диапазон изменения магнитной индукции от 0 гаусс до 600 гаусс – то есть, ΔB = 600 гаусс. Кривые потери для мягких магнитных материалов подразумевают биполярный режим работы (сердечник возбуждается в первом и третьем квадрантах петли гистерезиса B-H). Следовательно, независимо от того, является ли схема биполярной или однополярной, значение магнитной индукции, которое действует, всегда равняется ½ΔB. В данном случае плотность магнитной индукции переменного поля равняется 300 гаусс. Из рисунка 5 видно, что при 300 гауссах на частоте 100 кГц плотность потерь составляет примерно 150 мВт/см³. По справочнику можно определить, что объем сердечника 58441-A2 равняется 21,3 см³, поэтому суммарные потери в сердечнике равняются произведению от умножения (150) на (21,3) – то есть, 3195 мВт. Программное обеспечение, использующее уравнения в привязке к кривым, вычислило потери в сердечнике, равняющиеся 3316 мВт.

Рост температуры вычисляется, исходя из указанной ниже аппроксимации.

Рост температуры (°C) = [Суммарные потери мощности (мВт)/площадь поверхности (см²)]^0,833

Согласно выходным данным программного обеспечения, суммарные потери мощности для катушки индуктивности High Flux равняются 5668 мВт. Сердечник 58438-A2 имеет без обмотки площадь поверхности 69,3 см², а с полной обмоткой – 94,3 см² (значения взяты из справочника). Программное обеспечение интерполирует площадь поверхности для коэффициента плотности намотки провода, равного 17%, и получает значение площади поверхности, равное 79,3 см². Рост температуры, вычисляемый в этом случае по приведенному выше уравнению, равняется примерно 35°C. Заметим, что данная оценка является довольно грубым приближением, поскольку характеристики тепловыделения зависят не только от величины потерь, но и от механической конфигурации, вида сборочных материалов и от течения воздуха.

Рисунок 5. Кривые потерь в сердечнике при высоком уровне потока намагничивания.

В общем, характеристики потерь, по которым MPP обладает преимуществом над другими материалами, позволяют использовать катушки индуктивности с меньшими габаритами и более высокими значениями к.п.д. Суммарные потери в случае MPP составляют на 15% меньше потерь материала, являющегося следующим в сторону увеличения потерь. Поскольку материал High Flux обладает более высокими потерями, чем MPP, для сохранения одинаковой величины потерь необходимо выбирать сердечник с более низкой магнитной проницаемостью. Это, однако, приводит к увеличению числа витков, росту потерь в меди и к некоторому увеличению общих габаритов модуля. Причина того, что пониженная магнитная проницаемость приводит к уменьшению плотности потока переменного поля (то есть, к уменьшенным потерям в сердечнике) является очевидной и состоит в том, что наклон кривых для материалов с пониженной магнитной проницаемостью имеет на графике кривых намагничивания меньшую крутизну (см. рис. 4). Материал Kool Mμ требует еще большего увеличения общих габаритов, но суммарные потери сравнимы с потерями для High Flux. И в этом случае возможен вариант с E-сердечником Kool Mμ, который имеет несколько меньшие потери, уменьшенную площадь основания, но увеличенную габаритную высоту.

E-сердечник Kool Mμ является самым экономичным из четырех рассмотренных вариантов; вместе с тем, преимущества от габаритов и к.п.д. тороидального сердечника MPP становятся менее очевидными из-за самой высокой стоимости данного сердечника. Сердечники High Flux и MPP имеют одинаковые габариты и сравнимы по цене, поскольку порошки 14μ являются более дорогостоящими в производстве и в штамповке, нежели порошки 26μ.

Для требуемой катушки индуктивности решение о выборе материала определяется комбинацией следующих ограничительных факторов: пространство, к.п.д., удобство сборки, суммарная стоимость, индуктивность в зависимости от характеристик нагрузки, роста и рабочей температуры. Среди порошковых сердечников материал MPP превосходит другие материалы по такому свойству, как потери в сердечнике, и обладает самым высоким значением применимой магнитной проницаемости. High Flux обладает преимуществами над другими материалами в случаях, когда определяющими ограничительными факторами является минимизация габаритов и намагничивание постоянным полем. Kool Mμ является более экономичным материалом, нежели MPP или High Flux, и является стандартным материалом как для тороидальных сердечников, так и для E-сердечников. Сердечники на основе распыленного железа (Iron powder cores) являются менее дорогостоящими, чем Kool Mμ, но серьезно ухудшают характеристики изделия.

1. Magnetics «Inductor Design Using Powder Cores» software PCD-3.1
2. Magnetics «Powder Cores Design Manual and Catalog»

 

Катушки индуктивности | Основы электроакустики

Катушки индуктивности

 

Катушки индуктивности применяют в качестве элементов коле­бательных контуров, дросселей и для связи одних цепей с другими.

Катушка индуктивности, которая служит для разделения посто­янного и переменного токов или токов разных частот, называется дросселем. Индуктивное сопротивление (Ом) катушки зависит от частоты и определяется по формуле Xi. — 2nfLt  где f — частота, Гц; L — индуктивность, Гн. Одна и та же катушка представляет собой разное сопротивление для токов разных частот. Для постоянного тока сопротивление любой катушки очень мало. Каждая катушка характеризуется индук­тивностью, добротностью, стабильностью и собственной емкостью.

Катушки с малой индуктивностью изготовляют без сердечника с небольшим числом витков. Для увеличения индуктивности катушку выполняют многослойной и вводят сердечник из ферромагнитного материала. Потери энергии в катушке должны быть как можно меньше. Поэтому ее стремятся выполнить так, чтобы получить наибольшую индуктивность при малом активном сопротивлении. Отношение индуктивного сопротивления катушки к активному сопротивлению на — дан­ной частоте называется добротностью катуш­ки и определяется по формуле Qil=Xtlfsa Индуктивность и другие параметры ка­тушки не должны меняться под влиянием внешних причин, т. е. катушка должна обла­дать стабильностью. Собственная (междувитковая) емкость катушки понижает ее доброт­ность и уменьшает стабильность

У однослойной катушки при сплошной намотке (виток к витку) индуктивность (мкГн) можно определить по формулегде w — число витков; l — длина намотки, см; D — диаметр катуш­ки, см. Для уменьшения собственной, емкости витки катушки наматыва­ют не вплотную, а на некотором расстоянии один от другого (на­мотка с принудительным шагом). Многослойные катушки выполняют простой намоткой «внавал» или специальной («универсалы»). Индуктивность (мкГн) многослойной хатушки можно определить по формулегде dcf — средний диаметр намотки, см; w — число витков; I — длина намотки, см; t — толщина намотки, см.

Для уменьшения собственной емкости многослойную катушку выполняют из отдельных секций. Секционированные катушки при­меняют в качестве контурных катушек и дросселей высокой частоты. Малую собственную емкость имеют многослойные катушки с намот­кой «универсалы», при которой провод зигзагом переходит с одного края катушки на другой Для устранения влияния электромагнитного поля катушки на соседние детали и, наоборот, внешних полей на катушку ее закры­вают металлическим экраном. Для высокочастотных катушек экран изготовляют из меди или алюминия толщиной 0,4 — 0,5 мм. Экран уменьшает индуктивность и добротность катушки и увеличивает ее собственную емкость. Чем ближе расположен экран к виткам катупь ки, тем сильнее изменяются ее параметры. Чтобы влияние экрана было небольшим, его диаметр и длину берут в два раза больше диаметра и длины намотки. Для низкочастотных катушек применят ют экраны из ферромагнитных материалов, например из листовой стали толщиной 0,5 — 1,5 мм. Для увеличения добротности и уменьшения габаритов катушки применяют сердечники из ферромагнитных материалов. Высокочас­тотные катушки имеют сердечники из карбонильного железа. Доб­ротность катушек с таким сердечником равна 400 — 500, а без сер­дечника — не более 200.

Для контурных катушек длинных и средних волн используют броневые сердечники. Низкочастотные дроссели имеют сердечники из листовой электротехнической стали. Толщину стальных листов берут 0,2 — 0,5 мм для дросселей, используемых в цепях звуковых частот, и около 0,5 мм — в Цепях переменного тока с частотой 50 Гц.

Индуктивность катушки возрастает с увеличением числа и диа­метра витков при их сближении, что учитывают при изготовлении катушки. Введение внутрь катушки сердечника из магнитодиэлектрика также увеличивает ее индуктивность. Если сердечник выполнен из диамагнитного материала, например латуни, то при его введении индуктивность катушки уменьшится. То же произойдет, если внутрь катушки ввести короткозамкнутый виток. На практике чаще всего индуктивность изменяют, перемещая сердечник внутри катушки. Катушка, индуктивность которой можно изменять в больших пределах, называется вариометром. Чаще всего вариометр состоит из двух катушек, взаимная индуктивность которых может меняться. Вариометры применяют главным образом в передатчиках для на­стройки колебательных контуров и подбора связи между контурами.

 

Схемы на все случаи жизни » Индуктивность. Катушки индуктивности

Индуктивностью (применительно к компонентам электрической цепи) называется идеализированный элемент электрической цепи, приближающийся по свойствам к катушке индуктивности, в которой накапливается энергия магнитного поля.

Катушка индуктивности представляет собой проводник, намотанный на сердечник. Сердечник может быть магнитным, либо немагнитным. Схематическое изображение катушки индуктивности показано на рис 1. При работе в электрической цепи катушка индуктивности препятствует изменению протекающего через нее тока. Иными словами, если ток, подаваемый в схему, которая содержит катушку, резко увеличить, то ток в схеме будет нарастать плавно до достижения своего максимального значения.

На рисунке 1 показаны условно-графические изображения катушек индуктивности различных типов [3].

Способность катушки индуктивности препятствовать изменению силы тока, протекающего через нее, носит название индуктивности этой катушки. Индуктивность обозначается буквой L, единицей ее измерения является Генри (Гн). Генри — большая единица индуктивности, значительно чаще используются миллигенри (мГн) = 10^-3 Гн и микрогенри (мкГн) = 10^-6 Гн.

Катушки могут иметь как постоянную, так и изменяемую индуктивность. На рисунке 1 показано схематическое изображение катушки с переменной индуктивностью (рисунки 1в и 1г). Катушки с переменной индуктивностью содержат подстроечный сердечник. Сердечник может изготавливаться из материала, который при введении внутрь катушки как увеличивает индуктивность (например, феррит), так и уменьшает (например, латунь).

Катушки индуктивности с воздушным сердечником, или катушки без сердечника, используются в тех случаях, когда индуктивность не превышает 5 мГн. Они наматываются на керамические или композитные сердечники. Сердечники из феррита или порошкообразного железа обычно используются для индуктивности до 200 мГн.

Тороидальные сердечники имеют кольцеобразную форму и позволяют получить высокую индуктивность при малых размерах. Их магнитное поле сосредоточено внутри сердечника.

Многослойные катушки индуктивности с железным сердечником используются для получения большой индуктивности от 0,1 до 100 Гн. Эта индуктивность зависит от величины тока, протекающего через катушку. Эти катушки иногда называют дросселями. Они используются в цепях фильтрации источников питания для удаления переменных составляющих выпрямленного постоянного тока.

Если постоянное напряжение приложено к катушке индуктивности L через резистор (рис.2) то, для того чтобы в цепи установился максимальный ток требуется время, прямо пропорциональное величине сопротивления и индуктивности. Постоянная времени цепи определяет время, требуемое для увеличения тока в проводнике от нуля до 63,2% или уменьшения до 36,8% от максимального значения. Постоянная времени определяется следующей формулой: t= L/R, где t — время в секундах, R — сопротивление в омах, L — индуктивность в Генри.

Для того, чтобы создать максимальное магнитное поле в катушке индуктивности требуется примерно пять постоянных времени цепи L/R. Такое же время требуется для того, чтобы магнитное поле исчезло.

Катушка индуктивности в цепи постоянного тока имеет очень малое сопротивление (с учетом сопротивления проводника) и не препятствует прохождению постоянного тока. Если к катушке индуктивности приложено переменное напряжение, оно создает магнитное поле. Магнитное поле в свою очередь индуцирует напряжение в витках катушки, которое называется электродвижущей силой (э.д.с) самоиндукции. Э.д.с. самоиндукции сдвинута по фазе на 180^° относительно приложенного напряжения и противодействует приложенному напряжению.

Реактивное сопротивление катушки индуктивности вычисляется по формуле: X_L = j*2*π*f*L, где j — означает поворот вектора по часовой стрелке на 90^°, L — индуктивность (Гн), f — частота (Гц).

Индуктивное сопротивление является функцией частоты приложенного переменного напряжения и индуктивности. Рост частоты увеличивает индуктивное сопротивление и вызывает увеличение противодействия току. Уменьшение частоты уменьшает индуктивное сопротивление и снижает противодействие току. Данное свойство катушек индуктивности используетя при построении различных электрических фильтров.

Список использованной литературы

1. Атабеков Г. И. Основы теории цепей: Учебник. 2-е изд.,испр.–СПб.: Издательство «Лань», 2006.–432 с.

2. Эрл Д.Гейтс. Введение в электронику: Учебник. — Ростов-на-Дону.: Издательство «Феникс», 1998 год, 640 стр.

3. ГОСТ 2.723-68. Единая система конструкторской документации. Обозначения условные графические в схемах. Катушки индуктивности, дроссели, трансформаторы, автотрансформаторы и магнитные усилители.

Общие сведения о катушках индуктивности

Применяемые в низкочастотных усилителях трансформаторы могут подразделяться на две основные категории: силовые или сетевые трансформаторы и сигнальные трансформаторы, используемые в качестве согласующих, выходных, либо повышающих, например, для картриджей звукоснимателей с подвижной катушкой. Совершенно аналогично катушки индуктивности могут предназначаться для работы в цепях прохождения сигнала, например в различных фильтрах, либо же они могут быть мощными дросселями, используемыми в высоковольтных источниках питания. Основной особенностью этих компонентов схем является применение в них магнитных материалов. Они представляют последнюю группу идеальных пассивных компонентов схем (резисторы, конденсаторы и катушки индуктивности, включая трансформаторы). В отличие от резисторов и конденсаторов, катушки индуктивности и трансформаторы, как правило, не являются промышленными изделиями, а изготавливаются вручную. Именно по этой причине многие разработчики стараются всячески избегать их применения. Такой подход нельзя признать разумным, так как он серьезно ограничивает возможности проектирования схем.

Катушка индуктивности запасает энергию магнитного поля. Прохождение тока любой величины по проводнику всегда сопровождается возникновением магнитного поля вокруг проводника. Поэтому проводник обладает индуктивностью. Можно увеличить индуктивность, свернув провод в спираль, или намотав его в виде катушки, а если внутрь такой катушки поместить железный сердечник (магнитопровод), то индуктивность возрастет многократно. Эта зависимость может быть приближенно выражена следующим соотношением:

в котором L — индуктивность,

μ₀ — магнитная проницаемость вакуума, в системе СИ равна 4π·10^-7 Гн/м,

μ_r— относительная магнитная проницаемость магнитного материала

сердечника,

А — площадь поперечного сечения магнитопровода,

I — длина магнитопровода,

N — количество витков катушки.

Относительная магнитная проницаемость, μ_r, является характеристикой магнитных свойств материала, и можно провести некоторую аналогию с ранее уже упоминавшейся относительной диэлектрической проницаемостью, характеризующей диэлектрические свойства диэлектриков. Относительная магнитная проницаемость имеет различные значения и может меняться от 1 для воздуха до примерно 5500 для железа. Длина магнитопровода отсчитывается по замкнутому контура от какой-то начальной точки, а площадь поперечного сечения магнитопровода просто принимается равной площади сечения магнитного сердечника. Поэтому, может показаться, что вышеприведенное уравнение без особых трудностей может быть использовано для расчета индуктивности.

К сожалению, параметр μ_r сильно зависит от плотности магнитного потока, на длину магнитопровода могут сильно повлиять воздушные зазоры, а часть магнитного потока рассеивается в окружающей среде. Каждая из этих проблем будет проанализирована по отдельности несколько позже, а сейчас надо просто признать, что очень часто оказывается просто невозможным точно рассчитать значение индуктивности катушки. Поэтому на практике зачастую приходится строить всевозможные предположения, добавлять лишние витки, измерять индуктивность в условиях, максимально близким к условиям реальной работы, а затем удалять витки катушки, пока не будет получена требуемая величина индуктивности.

При каждом обсуждении свойств магнитных материалов, обычно используется зависимость, которая называется кривой (начальной) намагниченности. Данная кривая выражает зависимость результирующей магнитной индукции поля, В, от изменения величины напряженности магнитного поля, Н, иногда для простоты называемой зависимостью В-Н (рис. 5.10). В целях дальнейшего изложения следует прежде всего отметить, что относительная магнитная проницаемость m пропорциональна градиенту (или углу наклона) данной кривой, а так как градиент изменяется при изменении напряженности магнитного поля, то это означает, что будет изменяться и μ.

Рис. 5.10 Кривая намагничивания: непостоянство угла наклона ведет к изменению магнитной проницаемости материала

Катушка индуктивности без магнитного сердечника

Можно полностью исключить проблему, связанную с изменением параметра m при изменении напряженности магнитного поля, если использовать катушку, в которой отсутствует сердечник, изготовленный из магнитного материала. Катушка индуктивности без магнитного сердечника (воздушная катушка индуктивности) характеризуется постоянным значением индуктивности при изменении величины сигнала, следовательно, такие катушки не вызывают искажений, что делает их особо популярными для использования в схемах кроссоверов высококачественных громкоговорителей. Определить площадь, через которую проходит магнитный поток, для данного случая достаточно сложно, так как теоретически магнитный поток распространяется в бесконечность, точно также невозможно точно определить и длину «магнитопровода». Тем ни менее, для катушек с различной геометрией были предложены приближенные соотношения, из которых ниже приводится формула для наиболее интересного, с практической точки зрения, случая оптимального (то есть наименьшего) значения сопротивления воздушной катушки, обмотка которой выполнена из медного провода. Формулы для приближенного расчета были предложены А. Н. Тайлом (A.N.Thiele):

в которых (рис. 5.11), R — сопротивление обмотки, Ом,

L — Индуктивность, мкГн,

d — диаметр провода, мм,

N — количество витков,

с — обобщенный параметр каркаса, связывающий его внешний и внутренний диаметры, а также длину слоя намотки,

l — длина провода, м.

Рис. 5.11 Относительные размеры бобины, используемой для намотки воздушной катушки индуктивности (в соответствии с приведенной формулой Таила)

Формула приводится с числовыми коэффициентами для частного случая, так как провод для катушки имеет стандартизованные значения диаметра, а величина сопротивления катушки не оказывает большого влияния на получаемый результат.

Если сопротивление будет отличаться от необходимого значения, следует использовать провод с другим поперечным сечением.

Естественно было бы выполнять все расчеты с использованием персонального компьютера, поэтому ниже приводится программа, написанная на языке QBASIC (хотя основное уравнение может быть с не меньшим успехом решено с использованием широкоформатных таблиц).

CLS

L = 1

PRINT «This program designs air-cored copper»

PRINT «wire coils according to the Thiele»

PRINT «formulae. L is in micro henries, d (wire»

PRINT «diameter) is in mm»

PRINT

PRINT «To quit, input L = 0.(1/2))*100\1)/100

PRINT

PRINT «You need»; N; «turns on a core of»; 2*c; «ram in diameter,»; c; «mm thick.»

PRINT «It will use»; Q; «meters of wire, and»

PRINT «will have a resistance of»; R; «Ohms.»

PRINT

LOOP

Эксперименты вскоре показали, что катушки индуктивности без магнитного сердечника имеют высокое сопротивление, и что они очень большие по своим размерам. Проблема сопротивления остается общей для всех катушек индуктивности и является основной причиной, определяющей неидельность их характеристик. Применение воздушных катушек индуктивности не ограничивается только кроссоверами громкоговорителей, но они также широко применяются в выходных фильтрах цифро-аналоговых преобразователей (ЦАП), в которых сопротивление обмотки не является определяющим фактором. Также катушки без сердечников получили широкое применение в радиочастотной технике.

Следует отметить, что в связи с используемыми упрощающими допущениями (не учитывается эффективность намотки, изменения диаметра провода и т. д.), использование данной формулы не позволяет получить точные результаты. В силу этого, рекомендуется при расчетах предусмотреть 5% увеличение параметров, а затем удалять витки с катушки, измеряя значение индуктивности с использованием измерительного моста.

В большом количестве измерительных мостов используется генератор, имеющий собственную частоту 1 кГц. При измерении индуктивности воздушных катушек относительно высокое значение сопротивления может подавить влияние индуктивной составляющей, в силу чего при измерениях с использованием мостовой схемы можно получить неверный результат. Если возможно для питания схемы моста использовать внешний источник переменного тока, то рекомендуется применять максимальное значение частоты, которое допускается использовать производителями измерительных мостов (как правило, частота составляет 20 кГц), что позволит более точно выполнить необходимые измерения.

Броневые сердечники с зазором

Одним из путей уменьшения сопротивления без внесения заметных искажений является использование катушки, в которой имеется магнитный сердечник с зазором. Магнитный сердечник с зазором значительно увеличивает индуктивность по сравнению с воздушной катушкой индуктивности. Однако так как воздушный зазор образует сравнительно высокое сопротивление для распространения магнитного потока, то он приглушает изменения в относительной магнитной проницаемости магнитного сердечника, имеющего низкое значение сопротивления магнитному потоку, в силу чего индуктивность катушки становится более стабильной. При увеличении величины зазора величина индуктивности снижается, и при увеличении зазора до бесконечно большого значения опять будет наблюдаться предельный случай катушки индуктивности без магнитного сердечника. Подобная конструкция была много лет назад использована отделом исследований Британской радиовещательной корпорации (Би-би-си) в катушках индуктивности кроссоверов пассивных громкоговорителей.

Катушка индуктивности с магнитным сердечником, имеющим зазор, может получиться совершенно непреднамеренно. Большое количество ферритовых сердечников, используемых для небольших катушек индуктивностей, изготавливаются в виде двух половинок, которые устанавливаются снаружи катушки и сопрягаются друг с дружкой наворачиванием половинок. Наличие пыли на сопрягаемых поверхностях приводит к увеличению зазора, и если половинки сердечника во время измерений индуктивности катушки плотно прижать одну к другой, то можно будет получить значительное увеличение индуктивности.

Если по индуктивности будет протекать постоянный ток, то очень важно, чтобы постоянный ток не вызвал переход материала сердечника в область насыщения, так как в этом случае значение индуктивности резко уменьшится, а сердечник будет сильно разогреваться. Катушки индуктивности, в которых сердечники изготовлены из железа и по катушкам которых протекают постоянная составляющая тока, обязательно имеют воздушные зазоры, для того, чтобы обеспечить максимальное значение индуктивности при максимальном значении переменного тока. При этом следует учитывать, что так как в области воздушного зазора происходит рассеяние магнитного потока, вызванного протеканием переменной составляющей, такие катушки индуктивности могут сильно влиять на соседние цепи схемы, вызывая в них паразитные наводки.

Собственная емкость катушек индуктивности

Если обмотка катушки индуктивности содержит большое количество витков, и существует разность потенциалов между отдельными витками и слоями витков, то следует ожидать, что катушка тесла будет иметь некоторую емкость, которая будет включена параллельно индуктивности самой катушки (рис. 5.12).

Рис. 5.12 Эквивалентная схема замещения реальной катушки индуктивности

Таким образом, возникает хорошо знакомая цепь с параллельным резонансом а это означает, что как только частота превысит резонансную, катушка индуктивности перестанет вести себя как индуктивность, а начнет проявлять свойства конденсатора. Самый простой способ определить величину такой паразитной емкости, это собрать тестовую схему (рис. 5.13).

Рис. 5.13 Использование фигур Лиссажу для определения частоты собственного резонанса катушки индуктивности

В осциллографе необходимо произвести переключение в режим работы с использованием и вертикального, и горизонтального входов «XY». При изменении частоты генератора получаемые на экране осциллографа фигуры Лиссажу будут изменяться от эллипса до прямой линии. Как раз та частота, при которой будет наблюдаться прямая линия, и будет соответствовать резонансной частоте катушке индуктивности.

 

Если необходимо, то можно будет рассчитать значение шунтирующей емкости, используя нижеприведенное выражение:

Мощные дроссели (катушки фильтров выпрямителей и т. п.), предназначенные для небольших ламповых усилителей, имеют, как правило, индуктивность 10—15 Гн и рассчитаны на токи 100—250 мкА. Для таких дросселей резонансная частота составляет от 3 до 12 кГц. На частотах, превышающих значение резонансной, дроссели не могут обеспечить эффективный барьер для шумов, генерируемых при выпрямлении переменного тока, или для ВЧ шумов, поступающих по сети питания.

Вопросы применения мощных дросселей будут рассмотрены позже.

 

Индуктивность

Чтобы увеличить свойство индуктивности, проводник может быть сформирован в виде петли или катушка. Катушку также называют индуктором. На рис. 2-3 показан проводник, сформированный в виде катушки. Ток через одну петлю создает магнитное поле, которое окружает петлю в направление, как показано на рисунке 2-3 (A). По мере увеличения тока магнитное поле расширяется и отрезает все петли, как показано на рисунке 2-3 (B). Ток в каждом контуре влияет на все остальные петли. Поле, пересекающее другую петлю, увеличивает сопротивление текущее изменение.

Рисунок 2-3. — Индуктивность.

Катушки индуктивности классифицируются по типу сердечника. Сердечник — центр индуктора так же, как сердцевина яблока — это центр яблока. Индуктор выполнен путем формирования моток проволоки вокруг сердечника. Материал сердечника обычно бывает двух основных типов: мягкое железо или воздух. Индуктор с железным сердечником и его схематическое обозначение (которое представлено с линиями в верхней части, указывающими на наличие железного сердечника) показаны на рисунок 2-4 (A).Катушка индуктивности с воздушным сердечником может быть не чем иным, как катушкой с проволокой, но она обычно катушка образована вокруг полой формы из какого-либо немагнитного материала, например картона. Этот материал служит только для сохранения формы катушки. Воздушное ядро индуктор и его схематическое обозначение показаны на рисунке 2-4 (B).

Рисунок 2-4. — Типы индукторов и условные обозначения.

Факторы, влияющие на индуктивность катушки Есть несколько физических факторов, которые влияют на индуктивность катушки.Они включают количество витков в катушке, диаметр катушка, длина катушки, тип материала, используемого в сердечнике, и количество слоев обмотка в катушках.

Индуктивность полностью зависит от физической конструкции схемы и может только измеряться специальными лабораторными приборами. Из упомянутых факторов рассмотрим в первую очередь как количество витков влияет на индуктивность катушки. На рисунке 2-5 показаны две катушки. Катушка (A) имеет два витка, а катушка (B) — четыре витка.В катушке (A) магнитное поле, создаваемое одним петля перерезает еще одну петлю. В катушке (B) магнитное поле, создаваемое одним контуром, отсекает три других. петли. Удвоение числа витков в катушке создаст поле вдвое более сильное, если используется тот же ток. Поле вдвое сильнее, сокращая вдвое больше оборотов, индуцируют в четыре раза большее напряжение. Следовательно, можно сказать, что индуктивность изменяется как квадрат числа витков .

Рисунок 2-5.- Коэффициент индуктивности (витки).

Второй фактор — диаметр катушки. На рисунке 2-6 видно, что катушка в поле зрения Диаметр B в два раза больше диаметра катушки A. Физически требуется больше проволоки, чтобы построить катушку. катушка большего диаметра, чем катушка малого диаметра, с равным числом витков. Следовательно, существует больше силовых линий, чтобы вызвать противоэдс в катушке с большей диаметр. Фактически, индуктивность катушки увеличивается прямо пропорционально поперечному сечению. площадь сердечника увеличивается на .Вспомните формулу площади круга: A = pr ² . Удвоение радиуса катушки увеличивает индуктивность в четыре раза.

Рисунок 2-6. — Коэффициент индуктивности (диаметр).

Третий фактор, влияющий на индуктивность катушки, — это длина катушки. На рис. 2-7 показаны два примера расстояния между змеевиками. Катушка (A) имеет три витка, довольно широко разнесены, образуя относительно длинную катушку. Катушка этого типа имеет мало потокосцеплений из-за большее расстояние между каждым поворотом.Следовательно, катушка (A) имеет относительно низкую индуктивность. Катушка (B) имеет близкорасположенные витки, что составляет относительно короткую катушку. Это близко расстояние увеличивает потокосцепление, увеличивая индуктивность катушки. Удвоение длина катушки при сохранении того же числа витков уменьшает значение индуктивности вдвое.

Рисунок 2 — 7. — Коэффициент индуктивности (длина катушки). ТЯЖЕЛО РАНО

Четвертый физический фактор — это тип материала сердечника, используемого в катушке.Рисунок 2-8 показаны две катушки: катушка (A) с воздушным сердечником и катушка (B) с сердечником из мягкого железа. В магнитный сердечник катушки (B) — лучший путь для магнитных силовых линий, чем немагнитный сердечник катушки (А). Высокая проницаемость магнитного сердечника из мягкого железа имеет меньшую сопротивление магнитному потоку, что приводит к появлению большего количества магнитных силовых линий. Это увеличение в магнитных силовых линиях увеличивается количество силовых линий, разрезающих каждую петлю катушки, тем самым увеличивая индуктивность катушки.Теперь должно быть очевидно, что индуктивность катушки увеличивается непосредственно по мере увеличения проницаемости материала сердечника .

Рисунок 2-8. — Коэффициент индуктивности (материал сердечника). МЯГКОЕ ЖЕЛЕЗНОЕ ЯДРО

Другой способ увеличения индуктивности — намотать катушку слоями. Рисунок 2-9 показаны три ядра с разным количеством слоев. Катушка на рисунке 2-9 (A) — плохая индуктор по сравнению с другими на рисунке, потому что его витки широко разнесены и наслоения нет.Движение потока, обозначенное пунктирными стрелками, не связывает эффективно, потому что есть только один слой витков. Более индуктивная катушка показана на рисунок 2-9 (B). Витки расположены близко друг к другу, провод намотан в два слоя. В два слоя связывают друг друга с большим количеством петель потока во время всех движений потока. Обратите внимание, что почти все витки, такие как X, находятся рядом с четырьмя другими витками (заштрихованы). Этот вызывает увеличение магнитной связи.

Рисунок 2-9.- Катушки различной индуктивности.

Катушку можно сделать еще более индуктивной, намотав ее в три слоя, как показано на рисунок 2-9 (С). Увеличенное количество слоев (площадь поперечного сечения) улучшает флюсовую связь даже больше. Обратите внимание, что некоторые повороты, такие как Y, лежат непосредственно рядом с шестью другими поворотами (заштрихованы). На практике наслоение может продолжаться через намного больше слоев. Важный факт следует помнить, однако, что индуктивность катушки увеличивается с каждым слоем добавил .

Как вы видели, на индуктивность катушки могут влиять несколько факторов, и все они факторы переменные. Многие катушки различной конструкции могут иметь одинаковую индуктивность. В Однако важно помнить, что индуктивность зависит от степень связи между проводником (проводниками) провода и электромагнитным полем . В прямая длина проводника, между одной частью проводника очень малая магнитная связь. дирижер и другой.Поэтому его индуктивность крайне мала. Было показано, что проводники становятся намного более индуктивными, когда они наматываются на катушки. Это правда, потому что между витками проводника, лежащими бок о бок в катушка.

Q.7 Перечислите пять факторов, влияющих на индуктивность катушки.

Индуктивность | Физика II

Индукция — это процесс, при котором ЭДС индуцируется изменением магнитного потока. До сих пор обсуждалось множество примеров, некоторые из которых более эффективны, чем другие.Трансформаторы, например, спроектированы так, чтобы быть особенно эффективными при наведении желаемого напряжения и тока с очень небольшими потерями энергии в другие формы. Есть ли полезная физическая величина, связанная с тем, насколько «эффективно» данное устройство? Ответ положительный, и эта физическая величина называется индуктивностью , . Взаимная индуктивность — это влияние закона индукции Фарадея для одного устройства на другое, например, первичная катушка, при передаче энергии вторичной обмотке в трансформаторе.См. Рис. 1, где простые катушки индуцируют ЭДС друг в друге.

Рис. 1. Эти катушки могут вызывать ЭДС друг в друге, как неэффективный трансформатор. Их взаимная индуктивность M указывает на эффективность связи между ними. Здесь видно, что изменение тока в катушке 1 вызывает ЭДС в катушке 2. (Обратите внимание, что « E ₂ индуцированная» представляет наведенную ЭДС в катушке 2.)

Во многих случаях, когда геометрия устройств фиксирована, магнитный поток изменяется за счет изменения тока.Поэтому мы сконцентрируемся на скорости изменения тока Δ I / Δ t как причине индукции. Изменение тока I ₁ в одном устройстве, катушка 1 на рисунке, индуцирует ЭДС ₂ в другом. Мы выражаем это в форме уравнения как

[латекс] {\ text {emf}} _ {2} = — M \ frac {\ Delta {I} _ {1}} {\ Delta t} \\ [/ latex],

, где M определяется как взаимная индуктивность между двумя устройствами. Знак минус является выражением закона Ленца.Чем больше взаимная индуктивность M , тем эффективнее связь. Например, катушки на рисунке 1 имеют небольшой размер M по сравнению с катушками трансформатора на рисунке 3 от Transformers. Единицами измерения для M являются (В с) / A = Ом ⋅ с, который назван генри (H) в честь Джозефа Генри. То есть 1 H = 1 Ω⋅s. Природа здесь симметрична. Если мы изменим ток I ₂ в катушке 2, мы индуцируем ЭДС ₁ в катушке 1, что равно

[латекс] {\ text {emf}} _ {1} = — M \ frac {\ Delta {I} _ {2}} {\ Delta t} \\ [/ latex],

, где M то же, что и для обратного процесса.Трансформаторы работают в обратном направлении с такой же эффективностью или взаимной индуктивностью M . Большая взаимная индуктивность M может быть или нежелательна. Мы хотим, чтобы трансформатор имел большую взаимную индуктивность. Но такой прибор, как электрическая сушилка для одежды, может вызвать опасную ЭДС на корпусе, если взаимная индуктивность между его катушками и корпусом велика. Один из способов уменьшить взаимную индуктивность M состоит в том, чтобы намотать катушки в обратном направлении, чтобы нейтрализовать создаваемое магнитное поле.(См. Рисунок 2.)

Рис. 2. Нагревательные катушки электрической сушилки для одежды могут быть намотаны в противоположную сторону, так что их магнитные поля нейтрализуют друг друга, что значительно снижает взаимную индуктивность относительно корпуса сушилки.

Самоиндукция , действие закона индукции Фарадея устройства на самого себя, также существует. Когда, например, увеличивается ток через катушку, магнитное поле и магнитный поток также увеличиваются, вызывая противоэдс, как того требует закон Ленца.И наоборот, если ток уменьшается, индуцируется ЭДС, которая препятствует уменьшению. Большинство устройств имеют фиксированную геометрию, поэтому изменение магнитного потока полностью связано с изменением тока Δ I через устройство. Индуцированная ЭДС связана с физической геометрией устройства и скоростью изменения тока. Выдается

[латекс] \ text {emf} = — L \ frac {\ Delta I} {\ Delta t} [/ latex],

, где L — собственная индуктивность устройства. Устройство, которое демонстрирует значительную самоиндукцию, называется индуктором и обозначено символом на рисунке 3.

Рисунок 3.

Знак минус является выражением закона Ленца, означающего, что ЭДС препятствует изменению тока. Единицами самоиндукции является генри (Гн), как и для взаимной индуктивности. Чем больше самоиндукция L устройства, тем сильнее оно сопротивляется любому изменению тока через него. Например, большая катушка с множеством витков и железным сердечником имеет большой L и не позволит току быстро меняться. Чтобы избежать этого эффекта, необходимо добиться небольшого размера L , например, за счет встречной намотки катушек, как показано на рисунке 2.Индуктор 1 H — это большой индуктор. Чтобы проиллюстрировать это, рассмотрим устройство с L = 1,0 Гн, через которое протекает ток 10 А. Что произойдет, если мы попытаемся быстро отключить ток, возможно, всего за 1,0 мс? ЭДС, заданная как ЭДС = — L (Δ I / Δ t ), будет противодействовать изменению. Таким образом, ЭДС будет индуцирована ЭДС = — L (Δ I / Δ t ) = (1,0 H) [(10 A) / (1,0 мс)] = 10 000 В. Положительный знак означает это большое напряжение идет в том же направлении, что и ток, противодействуя его уменьшению.Такие большие ЭДС могут вызвать дуги, повредить коммутационное оборудование, и поэтому может потребоваться более медленное изменение тока. Есть применение для такого большого наведенного напряжения. Во вспышках камеры используются батарея, два индуктора, которые работают как трансформатор, и система переключения или генератор для создания больших напряжений. (Помните, что нам нужно изменяющееся магнитное поле, вызванное изменяющимся током, чтобы вызвать напряжение в другой катушке.) Система генератора будет делать это много раз, когда напряжение батареи повышается до более чем тысячи вольт.(Вы можете услышать пронзительный вой от трансформатора, когда конденсатор заряжается.) Конденсатор сохраняет высокое напряжение для последующего использования для питания вспышки. (См. Рисунок 4.)

Рис. 4. Благодаря быстрому переключению катушки индуктивности можно использовать батареи 1,5 В для индукции ЭДС в несколько тысяч вольт. Это напряжение можно использовать для хранения заряда в конденсаторе для последующего использования, например, в насадке для вспышки камеры.

Можно рассчитать L для индуктора, учитывая его геометрию (размер и форму) и зная создаваемое магнитное поле.В большинстве случаев это сложно из-за сложности создаваемого поля. Таким образом, в этом тексте индуктивность L обычно является заданной величиной. Единственным исключением является соленоид, потому что он имеет очень однородное поле внутри, почти нулевое поле снаружи и простую форму. Поучительно вывести уравнение для его индуктивности. Начнем с того, что наведенная ЭДС определяется законом индукции Фарадея как ЭДС = — Н (Δ Φ / Δ t ) и, согласно определению самоиндукции, как ЭДС = — L . (Δ I / Δ т ).Приравнивая эти доходности к

[латекс] \ text {emf} = — N \ frac {\ Delta \ Phi} {\ Delta t} = — L \ frac {\ Delta I} {\ Delta t} \\ [/ latex]

Решение для L дает

[латекс] L = N \ frac {\ Delta \ Phi} {\ Delta I} \\ [/ latex]

Это уравнение для самоиндукции L устройства всегда верно. Это означает, что самоиндукция L зависит от того, насколько эффективен ток для создания магнитного потока; чем эффективнее, тем больше Δ Φ / Δ I .Давайте воспользуемся этим последним уравнением, чтобы найти выражение для индуктивности соленоида. Поскольку площадь A, соленоида является фиксированной, изменение магнитного потока составляет Δ Φ = Δ ( B A ) = A Δ B . Чтобы найти Δ B , заметим, что магнитное поле соленоида определяется выражением [латекс] B = {\ mu} _ {0} {nI} = {\ mu} _ {0} \ frac {NI} { \ ell} \\ [/ латекс]. (Здесь = / , где — количество катушек, а ℓ — длина соленоида. {2} \ влево (1.{2} \ right)} {0.100 \ text {m}} \\ & = & 0.632 \ text {mH} \ end {array} \\ [/ latex].

Обсуждение

Этот соленоид среднего размера. Его индуктивность около миллигенри также считается умеренной.

Одно из распространенных применений индуктивности используется в светофорах, которые могут определить, когда автомобили ждут на перекрестке. Электрическая цепь с индуктором размещается на дороге под местом остановки ожидающей машины. Кузов автомобиля увеличивает индуктивность, и схема изменяется, посылая сигнал светофору об изменении цвета.Точно так же металлоискатели, используемые для безопасности аэропортов, используют ту же технику. Катушка или индуктор в корпусе металлоискателя действует как передатчик и как приемник. Импульсный сигнал в катушке передатчика вызывает сигнал в приемнике. На самоиндукцию цепи влияет любой металлический предмет на пути. Такие детекторы могут быть настроены на чувствительность, а также могут указывать приблизительное местонахождение обнаруженного на человеке металла. (Но они не смогут обнаружить пластиковую взрывчатку, подобную той, которая была обнаружена на «бомбардировщике в нижнем белье.”) См. Рисунок 5.

Рис. 5. Знакомые ворота безопасности в аэропорту могут не только обнаруживать металлы, но и указывать их приблизительную высоту над полом. (Источник: Alexbuirds, Wikimedia Commons)

Самоиндуктивность и индукторы — Университетская физика, том 2

Цели обучения

К концу этого раздела вы сможете:

• Сопоставьте скорость изменения тока с наведенной ЭДС, создаваемой этим током в той же цепи
• Вывести самоиндукцию цилиндрического соленоида
• Вывести самоиндукцию для прямоугольного тороида

Взаимная индуктивность возникает, когда ток в одной цепи создает изменяющееся магнитное поле, которое индуцирует ЭДС в другой цепи.Но может ли магнитное поле повлиять на ток в исходной цепи, создавшей поле? Ответ положительный, и это явление называется самоиндуктивностью .

Катушки индуктивности

(рисунок) показывает некоторые силовые линии магнитного поля, возникающие из-за тока в кольцевой проволочной петле. Если ток постоянный, магнитный поток через контур также постоянен. Однако, если бы ток I изменялся со временем — скажем, сразу после замыкания переключателя S — тогда соответственно изменился бы магнитный поток.Тогда закон Фарадея говорит нам, что в цепи будет индуцирована ЭДС, где

Поскольку магнитное поле, создаваемое токоведущим проводом, прямо пропорционально току, поток, создаваемый этим полем, также пропорционален току; то есть

Магнитное поле создается током I в контуре. Если бы I менялись со временем, магнитный поток через петлю также изменился бы, и в петле была бы индуцирована ЭДС.

Это также можно записать как

, где коэффициент пропорциональности L известен как самоиндукция проволочной петли.Если петля имеет N витков, это уравнение принимает вид

По соглашению, положительное значение нормали к петле связано с током по правилу правой руки, поэтому на (Рисунок) нормаль направлена ​​вниз. В соответствии с этим соглашением положительное значение на (Рисунок), поэтому L всегда имеет положительное значение .

Для контура с N витков, поэтому наведенная ЭДС может быть записана в терминах самоиндукции как

При использовании этого уравнения для определения L проще всего игнорировать знаки и вычислить L как

Поскольку самоиндукция связана с магнитным полем, создаваемым током, любая конфигурация проводников обладает самоиндукцией.Например, помимо проволочной петли, длинный прямой провод имеет самоиндукцию, как и коаксиальный кабель. Коаксиальный кабель чаще всего используется в индустрии кабельного телевидения, и его также можно найти для подключения к кабельному модему. Коаксиальные кабели используются из-за их способности передавать электрические сигналы с минимальными искажениями. Коаксиальные кабели имеют два длинных цилиндрических проводника, которые обладают током и самоиндукцией, что может иметь нежелательные эффекты.

Элемент схемы, используемый для обеспечения самоиндукции, известен как индуктор.Он представлен символом, показанным на (Рисунок), который напоминает катушку с проводом, основную форму индуктора. (Рисунок) показывает несколько типов индукторов, обычно используемых в схемах.

Символ, обозначающий катушку индуктивности в цепи.

Катушки индуктивности разнообразные. Независимо от того, заключены ли они в капсулу, как показанные три верхних, или намотаны в катушку, как самая нижняя, каждая представляет собой просто относительно длинную катушку провода. (Источник: Windell Oskay)

В соответствии с законом Ленца отрицательный знак на (рис.) Указывает, что наведенная ЭДС на катушке индуктивности всегда имеет полярность, которая противодействует изменению тока.Например, если бы ток, протекающий от A к B на (Рисунок) (a), увеличивался, наведенная ЭДС (представленная воображаемой батареей) имела бы указанную полярность, чтобы противодействовать увеличению. Если бы ток от A до B уменьшался, то индуцированная ЭДС имела бы противоположную полярность, опять же, чтобы противодействовать изменению тока ((Рисунок) (b)). Наконец, если бы ток через катушку индуктивности был постоянным, в катушке не было бы индуцированной ЭДС.

Индуцированная ЭДС на катушке индуктивности всегда препятствует изменению тока. Это можно представить себе как воображаемую батарею, заставляющую течь ток, чтобы противодействовать изменению в (а) и усиливать изменение в (б).

Одно из распространенных применений индуктивности — это возможность светофора определять, когда автомобили ждут на перекрестке. Электрическая цепь с индуктором размещается на дороге под местом остановки ожидающего автомобиля.Кузов автомобиля увеличивает индуктивность, и схема изменяется, посылая сигнал на светофор, чтобы изменить цвет. Точно так же металлоискатели, используемые для безопасности аэропортов, используют ту же технику. Катушка или индуктор в корпусе металлоискателя действует как передатчик и как приемник. Импульсный сигнал от катушки передатчика вызывает сигнал в приемнике. На самоиндукцию цепи влияет любой металлический объект на пути ((Рисунок)). Металлоискатели можно настроить на чувствительность, а также они могут определять присутствие металла на человеке.

Знакомые ворота безопасности в аэропорту не только обнаруживают металлы, но также могут указывать их приблизительную высоту над полом. (кредит: «Alexbuirds» / Wikimedia Commons)

Во вспышках фотокамер обнаруживаются большие наведенные напряжения. Во вспышках камеры используются аккумулятор, два индуктора, которые работают как трансформатор, и система переключения или генератор для создания больших напряжений. Вспомните из статьи «Колебания при колебаниях», что «колебание» определяется как колебание величины или повторяющиеся регулярные колебания величины между двумя крайними значениями вокруг среднего значения.Также вспомните (из «Электромагнитная индукция об электромагнитной индукции»), что нам нужно изменяющееся магнитное поле, вызванное изменяющимся током, чтобы вызвать напряжение в другой катушке. Система генератора делает это много раз, когда напряжение батареи повышается до более чем 1000 вольт. (Вы можете услышать пронзительный свист трансформатора, когда конденсатор заряжается.) Конденсатор сохраняет высокое напряжение для последующего использования для питания вспышки.

Самоиндуктивность катушки Индуцированная ЭДС 2.0 В измеряется на катушке из 50 плотно намотанных витков, в то время как ток через нее равномерно увеличивается от 0,0 до 5,0 А за 0,10 с. а) Какова собственная индуктивность катушки? (б) Каков поток через каждый виток катушки при токе 5,0 А?

Стратегия

Обе части этой проблемы предоставляют всю информацию, необходимую для решения самоиндукции в части (а) или потока через каждый виток катушки в части (b). Необходимые уравнения (рисунок) для части (a) и (рисунок) для части (b).

Решение

1. Игнорируя отрицательный знак и используя величины, мы получаем, из (Рисунок),
   
2. Из (Рисунок), магнитный поток выражается в единицах тока так
   

Значение Самоиндукция и магнитный поток, вычисленные в частях (a) и (b), являются типичными значениями для катушек, используемых в современных устройствах. Если ток не меняется во времени, поток не изменяется во времени, поэтому ЭДС не индуцируется.

Проверьте свое понимание Ток течет через катушку индуктивности на (Рисунок) от B до A вместо A до B , как показано.Увеличивается или уменьшается ток, чтобы создать ЭДС, показанную на диаграмме (а)? На диаграмме (б)?

а. уменьшение; б. увеличение; Поскольку ток течет в противоположном направлении диаграммы, чтобы получить положительную ЭДС в левой части диаграммы (а), нам нужно уменьшить ток влево, что создает усиленную ЭДС, где положительный конец находится слева. Чтобы получить положительную ЭДС в правой части диаграммы (b), нам нужно увеличить ток слева, что создает усиленную ЭДС там, где положительный конец находится справа.

Проверьте свое понимание Изменяющийся ток индуцирует ЭДС 10 В на катушке индуктивности 0,25 Гн. С какой скоростью меняется ток?

Хороший подход к расчету самоиндукции катушки индуктивности состоит из следующих шагов:

Стратегия решения проблем: самоиндуктивность

1. Предположим, что через катушку индуктивности протекает ток I .
2. Определите магнитное поле, создаваемое током.Если есть соответствующая симметрия, вы можете сделать это с помощью закона Ампера.
3. Получить магнитный поток,
4. При известном магнитном потоке самоиндукция может быть определена по формуле (Рисунок),.

Чтобы продемонстрировать эту процедуру, мы теперь вычисляем самоиндуктивности двух катушек индуктивности.

Цилиндрический соленоид

Рассмотрим длинный цилиндрический соленоид длиной l , площадью поперечного сечения A и N витков провода.Мы предполагаем, что длина соленоида настолько больше, чем его диаметр, что мы можем считать, что магнитное поле распространяется по всей внутренней части соленоида, то есть мы игнорируем концевые эффекты в соленоиде. При токе I , протекающем через катушки, магнитное поле, создаваемое внутри соленоида, составляет

.

, поэтому магнитный поток на один виток равен

Используя (рисунок), находим для самоиндукции соленоида

Если — количество витков на единицу длины соленоида, то можно записать (рисунок) как

где — объем соленоида.Обратите внимание, что самоиндукция длинного соленоида зависит только от его физических свойств (таких как количество витков провода на единицу длины и объема), а не от магнитного поля или тока. Это верно для индукторов в целом.

Онлайн-тест по базовой электротехнике

Этот набор онлайн-тестов «Базовая электротехника» посвящен «Факторам, определяющим индуктивность катушки».

1. Что происходит с индуктивностью катушки при увеличении количества витков в катушке?
a) Увеличивается
b) Уменьшается
c) Остается прежним
d) Обнуляется
Просмотр ответа

Ответ: a
Объяснение: Индуктивность прямо пропорциональна квадрату количества витков в катушке, следовательно, как число витков увеличивается, индуктивность тоже увеличивается.

2. Что происходит с индуктивностью при уменьшении напряженности магнитного поля?
a) Увеличивается
b) Уменьшается
c) Остается прежним
d) Становится нулевым
Просмотр ответа

Ответ: b
Пояснение: Индуктивность прямо пропорциональна напряженности магнитного поля в катушке, следовательно, сила магнитного поля уменьшается , индуктивность уменьшается.

3. Что происходит с индуктивностью, когда ток в катушке удваивается по сравнению с исходным значением?
a) становится наполовину
b) становится четырехкратным
c) становится двойным
d) остается таким же
Посмотреть ответ

Ответ: d
Объяснение: ϕ прямо пропорционально i.
Φ = Li, где L — константа пропорциональности.
Итак, когда ток удваивается, ϕ также становится двойным, сохраняя L таким же.

4. Когда катушка намотана на ферромагнитный сердечник, почему трудно определить индуктивность?
a) Изменение магнитного потока больше не пропорционально изменению тока
b) В катушке нет тока
c) В катушке нет потока
d) Значение тока слишком велико для измерения
Просмотр Ответ

Ответ: a
Объяснение: Когда катушка наматывается на ферромагнитный сердечник, трудно определить индуктивность, потому что изменение магнитного потока больше не пропорционально изменению тока.

5. Что происходит с индуктивностью при увеличении площади поперечного сечения катушки?
a) Увеличивается
b) Уменьшается
c) Остается прежним
d) Становится нулевым
Просмотр ответа

Ответ: a
Объяснение: L = µ ₀ * N ² * A / l, следовательно, как площадь сечения A увеличивается, индуктивность также увеличивается.

6. Что происходит с индуктивностью при увеличении длины магнитной цепи?
a) Увеличивается
b) Уменьшается
c) Остается прежним
d) Обнуляется
Просмотр ответа

Ответ: b
Пояснение: L = µ ₀ * N ² * A / l, следовательно, как длина магнитопровода l увеличивается, индуктивность уменьшается.

7. Если ток изменяется с 20 А на 10 А за 5 секунд, а значение индуктивности равно 1 Гн, рассчитайте наведенную ЭДС.
a) 8V
b) 6V
c) 4V
d) 2V
Просмотреть ответ

Ответ: d
Объяснение: мы знаем, что:
emf = L (i2-i1) / t
Подставляя значения из вопроса, мы получаем ЭДС = 2В.

Серия Sanfoundry Global Education & Learning — Основы электротехники.

Чтобы попрактиковаться во всех областях базовой электротехники для онлайн-тестов, представляет собой полный набор из 1000+ вопросов и ответов с несколькими вариантами ответов .

Примите участие в конкурсе сертификации Sanfoundry, чтобы получить бесплатную Почетную грамоту. Присоединяйтесь к нашим социальным сетям ниже и будьте в курсе последних конкурсов, видео, стажировок и вакансий!

Индукторы

― Часть 2 Основы индукторов ② ｜ Электроника ABC ｜ TDK Techno Magazine

Поведение индуктора на постоянном токе

Переходная характеристика катушки

Из-за эффекта самоиндукции катушки (индукторы) создают электродвижущую силу (индуктивную электродвижущую силу), которая ориентирована так, чтобы противодействовать изменению тока.Следовательно, когда на катушку подается напряжение, ток не начинает течь сразу, а когда напряжение снимается, ток не прекращается немедленно. Неравномерное изменение тока или напряжения, которое происходит, например, в точке включения или выключения переключателя, называется переходной характеристикой (переходным явлением) катушки. Например, в схеме, показанной ниже, где катушка и неоновая лампа (напряжение начала разряда не менее нескольких десятков вольт) подключены параллельно, простое замыкание переключателя батареи (напряжение всего несколько вольт) не приведет к включите неоновую лампу.Но если выключатель разомкнут, когда через катушку протекает ток, загорится неоновая лампа. Электродвижущая сила (V), создаваемая катушкой из-за эффекта самоиндукции, пропорциональна коэффициенту изменения тока (ΔI / Δt). Когда переключатель установлен в положение ON, ток постепенно увеличивается, и поэтому электродвижущая сила не превышает напряжения источника питания. Но когда переключатель установлен в положение OFF, протекающий ток мгновенно отключается, что означает, что коэффициент изменения тока большой, вызывая создание большой электродвижущей силы, достаточной для зажигания неоновой лампы.

Энергия, запасаемая катушкой

В приведенной выше схеме можно зажечь неоновую лампу, потому что катушка накапливает энергию. Эта энергия пропорциональна индуктивности катушки и квадрату тока. Когда переключатель установлен в положение OFF, накопленная энергия мгновенно высвобождается, создавая высокую электродвижущую силу.

Поведение катушки переменного тока

Индуктивное реактивное сопротивление (XL)

Катушка (индуктор) плавно пропускает постоянный ток, но имеет сопротивление переменному току.Сопротивление увеличивается по направлению к более высоким частотам. Этот эффект называется индуктивным реактивным сопротивлением (XL) катушки. Следующее соотношение существует между частотой переменного тока (f) и индуктивностью (L).

Форма кривой напряжения и тока в цепи переменного тока с катушкой

Переменный ток от коммерческой розетки переменного тока имеет синусоидальную форму.Когда катушка подключена к источнику переменного тока, эффект самоиндукции создает электродвижущую силу, ориентированную таким образом, чтобы противодействовать изменению тока. Таким образом, изменение тока задерживается на 90 градусов (1/4 цикла) по отношению к изменению напряжения.

Намагничивание сердечника и магнитная проницаемость

Кривая намагничивания и магнитное насыщение

Магнитный поток (Φ), создаваемый в катушке, пропорционален индуктивности (L) и протекающему току (I).Поскольку индуктивность пропорциональна магнитной проницаемости, использование магнитного материала с высокой магнитной проницаемостью и приложение большого тока приведет к созданию более сильного магнитного потока. Однако есть пределы способности магнитного материала собирать магнитный поток, и когда ток увеличивается до определенной точки, сердечник достигает магнитного насыщения. Плотность магнитного потока (B) в этой точке называется максимальной плотностью магнитного потока (Bm).

Процесс намагничивания сердечника и изменение магнитной проницаемости

Когда сердечник намагничивается, магнитная проницаемость сердечника изменяется.Как показано на графике ниже, магнитная проницаемость (μ) выражается градиентом кривой намагничивания сердечника (θ). Начальный градиент около начала кривой — это начальная магнитная проницаемость (μ0). Эта начальная магнитная проницаемость — это то, что обычно называют магнитной проницаемостью, и это также значение, которое указано в каталогах для ферритовых материалов. Увеличение тока в катушке и, таким образом, увеличение намагниченности в конечном итоге приведет к достижению максимальной магнитной проницаемости.Это называется максимальной магнитной проницаемостью (мкм), после которой значение снова падает.

Потери на вихревые токи в сердечнике

Когда в катушку подается переменный ток, создается электродвижущая сила, которая противодействует изменению магнитного потока, и в сердечнике течет концентрический ток. Это называется вихревым током, и он лишает систему мощности RI2 (R: сопротивление, I: ток), которая уходит в виде джоулева тепла.Это называется потерей на вихревые токи. У металлических сердечников с низким электрическим сопротивлением потери на вихревые токи более выражены. Ламинированные сердечники, используемые для силовых трансформаторов, представляют собой попытку уменьшить потери на вихревые токи. Однако потери будут увеличиваться по направлению к более высоким частотам, что приведет к выделению большего количества тепла. Поскольку феррит имеет высокое удельное сопротивление, потери на вихревые токи низкие, что делает этот материал пригодным для многих применений, таких как высокочастотные катушки и высокочастотные трансформаторы.

Индуктивность, импеданс и потери — Блог о пассивных компонентах

L.1.7 Индуктивность L

Не только магнитные материалы обладают магнитным полем, каждый проводник с током сам создает магнитное поле.

Рис. 1.23: Магнитные поля токопроводящих проводов

Энергия может временно храниться в магнитном поле.Этот эффект технически используется в катушках, состоящих из одной или нескольких проволочных обмоток. Синонимичный термин «индуктор» утвердился.

Существуют различные типы индукторов или катушек:

• Воздушные змеевики (без феррита)
• Дроссельные катушки с сердечником из железного порошка или ферритовым сердечником
• Катушка с тороидальным сердечником
• Катушка сердечника стержня
Типы
• SMD становятся все более важными из-за их небольшого размера. Помимо индукторов SMD с намоткой, все большее распространение получают индукторы для многопользовательской игры.

Все катушки имеют особое поведение, более подробно описанное в следующих определениях.

1.7.1 Определение индуктивности L

Элемент схемы, который реагирует на изменение тока противодавлением, проявляет индуктивные свойства. Катушка индуктивности — это пассивный компонент, который, как сопротивление переменному току, создает противодействующее напряжение — напряжение самоиндукции.

Напряжение самоиндукции (U _ind ) на выводах индуктора зависит от скорости изменения тока (di / dt) и константы пропорциональности, индуктивности (L):

Индуктивность (L ) катушки зависит от материала сердечника, геометрии материала сердечника, витков обмотки и типа обмоток.Следующее уравнение обычно применяется для расчета индуктивности (L):

Единицей измерения индуктивности (L) является Генри (H) = Vs / A .

Индуктивность сердечников со вставленным воздушным зазором можно рассчитать по следующей формуле:

l _{среднее значение} = средняя длина магнитного пути в сердечнике (без воздушного зазора)
l _зазор = длина пути воздушный зазор (ы)
μ _r = относительная проницаемость

Эта формула, вставленная в формулу для расчета общей индуктивности, дает:

Это также позволяет определить ширину воздушного зазора, если известны требуемая индуктивность L и другие параметры.Здесь необходимо иметь в виду, что приведенная выше формула применима только в том случае, если μ _r велико, а длина воздушного зазора намного меньше средней длины в сердечнике.

Чтобы учесть паразитные эффекты и их влияние на индуктивность, Маклайман предлагает следующую форму расчета паразитных эффектов F:

w _h = высота обмотки
l _зазор = длина пути воздушного зазора ( s)
A _зазор = площадь поперечного сечения воздушного зазора
F = коэффициент рассеяния

В результате индуктивность L _F изменяется на расчетное значение L _{зазора в} раз больше коэффициента рассеяния F:

Положительное влияние воздушного зазора заключается в увеличении тока насыщения для сердечника того же размера.Недостатком является то, что для достижения заданного значения L количество витков теперь должно быть увеличено, и поэтому, если нет места для обмотки, для более толстого или более одного провода в бифилярной или трехзаходной обмотке сопротивление постоянному току обмотки тоже увеличивается.

Ни при каких обстоятельствах не следует уменьшать количество витков для компенсации паразитного эффекта — это дополнительно увеличивает индукцию и может привести к преждевременному насыщению.

Требуемая ширина воздушного зазора для данной индуктивности L с учетом паразитного фактора F может быть рассчитана в первом приближении следующим образом:

1.7.2 Определение значения A _L

Чтобы избавить пользователя от расчета эффективной магнитной длины (l _eff ) и площади (A _eff ), для тороидальных сердечников и гильз указано соответствующее значение A _L . Он представляет собой эффективную индуктивность для одной обмотки и должен быть умножен на квадрат витков обмотки (N), чтобы получить фактическую индуктивность (L).

Величина (A _L ) — это индуктивность (L) при условии N = 1 витков обмотки.Таким образом, учитывая значение A _L , можно найти необходимое количество обмоток катушки, не прибегая к долгому пути рассмотрения геометрических данных сердечника:

Пример:
Требуемая индуктивность 100 мкГн; сердечник имеет значение A _L , равное 250 нГн / Н ²

Результат:
Для создания индуктивности 100 мкГн сердечник должен иметь 20 обмоток.

1.7.3 Импеданс Z

Если катушка индуктивности работает от переменного напряжения, очевидно, что она имеет другое сопротивление, чем при работе на постоянном токе.

Сопротивление переменного напряжения, приложенного к клеммам катушки, называется сопротивлением (Z) .

Рис. 1.24: Взаимосвязь между импедансом, реактивным сопротивлением и сопротивлением

Импеданс (Z) зависит от частоты и складывается из геометрической суммы сопротивления потерь (R) и реактивного сопротивления (X _L ) идеальной катушки (L).

Реактивное сопротивление X _L определяется следующим образом:

Наблюдение:

Импеданс растет с увеличением частоты.

Эта линейная зависимость продолжается до бесконечно высоких частот для идеальной катушки.

Рис. 1.25: Кривая импеданса для реальных катушек индуктивности

Однако из-за частотной зависимости проницаемости и конструкции катушки и паразитной емкости применимость катушек на высоких частотах ограничена.

Импеданс быстро уменьшается от собственной резонансной частоты; индуктивный характер катушки исчезает.

1.7.4 Собственная резонансная частота (SFR)

Рис. 1.26: Эквивалентная схема реальной индуктивности

Каждая катушка индуктивности также имеет емкостную связь, возникающую из ее обмоток или многослойных элементов. Эти паразитные емкости обозначены конденсатором (C) в эквивалентной схеме. Этот конденсатор в катушке образует параллельный резонансный контур с индуктивностью.

На собственной резонансной частоте входная энергия колеблется между элементами индуктивности и емкости.Внешняя энергия больше не поглощается (идеальная катушка).

Если катушка работает выше своего резонанса, она становится все более емкостной. На практике катушки должны работать намного ниже их резонансной частоты.

1,7,5 R потери

Активная мощность (тепловые потери) не рассеивается в реактивном сопротивлении X _L из-за сдвига фаз 90 ° между напряжением и током. Общие потери в катушке можно объединить в сопротивление потерь (R), которое последовательно соединено с идеальной индуктивностью (L).В результате получается эквивалентная схема реальной индуктивности (см. Рисунок 1.26).

Поскольку потери в R зависят от частоты, сопротивление постоянному току (DCR) также всегда определяется в технических характеристиках. Это зависит от материала используемого провода или типа конструкции индукторов SMD и определяется при комнатной температуре путем простого измерения сопротивления.

Размер сопротивления DCR напрямую влияет на повышение температуры катушки. Поэтому следует избегать длительного превышения текущего номинального значения.Общие потери в катушке состоят как из потерь в сопротивлении постоянному току DCR, так и из следующих частотно-зависимых компонентов:

• Потери в материале сердечника (потери на магнитный гистерезис, вихретоковые потери)
• Дополнительные потери в проводнике от скин-эффекта (смещение тока на высоких частотах)
• Потери магнитного поля соседних обмоток (эффект близости)
• Радиационные потери
• Потери от дополнительной магнитной защиты (WE-MI)

Все эти компоненты потерь можно объединить в сопротивление потерь (R).Это сопротивление потерь в первую очередь отвечает за определение качества катушки индуктивности. К сожалению, математическое определение сопротивления потерь R невозможно.

Поэтому индукторы обычно измеряются во всем частотном диапазоне с помощью анализатора импеданса. Это измерение обеспечивает отдельные компоненты X _L (f), R (f) и Z (f). Добротность определяется как характеристика качества индуктора.

1.7.6 Потери в меди

Потери в меди для индуктивных компонентов состоят из потерь на постоянный ток и потерь на вихревые токи.Потери постоянного тока рассчитываются по закону Ома:

P _В = потеря мощности
R = сопротивление постоянному току
I _RMS = эффективный ток

На более высоких частотах также есть потери из-за скин-эффекта и эффекта близости. Эти потери от вихревых токов можно напрямую объяснить законом Фарадея. Ток, протекающий по проводнику, создает вокруг него магнитное поле.

Это магнитное поле быстро изменяется из-за высокой частоты, так что в проводнике и в соседних проводниках индуцируется напряжение.Это напряжение генерирует ток, противодействующий исходному току. Таким образом, в проводнике, а также в соседних проводниках возникают дополнительные токи.

Рассматривая одиночный проводник, говорят о скин-эффекте. Для проводников, по которым протекают токи высокой частоты, ток течет только по внешней обшивке проводника (рисунок 1.27). Глубина проникновения, при которой плотность тока упала до значения 1 / e, определяется по формуле:

δ = глубина проникновения
ρ = удельное сопротивление
ω = угловая частота 2 πf
μ = проницаемость проводника (для меди μ ₀ )

Глубина проникновения при 50 Гц равна 9.38 мм, при 10 кГц — 0,66 мм.

Рис. 1.27: Распределение тока в проводнике на высокой частоте. В качестве примера приведен диаметр проволоки, в 7 раз превышающий глубину проплавления.

Эффект близости играет гораздо большую роль для трансформаторов, когда соседние проводники генерируют поля, смещенные током. Возможность расчета потерь на вихревые токи для простых геометрий описана Доуэллом. Теория была развита Карстеном. Математическое описание выходит далеко за рамки этой книги.

Здесь гораздо важнее описать имеющиеся варианты ограничения потерь на вихревые токи. Потери на вихревые токи зависят от величины магнитного поля. Таким образом, способ ограничения потерь на вихревые токи заключается в ограничении напряженности магнитного поля.

Это может быть достигнуто, например, путем чередования обмоток, т.е. наматывается половина первичной обмотки, затем вторичная обмотка, а затем вторая половина первичной обмотки. Это снижает абсолютную величину магнитного поля и, следовательно, потери на вихревые токи.На рисунке 1.28 показан профиль поля H в обмотке из медной фольги со структурой обмотки первичная — вторичная и половина первичной вторичной обмоток — половина первичной.

Напряженность магнитного поля внутри обмотки возрастает изнутри наружу, потому что все больше витков (все большие токи) ограничиваются силовыми линиями. Магнитное поле вторичной обмотки противоположно исходному полю. Это снова служит для уменьшения магнитного поля. Уменьшение величины поля H очевидно.

Рис. 1.28: Профиль магнитного поля в трансформаторе с различными конфигурациями обмоток.

Тонкие плоские проводники, например медная фольга, также может использоваться для намотки. Толщина должна быть порядка глубины проникновения. Это следует использовать только для небольшого числа витков, потому что при большем количестве обмоток большое количество слоев вызывает более высокие потери на вихревые токи.

Еще одним вариантом уменьшения вихревых токов является намотка более тонкими изолированными проводами, а не толстыми.Здесь необходимо следить за тем, чтобы отдельные провода, подключенные параллельно, имели одинаковое распределение тока. ВЧ-литц-провода предлагают здесь вариант, при котором отдельные провода скручиваются друг с другом, так что в среднем каждый провод имеет одинаковое положение в магнитном поле. С этим вариантом также нужно следить, чтобы количество слоев не было слишком большим.

1.7.7 Определение добротности Q

Компонент входящей извне энергии, преобразованной в тепло в сопротивлении потерь R, не влияет на энергию, запасенную в магнитном поле.Чем больше эти потери, тем хуже индуктор действует как буфер.

Это определяет качество как фактор качества Q следующим образом:

Практические значения:

• Воздушный змеевик Q до 400
• Ферритовый дроссель Q до 150
• Многопользовательские индукторы SMD Q до 60

График качества-частоты помогает выбрать лучшую конструкцию индуктора для конкретного применения.

Фиг.1.29: График добротности-частота

Наблюдения:

• Качество повышается до максимального значения, а затем снижается.
• Допускаются постоянные малые потери в сопротивлении R индуктора вплоть до пикового значения качества.
• За пределами пикового значения становятся очевидными значительные потери, а также изменяется индуктивность из-за нелинейности ферритового материала.
• Рабочий диапазон с наименьшими потерями может быть определен до критической точки качества.Если индуктор используется на более высоких частотах, потери быстро увеличиваются.

1.7.8 Температурный режим

Рис. 1.30: Температурный дрейф многослойного индуктора

Катушки с ферромагнитным сердечником демонстрируют переменную индуктивность в зависимости от температуры окружающей среды. Если к стабильности цепей фильтров с индукторами
предъявляются высокие требования (например, в измерительной технике), целесообразно выбрать катушку с почти линейной температурной кривой.В этом случае изменение индуктивности ΔL относительно номинальной индуктивности L катушки является наименьшим. На рисунке 1.30 показан этот график для многослойной катушки индуктивности.

1.7.9 Номинальный ток

Номинальный ток, который может выдерживать индуктор, более точно определен в главе о компонентах для различных продуктов.

Номинальный ток обычно связан с заявлением о самонагреве компонента. Если компонент работает при номинальном токе, он нагревается выше температуры окружающей среды на температуру, указанную в техническом паспорте.

Затем необходимо выяснить, подходит ли полученная температура компонента для данного применения. В противном случае необходимо выбрать компонент с более высокой допустимой нагрузочной способностью по номинальному току. Необходимо убедиться, что при работе при номинальном токе деталь не превышает рабочую температуру (в противном случае необходимо снижение номинальных характеристик).

Пример:
Экранированный многослойный индуктор (WE-MI) Максимальное значение номинального тока достигается, если повышение температуры компонента превышает 20 ° C для выбранного испытательного тока.

1.7.10 Ток насыщения

Ток насыщения катушки индуктивности — это ток, при котором значение индуктивности упало на процент, указанный в таблице данных.

Пример:
Дроссели накопителя серии WE-PD

Здесь ток насыщения определяет ток, при котором индуктивность упала на 10%.

Примечание!
Пиковый ток, протекающий через катушку индуктивности, в момент включения может быть значительно выше, чем при нормальной работе, особенно для приложений с коммутационным контроллером или приложений с высокими емкостными нагрузками или высокими пусковыми токами.Это может привести к полному насыщению компонента и, следовательно, к возможным последующим неисправностям электроники. Желательно понимать и ограничивать ток или активировать функции плавного пуска.

Рис. 1.31: График индуктивности-тока

---

ABC CLR: Глава L Индукторы

Индуктивность, импеданс и потери

Контент, лицензированный EPCI: Würth Elektronik eiSos, Trilogy of Magnetics, распечатки справочника можно заказать здесь.

Содержание этой страницы находится под международной лицензией Creative Commons Attribution-ShareAlike 4.0.

Как сделать индуктор с воздушным сердечником-Formula

S Иногда вы не можете найти конкретный индуктор на рынке. На самом деле с этой проблемой сталкивается большинство любителей электроники, и проблема становится более серьезной, если ваш проект связан с радиочастотами.Катушки индуктивности, необходимые для РЧ-цепей (антенна, тюнер, усилитель и т. Д.), Практически невозможно найти на рынке, и единственное решение — не что иное, как их приготовление в домашних условиях.

Приложив немного практики и терпения, вы сможете сконструировать почти все индукторы с воздушным сердечником в домашних условиях. Индуктивность индуктора с воздушным сердечником может быть представлена ​​с помощью упрощенной формулы, показанной ниже, и для расчета индуктивности индуктора с воздушным сердечником можно использовать то же уравнение.

L = [d ² n ² ] / [18d + 40l]

• Где ‘L’ — индуктивность в Micro Henries [мкГн]
• ‘d’ — диаметр катушки от одного центра провода до другого центра провода.Следует указывать в дюймах.
• ‘l’ — длина катушки в дюймах.
• «n» — количество витков.

Примечания:

• Длина катушки, используемой в индукторе, должна быть равна или 0,4 диаметра катушки.
• Как показано в уравнении, индуктивность индуктора с воздушным сердечником изменяется как квадрат числа витков. Таким образом, значение «l» умножается в четыре раза, если значение «n» удваивается.Значение «l» умножается на два, если значение «n» увеличивается до 40%.

Намотка катушки.

• Катушка должна быть сначала намотана на пластмассовый каркас соответствующего диаметра (равного требуемому диаметру сердечника).
• Обмотка должна быть плотной, а соседние витки должны располагаться как можно ближе.
• После завершения намотки медленно извлеките сердечник, не трогая катушку.
• Теперь нанесите тонкий слой эпоксидной смолы на поверхность змеевика для механической поддержки.
• Удалите изоляцию с концов катушки.

Пример

Предположим, вы хотите сделать катушку индуктивности с индуктивностью 10 мкГн.