Катушка в электрической цепи: Катушка индуктивности. Устройство и принцип работы.

Катушка индуктивности. Устройство и принцип работы.

Приветствую всех на нашем сайте!

Мы продолжаем изучать электронику с самых основ, и темой сегодняшней статьи будет катушка индуктивности. Забегая вперед скажу, что сначала мы обсудим теоретические аспекты, а несколько будущих статей посвятим целиком и полностью рассмотрению различных электрических схем, в которых используются катушки индуктивности, а также элементы, которые мы изучили ранее в рамках нашего курса – резисторы и конденсаторы.

Устройство и принцип работы катушки индуктивности.

Как уже понятно из названия элемента – катушка индуктивности, в первую очередь, представляет из себя именно катушку 🙂 То есть большое количество витков изолированного проводника. Причем наличие изоляции является важнейшим условием – витки катушки не должны замыкаться друг с другом. Чаще всего витки наматываются на цилиндрический или тороидальный каркас:

Важнейшей характеристикой катушки индуктивности является, естественно, индуктивность, иначе зачем бы ей дали такое название 🙂 Индуктивность – это способность преобразовывать энергию электрического поля в энергию магнитного поля.

{-7}\medspace\frac{Гн}{м}

\mu – магнитная проницаемость магнитного материала сердечника. А что это за сердечник и для чего он нужен? Сейчас выясним. Дело все в том, что если катушку намотать не просто на каркас (внутри которого воздух), а на магнитный сердечник, то индуктивность возрастет многократно. Посудите сами – магнитная проницаемость воздуха равна 1, а для никеля она может достигать величины 1100. Вот мы и получаем увеличение индуктивности более чем в 1000 раз

S – площадь поперечного сечения катушки

N – количество витков

l – длина катушки

Из формулы следует, что при увеличении числа витков или, к примеру, диаметра (а соответственно и площади поперечного сечения) катушки, индуктивность будет увеличиваться. А при увеличении длины – уменьшаться. Таким образом, витки на катушке стоит располагать как можно ближе друг к другу, поскольку это приведет к уменьшению длины катушки.

С устройством катушки индуктивности мы разобрались, пришло время рассмотреть физические процессы, которые протекают в этом элементе при прохождении электрического тока.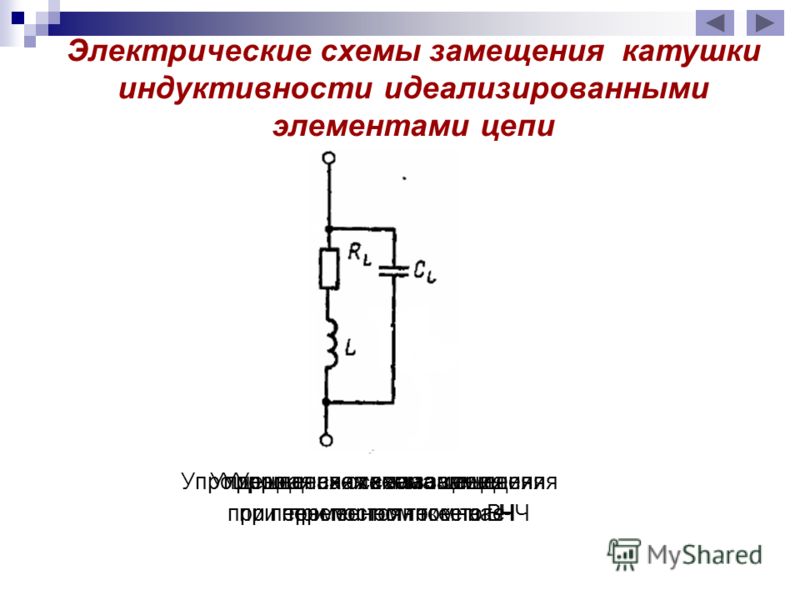 Для этого мы рассмотрим две схемы – в одной будем пропускать через катушку постоянный ток, а в другой -переменный!

Катушка индуктивности в цепи постоянного тока.

Итак, в первую очередь, давайте разберемся, что же происходит в самой катушке при протекании тока. Если ток не изменяет своей величины, то катушка не оказывает на него никакого влияния. Значит ли это, что в случае постоянного тока использование катушек индуктивности и рассматривать не стоит? А вот и нет 🙂 Ведь постоянный ток можно включать/выключать, и как раз в моменты переключения и происходит все самое интересное. Давайте рассмотрим цепь:

Резистор выполняет в данном случае роль нагрузки, на его месте могла бы быть, к примеру, лампа. Помимо резистора и индуктивности в цепь включены источник постоянного тока и переключатель, с помощью которого мы будем замыкать и размыкать цепь. Что же произойдет в тот момент когда мы замкнем выключатель?

Ток через катушку начнет изменяться, поскольку в предыдущий момент времени он был равен 0.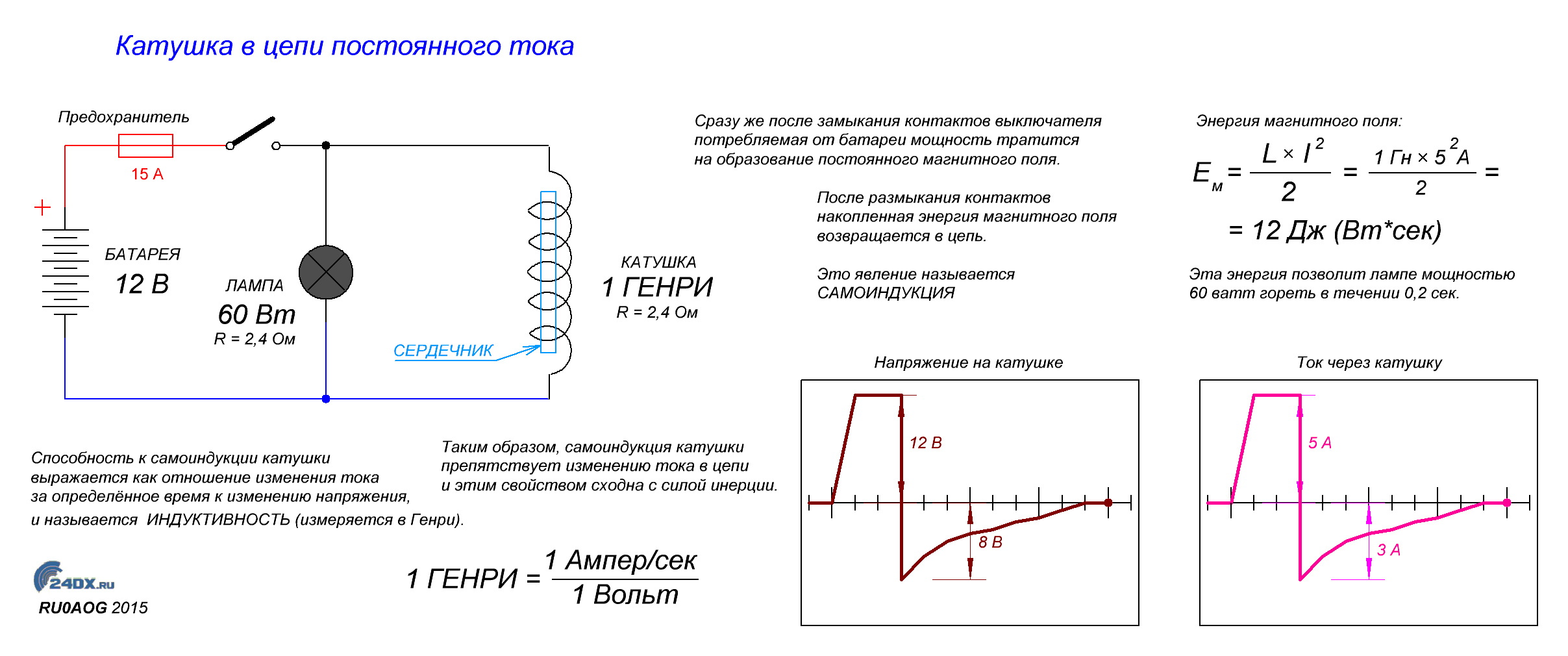 Изменение тока приведет к изменению магнитного потока внутри катушки, что, в свою очередь, вызовет возникновение ЭДС (электродвижущей силы) самоиндукции, которую можно выразить следующим образом:

\varepsilon_s = -\frac{d\Phi}{dt}

Возникновение ЭДС приведет к появлению индукционного тока в катушке, который будет протекать в направлении, противоположном направлению тока источника питания. Таким образом, ЭДС самоиндукции будет препятствовать протеканию тока через катушку (индукционный ток будет компенсировать ток цепи из-за того, что их направления противоположны). А это значит, что в начальный момент времени (непосредственно после замыкания выключателя) ток через катушку I_L будет равен 0. В этот момент времени ЭДС самоиндукции максимальна. А что же произойдет дальше? Поскольку величина ЭДС прямо пропорциональна скорости изменения тока, то она будет постепенно ослабевать, а ток, соответственно, наоборот  будет возрастать. Давайте посмотрим на графики, иллюстрирующие то, что мы обсудили:

На первом графике мы видим входное напряжение цепи – изначально цепь разомкнута, а при замыкании переключателя появляется постоянное значение.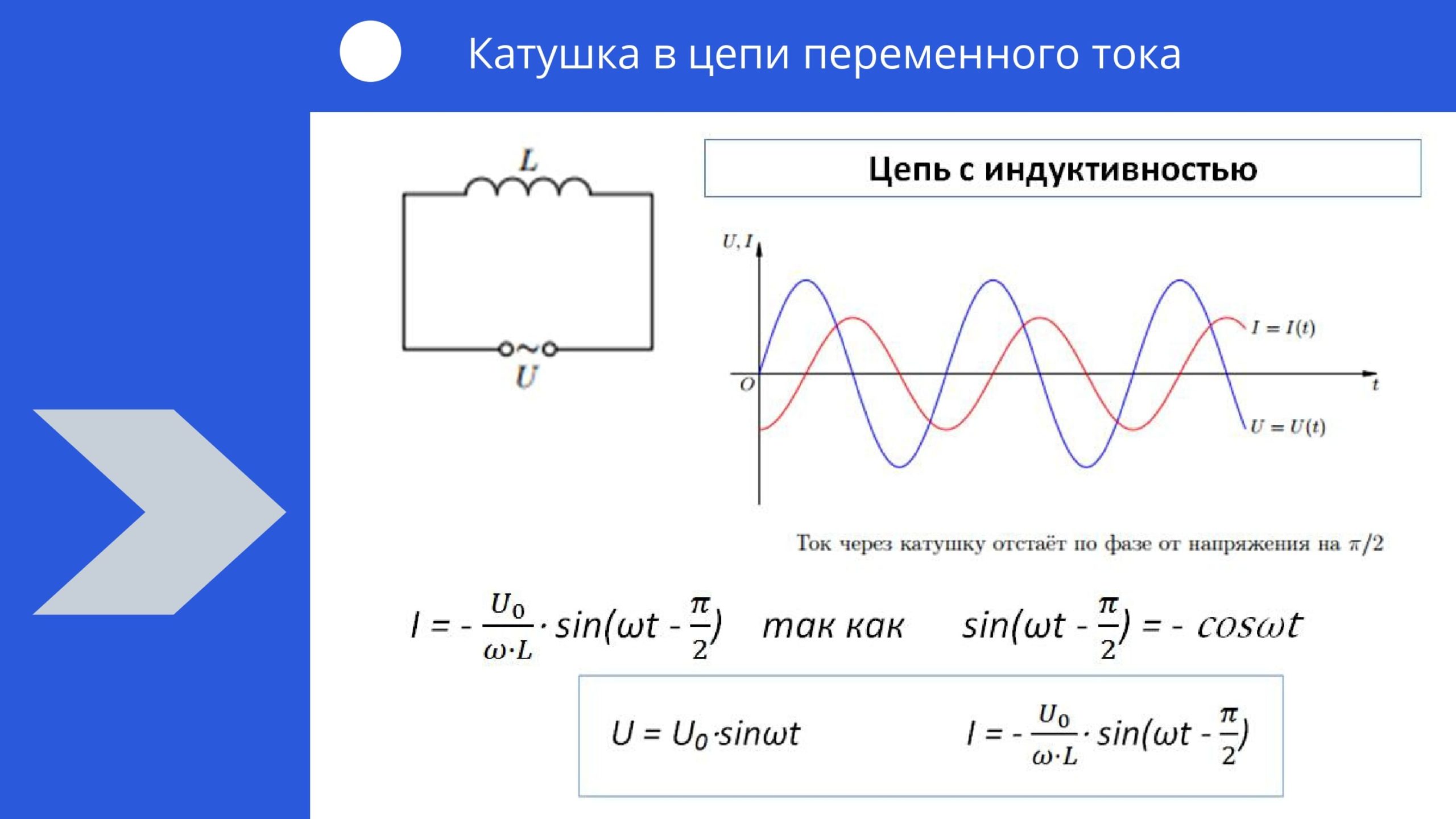 На втором графике мы видим изменение величины тока через катушку индуктивности. Непосредственно после замыкания ключа ток отсутствует из-за возникновения ЭДС самоиндукции, а затем начинает плавно возрастать.

Напряжение на катушке наоборот в начальный момент времени максимально, а затем уменьшается. График напряжения на нагрузке будет по форме (но не по величине) совпадать с графиком тока через катушку (поскольку при последовательном соединении ток, протекающий через разные элементы цепи одинаковый). Таким образом, если в качестве нагрузки мы будем использовать лампу, то они загорится не сразу после замыкания переключателя, а с небольшой задержкой (в соответствии с графиком тока).

Аналогичный переходный процесс в цепи будет наблюдаться и при размыкании ключа. В катушке индуктивности возникнет ЭДС самоиндукции, но индукционный ток в случае размыкания будет направлен в том же самом направлении, что и ток в цепи, а не в противоположном, поэтому запасенная энергия катушки индуктивности пойдет на поддержание тока в цепи:

После размыкания ключа возникает ЭДС самоиндукции, которая препятствует уменьшению тока через катушку, поэтому ток достигает нулевого значения не сразу, а по истечении некоторого времени.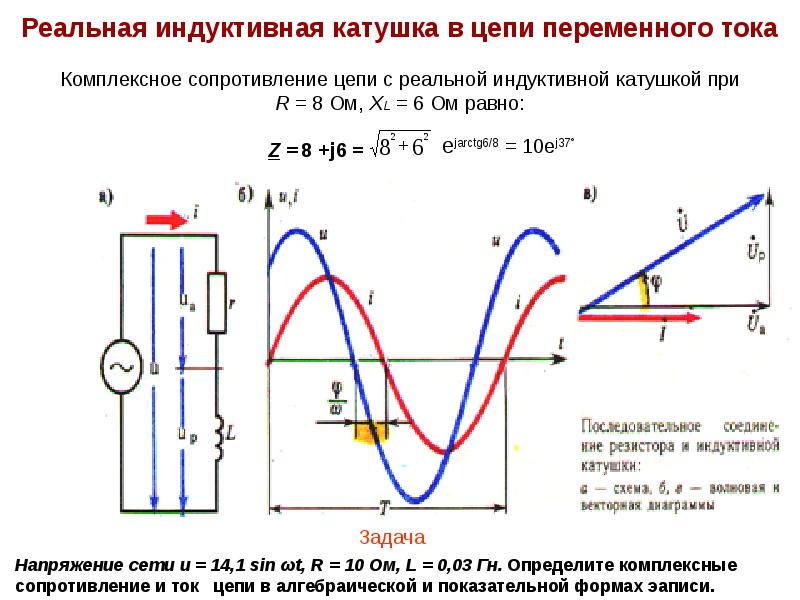

Напряжение же в катушке по форме идентично случаю замыкания переключателя, но противоположно по знаку. Это связано с тем, что изменение тока, а соответственно и ЭДС самоиндукции в первом и втором случаях противоположны по знаку (в первом случае ток возрастает, а во втором убывает).

Кстати, я упомянул, что величина ЭДС самоиндукции прямо пропорциональна скорости изменения силы тока, так вот, коэффициентом пропорциональности является ни что иное как индуктивность катушки:

\varepsilon_s = -L\medspace\frac{dI}{dt}

На этом мы заканчиваем с катушками индуктивности в цепях постоянного тока и переходим к цепям переменного тока.

Катушка индуктивности в цепи переменного тока.

Рассмотрим цепь, в которой на катушку индуктивности подается переменный ток:

Давайте посмотрим на зависимости тока и ЭДС самоиндукции от времени, а затем уже разберемся, почему они выглядят именно так:

Как мы уже выяснили ЭДС самоиндукции у нас прямо пропорциональна и противоположна по знаку скорости изменения тока:

\varepsilon_L = -L\medspace\frac{dI}{dt}

Собственно, график нам и демонстрирует эту зависимость! Смотрите сами – между точками 1 и 2 ток у нас изменяется, причем чем ближе к точке 2, тем изменения меньше, а в точке 2 в течении какого-то небольшого промежутка времени ток и вовсе не изменяет своего значения. Соответственно скорость изменения тока максимальна в точке 1 и плавно уменьшается при приближении к точке 2, а в точке 2 равна 0, что мы и видим на графике ЭДС самоиндукции. Причем на всем промежутке 1-2 ток возрастает, а значит скорость его изменения положительна, в связи с этим на ЭДС на всем этом промежутке напротив принимает отрицательные значения.

Аналогично между точками 2 и 3 – ток уменьшается – скорость изменения тока отрицательная и увеличивается – ЭДС самоиндукции увеличивается и положительна. Не буду расписывать остальные участки графика – там все процессы протекают по такому же принципу 🙂

Кроме того, на графике можно заметить очень важный момент – при увеличении тока (участки 1-2 и 3-4) ЭДС самоиндукции и ток имеют разные знаки (участок 1-2: \varepsilon < 0, i > 0, участок 3-4: \varepsilon > 0, i < 0). Таким образом, ЭДС самоиндукции препятствует возрастанию тока (индукционные токи направлены “навстречу” току источника).

А на участках 2-3 и 4-5 все наоборот – ток убывает, а ЭДС препятствует убыванию тока (поскольку индукционные токи будут направлены в ту же сторону, что и ток источника и будут частично компенсировать уменьшение тока).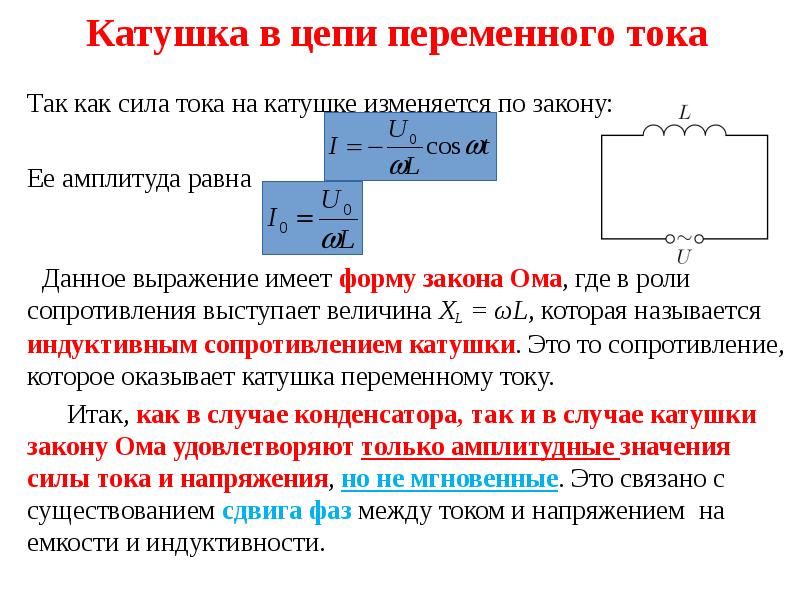

И в итоге мы приходим к очень интересному факту – катушка индуктивности оказывает сопротивление переменному току, протекающему по цепи. А значит она имеет сопротивление, которое называется индуктивным или реактивным и вычисляется следующим образом:

X_L = w\medspace L

Где w – круговая частота: w = 2 \pi f. [/latex]f[/latex] – это частота переменного тока. Таким образом, чем больше частота тока, тем большее сопротивление будет ему оказывать катушка индуктивности. А если ток постоянный (f = 0), то реактивное сопротивление катушки равно 0, соответственно, она не оказывает влияния на протекающий ток.

Давайте вернемся к нашим графикам, которые мы построили для случая использования катушки индуктивности в цепи переменного тока. Мы определили ЭДС самоиндукции катушки, но каким же будет напряжение u? Здесь все на самом деле просто! По 2-му закону Кирхгофа:

u + \varepsilon_L = 0

А следовательно:

u = – \varepsilon_L

Построим на одном графике зависимости тока и напряжения в цепи от времени:

Как видите ток и напряжение сдвинуты по фазе (ссылка) друг относительно друга, и это является одним из важнейших свойств цепей переменного тока, в которых используется катушка индуктивности:

При включении катушки индуктивности в цепь переменного тока в цепи появляется сдвиг фаз между напряжением и током, при этом ток отстает по фазе от напряжения на четверть периода. 

Вот и с включением катушки в цепь переменного тока мы разобрались!

На этом, пожалуй, закончим сегодняшнюю статью, она получилась уже довольно объемной, поэтому разговор о катушках индуктивности мы продолжим в следующий раз. Так что до скорых встреч, будем рады видеть вас на нашем сайте!

Катушка индуктивности

Катушка индуктивности – электронный компонент, представляющий собой винтовую либо спиральную конструкцию, выполненную с применением изолированного проводника.  Основным свойством катушки индуктивности, как понятно из названия – индуктивность. Индуктивность – это свойство преобразовать энергию электрического тока в энергию магнитного поля. Величина индуктивности для цилиндрической или кольцевой катушки равна 

Где  ψ — потокосцепление, µ0 = 4π*10-7 – магнитная постоянная, N – количество витков, S – площадь поперечного сечения катушки, l — длина средней линии потока.

Также катушке индуктивности присущи такие свойства как небольшая ёмкость и малое активное сопротивление, а идеальная катушка и вовсе их лишена. Применение данного электронного компонента отмечается практически повсеместно в электротехнических устройствах. Цели применения различны:

— подавление помех в электрической цепи;
— сглаживание уровня пульсаций;
— накопление энергетического потенциала;
— ограничение токов переменной частоты;
— построение резонансных колебательных контуров;
— фильтрация частот в цепях прохождения электрического сигнала;
— формирование области магнитного поля;
— построение линий задержек, датчиков и т.д.

Энергия магнитного поля катушки индуктивности

Электрический ток способствует накоплению энергии в магнитном поле катушки. Если отключить подачу электричества, накопленная энергия будет возвращена в электрическую цепь. Значение напряжения при этом в цепи катушки возрастает многократно. Величина запасаемой энергии в магнитном поле равна примерно тому значению работы, которое необходимо получить, чтобы обеспечить появление необходимой силы тока в цепи. Значение энергии, запасаемой катушкой индуктивности можно рассчитать с помощью формулы.

 

Реактивное сопротивление

При протекании переменного тока, катушка обладает кроме активного, еще и реактивным сопротивлением, которое находится по формуле 

По формуле видно, что в отличие от конденсатора, у катушки с увеличением частоты, реактивное сопротивление растет, это свойство применяется в фильтрах частот.

При построении векторных диаграмм важно помнить, что в катушке, напряжения опережает ток на 90 градусов.

Добротность катушки

Еще одним важным свойством катушки является добротность. Добротность показывает отношение реактивного сопротивления катушки к активному. 

Чем выше добротность катушки, тем она ближе к идеальной, то есть она обладает только главным своим свойством – индуктивностью.

Конструкции катушек индуктивности

Конструктивно катушки индуктивности могут быть представлены в разном исполнении. Например, в исполнении однослойной или многослойной намотки проводника. При этом намотка провода может выполняться на диэлектрических каркасах разных форм: круглых, квадратных, прямоугольных. Нередко практикуется изготовление бескаркасных катушек. Широко применяется методика изготовления катушек тороидального типа. 

Витки проводника, как правило, наматываются плотно один к одному. Однако в некоторых случаях намотка производится с шагом. Подобная методика отмечается, к примеру, когда изготавливаются высокочастотные дроссели. Намотка провода с шагом способствует снижению образования паразитной ёмкости, так же как и намотка, выполненная отдельными секциями. 

Индуктивность катушки можно изменять,  добавляя в конструкцию катушки ферромагнитный сердечник. Внедрение сердечников отражается на подавлении помех. Поэтому практически все дроссели, предназначенные для подавления высокочастотных помех, как правило, имеют ферродиэлектрические сердечники, изготовленные на основе феррита, флюкстрола, ферроксона, карбонильного железа. Низкочастотные помехи хорошо сглаживаются катушками на пермалоевых сердечниках или на сердечниках из электротехнической стали.

Просмотров:

Что такое катушка индуктивности и для чего она нужна? | ASUTPP

Я получил письма от многих из вас с просьбой рассказать простыми словами о катушке индуктивности.

Это действительно хорошая просьба и желание). Потому что катушка индуктивности — это довольно странный компонент. Её невероятно легко сделать. Но немного сложнее понять как она работает.

Катушка индуктивности

Катушка индуктивности

Катушка индуктивности (иногда называют ее индуктором или дросселем) — это просто катушка проволоки, которая намотана вокруг какого-нибудь сердечника. Ядро сердечника может быть просто воздухом или магнитом.

Когда вы подаете ток через катушку, вокруг неё создается магнитное поле.

При использовании магнитного сердечника магнитное поле будет намного сильнее.

Как работает катушка индуктивности?

Ток через любой провод создаст магнитное поле. Катушка индуктивности имеет проволочную форму, поэтому магнитное поле будет намного сильнее.

Причина, по которой индуктор работает так, как он работает, заключается в этом магнитном поле. Отсюда вытекают и следующие свойства катушки.

Свойства катушки индуктивности:

• Скорость изменения тока через катушку ограничена и определяется индуктивностью катушки.
• Сопротивление (модуль импеданса) катушки растет с увеличением частоты текущего через неё тока.
• Катушка индуктивности при протекании тока запасает энергию в своём магнитном поле. При отключении внешнего источника тока катушка отдаст запасенную энергию, стремясь поддержать величину тока в цепи. При этом напряжение на катушке нарастает, вплоть до пробоя изоляции или возникновения дуги на коммутирующем ключе.

Катушка индуктивности в электрической цепи для переменного тока имеет не только собственное омическое (активное) сопротивление, но и реактивное сопротивление переменному току, нарастающее при увеличении частоты, поскольку при изменении тока в катушке возникает ЭДС самоиндукции, препятствующая этому изменению.

Более детально о принципе работы катушек индуктивности вы можете почитать на сайте.

Для чего вы можете использовать их?

Я почти никогда не использую катушки индуктивности. Главным образом потому, что я работаю в основном с цифровыми схемами. Но я использовал их иногда для создания фильтров, генераторов и блоков питания.

Вы часто найдете катушки индуктивности в аналоговой электронике переменного тока, такой как радиооборудование.

Катушка индуктивности в цепи переменного тока

Принцип работы

Чтобы понять принцип действия катушки индукции, следует знать:

• вокруг движущихся электрически заряженных частиц (электрический ток) возникает электромагнитное поле. Если проводник с протекающим током смотан в катушку, поле многократно усиливается. Еще большим оно становится при использовании металлического сердечника, что объясняется высокой магнитопроницаемостью металлов по сравнению с воздухом;
• переменное магнитное поле наводит в проводнике ЭДС (закон электромагнитной индукции, открытый М. Фарадеем).

Способность катушки превращать электрическую энергию в магнитное поле, называется индуктивностью. Она измеряется в генри (Гн), в формулах обозначается литерой L. Катушка индуктивностью в 1 Гн при изменении силы тока со скоростью dI = 1 А/с (ампер в секунду) создает ЭДС в 1 В. Индуктивность катушки зависит от ее длины, потому шаг витков стремятся делать как можно меньшим.

Сердечник в катушке может быть регулируемым, тогда элемент имеет переменную индуктивность. Также применяют катушки вовсе без сердечника. Если катушка включена в цепь постоянного тока, то весь эффект от нее состоит в создании электромагнитного поля. Так устроены, например, электрические магниты для захвата металлолома, устанавливаемые на погрузочных кранах.

При проведении эксперимента надо ограничить ток в цепи, посредством включенной последовательно с катушкой нагрузки, иначе возникнет короткое замыкание.

Мощность в индукторе

Мы знаем, что индуктор в цепи противостоит потоку тока I через него, потому что поток этого тока индуцирует ЭДС, которая противостоит ему, закон Ленца. Затем необходимо выполнить работу от внешнего источника батареи, чтобы ток протекал против этой индуцированной ЭДС. Мгновенная мощность, используемая для форсирования тока I по отношению к этой самоиндуцированной ЭДС (V _L), определяется как:

Мощность в цепи задается как P = V * I, поэтому:

Идеальный индуктор не имеет сопротивления, только индуктивность, поэтому R = 0 Ом, и поэтому мощность в катушке не рассеивается, поэтому можно сказать, что идеальный индуктор имеет нулевую потерю мощности.

Обзор пассивных компонентов

Современная радиоэлектронная аппаратура (РЭА) содержит огромное количество электрорадиокомпонентов, т.е. самостоятельных  изделий, выполняющих определенные функции. Электрорадиоэлементы подразделяют на активные и пассивные. К активным относятся транзисторы,  микросхемы ,электронные лампы и т.д., т. е. элементы, способные усиливать или преобразовывать электрические сигналы. К пассивным относятся резисторы, катушки индуктивности, конденсаторы, трансформаторы, коммутационные элементы, т. е. такие элементы, которые предназначены для перераспределения электрической энергии.

Сетевая инфраструктура современного офиса состоит из множества составляющих, правильный выбор которых имеет существенное значение для успешной работы всей инфраструктуры в целом. Пассивные компоненты  играют при этом также немаловажную  роль, обеспечивают среде передачу данных, а также внешний вид, эстетику. Пассивным элементом схемы называется элемент, не имеющий внутренних источников энергии, и выполняющий либо накопление энергии (конденсатор, индуктивность), либо ее рассеяние (резистор).

Пассивные компоненты по сути соответствует пассивному элементу схемы. Пассивные компоненты характеризуются малыми размерами, малым числом выводов (как правило, два-три), низкой стоимостью и, как правило, достаточно высокой стойкостью к воздействиям при сборке узлов. Пассивные элементы могут выступать как дискретные компоненты и как элементы интегральных микросхем. В РЭА интегральные микросхемы  имеют очень большой удельный вес, но пассивные компоненты являются все же самыми распространенными изделиями электронной промышленности.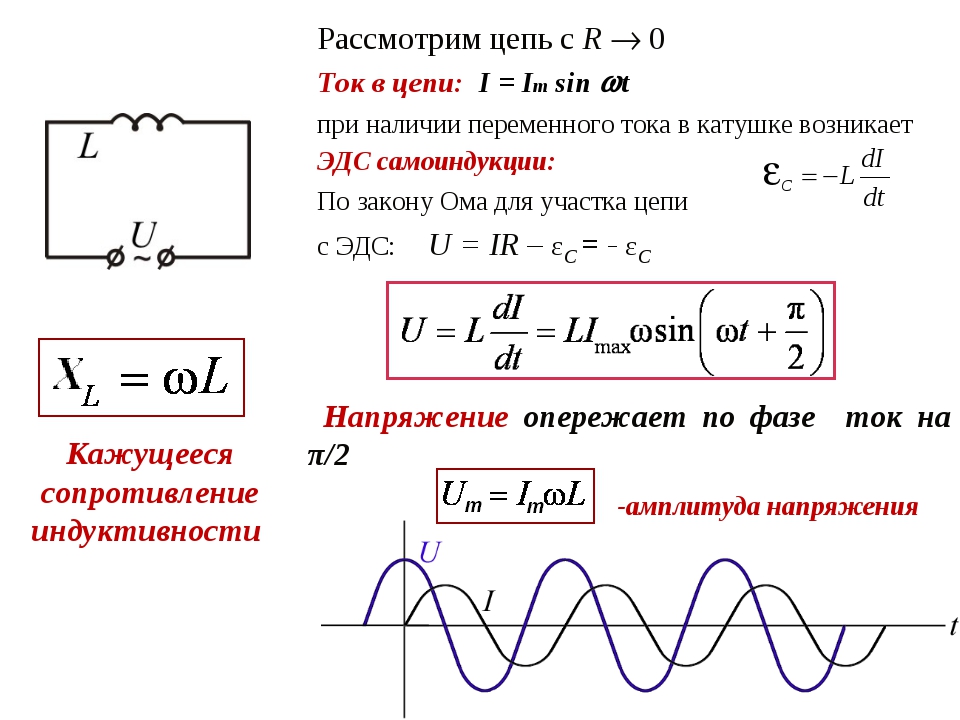 Это можно объяснить  тем, что некоторые элементы трудно выполнить в микросхемном исполнении. Практически невозможно в ИМС изготовить конденсаторы большой емкости, резисторы с большим сопротивлением, сложности в разработке интегральных катушек индуктивности и трансформаторов. Кроме того технические характеристики дискретных элементов лучше, чем интегральных.

Катушки индуктивности разных размеров

Предыдущая
РадиодеталиЧто такое подстроечный резистор: описание устройства и область его применения
Следующая
РадиодеталиДроссели в электрике: что это и где используются?

Назначение и принцип действия

Специалисты задаются вопросом, зачем нужна токовая катушка индуктивности в цепи, и для этого необходимо разобраться в показателях. Коэффициент ЭДС (электродвижущая сила) показывает разницу между энергией и магнитным потоком. Устройства самоиндукции способны влиять на изменения в цепи. Чаще всего дроссели применяются в силовых установках. Они способны контролировать уровень напряжения, не допускают разрыва цепи.

Устройства самоиндукции

Также компоненты устанавливаются на пару с конденсаторами либо резисторами. Благодаря работе катушки фильтры находятся в безопасности. Теперь вызывает интерес, как включается индукционная катушка. Принцип работы построен на изоляции проводников. В конструкции используется электрический каркас с различным сечением. За счёт намоток обеспечивается распределение ёмкости на дросселе.

Интересно! Витки наматываются с определенным шагом, многое зависит от типа катушки.

Свойства катушки индуктивности

Свойства катушки индуктивности:

• Скорость изменения тока через катушку ограничена и определяется индуктивностью катушки.
• Сопротивление (модуль импеданса) катушки растет с увеличением частоты текущего через неё тока.
• Катушка индуктивности при протекании тока запасает энергию в своём магнитном поле. При отключении внешнего источника тока катушка отдаст запасенную энергию, стремясь поддержать величину тока в цепи. 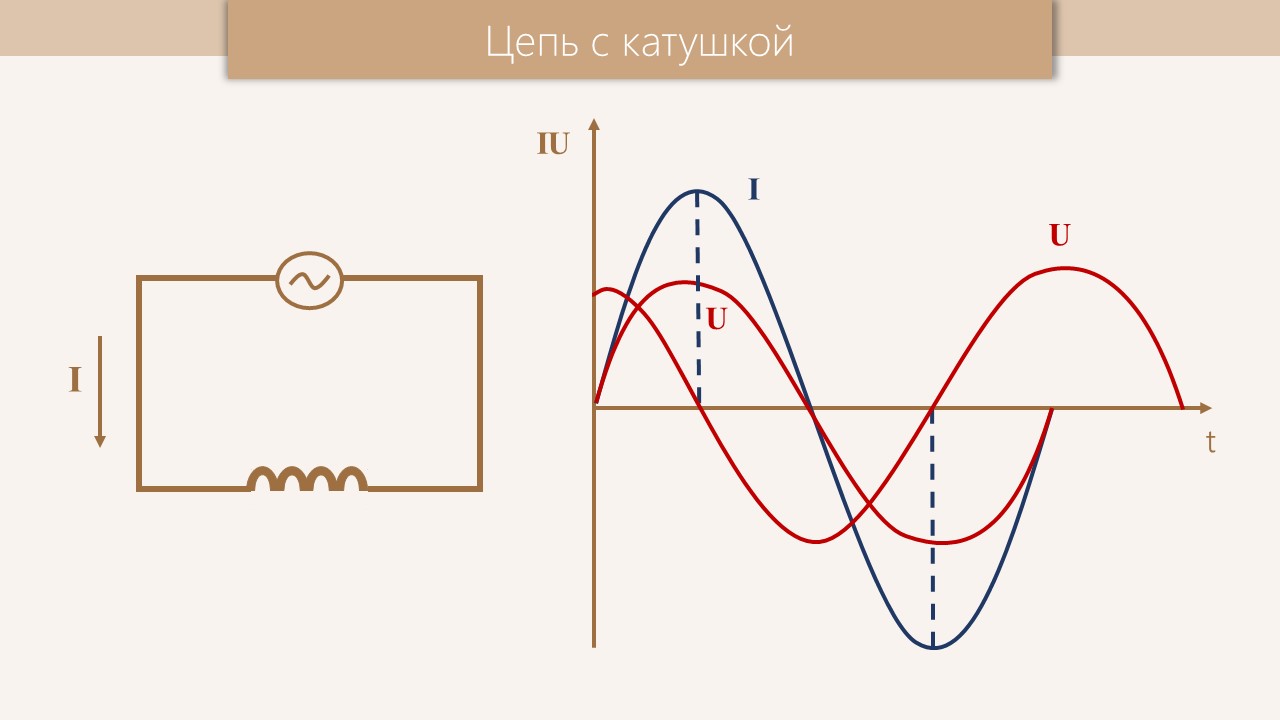При этом напряжение на катушке нарастает, вплоть до пробоя изоляции или возникновения дуги на коммутирующем ключе.

Катушка индуктивности в электрической цепи для переменного тока имеет не только собственное омическое (активное) сопротивление, но и реактивное сопротивление переменному току, нарастающее при увеличении частоты, поскольку при изменении тока в катушке возникает ЭДС самоиндукции, препятствующая этому изменению.

Катушка индуктивности обладает реактивным сопротивлением, модуль которого XL=ωL{\displaystyle X_{L}=\omega L}, где L{\displaystyle L} — индуктивность катушки, ω{\displaystyle \omega } — циклическая частота протекающего тока. Соответственно, чем больше частота тока, протекающего через катушку, тем больше её сопротивление.

Катушка с током запасает энергию в магнитном поле, равную работе, которую необходимо совершить для установления текущего тока I{\displaystyle I}. Эта энергия равна:

Векторная диаграмма в виде комплексных амплитуд для идеальной катушки индуктивности в цепи синусоидального напряжения

Катушка индуктивности в переменном напряжении — аналог подверженного механическим колебаниям тела с массой. {2}{\mbox{.}}}

При изменении тока в катушке возникает ЭДС самоиндукции, значение которой:

ε=−LdIdt.{\displaystyle \varepsilon =-L{dI \over dt}{\mbox{.}}}

Для идеальной катушки индуктивности (не имеющей паразитных параметров) ЭДС самоиндукции равна по модулю и противоположна по знаку напряжению на концах катушки:

|ε|=−ε=U.{\displaystyle |\varepsilon |=-\varepsilon =U{\mbox{.}}}

При замыкании катушки с током на резистор происходит переходной процесс, при котором ток в цепи экспоненциально уменьшается в соответствии с формулой:

I=Iexp(−tT),{\displaystyle I=I_{0}exp(-t/T){\mbox{,}}}

где : I{\displaystyle I} — ток в катушке,

I{\displaystyle I_{0}} — начальный ток катушки,

t{\displaystyle t} — текущее время,

T{\displaystyle T} — постоянная времени.

Постоянная времени выражается формулой:

T=L(R+Ri),{\displaystyle T=L/(R+R_{i}){\mbox{,}}}

где R{\displaystyle R} — сопротивление резистора,

Ri{\displaystyle R_{i}} — омическое сопротивление катушки.

При закорачивании катушки с током процесс характеризуется собственной постоянной времени Ti{\displaystyle T_{i}} катушки:

Ti=LRi.{\displaystyle T_{i}=L/R_{i}{\mbox{.}}}

При стремлении Ri{\displaystyle R_{i}} к нулю, постоянная времени стремится к бесконечности, именно поэтому в сверхпроводящих контурах ток течёт «вечно».

В цепи синусоидального тока, ток в катушке по фазе отстаёт от фазы напряжения на ней на π/2.

Явление самоиндукции аналогично проявлению инертности тел в механике, если аналогом индуктивности принять массу, тока — скорость, напряжения — силу, то многие формулы механики и поведения индуктивности в цепи принимают похожий вид:

F =mdvdt{\displaystyle F\ =m{dv \over dt}} |ε|=LdIdt{\displaystyle |\varepsilon |=L{dI \over dt}},

где

F {\displaystyle F\ } |ε|{\displaystyle |\varepsilon |} U {\displaystyle U\ } ; m {\displaystyle m\ } L {\displaystyle L\ } ; dv {\displaystyle dv\ } dI {\displaystyle dI\ }

Ecoxp=12LI2{\displaystyle E_{\mathrm {coxp} }={1 \over 2}LI^{2}} Ekinet=12mv2{\displaystyle E_{\mathrm {kinet} }={1 \over 2}mv^{2}}

Ток и напряжение в индукторе

Сколько индуктивного напряжения будет генерироваться индуктором, зависит от скорости изменения тока.  В нашем уроке об электромагнитной индукции закон Ленца гласил: «Направление индуцированной ЭДС таково, что оно всегда будет противостоять изменению, которое его вызывает». Другими словами, индуцированная ЭДС всегда будет противопоставлять движение или изменение, которые изначально вызвали индуцированную ЭДС.

Таким образом, при уменьшении тока полярность напряжения будет действовать как источник, а при увеличении тока полярность напряжения будет действовать как нагрузка. Таким образом, при одинаковой скорости изменения тока через катушку, увеличение или уменьшение величины индуцированной ЭДС будет одинаковым.

Конструкция

Конструктивно выполняется в виде винтовых или винтоспиральных (диаметр намотки изменяется по длине катушки) катушек однослойных или многослойных намоток изолированного одножильного или многожильного (литцендрат) проводника на диэлектрическом каркасе круглого, прямоугольного или квадратного сечения, часто на тороидальном каркасе или, при использовании толстого провода и малом числе витков — без каркаса. Иногда, для снижения распределённой паразитной ёмкости, при использовании в качестве высокочастотного дросселя однослойные катушки индуктивности наматываются с «прогрессивным» шагом — шаг намотки плавно изменяется по длине катушки.
Намотка может быть как однослойной (рядовая и с шагом), так и многослойной (рядовая, внавал, типа «универсал»). Намотка «универсал» имеет меньшую паразитную ёмкость. Часто, опять же, для снижения паразитной ёмкости, намотку выполняют секционированной, группы витков отделяются пространственно (обычно по длине) друг от друга.

Для увеличения индуктивности катушки часто снабжают замкнутым или разомкнутым ферромагнитным сердечником. Дроссели подавления высокочастотных помех имеют ферродиэлектрические сердечники: ферритовые, флюкстроловые, из карбонильного железа. Дроссели, предназначенные для сглаживания пульсаций промышленной и звуковой частот, имеют сердечники из электротехнических сталей или магнитомягких сплавов (пермаллоев). Также сердечники (в основном ферромагнитные, реже диамагнитные) используют для изменения индуктивности катушек в небольших пределах путём изменения положения сердечника относительно обмотки. На сверхвысоких частотах, когда ферродиэлектрики теряют свою магнитную проницаемость и резко увеличивают потери, применяются металлические (латунные) сердечники.

На печатных платах электронных устройств также иногда делают плоские «катушки» индуктивности: геометрия печатного проводника выполняется в виде круглой или прямоугольной спирали, волнистой линии или в виде меандра. Такие «катушки индуктивности» часто используются в сверхбыстродействующих цифровых устройствах для выравнивания времени распространения группы сигналов по разным печатным проводникам от источника до приемника, например, в шинах данных и адреса.

Терминология

Стандартизированные термины:

Индуктивная катушка — элемент электрической цепи, предназначенный для использования его индуктивности (ГОСТ 19880-74, см. термин 106).

Катушка индуктивности — индуктивная катушка, являющаяся элементом колебательного контура и предназначенная для использования её добротности (ГОСТ 20718-75, см. термин 1).

Электрический реактор — индуктивная катушка, предназначенная для использования её в силовой электрической цепи (ГОСТ 18624-73, см. термин 1). Одним из видов реактора является токоограничивающий реактор, например, для ограничения тока короткого замыкания ЛЭП.

При использовании для подавления помех, сглаживания пульсаций электрического тока, изоляции (развязки) по высокой частоте разных частей схемы и накопления энергии в магнитном поле сердечника часто называют дросселем, а иногда реактором. Стоит отметить, что такое толкование нестандартизированного термина «дроссель» (являющегося калькой с нем. Drossel) пересекается со стандартизированными терминами. В случае если работа данного элемента цепи основана на добротности катушки, то такой элемент следует называть «катушкой индуктивности», в противном случае «индуктивной катушкой».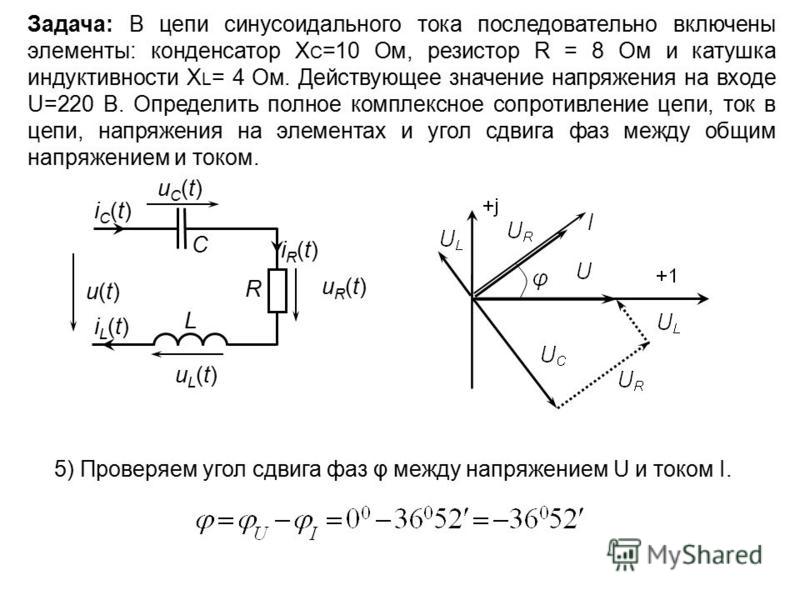

Цилиндрическую катушку индуктивности, длина которой намного превышает диаметр, называют соленоидом, магнитное поле внутри длинного соленоида однородно. Кроме того, зачастую соленоидом называют устройство, выполняющее механическую работу за счёт магнитного поля при втягивании ферромагнитного сердечника, или электромагнитом. В электромагнитных реле называют обмоткой реле, реже — электромагнитом.

Нагревательный индуктор — специальная катушка индуктивности, рабочий орган установок индукционного нагрева.

При использовании для накопления энергии (например, в схеме импульсного стабилизатора напряжения) называют индукционным накопителем или накопительным дросселем.

Самоиндукция

Катушка индуктивности обладает также очень интересным свойством. При подаче на катушку постоянного напряжения, в катушке возникает на короткий промежуток времени противоположное напряжение.

Это противоположное напряжение называется ЭДС самоиндукции. Эта ЭДС зависит от значения индуктивности катушки. Поэтому, в момент подачи напряжения на катушку сила тока в течение долей секунд плавно меняет свое значение от 0 до некоторого значения, потому что напряжение, в момент подачи электрического тока, также меняет свое значение от ноля и до установившегося значения. Согласно Закону Ома:

где

I – сила тока в катушке , А 

U – напряжение в катушке, В 

 R – сопротивление катушки, Ом

Как мы видим по формуле, напряжение меняется от нуля и до напряжения, подаваемого в катушку, следовательно и ток тоже будет меняться от нуля и до какого то значения. Сопротивление катушки для постоянного тока также постоянное.

И второй феномен в катушке индуктивности заключается в том, что если мы разомкнем цепь катушка индуктивности – источник тока, то у нас ЭДС самоиндукции будет суммироваться к напряжению, которое мы уже подали на катушку.

То есть как только мы разрываем цепь, на катушке напряжение в этот момент может быть  в разы больше, чем было до размыкания  цепи, а сила тока в цепи катушки будет тихонько падать, так как ЭДС самоиндукции будет поддерживать убывающее напряжение.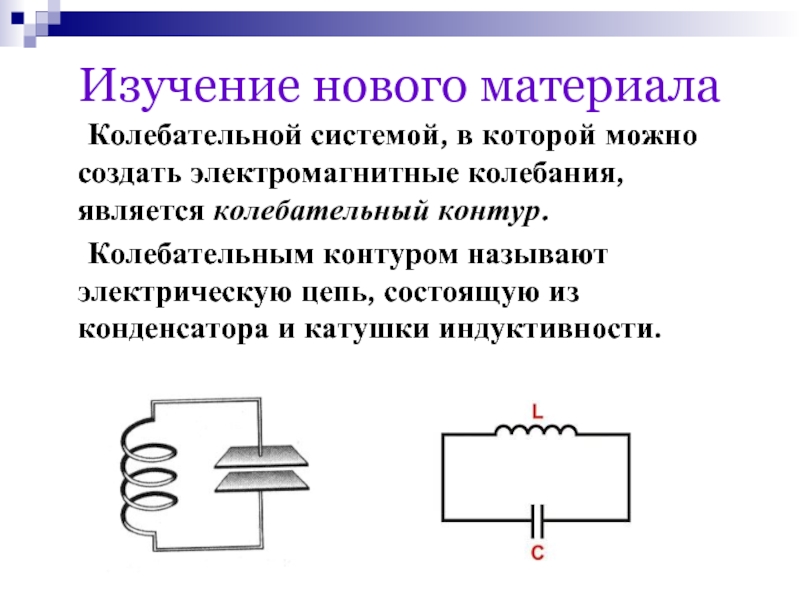

Сделаем первые выводы о работе катушки индуктивности при подаче на нее постоянного тока. При подаче на катушку электрического тока, сила тока будет плавно увеличиваться, а при снятии электрического тока с катушки, сила тока будет плавно убывать до нуля. Короче говоря, сила тока в катушке мгновенно измениться не может.

Маркировка

При рассмотрении катушек индуктивности оценивается цветовая и кодовая маркировка. Если смотреть на первые цифры, отображается показатель индуктивности. Далее учитывается параметр отклонения:

• Серебряный 0,01 мкГн, 10%.
• Золотой 0,1 мкГн, 5%.
• Черный 0,1мкГн, 20%.
• Коричневый 1,1 мкГн.
• Красный 2, 2 мкГн.
• Оранжевый 1 мкГн.
• Желтый 4 мкГн.
• Зеленый 5 мкГн.
• Голубой 6 мкГн.
• Фиолетовый 7мкГн.
• Серый 8 мкГн.
• Белый 9 мкГн.

Маркировка

В нестабильной цепи переменного электрического тока не обойтись без катушки индуктивности. Выше описаны основные типы изолированных проводников, продемонстрированы их параметры. Учитывается уровень частоты, а также свойства.

Приветствую всех на нашем сайте!

Мы продолжаем изучать электронику с самого начала, то есть с самых основ и темой сегодняшней статьи будет принцип работы и основные характеристики катушек индуктивности. Забегая вперед скажу, что сначала мы обсудим теоретические аспекты, а несколько будущих статей посвятим целиком и полностью рассмотрению различных электрических схем, в которых используются катушки индуктивности, а также элементы, которые мы изучили ранее в рамках нашего курса – резисторы и конденсаторы.

Катушка индуктивности в цепи переменного тока.

Рассмотрим цепь, в которой на катушку индуктивности подается переменный ток:

Давайте посмотрим на зависимости тока и ЭДС самоиндукции от времени, а затем уже разберемся, почему они выглядят именно так:

Как мы уже выяснили ЭДС самоиндукции у нас прямо пропорциональна и противоположна по знаку скорости изменения тока:

Собственно, график нам и демонстрирует эту зависимость Смотрите сами – между точками 1 и 2 ток у нас изменяется, причем чем ближе к точке 2, тем изменения меньше, а в точке 2 в течении какого-то небольшого промежутка времени ток и вовсе не изменяет своего значения.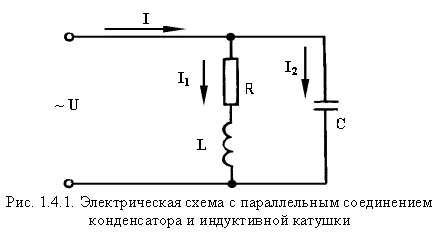 Соответственно скорость изменения тока максимальна в точке 1 и плавно уменьшается при приближении к точке 2, а в точке 2 равна 0, что мы и видим на графике ЭДС самоиндукции. Причем на всем промежутке 1-2 ток возрастает, а значит скорость его изменения положительна, в связи с этим на ЭДС на всем этом промежутке напротив принимает отрицательные значения.

Аналогично между точками 2 и 3 – ток уменьшается – скорость изменения тока отрицательная и увеличивается – ЭДС самоиндукции увеличивается и положительна. Не буду расписывать остальные участки графика – там все процессы протекают по такому же принципу

Кроме того, на графике можно заметить очень важный момент – при увеличении тока (участки 1-2 и 3-4) ЭДС самоиндукции и ток имеют разные знаки (участок 1-2: 0″ title=»Rendered by QuickLaTeX.com» />, участок 3-4: 0″ title=»Rendered by QuickLaTeX.com» />,

Где – круговая частота: . – это частота переменного тока.

Таким образом, чем больше частота тока, тем большее сопротивление будет ему оказывать катушка индуктивности. А если ток постоянный ( = 0), то реактивное сопротивление катушки равно 0, соответственно, она не оказывает влияния на протекающий ток.

Давайте вернемся к нашим графикам, которые мы построили для случая использования катушки индуктивности в цепи переменного тока. Мы определили ЭДС самоиндукции катушки, но каким же будет напряжение ? Здесь все на самом деле просто По 2-му закону Кирхгофа:

А следовательно:

Построим на одном графике зависимости тока и напряжения в цепи от времени:

Как видите ток и напряжение сдвинуты по фазе (ссылка) друг относительно друга, и это является одним из важнейших свойств цепей переменного тока, в которых используется катушка индуктивности:

При включении катушки индуктивности в цепь переменного тока в цепи появляется сдвиг фаз между напряжением и током, при этом ток отстает по фазе от напряжения на четверть периода.

Вот и с включением катушки в цепь переменного тока мы разобрались

На этом, пожалуй, закончим сегодняшнюю статью, она получилась уже довольно объемной, поэтому дальнейший разговор о катушках индуктивности мы будем вести в следующий раз. Так что до скорых встреч, будем рады видеть вас на нашем сайте!

В данной статье мы подробно рассмотрим индуктор. Отдельно разберем индуктор на схеме, обратную ЭДС генерируемую индуктором, постоянную времени индуктора, ток и напряжение в индукторе, а так же мощность и энергию в индукторе.

Реальная катушка в цепи переменного тока

Реальная катушка в отличии от идеальной имеет не только индуктивность, но и активное сопротивление, поэтому при протекании переменного тока в ней сопровождается не только изменением энергии в магнитном поле, но и преобразованием электрической энергии в другой вид. В частности, в проводе катушки электрическая энергия преобразуется в тепло в соответствии с законом Ленца — Джоуля.

Ранее было выяснено, что в цепи переменного тока процесс преобразования электрической энергии в другой вид характеризуется активной мощностью цепи Р, а изменение энергии в магнитном поле — реактивной мощностью Q.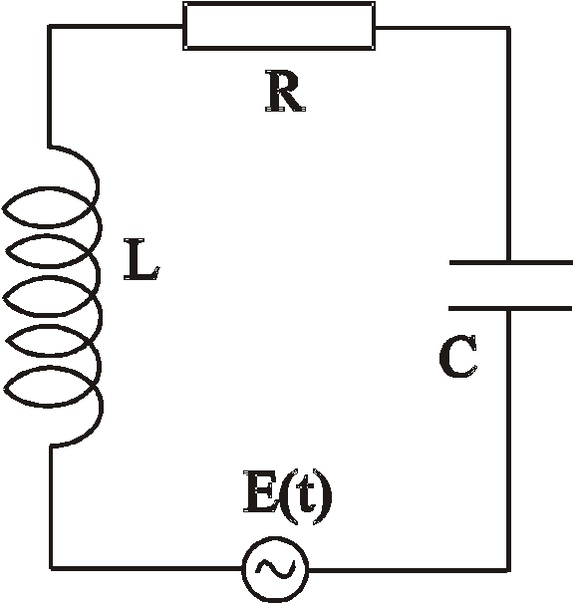

В реальной катушке имеют место оба процесса, т. е. ее активная и реактивная мощности отличны от нуля. Поэтому одна реальная катушка в схеме замещения должна быть представлена активным и реактивным элементами.

Схема замещения катушки с последовательным соединением элементов

В схеме с последовательным соединением элементов реальная катушка характеризуется активным сопротивлением R и индуктивностью L.

Активное сопротивление определяется величиной мощности потерь

R = P/I²

а индуктивность — конструкцией катушки. Предположим, что ток в катушке (рис. 13.9, а) выражается уравнением i = I_msinωt. Требуется определить напряжение в цепи и мощность.
При переменном токе в катушке возникает э. д. с. самоиндукции e_L поэтому ток зависит от действия приложенного напряжения и эдс e_L. Уравнение электрического равновесия цепи, составленное по второму закону Кирхгофа, имеет вид:

Приложенное к катушке напряжение состоит из двух слагаемых,одно из которых u_R равно падению напряжения в активном сопротивлении, а другое u_L уравновешивает эдс самоиндукции.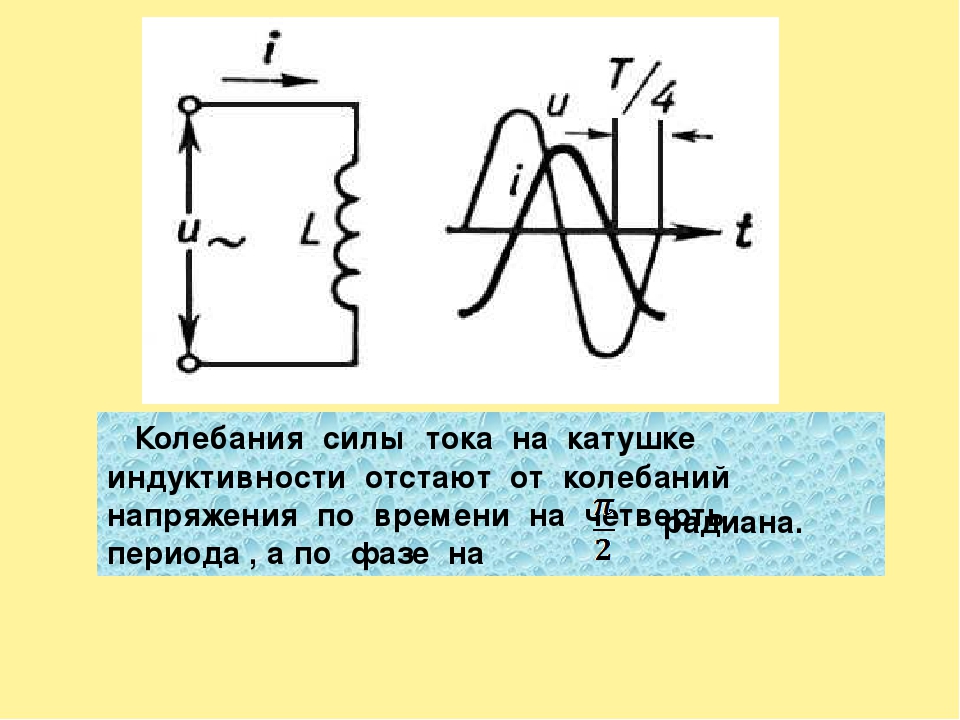

В соответствии с этим катушку в схеме замещения можно представить активным и индуктивным сопротивлениями, соединенными последовательно (рис. 13.9, б).
Дополнительно заметим, что оба слагаемых в правой части равенства (13.12) являются синусоидальными функциями времени. Согласно выводам полученных в этих предыдущих двух (первая, вторая) статьях получим — u_R совпадает по фазе с током, U_L опережает ток на 90°.

Поэтому:

u = R*I_msinωt  + ωLI_msin(ωt+π/2).

Векторная диаграмма реальной катушки и полное её сопротивление

Несовпадение по фазе слагаемых в выражении (13.12) затрудняет определение амплитуды и действующей величины приложенного к цепи напряжения U. Поэтому воспользуемся векторным способом сложения синусоидальных величин. Амплитуды составляющих общего напряжения

U_mR = RI_m;       U_mL = ωLI_m ,

а действующие величины

U_R = RI; U_L = X_LI .

Вектор общего напряжения

U = U_R + U_L

Для того чтобы найти величину вектора U, построим векторную диаграмму (рис. 13.10, а), предварительно выбрав масштабы тока Mi и напряжения Мu.

За исходный вектор диаграммы принимаем вектор тока I. Направление этого вектора совпадает с положительным направлением оси, от которой отсчитываются фазовые углы (начальная фаза заданного тока Ψi =0). Как и ранее, эту ось удобно (но не обязательно) направить по горизонтали.

Вектор U_R по направлению совпадает с вектором тока I, а вектор U_L направлен перпендикулярно вектору I с положительным углом.

Из диаграммы видно, что вектор тока I общего напряжения U отражает вектор тока I на угол φ>0, но φ<90°, а по величине равен гипотенузе прямоугольного треугольника, катетами которого являются векторы падений напряжения в активном и индуктивном сопротивлениях U_R и U_L :

U_R = Ucosφ 

Проекция вектора напряжения U на направление вектора тока называется активной составляющей вектора напряжения и обозначается U_a. Для катушки по схеме рис. 13.9 при U_a = U_R

U = Usinφ                                                        (13.14)

Проекция вектора напряжения U на направление, перпендикулярное вектору тока, называется реактивной составляющей вектора напряжения и обозначается U_p. Для катушки U_p = U_L

 

 

 

При токе i = Imsinωt уравнение напряжения можно записать на основании векторной диаграммы в виде

U = U_msin(ωt+φ)

Стороны треугольника напряжений, выраженные в единицах напряжения, разделим на ток I. Получим подобный треугольник сопротивлений (рис. 13.10, б), катетами которого являются активное R = U_R/I и индуктивное X_L = U_L/I, сопротивления, а гипотенузой величина Z = U/I.

Отношение действующего напряжения к действующему току данной цепи называется полным сопротивлением цепи.
Стороны треугольника сопротивлений нельзя считать векторами, так как сопротивления не являются функциями времени.
Из треугольника сопротивлений следует

 

 

Понятие о полном сопротивлении цепи Z позволяет выразить связь между действующими величинами напряжения и тока формулой, подобной формуле Ома:

 

 

Из треугольников сопротивления и напряжения определяются

cosφ = U_R/U = R/Z;    sinφ = U_L/U = X_L/Z;    tgφ = U_L/U_R = X_L/R. (13.18)

Мощность реальной катушки

Мгновенная мощность катушки

p = ui = U_msin(ωt+φ) * I_msinωt

Из графика мгновенной мощности (рис. 13.11) видно, что в течение периода мощность четыре раза меняет знак; следовательно, направление потока энергии и в данном случае в течение периода меняется. Относительно некоторой оси t’, сдвинутой параллельно оси t на величину Р, график мгновенно мощности является синусоидальной функцией двойной частоты.
При положительном значении мощности энергия переходит от источника в приемник, а при отрицательном — наоборот. Нетрудно заметить, что количество энергии, поступившей в приемник (положительная площадь), больше возвращенной обратно (отрицательная площадь).

Следовательно, в цепи с активным сопротивлением и индуктивностью часть энергии, поступающей от генератора, необратимо превращается в другой вид энергии, но некоторая часть возвращается обратно. Этот процесс повторяется в каждый период тока, поэтому в цепи наряду с непрерывным превращением электрической энергии в другой вид энергии (активная энергия) часть ее совершает колебания между источником и приемником (реактивная энергия).

Скорость необратимого процесса преобразования энергии оценивается средней мощностью за период, или активной мощностью Р, скорость обменного процесса характеризуется реактивной мощностью Q.

Согласно выводам полученных в этих предыдущих  (первая, вторая) статьях — в активном сопротивлении P = U_RI   Q = 0;  а в индуктивном Р = 0; Q = U_LI. 

Активная мощность всей цепи равна активной мощности в сопротивлении R, а реактивная — реактивной мощности в индуктивном сопротивлении X_L. Подставляя значения U_R = Ucosφ и U_L = Usinφ, определяемые из треугольника напряжений по формулам (13.18), получим:

                   P = UIcosφ                                (13.19)

                    Q = UIsinφ                                (13.20)

Кроме активной и реактивной мощностей пользуются понятием полной мощности S, которая определяется произведением действующих величин напряжения и тока цепи;

                   S = UI = I²Z                                (13.21)

Величину полной мощности можно получить из выражения (13.22), которое легко доказать на основании формул (13.19) и (13.20):

                        (13.22)                         

Мощности S, Р, Q графически можно выразить сторонами прямоугольного треугольника (см. рис. 13.10, в). Треугольник мощностей получается из треугольника напряжений, если стороны последнего, выраженные в единицах напряжения, умножить на ток. Из треугольника мощностей можно определить

cosφ = P/S;       sinφ = Q/S;     tgφ = Q/P.             (13.23)

Полная мощность имеет ту же размерность, что Р и Q, но для различия единицу полной мощности называют вольт-ампер (В · А).

Активная мощность Р меньше или равна полной мощности цепи.
Отношение активной мощности цепи к ее полной мощности P/S =
= cosφ называют коэффициентом мощности.

Назначение приемников электрической энергии — преобразование
ее в другие виды энергии. Поэтому колебания энергии в цепи не только
бесполезны, но и вредны, так как при этом в приемнике не совершается
полного преобразования электрической энергии в работу или тепло,
а в соединительных проводах она теряется.

Схема замещения реальной катушки с параллельным соединением элементов

Для реальной катушки можно составить и другую расчетную схему — с параллельным соединением двух ветвей: с активной G и индуктивной B_L проводимостями. На рис. 13.12, б эта схема показана в сравнении со схемой последовательного соединения активного и индуктивного сопротивлений (рис. 13.12, а), рассмотренной ранее.
Покажем, что схемы рис. 13.12, а, б эквивалентны в том смысле, что при одинаковом напряжении сохраняются неизменными ток в неразветвленной части цепи, активная и реактивная мощности.

Вектор тока I можно разложить на две взаимно перпендикулярные составляющие и в соответствии со схемой и векторной диаграммой на рис. 13.12, б выразить векторным равенством

                                             I = I_G + I_L                                           (13.24)

Для схемы параллельного соединения активного и индуктивного элементов общим является приложенное напряжение, а токи разные: I_G —ток в ветви с активной проводимостью, по фазе совпадает с напряжением; I_L — ток в ветви с индуктивной проводимостью, по фазе отстает от напряжения на угол 90°.

Вектор тока I и его составляющие I_G и I_L образуют прямоугольный треугольник, поэтому

Составляющая тока в активном элементе

I_G = Icosφ

Проекция вектора тока I на направление напряжения называется активной составляющей вектора тока и обозначается I_а. Для катушки по схеме на рис. 13.12, б I_a = I_G.

Составляющая тока в реактивном элементе

I_L = Isinφ

Проекция вектора тока I на направление, перпендикулярное вектору напряжения, называется реактивной составляющей вектора тока и обозначается Iр. Для катушки I_р = I_L .

Стороны треугольника токов, выраженные в единицах тока, можно разделить на напряжение U и получить подобный треугольник проводимостей, катетами которого являются активная G = I_G/U и индуктивная В_L = I_L/U проводимости, а гипотенузой — величина Y = I/U, называемая полной проводимостью цепи.

Из треугольника проводимостей и с учетом ранее полученных выражений из треугольника сопротивлений получим

Катушка индуктивности на схеме — Весёлый Карандашик

2013, Апрель 3 , Среда

Самая простая электрическая цепь, состоящая  из электрического проводника в виде обычного изолированного провода, и источника переменного тока, представляющего собой понижающий трансформатор, подключённый к бытовой электрической сети, будет примером для описания в этом материале.

В электрической цепи, в которой протекает переменный ток, на величину этого проходящего электрического тока влияет и сопротивление проводника, включённого в цепь, и  магнитное поле вокруг проводника, создаваемого при прохождении тока через этот проводник. Получается, что электрическая цепь с переменным током обладает ещё и своими магнитными свойствами, характеризующими величиной, какой является индуктивность. В данном случае —  это индуктивность проводника или всей электрической цепи.

Доступными словами будет сказано, чем больше по величине проходящий через проводник переменный ток, тем больше по величине будет создаваемое вокруг этого же проводника переменное магнитное поле.

Но не все проводники обладают одинаковой электрической проводимостью. Каждый материал, используемый для изготовления проводника, обладает своими свойствами, от которых зависит и величина сопротивления электрическому току, называемая активным сопротивлением проводника, и величина индуктивного сопротивления, определяемое индуктивностью проводника, то есть своими магнитными свойствами.

Электрический дроссель.

У прямого проводника сопротивление переменному току, создаваемое магнитным полем проводника, индуктивность небольшая. А если этот же проводник свернуть в катушку, то его индуктивность сразу и на много увеличится. Увеличится его индуктивное сопротивление переменному току и электрический ток в такой цепи уменьшится. Для переменного тока индуктивность полученной катушки является преградой и вокруг катушки образуется электромагнитное поле, величина которого будет зависеть от силы проходящего через катушку переменного тока. А для постоянного тока индуктивность не оказывает такого влияния, как для переменного тока, а определяет своё влияние только лишь активным сопротивлением проводника. Получается, что индуктивная катушка, обладающая большим сопротивлением для переменного тока и очень малым сопротивлением постоянному, будет характеризовать устройство, именуемое электрическим дросселем.

Любой электрический проводник, свёрнутый в катушку, в действующей электрической цепи с переменным током будет представлять собой катушку индуктивности, выполняющую роль  дросселя, вариометра(изменяющего индуктивность) или реактора и зависеть от величины и частоты проходящего через катушку тока.

Единицой индуктивности является генри(Гн).

Графическое изображение индуктивных элементов на схеме.

Катушки индуктивности могут иметь винтовую, спиральную или винтоспиральную намотку из изолированного проводника и иметь значительную индуктивность и малое активное сопротивление и малую электрическую ёмкость. Катушки наматываются на каркас с использованием сердечников или без них.

Волнообразная линия, нарисованная параллельно рисунку сердечника или без него и есть наш катушка индуктивности. Напоминает изображение части электрического трансформатора.

Так же как у трансформатора указывается начало обмотки толстой жирной точкой и указывается сердечник, если имеется, а вот обозначается на схеме буквой (L). Рядом устанавливается дополнительный буквенный символ, в зависимости от типа дросселя : L — LL(дроссель ламп люминесцентного освещения), G — LG(реактор), R — LR(обмотка возбуждения генератора).

Катушка индуктивности сама по себе является конструктивной составляющей единицей устройства, а дроссель, вариометр, реактор — это уже целая функционирующая единица устройства, конструкция которого определяется его назначением. То есть, используемая в электросхеме индуктивная  катушка в действующей цепи будет являться или дросселем или реактором или вариометром. В неработающей системе катушка индуктивности  будет только катушкой и не больше.  Это моё мнение и его никому не навязываю, только лишь делюсь.

---

«Катушка индуктивности на схеме»

Катушки индуктивности могут иметь винтовую, спиральную или винтоспиральную намотку из изолированного проводника и иметь значительную индуктивность и малое активное сопротивление и малую электрическую ёмкость. Катушки наматываются на каркас с использованием сердечников или без них. Волнообразная линия, нарисованная параллельно рисунку сердечника или без него и есть наш катушка индуктивности. Напоминает изображение части электрического трансформатора.

Игорь Александрович

«Весёлый Карандашик»

Резистор, индуктивная катушка и конденсатор в цепи синусоидального тока

Лекция № 4 Резистор, индуктивная катушка и конденсатор в цепи синусоидального тока.

Термин «сопротивление» для цепей переменного тока, оказывается недостаточно полным, поскольку сопротивление переменному току оказывают не только те элементы цепи, в которых выделяется энергия в виде теплоты (их называют активными сопротивлениями), но и те элементы цепи, в которых энергия периодически запасается в электрическом или магнитном полях. Такие элементы цепи называют реактивными сопротивлениями. Реактивными сопротивлениями обладают индуктивности и емкости.

Активное сопротивление в цепи синусоидального тока.

Если по активному сопротивлению течет ток тогда

по закону Ома

или

где

Т. е. в активном сопротивлении элемента цепи комплекс тока совпадает с комплексом напряжения

Рис. 4.1 – Графики мгновенных значений

Мгновенная мощность

=

или

т. е. мгновенная мощность имеет постоянную составляющую и переменную составляющую меняющуюся с частотой равной (на рис. 4.1)

Индуктивность в цепи переменного синусоидального тока.

Практически любая обмотка (катушка) обладает некоторой индуктивностью и активным сопротивлением .

Схема замещения катушки может быть представлена в виде последовательного соединения индуктивности и активного сопротивления .

Выделим из схемы одну индуктивность

  

Рис. 4.2

Если через индуктивность течет ток , то в катушке наводится ЭДС самоиндукции — .

Для прохождения переменного тока через индуктивность необходимо, чтобы на ее зажимах было напряжение , равное и противоположно направленное .

,

где — индуктивное сопротивление

где — частота, Гц,

— индуктивность, Гн.

Движению переменного тока через индуктивность оказывается сопротивление за счет накопления энергии , это сопротивление называется индуктивным.

Размерность индуктивного сопротивления

.

Значение тока в цепи с индуктивностью опережает ЭДС самоиндукции на 90°, но т. к. вектор напряжения на катушке индуктивности направлен в противоположную сторону ЭДС.

т. е.

т. о. в цепи с индуктивностью вектор тока отстает от вектора напряжения на угол 90°.

Действующее значение тока в цепи с индуктивностью равно действующему значению напряжения, деленному на индуктивное сопротивление.

т. е. 

Приведенная формула похожа на закон Ома. Это внешнее сходство позволяет определить ток в цепи с индуктивностью, подобно тому, как в цепи с активным сопротивлением. Но нужно помнить, что индуктивное сопротивление с физической точки зрения с обычным сопротивлением ничего общего не имеет.

Понятие об индуктивном сопротивлении формально введено для облегчения расчета.

Оно заменяет фактическое влияние ЭДС самоиндукции на ток в цепи.

Мгновенная и реактивная мощность

Мгновенное значение мощности или

График изменения мощности представляет собой синусоиду двойной частоты с амплитудой

.

Наибольшее значение мощности в цепи с индуктивностью равно произведению действующих значений напряжения и тока.

В первую четверть периода, когда ток в цепи увеличивается, энергия накапливается в магнитном поле катушки за счет энергии источника. Катушка в это время является приемником энергии: ток направлен против ЭДС самоиндукции.

Во вторую четверть периода, когда ток уменьшается, энергия возвращается в сеть (источнику). Направление ЭДС самоиндукции и тока совпадают. Катушка является источником энергии.

В следующую половину периода процесс повторяется.

Средняя активная мощность за период равна нулю , т. к. в цепи с индуктивностью преобразования электрической энергии в другие виды энергии не происходит.

Цепь с емкостью –

К конденсатору с идеальным диэлектриком, т. е. в нем нет потерь энергии, подведено напряжение

    

Определим ток и мощность

Ток в цепи.

Заряд конденсатора пропорционален напряжению между его обкладками, поэтому изменение напряжения сопровождается изменением заряда.

Скорость изменения заряда пропорциональна скорости изменения напряжения.

но скорость изменения заряда равна электрическому току

т. к.

то

Сопоставляя:

получаем, что ток через конденсатор по фазе опережает напряжение на конденсаторе на угол 90°. На векторной диаграмме вектор тока опережает вектор напряжения на угол 90°.

Амплитуда тока

Действующее значение тока

или

где — реактивное сопротивление конденсатора

Построение графика мгновенной мощности конденсатора выполняют также как и для индуктивной катушки.

т. к.

В первую четверть периода, когда напряжение на конденсаторе возрастает, энергия накапливается в электрическом поле конденсатора за счет работы источника, конденсатор в это время заряжается, т. е. является приемником энергии. Направления тока и напряжения совпадают.

Во вторую четверть периода, когда напряжение уменьшается, энергия в том же количестве возвращается в сеть к источнику. Ток направлен против напряжения сети – конденсатор является источником энергии ( разряжается ) и так в 3й и 4й части периода.

Активная мощность равна нулю, а реактивная

Установившийся режим в простейшей неразветвленной цепи с сосредоточенными параметрами.

Электрические цепи характеризуются двумя режимами: переходным и установившимся.

Переходные режимы возникают в результате перераспределения энергии электрических и магнитных полей в и при резком изменении параметров электрической цепи.

Простейшая электрическая цепь переменного тока с

Общее сопротивление такой цепи

где — реактивное сопротивление

или

где

Если по цепи протекает ток, то:

или

в комплексной форме

Отсюда или

— закон Ома в комплексной форме

где — комплексное сопротивление

— модуль комплексного сопротивления

Величина обратная комплексному сопротивлению называется комплексной проводимостью.

(сименс)

Умножая на сопряженный комплекс получаем

где — активная проводимость,

— реактивная проводимость.

,

по модулю

Умножив сопротивление на ток получим треугольник U.

Напряжение можно представить в виде двух составляющих

  

Цепь                 

Пусть

По второму закону Кирхгофа

где и — синусоидальные напряжения 

В комплексной форме

тогда

или

где — комплекс полного сопротивления индуктивной катушки (цепи )

Показательная форма записи

где — модуль комплекса полного сопротивления цепи

— аргумент.

Если , а ,

тогда

где , а

Если ток , то .

— Комплекс тока в цепи с равен комплексу напряжения деленному на комплекс полного сопротивления катушки.

Умножив треугольники на получим:

– полная мощность (ВА)

— реактивная мощность (ВАp)

— активная мощность (Вт)

или

— коэффициент мощности, зависит от соотношения и по его величине судят о том, какую часть полной мощности цепи составляет активная мощность.

Активную мощность измеряют ваттметром.

Цепь

Пусть .

По второму закону Кирхгофа

, т. к. напряжение отстает от тока

или

– комплекс полного сопротивления

— модуль комплекса

— аргумент

Напряжение на входе цепи отстает от тока на угол сдвига фаз

т. о. , т. к.

Аналогично цепи

или

Сложные цепи, состоящие из последовательных и параллельных участков

Расчет

1. При расчете цепи определяют активные и реактивные проводимости параллельных ветвей

; ; ; .

2. Далее определяют активную и реактивную проводимость разветвления аb

3.Преобразуют схему в эквивалентную

4.Определяют активное и реактивное сопротивление всей цепи

тогда ; ; ; ,

где , а .

Построение векторной диаграммы (по активным и реактивным составляющим).

Лучше построение векторной диаграммы начать с последней ветви и идти к началу цепи, т. е.к общему току и напряжению.

В нашем случае построение начнем с напряжения — откладываем его произвольно в масштабе.

Топографическая диаграмма:

при последовательном соединении напряжений и параллельных токов.

Топографическая диаграмма – такая векторная диаграмма, каждая точка которой соответствует определенной точке электрической цепи.

   

Резонанс при последовательном и параллельном соединении элементов

Резонанс – такой режим цепи содержащей , индуктивность и емкость, при котором ее входное сопротивление (или проводимость) имеет активный характер.

В зависимости от вида цепи (последовательное или параллельное соединение) существует резонанс напряжений и токов.

1. Последов. соединение R, L,C.

Условие резонанса:

или

т. к. , а , т. о.

, т. е. или

где — резонансная угловая частота.

при резонансе

При последовательном соединении и в резонансном режиме , т. е. имеется резонанс напряжений.

При резонансе значения и могут значительно превышать напряжения на зажимах.

Ток при резонансе

или , т. к. , а

т. о. , делим на , сокращаем

,

где — характеристическое (волновое) сопротивление контура имеет размерность сопротивления.

т. к. ; ; .

Отношение напряжения на индуктивности (или емкости) к напряжению на зажимах цепи при резонансе называется добротностью контура.

.

Величина обратная называется затуханием ()

Параллельное соединение

Условие резонанса: , т. е .

При равенстве реактивных проводимостей ветвей противоположные по фазе реактивные составляющие токов и равны по величине.

Такой режим работы цепи называют резонансом токов.

,

,

тогда

или ,

т. к. , то .

т. е. общий ток носит чисто активный характер (совпадает с ) и может быть меньше и .

Символический метод анализа электрических цепей синусоидального тока.

В режиме синусоидального тока можно перейти от уравнений составленных для мгновенных значений (дифференциальных уравнений) к алгебраическим уравнениям, составленным относительно комплексов тока и ЭДС.

Например ,

Для схемы:

или

,

т. к. амплитуда действующего напряжения на , то знак говорит о том, что опережает на 90°.

Для емкости — напряжение отстает от тока на 90°.

Если – комплексная амплитуда действующей ЭДС, то

и ,

т. о.умножение на равносильно повороту вектора на 90°, а на — на “-90°”.

Три формы записи комплексных чисел:

— алгебраическая форма,

— показательная форма,

— тригонометрическая.

Операции с комплексными числами

Сложение и вычитание комплексных чисел производится в алгебраической форме.

.

Деление и умножение производится в показательной форме:

;.

,

где , а .

Общие сведения об индуктивности »Электроника

Понимание основ индуктивности позволяет более эффективно использовать катушки индуктивности и трансформаторы.

---

Учебное пособие по индуктивности и трансформатору Включает:
Индуктивность Символы Закон Ленца Собственная индуктивность Расчет индуктивного реактивного сопротивления Теория индуктивного реактивного сопротивления Индуктивность проволоки и катушек Трансформеры

---

Индуктивность — ключевой параметр в электрических и электронных схемах.Подобно сопротивлению и емкости, это базовое электрическое измерение, которое в той или иной степени влияет на все цепи.

Индуктивность используется во многих областях электрических и электронных систем и схем. Компоненты могут быть разных форм и называться разными именами: катушки, катушки индуктивности, дроссели, трансформаторы и т. Д. . . Каждый из них также может иметь множество различных вариантов: с сердечником и без сердечника, а материалы сердечника могут быть разных типов.

Понимание индуктивности и различных форм и форматов катушек индуктивности и трансформаторов помогает понять, что происходит в электрических и электронных цепях.

Термин индуктивность был введен Оливером Хевисайдом в 1886 году. Обычно символ L используется для обозначений индукторов, показанных на принципиальных схемах, и индуктивности в уравнениях в честь физика Генриха Ленца.

Основы индуктивности

Индуктивность — это способность катушки индуктивности накапливать энергию в магнитном поле, создаваемом потоком электрического тока.

Энергия требуется для создания магнитного поля, и эта энергия должна высвобождаться при падении поля.

В результате магнитного поля, связанного с протеканием тока, индукторы генерируют противоположное напряжение, пропорциональное скорости изменения тока в цепи.

Индуктивность возникает из-за магнитного поля, создаваемого электрическими токами, протекающими в электрической цепи. Обычно катушки с проволокой используются, поскольку катушка увеличивает связь магнитного поля и усиливает эффект.

Есть два способа использования индуктивности:

• Самоиндукция: Самоиндукция — это свойство цепи, часто катушки, в результате чего изменение тока вызывает изменение напряжения в этой цепи из-за магнитного эффекта, вызванного протеканием тока.Можно видеть, что самоиндукция применяется к одной цепи — другими словами, это индуктивность, обычно в пределах одной катушки. Этот эффект используется в одиночных катушках или дросселях.
  
• Взаимная индуктивность: Взаимная индуктивность — это индуктивный эффект, когда изменение тока в одной цепи вызывает изменение напряжения во второй цепи в результате магнитного поля, которое связывает обе цепи. Этот эффект используется в трансформаторах.

Определение единиц индуктивности

При обозначении катушки индуктивности на принципиальной схеме или в уравнении обычно используется символ «L».На принципиальных схемах индукторы обычно пронумерованы, L1, L2 и т. Д.

Единицей индуктивности в системе СИ является генри, H, который можно определить как скорость изменения тока и напряжения.

Определение генри:

Индуктивность цепи равна одному генри, если скорость изменения тока в цепи составляет один ампер в секунду, и это приводит к электродвижущей силе в один вольт.

Один генри равен 1 Вб / А.

Индуктивность — что происходит

Когда ток течет внутри проводника, будь то прямой или в форме катушки, вокруг него создается магнитное поле, и это влияет на то, как нарастает ток после замыкания цепи.

С точки зрения того, как индуктивность влияет на электрическую цепь, это помогает посмотреть, как работает цепь, сначала для постоянного, а затем для переменного тока. Хотя они следуют одним и тем же законам и имеют одинаковые результаты, это помогает объяснению, пример постоянного тока проще, и тогда это объяснение можно использовать в качестве основы для случая переменного тока.

• Постоянный ток: По мере создания цепи ток начинает течь.Когда ток увеличивается до постоянного значения, создаваемое магнитное поле приобретает окончательную форму. Когда это происходит, магнитное поле изменяется, поэтому это индуцирует напряжение обратно в саму катушку, как и следовало ожидать в соответствии с законом Ленца.
  Катушка индуктивности в цепи с батареей и резистором Постоянная времени T в секундах цепи, которая будет включать значение индуктивности L Генри и соответствующее сопротивление цепи R Ом, может быть рассчитана как L / R. T — это время, за которое ток I amps повысится до 0.63 от его окончательного установившегося значения V / R. Энергия, запасенная в магнитном поле, составляет 1/2 L I ² .
  Повышение тока при приложении постоянного напряжения к катушке индуктивности Когда ток отключается, это означает, что фактически сопротивление цепи внезапно возрастает до бесконечности. Это означает, что отношение L / R становится очень малым, и магнитное поле очень быстро падает. Это представляет собой большое изменение магнитного поля, и, соответственно, индуктивность пытается поддерживать ток, и устанавливается обратная ЭДС, чтобы противодействовать этому, возникающему из-за энергии, хранящейся в магнитном поле.Напряжение означает, что на контакте переключателя могут появиться искры, особенно при разрыве контакта. Это приводит к появлению ямок на контактах и ​​износу любых механических переключателей. В электронных схемах эта обратная ЭДС может разрушить полупроводниковые устройства, поэтому часто используются способы уменьшения этой обратной ЭДС.
• Переменный ток: Для случая прохождения переменного тока через катушку индуктивности используются те же основные принципы, но, поскольку форма волны повторяется, мы склонны смотреть на то, как реагирует катушка индуктивности, несколько иначе: так удобнее.

  По самой своей природе форма переменного сигнала постоянно меняется. Это означает, что результирующее магнитное поле всегда будет изменяться, и всегда будет создаваться наведенная обратная ЭДС. Результатом этого является то, что индуктор препятствует прохождению через него переменного тока из-за индуктивности. Это в дополнение к вызванному сопротивлением омическому сопротивлению провода.

  Это означает, что если омическое сопротивление катушки индуктивности низкое, она будет пропускать постоянный ток, постоянный ток с небольшими потерями, но может иметь высокое сопротивление для любого высокочастотного сигнала.Эта характеристика катушки индуктивности может использоваться для обеспечения того, чтобы любые высокочастотные сигналы не проходили через катушку индуктивности.

Еще одним аспектом индуктивности является то, что реактивное сопротивление катушки индуктивности и реактивное сопротивление конденсатора могут действовать вместе в цепи, подавляя друг друга. Это называется резонансом и широко используется в полосовых фильтрах.

Индуктивность проводов и катушек

Прямые провода и катушки имеют индуктивность. Обычно катушки используются для индукторов, потому что соединение магнитного поля между различными витками катушки увеличивает индуктивность и позволяет удерживать провод в меньшем объеме.

Для большинства низкочастотных приложений индуктивностью прямого провода можно пренебречь, но по мере увеличения частоты в диапазоне УКВ и за его пределы индуктивность самого провода может стать значительной, и соединения должны быть короткими, чтобы минимизировать влияние. .

Доступно

расчетов, позволяющих достаточно точно рассчитать индуктивность проводов, но индуктивность катушек немного сложнее и зависит от множества факторов, включая форму катушки и постоянную материала внутри и вокруг катушки. .

Индуктивность — ключевой аспект проводов и катушек. Индуктивность — это незаменимая характеристика, которая может быть очень полезна во многих схемах.

Дополнительные концепции и руководства по основам электроники:
Voltage Текущий Власть Сопротивление Емкость Индуктивность Трансформеры Децибел, дБ Законы Кирхгофа Q, добротность Радиочастотный шум
Вернуться в меню «Основные понятия электроники».. .

Важность индуктивности катушки

В этом блоге мы исследуем индуктивность; одно из основных свойств электрической схемы или электронного устройства. Индуктивность определяется как свойство электрической цепи или устройства, которое препятствует изменению тока. Важно отметить, что индуктивность не противодействует току, а скорее противодействует изменению тока, протекающего в цепи.

Единицей индуктивности является генри (Гн), и она зависит от физических свойств цепи, а не от электрических характеристик, поскольку здесь нет тока или напряжения.Кроме того, индуктивность прямо пропорциональна «количеству витков», «площади, окруженной катушкой» и обратно пропорциональна «длине катушки».

Символ, используемый для обозначения индуктивности, — это заглавная буква L. Индуктивность (или, точнее, самоиндуктивность) катушки можно найти с помощью следующего уравнения:

Применяемая формула в электрических цепях:

Обзор процесса индуктивности

Чтобы понять процесс индуктивности и принцип его работы, давайте рассмотрим иллюстрированный источник постоянного тока с переключателем и катушкой (рисунок 1).Когда переключатель замкнут, по цепи течет ток. Здесь мы используем поток электронов, показанный красными стрелками, как направление электронов. Когда мы замыкаем переключатель, ток, протекающий от батареи, увеличивается в каждой катушке. Принимая во внимание правило большого пальца левой руки, ток течет прочь, а магнитный поток течет против часовой стрелки и расширяется наружу. Принимая во внимание Катушку 1 и Катушку 2, как на рисунке; Поток от катушки 1 проходит через катушку 2, создавая индуцированное напряжение.Закон Ленца и закон Фарадея — это два закона, применяемые для понимания этого процесса. Индуцированное напряжение всегда будет создавать поток, противоположный исходному потоку, который его вызвал. Таким образом, наше приложенное напряжение пытается направить ток в катушку, а индуцированное напряжение работает против этого. Он не останавливает ток, он просто замедляет его. Если по закону Ома сила тока будет 10 ампер, он не изменится мгновенно с 0 до 10, вместо этого потребуется некоторое время в зависимости от индуктивности, обеспечиваемой катушкой индуктивности.

Рисунок 1

В следующем случае мы попытаемся уменьшить ток, в той же цепи с 10 А, как установлено, магнитный поток связывает все витки в катушке. Когда мы размыкаем переключатель, поток возвращается к исходному проводнику. Движение потока прекращается, когда ток перестает изменяться. Уменьшение магнитного потока на каждом витке катушки проводника вызывает относительное движение между магнитными полями, что приводит к сильному индуцированному напряжению. Действие по уменьшению тока / напряжения до нуля путем удаления приложенного напряжения приводит к непрерывному изменению магнитного потока, который индуцирует напряжение, пытаясь противодействовать причине.Таким образом, схема пытается поддерживать ток, что приводит к задержке в скорости уменьшения тока, а не снижает ее мгновенно. Это называется индуктивным ударом. Происходящий процесс — это просто возвращение энергии обратно в цепь из магнитных полей. Величина индуцируемого напряжения зависит от таких факторов, как величина магнитного потока, количество витков и время.

Разрыв цепи может вызвать очень высокое наведенное напряжение в катушке, так как время очень короткое, а магнитный поток очень быстро спадает.Если нет пути для прохождения этой энергии, мы можем получить дугу через переключатели или дугу рядом с другими подключенными устройствами, что может вызвать повреждения. Таким образом, настоятельно рекомендуется соблюдать некоторые меры предосторожности при обнаружении характеристик индуктивности в электронных схемах.

Профилактические меры по предотвращению дугового разряда

Индуктивный ток, создаваемый в цепи постоянного тока, имеет высокую силу, когда поток, связанный с катушкой, мгновенно падает.Поэтому важно принять превентивные меры для устранения повреждений, предоставив альтернативный путь для энергии. Например, трансформатор тока является высокоиндуктивным устройством, поскольку у него много витков катушки, и количество витков катушки имеет большое влияние на генерируемый ток (L = µ N2A / l, где N = кол-во поворотов) .

Рисунок 2: Принцип противодействия ЭДС

Если амперметр, присоединенный к катушке, как показано на рисунке 2, снимается, пока цепь горячая, цепь с высокой индуктивностью прерывается.Разрыв цепи приводит к схлопыванию потока по виткам катушки, создавая чрезвычайно высокое индуцированное напряжение, которое может вызвать электрическую дугу длиной 4-5 дюймов. Эта электрическая дуга может причинить травму человеку, пытающемуся отключить амперметр от цепи.

Это похоже на шунтирующую обмотку двигателя постоянного тока, которая представляет собой еще одну высокоиндуктивную цепь. Шунтирующий двигатель постоянного тока также удовлетворяет всем характеристикам, которые генерируют высокоиндуктивный ток. Шунтирующий двигатель обычно находится под напряжением, и в другую часть двигателя вносятся изменения, чтобы обеспечить альтернативный путь для протекания индуктивного тока.Это сделано для того, чтобы переключение поля шунта могло вызвать серьезные повреждения и сократить срок службы контактов. Даже в небольших катушках, используемых в схемах ПЛК, возникает обратная подача и некоторые повреждения.

Параллельный двигатель

Самый простой способ устранить повреждение, вызванное током обратной связи, — это подключить резистор к катушке индуктивности. Это обеспечивает путь для индуктора, чтобы управлять энергией, но, когда он находится под напряжением в течение более длительного периода, это может быть неэффективным, поскольку все это время будет иметь место потеря мощности на резисторе.Эту проблему можно решить, включив диод последовательно с резистором, чтобы диод блокировал ток во время нормальной работы. Это снижает рассеиваемую мощность на резисторе. Питание подается через резистор только тогда, когда цепь разомкнута, вызывая индуктивный удар.

Помимо использования одного резистора и последовательной комбинации резистор-диод, конденсатор также может устранить повреждения, вызванные индуктивным током. Энергия, генерируемая во время обратной подачи индуктивного тока, рассеивается в конденсаторе, а оставшийся ток течет обратно от конденсатора к катушке индуктивности, тем самым защищая контакты переключателя, а также любые другие соприкасающиеся устройства.Подводя итог, можно сказать, что индуктивность — это свойство цепи, которая препятствует изменению тока в этой цепи.

До сих пор мы рассматривали индуктивность, вызванную цепью постоянного тока, но когда мы посмотрим на индуктивность, вызванную переменным током, который непрерывно изменяется во времени, формируется реактивная индуктивность, зависящая не только от индуктивности катушки, но и также от частоты сигнала переменного тока, как показано на рисунке 3.

Рисунок 3

Мы надеемся, что это было полезно для вас, как для технического специалиста, или для студента, приступившего к работе.Если у вас есть какие-либо вопросы о программах по электронике или электромеханику, вы можете связаться с одним из наших консультантов по программе по бесплатному телефону 1-888-553-5333 или по электронной почте [email protected].

цепей переменного тока | Безграничная физика

Индуктивность

Индукция — это процесс, при котором ЭДС индуцируется изменением магнитного потока, например изменением тока в проводнике.

Цели обучения

Опишите свойства индуктора

Ключевые выводы

Ключевые моменты

• В случае электроники индуктивность — это свойство проводника, благодаря которому изменение тока в проводнике создает напряжение как в самом проводнике, называемое самоиндукцией, так и в любых соседних проводниках, называемое взаимной индуктивностью.
• Согласно закону Ленца, изменяющийся электрический ток в цепи с индуктивностью индуцирует пропорциональное напряжение, которое противодействует изменению тока.
• Взаимная индуктивность обозначена. Изменение тока I ₁ в одном устройстве, катушка 1 на рисунке, индуцирует ЭДС ₂ в другом. Мы выражаем это в форме уравнения как [латекс] \ text {emf} _2 = — \ text {M} \ frac {\ Delta \ text {I} _1} {\ Delta \ text {t}} [/ latex]. M то же самое для обратного процесса.
• Самоиндукция — это действие закона индукции Фарадея устройства на самого себя. Индуцированная ЭДС связана с физической геометрией устройства и скоростью изменения тока, задаваемой [latex] \ text {emf} = — \ text {L} \ frac {\ Delta \ text {I}} {\ Delta \ text {t}} [/ латекс].
• Устройство, которое демонстрирует значительную самоиндукцию, называется индуктором и обозначается символом в.

Ключевые термины

• взаимная индуктивность : отношение напряжения в цепи к изменению тока в соседней цепи.
• самоиндукция : Отношение напряжения к изменению тока в той же цепи.
• индуктор : Пассивное устройство, которое вводит индуктивность в электрическую цепь.

Индуктивность

ОБЗОР

Индукция — это процесс, при котором ЭДС индуцируется изменением магнитного потока. В частности, в случае электроники индуктивность — это свойство проводника, благодаря которому изменение тока в проводнике создает напряжение как в самом проводнике (самоиндукция), так и в любых соседних проводниках (взаимная индуктивность).Этот эффект основан на двух фундаментальных физических наблюдениях: во-первых, постоянный ток создает постоянное магнитное поле, а во-вторых, что изменяющееся во времени магнитное поле индуцирует напряжение в соседнем проводнике (закон индукции Фарадея). Согласно закону Ленца, изменяющийся электрический ток через цепь с индуктивностью индуцирует пропорциональное напряжение, которое противодействует изменению тока (если бы это было не так, можно легко увидеть, что энергия не может быть сохранена, при этом изменяющийся ток усиливает изменение тока. петля положительной обратной связи).

ВЗАИМНАЯ ИНДУКТИВНОСТЬ

Взаимная индуктивность — это влияние закона индукции Фарадея для одного устройства на другое, например, первичная катушка, при передаче энергии вторичной обмотке в трансформаторе. Посмотрите, где простые катушки наводят друг на друга ЭДС.

Взаимная индуктивность катушек : Эти катушки могут вызывать ЭДС друг в друге, как неэффективный трансформатор. Их взаимная индуктивность M указывает на эффективность связи между ними. Здесь видно, что изменение тока в катушке 1 вызывает ЭДС в катушке 2.(Обратите внимание, что «E2 индуцированная» представляет наведенную ЭДС в катушке 2.)

Во многих случаях, когда геометрия устройств фиксирована, магнитный поток изменяется за счет изменения тока. Поэтому мы сконцентрируемся на скорости изменения тока Δ I / Δ t как причине индукции. Изменение тока I ₁ в одном устройстве, катушка 1 на рисунке, индуцирует ЭДС ₂ в другом. Мы выражаем это в форме уравнения как

[латекс] \ text {emf} _2 = — \ text {M} \ frac {\ Delta \ text {I} _1} {\ Delta \ text {t}} [/ latex]

, где M определяется как взаимная индуктивность между двумя устройствами.Знак минус является выражением закона Ленца. Чем больше взаимная индуктивность M , тем эффективнее связь. Единицы измерения для M : (В · с) / A = Ω · с, который назван генри (H) в честь Джозефа Генри (обнаружил самоиндукцию). То есть 1 H = 1 Ом.

Природа здесь симметрична. Если мы изменим ток I ₂ в катушке 2, мы индуцируем ЭДС ₁ в катушке 1, что равно

[латекс] \ text {emf} _1 = — \ text {M} \ frac {\ Delta \ text {I} _2} {\ Delta \ text {t}} [/ latex]

, где M то же, что и для обратного процесса.Трансформаторы работают в обратном направлении с такой же эффективностью или взаимной индуктивностью M.

Большая взаимная индуктивность M может быть или нежелательна. Мы хотим, чтобы трансформатор имел большую взаимную индуктивность. Но такой прибор, как электрическая сушилка для одежды, может вызвать опасную ЭДС на корпусе, если взаимная индуктивность между его катушками и корпусом велика. Один из способов уменьшить взаимную индуктивность M состоит в том, чтобы намотать катушки противотоком для подавления создаваемого магнитного поля.(Видеть ).

Противоточная намотка : Нагревательные катушки электрической сушилки для белья могут иметь встречную намотку, так что их магнитные поля нейтрализуют друг друга, что значительно снижает взаимную индуктивность по сравнению с корпусом сушилки.

САМОИНДУКЦИЯ

Самоиндуктивность, действие закона индукции Фарадея устройства на самого себя, также существует. Когда, например, увеличивается ток через катушку, магнитное поле и магнитный поток также увеличиваются, вызывая противоэдс, как того требует закон Ленца.И наоборот, если ток уменьшается, индуцируется ЭДС, которая препятствует уменьшению. Большинство устройств имеют фиксированную геометрию, и поэтому изменение магнитного потока полностью связано с изменением тока ΔI через устройство. Индуцированная ЭДС связана с физической геометрией устройства и скоростью изменения тока. Выдается

[латекс] \ text {emf} = — \ text {L} \ frac {\ Delta \ text {I}} {\ Delta \ text {t}} [/ latex]

, где L — собственная индуктивность устройства.Устройство, которое демонстрирует значительную самоиндукцию, называется индуктором и обозначается символом в.

.

Символ индуктивности

Знак минус является выражением закона Ленца, означающего, что ЭДС препятствует изменению тока. Единицами самоиндукции являются генри (Гн), как и для взаимной индуктивности. Чем больше самоиндукция L устройства, тем сильнее оно сопротивляется любому изменению тока через него. Например, большая катушка с множеством витков и железным сердечником имеет большой L и не позволит току быстро меняться.Чтобы избежать этого эффекта, необходимо добиться небольшого L, например, за счет встречной намотки катушек, как в.

СОЛЕНОИДЫ

Можно рассчитать L для катушки индуктивности, учитывая ее геометрию (размер и форму) и зная создаваемое ею магнитное поле. В большинстве случаев это сложно из-за сложности создаваемого поля. Индуктивность L обычно является заданной величиной. Единственным исключением является соленоид, потому что он имеет очень однородное поле внутри, почти нулевое поле снаружи и простую форму.{2} \ text {A}} {\ mathscr {\ text {l}}} [/ latex] (соленоид).

Поучительно вывести это уравнение, но это оставлено читателю в качестве упражнения. (Подсказка: начните с того, что отметьте, что индуцированная ЭДС определяется законом индукции Фарадея как ЭДС = −N (Δ / Δt), а по определению самоиндукции задается как ЭДС = −L (ΔI // Δt) и приравняем эти два выражения). Обратите внимание, что индуктивность зависит только от физических характеристик соленоида, в соответствии с его определением.

RL Схемы

Цепь RL состоит из катушки индуктивности и резистора, включенных последовательно или параллельно друг другу, с током, управляемым источником напряжения.{\ frac {- \ text {t}} {\ tau}}) [/ latex]. Конечный ток по прошествии длительного времени будет [латекс] \ текст {I} _0 [/ латекс].

Характеристическая постоянная времени определяется выражением [latex] \ tau = \ frac {\ text {L}} {\ text {R}} [/ latex], где R — сопротивление, а L — индуктивность. Это время, необходимое для того, чтобы ток в только что замкнутой цепи снизился с нуля до [latex] 0,632 \ cdot \ text {I} _0 [/ latex].

Когда источник напряжения отключен от катушки индуктивности, ток будет спадать в соответствии с [латексом] \ text {I} = \ text {I} _ {0} \ text {e} ^ {\ frac {- \ text {t }} {\ tau}} [/ латекс].В первом временном интервале τ ток падает в раз [латекс] \ frac {1} {\ text {e}} [/ latex] до [latex] 0,368 \ cdot \ text {I} _0 [/ latex].

Ключевые термины

• характеристическая постоянная времени : Обозначается $ \ tau $, в цепях RL она задается $ \ tau = \ frac {L} {R} $, где R — сопротивление, а L — индуктивность. Когда переключатель замкнут, это время, необходимое для того, чтобы сила тока уменьшилась с коэффициентом 1 / e.
• катушка индуктивности : Устройство или компонент схемы, который демонстрирует значительную самоиндукцию; устройство, которое хранит энергию в магнитном поле.

Цепи RL

Цепь резистор-индуктор (цепь RL) состоит из резистора и катушки индуктивности (последовательно или параллельно), приводимых в действие источником напряжения.

Обзор

Напомним, что индукция — это процесс, при котором ЭДС индуцируется изменением магнитного потока. Взаимная индуктивность — это действие закона индукции Фарадея одного устройства на другое, в то время как самоиндукция — это действие закона индукции Фарадея устройства на самого себя.Катушка индуктивности — это устройство или компонент схемы, который демонстрирует самоиндукцию.

Энергия индуктора

Мы знаем из закона Ленца, что индукторы противодействуют изменениям тока. Мы можем думать об этой ситуации с точки зрения энергии. Энергия хранится в магнитном поле. Требуется время, чтобы накопить энергию, а также время, чтобы истощить ее; следовательно, есть противодействие быстрым изменениям. В индукторе магнитное поле прямо пропорционально току и индуктивности устройства.{2} [/ латекс].

Катушки индуктивности в цепях

Мы знаем, что ток через катушку индуктивности L нельзя включить или выключить мгновенно. Изменение тока изменяет магнитный поток, вызывая противодействие изменению ЭДС (закон Ленца). Как долго длится противостояние? Текущий будет потоком и можно выключить , но сколько времени это займет? На следующем рисунке показана схема переключения, которую можно использовать для измерения тока через катушку индуктивности как функции времени.

Ток в цепи RL : (a) Цепь RL с переключателем для включения и выключения тока. В положении 1 батарея, резистор и катушка индуктивности включены последовательно, и устанавливается ток. В положении 2 аккумулятор извлекается, и ток в конечном итоге прекращается из-за потери энергии в резисторе. (b) График роста тока в зависимости от времени, когда переключатель перемещен в положение 1. (c) График уменьшения тока, когда переключатель перемещен в положение 2.

Когда переключатель сначала перемещается в положение 1 (при t = 0 ), ток равен нулю и в конечном итоге возрастает до I ₀ = В / R , где R — полное сопротивление цепи, а V — напряжение батареи.{\ frac {- \ text {t}} {\ tau}}) [/ latex]

— это ток в цепи RL при включении. (Обратите внимание на сходство с экспоненциальным поведением напряжения на зарядном конденсаторе.) Начальный ток равен нулю и приближается к I ₀ = В / R с характеристической постоянной времени для цепи RL , задаваемой формулой :

[латекс] \ tau = \ frac {\ text {L}} {\ text {R}} [/ latex],

, где [latex] \ tau [/ latex] имеет единицы измерения в секундах, поскольку [latex] 1 \ text {H} = 1 \ Omega \ cdot \ text {s} [/ latex].В первый период времени [латекс] \ тау [/ латекс] ток возрастает от нуля до 0,632I ₀ , так как I = I ₀ (1-e ^-1 ) = I ₀ ( 1−0,368) = 0,632I ₀ . В следующий раз ток составит 0,632 от остатка. Хорошо известным свойством экспоненциальной функции является то, что конечное значение никогда не достигается точно, но 0,632 остатка от этого значения достигается за каждое характерное время [латекс] \ тау [/ латекс]. Всего за несколько кратных промежутков времени [латекс] \ тау [/ латекс] конечное значение почти достигнуто (см. Часть (b) на рисунке выше).

Характерное время [латекс] \ тау [/ латекс] зависит только от двух факторов: индуктивности L и сопротивления R . Чем больше индуктивность L , тем она больше, что имеет смысл, поскольку большая индуктивность очень эффективна в противодействии изменению. Чем меньше сопротивление R, тем больше [латекс] \ тау [/ латекс]. Опять же, это имеет смысл, поскольку небольшое сопротивление означает большой конечный ток и большее изменение, чтобы достичь его. В обоих случаях (большой L и маленький R) больше энергии хранится в катушке индуктивности, и требуется больше времени для ее ввода и вывода.

Когда переключатель на (a) перемещается в положение 2 и отключает батарею из цепи, ток падает из-за рассеивания энергии резистором. Однако это также не происходит мгновенно, поскольку катушка индуктивности противодействует уменьшению тока, создавая ЭДС в том же направлении, что и батарея, управляющая током. Кроме того, в катушке индуктивности накапливается определенное количество энергии, (1/2) LI ₀ ² , и она рассеивается с конечной скоростью. Когда ток приближается к нулю, скорость убывания замедляется, поскольку скорость рассеяния энергии составляет I ² R.{\ frac {- \ text {t}} {\ tau}} [/ latex]

В (c), в первый период времени [latex] \ tau = \ text {L} / \ text {R} [/ latex] после включения переключателя, ток падает до 0,368 от своего начального значения, поскольку I = I ₀ e ⁻¹ = 0,368I ₀ . В каждый последующий раз [латекс] \ тау [/ латекс] ток падает до 0,368 от предыдущего значения, а через несколько кратных [латекс] \ тау [/ латекс] ток становится очень близким к нулю.

Цепь серии

RLC: на больших и малых частотах; Фазорная диаграмма

Отклик цепи RLC зависит от частоты возбуждения — на достаточно больших частотах преобладает индуктивный (емкостной) член.

Цели обучения

Различать поведение цепей серии RLC на больших и малых частотах

Ключевые выводы

Ключевые моменты

• RLC-схемы можно описать (обобщенным) законом Ома. Что касается фазы, когда прикладывается синусоидальное напряжение, ток отстает от напряжения на 90 ° по фазе в цепи с индуктором, в то время как ток опережает напряжение на 90 ° в цепи с конденсатором.
• На достаточно больших частотах [латекс] (\ nu \ gg \ frac {1} {\ sqrt {2 \ pi \ text {LC}}}) [/ latex] схема почти эквивалентна цепи переменного тока только с индуктор.Следовательно, среднеквадратичный ток будет Vrms / XL, а ток отстает от напряжения почти на 90 °.
• На достаточно малых частотах [латекс] (\ nu \ ll \ frac {1} {\ sqrt {2 \ pi \ text {LC}}}) [/ latex] схема почти эквивалентна цепи переменного тока с одним конденсатор. Следовательно, среднеквадратичное значение тока будет равно V _{среднеквадратичное значение} / X _C, , а ток опережает напряжение почти на 90 ^∘ .

Ключевые термины

• Закон Ленца : Закон электромагнитной индукции, который гласит, что электродвижущая сила, индуцированная в проводнике, всегда имеет такое направление, что возникающий ток будет противодействовать изменению, вызвавшему его; этот закон является формой закона сохранения энергии.
• резонанс : Увеличение амплитуды колебаний системы под действием периодической силы, частота которой близка к собственной частоте системы.
• rms : Среднеквадратичное значение: статистическая мера величины изменяющейся величины.

В предыдущих версиях Atoms мы узнали, как последовательная цепь RLC, показанная на рисунке, реагирует на источник переменного напряжения. Объединив закон Ома (I _{действующее значение} = V _{действующее значение} / Z; I _{среднеквадратичное значение} и V _{среднеквадратичное значение} представляют собой среднеквадратичное значение тока и напряжения) и выражения для импеданса Z из:

Последовательная цепь RLC : Последовательная цепь RLC: резистор, катушка индуктивности и конденсатор (слева).2}} [/ латекс].

Из уравнения мы исследовали условия резонанса для контура. Мы также изучили фазовые соотношения между напряжениями на резисторе, конденсаторе и катушке индуктивности: при приложении синусоидального напряжения ток отстает от напряжения на 90º по фазе в цепи с катушкой индуктивности, в то время как ток опережает напряжение на 90 ^∘ . в цепи с конденсатором. Теперь мы исследуем отклик системы в пределах больших и малых частот.

на больших частотах

На достаточно больших частотах [латекс] (\ nu \ gg \ frac {1} {\ sqrt {2 \ pi \ text {LC}}}) [/ latex], X _L намного больше, чем X _C .Если частота достаточно высока, так что X _L также намного больше, чем R, то в импедансе Z преобладает индуктивный член. Когда [латекс] \ text {Z} \ приблизительно \ text {X} _ \ text {L} [/ latex], схема почти эквивалентна цепи переменного тока с одним индуктором. Следовательно, среднеквадратичный ток будет составлять V _{, действующее значение} / X _L , а ток отстает от напряжения почти на 90 ^∘ . Этот отклик имеет смысл, потому что на высоких частотах закон Ленца предполагает, что полное сопротивление катушки индуктивности будет большим.

на малых частотах

В импедансе Z на малых частотах [латекс] (\ nu \ ll \ frac {1} {\ sqrt {2 \ pi \ text {LC}}}) [/ latex] преобладает емкостной член, предполагая, что частота достаточно высока, так что X _C намного больше R. Когда [latex] \ text {Z} \ приблизительно \ text {X} _ \ text {C} [/ latex], схема почти эквивалентна AC схема только с конденсатором. Следовательно, среднеквадратичное значение тока будет равно V _{среднеквадратичное значение} / X _C, , а ток опережает напряжение почти на 90 ^∘ .

Резисторы в цепях переменного тока

В цепи с резистором и источником питания переменного тока по-прежнему действует закон Ома ( В, = IR ).

Цели обучения

Применить закон Ома для определения силы тока и напряжения в цепи переменного тока

Ключевые выводы

Ключевые моменты

• При напряжении переменного тока, определяемом следующим образом: [latex] \ text {V} = \ text {V} _0 \ sin (2 \ pi \ nu \ text {t}) [/ latex], ток в цепи определяется как : [latex] \ text {I} = \ frac {\ text {V} _0} {\ text {R}} \ sin (2 \ pi \ nu \ text {t}) [/ latex] Это выражение происходит от Ohm закон: [латекс] \ text {V} = \ text {IR} [/ latex].2} {2 \ text {R}} [/ латекс].

Ключевые термины

• Закон Ома : Согласно наблюдениям Ома, постоянный ток, протекающий в электрической цепи, состоящей только из сопротивлений, прямо пропорционален приложенному напряжению.

Постоянный ток (DC) — это поток электрического заряда только в одном направлении. Это установившееся состояние цепи постоянного напряжения. Однако в большинстве известных приложений используется источник переменного напряжения. Переменный ток (AC) — это поток электрического заряда, который периодически меняет направление.Если источник периодически меняется, особенно синусоидально, цепь называется цепью переменного тока. Примеры включают коммерческую и бытовую энергетику, которая удовлетворяет многие наши потребности. показывает графики зависимости напряжения и тока от времени для типичных источников постоянного и переменного тока. Напряжение и частота переменного тока, обычно используемые в домах и на предприятиях, различаются по всему миру.

Синусоидальное напряжение и ток : (a) Напряжение и ток постоянного тока постоянны во времени после установления тока.(б) График зависимости напряжения и тока от времени для сети переменного тока 60 Гц. Напряжение и ток синусоидальны и совпадают по фазе для простой цепи сопротивления. Частоты и пиковое напряжение источников переменного тока сильно различаются.

Мы изучили закон Ома:

[латекс] \ text {I} = \ frac {\ text {V}} {\ text {R}} [/ latex]

, где I — ток, В, — напряжение, а R — сопротивление цепи. Закон Ома применяется как к цепям переменного тока, так и к цепям постоянного тока.Следовательно, при напряжении переменного тока, определяемом по формуле:

[латекс] \ text {V} = \ text {V} _0 \ sin (2 \ pi \ nu \ text {t}) [/ latex]

, где В ₀ — пиковое напряжение, а [латекс] \ nu [/ latex] — частота в герцах, ток в цепи задается как:

[латекс] \ text {I} = \ frac {\ text {V} _0} {\ text {R}} \ sin (2 \ pi \ nu \ text {t}) [/ latex]

В этом примере, в котором у нас есть резистор и источник напряжения в цепи, напряжение и ток считаются синфазными, как показано на (b). 2} {\ text {R}} \ cdot \ sin (2 \ pi \ nu \ text {t}) [/ latex]

Чтобы найти среднюю мощность, потребляемую этой схемой, нам нужно взять среднее значение функции по времени.2} {2 \ text {R}} [/ latex]

Конденсаторы в цепях переменного тока: емкостное сопротивление и фазовые диаграммы

Напряжение на конденсаторе отстает от тока. Из-за разности фаз для описания этих схем полезно вводить векторы.

Цели обучения

Объясните преимущества использования векторного представления

Ключевые выводы

Ключевые моменты

• Когда конденсатор подключен к переменному напряжению, максимальное напряжение пропорционально максимальному току, но максимальное напряжение не возникает одновременно с максимальным током.
• Если источник переменного тока подключен к резистору, то ток и напряжение будут пропорциональны друг другу. Это означает, что ток и напряжение будут «пиковыми» одновременно.
• Среднеквадратичное значение тока в цепи, содержащей только конденсатор C, определяется другой версией закона Ома как [латекс] \ text {I} _ {\ text {rms}} = \ frac {\ text {V} _ {\ text {rms}} {\ text {X} _ \ text {C}} [/ latex], где [latex] \ text {X} _ \ text {c} [/ latex] — это емкостное реактивное сопротивление.

Ключевые термины

• среднеквадратичное значение : Среднеквадратичное значение: статистическая мера величины переменной величины.

В предыдущем Atom «Резисторы в цепях переменного тока» мы представили источник питания переменного тока и изучили, как резисторы ведут себя в цепях переменного тока. Там мы использовали закон Ома (V = IR), чтобы получить соотношение между напряжением и током в цепях переменного тока. В этом и последующих разделах «Атомы» мы обобщим закон Ома, чтобы мы могли использовать его, даже если в цепи присутствуют конденсаторы и катушки индуктивности. Чтобы добраться туда, мы сначала представим очень общий графический способ представления синусоидальной волны с помощью фазора.

Конденсаторы в цепях переменного тока с фазорами

Phasor

Ключевая идея представления вектора состоит в том, что сложный, изменяющийся во времени сигнал может быть представлен как произведение комплексного числа (которое не зависит от времени) и сложного сигнала (которое зависит от времени). Фазоры разделяют зависимости от A (амплитуда), [latex] \ nu [/ latex] (частота) и θ (фаза) на три независимых фактора. Это может быть особенно полезно, потому что частотный коэффициент (который включает временную зависимость синусоиды) часто является общим для всех компонентов линейной комбинации синусоид.{\ text {i} \ theta} [/ латекс]. Поскольку векторы представлены величиной (или модулем) и углом, они графически представлены вращающейся стрелкой (или вектором) в плоскости x-y.

Рис. 3 : Вектор можно рассматривать как вектор, вращающийся вокруг начала координат в комплексной плоскости. Функция косинуса — это проекция вектора на действительную ось. Его амплитуда — это модуль вектора, а его аргумент — полная фаза \ omega t + \ theta. Фазовая постоянная \ theta представляет собой угол, который вектор образует с действительной осью при t = 0.

Конденсаторы в цепях переменного тока

Ранее в предыдущем Atom мы изучали, как напряжение и ток меняются со временем. Если источник переменного тока подключен к резистору, то ток и напряжение будут пропорциональны друг другу. Это означает, что ток и напряжение будут «пиковыми» одновременно. Мы говорим, что ток и напряжение совпадают по фазе.

Когда конденсатор подключен к переменному напряжению, максимальное напряжение пропорционально максимальному току, но максимальное напряжение не возникает одновременно с максимальным током.Ток имеет максимум (пик) за четверть цикла до пика напряжения. Инженеры говорят, что «ток опережает напряжение на 90 ». Это показано на.

.

Рис. 2 : Пик тока (имеет максимум) за четверть волны до напряжения, когда конденсатор подключен к переменному напряжению.

Для цепи с конденсатором мгновенное значение V / I непостоянно. Однако значение V _max / I _max полезно и называется емкостным реактивным сопротивлением (X _C ) компонента.Поскольку это по-прежнему напряжение, деленное на ток (например, сопротивление), единицей измерения является ом. Значение X _C (C означает конденсатор) зависит от его емкости (C) и частоты (f) переменного тока. [латекс] \ text {X} _ \ text {C} = \ frac {1} {2 \ pi \ nu \ text {C}} [/ latex].

Конденсатор влияет на ток, имея возможность полностью его отключить, когда он полностью заряжен. Поскольку применяется переменное напряжение, возникает среднеквадратичный ток, но он ограничивается конденсатором.Это считается эффективным сопротивлением конденсатора переменному току, поэтому среднеквадратичное значение тока I _{, действующее значение} в цепи, содержащей только конденсатор C, определяется другой версией закона Ома как [латекс] \ text {I} _ {\ text {rms}} = \ frac {\ text {V} _ {\ text {rms}}} {\ text {X} _ \ text {C}} [/ latex], где V _rms — это действующее значение напряжения. Обратите внимание, что X _C заменяет R в версии закона Ома для постоянного тока.

Фазовое представление

Поскольку напряжение на конденсаторе отстает от тока, вектор, представляющий ток и напряжение, будет иметь вид.На схеме стрелки вращаются против часовой стрелки с частотой [латекс] \ ню [/ латекс]. (Следовательно, ток ведет к напряжению.) В следующих атомах мы увидим, как эти векторы можно использовать для анализа цепей RC, RL, LC и RLC.

Рис. 4 : Фазорная диаграмма для цепи переменного тока с конденсатором

Индукторы в цепях переменного тока: индуктивно-реактивные и фазовые диаграммы

В цепи переменного тока с катушкой индуктивности напряжение на катушке индуктивности «ведет» ток в соответствии с законом Ленца.

Цели обучения

Объясните, почему напряжение на катушке индуктивности «опережает» ток в цепи переменного тока с катушкой индуктивности

Ключевые выводы

Ключевые моменты

• С индуктором в цепи переменного тока напряжение опережает ток на одну четверть цикла или на фазовый угол 90º.
• Среднеквадратичный ток I _{среднеквадратичное значение} через катушку индуктивности L определяется версией закона Ома: [латекс] \ text {I} _ {\ text {rms}} = \ frac {\ text {V} _ { \ text {rms}}} {\ text {X} _ \ text {L}} [/ latex].X _L называется индуктивным реактивным сопротивлением, которое задается как [латекс] \ text {X} _ \ text {L} = 2 \ pi \ nu \ text {L} [/ latex].
• Фазоры — это векторы, вращающиеся против часовой стрелки. Вектор для катушки индуктивности показывает, что напряжение опережает ток по фазе 90º.

Ключевые термины

• Закон Ленца : Закон электромагнитной индукции, который гласит, что электродвижущая сила, индуцированная в проводнике, всегда имеет такое направление, что возникающий ток будет противодействовать изменению, вызвавшему его; этот закон является формой закона сохранения энергии.
• rms : Среднеквадратичное значение: статистическая мера величины изменяющейся величины.
• вектор : представление комплексного числа в терминах комплексной экспоненты.

Предположим, индуктор подключен непосредственно к источнику переменного напряжения, как показано на рисунке. Разумно предположить, что сопротивление пренебрежимо мало, потому что на практике мы можем сделать сопротивление индуктора настолько малым, что оно окажет незначительное влияние на схему. График показывает напряжение и ток как функции времени.(б) начинается с максимального напряжения. Обратите внимание, что ток начинается с нуля, затем повышается до своего пика после управляющего им напряжения (как показано в предыдущем разделе, когда было включено напряжение постоянного тока).

Источник переменного напряжения, подключенный последовательно с индуктором : (a) Источник переменного напряжения, подключенный последовательно с индуктором, имеющим незначительное сопротивление. (б) График зависимости тока и напряжения на катушке индуктивности от времени.

Когда напряжение становится отрицательным в точке а, ток начинает уменьшаться; оно становится нулевым в точке b, где напряжение является самым отрицательным.Затем ток становится отрицательным, снова вслед за напряжением. Напряжение становится положительным в точке c, где оно начинает делать ток менее отрицательным. В точке d ток проходит через ноль, когда напряжение достигает своего положительного пика, чтобы начать следующий цикл. Следовательно, когда на катушку индуктивности подается синусоидальное напряжение, оно опережает ток на одну четверть цикла или на фазовый угол 90º.

Ток отстает от напряжения, поскольку индукторы препятствуют изменению тока. Изменение тока вызывает ЭДС.Это считается эффективным сопротивлением катушки индуктивности переменному току. Среднеквадратичный ток I _RMS через катушку индуктивности L определяется версией закона Ома: [латекс] \ text {I} _ {\ text {rms}} = \ frac {\ text {V} _ {\ text { rms}}} {\ text {X} _ \ text {L}} [/ latex] где V _rms — среднеквадратичное значение напряжения на катушке индуктивности, а [латекс] \ text {X} _ \ text {L} = 2 \ pi \ nu \ text {L} [/ latex] с [latex] \ nu [/ latex] частота источника переменного напряжения в герцах. X _L называется индуктивным реактивным сопротивлением. Поскольку катушка индуктивности препятствует прохождению тока, X _L имеет единицы измерения Ом (1 Гн = 1 Ом · с, так что частота, умноженная на индуктивность, имеет единицы (циклов / с) (Ом · с) = Ом), что соответствует его роли в качестве эффективное сопротивление.

Представление векторов

Напряжение на катушке индуктивности «ведет» ток в соответствии с законом Ленца. Следовательно, вектор, представляющий ток и напряжение, будет иметь вид. Опять же, вектора — это векторы, вращающиеся против часовой стрелки с частотой [latex] \ nu [/ latex] (вы можете видеть, что напряжение опережает ток) . В последующих выпусках Atoms будет обсуждаться, как эти векторы можно использовать для анализа цепей RC, RL, LC и RLC.

Векторная диаграмма : Векторная диаграмма для цепи переменного тока с индуктором.

Фазоры для индукторов в цепях переменного тока

Резонанс в цепях RLC

Резонанс — это тенденция системы к колебаниям с большей амплитудой на некоторых частотах — в последовательной цепи RLC он возникает на [latex] \ nu_0 = \ frac {1} {2 \ pi \ sqrt {\ text {LC}} }[/латекс].

Цели обучения

Сравнить резонансные характеристики цепей с высоким и низким сопротивлением

Ключевые выводы

Ключевые моменты

• Условие резонанса последовательной цепи RLC может быть получено приравниванием X _L и X _C , так что два противоположных вектора компенсируют друг друга.
• В резонансе влияние катушки индуктивности и конденсатора компенсируется, так что Z = R, а I _{среднеквадратичное значение} является максимальным.
• Цепи с более высоким сопротивлением не так сильно резонируют по сравнению с цепями с более низким сопротивлением, и при этом они не будут такими избирательными, например, в радиоприемнике.

Ключевые термины

• реактивное сопротивление : Противодействие изменению протекания тока в цепи переменного тока из-за индуктивности и емкости; мнимая часть импеданса.
• rms : Среднеквадратичное значение: статистическая мера величины изменяющейся величины.
• импеданс : мера сопротивления течению переменного тока в цепи; совокупность его сопротивления, индуктивного и емкостного сопротивления. Обозначается символом Z.

Резонанс — это тенденция системы к колебаниям с большей амплитудой на одних частотах, чем на других. Частоты, при которых амплитуда отклика является относительным максимумом, известны как резонансные частоты системы.2}} [/ latex],

, где I _rms и V _rms — среднеквадратичные значения тока и напряжения соответственно. Реактивные сопротивления изменяются в зависимости от частоты [латекс] \ nu [/ latex], при этом X _L большое на высоких частотах и ​​X _C большое на низких частотах, представленных как:

[латекс] \ text {X} _ \ text {L} = 2 \ pi \ nu \ text {L}, \ text {X} _ \ text {C} = \ frac {1} {2 \ pi \ nu \ text {C}} [/ латекс].

На некоторой промежуточной частоте [latex] \ nu_0 [/ latex] реактивные сопротивления будут равны и отменены, что дает Z = R — это минимальное значение для импеданса, а максимальное значение для I _rms .Мы можем получить выражение для [latex] \ nu_0 [/ latex], взяв X _L = X _C . Подставляя определения X _L и X _C , получаем:

[латекс] \ nu_0 = \ frac {1} {2 \ pi \ sqrt {\ text {LC}}} [/ латекс].

[латекс] \ nu_0 [/ latex] — это резонансная частота последовательной цепи RLC. Это также собственная частота, на которой цепь будет колебаться, если не будет управляться источником напряжения. В [latex] \ nu_0 [/ latex] эффекты катушки индуктивности и конденсатора нейтрализуются, так что Z = R, а I _{среднеквадратичное значение} является максимальным.Резонанс в цепях переменного тока аналогичен механическому резонансу, где резонанс определяется как вынужденные колебания (в данном случае вызванные источником напряжения) на собственной частоте системы.

Приемник в радиостанции — это RLC-цепь, которая лучше всего колеблется на своем [latex] \ nu_0 [/ latex]. Переменный конденсатор часто используется для регулировки резонансной частоты, чтобы получить желаемую частоту и отклонить другие. представляет собой график зависимости тока от частоты, иллюстрирующий резонансный пик в I _rms в [латексе] \ nu_0 = \ text {f} _0 [/ latex].Две кривые относятся к двум разным схемам, которые различаются только величиной сопротивления в них. Пик ниже и шире для цепи с более высоким сопротивлением. Таким образом, цепи с более высоким сопротивлением не резонируют так сильно, и они не будут такими избирательными, например, в радиоприемнике.

Зависимость тока от частоты : График зависимости тока от частоты для двух цепей серии RLC, различающихся только величиной сопротивления. Оба имеют резонанс при f0, но для более высокого сопротивления он ниже и шире.Источник управляющего переменного напряжения имеет фиксированную амплитуду V0.

Мощность

Мощность, подаваемая в цепь переменного тока серии RLC, рассеивается сопротивлением в цепи и определяется как [латекс] \ text {P} _ {\ text {avg}} = \ text {I} _ {\ text {rms }} \ text {V} _ {\ text {rms}} \ cos {\ phi} [/ latex]. Здесь [latex] \ phi [/ latex] называется фазовым углом.

Цели обучения

Рассчитать мощность, подаваемую в цепь переменного тока серии RLC с учетом тока и напряжения.

Ключевые выводы

Ключевые моменты

• Фазовый угол ϕ — это разность фаз между напряжением источника V и током I.См. Векторную диаграмму в.
• На резонансной частоте или в чисто резистивной цепи Z = R, так что cosϕ = 1. Это означает, что ϕ = 0º и что напряжение и ток синфазны.
• Среднюю мощность, рассеиваемую в цепи RLC, можно рассчитать, взяв среднее во времени мощность, P (t) = I (t) V (t), за период.

Ключевые термины

• среднеквадратичное значение : Среднеквадратичное значение: статистическая мера величины переменной величины.

Если ток изменяется в зависимости от частоты в цепи RLC, то мощность, подаваемая на него, также зависит от частоты.Однако средняя мощность — это не просто ток, умноженный на напряжение, как в чисто резистивных схемах. Как было замечено в предыдущих атомах, напряжение и ток в цепи RLC не совпадают по фазе. Между напряжением источника V и током I существует фазовый угол ϕ, равный

.

[латекс] \ cos {\ phi} = \ frac {\ text {R}} {\ text {Z}} [/ latex], как показано на рисунке

Векторная диаграмма для последовательной цепи RLC : Векторная диаграмма для последовательной цепи RLC. \ phi — фазовый угол, равный разности фаз между напряжением и током.

Например, на резонансной частоте [латекс] (\ nu_0 = \ frac {1} {2 \ pi \ sqrt {\ text {LC}}}) [/ latex] или в чисто резистивной цепи Z = R, так что cosϕ = 1. Это означает, что ϕ = 0º и что напряжение и ток синфазны, как и ожидалось для резисторов. На других частотах средняя мощность меньше, чем в резонансе, потому что напряжение и ток не совпадают по фазе, а I _{среднеквадратичное значение} ниже.

Тот факт, что напряжение и ток источника не совпадают по фазе, влияет на мощность, подаваемую в цепь.Можно показать, что средняя мощность

[латекс] \ text {P} _ {\ text {avg}} = \ text {I} _ {\ text {rms}} \ text {V} _ {\ text {rms}} \ cos {\ phi} [/ латекс]

(уравнение, полученное путем взятия среднего значения мощности по времени, P (t) = I (t) V (t), за период. I (t) и V (t) — это ток и напряжение в момент времени t). Таким образом, cosϕ называется коэффициентом мощности, который может находиться в диапазоне от 0 до 1. Коэффициенты мощности, близкие к 1, желательны, например, при проектировании эффективного двигателя. На резонансной частоте cosϕ = 1.

Мощность, подаваемая в цепь переменного тока серии RLC, рассеивается только за счет сопротивления.Катушка индуктивности и конденсатор имеют входную и выходную энергию, но не рассеивают энергию из цепи. Скорее, они передают энергию вперед и назад друг другу, а резистор рассеивает именно то количество, которое источник напряжения дает цепи. Это предполагает отсутствие значительного электромагнитного излучения от катушки индуктивности и конденсатора (например, радиоволн).

Схема аналогична колесу автомобиля, движущегося по гофрированной дороге, как показано на рисунке. Равномерно расположенные неровности дороги аналогичны источнику напряжения, приводящему колесо в движение вверх и вниз.Амортизатор аналогичен демпфирующему сопротивлению и ограничивающему амплитуду колебаний. Энергия внутри системы перемещается между кинетической (аналогично максимальному току и энергии, запасенной в индукторе) и потенциальной энергией, запасенной в автомобильной пружине (аналогично отсутствию тока и энергии, запасенной в электрическом поле конденсатора). Амплитуда движения колес максимальна, если неровности дороги встречаются с резонансной частотой.

Принудительное демпфированное движение колеса на автомобильной пружине : Принудительное, но демпфированное движение колеса на автомобильной пружине аналогично цепи переменного тока серии RLC.Амортизатор гасит движение и рассеивает энергию аналогично сопротивлению в цепи RLC. Масса и пружина определяют резонансную частоту.

Теория работы магнето-системы высокого напряжения — Вторичная электрическая цепь

Вторичная цепь содержит вторичные обмотки катушки, ротор распределителя, крышку распределителя, провод зажигания и свечу зажигания. Вторичная обмотка состоит из обмотки, содержащей примерно 13 000 витков тонкого изолированного провода; один конец которого электрически заземлен к первичной катушке или сердечнику катушки, а другой конец подключен к ротору распределителя.Первичная и вторичная обмотки заключены в непроводящий материал. Затем весь узел крепится к полюсным наконечникам винтами и зажимами.

Когда первичная цепь замкнута, ток, протекающий через первичную катушку, создает магнитные силовые линии, которые пересекают вторичные обмотки, создавая электродвижущую силу. Когда ток в первичной цепи прекращается, магнитное поле, окружающее первичные обмотки, разрушается, в результате чего вторичные обмотки перерезаются силовыми линиями.

Сила напряжения, индуцированного во вторичных обмотках, когда все другие факторы постоянны, определяется количеством витков провода. Поскольку у большинства высоковольтных магнето есть много тысяч витков провода во вторичной обмотке катушки, во вторичной цепи генерируется очень высокое напряжение, часто достигающее 20 000 вольт. Наведенное во вторичной катушке высокое напряжение направляется к распределителю, который состоит из двух частей: вращающейся и неподвижной. Вращающаяся часть называется ротором распределителя, а неподвижная часть — блоком распределителя.Вращающаяся часть, которая может иметь форму диска, барабана или пальца, изготовлена ​​из непроводящего материала со встроенным проводником. Стационарная часть состоит из блока, также сделанного из непроводящего материала, который содержит клеммы и клеммные колодки, в которые крепится проводка провода зажигания, соединяющая распределитель со свечой зажигания. Это высокое напряжение используется для перепрыгивания через воздушный зазор электродов свечи зажигания в цилиндре для воспламенения топливно-воздушной смеси.

Когда магнит перемещается в положение E-зазора для No.1 цилиндр и точки прерывания просто разделяются или открываются, ротор распределителя совмещается с электродом № 1 в блоке распределителя. Вторичное напряжение, индуцируемое при размыкании точек прерывателя, попадает в ротор, где образует небольшой воздушный зазор с электродом № 1 в блоке.

Рисунок 4-10. Связь между номерами клемм распределителя и номерами цилиндров.

Поскольку распределитель вращается с половинной частотой вращения коленчатого вала на всех четырехтактных двигателях, блок распределителя имеет столько же электродов, сколько цилиндров двигателя, или столько же электродов, сколько цилиндров, обслуживаемых магнето.Электроды расположены по окружности вокруг распределительного блока, так что, когда ротор вращается, цепь замыкается на другой цилиндр и свечу зажигания каждый раз, когда происходит совмещение между пальцем ротора и электродом в распределительном блоке. Электроды распределительного блока пронумерованы последовательно в направлении движения ротора распределителя. [Рис. 4-10]

Номера распределителей представляют порядок искрообразования от магнето, а не номера цилиндров двигателя.Электрод-распределитель с маркировкой «1» подключается к свече зажигания в цилиндре №1; электрод-распределитель с пометкой «2» ко второму зажигающемуся цилиндру; распределительный электрод с пометкой «3» к третьему цилиндру, который будет поджигаться, и так далее.

На Рисунке 4-10 палец ротора распределителя совмещен с электродом распределителя, помеченным «3», который запускает цилиндр № 5 девятицилиндрового радиального двигателя. Поскольку порядок зажигания девятицилиндрового радиального двигателя составляет 1-3-5-7-9-2-4-6-8, третий электрод в порядке зажигания магнето обслуживает электрод №5 цилиндр.

Летный механик рекомендует

Электрическая цепь состоит из генератора энергии, катушки, …

Контекст 1

… Цикл AMR состоит из четырех основных процессов (рис. 1): (1) намагничивание (магнитокалорический эффект вызывает повышение температуры материала регенератора), (2) поток жидкости в сильном и постоянном магнитном поле из холодного резервуара через регенератор в горячий резервуар, (3) размагничивание (магнитокалорический эффект вызывает снижение температуры…

Контекст 2

… рабочий цикл электромагнита с рекуперацией магнитной энергии разделен на четыре временных интервала (которые соответствуют четырем термодинамическим процессам), как показано на рис. 1. Во время процесса 1 ( Рис 1.), что соответствует намагничиванию (от t0 до t1), ток увеличивается со временем; энергия, накопленная в предыдущем цикле, передается от конденсатора к катушке. Во время процесса 3 (рис. 1), который соответствует размагничиванию (от t2 до t3), ток уменьшается со временем; файл…

Контекст 3

… рабочий цикл электромагнита с рекуперацией магнитной энергии разделен на четыре временных интервала (которые соответствуют четырем термодинамическим процессам), как показано на рис. 1. Во время процесса 1 ( Рис 1.), что соответствует намагничиванию (от t0 до t1), ток увеличивается со временем; энергия, накопленная в предыдущем цикле, передается от конденсатора к катушке. Во время процесса 3 (рис. 1), который соответствует размагничиванию (от t2 до t3), ток уменьшается со временем; энергия передается от катушки к конденсатору….

Контекст 4

… разделен на четыре временных интервала (которые соответствуют четырем термодинамическим процессам), как показано на рис. 1. Во время процесса 1 (рис. 1.), который соответствует при намагничивании (от t0 до t1) ток увеличивается со временем; энергия, накопленная в предыдущем цикле, передается от конденсатора к катушке. Во время процесса 3 (рис. 1), который соответствует размагничиванию (от t2 до t3), ток уменьшается со временем; энергия передается от катушки к конденсатору.Из-за различных потерь в электронных компонентах электрической цепи не вся магнитная энергия передается между катушкой и конденсатором. …

Контекст 5

… два дополнительных процесса связаны с теплопередачей во время потока жидкости через пористую матрицу AMR. Эти два процесса в термодинамическом цикле AMR протекают в постоянном магнитном поле. Во время сильнополевого течения жидкости (процесс 2 на рис. 1), который соответствует временному интервалу от t1 до t2, конвективная теплопередача приводит к нагреву рабочего тела (охлаждению AMR).В этом конкретном процессе источник питания напряжения активен. Однако во время процесса течения жидкости в слабом поле, который соответствует интервалу времени от t3 до t4 (процесс 4 на рис. 1), нет электрического …

Контекст 6

… поток жидкости (процесс 2 в На рис. 1), что соответствует временному интервалу от t1 до t2, конвективный теплообмен приводит к нагреву рабочего тела (охлаждению АМР). В этом конкретном процессе источник питания напряжения активен. Однако во время процесса течения жидкости в слабом поле, который соответствует временному интервалу от t3 до t4 (процесс 4 на рис.1) в электронике не течет электрический ток …

Контекст 7

… мощность Pmag, необходимая для выполнения с помощью магнита. Полезный вклад магнитной энергии для AMR (магнитная работа) был рассчитан с использованием численной модели [74], [75], и был рассмотрен уплотненный слой гадолиния. В каждом из магнитных узлов длина AMR составляла 60 мм (направление потока жидкости), а высота воздушного зазора составляла 4 мм (см. Также рис. A1). В электромагните АМР считался прямоугольным и шириной 40 мм.Во вращающемся узле с постоянными магнитами считалось, что восемь AMR заполняют весь цилиндрический воздушный зазор между ротором и статором (с общим средним периметром 320 мм). Пористость AMR уплотненного слоя, которая состояла из …

Context 8

… и C2, была рассчитана по формуле. (D.12). Энергоэффективность для электромагнита типа A была рассчитана при максимальной рабочей частоте 0,5 Гц с использованием уравнения. …

Контекст 9

… рабочий цикл можно разделить на четыре временных интервала (которые также соответствуют четырем термодинамическим процессам), как показано на рис. …

Контекст 10

… для расчета энергии элементов электронной схемы в каждый процесс MC (см. также Рис.1 и Рис. 2). …

Контекст 11

… теоретически определить электрический ток í µí ° ¼ 1 и í µí ° í µí ± ší µí ± Ží µí ± ¥, цепь LRC с недостаточным сбросом должна быть считается. Зависимость электрического тока от времени показана на рис.C1 справа. Решение этого дифференциального уравнения второго порядка приводит к действительной и мнимой части в экспоненциальной форме [87]. Для расчета потребляемой энергии необходимо проанализировать напряжение питания. Электрическая цепь во время процесса потока жидкости в сильном поле на самом деле представляет собой простую цепь LR, как показано на рис. C2. …

Молекулярные выражения: электричество и магнетизм

Индуктивность

Индуктивность — это свойство электрической цепи, с помощью которого изменяющееся магнитное поле создает электродвижущую силу или напряжение в этой цепи или в соседней цепи.Индуктивность также определяется как свойство электрической цепи, противодействующей любому изменению тока. В 1831 году английский ученый Майкл Фарадей обнаружил, что изменяющееся магнитное поле в цепи индуцирует ток в соседней цепи. Примерно в то же время это открытие независимо сделал американский ученый Джозеф Генри. Генерация электродвижущей силы и тока изменяющимся магнитным полем называется электромагнитной индукцией. Электрогенераторы работают по принципу индуктивности.

Линии магнитного поля

Чтобы лучше понять индуктивность, полезно иметь представление о силовых линиях магнитного поля. Все магниты окружены магнитным полем, также называемым магнитным потоком. Магнитное поле можно представить как состоящее из силовых линий или силовых линий. Силы магнитного притяжения и отталкивания движутся по силовым линиям. Шаблон силовых линий магнитного поля можно увидеть в нашем интерактивном руководстве по Java Magnetic Field Lines.

	Интерактивное учебное пособие по Java

Открытия Фарадея

Фарадей сделал свое открытие электромагнитной индукции в эксперименте с использованием двух катушек проволоки, намотанных вокруг противоположных сторон кольца из мягкого железа, аналогично экспериментальной установке на Рисунке 1 ниже.

Первая катушка справа прикреплена к батарее.Вторая катушка содержит компас, который действует как гальванометр для определения протекания тока. Когда переключатель замкнут, через первую катушку проходит ток, и железное кольцо намагничивается. Когда переключатель в первый раз замыкается, компас во второй катушке на мгновение отклоняется и немедленно возвращается в исходное положение. Отклонение компаса указывает на то, что возникла электродвижущая сила, заставившая на мгновение протекать ток во второй катушке. Фарадей также заметил, что при размыкании переключателя компас снова на мгновение отклоняется, но в противоположном направлении.

Фарадей знал, что катушка с проводом, по которой протекает электрический ток, создает магнитное поле. Поэтому он предположил, что изменяющееся магнитное поле индуцирует ток во второй катушке. Замыкание и размыкание переключателя вызывают изменение магнитного поля: расширение и сжатие соответственно. Вы можете провести эксперимент Фарадея в нашем интерактивном учебном пособии по Java Faraday’s Experiment.

	Интерактивное учебное пособие по Java

Фарадей продемонстрировал, что его гипотеза верна, перемещая простой стержневой магнит назад и вперед внутри катушки.Он заметил, что ток индуцировался в катушке только во время движения магнита. Он также заметил, что в катушке индуцировался ток, когда катушка перемещалась рядом с неподвижным постоянным магнитом. Он обнаружил, что именно относительное движение между проводником и магнитным полем производит ток. Чтобы генерировать ток, либо проводник может перемещаться через поле, либо поле может проходить мимо проводника. Для возникновения электромагнитной индукции необходимо изменение магнитного потока.Проведите этот эксперимент с помощью нашего 2-го экспериментального интерактивного учебного пособия по Java Faraday’s 2nd Experiment.

	Интерактивное учебное пособие по Java

Закон электромагнитной индукции Фарадея

Связь между изменением магнитного потока и индуцированной электродвижущей силой известна как закон электромагнитной индукции Фарадея:

Величина электромагнитной силы, индуцированной в цепи, пропорциональна скорости изменения магнитного потока, проходящего через цепь.

Математически закон Фарадея записывается как:

E = — (DF / Dt)

, где E — индуцированная электродвижущая сила в вольтах, DF — изменение магнитной силы в сетках, а Dt — количество времени в секундах, в течение которого происходит изменение магнитной силы.

Из приведенной выше формулы мы видим, что величина индуцированного напряжения определяется двумя факторами:

1. Величина магнитного потока
   Чем больше количество силовых линий магнитного поля, пересекающих проводник, тем больше индуцированное напряжение.
2. Скорость, с которой силовые линии магнитного поля пересекают проводник
   Чем быстрее силовые линии пересекают проводник или проводник пересекает силовые линии, тем больше индуцированное напряжение. Вы можете наблюдать это, варьируя скорость, с которой вы перемещаете магнит, в нашем 2-м экспериментальном интерактивном руководстве по Java Фарадея.

Закон Ленца

Знак минус в законе Фарадея указывает направление или полярность индуцированного напряжения.В 1833 году русский физик Генрих Ленц открыл взаимосвязи между силами, напряжениями и токами электромагнитной индукции. Закон Ленца гласит:

Индуцированная электродвижущая сила генерирует ток, который индуцирует противодействующее магнитное поле, которое противодействует магнитному полю, генерирующему ток.

Например, когда внешнее магнитное поле приближается к кольцевому проводнику, ток, который создается в кольце, будет индуцировать собственное магнитное поле, противоположное приближающемуся внешнему магнитному полю.С другой стороны, когда внешнее магнитное поле удаляется от кольца, индуцированное магнитное поле в кольце меняет направление на противоположное и противодействует изменению направления внешнего магнитного поля. Вы можете увидеть закон Ленца в действии в нашем интерактивном учебном пособии по Java Lenz’s Law.

	Интерактивное учебное пособие по Java

Самоиндуктивность

Мы знаем, что ток, протекающий по проводнику, создает магнитное поле вокруг проводника.Когда ток увеличивается, уменьшается или меняет направление, магнитное поле изменяется. Магнитное поле расширяется, сжимается или меняет направление в ответ на изменения тока. Изменяющееся магнитное поле индуцирует дополнительную электродвижущую силу или напряжение в проводнике. Возникновение этого дополнительного напряжения называется самоиндукцией, потому что оно индуцируется внутри самого проводника. Направление самоиндуцированной электродвижущей силы или напряжения противоположно направлению тока, который его генерировал.Это соответствует закону Ленца, который можно выразить следующим образом:

Индуцированная электродвижущая сила (напряжение) в любой цепи всегда направлена ​​против тока, создавшего ее.

Эффект самоиндукции в цепи заключается в противодействии любому изменению тока, протекающего в цепи. Например, когда напряжение подается на цепь, ток начинает течь во всех частях цепи. Этот ток индуцирует вокруг себя магнитное поле.По мере расширения поля в цепи создается противодействующее напряжение, иногда называемое обратным напряжением. Это обратное напряжение вызывает протекание тока в направлении, противоположном направлению основного тока. Индуктивность на этом этапе препятствует нарастанию тока. Когда индуцированное магнитное поле становится устойчивым, оно перестает индуцировать обратное напряжение.

Когда ток в цепи отключается, индуцированное магнитное поле начинает разрушаться. Когда поле схлопывается, оно генерирует напряжение в том направлении, которое на мгновение продлевает основной ток.Когда индуцированное магнитное поле полностью схлопывается, индуцированное напряжение и ток прекращаются. Опять же, самоиндукция препятствует изменению тока. Он препятствует нарастанию тока и задерживает его пробой. Вы можете увидеть влияние самоиндукции на ток в нашем интерактивном руководстве по Java Self-Inductance.

	Интерактивное учебное пособие по Java

Взаимная индуктивность

В эксперименте Фарадея с двумя катушками на кольце из проводящего железа он обнаружил, что изменяющееся магнитное поле в одной катушке индуцирует электродвижущую силу или напряжение во второй катушке.Это явление называется взаимной индуктивностью. Взаимная индуктивность возникает, когда изменяющееся магнитное поле в одной цепи индуцирует напряжение в соседней цепи.

В соответствии с законом Ленца направление индуцированной электродвижущей силы или напряжения противоположно направлению тока, который его генерировал. Снова глядя на эксперимент Фарадея ниже, мы обнаруживаем, что когда напряжение подается на катушку справа, в железном кольце индуцируется магнитное поле. По мере расширения поля во второй катушке слева генерируется напряжение.Это вторичное напряжение вызывает ток во второй катушке. Этот вторичный ток протекает в направлении, противоположном току в первой катушке. Когда индуцированное магнитное поле в кольце становится устойчивым, ток перестает течь во второй катушке.

Когда ток в первой катушке отключается, индуцированное магнитное поле в кольце начинает разрушаться. Когда поле схлопывается, во второй катушке снова возникает напряжение.Результирующий ток во второй катушке имеет направление, противоположное ранее наведенному току. Когда магнитное поле в кольце полностью схлопывается, индуцированное напряжение и ток во вторичной катушке прекращаются. Вы можете провести этот эксперимент в нашем интерактивном учебном пособии по Java Faraday’s Experiment.

	Интерактивное учебное пособие по Java

Катушки индуктивности

Дроссели — это электрические устройства, предназначенные для обеспечения индуктивности в цепи.Индуктор — это просто катушка с проволокой. Самоиндукция возникает в цепи, даже если проводники абсолютно прямые. Однако самоиндукция в прямом проводе очень мала. Индуктивность намного более значительна, когда проводники скручены, потому что магнитное поле каждого витка катушки пересекает соседние витки катушки. Для увеличения индуктивности индуктор может иметь железный сердечник. Помещение железа внутрь катушки значительно увеличивает силу ее магнитных полей.

Факторы, влияющие на индуктивность катушки

На индуктивность катушки влияют три фактора:

1. Количество витков в катушке
   Чем больше количество витков в катушке, тем больше индуктивность.Это верно, потому что чем больше витков в катушке, тем больше количество взаимодействий магнитного поля.
2. Площадь сечения катушки
   Чем больше площадь поперечного сечения катушки, тем больше индуктивность. Этот фактор тесно связан с количеством витков в катушке. Он включает рассмотрение расстояния между витками. Поскольку магнитное поле становится слабее по мере его движения, витки, которые расположены близко друг к другу, обеспечивают взаимодействия там, где поля наиболее сильны.
3. Проницаемость керна
   Проницаемость относится к способности материала проводить магнитные силовые линии. Железо имеет гораздо большую проницаемость, чем воздух. Следовательно, катушка с железным сердечником имеет большую индуктивность, чем катушка с сердечником, содержащим только воздух.

Расчет наведенного напряжения в катушке

Закон Фарадея можно использовать для определения полной наведенной электродвижущей силы или напряжения в катушке.Предполагая, что витки катушки плотно намотаны, полное наведенное напряжение катушки можно рассчитать по следующей формуле:

E = — N (DF / Dt)

, где E — индуцированная электродвижущая сила в вольтах, N — количество витков в катушке, DF — изменение магнитной силы в веберах, а Dt — время в секундах, в течение которого происходит изменение магнитной силы.

Измерение индуктивности

Символ индуктивности — заглавная буква L в честь Генриха Ленца. Единицей измерения индуктивности является генри, названный в честь Джозефа Генри, сокращенно ч . Один ген индуктивности существует, когда один вольт электродвижущей силы индуцируется при изменении тока со скоростью один ампер в секунду. Математически это записывается как:

L = E / (DI / Dt)

, где L — индуктивность в генри, E — индуцированная электродвижущая сила в вольтах, DI — изменение тока в амперах, а Dt — время в секундах, в течение которого происходит изменение тока. .

Катушки индуктивности в последовательной цепи

Последовательная цепь — это цепь, в которой ток имеет только один путь. В последовательной цепи весь ток проходит через каждый из компонентов в цепи. Схема на рисунке 2 имеет три последовательно включенных индуктора.

Если катушки индуктивности экранированы или расположены достаточно далеко друг от друга, чтобы предотвратить взаимную индуктивность, общая индуктивность цепи является накопительной. Полная индуктивность такой цепи — это сумма всех индукторов в цепи.Поэтому для расчета общей индуктивности последовательной цепи используйте следующую формулу:

L _T = L ₁ + L ₂ + L ₃ . . .

, где L _T — общая индуктивность в цепи, а L ₁ через L ₃ . . . — это номинальные значения индуктивности отдельных катушек индуктивности в цепи.

Используя эту формулу, общую индуктивность последовательной цепи на Рисунке 2 можно рассчитать следующим образом:

L _T = 50 + 40 + 20

L _T = 110 м h

Катушки индуктивности в параллельных цепях

Параллельная цепь — это цепь, в которой компоненты расположены так, что путь для тока разделен.Схема на Рисунке 3 имеет три параллельно включенных индуктора.

Параллельное соединение катушек индуктивности всегда снижает общую индуктивность цепи. Если индукторы экранированы или расположены достаточно далеко друг от друга, чтобы предотвратить взаимную индуктивность, общую индуктивность цепи можно рассчитать по следующей формуле:

L _T = 1 ÷ (1 / L ₁ + 1 / L ₂ + 1 / L ₃ ….)

, где L _T — полная индуктивность в цепи, а L ₁ через L ₃ .. . — это номинальные значения индуктивности отдельных катушек индуктивности в цепи.

Используя эту формулу, общую индуктивность указанной выше параллельной цепи можно рассчитать следующим образом:

L _T = 1 ÷ (1/5 + 1/15 + 1/30)

L _T = 1 ÷ (0,2 + 0,066 + 0,033)

L _T = 1 ÷ 0,299

L _T = 3.344 мч

Индуктивное реактивное сопротивление

Эффект самоиндукции в катушке заключается в противодействии любому изменению тока, протекающего в катушке. Например, когда на катушку подается напряжение, в катушке начинает течь ток. Этот ток индуцирует вокруг себя магнитное поле. По мере расширения поля в катушке генерируется противодействующее напряжение, иногда называемое обратным напряжением. Это обратное напряжение противодействует основному току. Это противодействие протеканию тока называется индуктивным реактивным сопротивлением и измеряется в омах.

Величина индуктивного сопротивления в цепи зависит от частоты и величины переменного тока, а также величины индуктивности. Индуктивное сопротивление цепи можно рассчитать по следующей формуле:

X _L = 2pfL

, где X _L — индуктивное реактивное сопротивление в омах, 2p — постоянная, полученная расчетным путем, которая обычно округляется до 6,28, f — частота приложенного переменного тока в герцах, а L — это постоянная. индуктивность цепи в генри.

Трансформаторы

Трансформаторы работают по принципу взаимной индуктивности. Трансформаторы используются для увеличения или уменьшения напряжений и токов переменного тока в цепях. Трансформатор обычно состоит из двух катушек провода, электрически изолированных друг от друга, намотанных на один и тот же сердечник. Одна катушка называется первичной катушкой; другой называется вторичной обмоткой. Первичная катушка — это входная катушка трансформатора, а вторичная катушка — это выходная катушка.Когда переменное напряжение подается на первичную катушку, оно вызывает изменяющееся магнитное поле в сердечнике. Взаимная индукция вызывает индуцирование напряжения во вторичной катушке.

Количество обмоток первичной и вторичной обмоток трансформатора определяет, как изменяется напряжение в цепи. Когда количество витков первичной катушки больше, чем количество вторичной катушки, индуцированное напряжение во вторичной катушке меньше, чем приложенное напряжение первичной катушки.Когда количество обмоток первичной обмотки меньше, чем количество обмоток вторичной обмотки, индуцированное напряжение во вторичной обмотке больше, чем приложенное напряжение первой обмотки. Если выходное напряжение трансформатора больше входного напряжения, он называется повышающим трансформатором. Если выходное напряжение трансформатора меньше входного напряжения, он называется понижающим трансформатором. Откройте для себя эффекты изменения входного напряжения и количества обмоток трансформатора в нашем интерактивном руководстве по Java Transformer.

	Интерактивное учебное пособие по Java

Повышающий трансформатор увеличивает напряжение. Однако увеличение напряжения сопровождается уменьшением тока. Обратное верно для понижающего трансформатора. Понижающий трансформатор снижает напряжение, но увеличивает ток. Это свойство трансформаторов делает их очень полезными и выгодными для передачи электроэнергии на большие расстояния.Повышающие трансформаторы используются на электростанциях для выработки очень высоких напряжений. Уменьшается выходной ток, что значительно снижает потери мощности из-за сопротивления в линиях передачи. Когда мощность достигает потребителей, используются понижающие трансформаторы для снижения напряжения и увеличения тока до уровня, необходимого для потребительских приложений.

Применение индуктивности

Свойства индукторов делают их очень полезными в различных приложениях.Например, индукторы противодействуют любым изменениям тока. Следовательно, индукторы можно использовать для защиты цепей от скачков тока. Катушки индуктивности также используются для стабилизации постоянного тока и для контроля или устранения переменного тока. Катушки индуктивности, используемые для устранения переменного тока выше определенной частоты, называются дросселями.

Генераторы

Одно из наиболее распространенных применений электромагнитной индуктивности — генерация электрического тока. Чтобы узнать, как работает генератор, посетите наш учебник по генераторам и двигателям .

Радиоприемники Катушки индуктивности

могут использоваться в цепях с конденсаторами для генерации и изоляции высокочастотных токов. Например, катушки индуктивности используются с конденсаторами в схемах настройки радиоприемников. На рисунке 4 переменный конденсатор подключен к схеме антенна-трансформатор. Передаваемые радиоволны вызывают прохождение индуцированного тока в антенне через первичную катушку индуктивности на землю.

Во вторичной катушке индуктивности индуцируется вторичный ток в противоположном направлении.Этот ток течет к конденсатору. Скачок тока в конденсаторе вызывает противодействующую электродвижущую силу. Эту противодействующую электродвижущую силу называют емкостным реактивным сопротивлением. Индуцированный поток тока через катушку также вызывает противодействующую электродвижущую силу. Это называется индуктивным реактивным сопротивлением. Таким образом, мы имеем в цепи как емкостное, так и индуктивное реактивное сопротивление.

На более высоких частотах индуктивное реактивное сопротивление больше, а емкостное реактивное сопротивление меньше. На более низких частотах все наоборот.Переменный конденсатор используется для выравнивания индуктивного и емкостного сопротивлений. Состояние, при котором реактивные сопротивления уравновешены, называется резонансом. Конкретная частота, которая изолирована выровненными реактивными сопротивлениями, называется резонансной частотой.

Радиосхема настраивается путем регулирования емкости переменного конденсатора для выравнивания индуктивного и емкостного реактивного сопротивления цепи для желаемой резонансной частоты или, другими словами, для настройки на желаемую радиостанцию.Наш интерактивный учебник по Java Radio Receiver демонстрирует, как катушки индуктивности и переменный конденсатор используются для настройки на радиочастоты.

	Интерактивное учебное пособие по Java

Металлоискатели

Работа металлоискателя основана на принципе электромагнитной индукции. Металлоискатели содержат одну или несколько катушек индуктивности.Когда металл проходит через магнитное поле, создаваемое катушкой или катушками, поле индуцирует электрические токи в металле. Эти токи называются вихревыми токами. Эти вихревые токи, в свою очередь, создают собственное магнитное поле, которое генерирует ток в детекторе, который питает сигнал, указывающий на присутствие металла. Наблюдайте за магнитными полями и вихревыми токами, генерируемыми металлоискателем, в нашем учебном пособии по металлоискателю для Java.

	Интерактивное учебное пособие по Java

НАЗАД НА ДОМ ЭЛЕКТРИЧЕСТВА И МАГНИТИЗМА

Вопросы или комментарии? Отправить нам письмо.

© 1995-2021, автор — Майкл В. Дэвидсон и Государственный университет Флориды. Все права защищены. Никакие изображения, графика, программное обеспечение, сценарии или апплеты не могут быть воспроизведены или использованы каким-либо образом без разрешения правообладателей. Использование этого веб-сайта означает, что вы соглашаетесь со всеми юридическими положениями и условиями, изложенными владельцами.

Этот веб-сайт поддерживается нашим

Команда разработчиков графики и веб-программирования
в сотрудничестве с оптической микроскопией в Национальной лаборатории сильного магнитного поля
.

Последнее изменение: пятница, 13 ноября 2015 г., 14:18

Счетчик доступа с 29 марта 1999 г .: 260997

10.3: Магнитные цепи — Разработка LibreTexts

Магнитные цепи включают такие приложения, как трансформаторы и реле. Очень простая магнитная цепь показана на рисунке \ (\ PageIndex {1} \).

Рисунок \ (\ PageIndex {1} \): Простая магнитная цепь.

Во-первых, он состоит из магнитопровода.Сердечник может состоять из одного материала, такого как листовая сталь, но также может использовать несколько секций и воздушный зазор (и). Вокруг сердечника находится по крайней мере один набор витков провода, то есть катушка, сформированная вокруг сердечника. Для трансформаторов используется несколько наборов витков (в простейшем случае один для первичной обмотки, а другой для вторичной). Как мы уже видели, прохождение тока через обмотки создает магнитный поток \ (\ Phi \) в сердечнике. Поскольку этот поток ограничен площадью поперечного сечения сердечника \ (A \), мы можем получить плотность потока \ (B \).

\ [B = \ frac {\ Phi} {A} \ label {10.4} \]

Где

\ (B \) — плотность магнитного потока в теслах,

\ (\ Phi \) — магнитный поток в веберах,

\ (A \) — площадь в квадратных метрах.

Вспомните из главы 9, что одна тесла определяется как один вебер на квадратный метр. Альтернативной единицей измерения, которая иногда используется, является гаусс (система единиц cgs), названная в честь Карла Фридриха Гаусса, немецкого математика и ученого.

\ [1 \ text {тесла} = 10 000 \ text {gauss} \ label {10.2} \ nonumber \]

\ [B = 0,3T \ nonumber \]

Закон Ома для магнитных цепей (закон Гопкинсона или Роуленда)

Между магнитными цепями и электрическими цепями проводится общая параллель, а именно закон Гопкинсона (закон Роуленда). Для электрических цепей закон Ома гласит:

\ [V = I R \ nonumber \]

Аналогично для магнитных цепей:

\ [\ boldsymbol {F} = \ Phi \ boldsymbol {R} \ label {10.6} \]

Где

\ (\ boldsymbol {F} \) — магнитодвижущая сила (или MMF) в ампер-витках,

\ (\ Phi \) — магнитный поток в веберах,

\ (\ boldsymbol {R} \) — сопротивление материала в ампер-витках / Вебере.

Магнитодвижущая сила сравнивается с напряжением источника или электродвижущей силой (ЭДС), магнитный поток сравнивается с потоком тока, а реактивное сопротивление заменяет сопротивление (то есть, с одной стороны, у нас есть материал, который сопротивляется потоку ток, а с другой стороны, материал, у которого есть «сопротивление» для установления магнитного потока). Кроме того, магнитодвижущая сила — это произведение тока, протекающего через катушку, и количества витков или витков в катушке:

\ [\ boldsymbol {F} = N I \ label {10.7} \]

Где

\ (\ boldsymbol {F} \) — магнитодвижущая сила в ампер-оборотах,

\ (N \) — количество витков или витков в катушке,

\ (I \) — ток в катушке в амперах.

Уравнение сопротивления имеет хорошую параллель с уравнением сопротивления (уравнение 2.11 из главы 2):

\ [R = \ frac {\ phi l} {A} \ nonumber \]

\ [\ boldsymbol {R} = \ frac {l} {\ mu A} \ label {10.8} \]

Где

\ (\ boldsymbol {R} \) — сопротивление в ампер-витках / по Веберу,

\ (l \) — длина материала в метрах,

\ (A \) — площадь поперечного сечения материала в квадратных метрах,

\ (\ mu \) — проницаемость материала в генри на метр.

Учитывая характеристики катушки и длину пути магнитной цепи, магнитный поток создает намагничивающую силу \ (H \).

\ [H = \ frac {N I} {l} \ label {10.9} \]

Где

\ (H \) — сила намагничивания в ампер-витках / метр,

\ (N \) — количество витков или витков в катушке,

\ (I \) — ток катушки в амперах,

\ (l \) — длина магнитного пути в метрах.

Уравнение \ ref {10.8} показывает, что ферромагнитные материалы (то есть материалы с высокой проницаемостью, такие как сталь) имеют низкое сопротивление. Практическая проблема здесь в том, что \ (\ mu \), в отличие от удельного сопротивления \ (\ rho \) резисторов, не является постоянной величиной для таких материалов. Он может значительно различаться, как видно на общей диаграмме, представленной на рисунке \ (\ PageIndex {2} \). В результате непрактично находить сопротивление таким же образом, как мы находим сопротивление. Однако еще не все потеряно.

Рисунок \ (\ PageIndex {2} \): Типичная кривая проницаемости для материала с высокой проницаемостью.

Плотность магнитного потока и соответствующая сила намагничивания для любого данного материала связаны следующим уравнением:

\ [B = \ mu H \ label {10.10} \]

Где

\ (B \) — плотность потока в теслах,

\ (\ mu \) — проницаемость материала в генри / метр,

\ (H \) — сила намагничивания в ампер-витках / метр.

Еще раз, хитрость здесь — проницаемость материала керна. Для воздуха мы можем использовать проницаемость свободного пространства \ (\ mu_0 \).{-6} H / m \ label {10.11} \]

Для других материалов, таких как листовая или литая сталь, мы пойдем другим путем; а именно кривую, полученную эмпирическим путем, которая отображает зависимость плотности потока \ (B \) от силы намагничивания \ (H \). Такие графы обычно называют «кривыми \ (BH \)». Пример показан на рисунке \ (\ PageIndex {3} \). Ясно, что эта кривая не является хорошей прямой линией или даже очевидной предсказуемой функцией. Сразу бросаются в глаза начальные крутые подъемы, за которыми следует сглаживание кривой.Это сплющивание соответствует насыщению магнитного материала. Напротив, график для воздуха покажет прямую линию с очень пологим уклоном. Как мы увидим, возможность достичь высокой плотности магнитного потока для данной силы намагничивания приведет к созданию эффективной и действенной магнитной цепи. Таким образом, хотя воздух обладает положительным свойством ненасыщения, результирующая плотность потока мала, что обычно приводит к снижению производительности.

Рисунок \ (\ PageIndex {3} \): Общая кривая \ (BH \).

Кривая BH

Процесс создания кривой \ (BH \) выглядит следующим образом. Сначала мы создаем ядро ​​исследуемого материала. Затем вокруг этого сердечника наматывается катушка с проволокой. Пример показан на рисунке \ (\ PageIndex {4} \). Здесь у нас есть базовый тороид с катушкой на \ (N \) витков.

Рисунок \ (\ PageIndex {4} \): Тороидальный сердечник с катушкой.

Начнем с того, что система находится в состоянии покоя и не находится под напряжением. На катушку подается небольшой ток \ (I \).Это создает намагничивающую силу согласно уравнению \ ref {10.9}. Будет соответствующая плотность потока согласно Уравнению \ ref {10.10}.

Затем ток увеличивается. Это приводит к увеличению силы намагничивания и соответствующему изменению плотности магнитного потока. Сила тока увеличивается до тех пор, пока кривая не станет плоской, указывая на то, что насыщение достигнуто. Эта траектория показана пунктирной линией на рисунке \ (\ PageIndex {5} \), начинающейся в точке \ (\ boldsymbol {a} \) с точкой \ (\ boldsymbol {b} \), обозначающей насыщение.Затем ток снижается. Это вызывает уменьшение намагничивающей силы, но, хотя плотность магнитного потока уменьшается, она не возвращается идеально по исходной траектории. Вместо этого кривая смещается над исходной.

Рисунок \ (\ PageIndex {5} \): Построение кривой BH.

Со временем ток упадет до нуля. Это соответствует точке \ (\ boldsymbol {c} \) на графике на рисунке \ (\ PageIndex {5} \). В этот момент, даже если в катушке нет тока, в сердечнике все еще есть магнитный поток.Результирующая магнитная индукция называется удерживающей способностью и является мерой остаточного магнетизма. Это явление позволяет намагничивать материалы.

Если мы теперь изменим направление тока катушки и начнем увеличивать его величину, плотность потока будет продолжать падать. В точке \ (\ boldsymbol {d} \) он достигнет нуля. Поскольку мы фактически принудили поток обратно к нулю, мы называем намагничивающую силу, необходимую для этого, коэрцитивной силой или коэрцитивной силой.

По мере увеличения величины тока плотность потока также увеличивается, но с противоположным знаком. В конце концов, в точке \ (\ boldsymbol {e} \) снова достигается насыщение. Еще раз, если величина тока уменьшается, величина плотности потока также будет уменьшаться, но не будет точно прослеживаться вдоль исходной траектории. На этот раз он пойдет по более низкому пути. Когда ток снижается до нуля в точке \ (\ boldsymbol {f} \), сохраняемость зеркала становится очевидной. Дальнейшее положительное увеличение тока показывает зеркальную коэрцитивность в точке \ (\ boldsymbol {g} \).Наконец, когда ток увеличивается до максимума, мы снова достигаем насыщения в точке \ (\ boldsymbol {b} \).

Если ток снова переключается таким образом, процесс повторяется, и снова выбирается внешний путь, указанный стрелками. Таким образом, конкретное значение силы намагничивания может привести к различным значениям плотности потока: это зависит от недавней истории материала. Этот эффект известен как гистерезис и встречается также в других областях.

Фактически, опубликованные кривые \ (BH \) следуют за серединой петли гистерезиса.Пример кривых \ (BH \) для трех различных материалов сердечника показан на рисунке \ (\ PageIndex {6} \) ¹ . Кривая A — для листовой стали (которая обычно используется в трансформаторах), кривая B — для литой стали, а кривая C — для чугуна. Мы будем использовать их в следующих примерах. Также доступны кривые для других материалов.

Рисунок \ (\ PageIndex {6} \): Кривые BH для: A. Листовой стали B. Литой стали C. Чугуна

Пример \ (\ PageIndex {2} \)

Предположим, что тороид на рисунке \ (\ PageIndex {4} \) изготовлен из литой стали, имеет катушку на 500 витков, поперечное сечение 2 см на 2 см и среднюю длину пути 50 см.Определите магнитный поток в паутине, если на катушку подается ток 0,3 ампер.

Мы будем использовать уравнение \ ref {10.9}, чтобы найти силу намагничивания, и по кривой \ (BH \) найти плотность потока.

\ [H = \ frac {N I} {l} \ nonumber \]

\ [H = \ frac {500 \ text {повороты} \ times 0,3 A} {0,5 м} \ nonumber \]

\ [H = 300At / m \ text {(ампер-оборотов на метр)} \ nonumber \]

Литая сталь

соответствует кривой B (зеленая) на рисунке \ (\ PageIndex {5} \). Приличная оценка плотности потока — 0.2 \ nonumber \]

\ [\ Phi = 2.08E-4Wb \ nonumber \]

KVL для магнитных цепей

Беглый просмотр уравнений \ ref {10.7} и \ ref {10.9} показывает, что:

\ [\ boldsymbol {F} = H l = N I \ label {10.12} \]

Продолжая аналогию с законом Ома, произведение ампер-витков катушки, \ (NI \), аналогично увеличению напряжения. Далее, произведение \ (Hl \) аналогично падению напряжения. Если мы затем расширим аналогию, включив в нее концепцию закона напряжения Кирхгофа, неудивительно, что сумма «подъемов» \ (NI \) должна равняться сумме «падений» \ (Hl \).В схеме на рисунке \ (\ PageIndex {4} \) есть один «подъем» и один «спад». Таким образом, магнитная цепь аналогична минимальной электрической цепи, показанной на рисунке \ (\ PageIndex {7} \). \ (\ boldsymbol {F} \) — магнитодвижущая сила, \ (NI \), а \ (\ boldsymbol {R} \) — сопротивление тороидального сердечника. Это сопротивление испытает «падение» \ (Hl \).

Рисунок \ (\ PageIndex {7} \): Аналог электрической схемы для магнитной системы на рисунке \ (\ PageIndex {4} \).

Ядро может состоять из двух или более различных материалов, что эквивалентно последовательной цепи. В этом случае таблица, подобная той, что представлена ​​на рисунке \ (\ PageIndex {8} \), может использоваться для помощи в вычислениях.2\))»> Рисунок \ (\ PageIndex {8} \): Формат таблицы, используемый для анализа магнитной цепи.

Пора привести несколько наглядных примеров. Мы рассмотрим простую систему, подобную показанной на рисунке \ (\ PageIndex {4} \), двухсекционный сердечник, сердечник с воздушным зазором и сердечник с двумя катушками.

Пример \ (\ PageIndex {3} \)

Предположим, что сердцевина на рисунке \ (\ PageIndex {9} \) сделана из листовой стали, имеет катушку из 200 витков, сечение 1 см на 1 см и среднюю длину пути 12 см. Определите ток катушки, необходимый для достижения магнитного потока 1E-4.

Рисунок \ (\ PageIndex {9} \): Магнитная система для примера \ (\ PageIndex {3} \).2\))»> 1E − 4 1 190 0.12 22,8

Это «падение» составляет 22,8 ампер-витков, а катушка имеет 200 витков. Следовательно, требуемый ток:

\ [I = \ frac {H l} {N} \ nonumber \]

\ [I = \ frac {22.8At} {200 т} \ nonumber \]

\ [I = 114 мА \ nonumber \]

Далее рассмотрим ядро ​​с двумя секциями.

Пример \ (\ PageIndex {4} \)

Учитывая магнитную систему, показанную на рисунке \ (\ PageIndex {10} \), предположим, что секция A изготовлена ​​из листовой стали, а секция B — из литой стали.Каждая часть имеет сечение 2 см на 2 см. Длина пути A составляет 12 см, а длина пути B — 4 см. Если в катушке 50 витков, определите ток катушки, необходимый для достижения магнитного потока 2E-4.

Рисунок \ (\ PageIndex {10} \): Магнитная система для примера \ (\ PageIndex {4} \).

Аналогичная схема состоит из одного источника и двух сопротивлений. Это показано на рисунке \ (\ PageIndex {11} \).

Следовательно:

\ [N I = H_ {лист} l_ {лист} + H_ {cast} l_ {cast} \ nonumber \]

В нашем столе будет две строки, одна для листовой стали, а вторая для литой стали.Первая строка потребует использования кривой A (листовая сталь) из рисунка \ (\ PageIndex {6} \), а вторая строка потребует использования кривой B (литая сталь).

Рисунок \ (\ PageIndex {11} \): Аналогичная электрическая схема для системы, показанной на рисунке \ (\ PageIndex {10} \).

Поток, как и ток в последовательном контуре, будет одинаковым в обеих секциях. Отсюда мы можем заполнить ряд других значений в таблице, чтобы получить:

Раздел	Флюс \ (\ Phi \) (Wb)	Площадь \ (А \) (м \ (^ 2 \))	Плотность потока Б (Т)	Сила намагничивания \ (H \) (Ат / м)	Длина \ (длина \) (м)	«Капля» \ (Hl \) (Ат)
Листовая сталь	2E − 4	4E − 4	0.2\))»> 4E − 4	0,5	290	0,04	11,6

Используя нашу аналогию с KVL, полное «падение» составляет 8,4 при + 11,6 ат, или 20 ампер. Катушка была указана как имеющая 50 витков. Следовательно:

\ [I = \ frac {H l} {N} \ nonumber \]

\ [I = \ frac {20 At} {50 т} \ nonumber \]

\ [I = 400 мА \ nonumber \]

Обратите внимание, что даже несмотря на то, что секция из литой стали короче секции из листовой стали, она дает большую «каплю»; точно так же, как резистор большего размера в электрической цепи.Это требует большего тока в катушке, чем если бы весь сердечник был сделан из листовой стали.

Наконец, должно быть очевидно, что потребление тока можно уменьшить, если у катушки будет больше витков. Здесь есть практический предел, потому что все витки должны входить в отверстие сердечника. Когда это пространство заполнится, единственный способ увеличить количество витков — использовать провод более тонкого сечения, но это увеличивает сопротивление провода и потери мощности, а также снижает максимальную допустимую нагрузку по току.

Обработка воздушных зазоров

В некоторых системах в сердечнике имеется воздушный зазор. Если для остатка останется только один материал, это создаст систему, подобную изображенной на рисунке \ (\ PageIndex {12} \). Основное наблюдение здесь заключается в том, что проницаемость воздуха намного ниже, чем у ферромагнитных материалов, и, таким образом, зазор будет иметь относительно большое сопротивление по сравнению с длиной его пути. Тогда возникает очевидный вопрос: зачем нам использовать пробел? Одна из возможностей — электромагнитное реле, внутреннее устройство которого показано на рисунке \ (\ PageIndex {13} \).

Рисунок \ (\ PageIndex {12} \): Аналогичная электрическая схема для системы с воздушным зазором.

Рисунок \ (\ PageIndex {13} \): Внутреннее устройство электрического реле.

Чтобы создать реле, мы помещаем одну часть сердечника на шарнир, который можно удерживать в открытом состоянии с помощью небольшой пружины. Это создает воздушный зазор (непосредственно слева от сердечника на рисунке). Если мы подадим достаточно большой ток, результирующего магнитного потока будет достаточно, чтобы преодолеть натяжение пружины и закрыть вторую деталь на первой (т.е., магнитное притяжение). Как только это происходит, зазор исчезает, уменьшая сопротивление вокруг петли. Система будет оставаться закрытой до тех пор, пока ток в катушке не отключится и восстанавливающая пружина снова не разорвет две части. Мы добавляем изолированные металлические контакты к движущейся секции, и в итоге мы получаем сверхмощный переключатель, который «приводится в действие» управляющим током, а не механическим рычагом, перемещаемым человеком.

Стоит повторить, что для воздушных зазоров вместо кривой \ (BH \) мы можем использовать Определение \ ref {10.2 \). Длина пути основного сердечника составляет 8 см, а длина пути зазора составляет 1 мм. Сколько витков потребуется катушке, чтобы при токе катушки 400 мА достигнуть магнитного потока 1,2E-4?

Рисунок \ (\ PageIndex {14} \): Магнитная система для примера \ (\ PageIndex {5} \).

Аналогичная схема состоит из одного источника и двух сопротивлений, одно для сердечника из листовой стали, а второе для воздушного зазора. Это показано на рисунке \ (\ PageIndex {12} \). Далее аналогичное соотношение KVL:

\ [N I = H_ {лист} l_ {лист} + H_ {пробел} l_ {пробел} \ nonumber \]

В этой таблице будет две строки: одна для сердечника из листовой стали и одна для воздушного зазора.2 \))

Плотность потока

Б (Т)

Сила намагничивания

\ (H \) (Ат / м)

Длина

\ (длина \) (м)

«Капля»

\ (Hl \) (Ат)

Листовая сталь 1.2\))»> 3E − 4 0,4 1E − 3

Используя нашу аналогию с KVL, общее «падение» составляет 5,0 при + 318,3 ат, или 523,3 ампера. Ток катушки был задан равным 400 мА.2 \) и длина жилы 20 см. Катушка одна состоит из 2000 витков, а вторая — из 500 витков. Если при токе 120 мА в катушке 1 достигается магнитный поток 2,4E-4, определите ток в катушке 2.

Рисунок \ (\ PageIndex {15} \): Магнитная система для примера \ (\ PageIndex {6} \).

Рисунок \ (\ PageIndex {16} \): Аналогичная электрическая схема для системы, показанной на рисунке \ (\ PageIndex {15} \).

Аналогичная схема состоит из двух источников напряжения и одного реактивного сопротивления для сердечника из листовой стали. 2 \))

Плотность потока

Б (Т)

Сила намагничивания

\ (H \) (Ат / м)

Длина

\ (длина \) (м)

«Капля»

\ (Hl \) (Ат)

Листовая сталь 2.2 \))

Плотность потока

Б (Т)

Сила намагничивания

\ (H \) (Ат / м)

Длина

\ (длина \) (м)

«Капля»

\ (Hl \) (Ат)

Листовая сталь 2.2\))»> 3E − 4 0,8 100 0,2 ​​ 20

Используя нашу аналогию с KVL, находим:

\ [N_2 I_2 = N_1 I_1 −H_ {лист} l_ {лист} \ nonumber \]

\ [N_2 I_2 = 2000 \ text {повороты} \ раз 120 мА −20 При \ nonumber \]

\ [N_2 I_2 = 240At −20 At \ nonumber \]

\ [N_2 I_2 = 220At \ nonumber \]

Катушка 2 была определена как имеющая 500 витков, поэтому ее ток равен:

.

\ [I_2 = \ frac {220 At} {500 витков} \ nonumber \]

\ [I_2 = 440 мА \ nonumber \]

Ключевым моментом является то, что предыдущий пример должен использовать переменный ток, чтобы функционировать, как описано.Постоянный ток не даст ожидаемых результатов. Причина этого восходит к определению 10.2.1 и уравнению 10.2.2: если поток не изменяется относительно проводящей катушки, в катушке не будет индуцироваться напряжение. Таким образом, хотя входной постоянный ток будет создавать поток в сердечнике, этот поток будет статическим и неизменным. Следовательно, вторая катушка не будет производить выходной сигнал. Напротив, переменный ток плавно изменяется по амплитуде и полярности. Это создает плавно изменяющийся магнитный поток, который, в свою очередь, позволяет индуцировать напряжение во второй катушке.

Предположим на мгновение, что в предыдущем примере использовался переменный ток, обратите внимание, что ток почти в четыре раза выше в катушке 2, чем в катушке 1. Если бы мы смогли уменьшить «падение» сердечника до нуля, возможно, за счет уменьшения сопротивления сердечника до пренебрежимо малого значения, то ток увеличился бы ровно в четыре раза (до 480 мА против 440 мА). Это то же самое, что отношение количества витков катушки один к количеству витков катушки два, и известно как отношение витков.