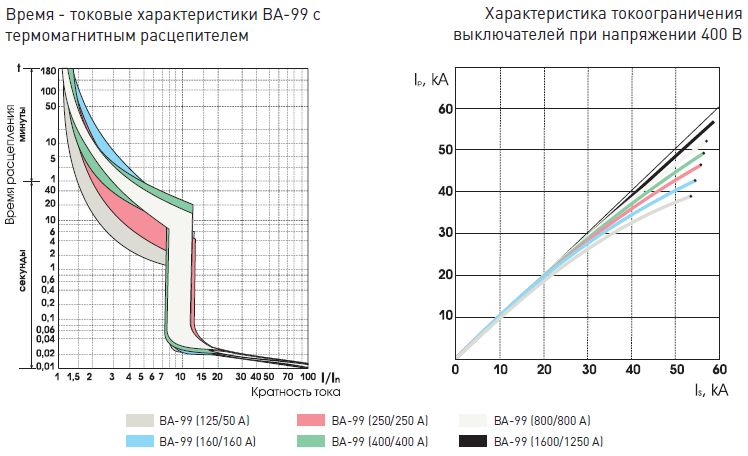
A, B, C и D
Автоматическими выключателями называются приборы, отвечающие за защиту электроцепи от повреждений, связанных с воздействием на нее тока большой величины. Слишком сильный поток электронов способен вывести из строя бытовую технику, а также вызвать перегрев кабеля с последующим оплавлением и возгоранием изоляции. Если вовремя не обесточить линию, это может привести к пожару, Поэтому, в соответствии с требованиями ПУЭ (Правила устройства электроустановок), эксплуатация сети, в которой не установлены электрические автоматы защиты, запрещена. АВ обладают несколькими параметрами, один из которых – время токовая характеристика автоматического защитного выключателя. В этой статье мы расскажем, чем различаются автоматические выключатели категории A, B, C, D и для защиты каких сетей они используются.
Особенности работы автоматов защиты сети
К какому бы классу ни относился автоматический выключатель, его главная задача всегда одна – быстро определить появление чрезмерного тока, и обесточить сеть раньше, чем будет поврежден кабель и подключенные к линии устройства.
Токи, которые могут представлять опасность для сети, подразделяются на два вида:
- Токи перегрузки. Их появление чаще всего происходит из-за включения в сеть приборов, суммарная мощность которых превышает ту, что линия способна выдержать. Другая причина перегрузки – неисправность одного или нескольких устройств.
- Сверхтоки, вызванные КЗ. Короткое замыкание происходит при соединении между собой фазного и нейтрального проводников. В нормальном состоянии они подключены к нагрузке по отдельности.
Устройство и принцип работы автоматического выключателя – на видео:
Токи перегрузки
Величина их чаще всего незначительно превышает номинал автомата, поэтому прохождение такого электротока по цепи, если оно не затянулось слишком надолго, не вызывает повреждения линии. В связи с этим мгновенного обесточивания в таком случае не требуется, к тому же нередко величина потока электронов быстро приходит в норму.
Время срабатывания защитного автоматического выключателя зависит от величины перегрузки: при небольшом превышении нормы оно может занять час и более, а при значительном – несколько секунд.
За отключение питания под воздействием мощной нагрузки отвечает тепловой расцепитель, основой которого является биметаллическая пластина.
Этот элемент нагревается под воздействием мощного тока, становится пластичным, изгибается и вызывает срабатывание автомата.
Токи короткого замыкания
Поток электронов, вызванный КЗ, значительно превосходит номинал устройства защиты, в результате чего последнее немедленно срабатывает, отключая питание. За обнаружение КЗ и немедленную реакцию аппарата отвечает электромагнитный расцепитель, представляющий собой соленоид с сердечником. Последний под воздействием сверхтока мгновенно воздействует на отключатель, вызывая его срабатывание.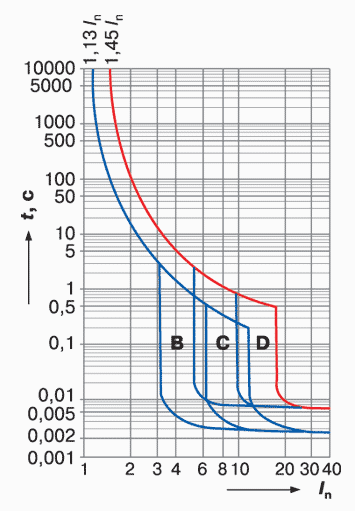 Этот процесс занимает доли секунды.
Этот процесс занимает доли секунды.
Однако существует один нюанс. Иногда ток перегрузки может также быть очень большим, но при этом не вызванным КЗ. Как же аппарат должен определить различие между ними?
На видео про селективность автоматических выключателей:
Здесь мы плавно переходим к основному вопросу, которому посвящен наш материал. Существует, как мы уже говорили, несколько классов АВ, различающихся по времятоковой характеристике. Наиболее распространенными из них, которые применяются в бытовых электросетях, являются устройства классов B, C и D. Автоматические выключатели, относящиеся к категории A, встречаются значительно реже. Они наиболее чувствительны и используются для защиты высокоточных аппаратов.
Между собой эти устройства различаются по току мгновенного расцепления. Его величина определяется кратностью тока, проходящего по цепи, к номиналу автомата.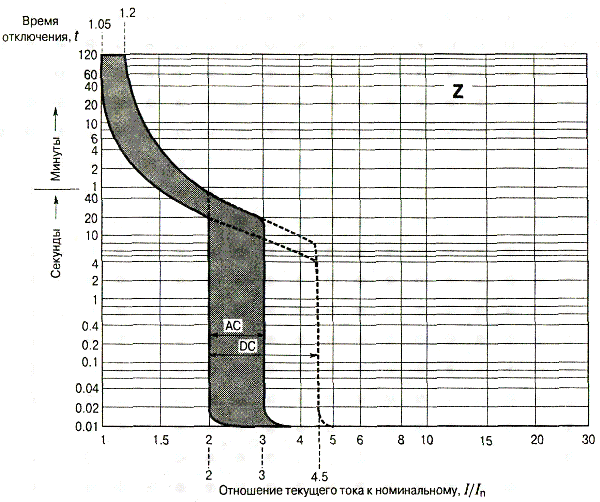
Характеристики срабатывания защитных автоматических выключателей
Класс АВ, определяющийся этим параметром, обозначается латинским литером и проставляется на корпусной части автомата перед цифрой, соответствующей номинальному току.
В соответствии с классификацией, установленной ПУЭ, защитные автоматы подразделяются на несколько категорий.
Автоматы типа МА
Отличительная черта таких устройств – отсутствие в них теплового расцепителя. Аппараты этого класса устанавливают в цепях подключения электрических моторов и других мощных агрегатов.
Защиту от перегрузок в таких линиях обеспечивает реле максимального тока, автоматический выключатель только предохраняет сеть от повреждений в результате воздействия сверхтоков короткого замыкания.
Приборы класса А
Автоматы типа А, как было сказано, обладают самой высокой чувствительностью. Тепловой расцепитель в устройствах с времятоковой характеристикой А чаще всего срабатывает при превышении силой тока номинала АВ на 30%.
Катушка электромагнитного расцепления обесточивает сеть в течение примерно 0,05 сек, если электроток в цепи превышает номинальный на 100%. Если по какой-либо причине после увеличения силы потока электронов в два раза электромагнитный соленоид не сработал, биметаллический расцепитель отключает питание в течение 20 – 30 сек.
Автоматы, имеющие времятоковую характеристику А, включаются в линии, при работе которых недопустимы даже кратковременные перегрузки. К таковым относятся цепи с включенными в них полупроводниковыми элементами.
Защитные устройства класса B
Аппараты категории B обладают меньшей чувствительностью, чем относящиеся к типу A. Электромагнитный расцепитель в них срабатывает при превышении номинального тока на 200%, а время на срабатывание составляет 0,015 сек. Срабатывание биметаллической пластины в размыкателе с характеристикой B при аналогичном превышении номинала АВ занимает 4-5 сек.
Оборудование этого типа предназначено для установки в линиях, в которые включены розетки, приборы освещения и в других цепях, где пусковое повышение электротока отсутствует либо имеет минимальное значение.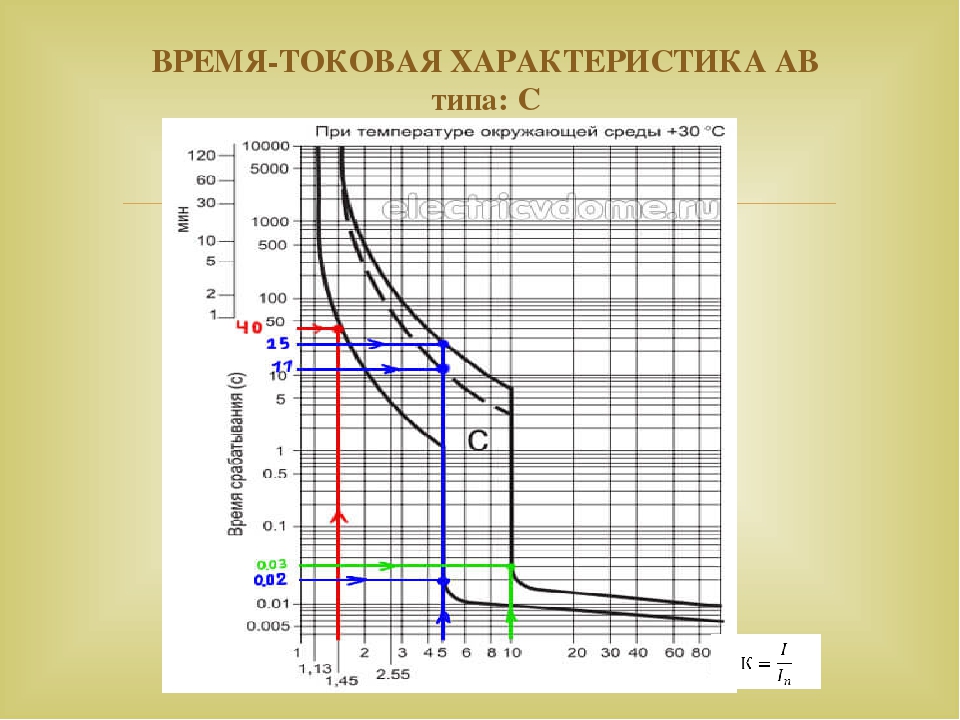
Автоматы категории C
Устройства типа C наиболее распространены в бытовых сетях. Их перегрузочная способность еще выше, чем у ранее описанных. Для того, чтобы произошло срабатывание соленоида электромагнитного расцепления, установленного в таком приборе, нужно, чтобы проходящий через него поток электронов превысил номинальную величину в 5 раз. Срабатывание теплового расцепителя при пятикратном превышении номинала аппарата защиты происходит через 1,5 сек.
Установка автоматических выключателей с времятоковой характеристикой C, как мы и говорили, обычно производится в бытовых сетях. Они отлично справляются с ролью вводных устройств для защиты общей сети, в то время как для отдельных веток, к которым подключены группы розеток и осветительные приборы, хорошо подходят аппараты категории B.
Это позволит соблюсти селективность защитных автоматов (избирательность), и при КЗ в одной из веток не будет происходить обесточивания всего дома.
Автоматические выключатели категории Д
Эти устройства имеют наиболее высокую перегрузочную способность.
Срабатывание теплового расцепителя в этом случае происходит через 0,4 сек.
Устройства с характеристикой D наиболее часто используются в общих сетях зданий и сооружений, где они играют подстраховочную роль. Их срабатывание происходит в том случае, если не произошло своевременного отключения электроэнергии автоматами защиты цепи в отдельных помещениях. Также их устанавливают в цепях с большой величиной пусковых токов, к которым подключены, например, электромоторы.
Защитные устройства категории K и Z
Автоматы этих типов распространены гораздо меньше, чем те, о которых было рассказано выше. Приборы типа K имеют большой разброс в величинах тока, необходимых для электромагнитного расцепления. Так, для цепи переменного тока этот показатель должен превышать номинальный в 12 раз, а для постоянного – в 18.
Этими особенностями обусловлено применение устройств типа K в цепях с исключительно индуктивной нагрузкой.
Приборы типа Z тоже имеют разные токи срабатывания соленоида электромагнитного расцепления, но разброс при этом не столь велик, как в АВ категории K. В цепях переменного тока для их отключения превышение токового номинала должно быть трехкратным, а в сетях постоянного – величина электротока должна быть в 4,5 раза больше номинальной.
Аппараты с характеристикой Z используются только в линиях, к которым подключены электронные устройства.
Наглядно про категории автоматов на видео:
Заключение
В этой статье мы рассмотрели время токовые характеристики защитных автоматов, классификацию этих устройств в соответствии с ПУЭ, а также разобрались, в каких цепях устанавливаются приборы различных категорий.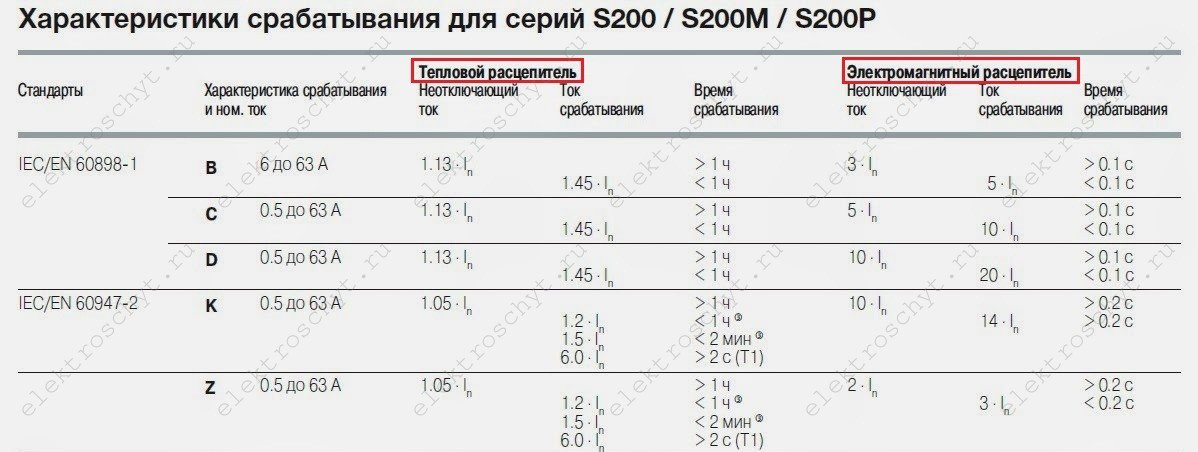 Полученная информация поможет вам определить, какое защитное оборудование следует использовать в сети, исходя из того, какие устройства к ней подключены.
Полученная информация поможет вам определить, какое защитное оборудование следует использовать в сети, исходя из того, какие устройства к ней подключены.
A, B, C, D, K и Z
На сегодняшний день автоматические выключатели стали незаменимым частью электрической цепи как на производстве, так и в быту. Все автоматические выключатели обладают множеством параметров, один из которых – время токовая характеристика. В данной статьи мы рассмотрим, чем отличаются автоматы с время токовой характеристиками категории A, B, C, D и где данные выключатели применяются.
Работа автоматического выключателя
Независимо от того к какому классу относится автоматический выключатель, его основная задача — это срабатывание в случае появления чрезмерного тока в сети, и прежде, чем произойдет повреждение защитного оборудования и кабеля автомат должен обесточить сеть.
В сети бывают 2 вида опасных для сети токов:
Сверхтоки вызванный КЗ. Причиной возникновения короткого замыкания является замыкание нейтрального и фазного проводника между собой. В обычном состоянии фазный и нейтральный провод подключены к нагрузке отдельно друг от друга.
Причиной возникновения короткого замыкания является замыкание нейтрального и фазного проводника между собой. В обычном состоянии фазный и нейтральный провод подключены к нагрузке отдельно друг от друга.
Токи перегрузки. Появление таких токов зачастую происходит в том случае, если суммарная мощность подключенных устройств к линии превышает предельно допустимую норму.
Токи перегрузки
Токи перегрузки зачастую бывают немного больше номинального значения тока автомата, поэтому токи перегрузки как правило не вызывают повреждение цепи в случае недолговременной продолжительности действия. Следовательно, нам не нужно мгновенно отключать сеть в данном случае (зачастую величина тока быстро приходит в норму). В каждом автоматическом выключателе предусмотрено определенное превышение силы тока, которое приводит к срабатыванию автомата.
Время срабатывания автоматического выключателя связано с величиной перегрузки. При значительном превышении номинала выключение автомата происходит за считанные секунды, а при небольшом превышении нормы, срабатывание автомата может произойти в течении часа и больше. Данная особенность обусловлена использованием в автомате биметаллической пластины, которая изгибается при нагреве током превышающего норму и тем самым приводит к срабатыванию автомата. Чем большее значение тока, тем быстрее изгибается пластина и тем раньше срабатывает автомат.
Данная особенность обусловлена использованием в автомате биметаллической пластины, которая изгибается при нагреве током превышающего норму и тем самым приводит к срабатыванию автомата. Чем большее значение тока, тем быстрее изгибается пластина и тем раньше срабатывает автомат.
Токи КЗ
При правильном выборе автомата, ток КЗ должен приводить к его мгновенному срабатыванию. За обнаружение и немедленную реакцию автомата отвечает электромагнитный расцепитель. Конструктивно расцепитель представляет собой соленоид с сердечником. Под воздействием сверхтока сердечник вызывает мгновенное срабатывание автомата и данное отключение должно происходить в течении доли секунд.
Здесь мы плавно переходим к основному вопросу, которому посвящен наш материал. Существует, как мы уже говорили, несколько классов АВ, различающихся по времятоковой характеристике. Наиболее распространенными из них, которые применяются в бытовых электросетях, являются устройства классов B, C и D. Автоматические выключатели, относящиеся к категории A, встречаются значительно реже. Они наиболее чувствительны и используются для защиты высокоточных аппаратов.
Автоматические выключатели, относящиеся к категории A, встречаются значительно реже. Они наиболее чувствительны и используются для защиты высокоточных аппаратов.
Теперь мы плавно переходим к главному вопросу связанному с срабатыванием автоматических выключателей в зависимости от его времятоковой характеристики. Между собой эти устройства различаются по току мгновенного расцепления. Его величина определяется кратностью тока, проходящего по цепи, к номиналу автомата.
Автоматы типа МА
Главная особенность подобных устройств – отсутствие в них теплового расцепителя. Обычно подобные устройства ставят для защиты электрических моторов и прочих мощных устройств.
Устройства класса А
Автоматы класса А имеют самый высокий порог чувствительности. В устройствах с времятоковой характеристикой А, тепловой расцепитель, как правило срабатывает в случае превышении воздействующей силы тока на 30% больше номинала выключателя.
Стоит учесть, что подобные автоматы устанавливаются в линии, в которой не допустимы даже кратковременные перегрузки. К примеру, это может быть цепь с полупроводниковыми элементами.
Защитные устройства класса B
Все устройства категории В имеют меньшую чувствительность, в сравнении с устройствами категории А. Срабатывание электромагнитного расцепителя в них происходит при превышении номинала автомата на 200%. При этом время срабатывания данных устройств составляет 0,015 сек.
Устройства категории В используются для установки в линиях, в которые включены приборы освещения, розетки и также в других цепях, в которых отсутствует пусковые токи или они имеют минимальное значение.
Устройства категории С
Устройства типа С весьма распространены в бытовых сетях. Устойчивость к перегрузкам у данных устройств выше, нежели у всех вышеперечисленных. Чтобы произошло срабатывание соленоида электромагнитного расцепителя, требуется превышение проходящего через расцепитель тока в 5 раз выше номинального значения. Тепловой расцепитель срабатывает в случае превышения номинала в 5 раз через 1,5 сек.
Тепловой расцепитель срабатывает в случае превышения номинала в 5 раз через 1,5 сек.
Как упоминалось ранее выключатели с времятоковой характеристикой С обычно устанавливаются в бытовых сетях. Данные устройства отлично работают в роли вводных устройств для защиты общей сети.
Вы можете купить автоматические выключатели категории С от лучших производителей:
Автоматы CHINT
Автоматы IEK
Автоматические выключатели категории D
Выключатели категории D имеют наиболее высокую перегрузочную способность. Электромагнитная катушка в устройстве срабатывает при превышении номинала автомата, как минимум в 10 раз.
Тепловой расцепитель срабатывает через 0,4 сек.
Зачастую устройства категории D применяются в общих сетях зданий и сооружений в роли страховки. Данные устройства срабатывают в том случае, если не произошло своевременное срабатывание автоматов защиты цепи в отдельных помещениях. Также автоматы категории D могут устанавливаться в цепях с большими пусковыми токами.
Также автоматы категории D могут устанавливаться в цепях с большими пусковыми токами.
Вы можете купить автоматические выключатели категории D здесь:
Автоматы CHINT
Автоматы IEK
Защитные устройства категории K и Z
Автоматы категории K и Z встречаются довольно редко. Устройства категории К имеют большой разброс в значениях тока, требуемых для электромагнитного расцепителя. К примеру, для цепи переменного тока данный показатель должен превышать номинал в 12 раз, а в случае применения в цепи постоянного тока, в 18 раз. Электромагнитный соленоид срабатывает через 0,02 сек. Тепловой расцепитель может сработать при превышении номинала всего на 5%.
Из-за своих свойств устройства категории К применяются в цепях с исключительно индуктивной нагрузкой.
Устройства категории Z также имеют различные токи срабатывания соленоида электромагнитного расцепителя, но разброс для данного варианта, не настолько большой, как в выключателях с категорией К. В цепи постоянного тока величина тока должна быть в 4,5 раза выше номинала, а в сетях переменного тока для срабатывания автомата, ток должен превысить автомат в 3 раза. Устройства категории Z обычно используют для защиты электроники.
В цепи постоянного тока величина тока должна быть в 4,5 раза выше номинала, а в сетях переменного тока для срабатывания автомата, ток должен превысить автомат в 3 раза. Устройства категории Z обычно используют для защиты электроники.
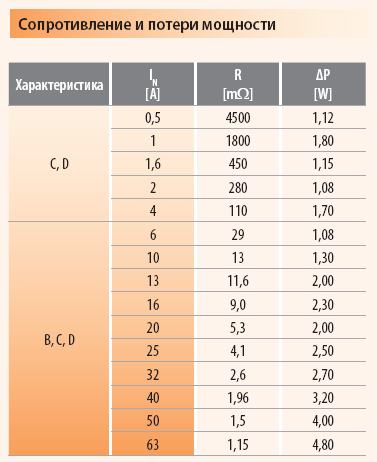
Технические характеристики автоматических выключателей
Рассмотрим технические характеристики автоматических выключателей, установленные требованиями стандартов МЭК 60898‑1 и МЭК 60898‑2, ГОСТ IEC 60898-1-2020 и ГОСТ IEC 60898-2-2011.
Вся информация, которую вы прочитаете ниже основана на материалах из книги Ю.В. Харечко [3], а также соответствующих ГОСТов.
Коммутационная износостойкость.
Коммутационная износостойкость представляет собой способность автоматического выключателя выполнять определенное число циклов оперирования, когда в его главной цепи протекает электрический ток, оставаясь после этого в предусмотренном состоянии.
При номинальном напряжении и токовой нагрузке в своей главной цепи, равной номинальному току, любой автоматический выключатель должен выдерживать не менее 4000 циклов электрического оперирования.
Под циклом оперирования понимают последовательность оперирований автоматического выключателя из одного положения в другое с возвратом в начальное положение. Каждый цикл оперирования состоит из замыкания главных контактов автоматического выключателя с последующим их размыканием.
После выполнения 4000 циклов включения номинальной электрической нагрузки с ее последующим отключением автоматический выключатель не должен быть чрезмерно изношенным, не должен иметь повреждений подвижных контактов главной цепи, а также ослабления электрических и механических соединений. Кроме того, не должна ухудшаться электрическая прочность изоляции автоматического выключателя, которую проверяют соответствующими испытаниями.
Номинальное рабочее напряжение (номинальное напряжение).
Под номинальным рабочим напряжением (номинальным напряжением) Uе понимают установленное изготовителем значение напряжения, при котором обеспечена работоспособность автоматического выключателя, особенно при коротком замыкании. Для одного автоматического выключателя может быть установлено несколько значений номинального напряжения, каждому из которых соответствует собственное значение номинальной коммутационной способности при коротком замыкании.
Для одного автоматического выключателя может быть установлено несколько значений номинального напряжения, каждому из которых соответствует собственное значение номинальной коммутационной способности при коротком замыкании.
В стандарте МЭК 60898‑1 и ГОСТ IEC 60898-1-2020 установлены следующие предпочтительные значения номинального напряжения для различных видов автоматических выключателей:
- для однополюсных – 120, 230, 230/400 В;
- для двухполюсных – 120/240, 230, 400 В;
- для трехполюсных и четырехполюсных – 240, 400 В.
Предпочтительные значения номинального напряжения, равные 120, 120/240 и 240 В, установлены стандартами для автоматических выключателей, предназначенных для использования в однофазных трехпроводных электрических системах переменного тока с номинальным напряжением 120/240 В.
Автоматические выключатели, имеющие значения номинального напряжения 230, 230/400 и 400 В, применяют в широко распространенных однофазных двухпроводных, трехфазных трехпроводных и четырехпроводных электрических системах переменного тока с номинальным напряжением 230 В, 400 и 230/400 В.
Помимо указанных выше в стандарте МЭК 60898-2 и ГОСТ IEC 60898-2-2011 установлены следующие предпочтительные значения номинального напряжения постоянного тока для универсальных автоматических выключателей:
для однополюсных – 125, 220 В;
для двухполюсных – 125/250, 220/440 В.
В обоих стандартах также сказано, что производитель должен указать в своей документации значение минимального напряжения, на которое рассчитан данный автоматический выключатель.
Номинальное напряжение изоляции Ui.
Номинальное напряжение изоляции Ui представляет собой установленное изготовителем напряжение, к которому отнесены напряжения испытания изоляции и расстояния утечки. Номинальное напряжение изоляции применяют для определения значений напряжения, используемых при испытании изоляции автоматического выключателя. Его также учитывают при установлении расстояний утечки автоматического выключателя. Когда отсутствуют другие указания, номинальное напряжение изоляции соответствует наибольшему номинальному напряжению автоматического выключателя. При этом значение наибольшего номинального напряжения автоматического выключателя не должно превышать значения его номинального напряжения изоляции.
При этом значение наибольшего номинального напряжения автоматического выключателя не должно превышать значения его номинального напряжения изоляции.
Номинальный ток In.
Номинальный ток In – установленный изготовителем электрический ток, который автоматический выключатель способен проводить в продолжительном режиме при определенной контрольной температуре окружающего воздуха.
Под продолжительным режимом в стандарте МЭК 60898‑1 и ГОСТ IEC 60898-1-2020 понимают такой режим, при котором главные контакты автоматического выключателя остаются замкнутыми, проводя установившийся электрический ток без прерывания в течение продолжительного времени (неделями, месяцами и даже годами).
Контрольной температурой окружающего воздуха называют такую температуру окружающего воздуха, при которой устанавливают время-токовую характеристику автоматического выключателя. Стандартная контрольная температура окружающего воздуха принята равной 30 °С.
В стандарте МЭК 60898‑1 и ГОСТ IEC 60898-1-2020 установлены следующие предпочтительные значения номинального тока: 6, 8, 10, 13, 16, 20, 25, 32, 40, 50, 63, 80, 100, 125 А.
Номинальная частота.
Характеристика «номинальная частота» определяет промышленную частоту, для которой разработан автоматический выключатель и с которой согласованы другие его характеристики. Автоматический выключатель может иметь несколько значений номинальной частоты. Автоматические выключатели, соответствующие требованиям стандарта МЭК 60898-2 и ГОСТ IEC 60898-2-2011, могут также функционировать при постоянном токе. Стандартные значения номинальной частоты автоматических выключателей равны 50 и 60 Гц.
Характеристика расцепления.
Характеристика расцепления каждого автоматического выключателя, с одной стороны, должна обеспечивать надежную защиту проводников электрических цепей от сверхтока. С другой стороны, она не должна допускать в стандартных условиях эксплуатации расцепления автоматического выключателя при протекании в его главной цепи электрического тока, равного номинальному току. Характеристика расцепления автоматического выключателя должна быть стабильной во время его эксплуатации и находиться в пределах соответствующей стандартной время-токовой зоны1.
Характеристика расцепления автоматического выключателя должна быть стабильной во время его эксплуатации и находиться в пределах соответствующей стандартной время-токовой зоны1.
Примечание 1: Эта характеристика автоматического выключателя в п. 8.6.1 ГОСТ IEC 60898-1-2020 названа нормальной время-токовой характеристикой, а п. 8.6.1 ГОСТ IEC 60898-2-2011 – стандартной время-токовой характеристикой. Однако время-токовая характеристика любого автоматического выключателя имеет вид кривой. В стандартах установлены граничные значения, в пределах которых должны находиться характеристики расцепления всех автоматических выключателей, т. е. в них заданы время-токовые зоны, которые находятся между граничными время-токовыми кривыми. Поэтому рассматриваемую характеристику логичнее поименовать стандартной время-токовой зоной. В п. 8.6.1 стандартов МЭК 60898‑1 и МЭК 60898-2 она названа именно так – «standard time-current zone».
Примечание 1 от Харечко Ю.В. из книги [3]
Основные параметры стандартных время-токовых зон представлены в таблицах 7 стандартов МЭК 60898‑1 и МЭК 60898‑2. Время-токовая характеристика любого качественного автоматического выключателя должна находиться в пределах его стандартной время-токовой зоны.
Ток мгновенного расцепления.
Под током мгновенного расцепления понимают минимальный электрический ток, вызывающий автоматическое срабатывание автоматического выключателя без выдержки времени.
В стандарте МЭК 60898‑1 и ГОСТ IEC 60898-1-2020 для каждого типа мгновенного расцепления установлены следующие стандартные диапазоны токов мгновенного расцепления1:
тип В – свыше 3 In до 5 In;
тип С – свыше 5 In до 10 In;
тип D – свыше 10 In до 20 In2.
Примечание 1: В стандарте МЭК 60898‑1 эта характеристика имеет наименование «стандартный диапазон мгновенного расцепления» («standard range of instantaneous tripping»).
Примечание 1 от Харечко Ю.В. из книги [3]Однако это название нельзя признать удачным. Мгновенное расцепление не может иметь какой-либо диапазон. Оно либо происходит, либо нет. В требованиях стандарта МЭК 60898‑1 и ГОСТ Р 50345 речь идет о диапазонах, в которых находятся минимальные электрические токи, вызывающие мгновенное расцепление автоматических выключателей, т. е. стандарты устанавливают диапазоны, в которых должны находиться токи мгновенного расцепления. Поэтому рассматриваемую характеристику автоматического выключателя в международном стандарте более правильно назвать стандартным диапазоном токов мгновенного расцепления, как она названа в п. 5.3.5 ГОСТ IEC 60898-1-2020.
Примечание 2: В стандарте МЭК 60898‑1 и ГОСТ IEC 60898-1-2020 указано, что для специальных автоматических выключателей, имеющих тип мгновенного расцепления D, верхняя граница может быть увеличена до 50 In.
Примечание 1 от Харечко Ю.В. из книги [3]
Для универсальных автоматических выключателей требованиями стандарта МЭК 60898‑2 и ГОСТ IEC 60898-2-2011 предусмотрены только два типа мгновенного расцепления – B и C. При этом для постоянного тока даны иные, чем для переменного тока, стандартные диапазоны токов мгновенного расцепления.
При этом для постоянного тока даны иные, чем для переменного тока, стандартные диапазоны токов мгновенного расцепления.
тип В – свыше 4 In до 7 In;
тип С – свыше 7 In до 15 In.
Если в главной цепи автоматического выключателя протекает электрический ток, величина которого равна нижней границе стандартного диапазона токов мгновенного расцепления (3 In, 5 In, 10 In переменного тока, а для универсальных автоматических выключателей также 4 In и 7 In постоянного тока), то автоматический выключатель должен расцепиться за промежуток времени более 0,1 с, но менее 45 с или 90 с (тип мгновенного расцепления B), 15 с или 30 с (тип мгновенного расцепления C) и 4 с или 8 с (тип мгновенного расцепления D) соответственно при номинальном токе до 32 А включительно и более 32 А, т. е. нижняя граница стандартного диапазона токов мгновенного расцепления не является током мгновенного расцепления.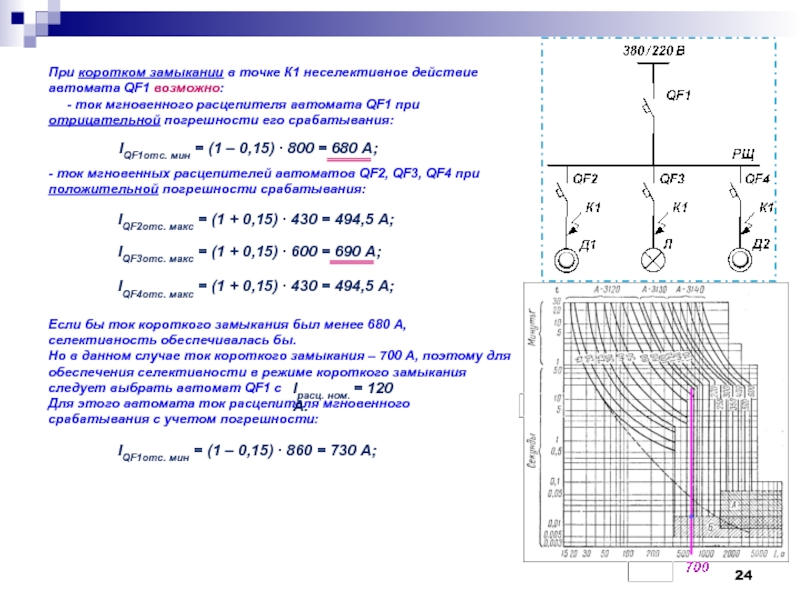
При протекании в главной цепи автоматического выключателя электрического тока, равного верхней границе стандартного диапазона токов мгновенного расцепления (5 In, 10 In, 20 In переменного тока или 7 In, 15 In постоянного тока), он должен расцепиться за промежуток времени менее 0,1 с, т. е. верхняя граница стандартного диапазона токов мгновенного расцепления представляет собой максимально допустимое значение тока мгновенного расцепления. Любой сверхток, превышающий верхнюю границу стандартного диапазона токов мгновенного расцепления, тем более
должен вызывать мгновенное расцепление автоматического выключателя.
В том случае, если значение электрического тока, протекающего в главной цепи автоматического выключателя, находится между нижней и верхней границами стандартного диапазона токов мгновенного расцепления, он может расцепиться либо с незначительной выдержкой времени (несколько секунд), либо без выдержки времени (менее 0,1 с). Фактическое время срабатывания конкретного автоматического выключателя определяется его индивидуальной время-токовой характеристикой. Ток мгновенного расцепления автоматического выключателя также определяется его индивидуальной время-токовой характеристикой.
Фактическое время срабатывания конкретного автоматического выключателя определяется его индивидуальной время-токовой характеристикой. Ток мгновенного расцепления автоматического выключателя также определяется его индивидуальной время-токовой характеристикой.
Стандарт МЭК 60898‑1 и ГОСТ IEC 60898-1-2020 классифицируют автоматические выключатели согласно их токам мгновенного расцепления по типам B, С и D, т. е. все автоматические выключатели подразделяют на три типа мгновенного расцепления: тип B, тип С и тип D. Конкретному типу мгновенного расцепления соответствует собственный стандартный диапазон токов мгновенного расцепления, а также собственная стандартная время-токовая зона. Для универсальных автоматических выключателей стандартом МЭК 60898‑2 и ГОСТ IEC 60898-2-2011 предусмотрены два типа мгновенного расцепления B и С.
Импульсное выдерживаемае напряжение.
Под импульсным выдерживаемым напряжением понимают наибольшее пиковое значение импульсного напряжения предписанной формы и полярности, которое не вызывает пробоя изоляции при установленных условиях. Номинальное импульсное выдерживаемое напряжение Uimp автоматического выключателя должно быть равным или превышать стандартные значения номинального импульсного выдерживаемого напряжения, которые установлены в таблицах 3 стандарта МЭК 60898‑1 и ГОСТ IEC 60898-1-2020 в зависимости от номинального напряжения электроустановки (см. табл. 1).
Номинальное импульсное выдерживаемое напряжение Uimp автоматического выключателя должно быть равным или превышать стандартные значения номинального импульсного выдерживаемого напряжения, которые установлены в таблицах 3 стандарта МЭК 60898‑1 и ГОСТ IEC 60898-1-2020 в зависимости от номинального напряжения электроустановки (см. табл. 1).
| Таблица 1. Стандартные значения номинального импульсного выдерживаемого напряжения | ||
| Номинальное импульсное выдерживаемое напряжение (Uimp), кВ | Номинальное напряжение электроустановки, В | |
| Трехфазные системы | Однофазная система с заземленной средней точкой | |
| 2,5 | — | 120/240 |
| 4 | 230/400, 250/440 | 120/240, 240 |
Предельная отключающая способность при коротком замыкании Icu.
Под предельной отключающей способностью при коротком замыкании Icu1 понимают отключающую способность, для которой предписанные условия соответственно установленной последовательности испытаний не предусматривают способности автоматического выключателя проводить в течение условного времени электрический ток, равный 0,85 его тока нерасцепления.
Примечание 1: В ГОСТ IEC 60898-1-2020 рассматриваемая характеристика автоматического выключателя имеет наименование «предельная наибольшая отключающая способность». В стандарте МЭК 60898‑1 эта характеристика названа иначе – «предельная отключающая способность при коротком замыкании» («ultimate short-circuit breaking capacity»). В национальных стандартах, распространяющихся на автоматические выключатели, вместо термина «предельная наибольшая отключающая способность» следует использовать термин «предельная отключающая способность при коротком замыкании». В требованиях стандарта МЭК 60898‑2 и ГОСТ IEC 60898-2-2011 не используют рассматриваемый термин.
Примечание 1 от Харечко Ю.В. из книги [3]
Номинальная коммутационная способность при коротком замыкании Icn.
Номинальная коммутационная способность при коротком замыкании Icn1 представляет собой значение предельной отключающей способности при коротком замыкании, установленное изготовителем для автоматического выключателя.
Примечание 1: В ГОСТ IEC 60898-1-2020 и ГОСТ IEC 60898-2-2011 рассматриваемая характеристика автоматического выключателя имеет наименование «номинальная наибольшая отключающая способность». В стандартах МЭК 60898‑1 и МЭК 60898‑2 эта характеристика названа иначе – «номинальная способность при коротком замыкании» («rated short-circuit capacity»). При этом под способностью при коротком замыкании (short-circuit capacity) в международных стандартах понимают (включающую и отключающую) способность при коротком замыкании (short-circuit (making and breaking) capacity), т.
Примечание 1 от Харечко Ю.В. из книги [3]е. коммутационную способность автоматического выключателя при коротком замыкании. Для устранения расхождений в наименованиях одной и той же характеристики автоматического выключателя в международных и национальных нормативных документах целесообразно использовать термин «номинальная коммутационная способность при коротком замыкании».
Характеристика «номинальная коммутационная способность при коротком замыкании» определяет максимальный ток короткого замыкания, который автоматический выключатель должен гарантированно включить, проводить определенное время и отключить при заданных стандартом условиях, например, при установленном в стандарте диапазоне коэффициентов мощности (см. таблицу 17 ГОСТ IEC 60898-1-2020). Автоматический выключатель тем более должен отключить любой ток короткого замыкания, значение которого не превышает его номинальной коммутационной способности при коротком замыкании.
Для понимания характера поведения автоматического выключателя после отключения им максимального тока короткого замыкания обратимся к требованиям, изложенным в п. 9.12.11.4.3 стандартов1. Каждый автоматический выключатель должен обеспечить одно отключение испытательной электрической цепи с ожидаемым током короткого замыкания, равным номинальной коммутационной способности при коротком замыкании, а также одно включение с последующим автоматическим отключением электрической цепи, в которой протекает указанный испытательный ток.
9.12.11.4.3 стандартов1. Каждый автоматический выключатель должен обеспечить одно отключение испытательной электрической цепи с ожидаемым током короткого замыкания, равным номинальной коммутационной способности при коротком замыкании, а также одно включение с последующим автоматическим отключением электрической цепи, в которой протекает указанный испытательный ток.
Примечание 1: В стандартах МЭК 60898‑1 и МЭК 60898‑2 этот пункт назван «Испытание при номинальной способности при коротком замыкании (Icn)», в ГОСТ IEC 60898-1-2020 и ГОСТ IEC 60898-2-2011 − «Испытание при номинальной наибольшей отключающей способности (Icn)». Этот пункт в международных и национальных стандартах целесообразно назвать иначе: «Испытание при номинальной коммутационной способности при коротком замыкании (Icn)».
Примечание 1 от Харечко Ю.В. из книги [3]
После проведения этого испытания качественный автоматический выключатель не должен иметь повреждений, ухудшающих его эксплуатационные свойства, а также должен выдержать установленные стандартом испытания на электрическую прочность и проверку характеристики расцепления.
Рассматриваемую характеристику автоматического выключателя используют для согласования ее численного значения с токами короткого замыкания в электроустановке здания. Значение номинальной коммутационной способности при коротком замыкании должно превышать или быть равным максимальному току короткого замыкания в месте установки автоматического выключателя.
Для автоматических выключателей бытового назначения в стандарте МЭК 60898‑1 и ГОСТ IEC 60898-1-2020 установлены следующие значения номинальной коммутационной способности при коротком замыкании:
- в диапазоне сверхтока до 10 000 А включительно – стандартные значения номинальной коммутационной способности при коротком замыкании, равные 1500, 3000, 4500, 6000, 10 000 А;
- в диапазоне сверхтока свыше 10 000 А до 25 000 А включительно – предпочтительное значение номинальной коммутационной способности при коротком замыкании, равное 20 000 А.
Указанные значения номинальной коммутационной способности при коротком замыкании имеют и универсальные автоматические выключатели.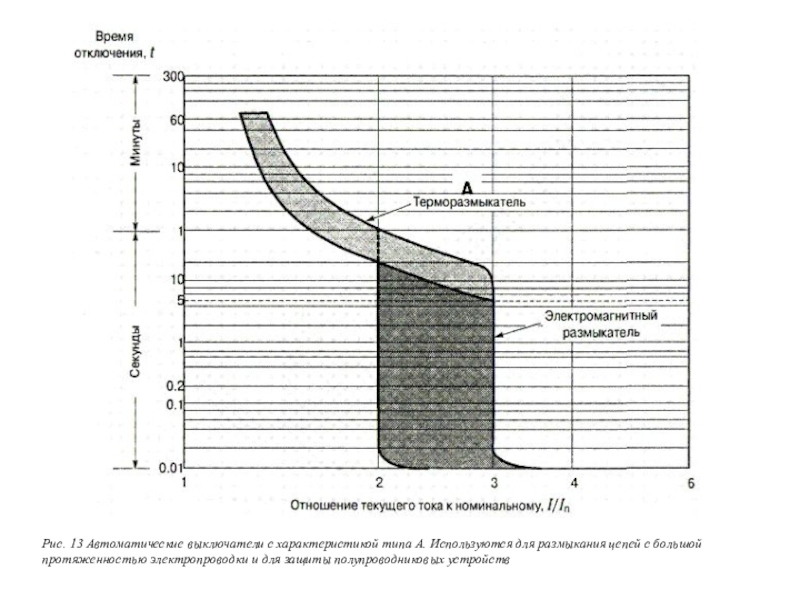
Включающая и отключающая способность при коротком замыкании.
Включающую и отключающую способность при коротком замыкании2 автоматического выключателя оценивают в стандарте МЭК 60898‑1 и ГОСТ IEC 60898-1-2020 по действующему значению переменной составляющей ожидаемого тока3, который он предназначен включать, проводить в течение его времени размыкания и отключать при определенных условиях.
Примечание 2: В ГОСТ IEC 60898-1-2020 рассматриваемая характеристика автоматического выключателя имеет наименование «наибольшая включающая и отключающая способность». В стандарте МЭК 60898‑1 эта характеристика названа иначе – «(включающая и отключающая) способность при коротком замыкании» («short-circuit (making and breaking) capacity»). В национальных стандартах, распространяющихся на автоматические выключатели, вместо термина «наибольшая включающая и отключающая способность» следует использовать термин «включающая и отключающая способность при коротком замыкании».
Примечание 2 от Харечко Ю.В. из книги [3]В стандарте МЭК 60898‑2 и ГОСТ IEC 60898-2-2011 не используют рассматриваемый термин.
Примечание 3: Ожидаемый ток – электрический ток, который будет протекать в электрической цепи, если каждый полюс коммутационного устройства заменить проводником с пренебрежимо малым полным сопротивлением.
Примечание 3 от Харечко Ю.В. из книги [3]
Время отключения и время дуги.
Для отключения сверхтока автоматическому выключателю требуется определенное время – время отключения, которое представляет собой интервал времени между началом времени размыкания и концом времени дуги. Началом времени размыкания считают момент, когда электрический ток в главной цепи автоматического выключателя достигнет уровня срабатывания его расцепителя сверхтока. Концом времени дуги является момент гашения электрических дуг во всех полюсах автоматического выключателя. Поэтому время отключения однополюсного автоматического выключателя приблизительно равно сумме времени размыкания и времени дуги в полюсе, а многополюсного автоматического выключателя – сумме времени размыкания и времени дуги в многополюсном автоматическом выключателе.
Рабочая отключающая способность при коротком замыкании Ics.
Номинальной коммутационной способности при коротком замыкании автоматического выключателя соответствует определенная рабочая отключающая способность при коротком замыкании Ics1 – отключающая способность, для которой предписанные условия соответственно установленной последовательности испытаний предусматривают способность автоматического выключателя проводить в течение условного времени электрический ток, равный 0,85 его тока нерасцепления.
Примечание 1: В ГОСТ IEC 60898-1-2020 и ГОСТ IEC 60898-2-2011 рассматриваемая характеристика автоматического выключателя имеет наименование «рабочая наибольшая отключающая способность». В стандартах МЭК 60898‑1 и МЭК 60898‑2 эта характеристика названа иначе – «рабочая отключающая способность при коротком замыкании» («service short-circuit breaking capacity»). Для устранения расхождений в наименованиях одной и той же характеристики автоматического выключателя в национальных нормативных документах вместо термина «рабочая наибольшая отключающая способность» следует использовать термин «рабочая отключающая способность при коротком замыкании».
Примечание 1 от Харечко Ю.В. из книги [3]
В стандарте МЭК 60898‑1 и ГОСТ IEC 60898-1-2020 между номинальной коммутационной способностью при коротком замыкании автоматического выключателя и его рабочей отключающей способностью при коротком замыкании установлены соотношения, представленные в табл. 2. Указанная информация приведена в таблицах 18 стандартов, в которых соотношение между рабочей отключающей способностью и номинальной коммутационной способностью задано посредством коэффициента, равного К = Ics/Icn.
Таблица 2. Соотношения между номинальной коммутационной способностью при коротком замыкании и рабочей отключающей способностью при коротком замыкании
| Номинальная коммутационная способность при коротком замыкании Icn | Рабочая отключающая способность при коротком замыкании Ics |
| Icn ≤ 6000 А | Ics = Icn |
| 6000 А < Icn ≤ 10 000 А | Ics = 0,75 Icn, но не менее 6000 А |
| Icn > 10 000 А | Ics = 0,5 Icn, но не менее 7500 А |
Рабочая отключающая способность при коротком замыкании значительно меньше номинальной коммутационной способности при коротком замыкании (при Icn > 6000 А).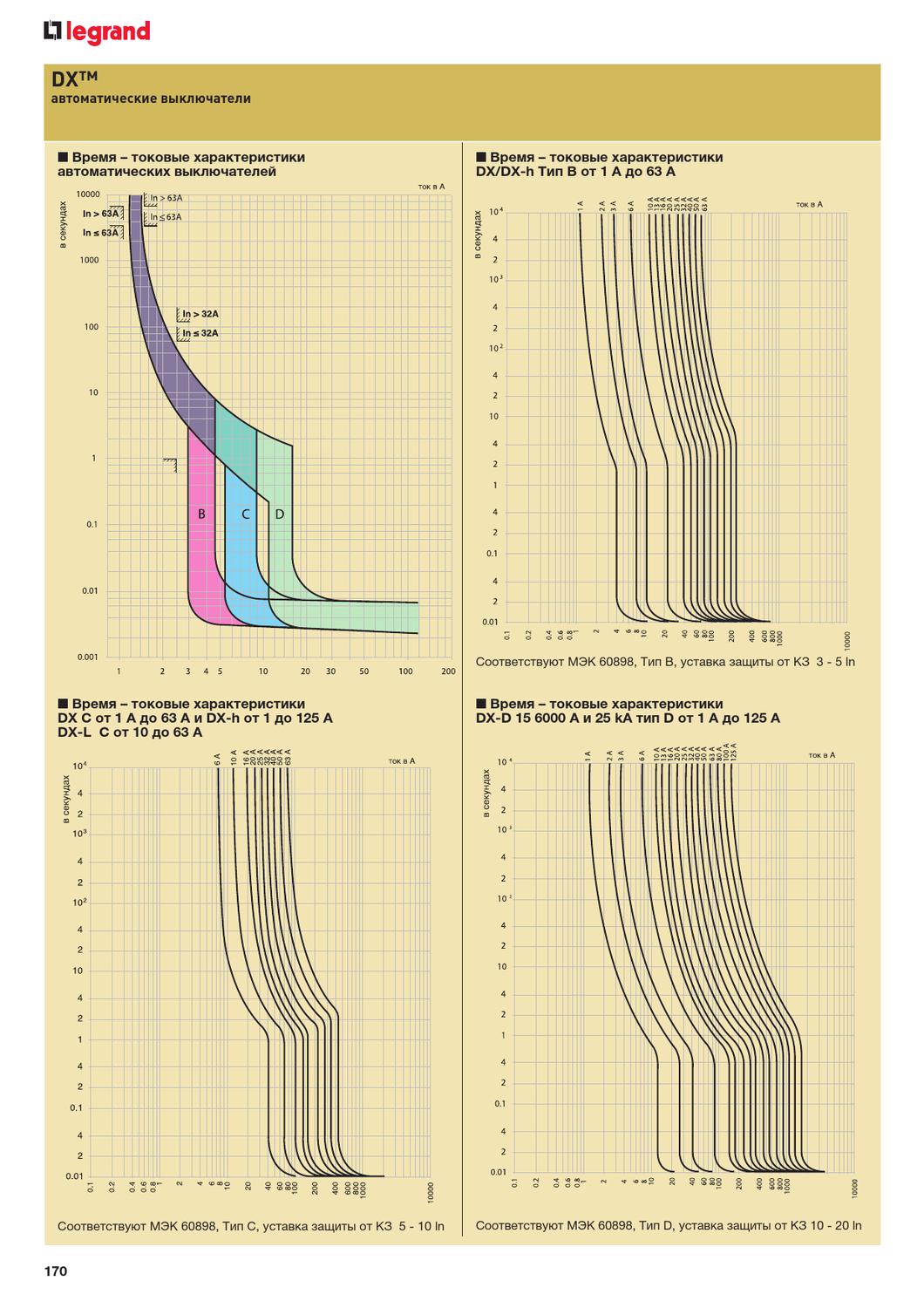 Поэтому каждый автоматический выключатель способен отключить электрический ток, равный рабочей отключающей способности при коротком замыкании, бóльшее число раз, чем электрический ток, равный номинальной коммутационной способности при коротком замыкании.
Поэтому каждый автоматический выключатель способен отключить электрический ток, равный рабочей отключающей способности при коротком замыкании, бóльшее число раз, чем электрический ток, равный номинальной коммутационной способности при коротком замыкании.
Однополюсный и двухполюсный автоматические выключатели должны обеспечить два отключения испытательной электрической цепи с ожидаемым током короткого замыкания в ней, равным рабочей отключающей способности при коротком замыкании, и одно включение указанной электрической цепи с последующим ее автоматическим отключением. Трехполюсный и четырехполюсный автоматические выключатели должны обеспечить одно отключение электрической цепи, в которой протекает указанный испытательный ток, а также два ее включения с последующим автоматическим отключением.
Однополюсный и двухполюсный универсальные автоматические выключатели должны обеспечить одно отключение электрической цепи с ожидаемым постоянным током короткого замыкания в ней, равным рабочей отключающей способности при коротком замыкании, а также два ее включения с последующим автоматическим отключением.
После проведения указанного испытания качественный автоматический выключатель не должен иметь повреждений, ухудшающих его эксплуатационные свойства. Автоматический выключатель также должен выдержать предписанные стандартами испытания на электрическую прочность и проверку его характеристики расцепления.
В требованиях подраздела 533.3 «Выбор устройств для защиты электропроводок от коротких замыканий» стандарта МЭК 60364‑5‑53 сказано, что, когда стандарт на защитное устройство определяет и рабочую отключающую способность при коротком замыкании, и номинальную предельную отключающую способность при коротком замыкании, допустимо выбирать защитное устройство на основе предельной отключающей способности при коротком замыкании для максимальных характеристик короткого замыкания.
Однако условия эксплуатации могут сделать желательным выбор защитного устройства по рабочей отключающей способности при коротком замыкании, например, когда защитное устройство устанавливают на вводе низковольтной электроустановки. Аналогичное требование, сформулированное с терминологическими ошибками, имеется в ГОСТ Р 50571.5.53-2013, который разработан на основе стандарта МЭК 60364‑5‑53:2002. Поэтому при согласовании характеристик автоматических выключателей с характеристиками электрических цепей в электроустановке здания значения их рабочих отключающих способностей при коротком замыкании целесообразно выбирать так, чтобы они превышали или были равными максимальным токам короткого замыкания в местах их установки.
Аналогичное требование, сформулированное с терминологическими ошибками, имеется в ГОСТ Р 50571.5.53-2013, который разработан на основе стандарта МЭК 60364‑5‑53:2002. Поэтому при согласовании характеристик автоматических выключателей с характеристиками электрических цепей в электроустановке здания значения их рабочих отключающих способностей при коротком замыкании целесообразно выбирать так, чтобы они превышали или были равными максимальным токам короткого замыкания в местах их установки.
Характеристика I2t.
Характеристика I2t представляет собой кривую, отражающую максимальные значения I2t автоматического выключателя как функцию ожидаемого тока в указанных условиях эксплуатации. Эта характеристика позволяет оценить способность автоматического выключателя ограничивать ожидаемый сверхток в защищаемых им электрических цепях. Некоторые виды электрооборудования, например устройства дифференциального тока без встроенной защиты от сверхтока, имеют ограничения по значению характеристики I2t. Поэтому при проектировании электроустановок зданий с помощью рассматриваемой характеристики проводят проверку возможности использования автоматических выключателей для обеспечения защиты подобного электрооборудования от токов короткого замыкания.
Поэтому при проектировании электроустановок зданий с помощью рассматриваемой характеристики проводят проверку возможности использования автоматических выключателей для обеспечения защиты подобного электрооборудования от токов короткого замыкания.
Значения характеристики I2t для конкретных электрических токов – так называемый «интеграл Джоуля» – интеграл квадрата силы тока по данному интервалу времени (t0, t1) – определяют по следующей формуле:
В стандарте EN 60898‑1 рассматриваемая характеристика положена в основу классификации автоматических выключателей, устанавливающей способность автоматических выключателей ограничивать ожидаемые сверхтоки в защищаемых ими электрических цепях. Автоматические выключатели подразделяют на три класса ограничения энергии.
Класс ограничения электроэнергии.
Характеристика «класс ограничения электроэнергии» и значения характеристики I2t, по которым автоматические выключатели могут быть отнесены к определенному классу, не предусмотрены ни в стандарте МЭК 60898‑1, ни в ГОСТ IEC 60898-1-2020.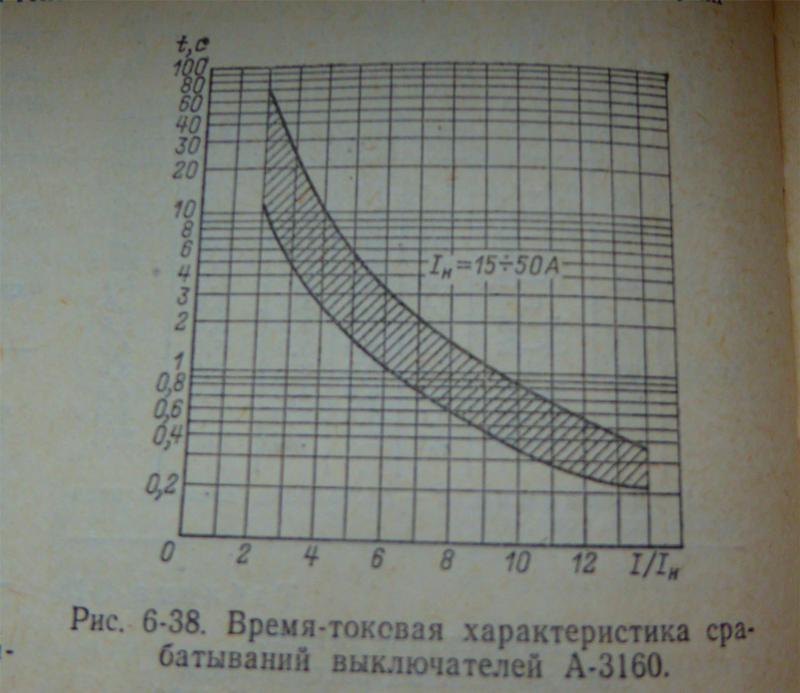 Однако в обоих стандартах отмечается, что в дополнение к характеристике I2t, обеспеченной производителем, автоматические выключатели могут быть классифицированы согласно их характеристике I2t. По требованию производитель должен сделать доступным характеристику I2t. Он может указать классификацию I2t и соответственно маркировать автоматические выключатели.
Однако в обоих стандартах отмечается, что в дополнение к характеристике I2t, обеспеченной производителем, автоматические выключатели могут быть классифицированы согласно их характеристике I2t. По требованию производитель должен сделать доступным характеристику I2t. Он может указать классификацию I2t и соответственно маркировать автоматические выключатели.
В табл. 3 представлены максимальные значения характеристики I2t автоматических выключателей по классам ограничения электроэнергии, значения которых заимствованы из изменения А11, внесенного в стандарт EN 60898 в 1994 г.
| Таблица 3. Предельные значения характеристики I2t для автоматических выключателей, А2с | |||||
| Номинальная коммутационная способность при коротком замыкании, А | Класс ограничения электроэнергии | ||||
| 1 | 2 | 3 | |||
| Тип мгновенного расцепления автоматического выключателя | |||||
| B и C | В | С | В | С | |
| Номинальный ток до 16 А включительно | |||||
| 3000 | Предельные значения не установлены | 31000 | 37000 | 15000 | 18000 |
| 4500 | 60000 | 75000 | 25000 | 30000 | |
| 6000 | 100000 | 120000 | 35000 | 42000 | |
| 10000 | 240000 | 290000 | 70000 | 84000 | |
| Номинальный ток свыше 16 А до 32 А включительно* | |||||
| 3000 | Предельные значения не установлены | 40000 | 50000 | 18000 | 22000 |
| 4500 | 80000 | 100000 | 32000 | 39000 | |
| 6000 | 130000 | 160000 | 45000 | 55000 | |
| 10000 | 310000 | 370000 | 90000 | 110000 | |
* Для автоматических выключателей с номинальным током 40 А могут быть применены максимальные значения, равные 120 % от указанных в таблице. Такие автоматические выключатели могут быть маркированы символом соответствующего класса ограничения электроэнергии. Такие автоматические выключатели могут быть маркированы символом соответствующего класса ограничения электроэнергии. | |||||
Автоматические выключатели, имеющие класс ограничения электроэнергии 2 и 3, представляют собой токоограничивающие автоматические выключатели, характеризующиеся малым временем отключения, в течение которого ток короткого замыкания не успевает достичь своего пикового значения. Применение токоограничивающих автоматических выключателей в электроустановках зданий позволяет уменьшить негативное воздействие токов короткого замыкания на низковольтное электрооборудование и, прежде всего, на проводники электрических цепей.
Современные автоматические выключатели бытового назначения, имеющие номинальный ток до 40 А и типы мгновенного расцепления B и C, как правило, представляют собой токоограничивающие автоматические выключатели и соответствуют третьему классу ограничения электроэнергии.
В стандарте МЭК 60898‑2 и ГОСТ IEC 60898-2-2011 дополнительно установлена следующая классификация универсальных автоматических выключателей по постоянной времени:
- автоматические выключатели, пригодные для электрических цепей постоянного тока с постоянной времени T ≤ 4 мс;
- автоматические выключатели, пригодные для электрических цепей постоянного тока с постоянной времени T ≤ 15 мс.
В ГОСТ IEC 60898-2-2011 приведено следующее пояснение: «Очевидно, что токи короткого замыкания не превышают значения 1500 А в тех установках, где в силу присоединенных нагрузок постоянная времени при нормальной эксплуатации может быть не более 15 мс. В электроустановках со значениями токов короткого замыкания свыше 1500 А постоянная времени T = 4 мс считается достаточной».
Список использованной литературы
- ГОСТ IEC 60898-1-2020
- ГОСТ IEC 60898-2-2011
- Харечко Ю.В. Краткий терминологический словарь по низковольтным электроустановкам. Часть 5// Приложение к журналу «Библиотека инженера по охране труда». – 2017. – № 2. – 160 c
Что такое время токовые характеристики автоматических выключателей
При нормальной работе электросети и всех приборов через автоматический выключатель протекает электрический ток. Однако если сила тока по каким-либо причинам превысила номинальные значения, происходит размыкание цепи из-за срабатывания расцепителей автоматического выключателя.
Характеристика срабатывания автоматического выключателя является очень важной характеристикой, которая описывает то, насколько время срабатывания автомата зависит от отношения силы тока, протекающего через автомат, к номинальному току автомата.
Данная характеристика сложна тем, что для ее выражения необходимо использование графиков. Автоматы с одним и тем же номиналом будут при разных превышениях тока по-разному отключаться в зависимости от типа кривой автомата (так иногда называется токовая характеристика), благодаря чему имеется возможность применять автоматы с разной характеристикой для разных типов нагрузки.
Тем самым, с одной стороны, осуществляется защитная токовая функция, а с другой стороны, обеспечивается минимальное количество ложных срабатываний – в этом и заключается важность данной характеристики.
В энергетических отраслях бывают ситуации, когда кратковременное увеличение тока не связано с появлением аварийного режима и защита не должно реагировать на такие изменения. Это же относится и к автоматам.
Это же относится и к автоматам.
При включении какого-нибудь мотора, к примеру, дачного насоса или пылесоса, в линии происходит достаточно большой бросок тока, который в несколько раз превышает нормальный.
По логике работы, автомат, конечно же, должен отключиться. К примеру, мотор потребляет в пусковом режиме 12 А, а в рабочем – 5. Автомат стоит на 10 А, и от 12 его вырубит. Что в таком случае делать? Если например поставить на 16 А, тогда непонятно отключится он или нет если заклинит мотор или замкнет кабель.
Можно было бы решить эту проблему, если его поставить на меньший ток, но тогда он будет срабатывать от любого движения. Вот для этого и было придумано такое понятие для автомата, как его «время токовая характеристика».
Какие существуют время токовые характеристики автоматических выключателей и их отличие между собой
Как известно основными органами срабатывания автоматического выключателя являются тепловой и электромагнитный расцепитель.
Тепловой расцепитель представляет собой пластину из биметалла, изгибающуюся при нагреве протекающим током. Тем самым в действие приводится механизм расцепления, при длительной перегрузке срабатывая, с обратнозависимой выдержкой времени. Нагрев биметаллической пластинки и время срабатывание расцепителя напрямую зависят от уровня перегрузки.
Электромагнитный расцепитель является соленоидом с сердечником, магнитное поле соленоида при определенном токе втягивает сердечник, приводящий в действие механизм расцепления – происходит мгновенное срабатывание при КЗ, благодаря чему пострадавший участок сети не будет дожидаться прогревания теплового расцепителя (биметаллической пластины) в автомате.
Зависимость времени срабатывания автомата от силы тока, протекающего через автомат, как раз и определяется время токовой характеристикой автоматического выключателя.
Наверное, каждый замечал изображение латинских букв B, C, D на корпусах модульных автоматов. Так вот они характеризуют кратность уставки электромагнитного расцепителя к номиналу автомата, обозначая его время токовую характеристику.
Эти буквы указывают ток мгновенного срабатывания электромагнитного расцепителя автомата. Проще говоря, характеристика срабатывания автоматического выключателя показывает чувствительность автомата – наименьший ток при котором автомат отключится мгновенно.
Автоматы имеют несколько характеристик, самыми распространенными из которых являются:
- — B — от 3 до 5 ×In;
- — C — от 5 до 10 ×In;
- — D — от 10 до 20 ×In.
Что означают цифры указанные выше?
Приведу небольшой пример. Допустим, есть два автомата одинаковой мощности (равные по номинальному току) но характеристики срабатывания (латинские буквы на автомате) разные: автоматы В16 и С16.
Диапазоны срабатывания электромагнитного расцепителя для В16 составляет 16*(3…5)=48…80А. Для С16 диапазон токов мгновенного срабатывания 16*(5…10)=80…160А.
При токе 100 А автомат В16 отключится практически мгновенно, в то время как С16 отключится не сразу а через несколько секунд от тепловой защиты (после того как нагреется его биметаллическая пластина).
В жилых зданиях и квартирах, где нагрузки чисто активные (без больших пусковых токов), а какие-нибудь мощные моторы включаются нечасто, самыми чувствительными и предпочтительными к применению являются автоматы с характеристикой B. На сегодняшний день очень распространена характеристика С, которую также можно использовать для жилых и административных зданий.
Что касается характеристики D, то она как раз годится для питания каких-либо электромоторов, больших двигателей и других устройств, где могут быть при их включении большие пусковые токи. Также через пониженную чувствительность при КЗ автоматы с характеристикой D могут быть рекомендованы для использования как вводные для повышения шансов селективности со стоящими ниже групповыми АВ при КЗ.
Согласитесь логично, что время срабатывания зависит от температуры автомата. Автомат отключится быстрее, если его тепловой орган (биметаллическая пластина) разогретый. И наоборот при первом включении когда биметалл автомата холодный время отключения будет больше.
Поэтому на графике верхняя кривая характеризует холодное состояние автомата, нижняя кривая характеризует горячее состояние автомата.
Пунктирной линией обозначен предельный ток срабатывания для автоматов до 32 А.
Что показано на графике время токовой характеристики
На примере 16-Амперного автомата, имеющего время токовую характеристику C, попробуем рассмотреть характеристики срабатывания автоматических выключателей.
На графике можно увидеть, как протекающий через автоматический выключатель ток влияет на зависимость времени его отключения. Кратность тока протекающего в цепи к номинальному току автомата (I/In) изображает ось Х, а время срабатывания, в секундах – ось У.
Выше говорилось, что в состав автомата входит электромагнитный и тепловой расцепитель. Поэтому график можно разделить на два участка. Крутая часть графика показывает защиту от перегрузки (работа теплового расцепителя), а более пологая часть защиту от КЗ (работа электромагнитного расцепителя).
Как видно на графике если к автомату С16 подключить нагрузку 23 А то он должен отключится за 40 сек. То есть при возникновении перегрузки на 45 % автомат отключится через 40 сек.
На токи большой величины, которые могут привести к повреждению изоляции электропроводки автомат способен реагировать мгновенно благодаря наличию электромагнитного расцепителя.
При прохождении через автомат С16 тока 5×In (80 А) он должен сработать через 0.02 сек (это если автомат горячий). В холодном состоянии, при такой нагрузке, он отключится в пределах 11 сек. и 25 сек. (для автоматов до 32 А и выше 32 А соответственно).
Если через автомат будет протекать ток равный 10×In, то он отключается за 0,03 секунды в холодном состоянии или меньше чем за 0,01 секунду в горячем.
К примеру, при коротком замыкании в цепи, которая защищена автоматом С16, и возникновении тока в 320 Ампер, диапазон времени отключения автомата будет составлять от 0,008 до 0,015 секунды. Это позволит снять питание с аварийной цепи и защитить от возгорания и полного разрушения сам автомат, закоротивший электроприбор и электропроводку.
Автоматы с какими характеристиками предпочтительнее использовать дома
В квартирах по возможности необходимо обязательно применять автоматы категории B, которые являются более чувствительными. Данный автомат отработает от перегрузки так же, как и автомат категории С. А вот о случае короткого замыкания?.
Если дом новый, имеет хорошее состояние электросети, подстанция находится рядом, а все соединения качественные, то ток при коротком замыкании может достигать таких величин, что его должно хватить на срабатывание даже вводного автомата.
Ток может оказаться малым при коротком замыкании, если дом является старым, а к нему идут плохие провода с огромным сопротивлением линии (особенно в сельских сетях, где большое сопротивление петли фаза-нуль) – в таком случае автомат категории C может не сработать вообще. Поэтому единственным выходом из этой ситуации является установка автоматов с характеристикой типа В.
Следовательно, время токовая характеристика типа В является определенно более предпочтительной, в особенности в дачной или сельской местности или в старом фонде.
В быту на вводной автомат вполне целесообразно ставить именно тип С, а на автоматы групповых линий для розеток и освещения – тип В. Таким образом будет соблюдена селективность, и где-нибудь в линии при коротком замыкании вводной автомат не будет отключаться и «гасить» всю квартиру.
Похожие материалы на сайте:
Понравилась статья — поделись с друзьями!
Категории автоматических выключателей
Автоматические выключатели, или проще говоря – автоматы, предназначены прежде всего для защиты наших бытовых приборов в квартире или частном доме от скачков электрического напряжения в сети, короткого замыкания и других факторов, способных вывести их из строя. Но надежная защита зависит не только от самых автоматов. Их еще нужно не только правильно установить, но и выбрать те, которые обеспечат эту самую надежную защиту. В этой статье речь пойдет о категориях автоматических выключателей, на которые они подразделяются. Рассмотрим чем отличаются автоматы с маркировкой «B» от таких же с виду автоматов с маркировкой «C» или «D».
В этой статье речь пойдет о категориях автоматических выключателей, на которые они подразделяются. Рассмотрим чем отличаются автоматы с маркировкой «B» от таких же с виду автоматов с маркировкой «C» или «D».
Конечно же, в строительных магазинах Вы вряд ли найдете автоматические выключатели такой редкой категории как «MA» «K» и «Z». Это специфические категории, используемые в промышленности, а не в быту. Но о них тоже стоит упомянуть, мало ли, попадутся вам на глаза или достанутся безвозмездно от какого-нибудь приятеля. Вы их установите, а достаточной защиты либо не получите, либо автомат будет срабатывать так часто, что в итоге его придется заменить.
Итак, поехали. Стоит отметить, что класс или категория автоматического выключателя обозначается большой латинской буквой, которая стоит перед цифрой, обозначающей номинальный ток.
Категория MA
Категория MA является, наверное, одной из самых редких. Особенностью этой категории автоматов является отсутствие в их конструкции теплового расцепителя, который срабатывает при токе перегрузки – ток, лишь незначительно превышающий номинальный, вызванный включением в сеть очень мощной нагрузки.
Эти автоматы срабатывают только на ток короткого замыкания, за который отвечает электромагнитное реле.
Особенность применения
Данные автоматы используются в основном на производстве и защищают электрическое оборудование в состав которого входят электрические двигатели и мощные силовые агрегаты. В момент запуска такого оборудования неизбежно возникают токи перегрузки, поэтому автоматы категории MA и не содержат тепловых расцепителей, чтобы они не вызывали ложных срабатываний.
Категория A
Автоматы этой категории содержат в своей конструкции и тепловой расцепитель и электромагнитное реле. Причем первый настроен так, что срабатывает даже при малейших превышениях тока нагрузки. В результате этого данная категория является одной из самых чувствительных.
Как правило, тепловой расцепитель у таких автоматов настроен на срабатывании при превышении тока нагрузки всего на 30 %.
Особенность применения
Используются такие автоматические выключатели в электрических сетях, которые запитывают особенно чувствительную аппаратуру. Это вычислительные системы, сервера, диагностическое и исследовательское оборудование.
Это вычислительные системы, сервера, диагностическое и исследовательское оборудование.
Категория B
Тепловой расцепитель автоматов категории B рассчитан на срабатывание при превышении номинального тока примерно в два раза. Они менее чувствительны чем предыдущая категория, но также обеспечивают достаточную защиту даже в высокоточных цепях.
Особенность применения
В основном автоматические выключатели категории B используются в бытовых сетях, которые питают розетки и светильники. Это наиболее подходящая категория для защиты домашней электропроводки.
Категория C
Автоматические выключатели категории C срабатывают при превышении номинального тока примерно в 5 раз. Они менее чувствительны, чем категория B.
Особенность применения
Автоматы этой категории также применяются в бытовых электрических сетях, но как правило устанавливаются не для защиты отдельных групп электроприборов, а для защиты всей сети или ее частей. Поэтому эти автоматы устанавливаются на ввод – в электрических щитках на лестничных площадках.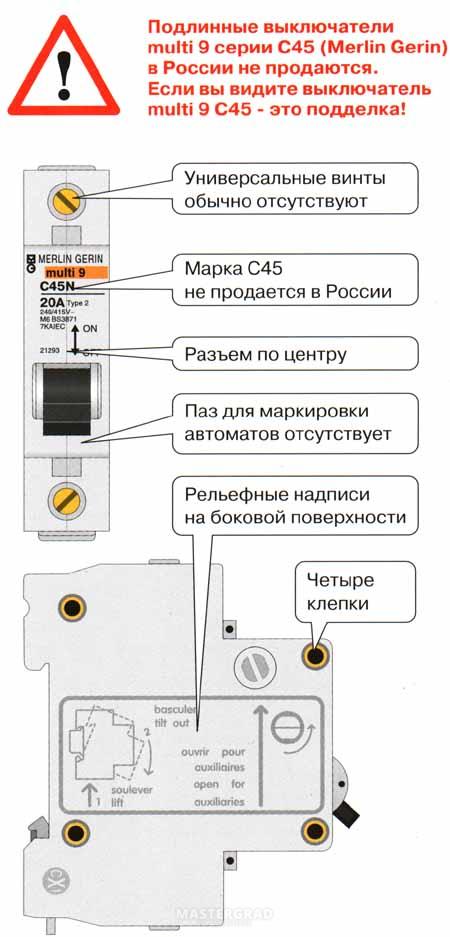
Категория D
Автоматические выключатели категории D срабатывают при превышении номинального тока, указанного на автомате, как минимум в 10 раз. Это наименее чувствительная категория. Следовательно, у них особая роль в обеспечении защиты – подстраховочная.
Особенности применения
Категория D устанавливается на вводе всего здания или его части и служит для обесточивания сети, когда автоматы более низких категорий по каким-либо причинам не сработали. Также эти автоматы, как и категория MA, используются в оборудовании, содержащей электродвигатели и силовые установки с большим пусковым током.
Категория K и Z
Это очень специфические автоматические выключатели. Срабатывание электромагнитного реле выключателя категории K, включенного в цепь переменного тока происходит при его 12 кратном превышении номинала. Для цепи постоянного тока этот показатель равен 18. При этом тепловой расцепитель должен сработать при перегрузке всего в 5 %.
Автоматические выключатели категории Z также имеют разные характеристики тока срабатывания для сетей переменного и постоянного тока. В первом случае превышение должно быть троекратным, а во втором – в 4,5 раза.
В первом случае превышение должно быть троекратным, а во втором – в 4,5 раза.
Особенности применения
Автоматические выключатели категории K используются в цепях с индуктивной нагрузкой. Это трансформаторы, преобразователи напряжения, электромагнитные устройства и прочее.
Категория Z в основном применяется в сетях где подключены какие-то специфические электронные устройства.
| < Предыдущая | Следующая > |
|---|
Типы и виды автоматических выключателей.
Основное предназначение автоматических выключателей—защита кабельно-проводниковой продукции (КПП), а также конечных потребителей от перегрузки выходных устройств и токов короткого замыкания. В этой главе я не буду рассматривать все типы, виды и категории автоматических выключателей, так как их есть великое множество, коснусь только тех, которые применяются для защиты жилых и офисно-магазинных помещений.
То есть, современные автоматы евростандарта, которые крепятся на DIN-рейку. Самые распространённые автоматы принадлежат следующим компаниям: «Аско (Украина)«, «ИЕК» (Россия), «ABB» и «Moeller» (Германия), «Schneider Elektrik» (Франция), «Hager» (Франция), «Sez» (Cловакия), «SIEMENS», и др. Автоматы больших габаритов, применяемые на предприятиях, здесь рассматриваться не будут.
Модульные автоматические выключатели распределяются по следующим характеристикам:
В—домовая, на освещение. В таком типе автоматов установка тока срабатывания магнитного расцепителя отрегулирована в пределах 3÷5 Iном. Тип В позволяет устранить короткое замыкание с малым значением тока короткого замыкания (если защищается линия большой длины). Чтобы исключить ложные срабатывания такие выключатели не используют в установках с большими пусковыми токами.
С—общепромышленная. Ток срабатывания магнитного расцепителя выставлен в пределах 5÷19 от Iном. Данный тип является универсальным и применяется при обычных нагрузках.
D—для защиты электродвигателей. Данный тип используется в устройствах с повышенными пусковыми токами при включении. Ток мгновенного расцепителя установлен в пределах от 10 до 20 Iном.
Модульный означает что это один автомат с одним рычажком, это и есть один модуль, который имеет толщину самого автомата около 18 мм (рис.1). Далее на рисунке видно винтовые зажимы (1). На них можно подключать провод или же кабель на суммарное значение до 25 мм². Рычажный выключатель (2) позволяет включать и выключать автоматический выключатель, а механический индикатор (3) сигнализирует о положении выключателя. Основные параметры, на которые следует обратить внимание при покупке автомата это его тип (категория) (4), подводимое напряжение (6) и ток срабатывания (в Амперах) (5) при перегрузке или же при коротком замыкании .
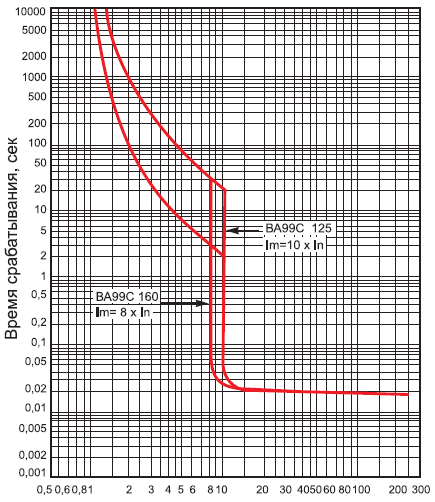
При выбивании автомата нужно сначала устранить причину поломки, а только потом включить автоматический выключатель. Если при повторном включении автомат сразу выбивает, то есть факт наличия короткого замыкания на выходе и нужно определять причину. А если он начинает выбивать через 10÷600 сек., то параметры автомата не соответствуют подводимой нагрузке. В этом случае нужно уменьшить нагрузку и попробовать снова включить. Если снова выбивает, то автомат можно считать непригодным, вероятнее всего внутри подгорели контакты, и из-за этого возникает повышенный ток, что и приводит к ложному срабатыванию. Определиться с неисправностью поможет грамотный электрик.Однофазные автоматы имеют следующий токовариат: 6; 10; 16; 20; 25; 32; 40; 50; 63 Ампер. Они бывают однополюсные и двухполюсные (1р+N). Последний имеет две пары винтовых зажимов: одна—вход фаза и ноль, а вторая—выход тех же. Двухполюсный занимает два модуля. Трёхфазные автоматы (на 380 В) бывают трёхполюсные (3р) и четырёхполюсные (3р+N).
Последние применяются в устройствах с трёхфазной электрической системой (чаще всего асинхронные электродвигатели), а также в местах с повышенными нагрузками, где её необходимо равномерно распределить. Трёхфазные автоматы чаще применяются на производстве, иногда в частных домах и в некоторых современных квартирах с электрическими плитами. В квартирах применяются однофазные автоматические выключатели (рис.1). О том, как устроен однофазный автоматический выключатель изнутри, можно посмотреть, нажав сюда .
Типы автоматических выключателей могут быть разными. Выбрать автомат нужно исходя из сечения провода и предстоящей нагрузки.
Виды дифавтоматов – в чем отличие между ними, и какие встречаются
В настоящее время выпускают огромное количество видов дифавтоматов на любой вкус. Чтобы выбрать среди них оптимальный вариант для конкретной электросети, нужно иметь представление об их классификации по функциональным возможностям. Это значительно облегчит выбор устройства. Пропустив их через сито нескольких наиболее важных характеристик, можно сильно сократить список подходящих приборов.
Это значительно облегчит выбор устройства. Пропустив их через сито нескольких наиболее важных характеристик, можно сильно сократить список подходящих приборов.
По типу сети и току утечки
Дифференциальные автоматы по типу контролируемой электрической сети делятся на однофазные напряжением 220 В и трехфазные с линейным напряжением 380 В, соответственно, разделяются на двухполюсников для однофазных и четырехполюсников для трехфазных сетей.
В зависимости от тока утечки, возникающего в контролируемой сети, дифавтоматы, как и УЗО, подразделяются на следующие категории.
Тип АС. Дифференциальный автомат этого вида реагирует на синусоидальный переменный ток утечки, который может появиться мгновенно или нарастать постепенно.
При превышении порогового значения тока отключения он срабатывает, разрывая защищаемую линию. На корпусе дифавтомата должно быть обозначение АС или символ переменного тока в рамке.
Тип А. Отличие устройства этой категории от первого типа состоит в том, что оно реагируют на мгновенное возникновение или постепенное увеличение переменного и постоянного (пульсирующего) тока утечки. При достижении значения уставки, дифавтомат срабатывает.
На его корпусе должно быть изображение буквы А или символа синусоиды и пульсирующего тока в рамке. Различия сказываются на цене. Эти дифавтоматы значительно дороже устройств первого типа из-за необходимости дополнительного контроля, пульсирующих токов.
Они имеют наибольшее распространение и рекомендуются в большинстве случаев. Это связано с большим количеством бытовой техники имеющей именно такого рода токи утечки. Некоторые производители прямо указывают на этот тип защитных приборов, для своих устройств.
Тип В. Дифавтоматы этого вида срабатывают при наличии переменного, постоянного или выпрямленного тока утечки. Независимо от того, как происходит превышение порогового значения, мгновенно или постепенно. Обычно используется на промышленных объектах.
На корпусе указываются символы постоянного, переменного и пульсирующего токов в рамке, как и в УЗО (кстати, на западе из принято называть дифреле).
В европейских странах тип АС практически не применяется. В России допускается применение всех типов устройств.
По току мгновенного расцепления
По время-токовой характеристике дифавтоматы, также как и автоматические выключатели делятся на несколько классов. Каждая категория указывает, во сколько раз ток мгновенного расцепления должен быть больше номинального, чтобы прибор сработал. По российскому ГОСТ Р 50345-99 этих категорий три:
- вид В. Приборы этой категории мгновенно срабатывают при превышении контролируемого тока в 3-5 раз по сравнению с номинальным током;
- вид С. Устройство с таким обозначением срабатывает в случае превышения номинального тока в 5-10 раз;
- вид D. Дифференциальный автомат относящийся к данному классу среагирует при токах превышения номинала в 10-20 раз.
На корпусах устройств буквы с обозначением вида электромагнитного расцепителя по току мгновенного расцепления стоят перед цифрами обозначающими значение номинального тока. То есть, если на приборе написано С16, значит номинальный ток равен 16 А, а мгновенного расцепления 80-160 А.
В европейском союзе имеются приборы дополнительного типа А. В устройствах данного вида ток мгновенного срабатывания в 2-3 раза больше номинального тока.
Есть еще несколько типов (K, Z), которые установили сами производители. Здесь уже лучше обратиться к инструкции по эксплуатации на данный тип устройства, возможно, это будет именно тот прибор, который Вам нужен.
По времени срабатывания
По задержке времени срабатывания дифавтоматы бывают селективные и мгновенного действия. Первые обычно устанавливаются на вводе электрощита. Их основная функция – защита от пожара при нарушениях изоляции электропроводки.
Имеют значения отключающего тока 100 мА, 300 мА, 500 мА. Время задержки отключения составляет 0,15-0,5 секунды. Дифавтоматы мгновенного действия имеют значения отключающего тока в пределах 6-30 мА. Срабатывание происходит за сотые доли секунды, быстродействующие реагируют через тысячные доли.
Номинальная отключающая способность
По номиналу отключения дифавтоматы, также как и автоматические выключатели делятся на несколько видов. На корпусе устройства в прямоугольнике стоит число 3000, 4500, 6000 или 10000. Оно указывает, какой ток короткого замыкания в амперах выдержит дифавтомат без нарушения работоспособности при дальнейшем применении.
Приборы с максимальным значением применяют в производственных помещениях, мастерских. Устройства со значением 6000 А обычно используют в зданиях с новой электропроводкой, способной кратковременно выдержать большие токи.
В сельской местности обычно применяют приборы со значением 4500 А, там проводка похуже и линии электроснабжения послабее.
По токоограничению
Как бы быстро ни срабатывали расцепители, но это происходит за какое-то конечное время. Механическое размыкание контактов приводит к возникновению электрической дуги, пока расстояние между контактами не станет настолько большим, что дуга уже не сможет формироваться.
Класс токоограничения показывает, за какой интервал времени происходит размыкание контактов с момента начала размыкания и до гашения дуги.
Этот параметр очень важен для длительного и безопасного функционирования электропроводки. Чем меньше время размыкания, тем меньше страдают провода электросети от токов короткого замыкания.
Смысл токоограничения дифавтомата заключается в отключении защищаемой линии раньше, чем короткое замыкание наберет полную силу. Здесь он работает, как автоматический выключатель. Это позволяет защитить изоляцию от чрезмерного нагрева проводов и возгорания.
Выделяют 3 класса:
- устройства 1 класса имеют время гашения дуги в дугогасительгой камере более 10 мс;
- приборы 2 класса осуществляют гашение электрической дуги за 6-10 мс;
- устройства 3 класса токоограничения производят это за 2,5-6 мс.
Чтобы определить класс, надо взглянуть на переднюю панель корпуса дифавтомата. Он виден в прямоугольной рамке под значением номинальной отключающей способности. Первый класс никак не обозначают.
Другие различия
Дифавтоматы различаются и по климатическому исполнению. На передней панели устройства внутри изображения снежинки указывается нижняя рабочая температура. Приборы подразделяются и по номинальной частоте контролируемой сети. Разновидности дифавтоматов на этом не заканчиваются.
Ко всему прочему дифференциальный автомат подразделяется на два вида: электронный и электромеханический. Первые компактнее, но имеют один недостаток, при отсутствии питающего напряжения на электронной плате они не работают. Это может произойти при обрыве нулевого провода.
В этот момент происходит перераспределение токов и необходимо срочно отключить электросеть, но электронный дифавтомат не поможет. Здесь справятся только второй (электромеханический) тип устройства, который не нуждается в дополнительном питании, чем отличается от первых, ему достаточно токов утечки.
Чисто внешне приборы отличить очень трудно. Самый простой способ использовать батарейку типа «Крона». При подключении к устройству в обход дифференциального трансформатора, электромеханический дифавтомат должен сработать, а электронный нет.
Стоит ли выбирать
Разобравшись с классификацией дифавтоматов по различным характеристикам, можно приступать к выбору необходимого для данной цепи устройства. Но на этом выбор прибора не заканчивается.
Теперь важно понять, а нужен ли автоматический выключатель дифференциального тока вообще, а может, стоит заменить его на два различных прибора: автоматический выключатель и устройство защитного отключения.
Этот вопрос возникает у многих специалистов. На первый взгляд применение дифавтомата несет только благо: экономится место в электрическом щите, упрощается монтаж. Но есть и несколько моментов заставляющих задуматься перед выбором.
Первое, цена дифавтомата больше стоимости автоматического выключателя и устройства защитного отключения. Это справедливо, если сравнивать приборы одного производителя.
Второй момент связан с тем, что при срабатывании дифавтомата невозможно понять причину отключения. Было ли это короткое замыкание или пробой изоляции. Соответственно и дальнейшие действия тоже становятся неясными.
И третье, все когда-нибудь выходит из строя. В случае с дифавтоматом, придется менять весь прибор. В случае с двумя устройствами, достаточно заменить один.
Кстати, чем сложнее устройство, тем менее оно надежно. Только учтя все преимущества и недостатки, можно сделать правильный выбор.
Теория автоматов | Британника
Теория автоматов , совокупность физических и логических принципов, лежащих в основе работы любого электромеханического устройства (автомата), которое преобразует информацию из одной формы в другую в соответствии с определенной процедурой. Реальные или гипотетические автоматы различной сложности стали незаменимыми инструментами для исследования и реализации систем, структура которых поддается математическому анализу.
Примером типичного автомата являются маятниковые часы.В таком механизме шестерни могут принимать только одно из конечного числа положений или состояний при каждом качании маятника. Каждое состояние с помощью спускового механизма определяет следующее последующее состояние, а также дискретный выход, который отображается как дискретные положения стрелок часов. Пока такие часы заводятся и их работа не нарушается, они будут продолжать работать без внешних воздействий, за исключением действия силы тяжести на маятник.
Более общие автоматы предназначены для реагирования на изменения внешних условий или на другие входные данные. Например, термостаты, автопилоты самолетов, системы наведения ракет, телефонные сети и средства управления некоторыми видами автоматических лифтов — все это формы автоматов.
Внутренние состояния таких устройств не определяются исключительно их начальным состоянием, как в случае с маятниковыми часами, но могут определяться вводом данных человеком-оператором, другим автоматом, событием или серией событий. в окружающей среде.Например, термостат может быть включен или выключен в зависимости от температуры. Самым известным универсальным автоматом является современный электронный компьютер, внутреннее состояние которого определяется вводом данных и который работает для получения определенного результата.
Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас Баярд Ранкин Р.Дж. НельсонПрирода и происхождение современных автоматов
Компоненты автоматов состоят из определенных материалов и устройств, таких как провода, транзисторы, рычаги, реле, шестерни и т. Д., И их работа основана на механике и электронике этих частей.Однако принципы их работы как последовательности дискретных состояний можно понять независимо от природы или расположения их компонентов. Таким образом, автомат можно рассматривать абстрактно как набор физически неопределенных состояний, входов, выходов и правил работы, а изучение автоматов — как исследование того, что с их помощью можно сделать. Этот способ абстракции дает математические системы, которые в некоторых отношениях напоминают логические системы. Таким образом, автомат можно описать как логически определенный объект, который может быть воплощен в форме машины, с термином автомат, обозначающим как физические, так и логические конструкции.
В 1936 году английский математик Алан Матисон Тьюринг в статье, опубликованной в журнале Proceedings of the London Mathematical Society («О вычислимых числах в приложении к проблеме Entscheidungsproblem»), задумал логическую машину, результаты которой можно было бы использовать для определения вычислимого числа. Для машины время считалось дискретным, а ее внутренняя структура в данный момент описывалась просто как одно из конечного набора состояний. Он выполнял свои функции путем сканирования неограниченной ленты, разделенной на квадраты, каждый из которых либо содержал конкретную информацию в виде одного из конечного числа символов, либо был пустым.Он мог сканировать только один квадрат за раз, и в любом внутреннем состоянии, кроме так называемого «пассивного», он мог перемещать ленту вперед или назад по одному квадрату за раз, стирать символ, печатать новый символ, если квадрат был пустым и изменял свое внутреннее состояние. Вычисленное число определялось символами («программа») на конечном участке ленты и правилами работы, которые включали остановку при достижении пассивного состояния. Выходное число затем интерпретировалось по символам, оставшимся на ленте после остановки машины.
Теория автоматов с середины 20-го века была значительно усовершенствована и часто находила практическое применение в гражданской и военной технике. Банки памяти современных компьютеров могут хранить большие (хотя и конечные) объемы информации. (Дополнительную информацию о компьютерах и их приложениях см. В разделе «Обработка информации».) Исходная машина Тьюринга не имела ограничений на банк памяти, потому что каждый квадрат на неограниченной ленте мог содержать информацию. Машина Тьюринга продолжает оставаться стандартной точкой отсчета в основных обсуждениях теории автоматов, и многие математические теоремы, касающиеся вычислимости, были доказаны в рамках первоначального предложения Тьюринга.
Иерархия Хомского в теории вычислений
Согласно иерархии Хомского, грамматики делятся на 4 типа:
Тип 0, известный как неограниченная грамматика. Тип 1 известен как контекстно-зависимая грамматика. Тип 2, известный как контекстно-свободная грамматика. Тип 3 Обычная грамматика.
Тип 0: неограниченная грамматика:
В типе 0
Грамматики типа 0 включают все формальные грамматики. Язык грамматики типа 0 распознается машиной Тьюринга.Эти языки также известны как языки с рекурсивным перечислением.
Грамматика Производство в форме
, где
— это (V + T) * V (V + T) *
V: переменные
T: терминалы.
— это (V + T) *.
В типе 0 должна быть хотя бы одна переменная на левой стороне производства.
Например,
Sab -> ba
A -> S.
Здесь переменными являются S, A и клеммы a, b.
Тип 1: контекстно-зависимая грамматика)
Грамматики типа 1 генерируют контекстно-зависимые языки.Язык, сгенерированный грамматикой, распознается автоматами с линейной связью
В Типе 1
I. Прежде всего грамматика Типа 1 должна быть Типа 0.
II. Грамматика Производство в форме
|| <= ||
, т.е. количество символов в меньше или равно
Например,
S -> AB
AB -> abc
B -> b
Тип 2: Грамматика без контекста:
Грамматика типа 2 генерируется контекстно-свободные языки.Язык, сгенерированный грамматикой, распознается автоматами Pushdown.
В Типе 2,
1. Прежде всего, это должен быть Тип 1.
2. Левая часть производства может иметь только одну переменную.
|| = 1.
Их нет ограничений на.
Например,
S -> AB
A -> a
B -> b
Тип 3: Обычная грамматика:
Грамматики типа 3 генерируют регулярные языки. Эти языки — это в точности все языки, которые могут быть приняты конечным автоматом.
Тип 3 — наиболее ограниченная форма грамматики.
Тип 3 должен быть только в данной форме:
V -> VT / T (правильная грамматика слева)
(или)
V -> TV / T (правильная грамматика справа )
например:
S -> a
Приведенная выше форма называется строго регулярной грамматикой.
Существует еще одна форма регулярной грамматики, называемая расширенной регулярной грамматикой.В таком виде:
V -> VT * / T *. (расширенная левосторонняя регулярная грамматика)
(или)
V -> T * V / T * (расширенная правосторонняя регулярная грамматика)
например:
S -> ab.
ССЫЛКИ
https://en.wikipedia.org/wiki/Chomsky_hierarchy
Пожалуйста, напишите комментарии, если вы обнаружите что-то неправильное или хотите поделиться дополнительной информацией по теме, обсужденной выше
Вниманию читателей! Не прекращайте учиться сейчас.Ознакомьтесь со всеми важными концепциями теории CS для собеседований SDE с помощью курса CS Theory Course по доступной для студентов цене и будьте готовы к отрасли.
Классификация Хомского | Формальные языки и компиляторы
В этой главе вы изучите четыре класса формальных языков, представленных Ноамом Хомским.
Самая известная классификация грамматик и языков, представленная Ноамом Хомским, разделена на четыре класса:
- Рекурсивно перечисляемые грамматики — распознаваемые машиной Тьюринга
- Контекстно-зависимые грамматики — распознаваемые линейно ограниченный автомат
- Контекстно-свободные грамматики — распознаваемые автоматом выталкивания
- Регулярные грамматики — распознаваемые конечным автоматом
0 — Рекурсивно перечисляемая грамматика002
, американский лингвист, философ, когнитивист и общественный деятель.Хомский хорошо известен в академическом и научном сообществе как один из отцов современной лингвистики и крупный деятель аналитической философии.
Грамматики типа 0 (неограниченные грамматики) включают все формальные грамматики. Они генерируют в точности все языки, которые может распознать машина Тьюринга. Эти языки также известны как языки с рекурсивным перечислением. Обратите внимание, что это отличается от рекурсивных языков, которые могут быть решены постоянно останавливающейся машиной Тьюринга.
Грамматики класса 0 слишком общие, чтобы описывать синтаксис языков программирования и естественных языков.
1 — Контекстно-зависимые грамматикиГрамматики типа 1 генерируют контекстно-зависимые языки. Эти грамматики имеют правила вида α A β → α γ β с нетерминалом A и строками терминалов и нетерминалов α, β и γ. Строки α и β могут быть пустыми, но строка γ должна быть непустой. Языки, описываемые этими грамматиками, — это в точности все языки, которые могут быть распознаны линейным ограниченным автоматом.
Пример:
- AB → CDB
- AB → CdEB
- ABcd → abCDBcd
- B → b
0 9-грамматика 13 9-грамматика 2
мм генерировать контекстно-свободные языки. Они определены правилами вида A → γ, где A — нетерминал, а γ — цепочка терминалов и нетерминалов. Эти языки — в точности все языки, которые могут быть распознаны недетерминированным автоматом выталкивания.Контекстно-свободные языки являются теоретической основой синтаксиса большинства языков программирования.Пример:
- A → aBc
Грамматики типа 3 генерируют регулярные языки. Такая грамматика ограничивает свои правила одним нетерминалом в левой части и правой частью, состоящей из одного терминала, за которым может следовать (или которому предшествуют, но не оба в одной и той же грамматике) один нетерминал.Правило S → ε также разрешено здесь, если S не появляется справа от любого правила. Эти языки — в точности все языки, которые могут быть определены конечным автоматом. Кроме того, это семейство формальных языков можно получить с помощью регулярных выражений. Обычные языки обычно используются для определения шаблонов поиска и лексической структуры языков программирования.
Пример:
- A → ε
- A → a
- A → abc
- A → B
- A → abcB
L
Если интересно 1 и L 2 являются обычными, также являются стандартными, следующие языки:
- L 1 ∪ L 2
- L 1 ∩ L 2
- 8
- L * L 2 = {xy: x ∈ L 1 ∧ y ∈ L 2 }
- L * = {ε} ∪ L ∪ L 2 ∪…
- Какую классификацию грамматики ввел Хомский?
- Какой класс грамматик соответствует машинам Тьюринга?
Если вы не знаете ответа на эти вопросы, прочтите еще раз содержание выше.
P автоматы — Scholarpedia
Введение
Рисунок 1: P-автомат с его средой и входными мультимножествами АвтоматыP представляют собой автоматоподобные принимающие варианты мембранных систем или P-систем. Общая модель представляет собой антипортовую систему P, в которой входные последовательности различаются как принятые или отклоненные входные последовательности. Входная последовательность — это последовательность мультимножеств объектов, которые входят в систему из окружающей среды во время вычислительных шагов P-автомата, начиная вычисление из своей начальной конфигурации.Принятие определяется набором конечных состояний, то есть вычислимым набором конфигураций, удовлетворяющих определенным условиям. Язык, принятый P-автоматом, получается из набора принятых входных последовательностей посредством отображения, которое упорядочивает слова по конечному алфавиту во входные последовательности. Детали конструкции можно найти в (Csuhaj-Varjú et al. 2010, ссылка 10).
Первыми вариантами P-автоматов были односторонние P-автоматы, имеющие только правила симпорта и специальные типы промоутеров (условия выбора объектов, которые могут быть переданы) (Csuhaj-Varjú, Vaszil 2002, ref.11), (Csuhaj-Varjú, Vaszil 2003, ссылка 12), а также анализ P-систем, которые принимают путем остановки конфигурации и отображают входное мультимножество в слово, которое является перестановкой объектов в мультимножестве (Freund, Oswald 2002, ссылка 15).
Некоторые формальные детали
P-автомат с (\ (n \) мембранами, \ (n \ ge 1 \)) является конструкцией \ [\ Pi = (V, \ mu, P_1, \ ldots, P_n, c_0, \ mathcal {F}) \, \] где
- \ (V \) — конечный алфавит объектов,
- \ (\ mu \) — мембранная структура с \ (n \) мембранами,
- \ (P_i \) — конечный набор правил антипорта, связанных с мембраной \ (i \) для всех \ (i \, \) \ (1 \ leq i \ leq n \, \)
- \ (c_0 \) — начальная конфигурация \ (\ Pi \, \) и
- \ (\ mathcal {F} \) — вычислимый набор принимающих конфигураций \ (\ Pi \.\)
Конфигурация P-автомата с \ (n \) мембранами на этапе вычисления представляет собой \ (n \) — кортеж мультимножеств объектов, которые присутствуют в соответствующих областях.
Когда правило антипорта \ ((x, out; y, in) \) применяется в области (\ (x \) и \ (y \) — мультимножества, состоящие из элементов \ (V \)), то объекты \ (y \) входят в область непосредственно из верхней области и в той же step объекты \ (x \) перемещаются в этот регион. В случае правил симпорта связь односторонняя, т.е.e., \ ((x, out) \) или \ ((y, in) \. \) Если правило антипорта связано с мультимножеством промотора \ (z \, \), то оно может применяться только в регионе если все элементы \ (z \) появляются в этой области. Если он связан с мультимножеством ингибиторов \ (z \, \), то ни один элемент \ (z \) должен присутствовать в регионе.
Автомат A P функционирует, изменяя свои конфигурации, определяемые отображением перехода \ (\ delta_X \), где \ (X \) относится к используемому вычислительному режиму (максимально параллельному, последовательному и т. Д.). Для двух конфигураций \ (c_1 \) и \ (c_2 \) из \ (\ Pi \, \) мы имеем \ (c_2 \ in \ delta_ {X} (v, c_1) \, \), если \ (\ Pi \ ) входит в конфигурацию \ (c_2 \) из конфигурации \ (c_1 \), применяя свои правила в режиме вычислений \ (X \), в то время как мультимножество объектов, попадающих в оболочку оболочки из окружающей среды, равно \ (v \. \)
Набор входных последовательностей, принимаемых \ (\ Pi \), функционирующим в режиме вычислений \ (X \), равен \ [A_ {X} (\ Pi) = \ {v_1 \ ldots v_s \ mid \] существуют конфигурации \ (c_0, c_1, \ ldots, c_s \) такие, что \ (c_ {i} \ in \ delta_X (v_i , c_ {i-1}) \, \) \ (1 \ leq i \ leq s \, \) и \ (c_s \ in {\ mathcal F} \} \.* \ mid w \ text {содержит равное количество символов} a \ text {и} b \} \] для \ (X \) — любой из максимально параллельных или последовательных режимов вычислений.
Принимающая мощность автоматов П
Класс языков, принимаемых универсальным вариантом P-автоматов, работающих в режиме максимально параллельных вычислений и применяющих несмываемое отображение к входным мультимножествам для получения языка, равен классу контекстно-зависимых языков. Если P-автоматы работают в режиме последовательных вычислений (1-ограниченный параллельный режим), то полученный языковой класс имеет сублогарифмическую пространственную сложность.Если отображение, примененное к входным мультимножествам, также может стирать, то языковой класс общих P-автоматов является классом рекурсивно перечислимых языков. Эти результаты были впервые опубликованы в (Csuhaj-Varjú et al. 2005, ссылка 8), (Csuhaj-Varjú et al. 2006, ссылка 9), см. (Csuhaj-Varjú et al. 2010, ссылка 10). подробности.
Было показано, что любой рекурсивно перечислимый язык приемлем как для односторонних P-автоматов, так и для анализа P-систем. Вычислительная полнота также может быть получена несколькими вариантами P-автоматов с дополнительными ограничениями на лежащие в основе P-системы или на способ их функционирования.Было показано, что любой рекурсивно перечислимый язык приемлем для P-автоматов с приоритетами (Cienciala, Ciencialová 2004, ссылка 4), P-автоматов с мембранными каналами (Oswald, Freund 2003, ссылка 21), (Freund, Oswald 2004, ссылка 16 ), P-автоматы с условными коммуникационными правилами, назначенными мембранам (Freund, Oswald 2004a, ссылка 17), или P-автоматы эволюции-коммуникации (Alhazov 2003, ref. 1).
Другие особенности P-автомата
АвтоматыP также могут определять языки по бесконечным алфавитам или языки, состоящие из бесконечных слов.В связи с тем, что максимально параллельный режим позволяет вводить объекты за один вычислительный шаг в неограниченном количестве копий, входные данные могут быть отображены в бесконечный алфавит. На основе этого наблюдения были построены конкретные варианты P-автоматов, называемые P-конечными автоматами, для реализации расширения обычных регулярных языков на регулярные языки над бесконечными алфавитами (Dassow, Vaszil 2006, ref. 14). Описание языков, состоящих из бесконечных слов, является следствием того факта, что P-автоматы допускают бесконечное количество циклов, т.е.е., бесконечные последовательности конфигураций. Аналоги \ (\ omega \) — машин Тьюринга в терминах P-автоматов, называемые \ (\ omega \) — P-автоматами, также могут быть построены для любого хорошо известного варианта режима приема \ (\ omega \) — Машины Тьюринга (Freund et al. 2004, ссылка 18).
Родственные варианты
Дополнительные варианты P-автоматов — это P-автоматы с состояниями (Madhu, Krithivasan 2003, ссылка 20), где отдельные наборы состояний связаны с регионами, активными P-автоматами, где лежащие в основе P-системы являются активными P-системами, а конструкция используется для анализируя предложения (Bel-Enguix, Gramatovici 2004, ref.2), (Bel-Enguix, Gramatovici 2006, ссылка 3) и P-автоматы с помеченными мембранами, которые заимствуют некоторые понятия из бранных исчислений (Csuhaj-Varjú, Vaszil 2008, ref. 13). P-автоматные аналоги классических автоматов сформулированы как мультимножественные автоматы Мили (Ciobanu, Gontineac 2006, ссылка 5), простые P-машины (Ciobanu, Gontineac 2006a, ссылка 6) и P-преобразователи (Ciobanu et al. 2006, ссылка 7). ). Комбинационные P-автоматы предоставляют методы для построения P-автоматов для принятия объединения, конкатенации, замыкания Клини или замыкания \ (\ omega \) языков (Long, Fu 2007, ref.19). Последние разработки в этой области — это системы DP, то есть распределенные системы P-автоматов, которые взаимодействуют и взаимодействуют друг с другом. Эта концепция наводит мост между теорией сложности связи и мембранными вычислениями (Паун, Перес-Хименес 2010, исх. 22).
Список литературы
1. А. Алхазов: Минимизация эволюции-коммуникации P систем и автоматов EC P. В: М. Кавальер, К. Мартин-Виде и Gh. Паун (ред.), Неделя мозгового штурма по мембранным вычислениям .Технический отчет 26/03 Исследовательской группы по математике Лингвистика, Университет Ровира и Вирджили, Таррагона, Испания, 2003 г., 23-31.
2. Г. Бел-Энгуикс и Р. Граматовичи: синтаксический анализ с активными P-автоматами. В: C. Martín-Vide, G. Mauri, Gh. Паун, Г. Розенберг и А. Саломаа (редакторы), Membrane Computing. Международный семинар, WMC 2003, Таррагона, Испания, 17-22 июля 2003 г. Пересмотренные документы . Конспект лекций по информатике 2933, Springer, Berlin, 2004, 31-42.
3.G. Bel-Enguix и R. Gramatovici: Синтаксический анализ с помощью P-автоматов. В: Г. Чобану, М. Перес-Хименес и Г. Паун (ред.), Применение мембранных вычислений . Серия Natural Computing, Springer, Berlin, 2006, 389-410.
4. L. Cienciala и L. Ciencialová: Мембранные автоматы с приоритеты. Журнал компьютерных наук и технологий 19 (1) (2004), 89-97.
5. Дж. Чобану и В. М. Гонтинеак: мультимножественные автоматы Мили. Международный журнал основ информатики 17 (2006), 111-126.
6. Г. Чобану и В. М. Гонтинеак: P-машины: автоматный подход к мембранные вычисления. В: H.-J. Hoogeboom, Gh. Паун, Дж. Розенберг и Арто Саломаа (ред.), Membrane Computing, 7-й международный семинар, WMC 2006, Лейден, Нидерланды, 17-21 июля 2006 г., исправленные, избранные и приглашенные документы. Конспект лекций по информатике 4361, Springer, Берлин, 2006 г., 314-329.
7. G. Ciobanu, Gh. Паун и Г. Стефанеску: П-преобразователи. Вычислительная техника нового поколения 24 (1) (2006), 1-28.
8. Э. Чухай-Варджу, О. Ибарра и Ги. Василь: О вычислительной сложность P-автоматов. В: C. Ferretti, G. Mauri и C. Zandron (ред.), DNA Computing, 10-й международный семинар по ДНК-вычислениям, DNA10, Милан, Италия, 7-10 июня, Revised Selected Papers . Конспект лекций по информатике 3384, Springer, 2005, 77-90.
9. Э. Csuhaj-Varjú, O.H. Ибарра и Ги. Васил: На вычислительная сложность P-автоматов. Natural Computing 5 (2) (2006), 109-126.
10. Э. Чухай-Варджу, М. Освальд и Ги. Васил: P-автоматы. Глава в Справочник по мембранным вычислениям . Gh. Паун, Дж. Розенберг и А. Саломаа (редакторы), Oxford University Press, 2010, 144-167.
11. Э. Чухай-Варджу и Ги. Васил: P-автоматы. В: Gh. Паун и К. Зандрон (ред.), Предварительные материалы семинара по мембранным вычислениям WMC-CdeA 2002, Куртя-де-Арджеш, Румыния, 19-23 августа 2002 г., Pub. № ~ 1 MolCoNet-IST-2001-32008, 2002, 177-192.
12.Э. Чухай-Варджу и Ги. Васил: P-автоматы или чисто коммуникативные принимающие P-системы. В: Gh. Паун, Дж. Розенберг, А. Саломаа и К. Зандрон (ред.), Мембранные вычисления. International Worskhop, WMC-CdeA 2002, Куртя-де-Арджеш, Румыния, 19-23 августа 2002 г., исправленные документы. Конспект лекций по компьютеру Science 2597, Springer, Berlin, 2003, 219-233.
13. Э. Чухай-Варджу и Ги. Васил: (Мем) бранные автоматы. Теоретическая информатика 404 (1-2) (2008), 52-60.
14.J. Dassow and Gy. Василь: P конечных автоматов и регулярные языки над счетно бесконечными алфавитами. В: H.-J. Hoogeboom, Gh. Паун, Г. Розенберг и А. Саломаа (ред.), Membrane Computing. 7-й международный семинар, WMC 2006, Лейден, Нидерланды, 17-21 июля 2006 г., Отредактированные, избранные и приглашенные доклады . Конспект лекций по информатике 4361, Springer-Verlag, Berlin, 2006, 367-381.
15. Р. Фройнд и М. Освальд: Краткое замечание по анализу P-систем. Бюллетень EATCS 78 (октябрь 2002 г.), 231-236.
16. Р. Фройнд и М. Освальд: P-автоматы с мембранными каналами. Искусственная жизнь и робототехника 8 (2004), 186-189.
17. Р. Фройнд и М. Освальд: P-системы с условной коммуникацией. правила, назначенные мембранам. Журнал автоматов, языков и комбинаторики 9 (4) (2004), 387-397.
18. Р. Фройнд, М. Освальд, Л. Штайгер \ [\ omega \] — P автоматы с правилами общения. В: C. Martín-Vide, G. Mauri, Gh. Паун, Г. Розенберг и А.Salomaa (ред.), Membrane Computing. Международный семинар, WMC 2003, Таррагона, Испания, 17-22 июля 2003 г. Пересмотренные документы . Конспект лекций на компьютере Science 2933, Springer, Berlin, 2004, 203-217.
19. Х. Лонг, Ю. Фу: Общий подход к построению комбинационных P-автоматов. Международный журнал компьютерной математики 84 (12) (2007), 1715-1730.
20. М. Мадху и К. Критхивасан: Об одном классе P автоматы. Международный журнал компьютерной математики 80 (9) (2003), 1111-1120.
21. Освальд М., Фройнд Р.: П-автоматы с мембранными каналами. В М. Сугисака, Х. Танака. (ред.), Proc. восьмого межд. Symp. по искусственной жизни и робототехнике, Беппу, Япония, , 2003, 275-278.
22. Gh. Паун, М.Дж. Перес-Хименес: Распределенное решение проблем в мембранных вычислениях: системы dP. Международный журнал компьютеров, связи и управления V (2) (2010), 238-250.
Внутренние ссылки
Дополнительная литература
E.Csuhaj-Varjú: P automata. В: G. Mauri, Gh. Паун, М. Перес-Хименес, Г. Розенберг и А. Саломаа (ред.), Мембранные вычисления: 5-й международный семинар, WMC 2004, Милан, Италия, 14-16 июня 2004 г. Пересмотренные избранные и приглашенные доклады. Конспект лекций по информатике 3365, Springer, 2005, 19-35.
Э. Чухай-Варджу: P Автоматы: концепции, результаты и новые аспекты. В: Gh. Паун, М. Перес-Хименес, А. Рискос-Нуньес, Г. Розенберг и А. Саломаа (ред.), Мембранные вычисления: 10-й международный семинар, WMC 2009, Куртя-де-Арджеш, Румыния, 24-27 августа 2009 г.Отредактированные избранные и приглашенные доклады. Конспект лекций по информатике 5957, Springer, 2010, 1-15.
М. Освальд: P Автоматы . Докторская диссертация, Венский технологический университет, 2003 г.
Гр. Василь: Мембранные системы, подобные автоматам — естественный способ описания сложных явлений. В: C. Campeanu, G. Pighizzini (eds.), 10-й международный семинар по описательной сложности формальных систем, 16-18 июля, Шарлоттаун, PE, Канада. Ход работы. Университет острова Принца Эдвардса, 2008 г., стр. 26–37.
Веб-страница системы P: http://ppage.psystems.eu
Computer Science Logo Style vol 3 ch 1: Automata Theory
Computer Science Logo Style vol 3 ch 1: Automata Theory Стиль логотипа компьютерных наук том 3: Помимо программирования 2 / e Copyright (C) 1997 MIT Программный файл для этой главы: fsm
Как я объяснил в предисловии к первому тому, одна из моих целей в написание этой серии книг было призвано отвлечь компьютерных любителей от взгляд на компьютерную экспертизу как на знание непонятных характеристик какого-то конкретного компьютера — как его программировать на машинном языке, что магические числа можно найти где в его памяти, как побороть копию схемы защиты на его дисках и тд.Проблема с такого рода специфический для машины опыт состоит в том, что он устаревает, когда ваш любимый компьютер делает. С моей точки зрения, одно из достоинств Logo как язык программирования заключается в том, что его структуры данных высокого уровня направляют ваши внимание от вопросов о том, что происходит где в памяти, позволяя вам вместо этого сосредоточиться на более абстрактном описании вашей проблемы.
Теория автоматов — еще один шаг в отвлечении вашего внимания от любых конкретный вид компьютера или конкретный язык программирования.В автоматах В теории мы рассматриваем математическую модель вычислений. Такая модель лишает вычислительную технику — «язык программирования» — до минимум, чтобы легко манипулировать этими теоретические машины (таких моделей несколько, для разных целей, как вы скоро увидите) математически, чтобы доказать свои способности. По большей части, эти математические модели не используются для практических задач программирования. Реальные языки программирования намного удобнее использовать.Но само гибкость, которая упрощает использование реальных языков, также усложняет их говорить формально. Урезанные теоретические машины предназначен для изучения математически.
Что такое математическая модель? Вскоре вы увидите один, который называется «конечный автомат».
Суть данного исследования заключается в том, что математические модели в некоторых важные способы, эквивалент реальным компьютерам и реальному программированию языков. Это означает, что любая проблема, которую можно решить на реальном компьютер можно решить с помощью этих моделей, и наоборот.Все, что мы можем Доказательство о моделях проливает свет на реальные проблемы компьютера а также программирование.
Теория автоматов задает следующие вопросы: Есть ли какие-нибудь проблемы, которые не может решить ни один компьютер, независимо от того, сколько времени и памяти он имеет? Может ли доказать , что конкретная компьютерная программа действительно решит конкретную проблему? Если компьютер может использовать два разные внешние устройства хранения (диски или ленты) одновременно, расширяет ли это спектр задач, которые он может решить по сравнению с машина только с одним таким устройством?
Есть еще более крупный вопрос, скрывающийся в основе автоматов. теория: решает ли человеческий разум проблемы так же, как компьютер делает? Подвержены ли люди тем же ограничениям, что и компьютеры? Теория автоматов на самом деле не дает ответа на этот вопрос, но идеи теории автоматов может помочь в поиске ответа.Подробнее об этом мы расскажем в главе об искусственном интеллекте.
Что такое вычисления?
Какие проблемы мы можем создать для наших абстрактных компьютеров? В теории автоматов мы хотим сосредоточить наше внимание на самих вычислениях, не на деталях устройств ввода и вывода. Поэтому мы не будем пытаться создавать математическая модель видеоигры.
А мы поиграем в игру. В этой игре компьютер имеет в виду правило.
Вы вводите строки букв, используя только буквы A , B и С .Компьютер сообщает вам, соответствует ли каждая строка правилу или
нет. Ваша задача — угадать правило. Например, предположим, что вы сделали
эти эксперименты:
| принято | отклонено |
|---|---|
ABC | CBA |
AAA | BBB |
ABCABCABC | BCABCABC |
A | BBBBBBB |
ACCCCCCCCC | CAAAAAAAAA |
Из этих примеров можно догадаться, что правило
«Строка должна начинаться с A .»Сделав предположение, вы сможете
проверьте это, попробовав больше примеров.
Программа для игры называется игра . Требуется один ввод,
число от 1 до 10. Я привел десять различных правил. Правила с 1 по 3
должно быть довольно легко угадать; правила с 8 по 10 должны быть почти невозможными.
(Не расстраивайтесь, если вы их не получите.)
Строка может иметь любую длину, включая нулевую (пустая строка). Каждый
когда вы набираете букву, программа сообщает,
набранный до сих пор подчиняется правилу.Программа указывает, является ли строка
принято или отклонено, отображая слово принять или отклонить на
экран. В частности, как только
при запуске игры программа сообщит вам, пустой ли
строка принимается этим правилом. Если вы наберете строку ABC , вы
на самом деле будет тестировать три строки: A, , AB, и ABC, . Ты
следует вводить по одной букве за раз, чтобы программа могла
ответьте на него, прежде чем перейти к следующему письму.Чтобы начать сначала с
другую строку, нажмите клавишу Return.
Вам стоит прекратить читать сейчас и попробовать игру. В следующих параграфах Я собираюсь рассказать о некоторых ответах, так что это ваш последний шанс. После того, как вы выяснили хотя бы некоторые правила, приходите вернуться к книге.
Конечные машины
Смысл изучения этой игры в том, что мы собираемся найти способ разработки абстрактный компьютер специального назначения, который понимает один конкретный правило.Затем мы можем задать вопросы о том, сколько информации компьютер нужно справиться с работой.
Вы уже видели слово состояние в связи с логотипом
черепаха. Его состояние включает его позицию и его заголовок. Итак, одна черепаха
состояние может быть «позиция [17 82] , заголовок 90 ». В принципе,
черепаха имеет бесконечных возможных состояний, потому что ее
позиция и заголовок не обязательно должны быть целыми числами. Его позиция может быть [14.142 14.142] , например.
Все, что содержит информацию, может находиться в разных состояниях. Как другой Например, выключатель света имеет два состояния. Некоторые лампы имеют четыре состояния: выкл., низкий, средний и высокий. Компьютер тоже имеет определенное количество состояний. Состояние компьютера включает в себя всю информацию в его памяти в какой-то момент. определенное время.
Машина с ограниченным числом состояний, как в примере выключатель света, называется конечным автоматом . Почти для всех в этой главе мы будем иметь дело с конечными автоматами. Ты можешь подумать что это налагает очень жесткие ограничения на виды вычислений, которые мы можем делать. Но обратите внимание, что в игре, в которую я просил вас сыграть, правило может принимать бесконечное количество возможных строк и отклонить бесконечное количество другие. Принятые или отклоненные строки могут быть любой длины. (Некоторые правила ограничивают длину строки, но другие допускают любую длину вообще.) в некотором смысле, конечный автомат все еще может выполнять бесконечно разные вычисления.
Рассмотрим для примера третью игру. Правило: «Принять
любая строка, которая начинается с AB . «Вот изображение конечного состояния
машина, которая реализует это правило:
Каждый пронумерованный кружок представляет состояние. В этой машине три
состояния. Стрелка start указывает, что машина запускается в состоянии
1. Состояние 3 показано двойным кружком , чтобы указать, что это принимает состояние . Другими словами, когда автомат находится в состоянии 3,
экран говорит, что принимает .Два других государства не
принимающие государства.
Каждый раз, когда вы вводите символ, машина переключается из одного состояния в другое.
Другой. Стрелка из состояния 1 в состояние 2 имеет A рядом с его
хвост. Это указывает на то, что когда автомат находится в состоянии 1, ввод переключает его в состояние 2. (Стрелка из состояния 3 на себя имеет
три буквы ABC на его хвосте. Это сокращенное обозначение
три отдельные стрелы с острием и хвостом в одном месте, по одной для каждой
письмо.)
Это изображение неполное. Полное описание машины
мы должны указать, что происходит на любом входе в любом состоянии. Другими словами,
из каждого круга должно выходить три стрелы, по одной
для A , B и C . Я решил принять соглашение, что
каждая машина имеет немаркированное состояние под названием отклонить . Любая отсутствующая стрелка
переходит в это состояние; как только машина находится в состоянии отказа, она остается
там навсегда.Итак, вот полная схема автомата для игры.
3:
С этого момента я не буду рисовать состояние отклонить , но вы должны
помните, что это действительно часть описания машины. Итак, эта машина
требуется четыре состояния, а не три.
Если первая введенная буква не A , машина переходит к reject государственный. Если первая буква — A , машина переходит в состояние 2. Затем,
если вторая буква B , машина переходит в состояние 3 и принимает
строка AB .Это самая короткая допустимая строка.
Каждая из трех стрелок из состояния 3 возвращается обратно в состояние
3 сам. (Помните, что хотя на картинке изображена только одна стрелка,
он обозначен тремя буквами, так что официально он представляет собой три
стрелки.) Это означает, что когда машина находится в состоянии 3, она остается
там, независимо от того, какие входы он получает. Любая строка, начинающаяся с AB , является
приемлемо.
Вот автомат для игры №2:
В этой машине начальное состояние также является принимающим
государственный. (Каждая машина имеет ровно одно начальное состояние, но может иметь любое
количество принимающих состояний.) Эта машина никогда не попадает в отклонение государственный. Это не значит, что он не отвергает никаких строк; все нечетной длины
строки отклоняются в состоянии 2. Но отклоненная строка может искупить себя путем
добавление еще одного входного символа, поэтому состояние 2 позволяет вернуться к принимающему
состояние 1.
Вот автомат для игры номер 5. (Обратите внимание, что я говорю «a машина », а не« машина »; всегда можно спроектировать другие машины, которые следовали бы тому же правилу.)
Вероятно, у вас было больше проблем с открытием правила 5, чем с правилом
2, и требуется больше времени, чтобы сказать правило английскими словами. Но , машины по двум нормам практически идентичны. (Помнить,
хотя, что машина с правилом 5 действительно имеет третье состояние, отклоняет состояние, которое не показано на схеме.)
Вот машины для правил 7 и 9. С этими машинами в качестве подсказок,
ты можешь разобраться в правилах? Вернитесь к программе game для тестирования
ваши гипотезы.
Вы также должны попрактиковаться в переводе в другом направлении, с
Английские правила машинных диаграмм. Вот пара, над чем стоит поработать: Правило 4:
«Чтобы быть принятой, строка должна состоять из удвоенных букв ( AA , BB и CC ), соединенные вместе. Правило 8:
строка должна содержать четное число A s. »
Недетерминированные машины
Вот правило 6: «Чтобы строка была принята, она должна начинаться с A и заканчиваться
с C .»Строки, принятые этим правилом, включают AC (самый короткий
возможно), ABC , AACC , ACAC , ABCABC и т. д.
Между начальным A и последним C принятая строка может
иметь любую комбинацию A s, B s и C s. Это естественно для
представьте, что строка состоит из трех частей: фиксированное начало, переменная
средний и фиксированный конец. Три части входных строк могут быть
удобно представлено в машине тремя состояниями, например:
Машина запускается в состоянии 1.Чтобы быть принятым, строка должна начинаться
с A . Следовательно, стрелка A ведет из состояния 1 в состояние 2. Любое
другой вход в состоянии 1 приводит к состоянию отклонить .
Когда машина находится в состоянии 2, она готова к средней части строка. В этой средней части допускается любое сочетание букв. Следовательно, есть три стрелки от состояния 2 к самому себе, одна для всевозможные буквы.
Наконец, стрелка C ведет из состояния 2 в состояние 3, сигнализируя об окончании
допустимой строки.Чтобы строка была принята, строка должна заканчиваться на C .
Проблема с этим станком: две стрелки C вывод из состояния 2. Первый — это цикл, возвращающийся в состояние 2; другой
переходит к состоянию 3. Эта ситуация отражает тот факт, что C обслуживает
две разные функции в этом правиле: C — необязательная часть
средняя часть строки, а также обязательный окончательный ввод
в строке.
Станок с двумя стрелками из одного состояния для одного и того же входа назвал недетерминированной машиной .Вот как такая машина может работать: если есть два варианта выбора машины текущее состояние и ввод, машина клонирует себя. Один из экземпляров следует за каждой стрелкой. С этого момента, если либо машина находится в Принимающее состояние строка принята.
Недетерминированные конечные автоматы сложнее чем детерминированные. «Покупает» ли добавленная сложность какие-либо добавленные мощность? Другими словами, может ли недетерминированная машина решать задачи что детерминированная машина не может? Оказывается, ответ на этот вопрос нет.Детерминированные машины столь же мощны как недетерминированные. Это важная теорема для автоматов. теория. Я не собираюсь доказывать это формально в этой книге, но хочу проиллюстрировать теорема, вот детерминированная машина, которая выполняет игру 6:
Эта машина похожа на недетерминированную версию. Он имеет такое же количество состояний и некоторые соединения идентичны. Однако состояние 3 более сложное. Также в этой машине больше не тот случай, когда каждое состояние машины точно соответствует к одной из трех частей входной строки.В частности, когда машина в состоянии 3 строка может заканчиваться, а может и не заканчиваться.
Представление машин в виде списков логотипов
Игра Программа использует конечные автоматы для представления правил
с помощью которого он принимает или отклоняет строки. (Машины должны быть детерминированными
чтобы программа работала.) Программы с логотипом не могут читать круги и стрелки,
Итак, машина представлена в виде списка. Какая информация есть на самом деле
содержится в диаграмме конечного автомата? На диаграмме видно, что существуют определенные
количество состояний (кружки), что есть определенные переходы из одного
состояние к другому (стрелки), что одно конкретное состояние является начальным состоянием
(стрелка начала), и что определенные состояния принимают их (двойная
круги).Как и в любом программном проекте, я мог выбрать много разных
способы представления этой информации в программе.
В выбранном мной конкретном представлении список машины состоит из трех членов. Первый член — это номер начального состояния. Второй член — это список стрелок; каждая стрелка сама по себе является списком, как я объясню через мгновение. Третий член списка машин — список принимающих состояний машины. Например здесь это снова машина для игры 3, в обеих формах:
[1 [[1 A 2] [2 B 3] [3 ABC 3]] [3]]
Число 1 — начальное состояние; список [3] — это
список принимающих состояний.(У этой машины есть только один принимающий
состояние.) Все остальное — список стрелок. Каждая стрелка — это тоже список
с тремя членами: начальное состояние (хвост стрелки), вход
буква или буквы и конечное состояние (острие стрелки). Первая стрелка в
эта машина
[1 A 2]
Это стрелка от состояния 1 к состоянию 2, связанная с
вход А .
Список [3 ABC 3] в этом аппарате представляет три стрелки, используя
такое же сокращение, как на диаграммах со стрелками и кругами.Я мог одинаково
хорошо изобразили эти стрелки по отдельности:
[1 [[1 A 2] [2 B 3] [3 A 3] [3 B 3] [3 C 3] ] [3]]
Как и на диаграммах со стрелками и кругами, я не представил явно
переходы в состояние отклоняют состояние в этих списках. Программа
написано так, что если он не находит переход для текущего состояния и
вход в список переходов, он переходит в состояние с номером -1, его
представление для отклонить состояние .
Вот еще несколько списков машин:
Игра 2: [1 [[1 ABC 2] [2 ABC 1]] [1]] Игра 7: [1 [[1 AB 1] [1 C 2] [2 C 1]] [1]] Игра 9: [1 [[1 AB 1] [1 C 2] [2 A 3] [2 B 1] [3 A 1]] [1]]
На этом этапе вы должны остановиться и поиграть с программой. Макияж, мириться
свои собственные правила. Процедура fsm принимает список машин в качестве входных данных.
и принимает строки на основе этой машины. ( Game использует fsm с особым
машины в качестве входных данных.) Попробуйте свои новые правила, чтобы убедиться, что вы создали
машины правильно.Затем попросите друга поиграть по вашим правилам.
Если вы оба читаете эту книгу вместе, вы можете устроить соревнование.
(Легко разработать правила, которые невозможно угадать, потому что
слишком много деталей. Если у вас есть соревнование, вы должны ограничить
до трех состояний на машину.)
Возможно, вам будет интересно прочитать программа fsm , которая
имитирует конечный автомат, когда дано описание машины
как его вход. Это довольно простая программа.Если вы думаете о машине
диаграмма состояний как своего рода «электрическая схема», которую можно использовать
при создании реальной версии этой конкретной машины эта программа Logo
это своего рода реализация универсального конечного автомата .
Текстовые редакторы: использование акцепторов
Вам может показаться, что принятие или отклонение строк — это не так уж и много как то, что вы обычно делаете с компьютерами. Вы можете задаться вопросом, как это Математическая модель связана с реальным компьютерным программированием. Там два ответа на этот вопрос.Во-первых, можно разработать конечные автоматы, которые имеют более универсальные выходы, чем просто да или нет. Вскоре я приведу пример. Но другой ответ что есть реальные ситуации, когда принятие или отклонение строки символов действительно возникает в практических вычислениях.
Один из примеров — реализация языков программирования. Когда Вы говорите, что
печать 2 + 2
— это официальная инструкция для логотипа, но
печать 2+
является незаконным, вы делаете более сложную версию того, что акцептор с конечным состоянием делает.
Команда search в хорошем текстовом редакторе использует конечные автоматы. В большинстве текстовых редакторов есть команда, позволяющая вы можете просмотреть файл в поисках определенной строки символов. Любитель редакторы позволяют искать не только одну строку, но и любую строка, которая следует правилу, которое может предоставить пользователь. Редактор находит строку, соответствует правилу с использованием конечного автомата. Конечно, люди, которые используют редакторам не нужно указывать свои правила поиска в форме конечный автомат! Программа редактирования принимает правила поиска в более простом виде. form и переводит их в форму FSM.Вот пример, обозначение используется ed, — стандартным редактором в операционной системе Unix.
Строка вида
спагетти
просто соответствует идентичной строке в файле, который вы редактируете. А немного более интересный случай
[Ss] пагетти
, что соответствует либо «спагетти», либо «спагетти» (с заглавной или строчной буквы «s»). Квадратные скобки означают, что Принимаются любые букв в скобках.В выражении
[Ss] paghet * i
звездочка соответствует любому номеру (включая ноль)
письмо перед ним (в данном случае буква t ). Этот пример
будет соответствовать любому из них:
Спагей Спагеттти спагетти спагети
Вы можете использовать это в поисковой команде, если плохо пишете! Скобу и звездочку можно комбинировать;
C [AD] * R
будет соответствовать любому из
АВТОМОБИЛЬ CDR CADDR CR
Или вы можете использовать
M [is] * p * i
, чтобы соответствовать названию известной реки.
Некоторые правила из игры, которую я представил ранее, можно представить в виде ed поисковые строки в соответствии с этими правилами. В первой игре
машина принимает любую строку, состоящую из A, s и B s. В
соответствующее выражение ed
[AB] *
В третьей игре используются строки, начинающиеся с последовательности AB , а затем все, что угодно. Это можно представить как
AB [ABC] *
Игра 10, которую, я уверен, вы не решали, принимает любую строку,
включает в себя последовательность ABCBA .В терминах ed это
[ABC] * ABCBA [ABC] *
Я не дал вам полного описания правил поиска ed . Я включил это только потому, что хочу, чтобы вы увидели, как «настоящая» программа использует идею конечных автоматов. Но в остальной части этого Глава Я хочу использовать другую нотацию, основанную на словах и списках логотипа.
Регулярные выражения
Обозначение, которое я собираюсь описать, допускает правило принятия, как и правила
в программе game или правилах поиска ed , чтобы
представлен в логотипе.Представление такого правила называется регулярное выражение. Я расскажу вам несколько правил того, что
выражение может выглядеть. Не путайте: любой конкретный регулярный
выражение — это правило, которое принимает строки букв. Я даю вам правила
которые принимают регулярные выражения — правила о правилах. В качестве грубой аналогии
«размер одного игрока X , а другого O » — это правило
специфическая игра Tic Tac Toe; «у каждого игрока должен быть шанс на победу»
это правило о том, какие правила игры приемлемы.
Алфавитная линейка. Любой символ в машинном
алфавит — это регулярное выражение. Представляем символ однобуквенным
Слово логотипа. В нашей игре в угадайку алфавит состоит из трех символов: A , B и C . Так
B
— регулярное выражение.
Правило конкатенации. Список, членами которого являются регулярные выражения.
представляет эти выражения одно за другим. Например, так как A — регулярное выражение, а B — регулярное выражение,
[A B]
— регулярное выражение, представляющее строку AB .(Уведомление
что слово логотипа AB не , а представляет эту строку; в
правило алфавита требует, чтобы каждая буква была представлена как отдельное слово.)
Правило альтернатив. Список, первым членом которого является слово или и
остальные члены которого являются регулярными выражениями, представляют любую строку,
соответствует любым из этих выражений. Например,
[ИЛИ [A A] B]
соответствует либо последовательности AA , либо одиночному символу B .Для удобства слово логотипа, содержащее более одной буквы (другие
чем слово или ) рассматривается как сокращение для или ing
отдельных букв. Например, ABC эквивалентно [ИЛИ AB C] .
Правило повторения. Список, содержащий ровно два элемента, в которых
первый — символ звездочки ( * ), второй — обычный
выражение, представляет собой строку, содержащую любое количество (включая ноль)
подстроки, соответствующие регулярному выражению.Так
[* [OR [A A] B]]
соответствует любому из этих:
B |
BB |
BAAB |
AAAAAA |
AABAA |
| (пустая строка) |
AABBBBBAA |
Число последовательных A s должно быть четным для строки A s и B s, чтобы соответствовать этому выражению.
Эти четыре правила составляют определение регулярного выражения. Это рекурсивное определение . Так же, как эффект рекурсивного Процедура создания логотипа определяется в терминах более простого случая той же процедуры, сложное регулярное выражение определяется в терминах более простых.
Вот десять правил игры из начала этой главы в форма регулярных выражений:
| 1. | [* AB] |
|---|---|
| 2. | [* [ABC ABC]] |
| 3. | [A B [* ABC]] |
| 4. | [* [ИЛИ [A A] [B B] [C C]]] |
| 5. | [* [ABC B]] |
| 6. | [A [* ABC] C] |
| 7. | [* [OR A B [C C]]] |
| 8. | [[* BC] [* [A [* BC] A [* BC]]]] |
| 9. | [[* AB] [* [C [OR B [A A]]] [* AB]]] |
| 10. | [[* ABC] A B C B A [* ABC]] |
Вам следует внимательно просмотреть эти примеры, убедившись, что вы понимаете, как регулярное выражение представляет ту же идею как в описании на английском языке или на схеме машины, которую вы видели ранее.
Необычные правила
Вы можете подумать, что любое правило для принятия или отклонения строки символов могут быть представлены как регулярное выражение.Но это не так. Например, рассмотрим правила распознавания обычных арифметические выражения:
| принято | отклонено |
|---|---|
2 + 3 | 23+ |
2 * (3 + 4) | 2 *) 3 + 4 ( |
-5 | /6 |
Задумайтесь на мгновение о том, балансирующие скобки.Иногда круглые скобки заключаются в круглые скобки, как в
((3 + 4) / (5 + 6))
Как бы вы изобразили эту часть арифметического выражения? правило в виде регулярного выражения? Вы не можете просто сказать что-то вроде
[[* (] что-то или другое [*)]]
означает «любое количество открытых скобок, что-нибудь, тогда любое количество закрывающих скобок ». Это позволит строкам вроде
(((7)))))
Но эту строку следует отклонить, потому что в ней слишком много близких круглые скобки.Вам не разрешается использовать закрывающую скобку, если вы не уже использовал подходящую открывающую скобку. Вы можете иметь любое количество вложенных круглые скобки, если они сбалансированы.
Можно изобрести другие виды формальных обозначений, более мощные, чем
регулярные выражения, которые позволят нам дать правила для правильно сформированных
арифметические выражения. В этом разделе я кратко представлю формальную
обозначение под названием производственные правила , достаточно мощное, чтобы описать
арифметические выражения.Сейчас в этой главе я не хочу обсуждать
детально проработанные правила производства; моя единственная причина представить их на
этот момент должен дать вам представление о том, как регулярные выражения вписываются в
большая вселенная возможных формальных систем. В следующих разделах я
есть что сказать о регулярных выражениях и конечных автоматах. Но
мы вернемся к правилам производства в главах 5 и 6, в которых нам понадобится
формальные обозначения, с помощью которых можно обсуждать более интересные языки, чем A — B — C язык данной главы.(В главе 5 мы будем
говорить о Паскале; в главе 6 мы займемся английским языком.)
Ключевой ингредиент, отсутствующий в нотации регулярных выражений, — это способ до имя своего рода подвыражение, чтобы имя можно было использовать в определение более сложных выражений. В частности, имя подвыражения может использоваться в собственном определении, чтобы разрешить рекурсивное определение правило.
Производственное правило имеет вид
название: расширение
Каждое правило представляет собой определение имени слева в терминах меньшие единицы, аналогично определению процедуры логотипа в терминах подпроцедур.Раскрывающая часть правила представляет собой строку символов включая оба члена «алфавита» системы (например, алфавит который лежит в основе языка регулярных выражений) и имен, определенных правила производства.
В качестве примера приведем набор производственных правил, определяющих язык арифметические выражения. Эти правила учитывают «порядок операции «для арифметики, которую вы изучали в начальной школе: умножение перед сложением. Выражение вроде
2/3 + 1/6
обычно интерпретируется как сумма двух членов , а именно две трети и одна шестая.Выражение может быть одним членом, суммой термины или разница в сроках. Вот как эта идея выражается в наборе правил производства; Я расскажу об обозначениях более подробно чуть позже.
Вертикальные полосы разделяют альтернативы. Первое правило, единственное
который определяет expr , содержит три альтернативы. Во-первых, выражение
может быть всего лишь одним термином. Во-вторых, выражение может быть меньшим
выражение плюс термин. В-третьих, выражение может быть выражением меньшего размера
минус срок.Символы внутри прямоугольников являются членами алфавита
язык арифметических выражений. (Я положил их в коробки, чтобы
их проще не путать с знаками препинания — двоеточиями и
вертикальные полосы — это часть самой нотации производственного правила.)
Вы видите, как подходят круглые скобки? Если строка типа 4 + 5 является
выражение, то (4 + 5) — множитель, поэтому 3 * (4 + 5) — член,
и так далее. Поскольку фактор — это разновидность термина, а термин — разновидность
выражение, множитель (4 + 5) можно рассматривать как выражение, и
поэтому его тоже можно заключить в круглые скобки.Таким образом, ((4 + 5)) также
приемлемый как фактор.
Регулярные выражения и конечные автоматы
Я намекнул на то, что на самом деле не сказал явно: Обычный выражения эквивалентны конечным автоматам. Другими словами, если вы можете выразить правило в виде регулярного выражения, вы можете создать конечный автомат, который выполняет это правило. Если ты не можешь писать регулярное выражение для правила, вы не можете создать конечное состояние машины тоже нет.
Вы можете подумать «ну и что?» Я представил два разных формальных нотации, конечные автоматы и регулярные выражения, и теперь я говоря вам, что эти два эквивалента.Так почему бы мне просто не выбрать один первое место и забыть о другом? У меня есть общий ответ и конкретный ответ на эти вопросы.
Общий ответ таков: сравнение различных формальных систем — вот что теория автоматов — это все. К концу этой книги вы будете познакомился с полдюжиной различных формальных систем. Некоторые больше сильнее других. Простое утверждение, что одна формальная система эквивалентен другому или более мощный, чем другой, не очень интересен; но если мы сможем понять причин , стоящих за этими утверждениями, тогда возможно, мы сможем применить знания на практике.На в самом конце этой книги, в главе 6, мы поговорим об особом формальном система, которая часто используется в программах искусственного интеллекта для распознавания Английские предложения. К тому времени вы должны знать достаточно о формальных системах, чтобы уметь понять, почему именно этот вариант — хороший выбор.
Конкретный ответ заключается в том, что конечные автоматы и регулярные выражения отличаются друг от друга интересным образом. Конечное состояние машина — это алгоритм , — последовательность шагов или процедура, которая может следовать, чтобы проверить, соответствует ли некоторая строка заданному правилу.Он говорит: «начни здесь, затем, если это произойдет, сделай это, тогда …» как процедура в Logo или большинстве других языков программирования. (Но мы видели, что конечный автомат похож на процедуру, написанную в ограниченном программировании язык, который не так гибок, как Logo.) Однако регулярное выражение , а не , последовательность шагов. Это больше похоже на описание результат , который мы хотим, оставив открытым точный рецепт того, как этого добиться. Люди часто создают проблемы подобным образом.Они вызывают сантехника и говорят: «сток в моей ванне идет обратно». Часть опыта водопроводчика чтобы иметь возможность перевести декларативную формулировку проблемы в процедурная форма , последовательность шагов, необходимых для устранения проблемы. Первым камнем преткновения в исследованиях искусственного интеллекта было кажущееся пропасть между процедурными знаниями, воплощенными в компьютерной программе, и декларативные знания, необходимые для человеческого поведения. В последнее время у людей есть изобрел декларативных языков программирования (самый известный это Prolog, но любая коммерческая программа для работы с электронными таблицами также в этой категории), что позволяют пользователю заявить о проблеме в декларативной форме.Программирование языковой интерпретатор автоматически переводит эту постановку задачи в последовательность шагов, которые должен выполнить компьютер.
При написании интерпретатора Пролога возникает много вопросов, выходящих за рамки данной статьи.
книга. Но мы можем сделать меньший шаг в области перевода с
декларативное обозначение к процессуальному. Я написал программу с логотипом,
перечислен в конце главы, что переводится с обычного
выражение в эквивалентный конечный автомат. Его процедура верхнего уровня, машина , принимает регулярное выражение в качестве входных данных и выводит машину
список в формате, который я показал ранее.
Как перевести
Общее утверждение, что регулярные выражения эквивалентны по мощности для конечных автоматов называется теоремой Клини, названной в честь математик Стивен К. Клини, его первооткрыватель. Вы можете найти доказательство этой теоремы в любом учебнике по теории автоматов. я не собираюсь чтобы дать здесь доказательство, но я укажу, как делается перевод в моей программе. В доказательстве используются те же идеи.
Помните, что определение регулярного выражения состоит из четырех частей.Правило алфавита обеспечивает фундаментальные строительные блоки; в
конкатенация, альтернативы и правила повторения создают большие регулярные
выражения рекурсивно из более мелких. Процесс перевода
следует тому же шаблону: мы начинаем с процедуры построения тривиального
машина с двумя состояниями, которая принимает только одну букву, затем мы добавляем три
правила объединения машин меньшего размера в большую машину. В следующих
абзацев, я покажу, как каждое правило отражается в станок программа.
Этот процесс строительства часто производит машины с большим количеством состояний, чем
нужно. Программа машины устраняет избыточные состояния как ее
Заключительный этап.
Правило алфавита гласит, что любой член алфавита машины
регулярное выражение. В программе символом может быть любое однобуквенное слово другое
чем * . Обозначение X переведено на автомат.
[1 [[1 X 2]] [2]]
(Вы увидите, что программа работает, комбинируя маленькие машины
в более крупные.Каждый раз программе приходится изобретать новую машину
указать, что он использует следующий свободный номер. Значит, государственные номера могут не
быть 1 и 2 в реальном примере.) Процедура ndletter справляется с этим
правило.
Далее следует правило конкатенации . Регулярное выражение
[A B]
соответствует строке из двух частей; в
первая подстрока соответствует A , а вторая соответствует В . В этом простом примере каждая «подстрока» соответствует только одному
письмо.В более сложной конкатенации, например
[[OR A C] [* B]]
есть разные варианты выбора для каждой подстроки. Например, что регулярное выражение соответствует строке
CBBB
, в котором буква C соответствует первой части
выражение и подстрока BBB соответствует второй части.
Чтобы преобразовать регулярное выражение такого типа (конкатенацию) в
конечного автомата, мы начинаем с рекурсивного перевода подвыражений
на более мелкие машины.Затем мы должны «соединить» две машины вместе.
Процедура ndconcat выполняет это соединение.
Начнем с простейшего из возможных примеров. Предположим, мы хотим перевести регулярное выражение
[A B]
Мы уже перевели два символа A и B в
машины:
Комбинированная машина должна запускаться в начальном состоянии первого составная машина, состояние 1. Комбинированная машина должна находиться в приемном состояние, когда оба компонентов машины удовлетворены; в другом словами, принимающие состояния комбинированной машины должны быть вторая машина компонентов.В данном случае это означает только состояние 4.
Чтобы соединить компоненты машин вместе, мы должны добавить переходы (стрелки)
между ними. В частности, всякий раз, когда первая компонентная машина попадает в
в принимающем состоянии комбинированная машина должна следовать тем же переходам
которые применяются к начальному состоянию второй компонентной машины. В этом
случай, когда комбинированная машина переходит в состояние 2 (принимающее состояние
первый компонент машины) он должен следовать тем же переходам, что и
применяются к состоянию 3 (начальное состояние второй машины).Здесь только один
такой переход, стрелка B в состояние 4. Это означает, что мы должны добавить
стрела
[2 B 4]
к комбинированной машине.
Состояние 3, хотя оно еще есть в машине, сейчас бесполезно. Машина не может перейти в состояние 3. Позже в процессе перевода другая процедура удаляет такие «осиротевшие» состояния от машины.
В качестве немного более сложного примера рассмотрим перевод регулярное выражение
[[OR A C] [* B]]
Начнем с предположения, что мы уже перевели два подвыражения отдельно:
(Мы еще не обсуждали правило альтернатив или повторение правило, поэтому я еще не объяснил, как переводятся эти подвыражения.А пока, пожалуйста, поверьте, что это изображение правильное. Мы получим к этим другим правилам в ближайшее время.)
Начальное состояние комбинированной машины — это начальное состояние первого компонент, состояние 1. В каждом состоянии принятия первой машины мы должны продублируйте переходы из начального состояния второй машины. В в этом примере начальное состояние второй машины имеет только переход
[4 B 5]
, но на первой машине есть два состояния приема, поэтому мы необходимо добавить две новые стрелки:
[2 B 5] [3 B 5]
Последняя деталь заключается в том, что в этом примере начальное состояние второй компонентный автомат, состояние 4, является состоянием приема.Это означает, что вторая подстрока может быть пустой. Поэтому принимающие состояния машина первого компонента также должна принимать состояния комбинированного машина. Вот результат:
Опять же, состояние 4 теперь «сирота» и будет устранено. позже в программе.
Правило альтернатив объединяет две машины параллельно, так сказать,
а не сериями. Он работает, изобретая новое состояние
это становится начальным состоянием комбинированной машины. Стрелки уходят
из нового состояния продублируйте стрелки из начальных состояний
комплектующие машины.Процедура ndor обрабатывает это правило.
В качестве примера приведем процесс перевода для
[OR A B]
(или его аббревиатура AB ). Начнем с двух отдельных машин:
Мы объединяем их, изобретая новое состояние 5:
Я не объяснил все детали процесса строительства. Например, должно ли новое состояние, состояние 5, быть принимающим? В этом пример быть не должно. Посмотрите, сможете ли вы придумать случай, в котором это могло бы быть; затем прочтите листинг программы, чтобы увидеть точный алгоритм, который делает это решение.Опять же, этот процесс построения может оставить неиспользуемые состояния для позже уборка.
Гораздо более серьезная проблема заключается в том, что конструкция или может
произвести недетерминированную машину. Например, вот машина
для
[ИЛИ [A B] [A C]]
Как и неиспользованные состояния, проблема недетерминизма
осталось до конца программы, когда процедура определяет, что переводит
недетерминированную машину в детерминированную.
(Правило конкатенации также может создавать недетерминированные машины, хотя
это не так вероятно.)
Последний случай, который необходимо рассмотреть, — это правило повторения . Это правило
действует только на одну машину меньшего размера, а не на две машины, как в предыдущем
два случая. Правило не требует никаких новых состояний. Он имеет два эффекта.
Один из них — добавить начальное состояние в список принимающих состояний. В
во-вторых, добавить стрелки из (старых) принимающих состояний, которые имитируют
стрелки из начального состояния. (Это в точности похоже на сращивание
двух машин в правиле конкатенации, но в этом случае мы конкатенируем
одна машина сама с собой!) Порядок действий ндманы делает это преобразование.Это тоже может привести к недетерминированной машине.
Вот пример правила:
Эти четыре правила объединены nondet ,
процедура, вход которой
регулярное выражение, вывод которого — машина (возможно, недетерминированная).
в nondet: regexp if и (wordp: regexp) (equalp count: regexp 1) [output ndletter: regexp] если wordp: regexp [вывод ndor reduce "предложение: regexp] если сначала равно: regexp "или [output ndor butfirst: regexp] если равняется сначала: regexp "* [вывод ndmany last: regexp] вывод ndconcat: regexp конец
Процедура верхнего уровня машина делает небольшую инициализацию
а затем выполняет свою работу по инструкции
оптимизировать вывод определить nondet: regexp
То есть сначала он создает то, что может быть недетерминированная машина затем, если необходимо, он переводит это в детерминированный (исключая сиротские состояния в процессе), то он получает Избавьтесь от любых избыточных состояний, которые могли быть созданы.
Делаем машину детерминированной
В первом томе этой серии мы исследовали технику поиска в глубину. и обход дерева в ширину. Учитывая древовидную структуру, эти алгоритмы позволяют нам «посетить» каждый узел дерева один раз.
Конечный автомат можно рассматривать как структуру почти как дерево. Начальное состояние машины соответствует корневому узлу; заявляет, что могут быть достигнуты стрелкой из данного состояния, являются дочерними элементами этого состояния.Но есть одно важное различие между деревьями и машинами: на дереве у каждого узла (кроме корневого) есть ровно один родитель. Дерево алгоритмы поиска зависят от этого факта, чтобы гарантировать посещение каждого узла только один раз. В машине стрелки из нескольких разных состояний могут привести к одно и то же государство, поэтому у государства может быть несколько «родителей». Техническое название для произвольного набора узлов со связями между ними является график. Если соединения односторонние, как в конечном диаграммы состояний, это называется ориентированным графом .
Поиск в графе похож на поиск в дереве, за исключением того, что мы должны
отслеживать, какие узлы мы уже посетили, чтобы не исследовать
один и тот же узел дважды. Процедура определения создает список с именем состояния , первоначально
пустой, в который каждый номер состояния добавляется как
программа исследует это состояние. Глубина первого обхода станка
осуществляется по процедуре nd.traverse ;
хотя эта процедура выглядит иначе, чем глубина.первый процедуры в томе 1, это
использует тот же базовый алгоритм. Учитывая состояние в качестве входных данных, он обрабатывает
это состояние и рекурсивно вызывает себя для всех дочерних элементов
это состояние — состояния, достижимые стрелками из состояния ввода. в отличие depth.first , а nd.traverse — это операция. Это
выводит новый список ходов (стрелки) для детерминированной версии
машина.
Что означает обработка состояния? Nd.traverse первые проверки
было ли это состояние уже обработано; если это так, он выводит пустой
list, потому что это состояние не будет вносить никаких новых ходов в машину.В противном случае он запоминает этот номер состояния как обработанный, находит
все ходы, начиная с этого состояния, и называет чек. И искать
недетерминизм. Check.nd берет первую доступную стрелу, хвост которой
находится в состоянии, которое мы обрабатываем, и ищет все стрелки с одинаковыми
хвост и с той же буквой. * Локальная переменная Heads будет содержать список всех номеров состояний.
достижимые этими стрелками. (Номера состояний отсортированы по возрастанию
порядок, а дубликаты устранены.Если в машине два полностью
одинаковые стрелки, что не приводит к недетерминизму.)
* Кстати
недет всегда
создает стрелки только из одной буквы; если две или более буквы идут от
одно и то же состояние в одно и то же состояние, отдельная стрелка создается для каждого из
их. Это делает список машин более длинным, но делает такие шаги
один — искать две стрелки с одной и той же буквой — проще. Однажды
была создана детерминированная машина, процедура optimize объединит
такие стрелки в сокращенную форму с
более одной буквы на стрелку.
Есть
три случая, которые должны сделать check.and . Во-первых, если есть
только один государственный номер в : головы , то недетерминизма для
это письмо, а чек. и включает стрелку из оригинала
машина как часть детерминированной машины. Во-вторых, если есть еще
чем один номер штата, проверка. и проверяет, видели ли мы уже
та же комбинация состояний результата. Если да, то мы уже создали
новое состояние, эквивалентное этой комбинации старых состояний, и проверка .nd создает новую стрелку, указывающую на это существующее новое состояние. Наконец, третий
Дело в том, что мы не видели такой комбинации состояний раньше. В
В этом случае проверка и должны создать новое состояние со стрелками, дублирующими
те из всех первоначальных состояний.
Другими словами, если есть стрелки
[[3 B 4] [3 B 7]]
, затем check. И изобретет новое состояние, которое является «псевдонимом».
для «четыре и семь». Если на той же машине есть стрелки
[[8 C 4] [8 C 7]]
, затем чек.nd будет использовать то же состояние псевдонима для этого
пару, не изобретая нового. Новый
состояние помечено стрелками, соответствующими стрелкам всех его компонентных состояний (4
и 7 в этом примере). Новое состояние может само содержать недетерминированный
ветвь, но это нормально, потому что новое состояние в конечном итоге будет обработано
по мере продолжения обхода машинного графа.
Вы могли подумать, что этот процесс может продолжаться вечно: каждый новый
состояние проверка. и изобретений окажутся недетерминированными, что
потребуется еще одно новое состояние для разрешения.К счастью, это
не бывает; процесс всегда рано или поздно заканчивается. (В следующий
в главе мы увидим, какой лимит на количество необходимых состояний
для детерминированной машины.)
Поскольку определяет, что использует алгоритм обхода графа для проверки
исходные состояния машины, она никогда не найдет «сиротские» состояния
которые не могут быть достигнуты стрелами из другого состояния. Вот почему
процесс создания детерминированной машины также устраняет сирот
состояния, без дополнительных усилий.
Устранение избыточных состояний
Машины, производимые компанией , определяют, что работоспособны, но часто уродливы;
они содержат намного больше состояний, чем необходимо. Процедура оптимизировать устраняет множество избыточностей, а также объединяет стрелки с одинаковыми
голова и хвост, но с разными буквами.
Сначала он просматривает список стрелок машины,
создание списка для каждого состояния, представляющего выходы из этого состояния:
[[* [A B]] C] Состояние 1: [[A 2] [C 4]] Состояние 2: [[B 3]] Состояние 3: [[A 2] [C 4]] Состояние 4: []
В этом аппарате состояния 1 и 3 имеют одинаковый список выхода.(В этих списках каждая стрелка представлена только двумя элементами; хвост стрелы в комплект не входит. Это потому, что состояния 1 и 3 будут не имеют идентичные списки, если были включены хвосты. Список государства 1 было бы
[[1 A 2] [1 C 4]]
и список состояния 3 будут иметь стрелки, начинающиеся с 3. В В программе двухчленная форма стрелки называется заглушкой . )
Программа должна внимательно следить за порядком, в котором она ставит заглушки в списке каждого штата, поэтому он не заканчивается
[[C 4] [A 2]]
для одного из штатов.Поэтому заглушка добавить испытывает проблемы
вставлять каждую заглушку в четко определенную позицию, а не просто добавлять
каждая новая заглушка в начале или в конце списка. Это также в stub.add , что стрелки, соединяющие одинаковые два состояния, но с разными
буквы объединены в единую стрелку.
Поскольку состояния 1 и 3 также согласны в своей приемлемости (а именно, они не
принимающие состояния), их можно объединить в одно состояние. Optimize.state может заменить каждую ссылку на состояние 3 ссылкой на
состояние 1.
Сумматор с конечным числом состояний
Я обещал ранее показать вам использование конечных автоматов и других чем принятие или отклонение строк. В этом разделе я выполню это обещание, создавая машину для сложения двух чисел. Мы представим числа в двоичной системе счисления, в которых каждая цифра представляет собой степень вместо 2 вместо 10.
Если вам раньше приходилось сталкиваться с двоичными числами, можете пропустить этот абзац. Так же, как обычное обозначение чисел основано на десяти цифрах от 0 до 9, двоичная запись основана на двух цифрах , 0 и 1.В обычном («десятичное») обозначение, сумма, которую каждая цифра вносит в общую зависит от того, где он находится в номере. Например, в числе 247 знак цифра 2 дает двести, а не просто две, потому что она находится в третьем отсчет позиции справа. Вклад каждой цифры — это значение сама цифра, умноженная на десять:
2 × 10 2 + 4 × 10 1 + 7 × 10 0(10 2 равно 100; 10 1 равно 10; 10 0 равно 1.) В двоичном формате вклад каждой цифры умножается на степень два, , так что двоичное число 10101 представляет
1 × 2 4 + 0 × 2 3 + 1 × 2 2 + 0 × 2 1 + 1 × 2 0что равно 16 + 4 + 1 (2 4 +2 2 +2 0 ) или 21. Компьютеры используют двоичную запись потому что легко построить электрические цепи, в которых каждый провод либо включен или выключен.В главе 2 мы поговорим о примере. Прямо сейчас я хочу показать что-то другое — не настоящую электронную машину, а абстрактную machine на основе идей, которые мы использовали в этой главе.
Машина будет складывать два двоичных числа, по одной позиции за раз, просто как вы сами складываете многозначные числа. Когда вы видите такую проблему, как
вы начинаете справа и говорите: «6 плюс 2 равно 8; 7 плюс 7 равно 14, что 4 переноски 1; 1 плюс 3 плюс 5 равно 9. «Конечный сумматор работает так же. способ, за исключением того, что цифры всегда 0 или 1.
Машина будет складывать любые числа, но чтобы объяснить, как это работает, я хочу рассмотрим конкретный пример. Допустим, мы хотим сложить 52 и 21. (Судя по Кстати, я выбрал эти числа не потому, что они называют карточные игры, а потому, что образец цифр в их двоичной форме удобен для объяснение, которое я хочу дать.) 52 в двоичном формате — это 110100 (32 + 16 + 4), а 21 — это 10101 (16 + 4 + 1). Я напишу это одно над другим, с парой дополнительных нулей слева, чтобы оставить место для возможного переноса:
0 0 1 1 0 1 0 0
0 0 0 1 0 1 0 1
Вспомните, как работает конечный автомат: в данный момент он
в каком-то состоянии , , затем он считывает какой-то входной символ и переходит к
другое состояние.В этой задаче, поскольку нам нужно сложить два числа, наиболее
естественный способ подумать об этом — дать машине два входа вовремя. Эта идея не совсем соответствует формальному определению
конечный автомат, но мы можем позволить автомату состоять из пар цифр, поэтому что-то вроде 01 будет одним вводом.
(Кстати, слово бит обычно используется как сокращение для
«двоичная цифра»). Так же, как вы добавили вертикальные пары цифр (первые 6 и 2,
затем 7 и 7 и т. д.) в предыдущем примере мы будем использовать вертикальные пары
биты в качестве входных данных для сумматора с конечным числом состояний, начиная с правого конца.Таким образом, первый ввод будет 01, затем 00, затем 11, затем 00, затем снова 11,
затем 10, а затем дважды 00. С этого момента в этом разделе, когда вы видите
что-то вроде 10, вы должны помнить, что это один вход для
конечный автомат, один символ, а не два подряд.
(На схеме ниже стрелка с надписью 01/10 представляет два
стрелки, одна для входа 01 и одна для входа 10 . Эти
две стрелки всегда будут переходить в одно и то же состояние, потому что 0 + 1 = 1 + 0.)
Нам нужно внести одно изменение в обозначения, используемые в схемах машин. Мы больше не хотим отмечать каждое состояние как принимающее (двойной кружок) или отклонение (одиночный кружок). Вместо этого каждое состояние производит вывод , который может быть любым произвольным символом. В этой машине выходы будет 0 или 1, представляя двоичные цифры суммы. Внутри каждый круг штата, вместо номера штата вы увидите что-то как «3/1»; это означает, что это состояние номер 3 и что выход из этого состояния — 1.
Вот машина:
Состояние 1, начальное состояние, не имеет выхода. Когда машина запускается заявить, что он еще не видел никаких цифр в слагаемых, поэтому он не может вычислить цифра суммы. Состояния 2 и 4 выводят нулевую цифру, а состояния 3 и 5 выводят единицу. (Как и входные данные, число, которое машина выходы представлены первым своим крайним правым битом. Машина работает таким образом, по той же причине, что и , вы, , складываете числа справа слева: это направление, в котором перемещается цифра «переноса». один столбец в другой.)
Почему два состояния с нулевым выходом и два с одним выходом состояния? Причина в том, что машина находится в состоянии 4 или 5, когда является переносом в следующую цифру суммы.
Давайте рассмотрим мой пример. Мы начинаем в состоянии 1. Первый вход символ 01, представляющий 0 в самой правой (двоичной) цифре 52 и 1 в крайней правой цифре 21. Машина переходит в состояние 3. и выводит 1.
Следующий ввод — 00, потому что оба числа имеют ноль в качестве второго. цифра.Машина переходит в состояние 2 и выводит 0.
Следующий вход — 11. Машина входит в состояние 4 и выдает 0. Находясь в состояние 4 означает, что есть перенос из этой позиции в следующую.
Вы можете закончить пример самостоятельно. Сумма должна быть 01001001, или 73.
Счетные и конечные машины
Ранее мы видели, что нельзя написать регулярное выражение для правила. это требует сбалансированных скобок. Поскольку регулярные выражения эквивалентно конечным автоматам, вы не удивитесь, узнав что конечные автоматы не умеют считать.
Фактически, они могут считать до определенного момента; просто каждое конечное состояние машина может считать только до фиксированного лимита. Например, вот конечный автомат, который принимает строки сбалансированных круглых скобок до четырех глубин:
Эта машина принимает такие строки:
() (()) () ()
(() ()) (((()))) (((()))) (())
Нет ограничений на длину строки this машина может справиться. Например, он примет это:
() () () () () () () () () () () () () ()
Но открывать не может более четырех круглых скобок сразу ; машина отклонит
((((()))))
Даже эта ограниченная счетная способность конечных автоматов имеет большое значение. практическая ценность.В конце концов, настоящие компьютеры имеют конечное состояние. машины. У любого реального компьютера есть конечный объем памяти, и это память может находиться в конечном числе состояний. Но число вполне огромный. Если на реальном компьютере есть программа для подсчета скобок это ограничено, скажем, 20 000 уровней скобок, никто не будет когда-нибудь замечаете, что предел не бесконечен.
(количество состояний на реальном компьютере может быть даже больше, чем у вас мышление. Каждый бит компьютерной памяти — это не состояние. Вместо этого, если компьютер имеет n бит памяти, он имеет 2 n состояний! Для Например, компьютер с тремя битами памяти может использовать эти биты для представляют восемь состояний:
0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1
Количество возможных состояний в типичном большом компьютере больше, чем количество атомов в галактике.)
Сейчас я расскажу о теоретической модели машины. с бесконечной памятью. Вы можете задаться вопросом, почему стоит изучать такие машины, так как любая реальная машина должна быть ограничена в памяти. В Ответ связан с моим примером о 20 000 уровней скобок. Теоретически можно написать регулярное выражение для таких струны. Чтобы показать вам, как это делается, вот регулярное выражение до трех уровней:
(Я нарисовал рамки вокруг реальных символов правил алфавита, чтобы чтобы вам было легче различать круглые скобки, которые являются символами во входных строках, и скобки, которые являются частью клей, который скрепляет регулярное выражение.)
Нет теоретической проблемы с расширением этого регулярного выражения. чтобы разрешить до 20 000 скобок. Но машина на основе этой техники будет очень большим и сложным. Вместо этого имеет смысл притвориться , что у компьютера бесконечный объем доступной памяти и используйте формальную систему (например, производственные правила, которые я вкратце упомянул) это зависит от бесконечной памяти. Такая формальная система приводит к более короткое и элегантное выражение правила сбалансированных круглых скобок.На практике мы можем предоставить достаточно памяти для любой из строк нашего программа действительно встретится.
Машины Тьюринга
Один из способов исследования бесконечных машин — это представить, что они представленные диаграммами состояний, как у конечных автоматов, но с бесконечным количеством состояний. Например, вот картинка счетчика круглых скобок бесконечной емкости:
Проблема с этой идеей в том, что трудно точно смоделировать то, что имеется в виду этот ряд точек справа.Мы не можем иметь полное формальное описание бесконечно сложной машины.
Вместо этого подумайте, что вы, , делаете, когда вам нужно решить проблему. слишком сложный, чтобы поместиться в вашей собственной памяти. Вы не строите себе больший мозг; вы получаете карандаш и бумагу. То есть вы используете внешнее хранилище . Вы можете представить, что ваш мозг — это конечное состояние. машина, но у нее есть доступ к бесконечному запасу бумаги.
Конечно, это разделение необходимой информации проблемы на конечное внутреннее состояние и бесконечное внешняя память также очевидным образом моделирует реальные компьютеры.Внутреннее состояние в модели представляет собой внутреннюю память компьютера, а внешняя память в модели представляет собой такие запоминающие устройства, как диски и ленты. Чтобы решить большую проблему, вам не нужно покупать компьютер побольше; вам просто нужно время от времени переключать дискеты.
Вы могли подумать, что математическая модель, о которой я говорю, была основанный на аналогии с реальными компьютерами, и что мой рассказ о конечных состояниях мозг это просто совпадение. Но на самом деле эта модель была изобретена Алан М.Тьюринг в 1936 году, еще до того, как появились компьютеры! Это было человек решение проблем, которые Тьюринг хотел смоделировать с помощью машины.
Что такое машина Тьюринга? Начните с представления конечного автомата с разными возможными выходами, как у сумматора, который мы видели ранее. Прикрепил к этой машине идет лента безграничной длины. Символы из некоторых алфавит, как и символы ввода и вывода машины, можно записать на ленте. Есть механизм чтения и записи, как у головок магнитной ленты, которая может перемещаться по ленте.
Так же, как каждое состояние машины может иметь выход, связанный с это, каждое состояние также может действовать, чтобы повлиять на ленту: она может перемещаться голову на один символ в любом направлении, и это может изменить символ в текущей позиции головы.
Фактически, мы упрощаем формальное описание машины на использование ленты в качестве устройства ввода / вывода, а также устройства хранения. То есть мы можем начать с некоторой последовательности уже написанных символов на ленте. Эта последовательность служит входными данными для машины; государственный переходы основаны на символе под головкой ленты, а не на символе из другого источника.Аналогично, выход из состояния (если есть) написано на ленте.
В чем-то аналогично концепции принимающего состояния в нашей предыдущей Например, машина Тьюринга может иметь остановок и состояний. Когда машина переходит в состояние остановки, она прекращает свою работу. Есть больше никаких переходов между состояниями. Выход из машины — это то, что последовательность символов, которые он оставляет записанными на ленте.
Тезис Тьюринга
Тьюринг изобрел свою абстрактную машину, потому что пытался формализовать идея эффективной процедуры : что означает указать техника для решения некоторой проблемы достаточно хорошо, чтобы мы могли быть уверены это действительно будет работать? В качестве аналогии подумайте о направлениях движения. отсюда куда-нибудь.Кто-то может передать вам листок бумаги с список инструкций типа «Когда вы доберетесь до АЗС налево, поверните направо «. Но иногда вы получаете указания, были недостаточно осторожны. Возможен резкий поворот направо и легкий Правый поворот доступен возле АЗС. Там может быть развилка дорога еще до того, как вы доберетесь до заправочной станции.
Идея Тьюринга состоит в том, что любая проблема, для которой существует любой эффективный Процедуру можно смоделировать с помощью машины Тьюринга. Фраза «любой эффективный процедура «включает в себя работу человеческого разума.Если Тьюринг прав, любую проблему, которую может решить человек, можно запрограммировать. для компьютера.
Это утверждение не может быть доказано или опровергнуто математически. потому что не существует предварительного формального определения «эффективной процедуры» с которыми можно сравнить машины Тьюринга. Кроме того, возможно, что представление о процедуре как-то не охватывает все виды думать, что люди делают. Может быть, это правда, например, что компьютеры потенциально так же могущественны, как и люди, в решении проблем, но «решают проблемы «может оказаться не подходящим описанием что происходит, когда мы чувствуем эмоции.Если это повернулось если быть правдой, мы, , должны ожидать, что компьютер станет мировым когда-нибудь чемпионом по шахматам, но мы, , не должны, , ожидать, что он станет поэт-чемпион мира.
Но этот возможный вывод подвергался критике с обеих сторон. Некоторый люди думают, что эмоции на самом деле — это вычислимые процедуры. Программа Кеннета Колби под названием Parry пытается моделировать поведение параноидального человека путем манипулирования переменными для таких эмоций, как гнев и страх.С другой стороны, некоторые люди думаю, что даже шахматы не относятся к сфере того, что люди делают это, выполняя эффективные процедуры в смысле Тьюринга. Эти люди говорят, что шахматный мастер не анализирует шахматную доску. шаг за шагом, как компьютер. Он смотрит на доску как единое целое, а важные функции просто возникают в уме каким-то процессом, который все еще остается довольно загадочным.
То, что является известным, так это то, что несколько других математических моделей эффективных было показано, что процедуры эквивалентны машинам Тьюринга, в в том же смысле, в котором регулярные выражения эквивалентны конечному состоянию машины.Например, все популярные языки программирования Эквивалент Тьюринга. Нет такой вещи, как вычисления, которые могут должно выполняться в Logo, но не в Pascal, или наоборот. (Конечно, один язык может быть более удобным , чем другой для данной задачи.)
Теорема об остановке
Я не буду вдаваться в конкретные примеры программирования машины Тьюринга здесь. Это заняло бы слишком много места для одной главы; если ты Заинтересованные вы должны продолжить тему в книге по теории автоматов.Но я хочу привести один пример теоретической ценности машин Тьюринга.
У вас, несомненно, был опыт написания программы Logo с ошибкой
что вызывает «бесконечный цикл» — вы запускаете программу, и она просто сидит там
навсегда, когда вместо этого предполагается вычислить и распечатать некоторые результаты.
Это неприятная ошибка, потому что вы никогда не уверены, что
программа действительно не работает или работает очень медленно. Может, если бы ты подождал
через минуту он придет к ответу.Было бы здорово, если бы
когда вы запускали программу, Logo может выводить сообщение об ошибке, например Эта программа имеет бесконечный цикл , как и для других ошибок?
Оказывается, бесконечные циклы, как правило, не могут быть обнаружены автоматически. Конечно, или бесконечных циклов очень легко обнаружить, и мы можем писать программы, которые ловят определенные категории бесконечного цикла. Но мы не можем написать программу, в которой гарантированно ловит бесконечное число циклы в программах на языке Logo или любом другом языке, эквивалентном Тьюрингу.В Тот факт, что это невозможно, называется теоремой об остановке.
Сложно понять, что говорит теорема об остановке, потому что он включает машины Тьюринга, которые манипулируют машинами Тьюринга как данными, которые это своего рода ссылка на себя, похожая на рекурсию. Самостоятельная ссылка всегда трудна о чем можно говорить и может привести к парадоксам, подобным классическому «Это утверждение ложно «. (Предложение в кавычках истинно или ложно? Если оно истинно, то оно должно быть ложным, потому что так сказано.Но если это ложь, и это говорит это ложь, это действительно должно быть правдой!) Так что давайте действовать осторожно.
Данные, записанные на ленту машины Тьюринга, представляют собой строку символов. Обычно мы выбираем символы для обозначения чего-то значимого; для Например, строка цифр может представлять число. Ранее в этой главе мы использовали строки символов вроде
[1 [[1 A 2] [2 B 3] [3 A 2]] [1 3]]
для представления конечного автомата. Нет причин, по которым мы
не мог поместить , эту строку символов на ленту машины Тьюринга
как его вход.Например, мы могли бы построить машину Тьюринга, которая бы работала
как моя программа fsm , имитирующая конечный автомат, который она нашла
написано на его ленте при запуске.
Разрешение машине Тьюринга моделировать конечный автомат не вызывает вопросы саморекламы. Но машина Тьюринга тоже формальная состав; его тоже можно представить в виде строки символов.
Поскольку представление машины Тьюринга может быть входом для другого
Машина Тьюринга, мы можем разработать машины Тьюринга, которые отвечают на вопросы о
Машины Тьюринга.Например, мы можем написать универсальный Тьюринг
машина, которая имитирует любую машину Тьюринга так же, как fsm любой конечный автомат.
Универсальная машина Тьюринга (симулятор машины Тьюринга) вроде полурешает проблема остановки. Предположим, мы хотим знать, будет ли данная машина останавливаться после запуска с заданным вводом. (Это все равно, что спросить, не определенная процедура логотипа будет завершена, если она будет вызвана с определенным входных данных.) Мы можем использовать универсальную машину Тьюринга, чтобы смоделировать ту, которую мы увлекающийся.Если машина сделает остановку , мы узнаем об этом. Но если рассматриваемая машина не останавливается , то симулятор тоже не остановится. У нас все еще будет проблема, которая была в первом место — как мы можем быть уверены, что оно не остановится, если мы дадим ему еще один минута?
Чтобы решить проблему остановки, нам нужна машина Тьюринга, которая принимает представление любой машины Тьюринга в качестве входных данных, точно так же, как универсальный Машина Тьюринга. Но этот должен быть гарантированно остановлен, даже если машина ввода не останавливалась.Вот что говорит теорема об остановке: мы не можем делать.
Доказательство теоремы о остановке в логотипе
Что позволяет поставить вопрос о том, может ли машина Тьюринга
решить, остановится ли другая машина Тьюринга для данной входной ленты,
тот факт, что «программа» одной машины Тьюринга может быть представлена как данные
для другой машины Тьюринга. Это также относится к процедурам с логотипом. В
в частности, процедуры более высокого порядка, такие как map и filter манипулировать другими процедурами, принимая их имена в качестве входных данных.Поэтому мы можем использовать Logo
процедуры, иллюстрирующие доказательство теоремы об остановке.
Будем рассматривать процедуру Logo с входом как аналог Тьюринга. машина со своей входной лентой. Мы хотим доказать, что логотипа не может быть процедура, которая могла бы сказать, останавливается ли такая процедура для данного ввода. Используемая нами техника называется доказательством от противоречия. В этом Мы предполагаем, что — это такая процедура, а затем покажем, что это предположение приводит к парадоксу.
Итак, давайте представим, что кто-то написал предикат логотипа haltp , который
принимает два входа: имя процедуры и входное значение для этого
процедура. Haltp выведет true , если процедура, которую он тестирует
в конечном итоге остановится при указанном вводе; haltp выходы false , если тестируемая процедура войдет в бесконечный цикл, например
рекурсивная процедура без правила остановки. (На практике, если подумать о
ваш собственный опыт отладки программ, легко определить,
вообще не имеет правила остановки, но не так-то просто убедиться, что остановка
правило всегда в конце концов будет удовлетворено.Подумайте о программе Pig Latin
дано слово из всех согласных в качестве входных. Мы хотим
в пиглатин: слово если сначала memberp: слово [a e i o u] [выходное слово: слово «ay] вывести пиглатинское слово bf: сначала слово: слово конец ? принт халтп салями "пиглатин" правда ? печать халтп "пиглатин" mxyzptlk ложный
Помните, что haltp сам должен всегда останавливаться , даже
в случае, когда пиглатин не остановится.)
Теперь рассмотрим эту процедуру с логотипом:
попробовать: proc если haltp: proc: proc [цикл] конец зацикливать петля конец
Поскольку haltp работает, мы предполагаем, что на любой логотип процедура с одним входом, она должна работать, в частности, на , попробуйте .Что произойдет, если мы скажем
? попробуйте "попробуйте "
Это останавливается или зацикливается? Предположим, это прекратится. try начинает свое
работать, оценивая выражение
haltp "попробовать" попробовать
Поскольку мы сказали, что попытка остановится, если попытка в качестве ввода, haltp выведет true . Из определения следует
попробуйте , этот try вызовет цикл и остановит , а не .Точно так же, если мы начнем с предположения, что try будет зацикливаться, тогда haltp должен выводить false и, следовательно, из определения попробуйте , вы увидите, что попробуйте остановится. Независимо от значения выходы haltp оказываются некорректными.
Это было предположение, что мы можем написать безошибочный haltp , который привел
мы оказались в этом противоречии, поэтому это предположение должно быть неверным. Мы не можем писать
процедура логотипа, которая автоматически обнаруживает бесконечные циклы в нашем
программы.Подобное доказательство может быть сделано на любом языке, на котором одна программа
может манипулировать другой программой как данными — то есть в любом эквиваленте Тьюринга
язык.
Листинг программы
;;; Интерпретатор конечных автоматов (FSM)
в игру: который
fsm thing word "mach: который
конец
в fsm: machine
открытый текст
setcursor [0 3]
localmake "start startpart: машина
localmake "перемещает movepart: machine
localmake "accept acceptpart: machine
fsm1: начало
конец
to fsm1: здесь
ifelse memberp: здесь: принять [принять] [отклонить]
fsm1 (fsmnext: здесь readchar)
конец
в fsmnext: здесь: ввод
пустой
если memberp: input (список char 13 char 10) ~
[print ifelse memberp: here: accept ["| ПРИНЯТЬ |] [" | ОТКАЗАТЬ |]
вывод: начало]
тип: ввод
catch "ошибка [вывод последней находки [fsmtest: здесь: ввод?]: перемещается]
выход -1
конец
в fsmtest: здесь: input: move
output and (equalp: здесь arrowtail: move) ~
(memberp: ввод со стрелкой, текст: перемещение)
конец
;; Отображение состояния машины
принять
дисплей "принять
конец
отказаться
отображать "отклонить
конец
заглушить
дисплей "|
конец
для отображения: текст
localmake "oldpos курсор
setcursor [15 1]
тип: текст
setcursor: oldpos
конец
;; Абстракция данных для машин
в началочасть: машина
сначала вывод: машина
конец
to movepart: machine
вывод первый бф: машина
конец
принять часть: машина
вывод последний: машина
конец
делать.машина: начало: движется: принять
вывод (список: начало: ходы: принять)
конец
;; Абстракция данных для стрелок
в arrowtail: arrow
вывод сначала: стрелка
конец
в arrowtext: arrow
вывод сначала, но сначала: стрелка
конец
к стрелке: стрелка
вывод последний: стрелка
конец
сделать.arrow: tail: text: head
вывод (список: хвост: текст: голова)
конец
;; Описание машин для игры в угадайку
make "mach2 [1 [[1 AB 1]] [1]]"
make "mach3 [1 [[1 ABC 2] [2 ABC 1]] [1]]"
make "mach4 [1 [[1 A 2] [2 B 3] [3 ABC 3]] [3]]"
make "mach5 [1 [[1 A 2] [1 B 3] [1 C 4] [2 A 1] [3 B 1] [4 C 1]] [1]]"
make "mach5 [1 [[1 ABC 2] [2 B 1]] [1]]"
make "mach6 [1 [[1 A 2] [2 AB 2] [2 C 3] [3 AB 2] [3 C 3]] [3]]"
make "mach7 [1 [[1 AB 1] [1 C 2] [2 C 1]] [1]]"
make "mach8 [1 [[1 A 2] [1 BC 1] [2 A 1] [2 BC 2]] [1]]"
make "mach9 [1 [[1 AB 1] [1 C 2] [2 A 3] [2 B 1] [3 A 1]] [1]]"
make "mach20 [1 [[1 A 2] [1 BC 1] [2 A 2] [2 B 3] [2 C 1]]"
[3 A 2] [3 B 1] [3 C 4] [4 A 2] [4 B 5] [4 C 1]
[5 A 6] [5 BC 1] [6 ABC 6]]
[6]]
;;; Преобразование регулярных выражений в автомат (МАШИНА)
на машину: regexp
localmake "nextstate 0"
output optimize определить nondet: regexp
конец
;; Первый шаг: создать возможно недетерминированную машину
в nondet: regexp
если и (wordp: regexp) (equalp count: regexp 1) ~
[выходной ndletter: regexp]
если wordp: regexp [вывод ndor reduce "предложение: regexp]
если сначала равно: regexp "или [output ndor butfirst: regexp]
если равняется сначала: regexp "* [вывод ndmany last: regexp]
вывод ndconcat: regexp
конец
;; Правило алфавита
на ndletter: письмо
localmake "от NewState
localmake "в NewState
вывод (make.машина: от
(список (make.arrow: from: letter: to))
(список: в))
конец
;; Правило конкатенации
кому: ndconcat: exprs
вывод reduce "строка (карта" nondet: exprs)
конец
в строку: machine1: machine2
вывод (make.machine (startpart: machine1)
(предложение (movepart: machine1)
(splice acceptpart: machine1: machine2)
(movepart: machine2))
(строка (acceptpart: machine1)
(начальная часть: машина2)
(acceptpart: machine2)))
конец
в строкуa: accept1: start2: accept2
если memberp: start2: accept2 [выходное предложение: accept1: accept2]
вывод: accept2
конец
;; Правило альтернатив
к ndor: exprs
localmake "newstart newstate"
localmake "машины (карта" nondet: exprs)
localmake "принимает карту.se "acceptpart: машины
вывод (make.machine: newstart
(предложение map.se "movepart: machines
map.se "or.splice: машины)
ifelse not emptyp find [memberp (startpart?)
(acceptpart?)]
: машины
[fput: newstart: принимает]
[: принимает])
конец
к or.splice: машина
карта вывода [newtail? : newstart] (стрелки.from.start: машина)
конец
;; Правило повторения
кому: ndmany: regexp
localmake "машина nondet: regexp
вывод (make.machine (startpart: machine)
предложение (movepart: machine)
(splice (acceptpart: machine): машина)
fput (начальная часть: машина) (acceptpart: машина))
конец
;; Генерировать ходы из набора заданных состояний (: принимает), дублируя
;; переходит из начального состояния некоторой машины (: machine).
;; Используется для правила конкатенации для соединения двух ранее разделенных машин;
;; используется для правила повторения, чтобы «соединить» машину с собой.соединять: принимает: машина
вывод map.se [copy.to.accepts?] (arrows.from.start: machine)
конец
до arrows.from.start: machine
выходной фильтр [equalp startpart: machine arrowtail?] movepart: machine
конец
to copy.to.accepts: move
карта вывода [newtail: move?]: принимает
конец
в newtail: arrow: tail
вывод make.arrow: tail (arrowtext: arrow) (arrowhead: стрелка)
конец
;; Сделайте новый государственный номер
Newstate
сделать "nextstate: nextstate + 1"
вывод: nextstate
конец
;; Второй шаг: превратить недетерминированный автомат в детерминированный
;; Также исключает «сиротские» (недоступные) состояния.определить: машина
localmake "перемещает movepart: machine
localmake "принимает acceptpart: machine
localmake "состояния []
localmake "join.state.list []
localmake "newmoves nd.traverse (начальная часть: машина)
вывод make.machine (startpart: machine) ~
: newmoves ~
фильтр [memberp? : состояния]: принимает
конец
к nd.traverse: состояние
если memberp: state: состояния [output []]
make "состояния fput: state: состояния
localmake "newmoves (check.nd filter [equalp arrowtail?: state]: move)
Выходное предложение: newmoves map.se "nd.traverse (карта" стрелка: newmoves)
конец
to check.nd: movelist
если emptyp: movelist [вывод []]
localmake "буква arrowtext first: movelist
localmake "карта сортировки голов" стрелка ~
filter [equalp: letter arrowtext?]: movelist
если пустоp, но сначала: головы ~
[сначала вывод fput: movelist
check.nd фильтр [not equalp: letter arrowtext?]
: movelist]
localmake "участник check.heads: Heads: join.state.list
если не пустоp: check.heads ~
[вывод fput make.стрелка: состояние: сначала буква, но сначала: check.heads ~
check.nd фильтр [not equalp: letter arrowtext?]
: movelist]
localmake "join.state newstate
сделать "join.state.list fput: Heads fput: join.state: join.state.list
сделать "ходы предложения: ходы ~
карта [make.arrow: join.state
arrowtext?
стрелка?] ~
фильтр [memberp arrowtail? : Heads]: движется
если не emptyp, найдите [memberp? : принимает]: головы ~
[make "принимает предложение: принимает: присоединяется.государственный]
вывод fput make.arrow: state: letter: join.state ~
check.nd фильтр [not equalp: letter arrowtext?]: movelist
конец
сортировать: список
если пустоp: список [вывод []]
вывод вставить сначала: сортировка списка, но сначала: список
конец
для вставки: значение: отсортировано
если пустоp: отсортировано [вывод (список: значение)]
если: значение = первое: отсортировано [вывод: отсортировано]
if: value Объединить избыточные состояния.
;; Также комбинирует стрелки с одинаковой головой и хвостом:
;; [1 A 2] [1 B 2] -> [1 AB 2].
оптимизировать: машина
localmake "массив stubarray: nextstate
foreach (movepart: machine) "массив.спасти
localmake "указывает sort fput (startpart: machine) ~
карта "стрелка movepart: машина
localmake "start startpart: машина
foreach reverse: состояния [optimize.state? ?отдых]
вывод (make.machine: start
map.se [fix.arrows? пункт ? : stubarray]: состояния
фильтр [memberp? : состояния] acceptpart: machine)
конец
в array.save: move
setitem (стрелка: перемещение): stubarray ~
stub.add (arrow.stub: move) (элемент (arrowtail: move): stubarray)
конец
заглушить.добавить: заглушка: список заглушек
если пустойp: список-заглушка [вывод (список: заглушка)]
if (stub.head: stub) (назад к содержанию)
НАЗАД
резьба главы СЛЕДУЮЩАЯ
Брайан Харви,
[email protected]
Теория вычислений — основные определения
В этом разделе описаны термины, которые часто используются в теории вычислений и теории автоматов. Прежде чем перейти к следующему разделу, вы должны понять термины, описанные ниже, поскольку они используются в большинстве концепций теории вычислений. Alphabets
Теория вычислений полностью основана на символах. Эти символы обычно представляют собой буквы и цифры.
Алфавиты определяются как — конечный набор символов.
Примеры:
∑ = {0, 1} — алфавит из двоичных цифр.
∑ = {A, B, C,…., Z} — алфавит.
Строки
Строка — это конечная последовательность символов, выбранная из некоторого алфавита . Обычно обозначается как w. Например, для алфавита ∑ = {0, 1} w = 010101 — это строка.
Длина строки обозначается как | w | и определяется как количество позиций для символа в строке. Для приведенного выше примера длина равна 6.
Пустая строка — это строка с нулевым количеством символов. Эта строка представлена как или λ.
Набор строк, включая пустую строку, в алфавите ∑ обозначается ∑ *.
Для ∑ = {0, 1} у нас есть набор строк как ∑ * = {є, 0, 1, 01, 10, 00, 11, 10101,…}.
и 1 = {0, 1}, ∑2 = {00, 01, 10, 11} и так далее.
∑ * содержит пустую строку є. Множество непустой строки обозначается ∑ +. Отсюда получаем:
∑ * = ∑ + U {є}
Реклама: Присоединяйтесь к Sanfoundry @ Linkedin
Конкатенация строк
Пусть w1 и w2 — две строки, тогда w1w2 обозначает их конкатенацию w. Конкатенация формируется путем создания копии w1, за которой следует копия w2.
Например, w1 = xyz, w2 = uvw
, затем w = w1w2 = xyzuvw
Также w13 = w1w1w1
Языки
Язык — это набор строк , все из которых выбираются из некоторого ∑ *, где ∑ — конкретный алфавит .Это означает, что язык L является подмножеством ∑ *. Примером может служить английский язык, где набор допустимых английских слов представляет собой набор строк в алфавите, который состоит из всех букв. Другой пример — язык программирования C, где алфавит — это подмножество символов ASCII, а программы — подмножество строк, которые могут быть сформированы из этого алфавита.
Объединение языков
Если L1 и L2 — два языка, их объединение можно определить как:
L = L1.L2, где L = {w: w = xy, где x є L1, y є L2}
Это означает, что все строки в языке L являются конкатенацией строк языков L1 и L2
Замыкание Клина
Если S — это набор слов, то под S * мы подразумеваем набор всех конечных строк, образованных конкатенацией слов из S, где любое слово может использоваться так часто, как нам нравится, и где нулевая строка также включены.
S * — это замыкание Клина для S. Мы можем рассматривать звезду Клина (S *) как операцию, которая делает бесконечный язык строк букв из алфавита.
Например, для ∑ = {a}
∑ * = {є, a, aa, aaa,….}
Конечные автоматы
Это устройства, которые принимают сгенерированный язык. Они принимают в качестве входных данных строку и выдают на выходе «да» (принято) или «нет» (отклонено). Это отличает их от преобразователей, которые принимают на входе строку и генерируют другую строку. В следующих уроках мы собираемся обсудить различные автоматы (единичный автомат).
Эти машины очень похожи на центральный процессор компьютера, но отсутствие памяти делает их более ограниченными.Компьютеры детерминированы. В данный момент они могут находиться только в одном состоянии. Конечные автоматы могут быть детерминированными или недетерминированными.
Конечный автомат состоит из 3 компонентов — входной ленты, считывающей головки и системы конечного управления. Считывающая головка считывает ввод с входной ленты, и система конечного управления принимает решение о действии. Система конечного управления начинается с начального состояния и может изменить или не изменить состояние на данном входе. Если после чтения входной строки машина переходит в одно из конечных состояний, входная строка считается принятой, в противном случае она отклоняется.
Конечный автомат называется конечным, потому что существует конечное число состояний, в которых он может существовать, а также конечное количество возможных входных символов. Изменение состояния определяется входом.
Sanfoundry Global Education & Learning Series — Более 100 учебных пособий по теории вычислений.
Если вы хотите просмотреть все учебные пособия и их примеры, перейдите к учебным пособиям по теории вычислений.
, чтобы получить бесплатную Почетную грамоту. Присоединяйтесь к нашим социальным сетям ниже и будьте в курсе последних конкурсов, видео, стажировок и вакансий!
IIS 10.0 Подробная ошибка — 404.11
Ошибка HTTP 404.11 — не найдено
Модуль фильтрации запросов настроен на отклонение запроса, содержащего двойную escape-последовательность.
Наиболее вероятные причины:
- Запрос содержал двойную escape-последовательность, а фильтрация запросов настроена на веб-сервере, чтобы отклонять двойные escape-последовательности.
Что можно попробовать:
- Проверьте конфигурацию / систему.webServer / security / requestFiltering @ allowDoubleEscaping в файле applicationhost.config или web.confg.