Подключение домофона своими руками: алгоритм действий
Просмотров: 4 905
Установка домофона в доме – это решение, которое направлено на то, чтобы увеличить уровень безопасности и защитить жильцов и их имущество от «непрошенных гостей».
Такого рода устройства применяются в качестве пропускных модулей, которые обеспечивают открывание входной двери в дом только с разрешения одного из жильцов.
Современные домофоны отличаются расширенными возможностями в плане того, что с их помощью можно не только вести переговоры с тем, кто хочет войти в дом, а и видеть его на внутреннем мониторе, который подключен к наружной камере домофона.
В том, как подключить домофон самостоятельно в многоквартирном доме, нет ничего сложного, и с этим может разобраться каждый, кто хоть немного владеет навыками электромонтажных работ.
Если же с установкой таких устройств может возникнуть проблема, то лучше обратиться в специализированную компанию, сотрудники которой подберут оптимальный вариант домофона и профессионально установят его.
Для тех, кто все-таки намерен осуществить подключение домофона в квартире своими руками полезной будет информация, представленная ниже.
Как устроен домофон
Домофон представляет собой устройство, с помощью которого организовывается своего рода система доступа в частный или многоквартирный дом. Наличие этого устройства исключит проникновение в квартиру без одобрения ее владельца.
Электронная схема домофона
В последнее время домофонами активно заменяют морально устаревшие кодовые замки.
В состав этих устройств входят следующие элементы:
- трубка домофона;
- вызывная панель;
- видеоаппаратура, если устройством предусмотрена возможность видеотрансляции;
- электрический замок;
- коммутатор.
Рассмотрим по отдельности, как работает каждый из этих узлов:
- Подключение трубки домофона осуществляется внутри помещения и используется для того, чтобы его владелец мог принять вызывной сигнал от гостя и при желании открыть ему дверь или попросту с ним пообщаться, используя для этой цели звуковую связь.
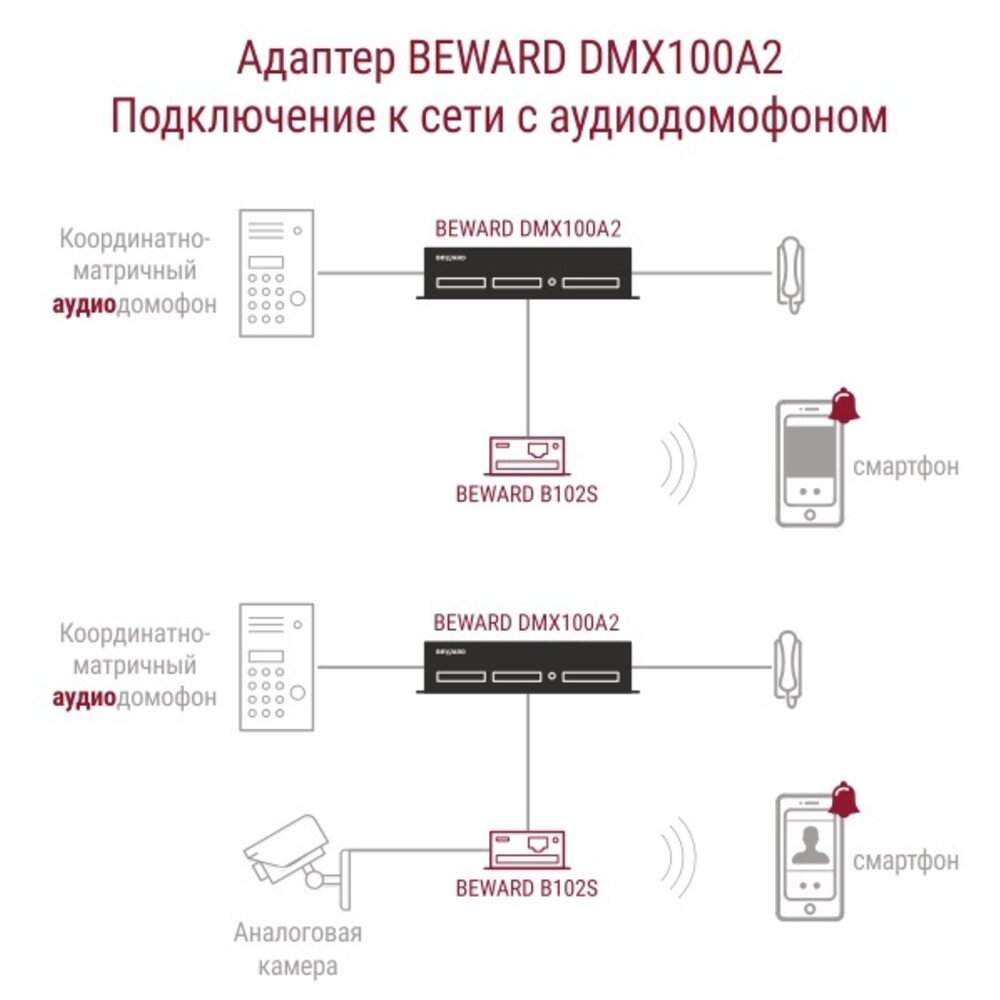 По умолчанию устройство абонента подключается к электрической запирающей системе и позволяет ею управлять.
По умолчанию устройство абонента подключается к электрической запирающей системе и позволяет ею управлять. - Вызывная панель используется с целью вызова абонента гостем, а также для введения соответствующего кода тем, кто имеет доступ к помещениям. Тому, кто собирается осуществлять подключение домофона в квартире важно помнить, что бывают разные вызывные панели – с кнопочными номеронабирателями, со специальным считывателем кода с электронного ключа или магнитной карточки или с визуальным определением. Последний тип является весьма редким и используется для охраны доступа к государственным или промышленным объектам, в жилом секторе он практически не применяется.
- Электрический замок представляет собой запирающее устройство, которое контролирует положение двери «Закрыто/Открыто». Замок подключается к абонентскому модулю домофона, с которого владелец может открыть дверь, пообщавшись с тем, кто к нему пришел. Наиболее широкое практическое применение получили замки с электромагнитной системой.

- Коммутатор потребуется в том случае, когда нужно разобраться, как установить домофон в многоквартирном доме своими руками. На таких объектах есть много различных абонентов и нужно адресовать сигнал вызова конкретному человеку. Для этой цели и применяется коммутатор, который вызов перенаправляет к одной квартире, а не ко всем сразу. При установке домофонов в частных домах потребность в коммутаторе попросту отпадает.
- В качестве дополнительных устройств безопасности могут использоваться видеосистемы, которые включают в свой состав наружную видеокамеру, устанавливаемую возле панели вызова и монитор, который может входить в один модуль с домофонной трубкой или использоваться в качестве отдельного устройства.
Виды домофонов
На сегодня существует несколько типов домофонов, которые применяются для защиты объектов недвижимости от «непрошенных гостей». В зависимости от типа устройства будет отличаться и процесс того, как подключить домофон.
Современные устройства делятся на две категории:
- Цифровые;
- Координатно-матричные.

Цифровые
Принцип работы цифрового домофона заключается в том, что при звонке с панели вызова происходит распознавание квартиры, куда он должен направляться по линии связи.
После того, как подключить трубку домофона в квартире, два провода двухпроводной линии связи будут обеспечивать доставку сигнала к требуемому абоненту.
Цифровой домофон
Чтобы произвести сопряжение используются специальные джамперы, посредством которых, с помощью витой пары, сигнал поступает к конкретной домофонной трубке. Преимуществом таких домофонов является то, что к одному контроллеру можно подключать как все квартиры на этаже, так и во всем подъезде.
Координатно-матричные
Схема подключения домофона этого типа более простая, поэтому и пользуется большей популярностью.
Устройства владеют в своем составе координатным модулем, который спряжен с коммутатором, способствующим подачу сигнала к конкретной трубке.
Подключение также осуществляется с помощью двух проводников, одному из которых отвечает номер единиц, а второму номер десяток.
Координатно-матричный домофон
Каждая из квартир имеет свой индивидуальный двухзначный номер, который обрабатывается модулятором и после это, используя коммутатор, уже и осуществляется подключение между конкретным абонентом и гостем.
Подключение домофона
Процедуру подключения следует разделить на два этапа – на первом из них производится установка оборудования внутри помещения, а на втором – монтаж устройств вне дома, перед входной дверью.
После завершения монтажных работ проводится проверка работоспособности системы и ее настройка перед тем, как ввести ее в эксплуатацию.
Инструкция по шагам
Чтобы система домофона могла функционировать, следует обеспечить ее надежное электропитание, которое поддерживается от блока питания постоянного напряжения. Подача электроэнергии к блоку осуществляется от обычной розетки 220 В или от электрощитка.
Подключение домофона к электропитанию
Кроме трубки домофона, от блока питания напряжение подается также к электрическому замку и вызывному устройству.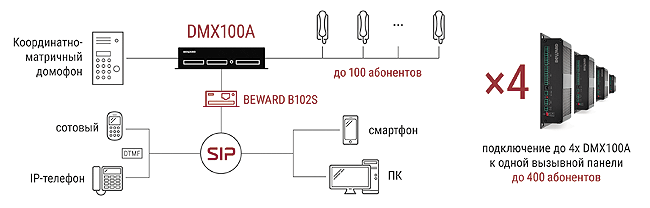
Далее следует определиться с тем, как подключить трубку домофона в квартире. Наиболее часто ее монтируют возле входной двери, для подключения трубки используется витая пара или двухпроводный кабель.
Если в составе домофона предусмотрен монитор видеонаблюдеия, то осуществляется и его подключение. Для монтажа внутренних элементов и крепления их к стенам используются обычные саморезы с дюбелями.
На этом монтажные работы внутри помещения заканчиваются и далее работы проводятся на улице, перед входной дверью.
Установка вызывной панели домофона
Перед этим предварительно нужно произвести прокладывание кабелей, которые будут подавать питание к электрическому замку, вызывному устройству и видеокамере, а также будут передавать звуковые и видеосигналы между устройствами, размещенными на улице и внутри помещения.
На улице подключение домофона своими руками включает в себя работы по монтажу вызывного устройства со встроенным микрофоном. Обычно его устанавливают возле входной двери, чтобы пришедшему удобно было общаться с владельцем дома или квартиры.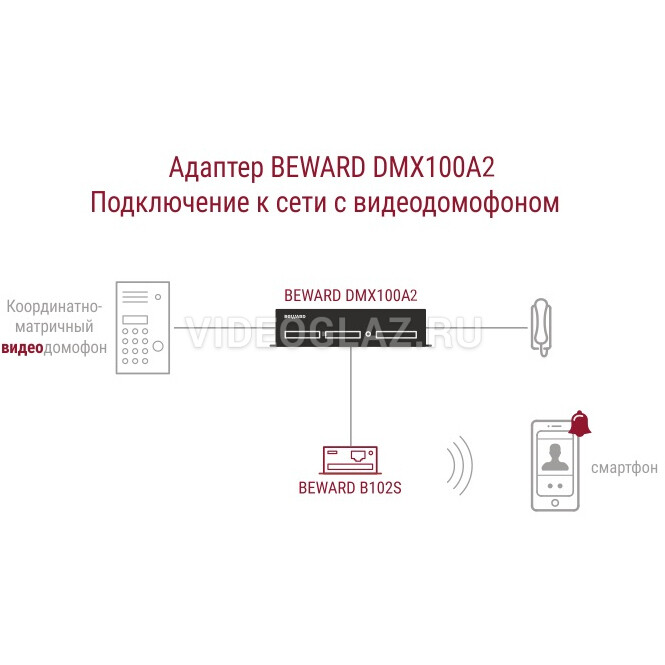
Возле вызывного устройства также производят установку и внешней видеокамеры, которая будет передавать изображение на внутренний монитор домофона.
Следующим шагом является подключение электромеханического или электромагнитного замка и его сопряжение с абонентским модулем домофона.
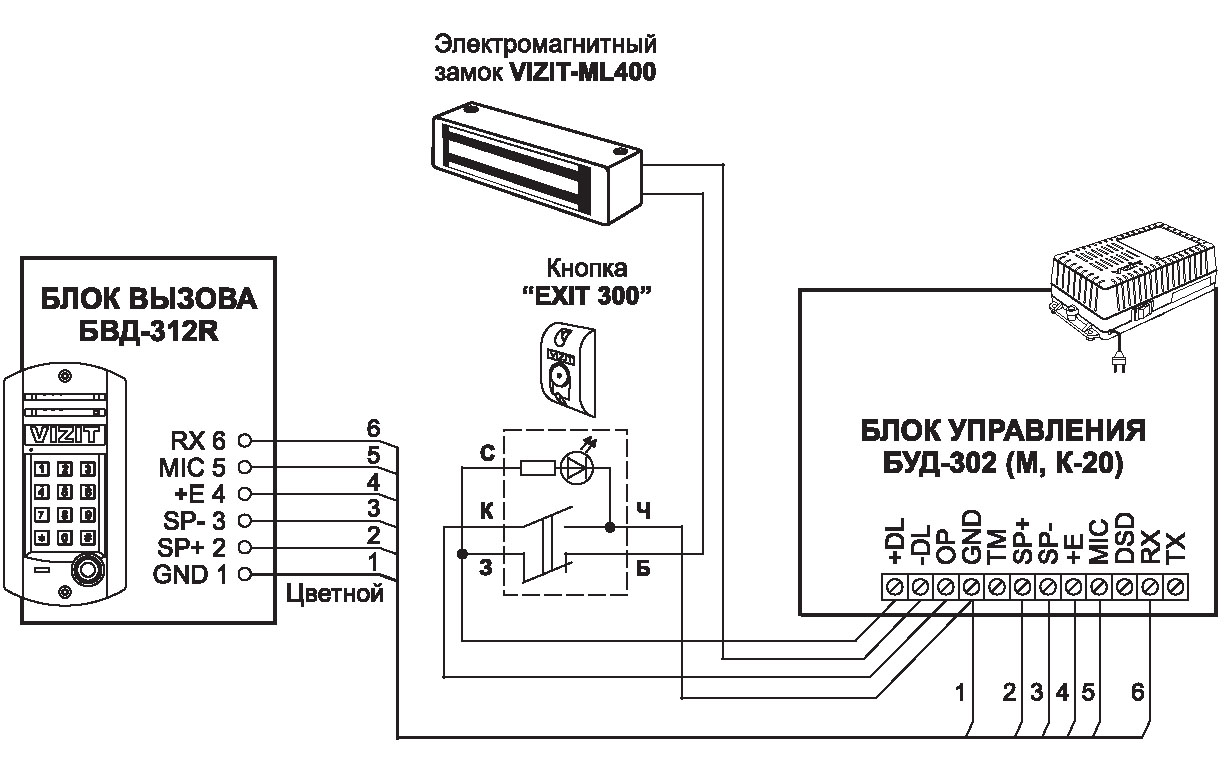
Установка электро-магнитного замка домофона
Провода, которые подключены к внешним устройствам следует защитить, используя для этого специальные гофры и пластмассовые короба.
Заключение
После того, как установить домофон в своем доме, никто из сторонних не сможет открыть входную дверь без разрешения на этого владельца дома.
Это довольно эффективный инструмент защиты себя и своего имущества от злоумышленников. Наличие в домофоне системы видеонаблюдения позволит еще и зафиксировать снимок того, кто приходил, когда никого не было дома.
Предложенная выше инструкция подскажет как подключить домофон самостоятельно, видео, которое можно найти в ютубе, еще более упростит реализацию этой задачи.
Если же процедура монтажа домофона окажется сложной, то всегда можно найти квалифицированную помощь у соответствующих организаций, которые специализируются на продаже и установке средств безопасности для жилых объектов.
Видео: Установка домофона. Или как самому установить видеодомофон и подключить его к многоквартирному дому
Домофон координатный его комплектность и главные достоинства
Компактные координатные домофоны – электронные механизмы переговорного типа. Они служат важным элементом систем безопасности жилых, производственных и офисных зданий, являются компонентом контроля и разрешают лицу, находящемуся внутри помещения, бесконтактно разрешать или запрещать доступ посетителя внутрь здания.
Координатный домофон, историческая справка
Данная разновидность домофонов является одной из старейших на рынке. Она была придумана и выполнена конструкторами в годы существования СССР, сразу после появления большого спектра полупроводников и интегральных микросхем.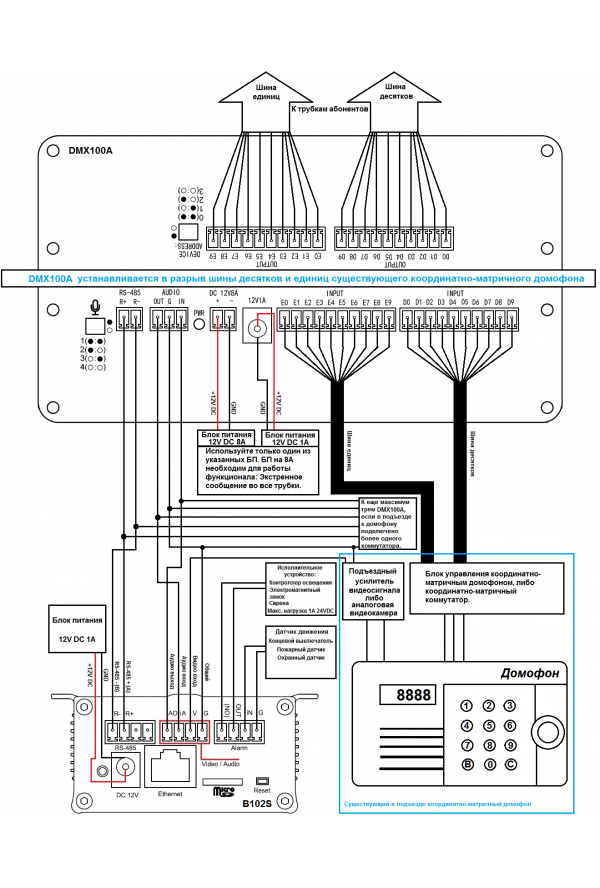
Первые устройства данного типа в электрической цепи использовали элементарные кремниевые транзисторы и простые логические микросхемы.
В них была выбрана самая неприхотливая матричная схема подключения абонентских устройств, присутствовало минимальное количество функций, доступных для координатно-матричного домофона, были включены функции голосовой связи и управления замком.
Пропуск посетителей в здание осуществлялся по простейшему однотипному ключу. Функцию электронной отмычки осуществлял резистор, который замыкал схему управления замком. Подключение каждого абонента осуществлялось при помощи двух электрических проводов и перемычки, протянутой до места, где была установлена трубка.
Современные домофоны: какими бывают
Современный домофон сегодня – это сложная специализированная микропроцессорная система, которая может устанавливаться в различных домах, офисах и производственных помещениях для организации контроля доступа и селекторной связи.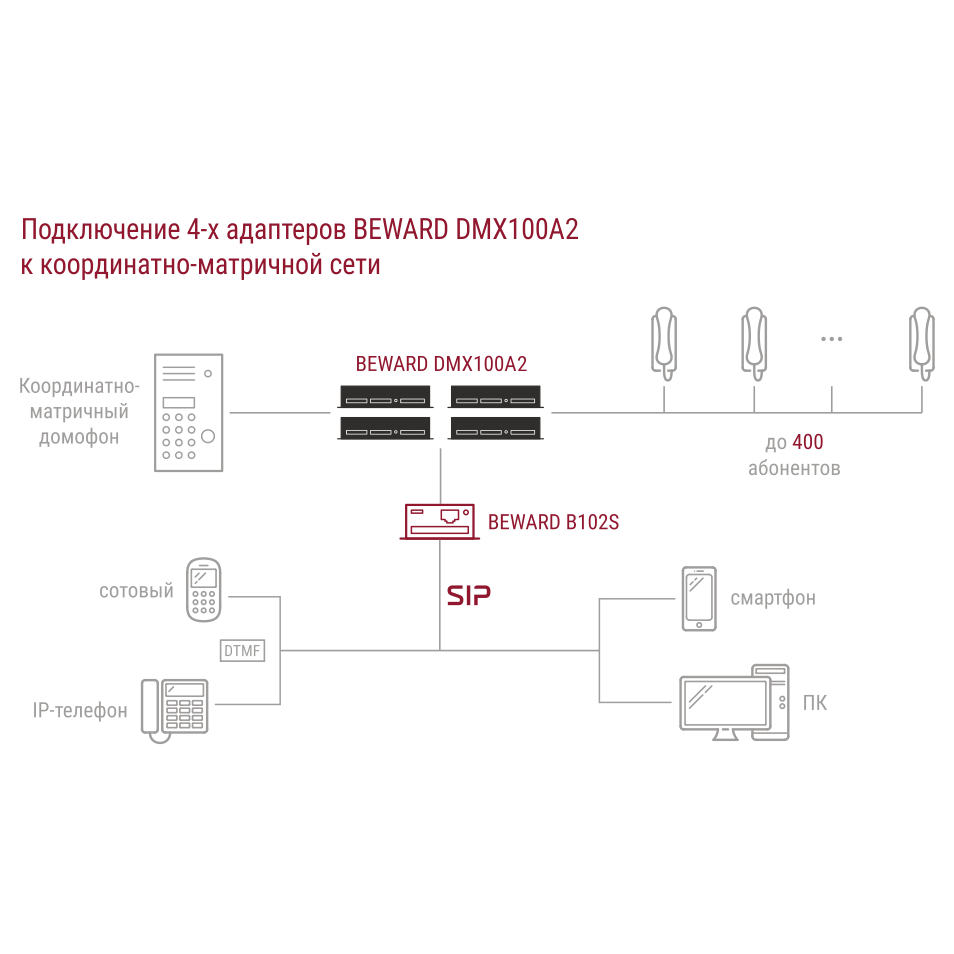
Устройство обладает высокой надежностью, простотой в эксплуатации, имеет современный привлекательный вид и работает совершенно по другому принципу, чем цифровой аналог.
В зависимости от числа подключения абонентов домофон может быть:- Одноабонентным;
- Многоабонентным.
Одноабонентный домофон устанавливается на двери или панели перед въездными воротами на частную территорию, закрытую зону или приватный дом.
Многоабонентный домофон устанавливается у входной двери или на входной двери в многоквартирном доме или многоофисном здании.
В зависимости от способа передачи информации домофон может быть:
- Видеодомофоном;
- Аудиодомофоном.
Видеодомофон наряду с переговорной связью позволяет человеку видеть визитера, что помогает понять, говорит гость по принуждению или нет.
Видеодомофоны в зависимости от вида экрана могут быть:
- Цветными;
- Черно-белыми;
- С маленьким, средним или крупным экраном;
- С экраном низкого, среднего и высокого разрешения.
Комплектность координатного подъездного домофона
Его принцип работы намного отличается от принципа работы цифровой модели. В роли связующего звена с квартирными трубками выступает коммутатор. Из него по всему подъезду отходят провода, имеющие множество жил, делящихся на единицы и десятки. Подразделение жил магистрали идет по цветам. Единица имеет следующие цвета: синий, красный, белый, зеленый, которые соответственно обозначены: 1, 2, 3 и т. д. Десяток состоит из 2 или 3 проводов в зависимости от количества квартир в подъезде.
Подключение трубок происходит на свой привод, и к каждой из них устанавливается определенный сигнал коммутатора. Такие трубки просты в строении, главное условие при их подключении заключается в том, что надо соблюдать полярность.
Стандартный домофон включает в себя несколько блоков:
- Вызывную панель координатного подъездного домофона.
 Панель может устанавливаться у входной двери, на двери или на специальной панели у ворот;
Панель может устанавливаться у входной двери, на двери или на специальной панели у ворот; - Коммутатор координатного подъездного домофона. Устройство передает звук к месту, где устанавливается трубка;
- Трубку. Трубка имеет кнопку открытия замка;
- Блок сопряжения координатного подъездного домофона. Он является специальным приспособлением, которое позволяет усовершенствовать аудиодомофон, при этом расширив его операции при помощи функции видео. Современные видеодомофоны с координатной системой часто комплектуются встроенным блоком сопряжения;
- Монитор. Может быть цветным или черно-белым, встречается только у видеодомофонов;
- Электронный открыватель. Устройство позволяет открывать и запирать входную дверь;
- Датчик движения. Устройство встречается у современных видеодомофонов.
Главные достоинства и недостатки домофона

Простая надежная комплектация. Цифровой домофон имеет более сложную комплектацию, поэтому предлагается покупателям по более высокой цене, часто ломается и требует особых условий эксплуатации.
Легкий ремонт. Конструкция координатного подъездного домофона имеет открытую архитектуру, предусматривает легкую замену поврежденных элементов без проведения перенастройки и переналадки всей системы.
Главным минусом домофона координатного типа является необходимость использовать огромное количество проводов при монтаже, которые переполняют кабель-каналы и уродуют отделку стен.
Спутывание проводов, идущих к трубке, приводит к переполюсовке и короткому замыканию в координатном блоке, что ведет к выходу из строя оборудования. Поломка в системе проявляется прослушиванием чужих вызовов, сторонних разговоров, невозможностью открыть входную дверь с помощью кнопки в помещении и в различных квартирах подъезда.
Аудиодомофоны координатные, что за устройства?
Аудиодомофоны (домофоны) – это простые, но весьма эффективные устройства обеспечения безопасности домов, квартир, офисов или загородных коттеджей.
Они представляют из себя двустороннее многопредметное переговорное устройство, которое состоит из вызывной панели, которая вмонтирована на наружной стороне двери и абонентской трубки, расположенной внутри здания. Трубка может иметь любой дизайн, всегда оборудуется кнопкой открытия входного замка.
Между собой вызывная панель и трубка соединяются двумя проводами. После нажатия кнопки вызывной панели трубка домофона издает сигнал, позволяет пользователю пообщаться с визитером, а также открыть ему входной замок.
Видеодомофоны координатные, чем отличаются от аудиодомофонов
У аудиодомофонов встроен только оригинальный гальваноразвязанный блок сопряжения и присутствует трубка. У видеодомофонов координатных с функцией открытия входной двери, в отличие от аудиодомофонов, предусмотрено еще и подключение монитора одной и более видеокамер.
Устройство легко подключается к координатным подъездным системам, может принимать голосовой и NTSC/PAL видеосигнал, имеет выбор нескольких мелодий вызова, может разрешать подключение нескольких мониторов, каналов видео.
Некоторые самые современные модели видеодомофонов координатных могут дополнительно вести запись видео и кадров на SD-карту и воспроизводить сохраненный материал на ПК или любое мобильное устройство. Они могут иметь сенсорные кнопки для подстройки монитора.
Основные функции видеодомофонов
Видеодомофон для координатных подъездных домофонов – это двухстороннее устройство, которое в реальном времени позволяет:
- Просматривать видео;
- В деталях рассматривать визитера;
- Вести переговоры с визитером;
- При необходимости отпирать входной замок.
В чем же заключается принцип работы видеодомофона? После того как визитер набрал номер квартиры, встроенный процессор координатного видеодомофона формирует сигнал и отсылает его на коммутатор.
Коммутатор получает сигнал, обрабатывает его и при помощи собственных электронных ключей подключает запрашиваемую трубку. Трубка издает сигнал, тем самым сообщает о приходе визитера.
Связь с визитером осуществляется через разговорную линию. Открытие входной двери выполняет трубка, оснащенная кнопкой для открытия электрозамка.
На видео рассказывается о том, как выбрать подходящий видеодомофон:
Факторы, которые влияют на стоимость
Стоимость видеодомофона зависит в первую очередь от:
- Вида монитора. Цена видеодомофона с цветным монитором будет намного выше стоимости аналогичного устройства с черно-белым экраном;
- Наличия сенсорного управления. Конструкция координатного подъездного домофона с сенсорами обойдется покупателю значительно дороже, чем аналогичная с кнопочным управлением;
- Укомплектованности оборудования трубкой или наличием громкой связи;
- Изысканности дизайна.
В настоящее время рынок позволяет выбрать координатный видеодомофон в любой дом, на любой вкус и кошелек – от бюджетных ретромоделей до ультрасовременных устройств, имеющих множество дополнительных функций.
Приобретение координатного подъездного домофона
Стандартизованные видеодомофоны в большинстве случаев не работают с подъездными многоквартирными аудиодомофонами, которых на рынке встречается огромное количество. Поэтому, прежде чем купить видеодомофон, следует:
- Изучить инструкцию, прилагаемую на видеодомофон, для координатных подъездных домофонов;
- Разобраться со схемой монтажа;
- Используя знания, провести монтаж;
- Если монтаж своими руками невозможен, обратиться за помощью к специалистам.
В настоящее время домофоны данного типа развиваются эволюционным путем. За время своего существования для них появились определенные стандарты, проверенные методы, схемы действий при возникновении нештатных ситуаций.
Активная конкуренция заставляет производителей совершенствовать свои продукты, предлагать клиентам более современные решения. Это признак того, что рынок координатных домофонов здоров, развивается и, возможно, в скором времени совершит качественный скачок вперед.
Домофон в умном доме
Кто-то решает этот вопрос с помощью SIP телефонии. То есть когда к
вам пришли гости и набрали на вызывной панели ваш номер квартиры — вы
получаете входящий звонок на ваш сотовый телефон.
У кого то есть фирменные приложения, которые позволяют получать как аудио, так и видео вызовы. Дьявол, как обычно, кроется в деталях.
Но если все-таки у застройщика появляется желание поставить в квартиры абонентские устройства типа трубок или мониторов, то вот тут начинается одна из самых дорогих частей системы — СКС (Структурированная Кабельная Система) для домофона. По сути — это дублирующая локальная сеть дома, которая строится параллельно провайдерской. Конечно, можно договориться с провайдером, чтобы он пустил в свою сеть, но тогда вы столкнетесь с тем, что для того, чтобы подключить трубку или монитор, вам придется подключиться именно к этому провайдеру. Я, по роду своей деятельности, именно таким способом и «окучивал» абонентскую базу. Очень удобно и в общем-то никого ни в чем не ограничивает. Но многие застройщики, столкнувшись с этим пару раз, предпочитают стоить отдельную сеть для домофонии. Поэтому в квартире появится еще один Ethernet кабель исключительно для домофона.
Очень удобно и в общем-то никого ни в чем не ограничивает. Но многие застройщики, столкнувшись с этим пару раз, предпочитают стоить отдельную сеть для домофонии. Поэтому в квартире появится еще один Ethernet кабель исключительно для домофона.
Что касается особенностей подобного типа домофонии, то возьмем двух самых страстных конкурентов на нашем рынке: Comelit и BasIP.
Comelit — это итальянская компания, которая заточена на европейский рынок. Имеет закрытую экосистему, которую невозможно интегрировать куда-либо. Правда в последних прошивках появилась возможность получать с вызывной панели RTSP поток камеры, но это все, что вы получите. Получать вызов куда-либо, кроме своего телефона или фирменного приложения, у вас не получится. Хотя SIP решение вполне имеет место быть.
BasIP — это, по сути, китайское
решение, которое интегрируется куда угодно, у них довольно дружелюбное
API и очень большой список интеграций как в личные кабинеты управляющих
компаний, так и в некоторые системы умного дома. Видео с камер вы можете
получить легко и просто.
Видео с камер вы можете
получить легко и просто.
И если сравнивать только по этим параметрам, то итальянцы проигрывают на корню. Но я уже говорил — дьявол кроется в деталях. Для эксплуатации BasIP вам потребуется покупать сервер, администрировать его, настраивать и перенастраивать, а обновление прошивок и тому подобное превращается в скакание по абонентам, у которых что-то отвалилось.
У итальянцев же все намного проще. Обновления устанавливаются удаленно и тихо, все настройки «приезжают» абонентам в почту файликом, который они просто открывают и вообще не задумываются о том, как оно работает.
И опыт эксплуатации показывает, что Comelit работает стабильнее настолько, что после установки системы, много лет нет ни одного звонка в техподдержку, кроме как по вопросам изготовления новых ключей или просьбы прислать файл настроек по причине смены смартфона.
Декартовы координаты и матрицы преобразования — Polymath Programmer
Если вы работаете в 3D, вам нужно знать о декартовой системе координат и матрицах преобразования. Декартовы координаты обычно используются для представления мира в 3D-программировании. Матрицы преобразования — это матрицы, представляющие операции над трехмерными точками и объектами. Типичные операции — это перемещение, вращение, масштабирование.
Декартовы координаты обычно используются для представления мира в 3D-программировании. Матрицы преобразования — это матрицы, представляющие операции над трехмерными точками и объектами. Типичные операции — это перемещение, вращение, масштабирование.
Двумерные декартовы координаты
Вы должны были видеть что-то подобное в своем классе математики:
[исходное изображение]
Римские буквы I, II, III и IV обозначают квадранты декартовой плоскости .Например, III представляет третий квадрант. Здесь особо нечего сказать, так что продолжаем…
Трехмерные декартовы координаты
А для трех измерений у нас есть это:
[исходное изображение]
Мне не нравится, как ось Z направлена вверх. Идея, вероятно, связана с листом бумаги, представляющим двумерную плоскость, образованную осями x и y. Бумага кладется на плоский горизонтальный стол, ось Z направляется вверх.
С математической точки зрения разницы нет.
Однако мне проще посмотреть на это так:
Декартова плоскость XY находится в вертикальном положении, представляя экран. Ось Z просто выступает за пределы экрана. Окно просмотра может охватывать все четыре квадранта плоскости XY. На рисунке показан только первый квадрант, поэтому я не высовываю вам глаз осью Z * улыбка *
Существует также так называемое правило правой руки и, соответственно, правило левой руки . Правило правой руки показывает, что ось z направлена за пределы экрана, как показано выше.Правило левой руки имеет ось z, указывающую на экрана. Соблюдайте правило правой руки:
Большой палец представляет ось x, указательный палец представляет ось y, а средний палец представляет ось z. Что касается правила левой руки, мы имеем:
Мы смотрим на другую сторону плоскости XY, но это то же самое. Ось z указывает в другом направлении. И да, у меня длинные пальцы. Моя рука может покрыть целую октаву на фортепиано.
В чем дело? Потому что ваш движок трехмерной графики по умолчанию может использовать определенное правило, и вы должны следовать ему. В противном случае вы можете найти ошибки, например, почему объект не отображается на экране. Потому что объект находился за камерой, когда вы думали, что он впереди. Выбранный вами графический движок также должен позволять вам использовать другое правило, если вы того пожелаете.
Если вам интересно, вот иллюстрация правила справа с осью Z, направленной вверх:
Мне все еще не нравится, когда ось Z направлена вверх.Меня это почему-то раздражает…
Масштабирование (или создание чего-то большего или меньшего)
Так как же увеличить или уменьшить что-либо в 3D? Вы применяете матрицу масштабирования. Давайте посмотрим на 2D-версию:
Если коэффициент масштабирования больше 1, вы увеличиваете объект. Если коэффициент масштабирования меньше 1, вы уменьшаете объект. Как вы думаете, что произойдет, если ваш коэффициент масштабирования равен 1? Или когда у вас коэффициент масштабирования отрицательный?
Как вы думаете, что произойдет, если ваш коэффициент масштабирования равен 1? Или когда у вас коэффициент масштабирования отрицательный?
Так как же коэффициент масштабирования выглядит в матрице масштабирования?
Если вы не знаете, что это значит, или не знаете, каким должен быть результат, просмотрите урок о матрицах и соответствующем программном коде.
Вы заметите, что существуют отдельные коэффициенты масштабирования для осей x и y. Это означает, что вы можете масштабировать их независимо. Например, у нас это:
А увеличиваем только по оси абсцисс:
Мы также можем увеличивать только по оси Y:
Ага, мне надоело рисовать 2D картинки, поэтому я решил сделать несколько 3D. Кстати, теперь у вас должна появиться возможность предложить 3D-версию матрицы масштабирования. Подсказка: просто добавьте коэффициент масштабирования для оси Z.
Вращение (или вращение до рвоты)
Вот как выглядит матрица вращения для двух измерений:
Этот символ похож на букву O с прорезью посередине? Это тета (произносится как th-ay-tuh), греческий алфавит. Обычно используется для обозначения неизвестных углов.
Обычно используется для обозначения неизвестных углов.
Я избавлю вас от математического вывода формулы. Просто используйте это.
Вы можете убедиться в этом, проведя простой эксперимент. Используйте вектор (1,0) или единичный вектор, лежащий на оси x.Подключите 90 градусов для теты, и вы должны получить (0,1), единичный вектор, лежащий на оси y.
Это вращение против часовой стрелки. Чтобы повернуть по часовой стрелке, просто используйте значение со сменой знака. Итак, у вас будет -90 градусов.
В зависимости от используемых математических библиотек может потребоваться использование радианов вместо градусов (что типично для большинства математических библиотек). Я уверен, что вы достаточно сообразительны, чтобы самостоятельно вычислить формулу преобразования градуса в радиан…
Теперь самое сложное.Трехмерная версия вращения… немного сложна. Вы видите, что то, что вы прочитали выше, на самом деле вращается вокруг предполагаемой оси Z. Подождите, это означает, что вы можете вращаться вокруг оси x! И ось Y! Сакребле! Можно вращать вокруг любой произвольной оси !
Я напишу об этом еще одну статью. Если вам это нравится, возможно, вам стоит взглянуть на эту статью о 3D-вращении. Я также коснусь концепции, в которой вы вращаетесь вокруг одной оси, а затем вращаетесь вокруг другой оси. Будьте готовы к тому, что в формуле будет много синусов и косинусов.Перестань плакать; это неприлично с вашей стороны.
Если вам это нравится, возможно, вам стоит взглянуть на эту статью о 3D-вращении. Я также коснусь концепции, в которой вы вращаетесь вокруг одной оси, а затем вращаетесь вокруг другой оси. Будьте готовы к тому, что в формуле будет много синусов и косинусов.Перестань плакать; это неприлично с вашей стороны.
Перевод (здесь ничего лингвистического)
Это означает, что вы перемещаете точки и объекты из одного положения в другое. Давайте посмотрим на одномерный пример:
Волнистый, неустойчивый на вид подражатель? Это дельта греческого алфавита. Дельта-x — стандартное обозначение для «изменения x». В этом случае «x» означает расстояние по оси x. В оставшейся части нашего обсуждения мы будем использовать версию, которую проще набирать, под названием «dx».
В двух измерениях у нас есть соответствующая dy для «изменения y». Обратите внимание, что ничто не мешает вам использовать отрицательные значения для dx или dy. На рисунке выше dx и dy отрицательны.
Вы должны представить себе случай 3D, потому что диаграмма может быть беспорядочной. Но это легко визуализировать. Сделайте то же самое для оси Z.
Так что же такое матрица преобразования для перевода? Во-первых, вам нужно увеличить размер матрицы и размер вектора на одно измерение.Точные причины связаны с аффинными преобразованиями и однородными координатами (я кратко упоминал их ранее).
Учтите: у вас есть точка (x, y, z), и вы хотите, чтобы она находилась в новой позиции (x + dx, y + dy, z + dz). Тогда матрица будет выглядеть так:
Обратите внимание, что для масштабирования важными записями являются диагональные записи. Для вращения есть синусы и косинусы, и они повсюду. Но для перевода «основная часть» матрицы на самом деле является единичной матрицей.Самое интересное происходит в столбце переулка в крайнем правом углу матрицы.
Это мне напомнило. Поскольку вы будете использовать все матрицы преобразования вместе, все матрицы должны быть одного размера. Таким образом, матрицы масштабирования и вращения тоже должны быть 4 на 4. Просто добавьте к ним ноль записей, кроме правой нижней записи, которая равна 1.
Таким образом, матрицы масштабирования и вращения тоже должны быть 4 на 4. Просто добавьте к ним ноль записей, кроме правой нижней записи, которая равна 1.
Заключение
Мы говорили о 2D и 3D декартовых координатах. Я также показал вам правила для правой и левой руки. Это формирует основу для изучения основных преобразований, таких как масштабирование, поворот и перемещение.
Есть еще две интересные матрицы преобразования: сдвиг и отражение. Я думал, что то, что у нас есть, пока достаточно. Вы можете провести собственное исследование. Когда возникнет ситуация, я расскажу об этих двух трансформациях.
Если вам понравилась эта статья и вы нашли ее полезной, поделитесь ею со своими друзьями. Вам также следует подписаться, чтобы получать последние статьи (это бесплатно).
Эта статья о преобразовании между растровыми, декартовыми и полярными координатами может оказаться полезной.
Эти книги по «преобразованию координат» могут оказаться полезными.
Рассчитайте координаты X, Y, Z в реальном мире по координатам изображения с помощью OpenCV — fdx labs
Как только я закончил свой прототип горизонтального перемещения робота-манипулятора и смог надежно совершать движения захвата и размещения, используя простые значения X, Y, Z, я решил создать реальный вариант использования, который мог бы показать его потенциал для реальных приложений.
Предоставить роботу компьютерное зрение кажется очень простым делом, и я многому научился, чем хочу поделиться, поскольку, скорее всего, вы найдете это полезным.
На всякий случай, если вы хотите сразу погрузиться, вы можете получить доступ к коду через мой проект робота Github HTA0.
Примечание. Я взял на себя смелость выделить то, что считаю наиболее важными. Я считаю, что вы обратитесь к репозиторию кода, а также к нескольким диаграммам, на которые я ссылаюсь ниже.
Координаты и системы отсчета
Вы можете прочитать мой пост на Medium об обзоре робота и посмотреть видео о его работе на Youtube.
Напоминаем, что это установка этого робота:
Робот-манипулятор с горизонтальным перемещением — HTA0По мере того, как я углубляюсь в этот блог, будет очень важно помнить о ссылках, которые я использовал:
Кадры координат робота, камеры и плана отсчетаКрасный — ось X, зеленый — ось Y и синий — ось Z, стрелки указывают в направлении положительного увеличения. Эта иллюстрация будет иметь решающее значение для понимания кода и того, как вы можете использовать его в своих собственных проектах (которые могут иметь разные системы отсчета в зависимости от вашего приложения).
Калибровка камеры OpenCV и трехмерная реконструкция
Формулы
Основная ссылка, которую я использовал для этого, — это документация OpenCV 2.4 и 3.0, использующая эти три страницы:
Выполнение шагов по калибровке камеры было действительно простым, но проблема для меня в этом путешествии заключалась в том, как вычислить реальные координаты X Y Z по точкам проекции данного изображения. Я искал это, и я не смог найти никаких ссылок, которые легко объясняли бы, как это сделать:
Основная проблема, которую я обнаружил с этой моделью точечного отверстия, заключается в том, что если вы хотите решить для X Y Z, это невозможно сделать, потому что вы не можете вычислить обратную матрицу R | t, поскольку она не квадратная.
Прежде чем я углублюсь в решение, важно понять модель и координаты камеры-обскуры:
И это важно, потому что, если ваша установка имеет значение z, отличное от нуля, модель камеры-обскуры упрощается до:
Модель обскуры, когда z не равно 0Чтобы это работало, я добавил коэффициент масштабирования и матрицу камеры, чтобы получить u, v, которые теперь позволяют вычислять X Y Z следующим образом:
решение для координат реального мира X Y Z Это был решающий шаг, который позволил мне найти рабочее решение, и во время работы над ним всплыл еще один интересный аспект.
Правильная калибровка внутренней камеры
Первым шагом к калибровке вашей установки является определение так называемых внутренних параметров вашей камеры, которые основаны на конструкции камеры, и одним из ключевых факторов для калибровки является искажение, вызванное кривизной объектив камеры.
Я выполнил шаги из OpenCV Camera Calibration и даже использовал много примеров кода, но нашел кое-что интересное.
Калибровка шахматной доскиСледуя примеру калибровки шахматной доски, я считаю, что рекомендуется использовать 10 или более изображений, и это не дает разъяснений о том, как «поставить» шахматную доску.
Я использовал предварительный просмотр «Неискажения», чтобы проверить свою работу, и обнаружил, что шаблон неискажения имеет множество вариаций, а именно:
Вариация функции устранения искажений в зависимости от используемых изображений и поз. В итоге я использовал около 40 изображений для калибровки и узнал, что для повышения «стабильности» масштабных коэффициентов мне нужно расположить шахматную доску в той же плоскости, где я хотел обнаруживать X Y Z.
Здесь вы можете найти скрипт Python для этой начальной калибровки.
Правильная калибровка перспективы
В моей настройке я использую одиночную фиксированную камеру , а это значит, что после калибровки перспективы модель должна начать работать. Чтобы добраться до этого момента, потребовался ряд дополнительных шагов, чтобы заставить его работать надежно, что я объясню.
Первый шаг — определить значения Cx, Cy и z для камеры, и мы используем новую матрицу камеры, чтобы найти, что Cx = 628 и Cy = 342.Если вы ссылаетесь на модель крошечного отверстия, они эквивалентны значениям пикселей u и v.
Из нашей внутренней калибровки мы получаем Cx и Cy. Затем мы вручную пытаемся найти точку пикселя u = 628 и v = 342:
. Мы находим cx в 628 и cy в 342 (пока игнорируем X, Y)И измеряем строчкой значение z:
Мы измеряем расстояние z, когда оно проецируется в позу, в данном случае эквивалентно ~ 43 см. Мы повторяем это измерение для каждой точки, но помните, что z верно только для центральной точки, а остальные точки мы измеряем как d * (который мы должны затем использовать x, y и тригонометрию, чтобы вычислить значение z, что мы делаем автоматически в коде).Наш лист выглядит так:
Мы повторяем это измерение для каждой точки, но помните, что z верно только для центральной точки, а остальные точки мы измеряем как d * (который мы должны затем использовать x, y и тригонометрию, чтобы вычислить значение z, что мы делаем автоматически в коде).Наш лист выглядит так:
Затем мы используем шаблон из 9 кругов, который я создал для вычисления точек изображения, которые являются информацией, которая нам нужна для расчета перспективы.
находим u и v для каждой из точекИ мы вводим это вручную в перспективную калибровку:
#ENTER (X, Y, d *)
# d * - это расстояние от вашей точки до объектива камеры. (d * = Z для центра камеры)
X_center = 10,9
Y_center = 10.7
Z_center = 43,4
worldPoints = np.array ([[X_center, Y_center, Z_center],
[5.5,3.9,46.8],
[14.2,3.9,47.0],
[22.8,3.9,47.4],
[5.5,10.6,44.2],
[14,2,10,6,43,8],
[22,8,10,6,44,8],
[5. 5,17.3,43],
[14,2,17,3,42,5],
[22.8,17.3,44.4]], dtype = np.float32)
# [u, v] center + 9 точек изображения
imagePoints = np.array ([[cx, cy],
[502,185],
[700,197],
[894 208],
[491 331],
[695 342],
[896 353],
[478 487],
[691 497],
[900,508]], dtype = np.float32)
5,17.3,43],
[14,2,17,3,42,5],
[22.8,17.3,44.4]], dtype = np.float32)
# [u, v] center + 9 точек изображения
imagePoints = np.array ([[cx, cy],
[502,185],
[700,197],
[894 208],
[491 331],
[695 342],
[896 353],
[478 487],
[691 497],
[900,508]], dtype = np.float32) И после запуска калибровки перспективы важно проверить коэффициент масштабирования s. Это важный шаг, учитывая, что результаты вашей внутренней калибровки камеры сильно различаются в надежности вычисления X Y Z, и вам следует постараться выполнить итерацию и получить как можно меньшую ошибку коэффициента масштабирования.
Я также обнаружил, что коэффициенты масштабирования меняют свои знаки в зависимости от количества точек и вычислений d * по сравнению с Z, и моя гипотеза заключается в том, что это основано в первую очередь на том, как системы отсчета для плоскости vs. камеры разные, что заставляет менять знаки при вычислении.
камеры разные, что заставляет менять знаки при вычислении.
Здесь вы можете найти сценарий Python для этого процесса.
Расчет реального мира X Y Z во время выполнения по координатам изображения
После того, как у вас есть надежная проверка прогнозов калибровки перспективы между точками мира и точками изображения, я создал два файла:
Процесс распознавания изображений выполняет выделение фона для идентификации объекта и фиксирует координаты u, v от его центра (координаты пикселей из обнаруженного изображения).
Процесс XYZ в реальном мире, затем загружает все выполненные нами начальные калибровки и вычисляет точки X Y Z, при этом «волшебство» происходит в этой конкретной функции:
def calculate_XYZ (self, u, v):
#Solve: Найдите в пикселях изображения мировые точки
uv_1 = np.array ([[u, v, 1]], dtype = np.float32)
uv_1 = uv_1. T
suv_1 = self.scalingfactor * uv_1
xyz_c = self.inverse_newcam_mtx.dot (suv_1)
xyz_c = xyz_c-сам.tvec1
XYZ = self.inverse_R_mtx.dot (xyz_c)
возврат XYZ
T
suv_1 = self.scalingfactor * uv_1
xyz_c = self.inverse_newcam_mtx.dot (suv_1)
xyz_c = xyz_c-сам.tvec1
XYZ = self.inverse_R_mtx.dot (xyz_c)
возврат XYZ Как только это заработает, вы можете потратить время на проверку ваших результатов, которые могут быть следующими:
Использование распечатки 9 точек изображения Использование объектовРассечение матрицы камеры, Часть 2: Внешняя матрица ←
22 августа 2012 г.
Добро пожаловать в третий пост из серии «Камера перспективы — Интерактивный тур». В прошлом посте мы узнали, как разложить матрицу камеры на произведение внутренней и внешней матриц.В следующих двух постах мы более подробно рассмотрим внешние и внутренние матрицы. Сначала мы рассмотрим различные способы взглянуть на внешнюю матрицу с интерактивной демонстрацией в конце.
Матрица внешней камеры
Внешняя матрица камеры описывает положение камеры в мире и направление, в котором она направлена. Те, кто знаком с OpenGL, знают это как «матрицу просмотра» (или свернутую в «матрицу просмотра модели»). Он состоит из двух компонентов: матрицы вращения R и вектора перемещения t , но, как мы скоро увидим, они не совсем соответствуют повороту и перемещению камеры.Сначала мы рассмотрим части внешней матрицы, а позже рассмотрим альтернативные способы описания позы камеры, которые более интуитивно понятны.
Внешняя матрица принимает форму жесткой матрицы преобразования: матрица вращения 3×3 в левом блоке и вектор-столбец переноса 3×1 справа:
\ [[R \, | \, \ boldsymbol {t}] = \ left [\ begin {array} {ccc | c} r_ {1,1} & r_ {1,2} & r_ {1,3} & t_1 \\ r_ {2,1} & r_ {2,2} & r_ {2,3} & t_2 \\ r_ {3,1} & r_ {3,2} & r_ {3,3} & t_3 \\ \ end {array} \ right] \]
Обычно можно увидеть версию этой матрицы с дополнительной строкой (0,0,0,1), добавленной внизу.Это делает матрицу квадратной, что позволяет нам дополнительно разложить эту матрицу на поворот , за которым следует перевод на :
\ [ \ begin {align} \слева [ \ begin {array} {c | c} R & \ boldsymbol {t} \\ \ hline \ boldsymbol {0} & 1 \ end {массив} \ right] & = \слева [ \ begin {array} {c | c} Я & \ boldsymbol {t} \\ \ hline \ boldsymbol {0} & 1 \ end {массив} \правильно ] \ раз \слева [ \ begin {array} {c | c} R & \ boldsymbol {0} \\ \ hline \ boldsymbol {0} & 1 \ end {массив} \правильно ] \\ знак равно \ left [\ begin {array} {ccc | c} 1 & 0 & 0 & t_1 \\ 0 & 1 & 0 & t_2 \\ 0 & 0 & 1 & t_3 \\ \ hline 0 & 0 & 0 & 1 \ end {array} \ right] \ times \ left [\ begin {array} {ccc | c} r_ {1,1} & r_ {1,2} & r_ {1,3} & 0 \\ r_ {2,1} & r_ {2,2} & r_ {2,3} & 0 \\ r_ {3,1} & r_ {3,2} & r_ {3,3} & 0 \\ \ hline 0 & 0 & 0 & 1 \ end {array} \ right] \ end {align} \]
Эта матрица описывает, как преобразовать точки в мировых координатах в координаты камеры. Вектор t можно интерпретировать как положение начала отсчета мира в координатах камеры, а столбцы R представляют направления мировых осей в координатах камеры.
Вектор t можно интерпретировать как положение начала отсчета мира в координатах камеры, а столбцы R представляют направления мировых осей в координатах камеры.
Важно помнить, что внешняя матрица описывает, как мир трансформируется относительно камеры . Это часто нелогично, потому что мы обычно хотим указать, как камера трансформируется относительно мира .Далее мы рассмотрим два альтернативных способа описания внешних параметров камеры, которые более интуитивно понятны, и способы их преобразования в форму внешней матрицы.
Построение внешней матрицы из позы камеры
Часто более естественно указать позу камеры напрямую, чем указывать, как точки мира должны преобразовываться в координаты камеры. К счастью, построить внешнюю матрицу камеры таким способом легко: просто создайте жесткую матрицу преобразования, которая описывает позу камеры, а затем возьмите ее обратную.
Пусть C будет вектор-столбцом, описывающий положение центра камеры в мировых координатах, и пусть \ (R_c \) будет матрицей вращения, описывающей ориентацию камеры относительно осей мировых координат. TC \\
\ hline
\ boldsymbol {0} & 1 \\
\ end {массив}
\ right] & \ text {(умножение матриц)}
\ end {align}
TC \\
\ hline
\ boldsymbol {0} & 1 \\
\ end {массив}
\ right] & \ text {(умножение матриц)}
\ end {align}
При применении инверсии мы используем тот факт, что инверсией матрицы вращения является ее транспонирование, а инвертирование матрицы переноса просто инвертирует вектор переноса.Т \\ \ boldsymbol {t} & = -RC \ end {align} \]
Некоторые тексты пишут внешнюю матрицу, заменяя -RC на t , что смешивает мировое преобразование ( R ) и нотацию преобразования камеры ( C ).
Обзорная камера
Читатели, знакомые с OpenGL, могут предпочесть третий способ определения позы камеры, используя (a) положение камеры, (b) то, на что она смотрит, и (c) направление «вверх».В унаследованном OpenGL это выполняется функцией gluLookAt (), поэтому мы назовем ее «обзорной» камерой. Пусть C будет центром камеры, p будет целевой точкой, а u направлен вверх. Алгоритм вычисления матрицы вращения (перефразирован из документации OpenGL):
Алгоритм вычисления матрицы вращения (перефразирован из документации OpenGL):
- Вычислить L = p — C.
- Нормализовать L.
- Вычислить s = L x u. (перекрестное произведение)
- Нормализовать s.
- Вычислить u ‘= s x L.
Тогда матрица внешнего вращения определяется по формуле:
\ [ R = \ left [ \ begin {array} {ccc} s_1 & s_2 & s_3 \\ u_1 ‘& u_2’ & u_3 ‘\\ -L_1 и -L_2 и -L_3 \ end {массив} \правильно] \]
(обновлено 21 мая 2014 г. — транспонированная матрица)
Вектор трансляции можно получить так же, как и раньше: t = -RC .
Попробуйте!
Ниже представлена интерактивная демонстрация трех различных способов параметризации внешних параметров камеры.Обратите внимание на то, как камера по-разному перемещается при переключении между тремя параметрами.
Для этого требуется браузер с поддержкой WebGL и включенным Javascript.
Javascript требуется для этой демонстрации.
Слева : сцена с камерой и просмотром. Виртуальная плоскость изображения отображается желтым цветом. Справа : изображение камеры.
Настройте внешние параметры, указанные выше.
Это параметризация, ориентированная на мир. Эти параметры описывают, как мир изменяется относительно камеры . Эти параметры соответствуют непосредственно записям в матрице внешней камеры.
При настройке этих параметров обратите внимание на то, как камера движется в мире (левая панель), и контрастируйте с параметризацией «ориентированной на камеру»:
- Вращение влияет на положение камеры (синее поле).
- Направление движения камеры зависит от текущего поворота.
- Положительное вращение перемещает камеру по часовой стрелке (или, что эквивалентно, вращает мир против часовой стрелки).

Также обратите внимание, как изменяется изображение (правая панель):
- Вращение никогда не перемещает начало мира (красный шар).
- При изменении \ (t_x \) сферы всегда перемещаются по горизонтали, независимо от вращения.
- Увеличение \ (t_z \) всегда перемещает камеру ближе к началу координат мира.
Настройте внешние параметры, указанные выше.
Это параметризация, ориентированная на камеру, которая описывает, как камера изменяется относительно мира . Эти параметры соответствуют элементам матрицы внешней камеры inverse .
При настройке этих параметров обратите внимание на то, как камера перемещается в мире
Matrix Market File Format
Формат файла Matrix MarketКод и библиотеки
Код для чтения и анализа графиков в формате mtx (как и во многих других форматах графиков):
Обратите внимание, что считыватели графиков в PMC и PGD довольно надежны и во многих случаях способны читать и определять тип формата графика. Кроме того, считыватели mtx в этих библиотеках могут читать файлы mtx, которые могут нарушать одну или несколько характеристик файла MTX.
Кроме того, считыватели mtx в этих библиотеках могут читать файлы mtx, которые могут нарушать одну или несколько характеристик файла MTX.
Комментарии к примечаниям обозначаются как минимум одним % .
Строка заголовка обычно является первой строкой, которая начинается по крайней мере с одного % и во многих случаях двух %% , за которым следует MatrixMarket и в большинстве случаев четыре поля, которые описывают сохраненные данные.
Как правило, первая строка без % представляет N M K , где N — количество строк, M — количество столбцов, а K — количество ненулевых значений в матрице.Для неориентированных графов первая строка без % представляет N N M , где N — количество узлов, а M — количество ребер. Например, первая строка выше — 4 4 6 и указывает, что количество узлов равно N = 4, а количество ребер — M = 6.
Графический файл с расширением . читается (PGD и PMC выше) с помощью этого (отчасти) строгого считывателя графов mtx.
Таким образом, если файл графика не соответствует указанному выше формату mtx (например,g., если граф является списком ребер, без строки заголовка или строки, которая кодирует количество строк, столбцов и ненулевых значений,
затем следует изменить расширение файла, чтобы он мог быть прочитан более гибким средством чтения графиков, обсуждаемым ниже.
Список краев: Эти коды разработаны так, чтобы быть максимально гибкими и допускать множество вариантов списков краев. Обратите внимание, что эти коды могут быть немного медленнее, чем считыватель mtx. Это связано с возможностью гибких форматов списков краев. Следовательно, этот считыватель должен выполнить множество проверок, чтобы выяснить точный формат входного файла, и выполнить любую необходимую предварительную обработку, которая может потребоваться.
Разделители: считыватель принимает списки краев, разделенные запятыми, пробелами или табуляцией.

Комментарии: комментарии разрешены и должны быть обозначены первым символом новой строки как # или%
Веса: Если список ребер содержит веса в 3-м столбце, они просто игнорируются. Пользователь может указать считывать веса, установив параметр wt или отметив, что график фактически является временным графиком.
Мультиграф: Когда список ребер содержит несколько ребер, мы просто удаляем повторяющиеся ребра.
Список ребер может также содержать пробелы в идентификаторах вершин (непоследовательные идентификаторы вершин) и начинаться с любого положительного целого числа. Самостоятельные петли убираются.
Предполагается, что список ребер неориентирован. Однако, если задан ориентированный граф, он просто рассматривается как неориентированный.
Формат файла MM / MTX
- Формат ASCII;
- разрешить строки комментариев, которые начинаются со знака процента;
- используйте «координатный» формат для разреженных матриц;
- используйте формат «массив» для общих плотных матриц;
Файл в формате Matrix Market состоит из четырех частей:
- Строка заголовка: содержит идентификатор и четыре текстовых поля;
- Строки комментариев: позволяют пользователю сохранять информацию и комментарии;
- Строка размера: указывает количество строк и столбцов, и количество ненулевых элементов;
- Строки данных: задают расположение записей матрицы
(неявно или явно) и их значения.
Строка заголовка имеет вид
% MatrixMarket объект формат поле симметрия или
% MatrixMarket объект формат поле симметрия Строка заголовка должна быть первой строкой файла, а заголовок строка должна начинаться со строки % MatrixMarket или %% MatrixMarket .Четыре поля, следующие за этой строкой,
- Объект обычно представляет собой матрицу , и это случай мы рассмотрим здесь. Еще одно юридическое значение вектор , формат которого аналогичен, но с некоторыми очевидные упрощения.
- Формат — это либо координата , либо массив ;
- поле либо вещественное , двойное , сложное , целое число или шаблон .

- симметрия либо общий (законный для реального, сложного, целочисленные поля или поля шаблона), симметричный (действительный, комплексный, целочисленный или шаблонный), кососимметричный (действительный, комплексный или целочисленный), или эрмитский (только комплекс).
Если поле матрицы представляет собой шаблон , то будут перечислены только местоположения ненулевых значений.Этот предполагает, очевидно, что мы используем координату формат!
Если симметрия матрицы равна симметрии или hermitian , то только записи на или под следует указать главную диагональ. Если симметрия является кососимметричным , то только записи строго под главной диагональю должны быть указаны.
Строки комментариев, если таковые имеются, должны следовать за строкой заголовка. Единственное требование — каждая строка комментария должна начинаться с
знак процента.
Единственное требование — каждая строка комментария должна начинаться с
знак процента.
Если формат был указан как массив , то Линия размера имеет вид:
м н.
где- м — количество строк в матрице;
- n — количество столбцов в матрице;
Если формат был указан как координата , то Линия размера имеет вид:
m n ненулевые
где- м — количество строк в матрице;
- n — количество столбцов в матрице;
- ненулевых — количество ненулевых элементов в матрице
(для общей симметрии), или количество ненулевых элементов
на диагонали или ниже (для симметричной или эрмитовой симметрии),
или количество ненулевых элементов ниже диагонали (для
кососимметричная симметрия).

Если формат был указан как массив , то должен быть точно следовать м * n строк данных, одна для каждая запись, перечисленная по столбцам, имеет форму
значение
где- значение — это значение записи. Если поле является комплексный , пара действительных чисел обязательна.
Если формат был указан как координата , то должен быть следовать ровно ненулевых строк данных, одна для каждая запись матрицы, которая должна быть указана, имеет вид
i j значение
где- i — строка записи;
- j — столбец записи;
- значение — это значение записи.Если поле является комплексный , пара действительных чисел обязательна.
 Если
значение формата было шаблон , тогда значение не
перечислено здесь; встречаются только значения i и j .
Если
значение формата было шаблон , тогда значение не
перечислено здесь; встречаются только значения i и j .
matrix () — CSS: каскадные таблицы стилей
Функция CSS matrix () определяет однородную матрицу 2D преобразования. Его результатом является тип данных .
Примечание: matrix (a, b, c, d, tx, ty) является сокращением для matrix3d (a, b, 0, 0, c, d, 0, 0, 0, 0, 1, 0, tx, ty, 0, 1) .
Функция matrix () задается с шестью значениями. Постоянные значения подразумеваются и не передаются в качестве параметров; остальные параметры описаны в порядке возрастания столбцов.
для tx и ty .Матрица( a , b , c , d , tx , ty )
Значения
- a b c d
- — это
<число>, описывающие линейное преобразование.
- tx ty
- Это
<номер>, описывающие применяемый перевод.
| Декартовы координаты на ℝ 2 | Однородные координаты на ℝℙ 2 | Декартовы координаты на ℝ 3 | Однородные координаты на ℝℙ 3 |
|---|---|---|---|
| acbd | actxbdty001 | actxbdty001 | ac0txbd0ty00100001 |
[a b c d tx ty] |
Значения представляют следующие функции:
matrix (scaleX (), skewY (), skewX (), scaleY (), translateX (), translateY ())
HTML
Normal
Изменено CSS
div {
ширина: 80 пикселей;
высота: 80 пикселей;
цвет фона: голубой;
}
. изменено {
преобразование: матрица (1, 2, -1, 1, 80, 80);
цвет фона: розовый;
}
изменено {
преобразование: матрица (1, 2, -1, 1, 80, 80);
цвет фона: розовый;
} Результат
Таблицы BCD загружаются только в браузере
Описание вращения в 2D | Академия роботов
Это должно быть нам хорошо знакомо: система координат, обозначенная A, и единственная точка. Мы можем описать точку вектором относительно кадра A. Ведущая буква A перед буквой P указывает на это. Я могу записать этот вектор в терминах его компонентов — его расстояний по оси XA и оси YA и единичных векторов XA и YA.Теперь давайте представим новую систему координат, кадр B, и у нее то же начало координат, которое повернуто на угол Тета. Я могу описать точку вектором относительно системы координат B, и я могу записать это в терминах единичных векторов XB и YB hat, и они обозначены здесь красным. Я могу писать выражения для шляпы XB в терминах cos Theta и sine Theta, и я могу написать выражение для шляпы YB в терминах минус синус Theta и cos Theta. Если я подставлю сюда эти два уравнения, я смогу написать это выражение. Затем я могу развернуть, переставить и исключить шляпу XA и шляпу YA. Следующее, на что следует обратить внимание, это то, что эти две системы координат имеют общее начало, тогда векторы AP и BP фактически идентичны. Коэффициенты шляпы XA должны быть одинаковыми, поэтому мы можем написать это. И коэффициенты шляпы YA должны быть одинаковыми, поэтому мы можем написать это. Возьмем эти два выражения. Слегка упростим, и теперь мы можем записать это в матричной форме. Если вы немного не уверены в этом шаге, просто умножьте его, и вы обнаружите, что у вас есть приведенные выше выражения.Теперь напишем векторную часть более лаконично. Вместо того, чтобы использовать его в терминах отдельных элементов, мы записываем его как символ P относительно конкретной системы координат. Таким образом, это выражение связывает вектор относительно кадра B с вектором относительно кадра A. Это достигается путем умножения компонентов вектора B на эту матрицу 2 x 2.
Затем я могу развернуть, переставить и исключить шляпу XA и шляпу YA. Следующее, на что следует обратить внимание, это то, что эти две системы координат имеют общее начало, тогда векторы AP и BP фактически идентичны. Коэффициенты шляпы XA должны быть одинаковыми, поэтому мы можем написать это. И коэффициенты шляпы YA должны быть одинаковыми, поэтому мы можем написать это. Возьмем эти два выражения. Слегка упростим, и теперь мы можем записать это в матричной форме. Если вы немного не уверены в этом шаге, просто умножьте его, и вы обнаружите, что у вас есть приведенные выше выражения.Теперь напишем векторную часть более лаконично. Вместо того, чтобы использовать его в терминах отдельных элементов, мы записываем его как символ P относительно конкретной системы координат. Таким образом, это выражение связывает вектор относительно кадра B с вектором относительно кадра A. Это достигается путем умножения компонентов вектора B на эту матрицу 2 x 2.
Мы можем сделать выражение еще более кратким и записать его так. И мы вводим символ R для представления матрицы вращения. Это очень краткий способ представления отношений между двумя векторами в разных системах координат, и они связаны матрицей вращения R.Здесь у нас есть то же выражение, что и раньше, и, чтобы быть немного более точным, немного более осторожным, мы добавим несколько меток к матрице R, и мы поместим ведущую A и конечную B. И это означает, что R является матрица вращения, которая вращает вектор от кадра B к кадру A. Важно отметить, что это не должно сбивать вас с толку: матрица R зависит от угла поворота от кадра A к кадру B. Порядок этих двух вещей различен и не выполняется Меня это не сбивает.
И мы вводим символ R для представления матрицы вращения. Это очень краткий способ представления отношений между двумя векторами в разных системах координат, и они связаны матрицей вращения R.Здесь у нас есть то же выражение, что и раньше, и, чтобы быть немного более точным, немного более осторожным, мы добавим несколько меток к матрице R, и мы поместим ведущую A и конечную B. И это означает, что R является матрица вращения, которая вращает вектор от кадра B к кадру A. Важно отметить, что это не должно сбивать вас с толку: матрица R зависит от угла поворота от кадра A к кадру B. Порядок этих двух вещей различен и не выполняется Меня это не сбивает.
Давайте посмотрим на матрицу вращения.Подобная матрица называется ортогональной матрицей или иногда ортонормированной матрицей. Каждый столбец в этой матрице представляет собой единичный вектор, и вы можете довольно легко это показать. Каждый столбец в матрице ортогонален другим столбцам. В этом случае есть только два столбца, и вы можете снова очень легко показать, что вектор, сформированный первым столбцом, ортогонален вектору, сформированному вторым столбцом. Скалярное произведение двух столбцов будет равно нулю. Действительно полезным свойством ортогональной матрицы является то, что ее инверсия совпадает с ее транспонированием.Вычислить инверсию матрицы довольно сложно, тогда как вычисление ее транспонирования действительно очень просто. Итак, замечательно, что у нас есть матрица, обратная к которой может быть вычислена очень просто, транспонируя элементы матрицы.
Скалярное произведение двух столбцов будет равно нулю. Действительно полезным свойством ортогональной матрицы является то, что ее инверсия совпадает с ее транспонированием.Вычислить инверсию матрицы довольно сложно, тогда как вычисление ее транспонирования действительно очень просто. Итак, замечательно, что у нас есть матрица, обратная к которой может быть вычислена очень просто, транспонируя элементы матрицы.
Еще одним свойством матрицы вращения является то, что ее определитель всегда равен 1. А это означает, что если я умножу любой вектор на эту матрицу, длина вектора не изменится. Это важное свойство матрицы вращения. Когда я поворачиваю вектор из одной системы координат в другую, его длина не изменяется.Математик сказал бы, что матрица вращения, подобная этой, принадлежит особой ортогональной группе размерности два. И, символически, мы бы написали, что, поскольку R является элементом — принадлежит — множеству SO (2), специальной ортогональной группе размерности 2. Вот выражение сверху. И, если я возьму матрицу вращения по другую сторону от знака равенства, я могу написать это. Это означает, что если я хочу повернуть вектор из системы координат A в систему координат B, я использую инверсную матрицу поворота из системы координат A в систему координат B.И помните, что инверсия матрицы вращения — это просто ее транспонирование.
Обозначения A и B в этом первом выражении являются полностью общими, и для меня вполне естественно поменять местами A и B, и теперь я могу написать это. Эти два уравнения эквивалентны. Итак, теперь я могу это написать, и это действительно важно. В нем говорится, что матрица вращения из системы координат B в систему координат A является инверсией матрицы вращения из системы координат A в систему координат B.Давайте посмотрим на некоторые конкретные примеры этого в MATLAB. Прежде всего, я собираюсь создать двумерную матрицу вращения, используя команду rot2 Toolbox для двумерной матрицы вращения. И я хочу попросить угол поворота 0 радиан. И вот матрица вращения 2 на 2, и это единичная матрица. У него единицы по диагонали и нули по недиагонали.
Я могу попросить вращение, которое соответствует углу, скажем, нулевой точке 2 радиана, и это та матрица вращения.Я также могу указать угол в градусах. Так, например, я мог бы запросить угол R, равный 30 градусам, и это соответствующая матрица вращения. Что я собираюсь сделать, так это поместить этот результат в переменную рабочего пространства R, и вот снова матрица поворота для поворота на положительные 30 градусов. Только что мы говорили об этой матрице вращения, имеющей ряд свойств, и одним из свойств было то, что столбцы ортогональны. Итак, я собираюсь создать переменную, которая представляет первый столбец матрицы, другую переменную, которая соответствует второму столбцу матрицы.И если я посмотрю на скалярное произведение этих двух векторов, мы увидим, что оно равно 0. Еще одно свойство, которое мы упомянули, заключается в том, что определитель матрицы равен положительной единице, и мы можем довольно легко это проверить.

