формула, мгновенный и средний расчет силы
В общем смысле этим термином обозначают энергетические изменения определенной системы. Классическая формула механической мощности устанавливает связь между работой и временем, которое понадобилось на завершение соответствующего процесса. В этой публикации дополнительно рассмотрены электрические и гидравлические параметры энергии, методики вычислений, измерительные приборы.
Механическая мощность характеризует скорость выполнения работы
Используемые обозначения
В стандартных формулах мощность часто обозначают буквой N без уточнения происхождения. Достаточно часто применяют P. В этом варианте понятен исходный смысл: от латинского слова potestas – действие, мощь, сила. В электротехнике часто применяют W (watt – англ., ватт). Дополнительными символами отмечают специфическое назначение NH – гидравлическая мощность от hydraulics.
Основные формулы
Когда рассчитывается средняя мощность формула содержит значения для определенных промежутков: ΔА (работа) и Δt (время).
Единицы измерения
В действующей системе единиц «СИ», утвержденной на международном уровне, мощность предлагается указывать в ваттах (один Вт = работе 1 Джоуль, сделанной за 1 секунду). Устаревшее обозначение «лошадиная сила» рекомендовано изъять из оборота. Для удобства применяют производные значения с определенными приставками (один киловатт (1кВт) = 10 в третьей степени ватт = 1 000 Вт).
Перевод 1 Вт в иные обозначения:
- килограмм-сила-метр в секунду (кгс*м/с) – 0,102;
- эрг в секунду (эрг/с) – 107;
- лошадиная сила (л.с.) метрическая/ английская – 1,36*10-3/ 1,34*10-3.
К сведению. Если в описании автомобиля указано 125 кВт, это равнозначно 170 л.с. (125*1,36=169,95).
Мощность в механике
В ходе исследования механических процессов необходимо учитывать точку приложения усилия и направление действия.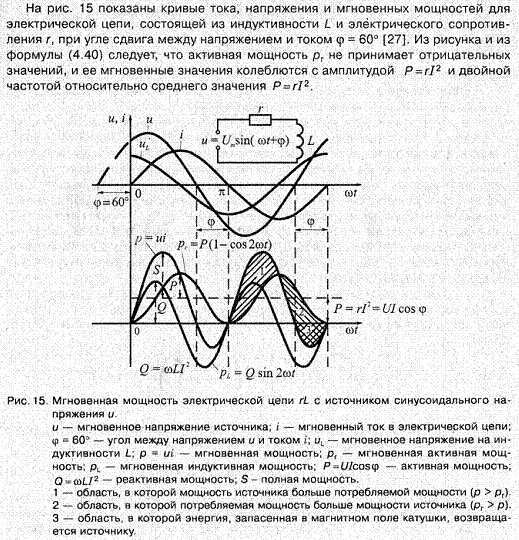
Рассчитать мощность можно по формуле (N=F*v) с учетом скорости движения (v) определенного тела. Если направления не совпадают, добавляют корректирующий множитель (cosα).
Электрическая мощность
В этой области не важны тяжесть предметов, сила трения, другие механические термины и определения. Тем не менее, суть рассматриваемой физической величины остается неизменной, подобны принципы отдельных вычислений.
Можно применить для расчета мгновенной мощности формулу:
P(a-b) = А/ Δt,
где:
- (a-b) – обозначают энергию, затраченную на перемещение заряда (q) из одной в другую точку;
- А – выполненная в ходе этого процесса работа.
Если взять все заряды (Q), напряжение в контрольных точках (U), нетрудно вычислить суммарную мощность:
P = (U/ Δt) * Q = U * Q/ Δt = U *I.
Последнее преобразование основано на классическом определении тока (количество зарядов, протекающих по соответствующему проводнику за определенное время).
Для пассивных цепей можно пользоваться законом Ома и соответствующими формулами без дополнительных коррекций. Учитывают (при наличии) источник электродвижущей силы (направление движения токов).
Формулы для расчета мощности и других параметров
При подключении техники к источникам переменного тока вычисления усложняются. Приходится интегрировать мгновенные значения с учетом определенных периодов, частоты и формы сигналов. На практике часто решают задачи по вычислению мощности потребителей, подключенных к источнику питания с синусоидальным током (напряжением).
Активная составляющая энергии в этом случае будет зависеть от фазового сдвига. Значение вычисляют по формуле:
Pa = U * I * cosϕ (для 220V).
При работе с трехфазными источниками пользуются измененным вариантом выражения:
Pa = √3 * U * I * cosϕ = 1,732 * U * I * cosϕ.
Реактивная переменная потребляется и возвращается в источник питания. Для расчета берут следующую зависимость базовых параметров:
Pq = U * I * sinϕ.
Полная мощность:
Ps = √( Pa2 + Pq2).
Приборы для измерения электрической мощности
С учетом основных компонентов формулы несложно понять, что значения необходимых параметров (ток и напряжение) можно узнать с помощью обычного мультиметра. По необходимому уровню точности выбирают методику и класс измерительного прибора.
Современный ваттметр может передавать информацию в режиме онлайн для удаленного контроля телеметрии
Специализированные изделия (ваттметры) способны отображать результаты исследований при работе в сетях постоянного и переменного тока. Специальные модификации (варметры) замеряют реактивную составляющую.
Гидравлическая мощность
Узнать производительность асинхронного электродвигателя насоса можно косвенным методом, по выполненной работе. Для этого умножают перепад измеренных (вход/ выход) давлений (ΔP) на количество перекачанной жидкости (V) в м куб. за секунду.
Пример:
- напор по манометрам – 220 кгс/ см кв.
; - производительность – 65 л/мин. = 3,9 куб. м/ час = 0,001083 куб. м /с.;
- мощность NH = ΔP * V = 220 * 100 (перевод см в м) * 0,001083 = 23,83 кВт.
;Мощность силы
Для решения практических задач меняют рассмотренные выражения необходимым образом. Расчет энергетических изменений отображает пример с падающим предметом:- в исходных данных известны высота и масса тела;
- требуется установить мощность силы формула которой отображает результат на половине пути при свободном падении;
- подставляют вместо базовых компонентов известные величины:
- F = m *g;
- V (скорость в определенной точке) = Vn (начальная скорость) + g*t.
- после завершения преобразований получают:
P = m*√(g3*h).
Мощность вращающихся объектов
Для расчета подобной системы применяют формулу:
N = M * w = (2π * M* n)/60,
где:
- M – момент силы;
- w – угловая скорость, характеризующая вращение;
- n – количество оборотов, которое совершает двигатель или другое устройство за 60 секунд.
Приведенные сведения используют с учетом целевого назначения и реальных условий. Так, в термодинамике необходимо помнить о зависимости эффективности системы от температуры окружающей среды. Тепловые потери нагревателя оценивают по соответствующей мощности на единицу площади поверхности. Аналогичным образом поступают при решении механических задач для расчета тяги, КПД, иных рабочих параметров. Как правило, приходится специальным коэффициентом компенсировать трение.
В электрических цепях ток ограничивает сопротивление проводника. Для небольших расстояний при малой мощности тщательные расчеты не нужны. Однако проект магистральной трассы обязательно содержит соответствующие вычисления. На основе полученных результатов делают выводы о среднегодовых экономических показателях. Следует помнить о необходимости учета искажений, которые добавляют при работе с переменным напряжением реактивные нагрузки.
Видео
3.1.1 Мгновенное значение.
По оси абсцисс отложено время t и величина ωt , пропорциональная времени и измеряемая в радианах.
Начальный фазный угол отсчитывается от начала синусоиды, т.е. от момента перехода синусоиды от отрицательных к положительным значе-
ниям до момента времени t =0 (начало координат). При | ψ1>0 начало си- | ||||||||||||||||||||||||
нусоиды сдвинуто влево, а при ψ2 <0 – вправо от начала координат. |
| ||||||||||||||||||||||||
|
| i, A |
| i1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| i2 |
|
|
|
| ||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
| Im2 |
|
|
|
| |||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||
|
|
|
|
| Im1 |
| 1 |
|
| Т |
| Т |
|
| 3 | Т | Т |
| |||||||
|
|
|
|
|
|
| 4 |
|
|
|
|
|
|
| |||||||||||
|
|
|
|
|
|
|
|
| 2 | 4 | t, c | ||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 3 |
|
|
|
|
| t, рад | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 2 | ||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 2 |
|
|
|
| ||||
1 >0 |
|
|
|
|
|
|
|
| 2 |
|
|
|
|
|
|
|
| ||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
| 2 <0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
|
|
|
|
|
|
| 1- 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 3.
1 – График синусоидальных токов одинаковой частоты, но с различными амплитудами и начальными фазами.
Если у нескольких синусоидальных функций, изменяющихся с одинаковой частотой, начала синусоид не совпадают, то говорят, что они сдвинуты друг относительно друга по фазе.
Сдвиг фаз измеряется разностью фаз, которая равна разности начальных фаз. На рисунке 3.1 ψ1 −ψ2 >0, т.е. ток i1 опережает по фазе ток
i2 на угол ψ1 −ψ2 , или, что тоже самое, ток i2 отстает по фазе от тока i1
на угол ψ1 −ψ2 .
Если у синусоидальных функций одной частоты одинаковые начальные фазы, то говорят, что они совпадают по фазе; если разность их фаз равна ±π , то говорят, что они противоположны по фазе (в противофазе). И, если разность их фаз равна ±π / 2 , то говорят, что они находятся в квадратуре.
Наибольшее распространение в электротехнике получил синусоидальный ток частотой 50 Гц, которая принята за стандартную в России. В США стандартной является частота f=60 Гц.
Лекция по теме: » Переменный ток»
Учебная дисциплина ОП.
03 Электротехника и электроника
«ОБЩАЯ ХАРАКТЕРИСТИКА ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА. НЕРАЗВЕТВЛЁННАЯ ЦЕПЬ ПЕРЕМЕННОГО ТОКА С АКТИВНО-ИНДУКТИВНЫМ, ЕМКОСТНЫМ СОПРОТИВЛЕНИЕМ. ВЕКТОРНЫЕ ДИАГРАММЫ. МОЩНОСТЬ ПЕРЕМЕННОГО ТОКА. КОЭФФИЦИЕНТ МОЩНОСТИ».
План лекции:
1.Переменный ток и его значение.
2. Характеристики переменного тока.
3.Максимакльное (амплитудное) и действующее (мгновенное) значение напряжения и силы тока.
4. Преобразование переменного тока в постоянный.
5.Основные элементы цепи переменного тока.
6. Резистор в цепи переменного тока.
7.Конденсатор в цепи переменного тока.
8.Катушка индуктивности в цепи переменного тока.
9. Мощность переменного тока. Коэффициент мощности.
10. Полное сопротивление в цепи переменного тока, содержащей резистор, конденсатор и катушку.
Сейчас невозможно представить себе нашу цивилизацию без электричества.
Телевизоры, холодильники, компьютеры – вся бытовая техника работает на нем. Основным источником энергии является переменный ток.
Электрический ток, питающий розетки в наших домах, является переменным.
А что это такое? Каковы его характеристики? Чем же переменный ток отличается от постоянного?
В известном опыте Фарадея при движении полосового магнита относительно катушки появлялся ток, что фиксировалось стрелкой гальванометра, соединенного с катушкой. Если магнит привести колебательное движение относительно катушки, то стрелка гальванометра будет отклоняться то в одну сторону, то в другую – в зависимости от направления движения магнита. Это означает, что возникающий в катушке ток меняет свое направление. Такой ток называют переменным.
Переменный электрический ток представляет собой электромагнитные вынужденные колебания. Переменный ток в отличие от постоянного имеет период, амплитуду и частоту.
Переменный ток— электрический ток, который с течением времени изменяется по величине и направлению или, в частном случае, изменяется по величине, сохраняя свое направление в электрической цепи неизменным.
Если говорить о переменном токе простыми словами, то можно сказать что в случае подключения электрической лампочки к сети переменного тока плюс и минус на ее контактах будут меняться местами с определенной частотой или иначе, ток будет менять свое направление с прямого на обратное.
Для чего нужен такой “переменчивый “ переменный ток, почему не использовать только постоянный?
Это сделано для того, чтобы получить возможность без особых потерь получать нужное напряжение в любом количестве способом применения трансформаторов.
Использование переменного тока позволяет передавать электроэнергию в промышленных масштабах на значительные расстояния с минимальными потерями.
Напряжение, которое подается мощными генераторами электростанций, составляет порядка 330 000-220 000 Вольт. Такое напряжение нельзя подавать в дома и квартиры, это очень опасно и сложно с технической стороны. Поэтому переменный электрический ток с электростанций подается на электрические подстанции, где происходит трансформация с высокого напряжения на более низкое, которое мы используем.
На рисунке обратное направление – это область графика ниже нуля.
Характеристики переменного тока:
Период — это время одного полного колебания.
Т – период, с
Амплитуда – это наибольшее положительное или отрицательное значение силы тока или напряжения.
Частота — это времени, в течение которого ток выполняет одно полное колебание, число полных колебаний за 1 с называется частотой тока и обозначается буквой f. Частота измеряется в герцах (Гц).
В промышленности и быту большинства стран используют переменный ток с частотой 50 Гц. В США частота промышленного тока 60 Гц.
Эта величина показывает количество изменений направления тока за одну секунду на противоположное и возвращение в исходное состояние.
Иными словами в электрической розетке, которая есть в каждом доме и куда мы включаем утюги и пылесосы, плюс с минусом на правой и левой клеммах розетки будет меняться местами с частотой 50 раз в секунду — это и есть, частота переменного тока.
Амплитуда – характеризует состояние переменного тока с течением времени.
Мгновенное и максимальное значения. Величину переменной электродвижущей силы, силы тока, напряжения и мощности в любой момент времени называют мгновенными значениями этих величин и обозначают соответственно строчными буквами (e, i, u, p).
Максимальным значением (амплитудой) переменной э. д. с. (или напряжения или тока) называется та наибольшая величина, которой она достигает за один период. Максимальное значение электродвижущей силы обозначается Еm, напряжения — Um, тока — Im.
Действующим (или эффективным) значением переменного тока называется такая сила постоянного тока, которая, протекая через равное сопротивление и за одно и то же время, что и переменный ток, выделяет одинаковое количество тепла.
Для синусоидального переменного тока действующее значение меньше максимального в 1,41 раз, т.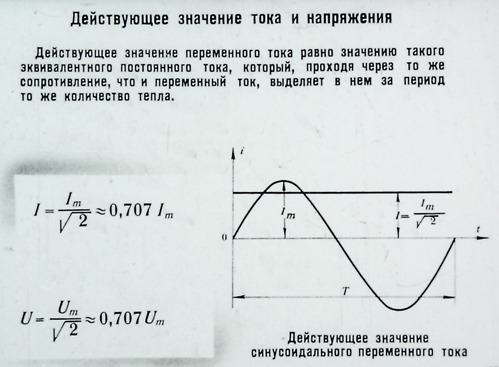
е. в раз.
Преобразование переменного тока в постоянный.
Из переменного тока, можно получить постоянный ток, для этого достаточно подключить сети переменного тока диодный мост или как его еще называют “выпрямитель”.
Из названия “выпрямитель” как нельзя лучше понятно, что делает диодный мост, он выпрямляет синусоиду переменного тока в прямую линию тем самым заставляя двигаться электроны в одном направлении.
Колебания силы тока в цепи резистора совпадают по фазе с колебаниями напряжения.
Видео по теме:«Переменный электрический ток. Получение переменного тока» см. по ссылке:
Вопросы для самоконтроля:
1.Что такое переменный электрический ток?
2. Почему переменный ток получил такое широкое распространение?
3.
Поясните, почему передача электроэнергии осуществляется с использованием переменного тока?
4.Что такое период, частота и фаза переменного тока?
5.Что называется действующим значением переменного тока? Какова связь действующих значений ЭДС, напряжения и тока с их амплитудными значениями?
6.По какой формуле определяется индуктивное сопротивление цепи переменному току?
7.По какой формуле определяется емкостное сопротивление цепи переменному току?
8.По какой формуле определяется сдвиг фаз между током и напряжением в цепях переменного тока?
9.По какой формуле вычисляется мощность переменного тока? Что называется коэффициентом мощности?
10.Как используется диод для выпрямления переменного тока?
Рассмотрим примеры решения задач:
Примеры решения расчетных задач
Задача 1. Определите сдвиг фаз колебаний напряжения и силы тока для электрической цепи, состоящей из последовательно включенных проводников с активным сопротивлением R = 1000 Ом, катушки индуктивностью L = 0,5 Гн и конденсатора емкостью С = 1 мкФ.
Определите мощность, которая выделяется в цепи, если амплитуда напряжения U0 = 100 В, а частота = 50 Гц.
Решение:
Сдвиг фаз между током и напряжением в цепях переменного тока определяется соотношением
(1)
здесь = 2 — циклическая частота. Следовательно,
Мощность, которая выделяется в цепи, определится по формуле
Для цепи переменного тока справедливо соотношение
где Z — полное сопротивление (импеданс) цепи:
Следовательно, мощность, которая выделяется в цепи
(2)
Подставив численные значения в (1), получим (минус означает, что напряжение отстает по фазе). Тогда . Подставив численные значения в (2), получим P = 0,5 Вт.
Ответ:
Задача 2. Конденсатор неизвестной емкости, катушка с индуктивностью L и сопротивлением R подключены к источнику переменного напряжения (рис. 1). Сила тока в цепи равна . Определите амплитуду напряжения между обкладками конденсатора.
Решение:
Из условия задачи видно, что сила тока и напряжение в цепи меняются синфазно. Это означает, что совпадают индуктивное и емкостное сопротивления.
(3)
Напряжение на конденсаторе будет равно
(4)
Поскольку , то
(5)
Подставляя (5) в (4), получим:
(6)
С учетом (3) соотношение (6) примет вид:
Поэтому амплитудное значение напряжения между обкладками конденсатора будет равно
Ответ:
Задача 3.
В электрической цепи из двух одинаковых конденсаторов емкости С и катушки с индуктивностью L, соединенных последовательно, в начальный момент времени один конденсатор имеет заряд q0, а второй не заряжен (рис. 2). Как будут изменяться со временем заряды конденсаторов и сила тока в контуре после замыкания ключа К?
Решение:
Цепь, приведенная на рис. 2, представляет собой колебательный контур. Сила тока в нем будет меняться по закону
(7)
Чтобы ответить на вопрос задачи, нужно найти максимальное значение силы тока I0 и частоту колебаний . Частоту колебаний можно определить по формуле
(8)
где Сэкв — емкость системы из двух последовательно соединенных конденсаторов емкостью С:
Подставляя значение Сэкв в (8), получим, что частота колебаний в контуре будет равна
(9)
Подставим значение частоты (9) в выражение для силы тока (7), тогда получим, что сила тока в цепи будет меняться по закону
(10)
Для определения I0 можно воспользоваться законом сохранения энергии.
Пусть в некоторый момент времени заряд одного из конденсаторов равен q1 , тогда заряд второго конденсатора будет q2 = q0 — q1 . В начальный момент времени энергия контура сосредоточена в электрическом поле заряженного конденсатора, в произвольный момент времени она перераспределяется между энергией электрического поля двух заряженных конденсаторов и энергией магнитного поля, сосредоточенного в катушке индуктивности. Следовательно, согласно закону сохранения энергии,
Отсюда можно найти зависимость силы тока от заряда q1.
Чтобы найти максимальное значение силы тока, нужно взять производную от I по q1 и приравнять ее к нулю.
Из последнего выражения видно, что максимальное значение силы тока достигается при . Следовательно,
Подставляя полученное значение для максимального значения силы тока в (10), получим, что сила тока в цепи будет меняться по закону
Чтобы найти закон изменения зарядов на пластинах конденсатора, воспользуемся выражением .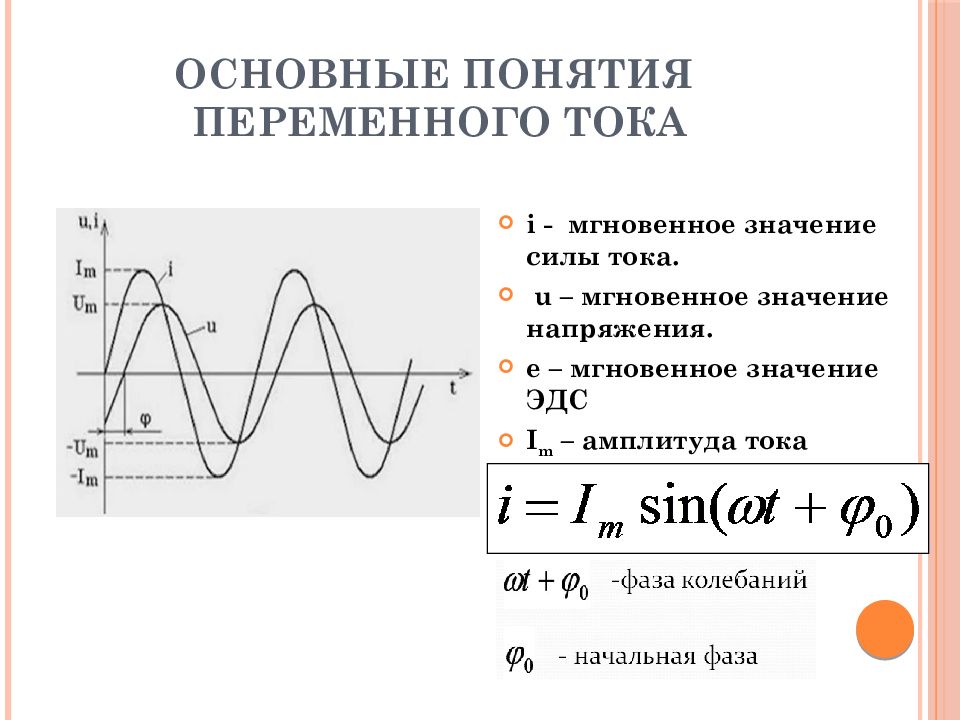
Преобразовав его, получим квадратное уравнение для q1:
Решая уравнение, получим:
Разные знаки означают, что в начальный момент времени любой конденсатор может либо иметь заряд q0, либо быть незаряженным. Пусть
Тогда
Ответ:
Задача 4. Имеются два колебательных контура с одинаковыми катушками и конденсаторами. В катушку одного из контуров вставили железный сердечник, увеличивший ее индуктивность в n = 4 раза. Найдите отношение резонансных частот контуров и их энергий, если максимальные заряды на конденсаторах одинаковы.
Решение:
Резонансные частоты контуров могут быть определены по формуле Томсона:
Отсюда
Ответ:
Задача 5.
Два сопротивления R1 и R2 и два диода подключены к источнику переменного тока с напряжением U так, как показано на рис. 3. Найдите среднюю мощность, выделяющуюся в цепи.
Решение:
Ток половину периода идет через один диод (например, 1). За это время на сопротивлении R1 выделяется средняя мощность
В течение второго полупериода ток идет через диод 2, выделяя на нем среднюю мощность
Таким образом, за полный период выделяется средняя мощность
Ответ:
Задачи для самостоятельного решения:
№ 1. В ц.п.т. с напряжением 220 В включена активная нагрузка сопротивлением 40 Ом. Определите ток цепи.
№ 2. Определите сопротивление конденсатора емкостью 5 мкФ при частоте 50 Гц.
№3. Определите сопротивление катушки индуктивностью 0,01 Гн при частоте 50 Гц.
№ 4. Определите ток, проходящий через катушку, индуктивное сопротивление которой 5 Ом, а активное сопротивление 1 Ом, если напряжение сети переменного тока 12 В.
№ 5. В ц.п.т. с напряжением 220 В включена эл.лампа, по спирали которой течет ток 5 А. Вычислите активную мощность этой лампы.
№ 6. В электрическую цепь напряжением 220 В последовательно включены реостат сопротивлением 5 Ом, катушка с активным сопротивлением 6 Ом и индуктивным сопротивлением 4 Ом, конденсатор с емкостным сопротивлением 3 Ом. Определите ток в цепи. Постройте векторную диаграмму токов и напряжений.
№ 7. В ц.п.т. с напряжением 220 В включены конденсатор емкостью 100 мкФ и катушка индуктивностью 0,05 Гн. Определите реактивную мощность цепи.
Постройте векторную диаграмму токов и напряжений.
№ 8.
В ц.п.т. с напряжением 380 В включены активное сопротивление 50 Ом и конденсатор емкостью 1000 мкФ. Определите полную мощность цепи.
Постройте векторную диаграмму токов, напряжений и мощностей.
№ 9. В ц.п.т. напряжением 110 В последовательно включены активное сопротивление 30 Ом, емкостное – 45 Ом и индуктивное — 50 Ом. Определите полное сопротивление этой цепи.
№ 10. В ц.п.т. с напряжением 220 В включены активное сопротивление 20 Ом, конденсатор емкостью 100 мкФ и катушка индуктивностью 0,05 Гн. Определите полную мощность цепи. Постройте векторную диаграмму токов, напряжений, мощностей.
Домашнее задание:
1.Выучить и законспектировать лекцию.
2. Разобрать и записать в тетрадь примеры решения задач, которые приведены в конце лекции.
3. Ответить на вопросы для самоконтроля.
4. Выполнить на оценку задания в тестовой форме:
Ответы (указав фамилию, имя, название теста и группу) прислать по следующему адресу в контакте: http://vk.
com/id216653613
Моделирование в электроэнергетике — Параметры электроэнергетического режима, записанные через изменение мгновенных значений электрических параметров
Параметры электроэнергетического режима, записанные через изменение мгновенных значений электрических параметров
Режим работы электроэнергетической системы в любой момент времени характеризуется изменяющимися мгновенными значениями тока и напряжения. Изменение данных параметров происходит с течением времени по закону, который можно записать следующим математическим выражением:
– амплитудные значения тока и напряжения;
– начальная фаза тока;
– начальная фаза напряжения;
– круговая частота (угловая частоты).
Как видно из представленных соотношений изменение тока и напряжения осуществляется с течением времени по синусоидальному закону (см. рис. 1). Основными величинами, которые определяют синусоидальный сигнал, являются: амплитуда, угловая частота и начальная фаза.
Рис.1.Изменение тока и напряжения с течением времени при произвольном выборе начало отсчета
Для описания характеристики интенсивности (силы действия) электрических параметров используется такое понятие, как действующее значение. Под действующим значением переменного тока понимают такое значение, при котором за время одного периода в проводнике выделяется столько же теплоты, сколько при постоянном токе. Математически данное утверждение записывается в следующем виде:
где I – постоянный ток;
i(t) – мгновенное значение переменного тока;
T – период изменения переменного тока.
В результате получаем, что действующее значение переменного тока определяется как среднеквадратичное значение переменного тока за период.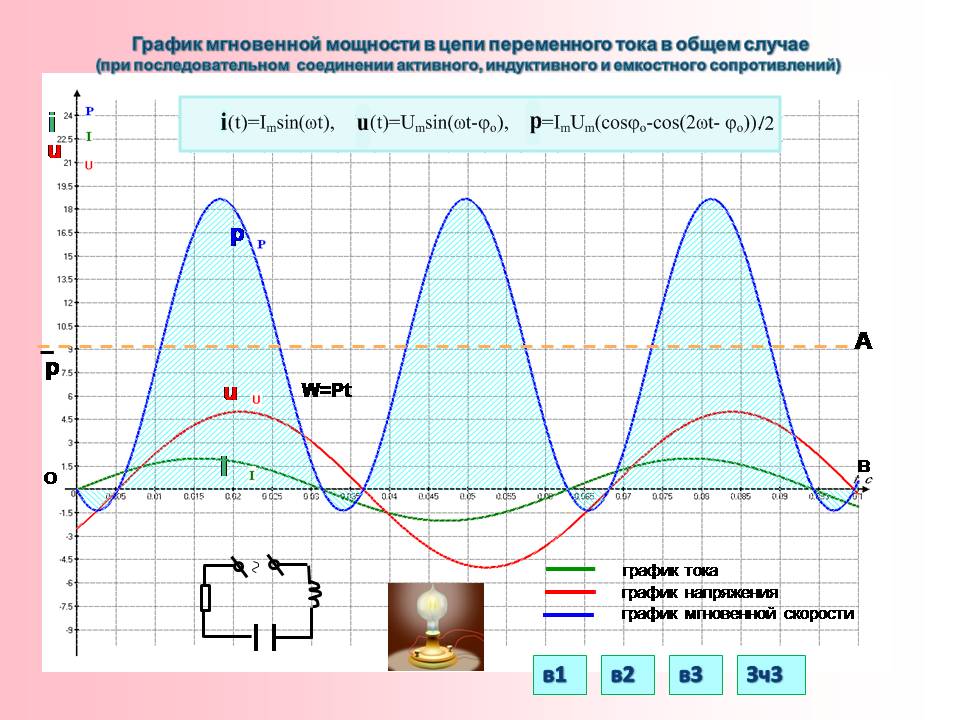
Аналогичным образом определяется действующее значение переменного напряжения:
В зарубежной литературе для обозначения действующего значения сигнала, используется аббревиатура RMS (rootmeansquare). Однако измерительные приборы, которые промаркированы аббревиатурой RMS, не всегда измеряют действующие значения сигнала по вышеописанному методу. В большинстве измерительных приборов старого образца применяется способ измерения действующих значений тока (или напряжения) основанный на измерении среднего выпрямленного значения за полупериод. Затем полученное среднее значение ставилось в соответствие действующему значению (градуировка прибора), так как действующее значение синусоидального сигнала может быть определено через среднее значение умноженное на коэффициент «1,1». Данный способ определения действующего значения был связан с тем, что принцип работы большинства аналоговых приборов (стрелочных приборов) основан на измерении какого-то действия за определенный промежуток времени, т.
е. определение среднего значения сигнала. В результате, измерительные приборы с меткой RMS могут отображать правильный результат только при синусоидальном сигнале.
Рис.2.Результат измерений действующих сигналов в зависимости от разной формы кривой
В современных устройствах (в микропроцессорной технике) применяются алгоритмы, которые определяют действующее значение тока за период в соответствии с вышеописанным методом. В результате полученные устройства показывают правильные результаты при любом негармоническом сигнале с некоторыми ограничениями по форме и частоте входного сигнала. Данные устройства в зарубежной литературе получили аббревиатуру TRMS (TrueRootMeanSquared – истинное среднеквадратичное значение).
Средним значением синусоидального тока (или напряжения) называется среднее арифметическое всех его значений за полупериод. Математически данное утверждение записывается в следующем виде:
Следует отметить, что среднее значение синусоидального тока (или напряжения) за период равно нулю, так как на протяжении первого полупериода ток имеет одно направление, а на протяжении второго полупериода – обратное.
Однако в случае выпрямления переменного тока, постоянный ток имеет одинаковое направление, и величина выпрямленного тока определяется среднеарифметическим всех мгновенных значений. Математически данное утверждение записывается в следующем виде:
Полная мощность в сети переменного тока
Величиной, которая определяет фактические электрические нагрузки на провода линий электропередачи или кабельные линии, обмотки силовых трансформаторов, аппаратуру распределительных устройств, является полная мощность электрической сети. Полная мощность – величина, равная произведению действующих значений периодического электрического тока в цепи и напряжения на ее зажимах. Полная мощность трехфазной сети переменного тока определяется следующим образом:
где – действующее значение фазного напряжения;
– действующее значение линейного напряжения;
– действующее значение фазного тока.
Полная мощность состоит из двух составляющих – активной и реактивной мощности.
Данные переменные связаны между собой следующим образом:
– активная мощность;
– реактивная мощность.
Активная мощность в сети переменного тока
Протекание синусоидальных токов по участкам электрической цепи сопровождается потреблением энергии. Так как ток и напряжение постоянно меняют своё значение, то потребляемая мощность будет меняться в каждый момент времени. Данная мощность называется мгновенной мощностью , которая определяется произведением мгновенного значения напряжения на мгновенное значение тока в этой цепи.
Рис.3.Изменение мгновенной мощности с течением времени.
Мгновенная мощность на графике обозначена заштрихованной областью. Из представленного графика видно, что мгновенная мощность имеет постоянную составляющую и гармоничную составляющую, частота которой в два раза больше частоты напряжения и тока.
Следует отметить, что мгновенная мощность в случае активно-индуктивной или активно-емкостной нагрузки может менять свой знак, который зависит от сдвига фаз между током и напряжением.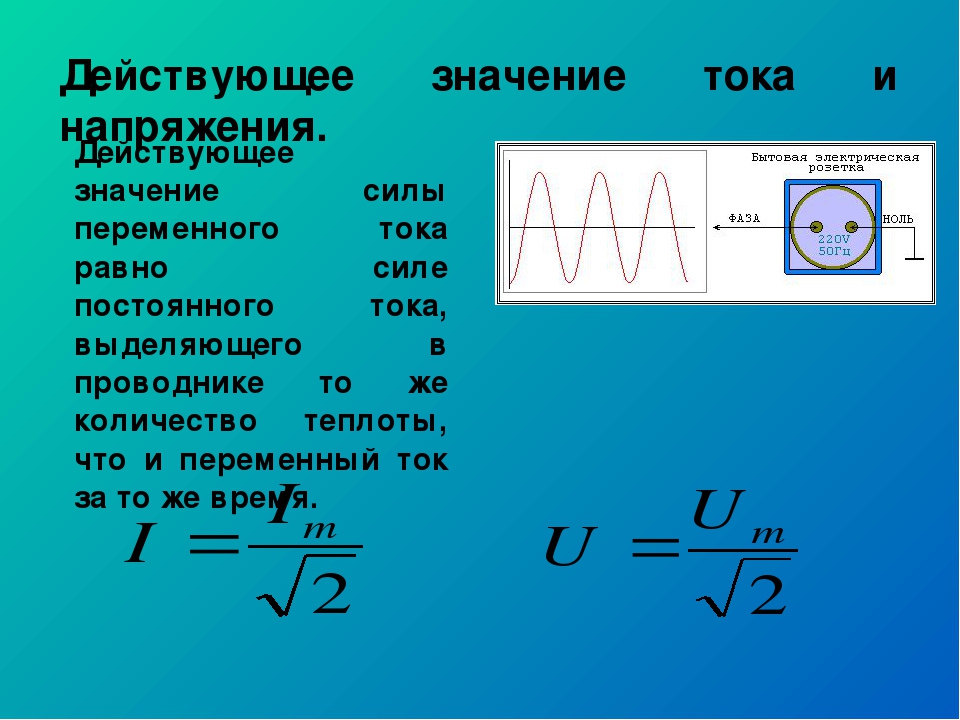
Когда мгновенная мощность отрицательна, то энергия возвращается из двухполюсника к источнику питания. Такой возврат энергии к источнику происходит за счет того, что энергия периодически запасается в магнитных и электрических полях соответственно индуктивных и емкостных элементов, входящих в состав двухполюсника.
Чтобы понять какое количество энергии потребляется в сети переменного тока, необходимо взять среднюю мощность за период. Таким образом, среднее арифметическое значение мгновенной мощности за период называется активной мощностью. Формула для определения активной мощности записывается следующим образом:
Введем понятия об угле сдвига между током и напряжением , который определяется разностью начальной фазы напряжения и начальной фазой тока. Формула для определения угла сдвига между током и напряжением записывается следующим образом:
Из представленной формулы видно, что сдвиг фаз между током и напряжением может быть как положительным, так и отрицательным:
— Положительный сдвиг фаз между током и напряжением указывает на то, что напряжение по фазе опережает ток (нагрузка активно-индуктивная).
— Отрицательный сдвиг фаз между током и напряжением указывает на то, что напряжение по фазе отстает от тока (нагрузка активно-емкостная).
Таким образом, формула для активной мощности в одной фазе может быть записана в следующем виде:
Для трехфазной сети переменного тока значение активной мощности будет определяться по следующему выражению:
Реактивная мощность в сети переменного тока
Реактивная мощность периодически циркулирует между источником и приемником, так как в процессе каждого периода реактивные элементы (емкость и индуктивность) накапливают энергию, а затем возвращают ее источнику. Реактивная мощность не может преобразоваться в тепловую или механическую энергию, таким образом, данная энергия не выполняет никакой работы. Реактивная мощность определяет небаланс между полной и активной мощностями.Таким образом, формула для определения реактивной мощности в одной фазе может быть записана в следующем виде:
Для трехфазной сети переменного тока значение реактивной мощности будет определяться по следующему выражению:
Следует отметить, что угол сдвига фаз между током и напряжением может быть как положительным, так и отрицательным:
— Положительный сдвиг фаз между током и напряжением указывает на то, что напряжение по фазе опережает ток — нагрузка активно-индуктивная.
В таком режиме работы сети реактивная мощность будет положительна
— Отрицательный сдвиг фаз между током и напряжением указывает на то, что напряжение по фазе отстает от тока (нагрузка активно-емкостная). В таком режиме работы сети реактивная мощность будет отрицательна
В качестве примера, рассмотрим один из способов измерения реактивной мощности в сети переменного тока с помощью одного ваттметра, который подключается специальным образом. Следует обратить внимание на то, что данный метод измерения является фиктивным, так как ваттметр осуществляет измерение только активной мощности в сети. В связи со специфичным подключением ваттметра измеренное значение активной мощности будет пропорциональна величине реактивной мощности в сети переменного тока.
В соответствии с данным методом ваттметр подключается по цепям тока — в рассечку любой фазы (например, фаза А), а по цепям напряжения — к линейному напряжению оставшихся фаз (например, к линейному напряжению В-С). Схема соединения ваттметра в сети переменного тока показана на схеме (см. рис.4).
Рис.4.Схема включения ваттметра для измерения мощности в симметричной трехфазной сети, которая по величине пропорциональна значению реактивной мощности, и векторная диаграмма
Вектор линейного напряжения будет определяться разностью фазных напряжений:
В результате к ваттметру подводится ток в фазе «А» и линейное напряжение, которое отстает от тока на угол:
Подключенный таким образом ваттметр будет измерять следующее значение активной мощности:
Полная реактивная мощность в сети переменного тока будет определяться следующим соотношением:
Таким образом, данный метод позволяет определить величину реактивной мощности в сети переменного тока, которая пропорциональна величине активной мощности, измеряемой ваттметром. Данным методом можно пользоваться только в симметричной трехфазной сети. Следует отметить, что данная схема используется редко, так как в случае незначительной асимметрии фаз применение данного метода дает значительную погрешность.
Для того, чтобы добавить Ваш комментарий к статье, пожалуйста, зарегистрируйтесь на сайте.
Урок 8. переменный электрический ток — Физика — 11 класс
Физика, 11 класс
Урок 8. Переменный электрический ток
Перечень вопросов, рассматриваемых на уроке:
1) Свойства переменного тока;
2) Понятия активного сопротивления, индуктивного и ёмкостного сопротивления;
3) Особенности переменного электрического тока на участке цепи с резистором;
4) Определение понятий: переменный электрический ток, активное сопротивление, индуктивное сопротивление, ёмкостное сопротивление.
Глоссарий по теме
Переменный электрический ток — это ток, периодически изменяющийся со временем.
Сопротивление элемента электрической цепи (резистора), в котором происходит превращение электрической энергии во внутреннюю называют активным сопротивлением.
Действующее значение силы переменного тока равно силе такого постоянного тока, при котором в проводнике выделяется то же количество теплоты, что и при переменном токе за то же время.
Величину ХC, обратную произведению ωC циклической частоты на электрическую ёмкость конденсатора, называют ёмкостным сопротивлением.
Величину ХL, равную произведению циклической частоты на индуктивность, называют индуктивным сопротивлением.
Основная и дополнительная литература по теме урока:
Мякишев Г.Я., Буховцев Б.Б., Чаругин В.М. Физика.11 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2014. – С. 86 – 95.
Рымкевич А.П. Сборник задач по физике. 10-11 класс. — М.: Дрофа, 2014. – С. 128 – 132.
Степанова. Г.Н. Сборник задач по физике. 10-11 класс. М., Просвещение 1999 г.
Е.А. Марон, А.Е. Марон. Контрольные работы по физике. М., Просвещение, 2004
Основное содержание урока
Сейчас невозможно представить себе нашу цивилизацию без электричества. Телевизоры, холодильники, компьютеры – вся бытовая техника работает на нем. Основным источником энергии является переменный ток.
Электрический ток, питающий розетки в наших домах, является переменным А что это такое? Каковы его характеристики? Чем же переменный ток отличается от постоянного? Об этом мы поговорим на данном уроке.
В известном опыте Фарадея при движении полосового магнита относительно катушки появлялся ток, что фиксировалось стрелкой гальванометра, соединенного с катушкой. Если магнит привести колебательное движение относительно катушки, то стрелка гальванометра будет отклоняться то в одну сторону, то в другую – в зависимости от направления движения магнита. Это означает, что возникающий в катушке ток меняет свое направление. Такой ток называют переменным.
Электрический ток, периодически меняющийся со временем по модулю и направлению, называется переменным током.
Переменный электрический ток представляет собой электромагнитные вынужденные колебания. Переменный ток в отличие от постоянного имеет период, амплитуду и частоту.
Сила тока и напряжение меняются со временем по гармоническому закону, такой ток называется синусоидальным. В основном используется синусоидальный ток. Колебания тока можно наблюдать с помощью осциллографа.
Если напряжение на концах цепи будет меняться по гармоническому закону, то и напряженность внутри проводника будет так же меняться гармонически. Эти гармонические изменения напряженности поля, в свою очередь вызывают гармонические колебания упорядоченного движения свободных частиц и, следовательно, гармонические колебания силы тока. При изменении напряжения на концах цепи, в ней с очень большой скоростью распространяется электрическое поле. Сила переменного тока практически во всех сечениях проводника одинакова потому, что время распространения электромагнитного поля превышает период колебаний.
Рассмотрим процессы, происходящие в проводнике, включенном в цепь переменного тока. Сопротивление проводника, в котором происходит превращение электрической энергии во внутреннюю энергию, называют активным. При изменении напряжения на концах цепи по гармоническому закону, точно так же меняется напряженность электрического поля и в цепи появляется переменный ток.
При наличии такого сопротивления колебания силы тока и напряжения совпадают по фазе в любой момент времени.
𝒾 — мгновенное значение силы тока;
ℐm— амплитудное значение силы тока.
– колебания напряжения на концах цепи.
Колебания ЭДС индукции определяются формулами:
При совпадении фазы колебаний силы тока и напряжения мгновенная мощность равна произведению мгновенных значений силы тока и напряжения. Среднее значение мощности равно половине произведения квадрата амплитуды силы тока и активного сопротивления.
Часто к параметрам и характеристикам переменного тока относят действующие значения. Напряжение, ток или ЭДС, которая действует в цепи в каждый момент времени — мгновенное значение (помечают строчными буквами — і, u, e). Однако оценивать переменный ток, совершенную им работу, создаваемое тепло сложно рассчитывать по мгновенному значению, так как оно постоянно меняется. Поэтому применяют действующее, которое характеризует силу постоянного тока, выделяющего за время прохождения по проводнику столько же тепла, сколько это делает переменный.
Действующее значение силы переменного тока равно силе такого постоянного тока, при котором в проводнике выделяется то же количество теплоты, что и при переменном токе за то же время.
Um — амплитудное значение напряжения.
Действующие значения силы тока и напряжения:
Электрическая аппаратура в цепях переменного тока показывает именно действующие значения измеряемых величин.
Конденсатор включенный в электрическую цепь оказывает сопротивление прохождению тока. Это сопротивление называют ёмкостным.
Величину ХC, обратную произведению циклической частоты на электрическую ёмкость конденсатора, называют ёмкостным сопротивлением.
Ёмкостное сопротивление не является постоянной величиной. Мы видим, что конденсатор оказывает бесконечно большое сопротивление постоянному току.
Если включить в электрическую цепь катушку индуктивности, то она будет влиять на прохождение тока в цепи, т.е. оказывать сопротивление току. Это можно объяснить явлением самоиндукции.
Величину ХL, равную произведению циклической частоты на индуктивность, называют индуктивным сопротивлением.
XL= ωL
Если частота равна нулю, то индуктивное сопротивление тоже равно нулю.
При увеличении напряжения в цепи переменного тока сила тока будет увеличиваться так же, как и при постоянном токе. В цепи переменного тока содержащем активное сопротивление, конденсатор и катушка индуктивности будет оказываться сопротивление току. Сопротивление оказывает и катушка индуктивности, и конденсатор, и резистор. При расчёте общего сопротивления всё это надо учитывать. Основываясь на этом закон Ома для переменного тока формулируется следующим образом: значение тока в цепи переменного тока прямо пропорционально напряжению в цепи и обратно пропорционально полному сопротивлению цепи.
Если цепь содержит активное сопротивление, катушку и конденсатор соединенные последовательно, то полное сопротивление равно
Закон Ома для электрической цепи переменного тока записывается имеет вид:
Преимущество применения переменного тока заключается в том, что он передаётся потребителю с меньшими потерями.
В электрической цепи постоянного тока зная напряжение на зажимах потребителя и протекающий ток можем легко определить потребляемую мощность, умножив величину тока на напряжение. В цепи переменного тока мощность равна произведению напряжения на силу тока и на коэффициент мощности.
Мощность цепи переменного тока
P=IU cosφ
Величина cosφ – называется коэффициентом мощности
Коэффициент мощности показывает какая часть энергии преобразуется в другие виды. Коэффициент мощности находят с помощью фазометров. Уменьшение коэффициента мощности приводит к увеличению тепловых потерь. Для повышения коэффициента мощности электродвигателей параллельно им подключают конденсаторы. Конденсатор и катушка индуктивности в цепи переменного тока создают противоположные сдвиги фаз. При одновременном включении конденсатора и катушки индуктивности происходит взаимная компенсация сдвига фаз и повышение коэффициента мощности. Повышение коэффициента мощности является важной народнохозяйственной задачей.
Разбор типовых тренировочных заданий
1. Рамка вращается в однородном магнитном поле. ЭДС индукции, возникающая в рамке, изменяется по закону e=80 sin 25πt. Определите время одного оборота рамки.
Дано: e=80 sin 25πt.
Найти: T.
Решение:
Колебания ЭДС индукции в цепи переменного тока происходят по гармоническому закону
Согласно данным нашей задачи:
Время одного оборота, т.е. период связан с циклической частотой формулой:
Подставляем числовые данные:
Ответ: T = 0,08 c.
2. Чему равна амплитуда силы тока в цепи переменного тока частотой 50 Гц, содержащей последовательно соединенные активное сопротивление 1 кОм и конденсатор емкости С = 1 мкФ, если действующее значение напряжения сети, к которой подключен участок цепи, равно 220 В?
Дано:
ν=50 Гц,
R=1 кОм=1000 Ом,
C=1 мкФ=10-6 Ф,
U=220 В.
Найти: Im
Решение:
Напишем закон Ома для переменного тока:
I=U/Z
Для амплитудных значений силы тока и напряжения, мы можем записать Im=Um/Z?
Полное сопротивление цепи равно:
Подставляя числовые данные находим полное сопротивление Z≈3300 Ом. Так как действующее значение напряжения равно:
то после вычислений получаем Im ≈0,09 Ом.
Ответ: Im ≈0,09 Ом.
2. Установите соответствие между физической величиной и прибором для измерения.
Физические величины | Физические приборы |
Сила тока | Омметр |
Напряжение | Вольтметр |
Сопротивление | Амперметр |
Мощность | Ваттметр |
Правильный ответ:
Физические величины | Физические приборы |
Сила тока | Амперметр |
Напряжение | Вольтметр |
Сопротивление | Омметр |
Мощность | Ваттметр |
Синусоидальный ток и основные характеризующие его величины.
Синусоидальный ток и основные характеризующие его величины.
Синусоидальный ток представляет собой ток, изменяющийся во времени по синусоидальному закону (рис. 3.1):
(3.1)
Максимальное значение функции называют амплитудой. Амплитуду тока обозначают Im.
Период Т — это время, за которое совершается одно полное колебание.
Рисунок 3.1
Частота f — число колебаний в 1 с (единица частоты f — герц (Гц) или с-1):
(3.2)
Угловая частота (единица угловой частоты — рад/с или с-1)
(3.3)
Аргумент синуса, т. е. ( t + ), называют фазой — характеризует состояние колебания (числовое значение) в данный момент времени t.
Любая синусоидально изменяющаяся функция определяется тремя величинами: амплитудой, угловой частотой и начальной фазой.
Синусоидальные токи и ЭДС сравнительно низких частот (до нескольких килогерц) получают с помощью синхронных генераторов (их изучают в курсе электрических машин). Синусоидальные токи и ЭДС высоких частот получают с помощью различных полупроводниковых генераторов (подробно рассматриваемых в курсе радиотехники и менее подробно — в курсе ТОЭ). Источник синусоидальной ЭДС и источник синусоидального тока обозначают на электрических схемах так же, как и источники постоянной ЭДС и тока, но обозначают их е и j(или e(t) и j (t)).
Среднее и действующее значения синусоидально изменяющейся величины.
Под средним значением синусоидально изменяющейся величины понимают ее среднее значение за полпериода. Среднее значение тока
(3.4)
т. е. среднее значение синусоидального тока составляет 2/ = 0,638 от амплитудного. Аналогично,
Eср = 2Em/ ; Uср = 2Um/ .
Широко применяют понятие действующего значения синусоидально изменяющейся величины (его называют также эффективным или среднеквадратичным). Действующее значение тока
(3.5)
Следовательно, действующее значение синусоидального тока равно 0,707 от амплитудного. Аналогично
Действующее значение синусоидального тока I численно равно значению такого постоянного тока, который за время, равное периоду синусоидального тока, выделяет такое же количество теплоты, что и синусоидальный ток.
Большинство измерительных приборов показывают действующее значение измеряемой величины.
Коэффициент амплитуды кa — это отношение амплитуды периодически изменяющейся функции к ее действующему значению. Для синусоидального тока
(3.6)
Под коэффициентом формы кф —понимают отношение действующего значения периодически изменяющейся функции к ее среднему за полпериода значению. Для синусоидального тока
(3.7)
Сложение и вычитание синусоидальных функций времени на комплексной плоскости. Векторная диаграмма.
Положим, что необходимо сложить два тока (i1 и i2) одинаковой частоты. Сумма их дает некоторый ток той же частоты:
Требуется найти амплитуду Iти начальную фазу ψ тока i. С этой целью ток i1 изобразим на комплексной плоскости (рис. 3.4) вектором = I1теjψ1, а ток i2 — вектором = I2теjψ2. Геометрическая сумма векторов и I2т даст комплексную амплитуду суммарного тока Iт = Iт e—jψ2 . Амплитуда тока Iт определяется длиной суммарного вектора, а начальная фаза ψ — углом, образованным этим вектором и осью + 1.
Рисунок 3.4
Для определения разности двух токов (ЭДС, напряжений) следует на комплексной плоскости произвести не сложение, а вычитание соответствующих векторов.
Обратим внимание на то, что если бы векторы , ,Iтстали вращаться вокруг начала координат с угловой скоростью ω, то взаимное расположение векторов относительно друг друга осталось бы без изменений.
Векторной диаграммойназывают совокупность векторов на комплексной плоскости, изображающих синусоидально изменяющиеся функции времени одной и той же частоты и построенных с соблюдением правильной ориентации их относительно друг друга по фазе. Пример на рис. 3.4.
Мгновенная мощность.
Протекание синусоидальных токов по участкам электрической цепи сопровождается потреблением энергии от источников. Скорость поступления энергии характеризуется мощностью. Под мгновенным значением мощности, или под мгновенной мощностью, понимают произведение мгновенного значения напряжения и на участке цепи на мгновенное значение тока i, протекающего по этому участку:
(3.14)
где р — функция времени.
Перед тем как приступить к изучению основ расчета сложных цепей синусоидального тока, рассмотрим соотношения между токами и напряжениями в простейших цепях, векторные диаграммы для них и кривые мгновенных значений различных величин. Элементами реальных цепей синусоидального тока являются резисторы, индуктивные катушки и конденсаторы. Протеканию синусоидального тока оказывают сопротивление резистивные элементы (резисторы) — в них выделяется энергия в виде теплоты — и реактивные элементы (индуктивные катушки и конденсаторы) — они то запасают энергию в магнитном (электрическом) поле, то отдают ее. Рассмотрим поведение этих элементов.
Комплексная проводимость.
Под комплексной проводимостью Y понимают величину, обратную комплексному сопротивлению Z:
(3.37)
Единица комплексной проводимости — См (Ом-1). Действительную часть ее обозначают через g, мнимую — через b.
Так как
то
(3.38)
Если X положительно, то и b положительно. При X отрицательном b также отрицательно.
При использовании комплексной проводимости закон Ома (3.35) запи-сывают так:
(3.39)
или
где Ia — активная составляющая тока;Ir — реактивная составляющая ; тока; U — напряжение на участке цепи, сопротивление которого равно Z.
Определение дуальной цепи.
Две электрические цепи называют дуальными, если закон изменения контурных токов в одной из них подобен закону изменения узловых потенциалов в другой. Исходную и дуальную ей схемы называют взаимно обратными.
В качестве простейшего примера на рис. 3.32изображены две дуальные цепи.
Рис.3.32.
Схема на рис. 3.32, а состоит из источника ЭДС Е и последовательно с ним включенных активного, индуктивного и емкостного элементов (R, L, С). Схема на рис. 3.32б состоит из источника тока J3и трех параллельных ветвей. Первая ветвь содержит активную проводимость gэ вторая — емкость Сэ, третья — индуктивность Zэ.
Для того чтобы показать, какого рода соответствие имеет место в дуальных цепях, составим для схемы на рис. 3.32, а уравнение по методу контурных токов:
(3.85)
а для схемы на рис. 3.32б — по методу узловых потенциалов, обозначив потенциал точки а через φа, положив равным нулю потенциал второго узла:
(3.86)
Если параметры gэ, Lэ. Сэ, схемы (рис. 3.32б) согласовать с параметрами R, L, С схемы (рис. 3.32а) таким образом, что
(3.87)
где к — некоторое произвольное число (масштабный множитель преоб-разования), Ом2, то
(3.88)
С учетом равенства (3.88) перепишем уравнение (3.86) следующим об-разом:
(3.89)
Из сопоставления уравнений (3.85) и (3.89) следует, что если ток Jэ источника тока в схеме на рис. 3.32б изменяется с той же угловой частотой, что и ЭДС Е в схеме на рис. 3.32а, и численно равен E , а параметры обеих схем согласованы в соответствии с уравнением (3.87), то при к = 1Ом 2. закон изменения во времени потенциала φ0 в схеме на рис. 3.32б совпадет с законом изменения во времени тока I в схеме на рис. 3.32а.
Если свойства какой-либо из схем изучены, то они полностью могут быть перенесены на дуальную ей схему.
Между входным сопротивлением Zисх исходного двухполюсника и входной проводимостью Yдуалдуального ему двухполюсника существует соотношение Zисх =k Yдуал
Из (3.88) получаем соотношение между частотной характеристикой чисто реактивного исходного двухполюсника Хисх(ω) и частотной характеристикой дуального ему тоже чисто реактивного двухполюсника b дуал (ω). Каждому элементу исходной схемы (схемы с источниками ЭДС E и параметрами R, L, С) отвечает свой элемент эквивалентной дуальной схемы (схемы с источниками тока J3 и параметрами gэ, Сэ, Lэ).
Синусоидальный ток и основные характеризующие его величины.
Синусоидальный ток представляет собой ток, изменяющийся во времени по синусоидальному закону (рис. 3.1):
(3.1)
Максимальное значение функции называют амплитудой. Амплитуду тока обозначают Im.
Период Т — это время, за которое совершается одно полное колебание.
Рисунок 3.1
Частота f — число колебаний в 1 с (единица частоты f — герц (Гц) или с-1):
(3.2)
Угловая частота (единица угловой частоты — рад/с или с-1)
(3.3)
Аргумент синуса, т. е. ( t + ), называют фазой — характеризует состояние колебания (числовое значение) в данный момент времени t.
Любая синусоидально изменяющаяся функция определяется тремя величинами: амплитудой, угловой частотой и начальной фазой.
Синусоидальные токи и ЭДС сравнительно низких частот (до нескольких килогерц) получают с помощью синхронных генераторов (их изучают в курсе электрических машин). Синусоидальные токи и ЭДС высоких частот получают с помощью различных полупроводниковых генераторов (подробно рассматриваемых в курсе радиотехники и менее подробно — в курсе ТОЭ). Источник синусоидальной ЭДС и источник синусоидального тока обозначают на электрических схемах так же, как и источники постоянной ЭДС и тока, но обозначают их е и j(или e(t) и j (t)).
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
Мгновенная мощность и средняя мощность
Мгновенная мощность — это количество энергии, перемещающееся в один момент времени. В общем, это определяется следующим образом: p (t) = v (t) x i (t), это уравнение 1.
НАЖМИТЕ ИЗОБРАЖЕНИЕ, ЧТОБЫ УВЕЛИЧИТЬ:
То есть значение мощности P в момент времени t равно напряжению во время t, умноженному на ток в момент t. Для синусоидального сигнала обратите внимание, что напряжение колеблется через ноль вольт дважды за цикл, поэтому мгновенная мощность равна нулю как минимум дважды за цикл.Если нагрузка имеет как сопротивление, так и реактивное сопротивление, тогда ток, который также колеблется через ноль дважды за цикл, смещается от момента, когда напряжение падает до нуля, и, таким образом, мгновенная мощность будет колебаться через ноль 4 раза за цикл, а именно, когда p (t) x 0V xi (t) = 0V и
p (t) xv (t) x 0V = 0V
Также обратите внимание, что мгновенная мощность может быть отрицательной для части цикла и положительной для части цикла, если в цепи есть как сопротивление, так и реактивное сопротивление. Знак указывает, в каком направлении течет мощность.
НАЖМИТЕ ИЗОБРАЖЕНИЕ, ЧТОБЫ УВЕЛИЧИТЬ:
p (t)> 0: мощность поглощается током
p (t) <0: мощность поглощается источником
Ваша первая формула не показывает переменную времени t, поэтому она может быть неточной при решении мгновенной мощности. Обычно мгновенное напряжение v (t) выражается как:
v (t) = Vm cos (wt + theta v), где w — омега
Ток i (t) может быть задан как синусоидальный сигнал аналогичного формата, но с другой фазой и амплитудой.i (t) = Im cos (wt + theta i), где w — омега.
Затем используйте уравнение 1 для вычисления мгновенной мощности или, если вы знаете напряжение и ток в один момент времени, просто умножьте их вместе, чтобы вычислить мгновенную мощность.
Что обычно более интересно, так это знать, сколько мощности выдает цепь за определенный период времени. Чтобы найти это, мы усредняем мгновенную мощность за интересующий период. Поскольку большинство приложений обеспечивают постоянную мощность, вам нужно только усреднить мощность за один цикл, чтобы найти среднюю мощность.Усреднение выполняется путем интегрирования:
Pavg = 1 по T, интеграл p (t) dt от 0 до T
При работе с синусоидами оказалось, что полезно определять среднеквадратичное значение (среднеквадратичное значение) напряжения v (t) и отдельно тока i (t). (Или измерьте их.) Обычно я слышу буквы «RMS», и я действительно не знаю, что это значит. Другие мои одноклассники тоже не знают, что такое RMS. Мы слышали его значение только от нашего учителя электроники и от нашего учителя электрических цепей.
Продолжая, насколько я помню, некоторые говорят, что если вы слышите, что мощность выражается в «RMS ваттах», но на самом деле имеется в виду, что выражаемая мощность является «средней мощностью», как определено выше. Это в отличие от производителей, которые любят выражать вещи в «пиковых ваттах», которые представляют собой пиковую мгновенную мощность (намного превышающую среднюю мощность). Чтобы вы не запутались, это так называемые RMS ватты.
Еще одна полезная характеристика средней мощности, Vrms и Irms, заключается в том, что эти значения эквивалентны значениям постоянного тока, необходимым для передачи такого же количества мощности с использованием постоянного тока.
Для дальнейшего объяснения перейдите по этой ссылке: http://www.powershow.com/view/11e3d5-NTFhN/CHAPTER_3_AC_POWER_ANALYSIS_powerpoint_ppt_presentation
http://www.youtube.com/watch?v=HsryuUsEh38
ПРИМЕР:
Рассчитайте мгновенную мощность, потребляемую пассивной линейной цепью, если:
Мое решение:
НАЖМИТЕ ИЗОБРАЖЕНИЕ, ЧТОБЫ УВЕЛИЧИТЬ:
>>> синус в косинус> просто вычтите 90 градусов из угла… (60 + (- 90)), затем подставьте полученные значения в формулу, приведенную для получения степени.
Средняя мощность
Средняя мощность P — это среднее значение мгновенной мощности за один период.
НАЖМИТЕ ИЗОБРАЖЕНИЕ, ЧТОБЫ УВЕЛИЧИТЬ:
- P не зависит от времени
- , когда theta v = theta i, это чисто резистивная нагрузка, P = 1/2 VmIm
- , когда тета v-тета i = положительный или отрицательный 90, это чисто резистивная нагрузка, P = 0
Наш учитель представил эти две важные цифры.Вспомните ICE и ELI.
ПРИМЕР:
А ток I = 10 <30 протекает через импеданс Z = 20 <-22. найти среднюю мощность, передаваемую на импеданс.
Мое решение:
Сначала я решил для напряжения, используя закон Ома, так как ток и импеданс уже даны.
Затем просто подставьте значения, указанные в формуле, чтобы получить ответ. Ответ должен быть равен P = 927,18W
.Для получения дополнительных сведений щелкните ссылки:
http: // www.youtube.com/watch?v=lcXWii1ffuI
Нравится:
Нравится Загрузка …
Связанные
Вычислить трехфазные мгновенные активные и реактивные мощности
Вычислить трехфазные мгновенные активные и реактивные powers
Библиотека
Simscape / Электрооборудование / Специализированные энергетические системы / Управление и измерения / Измерения
Simscape / Электрооборудование / Специализированные энергосистемы / Основные блоки / Измерения / Дополнительные измерения
Описание
Блок питания (3-фазный, мгновенный) вычисляет трехфазный мгновенная активная мощность P (в ваттах) и реактивная мощность Q (в варах) связаны с периодическим набором трехфазных напряжений и токов.Эти формулы используются для выполнения расчетов:
P = Va⋅Ia + Vb⋅Ib + Vc⋅IcQ = 13 [(Vb − Vc) ⋅Ia + (Vc − Va) ⋅Ib + (Va − Vb) ⋅Ic]
По этим формулам ток, протекающий в цепи RL, создает положительный P и положительный Q.
Расчетная мгновенная реактивная мощность точна только для сбалансированные трехфазные напряжения и токи без гармоник.
Входы и выходы
-
Vabc Трехфазный сигнал напряжения.
-
Iabc Трехфазный токовый сигнал.
-
P Трехфазная мгновенная активная мощность P, в ваттах.
-
Q Трехфазная мгновенная реактивная мощность Q в вар.
Примеры
Модель power_ThreePhasePower сравнивает выходы блока с Power (положительная последовательность)
блок и блок Power (dq0, Instantaneous). Это показывает, что
Блок питания (3-фазный, мгновенный) дает точные результаты, когда напряжение
и токи сбалансированы и свободны от гармоник.Когда напряжение питания
становится неуравновешенным, на выходе P наблюдается пульсация, и появляется ошибка
на выходе Q.
Время выборки модели параметрируется набором переменных Ts.
значение по умолчанию 50e-6 с. Установите для Ts значение 0 в командном окне и
изменить Тип моделирования параметр Powergui
блок к Непрерывный для моделирования модели
в непрерывном режиме.
Представлен в R2013a
PPT — Презентация PowerPoint мгновенной мощности, скачать бесплатно
Мгновенная мощность реальная (или средняя) мощность (Вт) Это фактическая мощность, потребляемая элементом. Примеры: Электрический нагреватель, электрическая плита, тостеры для духовки, утюг и т. Д. реактивная мощность Реактивная мощность, потребляемая или передаваемая элементом. Реактивная мощность представляет собой энергию, запасенную в реактивных элементах (катушках индуктивности и конденсаторах).Единица измерения — вольт-ампер, реактивная (ВАР)
Мгновенная мощность фактическая (или средняя) мощность (Вт), реактивная мощность (вольт-ампер, реактивная (ВАР))
Комплексная мощность Ранее мы нашли удобно вводить синусоидальные напряжение и ток в терминах комплексного числа вектор. Определение Пусть комплексная мощность представляет собой комплексную сумму активной и реактивной мощности
Преимущества использования комплексной мощности — Мы можем вычислить среднюю и реактивную мощность от комплексной степени S — комплексная степень обеспечивают геометрическую интерпретацию: Геометрические отношения для прямоугольного треугольника означают, что четыре измерения степенного треугольника (, P, Q, ) могут быть определены, если известны любые два из четырех
Вычисления мощности были Сопряжены с вектором тока Схема
В любой схеме сохранение компл. ex мощность достигается Это означает, что в любой цепи достигается сохранение средней мощности и сохранение реактивной мощности. Однако полная мощность (величина комплексной мощности) не сохраняется
Ex: 6.13 Определите среднюю и реактивную мощность, выдаваемую источником. Вектор тока на выходе из источника: Средняя мощность, отдаваемая источником:
Реактивная мощность, отдаваемая источником: А комплексная мощность, отдаваемая источником, составляет
Определите среднюю мощность и реактивная мощность, подаваемая на каждый элемент Напряжение на элементах составляет: Таким образом, комплексная мощность, подаваемая на каждый элемент, составляет
показывает, что достигается сохранение комплексной мощности, средней мощности и реактивной мощности.
6.6.1 Соотношение мощностей для резистора Напряжение и ток синфазны, поэтому средняя мощность равна: Реактивная мощность равна нулю для резистора
6.6.1 Соотношение мощностей для индуктора Напряжение опережает ток на 90, так что
6.6.1 Соотношение мощностей для конденсатора Ток опережает напряжение на 90, так что
Коэффициент мощности Вызов мгновенной мощности p (t) Угол qv — qi играет роль в вычислении средней и реактивной мощности Угол qv — qi называется углом коэффициента мощности. Теперь мы определяем следующее: Коэффициент мощности
Коэффициент мощности Знание коэффициента мощности pf не говорит вы — угол коэффициента мощности, т.к. для полного описания этого угла мы используем описательные фразы «отстающий коэффициент мощности» и «ведущий коэффициент мощности». «Отстающий коэффициент мощности» означает, что c urrentlagsvoltage, следовательно, индуктивная нагрузка. Опережающий коэффициент мощности означает, что ток ведет к напряжению, следовательно, и емкостная нагрузка
6.6.2 Коэффициент мощности Начиная с
Цепь
Цепь
EX: 6.15 Определите среднюю и реактивную мощность, передаваемую на полное сопротивление нагрузки и коэффициент мощности нагрузки Средняя мощность
EX: 6.15 Определите среднюю и реактивную мощность, передаваемую на полное сопротивление нагрузки и коэффициент мощности нагрузки ИЛИ
EX: 6.15 Определите среднюю и реактивную мощность, передаваемую , на полное сопротивление нагрузки и коэффициент мощности нагрузки ИЛИ
Это также можно вычислить из комплексной мощности , подаваемой на нагрузку. Коэффициент мощности нагрузки: нагрузка отстает, потому что ток отстает от напряжения
Типичное распределение мощности схема Потребитель взимается за среднюю мощность, потребляемую нагрузкой. Нагрузке требуется определенная полная полная мощность
Ex 6.16 Предположим, что значение напряжения нагрузки составляет 170 В. Сопротивление линии составляет 0,1 Ом. Для нагрузки требуется 10 кВт средней мощности. Изучите потери в линии при коэффициенте мощности нагрузки, равном единице, и при коэффициенте мощности 0,7 при отставании. Ток нагрузки получается из Для коэффициента мощности, равного единице, это для коэффициента мощности 0,7. Мощность, потребляемая в линии, теряет 720 Вт дополнительной мощности, которая будет генерироваться, если pf равен 0,7 для питания нагрузки
Коррекция коэффициента мощности Ex: 6.17: в Прим. 6.16 определить значение конденсатора на нагрузке, чтобы скорректировать коэффициент мощности до единицы, если частота сети составляет 60 Гц. (Отрицательный из-за запаздывания) Угол тока равен: Таким образом, ток в нагрузке равен: Ток через добавленный конденсатор равен: Следовательно, общий ток. Решение этой проблемы для нейтрализации реактивной составляющей дает: C = 120,02 / (2 * 3,14 * 60 * 170) = 0,001873F
Корректировка коэффициента мощности Ex: 6.17: в Ex 6.16 определите значение конденсатора на нагрузке, чтобы скорректировать коэффициент мощности от 0.7 к единице, если частота сети 60 Гц. Из примера 6.16 Для коэффициента мощности 0,7 коэффициент мощности 0,7 с запаздыванием Ток через добавленный конденсатор равен: Следовательно, общий ток, коэффициент мощности Unity Мнимая составляющая линейного тока равна нулю
Средняя мощность, подаваемая на нагрузку, составляет:
6.6.3 Максимальная передача мощности Конфигурация источник-нагрузка Определите полное сопротивление нагрузки, чтобы на эту нагрузку подавалась максимальная средняя мощность.Представьте источник и импедансы нагрузки в виде действительной и мнимой частей: Ток нагрузки:
Средняя мощность, подаваемая на нагрузку: Поскольку реактивное сопротивление может быть отрицательным и иметь максимальное значение, мы выбираем, оставляя дифференцировать с учетом к RL и установить на ноль для определения требуемого RL, который равен RL = RS Следовательно: В этом случае нагрузка согласована с источником. Максимальная мощность, подаваемая на нагрузку, составляет:
6.6.4 Суперпозиция средней мощности Расчет средней мощности, когда цепь содержит более одного источника
Мгновенная мощность, подаваемая на элемент, составляет Замена с использованием идентификатора
Использование идентификатора
Средние мощности, передаваемые источниками по отдельности Предположим, что две частоты являются целыми числами, кратными некоторой частоте, поскольку мгновенная мощность становится
Усреднение мгновенной мощности за общий период ТАК: мы можем наложить средние мощности, передаваемые источниками с разными частотами, но мы не можем, как правило, применять суперпозицию к средней мощности, если источники имеют одинаковую частоту.где
Пример 6.18: Определить среднюю мощность, выдаваемую двумя источниками схемы Следовательно, средняя мощность, отдаваемая источником напряжения, равна. Это можно подтвердить, исходя из средней мощности, передаваемой на два резистора
деление по току: Напряжение на источнике тока равно. Следовательно, средняя мощность, отдаваемая источником тока, равна. Это можно снова подтвердить, вычислив среднюю мощность, подаваемую на два резистора: поскольку частоты не совпадают, общая средняя передаваемая мощность равна сумма средних мощностей, отданных отдельно каждым источником
EX 6.19. Определите среднюю мощность, передаваемую двумя источниками . Поскольку оба источника имеют одинаковую частоту, мы не можем использовать суперпозицию. Итак, мы включаем оба источника в одну векторную схему. Общая средняя мощность, отдаваемая источниками, равна средней мощности, подаваемой на резистор. Мы используем суперпозицию в векторной схеме, чтобы найти ток через резистор
Векторный ток равен: Следовательно, средняя мощность, подаваемая на резистор резистор равен Обратите внимание, что мы не можем накладывать средние мощности, подаваемые на резисторы от отдельных источников. Мы можем вычислить эту общую среднюю мощность, напрямую вычислив среднюю мощность, подаваемую источниками из векторной схемы. Напряжение на источнике тока равно средней мощности. от источника напряжения Средняя мощность, отдаваемая источником тока, составляет Общая средняя мощность, отдаваемая источниками, составляет
6.6.5 Эффективные (среднеквадратичные) значения периодических сигналов Синусоидальная форма волны — одна из более общих периодических форм сигналов Подайте периодический источник тока с периодом T на резистор R Мгновенная мощность, подаваемая на резистор, составляет Средняя мощность, подаваемая на резистор, следовательно, средняя мощность Эта периодическая форма сигнала, подаваемая на резистор, может рассматриваться как эквивалентная форме сигнала постоянного тока, значение которой равно. Это называется эффективным значением формы сигнала или среднеквадратичным среднеквадратичным значением сигнала
Ex 6.20 Определите среднеквадратичное значение формы сигнала тока и среднюю мощность, которую он может передать на резистор. Среднеквадратичное значение формы сигнала равно
Среднеквадратичное значение напряжения и тока в векторных схемах. Синусоида. имеет среднеквадратичное значение. Следовательно, средняя мощность, подаваемая на резистор синусоидальным напряжением или формой волны тока, составляет. В общем, средняя мощность, подаваемая на элемент, равна. коэффициент ½ удаляется из всех выражений средней мощности.Однако выражения во временной области требуют, чтобы величина умножалась на квадратный корень из 2, поскольку X — это пиковое значение формы сигнала. Обычное бытовое напряжение указано как 120 В. Это среднеквадратичное значение пика 170 В.
Ex 6.21 Определите среднюю мощность, отдаваемую источником , и ток во временной области i (t) Схема фазора со среднеквадратичным, а не пиковым током. Следовательно, средняя мощность, подаваемая источником, равна. текущий —
Коммерческое распределение электроэнергии
Представление во временной области
Использование векторов
Как определить мгновенную скорость изменения функции в точке?
Наука
- Анатомия и физиология
- Астрономия
- Астрофизика
- Биология
- Химия
- наука о планете Земля
- Наука об окружающей среде