Мощность переменного тока это: мощность переменного тока — Мир Антенн

Содержание

Мощность переменного тока. Работа переменного тока

Господа, всех вас в очередной раз приветствую! В сегодняшней статье я бы хотел поднять темы, касающиеся мощности и энергии (работы) в цепях переменного тока. Сегодня мы узнаем, что это такое и научимся их определять. Итак, погнали.

Прежде чем начать что-либо обсуждать про переменный ток, давайте-ка вспомним, как мы определяли мощность в случае постоянного тока. Да-да, у нас была отдельная статейка на эту тему, помните? Если нет, то напоминаю, что в случае постоянного тока мощность в цепи считается очень просто, по одной из этих трех замечательных формул:

где P – искомая мощность, которая выделяется на резисторе R;

I – сила тока в цепи через резистор R;

U – напряжение на резисторе R.

Это все здорово. Но как быть в случае переменного тока, а в частности – синусоидального? Ведь там у нас колбасится синус, значения тока и напряжения все время меняются, сейчас они одни, через мгновение – уже другие, т.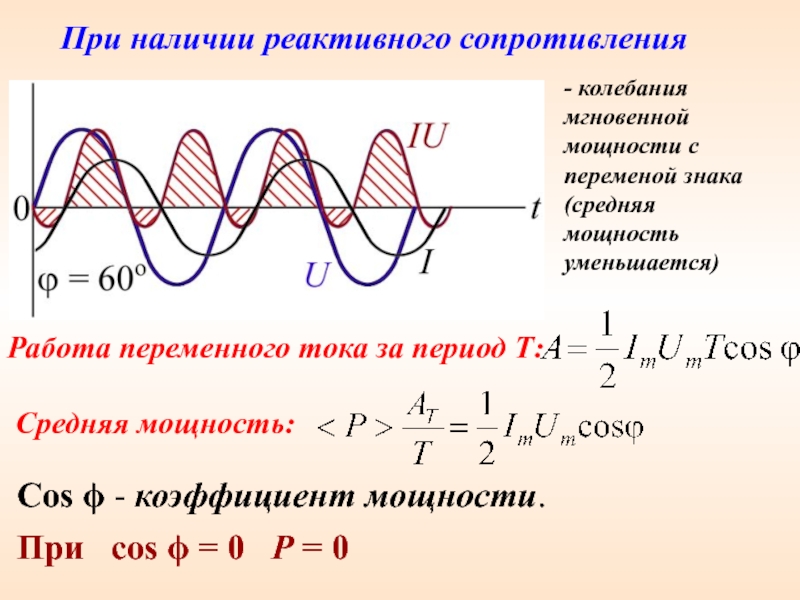

е., выражаясь научным языком, они являются функциями времени. Пользуясь знаниями, полученными нами в предыдущей вводной статье, мы можем записать вот такой закон изменения силы тока:

Мы не будем сейчас повторять что здесь есть что, все это было досконально рассмотрено в прошлый раз.

Абсолютно аналогично можно записать зависимость напряжения от времени для переменного синусоидального тока

Пока что считаем, что у нас в цепи только резисторы (конденсаторы и индуктивности отсутствуют), следовательно, напряжение и ток совпадают по фазе между собой. Не понятно почему так? Ничего, в будущем разберем это подробно. Пока же для нас это значит только то, что фазы как в законе изменения тока, так и в законе изменения напряжения можно выкинуть.

.. Такая идея пришла? Это просто замечательно! Давайте ее сейчас же реализуем! Поскольку у нас и ток, и напряжения зависят от времени, все три полученные новые формула для мощности абсолютно также будет зависеть от времени.

Ох, прям в глазах рябит от синусов . Но ведь все довольно просто и очевидно откуда, что получилось, не так ли? По вот этим вот самым формулам можно рассчитать мгновенную мощность в определенный момент времени. Фишка в том, что если через резистор течет переменный ток, то в каждое мгновение времени на нем будет выделяться вообще говоря разная мощность: иначе и быть не может, раз амплитуда тока через резистор все время разная. Другое дело, что визуально, при большой частоте изменения тока, мы скорее всего это не заметим: температура резистора не будет хаотично скакать в такт изменения мощности, которая на нем выделяется. Это будет потому, что сам резистор благодаря его массе и теплоемкости синтегрирует эти перепады температуры.

Итак, с мощностью более-менее понятно. А как быть с энергией? Ну, то есть с теплом, которое выделяется на резисторе? Как оценить эту самую энергию? Для этого нам надо вспомнить, как же связаны между собой мощность и энергия. Мы уже затрагивали эту тему в статье про мощность в цепи постоянного тока. Тогда этот вопрос решился просто: при постоянном токе достаточно умножить мощность (которая там не зависит от времени и все время одинакова) на время наблюдения и получить выделяющуюся за это самое время наблюдения энергию. С переменным током все посложнее, потому что тут мощность зависит от времени. И, увы, тут не обойтись без интегралов… Что это вообще такое этот самый интеграл? Как, вероятно, многие из вас знают,

интеграл – это просто площадь под графиком. В данном конкретном случае под графиком зависимости мощности от времени P(t). Да, вот так вот все просто.

Итак, энергия (или работа, что по сути одно и то же) в цепи переменного тока считается следующим образом

В этой формуле Q – это искомая работа (энергия) переменного тока (измеряется все так же в джоулях), P(t) – закон изменения мощности от времени, а Т – собственно, сам отрезок времени, который мы рассматриваем, и в течении которого ток работает.

Вообще говоря, это выражение можно рассматривать как общий случай и для постоянного тока, и для переменного (при этом переменный ток может быть любой формы, не обязательно синусоидальный). Во всех эих случаях можно считать энергию через вот этот вот интеграл. Если же мы подставим сюда P(t)=const (случай постоянного тока), то исходя из особенности взятия интеграла от константы результат расчета будет абсолютно таким же, как если бы мы просто умножили мощность на время, поэтому нет никакого смысла так заморачиваться и рассматривать интегралы в теме постоянного тока. Но полезно это знать, что бы была некая единая картина. Сейчас же, господа, я прошу вас запомнить главный вывод из всей этой болтовни –

если мы хотим найти выделившуюся энергия за время T (без разницы какой ток – постоянный или переменный), то это можно сделать, найдя площадь под графиком зависимости мощности от времени на интервале от 0 до Т.

Если брать токи синусоидальные и подставлять конкретные выражения для зависимости мощности от времени, то энергию можно посчитать по одной из следующих формул

Господа, скажу сразу, в своих статьях я не буду рассказывать, как брать интегралы. Я надеюсь, что вы это знаете. А если нет – ничего страшного, не спешите закрывать статью. Я буду стараться строить изложение таким образом, чтобы незнание интегралов не привело в вашем сознании к fatal error . Очень часто их вообще не требуется считать ручками, а можно посчитать в специализированных программах или даже онлайн на многочисленных сайтах.

Давайте теперь разберем все вышесказанное на конкретном примере. Господа, специально для вас я подготовил рисуночек 1. Взгляните на него. Изображение кликабельно.

Рисунок 1 – Зависимость мощности от времени для переменного и постоянного тока

Там два графика: на верхнем показана зависимость мощности от времени для случая переменного синусоидального тока, а на нижнем – для случая постоянного тока. Как я их построил? Очень просто. Для первого графика я взял вот эту ранее написанную нами формулу.

Будем полагать, что амплитуда синусоидального тока равна I_m=1 A, сопротивление резистора, на котором рассеивается мощность, равно R=5 Ом, а частота синуса равна f = 1 Гц, что соответствует круговой частоте

То есть формула, по которой мы строим график мощности переменного тока, имеет вид

Именно по этой формуле построен верхний график на рисунке 1.

А как быть с нижним графиком? Господа, ну тут совсем все просто. Я исходил из того, что через тот же самый резистор R=5 Ом течет постоянный ток величиной I=1 А. Тогда, как должно быть понятно из закона Джоуля-Ленца, на данном резисторе будет рассеиваться вот такая вот мощность

Поскольку ток постоянный, то эта мощность будет одинаковой в любой момент времени. А для таких замечательнейших случаев эталонной стабильности великая и могучая математика предусматривает график в виде прямой. Что мы и видим на нижнем графике рисунка 1.

Понятное дело, что раз через наши пятиомные резисторы течет ток, то на них выделяется некоторая мощность и рассеивается некоторое количество энергии. Иными словами, резистор греется за счет выделяющейся на нем энергии. Мы уже обсуждали, что эта энергия считается через интеграл. Но, как мы уже говорили, есть и графическое представление этого интеграла – он равен площади под графиком. Эту площадь я заштриховал на рисунке 1. То есть, если мы найдем, чему равна площадь под верхним и нижним графиками, то мы определим, какое количество энергии выделилось в первом и втором случае.

Ну, с нижним графиком вообще все просто. Там – прямоугольник высотой 5 Вт и шириной 2 секунды. Поэтому площадь (то бишь энергия) находится элементарно

Отметим, что этот результат в точности совпадает с формулой, полученной нам для расчета энергии постоянного тока в одной из прошлых статей.

Со верхним графиком все не так просто. Там у нас неправильная форма и просто так сразу нельзя сказать, чему равна эта площадь. Вернее, сказать можно – она равна вот такому вот интегралу

Результат вычисления этого интеграла равен конкретному числу и это число – как раз наша искомая энергия, которая выделилась на резисторе. Мы не будем расписывать взятие этого интеграла. Посчитать такой интеграл ручками не составит труда для человека, хотя бы поверхностного знакомого с математикой. Если же все-таки это вызывает затруднение, или просто лень самому считать – есть огромное количество САПРа, которое сделает это за вас. Либо можно посчитать этот интеграл на каком-либо сайте: по запросу в гугле «интегралы онлайн» выдается достаточное количество результатов. Итак, сразу переходим к ответу и он равен

Вот так вот. Энергия, которая выделяется на резисторе при протекании синусоидального тока с амплитудой 1 А почти в два раза меньше энергии, которая будет выделяться в случае, если течет постоянный ток величиной 1 А. Оно и понятно – даже визуально на рисунке 1 площадь под верхним графиком заметно ниже, чем под нижним.

Как-то так, господа. Теперь вы знаете, как рассчитать мощность и энергию в цепи переменного тока. Однако сегодня мы рассмотрели довольно сложный путь. Оказывается, есть методы попроще, с использованием так называемых действующих величин тока и напряжения. Но об этом в следующей статье.

А пока что – всем вам огромной удачи, спасибо, что прочитали, и пока!

Вступайте в нашу группу Вконтакте

Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it.

Переменный ток, мощность переменного тока

В свое время Эдисон и Тесла были противниками в вопросе использования электрического тока в энергетике. Тесла считал, что необходимо использовать переменный ток, а Эдисон – что нужно применять постоянный ток. У второго ученого было больше возможностей, так как он занимался бизнесом, однако Тесла в конечном итоге удалось победить, так как он был попросту прав.

Вступление

Переменный ток значительно эффективнее использовать для передачи энергии. Обсудим, как вычисляется мощность переменного тока, ведь переменный ток — это мощность, которая передается на расстоянии.

Вычисление мощности

Допустим, у нас имеется генератор переменного напряжения, который подключен к нагрузке. На выходе генератора, между двумя точками на клеммах, напряжение меняется по гармоническому закону, а нагрузка взята произвольная: катушки, активное сопротивление, конденсаторы, электромотор.

В цепи нагрузки течет ток, который меняется по гармоническому закону. Наша задача – установить, чему равна мощность потребляемой нагрузки от генератора. В распоряжении имеем генератор. В качестве исходных данных представлено направление на входе, которое будет меняться по гармоничному правилу:

(U(t) = U(m) cos w t)

Нагрузка – самое произвольное понятие.

Сила тока в нагрузке и, соответственно, в проводах, которые подводят мощность к нагрузке, будет меняться. Частота колебаний тока выйдет такая же, как частота колебаний напряжения, но существует также понятие сдвига фазы в промежутках колебаний тока и напряжения:

(I (t) = I (m) cos w t)

Дальнейшие вычисления

Показатели мощность будут равны произведению:

P (t) = I (t) U (t)

Этот закон остаётся справедливым как для переменного тока с мощностью, которую необходимо было вычислить, так и для постоянного.

(I (t) = I (m) cos (wt + J)

Мощность переменного тока при переменном токе вычисляется при помощи трех формул.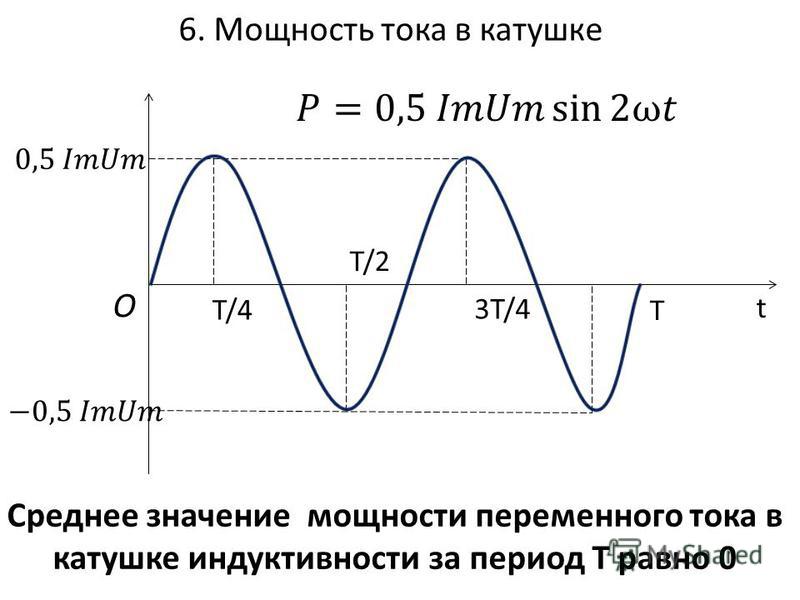 Представленные выше расчеты относятся к основной формуле, которая вытекает из определения силы тока и напряжения.

Если участок цепи однородный и можно пользоваться законом Ома для этого участка цепи, здесь такие вычисления использовать нельзя, так как нам неизвестен характер нагрузки.

Определяем результат

Подставим показатели силы тока и напряжения в данную формулу, и тут нам на помощь придет знание тригонометрических формул:

cosa cosb = cos(a +b) + cos(a — b) / 2

Воспользуемся этой формулой и получим вычисления:

P(t) = I(m) U (m) cos (wt + J) cos wt

После упрощения результатов получим:

P(t) = I(m) U (m)/2 cos (wt + J) + I(m) U (m) cosJ

Посмотрим на эту формулу. Здесь первое слагаемое зависит от времени, меняясь по гармоническому закону, а второе является величиной постоянной. Мощность переменного тока при переменном токе складывается из постоянной и переменной составляющей.

Если мощность положительна, значит, нагрузка потребляет энергию от генератора. При отрицательной мощности, наоборот, нагрузка раскручивает генератор.

Найдем среднее значение мощности за период времени. Для этого работу, совершенную электрическим током, поделим на величину этого периода.

Мощность трехфазной цепи переменного тока– это сумма переменной и постоянной составляющих.

Активная и реактивная мощность

Многие физические процессы можно представить аналогиями друг друга. На этой базе постараемся раскрыть суть понятий активной мощности цепи переменного тока и реактивной мощности цепи переменного тока.

Стакан представляет собой электростанцию, вода – электроэнергию, трубочка – кабель или провод. Чем выше поднимается стакан, тем больше напряжение или давление.

Параметры мощности в сети переменного тока активного или реактивного типа зависят от тех элементов, которые потребляют такую энергию. Активная – энергия индуктивности и ёмкости.

Покажем это на конденсаторе, ёмкости и стакане. Активными называются те элементы, которые способны преобразовывать энергию в другой вид. К примеру, в тепло (утюг), свет (лампочка), движение (мотор).

Реактивная энергия

При имитации реактивной энергии напряжение увеличивается, и ёмкость заполняется. При уменьшении напряжения накопленная энергия возвращается по проводу обратно в электростанцию. Так повторяется циклически.

Сам смысл реактивных элементов заключается в накоплении энергии, которая потом обратно возвращается или используется для других функций. Но никуда не тратится. Основной минус этой производной в том, что виртуальный трубопровод, по которому как-бы идет энергия, имеет сопротивление, и на нем тратится процент экономии.

Полной мощности цепи переменного тока требуются затраты определенного процента усилий. По этой причине на крупных предприятиях идет борьба с реактивной составляющей полной мощности.

Активная мощность – это та энергия, которая потребляется или преобразуется в другие виды – свет, тепло, движение, то есть в какую-либо работу.

Опыт

Для опыта возьмем стакан, которые служит активной составляющей мощности. Он представляет часть энергии, которую необходимо потребить или преобразовать в другой вид.

Часть энергии воды можно выпить. Полная мощность переменного тока коэффициент мощности — это показатель, который складывается из реактивной и активной составляющих: энергии, текущей по водопроводу и той, которая преобразуется.

Как выглядит полная мощность в нашей аналогии? Часть воды выпиваем, а оставшаяся будет продолжать бежать по трубке. Так как у нас есть реактивный ёмкостной элемент – конденсатор или ёмкость, воду опускаем и начинаем имитировать увеличение и уменьшение напряжения. При этом видно, как вода перетекает в двух направлениях. Следовательно, в этом процессе применяется и активная, и реактивная составляющая. Вместе это – полная мощность.

Преобразование мощности

Активная мощность преобразовывается в другой вид энергии, к примеру, в механическое движение или нагрев. Реактивная мощность, которая накапливается в реактивном элементе, позднее возвращается назад.

Полная мощность – это геометрическая сумма активной и реактивной мощности.

Для произведения вычислений используем тригонометрические функции. Физический смысл расчетов такой. Возьмем прямоугольный треугольник, в котором одна из сторон равна 90 градусов. Одна из сторон – это его гипотенуза. Есть прилежащий и противолежащий относительно прямого угла катеты.

Косинус представлен отношением, которое предопределяет длина прилегающего катета относительно длины гипотенузы.

Синусом угла является вид отношения, которое составляет длина противолежащего катета относительно гипотенузы. Зная угол и длину любой из сторон, можно вычислить все остальные углы и длину.

В данном треугольнике можно взять длину гипотенузы и прилежащего катета и вычислить этот угол с помощью тригонометрической функции косинусов. Мощность постоянного и переменного тока вычисляется с применением таких знаний.

Для вычисления угла можно применять обратную функцию от косинуса. Получим необходимый результат вычислений. Чтобы вычислить длину противолежащего катета, можно вычислить синус и получить соотношение противолежащего катета к гипотенузе.

Вычисление мощности цепи переменного тока по формуле предложено в этом описании.

В цепях постоянного тока мощность равна произведению напряжения на ток. В цепях переменного тока также работает это правило, но его трактовка будет не совсем правильной.

Индуктивность

Помимо активных элементов, действуют реактивные элементы – индуктивность и ёмкость. В цепях постоянного тока, где амплитудное значение напряжения токов не меняется во времени, работа данного сопротивления будет происходить только во времени. Индуктивность и ёмкость могут негативным образом влиять на сеть.

Активная мощность, которую имеет трехфазная цепь переменного тока, может выполнять полезную работу, а реактивная не выполняет никакой полезной работы, а только расходуется на преодоление реактивных сопротивлений индуктивности и ёмкости.

Попытаемся выполнить опыт. Возьмем источник переменного напряжения на 220 Вт с частотой 50Гц, датчик напряжения и тока источника, нагрузка, которая составляет активное 1Ом и индуктивное 1ОМ сопротивление.

Также есть выключатель, который подключится в определенный момент, активно-ёмкостная нагрузка. Запустим такую систему. Для удобства рассмотрения введем коэффициенты поправки напряжения.

Запускаем устройство

При запуске устройства видно, что напряжение и ток сети не совпадают по фазе. Наблюдается переход через 0, при котором существует угол – коэффициент мощности сети. Чем меньше этот угол, тем выше коэффициент мощности, который указывается на всех устройствах переменного тока, к примеру, электрических машинах или сварочных трансформаторах.

Угол зависит от величины индуктивного сопротивления нагрузки. Когда сдвиг уменьшается, увеличивается ток сети. Представим, что сопротивление катушки уменьшить нельзя, но надо улучшить косинус сети. Для этого и нужны конденсаторы, которые, в отличие от индуктивности, опережают напряжение и могут взаимно компенсировать реактивную мощность.

В момент подключения конденсаторной батареи за 0,05 с происходит резкое снижение косинуса, практически до 0. Также идет резкое снижение тока, который без конденсаторной батареи имел амплитудное значение намного ниже, чем при включении конденсаторной батареи.

Фактически подключением конденсаторной батареи удалось снизить мощность тока, потребляемого из сети. Это является положительным моментом и позволяет снижать ток сети и экономить на сечение кабелей, трансформаторах, силовом оборудовании.

Если произойдет отключение индуктивной нагрузки и останется активное сопротивление, произойдет процесс, когда косинус сети после подключения конденсаторной батареи приведет к фазовому сдвигу и большому скачку тока, который идёт в сеть, а не потребляется из неё, что происходит в генераторном режиме реактивной мощности.

Итоги

Активная мощность опять остается постоянной и равна нулю, так как нет индуктивного сопротивления. Начался процесс генерации реактивной мощности в сеть.

Следовательно, компенсировать реактивную мощность на крупных предприятий, потребляемых колоссальные её объёмы из энергосистем, — это приоритетная задача, так как это позволяет экономить не только на электрооборудовании, но и на затратах по оплате самой реактивной мощности.

Такое понятие регламентируется, и предприятие оплачивает и потребляемую, и генерируемую мощность. Здесь устанавливаются автоматические компенсаторы, обеспечивающие поддержку баланса мощности на заданном уровне.

При отключении мощной нагрузки, если не выключить из сети компенсирующее устройство, будет происходить генерация реактивной мощности в сеть, что создаст проблемы в энергосистеме.

В быту компенсация реактивной мощности не имеет смысла, так как потребление мощности здесь значительно ниже.

Активная и реактивная мощность – понятия школьного курса физики.

Как регулировать мощность переменного тока / Хабр

Решил как-то отец собрать для дачи некое устройство, в котором, по его заверению, можно будет варить сыр. Устройство сие вид имело могучий и представляло из себя железный короб, подозрительно напоминающий старую стиральную машинку. Внутрь короба (все также добротно!) были вмонтированы три тэна по 1700 Ватт каждый. В общем сыра должно было хватить на небольшой посёлок.

Изделие (внешне выглядящее как что-то из безумного макса), должно быть весьма технологичным и поддерживать заданную температуру в максимально узких пределах. Для этого рядом появилась ещё одна коробка с симисторами, к которым подключались ТЭНы и схема, выдающая высокий уровень при переходе синусоиды через ноль. А у меня появился интересный проект.

Итак нам нужно выходить на заданную температуру и поддерживать её, с этим должен справляться алгоритм ПИД регулятора. Глубоко вдаваться в его работу не буду, скажу лишь что он получает на вход текущую ошибку, а на выходе выдает какое-то число в заданных пределах. У меня таким числом будет мощность выдаваемая на ТЭН, хотя в принципе, это может быть любой инерционный процесс, например обороты двигателя. Что важно для ПИД регулятора, это чтобы выходная величина производила воздействие линейно. Поэтому попробуем разобраться в способах регулировки мощности и их линейности.

Как вообще регулируется мощность?

Мощность — это произведение силы тока на напряжение. Если представить это произведение графически, то для постоянного тока, это будет площадь прямоугольника со сторонами равными напряжению и току

Так как при постоянном сопротивлении и напряжении ток тоже будет постоянным, то заменим ось тока на ось времени. Сопротивление я беру постоянным для объяснения принципа регулирования.

Тогда при заданном напряжении (12 В) и сопротивлении в 12 Ом, по закону Ома: I=U/R, получаем ток равный 1 А, и соответственно мощность за единицу времени будет равна 12 Вт. При другом сопротивлении мощность, естественно тоже изменится.

Теперь, если мы хотим регулировать мощность за единицу времени, нам нужно как-то изменять площадь фигуры за единицу времени. Самым чистым способом будет просто изменять напряжение, тогда и мощность будет пропорционально изменяться. Но контроллер, как и любые цифровые устройства, не умеет плавно изменять напряжение на ножках, он может либо «поднимать» их до высокого уровня, либо «опускать» до низкого уровня. Этот недостаток он компенсирует скоростью, даже самый дохленький современный МК может работать на частотах в миллионы тактов в секунду. Чтобы регулировать мощность, контроллер будет очень быстро «дрыгать» ножкой, тем самым изменяя результирующая площадь импульса за единицу времени.

На этом принципе устроена широтно-импульсная модуляция, она же ШИМ. Изменяя время (ширину) импульса за период мы изменяем выдаваемую мощность. На рисунке выше, показано два периода ШИМа. Каждый период имеет отношение площади импульса к площади всего периода 0.5, те половину времени периода контроллер выдает высокий уровень сигнала, другую половину низкий. Отношение времени высокого уровня сигнала к времени низкого называется скважностью. Красная линия на графике отражает результирующую мощность за единицу времени, по ней видно что при скважности 0.5 мощность также упала на половину (с 12 до 6 Вт). Хорошая новость состоит в том, что, ШИМ в контроллерах реализован аппаратно. Так что для регулирования чего-то достаточно его запустить и, по необходимости, изменять скважность.

Для постоянного тока, режим ШИМа оптимален, причем чем более инерционный прибор мы к нему подключаем, тем меньшую частоту ШИМа можно использовать. Для большого ТЭНа достаточно чуть ли не одного герца, а вот для светодиодов лучше использовать частоту побольше. Кстати частота ШИМа в подсветке экрана ноутбука, зачастую оказывается чуть ли не решающим фактором при покупке, так как, при слишком низкой частоте, глаза будут быстро уставать.

Если попробовать провернуть трюк с ШИМом для переменного напряжения, мы увидим что все сломалось и мощность перестала регулироваться линейно

одинаковые промежутки времени стали давать нам разную площадь, а значит разную мощность. Однако, если разбить полученные отрезки на на ещё более мелкие, то процентное соотношение ширины импульса к ширине кусочка будет выравниваться.

Если мы возьмем равный процент выдаваемой мощности от каждого кусочка, в результате мы получим такой же процент, от мощности всей волны, а на выходе мы получим линейный регулятор мощности для переменного тока. Причем чем большую частоту будет иметь ШИМа, тем на большее количество кусочков он разобьет синусоиду, а значит мы получим большую линейность.

Это было бы решением всех проблем, но в моем случае устройством коммутировавшим нагрузку был не быстрый транзистор, а симистор — медленный прибор, с максимальными рабочими частотами в пределах нескольких сотен герц, к тому же симистор можно только открыть, закроется он сам при переходе через ноль. На таких частотах управлять переменным напряжением которое имеет частоту 50 Гц, линейно не получится. Поэтому здесь нужно использовать какой-то другой подход и как раз для него, помимо симисторов, была установлена схема перехода через ноль.

В случае с симисторами лучше разбить синусоиду на куски с одинаковыми площадями и записать время каждого такого кусочка в таблицу. Тогда каждое последующее значение из таблицы будет линейно увеличивать мощность.

На графике выше полуволна синусоиды разбита на части разные по времени, но имеющие одинаковую площадь, а значит несущие в себе одинаковую мощность. Все что нам останется сделать это загрузить таблицу с временными интервалам в наш котроллер, синхронизировать какой-то из его таймеров с частотой синусоиды, для этого используется схема перехода через ноль, и просто брать из таблички нужное значение, в течении которого будет высокий уровень. Суть метода похожа на ШИМ, но немного доработанный и синхронизированный с источником переменного напряжения.

Расчёт таблицы мощности

Теперь можно перейти непосредственно к расчёту.

Изначально задача заключается в том чтобы разбить синусоиду на нужное нам количество кусочков, каждый из которых будет иметь одинаковую площадь. На этом моменте, обычно проступает холодный пот, так-как площадь под графиком это и есть геометрическое определение интеграла.2(t).

Неопределённый интеграл от квадрата синуса

Теперь нужно подобрать пределы для определенных интегралов. Выберем, насколько частей мы хотим разбить нашу синусоиду: я выбрал сто, чтобы можно было регулировать мощность с шагом в 1%.

Итак мы нашли чему будет равен неопределённый интеграл и даже выбрали шаг. Теперь нужно подобрать пределы интегрирования. Смысл их подбора заключается в том, чтобы значение определенного интеграла было постоянным при их смене. Напомню, что неопределенный интеграл это формула, а определённый вполне конкретное число. Определённый интеграл считается по формуле:

То есть мы берем неопределённый интеграл, подставляем в него верхнее число, затем нижнее, и вычитаем второе из первого.

Наш неопределённый интеграл является смешанной тригонометрической функцией, а значит не имеет общего аналитического решения. Чаще всего такие функции решаются либо числовыми, либо графическими методами. Графический метода заключается в том что мы строим графики для правой и левой части уравнения их пересечение будет решением уравнения. На рисунке показано решение уравнения для 0.2

Наряду с графическим методом можно использовать численный, то есть подбор решения. Будем подставлять в неопределённый интеграл числа до тех пор пока не найдём решение). Можно использовать лист и бумажку чтобы попрактиковаться в математике, можно онлайн калькулятор, я же буду использовать Python и библиотеки numpy:

import numpy as np
rad_arr=list()
#записываем неопределённый интеграл
integral=lambda rad: (rad/2)-(math.sin(2*rad)/4)
#составляем простенький цикл для подбора решений
for x in np.arange(0, 0.78, 0.015):
  #шаг подбора
	for xx in np.arange(0, 3, 0.00001):
		if func(xx) >= x:
			print(xx)
      rad_arr.append
			break;

Отлично мы получили массив чисел (пределов интегрирования!), валидность этих чисел можно проверить подставив их в интеграл. В результате должна получится площадь равная выбранному шагу! Теперь, если подставить полученные числа на график мощности, должна получится следующая картина:

Если все сошлось, то можно двигаться дальше и задать получившимся числам размерность времени, потому что сейчас они в радианах. Чтобы это сделать нужно выяснить угловую скорость, для частоты сети, то есть количество радиан в секунду.

Тогда узнаем сколько сколько длится одна радиана

Теперь, значения задержек в радианах, превратим во время, умножив каждое значение на период радианы (T). Проверим ход своей мысли: действительно-ли получится время задержки, если умножить задержку, на период? Задержка имеет размерность радиан, период — секунд за радиану, мы хотим их перемножить. Тогда рад * ( сек / рад ) = сек. Мы получили время, а значит ход мыслей должен быть верным.

Для расчётов я опять предпочту python:

#стандартная частота сети
frequency = 50
#находим частоту в радианах
rad_per_s=frequency*(2*math.pi)
#находим период радианы
s_per_rad=1/rad_per_s
#находим задержки используя полученный ранее массив
delay_arr=[x*s_per_rad for x in rad_arr]

На этом моменте мы получили универсальную таблицу задержек, теперь необходимо конвертировать её специально под микроконтроллер.

Расчёт таймера МК и перевод таблицы

Время необходимо перевести в понятную для МК величину — количество переполнений таймера. Но сначала необходимо определится с частотой таймера: чем выше частота, тем точнее он будет отмерять время, но с другой стороны, тем меньше времени будет оставаться на выполнение остальной программы. Здесь необходимо найти золотую середину.

Для определения минимально допустимой частоты таймера, надо найти числа в массиве с минимальной разностью между ними. Разность тем меньше, чем ближе в максимуму синусоиды мы двигаемся. Тогда возьмем задержку при которой синусоида достигает единицы и число перед ним, после чего найдем их разность:

5 мс — 4.9363 мс = 0.0636 мс

Получившееся число является максимально допустимым периодом между прерываниями таймера, тогда через него найдём минимально допустимую частоту

1 / 0.0636 = 15 КГц

Значит для заданной точности в 1% будет достаточно таймера с частотой 15КГц. Частота МК составляет 16 МГц, значит между прерываниями будет 1000 тактов процессора, этого достаточно для выполнения остальной части программы, так что можно смело настраивать таймер на заданную частоту.

Для настройки таймера на определенную частоту, не кратную тактирующей используется режим таймера CTC — Clear Timer on Compare. В этом режиме таймер досчитывает до заданного числа и сбрасывается, после чего операция повторяется. Число при котором будет происходить совпадение считается по формуле

Число = Тактовая частота МК / предделитель таймера / выбранная частота

Частота выбрана, теперь нужно перевести таблицу в тики таймера. Делать я это буду опять на Python

#задаем частоту таймера
generator_freg=15000
#получаем время одного периода таймера
one_tick=1/generator_freq
#получаем массив с тиками таймера
tick_arr=[x/one_tick for x in delay_arr]

В общем-то на этом весь расчёт окончен, остается только отзеркалить получившийся массив для второй половины полуволны и загрузить в МК. Далее по прерыванию от синхроимпульса, нужно подать низкий уровень, на ножку управления симистором, запустить таймер и считать его переполнения (совпадения, тк. у нас режим CTC). Как только количество переполнений достигнет нужного числа из таблички, подаем высокий уровень на управляющую ножку. На этом линейный регулятор мощности переменного напряжения готов!

Заключение

Надеюсь статья была понятна и её было интересно читать. В дополнение хотелось бы сказать, сигнал перехода через ноль не приходит идеально вовремя, поэтому может потребоваться дополнительная коррекция, чтобы это исправить.

Код расчетов на python

import math
import numpy as np

rad_arr=list()
integral=lambda rad: (rad/2)-(math.sin(2*rad)/4)
for x in np.arange(0, 0.78, 0.015):
  for xx in np.arange(0, 3, 0.00001):
		if func(xx) >= x:
			print(xx)
      rad_arr.append
			break;

frequency = 50
rad_per_s = frequency * (2 * math.pi)
s_per_rad = 1 / rad_per_s

delay_arr = [x * s_per_rad for x in rad_arr]

generator_freg = 15000
one_tick = 1 / generator_freg

tick_arr = [x / one_tick for x in delay_arr]

print(tick_arr)

Также, если кому-то будет интересно, могу поделится исходником готового регулятора для ардуино.

Мощность — это… Что такое Мощность?

Мо́щность — физическая величина, равная в общем случае скорости изменения энергии системы. В более узком смысле мощность равна отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени.

Различают среднюю мощность за промежуток времени

и мгновенную мощность в данный момент времени:

Интеграл от мгновенной мощности за промежуток времени равен полной переданной энергии за это время:

Единицы измерения

В системе СИ единицей измерения мощности является ватт, равный одному джоулю, делённому на секунду.

Другой распространённой единицей измерения мощности является лошадиная сила.

Соотношения между единицами мощности
Единицы	Вт	кВт	МВт	кгс·м/с	эрг/с	л. с.(мет.)	л. с.(анг.)
1 ватт	1	10⁻³	10⁻⁶	0,102	10⁷	1,36·10⁻³	1,34·10⁻³
1 киловатт	10³	1	10⁻³	102	10¹⁰	1,36	1,34
1 мегаватт	10⁶	10³	1	102·10³	10¹³	1,36·10³	1,34·10³
1 килограмм-сила-метр в секунду	9,81	9,81·10⁻³	9,81·10⁻⁶	1	9,81·10⁷	1,33·10⁻²	1,31·10⁻²
1 эрг в секунду	10⁻⁷	10⁻¹⁰	10⁻¹³	1,02·10⁻⁸	1	1,36·10⁻¹⁰	1,34·10⁻¹⁰
1 лошадиная сила (метрическая)	735,5	735,5·10⁻³	735,5·10⁻⁶	75	7,355·10⁹	1	0,9863
1 лошадиная сила (английская)	745,7	745,7·10⁻³	745,7·10⁻⁶	76,04	7,457·10⁹	1,014	1

Мощность в механике

Если на движущееся тело действует сила, то эта сила совершает работу. Мощность в этом случае равна скалярному произведению вектора силы на вектор скорости, с которой движется тело:

где F — сила, v — скорость, — угол между вектором скорости и силы.

Частный случай мощности при вращательном движении:

M — момент силы, — угловая скорость, — число пи, n — частота вращения (число оборотов в минуту, об/мин.).

Электрическая мощность

Электри́ческая мощность — физическая величина, характеризующая скорость передачи или преобразования электрической энергии. При изучении сетей переменного тока, помимо мгновенной мощности, соответствующей общефизическому определению, вводятся также понятия активной мощности, равной среднему за период значению мгновенной, реактивной мощности, которая соответствует энергии, циркулирующей без диссипации от источника к потребителю и обратно, и полной мощности, вычисляемой как произведение действующих значений тока и напряжения без учёта сдвига фаз.

Приборы для измерения мощности

См. также

Ссылки

Ноутбуки HP — Использование адаптера питания переменного тока и устранение его неполадок

Правильное использование адаптера питания переменного тока обеспечит оптимальную производительность.

Подключение к источнику питания. Подсоедините кабель питания к электрической розетке, расположенной в легкодоступном месте.

ОСТОРОЖНО:

При тестировании адаптеров для сертификации ноутбуки HP подключались к адаптеру питания с заземлением. Если адаптер питания без заземления подвергается воздействию скачков мощности или электростатического разряда, это может привести к повреждению устройства.

Всегда подсоединяйте адаптер питания к заземленной розетке.
ОСТОРОЖНО:
Если подключить ноутбук к розетке без заземления, то при прикосновении к нему во время работы вы можете почувствовать пощипывание.
Если кабель питания оснащен трехконтактной вилкой, подключайте его в заземленную трехконтактную розетку. Не отсоединяйте заземляющий контакт вилки кабеля питания; например подключая двухконтактный адаптер. Заземление очень важно для обеспечения безопасной эксплуатации.
Если подача питания нестабильна, подключите адаптер к хорошему сетевому фильтру.

Использование адаптера питания. При подключении через внешний адаптер переменного тока аккумулятор будет заряжаться, а значок уровня заряда аккумулятора на панели задач изменит свой внешний вид.

Используйте только адаптеры питания, поставляемые в комплекте с компьютером, а также сменные адаптеры, поставляемые HP, или совместимые сменные адаптеры, приобретаемые у компании HP.
Кладите адаптер на твердую ровную поверхность.
Прим.:
НЕ располагайте адаптер питания в местах с недостаточной естественной вентиляцией и охлаждением – под шкафами, вблизи вытяжных вентиляторов или обогревателей и т.п., и не накрывайте его другими предметами (книгами, покрывалами или одеждой), чтобы температура воздуха вокруг него не превышала 35 °C (95 °F). В результате перегрева адаптер питания переменного тока может переключиться в режим тепловой защиты. Перед повторным использованием дайте адаптеру питания переменного тока остыть около пяти (5) минут.
Подключайте устройство к внешнему адаптеру переменного тока при зарядке или калибровке аккумулятора, установке или внесении изменений в системное программное обеспечение (например, драйверы и обновления), а также при записи данных на CD или DVD.
При постоянном использовании внешнего адаптера переменного тока следует регулярно выполнять калибровку аккумулятора или полностью его отсоединять после полной подзарядки, чтобы продолжить работу от внешнего питания переменного тока. Если аккумулятор использовать постоянно, не давая ему иногда полностью разряжаться, это может привести к уменьшению его срока службы.
Если запущено слишком много приложений или заряжается аккумулятор, адаптер питания может нагреваться при достижении предела мощности.
Использование нерекомендованных адаптеров питания приводит к ограничениям в работе док-станций. Используйте док-станцию, специально рекомендованную для вашего ноутбука. Используйте адаптер переменного тока, входящий в комплект поставки док-станции.
Если компьютер отключен от внешнего адаптера переменного тока, он будет питаться от аккумулятора, и уровень яркости дисплея автоматически уменьшится для экономии заряда. Чтобы увеличить яркость экрана в ОС Windows, найдите и откройте пункт Изменить уровень яркости, а затем с помощью ползунка настройте уровень яркости.

Отсоединение и перенос адаптера. При переноске ноутбука отсоединяйте от него шнур питания, мышь и другие периферийные устройства.

Всегда при отключении питания компьютера извлекайте штепсель кабеля питания из электрической розетки переменного тока, и только затем извлекайте его из разъема компьютера.
Не оставляйте внешние устройства или адаптер переменного тока подключенными к ноутбуку по время его переноски. Изгибы, кручения или прочие деформации кабелей этих устройств могут привести к повреждению их разъемов.

Работа и мощность переменного тока.

Энергетика Работа и мощность переменного тока.

просмотров — 350

Мощность цепи переменного тока

Согласно определению, мощность — ϶ᴛᴏ произведение тока на напряжение. В случае если — мгновенная мощность, то

. (1)

Введём в рассмотрение среднюю мощность за период:

т. е. средняя мощность равна постоянной составляющей мгновенной скорости (не зависит от времени).

Для цепи переменного тока имеется постоянный поток энергии от источника в нагрузку, который не зависит от времени (первое слагаемое в (1)) и равен средней мощности и колеблющейся части мощности, которая с частотой колеблется между источником и нагрузкой (вторая часть уравнения (1)).

В случае если в качестве нагрузки использовать идеальную индуктивность или идеальную ёмкость, тогда сдвиг фаз и . То есть, необратимого потока из источника в нагрузку нет, а имеются только колебания между источником и нагрузкой. Такие сопротивления называются безватными сопротивлениями.

(2) — характеристика технических устройств, где — активная мощность, — полная мощность.

показывает, какую часть от полной мощности составляет активная мощность.

Из (2) имеем:

то есть, чем выше , тем при меньшем значении тока в цепи идёт преобразование электрической энергии в другие виды энергий.

Резонанс токов.

В цепи на рисунке справа . .

При следует, что .

Значит, общий ток будет минимален: .

Переменный ток и его мощность

Энергия, поставляемая источником электродвижущей силы во внешнюю цепь, испытывает превращения в другие виды энергии. Если в цепи имеется только активное сопротивление, то вся энергия превращается в тепло, выделяемое на сопротивлении . Между током и напряжением сдвиг фаз отсутствует. Кроме того, в течение малого промежутка времени переменный ток можно рассматривать как постоянный. Поэтому мгновенная мощность, развиваемая переменным током на сопротивлении:

Хотя ток и напряжение бывают как положительными, так и отрицательными, мощность, равная их произведению, всегда положительна. Однако она пульсирует, изменяясь от нуля до максимального значения с частотой, равной удвоенной частоте переменного тока. На рис. 7.12 показана временная зависимость тока, напряжения и мощности переменного тока, выделяемой на активном сопротивлении. Ясно, что средняя передаваемая мощность меньше максимальной и равна половине максимальной мощности. Среднее значение и за период равно . Это можно объяснить следующим образом: , а за полный цикл среднее значение равно среднему значению . Поэтому среднее значение мощности будет равно

Коэффицие́нт мо́щности — безразмерная физическая величина, характеризующая потребителя переменного электрического тока с точки зрения наличия в нагрузке реактивной составляющей. Коэффициент мощности показывает, насколько сдвигается по фазе переменный ток, протекающий через нагрузку, относительно приложенного к ней напряжения.

Численно коэффициент мощности равен косинусу этого фазового сдвига.

Как известно, потребляемая от источника переменного тока энергия складывается из двух составляющих:

1. Активной энергии

2. Реактивной энергии

1. Активная энергия целиком и безвозвратно преобразуется приемником в другие виды энергии .
Пример: Протекая через резистор, ток совершает активную работу, что выражается в увеличении тепловой энергии резистора. Вне зависимости от фазы протекающего тока, резистор преобразует его энергию в тепловую. Резистору не важно в каком направлении течет по нему ток, важна лишь его величина: чем он больше, тем больше тепла высвободится на резисторе (количество выделенного тепла равно произведению квадрата тока и сопротивления резистора ).

Реактивная энергия — та часть потребляемой энергии, которая в следующую четверть периода будет целиком отдана обратно источнику

РЕЗОНАНС НАПРЯЖЕНИЙ

Известно, что в механической системе резонанс наступает при равенстве собственной частоты колебаний системы и частоты колебаний возмущающей силы, действующей на систему. Колебания механической системы, например колебания маятника, сопровождаются периодическим переходом кинетической энергии в потенциальную и наоборот. При резонансе механической системы малые возмущающие силы могут вызывать большие колебания системы, например большую амплитуду колебаний маятника.
В цепях переменного тока, где есть индуктивность и емкость, могут возникнуть явления резонанса, которые аналогичны явлению резонанса в механической системе. Полная аналогия – равенство собственной частоты колебаний электрического контура частоте возмущающей силы (частоте напряжения сети) – возможна не во всех случаях.
В общем случае под резонансом электрической цепи понимают такое состояние цепи, когда ток и напряжение совпадают по фазе, и, следовательно, эквивалентная схема цепи имеет место при определенном соотношении ее параметров r , L , C , когда резонансная частота цепи равна частоте приложенного к ней напряжения.
Резонанс в электрической цепи сопровождается периодическим переходом энергии электрического поля емкости в энергию магнитного поля и наоборот.
При резонансе в электрической цепи малые напряжения, приложенные к цепи, могут вызвать значительные токи и напряжения на отдельных участках. В цепи, где r , L , C соединены последовательно, может возникнуть резонанс напряжений, а в цепи, где r , L , C соединены параллельно, – резонанс токов .
Резона́нс — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при совпадении частоты собственных колебаний с частотой колебаний вынуждающей силы

резонансную частоту можно найти из выражения

где ; f — резонансная частота в герцах; L — индуктивность в генри; C — ёмкость в фарадах.

16. 1. Работа тока

Электрический ток, конечно же, не стал бы так широко использоваться, если бы не одно обстоятельство. Работу тока или же электроэнергию легко преобразовывать в любую нужную нам энергию или работу: тепловую, механическую, магнитную…

Для практического применения тока прежде всего хочется знать, какую работу можно обратить в свою пользу. Выведем формулу для определения работы тока:

Так как все величины, входящие в формулу, можно измерить соответствующими приборами (амперметр, вольтметр, часы), формула является универсальной.

Формулу можно также записать в несколько ином виде, используя закон Ома:

Если в исходную формулу для работы тока подставить силу тока, записанную таким образом, то получим:

Если же из закона Ома выразить напряжение, то тогда:

Использование этих формул удобно, когда в цепи присутствует какое-то одно соединение: параллельное для первого случая и последовательное для второго

В свое время Эдисон и Тесла были противниками в вопросе использования электрического тока в энергетике. Тесла считал, что необходимо использовать переменный ток, а Эдисон — что нужно применять постоянный ток. У второго ученого было больше возможностей, так как он занимался бизнесом, однако Тесла в конечном итоге удалось победить, так как он был попросту прав.

Вступление

Вычисление мощности

В цепи нагрузки течет ток, который меняется по гармоническому закону. Наша задача — установить, чему равна мощность потребляемой нагрузки от генератора. В распоряжении имеем генератор. В качестве исходных данных представлено направление на входе, которое будет меняться по гармоничному правилу:

(I (t) = I (m) cos w t)

Дальнейшие вычисления

Показатели мощность будут равны произведению:

P (t) = I (t) U (t)

(I (t) = I (m) cos (wt + J)

Определяем результат

cosa cosb = cos(a +b) + cos(a — b) / 2

Воспользуемся этой формулой и получим вычисления:

P(t) = I(m) U (m) cos (wt + J) cos wt

После упрощения результатов получим:

P(t) = I(m) U (m)/2 cos (wt + J) + I(m) U (m) cosJ

Мощность трехфазной цепи переменного тока- это сумма переменной и постоянной составляющих.

Активная и реактивная мощность

Стакан представляет собой электростанцию, вода — электроэнергию, трубочка — кабель или провод. Чем выше поднимается стакан, тем больше напряжение или давление.

Параметры мощности в сети переменного тока активного или реактивного типа зависят от тех элементов, которые потребляют такую энергию. Активная — энергия индуктивности и ёмкости.

Реактивная энергия

Активная мощность — это та энергия, которая потребляется или преобразуется в другие виды — свет, тепло, движение, то есть в какую-либо работу.

Опыт

Как выглядит полная мощность в нашей аналогии? Часть воды выпиваем, а оставшаяся будет продолжать бежать по трубке. Так как у нас есть реактивный ёмкостной элемент — конденсатор или ёмкость, воду опускаем и начинаем имитировать увеличение и уменьшение напряжения. При этом видно, как вода перетекает в двух направлениях. Следовательно, в этом процессе применяется и активная, и реактивная составляющая. Вместе это — полная мощность.

Преобразование мощности

Полная мощность — это геометрическая сумма активной и реактивной мощности.

Для произведения вычислений используем тригонометрические функции. Физический смысл расчетов такой. Возьмем прямоугольный треугольник, в котором одна из сторон равна 90 градусов. Одна из сторон — это его гипотенуза. Есть прилежащий и противолежащий относительно прямого угла катеты.

Вычисление мощности цепи переменного тока по формуле предложено в этом описании.

Индуктивность

Помимо активных элементов, действуют реактивные элементы — индуктивность и ёмкость. В цепях постоянного тока, где амплитудное значение напряжения токов не меняется во времени, работа данного сопротивления будет происходить только во времени. Индуктивность и ёмкость могут негативным образом влиять на сеть.

Запускаем устройство

При запуске устройства видно, что напряжение и ток сети не совпадают по фазе. Наблюдается переход через 0, при котором существует угол — коэффициент мощности сети. Чем меньше этот угол, тем выше коэффициент мощности, который указывается на всех устройствах переменного тока, к примеру, электрических машинах или сварочных трансформаторах.

Итоги

Активная и реактивная мощность — понятия школьного курса физики.

Как мы видели, в цепи синусоидального переменного тока, вообще говоря, возникает сдвиг по фазе между приложенным напряжением и током:

Мгновенная мощность. Сдвиг фаз зависит от соотношения между активным и реактивными сопротивлениями и тем самым от частоты Поскольку напряжение и ток в цепи изменяются с частотой , то при подсчете работы тока нужно рассматривать настолько малый промежуток времени чтобы значения напряжения и тока можно было считать постоянными:

Отсюда получается следующее выражение для мгновенной мощности тока:

Подставив сюда значения из (1), получаем

Воспользовавшись тригонометрическим тождеством

перепишем (4) в следующем виде:

Выражение для мгновенной мощности (5) состоит из двух слагаемых: одно из них не зависит от времени, а второе осциллирует с удвоенной частотой Это значит, что дважды за каждый период изменения приложенного напряжения изменяется направление потока энергии: в течение какой-то части периода энергия поступает в цепь от источника переменного напряжения, а в течение другой части возвращается обратно. Средний за период поток энергии положителен, т. е. энергия поступает в цепь от источника.

Средняя мощность. Действующие значения. Если интересоваться работой переменного тока за промежуток времени, сравнимый с периодом то в выражении (15) для мощности следует учитывать оба слагаемых. При вычислении работы, совершаемой током за промежуток времени, значительно превышающий период, вклад второго слагаемого будет пренебрежимо малым. В этом случае вместо (5) можно пользоваться выражением для средней мощности Р:

Часто эту формулу записывают в виде

где I и — так называемые действующие значения силы тока и напряжения, в раз меньшие соответствующих амплитудных значений:

Использование действующих значений вместо амплитудных удобно потому, что в нагрузке с чисто активным сопротивлением, где выражение (7) для мощности будет таким же, как и для постоянного тока.

Потери в линиях передачи. Потребителю обычно подается напряжение определенной величины поэтому одна и та же мощность Р будет потребляться при разных значениях тока в цепи I в зависимости от сдвига фазы между током и напряжением. При

малых значениях ток должен быть большим, что приводит к большим тепловым потерям в подводящих проводах линии передачи.

Если — сопротивление линии передачи, то рассеиваемая мощность тепловых потерь в линии равна . Выражая ток в цепи с помощью (7), для получаем

Для уменьшения потерь следует добиваться как можно меньшего сдвига фазы между током и напряжением в нагрузке.

Большинство современных потребителей электрической энергии синусоидального тока представляют собой нагрузки индуктивного характера, токи в которых отстают по фазе от напряжения источника питания. Эквивалентную схему такого потребителя можно изобразить в виде последовательно соединенных активного сопротивления и индуктивности (рис. 143а). Соответствующая векторная диаграмма показана на рис. 144а. Ток через нагрузку отстает от приложенного напряжения на определенный угол Потребляемая нагрузкой мощность согласно (7) равна

Рис. 143. Эквивалентная схема потребителя с индуктивной нагрузкой (а) и включение вспомогательного конденсатора для увеличения

Рис. 144. Векторные диаграммы для цепей, изображенных на рис. 143

Из этой формулы видно, что при напряжении такую же мощность можно было бы получить и при любом другом токе таком, что изображающий его вектор (показанный штриховой линией на рис. 144а) оканчивается на перпендикуляре опущенном из конца на направление так как при этом Но если то и при той же мощности тепловые потери в подводящих проводах будут меньше.

Уменьшение потерь. Как же добиться того, чтобы сдвиг фаз между напряжением и током в цепи уменьшился? Легко сообразить, что для этого можно подсоединить параллельно нагрузке вспомогательный конденсатор (рис. 1436). Векторная диаграмма в этом случае будет иметь вид, изображенный на рис. 144б. Векторы, изображающие приложенное напряжение и ток через нагрузку останутся неизменными, а полный ток в неразветвленной цепи, равный сумме токов через нагрузку и вспомогательный конденсатор, будет изображаться вектором Подбирая емкость конденсатора, можно добиться того, чтобы сдвиг по фазе принял заданное значение 9.

Из рис. 1446 видно, что длина вектора равна

Но и с помощью (10) находим Амплитудное значение тока в конденсаторе связано с амплитудным значением подаваемого напряжения формулой Подставляя в (11), находим

Таким образом, существует достаточно простой и эффективный способ снижения потерь в линиях передачи энергии переменного тока, связанных с реактивным характером сопротивления нагрузки: подключение конденсатора к индуктивной нагрузке позволяет получить равное нулю значение сдвига фаз 9.

Высоковольтные линии передачи. Но даже в том случае, когда сопротивление нагрузки является чисто активным и сдвиг фаз между напряжением и током отсутствует, т. е. тепловые потери в линии передачи все равно неизбежны. Можно ли их каким-либо способом уменьшить? Ответ на этот вопрос дает формула (9). Из нее видно, что при заданном значении передаваемой потребителю мощности Р уменьшить тепловые потери в линии можно, либо уменьшая сопротивление проводов линии передачи, либо повышая напряжение переменного тока, подаваемого потребителю. Уменьшение сопротивления линии в настоящее время возможно лишь до известных пределов, поэтому до создания эффективных сверхпроводящих линий электропередачи с потерями приходится бороться повышением напряжения.

Трансформатор. Для преобразования напряжения на электростанциях и у потребителей используются трансформаторы (рис. 145). Трансформатор имеет сердечник замкнутой формы из магнитомягкого (легко перемагничиваемого) материала, который несет на себе две обмотки: первичную и вторичную. Концы первичной обмотки (вход трансформатора) подключают к сети

переменного тока, а концы вторичной обмотки (выход) — к потребителю электрической энергии. ЭДС электромагнитной индукции, возникающая во вторичной обмотке, пропорциональна числу витков в ней.

Рис. 145. Трансформатор: общий вид, схематическое устройство и условное изображение на схемах

Поэтому, изменяя это число витков, можно изменять в широких пределах напряжение на выходе трансформатора.

Рассмотрим принцип действия трансформатора. Пусть сначала вторичная обмотка трансформатора разомкнута, а на первичную подается переменное синусоидальное напряжение. Это режим холостого хода. Как и всякую катушку индуктивности, первичную обмотку трансформатора можно рассматривать как последовательно соединенные индуктивность и активное сопротивление Напряжение на индуктивном сопротивлении первичной обмотки опережает по фазе ток и, следовательно, напряжение на ее активном сопротивлении на угол, равный Поэтому амплитудные значения поданного на первичную обмотку напряжения и напряжений на и связаны соотношением

Разумеется, непосредственно измерить и по отдельности невозможно, так как первичная обмотка, строго говоря, не есть последовательно соединенные индуктивность и активное сопротивление каждый элемент обмотки обладает одновременно индуктивностью и сопротивлением. Это так называемая цепь с распределенными параметрами. Но при расчете можно заменить реальную обмотку на цепь с сосредоточенными параметрами — катушку индуктивности и резистор, соединенные последовательно, поскольку через каждый элемент исходной цепи идет один и тот же ток.

Напряжение на индуктивности в каждый момент времени компенсирует возникающую в первичной обмотке ЭДС самоиндукции поэтому

Если весь магнитный поток, создаваемый током первичной обмотки, целиком, т. е. без рассеяния, пронизывает вторичную

обмотку, то индуцируемая в каждом витке вторичной обмотки ЭДС будет такой же, как и в каждом витке первичной обмотки. Поэтому отношение электродвижущих сил в первичной и вторичной обмотках равно отношению чисел витков:

На выходе разомкнутой вторичной обмотки существует напряжение, равное индуцируемой в ней ЭДС:

Подставляя сюда из (15) и учитывая (14), получаем

Режим холостого хода. Таким образом, значение напряжения на разомкнутой вторичной обмотке трансформатора пропорционально не подаваемому на первичную обмотку напряжению а лишь напряжению на индуктивном сопротивлении первичной обмотки Отсюда сразу становится ясна роль сердечника трансформатора. В самом деле, из формулы (13) следует, что напряжение на индуктивности будет тем ближе к подаваемому на вход трансформатора напряжению чем больше будет индуктивное сопротивление первичной обмотки по сравнению с ее активным сопротивлением Наличие сердечника из материала с высокой магнитной проницаемостью приводит к многократному увеличению индуктивности . У такого трансформатора на холостом ходу Знак минус означает, что эти напряжения находятся в противофазе. Благодаря большому индуктивному сопротивлению первичной обмотки ток в ней при разомкнутой вторичной цепи мал.

Трансформатор под нагрузкой. При замыкании вторичной цепи трансформатора на некоторую нагрузку во вторичной обмотке появляется ток. Создаваемый этим током магнитный поток направлен так, что, согласно закону Ленца, препятствует изменению магнитного потока, создаваемого током в первичной обмотке. Если бы при этом ток в первичной обмотке остался неизменным, то это привело бы к уменьшению магнитного потока. Значит, включение нагрузки во вторичную цепь эквивалентно уменьшению индуктивности первичной цепи.

Но уменьшение индуктивного сопротивления немедленно приводит к увеличению тока в первичной обмотке, к уменьшению сдвига по фазе между напряжением и током и, следовательно, к увеличению потребляемой от внешней цепи мощности. Таким образом, если на холостом ходу трансформатор представляет собой почти чисто

индуктивное сопротивление, то по мере увеличения нагрузки трансформатора, т. е. тока во вторичной цепи, характер сопротивления первичной обмотки трансформатора становится ближе к активному.

Если потери энергии в самом трансформаторе малы, то на основании закона сохранения энергии потребляемая трансформатором мощность целиком передается нагрузке. Тогда с помощью (6) можно написать

где — сдвиги фаз между током и напряжением в первичной и вторичной цепях.

Приведенное выше рассмотрение работы трансформатора относится к идеализированному случаю трансформатора без потерь. В реальном трансформаторе всегда имеются потери, связанные с выделением джоулевой теплоты в обмотках, с токами Фуко, с необратимыми явлениями при перемагничивании сердечника и с рассеянием магнитного потока. Но в современных трансформаторах суммарные потери не превышают нескольких процентов от передаваемой мощности. Коэффициент полезного действия трансформаторов очень высок и лежит в пределах 95-99,5%.

Выпрямление переменного тока. Для многих практических применений необходимо преобразовать переменный синусоидальный ток в ток одного направления. Этой цели служат выпрямители, действие которых основано на односторонней проводимости ламповых и полупроводниковых диодов.

Понять действие выпрямителя можно, не вникая в физическую природу самого механизма односторонней проводимости.

Простейшая схема выпрямителя приведена на рис. 146а. Это однополупериодный выпрямитель, в котором ток через нагрузку течет только в течение одной половины каждого периода приложенного синусоидального напряжения.

Рис. 146. Схемы выпрямителей: однополупериодного (а), двухполупериодного (б) и с удвоением напряжения (в)

В мостиковой схеме выпрямителя, показанной на рис. 1466, ток через нагрузку идет в одном и том же направлении в течение обеих половин каждого периода. Но в таком двухполупериодном выпрямителе ток все-таки тоже пульсирует. Для сглаживания этих

пульсаций используют так называемые электрические фильтры, если требуется не только получить ток одного направления, но и постоянное напряжение.

В приведенных на рис. 146 а,б схемах максимальное значение напряжения на нагрузке (при идеальных диодах) равно амплитудному значению приложенного синусоидального напряжения. В показанной на рис. 146 в схеме выпрямителя напряжение на нагрузке практически вдвое больше амплитудного значения приложенного напряжения, если время разрядки конденсаторов через сопротивление нагрузки значительно превышает период Т синусоидального напряжения. Это так называемая схема с удвоением напряжения.

Задачи

1. Активное сопротивление первичной обмотки трансформатора составляет ее индуктивного сопротивления Какое напряжение будет на разомкнутой вторичной обмотке, имеющей вдвое больше витков, если первичную обмотку включить в сеть напряжением 220 В?

Решение. Напряжение на разомкнутой вторичной обмотке связано с напряжением на индуктивном сопротивлении первичной обмотки соотношением (17). Поэтому в рассматриваемом случае для действующих значений имеем дросселя, если сопротивление кипятильника (реактивная нагрузка) и

В каких случаях при расчете работы переменного тока можно пользоваться выражением (6) для средней мощности, а не выражением (5) для мгновенной мощности?

Каким образом можно уменьшить тепловые потери в линиях электропередачи, изменяя характер сопротивления нагрузки? Почему в сетях переменного тока потребитель энергии должен обладать практически активным в целом сопротивлением?

В чем преимущество использования линий высокого напряжения для передачи электроэнергии?

Какую роль в трансформаторе играет сердечник из материала с высокой магнитной проницаемостью? Почему железный сердечник трансформатора собирают из отдельных изолированных пластин?

Из формулы (17) следует, что коэффициент трансформации напряжения определяется отношением чисел витков Казалось бы, при отношении потери в трансформаторе будут тем меньше, чем меньше значения так как с увеличением числа витков растет активное сопротивление. Почему же у трансформаторов обмотки обычно содержат большое число витков?

Можно ли включать трансформатор в сеть постоянного тока?

Нарисуйте графики зависимости силы тока от времени в нагрузке выпрямителей, схемы которых показаны на рис. 146 а,б.

Объясните, почему в схеме выпрямителя на рис. 146 в происходит удвоение напряжения на нагрузке. Предложите схему выпрямителя, в котором на нагрузке происходило бы утроение напряжения.

Details 26 February 2017

Господа, всех вас в очередной раз приветствую! В сегодняшней статье я бы хотел поднять темы, касающиеся мощности и энергии (работы) в цепях переменного тока . Сегодня мы узнаем, что это такое и научимся их определять. Итак, погнали.

Прежде чем начать что-либо обсуждать про переменный ток, давайте-ка вспомним, как мы определяли мощность в случае постоянного тока . Да-да, у нас была отдельная статейка на эту тему, помните? Если нет, то напоминаю, что в случае постоянного тока мощность в цепи считается очень просто, по одной из этих трех замечательных формул:

где P — искомая мощность, которая выделяется на резисторе R;

I — сила тока в цепи через резистор R;

U — напряжение на резисторе R.

Это все здорово. Но как быть в случае переменного тока , а в частности — синусоидального? Ведь там у нас колбасится синус, значения тока и напряжения все время меняются, сейчас они одни, через мгновение — уже другие, т.е., выражаясь научным языком, они являются функциями времени. Пользуясь знаниями, полученными нами в предыдущей вводной статье , мы можем записать вот такой закон изменения силы тока:

Мы не будем сейчас повторять что здесь есть что, все это было досконально рассмотрено в прошлый раз .

И вот глядя на эти три строчки с формул и сопоставляя их между собой, не приходит ли вам на ум какая-либо идея? Например, что можно бы подставить ток или напряжение в формулу для мощности… Такая идея пришла? Это просто замечательно! Давайте ее сейчас же реализуем! Поскольку у нас и ток, и напряжения зависят от времени, все три полученные новые формула для мощности абсолютно также будет зависеть от времени.

Ох, прям в глазах рябит от синусов . Но ведь все довольно просто и очевидно откуда, что получилось, не так ли? По вот этим вот самым формулам можно рассчитать мгновенную мощность в определенный момент времени. Фишка в том, что если через резистор течет переменный ток, то в каждое мгновение времени на нем будет выделяться вообще говоря разная мощность : иначе и быть не может, раз амплитуда тока через резистор все время разная. Другое дело, что визуально, при большой частоте изменения тока, мы скорее всего это не заметим: температура резистора не будет хаотично скакать в такт изменения мощности, которая на нем выделяется. Это будет потому, что сам резистор благодаря его массе и теплоемкости синтегрирует эти перепады температуры.

Итак, с мощностью более-менее понятно. А как быть с энергией? Ну, то есть с теплом, которое выделяется на резисторе? Как оценить эту самую энергию? Для этого нам надо вспомнить, как же связаны между собой мощность и энергия. Мы уже затрагивали эту тему в статье про мощность в цепи постоянного тока . Тогда этот вопрос решился просто: при постоянном токе достаточно умножить мощность (которая там не зависит от времени и все время одинакова) на время наблюдения и получить выделяющуюся за это самое время наблюдения энергию. С переменным током все посложнее, потому что тут мощность зависит от времени. И, увы, тут не обойтись без интегралов… Что это вообще такое этот самый интеграл? Как, вероятно, многие из вас знают, интеграл — это просто площадь под графиком . В данном конкретном случае под графиком зависимости мощности от времени P(t) . Да, вот так вот все просто.

Итак, энергия (или работа, что по сути одно и то же) в цепи переменного тока считается следующим образом

В этой формуле Q — это искомая работа (энергия) переменного тока (измеряется все так же в джоулях), P(t) — закон изменения мощности от времени, а Т — собственно, сам отрезок времени, который мы рассматриваем, и в течении которого ток работает.

Господа, скажу сразу, в своих статьях я не буду рассказывать, как брать интегралы. Я надеюсь, что вы это знаете. А если нет — ничего страшного, не спешите закрывать статью. Я буду стараться строить изложение таким образом, чтобы незнание интегралов не привело в вашем сознании к fatal error . Очень часто их вообще не требуется считать ручками, а можно посчитать в специализированных программах или даже онлайн на многочисленных сайтах.

Рисунок 1 — Зависимость мощности от времени для переменного и постоянного тока

Там два графика: на верхнем показана зависимость мощности от времени для случая переменного синусоидального тока, а на нижнем — для случая постоянного тока. Как я их построил? Очень просто. Для первого графика я взял вот эту ранее написанную нами формулу.

Будем полагать, что амплитуда синусоидального тока равна I m =1 A , сопротивление резистора, на котором рассеивается мощность, равно R=5 Ом , а частота синуса равна f = 1 Гц , что соответствует круговой частоте

То есть формула, по которой мы строим график мощности переменного тока, имеет вид

Именно по этой формуле построен верхний график на рисунке 1.

А как быть с нижним графиком? Господа, ну тут совсем все просто. Я исходил из того, что через тот же самый резистор R=5 Ом течет постоянный ток величиной I=1 А . Тогда, как должно быть понятно из закона Джоуля-Ленца , на данном резисторе будет рассеиваться вот такая вот мощность

Понятное дело, что раз через наши пятиомные резисторы течет ток, то на них выделяется некоторая мощность и рассеивается некоторое количество энергии. Иными словами, резистор греется за счет выделяющейся на нем энергии. Мы уже обсуждали, что эта энергия считается через интеграл. Но, как мы уже говорили, есть и графическое представление этого интеграла — он равен площади под графиком. Эту площадь я заштриховал на рисунке 1. То есть, если мы найдем, чему равна площадь под верхним и нижним графиками, то мы определим, какое количество энергии выделилось в первом и втором случае.

Ну, с нижним графиком вообще все просто. Там — прямоугольник высотой 5 Вт и шириной 2 секунды. Поэтому площадь (то бишь энергия) находится элементарно

Со верхним графиком все не так просто. Там у нас неправильная форма и просто так сразу нельзя сказать, чему равна эта площадь. Вернее, сказать можно — она равна вот такому вот интегралу

Результат вычисления этого интеграла равен конкретному числу и это число — как раз наша искомая энергия, которая выделилась на резисторе. Мы не будем расписывать взятие этого интеграла. Посчитать такой интеграл ручками не составит труда для человека, хотя бы поверхностного знакомого с математикой. Если же все-таки это вызывает затруднение, или просто лень самому считать — есть огромное количество САПРа, которое сделает это за вас. Либо можно посчитать этот интеграл на каком-либо сайте: по запросу в гугле «интегралы онлайн» выдается достаточное количество результатов. Итак, сразу переходим к ответу и он равен

Вот так вот. Энергия, которая выделяется на резисторе при протекании синусоидального тока с амплитудой 1 А почти в два раза меньше энергии, которая будет выделяться в случае, если течет постоянный ток величиной 1 А. Оно и понятно — даже визуально на рисунке 1 площадь под верхним графиком заметно ниже, чем под нижним.

А пока что — всем вам огромной удачи, спасибо, что прочитали, и пока!

Вступайте в нашу

21 сентября 2017

В свое время Эдисон и Тесла были противниками в вопросе использования электрического тока в энергетике. Тесла считал, что необходимо использовать переменный ток, а Эдисон — что нужно применять постоянный ток. У второго ученого было больше возможностей, так как он занимался , однако Тесла в конечном итоге удалось победить, так как он был попросту прав.

Вступление

Вычисление мощности

Допустим, у нас имеется генератор переменного напряжения, который подключен к нагрузке. На выходе генератора, между двумя точками на клеммах, напряжение меняется по гармоническому , а нагрузка взята произвольная: катушки, активное сопротивление, конденсаторы, электромотор.

(I (t) = I (m) cos w t)

Дальнейшие вычисления

Показатели мощность будут равны произведению:

P (t) = I (t) U (t)

(I (t) = I (m) cos (wt + J)

Определяем результат

cosa cosb = cos(a +b) + cos(a — b) / 2

Воспользуемся этой формулой и получим вычисления:

P(t) = I(m) U (m) cos (wt + J) cos wt

После упрощения результатов получим:

P(t) = I(m) U (m)/2 cos (wt + J) + I(m) U (m) cosJ

Мощность трехфазной цепи переменного тока- это сумма переменной и постоянной составляющих.

Активная и реактивная мощность

Реактивная энергия

Опыт

Пре мощности

Полная мощность — это геометрическая сумма активной и реактивной мощности.

Для произведения вычислений используем тригонометрические функции. Физический смысл расчетов такой. Возьмем прямоугольный треугольник, в котором одна из сторон равна 90 градусов. Одна из сторон — это его гипотенуза. Есть прилежащий и противолежащий относительно прямого угла катеты.

Косинус представлен , которое предопределяет длина прилегающего катета относительно длины гипотенузы.

Вычисление мощности цепи переменного тока по формуле предложено в этом описании.

Индуктивность

Запускаем устройство

При запуске устройства видно, что напряжение и ток сети не совпадают по фазе. Наблюдается переход через 0, при котором существует угол — коэффициент мощности сети. Чем меньше этот угол, тем выше коэффициент мощности, который указывается на всех устройствах переменного тока, к примеру, электрических или сварочных трансформаторах.

Итоги

Активная и реактивная мощность — понятия школьного курса физики.

Источник: fb.ru

В чем разница между питанием переменного и постоянного тока?

В эту забавную пятницу мы рассмотрим разницу между переменным и постоянным током. Мы начнем с «Текущей войны» Эдисона и Теслы в 1880-х годах, когда каждый боролся за свой тип электричества. Затем мы сравним их и посмотрим на плюсы и минусы каждого, в том числе на то, почему оба необходимы для современных технологий. Наконец, мы поговорим о различиях в стандартах на электроэнергию во всем мире.

Война течений началась в 1880-х годах между двумя очень известными именами: Томасом Эдисоном и Николой Тесла.Томас Эдисон разработал электричество постоянного тока или постоянного тока, которое какое-то время было единственным доступным источником электроэнергии. Проблема с постоянным током заключается в том, что трудно преобразовать его в более высокие или более низкие напряжения, что ограничивает его способность эффективно преодолевать большие расстояния. Электростанции постоянного тока должны были быть расположены на расстоянии мили от зданий, которые они питали, что было совершенно невозможно для сельской местности. Тесла придумал переменный ток, который вращается с частотой (в США — 60 раз в секунду) и может быть преобразован в другие напряжения с помощью трансформатора.У Эдисона были патенты на DC и он не хотел терять деньги, поэтому он начал дискредитировать AC — он лоббировал законодательные органы штата, распространял дезинформацию и даже пытался повлиять на общественное мнение, убивая бродячих животных током переменного тока, чтобы доказать его опасность.

Никола Тесла. Изображения предоставлены: WorldStandards

Thomas Edison. Изображение предоставлено: WorldStandards

Все изменилось на Всемирной выставке в Чикаго в 1893 году. Согласно Energy.gov, «General Electric предложила электрифицировать ярмарку с использованием постоянного тока Эдисона за 554000 долларов, но проиграла Джорджу Вестингаузу, который сказал, что может привести в действие электричество. справедливо всего за 399000 долларов с использованием переменного тока Tesla.[…] В том же году компания Niagara Falls Power Company решила заключить с Westinghouse, которая получила лицензию на патент на многофазный асинхронный двигатель переменного тока Tesla, контракт на производство электроэнергии из Ниагарского водопада ». В ноябре 1896 года General Electric полностью поддержала AC, и их недавно построенная гидроэлектростанция на Ниагарском водопаде осветила Буффало, штат Нью-Йорк. Казалось, сила переменного тока наконец-то восторжествовала над постоянным током.

Если в 1893 году мощность переменного тока победила постоянный ток, почему мы используем и то, и другое сегодня? Некоторое время переменный ток был доминирующей формой электричества, но сегодня мы используем постоянный ток каждый день, особенно в портативных устройствах.Давайте посмотрим на прямое сравнение переменного и постоянного тока. В простейшем случае электрический ток — это поток электронов. Основное различие между двумя типами тока — это направление: постоянный ток прямой, то есть он течет только в одном направлении. Вы можете думать об этом как о батарее с положительным и отрицательным полюсами, она должна быть установлена в одну сторону, чтобы через нее мог течь ток (я знаю, о чем вы думаете, подпружиньте плоский конец батареи. инженер-электрик, теперь вы закатываете глаза).Переменный ток имеет колеблющееся повторение, которое выглядит как волновой узор на графике, по сравнению с постоянным током, который выглядит как плоская линия. Волновой рисунок — это герц, или количество колебаний в секунду. Электропитание переменного тока более удобно для достижения высокого напряжения для передачи на большие расстояния, поэтому наши лампы и большая часть бытовой электроники, которые подключаются к стене, используют переменный ток. Однако с телефоном в ваш дом протекает переменный ток, который затем заряжает ваш телефон, аккумулятор которого работает от постоянного тока. То же самое и с ноутбуками, поэтому у них есть кирпич между стеной и компьютером — мощность должна быть преобразована в постоянный ток для внутренней батареи.

Синусоидальное напряжение переменного тока. Кредит изображения: Sparkfun

Напряжение постоянного тока. Кредит изображения: Sparkfun

Но так было не всегда, долгое время доминировал AC. Важным поворотным моментом для питания постоянного тока стали 1970-е годы, когда была изобретена полупроводниковая электроника. Было намного экономичнее преобразовывать переменный ток в постоянный, и некоторое оборудование могло генерировать очень высокое постоянное напряжение. Кроме того, для многих электронных устройств требуется постоянный ток; Согласно сайту Sciencing.com: «Постоянный ток используется в любом устройстве, имеющем печатную плату, потому что микросхемы в этих устройствах требуют постоянного однонаправленного потока электронов для работы и хранения данных.Это означает, что ваш настольный компьютер, игровая система и телевизор используют постоянный ток и содержат полный мостовой выпрямитель для преобразования переменного тока из настенной розетки в постоянный. Некоторые из этих устройств также содержат жесткие диски, приводимые в действие двигателями, которые, как вы уже догадались, требуют постоянного тока. С ростом количества электроники, который продолжается с тех пор: персональных компьютеров, сотовых телефонов, смарт-телевизоров, электромобилей и многого другого, DC вернулся с удвоенной силой и стал использоваться повсюду.

Краткое примечание об отправке энергии на большие расстояния.Поскольку большая часть мира подключена к переменному току, это то, что мы используем, но удивительно, что некоторые линии постоянного тока высокого напряжения или HVDC на самом деле могут доставлять электроэнергию с меньшими потерями, чем переменный ток, на большие расстояния. Эти линии могут даже позволить несколько систем переменного тока, например, 50 Гц в Европе и 60 Гц в США, подключаться к одной и той же линии. Однако повышенная стоимость и снижение надежности означают, что линии переменного тока все еще более распространены.

Tesla на зарядном устройстве 240в. Кредит изображения: JSR Electrical.

Если все используют кондиционер, почему в разных частях света используются разные стандарты, например, в Европе и США? Например, в Америке и Японии стандартная система на 100–127 вольт, но в Европе и большей части мира используется вдвое большее напряжение, 220–240 вольт.Никола Тесла провел тщательные вычисления, чтобы выбрать число 60 Гц как лучшую частоту. Что еще более странно, системы с более низким напряжением работают с частотой 60 Гц, или 60 колебаний в секунду, в то время как остальной мир работает с частотой 50 Гц. Согласно WorldStandards : «Когда немецкая компания AEG построила один из первых европейских генерирующих объектов, ее инженеры решили зафиксировать частоту на уровне 50 Гц, поскольку число 60 не соответствовало стандартной метрической последовательности единиц (1, 2, 5 ).В то время у AEG была виртуальная монополия, и их стандарт распространился на весь остальной континент. В Великобритании распространялись разные частоты, и только после Второй мировой войны был установлен стандарт 50-цикла ».

Первоначально стандарт напряжения был 120В и в Европе. Работая с медным проводом определенного диаметра, Европа сочла необходимым увеличить напряжение для меньших потерь и меньшего падения напряжения. Соединенные Штаты хотели сделать то же самое, но когда это рассматривалось в 50-х и 60-х годах, многие американские домохозяйства имели бытовую технику, такую как стиральные машины и холодильники, и стоимость их замены была непомерно высокой.В большинстве европейских домохозяйств такой бытовой техники еще не было, и переключиться было проще. Пребывание при таком более низком напряжении на самом деле вызывало в США проблемы с разбросом высокого и низкого напряжения. Решением было подать 240 вольт на каждое здание, а затем разделить его на две линии по 120 вольт. Хотя некоторые приборы, такие как сушилки и духовки, используют 240 В в Северной и Южной Америке, некоторые из этих приборов по-прежнему не работают с европейской мощностью из-за разницы фаз 60 Гц и 50 Гц.

Карта напряжений: 120 В красным и 240 В синим.Кредит изображения: WorldStandards.

Без великой работы Эдисона и Теслы наша повседневная жизнь, как мы ее знаем сегодня, была бы невозможна. Оказывается, переменный ток отлично подходит для некоторых целей, например, для путешествий на большие расстояния, а постоянный ток отлично подходит для других целей, таких как компьютеры, светодиоды и электромобили. В любом случае, это сила!

Источники:

https://www.energy.gov/articles/war-currents-ac-vs-dc-power

https://learn.sparkfun.com/tutorials/alternating-current- ac-vs-direct-current-dc / all #: ~: text = In% 20direct% 20current% 20 (DC)% 2C, потому что% 20the% 20current% 20changes% 20direction.

https://engineering.mit.edu/engage/ask-an-engineer/whats-the-difference-between-ac-and-dc/

https://sciencing.com/uses- direct-current-7394786.html

https://www.worldstandards.eu/electricity/history/why-no-standard-voltage/

https://jsrelectrical.com/electric-car-chargers /

Переменный ток — Energy Education

Переменный ток (AC) — это тип электрического тока, вырабатываемого подавляющим большинством электростанций и используемого в большинстве систем распределения электроэнергии.Переменный ток дешевле генерировать и имеет меньше потерь энергии, чем постоянный ток при передаче электроэнергии на большие расстояния. ^[1] Хотя для очень больших расстояний (более 1000 км) постоянный ток часто может быть лучше. В отличие от постоянного тока направление и сила переменного тока меняются много раз в секунду.

Недвижимость

Рис. 1. Анимация из моделирования ^[2] переменного тока PhET, которое было значительно замедлено.См. Постоянный ток для сравнения.

Переменный ток меняет направление потока заряда (60 раз в секунду в Северной Америке (60 Гц) и 50 раз в секунду в Европе (50 Гц)). Обычно это вызвано синусоидально изменяющимися током и напряжением, которые меняют направление, создавая периодическое движение назад и вперед для тока (см. Рисунок 1). Несмотря на то, что этот ток течет вперед и назад много раз в секунду, энергия по-прежнему непрерывно течет от электростанции к электронным устройствам.{2} R [/ math]

Мощность, передаваемая по линии, однако, имеет другое выражение:

[математика] P_ {передано} = IV [/ математика]

Как видно из первого уравнения, потери мощности при передаче пропорциональны квадрату тока через провод. Следовательно, предпочтительно минимизировать ток через провод, чтобы уменьшить потери энергии.Конечно, минимизация сопротивления также снизит потери энергии, но ток оказывает гораздо большее влияние на количество потерянной энергии из-за того, что его значение возводится в квадрат. Второе уравнение показывает, что если напряжение увеличивается, ток уменьшается эквивалентно для передачи той же мощности. Следовательно, напряжение в линиях передачи очень высокое, что снижает ток, что, в свою очередь, сводит к минимуму потери энергии при передаче. Вот почему переменный ток предпочтительнее постоянного тока для передачи электричества, так как намного дешевле изменить напряжение переменного тока.Однако существует предел, при котором более нецелесообразно использовать переменный ток по сравнению с постоянным током (см. Передача HVDC).

Использование и преимущества

Большинство устройств (например, большие заводские динамо-машины), которые напрямую подключены к электросети, работают на переменном токе, а электрические розетки в домах и коммерческих помещениях также подают переменный ток. Устройства, которым требуется постоянный ток, например ноутбуки, обычно имеют адаптер переменного тока, который преобразует переменный ток в постоянный.^[5]

Переменный ток является предпочтительным во всем мире, поскольку он имеет много явных преимуществ по сравнению с постоянным током. Для полной разбивки различий между ними см. AC vs DC. Некоторые преимущества включают: ^[6]

Дешевое и эффективное повышение напряжения с помощью трансформаторов. Как объяснялось выше, это позволяет осуществлять энергоэффективную передачу электроэнергии по линиям электропередач. Эта эффективная передача энергии экономит энергетическим компаниям и потребителям много денег и помогает уменьшить загрязнение, поскольку электростанциям не нужно компенсировать потерю электроэнергии за счет использования большего количества топлива.
Низкие затраты на техническое обслуживание высокоскоростных двигателей переменного тока.
Легко прервать ток (например, с помощью автоматического выключателя) из-за того, что ток естественным образом стремится к нулю каждые 1/2 цикла. Например, автоматический выключатель может отключать примерно 1/20 постоянного тока от переменного тока.

Phet Simulation

Университет Колорадо любезно разрешил нам использовать следующую симуляцию Фета, которая исследует, как работает переменный ток.

Дополнительная информация

Для получения дополнительной информации см. Соответствующие страницы ниже:

Ссылки

Узнать | OpenEnergyMonitor

Введение в питание переменного тока

Общие сведения о питании переменного тока

Энергомонитор всего дома измеряет энергию, потребляемую приборами, подключенными к домашней электросети.Чтобы понять, как это происходит, полезно знать кое-что о том, как приборы взаимодействуют с электрической системой.

Не все приборы одинаково взаимодействуют с электросетью. В этой статье сначала будут обсуждаться резистивные нагрузки и расчет потребляемой мощности. Затем мы переходим к обсуждению реактивных нагрузок и немного о нелинейных нагрузках. Наконец, он покажет, как мы измеряем направление потока энергии, что важно, если энергия генерируется, а также потребляется.

Резистивные нагрузки

Лампы накаливания, чайники, утюги, электрические водонагреватели, электрические плиты — все довольно просто. Они используют всю отданную им энергию. Это резистивные нагрузки, что означает, что их потребляемый ток равен напряжению, деленному на их сопротивление (закон Ома). Чисто резистивная нагрузка дает выходной сигнал напряжения и тока, аналогичный приведенному ниже:

Диаграмма 1 — Соотношение фаз напряжения и тока в резистивной нагрузке

Желтая линия — мощность в данный момент времени (в любой данный момент она называется мгновенной мощностью , ), которая равна произведению напряжения и тока в данный момент времени.Обратите внимание, сила всегда положительная. В этом случае положительное направление — это энергия, текущая к нагрузке.

Частично реактивные нагрузки

Однако такие вещи, как холодильники, стиральные машины, сверлильные станки и аппараты для дуговой сварки, не так просты, поскольку эти устройства потребляют определенное количество энергии, а затем возвращают часть энергии обратно в сеть. Они имеют индуктивные (например, двигатели) или емкостные (например, аппараты для дуговой сварки) компоненты в дополнение к резистивному компоненту. Частично индуктивная нагрузка дает выходные сигналы напряжения и тока, подобные приведенным ниже:

Диаграмма 2 — Соотношение фаз напряжения и тока в частично реактивной нагрузке

Обратите внимание, что желтая линия теперь на некоторое время становится отрицательной, положительный бит — это энергия, текущая к нагрузке, а отрицательный бит — энергия, текущая обратно от нагрузки.

Еще одна вещь, которую следует учитывать, — это то, что формы сигналов напряжения и тока смещены друг от друга. Представьте себе зарядку довольно большого конденсатора с помощью резистора последовательно (так, чтобы он не мог заряжаться мгновенно): для начала конденсатор разряжается. Напряжение питания возрастает и превышает напряжение на конденсаторе, поэтому ток течет в конденсатор (положительное направление на графике), что вызывает повышение напряжения на конденсаторе. Напряжение питания падает. Теперь напряжение на заряженном конденсаторе выше, чем напряжение питания.Ток начинает течь обратно в направлении источника питания (отрицательное направление на графике). Это приводит к тому, что текущая форма волны выглядит так, как если бы она была сдвинута, как показано на графике. (Это называется фазовым сдвигом).

Реальная мощность, реактивная мощность и полная мощность

Если посмотреть на приведенные выше графики напряжения, тока и мощности при частоте сети, потребляемая мощность колеблется 50/60 раз в секунду. Мы не можем угнаться за изменениями на этой скорости, поэтому у нас есть более полезное значение мощности: среднее значение мгновенной мощности, которое мы называем реальной мощностью или активной мощностью .

Реальная мощность часто определяется как мощность, используемая устройством для выполнения полезной работы. Ссылаясь на график выше, положительные биты — это мощность, поступающая на нагрузку от источника питания, а отрицательные биты — это мощность, возвращающаяся к источнику питания от нагрузки. Мощность, которая фактически использовалась нагрузкой, то есть мощность, которая была включена, за вычетом мощности, возвращаемой обратно, является реальной мощностью.

Реактивная мощность или мнимая мощность — это мера мощности, передаваемой между нагрузкой и источником питания, которая не выполняет полезной работы.

Еще одним полезным показателем мощности является полная мощность , которая является произведением среднеквадратичного (RMS) напряжения и RMS-тока. Для чисто резистивных нагрузок активная мощность равна полной мощности. Но для всех остальных нагрузок реальная мощность меньше полной мощности. Полная мощность — это мера реальной и реактивной мощности, но не сумма двух, так как сумма двух не учитывает разности фаз.

Соотношение между реальной, реактивной и полной мощностью для ИДЕАЛЬНЫХ синусоидальных нагрузок:

Реальная мощность = Полная мощность x cosΦ

Реактивная мощность = Полная мощность x sin Φ

cosΦ также известен как коэффициент мощности.

Однако примечание о нелинейных нагрузках:

Это соотношение коэффициента мощности действительно только для линейных синусоидальных нагрузок. Большинство источников питания для устройств постоянного тока, таких как портативные компьютеры, создают нелинейную нагрузку на сеть. Их текущий розыгрыш часто выглядит так:

Мы все еще можем рассчитать коэффициент мощности по следующему уравнению:

Коэффициент мощности = фактическая мощность / полная мощность

но отношение

(полная мощность) ² = (активная мощность) ² + (реактивная мощность) ²

, которое верно для чистых синусоидальных волн, больше не является правильным.Кроме того, коэффициент мощности = cosΦ , поскольку необходимо учитывать влияние гармоник более высокого порядка на формы сигналов как напряжения, так и тока.

Значение коэффициента мощности измеряет, насколько эффективность сети зависит от ОБЕИХ фазовой задержки φ И содержания гармоник входного тока.

Ссылка: понимание коэффициента мощности от L Wuidart

Определение направления потока мощности

До сих пор в этой статье предполагалось, что нагрузка потребляет мощность.Однако если мы генерируем электроэнергию, то направление тока меняется на противоположное. Но поскольку ток переменный, направление все равно меняется на противоположное, 50 (или 60) раз в секунду. Нам нужна ссылка для сравнения текущего направления. К счастью, у нас есть это в виде напряжения. На диаграмме 1 волны напряжения и тока как нарастали, так и падали вместе. Когда напряжение было положительным (выше оси X), ток был положительным, а когда напряжение было отрицательным (ниже оси x), ток был отрицательным.Мощность равна произведению напряжения и тока, поэтому мощность всегда была положительной — вся кривая мощности находится выше оси X.

Если дом вырабатывает электроэнергию, направление тока меняется на противоположное по сравнению с нашим предыдущим примером. Теперь, когда напряжение положительное (выше оси X), ток отрицательный (ниже оси X), а когда напряжение отрицательное, ток положительный. Мощность всегда отрицательная — вся кривая мощности находится ниже оси X.

Диаграмма 4 — Соотношение фаз напряжения и тока при выработке энергии.

Знак мощности, следовательно, указывает, потребляется или генерируется мощность.

Подводя итоги

Есть много параметров, которые мы можем измерить в отношении использования энергии в системах переменного тока. У каждого есть свои достоинства. Для измерения энергии в домах реальная мощность, вероятно, будет наиболее полезной величиной, поскольку она показывает, сколько энергии фактически потребляют все ваши приборы, и это то, за что вам выставляет счет коммунальное предприятие.

Далее: Теория мощности переменного тока — Математика Arduino — Как рассчитываются действительная и полная мощность, среднеквадратичное напряжение и ток, а также коэффициент мощности.

Дополнительная литература

https://en.wikipedia.org/wiki/AC_power

Мощность в резистивных и реактивных нагрузках: https://www.allaboutcircuits.com/vol_2/chpt_11/1.html

Однофазные системы питания: https://www.allaboutcircuits.com/vol_2/chpt_10/1.html

Блок питания

Трехфазные источники питания переменного тока серии AC6900

Максимальная частота: 550 Гц

Максимальная выходная мощность: 3000 ВА

Максимальный среднеквадратичный ток: 10 А

Быстрый просмотр

Что такое частота? | Fluke

Частота переменного тока — это количество циклов в секунду синусоидального сигнала переменного тока.Частота — это скорость изменения направления тока в секунду. Он измеряется в герцах (Гц), международной единице измерения, где 1 герц равен 1 циклу в секунду.

Герц (Гц) = Один герц равен одному циклу в секунду.
Цикл = Одна полная волна переменного тока или напряжения.
Чередование = половина цикла.
Период = время, необходимое для создания одного полного цикла сигнала.

В самом основном, частота — это то, как часто что-то повторяется.В случае электрического тока частота — это количество раз, когда синусоидальная волна повторяет или завершает цикл от положительного к отрицательному.

Чем больше циклов происходит в секунду, тем выше частота.

Пример: Если переменный ток имеет частоту 3 Гц (см. Диаграмму ниже), это означает, что его форма волны повторяется 3 раза за 1 секунду.

Частота обычно используется для описания работы электрического оборудования. Ниже приведены некоторые распространенные диапазоны частот:

Частота сети питания (обычно 50 Гц или 60 Гц).
Преобразователи частоты, которые обычно используют несущую частоту 1–20 килогерц (кГц).
Диапазон звуковых частот: от 15 Гц до 20 кГц (диапазон человеческого слуха).
Радиочастота: 30-300 кГц.
Низкая частота: от 300 кГц до 3 мегагерц (МГц).
Средняя частота: 3-30 МГц.
Высокая частота: 30-300 МГц.

Цепи и оборудование часто предназначены для работы с фиксированной или переменной частотой. Оборудование, предназначенное для работы на фиксированной частоте, работает ненормально, если оно работает на частоте, отличной от указанной.Например, двигатель переменного тока, предназначенный для работы на частоте 60 Гц, работает медленнее, если частота падает ниже 60 Гц, и быстрее, если она превышает 60 Гц. Для двигателей переменного тока любое изменение частоты вызывает пропорциональное изменение скорости двигателя. Другой пример: уменьшение частоты на 5% приводит к снижению скорости двигателя на 5%.

Как измерить частоту

Цифровой мультиметр, который включает режим частотомера, может измерять частоту сигналов переменного тока, а также может предлагать следующее:

Запись MIN / MAX, что позволяет записывать измерения частоты в течение определенного периода или таким же образом записываются измерения напряжения, тока или сопротивления.
Автоматический выбор диапазона, который автоматически выбирает частотный диапазон, кроме случаев, когда измеренное напряжение выходит за пределы диапазона измерения частоты.

Электросети различаются в зависимости от страны. В США сетка основана на высокостабильном сигнале с частотой 60 Гц, что означает, что она циклически повторяется 60 раз в секунду.

В США для электроснабжения домашних хозяйств используется однофазный источник питания переменного тока на 120 вольт. Мощность, измеренная в настенной розетке дома в США, будет давать синусоидальные волны, колеблющиеся в пределах ± 170 вольт, при измерении истинного среднеквадратичного напряжения на уровне 120 вольт.Частота колебаний составит 60 циклов в секунду.

Hertz назван в честь немецкого физика Генриха Герца (1857–1894), который первым начал передавать и принимать радиоволны. Радиоволны распространяются с частотой один цикл в секунду (1 Гц). (Точно так же часы отсчитывают 1 Гц.)

Ссылка: Принципы цифрового мультиметра, автор — Глен А. Мазур, American Technical Publishers.

Physics4Kids.com: Электричество и магнетизм: переменный ток

В нашем мире есть два основных типа тока.Один из них — постоянный ток (DC), который представляет собой постоянный поток электронов в одном направлении. Другой — переменный ток, который представляет собой поток зарядов, меняющий направление. Такие ученые, как Charles Proteus Steinmetz и Nikola Tesla , добились больших успехов, когда мощность переменного тока была просто научным экспериментом. Заряды (электроны) всегда должны течь, чтобы иметь ток. Однако поток зарядов не всегда должен быть в одном направлении. В переменном токе заряды движутся в одном направлении в течение очень короткого времени, а затем меняют направление.Это происходит снова и снова.

Ученые описывают цикл переключения направлений как частота . Частота измеряется в Гц (Гц). Говорят, что токи, которые циклируют чаще в течение определенного промежутка времени, имеют более высокую частоту. Переменный ток переключает 60 раз в секунду в США.

Поскольку Интернет является глобальным ресурсом, мы также должны упомянуть, что в мире существуют разные частоты переменного тока. Хотя все мы используем переменный ток, переключение происходит по-разному в течение определенного периода времени.В большинстве стран используются частоты переменного тока 50 или 60 герц.

Почему мы используем электроэнергию переменного тока во всем мире? Дешевле и проще изготавливать устройства для питания переменного тока. Это дешевле, потому что вы можете очень легко увеличивать и уменьшать ток для сети переменного тока. Выключатели питания переменного тока также дешевле в производстве. Вероятно, самым большим преимуществом переменного тока является то, что вы можете использовать высокое напряжение с малыми токами, чтобы уменьшить потери при передаче энергии. Помните, что потеря энергии увеличивается с увеличением количества столкновений, а уменьшение тока уменьшает количество столкновений (и снижает нагрев проводов).Вы можете передавать энергию постоянным током, но при передаче постоянного тока теряется много энергии. Вам придется приложить гораздо больше усилий, чтобы передать мощность постоянного тока на такое же расстояние. БОЛЬШОЕ ПРИМЕЧАНИЕ: НИКОГДА не прикасайтесь к розеткам в доме . Вы получите удар током. Электричество — это нечто большее, чем напряжение. Это текущий , который убьет вас.

Проще всего увидеть в действии мощность переменного тока — это ваш дом. Все приборы и свет в вашем доме, вероятно, отключены от сети переменного тока. Существуют также преобразователи мощности, которые преобразуют мощность постоянного тока в мощность переменного тока, когда вам нужно электричество, и вокруг нет розеток (например, в кемпинге).

Или выполните поиск на сайтах по определенной теме.

Универсальный источник переменного тока и анализатор переменного тока. Испытайте преимущество Extech.

Производство этого продукта снято с производства.

Передние (100 Вт) и задние (2000 Вт) универсальные выходные разъемы

Особенности:

Измерение мощности в режиме ожидания (от 10 мВт до 100 Вт) для настольных ПК и ноутбуков, ЖК-телевизоров, адаптеров переменного тока / зарядных устройств
Для тестирования продуктов от 85 до 250 В переменного тока, от 45 до 65 Гц
Стандартное измерение мощности:
- от 100 мВт до 1000 Вт (110 В)
- от 100 мВт до 2000 Вт (220 В)
Измерение качества электроэнергии (Вт, коэффициент мощности, напряжение, ток, гармоники)
Функция затрат рассчитывает стоимость за день, месяц и год
99 ячеек памяти для предустановленных настроек выходного напряжения и частоты
Программируемая пользователем защита от перегрузки по току
Программируется через встроенный интерфейс RS-232
В режиме сбора данных показания записываются на ваш компьютер с программируемой пользователем частотой дискретизации от 2 до 65 535 секунд
В комплекте шнур питания переменного тока, кабель RS-232 — USB и программное обеспечение

Технические характеристики:

Технические характеристики	Диапазон	Разрешение	Точность
Передняя панель
Выходное напряжение	от 85 до 250 В (регулируется)	0.1В	± 1%
Выходная частота	от 45 до 65 Гц (регулируется)	0,01 Гц	± 0,1 Гц
Мощность	от 10 мВт до 100 Вт	00,1 мВт	± (1% + 0,05 Вт)
Переменный ток	от 5 мА до 1,5 А	2 / 15A через розетки	0,1 мА
Коэффициент мощности	от 0 до 1	0.001	± 0,04
Задняя панель
Выходное напряжение	линейное напряжение	0,1 В	± 1%
Выходная частота	частота сети	0,01 Гц	± 0,1 Гц
Мощность	от 100 мВт до 2000 Вт	0,1 мВт	± (1% + 0,5 Вт)
Переменный ток	от 5 мА до 10 А	0.1 мА	± 1%
Коэффициент мощности	от 0 до 1	0,001	± 0,04
Гармоники (в амперах)	от 1 до 50 порядка	0,1 мА	± 1,4% (1-10 место)
THD	от 0,0 до 999,9%	0,1%
Источник питания	110 или 220В; От 45 до 65 Гц
Размер	12 х 10.2 x 5,9 дюйма (305 x 260 x 151 мм)
Масса	9,9 кг (21,8 фунта)

Особенности:

Измерение мощности в режиме ожидания (от 10 мВт до 100 Вт) для настольных ПК и ноутбуков, ЖК-телевизоров, адаптеров переменного тока / зарядных устройств
Для тестирования продуктов от 85 до 250 В переменного тока, от 45 до 65 Гц
Стандартное измерение мощности:
- от 100 мВт до 1000 Вт (110 В)
- от 100 мВт до 2000 Вт (220 В)
Измерение качества электроэнергии (Вт, коэффициент мощности, напряжение, ток, гармоники)
Функция затрат рассчитывает стоимость за день, месяц и год
99 ячеек памяти для предустановленных настроек выходного напряжения и частоты
Программируемая пользователем защита от перегрузки по току
Программируется через встроенный интерфейс RS-232
В режиме сбора данных показания записываются на ваш компьютер с программируемой пользователем частотой дискретизации от 2 до 65 535 секунд
В комплекте шнур питания переменного тока, кабель RS-232 — USB и программное обеспечение

Технические характеристики:

Технические характеристики	Диапазон	Разрешение	Точность
Передняя панель
Выходное напряжение	от 85 до 250 В (регулируется)	0.1В	± 1%
Выходная частота	от 45 до 65 Гц (регулируется)	0,01 Гц	± 0,1 Гц
Мощность	от 10 мВт до 100 Вт	00,1 мВт	± (1% + 0,05 Вт)
Переменный ток	от 5 мА до 1,5 А	2 / 15A через розетки	0,1 мА
Коэффициент мощности	от 0 до 1	0.001	± 0,04
Задняя панель
Выходное напряжение	линейное напряжение	0,1 В	± 1%
Выходная частота	частота сети	0,01 Гц	± 0,1 Гц
Мощность	от 100 мВт до 2000 Вт	0,1 мВт	± (1% + 0,5 Вт)
Переменный ток	от 5 мА до 10 А	0.1 мА	± 1%
Коэффициент мощности	от 0 до 1	0,001	± 0,04
Гармоники (в амперах)	от 1 до 50 порядка	0,1 мА	± 1,4% (1-10 место)
THD	от 0,0 до 999,9%	0,1%
Источник питания	110 или 220В; От 45 до 65 Гц
Размер	12 х 10. Рубрика: Рубрика:Разное Навигация по записям « Разборка наушников: Как разобрать наушники defender — В ушах Замена подшипника компрессора кондиционера ниссан альмера н16: Подшипник компрессора кондиционера Ниссан Альмера Н16 » Читайте также Глухозаземленная и изолированная нейтраль отличия: Режимы работы нейтрали в электроустановках и электрических сетях Что такое дребезг контактов: Дребезг контактов, и как с ним бороться Релейная защита трансформатора: Релейная защита силовых трансформаторов Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт Найти: Рубрики Антенна Настройка Подключение Радиолюбителям Ремонт Ресивер Своими руками Усилитель Установка Разное © 2019 Мир антенн. Все права защищены. Карта сайта

Мощность переменного тока. Работа переменного тока

Переменный ток, мощность переменного тока

Вступление

Вычисление мощности

Дальнейшие вычисления

Определяем результат

Активная и реактивная мощность

Реактивная энергия

Опыт

Преобразование мощности

Индуктивность

Запускаем устройство

Итоги

Как регулировать мощность переменного тока / Хабр

Как вообще регулируется мощность?

Расчёт таблицы мощности

Расчёт таймера МК и перевод таблицы

Заключение

Мощность — это… Что такое Мощность?

Единицы измерения

Мощность в механике

Электрическая мощность

Приборы для измерения мощности

См. также

Ссылки

Ноутбуки HP — Использование адаптера питания переменного тока и устранение его неполадок

Работа и мощность переменного тока.

Энергетика Работа и мощность переменного тока.

Читайте также

Переменный ток и его мощность

Вступление

Вычисление мощности

Дальнейшие вычисления

Определяем результат

Активная и реактивная мощность

Реактивная энергия

Опыт

Преобразование мощности

Индуктивность

Запускаем устройство

Итоги

Задачи

Вступление

Вычисление мощности

Дальнейшие вычисления

Определяем результат

Активная и реактивная мощность

Реактивная энергия

Опыт

Пре мощности

Индуктивность

Запускаем устройство

Итоги

В чем разница между питанием переменного и постоянного тока?

Переменный ток — Energy Education

Недвижимость

Использование и преимущества

Phet Simulation

Дополнительная информация

Ссылки

Узнать | OpenEnergyMonitor

Введение в питание переменного тока

Общие сведения о питании переменного тока

Резистивные нагрузки

Частично реактивные нагрузки

Реальная мощность, реактивная мощность и полная мощность

Определение направления потока мощности

Подводя итоги

Дополнительная литература

Трехфазные источники питания переменного тока серии AC6900

Что такое частота? | Fluke

Как измерить частоту

Physics4Kids.com: Электричество и магнетизм: переменный ток

Универсальный источник переменного тока и анализатор переменного тока. Испытайте преимущество Extech.

Передние (100 Вт) и задние (2000 Вт) универсальные выходные разъемы

Особенности:

Технические характеристики:

Особенности:

Технические характеристики:

Читайте также