Напряжение максимальное: максимальное напряжение — это… Что такое максимальное напряжение?

Максимальное напряжение на конденсаторе формула. Энергия заряженного конденсатора. применение конденсаторов

Печать

Конденсатор – электронный компонент, предназначенный для накопления электрического заряда. Способность конденсатора накапливать электрический заряд зависит от его главной характеристики – емкости . Емкость конденсатора (С) определяется как соотношение количества электрического заряда (Q) к напряжению (U).

Емкость конденсатора измеряется в фарадах (F) – единицах, названых в честь британского ученого физика Майкла Фарадея. Емкость в один фарад (1F) равняется количеству заряда в один кулон (1C), создающему напряжение на конденсаторе в один вольт (1V). Вспомним, что один кулон (1С) равняется величине заряда, прошедшего через проводник за одну секунду (1sec) при силе тока в один ампер (1A).

Однако кулон, это очень большое количество заряда относительно того, сколько способно хранить большинство конденсаторов.

По этой причине, для измерения емкости обычно используют микрофарады (µF или uF), нанофарады (nF) и пикофарады (pF).

• 1µF = 0.000001 = 10 -6 F

• 1nF = 0.000000001 = 10 -9 F

• 1pF = 0.000000000001 = 10 -12 F

Плоский конденсатор

Существует множество типов конденсаторов различной формы и внутреннего устройства. Рассмотрим самый простой и принципиальный — плоский конденсатор. Плоский конденсатор состоит из двух параллельных пластин проводника (обкладок), электрически изолированных друг от друга воздухом, или специальным диэлектрическим материалом (например бумага, стекло или слюда).

Устройство конденсатора

Заряд конденсатора. Ток

По своему предназначению конденсатор напоминает батарейку, однако все же он сильно отличается по принципу работы, максимальной емкости, а также скорости зарядки/разрядки.

Рассмотрим принцип работы плоского конденсатора. Если подключить к нему источник питания, на одной пластине проводника начнут собираться отрицательно заряженные частицы в виде электронов, на другой – положительно заряженные частицы в виде ионов.

Поскольку между обкладками находиться диэлектрик, заряженные частицы не могут «перескочить» на противоположную сторону конденсатора. Тем не менее, электроны передвигаются от источника питания — до пластины конденсатора. Поэтому в цепи идет электрический ток.

В самом начале включения конденсатора в цепь, на его обкладках больше всего свободного места. Следовательно, начальный ток в этот момент встречает меньше всего сопротивления и является максимальным. По мере заполнения конденсатора заряженными частицами ток постепенно падает, пока не закончится свободное место на обкладках и ток совсем не прекратится.

Время между состояниями «пустого» конденсатора с максимальным значением тока, и «полного» конденсатора с минимальным значением тока (т.е. его отсутствием), называют

переходным периодом заряда конденсатора.

Напряжение

В самом начале переходного периода зарядки, напряжение между обкладками конденсатора равняется нулю. Как только на обкладках начинают появляться заряженные частицы, между разноименными зарядами возникает напряжение. Причиной этому является диэлектрик между пластинами, который «мешает» стремящимся друг к другу зарядам с противоположным знаком перейти на другую сторону конденсатора.

На начальном этапе зарядки, напряжение быстро растет, потому что большой ток очень быстро увеличивает количество заряженных частиц на обкладках. Чем больше заряжается конденсатор, тем меньше ток, и тeм медленнее растет напряжение. В конце переходного периода, напряжение на конденсаторе полностью прекратит рост, и будет равняться напряжению на источнике питания.

Как видно на графике, сила тока конденсатора напрямую зависит от изменения напряжения.

Формула для нахождения тока конденсатора во время переходного периода:

• Ic — ток конденсатора

• C — Емкость конденсатора

• ?Vc/?t – Изменение напряжения на конденсаторе за отрезок времени

После того как конденсатор зарядился, отключим источник питания и подключим нагрузку R. Так как конденсатор уже заряжен, он сам превратился в источник питания. Нагрузка R образовала проход между пластинами. Отрицательно заряженные электроны, накопленные на одной пластине, согласно силе притяжения между разноименными зарядами, двинутся в сторону положительно заряженных ионов на другой пластине.

В момент подключения R, напряжение на конденсаторе то же, что и после окончания переходного периода зарядки. Начальный ток по закону Ома будет равняться напряжению на обкладках, разделенном на сопротивление нагрузки.

Как только в цепи пойдет ток, конденсатор начнет разряжаться. По мере потери заряда, напряжение начнет падать. Следовательно, ток тоже упадет. По мере понижения значений напряжения и тока, будет снижаться их скорость падения.

Время зарядки и разрядки конденсатора зависит от двух параметров – емкости конденсатора C и общего сопротивления в цепи R. Чем больше емкость конденсатора, тем большее количество заряда должно пройти по цепи, и тем больше времени потребует процесс зарядки/разрядки (ток определяется как количество заряда, прошедшего по проводнику за единицу времени). Чем больше сопротивление R, тем меньше ток. Соответственно, больше времени потребуется на зарядку.

Продукт RC (сопротивление, умноженное на емкость) формирует временную константу

? (тау). За один ? конденсатор заряжается или разряжается на 63%. За пять ? конденсатор заряжается или разряжается полностью.

Для наглядности подставим значения: конденсатор емкостью в 20 микрофарад, сопротивление в 1 килоом и источник питания в 10В. Процесс заряда будет выглядеть следующим образом:

Устройство конденсатора. От чего зависит емкость?

Емкость плоского конденсатора зависит от трех основных факторов:

• Площадь пластин — A

• Расстояние между пластинами – d

• Относительная диэлектрическая проницаемость вещества между пластинами — ?

Чем больше площадь пластин конденсатора, тем больше заряженых частиц могут на них разместится, и тем больше емкость.

Расстояние между пластинами

Емкость конденсатора обратно пропорциональна расстоянию между пластинами.

Для того чтобы объяснить природу влияния этого фактора, необходимо вспомнить механику взаимодействия зарядов в пространстве (электростатику).

Если конденсатор не находится в электрической цепи, то на заряженные частицы, расположенные на его пластинах влияют две силы. Первая — это сила отталкивания между одноименными зарядами соседних частиц на одной пластине. Вторая – это сила притяжения разноименных зарядов между частицами, находящимися на противоположных пластинах. Получается, что чем ближе друг к другу находятся пластины, тем больше суммарная сила притяжения зарядов с противоположным знаком, и тем больше заряда может разместится на одной пластине.

Относительная диэлектрическая проницаемость

Не менее значимым фактором, влияющим на емкость конденсатора, является такое свойство материала между обкладками как относительная диэлектрическая проницаемость? . Это безразмерная физическая величина, которая показывает

во сколько раз сила взаимодействия двух свободных зарядов в диэлектрике меньше, чем в вакууме.

Материалы с более высокой диэлектрической проницаемостью позволяют обеспечить большую емкость. Объясняется это эффектом поляризации – смещением электронов атомов диэлектрика в сторону положительно заряженной пластины конденсатора.

Поляризация создает внутренне электрическое поле диэлектрика, которое ослабляет общую разность потенциала (напряжения) конденсатора. Напряжение U препятствует притоку заряда Q на конденсатор. Следовательно, понижение напряжения способствует размещению на конденсаторе большего количества электрического заряда.

Ниже приведены примеры значений диэлектрической проницаемости для некоторых изоляционных материалов, используемых в конденсаторах.

• Бумага – от 2.5 до 3.5

• Стекло – от 3 до 10

• Слюда – от 5 до 7

• Порошки оксидов металлов – от 6 до 20

Номинальное напряжение

Второй по значимости характеристикой после емкости является максимальное номинальное напряжение конденсатора . Данный параметр обозначает максимальное напряжение, которое может выдержать конденсатор. Превышение этого значения приводит к «пробиванию» изолятора между пластинами и короткому замыканию. Номинальное напряжение зависит от материала изолятора и его толщины (расстояния между обкладками).

Следует отметить, что при работе с переменным напряжением нужно учитывать именно пиковое значение (наибольшее мгновенное значение напряжения за период). Например, если эффективное напряжение источника питания будет 50В, то его пиковое значение будет свыше 70В. Соответственно необходимо использовать конденсатор с номинальным напряжением более 70В. Однако на практике, рекомендуется использовать конденсатор с номинальным напряжением не менее в два раза превышающим максимально возможное напряжение, которое будет к нему приложено.

Ток утечки

Также при работе конденсатора учитывается такой параметр как ток утечки. Поскольку в реальной жизни диэлектрик между пластинами все же пропускает маленький ток, это приводит к потере со временем начального заряда конденсатора.

Если соединить резистор и конденсатор, то получится пожалуй одна из самых полезных и универсальных цепей.

О многочисленных способах применения которой я сегодня и решил рассказать. Но вначале про каждый элемент в отдельности:

Резистор — его задача ограничивать ток. Это статичный элемент, чье сопротивление не меняется, про тепловые погрешности сейчас не говорим — они не слишком велики. Ток через резистор определяется законом ома —

I=U/R , где U напряжение на выводах резистора, R — его сопротивление.

Конденсатор штука поинтересней. У него есть интересное свойство — когда он разряжен то ведет себя почти как короткое замыкание — ток через него течет без ограничений, устремляясь в бесконечность. А напряжение на нем стремится к нулю. Когда же он заряжен, то становится как обрыв и ток через него течь перестает, а напряжение на нем становится равным заряжающему источнику. Получается интересная зависимость — есть ток, нет напряжения, есть напряжение — нет тока.

Чтобы визуализировать себе этот процесс, представь ган… эмм.. воздушный шарик который наполняется водой. Поток воды — это ток. Давление воды на упругие стенки — эквивалент напряжения. Теперь смотри, когда шарик пуст — вода втекает свободно, большой ток, а давления еще почти нет — напряжение мало. Потом, когда шарик наполнится и начнет сопротивляться давлению, за счет упругости стенок, то скорость потока замедлится, а потом и вовсе остановится — силы сравнялись, конденсатор зарядился. Есть напряжение натянутых стенок, но нет тока!

Теперь, если снять или уменьшить внешнее давление, убрать источник питания, то вода под действием упругости хлынет обратно. Также и ток из конденсатора потечет обратно если цепь будет замкнута, а напряжение источника ниже чем напряжение в конденсаторе.

Емкость конденсатора. Что это?
Теоретически, в любой идеальный конденсатор можно закачать заряд бесконечного размера. Просто наш шарик сильней растянется и стенки создадут большее давление, бесконечно большое давление.
А что же тогда насчет Фарад, что пишут на боку конденсатора в качестве показателя емкости? А это всего лишь зависимость напряжения от заряда (q = CU). У конденсатора малой емкости рост напряжения от заряда будет выше.

Представь два стакана с бесконечно высокими стенками. Один узкий, как пробирка, другой широкий, как тазик. Уровень воды в них — это напряжение. Площадь дна — емкость. И в тот и в другой можно набузолить один и тот же литр воды — равный заряд. Но в пробирке уровень подскочит на несколько метров, А в тазике будет плескаться у самого дна. Также и в конденсаторах с малой и большой емкостью.
Залить то можно сколько угодно, но напряжение будет разным.

Плюс в реале у конденсаторов есть пробивное напряжение, после которого он перестает быть конденсатором, а превращается в годный проводник:)

А как быстро заряжается конденсатор?
В идеальных условиях, когда у нас бесконечно мощный источник напряжения с нулевым внутренним сопротивлением, идеальные сверхпроводящие провода и абсолютно безупречный конденсатор — этот процесс будет происходить мгновенно, с временем равным 0, равно как и разряд.

Но в реальности всегда существуют сопротивления, явные — вроде банального резистора или неявные, такие как сопротивление проводов или внутреннее сопротивление источника напряжения.
В этом случае скорость заряда конденсатора будет зависить от сопротивлений в цепи и емкости кондера, а сам заряд будет идти по экспоненциальному закону .

А у этого закона есть пара характерных величин:

• Т — постоянная времени , это время при котором величина достигнет 63% от своего максимума. 63% тут взялись не случайно, тут прямая завязка на такую формулу VALUE T =max—1/e*max.
• 3T — а при троекратной постоянной значение достигнет 95% своего максимума.

Постоянная времени для RC цепи Т=R*C .

Чем меньше сопротивление и меньше емкость, тем быстрей конденсатор заряжается. Если сопротивление равно нулю, то и время заряда равно нулю.

Рассчитаем за сколько зарядится на 95% конденсатор емкостью 1uF через резистор в 1кОм:
T= C*R = 10 -6 * 10 3 = 0.001c
3T = 0.003c через такое время напряжение на конденсаторе достигнет 95% от напряжения источника.

Разряд пойдет по тому же закону, только вверх ногами. Т.е. через Твремени в на конденсаторе остаенется всего лишь 100% — 63% = 37% от первоначального напряжения, а через 3T и того меньше — жалкие 5%.

Ну с подачей и снятием напряжения все ясно. А если напряжение подали, а потом еще ступенчато подняли, а разряжали также ступеньками? Ситуация тут практически не изменится — поднялось напряжение, конденсатор дозарядился до него по тому же закону, с той же постоянной времени — через время 3Т его напряжение будет на 95% от нового максимума.
Чуть понизилось — подразрядился и через время 3Т напряжение на нем будет на 5% выше нового минимума.
Да что я тебе говорю, лучше показать. Сварганил тут в мультисиме хитровыдрюченный генератор ступечнатого сигнала и подал на интегрирующую RC цепочку:

Видишь как колбасится:) Обрати внимание, что и заряд и разряд, вне зависимости от высоты ступеньки, всегда одной длительности!!!

А до какой величины конденсатор можно зарядить?
В теории до бесконечности, этакий шарик с бесконечно тянущимися стенками. В реале же шарик рано или поздно лопнет, а конденсатор пробьет и закоротит. Вот поэтому у всех конденсаторов есть важный параметр — предельное напряжение . На электролитах его часто пишут сбоку, а на керамических его надо смотреть в справочниках. Но там оно обычно от 50 вольт. В общем, выбирая кондер надо следить, чтобы его предельное напряжение было не ниже того которое в цепи. Добавлю что при расчете конденсатора на переменное напряжение следует выбирать предельное напряжение в 1.4 раза выше. Т.к. на переменном напряжении указывают действующее значение, а мгновенное значение в своем максимуме превышает его в 1.4 раза.

Что следует из вышеперечисленного? А то что если на конденсатор подать постоянное напряжение, то он просто зарядится и все. На этом веселье закончится.

А если подать переменное? То очевидно, что он будет то заряжаться, то разряжаться, а в цепи будет туда и обратно гулять ток. Движуха! Ток есть!

Выходит, несмотря на физический обрыв цепи между обкладками, через конденсатор легко протекает переменный ток, а вот постоянному слабо.

Что нам это дает? А то что конденсатор может служить своего рода сепаратором, для разделения переменного тока и постоянного на соответствующие составляющие.

Любой изменяющийся во времени сигнал можно представить как сумму двух составляющих — переменной и постоянной.

Например, у классической синусоиды есть только переменная часть, а постоянная равна нулю. У постоянного же тока наоборот. А если у нас сдвинутая синусоида? Или постоянная с помехами?

Переменная и постоянная составляющие сигнала легко разделяются!
Чуть выше я тебе показал как конденсатор дозаряжается и подразряжается при изменениях напряжения. Так что переменная составляющая сквозь кондер пройдет на ура, т.к. только она заставляет конденсатор активно менять свой заряд. Постоянная же как была так и останется и застрянет на конденсаторе.

Но чтобы конденсатор эффективно разделял переменную составляющую от постоянной частота переменной составляющей должна быть не ниже чем 1/T

Возможны два вида включения RC цепочки:
Интегрирующая и дифференцирующая . Они же фильтр низких частот и фильтр высоких частот.

Фильтр низких частот без изменений пропускает постоянную составляющую (т.к. ее частота равна нулю, ниже некуда) и подавляет все что выше чем 1/T. Постоянная составляющая проходит напрямую, а переменная составляющая через конденсатор гасится на землю.
Такой фильтр еще называют интегрирующей цепочкой потому, что сигнал на выходе как бы интегрируется. Помнишь что такое интеграл? Площадь под кривой! Вот тут она и получается на выходе.

А дифференцирующей цепью ее называют потому, что на выходе у нас получается дифференциал входной функции, который есть не что иное как скорость изменения этой функции.

• На участке 1 происходит заряд конденсатора, а значит через него идет ток и на резисторе будет падение напряжения.
• На участке 2 происходит резкое увеличение скорости заряда, а значит и ток резко возрастет, а за ним и падение напряжения на резисторе.
• На участке 3 конденсатор просто удерживает уже имеющийся потенциал. Ток через него не идет, а значит на резисторе напряжение тоже равно нулю.
• Ну и на 4м участке конденсатор начал разряжаться, т.к. входной сигнал стал ниже чем его напряжение. Ток пошел в обратную сторону и на резисторе уже отрицательное падение напряжения.

А если подать на вход прямоугольнй импульс, с очень крутыми фронтами и сделать емкость конденсатора помельче, то увидим вот такие иголки:

прямоугольник. Ну, а чо? Правильно — производная от линейной функции есть константа, наклон этой функции определяет знак константы.

Короче, если у тебя сейчас идет курс матана, то можешь забить на богомерзкий Mathcad, отвратный Maple, выбросить из головы матричную ересь Матлаба и, достав из загашников горсть аналоговой рассыпухи, спаять себе истинно ТРУЪ аналоговый компьютер:) Препод будет в шоке:)

Правда на одних только резисторах кондерах интеграторы и диффернциаторы обычно не делают, тут юзают операционные усилители. Можешь пока погуглить на предмет этих штуковин, любопытная вещь:)

А вот тут я подал обычный приямоугольный сигнал на два фильтра высоких и низких частот. А выходы с них на осциллограф:

Вот, чуть покрупней один участок:

При старте кондер разряжен, ток через него вваливат на полную, а напряжение на нем мизерное — на входе RESET сигнал сброса. Но вскоре конденсатор зарядится и через время Т его напряжение будет уже на уровне логической единицы и на RESET перестанет подаваться сигнал сброса — МК стартанет.
А для AT89C51 надо с точностью наоборот RESET организовать — вначале подать единицу, а потом ноль. Тут ситуация обратная — пока кондер не заряжен, то ток через него течет большой, Uc — падение напряжения на нем мизерное Uc=0. А значит на RESET подается напряжение немногим меньше напряжения питания Uпит-Uc=Uпит.
Но когда кондер зарядится и напряжение на нем достигнет напряжения питания (Uпит=Uс), то на выводе RESET уже будет Uпит-Uc=0

Аналоговые измерения
Но фиг сними с цепочками сброса, куда прикольней использовать возможность RC цепи для замера аналоговых величин микроконтроллерами в которых нет АЦП.
Тут используется тот факт, что напряжение на конденсаторе растет строго по одному и тому же закону — экспоненте. В зависимости от кондера, резистора и питающего напряжения. А значит его можно использовать как опорное напряжение с заранее известными параметрами.

Работает просто, мы подаем напряжение с конденсатора на аналоговый компаратор, а на второй вход компаратора заводим измеряемое напряжение. И когда хотим замерить напряжение, то просто вначале дергаем вывод вниз, чтобы разрядить конденсатор. Потом возвращем его в режим Hi-Z, cбрасываем и запускаем таймер. А дальше кондер начинает заряжаться через резистор и как только компаратор доложит, что напряжение с RC догнало измеряемое, то останавливаем таймер.

Зная по какому закону от времени идет возрастание опорного напряжения RC цепи, а также зная сколько натикал таймер, мы можем довольно точно узнать чему было равно измеряемое напряжение на момент сработки компаратора. Причем, тут не обязательно считать экспоненты. На начальном этапе зарядки кондера можно предположить, что зависимость там линейная. Или, если хочется большей точности, аппроксимировать экспоненту кусочно линейными функциями, а по русски — отрисовать ее примерную форму несколькими прямыми или сварганить таблицу зависимости величины от времени, короче, способов вагон просто.

Если надо заиметь аналоговую крутилку, а АЦП нету, то можно даже компаратор не юзать. Дрыгать ножкой на которой висит конденсатор и давать ему заряжаться через перменный резистор.

По изменению Т, которая, напомню T=R*C и зная что у нас С = const, можно вычислить значение R. Причем, опять же необязательно подключать тут математический аппарат, в большинстве случаев достаточно сделать замер в каких-нибудь условных попугаях, вроде тиков таймера. А можно пойти другим путем, не менять резистор, а менять емкость, например, подсоединяя к ней емкость своего тела… что получится? Правильно — сенсорные кнопки!

Если что то непонятно, то не парься скоро напишу статью про то как прикрутить к микроконтроллеру аналоговую фиговину не используя АЦП. Там подробно все разжую.

Как и любая система заряжен-ных тел, конденсатор обладает энер-гией. Вычислить энергию заряжен-ного плоского конденсатора с одно-родным полем внутри него не-сложно.

Энергия заряженного конденса-тора.

Для того чтобы зарядить конденсатор, нужно совершить рабо-ту по разделению положительных и отрицательных зарядов. Согласно закону сохранения энергии эта ра-бота равна энергии конденсатора. В том, что заряженный конденсатор обладает энергией, можно убедиться, если разрядить его через цепь, со-держащую лампу накаливания, рас-считанную на напряжение в не-сколько вольт (рис. 4). При раз-рядке конденсатора лампа вспыхи-вает. Энергия конденсатора пре-вращается в другие формы: тепло-вую, световую.

Выведем формулу для энергии плоского конденсатора .

Напряженность поля, созданного зарядом одной из пластин, равна Е/2, где Е — напряженность поля в конденсаторе. В однородном поле одной пластины находится заряд q, распределенный по поверхности дру-гой пластины (рис. 5). Согласно формуле W p = qEd. для потенциальной энергии заряда в однородном поле энергия конденсатора равна:

Можно доказать, что эти форму-лы справедливы для энергии любого конденсатора, а не только для плос-кого.

Энергия электрического поля.

Согласно теории близкодействия вся энергия взаимодействия заряженных тел сконцентрирована в электриче-ском поле этих тел. Значит, энергия может быть выражена через основную характеристику поля — напря-женность.

Так как напряженность электри-ческого поля прямо пропорциональ-на разности потенциалов

(U = Ed), то согласно формуле

энергия конденсатора прямо пропор-циональна напряженности электри-ческого поля внутри него: W p ~ E 2 . Детальный расчет дает следующее значение для энергии поля, приходя-щейся на единицу объема, т.е. для плотности энергии:

где ε 0 — электрическая постоянная

Применение конденсаторов.

Энер-гия конденсатора обычно не очень велика — не более сотен джоулей. К тому же она не сохраняется долго из-за неизбежной утечки заряда. Поэтому заряженные конденсаторы не могут заменить, например, акку-муляторы в качестве источников электрической энергии.

Но это совсем не означает, что конденсаторы как накопители энергии не получили практического при-менения. Они имеют одно важное свойство: конденсаторы могут на-капливать энергию более или менее длительное время, а при разрядке через цепь малого сопротивления они отдают энергию почти мгновенно. Именно это свойство используют широко на практике.

Лампа-вспышка, применяемая в фотографии, питается электрическим током разряда конденсатора, заря-жаемого предварительно специаль-ной батареей. Возбуждение кванто-вых источников света — лазеров осу-ществляется с помощью газораз-рядной трубки, вспышка которой происходит при разрядке батареи конденсаторов большой электроем-кости.

Однако основное применение кон-денсаторы находят в радиотехнике. С этим вы познакомитесь в XI классе.

Энергия конденсатора пропор-циональна его электроемкости и квадрату напряжения между плас-тинами. Вся эта энергия сосредото-чена в электрическом поле. Плот-ность энергии поля пропорциональна квадрату напряженности поля.

Рис. 1 Рис. 2

ЗАКОНЫ ПОСТОЯННОГО ТОКА.

Неподвижные электрические заряды редко используются на практике. Для того чтобы заставить электрические заряды слу-жить нам, их нужно привести в движение — создать электрический ток. Электрический ток освещает квартиры, приводит в дви-жение станки, создает радиоволны, циркулирует во всех электрон-но-вычислительных машинах.

Мы начнем с наиболее простого случая движения заряжен-ных частиц — рассмотрим постоянный электрический ток.

ЭЛЕКТРИЧЕСКИЙ ТОК. СИЛА ТОКА

Дадим строгое определение тому, что называют электрическим током.

Напомним, какой величиной ха-рактеризуется ток количественно.

Найдем, как быстро движутся электроны по проводам в вашей квартире.

При движении заряженных час-тиц в проводнике происходит перенос электрического заряда с одного места в другое. Однако если заряженные частицы совершают беспорядочное тепловое движение, как, например, свободные электроны в металле, то переноса заряда не про-исходит (рис.1). Электриче-ский заряд перемещается через по-перечное сечение проводника лишь в том случае, если наряду с беспорядочным движением электроны участвуют в упорядоченном движении (рис. 2). В этом случае говорят, что в проводнике устанавливается электрический ток.

Из курса физики VIII класса вы знаете, что электрическим током называют упорядоченное (направ-ленное) движение заряженных частиц.

Электрический ток возникает при упорядоченном перемещении свобод-ных электронов или ионов.

Если перемещать нейтральное в целом тело, то, несмотря на упо-рядоченное движение огромного чис-ла электронов, и атомных ядер, электрический ток не возникает. Полный заряд, переносимый через любое сечение проводника, будет при этом равным нулю, так как заряды разных знаков с одинаковой средней скоростью.

Электрический ток имеет определенное направление. За направление тока принимают направление движения положительно заряженных частиц. Если ток образован движением отрицательно заряженных частиц, то направление тока считают противоположным направлению дви-жения частиц.

Действия тока. Движение частиц в проводнике мы непосредственно не видим. О наличии электрического тока приходится судить по тем дей-ствиям или явлениям, которые его сопровождают.

Во-первых, проводник, по которо-му течет ток, нагревается.

Во-вторых, электрический ток мо-жет изменять химический состав проводника, например, выделять его химические составные части (медь из раствора медного купороса и т.д.).

В-третьих, ток оказывает силовое воздействие на соседние токи и на-магниченные тела. Это действие то-ка называется магнитным. Так, маг-нитная стрелка вблизи проводника с током поворачивается. Магнитное действие тока в отличие от химиче-ского и теплового является основ-ным, так как проявляется у всех без исключения проводников.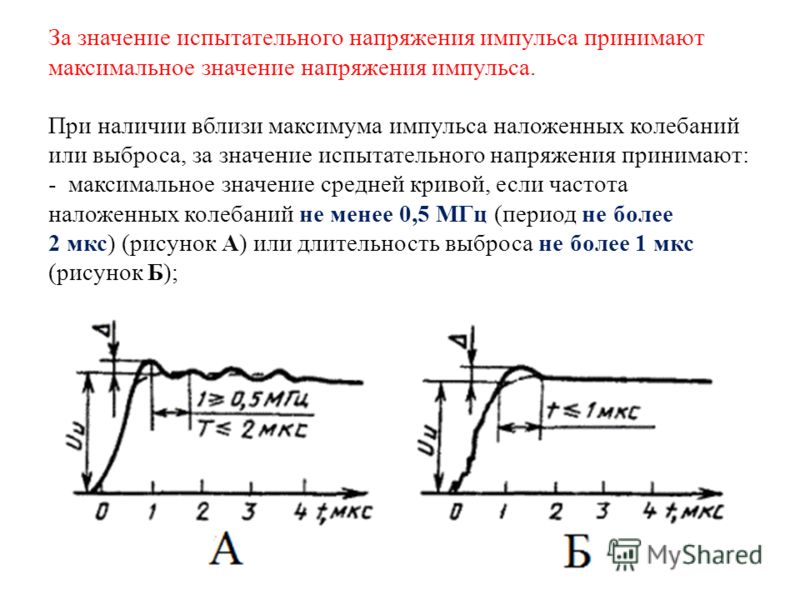 Хими-ческое действие тока наблюдается лишь у растворов и расплавов электролитов, а нагревание отсут-ствует у сверхпроводников.

Сила тока.

Если в цепи уста-навливается электрический ток, то это означает, что через поперечное сечение проводника все время пере-носится электрический заряд. Заряд, перенесенный в единицу времени, служит основной количественной ха-рактеристикой тока, называемой си-лой тока.

Таким образом, сила тока равна отношению заряда q, переносимого через поперечное сечение провод-ника за интервал времени t, к этому интервалу времени. Если сила тока со временем не меняется, то ток на-зывают постоянным.

Сила тока, подобно заряду, — ве-личина скалярная. Она может быть как положительной, так и отрица-тельной. Знак силы тока зависит от того, какое из направлений вдоль проводника принять за положитель-ное. Сила тока / > 0, если направ-ление тока совпадает с условно вы-бранным положительным направле-нием вдоль проводника. В против-ном случае /

Сила тока зависит от заряда, переносимого каждой частицей, кон-центрации частиц, скорости их направленного движения и площади поперечного сечения проводника. По-кажем это.

Пусть проводник (рис. 3) имеет поперечное сечение площадью S. За положительное направление в проводнике примем направление сле-ва направо. Заряд каждой частицы равен q 0 . В объеме проводника, ограниченном поперечными сечениям-и 1 и 2, содержится nSl частиц, где п — концентрация частиц. Их общий заряд q = q Q nSl. Если частицы движутся слева направо со средней скоростью υ, то за время

Все частицы, заключенные в рассматриваемом объеме, пройдут через поперечное сечение 2. Поэтому сила тока равна:

формуле (2) где е — модуль заряда электрона.

Пусть, например, сила тока I = 1 А, а площадь по-перечного сечения проводника S = 10 -6 м 2 . Модуль заряда электрона е = 1,6 — 10 -19 Кл. Число электронов в 1 м 3 меди равно числу атомов в этом объеме, так как один из ва-лентных электронов каждого атома меди коллективизирован и является свободным. Это число есть п = 8,5 · 10 28 м -3 Следовательно,

Рис №1. Рис №2 Рис №3

УСЛОВИЯ, НЕОБХОДИМЫЕ ДЛЯ СУЩЕСТВОВАНИЯ ЭЛЕКТРИЧЕСКОГО ТОКА

Что необходимо для создания электрического тока? Подумайте над этим сами и только потом прочтите этот параграф.

Для возникновения и существо-вания постоянного электрического тока в веществе необходимо, во-первых, наличие свободных заряжен-ных частиц. Если положительные и отрицательные заряды связаны друг с другом в атомах или молекулах , то их перемещение не приведет к по-явлению электрического тока.

Наличия свободных зарядов еще недостаточно для возникновения то-ка. Для создания и поддержания упорядоченного движения, заряжен-ных частиц необходима, во-вторых, сила, действующая на них в опре-деленном направлении. Если эта сила перестанет действовать, то упорядоченное движение заряженных частиц прекратится из-за сопротив-ления, оказываемого их движению ионами кристаллической решетки металлов или нейтральными молеку-лами электролитов .

На заряженные частицы, как мы знаем, действует электрическое поле с силой . Обычно именно электрическое поле внутри провод-ника служит причиной, вызываю-щей и поддерживающей упорядочен-ное движение заряженных частиц. Только в статическом случае, когда заряды покоятся, электрическое поле внутри проводника равно нулю.

Если внутри проводника имеется электрическое поле, то между конца-ми проводника в соответствии с фор-мулой существует разность потенциалов. Когда разность потен-циалов не меняется во времени, то в проводнике устанавливается по-стоянный электрический ток. Вдоль проводника потенциал уменьшается от максимального значения на одном конце проводника до минималь-ного — на другом. Это уменьшение потенциала можно обнаружить на простом опыте.

Возьмем в качестве проводника не очень сухую деревянную палку и подвесим ее горизонтально. (Такая палка хотя и плохо, но все же про-водит ток.) Источником напряжения пусть будет электростатическая ма-шина, Для регистрации потенциала различных участков проводника от-носительно земли можно использо-вать листочки металлической фоль-ги, прикрепленные к палке. Один полюс машины соединим с землей, а второй — с одним концом проводни-ка (палки). Цепь окажется незамк-нутой. При вращении рукоятки ма-шины мы обнаружим, что все лис-точки отклоняются на один и тот же угол (рис. 1).

Значит, потен-циал всех точек проводника отно-сительно земли одинаков. Так и должно быть при равновесии заря-дов на проводнике. Если теперь дру-гой конец палки заземлить, то при вращении рукоятки машины карти-на изменится. (Так как земля — проводник, то заземление провод-ника делает цепь замкнутой.) У за-земленного конца листочки вообще не разойдутся: потенциал этого кон-ца проводника практически равен потенциалу земли (падение потен-циала в металлической проволоке мало). Максимальный угол расхож-дения листочков будет у конца про-водника, присоединенного к машине (рис. 2). Уменьшение угла рас-хождения листочков по мере удале-ния от машины свидетельствует о падении потенциала вдоль провод-ника.

Электрический ток может быть получен только в веществе, в котором имеются свободные заряженные частицы. Чтобы они пришли в движение, нужно создать в проводнике электрическое поле.

Рис №1 Рис №2

ЗАКОН ОМА ДЛЯ УЧАСТКА ЦЕПИ. СОПРОТИВЛЕНИЕ

В VIII классе изучался закон Ома . Этот закон прост, однако столь важен, что его необходимо повторить.

Вольт — амперная характеристика.

В предыдущем параграфе было уста-новлено, что для существования то-ка в проводнике необходимо создать разность потенциалов на его концах. Сила тока в проводнике определяет-ся этой разностью потенциалов. Чем больше разность потенциалов, тем больше напряженность электриче-ского поля в проводнике и, следо-вательно, тем большую скорость на-правленного движения приобретают заряженные частицы. Согласно фор-муле, это означает увеличение силы тока.

Для каждого проводника — твер-дого, жидкого и газообразного — существует определенная зависи-мость силы тока от приложенной разности потенциалов на концах про-водника. Эту зависимость выражает так называемая вольт — амперная ха-рактеристика проводника. Ее нахо-дят, измеряя силу тока в проводнике при различных значениях напряже-ния. Знание вольт — амперной характе-ристики играет большую роль при изучении электрического тока.

Закон Ома.

Наиболее простой вид имеет вольт — амперная характеристи-ка металлических проводников и растворов электролитов. Впервые (для металлов) ее установил немец-кий ученый Георг Ом, поэтому зависимость силы тока от напря-жения носит название закона Ома. На участке цепи, изображенной на рисунке 109, ток направлен от точки 1 к точке 2. Разность потен-циалов (напряжение) на концах проводника равна: U = φ 1 — φ 2. Так как ток направлен слева направо, то напряженность электрического поля направлена в ту же сторону и φ 1 > φ 2

Согласно закону Ома для участка цепи сила тока прямо пропорцио-нальна приложенному напряжению U и обратно пропорциональна сопро-тивлению проводника R:

Закон Ома имеет очень простую форму, но доказать эксперименталь-но его справедливость довольно трудно. Дело в том, что разность по-тенциалов на участке металлическо-го проводника даже при большой силе тока мала, так как мало сопро-тивление проводника.

Электрометр, о котором шла речь, непригоден для измерения столь малых напряжений: его чув-ствительность слишком мала. Нужен несравненно более чувствительный прибор. Тогда, измеряя силу тока амперметром, а напряжение чув-ствительным электрометром, можно убедиться в том, что сила тока пря-мо пропорциональна напряжению. Применение же обычных приборов для измерения напряжения — вольт-метров — основано на использовании закона Ома.

Принцип устройства, вольтметра такой же, как и ампер-метра. Угол поворота стрелки прибо-ра пропорционален силе тока. Сила тока, проходящего по вольтметру, определяется напряжением между точками цепи, к которой он под-ключен. Поэтому, зная сопротивле-ние вольтметра, можно по силе тока определить напряжение. На практике прибор градуируют так, чтобы он сразу показывал напряжение в воль-тах.

Сопротивление. Основная элек-трическая характеристика проводни-ка — сопротивление. От этой вели-чины зависит сила тока в провод-нике при заданном напряжении. Со-противление проводника представля-ет собой как бы меру противо-действия проводника установлению в нем электрического тока. С помощью закона Ома можно определить сопротивление проводника:

Для этого нужно измерить напря-жение и силу тока.

Сопротивление зависит от мате-риала проводника и его геометри-ческих размеров. Сопротивление про-водника длиной l с постоянной пло-щадью поперечного сечения S равно:

где р — величина, зависящая от рода вещества и его состояния (от тем-пературы в первую очередь). Вели-чину р называют удельным сопро-тивлением проводника. Удельное со-противление численно равно сопро-тивлению проводника, имеющего форму куба с ребром 1 м, если ток направлен вдоль нормали к двум противоположным граням куба.

Единицу сопротивления провод-ника устанавливают на основе зако-на Ома и называют ее ом. Провод-ник имеет сопротивление 1 Ом, если при разности потенциалов 1 В сила тока в нем 1 А.

Единицей удельного сопротивле-ния является 1 Ом?м. Удельное со-противление металлов мало. Диэлектрики обладают очень большим удельным сопротивлением. В табли-це на форзаце приведены примеры значений удельного сопротивления некоторых веществ.

Значение закона Ома.

Закон Ома определяет силу тока в электриче-ской цепи при заданном напря-жении и известном сопротивлении. Он позволяет рассчитать тепловые, химические и магнитные действия тока, так как они зависят от силы тока. Из закона Ома вытекает, что замыкать обычную осветительную сеть проводником малого сопротив-ления опасно. Сила тока окажется настолько большой, что это может иметь тяжелые последствия.

Закон Ома — основа всей элект-ротехники постоянных токов. Формулу — надо хорошо понять и твердо запомнить.

ЭЛЕКТРИЧЕСКИЕ ЦЕПИ. ПОСЛЕДОВАТЕЛЬНОЕ И ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЯ ПРОВОДНИКОВ

От источника тока энергия может быть передана по проводам к устрой-ствам, потребляющим энергию: Элек-трической лампе, радиоприемнику и др. Для этого составляют электри-ческие цепи различной сложности. Электрическая цепь состоит из источника энергии, устройств, по-требляющих электрическую энергию, соединительных проводов и выклю-чателей для замыкания цепи. Часто и электрическую цепь включают приборы, контролирующие силу тока и напряжение на различных участ-ках цепи, — амперметры и вольт-метры.

К наиболее простым и часто встречающимся соединениям провод-ников относятся последовательное и параллельное соединения.

Последовательное соединение проводников.

При последовательном соединении электрическая цепь не имеет разветвлений. Все проводники включают в цепь поочередно друг за другом. На рисунке 1 показано последовательное соединение двух проводников 1 и 2, имеющих сопротивления R 1 , и R 2 . Это могут быть две лампы, две обмотки элект-родвигателя и др.

Сила тока в обоих проводниках одинакова, т. е. (1)

так как в проводниках электриче-ский заряд в случае постоянного тока не накапливается и через любое поперечное сечение проводника за определенное время проходит один и тот же заряд.

Напряжение на концах рассмат-риваемого участка цепи складывает-ся из напряжений на — первом и вто-ром проводниках:

Надо надеяться, что с доказатель-ством этого простого соотношения вы справитесь сами.

Применяя закон Ома для всего участка в целом и для участков с сопротивлениями R 1 и R 2 , можно до-казать, что полное сопротивление всего участка цепи при последова-тельном соединении равно:

Это правило можно применить для любого числа последовательно соединенных проводников.

Напряжения на проводниках и их сопротивления при последователь-ном соединении связаны соотноше-нием:

Докажите это равенство.

Параллельное соединение про-водников.

На рисунке 2 показано параллельное соединение двух про-водников 1 и 2с сопротивлениями R 1 и R 2 . В этом случае электриче-ский ток 1 разветвляется на две час-ти. Силу тока в первом и втором про-водниках обозначим через I 1 и I 2 . Так как в точке а — разветвлении проводников (такую точку называют узлом) — электрический заряд не на-капливается, то заряд, поступающий в единицу времени в узел, равен заряду, уходящему из узла за это же время. Следовательно, I = I 1 + I 2

Напряжение U на концах про-водников, соединенных параллельно, одно и то же.

В осветительной сети поддержи-вается напряжение 220 или 127 В. На это напряжение рассчитаны при-боры, потребляющие электрическую энергию. Поэтому параллельное сое-динение — самый распространенный способ соединения различных потре-бителей. В этом случае выход из строя одного прибора не отражается на работе остальных, тогда как при последовательном соединении выход из строя одного прибора размы-кает цепь.

Применяя закон Ома для всего участка в целом и для участков с сопротивлениями R 1 и R 2 , можно доказать, что величина, обратная полному сопротивлению участка ab, равна сумме величин, обратных сопротивлениям отдельных провод-ников:

Сила тока в каждом из провод-ников и сопротивления проводников при параллельном соединении свя-заны соотношением

Различные проводники в цепи соединяются друг с другом после-довательно или параллельно. В пер-вом случае сила тока одинакова во всех проводниках, а во втором слу-чае одинаковы напряжения на про-водниках. Чаще всего к осветитель-ной сети различные потребители тока подключаются параллельно.

ИЗМЕРЕНИЕ СИЛЫ ТОКА И НАПРЯЖЕНИЯ

Как измерить силу тока ампер-метром, а напряжение вольтметром, должен знать каждый.

Измерение силы тока.

Для изме-рения силы тока в проводнике ам-перметр включают последовательно с этим проводником (рис. 1). Но нужно иметь в виду, что сам ампер-метр обладает некоторым сопротив-лением R a . Поэтому сопротивление участка цепи с включенным ампер-метром увеличивается, и при неиз-менном напряжении сила тока умень-шается в соответствии с законом Ома. Чтобы амперметр оказывал как можно меньшее влияние на силу тока, измеряемую им, его сопротив-ление делают очень малым. Это нужно помнить и никогда не пытать-ся измерять силу тока в освети-тельной сети, подключая амперметр к розетке. Произойдет короткое за-мыкание; сила тока при малом со-противлении прибора достигнет столь большой величины, что обмотка ам-перметра сгорит.

Измерение напряжения.

Для того чтобы измерить напряжение на участке цепи с сопротивлением R, к нему параллельно подключают вольтметр. Напряжение на вольтметре совпа-дает с напряжением на участке цепи (рис. 2).

Если сопротивление вольтметра R B , то после включения его в цепь сопротивление участка будет уже не R, а . Из-за этого измеряемое напряжение на участ-ке цепи уменьшится. Для того чтобы вольтметр не вносил заметных иска-жений в измеряемое напряжение, его сопротивление должно быть большим по сравнению с сопротивлением участка цепи, на котором измеряется напряжение. Вольтметр можно вклю-чать в сеть без риска, что он сгорит, если только он рассчитан на напря-жение, превышающее напряжение сети.

Амперметр включают последова-тельно с проводником, в котором измеряют силу тока. Вольтметр включают параллельно проводнику, на котором измеряют напряжение.

РАБОТА И МОЩНОСТЬ ПОСТОЯННОГО ТОКА

Электрический ток получил такое широкое применение потому, что он несет с собой энергию. Эта энергия может быть превращена в любую форму.

При упорядоченном движении за-ряженных частиц в проводнике электрическое поле совершает ра-боту; ее принято называть работой тока. Сейчас мы напомним сведения о работе и мощности тока из курса физики VIII класса.

Работа тока.

Рассмотрим произ-вольный участок цепи. Это, может быть однородный проводник, напри-мер нить лампы накаливания, обмот-ка электродвигателя и др. Пусть за время t через поперечное сечение проводника проходит заряд q. Тогда электрическое поле совершит работу A = qU.

Так как сила тока , то эта работа равна:

Работа тока на участке цепи равна произведению силы тока, на-пряжения и времени, в течение ко-торого совершалась работа.

Согласно закону сохранения энергии эта работа должна быть рав-на изменению энергии рассматри-ваемого участка цепи. Поэтому энер-гия, выделяемая на данном участке цепи за время At, равна работе тока (см. формулу (1)).

В случае если на участке цепи не совершается механическая рабо-та и ток не производит химических действий, происходит только нагре-вание проводника. Нагретый про-водник отдает теплоту окружающим телам.

Нагревание проводника происхо-дит следующим образом. Электриче-ское поле ускоряет электроны. После столкновения с ионами кристалличе-ской решетки они передают ионам свою энергию. В результате энергия беспорядочного движения ионов око-ло положений равновесия возраста-ет. Это и означает увеличение внут-ренней энергии. Температура про-водника при этом повышается, и он начинает передавать теплоту окру-жающим телам. Спустя небольшое время после замыкания цепи процесс устанавливается, и температура пе-рестает изменяться со временем. К проводчику за счет работы элект-рического поля непрерывно поступа-ет энергия. Но его внутренняя энер-гия остается неизменной, так как проводник передает окружающим те-лам количество теплоты, равное ра-боте тока. Таким образом, формула (1) для работы тока определяет количество теплоты, передаваемое проводником другим телам.

Если в формуле (1) выразить либо напряжение через силу тока, либо силу тока через напряжение с помощью закона Ома для участка цепи, то получим три эквивалентные формулы:

(2)

Формулой A = I 2 R t удобно пользоваться для последовательного соединения проводников, так как сила тока в этом случае одинакова во всех проводниках. При парал-лельном соединении удобна формула , так как напряжение на всех проводниках одинаково.

Закон Джоуля — Ленца.

Закон, определяющий количество теплоты, которое выделяет проводник с то-ком в окружающую среду, был впервые установлен эксперименталь-но английским ученым Д. Джоу-лем (1818-1889) и русским ученым Э. X. Ленцем (1804-1865). Закон Джоуля — Ленца был сформулиро-ван следующим образом: количество теплоты, выделяемое проводником с током, равно произведению квад-рата силы тока, сопротивления про-водника и времени прохождения то-ка по проводнику:

(3)

Мы получили этот закон с по-мощью рассуждений, основанных на законе сохранения энергии. Формула (3) позволяет вычислить количе-ство теплоты, выделяемое на любом участке цепи, содержащем какие угодно проводники.

Мощность тока.

Любой электри-ческий прибор (лампа, электродвигатель) рассчитан на потребление определенной энергии в единицу вре-мени. Поэтому наряду с работой то-ка очень важное значение имеет по-нятие мощность тока. Мощность то-ка равна отношению работы тока за время t к этому интервалу времени.

Согласно этому определению

(4)

Это выражение для мощности можно переписать в нескольких эквивалентных формах, если исполь-зовать закон Ома для участка цепи:

На большинстве приборов ука-зана потребляемая ими мощность.

Прохождение по проводнику электрического тока сопровождается выделением в нем энергии. Эта энер-гия определяется работой тока: про-изведением перенесенного заряда и напряжения на концах проводника.

ЭЛЕКТРОДВИЖУЩАЯ СИЛА.

Любой источник тока характеризуется электродвижущей силой, или ЭДС. Так, на круглой батарейке для карманного фонарика написано: 1,5 В. Что это значит?

Соедините проводником два ме-таллических шарика, несущих за-ряды противоположных знаков. Под влиянием электрического поля этих зарядов в проводнике возникает электрический ток (рис. 1). Но этот ток будет очень кратковремен-ным. Заряды быстро нейтрализуют-ся, потенциалы шариков станут одинаковыми, и электрическое поле ис-чезнет.

Сторонние силы.

Для того чтобы ток был постоянным, надо поддер-живать постоянное напряжение меж-ду шариками. Для этого необходимо устройство (источник тока), которое перемещало бы заряды от одного шарика к другому в направлении, противоположном направлению сил, действующих на эти заряды со сто-роны электрического поля шариков. В таком устройстве на заряды, кро-ме электрических сил, должны дей-ствовать силы не электростатического происхождения (рис. 2). Одно лишь электрическое поле заряжен-ных частиц (кулоновское поле) не способно поддерживать постоянный ток в цепи.

Любые силы, действующие на электрически заряженные частицы, за исключением сил электростати-ческого происхождения (т. е. кулоновских), называют сторонними си-лами.

Вывод о необходимости сторон-них сил для поддержания посто-янного тока в цепи станет еще оче-виднее, если обратиться к закону сохранения энергии. Электростатиче-ское поле потенциально. Работа это-го поля при перемещении заряжен-ных частиц вдоль замкнутой электри-ческой цепи равна нулю. Прохож-дение же тока по проводникам сопровождается выделением энер-гии — проводник нагревается. Сле-довательно, в любой цепи должен быть какой-то источник энергии, по-ставляющий ее в цепь. В нем, по-мимо кулоновских сил, обязательно должны действовать сторонние не- потенциальные силы. Работа этих сил вдоль замкнутого контура долж-на быть отлична от нуля. Именно в процессе совершения работы этими силами заряженные частицы приобретают внутри источника тока энер-гию и отдают ее затем проводникам электрической цепи.

Сторонние силы приводят в дви-жение заряженные частицы внутри всех источников тока: в генераторах на электростанциях, в гальваниче-ских элементах, аккумуляторах и т.д.

При замыкании цепи создается электрическое поле во всех провод-никах цепи. Внутри источника тока заряды движутся под действием сторонних сил против кулоновских сил (электроны от положительно заряженного электрода к отрица-тельному), а во всей остальной цепи их приводит в движение электриче-ское поле (см. рис. 2).

Аналогия между электрическим током и течением жидкости.

Чтобы лучше понять механизм возникнове-ния тока, обратимся к сходству меж-ду электрическим током в провод-нике и течением жидкости по трубам.

На любом участке горизонталь-ной трубы жидкость течет за счет разности давлений на концах участ-ка. Жидкость перемещается в сторо-ну уменьшения давления. Но сила давления в жидкости — это вид сил упругости, которые являются потен-циальными, подобно кулоновским силам. Поэтому работа этих сил на замкнутом пути равна нулю и одни эти силы не способны вызвать длительную циркуляцию жидкости по трубам. Течение жидкости сопро-вождается потерями энергии вслед-ствие действия сил трения. Для цир-куляции воды необходим насос.

Поршень этого насоса действует на частички жидкости и создает по-стоянную разность давлений на вхо-де и выходе насоса (рис. 3). Благодаря этому жидкость течет по трубе. Насос подобен источнику тока, а роль сторонних сил играет сила, действующая на воду со стороны движущегося поршня. Внутри на-соса жидкость течет от участков с меньшим давлением к участкам с большим давлением. Разность дав-лений аналогична напряжению.

Природа сторонних сил.

Природа сторонних сил может быть разнооб-разной. В генераторах электростанций сторонняя сила — это сила, дей-ствующая со стороны магнитного поля на электроны в движущемся проводнике. Об этом кратко гово-рилось в курсе физики VIII класса.

В гальваническом элементе, на-пример элементе Вольта, действуют химические силы. Элемент Вольта состоит из цинкового и медного электродов, помещенных в раствор серной кислоты. Химические силы вызывают растворение цинка в кис-лоте. В раствор переходят положи-тельно заряженные ионы цинка, а сам цинковый электрод при этом заряжается отрицательно. (Медь очень мало растворяется в серной — кислоте.) Между цинковым и мед-ным электродами появляется раз-ность потенциалов, которая обуслов-ливает ток в замкнутой электриче-ской цепи.

Электродвижущая сила.

Дейст-вие сторонних сил характеризуется важной физической величиной, на-зываемой электродвижущей силой (сокращенно ЭДС).

Электродви-жущая сила в замкнутом контуре представляет собой отношение рабо-ты сторонних сил при перемещении заряда вдоль контура к заряду:

Электродвижущую силу выража-ют в вольтах.

Можно говорить об электродви-жущей силе на любом участке цепи. Это удельная работа сторонних сил (работа по перемещению единич-ного заряда) не во всем контуре, а только на данном участке. Электро-движущая сила гальванического эле-мента есть работа сторонних сил при перемещении единичного положи-тельного заряда внутри элемента от одного полюса к другому. Работа сторонних сил не может быть вы-ражена через разность потенциалов, так как сторонние силы не потенциальные и их работа зависит от формы траектории. Так, например, работа сторонних сил при переме-щении заряда между клеммами ис-точника тока вне самого источника равна нулю.

Теперь вы знаете, что такое ЭДС. Если на батарейке написано 1,5 В, то это означает, что сторонние силы (химические в данном случае) совер-шают работу 1,5 Дж при переме-щении заряда в 1 Кл от одного полюса батарейки к другому. Постоянный ток не может существовать в замкнутой цепи, если в ней не действуют сторонние силы, т. е. нет ЭДС

Рис №1 Рис №2 Рис №3

ЗАКОН ОМА ДЛЯ ПОЛНОЙ ЦЕПИ

Электродвижущая сила опреде-ляет силу тока в замкнутой электри-ческой цепи с известным сопротив-лением.

Спомощью закона сохранения энергии найдем зависимость силы тока от ЭДС и сопротивления.

Рассмотрим простейшую полную (замкнутую) цепь, состоящую из источника тока (гальванического элемента, аккумулятора или гене-ратора) и резистора сопротивле-нием R (рис. 1). Источник тока имеет ЭДС εи сопротивление r. Сопротивление источника часто на-зывают внутренним сопротивлением в отличие от внешнего сопротивле-ния R цепи. В генераторе r — это сопротивление обмоток, а в гальва-ническом элементе — сопротивление раствора электролита и электродов.

Закон Ома для замкнутой цепи связывает силу тока в цепи, ЭДС и полное сопротивление R + r цепи. Эта связь может быть установлена теоретически, если использовать за-кон сохранения энергии и закон Джоуля — Ленца.

Пусть за время t через попе-речное сечение проводника пройдет электрический заряд q. Тогда рабо-ту сторонних сил при перемещении заряда?qможно записать так: А ст = ε · q. Согласно определению силы тока q = It. Поэтому

(1)

При совершении этой работы на внутреннем и внешнем участках цепи, сопротивления которых r и R, выделяется некоторое количество теплоты. По закону Джоуля — Лен-ца оно равно:

Q = I 2 R · t + I 2 r · t. (2)

Согласно закону сохранения энергии A = Q. Приравнивая (1) и (2), получим:

ε = IR + Ir (3)

Произведение силы тока и сопро-тивления участка цепи часто назы-вают падением напряжения на этом участке. Таким образом, ЭДС равна сумме падений напряжений на внут-реннем и внешнем участках замкну-той цепи.

Обычно закон Ома для замкну-той цепи записывают в форме

(4)

По назначению конденсатор можно сравнить с батарейкой. Но имеется принципиальное отличие в работе данных элементов. Существуют отличия в предельной емкости и скорости зарядки конденсатора и батарейки.

Формула заряда конденсатора

где q – величина заряда одной из обкладок конденсатора, а – разность потенциалов между его обкладками.

Электроемкость конденсатора — это величина, которая зависит то размеров и устройства конденсатора.

Заряд на пластинах плоского конденсатора равен:

где – электрическая постоянная; – площадь каждой (или наименьшей) пластины; – расстояние между пластинами; – диэлектрическая проницаемость диэлектрика, который находится между пластинами конденсатора.

Заряд на обкладках цилиндрического конденсатора вычисляется при помощи формулы:

где l – высота цилиндров; – радиус внешней обкладки; – радиус внутренней обкладки.

Заряд на обкладках сферического конденсатора найдем как:

Заряд конденсатора связан с энергией поля (W) внутри него:

Из формулы (6) следует, что заряд можно выразить как:

Рассмотрим последовательное соединение из N конденсаторов (рис. 1).

Здесь (рис.1) положительная обкладка одного конденсатора соединяется с отрицательной обкладкой следующего конденсатора. При таком соединении, обкладки соседних конденсаторов создают единый проводник. У всех конденсаторов, соединенных последовательно на обкладках имеются равные по величине заряды.

При параллельном соединении конденсаторов (рис.2), соединяют обкладки, имеющие заряды одного знака. Суммарный заряд соединения (q) равен сумме зарядов конденсаторов.

Примеры решения задач по теме «Заряд конденсатора»

ru.solverbook.com

Формула емкости конденсатора, С

Если q – величина заряда одной из обкладок конденсатора, а – разность потенциалов между его обкладками, то величина C, равная:

называется емкостью конденсатора. Это постоянная величина, которая зависит то размеров и устройства конденсатора.

Рассмотрим два одинаковых конденсатора, разница между которым заключается только в том, что между обкладками одного вакуум (или часто говорят воздух), между обкладками другого находится диэлектрик. В таком случае при равных зарядах на конденсаторах разность потенциалов воздушного конденсатора будет в раз меньше, чем между обкладками второго. Значит емкость конденсатора с диэлектриком (C) в раз больше, чем воздушного ():

где – диэлектрическая проницаемость диэлектрика.

За единицу емкости конденсатора принимают емкость такого конденсатора, который единичным зарядом (1 Кл) заряжается до разности потенциалов, равной одному вольту (в СИ). Единицей емкости конденсатора (как и любой эклектической емкости) в международной системе единиц (СИ) служит фарад (Ф).

Формула электрической емкости плоского конденсатора

Поле между обкладками плоского конденсатора обычно считают однородным. Его однородность нарушается только около краев. При вычислении емкости плоского конденсатора этими краевыми эффектами часто пренебрегают. Это следует делать, если расстояние между пластинами мало в сравнении с их линейными размерами. Для расчета емкости плоского конденсатора применяют формулу:

Электрическая емкость плоского конденсатора, который содержит N слоев диэлектрика толщина каждого , соответствующая диэлектрическая проницаемость i-го слоя , равна:

Формула электрической емкости цилиндрического конденсатора

Цилиндрический конденсатор представляется собой две соосных (коаксиальных) цилиндрические проводящие поверхности, разного радиуса, пространство между которыми заполняет диэлектрик. Электрическая емкость цилиндрического конденсатора вычисляется как:

Формула электрической емкости сферического конденсатора

Сферическим конденсатором называют конденсатор, обкладками которого являются две концентрические сферические проводящие поверхности, пространство между ними заполнено диэлектриком. Емкость такого конденсатора находят как:

где – радиусы обкладок конденсатора.

Примеры решения задач по теме «Емкость конденсатора»

ru.solverbook.com

Ёмкость конденсатора — Все формулы

Электрическая ёмкость — характеристика проводника (конденсатора), мера его способности накапливать электрический заряд.

Конденсатор состоит из двух проводников (обкладок), которые разделены диэлектриком. На емкость конденсатора не должны влиять окружающие тела, поэтому проводникам придают такую форму, чтобы поле, которое создается накапливаемыми зарядами, было сосредоточено в узком зазоре между обкладками конденсатора. Этому условию удовлетворяют: 1) две плоские пластины; 2) две концентрические сферы; 3) два коаксиальных цилиндра. Поэтому в зависимости от формы обкладок конденсаторы делятся на плоские, сферические и цилиндрические.

Так как поле сосредоточено внутри конденсатора, то линии напряженности начинаются на одной обкладке и кончаются на другой, поэтому свободные заряды, которые возникают на разных обкладках, равны по модулю и противоположны по знаку. Под емкостью конденсатора понимается физическая величина, равная отношению заряда Q, накопленного в конденсаторе, к разности потенциалов (φ1 — φ2) между его обкладками

Для получения больших ёмкостей конденсаторы соединяют параллельно. При этом напряжение между обкладками всех конденсаторов одинаково. Общая ёмкость батареи параллельно соединённых конденсаторов равна сумме ёмкостей всех конденсаторов, входящих в батарею.

Конденсаторы можно классифицировать по следующим признакам и свойствам:

1) по назначению — конденсаторы постоянной и переменной емкости;

2) по форме обкладок различают конденсаторы плоские, сферические, цилиндрические и др.;

3) по типу диэлектрика — воздушные, бумажные, слюдяные, керамические, электролитические и т.д.

Так же есть:

Энергия конденсатора:

Ёмкость цилиндрического конденсатора:

Ёмкость плоского конденсатора:

Емкость сферического конденсатора:

В формуле мы использовали:

Электрическая ёмкость (ёмкость конденсатора)

Потенциал проводника (Напряжение)

Потенциал

Относительная диэлектрическая проницаемость

Электрическая постоянная

Площадь одной обкладки

Расстояние между обкладками

xn--b1agsdjmeuf9e.xn--p1ai

Заряд конденсатора, теория и примеры задач

Определение и заряд конденсатора

Возможность конденсатора накопить электрический заряд зависит от главной характеристики конденсатора – емкости (C).

По своему назначению конденсатор можно уподобить батарейке. Однако существует принципиальное отличие в принципах работы этих элементов. Отличаются, также максимальные емкости и скорости зарядки и разряда конденсатора и батарейки.

Если к конденсатору присоединить источник напряжения (рис.1), то на одной из пластин конденсатора станут накапливаться отрицательные заряды (электроны), на другой положительные частицы (положительные ионы). Между обкладками конденсатора находится диэлектрик, вследствие этого, заряды не могут перебраться на противоположную пластину. Однако заметим, что электроны двигаются от источника тока до пластины конденсатора.

При первоначальном соединении конденсатора и источника тока на обкладках конденсатора много свободного места. Это означает, что сопротивление току этот момент времени минимально, сам ток максимален. В ходе зарядки конденсатора сила тока в цепи постепенно падает, до того момента пока не закончится свободное место на обкладках. При полной зарядке конденсатора ток в цепи прекратится.

Время, которое затрачивается на зарядку конденсатора от нулевого заряда (максимального тока) до полностью заряженного конденсатора (минимальная или нулевая сила тока) называют переходным периодом заряда конденсатора. На практике процесс зарядки конденсатора считают законченным, если сила тока уменьшилась до 1% от начальной величины.

Величина заряда конденсатора (q) связана с его емкостью (C) и разностью потенциалов (U) между его обкладками как:

Примеры решения задач

ru.solverbook.com

Формула электроемкости конденсатора

Обкладки должны иметь такую форму и быть расположены так относительно друг друга, что поле, которое создается данной системой, было максимально сосредоточено в ограниченной области пространства, между обкладками.

Назначение конденсатора в том, чтобы накапливать и отдавать в электрической цепи заряд.

Основной характеристикой конденсатора является электрическая емкость (C). Электрическая емкость конденсатора – это взаимная емкость принадлежащих ему обкладок:

q – величина заряда на обкладке; – разность потенциалов между обкладками.

Электрическая ёмкость конденсатора зависит от диэлектрической проницаемости диэлектрика, который заполняет пространство между его обкладками. Если пространство между обкладками одного конденсатора заполнено диэлектриком с проницаемостью равной , а у второго конденсатора воздух между пластинами, то емкость конденсатора с диэлектриком (C) в раз больше, чем емкость воздушного конденсатора ():

Формула электроемкости основных типов конденсаторов

При расчете электроемкости плоского конденсатора нарушением однородности поля около краёв обкладок обычно пренебрегают. Это становится возможным, если расстояние между пластинами существенно меньше, чем линейные размеры обкладок. В таком случае электрическую емкость плоского конденсатора вычисляют при помощи формулы:

где – электрическая постоянная; S – площадь каждой (или наименьшей) пластины; d – расстояние между пластинами.

Если плоский конденсатор между обкладками имеет N слоев диэлектрика, при этом толщина каждого слоя равна , а диэлектрическая проницаемость , то его электрическую емкость рассчитывают при помощи формулы:

Цилиндрический конденсатор составляют две соосных (коаксиальных) цилиндрические проводящие поверхности, разного радиуса, пространство между которыми заполнено диэлектриком. При этом емкость цилиндрического конденсатора находят как:

где l – высота цилиндров; – радиус внешней обкладки; – радиус внутренней обкладки.

У сферического конденсатора обкладками служат две концентрические сферические проводящие поверхности, пространство обкладками заполняет диэлектрик. Емкость сферического конденсатора вычисляют как:

где – радиусы обкладок конденсатора. Если , то можно считать, что , тогда, мы имеем:

так как – площадь поверхности сферы, и если обозначить , то получим формулу для емкости плоского конденсатора (3). Если расстояние между обкладками сферического и цилиндрического конденсаторов малы (в сравнении с их радиусами), то в приближенных расчетах используют формулу емкости для плоского конденсатора.

Электрическую емкость для линии из двух проводов находят как:

где d – расстояние между осями проводов; R – радиус проводов; l – длина линии.

Формулы для вычисления электрической емкости соединений конденсаторов

Если конденсаторы соединены параллельно, то суммарная емкость батареи (C) находится как сумма емкостей отдельных конденсаторов ():

При последовательном соединении конденсаторов емкость батареи вычисляют как:

Если последовательно соединены N конденсаторов, с емкостями то емкость батареи найдем как:

Сопротивление конденсатора

Если конденсатор включен в цепь с постоянного тока, то сопротивление конденсатора можно считать бесконечно большим.

При включении конденсатора в цепь переменного тока, его сопротивление носит название емкостного, и вычисляют его с помощью формулы:

где – частота переменного тока; – угловая частота тока; C – емкость конденсатора.

Энергия поля конденсатора

Электрическое поле локализованное между пластинами конденсатора обладает энергией, которую можно вычислить при помощи формулы:

где –энергия поля конденсатора; q – заряд конденсатора; C – емкость конденсатора; – разность потенциалов между обкладками конденсатора.

Энергия поля плоского конденсатора:

Примеры решения задач по теме «Электроемкость конденсатора»

ru.solverbook.com

Как найти заряд конденсатора 🚩 как определить величину заряда 🚩 Естественные науки

В обычном (без плагинов и модов) варианте Minecraft такого понятия, как конденсатор, не существует. Вернее, устройство, выполняющее его функции, имеется, но название у него совершенно другое — компаратор. Некоторая путаница в этом плане произошла еще в период разработки такого прибора. Сперва — в ноябре 2012-го — представители Mojang (компании-создателя игры) объявили о скором появлении в геймплее конденсатора. Однако через месяц они высказались уже о том, что как такового этого прибора не будет, а вместо него в игре будет компаратор.

Подобное устройство существует для проверки заполненности расположенных позади него контейнеров. Таковыми могут быть сундуки (в том числе в виде ловушек), варочные стойки, раздатчики, выбрасыватели, печи, загрузочные воронки и т.п.

Помимо этого, его часто используют для сравнения двух сигналов редстоуна между собою — он выдает результат в соответствии с тем, как было запрограммировано в данной цепи, и с тем, какой режим выбран для самого механизма. В частности, компаратор может разрешить зажигание факела, если первый сигнал больше либо равен другому.

Также порой конденсатор-компаратор устанавливают рядом с проигрывателем, подключая его входом к последнему. Когда в звуковоспроизводящем устройстве проигрывается какая-либо пластинка, вышеупомянутый прибор будет выдавать сигнал, равный по силе порядковому номеру диска.

Скрафтить такой компаратор несложно, если имеется достаточно трудно добываемый ресурс — адский кварц. Его надо поставить в центральный слот верстака, над ним и по бокам от него установить три красных факела, а в нижнем ряду — такое же количество каменных блоков.

В большом количестве модов попадаются конденсаторы, имеющие самое разное предназначение. К примеру, в Galacticraft, где у геймеров есть возможность слетать на многие планеты для ознакомления с тамошними реалиями, появляется рецепт крафта кислородного конденсатора. Он служит для создания механизмов вроде коллектора и накопителя газа для дыхания, а также рамки воздушного шлюза. Для его изготовления четыре стальных пластины размещаются по углам верстака, в центре — оловянная канистра, а под нею — воздуховод. Остальные три ячейки занимают пластины из олова.

В JurassiCraft существует конденсатор потока — некий телепорт, позволяющий переместиться в удивительный игровой мир, кишащий динозаврами. Для создания такого прибора нужно поместить в два крайних вертикальных ряда шесть железных слитков, а в средний — два алмаза и между ними единицу пыли редстоуна. Дабы устройство заработало, надо поставить его на свинью либо вагонетку, а затем щелкнуть по нему правой клавишей мыши, быстро запрыгнув туда. При этом требуется поддержание высокой скорости устройства.

С модом Industrial Craft2 у игрока появляется возможность создавать как минимум два вида тепловых конденсаторов — красный и лазуритовый. Они служат исключительно для охлаждения ядерного реактора и для накопления его энергии и хороши для циклических сооружений такого типа. Остужаются они сами, соответственно, красной пылью или лазуритом.

Красный теплоконденсатор делается из семи единиц пыли редстоуна — их надо установить в виде буквы П и расставить под ними теплоотвод и теплообменник. Крафтинг же лазуритового устройства чуть посложнее. Для его создания четыре единицы пыли редстоуна расставляются по углам станка, в центр пойдет блок лазурита, по бокам от него — два красных тепловых конденсатора, сверху — теплоотвод реактора, а снизу — его же теплообменник.

В ThaumCraft, где сделан акцент на настоящем чародействе, конденсаторы тоже используются. Например, один из них — кристаллический — существует для аккумуляции и отдачи магии. Причем, что интересно, создавать его и многие другие вещи разрешено лишь после изучения особого элемента геймплея — исследования, проводимого за специальным столом и с определенными приборами.

Делается такой конденсатор из восьми тусклых осколков, в центр которых на верстаке помещается мистический деревянный блок. К сожалению, подобный прибор — равно как и его составляющие — просуществовал лишь до ThaumCraft 3, а в четвертой версии мода был упразднен.

www.kakprosto.ru

Соединение конденсаторов: формулы

Содержание:

1. Последовательное соединение
2. Онлайн калькулятор
3. Смешанное соединение
4. Параллельное соединение
5. Видео

В электронных и радиотехнических схемах широкое распространение получило параллельное и последовательное соединение конденсаторов. В первом случае соединение осуществляется без каких-либо общих узлов, а во втором варианте все элементы объединяются в два узла и не связаны с другими узлами, если это заранее не предусмотрено схемой.

Последовательное соединение

При последовательном соединении два и более конденсаторов соединяются в общую цепь таким образом, что каждый предыдущий конденсатор соединяется с последующим лишь в одной общей точке. Ток (i), осуществляющий зарядку последовательной цепи конденсаторов будет иметь одинаковое значение для каждого элемента, поскольку он проходит только по единственно возможному пути. Это положение подтверждается формулой: i = ic1 = ic2 = ic3 = ic4.

В связи с одинаковым значением тока, протекающего через конденсаторы с последовательным соединением, величина заряда, накопленного каждым из них, будет одинаковой, независимо от емкости. Такое становится возможным, поскольку заряд, приходящий с обкладки предыдущего конденсатора, накапливается на обкладке последующего элемента цепи. Поэтому величина заряда у последовательно соединенных конденсаторов будет выглядеть следующим образом: Qобщ= Q1 = Q2 = Q3.

Если рассмотреть три конденсатора С1, С2 и С3, соединенные в последовательную цепь, то выясняется, что средний конденсатор С2 при постоянном токе оказывается электрически изолированным от общей цепи. В конечном итоге величина эффективной площади обкладок будет уменьшена до площади обкладок конденсатора с самыми минимальными размерами. Полное заполнение обкладок электрическим зарядом, делает невозможным дальнейшее прохождение по нему тока. В результате, движение тока прекращается во всей цепи, соответственно прекращается и зарядка всех остальных конденсаторов.

Общее расстояние между обкладками при последовательном соединении представляет собой сумму расстояний между обкладками каждого элемента. В результате соединения в последовательную цепь, формируется единый большой конденсатор, площадь обкладок которого соответствует обкладкам элемента с минимальной емкостью. Расстояние между обкладками оказывается равным сумме всех расстояний, имеющихся в цепи.

Падение напряжения на каждый конденсатор будет разным, в зависимости от емкости. Данное положение определяется формулой: С = Q/V, в которой емкость обратно пропорциональна напряжению. Таким образом, с уменьшением емкости конденсатора на него падает более высокое напряжение. Суммарная емкость всех конденсаторов вычисляется по формуле: 1/Cобщ = 1/C1 + 1/C2 + 1/C3.

Главная особенность такой схемы заключается в прохождении электрической энергии только в одном направлении. Поэтому в каждом конденсаторе значение тока будет одинаковым. Каждый накопитель в последовательной цепи накапливает равное количество энергии, независимо от емкости. То есть емкость может воспроизводиться за счет энергии, присутствующей в соседнем накопителе.

Онлайн калькулятор, для расчета емкости конденсаторов соединенных последовательно в электрической цепи.

Смешанное соединение

Параллельное соединение конденсаторов

Параллельным считается такое соединение, при котором конденсаторы соединяются между собой двумя контактами. Таким образом в одной точке может соединяться сразу несколько элементов.

Данный вид соединения позволяет сформировать единый конденсатор с большими размерами, площадь обкладок которого будет равна сумме площадей обкладок каждого, отдельно взятого конденсатора. В связи с тем, что емкость конденсаторов находится в прямой пропорциональной зависимости с площадью обкладок, общая емкость составить суммарное количество всех емкостей конденсаторов, соединенных параллельно. То есть, Собщ = С1 + С2 + С3.

Поскольку разность потенциалов возникает лишь в двух точках, то на все конденсаторы, соединенные параллельно, будет падать одинаковое напряжение. Сила тока в каждом из них будет отличаться, в зависимости от емкости и значения напряжения. Таким образом, последовательное и параллельное соединение, применяемое в различных схемах, позволяет выполнять регулировку различных параметров на тех или иных участках. За счет этого получаются необходимые результаты работы всей системы в целом.

electric-220.ru

Во всех электронных устройствах используются конденсаторы. При их конструировании или изготовлении своими руками параметры устройств рассчитываются по специальным формулам.

Расчёт конденсаторов

Один из главных параметров таких устройств – ёмкость. Рассчитать её можно по следующей формуле:

• C – ёмкость,
• q – заряд одной из обкладок элемента,
• U – разность потенциалов между обкладками.

В электротехнике вместо понятия «разность потенциалов между обкладками» используется «напряжение на конденсаторе».

Ёмкость элемента не зависит от конструкции и размеров устройства, а только от напряжения на нём и заряда обкладок. Но эти параметры могут изменяться в зависимости от расстояния между ними и материала диэлектрика. Это учитывается в формуле:

С=Co*ε, где:

• С – реальная ёмкость,
• Со – идеальная, при условии, что между пластинами вакуум или воздух,
• ε – диэлектрическая проницаемость материала между ними.

Например, если в качестве диэлектрика используется слюда, «ε» которой 6, то ёмкость такого устройства в 6 раз больше, чем воздушного, а при изменении количества диэлектрика меняются параметры конструкции. На этом принципе основана работа ёмкостного датчика положения.

Единицей ёмкости в системе СИ является 1 фарад (F). Это большая величина, поэтому чаще применяются микрофарады (1000000mkF=1F) и пикофарады (1000000pF=1mkF).

Расчет плоской конструкции

• ε – диэлектрическая проницаемость изолирующего материала,
• d – расстояние между пластинами.

Расчет конструкции цилиндрической формы

Цилиндрический конденсатор – это две соосные трубки различного диаметра, вставленные друг в друга. Между ними находится диэлектрик. При радиусе цилиндров, близком друг к другу и намного большем, чем расстояние между ними, цилиндрической формой можно пренебречь и свести расчёт к формуле, аналогичной той, по которой рассчитывается плоский конденсатор.

Вычисляются параметры такого устройства по формуле:

C=(2π*l*R*ε)/d, где:

• l – длина устройства,
• R – радиус цилиндра,
• ε – диэлектрическая проницаемость изолятора,
• d – его толщина.

Расчёт сферической конструкции

Есть устройства, обкладки которых представляют собой два шара, вложенные друг в друга. Формула ёмкости такого прибора:

C=(4π*l*R1*R2*ε)/(R2-R1), где:

• R1 – радиус внутренней сферы,
• R2 – радиус внешней сферы,
• ε – диэлектрическая проницаемость.

Ёмкость одиночного проводника

Кроме конденсаторов, способностью накапливать заряд обладают отдельные проводники. Одиночным проводником считается такой проводник, который бесконечно далёк от других проводников. Параметры заряженного элемента рассчитывается по формуле:

• Q – заряд,
• φ – потенциал проводника.

Объём заряда определяется размером и формой устройства, а также окружающей средой. Материал прибора значения не имеет.

Способы соединения элементов

Не всегда есть в наличии элементы с необходимыми параметрами. Приходится соединять их различными способами.

Параллельное соединение

Это такое соединение деталей, при котором к одной клемме или контакту присоединяются первые обкладки каждого конденсатора. При этом вторые обкладки присоединяются к другой клемме.

При таком соединении напряжение на контактах всех элементов будет одинаковым. Заряд каждого из них происходит независимо от остальных, поэтому общая ёмкость равна сумме всех величин. Её находят по формуле:

где C1-Cn – параметры деталей, участвующих в параллельном соединении.

Важно! Конденсаторы имеют предельное допустимое напряжение, превышение которого приведёт к выходу элемента из строя. При параллельном соединении устройств с различным допустимым напряжением этот параметр получившейся сборки равен элементу с наименьшим значением.

Последовательное соединение

Это такое соединение, при котором к клемме присоединяется только одна пластина первого элемента. Вторая пластина присоединяется к первой пластине второго элемента, вторая пластина второго – к первой пластине третьего и так далее. Ко второй клемме присоединяется только вторая обкладка последнего элемента.

При таком соединении заряд на обкладках конденсатора в каждом приборе будет равен остальным, однако напряжение на них будет разным: для зарядки устройств большей ёмкости тем же зарядом требуется меньшая разность потенциалов. Поэтому вся цепочка представляет собой одну конструкцию, разность потенциалов которой равна сумме напряжений на всех элементах, а заряд конденсатора равен сумме зарядов.

Последовательное соединение увеличивает допустимое напряжение и уменьшает общую ёмкость, которая меньше самого меньшего элемента.

Рассчитываются эти параметры следующим образом:

• Допустимое напряжение:

Uобщ=U1+U2+U3+…Un, где U1-Un – напряжение на конденсаторе;

• Общая ёмкость:

1/Собщ=1/С1+1/С2+1/С3+…1/Сn, где С1-Сn – параметры каждого устройства.

Интересно. Если в цепи только два элемента, то можно воспользоваться упрощённой формулой: Собщ=(С1*С2)/(С1+С2).

Смешанное соединение

Это такое соединение, в котором есть детали, соединённые последовательно, и есть соединённые параллельно. Параметры всей цепи рассчитывается в следующей последовательности:

1. определяются группы элементов, соединённые параллельно;
2. для каждой группы в отдельности рассчитывается эквивалентные значения;
3. рядом с каждой группой параллельно соединённых деталей пишутся получившиеся величины;
4. получившаяся схема эквивалентна последовательной схеме и рассчитывается по соответствующим формулам.

Знание формул, по которым можно найти емкость при изготовлении конденсаторов или их соединении необходимо при конструировании электронных схем.

Видео

Напряжение цепи переменного тока | Электрикам

Переменное напряжение — это напряжение, которое изменяется с течением времени. Далее будем рассматривать только гармоническое переменное напряжение (изменяется по синусоиде).

u = U_msin(2πt + Ψ ) = U_msin(ωt + Ψ )

Где u = u(t) — мгновенное значение переменного напряжения [В].

U_m — максимальное значение напряжения (амплитудное значение) [В].

f — частота  равная числу колебаний в 1 секунду (единица частоты f — герц (Гц) или с^-1)

ω — угловая частота (омега) (единица угловой частоты — рад/с или с^-1)

ω = 2πf = 2π/T

Аргумент синуса, т. е. (ωt + Ψ), называют фазой. Фаза характеризует состояние колебания (числовое значение) в данный момент времени t.

U — Действующее значение напряжения [В]:

Рассмотрим параметры напряжения в бытовой электросети.

Все мы знаем, что у нас дома в розетке поступает переменный ток, с напряжением 220 вольт и частотой 50 герц (в идеальных условиях) на самом деле допускается не большая погрешность как в меньшую, так и в большую сторону так, что не удивляйтесь если ваш вольтметр покажет не 220, а например 210 или даже 230 В.).

Большинство приборов измеряет не амплитудное, а действующее значение переменного напряжения, тока, мощности так, что если мы говорим что у нас напряжение сети 220, 380 В и т. д. то имеется виду именно действующие значения.

• Действующее значение напряжения U = 220 В.
• Амплитудное значение напряжения цепи переменного тока U_m = U*√2 = 220 *√2 = 311 В.
• Угловая частота ω = 2πf = 3,14*2*50 = 314 рад/с.
• Начальная фаза Ψ = 0 град.
• Мгновенное значение u  = 311sin(314t) В.

Почему светодиод имеет максимальное напряжение?

Светодиод имеет «максимальное напряжение», потому что его сопротивление резко уменьшается — как и в любом другом диоде — так как его прямое напряжение увеличивается выше колена, и это увеличение напряжения на светодиоде связано с увеличением тока через него (из-за уменьшение его прямого сопротивления) увеличивает мощность, которую должен рассеивать светодиод, и, следовательно, его рабочую температуру. Затем, если ток через соединение светодиода поднимется выше его абсолютного максимального значения, его срок службы будет сокращен, и волшебный дым рано или поздно исчезнет.

В случае CREE XP-G, на который вы ссылались, я взял график Forward Voltage VS Forward current из таблицы данных и наложил его на график производного Forward Voltage VS Forward Resistance, как показано ниже. Скорее грубо, потому что я не делал никакой подгонки кривой, но легко увидеть огромное изменение прямого сопротивления для небольшого изменения прямого напряжения на 250 милливольт с 2,5 до 2,75 вольт.

Из-за этой чрезвычайной чувствительности к напряжению и из-за того, что местоположение колена диода нельзя предсказать с большой уверенностью, светодиоды обычно не приводятся в действие источниками необработанного напряжения, а являются источниками постоянного тока или источников напряжения с ограничением тока, разработанными так, чтобы никогда не допустить продукта тока через светодиод и падение напряжения на светодиоде, чтобы превысить номинальную мощность светодиода.

Для мощных недорогих светодиодов, таких как XP-G, источник постоянного тока может быть использован с хорошим преимуществом, поскольку он будет поддерживать постоянный ток через светодиод независимо от изменений в Vf светодиода или входного напряжения постоянного тока. поставка. Чаще всего, однако, резистор используется последовательно с источником напряжения, чтобы ограничить ток через светодиод.

Значение резистора определяется путем вычитания указанного минимального значения Vf светодиода из максимального выходного напряжения источника, а затем деления этой разности на требуемый ток светодиода. Это сопротивление гарантирует, что «максимальное напряжение» светодиода никогда не будет превышено, и вы можете видеть, что нет предела (хорошо …) разрешенному напряжению источника, так как резистор избавится от всего, в чем светодиод не нуждается ,

Максимальное напряжение — генератор — Большая Энциклопедия Нефти и Газа, статья, страница 1

Максимальное напряжение — генератор

Cтраница 1

Максимальное напряжение генератора составляет 150 кв; величина тока не превышает 400 ма.  [2]

Ограничение максимального напряжения генератора Итмакс производится путем настройки возбудителя, а ограничение по току — с помощью реле максимального тока. Недостаток рассматриваемой системы состоит в применении вращающегося коллекторного возбудителя специальной конструкции, имеющего значительные вес и габариты.  [3]

Скорость и реализуется IB этом случае, как правило, при максимальном напряжении генератора.  [4]

На современных тепловозах применяется также автоматическое ограничение напряжения тягового генератора при больших скоростях движения, что позволяет уменьшить габаритные размеры генератора и защитить элементы силовой цепи тепловоза ( линия вг) от высокого напряжения. Максимальное напряжение генератора ( обычно около 700 В) ограничивается допустимым значением среднего напряжения между коллекторными пластинами.  [6]

При появлении зарядов на кондукторе возникает электрическое поле, тангенциальная по отношению к ленте составляющая которого уменьшается по мере удаления от кондуктора. Поэтому максимальное напряжение генератора зависит от размеров кондуктора, формы электрического поля, образуемого кондуктором и сосудом ( котлом), в котором располагается ЭСГ, и от величины электрической прочности среды, окружающей генератор. Лучшей формой для электрода высокого напряжения является шаровая.  [7]

При большой частоте вращения напряжение возрастает настолько, что включенные потребители могут выйти из строя. Поэтому максимальное напряжение генератора ограничивается регулятором напряжения. По мере увеличения числа включенных потребителей при постоянном напряжении, которое поддерживает регулятор, увеличивается ток нагрузки генератора. Максимальный ток нагрузки лимитируется ограничителем тока.  [8]

Что является условием самовозбуждения генератора параллельного возбуждения. Чем обусловливается минимальное и максимальное напряжение генератора с параллельным возбуждением при номинальной скорости вращения.  [9]

Возбудитель должен обеспечивать длительную работу генератора в любой точке гиперболической части его характеристики. Наиболее тяжелым для возбудителя является режим максимального напряжения генератора, которому соответствует наибольший ток возбуждения. Поэтому номинальную ( расчетную) мощность возбудителя следует выбирать по режиму, соответствующему началу гиперболической части характеристики. Эта мощность составляет практически 1 — 2 % номинальной мощности генератора.  [11]

Действие импульсного генератора основано на параллельной зарядке через сопротивление 20 емкостных каскадов и на их последовательной разрядке на цепь. Двадцать каскадов, включающих в себя 100 конденсаторов, могут соединяться последовательно и параллельно в различных комбинациях, что позволяет получать широкий интервал напряжений и емкостей. Каждый каскад имеет емкость 0 1 мкф и может заряжаться до максимального напряжения 150000 в. Генератор позволяет, следовательно, получать 3 — Ю8 в при последовательном соединении 20 каскадов. Емкость в этом случае составляет 4500 эл. Последовательное соединение каскадов осуществляется через промежуточные шаровые разрядники. Расстояние между шарами является мерой максимального напряжения генератора в данном опыте. Катодный осциллограф, присоединенный к цепи трубки, позволяет измерять изменение приложенного напряжения во времени. Разрядка может производиться через каждые 2 сек. Обычно мы работаем при более низкой частоте импульсов.  [12]

Страницы:      1

Максимальное механическое напряжение — путь к росту. | by Elkin A.V.

Для достижения роста мышц нам предлагают кучи методик — статико-динамика, время под нагрузкой, ощущение мышцы, максимальный памп, максимальное разнообразие нагрузок… Что же выбрать?

Перво-наперво нужно понять, что является стимулом для гипертрофии. Наука достаточно однозначно выделяет механическое напряжение, которое должно испытать каждое мышечное волокно, как основной стимул для роста (4, 1, 2, 3, 5, 6, 7).

Почему каждое мышечное волокно, а не мышца целиком?

Каждая мышца состоит из множества клеток — мышечных волокон. Мышечные волокна вовлекаются в работу по определенному принципу: при небольшом сигнале из мозга идет активация самых выносливых, однако имеющих слабый потенциал для роста (8, 9, 10), мышечных волокон 1 типа. Мышечные волокна 2а и 2х типа вовлекаются в работу при суб- и максимальных усилиях и имеют совершенно иную регуляцию в ответ на различные стимулы, обладая значительным потенциалом для роста.

Таким образом, одно из основных условий для достижения максимальной гипертрофии — создание максимального усилия при работе данной группы мышц.

Что такое механическое напряжение, которое испытывает мышечное волокно?

Механическое напряжение —это сила растяжения, воздействующая на структурные компоненты мышечного волокна (экстраклеточный матрикс, костамеры, десмин, Z-диски). Именно данное напряжение “считывается” многочисленными сенсорами мышечной клетки, расположенными в разных областях цитоскелета. Степень полученного (созданного) механического напряжения коррелирует со степенью роста (11, 12, 13).

Как же создать заветное значительное механическое напряжение для инициации процессов роста?

Степень механического напряжения определяется следующими факторами:

1) Скоростью сокращения. Вкратце — чем выше скорость сокращения мышечного волокна, тем меньше усилия оно создает и испытывает. Мышечные волокна испытывают максимальное напряжение при минимальных скоростях, и при активном удлинении мышцы (так называемая негативная фаза). Следует заметить: для того, чтобы полный пул мышечных волокон 2 типа был активирован и сокращался медленно, веса должны быть либо суб-максимальными, либо малыми, но работа должна быть выполнена до отказа.

2) Положение (степень растяжения), в котором находится мышечное волокно в данный момент. Активированное мышечное волокно создает минимальное количество усилия, когда сокращено. По мере удлинения, количество создаваемого усилия увеличивается. Активированное мышечное волокно испытывает максимальное напряжение при удлиненном положении.

3) Утомление (!на уровне мышечного волокна!) негативно влияет на создание усилия (и, соответственно, степень механического напряжения).

Для максимального роста требуются тренировки обеспечивающие создание максимального напряжения на мышечные волокна 2 типа: в основном это работа с суб-максимальными весами, либо малыми весами, но до отказа, а так же работа в полную амплитуду или применение эксцентрического (негативный) метода. (При условии идеальной кондиции других переменных: питание, тренировочный объем, восстановление, уровень стресса и др).

Если ваша цель гипертрофия, то маловероятно ее вам обеспечат:
упражнения “на ощущения” (особенно для крупных мышечных групп, таких как ягодичные), либо “функциональный” тренинг или кроссфит, либо применение любых других методик, в которых не выполняются условия, описанные выше (либо включаются смешивающе факторы, такие как чрезмерный тренировочный объем или утомление).

Распределительная коробка Светозар для наружного монтажа максимальное напряжение 400 В IP 54 4 ввода 65x65x40 мм SV-54954 — цена, отзывы, характеристики, фото

• Количество вводов, шт 4
• Степень защиты, IP 54
• Материал пластик
• Конструкция квадратная
• Цвет белый
• Количество в упаковке, шт 1
• Тип проводки открытая
• Назначение для наружного монтажа
• Длина, мм 65
• Ширина, мм 65
• Глубина, мм 40
• Max температура эксплуатации, °С 300
• Min температура эксплуатации, °С -20
• Показать еще

Этот товар из подборок

Параметры упакованного товара

Единица товара: Штука
Вес, кг: 0,05

Длина, мм: 45
Ширина, мм: 80
Высота, мм: 80

Произведено

• Россия — родина бренда
• Россия — страна производства*
• Информация о производителе

* Производитель оставляет за собой право без уведомления дилера менять характеристики, внешний вид, комплектацию товара и место его производства.

Указанная информация не является публичной офертой

На данный момент для этого товара нет расходных материалов

Максимальное напряжение Ryzen | Te4h

Важным параметром функционирования современных процессоров есть напряжение питания. Данный параметр определяет множество различных характеристик, влияющих на производительность устройства. Это частота, температура под нагрузкой, потребление электроэнергии, максимальная частота памяти. Изменение этого параметра напрямую влияет на производительность. Однако, стоит отметить, что чрезмерное увеличение напряжения приводит к выходу процессора из строя.

Современные процессоры в процессе работы динамически регулируют напряжение питания. В зависимости от этой величины процессор настраивает частоту работы. Частоты чипа делятся на несколько категорий: базовая частота Base, частота пиковой производительности Boost, максимальная частота OС. В этой статье мы собрали информацию про безопасное напряжение для ryzen различных поколений.

Содержание статьи:

Напряжение процессоров Ryzen

Напряжение питания Ryzen зависит от частоты. Чем выше частота, тем выше напряжение необходимо процессору для стабильной работы. Рассмотрим три категории частот, о которых будем говорить далее:

• Базовая частота работы Ryzen (Base) — это значение частоты в МГц, заданное производителем при изготовлении процессора. Ей соответствует своё напряжение питания. Будем называть его Base.
• Частота Turbo Boost. Для повышения производительности процессоров в компании AMD разработали технологию PBO, которая автоматически повышает частоту процессора при увеличении нагрузки если это позволяет охлаждение и питание. Обычно, на максимальной частоте могут работать одновременно 1-2 ядра процессора. При этом оставшиеся ядра имеют более низкую частоту. Для повышения частоты до максимального предела Turbo Boost нужно повысить напряжения питания. Назовём его Boost.
• Частота OC. Пользователи могут вручную поднять частоту процессора ещё выше частоты Turbo Boost для получения максимальной производительности. При этом напряжение питания является очень высоким, что приводит к большому потреблению электроэнергии и сильному нагреву процессора. Нагрев, в свою очередь, требует качественных систем охлаждения, способных отвести выделяемое тепло. В случае, если кулер не соответствует нужным требованиям, происходит перегрев и выключение компьютера. В редких случаях возможен выход из стоя различных узлов компьютера. Данной частоте соответствуют значения напряжения, близкие к максимальным, — OC.

Рассмотрим таблицы частот и напряжений питания процессоров фирмы AMD семейств Ryzen и Ryzen Threadripper. Условные обозначения в таблицах:

• ? — точное значение не было найдено;
• ≈ — величина приблизительна указана на основе данных похожей модели.

Первая таблица напряжений Ryzen относится к линейке Summit Ridge, сюда входит процессор Ryzen 1600 и другие:

Процессор	Ядра/Потоки	Частота (Base, ГГц)	Напр. (Base, мВ)	Частота (Boost, ГГц)	Напр. (Boost, мВ)	Частота (OC, ГГц)	Напр. (OC, мВ)	TDP, Вт
Ryzen 3 1200	4/4	3.1	1175	3.4	≈1175	4.0	1400	65
Ryzen 3 1300X	4/4	3.5	1225	3.7	?	4.0	1400	65
Ryzen 5 1400	4/8	3.2	≈1225	3.4	1250	3.8	1350	65
Ryzen 5 1500X	4/8	3.5	≈1375	3.7	≈1300	3.9	≈1400	65
Ryzen 5 1600	6/12	3.2	≈1375	3.6	?	3.9	1425	65
Ryzen 5 1600X	6/12	3.6	≈1300	4.0	?	4.0	1400	95
Ryzen 7 1700	8/16	3.0	1250	3.7	1250	3.9	1400	65
Ryzen 7 1700X	8/16	3.4	1250	3.8	≈1275	4.0	1400	95
Ryzen 7 1800X	8/16	3.6	1275	4.0	1400	4.1	1400	95

Таблица напряжений процессоров Ryzen Threadripper поколения Whitehaven, 1000-ная серия:

Процессор	Ядра/Потоки	Частота (Base, ГГц)	Напр. (Base, мВ)	Частота (Boost, ГГц)	Напр. (Boost, мВ)	Частота (OC, ГГц)	Напр. (OC, мВ)	TDP, Вт
Ryzen Threadripper 1900X	8/16	3.8	1425	4.0	1425	≈4.2	?	180
Ryzen Threadripper 1920X	12/24	3.5	≈1225	4.05	1350	4.0	1350	180
Ryzen Threadripper 1950X	16/32	3.4	1150	4.0	?	3.9	1400	180

Как видите, максимальное напряжение Ryzen для этой серии составило 1,4 вольта. Больше не следует ставить даже при разгоне. Рассмотрим следующее поколение. Таблица напряжений линейки процессоров Pinnacle Ridge, 2000-ная серия:

Процессор	Ядра/Потоки	Частота (Base, ГГц)	Напр. (Base, мВ)	Частота (Boost, ГГц)	Напр. (Boost, мВ)	Частота (OC, ГГц)	Напр.(OC, мВ)	TDP, Вт
Ryzen 3 2300X	4/4	3.5	?	4.0	?	4.3	1400	65
Ryzen 5 2500X	4/8	3.6	?	4.0	?	4.3	?	65
Ryzen 5 1600 refresh	6/12	3.2	?	3.6	1250	?	?	65
Ryzen 5 2600	6/12	3.4	1225	3.9	≈1225	4.2	≈1475	65
Ryzen 5 2600X	6/12	3.6	1275	4.2	1475	4.2	1475	95
Ryzen 5 2600X MAX	6/12	3.6	≈1275	4.2	≈1475	≈4.2	≈1475	95
Ryzen 7 2700E	8/16	2.8	?	4.0	?	≈4.1	≈1475	45
Ryzen 7 2700	8/16	3.2	1175	4.1	≈1450	4.1	1450	65
Ryzen 7 2700 MAX	8/16	3.2	1175	4.1	≈1450	≈4.1	≈1450	65
Ryzen 7 PRO 2700X	8/16	3.6	≈1250	4.1	?	≈4.3	≈1475	105
Ryzen 7 2700X	8/16	3.7	1250	4.3	≈1475	4.3	1475	105

Таблица напряжений линейки Threadripper линейки Colfax, 2000-ная серия:

Наименование	Ядра/Потоки	Частота (Base, ГГц)	Напр. (Base, мВ)	Частота (Boost, ГГц)	Напр. (Boost, мВ)	Частота (OC, ГГц)	Напр.(OC, мВ)	TDP, Вт
Ryzen Threadripper 2920X	12/24	3.5	1100	4.3	≈1475	4.0	1275	180
Ryzen Threadripper 2950X	16/32	3.5	≈1300	4.4	≈1450	4.15	1475	180
Ryzen Threadripper 2970WX	24/48	3.0	?	4.2	≈1450	4.0	1375	250
Ryzen Threadripper 2990WX	32/64	3.0	?	4.2	≈1425	4.0	1425	250

Здесь максимальное напряжение вырастало до 1,475 вольт. Далее последнее, на момент написания статьи, поколение. Таблица напряжений линейки процессоров Ryzen 3000 Matisse:

Наименование	Ядра/Потоки	Частота (Base, ГГц)	Напр. (Base, мВ)	Частота (Boost, ГГц)	Напр. (Boost, мВ)	Частота (OC, ГГц)	Напр. (OC, мВ)	TDP, Вт
Ryzen 5 3500	6/6	3.6	≈0.925	4.1	≈1425	≈4.1	≈1425	65
Ryzen 5 3500X	6/6	3.6	≈0.925	4.1	1425	4.1	1425	65
Ryzen 5 3600	6/12	3.6	0.925	4.2	?	4.1	1400	65
Ryzen 5 Pro 3600	6/12	3.6	≈0.925	4.2	?	≈4.2	≈1350	65
Ryzen 5 3600X	6/12	3.8	≈1000	4.4	?	4.3	1350	95
Ryzen 7 Pro 3700	8/16	3.6	≈0.925	4.4	?	4.3	1450	65
Ryzen 7 3700X	8/16	3.6	≈0.925	4.4	?	4.3	1450	65
Ryzen 7 3800X	8/16	3.9	1000	4.5	1450	4.4	1475	105
Ryzen 9 3900	12/24	3.1	?	4.3	?	?	?	65
Ryzen 9 Pro 3900	12/24	3.1	?	4.3	?	?	?	65
Ryzen 9 3900X	12/24	3.8	1000	4.6	?	4.2	1400	105
Ryzen 9 3950X	16/32	3.5	1000	4.7	?	4.4	1450	105

Таблица вольтажа Ryzen Threadripper 3000 Castle Peak:

Наименование	Ядра/Потоки	Частота (Base, ГГц)	Напр. (Base, мВ)	Частота (Boost, ГГц)	Напр. (Boost, мВ)	Частота (OC, ГГц)	Напр. (OC, мВ)	TDP, Вт
Ryzen Threadripper 3960X	24/48	3.8	1100	4.5	?	≈4.1	≈1250	280
Ryzen Threadripper 3970X	32/64	3.7	1000	4.5	?	4.1	1250	280
Ryzen Threadripper 3990X	64/128	2.9	1050	4.3	?	3.7	1150	280

В последнем, на данный момент, поколении безопасное напряжение для ryzen снова намного ниже, но оно больше зависит от модели процессора.

Как посмотреть напряжение Ryzen

В BIOS название пункта напряжения питания процессора — CPU Vcore Voltage (CPU Core Voltage, CPU Vcore). Данную величину можно посмотреть на закладке H/W Monitor (Monitor, System Info).

Для того, чтобы посмотреть напряжение процессора в Windows, можно использовать утилиту CPU-Z. Значение называется Core Voltage и находится на закладке CPU.

Можно также использовать программу HWiNFO64. Параметр VID в таблице, строка CPU Status.

Выводы

Сегодня мы познакомились с напряжениями питания семейств процессоров Ryzen и Ryzen Threadripper. Благодаря этим данным вы сможете подобрать безопасное напряжение для ryzen при разгоне и не сжечь свой процессор. Также нами были рассмотрены способы узнать напряжения в BIOS и операционной системе Windows. Для Windows предложены две утилиты для данных целей — CPU-Z и HWiNFO64.

Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.

домашних заданий и упражнений — Рассчитайте максимальное напряжение, которое можно приложить к нескольким конденсаторам?

домашнее задание и упражнения — Рассчитать максимальное напряжение, которое можно приложить к нескольким конденсаторам? — Обмен физическими стеками

Сеть обмена стеков

Сеть Stack Exchange состоит из 176 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.

Посетить Stack Exchange

2. 0
3. +0
6. Авторизоваться Зарегистрироваться

Physics Stack Exchange — это сайт вопросов и ответов для активных исследователей, ученых и студентов-физиков.Регистрация займет всего минуту.

Зарегистрируйтесь, чтобы присоединиться к этому сообществу

Кто угодно может задать вопрос

Кто угодно может ответить

Лучшие ответы голосуются и поднимаются наверх

Спросил 4 года, 4 месяца назад

Просмотрено 2k раз

$ \ begingroup $ Закрыто. Это вопрос не по теме. В настоящее время он не принимает ответы.

---

Хотите улучшить этот вопрос? Обновите вопрос, чтобы он соответствовал теме Physics Stack Exchange.

Закрыт 4 года назад.

Как рассчитать максимальное напряжение, которое может быть приложено к этой цепи до того, как конденсаторы разорвутся.

Номинальное напряжение каждого конденсатора 60 В.

Мои решения:
Максимум правого провода составляет 60 + 60 + 60 = 180 В.
Максимум левого провода составляет (60) + 60 = 120 В.

Таким образом, максимальное напряжение составляет 120 В. Это правильно?

Создан 18 дек.

ThewThew

10333 бронзовых знака

$ \ endgroup $ 1 $ \ begingroup $

Боюсь, это так же просто, как и метод, который вы использовали, потому что если напряжение на двух параллельных конденсаторах составляет $ V $, то напряжение на конденсаторе, последовательно соединенном с ними, не равно $ V $.
Причина этого в том, что общий заряд параллельной комбинации конденсаторов должен быть таким же, как заряд конденсатора, соединенного последовательно с ними.
Итак, вам нужно решить, как напряжение, приложенное ко всему устройству, распределяется между двумя конденсаторами, включенными параллельно, и конденсатором, включенным последовательно с ними.

Создан 18 дек.

Фарчер

6,777 золотых знаков5454 серебряных знака148148 бронзовых знаков

$ \ endgroup $ 2 Physics Stack Exchange лучше всего работает с включенным JavaScript

Ваша конфиденциальность

Нажимая «Принять все файлы cookie», вы соглашаетесь с тем, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в ​​отношении файлов cookie.

Принимать все файлы cookie Настроить параметры

Предел максимального падения напряжения — Руководство по электрическому монтажу

Максимально допустимое падение напряжения варьируется от страны к стране.Типичные значения для низковольтных установок приведены ниже на Рис. G27.

Рис. G27 — Максимальное падение напряжения между исходной точкой установки и любой точкой нагрузки (IEC60364-5-52, таблица G.52.1)

Тип установки	Цепи освещения	Другое применение (обогрев и электроэнергия)
Низковольтные установки, питаемые напрямую от общественной низковольтной распределительной сети	3%	5%
Низковольтная установка с питанием от частной сети низкого напряжения	6%	8%

Эти пределы падения напряжения относятся к нормальным установившимся условиям работы и не применяются во время пуска двигателя, одновременного (случайного) переключения нескольких нагрузок и т. Д.как указано в разделе «Оценка фактического максимального потребления кВА (коэффициенты разнообразия и использования и т. д.)». Когда падение напряжения превышает значения, указанные на Рис. G27, для исправления ситуации необходимо использовать кабели (провода) большего размера.

Значение 8%, хотя и разрешено, может привести к проблемам с нагрузкой двигателя; Например:

• Обычно для удовлетворительной работы двигателя требуется напряжение в пределах ± 5% от его номинального номинального значения в установившемся режиме,
• Пусковой ток двигателя может в 5-7 раз превышать значение полной нагрузки (или даже больше).Если при токе полной нагрузки происходит падение напряжения на 8%, то во время запуска произойдет падение на 40% или более. В таких условиях двигатель либо:
  • Опрокидывание (то есть оставаться в неподвижном состоянии из-за недостаточного крутящего момента для преодоления момента нагрузки) с последующим перегревом и возможным отключением
  • Или ускоряться очень медленно, так что сильноточная нагрузка (с возможным нежелательным воздействием низкого напряжения на другое оборудование) продолжится после нормального периода запуска

• Наконец, падение напряжения на 8% представляет собой постоянную потерю мощности , что при длительных нагрузках будет значительным тратой (измеренной) энергии.По этим причинам не рекомендуется достигать максимального значения 8% в устойчивых рабочих условиях в цепях, которые чувствительны к проблемам пониженного напряжения (см. Рис. G28).

Рис. G28 — Максимальное падение напряжения (значения, указанные здесь, относятся к цепям, отличным от цепей освещения)

Напряжение в точке максимальной мощности — Vmp

Чтобы получить максимальное количество энергии от солнечного элемента, он должен работать при максимальном напряжении питания.Максимальное напряжение мощности дополнительно описывается V _MP , максимальным напряжением мощности и I _MP , током в точке максимальной мощности.

Максимальное напряжение питания возникает, когда дифференциал мощности, производимой элементом, равен нулю.

Исходя из уравнения IV для солнечного элемента:

I = IL-I0eVVt

Vt = nkTq для упрощения записи при выводе, где kT / q ~ 0,026 вольт, а n — коэффициент идеальности.Фактор идеальности зависит от рабочей точки. Для этих уравнений правильным значением является среднее значение от V _MP до V _OC .

Мощность, производимая элементом, является произведением напряжения и тока, т. Е. P = IV.

P = VIL-VI0eVVt

Использование дифференцирования по частям для второго члена: u = VI0, u ‘= I0, v = eVVt, v’ = 1VteVVt

Разница мощности по напряжению:

дПдВ = IL-VI01VteVVt + I0eVVt

Vmp возникает, когда dPdV = 0

VmpI01VteVmpVt-I0eVmpVt = IL

Подробные инструкции по преобразованию и упрощению:

VmpVteVmpVt-eVmpVt = ILI0

эВmpVtVmpVt-1 = ILI0

VmpVt + ln⁡VmpVt-1 = lnILI0

Vmp = VtlnILI0-ln⁡VmpVt-1

Использование Voc = VtlnILI0

Vmp = Voc-ln⁡VmpVt-1 Неявное уравнение, приведенное выше, не имеет простого решения, но быстро сходится с итерацией.Первоначальная оценка VMP = 0,9 VOC дает точное решение за две итерации.

Использование функций Ламберта

Точное решение для определения максимального напряжения мощности — с помощью функций Ламберта. Это трансцендентные функции, похожие на и или тригонометрические функции. Lambert доступен в самых продвинутых математических пакетах, таких как Maple, Mathematica и Python с SciPy, но их нет на большинстве портативных калькуляторов.

Как и выше, нам нужно найти напряжение, когда производная мощности равна нулю

P = VIL-VI0eVVt

0 = IL-I0exp⁡VVt1 + VVt

Поскольку V / Vt намного больше 1, мы можем удалить член +1: ILI0 = exp⁡VVt × VVt

Ламберт дает решение в форме: Y = XeX⇔X = W (Y).Используя это соотношение, предыдущий эквивалент становится:

VVt = W⁡JLJ0

, чтобы мы получили простое выражение для Vmp.

Vmp = VtW⁡JLJ0

В качестве альтернативы, используя полное уравнение выше для dP / dV = 0 и не отбрасывая член +1, решение становится:

Vmp = VtW⁡eJLJ0-1

Математика частично подтверждена с использованием Wolfram Alpha

J = JL − J0 [exp (VVt) −1] J = J_ {L} — J_ {0} \ left \ lbrack \ exp \ left (\ frac {V} {V_ {t}} \ right) — 1 \ вправо \ rbrack

Мощность = В x Дж

P = VJL-VJ0 [exp (VVt) -1]

Потеряйте -1, так как мы выше 100 мВ

Свод правил штата Калифорния, раздел 8, раздел 2510.1. Максимальное напряжение.

Эта информация предоставляется бесплатно Департаментом производственных отношений. со своего веб-сайта www.dir.ca.gov. Эти правила предназначены для удобство пользователя, и не дается никаких заверений или гарантий, что информация актуален или точен. См. Полный отказ от ответственности на странице https://www.dir.ca.gov/od_pub/disclaimer.html.

Подраздел 5. Приказы по электробезопасности
Группа 1.Приказы по электробезопасности при низком напряжении
Статья 51. Светильники, патроны, лампы и розетки.

---

---

Напряжение на землю. Патроны, светильники или стандартные розетки на 15 ампер или менее не должны питаться напряжением, превышающим 150 вольт на землю.

ИСКЛЮЧЕНИЕ: № 1: Допускается напряжение питания от 150 до 300 вольт относительно земли при соблюдении всех следующих условий: a. Осветительные приборы будут обслуживать только квалифицированные специалисты;

г.Светильники одобрены для напряжения питания;

г. Светильники, кроме стационарных электроразрядных, устанавливаются на высоте не менее 8 футов над полом. Если условия не позволяют 8 футов, светильник должен быть установлен на доступной высоте при условии, что светильники должным образом защищены; а также

г. Встроенные выключатели освещения, если они используются, не должны быть легко доступны.

ИСКЛЮЧЕНИЕ: № 2: Напряжение питания может превышать 300 вольт для стационарных светильников на высоте 18 футов или более.

ПРИМЕЧАНИЕ: Уполномоченный орган: Раздел 142.3 Трудового кодекса. Ссылка: раздел 142.3 Трудового кодекса.

ИСТОРИЯ

1. Отмена статьи 51 (разделы 2510.3-2510.81, не последовательно) и новой статьи 51 (разделы 2510.1-2510.58, не последовательно), поданных 8-9-79; начиная с тридцатого дня после этого (Регистр 79, № 32). Предыдущую историю см. Регистр 78, № 5.

2. Изменение исключения №1 поданная 9-7-79; начиная с тридцатого дня после этого (Регистр 79, № 36).

3. Поправка, исключающая подпункт (а) только обозначение, подана 8-27-86; начиная с тридцатого дня после этого (Регистр 86, № 37).

Вернуться к статье 51 Содержание

Как мне прочитать спецификации солнечных батарей?

Эми Боде 13 апреля 2016

Панели солнечных батарей

Impp, isc, максимальная номинальная мощность, noct, номинальное напряжение, Pmax, солнечные панели, спецификации, стандартные условия испытаний, stc, Vmpp, вок

Существует несколько терминов и рейтингов, связанных с техническими данными солнечной панели.Выяснение того, что означает, что для спецификаций, может быть довольно запутанным. Мы собираемся объяснить каждый из них, чтобы прояснить это.

Условия испытаний и солнечные панели

Стандартные условия испытаний (STC)

STC — это набор критериев, по которым тестируется солнечная панель. Поскольку напряжение и ток изменяются в зависимости от температуры и интенсивности света, среди других критериев, все солнечные панели испытываются в одних и тех же стандартных условиях испытаний. Это включает температуру ячеек 25 ℃ (77 ℉), интенсивность света 1000 ватт на квадратный метр, что в основном соответствует солнцу в полдень, и плотность атмосферы, равную 1.5, или угол, под которым солнце перпендикулярно солнечной панели на высоте 500 футов над уровнем моря.

Нормальная рабочая температура ячейки (NOCT)

Не знаю, как вы, но летом был на крыше, и могу вас заверить, солнечные батареи не стоят 77 ℉. Они нагреваются намного сильнее, чем на солнце, более 100.

NOCT дает более реалистичный взгляд на реальные условия в мире и дает вам рейтинги мощности, которые вы, вероятно, действительно увидите в своей солнечной системе.Вместо 1000 ватт на квадратный метр он использует 800 ватт на квадратный метр, что ближе к преимущественно солнечному дню с рассеянными облаками. Он использует температуру воздуха 20 ℃ (68 ℉), а не температуру солнечного элемента, и включает в себя ветер со скоростью 2,24 миль в час, охлаждающий заднюю часть установленной на земле солнечной панели (более распространенной в больших солнечных полях, чем в жилых массивах, установленных на крыше). Эти рейтинги будут ниже STC, но более реалистичны.

Характеристики номинальной мощности и солнечные панели

Номинальная мощность для солнечных панелей при различной интенсивности света (Вт / м2).«Изгиб» кривых — это место, где вырабатывается наибольшая мощность, а напряжение и ток оптимизируются.

Напряжение холостого хода (Voc)

Напряжение холостого хода — это сколько вольт выводит солнечная панель без нагрузки. Если вы просто измеряете с помощью вольтметра положительный и отрицательный выводы, вы увидите Voc. Поскольку солнечная панель ни к чему не подключена, на нее нет нагрузки и она не производит тока.

Это очень важное число, так как это максимальное напряжение, которое солнечная панель может выдавать в стандартных условиях тестирования, поэтому это число, которое следует использовать при определении, сколько солнечных панелей вы можете последовательно подключить к инвертору или контроллеру заряда. .

Voc потенциально будет кратковременно воспроизводиться утром, когда впервые встанет солнце и панели будут максимально холодными, но подключенная электроника еще не вышла из спящего режима.

Помните, предохранители и прерыватели защищают провода от перегрузки по току, а не от перенапряжения. Итак, если вы подадите слишком большое напряжение на большую часть электроники, вы повредите их.

Ток короткого замыкания (Isc)

Ток короткого замыкания — это количество ампер (т. Е. Тока), которое вырабатывают солнечные панели, когда они не подключены к нагрузке, но когда плюс и минус проводов панелей напрямую соединены друг с другом.Если вы просто измерите амперметром положительный и отрицательный провода, вы увидите Isc. Это самый высокий ток, который солнечные панели будут производить в стандартных условиях испытаний.

При определении того, сколько ампер может выдержать подключенное устройство, например, контроллер заряда солнечной батареи или инвертор, используется Isc, обычно умноженный на 1,25 для 80% требований Национального электрического кодекса (NEC).

Максимальная точка мощности (Pmax)

Pmax — это лучшая точка выходной мощности солнечной панели, расположенная в «изгибе» кривых на графике выше.Именно здесь комбинация вольт и ампер приводит к максимальной мощности (вольт x ампер = ватт).

Когда вы используете контроллер заряда или инвертор с отслеживанием точки максимальной мощности (MPPT), это точка, в которой электроника MPPT пытается поддерживать напряжение и ток на уровне, чтобы максимизировать выходную мощность. Мощность солнечной панели указана как Pmax, где Pmax = Vmpp x Impp (см. Ниже).

Максимальное напряжение точки питания (Vmpp)

Vmpp — это напряжение при максимальной выходной мощности.Это фактическое напряжение, которое вы хотите видеть, когда оно подключено к солнечному оборудованию MPPT (например, контроллеру заряда солнечной батареи MPPT или сетевому инвертору) в стандартных условиях тестирования.

Максимальный ток точки питания (Impp)

Impp — это ток (в амперах) при максимальной выходной мощности. Это фактическая сила тока, которую вы хотите видеть при подключении к солнечному оборудованию MPPT в стандартных условиях испытаний.

Пример стандартных условий испытаний (STC) и нормальной рабочей температуры элемента (NOCT) для солнечных панелей SolarWorld SunModule.

Номинальное напряжение

Номинальное напряжение — это то, что смущает многих. Это не настоящее напряжение, которое вы будете измерять. Номинальное напряжение — это категория.

Например, солнечная панель с номинальным напряжением 12 В имеет напряжение Voc около 22 В и напряжение Vmp около 17 В. Он используется для зарядки аккумулятора на 12 В (что на самом деле составляет около 14 В).

Номинальное напряжение позволяет людям узнать, какое оборудование используется вместе. Они похожи на Geranimals®, где вы сопоставляете животных на этикетках одежды, чтобы они соответствовали одежде (примечание редактора : большинство из нас здесь, в altE, понятия не имеют, что такое Geranimals®, о которых говорит Эми, но мы надеемся, что вы, ребята, сможете собрать воедино то, что она записывает ).

Солнечная панель на 12 В используется с контроллером заряда на 12 В, аккумуляторной батареей на 12 В и инвертором на 12 В. Вы можете создать солнечную батарею на 24 В, последовательно соединив две солнечные панели на 12 В. Панели на 12 В являются обычным явлением, например, Kyocera 145W, и некоторые производители, такие как Canadian Solar и SolarWorld, производят панели на 24 В.

Солнечные панели 12 В заряжают аккумулятор 12 В с помощью традиционного контроллера заряда 12 В с ШИМ.

Это начинает усложняться, когда вы уходите от солнечных систем, основанных на батареях, и 12-вольтные приращения больше не нужны.Сетевые солнечные панели с 60 элементами часто называют панелями с номинальным напряжением 20 В, как солнечная панель SolarWorld SunModule 290W.

У них слишком высокое напряжение для зарядки аккумуляторной батареи на 12 В с помощью традиционного контроллера заряда, но слишком низкое напряжение для зарядки аккумуляторной батареи на 24 В. Контроллеры заряда MPPT могут изменять выходное напряжение, чтобы их можно было использовать в системе батарей, см. Наш блог, в котором обсуждаются преимущества контроллера заряда MPPT по сравнению с контроллером заряда PWM.

Солнечная панель с номинальным напряжением 20 В проходит через контроллер заряда солнечной батареи MPPT, поэтому она может эффективно заряжать аккумулятор на 12 В.

Номинал	12 В	20 В	24 В
Кол-во ячеек	36	60	72
Напряжение холостого хода (Voc)	22V	38V	46V
Макс.мощность вольт (Вмп)	18V	31В	36V

Вверху: приблизительные значения напряжения для определения номинального напряжения солнечных панелей.

Следите за новостями

Теперь вы можете прочитать этикетку солнечной панели и выяснить, каковы ее характеристики. Следите за обновлениями, и в ближайшее время мы напишем в блоге, как все эти характеристики объединяются. Мы рассмотрим пример того, как определить размер системы с учетом деталей.

Следующие две вкладки изменяют содержимое ниже.

Эми Боде работает в сфере солнечной энергетики в магазине altE с 2007 года. Она была торговым представителем, инструктором и всесторонним евангелистом в области солнечной энергии, разделяя свою страсть к солнечной энергии по всему миру.В свободное от работы время она занимается парусным спортом или катается на лыжах, в зависимости от сезона, но, скорее всего, она все еще говорит о солнечных батареях на лодке или на склонах.

Почему минимальные и максимальные значения напряжения питания устройства в инструменте Power Delivery Network (PDN) отличаются от рекомендуемых условий эксплуатации в техническом паспорте устройства Altera?

Минимальные и максимальные значения напряжения питания в инструменте PDN, указанные в процентах пульсаций, отличаются по сравнению с минимальным и максимальным напряжением, указанным в технических характеристиках устройства Altera®, рекомендуемых для рабочих условий.Пульсации напряжения питания и напряжения, указанные в паспорте, для рекомендуемых условий эксплуатации отражаются в различных формах в системе подачи энергии.

Напряжение, указанное в техническом описании устройства, относится к постоянному току. Пульсация модуля регулятора напряжения (VRM) отображается как изменение уровня напряжения источника питания. Устройства Altera® предназначены для работы в определенном диапазоне напряжений, который считается спецификацией постоянного тока, которая, в свою очередь, преобразуется в требования к спецификации пульсаций модуля регулятора напряжения (VRM).

Значения пульсации в инструменте PDN приведены для условий переменного тока. Пульсации, вызванные активностью переключения устройства, отображаются как шум, добавленный к напряжению от источника питания. Altera предоставляет рекомендации по допустимому уровню шума шины питания, который отображается как максимальная пульсация шины питания в инструменте PDN.

Два типа спецификаций напряжения имеют разные соображения и требуют разных методологий проектирования (модель VRM или развязка). Обычно при проектировании систем подачи энергии рассматривают две спецификации напряжения отдельно и обеспечивают соответствие этим двум спецификациям.

Например, если типичная спецификация VCCIO составляет 3,0 В в техническом описании, VRM должен быть настроен на отправку 3,0 В, а не 3,15 В (где 3,15 В — максимальное рекомендуемое напряжение). VRM не идеален, и выходное напряжение будет медленно колебаться. Это колебание необходимо контролировать в определенном диапазоне, чтобы колебания не влияли на нормальную работу устройства. Этот диапазон указан в спецификации постоянного тока из технического описания устройства.

Коммутационная активность устройства приводит к возникновению переходных шумов (высокочастотных всплесков) на шинах источника питания.Этот шум может вызвать проблемы с функциональностью, если он слишком высокий. Шум необходимо ослаблять в пределах диапазона, который определяется как% от напряжения источника питания. Этот диапазон указан в инструменте PDN в качестве ориентира. Различные шины имеют разные спецификации из-за их чувствительности к шуму переходного напряжения, а также из-за того, какой ток потребляет шина питания. Эти факторы влияют на способ разъединения шин питания.

Таким образом, минимальное и максимальное значения напряжения постоянного тока, указанные в паспорте, должны соответствовать конструкции источника питания.Рекомендации PDN по пульсации должны соответствовать конструкции сети подачи питания, которая включает в себя разделительные конденсаторы, плоскую емкость, а также корпус и емкость кристалла, если она доступна для устройства.

TENS под капотом: максимальное напряжение

Этот пост является первым в серии, посвященной работе устройств TENS (чрескожная электрическая стимуляция нервов). Мы намерены проникнуть «под капот» этих ценных обезболивающих, чтобы помочь вам понять их работу, и мы изучим ключевые технические характеристики и принципы работы.Мы надеемся, что эта информация будет полезна при выборе устройства TENS для ваших конкретных нужд.

В этом посте мы обращаемся к одному из наиболее важных технических атрибутов устройства TENS — , максимальное напряжение . Прочтите, чтобы узнать, что это такое и почему это важно для эффективного обезболивания.

Стимуляция нервов

TENS обеспечивает облегчение боли, пропуская электрический ток между электродами, расположенными на коже. Ток проходит через кожу под электродами и через тело, стимулируя близлежащие нервы.Этот ток инициирует нервные импульсы, называемые потенциалами действия , которые проходят в спинной и головной мозг, чтобы активировать сложную неврологическую цепь, обеспечивающую облегчение боли.

Почему важно максимальное напряжение?

Как устройство TENS вырабатывает ток стимуляции? Хотя протекание тока через электрод и кожу сложно, основную концепцию можно понять с помощью закона Ома, который вы, возможно, помните из школьной физики:

Напряжение = Ток x Сопротивление

Сопротивление — это тенденция вашей кожи препятствовать электрическому току. Текущий.Сухая кожа имеет более высокое сопротивление, чем гидратированная кожа, потому что сухая кожа действует как барьер для электрического тока. Закон Ома гласит, что по мере увеличения сопротивления требуется большее напряжение для генерации того же тока.

Большинству людей требуется от 15 до 50 миллиампер (миллиампер — это 1000 ^или ампер) для сильной, но комфортной стимуляции для облегчения боли. Предположим, вам нужно 25 миллиампер, у вас здоровая и хорошо увлажненная кожа, а значит, сопротивление составляет 1000 Ом.Тогда вам нужно (25/1000 x 1000) = 25 вольт, которое может обеспечить большинство внебиржевых устройств TENS.

А что, если для снятия боли вам нужно 50 миллиампер и у вас сухая кожа с сопротивлением 2000 Ом? Теперь вам нужно (50/1000 * 2000) = 100 вольт. Немногие внебиржевые устройства могут генерировать такое высокое напряжение. Более высокое максимальное напряжение может иметь решающее значение, обеспечивая гибкость в случаях, когда требуется более высокий ток стимуляции и имеет большее сопротивление кожи.