Нечетные гармоники: Нечетные гармоники и четные гармоники

Нечетные гармоники и четные гармоники

1. Определение:
 Нечетная гармоника: сдвиг нечетной гармоники на половину периода, и он точно инвертируется по сравнению с исходной формой волны.
 Четная гармоника: сдвиньте сигнал четной гармоники на половину периода, чтобы он совпадал с исходной формой волны.

 например:
 Основная частота - 50 Гц, вторая гармоника - 100 Гц, третья гармоника - 150 Гц, четвертая гармоника - 200 Гц и так далее.
 Искаженные формы волны тока могут включать в себя вторую гармонику, третью гармонику, четвертую гармонику и т. Д.

 2. Гармонические искажения относятся к воспроизведению динамика из-за явления резонанса во время рабочего процесса динамика.
   Хотя исходным звуковым сигналом является только сигнал основной частоты в динамике, неизбежно возникнет резонанс (на основе исходной звуковой волны).
 Вторая, третья и даже кратные гармоники генерируются в верхней части), так что в звуковом сигнале больше нет только сигнала основной частоты, но также включаются гармоники и их кратные.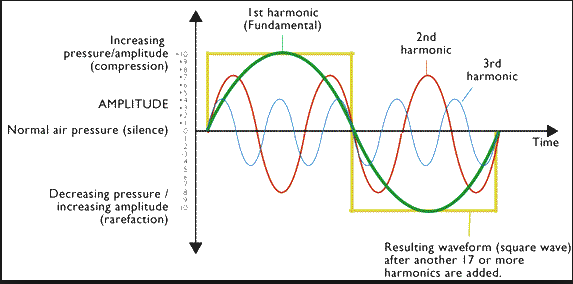  
 Эти сигналы умножителя вызовут искажения при воспроизведении динамика.

   В некоторых руководствах по продукту полное гармоническое искажение усилителя мощности выражается как THD <0,5%, 1 Вт, поэтому кажется, что общее гармоническое искажение невелико, но оно связано только с выходной мощностью.
 Общее гармоническое искажение составляет 1 Вт, что отличается от полного гармонического искажения, полученного в условиях измерения, требуемых стандартом.

 3. Примеры гармонических искажений
 <1>. Чаще всего прерывание звука вызвано высокочастотным искажением (срезание синусоидальной волны).
 <2>. Когда громкость максимальна, звук прерывается очень серьезно, что связано с коэффициентом усиления усилителя мощности. Коэффициент усиления не должен быть слишком большим, что приведет к общему гармоническому искажению.
 <3>. GAIN увеличивается, амплитуда сигнала увеличивается, а когда форма волны становится прямоугольной, возникает искажение. Если оно длится долгое время, динамик перегорит.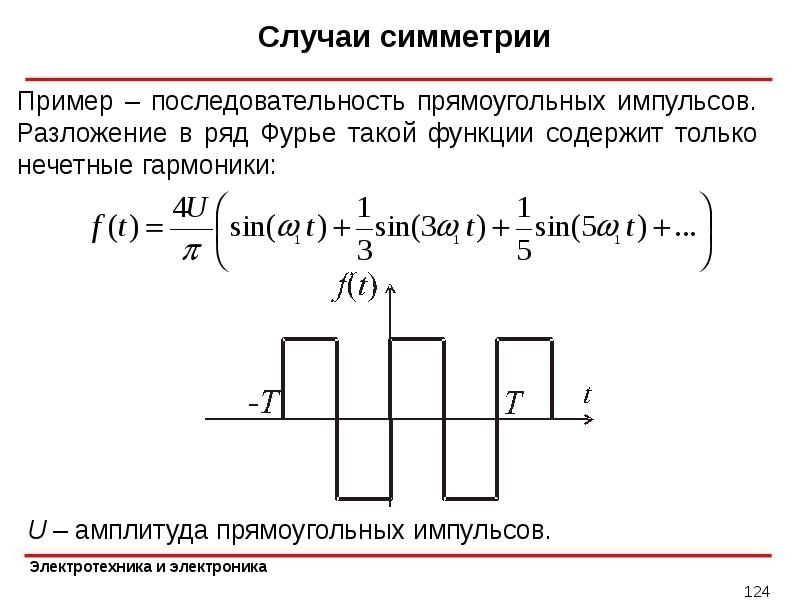
  <4>. Если низкочастотный сигнал приходит с большой амплитудой, звук прерывается. Рекомендуется установить частоту среза входного фильтра на 500 Гц.
 <5>. Максимальное искажение обусловлено главным образом тем, что оно превышает динамический диапазон усилителя мощности. Например, динамический диапазон усилителя мощности класса AB мощностью 0,5 Вт составляет всего около 5,5 В, в то время как динамический диапазон усилителя мощности класса D может достигать 2 В постоянного тока, что составляет 3,8 В постоянного тока. Динамический диапазон может достигать около 7 В, конечно, он будет урезан, если динамический диапазон будет превышен.

4. Подробнее о спектральном анализе сигналов | 7. Смешивание частот | Часть2

4. Подробнее о спектральном анализе сигналов

Подробнее о спектральном анализе сигналов

Компьютерный анализ Фурье (в частности алгоритм БПФ) является мощным инструментом, позволяющим лучше понять сигналы и связанные с ними спектральные компоненты. Математический алгоритм этого анализа запрограммирован в программе SPICE (в качестве параметра .fourier), а так же в различных измерительных приборах, которые выполняют анализ Фурье измеренных сигналов в режиме реального времени. Данная статья посвящена использованию таких инструментов и анализу различных сигналов.

Давайте начнем с простого синусоидального сигнала, частота которого составляет 523,25 Гц. В качестве примера мы взяли ноту «До» пианино, которая на одну октаву выше «middle C». На самом деле сигнал, измеренный для этой демонстрации, был создан клавишным электронным музыкальным инструментом, позволившим получить наиболее идеальную синусоиду. Нижеприведенный рисунок представляет собой экран осциллографа, показывающий амплитуду (напряжение) данного сигнала в течении длительного времени:

 

На экране осциллографа синусоида выглядит как волнистая кривая. Горизонтальная ось экрана обозначена словом «Время» и стрелкой в направлении увеличения времени. Сама кривая, конечно же, представляет собой циклическое увеличение и уменьшение напряжения с течением времени.

Приглядевшись внимательно к рисунку можно заметить неидеальность синусоидальной волны. Это обусловлено особенностями конкретного измерительного оборудования, используемого для анализа сигнала.

Если мы посмотрим на этот же сигнал в анализаторе спектра, то увидим совершенно другой результат:

 

Как видите, горизонтальная ось данного экрана обозначена словом «Частота», показывающим какой параметр мы анализируем. Единственный пик на кривой говорит нам о том, что в анализируемом сигнале преобладает только одна частота (фундаментальная). Если бы сетка экрана была помечена цифрами, то мы бы увидели, что этот пик приходится на частоту 523.25 Гц. Высота пика представляет собой амплитуду сигнала (напряжение).

Если мы смешаем три разных синусоидальных тона электронного клавишного инструмента (ноты До-Ми-Соль или До-мажорный аккорд) и измерим результат, то экраны осциллографа и анализатора спектра отобразят этот сложный сигнал следующим образом:

 

Экран осциллографа показывает волну с большим количеством пиков, чем в предыдущем примере, что является прямым результатом смешивания трех частот.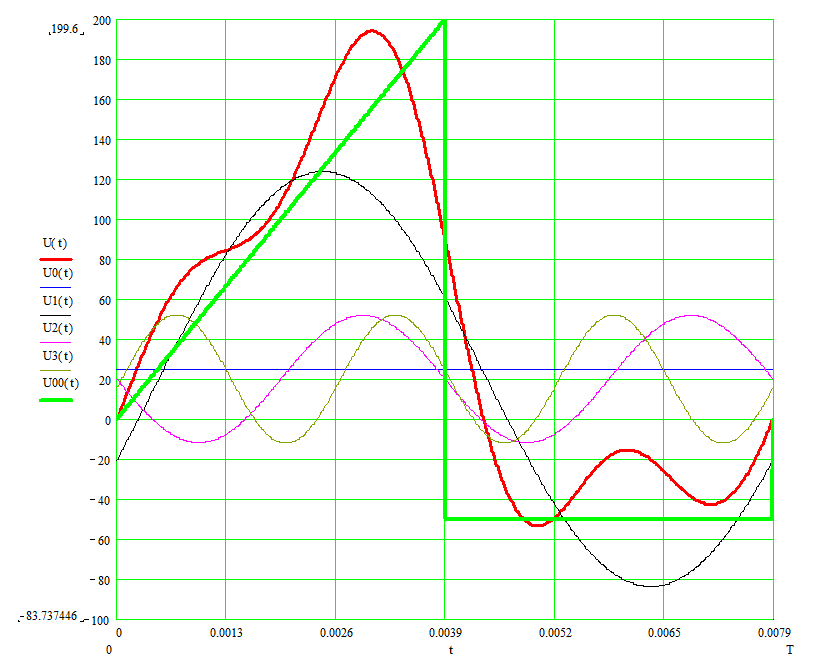 Как вы наверное заметили, некоторые из этих пиков превышают пиковые значения однотонового сигнала, а некоторые наоборот, имеют меньшие значения. Все это происходит потому, что три различных сигнала поочередно усиливают и ослабляют друг друга в соответствии с изменениями их фазовых сдвигов во времени.

 

Показания анализатора спектра интерпретировать гораздо легче: каждый «тон» здесь представлен собственным пиком на кривой. Различие в высотах этих пиков объясняется «особенностями» испытательного оборудования, а не характеристиками самого музыкального аккорда.

Как уже было сказано ранее, устройство, используемое для создания этих сигналов, представляет собой клавишный электронный музыкальный инструмент. Для первых экспериментов данный инструмент был выбран в связи с тем, что производимые им сигналы наиболее близко напоминают синусоиду. Сигнал, производимый другим музыкальным инструментом — трубой — не так прост, как рассмотренные выше:

 

Фундаментальная (основная) частота этого сигнала такая же, как и в первом примере — 523,25 Гц, но его форма далека от чистой синусоиды.

Зная, что любой повторяющийся несинусоидальный сигнал эквивалентен последовательности синусоидальных сигналов с различными амплитудами и частотами, мы ожидали, что увидим несколько пиков на экране анализатора спектра:

 

Наши ожидания оправдались! Фундаментальная частота 523,25 Гц представлена крайним левым пиком, а каждая последующая гармоника представлена собственным пиком на экране анализатора спектра. Вторя гармоника двукратна фундаментальной частоте (1046,5 Гц), третья гармоника трехкратна фундаментальной частоте (1569,75 Гц), и так далее. Этот рисунок показывает только первые шесть гармоник сложного сигнала, но на самом деле их гораздо больше.

Давайте проанализируем другой сложный сигнал, произведенный таким музыкальным инструментом, как аккордеон. Показания осциллографа и анализатора спектра в этом случае будут следующими:

 

 

Обратите внимание на различия в величинах амплитуд гармоник (высот пиков) трубы и аккордеона, отображенные на соответствующих экранах анализаторов спектров.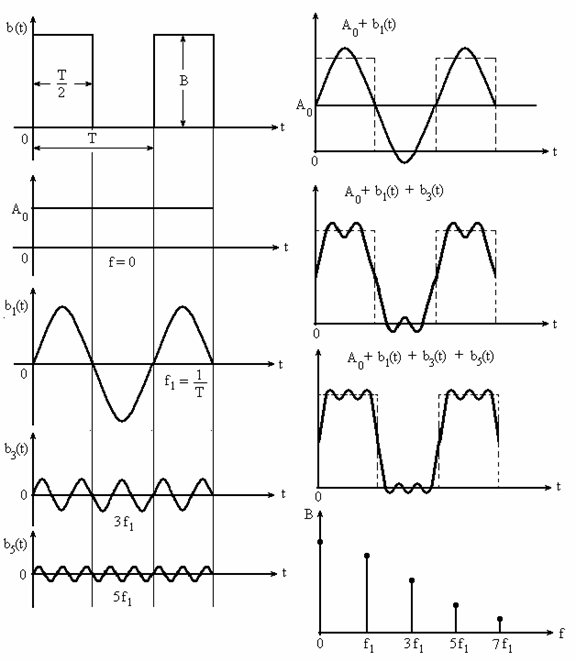

Оба прибора отображают с первой (фундаментальной) по шестую гармоники, но их пропорции не совпадают. Это говорит о том, что каждый инструмент имеет уникальную гармоническую сигнатуру в своем тоне. Примите во внимание, что эти сложные сигналы представляют собой одну ноту, проигранную двумя разными инструментами. Несколько нот, сыгранных, например, на аккордеоне, создадут гораздо более сложную смесь частот, чем представлено здесь.

Аналитические возможности осциллографа и анализатора спектра позволяют нам сформировать общие представления о сигналах и их гармонических спектрах на примерах реальных осциллограмм. Мы уже знаем, что любое отклонение сигнала от синусоидальной формы приводит к эквивалентной смеси нескольких синусоидальных сигналов различных амплитуд и частот. Однако, анализ большего количества сигналов, имеющих разные формы, позволяет получить нам больше конкретики. Обратите внимание на временной и частотный анализ сигнала, форма которого близка к прямоугольной:

 

 

Согласно показаниям анализатора спектра, этот сигнал не содержит четных гармоник, в его составе есть только нечетные гармоники. Несмотря на то, что экран прибора не показывает частоты дальше шестой гармоники, последовательность нечетных гармоник в порядке убывания амплитуды будет продолжаться бесконечно. Это не должно вас удивлять, так как ранее при помощи SPICE анализа мы с вами убедились, что прямоугольный сигнал состоит из бесконечности нечетных гармоник. Однако, тоны трубы и аккордеона содержат как четные, так и нечетные гармоники. Эта разница в содержании гармоник заслуживает внимания. Давайте продолжим наше исследование и проанализируем треугольный сигнал:

 

 

В этом сигнале практически отсутствуют четные гармоники, все значимые пики частот на экране анализатора спектра принадлежат нечетным гармоникам. Крошечные пики можно увидеть на второй, четвертой и шестой гармониках, но они обусловлены неидеальностью конкретного треугольного сигнала. Идеальный треугольный сигнал не производит четных гармоник, точно так же, как их не производит идеальный прямоугольный сигнал. Из проведенных исследований очевидно, что гармонический спектр треугольного сигнала не идентичен спектру прямоугольного сигнала: соответствующие гармонические пики имеют разную высоту.

Тем не менее, два этих сигнала идентичны в том, что у них отсутствуют четные гармоники.

Давайте исследуем еще один сигнал, очень похожий на треугольный. Называется этот сигнал пилообразным, и отличается от треугольного тем, что время его нарастания превышает время падения. На экране осциллографа данный сигнал будет выглядеть подстать своему названию:

 

Когда мы проведем спектральный анализ этого сигнала, то увидим результат, довольно сильно отличающийся от спектрального анализа треугольного сигнала. Здесь мы увидим довольно сильное присутствие четных гармоник (второй и четвертой):

 

Отличие сигналов имеющих четные гармоники от сигналов не имеющих четных гармоник заключается в различии форм этих сигналов. Данное различие определяется симметрией выше и ниже горизонтальной центральной (осевой) линии. Сигнал, который симметричен выше и ниже центральной линии не будет содержать четных гармоник:

 

Все вышепоказанные сигналы (прямоугольный, треугольный, синусоидальный) обладают такой симметрией, а следовательно, не содержат четных гармоник.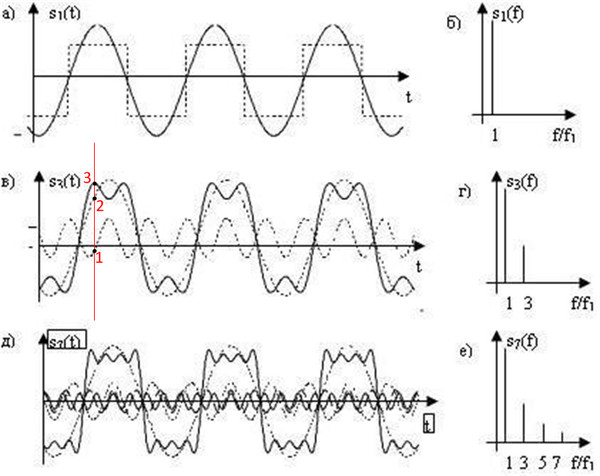 Сигналы, производимые трубой и аккордеоном, а также пилообразные сигналы не симметричны относительно центральной линии, а значит, они содержат четные гармоники.

 

Не стоит путать принцип симметрии центральной линии с симметрией вокруг нулевой линии. Во всех рассмотренных примерах центральная линия на экране осциллографа совпадает с нулевой (0 вольт). Если нулевая линия будет смещена вверх или вниз, то это никак не отразится на гармоническом содержании сигнала. Для примера мы покажем те же самые сигналы, нулевая линия в которых смещена относительно осевой:

 

 

Почему это эмпирическое правило гармоник так важно знать? Оно может помочь вам понять взаимоотношения между гармониками в цепях переменного тока и конкретными компонентами схемы. Поскольку большинство источников искажения синусоидальных сигналов в силовых цепях переменного тока, как правило, симметричны, четные гармоники в них можно увидеть достаточно редко. Это полезно знать, если вы проектируете системы энергоснабжения и заранее планируете устранение или минимизацию гармоник. В этом случае вам нужно будет позаботиться только о нечетных гармониках. Кроме того, если вам придется измерять гармоники в цепи переменного тока при помощи анализатора спектра или частотомера, вы будете знать, что что-то в этой цепи дает несимметричные искажения синусоидального сигнала напряжения или тока, и эта подсказка может быть полезной в локализации источника проблемы (вам нужно искать компоненты или условия, которые наиболее вероятно искажают один полупериод сигнала больше, чем другой).

Теперь вам должно быть понятно, почему сигнал, произведенный схемой выпрямителя из предыдущей статьи, содержит такие сильные четные гармоники. У этого сигнала вообще нет никакой симметрии относительно центральной (осевой) линии.

Гармоники в многофазных энергетических системах — многофазные цепи переменного тока

Гармоники в полифазных энергетических системах

Глава 10 — Многофазные цепи переменного тока

В главе о смешанных частотах мы рассмотрели концепцию гармоник в системах переменного тока: частоты, которые являются целыми кратными основной частоте источника. При системах переменного тока, где сигнал источника напряжения, поступающий от генератора переменного тока (генератор переменного тока), должен быть одночастотной синусоидальной волной, неискаженной, не должно быть гармонического содержимого.,, Идеально.

Это было бы верно, если бы не нелинейные компоненты . Нелинейные компоненты непропорционально распределяют ток относительно напряжения источника, вызывая несинусоидальные сигналы тока. Примеры нелинейных компонентов включают газоразрядные лампы, полупроводниковые устройства управления мощностью (диоды, транзисторы, SCR, TRIAC), трансформаторы (ток намагничивания первичной обмотки обычно несинусоидален из-за кривой насыщения B / H сердечника) и электродвигатели (опять же, когда магнитные поля в сердечнике двигателя работают вблизи уровней насыщения). Даже лампы накаливания генерируют незначительно несинусоидальные токи, так как сопротивление нити изменяется в течение всего цикла из-за быстрых колебаний температуры. Как мы узнали в главе с неоднородными частотами, любое искажение формы волны с синусоидальной формой представляет собой наличие гармонических частот.

Когда рассматриваемая несинусоидальная волновая форма симметрична выше и ниже ее средней осевой линии, гармонические частоты будут нечетными целыми кратными только основной частоте источника, без четных целых кратных. (Рис. Ниже). Большинство нелинейных нагрузок создают такие формы тока, как это, и поэтому четные гармоники (2, 4, 6, 8, 10, 12 и т. Д.) Отсутствуют или минимально присутствуют в большинстве систем переменного тока.

Примеры только симметричных осциллограмм — нечетные гармоники.

Примеры несимметричных осциллограмм с присутствующими четными гармониками приведены для ссылки на рис. Ниже.

Примерами несимметричных сигналов являются четные гармоники.

Несмотря на то, что половина возможных гармонических частот устраняется типично симметричным искажением нелинейных нагрузок, нечетные гармоники все еще могут вызывать проблемы. Некоторые из этих проблем являются общими для всех энергосистем, однофазных или иных. Например, перегрев трансформатора из-за потерь в вихревых токах может происходить в любой силовой системе переменного тока, где имеется значительное гармоническое содержание.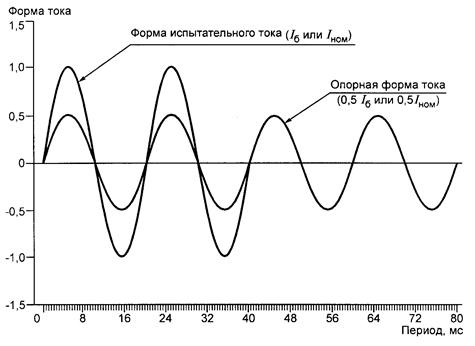 Однако есть некоторые проблемы, вызванные гармоническими токами, характерными для многофазных энергетических систем, и именно эти проблемы специально посвящены этому разделу.

Полезно иметь возможность имитировать нелинейные нагрузки в SPICE, чтобы избежать много сложной математики и получить более интуитивное понимание гармонических эффектов. Во-первых, мы начнем симуляцию с очень простой схемы переменного тока: одного источника синусоидального напряжения с чисто линейной нагрузкой и всех связанных сопротивлений: (рис. Ниже)

SPICE с единственным источником синусоидальной волны.

Сопротивления R- _{источника} и R- _линии в этой схеме делают больше, чем просто имитируют реальный мир: они также обеспечивают удобные шунтирующие сопротивления для измерения токов в моделировании SPICE: считывая напряжение на сопротивление 1 Ом, вы получаете прямую индикацию тока через это, так как E = IR.

Моделирование SPICE этой схемы (список SPICE: «Моделирование линейной нагрузки») с помощью анализа Фурье по напряжению, измеренному по _линии R, должно показать нам гармоническое содержание тока линии этой схемы. Будучи полностью линейным по своей природе, мы не должны ожидать гармоник, кроме 1-го (фундаментального) 60 Гц, предполагая источник 60 Гц. См. Вывод SPICE «Фурье-компоненты переходного отклика v (2, 3)» и рис. Ниже.

 Моделирование линейной нагрузки vsource 1 0 sin (0 120 60 0 0) rsource 1 2 1 rline 2 3 1 rload 3 0 1k .options itl5 = 0 .tran 0.5m 30m 0 1u .plot tran v (2, 3) .four 60 v (2, 3) .end 

 Фурье-компоненты переходного отклика v (2, 3) dc component = 4.028E-12 гармоническая частота Фурье нормализованная фаза нормализованная фаза (hz) компонента компонента (град) (6) 1 6.000E + 01 1.198E-01 1.000000 -72.000 0.000 2 1.200E + 02 5.793E-12 0.000000 51.122 123.122 3 1.800E + 02 7.407E-12 0.000000 -34.624 37.376 4 2.400E + 02 9.056E-12 0.000000 4.267 76.267 5 3.000E + 02 1.651E-11 0.000000 -83.461 - 11.461 6 3.600E + 02 3.931E-11 0.000000 36.399 108.399 7 4.200E + 02 2.338E-11 0.000000 -41.343 30.657 8 4.800E + 02 4.716E-11 0.000000 53.324 125.324 9 5.400E + 02 3. 453E-11 0.000000 21.691 93.691 суммарное гармоническое искажение = 0, 000000% 

График частотной области одночастотной составляющей. См. Список SPICE: «Моделирование линейной нагрузки».

В списке соединений SPICE появляется команда .plot, и обычно это приведет к выходу синусоидального графика. В этом случае, однако, я намеренно пропустил отображение формы сигнала для краткости — команда .plot находится в списке соединений просто для удовлетворения причуды функции преобразования Фурье SPICE.

Никакое дискретное преобразование Фурье не является совершенным, и поэтому мы видим очень малые гармонические токи, указанные (в диапазоне пико-ампер!) Для всех частот вплоть до 9-й гармоники (в таблице), которая до тех пор, пока SPICE не выполняет анализ Фурье, Мы показываем 0.1198 ампер (1.198E-01) для «фурье-составляющей» 1-й гармоники или основной частоты, которая является нашим ожидаемым током нагрузки: около 120 мА при заданном напряжении 120 В и сопротивлении нагрузки 1 кОм.

Затем я хотел бы моделировать нелинейную нагрузку, чтобы генерировать гармонические токи. Это можно сделать двумя принципиально разными способами. Один из способов — спроектировать нагрузку с использованием нелинейных компонентов, таких как диоды или другие полупроводниковые устройства, которые легко имитировать с помощью SPICE. Другой — добавить некоторые источники переменного тока параллельно нагрузочному резистору. Последний метод часто предпочитается инженерами для имитации гармоник, поскольку источники тока известного значения лучше подходят для математического сетевого анализа, чем компоненты с очень сложными характеристиками реакции. Поскольку мы позволяем SPICE выполнять всю математическую работу, сложность полупроводникового компонента не вызовет у нас никаких проблем, но поскольку источники тока могут быть точно настроены для создания любого произвольного количества тока (удобная функция), я буду выберите последний подход, показанный на рисунке ниже и в списке SPICE: «Моделирование нелинейной нагрузки».

Цепь SPICE: источник 60 Гц с добавленной 3-й гармоникой.

 Моделирование нелинейной нагрузки vsource 1 0 sin (0 120 60 0 0) rsource 1 2 1 rline 2 3 1 rload 3 0 1k i3har 3 0 sin (0 50m 180 0 0) . options itl5 = 0 .tran 0.5m 30m 0 1u. plot tran v (2, 3) .four 60 v (2, 3) .end 

В этой схеме мы имеем источник тока 50 мА и частоту 180 Гц, что в три раза превышает частоту источника 60 Гц. При подключении параллельно нагрузочному резистору 1 кОм его ток будет добавляться с резистором, чтобы сделать несинусоидальный общий ток линии. Я покажу график осциллограмм в рисунке ниже, чтобы вы могли видеть эффекты этого тока третьей гармоники на общий ток, который обычно был бы простой синусоидальной волной.

SPICE во временной области с суммой источника 60 Гц и третьей гармоники 180 Гц.

 Фурье-компоненты переходного отклика v (2, 3) dc component = 1, 349E-11 гармоническая частота Фурье нормализованная фаза нормализованная фаза (hz) компонента компонента (град.) 1 6000E + 01 1.198E-01 1.000000 -72.000 0.000 2 1.200E + 02 1, 609E-11 0, 000000 67, 570 139, 570 3 1, 800E + 02 4, 990E-02 0, 416667 144 000 216 000 4 2, 400E + 02 1.074E-10 0, 000000 -169, 546 -97, 546 5 3, 000E + 02 3, 871E-11 0, 000000 169, 582 241, 582 6 3. 600E + 02 5.736E-11 0.000000 140.845 212.845 7 4.200E + 02 8.407E-11 0.000000 177.071 249.071 8 4.800E + 02 1.329E-10 0.000000 156.772 228.772 9 5.400E + 02 2.619E-10 0.000000 160.498 232.498 общая гармоника искажение = 41, 666663% 

SPICE Фурье с изображением источника 60 Гц и третьей гармоники 180 Гц.

В анализе Фурье (см. Figureabove и «Фурье-компоненты переходного отклика v (2, 3)») смешанные частоты не смешиваются и представлены отдельно. Здесь мы видим те же 0, 1198 ампер 60 Гц (основной) ток, что и в первом симуляторе, но появляясь в третьей гармонической строке, мы видим 49, 9 мА: наш 50 мА, источник тока 180 Гц на работе. Почему бы нам не увидеть весь 50 мА через строку «# 02324.png»> ниже и список SPICE: «Моделирование нелинейной нагрузки».

Нелинейная нагрузка: присутствуют 1, 3, 5, 7 и 9 гармоники.

 Моделирование нелинейной нагрузки vsource 1 0 sin (0 120 60 0 0) rsource 1 2 1 rline 2 3 1 rload 3 0 1k i3har 3 0 sin (0 50m 180 0 0) i5har 3 0 sin (0 50m 300 0 0) i7har 3 0 sin (0 50m 420 0 0) i9har 3 0 sin (0 50m 540 0 0) . options itl5 = 0 .tran 0.5m 30m 0 1u .plot tran v (2, 3) .four 60 v (2, 3) .конец 

 Фурье-компоненты переходного отклика v (2, 3) dc component = 6.299E-11 гармоническая частота Фурье нормализованная фаза нормализованная фаза (hz) компонента компонента (град) (6) 1 6.000E + 01 1.198E-01 1.000000 -72.000 0.000 2 1.200E + 02 1.900E-09 0.000000 -93.908 -21.908 3 1.800E + 02 4.990E-02 0.416667 144.000 216.000 4 2.400E + 02 5.469E-09 0.000000 -116.873 -44.873 5 3.000E + 02 4.990E-02 0.416667 0.000 72.000 6 3.600E + 02 6.271E-09 0.000000 85.062 157.062 7 4.200E + 02 4.990E-02 0.416666 -144.000 -72.000 8 4.800E + 02 2.742E-09 0.000000 -38.781 33.219 9 5.400E + 02 4.990E-02 0, 416666 72 000 144 000 суммарное гармоническое искажение = 83, 333296% 

Фурье-анализ: «Фурье-компоненты переходного отклика v (2, 3)».

Как видно из анализа Фурье (рис. Выше), каждый гармонический источник тока одинаково представлен в линейном токе при 49, 9 мА каждый. Пока это всего лишь однофазное силовое моделирование.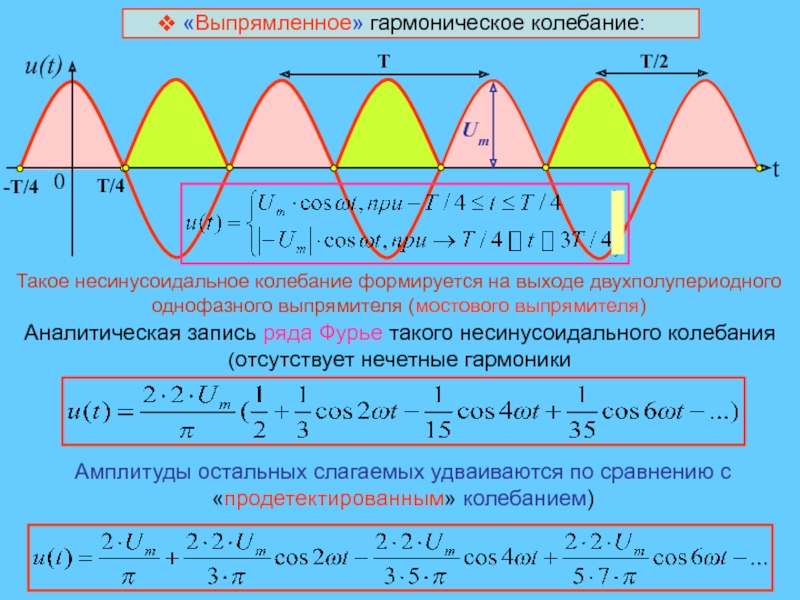 Все становится интереснее, когда мы делаем это трехфазное моделирование. Будут проведены два анализа Фурье: один для напряжения на линейном резисторе и один для напряжения на нейтральном резисторе. Как и ранее, напряжение считывания при фиксированных сопротивлениях 1 Ом каждый дает прямые указания на ток через эти резисторы. См. Рис. Ниже и список SPICE «YY источник / загрузка 4-проводной системы с гармониками».

Цепь SPICE: анализ «линейного тока» и «нейтрального тока», источника питания / нагрузки YY 4-проводной системы с гармониками.

 YY источник / нагрузка 4-проводная система с гармониками * * источник напряжения фазы 1 и r (120 v / 0 град) vsource1 1 0 sin (0 120 60 0 0) rsource1 1 2 1 * * источник напряжения фазы 2 и r (120 v / 120 градусов) vsource2 3 0 sin (0 120 60 5.55555m 0) rsource2 3 4 1 * * источник напряжения фазы 3 и r (120 v / 240 град.) Vsource3 5 0 sin (0 120 60 11.1111m 0) rsource3 5 6 1 * * сопротивление линии и нейтрального провода rline1 2 8 1 rline2 4 9 1 rline3 6 10 1 rneutral 0 7 1 * * фаза 1 нагрузки rload1 8 7 1k i3har1 8 7 sin (0 50m 180 0 0) i5har1 8 7 sin (0 50m 300 0 0) i7har1 8 7 sin (0 50m 420 0 0) i9har1 8 7 sin (0 50m 540 0 0) * * фаза 2 нагрузки rload2 9 7 1k i3har2 9 7 sin (0 50m 180 5. 55555m 0) i5har2 9 7 sin (0 50m 300 5.55555m 0) i7har2 9 7 sin (0 50m 420 5.55555m 0) i9har2 9 7 sin (0 50m 540 5.55555m 0) * * фаза 3 нагрузки rload3 10 7 1k i3har3 10 7 sin (0 50m 180 11.1111m 0) i5har3 10 7 sin (0 50m 300 11.1111m 0) i7har3 10 7 sin (0 50m 420 11.1111m 0) i9har3 10 7 sin (0 50m 540 11.1111m 0) * * анализ материала .options itl5 = 0 .tran 0.5m 100m 12m 1u .plot tran v (2, 8) .four 60 v (2, 8) .plot tran v (0, 7) .four 60 v (0, 7) .end 

Фурье-анализ линейного тока:

 Фурье-компоненты переходного отклика v (2, 8) dc component = -6.404E-12 гармоническая частота Фурье нормализованная фаза нормализованная нет (hz) составляющая компонента (град) фаза (град) 1 6.000E + 01 1.198E-01 1.000000 0.000 0.000 2 1.200E + 02 2.218E-10 0.000000 172.985 172.985 3 1.800E + 02 4.975E-02 0.415423 0.000 0.000 4 2.400E + 02 4.236E-10 0.000000 166.990 166.990 5 3.000E + 02 4.990E-02 0.416667 0.000 0.000 6 3.600 E + 02 1.877E-10 0.000000 -147.146 -147.146 7 4. 200E + 02 4.990E-02 0.416666 0.000 0.000 8 4.800E + 02 2.784E-10 0.000000 -148.811 -148.811 9 5.400E + 02 4.975E-02 0.415422 0.000 0.000 полное гармоническое искажение = 83.209009 процентов 

Фурье-анализ линейного тока в сбалансированной системе YY

Фурье-анализ нейтрального тока:

 Компоненты Фурье переходного отклика v (0, 7) постоянная составляющая = 1, 819E-10 гармоническая частота Фурье нормализованная фаза нормализованная нет (hz) составляющая компонента (град) фаза (град) 1 6.000E + 01 4.337E-07 1.000000 60.018 0.000 2 1.200E + 02 1.869E-10 0.000431 91.206 31.188 3 1.800E + 02 1.493E-01 344147.7638 -180.000 -240.018 4 2.400E + 02 1.257E-09 0.002898 -21.103 -81.121 5 3.000E + 02 9.023E-07 2.080596 119.981 59.963 6 3.600E + 02 3.396E-10 0.000783 15.882 -44.136 7 4.200E + 02 1.264E-06 2.913955 59.993 -0.025 8 4.800E + 02 5.975E-10 0.001378 35.584 -24.434 9 5.400E + 02 1.493E-01 344147.4889 -179, 999 -240, 017 

Фурье-анализ нейтрального тока показывает, кроме гармоник! Сравнение с текущим потоком в Figureabove

Это сбалансированная система питания YY, каждая из которых идентична однофазной системе переменного тока, смоделированной ранее. Следовательно, неудивительно, что анализ Фурье для линейного тока в одной фазе трехфазной системы почти идентичен анализу Фурье для линейного тока в однофазной системе: основной (60 Гц) токовый ток 0, 1198 А и нечетные гармонические токи приблизительно 50 мА каждый. См. Figureabove и Fourier analysis: «Фурье-компоненты переходного отклика v (2, 8)»

Здесь должно быть неожиданно проанализировать ток нейтрального проводника, определяемый падением напряжения на R- _{нейтральном} резисторе между узлами SPICE 0 и 7. (Рисунок выше). При сбалансированной трехфазной нагрузке Y мы ожидаем, что нейтральный ток равным нулю. Каждый фазовый ток, который сам по себе проходил через нейтральный провод обратно к фазе подачи на источнике Y, должен отменить друг друга в отношении нейтрального проводника, потому что они все одинаковы и все смещены на 120 ^o друг от друга. В системе без гармонических токов это то, что происходит, оставляя нулевой ток через нейтральный проводник. Однако мы не можем сказать то же самое для гармонических токов в одной и той же системе.

Обратите внимание, что основная частота (60 Гц или первая гармоника) практически отсутствует у нейтрального проводника. Наш анализ Фурье показывает только 0.4337 мкА 1-й гармоники при считывании напряжения через _{нейтраль} R. То же самое можно сказать и о 5-й и 7-й гармониках, причем оба этих течения имеют незначительную величину. Напротив, 3-я и 9-я гармоники сильно представлены в нейтральном проводнике с 149, 3 мА (1, 493E-01 вольт по 1 Ом) каждый! Это почти 150 мА, или в три раза больше значений текущих источников, индивидуально. При трех источниках на каждую гармоническую частоту в нагрузке появляется, что третий и девятый гармонические токи в каждой фазе складываются для формирования нейтрального тока. См. Анализ Фурье: «Компоненты Фурье переходного отклика v (0, 7)»

Это именно то, что происходит, хотя может быть и не понятно, почему это так. Ключ к пониманию этого проясняется во временном графе фазных токов. Изучите этот график сбалансированных фазных токов с течением времени с последовательностью фаз 1-2-3. (Figurebelow)

Фазовая последовательность 1-2-3-1-2-3-1-2-3 с равноотстоящими волнами.

Поскольку три фундаментальных сигнала одинаково сдвинуты по оси времени графика, легко увидеть, как они будут взаимно компенсировать друг друга, чтобы получить нулевой ток в нейтральном проводнике. Давайте рассмотрим, однако, что форма волны третьей гармоники для фазы 1 будет выглядеть как наложенная на график в рисунке ниже.

Форма волны третьей гармоники для фазы-1, наложенная на трехфазные фундаментальные формы волны.

Наблюдайте, как этот гармонический сигнал имеет одно и то же фазовое отношение к 2-й и 3-й фундаментальным формам волны, как это происходит с 1-м: в каждом положительном полупериоде любой из основных форм волны вы найдете ровно два положительных полуцикла и одну отрицательную половину -цикл гармонического сигнала. Это означает, что волны третьей гармоники трех осциллограмм с фазовой сдвиговой фазой с фазовой сдвиговой фазой фактически находятся в фазе друг с другом. Показатель фазового сдвига 120 ^o, обычно принимаемый в трехфазных системах переменного тока, применяется только к основным частотам, а не к их гармоническим кратным!

Если бы мы построили все три волны третьей гармоники на одном и том же графике, мы бы увидели, что они точно перекрываются и появляются как единый единый сигнал (выделен жирным шрифтом (рис.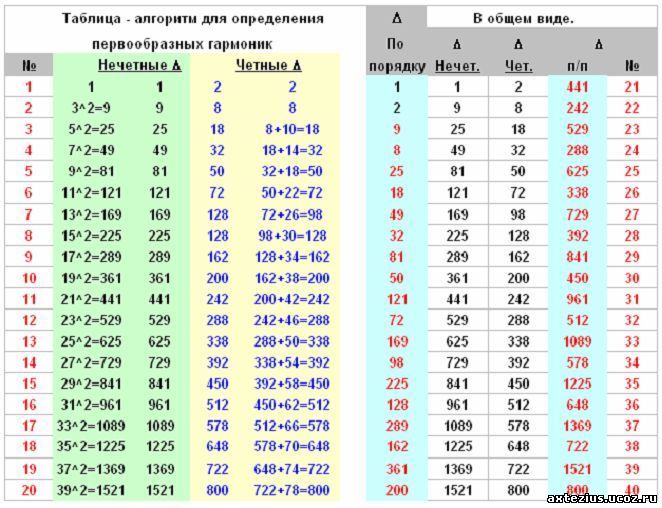 Ниже)

Третьи гармоники для фаз 1, 2, 3 все совпадают, когда они накладываются на основные трехфазные формы волны.

Для более математически наклонного, этот принцип может быть выражен символически. Предположим, что A представляет собой одну форму волны, а B — другую, причем на одной и той же частоте, но сдвинутую на 120 ^o друг от друга по фазе. Назовем 3-ю гармонику каждой формы A ‘ и B’ соответственно. Фазовый сдвиг между A ‘ и B’ не равен 120 ^o (это фазовый сдвиг между A и B ), но в 3 раза больше, потому что формы A ‘ и B’ чередуются в три раза быстрее, чем A и B. Сдвиг между формами колебаний только точно выражается через фазовый угол, когда предполагается та же угловая скорость. При связывании сигналов различной частоты наиболее точным способом представления сдвига фазы является время ; и сдвиг во времени между А ‘ и В’ эквивалентен 120 ^о на частоте в три раза ниже или 360 ^° на частоте А ‘ и В’ .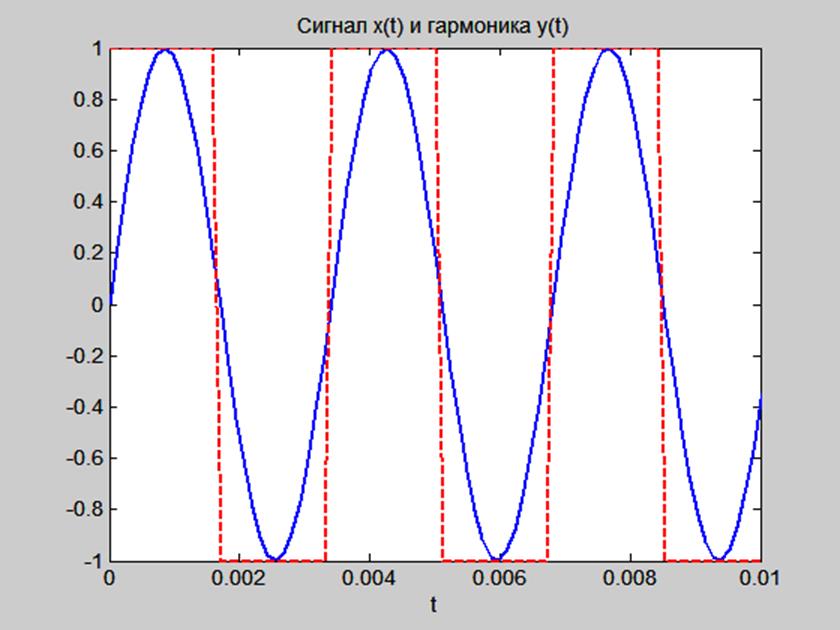 Фазовый сдвиг на 360 ^o является таким же, как сдвиг фазы 0 ^o, что означает отсутствие сдвига фазы вообще. Таким образом, A ‘ и B’ должны находиться в фазе друг с другом:

Эта характеристика 3-й гармоники в трехфазной системе также справедлива для любых целых кратных 3-й гармоники. Таким образом, не только волны третьей гармоники каждой основной формы волны находятся в фазе друг с другом, но и 6-я гармоника, 9-я гармоника, 12-я гармоника, 15-я гармоника, 18-я гармоника, 21-я гармоника и т. Д. Поскольку в системах, где искажение формы волны симметрично относительно осевой линии, появляются только нечетные гармоники, и большинство нелинейных нагрузок создают симметричные искажающие четность кратные 3-й гармоники (6, 12, 18 и т. Д.), Как правило, несущественны, оставляя только нечетные кратные (3, 9, 15, 21 и т. д.) для значительного вклада в нейтральные токи.

В многофазных энергосистемах с некоторым количеством фаз, отличных от трех, этот эффект возникает с гармониками одного и того же кратного. Например, гармонические токи, которые добавляются в нейтральный проводник связанной с звездой 4-фазной системы, где фазовый сдвиг между фундаментальными волнами составляет 90 ^o, будет 4, 8, 12, 16, 20 и т. Д.

Из-за их обилия и значимости в трехфазных энергетических системах 3-я гармоника и ее кратные имеют свое особое имя: триплекс-гармоники . Все триплетные гармоники добавляют друг к другу в нейтральном проводнике 4-проводной нагрузки с Y-соединением. В энергетических системах, содержащих существенную нелинейную нагрузку, триплексные гармонические токи могут иметь достаточно большую величину, чтобы вызвать перегрев нейтральных проводников. Это очень проблематично, так как другие соображения безопасности не позволяют нейтральным проводникам иметь максимальную токовую защиту, и, таким образом, не предусмотрено автоматическое прерывание этих высоких токов.

На следующем рисунке показано, как триплетные гармонические токи, созданные при нагрузке, добавляются в нейтральный проводник. Символ «ω» используется для представления угловой скорости и математически эквивалентен 2πf. Итак, «ω» представляет основную частоту, «3ω» представляет собой 3-ю гармонику, «5ω» представляет собой 5-ю гармонику и т. Д .: (рис. Ниже)

«YY» Triplen source / load: гармонические токи добавляют в нейтральный проводник.

Чтобы смягчить эти трипликационные токи с добавками, можно попытаться полностью удалить нейтральный провод. Если нет нейтрального провода, в котором триплетные токи могут течь вместе, то они не будут, правый «# 02330.png»> ниже представляет собой графическое резюме вышеупомянутых эффектов.

Трехпроводная система «YY» (без нейтральной): трипленовые напряжения появляются между «Y» -центрами. Нагрузочные напряжения появляются во всех фазах нагрузки. Непрямые токи появляются в линейных проводниках.

Таким образом, снятие нейтрального проводника приводит к «горячей» центральной точке нагрузки «Y», а также к фазовым напряжениям гармонической нагрузки равной величины, все из которых состоят из трех частот.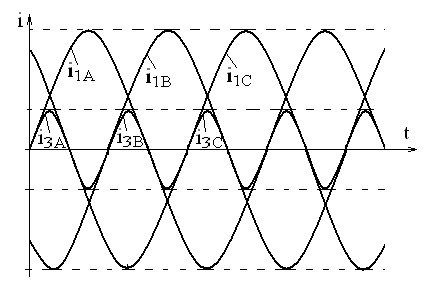 В предыдущей симуляции, где у нас была 4-проводная система с Y-соединением, нежелательным эффектом от гармоник был чрезмерный нейтральный ток, но по крайней мере каждая фаза нагрузки принимала напряжение, почти свободное от гармоник.

Поскольку удаление нейтрального провода, похоже, не работает в устранении проблем, вызванных гармониками, возможно, переключение на конфигурацию Δ. Давайте попробуем источник Δ вместо Y, сохраняя нагрузку в ее нынешней конфигурации Y и посмотрим, что произойдет. Измеряемыми параметрами будут ток линии (напряжение по _линии R, узлы 0 и 8), напряжение фазы нагрузки (узлы 8 и 7) и ток фазы источника (напряжение через _{источник} R, узлы 1 и 2). (Figurebelow)

Источник / мощность Delta-Y с гармониками

 Delta-Y источник / нагрузка с гармониками * * источник напряжения фазы 1 и r (120 v / 0 deg) vsource1 1 0 sin (0 207.846 60 0 0) rsource1 1 2 1 * * источник напряжения фазы 2 и r (120 v / 120 deg ) vsource2 3 2 sin (0 207.846 60 5. 55555m 0) rsource2 3 4 1 * * источник напряжения фазы 3 и r (120 v / 240 град) vsource3 5 4 sin (0 207.846 60 11.1111m 0) rsource3 5 0 1 * * line сопротивления rline1 0 8 1 rline2 2 9 1 rline3 4 10 1 * * фаза 1 нагрузки rload1 8 7 1k i3har1 8 7 sin (0 50m 180 9.72222m 0) i5har1 8 7 sin (0 50m 300 9.72222m 0) i7har1 8 7 sin (0 50m 420 9.72222m 0) i9har1 8 7 sin (0 50m 540 9.72222m 0) * * фаза 2 нагрузки rload2 9 7 1k i3har2 9 7 sin (0 50m 180 15.2777m 0) i5har2 9 7 sin (0 50m 300 15.2777m 0) i7har2 9 7 sin (0 50m 420 15.2777m 0) i9har2 9 7 sin (0 50m 540 15.2777m 0) * * фаза 3 нагрузки rload3 10 7 1k i3har3 10 7 sin (0 50m 180 4.16666m 0 ) i5har3 10 7 sin (0 50m 300 4.16666m 0) i7har3 10 7 sin (0 50m 420 4.16666m 0) i9har3 10 7 sin (0 50m 540 4.16666m 0) * * анализ материала .options itl5 = 0 .tran 0.5m 100m 16m 1u .plot tran v (0, 8) v (8, 7) v (1, 2) .four 60 v (0, 8) v (8, 7) v (1, 2) .end 

Примечание. Следующий абзац предназначен для тех любопытных читателей, которые следуют каждой детали моих списков SPICE.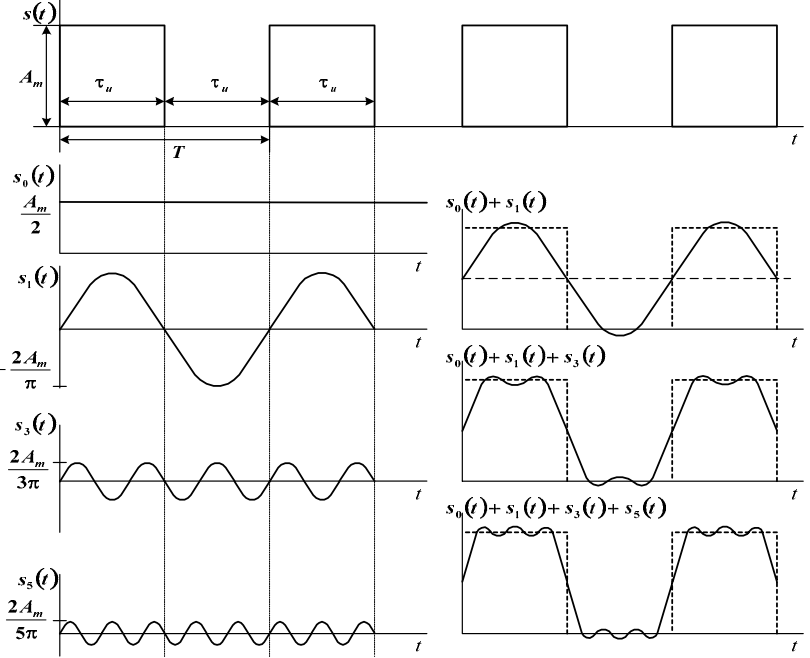 Если вы просто хотите узнать, что происходит в цепи, пропустите этот параграф! При моделировании цепей, имеющих источники переменного тока различной частоты и различной фазы, единственный способ сделать это в SPICE — это настроить источники с временем задержки или смещением фазы, указанным в секундах. Таким образом, источник 0 ^o имеет эти пять задающих цифр: «(0 207.846 60 0 0)», что означает 0 вольт смещения постоянного тока, амплитуду амплитуды 207, 846 вольт (в 120 раз больше квадратного корня из трех, чтобы обеспечить, чтобы напряжения фазы нагрузки оставались на 120 вольт каждый), 60 Гц, 0 временной задержки и 0 коэффициента затухания. Источник с сдвигом фазы 120 ^o имеет следующие цифры: «(0 207.846 60 5.55555m 0)», все равно, что и первый, за исключением коэффициента временной задержки 5, 55555 миллисекунд или 1/3 полного периода 16, 6667 миллисекунд для 60 Гц. Источник 240o должен быть задержан с задержкой по времени вдвое больше, чем эквивалент 240/360 из 16. 6667 миллисекунд или 11.1111 миллисекунды. Это для источника с Δ-связью. С другой стороны, для нагрузки с Y-соединением требуется другой набор величин задержки времени для источников гармонического тока, поскольку фазные напряжения в нагрузке Y не находятся в фазе с фазными напряжениями источника Δ. Если напряжение источника _{переменного тока} V _AC, V _BA и V _CB указано на значениях 0 ^o, 120 ^o и 240 ^o соответственно, тогда напряжения нагрузки V _A, V _B и V _C будут иметь фазовые углы -30 ^o, 90 ^o и 210 ^o соответственно. Это неотъемлемое свойство всех схем Δ-Y, а не причуда SPICE. Поэтому, когда я задал время задержки для источников гармоник, мне пришлось установить их в 15.2777 миллисекундах (-30 ^o, или +330 ^o ), 4.16666 миллисекундах (90 ^o ) и 9.72222 миллисекундах (210 ^o ). Последнее замечание: при задержке источников переменного тока в SPICE они не «включаются» до истечения времени задержки, что означает, что любой математический анализ до этого момента будет ошибкой. Следовательно, я установил строку анализа переходного процесса .tran, чтобы провести анализ до 16 миллисекунд после старта, что дает возможность задействовать все источники в времени списка соединений до проведения любого анализа.

Результат этого анализа почти столь же разочаровывает, как и последний. (Рис. Ниже) Линейные токи остаются неизменными (единственное существенное гармоническое содержание — 5-я и 7-я гармоники), а напряжения фазы нагрузки также остаются неизменными с полными 50 вольтами трехчастотных гармонических (3-й и 9-й) частот по каждому компоненту нагрузки. Ток фазы источника представляет собой долю тока линии, что не должно удивлять. Здесь представлены 5-я и 7-я гармоники с незначительными триплетными гармониками:

Фурье-анализ линейного тока:

 Компоненты Фурье переходного отклика v (0, 8) dc component = -6.850E-11 гармоническая частота Фурье нормализованная фаза нормализованная фаза (hz) компонента (град) фаза (град) 1 6.000E + 01 1. 198E-01 1.000000 150.000 0.000 2 1.200E + 02 2.491E-11 0, 000000 159, 723 9, 722 3 1, 800E + 02 1, 506E-06 0, 000013 0, 005 -149, 996 4 2, 400E + 02 2, 033E-11 0, 000000 52, 772 -97, 228 5 3, 000E + 02 4, 994E-02 0, 416682 30, 002 - 119.998 6 3.600E + 02 1.234E-11 0.000000 57.802 -92.198 7 4.200E + 02 4.993E-02 0.416644 -29.998 -179.998 8 4.800E + 02 8.024E-11 0.000000 -174.200 -324.200 9 5.400E + 02 4.518E- 06 0, 000038 -179.995 -329.995 полное гармоническое искажение = 58, 925038 процентов 

Фурье-анализ напряжения фазы нагрузки:

 Фурье-компоненты переходного отклика v (8, 7) dc component = 1, 259E-08 гармоническая частота Фурье нормализованная фаза нормализованная фаза (hz) компонента компонента (град.) 1 6000E + 01 1.198E + 02 1.000000 150.000 0.000 2 1.200E + 02 1.941E-07 0, 000000 49, 693 -100, 307 3 1.800E + 02 5.000E + 01 0.417222 -89.998 -239.998 4 2.400E + 02 1.519E-07 0.000000 66.397 -83.603 5 3.000E + 02 6.466E-02 0.000540 - 151.112 -301.112 6 3. 600E + 02 2.433E-07 0.000000 68.162 -81.838 7 4.200E + 02 6.931E-02 0.000578 148.548 -1.453 8 4.800E + 02 2.398E-07 0.000000 -174.897 -324.897 9 5.400E + 02 5.000E +01 0, 417221 90, 006 -5, 995 суммарное гармоническое искажение = 59, 004109 процентов 

Фурье-анализ тока фазы источника:

 Компоненты Фурье переходного отклика v (1, 2) dc component = 3.564E-11 гармоническая частота Фурье нормированная фаза нормализованная фаза (hz) компонента (град.) (6) 2 1.200E + 02 1, 525E-11 0, 000000 -156, 674 -156, 493 3 1, 800E + 02 1, 422E-06 0, 000021 -179, 996 -179, 815 4 2, 400E + 02 2, 949E-11 0, 000000 -110, 570 -110, 390 5 3, 000E + 02 2, 883E- 02 0.417440 -179.996 -179.815 6 3.600E + 02 2.324E-11 0, 000000 -91, 926 -91, 745 7 4.200E + 02 2.883E-02 0.417398 -179.994 -179.813 8 4.800E + 02 4.140E-11 0.000000 -39.875 -39.694 9 5.400 E + 02 4.267E-06 0, 000062 0, 006 0, 1886 суммарное гармоническое искажение = 59, 031969 процентов 

«Δ-Y» источник / нагрузка: Трипленовые напряжения появляются на фазах нагрузки. Непрямые токи появляются в линейных проводниках и в обмотках фазы источника.

Действительно, единственным преимуществом конфигурации Δ-Y с точки зрения гармоник является то, что нагрузка, представляющая опасность удара, больше не является центральной точкой. В противном случае компоненты нагрузки получат одинаковые гармонически насыщенные напряжения, а линии видят те же токи, что и в трехпроводной системе Y.

Если бы мы перенастроили систему на Δ-Δ-компоновку (рис. Ниже), которая должна гарантировать, что каждый компонент нагрузки получает негармоническое напряжение, так как каждая фаза нагрузки будет напрямую подключаться параллельно с каждой фазой источника. Полное отсутствие каких-либо нейтральных проводов или «центральных точек» в системе Δ-Δ предотвращает появление странных напряжений или аддитивных токов. Казалось бы, это идеальное решение. Давайте моделируем и наблюдаем, анализируя линейный ток, напряжение фазы нагрузки и ток фазы источника. См. Список SPICE: «Источник / загрузка Delta-Delta с гармониками», «Анализ Фурье: компоненты Фурье переходного отклика v (0, 6)» и «Фурье-компоненты переходного отклика v (2, 1)».

Delta-Delta источник / нагрузка с гармониками.

 Delta-Delta источник / нагрузка с гармониками * * источник напряжения фазы 1 и r (120 v / 0 deg) vsource1 1 0 sin (0 120 60 0 0) rsource1 1 2 1 * * источник напряжения фазы 2 и r (120 v / 120 deg ) vsource2 3 2 sin (0 120 60 5.55555m 0) rsource2 3 4 1 * * источник напряжения фазы 3 и r (120 v / 240 град.) vsource3 5 4 sin (0 120 60 11.1111m 0) rsource3 5 0 1 * * line сопротивления rline1 0 6 1 rline2 2 7 1 rline3 4 8 1 * * фаза 1 нагрузки rload1 7 6 1k i3har1 7 6 sin (0 50m 180 0 0) i5har1 7 6 sin (0 50m 300 0 0) i7har1 7 6 sin ( 0 50 м 420 0 0) i9har1 7 6 sin (0 50m 540 0 0) * * фаза 2 нагрузки rload2 8 7 1k i3har2 8 7 sin (0 50m 180 5.55555m 0) i5har2 8 7 sin (0 50m 300 5.55555m 0 ) i7har2 8 7 sin (0 50m 420 5.55555m 0) i9har2 8 7 sin (0 50m 540 5.55555m 0) * * фаза 3 нагрузки rload3 6 8 1k i3har3 6 8 sin (0 50m 180 11.1111m 0) i5har3 6 8 sin (0 50m 300 11.1111m 0) i7har3 6 8 sin (0 50m 420 11.1111m 0) i9har3 6 8 sin (0 50m 540 11. 1111m 0) * * анализ материала .options itl5 = 0 .tran 0.5m 100m 16m 1u. plot tran v (0, 6) v (7, 6) v (2, 1) i (3har1) .four 60 v (0, 6) v (7, 6) v (2, 1) .end 

Фурье-анализ линейного тока:

 Компоненты Фурье переходного отклика v (0, 6) dc component = -6.007E-11 гармоническая частота Фурье нормированная фаза нормализованная нет (hz) составляющая компонента (град) фаза (град) 1 6.000E + 01 2.070E-01 1.000000 150.000 0.000 2 1.200E + 02 5.480E-11 0.000000 156.666 6.666 3 1.800E + 02 6.257E-07 0.000003 89.990 -60.010 4 2.400E + 02 4.911E-11 0.000000 8.187 -141.813 5 3.000E + 02 8.626E-02 0.416664 -149.999 -300.000 6 3.600E + 02 1.089E-10 0.000000 -31.997 -181.997 7 4.200E + 02 8.626E-02 0.416669 150.001 0.001 8 4.800E + 02 1.578E-10 0.000000 -63.940 -213.940 9 5.400E + 02 1.877E- 06 0.000009 89.987 -60.013 полное гармоническое искажение = 58.925538% 

Фурье-анализ напряжения фазы нагрузки:

 Фурье-компоненты переходного отклика v (7, 6) dc component = -5. 680E-10 гармоническая частота Фурье нормированная фаза нормализованная нет (hz) составляющая компонента (град) фаза (град) 1 6.000E + 01 1.195E + 02 1.000000 0.000 0.000 2 1.200E + 02 1.039E-09 0.000000 144.749 144.749 3 1.800E + 02 1.251E-06 0.000000 89.974 89.974 4 2.400E + 02 4.215E-10 0.000000 36.127 36.127 5 3.000E + 02 1.992E-01 0.001667 -180.000 -180.000 6 3.600E + 02 2.499E-09 0.000000 -4.760 -4.760 7 4.200E + 02 1.992E-01 0.001667 -180.000 -180.000 8 4.800E + 02 2.951E-09 0.000000 -151.385 -151.385 9 5.400E + 02 3.752E- 06 0, 000000 89, 905 89, 905 суммарное гармоническое искажение = 0, 235702 процента 

Фурье-анализ тока фазы источника:

 Фурье-компоненты переходного отклика v (2, 1) dc component = -1.923E-12 гармоническая частота Фурье нормированная фаза нормализованная нет (hz) составляющая компонента (град) фаза (град) 1 6000E + 01 1.194E-01 1.000000 179.940 0.000 2 1.200E + 02 2, 569E-11 0, 000000 133, 491 -46, 449 3 1.800E + 02 3.129E-07 0, 000003 89, 985 -89, 955 4 2, 400E + 02 2, 657E-11 0, 000000 23, 368 -156, 571 5 3, 000E + 02 4, 980E-02 0, 416918 - 180.000 -359.939 6 3.600E + 02 4.595E-11 0.000000 -22.475 -202.415 7 4.200E + 02 4.980E-02 0.416921 -180.000 -359.939 8 4.800E + 02 7.385E-11 0.000000 -63.759 -243.699 9 5.400E + 02 9.385E-07 0.000008 89.991 -89.949 общее гармоническое искажение = 58.961298 процентов 

Как было предсказано ранее, напряжение фазы нагрузки является почти чистой синусоидальной волной с незначительным содержанием гармоник благодаря прямому соединению с фазами источника в системе Δ-Δ. Но что случилось с триплексными гармониками «# 02333.png»>.

Δ-Δ источник / нагрузка: фазы нагрузки получают неискаженное синусоидальное напряжение. Трифрановые токи ограничены циркуляцией в фазах нагрузки. Нетерритонные токи возникают в линейных проводниках и в обмотках фазы источника.

Это основное преимущество конфигурации Δ-Δ: триплексные гармонические токи остаются ограниченными в любом наборе компонентов, создающих их, и не «распространяются» на другие части системы.

• ОБЗОР:
• Нелинейными компонентами являются те, которые вытягивают несинусоидальную (несинусоидальную) форму тока при возбуждении синусоидальным (синусоидальным) напряжением. Так как любое искажение первоначально чистой синусоидальной волны представляет собой гармонические частоты, можно сказать, что нелинейные компоненты генерируют гармонические токи.
• Когда искажение синусоидальной волны симметрично выше и ниже средней центральной линии формы волны, единственные присутствующие гармоники будут нечетными, а не четными.
• Третья гармоника и ее целочисленные кратные (6, 9, 12, 15) известны как триплексные гармоники. Они находятся в фазе друг с другом, несмотря на то, что их соответствующие основные формы колебаний не совпадают друг с другом.
• В 4-проводной системе YY гармонические токи триплета добавляют в нейтральный проводник.
• Триплинные гармонические токи в Δ-связном множестве компонентов циркулируют внутри петли, образованной Δ.

Уменьшение искажений подавлением (компенсацией)

Как известно, каскад усиления, построенный по схеме с общим катодом, инвертирует усиливаемый сигнал. В предыдущем параграфе уже обращалось внимание, что в усилителях на лампах-триодах, определяющим фактором в искажениях является асимметричное усиление положительных и отрицательных полуволн аудиосигнала, в следствие нелинейности характеристик ламп. Теоретически, если два усилителя с общим катодом на одинаковых триодах работают в каскаде, и каждый каскад инвертирует сигнал, искажения второго триода являются инвертированными по отношению к искажениям, первого триода, и должно происходить их подавление за счет компенсации. Тем не менее, маловероятно, что это происходит в значительном диапазоне. Искажения пропорциональны уровню сигнала, и, потому что обе лампы обладают усилением, второй каскад работает с существенно более высоким уровнем сигнала, и, следовательно, генерирует большие искажения, чем первый каскад. Таким образом, хоть и происходит небольшое подавление искажений в следствие компенсации, но выигрыш всего лишь пропорционален ~ 1/А2, где А2 — коэффициент усиления по напряжению второго каскада. Например, если второй каскад построен на триоде типа 76 (μ = 13), и коэффициент его усиления Аv= 10, то можно уменьшить искажения от 1 % до 0,9%, что вероятнее всего меньше, чем разброс уровня искажений в разных экземплярах любых электронных ламп. Исходя из вышеизложенного, возникает вопрос возможно ли, выбрав лампу второго каскада намного более линейную, чем лампа первого каскада, добиться того чтобы их искажения полностью компенсировали друг друга, будучи равными и противофазными? Лампы с низким значением внутреннего статического коэффициента усиления μ являются наиболее линейными. В этом смысле, в качестве лампы второго каскада неплохо подошел бы тип 845 (μ = 5,3), который может обеспечить коэффициент усиления Av = 4. Для компенсации искажений, первый каскад должен генерировать нелинейный продукт в четыре раза интенсивнее, чем второй. Этого удобнее всего достичь регулировкой напряжения смещения первой лампы, то есть подбором ее рабочей точки. Тем не менее, компенсация искажений таким способом критически зависима от коэффициентов усиления ламп, и во многом определяется значением сопротивления нагрузки RH. Также важный вклад вносит и громкоговоритель, являющийся нагрузкой усилителя, поскольку его полное сопротивление меняется с частотой. На практике рассмотренным способом можно достичь снижения уровня нелинейных искажений по 2-й гармонике на 6 дБ. Подавление искажений методом компенсации надежно достигается только в том случае, если электронные лампы двух каскадов являются идентичными и имеют одинаковые режимы и нагрузки. Подавление искажений в двухтактном каскаде Двухтактные каскады очень широко применяется в качестве оконечных ступеней усилителей мощности и будут подробно рассмотрены. Особенностью работы двухтактного каскада является то, что при условии симметрии схемы, на вторичной обмотке выходного трансформатора наводится напряжение только на нечетных гармониках, а все четные гармоники подавляются. Если лампы, образующие двухтактный каскад, будут генерировать нелинейный продукт преимущественно на второй гармонике, что свойственно триодам, уровень нелинейных искажений двухтактного каскада теоретически окажется очень низким. Таким образом, двухтактный выходной каскад усилителя, построенный на триодах, работающих в режиме класса А с трансформаторным выходом удовлетворяет практически всем условиям для подавления нелинейных искажений. При работе в режимах класса АВ или В неизбежно будут возникать специфические искажения, вследствие нелинейности статических характеристик ламп в области отсечки анодного тока, а потому, если требуется низкий уровень нелинейных искажений, всегда нужно отдавать предпочтение режиму класса А. Говоря о хорошем подавлении нелинейного продукта на четных гармониках в двухтактном усилителе, нельзя не забывать о том, что пока две электронные лампы двухтактного каскада не будут точно согласованы друге другом по коэффициенту усиления и не будет обеспечен баланс по постоянному току, то подавление четных гармоник не будет полным в следствие асимметрии схемы. На практике в двухтактном каскаде обычно, удается достичь подавления четных гармоник примерно на 14 дБ, потому что сильная связь между двумя первичными полуобмотками выходного трансформатора облегчает задачу установить баланс по переменному току. Подавление искажений в дифференциальной паре Дифференциальная пара с приемником неизменяющегося (стабильного) тока теоретически обеспечивает оптимальные условия для подавления нелинейных искажений, потому что ток полезного сигнала вынужден проходить между двумя электронными лампами без потерь. При условии, что эквивалентные сопротивления нагрузок обеих ламп согласованы, размах напряжения на каждом аноде должен быть одинаковым, а сами анодные напряжения противофазными, теоретически обеспечивая идеальное подавление нелинейного продукта на 2-й гармонике. Резисторы анодной нагрузки могут быть легко согласованы с точностью до 0,2% путем измерения падающих на них напряжений по цифровому вольтметру. Если к каждому аноду дифференциальной пары подключен в качестве нагрузки катодный повторитель, то паразитная емкость становится небольшой, так что на звуковых частотах любой разбаланс является незначительным. Даже при частоте полезного сигнала 20 кГц, реактивное сопротивление Хс= 1,6 МОм для входной емкости величиной 5 пФ обычного катодного повторителя, существенно больше, чем сопротивление резисторов анодной нагрузки, которое часто выбирается равным 47 кОм. В качестве примера, лампа двойной триод типа 6SN7GT компании Маллард с хорошо согласованными половинами сравнивалась в различных схемах (классический усилитель с общим катодом, дифференциальная пара и μ-повторитель) при величине анодного тока Ia = 7,5 мА, анодном напряжении 230 В, и размахом сигнала +14 дБ на аноде. Были выполнены измерения между анодами дифференциальной пары на уровне +20 дБ, соответствующим +14 дБ на каждом аноде (рис. 4.14). В табл. 4.4. можно видеть, что дифференциальная пара подавляет четные нелинейные гармонические искажения на 26 дБ, но суммирует нечетные гармоники. Хотя уровень 0,0035% 3-й гармоники не представляет проблемы, это показывает, что идеальная дифференциальная должна строиться на лампах, которые создают небольшое количество искажений на нечетных гармониках. И наоборот, μ-повторитель не так эффективно уменьшает 2-ую гармонику, но уровень всех других гармоник был ниже пределов надежного измерения измерителя искажений. Таблица 4.4 Гармоника С общим катодом Дифференциальная пара μ-повторитель 2-я -51 дБ -77 дБ -68 дБ 3-я -93 дБ -89 дБ — 4-я (-106 дБ) — —

Нечетная гармоника — обзор

2.3 Работа с гармониками

Работа ЛСЭ на нечетной гармонике основной длины волны была впервые предложена Мадей и Табером [32]. Полную теорию гармонической генерации дал Колсон в 1981 г. [33]. Коэффициент усиления гармоники может быть выше, чем у основной гармоники. Если использовать этот подход для генерации на короткой длине волны без увеличения энергии ускорителя, параметр вигглера K должен быть больше единицы, чтобы гармоническое усиление было выше, чем усиление на основной частоте.Коэффициент усиления на гармонике намного более чувствителен к ухудшению из-за разброса энергии и эмиттанса электронного пучка, а также качества поля вигглера, поэтому на практике коэффициент усиления гармоники редко бывает выше, чем усиление на основной частоте для большинства существующих систем.

Экспериментальная проверка генерации третьей гармоники была продемонстрирована в 1987 г. в Стэнфорде [34], в 1988 г. в LANL [35] и в 1992 г. в Орсе [28]. Генерация на гармониках выше третьей пока не продемонстрирована. Уоррен предположил, что работа с очень высокими гармониками может быть хорошим способом работы с компактным ЛСЭ [36].Приведенный ниже анализ представляет собой краткое изложение его подхода. Примерная формула усиления для ЛСЭ с линейно поляризованным вигглером имеет вид

(3) g = 0⋅004IγQNβ2ηɛηγηfημ,

, где I — пиковый ток, N _β = N _W K / γ — количество периодов бетатрона в вигглере, Q — коэффициент, который зависит от параметра вигглера и номера гармоники h :

(4) Q = h31 + K2 [J (h − 1) / 2 (hξ) −J (h − 1) / 2 (hξ)] 2,

где переменная ξ равна

(5) ξ = K22 (1 + K2),

η _γ равно ухудшение усиления из-за разброса по энергии,

(6) ηγ = [1+ (42hNσγ / γ) 2] -1,

η _ε — ухудшение усиления из-за среднеквадратичного эмиттанса ε (эмиттанс равен мера площади поперечного фазового пространства, занимаемой распределением электронного пучка)

(7) ηɛ = [1 + ηγ (4π2ɛNβ / λ) 2] −1/2

η _f — коэффициент заполнения для оптическая мода

(8) ηf = (1 + 4πɛ / λ) −1, 9 0007

и η _μ — ухудшение усиления из-за эффектов проскальзывания

(9) ημ = [1+ (hNλ / 3σz)] — 1,

, где σ _z — среднеквадратичная длина электронного импульса.Ухудшение усиления из-за разброса энергии и эмиттанса аналогично эффектам неоднородного уширения в обычных лазерах и возникает из-за того, что некоторые электроны имеют резонансную длину волны, которая отличается от резонансной длины волны среднего электрона на большую часть ширины полосы усиления. Уменьшение усиления из-за коэффициента заполнения просто является результатом интеграла перекрытия между оптической модой и электронным пучком. Уравнение (8) предполагает, что оптическая мода и электронный пучок оптимально сфокусированы в области усиления.Поскольку усиливающая среда может влиять на реальную перетяжку оптической моды, это уравнение является приближенным. Коды трехмерного моделирования можно использовать для более точной оценки этого члена. Уменьшение усиления из-за проскальзывания происходит, когда преобразование Фурье формы электронного сгустка во времени имеет спектральную ширину полосы, сравнимую или большую, чем ширина полосы усиления. Это уменьшает связь электронного луча с оптическим импульсом.

Учитывая параметры электронного пучка, такие как эмиттанс ε, разброс по энергии σ _γ , пиковый ток I и энергия γ, можно спроектировать ондулятор, который дает параметр уменьшения усиления η _ε или η _γ из 0.5. Уоррен показал, что при больших значениях ε / λ гармоника, при которой оба коэффициента ухудшения усиления равны 0,5, может быть довольно высокой. К сожалению, в этом случае усиление обычно слишком мало, чтобы быть полезным. Для малых значений ε / λ все еще можно спроектировать вигглер, который устанавливает η _γ равным 0,5, и обнаруживается, что значения η _ε и η _f всегда больше 0,5. Если кто-то хочет работать с высокой гармоникой, количество периодов вигглера обычно довольно мало.Поскольку уменьшение усиления из-за проскальзывания одинаково для всех гармоник, значение η _μ обычно близко к единице.

Значение Q для данного номера гармоники и оптимального K меняется очень мало. Это показано в таблице 1, в которой перечислены оптимальные значения для Q и K , для которых встречается максимальное значение. Также перечислены значения K , для которых значение Q падает на 10% и 50% от своего пикового значения.Как видно из таблицы 1, оптимальное значение для Q мало меняется от h = 3 до h = 15. Это означает, что если коэффициент уменьшения неоднородного усиления, коэффициент проскальзывания и коэффициент заполнения не ухудшаться очень быстро с номером гармоники, усиление будет практически независимым от гармоники. Кроме того, значения для K _{90 %} находятся в доступном диапазоне от 1 до 2. Warren et al. указали, что параметры вигглера, близкие к единице, могут быть достигнуты для периодов всего 3 мм с помощью импульсного электромагнитного вигглера [37].Попытки управлять ЛСЭ с использованием такого вигглера пока не увенчались успехом [38].

ТАБЛИЦА 1. Максимальные значения для Q при нескольких числах гармоник и параметры вигглера, для которых имеют место максимум, 90% максимума и половина максимума

h	Q max	K макс	K 90%	K 50%
3	0,36064	1,064	0.832	0,566
5	0,30946	1,428	1,158	0,852
7	0,28843	1,684	1,560	1.200
11	0,26901	2,057	1,709	1,327
15	0,259521	2.337	1,953	1,533

В качестве примера системы, которая может достичь широкополосной перестройки с помощью гармонической генерации, я рассчитал коэффициент усиления в зависимости от длины волны для лазера, работающего в инфракрасном диапазоне, с использованием электронного луча с параметрами, аналогичными тем, что присутствует в фотоэлектронном инжекторе LANL APEX, работающем при 20 МэВ [39], или в установке Princeton CIRFEL [31]. Такое устройство было бы довольно компактным и могло бы генерировать генерацию от 3 до 80 мкм с коэффициентом усиления более 30%.На каждой гармонике длина волны будет изменяться путем настройки энергии электронного пучка.

Как сгенерировать нечетные и четные гармоники в Reason?

Почти все устройства в Reason, которые способны перегрузить сигнал, будут генерировать НЕЧЕТНЫЕ и / или ЧЕТНЫЕ обертоны / гармоники. Большинство из них используют и то, и другое, некоторые — НЕЧЕТНЫЕ или ЧЕТНЫЕ гармоники. Если вы не знакомы с этими концепциями, настоятельно рекомендуется использовать старую добрую статью Джека Эндино. Но что ж, я объясню это как можно проще в блоге ниже.Джек утверждает, что ленточные устройства генерируют обертоны ODD, а трубка может воспроизводить как ODD, так и EVEN обертоны.

ЧЕТНЫЕ гармоники — это частоты, которые являются 2, 4, 6, 8 и т. Д. Умножениями основной / основной частоты.
НЕЧЕТНЫЕ (также называемые НЕЧЕТНЫМИ) гармоники — это 3, 5, 7 и т. Д. Умножения основной / основной частоты.

Таким образом, разница между ними — либо четное число в качестве множителя, либо нечетное число в качестве множителя. Все просто, правда?

Список НЕЧЕТНЫХ и ЧЕТНЫХ

Я часто использую чистую синусоидальную волну, используя фантастический Wavetable OSC в Thor для генерации тона A3 / 440 Гц.ЧЕТНЫЕ и НЕЧЕТНЫЕ гармоники A3 / 440 Гц тогда следующие:
# 1 A3 (основная / основная)
# 2 ЧЕТНАЯ — A4 — октава
# 3 НЕЧЕТНАЯ — E5 — идеальная квинта
# 4 ЧЕТНАЯ — A5 — на 2 октавы выше
# 5 ODD — C # 6 — мажорная треть на 3 октавы выше
# 6 EVEN — E6 — идеальная квинта на 3 октавы выше
# 7 ODD — G6 — доминирующая семерка на 3 октавы выше
# 8 EVEN — A6 — на 3 октавы выше

Вот изображение, сделанное с помощью Ableton Spectrum:

Цифры, как вы можете видеть, соответствуют приведенному выше списку.Первые 3 гармоники (2, 3 и 4 как множители) очень хороши, только октавы и идеальная квинта! Но, как вы можете видеть, все тоны — это музыкальные частоты, которые соответствуют названиям нот в нашей модальной системе.

Сейчас много споров о том, что звучит лучше, ЧЕТНОЕ или НЕЧЕТНОЕ / НЕЧЕТКОЕ? Посмотрите это видео, например:

На мой взгляд, это смесь гармоник НЕЧЕТНЫХ и ЧЕТНЫХ, которая создает наилучшую насыщенность. И уровень, на котором они генерируются.Хотя я упомянул только первые 7 гармоник, большинство устройств насыщения будут генерировать обертоны, которые будут намного выше этого. Некоторые даже выходят за пределы 20 кГц (за пределы 10-й октавы!) И могут даже вызвать проблемы с псевдонимом!

Очень высокие гармоники могут привести к тонкому звуку. Так что добавление фильтра нижних частот перед искажением может быть очень полезно, например, с помощью прекрасного Reason Pulveriser. И не забывайте, что использование фильтра высоких частот перед перегрузкой — отличный способ минимизировать неприятные интермодуляции.

Только ЧЕТНЫЕ гармоники?

Как генерировать только ЧЕТНЫЕ гармоники в Reason? Создатель в Торе может доставить. Требуется особый трюк, чтобы открыть гейт Фильтра 1 в Thor, чтобы вы могли пропустить через него аудиосигнал. А поскольку это МОНО, вам нужно 2 Тора для обработки входа СТЕРЕО.

Rectify Shaper выдает только ЧЕТНЫЕ гармоники. И если вы включите Drive до упора, это убьет 1-ю частоту, основную частоту! Это как если бы вы сместили весь аудиосигнал на октаву! 🙂 Довольно круто, правда?

Unipulse Shaper также выдает только ЧЕТНЫЕ гармоники.Но он всегда убивает первую, корневую частоту, независимо от величины Drive. Его процесс насыщения генерирует больше высоких частот, чем Rectify Shaper. Вкратце: Rectify теплее, чем Unipulse.

Только нечетные гармоники?

Формирователь бипульсов в компании Thor передает только нечетные гармоники. То же, что и Echo , используя настройку OVDR . И устройство Synchronous с настройками Dist 1 и Dist 2 . А также Soft Shaper , Hard Clip Shaper , Saturate Shaper и Sine Shaper в Thor будут передавать только нечетные гармоники.

Отлично подходит для получения красивой ленты, такой как насыщенность!

Пульверизатор имеет несколько отличных функций насыщения: он генерирует только нечетные гармоники при более низких настройках привода (или когда вы не слишком сильно нажимаете на его вход), но также начинает добавлять ЧЕТНЫЕ гармоники к сигналу, когда вы поднимаете привод / Вход. Таким образом, он может воспроизводить нечетные или нечетные + четные гармоники в зависимости от количества возбуждения / входа.

Пожалуйста, не ослепляйте наукой! Я тоже. Отправка тона 440 Гц через устройства — это не то, чем вы хотите заниматься в реальной жизни в течение длительного времени.Лучше примените немного насыщенности к классному звуку. Просто экспериментируйте, используя свои уши. Добавьте немного овердрайва к гитарам, басу, барабанам, вокалу, чему угодно. Обертоны — прекрасное дополнение к сигналу.

Похожие сообщения

Нечетное и четное гармоническое искажение

Хорошо, позвольте мне попытаться сделать это немного более понятным:

Мы говорим здесь не только об искажении, но и о том, как все искажается. Возьмем чистую синусоидальную волну 1000 Гц.Он должен оставаться чистой синусоидой независимо от того, играете ли вы громко или тихо. Никаких обертонов. Этого не происходит в реальном мире, когда вы начинаете проталкивать этот сигнал через кучу электроники.

Если вы, например, перегрузите усилитель синусоидой, генерируются дополнительные ноты (которых нет в исходном сигнале). Они точно кратны исходному сигналу с частотой 1000 Гц. Таким образом, в дополнение к исходному сигналу 1000 Гц вы можете получить различные уровни добавленных нот: 2000, 3000, 4000, 5000, 6000, 7000 и т. Д.Четные кратные называются «четными гармониками», а нечетные кратные — «нечетными гармониками».

Четные гармоники 2000 Гц, 4000 Гц и 8000 Гц подходят; они идеальные октавы исходной ноты и могут добавить звуку жирности и теплоты. Лампы отлично подходят для искажения, потому что они, естественно, генерируют больше этих ровных гармоник при чрезмерном возбуждении.

Проблема заключается в нечетных гармониках (генерируемых большим количеством транзисторов). Эти ноты гармонического искажения 3000 Гц и 5000 Гц фактически конфликтуют в музыкальном плане с обычными нотами, встречающимися в музыкальных гаммах.

В большей части музыки, которую мы слышим, используется так называемая «темперированная гамма». «Высота» некоторых нот отрегулирована так, чтобы все ноты звучали приятнее для наших западных ушей. Итак, когда мы играем аккорд «C», ноты «G» и «E» были «отрегулированы по высоте», чтобы они хорошо звучали с основной основной нотой «C».

Но гармонические искажения наплевать на «умеренную шкалу». Он будет издавать идеальные 3 и 5 кратные исходной ноты, и это будет конфликтовать с некоторыми настоящими нотами, которые мы играем.

То, как вещи искажаются, может быть очень важным, и это то, о чем мы здесь говорим. Лампы склонны отдавать предпочтение октавам, когда они искажаются, и искажение обычно очень постепенное. Транзисторы предпочитают нечетные кратные искажения и могут срабатывать быстро и сильно, когда вы достигнете своего предела.

Эти искажения присутствуют практически во всем, что мы используем в студии, от микрофонов до динамиков; все они будут искажаться, если выйти за их пределы. Но часто важно понимать, как они искажаются, чтобы использовать это в своих интересах.

Недавно в ветке про кавер-версию песни я фактически предложил пропустить основной вокал через коробку дисторшна, чтобы добавить песне немного песка; все согласились, что искаженный вокал звучал лучше, чем чистый вокал — для этой песни.

Итак, теперь все это имеет немного больше смысла?

Механизм возникновения электромагнитного шума | Базовый курс по шумоподавлению

2-4. Гармоники в цифровом сигнале

Как описано в Разделе 2-3, одним из типов источников шума, генерируемых цифровой схемой, являются гармоники.Если вы можете хорошо контролировать гармоники, вы можете эффективно реализовать подавление шума для цифровых схем. В этом разделе описывается основная природа гармоник, содержащихся в цифровых сигналах.

2-4-1. Характер гармоник с точки зрения шума

(1) Цифровой сигнал состоит из гармоник

Как правило, все волны с постоянным периодом цикла могут быть разбиты на основную волну с циклической частотой и гармоники с частотами, кратными циклической частоте. ^{[Ссылка 2]} Множитель основной волны называется гармоническим порядком.
В случае точно повторяющихся волн нет других частотных составляющих, кроме этих. Многие цифровые сигналы имеют повторяющуюся форму волны. Следовательно, когда измеряется частотное распределение (называемое «спектром»), оно точно разбивается на гармоники, показывая дискретно распределенный спектр.

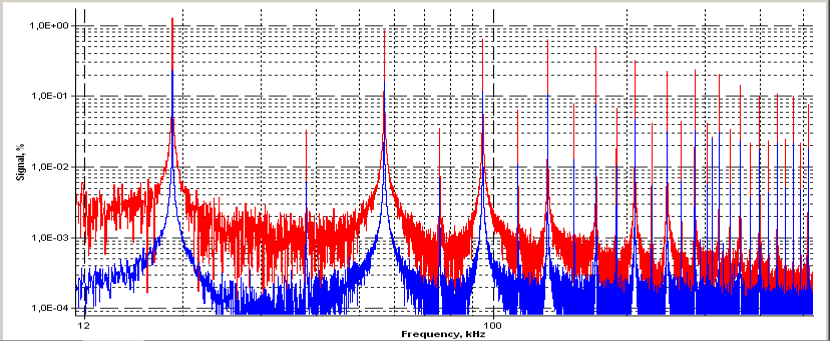
(2) Измерение гармоник тактового сигнала

На рис. 2-4-1 показан пример гармоник тактового сигнала 33 МГц, измеренных анализатором спектра.Участки, которые выступают вверх, как игла, являются гармониками и точно наблюдаются в интервале 33 МГц. Вы можете видеть, что нечетные и четные гармоники имеют разную тенденцию. Нижняя часть около 40 дБ или ниже указывает на фоновый шум анализатора спектра.

(3) Как найти источник шума по частоте шума

Вышеупомянутая природа гармоник пригодится при поиске источника шума на основе частоты шума. Измерение интервала спектра шума позволяет нам по аналогии думать о циклической частоте сигнала, вызывающего шум.Например, предположим, что мы наблюдали шум, подобный показанному на рис. 2-4-2, в электронном устройстве. Интервал частот с сильным шумом вроде как 33MHz. Поэтому считается, что этот шум вызван схемой, которая работает синхронно с тактовой частотой 33 МГц.
Даже если в этом электронном устройстве одновременно используются схемы с близкой циклической частотой, такой как 33,3 МГц или 34 МГц, такую ​​частоту можно разделить, если вы можете точно измерить частоту шума и интервал.Например, если на рис. 2-4-2 присутствует шум на частоте 330 МГц, мы можем предположить, что он вызван схемой с частотой 33,0 МГц, а не 33,3 МГц. Это потому, что ни сигнал 33,3 МГц, ни 34 МГц не содержит гармоники 330 МГц.

(4) Не содержит частот, кроме целых кратных

Кроме того, циклический сигнал не имеет частотной составляющей ниже основной частоты. Например, сигнал 100 МГц никогда не будет генерировать шум 20, 50 или 90 МГц. Если вы обнаружите шум на любой из этих частот, считается, что он вызван разделенным по частоте сигналом, а не исходным сигналом.
Цифровые схемы часто работают синхронно с тактовым сигналом, и многие из них работают на частоте 1 / N от тактового сигнала (так называемое «частотное деление»). В этом случае гармоники представляют собой целые кратные частоты сигнала с разделением по частоте. Однако, если две или более схемы работают с одним и тем же тактовым сигналом, который был разделен по частоте, гармоники тактового сигнала и гармоники частотно-разделенного сигнала перекрываются друг с другом, что затрудняет их различение.

2-4-2. Составной сигнал гармоник

(1) Добавление синусоидальных волн приближает его к цифровой форме волны

Как форма волны цифрового сигнала и включенные гармоники связаны друг с другом? На рис. 2-4-3 показаны изменения формы сигнала при добавлении гармоник малого порядка к основной волне. Вы можете видеть, что синусоидальная форма исходной основной волны приближается к прямоугольной по мере того, как к ней добавляется каждая гармоника.

(2) Высшие гармоники меньше влияют на форму сигнала

Напротив, при вычитании гармоник более высокого порядка из идеальной прямоугольной формы волны она становится ближе к синусоидальной волне.Однако изменение мягкое. В качестве примера на рис. 2-4-4 показаны формы сигналов, в которых наивысшая гармоника удаляется одна за другой из формы сигнала, которая была добавлена ​​до гармоники 17-го порядка.

(3) Форма волны при нагрузке 50% с сильными нечетными гармониками

При создании формы волны с коэффициентом заполнения 50% суммируются только нечетные гармоники. Если вы создаете сигнал без коэффициента заполнения 50%, вам также потребуются четные гармоники, как описано в разделе 2-4-5. Здесь скважность означает отношение уровня сигнала «Высокий» за один цикл.
В реальных сигналах коэффициент заполнения никогда не будет составлять всего 50%. Таким образом, четные гармоники также включены, как показано на рис. 2-4-1.

(4) Уменьшение шума путем отсечения гармоник более высокого порядка

Как указано выше, компоненты с относительно низкой частотой (более низкого порядка) среди гармоник цифрового сигнала важны для поддержания формы сигнала, в то время как компоненты с более высокой частотой (более высокого порядка) могут считаться менее важными.
Однако, как описано в Разделе 2-3-6 Гармоники в сигнале, гармоники более высокого порядка имеют более высокие частоты и, следовательно, легко излучаются и вызывают шум.Следовательно, подавление шума реализуется путем устранения гармоник более высокого порядка до такой степени, чтобы не вызывать проблем с формой сигнала. Обычно сохраняется до 3-7 гармоник, а любые гармоники более высокого порядка удаляются. На рис. 2-4-5 показаны результаты измерения форм сигналов и шума при устранении гармоник с помощью фильтра нижних частот. Цифровой сигнал без гармоник имеет форму волны с закругленными углами, как это, вместо приличных квадратных углов.

(5) Устранение гармоник с помощью фильтров подавления электромагнитных помех для сигналов.

Фильтры подавления электромагнитных помех для сигналов — это фильтры, которые используются для этой цели.На рис. 2-4-5 фильтр подавления электромагнитных помех с частотой среза 150 МГц использовался для сигнала 20 МГц. Следовательно, форма волны на рисунке (b) содержит до 7-й гармоники (140 МГц). Фильтры подавления электромагнитных помех будут дополнительно описаны в следующих разделах.

2-4-3. Тренд частот гармоник

(1) Природа гармоник трапецеидальной волны

Давайте посмотрим на тенденцию изменения уровней гармоник в цифровом сигнале. Если форма волны напряжения цифрового сигнала имеет идеальную трапециевидную форму, как показано на рис.2-4-6, можно найти несколько тенденций.
Рисунок 2-4-6 (b) показывает огибающую гармоник, включенных в трапециевидную волну. Как показано на рисунке, если частота отложена по логарифмической оси, огибающая гармоник образует простую многоугольную линию с двумя точками перегиба (A, B). ^{[Ссылка 2]}
A — точка частоты, определяемая шириной импульса сигнала t _p . Чем уже становится ширина импульса, тем больше A смещается в сторону более высоких частот.
B — частотная точка, определяемая временем нарастания (спада) сигнала t _r . Чем короче становится этот период, тем больше B смещается в сторону более высоких частот. (При условии, что время нарастания и спада одинаковы для упрощения тренда)

(2) Для управления уровнями гармоник

Огибающая гармоник имеет тенденцию иметь постоянный уровень от постоянного тока до точки A (область a), уменьшаясь в соответствии с частотой со скоростью 20 дБ / дек.(20 дБ на каждую декаду частоты) от точки A до точки B (область b), а затем резко уменьшается со скоростью 40 дБ / дек. от точки B к стороне более высоких частот. (Область c). Следовательно, желательно сместить точки A и B в сторону более низких частот с точки зрения подавления шума.
См. Ссылку ^{[Ссылка 2]} , который показывает теоретическую формулу, выражающую эту тенденцию.

(3) Сравните теоретическую кривую с фактическим измерением.

Приведенные выше частотные характеристики лишь указывают на общую тенденцию.На отдельные уровни гармоник может влиять рабочий цикл и т. Д., И они могут быть немного меньше, чем эта огибающая (конкретная гармоника может быть очень маленькой).
На рис. 2-4-7 показан пример сравнения тенденции на рис. 2-4-6 с фактическим измерением. На рис. 2-4-7 (a) показан случай продолжительности включения 50%, а на (b) показан случай продолжительности включения 20%.
Формы сигналов напряжения, измеренные осциллографом, показаны в левой части рисунка, а спектры, измеренные анализатором спектра, показаны в середине.Наблюдались те же гармоники, что и на рис. 2-4-1. В случае коэффициента заполнения 20% на рис. 2-4-7 (b) вы можете видеть, что уровни четных гармоник почти такие же большие, как уровни нечетных гармоник.
В правой части рисунка ось частот спектров в середине преобразована в логарифмическую ось, чтобы их можно было сравнить с огибающей на рис. 2-4-6. Для справки, красные линии обозначают теоретические конверты. Можно сказать, что конверт рис.2-4-6 хорошо соответствуют реальным измерениям в диапазоне частот ниже 100 МГц. В более высоком диапазоне частот выше 200 МГц фактические измерения меньше теоретических значений. Считается, что это связано с тем, что генератор сигналов, используемый для эксперимента, не мог выдавать точные трапециевидные волны из-за своего верхнего предела в генерации частоты.

(4) Разработка электронных устройств с меньшим уровнем шума

Следующие тренды получены из формы огибающей, показанной на рис.2-4-6 (б).

1. (я) Чем выше становится циклическая частота сигнала, тем уже ширина импульса. Следовательно, точка A перемещается в сторону более высокой частоты, что приводит к большему шуму.
2. (ii) По мере того, как время нарастания становится короче (скорость сигнала увеличивается), точка B перемещается в сторону более высокой частоты, что приводит к увеличению шума.

Чтобы спроектировать схему, вызывающую меньший выступ, полезно избегать этих тенденций и сдвигать точки A и B в сторону низких частот.Если вы не можете избежать вышеуказанных тенденций в своей конструкции, будет легче выполнить подавление шума, если сигнальная линия будет снабжена контактными площадками для подключения фильтров подавления электромагнитных помех.
При наблюдении гармоник реального цифрового сигнала трудно наблюдать область a. Это связано с тем, что многие цифровые сигналы имеют коэффициент заполнения, близкий к 50%, и, таким образом, точка А находится на стороне более низкой частоты основной частоты.

2-4-4. Влияние времени нарастания сигнала

(1) Изменение времени нарастания тактового сигнала 10 МГц

Инжир.2-4-6 показали, что замедление скорости нарастания формы волны перемещает точку B в сторону более низких частот и, таким образом, подавляет уровни гармоник. На рис. 2-4-8 показан пример, подтверждающий эту тенденцию расчетом.
Здесь гармоники рассчитываются на основе циклической частоты 10 МГц, скважности 50% и величины напряжения 1 В. В левой части рисунка показана предполагаемая форма волны сигнала, а в середине показаны результаты расчета спектра гармоник. Как и на рис. 2-4-7, правые графики показывают результаты с частотной осью, преобразованной в логарифмическую ось.Правые графики показывают каждый спектр точками и перекрывают огибающую, показанную на рис. 2-4-7. Уровень спектра был рассчитан как среднеквадратическое значение, исходя из предположения, что для измерения используется анализатор спектра. То же самое относится ко всем следующим данным.

(2) Точка B появляется на частоте 30 МГц при времени нарастания 10 нс

На рис. 2-4-8 (а) показан случай быстрого подъема ( т _р = 0,1 нс), а (б) — случай медленного нарастания ( т _р = 10 нс).Точка B конверта, рассчитанная по формуле на рис. 2-4-6, составляет прибл. 3 ГГц при условии (а), что значительно отклоняется от диапазона отображения (до 1 ГГц) графика. При условии (b) прибл. 30 МГц.
Результаты расчетов на рис. 2-4-8 (a) показывают, что спектр гармоник имеет тенденцию просто уменьшаться со скоростью 20 дБ / дек. Кроме того, было подтверждено, что точка B не видна в пределах диапазона отображения графика (до 1 ГГц).
Напротив, результаты расчетов на рис.2-4-6 (b) показывает, что гармоники резко уменьшаются со скоростью 40 дБ / дек. выше частотного диапазона более 30 МГц. Точка перегиба, которая считается точкой B, возможно, существует где-то здесь.

(3) Уменьшается на 20 дБ или более при 500 МГц

Сравнивая спектры в середине друг с другом, (б) при медленном нарастании сигнала уровни гармоник меньше, чем у других во всем частотном диапазоне, за исключением очень маленького диапазона в нижней части диапазона. Разница достигает более 20 дБ на частоте 500 МГц.
Из приведенных выше результатов расчетов ясно, что замедление скорости нарастания сигнала эффективно для подавления гармоник. Чтобы создать схему, которая вызывает меньше шума, эффективно выбрать ИС, которая работает как можно медленнее, чтобы не создавать проблем для работы схемы. Также эффективно использовать фильтры подавления электромагнитных помех для сигнала.

2-4-5. Влияние скважности формы сигнала на гармоники

(1) Изменяет скважность тактового сигнала 10 МГц

Одним из типов типичных цифровых сигналов, которые легко вызывают шум, является тактовый сигнал.Тактовые сигналы обычно имеют форму волны с коэффициентом заполнения около 50%. Как упоминалось ранее, если скважность близка к 50%, сигнал содержит сильные нечетные гармоники, в то время как четные гармоники имеют тенденцию быть слабыми. Уровни четных гармоник могут значительно изменяться в зависимости от продолжительности включения. (Изменения нечетных гармоник также велики в высокочастотном диапазоне, где порядки гармоник высоки). На рис. 2-4-9 показан пример, подтверждающий эту тенденцию расчетом.

(2) Гармоники сгруппированы в нечетную и четную группы

На рисунке сравниваются гармоники, в которых коэффициент заполнения постепенно изменяется с 50% (а) до 49.9% (b), а затем до 49% (c) на основе идеального быстрорастущего цифрового сигнала, показанного на рис. 2-4-8 (a). Эти результаты расчетов показывают, что четные и нечетные гармоники выстраиваются вдоль зеленой и желтой линий соответственно, указывая на различную тенденцию между четными и нечетными порядками.
На рис. 2-4-9 (a), который имеет скважность 50%, нечетные гармоники выстраиваются вдоль огибающей, показанной на рис. 2-4-6, в то время как четные гармоники не наблюдаются.

(3) Изменение режима на 1% может привести к разнице в 10 дБ

Напротив, рис.2-4-9 (b), который имеет коэффициент заполнения 49,9%, показывает четные гармоники, хотя уровни все еще низкие. На рис. 2-4-9 (c), где коэффициент заполнения изменен на 49%, показаны повышенные уровни четных гармоник, которые даже выше, чем нечетные гармоники в определенном диапазоне частот. При наблюдении за диапазоном более высоких частот более 1 ГГц или вычислении случая, когда коэффициент заполнения значительно отклоняется от 50%, вы можете наблюдать тенденцию, согласно которой относительное соотношение (выше / ниже) уровней четной и нечетной гармоник переключается в цикл.Пожалуйста, используйте MEFSS, чтобы подтвердить эту тенденцию.
Как указано выше, изменение коэффициента заполнения даже на 1%, которое трудно определить с помощью осциллографа, может вызвать изменение на несколько десятков дБ уровней четных гармоник и гармоник более высокого порядка. Нет значительных изменений в общей форме спектра, который все еще соответствует огибающей, показанной на рис. 2-4-5. Однако при рассмотрении каждого спектра в отдельности эти влияния кажутся значительными. Обратите внимание на это расположение, поскольку оно может серьезно повлиять на воспроизводимость измерения шума.
Что касается принятия решения о том, прошел или не прошел регулирование шума, оно считается неудачным, даже если только одна часть спектра превышает. Если такой компонент значительного отклонения близок к предельному, требуются тщательные измерения.

2-4-6. Гармоники напряжения и гармоники тока

(1) Сравните форму волны напряжения с кривой тока

Вышеупомянутое расположение гармоник основано на предположении, что форма волны напряжения имеет прямоугольную форму.Следует отметить, что даже несмотря на то, что реальная схема имеет прямоугольную форму волны для формы волны напряжения, форма волны тока может быть другой. Это означает, что шумовое излучение может иметь различную тенденцию в зависимости от того, в основном ли оно связано с напряжением или током.
На рис. 2-4-10 показаны результаты форм сигналов и спектров, рассчитанных MEFSS для случая установки конденсатора 5 пФ в качестве нагрузки при использовании цифровой схемы C-MOS. Форма волны напряжения близка к идеальному цифровому импульсу, а значения спектра гармоник близки к значениям огибающей, показанной на рис.2-4-6 (форма немного отличается из-за емкостной нагрузки, что указывает на точку минимума около 500 МГц).

(2) Ток содержит больше гармоник

Напротив, ток течет только в моменты нарастания и спада, как показано на рисунке. Спектр такой формы волны имеет постоянный уровень вплоть до высокой частоты в несколько сотен МГц (в зависимости от времени нарастания), как показано на рисунке. Следовательно, если возникает шум из-за тока, вероятно, шум вызван высокими частотами.Таким образом, MEFSS также может рассчитывать спектр формы волны тока.
В результатах измерений шума, показанных на рис. 2-3-14, почти не видно спектра напряжения выше 500 МГц на (b), в то время как спектр шума излучения на (c) показывает сильное излучение. Следовательно, можно считать, что причиной эмиссии шума в этом эксперименте был электрический ток как одна из причин, указывающих на различия в частотных распределениях между источником шума и излучаемым шумом.(В отличие от этого эксперимента, есть случаи, когда напряжение вызывает шумовое излучение)

(3) Ток имеет игольчатую заостренную форму волны

На рис. 2-4-10 причина того, что гармоники тока не затухают до высокой частоты, понятна, если вы думаете, что это потому, что форма волны тока имеет форму тонких пиков. Рассматривая модель трапецеидальной волны на рис. 2-4-6, форма волны пиковой формы, как и форма волны тока, может рассматриваться как трапецеидальная волна с очень малым коэффициентом заполнения.Для огибающей трапецеидальной волны с малым коэффициентом заполнения точка A смещается в сторону высоких частот, сохраняя постоянный уровень вплоть до высоких частот. Таким образом, гармоники формы волны тока можно наблюдать вплоть до высокой частоты без ослабления.
Обратите внимание, что модель трапецеидальной волны на рис. 2-4-6 отличается от формы волны тока, поскольку пики формы волны тока направлены вверх и вниз. Следовательно, модель трапецеидальной волны с малой скважностью имеет более сильные четные гармоники при смещении точки А.Однако эта тенденция слабее в текущей форме волны.

2-4-7. Влияние изменения формы импульса резонансом

(1) Резонанс вызывает искажение формы импульса

Поскольку приведенное выше объяснение предполагает, что форма импульса цифрового сигнала является идеальной прямоугольной формой волны, требуется коррекция, если форма волны отклоняется от прямоугольной формы волны из-за условий схемы. Одной из причин искажения формы импульса является резонанс ИС драйвера, ИС приемника и проводки.В этом разделе описаны примеры изменений в спектре, когда форма волны искажена резонансом.
Если пренебречь влиянием проводки, цифровую схему C-MOS можно рассматривать как очень простую схему, как показано на модельной диаграмме на рис. 2-4-10, что позволяет нам получить почти идеальную форму импульса при моделировании.

(2) Пример увеличения шума, вызванного звонком из-за длинной проводки

Как будет выглядеть осциллограмма, если к этой схеме добавить влияние проводки? Результаты расчета представлены на рис.2-4-10. На рис. 2-4-11 сравниваются формы сигналов между схемой с проводом и схемой без провода, предполагая, что провод длинный (20 см), так что влияние становится очевидным. Когда есть провод, сигнал сильно зазвонит. Соответственно, вы можете увидеть тенденцию к значительному увеличению гармоник около 150 МГц. (Чтобы наблюдать звон, напряжение было измерено в более широком диапазоне, чем на рис. 2-4-10)

(3) Подтвердить звонок экспериментально

Такой звон часто наблюдается в реальных цифровых схемах.На рис. 2-4-12 показан пример результата измерения, когда подключен провод длиной 20 см. Хотя он не такой сильный, как в моделировании на рис. 2-4-11, звон возникает в аналогичном цикле, показывая тенденцию к значительному увеличению гармоник около 150 МГц. Следовательно, если цифровая схема подключает более длинную сигнальную линию, форма сигнала, скорее всего, будет страдать от звона. В этом случае частота вызывного сигнала может вызвать более высокие уровни гармоник и, следовательно, вызвать проблемы с шумом.
Звонок результата измерения на рис.2-4-12 относительно меньше результата измерения на рис. 2-4-11. Считается, что это происходит из-за затухания за короткий период времени, поскольку в реальных схемах более или менее есть некоторые потери в ИС и скручивании. Величина напряжения также меньше, она составляет менее 3 В на рис. 2-4-12.
Кроме того, для измерения используется пробник на полевых транзисторах с полосой частот 2,5 ГГц в качестве пробника напряжения, который имеет отношение напряжений 10: 1. Следовательно, значения спектра, показанные на рис. 2-4-12, на 20 дБ меньше фактических значений.

(4) Индуктивность в проводке вызывает резонанс и, в свою очередь, вызывает звон

Звон, показанный на рис. 2-4-11, считается результатом резонансного контура, создаваемого внутри сигнального контура из-за индуктивности проводки. На Рис. 2-4-13 (a) показана модельная диаграмма.
На рис. 2-4-13 (a) индуктивность и электростатическая емкость проводки описаны в виде сосредоточенных параметров. Такое расположение позволяет нам понять, что в сигнальном контуре был создан RLC-последовательный резонансный контур.
При увеличении звона, генерируемого в нарастающей части сигнала на рис. 2-4-11, вы можете увидеть затухающую осциллирующую форму волны с периодом прибл. 7ns, как показано на рис. 2-4-13 (b). Цикл 7 нс равен 143 МГц по частоте, что почти соответствует частоте (150 МГц) нарастающей гармоники, наблюдаемой на рис. 2-4-11.

(5) Какая индуктивность в проводке?

Индуктивность и электростатическая емкость для 20-сантиметрового провода, принятые на рис.2-4-11 рассчитаны на прибл. 140 нГн и 10 пФ соответственно на основе параметров единичной длины, указанных в теории передачи. Если эти значения применяются к последовательному резонансному контуру RLC, показанному на рис. 2-4-13 (a), резонансная частота оценивается как прибл. 110 МГц. Хотя этот результат на 30% меньше, чем 150 МГц, наблюдаемый на рис. 2-4-11, в целом он согласуется, и поэтому упрощенная модель на рис. 2-4-13 (а) считается подходящей для понимания механизма звон.
Если вам нужно более точно оценить резонансную частоту, проводку следует рассматривать как линию передачи, а не использовать сосредоточенные параметры, такие как индуктивность и электростатическая емкость. (Пожалуйста, обратитесь к техническим книгам, чтобы узнать, как рассчитать параметры единичной длины проводки и как обращаться с проводкой как с линией передачи. ^{[Ссылка 5,6,7]} )

(6) Поглощение звона ферритовой шайбой

Обычно для подавления резонанса используются демпфирующие резисторы.Если вы хотите одновременно уменьшить шум, эффективно использовать ферритовый шарик вместо демпфирующих резисторов. На рис. 2-4-14 показан результат расчета при использовании ферритовой бусины в предыдущей модели. Кроме того, на рис. 2-4-15 показан результат расчета, в котором ферритовая бусина используется в испытательной схеме, показанной на рис. 2-4-12.
Поскольку на Рис. 2-4-14 и Рис. 2-4-15 была прикреплена ферритовая бусина, звон был ослаблен, и нарастание гармоник около 150 МГц исчезло, а также снизились уровни гармоник в весь частотный диапазон до 500 МГц одновременно.Таким образом, ферритовые бусины могут эффективно подавлять не только резонанс, но и нежелательные гармоники. Ферритовые шарики широко используются для устранения шума, вызванного гармониками цифрового сигнала.

2-4-8. Устранение гармоник фильтром подавления электромагнитных помех

(1) Фильтр подавления электромагнитных помех устраняет гармоники, которые могут вызывать шум

Использование фильтра подавления электромагнитных помех, такого как ферритовый шарик, позволяет полностью устранить нежелательные гармоники в цифровой схеме и, таким образом, подавить шум от гармоник.Хотя фильтр подавления электромагнитных помех и то, как он используется, будут описаны в отдельной главе, в этом разделе будет описан пример его эффектов.
Хотя подавление гармоник может быть достигнуто до некоторой степени за счет замедления времени нарастания с использованием низкоскоростной ИС (как описано выше) или деталей общего назначения, таких как резистор, большего эффекта можно добиться с помощью фильтров подавления электромагнитных помех. Даже если он выглядит как одна и та же форма сигнала, разница в эффекте подавления шума может составлять 10 дБ или более.

(2) Используйте фильтр среза 50 МГц для тактового сигнала 20 МГц

На рис. 2-4-16 показан пример эксперимента, который устранил шум тактового генератора 20 МГц с использованием фильтра подавления электромагнитных помех. Здесь случай использования трехполюсного конденсатора и случай использования π -типа с частотой среза 50 МГц (более крутая частотная характеристика) сравниваются между собой. Хотя эффект шумоподавления превосходен в обоих случаях, вы можете видеть, что изменения формы сигнала и времени нарастания не обязательно соответствуют эффекту подавления шума.В π Фильтр -типа, по-видимому, способен устранять шум, сохраняя при этом форму импульса сигнала и время нарастания.

(3) Шум выглядит иначе на осциллографе или анализаторе спектра.

Это связано с тенденцией, согласно которой относительно низкочастотные компоненты, кажется, выделяются в форме сигнала, в то время как относительно более высокочастотные составляющие выделяются при измерении шума. Поскольку наблюдение за формой сигнала показывает форму волны, в которой складываются все частоты, более низкие гармоники с большой амплитудой оказывают более сильное влияние.Напротив, измерение шума дискретно наблюдает каждую частоту и больше зависит от высокочастотных составляющих (более высокого порядка) из-за того, что оно легко излучается антенной меньшего размера.

(4) Фильтр подавления электромагнитных помех для сигналов

Если вы используете фильтр с крутой частотной характеристикой, как у π -типа фильтра подавления электромагнитных помех, показанного на рис. 2-4-16, шум может быть эффективно подавлен при сохранении качества сигнала. Этот тип фильтра подавления электромагнитных помех будет дополнительно описан в следующих разделах.

Начало страницы

---

«2-4. Гармоники в цифровом сигнале »- Ключевые моменты

• Цифровой сигнал состоит из гармоник.
• Форма сигнала может поддерживаться гармониками более низкого порядка. Нежелательные гармоники более высокого порядка могут вызывать шум.
• Время нарастания существенно влияет на уровни высших гармоник.
• Фильтр подавления электромагнитных помех позволяет эффективно устранять нежелательные гармоники.

Что такое гармоника? — Определение с сайта WhatIs.com

Гармоника — это сигнал или волна, частота которой является целым (целочисленным) кратным частоте некоторого опорного сигнала или волны. Термин может также относиться к отношению частоты такого сигнала или волны к частоте опорного сигнала или волны.

Пусть f представляет основную или основную частоту сигнала переменного тока, электромагнитного поля или звуковой волны.Эта частота, обычно выражаемая в герцах, является частотой, на которой содержится большая часть энергии или на которой, как определено, должен возникать сигнал. Если сигнал отображается на осциллографе, форма сигнала будет повторяться с частотой, соответствующей f Гц.

Для сигнала с основной частотой f вторая гармоника имеет частоту 2 f , третья гармоника имеет частоту 3 f и т. Д. Пусть w представляет длину волны сигнала или волны в указанной среде.Вторая гармоника имеет длину волны Вт /2, третья гармоника имеет длину волны Вт /3 и так далее. Сигналы, возникающие на частотах 2 f , 4 f , 6 f и т. Д., Называются четными гармониками; сигналы на частотах 3 f , 5 f , 7 f и т. д. называются нечетными гармониками. Теоретически сигнал может иметь бесконечно много гармоник.

Почти все сигналы содержат энергию на гармонических частотах в дополнение к энергии на основной частоте.Если вся энергия в сигнале содержится на основной частоте, то этот сигнал представляет собой идеальную синусоидальную волну. Если сигнал не является идеальной синусоидальной волной, тогда некоторая энергия содержится в гармониках. Некоторые формы волны содержат большое количество энергии на гармонических частотах. Примерами являются прямоугольные волны, пилообразные волны и треугольные волны.

В беспроводной связи и радиовещании передатчики сконструированы таким образом, что они излучают минимум энергии на гармонических частотах. Обычно беспроводное устройство предназначено для использования только на одной частоте.Выходной сигнал на гармонических частотах может создавать помехи для других средств связи или вещания. Например, широковещательный сигнал на частоте 90,5 МГц (в стандартном диапазоне FM) будет иметь вторую гармонику на частоте 181 МГц, третью гармонику на частоте 271,5 МГц, четвертую гармонику на частоте 362 МГц и так далее. Некоторые или все эти гармонические сигналы, если они сильные, могут нарушить работу других беспроводных услуг.

4 способа добавления, усиления или возбуждения верхних гармоник

В миксе часто встречаются скучные элементы.Инструмент может быть правильным, партия, которую он играет, может быть правильной, но это все равно не звучит захватывающе. Добавляя верхние гармоники, мы можем придать звуку более полный, грубый и яркий характер — конечно, в зависимости от исходного сигнала. Эти дополнительные частоты могут создавать интересные тембры, которые ваша аудитория может наслаждаться прослушиванием за другим.

В этой статье мы рассмотрим четыре процесса, которые можно использовать для добавления или увеличения верхних гармоник, чтобы оживить скучный элемент микса. Это будет включать искажение, насыщение, сжатие и гармоническое возбуждение.

Общие сведения о гармониках

Чтобы понять, почему некоторые из этих процессоров вводят новую частотную информацию в существующий аудиосигнал, мы должны сначала быстро охватить концепцию гармоник.

Анатомически звук — это волна, колеблющаяся с определенной частотой. Эта базовая частота называется основной частотой и математически определяет любые дополнительные частоты, которые могут быть обнаружены в аудиосигнале.

Синусоида

Простейшая волна — это синусоида, непрерывная и плавная кривая, колеблющаяся между положительным и отрицательным значением.

Синусоида

Синусоидальную волну легко различить по характерному округлому тембру. Это связано с его довольно простым частотным составом. Обратите внимание на спектральный анализатор ниже, что синусоидальная волна имеет одиночный всплеск на частоте 198 Гц.

Частота синусоидальной волны

Для пояснения: высокочастотный контент, который вы видите в спектральном анализаторе, — это скрытый шум в моей аудиосистеме или минимальный уровень шума.Обратите внимание, что все это ниже -114 дБ, что практически не слышно по сравнению с синусоидальной волной.

Более сложные формы волны — любая форма, кроме синусоидальной волны — будут содержать дополнительные тона на других частотах, которые гармонически связаны с основной частотой.

Эти дополнительные тона называются гармониками, общий набор которых находится в целых числах, кратных основной частоте. Следовательно, тон с частотой 100 Гц может иметь гармоники с частотой 100 Гц, 200 Гц, 300 Гц, 400 Гц и т. Д.

Синусоидальная волна имеет одну гармонику, первую гармонику, которая находится на частоте, выраженной как основная частота x 1. Это, очевидно, все еще тот же шаг, что и основная частота, что означает, что частотный состав синусоидальной волны состоит только из основной частоты. .

Три из наиболее известных сложных волн — это пилообразная, квадратная и треугольная волны. Эти волны различаются тем, включают ли они гармоники, расположенные на кратных четных числах основной частоты — «четные гармоники» — или находящиеся на кратных нечетных числах — «нечетные гармоники» — или и то, и другое.Амплитуда этих гармоник также может отличаться.

Как правило, мы склонны считать четные гармоники менее резкими и более приятными, чем нечетные.

Пилообразная волна

Пилообразная волна содержит все гармоники, как четные, так и нечетные, кратные основной гармонике. Благодаря включению всех гармоник тембр пилообразной волны получается ярким и резким.

Пилообразная волна

Частотный состав пилообразной волны

Прямоугольная волна

Прямоугольная волна содержит все нечетные гармоники.Хотя прямоугольная волна обычно не такая яркая, как пилообразная, она все же имеет довольно резкий тембр.

Прямоугольная волна

Частота прямоугольной волны

Треугольник волна

Треугольная волна, как и прямоугольная волна, включает в себя все нечетные гармоники. Гармоники обычно имеют более низкие амплитуды, чем основная частота, и уменьшаются по амплитуде по мере того, как мы поднимаемся вверх по звуковому частотному спектру.Однако амплитуды гармоник в треугольной волне уменьшаются намного быстрее, чем в прямоугольной. Из-за этого треугольная волна более резкая, чем синусоида, но не такая яркая, как прямоугольная волна.

Треугольная волна

Частотное содержание треугольной волны

Обратите внимание, что фактически нет разницы между одной из высших гармоник в сложной волне — например, пилообразной, прямоугольной или треугольной волной — и синусоидальной волной на частоте и амплитуде этой гармоники.

Согласно открытиям математика 18 века Джозефа Фурье, мы можем эффективно воссоздать гармонический состав сложной волны, используя серию синусоидальных волн, расположенных на соответствующих частотах. Эти волны, если их суммировать в один звуковой сигнал, будут звучать как сложная волна.

Используя ту же логику, если мы можем каким-то образом сделать звуковой сигнал, такой как синусоида, более похожим на прямоугольную волну, мы можем ввести дополнительные гармоники в ранее простой сигнал. Это более или менее способ, которым следующие процессоры создают и увеличивают математически связанные верхние гармоники из входного сигнала, который изначально не содержит этих частот.

Искажения

Distortion используется для добавления верхних гармоник на протяжении десятилетий. Подумайте о звуковых различиях между электрогитарой с искажениями и ее чистой, неискаженной копией. Кажется, что искаженная гитара имеет более богатую гармоническую составляющую, заполняя частотный спектр более плотно, чем чистый сигнал.

В аналоговом или цифровом контексте искажение является результатом того, что амплитуда сигнала превышает пределы аудиосистемы. У системы нет способа точно записать эти пики, она только распознает, что сигнал приближается к пределу и находится где-то выше него.

Поскольку система не может точно воссоздать сигнал, выходящий за предел, система устанавливает амплитуду сигнала на максимально возможное значение: сам предел. В результате форма волны сигнала на этих пиках по существу обрезается.

Мы называем это жестким ограничением, когда сигнал остается неизменным до тех пор, пока он не достигнет предела, когда пики затем полностью сглаживаются, пока сигнал снова не перейдет в воспроизводимую амплитуду.

Жесткая клипса

Обратите внимание, что по мере сглаживания пиков синусоидальной волны она становится все более и более похожей на прямоугольную волну.Как мы упоминали ранее, прямоугольная волна содержит нечетные гармоники и поэтому имеет резкий и ломкий тон.

Это «квантование» аудиосигнала производит высшие гармоники, которые гармонично связаны с частотой исходного аудиосигнала.

Hard clipping может иметь агрессивный звук, полностью разрушающий целостность аудиосигнала, если довести его до крайности. Из-за чрезмерного введения верхних гармоник частотная составляющая исходного сигнала становится менее понятной, в результате чего выходной сигнал все меньше и меньше представляет исходный сигнал.

На этих экстремальных уровнях искажение отлично подходит для добавления зернистости и создания агрессивного тона. В приведенных ниже аудио примерах я продемонстрировал этот драйв на басу, электрическом пианино и вокале с использованием Trash 2.

Вот сухие звуки:

Вот те же звуки с сильным искажением:

Сильно искаженные басы

Электропианино с сильными искажениями

Сильно искаженный вокал

На более умеренных уровнях или в случае лампового искажения, которое создает ровные гармоники, искажение может иметь «согревающий» эффект, слегка добавляя верхние гармоники для создания более плотного звука.Ниже я продемонстрировал более легкое искажение, используя те же звуки:

Слегка искаженные басы

Электропианино со слабым искажением

Слегка искаженный вокал

Насыщенность

Насыщенность очень похожа на искажение как по своей причине, так и по звуковому характеру.Однако различий достаточно, чтобы заметить разницу.

Общий эффект насыщенности в современном цифровом аудиопроизводстве связан с эффектом насыщенности ленты в контексте аналоговой записи. Опять же, как и в случае искажения, насыщение возникает, когда амплитуда сигнала превышает пределы, при которых он может быть записан и воссоздан.

Однако магнитная лента, используемая в аналоговой записи, не реагирует как электрическая цепь или цифровая аудиосистема. Вместо этого из-за химического состава магнитной ленты возникает более легкий, похожий на сжатие эффект.

Мы называем это мягким ограничением, поскольку пики аудиосигнала более мягко округляются при приближении к системному пределу, а не полностью обрезаются, как при жестком ограничении.

Мягкая клипса

В итоге насыщенность вообще довольно приятный эффект. Он может добавить теплоту мягкого искажения, и его часто можно использовать сильнее, чем искажение, без полного прерывания аудиосигнала.

Поскольку насыщенность не привносит резкость искажения, она отлично подходит для добавления верхних гармоник к «жирным» низкочастотным звукам, а также для склеивания групп элементов вместе.

Я пропустил предыдущие три звука через некоторое насыщение, используя тип искажения Trash 2 «Tape Saturation», чтобы продемонстрировать звуковые различия между насыщенностью и искажением:

Слегка искаженный вокал

Слегка искаженный вокал

Слегка искаженный вокал

Жесткое сжатие

Вы должны заметить, что и искажение, и насыщенность действуют путем сжатия пиков аудиосигнала, когда его амплитуда превышает определенный порог.Этот процесс должен показаться довольно знакомым, поскольку он является основой для обычного сжатия.

Следовательно, поскольку искажение и насыщенность могут создавать и увеличивать верхние гармоники, стандартная компрессия может вызвать аналогичный эффект.

Основное различие между сжатием и искажением / насыщением заключается в том, что сжатие обычно действует намного медленнее, поскольку искажение и насыщение фактически не имеют времени атаки. Следовательно, умеренное сжатие обычно не приводит к отсечению, вызванному двумя предыдущими процессорами.

Однако жесткое сжатие с достаточно быстрым временем атаки и достаточно высоким коэффициентом — как в случае с лимитером — может начать имитировать эффекты клиппирования. Следовательно, мы можем использовать жесткое сжатие или жесткое параллельное сжатие для достижения результатов, аналогичных искажению или насыщению.

Как правило, искажение — это более специализированный способ создания агрессивного звука, чем жесткая компрессия. Однако мы можем использовать жесткое параллельное сжатие, чтобы добиться более динамичного звука, сохраняя при этом способность балансировать жестко сжатый сигнал с необработанным сигналом.

Опять же, я обработал предыдущие три звука с помощью жесткого параллельного сжатия:

Параллельная обработка может использоваться для реализации любого из эффектов, которые мы сегодня обсуждаем. Зайдите сюда для более подробного обсуждения параллельного сжатия, искажения и насыщенности.

Возбуждение гармоник

Возбудители гармоник очень похожи на искажение и насыщение, поскольку они добавляют верхние гармоники в процессе искажения.Основное отличие состоит в том, что они имеют тенденцию вводить верхние гармоники только в определенном диапазоне частотного спектра.

Aphex Aural Exciter, представленный в 1970-х годах, функционировал, в основном, путем параллельного искажения исходной версии исходного сигнала с прошедшими верхними частотами.

Ауральный возбудитель Aphex

Исключительно искажая эту полосу частот и смешивая этот новый сигнал с исходным, гармоническое возбуждение обеспечивает резкость, связанную с гармониками, которую невозможно воспроизвести с помощью стандартных методов эквалайзера.

Таким образом, гармонические возбудители отлично подходят для обработки вокала, чтобы увеличить присутствие и разборчивость, а также мастер-шина, чтобы добавить немного воздуха в микс. Поскольку возбудитель может легко сделать звук ярче, лучше использовать его умеренно.

Современные плагины возбуждения, такие как возбудители в Neutron 3 и Ozone 9, также могут выполнять возбуждение в других частотных диапазонах. По сути, это делает их многополосными модулями искажения.

В следующих аудио примерах я обработал бас, электрическое пианино и вокал с помощью Exciter из Ozone 9.Чтобы имитировать эффект старого возбудителя, я слегка проделал это на высоких частотах.

Bass — возбужденный

Электропианино — Excited

вокал — возбужденный

Заключение

С помощью этих методов в отдельные элементы, группы элементов или даже весь микс можно придать некоторую жизнь с введением верхних гармоник.Это может привести к более полному, теплому или жесткому звучанию в зависимости от того, насколько сильно вы нажимаете на процессоры эффектов.

Включив блок искажения, насыщения, сжатия или гармонического возбуждения, мы можем создавать агрессивные и характерные звуки, которые придают дорожке много энергии.

И с более тонким подходом мы можем сделать звучание элемента более впечатляющим для слушателя, не становясь при этом властным, оживляя впечатления слушателя и делая трек более приятным для слуха.oob_n \ sin nt`

`= (a_0) / 2 + a_1 \ cos t« + \ a_2 \ cos 2t` `+ \ a_3 \ cos 3t + …` `+ \ b_1 \ sin t« + \ b_2 \ sin 2t` ` + \ b_3 \ sin 3t + … `

Мы можем переупорядочить эту серию и записать ее как:

`f (t) = (a_0) / 2 + (a_1 \ cos t + b_1 \ sin t)` `+ (a_2 \ cos 2t + b_2 \ sin 2t)` `+ (a_3 \ cos 3t + b_3 \ sin 3t ) + … `

Член ( a ₁ cos t + b ₁ sin t ) известен как основной .

Термин ( a ₂ cos 2 t + b ₂ sin 2 t ) называется второй гармоникой .

Термин ( a ₃ cos 3 t + b ₃ sin 3 t ) называется третьей гармоникой , и т. д.

Нечетные гармоники

Ряд Фурье будет содержать нечетных гармоник , если `f (t + π) = — f (t)`.

Пример 1

График функции `f (t)`, где `f (t + π) = — f (t)`.

В этом случае разложение Фурье будет иметь вид:

`f (t) = (a_0) / 2 + (a_1 \ cos t + b_1 \ sin t)` `+ \ (a_3 \ cos 3t + b_3 \ sin 3t)` `+ \ (a_5 \ cos 5t + b_5 \ sin 5t) + … `

Все гармоники нечетные .

Четные гармоники

Ряд Фурье будет содержать четных гармоник , если `f (t + π) = f (t)`. То есть в нем есть точка «пи».

График функции `f (t)`, где `f (t + π) = f (t)`.

В этом случае разложение Фурье будет иметь вид:

`f (t) = (a_0) / 2 + (a_2 \ cos 2t + b_2 \ sin 2t)` `+ \ (a_4 \ cos 4t + b_4 \ sin 4t)` `+ \ (a_6 \ cos 6t + b_6 \ грех 6т) +…`

Всего гармоник , даже .

Пример 2

Определите наличие нечетных или четных гармоник для следующие функции.

(a) `f (t) =` `{{: (-t-pi / 2″, «, -pi <= t <0), (t-pi / 2", ", 0 <= t < pi):} `

`f (t) = f (t + 2π)`.

Ответ

Из графика видно, что `f (t + π) = — f (t)`.

Например, мы замечаем, что `f (2) = 0,4`, приблизительно. Если теперь переместить единицы «π» вправо (или примерно на «2 + 3.14 = 5,14 ‘), видим, что значение функции равно

`f (5,14) = -0,4`.

То есть `f (t + π) = — f (t)`.

Такое же поведение будет происходить для любого значения `t`, которое мы выбрали.

Таким образом, ряд Фурье будет иметь нечетное гармоники .

Это означает, что в нашем разложении Фурье мы увидим только такие термины:

`f (t) = (a_0) / 2 + (a_1 \ cos t + b_1 \ sin t)` `+ \ (a_3 \ cos 3t + b_3 \ sin 3t)` `+ \ (a_5 \ cos 5t + b_5 \ грех 5т) +…`

[ Примечание: Не путайте с нечетными функциями и нечетными гармониками . В этом примере у нас есть четная функция (поскольку она симметрична относительно оси y ), но поскольку функция имеет свойство `f (t + π) = — f (t)`, то мы знайте, что он имеет нечетных гармоник только .

Тот факт, что это четная функция, не влияет на характер гармоник и может быть проигнорирован.]

Помимо: Музыкальные гармоники

Игра гармоник на гитаре.(-t + pi), если, pi {: <=:} t <2pi):} `

`f (t) = f (t + π)`.

Ответ

График функции `f (t)`, где `f (t + π) = f (t)`.

Как гласит вопрос, функция периодическая с периодом «пи».

Итак, делаем вывод, что ряд Фурье будет иметь даже гармоники , и будет иметь вид:

`(a_0) / 2 + (a_2 \ cos 2t + b_2 \ sin 2t)` `+ \ (a_4 \ cos 4t + b_4 \ sin 4t)` `+ \ (a_6 \ cos 6t + b_6 \ sin 6t) +. ..`

.