Номинальная мощность формула – Формула мощности тока. Фактическая и номинальная мощность. КПД электрического прибора :: SYL.ru

формула, правила расчета, виды и классификация электродвигателей — OneKu

Содержание статьи:

В электромеханике существует много приводов, которые работают с постоянными нагрузками без изменения скорости вращения. Их используют в промышленном и бытовом оборудовании как, например, вентиляторы, компрессоры и другие. Если номинальные характеристики неизвестны, то для расчетов используют формулу мощности электродвигателя. Вычисления параметров особенно актуальны для новых и малоизвестных приводов. Калькуляция выполняется с использованием специальных коэффициентов, а также на основе накопленного опыта работы с подобными механизмами. Данные необходимы для правильной эксплуатации электрических установок.

Вам будет интересно:Что в физике означает g? Закон Всемирного тяготения, ускорение свободного падения и вес тела

Что такое электродвигатель?

Электрический двигатель представляет собой устройство, которое преобразует электрическую энергию в механическую. Работа большинства агрегатов зависит от взаимодействия магнитного поля с обмоткой ротора, которая выражается в его вращении. Функционируют они от источников питания постоянного или переменного тока. В качестве питающего элемента может выступать аккумулятор, инвертор или розетка электросети. В некоторых случаях двигатель работает в обратном порядке, то есть преобразует механическую энергию в электрическую. Такие установки находят широкое применение на электростанциях, работающие от потока воздуха или воды.

Электродвигатели классифицируют по типу источника питания, внутренней конструкции, применению и мощности. Также приводы переменного тока могут иметь специальные щетки. Они функционируют от однофазного, двухфазного или трехфазного напряжения, имеют воздушное или жидкостное охлаждение. Формула мощности электродвигателя переменного тока

P = U х I,

где P — мощность, U — напряжение, I — сила тока.

Приводы общего назначения со своими размерами и характеристиками находят применение в промышленности. Самые большие двигатели мощностью более 100 Мегаватт используют на силовых установках кораблей, компрессорных и насосных станций. Меньшего размера используют в бытовых приборах, как пылесос или вентилятор.

Конструкция электрического двигателя

Привод включает в себя:

• Ротор.
• Статор.
• Подшипники.
• Воздушный зазор.
• Обмотку.
• Коммутатор.

Ротор — единственная подвижная деталь привода, которая вращается вокруг своей оси. Ток, проходя через проводники, образует индукционное возмущение в обмотке. Формируемое магнитное поле взаимодействует с постоянными магнитами статора, что приводит в движение вал. Их рассчитывают по формуле мощности электродвигателя по току, для которой берется КПД и коэффициент мощности, в том числе все динамические характеристики вала.

Подшипники расположены на валу ротора и способствуют его вращению вокруг своей оси. Внешней частью они крепятся к корпусу двигателя. Вал проходит через них и выходит наружу. Поскольку нагрузка выходит за пределы рабочей зоны подшипников, ее называют нависающей.

Статор является неподвижным элементом электромагнитной цепи двигателя. Может включать в себя обмотку или постоянные магниты. Сердечник статора выполнен из тонких металлических пластин, которые называют пакетом якоря. Он призван снижать потери энергии, что часто происходит с твердыми стержнями.

Вам будет интересно:Корневое давление — это важный параметр в жизни растения

Воздушный зазор — расстояние между ротором и статором. Эффективным является небольшой промежуток, так как он влияет на низкий коэффициент работы электродвигателя. Ток намагничивания растет с увеличением размера зазора. Поэтому его всегда стараются делать минимальным, но до разумных пределов. Слишком маленькое расстояние приводит к трению и ослаблению фиксирующих элементов.

Обмотка состоит из медной проволоки, собранной в одну катушку. Обычно укладывается вокруг мягкого намагниченного сердечника, состоящего из нескольких слоев металла. Возмущение индукционного поля происходит в момент прохождения тока через провода обмотки. В этот момент установка переходит в режим конфигурации с явными и неявными полюсами. В первом случае магнитное поле установки создает обмотка вокруг полюсного наконечника. Во втором случае, в распределенном поле рассредотачивается слотов полюсного наконечника ротора. Двигатель с экранированными полюсами имеет обмотку, которое сдерживает магнитное возмущение.

Коммутатор используют для переключения входного напряжения. Состоит из контактных колец, расположенных на валу и изолированных друг от друга. Ток якоря подается на щетки контактов ротационного коммутатора, который приводит к изменению полярности и заставляет вращаться ротор от полюса к полюсу. При отсутствии напряжения мотор прекращает крутиться. Современные установки оборудованы дополнительными электронным средствами, которые контролируют процесс вращения.

Принцип действия

По закону Архимеда ток в проводнике создает магнитное поле, в котором действует сила F1. Если из этого проводника изготовить металлическую рамку и поместить ее в поле под углом 90°, то края будут испытывать силы, направленные в противоположную сторону относительно друг друга. Они создают крутящий момент относительно оси, который начинает ее вращать. Витки якоря обеспечивают постоянное кручение. Поле создается электрическими или постоянными магнитами. Первый вариант выполнен в виде обмотки катушки на стальном сердечнике. Таким образом, ток рамки генерирует индукционное поле в обмотке электромагнита, которое порождает электродвижущую силу.

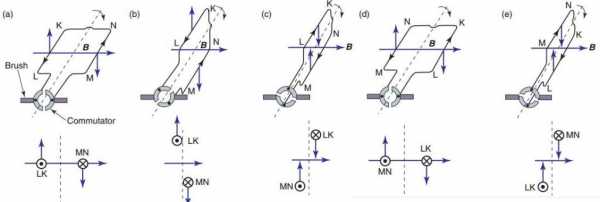
Рассмотрим более подробно работу асинхронных двигателей на примере установок с фазным ротором. Такие машины работают от переменного тока с частотой вращения якоря, не равной пульсации магнитного поля. Поэтому их еще называют индукционными. Ротор приводится в движение за счет взаимодействия электрического тока в катушках с магнитным полем.

Когда во вспомогательной обмотке отсутствует напряжение, устройство находится в состоянии покоя. Как только на контактах статора появляется электрический ток, образуется постоянное в пространстве магнитное поле с пульсацией +Ф и -Ф. Его можно представить в виде следующей формулы:

nпр = nобр = f1 × 60 ÷ p = n1

где:

nпр — количество оборотов, которое совершает магнитное поле в прямом направлении, об/мин;

nобр — число оборотов поля в обратном направлении, об/мин;

f1 — частота пульсации электрического тока, Гц;

p — количество полюсов;

n1 — общее число оборотов в минуту.

Испытывая пульсации магнитного поля, ротор получает начальное движение. По причине неоднородности воздействия потока, он будет развиваться крутящий момент. По закону индукции, в короткозамкнутой обмотке образуется электродвижущая сила, которая генерирует ток. Его частота пропорциональна скольжению ротора. Благодаря взаимодействию электрического тока с магнитным полем создается крутящий момент вала.

Для расчетов производительности существуют три формулы мощности асинхронного электродвигателя. По сдвигу фаз используют

Вам будет интересно:Чем наблюдение отличается от эксперимента в школе

S = P ÷ cos (alpha), где:

S — полная мощность, измеряемая в Вольт-Амперах.

P — активная мощность, указываемая в Ваттах.

alpha — сдвиг фаз.

Под полной мощностью понимаются реальный показатель, а под активной — расчетный.

Виды электродвигателей

По источнику питания приводы разделяют на работающие от:

• Постоянного тока.
• Переменного тока.

По принципу работы их, в свою очередь, делят на:

• Коллекторные.
• Вентильные.
• Асинхронные.
• Синхронные.

Вентильные двигатели не относят к отдельному классу, так как их устройство является вариацией коллекторного привода. В их конструкцию входит электронный преобразователь и датчик положения ротора. Обычно их интегрируют вместе с платой управления. За их счет происходит согласованная коммутация якоря.

Синхронные и асинхронные двигатели работают исключительно от переменного тока. Управление оборотами происходит с помощью сложной электроники. Асинхронные делятся на:

• Трехфазные.
• Двухфазные.
• Однофазные.

Теоретическая формула мощности трехфазного электродвигателя при соединении в звезду или треугольником

P = 3 * Uф * Iф * cos(alpha).

Однако для линейных значений напряжения и тока она выглядит как

P = 1,73 × Uф × Iф × cos(alpha).

Это будет реальный показатель, сколько мощности двигатель забирает из сети.

Синхронные подразделяются на:

• Шаговые.
• Гибридные.
• Индукторные.
• Гистерезисные.
• Реактивные.

В своей конструкции шаговые двигатели имеют постоянные магниты, поэтому их не относят к отдельной категории. Управление работой механизмов производится с помощью частотных преобразователей. Существуют также универсальные двигатели, которые функционируют от постоянного и переменного тока.

Общие характеристики двигателей

Все моторы имеют общие параметры, которые используются в формуле определения мощности электродвигателя. На их основе можно рассчитать свойства машины. В разной литературе они могут называться по-разному, но означают они одно и то же. В список таких параметров входит:

• Крутящий момент.
• Мощность двигателя.
• Коэффициент полезного действия.
• Номинальное количество оборотов.
• Момент инерции ротора.
• Расчетное напряжение.
• Электрическая константа времени.

Вышеуказанные параметры необходимы, прежде всего, для определения эффективности электрических установок, работающих за счет механической силы двигателей. Расчетные величины дают лишь приблизительное представление о реальных характеристиках изделия. Однако эти показатели часто используют в формуле мощность электродвигателя. Именно она определяет результативность машин.

Вращательный момент

Этот термин имеет несколько синонимов: момент силы, момент двигателя, Вращательный момент, вертящий момент. Все они используются для обозначения одного показателя, хотя с точки зрения физики эти понятия не всегда тождественны.

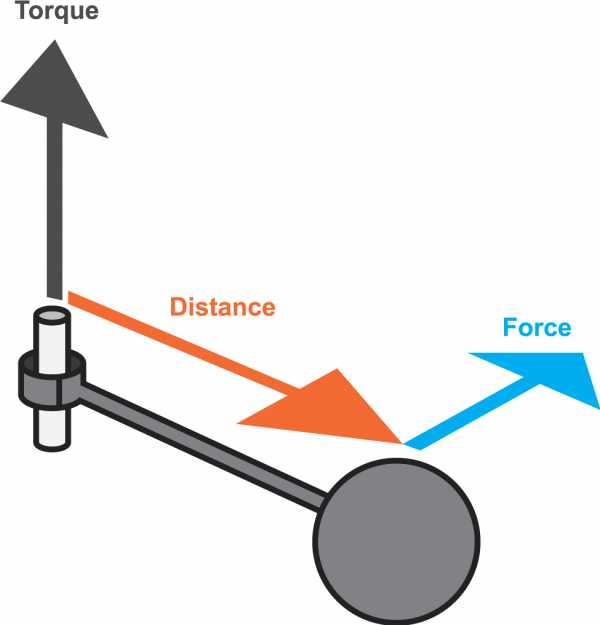
В целях унификации терминологии были разработаны стандарты, которые приводят все к единой системе. Поэтому в технической документации всегда используются словосочетание «крутящий момент». Он представляет собой векторную физическую величину, которая равна произведению векторных значений силы и радиуса. Вектор радиуса проводится от оси вращения к точке приложенной силы. С точки зрения физики разница между крутящим и вращательным моментом заключается в точке прикладывания силы. В первом случае это внутреннее усилие, во втором — внешнее. Измеряется величина в ньютон-метрах. Однако в формуле мощности электродвигателя крутящий момент используется как основное значение.

Рассчитывается он как

M = F × r, где:

M — крутящий момент, Нм;

F — прикладываемая сила, H;

r — радиус, м.

Для расчета номинального вращающего момента привода используют формулу

Мном = 30Рном ÷ pi × нном, где:

Рном — номинальная мощность электрического двигателя, Вт;

нном — номинальное число оборотов, мин-1.

Соответственно, формула номинальной мощности электродвигателя бедует выглядеть следующим образом:

Рном = Мном * pi*нном / 30.

Обычно все характеристики указаны в спецификации. Но бывает, что приходится работать с совершенно новыми установками, информацию о которых найти очень сложно. Для расчета технических параметров таких устройств берут данные их аналогов. Также всегда известны только номинальные характеристики, которые даются в спецификации. Реальные данные необходимо рассчитывать самостоятельно.

Мощность двигателя

В общем смысле данный параметр представляет собой скалярную физическую величину, которая выражена в скорости потребления или преобразования энергии системы. Он показывает, какую работу механизм выполнит за определенную единицу времени. В электротехнике характеристика отображает полезную механическую мощность на центральном вале. Для обозначения показателя используют литеру P или W. Основной единицей измерения является Ватт. Общая формула расчета мощности электродвигателя может быть представлена как:

P = dA ÷ dt, где:

A — механическая (полезная) работа (энергия), Дж;

t — затраченное время, сек.

Механическая работа также является скалярной физической величиной, выражаемой действием силы на объект, и зависящей от направления и перемещения этого объекта. Она представляет собой произведение вектора силы на путь:

dA = F × ds, где:

s — пройденное расстояние, м.

Она выражает дистанцию, которую преодолеет точка приложенной силы. Для вращательных движений она выражается как:

ds = r × d(teta), где:

teta — угол оборота, рад.

Таким образом можно вычислить угловую частоту вращения ротора:

omega = d(teta) ÷ dt.

Из нее следует формула мощности электродвигателя на валу: P = M × omega.

Коэффициент полезного действия электромотора

КПД — это характеристика, которая отражает эффективность работы системы при преобразовании энергии в механическую. Выражается отношением полезной энергии к потраченной. По единой системе единиц измерений он обозначается как «eta» и является безразмерным значением, исчисляемым в процентах. Формула КПД электродвигателя через мощность:

eta = P2 ÷ P1, где:

P1 — электрическая (подаваемая) мощность, Вт;

P2 — полезная (механическая) мощность, Вт;

Также он может быть выражен как:

eta = A ÷ Q × 100 %, где:

A — полезная работа, Дж;

Q — затраченная энергия, Дж.

Чаще коэффициент вычисляют по формуле потребляемой мощности электродвигателя, так как эти показатели всегда легче измерить.

Снижение эффективности работы электродвигателя происходит по причине:

• Электрических потерь. Это происходит в результате нагрева проводников от прохождения по ним тока.
• Магнитных потерь. Вследствие излишнего намагничивания сердечника появляется гистерезис и вихревые токи, что важно учитывать в формуле мощности электродвигателя.
• Механических потерь. Они связаны с трением и вентиляцией.
• Дополнительных потерь. Они появляются из-за гармоник магнитного поля, так как статор и ротор имеют зубчатую форму. Также в обмотке присутствуют высшие гармоники магнитодвижущей силы.

Следует отметить, что КПД является одним из самых важных компонентов формулы расчета мощности электродвигателя, так как позволяет получить цифры, наиболее приближенные к действительности. В среднем этот показатель варьирует от 10% до 99%. Она зависит от конструктивного устройства механизма.

Номинальное количество оборотов

Вам будет интересно:Самый мощный тепловоз в мире. Самые мощные российские модели

Еще одним ключевым показателем электромеханических характеристик двигателя является частота вращения вала. Он выражается в числе оборотов в минуту. Часто его используют в формуле мощности электродвигателя насоса, чтобы узнать его производительность. Но необходимо помнить, что показатель всегда разный для холостого хода и работы под нагрузкой. Показатель представляет физическую величину, равной количеству полных оборотов за некий промежуток времени.

Расчетная формула частоты оборотов:

n = 30 × omega ÷ pi, где:

n — частота вращения двигателя, об/мин.

Для того, чтобы найти мощность электродвигателя по формуле оборотистости вала, необходимо привести ее к расчету угловой скорости. Поэтому P = M × omega будет выглядеть следующим образом:

P = M × (2pi × n ÷ 60) = M × (n ÷ 9,55), где

t = 60 секунд.

Момент инерции

Этот показатель представляет собой скалярную физическую величину, которая отражает меру инертности вращательного движения вокруг собственной оси. При этом масса тела является величиной его инертности при поступательном движении. Основная характеристика параметра выражена распределением масс тела, которая равна сумме произведений квадрата расстояния от оси до базовой точки на массы объекта.В Международной системе единиц измерения он обозначается как кг·м2 и имеет рассчитывается по формуле:

J = ∑ r2 × dm, где

J — момент инерции, кг·м2 ;

m — масса объекта, кг.

Моменты инерции и силы связаны между собой соотношением:

M — J × epsilon, где

epsilon — угловое ускорение, с-2.

Показатель рассчитывается как:

epsilon = d(omega) × dt.

Таким образом, зная массу и радиус ротора, можно рассчитать параметры производительности механизмов. Формула мощности электродвигателя включает в себя все эти характеристики.

Расчетное напряжение

Его еще называют номинальным. Оно представляет собой базовое напряжение, представленное стандартным набором вольтажа, которые определяется степенью изоляции электрического оборудования и сети. В действительности оно может отличаться в разных точках оборудования, но не должно превышать предельно допустимых норм рабочих режим, рассчитанных на продолжительное функционирование механизмов.

Для обычных установок под номинальным напряжением понимают расчетные величины, для которых они предусмотрены разработчиком в нормальном режиме работы. Перечень стандартного вольтажа сети предусмотрен в ГОСТ. Эти параметры всегда описаны в технических характеристиках механизмов. Для расчета производительности используют формулу мощности электродвигателя по току:

P = U × I.

Электрическая константа времени

Представляет собой время, необходимое для достижения уровня тока до 63 % после подачи напряжения на обмотки привода. Параметр обусловлен переходными процессами электромеханических характеристик, так как они быстротечны ввиду большого активного сопротивления. Общая формула расчета постоянной времени:

te = L ÷ R.

Однако электромеханическая константа времени tm всегда больше электромагнитной te. Первый параметр получается из уравнения динамических характеристики двигателя при сохранении условии, когда ротор разгоняется с нулевой скоростью до максимальных оборотов холостого хода. В этом случае уравнение принимает вид

M = Mст + J × (d(omega) ÷ dt), где

Mст = 0.

Отсюда получаем формулу:

M = J × (d(omega) ÷ dt).

По факту электромеханическую константу времени рассчитывают по пусковому момент — Mп. Механизм, работающий в идеальных условиях, с прямолинейными характеристиками будем иметь формулу:

M = Mп × (1 — omega ÷ omega0), где

omega0 — скорость на холостом ходу.

Такие расчеты используют в формуле мощности электродвигателя насоса, когда ход поршня напрямую зависит от оборотистости вала.

Основные формулы расчета мощности двигателей

Для вычисления реальных характеристик механизмов всегда нужно учитывать много параметров. в первую очередь нужно знать, какой ток подается на обмотки электродвигателя: постоянный или переменный. Принцип их работы отличается, следовательно, отличаются метод вычислений. Если упрощенный вид расчета мощности привода выглядит как:

Pэл = U × I, где

I — сила тока, А;

U — напряжение, В;

Pэл — подведенная электрическая мощность. Вт.

В формуле мощности электродвигателя переменного тока необходимо также учитывать сдвиг фаз (alpha). Соответственно, расчеты для асинхронного привода выглядят как:

Pэл = U × I × cos(alpha).

Кроме активной (подведенной) мощности существует также:

• S — реактивная, ВА. S = P ÷ cos(alpha).
• Q — полная, ВА. Q = I × U × sin(alpha).

В расчетах также необходимо учитывать тепловые и индукционные потери, а также трение. Поэтому упрощенная модель формулы для электродвигателя постоянного тока выглядит как:

Pэл = Pмех + Ртеп +Ринд + Ртр, где

Рмех — полезная вырабатываемая мощность, Вт;

Ртеп — потери на образование тепла, ВТ;

Ринд — затраты на заряд в индукционной катушке, Вт;

Рт — потери в результате трения, Вт.

Заключение

Электродвигатели находят применение практически во всех областях жизни человека: в быту, в производстве. Для правильного использования привода необходимо знать не только его номинальные характеристики, но и реальные. Это позволит повысить его эффективность и снизить затраты.

Источник

1ku.ru

Выбор мощности собственных нужд, расчет, формула, таблица мощности потребителей

Номинальную мощность трансформаторов собственных нужд выбирают в соответствии с их расчетной нагрузкой Sрасч. Последняя определяется суммой мощностей всех электроприемников, которые присоединены к данному трансформатору.

При определении Sрасч возникают трудности из-за зависимости Sрасч от Кзгр, cos, наличия резервных и нормально не работающих механизмов СН, а также трансформаторов второй ступени напряжения 6/0,4 кВ. Поэтому проектные организации применяют упрощенную методику определения Sрасч через расчетные переводные коэффициенты Красч для групп электродвигателей и для трансформаторов второй ступени.

Расчетная нагрузка, кВА, на трансформатор собственных нужд первой ступени трансформации составляет:

где Красч д1 – расчетный переводной коэффициент для группы двигателей первой ступени напряжения (6 кВ) общим числом nд1;

Ррасч д1 – расчетная мощность на валу каждого из двигателей первой ступени, кВт;

Красч т2 – расчетный переводной коэффициент для группы трансформаторов второй ступени трансформации общим числом nт2;

Sрасч т2 – расчетная мощность каждого из трансформаторов второй ступени, кВА.

В коэффициенте Красч д1 кроме численного значения заложено приве дение размерности активной мощности (кВт) к полной мощности (кВА).

Поэтому несмотря на то, что Ррасч д1 измеряется в кВт, итоговое значение Sрасч т1 имеем в кВА.В величину Sрасч т1 включают и электродвигатели резервных агрегатов СН, и резервных трансформаторов второй ступени, а также электродвигатели и трансформаторы надежного питания, работающие в нормальном режиме.

Электроприемники, работающие эпизодически (например, электродвигатели резервного возбудителя, насоса кислотной промывки), а также электродвигатели механизмов систем расхолаживания, работающие только в аварийном режиме при определении Sрасч т1 не учитывают. На основе опыта проектирования и эксплуатации принято Красч д1 = Красч т2 = 0,9.

Величина Ррасч д1 может быть найдена через номинальную мощность двигателя Рн д1, если известен его коэффициент загрузки:

Величина Ррасч д1 может быть найдена также из выражения для мощности, потребляемой на валу механизма, которая находится без участия Кзгр по формуле (98).

Величина Sрасч т2 может быть найдена через номинальную мощность трансформатора Sн т2, если известен его коэффициент загрузки:

Определение расчетной нагрузки на резервный (пускорезервный) трансформатор собственных нужд производится аналогично. В любом случае резервный трансформатор собственных нужд должен обеспечить длительную замену рабочего. В схемах без выключателя между генератором и повысительным трансформатором должна обеспечиваться замена рабочего выбранного трансформатора и одновременно пуск или останов другого реакторного блока. При этом в величине Sрасч от запускаемого (останавливаемого) блока учитываются только электроприемники, работающие при пуске или останове.

Расчетную нагрузку трансформаторов второй ступени также определяют через расчетные переводные коэффициенты, но ввиду неоднородности состава электроприемников их разбивают на четыре группы с соответствующими значениями обобщенных переводных коэффициентов

где Рн1 – суммарная номинальная мощность постоянно работающих электродвигателей второй ступени единичной мощностью от 70 до 200 кВт;

Рн2 – суммарная номинальная мощность периодически работающих электродвигателей второй ступени единичной мощностью менее 100 кВт;

Рн3 – суммарная номинальная мощность электродвигателей задвижек, колонок дистанционного управления и т.д.; ?Рн4 – суммарная номинальная нагрузка освещения и электрообогрева.

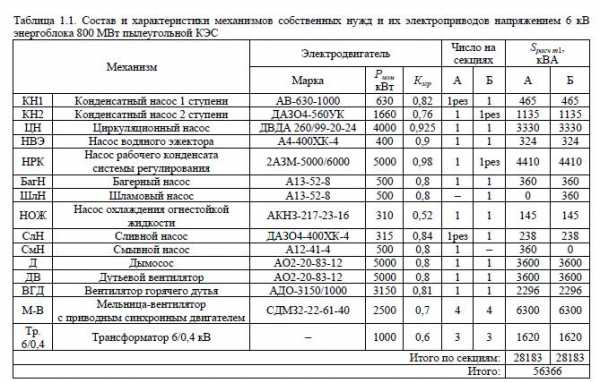
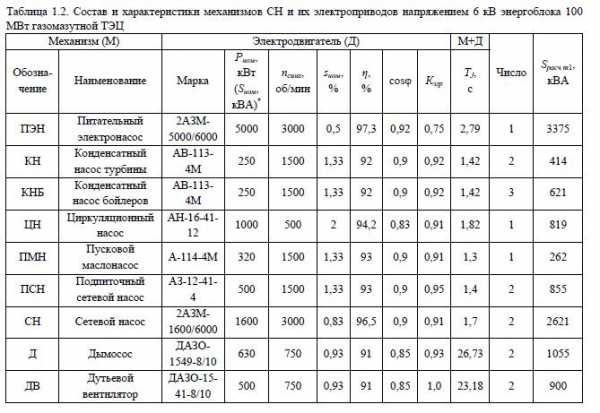
В виде примера определена нагрузка (табл.1.1) на рабочий ТСН (двухобмоточный с расщепленными обмотками низшего напряжения) энергоблока 800 МВт, а в табл.1.2 – нагрузка на рабочий ТСН (двухобмоточный без расщепления) энергоблока 100 МВт.

В табл.1.1, 1.2 число и мощность трансформаторов 6/0,4 кВ приняты по аналогии с действующими блоками. При этом не требуется вычислений по формулам (1.3) и (1.4) для двигателей на напряжении 0,4 кВ, а для двигателей на напряжении 6 кВ Ррасч д1 определяется через Кзгр – формула (1.2).

На основании величины расчетной нагрузки на трансформатор (Sрасч т1 = 51,15 МВА по табл.1.1 и Sрасч т2 = 14,78 МВА по табл.1.2) выбирается его тип.

Применительно к АЭС выбор мощности ТСН представлен в работе , в табл.15 приложения для блока РБМК-1000, схема которого представлена на рис.10, стр.58 . В табл.15 знаком * обозначены потребители, не участвующие в расчете мощности трансформаторов.

pue8.ru

Номинальная мощность электроприемников. — КиберПедия

Номинальная активная мощность ЭП (PНОМ) – это мощность, потребляемая из сети при номинальной нагрузке ЭП, при которой он должен работать длительное время в установившемся режиме без превышения допустимой температуры.

Для длительного режима работы ЭП номинальная мощность равна паспортной величине (P_ПАСП)

P_НОМ=P_ПАСП.

Для приемников работающих в повторно-кратковременном режиме номинальную мощность определяют по паспортной мощности путем приведения ее к длительному режиму работы (ПВ=1) в соответствии с формулами: , или ,

где ПВ_ПАСП — паспортная величина, о.е.; kВ — коэффициент включения рассчитывается по графику нагрузки ЭП.

Для электродвигателей мощность, потребляемая из сети, называется присоединенной мощностью (PПР) и определяется по выражению

,

где P_НОМ — номинальная мощность, развиваемая на валу двигателя, кВт;

ηНОМ — номинальный КПД электродвигателя, о.е.

Номинальная реактивная мощность ЭП (QНОМ) – реактивная мощность, потребляемая им из сети при номинальной активной мощности и номинальном напряжении.

Для ЭП, работающего в длительном режиме, величина QНОМ вычисляется по формуле

,

где tgφ — соответствует номинальному cosφ ЭП (cosφ — паспортная величина).

Для ЭП, работающего в повторно-кратковременном режиме, величина QНОМ вычисляется по формуле .

 

Номинальная полная мощность ЭП (sн)

.

Номинальный ток (I_НОМ)

трехфазного ЭП:

.

однофазного ЭП:

.

 

Номинальный коэффициент активной мощности (cosφ)

.

Номинальные напряжения.

Номинальное напряжение — это базисное напряжение из стандартизированного ряда напряжений, определяющих уровень изоляции сети и электрооборудования.

Действительные напряжения в различных точках системы могут несколько отличаться от номинального, однако они не должны превышать наибольшие рабочие напряжения, установленные для продолжительной работы.

Номинальным напряжением у источников и приёмников электроэнергии (генераторов, трансформаторов) называется такое напряжение, на которое они рассчитаны в условиях нормальной работы. Номинальные напряжения электрических сетей и присоединяемых к ним источников и приёмников электрической энергии устанавливаются ГОСТом.

Номинальное напряжение, кВ	Наибольшее рабочее напряжение, кВ
до 1000В
0,23
0,4
0,66
свыше 1000В
	3,6
	7,2
	17,5
	40,5

 

Род и частота тока

Токи различного рода неодинаково опасны (при прочих равных условиях) для организма. Наиболее опасным следует считать переменный ток промышленной частоты 50 – 60 Гц. Он сильно воздействует на центральную нервную систему и производит сильные сокращения мышц, которые во многих случаях удерживают человека в контакте с частями, находящимися под напряжением, лишая возможности самостоятельно освободится от ТВЧ.

По этому вопросу существует несколько теорий, но ни одна из них не отвечает высоким требованиям современной физиологической науки. Однако, грубо в приближенной форме можно объяснить это явление.

При прикосновении к ТВЧ, находящимся под напряжением, в живой клетке происходит расщепление внутриклеточного вещества на ионы, которые устремляются к внешним оболочкам клеток.

При частоте 50 Гц и близких к ней скорость ионов оказывается достаточной, чтобы за период изменения тока, пройти длину клетки. Это соответствует наибольшему возмущению в клетке и нарушению биохимических процессов в ней.

Дальнейшее повышение частоты, несмотря на рост тока, проходящего через человека, сопровождается снижением опасности поражения, которая полностью исчезает при частоте 450 – 500 кГц.

Токи частотой 450 – 500 кГц и более не могут вызвать смертельного поражения вследствие прекращения работы сердца или легких, а также других жизненно важных органов.

Правда, эти токи сохраняют опасность ожогов, как при возникновении электрической дуги, так и при прохождении их непосредственно через тело человека.

Постоянный токпримерно в 4 – 5 раз безопаснее переменного частотой 50 Гц. Проходя через тело человека, он вызывает более слабые сокращения мышц и менее неприятные ощущения по сравнению с переменным током того же значения. Лишь в момент замыкания и размыкания цепи тока человек испытывает кратковременное болезненное ощущение вследствие внезапного судорожного сокращения мышц, подобное тому, которое возникает при переменном токе примерно того же значения.

 

cyberpedia.su

Формула определения мощности

Электрическая мощность

Классическая электродинамика

Электричество · Магнетизм

Электростатика Закон Кулона Теорема Гаусса Электрический дипольный момент Электрический заряд Электрическая индукция Электрическое поле Электростатический потенциал Магнитостатика Закон Био — Савара — Лапласа Закон Ампера Магнитный момент Магнитное поле Магнитный поток Магнитная индукция Электродинамика Векторный потенциал Диполь Потенциалы Лиенара — Вихерта Сила Лоренца Ток смещения Униполярная индукция Уравнения Максвелла Электрический ток Электродвижущая сила Электромагнитная индукция Электромагнитное излучение Электромагнитное поле Электрическая цепь Закон Ома Законы Кирхгофа Индуктивность Радиоволновод Резонатор Электрическая ёмкость Электрическая проводимость Электрическое сопротивление Электрический импеданс Ковариантная формулировка Тензор электромагнитного поля Тензор энергии-импульса 4-потенциал 4-ток Известные учёные Генри Кавендиш Майкл Фарадей Никола Тесла Андре-Мари Ампер Густав Роберт Кирхгоф Джеймс Клерк (Кларк) Максвелл Генри Рудольф Герц Альберт Абрахам Майкельсон Роберт Эндрюс Милликен

См. также: Портал:Физика

Электрическое напряжение
Сила тока
Электрическая мощность
Электрическое сопротивление

Электри́ческая мо́щность — физическая величина, характеризующая скорость передачи или преобразования электрической энергии.

Мгновенная электрическая мощность

Мгновенной мощностью называется произведение мгновенных значений напряжения и силы тока на каком-либо участке электрической цепи.

По определению, электрическое напряжение — это отношение работы электрического поля, совершенной при переносе пробного электрического заряда из точки A {\displaystyle A} в точку B {\displaystyle B} , к величине пробного заряда. То есть можно сказать, что электрическое напряжение равно работе по переносу единичного заряда из точки A {\displaystyle A} в точку B {\displaystyle B} . Другими словами, при движении единичного заряда по участку электрической цепи он совершит работу, численно равную электрическому напряжению, действующему на участке цепи. Умножив работу на количество единичных зарядов, мы, таким образом, получаем работу, которую совершают эти заряды при движении от начала участка цепи до его конца. Мощность, по определению, — это работа в единицу времени. Введём обозначения:

U {\displaystyle U}  — напряжение на участке A − B {\displaystyle A-B} (принимаем его постоянным на интервале Δ t {\displaystyle \Delta t} ), Q {\displaystyle Q}  — количество зарядов, прошедших от A {\displaystyle A} к B {\displaystyle B} за время Δ t {\displaystyle \Delta t} , A {\displaystyle A}  — работа, совершённая зарядом Q {\displaystyle Q} при движении по участку A − B {\displaystyle A-B} , P {\displaystyle P}  — мощность.

Записывая вышеприведённые рассуждения, получаем:

P A − B = A Δ t {\displaystyle P_{A-B}={\frac {A}{\Delta t}}}

Для единичного заряда на участке A − B {\displaystyle A-B} :

P e ( A − B ) = U Δ t {\displaystyle P_{e(A-B)}={\frac {U}{\Delta t}}}

Для всех зарядов:

P A − B = U Δ t ⋅ Q = U ⋅ Q Δ t {\displaystyle P_{A-B}={\frac {U}{\Delta t}}\cdot {Q}={U}\cdot {\frac {Q}{\Delta t}}}

Поскольку ток есть электрический заряд, протекающий по проводнику в единицу времени, то есть I = Q Δ t {\displaystyle I={\frac {Q}{\Delta t}}} по определению, в результате получаем:

P A − B = U ⋅ I {\displaystyle P_{A-B}=U\cdot I} .

Полагая время бесконечно малым, можно принять, что величины напряжения и тока за это время тоже изменятся бесконечно мало. В итоге получаем следующее определение мгновенной электрической мощности:

мгновенная электрическая мощность p ( t ) {\displaystyle p(t)} , выделяющаяся на участке электрической цепи, есть произведение мгновенных значений напряжения u ( t ) {\displaystyle u(t)} и силы тока i ( t ) {\displaystyle i(t)} на этом участке:

p ( t ) = u ( t ) ⋅ i ( t ) . {\displaystyle p(t)=u(t)\cdot i(t).}

Если участок цепи содержит резистор c электрическим сопротивлением R {\displaystyle R} , то

p ( t ) = i ( t ) 2 ⋅ R = u ( t ) 2 R {\displaystyle p(t)=i(t)^{2}\cdot R={\frac {u(t)^{2}}{R}}} .

Дифференциальные выражения для электрической мощности

Мощность, выделяемая в единице объёма, равна:

w = d P d V = E ⋅ j {\displaystyle w={\frac {dP}{dV}}=\mathbf {E} \cdot \mathbf {j} } ,

где E {\displaystyle \mathbf {E} }  — напряжённость электрического поля, j {\displaystyle \mathbf {j} }  — плотность тока. Отрицательное значение скалярного произведения (век

zna4enie.ru

9.7. Выбор по мощности двигателей номинального продолжительного режима работы

Искусство выбора двигателей по мощности состоит в том, чтобы на основании расчетных данных, полученных из нагру­зочной диаграммы двигателя, обеспечить наиболее близкое соответствие его температурного режима номинальному. При этом, как было показано в § 9.5,должно выполняться усло­вие сохранения срока службы изоляции и отсутствия недопу­стимых пиков температуры.

Отметим, что, как правило, в общем случае задача выбора двигателя по мощности решается в два или более этапов. Как это было показано в § 9.6,точная нагрузочная диаграмма двигателя, на основании которой можно было бы получить необходимые данные для оценки графика мощности или момента двигателя и тем более потерь, может быть построена только при известных данных двигателя и уточненном харак­тере движения. Момент инерции ротораJ_poти жесткость механической характеристикиопределяют Т_м, а КПД опреде­ляет потери. Момент инерции существенно влияет на вид кривойM(t), а зависимость КПД от нагрузки—на потери. В связи с этим на первом этапе двигатель предварительно выбирается, затем производится уточнение кривой М (t) и харак­тера движения, построение графика потерь или графика вели­чины, косвенно оценивающей потери, и далее проверка пред­варительно выбранного двигателя по уточненным данным.

Если разница номинальной и расчетной мощностей больше, чем разница мощностей выбранного двигателя и ближайшего, имеющего меньшую мощность, следует повторить указанные этапы проверки с двигателем меньшей мощности. Если при проверке номинальная мощность оказалась меньше расчетной, следует перейти к двигателю ближайшей большей мощности.

Рассмотрим процесс выбора по мощности двигателей номи­нального режима S1 для различных нагрузочных диаграмм. Наиболее просто задача выбора двигателя номинального про­должительного режима работы решается при непрерывном режиме работы механизма, имеющего неизменную нагрузку:M_с=const. Таким образом должен быть выбран двигатель, мощность которого больше или равна мощности, полученной по нагрузочной диаграмме двигателя:

(9.97)

Выполнение условия (9.97)обеспечивает выполнение условия эквивалентности данного режима работы номинальному в виде(9.93),так как при этом. Однако, как следует из (9.91)и (9.92),даже в этом простейшем случае следует убедиться, что_среды <_{среды, ном}, А »А_ном. При выборе двигателя по условию (9.97)нельзя допустить существенного отклонения его номинальной скорости от требуемой по нагру­зочной диаграмме, так как при_ном >_мехбудет выбран двигатель с меньшим номинальным моментом, чем это необходимо по нагрузочной диаграмме; в другом случае при_ном <_мехбудет снижена производительность механизма,

Производить проверку двигателя по мощности, как правило, нет необходимости. Нужно лишь проверить его по пусковому моменту, т. е. проверить выполнение неравенства

так как для многих механизмов максимальный момент при трогании может превосходить пусковой момент двигателя.

Нагрузка механизмов непрерывного действия не ограничи­вается случаем М_с =const. На рис. 9.26показан характер­ный случай меняющейся во времени нагрузкиP(t) и в об­щем виде соответствующий ему график мощности потерьР(t).

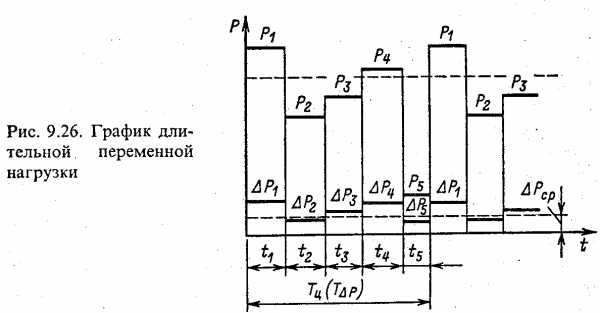
На первом этапе рассмотрим ситуацию, когда произво­дится грубая оценка необходимой мощности двигателя и вы­бирается двигатель для режима S1 с номинальной мощ­ностью

(9.98)

где Р_c,ср —средняя статическая мощность за цикл;k₃ = 1,1  1,3 –коэффициент запаса, который принимается тем больше, чем больше предполагаемый вклад неучтенного ди­намического момента.

После предварительного выбора двигателя по условию (9.98) строят график P(t) (рис. 9.26) и производят про­верку двигателя по условиям нагрева. В этом случае двигатель следует проверить и по условию эквивалентности тепловых режимов, опираясь на соотношение эквивалентности в виде (9.93), проверяя лишь наличие условий, гарантиру­ющих малые значения приращения скорости старения d =т. е. ориентировочно сопоставив отношения и T_р/T_и в (9.88) при данном k.

Использование в рассмотренном случае соотношений (9.91) – (9.93)метода средних потерь при проверке по нагреву не всегда удобно и не всегда необходимо. На базе этого метода можно обосновать более простые методы эквивалентирования режимов двигателей. Идея этих методов состоит в замене соотношений для средних потерь соот­ношением других величин, которые пропорциональны сред­ним потерям. Обобщим выражения для потерь в двигате­лях постоянного и переменного тока в виде

(9.99)

где I =I_ядля двигателя постоянного тока, I =I₂’ для асин­хронного и I =I_ядля синхронного двигателя;R* = R,для двигателя постоянного тока независимого возбуждения, R* = R_я + R_вдля двигателя последовательного возбуждения,R*=3(1 +R₁/R₂‘) для асинхронного двигателя,R* = 3R₁для синхронного.

В постоянные потери асинхронного двигателя входит сос­тавляющая I²R₁— составляющая потерь от тока намагничи­вания, который принят неизменным для линейного участка механической характеристики асинхронного двигателя. Для двигателя независимого возбуждения и синхронного в по­стоянные потери входят потери на возбуждение.

Записав выражение для средних потерь в соответствии с (9.99) в виде

(9.100)

можно увидеть, что при равенстве средних за цикл посто­янных потерь и «сопротивлений» R* средние суммарные потери в данном режиме можно сравнивать с номинальными ΔРном» сопоставляя так называемыйэквивалентный ток

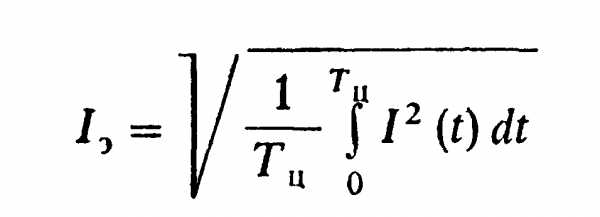(9.101)

с номинальным.

Из (9.100) и (9.101) следует, что эквивалентный ток дви­гателя в данном режиме — это такой неизменный ток, при котором выделится такое же количество теплоты при том же сопротивлении R*, что и при реальном токе—I(t).

Метод, основанный на сравнении эквивалентных токов, получил название метода эквивалентного тока.Применение этого метода правомерно при соблюдении условий, накла­дываемых на применение метода средних потерь, а так­же при равенстве средних «постоянных» потерь и сопро­тивления R*. Условие соответствия номинальной мощности выбранного двигателя мощности, необходимой для данного режима, запишется в этом случае в видеIэIном.

Если известно, что в режиме, для которого выбирается двигатель, соблюдается условие Μ=сI,то подстановка его в выражение (9.101) дает

(9.102)

При наложенном дополнительном условии о пропорци­ональности между током н моментом расчетной величиной, пропорциональной средним потерям, окажется эквивалентный момент, определенной выражением (9.102), при этом двигатель выбран правильно, если Мэ  Μном.

Наконец, если можно считать, что скорость двигателя меняется мало и справедливы Ρ=Мω_си Μ=Р/ω_с, то можно определить эквивалентную мощность аналогично (9.101), (9.102) в виде

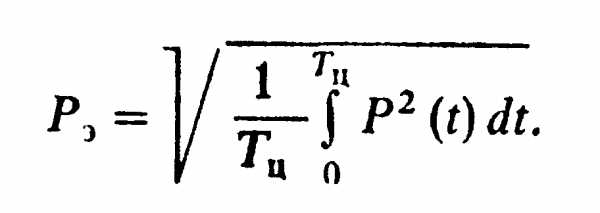(9.103)

При практических расчетах, связанных с определением за цикл или любой другой отрезок времени средних значений мощности потерь или эквивалентных величин, часто интегри­рование (9.98), (9.99), (9.101), (9.103) удобно заменить сумми­рованием, разбив графики на участки с примерно постоян­ными значениями переменных. В этом случае формулы для эквивалентных величин примут вид

(9.104)

(9.105)

(9.106)

Полученные соотношения методов эквивалентных величин позволяют рекомендовать их и на стадии предварительного выбора двигателей (методы эквивалентной мощности, экви­валентного момента), если можно обосновать выполнение усло­вий их применимости. Например, лучше в случае ω=const,Φ=const, ΔРс=const,R=constпри предварительном выборе мощности в качестве расчетной: принять не среднюю мощность, а эквивалентную, т. е. среднеквадратическую (9.106).

Полученные выше соотношения справедливы при условии неизменности условий охлаждения двигателей, т. е. постоянства коэффициента теплоотдачи А. Учет изменения теплоотдачи в целях определения параметров температурного режима — за­дача весьма сложная. Однако при некоторых условиях учесть изменения теплоотдачи для обоснования рассмотренных выше методов можно достаточно просто. Предположим, что в соот­ветствии с оценками по (9.77) максимально возможное откло­нение температуры от среднего значения мало при всех воз­можных значениях коэффициента А,при этом можно принятьτ=const. Условие постоянства температуры позволяет запи­сать интегральное соотношение, отражающее тот факт, что при τ=τ_ср=const средняя мощность потерь за цикл должна быть равна средней мощности теплоотвода в охлаждающую среду: .

Из этого выражения вытекает

откуда следует, что

(9.107)

Поэтому при подсчетах средней мощности потерь или зна­чений эквивалентных величин для учета ухудшения теплоот­дачи на отдельных участках цикла время работы на этом этапе следует умножить на среднее значение коэффициента тепло­отдачи. Например, формула для подсчета эквивалентного тока (9.104) примет вид

В любом случае при переменной нагрузке, так как Мmах>Мэ>Мср, необходимо проверить кроме пускового момента, если возможен пуск под нагрузкой, также перегрузочную спо­собность двигателя.

Во избежание останова двигателя при пиках нагрузки должно выполняться условие

Для коллекторных двигателей проверяется перегрузочная способность по току, ограниченная током, допустимым по условиям коммутации.

Сглаживание нагрузочной диаграммы двигателя при увели­чении Jyимеет важное практическое значение не только в связи с тем, как это было отмечено выше, что снижает мак­симальный момент двигателя, но и в связи с тем, что позво­ляет снизить эквивалентный момент и, следовательно, сни­зить в ряде случаев установленную мощность. Действительно, это легко показать, если эквивалентный момент записать в виде

где σ {Μ} —среднее квадратическое отклонение момента от среднего значения (действующее значение переменной состав­ляющей момента).

Например, при синусоидальном графике момента с ампли­тудой ΔΜ

Поскольку параметры нагрузочной диаграммы механизма и двигателя в рассматриваемом случае связаны через параметры инерционного звена, удобно воспользоваться соотношениями (9.73), (9.77), которые были получены для связи параметров графика потерь и температуры τ.Меняя в (9.73), (9.77) соответ­ствующие параметры, получаем оценки максимального мо­мента двигателя и эквивалентного момента в виде

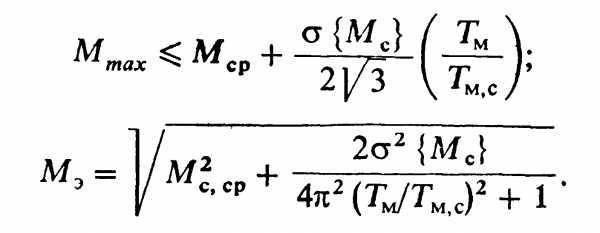(9.108)

Полученные соотношения позволяют пояснить эффектив­ность увеличения Тм путем увеличения суммарного момента инерции привода.

Ряд механизмов имеет нагрузочную диаграмму с относи­тельно малым временем работы с максимальной нагрузкой и продолжительным участком холостого хода (прессы, штампы).

Для таких механизмов характерно большое отношение λ’=Мmax/Мэ, существенно превышающее перегрузочную спо­собность двигателей по моменту. Если не принять мер к вырав­ниванию нагрузочной диаграммы двигателей, то придется выби­рать его мощность, ориентируясь на максимальный момент.

Однако практически выгоднее искусственно увеличить J_Σ привода путем введения дополнительного маховика (махови­ковый привод). Это приведет к увеличению Тм и, как следует из (9.108), к приближению Мэ к Мс.ср. В пределе приJ_Σ→∞, Т_m→∞Mэ=Mc,cpи двигатель может быть выбран по сред­ней мощности

Реальные значения Тм ограничены, с одной стороны, возмож­ностями конструктивного выполнения маховика больших раз­меров и его установки в кинематической цепи, а с другой стороны, допустимыми потерями при пуске электропривода, которые возрастут с увеличением J_Σ. Тем не менее, определив Мс,ср для диаграммы с резкопеременной нагрузкой и задавшись приемлемыми значениями М_MAXи М_Э, можно с учетом (9.108) определить требуемое значение Тм и соответственноJ_ΣиJmax. Важно также отметить, что в этом случае снижаются и потери в приводе, как это было рассмотрено в § 9.3.

При выборе двигателей номинального продолжительного режима работы для режимов типа повторно-кратковременных рассмотрим случай, отвечающий соотношению эквивалент­ности (9.92), записав его следующим образом:

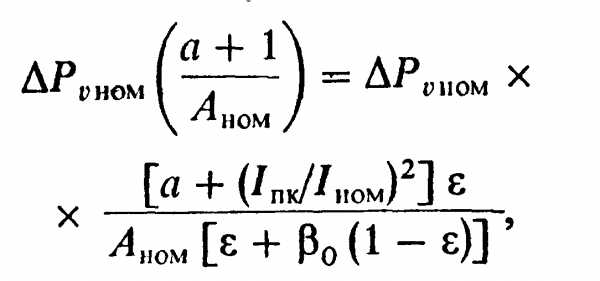(9.109)

где в правой части равенства числитель есть средние потери за цикл при токе нагрузки Iпк, знаменатель — средний коэффи­циент теплоотдачи;а —коэффициент потерь; βο —коэффи­циент ухудшения теплоотдачи для неподвижного двигателя.

Преобразуя (9.109), получаем выражение эквивалентной токовой нагрузки двигателя продолжительного номинального режима при работе в повторно-кратковременном режиме с заданным значением ε

(9.110)

Полученное значение тока при проверке двигателя сравни­вается с эквивалентным током нагрузочной диаграммы. При выборе двигателя при Фном=Φ=constсопоставляются вели­чины Μпк=c·Iпк и Мэ графика нагрузки. Если же работа в период включенного состояния происходит при ω=const, то можно воспользоваться сопоставлением допустимой мощности дви­гателя в этом режиме Рпк=Iпк·ω₀и мощности нагрузки в период работы двигателя.

Если постоянными потерями пренебречь и рассматривать двигатели, для которых β₀≈1, то выражение (9.110) примет вид

(9.111)

Практически возможности использования двигателей номи­нального продолжительного режима для работы в повторнократковременных режимах ограничены. При изменении режима работы во времени ε=t_р/Тц, максимально допустимые токовые нагрузки двигателей (максимальные моменты) не меняются, а номинальные возрастают, что приводит к снижению пере­грузочной способности λ(рис. 9.27). Еще более важен учет этих ограничений при выборе двигателя для работы в кратко­временном режиме. Простейший график работы двигателя в кратковременном режиме приведен на рис. 9.28. Исходя из определения кратковременного режима работы, можно для установления превышения температуры ограничиться рас­смотрением лишь одного периода. Используя (9.68), записываем

Если выбрать двигатель, рассчитанный для продолжитель­ного режима, с мощностью, равной мощности при кратко­временном режиме работы Рк,ном то превышение температуры не достигнет установившегося значения τ_ук концу рабочего периода t_ρ,как это видно на рис. 9.28 (кривая 1), поэтому в рассматриваемом случае двигатель недоиспользовался бы по нагреву.

При полном использовании по мощности в этом режиме превышение температуры к концу рабочего периода tpдолжно быть равным τ_доп(рис. 9.28, кривая 2). В этом случае двигатель может развивать мощность большую, чем была бы допустима для него мощность в продолжительном режиме, а «установив­шаяся» температура, если бы он развивал эту мощность дли­тельно, была бы равнаτ`_у > τ_у > τ_доп.

Связь τ`_у и τ_уопределяется выражением

(9.112)

где Тн.ср=(Тн.нач + Тн,кон)/2 — среднее значение постоянной вре­мени нагрева; τ_у=ΔРном/А=ΔΡк/Α; ΔPκ —потери мощно­сти в двигателе при кратковременной нагрузке.

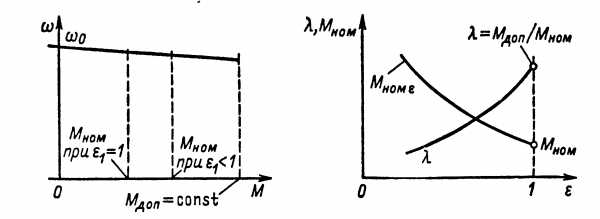
Рис. 9.27. Изменение перегрузочной способности λ=f(ε)двигателей

Отношение потерь при кратковременной нагрузке к потерям, допустимым в длительном режиме, называется коэффициен­том термической перегрузкии может быть получено из (9.112):

(9.113)

Зависимость р_терм=f(t_p/Tн.cp) приведена на рис. 9.29. По коэффициенту термической перегрузки можно найти коэффи­циент механической перегрузки, равный отношению мощностиΡк к мощности при продолжительной нагрузке Рном» то есть р_м=Рк/Рном.

Действительно,

(9.114)

(9.115)

где а=ΔРс/ΔР_V.ном— отношение постоянных потерь к пере­менным при номинальной нагрузке.

Подставляя в (9.115) значение р_термиз (9.113), получаем

(9.116)

По (9.16) и заданному коэффициенту аможет быть построена зависимость допустимого коэффициента механической пере­грузки р_мот относительного времени работы t_p/Τн,cр(рис. 9.29).

Пренебрегая постоянными потерями (а=0), выражение (9.116) можно записать в виде

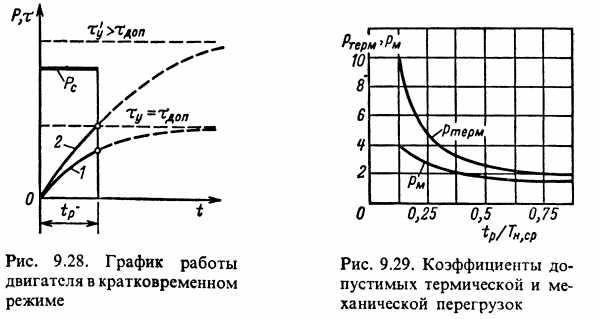
Если нагрузка в рабочий период меняется, то ηрасчетные формулы вводится вместо Ρк эквивалентная мощность за времяt_р.

Выбор мощности двигателей номинального продолжитель­ного режима для работы в кратковременном режиме произво­дится из допустимых нагрева и перегрузки, при этом номиналь­ные мощности равны: Рном = Рк/Ртерм; Рном.mах=Рк/λдв, где λ -допустимая перегрузочная способность двигателя, значения которой указаны ниже:

Двигатель постоянного тока . . . . . . 2—2,5

Асинхронный двигатель с короткозамкнутым ротором

нормального исполнения . . . . . . 1,7—2,2

То же с контактными кольцами . . . . 2—2,5

Синхронные двигатели …………. 2—2,5

При задании графика нагрузки в виде i=f(t) или Μ=(t) в расчетные формулы вместо мощности Ρк вводится соответ­ствующее значение тока или момента.

Из анализа кривых на рис. 9.29 видно, что уже при t_p/Tн.cp=0,35 и допустимой перегрузке по нагреву коэффициент механиче­ской перегрузки становится равным 2,5, что для двигателей постоянного тока оказывается предельным. Асинхронные же двигатели допускают еще меньшую перегрузку, поэтому двига­тели, предназначенные для продолжительного режима работы и используемые в кратковременном режиме, редко рассчиты­ваются по условиям допустимого нагрева и в большинстве случаев недоиспользуются по нагреву. Для лучшего исполь­зования двигателей по нагреву при небольших значенияхt_ρ/Тн,ср необходимо применять двигатели специального испол­нения, отличающиеся повышенной перегрузочной способно­стью; асинхронные двигатели с короткозамкнутым ротором должны также иметь больший пусковой момент.

studfiles.net

Как рассчитать номинальную потребляемую мощность?

Что-то некоторые отвечающие сами блудят.. . На счет понятий, все правильно, -кто Николаю N сказал, что нет понятия НОМИНАЛЬНАЯ ПОТРЕБЛЯЕМАЯ МОЩНОСТЬ? Признавайтесь… ! Мощность номинальная потребляемая, так и будет- 60Вт. А вот полная мощность, будет иной, если лампа питается от источника переменного тока, даже если это лампа накаливания, то полная мощность выраженная в ВА, будет на ГРАМУЛЬКУ больше.. . Лампы с ПРА, имеют COS ФИ отличный от 1, поэтому полная мощность ВА, будет существенно больше номинальной в Вт.. . Реактивная мощность, потребляемая лампами, как правило не где не прописывается, и спрос на ее величину, возникает только у БОТАНИКОВ.. . Путем простых фактических замеров тока и напряжения, вы как раз определите полную потребляемую мощность в ВА.. .

лампа накаливания? если да, то мощность 60 ватт.. . точнее только взять и измерить.. . если люминесцентная с ПРА то потребляемая мощность будет больше 60 ватт, т. к. ПРА часть энергии будет рассеивать…

Номинальная мощность — она и в Африке номинальная — 60 Вт . Но нет такого понятия «номинальная потребляемая мощность». Есть мощность потребляемая нагрузкой (светильником) в номинальном режиме. Но не указан тип лампы — накаливания, люминисцентная, ДРЛ или др. Если не накаливания, то не указан вид мощности — активная, реактивная или полная ?

touch.otvet.mail.ru

Что такое номинальная мощность электродвигателя и как она расчитывается

Одна из естественных характеристик электродвигателя – его номинальная (эффективная) мощность P_ном, которая для машин переменного и постоянного тока является механической мощностью на валу.

Это мощность двигателя, с которой он мог бы работать в номинальном режиме — режиме эффективной работы на протяжении длительного времени (не менее нескольких часов). Номинальная мощность измеряется в Вт (кВт) или лошадиных силах (л.с.) и указывается на щитке электрической машины вместе с остальными основными характеристиками.

номинальная мощность электродвигателя

При нагрузках, меньших P_ном, мощность двигателя развивается в полной мере. При загрузке двигателя до номинальной мощности на сравнительно короткий промежуток времени можно считать, что он не используется в полную силу. В такой ситуации бывает целесообразна его кратковременная перегрузка, предел которой определяется перегрузочной мощностью двигателя.

В паспорте электродвигателя заводом-изготовителем всегда указываются номинальные величины мощности P_ном, напряжения U_ном, коэффициента мощности cosϕ_ном, номинальная угловая скорость двигателя ω_ном.

Расчет номинальной мощности

Метод эквивалентного тока

Применим для расчета номинальной мощности при обязательном соблюдении во время работы неизменности показателей мощности потерь в обмотках двигателя, складывающейся из постоянной и переменной величин мощности, сопротивлений обмоток ротора и статора, потерь на механическое трение. Зная номинальный коэффициент мощности, показатели эквивалентного тока и номинального напряжения, возможно рассчитать номинальную мощность электродвигателя:

P_ном ≥ I_эк ∙ U_ном ∙cosϕ_ном,

где I_эк – показатель эквивалентного тока,

U_ном – номинальное напряжение,

cosϕ_ном – номинальный коэффициент мощности, повышающийся с увеличением мощности и номинальной угловой скорости вращения ротора, а также зависящий от нагрузки. Для большинства электродвигателей составляет 0,8-0,9.

Метод эквивалентного момента

Электродвигатели любого типа имеют пропорциональный произведению тока и величине магнитного потока вращающий момент. Метод эквивалентного момента для расчета номинальной мощности используется в тех случаях, когда условия применяемой нагрузки определяют непосредственно требуемый от двигателя момент, а не ток. Для синхронных и асинхронных машин переменного тока коэффициент мощности cosϕ приближенно принимается за постоянную величину:

P_ном = М_вр ∙ ω_ном,

где М_вр – значение вращающего момента,

ω_ном – номинальная угловая скорость двигателя.

Определение номинальной мощности опытным путем

Указанная в паспорте или щитке устройства номинальная мощность будет равна этому значению только при оптимальной нагрузке на вал, определяемой заводом-изготовителем для номинального режима. На что ориентироваться, если по каким-то причинам не сохранился паспорт или стерлись надписи на табличке?

Помогут практические измерения и счетчик электроэнергии:

1. Необходимо полностью отключить все прочие источники потребления электроэнергии: освещение, электроприборы и т.д.

2. В случае использования электронного счетчика следует подключить двигатель под нагрузкой на 5-6 минут, на электронном дисплее отобразиться величина нагрузки в кВт.

Дисковый счетчик проводит измерения в кВт∙час. Следует записать последние показания и включить двигатель на 10 минут с точностью до секунды. После остановки электромашины отнять из полученного значения записанные показания и умножить на 6. Полученное число и будет являться активной механической мощностью двигателя.

1. Для маломощных двигателей можно подсчитать количество оборотов диска счетчика, для каждого из которых указана, чему равна величина полных оборотов в единицах мощности. Несложные расчеты помогут определить искомую величину мощности.

При использовании этого метода важно правильно подобрать нагрузку, поскольку при ее недостаточности или перегрузке определяемый показатель будет далек от номинальной мощности электродвигателя.

Пишите комментарии, дополнения к статье, может я что-то пропустил.

Загляните на карту сайта, буду рад если вы найдете на моем сайте еще что-нибудь полезное.

Всего доброго.

• Twitter
• Google
• Печать
• Reddit
• Facebook
• LinkedIn
• по электронной почте

elektrik-orenburg.ru