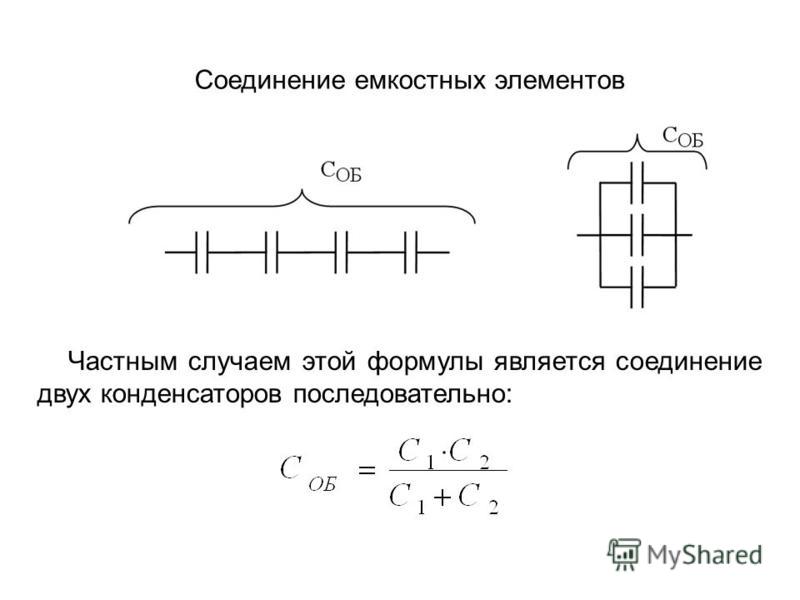
Параллельное соединение конденсаторов формула: Параллельное соединение конденсаторов – общая емкость, заряд, формула кратко

Параллельное соединение конденсаторов – общая емкость, заряд, формула кратко

4.8

Средняя оценка: 4.8

Всего получено оценок: 46.

Обновлено 20 Ноября, 2020

4.8

Средняя оценка: 4.8

Всего получено оценок: 46.

Обновлено 20 Ноября, 2020

Компоненты электрической цепи могут быть соединены различными способами, чаще всего используется параллельное и последовательное соединение. Рассмотрим работу параллельно соединенных конденсаторов.

Виды соединений в электрической цепи

Любая электрическая цепь состоит из одного или нескольких источников тока и одного или нескольких потребителей. Все эти компоненты связаны между собой проводниками.

Как бы ни сложна была электрическая цепь, в ней всегда можно выделить узлы и звенья:

• узел — это точка, в которой сходятся три и более проводника;
• звено — это участок цепи между двумя соседними узлами.

Каждое звено может быть простым проводником, может состоять из одного потребителя, а может содержать несколько потребителей, соединенных «цепочкой», один за другим.

Такое соединение потребителей называется последовательным.

Если несколько звеньев подключаются к одним и тем же двум узлам, такое соединение называется параллельным.

Если три и более звена соединяются так, что некоторые звенья будут соединены параллельно, а некоторые — последовательно, то такое соединение называется смешанным.

Рис. 1. Виды соединений в электрической цепи.

Параллельное соединение конденсаторов

При параллельном соединении к двум выводам звена подключается каждый из соединенных конденсаторов. Получается, что при подключении к внешней цепи электрический ток будет поступать сразу на все конденсаторы. Произведем расчет емкости такой батареи конденсаторов.

Напомним, что емкость конденсатора показывает, насколько легко сообщить конденсатору заряд, и равна отношению заряда к напряжению на обкладках:

$$C={q\over U}$$

Если сообщить батарее конденсаторов некоторый заряд, то по закону сохранения этот заряд может лишь распределиться между конденсаторами, однако суммарно он останется прежним:

$$q_{общ}=q_1+q_2+…+q_n$$

При параллельном соединении конденсаторов напряжение на каждом из них будет одинаково.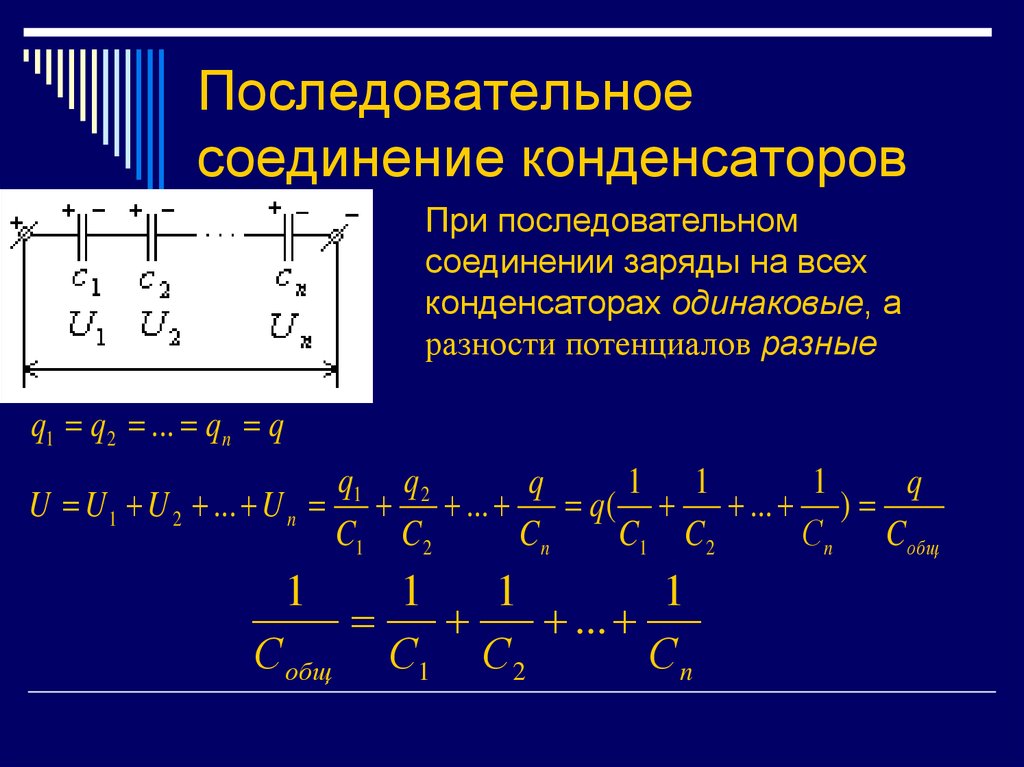 Действительно, если на каком-то из конденсаторов напряжение было бы больше, то заряд из этого конденсатора сразу же перешел бы к другому, тем самым уменьшив напряжение на первом и увеличив на втором.

Таким образом, общая емкость батареи конденсаторов равна:

$$C_{общ}={q_1+q_2+…+q_n\over U}={q_1\over U}+{q_2\over U}+…+{q_n\over U}$$

Каждый компонент полученной суммы равен отношению заряда на одном из конденсаторов к напряжению на нем, а это — емкость данного конденсатора. Заменяя каждую дробь на соответствующую емкость, получаем формулу для определения общей емкости параллельно соединенных конденсаторов:

$$C_{общ}=C_1+C_2+…+Cn$$

При параллельном соединении конденсаторов общая емкость батареи равна сумме емкостей отдельных элементов.

Рис. 2. Параллельное соединение конденсаторов.

Использование параллельного соединения конденсаторов

Казалось бы, смысла в параллельном соединении конденсаторов нет. Зачем брать два конденсатора, если можно взять один, большей емкости?

Основная причина состоит в том, что выпускаемые номиналы конденсаторов имеют не любые значения.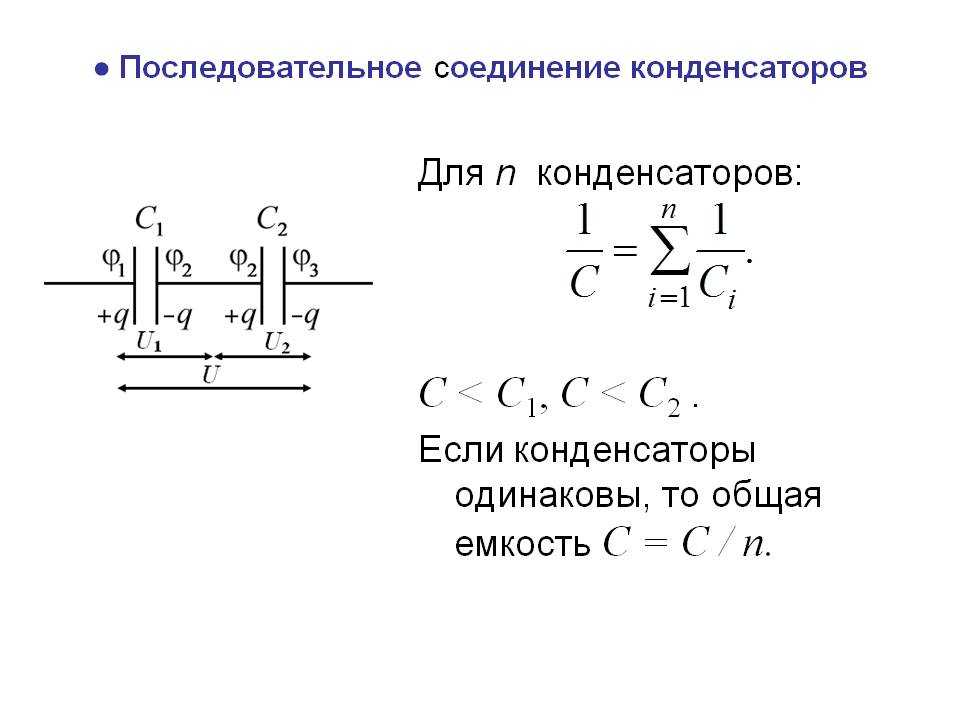 Например, конденсаторы емкостью 7 мкФ не выпускаются. Однако выпускаются конденсаторы емкостью 6,8 мкФ и 0,2 мкФ. Соединив их параллельно, можно получить требуемые 7 мкФ.

Рис. 3. Стандартные ряды номиналов радиодеталей.

Существует еще одна причина использования параллельного соединения конденсаторов — их неидеальность. Например, у больших конденсаторов имеется заметная на высоких частотах паразитная индуктивность. Из-за этого высокочастотная составляющая сигнала, которая в идеале должна легко проходить через большую емкость конденсатора, не проходит через него. Поэтому в этом случае параллельно конденсатору большой емкости ставится еще один, малой емкости, но имеющий очень малую паразитную индуктивность, которой можно пренебречь. В результате высокочастотная составляющая будет проходить через него.

Что мы узнали?

Общая емкость конденсаторов при параллельном соединении равна сумме емкостей отдельных конденсаторов. Такое соединение используется чаще всего для того, чтобы получить номиналы, не выпускающиеся промышленностью.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

Пока никого нет. Будьте первым!

Оценка доклада

4.8

Средняя оценка: 4.8

Всего получено оценок: 46.

---

А какая ваша оценка?

Параллельное и последовательное соединение конденсаторов (формулы, законы для вычисления емкости и напряжения)

Содержание

1. Отличия параллельного и последовательного соединения конденсаторов
2. Смешанное подключение
3. Общая емкость и распределение напряжений между элементами при разных типах включения
4. Примеры подключений

Электрические схемы могут содержать элементы, основным параметром которых является емкость. Чаще всего это конденсаторы (также в этом качестве используются, например, варикапы, ионисторы и т.п.). Такие элементы можно соединять параллельно или последовательно и получать участки схемы с иными параметрами.

Отличия параллельного и последовательного соединения конденсаторов

При параллельном (parallel) подключении обкладки конденсаторов соединяются в одной точке, а противоположные – в другой. К этим точкам подключается источник напряжения. Наглядно продемонстрировать такую схему можно на примере полярных приборов (например, электролитических конденсаторов), когда все положительные электроды соединяются между собой и подключаются к плюсу питания.

Отрицательные обкладки также соединяются в один узел, на который подается минус питающего напряжения. У неполярных элементов нет разделения на положительные и отрицательные электроды, они соединяются произвольным образом, но по тому же принципу (в этом случае на батарею можно подавать и двухполярное напряжение). Каждый конденсатор подключен непосредственно к источнику питания, поэтому напряжение на каждой банке одинаково.

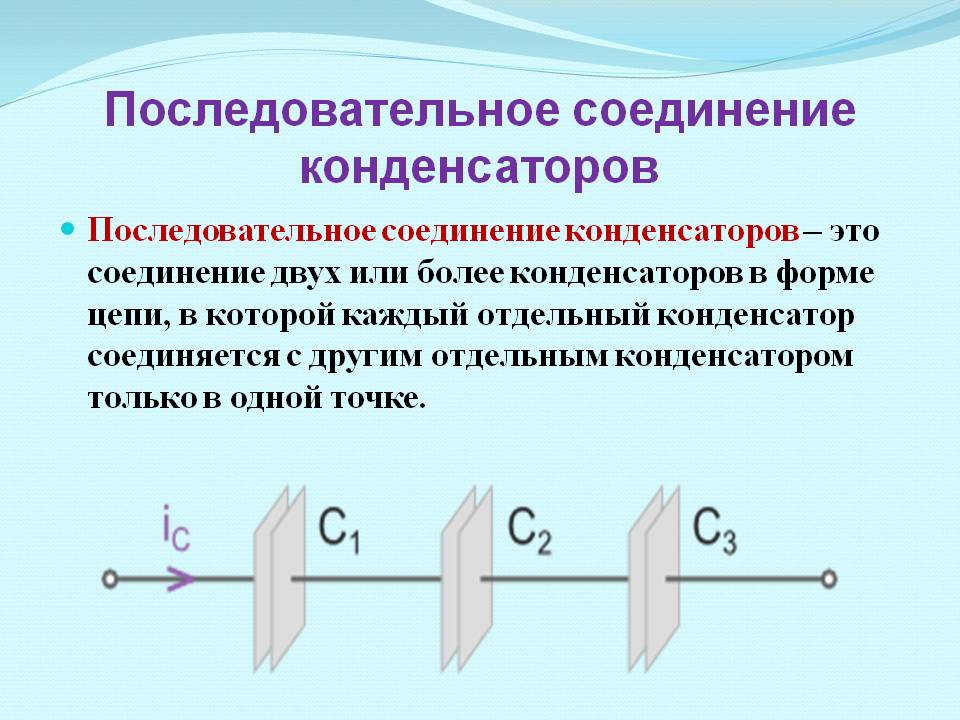
Параллельное включение элементов.

При последовательном (serial) соединении одна обкладка каждого элемента подключается к выводу соседнего конденсатора, а другая – к выводу другой ячейки. Напряжение подается на свободные выводы крайних элементов.

Батарея из последовательно соединенных ячеек.

Смешанное подключение

Также существует смешанное соединение элементов, когда часть ячеек включена параллельно, часть последовательно. Такие схемы несколько сложнее для анализа.

Батарея из смешанно соединенных конденсаторов.

Общая емкость и распределение напряжений между элементами при разных типах включения

Емкость конденсаторов зависит, в том числе, и от площади обкладок. Если однотипные элементы соединить параллельно, это можно рассматривать как суммирование всех площадей обкладок, что означает сложение емкостей банок, входящих в батарею. Очевидно, что это же правило действует и для разнотипных элементов. Аналитическим путем к этому можно прийти в результате следующих рассуждений:

• очевидно, что при таком подключении на каждом элементе напряжения будут равны (U₁=U₂=U);
• запасенные заряды всех пластин суммируются (q=q₁+q₂);
• тогда общая емкость равна С=U*q=U*(q₁+q₂)=U*q₁+U*q₂=C1+C2.

Напряжение и заряды при параллельном включении элементов.

Эта же формула действует при параллельном соединении n конденсаторов:

С=С₁+С₂+..+C_n.

Последовательное соединение емкостей.

Если соединить в последовательную цепь, например, три конденсатора различной емкости и полностью их зарядить до напряжения U, то выяснится, что:

• заряды –q1 и q2, -q2 и q3 равны между собой, так как обкладки с этими зарядами электрически соединены;
• заряды q1 и –q1, q2 и –q2, q3 и –q3 равны между собой по абсолютной величине, но противоположны по знаку.

Конденсаторы в таком включении получают равный заряд q, но при разной емкости получится, что напряжения на каждом элементе равны:

• U₁=q/ C₁;
• U₂=q/ C₂;
• U₃= q/ C₃.

Напряжения распределяются пропорционально емкостям (при равных параметрах на каждой банке падает одинаковое сопротивление).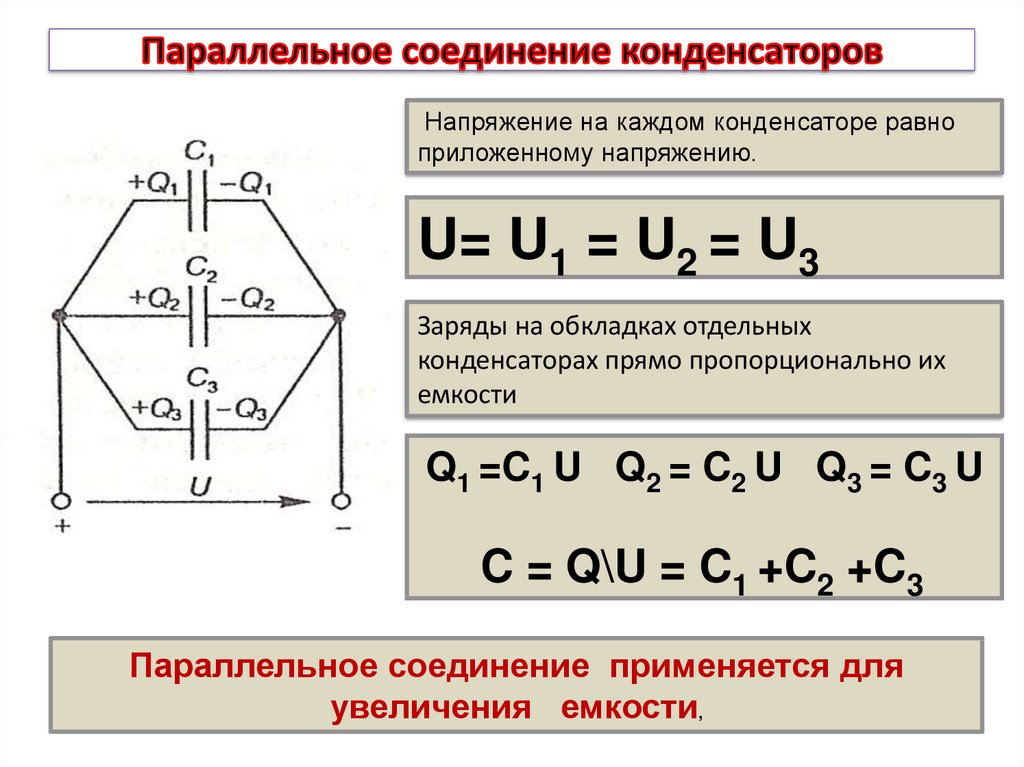 А общая емкость равна С=q/(U₁+U₂+U₃), отсюда 1/С=( U₁+U₂+U₃)/q=1/С₁+1/С₂+1/С₃.

Для n элементов, подключенных в последовательную цепь:

1/С=1/С₁+1/С₂+..+1/С_n.

Формула выглядит громоздко, но для цепи из двух элементов можно пользоваться приведенным видом С= С₁* С₂/( С₁+ С₂).

Для предварительного анализа схем, состоящих из емкостных элементов, подключенных различными способами, надо запомнить несколько законов:

• при параллельном соединении емкости складываются, суммарная емкость всегда больше, чем у элемента с самым большим значением емкости;
• напряжения при параллельном соединении одинаковы на каждом элементе цепи;
• при последовательном соединении итоговая емкость будет меньше наименьшего значения емкости любого элемента;
• напряжения на последовательно включенных звеньях распределяются пропорционально емкости.

Анализ и расчет схем со смешанным подключением элементов надо начинать с приведения цепи к единому виду, где конденсаторы будут включены либо только последовательно, либо только в параллель.

Преобразование к последовательному виду.

Так, схема на рисунке содержит три элемента, два из которых включены в параллель, и один последовательно. Удобно С1 и С3 заменить одним эквивалентным звеном С – при этом останутся только последовательные звенья. Остается выполнить расчет схемы, а потом вернуться к изначальной цепи.

Преобразование к последовательному виду.

Рекомендуем видео-урок по физике.

Примеры подключений

Параллельное соединение применяется в тех случаях, когда надо увеличить итоговую емкость.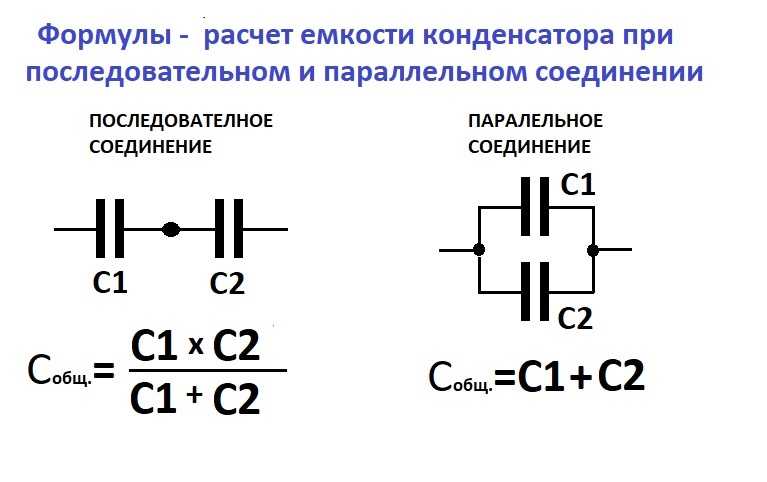 По экономическим или компоновочным причинам использование одного элемента с необходимыми параметрами может быть невозможно или нерационально. Поэтому собирают батарею из конденсаторов так, чтобы сумма емкостей давала необходимое значение. Такая схема применяется, например, для фильтров блоков питания в целях увеличения емкости сглаживающего фильтра.

Другой вариант параллельного включения – когда емкость надо точно настраивать по месту, а подстроечного конденсатора с необходимыми пределами или нет в наличии, или не существует. Тогда параллельно конденсатору постоянной емкости включают подстроечный элемент. После монтажа устройства во время настройки устанавливается точное значение.

Параллельно включенный прибор с постоянными параметрами и подстроечник.

Последовательное включение нескольких элементов дает увеличение рабочего напряжения цепочки, но уменьшает общую емкость. К тому же купить приборы на высокое напряжение (до нескольких киловольт) несложно, поэтому последовательные цепи в целях достижения необходимых параметров применяются нечасто. Обычно такое включение используется в емкостных делителях напряжения. В отличие от резистивных компонентов, через реактивные элементы не протекает активный ток, поэтому не надо решать задачу отвода тепла. Такие делители можно применять, к примеру, в индикаторах наличия высокого напряжения. Несколько киловольт на входе подбором номиналов банок делятся так, что напряжение на нижнем элементе безопасно для индикаторной лампы.

Индикатор высокого напряжения.

Также такой делитель можно найти в схемах импульсных источников питания с полумостовой схемой. Таким способом образуется средняя точка с потенциалом, равным половине питания.

Фрагмент схемы блока питания с фильтром-делителем и выравнивающими резисторами.

 

Еще один пример применения последовательного соединения элементов – в умножителях напряжения. В них нагрузочная способность источника питания зависит от емкости, поэтому в умножителях также применяются оксидные конденсаторы.

Последовательная батарея для умножителя.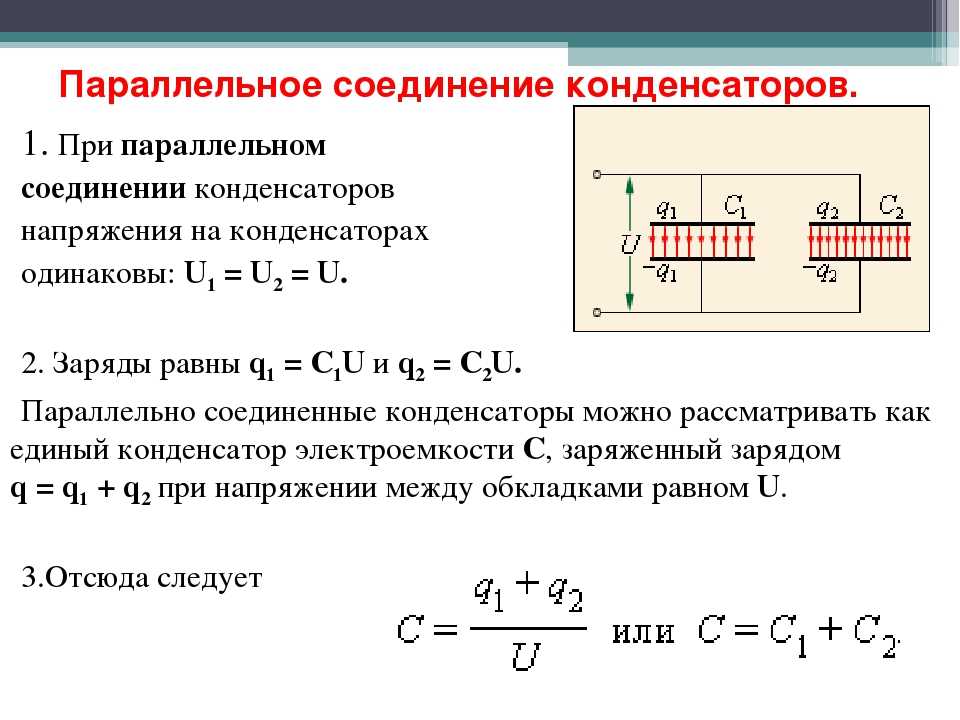

Смешанное включение встречается гораздо реже. Один из примеров такой схемы – колебательный контур с переменной частотой настройки. Его резонанс зависит, в том числе, от емкости конденсатора, и перестройка по частоте зависит от пределов изменения емкости. Ряд конденсаторов переменной емкости, выпускаемый промышленностью, довольно ограничен, поэтому для достижения необходимых границ параллельно и последовательно с КПЕ включают «растягивающие» конденсаторы.

КПЕ с «растягивающими» элементами.

Если имеется конденсатор с пределами изменения характеристик от 10 до 430 пФ, при подключении добавочных конденсаторов пределы изменения емкости получаются:

С1, пФ	С2, пФ	Новые пределы изменения, пФ
15	40	15..36
25	100	25..82

Знание свойств соединения емкостных элементов позволяет быстро анализировать процессы, происходящие в электрических схемах. Также понимание, как изменяются характеристики цепи при различных видах подключения, позволяет комбинировать имеющиеся элементы, создавая участки схем с новыми параметрами.

19.6 Конденсаторы, включенные последовательно и параллельно – College Physics

Глава 19 Электрический потенциал и электрическое поле

Резюме

• Выведите выражения для полной емкости при последовательном и параллельном подключении.
• Определите последовательное и параллельное соединение конденсаторов.
• Рассчитайте эффективную емкость при последовательном и параллельном подключении по отдельным емкостям.

Несколько конденсаторов могут быть соединены вместе в различных приложениях. Несколько соединений конденсаторов действуют как один эквивалентный конденсатор. Общая емкость этого эквивалентного одиночного конденсатора зависит как от отдельных конденсаторов, так и от того, как они соединены. Существует два простых и распространенных типа соединений, называемых 9.0017 серии и параллельно , для которых мы можем легко рассчитать общую емкость.

Некоторые более сложные соединения также могут быть связаны с комбинациями последовательного и параллельного соединения.

На рис. 1(а) показано последовательное соединение трех конденсаторов с приложенным напряжением. Как и для любого конденсатора, емкость комбинации связана с зарядом и напряжением соотношением [latex]{C = \frac{Q}{V}}[/latex].

Обратите внимание на рис. 1, что противоположные заряды величиной [латекс]{Q}[/латекс] текут по обеим сторонам первоначально незаряженной комбинации конденсаторов при приложении напряжения [латекс]{В}[/латекс]. Сохранение заряда требует, чтобы на пластинах отдельных конденсаторов создавались заряды равной величины, поскольку в этих изначально нейтральных устройствах заряд только разделяется. Конечным результатом является то, что комбинация напоминает один конденсатор с эффективным расстоянием между пластинами больше, чем у отдельных конденсаторов по отдельности. (См. рис. 1(b).) Большее расстояние между пластинами означает меньшую емкость.

Общей особенностью последовательного соединения конденсаторов является то, что общая емкость меньше любой из отдельных емкостей.

Рисунок 1. (а) Конденсаторы, соединенные последовательно. Величина заряда на каждой пластине равна Q . (b) Эквивалентный конденсатор имеет большее расстояние между пластинами d . Последовательные соединения дают общую емкость меньше, чем у любого из отдельных конденсаторов.

Мы можем найти выражение для общей емкости, рассматривая напряжение на отдельных конденсаторах, показанных на рисунке 1. Решение [латекс]{С = \frac{Q}{V}}[/латекс] для [латекс]{В} [/latex] дает [latex]{V = \frac{Q}{C}}[/latex]. Таким образом, напряжения на отдельных конденсаторах равны [латекс]{V_1 = \frac{Q}{C_1}}[/latex], [латекс]{V_2 = \frac{Q}{C_2}}[/latex] и [ латекс]{V_3 = \frac{Q}{C_3}}[/латекс]. Общее напряжение представляет собой сумму отдельных напряжений:

[латекс] {V = V_1 + V_2 + V_3}. [/латекс]

Теперь, называя общую емкость [латекс]{C_S}[/латекс] последовательной емкостью, считайте, что

[латекс] {V =} [/латекс] [латекс] {\ гидроразрыва {Q} {C_S}} [/ латекс] [латекс] { = V_1 + V_2 + V_3}. [/латекс]

Введя выражения для [латекс]{V_1}[/латекс], [латекс]{V_2}[/латекс] и [латекс]{V_3}[/латекс], мы получим

[латекс] {\ гидроразрыва {Q} {C_S} = \ гидроразрыва {Q} {C_1} + \ гидроразрыва {Q} {C_2} + \ гидроразрыва {Q} {C_3}}. [/латекс]

Отменяя [латекс]{Q}[/латекс], мы получаем уравнение для полной емкости последовательно [латекс]{C_S}[/латекс] равной

[латекс] {\ гидроразрыва {1} {C_S}} [/ латекс] [латекс] {=} [/ латекс] [латекс] {\ гидроразрыва {1} {C_1}} [/ латекс] [латекс] {+ } [/латекс] [латекс] {\ гидроразрыва {1} {C_2}} [/ латекс] [латекс] {+} [/латекс] [латекс] {\ гидроразрыва {1} {C_3}} [/латекс] [ латекс]{+ \cdots},[/латекс]

, где «…» указывает, что выражение справедливо для любого количества последовательно соединенных конденсаторов.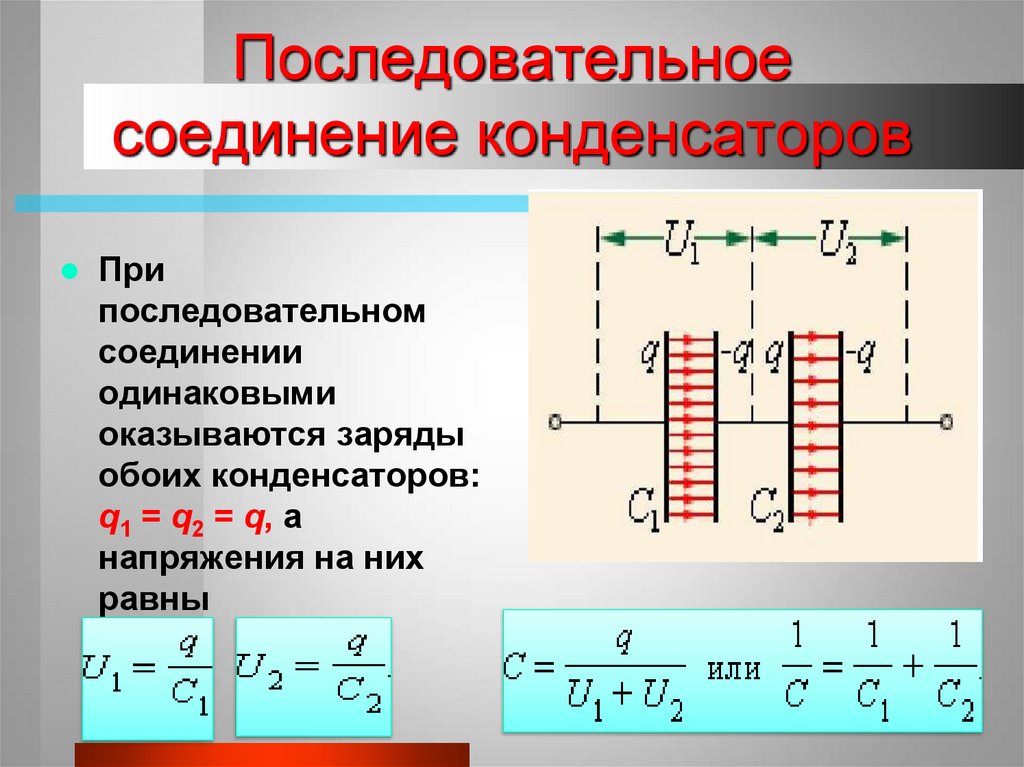 Выражение этой формы всегда приводит к тому, что общая емкость [латекс]{C_S}[/латекс] меньше любой из отдельных емкостей [латекс]{С_1}[/латекс], [латекс]{С_2}[/латекс]. ], …, как показано в следующем примере.

Суммарная последовательная емкость,

C _с

Полная последовательная емкость: [латекс] {\ frac {1} {C_S} = \ frac {1} {C_1} + \ frac {1} {C_2} + \frac{1}{C_3} + \cdots}[/latex]

Пример 1: Что такое последовательная емкость?

Найдите общую емкость трех последовательно соединенных конденсаторов, если их индивидуальные емкости равны 1000, 5000 и 8000 [латекс]\мк\текстбф{Ф}[/латекс].

Стратегия

Имея данную информацию, общую емкость можно найти, используя уравнение для последовательной емкости.

Решение

Ввод данных емкостей в выражение для [латекс]{\ гидроразрыва {1} {C_S}} [/латекс] дает [латекс] {\ гидроразрыва {1} {C_S} = \ гидроразрыва {1 {C_1} + \frac{1}{C_2} + \frac{1}{C_3}}[/latex].

[латекс] {\ гидроразрыва {1} {C_S}} [/ латекс] [латекс] {=} [/ латекс] [латекс] {\ гидроразрыва {1} {1,000 \; \ мю \ textbf {F}} }[/латекс] [латекс]{+}[/латекс] [латекс]{\гидроразрыва{1}{5.000 \;\textbf{F}}}[/латекс] [латекс]{+}[/латекс] [ латекс] {\ гидроразрыва {1} {8.000 \; \ mu \ textbf {F}}} [/ латекс]  [латекс] {=} [/латекс] [латекс] {\ гидроразрыва {1,325} {\ му \ textbf { F}}}[/латекс]

Инвертирование для нахождения [латекс]{C_S}[/латекс] дает [латекс]{C_S = \frac{\mu \textbf{F}}{1,325} = 0,755 \;\mu \textbf{F}}[/ латекс].

Обсуждение

Суммарная последовательная емкость [латекс]{C_s}[/латекс] меньше наименьшей индивидуальной емкости, как и было обещано. При последовательном соединении конденсаторов сумма меньше частей. На самом деле, это меньше, чем любой человек. Обратите внимание, что иногда возможно и более удобно решить уравнение, подобное приведенному выше, путем нахождения наименьшего общего знаменателя, который в этом случае (показывая только вычисления целых чисел) равен 40. Таким образом,

[латекс] {\ гидроразрыва {1} {C_S}} [/ латекс] [латекс] {=} [/ латекс] [латекс] {\ гидроразрыва {40} {40 \; \ mu \ textbf {F}} }[/латекс] [латекс]{+}[/латекс] [латекс]{\гидроразрыва{8}{40 \;\mu \textbf{F}}}[/латекс] [латекс]{+}[/латекс ] [латекс] {\ гидроразрыва {5} {40 \; \ mu \ textbf {F}}} [/ латекс] [латекс] {=} [/ латекс] [латекс] {\ гидроразрыва {53} {40 \; \mu \textbf{F}}},[/latex]

, так что

[latex]{C_S =}[/latex] [latex]{\frac{40 \;\mu \textbf{F}}{ 53}}[/латекс] [латекс]{= 0,755 \; \mu \textbf{F}}.[/latex]

На рис. 2(а) показано параллельное соединение трех конденсаторов с приложенным напряжением. Здесь общую емкость найти проще, чем в последовательном случае. Чтобы найти эквивалентную общую емкость [латекс]{\текст{С}_{\текстбф{р}}}[/латекс], сначала отметим, что напряжение на каждом конденсаторе равно [латекс]{В}[/латекс], такие же, как и у источника, так как они подключены непосредственно к нему через проводник. (Проводники являются эквипотенциальными, поэтому напряжение на конденсаторах такое же, как и на источнике напряжения. ) Таким образом, конденсаторы имеют на себе такие же заряды, как если бы они были подключены к источнику напряжения по отдельности. Общий заряд [латекс]{Q}[/латекс] представляет собой сумму отдельных сборов:

[латекс] {Q = Q_1 + Q_2 + Q_3}.[/латекс]

Рис. 2. (a) Параллельное подключение конденсаторов. Каждый из них подключен непосредственно к источнику напряжения, как если бы он был один, и поэтому общая емкость при параллельном подключении представляет собой просто сумму отдельных емкостей. (b) Эквивалентный конденсатор имеет большую площадь пластины и, следовательно, может удерживать больше заряда, чем отдельные конденсаторы.

Используя соотношение [латекс]{Q = CV}[/латекс], мы видим, что общий заряд равен [латекс]{Q = C_{\textbf{p}}V}[/латекс], а отдельные заряды равны [латекс]{Q_1 = C_1 V}[/латекс] ,  [латекс]{Q_2 = C_2 V}[/латекс] , и [латекс]{Q_3 = C_3 V}[/латекс]. Ввод их в предыдущее уравнение дает

[латекс] {C_{\textbf{p}} V = C_1 V + C_2 V + C_3 V} . [/latex]

Исключая [латекс]{V}[/латекс] из уравнения, мы получаем уравнение для полной емкости параллельно [латекс]{С_{\textbf{p}}}[/латекс]:

[латекс]{C_{\textbf{p}} = C_1 + C_2 + C_3 \cdots}[/латекс] .

Общая емкость при параллельном подключении представляет собой просто сумму отдельных емкостей. (Опять «…» указывает, что выражение справедливо для любого количества конденсаторов, соединенных параллельно.) Так, например, если бы конденсаторы в приведенном выше примере были соединены параллельно, их емкость была бы

[латекс]{C_{\textbf{p}} = 1,000 \;\mu \textbf{F} + 5,000 \;\mu \textbf{F} + 8,000 \;\mu \textbf{F} = 14,000 \; \mu \textbf{F}}.[/latex]

Эквивалентный конденсатор для параллельного соединения имеет значительно большую площадь пластин и, следовательно, большую емкость, как показано на рис. 2(b).

Суммарная емкость при параллельном подключении,

C _p [латекс] {C_{\textbf{p}}}[/latex]

Суммарная емкость при параллельном подключении [латекс]{C_{\textbf{p}} = C_1 + C_2 + C_3 + \cdots}[/латекс]

Более сложные соединения конденсаторов иногда могут представлять собой комбинации последовательного и параллельного соединения.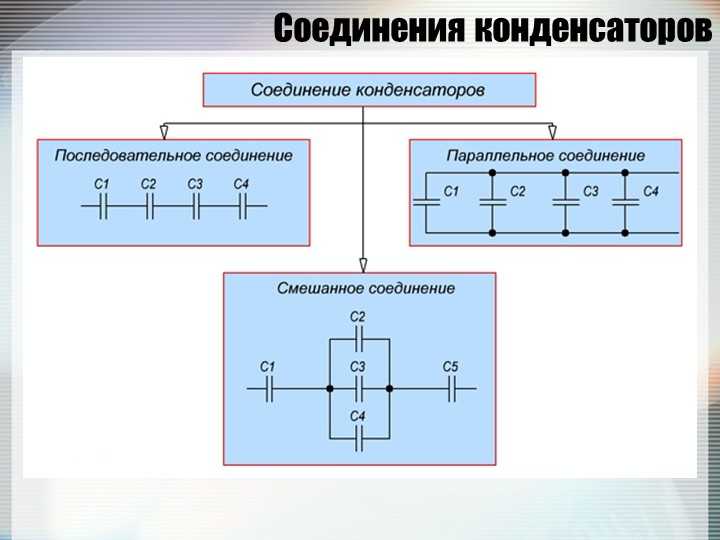 (См. рис. 3.) Чтобы найти общую емкость таких комбинаций, мы идентифицируем последовательные и параллельные части, вычисляем их емкости, а затем находим общую емкость.

Рис. 3. (а) Эта схема содержит как последовательное, так и параллельное соединение конденсаторов. См. Пример 2 для расчета общей емкости цепи. (b) C ₁ и C ₂ расположены последовательно; их эквивалентная емкость C _S меньше любого из них. (c) Обратите внимание, что C _S находится параллельно с C ₃ . Таким образом, общая емкость равна сумме C _S и C ₃ .

Смесь последовательных и параллельных емкостей

Найдите общую емкость комбинации конденсаторов, показанной на рисунке 3. Предположим, что емкости на рисунке 3 известны с точностью до трех знаков после запятой ([latex]{C_1 = 1,000 \;\mu\textbf {F}}[/латекс], [латекс]{C_2 = 5.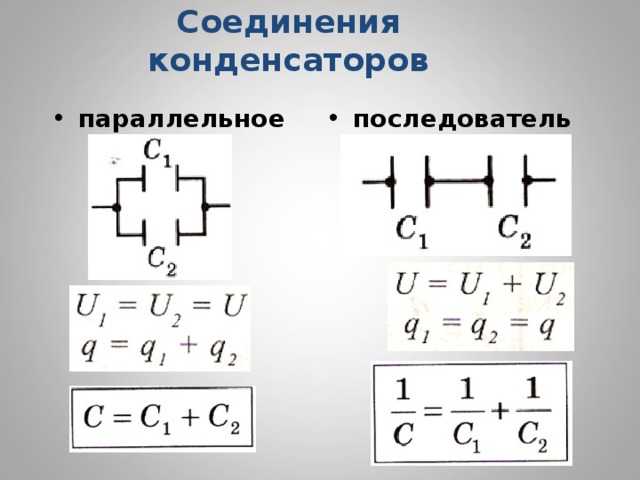 000 \;\mu \textbf{F}}[/латекс] и [латекс]{C_3 = 8.000 \;\mu \textbf{F}}[ /latex]) и округлить ответ до трех знаков после запятой.

Стратегия

Чтобы найти общую емкость, мы сначала определяем, какие конденсаторы соединены последовательно, а какие — параллельно. Конденсаторы [латекс]{C_1}[/латекс] и [латекс]{С_2}[/латекс] включены последовательно. Их комбинация, обозначенная на рисунке [латекс]{C_S}[/латекс], параллельна [латекс]{С_3}[/латекс].

Решение

Поскольку [латекс]{C_1}[/латекс] и [латекс]{С_2}[/латекс] соединены последовательно, их общая емкость определяется как [латекс]{\ гидроразрыва {1} {C_S } = \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3}}[/latex]. Ввод их значений в уравнение дает

[латекс] {\ гидроразрыва {1} {C_1}} [/ латекс] [латекс] {+} [/ латекс] [латекс] {\ гидроразрыва {1} {C_2}} [/ латекс] [латекс] { =} [/латекс] [латекс] {\ гидроразрыва {1} {1,000 \; \ mu \ textbf {F}}} [/ латекс] [латекс] {+} [/латекс] [латекс] {\ гидроразрыва {1 }{5. 000 \;\mu \textbf{F}}}[/latex] [латекс]{=}[/latex] [латекс]{\frac{1.200}{\mu \textbf{F}}}.[/ латекс]

Инвертирование дает

[латекс]{C_{\textbf{S}} = 0,833 \;\mu \textbf{F}} .[/latex]

Эта эквивалентная последовательная емкость подключена параллельно третьему конденсатору ; таким образом, общее количество равно сумме

[латекс]\begin{array}{r @{{}={}} l} {C_{\text{tot}}} & {C_S + C_S} \\[1em] & {0,833 \;\mu \textbf{F} + 8.000 \;\mu \textbf{F}} \\[1em] & {8.833 \;\mu \textbf{F}}. \end{array}[/latex]

Обсуждение

Этот метод анализа комбинаций конденсаторов по частям до тех пор, пока не будет получена сумма, может быть применен к большим комбинациям конденсаторов.

 

• Общая емкость последовательно [латекс] {\ frac {1} {C _ {\ textbf {S}}} = \ frac {1} {C_1} + \ frac {1} {C_2} + \ frac {1} C_3} + \cdots }[/латекс]
• Общая емкость при параллельном соединении [латекс] {C_{\textbf{p}} = C_1 + C_2 + C_3 + \cdots}[/latex]
• Если цепь содержит комбинацию конденсаторов, соединенных последовательно и параллельно, определите последовательные и параллельные части, вычислите их емкости, а затем найдите общую сумму.

 

 

Емкость — Последовательное и параллельное соединение конденсаторов

Уровень 3 (с высшей математикой)

Уровень 3 требует основ векторного исчисления, дифференциального и интегрального исчисления. Подходит для студентов и старшеклассников.

Обновлено Александром Фуфаевым от 14.10.2022

Содержание

1. Суммарная емкость последовательного соединения конденсаторов Здесь мы выводим формулу полной емкости (эквивалентной емкости) при последовательном соединении конденсаторов.
2. Суммарная емкость параллельного соединения конденсаторов Hier leiten wir eine Formel für die Gesamtkapazität (Ersatzkapazität) her, wenn Kondensatoren parallel geschaltet sind.

Здесь мы хотим получить общая емкость \(C\) цепи, в которой два конденсатора соединены последовательно или параллельно . Один конденсатор имеет емкость \(C_1\), а другой конденсатор имеет емкость \(C_2\). Общая емкость также называется эквивалентной емкостью , потому что мы можем заменить отдельные емкости \(C_1\) и \(C_2\) на \(C\) без изменения функциональности схемы.

Суммарная емкость последовательного соединения конденсаторов

Последовательное соединение двух конденсаторов.

Рассмотрим цепь с переменным напряжением. Для этого возьмем два конденсатора с емкостями \(C_1\) и \(C_2\). Мы применяем переменное напряжение \(U(t)\) к этим двум конденсаторам, как показано на рисунке 1. Таким образом, мы построили серию конденсаторов .

Величина заряда пластин конденсатора :
Приложенное переменное напряжение вызывает переменный электрический ток \( \class{red}{I(t)} \), который заряжает и разряжает два конденсатора. Поскольку в последовательной цепи нет узлов, в которых ток мог бы разделиться, через два конденсатора протекает один и тот же ток \( \class{red}{I}(t) \). Ток определяется как заряд \(\class{red}{Q(t)}\) за раз \(t\):

Определение электрического тока

Формула якоря $$ \begin{align} \class{ red}{I(t)} ~=~ \frac{\class{red}{Q(t)}}{t} \end{align} $$

В момент времени \(t\) в обоих конденсаторах количество заряда \(\class{red}{Q(t)} ~=~ \class{red}{I(t)} \, t \) сохраняется. Поскольку ток через оба конденсатора одинаков, величина заряда \( \class{red}{Q(t)} \) в момент времени \(t\) одинакова на обоих конденсаторах.

Напряжение на конденсаторах :
Приложенное переменное напряжение \( U(t) \) представляет собой общее напряжение, которое падает на обоих конденсаторах. Это сумма напряжения \(U_1(t)\), приложенного между электродами первого конденсатора, и напряжения \(U_2(t)\), приложенного между электродами второго конденсатора:

Общее напряжение равно сумме отдельных напряжений

Привязка к формуле $$ \begin{align} U(t) ~=~ U_1(t) ~+~ U_2(t) \end{align} $$

Мы вводим емкость в игру, используя связь между зарядом и напряжением (\ (\ class {red} {Q} = C \, U \)).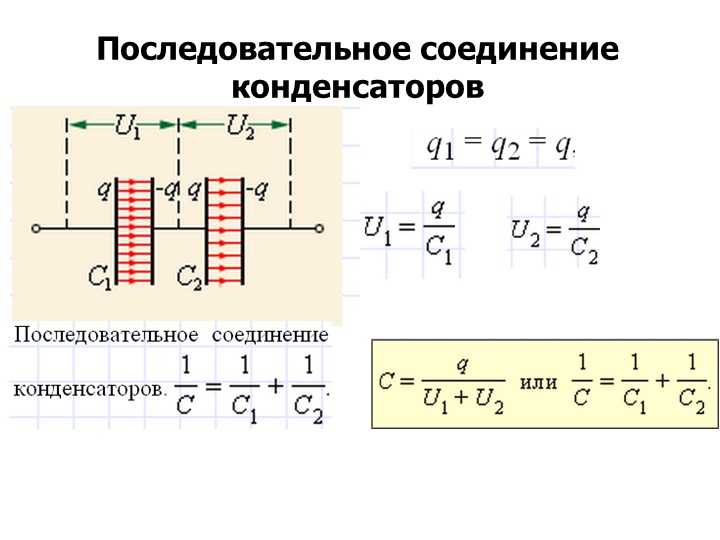 Для первого и второго конденсатора имеем следующие уравнения:

Уравнения для заряда конденсаторов

Якорь формулы $$ \begin{align} \class{red}{Q(t)} &~=~ C_1 \, U_1(t) \\\\
\class {red}{Q(t)} &~=~ C_2 \, U_2(t) \end{align} $$

Общая емкость \(C\) последовательной цепи связана с полным напряжением \ ( U(t) \) так же, как отдельные емкости в 3 :

Общий заряд пропорционален общему напряжению

Формула привязки $$ \begin{align} \class{red}{Q( t)} ~=~ C \, U(t) \end{align} $$

Эти уравнения утверждают, что заряд \( \class{red}{Q(t)} \) на пластинах конденсатора пропорционален соответствующему напряжению между пластинами конденсатора, где константа пропорциональности — это емкость. Переставьте оба уравнения 3 и 4 для напряжения:

Уравнения для всех напряжений

Якорь формулы $$ \begin{align} U_1(t) &~=~ \frac{\class{red}{ Q(t)}}{C_1} \\\\
U_2(t) &~=~ \frac{\class{red}{Q(t)}}{C_2} \\\\
U(t) &~=~ \frac{\class{red}{Q(t)}}{C} \end{align} $$

Теперь можно заменить напряжения в 3 и 4 с теми, что в 5 :

Уравнения для полного напряжения и заряда на общую емкость

Якорь формулы $$ \begin{align} U(t) &~=~ U_1(t) ~+~ U_2(t) \\\\
\ frac {\ class {red} {Q (t)}} {C} &~=~ \ frac {\ class {red} {Q (t)}} {C_1} ~+~ \ frac {\class{red}{Q(t)}}{C_2} \end{align} $$

Разделите обе части на заряд \(\class{red}{Q(t)}\), чтобы исключить его:

Обратная общая емкость есть обратная сумма двух отдельных емкостей

Привязка к формуле $$ \begin{align} \frac{1}{C} ~=~ \frac{1}{C_1} ~+~ \frac{ 1}{C_2} \end{align} $$

Это уравнение можно преобразовать для \(C\):

Формула: Эквивалентная емкость двух последовательно соединенных конденсаторов

Формула привязки $$ \begin{align } C ~=~ \frac{C_1\, C_2}{C_1 ~+~ C_2} \end{align} $$

Если у вас более двух конденсаторов, вы можете повторить все вышеописанные шаги, чтобы вывести следующую формулу:

Суммарная емкость последовательной цепи

Якорь формулы $$ \begin{align} \frac{1}{C} ~=~ \frac{1}{C_1} ~+~ \frac{1}{C_2 } ~+~. .. ~+~ \frac{1}{C_n} \end{align} $$

Здесь \(C_n\) обозначает емкость \(n\)-го конденсатора.

Суммарная емкость при параллельном соединении конденсаторов

Параллельное соединение двух конденсаторов.

Рассмотрим немного другую схему. Снова берем два конденсатора с емкостями \(C_1\) и \(C_2\). Мы применяем переменного напряжения \( U(t) \) на эти два конденсатора, но на этот раз, как показано на рисунке 2. Таким образом, мы построили параллельную цепь конденсаторов.

Ток через конденсатор :
В параллельной цепи общий ток \( \class{red}{I(t)} \) разделяется в узлах на конденсаторы. Теперь мы не можем предположить, что ток через оба конденсатора одинаков. Поэтому ток через первый конденсатор обозначим как \( \class{red}{I_1(t)} \) и через второй конденсатор как \( \class{red}{I_2(t)} \). Общий ток, конечно, должен быть суммой двух отдельных токов из-за сохранения заряда:

Общий ток представляет собой сумму отдельных токов

Якорь формулы $$ \begin{align} \class{red}{I(t)} ~=~ \class{red}{I_1(t)} ~+~ \class{red}{I_2(t)} \end{align} $$

Заряд на пластинах конденсатора :
Мы можем использовать определение тока (как заряд за время) в 2 , чтобы получить уравнение для общего заряда \(\class{red}{Q(t)}\):

Общий заряд за раз представляет собой сумму отдельных зарядов за раз

Якорь формулы $$ \begin{align} \frac{\class{red}{Q(t)}}{t} ~=~ \frac{\class{red}{Q_1(t)}}{t} ~ +~ \frac{\class{red}{Q_2(t)}}{t} \end{align} $$

Разделите обе части на время \(t\):

Общий заряд равен сумме отдельные расходы

Якорь формулы $$ \begin{align} \class{red}{Q(t)} ~=~ \class{red}{Q_1(t)} ~+~ \class{red}{Q_2( t)} \end{align} $$

В отличие от последовательной цепи заряд конденсаторов в параллельной цепи разный.