Параллельное соединение конденсаторов расчет: Параллельное соединение конденсаторов, Емкость параллельно соединенных конденсаторов | Формулы и расчеты онлайн

Тест Параллельное соединение конденсаторов по физике онлайн

Сложность: обновляется.Последний раз тест пройден 6 часов назад.

Перед прохождением теста рекомендуем прочитать:

1. Вопрос 1 из 10

   Точка в электрической цепи, где сходятся три и более проводников, называется:

   • Правильный ответ
   • Неправильный ответ
   • Пояснение: Узел — это точка, в которой сходятся три и более проводника.
   • Вы и еще 62% ответили правильно
   • 62% ответили правильно на этот вопрос

   В вопросе ошибка?

   Следующий вопросОтветить

2. Вопрос 2 из 10

   Участок цепи между двумя соседними узлами, называется:

   • Правильный ответ
   • Неправильный ответ
   • Пояснение: Звено — это участок цепи между двумя соседними узлами.
   • Вы и еще 77% ответили правильно
   • 77% ответили правильно на этот вопрос

   В вопросе ошибка?

   Ответить

3. Вопрос 3 из 10

   Соединение, в котором потребители соединены цепочкой, один за другим, называется:

   • Правильный ответ
   • Неправильный ответ
   • Пояснение: Звено может содержать несколько потребителей, соединенных цепочкой, один за другим. Такое соединение потребителей называется последовательным.
   • Вы и еще 54% ответили правильно
   • 54% ответили правильно на этот вопрос

   В вопросе ошибка?

   Ответить

4. Вопрос 4 из 10

   Соединение, в котором несколько звеньев подключаются к одним и тем же двум узлам, называется:

   • Правильный ответ
   • Неправильный ответ
   • Пояснение: Если несколько звеньев подключаются к одним и тем же двум узлам, такое соединение называется параллельным.
   • Вы и еще 54% ответили правильно
   • 54% ответили правильно на этот вопрос

   В вопросе ошибка?

   Ответить

5. Вопрос 5 из 10

   Соединение, в котором два звена соединены параллельно, а к ним присоединено последовательное звено, называется:

   • Правильный ответ
   • Неправильный ответ
   • Пояснение: Если три и более звена соединяются так, что некоторые звенья будут соединены параллельно, а некоторые — последовательно, то такое соединение называется смешанным.
   • Вы и еще 54% ответили правильно
   • 54% ответили правильно на этот вопрос

   В вопросе ошибка?

   Ответить

6. Вопрос 6 из 10

   Если на одном конденсаторе при параллельном соединении напряжение $U$, то на другом конденсаторе напряжение будет равно:

   • Правильный ответ
   • Неправильный ответ
   • Пояснение: При параллельном соединении конденсаторов напряжение на каждом из них будет одинаково.
   • Вы и еще 69% ответили правильно
   • 69% ответили правильно на этот вопрос

   В вопросе ошибка?

   Ответить

7. Вопрос 7 из 10

   Емкость параллельного соединения конденсаторов находится по формуле:

   • Правильный ответ
   • Неправильный ответ
   • Пояснение: При параллельном соединении емкость конденсаторов суммируется, то есть верна четвертая формула.
   • Вы ответили лучше 69% участников
   • 31% ответили правильно на этот вопрос

   В вопросе ошибка?

   Ответить

8. Вопрос 8 из 10

   Параллельное подсоединение конденсаторов используется потому, что:

   • Правильный ответ
   • Неправильный ответ
   • Пояснение: Основная причина состоит в том, что выпускаемые номиналы конденсаторов имеют не любые значения.
   • Вы ответили лучше 92% участников
   • 8% ответили правильно на этот вопрос

   В вопросе ошибка?

   Ответить

9. Вопрос 9 из 10

   Если имеется конденсатор 10 мкФ, а надо получить емкость 2 мкФ, то необходимо параллельно подключить конденсатор емкостью:

   • Правильный ответ
   • Неправильный ответ
   • Пояснение: При параллельном соединении емкость суммируется, поэтому подключая к конденсатору другие конденсаторы, никак невозможно уменьшить его емкость.
   • Вы и еще 54% ответили правильно
   • 54% ответили правильно на этот вопрос

   В вопросе ошибка?

   Ответить

10. Вопрос 10 из 10

    Для уменьшения паразитной индуктивности реального конденсатора большой емкости необходимо подключить параллельно конденсатор:

    • Правильный ответ
    • Неправильный ответ
    • Пояснение: У больших конденсаторов имеется заметная на высоких частотах паразитная индуктивность. В этом случае параллельно конденсатору большой емкости ставится еще один, малой емкости, но имеющий очень малую паразитную индуктивность, которой можно пренебречь.
    • Вы ответили лучше 85% участников
    • 15% ответили правильно на этот вопрос

    В вопросе ошибка?

    Ответить

Доска почёта

Чтобы попасть сюда — пройдите тест.

Рейтинг теста

Средняя оценка: обновляется.

А какую оценку получите вы? Чтобы узнать — пройдите тест.

Тема1. Электрическое поле. Расчет электрических цепей при последовательном, параллельном и смешанном соединении конденсаторов

Т.Н.ЛУКОЯНОВА

Методические указания к выполнению контрольной работы по дисциплине

«Электротехника и электроника»

 

 

2016 г.

 

ВВЕДЕНИЕ

 

Подготовка в средней профессиональной школе специалистов технических специальностей, связанных с машиностроением в области электротехники и электроники, нацелена на то чтобы выпускники умели выбирать необходимые электротехнические, электронные и электроизмерительные устройства и могли их правильно эксплуатировать Задача средних специальных учебных заведений (ссузов) обеспечить все необходимые условия для овладения студентами профессионально значимыми компетенциями, развития конкретных личностных качеств будущего специалиста, определяющих его готовность к творческой профессиональной деятельности.

В этой связи при обучении дисциплине «Электротехника и электроника», в средних специальных учебных заведениях возникает необходимость дать студентам требуемые теоретические знания, выработать у них твердые практические навыки, в том числе исследовательского характера.

Настоящее учебное пособие предназначено для обучения студентов техникумом и колледжей дисциплине «Электротехника и электроника» по специальности «Технология машиностроения».

Содержание методических указаний соответствует требованиям федеральных государственных образовательных стандартов среднего профессионального образования третьего поколения дисциплины «Электротехника и электроника».

 

 

Пример 1

Определите емкость батареи конденсаторов С₁ = 2,8 мкФ, С₂ = 0,3 мкФ, С₃ = 0,5 мкФ, С₄ = 2 мкФ, С₅ = 6 мкФ, С₆ = 3 мкФ, С₇ = 5 мкФ, схема соединения которых дана на рис. 1.

Рис.1

 

Решение:

С₂₃₄= С₂+С₃+С₄; ;

	С1		С234			С56
											С5
							С7

 

Рис. 2

С₅₆₇= С₅₆ + С₇;

	С1		С234	С567
								С5

 

Рис.3

Ответ: 1,2 мкФ.

 

Пример 2

Напряжение на зажимах цепи равно U = 100 В (Рис.4), емкости конденсаторов: С₁ = 6 мкФ; С₂ = 1,5 мкФ, С₃ = С₄ = 3 мкФ; С₅ = 6 мкФ. Определите эквивалентную емкость батареи и напряжения на конденсаторах.

 

 

	С1		С2	С3
									С5
				С4	С5

Рис. 4

 

 

Решение:

 

 

Ответ: 2 мкФ; 33,3 В; 44,5 В; 22,2 В; 44,5 В; 22,2 В.

Пример 3

К двум последовательно соединенным плоским конденсаторам с емкостями С₁ = 4 мкФ и С₂ = 12 мкФ подвели напряжение U, что вызвало появление на обкладках конденсаторов одинаковых зарядов Q = 0,003 Кл.

Изоляции и площади обкладок обоих конденсаторов, одинаковы, расстояние между обкладками первого конденсатора d₁ = 3 мм. Определите напряжение на выводах обоих конденсаторов, общее напряжение, расстояние между обкладками второго конденсатора, емкость эквивалентного плоского конденсатора и расстояние между его обкладками, считая, площадь обкладок одинаковой у обоих конденсаторов.

Расчетные формулы:

U₁ = ; U₂ = ; U = U₁+ U₂; С = ;

С₁ = ; С₂ = ; ; d = d₁+d₂.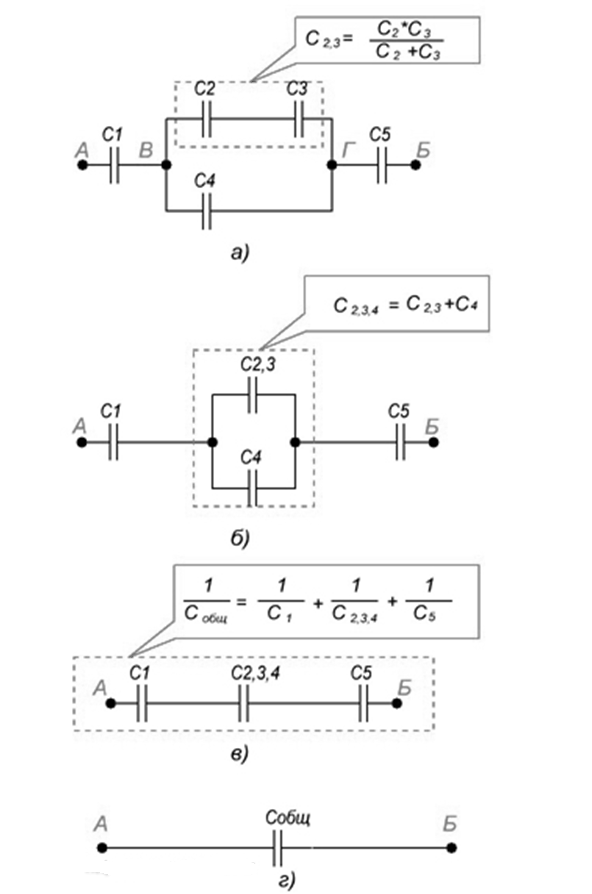

 

Ответ: 750 В; 250 В; 1000 В; 3 мкФ; 4 мм.

Пример 4

Определите напряжение на зажимах цепи и на каждом конденсаторе:

С₁ = 2 мкФ; С₂ = 3 мкФ; С₃ = 6 мкФ. Заряд батареи конденсаторов Q = 200·10^-6 Кл.

				С1
								С5
		С2			С3

 

Ответ: 50 В; 33,3 В; 16,7 В.

Ответы

Тема 9

Пример 1

Ответ: 19745223 Гн^-1.

Пример 2

Ответ: 6972 А

Пример 3

Ответ: w ≈ 2400 витков

Пример 4

Ответ: w ≈ 1776 витков

Пример 5

Ответ: ≈ 337 витков

Пример 6

Ответ: ≈ 437 витков

Список литературы

1. Полещук В.И. Задачник по электротехнике и электронике: учеб.пособие для студ. сред. проф.образования. – 4-е изд., стер. – М.: Издательский центр «Академия», 2008. – 224 с.

 

 

Т.Н.ЛУКОЯНОВА

Методические указания к выполнению контрольной работы по дисциплине

«Электротехника и электроника»

 

 

2016 г.

 

ВВЕДЕНИЕ

 

Подготовка в средней профессиональной школе специалистов технических специальностей, связанных с машиностроением в области электротехники и электроники, нацелена на то чтобы выпускники умели выбирать необходимые электротехнические, электронные и электроизмерительные устройства и могли их правильно эксплуатировать Задача средних специальных учебных заведений (ссузов) обеспечить все необходимые условия для овладения студентами профессионально значимыми компетенциями, развития конкретных личностных качеств будущего специалиста, определяющих его готовность к творческой профессиональной деятельности.

В этой связи при обучении дисциплине «Электротехника и электроника», в средних специальных учебных заведениях возникает необходимость дать студентам требуемые теоретические знания, выработать у них твердые практические навыки, в том числе исследовательского характера.

Настоящее учебное пособие предназначено для обучения студентов техникумом и колледжей дисциплине «Электротехника и электроника» по специальности «Технология машиностроения».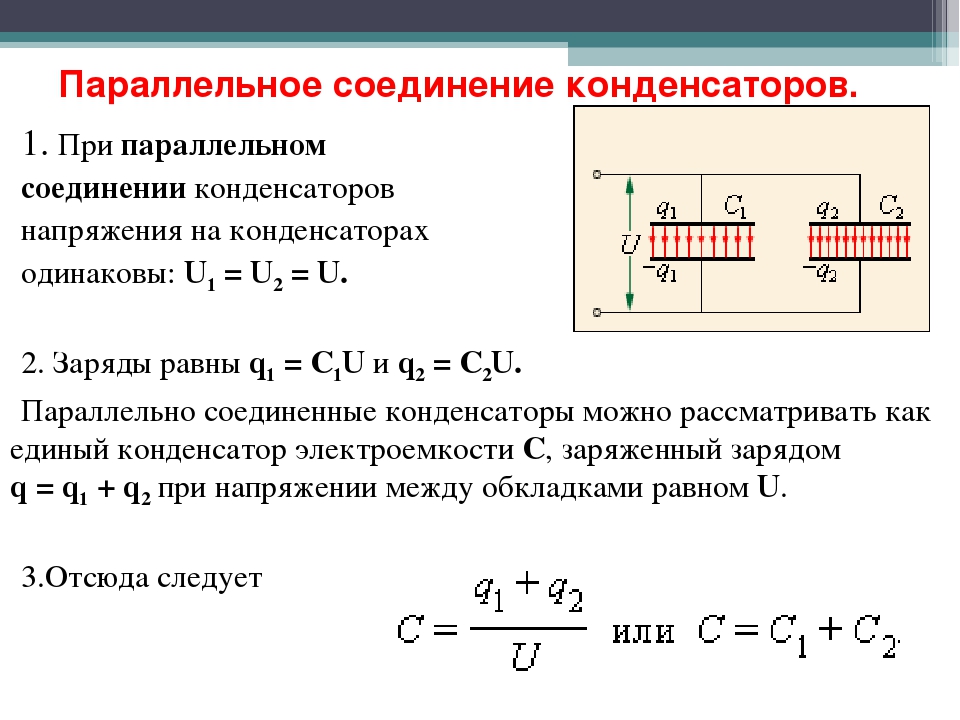

Содержание методических указаний соответствует требованиям федеральных государственных образовательных стандартов среднего профессионального образования третьего поколения дисциплины «Электротехника и электроника».

 

 

Тема1. Электрическое поле. Расчет электрических цепей при последовательном, параллельном и смешанном соединении конденсаторов

Устройство из двух изолированных друг от друга металлических проводников называют конденсатором. Простейший плоский конденсатор состоит из двух параллельно расположенных металлических пластин – обкладок, разделенных каким-либо диэлектриком, толщина которого мала по сравнению с линейными размерами проводников. Если пластины конденсатора присоединены к источнику питания с постоянным напряжением U, то на них образуются равные по значению, но противоположные по знаку электрические заряды +Q и –Q. Отношение заряда одной из обкладок Q к приложенному напряжению называется емкостью: . Электрическое напряжение обозначается буквой U, единицей измерения служит вольт [В], единицей измерения емкости служит фарад [Ф], это емкость такого конденсатора, у которого при заряде каждой пластины в один кулон [Кл] напряжение между пластинами равно одному вольту.

Конденсаторы различаются формой электродов, типом диэлектрика (слюда, бумага, керамика) и емкостью. В электролитических конденсаторах диэлектриком служит тонкая пленка окиси алюминия с высокой диэлектрической проницаемостью. Такие конденсаторы имеют большую емкость при небольших размерах и применяются только в цепях постоянного тока. Каждый конденсатор характеризуется номинальной емкостью и напряжением, которое длительное время выдерживает его диэлектрик. Воздушные конденсаторы, состоящие из системы подвижных пластин и системы неподвижных пластин, применяются в качестве регулируемых небольших переменных емкостей.

Емкость плоского конденсатора прямо пропорциональна проницаемости диэлектрика ε_а, площади пластин S и обратно пропорциональна расстоянию между пластинами d: = , где ε_а — абсолютная диэлектрическая проницаемость; ε – диэлектрическая проницаемость среды показывающая, во сколько раз напряженность поля в вакууме больше, чем в диэлектрике; ε₀ -электрическая постоянная [ε_о = = 8,85·10^-12 ].

Для получения нужной емкости или при напряжении сети, превышающем номинальное напряжение, конденсаторы соединяются последовательно, или смешано. При последовательном соединении на электродах всех конденсаторов будут одинаковые заряды, так как от источника питания они поступают только на внешние электроды, а на внутренних электродах они получаются только за счет разделения зарядов, ранее нейтрализовавших друг друга. Обозначив заряд одного электрода через Q можно написать для двух последовательно

соединенных конденсаторов: U₁ = и U₂ = или: = + .

Эквивалентная емкость при последовательном соединении конденсаторов рассчитывается по формуле: . При параллельном соединении конденсаторов напряжения на всех конденсаторах одинаковы, а заряды в общем случае имеют разные значения. Заряд, полученный всеми параллельно соединенными конденсаторами равен сумме зарядов и соответственно эквивалентная емкость: С = С₁+С₂+. .

Пример 1

Определите емкость батареи конденсаторов С₁ = 2,8 мкФ, С₂ = 0,3 мкФ, С₃ = 0,5 мкФ, С₄ = 2 мкФ, С₅ = 6 мкФ, С₆ = 3 мкФ, С₇ = 5 мкФ, схема соединения которых дана на рис. 1.

Соединение конденсаторов — Студопедия

В электрических цепях применяются различные способы соединения конденсаторов. Соединение конденсаторовможет производиться: последовательно, параллельно и последовательно-параллельно (последнее иногда называют смешанное соединение конденсаторов). Существующие виды соединения конденсаторов показаны на рисунке 1.

Рисунок 1. Способы соединения конденсаторов.

Параллельное соединение конденсаторов.

Если группа конденсаторов включена в цепь таким обра­зом, что к точкам включения непосредственно присоединены пластины всех конденсаторов, то такое соединение называется параллельным соединением конденсаторов (рисунок 2. ).

Рисунок 2. Параллельное соединение конденсаторов.

При заряде группы конденсаторов, соединенных параллель­но, между пластинами всех конденсаторов будет одна и та же разность потенциалов, так как все они заряжаются от одного и того же источника тока. Общее же количе­ство электричества на всех конденсаторах будет равно сумме количеств электричества, помещающихся на каждом из кон­денсаторов, так как заряд каждого их конденсаторов проис­ходит независимо от заряда других конденсаторов данной группы. Исходя из этого, всю систему параллельно соединен­ных конденсаторов можно рассматривать как один эквива­лентный (равноценный) конденсатор. Тогда общая емкость конденсаторов при параллельном соединении равна сумме емкостей всех соединенных конденсаторов.

Обозначим суммарную емкость соединенных в батарею конденсаторов бук­вой Собщ, емкость первого конденсатора С1 емкость второго С2 и емкость третьего С3. Тогда для параллельного соединения конденсаторов будет справедлива следующая формула:

Последний знак + и многоточие указывают на то, что этой формулой можно пользоваться при четырех, пяти и во­обще при любом числе конденсаторов.

Последовательное соединение конденсаторов.

Если же соединение конденсаторов в батарею производится в виде цепочки и к точкам включения в цепь непосредственно присоединены пластины только первого и последнего конденсаторов, то такое соединение конденсаторов называется последо­вательным (рисунок 3).

Рисунок 2. Последовательное соединение конденсаторов.

При последовательном соединении все конденса­торы заряжаются одинаковым количеством электричества, так как непосредственно от источника тока заряжаются только крайние пластины (1 и 6), а остальные пластины (2, 3, 4 и 5) заря­жаются через влияние. При этом заряд пла­стины 2 будет равен по величине и противо­положен по знаку за­ряду пластины 1, заряд пластины 3 будет равен по величине и противоположен по знаку заряду пла­стины 2 и т. д.

Напряжения на различных конденсаторах будут, вообще говоря, различными, так как для заряда одним и тем же количеством электричества конденсаторов различной емкости всегда требуются различные напряжения.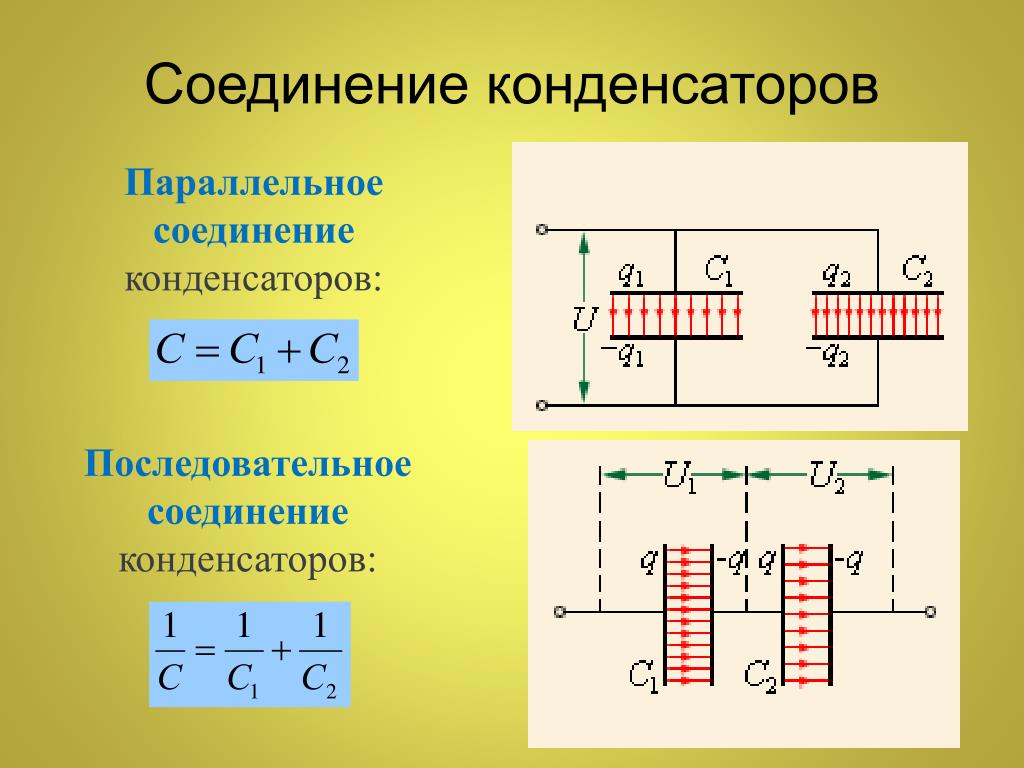 Чем меньше емкость конденсатора, тем большее напряжение необходимо для того, чтобы зарядить этот конденсатор требуемым количеством электричества, и наоборот.

Таким образом, при заряде группы конденсаторов, соединенных последовательно, на конденсаторах малой емкости напряжения будут больше, а на конденсаторах большой емкости — меньше.

Аналогично предыдущему случаю можно рассматривать всю группу конденсаторов, соединенных последовательно, как один эквивалентный конденсатор, между пластинами которого существует напряжение, равное сумме напряжений на всех конденсаторах группы, а заряд которого равен заряду любого из конденсаторов группы.

Возьмем самый маленький конденсатор в группе. На нем должно быть самое большое напряжение. Но напряжение на этом конденсаторе составляет только часть общего напряже­ния, существующего на всей группе конденсаторов. Напря­жение на всей группе больше напряжения на конденсаторе, имеющем самую малую емкость. А отсюда непосредственно следует, что общая емкость группы конденсаторов, соединен­ных последовательно, меньше емкости самого малого конден­сатора в группе.

Для вычисления общей емкости при последовательном со­единении конденсаторов удобнее всего пользоваться следую­щей формулой:

Для частного случая двух последовательно соединенных конденсаторов формула для вычисления их общей емкости будет иметь вид:

Последовательно-параллельное (смешанное) соединение конденсаторов

Последовательно-параллельным соединением конденсаторов называется цепь имеющая в своем составе участки, как с параллельным, так и с последовательным соединением конденсаторов.

На рисунке 4 приведен пример участка цепи со смешанным соединением конденсаторов.

Рисунок 4. Последовательно-параллельное соединение конденсаторов.

При расчете общей емкости такого участка цепи с последовательно-параллельным соединением конденсаторов этот участок разбивают на простейшие участки, состоящие только из групп с последовательным или параллельным соединением конденсаторов. Дальше алгоритм расчета имеет вид:

1. Определяют эквивалентную емкость участков с последовательным соединением конденсаторов.

2. Если эти участки содержат последовательно соединенные конденсаторы, то сначала вычисляют их емкость.

3. После расчета эквивалентных емкостей конденсаторов перерисовывают схему. Обычно получается цепь из последовательно соединенных эквивалентных конденсаторов.

4. Рассчитывают емкость полученной схемы.

Один из примеров расчета емкости при смешанном соединении конденсаторов приведен на рисунке 5.

Рисунок 5. Пример расчета последовательно-параллельного соединения конденсаторов.

Формула расчета последовательного соединения конденсатора

У многих радиолюбителей, особенно приступающих впервые к конструированию электросхем, возникает вопрос, как надо подключить конденсатор требуемой ёмкости? Когда, к примеру, в каком-то месте схемы нужен конденсатор ёмкостью 470 мкФ, и такой элемент есть в наличии, то проблемы не возникнет. Но когда требуется поставить конденсатор на 1000 мкФ, а присутствуют только элементы неподходящей емкости, на помощь приходят схемы из нескольких конденсаторов, соединённых вместе. Соединять элементы можно, применяя параллельное и последовательное соединение конденсаторов по отдельности или по комбинированному принципу.

Последовательное соединение конденсаторов

Схема последовательного соединения

Когда применяется схема последовательного соединения конденсаторов, заряд каждой детали эквивалентен. С источником соединены только внешние пластины, другие – заряжаются перераспределением электрозарядов между ними. Все конденсаторы сохраняют аналогичное количество заряда на своих обкладках. Это объясняется тем, что на каждый последующий элемент поступает заряд от соседнего. Вследствие этого справедливо уравнение:

q = q1 = q2 = q3 = …

Известно, что при последовательном соединении резисторных элементов их сопротивления суммируются, но емкость конденсатора, включенного в такую электроцепь, рассчитывается по-другому.

Падение напряжения на отдельном конденсаторном элементе зависит от его емкости. Если в последовательной электроцепи имеется три конденсаторных элемента, составляется выражение для напряжения U  на основании закона Кирхгофа:

U = U1 + U2 + U3,

при этом U= q/C, U1 = q/C1, U2 = q/C2, U3 = q/C3.

Подставляя значения для напряжений в обе части уравнения, получается:

q/C = q/C1 + q/C2 + q/C3.

Так как электрозаряд q – величина одинаковая, на нее можно поделить все части полученного выражения.

Результирующая формула для емкостей конденсаторов:

1/С = 1/С1 + 1/С2 + 1/С3.

Важно! Если конденсаторы подключаются в последовательную электроцепь, показатель, обратный результирующей емкости, равен совокупности обратных значений единичных емкостей.

Особенности последовательного соединения

Пример. Три конденсаторных элемента подключены в последовательную цепь и обладают емкостями: С1 = 0,05 мкф, С2 = 0,2 мкФ, С3 = 0,4 мкФ. Рассчитать общую емкостную величину:

1. 1/С = 1/0,05 + 1/0,2 + 1/0,4 = 27,5;
2. С = 1/27,5 = 0,036 мкФ.

Важно! Когда конденсаторные элементы включены в последовательную электроцепь, общее емкостное значение не превышает наименьшей емкости отдельного элемента.

Если цепь состоит всего из двух компонентов, формула переписывается в таком виде:

С = (С1 х С2)/(С1 + С2).

В случае создания цепи из двух конденсаторов с идентичным емкостным значением:

С = (С х С)/(2 х С) = С/2.

Последовательно включенные конденсаторы имеют реактивное сопротивление, зависящее от частоты протекающего тока. На каждом конденсаторе напряжение падает из-за наличия этого сопротивления, поэтому на основе такой схемы создается емкостной делитель напряжения.

Емкостной делитель напряжения

Формула для емкостного делителя напряжения:

U1 = U x C/C1, U2 = U x C/C2, где:

• U – напряжение питания схемы;
• U1, U2 – падение напряжения на каждом элементе;
• С – итоговая емкость схемы;
• С1, С2 – емкостные показатели единичных элементов.

Вычисление падений напряжения на конденсаторах

К примеру, имеются сеть переменного тока 12 В и две альтернативных электроцепи подсоединения последовательных конденсаторных элементов:

• первая – для подключения одного конденсатора С1 = 0,1 мкФ, другого С2 = 0,5 мкФ;
• вторая – С1 = С2 = 400 нФ.

Первый вариант

1. Итоговая емкость электросхемы С = (С1 х С2)/(С1 + С2) = 0,1 х 0,5/(0,1 + 0,5) = 0,083 мкФ;
2. Падение напряжения на одном конденсаторе: U1 = U x C/C1 = 12 x 0,083/0,1 = 9,9 В
3. На втором конденсаторе: U2 = U x C/C2 = 12 х 0,083/0,5 = 1,992 В.

Второй вариант

1. Результирующая емкость С = 400 х 400/(400 + 400) = 200 нФ;
2. Падение напряжения U1 = U2 = 12 x 200/400 = 6 В.

Согласно расчетам, можно сделать выводы, что если подключаются конденсаторы равных емкостей, вольтаж делится поровну на обоих элементах, а когда емкостные значения различаются, то на конденсаторе с меньшей емкостной величиной напряжение увеличивается, и наоборот.

Параллельное и комбинированное соединение

Параллельное соединение конденсаторов представляется иным уравнением. Для определения общего емкостного значения надо просто найти совокупность всех величин по отдельности:

С = С1 + С2 + С3 + …

Напряжение к каждому элементу будет прикладываться идентичное. Следовательно, для усиления емкости надо соединить несколько деталей параллельно.

Если соединения смешанные, последовательно-параллельные, то для таких контуров применяют эквивалентные, или упрощенные, электросхемы. Каждую область цепи рассчитывают отдельно, а затем, представляя их вычисленными емкостями, объединяют в простую цепь.

Варианты получения эквивалентных схем

Особенности замены конденсаторов

К примеру, в наличии сеть переменного тока 12 В и две альтернативных группы последовательных конденсаторных элементов.

Конденсаторы подсоединяются в последовательный контур для увеличения напряжения, под которым они остаются работоспособными, но их общая емкость падает в соответствии с формулой для ее расчета.

Часто применяется смешанное соединение конденсаторов, чтобы создать нужную емкостную величину и увеличить напряжение, которое детали способны выдержать.

Можно привести вариант, как соединить несколько компонентов, чтобы выйти на нужные параметры. Если требуется конденсаторный элемент 80 мкФ при напряжении 50 В, но есть только конденсаторы 40 мкФ на 25 В, необходимо образовать следующую комбинацию:

1. Два конденсатора 40 мкФ/25 В подсоединить последовательно, что позволит иметь в общей сложности 20 мкФ /50 В;
2. Теперь вступает в действие параллельное включение конденсаторов. Пара конденсаторных групп, включенных последовательно, созданных на первом этапе, соединяются параллельно, получится 40 мкФ / 50 В;
3. Две собранные в итоге группы соединить параллельно, в результате получим 80 мкФ/50 В.

Важно! Для того чтобы усилить конденсаторы по напряжению, возможно их объединить в последовательную электросхему. Увеличение общей емкостной величины достигается параллельным подключением.

Что необходимо учитывать при создании последовательной цепи:

1. При соединениях конденсаторов оптимальный вариант – брать элементы с мало различающимися или с одинаковыми параметрами, вследствие большой разницы в напряжениях разряда;
2. Для баланса токов утечки на каждый конденсаторный элемент (в параллель) включается уравнительное сопротивление.

Получение неполярного конденсатора

Включение в последовательную цепь всегда должно происходить с соблюдением «плюса» и «минуса» конденсаторов. Если их соединить одноименными полюсами, то такое сочетание уже теряет поляризованность. При этом емкость созданной группы будет равна половине от емкостного значения одной из деталей. Такие конденсаторы возможно применять в качестве пусковых на электромоторах.

Видео

Оцените статью:

Последовательный и параллельный калькулятор емкости

[1] 2020/11/19 01:33 Мужской / До 20 лет / Другое / Очень /

Цель использования

Выяснение, какая комбинация конденсаторов у меня под рукой создать нужное мне значение в данной схеме

Комментарий / запрос

Возможность добавления более двух конденсаторов

[2] 2020/08/13 03:32 Мужчина / Уровень 30 лет / Инженер / Полезно /

Цель использования

Проверить мою собственную работу по созданию задач, которые должны решить младшие технические специалисты

[3] 2019/11/15 17:26 Мужчина / 20-летний уровень / Средняя школа / Университет / аспирант / Полезно /

Цель использования

ДЛЯ ПОНИМАНИЯ

Комментарий / Запрос

ДЛЯ ПОЛУЧЕНИЯ ЗНАНИЙ

[4] 10. 04.2019 15:25 Мужской / Уровень 30 лет / Самостоятельно занятые люди / Очень /

Цель использования

Генератор Колпитца на УКВ , рассчитайте общую емкость на двух диодах варикапа, используемых для настройки, а также общую емкость на делителе обратной связи.

[5] 2019/03/08 07:04 Мужчина / 60 лет и старше / Пенсионер / Очень /

Цель использования

Помимо того, что я радиолюбитель, я также занимаюсь изготовлением кристаллических радиоприемников .
Для многих конструкций требуется воздушный конденсатор емкостью 500 пФ, но все, что я смог найти, это 630 пФ.
Итак, используя ваш калькулятор, я смог увидеть, сколько емкости мне нужно было добавить последовательно, чтобы снизить емкость конденсатора 630 пФ до 500 пФ.

Отлично сработало, мои искренние благодарности.

[6] 2018/08/27 21:07 Мужской / 40-летний уровень / Другое / Очень /

Цель использования

За исключением правильных значений на двух крышках. Используется для расчета заменяемых колпачков для старой магнитофонной деки.

Комментарий / запрос

Очень полезно

[7] 2018/08/17 13:15 Мужской / 40-летний уровень / Самозанятые люди / Очень /

Цель использования

рассчитать шину питания для ламповый усилитель

[8] 2018/08/12 01:16 Мужчина / 60 лет и старше / Офисный работник / Государственный служащий / Полезно /

Цель использования

Устранение неисправностей источника питания.У него был счетчик, который показывал максимум 10000 мкФ. Итак, мне пришлось последовательно соединить два одинаковых, чтобы проверить значение крышки фильтра.

[9] 2018/08/06 18:40 Мужчина / Уровень 20 лет / Инженер / Очень /

Цель использования

Расчет емкости для настройки антенны

[10] 2018/06 / 13 16:08 Мужской / 50-летний уровень / Высшая школа / Университет / аспирант / Очень /

Цель использования

Два последовательно соединенных диода общей емкости для планирования антенны.

Конденсатор в последовательной, параллельной и цепи переменного тока

Конденсатор — один из наиболее часто используемых электронных компонентов. Он имеет способность накапливать энергию внутри себя в виде электрического заряда, создающего статическое напряжение (разность потенциалов) на его пластинах. Проще говоря, конденсатор похож на небольшую перезаряжаемую батарею. Конденсатор представляет собой просто комбинацию двух параллельных проводящих или металлических пластин, которые электрически разделены хорошим изолирующим слоем (также называемым диэлектриком ) , состоящим из вощеной бумаги, слюды, керамики, пластика и т. Д.

Существует множество применений конденсатора в электронике, некоторые из них перечислены ниже:

• Накопитель энергии
• Регулировка мощности
• Коррекция коэффициента мощности
• Фильтрация
• Генераторы

Теперь вопрос , как конденсатор работает ? Когда вы подключаете источник питания к конденсатору, он блокирует постоянный ток из-за изолирующего слоя и позволяет напряжению присутствовать на пластинах в виде электрического заряда. Итак, вы знаете, как работает конденсатор и каково его использование или применение, но вы должны научиться этому, как использовать конденсатор в электронных схемах.

Как подключить конденсатор в электронную схему?

Здесь мы собираемся продемонстрировать вам подключение конденсатора и связанный с ним эффект на примерах.

• Конденсатор серии
• Параллельный конденсатор
• Конденсатор в цепи переменного тока

Конденсатор в последовательной цепи

В схеме, когда вы соединяете конденсаторы последовательно, как показано на изображении выше, общая емкость уменьшается.Ток, проходящий через конденсаторы последовательно, равен (т.е. i _T = i ₁ = i ₂ = i _{3 =} i _n ). Следовательно, заряд, накопленный конденсаторами, также одинаков (то есть Q _T = Q ₁ = Q ₂ = Q ₃ ), потому что заряд, накопленный пластиной любого конденсатора, исходит от пластины соседнего конденсатор в цепи.

Применяя Закон Кирхгофа (KVL) в цепи, мы получаем

  V  T  = V  C1  + V  C2  + V  C3 … уравнение (1)  

Как известно,

  Q = CV 
  Итак, V = Q / C  

Где, V _C1 = Q / C ₁ ; V _C2 = Q / C ₂ ; V _C3 = Q / C ₃

Теперь, подставив указанные выше значения в уравнение (1)

   (1 / C  T ) = (1 / C  1 ) + (1 / C  2 ) + (1 / C  3 )  

Для n последовательно подключенных конденсаторов уравнение будет

  (1 / C  T ) = (1 / C  1 ) + (1 / C  2 ) + (1 / C  3 ) +….+ (1 / Cn)  

Следовательно, приведенное выше уравнение является уравнением конденсаторов серии .

Где, C _T = Общая емкость цепи

C ₁ … n = емкость конденсаторов

Уравнение емкости для двух особых случаев определяется ниже:

Случай I: , если есть два конденсатора, соединенных последовательно, с разными значениями, емкость будет выражена как:

  (1 / C  T ) = (C  1  + C  2 ) / (C  1  * C  2 ) 
  Или, C  T  = (C  1  * C  2 ) / (C  1  + C  2 )… уравнение (2)  

Случай II: , если два конденсатора включены последовательно, с одинаковым значением емкость будет выражаться как:

  (1 / C  T ) = 2 / C  2  = 2 / C 
  Или, C  T  = C / 2  

Пример цепи последовательного конденсатора:

Теперь, в приведенном ниже примере мы покажем вам, как рассчитать общую емкость и индивидуальное среднеквадратичное падение напряжения на каждом конденсаторе.

Как и на приведенной выше принципиальной схеме, есть два конденсатора , соединенных последовательно с разными номиналами. Значит, падение напряжения на конденсаторах также неодинаково. Если мы подключим два конденсатора с одинаковым значением, падение напряжения также будет одинаковым.

Теперь для определения общего значения емкости воспользуемся формулой из уравнения (2)

  Итак, C  T  = (C  1  * C  2 ) / (C  1  + C  2 ) 
  Здесь C  1  = 4.7 мкФ и C  2  = 1 мкФ 
  C  T  = (4,7 мкФ * 1 мкФ) / (4,7 мкФ + 1 мкФ) 
  C  T  = 4,7 мкФ / 5,7 мкФ 
  C  T  = 0,824 мкФ  

Теперь падение напряжения на конденсаторе C ₁ составляет:

  VC  1  = (C  T  / C  1 ) * V  T  
  VC  1  = (0,824 мкФ / 4,7 мкФ) * 12 
  VC  1  = 2,103V  

Теперь падение напряжения на конденсаторе C ₂ составляет:

  VC  2  = (C  T  / C  2 ) * V  T  
  VC  2  = (0. 824 мкФ / 1 мкФ) * 12 
  VC  2  = 9,88 В  

Конденсатор в параллельной цепи

При параллельном подключении конденсаторов общая емкость будет равна сумме емкостей всех конденсаторов. Потому что верхняя пластина всех конденсаторов соединена вместе, как и нижняя пластина. Таким образом, при соприкосновении друг с другом эффективная площадь пластин также увеличивается. Следовательно, емкость пропорциональна отношению площади и расстояния.

Применяя Текущий закон Кирхгофа (KCL) в вышеуказанной схеме,

  i  T  = i  1  + i  2  + i  3   

Как известно, ток через конденсатор выражается как;

  i = C (dV /   dt  ) 
  Итак, i  T  = C  1  (dV /   dt  ) + C  2  (dV /   dt  ) + C  3  (dV /   dt  )
  А,
   i    T     = (C  1  + C  2  + C  3 ) * (dV /   dt  ) 
  i  T  = C  T  (dV /   dt  )… уравнение (3)  

Из уравнения (3) уравнение параллельной емкости:

  C  T  = C  1  + C  2  + C  3   

Для n конденсаторов, подключенных параллельно, уравнение выше выражается как:

  C  T  = C  1  + C  2  + C  3  +… + Cn  

Пример параллельной цепи конденсатора

На приведенной ниже принципиальной схеме три конденсатора подключены параллельно . Поскольку эти конденсаторы подключены параллельно, эквивалентная или общая емкость будет равна сумме индивидуальных емкостей.

  C  T  = C  1  + C  2  + C  3  
  Где, C  1  = 4,7 мкФ; C  2  = 1 мкФ и C  3  = 0,1 мкФ 
  Итак, C  T  = (4,7 +1 + 0,1) мкФ 
  C  T  = 5,8 мкФ  

Конденсатор в цепях переменного тока

Когда конденсатор подключен к источнику постоянного тока, конденсатор начинает медленно заряжаться.И, когда напряжение зарядного тока конденсатора равно напряжению питания, это считается полностью заряженным. Здесь в этом состоянии конденсатор работает как источник энергии, пока подается напряжение. Кроме того, конденсаторы не позволяют току проходить через него после полной зарядки.

Когда на конденсатор подается переменное напряжение, как показано на чисто емкостной схеме выше. Затем конденсатор непрерывно заряжается и разряжается до каждого нового уровня напряжения (заряжается при положительном уровне напряжения и разряжается при отрицательном уровне напряжения).Емкость конденсатора в цепях переменного тока зависит от частоты входного напряжения, подаваемого в цепь. Сила тока прямо пропорциональна скорости изменения напряжения, приложенного к цепи.

  i = dQ /   dt   = C (dV /   dt  )  

Векторная диаграмма конденсатора в цепи переменного тока

Как вы видите на векторной диаграмме конденсатора переменного тока на изображении ниже, ток и напряжение представлены в виде синусоидальной волны.При наблюдении при 0 ° зарядный ток достигает своего пикового значения из-за постоянного увеличения напряжения в положительном направлении.

Теперь, при 90 °, ток через конденсатор не протекает, поскольку напряжение питания достигает максимального значения.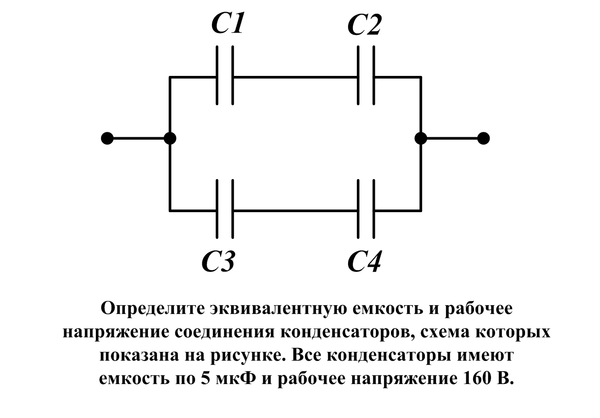 При 180 ° напряжение начинает медленно снижаться до нуля, а ток достигает максимального значения в отрицательном направлении. И снова заряд достигает своего пикового значения на 360 °, потому что напряжение питания находится на минимальном значении.

Таким образом, из приведенного выше сигнала мы можем видеть, что ток опережает напряжение на 90 °.Итак, мы можем сказать, что напряжение переменного тока отстает от тока на 90 ° в идеальной конденсаторной цепи .

Реактивное сопротивление конденсатора (Xc) в цепи переменного тока

Рассмотрим приведенную выше принципиальную схему, поскольку мы знаем, что входное напряжение переменного тока выражается как

  V = V  м  Sin  wt   

А, заряд конденсатора Q = CV,

Итак, Q = CV _м Sin _wt

А, ток через конденсатор, i = dQ / dt

Итак,

  i = d (CV  m  Sin  wt ) / dt 
  i = C * d (V  m  Sin  wt ) / dt 
  i = C * V  m  Cos  wt  * w 
  i = w * C * V  m  Sin (wt + π / 2) 
  ат, wt = 0 
  sin (wt + π / 2) = 1 
 , следовательно, i  m  = wCV  m  
  V  м  / i  м  = 1 / wC  

Как известно, w = 2πf

Итак,

  Емкостное реактивное сопротивление (Xc) = V  м  / i  м  = 1 / 2πfC  

Пример емкостного реактивного сопротивления в цепи переменного тока

диаграмма

Давайте рассмотрим значение C = 2.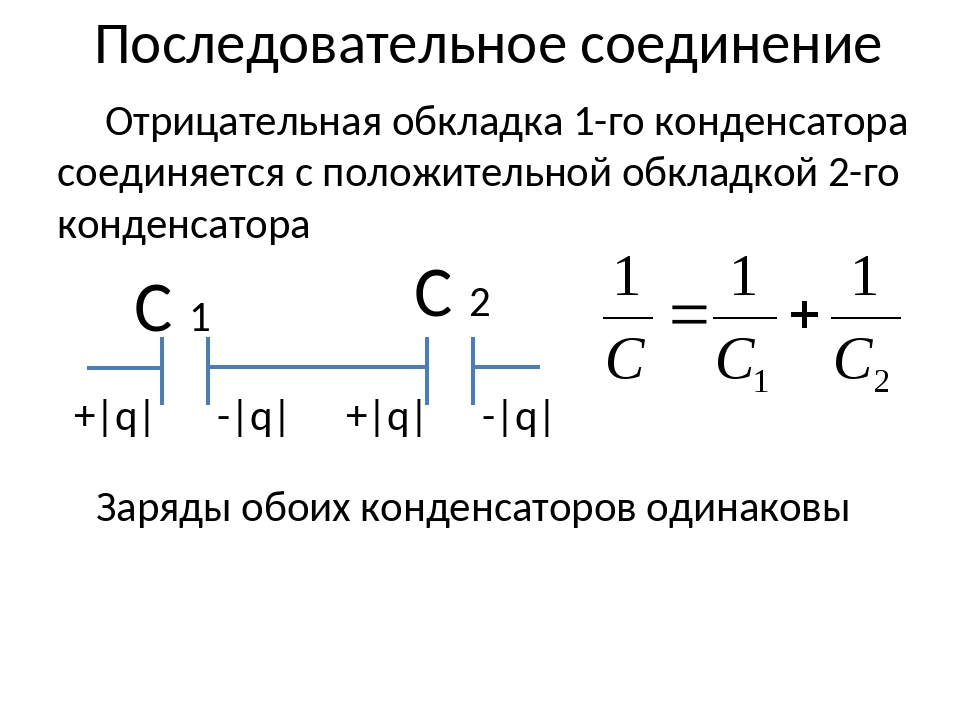 2uf и напряжение питания V = 230 В, 50 Гц

  Теперь емкостное реактивное сопротивление (Xc) = V  м  / i  м  = 1 / 2πfC 
  Здесь C = 2,2 мкФ и f = 50 Гц 
  Итак, Xc = 1/2 * 3,1414 * 50 * 2,2 * 10 -6  
  Xc = 1446,86 Ом  

Конденсаторы последовательно и параллельно с примерами

Последовательные и параллельные конденсаторы

Системы с более чем одним конденсатором имеют эквивалентную емкость.Конденсаторы можно соединять между собой двумя способами. Их можно подключать последовательно и параллельно. Сначала мы увидим конденсаторы, включенные параллельно.

В этой цепи конденсаторы включены параллельно.

Потому что левые стороны конденсаторов подключены к потенциалу a, а правые стороны конденсаторов подключены к потенциалу b. Другими словами, мы можем сказать, что каждый конденсатор имеет одинаковую разность потенциалов. Находим заряд каждого конденсатора как;

Q ₁ = C ₁ .V

Q ₂ = C ₂ .V

Q ₃ = C ₃ .V

Общий заряд системы определяется сложением каждого заряда.

Q _итого = C _экв .V

Q _итого = Q ₁ + Q ₂ + Q ₃ = C ₁ .V + C ₂ .V + C ₃ .V = V. (C ₁ + C ₂ + C ₃ ) = C _экв.

C _экв = C ₁ + C ₂ + C ₃

Как видите, мы нашли эквивалентную емкость системы как C ₁ + C ₂ + C ₃

Теперь посмотрим последовательно включенные конденсаторы;

В конденсаторах, подключенных последовательно, каждый конденсатор имеет одинаковый поток заряда от батареи. В этой схеме заряд + Q течет от положительной части батареи к левой пластине первого конденсатора и притягивает заряд –Q на правой пластине, с той же идеей заряд -Q течет от батареи к правой пластине. третьего конденсатора и притягивает + Q на левой пластине. Таким же образом заряжаются и другие конденсаторы. Подводя итог, можно сказать, что каждый конденсатор имеет одинаковый заряд с батареей.

C ₁ .V ₁ = Q

С ₂ .V ₂ = Q, V = V ₁ + V ₂ + V ₃ и Q = C _экв .V

C ₃ .V ₃ = Q

Пример: вычислить эквивалентную емкость между точками a и b.

Что такое жесткость пружины при параллельном и последовательном подключении?

Физика

Наука

• Анатомия и физиология
• Астрономия
• Астрофизика
• Биология
• Химия
• наука о планете Земля
• Наука об окружающей среде

.