Параллельное соединение резистора и конденсатора расчет сопротивления: Последовательное и параллельное соединение проводников, резисторов, конденсаторов и катушек индуктивности. Онлайн расчёты. — Мир Антенн

Содержание

Последовательное и параллельное соединение проводников, резисторов, конденсаторов и катушек индуктивности. Онлайн расчёты.

«- Я тебе как электрику объясняю: Надя спит с мужиками последовательно, а Света параллельно. Кто из них шмара вавилонская?
— Ну, Света наверное.
— Вот! А мне, как кладовщику, видится немного другое: «поблядушка обыкновенная» — 2 штуки! »

«- А теперь скажи мне отрок, как течёт электричество по проводам электрическим, и цепям рукотворным, последовательным да параллельным, от плюса к минусу со скоростью света в вакууме?
— С Божьей помощью, батюшка! С Божьей помощью…»

Ну да ладно, достаточно! Шутки — штуками, а пора бы уже дело делать. Так что «Копайте пока здесь! А я тем временем схожу узнаю — где надо…», а заодно набросаю пару-тройку калькуляторов на заданную тему.

Итак.
При последовательном соединении проводников сила тока во всех проводниках одинакова, при этом общее напряжение в цепи равно сумме напряжений на концах каждого из проводников.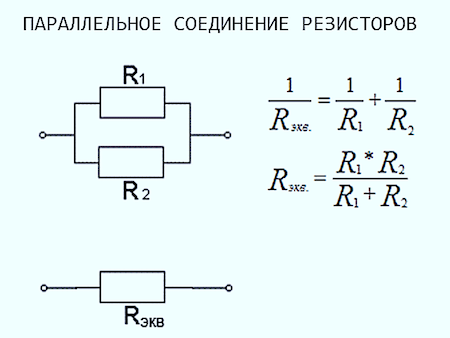

При параллельном соединении падение напряжения между двумя узлами, объединяющими элементы цепи, одинаково для всех элементов, а сила тока в цепи равна сумме сил токов в отдельных параллельно соединённых проводниках.
Поясним рисунком с распределением напряжений, токов и формулами.

Рис.1

Расчёт проведём для 4 резисторов (проводников), соединённых последовательно или параллельно. Если элементов в цепи меньше, то оставляем лишние поля в таблице не заполненными.
Заодно, при желании узнать распределение значений токов и напряжений на каждом из элементов при последовательном и параллельном соединениях, есть возможность ввести величину общего напряжения в цепи U. А есть возможность не вводить…
Короче, все вводные, помеченные * — к заполнению не обязательны.

РАСЧЁТ СОПРОТИВЛЕНИЙ ПРИ ПАРАЛЛЕЛЬНОМ И ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ

проводников

Теперь, что касается последовательных и параллельных соединений конденсаторов и катушек индуктивности.
Схема, приведённая на Рис.1 для проводников и резисторов, остаётся в полной силе и для катушек с конденсаторами, распределение напряжений и токов тоже никуда не девается, трансформируется лишь осмысление того, что токи эти и напряжения обязаны быть переменными.
Почему переменными?
А потому, что для постоянных значений этих величин — сопротивление конденсаторов составляет в первом приближении бесконечность, а катушек — ноль, соответственно и токи будут равны либо нулю, либо бесконечности, а для переменных значений иметь ярко выраженную зависимость от частоты.

Поэтому, для желающих рассчитать величины напряжений и токов в последовательных или параллельных цепях, состоящих из конденсаторов и катушек индуктивности, имеет полный смысл выяснить на странице ссылка на страницу значения реактивных сопротивлений данных элементов при интересующей Вас частоте и подставить эти значения в таблицу для расчёта проводников и резисторов.

А в качестве общего напряжения в цепи — подставлять действующее значение амплитуды переменного тока.

Ну а теперь приведём таблицы для расчёта значений ёмкостей и индуктивностей при условии последовательного и параллельного соединений конденсаторов и катушек в количестве от 2 до 4 штук.
Расчёт поведём на основании хрестоматийных формул:

С = С₁+ С₂+….+ С_n и 1/L = 1/L₁+ 1/L₂

+…+ 1/L_n для параллельных цепей и
L = L₁ + L₂ +….+ L_n и 1/С = 1/С₁+ 1/С₂+…+ 1/С_n для последовательных.

Как и в предыдущей таблице вводные, помеченные * — к заполнению не обязательны.

РАСЧЁТ ЁМКОСТИ ПРИ ПАРАЛЛЕЛЬНОМ И ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ
конденсаторов

Ну и в завершении ещё одна таблица.

РАСЧЁТ ИНДУКТИВНОСТИ ПРИ ПАРАЛЛЕЛЬНОМ И ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ
катушек

Тут важно заметить, что приведённые в последней таблице расчёты верны только для индуктивно не связанных катушек, то есть для катушек, намотанных на разных каркасах и расположенных на значительных расстояниях друг от друга, во избежание, пересечения взаимных магнитных полей.

Расчёт сопротивления резисторов и ёмкости конденсаторов

Автор: admin, 22 Мар 2013

Расчёт сопротивления резисторов и ёмкости конденсаторов

В этой статье рассмотрим как можно с помощью параллельного и последовательного включения резисторов и конденсаторов подобрать нужный номинал радиодетали, при отсутствии нужного. Расчёт производится по формулам расчёта сопротивления и ёмкости для параллельного и последовательного включения, а также с помощью удобной таблицы подбора ёмкости и сопротивления.

Резисторы

Широко применяются в радиоприёмниках, усилителях сигналов и во многих других схемах. Они служат для ограничения тока, создания падения напряжения, регулирования частоты, громкости и других сигналов. Обозначаются на схемах буквой R. Сопротивление резистора измеряется в Омах. Для больших сопротивлений используют единицы: килоомы (1кОм=1000Ом), мегаомы (1Мом=1000кОм). Кроме сопротивления резисторы характеризуются мощностью рассеяния, это такая наибольшая мощность, которую резистор может выдержать длительное время. Мощность рассеяния измеряется в ваттах (Вт). Ещё один показатель — это наибольшее возможное отклонение действительного сопротивления от номинального, указанного на резисторе, выражается в %. Резисторы бывают постоянные (не изменяют своего сопротивления) и переменные(изменяют сопротивление в зависимости от положения движка резистора).

Иногда, при сборке схемы не оказывается под рукой резистора нужного номинала. В этом случае в большинстве случаев можно заменить резистор на ближайший по номиналу — например вместо 110 Ом можно использовать резистор номиналом 100 или 120 Ом. А если нет и ближайшего по номиналу или требуется точное значение сопротивления, то можно составить нужное сопротивление с помощью последовательного или параллельного соединения нескольких резисторов.

Последовательное соединение резисторов:

последовательное соединение резисторов

При последовательном соединении резисторов их общее сопротивление равно их сумме: Rобщ = R1+R2+…+Rn.

Параллельное соединение резисторов:

параллельное соединение резисторов

При параллельном соединении резисторов их общее сопротивление рассчитывается по формуле:

1/Rобщ = 1/R1 + 1/R2 +…+1/Rn или

Rобщ = 1/(1/R1 + 1/R2 +…+1/Rn).

На практике для подбора нужного сопротивления обычно включают параллельно два резистора, в этом случае формула примет вид:

Rобщ = R1*R2/(R1+R2).

Ещё можно отметить, что при включении резисторов одинакового сопротивления, то их общее сопротивление будет равно половине сопротивления каждого их них. Мощность рассеяния, в этом случае, увеличится в 2 раза. Также при параллельном соединении общее сопротивление всегда меньше наименьшего из включенных в параллель резисторов.

Конденсаторы

Конденсаторы, как и резисторы, тоже очень широко применяются. Конденсатор это накопитель энергии, в простейшем виде это две пластины, между которыми находится диэлектрик, в качестве диэлектрика может быть просто воздух. Конденсаторы также бывают постоянной и переменной ёмкости. Единицей ёмкости является фарада(Ф). На практике используют меньшие ёмкости, их выражают в микрофарадах(1Ф=1 000 000 мкФ), нанофарадах(1мкФ = 1 000 нФ), пикофарадах(1нФ=1 000 пФ). Также конденсаторы характеризуются рабочим напряжением, выражаемом в вольтах (В). Превышение на конденсаторе напряжения выше рабочего может привести к «пробою» диэлектрика конденсатора.

Конденсатор не проводит постоянный ток, а переменному току оказывает сопротивление, которое вычисляется по формуле:

Хс = 1/(2πfC), где

Хс — емкостное сопротивление конденсатора, Ом;
π — математическая константа, примерно равная 3,1416;
f — частота переменного тока, Гц;
С — ёмкость конденсатора, Ф.

Рассмотрим как можно собрать нужную ёмкость из имеющихся под рукой.

Последовательное включение конденсаторов:

Последовательное соединение конденсаторов

При последовательном соединении конденсаторов их общая ёмкость рассчитывается по формуле, очень похожей на формулу для параллельного включения резисторов:

Собщ = 1/(1/С1+1/С2+…+1/Сn).

Но чаще тоже используют два конденсатора, тогда формула упрощается:

Собщ = С1*С2/(С1+С2).

Также, при включении конденсаторов с одинаковой ёмкостью их общая ёмкость будет в два раза меньше ёмкости каждого из них. Рабочее напряжение такого сборного конденсатора увеличится в 2 раза.

Параллельное включение конденсаторов:

Параллельное соединение конденсаторов

При параллельном соединении конденсаторов их общая ёмкость будет равна сумме всех емкостей.

Собщ = С1+С2+…+Сn.

При необходимости можно делать даже комбинированные соединения и параллельные и последовательные, в этом случае высчитывается ёмкость(или сопротивление) по одинаковым группам соединений, получают промежуточные значения, например Собщ1, Собщ2. ., а потом уже из них высчитывают общее значение.

Но, как правило, более двух деталей для составления нужного номинала не используют, для параллельного соединения конденсаторов и последовательного резисторов всё просто — считаем сумму. А для последовательного соединения конденсаторов и параллельного соединения резисторов нужно считать, поэтому будет удобно пользоваться заранее составленной таблицей, которая подойдёт для обоих радиоэлементов.

Таблица расчёта общего сопротивления (ёмкости) для двух параллельно соединённых резисторов (двух последовательно соединённых конденсаторов)

Таблица расчёта общего сопротивления(ёмкости)

По горизонтали смотрим значения, выделенные зелёным цветом, первого резистора(конденсатора) по вертикали второго. На перекрестии этих двух значений и будет общее сопротивление (ёмкость).

Будет интересно почитать:

Рубрики: Электронные устройства, Электросхемы
Метки: электроника, электросхема

Формула расчета сопротивления при параллельном соединении резистора

Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы.

Схема параллельного соединения резисторов показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:

Формула параллельного соединения резисторов

Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:

Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:

При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.

Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:

Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов.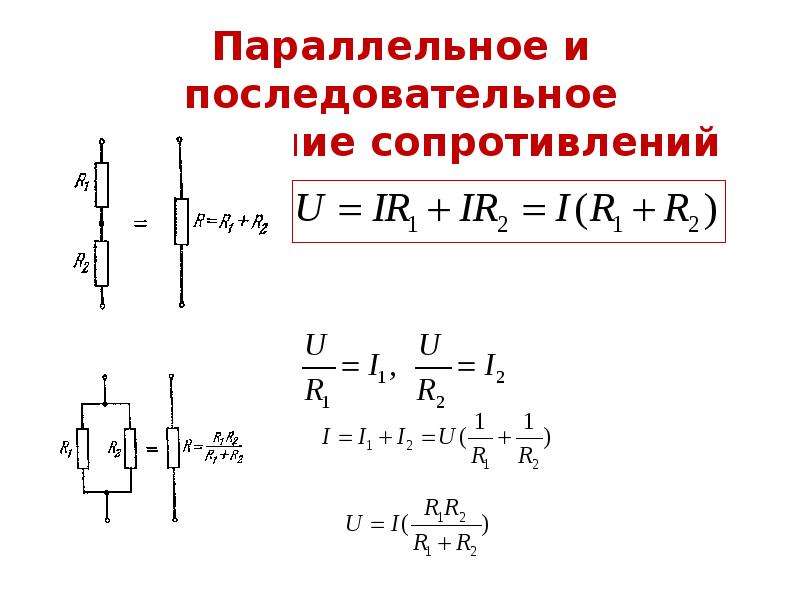 При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:

Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.

Пример расчета №2

Найти общее сопротивление R из трех параллельно соединенных резисторов:

Общее сопротивление R рассчитывается по формуле:

Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.

Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.

Как рассчитать сложные схемы соединения резисторов

Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:

Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).

Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:

В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:

Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.

Ток, протекающий в цепи параллельно соединенных резисторах

Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.

Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).

Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .

Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».

Таким образом, протекающий общий ток в цепи можно определить как:
I = I1 + I2
Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:
Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА
Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА
Таким образом, общий ток будет равен:
I = 0,545 мА + 0,255 мА = 0,8 мА
Это также можно проверить, используя закон Ома:
I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)
где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)
И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.

Параллельное соединение резисторов — онлайн калькулятор

Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:

Подведем итог

Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.

Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора, входящего в параллельное соединение.

Источник: http://www.joyta.ru/7362-parallelnoe-soedinenie-rezistorov/

Последовательное и параллельное соединение резисторов

Последовательное соединение – это соединение двух или более резисторов в форме цепи, в которой каждый отдельный резистор соединяется с другим отдельным резистором только в одной точке.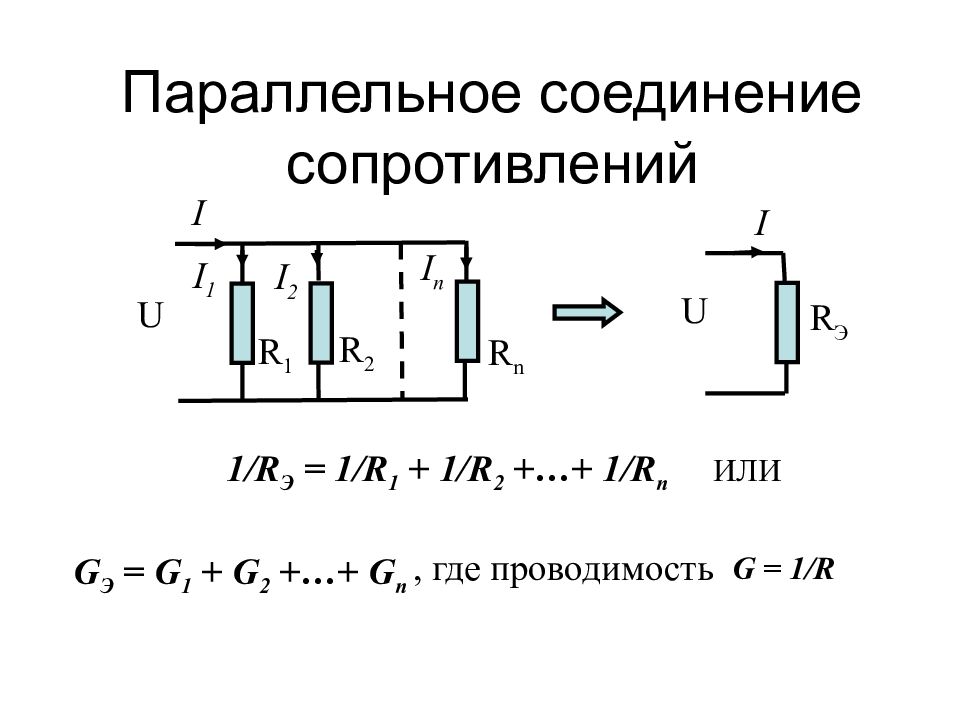

Общее сопротивление Rобщ

При таком соединении, через все резисторы проходит один и тот же электрический ток. Чем больше элементов на данном участке электрической цепи, тем «труднее» току протекать через него. Следовательно, при последовательном соединении резисторов их общее сопротивление увеличивается, и оно равно сумме всех сопротивлений.

Напряжение при последовательном соединении

Напряжение при последовательном соединении распределяется на каждый резистор согласно закону Ома:

Т.е чем большее сопротивление резистора, тем большее напряжение на него падает.

Параллельное соединение резисторов

Параллельное соединение – это соединение, при котором резисторы соединяются между собой обоими контактами. В результате к одной точке (электрическому узлу) может быть присоединено несколько резисторов.

Общее сопротивление Rобщ

При таком соединении, через каждый резистор потечет отдельный ток. Сила данного тока будет обратно пропорциональна сопротивлению резистора. В результате общая проводимость такого участка электрической цепи увеличивается, а общее сопротивление в свою очередь уменьшается.

Таким образом, при параллельном подсоединении резисторов с разным сопротивлением, общее сопротивление будет всегда меньше значения самого маленького отдельного резистора.

Формула общей проводимости при параллельном соединении резисторов:

Формула эквивалентного общего сопротивления при параллельном соединении резисторов:

Для двух одинаковых резисторов общее сопротивление будет равно половине одного отдельного резистора:

Соответственно, для n одинаковых резисторов общее сопротивление будет равно значению одного резистора, разделенного на n.

Напряжение при параллельном соединении

Напряжение между точками A и B является как общим напряжением для всего участка цепи, так и напряжением, падающим на каждый резистор в отдельности. Поэтому при параллельном соединении на все резисторы упадет одинаковое напряжение.

Электрический ток при параллельном соединении

Через каждый резистор течет ток, сила которого обратно пропорциональна сопротивлению резистора. Для того чтобы узнать какой ток течет через определенный резистор, можно воспользоваться законом Ома:

Смешанное соединение резисторов

Смешанным соединением называют участок цепи, где часть резисторов соединяются между собой последовательно, а часть параллельно. В свою очередь, смешанное соединение бывает последовательного и параллельного типов.

Общее сопротивление Rобщ

Для того чтобы посчитать общее сопротивление смешанного соединения:

Цепь разбивают на участки с только пареллельным или только последовательным соединением.
Вычисляют общее сопротивление для каждого отдельного участка.
Вычисляют общее сопротивление для всей цепи смешанного соединения.

Так это будет выглядеть для схемы 1:

Также существует более быстрый способ расчета общего сопротивления для смешанного соединения.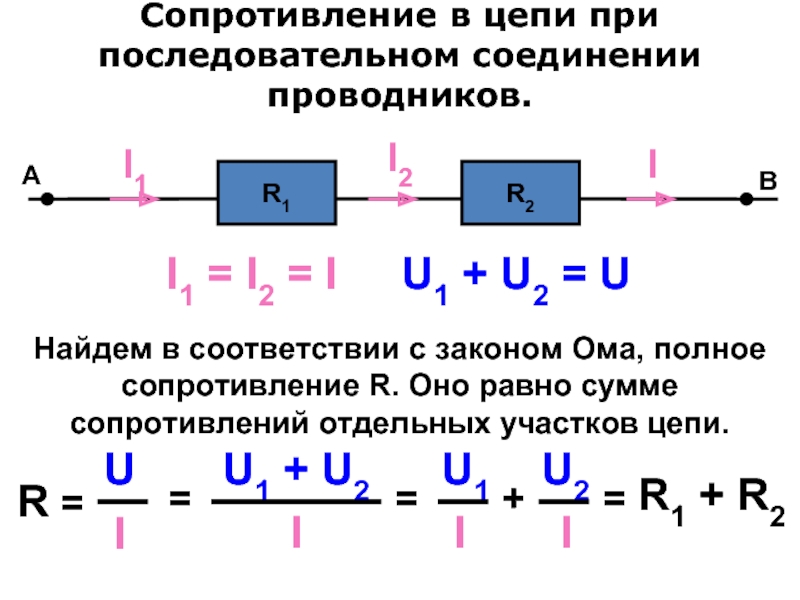 Можно, в соответствии схеме, сразу записывать формулу следующим образом:

Если резисторы соединяются последоватеьно — складывать.
Если резисторы соединяются параллельно — использовать условное обозначение «||».
Подставлять формулу для параллельного соединения где стоит символ «||».

Так это будет выглядеть для схемы 1:

После подстановки формулы параллельного соединения вместо «||»:

Источник: http://hightolow.ru/resistor3.php

Параллельное соединение сопротивлений в электрической цепи. Параллельное соединение конденсаторов и катушек

Параллельное соединение электрических элементов (проводников, сопротивлений, емкостей, индуктивностей) — это такое соединение, при котором подключенные элементы цепи имеют два общих узла подключения.

Другое определение: сопротивления подключены параллельно, если они подключены одно и той же паре узлов.

Графическое обозначение схемы параллельного соеднинения

На приведенном рисунке показана схема параллельное подключения сопротивлений R1, R2, R3, R4. Из схемы видно, что все эти четыре сопротивления имеют две общие точки (узла подключения).

В электротехнике принято, но не строго требуется, рисовать провода горизонтально и вертикально. Поэтому эту же схему можно изобразить, как на рисунке ниже. Это тоже параллельное соединение тех же самых сопротивлений.

Формула для расчета параллельного соединения сопротивлений

При параллельном соединении обратная величина от эквивалентного сопротивления равна сумме обратных величин всех параллельно подключенных сопротивлений. Эквивалентная проводимость равна сумме всех параллельно подключенных проводимостей электрической схемы.

Для приведенной выше схемы эквивалентное сопротивление можно рассчитать по формуле:

В частном случае при подключении параллельно двух сопротивлений:

Эквивалентное сопротивление цепи определяется по формуле:

В случае подключения «n» одинаковых сопротивлений, эквивалентное сопротивление можно рассчитать по частной формуле:

Формулы для частного рассчета вытекают из основной формулы.

Формула для расчета параллельного соединения емкостей (конденсаторов)

При параллельном подключении емкостей (конденсаторов) эквивалентная емкость равна сумме параллельно подключенных емкостей:

Формула для расчета параллельного соединения индуктивностей

При параллельном подключении индуктивностей, эквивалентная индуктивность рассчитывается так же, как и эквивалентное сопротивление при параллельном соединении:
Необходимо обратить внимание, что в формуле не учтены взаимные индуктивности.

Пример свертывания параллельного сопротивления

Для участка электрической цепи необходимо найти параллельное соединение сопротивлений выполнить их преобразование до одного.

Из схемы видно, что параллельно подключены только R2 и R4. R3 не параллельно, т.к. одним концом оно подключено к источнику ЭДС E1. R1 — одним концом подключено к R5, а не к узлу. R5 — одним концом подключено к R1, а не к узлу. Можно так же говорить, что последовательное соединение сопротивлений R1 и R5 подключено параллельно с R2 и R4.

Рассчитать эквивалентное сопротивлений R14 можно по формуле для двух сопротивлений.

Ток при параллельном соединении

При параллельном соединении сопротивлений ток через каждое сопротивление в общем случае разный. Величина тока обратно пропорциональна величине сопротивления.

Напряжение при параллельном соединении

При параллельном соединении разность потенциалов между узлами, объединяющими элементы цепи, одинакова для всех элементов.

Применение параллельного соединения

1. В промышленности изготавливаются сопротивления определенных величин. Иногда необходимо получить значение сопротивления вне данных рядов. Для этого можно подключить несколько сопротивлений параллельно. Эквивалентное сопротивление всегда будет меньше самого большого номинала сопротивления.

2. Делитель токов.

Источник: https://kurstoe.ru/osnovnie-svedeniya/preobrazovanie-tcepej/parallelnoe-soedinenie.html

Последовательное и параллельное соединение резисторов

Последовательное и параллельное соединение резисторов в схемах являются самыми распространенными, также — это база для расчета более сложных схем.

Последовательное подключение

Начнем с последовательного соединения. По этой схеме каждый резистор подключается с другим только в одной точке, их может быть в цепи 2, 3 и больше.

Рис. Последовательное подключение.

Обозначение:

Обозначим сопротивления: R1, R2, R3 и напряжение источника в цепи Uц. При подключении источника питания в ней начнет протекать ток Iц. В цепи с последовательным соединением ток протекает по всем резисторам один за другим.

Поскольку ток течет через все резисторы их сопротивления и ток суммируется, Iц = I1+I2+I3, Rц = R1 +R2 + R3, чем больше отдельно взятое сопротивление, тем тяжелее электронам преодолевать участок цепи. Мощность резисторов при последовательном и параллельном соединении рассчитывается по разным формулам.

В последовательных цепях — складываем, в параллельных — это обратно пропорциональная величина.

Параллельное соединение

Рис. Параллельное подключение.

Данный вид подключения характерен тем, что все элементы цепи соединяется выводами в одной точке друг другу, т.е. точка входа и выхода всех нагрузок сходятся в одну точку (или еще одно обозначение на схемах — //). Электроток, двигаясь по проводнику, дойдя до общего соединения делится на количество имеющихся веток. Если представить движение воды в трубе, то можно сказать, что вода двигающиеся по одной трубе, равномерно перетекает в несколько отводов, подсоединенных к ней. В нашем случае заряженные электроны, двигающиеся по проводнику, также растекаются на количества предложенных веток в узле. Более наглядно это можно представить в виде формул: 1. Каждый вид соединения находится под одинаковым напряжением: U = U1 = U2; 2. Суммарная сила тока равняется суммарному значению тока каждого участка I = I1 + I2; 3. Сопротивление цепи равно сумме величина обратных сопротивлению участка: 1/R = 1/R1 + 17R2 + . . . + 1/Rn; 4. Сила тока пропорциональна сопротивлению каждого участка I1/I2=R2/R1.

Далее рассмотрим схему как работает не только последовательное параллельное, но и смешанное соединение резисторов.

Смешанное подключение

Рис. Смешанное подключение резисторов

В электрических схемах используются не только типовые схемы, но и смешанное, созданное из критерий определенных требований. Чаще всего в схемах встречается третий вариант, представляющий набор из элементарных типов схем. В смешанных участках учитываются не только элементы, но и направления движения тока. При вычислении мощности резисторов смешанного подключения используются формулы для параллельного и последовательного соединения резисторов, формула также является составной.

Основные законы электротехники, наиболее часто используемые для расчетов

Рассмотрим основные законы электротехники и свойства последовательного и параллельного соединения резисторов для участка цепи

Закон Ома

Напряжение находится по закону Ома по формуле I=U/R — чем больше сопротивление, тем меньше ток. Напряжение можно найти из этой же формулы. U=R*I, ток умножается на сопротивление. Запишем эту формулу для каждого участка U1=R1· I1, Un=Rn · In.

Законы Кирхгофа

Первый закон

Ещё один очень важный закон — это закон Кирхгофа. Для участка цепи постоянного тока их два.

Рис. иллюстрация к пояснению действия первого закона Кирхгофа.

Первый закон имеет формулировку: Сумма всех токов, входящих в узел и выходящих из него равна нулю. Если посмотреть на схему, I1 — это ток, который заходит в узел, I2 и I3 — это электроны, которые вытекают из него. Применяя формулировку первого закона можно записать формулу по-другому:

I1-I2+I3=0. В этой формуле знаки плюс имеют значения, которые прибывают в узел, минус, который отходит от него.

Второй закон Кирхгофа

Рис. иллюстрация к пояснению действия второго закона Кирхгофа.

Если к цепи с включенными сопротивлениями подключен один источник ЭДС (батарея питания) тогда всё понятно, можно обойтись законом Ома. А, если, источников несколько и схема с различным схемным расположением элементов, тогда вступает в силу второй закон, который гласит: сумма токов всех источников питания для замкнутого контура, равна сумме падений напряжения на всех сопротивлениях участка в этом контуре. E1- Е2 = — UR1 — UR2 или E1 = Е2 — UR1 — UR2.

Параллельное и последовательное соединение резисторов, решение задач

Алгоритм расчёта смешанных подключений находится в тех же правилах, что и в элементарных схемах расчета последовательного и параллельного соединения резисторов. Ничего нового нет: нужно правильно разбить предложенную схему на пригодные для расчета участки. Участки, с элементами, подключены поочередно либо параллельно.

Рис. Порядок замещения при расчете сложных позиций более простыми.

Для решения задачи на последовательное и параллельное соединение резисторов необходимо правильно оценить цепи элементов. Рассмотрим схему №1 на рис.

На схеме присутствует параллельная и последовательная часть соединения элементов. Для расчета очень важно аккуратно, шаг за шагом упрощать цепи и не брать сразу всю схему (рис.1).

Как же правильно определить параллельное и последовательное соединение резисторов?

Для примера расчета возьмем резисторы R3, R4, которые подключены параллельно. Эквивалентный резистор этих элементов, будет равенRэ. = 1/R34 =1/R3 + 1/R4, после преобразования формулы и приведения к одному знаменателю получим R34 = R3 · R4 / (R3 + R4). Э. = 1/3+1/4 /(3+4) =1,7 Ом.

Далее видно, что приведённая эквивалентное R эк и R6 соединены последовательно, чтобы узнать сопротивление их необходимо сложить, тогда общее сопротивление будет равно R346 = R34 + R6, тогда Rэк346 = 1,7 + 6 = 7, 7 Ом. Заменяем на схеме одним общим элементом, теперь, позиция упрощается еще больше (рис 3).

Теперь образовалась ситуация — включение трех элементов в //. Как вычисляется такое соединение нам уже известно, 1/ R23465 = 1/ R2 +1/R346 + 1/R5 после вычисления правой части получаем 0,82 Ом. После окончательного вычисления получаем R23465 = 2,1 Ом. Здесь следует обратить внимание, что общее сопротивление получилось меньше самого меньшего из трех.

Заменяем эти сопротивление одним эквивалентным R23465. В конечном итоге все выглядит уже намного проще. Rц = Rэк + R1+ R2. R об. = R ц = 1,21 +7+1 =9,21 Ом. Из приведенного алгоритма расчёта видно, как из сложной схемы путем простого математического вычисления и применения правил сокращения резисторов участок становится простой и понятной.

Схема с подключением сопротивлений «треугольником»

Рис. Расчетная схема соединения резисторов в треугольник.

Иногда некоторые затруднения возникают при разборе схемы соединения в треугольник.

Рассмотрим на примере рисунка расчет резисторов по этому подключению. Из схемы видно, что R1 и R2 соединены последовательно Rэ12 будет соединяться R3 последовательно.

Затем Rэ123 соединяется с сопротивлением R4, R5 в последовательную цепь. Затем все это объединяется с Rэ в //.

Проведем несложные вычисления учитывая, что R1, R2, R4, R5 равняется 1 Ом. R3, R7 — 2 Ом.

RЭ1,2 = R1+R2 = 1+1=2 Ом.

Вычисляем параллельное подключение: Rэ 12 с R3. Rэ1,3 = (Rэ12*R3) /(Rэ12+R3) = (2*2) /(2+2) = 1Ом.

Далее мы видим последовательное: RЭ123 + R4 + R5 = 1+1+1 = 3 Ом. И последнее — Rэ123 4 5 с R6 — параллельное.

Общее сопротивление цепи Rц = Rоб = (RЭ1,2,3,4,5 *R6) /(RЭ1,2,3,4,5+R6) = (3 * 2) / (3+2) = 1,2 Ом. Как видно, что расчет подобного варианта также не сложный.

Расчет последовательного и параллельного подключения резисторов онлайн

Подсчитать значение мощность и сопротивлений подставляя их в формулы можно только в учебных целях, или, когда объемы не очень большие.

Наиболее практичный вариант расчета является онлайн калькуляторы, которые расположены на многочисленных интернет ресурсах.

Для расчёта любой сложности нужно правильно определить тип соединения резисторов последовательное или параллельное и внести данные для расчета в поля калькулятора.

Также такая форма расчета подойдет и для проверки результатов решения учебных задач.

Последовательное и параллельное соединение резисторов и конденсаторов

Электрические цепи состоят не только из резисторов, в них применяется большое количество различных деталей, например, конденсатор, которые подключаются в последовательное, // и смешанное соединение.

Рис. Замещения последовательно включенных элементов.

Определение этому элементу можно дать следующее: Конденсатор — это совокупность проводящих тел служащий для накопления электрического заряда. Элементарный конденсатор имеет две пластины, форма этих пластин может быть различной: сферической, круглой, цилиндрической, прямоугольной — по форме пластин разделяется и тип конденсатора.

Важное свойство. Одно из важных свойств конденсатора: если заряжается одна пластина конденсатора, то благодаря явлению электростатической индукции заряжается и вторая половина, но с противоположным знаком.

Устройство конденсатора

Плоский конденсатор состоит из двух плоских пластин отстоящих друг от друга на маленькое расстояние. У конденсатора к двум пластинам припаивается вывод всего их получается два.

Типовые схемы подключения конденсаторов

Рассмотрим различные виды подключения конденсатора.

Последовательное

Первый вид — это последовательное соединение. Предположим, что емкость этих конденсаторов будут равны.

Тогда заряды также будут равны: q1=q2=q3, как и в примере с резисторами, сложный тип позиций с конденсатором можно упростить, заменив несколько элементов одним.

У элементов соединенных друг за другом, общая емкость будет обратно пропорциональная всем имеющимся элементам. То есть: Rэк будет равняться 1/С1 + 1/С2 +…. 1/Сn/

Напряжение складывается, U эк = U1 + U2+ … Un.

Параллельное

Второй тип подключения конденсаторов — это соединение в паралель

Рис. Схема замещения элементов, включенных в параллель.

Соответственно эти конденсаторов обозначены C1, C2, … Cn заряды: Q1, Q2, … Qn и напряжение: U1, U2, … Un.
У элементов в // емкость складывается Сэ = C1 + C2 + … C n. Напряжение Un на каждом конденсаторе будет равно напряжению на эквивалентном
Uэ = U1 = U2 =… = Un — это особенность параллельного подсоединения всех элементов цепи.
Емкость будет складываться из суммы отдельных элементов Сэ =С1 + С2 + … Сп.

Рис. Расчетные позиции элементов при различном включении.

Простая позиция, которая не требует преобразования №1 — последовательное подключение. По известной формуле для этих поз. запишем 1/Сэ = 1/С1 +1/С2 +1/С3, подставив формулу значения, которые даны в условии задачи, получим 1/Сэ = 1/С1 +1/С2 +1/С3 = 59 мФ.

Не требует преобразования и 2 схема: емкость общего конденсатора будет равняться сумме конденсаторов которые включены в параллельной цепи: Сэ =С1 +С2 +С3 Сэ = 100 + 200 + 500 = 800 мФ.

Рассмотрев рис. №3 видно, что пара конденсаторов включена параллельно и один последовательно. Алгоритм преобразования таких цепей мы уже рассматривали, поэтому: сразу же находим емкость конденсатора Сэ соединения: Сэ = С1+С2 = 200+500 = 700 мФ.

Теперь находим общие эквивалентную емкость элементов с последовательным подключением 1/Сэ = 1/С2,3 +1/ С1 = 89 мф. Практическая задача решена.

Источник: http://themechanic.ru/posledovatelnoe-i-parallelnoe-soedinenie-rezistorov/

Соединение резисторов

Радиоэлектроника для начинающих

О том, как соединять конденсаторы и рассчитывать их общую ёмкость уже рассказывалось на страницах сайта. А как соединять резисторы и посчитать их общее сопротивление? Именно об этом и будет рассказано в этой статье.

Резисторы есть в любой электронной схеме, причём их номинальное сопротивление может отличаться не в 2 – 3 раза, а в десятки и сотни раз. Так в схеме можно найти резистор на 1 Ом, и тут же неподалёку на 1000 Ом (1 кОм)!

Поэтому при сборке схемы либо ремонте электронного прибора может потребоваться резистор с определённым номинальным сопротивлением, а под рукой такого нет. В результате быстро найти подходящий резистор с нужным номиналом не всегда удаётся. Это обстоятельство тормозит процесс сборки схемы или ремонта. Выходом из такой ситуации может быть применение составного резистора.

Знания о правильном соединении резисторов и расчёте их общего сопротивления выручают и ремонтников, восстанавливающих неисправную электронику, и радиолюбителей, занятых сборкой своего электронного устройства.

Последовательное соединение резисторов

В жизни последовательное соединение резисторов имеет вид:
Последовательно соединённые резисторы серии МЛТ
Принципиальная схема последовательного соединения выглядит так:

На схеме видно, что мы заменяем один резистор на несколько, общее сопротивление которых равно тому, который нам необходим.

Подсчитать общее сопротивление при последовательном соединении очень просто. Нужно сложить все номинальные сопротивления резисторов входящих в эту цепь. Взгляните на формулу.

Общее номинальное сопротивление составного резистора обозначено как Rобщ.
Номинальные сопротивления резисторов включённых в цепь обозначаются как R1, R2, R3,…RN.
Применяя последовательное соединение, стоит помнить одно простое правило:

Из всех резисторов, соединённых последовательно главную роль играет тот, у которого самое большое сопротивление. Именно он в значительной степени влияет на общее сопротивление.

Что это значит?

Так, например, если мы соединяем три резистора, номинал которых равен 1, 10 и 100 Ом, то в результате мы получим составной на 111 Ом.

Если убрать резистор на 100 Ом, то общее сопротивление цепочки резко уменьшиться до 11 Ом! А если убрать, к примеру, резистор на 10 Ом, то сопротивление будет уже 101 Ом.

Как видим, резисторы с малыми сопротивлениями в последовательной цепи практически не влияют на общее сопротивление.

Параллельное соединение резисторов

Можно соединять резисторы и параллельно:
Два резистора МЛТ-2, соединённых параллельно
Принципиальная схема параллельного соединения выглядит следующим образом:

Для того чтобы подсчитать общее сопротивление нескольких параллельно соединённых резисторов понадобиться знание формулы. Выглядит она вот так:

Эту формулу можно существенно упростить, если применять только два резистора. В таком случае формула примет вид:

Есть несколько простых правил, позволяющих без предварительного расчёта узнать, каково должно быть сопротивление двух резисторов, чтобы при их параллельном соединении получить то, которое требуется.

Если параллельно соединены два резистора с одинаковым сопротивлением, то общее сопротивление этих резисторов будет ровно в два раза меньше, чем сопротивление каждого из резисторов, входящих в эту цепочку.

Это правило исходит из простой формулы для расчёта общего сопротивления параллельной цепи, состоящей из резисторов одного номинала. Она очень проста. Нужно разделить номинальное сопротивление одного из резисторов на общее их количество:

Здесь R1 – номинальное сопротивление резистора. N – количество резисторов с одинаковым номинальным сопротивлением.

Ознакомившись с приведёнными формулами, вы скажите, что все они справедливы для расчёта ёмкости параллельно и последовательно соединённых конденсаторов. Да, только в отношении конденсаторов всё действует с точностью до «наоборот”. Узнать подробнее о соединении конденсаторов можно здесь.

Проверим справедливость показанных здесь формул на простом эксперименте.

Возьмём два резистора МЛТ-2 на 3 и 47 Ом и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.

Замер общего сопротивления при последовательном соединении
Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.
Измерение сопротивления при параллельном соединении
Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:

При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.

Что ещё нужно учитывать при соединении резисторов?

Во-первых, обязательно учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом и мощностью 1 Вт. Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?

Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А), а сопротивление каждого из них равно 50 Ом, тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт. В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт.

Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.

Подробнее о мощности рассеивания резистора читайте тут.

Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.

Главная » Радиоэлектроника для начинающих » Текущая страница

Также Вам будет интересно узнать:

Источник: https://go-radio.ru/connection-of-resistors.html

Параллельное соединение резисторов

Господа, в прошлый раз мы с вами говорили про последовательное сопротивление резисторов. Сегодня я бы хотел вам рассказать про другой возможный вид соединения – параллельное.

Чем различается последовательное и параллельное соединение я уже писал в предыдущей статье. Но все-таки вытащу сюда картинку из той прошлой статьи, я ж знаю, что вам будет лень ходить по ссылкам .

А) – Последовательное соединение
В) – Параллельное соединение
Рисунок 1 – Последовательное и параллельное соединение
Как мы видим из рисунка 1, параллельное соединение – это такое соединение, при котором одни концы всех резисторов соединены в один узел, а другие концы – в другой узел.

Сейчас наша задача будет разобраться, как ведут себя токи, напряжения, сопротивления и мощности при таком подключении. Для этого прошу вас взглянуть на рисунок 2, где подробно разрисован расклад дел для параллельного соединения. Будем полагать, что мы знаем величины R1, R2 и R3, а также величину приложенного к схеме напряжения U. Про токи же мы ничего не знаем.

Рисунок 2 – Параллельное соединения

Что мы видим на рисунке 2? Ну, в первую очередь – два узла А и B. В узел А сходятся одни концы всех резисторов, а в узел В – другие концы. Пусть узел А имеет потенциал φ1, а узел В – потенциал φ2. Из рисунка 2 видно, что для всех резисторов R1, R2 и R3 у нас одна и та же разность потенциалов U.

Как следует из статьи про потенциалы, это означает, что напряжение на всех резисторах у нас одинаково и равно приложенному напряжению U. Это важный вывод, его следует хорошо запомнить.

С токами дело обстоит по-другому. Проанализируем рисунок 2 слева направо. Пусть у нас в цепи течет ток I. Течет он себе, течет, никого не трогает и тут вдруг натыкается на узел А. Что в этом случае говорит полюбившаяся вам статья про первый закон Кирхгофа? А то, что ток I в узле А разделится на три тока I1, I2, I3. При этом будет выполняться равенство

То есть через резистор R1 будет протекать ток I1, через резистор R2 – ток I2, а через резистор R3 – ток I3.

Итак, у нас в системе уже тихо-мирно текут себе три тока. И все хорошо, пока они не наткнуться на узел В. Тут снова вступает в силу первый закон Кирхгофа. Эти три тока I1, I2, I3 вновь соединятся в один ток I. Причем после узла В ток будет иметь такую же величину I, какой он был до узла А.

То есть если все вышесказанное воплотить в лаконичный язык наскальной живописи, положение дел можно представить себе вот так

Как же найти эти самые токи I1, I2, I3? Господа, полагаю, вы уже догадались, что на помощь нам придет горячо нами всеми любимый закон Ома. Действительно, мы знаем сопротивления резисторов и, кроме того, нам известно, что на всех них падает одно и тоже напряжение U. Поэтому легко находим токи

Отлично, мы разобрались с напряжениями и с токами в такой схеме. А помните в статье про последовательное сопротивление мы ловко преобразовали три резистора в один с эквивалентным им сопротивлением? Нельзя ли и здесь сделать что-то подобное? Оказывается, вполне себе можно. Как мы помним, токи в схеме распределены таким вот образом

Обзовем эквивалентное сопротивление буковкой R. И подставим в это выражение только что найденные нами токи I1, I2, I3
Видим, что здесь без проблем можно сократить левую и правую части на U. Получаем
Господа, важный вывод: при параллельном соединении резисторов обратное эквивалентное сопротивление равно сумме обратных сопротивлений отдельных резисторов.
То есть для упрощения различных расчетов электрических схем такую вот цепочку параллельно соединенных резисторов можно заменить одним резистором с соответствующим сопротивлением, как показано на рисунке 3.
Рисунок 3 – Преобразование параллельного соединение

Весьма частый случай на практике, когда соединены параллельно не много резисторов, а всего два. Поэтому полезно знать наизусть итоговое сопротивление такой схемы. Давайте посмотрим, чему оно равно:

То есть, если у вас два сопротивления соединены параллельно, то по этой формуле вы легко высчитаете общее сопротивление. Рассмотрим пример. Пусть у нас параллельно соединены два резистора 10 кОм и 15 кОм. Чему равно их общее сопротивление?

Заметьте, господа, итоговое сопротивление у нас получилось 6 кОм, что меньше 10 кОм и 15 кОм. То есть при параллельном соединении общее сопротивление меньше любого из составляющих.

Это всегда верно для любого количества резисторов, а не только для двух. Итоговое сопротивление всегда уменьшается (в отличии от последовательного сопротивления, где итоговое сопротивление всегда растет).

Этот факт полезно запомнить.

Еще один часто встречающийся на практике случай – когда параллельно соединены несколько резисторов с одинаковым сопротивлением. Допустим, каждый из них обладает сопротивлением R1 и всего их N штук. Тогда по нашей общей формуле для эквивалентного сопротивления

То есть при параллельном соединении N одинаковых резисторов с сопротивлением R1 итоговое сопротивление будет в N раз меньше этого самого сопротивления R1.
Так-с, с током разобрались, с напряжением разобрались, с эквивалентным сопротивлением вроде тоже…осталась мощность. Для этого воспользуемся вот этим выражением, которое мы писали чуть выше в статье
Умножим левую и правую части на напряжение U.
Как мы помним из статьи про мощность произведение тока на напряжение есть мощность. То есть мы можем записать
где Р – мощность, выдаваемая источником;
P1 – мощность, рассеиваемая на резисторе R1;
P2 – мощность, рассеиваемая на резисторе R2;
P3 – мощность, рассеиваемая на резисторе R3.

Заметьте, господа, формула в точности такая же, как и для случая последовательного соединения резисторов. И там и там мощность, выдаваемая источником, равна сумме мощностей, рассеиваемых на резисторах цепи.

Итак, господа, мы рассмотрели основные соотношения при параллельном соединении резисторов. Теперь осталось поговорить, где это параллельное соединение можно использовать и для чего.

1) Ну, во-первых, параллельное соединение применяют во всех случаях, когда хотят запитать несколько нагрузок от одного источника напряжения. При этом пользуются тем свойством, что при параллельном соединении напряжения на всех нагрузках одинаково.

То есть, допустим, вы берете источник напряжения, выставляете на нем напряжение 5 В и цепляете к этому источнику сразу несколько своих устройств. Узлами А и В в этом случае будут клеммы источника. На каждое из устройств в этом случае придет напряжение 5 В.

Да и все устройства в вашей квартире (лампочки, компьютеры, телевизоры и все прочее) соединены между собой параллельно.

2) Второе возможное применение встречается не так часто, но, думаю, о нем тоже следует рассказать. Допустим, вы делаете какую-то схему, где необходим очень точный подгон сопротивления. Скажем, надо получить сопротивление 6 кОм. Такое сопротивление найти нелегко, их просто не продают. Зато у вас есть два сопротивления 10 кОм и 15 кОм.

Вы их соединяете параллельно и получаете требуемые 6 кОм. Как показывает практика, 3 параллельных резисторов достаточно для получения итогового результирующего сопротивления требуемого номинала с весьма хорошей точностью. Конечно, таких вещей лучше избегать и, если есть возможность, всегда стараться применять стандартные сопротивления.

Но бывают случаи, когда это невозможно, и тогда приходит на помощь этот метод.

3) Третий пункт будет немного похож на первый. Его суть заключается в следующим. Допустим, нам надо снять с источника питания 10 Вт мощности. А у нас в наличии только резисторы, которые позволяют рассеивать на себе 1 Вт. Что делать? Можно соединить 10 резисторов параллельно и с каждого снимать по 1 Вт. Мы же помним нашу формулу

Конечно, лучше брать не 10 резисторов, а хотя бы 15 и рассеивать на них меньше, чем 1 Вт. Работать на пределе никогда не следует.

Кстати, тут очень вовремя к моменту написания статьи пришли платы с производства! Господа, прошу вас взглянуть на рисунок 4.

Рисунок 4 – Плата нагревателя

На нем изображена плата нагревателя (флешка для масштаба). В чем суть? Имеется весьма сложное устройство, предназначенное для работы в арктических условиях.

Найти же компоненты, которые надежно функционировать при температурах минус 55 градусов и при этом стоят адекватных денег и обладают адекватными размерами бывает непросто. Обычно элементная база в лучшем случае рассчитана на минус 40 градусов.

И было принято решение разработать вот такой вот нагреватель для прогрева чувствительных к холоду аналоговых узлов устройства. Он управляется с микроконтроллера и автоматически включается при температурах меньше минус 40 градусов.

Как вы можете видеть из рисунка 4, этот нагреватель представляет собой 30 параллельно соединенных резисторов с сопротивлениями 150 Ом. Каждый резистор, согласно документации, способен рассеивать до 1 Вт мощности. Используя изученные формулки, мы можем посчитать, что в сумме такая система обладает сопротивлением

и теоретически может рассеивать мощность

Ну, с сопротивлением вопросов нет, оно действительно равно 5 Ом. Ну, плюс-минус 5 % на допуск резисторов, что в данном случае вообще не критично. А вот с мощностью тут не так все однозначно. Помните про закон Джоуля-Ленца, который мы рассматривали? Резисторы будут греться, причем не слабо.

Как показывает практика, если нагружать резисторы по полной, то есть рассеивать на каждом по 1 Вт, то в течении нескольких секунд их температура улетит за 150 градусов. Такая высокая температура критична для резистора и может привести к его разрушению.

Я был готов к такому развитию событий, поэтому заложил для платы нагревателя максимальное напряжение 9 вольт. Это значит, что на каждом резисторе будет выделяться

что почти в два раза меньше максимально допустимой мощности в 1 Вт. В сумме на всей плате выделялось, соответственно

Эксперимент показал, что резисторы достигли температуры с комнатных 25 градусов до критичных 120 градусов приблизительно за 10 секунд работы и температура продолжала уверенно расти.

Очевидно, если оставить на длительное время включенным такой нагреватель при комнатной температуре, он неминуемо выйдет из строя.

Возможно, при работе на минус 55 градусах перегрев бы не был столь критичным, однако хотелось исключить вариант спалить плату на столе, поэтому я понизил напряжение, подаваемое на плату на 3 вольта: стал подавать 6 вольт. Теперь на каждом резисторе рассеивалось

а на всей плате

Теперь температура поднималась до 100-110 градусов примерно за 30-40 секунд работы и оставалась на этом уровне (выходила в точку термодинамического равновесия). Эта температура вполне подходит для нагревателя.

Однако пока это были лишь эксперименты на столе при комнатной температуре, главный эксперимент – в термокамере на минус 55 градусах – впереди. Возможно, по его результатам потребуется чуть увеличить рассеиваемую мощность.

А может все останется как есть и этой мощности будет достаточно для вывода девайса на режим за адекватное время, время покажет .

На сегодня все, господа. Удачи вам и до новых встреч!

Источник: http://myelectronix.ru/postoyannyy-tok/40-parallelnoe-soedinenie-rezistorov

Как отличается параллельное и последовательное соединение резисторов?

Большое разнообразие схем основано на двух видах соединений – последовательное параллельное. Для каждого типа существуют свои собственные законы и принципы. Именно это и позволяет создавать устройства с самыми различными техническими параметрами, в том числе и резисторы. Что же такое резистор?

Резистор – радиодеталь, созданная для контроля напряжения и тока в цепи, увеличивая либо понижая его. Резисторы могут быть двух видов – постоянные и переменные. Так, например, светодиоды требуют для себя совсем небольшого тока. Для этого в электрическую цепочку перед светодиодом устанавливается резистор, который обеспечивает необходимое напряжение для работы последнего.

В статье подробны рассмотрены все аспекты последовательного и параллельного подключения резисторов. Бонусом к статье являются видеоролик и детальная информационная статья на рассматриваемую тему.

Последовательное подключение

Начнем с последовательного соединения. По этой схеме каждый резистор подключается с другим только в одной точке, их может быть в цепи 2, 3 и больше. Обозначим сопротивления: R1, R2, R3 и напряжение источника в цепи Uц. При подключении источника питания в ней начнет протекать ток Iц. В цепи с последовательным соединением ток протекает по всем резисторам один за другим.

Последовательное соединение характеризуется тем, что элементы идут друг за другом. Конец одного подключается к началу другого. При подключении полученной цепочки к источнику тока получается кольцо.

Теоретическая часть

Последовательное соединение характерно тем, что через все элементы протекает ток одинаковой силы. То есть, если цепочка состоит из двух резисторов R1 и R2 (как на рисунке ниже), то ток протекающий через каждое из них и любую другую часть цепи будет одинаковой (I = I1 = I2).

Суммарное сопротивление всей цепи последовательно соединенных резисторов считается как сумма сопротивлений всех ее элементов. То есть, номиналы складывают. R = R1 + R2 — это и есть формула расчета сопротивления при последовательном соединении резисторов. Если элементов больше двух, будет просто больше слагаемых.

Еще одно свойство последовательного соединения — на каждом элементе напряжение отличается. Ток в цепи одинаковый, а напряжение на резисторе зависит от его номинала.

Последовательное подключение.

Примеры расчета

Давайте рассмотрим пример. Цепь представлена на рисунке выше. Есть источник тока и два сопротивления. Пусть R1=1,2 кОм, R2= 800 Ом, а ток в цепи 2 А. По закону Ома U = I * R. Подставляем наши значения:

U1 = R1 * I = 1200 Ом * 2 А = 2400 В;
U2 = R2 * I = 800 Ом * 2А = 1600 В.

Будет интересно➡ SMD резисторы: что это такое и для чего используются?

Общее напряжение цепи считается как сумма напряжений на резисторах: U = U1 + U2 = 2400 В + 1600 В = 4000 В. Полученную цифру можно проверить. Для этого найдем суммарное сопротивление цепи и умножим его на ток. R = R1 + R2 = 1200 Ом + 800 Ом = 2000 Ом.

Если подставить в формулу напряжения при последовательном соединении сопротивлений, получаем: U = R * I = 2000 Ом * 2 А = 4000 В. Получаем, что общее напряжение данной цепи 4000 В.

А теперь посмотрите на схему. На первом вольтметре (возле резистора R1) показания будут 2400 В, на втором — 1600 В. При этом напряжение источника питания — 4000 В. Последовательное соединение – это соединение двух или более резисторов в форме цепи, в которой каждый отдельный резистор соединяется с другим отдельным резистором только в одной точке.

Материал по теме: Как проверить варистор мультиметром.

Общее сопротивление Rобщ

Параллельное соединение резисторов

Параллельное соединение – это соединение, при котором резисторы соединяются между собой обоими контактами. В результате к одной точке (электрическому узлу) может быть присоединено несколько резисторов.

Параллельное подключение резисторов.

Общее сопротивление Rобщ

Если посмотреть на изображение параллельного соединения, заметно, что ко всем элементам прилагается одинаковое напряжение.

То есть, при параллельном соединении резисторов, на каждом из них будет одинаковое напряжение U = U1 = U2 = U3. Получается, что ток разделяется на несколько «ручейков».

То есть, при параллельном соединении резисторов сила тока, протекающего через каждый из элементов, отличается. I = I1+I2+I3. И зависит сила тока (согласно тому же закону Ома) от сопротивления каждого участка цепи.

В случае с параллельным соединением резисторов — от их номинала.

Предлагаем также почитать интересный материал про малоизвестные факты о двигателях постоянного тока в другой нашей статье.

Схема параллельного соединения

Общее сопротивление участка цепи при таком соединении становится ниже. Его высчитывают по формуле: 1/R = 1/R1 + 1/R + 1/R3+. Такая форма хоть и понятна, но неудобна.

Формула расчета сопротивления параллельно подключенных резисторов получается тем сложнее, чем больше элементов соединены параллельно.

Но больше двух-трех редко кто объединяет, так что на практике достаточно знать только две формулы приведенные ниже.

Если подставить значения в эти формулы, то заметим, что результат будет меньше, чем сопротивление резистора с наименьшим номиналом. Это стоит запомнить: результирующее сопротивление включенных параллельно резисторов будет ниже самого маленького номинала. Давайте сначала рассчитаем параллельное соединение двух резисторов разного номинала и посмотрим что получится.

Соединили параллельно 150 Ом и 100 Ом. Считаем результирующее: 150*100 / (150+100) = 15000/250 = 60 Ом. Если соединить 150 Ом и 50 Ом, получим: 150*50 / (150+50) = 7500 / 200 = 37,5 Ом.

Как видим, в обоих случаях результат оказывается меньше чем самый низкий номинал соединенных деталей. Этим и пользуются, если в наличии нет сопротивления небольшого номинала.

Проблема только в том, что подбирать сложновато: надо каждый раз считать используя калькулятор.

Как высчитывать сопротивление составных резисторов

Возможно, вам будет проще, если знать, что соединив два одинаковых резистора параллельно, получим результат в два раза меньше. Например, соединив параллельно два резистора по 100 Ом получим составное сопротивление 50 Ом. Проверим? Считаем: 100*100 / (100+100) = 10000 / 200 = 50 Ом. При соединении параллельно трех резисторов, считать приходится больше, так как формула сложнее.

Если подключить параллельно 150 Ом, 100 Ом и 50 Ом, результирующее будет 27,3 Ом. Попробуем с более низкими номиналами. Если параллельно включены 20 Ом, 15 Ом и 10 Ом. Получим результирующее сопротивление 4,61 Ом. Вот вам подтверждение правила. Суммарное сопротивление параллельно соединенных резисторов меньше чем самый низкий номинал.

Параллельное соединение резисторов

Параллельное соединение резисторов это соединение, в котором начала всех резисторов соединены в одну общую точку (А), а концы в другую общую точку. При этом по каждому резистору течет свой ток. При параллельном соединении при протекании тока из точки А в точку Б, он имеет несколько путей.

Таким образом, увеличение числа параллельно соединенных резисторов ведет к увеличению путей протекания тока, то есть к уменьшению противодействия протеканию тока. А это значит, чем большее количество резисторов соединить параллельно, тем меньше станет значение общего сопротивления такого участка цепи.

Общее сопротивление параллельно соединенных резисторов определяется следующим отношением: 1/Rобщ= 1/R1+1/R2+1/R3+…+1/Rn.

Формулы расчета параллельного и последовательного подключения.

Следует отметить, что здесь действует правило «меньше – меньшего». Это означает, что общее сопротивление всегда будет меньше сопротивления любого параллельно включенного резистора. Общее сопротивление для двух параллельно соединенных резисторов рассчитывается по следующей формуле: Rобщ= R1*R2/R1+R2.

Если имеет место два параллельно соединенных резистора с одинаковыми сопротивлениями, то их общее сопротивление будет равно половине сопротивления одного из них. Параллельное соединение резисторов. При параллельном соединении резисторов нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви.

Заменяя лампы резисторами с сопротивлениями R1, R2, R3, При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Поэтому согласно закону Ома: I1=U/R1; I2=U/R2; I3=U/R3.

Источник: https://ElectroInfo.net/radiodetali/rezistory/kak-otlichaetsja-parallelnoe-i-posledovatelnoe-soedinenie-rezistorov.html

Параллельное соединение резисторов: расчет и формулы

В случае последовательного соединения прохождение тока осуществляется только через один проводник. Параллельное соединение резисторов предполагает распределение электрического тока среди нескольких проводников. При добавлении еще одного резистора в электрическую цепь, ток будет частично проходить через разные резисторы.

Схемы последовательного и параллельного соединения

Если рассматривать соединение на примере громкоговорителя, то при последовательном соединении с усилителем мощности подключается только один динамик, поскольку прохождение тока осуществляется только через один проводник. Подключение второго громкоговорителя может быть выполнено разными способами.

При последовательном соединении по обоим устройствам будет протекать одинаковый ток. В этом случае общее сопротивление приборов представляет собой сумму отдельно взятых сопротивлений.

При параллельном соединении протекание тока будет происходить по двум направлениям. Здесь общее значение сопротивления в отличие от последовательного соединения, наоборот, будет уменьшаться. То есть, при параллельном соединении двух сопротивлений, их общее значение будет составлять половину каждого из них.

Если последовательное и параллельное соединение резисторов рассматривается с точки зрения радиоэлектроники, необходимо четко представлять себе, что представляет собой данный элемент и какова его роль в электронных схемах. Эта деталь является неотъемлемой частью многих устройств, благодаря такому свойству, как сопротивление электрическому току. Резисторы могут быть двух типов – постоянными и переменными, то есть подстроечными. При создании тех или иных электрических схем требуется резистор установленного номинала, которого в данный момент может не оказаться в наличии. Поэтому приходится использовать элементы с другими номинальными значениями, формула для каждого из которых подтверждает их физические свойства.

Последовательное соединение считается наиболее простым. Оно используется, когда необходимо увеличить общее сопротивление электрической цепи. В этом случае все сопротивления резисторов просто складываются и дают общую сумму. При параллельном соединении, наоборот, можно снизить результирующее сопротивление или увеличить мощность за счет нескольких подключенных резисторов.

Отличие параллельного и последовательного соединения

Последовательное и параллельное соединение резисторов отличаются между собой значениями напряжения. В каждой части параллельных контуров этот показатель будет одинаковым. Однако, при одном и том же напряжении, сила тока в контурах будет разной. Кроме того, сопротивление резисторов при параллельном соединении будет существенно отличаться от того же показателя при последовательном соединении.

В процессе использования последовательной схемы наблюдаются обратные явления. Сила тока в каждом сопротивлении будет одна и та же, а напряжение на каждом участке будет отличаться. Это связано с тем, что во время протекания тока, каждый резистор частично забирает приложенное напряжение. Из-за различного сопротивления резисторов, при последовательном соединении, напряжение в цепи может падать. Для того чтобы подтвердить данное явление, выполняется расчет сопротивления. Все падения напряжения в общей сумме равняются общему напряжению, которое было приложено. Для проведения вычислений используются формулы, с помощью которых можно получить наиболее точные результаты.

Таким образом, параллельное соединение резисторов, находящихся под одинаковым напряжением, не влияет на режим работы каждого из них. То есть, они совершенно не зависят друг от друга, и ток, проходящий по одному приемнику, не может существенно влиять на другие приемники.

Формула расчета параллельного соединения резисторов

Свои особенности имеет и ток при параллельном соединении резисторов. Попадая в первый узел соединения, он разделяется на столько частей, сколько имеется резисторов, подключенных параллельно. То есть, через сопротивление R1 будет протекать ток I1, а через R2 – ток I2. При попадании во второй узел, они вновь соединяются в один общий ток: I = I1 + I2.

Если какой-либо резистор вышел из строя, то остальные будут нормально функционировать. В этом заключается основное преимущество параллельного соединения. Особенно, это касается двигателей и электрических ламп, работающих от определенного номинального напряжения.

Расчет общего номинального сопротивления осуществляется с помощью формулы: R(общ)=1/(1/R1+1/R2+1/R3+1/R n), где R(общ) – является общим сопротивлением, а R1, R2, R3 и Rn – параллельно подключенными резисторами. Если выполняется параллельное соединение двух резисторов, при котором используется всего лишь два элемента, то в этом случае для расчетов используется следующая схема: R(общ)=R1хR2/R1+R2.

Очень часто в радиоэлектронике приходится пользоваться следующим правилом: если резисторы, подключенные параллельно, имеют один и тот же номинал, то итоговое сопротивление высчитывается путем деления номинала на число подключенных элементов. Такое параллельное соединение резисторов формула представляется следующим образом: R(общ)=R1\n, где R(общ) представляет собой сопротивление, R – номинал параллельно подключенного резистора, n – число подключенных элементов.

Для того чтобы рассчитать параллельное соединение резисторов, следует учитывать, что итоговое сопротивление всех подключенных элементов будет всегда ниже, чем сопротивление резистора с самым низким номиналом. В качестве примера можно рассмотреть схему с тремя резисторами, сопротивления которых составляют 30, 100 и 150 Ом. При использовании основной формулы будет получен следующий результат: R(общ)=1/(1/30+1/100+1/150) =1/(0,03+0,01+0,007)=1/0,047=21,28Ом. Таким образом, три резистора, соединенные параллельно, с минимальным номиналом 30 Ом, в итоге дадут общее сопротивление электрической цепи 21,28 Ом.

Онлайн калькулятор

В случае больших объемов вычислений, расчет параллельного соединения резисторов выполняется с помощью онлайн-калькулятора.

Как считать сопротивление при параллельном соединении

Как правильно соединять резисторы?

Для того чтобы собрать составной резистор нужно соединить несколько резисторов параллельно или последовательно и тем самым получить нужное нам номинальное сопротивление. На практике это пригождается постоянно. Знания о правильном соединении резисторов и расчёте их общего сопротивления выручают и ремонтников, восстанавливающих неисправную электронику, и радиолюбителей, занятых сборкой своего электронного устройства.

Последовательное соединение резисторов.

В жизни последовательное соединение резисторов имеет вид:

Последовательно соединённые резисторы серии МЛТ

Принципиальная схема последовательного соединения выглядит так:

Общее номинальное сопротивление составного резистора обозначено как R_общ.

Номинальные сопротивления резисторов включённых в цепь обозначаются как R₁, R₂, R₃,…R_N.

Применяя последовательное соединение, стоит помнить одно простое правило:

Так, например, если мы соединяем три резистора, номинал которых равен 1, 10 и 100 Ом, то в результате мы получим составной на 111 Ом. Если убрать резистор на 100 Ом, то общее сопротивление цепочки резко уменьшиться до 11 Ом! А если убрать, к примеру, резистор на 10 Ом, то сопротивление будет уже 101 Ом. Как видим, резисторы с малыми сопротивлениями в последовательной цепи практически не влияют на общее сопротивление.

Параллельное соединение резисторов.

Можно соединять резисторы и параллельно:

Два резистора МЛТ-2, соединённых параллельно

Принципиальная схема параллельного соединения выглядит следующим образом:

Здесь R₁ – номинальное сопротивление резистора. N – количество резисторов с одинаковым номинальным сопротивлением.

Проверим справедливость показанных здесь формул на простом эксперименте.

Возьмём два резистора МЛТ-2 на 3 и 47 Ом и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.

Замер общего сопротивления при последовательном соединении

Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.

Измерение сопротивления при параллельном соединении

Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:

Что ещё нужно учитывать при соединении резисторов?

Во-первых, обязательно учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом и мощностью 1 Вт. Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?

Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А), а сопротивление каждого из них равно 50 Ом, тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт. В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт.

Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.

Подробнее о мощности рассеивания резистора читайте тут.

Формула параллельного соединения резисторов

Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:

Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:

Параллельное соединение резисторов — расчет

Пример №1

Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.

Пример расчета №2

Найти общее сопротивление R из трех параллельно соединенных резисторов:

Общее сопротивление R рассчитывается по формуле:

Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.

Как рассчитать сложные схемы соединения резисторов

Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).

Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:

Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.

Ток, протекающий в цепи параллельно соединенных резисторах

Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».

Таким образом, протекающий общий ток в цепи можно определить как:

Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:

Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА

Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА

Таким образом, общий ток будет равен:

I = 0,545 мА + 0,255 мА = 0,8 мА

Это также можно проверить, используя закон Ома:

I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)

где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)

И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.

Параллельное соединение резисторов — онлайн калькулятор

Подведем итог

Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.

При проектировании электрических схем возникает необходимость использования последовательного и параллельного соединений резисторов. Соединения применяются также и при ремонтах электрооборудования, поскольку в некоторых ситуациях невозможно найти эквивалентный номинал резистора. Выполнить расчет просто, и справиться с этой операцией может каждый.

Типы проводников

Проводимость веществом электрического тока связана с наличием в нем свободных носителей заряда. Их количество определяется по электронной конфигурации. Для этого необходима химическая формула вещества, при помощи которой можно вычислить их общее число. Значение для каждого элемента берется из периодической системы Дмитрия Ивановича Менделеева.

Электрический ток — упорядоченное движение свободных носителей заряда, на которые воздействует электромагнитное поле. При протекании тока по веществу происходит взаимодействие потока заряженных частиц с узлами кристаллической решетки, при этом часть кинетической энергии частицы превращается в тепловую энергию. Иными словами, частица «ударяется» об атом, а затем снова продолжает движение, набирая скорость под действием электромагнитного поля.

Процесс взаимодействия частиц с узлами кристаллической решетки называется электрической проводимостью или сопротивлением материала. Единицей измерения является Ом, а определить его можно при помощи омметра или расчитать. Согласно свойству проводимости, вещества можно разделить на 3 группы:

Проводники (все металлы, ионизированный газ и электролитические растворы).
Полупроводники (Si, Ge, GaAs, InP и InSb).
Непроводники (диэлектрики или изоляторы).

Проводники всегда проводят электрический ток, поскольку содержат в своем атомарном строении свободные электроны, анионы, катионы и ионы. Полупроводники проводят электричество только при определенных условиях, которые влияют на наличие или отсутствие свободных электронов и дырок. К факторам, влияющим на проводимость, относятся следующие: температура, освещенность и т. д. Диэлектрики вообще не проводят электричество, поскольку в их структуре вообще отсутствуют свободные носители заряда. При выполнении расчетов каждый радиолюбитель должен знать зависимость сопротивления от некоторых физических величин.

Зависимость сопротивления

Значение электропроводимости зависит от нескольких факторов, которые необходимо учитывать при расчетах, изготовлении элементов резистивной нагрузки (резисторов), ремонте и проектировании устройств. К этим факторам необходимо отнести следующие:

Температура окружающей среды и материала.
Электрические величины.
Геометрические свойства вещества.
Тип материала, из которого изготовлен проводник (полупроводник).

К электрическим величинам можно отнести разность потенциалов (напряжение), электродвижущую силу (ЭДС) и силу тока. Геометрией проводника является его длина и площадь поперечного сечения.

Электрические величины

Зависимость величины электропроводимости от параметров электричества определяется законом Ома. Существует две формулировки: одна — для участка, а другая — для полной цепи. В первом случае соотношение определяются, исходя из значений силы тока (I) и напряжения (U) простой формулой: I = U / R. Из соотношения видна прямо пропорциональная зависимость тока от величины напряжения, а также обратно пропорциональная от сопротивления. Можно выразить R: R = U / I.

Для расчета электропроводимости всего участка следует воспользоваться соотношением между ЭДС (e), силой тока (i), а также внутренним сопротивлением источника питания (Rвн): i = e / (R+Rвн). В этом случае величина R вычисляется по формуле: R = (e / i) — Rвн. Однако при выполнении расчетов необходимо учитывать также геометрические параметры и тип проводника, поскольку они могут существенно повлиять на вычисления.

Тип и геометрические параметры

Свойство вещества к проводимости электричества определяется структурой кристаллической решетки, а также количеством свободных носителей. Исходя из этого, тип вещества является ключевым фактором, который определяет величину электропроводимости. В науке коэффициент, определяющий тип вещества, обозначается литерой «р» и называется удельным сопротивлением. Его значение для различных материалов (при температуре +20 градусов по Цельсию) можно найти в специальных таблицах.

Иногда для удобства расчетов используется обратная величина, которая называется удельной проводимостью (σ). Она связана с удельным сопротивлением следующим соотношением: p = 1 / σ. Площадь поперечного сечения (S) влияет на электрическое сопротивление. С физической точки зрения, зависимость можно понять следующим образом: при малом сечении происходят более частые взаимодействия частиц электрического тока с узлами кристаллической решетки. Поперечное сечение можно вычислить по специальному алгоритму:

Измерение геометрических параметров проводника (диаметр или длину сторон) при помощи штангенциркуля.
Визуально определить форму материала.
Вычислить площадь поперечного сечения по формуле, найденной в справочнике или интернете.

В случае когда проводник имеет сложную структуру, необходимо вычислить величину S одного элемента, а затем умножить результат на количество элементов, входящих в его состав. Например, если провод является многожильным, то следует вычислить S для одной жилы. После этого нужно умножить, полученную величину S, на количество жил. Зависимость R от вышеперечисленных величин можно записать в виде соотношения: R = p * L / S. Литера «L» является длиной проводника. Однако для получения точных расчетов необходимо учитывать температурные показатели внешней среды и проводника.

Температурные показатели

Существует доказательство зависимости удельного сопротивления материала от температуры, основанное на физическом эксперименте. Для проведения опыта нужно собрать электрическую цепь, состоящую из следующих элементов: источника питания, нихромовой спирали, соединительных проводов амперметра и вольтметра. Приборы нужны для измерения значений силы тока и напряжения соответственно. При протекании электричества происходит нагревание нихромовой пружины. По мере ее нагревания, показания амперметра уменьшаются. При этом происходит существенное падение напряжения на участке цепи, о котором свидетельствуют показания вольтметра.

В радиотехнике уменьшение величины напряжение называется просадкой или падением. Формула зависимости р от температуры имеет следующий вид: p = p0 * [1 + a * (t — 20)]. Значение p0 — удельное сопротивление материала, взятого из таблицы, а литера «t» — температура проводника.

Температурный коэффициент «а» принимает следующие значения: для металлов — a>0, а для электролитических растворов — a Объединение резистивных радиокомпонентов

Для получения необходимого номинала сопротивления применяются два типа соединения резисторов: параллельное и последовательное. Если их соединить параллельно, то нужно два вывода одного резистора подключить к двум выводам другого. Если соединение является последовательным, то один вывод резистора соединяется с одним выводом другого резистора. Соединения используются для получения необходимых номиналов сопротивлений, а также для увеличения рассеивания мощности тока, протекающего по цепи.

Каждое из соединений обладает определенными характеристиками. Кроме того, последовательно или параллельно могут объединяться несколько резисторов. Соединения также могут быть смешанными, т. е. применяться оба типа объединения радиокомпонентов.

Параллельное соединение

При параллельном подключении значение напряжения на всех резисторах одинаковое, а сила тока — обратно пропорциональна их общему сопротивлению. В интернете web-разработчики создали для расчета величины общего сопротивления параллельного соединения резисторов онлайн-калькулятор.

Рассчитывается общее сопротивление при параллельном соединении по формуле: 1 / Rобщ = (1 / R1) + (1 / R2) + …+ (1 / Rn). Если выполнить математические преобразования и привести к общему знаменателю, то получится удобная формула параллельного соединения для расчета Rобщ. Она имеет следующий вид: Rобщ = (R1 * R2 * … * Rn) / (R1 + R2 + … + Rn). Если необходимо рассчитать величину Rобщ только для двух радиокомпонентов, то формула параллельного сопротивления имеет следующий вид: Rобщ = (R1 * R2) / (R1 + R2).

При ремонте или проектировании схемы устройства возникает задача объединения нескольких резистивных элементов для получения конкретной величины сопротивления. Например, значение Rобщ для определенной цепочки элементов равно 8 Ом, которое получено при расчетах. Перед радиолюбителем стоит задача, какие нужно подобрать номиналы для получения нужного значения (в стандартном ряду резисторов отсутствует радиокомпонент с номиналом в 8 Ом, а только 7,5 и 8,2). В этом случае нужно найти сопротивление при параллельном соединении резистивных элементов. Посчитать значение Rобщ для двух элементов можно следующим образом:

Номинал резистора в 16 Ом подойдет.
Подставить в формулу: R = (16 * 16) / (16 + 16) = 256 / 32 = 8 (Ом).

В некоторых случаях следует потратить больше времени на подбор необходимых номиналов. Можно применять не только два, но и три элемента. Сила тока вычисляется с использованием первого закона Кирхгофа. Формулировка закона следующая: общее значение тока, входящего и протекающего по цепи, равен выходному его значению. Величина силы тока для цепи, состоящей из двух резисторов (параллельное соединение) рассчитывается по такому алгоритму:

Ток, протекающий через R1 и R2: I1 = U / R1 и I2 = U / R2 соответственно.
Общий ток — сложение токов на резисторах: Iобщ = I1 + I2.

Например, если цепь состоит из 2 резисторов, соединенных параллельно, с номиналами в 16 и 7,5 Ом. Они запитаны от источника питания напряжением в 12 В. Значение силы тока на первом резисторе вычисляется следующим способом: I1 = 12 / 16 = 0,75 (А). На втором резисторе ток будет равен: I2 = 12 / 7,5 = 1,6 (А). Общий ток определяется по закону Кирхгофа: I = I1 + I2 = 1,6 + 0,75 = 2,35 (А).

Последовательное подключение

Последовательное включение резисторов также применяется в радиотехнике. Методы нахождения общего сопротивления, напряжения и тока отличаются от параллельного подключения. Основные правила соединения следующие:

Ток не изменяется на участке цепи.
Общее напряжение равно сумме падений напряжений на каждом резисторе.
Rобщ = R1 + R2 + … + Rn.

Пример задачи следующий: цепочка, состоящая из 2 резисторов (16 и 7,5 Ом), питается от источника напряжением 12 В и током в 0,5 А. Необходимо рассчитать электрические параметры для каждого элемента. Порядок расчета следующий:

I = I1 = I2 = 0,5 (А).
Rобщ = R1 + R2 = 16 + 7,5 = 23,5 (Ом).
Падения напряжения: U1 = I * R1 = 0,5 * 16 = 8 (В) и U2 = I * R2 = 0,5 * 7,5 = 3,75 (В).

Не всегда выполняется равенство напряжений (12 В не равно 8 + 3,75 = 11,75 В), поскольку при этом расчете не учитывается сопротивление соединительных проводов. Если схема является сложной, и в ней встречается два типа соединений, то нужно выполнять расчеты по участкам. В первую очередь, рассчитать для параллельного соединения, а затем для последовательного.

Таким образом, параллельное и последовательное соединения резисторов применяются для получения более точных значений сопротивлений, а также при отсутствии необходимого номинала радиокомпонента при проектировании или ремонте устройств.

Последовательное и параллельное соединение. Применение и схемы

В электрических цепях элементы могут соединяться по различным схемам, в том числе они имеют последовательное и параллельное соединение.

Последовательное соединение

При таком соединении проводники соединяются друг с другом последовательно, то есть, начало одного проводника будет соединяться с концом другого. Основная особенность данного соединения заключается в том, что все проводники принадлежат одному проводу, нет никаких разветвлений. Через каждый из проводников будет протекать один и тот же электрический ток. Но суммарное напряжение на проводниках будет равняться вместе взятым напряжениям на каждом из них.

Рассмотрим некоторое количество резисторов, соединенных последовательно. Так как нет разветвлений, то количество проходящего заряда через один проводник, будет равно количеству заряда, прошедшего через другой проводник. Силы тока на всех проводниках будут одинаковыми. Это основная особенность данного соединения.

Это соединение можно рассмотреть иначе. Все резисторы можно заменить одним эквивалентным резистором.

Ток на эквивалентном резисторе будет совпадать с общим током, протекающим через все резисторы. Эквивалентное общее напряжение будет складываться из напряжений на каждом резисторе. Это является разностью потенциалов на резисторе.

Если воспользоваться этими правилами и законом Ома, который подходит для каждого резистора, можно доказать, что сопротивление эквивалентного общего резистора будет равно сумме сопротивлений. Следствием первых двух правил будет являться третье правило.

Применение

Последовательное соединение используется, когда нужно целенаправленно включать или выключать какой-либо прибор, выключатель соединяют с ним по последовательной схеме. Например, электрический звонок будет звенеть только тогда, когда он будет последовательно соединен с источником и кнопкой. Согласно первому правилу, если электрический ток отсутствует хотя бы на одном из проводников, то его не будет и на других проводниках. И наоборот, если ток имеется хотя бы на одном проводнике, то он будет и на всех других проводниках. Также работает карманный фонарик, в котором есть кнопка, батарейка и лампочка. Все эти элементы необходимо соединить последовательно, так как нужно, чтобы фонарик светил, когда будет нажата кнопка.

Иногда последовательное соединение не приводит к нужным целям. Например, в квартире, где много люстр, лампочек и других устройств, не следует все лампы и устройства соединять последовательно, так как никогда не требуется одновременно включать свет в каждой из комнат квартиры. Для этого последовательное и параллельное соединение рассматривают отдельно, и для подключения осветительных приборов в квартире применяют параллельный вид схемы.

Параллельное соединение

В этом виде схемы все проводники соединяются параллельно друг с другом. Все начала проводников объединены в одну точку, и все концы также соединены вместе. Рассмотрим некоторое количество однородных проводников (резисторов), соединенных по параллельной схеме.

Этот вид соединения является разветвленным. В каждой ветви содержится по одному резистору. Электрический ток, дойдя до точки разветвления, разделяется на каждый резистор, и будет равняться сумме токов на всех сопротивлениях. Напряжение на всех элементах, соединенных параллельно, является одинаковым.

Все резисторы можно заменить одним эквивалентным резистором. Если воспользоваться законом Ома, можно получить выражение сопротивления. Если при последовательном соединении сопротивления складывались, то при параллельном будут складываться величины обратные им, как записано в формуле выше.

Применение

Если рассматривать соединения в бытовых условиях, то в квартире лампы освещения, люстры должны быть соединены параллельно. Если их соединить последовательно, то при включении одной лампочки мы включим все остальные. При параллельном же соединении мы можем, добавляя соответствующий выключатель в каждую из ветвей, включать соответствующую лампочку по мере желания. При этом такое включение одной лампы не влияет на остальные лампы.

Все электрические бытовые устройства в квартире соединены параллельно в сеть с напряжением 220 В, и подключены к распределительному щитку. Другими словами, параллельное соединение используется при необходимости подключения электрических устройств независимо друг от друга. Последовательное и параллельное соединение имеют свои особенности. Существуют также смешанные соединения.

Работа тока

Последовательное и параллельное соединение, рассмотренное ранее, было справедливо для величин напряжения, сопротивления и силы тока, являющихся основными. Работа тока определяется по формуле:

А = I х U х t, где А – работа тока, t – время течения по проводнику.

Для определения работы при последовательной схеме соединения, необходимо заменить в первоначальном выражении напряжение. Получаем:

А=I х (U1 + U2) х t

Раскрываем скобки и получаем, что на всей схеме работа определяется суммой на каждой нагрузке.

Точно также рассматриваем параллельную схему соединения. Только меняем уже не напряжение, а силу тока. Получается результат:

А = А1+А2

Мощность тока

При рассмотрении формулы мощности участка цепи снова необходимо пользоваться формулой:

Р=U х I

После аналогичных рассуждений выходит результат, что последовательное и параллельное соединение можно определить следующей формулой мощности:

Р=Р1 + Р2

Другими словами, при любых схемах общая мощность равна сумме всех мощностей в схеме. Этим можно объяснить, что не рекомендуется включать в квартире сразу несколько мощных электрических устройств, так как проводка может не выдержать такой мощности.

Влияние схемы соединения на новогоднюю гирлянду

После перегорания одной лампы в гирлянде можно определить вид схемы соединения. Если схема последовательная, то не будет гореть ни одной лампочки, так как сгоревшая лампочка разрывает общую цепь. Чтобы выяснить, какая именно лампочка сгорела, нужно проверять все подряд. Далее, заменить неисправную лампу, гирлянда будет функционировать.

При применении параллельной схемы соединения гирлянда будет продолжать работать, даже если одна или несколько ламп сгорели, так как цепь не разорвана полностью, а только один небольшой параллельный участок. Для восстановления такой гирлянды достаточно увидеть, какие лампы не горят, и заменить их.

Последовательное и параллельное соединение для конденсаторов

При последовательной схеме возникает такая картина: заряды от положительного полюса источника питания идут только на наружные пластины крайних конденсаторов. Конденсаторы, находящиеся между ними, передают заряд по цепи. Этим объясняется появление на всех пластинах равных зарядов с разными знаками. Исходя из этого, заряд любого конденсатора, соединенного по последовательной схеме, можно выразить такой формулой:

q_общ= q1 = q2 = q3

Для определения напряжения на любом конденсаторе, необходима формула:

U= q/С

Где С — емкость. Суммарное напряжение выражается таким же законом, который подходит для сопротивлений. Поэтому получаем формулу емкости:

С= q/(U1 + U2 + U3)

Чтобы сделать эту формулу проще, можно перевернуть дроби и заменить отношение разности потенциалов к заряду емкости. В результате получаем:

1/С= 1/С1 + 1/С2 + 1/C3

Немного иначе рассчитывается параллельное соединение конденсаторов.

Общий заряд вычисляется как сумма всех зарядов, накопившихся на пластинах всех конденсаторов. А величина напряжения также вычисляется по общим законам. В связи с этим формула суммарной емкости при параллельной схеме соединения выглядит так:

С= (q1 + q2 + q3)/U

Это значение рассчитывается как сумма каждого прибора в схеме:

С=С1 + С2 + С3

Смешанное соединение проводников

В электрической схеме участки цепи могут иметь и последовательное и параллельное соединение, переплетающихся между собой. Но все законы, рассмотренные выше для отдельных видов соединений, справедливы по-прежнему, и используются по этапам.

Сначала нужно мысленно разложить схему на отдельные части. Для лучшего представления ее рисуют на бумаге. Рассмотрим наш пример по изображенной выше схеме.

Удобнее всего ее изобразить, начиная с точек Б и В. Они расставляются на некотором расстоянии между собой и от края листа бумаги. С левой стороны к точке Б подключается один провод, а справа отходят два провода. Точка В наоборот, слева имеет две ветки, а после точки отходит один провод.

Далее нужно изобразить пространство между точками. По верхнему проводнику расположены 3 сопротивления с условными значениями 2, 3, 4. Снизу будет идти ток с индексом 5. Первые 3 сопротивления включены в схему последовательно, а пятый резистор подключен параллельно.

Остальные два сопротивления (первый и шестой) подключены последовательно с рассматриваемым нами участком Б-В. Поэтому схему дополняем 2-мя прямоугольниками по сторонам от выбранных точек.

Теперь используем формулу расчета сопротивления:

Первая формула для последовательного вида соединения.
Далее, для параллельной схемы.
И окончательно для последовательной схемы.

Аналогичным образом можно разложить на отдельные схемы любую сложную схему, включая соединения не только проводников в виде сопротивлений, но и конденсаторов. Чтобы научиться владеть приемами расчета по разным видам схем, необходимо потренироваться на практике, выполнив несколько заданий.

Параллельное соединение сопротивлений | Электрикам

Параллельным соединением резисторов (или приемников энергии, ветвей, сопротивлений) называется такое, при котором к одним и тем же двум узлам электрической цепи (рисунок 1) присоединены несколько резисторов (ветвей).

Рис. 1 Изображение параллельного соединения трех резисторов

Проводимость при параллельном соединении

Сопротивление при параллельном соединении:

Для трёх параллельно соединенных сопротивлений

Для двух параллельно соединенных сопротивлений

Для ветвей с одинаковым сопротивлением где n количество ветвей

Ток при параллельном соединении

Мощность при параллельном соединении

Доказательство

Так как резисторы присоединены к одним и тем же узлам, то каждый из них находится под одинаковым напряжением U. Согласно закону Ома токи в сопртивлениях определяются по формулам

Из этих формул следует, что токи в параллельных ветвях с сопротивлениями распределяются прямо пропорционально проводимостям ветвей или обратно пропорционально их сопротивлениям. Ряд параллельно соединенных резисторов можно заменить эквивалентным с сопротивлением R, значение которого должно быть таким, чтобы при том же напряжении на выводах ток в эквивалентном резисторе был равен сумме токов в отдельных ветвях:

Эквивалентная проводимость

(1)

т. е. эквивалентная проводимость параллельного соединения резисторов равна сумме проводимостей всех параллельных ветвей. Следовательно, эквивалентное сопротивление будет меньше самого малого из параллельно соединенных резисторов.
Формула (1) дает возможность определить и эквивалентное сопротивление параллельного соединения резисторов. Например, при трех ветвях эквивалентная проводимость

и эквивалентное сопротивление

Для двух резисторов

Если сопротивление ветвей одинаково R1 = R2 = R3, то можно воспользоваться формулой

в общем случае при соединении n резисторов с одинаковым сопротивлением R1 эквивалентное сопротивление равно

Мощности параллельно соединенных резисторов равна сумме мощностей всех резисторов

Импеданс R и C параллельно Калькулятор

Цель использования: Рассчитать параметр паразитной емкости на печатной плате плата

Цель использования: Разработка емкостной навигационной системы

Цель использования: Проверка домашнего задания

Цель использования: При обратном, т.е.е. известны разные значения угла и импеданса, каковы значения сопротивления и емкости?
Комментарий / запрос: При обратном, т.е. известны разные значения угла и импеданса, каковы значения сопротивления и емкости?

Цель использования: Сравните результаты с индивидуальной конструкцией анализатора импеданса.

Цель использования: Убедитесь, что я правильно рассчитываю полное сопротивление для параллельная цепь переменного тока для класса электроники.

Цель использования: Определение значений R, C для желаемого гистерезиса, используемого с операционным усилителем (Horowitz & Hill стр. 134-5)

Цель использования: bangin ur mom

Цель использования: Проверь мою интуицию в задаче домашнего задания

Цель использования: Проверка прибора Fluke RCL, чтобы убедиться, что он все еще функционирует нормально
действительно оценил вашу точную программу

Параллельно резисторов и конденсаторов

Введение

В этом заключительном разделе мы исследуем частотную характеристику цепей, содержащих резисторы и конденсаторы в параллельных комбинациях.Как и в предыдущем разделе, мы можем использовать анализ постоянного тока параллельных цепей резисторов в качестве отправной точки, а затем учесть фазовое соотношение между током, протекающим через резистор и компоненты конденсатора.

Анализ параллельных цепей RC

Как мы видели ранее, в параллельной цепи у тока есть несколько альтернативных путей, и выбранный маршрут зависит от относительного «сопротивления» каждой ветви. На рисунке ниже показано параллельное соединение одного резистора и конденсатора между точками A и B .

Для расчета полного импеданса (сопротивления) этой цепи мы снова используем емкостное реактивное сопротивление Xc как эквивалентное сопротивление конденсатора. Затем мы используем те же правила, что и для последовательного суммирования резисторов, помня, что теперь мы имеем дело с векторными величинами. Вы помните, что правило суммирования резисторов, включенных параллельно, дает

.
, рассматривая R2 выше как емкостное реактивное сопротивление и немного алгебры комплексных чисел, мы можем показать, что величина импеданса и фазовый угол задаются следующим образом
Теперь мы рассмотрим реакцию схемы, как указано выше, с емкостным сопротивлением 50 Ом и сопротивлением 100 Ом
Z = 100 x 50 / (100 2 + 50 2) ½ = 44.7 °
, а угол составляет -63,4 °. Частотная характеристика схемы этого типа показана ниже в виде векторов и боде.
Видно, что фазовый угол изменяется от 0 ° на низких частотах, когда ток почти полностью протекает через плечо резистора, до -90 ° на высоких частотах, когда ток протекает через ветвь, содержащую конденсатор.
Калькулятор импеданса параллельной RC-цепи
• Калькуляторы электрических, радиочастот и электроники • Онлайн-преобразователи единиц
Этот калькулятор определяет импеданс и угол сдвига фаз конденсатора и резистора, подключенных параллельно для заданной частоты синусоидального сигнала.
Пример: Рассчитайте полное сопротивление конденсатора 500 мкФ и резистора 0,2 Ом на частоте 25 кГц.
Вход
Сопротивление, R
миллиом (мОм) Ом (Ом) килоом (кОм) мегом (МОм)
Емкость, C
фарад (F) микрофарад (мкФ, мкФ) нанофара (пФ)
Частота, f
герц (Гц) миллигерц (мГц) килогерц (кГц) мегагерц (МГц) гигагерц (ГГц)
Выход
Угловая частота ω = 9 рад / с X _C = Ом
Общее сопротивление RC | Z _RC | = Ом
Разность фаз φ = ° = рад
Введите значения сопротивления, емкости и частоты, выберите единицы измерения и нажмите или коснитесь кнопки Calculate .Попробуйте ввести нулевые или бесконечно большие значения, чтобы увидеть, как ведет себя эта схема. Бесконечная частота не поддерживается. Чтобы ввести значение Infinity , просто введите inf в поле ввода.
Этот калькулятор определяет импеданс и угол разности фаз по следующим формулам:
где:
Z _RC — полное сопротивление RC-цепи в Ом (Ом),
ω = 2πf — угловая частота в рад / с,
f — частота в герцах (Гц),
R — сопротивление в омах (Ом),
C — емкость в фарадах (F)
φ — фазовый сдвиг между полным напряжением В _T и полным током I _T в градусах (°) и радианах, а
j — это мнимая единица.
Для расчета введите емкость, сопротивление и частоту, выберите единицы измерения, и результат для импеданса RC будет показан в омах, а для разности фаз — в градусах.
График импеданса параллельной RC-цепи Z _RC от частоты f для заданной емкости и сопротивления показывает обратную пропорциональность частоте
Для параллельной RС-цепи импеданс является комплексным числом и определяется как
Приложенное напряжение В _T одинаково как для резистора, так и для конденсатора.Общий ток I _T делится на два тока ответвления: I _C и I _R :
Согласно закону Кирхгофа, общий ток I _{T I _T — это векторная сумма двух токов ответвления I _C и I _R , которые не совпадают по фазе на 90 ° друг с другом. Следовательно,}
На векторной диаграмме для параллельной RC-цепи видно, что волна полного тока опережает волну полного напряжения.Угол поворота составляет менее 90 ° и более 0 °. При 90 ° резистор удаляется из цепи (цепь чисто емкостная), а при 0 ° конденсатор удаляется из цепи (цепь чисто резистивная)
Импеданс измеряется в омах, как и сопротивление. Так же, как сопротивление, импеданс показывает величину сопротивления компонента потоку электрического тока. Но чем импеданс отличается от простого сопротивления? Разница заключается в зависимости импеданса от частоты сигнала.Сопротивление не зависит от частоты и от нее зависит полное сопротивление конденсаторов. Импеданс конденсаторов увеличивается с уменьшением частоты. Емкость конденсатора оказывает такое же влияние на импеданс, как и частота. Чем выше емкость, тем ниже сопротивление и наоборот.
Этот калькулятор разработан для идеальных конденсаторов. Настоящие конденсаторы всегда имеют некоторую индуктивность, а иногда и сопротивление. Используйте наш калькулятор импеданса RLC для расчета импеданса реальных конденсаторов.
Режимы отказа
Что делать, если что-то пойдет не так в этой цепи? Щелкните или коснитесь соответствующей ссылки, чтобы просмотреть калькулятор в различных режимах отказа:
Специальные режимы
Щелкните или коснитесь соответствующей ссылки, чтобы просмотреть калькулятор в различных специальных режимах:
Различные режимы постоянного тока
Короткое замыкание
Обрыв цепи
Чисто емкостная схема
Примечания
В наших объяснениях поведения этой схемы нулевая частота означает постоянный ток.Если f = 0, мы предполагаем, что схема подключена к идеальному источнику постоянного напряжения.
При нулевой частоте мы считаем реактивное сопротивление конденсатора равным нулю, если его емкость бесконечно велика. Если конденсатор имеет конечную емкость, его реактивное сопротивление при нулевой частоте бесконечно велико и для источника постоянного напряжения оно представляет собой разомкнутую цепь или, другими словами, удаленный конденсатор.
Последовательные и параллельные резисторы
Цели обучения
К концу этого раздела вы сможете:
Нарисуйте цепь с резисторами, включенными параллельно и последовательно.
Рассчитайте падение напряжения тока на резисторе, используя закон Ома.
Контраст — способ расчета общего сопротивления для резисторов, включенных последовательно и параллельно.
Объясните, почему полное сопротивление параллельной цепи меньше наименьшего сопротивления любого из резисторов в этой цепи.
Рассчитайте общее сопротивление цепи, которая содержит смесь резисторов, подключенных последовательно и параллельно.
Большинство схем имеет более одного компонента, называемого резистором , который ограничивает поток заряда в цепи.Мера этого предела расхода заряда называется сопротивлением . Простейшие комбинации резисторов — это последовательное и параллельное соединение, показанное на рисунке 1. Общее сопротивление комбинации резисторов зависит как от их индивидуальных значений, так и от способа их подключения.
Рис. 1. (a) Последовательное соединение резисторов. (б) Параллельное соединение резисторов.
Когда резисторы в серии ? Резисторы включены последовательно всякий раз, когда поток заряда, называемый током , должен проходить через устройства последовательно.Например, если ток течет через человека, держащего отвертку, в землю, то R ₁ на Рисунке 1 (a) может быть сопротивлением вала отвертки, R ₂ сопротивлением ее ручки , R ₃ сопротивление тела человека и R ₄ сопротивление его обуви. На рисунке 2 показаны резисторы, последовательно подключенные к источнику напряжения . Кажется разумным, что полное сопротивление является суммой отдельных сопротивлений, учитывая, что ток должен проходить через каждый резистор последовательно.(Этот факт был бы преимуществом для человека, желающего избежать поражения электрическим током, который мог бы уменьшить ток, надев обувь с высоким сопротивлением на резиновой подошве. Это могло бы стать недостатком, если бы одно из сопротивлений было неисправным шнуром с высоким сопротивлением. прибор, уменьшающий рабочий ток.)
Рис. 2. Три резистора, подключенных последовательно к батарее (слева), и эквивалентное одиночное или последовательное сопротивление (справа).
Чтобы убедиться, что последовательно соединенные сопротивления действительно складываются, давайте рассмотрим потерю электроэнергии, называемую падением напряжения , в каждом резисторе на Рисунке 2.Согласно закону Ома , падение напряжения В на резисторе при протекании через него тока рассчитывается по формуле В = IR , где I равно току в амперах (A) и R — сопротивление в Ом (Ом). Другой способ представить это: В, — это напряжение, необходимое для протекания тока I через сопротивление R . Таким образом, падение напряжения на R ₁ составляет В ₁ = IR ₁, что на R ₂ составляет В ₂ = IR ₂, и что для R ₃ это V ₃ = IR ₃.Сумма этих напряжений равна выходному напряжению источника; то есть
V = V ₁ + V ₂ + V ₃.
Это уравнение основано на сохранении энергии и сохранении заряда. Электрическая потенциальная энергия может быть описана уравнением PE = qV , где q — электрический заряд, а V — напряжение. Таким образом, энергия, подаваемая источником, составляет кв , а энергия, рассеиваемая резисторами, составляет
.
qV ₁ + qV ₂ + qV ₃.
Установление связей: законы сохранения
Вывод выражений для последовательного и параллельного сопротивления основан на законах сохранения энергии и сохранения заряда, которые утверждают, что общий заряд и полная энергия постоянны в любом процессе. Эти два закона непосредственно участвуют во всех электрических явлениях и будут многократно использоваться для объяснения как конкретных эффектов, так и общего поведения электричества.
Эти энергии должны быть равны, потому что в цепи нет другого источника и другого назначения для энергии.Таким образом, qV = qV ₁ + qV ₂ + qV ₃. Плата q отменяется, давая V = V ₁ + V ₂ + V ₃, как указано. (Обратите внимание, что одинаковое количество заряда проходит через батарею и каждый резистор за заданный промежуток времени, поскольку нет емкости для хранения заряда, нет места для утечки заряда и заряд сохраняется.) Теперь подстановка значений для отдельных напряжений дает
V = IR ₁ + IR ₂ + IR ₃ = I ( R ₁ + R ₂ 9017 9010 ).
Обратите внимание, что для эквивалентного сопротивления одной серии R _с, мы имеем
В = ИК _с.
Это означает, что полное или эквивалентное последовательное сопротивление R _с трех резисторов составляет R _с = R ₁ + R ₂ + R ₃.Эта логика действительна в общем для любого количества резисторов, включенных последовательно; таким образом, полное сопротивление R _с последовательного соединения составляет
R _с = R ₁ + R ₂ + R ₃ +…,
, как предлагается. Поскольку весь ток должен проходить через каждый резистор, он испытывает сопротивление каждого, а последовательно соединенные сопротивления просто складываются.
Пример 1. Расчет сопротивления, тока, падения напряжения и рассеиваемой мощности: анализ последовательной цепи
Предположим, что выходное напряжение батареи на рисунке 2 равно 12.0 В, а сопротивления равны R ₁ = 1,00 Ом, R ₂ = 6,00 Ом и R ₃ = 13,0 Ом. а) Каково полное сопротивление? (б) Найдите ток. (c) Рассчитайте падение напряжения на каждом резисторе и покажите, как они складываются, чтобы равняться выходному напряжению источника. (d) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами.
Стратегия и решение для (а)
Общее сопротивление — это просто сумма отдельных сопротивлений, определяемая следующим уравнением:
[латекс] \ begin {array} {lll} {R} _ {\ text {s}} & = & {R} _ {1} + {R} _ {2} + {R} _ {3} \ \ & = & 1.00 \ text {} \ Omega + 6.00 \ text {} \ Omega + 13.0 \ text {} \ Omega \\ & = & 20.0 \ text {} \ Omega \ end {array} \\ [/ latex].
Стратегия и решение для (b)
Ток определяется по закону Ома, В = IR . Ввод значения приложенного напряжения и общего сопротивления дает ток для цепи:
[латекс] I = \ frac {V} {{R} _ {\ text {s}}} = \ frac {12.0 \ text {V}} {20.0 \ text {} \ Omega} = 0.60 \ text {A }\\[/латекс].
Стратегия и решение для (c)
Напряжение — или падение IR — на резисторе определяется законом Ома.Ввод тока и значения первого сопротивления дает
.
В ₁ = IR ₁ = (0,600A) (1,0 Ом) = 0,600 В.
Аналогично
В ₂ = ИК ₂ = (0,600 A) (6,0 Ом) = 3,60 В
и
V3 = IR ₃ = (0,600 A) (13,0 Ом) = 7,80 В.
Обсуждение для (c)
Три капли IR добавляют к 12.0 В, прогноз:
V ₁ + V ₂ + V ₃ = (0,600 + 3,60 + 7,80) V = 12,0 В.
Стратегия и решение для (d)
Самый простой способ рассчитать мощность в ваттах (Вт), рассеиваемую резистором в цепи постоянного тока, — это использовать закон Джоуля , P = IV , где P — электрическая мощность. В этом случае через каждый резистор протекает одинаковый полный ток.Подставляя закон Ома V = IR в закон Джоуля, мы получаем мощность, рассеиваемую первым резистором, как
P ₁ = I ² R ₁ = (0,600 A) ² (1,00 Ом) = 0,360 Вт
Аналогично
P ₂ = I ² R ₂ = (0,600 A) ² (6,00 Ом) = 2,16 Вт
и
P ₃ = I ² R ₃ = (0.{2}} {R} \\ [/ latex], где В, — это падение напряжения на резисторе (а не полное напряжение источника). Будут получены те же значения.
Стратегия и решение для (e)
Самый простой способ рассчитать выходную мощность источника — использовать P = IV , где В, — напряжение источника. Это дает
P = (0,600 A) (12,0 В) = 7,20 Вт.
Обсуждение для (e)
Обратите внимание, что по совпадению общая мощность, рассеиваемая резисторами, также равна 7.20 Вт, столько же, сколько мощность, выдаваемая источником. То есть
P ₁ + P ₂ + P ₃ = (0,360 + 2,16 + 4,68) W = 7,20 Вт
Мощность — это энергия в единицу времени (ватт), поэтому для сохранения энергии требуется, чтобы выходная мощность источника была равна общей мощности, рассеиваемой резисторами.
Основные характеристики резисторов серии
Последовательные сопротивления добавить: R _с = R ₁ + R ₂ + R ₃ +….
Одинаковый ток протекает последовательно через каждый резистор.
Отдельные последовательно включенные резисторы не получают полное напряжение источника, а делят его.
На рисунке 3 показаны резисторы параллельно , подключенные к источнику напряжения. Резисторы включены параллельно, когда каждый резистор подключен непосредственно к источнику напряжения с помощью соединительных проводов с незначительным сопротивлением. Таким образом, к каждому резистору приложено полное напряжение источника. Каждый резистор потребляет такой же ток, как если бы он один был подключен к источнику напряжения (при условии, что источник напряжения не перегружен).Например, автомобильные фары, радио и т. Д. Подключены параллельно, так что они используют полное напряжение источника и могут работать полностью независимо. То же самое и в вашем доме, или в любом другом здании. (См. Рисунок 3 (b).)
Рис. 3. (a) Три резистора, подключенных параллельно батарее, и эквивалентное одиночное или параллельное сопротивление. (б) Электроснабжение в доме. (Источник: Dmitry G, Wikimedia Commons)
Чтобы найти выражение для эквивалентного параллельного сопротивления R _p, давайте рассмотрим протекающие токи и их связь с сопротивлением.Поскольку каждый резистор в цепи имеет полное напряжение, токи, протекающие через отдельные резисторы, равны [латекс] {I} _ {1} = \ frac {V} {{R} _ {1}} \\ [/ latex] , [латекс] {I} _ {2} = \ frac {V} {{R} _ {2}} \\ [/ latex] и [латекс] {I} _ {3} = \ frac {V} {{R} _ {3}} \\ [/ латекс]. Сохранение заряда подразумевает, что полный ток I , производимый источником, является суммой этих токов:
I = I ₁ + I ₂ + I ₃.
Подстановка выражений для отдельных токов дает
[латекс] I = \ frac {V} {{R} _ {1}} + \ frac {V} {{R} _ {2}} + \ frac {V} {{R} _ {3}} = V \ left (\ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2}} + \ frac {1} {{R} _ {3}} \ справа) \\ [/ латекс].
Обратите внимание, что закон Ома для эквивалентного одиночного сопротивления дает
[латекс] I = \ frac {V} {{R} _ {p}} = V \ left (\ frac {1} {{R} _ {p}} \ right) \\ [/ latex].
Члены в скобках в последних двух уравнениях должны быть равны. Обобщая для любого количества резисторов, общее сопротивление R _p параллельного соединения связано с отдельными сопротивлениями на
[латекс] \ frac {1} {{R} _ {p}} = \ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2}} + \ гидроразрыв {1} {{R} _ {\ text {.} 3}} + \ text {.} \ Text {…} \\ [/ latex]
Это соотношение приводит к общему сопротивлению R _p, которое меньше наименьшего из отдельных сопротивлений. (Это видно в следующем примере.) При параллельном подключении резисторов от источника течет больше тока, чем протекает по любому из них по отдельности, поэтому общее сопротивление ниже.
Пример 2. Расчет сопротивления, тока, рассеиваемой мощности и выходной мощности: анализ параллельной цепи
Пусть выходное напряжение батареи и сопротивления в параллельном соединении на Рисунке 3 будут такими же, как в ранее рассмотренном последовательном соединении: В = 12.0 В, R ₁ = 1,00 Ом, R ₂ = 6,00 Ом и R ₃ = 13,0 Ом. а) Каково полное сопротивление? (б) Найдите полный ток. (c) Рассчитайте токи в каждом резисторе и покажите, как они складываются, чтобы равняться общему выходному току источника. (d) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами.
Стратегия и решение для (а)
Общее сопротивление для параллельной комбинации резисторов находится с помощью следующего уравнения.Ввод известных значений дает
[латекс] \ frac {1} {{R} _ {p}} = \ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2}} + \ frac {1} {{R} _ {3}} = \ frac {1} {1 \ text {.} \ text {00} \ text {} \ Omega} + \ frac {1} {6 \ text {. } \ text {00} \ text {} \ Omega} + \ frac {1} {\ text {13} \ text {.} 0 \ text {} \ Omega} \\ [/ latex].
Таким образом,
[латекс] \ frac {1} {{R} _ {p}} = \ frac {1.00} {\ text {} \ Omega} + \ frac {0 \ text {.} \ Text {1667}} {\ текст {} \ Omega} + \ frac {0 \ text {.} \ text {07692}} {\ text {} \ Omega} = \ frac {1 \ text {.} \ text {2436}} {\ text { } \ Omega} \\ [/ латекс].
(Обратите внимание, что в этих расчетах каждый промежуточный ответ отображается с дополнительной цифрой.) Мы должны перевернуть это, чтобы найти полное сопротивление R _p. Это дает
[латекс] {R} _ {\ text {p}} = \ frac {1} {1 \ text {.} \ Text {2436}} \ text {} \ Omega = 0 \ text {.} \ Text { 8041} \ text {} \ Omega \\ [/ latex].
Общее сопротивление с правильным количеством значащих цифр составляет R _p = 0,804 Ом
Обсуждение для (а)
R _p, как и предполагалось, меньше наименьшего индивидуального сопротивления.
Стратегия и решение для (b)
Полный ток можно найти из закона Ома, заменив полное сопротивление R _p. Это дает
[латекс] I = \ frac {V} {{R} _ {\ text {p}}} = \ frac {\ text {12.0 V}} {0.8041 \ text {} \ Omega} = \ text {14} \ text {.} \ text {92 A} \\ [/ latex].
Обсуждение для (б)
Ток I для каждого устройства намного больше, чем для тех же устройств, подключенных последовательно (см. Предыдущий пример).Схема с параллельным соединением имеет меньшее общее сопротивление, чем резисторы, включенные последовательно.
Стратегия и решение для (c)
Отдельные токи легко вычислить по закону Ома, поскольку каждый резистор получает полное напряжение. Таким образом,
[латекс] {I} _ {1} = \ frac {V} {{R} _ {1}} = \ frac {12.0 \ text {V}} {1.00 \ text {} \ Omega} = 12.0 \ text {A} \\ [/ латекс].
Аналогично
[латекс] {I} _ {2} = \ frac {V} {{R} _ {2}} = \ frac {12.0 \ text {V}} {6.00 \ text {} \ Omega} = 2 \ text {.} \ text {00} \ text {A} \\ [/ latex]
и
[латекс] {I} _ {3} = \ frac {V} {{R} _ {3}} = \ frac {\ text {12} \ text {.} 0 \ text {V}} {\ text {13} \ text {.} \ Text {0} \ text {} \ Omega} = 0 \ text {.} \ Text {92} \ text {A} \\ [/ latex].
Обсуждение для (c)
Общий ток складывается из отдельных токов:
I ₁ + I ₂ + I ₃ = 14,92 A.
Это соответствует сохранению заряда.{2}} {13.0 \ text {} \ Omega} = 11.1 \ text {W} \\ [/ latex].
Обсуждение для (d)
Мощность, рассеиваемая каждым резистором параллельно, значительно выше, чем при последовательном подключении к тому же источнику напряжения.
Стратегия и решение для (e)
Общую мощность также можно рассчитать несколькими способами. Выбрав P = IV и введя полный ток, получим
P = IV = (14,92 A) (12,0 В) = 179 Вт.
Обсуждение для (e)
Общая мощность, рассеиваемая резисторами, также составляет 179 Вт:
P ₁ + P ₂ + P ₃ = 144 Вт + 24,0 Вт + 11,1 Вт = 179 Вт
Это соответствует закону сохранения энергии.
Общее обсуждение
Обратите внимание, что как токи, так и мощность при параллельном подключении больше, чем для тех же устройств, подключенных последовательно.
Основные характеристики параллельных резисторов
Параллельное сопротивление определяется из [latex] \ frac {1} {{R} _ {\ text {p}}} = \ frac {1} {{R} _ {1}} + \ frac {1} { {R} _ {2}} + \ frac {1} {{R} _ {3}} + \ text {…} \\ [/ latex], и оно меньше любого отдельного сопротивления в комбинации.
Каждый резистор, включенный параллельно, имеет такое же полное напряжение, что и источник. (В системах распределения электроэнергии чаще всего используются параллельные соединения для питания бесчисленных устройств, обслуживаемых одним и тем же напряжением, и для того, чтобы они могли работать независимо.)
Параллельные резисторы не получают суммарный ток каждый; они делят это.
Сочетания последовательного и параллельного
Более сложные соединения резисторов иногда представляют собой просто комбинации последовательного и параллельного. Они часто встречаются, особенно если учесть сопротивление провода. В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно. Комбинации последовательного и параллельного подключения можно свести к одному эквивалентному сопротивлению, используя технику, показанную на рисунке 4.Различные части идентифицируются как последовательные или параллельные, уменьшаются до их эквивалентов и далее уменьшаются до тех пор, пока не останется единственное сопротивление. Процесс занимает больше времени, чем труден.
Рис. 4. Эта комбинация из семи резисторов имеет как последовательные, так и параллельные части. Каждое из них идентифицируется и приводится к эквивалентному сопротивлению, а затем уменьшается до тех пор, пока не будет достигнуто единичное эквивалентное сопротивление.
Самая простая комбинация последовательного и параллельного сопротивления, показанная на рисунке 4, также является наиболее поучительной, поскольку она используется во многих приложениях.Например, R ₁ может быть сопротивлением проводов от автомобильного аккумулятора к его электрическим устройствам, которые подключены параллельно. R ₂ и R ₃ могли быть стартером и светом салона. Ранее мы предполагали, что сопротивление провода незначительно, но, когда это не так, оно имеет важные последствия, как показывает следующий пример.
Пример 3. Расчет сопротивления,
IR Падение, ток и рассеиваемая мощность: объединение последовательных и параллельных цепей
На рис. 5 показаны резисторы из двух предыдущих примеров, подключенные другим способом — комбинацией последовательного и параллельного подключения.Мы можем считать R ₁ сопротивлением проводов, ведущих к R ₂ и R ₃. (а) Найдите полное сопротивление. (b) Что такое падение IR в R ₁? (c) Найдите текущие значения от I ₂ до R ₂. (d) Какую мощность рассеивает R ₂?
Рис. 5. Эти три резистора подключены к источнику напряжения, так что R ₂ и R ₃ параллельны друг другу, и эта комбинация последовательно с R ₁.
Стратегия и решение для (а)
Чтобы найти полное сопротивление, отметим, что R ₂ и R ₃ находятся параллельно, и их комбинация R _p находится последовательно с R ₁. Таким образом, полное (эквивалентное) сопротивление этой комбинации составляет
.
R _tot = R ₁ + R _p.
Сначала находим R _p, используя уравнение для параллельных резисторов и вводя известные значения:
[латекс] \ frac {1} {{R} _ {\ text {p}}} = \ frac {1} {{R} _ {2}} + \ frac {1} {{R} _ {3 }} = \ frac {1} {6 \ text {.} \ text {00} \ text {} \ Omega} + \ frac {1} {\ text {13} \ text {.} 0 \ text {} \ Omega} = \ frac {0.2436} {\ text {} \ Омега} \\ [/ латекс].
Инвертирование дает
[латекс] {R} _ {\ text {p}} = \ frac {1} {0,2436} \ text {} \ Omega = 4.11 \ text {} \ Omega \\ [/ latex].
Таким образом, общее сопротивление равно
.
R _tot = R ₁ + R _p = 1,00 Ом + 4,11 Ом = 5,11 Ом.
Обсуждение для (а)
Общее сопротивление этой комбинации является промежуточным между значениями чистой серии и чистой параллели (20.0 Ом и 0,804 Ом соответственно), найденные для тех же резисторов в двух предыдущих примерах.
Стратегия и решение для (b)
Чтобы найти падение IR в R ₁, отметим, что полный ток I протекает через R ₁. Таким образом, его падение IR составляет
В ₁ = ИК ₁
Мы должны найти I , прежде чем сможем вычислить V ₁.Полный ток I находится с помощью закона Ома для схемы. То есть
[латекс] I = \ frac {V} {{R} _ {\ text {tot}}} = \ frac {\ text {12.0} \ text {V}} {5.11 \ text {} \ Omega} = 2.35 \ text {A} \\ [/ latex].
Вводя это в выражение выше, мы получаем
В ₁ = IR ₁ = (2,35 А) (1,00 Ом) = 2,35 В.
Обсуждение для (б)
Напряжение, приложенное к R ₂ и R ₃, меньше общего напряжения на величину В ₁.Когда сопротивление провода велико, это может существенно повлиять на работу устройств, представленных R ₂ и R ₃.
Стратегия и решение для (c)
Чтобы найти ток через R ₂, мы должны сначала найти приложенное к нему напряжение. Мы называем это напряжение В _p, потому что оно приложено к параллельной комбинации резисторов. Напряжение, приложенное как к R ₂, так и к R ₃, уменьшается на величину В ₁, и поэтому оно составляет
V _p = V — V ₁ = 12.0 В — 2,35 В = 9,65 В.
Теперь ток I ₂ через сопротивление R ₂ находится по закону Ома:
[латекс] {I} _ {2} = \ frac {{V} _ {\ text {p}}} {{R} _ {2}} = \ frac {9.65 \ text {V}} {6.00 \ текст {} \ Omega} = 1,61 \ text {A} \\ [/ latex].
Обсуждение для (c)
Ток меньше, чем 2,00 А, которые протекали через R ₂, когда он был подключен параллельно батарее в предыдущем примере параллельной цепи.
Стратегия и решение для (d)
Мощность, рассеиваемая на R ₂ определяется на
P ₂ = ( I ₂) ² R ₂ = (1,61 A) ² (6,00 Ом) = 15,5 Вт
Обсуждение для (d)
Мощность меньше 24,0 Вт, рассеиваемых этим резистором при параллельном подключении к источнику 12,0 В.
Одним из следствий этого последнего примера является то, что сопротивление в проводах снижает ток и мощность, подаваемую на резистор.Если сопротивление провода относительно велико, как в изношенном (или очень длинном) удлинителе, то эти потери могут быть значительными. Если потребляется большой ток, падение IR в проводах также может быть значительным.
Например, когда вы роетесь в холодильнике и включается мотор, свет холодильника на мгновение гаснет. Точно так же вы можете увидеть тусклый свет в салоне, когда вы запускаете двигатель вашего автомобиля (хотя это может быть связано с сопротивлением внутри самой батареи).
То, что происходит в этих сильноточных ситуациях, показано на рисунке 6. Устройство, обозначенное как R ₃, имеет очень низкое сопротивление, поэтому при его включении протекает большой ток. Этот повышенный ток вызывает большее падение IR в проводах, представленных R ₁, снижая напряжение на лампочке (которое составляет R ₂), которое затем заметно тускнеет.
Рис. 6. Почему гаснет свет при включении большого прибора? Ответ заключается в том, что большой ток, потребляемый двигателем прибора, вызывает значительное падение напряжения в проводах и снижает напряжение на свету.
Проверьте свое понимание
Можно ли любую произвольную комбинацию резисторов разбить на последовательную и параллельную? Посмотрите, сможете ли вы нарисовать принципиальную схему резисторов, которые нельзя разбить на комбинации последовательно и параллельно.
Решение Нет, есть много способов подключения резисторов, которые не являются комбинациями последовательного и параллельного, включая петли и переходы. В таких случаях правила Кирхгофа, которые будут включены в Правила Кирхгофа, позволят вам проанализировать схему.
Стратегии решения проблем для последовательных и параллельных резисторов
Нарисуйте четкую принципиальную схему, пометив все резисторы и источники напряжения. Этот шаг включает список известных проблем, поскольку они отмечены на вашей принципиальной схеме.
Определите, что именно необходимо определить в проблеме (определите неизвестные). Письменный список полезен.
Определите, включены ли резисторы последовательно, параллельно или в комбинации последовательно и параллельно.Изучите принципиальную схему, чтобы сделать эту оценку. Резисторы включены последовательно, если через них должен последовательно проходить один и тот же ток.
Используйте соответствующий список основных функций для последовательных или параллельных подключений, чтобы найти неизвестные. Есть один список для серий, а другой — для параллелей. Если ваша проблема представляет собой комбинацию последовательного и параллельного соединения, уменьшайте ее поэтапно, рассматривая отдельные группы последовательных или параллельных соединений, как это сделано в этом модуле и примерах. Особое примечание: при обнаружении R необходимо соблюдать осторожность.
Проверьте, являются ли ответы разумными и последовательными. Единицы и числовые результаты должны быть разумными. Общее последовательное сопротивление должно быть больше, а общее параллельное сопротивление, например, должно быть меньше. Мощность должна быть больше для одних и тех же устройств, подключенных параллельно, по сравнению с последовательными и т. Д.
Сводка раздела
Концептуальные вопросы
1. Переключатель имеет переменное сопротивление, близкое к нулю в замкнутом состоянии и очень большое в разомкнутом, и он включен последовательно с устройством, которым он управляет.Объясните влияние переключателя на рис. 7 на ток в разомкнутом и замкнутом состоянии.
Рис. 7. Переключатель обычно включается последовательно с источником сопротивления и напряжения. В идеале переключатель имеет почти нулевое сопротивление в замкнутом состоянии, но имеет чрезвычайно большое сопротивление в разомкнутом состоянии. (Обратите внимание, что на этой диаграмме скрипт E представляет напряжение (или электродвижущую силу) батареи.)
2. Какое напряжение на разомкнутом переключателе на Рисунке 7?
3. На разомкнутом переключателе есть напряжение, как на Рисунке 7.Почему же тогда мощность, рассеиваемая разомкнутым переключателем, мала?
4. Почему мощность, рассеиваемая замкнутым переключателем, как на Рисунке 7, мала?
5. Студент в лаборатории физики по ошибке подключил электрическую лампочку, батарею и выключатель, как показано на рисунке 8. Объясните, почему лампочка горит, когда выключатель разомкнут, и гаснет, когда он замкнут. (Не пытайтесь — батарея сильно разряжается!)
Рис. 8. Ошибка подключения: включите этот переключатель параллельно устройству, обозначенному [латекс] R [/ латекс].(Обратите внимание, что на этой диаграмме скрипт E представляет напряжение (или электродвижущую силу) батареи.)
6. Зная, что сила удара зависит от величины тока, протекающего через ваше тело, вы бы предпочли, чтобы он был включен последовательно или параллельно с сопротивлением, таким как нагревательный элемент тостера, если он поражен им? Объяснять.
7. Были бы ваши фары тусклыми при запуске двигателя автомобиля, если бы провода в вашем автомобиле были сверхпроводящими? (Не пренебрегайте внутренним сопротивлением батареи.) Объяснять.
8. Некоторые гирлянды праздничных огней соединены последовательно для экономии затрат на проводку. В старой версии использовались лампочки, которые при перегорании прерывали электрическое соединение, как открытый выключатель. Если одна такая лампочка перегорит, что случится с остальными? Если такая цепочка работает от 120 В и имеет 40 одинаковых лампочек, каково нормальное рабочее напряжение каждой? В более новых версиях используются лампы, которые при перегорании закорачивают, как замкнутый выключатель. Если одна такая лампочка перегорит, что случится с остальными? Если такая цепочка работает от 120 В и в ней осталось 39 идентичных лампочек, каково тогда рабочее напряжение каждой?
9.Если две бытовые лампочки мощностью 60 и 100 Вт подключить последовательно к бытовой электросети, какая из них будет ярче? Объяснять.
10. Предположим, вы проводите физическую лабораторию, в которой вас просят вставить резистор в цепь, но все прилагаемые резисторы имеют большее сопротивление, чем запрошенное значение. Как бы вы соединили доступные сопротивления, чтобы попытаться получить меньшее запрошенное значение?
11. Перед Второй мировой войной некоторые радиостанции получали питание через «шнур сопротивления», который имел значительное сопротивление.Такой резистивный шнур снижает напряжение до желаемого уровня для ламп радиоприемника и т.п., и это экономит расходы на трансформатор. Объясните, почему шнуры сопротивления нагреваются и тратят энергию при включенном радио.
12. У некоторых лампочек есть три уровня мощности (не включая ноль), получаемые от нескольких нитей накала, которые индивидуально переключаются и соединяются параллельно. Какое минимальное количество нитей необходимо для трех режимов мощности?
Задачи и упражнения
Примечание. Можно считать, что данные, взятые из цифр, имеют точность до трех значащих цифр.
1. (a) Каково сопротивление десяти последовательно соединенных резисторов сопротивлением 275 Ом? (б) Параллельно?
2. (a) Каково сопротивление последовательно соединенных резисторов 1,00 × 10 ² Ом, 2,50 кОм и 4,00 кОм? (б) Параллельно?
3. Какое наибольшее и наименьшее сопротивление можно получить, соединив резисторы на 36,0 Ом, 50,0 Ом и 700 Ом?
4. Тостер на 1800 Вт, электрическая сковорода на 1400 Вт и лампа на 75 Вт подключены к одной розетке в цепи 15 А, 120 В.(Три устройства работают параллельно, если подключены к одной розетке.) а) Какой ток потребляет каждое устройство? (b) Перегорит ли эта комбинация предохранитель на 15 А?
5. Фара мощностью 30,0 Вт и стартер мощностью 2,40 кВт обычно подключаются параллельно в систему на 12,0 В. Какую мощность потребляли бы одна фара и стартер при последовательном подключении к батарее 12,0 В? (Не обращайте внимания на любое другое сопротивление в цепи и любое изменение сопротивления в двух устройствах.)
6.(a) Для батареи 48,0 В и резисторов 24,0 Ом и 96,0 Ом найдите для каждого из них ток и мощность при последовательном соединении. (b) Повторите, когда сопротивления включены параллельно.
7. Ссылаясь на пример комбинирования последовательных и параллельных цепей и рисунок 5, вычислите I ₃ двумя следующими способами: (a) из известных значений I и I ₂; (б) используя закон Ома для R ₃. В обеих частях явно показано, как вы следуете шагам, описанным в описании стратегии решения проблем для последовательных и параллельных резисторов выше.
Рис. 5. Эти три резистора подключены к источнику напряжения, так что R ₂ и R ₃ параллельны друг другу, и эта комбинация последовательно с R ₁.
8. Ссылаясь на рисунок 5: (a) Вычислите P ₃ и обратите внимание на его сравнение с P ₃, найденным в первых двух примерах задач в этом модуле. (b) Найдите полную мощность, отдаваемую источником, и сравните ее с суммой мощностей, рассеиваемых резисторами.
9. См. Рисунок 6 и обсуждение затемнения света при включении тяжелого прибора. (а) Учитывая, что источник напряжения составляет 120 В, сопротивление провода составляет 0,400 Ом, а номинальная мощность лампы составляет 75,0 Вт, какая мощность будет рассеиваться лампой, если при включении двигателя через провода пройдет в общей сложности 15,0 А? Предположите незначительное изменение сопротивления лампы. б) Какая мощность потребляет двигатель?
Рис. 6. Почему гаснет свет при включении большого прибора? Ответ заключается в том, что большой ток, потребляемый двигателем прибора, вызывает значительное падение напряжения в проводах и снижает напряжение на свету.
10. Линия электропередачи на 240 кВ, имеющая 5,00 × 10 ², подвешена к заземленным металлическим опорам с помощью керамических изоляторов, каждый из которых имеет сопротивление 1,00 × 10 ⁹ Ом (рисунок 9 (a)). Какое сопротивление на землю у 100 изоляторов? (b) Рассчитайте мощность, рассеиваемую 100 из них. (c) Какая доля мощности, переносимой линией, составляет это? Ясно покажите, как вы следуете шагам, описанным выше в описании стратегии решения проблем для последовательных и параллельных резисторов .
Рис. 9. Высоковольтная линия электропередачи (240 кВ) 5,00 × 10 ² подвешена к заземленной металлической опоре электропередачи. Ряд керамических изоляторов обеспечивает сопротивление 1,00 × 10 ⁹ Ом каждый.
11. Покажите, что если два резистора R ₁ и R ₂ объединены и один намного больше другого ( R ₁ >> R ₂): (a ) Их последовательное сопротивление почти равно большему сопротивлению R ₁.(b) Их параллельное сопротивление почти равно меньшему сопротивлению R ₂.
12. Необоснованные результаты Два резистора, один с сопротивлением 145 Ом, подключены параллельно, чтобы получить общее сопротивление 150 Ом. а) Каково значение второго сопротивления? б) Что неразумного в этом результате? (c) Какие предположения необоснованны или непоследовательны?
13. Необоснованные результаты Два резистора, один из которых имеет сопротивление 900 кОм, соединены последовательно, чтобы получить общее сопротивление 0.500 МОм. а) Каково значение второго сопротивления? б) Что неразумного в этом результате? (c) Какие предположения необоснованны или непоследовательны?
Глоссарий
серия:
последовательность резисторов или других компонентов, включенных в цепь один за другим
резистор:
компонент, обеспечивающий сопротивление току, протекающему по электрической цепи
сопротивление:
, вызывая потерю электроэнергии в цепи
Закон Ома:
соотношение между током, напряжением и сопротивлением в электрической цепи: В = IR
напряжение:
электрическая потенциальная энергия на единицу заряда; электрическое давление, создаваемое источником питания, например аккумулятором
падение напряжения:
потеря электроэнергии при прохождении тока через резистор, провод или другой компонент
текущий:
поток заряда через электрическую цепь мимо заданной точки измерения
Закон Джоуля:
соотношение между потенциальной электрической мощностью, напряжением и сопротивлением в электрической цепи, определяемое по формуле: [latex] {P} _ {e} = \ text {IV} [/ latex]
параллельно:
разводку резисторов или других компонентов в электрической цепи, так что каждый компонент получает одинаковое напряжение от источника питания; часто изображается на диаграмме в виде лестницы, где каждый компонент находится на ступеньке лестницы
Избранные решения проблем и упражнения
1.(а) 2,75 кОм (б) 27,5 Ом
3. (а) 786 Ом (б) 20,3 Ом
5. 29,6 Вт
7. (а) 0,74 А (б) 0,742 А
9. (а) 60,8 Вт (б) 3,18 кВт
11. (a) [латекс] \ begin {array} {} {R} _ {\ text {s}} = {R} _ {1} + {R} _ {2} \\ \ Rightarrow {R} _ {\ text {s}} \ приблизительно {R} _ {1} \ left ({R} _ {1} \ text {>>} {R} _ {2} \ right) \ end {array} \\ [/ латекс]
(b) [латекс] \ frac {1} {{R} _ {p}} = \ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2} } = \ frac {{R} _ {1} + {R} _ {2}} {{R} _ {1} {R} _ {2}} \\ [/ latex],
, так что
[латекс] \ begin {array} {} {R} _ {p} = \ frac {{R} _ {1} {R} _ {2}} {{R} _ {1} + {R} _ {2}} \ приблизительно \ frac {{R} _ {1} {R} _ {2}} {{R} _ {1}} = {R} _ {2} \ left ({R} _ {1 } \ text {>>} {R} _ {2} \ right) \ text {.} \ end {array} \\ [/ latex]
13. (a) –400 кОм (b) Сопротивление не может быть отрицательным. (c) Считается, что последовательное сопротивление меньше, чем у одного из резисторов, но должно быть больше, чем у любого из резисторов.
электрических цепей — Ток при параллельном соединении конденсатора и резистора?
Интересно то, что OP не включал принципиальную схему ( 3 ), что, возможно, является более знакомой ситуацией?
В схеме 1 резистор $ S $ равен нулю, а в схеме 3 резистор $ P $ бесконечен, поэтому схемы 1 и 3 являются вариациями схемы 2 .
Во всех трех цепях конденсатор $ C $ вначале остается незаряженным, и конечное значение напряжения на конденсаторе достигает постоянного значения, определяемого значениями напряжения питания $ V $ и сопротивлениями резисторов.
Для цепей 1 и 3 конечное напряжение на конденсаторе составляет $ V $, в то время как для цепи 2 конечное напряжение составляет $ \ left (\ frac {P} {P + S} \ right) \, В $ с цепочкой резисторов, выступающих в качестве делителя потенциала.
Обратите внимание, что как $ S \ to 0 $, тогда $ \ left (\ frac {P} {P + S} \ right) \, V \ to V $, который является контуром 1 , и как $ P \ to \ infty $, затем $ \ left (\ frac {P} {P + S} \ right) \, V \ to V $, который является контуром 3 .
В каждой цепи напряжение на конденсаторе будет равно $ V _ {\ rm C} (t) = V _ {\ rm final} \ left (1 — \ exp \ left (\ frac t \ tau \ right) \ right ) $, где $ \ tau $ — постоянная времени схемы.
Постоянная времени представляет собой произведение значения емкости и значения сопротивления, $ R _ {\ rm effective} C _ {\ rm effective} $.
Для контура 3 постоянная времени равна $ SC $, а для контура 1 постоянная времени равна 0 $, а для контура 2 будет находиться где-то между этими двумя значениями.
Ток в конденсаторной ветви цепи $ I _ {\ rm C} (t) = I _ {\ rm initial} \ exp \ left (\ frac t \ tau \ right) $, где $ I _ {\ rm initial} = \ frac VS $, поскольку изначально все напряжение питания должно быть на резисторе $ S $, поскольку на конденсаторе нет напряжения.
Я пытаюсь показать, что знание того, что происходит в схеме 3 , можно использовать для прогнозирования того, что происходит в схемах 1 и 2 .
Найти постоянную времени $ \ tau $ для каждой цепи немного сложнее.
Предположим, что источника напряжения нет, конденсатор заряжен и при замкнутом переключателе конденсатор разряжается.
Постоянная времени схемы равна $ \ left (\ frac {SP} {S + P} \ right) \, C $, где $ \ left (\ frac {SP} {S + P} \ right) $ — это действующий из двух резисторов сопротивлением $ S $ и $ P $, включенных параллельно.
Это также постоянная времени цепи, когда конденсатор заряжается, давая $ \ tau \ to 0 $ как $ S \ to 0 $, что является контуром 1 и $ \ tau \ to SC $ как $ P \ to \ infty $ — контур 3 .
Это не доказательство, которое можно сделать с помощью анализа схем, а способ получить «ответ», используя ранее полученные знания.
Возможно, мой ответ также показывает, что, возможно, лучше включить в анализ «лишние» компоненты, а затем посмотреть, что произойдет, если их значение будет очень маленьким или очень большим?
Такой подход поможет справиться с невозможностью достижения бесконечного тока и невозможностью мгновенного изменения тока путем включения в цепь «паразитного» сопротивления, емкости и индуктивности.
Для стандартного лабораторного эксперимента такое уточнение обычно не требуется, но может быть очень важным в некоторых областях, например, при цифровом переключении, как это происходит в компьютерных схемах.
параллельная RC-цепь | Диаграмма фазора | Импеданс и мощность
В этом руководстве рассматриваются анализ параллельной RC-цепи, фазорная диаграмма, треугольник импеданса и мощности, а также несколько решенных примеров с ответами на вопросы для обзора.
В этом руководстве рассматривается комбинация резистора и конденсатора, подключенных параллельно источнику переменного тока, как показано на рис. 1 , называется параллельной цепью RC .
Условия, которые существуют в параллельных цепях RC , и методы, используемые для их решения, очень похожи на те, которые используются для параллельных цепей RL . Напряжение имеет одинаковое значение на каждой параллельной ветви и служит основой для выражения любых разностей фаз. Принципиальная разница — это соотношение фаз.
В чистом конденсаторе ток опережает напряжение на 90 градусов, в то время как в чистой катушке индуктивности ток отстает от напряжения на 90 градусов.
Рисунок 1 Параллельная цепь RC .
Фазорная схема параллельной RC-цепи
Взаимосвязь между напряжением и токами в параллельной цепи RC проиллюстрирована на векторной (векторной) диаграмме на рисунке 2 и резюмирована следующим образом:
опорный вектор обозначен E и представляет собой напряжение в цепи, общее для всех элементов.
Поскольку ток через резистор синфазен с напряжением на нем, I _R (8 A) показано наложенным на вектор напряжения.
Конденсаторный ток I _C (12 А) опережает напряжение на 90 градусов и расположен в восходящем направлении, опережая вектор напряжения на 90 градусов.
Сложение векторов I _R и I _C дает результат, который представляет собой общий (IT) или линейный ток (14.4 А).
Угол тета (θ) представляет собой фазу между приложенным линейным напряжением и током.
Рисунок 2 Векторная (векторная) схема Parallel RC .
В параллельной цепи RC линейный ток опережает приложенное напряжение на некоторый фазовый угол меньше 90 градусов, но больше 0 градусов. Точный угол зависит от того, больше ли емкостной или резистивный ток.Если есть на больше емкостного тока, угол будет ближе к 90 градусам, , а если резистивный ток больше, угол будет ближе к 0 градусам.
Значение фазового угла можно рассчитать из значений двух токов ответвления с помощью следующего уравнения:
Ток в параллельной RC-цепи, пример 1
Для параллельной RC-цепи , показанной на рисунке 3 , определите:
Ток, протекающий через резистор.
Ток через конденсатор.
Общий линейный ток.
Фазовый угол между напряжением и полным током.
Выразите все токи в полярных обозначениях.
Используйте калькулятор, чтобы преобразовать все токи в прямоугольную форму.
Рисунок 3 Схема , пример 1.
Решение:
\ [\ text {a} \ text {. } {{\ text {I}} _ {\ text {R}}} \ text {=} \ frac {\ text {E}} {\ text {R}} \ text {=} \ frac {\ text { 120 В}} {\ text {10} \! \! \ Omega \! \! \ Text {}} \ text {= 12A} \]
\ [\ text {b} \ text {.{\ text {o}}} \\\ end {matrix} \]
\ [\ text {f} \ text {.} \ begin {matrix} \ text {} {{\ text {I}} _ { \ text {T}}} \ text {= 12 + j6} & {{\ text {I}} _ {\ text {R}}} \ text {= 12 + j0} & {{\ text {I}} _ {\ text {C}}} \ text {= 0 + j6} \\\ end {matrix} \]
Сопротивление параллельной RC-цепи
Импеданс ( Z ) параллельного RC-цепи Схема аналогична схеме параллельной RL и резюмируется следующим образом:
Импеданс можно рассчитать непосредственно из значений сопротивления и емкостного реактивного сопротивления с помощью уравнения
Импеданс можно рассчитать с помощью уравнение закона
Импеданс параллельной цепи RC всегда меньше, чем сопротивление или емкостное реактивное сопротивление отдельных ветвей.
Импеданс в параллельной RC-цепи Пример 2
Для параллельной RC цепи, показанной на рисунке 4 определите:
Ток, протекающий через резистор ( I _R ).
Ток, протекающий через конденсатор ( I _C ).
Полный линейный ток ( I _T ).
Импеданс ( Z ).
Фазовый угол между напряжением и полным током.
Если цепь более резистивная или емкостная.
Рисунок 4 Схема для примера 2.
Решение:
\ [\ text {a} \ text {. } {{\ text {I}} _ {\ text {R}}} \ text {=} \ frac {\ text {E}} {\ text {R}} \ text {=} \ frac {\ text { 240V}} {\ text {200} \! \! \ Omega \! \! \ Text {}} \ text {= 1} \ text {.2A} \]
\ [\ text {b} \ text { . } {{\ text {I}} _ {\ text {C}}} \ text {=} \ frac {\ text {E}} {{{\ text {X}} _ {\ text {C}}} } \ text {=} \ frac {\ text {240V}} {\ text {100} \! \! \ Omega \! \! \ text {}} \ text {= 2} \ text {.{o}} \]
ф. Схема более емкостная по своей природе, потому что емкостной ток больше, чем резистивный ток.
Питание в параллельной RC-цепи
Компоненты питания для параллельной RC-цепи RC показаны на Рисунке 5 . Применяемые формулы такие же, как и для параллельной цепи RL :
Рисунок 5 Силовые компоненты параллельной цепи RC .
Коэффициент мощности параллельной RC-цепи
Коэффициент мощности параллельной RC-цепи RC всегда опережает. Каждый раз, когда сопротивление ответвления увеличивается, через него проходит меньше тока, и цепь становится более емкостной, что приводит к снижению коэффициента мощности. Обратное верно, если сопротивление уменьшается.
Используя значения тока или сопротивления и импеданса, коэффициент мощности можно определить следующим образом:
Пример расчета параллельной RC-цепи 3
Для параллельной RC-цепи , показанной на рисунке 6 , определите:
Емкостное реактивное сопротивление конденсатора ( X _C ).
Ток, протекающий через конденсатор ( I _C ).
Реактивная мощность конденсатора (ВАР).
Ток, протекающий через резистор ( I _R ).
Истинная мощность (Вт).
Общий ток в линии ( I _T ).
Полное сопротивление цепи ( Z ).
Полная мощность (ВА).
Коэффициент мощности (PF).
Фазовый угол цепи θ.
Рисунок 6 Схема для примера 3.
Решение:
Шаг 1 . Составьте таблицу и запишите все известные значения.
Шаг 2 . Рассчитайте емкостное реактивное сопротивление конденсатора и введите значение в таблицу.
Шаг 3 . Рассчитайте ток, протекающий через конденсатор, и введите значение в таблицу.
Шаг 4 . Рассчитайте реактивную мощность конденсатора и введите значение в таблицу.
Шаг 5 . Рассчитайте ток, протекающий через резистор, и введите значение в таблицу.
Шаг 6 . Рассчитайте истинную мощность и введите значение в таблицу.
Шаг 7 . Рассчитайте общий ток линии и введите значение в таблицу.
Шаг 8 . Рассчитайте полное сопротивление и введите значение в таблицу.
Шаг 9 . Рассчитайте полную мощность и введите значение в таблицу.
Шаг 10. Рассчитайте коэффициент мощности и введите значение в таблицу.
Шаг 11. Рассчитайте фазовый угол цепи θ и введите значение в таблицу.
Контрольные вопросы
В чем основное различие между параллельной схемой RL и RC ?
Предположим, что сопротивление резистивной составляющей параллельной цепи RC увеличено.Какое влияние это окажет на фазовый угол схемы?
Параллельная цепь RC подключена к источнику 100 В, 60 Гц. Измеренный ток, протекающий через резистор, составляет 10 ампер. Измеренный ток, протекающий через конденсатор, составляет 10 ампер. Определите:
Линейный ток ( I _T ).
Импеданс ( Z ).
Истинная мощность (Вт).
Реактивная мощность (ВАР).
Полная мощность (ВА).
ПФ в процентах.
Для схемы, показанной на рисунке 7 , определите:
Рисунок 7 Схема для обзора вопроса 4.
Величина тока, протекающего через резистор.
Емкостное реактивное сопротивление конденсатора.
Величина тока, протекающего через конденсатор.
Линейный ток.
Полная мощность.
ПФ в процентах.
5.Заполните таблицу для всех заданных и неизвестных величин для параллельной цепи RC , показанной на Рисунке 8 .
Рисунок 8 Схема для вопроса 5 обзора.
Контрольные вопросы — ответы
Принципиальная разница заключается в соотношении фаз. В чистом конденсаторе ток опережает напряжение на 90 °, в то время как в чистой катушке индуктивности ток отстает от напряжения на 90 °.
Если сопротивление RC-цепи увеличивается, резистивный ток будет уменьшаться, и цепь станет более емкостной, а фазовый угол станет больше.
(а) 14,14 А, (б) 7,07 Ом, (в) 1000 Вт, (г) 1000 ВАр, (д) 1414 ВА, (е) 70,7%, опережение
(а) 80 А, (б) 1,77 Ом, (c) 67,8 A, (d) 105 A, (e) 12600 VA, (f) 76,2%, ведущий
E I C R / X _C / Z W / VA / VARs PF
R 440 В 20 A N / A 227 Ом 8800 Вт 0
C 440 V 11.1 A 67 мкФ 39,6 Ом 4884 VAR 90
Всего 440 В 22,9 A N / A 19,2 Ом 10076 VA32 87,3%
Серия
и параллельные схемы — learn.sparkfun.com
Добавлено в избранное Любимый 54 Серия
и параллельные схемы
Простые схемы (состоящие всего из нескольких компонентов) обычно довольно просты для понимания новичками.Но, когда на вечеринку приходят другие компоненты, все может запутаться. Куда идет ток? Что делает напряжение? Можно ли это упростить для облегчения понимания? Не бойся, бесстрашный читатель. Ценная информация приводится ниже.
В этом руководстве мы сначала обсудим разницу между последовательными и параллельными схемами, используя схемы, содержащие самые основные компоненты — резисторы и батареи, — чтобы показать разницу между двумя конфигурациями. Затем мы рассмотрим, что происходит в последовательных и параллельных цепях, когда вы комбинируете компоненты разных типов, например конденсаторы и катушки индуктивности.
рассматривается в этом учебном пособии
Как выглядят конфигурации последовательной и параллельной цепей
Как пассивные компоненты действуют в этих конфигурациях
Как источник напряжения будет воздействовать на пассивные компоненты в этих конфигурациях
Рекомендуемая литература
Вы можете посетить эти руководства по основным компонентам, прежде чем погрузиться в построение схем в этом руководстве.
Видео

Цепи серии
Узлы и текущий поток
Прежде чем мы углубимся в это, мы должны упомянуть, что такое узел .Ничего особенного, просто представление электрического соединения между двумя или более компонентами. Когда схема моделируется на схеме, эти узлы представляют собой провода между компонентами.
Пример схемы с четырьмя узлами уникального цвета.
Это полдела на пути к пониманию разницы между последовательным и параллельным. Нам также нужно понять , как ток течет по цепи. Ток течет от высокого напряжения к более низкому напряжению в цепи.Некоторое количество тока будет проходить по каждому пути, который может пройти, чтобы добраться до точки с наименьшим напряжением (обычно называемой землей). Используя приведенную выше схему в качестве примера, вот как будет течь ток, когда он проходит от положительной клеммы аккумулятора к отрицательной:
Ток (обозначенный синей, оранжевой и розовой линиями), протекающий по той же примерной схеме, что и выше. Разные токи обозначены разными цветами.
Обратите внимание, что в некоторых узлах (например, между R ₁ и R ₂) ток на входе такой же, как на выходе.В других узлах (в частности, в трехстороннем переходе между R ₂, R ₃ и R ₄) основной (синий) ток разделяется на два разных. Это ключевое различие между последовательным и параллельным подключением!
Определение цепей серии
Два компонента соединены последовательно, если они имеют общий узел и если через них протекает один и тот же ток . Вот пример схемы с тремя последовательными резисторами:
В вышеуказанной цепи есть только один способ протекания тока.Начиная с положительной клеммы аккумулятора, ток сначала будет встречать R ₁. Оттуда ток будет течь прямо к R ₂, затем к R ₃ и, наконец, обратно к отрицательной клемме батареи. Обратите внимание, что у текущего есть только один путь. Эти компоненты включены последовательно.
Параллельные схемы
Определение параллельных цепей
Если компоненты используют два общих узла , они работают параллельно.Вот пример схемы трех резисторов, подключенных параллельно батарее:
От положительной клеммы аккумуляторной батареи ток течет к R ₁ … и R ₂, и R ₃. Узел, который подключает аккумулятор к R ₁, также подключен к другим резисторам. Другие концы этих резисторов аналогично связываются вместе, а затем снова подключаются к отрицательной клемме батареи. Существует три различных пути, по которым ток может пройти перед возвращением в батарею, и соответствующие резисторы считаются параллельными.
Если все последовательные компоненты имеют одинаковые токи, протекающие через них, все параллельные компоненты имеют одинаковое падение напряжения на них — series: current :: parallel: Voltage.
Совместная работа последовательных и параллельных цепей
Оттуда мы можем смешивать и сочетать. На следующем снимке мы снова видим три резистора и батарею. С положительной клеммы аккумуляторной батареи ток сначала достигает R ₁. Но на другой стороне R ₁ узел разделяется, и ток может идти как на R ₂, так и на R ₃.Затем пути тока через R ₂ и R ₃ снова связываются вместе, и ток возвращается к отрицательному выводу батареи.
В этом примере R ₂ и R ₃ параллельны друг другу, а R ₁ последовательно с параллельной комбинацией R ₂ и R ₃.
Расчет эквивалентных сопротивлений в последовательных цепях
Вот информация, которая может оказаться для вас более полезной.Когда мы соединяем резисторы таким образом, последовательно и параллельно, мы меняем способ протекания тока через них. Например, если у нас есть питание 10 В через 10 кОм; резистора, закон Ома гласит, что у нас протекает ток 1 мА.
Если потом поставить еще 10к & ом; резистор, включенный последовательно с первым и оставив питание без изменений, мы сократили ток вдвое, потому что сопротивление увеличилось вдвое.
Другими словами, по-прежнему существует только один путь для прохождения тока, и мы только усложнили прохождение тока.Насколько сложнее? 10к & Ом; + 10к & Ом; = 20 кОм ;. Вот как мы рассчитываем последовательно включенные резисторы — всего суммируем их значения .
Если выразить это уравнение в более общем виде: полное сопротивление Н — произвольное количество резисторов — это их общая сумма.
Расчет эквивалентных сопротивлений в параллельных цепях
А как насчет параллельных резисторов? Это немного сложнее, но ненамного.Рассмотрим последний пример, в котором мы начали с источника питания 10 В и 10 кОм; резистор, но на этот раз мы добавляем еще 10кОм; параллельно, а не последовательно. Теперь у тока есть два пути. Поскольку напряжение питания не изменилось, закон Ома гласит, что первый резистор по-прежнему будет потреблять 1 мА. Но то же самое и со вторым резистором, и теперь у нас есть в общей сложности 2 мА, поступающие от источника питания, что вдвое превышает первоначальный 1 мА. Это означает, что мы уменьшили общее сопротивление вдвое.
Пока можно сказать, что 10к & ом; || 10к & Ом; = 5 кОм; («||» примерно переводится как «параллельно»), у нас не всегда будет 2 одинаковых резистора.Что тогда?
Уравнение для добавления произвольного количества резисторов параллельно:
Если обратные значения вам не подходят, мы также можем использовать метод, называемый «произведение на сумму», когда у нас есть два параллельных резистора:
Однако этот метод подходит только для двух резисторов в одном расчете. Мы можем объединить более 2 резисторов этим методом, взяв результат R1 || R2 и вычисление этого значения параллельно с третьим резистором (снова как произведение на сумму), но обратный метод может быть меньше работы.
Время эксперимента — Часть 1
Что вам понадобится:
Давайте проведем простой эксперимент, чтобы доказать, что все работает именно так, как мы говорим.
Во-первых, мы собираемся подключить 10 кОм; последовательно подключите резисторы и наблюдайте, как они складываются самым необычным образом. Используя макетную плату, поместите один 10 кОм; резистор, как показано на рисунке, и измерьте его мультиметром. Да, мы уже знаем, что будет указано, что оно составляет 10 кОм, но это то, что мы в бизнесе называем «проверкой работоспособности».Убедившись, что мир существенно не изменился с тех пор, как мы в последний раз смотрели на него, поместите еще один аналогично, но с выводами каждого резистора, электрически подключенными через макетную плату, и снова произведите измерения. Теперь измеритель должен показывать что-то близкое к 20 кОм.
Вы можете заметить, что сопротивление, которое вы измеряете, может быть не совсем таким, каким должно быть резистор. Резисторы имеют определенный допуск , что означает, что они могут быть отключены на определенный процент в любом направлении.Таким образом, вы можете прочитать 9.99k & ohm; или 10.01кОм. Пока оно близко к правильному значению, все должно работать нормально.
Читатель должен продолжать это упражнение до тех пор, пока не убедится, что он знает, что будет в результате, прежде чем делать это снова, или у них закончатся резисторы, которые можно вставить в макет, в зависимости от того, что наступит раньше.
Время эксперимента — Часть 2
Теперь давайте попробуем это с резисторами в параллельной конфигурации .Поместите один 10 кОм; резистор в макетной плате, как и раньше (мы полагаем, что читатель уже считает, что один резистор 10 кОм будет измерять на мультиметре что-то близкое к 10 кОм). Теперь поместите второй 10k & ohm; резистор рядом с первым, следя за тем, чтобы выводы каждого резистора находились в электрически соединенных рядах. Но перед тем, как измерить комбинацию, вычислите, используя метод «произведение над суммой» или обратный метод, каким должно быть новое значение (подсказка: оно будет 5 кОм;).Затем измерьте. Это что-то близкое к 5к & ом ;? Если это не так, дважды проверьте отверстия, в которые вставлены резисторы.
Повторите упражнение с резисторами 3, 4 и 5. Расчетные / измеренные значения должны быть 3,33 кОм, 2,5 кОм; и 2кОм соответственно. Все ли получилось по плану? Если нет, вернитесь и проверьте свои соединения. Если это так, EXCELSIOR! Прежде чем продолжить, выпейте молочный коктейль. Ты заслужил это.
Практические правила для последовательных и параллельных резисторов
Есть несколько ситуаций, которые могут потребовать творческих комбинаций резисторов.Например, если мы пытаемся установить очень конкретное опорное напряжение, вам почти всегда потребуется очень определенное соотношение резисторов, значения которых вряд ли будут «стандартными» значениями. И хотя мы можем получить очень высокую степень точности значений резисторов, мы, возможно, не захотим ждать X дней, необходимых для доставки чего-либо, или платить цену за нестандартные значения, отсутствующие на складе. Так что в крайнем случае мы всегда можем создать собственные номиналы резисторов.
Совет №1: Равнопараллельные резисторы
Добавление N резисторов с одинаковым номиналом R , включенных параллельно, дает нам R / N Ом.Допустим, нам нужен 2,5 кОм; резистор, но все, что у нас есть, это ящик, полный 10 кОм. Объединение четырех из них параллельно дает нам 10 кОм / 4 = 2,5 кОм.
Совет № 2: Допуск
Знайте, какую терпимость вы можете терпеть. Например, если вам нужен 3.2k & ohm; резистор, можно было поставить 3 10кОм; резисторы параллельно. Это даст вам 3,3 кОм, что составляет около 4% отклонения от необходимого значения. Но если схема, которую вы строите, должна иметь допуск ближе, чем 4%, мы можем измерить наш запас в 10 кОм, чтобы увидеть, какие из них являются самыми низкими значениями, потому что они также имеют допуск.По идее, если заначка 10к & ом; резисторы имеют допуск 1%, мы можем получить только 3,3 кОм. Но производители запчастей, как известно, допускают именно такого рода ошибки, поэтому стоит немного покопаться.
Совет № 3: Номинальная мощность при последовательном / параллельном подключении
Такая комбинация резисторов последовательно и параллельно работает и для номинальных мощностей. Допустим, нам нужен 100 & Ом; резистор рассчитан на 2 Вт (Вт), но все, что у нас есть, это связка 1 кОм; резисторы на четверть ватта (Вт) (а сейчас 3 часа ночи, вся Mountain Dew исчезла, а кофе остыл).Вы можете объединить 10 из 1 кОм, чтобы получить 100 Ом; (1 кОм / 10 = 100 Ом), а номинальная мощность будет 10×0,25 Вт или 2,5 Вт. Не очень красиво, но это поможет нам завершить финальный проект и даже может принести нам дополнительные баллы за способность думать на ногах.
Нам нужно быть немного более осторожными, когда мы объединяем резисторы разных номиналов параллельно, когда речь идет об общем эквивалентном сопротивлении и номинальной мощности. Для читателя это должно быть совершенно очевидно, но …
Совет № 4: разные резисторы параллельно
Суммарное сопротивление двух резисторов разного номинала всегда меньше, чем резистор наименьшего номинала.Читатель будет поражен тем, сколько раз кто-то объединяет значения в своей голове и приходит к значению, которое находится посередине между двумя резисторами (1 кОм || 10 кОм; НЕ равняется чему-либо около 5 кОм ;!). Общее параллельное сопротивление всегда будет приближаться к резистору с наименьшим значением. Сделайте себе одолжение и прочитайте совет №4 10 раз.
Совет № 5: Параллельное рассеивание мощности
Мощность, рассеиваемая при параллельной комбинации резисторов разного номинала, не распределяется между резисторами равномерно, поскольку токи не равны.Используя предыдущий пример (1k & ohm; || 10k & ohm;), мы видим, что 1k & ohm; будет потреблять в 10 раз больше тока 10 кОм. Поскольку закон Ома гласит, что мощность = напряжение x ток, отсюда следует, что 1 кОм; резистор рассеивает в 10 раз мощность, превышающую 10 кОм.
В конечном счете, уроки советов 4 и 5 заключаются в том, что мы должны уделять больше внимания тому, что мы делаем при параллельном соединении резисторов разного номинала. Но советы 1 и 3 предлагают несколько удобных ярлыков, когда значения совпадают.
Конденсаторы серии
и параллельные
Объединение конденсаторов аналогично объединению резисторов … только наоборот. Как бы странно это ни звучало, это абсолютная правда. Почему это могло быть?
Конденсатор — это две пластины, расположенные очень близко друг к другу, и его основная функция — удерживать целую группу электронов. Чем больше значение емкости, тем больше электронов она может удерживать. Если размер пластин увеличивается, емкость увеличивается, потому что физически больше места для электронов.А если пластины отодвинуть дальше друг от друга, емкость падает, потому что напряженность электрического поля между ними уменьшается с увеличением расстояния.
Теперь предположим, что у нас есть два конденсатора по 10 мкФ, соединенных последовательно, и предположим, что они оба заряжены и готовы к разрядке в друга, сидящего рядом с вами.
Помните, что в последовательной цепи есть только один путь для прохождения тока. Отсюда следует, что количество электронов, выходящих из колпачка внизу, будет таким же, как и количество электронов, выходящих из колпачка наверху.Значит, емкость не увеличилась?
На самом деле все еще хуже. Разместив конденсаторы последовательно, мы эффективно раздвинули пластины дальше друг от друга, потому что расстояние между пластинами двух конденсаторов складывается. Так что у нас нет 20 мкФ или даже 10 мкФ. У нас 5 мкФ. Результатом этого является то, что мы добавляем значения последовательного конденсатора так же, как мы добавляем значения параллельного резистора. И метод «произведение над суммой», и метод взаимности действительны для последовательного добавления конденсаторов.
Может показаться, что нет смысла добавлять конденсаторы последовательно. Но следует отметить, что мы получили вдвое большее напряжение (или номинальное напряжение). Как и в случае с батареями, когда мы соединяем конденсаторы последовательно, напряжения складываются.
Добавление конденсаторов параллельно похоже на последовательное добавление резисторов: значения просто складываются, никаких уловок. Почему это? Их параллельное расположение эффективно увеличивает размер пластин без увеличения расстояния между ними.Чем больше площадь, тем больше емкость. Простой.
Время эксперимента — Часть 3
Что вам понадобится:
Давайте посмотрим на некоторые последовательно и параллельно соединенные конденсаторы в действии. Это будет немного сложнее, чем примеры резисторов, потому что измерить емкость напрямую мультиметром труднее.
Давайте сначала поговорим о том, что происходит, когда конденсатор заряжается с нуля вольт. Когда ток начинает идти в один из выводов, равное количество тока выходит из другого.А если последовательно с конденсатором нет сопротивления, может быть довольно большой ток. В любом случае ток течет до тех пор, пока конденсатор не начнет заряжаться до значения приложенного напряжения, и медленнее будет стекать до тех пор, пока напряжения не станут равными, когда ток полностью прекратится.
Как указано выше, потребляемый ток может быть довольно большим, если нет сопротивления последовательно с конденсатором, а время зарядки может быть очень коротким (например, миллисекунды или меньше). Для этого эксперимента мы хотим иметь возможность наблюдать за зарядом конденсатора, поэтому мы собираемся использовать 10 кОм; резистор, включенный последовательно, чтобы замедлить действие до точки, где мы его легко увидим.Но сначала нам нужно поговорить о том, что такое постоянная времени RC.
В приведенном выше уравнении говорится, что одна постоянная времени в секундах (называемая тау) равна сопротивлению в омах, умноженному на емкость в фарадах. Простой? Нет? Продемонстрируем на следующей странице.
Время эксперимента — часть 3, продолжение …
В первой части этого эксперимента мы собираемся использовать один резистор 10 кОм и один резистор 100 мкФ (что равно 0,0001 фарад). Эти две части создают постоянную времени в 1 секунду:
При зарядке нашего конденсатора 100 мкФ через 10 кОм; резистора, мы можем ожидать, что напряжение на цоколе вырастет примерно до 63% от напряжения питания за 1 постоянную времени, которая составляет 1 секунду.После 5 постоянных времени (в данном случае 5 секунд) конденсатор заряжается примерно на 99% до напряжения питания, и он будет следовать кривой заряда, похожей на график ниже.
Теперь, когда мы это знаем, мы собираемся подключить схему, показанную на схеме (убедитесь, что полярность на этом конденсаторе правильная!).
С помощью нашего мультиметра, установленного для измерения вольт, проверьте выходное напряжение батареи при включенном переключателе. Это наше напряжение питания, и оно должно быть около 4.5В (будет немного больше, если батарейки новые). Теперь подключите схему, убедившись, что переключатель на батарейном блоке находится в положении «ВЫКЛ», прежде чем вставлять его в макетную плату. Также позаботьтесь о том, чтобы красный и черный провода были в нужных местах. Если это более удобно, вы можете использовать зажимы типа «крокодил», чтобы прикрепить измерительные щупы к ножкам конденсатора для измерения (вы также можете немного раздвинуть эти ножки, чтобы упростить задачу).
Когда мы убедимся, что схема выглядит правильно, а наш счетчик включен и настроен на считывание вольт, переведите переключатель на батарейном блоке в положение «ВКЛ».Примерно через 5 секунд показания счетчика должны быть довольно близкими к напряжению аккумуляторной батареи, что демонстрирует, что уравнение верное, и мы знаем, что делаем. Теперь выключите выключатель. Он все еще довольно хорошо держит это напряжение, не так ли? Это потому, что ток не может разрядить конденсатор; у нас разомкнутая цепь. Для разряда конденсатора можно использовать еще один резистор на 10 кОм параллельно. Примерно через 5 секунд он вернется к почти нулевому значению.
Experiment Time — Часть 3, и даже больше…
Теперь мы переходим к интересным моментам, начиная с подключения двух конденсаторов последовательно. Помните, что мы сказали, что результат будет аналогичен параллельному соединению двух резисторов. Если это правда, мы можем ожидать (используя произведение над суммой)
Что это будет делать с нашей постоянной времени?
Имея это в виду, подключите другой конденсатор последовательно с первым, убедитесь, что измеритель показывает ноль вольт (или около того), и переведите переключатель в положение «ON».Зарядка до напряжения аккумуляторной батареи занимала примерно половину времени? Это потому, что емкость вдвое меньше. Электронный бензобак стал меньше, поэтому на его зарядку уходит меньше времени. Для этого эксперимента предлагается третий конденсатор, просто чтобы доказать это, но мы держим пари, что читатель сможет увидеть надпись на стене.
Теперь мы попробуем подключить конденсаторы параллельно, помня, что мы говорили ранее, что это будет похоже на добавление резисторов последовательно. Если это правда, то мы можем ожидать 200 мкФ, верно? Тогда наша постоянная времени станет
Это означает, что теперь потребуется около 10 секунд, чтобы увидеть, как параллельные конденсаторы заряжаются до напряжения питания 4.5В.
Для доказательства начнем с нашей исходной схемы на 10 кОм; последовательно подключены резистор и один конденсатор емкостью 100 мкФ, как показано на первой схеме этого эксперимента. Мы уже знаем, что конденсатор заряжается примерно за 5 секунд. Теперь подключите второй конденсатор параллельно. Убедитесь, что показания измерителя близки к нулю (разрядите через резистор, если он не показывает нулевое значение), и переведите переключатель на батарейном блоке в положение «ON». Нужно много времени, не правда ли? Разумеется, мы увеличили размер электронного бензобака, и теперь на его заполнение уходит больше времени.Чтобы убедиться в этом, попробуйте добавить третий конденсатор емкостью 100 мкФ и понаблюдайте, как он заряжается в течение долгого времени.
Дроссели серии
и параллельные индукторы
Катушки индуктивности серии
и параллельные
Случаи, когда индукторы необходимо добавлять последовательно или параллельно, довольно редки, но не редкость. В любом случае, давайте рассмотрим их, чтобы быть полными.
Вкратце, они складываются так же, как и резисторы, то есть они складываются со знаком плюс, когда соединены последовательно, и с превышением произведения при параллельном соединении.Сложность возникает, когда они размещаются близко друг к другу, чтобы иметь взаимодействующие магнитные поля, намеренно или нет. По этой причине предпочтительнее иметь один компонент, чем два или более, хотя большинство индукторов экранированы для предотвращения взаимодействия магнитных полей.
В любом случае достаточно сказать, что они добавляют, как резисторы. Дополнительная информация о катушках индуктивности выходит далеко за рамки этого руководства.
Ресурсы и дальнейшее развитие
Теперь, когда вы знакомы с основами последовательных и параллельных схем, почему бы не ознакомиться с некоторыми из этих руководств?
Делители напряжения — Одна из самых простых и повторяющихся схем — это делитель напряжения.Это схема, которая действительно основана на концепциях, рассмотренных в этом руководстве.
Что такое Ардуино? — Теперь, когда у вас есть основы схемотехники, вы можете перейти непосредственно к изучению микроконтроллеров с одной из самых популярных платформ: Arduino.
Основы коммутатора
— В этом руководстве мы говорили о некоторых наиболее основных элементах схемы, но это не был один из них. Переключатели являются важным компонентом практически в каждом электронном проекте.Узнайте все о переключателях в этом руководстве
Шитье проводящей нитью — схемы не обязательно должны состоять из макетов и проводов. Электронный текстиль использует токопроводящую нить для вшивания светильников и другой электроники в одежду или другую ткань.
.

	E	I	C	R / X _C / Z	W / VA / VARs	PF
R	440 В	20 A	N / A	227 Ом 8800 Вт	0
C	440 V	11.1 A	67 мкФ	39,6 Ом	4884 VAR	90
Всего	440 В	22,9 A	N / A	19,2 Ом 10076 VA32	87,3%