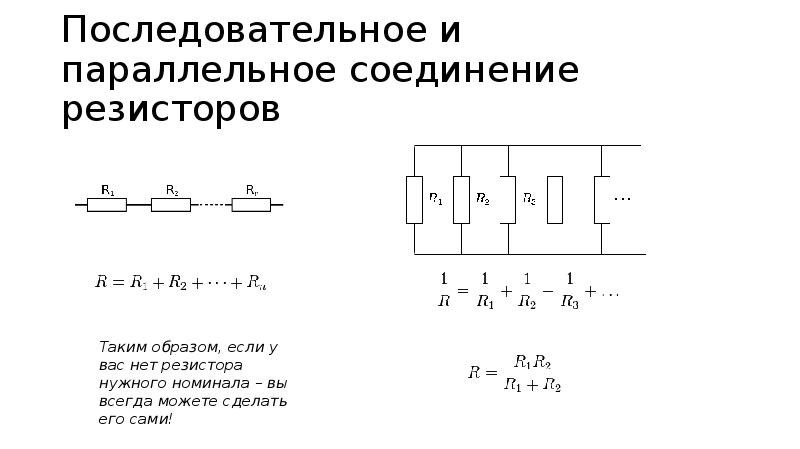
Параллельное соединение резисторов схема: Схемы соединения резисторов — Мир Антенн

Содержание

Схемы соединения резисторов

Последовательное соединение резисторов

I_общ = I₁ = I₂ = I₃

U_общ = U₁ + U₂ + U₃

Параллельное соединение резисторов

I_общ = I₁ + I₂ + I₃

U_общ = U₁ = U₂ = U₃

Реостат

Реостат – это переменный резистор, который включается в цепь последовательно с потребителем нагрузки.

Изменяя положение ползунка, в цепи меняется ток от 0 до max.

Реостат применяется для изменения тока в цепи.

В электрических схемах встречается понятие – реостатное включение нагрузки.

Реостатное включение нагрузки

T₁ I =

U_ист

R_р + R_н

→ max

R_P = 0

T₂ I =

U_ист

R_р + R_н

→ min

Гасящий резистор

В радиосхемах возникает необходимость подавать на потребитель напряжение меньше чем развивает источник, тогда между источником и нагрузкой включается гасящий резистор.

Применение – в схеме создания напряжения смещения на участке эмиттер-база транзистора.

Гасящий резистор

U_гас = U_ист – U_Rн

P_Rгас = I² – R_гас

Делитель напряжения

Делитель напряжения – это цепь, состоящая из нескольких последовательно соединённых резисторов обеспечивающих подачу на потребитель некоторой части напряжения источника.

Потенциометр

Потенциометр – это переменный резистор, с части которого снимается напряжения источника.

Потенциометр

Применение – регулировка громкости на входе усилителя низкой частоты.

Последовательное и параллельное соединение резисторов.

Как я и обещал в статье про переменные резисторы (ссылка), сегодня речь пойдет о возможных способах соединения, в частности о последовательном соединении резисторов и о параллельном.

Последовательное соединение резисторов.

Давайте начнем с рассмотрения цепей, элементы которой соединены последовательно. И хоть мы и будем рассматривать только резисторы в качестве элементов цепи в данной статье, но правила, касающиеся напряжений и токов при разных соединениях будут справедливы и для других элементов. Итак, первая цепь, которую мы будем разбирать выглядит следующим образом:

Здесь у нас классический случай последовательного соединения — два последовательно включенных резистора.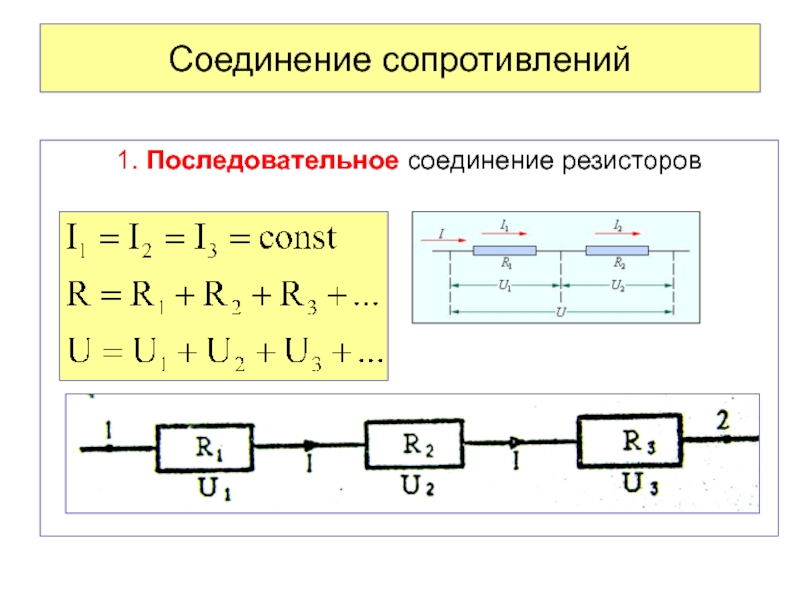 Но не будем забегать вперед и рассчитывать общее сопротивление цепи, а для начала рассмотрим все напряжения и токи. Итак, первое правило заключается в том, что протекающие по всем проводникам токи при последовательном соединении равны между собой:

I = I_1 = I_2

А для определения общего напряжения при последовательном соединении, напряжения на отдельных элементах необходимо просуммировать:

U = U_1 + U_2

В то же время, по закону Ома для напряжений, сопротивлений и токов в данной цепи справедливы следующие соотношения:

U_1 = I_1R_1 = IR_1

U_2 = I_2R_2 = IR_2

Тогда для вычисления общего напряжения можно будет использовать следующее выражение:

U = U_1 + U_2 = IR_2 + IR_2 = I(R_1 + R_2)

Но для общего напряжение также справедлив закон Ома:

U = IR_0

Здесь R_0 — это общее сопротивление цепи, которое исходя из двух формул для общего напряжения равно:

R_0 = R_1 + R_2

Таким образом, при последовательном соединении резисторов общее сопротивление цепи будет равно сумме сопротивлений всех проводников.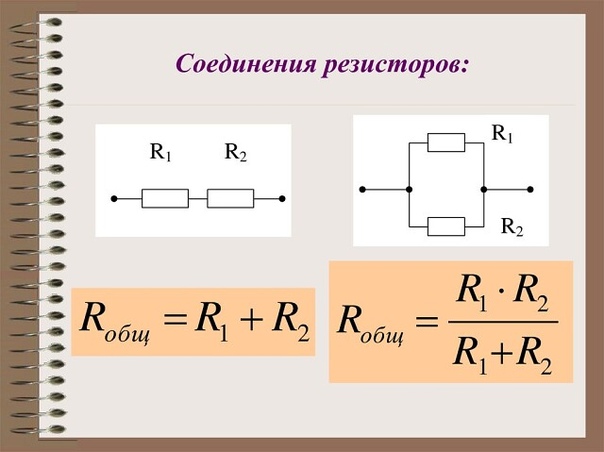

Например для следующей цепи:

Общее сопротивление будет равно:

R_0 = R_1 + R_2 + R_3 + R_4 + R_5 + R_6 + R_7 + R_8 + R_9 + R_{10}

Количество элементов значения не имеет, правило, по которому мы определяем общее сопротивление будем работать в любом случае 🙂 А если при последовательном соединении все сопротивления равны (R_1 = R_2 = … = R), то общее сопротивление цепи составит:

R_0 = nR

В данной формуле n равно количеству элементов цепи. С последовательным соединением резисторов мы разобрались, давайте перейдем к параллельному.

Параллельное соединение резисторов.

При параллельном соединении напряжения на проводниках равны:

U_1 = U_2 = U

А для токов справедливо следующее выражение:

I = I_1 + I_2

То есть общий ток разветвляется на две составляющие, а его значение равно сумме всех составляющих. По закону Ома:

I_1 = \frac{U_1}{R_1} = \frac{U}{R_1}

I_2 = \frac{U_2}{R_2} = \frac{U}{R_2}

Подставим эти выражения в формулу общего тока:

I = \frac{U}{R_1} + \frac{U}{R_2} = U\medspace (\frac{1}{R1} + \frac{1}{R2})

А по закону Ома ток:

I = \frac{U}{R_0}

Приравниваем эти выражения и получаем формулу для общего сопротивления цепи:

\frac{1}{R_0} = \frac{1}{R_1} + \frac{1}{R_2}

Данную формулу можно записать и несколько иначе:

R_0 = \frac{R_1R_2}{R_1 + R_2}

Таким образом, при параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.

Аналогичная ситуация будет наблюдаться и при большем количестве проводников, соединенных параллельно:

\frac{1}{R_0} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \frac{1}{R_4} + \frac{1}{R_5} + \frac{1}{R_6}

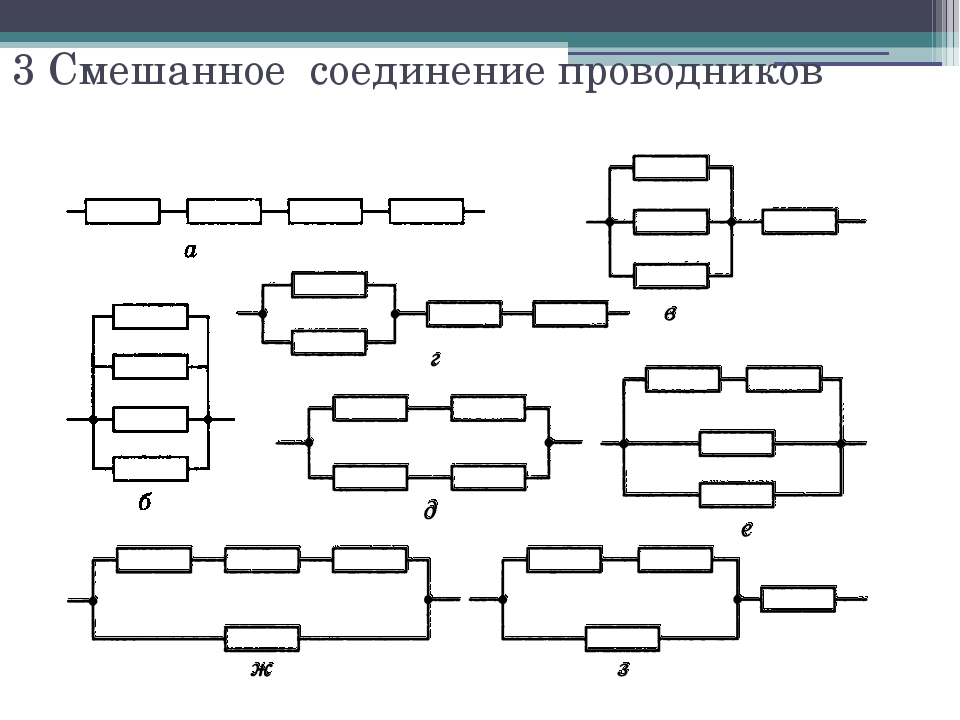
Смешанное соединение резисторов.

Помимо параллельного и последовательного соединений резисторов существует еще смешанное соединение. Из названия уже понятно, что при таком соединении в цепи присутствуют резисторы, соединенные как параллельно, так и последовательно. Вот пример такой цепи:

Давайте рассчитаем общее сопротивление цепи. Начнем с резисторов R_1 и R_2 — они соединены параллельно. Мы можем рассчитать общее сопротивление для этих резисторов и заменить их в схеме одним единственным резистором R_{1-2}:

R_{1-2} = \frac{R1\cdot R2}{R1 + R2} = 1

Теперь у нас образовались две группы последовательно соединенных резисторов:

Заменим эти две группы двумя резисторами, сопротивление которых равно:

R_{1-2-3} = R_{1-2} + R_3 = 5

R_{4-5} = R_4 + R_5 = 24

Как видите, схема стала уже совсем простой 🙂 Заменим группу параллельно соединенных резисторов R_{1-2-3} и R_{4-5} одним резистором R_{1-2-3-4-5}:

R_{1-2-3-4-5}\enspace = \frac{R_{1-2-3}\medspace\cdot R_{4-5}}{R_{1-2-3} + R_{4-5}} = \frac{5\cdot24}{5 + 24} = 4. 14

И в итоге у нас на схеме осталось только два резистора соединенных последовательно:

Общее сопротивление цепи получилось равным:

R_0 = R_{1-2-3-4-5}\medspace +\medspace R_6 = 4.14 + 10 = 14.14

Таким вот образом достаточно большая схема свелась к простейшему последовательному соединению двух резисторов!

Тут стоит отметить, что некоторые схемы невозможно так просто преобразовать и определить общее сопротивление — для таких схем нужно использовать правила Кирхгофа, о которых мы обязательно поговорим в будущих статьях. А сегодняшняя статья на этом подошла к концу, до скорых встреч на нашем сайте!

Проверка формул для расчёта эквивалентных сопротивлений при последовательном, параллельном и смешанном соединении

СОДЕРЖАНИЕ

1. Цель работы 2

2. Приборы и оборудование 2

Техника безопасности 2

4. Порядок выполнения работы 2

5. Содержание отчета 4

6. Контрольные вопросы 4

7. Рекомендуемая литература 4

Приложение 1. Теоретические сведения 5

Приложение 2. Задание для домашней подготовки к работе. 7

1. цель работы

1.1 Приобрести навыки выполнения различных видов соединений резисторов.

1.2 Произвести опытную проверку формул для расчёта эквивалентных сопротивлений при последовательном, параллельном и смешанном их соединениях.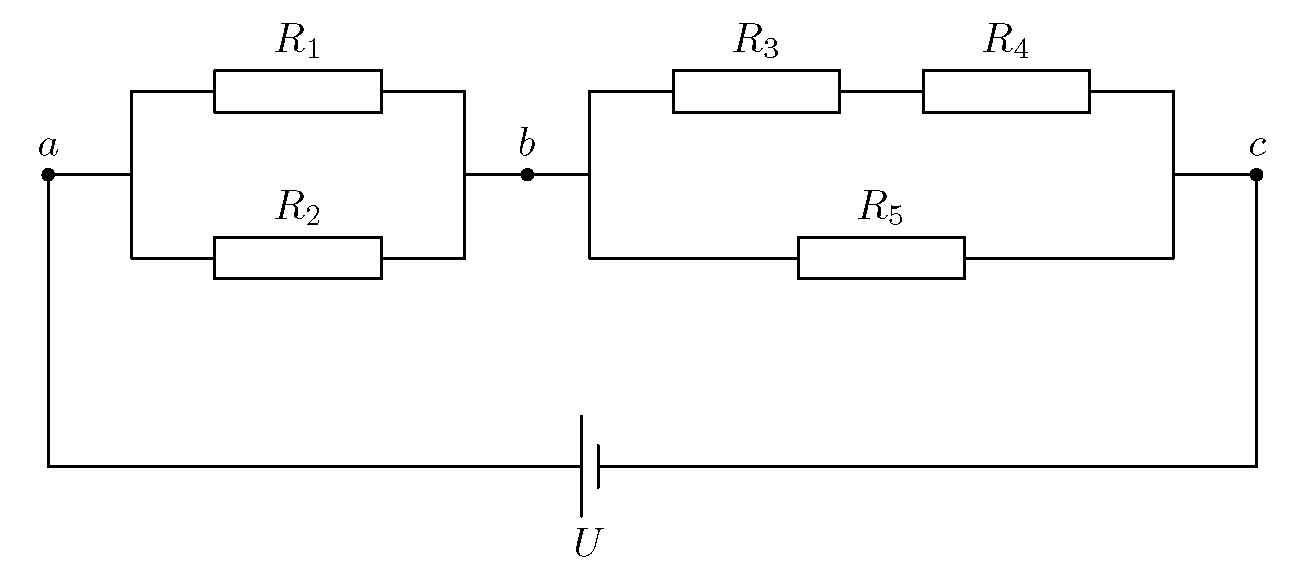

2. приборы и оборудование

Таблица 1

№ п/п	Наименование прибора	Услов. обозн.	Тип	Завод. номер	Измерительная система		Класс точно-сти	Род тока	Пре-делы измер.	Цена дел.
№ п/п	Наименование прибора	Услов. обозн.	Тип	Завод. номер	название	Усл. обозн.	Класс точно-сти	Род тока	Пре-делы измер.	Цена дел.
1	Амперметр	РА1
2	Амперметр	РА2
3	Вольтметр	PV

3. техника безопасности

3.1 Сборку схем и переключения в них, производить только при отключенной от источника цепи.

3.2 Электрическую цепь или стенд включать только с разрешения преподавателя.

3.3 При сборке схем использовать только соединительные провода с исправной изоляцией.

3.4 По окончании работы отключить цепь от источника, показать преподавателю результаты измерений и расчета для проверки, привести рабочее место в порядок.

4. порядок выпонения работы

4.1 Измерение тока и напряжения. Расчёт сопротивлений резисторов R1, R2, R3.

4.1.1 На базе стенда ЛЭС-4 собрать электрическую цепь (рис. 1) и показать ее преподавателю для проверки.

4.1.2 Начертить схему замещения электрической цепи (рис.1).

4.1.3 Поочерёдно подключая к зажимам 1, 2 используемые в опыте резисторы произвести замеры тока и напряжения.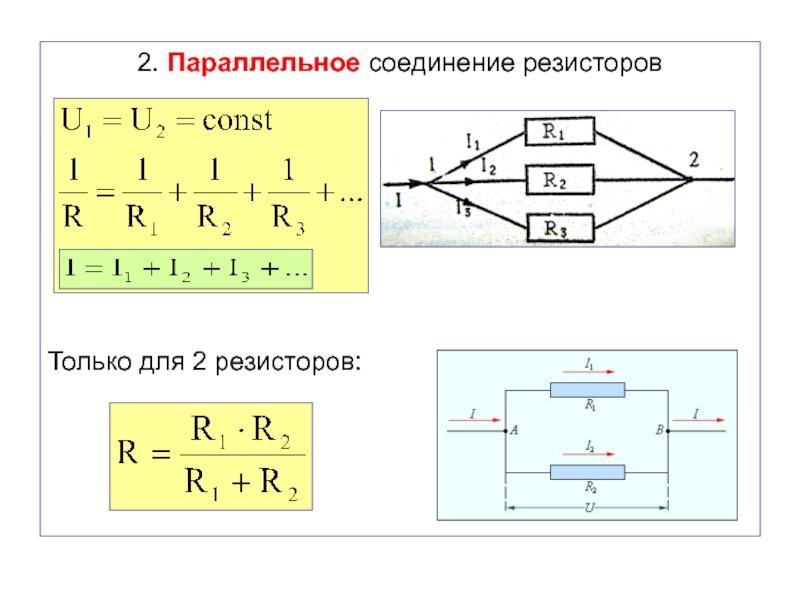 Используя закон Ома рассчитайте их сопротивления. Результаты измерений и расчёта занесите в табл.2.

Таблица 2

Резистор	Измерено		Вычислено
Резистор	U, B	I, A	R, Oм
R1
R2
R3

4. 2. Последовательное соединение резисторов R1, R2, R3. Измерение тока и напряжения.

4.2.1. Соединить последовательно резисторы R1, R2, R3 и подключить к зажимам 1, 2 электрической цепи (рис.1).

4.2.2. Включить стенд, измерить ток и напряжение. Показания вольтметра и амперметра записать в табл.3.

4.2.3. Начертить схему замещения цепи с последовательно соединёнными резисторами R1, R2, R3.

Таблица 3

Вид соединения резисторов	Измерено		Вычислено
Вид соединения резисторов	U, B	I, A	По закону Ома R_Э	По формуле R_Э
Последовательное
Параллельное
Смешанное

4. 2.4. Произвести расчёт эквивалентного сорпотивления по закону Ома и, исходя из вида соединения резисторов по формуле. Результаты расчёта записать в табл.3.

4.3. Параллельное соединение резисторов R1, R2, R3. Измерение тока и напряжения.

4.3.1. Соединить параллельно резисторы R1, R2, R3 и подключить к зажимам 1, 2 электрической цепи (рис.1).

4.3.2. Включить стенд , измерить ток и напряжение. Показания вольтметра и амперметра записать в таблицу 3.

4.3.3.Начертить схему замещения цепи с параллельно соединёнными резисторами R1, R2, R3.

4.3.4. Произвести расчёт эквивалентного сорпотивления по закону Ома и, исходя из вида соединения резисторов по формуле. Результаты расчёта записать в табл.3.

4.4. Смешанное соединение резисторов R1, R2, R3. Измерение тока и напряжения.

4.4.1. Соединить резисторы R2, R3 параллельно и подключить их к резистору R1 последовательно. Смешанное соединение резистора R1, R2, R3 подключить к зажимам 1, 2 электрической цепи (рис.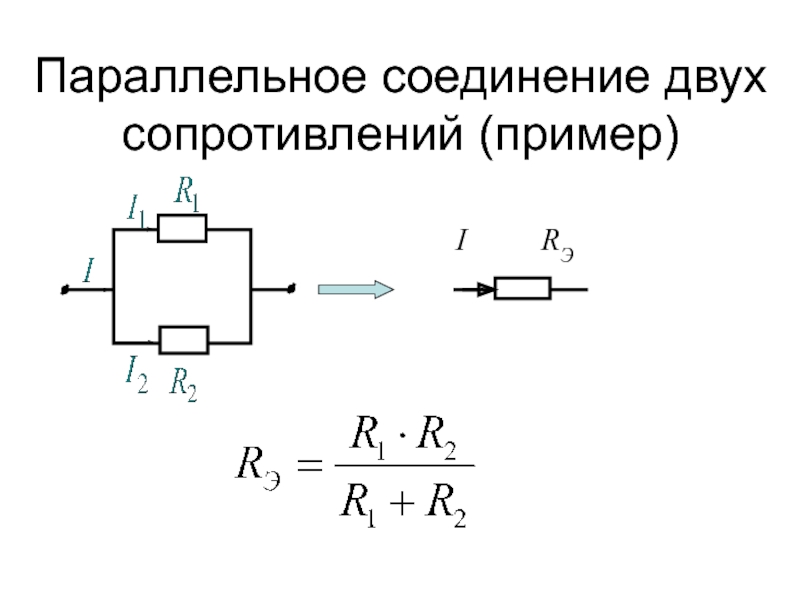 1).

4.4.2. Включить стенд , измерить ток и напряжение. Показания вольтметра и амперметра записать в таблицу 3.

4.4.3. Начертить схему замещения цепи с смешанным соединением резисторов R1, R2, R3.

4.4.4. Произвести расчёт эквивалентного сорпотивления по закону Ома и, исходя из вида соединения резисторов по формуле. Результаты расчёта записать в табл.3.

4.5. По результатам работы сделать вывод, отвечающий на вопросы цели работы.

5. СОДЕРЖАНИЕ ОТЧЕТА

5.1 Цель работы.

5.2 Приборы и оборудование.

5.3 Выполнение рабочего задания.

5.3.1. Наименование задания.

5.3.2. Схемы электрических цепей.

5.3.3. Схема замещения.

5.3.4. Таблицы результатов измерений и вычислений.

5.3.5. Основные расчетные формулы.

5.4 Выводы по работе.

6. контрольные вопросы

6.1 Что называют последовательным и параллельным соединением?

6. 2 Запишите формулы для расчёта эквивалентного сопротивления при последовательном и параллельном соединении.

6.3 На каком из 2-х последовательно соединённых разных по величине резисторов будет больше падение напряжения?

6.4 В какой из 2-х параллельных ветвей, имеющих разное сопротивление будет больше ток?

6.5 Как рассчитать проводимость ветвей?

7. рекомендуемая литература

7.1 Евдокимов Ф.Е. «Теоретические основы электротехники», М. «Высшая школа», 1975.

приложение 1

Теоретические сведения

Последовательное соединение резисторов – это такое соединение, когда к концу одного резистора присоединяется начало второго, к концу второго начало третьего и т.д. и при этом образуется неразветвлённая цепь или участок цепи. При последовательном соединении ток во всех резисторах одинаков.

Рис.5

Для последовательного соединения выполняется:

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

Параллельное соединение резисторов – это такое соединение, когда начала всех резисторов соединены в одну точку, а их концы в другую.

Рис.6

Для параллельного соединения характерно одинаковое падение напряжения на каждом резисторе и всём участке: U = U1 = U2 = U3

При параллельном соединении резисторов выполняется:

(10)

(11)

(12)

(13)

(14)

(15)

(16)

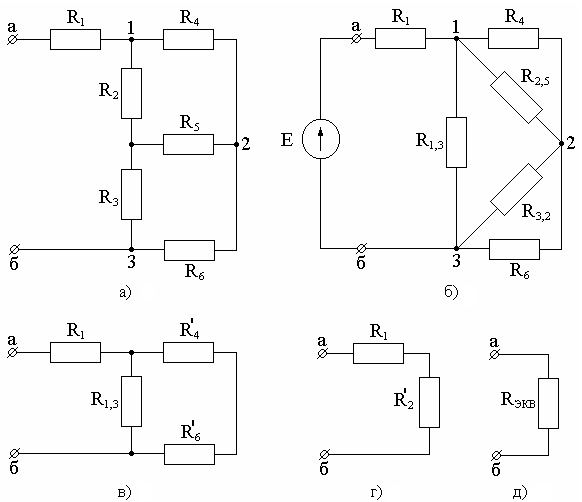
На рис.7 изображено смешанное соединение резисторов.

Рис.7

Резисторы R2, R3, R4 соединены параллельно, для них выполняются закономерности параллельного соединения, а резисторы R1, R2,3,4 и R5 соединены последовательно.

приложение 2

задание для домашней подготовки к работе

Ознакомиться по учебнику, конспекту с материалом о последовательном

Суммарное сопротивление при последовательном соединении. Последовательное и параллельное соединение сопротивлений

Содержание:

Все известные виды проводников обладают определенными свойствами, в том числе и электрическим сопротивлением. Это качество нашло свое применение в резисторах, представляющих собой элементы цепи с точно установленным сопротивлением. Они позволяют выполнять регулировку тока и напряжения с высокой точностью в схемах. Все подобные сопротивления имеют свои индивидуальные качества. Например, мощность при паралл ельном и последовательном соединении резисторов будет различной. Поэтому на практике очень часто используются различные методики расчетов, благодаря которым возможно получение точных результатов.

Свойства и технические характеристики резисторов

Как уже отмечалось, резисторы в электрических цепях и схемах выполняют регулировочную функцию. С этой целью используется закон Ома, выраженный формулой: I = U/R. Таким образом, с уменьшением сопротивления происходит заметное возрастание тока. И, наоборот, чем выше сопротивление, тем меньше ток. Благодаря этому свойству, резисторы нашли широкое применение в электротехнике. На этой основе создаются делители тока, использующиеся в конструкциях электротехнических устройств.

Помимо функции регулировки тока, резисторы применяются в схемах делителей напряжения. В этом случае закон Ома будет выглядеть несколько иначе: U = I x R. Это означает, что с ростом сопротивления происходит увеличение напряжения. На этом принципе строится вся работа устройств, предназначенных для деления напряжения. Для делителей тока используется паралл ельное соединение резисторов, а для — последовательное.

На схемах резисторы отображаются в виде прямоугольника, размером 10х4 мм. Для обозначения применяется символ R, который может быть дополнен значением мощности данного элемента. При мощности свыше 2 Вт, обозначение выполняется с помощью римских цифр. Соответствующая надпись наносится на схеме возле значка резистора. Мощность также входит в состав , нанесенной на корпус элемента. Единицами измерения сопротивления служат ом (1 Ом), килоом (1000 Ом) и мегаом (1000000 Ом). Ассортимент резисторов находится в пределах от долей ома до нескольких сотен мегаом. Современные технологии позволяют изготавливать данные элементы с довольно точными значениями сопротивления.

Важным параметром резистора считается отклонение сопротивления. Его измерение осуществляется в процентах от номинала. Стандартный ряд отклонений представляет собой значения в виде: + 20, + 10, + 5, + 2, + 1% и так далее до величины + 0,001%.

Большое значение имеет мощность резистора. По каждому из них во время работы проходит электрический ток, вызывающий нагрев. Если допустимое значение рассеиваемой мощности превысит норму, это приведет к выходу из строя резистора. Следует учитывать, что в процессе нагревания происходит изменение сопротивления элемента. Поэтому если устройства работают в широких диапазонах температур, применяется специальная величина, именуемая температурным коэффициентом сопротивления.

Для соединения резисторов в схемах используются три разных способа подключения — паралл ельное, последовательное и смешанное. Каждый способ обладает индивидуальными качествами, что позволяет применять данные элементы в самых разных целях.

Мощность при последовательном соединение

При соединение резисторов последовательно электрический ток по очереди проходит через каждое сопротивление. Значение тока в любой точке цепи будет одинаковым. Данный факт определяется с помощью закона Ома. Если сложить все сопротивления, приведенные на схеме, то получится следующий результат: R = 200+100+51+39 = 390 Ом.

Учитывая напряжение в цепи, равное 100 В, сила тока будет составлять I = U/R = 100/390 = 0,256 A.На основании полученных данных можно рассчитать мощность резисторов при последовательном соединении по следующей формуле: P = I 2 x R = 0,256 2 x 390 = 25,55 Вт.

P 1 = I 2 x R 1 = 0,256 2 x 200 = 13,11 Вт;
P 2 = I 2 x R 2 = 0,256 2 x 100 = 6,55 Вт;
P 3 = I 2 x R 3 = 0,256 2 x 51 = 3,34 Вт;
P 4 = I 2 x R 4 = 0,256 2 x 39 = 2,55 Вт.

Если сложить полученные мощность, то полная Р составит: Р = 13,11+6,55+3,34+2,55 = 25,55 Вт.

Мощность при паралл ельном соединение

При паралл ельном подключении все начала резисторов соединяются с одним узлом схемы, а концы — с другим. В этом случае происходит разветвление тока, и он начинает протекать по каждому элементу. В соответствии с законом Ома, сила тока будет обратно пропорциональна всем подключенным сопротивлениям, а значение напряжения на всех резисторах будет одним и тем же.

Прежде чем вычислять силу тока, необходимо выполнить расчет полной проводимости всех резисторов, применяя следующую формулу:

1/R = 1/R 1 +1/R 2 +1/R 3 +1/R 4 = 1/200+1/100+1/51+1/39 = 0,005+0,01+0,0196+0,0256 = 0,06024 1/Ом.
Поскольку сопротивление является величиной, обратно пропорциональной проводимости, его значение составит: R = 1/0,06024 = 16,6 Ом.
Используя значение напряжения в 100 В, по закону Ома рассчитывается сила тока: I = U/R = 100 x 0,06024 = 6,024 A.
Зная силу тока, мощность резисторов, соединенных паралл ельно, определяется следующим образом: P = I 2 x R = 6,024 2 x 16,6 = 602,3 Вт.
Расчет силы тока для каждого резистора выполняется по формулам: I 1 = U/R 1 = 100/200 = 0,5A; I 2 = U/R 2 = 100/100 = 1A; I 3 = U/R 3 = 100/51 = 1,96A; I 4 = U/R 4 = 100/39 = 2,56A. На примере этих сопротивлений прослеживается закономерность, что с уменьшением сопротивления, сила тока увеличивается.

Существует еще одна формула, позволяющая рассчитать мощность при паралл ельном подключении резисторов: P 1 = U 2 /R 1 = 100 2 /200 = 50 Вт; P 2 = U 2 /R 2 = 100 2 /100 = 100 Вт; P 3 = U 2 /R 3 = 100 2 /51 = 195,9 Вт; P 4 = U 2 /R 4 = 100 2 /39 = 256,4 Вт. Сложив мощности отдельных резисторов, получится их общая мощность: Р = Р 1 +Р 2 +Р 3 +Р 4 = 50+100+195,9+256,4 = 602,3 Вт.

Таким образом, мощность при последовательном и паралл ельном соединении резисторов определяется разными способами, с помощью которых можно получить максимально точные результаты.

Содержание:

Течение тока в электрической цепи осуществляется по проводникам, в направлении от источника к потребителям. В большинстве подобных схем используются медные провода и электрические приемники в заданном количестве, обладающие различным сопротивлением. В зависимости выполняемых задач, в электрических цепях используется последовательное и параллельное соединение проводников. В некоторых случаях могут быть применены оба типа соединений, тогда этот вариант будет называться смешанным. Каждая схема имеет свои особенности и отличия, поэтому их нужно обязательно заранее учитывать при проектировании цепей, ремонте и обслуживании электрооборудования.

Последовательное соединение проводников

В электротехнике большое значение имеет последовательное и параллельное соединение проводников в электрической цепи. Среди них часто используется схема последовательного соединения проводников предполагающая такое же соединение потребителей. В этом случае включение в цепь выполняется друг за другом в порядке очередности. То есть, начало одного потребителя соединяется с концом другого при помощи проводов, без каких-либо ответвлений.

Свойства такой электрической цепи можно рассмотреть на примере участков цепи с двумя нагрузками. Силу тока, напряжение и сопротивление на каждом из них следует обозначить соответственно, как I1, U1, R1 и I2, U2, R2. В результате, получились соотношения, выражающие зависимость между величинами следующим образом: I = I1 = I2, U = U1 + U2, R = R1 + R2. Полученные данные подтверждаются практическим путем с помощью проведения измерений амперметром и вольтметром соответствующих участков.

Таким образом, последовательное соединение проводников отличается следующими индивидуальными особенностями:

Сила тока на всех участках цепи будет одинаковой.
Общее напряжение цепи составляет сумму напряжений на каждом участке.
Общее сопротивление включает в себя сопротивления каждого отдельного проводника.

Данные соотношения подходят для любого количества проводников, соединенных последовательно. Значение общего сопротивления всегда выше, чем сопротивление любого отдельно взятого проводника. Это связано с увеличением их общей длины при последовательном соединении, что приводит и к росту сопротивления.

Если соединить последовательно одинаковые элементы в количестве n, то получится R = n х R1, где R — общее сопротивление, R1 — сопротивление одного элемента, а n — количество элементов. Напряжение U, наоборот, делится на равные части, каждая из которых в n раз меньше общего значения. Например, если в сеть с напряжением 220 вольт последовательно включаются 10 ламп одинаковой мощности, то напряжение в любой из них составит: U1 = U/10 = 22 вольта.

Проводники, соединенные последовательно, имеют характерную отличительную особенность. Если во время работы отказал хотя-бы один из них, то течение тока прекращается во всей цепи. Наиболее ярким примером является , когда одна перегоревшая лампочка в последовательной цепи, приводит к выходу из строя всей системы. Для установления перегоревшей лампочки понадобится проверка всей гирлянды.

Параллельное соединение проводников

В электрических сетях проводники могут соединяться различными способами: последовательно, параллельно и комбинированно. Среди них параллельное соединение это такой вариант, когда проводники в начальных и конечных точках соединяются между собой. Таким образом, начала и концы нагрузок соединяются вместе, а сами нагрузки располагаются параллельно относительно друг друга. В электрической цепи могут содержаться два, три и более проводников, соединенных параллельно.

Если рассматривать последовательное и параллельное соединение, сила тока в последнем варианте может быть исследована с помощью следующей схемы. Берутся две лампы накаливания, обладающие одинаковым сопротивлением и соединенные параллельно. Для контроля к каждой лампочке подключается собственный . Кроме того, используется еще один амперметр, контролирующий общую силу тока в цепи. Проверочная схема дополняется источником питания и ключом.

После замыкания ключа нужно контролировать показания измерительных приборов. Амперметр на лампе № 1 покажет силу тока I1, а на лампе № 2 — силу тока I2. Общий амперметр показывает значение силы тока, равное сумме токов отдельно взятых, параллельно соединенных цепей: I = I1 + I2. В отличие от последовательного соединения, при перегорании одной из лампочек, другая будет нормально функционировать. Поэтому в домашних электрических сетях используется параллельное подключение приборов.

С помощью такой же схемы можно установить значение эквивалентного сопротивления. С этой целью в электрическую цепь добавляется вольтметр. Это позволяет измерить напряжение при параллельном соединении, сила тока при этом остается такой же. Здесь также имеются точки пересечения проводников, соединяющих обе лампы.

В результате измерений общее напряжение при параллельном соединении составит: U = U1 = U2. После этого можно рассчитать эквивалентное сопротивление, условно заменяющее все элементы, находящиеся в данной цепи. При параллельном соединении, в соответствии с законом Ома I = U/R, получается следующая формула: U/R = U1/R1 + U2/R2, в которой R является эквивалентным сопротивлением, R1 и R2 — сопротивления обеих лампочек, U = U1 = U2 — значение напряжения, показываемое вольтметром.

Следует учитывать и тот фактор, что токи в каждой цепи, в сумме составляют общую силу тока всей цепи. В окончательном виде формула, отражающая эквивалентное сопротивление будет выглядеть следующим образом: 1/R = 1/R1 + 1/R2. При увеличении количества элементов в таких цепях — увеличивается и число слагаемых в формуле. Различие в основных параметрах отличают друг от друга и источников тока, позволяя использовать их в различных электрических схемах.

Параллельное соединение проводников характеризуется достаточно малым значением эквивалентного сопротивления, поэтому сила тока будет сравнительно высокой. Данный фактор следует учитывать, когда в розетки включается большое количество электроприборов. В этом случае сила тока значительно возрастает, приводя к перегреву кабельных линий и последующим возгораниям.

Законы последовательного и параллельного соединения проводников

Данные законы, касающиеся обоих видов соединений проводников, частично уже были рассмотрены ранее.

Для более четкого их понимания и восприятия в практической плоскости, последовательное и параллельное соединение проводников, формулы следует рассматривать в определенной последовательности:

Последовательное соединение предполагает одинаковую силу тока в каждом проводнике: I = I1 = I2.
параллельное и последовательное соединение проводников объясняет в каждом случае по-своему. Например, при последовательном соединении, напряжения на всех проводниках будут равны между собой: U1 = IR1, U2 = IR2. Кроме того, при последовательном соединении напряжение составляет сумму напряжений каждого проводника: U = U1 + U2 = I(R1 + R2) = IR.
Полное сопротивление цепи при последовательном соединении состоит из суммы сопротивлений всех отдельно взятых проводников, независимо от их количества.
При параллельном соединении напряжение всей цепи равно напряжению на каждом из проводников: U1 = U2 = U.
Общая сила тока, измеренная во всей цепи, равна сумме токов, протекающих по всем проводникам, соединенных параллельно между собой: I = I1 + I2.

Для того чтобы более эффективно проектировать электрические сети, нужно хорошо знать последовательное и параллельное соединение проводников и его законы, находя им наиболее рациональное практическое применение.

Смешанное соединение проводников

В электрических сетях как правило используется последовательное параллельное и смешанное соединение проводников, предназначенное для конкретных условий эксплуатации. Однако чаще всего предпочтение отдается третьему варианту, представляющему собой совокупность комбинаций, состоящих из различных типов соединений.

В таких смешанных схемах активно применяется последовательное и параллельное соединение проводников, плюсы и минусы которых обязательно учитываются при проектировании электрических сетей. Эти соединения состоят не только из отдельно взятых резисторов, но и довольно сложных участков, включающих в себя множество элементов.

Смешанное соединение рассчитывается в соответствии с известными свойствами последовательного и параллельного соединения. Метод расчета заключается в разбивке схемы на более простые составные части, которые считаются отдельно, а потом суммируются друг с другом.

Параллельное соединение резисторов. При параллельном соединении резисторов нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви (рис. 26, а). Заменяя

лампы резисторами с сопротивлениями R1, R2, R3, получим схему, показанную на рис. 26, б.
При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Поэтому согласно закону Ома:

I 1 =U/R 1 ; I 2 =U/R 2 ; I 3 =U/R 3 .

Ток в неразветвленной части цепи согласно первому закону Кирхгофа I = I 1 +I 2 +I 3 , или

I = U / R 1 + U / R 2 + U / R 3 = U (1/R 1 + 1/R 2 + 1/R 3) = U / R эк (23)

Следовательно, эквивалентное сопротивление рассматриваемой цепи при параллельном соединении трех резисторов определяется формулой

1/R эк = 1/R 1 + 1/R 2 + 1/R 3 (24)

Вводя в формулу (24) вместо значений 1/R эк, 1/R 1 , 1/R 2 и 1/R 3 соответствующие проводимости G эк, G 1 , G 2 и G 3 , получим: эквивалентная проводимость параллельной цепи равна сумме проводимостей параллельно соединенных резисторов :

G эк = G 1 + G 2 +G 3 (25)

Таким образом, при увеличении числа параллельно включаемых резисторов результирующая проводимость электрической цепи увеличивается, а результирующее сопротивление уменьшается.
Из приведенных формул следует, что токи распределяются между параллельными ветвями обратно пропорционально их электрическим сопротивлениям или прямо пропорционально их проводимостям. Например, при трех ветвях

I 1: I 2: I 3 = 1/R 1: 1/R 2: 1/R 3 = G 1 + G 2 + G 3 (26)

В этом отношении имеет место полная аналогия между распределением токов по отдельным ветвям и распределением потоков воды по трубам.
Приведенные формулы дают возможность определить эквивалентное сопротивление цепи для различных конкретных случаев. Например, при двух параллельно включенных резисторах результирующее сопротивление цепи

R эк =R 1 R 2 /(R 1 +R 2)

при трех параллельно включенных резисторах

R эк =R 1 R 2 R 3 /(R 1 R 2 +R 2 R 3 +R 1 R 3)

При параллельном соединении нескольких, например n, резисторов с одинаковым сопротивлением R1 результирующее сопротивление цепи Rэк будет в n раз меньше сопротивления R1, т.е.

R эк = R1 / n (27)

Проходящий по каждой ветви ток I1, в этом случае будет в п раз меньше общего тока:

I1 = I / n (28)

При параллельном соединении приемников, все они находятся под одним и тем же напряжением, и режим работы каждого из них не зависит от остальных. Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются включенными. Поэтому параллельное соединение имеет существенные преимущества перед последовательным, вследствие чего оно получило наиболее широкое распространение. В частности, электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, всегда включают параллельно.
На электровозах постоянного тока и некоторых тепловозах тяговые двигатели в процессе регулирования скорости движения нужно включать под различные напряжения, поэтому они в процессе разгона переключаются с последовательного соединения на параллельное.

Каждый в этой жизни сталкивался с резисторами. Люди с гуманитарными профессиями, как и все, изучали в школе на уроках физики проводники электрического тока и закон Ома.

С резисторами также имеют дело студенты технических университетов и инженеры различных производственных предприятий. Перед всеми этими людьми, так или иначе, вставала задача расчёта электрической цепи при различных видах соединения резисторов. В данной статье речь пойдёт о расчёте физических параметров, характеризующих цепь.

Виды соединений

Резистор — пассивный элемент , присутствующий в каждой электрической цепи. Он предназначен для того, чтобы сопротивляться электрическому току. Существует два вида резисторов:

Постоянные.
Переменные.

Зачем же спаивать проводники друг с другом? Например, если для какой-то электрической цепи нужно определённое сопротивление. А среди номинальных показателей нужного нет. В таком случае необходимо подобрать элементы схемы с определёнными значениями сопротивления и соединить их. В зависимости от вида соединения и сопротивлений пассивных элементов мы получим какое-то определённое сопротивление цепи. Оно называется эквивалентным. Его значение зависит от вида спайки проводников. Существует три вида соединения проводников:

Последовательное.
Параллельное.
Смешанное.

Значение эквивалентного сопротивления в цепи считается достаточно легко. Однако, если резисторов в схеме очень много, то лучше воспользоваться специальным калькулятором, который считает это значение. При ведении расчёта вручную, чтобы не допускать ошибок, необходимо проверять, ту ли формулу вы взяли.

Последовательное соединение проводников

В последовательной спайке резисторы идут как бы друг за другом. Значение эквивалентного сопротивления цепи равно сумме сопротивлений всех резисторов. Особенность схем с такой спайкой заключается в том, что значение тока постоянно . Согласно закону Ома, напряжение в цепи равно произведению тока и сопротивления. Так как ток постоянен, то для вычисления напряжения на каждом резисторе, достаточно перемножить значения. После этого необходимо сложить напряжения всех резисторов, и тогда мы получим значение напряжения во всей цепи.

Расчёт очень простой. Так как с ним имеют дело в основном инженеры-разработчики, то для них не составит труда сосчитать всё вручную. Но если резисторов очень много, то проще воспользоваться специальным калькулятором.

Примером последовательного соединения проводников в быту является ёлочная гирлянда.

Параллельное соединение резисторов

При параллельном соединении проводников эквивалентное сопротивление в цепи считается по-другому. Немного сложнее, чем при последовательном.

Его значение в таких цепях равняется произведению сопротивлений всех резисторов, делённому на их сумму. А также есть и другие варианты этой формулы. Параллельное соединение резисторов всегда снижает эквивалентное сопротивление цепи. То есть, его значение всегда будет меньше, чем наибольшее значение какого-то из проводников.

В таких схемах значение напряжения постоянно . То есть значение напряжения во всей цепи равно значениям напряжений каждого из проводников. Оно задаётся источником напряжения.

Сила тока в цепи равна сумме всех токов, протекающих через все проводники. Значение силы тока, протекающего через проводник. равно отношению напряжения источника к сопротивлению этого проводника.

Примеры параллельного соединения проводников:

Освещение.
Розетки в квартире.
Производственное оборудование.

Для расчёта схем с параллельным соединением проводников лучше пользоваться специальным калькулятором. Если в схеме много резисторов, спаянных параллельно, то гораздо быстрее вы посчитаете эквивалентное сопротивление с помощью этого калькулятора.

Смешанное соединение проводников

Этот вид соединения состоит из каскадов резисторов . Например, у нас есть каскад из 10 проводников, соединённых последовательно, и после него идёт каскад из 10 проводников, соединённых параллельно. Эквивалентное сопротивление этой схемы будет равно сумме эквивалентных сопротивлений этих каскадов. То есть, по сути, здесь последовательное соединение двух каскадов проводников.

Многие инженеры занимаются оптимизацией различных схем. Её целью является уменьшение количества элементов в схеме за счёт подбора других, с подходящими значениями сопротивлений. Сложные схемы разбиваются на несколько небольших каскадов, ведь так гораздо проще вести расчёты.

Сейчас, в двадцать первом веке, инженерам стало гораздо проще работать. Ведь несколько десятилетий назад все расчёты производились вручную. А сейчас программисты разработали специальный калькулятор для расчёта эквивалентного сопротивления цепи. В нём запрограммированы формулы, по которым ведутся расчёты.

В этом калькуляторе можно выбрать вид соединения, и потом ввести в специальные поля значения сопротивлений. Через несколько секунд вы уже увидите это значение.

Элементы электрической цепи можно соединить двумя способами. Последовательное соединение подразумевает подключение элементов друг к другу, а при параллельном соединении элементы являются частью параллельных ветвей. Способ соединения резисторов определяет метод вычисления общего сопротивления цепи.

Шаги

Последовательное соединение

Определите, является ли цепь последовательной. Последовательное соединение представляет собой единую цепь без каких-либо разветвлений. Резисторы или другие элементы расположены друг за другом.

Сложите сопротивления отдельных элементов. Сопротивление последовательной цепи равно сумме сопротивлений всех элементов, входящих в эту цепь. Сила тока в любых частях последовательной цепи одна и та же, поэтому сопротивления просто складываются.

Например, последовательная цепь состоит из трех резисторов с сопротивлениями 2 Ом, 5 Ом и 7 Ом. Общее сопротивление цепи: 2 + 5 + 7 = 14 Ом.

Если сопротивление каждого элемента цепи не известно, воспользуйтесь законом Ома: V = IR, где V – напряжение, I – сила тока, R – сопротивление. Сначала найдите силу тока и общее напряжение.

Подставьте известные значения в формулу, описывающую закон Ома. Перепишите формулу V = IR так, чтобы обособить сопротивление: R = V/I. Подставьте известные значения в эту формулу, чтобы вычислить общее сопротивление.

Например, напряжение источника тока равно 12 В, а сила тока равна 8 А. Общее сопротивление последовательной цепи: R O = 12 В / 8 А = 1,5 Ом.

Параллельное соединение

Определите, является ли цепь параллельной. Параллельная цепь на некотором участке разветвляется на несколько ветвей, которые затем снова соединяются. Ток течет по каждой ветви цепи.
Вычислите общее сопротивление на основе сопротивления каждой ветви. Каждый резистор уменьшает силу тока, проходящего через одну ветвь, поэтому она оказывает небольшое влияние на общее сопротивление цепи. Формула для вычисления общего сопротивления: , где R 1 – сопротивление первой ветви, R 2 – сопротивление второй ветви и так далее до последней ветви R n .
Вычислите сопротивление по известной силе тока и напряжению. Сделайте это, если сопротивление каждого элемента цепи не известно.
Подставьте известные значения в формулу закона Ома. Если известны значения общей силы тока и напряжения в цепи, общее сопротивление вычисляется по закону Ома: R = V/I.
- Например, напряжение в параллельной цепи равно 9 В, а общая сила тока равна 3 А. Общее сопротивление: R O = 9 В / 3 А = 3 Ом.
Поищите ветви с нулевым сопротивлением. Если у ветви параллельной цепи вообще нет сопротивления, то весь ток будет течь через такую ветвь. В этом случае общее сопротивление цепи равно 0 Ом.

Комбинированное соединение

Разбейте комбинированную цепь на последовательную и параллельную. Комбинированная цепь включает элементы, которые соединены как последовательно, так и параллельно. Посмотрите на схему цепи и подумайте, как разбить ее на участки с последовательным и параллельным соединением элементов. Обведите каждый участок, чтобы упростить задачу по вычислению общего сопротивления.

Например, цепь включает резистор, сопротивление которого равно 1 Ом, и резистор, сопротивление которого равно 1,5 Ом. За вторым резистором схема разветвляется на две параллельные ветви – одна ветвь включает резистор с сопротивлением 5 Ом, а вторая – с сопротивлением 3 Ом. Обведите две параллельные ветви, чтобы выделить их на схеме цепи.

Найдите сопротивление параллельной цепи. Для этого воспользуйтесь формулой для вычисления общего сопротивления параллельной цепи: 1 R O = 1 R 1 + 1 R 2 + 1 R 3 + . . . 1 R n {\displaystyle {\frac {1}{R_{O}}}={\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}+{\frac {1}{R_{3}}}+…{\frac {1}{R_{n}}}} .

Упростите цепь. После того как вы нашли общее сопротивление параллельной цепи, ее можно заменить одним элементом, сопротивление которого равно вычисленному значению.

В нашем примере избавьтесь от двух параллельных ветвей и замените их одним резистором с сопротивлением 1,875 Ом.

Сложите сопротивления резисторов, соединенных последовательно. Заменив параллельную цепь одним элементом, вы получили последовательную цепь. Общее сопротивление последовательной цепи равно сумме сопротивлений всех элементов, которые включены в эту цепь.

Последовательное и параллельное соединение

В данной статье речь пойдет о последовательном и параллельном соединении проводников. На примерах будут рассмотрены данные соединения и как при таких соединениях будут изменяться такие величины как:

ток;
напряжение;
сопротивление.

В таблице 1.8 [Л2, с.24] приведены схемы и формулы по определению сопротивлений, токов и напряжений при параллельном и последовательном соединении.

Последовательное соединение

Последовательным соединением называются те участки цепи, по которым всегда проходят одинаковые токи.

При последовательном соединении:

сила тока во всех проводниках одинакова;
напряжение на всём соединении равно сумме напряжений на отдельных проводниках;
сопротивление всего соединения равно сумме сопротивлений отдельных проводников.

Пример 1

Последовательно подключены две лампы накаливания одинаковой мощности Рл1=Рл2=100 Вт к сети с напряжением Uн=220В. Сопротивление нити в лампах составляет Rл1=Rл2=122 Ом. Номинальное напряжение для ламп равно 220 B. На рис.1 показано последовательное включение ламп.

Решение

Составляем схему замещения, выражая каждую из входящих элементов цепи (в данном случае лампы накаливания) в виде сопротивлений.

1. Определяем ток протекающей по участкам цепи:

Iн = Uн/Rл1+ Rл2 = 220/122+122 = 0,9 A

2. Определяем напряжение на каждой из ламп накаливания, так как мощность ламп у нас одинаковая, то и напряжение для каждой из ламп будет одинаково:

Uл1=Uл2 = Iн*R = 0,9*122 = 110 B

Как мы видим напряжение источника (в данном примере 220 В) разделиться поровну, между обоими последовательно включенными лампами. При этом лампы будут ели светит, их накал будет неполным.

Для того чтобы лампы горели с полным накалом, нужно увеличить напряжение источника с 220В до 440В, при этом на каждой из ламп установиться номинальное (рабочее) напряжение равное 220В.

Пример 2

Последовательно подключены две лампы накаливания мощность Рл1 = 100 Вт и Рл2 = 75 Вт к сети с напряжением Uн=220В. Сопротивление нити в лампах составляют Rл1= 122 Ом для стоваттной лампы и Rл2= 153 Ом для семидесяти пяти ватной лампы.

Решение

1. Определяем ток протекающей по участкам цепи:

Iн = Uн/Rл1+ Rл2 = 220/100+75 = 0,8 A

2. Определяем напряжение на каждой из ламп накаливания:

Uл1= Iн*Rл1 = 0,8*122 = 98 B
Uл2= Iн*Rл2 = 0,8*153 = 122 B

Исходя из результатов расчетов, более мощная лампа 100 Вт получает при этом меньшее напряжение. Но ток в двух последовательно включенных даже разных лампах остается одинаковым. Например, если одна из ламп перегорит (порвется ее нить накаливания), погаснут обе лампы.

Данное соединение лампочек, например, используется в трамвайном вагоне для освещения салона.

Параллельное соединение

Параллельное соединение – это соединение, при котором начала всех проводников присоединяются к одной точке цепи, а их концы к другой.

Точки цепи, к которым сходится несколько проводов, называют узлами. Участки цепи, соединяющие между собой узлы, называют ветвями.

При параллельном соединении:

напряжение на всех проводниках одинаково;
сила тока в месте соединения проводников равна сумме токов в отдельных проводниках;
величина, обратная сопротивлению всего соединения, равна сумме величин, обратных сопротивлениям отдельных проводников.

Пример 3

Определить токи и напряжения всех участков цепи (рис.5), если известно:

Номинальное напряжение сети Uн = 220В;
Сопротивление нити в лампах HL1 и HL2 составляют Rл1 = Rл2 = 122 Ом.
Сопротивление нити в лампе HL3 составляют Rл3 = 153 Ом.

Решение

Составляем схему замещения для схемы, представленной на рис.5.

1. Определяем проводимость всей цепи [Л1, с.47] и согласно таблицы 1.8:

2. Определяем сопротивление всей цепи [Л1, с.47]:

3. Определяем силу тока цепи по закону Ома:

4. Определяем токи для каждой цепи [Л1, с.47]:

5. Выполним проверку, согласно которой, сила тока в месте соединения проводников равна сумме токов в отдельных проводниках:

Iл1+ Iл2+ Iл3=Iобщ.=1,8+1,8+1,44=5,04=5,04 (условие выполняется)

Смешанное соединение

Смешанным соединением – называется последовательно-параллельное соединение сопротивлений или участков цепи.

Пример 4

Определить токи и напряжения всех участков цепи (рис.7), если известно:

Номинальное напряжение сети Uн = 220В;
Сопротивление нити в лампах HL1, HL2, HL3 составляют Rл1 = Rл2 = Rл3 = 122 Ом.
Сопротивление нити в лампе HL4 составляют Rл4 = 153 Ом.
Результаты расчетов для участка цепи ВС (параллельное соединение проводников) применим из примера 3:
Сопротивление цепи ВС составляет Rвс = 43,668 Ом.

Решение

Составляем схему замещения для схемы, представленной на рис.7.

1. Определяем сопротивление всей цепи:

Rобщ = Rав+Rвс = Rл1+Rвс = 122+43,688 = 165,688 Ом

2. Определяем силу тока цепи, согласно закона Ома:

3. Определяем напряжение на первом сопротивлении:

Uав=Uл1= Iобщ*Rл1 = 1,33*122 = 162 B

4. Определяем напряжение на участке ВС:

Uвс= Iобщ*Rвс = 1,33*43,688 = 58,1 B

5. Определяем токи для каждой цепи участка ВС:

6. Выполним проверку для участка цепи ВС:

Iл2+ Iл3+ Iл4= Iобщ.=0,48+0,48+0,38=1,33=1,33 (условие выполняется)

Литература:

Общая электротехника с основами электроники, В.С. Попов, 1972 г.
Справочная книга электрика. В.И. Григорьева. 2004 г.

Всего наилучшего! До новых встреч на сайте Raschet.info.

Последовательное соединение схема формула. Последовательное и параллельное соединение

Содержание:

Во всех электрических схемах используются резисторы, представляющие собой элементы, с точно установленным значением сопротивления. Благодаря специфическим качествам этих устройств, становится возможной регулировка напряжения и силы тока на любых участках схемы. Данные свойства лежат в основе работы практически всех электронных приборов и оборудования. Так, напряжение при параллельном и последовательном соединении резисторов будет отличаться. Поэтому каждый вид соединения может применяться только в определенных условиях, чтобы та или иная электрическая схема могла в полном объеме выполнять свои функции.

Напряжение при последовательном соединении

При последовательном соединении два резистора и более соединяются в общую цепь таким образом, что каждый из них имеет контакт с другим устройством только в одной точке. Иначе говоря, конец первого резистора соединяется с началом второго, а конец второго — с началом третьего и т.д.

Особенностью данной схемы является прохождение через все подключенные резисторы одного и того же значения электрического тока. С возрастанием количества элементов на рассматриваемом участке цепи, течение электрического тока становится все более затрудненным. Это происходит из-за увеличения общего сопротивления резисторов при их последовательном соединении. Данное свойство отражается формулой: R общ = R 1 + R 2 .

Распределение напряжения, в соответствии с законом Ома, осуществляется на каждый резистор по формуле: V Rn = I Rn x R n . Таким образом, при увеличении сопротивления резистора, возрастает и падающее на него напряжение.

Напряжение при параллельном соединении

При параллельном соединении, включение резисторов в электрическую цепь выполняется таким образом, что все элементы сопротивлений подключаются друг к другу сразу обоими контактами. Одна точка, представляющая собой электрический узел, может соединять одновременно несколько резисторов.

Такое соединение предполагает течение отдельного тока в каждом резисторе. Сила этого тока находится в обратно пропорциональной . В результате, происходит увеличение общей проводимости данного участка цепи, при общем уменьшении сопротивления. В случае параллельного соединения резисторов с различным сопротивлением, значение общего сопротивления на этом участке всегда будет ниже самого маленького сопротивления отдельно взятого резистора.

На представленной схеме, напряжение между точками А и В представляет собой не только общее напряжение для всего участка, но и напряжение, поступающее к каждому отдельно взятому резистору. Таким образом, в случае параллельного соединения, напряжение, подаваемое ко всем резисторам, будет одинаковым.

В результате, напряжение при параллельном и последовательном соединении будет отличаться в каждом случае. Благодаря этому свойству, имеется реальная возможность отрегулировать данную величину на любом участке цепи.

Параллельное соединение электрических элементов (проводников, сопротивлений, емкостей, индуктивностей) — это такое соединение, при котором подключенные элементы цепи имеют два общих узла подключения.

Другое определение: сопротивления подключены параллельно, если они подключены одно и той же паре узлов.

Графическое обозначение схемы параллельного соеднинения

На приведенном рисунке показана схема параллельное подключения сопротивлений R1, R2, R3, R4. Из схемы видно, что все эти четыре сопротивления имеют две общие точки (узла подключения).

В электротехнике принято, но не строго требуется, рисовать провода горизонтально и вертикально. Поэтому эту же схему можно изобразить, как на рисунке ниже. Это тоже параллельное соединение тех же самых сопротивлений.

Формула для расчета параллельного соединения сопротивлений

При параллельном соединении обратная величина от эквивалентного сопротивления равна сумме обратных величин всех параллельно подключенных сопротивлений. Эквивалентная проводимость равна сумме всех параллельно подключенных проводимостей электрической схемы.

Для приведенной выше схемы эквивалентное сопротивление можно рассчитать по формуле:

В частном случае при подключении параллельно двух сопротивлений:

Эквивалентное сопротивление цепи определяется по формуле:

В случае подключения «n» одинаковых сопротивлений, эквивалентное сопротивление можно рассчитать по частной формуле:

Формулы для частного рассчета вытекают из основной формулы.

Формула для расчета параллельного соединения емкостей (конденсаторов)

При параллельном подключении емкостей (конденсаторов) эквивалентная емкость равна сумме параллельно подключенных емкостей:

Формула для расчета параллельного соединения индуктивностей

При параллельном подключении индуктивностей, эквивалентная индуктивность рассчитывается так же, как и эквивалентное сопротивление при параллельном соединении:

Необходимо обратить внимание, что в формуле не учтены взаимные индуктивности.

Пример свертывания параллельного сопротивления

Для участка электрической цепи необходимо найти параллельное соединение сопротивлений выполнить их преобразование до одного.

Из схемы видно, что параллельно подключены только R2 и R4. R3 не параллельно, т.к. одним концом оно подключено к E1. R1 — одним концом подключено к R5, а не к узлу. R5 — одним концом подключено к R1, а не к узлу. Можно так же говорить, что последовательное соединение сопротивлений R1 и R5 подключено параллельно с R2 и R4.

Ток при параллельном соединении

При параллельном соединении сопротивлений ток через каждое сопротивление в общем случае разный. Величина тока обратно пропорциональна величине сопротивления.

Напряжение при параллельном соединении

При параллельном соединении разность потенциалов между узлами, объединяющими элементы цепи, одинакова для всех элементов.

Применение параллельного соединения

1. В промышленности изготавливаются сопротивления определенных величин. Иногда необходимо получить значение сопротивления вне данных рядов. Для этого можно подключить несколько сопротивлений параллельно. Эквивалентное сопротивление всегда будет меньше самого большого номинала сопротивления.

2. Делитель токов.

Содержание:

Последовательное соединение проводников

Сила тока на всех участках цепи будет одинаковой.
Общее напряжение цепи составляет сумму напряжений на каждом участке.
Общее сопротивление включает в себя сопротивления каждого отдельного проводника.

Параллельное соединение проводников

Законы последовательного и параллельного соединения проводников

Данные законы, касающиеся обоих видов соединений проводников, частично уже были рассмотрены ранее.

Последовательное соединение предполагает одинаковую силу тока в каждом проводнике: I = I1 = I2.
параллельное и последовательное соединение проводников объясняет в каждом случае по-своему. Например, при последовательном соединении, напряжения на всех проводниках будут равны между собой: U1 = IR1, U2 = IR2. Кроме того, при последовательном соединении напряжение составляет сумму напряжений каждого проводника: U = U1 + U2 = I(R1 + R2) = IR.
Полное сопротивление цепи при последовательном соединении состоит из суммы сопротивлений всех отдельно взятых проводников, независимо от их количества.
При параллельном соединении напряжение всей цепи равно напряжению на каждом из проводников: U1 = U2 = U.
Общая сила тока, измеренная во всей цепи, равна сумме токов, протекающих по всем проводникам, соединенных параллельно между собой: I = I1 + I2.

Смешанное соединение проводников

В предыдущем конспекте был установлено, что сила тока в проводнике зависит от напряжения на его концах. Если в опыте менять проводники, оставляя напряжение на них неизменным, то можно показать, что при постоянном напряжении на концах проводника сила тока обратно пропорциональна его сопротивлению. Объединив зависимость силы тока от напряжения и его зависимость от сопротивления проводника, можно записать: I = U/R . Этот закон, установленный экспериментально, называется закон Ома (для участка цепи).

Закон Ома для участка цепи : сила тока в проводнике прямо пропорциональна приложенному к его концам напряжению и обратно пропорциональна сопротивлению проводника. Прежде всего закон всегда верен для твёрдых и жидких металлических проводников. А также для некоторых других веществ (как правило, твёрдых или жидких).

Потребители электрической энергии (лампочки, резисторы и пр.) могут по-разному соединяться друг с другом в электрической цепи. Д ва основных типа соединения проводников : последовательное и параллельное. А также есть еще два соединения, которые являются редкими: смешанное и мостовое.

Последовательное соединение проводников

При последовательном соединении проводников конец одного проводника соединится с началом другого проводника, а его конец — с началом третьего и т.д. Например, соединение электрических лампочек в ёлочной гирлянде. При последовательном соединении проводников ток проходит через все лампочки. При этом через поперечное сечение каждого проводника в единицу времени проходит одинаковый заряд. То есть заряд не скапливается ни в какой части проводника.

Поэтому при последовательном соединении проводников сила тока в любом участке цепи одинакова: I 1 = I 2 = I .

Общее сопротивление последовательно соединённых проводников равно сумме их сопротивлений : R 1 + R 2 = R . Потому что при последовательном соединении проводников их общая длина увеличивается. Она больше, чем длина каждого отдельного проводника, соответственно увеличивается и сопротивление проводников.

По закону Ома напряжение на каждом проводнике равно: U 1 = I* R 1 , U 2 = I*R 2 . В таком случае общее напряжение равно U = I ( R 1 + R 2) . Поскольку сила тока во всех проводниках одинакова, а общее сопротивление равно сумме сопротивлений проводников, то полное напряжение на последовательно соединённых проводниках равно сумме напряжений на каждом проводнике : U = U 1 + U 2 .

Из приведённых равенств следует, что последовательное соединение проводников используется в том случае, если напряжение, на которое рассчитаны потребители электрической энергии, меньше общего напряжения в цепи.

Для последовательного соединения проводников справедливы законы :

1) сила тока во всех проводниках одинакова; 2) напряжение на всём соединении равно сумме напряжений на отдельных проводниках; 3) сопротивление всего соединения равно сумме сопротивлений отдельных проводников.

Параллельное соединение проводников

Примером параллельного соединения проводников служит соединение потребителей электрической энергии в квартире. Так, электрические лампочки, чайник, утюг и пр. включаются параллельно.

При параллельном соединении проводников все проводники одним своим концом присоединяются к одной точке цепи. А вторым концом к другой точке цепи. Вольтметр, подключенный к этим точкам, покажет напряжение и на проводнике 1, и на проводнике 2. В таком случае напряжение на концах всех параллельно соединённых проводников одно и то же: U 1 = U 2 = U .

При параллельном соединении проводников электрическая цепь разветвляется. Поэтому часть общего заряда проходит через один проводник, а часть — через другой. Следовательно при параллельном соединении проводников сила тока в неразветвлённой части цепи равна сумме силы тока в отдельных проводниках: I = I 1 + I 2 .

В соответствии с законом Ома I = U/R, I 1 = U 1 /R 1 , I 2 = U 2 /R 2 . Отсюда следует: U/R = U 1 /R 1 + U 2 /R 2 , U = U 1 = U 2 , 1/R = 1/R 1 + 1/R 2 Величина, обратная общему сопротивлению параллельно соединенных проводников, равна сумме величин, обратных сопротивлению каждого проводника.

При параллельном соединении проводников их общее сопротивление меньше, чем сопротивление каждого проводника. Действительно, если параллельно соединены два проводника, имеющие одинаковое сопротивление г , то их общее сопротивление равно: R = г/2 . Это объясняется тем, что при параллельном соединении проводников как бы увеличивается площадь их поперечного сечения. В результате уменьшается сопротивление.

Из приведённых формул понятно, почему потребители электрической энергии включаются параллельно. Они все рассчитаны на определённое одинаковое напряжение, которое в квартирах равно 220 В. Зная сопротивление каждого потребителя, можно рассчитать силу тока в каждом из них. А также соответствие суммарной силы тока предельно допустимой силе тока.

Для параллельного соединения проводников справедливы законы:

1) напряжение на всех проводниках одинаково; 2) сила тока в месте соединения проводников равна сумме токов в отдельных проводниках; 3) величина, обратная сопротивлению всего соединения, равна сумме величин, обратных сопротивлениям отдельных проводников.

Параллельное и последовательное соединение проводников – способы коммутации электрической цепи. Электрические схемы любой сложности можно представить посредством указанных абстракций.

Определения

Существует два способа соединения проводников, становится возможным упростить расчет цепи произвольной сложности:

Конец предыдущего проводника соединен непосредственно с началом следующего — подключение называют последовательным. Образуется цепочка. Чтобы включить очередное звено, нужно электрическую схему разорвать, вставив туда новый проводник.
Начала проводников соединены одной точкой, концы – другой, подключение называется параллельным. Связку принято называть разветвлением. Каждый отдельный проводник образует ветвь. Общие точки именуются узлами электрической сети.

На практике чаще встречается смешанное включение проводников, часть соединена последовательно, часть – параллельно. Нужно разбить цепь простыми сегментами, решать задачу для каждого отдельно. Сколь угодно сложную электрическую схему можно описать параллельным, последовательным соединением проводников. Так делается на практике.

Использование параллельного и последовательного соединения проводников

Термины, применяемые к электрическим цепям

Теория выступает базисом формирования прочных знаний, немногие знают, чем напряжение (разность потенциалов) отличается от падения напряжения. В терминах физики внутренней цепью называют источник тока, находящееся вне – именуется внешней. Разграничение помогает правильно описать распределение поля. Ток совершает работу. В простейшем случае генерация тепла согласно закону Джоуля-Ленца. Заряженные частицы, передвигаясь в сторону меньшего потенциала, сталкиваются с кристаллической решеткой, отдают энергию. Происходит нагрев сопротивлений.

Для обеспечения движения нужно на концах проводника поддерживать разность потенциалов. Это называется напряжением участка цепи. Если просто поместить проводник в поле вдоль силовых линий, ток потечет, будет очень кратковременным. Процесс завершится наступлением равновесия. Внешнее поле будет уравновешено собственным полем зарядов, противоположным направлением. Ток прекратится. Чтобы процесс стал непрерывным, нужна внешняя сила.

Таким приводом движения электрической цепи выступает источник тока. Чтобы поддерживать потенциал, внутри совершается работа. Химическая реакция, как в гальваническом элементе, механические силы – генератор ГЭС. Заряды внутри источника движутся в противоположную полю сторону. Над этим совершается работа сторонних сил. Можно перефразировать приведенные выше формулировки, сказать:

Внешняя часть цепи, где заряды движутся, увлекаемые полем.
Внутренняя часть цепи, где заряды движутся против напряженности.

Генератор (источник тока) снабжен двумя полюсами. Обладающий меньшим потенциалом называется отрицательным, другой – положительным. В случае переменного тока полюсы непрерывно меняются местами. Непостоянно направление движения зарядов. Ток течет от положительного полюса к отрицательному. Движение положительных зарядов идет в направлении убывания потенциала. Согласно этому факту вводится понятие падения потенциала:

Падением потенциала участка цепи называется убыль потенциала в пределах отрезка. Формально это напряжение. Для ветвей параллельной цепи одинаково.

Под падением напряжения понимается и нечто иное. Величина, характеризующая тепловые потери, численно равна произведению тока на активное сопротивление участка. Законы Ома, Кирхгофа, рассмотренные ниже, формулируются для этого случая. В электрических двигателях, трансформаторах разница потенциалов может значительно отличаться от падения напряжения. Последнее характеризует потери на активном сопротивлении, тогда как первое учитывает полную работу источника тока.

При решение физических задач для упрощения двигатель может включать в свой состав ЭДС, направление действия которой противоположно эффекту источника питания. Учитывается факт потери энергии через реактивную часть импеданса. Школьный и вузовский курс физики отличается оторванностью от реальности. Вот почему студенты, раскрыв рот, слушают о явлениях, имеющих место в электротехнике. В период, предшествующий эпохе промышленной революции, открывались главные законы, ученый должен объединять роль теоретика и талантливого экспериментатора. Об этом открыто говорят предисловия к трудам Кирхгофа (работы Георга Ома на русский язык не переведены). Преподаватели буквально завлекали люд дополнительными лекциями, сдобренными наглядными, удивительными экспериментами.

Законы Ома и Кирхгофа применительно к последовательному и параллельному соединению проводников

Для решения реальных задач используются законы Ома и Кирхгофа. Первый выводил равенство чисто эмпирическим путем – экспериментально – второй начал математическим анализом задачи, потом проверил догадки практикой. Приведем некоторые сведения, помогающие решению задачи:

Посчитать сопротивления элементов при последовательном и параллельном соединении

Алгоритм расчета реальных цепей прост. Приведем некоторые тезисы касательно рассматриваемой тематики:

При последовательном включении суммируются сопротивления, при параллельном — проводимости:
1. Для резисторов закон переписывается в неизменной форме. При параллельном соединении итоговое сопротивление равняется произведению исходных, деленному на общую сумму. При последовательном – номиналы суммируются.
2. Индуктивность выступает реактивным сопротивлением (j*ω*L), ведет себя, как обычный резистор. В плане написания формулы ничем не отличается. Нюанс, для всякого чисто мнимого импеданса, что нужно умножить результат на оператор j, круговую частоту ω (2*Пи*f). При последовательном соединении катушек индуктивности номиналы суммируются, при параллельном – складываются обратные величины.
3. Мнимое сопротивление емкости записывается в виде: -j/ω*С. Легко заметить: складывая величины последовательного соединения, получим формулу, в точности как для резисторов и индуктивностей было при параллельном. Для конденсаторов все наоборот. При параллельном включении номиналы складываются, при последовательном – суммируются обратные величины.

Тезисы легко распространяются на произвольные случаи. Падение напряжения на двух открытых кремниевых диодах равно сумме. На практике составляет 1 вольт, точное значение зависит от типа полупроводникового элемента, характеристик. Аналогичным образом рассматривают источники питания: при последовательном включении номиналы складываются. Параллельное часто встречается на подстанциях, где трансформаторы ставят рядком. Напряжение будет одно (контролируются аппаратурой), делятся между ветвями. Коэффициент трансформации строго равен, блокируя возникновение негативных эффектов.

У некоторых вызывает затруднение случай: две батарейки разного номинала включены параллельно. Случай описывается вторым законом Кирхгофа, никакой сложности представить физику не может. При неравенстве номиналов двух источников берется среднее арифметическое, если пренебречь внутренним сопротивлением обоих. В противном случае решаются уравнения Кирхгофа для всех контуров. Неизвестными будут токи (всего три), общее количество которых равно числу уравнений. Для полного понимания привели рисунок.

Пример решения уравнений Кирхгофа

Посмотрим изображение: по условию задачи, источник Е1 сильнее, нежели Е2. Направление токов в контуре берем из здравых соображений. Но если бы проставили неправильно, после решения задачи один получился бы с отрицательным знаком. Следовало тогда изменить направление. Очевидно, во внешней цепи ток течет, как показано на рисунке. Составляем уравнения Кирхгофа для трех контуров, вот что следует:

Работа первого (сильного) источника тратится на создание тока во внешней цепи, преодоление слабости соседа (ток I2).
Второй источник не совершает полезной работы в нагрузке, борется с первым. Иначе не скажешь.

Включение батареек разного номинала параллельно является безусловно вредным. Что наблюдается на подстанции при использовании трансформаторов с разным передаточным коэффициентом. Уравнительные токи не выполняют никакой полезной работы. Включенные параллельно разные батарейки начнут эффективно функционировать, когда сильная просядет до уровня слабой.

Как различать последовательное и параллельное соединение. Соединение резисторов параллельно и последовательно

Определения

Конец предыдущего проводника соединен непосредственно с началом следующего — подключение называют последовательным. Образуется цепочка. Чтобы включить очередное звено, нужно электрическую схему разорвать, вставив туда новый проводник.
Начала проводников соединены одной точкой, концы – другой, подключение называется параллельным. Связку принято называть разветвлением. Каждый отдельный проводник образует ветвь. Общие точки именуются узлами электрической сети.

Использование параллельного и последовательного соединения проводников

Термины, применяемые к электрическим цепям

Внешняя часть цепи, где заряды движутся, увлекаемые полем.
Внутренняя часть цепи, где заряды движутся против напряженности.

Падением потенциала участка цепи называется убыль потенциала в пределах отрезка. Формально это напряжение. Для ветвей параллельной цепи одинаково.

Законы Ома и Кирхгофа применительно к последовательному и параллельному соединению проводников

Посчитать сопротивления элементов при последовательном и параллельном соединении

Алгоритм расчета реальных цепей прост. Приведем некоторые тезисы касательно рассматриваемой тематики:

При последовательном включении суммируются сопротивления, при параллельном — проводимости:
1. Для резисторов закон переписывается в неизменной форме. При параллельном соединении итоговое сопротивление равняется произведению исходных, деленному на общую сумму. При последовательном – номиналы суммируются.
2. Индуктивность выступает реактивным сопротивлением (j*ω*L), ведет себя, как обычный резистор. В плане написания формулы ничем не отличается. Нюанс, для всякого чисто мнимого импеданса, что нужно умножить результат на оператор j, круговую частоту ω (2*Пи*f). При последовательном соединении катушек индуктивности номиналы суммируются, при параллельном – складываются обратные величины.
3. Мнимое сопротивление емкости записывается в виде: -j/ω*С. Легко заметить: складывая величины последовательного соединения, получим формулу, в точности как для резисторов и индуктивностей было при параллельном. Для конденсаторов все наоборот. При параллельном включении номиналы складываются, при последовательном – суммируются обратные величины.

Пример решения уравнений Кирхгофа

Работа первого (сильного) источника тратится на создание тока во внешней цепи, преодоление слабости соседа (ток I2).
Второй источник не совершает полезной работы в нагрузке, борется с первым. Иначе не скажешь.

Если нам надо, чтобы электроприбор работал, мы должны подключить его к . При этом ток должен проходить через прибор и возвращаться вновь к источнику, то есть цепь должна быть замкнутой.

Но подключение каждого прибора к отдельному источнику осуществимо, в основном, в лабораторных условиях. В жизни же приходится иметь дело с ограниченным количеством источников и довольно большим количеством потребителей тока. Поэтому создают системы соединений, позволяющие нагрузить один источник большим количеством потребителей. Системы при этом могут быть сколь угодно сложными и разветвленными, но в их основе лежит всего два вида соединения: последовательное и параллельное соединение проводников. Каждый вид имеет свои особенности, плюсы и минусы. Рассмотрим их оба.

Последовательное соединение проводников

Последовательное соединение проводников – это включение в электрическую цепь нескольких приборов последовательно, друг за другом. Электроприборы в данном случае можно сравнить с людьми в хороводе, а их руки, держащие друг друга – это провода, соединяющие приборы. Источник тока в данном случае будет одним из участников хоровода.

Напряжение всей цепи при последовательном соединении будет равно сумме напряжений на каждом включенном в цепь элементе. Сила тока в цепи будет одинакова в любой точке. А сумма сопротивлений всех элементов составит общее сопротивление всей цепи. Поэтому последовательное сопротивление можно выразить на бумаге следующим образом:

I=I_1=I_2=⋯=I_n ; U=U_1+U_2+⋯+U_n ; R=R_1+R_2+⋯+R_n ,

Плюсом последовательного соединения является простота сборки, а минусом – то, что если один элемент выйдет из строя, то ток пропадет во всей цепи. В такой ситуации неработающий элемент будет подобен ключу в выключенном положении. Пример из жизни неудобства такого соединения наверняка припомнят все люди постарше, которые украшали елки гирляндами из лампочек.

Если в такой гирлянде выходила из строя хотя бы одна лампочка, приходилось перебирать их все, пока не найдешь ту самую, перегоревшую. В современных гирляндах эта проблема решена. В них используют специальные диодные лампочки, в которых при перегорании сплавляются вместе контакты, и ток продолжает беспрепятственно проходить дальше.

Параллельное соединение проводников

При параллельном соединении проводников все элементы цепи подключаются к одной и той же паре точек, можно назвать их А и В. К этой же паре точек подключают источник тока. То есть получается, что все элементы подключены к одинаковому напряжению между А и В. В то же время ток как бы разделяется на все нагрузки в зависимости от сопротивления каждой из них.

Параллельное соединение можно сравнить с течением реки, на пути которой возникла небольшая возвышенность. Вода в таком случае огибает возвышенность с двух сторон, а потом вновь сливается в один поток. Получается островок посреди реки. Так вот параллельное соединение – это два отдельных русла вокруг острова. А точки А и В – это места, где разъединяется и вновь соединяется общее русло реки.

Напряжение тока в каждой отдельной ветви будет равно общему напряжению в цепи. Общий ток цепи будет складываться из токов всех отдельных ветвей. А вот общее сопротивление цепи при параллельном соединении будет меньше сопротивления тока на каждой из ветвей. Это происходит потому, что общее сечение проводника между точками А и В как бы увеличивается за счет увеличения числа параллельно подключенных нагрузок. Поэтому общее сопротивление уменьшается. Параллельное соединение описывается следующими соотношениями:

U=U_1=U_2=⋯=U_n ; I=I_1+I_2+⋯+I_n ; 1/R=1/R_1 +1/R_2 +⋯+1/R_n ,

где I — сила тока, U- напряжение, R – сопротивление, 1,2,…,n – номера элементов, включенных в цепь.

Огромным плюсом параллельного соединения является то, что при выключении одного из элементов, цепь продолжает функционировать дальше. Все остальные элементы продолжают работать. Минусом является то, что все приборы должны быть рассчитаны на одно и то же напряжение. Именно параллельным образом устанавливают розетки сети 220 В в квартирах. Такое подключение позволяет включать различные приборы в сеть совершенно независимо друг от друга, и при выходе их строя одного из них, это не влияет на работу остальных.

Нужна помощь в учебе?

Предыдущая тема: Расчёт сопротивления проводников и реостаты: формулы
Следующая тема:&nbsp&nbsp&nbspРабота и мощность тока

Ток в электроцепи проходит по проводникам от источника напряжения к нагрузке, то есть к лампам, приборам. В большинстве случаев в качестве проводника используются медные провода. В цепи может быть предусмотрено несколько элементов с разными сопротивлениями. В схеме приборов проводники могут быть соединены параллельно или последовательно, также могут быть смешанные типы.

Элемент схемы с сопротивлением называется резистором, напряжение данного элемента является разницей потенциалов между концами резистора. Параллельное и последовательное электрическое соединение проводников характеризуется единым принципом функционирования, согласно которому ток протекает от плюса к минусу, соответственно потенциал уменьшается. На электросхемах сопротивление проводки берется за 0, поскольку оно ничтожно низкое.

Параллельное соединение предполагает, что элементы цепы подсоединены к источнику параллельно и включаются одновременно. Последовательное соединение означает, что проводники сопротивления подключаются в строгой последовательности друг за другом.

При просчете используется метод идеализации, что существенно упрощает понимание. Фактически в электрических цепях потенциал постепенно снижается в процессе перемещения по проводке и элементам, которые входят в параллельное или последовательное соединение.

Последовательное соединение проводников

Схема последовательного соединения подразумевает, что они включаются в определенной последовательности один за другим. Причем сила тока во всех из них равна. Данные элементы создают на участке суммарное напряжение. Заряды не накапливаются в узлах электроцепи, поскольку в противном случае наблюдалось бы изменение напряжения и силы тока. При постоянном напряжении ток определяется значением сопротивления цепи, поэтому при последовательной схеме сопротивление меняется в случае изменения одной нагрузки.

Недостатком такой схемы является тот факт, что в случае выхода из строя одного элемента остальные также утрачивают возможность функционировать, поскольку цепь разрывается. Примером может служить гирлянда, которая не работает в случае перегорания одной лампочки. Это является ключевым отличием от параллельного соединения, в котором элементы могут функционировать по отдельности.

Последовательная схема предполагает, что по причине одноуровневого подключения проводников их сопротивление в любой точки сети равно. Общее сопротивление равняется сумме уменьшения напряжений отдельных элементов сети.

При данном типе соединения начало одного проводника подсоединяется к концу другого. Ключевая особенность соединения состоит в том, что все проводники находятся на одном проводе без разветвлений, и через каждый из них протекает один электроток. Однако общее напряжение равно сумме напряжений на каждом. Также можно рассмотреть соединение с другой точки зрения – все проводники заменяются одним эквивалентным резистором, и ток на нем совпадает с общим током, который проходит через все резисторы. Эквивалентное совокупное напряжение является суммой значений напряжения по каждому резистору. Так проявляется разность потенциалов на резисторе.

Использование последовательного подключения целесообразно, когда требуется специально включать и выключать определенное устройство. К примеру, электрозвонок может звенеть только в момент, когда присутствует соединение с источником напряжения и кнопкой. Первое правило гласит, что если тока нет хотя бы на одном из элементов цепи, то и на остальных его не будет. Соответственно при наличии тока в одном проводнике он есть и в остальных. Другим примером может служить фонарик на батарейках, который светит только при наличии батарейки, исправной лампочки и нажатой кнопки.

В некоторых случаях последовательная схема нецелесообразна. В квартире, где система освещения состоит из множества светильников, бра, люстр, не стоит организовывать схему такого типа, поскольку нет необходимости включать и выключать освещение во всех комнатах одновременно. С этой целью лучше использовать параллельное соединение, чтобы иметь возможность включения света в отдельно взятых комнатах.

Параллельное соединение проводников

В параллельной схеме проводники представляют собой набор резисторов, одни концы которых собираются в один узел, а другие – во второй узел. Предполагается, что напряжение в параллельном типе соединения одинаковое на всех участках цепи. Параллельные участки электроцепи носят название ветвей и проходят между двумя соединительными узлами, на них имеется одинаковое напряжение. Такое напряжение равно значению на каждом проводнике. Сумма показателей, обратных сопротивлениям ветвей, является обратной и по отношению к сопротивлению отдельного участка цепи параллельной схемы.

При параллельном и последовательном соединениях отличается система расчета сопротивлений отдельных проводников. В случае параллельной схемы ток уходит по ветвям, что способствует повышению проводимости цепи и уменьшает совокупное сопротивление. При параллельном подключении нескольких резисторов с аналогичными значениями совокупное сопротивление такой электроцепи будет меньше одного резистора число раз, равное числу .

В каждой ветви предусмотрено по одному резистору, и электроток при достижении точки разветвления делится и расходится к каждому резистору, его итоговое значение равно сумме токов на всех сопротивлениях. Все резисторы заменяются одним эквивалентным резистором. Применяя закон Ома, становится понятным значение сопротивления – при параллельной схеме суммируются значения, обратные сопротивлениям на резисторах.

При данной схеме значение тока обратно пропорционально значению сопротивления. Токи в резисторах не взаимосвязаны, поэтому при отключении одного из них это никоим образом не отразится на остальных. По этой причине такая схема используется во множестве устройств.

Рассматривая возможности применения параллельной схемы в быту, целесообразно отметить систему освещения квартиры. Все лампы и люстры должны быть соединены параллельно, в таком случае включение и отключение одного из них никак не влияет на работу остальных ламп. Таким образом, добавляя выключатель каждой лампочки в ветвь цепи, можно включать и отключать соответствующий светильник по необходимости. Все остальные лампы работают независимо.

Все электроприборы объединяются параллельно в электросеть с напряжением 220 В, затем они подключаются к . То есть все приборы подключаются независимо от подключения прочих устройств.

Законы последовательного и параллельного соединения проводников

Для детального понимания на практике обоих типов соединений, приведем формулы, объясняющие законы данных типов соединений. Расчет мощности при параллельном и последовательном типе соединения отличается.

При последовательной схеме имеется одинаковая сила тока во всех проводниках:

Согласно закону Ома, данные типы соединений проводников в разных случаях объясняются иначе. Так, в случае последовательной схемы, напряжения равны друг другу:

U1 = IR1, U2 = IR2.

Помимо этого, общее напряжение равно сумме напряжений отдельно взятых проводников:

U = U1 + U2 = I(R1 + R2) = IR.

Полное сопротивление электроцепи рассчитывается как сумма активных сопротивлений всех проводников, вне зависимости от их числа.

В случае параллельной схемы совокупное напряжение цепи аналогично напряжению отдельных элементов:

А совокупная сила электротока рассчитывается как сумма токов, которые имеются по всем проводникам, расположенным параллельно:

Чтобы обеспечить максимальную эффективность электрических сетей, необходимо понимать суть обоих типов соединений и применять их целесообразно, используя законы и рассчитывая рациональность практической реализации.

Смешанное соединение проводников

Последовательная и параллельная схема соединения сопротивления могут сочетаться в одной электросхеме при необходимости. К примеру, допускается подключение параллельных резисторов по последовательной или их группе, такое тип считается комбинированным или смешанным.

В таком случае совокупное сопротивление рассчитывается посредством получения сумм значений для параллельного соединения в системе и для последовательного. Сначала необходимо рассчитывать эквивалентные сопротивления резисторов в последовательной схеме, а затем элементов параллельного. Последовательное соединение считается приоритетным, причем схемы такого комбинированного типа часто используются в бытовой технике и приборах.

Итак, рассматривая типы подключений проводников в электроцепях и основываясь на законах их функционирования, можно полностью понять суть организации схем большинства бытовых электроприборов. При параллельном и последовательном соединениях расчет показателей сопротивления и силы тока отличается. Зная принципы расчета и формулы, можно грамотно использовать каждый тип организации цепей для подключения элементов оптимальным способом и с максимальной эффективностью.

Последовательным называют такое соединение элементов цепи, при котором во всех включенных в цепь элементах возникает один и тот же ток I (рис. 1.4).

На основании второго закона Кирхгофа (1.5) общее напряжение U всей цепи равно сумме напряжений на отдельных участках:

U = U 1 + U 2 + U 3 или IR экв = IR 1 + IR 2 + IR 3 ,

откуда следует

R экв = R 1 + R 2 + R 3 .

Таким образом, при последовательном соединении элементов цепи общее эквивалентное сопротивление цепи равно арифметической сумме сопротивлений отдельных участков. Следовательно, цепь с любым числом последовательно включенных сопротивлений можно заменить простой цепью с одним эквивалентным сопротивлением R экв (рис. 1.5). После этого расчет цепи сводится к определению тока I всей цепи по закону Ома

и по вышеприведенным формулам рассчитывают падение напряжений U 1 , U 2 , U 3 на соответствующих участках электрической цепи (рис. 1.4).

Недостаток последовательного включения элементов заключается в том, что при выходе из строя хотя бы одного элемента, прекращается работа всех остальных элементов цепи.

Электрическая цепь с параллельным соединением элементов

Параллельным называют такое соединение, при котором все включенные в цепь потребители электрической энергии, находятся под одним и тем же напряжением (рис. 1.6).

В этом случае они присоединены к двум узлам цепи а и b, и на основании первого закона Кирхгофа можно записать, что общий ток I всей цепи равен алгебраической сумме токов отдельных ветвей:

I = I 1 + I 2 + I 3 , т.е.

откуда следует, что

В том случае, когда параллельно включены два сопротивления R 1 и R 2 , они заменяются одним эквивалентным сопротивлением

Из соотношения (1.6), следует, что эквивалентная проводимость цепи равна арифметической сумме проводимостей отдельных ветвей:

g экв = g 1 + g 2 + g 3 .

По мере роста числа параллельно включенных потребителей проводимость цепи g экв возрастает, и наоборот, общее сопротивление R экв уменьшается.

Напряжения в электрической цепи с параллельно соединенными сопротивлениями (рис. 1.6)

U = IR экв = I 1 R 1 = I 2 R 2 = I 3 R 3 .

Отсюда следует, что

т.е. ток в цепи распределяется между параллельными ветвями обратно пропорционально их сопротивлениям.

По параллельно включенной схеме работают в номинальном режиме потребители любой мощности, рассчитанные на одно и то же напряжение. Причем включение или отключение одного или нескольких потребителей не отражается на работе остальных. Поэтому эта схема является основной схемой подключения потребителей к источнику электрической энергии.

Электрическая цепь со смешанным соединением элементов

Смешанным называется такое соединение, при котором в цепи имеются группы параллельно и последовательно включенных сопротивлений.

Для цепи, представленной на рис. 1.7, расчет эквивалентного сопротивления начинается с конца схемы. Для упрощения расчетов примем, что все сопротивления в этой схеме являются одинаковыми: R 1 =R 2 =R 3 =R 4 =R 5 =R. Сопротивления R 4 и R 5 включены параллельно, тогда сопротивление участка цепи cd равно:

В этом случае исходную схему (рис. 1.7) можно представить в следующем виде (рис. 1.8):

На схеме (рис. 1.8) сопротивление R 3 и R cd соединены последовательно, и тогда сопротивление участка цепи ad равно:

Тогда схему (рис. 1.8) можно представить в сокращенном варианте (рис. 1.9):

На схеме (рис. 1.9) сопротивление R 2 и R ad соединены параллельно, тогда сопротивление участка цепи аb равно

Схему (рис. 1.9) можно представить в упрощенном варианте (рис. 1.10), где сопротивления R 1 и R ab включены последовательно.

Тогда эквивалентное сопротивление исходной схемы (рис. 1.7) будет равно:

Рис. 1.10

Рис. 1.11

В результате преобразований исходная схема (рис. 1.7) представлена в виде схемы (рис. 1.11) с одним сопротивлением R экв. Расчет токов и напряжений для всех элементов схемы можно произвести по законам Ома и Кирхгофа.

ЛИНЕЙНЫЕ ЦЕПИ ОДНОФАЗНОГО СИНУСОИДАЛЬНОГО ТОКА.

Получение синусоидальной ЭДС. . Основные характеристики синусоидального тока

Основным преимуществом синусоидальных токов является то, что они позволяют наиболее экономично осуществлять производство, передачу, распределение и использование электрической энергии. Целесообразность их использования обусловлена тем, что коэффициент полезного действия генераторов, электрических двигателей, трансформаторов и линий электропередач в этом случае оказывается наивысшим.

Для получения в линейных цепях синусоидально изменяющихся токов необходимо, чтобы э. д. с. также изменялись по синусоидальному закону. Рассмотрим процесс возникновения синусоидальной ЭДС. Простейшим генератором синусоидальной ЭДС может служить прямоугольная катушка (рамка), равномерно вращающаяся в однородном магнитном поле с угловой скоростью ω (рис. 2.1, б ).

Пронизывающий катушку магнитный поток во время вращения катушки abcd наводит (индуцирует) в ней на основании закона электромагнитной индукции ЭДС е . Нагрузку подключают к генератору с помощью щеток 1 , прижимающихся к двум контактным кольцам 2 , которые, в свою очередь, соединены с катушкой. Значение наведенной в катушке abcd э. д. с. в каждый момент времени пропорционально магнитной индукции В , размеру активной части катушки l = ab + dc и нормальной составляющей скорости перемещения ее относительно поля v н :

e = Blv н (2.1)

где В и l — постоянные величины, a v н — переменная, зависящая от угла α. Выразив скорость v н через линейную скорость катушки v , получим

e = Blv·sinα (2.2)

В выражении (2.2) произведение Blv = const. Следовательно, э. д. с., индуцируемая в катушке, вращающейся в магнитном поле, является синусоидальной функцией угла α .

Если угол α = π/2 , то произведение Blv в формуле (2.2) есть максимальное (амплитудное) значение наведенной э. д. с. E m = Blv . Поэтому выражение (2.2) можно записать в виде

e = E m sinα (2.3)

Так как α есть угол поворота за время t , то, выразив его через угловую скорость ω , можно записать α = ωt , a формулу (2.3) переписать в виде

e = E m sinωt (2.4)

где е — мгновенное значение э. д. с. в катушке; α = ωt — фаза, характеризующая значение э. д. с. в данный момент времени.

Необходимо отметить, что мгновенную э. д. с. в течение бесконечно малого промежутка времени можно считать величиной постоянной, поэтому для мгновенных значений э. д. с. е , напряжений и и токов i справедливы законы постоянного тока.

Синусоидальные величины можно графически изображать синусоидами и вращающимися векторами. При изображении их синусоидами на ординате в определенном масштабе откладывают мгновенные значения величин, на абсциссе — время. Если синусоидальную величину изображают вращающимися векторами, то длина вектора в масштабе отражает амплитуду синусоиды, угол, образованный с положительным направлением оси абсцисс, в начальный момент времени равен начальной фазе, а скорость вращения вектора равна угловой частоте. Мгновенные значения синусоидальных величин есть проекции вращающегося вектора на ось ординат. Необходимо отметить, что за положительное направление вращения радиус-вектора принято считать направление вращения против часовой стрелки. На рис. 2.2 построены графики мгновенных значений э. д. с. е и е» .

Если число пар полюсов магнитов p ≠ 1 , то за один оборот катушки (см. рис. 2.1) происходит p полных циклов изменения э. д. с. Если угловая частота катушки (ротора) n оборотов в минуту, то период уменьшится в pn раз. Тогда частота э. д. с., т. е. число периодов в секунду,

f = Pn / 60

Из рис. 2.2 видно, что ωТ = 2π , откуда

ω = 2π / T = 2πf (2.5)

Величину ω , пропорциональную частоте f и равную угловой скорости вращения радиус-вектора, называют угловой частотой. Угловую частоту выражают в радианах в секунду (рад/с) или в 1 / с.

Графически изображенные на рис. 2.2 э. д. с. е и е» можно описать выражениями

e = E m sinωt; e» = E» m sin(ωt + ψ e» ) .

Здесь ωt и ωt + ψ e» — фазы, характеризующие значения э. д. с. e и e» в заданный момент времени; ψ e» — начальная фаза, определяющая значение э. д. с. е» при t = 0. Для э. д. с. е начальная фаза равна нулю (ψ e = 0 ). Угол ψ всегда отсчитывают от нулевого значения синусоидальной величины при переходе ее от отрицательных значений к положительным до начала координат (t = 0). При этом положительную начальную фазу ψ (рис. 2.2) откладывают влево от начала координат (в сторону отрицательных значений ωt ), а отрицательную фазу — вправо.

Если у двух или нескольких синусоидальных величин, изменяющихся с одинаковой частотой, начала синусоид не совпадают по времени, то они сдвинуты друг относительно друга по фазе, т. е. не совпадают по фазе.

Разность углов φ , равная разности начальных фаз, называют углом сдвига фаз. Сдвиг фаз между одноименными синусоидальными величинами, например между двумя э. д. с. или двумя токами, обозначают α . Угол сдвига фаз между синусоидами тока и напряжения или их максимальными векторами обозначают буквой φ (рис. 2.3).

Когда для синусоидальных величин разность фаз равна ±π , то они противоположны по фазе, если же разность фаз равна ±π/2 , то говорят, что они находятся в квадратуре. Если для синусоидальных величин одной частоты начальные фазы одинаковы, то это означает, что они совпадают по фазе.

Синусоидальные напряжение и ток, графики которых представлены на рис. 2.3, описываются следующим образом:

u = U m sin(ω t + ψ u ) ; i = I m sin(ω t + ψ i ) , (2.6)

причем угол сдвига фаз между током и напряжением (см. рис. 2.3) в этом случае φ = ψ u — ψ i .

Уравнения (2.6) можно записать иначе:

u = U m sin(ωt + ψ i + φ) ; i = I m sin(ωt + ψ u — φ) ,

поскольку ψ u = ψ i + φ и ψ i = ψ u — φ .

Из этих выражений следует, что напряжение опережает по фазе ток на угол φ (или ток отстает по фазе от напряжения на угол φ ).

Формы представления синусоидальных электрических величин.

Любая, синусоидально изменяющаяся, электрическая величина (ток, напряжение, ЭДС) может быть представлена в аналитическом, графическом и комплексном видах.

1). Аналитическая форма представления

I = I m ·sin(ω·t + ψ i ), u = U m ·sin(ω·t + ψ u ), e = E m ·sin(ω·t + ψ e ),

где I , u , e – мгновенное значение синусоидального тока, напряжения, ЭДС, т. е. Значения в рассматриваемый момент времени;

I m , U m , E m – амплитуды синусоидального тока, напряжения, ЭДС;

(ω·t + ψ ) – фазовый угол, фаза; ω = 2·π/Т – угловая частота, характеризующая скорость изменения фазы;

ψ i , ψ u , ψ e – начальные фазы тока, напряжения, ЭДС отсчитываются от точки перехода синусоидальной функции через нуль к положительному значению до начала отсчета времени (t = 0). Начальная фаза может иметь как положительное так и отрицательное значение.

Графики мгновенных значений тока и напряжения показаны на рис. 2.3

Начальная фаза напряжения сдвинута влево от начала отсчёта и является положительной ψ u > 0, начальная фаза тока сдвинута вправо от начала отсчёта и является отрицательной ψ i φ . Сдвиг фаз между напряжением и током

φ = ψ u – ψ i = ψ u – (- ψ i) = ψ u + ψ i .

Применение аналитической формы для расчёта цепей является громоздкой и неудобной.

На практике приходится иметь дело не с мгновенными значениями синусоидальных величин, а с действующими. Все расчёты проводят для действующих значений, в паспортных данных различных электротехнических устройств указаны действующие значения (тока, напряжения), большинство электроизмерительных приборов показывают действующие значения. Действующий ток является эквивалентом постоянного тока, который за одно и то же время выделяет в резисторе такое же количество тепла, как и переменный ток. Действующее значение связано с амплитудным простым соотношением

2). Векторная форма представления синусоидальной электрической величины – это вращающийся в декартовой системе координат вектор с началом в точке 0, длина которого равна амплитуде синусоидальной величины, угол относительно оси х – её начальной фазе, а частота вращения – ω = 2πf . Проекция данного вектора на ось у в любой момент времени определяет мгновенное значение рассматриваемой величины.

Рис. 2.4

Совокупность векторов, изображающих синусоидальные функции, называют векторной диаграммой, рис. 2.4

3). Комплексное представление синусоидальных электрических величин сочетает наглядность векторных диаграмм с проведением точных аналитических расчётов цепей.

Рис. 2.5

Ток и напряжение изобразим в виде векторов на комплексной плоскости, рис.2.5 Ось абсцисс называют осью действительных чисел и обозначают +1 , ось ординат называют осью мнимых чисел и обозначают +j . (В некоторых учебниках ось действительных чисел обозначают Re , а ось мнимых – Im ). Рассмотрим векторы U и I в момент времени t = 0. Каждому из этих векторов соответствует комплексное число, которое может быть представлено в трех формах:

а). Алгебраической

U = U ’+ jU «

I = I ’ – jI «,

где U «, U «, I «, I » – проекции векторов на оси действительных и мнимых чисел.

б). Показательной

где U , I – модули (длины) векторов; е – основание натурального логарифма; поворотные множители, т. к. умножение на них соответствует повороту векторов относительно положительного направления действительной оси на угол, равный начальной фазе.

в). Тригонометрической

U = U ·(cosψ u + j sinψ u)

I = I ·(cosψ i – j sinψ i).

При решении задач в основном применяют алгебраическую форму (для операций сложения и вычитания) и показательную форму (для операций умножения и деления). Связь между ними устанавливается формулой Эйлера

е j ·ψ = cosψ + j sinψ .

Неразветвлённые электрические цепи

Нужно вычислить сопротивление последовательной, параллельной или комбинированной цепей? Нужно, если вы не хотите сжечь плату! Эта статья расскажет вам, как это сделать. Перед чтением, пожалуйста, уясните, что у резисторов нет «начала» и нет «конца». Эти слова вводятся для облегчения понимания изложенного материала.

Шаги

Сопротивление последовательной цепи

Сопротивление параллельной цепи

Сопротивление комбинированной цепи

Некоторые факты

Каждый электропроводный материал имеет некоторое сопротивление, являющееся сопротивляемостью материала электрическому току.
Сопротивление измеряется в Омах. Символ единицы измерения Ом — Ω.
Разные материалы имеют разные значения сопротивления.
- Например, сопротивление меди 0.0000017 Ом/см 3
- Сопротивление керамики около 10 14 Ом/см 3
Чем больше значение сопротивления, тем выше сопротивляемость электрическому току. Медь, которая часто используется в электрических проводах, имеет очень малое сопротивление. С другой стороны, сопротивление керамики очень велико, что делает ее прекрасным изолятором.
Работа всей цепи зависит от того, какой тип соединения вы выберете для подключения резисторов в этой цепи.
U=IR. Это закон Ома, установленный Георгом Омом в начале 1800х. Если вам даны любые две из этих переменных, вы легко найдете третью.
- U=IR: Напряжение (U) есть результат умножения силы тока (I) * на сопротивление (R).
- I=U/R: Сила тока есть частное от напряжение (U) ÷ сопротивление (R).
- R=U/I: Сопротивление есть частное от напряжение (U) ÷ сила тока (I).

Запомните: при параллельном соединении существует несколько путей прохождения тока по цепи, поэтому в такой цепи общее сопротивление будет меньше сопротивления каждого отдельного резистора. При последовательном соединении ток проходит через каждый резистор в цепи, поэтому сопротивление каждого отдельного резистора добавляется к общему сопротивлению.
Общее сопротивление в параллельной цепи всегда меньше сопротивления одного резистора с самым низким сопротивлением в этой цепи. Общее сопротивление в последовательной цепи всегда больше сопротивления одного резистора с самым высоким сопротивлением в этой цепи.

Цепи резисторов серии

и параллельные

Электронные компоненты подключаются разными способами. Две простейшие формы подключения — последовательное и параллельное. соединения.

Если компоненты соединены последовательно в цепи, то цепь называется последовательной. Если резисторы соединены последовательно в цепи, тогда цепь говорят, что это цепь последовательного резистора.

Если компоненты соединены в цепи параллельно, то цепь называется параллельной. Если резисторы соединены параллельно в цепи, тогда цепь называется параллельной схемой резистора.

Резистор серии

цепь

А Схема последовательного резистора — это электронная схема, в которой все резисторы подключаются друг за другом по одному и тому же пути так что одинаковый ток течет через все и каждый резистор.

полное сопротивление такой цепи получается простым суммируя значения сопротивлений отдельных резисторов.

R _T = ₁ + ₂ + ₃ + ₄ рандов …… ..и т. Д.

Для Например, если пять резисторов соединены последовательно. Тогда полное сопротивление цепи равно:

R _T = ₁ + ₂ + ₃ + ₄ рандов + Р ₅

Все ток, протекающий через первый резистор, не имеет другого путь идти.Следовательно, он также должен пройти через второй резистор, третий резистор, четвертый резистор и так далее.

Пример:

А Схема последовательного резистора показана на рисунке ниже. Этот схема состоит из пяти резисторов, которые включены в последовательный и источник постоянного напряжения.

Если Значения пяти резисторов равны: R ₁ = 4 Ом, R ₂ = 4 Ом, R ₃ = 2 Ом, R ₄ = 2 Ом, R ₅ = 3 Ом и батарея постоянного тока = 15 В, тогда

Общее сопротивление это R _T = ₁ + ₂ + ₃ + ₄ рандов + R ₅ = 4 + 4 + 2 + 2 + 3 = 15 Ом.

Вспомните формулу закона Ома, V = I R

Зная любые две переменные в выше уравнения, мы можем легко найти оставшиеся неизвестные Переменная.

Нам известно значение полного сопротивления, т.е. R _T = 15 Ом и значение напряжения I.e. V = 15 В

Теперь нужно найти оставшееся неизвестное текущее значение I.

Текущий текущий через каждый резистор будет 1 А.

Напряжение на каждый резистор в последовательной цепи отличается. Если все резисторы в последовательной цепи имеют одинаковое значение сопротивления тогда напряжение через каждый резистор такой же. С другой стороны, если каждый резистор имеет другое значение сопротивления, то напряжение на каждом резисторе различается.

Напряжение на резистор (R ₁) составляет В ₁ = I × R ₁ = 1 × 4 = 4 В

Напряжение на резистор (R ₂) составляет В ₂ = I × R ₂ = 1 × 4 = 4 В

Напряжение на резистор (R ₃) составляет В ₃ = I × R ₃ = 1 × 2 = 2 В

Напряжение на резистор (R ₄) составляет В ₄ = I × R ₄ = 1 × 2 = 2 В

Напряжение на резистор (R ₅) составляет В ₅ = I × R ₅ = 1 × 3 = 3 В

Суммарное напряжение в последовательная цепь равна сумме всех отдельных напряжения в сумме

И.е. В _Т = В ₁ + V ₂ + V ₃ + V ₄ + ………. + V _N

В нашей схеме общее напряжение равно сумме разностей потенциалов по R _1,, _{R ₂, R ₃, ₄ и ₅.}

Т.е. В _Т = В ₁ + В ₂ + В ₃ + В ₄ + В ₅ = 4 + 4 + 2 + 2 + 3 = 15 В.

Параллельный схема резистора

А Схема параллельного резистора — это электронная схема, в которой все резисторы соединены бок о бок в разных пути, чтобы один и тот же ток не проходил через каждый резистор. Параллельная схема показывает несколько путей к электрический ток течет.

ток в параллельной цепи прерывается, с некоторым током течет вдоль каждой параллельной ветви и повторно комбинируется, когда ветви снова встречаются.Следовательно, электрический ток через каждый резистор будет другим. Однако напряжение на каждый резистор такой же.

полное сопротивление параллельной цепи резистора получается как сложение обратных величин (1 / R) значений сопротивления отдельные резисторы, а затем взяв обратную величину общий.

Для Например, если три резистора подключены параллельно.потом полное сопротивление цепи

Пример:

А Схема параллельного резистора показана на рисунке ниже. Этот схема состоит из трех резисторов, которые включены в параллельный и источник постоянного напряжения.

Если Значения трех резисторов равны: R ₁ = 8 Ом, R ₂ = 8 Ом, R ₃ = 4 Ом и батарея постоянного тока = 14 В, затем

общее сопротивление

Суммарный ток по контуру —

Как напряжение на каждом резисторе одинаково параллельно схема, мы можем использовать Ом закон чтобы найти ток отдельной ветви следующим образом.

ток через резистор (R ₁) _{is I ₁ = V / R ₁ = 14/8 =
1,75 А}

ток через резистор (R ₂) _{is I ₂ = V / R ₂ = 14/8 =
1,75 А}

ток через резистор (R ₃) _{is I ₃ = V / R ₃ = 14/4 =
3.5 А}

Тогда общая ток равен сумме токов отдельных ветвей

Т.е. Я _Т = Я ₁ + I ₂ + I ₃ = 1,75 + 1,75 + 3,5 = 7 А

Что такое параллельная цепь — как сделать, характеристики, применение

Поведение схемы полностью зависит от конфигурации ее компонентов схемы.В зависимости от конфигурации подключения эти схемы делятся на параллельные и последовательные схемы. В этом посте раскрывается смысл параллельной схемы, как создать параллельную схему, ее различные характеристики, приложения, преимущества и недостатки.

Что такое параллельная цепь

Схема называется параллельной схемой, когда два или более компонентов подключены к одному и тому же узлу, и обе стороны компонентов подключены непосредственно к батарее или любому другому источнику.Ток в параллельной цепи имеет два или более путей протекания через него.

Наиболее распространенным примером параллельной схемы является подключение автомобильных фар. Если фары автомобиля были включены последовательно, то при выходе из строя одного из фар другой также выключится, что означает потерю запаса прочности.

Рис. 1 — Пример автомобильных фар, подключенных в параллельную цепь

Как сделать параллельную цепь

Два или более компонентов схемы соединены через общий источник напряжения для образования параллельной цепи.На рисунке ниже показана типичная параллельная схема, в которой резисторы (R1, R2, R3, R4) подключены параллельно. Обе стороны резисторов подключены непосредственно к источнику напряжения. Параллельный путь называется ветвью, и напряжение на всех ветвях одинаковое, но ток может быть разным.

Рис. 2 — Принципиальная схема параллельной цепи

Характеристики параллельной цепи

Основные характеристики параллельной цепи перечислены ниже:

Токи ответвления в параллельной цепи

по Ом закон, I = E / R. Это означает, что каждый резистор в этой цепи будет потреблять ток от источника. Следовательно, полный ток, потребляемый от источника, равен сумме токов ответвления, и ток, протекающий по каждому пути, зависит от сопротивления ответвления. Однако напряжение остается прежним и создает разность потенциалов на его выводах.

Общий ток (I _t) можно рассчитать по формуле:

I _t = I ₁ + I ₂ + I ₃ +….I _n

Где (I ₁ + I ₂ + I ₃ +… .I _n) — токи ответвления

. R1 и R2) с разными значениями (10 Ом и 5 Ом) соответственно. Напряжение 10 В подается на резисторы, в результате чего ток 1 А, потребляемый от батареи через R1, и 2 А, протекающий через R2, выводится из уравнения I = E / R .

Следовательно, два тока ответвления в цепи равны 1А и 2А, что в сумме составляет 3А.

I _t = 1 + 2 = 3A

Сопротивления в параллельной цепи

Суммарные сопротивления любого количества резисторов рассчитываются по формуле:

Взаимно R1 = 1 / R1 = 1/10 = 0,1

Величина, обратная R2 = 1 / R2 = 1/5 = 0,2

Сумма указанных выше обратных величин = 0,3

R _t = 1 / 0,3 = 3,33 Ом

Мощность в параллельной цепи

Один раз известны значения общего тока и приложенного напряжения. Мощность может быть рассчитана по формуле P = EI .В приведенном выше примере приложенное напряжение (E) = 10 В и I = 3 A

∴P = 10 x 3 = 30 Вт

Применения параллельной цепи

Применения параллельных цепей включают:

Электропроводка к розеткам электропитания в каждом доме в виде параллельных цепей.
В источниках питания постоянного тока в автомобильной промышленности используются параллельные схемы.
Компьютерное оборудование разработано с использованием параллельных цепей.

Преимущества параллельной схемы

Преимущества параллельной схемы включают:

Равное напряжение распределяется на каждый компонент в цепи.
На ток не влияет даже при добавлении или удалении дополнительных компонентов (резисторов) из схемы.

Недостатки параллельной схемы

Недостатки параллельных схем перечислены ниже:

Она более сложна в проектировании по сравнению с последовательными схемами.
Дорого в сборке.
Короткое замыкание при параллельном подключении может быть опасным.
Даже если один из компонентов неисправен, ток все равно может проходить через цепь.

  Также читают: 
 Цепь серии  - принцип работы, характеристики, применение, преимущества 
  Что такое цифровой вольтметр - как он работает, типы, применение, преимущества 
  Что такое технология Li-Fi - Как это работает, применение и преимущества

Последовательные и параллельные резисторы — Электрические цепи — WJEC — GCSE Physics (Single Science) Revision — WJEC

Последовательные резисторы

Когда резисторы подключены в серии, ток через каждый резистор одинаков.Другими словами, ток одинаков во всех точках последовательной цепи.

При последовательном соединении резисторов общее напряжение (или разность потенциалов) на всех резисторах равно сумме напряжений на каждом резисторе.

Другими словами, напряжения в цепи складываются с напряжением источника питания.

Общее сопротивление ряда последовательно включенных резисторов равно сумме всех отдельных сопротивлений.

В этой схеме действует следующее.

I ₁ = I ₂ = I ₃

V _T = V ₁ + V ₂ + V ₃

и, R _T = R ₁ + R ₂ + R ₃

Последовательное добавление компонентов увеличивает общее сопротивление в цепи.

Параллельные резисторы

При параллельном подключении резисторов ток питания равен сумме токов, протекающих через каждый резистор.Токи в ветвях параллельной цепи складываются с током питания.

При параллельном подключении резисторов они имеют одинаковую разность потенциалов. Любые параллельные компоненты имеют одинаковую разность потенциалов.

Это уравнение используется для расчета общего сопротивления двух параллельно включенных резисторов.

\ [\ frac {1} {R} = \ frac {1} {R} _ {1} + \ frac {1} {R} _ {2} \]

Для расчета общего сопротивления трех резисторов подключенные параллельно, мы добавляем в уравнение третий резистор (и так далее).

\ [\ frac {1} {R} = \ frac {1} {R} _ {1} + \ frac {1} {R} _ {2} + \ frac {1} {R} _ {3 } \]

Параллельное добавление компонентов снижает общее сопротивление в цепи.

Вопрос

Вычислите сопротивление этой параллельной комбинации.

Показать ответ

\ [\ frac {1} {R} = \ frac {1} {R} _ {1} + \ frac {1} {R} _ {2} + \ frac {1} {R} _ {3} \]

\ [\ frac {1} {R} = \ frac {1} {3} + \ frac {1} {6} + \ frac {1} {9} \]

R = 1,64 Ом

Общее сопротивление меньше, чем у наименьшего резистора.

Введение в последовательные, параллельные и последовательно-параллельные соединения

Последовательные, параллельные и последовательно-параллельные схемы, их сравнение и применения

Почему параллельное соединение предпочтительнее последовательного?

Сегодня невозможно переоценить использование, применение и важность последовательного и параллельного соединения цепей. Применение последовательного и параллельного подключения цепей можно увидеть в наших домах, школьных залах и в наших уличных фонарях.Одним нажатием кнопки включаются все качели в наших гостиных. некоторые говорят, что у бобов в их домах должны быть разные переключатели.

Что ж, это не волшебство, когда одним переключателем управляет более трех электрических бобов или нагрузок. Нагрузка — это что угодно, то есть это могут быть приборы, электрические качалки или даже потолочные вентиляторы, которые потребляют электроэнергию при подключении к источнику питания. Электрические бобы, телевизоры, холодильники и т. Д. Можно назвать грузом.Бобы преобразуют электрическую энергию в световую и тепловую форму энергии. Вентиляторы преобразуют электрическую энергию в механическую.

Тип подключения к нашим потолочным вентиляторам и электробобам будет определять, будут ли они иметь общий выключатель или нет. Последовательное соединение цепи дает нам возможность подключить более двух нагрузок к общему выключателю. Уличные фонари — очень хороший тому пример. Параллельное соединение цепи позволяет нам подключать нагрузки к их индивидуальному переключателю.Подходит как последовательное, так и параллельное соединение, но одно предпочтительнее другого по той или иной причине. Прежде чем мы поговорим о том, почему параллельное соединение предпочтительнее последовательного, давайте вспомним, какие последовательные и параллельные соединения являются первыми.

Последовательная цепь

Последовательная цепь — это цепь, в которой резисторы или нагрузки подключены встык, так что в цепи будет только один путь, по которому протекает электрический ток.Таким образом, когда несколько резисторов соединены последовательно, эффективное сопротивление (общее сопротивление в цепи) получается путем алгебраического сложения отдельных сопротивлений. То есть, если у нас есть резисторы с сопротивлением R1, R2, R3… Rn , соединенные последовательно , то;

R _eff = R _T = R ₁ + R ₂ + R ₃ +… R _n.

При последовательном соединении один и тот же ток течет по всем ветвям схемы, но разное напряжение на нем, что заставляет резисторы иметь разное напряжение на них.На каждом резисторе или нагрузке будет падение напряжения. Приложенное напряжение равно сумме падений напряжения на различных частях цепи. Падение напряжения пропорционально тому, что ток сопротивления одинаков во всей цепи. Когда нагрузки подключаются последовательно, они имеют тенденцию иметь общий выключатель. Такая связь используется в школьных залах, уличных фонарях.

Как подключить фары последовательно?

Использование и применение последовательного соединения

Некоторые люди подключают сигнальные огни в своих домах последовательно, в результате чего у них будет общий выключатель.Проблема с таким типом подключения заключается в том, что при возникновении проблемы с нагрузкой другая подключенная система выйдет из строя. Это тип подключения по схеме «все или ничего». Пока нагрузка не получит энергию до того, как она передаст ее другой, и одна из них не выйдет из строя, будет отключение электроэнергии.

Последовательные соединения схем распространены и широко используются в электрическом оборудовании. Нити трубки в небольших радиоприемниках обычно идут последовательно. Устройства управления током всегда подключаются последовательно с устройством, которое они защищают.Предохранители соединены последовательно с устройством, которое они защищают. Автоматическое отопительное оборудование имеет термостат, электромагнитные катушки и предохранительные выключатели, соединенные последовательно с источником напряжения и т. Д.

Недостатки последовательной цепи

Разрыв в проводе отказ или удаление любой отдельной лампы приведет к разрыву цепи и приведению к прекращению работы всех остальных, поскольку в цепи протекает только один единственный путь тока.
При добавлении дополнительных ламп в цепь последовательного освещения все они будут иметь меньшую яркость.потому что напряжение распределяется по последовательной цепи. Если мы добавим больше нагрузок в последовательной цепи, падение напряжения возрастет, что не является хорошим признаком для защиты электроприборов.
представляет собой проводку типа «ВСЕ или НЕТ», что означает, что все устройства будут работать одновременно или все они отключатся, если произойдет сбой в любом из подключенных устройств в последовательной цепи.
Высокое напряжение питания необходимо, если нам нужно добавить дополнительную нагрузку (лампочки, электрические обогреватели, кондиционер и т. Д.) В последовательную цепь.Например, если пять ламп 220 В должны быть подключены последовательно, то напряжение питания должно быть: 5 x 220 В = 1,1 кВ.
Общее сопротивление последовательной цепи увеличивается (а ток уменьшается), когда в цепь добавляется дополнительная нагрузка.
В соответствии с будущими потребностями, в последовательную цепь тока следует добавлять только те электроприборы, если они имеют тот же номинальный ток, что и ток, одинаковый в каждой точке последовательной цепи. Однако мы знаем, что электрические приборы и устройства i.е. лампочки, вентилятор, обогреватель, кондиционер и т. д. имеют разный номинальный ток, поэтому они не могут быть подключены последовательно для бесперебойной и эффективной работы. Фары, подключенные последовательно

Преимущества последовательного подключения

Меньше размер провода кабеля требуется при последовательном подключении.
Мы используем для защиты цепи для последовательного соединения предохранителей и автоматических выключателей с другими приборами.
нелегко получить накладные расходы из-за высокого сопротивления, когда в цепь добавляется дополнительная нагрузка.
Срок службы батареи в последовательной цепи больше, чем в параллельной.
Это самый простой способ подключения электропроводки, который позволяет легко обнаружить и устранить неисправность по сравнению с параллельным или последовательно-параллельным подключением.

Параллельная цепь

Резисторы, нагрузки считаются подключенными параллельно, когда конец каждого из резисторов или нагрузок имеет общую точку или соединение, а другие концы также подключены к общей точке или соединению.Такие схемы известны как параллельные схемы.

Лампочки, подключенные параллельно

В отличие от последовательного подключения, при нахождении общего (эффективного) сопротивления в параллельной цепи берется величина, обратная отдельному сопротивлению. Таким образом, когда несколько сопротивлений соединены параллельно, величина, обратная величине эффективного сопротивления, определяется арифметической или алгебраической суммой величины, обратной величине отдельного сопротивления.

1 / R _eff или 1 / R _T = 1 / R ₁ + 1 / R ₂ + 1 / R ₃… 1 / R _n.

Параллельное соединение цепи имеет одинаковое напряжение, протекающее по всем ветвям цепи. У разных резисторов свои токи.

Использование и применение параллельного соединения

Параллельное соединение используется очень часто. Различные лампы и электроприборы в наших домах подключаются параллельно, так что каждая из ламп или бобышек и приборов может работать независимо. Чтобы мы могли управлять отдельными лампами или нагрузками, они должны быть подключены параллельно.

Преимущества параллельной схемы

Каждое подключенное электрическое устройство и устройство не зависят от других. Таким образом, включение / выключение устройства не повлияет на другие устройства и их работу.
В случае обрыва кабеля или снятия какой-либо лампы все цепи и подключенные нагрузки не разорвутся, другими словами, другие светильники / лампы и электроприборы по-прежнему будут работать без сбоев.
Если добавить больше ламп в параллельные цепи освещения, их яркость не будет уменьшена (как это происходит только в последовательных цепях освещения).Потому что напряжение одинаково в каждой точке параллельной цепи. Короче говоря, они получают то же напряжение, что и напряжение источника.
Можно добавить дополнительные осветительные приборы и точки нагрузки в параллельных цепях в соответствии с будущими потребностями, если цепь не будет перегружена.
Добавление дополнительных устройств и компонентов не приведет к увеличению сопротивления, но уменьшит общее сопротивление цепи, особенно когда используются устройства с высоким номинальным током, такие как кондиционер и электрические обогреватели.
параллельная проводка более надежна, безопасна и проста в использовании. Неисправности в параллельных цепях освещения.

Недостатки параллельных подключений.
При добавлении дополнительной лампочки в параллельную цепь требуется больше тока.
Батарея разряжается быстрее при установке постоянного тока.
Схема параллельного подключения более сложна по сравнению с последовательным подключением.
Связанное сообщение: Какая лампа светится ярче при последовательном и параллельном подключении и почему?
Последовательно-параллельные соединения и схемы
Схема не является последовательной или параллельной на следующем рисунке, т.е. это последовательно-параллельная схема. Первые три лампы (B ₁, B ₂ и B ₃) подключены параллельно, а переключатели (S ₁, S ₂ и S ₃) подключены последовательно соответственно.B ₇, B ₈, B ₉ и B ₁₀ соединены последовательно друг с другом, в то время как они параллельны первым трем лампочкам (B ₁, B ₂ и B ₃) в то время как переключатели (S5 и S6) подключены параллельно к лампе (B ₁₀). Кроме того, лампы (B ₄, B ₅ и B ₆) и выключатель (S ₇) включены последовательно друг с другом, в то время как они параллельны (B ₁, B ₂ и B ₃) и так далее.
Поскольку схема является комбинацией последовательной и параллельной, мы не можем упростить ток, напряжение, сопротивление и мощность с помощью простого закона Ома. Мы должны применить различные теоремы, такие как теоремы Нортона, Тевенина, теоремы о максимальной передаче мощности и т. Д., Или упростим схему в основных последовательных и параллельных схемах, чтобы найти все эти величины.
Наиболее распространенная в настоящее время установка бытовой электропроводки с использованием этого метода электропроводки.
Последовательная параллельная световая цепь и соединение
Сравнение последовательного и параллельного подключения
Ниже в данной таблице показаны основные различия между последовательным и параллельным подключением.
9 0707 Чтобы найти электрическую мощность (P)
S Нет Последовательная цепь Параллельная цепь
Ток (I) Ток одинаковый в каждой точке в последовательной цепи I16: 1 2 I ₂ = I ₃ =…. I _n
Ток в последовательной цепи складывается:
I ₁ + I ₂ + I ₃ +…. I _n
Напряжение (В) Напряжение складывается в последовательной цепи:
В ₁ + В ₂ + В ₃ +….V _n
Напряжения одинаковы в каждой точке параллельной цепи:
V ₁ = V ₂ = V ₃ =…. V _n
Сопротивление (R) и найти (R) Сопротивления складываются в последовательной цепи:
R ₁ + R ₂ + R ₃ +… R _{n =} R _eff = R _T
Сопротивление делится при увеличении нагрузки в цепи.
1 / R _T = 1 / R ₁ + 1 / R ₂ + 1 / R ₃… 1 / R _n
или
I = G ₁ + G ₂ + G ₃ +… G _n
Чтобы найти ток (I) I = V ₁ / R ₁ = V ₂ / R ₂ = V ₃ / R ₃ = V _n / R _n I = V ₁ / R ₁ + V ₂ / R ₂ + V ₃ / R ₃ + V _n / R _n
Для определения напряжения (В) V = I ₁ R ₁ + I ₂ R ₂ + I ₃ R ₃ +… I _n R _n V = I ₁ R ₁ = I ₂ R ₂ = I ₃ R ₃ =… I _n R _н
P = I ² R ₁ + I ² R ₂ +… I ² R _n
или
P = V ₁ ² / R ₁ + V ₂ ² / R ₂ +… V _n ^2/ R _n
P = V ² / R ₁ + V ² / R ₂ +… V ^2/ R _n
или
P = I ₁ ² R ₁ + I ₂ ² R ₂ +… I _n ² R _n
Правило делителя тока и напряжения В ₁ = В _T (R ₁ / R _T ), V ₂ = V _T (R ₂ / R _T) I ₁ = I _T (G ₁ / G _{T 900 17), I ₂ = I _T (G ₂ / G _T)}
Пути прохождения электрического тока Только один путь Два или несколько путей
Яркость лампы Диммер, если добавлено больше ламп (P = V x I) Ярче из-за того же напряжения
При обрыве цепи Вся цепь бесполезна Остальное цепь будет по-прежнему работать
Состояние батареи Медленная разрядка батареи (Ач-номинал батареи) Быстрая разрядка батареи (время работы батареи в А-ч и токи)
Приложения Используется для защиты цепи во время подключение предохранителей и автоматических выключателей последовательно с подключенными приборами Используется в большинстве бытовых электропроводок
Преимущества параллельного соединения по сравнению с последовательным соединением
Последовательное соединение — это соединение всех или отсутствующих схем.Это означает, что если одно из устройств выйдет из строя, все другие устройства также выйдут из строя, поэтому этот тип подключения хорош только тогда, когда мы хотим защитить устройство. Когда плавкий предохранитель сгорает, например, из-за высокого тока, тогда устройство подключается к нему. защита не будет повреждена, потому что ток больше не будет достигать ее. В то время как последовательное соединение является полным или нулевым, параллельное соединение дает вам возможность дать нагрузкам и приборам их индивидуальный переключатель. Параллельное соединение обеспечивает сопротивление протеканию тока по сравнению с последовательным соединением.
Недостатки последовательной схемы освещения
Резисторы сопротивлением 100 Ом и 150 Ом, подключенные параллельно, будут иметь меньшее влияние на электрический ток по сравнению с резисторами 50 Ом и 40 Ом, подключенными последовательно. В электронных устройствах параллельное соединение имеет первостепенное значение. Все элементы в блоке питания подключены параллельно. Параллельное соединение продлевает срок службы электроэнергии. Сами элементы имеют свое внутреннее сопротивление, поэтому, если они были подключены последовательно, некоторая часть энергии будет потеряна, преодолевая внутреннее сопротивление, поскольку его влияние выше, когда они соединены последовательно, чем когда параллельно.
Связанные сообщения:
Резисторы параллельно
Обзор
Резисторы в цепи могут быть подключены последовательно или параллельно. Общее сопротивление комбинации резисторов зависит как от их индивидуальных значений, так и от способа их подключения.
Параллельные резисторы
Сопротивления параллельны, когда каждый резистор подключен непосредственно к источнику напряжения путем соединения проводов с незначительным сопротивлением. Таким образом, к каждому резистору приложено полное напряжение источника.
Параллельные резисторы
Параллельное соединение резисторов.
Каждый резистор потребляет такой же ток, как если бы он был единственным резистором, подключенным к источнику напряжения. Это верно для схем в доме или квартире. Каждая розетка, подключенная к устройству («резистор»), может работать независимо, и ток не должен проходить через каждое устройство последовательно.
Закон Ома и параллельные резисторы
Каждый резистор в цепи имеет полное напряжение.Согласно закону Ома токи, протекающие через отдельные резисторы, равны $ I_1 = \ frac {V} {R_1} $, $ I_2 = \ frac {V} {R_2} $ и $ I_3 = \ frac {V} {R_3 } $. Сохранение заряда подразумевает, что полный ток является суммой этих токов:
Резисторы параллельные
Три резистора, подключенных параллельно к батарее, и эквивалентное одиночное или параллельное сопротивление.
$ I = I_1 + I_2 + I_3. $
Подстановка выражений для отдельных токов дает:
$ I = \ frac {V} {R_1} + \ frac {V} {R_2} + \ frac {V} {R_3} $
или
$ I = V (\ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3}) $
Это означает, что полное сопротивление в параллельной цепи равно сумме инверсии каждого отдельного сопротивления.Следовательно, для каждой цепи с числом $ n $ или параллельно подключенными резисторами
$ R_ {n \; (parallel)} = \ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3} … + \ frac {1} {R_n}. $
Это соотношение приводит к общему сопротивлению, которое меньше наименьшего из отдельных сопротивлений. Когда резисторы соединены параллельно, от источника течет больше тока, чем протекает для любого из них по отдельности, поэтому общее сопротивление ниже.
Каждый резистор, включенный параллельно, имеет одинаковое полное напряжение источника, приложенного к нему, но делит общий ток между ними.Примером может служить соединение двух лампочек в параллельную цепь с аккумулятором на 1,5 В. В последовательной цепи две лампочки будут вдвое менее тусклыми при подключении к одному источнику батареи. Однако, если бы две лампочки были подключены параллельно, они были бы столь же яркими, как если бы они были подключены к батарее по отдельности. Поскольку к обеим лампочкам подается одинаковое полное напряжение, батарея также разряжается быстрее, так как она, по сути, поставляет полную энергию обеим лампочкам.В последовательной цепи батарея будет работать столько же, сколько и с одной лампочкой, только тогда яркость будет разделена между лампочками.
4.1 Последовательные и параллельные резисторы
Последовательные резисторы
Когда резисторы включены последовательно? Резисторы включены последовательно всякий раз, когда поток заряда, называемый током, должен проходить через устройства последовательно. Например, если ток протекает через человека, держащего отвертку, в землю, тогда R1.R1. на рисунке 4.2 (a) может быть сопротивлением стержня отвертки, R2R2 сопротивлением ее ручки, R3R3 сопротивлением тела человека и R4R4 сопротивлением ее обуви.
На рис. 4.3 показаны резисторы, последовательно подключенные к источнику напряжения. Кажется разумным, что полное сопротивление является суммой отдельных сопротивлений, учитывая, что ток должен проходить через каждый резистор последовательно. Этот факт был бы преимуществом для человека, желающего избежать поражения электрическим током, который мог бы уменьшить ток, надев обувь на резиновой подошве с высоким сопротивлением.Это могло быть недостатком, если бы одно из сопротивлений было неисправным шнуром с высоким сопротивлением к прибору, который уменьшал бы рабочий ток.
Рисунок 4.3 Три резистора, подключенных последовательно к батарее (слева) и эквивалентному одиночному или последовательному сопротивлению (справа).
Чтобы убедиться, что последовательно соединенные сопротивления действительно складываются, давайте рассмотрим потерю электроэнергии, называемую падением напряжения, в каждом резисторе на рис. 4.3.
Согласно закону Ома падение напряжения V, V на резисторе при протекании через него тока рассчитывается по формуле V = IR, V = IR, где II равно току в амперах (A), а RR — это сопротивление в Ом Ом.Ω. Другой способ представить это: VV — это напряжение, необходимое для протекания тока II через сопротивление RR
.
Таким образом, падение напряжения на R1R1 равно V1 = IR1, V1 = IR1, что на R2R2 равно V2 = IR2, V2 = IR2, а на R3R3 равно V3 = IR3.V3 = IR3. Сумма этих напряжений равна выходному напряжению источника; то есть
4,1 В = V1 + V2 + V3. V = V1 + V2 + V3.
Это уравнение основано на сохранении энергии и сохранении заряда. Электрическая потенциальная энергия может быть описана уравнением PE = qV, PE = qV, где qq — электрический заряд, а VV — напряжение.Таким образом, энергия, подводимая источником, равна qV, qV, а энергия, рассеиваемая резисторами, равна
. 4.2 qV1 + qV2 + qV3. QV1 + qV2 + qV3.
Связи: законы сохранения
Вывод выражений для последовательного и параллельного сопротивления основан на законах сохранения энергии и сохранения заряда, которые утверждают, что общий заряд и полная энергия постоянны в любом процессе. Эти два закона непосредственно участвуют во всех электрических явлениях и будут многократно использоваться для объяснения как конкретных эффектов, так и общего поведения электричества.
Эти энергии должны быть равны, потому что в цепи нет другого источника и другого назначения для энергии. Таким образом, qV = qV1 + qV2 + qV3.qV = qV1 + qV2 + qV3. Заряд qq аннулируется, давая V = V1 + V2 + V3, V = V1 + V2 + V3, как указано. (Обратите внимание, что одинаковое количество заряда проходит через батарею и каждый резистор за заданный промежуток времени, поскольку нет емкости для хранения заряда, нет места для утечки заряда и заряд сохраняется.)
Теперь подстановка значений отдельных напряжений дает
4.3 V = IR1 + IR2 + IR3 = I (R1 + R2 + R3). V = IR1 + IR2 + IR3 = I (R1 + R2 + R3).
Обратите внимание, что для эквивалентного одиночного последовательного сопротивления Rs, Rs мы имеем
Это означает, что полное или эквивалентное последовательное сопротивление RsRs трех резисторов равно Rs = R1 + R2 + R3.Rs = R1 + R2 + R3.
Эта логика действительна в общем для любого количества резисторов, включенных последовательно; таким образом, полное сопротивление RsRs последовательного соединения составляет
4.5 Rs = R1 + R2 + R3 + …, Rs = R1 + R2 + R3 + …,
, как предлагается. Поскольку весь ток должен проходить через каждый резистор, он испытывает сопротивление каждого, а последовательно соединенные сопротивления просто складываются.
Пример 4.1 Расчет сопротивления, тока, падения напряжения и рассеиваемой мощности: анализ последовательной цепи
Предположим, что выходное напряжение батареи на рисунке 4.3 составляет 12,0 В и 12,0 В, а сопротивления равны R1 = 1,00 Ом, R1 = 1,00 Ом, R2 = 6,00 Ом, R2 = 6,00 Ом и R3 = 13,0 Ом. R3 = 13,0 Ом. . а) Каково полное сопротивление? (б) Найдите ток. (c) Рассчитайте падение напряжения на каждом резисторе и покажите, что в сумме они равны выходному напряжению источника. (d) Рассчитайте мощность, рассеиваемую каждым резистором.(e) Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами.
Стратегия и решение для (а)
Общее сопротивление — это просто сумма отдельных сопротивлений, определяемая уравнением
. 4,6 Rs = R1 + R2 + R3 = 1,00 Ом + 6,00 Ом + 13,0 Ом = 20,0 Ом. Rs = R1 + R2 + R3 = 1,00 Ом + 6,00 Ом + 13,0 Ом = 20,0 Ом.
Стратегия и решение для (b)
Ток определяется по закону Ома, V = IR.V = IR. Ввод значения приложенного напряжения и общего сопротивления дает ток для цепи.
4,7 I = VRs = 12,0 В 20,0 Ом = 0,600 AI = VRs = 12,0 В 20,0 Ом = 0,600 A
Стратегия и решение для (c)
Напряжение — или падение IRIR — на резисторе определяется законом Ома. Ввод тока и значения первого сопротивления дает
. 4,8 В1 = IR1 = (0,600 А) (1,0 Ом) = 0,600 В. V1 = IR1 = (0,600 А) (1,0 Ом) = 0,600 В.
Аналогично
4,9 В2 = IR2 = (0,600 А) (6,0 Ом) = 3,60 В V2 = IR2 = (0,600 А) (6,0 Ом) = 3,60 В
и
4,10 V3 = IR3 = (0,600 A) (13,0 Ом) = 7,80 В. V3 = IR3 = (0,600 A) (13.0 Ом) = 7,80 В.
Обсуждение для (c)
Три капли IRIR в сумме дают 12,0 В, 12,0 В, как и предполагалось.
4,11 V1 + V2 + V3 = (0,600 + 3,60 + 7,80) V = 12,0 VV1 + V2 + V3 = (0,600 + 3,60 + 7,80) V = 12,0 В
Стратегия и решение для (d)
Самый простой способ рассчитать мощность в ваттах (Вт), рассеиваемую резистором в цепи постоянного тока, — это использовать закон Джоуля, P = IV, P = IV, где PP — электрическая мощность. В этом случае через каждый резистор протекает одинаковый полный ток. Подставляя закон Ома V = IRV = IR в закон Джоуля, мы получаем мощность, рассеиваемую первым резистором, как
4.12 P1 = I2R1 = (0,600 A) 2 (1,00 Ом) = 0,360 Вт. P1 = I2R1 = (0,600 A) 2 (1,00 Ом) = 0,360 Вт.
Аналогично
4,13 P2 = I2R2 = (0,600 A) 2 (6,00 Ом) = 2,16 WP2 = I2R2 = (0,600 A) 2 (6,00 Ом) = 2,16 Вт
и
4,14 P3 = I2R3 = (0,600 A) 2 (13,0 Ом) = 4,68 Вт. P3 = I2R3 = (0,600 A) 2 (13,0 Ом) = 4,68 Вт.
Обсуждение для (д)
Мощность также можно рассчитать, используя P = IVP = IV или P = V2R, P = V2R, где VV — это падение напряжения на резисторе (а не полное напряжение источника). Будут получены те же значения.
Стратегия и решение для (e)
Самый простой способ рассчитать выходную мощность источника — использовать P = IV, P = IV, где VV — напряжение источника. Это дает
4,15 P = (0,600 A) (12,0 В) = 7,20 Вт. P = (0,600 A) (12,0 В) = 7,20 Вт.
Обсуждение для (e)
По совпадению обратите внимание, что общая мощность, рассеиваемая резисторами, также составляет 7,20 Вт, что соответствует мощности, выдаваемой источником. То есть
4,16 P1 + P2 + P3 = (0,360 + 2,16 + 4,68) W = 7.20 W. P1 + P2 + P3 = (0,360 + 2,16 + 4,68) W = 7,20 Вт.
Мощность — это энергия в единицу времени (ватт), поэтому для сохранения энергии требуется, чтобы выходная мощность источника была равна общей мощности, рассеиваемой резисторами.
Основные характеристики резисторов серии
Последовательные сопротивления складываются Rs = R1 + R2 + R3 + …. Rs = R1 + R2 + R3 + ….
Один и тот же ток последовательно проходит через каждый резистор.
Отдельные последовательно включенные резисторы не получают полное напряжение источника, а скорее делят его.
L4: Последовательные и параллельные резисторы
Содержание
Эквивалентные сопротивления
Последовательные резисторы
Последовательный пример 1: Решить для тока
Шаг 1: Решить для общего сопротивления
Шаг 2: Решить для тока I с эквивалентом сопротивление
Пример серии 2: Решить для тока
Проверить нашу работу в симуляторе цепи
Делители напряжения
Пример 1: Решить для напряжения на VB
Шаг 1: Решить для тока через схема
Шаг 2: Рассчитайте падение напряжения на резисторах
Шаг 3: Теперь вычислите VB
Шаблон делителя напряжения
Получение уравнения делителя напряжения
Параллельные резисторы
Параллельный пример 1: Решите параллельный пример 1: Решите \ (I_ {Total} \)
Шаг 1. Обратите внимание, что \ (I_ {Total} \) разбивает int o ветви
Шаг 2: Определите и назовите узлы
Шаг 3: Определите \ (V_A \)
Шаг 4: Решите для \ (I_1 \) и \ (I_2 \)
Шаг 5: Наконец, решите для \ (I_ {Total} \)
Шаг 6: Используйте эквивалентное сопротивление для проверки нашей работы
Проверьте нашу работу в симуляторе цепей
Activity
Ресурсы
Следующий урок
По закону Ома На уроке мы проанализировали относительно простые схемы с одним резистором.Эти схемы помогли нам заложить основу и концептуальное понимание закона Ома и того, как его применять; однако большинство схем не так просты.
В этом уроке мы собираемся распространить закон Ома на более сложные схемы: резисторы серии и резисторы параллельно . Вкратце:
Последовательные резисторы делят напряжение и являются одной из наиболее распространенных (и полезных) схемотехнических схем при работе с микроконтроллерами и резистивными датчиками, такими как потенциометры, силовые резисторы и фотоэлементы.
Параллельно подключенные резисторы делят ток (и больше тока проходит по цепям с меньшим сопротивлением). Параллельные схемы полезны, например, для питания нескольких светодиодов.
Рисунок. Пример резисторов серии (слева) и параллельных резисторов (справа). Изображения сделаны в PowerPoint.
Эквивалентные сопротивления
Используя законы Кирхгофа для цепей, мы можем получить «эквивалентные» сопротивления для последовательных и параллельных цепей.
Для последовательных резисторов суммируем сопротивления, чтобы найти совокупное сопротивление \ (R_ {эквивалент} \):
\ [R_ {эквивалент} = R_ {1} + R_ {2} + … + R_ {N-1 } + R_ {N} \]
Для параллельных резисторов все немного сложнее:
\ [R_ {эквивалент} = \ frac {1} {\ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + … + \ frac {1} {R_ {N-1}} + \ frac {1} {R_ {N}}} \]
Да, уравнение параллельного сопротивления немного загадочно но вы можете получить его самостоятельно (или даже забыть все вместе), если знаете закон Ома и законы Кирхгофа.
Для нас наиболее важной и полезной концепцией является то, что резисторы серии делят напряжение (мы будем использовать это позже в схемах микроконтроллера) и что параллельных резисторов делят ток (с больше тока, протекающего через ветви с меньшим сопротивлением). Изображение ниже пытается кратко объяснить это.
Рисунок. Обзор того, как работают резисторы серии (ток одинаков на каждом резисторе, но напряжение делится на ) и как работают параллельные резисторы (напряжение одинаково на каждом резисторе, но ток делится на ).Найдите минутку, чтобы изучить и понять, почему это может быть. Щелкните изображение правой кнопкой мыши и выберите «Открыть в новой вкладке», чтобы увеличить. Изображение сделано в PowerPoint.
И хотя способность вручную понимать и анализировать схему важна для физических вычислений, если вы запутаетесь, вы всегда можете использовать симулятор схем, например CircuitJS.
Резисторы серии
Резисторы последовательно подключаются по очереди: голова к хвосту.
Рисунок. Компоненты расположены последовательно, если они соединены встык (или конец к концу) в последовательности, как указано выше.Изображение слева из Академии Хана. Изображение сделано в PowerPoint.
Из закона Ома мы знаем, что на резисторах падает напряжение (действительно, падение напряжения \ (V_ {R} \) на резисторе \ (R \) равно \ (V_ {R} = I * R \)) . Таким образом, несколько резисторов «в ряд» (последовательно) по будут вызывать падение напряжения, а величина этого падения пропорциональна резистору (большее сопротивление, большее падение напряжения).
Обычно, когда мы пытаемся проанализировать схему с несколькими конфигурациями резисторов (последовательными, параллельными или комбинациями), первым шагом является определение эквивалентного сопротивления .То есть, как мы можем объединить все сопротивление в цепи в одно значение (называемое \ (R_ {total} \) или \ (R_ {эквивалент} \)), которое позволяет нам применять закон Ома ко всей цепи. В случае расчета по току это будет \ (I = \ frac {V} {R_ {total}} \)
Итак, давайте попробуем!
Серия
, пример 1: Решить для тока
Давайте начнем с простейшей схемы последовательного резистора: батареи 9 В с последовательно включенными резисторами 100 Ом и 1 кОм.
Рисунок. Простая схема с двумя последовательными резисторами (100 Ом и 1 кОм) и батареей на 9 В. Сколько тока \ (I \) протекает по этой цепи?
Шаг 1: Найдите общее сопротивление
Первый шаг — вычислить общее сопротивление в нашей цепи. Мы знаем, что мы суммируем сопротивления последовательно, поэтому: \ (R_ {Total} = R_ {1} + R_ {2} \ Rightarrow 100Ω + 1000Ω \ Rightarrow 1100Ω \). Общее сопротивление составляет \ (1100 Ом \).
Рисунок. Чтобы найти эквивалентное сопротивление этой цепи (назовем это \ (R_ {Total} \)), мы можем объединить последовательные резисторы, суммируя их.
Шаг 2: Решите для тока I с эквивалентным сопротивлением
Теперь мы можем использовать это эквивалентное значение сопротивления \ (R_ {Total} \), чтобы найти ток \ (I \), используя закон Ома: \ (I = 9V / 1100Ω \ Rightarrow 0.0082A \ Rightarrow 8.2mA \)
Рис. Теперь мы решаем по току \ (I \) просто по закону Ома: \ (I = 9V / 1100Ω \ Rightarrow 8.2mA \)
Вот и все. Мы сделали это! Полный ток равен \ (I = 8,2 мА \).
Серия, пример 2: Решить для текущего
Чтобы укрепить понимание, давайте попробуем еще раз, но с тремя резисторами вместо двух.На этот раз \ (R_ {1} = 2,2 кОм \), \ (R_ {2} = 1 кОм \) и \ (R_ {3} = 470 Ом \).
Опять же, мы начинаем с нахождения \ (R_ {Total} \), что составляет:
\ [R_ {Total} = R_ {1} + R_ {2} + R_ {3} \\ R_ {Total} = 2200 Ом. + 1000Ω + 470Ω \\ R_ {Total} = 3670Ω \]
Затем мы можем использовать это эквивалентное значение сопротивления для определения тока \ (I \), который равен \ (I = \ frac {9V} {3670Ω} \ Rightarrow 0,0025 A \ Стрелка вправо 2,5 мА \).
Рисунок. На изображении выше мы вычисляем ток с тремя последовательными резисторами.Сначала просуммируйте сопротивления (потому что они включены последовательно), а затем используйте это совокупное сопротивление (\ (R_ {Total} \)), чтобы определить ток по закону Ома: \ (I = \ frac {V} {R_ {Total}} \ Rightarrow \ frac {9V} {3670Ω $} \ Rightarrow 2.5mA \)
Проверьте нашу работу в симуляторе схем
Мы можем проверить нашу работу в нашем любимом симуляторе схем, который вам нравится. 🙂
Я буду использовать открытый инструмент CircuitJS. Конкретная симуляция здесь.
Мы можем щелкнуть по проводам, чтобы волшебным образом показать, какой ток проходит по ним, или показать их электрический потенциал (напряжение) относительно земли.И, конечно же, вы увидите, что действительно \ (2,5 мА \) проходит по цепи. Что еще вы наблюдаете?
Хорошо, вспомните, как мы подчеркивали, что напряжения делятся на , или , на последовательно соединенных резисторах. Вы тоже это ясно видите! Напряжение составляет \ (9 В \) в верхнем узле, но падает на \ (5,4 В \) на резисторе \ (2,2 кОм \) до \ (3,6 В \), которое затем падает на \ (2,4 В \) в течение резистор \ (1 кОм \) оставляет только \ (1,2 В \) электрического потенциала, прежде чем окончательно упасть до \ (0 В \) или \ (GND \) на резисторе \ (470 Ом \).Мы поговорим об этом позже!
Рисунок. В этом видео показано моделирование CircuitJS базовой схемы с тремя последовательными резисторами. Здесь вы можете поиграть со схемой.
Делители напряжения
Представление о том, что резисторы серии делят напряжение , является критически важным понятием при работе с микроконтроллерами. Итак, это заслуживает отдельного внимания.
Главное, что нужно запомнить: падение напряжения на каждом резисторе (это всегда так, а не только в конфигурации последовательной цепи).Таким образом, между каждым резистором у нас есть разный электрический потенциал или напряжение. А поскольку микроконтроллеры «считывают» напряжение, а не ток, мы можем использовать это свойство для управления динамическим вводом в наш микроконтроллер!
Давайте рассмотрим несколько примеров.
Пример 1: Решить для напряжения на VB
С этой идеей падения напряжения на каждом резисторе, давайте посмотрим, как рассчитать напряжение в узле \ (V_ {B} \) относительно земли (и помните, что узел — это просто любая точка соединения с двумя или более соединениями в цепи).
Прежде чем продолжить наш пример, остановитесь и спросите себя: как бы вы рассчитали напряжение в \ (V_ {B} \)?
Шаг 1: Найдите ток в цепи
Как и раньше, первый шаг — найти ток в цепи. Мы делаем это снова, найдя эквивалентное сопротивление \ (R_ {Total} \) и используя закон Ома. Итак, \ (I = \ frac {V} {R_ {Total}} \ Rightarrow \ frac {9V} {250Ω} \ Rightarrow 36mA \).
Шаг 2: Расчет падения напряжения на резисторах
Теперь, когда мы знаем общий ток, протекающий по нашей цепи (\ (36 мА \)), мы можем использовать это для вычисления удельного падения напряжения на каждом резисторе.Назовем падение напряжения более \ (R_ {1} \): \ (V_ {1} \) и падение напряжения более \ (R_ {2} \): \ (V_ {2} \). И поскольку нас интересует вычисление напряжения, мы будем использовать эту формулировку закона Ома: \ (V = I * R \).
Таким образом:
\ [{V_1} = I * R_1 \ Rightarrow 0.0036A * 100Ω \ Rightarrow 3.6V \\ {V_2} = I * R_2 \ Rightarrow 0.0036A * 150Ω \ Rightarrow 5.4V \]
И так же Быстрая проверка нашей работы (и не вдаваясь в подробности), мы знаем из схем Кирхгофа, что \ (V_ {Total} = V_1 + V_2 \ Rightarrow 9V = 3.6 В + 5,4 В \ Стрелка вправо 9 В = 9 В \). Итак, пока все идет хорошо!
Шаг 3: Теперь вычислите VB
Теперь вычислить \ (V_B \) тривиально. Мы знаем, что \ (V_A = 9V \) и \ (R_1 \) вызывает падение напряжения \ (3.6V \). Итак, \ (V_B \) должен быть равен \ (9V — 3.6V \), что составляет 5,4V.
Схема делителя напряжения
Подобную конфигурацию с двумя резисторами мы называем делителем напряжения именно потому, что, как вы можете видеть, он делит напряжения.В этом случае мы использовали последовательно резисторы \ (100 Ом \) и \ (150 Ом \) для вывода \ (5,4 В \) на \ (V_B \).
Используя закон Ома, мы можем вывести уравнение делителя напряжения для \ (V_B \) в терминах входного напряжения (\ (V_A \)) в нашу сеть делителя напряжения и двух резисторов: верхнего резистора \ (R_1 \) и нижний резистор \ (R_2 \).
Это уравнение делителя напряжения, таким образом, выглядит следующим образом: \ (V_ {B} = V_ {A} * \ frac {R_2} {R_1 + R_2} \)
Или чаще записывается как \ (V_ {out} = V_ { in} * \ frac {R_2} {R_1 + R_2} \)
Рис. Схема и уравнение делителя напряжения. Изображение сделано в PowerPoint. См. Академию Хана для получения дополнительной информации.
Важно, что, как вы можете понять из уравнения, значение имеет , а не абсолютное сопротивление, а скорее отношение \ (R_1 \) к \ (R_2 \), которое контролирует \ (V_ {out} \). Таким образом, для целей деления напряжений , установка \ (R_1 = 100Ω \) и \ (R_2 = 100Ω \) будет такой же, как \ (R_1 = 2.2kΩ \) и \ (R_2 = 2.2kΩ \), они оба делят напряжения равномерно. Итак, \ (V_ {out} \) будет равно \ (4.5V \), если \ (V_ {in} = 9V \).
Однако величина тока между двумя цепями будет значительно отличаться от первой: \ (I = \ frac {9V} {200Ω} \ Rightarrow 45mA \) и второй: \ (I = \ frac {9V} {4.4kΩ} \ Rightarrow 2.0mA \).
Разве не было бы круто динамически управлять одним из этих значений резистора для вывода переменного напряжения на уровне \ (V_ {out} \)? Да! И это основа потенциометра, о котором мы узнаем на следующем уроке.
Получение уравнения делителя напряжения
Учитывая то, что вы изучаете о схемах, теперь у вас есть знания, чтобы вывести уравнение делителя напряжения или, по крайней мере, понять , как оно выводится из .Давайте взглянем!
Рисунок. Вывод уравнения делителя напряжения. См. Академию Хана для получения дополнительной информации.
Используя приведенный выше рисунок, давайте определим и запишем то, что мы знаем. Мы знаем, что падение напряжения на \ (R2 \) равно \ (V_ {out} \) (действительно, это одно и то же) и что \ (V_R2 = I * R2 \):
\ [V_ {out } = V_ {R2} = I * R2 \]
Мы также знаем, что \ (V_in \) равно \ (V_R1 + V_R2 \) с учетом закона Кирхгофа о напряжении.
\ [V_ {in} = V_ {R1} + V_ {R2} \]
Используя закон Ома, мы можем заменить \ (I * R1 \) на \ (V_ {R1} \) и \ (I * R2 \ ) для \ (V_ {R2} \).
\ [V_ {in} = I * R1 + I * R2 \]
Теперь переставим уравнение \ (V_ {in} \), используя алгебру:
\ [V_ {in} = I * (R1 + R2) \ Стрелка вправо I = \ frac {V_ {in}} {(R1 + R2)} \]
Возвращаясь к \ (V_ {out} = I * R2 \), мы можем заменить \ (I \), учитывая формулировку выше:
\ [V_ {out} = I * R2 = \ frac {V_ {in}} {(R1 + R2)} * R2 \]
Наконец, измените приведенное выше, чтобы получить популярное уравнение делителя напряжения:
\ [V_ {out } = V_ {in} * \ frac {R2} {(R1 + R2)} \]
Примечание: для выполнения этого уравнения делителя напряжения ток \ (I \), протекающий через \ (R_1 \), должен быть ( в основном) равным \ (R_2 \).То есть, если мы подключим ответвление к \ (V_ {out} \), как мы это делали ниже, тогда эта ветвь должна иметь очень высокое сопротивление, чтобы в эту ветвь «просачивался» очень небольшой ток. То есть \ (R_ {Load} \) должно быть больше, чем \ (R1 + R2 \). Однако в случае входов микроконтроллера это , к счастью, случай, к которому мы вернемся позже.
Рисунок. Уравнение делителя напряжения выполняется только тогда, когда \ (R_ {Load} \) велико, что будет, когда мы начнем использовать микроконтроллеры (которые считывают изменения уровней напряжения и имеют «высокий входной импеданс»)
Параллельные резисторы
Принимая во внимание Резисторы серии имеют одинаковый ток, но делят напряжение, * параллельные резисторы * имеют такое же напряжение, но делят ток.Компоненты, включенные параллельно, выглядят так:
Рис. Компоненты работают параллельно, если их голова совместно использует узел, а их хвост — общий узел. Изображение слева из Академии Хана. Изображение сделано в PowerPoint.
Параллельный пример 1: Решите для \ (I_ {Total} \)
В приведенной ниже схеме у нас есть два параллельных резистора \ (R_1 = 100 Ом \) и \ (R_2 = 1 кОм \). Давайте решим полный ток \ (I_ {Total} \) в цепи.
Шаг 1. Обратите внимание на то, что \ (I_ {Total} \) разбивается на ветви
Первое, что нужно признать, это то, что \ (I_ {Total} \) разбивается на две ветви.Назовем ток в этих двух ветвях \ (I_1 \) и \ (I_2 \). Из законов Кирхгофа мы знаем, что \ (I_ {Total} = I_1 + I_2 \). Это связано с сохранением энергии — в нашем контуре не теряются заряды (они просто текут вокруг и вокруг).
Шаг 2: Идентифицируйте и присвойте имя узлам
Также обратите внимание на то, что в нашей цепи только два узла . Мы можем пометить их как \ (Узел A \) и \ (Узел B \).
Шаг 3: Определите \ (V_A \)
Поскольку \ (Узел A \) напрямую подключен к положительной клемме батареи, он имеет электрический потенциал 9 В.Назовем это \ (V_A = 9V \). Точно так же \ (Узел B \) напрямую подключен к отрицательному выводу батареи, поэтому давайте назовем его \ (GND \) или \ (OV \).
Шаг 4: Решите для \ (I_1 \) и \ (I_2 \)
Используя закон Ома, теперь мы можем решить для \ (I_1 \) и \ (I_2 \), где: \ (I_1 = \ frac {V_A} {R_1} \) и \ (I_2 = \ frac {V_A} {R_2} \). Таким образом, \ (I_1 = \ frac {9V} {100Ω} \ Rightarrow 90mA \) и \ (I_2 = \ frac {9V} {1000Ω} \ Rightarrow 9mA \).
Остановитесь на мгновение.Подумайте об этих результатах. Имеют ли смысл концептуально?
Используя закон Ома, мы обнаружили, что через ветвь \ (I_2 \) протекает ток , в 10 раз превышающий , чем через ветвь \ (I_1 \). Действительно, это точно соответствует соотношению двух резисторов \ (R_1 \) к \ (R_2 \) — \ (R_2 \) на в 10 раз больше, чем на , чем \ (R_1 \), и, таким образом, будет ограничивать гораздо больший ток. Это имеет смысл: точно так же, как больше воды будет течь через ветвь с меньшим сопротивлением, также будет больше тока течь по пути с меньшим сопротивлением.
Шаг 5: Наконец, решите для \ (I_ {Total} \)
Наконец, мы можем использовать \ (I_ {Total} = I_1 + I_2 \) для решения \ (I_ {Total} \). В этом случае \ (I_ {Total} = 90 мА + 9 мА \ Rightarrow 99 мА \).
Шаг 6: Используйте эквивалентное сопротивление для проверки нашей работы
Помните, как мы ввели уравнение для эквивалентного сопротивления в параллельных цепях резисторов? Уравнение:
\ [R_ {эквивалент} = \ frac {1} {\ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + … + \ frac {1 } {R_ {N-1}} + \ frac {1} {R_ {N}}} \]
Кстати, если вам интересно узнать о его происхождении, посмотрите этот урок Khan Academy — но, вкратце, вы можно вывести его из закона Ома (и шагов, которые мы выполнили выше).
Мы можем использовать это уравнение для более быстрого решения для \ (I_ {Total} \), которое равно \ (I_ {Total} = \ frac {V_A} {R_ {equal}} \).
Мы знаем, что \ ({R_ {equal} = \ frac {1} {\ frac {1} {100Ω} + \ frac {1} {1kΩ}}} \ Rightarrow 90.9Ω \)
Таким образом, \ ( I_ {Total} = \ frac {9V} {90.91Ω} \ Rightarrow 99mA \).
Проверить нашу работу на симуляторе схем
Мы также можем проверить нашу работу на симуляторе схем. Я построил такую же схему в CircuitJS, которую вы можете просмотреть здесь.
Соответствует ли визуализация вашим ожиданиям?
Рисунок. В этом видео показано моделирование CircuitJS базовой параллельной схемы с двумя резисторами. Здесь вы можете поиграть со схемой.
Activity
Придумайте две цепи последовательных резисторов и две параллельные цепи резисторов. Используя то, что вы узнали, вручную решите для текущий в каждой цепи (карандаш + бумага или в цифровом виде). Покажите свою пошаговую работу. Проверьте свою работу, построив симуляцию в CircuitJS.
В свои журналы прототипирования включите эскиз схемы (может быть изображение смартфона, состоящее из бумаги + карандаша), вашу ручную работу, которую нужно решить для текущего \ (I \) (опять же, может быть бумага + карандаш), и снимок экрана. схемы CircuitJS вместе с прямой ссылкой.(Помните, что вы можете создать ссылку CircuitJS, выбрав «Файл» -> «Экспортировать как ссылку»).
Ресурсы
Следующий урок
В следующем уроке мы узнаем больше о резисторах, о том, как они сделаны, как их использовать, как они характеризуются и как рассчитать их рассеиваемую мощность.
Предыдущая: Схема Следующая: Резисторы
Все материалы с открытым исходным кодом созданы лабораторией Makeability Lab и профессором Джоном Э.

S Нет	Последовательная цепь	Параллельная цепь
Ток (I)	Ток одинаковый в каждой точке в последовательной цепи I16: 1 2 I ₂ = I ₃ =…. I _n	Ток в последовательной цепи складывается: I ₁ + I ₂ + I ₃ +…. I _n
Напряжение (В)	Напряжение складывается в последовательной цепи: В ₁ + В ₂ + В ₃ +….V _n	Напряжения одинаковы в каждой точке параллельной цепи: V ₁ = V ₂ = V ₃ =…. V _n
Сопротивление (R) и найти (R)	Сопротивления складываются в последовательной цепи: R ₁ + R ₂ + R ₃ +… R _{n =} R _eff = R _T	Сопротивление делится при увеличении нагрузки в цепи. 1 / R _T = 1 / R ₁ + 1 / R ₂ + 1 / R ₃… 1 / R _n или I = G ₁ + G ₂ + G ₃ +… G _n
Чтобы найти ток (I)	I = V ₁ / R ₁ = V ₂ / R ₂ = V ₃ / R ₃ = V _n / R _n	I = V ₁ / R ₁ + V ₂ / R ₂ + V ₃ / R ₃ + V _n / R _n
Для определения напряжения (В)	V = I ₁ R ₁ + I ₂ R ₂ + I ₃ R ₃ +… I _n R _n	V = I ₁ R ₁ = I ₂ R ₂ = I ₃ R ₃ =… I _n R _н
P = I ² R ₁ + I ² R ₂ +… I ² R _n или P = V ₁ ² / R ₁ + V ₂ ² / R ₂ +… V _n ^2/ R _n	P = V ² / R ₁ + V ² / R ₂ +… V ^2/ R _n или P = I ₁ ² R ₁ + I ₂ ² R ₂ +… I _n ² R _n
Правило делителя тока и напряжения	В ₁ = В _T (R ₁ / R _T ), V ₂ = V _T (R ₂ / R _T)	I ₁ = I _T (G ₁ / G _{T 900 17), I ₂ = I _T (G ₂ / G _T)}
Пути прохождения электрического тока	Только один путь	Два или несколько путей
Яркость лампы	Диммер, если добавлено больше ламп (P = V x I)	Ярче из-за того же напряжения
При обрыве цепи	Вся цепь бесполезна	Остальное цепь будет по-прежнему работать
Состояние батареи	Медленная разрядка батареи (Ач-номинал батареи)	Быстрая разрядка батареи (время работы батареи в А-ч и токи)
Приложения	Используется для защиты цепи во время подключение предохранителей и автоматических выключателей последовательно с подключенными приборами	Используется в большинстве бытовых электропроводок