Параллельное сопротивление расчет: Онлайн-калькулятор расчета последовательного и параллельного соединения резисторов — Мир Антенн

Содержание

Физическая формула расчета (определения) эквивалентного сопротивления в цепи

Если электрическая цепь содержит несколько резисторов, то для подсчёта её основных параметров (силы тока, напряжения, мощности) удобно все резистивные устройства заменить на одно эквивалентное сопротивление цепи. Только для него должно выполняться следующее требование: его сопротивление должно быть равным суммарному значению сопротивлений всех элементов, то есть показания амперметра и вольтметра в обычной схеме и в преобразованной не должны измениться. Такой подход к решению задач называется методом свёртывания цепи.

Метод свёртывания цепи

Внимание! Расчёт эквивалентного (общего или суммарного) сопротивления в случае последовательного или параллельного подключения выполняется по разным формулам.

Последовательное соединение элементов

В случае последовательного подключения все приборы соединяются последовательно друг с другом, а собранная цепь не имеет разветвлений.

При таком подключении сила тока, проходящая через каждый резистор, будет одинаковая, а общее падение напряжения складывается из суммарных падений напряжения на каждом из приборов.

Последовательное подключение приборов

Чтобы определить суммарное значение в этом случае, воспользуемся законом Ома, который записывается следующим образом:

I = U/R.

Из вышестоящего выражения получаем значение R:

R = U/I (1).

Поскольку при последовательном соединении:

I = I1 = I2 =…= IN (2),
U = U1 + U2 +…+ UN (3),

формула для расчёта эквивалентного сопротивления (Rобщ или Rэкв) из (1) – (3) будет иметь вид:

Rэкв = (U1 + U2 + …+ UN)/I,
Rэкв = R1 + R2 + … + RN (4).

Таким образом, если имеется N последовательно соединённых одинаковых элементов, то их можно заменить на одно устройство, у которого:

Rобщ = N·R (5).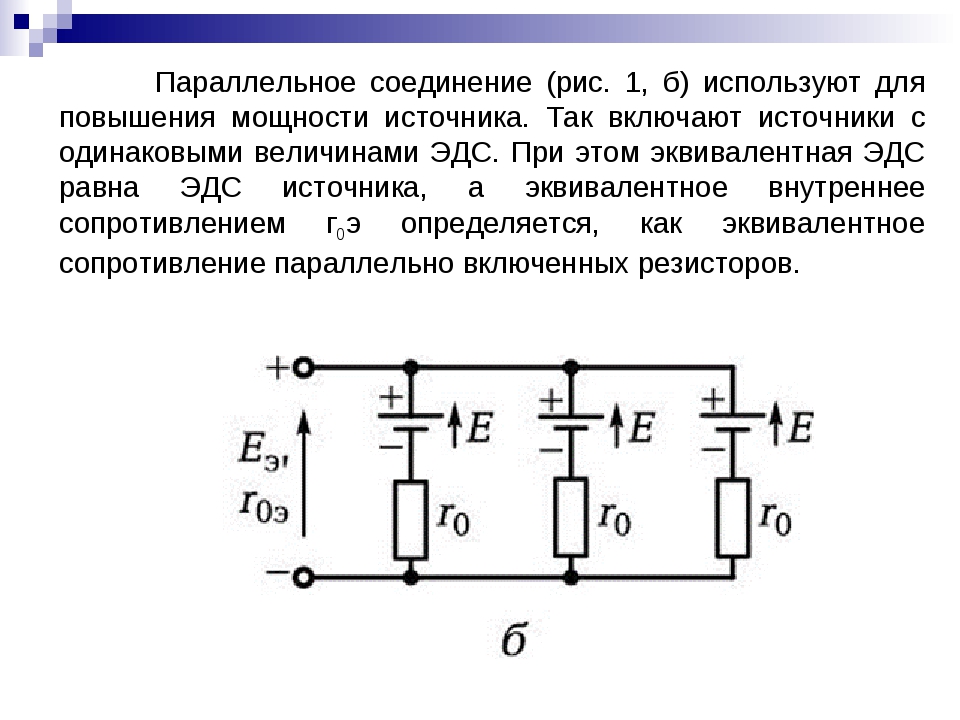

Параллельное соединение

При таком подключении входы от всех устройств соединены в одной точке, выходы – в другой точке. Эти точки в физике и электротехнике называются узлами. На электрических схемах узлы представляют собой места разветвления проводников и обозначаются точками.

Параллельное соединение

Расчет эквивалентного сопротивления также выполняем с помощью закона Ома.

В этом случае общее значение силы тока складывается из суммы сил токов, протекающих по каждой ветви, а величина падения напряжения для каждого устройства и общее напряжение одинаковые.

Если имеются N резистивных устройств, подключенных таким образом, то:

I = I1 + I2 + … + IN (6),

U = U1 = U2 = … = UN (7).

Из выражений (1), (6) и (7) имеем:

Rобщ = U/(I1 + I2 + …+ IN),
1/Rэкв = 1/R1 + 1/R2 +…+ 1/RN (8).

Если имеется N одинаковых резисторов, имеющих подключение данного типа, то формула (8) преобразуется следующим образом:

Rобщ = R · R / N·R = R / N (9).

Если соединены несколько катушек индуктивности, то их суммарное индуктивное сопротивление рассчитывается так же, как и для резисторов.

Расчёт при смешанном соединении устройств

В случае смешанного подключения присутствуют участки с последовательным и параллельным подключениями элементов.

При решении задачи используют метод сворачивания цепи (метод эквивалентных преобразований). Его используют для вычисления параметров в том случае, если есть один источник энергии.

Предположим, задана следующая задача. Электрическая схема (см. рис. ниже) состоит из 7 резисторов. Рассчитайте токи на всех резисторах, если имеются следующие исходные данные:

R1 = 1Ом,
R2 = 2Ом,
R3 = 3Ом,
R4 = 6Ом,
R5 = 9Ом,
R6 = 18Ом,
R7 = 2,8Ом,
U = 32В.

Электрическая схема

Из закона Ома имеем:

I = U/R,

где R – суммарное сопротивление всех приборов.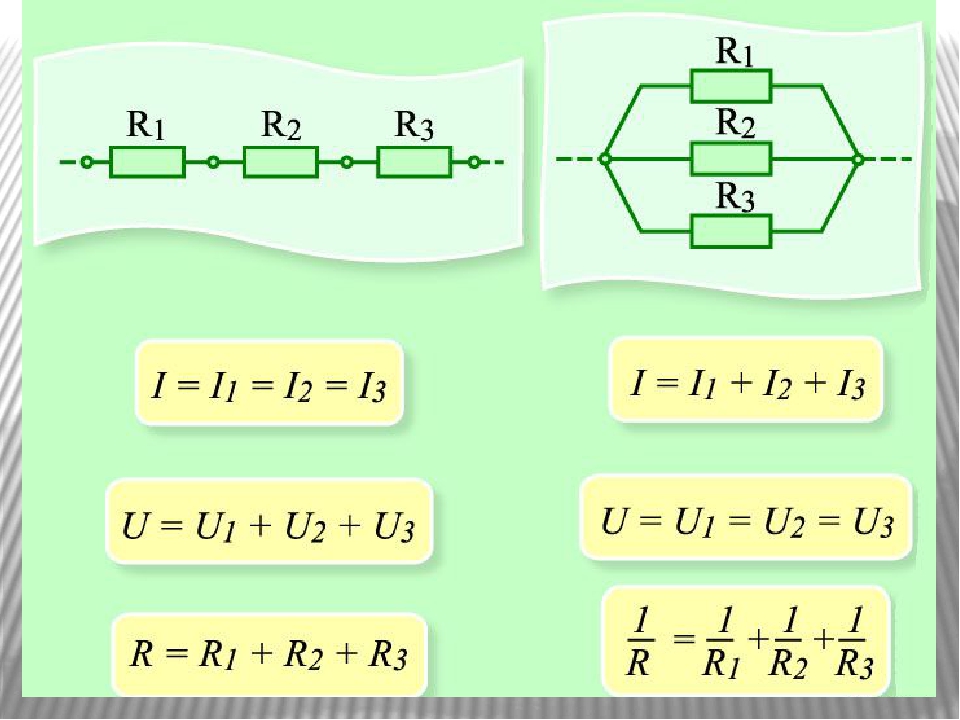

Его будем находить, воспользовавшись методом сворачивания цепи.

Элементы R2 и R3 подключены параллельно, поэтому их можно заменить на R2,3, величину которого можно рассчитать по формуле:

R2,3= R2·R3 / (R2+R3).

R4, R5 и R6 также включены параллельно, и их можно заменить на R4,5,6, которое вычисляется следующим образом:

1/R4,5,6 = 1/R4+1/R5+1/R6.

Таким образом, схему, изображённую на картинке выше, можно заменить на эквивалентную, в которой вместо резисторов R2, R3 и R4, R5, R6 используются R2,3 и R4,5,6.

Эквивалентная схема

Согласно картинке выше, в результате преобразований получаем последовательное соединение резисторов R1, R2,3, R4,5,6 и R7.

Rобщ может быть найдено по формуле:

Rобщ = R1 + R2,3 + R4,5,6 + R7.

Подставляем числовые значения и рассчитываем R для определённых участков:

R2.3 = 2Ом·3Ом / (2Ом + 3Ом) = 1,2Ом,
1/R4,5,6 = 1/6Ом + 1/9Ом + 1/18Ом = 1/3Ом,
R4,5,6 = 3Ом,
Rэкв = 1Ом + 1,2Ом + 3Ом + 2,8Ом= 8Ом.

Теперь, после того, как нашли Rэкв, можно вычислять значение I:

I = 32В / 8Ом = 4А.

После того, как мы получили величину общего тока, можно вычислить силу тока, протекающую на каждом участке.

Поскольку R1, R2,3, R4,5,6 и R7 соединены последовательно, то:

I1 = I2,3 = I4,5,6 = I7 = I = 4А.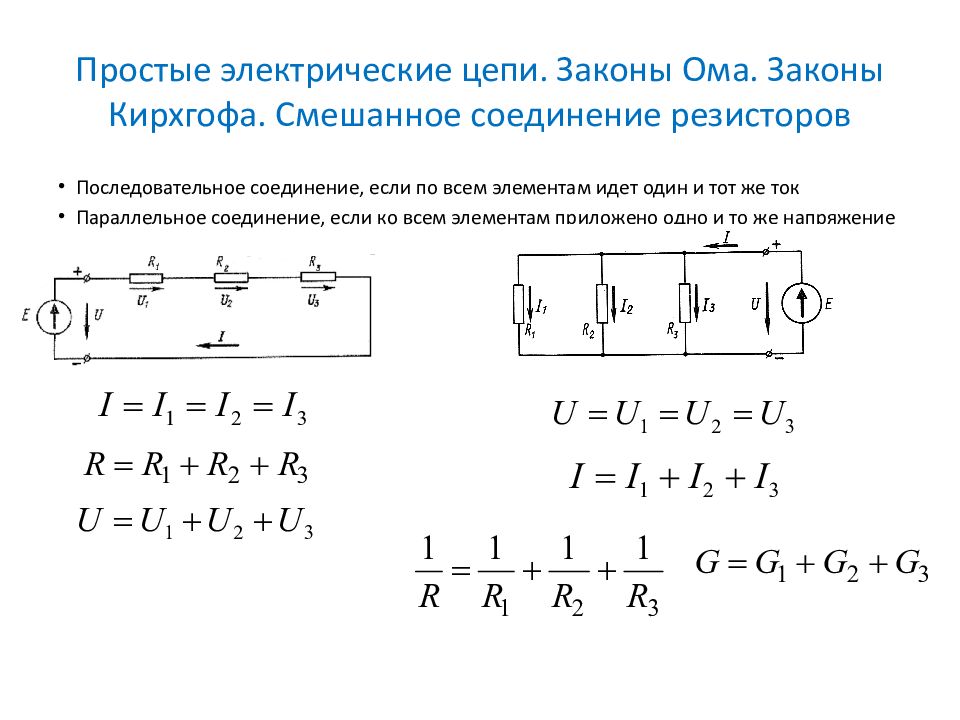

На участке R2,3 напряжение находим по формуле:

U2,3 = I2,3·R2,3,
U2,3 = 4А·1,2Ом = 4,8В.

Поскольку R2 и R3 подключены параллельно, то U2,3 = U2 = U3, следовательно:

I2 = U2 / R2,
I2 = 4,8В / 2Ом = 2,4А,
I3 = U3 / R3,
I3 = 4,8В / 3Ом = 1,6А.

Проверяем правильность решения:

I2,3 = I2 + I3,
I2,3 = 2,4А + 1,6А = 4А.

На участке R4,5,б напряжение также находим, исходя из закона Ома:

U4,5,6 = I4,5,6·R4,5,6,
U4,5,6 = 4А·3Ом = 12В.

Так как R4, R5, Rб подключены параллельно друг к другу, то:

U4,5,6 = U4 = U5 = U6 = 12В.

Вычисляем I4, I5, I6:

I4 = U4 / R4,
I4 = 12В / 6Ом = 2А,
I5 = U5 / R5,
I5 = 12В / 9Ом » 1,3А,
I6 = U6 / R6,
I5 = 12В / 18Ом » 0,7А.

Проверяем правильность решения:

I4,5,6 = 2А + 1,3А + 0,7А = 4А.

Чтобы автоматизировать выполнение расчётов эквивалентных значений для различных участков цепи, можно воспользоваться сервисами сети Интернет, которые предлагают на их сайтах выполнить онлайн вычисления нужных электрических характеристик. Сервис обычно имеет встроенную специальную программу – калькулятор, которая помогает быстро выполнить расчет сопротивления цепи любой сложности.

Таким образом, использование метода эквивалентных преобразований при расчёте смешанных соединений различных устройств позволяет упростить и ускорить выполнение вычислений основных электрических параметров.

Видео

Оцените статью:

Онлайн калькулятор расчета параллельного соединения резисторов

Соединение резисторов, при котором одноименные выводы каждого из элементов собираются в одну точку, называется параллельным.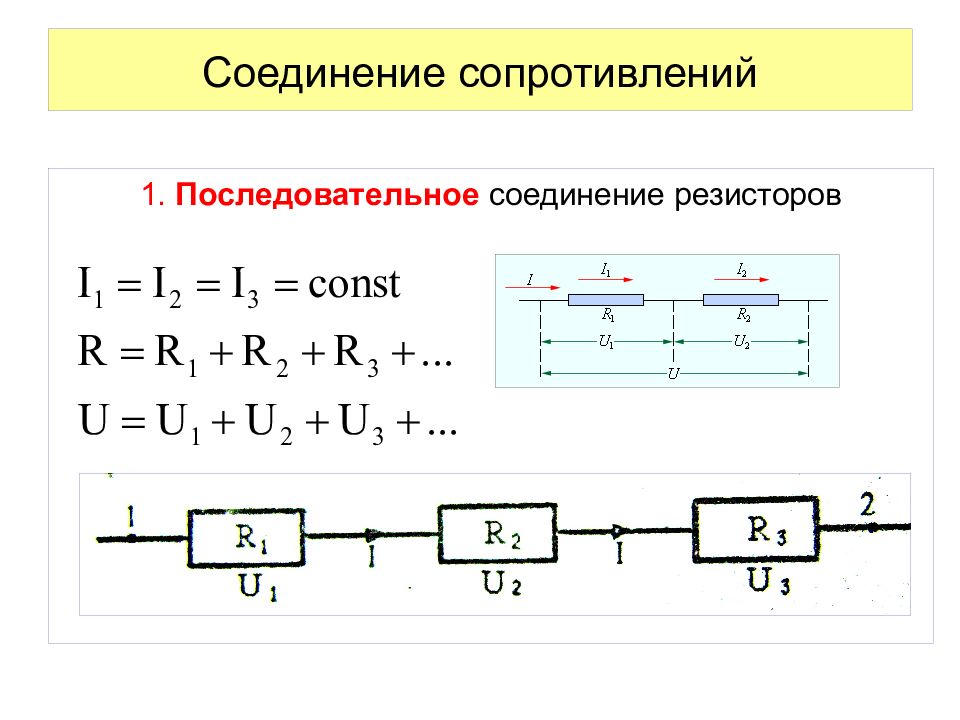 При этом ко всем резисторам подводится один и тот же потенциал, но величина тока через каждый из них будет отличаться. Для составления схем или при замене резисторов в уже существующих цепях важно знать их суммарное сопротивление, как показано на рисунке:

Параллельное соединение резисторов

Данный калькулятор позволяет рассчитать суммарное сопротивление параллельно соединенных резисторов с любым количеством элементов.

Для этого вам необходимо:

Указать в графе «количество резисторов» их число, в нашем примере их три;
После того, как вы укажите количество элементов, в поле ниже появится три окошка для ввода значения сопротивления каждого из элементов, к примеру, у вас резисторы сопротивлением 20, 30 и 60 Ом;

Далее нажмите кнопку «рассчитать» и в окошке «параллельное сопротивление в цепи» вы получите значение сопротивления в 10 Ом.

Чтобы рассчитать другую цепь или при подборе других элементов, нажмите кнопку «сбросить», чтобы обнулить значение параллельно включенных элементов калькулятора.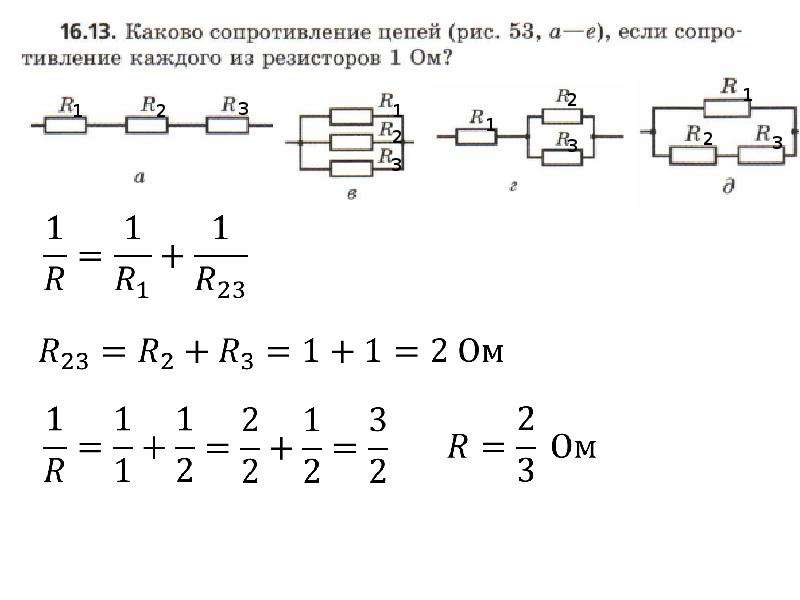

Для расчета суммарного сопротивления калькулятором используется такое соотношение:

Где,

R_сум— суммарное сопротивление параллельно соединенных элементов
R₁ — сопротивление первого резистора;
R₂ — сопротивление второго резистора;
R₃ — сопротивление третьего резистора;
R_n — сопротивление n-ого элемента.

Таким образом, в рассматриваемом примере параллельно включены три резистора, поэтому формула для определения суммарного сопротивления будет иметь такой вид:

Чтобы выразить величину суммарного сопротивления необходимо умножить обе половины уравнения на произведение сопротивлений всех трех резисторов. После этого перенести составляющие элементы по правилу пропорции и получить значение сопротивления:

Как видите, расчет параллельного сопротивления резисторов вручную требует немалых усилий, поэтому куда проще его сделать на нашем онлайн калькуляторе.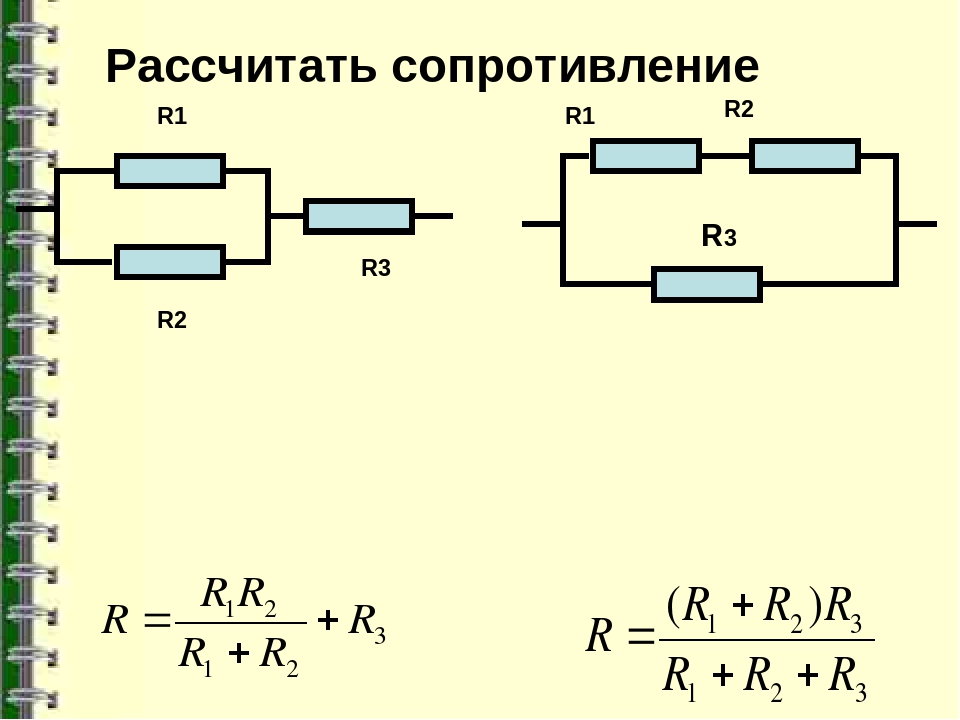

Обратите внимание, при наличии элементов с сопротивлением в разной размерности Ом, кОм, МОм, их необходимо привести к одной величине, прежде чем производить расчет. К примеру, в Ом и указывать в поле калькулятора для расчета параллельного соединения резисторов значение непосредственно в Омах.

Как считается параллельное сопротивление. Сопротивление при параллельном соединении: формула расчета

Каждый в этой жизни сталкивался с резисторами. Люди с гуманитарными профессиями, как и все, изучали в школе на уроках физики проводники электрического тока и закон Ома.

С резисторами также имеют дело студенты технических университетов и инженеры различных производственных предприятий. Перед всеми этими людьми, так или иначе, вставала задача расчёта электрической цепи при различных видах соединения резисторов. В данной статье речь пойдёт о расчёте физических параметров, характеризующих цепь.

Виды соединений

Резистор — пассивный элемент , присутствующий в каждой электрической цепи. Он предназначен для того, чтобы сопротивляться электрическому току. Существует два вида резисторов:

Постоянные.
Переменные.

Зачем же спаивать проводники друг с другом? Например, если для какой-то электрической цепи нужно определённое сопротивление. А среди номинальных показателей нужного нет. В таком случае необходимо подобрать элементы схемы с определёнными значениями сопротивления и соединить их. В зависимости от вида соединения и сопротивлений пассивных элементов мы получим какое-то определённое сопротивление цепи. Оно называется эквивалентным. Его значение зависит от вида спайки проводников. Существует

три вида соединения проводников:

Последовательное.
Параллельное.
Смешанное.

Значение эквивалентного сопротивления в цепи считается достаточно легко. Однако, если резисторов в схеме очень много, то лучше воспользоваться специальным калькулятором, который считает это значение. При ведении расчёта вручную, чтобы не допускать ошибок, необходимо проверять, ту ли формулу вы взяли.

Последовательное соединение проводников

В последовательной спайке резисторы идут как бы друг за другом. Значение эквивалентного сопротивления цепи равно сумме сопротивлений всех резисторов. Особенность схем с такой спайкой заключается в том, что

значение тока постоянно . Согласно закону Ома, напряжение в цепи равно произведению тока и сопротивления. Так как ток постоянен, то для вычисления напряжения на каждом резисторе, достаточно перемножить значения. После этого необходимо сложить напряжения всех резисторов, и тогда мы получим значение напряжения во всей цепи.

Расчёт очень простой. Так как с ним имеют дело в основном инженеры-разработчики, то для них не составит труда сосчитать всё вручную. Но если резисторов очень много, то проще воспользоваться специальным калькулятором.

Примером последовательного соединения проводников в быту является ёлочная гирлянда.

Параллельное соединение резисторов

При параллельном соединении проводников эквивалентное сопротивление в цепи считается по-другому.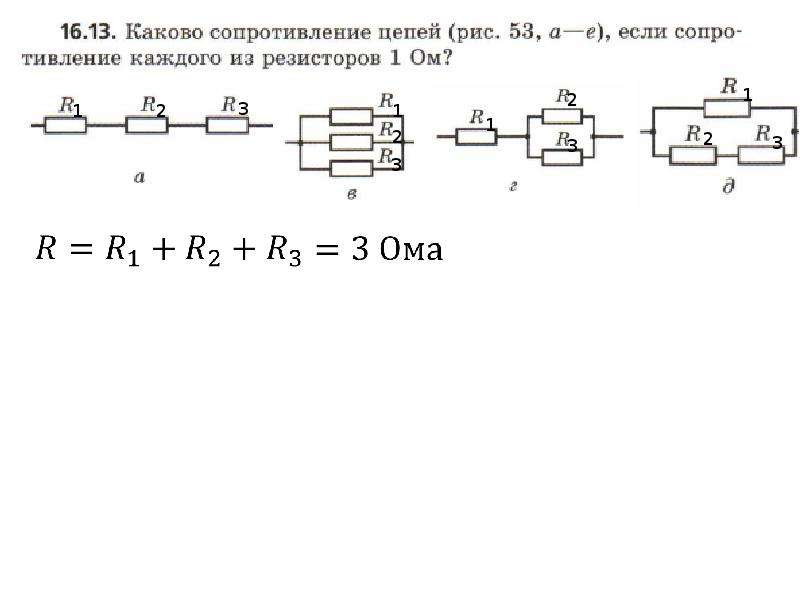 Немного сложнее, чем при последовательном.

Его значение в таких цепях равняется произведению сопротивлений всех резисторов, делённому на их сумму. А также есть и другие варианты этой формулы. Параллельное соединение резисторов всегда снижает эквивалентное сопротивление цепи. То есть, его значение всегда будет меньше, чем наибольшее значение какого-то из проводников.

В таких схемах значение напряжения постоянно . То есть значение напряжения во всей цепи равно значениям напряжений каждого из проводников. Оно задаётся источником напряжения.

Сила тока в цепи равна сумме всех токов, протекающих через все проводники. Значение силы тока, протекающего через проводник. равно отношению напряжения источника к сопротивлению этого проводника.

Примеры параллельного соединения проводников:

Освещение.
Розетки в квартире.
Производственное оборудование.

Для расчёта схем с параллельным соединением проводников лучше пользоваться специальным калькулятором.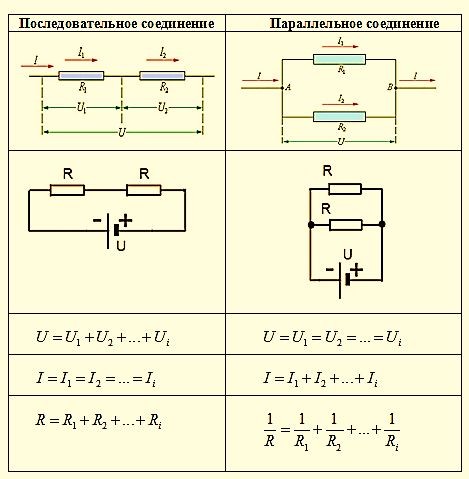

Если в схеме много резисторов, спаянных параллельно, то гораздо быстрее вы посчитаете эквивалентное сопротивление с помощью этого калькулятора.

Смешанное соединение проводников

Этот вид соединения состоит из каскадов резисторов . Например, у нас есть каскад из 10 проводников, соединённых последовательно, и после него идёт каскад из 10 проводников, соединённых параллельно. Эквивалентное сопротивление этой схемы будет равно сумме эквивалентных сопротивлений этих каскадов. То есть, по сути, здесь последовательное соединение двух каскадов проводников.

Многие инженеры занимаются оптимизацией различных схем. Её целью является уменьшение количества элементов в схеме за счёт подбора других, с подходящими значениями сопротивлений. Сложные схемы разбиваются на несколько небольших каскадов, ведь так гораздо проще вести расчёты.

Сейчас, в двадцать первом веке, инженерам стало гораздо проще работать. Ведь несколько десятилетий назад все расчёты производились вручную.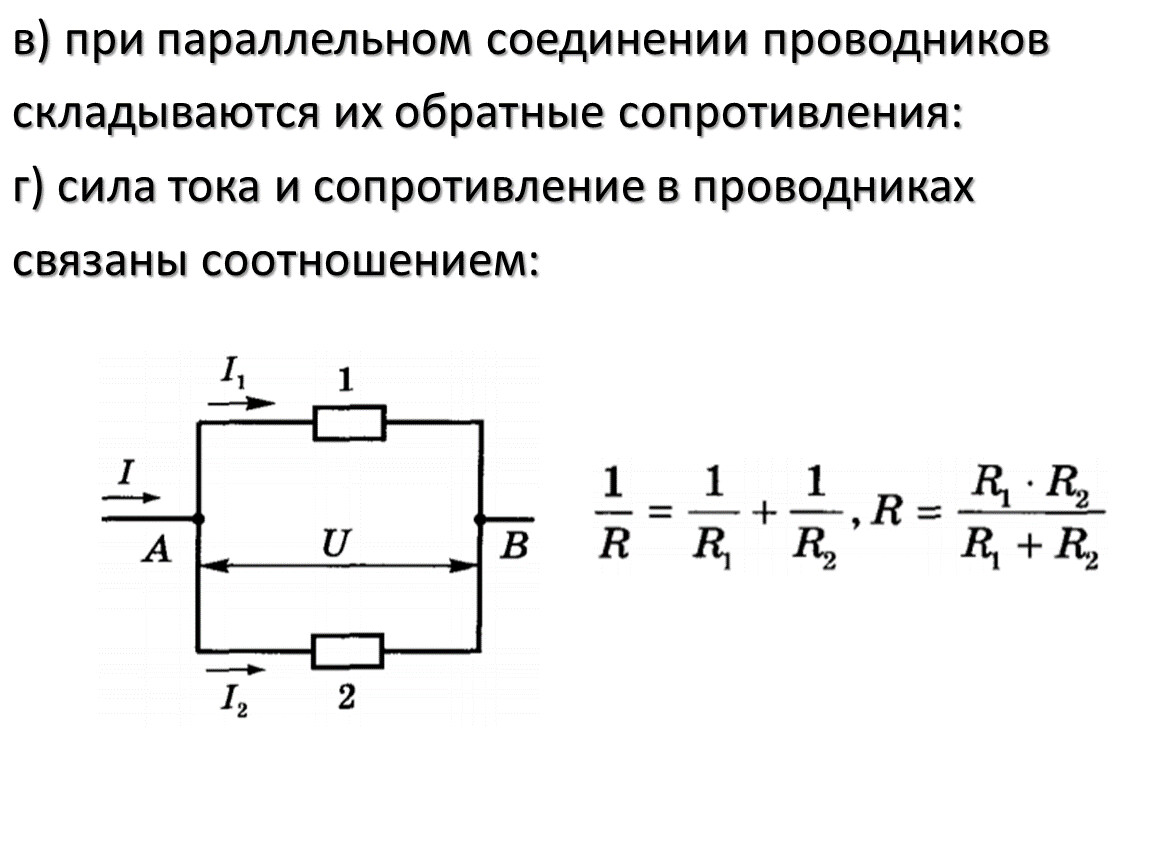

А сейчас программисты разработали специальный калькулятор для расчёта эквивалентного сопротивления цепи. В нём запрограммированы формулы, по которым ведутся расчёты.

В этом калькуляторе можно выбрать вид соединения, и потом ввести в специальные поля значения сопротивлений. Через несколько секунд вы уже увидите это значение.

Проверим справедливость показанных здесь формул на простом эксперименте.

Возьмём два резистора МЛТ-2 на 3 и 47 Ом и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.

Замер общего сопротивления при последовательном соединении

Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.

Измерение сопротивления при параллельном соединении

Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку.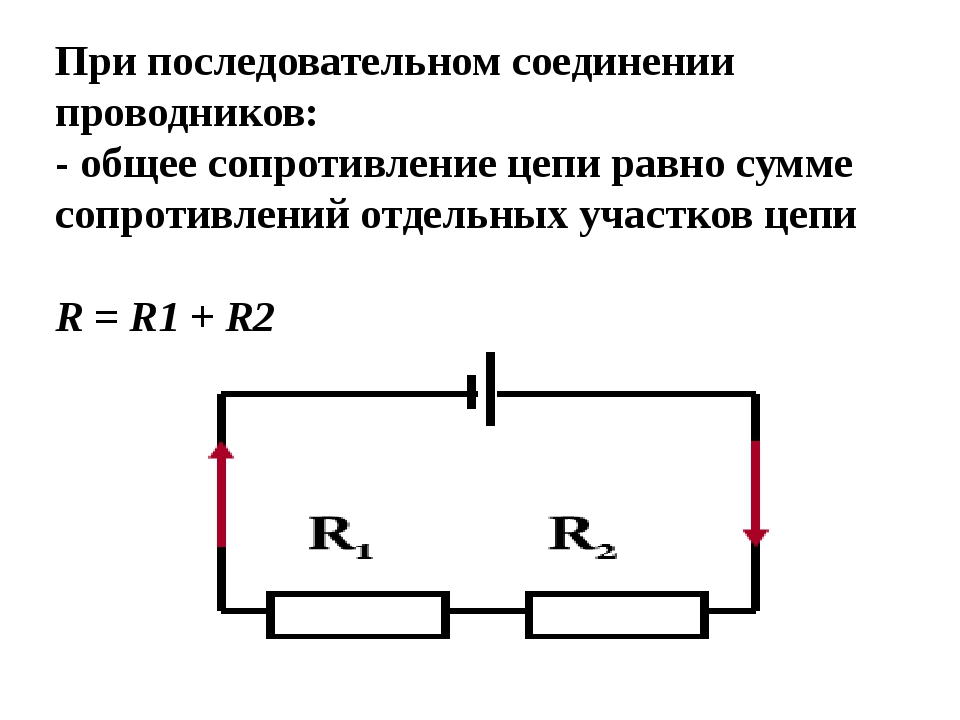

Отсюда вытекает ещё одно известное правило, которое можно применять на практике:

При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.

Что ещё нужно учитывать при соединении резисторов?

Во-первых, обязательно учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом и мощностью 1 Вт . Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?

Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А ), а сопротивление каждого из них равно 50 Ом , тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт . В результате на каждом из них выделится по

0,5 Вт мощности. В сумме это и будет тот самый 1 Вт .

Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.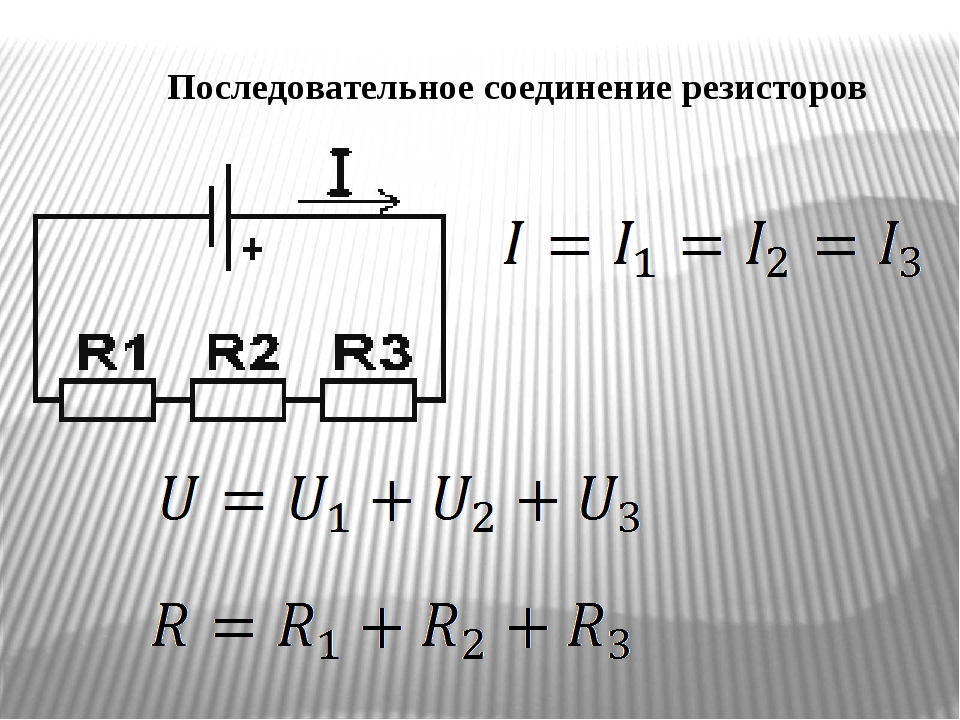

Подробнее о мощности рассеивания резистора читайте .

Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.

Последовательное соединение – это соединение двух или более резисторов в форме цепи, в которой каждый отдельный резистор соединяется с другим отдельным резистором только в одной точке.

Общее сопротивление R общ

При таком соединении, через все резисторы проходит один и тот же электрический ток. Чем больше элементов на данном участке электрической цепи, тем «труднее» току протекать через него. Следовательно, при последовательном соединении резисторов их общее сопротивление увеличивается, и оно равно сумме всех сопротивлений.

Напряжение при последовательном соединении

Напряжение при последовательном соединении распределяется на каждый резистор согласно закону Ома:

Т.е чем большее сопротивление резистора, тем большее напряжение на него падает.

Параллельное соединение – это соединение, при котором резисторы соединяются между собой обоими контактами. В результате к одной точке (электрическому узлу) может быть присоединено несколько резисторов.

Общее сопротивление R общ

При таком соединении, через каждый резистор потечет отдельный ток. Сила данного тока будет обратно пропорциональна сопротивлению резистора. В результате общая проводимость такого участка электрической цепи увеличивается, а общее сопротивление в свою очередь уменьшается.

Таким образом, при параллельном подсоединении резисторов с разным сопротивлением, общее сопротивление будет всегда меньше значения самого маленького отдельного резистора.

Формула общей проводимости при параллельном соединении резисторов:

Формула эквивалентного общего сопротивления при параллельном соединении резисторов:

Для двух одинаковых резисторов общее сопротивление будет равно половине одного отдельного резистора:

Соответственно, для n одинаковых резисторов общее сопротивление будет равно значению одного резистора, разделенного на n.

Напряжение при параллельном соединении

Напряжение между точками A и B является как общим напряжением для всего участка цепи, так и напряжением, падающим на каждый резистор в отдельности. Поэтому при параллельном соединении на все резисторы упадет одинаковое напряжение.

Через каждый резистор течет ток, сила которого обратно пропорциональна сопротивлению резистора. Для того чтобы узнать какой ток течет через определенный резистор, можно воспользоваться законом Ома:

Смешанным соединением называют участок цепи, где часть резисторов соединяются между собой последовательно, а часть параллельно. В свою очередь, смешанное соединение бывает последовательного и параллельного типов.

Общее сопротивление R общ

Цепь разбивают на участки с только пареллельным или только последовательным соединением.
Вычисляют общее сопротивление для каждого отдельного участка.
Вычисляют общее сопротивление для всей цепи смешанного соединения.

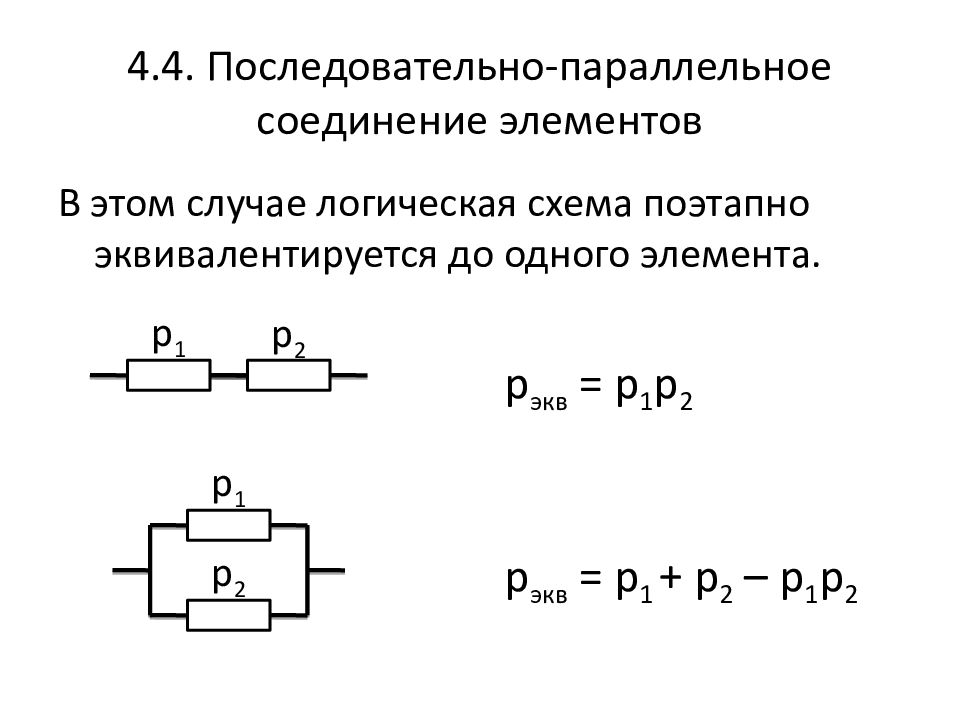
Также существует более быстрый способ расчета общего сопротивления для смешанного соединения. Можно, в соответствии схеме, сразу записывать формулу следующим образом:

Если резисторы соединяются последоватеьно — складывать.
Если резисторы соединяются параллельно — использовать условное обозначение «||».
Подставлять формулу для параллельного соединения где стоит символ «||».

Так это будет выглядеть для схемы 1:

Определение параллельного соединения

Параллельное соединение электрических элементов (проводников, сопротивлений, емкостей, индуктивностей) — это такое соединение, при котором подключенные элементы цепи имеют два общих узла подключения.

Другое определение: сопротивления подключены параллельно, если они подключены одно и той же паре узлов.

Графическое обозначение схемы параллельного соеднинения

На приведенном рисунке показана схема параллельное подключения сопротивлений R1, R2, R3, R4.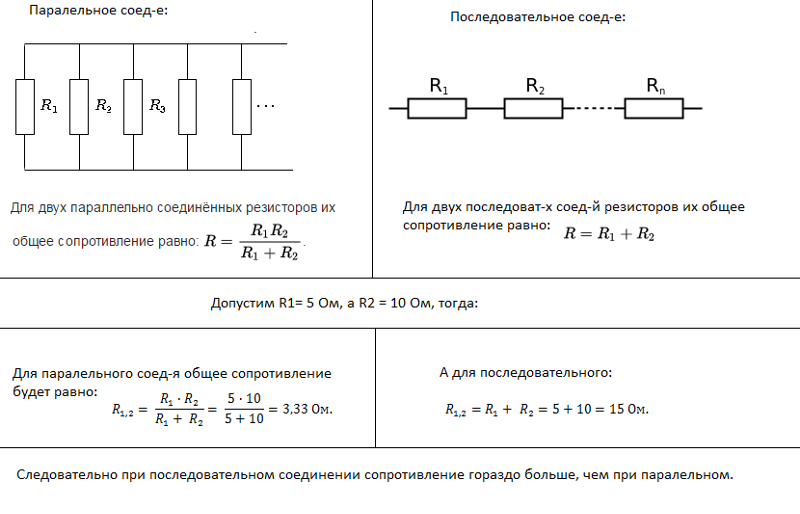 Из схемы видно, что все эти четыре сопротивления имеют две общие точки (узла подключения).

В электротехнике принято, но не строго требуется, рисовать провода горизонтально и вертикально. Поэтому эту же схему можно изобразить, как на рисунке ниже. Это тоже параллельное соединение тех же самых сопротивлений.

Формула для расчета параллельного соединения сопротивлений

При параллельном соединении обратная величина от эквивалентного сопротивления равна сумме обратных величин всех параллельно подключенных сопротивлений. Эквивалентная проводимость равна сумме всех параллельно подключенных проводимостей электрической схемы.

Для приведенной выше схемы эквивалентное сопротивление можно рассчитать по формуле:

В частном случае при подключении параллельно двух сопротивлений:

Эквивалентное сопротивление цепи определяется по формуле:

В случае подключения «n» одинаковых сопротивлений, эквивалентное сопротивление можно рассчитать по частной формуле:

Формулы для частного рассчета вытекают из основной формулы.

Формула для расчета параллельного соединения емкостей (конденсаторов)

При параллельном подключении емкостей (конденсаторов) эквивалентная емкость равна сумме параллельно подключенных емкостей:

Формула для расчета параллельного соединения индуктивностей

При параллельном подключении индуктивностей, эквивалентная индуктивность рассчитывается так же, как и эквивалентное сопротивление при параллельном соединении:

Необходимо обратить внимание, что в формуле не учтены взаимные индуктивности.

Пример свертывания параллельного сопротивления

Для участка электрической цепи необходимо найти параллельное соединение сопротивлений выполнить их преобразование до одного.

Из схемы видно, что параллельно подключены только R2 и R4. R3 не параллельно, т.к. одним концом оно подключено к E1. R1 — одним концом подключено к R5, а не к узлу. R5 — одним концом подключено к R1, а не к узлу. Можно так же говорить, что последовательное соединение сопротивлений R1 и R5 подключено параллельно с R2 и R4.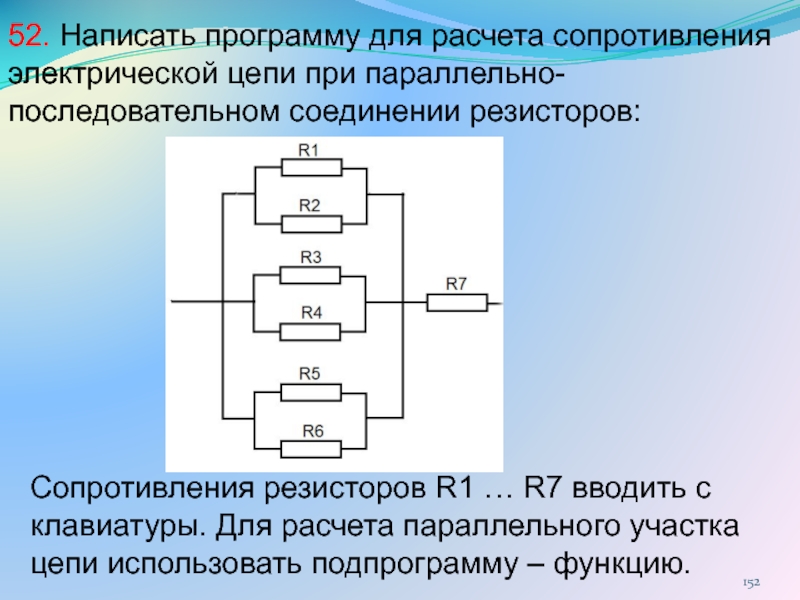

Ток при параллельном соединении

При параллельном соединении сопротивлений ток через каждое сопротивление в общем случае разный. Величина тока обратно пропорциональна величине сопротивления.

Напряжение при параллельном соединении

При параллельном соединении разность потенциалов между узлами, объединяющими элементы цепи, одинакова для всех элементов.

Применение параллельного соединения

1. В промышленности изготавливаются сопротивления определенных величин. Иногда необходимо получить значение сопротивления вне данных рядов. Для этого можно подключить несколько сопротивлений параллельно. Эквивалентное сопротивление всегда будет меньше самого большого номинала сопротивления.

2. Делитель токов.

На практике нередко встречается задача нахождения сопротивления проводников и резисторов при различных способах соединения. В статье рассмотрено, как рассчитывается сопротивление при и некоторые другие технические вопросы.

Сопротивление проводника

Все проводники имеют свойство препятствовать течению электрического тока, его принято называть электрическим сопротивлением R, оно измеряется в омах. Это основное свойство проводниковых материалов.

Для ведения электротехнических расчётов применяется удельное сопротивление — ρ Ом·м/мм 2 . Все металлы — хорошие проводники, наибольшее применение получили медь и алюминий, гораздо реже применяется железо. Лучший проводник — серебро, оно применяется в электротехнической и электронной промышленности. Широко распространены сплавы с высоким значением сопротивления.

При расчёте сопротивления используется известная из школьного курса физики формула:

R = ρ · l/S, S — площадь сечения; l — длина.

Если взять два проводника, то их сопротивление при параллельном соединении станет меньше из-за увеличения общего сечения.

и нагрев проводника

Для практических расчётов режимов работы проводников применяется понятие плотности тока — δ А/мм 2 , она вычисляется по формуле:

δ = I/S, I — ток, S — сечение.

Ток, проходя по проводнику, нагревает его. Чем больше δ, тем сильнее нагревается проводник. Для проводов и кабелей разработаны нормы допустимой плотности, которые приводятся в Для проводников нагревательных устройств существуют свои нормы плотности тока.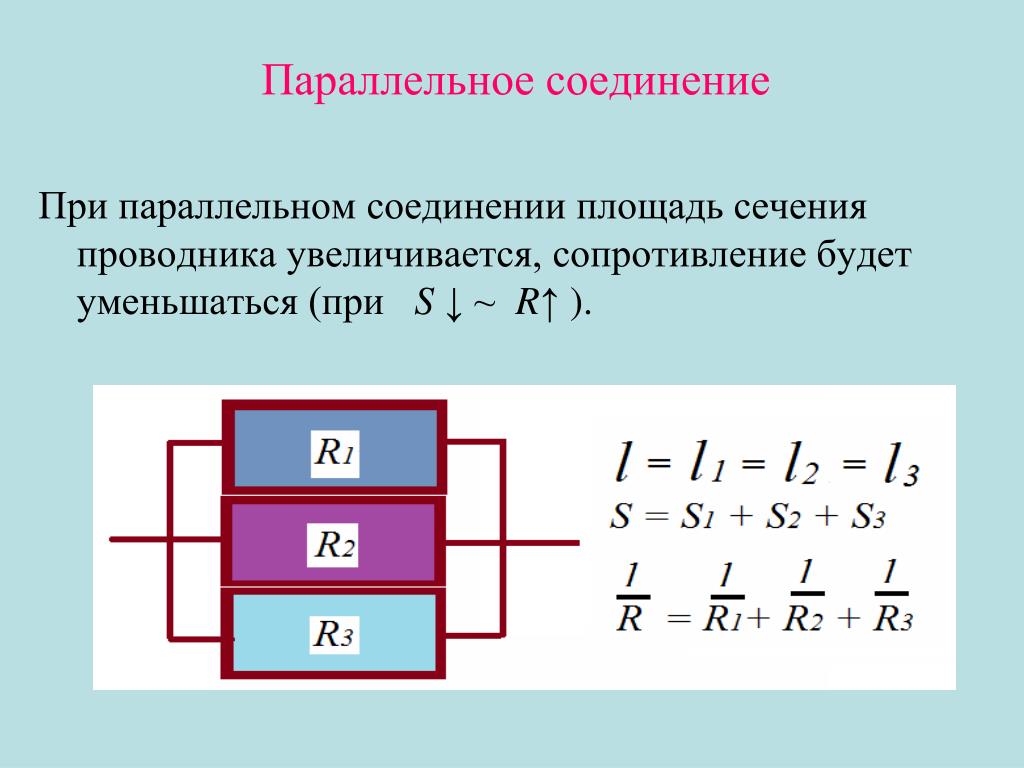

Если плотность δ выше допустимой, может произойти разрушение проводника, например, при перегреве кабеля у него разрушается изоляция.

Правилами регламентируется производить расчёт проводников на нагрев.

Способы соединения проводников

Любой проводник гораздо удобнее изображать на схемах как электрическое сопротивление R, тогда их легко читать и анализировать. Существует всего три способа соединения сопротивлений. Первый способ самый простой — последовательное соединение.

На фото видно, что полное сопротивление равно: R = R 1 + R 2 + R 3 .

Второй способ более сложный — параллельное соединение. Расчёт сопротивления при параллельном соединении выполняется поэтапно. Рассчитывается полная проводимость G = 1/R, а затем полное сопротивление R = 1/G.

Можно поступить и по-другому, прежде рассчитать общее сопротивление при R1 и R2, после этого повторить операцию и найти R.

Третий способ соединения наиболее сложный — смешанное соединение, то есть присутствуют все рассмотренные варианты. Схема приведена на фото.

Для расчёта этой схемы её следует упростить, для этого заменяют резисторы R2 и R3 одним R2,3. Получается несложная схема.

R2,3,4 = R2,3 · R4/(R2,3 + R4).

Схема становится ещё проще, в ней остаются резисторы, имеющие последовательное соединение. В более сложных ситуациях используется этот же метод преобразования.

Виды проводников

В электронной технике, при производстве проводники представляют собою тонкие полоски медной фольги. Ввиду малой длины сопротивление у них незначительно, им во многих случаях можно пренебречь. Для этих проводников сопротивление при параллельном соединении уменьшается вследствие увеличения сечения.

Большой раздел проводников представляют обмоточные провода. Они выпускаются разных диаметров — от 0,02 до 5,6 миллиметра. Для мощных трансформаторов и электродвигателей выпускаются медные шинки прямоугольного сечения. Иногда при ремонте заменяют провод большого диаметра на несколько параллельно соединённых меньшего размера.

Особый раздел проводников представляют провода и кабели, промышленность предоставляет широчайший выбор марок для самых различных нужд. Нередко приходится заменять один кабель на несколько, меньшего сечения. Причины этого бывают самые различные, например, кабель сечением 240 мм 2 очень трудно прокладывать по трассе с крутыми изгибами. Его заменяют на 2×120 мм 2 , и проблема решена.

Расчёт проводов на нагрев

Проводник нагревается протекающим током, если его температура превысит допустимую, наступает разрушение изоляции. ПУЭ предусматривает расчёт проводников на нагрев, исходными данными для него являются сила тока и условия внешней среды, в которой проложен проводник. По этим данным из таблиц в ПУЭ выбирается рекомендуемое проводника или кабеля).

На практике встречаются ситуации, когда нагрузка на действующий кабель сильно возросла. Существует два выхода ‒ заменить кабель на другой, это бывает дорого, или параллельно ему проложить ещё один, чтобы разгрузить основной кабель. В этом случае сопротивление проводника при параллельном соединении уменьшается, следовательно падает выделение тепла.

Чтобы правильно выбрать сечение второго кабеля, пользуются таблицами ПУЭ, важно при этом не ошибиться с определением его рабочего тока. В этой ситуации охлаждение кабелей будет даже лучше, чем у одного. Рекомендуется рассчитать сопротивление при параллельном соединении двух кабелей, чтобы точнее определить их тепловыделение.

Расчёт проводников на потерю напряжения

При расположении потребителя R н на большом расстоянии L от источника энергии U 1 возникает довольно большое на проводах линии. К потребителю R н поступает напряжение U 2 значительно ниже начального U 1 . Практически в качестве нагрузки выступает различное электрооборудование, подключаемое к линии параллельно.

Для решения проблемы производят расчет сопротивления при параллельном соединении всего оборудования, так находится сопротивление нагрузки R н. Далее следует определить сопротивление проводов линии.

R л = ρ · 2L/S,

Здесь S — сечение провода линии, мм 2 .

Последовательное и параллельное соединение резисторов

Последовательное соединение резисторов

Общее сопротивление R

_общ

Напряжение при последовательном соединении

Напряжение при последовательном соединении распределяется на каждый резистор согласно закону Ома:

Т.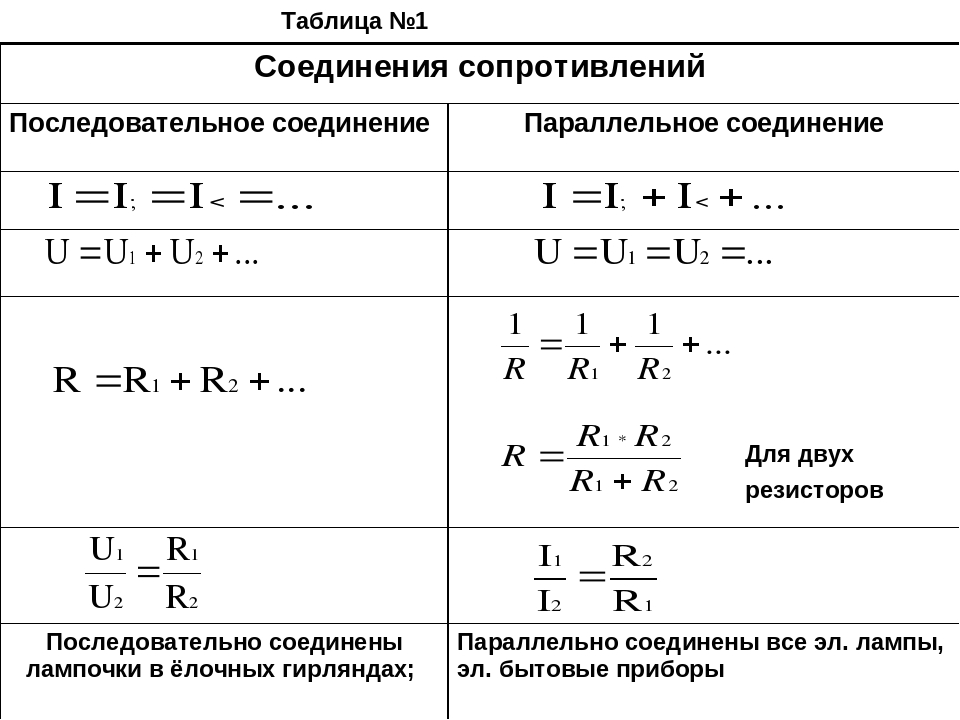 е чем большее сопротивление резистора, тем большее напряжение на него падает.

Параллельное соединение резисторов

Общее сопротивление R

_общ

Формула общей проводимости при параллельном соединении резисторов:

Формула эквивалентного общего сопротивления при параллельном соединении резисторов:

Для двух одинаковых резисторов общее сопротивление будет равно половине одного отдельного резистора:

Напряжение при параллельном соединении

Электрический ток при параллельном соединении

Смешанное соединение резисторов

Общее сопротивление R

_общ

Для того чтобы посчитать общее сопротивление смешанного соединения:

Цепь разбивают на участки с только пареллельным или только последовательным соединением.
Вычисляют общее сопротивление для каждого отдельного участка.
Вычисляют общее сопротивление для всей цепи смешанного соединения.

Так это будет выглядеть для схемы 1:

Если резисторы соединяются последоватеьно — складывать.
Если резисторы соединяются параллельно — использовать условное обозначение «||».
Подставлять формулу для параллельного соединения где стоит символ «||».

Так это будет выглядеть для схемы 1:

После подстановки формулы параллельного соединения вместо «||»:

последовательное, параллельное, смешанное соединение. Расчет сопротивления

электрика, сигнализация, видеонаблюдение, контроль доступа (СКУД), инженерно технические системы (ИТС)

Резисторы между собой могут быть соединены двумя основными способами: последовательно и параллельно. Смешанное соединение резисторов является их комбинацией.

Сочетания любых соединений резисторов можно привести к одному резистору, расчетом сопротивления которого (R) мы сейчас займемся.

ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ РЕЗИСТОРОВ

Давайте рассчитаем общее сопротивление такой цепи (рисунок 1). Для этого нам понадобится закон Ома — I=U/R и закон Кирхгофа — I=I₁+I₂+..In

С учетом этого имеем:

I=U/R
I₁=U/R₁
I₂=U/R₂
In=U/Rn
U/R=U/R₁+U/R₂+…U/Rn
1/R=1/R₁+1/R₂+…1/Rn

Последняя формула является основной для расчета сопротивления цепи параллельно соединенных резисторов. Для двух резисторов ее можно записать более удобно: R=(R₁*R₂)/(R₁+R₂).

Отсюда следует, что в случае параллельного соединения двух одинаковых по номиналу резисторов (R₁=R₂) их общее сопротивление будет вдвое меньше любого из них.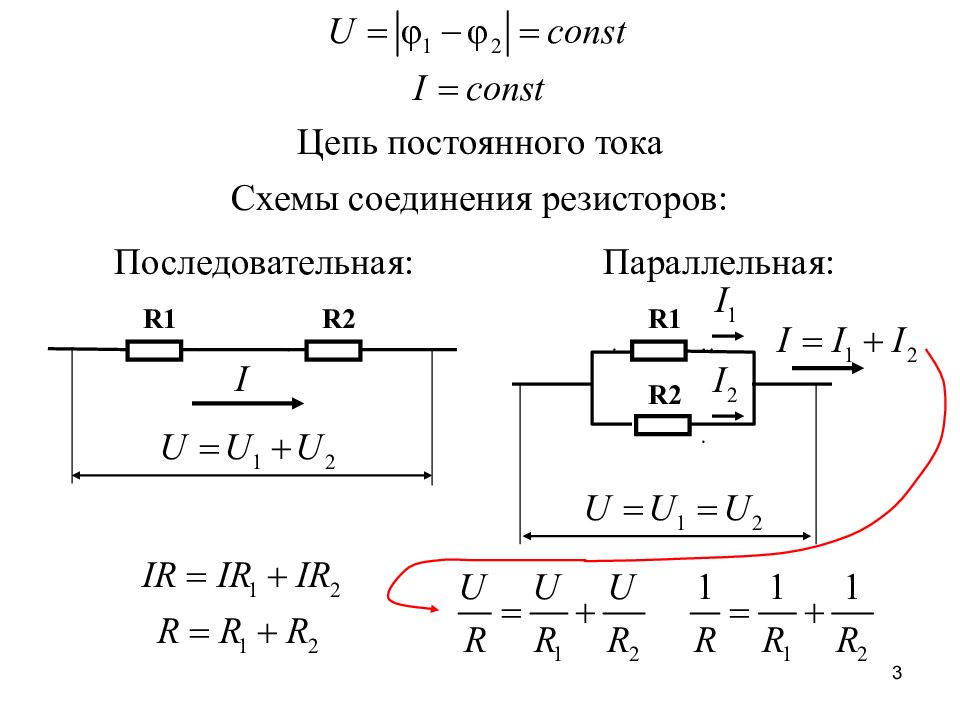 Это полезно помнить.

ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ РЕЗИСТОРОВ

Используя уже упомянутые законы для цепи последовательно соединенных резисторов (рисунок 2) можем записать:

U=I*R
I=I₁=I₂=…In
U=U₁+U₂+…Un
I*R=I*R₁+I*R₂+…I*Rn
R=R₁+R₂+…Rn

То есть общее сопротивление резисторов при последовательном соединении равно сумме их сопротивлений.

СМЕШАННОЕ СОЕДИНЕНИЕ РЕЗИСТОРОВ

Такое соединение всегда можно представить как комбинацию последовательного и параллельного соединений (рис.3).

Расчет общего сопротивления цепи при этом производится поэтапно. В приведенном примере рассчитываем:

последовательное сопротивление резисторов Rпосл=R₁+R₂
параллельное соединение R=(Rпосл*R₃)/(Rпосл+R₃)

Безусловно, могут встретиться более сложные варианты, но методика расчета их сопротивления та же.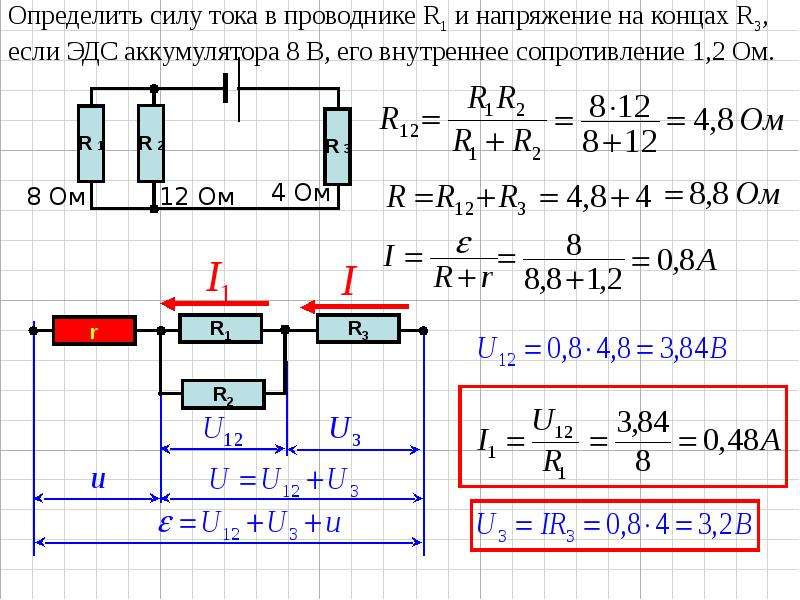

Несколько слов про то, когда возникает необходимость соединять резисторы тем или иным способом:

Отсутствие «под рукой» резистора нужного номинала. При этом следует помнить, что погрешности резисторов будут суммироваться.
Например, для рисунка 3.a, если фактическая погрешность R₁ составляет +10%, а R₂ имеет +15%, то для Rпосл она будет +25%.
Здесь следует обращать внимание на знак, то есть для -10% и +15% в результате получим +5%.
Необходимость получить большую мощность.
Здесь надо учесть, что при одинаковых номиналах сопротивлений и мощностей соединяемых резисторов, как при последовательном, так и при параллельном их соединении итоговая мощность будет равна сумме мощностей.
В противном случае следует ее рассчитать, используя закон Ома и формулу для определения рассеиваемой мощности P=I*U.

Про мощность и номиналы резисторов можно почитать здесь.

Представленные на сайте материалы имеют информационный характер и не могут быть использованы в качестве руководящих и нормативных документов

Формулы параллельного, последовательного и смешанного соединения резисторов

Автор Aluarius На чтение 7 мин. Просмотров 4.3k. Опубликовано 18.05.2020

Ни одна электрическая схема не обходится без резисторов. Что это такое, для чего он нужен и какими способами их подключают в электрическую цепь рассмотрим подробно.

Что такое резистор и для чего он нужен

Резистор – пассивный элемент электрической цепи, который поглощает энергию тока и преобразовывает её в тепло за счет сопротивления потоку электронов в цепи.

Зависимость тока от сопротивления описывается законом Ома и рассчитывается по формуле I = U/R.

Свойство резисторов ограничивать ток и снижать напряжение используется во многих электронных устройствах и бытовых приборах.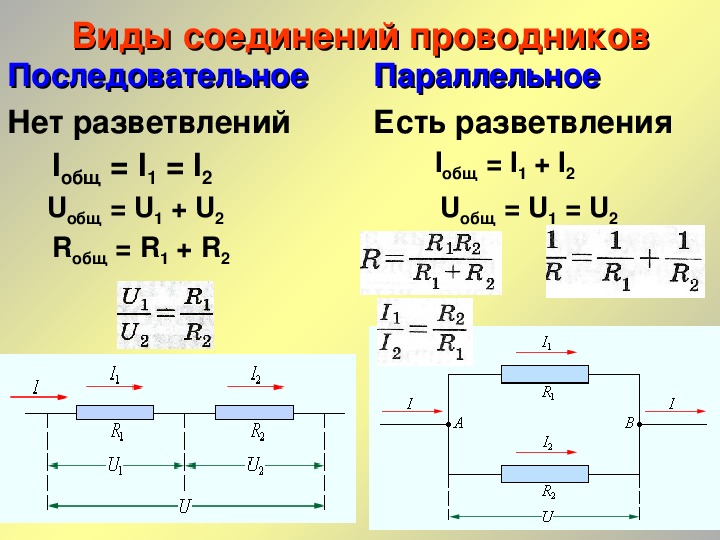

Справка: Резисторы бывают двух видов – постоянные и переменные, во втором случае сопротивление проводника изменяется механическим путем (вручную).

Последовательное и параллельное соединение резисторов – основные способы соединения резистивных элементов.

Внимание! Резистор не имеет полярности, длина выводов с обоих концов одинакова, поэтому для лучшего понимания сути соединения предлагается называть выводы:

С правого края – правый.
С левого края – левый.

Понятие параллельного подключения резисторов

При параллельном подключении правые выводы всех резисторов соединяются в один узел, левые – во второй узел.

При параллельном включении резисторов ток в цепь разветвляется по отдельным ветвям, протекая через каждый элемент – по закону Ома величина тока обратно пропорциональна сопротивлению, напряжение на всех элементах одинаковое.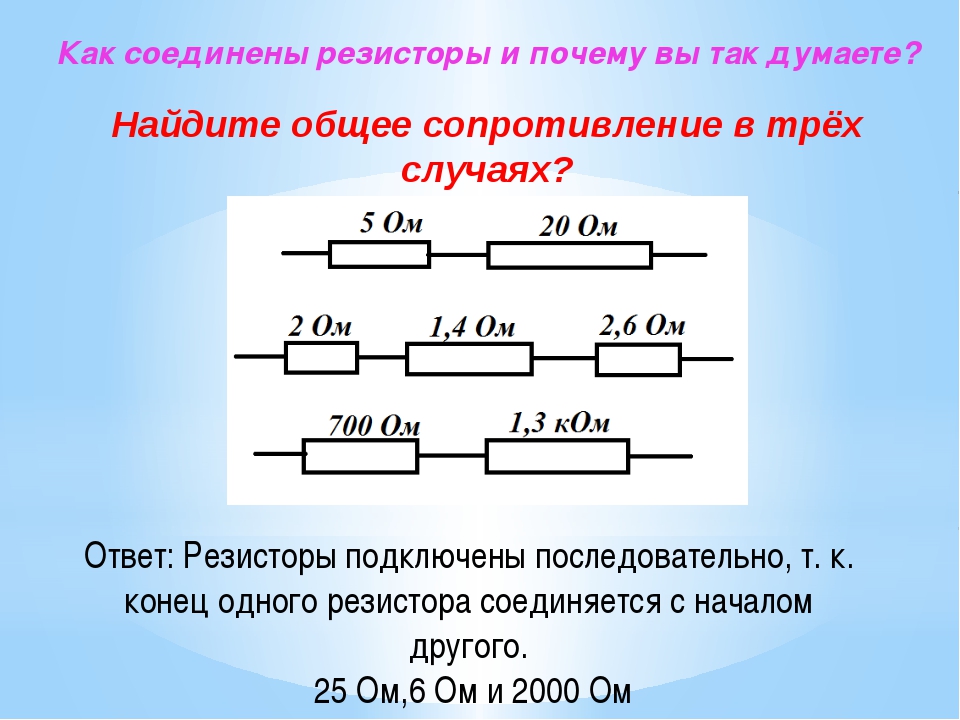

Справка: Ветвь – фрагмент электрической цепи, содержащий один или несколько последовательно соединенных компонентов от узла до узла.

Последовательное подключение

При последовательном соединении резисторы нужно подключить в цепь друг за другом – правый вывод одного резистора к левому второго, правый второго – к левому третьего и так далее в зависимости от количества соединяемых элементов.

При последовательном соединении ток, не изменяя своей величины, течет через все резистивные элементы.

Смешанное подключение

При смешанном подключении в одной схеме сочетаются несколько видов соединений – последовательное, параллельное соединение резисторов и их комбинации. Самую сложную электрическую схему, состоящую из источников питания, диодов, транзисторов, конденсаторов и других радиоэлектронных элементов можно заменить резисторами и источниками напряжения, параметры которых изменяются в каждый момент времени. О параллельном соединении резистора и конденсатора читайте тут.

Смешанная схема делится на фрагменты, ток и напряжение рассчитывается для каждого отдельно в зависимости от того, как они соединены на выбранном сегменте электрической схемы.

Важно! Для расчета сопротивления резистора в схеме применяют отдельные формулы для каждого конкретного элемента в зависимости от вида соединения.

Что ещё нужно учитывать при подключении резисторов

Важный показатель в работе резистивного элемента мощность рассеивания – переход электрической энергии в тепловую, вызывающую нагрев элемента.

При превышении допустимой мощности рассеивания резисторы будут сильно греться и могут сгореть, поэтому при расчете схем соединения надо учитывать этот параметр – важно знать насколько изменится мощность резистивных элементов при включении в электрическую цепь.

Какая мощность тока при последовательном и параллельном соединении

Определение мощности отдельного резистивного элемента производится по формуле

P = U²/R или P = I²R , которую можно вывести из формулы расчета мощности электрической цепи P = UI по закону Ома.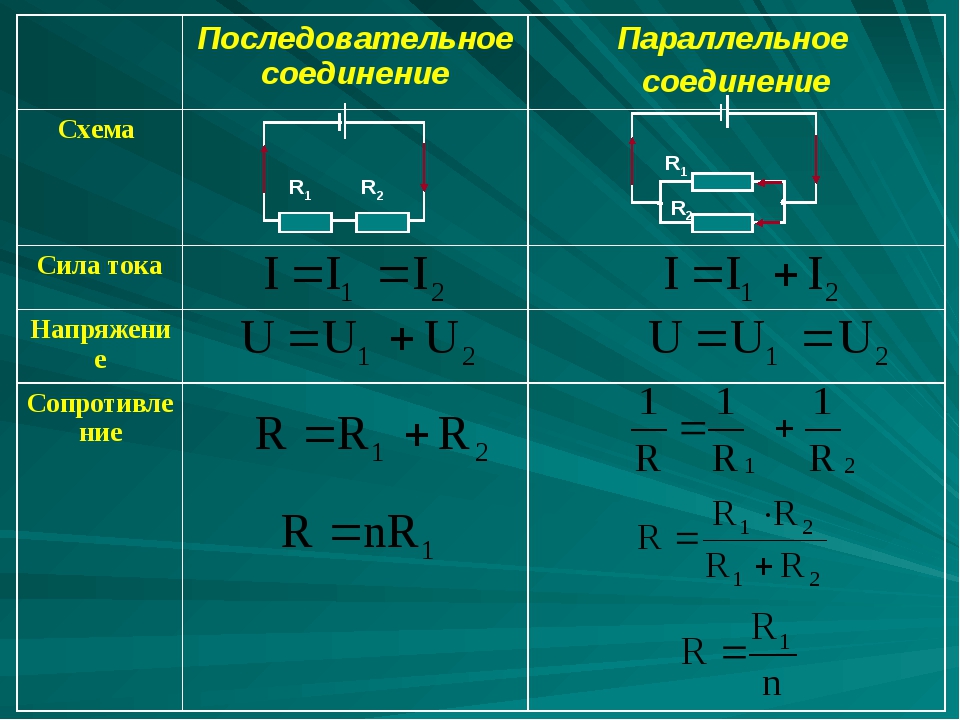

Мощность при параллельном соединении

Рассчитав сопротивление каждого элемента в отдельности, считаем мощность каждого по формуле P = I²R, где

R – не номинальное сопротивление резистивного элемента, а рассчитанное для данной цепи;
I – сила тока в цепи.

При параллельном соединении через меньший резистор протекает больший ток – мощность рассеивания на этом резистивном элементе будет больше, чем на остальных.

Важно! При расчете параллельной цепи следует учитывать мощность сопротивления с самым маленьким номиналом.

Мощность при последовательном соединении

Вычислив сопротивление каждого резистивного элемента по отдельности, рассчитываем мощность каждого по формуле P = U²/R, где

R – рассчитанное нами сопротивление для определенной схемы;
U – падение напряжения на данном резистивном элементе.

Справка: Полную мощность цепи при последовательном и параллельном соединении можно найти, сложив вычисленные мощности отдельных элементов, входящих в цепь Pобщ = P₁+P₂+P₃+…+Pn.

Как правильно рассчитать сопротивление

Применяется закон Ома для участка цепи – расчет сопротивления делается по формуле R = U/I, где

U – падение напряжение на конкретном резистивном элементе;
I – ток, протекающий через него.

При последовательном соединении

Для двух элементов считаем Rобщ = R₁+R₂.

Для нескольких сопротивлений разного номинала Rобщ = R₁+R₂+R₃+…+Rn.

При параллельном соединении

Расчет для двух резисторов делаем по формуле Rобщ = (R₁×R₂)/(R₁+R₂).

Сопротивление параллельных резисторов с разным номиналом рассчитываем по формуле

Rобщ = 1/(1/R₁+1/R₂+1/R₃+…+1/Rn).

Для элементов, соединенных в параллель, суммарное сопротивление всегда ниже наименьшего номинального.

Как рассчитать сложные схемы соединения резисторов

Сложные схемы рассчитываются путем группировки по параллельному и последовательному способу соединения.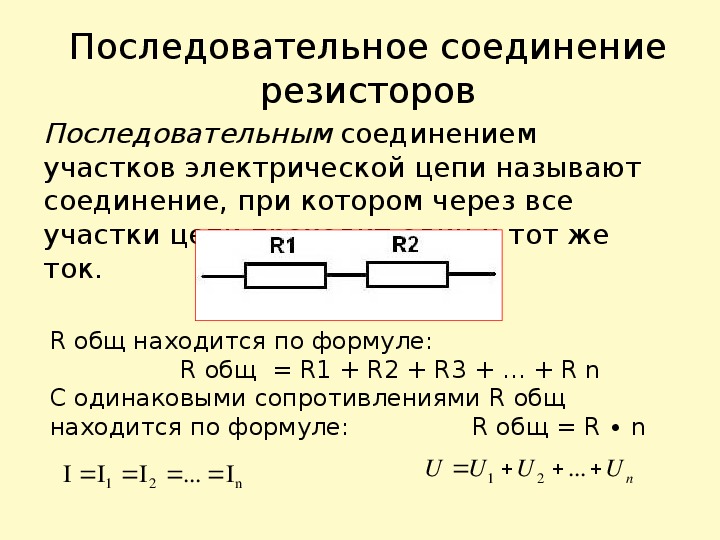

Перед нами сложная схема – задача рассчитать общее сопротивление:

R₂, R₃, R₄ объединим в последовательную группу – применим формулу R_2,3,4 = R₂+R₃+_R4.
R₅ и R_2,3,4 – параллельно соединенные резисторы, рассчитаем R_5,2,3,4 = 1/ (1/R₅+1/R_2,3,4).
R_5,2,3,4, R₁, R₆ опять объединяем в последовательную группу – суммируя величины, получаем Rобщ = R_5,2,3,4+R₁+R₆.

Для больших схем существуют специальные методы, облегчающие расчет. Один из таких методов – эквивалентное преобразование «треугольника» в «звезду». Такая система расчета применяется в том случае, когда невозможно по схеме определить последовательное или параллельное подключение резисторов.

Преобразование «звезда-треугольник»

Для соединения резистивных элементов, кроме вышеописанных способов, существует несколько других видов соединения:

«звезда» – соединение трех ветвей с одним общим узлом;
«треугольник» – соединение ветвей схемы в виде треугольника, сторонами которого служат ветви, вершины представляют узлы.

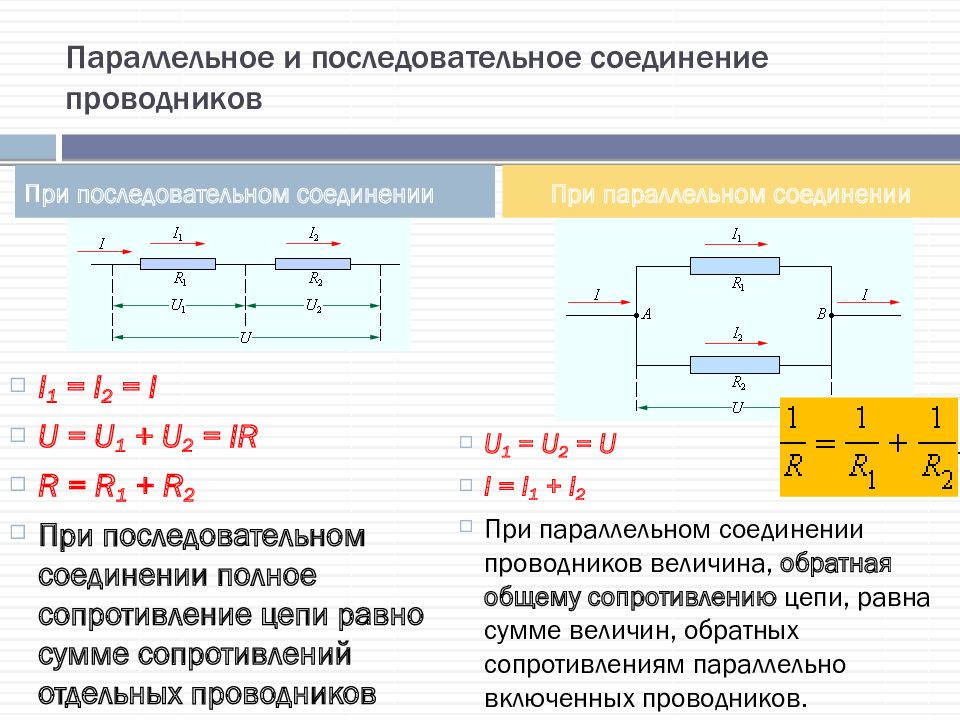
Справка: Узел – точка, в которой соединяются три и более проводника электрической цепи.

Эквивалентность замены предполагает стабильность токов, входящих в каждый узел, при одинаковых напряжения между одноименными узлами «треугольника» и «звезды».

Сопротивление резистора луча «звезды» равно произведению сопротивлений резисторов прилегающих сторон «треугольника», деленному на сумму сопротивлений резисторов трех сторон «треугольника».

R_A = R_AB R_AC/(R_AB+R_AC+R_DC).

Сопротивление резисторов сторон «треугольника» равно сумме произведения сопротивлений резисторов двух прилегающих лучей «звезды», деленного на сопротивление третьего луча.

R_AB=(R_AR_B+R_AR_C+R_BR_С)/R_C

О разнице подключения звезда и треугольник читайте здесь.

Чему равна сила тока в цепи при параллельном соединении резисторов

Согласно правилу Кирхгофа ток, поступающий в узел, равен току, выходящему из узла, – величина тока до группы параллельных резисторов и после нее должна быть неизменной.

Ток в группе параллельных резисторов распределяется по цепи в зависимости от их номинала, после прохождения через сопротивления суммируется в узле и выходит из него неизменным I = I₁+I₂+I₃+…+In.

Как определить величину эквивалентного сопротивления при последовательном соединении резисторов

Справка: Эквивалентом сопротивления называется замена части схемы, состоящей из нескольких резистивных элементов, одним элементом.

Для последовательного соединения эквивалентное сопротивление равно сумме сопротивлений резисторов, включенных в группу, для расчета применяется формула Rэкв = R₁+R₂+…+Rn.

Например: Нужно посчитать эквивалентное сопротивление данной схемы.

Решение задачи производится путем разделения резистивных элементов на системные группы.

Выделяем первую группу из последовательно соединенных элементов – R₂, R₃, R₄.

Считаем сопротивление Rобщ₁ = R₂+R₃+R₄.

Выделяем вторую группу из последовательных элементов R₁, R₅, R₆.

Считаем сопротивление Rобщ₂= R₁+R₅+R₆.

Получаем величину двух эквивалентных сопротивлений Rобщ₁ и Rобщ₂, соединенных параллельно.

Делаем расчет всей схемы Rэкв= Rобщ₁× Rобш₂/ (Rобщ₁+ Rобщ₂).

Зная способы соединения и формулы расчета можно рассчитать любую сложную схему соединения резистивных элементов, однако существует множество онлайн калькуляторов, которые сделают это быстрей человека, достаточно только ввести нужные параметры компонентов схемы.

формула расчета расчета общего сопротивления

Параллельное соединение резисторов, наряду с последовательным, является основным способом соединения элементов в электрической цепи. Во втором варианте все элементы установлены последовательно: конец одного элемента соединен с началом следующего. В такой схеме сила тока на всех элементах одинаковая, а падение напряжений зависит от сопротивления каждого элемента. В последовательном соединении есть два узла. К одному подсоединены начала всех элементов, а ко второму их концы. Условно для постоянного тока можно обозначить их как плюс и минус, а для переменного как фазу и ноль. Благодаря своим особенностям находит широкое применение в электрических схемах, в том числе и со смешанным соединением. Свойства одинаковы для постоянного и переменного тока.

Расчет общего сопротивления при параллельном соединении резисторов

В отличие от последовательного соединения, где для нахождения общего сопротивления достаточно сложить значение каждого элемента, для параллельного то же самое будет справедливо для проводимости. А так как она обратно пропорциональна сопротивлению, получим формулу, представленную вместе со схемой на следующем рисунке:

Необходимо отметить одну важную особенность расчета параллельного соединения резисторов: общее значение будет всегда меньше, чем самое маленькое из них. Для резисторов справедливо как для постоянного, так и для переменного тока. Катушки и конденсаторы имеют свои особенности.

Сила тока и напряжение

При расчете параллельного сопротивления резисторов необходимо знать, как рассчитать напряжение и силу тока. В этом случае нам поможет закон Ома, определяющий связь между сопротивлением, силой тока и напряжением.

Исходя из первой формулировки закона Кирхгофа, получим, что сумма сходящихся в одном узле токов равна нулю. Направление выбираем по направлению протекания тока. Таким образом, положительным направлением для первого узла можно считать входящий ток от источника питания. А отрицательными будут отходящие из каждого резистора. Для второго узла картина противоположна. Исходя из формулировки закона, получим, что суммарный ток равен сумме токов, проходящих через каждый параллельно соединенный резистор.

Итоговое напряжение же определяется по второму закону Кирхгофа. Оно одинаково для каждого резистора и равно общему.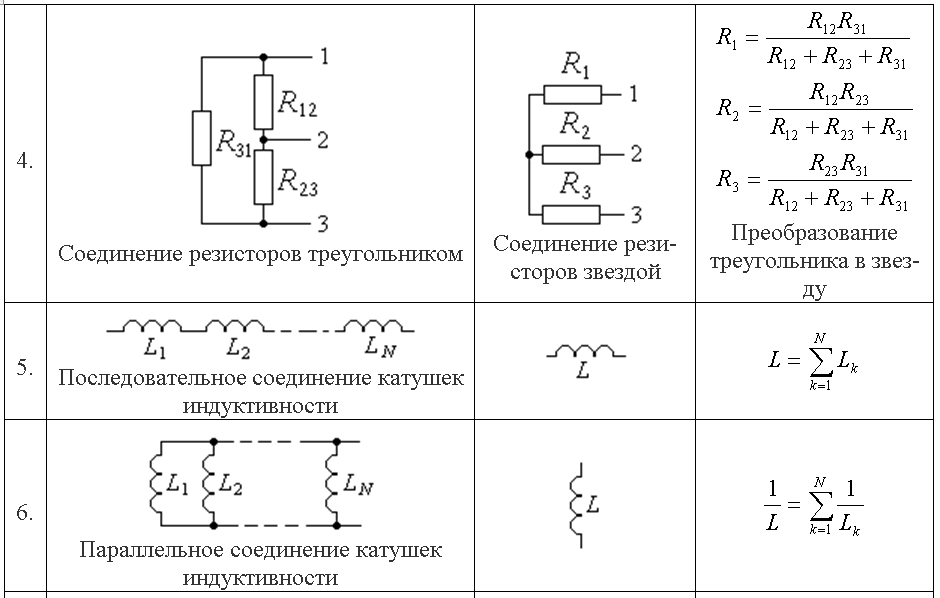 Эта особенность используется для подключения розеток и освещения в квартирах.

Пример расчета

В качестве первого примера приведем расчет сопротивления при параллельном соединении одинаковых резисторов. Сила тока, протекающая через них, будет одинаковой. Пример расчета сопротивления выглядит так:

По этому примеру прекрасно видно, что общее сопротивление ниже в два раза, чем каждое из них. Это соответствует тому, что суммарная сила тока в два раза выше, чем у одного. А также прекрасно соотносится с увеличением проводимости в два раза.

Второй пример

Рассмотрим пример параллельного соединения трех резисторов. Для расчета используем стандартную формулу:

Похожим образом рассчитываются схемы с большим количеством параллельно соединенных резисторов.

Пример смешанного соединения

Для смешанного соединения, например, представленного ниже, расчет будет производиться в несколько этапов.

Для начала последовательные элементы можно условно заменить одним резистором, обладающим сопротивлением, равным сумме двух заменяемых.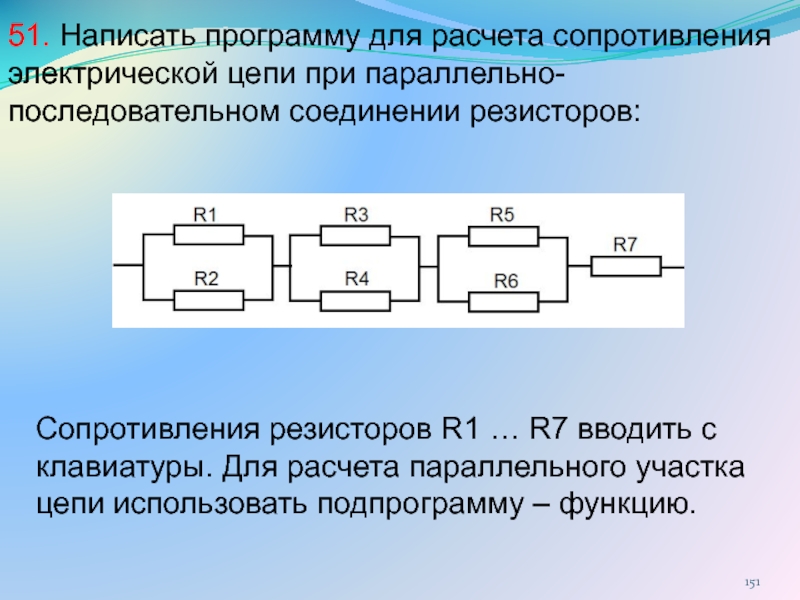 Далее общее сопротивление считаем тем же способом, что и для предыдущего примера. Данный метод подойдет и для других более сложных схем. Последовательно упрощая схему, можно получить необходимое значение.

Например, если вместо резистора R3 будут подключены два параллельных, потребуется сначала рассчитать их сопротивление, заменив их эквивалентным. А далее то же самое, что и в примере выше.

Применение параллельной схемы

Параллельное соединение резисторов находит свое применение во многих случаях. Последовательное подключение увеличивает сопротивление, а для нашего случая оно уменьшится. Например, для электрической цепи требуется сопротивление в 5 Ом, но есть только резисторы на 10 Ом и выше. Из первого примера мы знаем, что можно получить в два раза меньшее значение сопротивления, если установить два одинаковых резистора параллельно друг другу.

Уменьшить сопротивление можно еще больше, например, если две пары параллельно соединенных резисторов соединить параллельно относительно друг друга.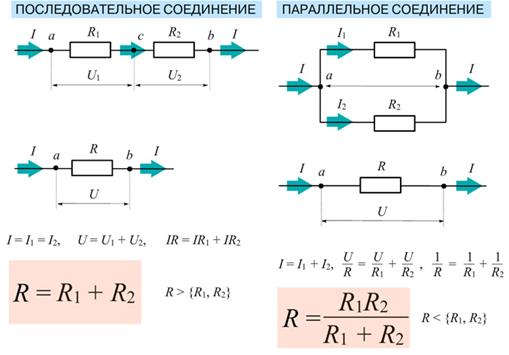 Можно уменьшить сопротивление еще в два раза, если резисторы имеют одинаковое сопротивление. Комбинируя с последовательным соединением, можно получить любое значение.

Второй пример — это использование параллельного подключения для освещения и розеток в квартирах. Благодаря такому подключению напряжение на каждом элементе не будет зависеть от их количества и будет одинаковым.

Еще один пример использования параллельного подключения — это защитное заземление электрооборудования. Например, если человек касается металлического корпуса прибора, на который произойдет пробой, получится параллельное соединения его и защитного проводника. Первым узлом будет место прикосновения, а вторым нулевая точка трансформатора. По проводнику и человеку будет течь разный ток. Величину сопротивления последнего принимают за 1000 Ом, хотя реальное значение зачастую гораздо больше. Если бы не было заземления, весь ток, протекающий в схеме, пошел бы через человека, так как он был бы единственным проводником.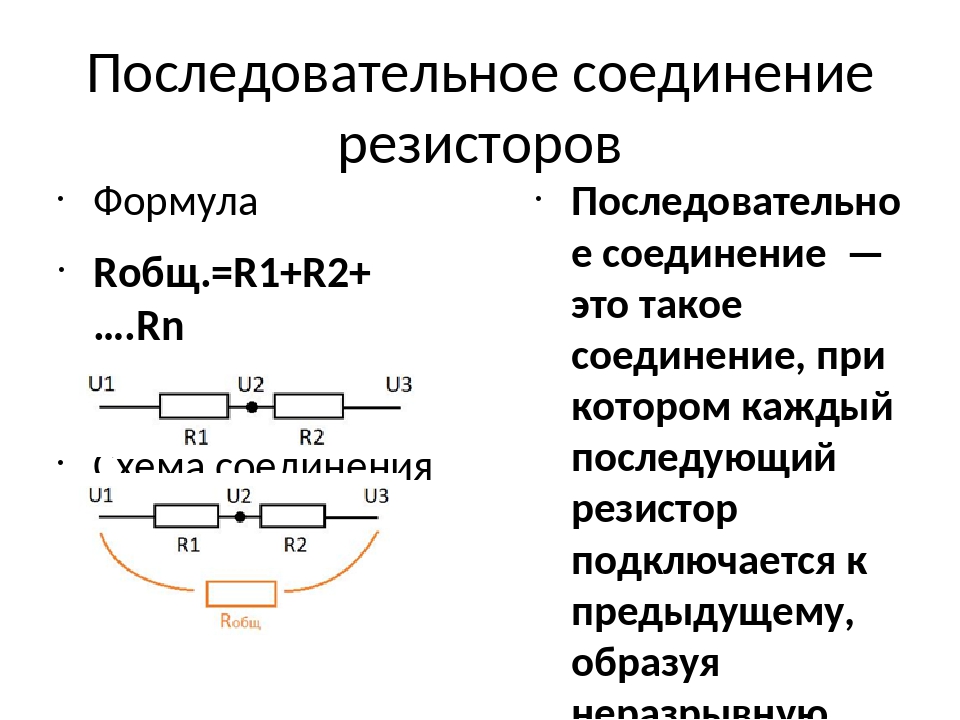

Параллельное соединение может использоваться и для батарей. Напряжение при этом остается прежним, однако в два раза возрастает их емкость.

Итог

При подключении резисторов параллельно, напряжение на них будет одинаковым, а ток равен сумме протекающих через каждый резистор. Проводимость будет ровняться сумме каждого. От этого и получается необычная формула суммарного сопротивления резисторов.

Необходимо учитывать при расчете параллельного соединения резисторов то, что итоговое сопротивление будет всегда меньше самого маленького. Это также можно объяснить суммированием проводимости резисторов. Последняя будет возрастать при добавлении новых элементов, соответственно и проводимость будет уменьшаться.

Учебное пособие по физике: Комбинированные схемы

Ранее в Уроке 4 упоминалось, что существует два разных способа соединения двух или более электрических устройств в цепь. Они могут быть соединены посредством последовательного или параллельного соединения. Когда все устройства в цепи соединены последовательными соединениями, тогда схема называется последовательной схемой. Когда все устройства в цепи соединены параллельными соединениями, тогда схема называется параллельной цепью.Третий тип схемы предполагает двойное использование последовательного и параллельного соединений в схеме; такие схемы называются составными схемами или комбинированными схемами. Схема, изображенная справа, является примером использования как последовательного, так и параллельного соединения в одной цепи. В этом случае лампочки A и B подключаются параллельно, а лампочки C и D подключаются последовательно. Это пример комбинированной схемы .

При анализе комбинированных цепей критически важно иметь твердое понимание концепций, относящихся как к последовательным цепям, так и к параллельным цепям.Поскольку оба типа соединений используются в комбинированных схемах, концепции, связанные с обоими типами схем, применяются к соответствующим частям схемы. Основные понятия, связанные с последовательными и параллельными цепями, представлены в таблице ниже.

Цепи серии

Ток одинаков на всех резисторах; этот ток равен току в батарее.
Сумма падений напряжения на отдельных резисторах равна номинальному напряжению батареи.
Общее сопротивление набора резисторов равно сумме отдельных значений сопротивлений,

R _to = R ₁ + R ₂ + R ₃ + …

Параллельные схемы

Падение напряжения одинаково на каждой параллельной ветви.
Сумма тока в каждой отдельной ветви равна току вне ветвей.
Эквивалентное или полное сопротивление набора резисторов определяется уравнением 1 / R _экв = 1 / R ₁ + 1 / R ₂ + 1 / R ₃ …

Каждое из вышеперечисленных понятий имеет математическое выражение. Комбинирование математических выражений вышеуказанных понятий с уравнением закона Ома (ΔV = I • R) позволяет провести полный анализ комбинированной схемы.

Анализ комбинированных цепей

Основная стратегия анализа комбинированных схем включает использование значения эквивалентного сопротивления для параллельных ветвей для преобразования комбинированной схемы в последовательную. После преобразования в последовательную схему анализ можно проводить обычным образом. Ранее в Уроке 4 был описан метод определения эквивалентного параллельного сопротивления, затем общее или эквивалентное сопротивление этих ветвей равно сопротивлению одной ветви, деленному на количество ветвей.

Этот метод соответствует формуле

1 / R _экв. = 1 / R ₁ + 1 / R ₂ + 1 / R ₃ + …

, где R ₁, R ₂ и R ₃ — значения сопротивления отдельных резисторов, подключенных параллельно. Если два или более резистора, находящихся в параллельных ветвях, не имеют одинакового сопротивления, необходимо использовать приведенную выше формулу.Пример этого метода был представлен в предыдущем разделе Урока 4.

Применяя свое понимание эквивалентного сопротивления параллельных ветвей к комбинированной схеме, комбинированную схему можно преобразовать в последовательную. Затем понимание эквивалентного сопротивления последовательной цепи можно использовать для определения общего сопротивления цепи. Рассмотрим следующие диаграммы ниже. Схема А представляет собой комбинированную схему с резисторами R ₂ и R ₃, размещенными в параллельных ветвях.Два параллельных резистора 4 Ом эквивалентны сопротивлению 2 Ом. Таким образом, две ветви можно заменить одним резистором с сопротивлением 2 Ом. Это показано на схеме B. Теперь, когда все резисторы включены последовательно, можно использовать формулу для общего сопротивления последовательных резисторов для определения общего сопротивления этой цепи: Формула для последовательного сопротивления составляет

_{рэндов до} = ₁ + ₂ рэндов + ₃ + …

Итак, на схеме B полное сопротивление цепи составляет 10 Ом.

После определения общего сопротивления цепи анализ продолжается с использованием закона Ома и значений напряжения и сопротивления для определения значений тока в различных местах. Весь метод проиллюстрирован ниже на двух примерах.

Пример 1:

Первый пример — самый простой случай — резисторы, включенные параллельно, имеют одинаковое сопротивление. Цель анализа — определить ток и падение напряжения на каждом резисторе.

Как обсуждалось выше, первым шагом является упрощение схемы путем замены двух параллельных резисторов одним резистором с эквивалентным сопротивлением. Два последовательно подключенных резистора 8 Ом эквивалентны одному резистору 4 Ом. Таким образом, два резистора ответвления (R ₂ и R ₃) можно заменить одним резистором с сопротивлением 4 Ом.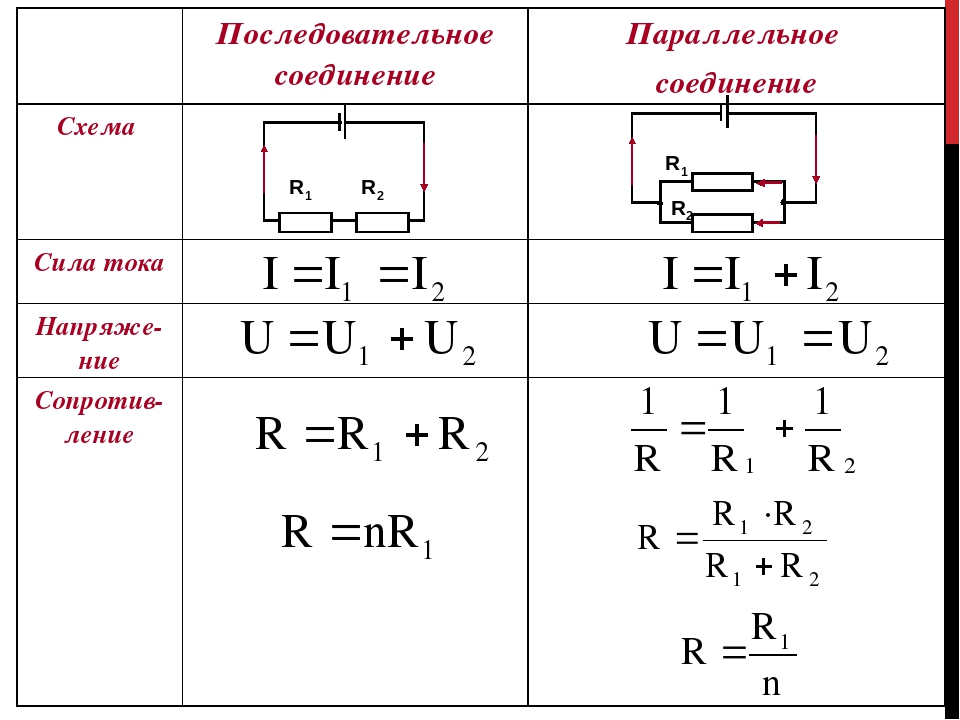 Этот резистор 4 Ом включен последовательно с R ₁ и R ₄. Таким образом, общее сопротивление составляет

. R _до = R ₁ + 4 Ом + R ₄ = 5 Ом + 4 Ом + 6 Ом

R _общ = 15 Ом

Теперь уравнение закона Ома (ΔV = I • R) можно использовать для определения полного тока в цепи.При этом необходимо использовать общее сопротивление и общее напряжение (или напряжение батареи).

I _tot = ΔV _tot / R _tot = (60 В) / (15 Ом)

I _до = 4 А

Расчет тока 4 А представляет собой ток в месте расположения батареи. При этом резисторы R ₁ и R ₄ включены последовательно, а ток в последовательно соединенных резисторах везде одинаков.Таким образом,

I _до = I ₁ = I ₄ = 4 А

Для параллельных ветвей сумма тока в каждой отдельной ветви равна току вне ветвей. Таким образом, I ₂ + I ₃ должно равняться 4 ампер. Существует бесконечное количество возможных значений I ₂ и I ₃, которые удовлетворяют этому уравнению. Поскольку значения сопротивления равны, значения тока в этих двух резисторах также равны.Следовательно, ток в резисторах 2 и 3 равен 2 А.

I ₂ = I ₃ = 2 А

Теперь, когда известен ток в каждом отдельном месте резистора, можно использовать уравнение закона Ома (ΔV = I • R) для определения падения напряжения на каждом резисторе. Эти расчеты показаны ниже.

ΔV ₁ = I ₁ • R ₁ = (4 А) • (5 Ом)
ΔV ₁ = 20 В
ΔV ₂ = I ₂ • R ₂ = (2 А) • (8 Ом)
ΔV ₂ = 16 В
ΔV ₃ = I ₃ • R ₃ = (2 А) • (8 Ом)
ΔV ₃ = 16 В
ΔV ₄ = I ₄ • R ₄ = (4 А) • (6 Ом)
ΔV ₄ = 24 В

На этом анализ завершен, и его результаты представлены на диаграмме ниже.

Пример 2:

Второй пример — более сложный случай — резисторы, включенные параллельно, имеют другое сопротивление. Цель анализа та же — определить ток и падение напряжения на каждом резисторе.

Как обсуждалось выше, первым шагом является упрощение схемы путем замены двух параллельных резисторов одним резистором с эквивалентным сопротивлением.Эквивалентное сопротивление резистора 4 Ом и 12 Ом, включенного параллельно, можно определить, используя обычную формулу для эквивалентного сопротивления параллельных ветвей:

1 / R _экв = 1 / R ₁ + 1 / R ₂ + 1 / R ₃ …

1 / R _экв = 1 / (4 Ом) + 1 / (12 Ом)

1 / R _экв. = 0,333 Ом ^-1

R _экв = 1 / (0,333 Ом ^-1)

R _экв = 3.00 Ом

На основании этого расчета можно сказать, что два резистора ответвления (R ₂ и R ₃) можно заменить одним резистором с сопротивлением 3 Ом. Этот резистор 3 Ом включен последовательно с R ₁ и R ₄. Таким образом, общее сопротивление составляет

. R _до = R ₁ + 3 Ом + R ₄ = 5 Ом + 3 Ом + 8 Ом

R _общ = 16 Ом

I _tot = ΔV _tot / R _tot = (24 В) / (16 Ом)

I _до = 1,5 А

Расчет тока 1,5 А представляет собой ток в месте расположения батареи. При этом резисторы R ₁ и R ₄ включены последовательно, а ток в последовательно соединенных резисторах везде одинаков.Таким образом,

I _до = I ₁ = I ₄ = 1,5 А

Для параллельных ветвей сумма тока в каждой отдельной ветви равна току вне ветвей. Таким образом, I ₂ + I ₃ должно равняться 1,5 А. Существует бесконечное множество значений I ₂ и I ₃, которые удовлетворяют этому уравнению. В предыдущем примере два параллельно включенных резистора имели одинаковое сопротивление; таким образом, ток распределялся поровну между двумя ветвями.В этом примере неравный ток в двух резисторах усложняет анализ. Ветвь с наименьшим сопротивлением будет иметь наибольший ток. Для определения силы тока потребуется использовать уравнение закона Ома. Но для его использования сначала необходимо знать падение напряжения на ветвях. Таким образом, направление решения в этом примере будет немного отличаться от более простого случая, проиллюстрированного в предыдущем примере.

Чтобы определить падение напряжения на параллельных ветвях, сначала необходимо определить падение напряжения на двух последовательно соединенных резисторах (R ₁ и R ₄).Уравнение закона Ома (ΔV = I • R) можно использовать для определения падения напряжения на каждом резисторе. Эти расчеты показаны ниже.

ΔV ₁ = I ₁ • R ₁ = (1,5 А) • (5 Ом)
ΔV ₁ = 7,5 В
ΔV ₄ = I ₄ • R ₄ = (1,5 А) • (8 Ом)
ΔV ₄ = 12 В

Эта схема питается от источника 24 В.Таким образом, совокупное падение напряжения заряда, проходящего по контуру цепи, составляет 24 вольта. Будет падение 19,5 В (7,5 В + 12 В) в результате прохождения через два последовательно соединенных резистора (R ₁ и R ₄). Падение напряжения на ответвлениях должно составлять 4,5 В, чтобы компенсировать разницу между общим значением 24 В и падением 19,5 В на R ₁ и R ₄. Таким образом,

ΔV ₂ = V ₃ = 4,5 В

Зная падение напряжения на параллельно соединенных резисторах (R ₁ и R ₄), можно использовать уравнение закона Ома (ΔV = I • R) для определения тока в двух ветвях.

I ₂ = ΔV ₂ / R ₂ = (4,5 В) / (4 Ом)
I ₂ = 1,125 А
I ₃ = ΔV ₃ / R ₃ = (4,5 В) / (12 Ом)
I ₃ = 0,375 A

На этом анализ завершен, и его результаты представлены на диаграмме ниже.

Разработка стратегии

Два приведенных выше примера иллюстрируют эффективную концептуально-ориентированную стратегию анализа комбинированных схем.Подход требовал твердого понимания концепций последовательностей и параллелей, обсуждавшихся ранее. Такие анализы часто проводятся, чтобы решить физическую проблему для указанного неизвестного. В таких ситуациях неизвестное обычно меняется от проблемы к проблеме. В одной задаче значения резистора могут быть заданы, а ток во всех ветвях неизвестен. В другой задаче могут быть указаны ток в батарее и несколько значений резистора, и неизвестная величина становится сопротивлением одного из резисторов.Очевидно, что разные проблемные ситуации потребуют небольших изменений в подходах. Тем не менее, каждый подход к решению проблем будет использовать те же принципы, что и при подходе к двум приведенным выше примерам проблем.

Начинающему студенту предлагаются следующие предложения по решению задач комбинированной схемы:

Если схематическая диаграмма не предоставлена, найдите время, чтобы построить ее. Используйте условные обозначения, такие как те, что показаны в примере выше.
При приближении к проблеме, связанной с комбинированной схемой, найдите время, чтобы организовать себя, записав известные значения и приравняв их к символу, например, I _—, I ₁, R ₃, ΔV ₂ и т. Д. Схема организации, использованная в двух приведенных выше примерах, является эффективной отправной точкой.
Знать и использовать соответствующие формулы для эквивалентного сопротивления последовательно соединенных и параллельно соединенных резисторов. Использование неправильных формул гарантирует неудачу.
Преобразуйте комбинированную схему в строго последовательную, заменив (по вашему мнению) параллельную секцию одним резистором, значение сопротивления которого равно эквивалентному сопротивлению параллельной секции.
Используйте уравнение закона Ома (ΔV = I • R) часто и надлежащим образом. Большинство ответов будет определено с использованием этого уравнения. При его использовании важно подставлять в уравнение соответствующие значения. Например, при вычислении I ₂ важно подставить в уравнение значения ΔV ₂ и R ₂.

Для дальнейшей практики анализа комбинированных схем рассмотрите возможность анализа проблем в разделе «Проверьте свое понимание» ниже.

Мы хотели бы предложить … Зачем просто читать об этом и когда можно с этим взаимодействовать? Взаимодействовать — это именно то, что вы делаете, когда используете одно из интерактивных материалов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного средства построения цепей постоянного тока.Вы можете найти его в разделе Physics Interactives на нашем сайте. Построитель цепей постоянного тока предоставляет учащемуся набор для построения виртуальных цепей. Вы можете легко перетащить источники напряжения, резисторы и провода на рабочее место, расположить и подключить их так, как вам нужно. Вольтметры и амперметры позволяют измерять ток и падение напряжения. Нажатие на резистор или источник напряжения позволяет изменять сопротивление или входное напряжение. Это просто. Это весело. И это безопасно (если вы не используете его в ванне).

Проверьте свое понимание

1. Комбинированная схема показана на схеме справа. Используйте диаграмму, чтобы ответить на следующие вопросы.

а. Ток в точке A равен _____ (больше, равен, меньше) току в точке B.

г. Ток в точке B равен _____ (больше, равен, меньше) ток в точке E.

г. Ток в точке G равен _____ (больше, равен, меньше) ток в точке F.

г. Ток в точке E равен _____ (больше, равен, меньше) току в точке G.

e. Ток в точке B равен _____ (больше, равен, меньше) ток в точке F.

ф. Ток в точке A равен _____ (больше, равен, меньше) ток в точке L.

г. Ток в точке H равен _____ (больше, равен, меньше) ток в точке I.

2. Рассмотрим комбинированную схему на схеме справа. Используйте диаграмму, чтобы ответить на следующие вопросы. (Предположим, что падение напряжения в самих проводах пренебрежимо мало.)

а. Разность электрических потенциалов (падение напряжения) между точками B и C составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками J и K.

г. Разность электрических потенциалов (падение напряжения) между точками B и K составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками D и I.

г. Разность электрических потенциалов (падение напряжения) между точками E и F составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками G и H.

e. Разность электрических потенциалов (падение напряжения) между точками J и K составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками D и I.

ф. Разность электрических потенциалов между точками L и A составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками B и K.

3.Используйте концепцию эквивалентного сопротивления, чтобы определить неизвестное сопротивление идентифицированного резистора, которое сделало бы схемы эквивалентными.

4. Проанализируйте следующую схему и определите значения общего сопротивления, общего тока, а также тока и падения напряжения на каждом отдельном резисторе.

5. Обращаясь к диаграмме в вопросе №4, определите …

а. … номинальная мощность резистора 4.
г. … скорость, с которой энергия потребляется резистором 3.

Параллельные схемы

Ваш браузер не поддерживает Java-апплеты

Схема с более чем одним Путь прохождения тока представляет собой параллельную цепь.

НАПРЯЖЕНИЕ В ПАРАЛЛЕЛЬНЫХ ЦЕПЯХ

Общее напряжение равно напряжение любого параллельного сопротивления.

ТОК В ПАРАЛЛЕЛЬНЫХ ЦЕПЯХ

Полный ток равен сумма тока каждого параллельного компонента.

ПАРАЛЛЕЛЬНОЕ СОПРОТИВЛЕНИЕ ЦЕПИ

Общее сопротивление может быть рассчитывается по закону Ома, если известны напряжение и полный ток.

Общее сопротивление всегда меньше наименьшего значения сопротивления.

Метод равных значений

Для параллельных сопротивлений в какие все резисторы имеют одинаковое значение, сопротивление можно рассчитать по формуле разделив номинал одного из резисторов на количество резисторов.

Взаимный метод

1 / R _T = 1 / R ₁ + 1 / R ₂ + 1 / R _N

R _EQ = 1 / (1 / R ₁ + 1 / R ₂ + … + 1 / R _N )

Метод произведения на сумму

Для расчета сопротивления двух резисторов параллельно можно использовать эту формулу:

R _EQ = (₁ * R ₂) / (₁ + ₂)

Правило приближения 10 к 1

Если подключены два резистора параллельно, и один резистор в 10 или более раз больше по стоимости, чем другой резистор, резистор большего номинала можно не учитывать.

ПРОВОДИМОСТЬ

Общая проводимость равна сумме проводимости каждого компонента.

ПИТАНИЕ В ПАРАЛЛЕЛЬНЫХ ЦЕПЯХ

Суммарная мощность равна сумма мощности каждого компонента. (Это то же самое, что и с серией схемы).

Правила для параллельных цепей постоянного тока

Такое же напряжение существует через каждую ветвь параллельной цепи и равно напряжению источника.
Ток через параллельная ветвь обратно пропорциональна величине сопротивления ветвь.
Полный ток параллельная цепь равна сумме отдельных токов ответвления цепь
Эквивалентное сопротивление параллельная цепь находится по общему уравнению Req = 1 / (1 / R1 + 1 / R2 + 1 / номер)
Общая мощность, потребляемая в параллельная схема равна сумме мощности, потребляемой индивидуумом резисторы.

ПАРАЛЛЕЛЬНЫЙ АНАЛИЗ ЦЕПЕЙ

Соблюдайте принципиальную схему внимательно или при необходимости нарисуйте.
Обратите внимание на указанные значения и значения, которые необходимо найти.
Выберите подходящий уравнения, которые будут использоваться при решении для неизвестных величин на основе известных количества.
Подставьте известные значения в выбранном вами уравнении и найдите неизвестное значение.

ПАРАЛЛЕЛЬНОЕ УСТРАНЕНИЕ НЕПОЛАДОК ЦЕПИ

Когда в ветви параллельной сети сопротивление ветви увеличивается и общее сопротивление цепи увеличивается. Это вызывает уменьшение общего Текущий.

Короткое замыкание всегда приводит в отсутствии тока, протекающего через другие ветви цепи.

Расчет тока в последовательно-параллельных цепях

Рисунок 1. Последовательно-параллельные резисторы.

В цепи с резисторами, включенными как последовательно, так и параллельно, рассматривать схему как комбинацию параллельных частей и последовательных части.

Используйте формулы сопротивления для определения общего сопротивления серийных и параллельных частей. Затем используйте закон Ома, чтобы вычислить напряжение падает поперек и токи через каждую часть.

В схеме на Рисунке 1 сначала используйте параллельное сопротивление формула для определения эквивалентного сопротивления R ₁₂₃ .

Тогда формула последовательного сопротивления говорит нам R _TOT = R ₁₂₃ + R ₄ . Итак, закон Ома дает полный ток цепи:

I _TOT равно как текущим I ₄ через R ₄ и текущему I ₁₂₃ вход / выход из параллельной части. Используя закон Ома:

Итак, зная значение В ₁₂₃ , снова применим закон Ома, чтобы найти ток I ₁ через параллельный резистор R ₁ :

и аналогично для I ₂ и I ₃ .

Пример

Для схемы на рисунке 1 предположим, что E = 9 В, R ₁ = 500 Ом, R ₂ = 1,0 кОм, R ₃ = 1,5 кОм и R ₄ = 220 Ом. Тогда R ₁₂₃ = 273 Ом и R _TOT = 493 Ом, поэтому

и, следовательно,

Аналогично для I ₂ и I ₃ .

Примечание: Важно осторожно обращаться с единицами измерения с метрическими префиксами. Выше мы отрегулировали десятичную точку и единицы измерения так, чтобы наша формула для тока давала вольт / Ом = ампер.

Онлайн-конвертеры единиц измерения

Случайный преобразователь

Онлайн-конвертеры единиц измерения

Конвертер длины и расстоянияКонвертер массыКонвертер сухого объема и общих измерений при варкеПреобразователь площадиКонвертер объёма и общих измерений при варкеПреобразователь температурыПреобразователь давления, напряжения, модуля ЮнгаПреобразователь энергии и работыПреобразователь силыПреобразователь силыКонвертер времениЛинейный конвертер скорости и скоростиКонвертер угла Хранение данныхКурсы обмена валютЖенская одежда и размеры обувиМужская одежда и размеры обувиКонвертер угловой скорости и частоты вращенияКонвертер ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаПреобразователь момента инерцииПреобразователь момента силыКонвертер крутящего моментаПреобразователь удельной энергии, теплоты сгорания (на единицу температуры) Преобразователь интерваловКонвертер коэффициента теплового расширенияПреобразователь теплового сопротивленияПреобразователь теплопроводности Конвертер удельной теплоемкости ter Конвертер скорости передачиКонвертер уровня звукаКонвертер чувствительности микрофонаКонвертер уровня звукового давления (SPL) Конвертер уровня звукового давления с выбираемым эталонным давлениемКонвертер яркостиКонвертер яркостиКонвертер яркостиКонвертер разрешения цифрового изображенияПреобразователь частоты и длины волныОптическая мощность (диоптрия) в преобразователь фокусного расстоянияПреобразователь оптической мощности (диоптрий) в увеличение (X) Конвертер электрического заряда Конвертер плотности зарядаКонвертер плотности поверхностного зарядаКонвертер объёмной плотности заряда Преобразователь электрического токаЛинейный преобразователь плотности токаПреобразователь плотности поверхностного токаПреобразователь напряженности электрического поляПреобразователь электрического потенциала и напряженияПреобразователь электрического сопротивленияКонвертер электрического сопротивленияПреобразователь электрической проводимостиПреобразователь электрической проводимостиПреобразователь емкостиПреобразователь индуктивностиПреобразователь реактивной мощности переменного токаПреобразователь единиц магнитного поля в ваттах и дБм Конвертер плотности потока Конвертер мощности поглощенной дозы излучения, Конвертер мощности дозы полного ионизирующего излученияРадиоактивность.Преобразователь радиоактивного распада Преобразователь радиационного облученияРадиация. Конвертер поглощенной дозы Конвертер метрических префиксов Конвертер передачи данных Конвертер единиц типографии и цифрового изображения Конвертер единиц измерения объема древесиныКалькулятор молярной массыПериодическая таблица

Этот онлайн-конвертер единиц измерения позволяет быстро и точно преобразовывать многие единицы измерения из одной системы в другую. Страница «Преобразование единиц» предоставляет решение для инженеров, переводчиков и для всех, чья деятельность требует работы с величинами, измеренными в различных единицах.

Вы можете использовать этот онлайн-конвертер для преобразования нескольких сотен единиц (включая метрическую, британскую и американскую) в 76 категорий или нескольких тысяч пар, включая ускорение, площадь, электрическую энергию, энергию, силу, длину, свет, массу, массовый расход, плотность, удельный объем, мощность, давление, напряжение, температура, время, крутящий момент, скорость, вязкость, объем и емкость, объемный расход и многое другое.
Примечание. Целые числа (числа без десятичной точки или показателя степени) считаются с точностью до 15 цифр, а максимальное количество цифр после десятичной точки равно 10.», То есть« умножить на десять в степени ». Электронная нотация обычно используется в калькуляторах, а также учеными, математиками и инженерами.

Стандартные преобразователи единиц

Конвертер длины и расстояния : метр, километр, сантиметр, миллиметр, нанометр, ярд, фут, дюйм, парсек, световой год, астрономическая единица, расстояние до Луны (от Земли до Луны), лига , миля, морская миля (международная), сажень, длина кабеля (международная), точка, пиксель, калибр, планковская длина…

Конвертер массы : грамм, килограмм, миллиграмм, тонна (метрическая), фунт, унция, камень (США), камень (Великобритания), карат, зерно, талант (библейский греческий), драхма (библейский греческий язык), денарий (библейский римский), шекель (библейский иврит), масса Планка, масса протона, атомная единица массы, масса электрона (покой), масса Земли, масса Солнца …

Сухой объем и стандартные измерения при приготовлении пищи : литр, бочка сухой (США), пинта сухой (США), квартовый сухой (США), peck (США), peck (Великобритания), bushel (США), bushel (UK), cor (библейский), homer (библейский), ephah (библейский) ), seah (библейский), omer (библейский), cab (библейский), log (библейский), кубометр.

Конвертер площади : миллиметр², сантиметр², метр², километр², гектар, акр, дюйм², фут², ярд², миля², сарай, круглый дюйм, поселок, роуд, стержень², окунь², усадьба, шест², сабин, арпент, куэрда, квадратная верста, квадратный аршин, квадратный фут, квадратный сажень, площадь Планка …

Конвертер объёма и общих единиц измерения температуры : метр³, километр³, миллиметр³, литр, гектолитр, миллилитр, капля, бочка (масло), бочка (США) ), баррель (Великобритания), галлон (США), галлон (Великобритания), кварта (США), кварта (Великобритания), пинта (США), пинта (Великобритания), баррель (нефть), баррель (США), баррель (Великобритания ), галлон (США), галлон (Великобритания), кварта (США), кварта (Великобритания), пинта (США), пинта (Великобритания), ярд³, фут³, дюйм³, регистровая тонна, 100 кубических футов…

Преобразователь температуры : кельвин, градус Цельсия, градус Фаренгейта, градус Ренкина, градус Реомюра, температура Планка.

Преобразователь давления, напряжения, модуля Юнга : паскаль, килопаскаль, мегапаскаль, миллипаскаль, микропаскаль, нанопаскаль, атмосферно-техническая, стандартная атмосфера, ksi, psi, ньютон / метр², бар, миллибар, килограмм-сила / метр², грамм- сила / сантиметр², тонна-сила (короткая) / фут², фунт-сила / фут², миллиметр ртутного столба (0 ° C), дюйм ртутного столба (32 ° F), сантиметр водяного столба (4 ° C), фут водяного столба (4 ° C) , метр морской воды…

Конвертер энергии и работы : джоуль, килоджоуль, мегаджоуль, миллиджоуль, мегаэлектронвольт, электрон-вольт, эрг, киловатт-час, мегаватт-час, ньютон-метр, килокалория (IT), калория (пищевая), Британские тепловые единицы (IT), мегабтеки (IT), тонна-час (охлаждение), тонна нефтяного эквивалента, баррель нефтяного эквивалента (США), мегатонна, тонна (взрывчатые вещества), килограмм в тротиловом эквиваленте, дин-сантиметр, грамм-сила-сантиметр, килограмм-сила-метр, килопонд-метр, фут-фунт, дюйм-фунт, энергия Планка …

Power Converter : ватт, киловатт, мегаватт, милливатт, лошадиные силы, вольт-ампер, ньютон-метр / секунда, джоуль / секунда, мегаджоуль в секунду, килоджоуль в секунду, миллиджоуль в секунду, джоуль в час, килоджоуль в час, эрг в секунду, британские тепловые единицы (IT) в час, килокалории (IT) в час…

Преобразователь силы : ньютон, килоньютон, миллиньютон, дин, джоуль / метр, джоуль / сантиметр, грамм-сила, килограмм-сила, тонна-сила (короткая), кип-сила, килопунт-сила, фунт-сила сила, унция-сила, фунтал, фунт-фут в секунду², pond, sthene, грав-сила, миллиграв-сила …

Преобразователь времени : секунда, миллисекунда, наносекунда, пикосекунда, минута, час, день, неделя, месяц, год, декада, век, тысячелетие, планковское время, год (юлианский), год (високосный), год (тропический), год (сидерический), год (григорианский), две недели, встряска…

Конвертер линейной скорости и скорости : метр в секунду, километр в час, километр в секунду, миля в час, фут в секунду, миля в секунду, узел, узел (Великобритания), скорость света в вакууме, космический скорость — первая, космическая скорость — вторая, космическая скорость — третья, скорость Земли, скорость звука в чистой воде, Мах (стандарт СИ), Мах (20 ° C и 1 атм), ярд / секунду …

Угол Преобразователь : градус, радиан, град, гон, минута, секунда, знак, мил, оборот, круг, поворот, квадрант, прямой угол, секстант.

Конвертер топливной экономичности, расхода топлива и экономии топлива : метр / литр, километр / литр, миля (США) / литр, морская миля / литр, морская миля / галлон (США), километр / галлон (США), литр / 100 км, галлон (США) / миля, галлон (США) / 100 миль, галлон (Великобритания) / миля, галлон (Великобритания) / 100 миль …

Конвертер чисел : двоичный, восьмеричный, десятичный, шестнадцатеричный, основание-3, основание-4, основание-5, основание-6, основание-7, основание-9, основание-10, основание-11, основание-12, основание-13, основание-14, основание-15, основание-20, основание-21, основание-22, основание-23, основание-24, основание-28, основание-30, основание-32, основание-34, основание-36…

Конвертер единиц информации и хранения данных : бит, байт, слово, четверное слово, MAPM-слово, блок, килобит (10³ бит), кибибит, кибибайт, килобайт (10³ байтов), мегабайт (10⁶) байтов), гигабайт (10⁹ байтов), терабайт (10¹² байтов), петабайт (10¹⁵ байтов), эксабайт (10¹⁸ байтов), гибкий диск (3,5 ED), гибкий диск (5,25 HD), Zip 250, Jaz 2 ГБ, CD (74 минут), DVD (2 слоя 1 сторона), диск Blu-ray (однослойный), диск Blu-ray (двухслойный) …

Обменный курс валюты : евро, доллар США, канадский доллар, британский фунт стерлингов, японская иена, швейцарский франк, аргентинское песо, австралийский доллар, бразильский реал, болгарский лев, чилийское песо, китайский юань, чешская крона, датская крона, египетский фунт, венгерский форинт, исландская крона, индийская рупия, индонезийская рупия, новый израильский шекель , Иорданский динар, малазийский ринггит, мексиканское песо, новозеландский доллар, норвежская крона, пакистанская рупия, филиппинское песо, румынский лей, российский рубль, саудовский риял, сингапурский доллар, Южноафриканский рэнд, южнокорейский вон, шведская крона, новый тайваньский доллар, тайский бат, турецкая лира, украинская гривна…

Размеры женской одежды и обуви : женские платья, костюмы и свитера, женская обувь, женские купальные костюмы, размер букв, бюст, дюймы, естественная талия, дюймы, заниженная талия, дюймы, бедра, дюймы, бюст, сантиметры, Естественная талия, сантиметры, Заниженная талия, сантиметры, Бедра, сантиметры, Длина стопы, мм, Торс, дюймы, США, Канада, Великобритания, Европа, континентальный, Россия, Япония, Франция, Австралия, Мексика, Китай, Корея ..

Размеры мужской одежды и обуви : мужские рубашки, мужские брюки / брюки, размер мужской обуви, размер букв, шея, дюймы, грудь, дюймы, рукав, дюймы, талия, дюймы, шея, сантиметры, грудь, сантиметры, Рукав, сантиметры, Талия, сантиметры, Длина стопы, мм, Длина стопы, дюймы, США, Канада, Великобритания, Австралия, Европа, континентальный, Япония, Россия, Франция, Италия, Испания, Китай, Корея, Мексика…

Механика

Преобразователь угловой скорости и частоты вращения : радиан / секунда, радиан / день, радиан / час, радиан / минута, градус / день, градус / час, градус / минута, градус / секунда, оборот / день, оборот / час, оборот / минута, оборот / секунда, оборот / год, оборот / месяц, оборот / неделя, градус / год, градус / месяц, градус / неделя, радиан / год, радиан / месяц, радиан / неделя.

Преобразователь ускорения : дециметр / секунда², метр / секунда², километр / секунда², гектометр / секунда², декаметр / секунда², сантиметр / секунда², миллиметр / секунда², микрометр / секунда², нанометр / секунда², пикометр / секунда², фемтометр / секунда² , аттометр / секунда², галлон, галилей, миля / секунда², ярд / секунда², фут / секунда², дюйм / секунда², ускорение свободного падения, ускорение свободного падения на Солнце, ускорение свободного падения на Меркурии, ускорение свободного падения на Венере , ускорение свободного падения на Луне, ускорение свободного падения на Марсе, ускорение свободного падения на Юпитере, ускорение свободного падения на Сатурне…

Конвертер плотности : килограмм / метр³, килограмм / сантиметр³, грамм / метр³, грамм / сантиметр³, грамм / миллиметр³, миллиграмм / метр³, миллиграмм / сантиметр³, миллиграмм / миллиметр³, экзаграмма / литр, петаграмм / литр, тераграмма / литр, гигаграмм / литр, мегаграмм / литр, килограмм / литр, гектограмм / литр, декаграмм / литр, грамм / литр, дециграмм / литр, сантиграмм / литр, миллиграмм / литр, микрограмм / литр, нанограмм / литр, пикограмм / литр , фемтограмм / литр, аттограмм / литр, фунт / дюйм³ …

Конвертер удельного объема : метр³ / килограмм, сантиметр³ / грамм, литр / килограмм, литр / грамм, фут³ / килограмм, фут³ / фунт, галлон (США ) / фунт, галлон (Великобритания) / фунт.

Преобразователь момента инерции : килограмм-метр², килограмм-сантиметр², килограмм-миллиметр², грамм-сантиметр², грамм-миллиметр², килограмм-сила-метр-секунда², унция-дюйм², унция-сила-дюйм-секунда², фунт-фут², фунт-сила-фут-секунда, фунт²-дюйм , фунт-сила-дюйм-секунда², ударный фут².

Конвертер момента силы : метр ньютон, метр килоньютон, метр миллиньютон, метр микроньютон, метр тонна-сила (короткий), метр тонна-сила (длинный), метр тонна-сила (метрический), метр килограмм-сила, грамм-сила-сантиметр, фунт-сила-фут, фунт-фут, фунт-дюйм.

Гидротрансформатор : ньютон-метр, ньютон-сантиметр, ньютон-миллиметр, килоньютон-метр, дин-сантиметр, дин-сантиметр, дин-миллиметр, килограмм-сила-метр, килограмм-сила-сантиметр, килограмм-сила-миллиметр, грамм-сила-метр, грамм- сила-сантиметр, грамм-сила-миллиметр, унция-сила-фут, унция-сила-дюйм, фунт-сила-фут, фунт-сила-дюйм.

Термодинамика — тепло

Конвертер удельной энергии, теплоты сгорания (на массу) : джоуль / килограмм, килоджоуль / килограмм, калория (IT) / грамм, калория (th) / грамм, британские тепловые единицы (IT) / фунт, BTU (th) / фунт, килограмм / джоуль, килограмм / килоджоуль, грамм / калория (IT), грамм / калория (th), фунт / BTU (IT), фунт / Btu (th), фунт / лошадиная сила-час, грамм / лошадиная сила (метрическая) -час, грамм / киловатт-час.

Конвертер удельной энергии, теплоты сгорания (на объем) : джоуль / метр³, джоуль / литр, мегаджоуль / метр³, килоджоуль / метр³, килокалория (IT) / метр³, калория (IT) / сантиметр³, терм / фут³, терм / галлон (Великобритания), британские тепловые единицы (IT) на фут³, британские тепловые единицы на фут³, CHU / фут³, метр³ / джоуль, литр / джоуль, галлон (США) / лошадиная сила-час, галлон (США) / лошадиная сила (метрическая система) )-час.

Конвертер теплопроводности : ватт / метр / K, ватт / сантиметр / ° C, киловатт / метр / K, калория (IT) / секунда / сантиметр / ° C, калория (th) / секунда / сантиметр / ° C , килокалория (IT) / час / метр / ° C, килокалория (th) / час / метр / ° C, BTU (IT) дюйм / секунда / фут² / ° F, BTU (th) дюйм / секунда / фут² / ° F , Btu (IT) фут / час / фут² / ° F, Btu (th) фут / час / фут² / ° F, BTU (IT) дюйм / час / фут² / ° F, BTU (th) дюйм / час / фут² / ° F.

Конвертер удельной теплоемкости : джоуль / килограмм / K, джоуль / килограмм / ° C, джоуль / грамм / ° C, килоджоуль / килограмм / K, килоджоуль / килограмм / ° C, калория (IT) / грамм / ° C, калория (IT) / грамм / ° F, калория (th) / грамм / ° C, килокалория (IT) / килограмм / ° C, килокалория (th) / килограмм / ° C, килокалория (IT) / килограмм / K , килокалория (th) / килограмм / K, килограмм-сила-метр / килограмм / K, фунт-сила-фут / фунт / ° R, Btu (IT) / фунт / ° F, Btu (th) / фунт / ° F, Btu (IT) / фунт / ° R, Btu (th) / фунт / ° R, Btu (IT) / фунт / ° C, CHU / фунт / ° C.

Конвертер плотности теплового потока : ватт / метр², киловатт / метр², ватт / сантиметр², ватт / дюйм², джоуль / секунда / метр², килокалория (IT) / час / метр², килокалория (IT) / час / фут², калория (IT) / минута / сантиметр², калория (IT) / час / сантиметр², калория (th) / минута / сантиметр², калория (th) / час / сантиметр², дина / час / сантиметр, эрг / час / миллиметр², фут-фунт / минута на фут², мощность в лошадиных силах на фут², мощность (метрическая) на фут², BTU (IT) / секунда на фут², BTU (IT) / минута на фут², Btu (IT) / час на фут², BTU (th) / секунда на дюйм² , Btu (th) / секунда / фут², Btu (th) / минута / фут², Btu (th) / час / фут², CHU / час / фут².

Преобразователь коэффициента теплопередачи : ватт / метр² / K, ватт / метр² / ° C, джоуль / секунда / метр² / K, килокалория (IT) / час / метр² / ° C, килокалория (IT) / час / фут² / ° C, BTU (IT) / секунда / фут² / ° F, Btu (th) / секунда / фут² / ° F, BTU (IT) / час / фут² / ° F, Btu (th) / час / фут² / ° F, CHU / час / фут² / ° C.

Гидравлика — жидкости

Конвертер объемного расхода : метр³ / секунда, метр³ / день, метр³ / час, метр³ / минута, сантиметр³ / день, сантиметр³ / час, сантиметр³ / минуту, сантиметр³ / секунда, литр / день, литр / час, литр / минута, литр / секунда, миллилитр / день, миллилитр / час, миллилитр / минута, миллилитр / секунда, галлон (США) / день, галлон (США) / час, галлон (США) / минута, галлон (США) в секунду, галлон (Великобритания) в день, галлон (Великобритания) в час, галлон (Великобритания) в минуту, галлон (Великобритания) в секунду, килобаррель (США) в день, баррель (США) в день…

Конвертер массового расхода : килограмм / секунда, грамм / секунда, грамм / минута, грамм / час, грамм / день, миллиграмм / минута, миллиграмм / час, миллиграмм / день, килограмм / минута, килограмм / час , килограмм / день, экзаграмм / секунда, петаграмма / секунда, тераграмма / секунда, гигаграмма / секунда, мегаграмм / секунда, гектограмм / секунда, декаграмма / секунда, дециграмма / секунда, сантиграмма / секунда, миллиграмм / секунда, микрограмм / секунда, тонна (метрическая) в секунду, тонна (метрическая) в минуту, тонна (метрическая) в час, тонна (метрическая) в день …

Конвертер молярной скорости потока : моль / секунда, экзамен / секунда, петамоль / секунда, терамоль / секунда, гигамоль / секунда, мегамоль / секунда, киломоль / секунда, гектомоль / секунда, декамоль / секунда, децимоль / секунда, сантимоль / секунда, миллимоль / секунда, микромоль / секунда, наномоль / секунда, пикомоль / секунда, фемтомоль / секунда, аттомоль в секунду, моль в минуту, моль в час, моль в день, миллимоль в минуту, миллимоль в час, миллимоль в день, километр в минуту, километр в час, километр в день.

Mass Flux Converter : грамм / секунда / метр², килограмм / час / метр², килограмм / час / фут², килограмм / секунда / метр², грамм / секунда / сантиметр², фунт / час / фут², фунт / секунда / фут².

Конвертер молярной концентрации : моль / метр³, моль / литр, моль / сантиметр³, моль / миллиметр³, километр / метр³, километр / литр, километр / сантиметр³, километр / миллиметр³, миллимоль / метр³, миллимоль / литр, миллимоль / сантиметр³, миллимоль / миллиметр³, моль / дециметр³, молярный, миллимолярный, микромолярный, наномолярный, пикомолярный, фемтомолярный, аттомолярный, зептомолярный, йоктомолярный.

Массовая концентрация в преобразователе раствора : килограмм / литр, грамм / литр, миллиграмм / литр, часть / миллион, гран / галлон (США), гран / галлон (Великобритания), фунт / галлон (США), фунт / галлон (Великобритания), фунт / миллион галлон (США), фунт / миллион галлон (Великобритания), фунт / фут³, килограмм / метр³, грамм / 100 мл.

Конвертер динамической (абсолютной) вязкости : паскаль-секунда, килограмм-сила секунда на метр², ньютон-секунда на метр², миллиньютон-секунда на метр², дин-секунда на сантиметр², равновесие, эксапуаз, петапуаз, терапуаз, гигапуаз, мегапуаз, килопуаз, гектопуаз, декапуаз, деципуаз, сантипуаз, миллипуаз, микропуаз, наноуаз, пикопуаз, фемтопуаз, аттопуаз, фунт-сила-секунда / дюйм², фунт-сила-секунда / фут², фунт-секунда / фут², грамм / сантиметр / секунда…

Конвертер кинематической вязкости : метр² / секунда, метр² / час, сантиметр² / секунда, миллиметр² / секунда, фут² / секунда, фут² / час, дюйм² / секунда, стоксы, экзастоки, петастоки, терастоки, гигастоки, мегастоксы, килостоки, гектостоки, декастоки, децистоки, сантистоки, миллистоки, микростоки, наностоки, пикостоки, фемтостоки, аттостоки.

Преобразователь поверхностного натяжения : ньютон на метр, миллиньютон на метр, грамм-сила на сантиметр, дина на сантиметр, эрг / сантиметр², эрг / миллиметр², фунт на дюйм, фунт-сила / дюйм.

Акустика — Звук

Преобразователь чувствительности микрофона : децибел относительно 1 вольт на 1 паскаль, децибел относительно 1 вольта на 1 микропаскаль, децибел относительно 1 вольта на 1 дин на квадратный сантиметр, децибел относительно 1 вольт на 1 микробар, вольт на паскаль, милливольт на паскаль, микровольт на паскаль.

Преобразователь уровня звукового давления (SPL) : ньютон на квадратный метр, паскаль, миллипаскаль, микропаскаль, дин / квадратный сантиметр, бар, миллибар, микробар, уровень звукового давления в децибелах.

Фотометрия — свет

Конвертер яркости : кандела на метр², кандела на сантиметр², кандела на фут², кандела на дюйм², килокандела на метр², стильб, люмен на метр² / стерадиан, люмен на сантиметр² / стерадиан², люмен на фут². стерадиан, нит, миллинит, ламберт, миллиламберт, фут-ламберт, апостиль, блондель, брил, скот.

Конвертер силы света : кандела, свеча (немецкий язык), свеча (Великобритания), десятичная свеча, свеча (пентан), пентановая свеча (мощность 10 свечей), свеча Хефнера, единица измерения яркости, десятичный буж, люмен / стерадиан, свеча (Международный).

Конвертер освещенности : люкс, метр-свеча, сантиметр-свеча, фут-свеча, фот, nox, кандела стерадиан на метр², люмен на метр², люмен на сантиметр², люмен на фут², ватт на сантиметр² (при 555 нм) .

Преобразователь частоты и длины волны : герцы, экзагерцы, петагерцы, терагерцы, гигагерцы, мегагерцы, килогерцы, гектогерцы, декагерцы, децигерцы, сантигерцы, единицы измерения длины волны, микрогерцы, микрогерцы, миллигерцы, микрогерцы, миллигерц , длина волны в петаметрах, длина волны в тераметрах, длина волны в гигаметрах, длина волны в мегаметрах, длина волны в километрах, длина волны в гектометрах, длина волны в декаметрах…

Конвертер оптической силы (диоптрии) в фокусное расстояние : Оптическая сила (диоптрическая сила или преломляющая сила) линзы или другой оптической системы — это степень, в которой система сходится или расходит свет. Он рассчитывается как величина, обратная фокусному расстоянию оптической системы и измеряется в инверсных метрах в СИ или, чаще, в диоптриях (1 диоптрия = м⁻¹)

Электротехника

Конвертер электрического заряда : кулон, мегакулон , килокулон, милликулон, микрокулон, нанокулон, пикокулон, абкулон, EMU заряда, статкулон, ESU заряда, франклин, ампер-час, миллиампер-час, ампер-минута, ампер-секунда, фарадей (на основе углерода 12), элементарный заряжать.

Преобразователь электрического тока : ампер, килоампер, миллиампер, биот, абампер, ЭДС тока, статампер, ЭДС тока, СГС э.м. единица, CGS e.s. единица, микроампер, наноампер, ток Планка.

Линейный преобразователь плотности тока : ампер / метр, ампер / сантиметр, ампер / дюйм, абампер / метр, абампер / сантиметр, абампер / дюйм, эрстед, гильберт / сантиметр, ампер / миллиметр, миллиампер / метр, миллиампер , миллиампер / сантиметр, миллиампер / миллиметр, микроампер / метр, микроампер / дециметр, микроампер / сантиметр, микроампер / миллиметр.

Преобразователь поверхностной плотности тока : ампер / метр², ампер / сантиметр², ампер / дюйм², ампер / мил², ампер / круговой мил, абампер / сантиметр², ампер / миллиметр², миллиампер / миллиметр², микроампер / миллиметр², миллиампер / миллиметр², миллиампер / миллиметр² миллиампер / сантиметр², микроампер / сантиметр², килоампер / сантиметр², ампер / дециметр², миллиампер / дециметр², микроампер / дециметр², килоампер / дециметр².

Преобразователь напряженности электрического поля : вольт на метр, киловольт на метр, киловольт на сантиметр, вольт на сантиметр, милливольт на метр, микровольт на метр, киловольт на дюйм, вольт на дюйм, вольт на мил, абвольт на сантиметр, статвольт / сантиметр, статвольт / дюйм, ньютон / кулон, вольт / микрон.

Преобразователь электрического потенциала и напряжения : вольт, милливольт, микровольт, нановольт, пиковольт, киловольт, мегавольт, гигавольт, теравольт, ватт / ампер, абвольт, EMU электрического потенциала, статвольт, ESU электрического потенциала, планковский электрический потенциал.

Преобразователь электрического сопротивления : Ом, мегаом, мкОм, вольт / ампер, обратный сименс, abohm, EMU сопротивления, статом, ESU сопротивления, квантованное сопротивление Холла, импеданс Планка, миллиом, кОм.

Преобразователь удельного электрического сопротивления : омметр, ом-сантиметр, ом-дюйм, микром-сантиметр, микром-дюйм, ом-сантиметр, статом-сантиметр, круговой мил-ом / фут, ом-кв.миллиметр на метр.

Преобразователь электрической проводимости : сименс, мегасименс, килосименс, миллисименс, микросименс, ампер / вольт, mho, gemmho, micromho, abmho, statmho, квантованная проводимость Холла.

Конвертер электропроводности : сименс / метр, пикосименс / метр, mho / метр, mho / сантиметр, abmho / метр, abmho / сантиметр, статмо / метр, статмо / сантиметр, сименс / сантиметр, миллисименс / метр, миллисименс / сантиметр, микросименс / метр, микросименс / сантиметр, единица электропроводности, коэффициент проводимости, доли на миллион, шкала 700, шкала частей на миллион, шкала 500, частей на миллион, шкала 640, TDS, частей на миллион, шкала 640, TDS, части на миллион, шкала 550, TDS, частей на миллион, шкала 500, TDS, частей на миллион, шкала 700.

Преобразователь емкости : фарад, экзафарад, петафарад, терафарад, гигафарад, мегафарад, килофарад, гектофарад, декафарад, децифарад, сентифарад, миллифарад, микрофарад, емкость, нанофарад, аттофарад, ед. , статфарад, ЭСУ емкости.

Преобразователь индуктивности : генри, эксагенри, петагенри, терагенри, гигагенри, мегагенри, килогенри, гектогенри, декагенри, децигенри, сантигенри, миллигенри, микрогенри, наногенри, пикогенри, атогенри, атогенри, энтогенри , статенри, ЭСУ индуктивности.

Преобразователь реактивной мощности переменного тока : реактивный вольт-ампер, реактивный милливольт-ампер, реактивный киловольт-ампер, реактивный мегавольт-ампер, реактивный гигавольт-ампер.

Американский калибр проводов : Американский калибр проводов (AWG) — это стандартизированная система калибра проводов, используемая в США и Канаде для измерения диаметров цветных электропроводящих проводов, включая медь и алюминий. Чем больше площадь поперечного сечения провода, тем выше его допустимая нагрузка по току.Чем больше номер AWG, также называемый калибром провода, тем меньше физический размер провода. Самый большой размер AWG — 0000 (4/0), а самый маленький — 40. В этой таблице перечислены размеры и сопротивления AWG для медных проводников. Используйте закон Ома для расчета падения напряжения на проводнике.

Магнитостатика, магнетизм и электромагнетизм

Преобразователь магнитного потока : Вебер, милливебер, микровебер, вольт-секунда, единичный полюс, мегалин, килолин, линия, максвелл, тесла-метр², тесла-сантиметр², гаусс-сантиметр², квант магнитного потока.

Конвертер плотности магнитного потока : тесла, Вебер / метр², Вебер / сантиметр², Вебер / дюйм², Максвелл / метр², Максвелл / сантиметр², Максвелл / дюйм², Гаусс, линия / сантиметр², линия / дюйм², гамма.

Радиация и радиология

Конвертер мощности поглощенной дозы излучения, суммарной мощности дозы ионизирующего излучения : серый цвет в секунду, эксагрей в секунду, петагрей в секунду, тераграрей в секунду, гигаграй в секунду, мегагрей в секунду, килограмм в секунду, гектограмм / секунда, декаграй / секунда, дециграй / секунда, сантигрей / секунда, миллиграй / секунда, микрогрей / секунда, наногрей / секунда, пикграй / секунда, фемтогрей / секунда, аттогрей / секунда, рад / секунда, джоуль / килограмм / секунда, ватт на килограмм, зиверт в секунду, миллизиверт в год, миллизиверт в час, микрозиверт в час, бэр в секунду, рентген в час…

Радиоактивность. Конвертер радиоактивного распада : беккерель, петабеккерель, терабеккерель, гигабеккерель, мегабеккерель, килобеккерель, миллибеккерель, кюри, килокюри, милликюри, микрокюри, нанокюри, пикокюри, резерфорд, одно / секунда, дезинтеграция.

Конвертер облучения : кулон на килограмм, милликулон на килограмм, микрокулон на килограмм, рентген, миллирентген, микрорентген, тканевый рентген, Паркер, респ.

Радиация. Конвертер поглощенной дозы : рад, миллирад, джоуль / килограмм, джоуль / грамм, джоуль / сантиграм, джоуль / миллиграмм, серый, эксагрей, петагрей, терагрей, гигагрей, мегагрей, килограмм, гектагрей, декаграй, декаграй, сантигрей, микрогрей, миллиграм , наногрей, пикограй, фемтогрей, аттогрей, зиверт, миллизиверт, микрозиверт …

Прочие преобразователи

Конвертер метрических префиксов : нет, yotta, zetta, exa, peta, tera, giga, mega, kilo, hecto, deka , деци, санти, милли, микро, нано, пико, фемто, атто, зепто, йокто.

Конвертер передачи данных : бит / секунда, байт / секунда, килобит / секунда (SI по умолчанию), килобайт / секунда (SI по умолчанию), кибибит / секунда, кибибайт / секунда, мегабит / секунда (SI по умолчанию) , мегабайт в секунду (SI по умолчанию), мебибит в секунду, мебибайт в секунду, гигабит в секунду (SI по умолчанию), гигабайт в секунду (SI по умолчанию), гибибит в секунду, гибибит в секунду, терабит в секунду (SI по умолчанию). .), терабайт в секунду (по умолчанию SI), тебибит в секунду, тебибайт в секунду, Ethernet, Ethernet (быстрый), Ethernet (гигабит), OC1, OC3, OC12, OC24, OC48 …

Типографика и цифровой Конвертер единиц изображения : твип, метр, сантиметр, миллиметр, символ (X), символ (Y), пиксель (X), пиксель (Y), дюйм, пика (компьютер), пика (принтер), точка (DTP / PostScript) ), point (компьютер), point (принтер), en, cicero, em, Didot point.

Конвертер величин объема пиломатериалов : кубический метр, кубический фут, кубический дюйм, футы для досок, тысяча футеров для досок, шнур, шнур (80 фут3), футы для шнура, узел, поддон, поперечина, стяжка переключателя.

Калькулятор молярной массы : Молярная масса — это физическое свойство, которое определяется как масса вещества, деленная на его количество в молях. Другими словами, это масса одного моля определенного вещества.

Периодическая таблица : Периодическая таблица представляет собой список всех химических элементов, упорядоченных слева направо и сверху вниз по их атомным номерам, электронным конфигурациям и повторяющимся химическим свойствам, расположенным в форме таблицы таким образом, чтобы элементы с аналогичные химические свойства отображаются в вертикальных столбцах, называемых группами.У некоторых групп есть имена, а также номера. Например, все элементы группы 1, кроме водорода, являются щелочными металлами, а элементы группы 18 — благородными газами, которые ранее назывались инертными газами. Различные строки таблицы называются периодами, потому что это расположение отражает периодическое повторение сходных химических и физических свойств химических элементов по мере увеличения их атомного номера. Элементы одного периода имеют одинаковое количество электронных оболочек.

У вас есть трудности с переводом единицы измерения на другой язык? Помощь доступна! Задайте свой вопрос в TCTerms , и вы получите ответ от опытных технических переводчиков в считанные минуты.

Калькулятор резистора

Ниже приведены инструменты для расчета значения сопротивления и допусков на основе цветовой кодировки резисторов, общего сопротивления группы резисторов, включенных параллельно или последовательно, и сопротивления проводника в зависимости от размера и проводимости.

Калькулятор цветового кода резистора

Используйте этот калькулятор, чтобы узнать значение сопротивления и допуск на основе цветовой кодировки резистора.

Вычислитель параллельных резисторов

Введите все значения сопротивления параллельно, разделенные запятой «,» и нажмите кнопку «Рассчитать», чтобы определить общее сопротивление.

Последовательный счетчик резисторов Введите все значения сопротивления последовательно, разделенные запятой «,» и нажмите кнопку «Рассчитать», чтобы определить общее сопротивление.

Сопротивление проводника

Используйте следующее для расчета сопротивления проводника. В этом калькуляторе предполагается, что проводник круглый.

Калькулятор закона Омса
Цветовой код резистора

Электронный цветовой код — это код, который используется для указания номинальных характеристик определенных электрических компонентов, например сопротивления резистора в Ом.Электронные цветовые коды также используются для оценки конденсаторов, катушек индуктивности, диодов и других электронных компонентов, но чаще всего используются для резисторов. Калькулятор рассчитывает только резисторы.

Как работает цветовая кодировка:

Цветовая кодировка резисторов является международным стандартом, определенным в IEC 60062. Цветовая кодировка резистора, показанная в таблице ниже, включает различные цвета, которые представляют значащие числа, множитель, допуск, надежность и температурный коэффициент.К какому из них относится цвет, зависит от положения цветовой полосы на резисторе. В типичном четырехполосном резисторе существует промежуток между третьей и четвертой полосами, чтобы указать, как следует считывать показания резистора (слева направо, причем одинокая полоса после промежутка является самой правой полосой). В объяснении ниже будет использоваться четырехполосный резистор (конкретно показанный ниже). Другие возможные варианты резистора будут описаны позже.

Составляющая значащей фигуры:

В типичном четырехполосном резисторе первая и вторая полосы представляют собой значащие цифры.Для этого примера обратитесь к рисунку выше с зеленой, красной, синей и золотой полосой. В приведенной ниже таблице зеленая полоса представляет собой цифру 5, а красная полоса — 2.

Множитель:

Третья синяя полоса — множитель. Таким образом, множитель по таблице равен 1 000 000. Этот множитель умножается на значащие числа, определенные из предыдущих диапазонов, в данном случае 52, в результате получается значение 52 000 000 Ом или 52 МОм.

Допуск:

Четвертая полоса присутствует не всегда, но когда она есть, представляет собой допуск.Это процентное значение, на которое может изменяться номинал резистора. Золотая полоса в этом примере указывает на допуск ± 5%, который может быть представлен буквой J. Это означает, что значение 52 МОм может изменяться до 5% в любом направлении, поэтому номинал резистора составляет 49,4 МОм. — 54,6 МОм.

Надежность, температурный коэффициент и другие вариации:

Кодированные компоненты имеют как минимум три полосы: две полосы значащих цифр и множитель, но есть и другие возможные варианты.Например, компоненты, изготовленные в соответствии с военными спецификациями, обычно представляют собой четырехполосные резисторы, которые могут иметь пятую полосу, которая указывает на надежность резистора с точки зрения процента отказов на 1000 часов работы. Также возможно иметь полосу 5 ^th, которая представляет собой температурный коэффициент, который указывает изменение сопротивления компонента в зависимости от температуры окружающей среды в единицах ppm / K.

Чаще встречаются пятиполосные резисторы, которые более точны из-за третьей значащей полосы числа.Это смещает положение множителя и диапазона допуска в положение 4 ^-го и 5 ^-го по сравнению с типичным четырехполосным резистором.

На самом точном резисторе может присутствовать полоса 6 ^и. Первые три диапазона будут значительными диапазонами цифр, 4 ^th — множителем, 5 ^th — допуском, а 6 ^th могут быть либо надежностью, либо температурным коэффициентом. Возможны и другие варианты, но это одни из наиболее распространенных конфигураций.

Цвет	1 ^st, 2 ^nd, 3 ^rd Band Значимые цифры	Множитель	Допуск	Температурный коэффициент
Черный	0	× 1		250 частей на миллион / К (ед.)
Коричневый	1	× 10	± 1% (Ж)	100 частей на миллион / K (S)
Красный	2	× 100	± 2% (Г)	50 частей на миллион / K (R)
Апельсин	3	× 1 К	± 0.05% (Вт)	15 частей на миллион / K (P)
Желтый	4	× 10 К	± 0,02% (П)	25 частей на миллион / K (Q)
Зеленый	5	× 100 К	± 0,5% (Г)	20 частей на миллион / K (Z)
Синий	6	× 1М	± 0.25% (С)	10 частей на миллион / K (Z)
Фиолетовый	7	× 10М	± 0,1% (В)	5 частей на миллион / K (M)
Серый	8	× 100М	± 0,01% (л)	1 частей на миллион / К (К)
Белый	9	× 1 г
Золото		× 0.1	± 5% (Дж)
Серебро		× 0,01	± 10% (К)
Нет			± 20% (М)

Резисторы — это элементы схемы, которые придают электрическое сопротивление. Хотя схемы могут быть очень сложными, и существует много различных способов размещения резисторов в цепи, резисторы в сложных схемах обычно могут быть разбиты и классифицированы как подключенные последовательно или параллельно.

Сопротивления параллельно:

Общее сопротивление резисторов, включенных параллельно, равно обратной сумме обратных величин каждого отдельного резистора. Обратитесь к уравнению ниже для пояснения:

R _итого =

1

	+	+	+ … +

Последовательные резисторы:

Общее сопротивление последовательно включенных резисторов — это просто сумма сопротивлений каждого резистора.Обратитесь к уравнению ниже для пояснения:

R _Всего = ₁ + ₂ + ₃ … + _R

Сопротивление проводника:

Где:
L — длина жилы
A — площадь поперечного сечения проводника
C — проводимость материала

Резистор, конденсатор и индуктор в последовательно-параллельном соединении

Резистор, конденсатор и индуктор в последовательном и параллельном соединении — формулы и уравнения

Следующие основные и полезные уравнения и формулы могут использоваться для проектирования, измерения, упрощения и анализа электрических цепей для различные компоненты и электрические элементы, такие как резисторы, конденсаторы и катушки индуктивности, соединенные последовательно и параллельно.

Сопротивление в последовательном и параллельном уравнениях

Сопротивление:

Общее эквивалентное сопротивление резисторов, подключенных последовательно или параллельно, определяется по следующей формуле:

Последовательное сопротивление:

Когда два или более двух резисторов подключены последовательно, как показано на рисунке, их эквивалентное сопротивление рассчитывается по формуле:

R _Eq = R ₁ + R ₂ + R ₃ +… R _n

Сопротивление параллельно:

, когда резисторы находятся в параллельной конфигурации, эквивалентное сопротивление становится:

Где

R _Eq — эквивалентное сопротивление всех резисторов (R ₁, R ₂, R ₃… R _n)

Похожие сообщения:

Дельта Δ до звезды Y (от Pi до Te e) Преобразование:

Соединение треугольником (Δ) также упоминается как соединение Pi , а соединение звезда (Y) также упоминается как соединение Tee (T) .

От треугольника (Δ) до звезды (Y) Межсоединение:

От звезды (Y) к треугольнику (Δ) Межсоединение

Подробнее и решено примеры, проверьте преобразование звезды в дельту и дельта в звезду.

Емкость в последовательном и параллельном уравнениях

Емкость:

Общая емкость конденсатора, подключенного параллельно и последовательно, приведена ниже:

Емкость последовательно:

Когда конденсаторы подключены последовательно В конфигурации эквивалентная емкость становится:

Параллельная емкость:

Емкость суммируется, когда они соединены вместе в параллельной конфигурации

C _Eq = C ₁ + C ₂ + C ₃ +… C _n

Где

C _Eq — эквивалентная емкость всех конденсаторов (C ₁, C ₂, C ₃… C _n )

Связанные сообщения:

Индуктивность в последовательном и параллельном уравнениях

Индуктивность:

9 0002 Расчет полной индуктивности катушек индуктивности внутри цепи аналогичен расчету резисторов.

Последовательная индуктивность:

Когда индукторы включены последовательно, как показано на рисунке, их индуктивности складываются.

L _Eq = L ₁ + L ₂ + L ₃ +… L _n

Параллельная индуктивность:

В параллельной комбинации эквивалентная индуктивность катушки индуктивности задаются как

Где

L _Eq — эквивалентная индуктивность всех катушек индуктивности (L ₁, L ₂, L ₃… L _n)

Связанные формулы и Уравнения Сообщений:

Цепи — ток, разность потенциалов, сопротивление и элементы в последовательной и параллельной цепях, сохранение заряда

Ячейки последовательно и параллельно

Ячейки в серии

Когда элементы соединены последовательно друг с другом и все они подключены в одном направлении, общая разность потенциалов, подаваемая в цепь, складывается из индивидуальных разностей потенциалов.

В _всего = В ₁ + В ₂ + В ₃

Идентичные ячейки параллельно друг другу

Когда идентичные элементы параллельны друг другу, полная разность потенциалов, подаваемая в цепь, равна разности потенциалов только одной из ячеек.

V _всего = V ₁ = V ₂ = V ₃

Итак, если три ячейки 2 В соединены параллельно друг с другом, разность потенциалов, подаваемая в цепь, составляет 2 В.

Резисторы последовательно и параллельно

Резисторы последовательно

Когда резисторов соединены последовательно друг с другом, общее сопротивление складывается из отдельных сопротивлений.

Резисторы, включенные параллельно

Когда резисторов соединены параллельно друг с другом, общее сопротивление определяется с помощью следующего уравнения.

Ток в последовательной и параллельной цепях

Сохранение заряда — «общий заряд, протекающий в стык проводов, должен равняться общему заряду, вытекающему из стыка».

Первый закон Кирхгофа — «сумма токов, протекающих в месте соединения проводов, должна равняться сумме токов, исходящих от места соединения проводов».

Ток в последовательных цепях .

Когда вы подключаете амперметр к последовательной цепи, ток остается неизменным, куда бы вы ни вставили амперметр.

Ток в параллельных цепях .

Суммарный ток, протекающий от ячейки к ветвям в цепи, всегда должен равняться току, протекающему через каждый компонент в ветвях цепи, когда они складываются.

Если компоненты имеют разное сопротивление, тогда ток через каждый компонент может быть разным, но когда вы складываете их вместе, они должны составлять общую сумму тока, выходящего из ячейки.