Соединение катушек — Основы электроники
Соединение катушек индуктивности при отсутствии взаимного влияния магнитных полей катушек.
Последовательное соединение катушек индуктивности.
Суммарная индуктивность двух или нескольких катушек, соединенных последовательно и расположенных на таком расстоянии друг от друга, что магнитное поле одной катушки не пересекает витков другой (рисунок 1), равна сумме их индуктивностей.
Рисунок 1. Последовательное соединение катушект индуктивности.
Цепь, изображенная на рисунке 1, обладает общей индуктивностью L, которая выражается так:
где L1, L2 и L3 — индуктивности отдельных катушек.
Параллельное соединение катушек индуктивности.
Индуктивность цепи, составленной из тех же катушек при параллельном их соединении (рисунок 2) и при соблюдении того же условия относительно их расположения (отсутствие магнитного взаимодействия), подсчитывается по следующей формуле:
Рисунок 2. Параллельное соединение катушек индуктивности.
Параллельное соединение катушек индуктивности.
Индуктивность двух катушек, соединенных параллельно, определяется по следующей формуле:
Как видим, формулы для подсчета результирующих индуктивностей катушек, соединенных последовательно или параллельно и не взаимодействующих между собой, совершенно тождественны с формулами для подсчета омического сопротивления цепи при последовательном и параллельном соединении резисторов.
Соединение катушек при наличии взаимного влияния их магнитных полей.
Если катушки, включенные в цепь последовательно, расположены близко друг к другу, т. е. так, что часть магнитного потока одной катушки пронизывает витки другой, т. е. между катушками существует индуктивная связь (рисунок 3а), то для определения их общей индуктивности приведенная выше формула будет уже непригодна. При таком расположении катушек могут быть два случая, а именно:
- Магнитные потоки обеих катушек имеют одинаковые направления
- Магнитные потоки обеих катушек направлены навстречу друг другу
Тот или другой случай будет иметь место в зависимости от направления витков обмотки катушек и от направлений токов в них.
Рисунок 3. Соединение катушек индуктивности: а)суммарная индуктивность увеличивается за счет взаимной индукции б)суммарная индуктивность уменьшается за счет взаимной индукции.
Если обе катушки намотаны в одну сторону и токи в них текут в одном направлении, то это будет соответствовать первому случаю; если же токи текут в противоположных направлениях (рисунок 3б), то будет иметь место второй случай.
Разберем первый случай, когда магнитные потоки направлены в одну сторону. Очевидно, при этих условиях витки каждой катушки будут пронизываться своим потоком и частью потока другой катушки, т. е. магнитные потоки в той и в другой катушке будут больше по сравнению с тем случаем, когда между катушками нет индуктивной связи. Увеличение магнитного потока, пронизывающего витки той или иной катушки, равносильно увеличению ее индуктивности. Поэтому общая индуктивность цепи в рассматриваемом случае будет больше суммы индуктивностей отдельных катушек, из которых составлена цепь.
Рассуждая таким же образом, мы придем к выводу, что для второго случая, когда потоки направлены навстречу друг другу, общая индуктивность цепи будет меньше суммы индуктивностей отдельных катушек.
Подсчет величины индуктивности цепи, составленной из двух соединенных последовательно катушек индуктивности L1 и L2 при наличии между ними индуктивной связи, производится по формуле:
В первом случае ставится знак + (плюс), а во втором случае знак — (минус).
Величина М, называемая коэффициентом взаимной индукции, представляет собой добавочную индуктивность, обусловленную частью магнитного потока, общей для обеих катушек.
На явлении взаимоиндукции основано устройство вариометров. Вариометр состоит из двух катушек, общая индуктивность которых может, по желанию, плавно изменяться в некоторых пределах. В радиотехнике вариометры применяются для настройки колебательных контуров приемников и передатчиков.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
Калькулятор взаимной индукции — последовательное соединение индуктивностей • Электротехнические и радиотехнические калькуляторы • Онлайн-конвертеры единиц измерения
Этот калькулятор определяет взаимоиндукцию и эквивалентную индуктивность двух связанных и соединенных последовательно катушек индуктивности.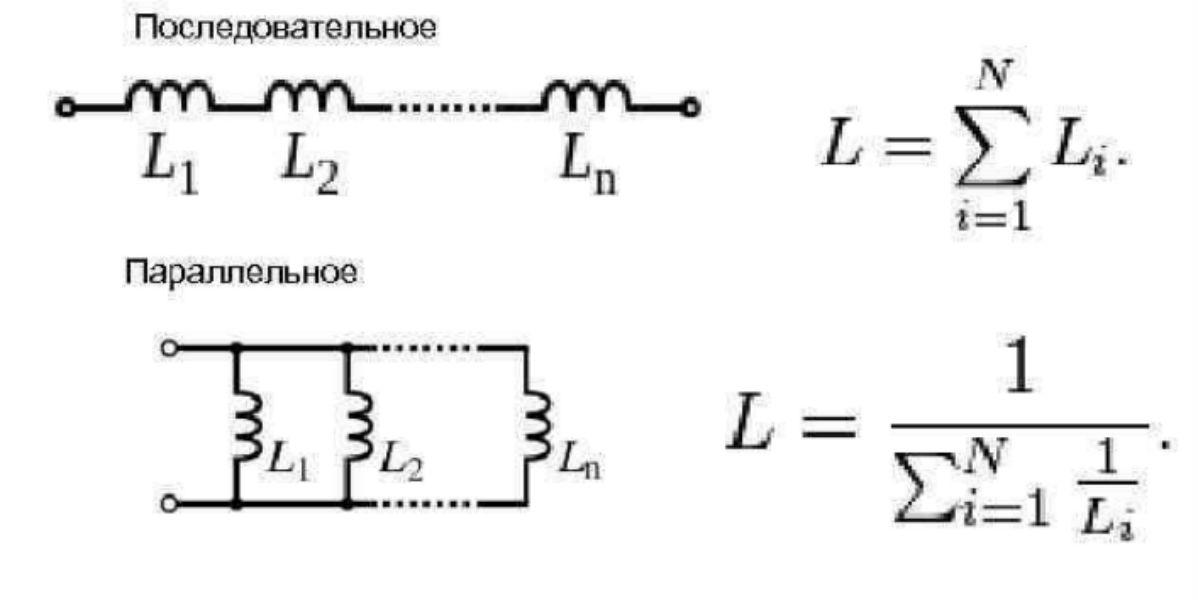
Пример. Рассчитать эквивалентную индуктивность двух катушек индуктивности 10 мкГн и 5 мкГн, соединенных последовательно и согласно с коэффициентом связи 0,5.
Входные данные
Индуктивность первой катушки, L1
генри (Гн)миллигенри (мГн)микрогенри (мкГн)наногенри (нГн)пикогенри (пГн)
Индуктивность второй катушки, L2
миллигенри (мГн)
Коэффициент связи, k
0 ≤ k ≤ 1
Тип включения катушек
Встречно
Согласно
Выходные данные
Взаимоиндукция
M миллигенри (мГн)
Полная индуктивность
Lt миллигенри (мГн)
Введите тип связи, величины индуктивностей и коэффициента связи, выберите единицы индуктивности в генри (Гн), миллигенри (мГн), микрогенри (мкГн) или пикогенри (пГн) и нажмите кнопку Рассчитать.
В Калькуляторе сопротивлений мы показали, что полное сопротивление соединенных последовательно резисторов равно сумме их сопротивлений.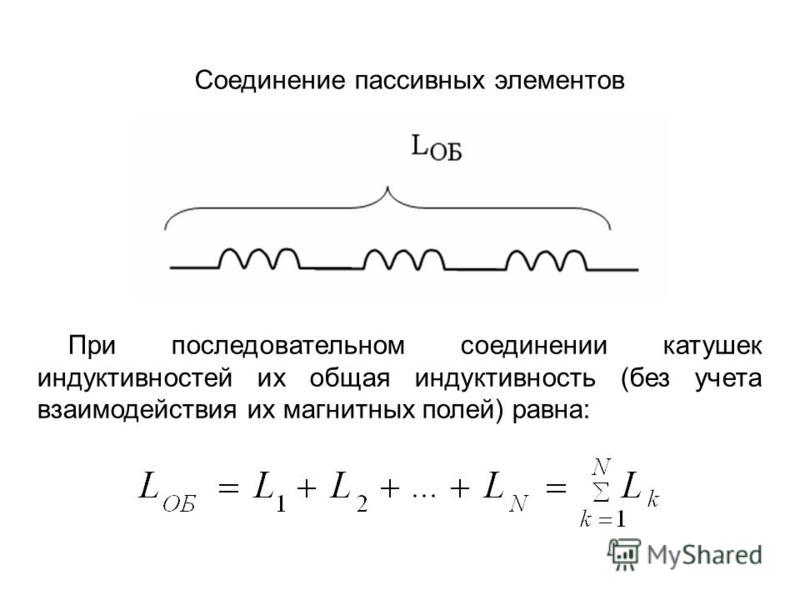 То же относится и к индуктивностям. Общая индуктивность определяется по аналогичному закону и если несколько соединенных последовательно катушек индуктивности не связаны между собой, их общая индуктивность равна сумме индуктивностей отдельных катушек. Если посмотреть на приведенную ниже иллюстрацию последовательно соединенных индуктивностей, мы увидим, что витки катушек составляют одну общую катушку и, следовательно, их индуктивности также складываются:
То же относится и к индуктивностям. Общая индуктивность определяется по аналогичному закону и если несколько соединенных последовательно катушек индуктивности не связаны между собой, их общая индуктивность равна сумме индуктивностей отдельных катушек. Если посмотреть на приведенную ниже иллюстрацию последовательно соединенных индуктивностей, мы увидим, что витки катушек составляют одну общую катушку и, следовательно, их индуктивности также складываются:
Это равенство работает только в том случае, если между отдельными катушками индуктивности нет связи. Отметим, что это бывает только в идеальном случае. В реальной жизни магнитные поля катушек пронизывают витки соседних катушек даже в том случае, если расстояние между ними достаточно велико. Если две индуктивности соединены последовательно и влияют одна на другую, то возможны две ситуации. Если магнитные потоки, образованные вокруг катушек в результате протекания в них тока, направлены в одну сторону, говорят, что такие катушки включены согласно.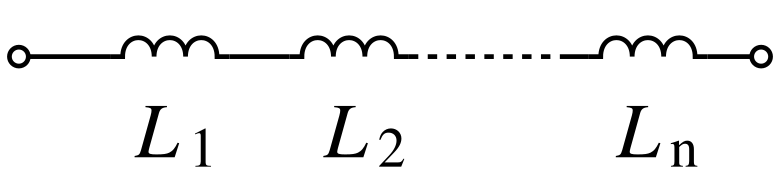 Если же магнитные потоки, образованные вокруг катушек в результате протекания в них тока, направлены в разные стороны, говорят, что такие катушки включены встречно.
Если же магнитные потоки, образованные вокруг катушек в результате протекания в них тока, направлены в разные стороны, говорят, что такие катушки включены встречно.
Последовательно соединенные катушки с согласным включением
Последовательно соединенные катушки с согласным включением
Рассмотрим две взаимно связанные катушки индуктивности L₁ и L₂, соединенные последовательно. Катушка L₁ индуктивно связана с катушкой L₂ и их взаимоиндукция равна M₁₂. Катушка L₂, в свою очередь, также индуктивно связана с катушкой L₁ и их взаимоиндукция равна M₂₁. Поскольку их магнитные поля направлены в одну сторону, они складываются. В результате складываются и индуктивности:
Согласно принципу обратимости, M₂₁ = M₁₂, следовательно, имеем
Здесь М — взаимоиндукция двух катушек, а L₁ и L₂ — самоиндукции двух катушек. В Калькуляторе взаимной индукции было показано, что взаимная индукция определяется как
Подставляя это в вышеприведенную формулу, получаем используемую в этом калькуляторе формулу для расчета общей индуктивности двух включенных согласно катушек индуктивности с коэффициентом связи k:
Последовательно соединенные катушки со встречным включением
Последовательно соединенные катушки со встречным включением
Если две катушки индуктивности L₁ и L₂ соединены, как показано на этом рисунке, то один и тот же ток, текущий в каждой катушке, направлен в противоположную сторону в каждой из них.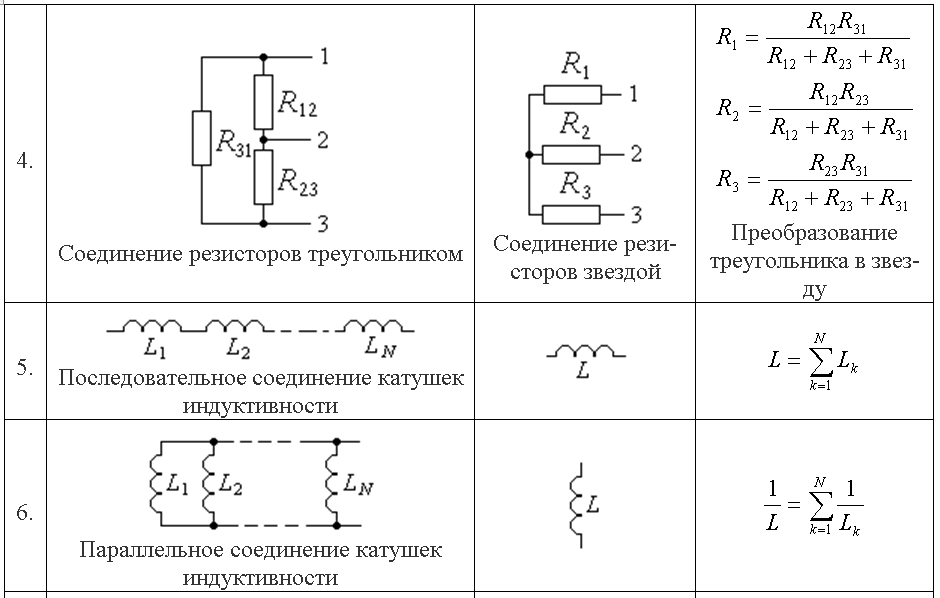 ЭДС, появляющаяся в катушке L₁ под влиянием взаимной индуктивности катушки L₂, направлена противоположно ЭДС, вызванной самоиндукцией катушки L₁. То же можно сказать относительно ЭДС в катушке L₂, вызванной магнитным полем катушки L₁. Мы видим, что в этом случае взаимная индукция уменьшает, иными словами «гасит» самоиндукцию. Поэтому вместо знака плюс в формуле общей индуктивности появляется знак минус:
ЭДС, появляющаяся в катушке L₁ под влиянием взаимной индуктивности катушки L₂, направлена противоположно ЭДС, вызванной самоиндукцией катушки L₁. То же можно сказать относительно ЭДС в катушке L₂, вызванной магнитным полем катушки L₁. Мы видим, что в этом случае взаимная индукция уменьшает, иными словами «гасит» самоиндукцию. Поэтому вместо знака плюс в формуле общей индуктивности появляется знак минус:
Эта формула и используется в данном калькуляторе для расчета общей индуктивности двух катушек со встречным включением L₁ и L₂ с коэффициентом связи k.
Катушки индуктивности на плате блока питания: трансформаторы отмечены красными стрелками, дроссели — синими стрелками
Параллельное соединение катушек индуктивности | ||||
I= . мА | X L = U L / I Ом | L = X L / ω, | Проверка | |
L =
I
Таблица 5.2.1
Соберите цепь с параллельным соединением катушек (рис. 5.2.2).
Предусмотрите в схеме
перемычки
измерения
мультиметром.
Включите
регулируемый
источник
синусоидального напряжения с параметрами Um = 10B и f = l кГц.
Таблица 5.2.2
Измерьте мультиметром
общий ток цепи I, токи параллельных
ветвей Ii
входе цепи U, занесите
данные измерений в табл. 5.2.2
5.2.2
1г, и напряжения на
Вычислите емкостные реактивные сопротивления Х, X L 1 , X L 2 ,
поформуле X
Определите индуктивности катушек и эквивалентную индуктивность цепи по формуле
L=X L / ω , где ω = 2 πf =
Проверьте вычислениями величину индуктивности L
Величина, описываемая соотношением между скоростью изменения тока и некоторой величиной, проявляющейся в проводнике при действии ЭДС самоиндукции, называется коэффициентом самоиндукции или индуктивностью проводника.
Индуктивность обозначается латинским символом L . Можно сформулировать и более простое определение: индуктивность , электротехническая величина показывающая, сколько энергии магнитного поля можно накопить в проводнике. При скручивание проводника в катушку его индуктивность увеличивается в разы. Чем выше L проводника, тем больше номинальное значение . Индуктивность измеряется единицей, получившей название генри. Сокращенно генри обозначается Гн .
Индуктивность измеряется единицей, получившей название генри. Сокращенно генри обозначается Гн .
Индуктивностью в 1 генри обладает катушка, в которой с изменением силы тока на 1 ампер в течение секундного временного интервала наводится ЭДС самоиндукции, равная 1 вольт.
Кроме генри используются величины: тысячная доля генри (миллигенри-мГн), миллионная доля генри (микрогенри — мкГн)
1 миллигенри (мГн) =1/1000 Гн = 10 -3 Гн;
1 микрогенги (мкГн) = 1/1000000 Гн = 1/1000 мГн =10 -6 Гн
Катушка индуктивности |
Катушка индуктивности, как следует из названия представляет из себя именно катушку, то есть имеется некоторое количество витков проводника (обычно медного) намотанных на каркасе. Причем наличие изоляции между витками и каркасом является важнейшим условием. Кроме того витки катушки индуктивности не должны замыкаться между собой. Чаще всего витки наматываются на тороидальный или цилиндрический каркас.
Винтовая, спиральная или винтоспиральная катушка из свёрнутого проводника, обладает значительно большой величиной индуктивности при относительно малом уровне емкости и низком активном сопротивлении.
Индуктивность катушки прямо пропорциональна квадрату числа витков, так как с увеличением количества витков увеличивается, число магнитных силовых линий, и число пересечений каждой силовой линии с проводником.
— увеличивается с увеличением площади витка катушки, так как возрастает уровень магнитного потока в катушке.
-уменьшается с увелечением осевой длины катушки, так как, чем она выше, тем меньшее число витков на единицу ее осевой длины и, следовательно, тем ниже магнитный поток.
Если в катушку добавить железный или стальной сердечник, то величина L возрастет многократно.
Разновидностей катушек индуктивности существуют великое множество. Они бывают высокочастотные, низкочастотные, с подстроечными сердечникам, катушки с отводами, катушки рассчитанные на большие напряжения. Катушки для СВЧ техники называют микрополосковыми линиями. Они совсем не похожи на катушки. (правый рисунок)
Катушки для СВЧ техники называют микрополосковыми линиями. Они совсем не похожи на катушки. (правый рисунок)
Катушка с сердечником может выглядеть так — рисунок слева, а с подстроечным сердечником, как на фотографии справа. Величина индуктивности в случае с подстроечным сердечником меняется в небольших пределах. Подстроечные катушки индуктивности используются в схемах, где необходима одноразовая подстройка. В дальнейшем ее обычно не регулируют.
Последовательное соединение катушек индуктивности
Суммарная индуктивность двух или более катушек, соединенных последовательно и расположенных на определенном расстоянии друг от друга так, что их магнитные поля не пересекали витки соседей, равна сумме их индуктивностей.
Параллельное соединение катушек
при параллельном их соединении и при соблюдении того же условия отсутствие магнитного взаимодействия относительно их расположения, расчет осуществляем по формулам:
Если катушки, соединенные в электрическую цепь последовательно, находятся близко друг к другу, и так, что часть магнитного потока одной пронизывает витки другой, т. е. между катушками присутствует индуктивная связь, то для расчета их общей индуктивности данная выше формула уже не подойдет. При таком расположении могут возникнуть два частных случая:
е. между катушками присутствует индуктивная связь, то для расчета их общей индуктивности данная выше формула уже не подойдет. При таком расположении могут возникнуть два частных случая:
Магнитные потоки катушек в цепи имеют одинаковые направления
Или наооборот их потоки направлены навстречу друг другу
Любой их них будет иметь место в зависимости от направления витков катушек и от направлений протекания токов в них.
Если обе катушки намотаны в одну сторону и токи в них протекают в одном попутном направлении, то-есть когда магнитные потоки направлены в одну сторону. При этих факторах витки каждой катушки будут пронизываться своим потоком и частью потока соседа, т. е. магнитные потоки в обоих катушках будут выше по сравнению с отсутствием индуктивной связи. Поэтому общая индуктивность схемы будет выше суммы ее составляющих отдельных катушек. Наоборот, когда потоки направлены навстречу друг другу, общая индуктивность схемы будет ниже суммы L отдельных катушек.
В первом случае, в расчетной формуле ставится знак плюс, а во втором знак минус.
Величина М приведенная в формуле, называется коэффициентом взаимной индукции , представляет собой некоторую добавочную индуктивность, обусловленную частью магнитного потока, общей для обеих катушек.
На явлении взаимоиндукции основан принцип работы вариометра . Он состоит из двух катушек, общая L которых может, по необходимости, плавно регулироваться в некотором диапазоне. В радиолюбительской практике вариометры используют для настройки колебательных контуров и передатчиков.
Индуктивное сопротивление отличается от классического омического тем, что при протекании через индуктивность переменного тока отсутствуют потери мощности.
В реальных условиях любая катушка индуктивности обладает и реальным омическим сопротивлением. Но если оно не очень большое по сравнению с индуктивным сопротивлением, то им можно условно пренебречь.
При этом происходит следующий эффект: в течение первой четверти периода, когда ток увеличивается, магнитное поле потребляет энергию из цепи, а в течение следующей четверти, когда ток снижается, возвращает ее в цепь. Поэтому, в среднем за период в индуктивном сопротивлении мощность не расходуется. Поэтому индуктивное сопротивление получило название реактивного.
Поэтому, в среднем за период в индуктивном сопротивлении мощность не расходуется. Поэтому индуктивное сопротивление получило название реактивного.
Индуктивное сопротивление одной и той же катушки будет отличаться для переменных токов разных частот. Чем выше частота, тем большее влияние на схему оказывает индуктивность и тем выше будет индуктивное сопротивление катушки. Наоборот, чем ниже частота переменного тока, тем индуктивное сопротивление ниже. При нулевой частоте (постоянный ток), индуктивное сопротивление нулевое.
Индуктивное сопротивление в формулах электротехники, обозначается как X L и измеряется в омах.
где X L — индуктивное сопротивление в омах; f-частота переменного тока в гц; L — индуктивность катушки в генри
Величину 2π×f называют круговой частотой и обозначают буквой ω (омега). Поэтому формулу выше можно представить так:
Отсюда следует, что при протекании через катушку постоянного тока (ω = 0). Поэтому, если, требуется пропустить по цепи постоянный ток, задержав переменный, то в цепь вводят последовательно катушку индуктивности.
Для преграждения пртекания токов низких звуковых частот используют катушки с железным сердечником, так называемые дроссели низкой частоты (НЧ), а для высоких радиочастот уже без железного сердечника, которые называют дроссели высокой частоты (ВЧ).
Катушка индуктивности в цепи переменного тока |
Если катушка индуктивности стоит в цепи переменного тока, то в ней, фаза тока всегда будет отставать от напряжения. В курсе этой лекции рассмотрим причины отставания фазы тока на элементарном примере, когда в идеальной цепи есть только индуктивное сопротивление, а омическое сопротивление отсутствует, точнее омическим сопротивлением провода катушки пренебрегаем, так как оно очень низкое.
| Катушка индуктивности |
Это — винтовая, спиральная или винтоспиральная катушка из свёрнутого проводника, обладающая значительно большой величиной индуктивности при относительно малом уровне ёмкости и низком активном сопротивлении
Индуктивность катушки прямо пропорциональна квадрату числа витков, так как с увеличением количества витков увеличивается, число магнитных силовых линий, и число пересечений каждой силовой линии с проводником.
— увеличивается с увеличением площади витка катушки, так как возрастает уровень магнитного потока в катушке.
-уменьшается с увелечением осевой длины катушки, так как, чем она выше, тем меньшее число витков на единицу ее осевой длины и, следовательно, тем ниже магнитный поток.
Соединение катушек
Соединение катушек индуктивности при отсутствии взаимного влияния магнитных полей катушек.
Последовательное соединение катушек индуктивности.
Суммарная индуктивность двух или нескольких катушек, соединенных последовательно и расположенных на таком расстоянии друг от друга, что магнитное поле одной катушки не пересекает витков другой (рисунок 1), равна сумме их индуктивностей.
Рисунок 1. Последовательное соединение катушект индуктивности.
Цепь, изображенная на рисунке 1, обладает общей индуктивностью L, которая выражается так:
где L1, L2 и L3 — индуктивности отдельных катушек.
Параллельное соединение катушек индуктивности.
Индуктивность цепи, составленной из тех же катушек при параллельном их соединении (рисунок 2) и при соблюдении того же условия относительно их расположения (отсутствие магнитного взаимодействия), подсчитывается по следующей формуле:
Рисунок 2. Параллельное соединение катушек индуктивности.
Индуктивность двух катушек, соединенных параллельно, определяется по следующей формуле:
Как видим, формулы для подсчета результирующих индуктивностей катушек, соединенных последовательно или параллельно и не взаимодействующих между собой, совершенно тождественны с формулами для подсчета омического сопротивления цепи при последовательном и параллельном соединении резисторов.
Соединение катушек при наличии взаимного влияния их магнитных полей.
Если катушки, включенные в цепь последовательно, расположены близко друг к другу, т. е. так, что часть магнитного потока одной катушки пронизывает витки другой, т. е. между катушками существует индуктивная связь (рисунок 3а), то для определения их общей индуктивности приведенная выше формула будет уже непригодна. При таком расположении катушек могут быть два случая, а именно:
1. Магнитные потоки обеих катушек имеют одинаковые направления
2. Магнитные потоки обеих катушек направлены навстречу друг другу
Тот или другой случай будет иметь место в зависимости от направления витков обмотки катушек и от направлений токов в них.
Рисунок 3. Соединение катушек индуктивности: а)суммарная индуктивность увеличивается за счет взаимной индукции б)суммарная индуктивность уменьшается за счет взаимной индукции.
Если обе катушки намотаны в одну сторону и токи в них текут в одном направлении, то это будет соответствовать первому случаю; если же токи текут в противоположных направлениях (рисунок 3б), то будет иметь место второй случай.
Разберем первый случай, когда магнитные потоки направлены в одну сторону. Очевидно, при этих условиях витки каждой катушки будут пронизываться своим потоком и частью потока другой катушки, т. е. магнитные потоки в той и в другой катушке будут больше по сравнению с тем случаем, когда между катушками нет индуктивной связи. Увеличение магнитного потока, пронизывающего витки той или иной катушки, равносильно увеличению ее индуктивности. Поэтому общая индуктивность цепи в рассматриваемом случае будет больше суммы индуктивностей отдельных катушек, из которых составлена цепь.
Рассуждая таким же образом, мы придем к выводу, что для второго случая, когда потоки направлены навстречу друг другу, общая индуктивность цепи будет меньше суммы индуктивностей отдельных катушек.
Подсчет величины индуктивности цепи, составленной из двух соединенных последовательно катушек индуктивности L1 и L2 при наличии между ними индуктивной связи, производится по формуле:
В первом случае ставится знак + (плюс), а во втором случае знак — (минус).
Величина М, называемая коэффициентом взаимной индукции , представляет собой добавочную индуктивность, обусловленную частью магнитного потока, общей для обеих катушек.
На явлении взаимоиндукции основано устройство вариометров . Вариометр состоит из двух катушек, общая индуктивность которых может, по желанию, плавно изменяться в некоторых пределах. В радиотехнике вариометры применяются для настройки колебательных контуров приемников и передатчиков.
Последовательное соединение резистора и катушки индуктивности — Студопедия
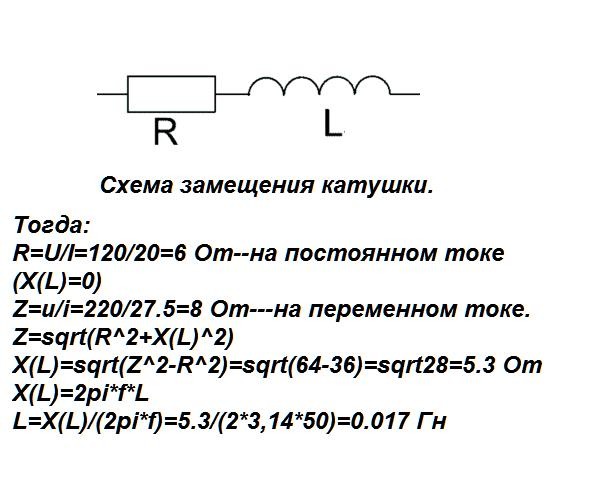
Реальная катушка индуктивности кроме индуктивности обладает активным сопротивлением . Цепь, состоящая из последовательно соединенных резистора и катушки индуктивности (рисунок 3.8а) обладает эквивалентным активным сопротивлением , где — активное сопротивление катушки индуктивности и индуктивным сопротивлением . Полное сопротивление такой цепи определяется из выражения , а ток в цепи . Этот ток будет одинаковым для всех элементов цепи, а приложенное напряжение распределится между элементами цепи, при этом напряжение на резисторе , совпадает по фазе с током, а напряжение на катушке индуктивности (где — полное сопротивление реальной катушки индуктивности) опережает ток на угол . Напряжение на катушке можно представить в виде двух составляющих – активной , совпадающей по фазе с током, и реактивной составляющей , опережающей ток на угол . Таким образом общее напряжение питания содержит две составляющие – активную и индуктивную . Результирующий угол сдвига . В данном случае угол считается положительным, так как ток отстает от напряжения .
Все соотношения для токов и напряжений этой схемы удобно представить в виде векторной диаграммы. Для цепей с последовательным соединением за основу диаграммы принимается величина, общая для всех элементов цепи – вектор тока , и относительно него под соответствующими углами откладываются векторы напряжений на отдельных элементах. Разновидностью векторных диаграмм является топографическая векторная диаграмма, на которой каждая точка диаграммы соответствует определенной точке электрической цепи. Топографическая векторная диаграмма для цепи с последовательным соединением резистора и катушки индуктивности имеет вид, показанный на рисунке 3.8б. Эта диаграмма имеет вид треугольника напряжений, образованного векторами , и . Делением всех сторон треугольника напряжений на ток получается подобный ему треугольник сопротивлений, а умножением сторон на ток — треугольник мощностей.
Рисунок 3.8 — Схема (а) и векторная диаграмма (б) цепи с последовательным соединением резистора и катушки индуктивности.
Последовательное соединение индуктивно связанных элементов цепи
Предположим, что две катушки или два каких-либо элемента цепи с сопротивлениями и , индуктивностями и и взаимной индуктивностью М соединены последовательно. Возможны два вида их включения — согласное (рис. 6.7, а) и встречное (рис. 6.7, б). При согласном включении токи в обоих элементах в любой момент времени направлены одинаково относительно одноименных выводов, поэтому магнитные потоки самоиндукции (или ) и взаимной индукции (или ), сцепленные с каждым элементом, складываются. При встречном включении токи в обоих элементах цепи в любой момент времени направлены противоположно относительно одноименных выводов, поэтому магнитные потоки самоиндукции и взаимной индукции, сцепленные с каждым элементом, вычитаются.
Индуктивность двух последовательно соединенных индуктивно связанных элементов
где и — потокосцепления первого и второго элементов, причем ; . Знак плюс относится к согласному, а знак минус к встречному включению. Следовательно,
В предельном случае идеальной связи (при k = 1) имеем . Если, кроме того, , то при согласном включении , а при встречном L=0 (при k<1 всегда L>0).
Полное сопротивление при согласном включении больше, чем при встречном. Этим можно пользоваться для определения опытным путем одноименных выводов индуктивно связанных элементов цепи, например, по показаниям вольтметра и амперметра.
Напряжения на элементах имеют по три составляющие:
Если индуктивность одного из элементов меньше взаимной индуктивности, то при встречном включении наблюдается своеобразный «емкостный» эффект. Пусть, например, , при этом в выражении
имеем , и, следовательно, напряжение отстает по фазе от тока , как в случае емкостного сопротивления. Конечно, реактивное сопротивление всей цепи в целом индуктивное, так как и ток отстает по фазе от напряжения .
На рис. 6.8 показаны векторные диаграммы для согласного и встречного включений при одинаковом значении тока в обоих случаях.
Входное комплексное сопротивление цепи получаем, учитывая (6.6):
где
Рис. 6.7
Рис. 6.8
Законы последовательного и параллельного соединения проводников
В основном элементы электрических цепей соединяют между собой параллельным либо последовательным методом. Электрику необходимо знать определения этих видов связей, иметь представление о различиях между ними и вариантах практического применения.
Последовательно соединенные проводники
Последовательное соединение
Этот способ подразумевает, что все приборы, входящие в состав электроцепи, связываются между собой проводами так, что во фрагменте цепи, где происходит включение, отсутствуют какие-либо узелки. При последовательном соединении проводников значение токовой силы в разных участках будет иметь одно и то же значение. Это связано с тем, что в безузловой цепи электронный заряд идет по одному и тому же проводнику. Чтобы вычислить общий показатель цепного напряжения, нужно сложить данные по всем фрагментам цепи:
U = U1 + U2 +…+Un.
При объединении аккумуляторных или гальванических единиц в одну батарею последовательный способ поможет увеличить рабочее напряжение.
Резисторы
Общее сопротивление цепи с последовательно связанными резисторами высчитывается по тому же правилу, что и напряжение: оно равно сумме показателей для каждого элемента.
Катушка индуктивности
Когда дроссели соединены последовательно так, чтобы магнитное поле каждой катушки не накладывалось на соседние дроссели, общая индуктивность такого соединения будет равна сложенным параметрам всех катушек:
L = L1+L2 +…+Ln.
Электрический конденсатор
Когда несколько конденсаторов соединяется между собой в цепь, соотношение их емкостей может быть описано такой формулой:
1/С = 1/С1 +1/С2 +…+ 1/Cn.
Мемристоры
Мемристивность цепи оценивается как сумма показателей всех подсоединенных компонентов:
M = M1 +M2 +… + Mn.
Выключатели
Если несколько таких устройств подсоединены в цепь последовательно, она будет замкнутой только при замыкании всех устройств. Если хоть один переключатель разомкнуть, цепь также размыкается. При выходе из строя какого-либо устройства остальные тоже перестанут функционировать. Это правило распространяется и на цепь из нескольких розеток.
Для домашней разводки проводов
Хотя данный способ потенциально мог бы принести потребителю определенные выгоды (экономия проводников, упрощение подключения заземления), на практике для подключения бытовых электроприборов он не используется. Это связано с тем, что неисправность одного из устройств приводит к прекращению функционирования остальных. Этот пример можно проиллюстрировать на елочной гирлянде: в ней используется именно рассматриваемый тип соединения, в случае перегорания какой-либо из ламп остальные затухают. Именно поэтому электроприборы в домашнюю сеть всегда подключаются параллельно.
Важно! При принятии решения соединить последовательно несколько устройств целесообразно составить таблицу их мощностей и оценить на предмет величины перепадов. Если подключить в одну электроцепь, например, нагреватель воды с большой мощностью, потребляющий много энергии, и маломощный прибор вроде старого приемника, более мощный прибор не сможет работать.
Практическое использование последовательной схемы
Для замены кабелей
Если соединить несколько кабелей в одну линию, в случае перегорания какого-либо из элементов ток будет пропадать на всей протяженности конструкции. Поэтому подключение параллельных проводников является более практичным вариантом. Его применяют в качестве замены толстого провода, подходящего для высокомощных нагрузок. Когда такого провода нет в наличии, подключают серию более тонких, в сумме они переносят ток, эквивалентный одному толстому. Нужные сечения находят расчетным путем, опираясь на данные о потерях напряжения. Такие конструкции широко применяются при обустройстве электролиний большой протяженности.
Параллельное соединение
Параллельное соединение проводников предполагает объединение связываемых сетью приборов посредством двух узловых соединений. В этом случае токовая сила на участке, не принадлежащем разветвлению, равна сумме значений этого параметра для каждого из параллельно подключенных кабелей. Значение напряжения, напротив, одинаковое для любого из элементов соединения:
U = U1 = U2 =…=Un.
Схема параллельного соединения
Резисторы
Когда эти элементы соединены параллельно, значения сопротивлений находятся в таком отношении между собой, что общая проводимость (параметр, обратно пропорциональный сопротивлению, то есть равный 1/R) равна сумме проводимостей всех резисторных элементов:
1/R = 1/R1 + 1/R2 + … + 1/Rn.
Катушка индуктивности
Общая индуктивность и показатели для каждой из подсоединенных дросселей находятся в таком соотношении:
1/L = 1/L1 + 1/L2 + … + 1/Ln.
Электрический конденсатор
Общая емкость в данном случае будет равной суммированным показателям отдельных приборов:
C = C1 +C2 +…+ Cn.
Мемристоры
При параллельном включении нескольких мемристоров в сеть соотношение их основных характеристик выражается такой формулой:
M = (M1-1 + M2-1 +…+ Mn-1)-1
Выключатели
В случае параллельного подключения нескольких таких устройств цепочка считается замкнутой, когда в этом положении находится хотя бы один переключатель.
Примеры использования
Последовательная схема применяется для соединения компонентов квартирного звонка, карманного фонаря (выключатель, лампа и батарея) и других устройств, в которых необходимо обеспечить активизацию при нажатии кнопки. На ней также построены елочные гирлянды.
Примерами параллельного соединения могут служить люстры и осветительные приборы в квартире. Если в этом случае воспользоваться последовательным вариантом, при включении любой лампы будут включаться и прочие, что совершенно не входит в цели монтажа. Кроме того, в этом случае цепь перестанет работать при неисправности одного из устройств. Подключая лампы параллельно, можно оснастить каждое разветвление собственным выключателем, тогда им можно будет управлять, не затрагивая других элементов.
Важно! В ПУЭ указывается, что силовые нагрузки можно соединять параллельно в том случае, если провод питания может выдержать суммарную нагрузку одновременно работающих устройств. Когда розетки будут установлены, от каждой из них к распредкоробке протягивают прямой провод.
Правила для различных соединений проводников
Для обоих вариантов соединения существуют правила подсчета различных параметров электрической цепи.
Законы последовательной цепи
Законы последовательного соединения имеют такой вид:
- ток на всех участках цепочки идентичен, тогда как напряжение на ее концах равно сумме значений для каждого ее участка;
- у соединенных конденсаторов электрозаряды на обкладках примут одинаковые значения;
- когда в такую цепь соединены резисторы, ток идет в начале через первый элемент, потом через второй и, последовательно проходя все устройства, доходит до последнего (общая величина спада напряжения равна суммированным потерям его для каждого из резисторов).
Законы параллельного соединения проводников
Здесь следующая картина:
- когда электроприбор перегорает, путь электротока не блокируется, а остальные приборы не выключаются;
- ток распределяется на все распараллеленные участки и принимает на них разные значения, напряжение везде остается прежним;
- при подключении конденсаторов заряд на каждом из них равен произведению напряжения (одинакового для всех) и емкости конкретного устройства, общая емкость равна суммированным показателям всех приборов.
Смешанное соедиение проводников
Смешанное соединение – сложная конфигурация из нескольких проводников, часть из которых коммуницируют параллельно, часть – последовательно. Чтобы рассчитать значения разных показателей (ток, сопротивление и т.д.) для такого соединения, его разбивают на структурные элементы и проводят вычисления для каждого из них. При подсчете данных для укрупненных единиц их можно заменять на эквивалентные.
Примеры смешанных схем
При соединении нескольких устройств в одну цепочку важно выбрать правильный способ соединения. Если он не будет соответствовать практическим задачам, устройства не будут функционировать корректно.
Видео
Последовательное соединение резистора и катушки индуктивности.
Параллельное соединение резистора и конденсатора.
В разветвленной цепи, состоящей из параллельно соединенных резистора и конденсатора (рисунок 3.11а), напряжение на обоих элементах схемы одинаково. Это напряжение создает в резисторе активный ток, совпадающий по фазе с напряжением: . При этом ток в конденсаторе чисто реактивный (не имеет активной составляющей) и опережает напряжение на угол : , где — реактивная проводимость конденсатора. Векторная диаграмма для параллельного соединения резистора и конденсатора показана на рисунке 3.11,б. За основу диаграммы принят вектор напряжения , относительно которого строятся векторы токов. Диаграмма так же имеет вид треугольника токов, из которого могут быть получены треугольники проводимостей и мощностей. В данном случае угол сдвига между током и напряжением считается отрицательным, так как вектор общего тока цепи опережает вектор напряжения .
Рисунок 3.11 — Схема (а) и векторная диаграмма (б) цепи с параллельным соединением резистора и конденсатора.
Последовательное соединение резистора и конденсатора.
Для цепи, состоящей из последовательно соединенных резистора и конденсатора (рисунок 3.9 а), характерны следующие соотношения:
— полное сопротивление цепи, где — емкостное сопротивление. Ток, протекающий по элементам цепи: . Падение напряжения на активном сопротивлении: , падение напряжения на конденсаторе: является чисто емкостным (не имеет активной составляющей) и отстает от тока на угол . Результирующий угол сдвига между током и напряжением : , в данном случае считается отрицательным, так как ток опережает напряжение. Векторная диаграмма соответствующая последовательному соединению резистора и конденсатора показана на рисунке 3.9б.
Рисунок 3.9 — Схема (а) и векторная диаграмма (б) цепи с последовательным соединением резистора и конденсатора.
Последовательное соединение резистора и катушки индуктивности.
Реальная катушка индуктивности кроме индуктивности обладает активным сопротивлением . Цепь, состоящая из последовательно соединенных резистора и катушки индуктивности (рисунок 3.8а) обладает эквивалентным активным сопротивлением , где — активное сопротивление катушки индуктивности и индуктивным сопротивлением . Полное сопротивление такой цепи определяется из выражения , а ток в цепи . Этот ток будет одинаковым для всех элементов цепи, а приложенное напряжение распределится между элементами цепи, при этом напряжение на резисторе , совпадает по фазе с током, а напряжение на катушке индуктивности (где — полное сопротивление реальной катушки индуктивности) опережает ток на угол . Напряжение на катушке можно представить в виде двух составляющих – активной , совпадающей по фазе с током, и реактивной составляющей , опережающей ток на угол . Таким образом общее напряжение питания содержит две составляющие – активную и индуктивную . Результирующий угол сдвига . В данном случае угол считается положительным, так как ток отстает от напряжения .
Все соотношения для токов и напряжений этой схемы удобно представить в виде векторной диаграммы. Для цепей с последовательным соединением за основу диаграммы принимается величина, общая для всех элементов цепи – вектор тока , и относительно него под соответствующими углами откладываются векторы напряжений на отдельных элементах. Разновидностью векторных диаграмм является топографическая векторная диаграмма, на которой каждая точка диаграммы соответствует определенной точке электрической цепи. Топографическая векторная диаграмма для цепи с последовательным соединением резистора и катушки индуктивности имеет вид, показанный на рисунке 3.8б. Эта диаграмма имеет вид треугольника напряжений, образованного векторами , и . Делением всех сторон треугольника напряжений на ток получается подобный ему треугольник сопротивлений, а умножением сторон на ток — треугольник мощностей.
Рисунок 3.8 — Схема (а) и векторная диаграмма (б) цепи с последовательным соединением резистора и катушки индуктивности.
Катушки индуктивности сериии параллельные | Катушки индуктивности
Когда катушки индуктивности соединены последовательно, общая индуктивность является суммой индуктивностей отдельных катушек индуктивности. Чтобы понять, почему это так, рассмотрим следующее: окончательная мера индуктивности — это величина напряжения, падающего на катушку индуктивности при заданной скорости изменения тока через нее.
Если катушки индуктивности соединены последовательно (таким образом, разделяя один и тот же ток и наблюдая одну и ту же скорость изменения тока), то общее падение напряжения в результате изменения тока будет складываться с каждой катушкой индуктивности, создавая большее общее напряжение. напряжения, чем любой из отдельных катушек индуктивности в отдельности.Более высокое напряжение при той же скорости изменения тока означает большую индуктивность.
Таким образом, общая индуктивность последовательных катушек индуктивности больше, чем любая из индуктивностей отдельных катушек индуктивности. Формула для расчета полной последовательной индуктивности имеет ту же форму, что и для расчета последовательного сопротивления:
При параллельном подключении катушек индуктивности общая индуктивность меньше индуктивности любой из параллельных катушек индуктивности.Опять же, помните, что окончательная мера индуктивности — это величина напряжения, падающего на катушку индуктивности при заданной скорости изменения тока через нее.
Поскольку ток через каждую параллельную катушку индуктивности будет составлять часть общего тока, а напряжение на каждой параллельной катушке индуктивности будет одинаковым, изменение общего тока приведет к меньшему падению напряжения на параллельном массиве, чем для любой из катушек индуктивности. рассматривается отдельно. Другими словами, при заданной скорости изменения тока на параллельных индукторах будет меньше падения напряжения, чем на любой из этих индукторов, рассматриваемых отдельно, потому что общий ток делится между параллельными ветвями.
Меньшее напряжение при той же скорости изменения тока означает меньшую индуктивность.
Таким образом, общая индуктивность меньше индуктивности любой из отдельных катушек индуктивности. Формула для расчета полной параллельной индуктивности имеет ту же форму, что и для расчета параллельных сопротивлений:
ОБЗОР:
- Индуктивности складываются последовательно.
- Параллельно уменьшаются индуктивности.
Катушки индуктивности серии
Катушка индуктивности — это пассивный элемент, который используется в электронных схемах для временного хранения электрической энергии в виде магнитного потока или просто магнитного поля. Индуктивность — это свойство любой катушки, которая может создавать магнитный поток, когда через нее проходит ток.
Любое устройство, обладающее свойством индуктивности, можно назвать индуктором. Обычно индуктор построен в виде катушки из медного материала вокруг сердечника из магнитной (железо) или немагнитной среды (например, воздуха).
Катушки индуктивности могут быть подключены последовательно или параллельно в зависимости от характеристик, требуемых схемой. Эти комбинации используются для проектирования более сложных сетей. Общая индуктивность цепи зависит от способа подключения катушек индуктивности, может быть последовательным или параллельным.
Кроме того, способ подключения индукторов таким образом, что одна индуктивность не влияет на другую, также изменяет общую индуктивность по сравнению с эффектом магнитной связи между индукторами.
Следовательно, индукторы располагаются на основе их взаимной индуктивности или магнитной связи в последовательной или параллельной комбинации.
Катушки индуктивности, подключенные последовательно
Предположим, что индукторы, подключенные в цепь, не имеют никакой связи между собой. Это означает, что нет никаких магнитных линий от одного индуктора, соединенного с другим, и, следовательно, не будет взаимного потока между катушками.
Соединение двух или более индукторов «конец в конец» называется «последовательным соединением индукторов».В этой связи индукторы соединены последовательно, так что эффективное количество витков индуктора увеличивается. Последовательное соединение катушек индуктивности показано на диаграмме ниже
Индуктивность последовательно соединенных катушек индуктивности рассчитывается как сумма индивидуальных индуктивностей каждой катушки, поскольку изменение тока через каждую катушку одинаково.
Это последовательное соединение аналогично последовательному соединению резисторов, за исключением того, что резисторы заменены индукторами.Если ток I протекает в последовательном соединении, а катушки L1, L2 и т. Д., Общий ток в последовательных катушках индуктивности определяется как
I Всего = I L1 = I L2 = I L3 . . . = I n
Если отдельные падения напряжения на каждой катушке в этом последовательном соединении равны VL1, VL2, V¬L3 и т. Д., Общее падение напряжения между двумя клеммами VT равно
В Всего = V L1 + V L2 + V L3 ….+ V n
Поскольку мы знаем, что падение напряжения может быть представлено в терминах собственной индуктивности L, это означает
В = L di / dt.
Это также можно записать как
LT di / dt = L1 di / dt + L2 di / dt + L3 di / dt +. . . + Ln di / dt
Следовательно, общая индуктивность составляет
L Всего = L 1 + L 2 + L 3 +… .. + L n
Это означает общую индуктивность последовательное соединение — это сумма индивидуальных индуктивностей всех катушек индуктивности.Вышеупомянутое уравнение верно, когда нет взаимного влияния индуктивности между катушками в этой последовательной конфигурации.
Взаимная индуктивность катушек индуктивности приведет к изменению значения общей индуктивности в последовательной комбинации катушек индуктивности.
Предположим, что есть две катушки индуктивности, подключенные последовательно к источнику переменного напряжения, который может генерировать переменный ток в цепи, как показано на рисунке выше.
Если в цепи нет взаимной индуктивности, то общая индуктивность задается как
L T = L 1 + L 2
Важно помнить, что общая индуктивность всегда больше, чем самый большой индуктор в последовательном расположении индукторов.
Катушки индуктивности, соединенные последовательно Пример
Пример 1: Если в цепи последовательно соединены 3 катушки индуктивности по 60 Генри, 30 Генри и 20 Генри, какова будет общая индуктивность серии?
Sol: Мы знаем, что формула для полной индуктивности серии L Total = L 1 + L 2 + L 3 +… .. + L n
Учитывая, что L 1 = 60 Генри
L 1 = 30 Генри
L 1 = 20 Генри
Общая индуктивность, L Всего = 60 + 30 + 20 = 110 Генри.
Взаимно соединенные индукторы в серии
Теперь представьте, что индукторы соединены таким образом, что магнитное поле одной катушки влияет на другую. Когда две или более катушки индуктивности соединены последовательно, на индуктивность одной катушки индуктивности будет влиять магнитное поле, создаваемое другой катушкой.
Это называется взаимной индуктивностью, а катушки — «взаимно подключенными индукторами». Эта взаимная индуктивность может увеличивать или уменьшать общую индуктивность последовательной цепи.
Фактором, влияющим на взаимную индуктивность последовательно соединенных катушек индуктивности, является расстояние между катушками и их ориентация.
Взаимосвязанные индукторы могут быть двух типов
1) Кумулятивно связанные или последовательные
2) Дифференциально связанные или последовательно встречные
Кумулятивно связанные индукторы последовательно
Если магнитные потоки, создаваемые индукторами, одинаковы направление протекания тока через них, тогда катушки известны как «кумулятивно связанные».
В этой последовательной вспомогательной или кумулятивно связанной схеме ток входит или покидает клеммы катушек в любой момент времени в одном направлении.
На рисунке ниже показано последовательное соединение двух индукторов.
Если мы пропустим ток через кумулятивно связанные катушки (между узлами A и D) в одном и том же направлении, падение напряжения каждой отдельной катушки повлияет на общую индуктивность серии.
Пусть собственная индуктивность катушки 1 равна L 1 , собственная индуктивность катушки 2 равна L 2 , а взаимная индуктивность между катушкой 1 и катушкой 2 равна M.
Самоиндуцированная ЭДС в катушке-1 составляет
e1 = — L 1 di / dt
Взаимная наведенная ЭДС в катушке-1 из-за изменения тока в катушке-2 составляет
eM1 = — M di / dt
Точно так же самоиндуцированная ЭДС в катушке-2 составляет
e2 = — L 2 di / dt
Взаимная наведенная ЭДС в катушке-2 из-за изменения тока в катушке-1 составляет
eM2 = — M di / dt
Следовательно, полная наведенная ЭДС в последовательной вспомогательной цепи задается как
e = — L 1 di / dt– L 2 di / dt– 2M di / dt
= — (L 1 + L 2 + 2M) di / dt
Если L T — полная индуктивность цепи, общая наведенная ЭДС будет эквивалентна
e = — L T di / dt
Подстановка в приведенном выше уравнении мы получаем
— L T di / dt = — (L 1 + L 2 + 2M) di / dt
Следовательно, L T = (L 1 + L 2 + 2M)
Кумулятивно связанные индукторы в серии Пример
Пример: Если две катушки индуктивностью 70 мГн и 30 мГн соединены последовательно, то найдите общую кумулятивную индуктивность последовательно соединенных катушек индуктивности.Учтите, что взаимная индуктивность комбинации двух катушек составляет 40 мГн.
Sol:
Учитывая, что L 1 = 70 мГн
L 2 = 30 мГн
M = 40 мГн
Применяя формулу для кумулятивно подключенных катушек индуктивности, LT = L1 + L2 + 2M
L T = 70 + 30 + 2 (40)
= 100 + 80
= 180 мГн
Следовательно, совокупная индуктивность катушки составляет 180 милли Генри.
Дифференциально связанные индукторы серии
Если магнитные потоки, создаваемые индукторами, направлены в противоположном направлении, то катушки известны как «дифференциально связанные».
В этом дифференциальном соединении или последовательном оппозиционном соединении ток поступает или покидает клеммы катушек в любой момент времени в противоположном направлении.
На рисунке ниже показано соединение двух катушек индуктивности в последовательном оппозиционном расположении.
В дифференциально связанных катушках поля магнитного потока могут создаваться в том же или противоположном направлении. Пусть собственная индуктивность катушек равна L1 и L2, а взаимная индуктивность равна M.
Здесь взаимная индуктивность будет добавлена к собственной индуктивности каждой катушки из-за конфигурации цепи.
Следовательно, полная наведенная ЭДС в последовательной встречной цепи задается как
e = — L 1 di / dt– L 2 di / dt + 2M di / dt
= — (L 1 + L 2 — 2M) di / dt
Если L T — это полная индуктивность цепи, общая наведенная ЭДС будет эквивалентна
e = — L T di / dt
Подставив указанное выше уравнение, получаем
— L T di / dt = — (L 1 + L 2 — 2M) di / dt
Следовательно, L T = (L 1 + L 2 — 2M)
Пример последовательного соединения индукторов с дифференциальной связью
Пример: Если две катушки индуктивности 70 мГн и 30 мГн соединены последовательно, то найдите общую дифференциальную индуктивность последовательно соединенных катушек индуктивности.Учтите, что взаимная индуктивность комбинации двух катушек составляет 40 мГн.
Sol:
Учитывая, что L 1 = 70 мГн
L 2 = 30 мГн
M = 40 мГн
Применяя формулу для дифференциально подключенных индукторов, LT = L1 + L2 — 2M
L T = 70 + 30-2 (40)
= 100-80
= 20 мГн
Следовательно, дифференциальная индуктивность катушки составляет 20 миллигенри.
Резюме
- Катушка индуктивности — это пассивный элемент, который используется в электронных схемах для хранения энергии в виде магнитного потока.Индуктивность измеряется в Генри.
- Количество рассеиваемой фактической мощности с током, протекающим в цепи, называется «индуктивным реактивным сопротивлением». Измеряется в омах. X L = 2 f L
- Самоиндукция — это свойство электрической цепи или контура, в котором собственное магнитное поле противодействует любому изменению тока
- Взаимная индуктивность — это способность катушки индуктивности, которая вызывает индукцию ЭДС в другой индуктор помещается очень близко к нему, когда ток в первом индукторе изменяется.
- Соединение двух или более индукторов «конец в конец» называется «последовательным соединением индукторов». Формула для общей индуктивности в серии: L T = L 1 + L 2
- Общая индуктивность последовательно соединенных катушек индуктивности всегда больше, чем самая большая индуктивность в этой серии.
- Если магнитные потоки, создаваемые катушками индуктивности, направлены в том же направлении, что и ток через них, то катушки известны как «кумулятивно связанные».L T = L 1 + L 2 + 2M
- Если магнитные потоки, создаваемые индукторами, имеют противоположное направление, то катушки известны как «дифференциально связанные». L T = L 1 + L 2 — 2M
Последовательные индукторы подробно описаны
Катушки индуктивности — это один из пассивных элементов (резисторы и конденсаторы), используемых в электрической цепи. Он хранит энергию в виде магнитного поля.
Теперь индукторы могут быть подключены двумя способами
- Катушки индуктивности серии
- Параллельные индукторы
В этой статье, в частности, мы будем изучать последовательное соединение индукторов. Мы знаем, что у индуктора есть положительный и отрицательный терминалы. Таким образом, если отрицательный вывод одного соединен с положительным выводом другого, то соединение считается последовательным. Ясно, что ток, протекающий через все последовательно включенные индукторы, будет одинаковым.
Катушки индуктивности в последовательной цепи
Если ток, протекающий во всех подключенных индукторах, одинаков, то соединение является последовательным. Эквивалентная индуктивность последовательно соединенных индукторов эквивалентна сумме всех отдельных индукторов, включенных последовательно.
Как показано выше, ток одинаков во всех трех индукторах,
т.е., I 1 = I 2 = I 3
Кроме того, мы знаем, что напряжение через катушку индуктивности равно
.В = L (ди / дт)
Уравнение эквивалентной индуктивности
Применяя закон Кирхгофа в приведенной выше схеме, имеем
В = В L1 + В L2 + В L3
As, V = L (di / dt)
Следовательно, V 1 = L1 (dI 1 / dt)
В 2 = L 2 (dI 2 / dt)
В 3 = L 3 (dI 3 / dt)
, подставляя значения V1, V2 и V 3 в первое уравнение, получаем
V = L 1 (dI 1 / dt) + L2 (dI2 / dt) + L3 (dI3 / dt)
Поскольку ток одинаков во всех трех, пусть I 1 = I2 = I3 = I
В = L 1 (dI / dt) + L2 (dI / dt) + L3 (dI / dt)
= (dI / dt) (L 1 + L2 + L3)
= L экв. (dI / dt)
, следовательно, L equi = (L 1 + L 2 + L 3 )
В общем случае L equi = (L 1 + L 2 + L 3 + ……..L n ) [для последовательно соединенных индукторов n]
Катушки индуктивности серии
Здесь следует помнить, что эквивалентная индуктивность двух или более катушек индуктивности, соединенных последовательно, больше, чем наибольшее значение индуктивности среди них.
Пример индукторов серии
Пусть четыре катушки индуктивности соединены последовательно со значениями 10 мГн, 20 мГн, 30 мГн и 40 мГн, без взаимной индуктивности между ними. Теперь для расчета эквивалентной индуктивности комбинации рассчитывается путем сложения всех индивидуальных индуктивностей.
Следовательно, L equi = L 1 + L 2 + L 3 + L 4
л экви = 10 + 20 + 30 + 40 = 100 мГн
Здесь также мы видим, что наибольшее значение индивидуальной индуктивности составляет 40 мГн, а эквивалентное значение больше этого (100 мГн).
Дроссели с взаимным соединением серии
Когда катушки индуктивности соединены последовательно, так что магнитное поле одного соединяется с другим, то влияние взаимной индуктивности либо уменьшает, либо увеличивает общую индуктивность в зависимости от магнитной связи.Расстояние между катушками и их ориентация друг к другу меняют влияние этой взаимной индуктивности.
Теперь эти взаимно соединенные индукторы могут быть двух типов:
- Суммарная индуктивность
- Противоположная полная индуктивность
Если ток, протекающий через катушку, и создаваемый магнитный поток идут в одном направлении, то говорят, что катушки кумулятивно связаны. Если направление тока противоположно направлению создаваемого магнитного потока, то говорят, что катушки соединены дифференциально.
Катушки индуктивности сериис накопительной связью
Как показано на рисунке ниже, когда ток, протекающий между двумя точками через кумулятивно связанные катушки, имеет одинаковое направление, поэтому падение напряжения на каждой катушке будет изменено с учетом влияния взаимной индуктивности. Собственные индуктивности (L) здесь также будут такими же, но будет добавлена взаимная индуктивность (M).
Кумулятивно связанные катушки
Таким образом, полная ЭДС, индуцированная в этих катушках, равна
.В = L1 (dI / dt) + L2 (dI / dt) 2M (dI / dt)
здесь 2M представляет влияние L 1 и L 2 друг на друга.
As V = L equi (di / dt)
поместив это в уравнение выше,
L equi (di / dt) = L 1 (dI / dt) + L 2 (dI / dt) 2M (dI / dt)
разделив приведенное выше уравнение на dI / dt, мы получим
L экв. = L 1 + L 2 + 2M
Если одна из катушек перевернута, так что один и тот же ток течет через каждую катушку, но в противоположном направлении, взаимная индуктивность, тогда существующая взаимная индуктивность будет иметь эффект компенсации на каждой катушке, как объяснено ниже.
Дроссели с дифференциальной связью серии
Катушки с дифференциальной связью
ЭДС, индуцированная в катушке 1 из-за эффекта взаимной индуктивности катушки 2, имеет противоположное направление по сравнению с направлением самоиндуцированной ЭДС. Это потому, что один и тот же ток теперь течет через каждую катушку в противоположном направлении. Принимая во внимание этот эффект компенсации, знак минус вводится с буквой M, когда магнитное поле двух катушек дифференциально соединено.
Это дает нам окончательное уравнение для расчета полной индуктивности дифференциально соединенных катушек как:
L экв. = L 1 + L2 — 2M
Таким образом, окончательное уравнение для последовательно включенных индукторов имеет следующий вид:
L экв. = L 1 + L 2 ± 2M
Пример концепции взаимной индуктивности
Пусть две катушки соединены последовательно с собственной индуктивностью 40 мГн и 50 мГн соответственно.Общая индуктивность комбинации составила 80 мГн. Найдите значение взаимной индуктивности, которое существует между двумя катушками между двумя катушками, предполагая, что они противостоят друг другу.
мы знаем,
L экв. = L 1 + L 2 — 2M
подставляя значения для каждой переменной, получаем
80 = 40 + 50-2 (М)
2M = 90 — 80
, следовательно, M = 5mH
Давайте рассмотрим еще один пример, чтобы лучше понять концепцию.
Предположим, две катушки индуктивности по 30 мГн соответственно соединены вместе в последовательной комбинации, так что их магнитные поля помогают друг другу, создавая кумулятивную связь. Их взаимная индуктивность составляет 5 мГн. Определите общую индуктивность последовательной комбинации.
L экв. = L 1 + L 2 + 2M
= 30 + 30 + 2 (5)
= 70 мГн
Серия индукторовКраткое описание серии
Мы знаем, что катушки индуктивности могут быть соединены последовательно, чтобы получить общее значение индуктивности, L equi , которое равно сумме отдельных подключенных катушек индуктивности (как и в случае последовательно соединенных резисторов).Однако, когда они соединены вместе, на значение также влияет взаимная индуктивность.
Корпус взаимной индуктивности бывает двух типов: последовательный и последовательно встречный. Это зависит от того, связаны ли катушки кумулятивно (в одном направлении) или дифференциально (в противоположном направлении). Соответственно, формула для полной индуктивности изменится в обоих случаях.
АДЖАЙ ДХИРАДЖ
Разработчик технического контента
Нравится:
Нравится Загрузка…
Возможно, вам также понравитсяЧто такое индуктивность? Последовательная и параллельная цепь
Индуктивность . — это свойство материала, благодаря которому он препятствует любому изменению величины и направления электрического тока, проходящего через проводник. Другими словами, это свойство катушки, в которой ЭДС индуцируется из-за изменения магнитного потока.
Индуктивность добавляется в цепь через катушку индуктивности.Индуктор — это в основном катушка из проводов, которая концентрирует магнитное поле в цепи.
Индуктивность обозначается (L), а единица измерения — Генри. Считается, что индуктивность равна одному Генри, когда ток в один ампер проходит через катушку или проводник изменяется со скоростью в секунду, а напряжение на катушке индуцируется со скоростью один вольт.
Состав:
Описание и типы индукторов
Катушка индуктивности образуется при скручивании провода конечной длины в катушку.Когда ток течет через катушку, образуется электромагнитное поле. Электромагнитное поле изменяется при изменении направления тока.
Это изменение электромагнитного поля индуцирует напряжение (v) на катушке и определяется уравнением, показанным ниже:
Где I — ток, протекающий через катушку индуктивности, в амперах.
Напряжение на катушке индуктивности будет равно нулю, если ток, протекающий через нее, останется постоянным. Это означает, что когда через индуктор протекает постоянный устойчивый ток, он ведет себя как короткозамкнутая катушка в установившемся состоянии.Если есть небольшое изменение направления или силы тока, появится индуктивность.
Если мы положим значение dt равным нулю (dt = 0) в уравнении (1), то увидим, что при мгновенном изменении тока в течение нулевого времени возникает бесконечное напряжение на катушке индуктивности, что не является допустимым условием и, таким образом, в катушке индуктивности нельзя резко изменить ток .
Таким образом, после переключения постоянного напряжения катушки индуктивности действуют как разомкнутые катушки.
Мощность, потребляемая индуктором, определяется по приведенному ниже уравнению:
Подставляя значение v из уравнения (1) в уравнение (2), мы получим степень как:
Энергия, поглощаемая индуктором, определяется как:
Катушка индуктивности накапливает конечное количество энергии, даже если напряжение на ней может быть незначительным.
Катушки индуктивности классифицируются в зависимости от различных факторов, таких как размер, используемый материал сердечника, тип обмотки и т. Д. Сердечник играет важную роль при выборе катушки индуктивности.
В зависимости от материала сердечника используются следующие типы индукторов:
- Индуктор с ферромагнитным или железным сердечником
- Индуктор с воздушным сердечником
- Индуктор с тороидальным сердечником
- Индуктор с ламинированным сердечником
- Индуктор с активным сердечником
Последовательное и параллельное соединение индуктора
Цепь индуктивности серииВ последовательной цепи индуктивности несколько индукторов подключены последовательно в цепи, и одинаковое количество тока будет протекать в каждой из подключенных индукторов.Например, если L 1 , L 2 , L 3 …… индукторы подключены последовательно, и ток I течет по цепи, как показано на рисунке ниже:
Ток на индукторе L 1 , L 2 , L 3 будет I 1 , I 2 , I 3 соответственно. Значение тока на каждой катушке индуктивности будет одинаковым.
IL 1 = IL 2 = IL 3 = I MN
Полная или эквивалентная индуктивность определяется уравнением
Цепь параллельного индуктора
Если несколько индукторов соединены параллельно друг с другом, то цепь называется параллельной цепью индуктивности.В этом типе схемы схема разделена на каждую ветвь схемы, как показано на рисунке ниже:
Ток I 1 протекает в катушке индуктивности L 1 , и аналогично, ток I 2 в L 2 и I 3 в L 3 индуктивности, а I T — это общее количество ток, протекающий в цепи. Эквивалентная индуктивность определяется уравнением, показанным ниже:
Применение индуктора
Некоторые из применений индуктора следующие
- Используется в электронном оборудовании, таком как радиоприемники
- В аппарате связи
- Электронные испытательные приборы
- Как накопитель энергии
- В датчиках, трансформаторах, двигателях и различных фильтрах.
Основное применение индукторов — накопление энергии в виде магнитного поля.
катушек индуктивности последовательно и параллельно | Энергия, накопленная в индукторе
Когда через проводник проходит ток, он оказывается окруженным электромагнитным полем. Это поле приводит к свойству, известному как индуктивность , (L), которое препятствует любому изменению тока. Индукторы — это компоненты, которые обладают этим свойством. В этом модуле мы обсудим основную конструкцию катушек индуктивности, как их можно комбинировать в последовательном и параллельном режимах и как они ведут себя в цепях.
Катушка индуктивности представляет собой электрический компонент, образованный катушкой из проволоки, которая проявляет свойство индуктивности. Величина индуктивности, которую демонстрирует катушка, измеряется в генри (H) .
Генри определяется как скорость изменения тока в один ампер в секунду, индуцирующего один вольт через катушку.
Однако Генри — довольно большая единица измерения, и индуктивность чаще всего измеряется в миллигенри (мГн) или микрогенри (мкГн).
Основная конструкция индуктораНа рисунке 1 показан основной индуктор с магнитными силовыми линиями и направлением тока. Сила тока, протекающего через катушку, пропорциональна величине поля; следовательно, изменяющийся ток вызовет изменение магнитного поля вокруг индуктора. Это изменяющееся поле вызывает на катушке наведенное напряжение . Это напряжение противоположно току и препятствует изменению тока.
Рисунок 1 — Базовый индуктор
На индуктивность катушки сильно влияет материал, вокруг которого наматывается провод. Внутренний материал, известный как сердечник , может быть немагнитным (воздух, дерево и т. Д.) Или магнитным (железо, сталь и т. Д.). Проницаемость сердечника является мерой его сопротивления магнитным силовым линиям. Поскольку силовые линии контролируют величину индуктивности, проницаемость сердечника (µ) напрямую связана с индуктивностью.{2}} \ times \ mu \ times A} {l} \]
Две другие характеристики индукторов — это сопротивление обмотки и емкость обмотки. Сопротивление обмотки является мерой сопротивления постоянному току провода, составляющего катушку. Емкость обмотки , , , — это побочный эффект, вызванный множеством витков провода, находящихся в непосредственной близости. Они могут повлиять на цепь, если катушка индуктивности слишком велика или частота очень высока; однако в большинстве схем их можно не учитывать при расчетах.{-5}} \ right)} {\ left (0,015 \ right)} = 40 мГн $
Серия индукторовНа картинке в вашей голове несколько индукторов, соединенных встык. Если вы будете двигать их все ближе и ближе друг к другу, они в конечном итоге будут похожи на большую катушку проволоки. Так работает последовательная индуктивная цепь. {d {{i} _ {t}}} / {} _ {dt}} \ text {} \ cdots \ текст {(b)} \]
Левая часть уравнения (b) представляет собой полное напряжение, деленное на скорость изменения тока.{d {{i} _ {t}}} / {} _ {dt}} = {{L} _ {3}} \]
Итак, общая индуктивность будет,
$ {{L} _ {T}} = {{L} _ {1}} + {{L} _ {2}} + {{L} _ {3}} \ text {} \ cdots \ text {(c)}
долл. СШАУравнение (c) утверждает, что при последовательном соединении катушек индуктивности общая индуктивность является суммой индивидуальных индуктивностей.
Если есть две или более катушки индуктивности одинакового номинала, соединенные последовательно, общая индуктивность может быть определена как;
$ {{L} _ {T}} = NL $
Где N — количество одинаковых катушек индуктивности, а L — значение одной катушки индуктивности.
Параллельные индукторыКатушки индуктивности также могут быть объединены в параллельные цепи. Последовательное подключение катушек индуктивности увеличивало общую индуктивность; поэтому, естественно, подключение катушек индуктивности параллельно должно уменьшить общую индуктивность.
Подобно тому, как последовательные индукторы действуют как последовательные резисторы, параллельные индукторы действуют как параллельные резисторы. Формула для определения полной индуктивности в параллельной цепи очень похожа на формулу для определения полного сопротивления в параллельной цепи.
Применяя закон Кирхгофа к следующему рисунку, мы можем определить, как соединяются параллельно включенные индукторы;
$ ~ {{i} _ {T}} = {{i} _ {1}} + {{i} _ {2}} + {{i} _ {3}} \ text {} \ cdots \ text {(d)} $
Чтобы выразить вышеприведенное уравнение как скорость изменения текущей производной с обеих сторон;
\ [\ frac {d {{i} _ {T}}} {dt} = \ frac {d {{i} _ {1}}} {dt} + \ frac {d {{i} _ { 2}}} {dt} + \ frac {d {{i} _ {3}}} {dt} \ text {} \ cdots \ text {(e)} \]
Поскольку напряжение на катушке индуктивности равно
$ {{V} _ {L}} = L \ frac {di} {dt} $
А также, поскольку V T — это полное напряжение на параллельной индуктивности,
$ \ frac {{{V} _ {T}}} {{{L} _ {T}}} = \ frac {{{V} _ {T}}} {{{L} _ {1}}} + \ frac {{{V} _ {T}}} {{{L} _ {2}}} + \ frac {{{V} _ {T}}} {{{L} _ {3}}} \ text {} \ cdots \ text { (f)} $
Разделив обе части уравнения (c) на V T , мы получим следующее уравнение;
$ \ frac {1} {{{L} _ {T}}} = \ frac {1} {{{L} _ {1}}} + \ frac {1} {{{L} _ {2 }}} + \ frac {1} {{{L} _ {3}}} \ text {} \ cdots \ text {(g)} $
Уравнение (g) утверждает, что обратная величина полной индуктивности равна сумма обратных величин отдельных индуктивностей, соединенных параллельно.
Если две или более параллельных катушки индуктивности равны. Полная индуктивность может быть определена путем деления значения одной из катушек индуктивности на количество равных катушек индуктивности.
$ {{L} _ {T}} = \ frac {L} {N} $
Где L — значение одного из одинаковых показателей, а N — количество одинаковых индукторов.
Снова представьте несколько катушек индуктивности, соединенных вместе, но на этот раз они включены параллельно. В параллельной цепи ток делится между ветвями; Таким образом, через каждую катушку индуктивности проходит меньше тока.Это приводит к меньшему наведенному напряжению, что приводит к меньшей общей индуктивности.
Энергия, запасенная в катушке индуктивностиМощность, поступающая в катушку индуктивности в любой момент времени, равна;
$ P = Vi = Li \ frac {di} {dt} $
Когда ток постоянный, производная равна нулю, и в индукторе не накапливается дополнительная энергия. Когда ток увеличивается, производная тока имеет положительное значение, а мощность — положительное значение. {2}} \ text {} \ cdots \ text {(h)} $
W L = энергия, запасенная в катушке индуктивности в момент времени t в Джоулях
i = ток в катушке индуктивности в момент времени t в амперах
Уравнение (e) указывает, что полная энергия в катушке индуктивности зависит только от мгновенного значения тока .Чтобы энергия, запасенная в катушке индуктивности, согласно уравнению (e), была положительной, ток и напряжение должны иметь одинаковые знаки, как показано на следующем рисунке:
Вы также можете прочитать:
Последовательные и параллельные резисторы
Последовательные и параллельные конденсаторы
Катушки индуктивности могут быть соединены вместе либо последовательно, либо параллельно, либо в комбинации последовательного и параллельного соединения для создания более сложных сетей, общая индуктивность которых является комбинацией отдельных катушек индуктивности.Однако существуют определенные правила для подключения катушек индуктивности последовательно или параллельно, и они основаны на том факте, что между отдельными индукторами не существует взаимной индуктивности или магнитной связи. |
Катушки индуктивности серии |
| Считается, что катушки индуктивности соединены последовательно, когда они соединены гирляндной цепочкой по прямой линии, конец в конец.В руководстве «Резисторы в серии » мы видели, что разные значения сопротивлений просто «складываются» вместе, и это также верно для индуктивности. Последовательные катушки индуктивности складываются вместе, потому что количество витков катушки эффективно увеличивается, а общая индуктивность цепи L T равна сумме всех отдельных индуктивностей, сложенных вместе. |
Индуктор в последовательной цепи |
Ток (I), протекающий через первую катушку индуктивности, L 1 , не имеет другого пути, кроме как пройти через вторую катушку индуктивности, третью и так далее.Затем через последовательно соединенные индукторы протекает общий ток , например: |
I L1 = I L2 = I L3 = I AB … и т. Д. |
В приведенном выше примере катушки индуктивности L 1 , L 2 и L 3 соединены последовательно между точками A и B. Сумма индивидуальных падений напряжения на каждой катушке индуктивности может быть найдена с помощью напряжения Кирхгофа. Закон (KVL) где, V T = V 1 + V 2 + V 3 , и мы знаем из предыдущих руководств по индуктивности, что самоиндуцированная ЭДС на катушке индуктивности задается как: V = L di / dt. |
Итак, взяв значения отдельных падений напряжения на каждой катушке индуктивности в нашем примере выше, общая индуктивность для последовательной комбинации будет равна: |
Разделив приведенное выше уравнение на di / dt, мы можем уменьшить его, чтобы получить окончательное выражение для расчета общей индуктивности цепи при последовательном соединении катушек индуктивности, которое дается как: |
Последовательные индукторы Уравнение |
L всего = L 1 + L 2 + L 3 +….. + L n и т. Д. |
Тогда общую индуктивность последовательной цепи можно найти, просто сложив вместе отдельные индуктивности последовательно соединенных индукторов, точно так же, как суммируя последовательно резисторы. Однако вышеприведенное уравнение справедливо только тогда, когда нет взаимной индуктивности или магнитной связи между двумя или более индукторами (они магнитно изолированы друг от друга). |
Один важный момент, который следует помнить о индукторах в последовательных цепях, общая индуктивность (L T ) любых двух или более индукторов, соединенных вместе последовательно, всегда будет на БОЛЬШЕ , чем значение самого большого индуктора в последовательной цепи. |
Пример № 1 |
Три индуктора 10 мГн, 40 мГн и 50 мГн соединены вместе в последовательной комбинации без взаимной индуктивности между ними. Рассчитайте общую индуктивность последовательной комбинации. |
Катушки индуктивности с взаимным соединением серии |
Когда катушки индуктивности соединены последовательно, так что магнитное поле одного соединяется с другим, эффект взаимной индуктивности либо увеличивает, либо уменьшает общую индуктивность в зависимости от величины магнитной связи.Эффект этой взаимной индуктивности зависит от расстояния между катушками и их ориентации друг относительно друга. Взаимно соединенные последовательно катушки индуктивности могут быть классифицированы как «вспомогательные» или «противодействующие» общей индуктивности. Если магнитный поток, создаваемый током, течет через катушки в одном и том же направлении, то говорят, что катушки кумулятивно связаны . Если ток течет через катушки в противоположных направлениях, то говорят, что катушки с дифференциальной связью , как показано ниже. |
Катушки индуктивности сериис накопительной связью |
Хотя ток, протекающий между точками A и D через две кумулятивно связанные катушки, имеет одно и то же направление, приведенное выше уравнение для падения напряжения на каждой из катушек необходимо изменить, чтобы учесть взаимодействие между двумя катушками из-за эффект взаимной индуктивности.Собственная индуктивность каждой отдельной катушки, L 1 и L 2 , соответственно, будет такой же, как и раньше, но с добавлением M, обозначающего взаимную индуктивность. |
Тогда полная ЭДС, индуцированная в кумулятивно связанных катушках, определяется как: |
Где: 2M представляет влияние змеевика L 1 на L 2 и аналогично змеевика L 2 на L 1 . |
Разделив приведенное выше уравнение на di / dt, мы можем уменьшить его, чтобы получить окончательное выражение для расчета полной индуктивности цепи, когда катушки индуктивности соединены кумулятивно, и это дается как: |
L всего = L 1 + L 2 + 2M |
Если одна из катушек перевернута так, что один и тот же ток течет через каждую катушку, но в противоположных направлениях, взаимная индуктивность M, существующая между двумя катушками, будет иметь эффект компенсации для каждой катушки, как показано ниже. |
Дроссели с дифференциальной связью серии |
ЭДС, индуцируемая в катушке 1 под действием взаимной индуктивности катушки 2, противоположна самоиндуцированной ЭДС в катушке 1, так как теперь один и тот же ток проходит через каждую катушку в противоположных направлениях. Чтобы учесть этот эффект компенсации, знак минус используется с M, когда магнитное поле двух катушек дифференциально соединено, что дает нам окончательное уравнение для расчета общей индуктивности цепи, когда индукторы дифференциально соединены как: |
L всего = L 1 + L 2 — 2M |
Тогда окончательное уравнение для последовательно соединенных индукторов имеет следующий вид: |
Пример №2 |
Два индуктора по 10 мГн соответственно соединены вместе в последовательной комбинации, так что их магнитные поля помогают друг другу, обеспечивая кумулятивную связь.Их взаимная индуктивность составляет 5 мГн. Рассчитайте общую индуктивность последовательной комбинации. |
Пример №3 |
Две последовательно соединенные катушки имеют самоиндукцию 20 мГн и 60 мГн соответственно. Общая индуктивность комбинации составила 100 мГн. Определите величину взаимной индуктивности, которая существует между двумя катушками, предполагая, что они помогают друг другу. |
Сводка серий индукторов |
Теперь мы знаем, что мы можем соединить вместе катушек индуктивности последовательно , чтобы получить общее значение индуктивности, L T , равное сумме отдельных значений, которые они складывают вместе, аналогично соединению резисторов последовательно.Однако последовательно соединенные друг с другом катушки индуктивности классифицируются как «помогающие» или «противодействующие» этой общей индуктивности в зависимости от того, связаны ли катушки кумулятивно (в одном направлении) или дифференциально (в противоположном направлении). В следующем уроке об индукторах мы увидим, что положение катушек при параллельном соединении индукторов также влияет на общую индуктивность L T цепи. |
Воспроизведено с разрешения Wayne Storr |
| (http: // www.electronics-tutorials.ws/inductor/series-inductors.html) |
без магнитной муфты ИНДУКТОРЫ СЕРИИ
БЕЗ МАГНИТНОЙ МУФТЫКогда индукторы хорошо экранированы или расположены достаточно далеко друг от друга, влияние взаимной индуктивности незначительно. Если нет взаимной индуктивности (магнитная связь), а катушки индуктивности соединены последовательно, общая индуктивность равна сумма индивидуальных индуктивностей.В виде формулы:
, где L T — полная индуктивность; L 1 , L 2 , L 3 — индуктивности L 1 , L 2 , L 3 ; и L n означает, что можно использовать любое количество (n) индукторов. Индуктивности катушек индуктивности последовательно складываются, как сопротивления последовательно соединенных резисторов.
ИНДУКТОРЫ СЕРИИС МАГНИТНОЙ МУФТОЙ
Когда две последовательно соединенные катушки индуктивности расположены так, что поле одной соединяет другую, комбинированная индуктивность определяется следующим образом:
Знак плюс используется с M, когда магнитные поля двух индукторов помогают друг друга, как показано на рисунке 2-14.Знак минус используется вместе с M, когда магнитное поле двух индукторов расположены напротив друг друга, как показано на рисунке 2-15. Фактор 2М счета для влияния L 1 на L 2 и L 2 на L 1 .
Рисунок 2-14. — Последовательные индукторы со вспомогательными полями.
Рисунок 2-15. — Последовательные индукторы с противолежащими полями.
Пример задачи:
Катушка 10 Н соединена последовательно с катушкой 5 Н, поэтому поля помогают друг другу.Их взаимная индуктивность 7 Гн. Какова суммарная индуктивность катушек?
Q.15 Две последовательно соединенные катушки индуктивности 7-H расположены рядом друг с другом; их коэффициент
сцепления 0,64. Какое значение имеет М?
Q.16 Цепь содержит две последовательные катушки индуктивности, выровненные таким образом, что их магнитные
поля противостоят друг другу. Какую формулу вы должны использовать для вычисления полной индуктивности в этом
схема?
Q.17 Магнитные поля двух катушек помогают друг другу.Индуктивность катушек
равны 3 H и 5 H соответственно. Взаимная индуктивность катушек 5 Гн.
индуктивность?
ПАРАЛЛЕЛЬНЫЕ ИНДУКТОРЫ БЕЗ МУФТЫ
Общая индуктивность (L T ) индукторов, включенных параллельно, вычисляется в том же способ расчета полного сопротивления параллельно включенных резисторов при условии, что коэффициент связи между катушками равен нулю.


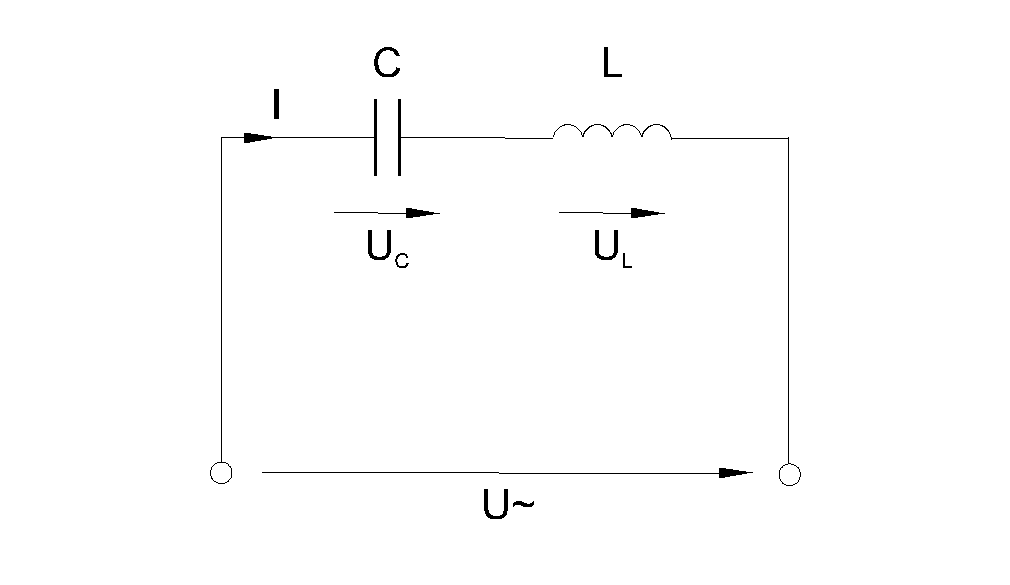


 Напряжение, приложенное
к каждой катушке, одинаково и равно U.
Экспериментальная часть
Задание
Докажите путем измерения токов и напряжений, что эквивалентная
индуктивность цепи с параллельным соединением катушек меньше индуктивности
наименьшей катушки и что измеренные индуктивные реактансы и индуктивности
связаны соотношением:
XL = w
L
Порядок выполнения эксперимента
Соберите цепь согласно схеме (рис. 5.4.2), подсоедините регулируемый
источник синусоидального напряжения с параметрами U = 5 В и f = 1
кГц.
Измерьте с помощью мультиметра или виртуальных приборов общий ток
цепи I,
Рис. 5.4.2
токи параллельных ветвей I1, I2, I3 и падения напряжение U на катушках,
занесите данные измерений в табл. 5.4.1
Таблица 5.4.1
Напряжение, приложенное
к каждой катушке, одинаково и равно U.
Экспериментальная часть
Задание
Докажите путем измерения токов и напряжений, что эквивалентная
индуктивность цепи с параллельным соединением катушек меньше индуктивности
наименьшей катушки и что измеренные индуктивные реактансы и индуктивности
связаны соотношением:
XL = w
L
Порядок выполнения эксперимента
Соберите цепь согласно схеме (рис. 5.4.2), подсоедините регулируемый
источник синусоидального напряжения с параметрами U = 5 В и f = 1
кГц.
Измерьте с помощью мультиметра или виртуальных приборов общий ток
цепи I,
Рис. 5.4.2
токи параллельных ветвей I1, I2, I3 и падения напряжение U на катушках,
занесите данные измерений в табл. 5.4.1
Таблица 5.4.1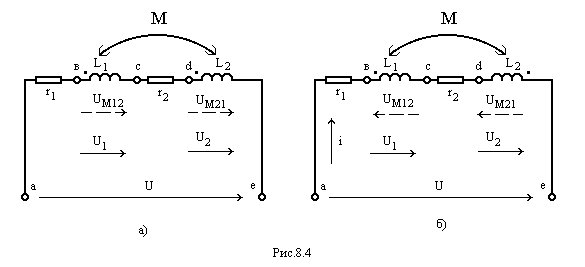 Определите индуктивности отдельных катушек и общую индуктивность
цепи по формуле L = XL ¤
w
.
Проверьте вычислениями величину индуктивности LЭ, найденную экспериментально.
Вычисление индуктивных реактансов:
XL1 = UL1 ¤
IL1 =
XL2 = UL2 ¤
IL2 =
XL3 = UL3 ¤
IL3 =
XLЭ = U ¤
I =
Вычисление индуктивностей:
L1 = XL1 ¤
w
=
L2 = XL2 ¤
w
=
L3 = XL3 ¤
w
=
LЭ = XLЭ ¤
w
=
Проверка общей индуктивности расчетом:
LЭ = 1 ¤
(1 ¤
L1 + 1 ¤ L2+ 1 ¤
L3) =.
Определите индуктивности отдельных катушек и общую индуктивность
цепи по формуле L = XL ¤
w
.
Проверьте вычислениями величину индуктивности LЭ, найденную экспериментально.
Вычисление индуктивных реактансов:
XL1 = UL1 ¤
IL1 =
XL2 = UL2 ¤
IL2 =
XL3 = UL3 ¤
IL3 =
XLЭ = U ¤
I =
Вычисление индуктивностей:
L1 = XL1 ¤
w
=
L2 = XL2 ¤
w
=
L3 = XL3 ¤
w
=
LЭ = XLЭ ¤
w
=
Проверка общей индуктивности расчетом:
LЭ = 1 ¤
(1 ¤
L1 + 1 ¤ L2+ 1 ¤
L3) =.  В идеальной катушке потерь активной мощности нет. В действительности
же возвращаемая энергия всегда меньше потребляемой из-за потерь энергии
в активном сопротивлении катушки.
Рис. 5.5.1
В идеальной катушке (при R=0) график мощности p(t) представляет
собой синусоиду двойной частоты (см. рис. 5.5.1) с амплитудой
QL = ULm ILm/2 = UL IL.
Это значение является максимальной мощностью, потребляемой или отдаваемой
идеальной катушкой индуктивности. Она называется индуктивной реактивной
мощностью.
Средняя (активная) мощность, потребляемая такой катушкой, равна
нулю.
Экспериментальная часть
Задание
Выведите кривые тока и напряжения катушки на экран виртуального
осциллографа, перенесите их на график и постройте кривую изменения
мгновенных значений мощности перемножением мгновенных значений напряжения
и тока.
Порядок выполнения эксперимента
Соберите цепь согласно схеме (рис. 5.5.2), подсоедините к ней регулируемый
источник синусоидального напряжения с параметрами: U=5…7B и f = 200
Гц. В качестве индуктивности с малым активным сопротивлением используйте
катушку трансформатора 300 витков, вставив между подковами разъемного
сердечника полоски бумаги в один слой (немагнитный зазор).
В идеальной катушке потерь активной мощности нет. В действительности
же возвращаемая энергия всегда меньше потребляемой из-за потерь энергии
в активном сопротивлении катушки.
Рис. 5.5.1
В идеальной катушке (при R=0) график мощности p(t) представляет
собой синусоиду двойной частоты (см. рис. 5.5.1) с амплитудой
QL = ULm ILm/2 = UL IL.
Это значение является максимальной мощностью, потребляемой или отдаваемой
идеальной катушкой индуктивности. Она называется индуктивной реактивной
мощностью.
Средняя (активная) мощность, потребляемая такой катушкой, равна
нулю.
Экспериментальная часть
Задание
Выведите кривые тока и напряжения катушки на экран виртуального
осциллографа, перенесите их на график и постройте кривую изменения
мгновенных значений мощности перемножением мгновенных значений напряжения
и тока.
Порядок выполнения эксперимента
Соберите цепь согласно схеме (рис. 5.5.2), подсоедините к ней регулируемый
источник синусоидального напряжения с параметрами: U=5…7B и f = 200
Гц. В качестве индуктивности с малым активным сопротивлением используйте
катушку трансформатора 300 витков, вставив между подковами разъемного
сердечника полоски бумаги в один слой (немагнитный зазор). Рис. 5.5.2
Включите виртуальные приборы V0, A1 и осциллограф.
«Подключите» два входа осциллографа к приборам V0 и A1, а остальные
отключите.
Установите параметры развёртки осциллографа так, чтобы на экране
было изображение примерно одного-двух периодов напряжения и тока.
Включите блок дополнительных приборов, выберите из меню приборы
«Активная мощность» и «Реактивная мощность» и подключите их к V1 и
A1. Запишите значения реактивной мощности QL и активной P. Убедитесь,
что P
Рис. 5.5.2
Включите виртуальные приборы V0, A1 и осциллограф.
«Подключите» два входа осциллографа к приборам V0 и A1, а остальные
отключите.
Установите параметры развёртки осциллографа так, чтобы на экране
было изображение примерно одного-двух периодов напряжения и тока.
Включите блок дополнительных приборов, выберите из меню приборы
«Активная мощность» и «Реактивная мощность» и подключите их к V1 и
A1. Запишите значения реактивной мощности QL и активной P. Убедитесь,
что P 5.5.1 на график (рис. 5.5.3).
5.5.1 на график (рис. 5.5.3). Например, напряжение u = Um sin (w
t+y
) изображается вектором длиной Um или Um/Ö
2, расположенным под углом y
к горизонтали. Векторные изображения синусоидальных
величин в дальнейшем будут подчеркиваться.
Например, напряжение u = Um sin (w
t+y
) изображается вектором длиной Um или Um/Ö
2, расположенным под углом y
к горизонтали. Векторные изображения синусоидальных
величин в дальнейшем будут подчеркиваться. …
…