При каких условиях возникает резонанс напряжений: Вопрос 3. В чем заключается явление резонанса напряжений и при каких условиях оно возникает? — Мир Антенн

Содержание

Вопрос 3. В чем заключается явление резонанса напряжений и при каких условиях оно возникает?

Ответ 3.1: В данной цепи при равенстве индуктивного и емкостного сопротивлений полное сопротивление цепи будет минимальным и чисто активным Z=R, а ток – максимальным .

Падения напряжения на индуктивном и емкостном элементах рассчитываются по закону Ома: , и т.к.величина напряжения на идеальной индуктивности U_Lравнанапряжению на емкости U_C_., но фазы напряженийU_Lи U_C противоположны (сдвинуты на 180°).

Режим работы цепи c последовательным соединением R,L,C элементов при котором и (или )называют резонансом напряжений.

Сумма комплексов напряжений Ū_Lи Ū_C равна нулю, следовательно и модуль суммы будет равен нулю.

Вольтметр, измеряющий падение напряжения (модуль комплекса напряжения) на участке цепи с идеальной индуктивностью и емкостью, покажет значение =0. При этом ток и напряжение_ВХ совпадает по фазе (коэффициент мощности ,φ₀=0). Активная мощность имеет наибольшее значение, равное полной мощностиS, в то время как реактивная мощность цепи оказывается равной нулю: .

При резонансе напряжения на емкости и на индуктивности могут значительно превышать подводимое напряжение U, если изначительно превышают R:

, .

Физическая причина возникновения повышенных напряжений – это колебания значительной энергии, запасаемой попеременно в электрическом поле емкостного и магнитном поле индуктивного элементов. При резонансе напряжений малые количества энергии, поступающей от источника и компенсирующие потери энергии в активном элементе – сопротивлении R, достаточны для поддержания незатухающих колебаний в системе относительно больших количеств энергии электрического и магнитного полей.

Причем в любой момент времени суммарная энергия электрического и магнитного полей остается постоянной.

Резонанс напряжений в промышленных электрических установках нежелательное и опасное явление, так как оно может привести к аварии вследствие недопустимого перегрева отдельных элементов электрической цепи или пробою изоляции.

**) Для мощных двигателей отношение сопротивлений обмоток X_L/R на промышленной частоте составляет несколько десятков. Напряжение питания двигателей обычно <380В. Поэтому в случае резонанса, напряжение на обмотке U_L

превысит напряжение питания в деcятки раз (U_L>>3800В).

В тоже время резонанс напряжений в электрических цепях переменного тока широко используется в радиотехнике в различных приборах и устройствах, основанных на резонансных явлениях.

Вопрос 4. Изменением каких параметров электрической цепи (см. Рис.1) можно получить резонанс напряжений ?

Ответ 4: При резонансе напряжений выравниваются реактивные сопротивления Х_L=X_C.

Т.к. Х_L=ω·L , а X_C=1/ωС , то равенства сопротивлений можно добиться тремя способами:

при постоянных ω и L изменяя величину емкости С;
при постоянных ω и С изменяя величину индуктивности L;
при постоянных L и С изменяя частоту ω. При резонансе .

Вопрос 5. С помощью каких приборов и по какому признаку можно судить о возникновении резонанса напряжений в электрической цепи?

Ответ 5: 1) В данной лабораторной установке опыты проводятся при постоянных величинах ω и L. По мере увеличения емкости от минимального до резонансного значения С₀=1/ωX_L, полное сопротивление цепи будет уменьшаться, при этом ток в цепи согласно формуле для тока будет расти. При резонансе он достигнет максимального значения .

Вывод 1

1: Амперметр покажет максимальное значение тока.

2) Т.к. U_L=I·X_L_,топадение напряжения на индуктивности U_L будет расти пропорционально росту тока. При резонансе напряжений, это напряжение будет максимальным. Однако вольтметр PV_К измеряет, согласно схеме замещения, падение напряжения на участке цепи из 2-х последовательно соединенных элементов: сопротивлений катушки R и индуктивности Х

L. Падение напряжения на сопротивлении Rравно U_R= I·R=U_вх, следовательнопри резонансе это напряжение также будет максимальным.

Вывод 2:

1)Вольтметр PV_Ктакже покажет максимальное значение

2)Падение напряжения на емкости С, измеряемое вольтметром PV_C_,равно: .

Т.к . ток в цепи один , а величины сопротивлений Х_L, X_C при резонансе одинаковы, то и напряжения одинаковы U_L =U_С. При этом U_вх
= U_R_. При резонансе =.Следовательно показания вольтметров PV

К и PV_Cбудут разными. Очевидно, что U_К> U_C.

Вывод 3: при резонансе показания вольтметра PV_Кбольше показания вольтметра PV_C .

4) Ваттметр PW измеряет активную мощность потребляемую цепью. Т.к. при резонансе ток максимальный, а активная мощность Р = I²·R, то и мощность P будет максимальной.

Вывод 4: Ваттметр покажет максимальное значение Р_макс = I₀²·R= U²_вх / R.

Резонанс напряжений, условие возникновения — Ремонт220

Автор Фома Бахтин На чтение 3 мин. Просмотров 9.3k. Опубликовано

10 марта Обновлено 19 ноября

Явление резонанса электрических напряжений наблюдается в цепи последовательного колебательного контура, состоящего из емкости (конденсатора), индуктивности и резистора (сопротивления). Для обеспечения энергетической подпитки колебательного контура в последовательную цепь включается также источник электродвижущей силы Е. Источник вырабатывает переменное напряжение с частотой W. При резонансе ток, циркулирующий в последовательной цепи, должен совпадать по фазе с э.д.с. Е. Это обеспечивается, если общее сопротивление схемы Z = R+J(WL – 1/WС) будет лишь активным, т.е. Z=R. Равенство:

(L – 1/WС) = 0 (1),

является математическим условием резонанса в колебательном контуре. При этом величина тока в цепи составит I = E/R. Если преобразовать равенство (1), то получим:

WL = 1/WС.

В этом выражении W – является резонансной частотой контура.

Важно то, что в процессе резонанса напряжение на индуктивности равно напряжению на конденсаторе и составляет:

UL = U = WL * I = WLE/R

Общая сумма энергий в индуктивности и емкости (магнитного и электрического полей) постоянна. Это объясняется тем, что между этими полями происходит колебательный обмен энергиями. Суммарное ее количество в любой момент неизменно. При этом обмена энергией между ее источником Е и цепью не происходит. Вместо этого имеет место непрерывное преобразование одного вида энергии в другой.

Для колебательных контуров применятся термин добротность, которая показывает, как соотносятся напряжение на реактивном элемента (емкость или индуктивность) и входное напряжение контура. Добротность вычисляется по формуле:

Q = WL/R

Для идеальной последовательной цепи с нулевым активным сопротивлением возникновение резонанса сопровождается незатухающими колебаниями.

На практике затухание колебаний компенсируется подпиткой контура от генератора колебаний с частотой резонанса.

Применение резонанса напряжений

Явление колебательного резонанса широко используется в радиоэлектронике. В частности, входная цепь любого радиоприемника представляет собой регулируемый колебательный контур. Его резонансная частота, изменяемая с помощью регулировки емкости конденсатора, совпадает с частотой сигнала радиостанции, которую необходимо принять.

В электроэнергетике возникновение резонанса напряжений вследствие сопутствующих ему перенапряжений чревато нежелательными последствиями. Например, в случае подключения к генератору или промежуточному трансформатору длинной кабельной линии (являющейся колебательным контуром с распределенной емкостью и индуктивностью), не соединенной на приемном конце с нагрузкой (это называется режимом холостого хода), весь контур может оказаться в резонансом состоянии. В такой ситуации напряжения, возникающие на некоторых участках цепи, могут оказаться выше расчетных.

Это может грозить пробоем изоляции кабеля и выходом его из строя. Такая ситуация предотвращается применением вспомогательной нагрузки.

Механизм возникновения электрического тока

Схема удивительного генератора СВЧ полей на разряднике Вина уникальное, в своём роде устройство

83046 Нагревание проводников электрическим током

Явление резонансов напряжений и токов в электроцепях и условия их возникновения

Любая электрическая цепь, содержащая элементы со свойствами индуктивности и ёмкости, может являться разновидностью колебательного контура – системы, в которой обязательно возникают незатухающие (в идеальном случае) колебания электроэнергии на частоте собственного резонанса. Определяют резонансную частоту параметры ёмкости – С и индуктивности – L. В общем случае, частота (F) описывается формулой:

Простейший контур

При подключении заряженного конденсатора к выводам катушки в последней возникает электродвижущая сила самоиндукции, начальный ток которой равен и противоположен по направлению току разряда. В течение разряда в катушке накапливается магнитная энергия, достигающая максимального значения, когда конденсатор полностью разряжается. Емкостное сопротивление при этом минимально, и катушка индуктивности накопленную энергию передаёт в конденсатор, далее начинается заряд напряжением противоположной полярности до момента полного преобразования магнитной энергии в ёмкость и последующей передачей обратно. При этих процессах токи, проходящие через конденсатор и индуктивность, больше тока всего контура, поэтому возникает резонанс токов.

Подключение конденсатора к катушке

Затухание колебаний происходит вследствие потерь энергии в проводниках схемы и катушки, утечек в конденсаторе. Реальный колебательный контур, в котором присутствуют условия резонанса, всегда используется с внешним источником колебаний – генератором, сетью переменного тока, радиосигналом.

Резонанс токов

В случае параллельного подключения индуктивности, ёмкости и нагрузки к источнику переменного напряжения с частотой, равной резонансной контура, наблюдается значительное увеличение тока через элементы контура и возрастание его сопротивления.

Параллельный контур

Свойства такого включения компонентов используются в заграждающих фильтрах различного назначения, пропускающих все частоты, кроме резонансной, при последовательном включении с сопротивлением нагрузки. При параллельном подключении контур не оказывает влияния на напряжение резонансной частоты. Если нагрузка обладает индуктивным сопротивлением, как асинхронный электродвигатель, то с параллельно включённым конденсатором они образуют колебательный контур. Если собственная его частота совпадает с частотой питающей сети, возрастает ток через нагрузку.

Резонанс напряжений

Подключение последовательного контура к генератору переменного напряжения частотой, равной собственной частоте контура, вызывает резонанс напряжений, при котором возрастают напряжения на индуктивности и ёмкости, с увеличением потребляемого тока от источника.

Последовательный контур

Сопротивление устройства на частоте резонанса минимально, что применяется в радиоприёмниках для настройки на частоту станции с помощью конденсатора переменной ёмкости. Как и при резонансе токов, последовательный контур применяется в фильтрах для подавления или пропускания определённых частот. В некоторых случаях возникновение резонанса напряжений приводят к нежелательным последствиям: кабель достаточной длины обладает значительной ёмкостью и индуктивностью и образует колебательный контур, при совпадении частоты сети и резонансной частоты кабеля возможен неконтролируемый рост напряжения с дальнейшим пробоем изоляции. В отдельных случаях последовательное включение конденсатора позволяет увеличить напряжение на индуктивной нагрузке – такая схема используется для запуска электродвигателей (пусковой конденсатор).

Условие резонанса любого типа возникает только при совпадении периодичности внешних воздействий с частотой собственных колебаний системы, на которую оказывается воздействие.

Явления резонанса применяются во множестве электронных и электротехнических устройствах. Магнетрон любой микроволновой печки – это резонатор, работающий как генератор колебаний СВЧ, феррорезонансный стабилизатор напряжения использует свойства параллельного колебательного контура.

Видео

Оцените статью:

Резонанс напряжений, условие возникновения

Резонанс токов (параллельный резонанс) — резонанс, происходящий в параллельном колебательном контуре при его подключении к источнику напряжения, частота которого совпадает c резонансной частотой контура.

Блок: 1/9 | Кол-во символов: 208
Источник: https://ru.wikipedia.org/wiki/%D0%A0%D0%B5%D0%B7%D0%BE%D0%BD%D0%B0%D0%BD%D1%81_%D1%82%D0%BE%D0%BA%D0%BE%D0%B2

Что это такое

Резонанс токов — разновидность состояния электрической цепи, когда общий вид токовых показателей совпадает по фазам уровню напряжения, а мощность реактивного вида равна нулю или же она представлена в активном виде.

. Резонанс токов

Этот вариант развития событий характерен для переменного тока и имеет не только положительные свойства, но и некоторые нежелательные последствия. Так, благодаря резонансу работает радиотехника, автоматика и проволочная телефония, но в то же время возникают перенапряжения и сбои в работе электрической системы.

Определение из учебного пособия

Блок: 2/6 | Кол-во символов: 589
Источник: https://rusenergetics.ru/ustroistvo/rezonans-tokov

При каких условиях возникает

Условием того, чтобы возникло это явление, является равные показатели проводниковой частоты, где BL=BC. То есть емкостная с индуктивной проводимостью должна быть равна. Только тогда подобное явление резонанса токов наблюдается в электрической цепи. Он при этом может быть как положительным, так и отрицательным. В любом радиоприемнике есть колебательный контур, который из-за индуктивного или емкостного изменения, настраивается на нужный сигнал радиоволны. В другом случае, это ведет к тому, что появляются скачки напряжения или ток в цепи и появляется аварийная ситуация.

В условиях лаборатории, он возникает во время, когда изменяется емкость и не изменяется индуктивность катушки L. В таком случае формула выглядит как Bc=C

При каких условиях возникает

Блок: 3/6 | Кол-во символов: 786
Источник: https://rusenergetics.ru/ustroistvo/rezonans-tokov

Собственная частота резонансного контура

Емкость конденсатора (С) в совокупности с индуктивностью катушки (L) определяют собственную частоту контура (Wc). Для приблизительных расчетов пользуются формулой Wc=1/√L*C. В этом случае речь идет об идеальных условиях, когда потерями пренебрегают по причине минимальных значений.

Для повышения точности применяют коэффициент затухания (Кз). С учетом этого фактора можно привести следующую зависимость между собственной и резонансной частотами:

Wo=√Wc2-2*Кз2.

Блок: 3/12 | Кол-во символов: 502
Источник: https://amperof. ru/bezopasnost/usloviya-rezonansa.html

Использование резонанса напряжений для передачи радиосигнала

Колебательный контур этого типа создают из последовательной комбинации трех базовых компонентов: резистор, конденсатор, индуктивность. Подходящим для резонанса условием является нулевое сопротивление цепи (комплексное). Для решения такой задачи следует изучить основные формулы.

Комплексное сопротивление Rк=R+j(wL-1/wC). Постоянный резистор (R) не зависит от частоты (w). Значит, придется оперировать с индукционными и емкостными элементами. Резонансный эффект получают при (wL-1/wC)=0. Для вычисления необходимых значений пользуются следующими расчетами:

Lп=1/w2*C;
Сп=1/w2*L;
Wп=1/√L*C.

Из приведенных данных понятно, что корректировать можно любой из параметров при одновременном сохранении двух других. В практической схемотехнике удобнее работать с частотой, поэтому рассмотрим подробнее применение такого варианта.

Последовательный контур с графиками

На рисунках показаны условия возникновения резонанса напряжений. В точке, обозначенной w0, наблюдается равенство индуктивной и емкостной составляющих на определенной частоте. Небольшой сдвиг влево по оси обусловлен резистивным компонентом цепи.

Напряжение на конденсаторе (Uc) при частоте резонанса (W0) равно волновому сопротивлению колебательного контура (p=√L/C). Аналогичная разница потенциалов будет на клеммах катушки при частоте W0. Данная особенность объясняет особое название процесса – «резонанс напряжений». Также в электротехнических расчетах применяют следующие определения:

Добротность – Q=p/R;
Затухание – 1/Q.

Отмеченные свойства используют в радиоприемной и передающей аппаратуре. Выделение контуром определенного диапазона позволяет выполнять настройку станции на определенную частоту с определенной параметрами цепи погрешностью. Для контроля избирательности оценивают амплитуду сигнала относительно резонансной частоты. Уровень отклонения на 3 дБ в обе стороны (0,7 от максимума) называют полосой пропускания.

Амплитудно-частотная характеристика (АЧХ) и полоса пропускания

Блок: 2/12 | Кол-во символов: 2012
Источник: https://amperof.ru/bezopasnost/usloviya-rezonansa.html

Примеры применения на практике

Классическим примером применения резонанса колебательных контуров является настройка радиоприёмника на частоту соответствующей радиостанции. В качестве рабочего элемента настроечного узла используется конденсатор с регулируемой ёмкостью. Вращение ручки настройки изменяет ёмкость конденсатора, а значит и резонансную частоту контура.

В момент совпадения резонансной частоты с рабочей частотой какой-либо радиостанции возникает резонанс напряжений, в результате которого резко возрастает амплитуда колебаний принятой радиоприёмником частоты. Специальные фильтры отделяют эти колебания от несущих радиочастот, а усилители усиливают полученные сигналы. В динамике появляются звуки, генерируемые передатчиком радиостанции.

Колебательные контуры, построенные на принципе последовательного соединения LC-элементов, применяются в цепях питания высокоомных нагрузок, потребляющих токи повышенного напряжения. Такие же устройства применяют в полосовых фильтрах.

Последовательный резонанс применяют при пониженных напряжениях сети. В этом случае используют реактивную энергию обмоток трансформатора, соединённых последовательно.

Конденсаторы и различные катушки индуктивности (рис. 5) входят в конструкцию практически всех аналоговых устройств. Они используются для настройки фильтров или для управления токами в отдельных узлах.

Катушки индуктивности

Важно знать, что резонансные контуры не увеличивают количество электрической энергии в цепях. Они лишь могут повышать напряжения, иногда до опасных значений. Постоянный ток не причиной резонансных явлений.

Наряду с полезными свойствами резонансных явлений, в практической электротехнике часто возникают ситуации, когда резонанс напряжений приносит вред. В основном это связано с нежелательным повышением параметров тока на участках цепей. Примером могут служить опасное резонансные явления в кабельных линиях без нагрузки, что может привести к пробоям изоляции. Чтобы этого не случилось, на концевых участках таких линий устанавливают балластные нагрузочные элементы.

Блок: 3/3 | Кол-во символов: 2059
Источник: https://www.asutpp.ru/rezonans-napryazheniy.html

Замечания

Колебательный контур, работающий в режиме резонанса токов, не является усилителем мощности. Он является усилителем тока.

Большие токи, циркулирующие в контуре, возникают за счет мощного импульса тока от генератора в момент включения, когда заряжается конденсатор. При значительном отборе мощности от контура эти токи «расходуются», и генератору вновь приходится отдавать значительный ток подзарядки. Поэтому внутри контура сопротивление должно быть сведено к минимуму чтобы уменьшить потери.

Если генератор слабый, большой ток подзарядки в момент его включения на колебательный контур может сжечь его. Выйти из положения можно, постепенно повышая напряжение на клеммах генератора (постепенно «раскачивая» контур).

Колебательный контур с низкой добротностью и катушкой небольшой индуктивности слишком плохо «накачивается» энергией (запасает мало энергии), что понижает КПД системы. Также катушка с маленькой индуктивностью и на низких частотах обладает малым индуктивным сопротивлением, что может привести к «короткому замыканию» генератора по катушке, и вывести генератор из строя.

Добротность колебательного контура пропорциональна L/C, колебательный контур с низкой добротностью плохо «запасает» энергию. Для повышения добротности колебательного контура используют несколько путей:

Повышение рабочей частоты;
По возможности увеличить L и уменьшить C. Если увеличить L с помощью увеличения витков катушки или увеличения длины провода не представляется возможным, используют ферромагнитные сердечники или ферромагнитные вставки в катушку; катушка обклеивается пластинками из ферромагнитного материала и т п.

При расчёте колебательного контура с катушкой небольшой индуктивности, нужно учитывать индуктивность соединительных шин (от катушки к конденсатору), соединительные провода конденсаторной батареи. Индуктивность соединительных шин может быть намного больше индуктивности катушки и серьёзно понизить частоту колебательного контура.

При реализации резонанса токов на трансформаторах, первичная и вторичная обмотки должны располагаться на разных кернах на магнитопроводе, иначе электромагнитные наводки от вторичной обмотки будут мешать резонансу. Поэтому годятся трансформаторы с П образным или Ш образным сердечником. В противном случае обмотки тщательно экранируют друг от друга фольгой.

Блок: 4/9 | Кол-во символов: 2298
Источник: https://ru.wikipedia.org/wiki/%D0%A0%D0%B5%D0%B7%D0%BE%D0%BD%D0%B0%D0%BD%D1%81_%D1%82%D0%BE%D0%BA%D0%BE%D0%B2

Как используется

Резонансные токи используются сегодня в некоторых фильтрующих системах, радиотехнике, электричестве, радиостанциях, асинхронных двигателях, высокоточных электрических сварных установках, колебательных генераторных электрических контурах и высокочастотных приборах. Нередко, когда они применяются, чтобы снизить генераторную нагрузку.

Обратите внимание! Простейшая цепь, где наблюдаются они, это параллельного вида колебательный контур. Такие контуры используются в современном промышленном индукционном котловом оборудовании и улучшают показатели КПД.

Сфера применения

Блок: 4/6 | Кол-во символов: 590
Источник: https://rusenergetics.ru/ustroistvo/rezonans-tokov

Последовательно-параллельный резонанс

Параллельно-последовательный резонанс выполненый на основе трансформаторов.

Параллельно-последовательный резонанс.

Кроме параллельного и последовательного резонанса существует также комбинированный, а точнее параллельно-последовательный. В простейшем варианте это две катушки с одинаковой индуктивностью соединённые последовательно. На одной из катушек реализован колебательный контур. При этом на половину проявляется эффект от параллельного резонанса и на половину проявляется эффект от последовательного резонанса. Поэтому при этом происходит частичное увеличение напряжения. Этот способ уместно применять в тех случаях когда генератор не может выдать нужное напряжение или напряжение в сети проседает. Но применяется такой способ только к тем потребителям, у которых нагрузка постоянная, потому что если нагрузка будет меняться, то резонанс будет сбиваться. Для такой схемы годятся не любые трансформаторы, а только те у которых обмотки не накладываются друг на друга и располагаются на разных кернах на против друг друга на сердечнике. Если вторичная обмотка намотана поверх первичной, то на таком трансформаторе параллельный резонанс не работает. Кроме этого существуют и более сложные схемы последовательно-параллельного резонанса использующие полупроводники, такие как транзисторы.

Блок: 3/9 | Кол-во символов: 1329
Источник: https://ru.wikipedia.org/wiki/%D0%A0%D0%B5%D0%B7%D0%BE%D0%BD%D0%B0%D0%BD%D1%81_%D1%82%D0%BE%D0%BA%D0%BE%D0%B2

Принцип действия

Токовый резонанс можно заметить во внутренней поверхности электрической цепи, которая имеет параллельное катушечное, резисторное и конденсаторное подсоединение. Главный принцип того, как работает стандартный аппарат, не сложен в понимании.

Когда включается электрическое питание, внутри конденсаторной установки накапливается заряд до номинального напряжения. В этом время отключается питающий источник и замыкается цепь в контур. Этот момент сопровождается переносом разряда на часть катушки. Далее показатели тока, которые проходят по катушке, генерируют магнитное поле. Создается электродвижущая самостоятельная индукционная сила по направлению встречному току. При полном конденсаторном разряде максимально увеличиваются токовые показатели. Объем энергии становится магнитным индукционным полем. В результате данный цикл повторяется, и катушечное поле преобразовывается в конденсаторный заряд.

Принцип работы

Блок: 5/6 | Кол-во символов: 930
Источник: https://rusenergetics.ru/ustroistvo/rezonans-tokov

Как правильно рассчитать

Токовый резонанс очень важно правильно рассчитать, если есть параллельное соединение, предотвращающая появление помех около системы. Для правильного расчета необходимо понять, какие показатели мощности в электросети. Средняя стандартная мощность, рассеивающаяся при резонансном контуре, выражается при помощи среднеквадратичных токовых показателей и напряжения. При резонансе мощностный коэффициент равен единице и формула имеет вид, как на картинке.

Формула расчета

Чтобы правильно определить нулевой импеданс, понадобиться воспользоваться стандартной формулой, которая дана ниже.

Формула резонансных кривых

Что касается аппроксимирования резонанса колебательных частот, это можно выяснить по следующей формуле.

Расчет колебательного контура

Обратите внимание! Для получения максимально точных данных по приведенным формулам, округлять данные не нужно. Благодаря этому получится грамотный расчет, который приведет к достойной экономии переменного тока, если речь идет о подсчете в целях снижения счетов.

В целом, резонанс токов — это то, что происходит в части параллельного колебательного контура, в случае его подключения к источнику напряжения, частота какого может совпадать с контурной. Возникает при условиях, когда цепь, имеющая параллельное соединение резисторной катушки и конденсатора, равна проводимости BL=BC. Правильно сделать весь необходимый подсчет можно по специальной формуле или, прибегая к использованию специальных измерительных инструментов в виде мультиметра.

Блок: 6/6 | Кол-во символов: 1511
Источник: https://rusenergetics.ru/ustroistvo/rezonans-tokov

Резонанс в линейных системах с одной степенью свободы

К этой группе можно причислить рассмотренные последовательные и параллельные электрические схемы. Механический пример – пружина с грузом, который способен перемещаться только по вертикальной прямой. Исключены порывы ветра, вибрации, другие «паразитные» внешние воздействия. В подобных условиях можно применять типовые формулы для систем линейного типа.

Отмеченная выше добротность является определяющим фактором для избирательности по частоте. Сужение ширины резонансного диапазона помогает улучшить характеристики приемных и передающих устройств. Кроме экономного расходования электроэнергии, при правильном расчете схемы существенно улучшается помехозащищенность.

Блок: 6/12 | Кол-во символов: 720
Источник: https://amperof.ru/bezopasnost/usloviya-rezonansa.html

Литература

Власов В. Ф. Курс радиотехники. М.: Госэнергоиздат, 1962. С. 928.
Изюмов Н. М., Линде Д. П. Основы радиотехники. М.: Госэнергоиздат, 1959. С. 512.

Блок: 8/9 | Кол-во символов: 157
Источник: https://ru.wikipedia.org/wiki/%D0%A0%D0%B5%D0%B7%D0%BE%D0%BD%D0%B0%D0%BD%D1%81_%D1%82%D0%BE%D0%BA%D0%BE%D0%B2

Ссылки

Резонанс токов

Circuits. A/C Circuits. Parallel Resonance

Частотно-модулированный преобразователь с последовательно- параллельным резонансом

Блок: 9/9 | Кол-во символов: 148
Источник: https://ru. wikipedia.org/wiki/%D0%A0%D0%B5%D0%B7%D0%BE%D0%BD%D0%B0%D0%BD%D1%81_%D1%82%D0%BE%D0%BA%D0%BE%D0%B2

Резонанс в реальных цепях

Для изучения описанных процессов надо собрать контур из соответствующих компонентов. Придется подготовить генератор с изменяющейся частотой выходного сигнала, осциллограф и другие измерительные инструменты. Чтобы получить достоверные результаты без лишних трудностей, пользуются специализированным программным обеспечением.

Теория и практика

В левой части рисунка размещены схема и амплитуда сигнала на выходе при подключении к выводам конденсатора параллельного контура. В правой – снимок экрана измерительной аппаратуры. Несложно убедиться в идентичности колебаний.

К сведению. С помощью ПО выполняют десятки экспериментов быстро и точно в обычных домашних условиях. Этот способ значительно упрощает создание электрических схем с оптимальными параметрами.

Блок: 9/12 | Кол-во символов: 785
Источник: https://amperof. ru/bezopasnost/usloviya-rezonansa.html

Частотные характеристики контура

Для любой схемы определить выходные параметры можно по параметрам входного сигнала, значениям емкости (индуктивности). Также применяют расчет по добротности контура:

параллельный: Q=1/w*L*C;
последовательный: Q= 1/w*C*R=wL/R.

Блок: 10/12 | Кол-во символов: 259
Источник: https://amperof.ru/bezopasnost/usloviya-rezonansa.html

Резонанс в линейных колебательных системах с несколькими степенями свободы

Такие расчеты понадобятся при конструировании двух последовательных контуров с индуктивной связью. В этом случае переменные колебательные процессы оказывают взаимное влияние. Фактически речь идет о распределенной системе.

Кроме схемотехники, в подобных ситуациях отдельно изучают коэффициент связи (Кс). При работе с трансформатором его вычисляют делением напряжений на первичной (вторичной) катушке, соответственно. Следует учесть реактивные характеристики, которые преобладают в рабочем диапазоне частот.

Узнав, что такое резонанс напряжений и токов, можно самостоятельно реализовать различные проекты. Тщательная предварительная подготовка необходима для создания схемы с хорошими эксплуатационными параметрами. Начинают с чертежей и расчетной части. Теоретические изыскания дополняют изготовлением макета и практическими испытаниями. Ускоряют подготовку конструкторской документации, а также выполняют эксперименты с применением программного обеспечения. В наиболее сложных ситуациях обращаются к опытным специалистам.

Блок: 11/12 | Кол-во символов: 1098
Источник: https://amperof.ru/bezopasnost/usloviya-rezonansa.html

Видео

Блок: 12/12 | Кол-во символов: 6
Источник: https://amperof. ru/bezopasnost/usloviya-rezonansa.html

Кол-во блоков: 23 | Общее кол-во символов: 16179
Количество использованных доноров: 5
Информация по каждому донору:

https://rusenergetics.ru/ustroistvo/rezonans-tokov: использовано 5 блоков из 6, кол-во символов 4406 (27%)
https://ru.wikipedia.org/wiki/%D0%A0%D0%B5%D0%B7%D0%BE%D0%BD%D0%B0%D0%BD%D1%81_%D1%82%D0%BE%D0%BA%D0%BE%D0%B2: использовано 5 блоков из 9, кол-во символов 4140 (26%)
https://www.asutpp.ru/rezonans-napryazheniy.html: использовано 1 блоков из 3, кол-во символов 2059 (13%)
https://amperof.ru/bezopasnost/usloviya-rezonansa.html: использовано 7 блоков из 12, кол-во символов 5382 (33%)
https://remont220.ru/stati/728-rezonans-napryazheniy-uslovie-vozniknoveniya/: использовано 3 блоков из 5, кол-во символов 192 (1%)

При каких параметрах цепи возникают резонанс тока и напряжения

В цепи переменного тока с активным сопротивлением, индуктивностью и емкостью, при их последовательным соединении, сила тока будет максимальной, ограниченной только активным сопротивлением.

Поэтому при равенстве индуктивного и емкостного сопротивлений в последовательной цепи наступает — резонанс напряжений.

Резонанс напряжений в энергосистемах иногда возникает непредвиденно и приводит к тому, что на отдельных установках возникают перенапряжения, в несколько раз превышающие рабочие напряжения.

Явление резонанса состоит в том, что напряжение на индуктивности и напряжение на емкости, т.е. частичные напряжения в цепи, могут получить очень большие значения, во мгого раз превышающие напряжение источника тока. Если при этом активное сопротивление цепи невелико, то сила тока в цепи должна сильно возрасти и при отсутствии в цепи активного сопротивления, достаточно самого небольшого напряжения, чтобы в случае резонанса вызвть ток, бесконечно большой силы. При этом вполне очевидно, что угол сдвига фаз равно нулю. . Таким образом электрическая цепь при резонансе напряжений, вследствие взаимокомпенсации индуктивных и емкостных сопротивлений, ведет себя по отношению к внешней ЭДС, как чисто активное сопротивление.

При параллельном соединении активного, индуктивного и емкостного сопротивлений и отсутствии сдвига фаз между током и напряжением на зажимах цепи наступает резонанс токов. Т.е. при равенстве индуктивного и емкостного сопротивлений в цепи параллельного включения их с активным ток в цепи достигает своего минимального значения.

Явление резонанса токов наступает вследствие взаимокомпенсации индуктивных и емкостных проводимостей, а потому электрическая цепь в этом случае ведет себя по отношению к внешней ЭДС, как чисто активная проводимость, следовательно, угол сдвига фаз в главной цепи при резонансе токов равен нулю.

Следует отметить, что при резонансе токов возможны случаи, когда токи в индуктивной катушке и в конденсаторе могут превосходить, и иногда намного, суммарный ток в цепи. При резонансе токов энергия магнитного поля индуктивности переходит в энергию электрического поля конденсатора и наоборот, а энергия от источника расходуется только в активных сопротивлениях.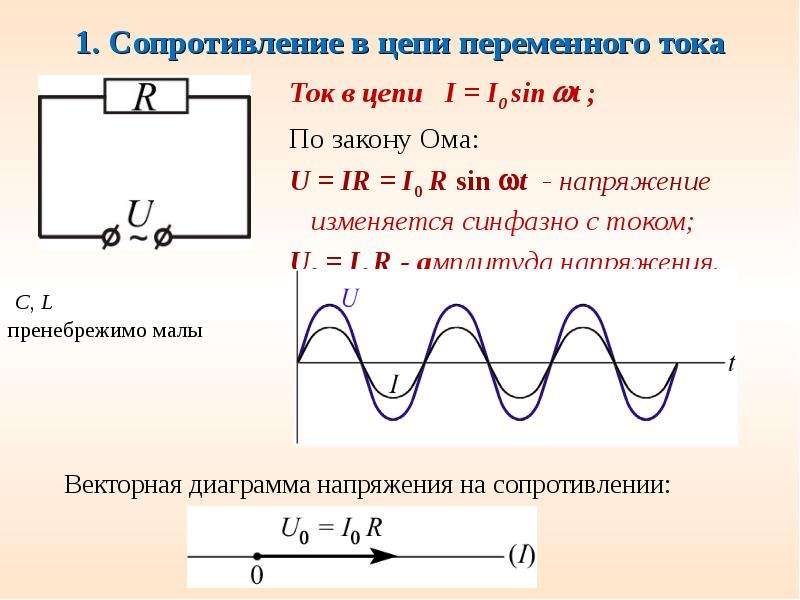

Условия возникновения резонанса в электрической цепи. Резонанс напряжений

Резонанс токов возникает в электрических цепях переменного тока при параллельном соединении ветвей с разнохарактерными (индуктивными и емкостными) реактивными сопротивлениями. В режиме резонанса токов реактивная индуктивная проводимость цепи оказывается равной ее реактивной емкостной проводимости, т.е. B L =B C .

Простейшей электрической цепью, в которой может наблюдаться резонанс токов, является цепь с параллельным соединением катушки индуктивности и конденсатора. Данная схема соответствует цепи, представленной на рис. 8, а , для которойR 2 = 0, а R 1 =R к (здесьR к – активное сопротивление катушки индуктивности). Полная проводимость такой цепиY =.

Условие резонанса токов (B L =B C) можно записать через соответствующие параметры электрической цепи. Так как реактивная проводимость катушки, имеющей активное сопротивлениеR к, определяется выражениемB L =X L /=L /(R к 2 + 2 L 2), а проводимость конденсатора без учета его активного сопротивления (R C = 0)B C =X C /= 1/X C =C , то условие резонанса может быть записано в виде

L /(+ 2 L 2) = C .

Из этого выражения следует, что резонанс токов в такой цепи можно получить при изменении одного из параметров R к,L ,C ипри постоянстве других. При некоторых условиях в подобных цепях резонанс может возникать и при одновременном изменении указанных параметров.

Простейшие резонансные цепи, состоящие из параллельно соединенных между собой катушки индуктивности и конденсатора, широко применяются в радиоэлектронике в качестве колебательных контуров, резонанс токов в которых достигается при некоторой определенной частоте поступающего на вход соответствующего устройства сигнала.

В лабораторных условиях наиболее часто резонанс токов достигается при неизменной индуктивности катушки L , путем изменения емкостиС батареи конденсаторов. С изменением емкостной проводимостиB C =C , пропорциональной емкости конденсатора, происходит изменение полной проводимостиY , общего токаI и коэффициента мощности cos. Указанные зависимости приведены на рис. 10,a . Анализ этих зависимостей показывает, что при увеличении емкости от нуля полная проводимость электрической цепи сначала уменьшается, достигает при (B L =B C) своего минимума, а затем возрастает с увеличениемС , в пределе стремясь к бесконечности. Общий токI =YU , потребляемый цепью, пропорционален полной проводимости. Поэтому характер его изменения подобен характеру изменения проводимости.

Коэффициент мощности cosс увеличением емкости сначала возрастает, а затем уменьшается, в пределе стремясь к нулю, так как cos=G /Y . В результате анализа указанных зависимостей можно установить, что резонанс токов характеризуется следующими явлениями.

a) б)

1. При резонансе токов полная проводимость всей электрической цепи приобретает минимальное значение и становится равной активной ее составляющей:

Y = =G .

2. Минимальное значение проводимости обусловливает минимальное значение тока цепи:

I = YU = GU .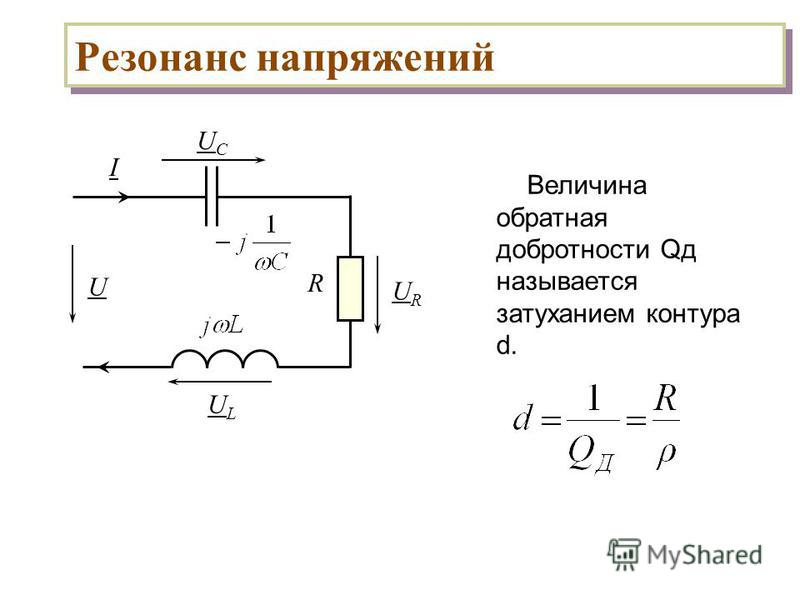

3. Емкостный ток I C и индуктивная составляющаяI L тока катушкиI к оказываются при этом равными по величине, а активная составляющая тока катушкиI а1 становится равной токуI , потребляемому из сети:

I р1 = I L = B L U = B C U = I C = I р2 ; I а = I а1 =GU = YU =I .

При этом реактивные составляющие токов I L иI C в зависимости от значений реактивных проводимостей могут приобретать теоретически весьма большие значения и намного превышать токI , потребляемый электрической цепью из сети.

4. Реактивная составляющая полной мощности цепи при B L =B C оказывается равной нулю:

Q = B L U 2  B C U 2 = Q L  Q C = 0.

При этом индуктивная и емкостная составляющие реактивной мощности также могут приобретать весьма большие значения, оставаясь равными друг другу.

5. Полная мощность цепи при резонансе равна ее активной составляющей:

S = YU 2 = GU 2 = P .

6. Коэффициент мощности всей цепи при резонансе:

cos = P /S = GU 2 /YU 2 = 1.

Напряжение и ток электрической цепи при резонансе токов совпадают по фазе. Векторная диаграмма, построенная для условий резонанса токов и применительно к рассматриваемой цепи, представлена на рис. 10, б . В табл. 2 методических указаний по выполнению работы обозначениямI L , I K , I C соответствуют обозначенияI р1 , I 1 , I р2 на векторной диаграмме токов (рис. 10,б ).

Резонанс токов находит широкое применение в силовых электрических цепях для повышения коэффициента мощности, так как это имеет большое технико-экономическое значение. Большинство промышленных потребителей переменного тока имеют активно-индуктивный характер; некоторые из них работают с низким коэффициентом мощности и потребляют значительную реактивную мощность. К таким потребителям могут быть отнесены асинхронные двигатели (особенно работающие с неполной нагрузкой), установки электрической сварки, высокочастотной закалки и т.д. Для уменьшения реактивной мощности и повышения коэффициента мощности параллельно потребителю включают батарею конденсаторов. Реактивная мощность конденсаторной батарей снижает общую реактивную мощность установки и тем самым увеличивает коэффициент мощности. Повышение коэффициента мощности приводит к уменьшению тока в проводах за счет снижения его реактивной составляющей и, соответственно, к уменьшению потерь энергии в генераторе и подводящих проводах.

Явление резонанса токов и напряжений наблюдается в цепях индуктивно-емкостного характера. Это явление нашло применение в радиоэлектронике, став основным способов настройки приемника на определенную волну. К сожалению, резонанс может нанести вред электрооборудованию и кабельным линиям. В физике резонансом является совпадение частот нескольких систем. Давайте рассмотрим, что такое резонанс напряжений и токов, какое значение он имеет и где используется в электротехнике.

Реактивные сопротивления индуктивности и емкости

Индуктивностью называется способность тела накапливать энергию в магнитном поле. Для нее характерно отставание тока от напряжения по фазе. Характерные индуктивные элементы — дросселя, катушки, трансформаторы, электродвигатели.

Емкостью называются элементы, которые накапливают энергию с помощью электрического поля. Для емкостных элементов характерно отставание по фазе напряжения от тока. Емкостные элементы: конденсаторы, варикапы.

Приведены их основные свойства, нюансы в пределах этой статьи во внимание не берутся.

Кроме перечисленных элементов другие также имеют определенную индуктивность и емкость, например в электрических кабелях распределенные по его длине.

Емкость и индуктивность в цепи переменного тока

Если в цепях постоянного тока емкость в общем смысле представляет собой разорванный участок цепи, а индуктивность — проводник, то в переменном конденсаторы и катушки представляют собой реактивный аналог резистора.

Реактивное сопротивление катушки индуктивности определяется по формуле:

Векторная диаграмма:

Реактивное сопротивление конденсатора:

Здесь w — угловая частота, f — частота в цепи синусоидального тока, L — индуктивность, C — емкость.

Векторная диаграмма:

Стоит отметить, что при расчете соединенных последовательно реактивных элементов используют формулу:

Обратите внимание, что емкостная составляющая принимается со знаком минус. Если в цепи присутствует еще и активная составляющая (резистор), то складывают по формуле теоремы Пифагора (исходя из векторной диаграммы):

От чего зависит реактивное сопротивление? Реактивные характеристики зависят от величины емкости или индуктивности, а также от частоты переменного тока.

Если посмотреть на формулу реактивной составляющей, то можно заметить, что при определенных значениях емкостной или индуктивной составляющей их разность будет равна нулю, тогда в цепи останется только активное сопротивление. Но это не все особенности такой ситуации.

Резонанс напряжений

Если последовательно с генератором соединить конденсатор и катушку индуктивности, то, при условии равенства их реактивных сопротивлений, возникнет резонанс напряжений. При этом активная часть Z должно быть как можно меньшей.

Стоит отметить, что индуктивность и емкость обладает только реактивными качествами лишь в идеализированных примерах. В реальных же цепях и элементах всегда присутствует активное сопротивление проводников, хоть оно и крайне мало.

При резонансе происходит обмен энергией между дросселем и конденсатором. В идеальных примерах при первоначальном подключении источника энергии (генератора) энергия накапливается в конденсаторе (или дросселе) и после его отключения происходят незатухающие колебания за счет этого обмена.

Напряжения на индуктивности и емкости примерно одинаковы, согласно :

Где X — это Xc емкостное или XL индуктивное сопротивление соответственно.

Цепь, состоящую из индуктивности и емкости, называют колебательным контуром. Его частота вычисляется по формуле:

Период колебаний определяется по формуле Томпсона:

Так как реактивное сопротивление зависит от частоты, то сопротивление индуктивности с ростом частоты увеличивается, а у ёмкости падает. Когда сопротивления равны, то общее сопротивление сильно снижается, что отражено на графике:

Основными характеристиками контура являются добротность (Q) и частота. Если рассмотреть контур в качестве четырехполюсника, то его коэффициент передачи после несложных вычислений сводится к добротности:

А напряжение на выводах цепи увеличивается пропорционально коэффициенту передачи (добротности) контура.

Uк=Uвх*Q

При резонансе напряжений, чем выше добротность, тем больше напряжение на элементах контура будет превышать напряжение подключенного генератора. Напряжение может повышаться в десятки и сотни раз. Это отображено на графике:

Потери мощности в контуре обусловлены только наличием активного сопротивления. Энергия из источника питания берется только для поддержания колебаний.

Коэффициент мощности будет равен:

Эта формула показывает, что потери происходят за счет активной мощности:

S=P/Cosф

Резонанс токов наблюдается в цепях, где индуктивность и емкость соединены параллельно.

Явление заключается в протекании токов большой величины между конденсатором и катушкой, при нулевом токе в неразветвленной части цепи. Это объясняется тем, что при достижении резонансной частоты общее сопротивление Z возрастает. Или простым языком звучит так – в точке резонанса достигается максимальное общее значение сопротивления Z, после чего одно из сопротивлений увеличивается, а другое снижается в зависимости от того растет или снижается частота. Это наглядно отображено на графике:

В общем, всё аналогично предыдущему явлению, условия возникновения резонанса токов следующие:

Частота питания аналогична резонансной у контура.
Проводимости у индуктивности и ёмкости по переменному току равны BL=Bc, B=1/X.

Применение на практике

Рассмотрим, какая польза и вред резонанса токов и напряжений. Наибольшую пользу явления резонанса принесли в радиопередающей аппаратуре. Простыми словами, а схеме приемника установлены катушка и конденсатор, подключенные к антенне. С помощью изменения индуктивности (например, перемещая сердечник) или величины емкости (например, воздушным переменным конденсатором) вы настраиваете резонансную частоту. В результате чего напряжение на катушке повышается и приемник ловит определенную радиоволну.

Вред эти явления могут на нести в электротехнике, например, на кабельных линиях. Кабель представляет собой распределенную по длине индуктивность и емкость, если на длинную линию подать напряжение в режиме холостого хода (когда на противоположном от источника питания конце кабеля нагрузка не подключена). Поэтому есть опасность того, что произойдет пробой изоляции, во избежание этого подключается нагрузочный балласт. Также аналогичная ситуация может привести к выходу из строя электронных компонентов, измерительных приборов и другого электрооборудования – это опасные последствия возникновения этого явления. (1/2)

Как устранить явление?

Увеличив активное сопротивление в цепи или изменив частоту.

Теперь вы знаете, что такое резонанс токов и напряжений, каковы условия его возникновения и варианты применения на практике. Для закрепления материала рекомендуем просмотреть полезное видео

Резонансом называют режим, когда в цепи, содержащей индуктивности и емкости, ток совпадает по фазе с напряжением . Входные реактивные сопротивление и проводимость равны нулю:
x = ImZ = 0 и B = ImY = 0. Цепь носит чисто активный характер:
Z = R ; сдвиг фаз отсутствует (j = 0).

Напряжения на индуктивности и емкости в этом режиме равны по величине и, находясь в противофазе, компенсируют друг друга. Все приложенное к цепи напряжение приходится на ее активное сопротивление (рис. 2.42, а ).

Рис. 2.42. Векторные диаграммы при резонансе напряжений (а) и токов (б)

Напряжения на индуктивности и емкости могут значительно превышать напряжения на входе цепи. Их отношение, называемое добротностью контура Q , определяется величинами индуктивного (или емкостного) и активного сопротивлений

Добротность показывает, во сколько раз напряжения на индуктивности и емкости при резонансе превышают напряжение, приложенное к цепи. В радиотехнических цепях она может достигать нескольких сотен единиц.

Из условия (2.33) следует, что резонанса можно достичь, изменяя любой из параметров – частоту, индуктивность, емкость. При этом меняются реактивное и полное сопротивления цепи, а вследствие этого – ток, напряжение на элементах и сдвиг фаз. Не приводя анализа формул, показываем графические зависимости некоторых из этих величин от емкости (рис. 2.43). Емкость , при которой наступает резонанс, можно определить из формулы (2.33):

Если, например, индуктивность контура L = 0,2 Гн, то при частоте 50 Гц, резонанс наступит при емкости

Рис. 2.43. Зависимости параметров режима от емкости

Аналогичные рассуждения можно провести и для цепи, состоящей из параллельно соединенных R , L и C (рис. 2.31, а ). Векторная диаграмма ее резонансного режима приведена на рис. 2.42, б .

Рассмотрим теперь более сложную цепь с двумя параллельными ветвями, содержащими активные и реактивные сопротивления
(рис. 2.44, а ).

Рис. 2.44. Разветвленная цепь (а ) и ее эквивалентная схема (б )

Для нее условием резонанса является равенство нулю ее реактивной проводимости: ImY = 0 . Это равенство означает, что мы должны мнимую часть комплексного выражения Y приравнять к нулю.

Определяем комплексную проводимость цепи. Она равна сумме комплексных проводимостей ветвей:

Приравнивая к нулю выражение, стоящее в круглых скобках, получаем:

или . (2.34)

Левая и правая части последнего выражения представляют собой не что иное, как реактивные проводимости первой и второй ветвей B 1 и B 2 . Заменяя схему на рис. 2.44, а эквивалентной (рис. 2.44, б ), параметры которой вычисляем по формуле (2. 31), и используя условие резонанса(B = B 1 – B 2 = 0), снова приходим к выражению (2.34).

Схеме на рис. 2.44, б соответствует векторная диаграмма, приведенная на рис. 2.45.

Резонанс в разветвленной цепи называется резонансом токов . Реактивные составляющие токов параллельных ветвей противоположны по фазе, равны по величине и компенсируют друг друга, а сумма активных составляющих токов ветвей дает общий ток.

Рис. 2.45. Векторная диаграмма резонансного режима разветвленной цепи

Пример 2.23. Считая R 2 и x 3 известными, определить величину x 1 , при которой в цепи наступит резонанс напряжений (рис. 2.46, а ). Для резонансного режима построить векторную диаграмму.

САМАРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ

Электрические цепи переменного тока Явление резонанса.

Выполнил:

Антропов А. И.

Проверила:

Бородина А. В.

Самара 2009

Электрические цепи переменного тока. Явление резонанса

Явление резонанса относится к наиболее важным с практической точки зрения свойствам электрических цепей. Оно заключается в том, что электрическая цепь, имеющая реактивные элементы обладает чисто резистивным сопротивлением .

Общее условие резонанса для любого двухполюсника можно сформулировать в виде Im[Z ]=0 или Im[Y ]=0, где Z и Y комплексное сопротивление и проводимость двухполюсника. Следовательно, режим резонанса полностью определяется параметрами электрической цепи и не зависит от внешнего воздействия на нее со стороны источников электрической энергии.

Для определения условий возникновения режима резонанса в электрической цепи нужно:

· найти ее комплексное сопротивление или проводимость;

· выделить мнимую часть и приравнять нулю.

Все параметры электрической цепи, входящие в полученное уравнение, будут в той или иной степени влиять на характеристики явления резонанса.

Уравнение Im[Z ]=0 может иметь несколько корней решения относительно какого-либо параметра. Это означает возможность возникновения резонанса при всех значениях этого параметра, соответствующих корням решения и имеющих физический смысл.

В электрических цепях резонанс может рассматриваться в задачах:

· анализа этого явления при вариации параметров цепи;

· синтеза цепи с заданными резонансными параметрами.

Электрические цепи с большим количеством реактивных элементов и связей могут представлять значительную сложность при анализе и почти никогда не используются для синтеза цепей с заданными свойствами, т.к. для них не всегда возможно получить однозначное решение. Поэтому на практике исследуются простейшие двухполюсники и с их помощью создаются сложные цепи с требуемыми параметрами.

Сдвиг фаз между током и напряжением. Понятие двухполюсника

Простейшими электрическими цепями, в которых может возникать резонанс, являются последовательное и параллельное соединения резистора, индуктивности и емкости. Соответственно схеме соединения, эти цепи называются последовательным и параллельным резонансным контуром . Наличие резистивного сопротивления в резонансном контуре по определению не является обязательным и оно может отсутствовать как отдельный элемент (резистор). Однако при анализе резистивным сопротивлением следует учитывать по крайней мере сопротивления проводников.

Последовательный резонансный контур представлен на рис. 1 а). Комплексное сопротивление цепи равно

Условием резонанса из выражения (1) будет

Таким образом, резонанс в цепи наступает независимо от значения резистивного сопротивления R когда индуктивное сопротивление x L = wL равно емкостному x C = 1/(wC ) . Как следует из выражения (2), это состояние может быть получено вариацией любого их трех параметров — L , C и w , а также любой их комбинацией. При вариации одного из параметров условие резонанса можно представить в виде

Все величины, входящие в выражение (3) положительны, поэтому эти условия выполнимы всегда, т.е. резонанс в последовательном контуре можно создать

· изменением индуктивности L при постоянных значениях C и w ;

· изменением емкости C при постоянных значениях L и w ;

· изменением частоты w при постоянных значениях L и C .

Наибольший интерес для практики представляет вариация частоты. Поэтому рассмотрим процессы в контуре при этом условии.

При изменении частоты резистивная составляющая комплексного сопротивления цепи Z остается постоянной, а реактивная изменяется. Поэтому конец вектора Z на комплексной плоскости перемещается по прямой параллельной мнимой оси и проходящей через точку R вещественной оси (рис. 1 б)). В режиме резонанса мнимая составляющая Z равна нулю и Z = Z = Z min = R , j = 0 , т.е. полное сопротивление при резонансе соответствует минимальному значению .

Индуктивное и емкостное сопротивления изменяются в зависимости от частоты так, как показано на рис. 2. При частоте стремящейся к нулю x C ®µ , x L ® 0 , и j® — 90° (рис. 1 б)). При бесконечном увеличении частоты — x L ®µ , x C ® 0 , а j® 90° . Равенство сопротивлений x L и x C наступает в режиме резонанса при частоте w 0 .

Рассмотрим теперь падения напряжения на элементах контура. Пусть резонансный контур питается от источника, обладающего свойствами источника ЭДС, т.е. напряжение на входе контура u = const, и пусть ток в контуре равен i =I m sinwt . Падение напряжения на входе уравновешивается суммой напряжений на элементах

Переходя от амплитудных значений к действующим, из выражения (4) получим напряжения на отдельных элементах контура

А при резонансной частоте

величина, имеющая размерность сопротивления и называемая волновым или характеристическим сопротивлением контура.

Следовательно, при резонансе

· напряжение на резисторе равно напряжению на входе контура;

· напряжения на реактивных элементах одинаковы и пропорциональны волновому сопротивлению контура;

· соотношение напряжения на входе контура (на резисторе) и напряжений на реактивных элементах определяется соотношением резистивного и волнового сопротивлений.

Отношение волнового сопротивления к резистивному r /R = Q , называется добротностью контура , а величина обратная D =1/Q — затуханием . Таким образом, добротность числено равна отношению напряжения на реактивном элементе контура к напряжению на резисторе или на входе в режиме резонанса. Добротность может составлять несколько десятков единиц и во столько же раз напряжение на реактивных элементах контура будет превышать входное. Поэтому резонанс в последовательном контуре называется резонансом напряжений .

Рассмотрим зависимости напряжений и тока в контуре от частоты. Для возможности обобщенного анализа перейдем в выражениях (5) к относительным единицам, разделив их на входное напряжение при резонансе

U =RI 0

где i =I /I 0 , u k =U k /U , v = w /w 0 — соответственно ток, напряжение и частота в относительных единицах, в которых в качестве базовых величин приняты ток I 0 , напряжение на входе U и частота w 0 в режиме резонанса.

Абсолютный и относительный ток в контуре равен

Из выражений (7) и (8) следует, что характер изменения всех величин при изменении частоты зависит только от добротности контура. Графическое представление их при Q =2 приведено на рис. 3 в логарифмическом (а) и линейном (б) масштабах оси абсцисс.

На рис. 3 кривые A (v), B (v) и C (v) соответствуют напряжению на индуктивности, емкости и резисторе или току в контуре. Кривые A (v)=u L (v) и B (v)=u C (v) имеют максимумы, напряжения в которых определяются выражением

, (9)

а относительные частоты максимумов равны

(10)

При увеличении добротности Q ®µA max = B max ®Q , а v 1 ®1.0 и v 2 ®1.0.

С уменьшением добротности максимумы кривых u L (v) и u С (v) смещаются от резонансной частоты, а при Q 2

Напряжение на резисторе и ток в контуре имеют при резонансной частоте максимум равный 1,0. Если на оси ординат отложить абсолютные значения тока или напряжения на резисторе, то для различных значений добротности они будут иметь вид, показанный на рис. 4. В целом они дают представление о характере изменения величин, но удобнее делать сопоставление в относительных единицах.

На рис. 5 представлены кривые рис. 4 в относительных единицах. Здесь видно, что увеличение добротности влияет на скорость изменения тока при изменении частоты.

Можно показать, что разность относительных частот, соответствующих значениям относительного тока

, равна затуханию контура D =1/Q =v 2 -v 1 .

Перейдем теперь к анализу зависимости фазового сдвига между током и напряжением на входе контура от частоты. Из выражения (1) угол j равен

При протекании электроэнергии по элементам электрической схемы возможно возникновение различных режимов; совпадение по фазе вектора токов и напряжений в цепях с емкостью и индуктивностью называют явлением электрического резонанса.

При нем исчезает реактивный характер нагрузки и выполняются все соотношения для активного сопротивления , когда Х=I m ∙Z, В= I m ∙Y, R=Z, φ=0 .

В электротехнике при последовательном соединении элементов индуктивной и емкостной нагрузки возможен резонанс напряжений. Рассмотрим его проявление для простейшей цепи с последовательно образованным контуром, когда резонанс проявится при случае Х=Х L -Х C =0 . Выразим Х L =Х C , а после подстановки их выражений получим соотношение:

φL=1/φC .

У индуктивности и емкости для рассматриваемого случая вектора напряжений находятся в противоположных фазах, уравновешивают друг друга. При этом, все напряжение, которое приложено на электрическую схему, воздействует на активное сопротивление. Диаграмма векторов представлена следующим видом:

Диаграмма демонстрирует, что величины напряжений на реактивных нагрузках при резонансе могут весьма значительно превышать входное напряжение схемы. Для оценки этого параметра введено термин добротности контура Q .

Q=U L /U=U C /U=x Lрез /R=x Cрез /R .

Она зависит от частоты, величины емкости или индуктивности. Изменяя любой из перечисленных параметров можно регулировать величину добротности. В радиотехнике она нашла широкое применение, где ее величина доводится до больших значений в несколько сотен единиц во время резонанса напряжений.

При этом возникают изменения реактивного и полного сопротивлений в схеме, следствием чего проявляются изменения токов, напряжений, углов сдвига фаз на различных приемниках электроэнергии.

Зависимость параметров электрической схемы при изменении значений емкости С O для создания резонанса демонстрирует график:

Величину С O выражает соотношение: С O =1/(ω2L) .

Вполне допустимо рассмотреть случай параллельного соединения нагрузок R, L и C . Для него будет справедлива векторная диаграмма вида:

На практике приходится иметь дело с более сложными соединениями элементов. Для примера можно взять разветвленную схему с 2-мя параллельными ветвями, включающими как активные, так и реактивные нагрузки.

У данной цепи резонанс наступает при равенстве нулю составляющей ее реактивной проводимости, когда I m ∙Y=0 . То есть, при рассматриваемом случае мнимая часть у комплексного выражения Y приравнена к нулю.

Найдем значение комплексной проводимости для схемы, которая выразится суммой всех проводимостей в ветвях.

Y=Y1+Y2=1/Z1+1/Z2=1/(R1+jx1)+1/(R2-jx2)=(R1-jx1)/(R 2 1+x 2 1)+(R2+jx2)/(R 2 2+x 2 2)=
R1/(R 2 1+x 2 1)+R2/(R 2 2+x 2 2)-j(x1/(R 2 1+x 2 1)-x2/(R 2 2+x 2 2)) .

Выражение, выделенное круглыми скобками, приравниваем к нулю и получаем соотношение:

x1/(R 2 1+x 2 1)=x2/(R 2 2+x 2 2) .

Данное соотношение может быть представлено развернутым видом:

φL/(R 2 1+(φL) 2)=(1/φC)/(R 2 2+(1/φC) 2) .

Мы получили выражение, не похожее на реактивные проводимости для 1-й и 2-й ветвей цепи с В1 и В2 . Сделаем замену рассматриваемой нами схемы на эквивалентную. У нее значения параметров определены расчетом для условий резонанса, когда В=В1-В2=0 :

Таким способом мы пришли к искомому выражению. Векторная диаграмма для полученной схемы разветвленной цепи может быть выражена так:

В разветвленных схемах возникает явление резонанса токов, когда реактивные части токов для противоположных ветвей направлены в противоположных направлениях и уравновешены между собой по величине. Общий ток в схеме формируется суммой составляющих активных токов в ветвях.

В чем заключается явление резонанса напряжений и при каком условии оно возникает? Перечислите

скільки нікелю виділиться на катоді при електролізі за 1 годину,якщо сила струму дорівнює 10А

Вивчення умови рівноваги важеляМета роботи: перевірити, при якому спів-відношенні сил і іх плечей важіль перебуваєв рівновазі. Перевірити правило моме … нтів.Прилади і матеріали: важіль на шта-тиві, набір важків, динамометр, лінійка зміліметровими поділками.Хід роботи1. Зрівноважте важіль, обертаючи гай-ки на його кінцях так, щоб він розмістив-ся горизонтально (мал. 284).2. Підвісьте два важки на лівій частиніважеля на відстані 10 см від осі обертання.Дослідом установіть, на якій відстані справавід осі обертання треба підвісити: 1) 1 ва-жок; 2) 2 важки; 3) 3 важки; 4) 4 важки.3. Вважаючи, що кожний тягарець ва-жить 1 H, запишіть дані та результативимірювань у таблицю.Мал.:40302010NoдослідуF, Hd, мF, Hd,, мFF,12344. Обчисліть відношення сил і відношення плечей дляідів. Зробіть висновки.5. Розрахуйте абсолютне значення моментів сил м, і Мравило моментів сил. Зробіть висновки.6. Підвісьте три важки справа від осі обертання важеля надопомогою динамометра визначте силу, яку треба прикласм від осі обертання справа від важків, щоб важіль бувпрямлені в цьому випадку сили, що діють на важіль? ВиконОбчисліть відношення значень сил і плечей для цього Еь висновки.Срочно

під час посріблення деталі за допомогою електролізу було витрачено 5.031 грам срібла. який заряд пройшов через електроліз . електрохімічний еквівалент … срібла 1.18×10в -6 степені

Автомобиль движется со скоростью 54км/ч по горизонтальной дороге. На какой угол наклонится автомобиль при резком торможении и каким будет его тормозно … й путь? Коэффициент трения скольжения 0,8. Центр масс автомобиля О расположен на равном расстоянии от передних и задних колес на высоте 50см над поверхностью земли. Расстояние между осями автомобиля 2м. Упругость всех пружин подвески одинакова и такова, что у неподвижного автомобиля на горизонтальной площадке их прогиб равен 10см, торможение всеми 4 колесами

В электронно лучевой трубке сила тока в электронном пучке i=600 мка, ускоряющее напряжение u= 10 кв. Определить силу давления f электронного пучка на … экран трубки, считая, что электроны поглощается экраном

найти фокусное расстояние собирающий линзы если экран расположен на расстоянии 80см а предмет расположен на расстоянии 25см

помогитеее выполнить задание

150Н *0,15/0.03=?решите пожалуйста

Знайти потужність яку розвиває двигун автомобіля маючи силу 3kH і швидкість 20м/с

як виконати дію додаваня за допомогою електровимірювальних приладів і реостатів для паралельного з’єднаня

Видеоурок: Резонанс в цепях переменного тока

Стенограмма видеозаписи

В этом видео мы узнаем о явлении резонанса в цепях переменного тока. Резонанс возникает, потому что оба емкостное и индуктивное реактивные сопротивления зависят от частоты переменного напряжение и ток. Начнем с обзора реактивного сопротивления, который обобщает противодействующее току качество сопротивления для резисторов до также включать катушки индуктивности и конденсаторы.

Резистор имеет особые свойства что его противостояние току зафиксировано. То есть сопротивление резистора, обычно обозначается символом 𝑅, не зависит от силы, направления или частоты напряжения в цепи. То же самое не относится к индукторам. и конденсаторы в цепях переменного тока. Хотя емкость 𝐶 и индуктивность 𝐿 не зависит от напряжения, сопротивления катушки индуктивности и конденсатора к току действительно зависит от частоты напряжения в цепи.

Для конденсатора более заряженный чем больше он противостоит току. Чем быстрее электродвижущая сила меняет направление, то есть чем выше его частота, тем меньше конденсатор заряжает перед повторной разрядкой. Таким образом, на более высоких частотах конденсатор имеет меньшее реактивное сопротивление. А индуктор, с другой стороны, создает магнитное поле. И чем сильнее магнитное поле тем меньше сопротивление индуктивности току.Однако это магнитное поле принимает время наращивать. Таким образом, чем выше частота электродвижущая сила, тем слабее будет магнитное поле перед изменением направления. В результате индуктивный реактивное сопротивление будет больше на более высоких частотах.

По формулам, емкостная реактивное сопротивление делится на угловую частоту времени напряжения и тока. емкость. Индуктивное реактивное сопротивление — это угловая частота напряжения и тока, умноженная на индуктивность.Обратите внимание, что обе эти формулы дают правильное качественное соотношение между реактивным сопротивлением и частотой. Емкостное реактивное сопротивление обратно пропорционально частоте, в то время как индуктивное реактивное сопротивление прямо пропорционально пропорционально частоте.

Значит, на более высоких частотах индуктивное реактивное сопротивление больше, а емкостное реактивное сопротивление меньше. , угловая частота, равна определяется как два 𝜋 радиана, умноженные на обычную частоту, или циклов в секунду.Мы используем 𝜔, потому что это помогает нам запишите эти формулы, просто не перенося множители двух 𝜋.

Последнее, что нам нужно вспомнить, это что для цепи с индуктивной и емкостной составляющими общая реактивное сопротивление — это не просто сумма индуктивного и емкостного сопротивлений. Это потому, что индукторы и конденсаторы также вносят фазовый сдвиг между током и ЭДС.Конденсаторы заставляют ток покидают ЭДС, в то время как катушки индуктивности заставляют ток отставать от ЭДС. Чистый эффект этих разных фазовые сдвиги заключаются в том, что правильная комбинация для полного реактивного сопротивления — это разница между двумя реактивными сопротивлениями индуктивное реактивное сопротивление минус емкостное реактивное сопротивление.

Резонанс возможен в цепь переменного тока именно потому, что полное реактивное сопротивление — это разница вместо суммы.Итак, давайте посмотрим, в чем разница между индуктивным и емкостным сопротивлениями может привести к резонансу. Рассмотрим простую схему приводится в действие источником переменного напряжения с подключенными катушкой индуктивности и конденсатором. ряд. Хотя мы ограничим наше обсуждение к последовательным цепям те же принципы применимы и к параллельным цепям.

В любом случае полное реактивное сопротивление в схема представляет собой индуктивное реактивное сопротивление минус емкостное реактивное сопротивление.Помните, что индуктивная и Емкостные реактивные сопротивления зависят от частоты противоположным образом. Итак, если мы изменим частоту от, скажем, от очень низкого значения до очень высокого, емкостное реактивное сопротивление изменится с от очень большого до очень маленького. Но индуктивное реактивное сопротивление будет изменение от очень маленького до очень большого. Это говорит о том, что может быть некоторая частота в середине нашего диапазона, для которой индуктивное реактивное сопротивление и емкостные реактивные сопротивления равны.

Если индуктивная и емкостная реактивные сопротивления равны, тогда их разность, полное реактивное сопротивление, равно нулю. Итак, индуктор и конденсатор Комбинация не обеспечивает противодействия току на этой частоте. Чтобы найти особую частоту, мы начнем с приравнивания частотно-зависимых формул для индуктивных и емкостное реактивное сопротивление. Чтобы найти 𝜔, мы умножим обе стороны на 𝜔 над 𝐿. Слева из наша формула отменяет знак в знаменателе.А справа из нашей формулы исключает в числителе. Это оставляет нам 𝜔 в квадрате равно единице, деленной на.

Если мы сейчас продолжим и возьмем квадратный корень из обеих частей этого равенства, мы получаем, что угловая частота в зависимости от полное реактивное сопротивление равно нулю, равно единице, деленной на квадратный корень из индуктивность катушки индуктивности умножена на емкость конденсатора.Мы часто пишем 𝜔 с нижним индексом нулевого значения, когда речь идет именно об этой частоте.

Явление индуктивного и емкостные реактивные сопротивления, которые точно компенсируются на определенной частоте, известны как резонанс. И ноль, частота на который возникает резонанс, называется резонансной частотой. Потому что при резонансе общая реактивное сопротивление равно нулю, индуктор и конденсатор в нашей цепи ведут себя как проводящие провода.Но это означает, что при резонансе идеальная схема, которую мы нарисовали, фактически представляет собой короткое замыкание. Если бы это была настоящая схема, короткое замыкание может вызвать серьезное повреждение различных компонентов и переменного тока. источник напряжения. Однако если бы это был настоящий цепи, будет некоторое сопротивление, присущее компонентам и провода.

Итак, давайте смоделируем это в реальной жизни ситуация с идеальной схемой, состоящей из катушки индуктивности, конденсатора, а также резистор.Здесь у нас есть схема с резистор, катушка индуктивности и конденсатор, включенные последовательно, с приводом от переменного напряжения. источник. Поскольку в этой схеме есть резистивные и реактивные элементы, полное сопротивление току определяется комбинация сопротивления и реактивного сопротивления, известная как импеданс. Размер импеданса равен квадратный корень из суммы квадратов сопротивления и полного реактивного сопротивления. Мы должны использовать это специальное комбинация, потому что реактивные компоненты изменяют фазу между ЭДС и током, а резистивные компоненты — нет.

Хорошо, давайте посмотрим, что будет с импеданс, когда мы возбуждаем цепь на резонансной частоте. Напомним, что при резонансе индуктивное и емкостное реактивные сопротивления равны. Таким образом, полное реактивное сопротивление равно нулю. Таким образом, полное сопротивление резонанса равно квадратный корень из в квадрате плюс ноль, который является квадратным корнем из в квадрате, что просто 𝑅. Итак, что касается резонанса, импеданс схема идентично сопротивлению.

Это говорит нам о нескольких важных вещи. Во-первых, поскольку общая реактивная вклад в импеданс равен нулю при резонансе, фазовый сдвиг отсутствует между током и ЭДС. Во-вторых, для генерала цепь переменного тока, закон Ома говорит нам, что напряжение равно току раз импеданс. При резонансе это становится напряжением равно току, умноженному на сопротивление, что является просто законом Ома для чисто резистивных цепи переменного тока.

Кроме того, оглядываясь на наши формула для величины импеданса, квадрат полного реактивного сопротивления всегда положителен, если только это ноль. Итак, о резонансе, когда всего реактивное сопротивление равно нулю, полное сопротивление минимизировано. Оглядываясь назад на закон Ома, если пиковое напряжение не меняется, затем по мере уменьшения сопротивления пиковый ток становится больше. Таким образом, минимальный импеданс подразумевает максимальный пиковый ток.

Теперь, когда мы увидели, что происходит когда мы запускаем цепь на резонансной частоте, давайте посмотрим, что происходит, когда мы управлять схемой на частотах, отличных от резонансной.Чтобы увидеть, как ток ведет себя на частот, отличных от резонансной, мы используем график с угловой частотой по горизонтальной оси и относительная амплитуда тока по вертикали ось. Относительная амплитуда для ток на определенной угловой частоте находится путем деления пикового тока на эту частоту пиковым током на резонансной частоте.

Итак, по определению, относительный амплитуда тока на резонансной частоте равна единице.Если на другой частоте ток имел пиковое значение, равное половине значения тока в резонансном частота, то относительная амплитуда тока на этой частоте будет одна половина. Использование относительного вместо абсолютного амплитуда позволяет этому обсуждению быть очень общим, поэтому оно применимо к широкому спектру резонансных явлений.

Возвращаясь, в частности, к нашему электронные схемы на частотах, увеличивающихся по сравнению с резонансными Частота индуктивного сопротивления все больше и больше.Итак, относительная амплитуда ток все меньше и меньше. Аналогично на частотах все меньше по сравнению с резонансной частотой, емкостное реактивное сопротивление равно все больше и больше. Итак, снова относительный амплитуда тока все меньше и меньше.

Этот график, который мы нарисовали на самом деле имеет форму, типичную для самых разных резонансных систем. Одна из самых ярких особенностей этого графика — острый пик на резонансной частоте.Мы говорим, что пик резкий потому что он намного уже, чем высокий. Физически это означает, что ток в нашей цепи будет намного больше при работе на резонансной частоте чем при работе на частотах не меньше или больше резонансных частота.

Для многих приложений, от измерительное оборудование для радиосвязи, полезно определять резкость резонансного пика.Это потому, что чем резче резидентный пик, тем более избирательно наша система реагирует на конкретный частота. То есть, чем острее пик, чем больше наши системы реагируют на изменения, тем меньше отклонения от резонансного частота.

Число, которое мы используем для количественной оценки резкость пика называется-или добротностью резонанса. Для последовательных цепей, подобных типу мы обсуждали, 𝑄-фактор равен угловой частоте резонанс, умноженный на индуктивность катушки индуктивности, деленную на сопротивление резистор.Есть еще несколько способов, которыми мы может определить 𝑄-фактор. Независимо от того, как мы это определяем, большие 𝑄-факторы соответствуют графикам с более резкими пиками вокруг резонансная частота. И меньшие 𝑄-факторы соответствуют к графикам, которые более широко разбросаны вокруг резонансной частоты.

Фактически оказывается, что ширина пика примерно на половине максимального значения примерно соответствует резонансной частоту, деленную на добротность.Это довольно хороший способ определить 𝑄, поскольку, просто взглянув на график, мы можем определить ширину пик, а также его частота, которая является резонансной частотой. Кроме того, если мы знаем любые три величин, фигурирующих в нашей полной формуле, мы можем использовать эту формулу, чтобы найти четвертый.

Хорошо, теперь, когда мы узнали насчет резонансной частоты и 𝑄-фактора, давайте поработаем Примеры.

Цепь состоит из резистора, конденсатор и катушка индуктивности, все из которых включены последовательно. Источник переменного напряжения подключен к цепи, и генерируется переменный ток. Как резонансная частота схему изменить, если индуктивность индуктора увеличится? (а) Резонансная частота уменьшается. (б) Резонансная частота увеличивается. (c) Резонансная частота не менять.

Нам задают вопрос о резонансная частота цепи переменного тока. В частности, для последовательной цепи с резистором, конденсатором и катушкой индуктивности вопрос спрашивает нас, что произойдет если индуктивность индуктора увеличена. Вот схема нашего схема. У нас есть переменное напряжение источник, резистор сопротивления 𝑅, индуктор индуктивности и конденсатор емкости 𝐶.Мы будем использовать символ 𝜔 для угловая частота источника напряжения.

Напомним, что резонанс произойдет в эта схема, когда разница между индуктивным и емкостным сопротивлениями, что , полное реактивное сопротивление равно нулю. Другими словами, резонанс — это когда индуктивное и емкостное сопротивления равны. У нас также есть формулы, которые связать угловую частоту с реактивным сопротивлением, поскольку индуктивное реактивное сопротивление — это угловая частота умножить на индуктивность и емкостное реактивное сопротивление, разделенное на угловую частоту, умноженное на емкость.Если мы приравняем эти выражения, как будет истинным на резонансной частоте, мы получим, что ничто равно единице делится на ноль, где ноль — резонансная угловая частота.

Если решить это равенство относительно 𝜔 ноль, мы находим, что резонансная угловая частота равна единице, деленной на корень квадратный из индуктивности индуктора, умноженной на емкость конденсатор. Эта формула связывает резонансные частота к индуктивности, поэтому давайте ответим на наш вопрос.По мере увеличения индуктивности квадратный корень из индуктивности, умноженной на емкость, увеличивается. Итак, знаменатель нашей дроби становится больше, что означает, что значение общей доли становится больше меньше. Но значение этой дроби равно просто резонансная частота. Так как индуктивность индуктор увеличивается, резонансная частота уменьшается. Интересно, что из нашего формула, что резонансная частота также уменьшится, если мы увеличим емкость конденсатора.Но если мы изменим сопротивление резистора, резонансная частота не изменится.

Давайте посмотрим на другой пример, имеет дело с резонансом более количественно.

Какая резонансная частота схема, показанная на схеме?

Схема состоит из источник переменного напряжения, подключенный к последовательной комбинации резистора 35 Ом, Индуктор на 7,5 Генри и конденсатор на 350 мкФ.И нас просят найти резонансная частота этого контура. Напомним, что индуктивное сопротивление в цепи — это угловая частота источника напряжения, умноженная на индуктивность. И емкостное реактивное сопротивление равно единице. деленное на угловую частоту источника напряжения, умноженную на емкость. При резонансе эти два реактивных сопротивления равны.

Если называть резонансный угловой частота 𝜔 ноль, тогда мы имеем, что 𝜔 ноль 𝐿 равно единице больше 𝜔 ноль 𝐶, которую мы можем решить напрасно.Когда мы решаем это уравнение относительно 𝜔 ноль, мы находим, что резонансная угловая частота равна единице, деленной на корень квадратный из индуктивности индуктора, умноженной на емкость конденсатор. Теперь это формула углового частота, но мы ищем только обычную частоту. Итак, нам нужно использовать отношение эта угловая частота в два раза больше обычной частоты.

Хорошо, давайте подключим наш определение угловой частоты в наше уравнение для резонансного углового частота.У нас есть в два раза 𝜋 раза больше резонансная частота равна единице, деленной на квадратный корень из индуктивности раз больше емкости. Чтобы воплотить это выражение в Окончательный вид нам нужен, просто делим обе стороны на две. Слева две делится на два 𝜋 равно одному, и мы просто остаемся с 𝑓 ничего. В правой части два 𝜋 просто становится частью знаменателя нашей дроби. Остается последний формула нам нужна.Резонансная частота равна единице делится на две, умноженные на квадратный корень из индуктивности, в генри, умноженный на емкость, в фарадах.

Итак, теперь нам просто нужно подключить значения. У нас есть индуктивность в Генри. Это 7,5 генри. Однако наша емкость дается в микрофарадах вместо фарадов. Чтобы преобразовать в фарады, вспомните, что есть один миллион микрофарад на фарад. Другими словами, один микрофарад — это эквивалентно 10 отрицательным шестым фарадам.Так как у нас 350 мкФ, наши Емкость эквивалентна 350 умноженным на 10 отрицательным шестым фарадам.

Подключение индуктивности и емкость в нашу формулу для резонансной частоты, это дает нам единицу, деленную на два 𝜋 умножить на квадратный корень из 350 умножить на 10 до отрицательной шестой фарад умноженной на 7,5 Генри. Оказывается, квадратный корень Один фарад, умноженный на один генри, равен одной секунде. Итак, мы можем переписать знаменатель с единицами измерения секунд.

Теперь, деленное на секунды — это единица герц, которая используется для частоты. Итак, теперь у нас есть выражение для резонансная частота. Это количество, умноженное на единицу герц, что является правильной единицей измерения частоты. Итак, теперь все, что нам нужно сделать, это оцените это число с помощью калькулятора. Когда мы делаем эту оценку, мы находим что все числовое выражение примерно равно 3,1. Итак, резонансная частота этого цепь 3.1 герц. Стоит отметить, что 35-Ω резистор не играл роли в нашем расчете резонансной частоты.

Хорошо, теперь, когда мы увидели примеры, давайте рассмотрим некоторые ключевые моменты, которые мы усвоили в этом уроке. В этом видео мы рассмотрели цепь, состоящая из источника переменного напряжения, возбуждающего резистор, катушки индуктивности, и конденсатор, все подключенные последовательно. Поскольку индуктивные и емкостные реактивное сопротивление зависит от частоты источника переменного напряжения, мы видели что можно было найти частоту, на которой полное реактивное сопротивление, индуктивное минус емкостное реактивное сопротивление равно нулю.

Приравнивая частотно-зависимый формулы для индуктивного и емкостного сопротивлений, мы смогли найти, что резонансная угловая частота равна единице, деленной на квадратный корень из индуктивность катушки индуктивности умножена на емкость конденсатора. Когда частота напряжения равна резонансной частоте, чистому влиянию катушек индуктивности и конденсаторы не должны препятствовать току в цепи.Это означает, что единственная оппозиция к току исходит от резистора, и поэтому импеданс идентичен сопротивление. Это тоже минимально возможный значение для импеданса, потому что вне резонанса, реактивный вклад в импеданс больше нуля. Соответственно тогда по закону Ома если импеданс минимален, то амплитуда тока максимальна.

Наконец, мы рассмотрели, как относительная амплитуда тока зависит от угловой частоты.Мы видели, что график с относительной амплитуда по вертикальной оси и угловая частота по горизонтальной оси показывает резкий пик на резонансной частоте. Это соответствует тому же величина управляющего напряжения, приводящая к гораздо большему току в резонансном частота, чем на более низких и более высоких частотах. Для количественной оценки резкости резонансный пик, мы определяем-или добротность как резонансную угловую частоту умноженное на индуктивность катушки индуктивности, деленную на сопротивление резистора.Большие значения 𝑄 соответствуют резонансы с более резкими пиками, а меньшие значения 𝑄 соответствуют резонансам с более широкими пиками.

Наконец, мы заявили, но не доказали что мы можем определить значение 𝑄 по графику, подобному этому, измеряя ширина пика, а также положение пика, которое является резонансной частотой. Итак, зная любые три из значений в нашей формуле для коэффициента качества, мы можем определить значение четвертое количество.

Электрическое сопротивление

— каков эффект резонанса в цепи RLC?

Рассматривайте вашу последовательную цепь LCR как систему driveN, а источник питания — как driveR. \ circ $.\ circ $ не совпадают по фазе друг с другом.
Импеданс индуктора $ \ omega L $ равен сопротивлению конденсатора $ \ frac {1} {\ omega C} $. Таким образом, напряжение питания равно напряжению на резисторе.

В электронике есть много примеров, когда резонанс имеет значение при использовании, и одним из примеров является простой радиоприемник, называемый кристаллическим набором.

Радиосигнал улавливается антенной и подается в настроенную цепь, состоящую из катушки индуктивности и конденсатора, включенных параллельно.
Если частота радиосигнала (driveR) такая же, как резонансная частота настроенной схемы (driveN), напряжение на этой частоте на конденсаторе очень велико, тогда как все другие частотные сигналы, принимаемые антенной, производят очень много меньшие напряжения на конденсаторе и поэтому не обнаруживаются остальной частью схемы, которая преобразует радиосигнал в звук.
Итак, настроенная схема выбирает сигнал от радиостанции, которую вы хотите слушать, и отклоняет все остальные сигналы.Резонансная частота настроенного контура в этом контуре контролируется изменением емкости конденсатора.

Цепи переменного тока серии

RLC | Физика

Цели обучения

К концу этого раздела вы сможете:

Рассчитайте полное сопротивление, фазовый угол, резонансную частоту, мощность, коэффициент мощности, напряжение и / или ток в последовательной цепи RLC.
Нарисуйте принципиальную схему последовательной цепи RLC.
Объясните значение резонансной частоты.

Когда один в цепи переменного тока, все катушки индуктивности, конденсаторы и резисторы препятствуют току. Как они себя ведут, когда все три встречаются вместе? Интересно, что их индивидуальные сопротивления в Ом не складываются просто так. Поскольку катушки индуктивности и конденсаторы ведут себя противоположным образом, они частично полностью нейтрализуют влияние друг друга. На рисунке 1 показана последовательная цепь RLC с источником переменного напряжения, поведение которой является предметом данного раздела.Суть анализа цепи RLC — это частотная зависимость X _L и X _C и их влияние на фазу напряжения по отношению к току (установлено в предыдущий раздел). Это приводит к частотной зависимости схемы с важными «резонансными» характеристиками, которые лежат в основе многих приложений, таких как радиотюнеры.

Рисунок 1. Последовательная цепь RLC с источником переменного напряжения.

Комбинированное влияние сопротивления R , индуктивного реактивного сопротивления X _L и емкостного реактивного сопротивления X _C определяется как полное сопротивление , аналог сопротивления переменного тока в цепи постоянного тока. Ток, напряжение и импеданс в цепи RLC связаны версией закона Ома для переменного тока:

[латекс] {I} _ {0} = \ frac {{V} _ {0}} {Z} \ text {или} {I} _ {\ text {rms}} = \ frac {{V} _ {\ text {rms}}} {Z} \\ [/ latex].

Здесь I ₀ — пиковый ток, V ₀ — пиковое напряжение источника и Z — полное сопротивление цепи. Единицы измерения импеданса — омы, и его влияние на схему такое, как и следовало ожидать: чем больше импеданс, тем меньше ток. Чтобы получить выражение для Z в терминах R , X _L и X _C, мы теперь рассмотрим, как напряжения на различных компонентах связаны с источником. Напряжение.Эти напряжения обозначены как V _R, V _L и V _C на рисунке 1. Для сохранения заряда ток должен быть одинаковым в каждой части цепи. всегда, так что мы можем сказать, что токи в R , L и C равны и синфазны. Но мы знаем из предыдущего раздела, что напряжение на катушке индуктивности В _L опережает ток на одну четверть цикла, напряжение на конденсаторе В _C следует за током на единицу. -четвертый цикл, и напряжение на резисторе В _R точно совпадает по фазе с током.На рисунке 2 показаны эти отношения на одном графике, а также показано общее напряжение в цепи V = V _R + V _L + V _C, где все четыре напряжения — мгновенные значения. Согласно правилу петли Кирхгофа, полное напряжение вокруг цепи В, также является напряжением источника. Из рисунка 2 видно, что в то время как V _R находится в фазе с током, V _L идет под углом 90º, а V _C следует под углом 90º.Таким образом, V _L и V _C сдвинуты по фазе на 180 ° (от пика до впадины) и имеют тенденцию к аннулированию, хотя и не полностью, если они не имеют одинаковой величины. Поскольку пиковые напряжения не выровнены (не совпадают по фазе), пиковое напряжение V ₀ источника не равно сумме пиковых напряжений на R , L и C . {2}} \\ [/ latex],

, который является сопротивлением цепи переменного тока серии RLC .Для схем без резистора принять R = 0; для тех, у кого нет индуктора, возьмите X _L = 0; а для тех, у кого нет конденсатора, возьмите X _C = 0.

Рис. 2. На этом графике показаны отношения напряжений в цепи RLC к току. Напряжения на элементах схемы в сумме равняются напряжению источника, которое, как видно, не совпадает по фазе с током.

Пример 1.Расчет импеданса и тока

Последовательная цепь RLC имеет резистор 40,0 Ом, индуктивность 3,00 мГн и конденсатор 5,00 мкФ. (a) Найдите полное сопротивление цепи при 60,0 Гц и 10,0 кГц, отметив, что эти частоты и значения для L и C такие же, как в Примере 1 и Примере 2 из раздела Реактивное, индуктивное и емкостное. (b) Если источник напряжения имеет В _{среднеквадратичное значение} = 120 В, что будет I _{среднеквадратичное значение} на каждой частоте?

Стратегия

Для каждой частоты мы используем [latex] Z = \ sqrt {{R} ^ {2} + \ left ({X} _ {L} — {X} _ {C} \ right) ^ {2}} \ \ [/ latex], чтобы найти импеданс, а затем закон Ома, чтобы найти ток. { 2}} \\ & = & \ sqrt {\ left (40.{2}} \\ & = & 190 \ text {} \ Omega \ text {at} 10.0 \ text {kHz} \ end {array} \\ [/ latex]

Обсуждение для (а)

В обоих случаях результат почти такой же, как и наибольшее значение, а импеданс определенно не является суммой отдельных значений. Ясно, что X _L доминирует на высокой частоте, а X _C доминирует на низкой частоте.

Решение для (b)

Ток I _{среднеквадратичное значение} можно найти, используя версию закона Ома по переменному току в уравнении I _{среднеквадратичное значение} = В _{среднеквадратичное значение}/ Z :

[латекс] {I} _ {\ text {rms}} = \ frac {{V} _ {\ text {rms}}} {Z} = \ frac {120 \ text {V}} {531 \ text { } \ Omega} = 0.226 \ text {A} \\ [/ latex] при 60,0 Гц

Наконец, на частоте 10,0 кГц мы находим

[латекс] {I} _ {\ text {rms}} = \ frac {{V} _ {\ text {rms}}} {Z} = \ frac {120 \ text {V}} {190 \ text { } \ Omega} = 0,633 \ text {A} \\ [/ latex] при 10,0 кГц

Обсуждение для (а)

Ток при 60,0 Гц такой же (до трех цифр), что и для одного конденсатора в примере 2 из раздела «Реактивное сопротивление, индуктивность и емкость». Конденсатор преобладает на низкой частоте. Ток на частоте 10,0 кГц лишь незначительно отличается от тока, обнаруженного для одной катушки индуктивности в Примере 1 из разделов «Реактивное сопротивление, индуктивность и емкость».{2}}} \\ [/ latex]

Реактивные сопротивления изменяются в зависимости от частоты: X _L большое на высоких частотах и X _C большое на низких частотах, как мы видели в трех предыдущих примерах. На некоторой промежуточной частоте f ₀ реактивные сопротивления будут равны и отменены, давая Z = R — это минимальное значение для импеданса и максимальное значение для I _rms результаты .Мы можем получить выражение для f ₀, взяв

X _L = X _C.

Замена определений X _L и X _C,

[латекс] 2 \ pi f_ {0} L = \ frac {1} {2 \ pi f_ {0} C} \\ [/ latex].

Решение этого выражения для f ₀ дает

[латекс] {f} _ {0} = \ frac {1} {2 \ pi \ sqrt {LC}} \\ [/ latex],

, где f ₀ — резонансная частота последовательной цепи RLC .Это также собственная частота , на которой цепь будет колебаться, если не будет управляться источником напряжения. При f ₀ влияние катушки индуктивности и конденсатора компенсируется, так что Z = R и I _{среднеквадратичное значение} является максимальным.

Резонанс в цепях переменного тока аналогичен механическому резонансу, где резонанс определяется как вынужденное колебание — в данном случае вызванное источником напряжения — на собственной частоте системы.Приемник в радиоприемнике представляет собой схему RLC , которая лучше всего колеблется на ее f ₀. Переменный конденсатор часто используется для настройки f ₀, чтобы получить желаемую частоту и отклонить другие. Фиг.3 представляет собой график зависимости тока от частоты, иллюстрирующий резонансный пик в I _{среднеквадратичное значение} при f ₀. Две кривые относятся к двум разным схемам, которые различаются только величиной сопротивления в них.Пик ниже и шире для цепи с более высоким сопротивлением. Таким образом, цепь с более высоким сопротивлением не так сильно резонирует и, например, не будет такой избирательной в радиоприемнике.

Рис. 3. График зависимости тока от частоты для двух последовательных цепей RLC, различающихся только величиной сопротивления. Оба имеют резонанс при f ₀, но для более высокого сопротивления он ниже и шире. Источник управляющего переменного напряжения имеет фиксированную амплитуду В ₀.

Пример 2. Расчет резонансной частоты и тока

Для той же последовательной цепи RLC , имеющей резистор 40,0 Ом, индуктивность 3,00 мГн и конденсатор 5,00 мкФ: (a) Найдите резонансную частоту. (b) Рассчитайте I _{среднеквадратичное значение} при резонансе, если В _{среднеквадратичное значение} равно 120 В.

Стратегия

Резонансная частота находится с помощью выражения в [latex] {f} _ {0} = \ frac {1} {2 \ pi \ sqrt {LC}} \\ [/ latex].{-6} \ text {F} \ right)}} = 1,30 \ text {кГц} \ end {array} \\ [/ latex]

Обсуждение для (а)

Мы видим, что резонансная частота находится между 60,0 Гц и 10,0 кГц, двумя частотами, выбранными в предыдущих примерах. Этого следовало ожидать, поскольку конденсатор преобладает на низкой частоте, а катушка индуктивности — на высокой. Их эффекты такие же на этой промежуточной частоте.

Решение для (b)

Ток определяется законом Ома.В резонансе два реактивных сопротивления равны и компенсируются, так что полное сопротивление равно только сопротивлению. Таким образом,

[латекс] {I} _ {\ text {rms}} = \ frac {{V} _ {\ text {rms}}} {Z} = \ frac {120 \ text {V}} {40.0 \ text { } \ Omega} = 3,00 \ text {A} \\ [/ latex].

Обсуждение для (б)

В резонансе ток больше, чем на более высоких и низких частотах, рассмотренных для той же цепи в предыдущем примере.

Питание в цепях переменного тока серии

RLC

Если ток изменяется с частотой в цепи RLC , то мощность, подаваемая на нее, также зависит от частоты.Но средняя мощность — это не просто ток, умноженный на напряжение, как в чисто резистивных цепях. Как видно на рисунке 2, напряжение и ток в цепи RLC не совпадают по фазе. Существует фазовый угол ϕ между напряжением источника В и током I , который можно найти из

[латекс] \ cos \ varphi = \ frac {R} {Z} \\ [/ latex]

Например, на резонансной частоте или в чисто резистивной цепи Z = R , так что [latex] \ text {cos} \ varphi = 1 \\ [/ latex].Это означает, что ϕ = 0º и что напряжение и ток синфазны, как и ожидалось для резисторов. На других частотах средняя мощность меньше, чем на резонансе. Причина в том, что напряжение и ток не совпадают по фазе, а также потому, что I _{действующее значение} ниже. Тот факт, что напряжение и ток источника не совпадают по фазе, влияет на мощность, подаваемую в цепь. Можно показать, что средняя мощность равна

[латекс] {P} _ {\ text {ave}} = {I} _ {\ text {rms}} {V} _ {\ text {rms}} \ cos \ varphi \\ [/ latex],

Таким образом, cos ϕ называется коэффициентом мощности , который может находиться в диапазоне от 0 до 1.Например, при разработке эффективного двигателя желательны коэффициенты мощности, близкие к 1. На резонансной частоте cos ϕ = 1.

Пример 3. Расчет коэффициента мощности и мощности

Для той же последовательной цепи RLC , имеющей резистор 40,0 Ом, индуктор 3,00 мГн, конденсатор 5,00 мкФ и источник напряжения с В _{среднеквадратичное значение} 120 В: (a) Рассчитайте коэффициент мощности и фазу угол для f = 60,0 Гц. (б) Какая средняя мощность при 50.0 Гц? (c) Найдите среднюю мощность на резонансной частоте цепи.

Стратегия и решение для (а)

Коэффициент мощности при 60,0 Гц находится из

[латекс] \ cos \ varphi = \ frac {R} {Z} \\ [/ latex].

Мы знаем Z = 531 Ом из Пример 1: Расчет импеданса и тока , так что

[латекс] \ cos \ varphi = \ frac {40.0 \ text {} \ Omega} {531 \ text {} \ Omega} = 0,0753 \ text {at} 60.0 \ text {Hz} \\ [/ latex].

Это небольшое значение указывает на то, что напряжение и ток значительно не совпадают по фазе.{-1} 0,0753 = \ text {85,7º} \ text {at} 60,0 \ text {Hz} \\ [/ latex].

Обсуждение для (а)

Фазовый угол близок к 90º, что согласуется с тем фактом, что конденсатор доминирует в цепи на этой низкой частоте (чистая цепь RC имеет напряжение и ток, сдвинутые по фазе на 90º).

Стратегия и решение для (b)

Средняя мощность при 60,0 Гц —

P _ср. = I _{среднеквадратичное значение} V _{среднеквадратичное значение} cos ϕ .

I _{среднеквадратичное значение} оказалось равным 0,226 А в Пример 1: Расчет импеданса и тока . Ввод известных значений дает

P _средн. = (0,226 A) (120 В) (0,0753) = 2,04 Вт при 60,0 Гц.

Стратегия и решение для (c)

На резонансной частоте мы знаем, что cos ϕ = 1, и I _{среднеквадратичное значение} оказалось равным 6,00 A в Пример 3: Расчет резонансной частоты и тока .Таким образом, P _ave = (3,00 A) (120 В) (1) = 360 Вт при резонансе (1,30 кГц)

Обсуждение

Как ток, так и коэффициент мощности больше в резонансе, производя значительно большую мощность, чем на высоких и низких частотах.

Мощность, подаваемая в цепь переменного тока серии RLC , рассеивается только за счет сопротивления. Катушка индуктивности и конденсатор имеют входную и выходную энергию, но не рассеивают ее из цепи. Скорее они передают энергию туда и обратно друг другу, а резистор рассеивает именно то, что источник напряжения вводит в цепь.Это предполагает отсутствие значительного электромагнитного излучения от катушки индуктивности и конденсатора, например радиоволн. Такое излучение может происходить и даже быть желательным, как мы увидим в следующей главе об электромагнитном излучении, но оно также может быть подавлено, как в случае в этой главе. Схема аналогична колесу автомобиля, движущегося по гофрированной дороге, как показано на рис. 4. Неровности дороги с равномерным интервалом аналогичны источнику напряжения, приводящему колесо в движение вверх и вниз. Амортизатор аналогичен демпфирующему сопротивлению и ограничивающему амплитуду колебаний.Энергия внутри системы перемещается между кинетической (аналогично максимальному току и энергии, хранящейся в индукторе) и потенциальной энергией, хранящейся в автомобильной пружине (аналогично отсутствию тока и энергии, хранящейся в электрическом поле конденсатора). Амплитуда движения колес максимальна, если неровности дороги встречаются на резонансной частоте.

Рис. 4. Вынужденное, но демпфированное движение колеса на автомобильной пружине аналогично цепи переменного тока серии RLC .Амортизатор гасит движение и рассеивает энергию, аналогично сопротивлению в цепи RLC . Масса и пружина определяют резонансную частоту.

Чистая цепь LC с незначительным сопротивлением колеблется с частотой f ₀, той же резонансной частотой, что и цепь RLC . Он может служить эталоном частоты или схемой часов — например, в цифровых наручных часах. При очень маленьком сопротивлении требуется лишь очень небольшая подводимая энергия для поддержания колебаний.Схема аналогична автомобилю без амортизаторов. Как только он начинает колебаться, он некоторое время продолжает работать на своей собственной частоте. На рисунке 5 показана аналогия между цепью LC и грузом на пружине.

Рис. 5. LC-контур аналогичен массе, колеблющейся на пружине без трения и без движущей силы. Энергия движется вперед и назад между катушкой индуктивности и конденсатором, точно так же, как она движется от кинетической к потенциальной в системе масса-пружина.

Исследование PhET: комплект для конструирования цепей (AC + DC), виртуальная лаборатория

Создавайте цепи с конденсаторами, катушками индуктивности, резисторами и источниками переменного или постоянного напряжения и проверяйте их с помощью лабораторных инструментов, таких как вольтметры и амперметры.

Щелкните, чтобы загрузить симуляцию. Запускать на Java.

Сводка раздела

Аналогом сопротивления переменного тока является сопротивление Z , комбинированное действие резисторов, катушек индуктивности и конденсаторов, определяемое версией закона Ома для переменного тока:
[латекс] {I} _ {0} = \ frac {{V} _ {0}} {Z} \ text {или} {I} _ {\ text {rms}} = \ frac {{V} _ {\ text {rms}}} {Z} \\ [/ latex],
, где I _o — пиковый ток, а V _o — пиковое напряжение источника.{2}} \\ [/ латекс].
Резонансная частота f ₀, при которой X _L = X _C , составляет
[латекс] {f} _ {0} = \ frac {1} {2 \ pi \ sqrt {LC}} \\ [/ latex]
В цепи переменного тока существует фазовый угол ϕ между напряжением источника В и током I , который можно найти из
[латекс] \ text {cos} \ varphi = \ frac {R} {Z} \\ [/ latex],
ϕ = 0º для чисто резистивной цепи или цепи RLC в резонансе.
Средняя мощность, подаваемая в цепь RLC , зависит от фазового угла и определяется выражением
[латекс] {P} _ {\ text {ave}} = {I} _ {\ text {rms}} {V} _ {\ text {rms}} \ cos \ varphi \\ [/ latex],
cos ϕ называется коэффициентом мощности, который находится в диапазоне от 0 до 1.

Концептуальные вопросы

1. Зависит ли резонансная частота цепи переменного тока от пикового напряжения источника переменного тока? Объясните, почему да или почему нет.

2. Предположим, у вас есть двигатель с коэффициентом мощности значительно меньше 1.Объясните, почему было бы лучше улучшить коэффициент мощности как метод улучшения выходной мощности двигателя, чем увеличивать входное напряжение.

Задачи и упражнения

1. Цепь RL состоит из резистора 40,0 Ом и катушки индуктивности 3,00 мГн. (a) Найдите его полное сопротивление Z при 60,0 Гц и 10,0 кГц. (b) Сравните эти значения Z со значениями, найденными в Пример 1: Расчет импеданса и тока , в котором также был конденсатор.

2. Схема RC состоит из резистора 40,0 Ом и конденсатора 5,00 мкФ. (а) Найдите его полное сопротивление при 60,0 Гц и 10,0 кГц. (b) Сравните эти значения Z со значениями, найденными в Пример 1: Расчет импеданса и тока , в котором также была катушка индуктивности.

3. Цепь LC состоит из индуктора 3,00 мГн и конденсатора 5,00 мкФ. (а) Найдите его полное сопротивление при 60,0 Гц и 10,0 кГц. (b) Сравните эти значения Z со значениями, найденными в Пример 1: Расчет импеданса и тока , в котором также был резистор.

4. Какова резонансная частота индуктора 0,500 мГн, подключенного к конденсатору 40,0 мкФ?

5. Для приема AM-радио вам нужна цепь RLC , которая может резонировать на любой частоте от 500 до 1650 кГц. Это достигается с помощью фиксированной катушки индуктивности 1,00 мкГн, подключенной к конденсатору переменной емкости. Какой диапазон емкости нужен?

6. Предположим, у вас есть запас индукторов от 1,00 нГн до 10,0Гн и конденсаторов от 1.От 00 пФ до 0,100 F. Каков диапазон резонансных частот, который может быть достигнут при сочетании одной катушки индуктивности и одного конденсатора?

7. Какая емкость необходима для получения резонансной частоты 1,00 ГГц при использовании катушки индуктивности 8,00 нГн?

8. Какая индуктивность необходима для создания резонансной частоты 60,0 Гц при использовании конденсатора 2,00 мкФ?

9. Самая низкая частота в диапазоне FM-радио — 88,0 МГц. (а) Какая индуктивность необходима для создания этой резонансной частоты, если она подключена к 2.Конденсатор 50 пФ? (b) Конденсатор регулируемый, что позволяет регулировать резонансную частоту до 108 МГц. Какой должна быть емкость на этой частоте?

10. Последовательная цепь RLC имеет резистор 2,50 Ом, индуктивность 100 мкГн и конденсатор 80,0 мкФ. (A) Найдите полное сопротивление цепи при 120 Гц. (b) Найдите полное сопротивление цепи на частоте 5,00 кГц. (c) Если источник напряжения имеет В _{среднеквадратичное значение} = 5,60 В, что будет I _{среднеквадратичное значение} на каждой частоте? (г) Какова резонансная частота контура? (e) Что такое I _RMS в резонансе?

11.Последовательная цепь RLC имеет резистор 1,00 кОм, индуктивность 150 мкГн и конденсатор 25,0 нФ. (а) Найдите полное сопротивление цепи при 500 Гц. (b) Найдите полное сопротивление цепи на частоте 7,50 кГц. (c) Если источник напряжения имеет В _{среднеквадратичное значение} = 408 В, что такое I _{среднеквадратичное значение} на каждой частоте? (г) Какова резонансная частота контура? (e) Что такое I _RMS в резонансе?

12. Последовательная цепь RLC имеет 2.Резистор 50 Ом, катушка индуктивности 100 мкГн и конденсатор 80,0 мкФ. (a) Найдите коэффициент мощности при f = 120 Гц. (б) Каков фазовый угол при 120 Гц? (c) Какая средняя мощность при 120 Гц? (d) Найдите среднюю мощность на резонансной частоте цепи.

13. Последовательная цепь RLC имеет резистор 1,00 кОм, индуктивность 150 мкГн и конденсатор 25,0 нФ. (a) Найдите коэффициент мощности при f = 7,50 Гц. б) Каков фазовый угол на этой частоте? (c) Какая средняя мощность на этой частоте? (d) Найдите среднюю мощность на резонансной частоте цепи.

14. Последовательная цепь RLC имеет резистор 200 Ом и катушку индуктивности 25,0 мГн. {2}} \\ [/ latex]

резонансная частота:: — частота, при которой полное сопротивление в цепи минимально, а также частота, с которой цепь будет колебаться, если она не будет управляться источником напряжения; рассчитывается по [latex] {f} _ {0} = \ frac {1} {2 \ pi \ sqrt {\ text {LC}}} \\ [/ latex]

фазовый угол:: обозначается как ϕ , величина, на которую напряжение и ток не совпадают по фазе друг с другом в цепи

Коэффициент мощности:: — величина, на которую мощность, передаваемая в цепи, меньше теоретического максимума цепи из-за того, что напряжение и ток не совпадают по фазе; рассчитывается по cos ϕ

Избранные решения проблем и упражнения

1.(a) 40,02 Ом при 60,0 Гц, 193 Ом при 10,0 кГц (b) При 60 Гц, с конденсатором, Z = 531 Ом, что в 13 раз больше, чем без конденсатора. Конденсатор имеет большое значение на низких частотах. На 10 кГц, с конденсатором Z = 190 Ом, примерно так же, как без конденсатора. Конденсатор оказывает меньшее влияние на высоких частотах.

3. (a) 529 Ом при 60,0 Гц, 185 Ом при 10,0 кГц (b) Эти значения близки к значениям, полученным в Пример 1: Расчет импеданса и тока , поскольку на низкой частоте преобладает конденсатор, а на высокой — индуктор доминирует.Таким образом, в обоих случаях резистор вносит небольшой вклад в общий импеданс.

5. От 9,30 нФ до 101 нФ

7. 3,17 пФ

9. (а) 1,31 мкГн (б) 1,66 пФ

11. (a) 12,8 кОм (b) 1,31 кОм (c) 31,9 мА при 500 Гц, 312 мА при 7,50 кГц (d) 82,2 кГц (e) 0,408 A

13. (а) 0,159 (б) 80,9º (в) 26,4 Вт (г) 166 Вт

15. 16.0 Вт

Узнайте о резонансе в последовательной цепи RLC

Резонанс возникает в тех системах, которые склонны колебаться на определенной частоте.Это называется собственной частотой системы или цепи. В последовательном резонансном контуре RLC частота приложенного переменного напряжения равна собственной частоте контура RLC. Амплитуда колебаний становится большой, и возникает резонанс. Например, ребенок на качелях имеет естественную частоту качания. Если кто-то толкает качели через равные промежутки времени с частотой, равной частоте качания, амплитуда колебаний становится очень большой. В этом случае возникает резонанс.2}} Z = R2 + (XL −XC) 2

На очень низких частотах индуктивный реактивное сопротивление, XL = ωL {X_L} = \ omega LXL = ωL, незначительно, но емкостное реактивное сопротивление, XC = 1ω C {X_C} = \ frac {1} {{\ omega {\ text {}} C}} XC = ω C1, очень высокое.

По мере увеличения частоты переменного ЭДС, приложенного к цепи, XL {X_L} XL продолжает увеличиваться, а XC {X_C} XC продолжает уменьшаться. Для значения ω = ωr \ omega = \ omega _ {r} ω = ωr.

XL = XC {X_L} = {X_C} XL = XC

т. Е.

ωrL = 1 / ωrC [ωr = 1 / LC] {\ omega _r} L = 1 / {\ omega _r} C \ left [{{\ omega _r} = 1 / \ sqrt {LC}} \ right] ωr L = 1 / ωr C [ωr = 1 / LC]

или

2πfr = 1 / √LC [fr = 1 / 2π√LC] 2 \ pi {f_r} = 1 / \ surd LC \ left [{{f_r} = 1/2 \ pi \ surd LC} \ right] 2πfr = 1 / √LC [fr = 1 / 2π√LC]

На определенной частоте

XL = XC {X_L} = {X_C} XL = XC

Следовательно, из (1) Z = R2 + 0Z = \ sqrt {{R ^ 2} + 0} Z = R2 + 0 = минимум, т.е.е., полное сопротивление цепи RLC равно минимальным и, следовательно, ток становится максимальным. Эта частота называется резонансной. частота.

В этой схеме энергия накапливается в два этапа:

· Когда ток течет через катушку индуктивности, энергия накапливается в виде магнитного поля. ·

. Когда конденсатор заряжается, энергия накапливается в виде статическое электрическое поле.

Сначала конденсатор заряжается, и когда конденсатор разряжается, ток вырабатывается.Благодаря этому току в индукторе индуцируется магнитное поле. Точно так же при сжатии магнитного поля конденсатор заряжается. Этот процесс продолжается, что приводит к электрическая энергия колеблется между электрическим и магнитным полями. На определенной частоте (резонансной частоте) индуктивное и емкостное реактивные сопротивления становятся равными. Это приводит к колебаниям электрической энергии между магнитным и электрическим полями индуктора и конденсатора. Это формирует гармонические колебания тока.В цепи RLC из-за наличия сопротивления со временем теряется энергия. Это формирует затухающие колебания.

Резонанс, резонансная частота, последовательный и параллельный резонанс

В сообщениях об индуктивности и емкости мы узнали, что оба состояния являются реактивными и могут препятствовать протеканию тока, но по противоположным причинам. Поэтому важно найти точку, в которой индуктивность и емкость компенсируют друг друга, чтобы добиться эффективной работы цепей переменного тока.

Резонансная частота

Резонанс возникает в цепи переменного тока, когда индуктивное реактивное сопротивление и емкостное реактивное сопротивление равны друг другу: X _L = X _C. Когда это происходит, полное реактивное сопротивление, X = X _L — X _C становится равным нулю, а полное сопротивление становится полностью резистивным. Поскольку индуктивное реактивное сопротивление и емкостное реактивное сопротивление зависят от частоты, можно привести цепь в резонанс, регулируя частоту приложенного напряжения.Резонансная частота (f _Res) — это частота, на которой возникает резонанс, или где X _L = X _C.

Уравнение ниже представляет собой математическое представление резонансной частоты.

, где
f _Res = резонансная частота (Гц)
L = индуктивность (H)
C = емкость (f)

Резонанс серии

Рисунок 9: Простая цепь R-C-L

В последовательной цепи R-C-L, как показано на рисунке 9, в резонансе чистое реактивное сопротивление цепи равно нулю, а полное сопротивление равно сопротивлению цепи; следовательно, выходной ток последовательного резонансного контура имеет максимальное значение для этого контура и определяется значением сопротивления.(Z = R)

Параллельный резонанс

Резонанс в параллельной цепи R-C-L возникает, когда реактивный ток в индуктивных ветвях равен реактивному току в емкостных ветвях (или когда X _L = X _C). Поскольку индуктивный и емкостной реактивные токи равны и противоположны по фазе, они компенсируют друг друга при параллельном резонансе.

Рисунок 10: Простая параллельная цепь R-C-L

Если конденсатор и катушка индуктивности, каждая с незначительным сопротивлением, соединены параллельно, а частота настроена так, чтобы реактивные сопротивления были точно равны, ток будет течь в катушке индуктивности и конденсаторе, но общий ток будет незначительным.

Параллельная цепь C-L будет иметь почти бесконечный импеданс. Конденсатор будет попеременно заряжаться и разряжаться через катушку индуктивности. Таким образом, в параллельном R-C-L, как на Рисунке 10, чистый ток, протекающий через цепь, минимален из-за высокого сопротивления, представленного параллельными X _L и X _C.

индуктивность; Резонанс индуктивности цепи LCR

; Резонанс цепи LCR

Содержание>
Индуктивность; Резонанс цепи LCR

Темы и файлы

Темы EM

Цепь LRC и переменный ток

Файл DataStudio

Перечень оборудования

Введение

Целью этого упражнения является изучение резонанса в цепи индуктор-резистор-конденсатор (LRC-цепи) путем изучения тока в цепи как функции частоты приложенного напряжения и определения того, что происходит с амплитудой тока в цепи. Цепь LRC, когда частота приложенного напряжения равна или близка к резонансной частоте цепи.Функция «ВЫХОД» интерфейса PASCO 750 будет использоваться для подачи напряжения на схему, а датчик напряжения и DataStudio будут использоваться для измерения напряжения на резисторе в цепи при изменении частоты напряжения. Напряжение, измеренное на резисторе, связано с током через резистор. Это действие также будет исследовать фазовое соотношение между приложенным напряжением и напряжением резистора при изменении частоты.

Фон

Когда вибрирующая механическая система приводится в движение, она колеблется со своей собственной частотой.Однако механическую систему можно заставить вибрировать с другой частотой. Амплитуда вибрации и, следовательно, энергия, передаваемая системе, зависит от разницы между собственной частотой и частотой вынужденной вибрации. Амплитуда становится очень большой, когда разница между собственной и вынужденной частотой становится очень маленькой. Это называется резонансом, а собственная частота системы иногда называется резонансной частотой. В резонансе для получения большой амплитуды требуется относительно небольшая энергия.Один из примеров резонанса — когда усиленный голос певца разбивается о стекло. Электрический резонанс аналогичен механическому резонансу. Энергия, передаваемая системе, максимальна при резонансе. Амплитуда переменного тока ( I _o ) в последовательной цепи LRC зависит от амплитуды приложенного напряжения ( В, _o ) и импеданса ( Z ). Поскольку импеданс зависит от частоты,

(2)

Z =

(X _L — X _C) ² + R ²

где X _L = индуктивное реактивное сопротивление = ω L , X _C = емкостное реактивное сопротивление = R = сопротивление и ω = угловая частота = 2 π f ( f = линейная частота), ток также зависит от частоты.Ток будет максимальным, когда цепь будет работать на резонансной частоте:

(3)

ω _res =

Можно показать, что в резонансе X _L = X _C и, таким образом, полное сопротивление ( Z ) уменьшается до R . В резонансе импеданс имеет наименьшее возможное значение, а ток — наибольшее возможное значение.Калькулятор резонансной частоты

для LC-контура

Если вы хотите рассчитать резонансную частоту LC-контура, не смотрите дальше — этот калькулятор резонансной частоты — инструмент для вас. Введите индуктивность и емкость, и вы сразу же найдете резонансную и угловую частоту. Мы также предлагаем некоторую теорию, поскольку это может быть удобно — ниже вы узнаете, как рассчитать резонансную частоту, а также дадим краткое определение того, что такое резонансная частота на самом деле.

Если вас интересуют электронные схемы, вы, вероятно, хотели бы знать, как получить некоторую долю входного напряжения — наш калькулятор делителя напряжения просто необходим для этой задачи.

Что такое контур LC (контур резервуара)?

LC-контур (также называемый резонансным контуром, резервуарным контуром или настроенным контуром) представляет собой идеализированный контур RLC с нулевым сопротивлением. Он содержит только катушку индуктивности и конденсатор в параллельной или последовательной конфигурации:


Параллельная цепь LC	Последовательный контур LC

Цепи

Tank обычно используются в качестве генераторов сигналов и полосовых фильтров — это означает, что они выбирают сигнал определенной частоты из более сложного сигнала.Они широко применяются в электронике — LC-схемы можно найти в усилителях, генераторах, тюнерах, радиопередатчиках и приемниках. Цепи LC и RC могут использоваться для фильтрации сигнала путем блокировки определенных частот.

Что такое резонансная частота?

Резонансная частота — это естественная незатухающая частота системы. Если мы применяем резонансную частоту, тогда колебания становятся максимальной амплитудой, и даже относительно небольшие силы могут создавать большие амплитуды.Однако, если выбрана любая другая частота, этот сигнал ослабляется. Есть много разных типов резонансов, например

механический и акустический,
электрика,
оптический,
орбитальный,
молекулярный.

Для LC-контуров резонансная частота определяется емкостью C и импедансом L.

Как рассчитать резонансную частоту?

Следующая формула описывает взаимосвязь в цепи LC:

f = 1 / (2 * π * √ (L * C))

Где:

f — резонансная частота
L — индуктивность цепи
С — емкость цепи

Откуда взялась эта формула? Резонанс в LC-цепи возникает, когда индуктивное сопротивление катушки индуктивности становится равным емкостному сопротивлению конденсатора.Итак:

xL = 2 * π * f * L
xC = 1 / (2 * π * f * C)

Тогда, преобразовав уравнение, находим:

xL = xC
2 * π * f * L = 1 / (2 * π * f * C)
так:
f² = 1 / (4 * π² * L * C)
и наконец:
f = 1 / (2 * π * √ (L * C))

Также угловая частота может быть вычислена по следующей известной формуле:

ω = 2 * π * f

Как пользоваться вычислителем резонансной частоты

С помощью нашего инструмента прогулка по парку:

Введите значение конденсатора .Например, у нас емкость равна 1 мкФ.
Тип индуктивности . Наша индуктивность в нашей LC-цепи равна 0,18 мГн.
Вычислитель резонансной частоты сделал свое дело! Мы быстро выяснили, что такое резонансная частота: 11,863 кГц.

Вопрос 3. В чем заключается явление резонанса напряжений и при каких условиях оно возникает?

Вопрос 4. Изменением каких параметров электрической цепи (см. Рис.1) можно получить резонанс напряжений ?

Вопрос 5. С помощью каких приборов и по какому признаку можно судить о возникновении резонанса напряжений в электрической цепи?

Резонанс напряжений, условие возникновения — Ремонт220

Применение резонанса напряжений

Механизм возникновения электрического тока

Схема удивительного генератора СВЧ полей на разряднике Вина уникальное, в своём роде устройство

83046 Нагревание проводников электрическим током

Явление резонансов напряжений и токов в электроцепях и условия их возникновения

Резонанс токов

Резонанс напряжений

Видео

Резонанс напряжений, условие возникновения

Что это такое

При каких условиях возникает

Примеры применения на практике

Замечания

Как используется

Последовательно-параллельный резонанс

Принцип действия

Как правильно рассчитать

Литература

Ссылки

При каких параметрах цепи возникают резонанс тока и напряжения

Условия возникновения резонанса в электрической цепи. Резонанс напряжений

Реактивные сопротивления индуктивности и емкости

Емкость и индуктивность в цепи переменного тока

Резонанс напряжений

Применение на практике

В чем заключается явление резонанса напряжений и при каком условии оно возникает? Перечислите

Видеоурок: Резонанс в цепях переменного тока

Стенограмма видеозаписи

— каков эффект резонанса в цепи RLC?

RLC | Физика

Цели обучения

Пример 1.Расчет импеданса и тока

Пример 2. Расчет резонансной частоты и тока

Питание в цепях переменного тока серии

Пример 3. Расчет коэффициента мощности и мощности

Сводка раздела

Концептуальные вопросы

Задачи и упражнения

Избранные решения проблем и упражнения

Узнайте о резонансе в последовательной цепи RLC

Резонанс, резонансная частота, последовательный и параллельный резонанс

Резонансная частота

Параллельный резонанс

индуктивность; Резонанс индуктивности цепи LCR

Темы и файлы

Темы EM

Файл DataStudio

Перечень оборудования

Введение

Фон

для LC-контура

Что такое контур LC (контур резервуара)?

Что такое резонансная частота?

Как рассчитать резонансную частоту?

Как пользоваться вычислителем резонансной частоты

Читайте также

Что делать, если грудничок не спит днем: советы по налаживанию режима сна

Антигистаминные препараты для новорожденных: лечение и профилактика аллергии у грудничков

Методика «Цветоник» М. Лазарева для музыкального развития детей

Добавить комментарий Отменить ответ