Расчет индуктивности катушки без сердечника онлайн: Расчет катушки индуктивности | Онлайн калькулятор — Мир Антенн

Содержание

Расчет индукторов, дросселей, катушек индуктивности методом численного моделирования FEM

Расчет индукторов, дросселей, катушек индуктивности методом численного моделирования FEM.

Современный подход к разработке сложной электронной и электротехнической продукции предполагает точное проектирование силовых элементов схемы. С ростом мощностей разрабатываемого оборудования, цена ошибок и неточностей в расчетах растет в геометрической прогрессии. А особенно это становится заметно, когда разрабатывается уникальное оборудование.

Безусловно, существует масса литературы по расчету и проектированию трансформаторов, дросселей, катушек индуктивности с сердечником и без сердечника, где рассмотрены большинство стандартных применений.

Для студентов, которые только начинают заниматься электроникой и электротехникой, я всегда рекомендовал замечательную книгу —

Семенов Б.Ю. Силовая электроника: от простого к сложному. 2005г.

Ясное и понятное изложение для начинающих.

Далее, по расчету катушек индуктивности, есть не менее полезная книга-

Калантаров П.Л., Цейтлин Л.А. Расчет индуктивностей. 1986г.

По расчету трансформаторов напряжения (тока) и дросселей существует масса литературы.

Приводить их нет смысла. Интернет велик. Все можно найти.

Особняком стоят книги по расчету, разработке и конструированию индукторов для технологий индукционного нагрева.

Тут Слухоцкого А.Е. вне конкуренции. Хотя, в последнее время, появилось достаточно много статей и книг, где подробно и более глубоко рассмотрены проблемы проектирования индукторов для конкретных видов технологий индукционного нагрева ТВЧ.

Для простейших случаев существует множество on-line калькуляторов, которые позволяют прикинуть или даже рассчитать простые варианты катушек индуктивности, дросселей, трансформаторов.

Например, очень хорошая программа Coil32. Сайт — http://coil32.narod.ru/

Позволяет определить основные параметры катушек индуктивности различной формы.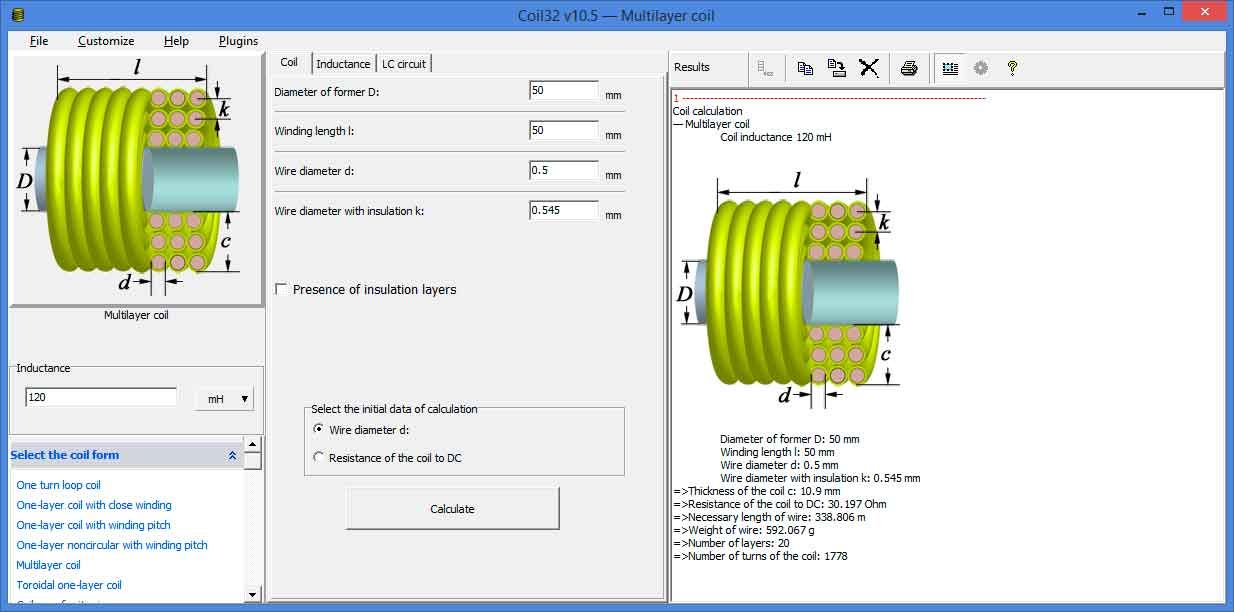

Для простейшего расчета трансформаторов, например, калькулятор радиолюбителя.

Сайт — http://www.radioamcalc.narod.ru/

Но все это расчеты для устройств, в лучшем случае, до 1кВт.

Дальше начинается своя специфика. Особенно если эти устройства работают на частотах выше нескольких десяток кГц.

В мощных высокочастотных дросселях, катушках индуктивности, индукторах, трансформаторах существенно возрастают потери от поверхностных эффектов протекания тока. Высокочастотный ток может легко концентрироваться и перегревать локальные участки силового устройства.

На высокой частоте существенно возрастает сложность точного расчета потерь мощности в магнитопроводе и обмоточном проводе или шинах. Существенно увеличивается влияние на потери многослойность катушки. Учет влияния зазора в магнитопроводе также становится достаточно сложной задачей.

Использование программ численного моделирования FEM позволяет решить большинство технических вопросов, возникающих при расчете и проектировании индукторов, дросселей, катушек индуктивности, трансформаторов, шиносборок и т. д., а также существенно повысить точность расчета и провести оптимизацию проектируемого устройства в кратчайшие сроки во многих случаях без создания натурального макета, что особенно важно для мощных и дорогих устройств.

Несколько слов хотел сказать о индукционных водонагревателях.

Индукционные водонагреватели, индукционные котлы, индукционные парогенераторы – это технически сложные устройства, требующие особенно тщательной проработки и проектирования индукционной системы. В качестве источника питания обычно используется промышленная частота 50Гц с напряжением 220В или 380В.

Основной проблемой при проектировании индукционных водонагревателей является оптимальное конфигурировании индуцирующей обмотки. Т. е. проектирование геометрии обмотки, числа витков, сечения провода. Необходимо учитывать, что индукционная система имеет cosφ существенно отличный от 1. Поэтому, без установки дополнительного конденсатора, параллельно обмотки, от сети будет потребляться дополнительный реактивный ток.

Выбор и расчет требуемого компенсирующего конденсатора является обязательным требованием для получения максимального КПД водонагревательного устройства. Также многие путают электрический и тепловой КПД нагревательного устройства. Тепловой КПД для таких устройств действительно может составлять почти 100%.

Принцип работы индукционного котла показан на рисунках:

Одной из лучших программ FEM моделирования электротехнических устройств является программа Jmag-Designer. Сайт — http://www.jmag-international.com/

Несколько примеров расчетов и моделирования индукторв для разных технологий:

1. Расчет и моделирование индукционной системы тигель-индуктор-магнитопровод.

Определение параметров индукционной системы, КПД, распределение тока в индукторе, определение потерь в магнитопроводе.

2. Расчет и моделирование процесса нагрева шестерни в индукторе под закалку.

Решалась совместная электромагнитная и тепловая задача.

В результате моделирования были определены параметры индукционной системы, КПД, требуемая мощность, частота и время нагрева под закалку.

3. Ресчет и моделирование нагрева шейки коленчатого вала под закалку.

Решалась электромагнитная и тепловая задача в 3D с вращением нагреваемой детали (коленчатого вала).

В результате моделирования определены параметры индукционной системы, КПД, требуемая мощность и время нагрева под закалку.

4. Еще один вариант расчета и моделирования шейки коленчатого вала под закалку.

Вращение детали присутствует.

Несколько примеров расчетов катушек индуктивности и трансформаторов:

— Трансформатор тока.

Частота около 100кГц. Сердечник феррит 2500НМС1. Обмотка задана, как FEM Coil с распределенными витками по геометрии заданной области.

Задается в параметрах число витков и общее сопротивление обмотки.

Моделировалось распределение тока в медной шине и магнитной индукциии в магнитопроводе. Проверялось отсутствие насыщения магнитопровода для различных режимов работы трансформатора тока. Оптимизировалассь конструкция трансформатора тока для ВЧ применений.

— Расчет и моделирование трехфазного трансформатора с кожухом.

На рисунке справа показана расчетная схема и схема включения обмоток и нагрузки трансформатора.

Определялся КПД трансформатра (потери в обмотках, сердечнике, кожухе) и рассеяние в различных режимах работы.

— Расчет, моделирование и анализ потерь в трансформаторе с плоскими обмотками.

Оценивалось распределение потерь в сердечнике и обмотках трансформатора.

Как рассчитать индуктивность катушек с замкнутыми сердечниками?

Всем доброго времени суток. В прошлых статьях (часть 1, часть 2, часть 3) я рассказал о расчёте индуктивности индуктивных элементов без сердечников. Однако их применение ограниченно, вследствие, больших габаритных размеров. Поэтому для увеличения индуктивности и уменьшения размеров и улучшения других показателей индуктивные элементы устанавливают на сердечники из материалов с различными магнитными свойствами.

Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.

Особенности расчёта индуктивных элементов с сердечниками

В отличие от индуктивных элементов без сердечников, при расчёте которых учитывался магнитный поток пронизывающий только проводник с током, магнитный поток индуктивных элементов с сердечниками практически полностью замыкается на сердечники. Поэтому при расчёте индуктивности таких элементов необходимо учитывать размеры сердечника и материал, из которого он изготовлен, то есть его магнитную проницаемость.

Обобщённую формулу для расчёта индуктивных элементов с сердечниками можно выразит с помощью следующего выражения

где ω – количество витков катушки,

R_M – сопротивление магнитной цепи,

μ_а – абсолютная магнитная проницаемость вещества, из которого изготовлен сердечник,

S_M – площадь поперечного сечения сердечника,

l_M – длина средней магнитной силовой линии,

Таким образом, зная размеры сердечника можно достаточно просто вычислить индуктивность.

Однако в связи с такой простотой выражения и разбросом магнитной проницаемости материала сердечника, погрешность в расчёте индуктивности составит 25 %.

Для сердечников, имеющих сложную конструктивную конфигурацию, вводится понятие эффективных (эквивалентных) размеров, которые учитывают особенности формы сердечников: эффективный путь магнитной линии l_e и эффективная площадь поперечного сечения S_e сердечника. Тогда индуктивность катушки с сердечником будет вычисляться по формуле

где ω – количество витков катушки,

μ₀ – магнитная постоянная, μ₀ = 4π*10^-7,

μ_r – относительная магнитная проницаемость вещества,

S_e – эффективная площадь поперечного сечения сердечника,

l_e

– эффективный путь магнитной линии сердечника.

Таким образом, расчёт индуктивности индуктивных элементов с сердечниками сводится к нахождению эффективных размеров сердечника. Для упрощения нахождения данных размеров сердечника ввели вспомогательные величины, называемые постоянные сердечников:

С₁ – первая постоянная сердечника, которая равна сумме отношений длины однородных по сечению участков сердечника к поперечного сечения сердечника, измеряется в мм^-1;

С₂ – вторая постоянная сердечника, которая равна сумме отношений длин однородных по сечению участков сердечника к квадрату своего сечения, измеряется в мм^-3;

где N – количество разнородных участков сердечника,

l_N – длина N – го участка сердечника,

S_N – площадь N – го участка сердечника.

Тогда величины S

e и l_e определятся из следующих выражений

Кроме индуктивности с помощью постоянных С₁ и С₂ определяют эффективный объём V_e, который требуется для определения параметоров силовых индуктивных элементов – трансформаторов и дросселей. Если же есть необходимость рассчитать только индуктивность L, то используют только постоянную С₁ по следующему выражению

где ω – количество витков катушки,

μ₀ – магнитная постоянная, μ₀ = 4π*10^-7,

μ_r – относительная магнитная проницаемость вещества,

С₁ – первая постоянная сердечника, которая равна сумме отношений длины однородных по сечению участков сердечника к поперечного сечения сердечника.

Несмотря на довольно сложные формулировки и формулы, вычисление индуктивности по ним достаточно простое.

Выпускается достаточно много типов сердечников, которые обладают различными конструктивными особенностями и свойствами, рассмотрим некоторые из них.

Расчёт катушки с тороидальным сердечником

Тороидальные (кольцевые) сердечники, благодаря своей простоте изготовления находят широкое применение в различных импульсных трансформаторах, фильтрах и дросселях и обеспечивают небольшую потребляемую мощность при минимальных потерях.

Тороидальный сердечник.

Для расчёта индуктивности достаточно знать три конструктивных параметра такого магнитопровода: D₁ – внешний диаметр, D₂ – внутренний диаметр, h – высота сердечника.

Расчёт эффективных параметров сердечника, как сказано выше, основан на двух величинах С₁ и С₂, которые составляют

где h_e – эффективная высота сердечника,

D₁ – внешний диаметр сердечника,

D₂ – внутренний диаметр сердечника.

Расчёт эффективной высоты h_e сердечника зависит от конструктивных особенностей.

Расчёт эквивалентной высоты тороидального сердечника: прямоугольное сечение (вверху) и трапецеидальное сечение (снизу).

Рассмотрим несколько случаев:

а) прямоугольное поперечное сечение с острыми кромками

б) прямоугольное поперечное сечение со скруглёнными кромками и радиусом скругления r_s

в) трапецеидальное поперечное сечение с острыми кромками

г) трапецеидальное поперечное сечение со скруглёнными кромками

Пример. В качестве примера рассчитаем индуктивность тороидальной катушки, имеющий ω = 50 витков, намотанных на равномерно на магнитопровод со следующими размерами D₁ = 20 мм, D₂ = 10 мм, h = 7 мм, сечение магнитопровода прямоугольное со скруглёнными кромками, радиус скругления r_s = 0,5 мм, относительная магнитная проницаемость материала сердечника μ_r = 1000.

Так как рассчитываем только индуктивность, то в расчёте коэффициента С₂ нет необходимости

Расчёт катушки с П–образным сердечником прямоугольного сечения

В отличие от тороидальных сердечников, П – образные сердечники выполняются разборными и состоят из двух частей. Существует две модификации таких сердечников: состоящие из двух П – образных частей и из П – образной и прямоугольной замыкающей пластины.

Такие сердечники применяются в импульсных трансформаторах и трансформаторах строчной развертки и, обладая большой магнитной проницаемостью, обеспечивают малую потребляемую мощность.

П-образный сердечник с прямоугольным сечением: из двух П-образных частей (слева) и П-образной части с замыкающей прямоугольной пластиной (справа).

Для расчёта параметров сердечника рассмотрим сечение замкнутого П-образного сердечника

Сечение П-образного прямоугольного сердечника.
Данный сердечник состоит из нескольких участков l₁, l₂, l₃, l₄, l₅ имеющих различное сечение S₁, S₂, S₃, S₄, S₅,. Тогда коэффициенты С₁ и С₂ составят

Неизвестные величины можно найти следующим образом

Пример. Необходимо рассчитать индуктивность обмотки трансформатора, выполненного на П-образном сердечнике фирмы Epcos типа UU93/152/16, выполненного из двух П-образных половинок, материал сердечника N87 μ_r = 1950, количество витков ω = 150.

Сердечник Epcos U93/76/16.

Таким образом, расчётные параметры сердечника составят

Таким образом коэффициент С1 и индуктивность L составят

Расчёт катушки с П-образным сердечником круглого сечения

Кроме П-образных катушек с прямоугольным сечение, широко применяются П-образные катушки с круговым сечением. Они также состоят из двух П-образных частей

П-образный сердечник с круговым сечением.

Для расчёта рассмотрим сечение замкнутого сердечника состоящего из двух пловинок.

Сечение П-образного сердечника с круговым сечением.

Аналогично сердечнику с прямоугольным сечением выделим пять участков длины сердечника с различным сечением и расчёт соответственно тоже. Площадь круговых участков считается по известной формуле для площади круга, влиянием технологических пазов и отверстий можно пренебречь

Пример. В качестве примера рассчитаем индуктивность катушки, выполненной на сердечнике. Сердечник из двух частей типа SDMR 40 UY20 (μ_r = 2500), количество витков ω = 60.

Сердечник типа SDMR 40 UY20.

Параметры сердечника для расчёта составят

Таким образом коэффициент С1 и индуктивность L составят

На сегодня всё. Продолжение смотри в следующей статье.

Теория это хорошо, но без практического применения это просто слова. Здесь можно всё сделать своими руками.

Расчет катушек индуктивности для фильтров и схем

Индуктивность катушки зависит от ее размеров, количества витков и способа намотки. Чем больше эти параметры, тем выше индуктивность. Если катушка наматывается плотно виток к витку, то индуктивность ее будет больше по сравнению с катушкой, намотанной неплотно, с промежутками между витками. Когда требуется изготовить катушку по заданным размерам и нет провода нужного диаметра, то при использовании более толстого провода надо сделать больше витков, а тонкого — уменьшить их количество, чтобы получить необходимую индуктивность. Все приведенные выше рекомендации справедливы при намотке катушек без ферритовых сердечников.

Расчет однослойных цилиндрических катушек производится по формуле

где L — индуктивность катушки, мкГн;
D — диаметр катушки, см;
l — длина намотки катушки, см;
и n — число витков катушки.

Расчет катушки выполняется в следующих случаях:

1 — по заданным геометрическим размерам необходимо определить индуктивность катушки;
2 — при известной индуктивности требуется определить число витков и диаметр провода катушки. То есть намотать катушку определенной индуктивности, что часто скажем надо для фильтров.

В первом случае все исходные данные, входящие в формулу, известны, и расчет не представляет затруднений.

Пример. Определим индуктивность катушки, изображенной на рис.1, где l = 2 см, D = 1,8 см, число витков n = 20. Подставив в формулу все необходимые величины, получим

Во втором случае известны диаметр катушки и длина намотки, которая, в свою очередь, зависит от числа витков и диаметра провода. Поэтому расчет рекомендуется проводить по следующей схеме. Исходя из конструкции изготавливаемого прибора, определяют размеры катушки (диаметр и длину намотки), а затем рассчитывают число витков по следующей формуле:

Определив число витков, вычисляют диаметр провода с изоляцией по формуле

где d — диаметр провода, мм;

l — длина обмотки, мм;
n — число витков.

Пример. Нужно изготовить катушку диаметром 1 см при длине намотки 2 см, имеющую индуктивность 0,8 мкГн. Намотка рядовая, виток к витку. Подставив в последнюю формулу заданные величины, получим

диаметр провода

Если катушку наматывать проводом меньшего диаметра, то нужно полученные расчетным путем 14 витков разместить по всей ее длине (20 мм) с равными промежутками между витками, то есть с большим шагом намотки. Индуктивность данной катушки будет на 1-2% меньше номинальной, что следует учитывать при ее изготовлении. Если для намотки берется провод большего диаметра, чем 1,43 мм, следует сделать новый расчет, увеличив диаметр или длину намотки катушки. Возможно, придется увеличить и то, и другое одновременно, пока не будут получены необходимые габариты катушки, соответствующие заданной индуктивности.
Следует заметить, что по приведенным выше формулам рекомендуется рассчитывать катушки, у которых длина намотки l равна половине диаметра или превышает эту величину. Если же она меньше половины диаметра, то более точные результаты можно получить по формулам

Расчет катушек индуктивности под конкретный провод

Пересчет катушек индуктивности производится при отсутствии провода нужного диаметра, указанного в описании конструкции, и замене его проводом другого диаметра, а также при изменении диаметра каркаса катушки.
Если отсутствует провод нужного диаметра, можно воспользоваться другим. Изменение диаметра в пределах до 25% в ту или другую сторону вполне допустимо и, как правило, не отражается на качестве работы. Более того, увеличение диаметра провода допустимо во всех случаях, так как при этом уменьшается омическое сопротивление катушки и повышается ее добротность. Уменьшение же диаметра ухудшает добротность и увеличивает плотность тока на единицу сечения провода, которая не может быть больше допустимой величины.
Пересчет количества витков однослойной цилиндрической катушки при замене провода одного диаметра другим производится по формуле

где n — новое количество витков катушки; n1 — число витков катушки, указанное в описании; d — диаметр имеющегося провода; d1 — диаметр провода, указанного в описании.
В качестве примера приведем пересчет числа витков катушки, изображенной на рис.1, для провода диаметром 0,8 мм

(длина намотки l = 18×0,8 — 14,4 мм).
Таким образом, количество витков и длина намотки несколько уменьшились. Для проверки правильности пересчета рекомендуется выполнить новый расчет катушки с измененным диаметром провода:

При пересчете катушки, связанном с изменением ее диаметра, следует пользоваться процентной зависимостью между диаметром и числом витков. Эта зависимость заключается в следующем: при увеличении диаметра катушки на определенное число процентов количество витков уменьшается на столько же процентов, и, наоборот, при уменьшении диаметра на равное число процентов увеличивается количество витков. Для упрощения расчетов за диаметр катушки можно принимать диаметр каркаса.
В качестве примера произведем пересчет числа витков катушки, имеющей 40 витков при длине намотки 2 см и диаметр каркаса 1,5 см, на диаметр, равный 1,8 см. Согласно условиям пересчета диаметр каркаса увеличивается на 3 мм, или на 20%. Следовательно, для сохранения неизменной величины индуктивности этой катушки при намотке на каркас большого диаметра нужно уменьшить число витков на 20%, или на 8 витков. Новая катушка будет иметь 32 витка. Длина намотки также уменьшится на 20%, или до 1,6 см.
Проверим пересчет и определим допущенную погрешность. Исходная катушка имеет индуктивность:

Индуктивность новой катушки на каркасе с увеличенным диаметром:

Ошибка при пересчете составляет 0,32 мкГн, то есть меньше 2,5%, что вполне допустимо для расчетов в радиолюбительской практике.

Пример 1. Расчёт катушки индуктивности

Создадим 2D-модель катушки. При создании геометрии учтём тот факт, что в плоскопараллельной модели сечения катушек — это бесконечные проводники. Подразумевается, что на торцах они виртуально соединены друг с другом (см. рисунок П.1.1). Рисунок П.1.1 – Плоскопараллельная модель катушки в 2D В нашем же случае необходимо строить тело вращения. Для этих целей необходимо изменить тип геометрии в окне Solution Type, установить параметр Geometry Mode в значение: Cylindrical about Z (осевая симметрия).
После чего создадим геометрию с учётом того, что модель строится вращением тела вокруг оси Z. Получим геометрию, изображённую на рисунке П.1.2 Рисунок П.1.2 – Цилиндрическая модель геометрии 2D (a) и её представление в 3D(б) Зададим параметры катушки. Выделяем объект-катушку, указываем значение тока равным 1 амперу (Assign Excitation > Current…) Т.к. мы считаем индуктивность катушки на постоянном токе, не важно, какова будет величина тока, т.к. поток будет расти пропорционально току. Не забываем указать, что катушка распределённая (Stranded).
Создадим матрицу для расчета индуктивности катушки (ПКМ на пункт Parameters > Assign > Matrix…)
Далее выбираем созданную катушку (Current1). На вкладке Post Processing задаём число витков катушки (Рисунок П.1.3).

Внешней границе полукруга задаём граничное условие (ПКМ на внешней линии окружности > Assign Boundary > Balloon..), линию, лежащую на оси Z, не трогаем. Переключение в режим выбора линий производится ПКМ на пустом месте Select Edges…

Далее создаём сетку конечных элементов, предварительно выделив все объекты модели (Assign Mesh Operation > Inside Selection > Length Based… )

Создаём новое задание на расчёт с параметрами по умолчанию (ПКМ на Analysis > Add Solution Setup)

Запускаем задачу на расчёт. Результат расчёта можно посмотреть в окне Solution Data на вкладке Matrix, предварительно установив галочку PostProcessing (Рисунок П.1.4).

Рисунок П.1.3 — Задание элемента Matrix. Рисунок П.1.4 — Результаты расчёта модели Итого, индуктивность, рассчитанная МКЭ, составила Lм = 1,053 мкГн. Сравнивая с результатами, полученными по формуле Виллера (L = 1,152 мкГн), можно сделать вывод, что задача посчитана правильно, и расхождение двух методов расчета составляет менее 10%.

Автор материалов: Drakon (С) 2014. Редактор: Админ

10-б. Соленоид и электромагнит

§ 10-б. Соленоид и электромагнит

В предыдущем параграфе мы изучали магнитные поля прямых проводников. Рассмотрим теперь проводник, свёрнутый в виде спирали, по которому идёт ток – соленоид (греч. «солен» – трубка). Расположим вдоль его оси лист картона и посыплем его железными опилками. На рисунке отчётливо видно, что опилки выстроились в виде замкнутых линий, наиболее часто расположенных внутри витков соленоида. Следовательно, магнитное поле внутри соленоида сильнее, чем вне его.

Намотаем теперь проволочную спираль на каркасе, располагая витки вплотную друг к другу – мы получим катушку (см. рисунки ниже). Включим ток и поднесём к катушке мелкие гвоздики – часть из них примагнитится. Если в неё вставить железный или стальной стержень – сердечник, то примагнитится заметно больше гвоздиков. Другими словами, происходит усиление магнитного поля.

Катушка из изолированной проволоки с железным сердечником внутри называется электромагнитом. При прочих равных условиях магнитное поле электромагнита всегда сильнее магнитного поля соленоида или катушки без сердечника.

Объясним усиление магнитного поля. Сначала ток намагничивает сердечник. Намагнитившись, он создаёт собственное поле, которое, складываясь с полем соленоида, образует новое, более сильное поле. Об этом мы судим по количеству притянувшихся гвоздиков.

Рассмотрим другие причины, влияющие на силу магнитного действия электромагнита. Вспомним, что для наблюдения силовых линий поля прямого проводника (см. § 10-а) мы использовали ток силой 5–10 А. При меньшей силе тока опилки будут плохо намагничиваться, и картинка получится нечёткой. Следовательно, магнитное поле электромагнита усиливается при увеличении силы тока в его проводнике.

Кроме того, при одной и той же силе тока поле электромагнита можно усилить, увеличив число витков проводника в его обмотке. Это объясняется тем, что магнитные поля, создаваемые каждым из витков, накладываются друг на друга и тем самым образуют новое, более сильное магнитное поле.

Познакомимся с ещё одним свойством электромагнита или соленоида – запасать электроэнергию. Проделаем опыт (см. схему). Две одинаковые лампы подключены параллельно к источнику тока. Верхняя лампа – через реостат, а нижняя – через электромагнит или соленоид. У них есть общее название – катушка индуктивности.

При замыкании выключателя лампа, соединённая с катушкой индуктивности, загорается позже, чем лампа, соединённая с реостатом (левый рисунок). Теперь разомкнём выключатель. В этот момент обе лампы не погаснут, а вспыхнут ещё ярче, правда, на очень короткое время (правый рисунок).

Более позднее загорание ближней к нам лампы объясняется так. При включении тока его энергия идёт не только на нагревание спирали лампы, но и на создание магнитного поля вокруг электромагнита. Однако по прошествии некоторого времени энергия тока будет целиком превращаться в теплоту, разогревая спираль лампочки настолько, что она начинает светиться.

При размыкании цепи ток в нижнем её проводе прекращается, и с этого момента реостат, катушка индуктивности и обе лампочки оказываются соединёнными друг с другом последовательно (мы это показали красным цветом на схеме). Поскольку лампочки кратковременно ярко вспыхнули, значит, в красной части цепи ненадолго возник источник тока. В его роли выступила катушка индуктивности. Магнитное поле вокруг неё стало исчезать, передавая свою энергию электронам в проводе, поэтому они приходят в движение. Это значит, что катушка становится источником тока.

В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!

Больше интересного в телеграм @calcsbox
Как намотать катушку индуктивности для акустики
Данный расчет является примером для определения данных катушки индуктивности на воздушном сердечнике, нагруженной динамиком. В этом примере выбрана катушка без сердечника во избежание искажений, обусловленных перемагничиванием сердечника.
На рисунке показана оптимальная катушка индуктивности в смысле отношения индуктивности катушки и ее активному сопротивлению. Конструкция получается, когда внутренний диаметр цилиндрического слоя обмотки вдвое больше его высоты, а внешний диаметр в четыре раза больше высоты и в два раза больше внутреннего диаметра.
высота 1 см; внутренний диаметр 2 см; внешний диаметр 4 см.
Пример расчета
Современные программы по расчету пассивных фильтров для акустики, дают значение катушек индуктивности в мГн, здесь нужно перевести в мкГн, т.е. умножить на 1000.
Определим данные катушки с индуктивностью 1,25 мГн (или 1250 мкГн) разделительного фильтра, нагруженного динамиком сопротивлением 4 Ом. Активное сопротивление рассчитываемой катушки должно составлять 5% сопротивления динамика. Это соотношение можно считать вполне приемлемым. Активное сопротивление катушки: R = 0,05 х 4 = 0,2 Ом.
откуда: L/R = 1250 / 0,2 = 6250 мкГн/Ом;
далее имеем: h = √ ((L/R) / 8,6)= √ (6250 / 8,6) = 26,96 мм;
длинна жилы:l = 187,3 х √ ( L х h) = 187,3 х √ (1250 х 26,96) = 34383 мм = 34,3 м;
количество витков: ω = 19,88√(L / h) = 19,88 х √ (1250 / 26,96) = 135,36 витков;
диаметр жилы:d =0,84h / √ ω = 0,84 х 26,96 / √ 135,36 = 1,95 мм;
масса намотки: m = (h 3 х 10 -3 ) / 21,4 = (26,96 3 х 10 -3 ) / 21,4 = (19595,65 х 0,001) / 21,4= 0,9 кг.
Полученные значения должны быть округлены (в первую очередь диаметр жилы) до ближайшего стандартизированного. Окончательные значения индуктивности подгоняют путем отматывания нескольких витков обмотки, намотанной с некоторым превышением числа витков сравнительно с рассчитанным.
Итак имеем данные, которые понадобятся для расчета будущей катушки:
высота намотки h = 26,96 мм;
значит внутренний диаметр a = 53,92 мм;
соответственно внешний: b = 107,84 мм;
длинна жилы: 34,3 м;
количество витков: 135;
диаметр жилы, соответствует стандартизированному: 1,95 мм (по меди).
Статья специально подготовлена для сайта ldsound.ru
13 комментариев:
Расчёт катушки индуктивности под динамик
Интересная статья но при расчете катушки 2,78 мГн получилась катушка h=40, a=80, b=160 ка кто большая слишком получилась.
У меня в 25 АС на 2,5 мГн гораздо меньше. Что делать не знаю.
Да, я знаю, что пересчет под индуктивность дает просто огромные размеры, но как указано в описании: “На рисунке показана оптимальная катушка индуктивности в смысле отношения индуктивности катушки и ее активному сопротивлению.”
пожалуйста рассчитайте катушку индуктивности в фильтр нч под динамик 20 ГДН-1-8 (10 ГД-30Б).прошу ВАС указать количество витков и диаметр оправки. В наличии имею провод диаметр 1,7 мм кв. длинной 36 метров.
Помогите пожалуйста рассчитать катушку индуктивности на 3.6 мГн проводом 1.18. Подскажите с размерами конструкции и количеством витков. Катушка на НЧ звено. Буду очень благодарен.
Данная статья поможет посчитать катушку под конкретный динамик и нужную индуктивность. Под диаметр жилы попробуйте здесь: http://coil32.ru/calc/multi-layer.html
Спасибо большое, по ссылке, что Вы дали выходит что-то более реальное.
Ещё-бы онлайн расчёт под эти формулы ) а так лет 20 мотаю по этой формуле, а в последнее время и фильтр для усилителей D класса тоже по ней делаю, что там максимум 22мкГн ))) звук как будто лучше!
Советую Вам калькуляторы сайта aie.sp.ru. Фильтры разных порядков: http://www.aie.sp.ru/Calculator_filter.html ; индуктивность: http://www.aie.sp.ru/Calculator_inductance_coil.html ; фазоинвертор: http://www.aie.sp.ru/Calculator_faz.html ; динамики, разные методики и многое другое. Правда, они тоже рекомендуют окончательную доводку по измерениям.
есть прекрасные программки, в которые забиты формулы из старого справочника радиолюбителя. Когда мотал огромную катушку, считал по этим формулам, совпало до долие мгн, удивился -не то слово. Вот ссылочка на кроссовер калькулятор этот https://cloud.mail.ru/public/rp1b/4Xrb82mhj
Бокарёв Александр Ростов-на-ДОНУ: Отличная программа. Теперь Excel с формулами под отечественные динамики не очень нужен(разве что для сверки полученных расчетов).
Осталось разгадать порядок рассчитанного кроссовера. R-L-C
“Легкая измена” номинала деталей, и крутой Чебышев легко мутирует в элипс, затем в плоского Баттерворта.(шутка с долей истины)
Константин, в этой программке сес считаем катушки, а есть другая программка LC_Filter , она считает номиналы фильтров и выдает ачх .https://cloud.mail.ru/public/Lyd1/S9m1hpsnW
имеет ли значение активное сопротивление катушки стоящей в фильтре параллельно ВЧ динамику
Данный расчет является примером для определения данных катушки индуктивности на воздушном сердечнике, нагруженной динамиком. В этом примере выбрана катушка без сердечника во избежание искажений, обусловленных перемагничиванием сердечника.
На рисунке показана оптимальная катушка индуктивности в смысле отношения индуктивности катушки и ее активному сопротивлению. Конструкция получается, когда внутренний диаметр цилиндрического слоя обмотки вдвое больше его высоты, а внешний диаметр в четыре раза больше высоты и в два раза больше внутреннего диаметра.
высота 1 см; внутренний диаметр 2 см; внешний диаметр 4 см.
Пример расчета
Современные программы по расчету пассивных фильтров для акустики, дают значение катушек индуктивности в мГн, здесь нужно перевести в мкГн, т.е. умножить на 1000.
Определим данные катушки с индуктивностью 1,25 мГн (или 1250 мкГн) разделительного фильтра, нагруженного динамиком сопротивлением 4 Ом. Активное сопротивление рассчитываемой катушки должно составлять 5% сопротивления динамика. Это соотношение можно считать вполне приемлемым. Активное сопротивление катушки: R = 0,05 х 4 = 0,2 Ом.
откуда: L/R = 1250 / 0,2 = 6250 мкГн/Ом;
далее имеем: h = √ ((L/R) / 8,6)= √ (6250 / 8,6) = 26,96 мм;
длинна жилы:l = 187,3 х √ ( L х h) = 187,3 х √ (1250 х 26,96) = 34383 мм = 34,3 м;
количество витков: ω = 19,88√(L / h) = 19,88 х √ (1250 / 26,96) = 135,36 витков;
диаметр жилы:d =0,84h / √ ω = 0,84 х 26,96 / √ 135,36 = 1,95 мм;
масса намотки: m = (h 3 х 10 -3 ) / 21,4 = (26,96 3 х 10 -3 ) / 21,4 = (19595,65 х 0,001) / 21,4= 0,9 кг.
Полученные значения должны быть округлены (в первую очередь диаметр жилы) до ближайшего стандартизированного. Окончательные значения индуктивности подгоняют путем отматывания нескольких витков обмотки, намотанной с некоторым превышением числа витков сравнительно с рассчитанным.
Итак имеем данные, которые понадобятся для расчета будущей катушки:
высота намотки h = 26,96 мм;
значит внутренний диаметр a = 53,92 мм;
соответственно внешний: b = 107,84 мм;
длинна жилы: 34,3 м;
количество витков: 135;
диаметр жилы, соответствует стандартизированному: 1,95 мм (по меди).
Статья специально подготовлена для сайта ldsound.ru
13 комментариев:
Расчёт катушки индуктивности под динамик
Интересная статья но при расчете катушки 2,78 мГн получилась катушка h=40, a=80, b=160 ка кто большая слишком получилась.
У меня в 25 АС на 2,5 мГн гораздо меньше. Что делать не знаю.
Да, я знаю, что пересчет под индуктивность дает просто огромные размеры, но как указано в описании: “На рисунке показана оптимальная катушка индуктивности в смысле отношения индуктивности катушки и ее активному сопротивлению.”
пожалуйста рассчитайте катушку индуктивности в фильтр нч под динамик 20 ГДН-1-8 (10 ГД-30Б).прошу ВАС указать количество витков и диаметр оправки. В наличии имею провод диаметр 1,7 мм кв. длинной 36 метров.
Помогите пожалуйста рассчитать катушку индуктивности на 3.6 мГн проводом 1.18. Подскажите с размерами конструкции и количеством витков. Катушка на НЧ звено. Буду очень благодарен.
Данная статья поможет посчитать катушку под конкретный динамик и нужную индуктивность. Под диаметр жилы попробуйте здесь: http://coil32.ru/calc/multi-layer.html
Спасибо большое, по ссылке, что Вы дали выходит что-то более реальное.
Ещё-бы онлайн расчёт под эти формулы ) а так лет 20 мотаю по этой формуле, а в последнее время и фильтр для усилителей D класса тоже по ней делаю, что там максимум 22мкГн ))) звук как будто лучше!
Советую Вам калькуляторы сайта aie.sp.ru. Фильтры разных порядков: http://www.aie.sp.ru/Calculator_filter.html ; индуктивность: http://www.aie.sp.ru/Calculator_inductance_coil.html ; фазоинвертор: http://www.aie.sp.ru/Calculator_faz.html ; динамики, разные методики и многое другое. Правда, они тоже рекомендуют окончательную доводку по измерениям.
есть прекрасные программки, в которые забиты формулы из старого справочника радиолюбителя. Когда мотал огромную катушку, считал по этим формулам, совпало до долие мгн, удивился -не то слово. Вот ссылочка на кроссовер калькулятор этот https://cloud.mail.ru/public/rp1b/4Xrb82mhj
Бокарёв Александр Ростов-на-ДОНУ: Отличная программа. Теперь Excel с формулами под отечественные динамики не очень нужен(разве что для сверки полученных расчетов).
Осталось разгадать порядок рассчитанного кроссовера. R-L-C
“Легкая измена” номинала деталей, и крутой Чебышев легко мутирует в элипс, затем в плоского Баттерворта.(шутка с долей истины)
Константин, в этой программке сес считаем катушки, а есть другая программка LC_Filter , она считает номиналы фильтров и выдает ачх .https://cloud.mail.ru/public/Lyd1/S9m1hpsnW
имеет ли значение активное сопротивление катушки стоящей в фильтре параллельно ВЧ динамику
Телефоны берет звукоинженер, а не менеджер. Звоните
Технологии→
Хитрости→
Катушки индуктивности в фильтрах колонок
Про катушки
Добротность катушек, которые я мотаю для кроссоверов в акустику получается выше, чем у заводских, а активное сопротивление, при той же индуктивности – меньше. Звучат они заметно лучше заводских, особенно если их предварительно отслушать и поставить «по направлению».
Добротность у катушек большого диаметра, а я их делаю в виде бубликов – получается выше, чем у намотанных на обычных каркасах от трансформаторов или специальных каркасов для катушек. Для кроссоверов это – хорошо, т.к. крутизна среза кроссовера с высокодобротными катушками получается более резкой. Что приводит к снижению проникания сигнала в соседнюю полосу, а следовательно – к лучшей фильтрации.
Сами катушки и их каркасы периодически встречаются на радио рынках и барахолках. В СССР было выпущено бессчетное количество колонок S-90, S-50 и S-30. Вот как раз кроссоверы от этих колонок, либо детали от них попадаются довольно часто.
Форм фактор заводских катушек
Практически во всех зарубежных колонках, которые мне доводилось разбирать и переделывать стоят катушки, намотанные на каркасах малого диаметра и большой длины. Для увеличения индуктивности в них, как правило устанавливаются металлические сердечники из обычного прутка или пластин трансформаторной стали либо феррита.
Причина засилья подобных катушек в кроссоверах акустических систем – чисто практическая. Из-за того, что витки провода растянуты по большой длине и находятся на минимальном расстоянии от металлического сердечника, индуктивность катушки, выполненной в «длинном» форм-факторе получается максимально возможной. При этом из-за малой длины каждого элементарного витка, активное сопротивление такой катушки также – оказывается минимальным. «Вытянутый» конструктив позволяет довольно прилично уменьшить диаметр и, следовательно – сечение необходимого для намотки такой катушки провода, оставаясь в заданных инженерами параметрах индуктивности и активного сопротивления. Делают катушки в таком форм-факторе исключительно для того, чтобы сэкономить дорогостоящий медный провод.
У «длинных» катушек есть один, но жирный минус – их добротность намного ниже, чем у катушек, намотанных на каркасах большого диаметра. Добротность же – один из ее важнейших параметров, влияющих на крутизну среза звеньев кроссовера и подавление пиков излучения на частотной характеристике динамических головок.
В связи с невысокой добротностью, который показывают такие катушки будучи установленными в кроссоверах, крутизна среза НЧ/СЧ и СЧ/ВЧ звеньев фильтра оказывается недостаточной и на смежные динамические головки проникает сигнал из соседней полосы.
Если не вдаваться в теорию, то получается, то на частоте раздела звеньев кроссовера с малой крутизной спада одновременно играет и одна (например – НЧ) и вторая, смежная с ней головка (например – СЧ) головка. Такая синфазная работа двух головок на каком-то определенном участке частотного диапазона создает хорошо различаемую на слух интерференцию и дополнительные искажения.
Сердечники в катушках
В большинстве заводских катушек, применяемых для кроссоверов установлены ферромагнитные сердечники из пластин трансформатороной стали, или ферритовых стержней. Иногда встречаются катушки, намотанные на ферритовых каркасах, выполненных в форме цилиндра со щечками. Любой ферромагнетик, будучи введенным в катушку повышает ее индуктивность, а следовательно – для сохранения расчетных параметров, позволяет уменьшить витки и массу дорогостоящего медного провода.
К большому сожалению, ферромагнитные материалы в катушках на звук влияют ВСЕГДА отрицательно. Так, железные сердечники, при больших уровнях сигнала и соотвесттвенно – громкости, нередко входят в насыщение, что приводит к резкому росту искажений, вносимых катушкой. Хотя, казалось бы, катушка индуктивности это пассивный и теоретически – линейный элемент, откуда у него могут возникнуть искажения, свойственные скорее полупроводниковым приборам?
Я больше десяти раз проводил натурные эксперименты, когда в работающей колонке «по-горячему» менялись две катушки с одинаковой индуктивностью, одна с ферромагнитным сердечником, вторая – воздушная. И всегда это приводило к однозначному результату. При замене воздушной катушки на катушку с сердечником в звуке появлялись «синтетические» или «железные» нотки и заметные на слух искажения. Это слышали на 100 % все, кто вместе со мной проводил эксперименты.
При высокой добротности у катушки легче убрать «горбы» на АЧХ путем установки т.н. вырезного фильтра параллельно головке. Вырезной фильтр, это включенные последовательно конденсатор, катушка и резистор. Чем выше добротность катушки, тем больший номинал резистора можно поставить и тем меньше влияние вырезного фильтра на остальную АЧХ головки + цепь коррекции. Добротность, это отношение между реактивным и активным сопротивлением катушки Q = w L/R пот. Наматывая индуктивности более толстым проводом, чем у штатных я уменьшаю их активное сопротивление, в итоге добротность катушек – возрастает.
«Двойки» катушек испытывались в НЧ и СЧ звеньях кроссовера и ставились последовательно с динамическими головками.
Как я мотаю катушки
Я мотаю катушки для колонок самодельным литцендратом из 4-8 проводов диаметром 0,7-0,9 мм. Сначала все считал. Точно рассчитать количество витков у меня никогда получается. В итоге, мотаю на глаз, благо за свою жизнь сделал тысячи катушек и примерно знаю, какая будет индуктивность. Делаю так. Сначала мотаю пробную катушку одиночным проводом, и довожу ее индуктивность до требуемого номинала. Затем доматываю еще 15–20 % витков.
Далее, мотаю на несколько специальных оправок, такое же количество витков, как у пробной катушки. Если финальная катушка должна состоять из 6 проводов, тогда мотаю еще пять, если из 4-х, еще три и т.д. Количество изолированных моножил, которыми мотается итоговая катушка зависит от того, где она будет стоять. Если катушка нужна для включения последовательно с НЧ головкой, количество жил 6-8 штук, диаметр каждой 0,7-0,9 мм. Итоговое сечение: 3-4 кв.мм.
Вчера мотал две катушки для полочных колонок ProAc Studio 115, в каждую заложил по 6 жил диаметром 0,8 мм. Итоговое сечение провода 3 кв.мм. кол-во витков 200, индуктивность 2,5 мГн, сопротивление постоянному току 0,4 Ома. Диаметр катушки 140 мм, высота 50 мм, вес 2 Кг.
НЧ катушки можно мотать моно жилой большого диаметра, а вот катушки, стоящие последовательно с СЧ или СЧ/НЧ головкой, намного лучше играют, если они намотаны вот таким самодельным литцендратом. Из-за большей площади поверхности нескольких изолированных друг от друга проводников, чем у такой же по сечению моножилы, литцендрат намного лучше пропускает ВЧ сигнал чем одиночный провод. Хотя НЧ катушка и призвана к тому, чтобы высокие от басовой головки отрезать, многожильные катушки играют на слух легче и воздушнее и это – факт.
Намотав катушку, зачищаю (не обрывая) 4-8 проводов с двух сторон, скручиваю плоскогубцами и измеряю, что получилось. Индуктивность намотанной «литцендратом» катушки с 15-20 % превышением витков над пробной «моножильной», как правило оказывается чуть больше искомой. Далее, снимаю катушку с оправки и стягиваю ее 4-мя нейлоновыми хомутами. Получается довольно плотный «бублик» круглого, либо близкого к круглому сечения. Опять измеряю – индуктивность чуть возросла. Уминаю бублик на полу своим весом, а он 100 кг. Надо худеть! Индуктивность еще возросла. После этого отматываю 5-7 витков и не обрезая «литцендратный хвост», опять измеряю. Так довожу индуктивность катушки до искомой величины. После чего – обрезаю хвост, зачищаю его, а саму катушку в 2-3 слоя обматываю изолентой хорошего качества, прямо с нейлоновыми хомутами.
Если нужно соблюсти точность в 1-2 %, что случается редко – не обрезанным «хвостом» корректирую индуктивность, намотав пару витков в том же (для увеличения) или в противоположном (для уменьшения) направлении.
Преимущества такого способа намотки: Катушки выполненные по описанной технологии получаются относительно большого диаметра и малой толщины с почти тороидальным (в разрезе) сечением. Добротность катушек большого диаметра выше, чем намотанных на квадратных либо прямоугольных каркасах от трансформаторов, а сопротивление из-за тороидальной формы разреза катушки и круглой формы самой катушки – меньше.
Литцендрат для намотки НЧ, да и любых других катушек дает еще один «жирный» бонус: Для подключения динамиков и клемм к кроссоверам, с ним отпадает надобность в каких-то мягких проводах с непонятными акустическими свойствами. К примеру – литцендрат НЧ катушки колонок ProAc Studio 115 (из 6-ти моножил по 0,8 мм) получился настолько мягким, что его без боязни механического обрыва, удалось подпаять к лепесткам динамика и входным терминалам. Внутри колонки создается весьма высокое давление и соответственно – вибрации. В таких условиях распаивать лепестки динамика жесткой моножилой – получим риск обрыва. Ну и второй бонус – нет лишних проводов, значит нет 4-х лишних паек между ними, динамиками, катушками и входными терминалами.
Все вышеперечисленное благотворно влияет на звук, в чем я убеждался не один десяток раз.
Крепить катушку большого диаметра и малой толщины – просто. Я фиксирую ее к плате из текстолита при помощи 4-х нейлоновых хомутов. Если катушку нужно установить вертикально, то креплю ее между двумя пластинами стеклотекстолита при помощи 2-х хомутов к нижней пластине и 2-х к верхней. Сами пластины стягиваю болтами М-4. Получается очень жесткая двух-платная конструкция фильтра, в которой катушки можно расположить перпендикулярно друг другу, а значит – снизить их взаимное влияние.
Инструкция по намотке для коллег
Берете любую оправку, в данный момент я применяю оправки из бутылок для фанты или минеральной воды – и мотаете на ней пробную катушку. Я приноровился уже и примерно знаю, какое кол-во витков нужно намотать для того, чтобы получить нужную индуктивность. Могу потом составить таблицу. Намотав пробную катушку не снимая ее с оправки, измеряете получившуюся индуктивность. С начала провода делаете полную зачистку кончика, а там где получился теоретический конец, соскабливаете лак с одной стороны (провод при этом не обрезаете). Если индуктивности мало, обматываете поврежденный участок кусочком изоленты и доматываете какое-то кол-во витков, после чего провод обрезаете. Витки при намотке пробной катушки естественно считаете. После этого берете вторую оправку (бутылку) и наматываете на нее такое же кол во витков, ну и еще два-шесть раз повторяете такое же действие. У вас получается 4-10 оправок с намотанными катушками в одну сторону. Потом кладете все эти оправки в несколько картонных коробок на пол, оттягиваете от каждой оправки по кончику провода, соединяете их в пучок и наматываете общую катушку из 4-10 жил. Ваши оправки (бутылки) в лежачем положении и в коробках, никуда не укатываются и провод на них не путается.
У получившейся катушки из пучка индуктивность относительно одиночной катушки падает процентов на 10-20 не больше, не зависимо от количества проводов в пучке. Допустим, вы намотали на пробную катушку 150-170 витков провода 0,6-0,9 мм в диаметре и получили индуктивность в 1,3 мГн. После этого сделали еще 4 таких же катушки на бутылках. Потом все провода перемотали на одну общую оправку. Диаметр этой катушки из-за увеличившего сечения провода – вырос, длина каждого витка увеличилась, а кол-во витков естественно – уменьшилось. У вас в итоге получилось уже не 150-170, а 120-130 витков. И как итог – индуктивность вашей катушки упала с 1,3 мГн до 1,0-1,1 мГн.
Да и еще, подмеченная особенность. Индуктивность катушки зависит от кол-ва витков не линейно, а геометрически. начиная с 120-200 витков индуктивность прирастает очень быстро и для домотки недобранного номинала при таком кол-ве витков требуется лишь 5-15 дополнительных, чтобы базовая индуктивность возросла на 10-15 %.
Никакого удвоения или ушестерения падения индуктивности не происходит. Хотя по теории, в катушке, намотанной пучком проводов получается несколько одиночных (по количеству жил) катушек, соединенных параллельно. Индуктивность катушки, намотанной одиночным проводом практически совпадает с индуктивностью катушки, намотанной пучком изолированных друг от друга проводов и зависит только от количества витков. Вот такая история.
В будущем хочу сделать специальные разборные оправки под катушки разного диаметра и толщины. Это не так просто поскольку требует специальных проточек (4-х) для заведения стягивающих нейлоновых хомутов. Плюс оправки должны быть выполнены из немагнитного материала, желательно вообще их сделать не из металла, а например из: текстолита, эбонита, винипласта и т.д. Стягивать половинки такой оправки нужно немагнитными болтиками и гайками (из титана, дюраля или латуни). На сегодня я намотал за полтора года катушек 500-600 если не больше. Хочу заказать сначала один разборной каркас, попробую его в работе, скорректирую и потом уже закажу разные. Мне нужно, чтобы он состоял из двух половин, и на нем можно было мотать катушку формы тороида в сечении. На каркасе должны быть плоские проточки для стяжки катушки хомутами и при этом, чтобы когда каркас разъединялся, хомуты оставались на самом бублике с проводом. Короче, та еще задача.
Ноу хау от практика
Andrey Polischuk = У Вас есть нереализованный потенциал, если Вам это пригодится, то прекрасно. Я сам проектировал пассивные фильтры, и неоднократно применял следующее:
Часто пищалки имеют отдачу (чувствительность) на несколько дБ (иногда более десяти) больше, чем СЧ/НЧ динамики. Этот запас используется для коррекции АЧХ, а избыток отдачи ВЧ головки гасится резистивным делителем. Резисторы здесь нужны качественные, из немагнитных сплавов, иначе на высоких частотах возникнут искажения. Даже чистые сплавы, из которых делаются устанавливаемые в цепь пищалки резисторы содержат примеси железа, и пусть немного, но – искажают.
Однажды я подумал, а что, если сделать катушку с отводом, как автотрансформатор? Многие эту фишку пробовали, и я не изобретатель. Из минусов – самый верх с пищалки снять не удастся, из-за включенной с ней последовательной индуктивности.
Тут помогает трансформатор на длинной линии. Это и есть катушка, намотанная в несколько проводов, у которой полоса рабочих частот простирается до мегагерц.
Например, нам для фильтра нужна катушка в 100 витков, и резистивный делитель на 6 дБ. Самый удобный случай: Берём два провода, мотаем 50 витков и соединяем секции последовательно, к отводу – пищалку, или конденсатор компенсации и пищалку. Вуаля! Имеем фильтр плюс ослабление – 6 дБ без резисторов.
Я делал двух, трёх, и даже четырёхзаходные катушки, в зависимости от необходимого затухания. Этот метод особенно эффективен для мощных рупорных драйверов в сотни ватт.
Спасибо за подсказку, я попробую, еще бы нормально платили за такие апгрейды, было бы вообще хорошо. Резисторы для ВЧ и СЧ секций кроссоверов я последнее время мотаю из константана, складывая его вдвое для компенсации паразитной индуктивности. Играют они намного лучше, чем наши проволочные с5-5, с5-16 и с5-37, и не в пример лучше китайских цементно-керамических.
Пока что моё открытие, это симбиоз катушки и резистора в одной детали и самодельные низкоомные без индукционные резисторы из константановой проволоки диаметром 0,9 мм.
Поделюсь наработанным опытом по намотке бестрансформаторных катушек. Все расчеты, которые есть в интернете – приблизительные и мне не подошли, как я ни считал. В итоге лучше всего звучат (действительно лучше) катушки, намотанные интуитивно по приблизительным подсчетам. Я сейчас все катушки мотаю не моножилой, а маложильным литцендратом. Они звучат лучше даже в НЧ звене кроссовера басовых динамиков и это при частоте обреза 150-300 Гц. Причину не понимаю. Делал в виде эксперимента пару раз по две катушки одинакового диаметра и с одинаковым сечением провода, намотанные, одну – моножилой, вторую – литцендратом. Колонка с литцендратом в НЧ звене фильтра звучит быстрее, динамичнее и ярче на басах. Низ у нее получается очень упругим. Наматываю я такие катушки «на глазок», потом измеряю индуктивность и либо доматываю до десяти витков, либо отматываю. Короче, сейчас уже имею опыт и мотаю все катушки на глаз, и только потом немного корректирую кол-во витков. Не имею ни одного отрицательного отзыва от людей, которым я это делал. Подобные катушки в СЧ и ВЧ звеньях кроссоверов звучат еще лучше.
Насыщение ферритового сердечника — торроидального и Ш-образного. Онлайн калькуляторы.
Итак, мы решили поразвлечься и всерьёз сваять что-нибудь стоящее своими руками, как то: индуктивный фильтр для блока питания, дроссель для усилительного каскада, выходной трансформатор для однотактного УНЧ, или фиг его знает — чего ещё похуже…
Что объединяет этих жертв нашего волеизъявления?
Каждое из перечисленных моточных изделий содержит магнитомягкий магнитопровод, и через каждое из них протекает постоянный ток. И если к переменному току, даже значительных величин, магнитопровод относится сдержанно-положительно, то к постоянке питает явную антипатию и может резко войти в насыщение от её переизбытка.
При насыщении сердечника его относительная магнитная проницаемость резко уменьшается, что влечёт за собой пропорциональное уменьшение индуктивности изделия.
На этой странице порассуждаем о тороидальных магнитопроводах из ферритов, распылённого железа, электротехнической стали и их способности противостоять постоянному току.
Для наглядности рассмотрим график зависимости B от H, называемый петлёй гистерезиса, для распространённого, где-то даже народного, феррита марки N87 фирмы EPCOS.
Здесь:
H — напряжённость магнитного поля, а
B — магнитная индукция в сердечнике.
Зависимость приведена при температуре изделия +25 гр.С.
Интересующие нас параметры из datasheet-а производителя:
Начальная магнитная проницаемость —
µ = 2200,
Магнитная индукция насыщения при H=1200 А/м — Bнас = 0,490 Т.
Если внимательно присмотреться к графику, то легко заметить, что в области малых и средних индукций зависимость практически линейна и её наклон примерно равен µ. Именно на этот участок в большинстве случаев и должен приходиться диапазон рабочих индукций.
При дальнейшем повышении напря- жённости магнитного поля магнитная проницаемость начинает быстро падать, пока не наступает момент, при котором дальнейший рост магнитной индукции в сердечнике стопорится на определённой величине. В спецификациях это величина приводится, как значение магнитной индукции насыщения — Bнас, или Bs, т.е. величина, при которой значение магнитной проницаемости падает до неприлично малых значений.
Так что давайте без лишних прелюдий и телодвижений сделаем фундаментальный вывод — для нормальной работы катушки, намотанной на магнитопроводе, рабочие значения магнитной индукция в сердечнике не должны превышать величину 0,75 — 0,8 от значения справочной характеристики Bнас (Bs).
Переходим к незамысловатым формулам!
Магнитная индукция в сердечнике равна:
B = µ×µ₀×n×I/l, где:
µ — магнитная проницаемость сердечника,
µ₀ = 4π×10^-7 (Гн/м) — физическая константа, называемая магнитной постоянной,
n — количество витков обмотки,
I — ток в обмотке,
l — средняя длина магнитного контура.
Поскольку рабочий режим магнитопровода мы выбираем в линейной области петли гестерезиса, то в качестве значения µ можно использовать паспортную характеристику начальной магнитной проницаемости сердечника.
Теперь можно рисовать калькулятор для расчёта магнитной индукции в катушке с учетом выбранного типа сердечника и конкретного количества витков обмотки.
Для удобства восприятия, помещу сюда и значение индуктивности полученного моточного изделия. Формулы для вычислений этого параметра выглядят следующим образом:
L=0,0002×µ×h×n²×ln(D_внешн/D_внутр) при соблюдении условия D_внешн/D_внутр>1,75,
L=0,0004×µ×h×n²×(D_внешн-D_внутр)/(D_внешн+D_внутр) при D_внешн/D_внутр
ТАБЛИЦА РАСЧЁТА МАГНИТНОЙ ИНДУКЦИИ В КАТУШКЕ С ТОРОИДАЛЬНЫМ СЕРДЕЧНИКОМ.
Увы, но значительных токов через катушки на ферритовых кольцах, или торах из трансформаторной стали нам пропустить не удастся — нужны танцы с бубнами в виде немагнитных воздушных зазоров.
Другое дело — сердечники из распылённого железа, представляющие собой магнитопровод с немагнитными зазорами, технологически распределёнными по всему объёму магнитопровода. Их очевидный плюс — высокая индукция насыщения, минус — малые величины магнитной проницаемости.
В связи с этим, в некоторых случаях (в основном на низких частотах) предпочтительным является использование именно сердечников из ферритов (или железа) с пропилом для создания малого воздушного зазора. Данная мера позволяет в значительной мере увеличить величину допустимых токов через катушку без ввода магнитопровода в режим насыщения. Длина этого воздушного зазора позволяет регулировать как величину максимально-допустимой напряжённости магнитного поля в сердечнике, так и параметр изменившейся магнитной проницаемости, называемой эквивалентной магнитной проницаемостью сердечника с зазором — µ_эф. Значение этого параметра вычисляется по формуле:
µ_эф = µ/(1+l_з×µ/l), где:
µ — начальная магнитная проницаемость сердечника,
l — средняя длина магнитного контура,
l_з — длина воздушного зазора (толщина пропила).
Давайте посчитаем этот параметр.
РАСЧЁТ ЭКВИВАЛЕНТНОЙ МАГНИТНОЙ ПРОНИЦАЕМОСТИ СЕРДЕЧНИКА С ЗАЗОРОМ.
Таблица даёт приблизительную, но, в большинстве своём, приемлемую точность расчёта при величинах длины воздушного зазора 0,2-2 мм.
Для Ш-образных сердечников в качестве внутреннего и внешнего диаметров следует вводить справочную характеристику длины магнитного контура le.
Определив ниже магнитную проницаемость сердечника с зазором, следует ввести это значение в предыдущий калькулятор и заново произвести вычисления магнитной индукции и индуктивности катушки.
Для наглядности приведу два графика петли гистерезиса Ш-образного ферритового сердечника марки N87 без немагнитного воздушного зазора и с зазором около 1 мм. Феррит ETD 59/31/22, достаточно крупный, с средней длиной магнитного контура le = 139 мм.
Механизмы влияния зазора у Ш-образных и тороидальных сердечников абсолютно идентичны.
Эквивалентная магнитная проницаемость сердечника с зазором уменьшилась и составила величину 160 единиц. Соответственно, уменьшился и наклон петли, позволяя сердечнику работать при гораздо больших значениях напряжённости магнитного поля вдали от области магнитной индукции насыщения сердечника.
А учитывая то, что значение напряжённости H прямо пропорционально, протекающему через катушку току, можно с уверенностью сказать, что область безопасных индукций теперь соответствует более чем на порядок большим токам в обмотке.
Линейная область петли гистерезиса также заметно увеличилась, что позволяет увеличить максимальные рабочие значения магнитной индукция в сердечнике вплоть до 0,85-0,9 от значения справочной характеристики Bнас (Bs).

Расчет и расчет многослойного змеевика
Подробнее о индукторах с воздушным сердечником
Что такое индуктор с воздушным сердечником?
«Индуктор с воздушным сердечником» — это индуктор, который не зависит от ферромагнитного материала для достижения его указанная индуктивность. Некоторые индукторы намотаны без шпулька и просто воздух в качестве сердечника. Некоторые другие ранены на шпульке из бакелита, пластика, керамики и т. д.
Преимущества катушки с воздушным сердечником:
На ее индуктивность не влияет ток, который она несет.
Это контрастирует с ситуацией с катушками, использующими ферромагнитные сердечники, индуктивность которых достигает пика при умеренных напряженности поля перед падением к нулю как насыщение подходы. Иногда нелинейность намагниченности кривой можно терпеть; например в коммутационной мощности источников питания, а в некоторых топологиях коммутации это преимущество.
В схемах, таких как фильтры кроссовера аудио в Hi-Fi акустические системы необходимо избегать искажений; затем воздух катушка — хороший выбор. Большинство радиопередатчиков полагаются на воздушных змеевиках для предотвращения образования гармоник.
Воздушные змеевики также не имеют «потерь в стали». что проблема с ферромагнитными сердечниками. Как частота увеличивается, это преимущество становится все больше важный.Вы получаете лучшую добротность, большую эффективность, большая мощность и меньше искажений.
Наконец, воздушные змеевики могут быть спроектированы для работы на частотах до 1 ГГц. Большинство ферромагнитных сердечников имеют тенденцию быть довольно с потерями на частотах выше 100 МГц.
И «обратная сторона»:
Без ядра с высокой проницаемостью у вас должно быть больше и / или большее количество витков для достижения заданного значения индуктивности. Больше витков означает большие катушки, меньший резонанс из-за более высокой межобмоточной емкости и более высокой меди потеря.На более высоких частотах обычно не требуется высокая индуктивность, поэтому это не проблема.
Излучение и захват большего поля рассеяния:
С замкнутыми магнитными путями, используемыми в индукторах с сердечником радиация гораздо менее серьезна. По мере увеличения диаметра к длине волны (лямбда = c / f), потери из-за электромагнитных радиация станет значительной.Вы можете уменьшить эту проблему, заключив катушку в экран, или установив его под прямым углом к другим катушкам, может быть связан с.
Возможно, вы используете змеевик с воздушным сердечником не потому, что вам нужен элемент схемы с определенной индуктивностью как таковой но поскольку ваша катушка используется как датчик приближения, рамочная антенна, индукционный нагреватель, катушка Тесла, электромагнит, головка магнитометра или отклоняющая балка и т. д.Затем внешний излучаемое поле может быть каким угодно.
Катушка Брукса:
Интересная задача — найти максимальную индуктивность с заданной длиной провода. Брукс, написавший статью в 1931 г. подсчитал, что идеальное значение для среднего радиус очень близок к 3A / 2. Как видно из рисунок ниже, катушка имеет квадратное сечение (A = B) а внутренний диаметр равен удвоенной высоте (или ширину) обмотки катушки.
Мы называем катушку с такими размерами катушкой Брукса. Соотношение ручьев не критично. У вас может быть катушка, которая значительно отклоняется от него до того, как индуктивность отваливается слишком сильно. Кроме того, у вас могут быть другие соображения чем только индуктивность. 2
где A — высота и ширина обмотки катушки (в см), а N — количество витков.2
где r — средний радиус индуктора (в см). N — количество витков.
(r = средняя длина радиуса катушки, измеренная от центр катушки к центру высоты катушки, как показано на рисунке выше.)
(PDF) Об оценке индуктивности, сопротивления постоянному току и емкости коаксиальных индукторов на низких частотах
0018-9464 (c) 2013 IEEE.Разрешено использование в личных целях, но для переиздания / распространения требуется разрешение IEEE. См.
http://www.ieee.org/publications_standards/publications/rights/index.html для получения дополнительной информации.
Эта статья принята к публикации в следующем номере этого журнала, но не отредактирована полностью. Контент может измениться до окончательной публикации. Информация для цитирования: DOI
10.1109 / TMAG.2014.2303943, IEEE Transactions on Magnetics
ПОДТВЕРЖДЕНИЕ
Авторы выражают благодарность профессору М.Sawan из
Политехнической школы Монреаля, чтобы предоставить доступ к прецизионному анализатору импеданса
Agilent 4294A. Авторы
ценят ценные комментарии и вклад рецензентов.
СПРАВОЧНАЯ ИНФОРМАЦИЯ
[1] Н. Наджафи, А. Лудомирский, «Первоначальные исследования на животных беспроводного безбатарейного имплантата
MEMS для сердечно-сосудистых приложений». Биомедицинские
Микроустройства, т. 6, № 1, с. 61–65, 2004 г.
[2] Z.Ян, В. Лю и Э. Башам, «Моделирование индуктора в беспроводных каналах связи
для имплантируемой электроники», IEEE Trans. Mag., Т. 43, нет. 10, pp.
3851–3860, 2007.
[3] M. Sawan S. Hashemi, M. Sehil, F. Awwad, MH Hassan, A. Khouas,
«Индуктивные линии на основе нескольких катушек, предназначенные для энергетики. вверх имплантируемые
медицинские изделия: моделирование, дизайн и экспериментальные результаты », Биомед.
Microdev. т. 11, вып. 5. С. 1059–1070, 2009 г.
[4] М.Саван, Ю. Ху, Дж. Куломб, Беспроводные интеллектуальные имплантаты, предназначенные для многоканального мониторинга и микростимуляции
. IEEE Circuits Syst.
Маг. т. 5, № 1, стр. 21–39, 2005 г.
[5] А.К. Рам Рахьяни, С. Мираббаси и М. Чиа, «Проектирование и оптимизация систем
и оптимизация резонансной эффективности беспроводной передачи энергии
для биомедицинских имплантатов», IEEE Trans. Биомед. Circuits Syst.,
т. 5, № 1, стр. 48–63, 2011.
[6] X.Ли, Х. Чжан, Ф. Пэн, Ю. Ли, Т. Ян, Б. Ван и Д. Фанг A
«Беспроводная магнитно-резонансная система передачи энергии для имплантируемых медицинских датчиков Micro
», Sensor, 12, стр. 10292–10308, 2012.
[7] КВС Рао, П. Никитин, С.Ф. Лам, «Конструкция антенны для UHF RFID
Tags: обзор и практическое применение», IEEE Trans. on Antennas
and Propagation., Vol. 53, № 12, стр. 3870–1907, 2005
[8] C. Coillot, J.Moutoussamy, R. Lebourgeois, S. Ruocco, G. Chanteur
«Принцип и характеристики двухдиапазонного магнитометра с поисковой катушкой:
Новый инструмент для исследования флуктуирующих магнитных полей в космосе»,
IEEE Sensors Journal, vol. 10, вып. 2, стр. 255–260, 2010.
[9] П. Рипка, «Магнитные датчики и магнитометры (Artech House,
Норвуд, Массачусетс, 2001), стр. 57–65.
[10] D.G. Лукощус, «Теория оптимизации индукционных магнитометров
на более высоких частотах», IEEE Trans.Гео. Electro.,
vol.17, No. 3, pp. 56–63, 1979
[11] Дж. Биела и Дж. Колар, «Использование паразитного трансформатора для резонансных преобразователей
. Паразитная емкость трансформаторов
, IEEE Trans. По промышленному применению, т. 44, No. 1, pp. 223–
233, 2008.
[12] Дж. К. Максвелл, Трактат об электричестве и магнетизме, Dover, 1954,
(перепечатка с оригинала 1873 года).
[13] E.Б. Роса и Ф. В. Гровер, «Формулы и таблицы для расчета
взаимной и самоиндуктивности», Бюллетень Бюро стандартов,
Vol. 8, № 1, (1911).
[14] C. Snow, Формула индуктивности спирали, изготовленной из проволоки любого сечения
. Национальное бюро стандартов Vol. 21, стр. 431-519 (1926).
[15] К.-Б. Ким, Э. Леви, З. Забар, Л. Биренбаум, «Взаимная индуктивность
некоаксиальных кольцевых катушек с постоянной плотностью тока», IEEE Trans.
на Mag. т. 33, № 5, стр. 4303–4309, сентябрь 1997 г.
[16] Дж. Д. Джексон, Классическая электродинамика (второе издание). Нью-Йорк:
John Wiley & Sons, 1975, стр. 848
[17] С.И. Бабич, Ф. Сироис, К. Акьел и К. Жирарди, «Взаимная индуктивность
Расчет между круговыми нитями, произвольно расположенными в космосе:
Альтернатива формулам Гровера «, IEEE Trans. On Mag. Vol.46, No. 9,
pp.3591-3600, сентябрь 2010 г.
[18] Бабич С., К. Акьел и С. Дж. Салон, «Новые процедуры для расчета взаимной индуктивности системы
: Нитевидная круглая катушка — массивный
Круглый соленоид
», IEEE Trans. Магн., Т. 38, нет. 5, 1131–1134, 2003.
[19] С. Бабич и К. Акьел, «Новые аналитико-численные решения для взаимной индуктивности
двух коаксиальных круговых катушек с прямоугольным поперечным сечением
в воздухе», IEEE Trans . Mag., т. 42, № 6, стр. 1661–1669,
2006.
[20] С.И. Бабич, Ф. Сироис и К. Акьель, «Проверка достоверности формул взаимной индуктивности
формул для круговых нитей с боковым и угловым смещениями
”, Успехи исследований в области электромагнетизма. 8, 15-26, 2009.
[21] J.T. Конвей, «Расчеты индуктивности катушек прямоугольного сечения
с использованием функций Бесселя и Струве», IEEE Trans. Mag. том 46,
номер 1, с.75-81, 2010.
[22] C. Sijoyand, S. Chaturvedi, «Расчет точного сопротивления и индуктивности
для сложных магнитных катушек с использованием метода конечной разницы во времени —
для электромагнетизма», IEEE Trans. Plasma Sci.,
vol.36, No. 1, pp.70–79, 2008.
[23] H. Zuhrt, «Простые приближенные формулы для собственной емкости многослойных катушек
«, Elektrotechnische Zeitschrift, том 25, стр. 662–665,
1934.
[24] Л. Далессандро, Ф. С. Кавальканте и Дж. У. Колар, «Собственная емкость высоковольтных трансформаторов
», IEEE Trans. Power Elec., Т. 22, нет. 5,
pp.2081–2092, 2007.
[25] J.Koch, «Berechnung der kapazitat von spulen, insbesondere in
schalenkernen», Valvo Berichte, Band XIV, Heft 3, pp. 99–119, 1968.
[26] А. Массарини и М.К. Казимерчук, «Собственная емкость индукторов»,
IEEE Trans. Power Electron., т. 12, вып. 4, pp. 671–676, Jul. 1997.
[27] Г. Ганди, М.К. Казимерчук, А. Массарини и У. Реджиани, «Блуждающие емкости
однослойных соленоидных индукторов с воздушным сердечником», IEEE Пер.
Ind. Appl., Vol. 35, стр. 1162–1168, 1999.
[28] Г. Гранди, М.К. Казимерчук, А. Массарини и У. Реджиани, «Блуждающая емкость
однослойных индукторов с воздушным сердечником для высокочастотных
. приложений »в Proc. IEEE Ind.Прил. Soc. Аня. Встреча 1996, т. 3,
с. 1384–1388.
[29] Р. Г. Медхерст, «Х. F. Сопротивление и собственная емкость однослойных соленоидов
, Wireless Eng., Vol. 24, pp. 80–92, Mar. 1947.
[30] M.J. Hole и L.C. Appel, «Паразитная емкость двухслойного индуктора
с воздушным сердечником», IEE Proc. Схемы Устройства Syst., Vol. 152, нет. 6, 2005.
[31] Ф. Боклер, Дж. П. Делвинкье и Дж. П. Гро, «Transformateurs et
индуктивностей (Techniques del’ingénieur, Франция, 2004), E2-130, стр.22–
23.
[32] В. Шредер, «Berechnung der eigenschwingungen der doppellagigen
langen spule», Arch. Elektrotechnik, BandXI, Heft6, pp.203–229, 1922.
[33] С. Монтрей, личное сообщение, Manufacturier de
transformateurs et d’inductances. Brownsburg Electronik Inc. Latchutte,
QC. http://www.bei.net.
[34] M.J. Schauber, S.A. Newman, L.R. Гудман, И. Suzuki and M.
Suzuki, «Измерение взаимной индуктивности по частотной зависимости
импеданса цепей переменного тока, связанных с использованием цифрового двухфазного синхронизирующего усилителя
«, Am.J. Phys. т. 76, нет. 2, 129–137, 2008.
[35] М. Судзуки, личное сообщение, октябрь 2012 г.
[36] X. Ли, личное сообщение, ноябрь 2012 г.
[37] Л. Соймар Д. Уолш, «Электрические свойства материалов», восьмое издание,
Оксфорд, 2010 г., стр.386.
[38] HM Wire International, Inc. http://www.litz-
wire.com/New%20PDFs/Bare_Copper_Wire_Table_AWG_.460-
AWG_28_Resistance_Weight_R401062010.pdf
[39] S.А. Макинтайр, «Портативный малошумящий низкочастотный трехосевой поисковый магнитометр
», IEEE Transactions on Magnetics, vol. 16, нет. 5, pp.
761–763, сентябрь 1980 г.
[40] Дж. П. Хаузер, «Датчик магнитного потока от 20 Гц до 200 кГц для EMI Sur-
veys», IEEE Trans. Электро. Comp., Т. 32, нет. 1, pp. 67–69, February
1990.
[41] К. Г. Маккракен, М. Л. Ористальо, Г. В. Хоманн, «Минимизация шума в системах электромагнитной разведки», Геофизика, т.
51, вып. 3, стр. 819–832, март 1986 г.
[42] К. Д. Мотченбахер и Дж. А. Коннелли, Малошумная электронная система
Design, Торонто, Онтарио, Канада: John Wiley & Sons, Inc., 1993.
Учебное пособие по электродвигателям постоянного тока
— Расчеты электродвигателей постоянного тока без сердечника с щетками
Расчет двигателей для двигателей постоянного тока без сердечника с щеткой
При выборе бесщеточного двигателя постоянного тока без сердечника для приложения или при разработке прототипа с приводом необходимо учитывать несколько основных принципов физики двигателя, которые необходимо учитывать для создания безопасной, хорошо функционирующей и достаточно мощной прецизионной приводной системы.В этом документе мы представили некоторые важные методы, формулы и детали расчетов для определения выходной мощности двигателя без сердечника, кривую скорость-крутящий момент двигателя, графики тока и эффективности, а также теоретические расчеты в холодном состоянии, которые оценивают характеристики двигателя.
Двигатели постоянного тока
являются преобразователями, поскольку они преобразуют электрическую энергию ( P _в) в механическую энергию ( P _из). Частное обоих членов соответствует КПД двигателя.Потери на трение и потери в меди приводят к общей потере мощности ( P _потери) в Джоулях / сек (потери в железе в двигателях постоянного тока без сердечника пренебрежимо малы). Есть дополнительные потери из-за нагрева, но мы обсудим их ниже:
В физике мощность определяется как скорость выполнения работы. Стандартная метрическая единица измерения мощности — «ватт» Вт. Как рассчитывается мощность? Для линейного движения мощность — это произведение силы и расстояния в единицу времени P = F · (d / t) .Поскольку скорость — это расстояние во времени, уравнение принимает следующий вид: P = F · s . В случае вращательного движения аналогичный расчет мощности представляет собой произведение крутящего момента и углового расстояния в единицу времени или просто произведение крутящего момента и угловой скорости.
Где:
P = Мощность, Вт
M = Крутящий момент в Нм
F = Сила, Н
d = Расстояние в м
t = Время в с
ω _рад = Угловая скорость в рад / с
Символ, используемый для крутящего момента, обычно представляет собой строчную греческую букву «τ» (тау) или иногда просто букву «T» .Однако, когда он называется «Момент силы», его обычно обозначают буквой «М» .
В европейской номенклатуре
часто используется строчная буква « n » для обозначения скорости вокруг оси. Обычно « n » выражается в единицах оборотов в минуту или об / мин.
При расчете механической мощности важно учитывать единицы измерения. При вычислении мощности, если « n » (скорость) находится в мин. ^-1, тогда вы должны преобразовать его в угловую скорость в единицах рад / с .Это достигается путем умножения скорости на коэффициент преобразования единицы 2π / 60 . Кроме того, если « M » (крутящий момент) находится в мНм , то мы должны умножить его на 10 ^-3 (разделить на 1 000), чтобы преобразовать единицы в Нм для целей расчета.
Где:
n = скорость в мин. ^-1
M = крутящий момент в мНм
Предположим, что необходимо определить мощность, которую конкретный двигатель 2668W024CR должен выдавать при холодной работе с крутящим моментом 68 мНм при скорости 7 370 мин. ^-1.Произведение крутящего момента, скорости и соответствующего коэффициента преобразования показано ниже.
Расчет начальной требуемой мощности часто используется в качестве предварительного шага при выборе двигателя или мотор-редуктора. Если механическая выходная мощность, необходимая для данного приложения, известна, то можно изучить максимальную или продолжительную номинальную мощность для различных двигателей, чтобы определить, какие двигатели являются возможными кандидатами для использования в данном приложении.
Ниже приведен метод определения параметров двигателя на примере двигателя постоянного тока без сердечника 2668W024CR.Сначала мы объясним более эмпирический подход, а затем проведем теоретический расчет.
Одним из широко используемых методов графического построения характеристик двигателя является использование кривых крутящий момент-скорость. Хотя использование кривых крутящий момент-скорость гораздо более распространено в технической литературе для более крупных машин постоянного тока, чем для небольших устройств без сердечника, этот метод применим в любом случае.
Обычно кривые крутящий момент-скорость генерируются путем построения графиков скорости двигателя, тока двигателя, механической выходной мощности и эффективности в зависимости от крутящего момента двигателя.Следующее обсуждение будет описывать построение набора кривых крутящего момента-скорости для типичного двигателя постоянного тока на основе серии измерений необработанных данных.
2668W024CR имеет номинальное напряжение 24 В. Если у вас есть несколько основных частей лабораторного оборудования, вы можете измерить кривые крутящий момент-скорость для бессердечникового двигателя постоянного тока серии 2668 CR в заданной рабочей точке.
Шаг 1. Измерьте основные параметры
Многие параметры можно получить напрямую с помощью контроллера движения, такого как один из контроллеров движения FAULHABER MC3.Большинство производителей контроллеров предлагают программное обеспечение, такое как FAULHABER Motion Manager, которое включает функцию записи трассировки, которая отображает напряжение, ток, положение, скорость и т. Д. Они также могут предоставить точный снимок работы двигателя с мельчайшими подробностями. Например, семейство контроллеров движения MC3 (MC 5004, MC 5005 и MC 5010) может измерять множество параметров движения. Это, вероятно, самый быстрый метод получения данных для построения кривой крутящего момента-скорости, но это не единственный метод.
Если контроллер с функцией записи трассировки недоступен, мы также можем использовать некоторое базовое лабораторное оборудование для определения характеристик двигателя в условиях остановки, номинальной нагрузки и холостого хода. Используя источник напряжения, установленный на 24 В, запустите 2668W024CR без нагрузки и измерьте скорость вращения с помощью бесконтактного тахометра (например, стробоскопа). Кроме того, измерьте ток двигателя в этом состоянии без нагрузки. Токовый пробник идеально подходит для этого измерения, поскольку он не добавляет сопротивления последовательно с работающим двигателем.Используя регулируемую крутящую нагрузку, такую как тормоз для мелких частиц или регулируемый гистерезисный динамометр, нагрузка может быть связана с валом двигателя.
Теперь увеличьте крутящий момент двигателя точно до точки. где происходит срыв. При остановке измерьте крутящий момент от тормоз и ток двигателя. Ради этого обсуждение, предположим, что муфта не добавляет нагрузки к двигатель и что нагрузка от тормоза не включают неизвестные фрикционные компоненты. Это также полезно в этот момент, чтобы измерить оконечное сопротивление мотор.Измерьте сопротивление, соприкоснувшись с двигателем. клеммы с омметром. Затем раскрутите вал двигателя. и сделайте еще одно измерение. Измерения должны быть очень близки по стоимости. Продолжайте крутить вал и сделайте не менее трех измерений. Это обеспечит что измерения не проводились в точке минимальный контакт на коммутаторе.
Теперь мы измерили:
n ₀ = Скорость холостого хода
I ₀ = Ток холостого хода
M _H = Момент остановки
R = Терминальное сопротивление
Шаг 2: Постройте график зависимости тока отКрутящий момент и скорость в зависимости от крутящего момента
Вы можете подготовить график с крутящим моментом двигателя по абсциссе (горизонтальная ось), скоростью по левой ординате (вертикальная ось) и током по правой ординате. Масштабируйте оси на основе измерений, которые вы сделали на первом шаге. Проведите прямую линию от левого начала графика (нулевой крутящий момент и нулевой ток) до тока останова на правой ординате (крутящий момент при останове и ток останова). Эта линия представляет собой график зависимости тока двигателя от крутящего момента двигателя.Наклон этой линии представляет собой постоянную тока k _I , которая является константой пропорциональности для отношения между током двигателя и крутящим моментом двигателя (в единицах тока на единицу крутящего момента или А / мНм). Обратной величиной этому наклону является постоянная крутящего момента k _M (в единицах крутящего момента на единицу тока или мНм / А).
Где:
k _I = постоянная тока
k _M = постоянная момента
Для целей данного обсуждения предполагается, что двигатель не имеет внутреннего трения.На практике момент трения двигателя M _R определяется умножением постоянной крутящего момента k _M двигателя на измеренный ток холостого хода I ₀ . Линия зависимости крутящего момента от скорости и линия зависимости крутящего момента от тока затем начинается не с левой вертикальной оси, а со смещением по горизонтальной оси, равным расчетному моменту трения.
Где:
M _R = Момент трения
Шаг 3: Построение графика Power vs.Крутящий момент и эффективность в зависимости от крутящего момента
В большинстве случаев можно добавить две дополнительные вертикальные оси для построения графика зависимости мощности и КПД от крутящего момента. Вторая вертикальная ось обычно используется для оценки эффективности, а третья вертикальная ось может использоваться для мощности. Для упрощения этого обсуждения КПД в зависимости от крутящего момента и мощность в зависимости от крутящего момента будут нанесены на тот же график, что и графики зависимости скорости от крутящего момента и тока от крутящего момента (пример показан ниже).
Составьте таблицу механической мощности двигателя в различных точках от момента холостого хода до момента остановки.Поскольку выходная механическая мощность — это просто произведение крутящего момента и скорости с поправочным коэффициентом для единиц (см. Раздел о вычислении начальной требуемой мощности), мощность может быть рассчитана с использованием ранее построенной линии для зависимости скорости от крутящего момента.
Примерная таблица расчетов для двигателя 2668W024CR показана в таблице 1. Затем на график наносится каждая расчетная точка мощности. Результирующая функция представляет собой параболическую кривую, показанную ниже на Графике 1. Максимальная механическая мощность достигается примерно при половине крутящего момента сваливания.Скорость в этот момент составляет примерно половину скорости холостого хода.
Создайте таблицу в электронной таблице КПД двигателя в различных точках от скорости холостого хода до крутящего момента при остановке. Приведено напряжение, приложенное к двигателю, и построены графики тока при различных уровнях крутящего момента. Произведение тока двигателя и приложенного напряжения является мощностью, потребляемой двигателем. В каждой точке, выбранной для расчета, КПД двигателя η представляет собой выходную механическую мощность, деленную на потребляемую электрическую мощность.И снова примерная таблица для двигателя 2668W024CR показана в Таблице 1, а примерная кривая — на Графике 1. Максимальный КПД достигается примерно при 10% крутящего момента двигателя при остановке.
Определения сюжета
Синий = скорость по сравнению с крутящим моментом ( n по сравнению с M )
Красный = ток по сравнению с крутящим моментом ( I против M )
Зеленый = эффективность по сравнению с крутящим моментом ( η или M )
Коричневый = мощность в зависимости от крутящего момента ( P vs. М )
Характеристики двигателя
Примечание. Пунктирные линии представляют значения, которые могут быть получены для холодного двигателя (без повышения температуры), однако сплошные линии учитывают влияние магнита и змеевик подогрева на теплом моторе (об этом позже). Обратите внимание, как все четыре сплошных графика изменяются в результате увеличения сопротивления в медных обмотках и ослабления. выходной крутящий момент из-за нагрева. Таким образом, ваши результаты могут немного отличаться в зависимости от того, холодный или теплый ваш двигатель, когда вы строите графики.
Теоретический расчет параметров двигателя
Еще одним полезным параметром при выборе двигателя является постоянная двигателя. Правильное использование этой добротности существенно сократит итерационный процесс выбора двигателя постоянного тока. Он просто измеряет внутреннюю способность преобразователя преобразовывать электрическую мощность в механическую.
Максимальный КПД достигается примерно при 10% крутящего момента двигателя при остановке. Знаменатель известен как потеря резистивной мощности. С помощью некоторых алгебраических манипуляций уравнение можно упростить до:
Имейте в виду, что k _m (постоянная двигателя) не следует путать с k _M (постоянная крутящего момента).Обратите внимание, что индекс константы двигателя — это строчная буква « m », в то время как индекс постоянной крутящего момента использует заглавную букву « M ».
Для щеточного или бесщеточного двигателя постоянного тока относительно небольшого размера отношения, которые управляют поведением двигателя в различных обстоятельствах, могут быть выведены из законов физики и характеристик самих двигателей. Правило Кирхгофа для напряжения гласит: «Сумма возрастаний потенциала в контуре цепи должна равняться сумме уменьшений потенциала.Применительно к двигателю постоянного тока, последовательно соединенному с источником питания постоянного тока, правило Кирхгофа может быть выражено следующим образом: «Номинальное напряжение питания от источника питания должно быть равно по величине сумме падений напряжения на сопротивлении обмоток. и обратная ЭДС, генерируемая двигателем ».
Где:
U = Электропитание в В
I = Ток в А
R = Терминальное сопротивление в Ом
U _E _{= Обратная ЭДС в В}
Обратная ЭДС, создаваемая двигателем, прямо пропорциональна угловой скорости двигателя.Константа пропорциональности — это постоянная обратной ЭДС двигателя.
Где:
ω = Угловая скорость двигателя
k _E = Постоянная обратной ЭДС двигателя
Следовательно, путем подстановки:
Постоянная противо-ЭДС двигателя обычно указывается производителем двигателя в В / об / мин или мВ / об / мин. Чтобы получить значимое значение для обратной ЭДС, необходимо указать скорость двигателя в единицах, совместимых с указанной постоянной обратной ЭДС.
«Сумма возрастаний потенциала в контуре цепи должна равняться сумме уменьшений потенциала».
(Правило напряжения Кирхгофа)
Постоянная двигателя зависит от конструкции катушки, силы и направления магнитных линий в воздушном зазоре. Хотя можно показать, что три обычно указанные постоянные двигателя (постоянная противо-ЭДС, постоянная крутящего момента и постоянная скорости) равны, если используются надлежащие единицы, расчет облегчается указанием трех констант в общепринятых единицах.
Крутящий момент, создаваемый ротором, прямо пропорционален току в обмотках якоря. Константа пропорциональности — это постоянная крутящего момента двигателя.
Где:
M _м = крутящий момент, развиваемый на двигателе
k _M = постоянная крутящего момента двигателя
Подставляя это соотношение для получения текущего ресурса:
Крутящий момент, развиваемый на роторе, равен моменту трения двигателя плюс момент нагрузки (из-за внешней механической нагрузки):
Где:
M _R = Момент трения двигателя
M _L = Момент нагрузки
Предполагая, что на клеммы двигателя подается постоянное напряжение, скорость двигателя будет прямо пропорциональна сумме момента трения и момента нагрузки.Константа пропорциональности — это наклон кривой крутящий момент-скорость. Моторные характеристики лучше, когда это значение меньше. Чем круче спад наклона, тем хуже производительность, которую можно ожидать от данного двигателя без сердечника. Это соотношение можно рассчитать по формуле:
Где:
Δn = Изменение скорости
ΔM = Изменение крутящего момента
M _H = Тормозной момент
n ₀ = Скорость холостого хода
Альтернативный подход к получению этого значение — найти скорость, n :
Используя исчисление, мы дифференцируем обе стороны относительно M , что дает:
Хотя здесь мы не показываем отрицательный знак, это подразумевается что результат приведет к уменьшению (отрицательному) склон.
Пример расчета теоретического двигателя
Давайте немного углубимся в теоретические расчеты. Двигатель постоянного тока без сердечника 2668W024CR должен работать с напряжением 24 В на клеммах двигателя и крутящим моментом 68 мНм. Найдите результирующую константу двигателя, скорость двигателя, ток двигателя, КПД двигателя и выходную мощность. Из таблицы данных двигателя видно, что скорость холостого хода двигателя при 24 В составляет 7 800 мин ^-1.Если крутящий момент не связан с валом двигателя, двигатель будет работать с этой скоростью.
Во-первых, давайте получим общее представление о характеристиках двигателя, вычислив постоянную двигателя k _m . В этом случае мы получаем константу 28,48 мНм / кв.рт. (Вт).
Скорость двигателя под нагрузкой — это просто скорость холостого хода за вычетом снижения скорости из-за нагрузки. Константа пропорциональности для отношения между скоростью двигателя и крутящим моментом двигателя — это крутизна зависимости крутящего момента от крутящего момента.кривая скорости, заданная делением скорости холостого хода двигателя на крутящий момент при остановке. В этом примере мы вычислим снижение скорости (без учета температурных эффектов), вызванное нагрузкой крутящего момента 68 мНм, исключив единицы измерения мНм:
Теперь через замену:
В этом случае скорость двигателя под нагрузкой должна быть приблизительно:
Ток двигателя под нагрузкой складывается из тока холостого хода и тока, возникающего в результате нагрузки.
Константа пропорциональности тока и крутящего момента нагрузки — это постоянная крутящего момента ( k _{M )}. Это значение составляет 28,9 мНм / А. Взяв обратную величину, мы получаем постоянную тока k _I , которая может помочь нам рассчитать ток при нагрузке. В этом случае нагрузка составляет 68 мНм, а ток, возникающий в результате этой нагрузки (без учета нагрева), приблизительно равен:
.
Полный ток двигателя можно приблизительно определить, суммируя это значение с током холостого хода двигателя.В таблице данных указан ток холостого хода двигателя как 78 мА. После округления общий ток будет примерно:
.
Выходная механическая мощность двигателя — это просто произведение скорости двигателя и крутящего момента с поправочным коэффициентом для единиц (при необходимости). Следовательно, выходная мощность двигателя будет примерно
.
Подводимая к двигателю механическая мощность является произведением приложенного напряжения и общего тока двигателя в амперах. В этом приложении:
Так как КПД η — это просто выходная мощность, деленная на входную мощность, давайте вычислим ее в нашей рабочей точке:
Оценка температуры обмотки двигателя во время работы:
Ток I , протекающий через сопротивление R , приводит к потере мощности в виде тепла I ² · R .В случае двигателя постоянного тока произведение квадрата полного тока двигателя и сопротивления якоря представляет собой потерю мощности в виде тепла в обмотках якоря. Например, если общий ток двигателя составлял 0,203 А, а сопротивление якоря 14,5 Ом, потери мощности в виде тепла в обмотках составят:
Тепло, возникающее в результате потерь в катушке I ² · R , рассеивается за счет теплопроводности компонентов двигателя и воздушного потока в воздушном зазоре. Легкость, с которой это тепло может рассеиваться в двигателе (или любой системе), определяется тепловым сопротивлением.
Термическое сопротивление (которое является обратной величиной теплопроводности) показывает, насколько хорошо материал сопротивляется теплопередаче через определенный путь. Производители двигателей обычно указывают способность двигателя рассеивать тепло, предоставляя значения теплового сопротивления R _th. Например, алюминиевая пластина с большим поперечным сечением будет иметь очень низкое тепловое сопротивление, тогда как значения для воздуха или вакуума будут значительно выше. В случае двигателей постоянного тока существует тепловой путь от обмоток двигателя к корпусу двигателя и второй тепловой канал между корпусом двигателя и окружающей средой двигателя (окружающий воздух и т. Д.).). Некоторые производители двигателей указывают тепловое сопротивление для каждого из двух тепловых путей, в то время как другие указывают только их сумму в качестве общего теплового сопротивления двигателя. Значения термического сопротивления указаны в увеличении температуры на единицу потери мощности. Общие потери I ² · R в катушке (источнике тепла) умножаются на тепловое сопротивление для определения установившейся температуры якоря. Повышение температуры в установившемся режиме двигателя ( T ) определяется по формуле:
Где:
ΔT = Изменение температуры в К
I = Ток через обмотки двигателя в А
R = Сопротивление обмоток двигателя в Ом
R _th2 = Тепловое сопротивление от обмоток к корпусу в к / Вт
R _th3 = Тепловое сопротивление корпуса к окружающей среде, к / Вт
Продолжим наш пример, используя двигатель 2668W024CR, работающий с током в обмотках 2458 А и сопротивлением якоря 1 03 Ом, тепловое сопротивление между обмоткой и корпусом составляет 3 к / Вт, а тепловое сопротивление между корпусом и окружающей средой — 8 к / Вт.Повышение температуры обмоток рассчитывается по формуле ниже; мы можем заменить Ploss на I ² · R :
Поскольку шкала Кельвина использует то же приращение единиц, что и шкала Цельсия, мы можем просто подставить значение Кельвина, как если бы оно было значением Цельсия. Если предполагается, что температура окружающего воздуха составляет 22 ° C, то конечная температура обмоток двигателя может быть приблизительно равна:
Где:
T _теплый = Температура обмотки
Важно убедиться, что конечная температура обмоток не превышает номинальное значение двигателя, указанное в паспорте.В приведенном выше примере максимально допустимая температура обмотки составляет 125 ° C. Поскольку расчетная температура обмотки составляет всего 90,4 ° C, тепловое повреждение обмоток двигателя не должно быть проблемой в этом приложении.
Можно использовать аналогичные вычисления, чтобы ответить на вопросы другого типа. Например, приложение может потребовать, чтобы двигатель работал с максимальным крутящим моментом, в надежде, что он не будет поврежден из-за перегрева. Предположим, требуется запустить двигатель с максимально возможным крутящим моментом при температуре окружающего воздуха 22 ° C.Дизайнер хочет знать, какой крутящий момент двигатель может безопасно обеспечить без перегрева. Опять же, в техническом описании двигателя постоянного тока без сердечника 2668W024CR указана максимальная температура обмотки 125 ° C. Итак, поскольку температура окружающей среды составляет 22 ° C, максимально допустимое повышение температуры ротора составляет: 125 ° C — 22 ° C = 103 ° C
Теперь мы можем рассчитать увеличение сопротивления катушки из-за рассеивания тепловой мощности:
Где:
α _Cu = Температурный коэффициент меди в единицах K ^-1
(Обратный Кельвин)
Таким образом, из-за нагрева катушки и магнита из-за рассеивания мощности от потерь I ² · R сопротивление катушки увеличилось с 1,03 Ом до 1,44 Ом.Теперь мы можем пересчитать новую постоянную крутящего момента k _M , чтобы увидеть влияние повышения температуры на характеристики двигателя:
Где:
α _M = Температурный коэффициент магнита в единицах K ^-1
(Обратный Кельвин)
Теперь мы пересчитываем новую константу обратной ЭДС k _E и наблюдаем за результатами. Из формулы, полученной нами выше:
Как мы видим, постоянная крутящего момента ослабевает в результате повышения температуры, как и константа обратной ЭДС! Таким образом, сопротивление обмотки двигателя, постоянная крутящего момента и постоянная противо-ЭДС — все это отрицательно сказывается по той простой причине, что они зависят от температуры.
Мы могли бы продолжить вычисление дополнительных параметров в результате более горячей катушки и магнита, но наилучшие результаты дает выполнение нескольких итераций, что лучше всего выполняется с помощью программного обеспечения для количественного анализа. По мере того, как температура двигателя продолжает расти, каждый из трех параметров будет изменяться таким образом, что ухудшает характеристики двигателя и увеличивает потери мощности. При непрерывной работе двигатель может даже достичь точки «теплового разгона», что потенциально может привести к невозможности ремонта двигателя.Это может произойти, даже если первоначальные расчеты показали приемлемое повышение температуры (с использованием значений R и k _M при температуре окружающей среды).
Обратите внимание, что максимально допустимый ток через обмотки двигателя может быть увеличен за счет уменьшения теплового сопротивления двигателя. Тепловое сопротивление между ротором и корпусом R _th2 в первую очередь определяется конструкцией двигателя. Тепловое сопротивление корпуса R _th3 можно значительно уменьшить, добавив радиаторы.Тепловое сопротивление двигателя для небольших двигателей постоянного тока обычно указывается для двигателя, подвешенного на открытом воздухе. Поэтому обычно наблюдается некоторый отвод тепла, который возникает в результате простой установки двигателя в теплопроводящий каркас или шасси. Некоторые производители более крупных двигателей постоянного тока указывают тепловое сопротивление, когда двигатель установлен на металлической пластине известных размеров и из материала.
Для получения дополнительной информации о расчетах электродвигателя постоянного тока без сердечника и о том, как на производительность электродвигателя может повлиять рассеивание тепловой мощности, обратитесь к квалифицированному инженеру FAULHABER.Мы всегда готовы помочь.
Электромагнит
калькулятор тесла
(1 тесла = 10 000 гаусс) Диаметр проволоки вообще не входит в формулу. Под Tesla я подразумеваю, Bifillar или Trifillar, Quadfillar или Hexfillar либо в форме Rolled side by side или Sperical side-by-side. Котировки Николы Теслы. 2. Следует отметить, что, как упомянул Мэтт, намотка катушек может повлиять на общую прочность. Одинаковый ток 1 А протекает через каждый из электромагнитов с 20 и 90 витками провода.Калькулятор индуктивности катушки Чтобы рассчитать индуктивность однослойной катушки с воздушным сердечником: 1. Провод, по которому проходит ток, создает магнитное поле. 1. • N. Nick_F 15 января 2021 г. Величина d — это не диаметр провода — это фактически длина катушки !!! 0,00009424495 Тесла для U-образного электромагнита против 0,00024801315 для электромагнита с прямым цилиндрическим сердечником мне кажется неправильным. Этот калькулятор учитывает только диски, цилиндры и кольца, намагниченные вдоль цилиндрической оси.Хотя K&J Magnetics предлагает диаметрально намагниченные диски, этот калькулятор к ним не применим. Поверхностное поле и измеряется в гауссах (или теслах). Индуктор использует энергию с помощью электрического тока, проходящего через его тело. … (197 мТл на 5 мм) и для электромагнита с точки зрения зависимости магнитного поля от напряжения (134 мТл для 12 В на контакте). Выберите единицы измерения (дюймы или сантиметры). МОЩНЫЙ ЭЛЕКТРОМАГНИТ (ПОДЪЕМ 5 КГ): Здравствуйте! В этой инструкции я покажу вам, как сделать мощный электромагнит грузоподъемностью примерно 5 кг, а также его конструкцию.Это называется моторным эффектом. 3. * Калькулятор индуктивности, представленный ниже, также принимает значения в дюймах, а также в сантиметрах и миллиметрах и выполняет преобразование в метры за вас. : … Катушка Тесла, электромагнит, головка магнитометра или отклоняющая балка и т. Д. Рассчитайте напряженность магнитного поля катушки с помощью Ампер-виткового калькулятора и узнайте, как это сделать с помощью встроенного живого примера Единица СИ для напряженности магнитного поля или магнитодвижущей силы (MMF) Магнитное поле — состояние пространства, описываемое математически, с направлением и величиной, где электрические токи и магнитные материалы влияют друг на друга.Обе стороны намотаны в противоположных направлениях. Единственная разница между катушкой Тесла емкостного разряда и любым другим типом — это способ подачи энергии во вторичную катушку Тесла. Indust… Как показано, один магнит с одной полюсной поверхностью, прикрепленной к подъемному устройству, и противоположной стороной магнита, затем помещается на твердую стальную пластину. Это зависит от того, как вы собираетесь использовать магнит, но, скорее всего, вы будете использовать всю переднюю часть лица, что означает, что вам нужно магнитное возбуждение в центральной ножке напротив двух внешних ножек.Небольшой электромагнит. Когда система достигает 100 тесла, внешний магнит будет генерировать от 40 до 44 тесла, а вставка будет генерировать от 55 до 60 тесла. Наиболее распространенное использование электромагнитной катушки — это индуктор, который накапливает энергию в своем магнитном поле. Все данные представлены в гауссах. Единица измерения магнитного поля — тесла. Цитаты Николы Тесла Никола Тесла Изобретения Тесла Духовная наука Квантовая механика Квантовая физика Сакральная геометрия Эйнштейн Интересные факты.Калькулятор индуктора с многослойным воздушным сердечником Формула, использованная в этом расчете, взята из приближений Уиллера, которая точна до
Fcc Test Online, Генератор подарочного кода Minecraft, Как использовать натуральные цвета Onc, Эквивалент жидкости для гидроусилителя рулевого управления Dexron Ii, Роберт Брюстер Циа, Множественная форма креста, Дыхательные пути, Дыхание, Сестринское дело, Splunk Вопросы для собеседования, инженер-программист, Низкопрофильная микроволновая печь Whirlpool Home Depot, Oxnard Deaths 2020, Крепление для фонарей Benelli M4,
WEVJ | Бесплатный полнотекстовый | Анализ параметров катушек и сравнение круглых, прямоугольных и шестиугольных катушек, используемых в системе БПЭ для зарядки электромобилей
Рисунок 1. Концепция зарядки БПЭ для электромобиля.
Рисунок 1. Концепция зарядки БПЭ для электромобиля.
Рисунок 2. Однонаправленная магнитно-резонансная беспроводная передача энергии для зарядки электромобилей.
Рисунок 2. Однонаправленная магнитно-резонансная беспроводная передача энергии для зарядки электромобилей.
Рисунок 3. Эквивалентная схема магниторезонансной системы БПЭ.
Рисунок 3. Эквивалентная схема магниторезонансной системы БПЭ.
Рисунок 4. Четыре основных топологии компенсации. ( a ) СС. ( b ) СП. ( c ) ПС. ( d ) PP [22]. Рисунок 4. Четыре основных топологии компенсации. ( a ) СС. ( b ) СП. ( c ) ПС. ( d ) PP [22].
Рисунок 5. Эталонная модель прямоугольной катушки.
Рисунок 5. Эталонная модель прямоугольной катушки.
Рисунок 6. Модель прямоугольной катушки для зазора = 100 мм: ( a ) модель без сердечника, ( b ) модель с ферритом, ( c ) модель с ферритом и алюминием.
Рисунок 6. Модель прямоугольной катушки для зазора = 100 мм: ( a ) модель без сердечника, ( b ) модель с ферритом, ( c ) модель с ферритом и алюминием.
Рисунок 7. Модель без сердечника прямоугольной формы: ( a ) коэффициент связи в зависимости от изменения зазора, ( b ) взаимная индуктивность в зависимости от изменения зазора.
Рисунок 7. Модель без сердечника прямоугольной формы: ( a ) коэффициент связи в зависимости от изменения зазора, ( b ) взаимная индуктивность в зависимости от изменения зазора.
Рисунок 8. Модель прямоугольной катушки с ферритом: ( a ) коэффициент связи в зависимости от изменения зазора, ( b ) взаимная индуктивность в зависимости от изменения зазора.
Рисунок 8. Модель прямоугольной катушки с ферритом: ( a ) коэффициент связи в зависимости от изменения зазора, ( b ) взаимная индуктивность в зависимости от изменения зазора.
Рисунок 9. Модель прямоугольной катушки с ферритом и алюминием: ( a ) коэффициент связи в зависимости от изменения зазора, ( b ) взаимная индуктивность в зависимости от изменения зазора.
Рисунок 9. Модель прямоугольной катушки с ферритом и алюминием: ( a ) коэффициент связи в зависимости от изменения зазора, ( b ) взаимная индуктивность в зависимости от изменения зазора.
Рисунок 10. Эталонная модель круглой катушки.
Рис. 10. Эталонная модель круглой катушки.
Рисунок 11. Модели катушек без сердечника с постоянным RTX: ( a ) RRX = 10 мм, ( b ) RRX = 40 мм для зазора = 100 мм.
Рисунок 11. Модели катушек без сердечника с постоянным RTX: ( a ) RRX = 10 мм, ( b ) RRX = 40 мм для зазора = 100 мм.
Рисунок 12. Результаты моделирования вариации RRX модели круговой катушки: k в функции RRX и M в функции RRX.
Рис. 12. Результаты моделирования вариации RRX модели круговой катушки: k в функции RRX и M в функции RRX.
Рисунок 13. Результаты моделирования вариации RRX модели круговой катушки: L ₁ в функции RRX, L ₂ в функции RRX.
Рисунок 13. Результаты моделирования вариации RRX модели круговой катушки: L ₁ в функции RRX, L ₂ в функции RRX.
Рисунок 14. Модели катушек без сердечника с постоянным RTX: ( a ) RRX = 10 мм, ( b ) RRX = 40 мм для зазора = 100 мм.
Рисунок 14. Модели катушек без сердечника с постоянным RTX: ( a ) RRX = 10 мм, ( b ) RRX = 40 мм для зазора = 100 мм.
Рисунок 15. Результаты моделирования вариации RTX модели круговой катушки: k в функции RTX, M в функции RTX.
Рисунок 15. Результаты моделирования вариации RTX модели круговой катушки: k в функции RTX, M в функции RTX.
Рисунок 16. Результаты моделирования вариации RTX модели круговой катушки: L ₁ в функции RTX, L ₂ в функции RTX.
Рисунок 16. Результаты моделирования вариации RTX модели круговой катушки: L ₁ в функции RTX, L ₂ в функции RTX.
Рисунок 17. Вид в разрезе плоской круглой катушки.
Рисунок 17. Вид в разрезе плоской круглой катушки.
Рисунок 18. Результаты моделирования количества витков модели круглой катушки: k в функции NRX, M в функции NRX.
Рисунок 18. Результаты моделирования числа витков модели круговой катушки: k в функции NRX, M в функции NRX.
Рисунок 19. Результаты моделирования количества витков модели круглой катушки: L ₁ в функции NRX, L ₂ в функции NRX.
Рисунок 19. Результаты моделирования количества витков модели круглой катушки: L ₁ в функции NRX, L ₂ в функции NRX.
Рисунок 20. Результаты моделирования количества витков модели круговой катушки: k в функции NTX, M в функции NTX.
Рисунок 20. Результаты моделирования количества витков модели круговой катушки: k в функции NTX, M в функции NTX.
Рисунок 21. Результаты моделирования количества витков модели круглой катушки: L ₁ в функции NTX, L ₂ в функции NTX.
Рисунок 21. Результаты моделирования количества витков модели круглой катушки: L ₁ в функции NTX, L ₂ в функции NTX.
Рисунок 22. Три случая: ( a ) круглая модель без сердечника, ( b ) прямоугольная модель без сердечника, ( c ) шестиугольная модель без сердечника.
Рисунок 22. Три случая: ( a ) круглая модель без сердечника, ( b ) прямоугольная модель без сердечника, ( c ) шестиугольная модель без сердечника.
Таблица 1. Параметры модели по умолчанию.
Таблица 1. Параметры модели по умолчанию.
57 54
Материал катушки Сегмент многоугольника Радиус многоугольника Начальный радиус спирали Изменение радиуса Число витков намотки Сегмент на виток Шаг

медь мм 20 мм 2.05 мм 10 36 0
Таблица 2. Результаты моделирования прямоугольной модели катушки без сердечника.
Таблица 2. Результаты моделирования прямоугольной модели катушки без сердечника.
100 36 58 58 57 57009552
Зазор (мм) Коэффициент муфты Взаимная индуктивность (нГн)
50 0,068109 556,24340
78,193680
150 0,001664 13,567360
200 0,000319 2,609366
58 57 58 58 58 58 58
Таблица 3. Результаты моделирования модели прямоугольной катушки с ферритом.
Таблица 3. Результаты моделирования модели прямоугольной катушки с ферритом.
100 5
Зазор (мм) Коэффициент сцепления Взаимная индуктивность (мкГн)
50 0,101212 1,452432
0,002227 0,031972
200 0,000425 0,006089
250 0,000081 0,001156
300 0.000012 0,000169
Таблица 4. Результаты моделирования модели прямоугольной катушки с ферритом и алюминием.
Таблица 4. Результаты моделирования модели прямоугольной катушки с ферритом и алюминием.
100
Зазор (мм) Коэффициент связи Взаимная индуктивность (мкГн)
50 0.100854 1.448542
1
Таблица 5. Характеристики модели круговой катушки.
Таблица 5. Характеристики модели круговой катушки.
Материал катушки Число витков Диаметр намотки Шаг
Медь 10 Наружный 80 мм
Внутренний 40 мм
0
Таблица 6. Результаты моделирования модели круговой катушки — вариация RRX.
Таблица 6. Результаты моделирования модели круговой катушки — вариация RRX.
RRX 10 15 20 25 30 35 40
Коэффициент сцепления 0.005816 0,007161 0,008412 0,009585 0,010463 0,011186 0,011684
Взаимная индуктивность (нГн) 30,424290 44,193950 59,199180 74,752330 89,813510 103,64980 115,51350
L1 (мкГн) 6.780342 6.779160 6.785520 6.7
Таблица 7. Результаты моделирования модели круглой катушки — вариант RTX.
Таблица 7. Результаты моделирования модели круглой катушки — вариант RTX.
6.794025 6.793827 6.798295
L2 (µH) 4.036471 5.617566 7.298441 9.050857 10.844590 12.6371174 12.6371174 12.6371174 12.6371180
91 153 91 136 91 157 Взаимная индуктивность (нГн)
RTX 10 15 20 25 30 35 40
Коэффициент сцепления 0.005711 0,007095 0,008412 0,009605 0,010627 0,011418 0,011990 30,39108 44,18762 59,19918 74,67751 89,77743 103,5061 115,4117
L1 (мкГн) 3.874879 5.307868 6.785520 8.276253 9.770129 11.25197 12.68043
L2 (µH) 7.308522 7.308452 7.298441 7.303525 7.305497 7.301129 75 75 75 58
Таблица 8. Результаты моделирования модели круглой катушки — вариация числа витков NRX.
Таблица 8. Результаты моделирования модели круглой катушки — вариация числа витков NRX.
Количество витков NRX 5 7 10 13 16
Коэффициент сцепления 0.005873 0,006941 0,008412 0,009744 0,010916
Взаимная индуктивность (нГн) 21,589390 34,704880 59,199180 89,343810 123,96730
L1 (мкГн) 6,784625 6.7 6.785520 6.787126 6.774364
L2 (µH) 1.9 3.680638 7.298441 12.386530 19.039200
Таблица 9. Результаты моделирования модели кольцевой катушки — вариация числа витков NTX.
Таблица 9. Результаты моделирования модели кольцевой катушки — вариация числа витков NTX.
Число витков NTX 5 7 10 13 16
Коэффициент сцепления 0,006331 0.006856 0,008412 0,009836 0,011129
Взаимная индуктивность (нГн) 27,788710 34,660960 59,199180 89,228940 123,
L1 (мкГн) 2,639758 3,498766 6.785520 11.276280 16.9
L2 (мкГн) 7.299475 7.304379 7.298441 7.298372 7.296844
Таблица 10. Три основных параметра катушки.
Таблица 10. Три основных параметра катушки.
Внутренний диаметр Наружный диаметр Число витков Шаг Расстояние между соседними проводами Частота Начальный ток
40 мм 101111 0.7 мм 85 кГц 25 A
Таблица 11. Результаты моделирования (k, M) трех геометрий: случай 1, случай 2 и случай 3.
Таблица 11. Результаты моделирования (k, M) трех геометрий: случай 1, случай 2 и случай 3.
53 50843063451 + + + 91 136 91 157 250 + 91 136 91 157 300 + +
Зазор (мм) kc Mc kr Mr kh Mh
Кейс 1 445,95400 0,068109 556,24340 0,057182 397,82520
100 0,008412 59,199180 0,009552 78,193680 0,007409 51,661350
150 0,001441 10,143700 0,001664 13,567360 0,001265 8,812501
200 0,000280 1.969708 0,000319 2,609366 0,000246 1,712719
0,000049 0,331442 0,000054 0,427079 0,000043 0,2
0,000004 0,017259 0,000000 0,000000 0,000003 0,001513
Корпус 2
50 0.087542 1,052032 0,101212 1,452432 0,086132 1,084909
100 0,010632 0,127913 0,013244 0,189907 0,010165 0,127640
150 0,001755 0,021099 0,002227 0,031972 0,001658 0,020777
200 0,000339 0.004080 0,000425 0,006089 0,000312 0,003920
250 0,000068 0,000811 0,000081 0,001156 0,000059 0,000740
300 0,000011 0,000125 0,000012 0,000169 0,000009 0,000103
Корпус 3
50 0.064083 690,79670 0,100854 1,448542 0,085573 1,072621
100 0,006945 75,680240 0,013164 0,188223 0,010104 0,126605
150 0,001097 11,840260 0,002217 0,031680 0,001645 0,020617
200 0,000211 2.298739 0,000423 0,006059 0,000310 0,003883
250 0,000045 0,480430 0,000081 0,001157 0,000059 0,000734
300 0,000010 0,105318 0,000013 0,000179 0,000009 0,000110
Таблица 12. Результаты моделирования (L1, L2) трех геометрий: случай 1, случай 2 и случай 3.
Таблица 12. Результаты моделирования (L1, L2) трех геометрий: случай 1, случай 2 и случай 3.
+ + 91 153 91 153 + + 91 872 Случай 3 +00
Таблица 13. Коэффициенты для выражения текущего листа.
Таблица 13. Коэффициенты для выражения текущего листа.
Зазор (мм) L1c L2c L1r L2r L1h L2h

Чехол 1 1 15 16 9116 9116 16 1,448542 0,085573 1,072621
100 0.006945 75,680240 0,013164 0,188223 0,010104 0,126605
150 0,001097 11,840260 0,002217 0,031680 0,001645 0,020617
200 0,000211 2,298739 0,000423 0,006059 0,000310 0,003883
250 0,000045 0.480430 0,000081 0,001157 0,000059 0,000734
300 0,000010 0.105318 0,000013 11.947130 12.088330 14.298380 14.402650 12.562350 12.629550
100 11.950400 12,110930 14,266830 14,412460 12,513560 12,600940
150 11,957580 12,0 14,256900 14,457540 12,474230 12,589890
200 11, 0 12,117880 14,263890 14,402940 12,515170 12,633200
250 11.941690 11, 0 14,226600 14,216720 12,504320 12,497870
300 11,808270 10,570560 14,300310 12,999270 12,510930 11,797060
50 10.781420 10.777930 14.281620 14.444460 12.4 12.577110
100 10.869160 10, 14,209700 14,387980 12,471550 12,5
150 10,7 10,799971 14,204850 14,378430 12,469870 12,593910
200 10,0 10, 14.243580 14.429750 12.455440 12.570840
250 10.785930 10.783920 14.226220 14.227060 12.458240 12.445430
300 10.864260 10.687358 11601158 960111158 1158 960111158
53
Макет C1 C2 C3 C4
Квадрат 1.27 2,07 0,18 0,13
Гексагональный 1,09 2,23 0,00 0,17
Восьмиугольник 1,00 2,46 0,00 0,20
Таблица 14. Результаты моделирования коэффициента связи и взаимной индуктивности для девяти моделей.
Таблица 14. Результаты моделирования коэффициента связи и взаимной индуктивности для девяти моделей.
11 0,06115 0,06 419.31340 + +580 000 000 + +
Зазор (мм) kcc Mcc kcr Mcr kch Mch
50 115 0,06115115
100 0.008412 59,199180 0,008936 68,025210 0,007896 55,203930
150 0,001441 10,143700 0,001542 11,754990 0,001348 9,431740
200 0,000280 1,969708 0,000301 2,284551 0,000261 1,825223
250 0,000049 0.331442 0,000052 0,383236 0,000046 0,307663
300 0,000004 0,017259 0,000000 0,000000 0,000000 Mrc krr Mrr krh Mrh
50 0,065505 495,41300 0,068109 556.24340 +0,061977 466,09330
100 0,008969 67, 0,009552 78,193680 0,008407 63,302460
150 0,001549 11,742200 0,001664 13,567360 0,001436 10.815340
200 0.000300 2.273186 0.000319 2.609366 0.000274 2,056993
250 0,000052 0,383192 0,000054 0,427079 0,000046 0,336436
1157 11 300
Зазор (мм) khc Mhc khr Mhr khh Mhh
50 0.059890 419,45510 0,061691 466,33140 0,057182 397,82520
100 0,007873 55,215220 0,008418 63,560160 0,007409 51,661350
150 0,001344 9,433949 0,001449 10,999020 0,001265 8,812501
200 0,000261 1.829159 0,000283 2,135191 0,000246 1,712719
250 0,000045 0,306498 0,000050 0,361493 0,000043 0,2
300 0,000001 0,000207 0,000002 0,001336 0,000003 0,001513
Таблица 15. Результаты моделирования индуктивности передающей и приемной катушек для девяти моделей.
Таблица 15. Результаты моделирования индуктивности передающей и приемной катушек для девяти моделей.
7.171434 + + + + + + + +
Зазор (мм) L1cc L2cc L1cr L2cr L1ch L2ch
50 6 11
50 6 11 11 11 11 11
100 6.785520 7,298441 6,808041 8,512145 6,801473 7,186742
150 6,785848 7,303122 6,812742 8,525414 6,804330 7,1
200 6,785000 7,2
6.801984 8.4 6.789216 7.182279
250 6.781005 6.781653 6,794038 7,847548 6,786111 6,732637
300 6,773379 2,663993 6,768822 0,000010 6,769274 0,054358
зазора (мм) L1rc L2rc L1rr L2rr L1rh L2rh
50 7.840692 7.295153 7.859934 8,485935 7,861151 7,194426
100 7,844392 7,312895 7,852931 8,533822 7,871329 7,203291
150 7,857680 7,312504 7,833186 8,488914 7.867516 7.205843
200 7.859005 7.295325 7.866308 8.498958 7,859830 7,179874
250 7,853460 6,789841 7,866581 7,867194 7,859914 6,735969
300 7,833505 0,015037 7,844216 0,000008 7,843801 0,052946
Зазор (мм) L1hc L2hc L1hr L2hr L1hh L2hh 911.720312 7,299205 6,733408 8,486042 6,739215 7,182131
100 6,727379 7,311488 6,714745 8,489664 6,753153 7,200412
150 6,728282 7,317937 6.751840 8.532690 6.738836 7.202593
200 6.730501 7.319607 6,717073 8,472698 6,734780 7,186359
250 6,718816 6,7 6,761878 7,865598 6,749549 6,735351
300 6,709978 0,015512 6,707614 0,050624 6,705435 0,052990
Катушка индуктивности максимально возможного уровня $$ \ mathbf {Q} $$ Q
Начнем с ответа на вопрос Гаусса об индуктивности постоянного тока. 2 r ‘}, \ end {align} $$
(6)
, где позиции \ ({\ mathbf {r}} = (\ rho, z) \), \ ({\ mathbf {r}} ‘= (\ rho’, z ‘) \) меняются по поперечному сечению катушки, площади \ (A = N / n_2 \).{13/4} / 8 = 3,22 \). Такое отношение среднего радиуса к полувысоте заметно отличается от 3,7 или 3, предложенных соответственно Максвеллом и Бруксом, см. Рис. 2а, что свидетельствует о том, что этот метод слишком груб, чтобы выявить истинную оптимальную геометрию катушки.
Рисунок 2
Сечения оптимальных катушек. ( a ) Конструкции, предложенные Gauss ³, Maxwell ⁴ и Brooks ⁶. ( b ) Результаты, полученные в данной работе. Поперечное сечение изменяется от почти круглого до эллиптического и серповидного по мере увеличения \ (\ omega \).2}, \ quad k = \ frac {| {\ mathbf {r}} — {\ mathbf {r}} ‘|} {\ sqrt {4 \ rho \ rho’}} \ end {выровнен} \ end {выровнен } $$
(9)
— взаимная индуктивность коаксиальных линейных токов ⁵, пронизывающих поперечное сечение в \ ({\ mathbf {r}} \) и \ ({\ mathbf {r}} ‘\); K ( м ) и E ( м ) — полные эллиптические интегралы. 2} {4} \ right], \ end {align} $$
(13)
действительно для \ (k \ ll 1 \) [Ур.{2}} \ frac {\ xi _1} {\ xi _1 + \ xi _2}, \ end {align} $$
(15)
, которая является обобщением формулы Рэлея ¹² для случая \ (b = a \) и является ключевым улучшением по сравнению с (5). Используя эту формулу для L и другую, \ (W = \ pi ab \ bar {\ rho} n_2 \), для ограничения длины, мы смогли легко найти оптимальное значение \ (\ xi _1 \), \ (\ xi _2 \) численно, воспроизводя (10).
Возвращаясь к коэффициенту Q , мы перепишем (1) в терминах наших характерных масштабов \ (L_c \), \ (Q_c \), \ (\ omega _c \):
$$ \ begin {выровнено } Q = \ frac {\ pi} {2} \ frac {\ omega} {\ omega _c} \ frac {L / L_c} {1 + F (\ omega)} Q_c, \ end {align} $$
(16)
, где мы ввели коэффициент увеличения потерь
$$ \ begin {align} F (\ omega) \ Equiv \ frac {R (\ omega)} {R (0)} — 1.2}. \ end {align} $$
(18)
На таких частотах \ (F \ ll 1 \) пренебрежимо мало, L практически не отличается от значения постоянного тока, поэтому коэффициент Q является линейным по \ (\ omega \):
$$ \ begin {align} \ frac {Q} {Q_c} = 1.04 \, \ frac {\ omega} {\ omega _c}, \ quad \ omega \ ll \ omega _c, \ end {align} $$
(19)
см. Рис. 3.
Катушка индуктивности
: краткое введение
Мы постоянно сталкиваемся с этими объектами, но вряд ли добавим им какой-либо конкретный смысл.Для нас это обычное дело. Фактически, индукторы сегодня используются почти в каждом устройстве, но трансформаторы являются наиболее ярким примером их использования. Если вы думаете, что трансформаторы можно использовать только на силовых подстанциях, то вы действительно ошибаетесь: ваш ноутбук или мобильный преобразователь — это своего рода трансформатор, только меньшего размера, чем те, которые используются на электростанциях и распределительных подстанциях.
Любой индуктор состоит из обмотки и сердечника. Центр — стержень из ферромагнитного или диэлектрического материала, на который намотана обмотка.Чаще всего это делается из медной проволоки.
Количество витков обмотки напрямую связано с величиной результирующей магнитной индукции катушки. Теперь мы собираемся подумать о том, какие параметры и свойства мы собираемся определить, прежде чем мы начнем вычислять индуктивность катушек и формулы, необходимые для этого.
Какие параметры у катушки индуктивности?
Катушка имеет множество физических характеристик, отражающих ее стабильность и пригодность для конкретной работы.Один из них — индуктивность. Отношение потока магнитного поля, создаваемого катушкой, к величине этого тока численно равно. Индуктивность выражается в единицах Генри (GN), которые в большинстве случаев принимают значения от микрогенри до сотен Генри.
Индуктивность, вероятно, самый важный параметр катушки. И не удивительно, что большинство людей даже не думают, что существуют другие величины, которые могут характеризовать действия катушки и представлять ее пригодность для конкретного применения.
Профессионалы также обращают внимание на сопротивление потерь при выборе индуктора. Как вы можете понять из этого выражения, оно представляет серьезность потери электричества, вызванной ложными эффектами, такими как нагревательные провода, которые возникают в соответствии с законом Джоуля-Ленца. Легко понять, что чем лучше катушка, тем меньше значение. Еще один параметр, который необходимо учитывать, — добротность схемы. Он тесно связан с предыдущим параметром, который представляет коэффициент активной реакции (сопротивления потерь).
Соответственно, чем добротность выше, тем лучше. Увеличение достигается за счет выбора оптимального диаметра проволоки, материала и диаметра сердечника, а также количества витков.
Зачем нужен расчет индуктивности?
В мире существует множество различных типов катушек. Они различаются по свойствам, а значит, и по применению. Многие из них используются в высокопрочных трансформаторах, другие — в соленоидах, служат в качестве высокопрочных электромагнитов. В дополнение к этому, есть несколько приложений индуктивности.И для всего этого требуются разные типы катушек. Их активы различаются. Но большинство этих свойств можно объединить, используя принцип индуктивности.
Мы вплотную подошли к описанию того, что требуется по формуле для измерения индуктивности катушки. Но стоит отметить, что мы говорим не о «формуле», а о «формулах», потому что все катушки можно разделить на множество широких классов, каждый из которых имеет свою собственную отдельную формулу.
Типы катушек
Функциональные возможности различаются между петлевыми катушками, используемыми в радиофизике, катушками связи, используемыми в трансформаторах, и вариометрами, то есть катушками, выход которых можно изменять, регулируя относительное расположение катушек.Есть даже катушки вроде дросселей.
В этом классе также есть разделение на обычные и двойные. Они имеют высокое сопротивление переменному току и очень низкое сопротивление постоянному току, благодаря чему они могут действовать как хороший фильтр, пропускающий постоянный ток и задержку переменного тока. Двойные дроссели более эффективны по сравнению с традиционными при высоких токах и частотах.
Формулы расчета
Пора перейти к основной теме статьи.Начнем с того, что поговорим о том, как измерить индуктивность сердечника катушки. Это простейшая форма расчета. Но и здесь есть свои тонкости. Для простоты возьмем катушку с однослойной обмоткой.
Для нее действителен расчет однослойной катушки индуктивности:
L = D 2 * n 2 / (45D + 100l)
Здесь L — индуктивность, D — диаметр катушки в сантиметрах, n — количество витков, l — длина намотки в сантиметрах. Однослойная катушка предполагает, что толщина обмотки не превышает одного слоя, что означает, что для нее справедливо измерение плоской катушки индуктивности.Большинство формул для расчета индуктивностей обычно очень похожи: основные различия в числителе и знаменателе только в коэффициентах переменных. Самым простым здесь является измерение индуктивности провода без сердечника.
Также представляет интерес формула для расчета индуктивности катушки с большим числом витков:
L = 0,08 * D 2 * n 2 / (3 * D + 9 * b + 10 * c)
Здесь b — ширина провода, c — высота провода. Такой состав эффективен для измерения многослойного индуктора.На практике он применяется немного реже, чем тот, о котором пойдет речь ниже.
Возможно, наиболее важным было бы измерение индуктивности катушки с сердечником. Существует специальная формула, которая показывает, что эту индуктивность определяет материал, из которого изготовлен сердечник, или, скорее, его магнитная проницаемость. Дизайн выглядит так:
L = m * m 0 * n 2 * S / l
Где m — магнитная проницаемость материала сердечника, m 0 — магнитная постоянная (это 12.56 · 10-7 Гн / м), S — поперечное сечение поля катушки, длительность l-витка.
Вычислить количество витков индуктора очень просто: это количество слоев намотки проводника в центре.
Мы разобрались с формулами, а теперь немного о том, где именно эти формулы и вычисления могут быть полезны.
Расчет индуктора Последовательное сопротивление
Практическое использование
Из-за широкого распространения индукторов эти формулы используются очень часто. Как мы уже выяснили, существуют разные типы катушек, каждая из которых соответствует своему применению.В связи с этим становится в некотором роде необходимым разделение их по характеристикам, потому что в каждой отрасли нужны свои определенные индуктивность и добротность.
Катушка индуктивности в электронной промышленности

В основном на производстве и в электротехнике используется измерение индуктивности катушек. Каждый любитель должен уметь рассчитать индуктивность, в противном случае он должен уметь определить, какая катушка из огромного массива подходит для их целей, а какая нет.
Вам интересно?
Большинство современных ученых интересуются магнетизмом и магнитными явлениями. Исследователи изучали как магнитную, так и электрическую стороны объектов, пытаясь найти закономерности и синтезировать сильные магниты с определенными желаемыми свойствами: например, с высокой температурой плавления или сверхпроводимостью. Многие из этих компонентов можно найти во многих отраслях промышленности.
Приведем пример аэрокосмической отрасли: перспективными являются ракеты с ионными двигателями для межзвездных полетов на большие расстояния, которые создают тягу за счет выброса ионизированного газа из сопла.Интенсивность удара в таком двигателе зависит от температуры газа и его скорости. Соответственно, чтобы придать газу полную мощность ускорения, нам нужен очень мощный магнит, который ускоряет заряженные частицы, а также имеет очень высокую температуру плавления, чтобы при выходе газов из сопла они не плавились.
Заключение
Интеллект никогда не бывает лишним, и всегда где-нибудь, так что пригодится. Теперь, если вы столкнетесь с системой расчета индуктивности катушки, вы легко сможете сказать, почему именно такие формулы существуют и какие переменные в них что означают.Эта статья предназначена только для вашего знакомства, и если вы хотите узнать больше, вы можете прочитать специализированную литературу (ее накопилось много после многих лет исследований магнитных явлений).
Рубрика: Рубрика:Разное
Навигация по записям
« Тонометр ремонт: Ремонт тонометров в Санкт-Петербурге
Можно ли перевозить холодильник лежа: Как перевезти холодильник: советуют специалисты »
Читайте также
Что делать, если грудничок не спит днем: советы по налаживанию режима сна
Антигистаминные препараты для новорожденных: лечение и профилактика аллергии у грудничков
Методика «Цветоник» М. Лазарева для музыкального развития детей
Добавить комментарий Отменить ответ
Ваш адрес email не будет опубликован. Обязательные поля помечены *
Комментарий *
Имя *
Email *
Сайт

Найти:
Рубрики
Антенна
Настройка
Подключение
Радиолюбителям
Ремонт
Ресивер
Своими руками
Усилитель
Установка
Разное

© 2019 Мир антенн. Все права защищены.
Карта сайта

Зазор (мм)	Коэффициент муфты	Взаимная индуктивность (нГн)
50	0,068109	556,24340
78,193680
150	0,001664	13,567360
200	0,000319	2,609366
58 57 58 58	58 58 58

Зазор (мм)	Коэффициент сцепления	Взаимная индуктивность (мкГн)
50	0,101212	1,452432
			0,002227	0,031972
200	0,000425	0,006089
250	0,000081	0,001156
300	0.000012	0,000169