Расчет индуктивности катушки с сердечником: Как рассчитать сердечник и витки самодельных катушек индуктивности

Рассчитать катушку индуктивности с помощью онлайн калькулятора

Катушки индуктивности являются неотъемлемым элементом различных радиоэлектронных схем. Основным её свойством является наличие большой индуктивности при малой емкости и низком активном сопротивлении. В этом обзоре описано, как выполнить самостоятельный расчет катушки индуктивности, какими внешними параметрами она должна обладать, что бы были достигнуты требуемые рабочие параметры.

Калькулятор расчета катушки индуктивности

Индуктивность можно рассчитать самостоятельно или выполнить онлайн расчет с помощью специального калькулятора. Для автоматического расчета наиболее часто используется программа Coil32. Её можно бесплатно скопировать с одноименного сайта либо воспользоваться онлайн калькулятором. Пользоваться этой программой достаточно просто.

При работе с ней сначала нужно выбрать тип изделия (однослойная или многослойная, с ферритовым сердечником или без него, возможны другие варианты).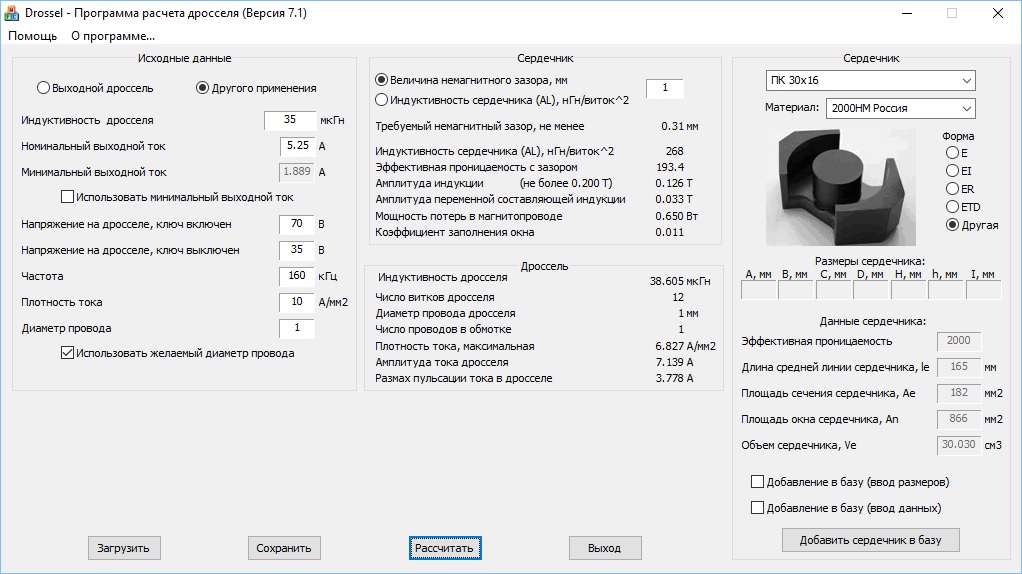

Задав в калькуляторе расчет геометрических параметров, диаметр провода, число витков, свойства сердечника можно с помощью программы получить ожидаемую индуктивность изделия. Для получения необходимой величины можно в расчетах изменять число витков и диаметр провода.

Собранное изделие по рассчитанным параметрам можно проверить с помощью тестера на соответствие необходимым параметрам. Такой прибор называется LC тестер. Он измеряет индуктивность катушек и ёмкость конденсаторов. При отклонении полученных параметров от заданной величины можно увеличить либо уменьшить количество витков проволоки на изделии.

При желании можно выполнить самостоятельно расчет индуктивности катушки без сердечника или с ним. Единой формулы нет, они строго индивидуальны для каждого случая. В общем случае они прямо пропорциональны количеству витков и диаметру витков. Например, расчет однослойной цилиндрической обмотки выполняют по формуле:

L = (D/10)2*n2/(4.5*D+10*l)

Где L – индуктивность в микро Генри, D – её диаметр в мм, L – длина в мм, n – число витков. Эта эмпирическая формула очень проста, она не учитывает диаметр проволоки, рабочую частоту на которой планируется применять изделие.

Расчет индуктивности катушки с сердечником более сложен. С его добавлением значение индуктивность сильно возрастает. В расчетах в формулу добавляются параметры магнитных свойств сердечника. Ещё более сложными являются формулы расчёта многослойных катушек или катушек тороидальной формы. При редком или первичном использовании лучше всего воспользоваться специальными калькуляторами. Полученные расчеты можно проверить по формулам вручную. В любом случае после изготовления можно проверить параметры собранного изделия и при необходимости их изменить.

 

Расчет многослойной катушки индуктивности онлайн

Онлайн помощник домашнего мастера

Катушки индуктивности являются неотъемлемым элементом различных радиоэлектронных схем. Основным её свойством является наличие большой индуктивности при малой емкости и низком активном сопротивлении.

В этом обзоре описано, как выполнить самостоятельный расчет катушки индуктивности, какими внешними параметрами она должна обладать, что бы были достигнуты требуемые рабочие параметры.

Калькулятор расчета катушки индуктивности

Индуктивность можно рассчитать самостоятельно или выполнить онлайн расчет с помощью специального калькулятора. Для автоматического расчета наиболее часто используется программа Coil32. Её можно бесплатно скопировать с одноименного сайта либо воспользоваться онлайн калькулятором. Пользоваться этой программой достаточно просто.

При работе с ней сначала нужно выбрать тип изделия (однослойная или многослойная, с ферритовым сердечником или без него, возможны другие варианты). Задав в калькуляторе расчет геометрических параметров, диаметр провода, число витков, свойства сердечника можно с помощью программы получить ожидаемую индуктивность изделия. Для получения необходимой величины можно в расчетах изменять число витков и диаметр провода.

Собранное изделие по рассчитанным параметрам можно проверить с помощью тестера на соответствие необходимым параметрам. Такой прибор называется LC тестер. Он измеряет индуктивность катушек и ёмкость конденсаторов. При отклонении полученных параметров от заданной величины можно увеличить либо уменьшить количество витков проволоки на изделии.

При желании можно выполнить самостоятельно расчет индуктивности катушки без сердечника или с ним. Единой формулы нет, они строго индивидуальны для каждого случая. В общем случае они прямо пропорциональны количеству витков и диаметру витков. Например, расчет однослойной цилиндрической обмотки выполняют по формуле:

L = (D/10)2*n2/(4.5*D+10*l)

Где L – индуктивность в микро Генри, D – её диаметр в мм, L – длина в мм, n – число витков. Эта эмпирическая формула очень проста, она не учитывает диаметр проволоки, рабочую частоту на которой планируется применять изделие.

Расчет индуктивности катушки с сердечником более сложен. С его добавлением значение индуктивность сильно возрастает. В расчетах в формулу добавляются параметры магнитных свойств сердечника.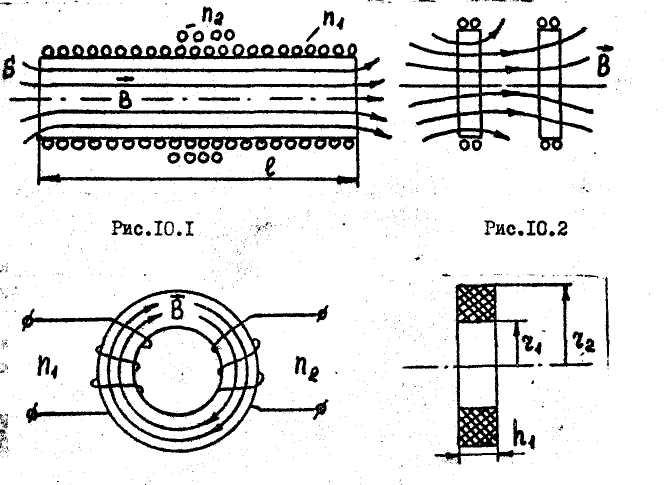 Ещё более сложными являются формулы расчёта многослойных катушек или катушек тороидальной формы. При редком или первичном использовании лучше всего воспользоваться специальными калькуляторами. Полученные расчеты можно проверить по формулам вручную. В любом случае после изготовления можно проверить параметры собранного изделия и при необходимости их изменить.

Конвертер величин

На рисунке выше показана однослойная катушка индуктивности: Dc — диаметр катушки, D — диаметр оправки или каркаса катушки, p — шаг намотки катушки, d — диаметр провода без изоляции и di — диаметр провода с изоляцией

Для расчета индуктивности LS применяется приведенная ниже формула из статьи Р. Уивера (R. Weaver) Численные методы расчета индуктивности:

Здесь

D — диаметр оправки или каркаса катушки в см,

l — длина катушки в см,

N — число витков и

L — индуктивность в мкГн.

Эта формула справедлива только для соленоида, намотанного плоским проводом. Это означает, что катушка намотана очень тонкой лентой без зазора между соседними витками. Она является хорошим приближением для катушек с большим количеством витков, намотанных проводом круглого сечения с минимальным зазором между витками. Американский физик Эдвард Беннетт Роса (Edward Bennett Rosa, 1873–1921) работавший в Национального бюро стандартов США (NBS, сейчас называется Национальное бюро стандартов и технологий (NIST) разработал так называемые корректирующие коэффициенты для приведенной выше формулы в форме (см. формула 10.1 в статье Дэвида Найта, David W. Knight):

Здесь LS — индуктивность плоской спирали, описанная выше, и

где ks — безразмерный корректирующий коэффициент, учитывающий разницу между самоиндукцией витка из круглого провода и витка из плоской ленты; km — безразмерный корректирующий коэффициент, учитывающий разницу в полной взаимоиндукции витков из круглого провода по сравнению с витками из плоской ленты; Dc — диаметр катушки в см, измеренный между центрами проводов и N — число витков.

Величина коэффициента Роса km определяется по формуле 10.18 в упомянутой выше статье Дэвида Найта:

Коэффициент Роса ks, учитывающий различие в самоиндукции, определяется по формуле 10.4 в статье Д. Найта:

Здесь p — шаг намотки (расстояние между витками, измеренное по центрам проводов) и d — диаметр провода. Отметим, что отношение p/d всегда больше единицы, так как толщина изоляции провода конечна, а минимально возможное расстояние между двумя соседними витками с очень тонкой изоляцией, расположенными без зазора, равна диаметру провода d.

Факторы, влияющие на индуктивность катушки

На индуктивность катушки влияют несколько факторов.

• Количество витков. Катушка с большим количеством витков имеет бóльшую индуктивность по сравнению с катушкой с меньшим количеством витков.
• Длина намотки. Две катушки с одинаковым количеством витков, но разной длиной намотки имеют разную индуктивность. Более длинная катушка имеет меньшую индуктивность. Это связано с тем, что магнитное поле менее компактной катушки более слабое и оно не может хорошо концентрироваться в растянутой катушке.
• Диаметр катушки. Две плотно намотанные катушки с одинаковым количеством витков и разными диаметрами имеют разную индуктивность. Катушка с бóльшим диаметром имеет бóльшую индуктивность.
• Сердечник. Для увеличения индуктивности в катушку часто вставляется сердечник из материала с высокой магнитной проницаемостью. Сердечники с более высокой магнитной проницаемостью позволяют получить более высокую индуктивность. Сердечники, изготовленные из магнитной керамики — феррита, часто используются в катушках и трансформаторах различных электронных устройств, так как у них очень низкие потери на вихревые токи.

Упрощенная эквивалентная схема реальной катушки индуктивности: Rw — сопротивление обмотки и ее выводов; L — индуктивность идеальной катушки; Rl — сопротивление вследствие потерь в сердечнике; и Cw — паразитная емкость катушки и ее выводов.

Эквивалентная схема реальной катушки индуктивности

В этом калькуляторе мы рассматривали идеальную катушку индуктивности. В то же время, в реальной жизни таких катушке не бывает. Катушки обычно конструируются с минимальными размерами таким образом, чтобы они помещались в миниатюрное устройство. Любую реальную катушку индуктивности можно представить в виде идеальной индуктивности, к которой параллельно подключены емкость и сопротивление, а еще одно сопротивление подключено последовательно. Параллельное сопротивление учитывает потери на гистерезис и вихревые токи в магнитном сердечнике. Это параллельное сопротивление зависит от материала сердечника, рабочей частоты и магнитного потока в сердечнике.

Паразитная емкость появляется в связи с тем, что витки катушки находятся близко друг к другу. Любые два витка провода можно рассмотреть как две обкладки маленького конденсатора. Витки разделяются изолятором, таким как воздух, изоляционный лак, лента или иной изоляционный материал.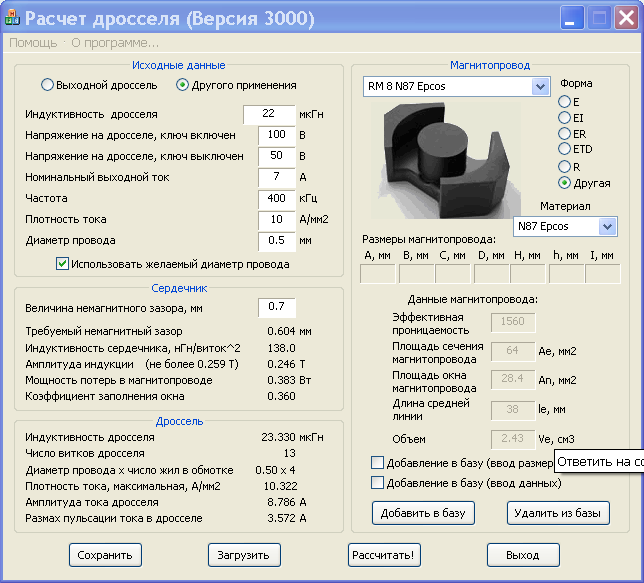

Относительная диэлектрическая проницаемость материалов, используемых для изоляции, увеличивает емкость обмотки. Чем выше эта проницаемость, тем выше емкость. В некоторых случаях дополнительная емкость может появиться также между катушкой и противовесом, если катушка расположена над ним. На высоких частотах реактивное сопротивление паразитной емкости может быть весьма высоким и игнорировать его нельзя. Для уменьшения паразитной емкости используются различные методы намотки катушек.

Для уменьшения паразитной емкости катушки с высокой добротностью для радиопередатчиков наматывают так, чтобы было достаточно большое расстояние между витками

Если индуктивность большая, то сопротивление обмотки (Rw на схеме) игнорировать уже нельзя. Тем не менее, оно мало по сравнению с реактивным сопротивлением больших катушке на высоких частотах. Однако, на низких частотах и на постоянном токе это сопротивление необходимо учитывать, так как в этих условиях через катушку могут протекать значительные токи.

Катушки индуктивности и обмотки в различных устройствах

Расчет индуктивности катушек (однослойных)

Как произвести расчет катушек индуктивности (однослойных, цилиндрических без сердечника)

Индуктивность катушки зависит от ее геометрических размеров, числа витков и способа намотки катушки. Чем больше диаметр, длина намотки и число витков катушки, тем больше ее индуктивность. То что делает катушка индуктивности в колебательных контурах является очень важным и от правильного расчета зависит добротность контура.

Если катушка индуктивности наматывается плотно виток к витку, то индуктивность ее будет больше по сравнению с катушкой, намотанной неплотно, с промежутками между витками. Когда требуется намотать катушку по заданным размерам и нет провода нужного диаметра, то при намотке ее более толстым проводом надо несколько увеличить, а тонким —    уменьшить число витков катушки, чтобы получить необходимую индуктивность.

Ресчет катушек индуктивности (однослойных, цилиндрических)

Рис. 1. Пример однослойной катушки индуктивности.

Все приведенные выше соображения справедливы при намотке катушек без ферритовых сердечников. Расчет однослойных цилиндрических катушек производится по формуле:

где:

• L — индуктивность катушки, мкГн;
• D — диаметр катушки, см;
• I — длина намотки катушки, см;
• n — число витков катушки.

При расчете катушки могут встретиться два случая:

• а) по заданным геометрическим размерам необходимо определить индуктивность катушки;
• б) при известной индуктивности определить число витков и диаметр провода катушки.

В первом случае все исходные данные, входящие в формулу, известны, и расчет не представляет затруднений.

Пример. Определим индуктивность катушки, изображенной на рис. 1; для этого подставим в формулу все необходимые величины:

Во втором случае известны диаметр катушки и длина намотки, которая, в свою очередь, зависит от числа витков и диаметра провода.

Поэтому расчет рекомендуется вести в следующей последовательности. Исходя из конструктивных соображений определяют размеры катушки, диаметр и длину намотки, а затем рассчитывают число витков по формуле:

После того как будет найдено число витков, определяют диаметр провода с изоляцией по формуле:

где:

• d — диаметр провода, мм,
• l — длина обмотки, мм,
• n — число витков.

Пример. Нужно изготовить катушку диаметром 1 см при длине намотки 2 см, имеющую индуктивность 0,8 мкГн. Намотка рядовая виток к витку.

Подставив в последнюю формулу заданные величины, получим:

Диаметр провода:

Если эту катушку наматывать проводом меньшего диаметра, то нужио полученные расчетным путем 14 витков разместить по всей длине катушки (20 мм) с равными промежутками между витками, т. е. с шагом намотки.

Индуктивность данной катушки будет на 1—2% меньше номинальной, что следует учитывать при изготовлении таких катушек.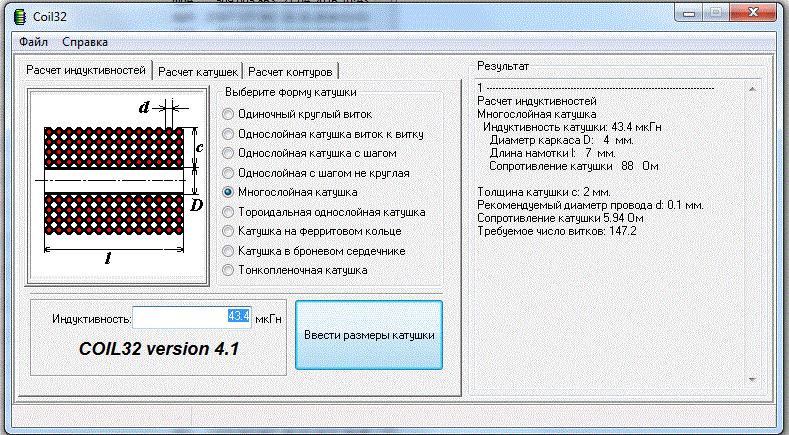 При намотке в случае необходимости более толстым проводом, чем 1,43 мм, следует сделать новый расчет, увеличив диаметр или длину намотки катушки.

Возможно, также придется увеличить и то и другое одновременно, пока не будут получепы необходимые габариты катушки, соответствующие заданной индуктивности.

Следует заметить, что по приведенным пыше формулам рекомендуется рассчитывать такие катушки, у которых длина намотки l равна или больше половины диаметра. Если же длина намотки меньше D половины диаметра то более точные результаты можно получить по формулам:

Как произвести пересчет катушек индуктивности (однослойных, цилиндрических)

Необходимость в пересчете катушек индуктивности возникает при отсутствии нужного диаметра провода, указанного в описании конструкции, и замене его проводом другого диаметра; при изменении диаметра каркаса катушки.

Если отсутствует провод нужного диаметра, что является наиболее частой причиной пересчета катушек, можно воспользоваться проводом другого диаметра.

Изменение диаметра провода в пределах до 25% в ту или другую сторону вполне допустимо и в большинстве конструкций не отражается на качестве их работы. Более того, увеличение диаметра провода допустимо во всех случаях, так как оно уменьшает омическое сопротивление катушки и повышает ее добротность.

Уменьшение же диаметра ухудшает добротность и увеличивает плотность тока на единицу сечения провода, которая не может быть больше определенной допустимой величины.

Пересчет числа витков однослойной цилиндрической катушки при замене провода одного диаметра другим производится по формуле:

где:

• n — повое число витков катушки;
• n1 — число витков катушки, указанное в описании;
• d— диаметр имеющеюся провода;
• d1 — диаметр провода, указанный в описании.

В качестве примера произведем пересчет числа витков катушки, изображенной на рис. 1, для провода диаметром 0,8 мм:

(длина намотки l= 18 X 0,8 = 14,4 мм, или 1,44 см).

Таким образом, число витков и длина намотки несколько уменьшились. Для проверки правильности пересчета рекомендуется выполнить новый расчет катушки с измененным диаметром провода:

При пересчете катушки, связанном с изменением ее диаметра, следует пользоваться процентной зависимостью между диаметром и числом витков катушки.

Эта зависимость заключается в следующем: при увеличении диаметра катушки на определенное число процентов количество витков ее уменьшается на столько же процентов, и, наоборот, при уменьшении диаметра увеличивается число витков на равное число процентов. Для упрощения расчетов за диаметр катушки можно принимать диаметр каркаса.

Рис. 2. Катушки индуктивности. Пример.

Так, для примера произведем пересчет числа витков катушки (рис. 2, а), имеющей диаметр 1,5 см, на диаметр, равный 1,8 см (рис. 2, б). Согласно условиям пересчета диаметр каркаса увеличивается на 3 мм, или на 20%.

Следовательно, для сохранения неизменной величины индуктивности этой катушки при намотке ее на каркасе большего диаметра нужно уменьшить число витков на 20%, или на 8 витков. Таким образом, новая катушка будет иметь 32 витка.

Проверим пересчет н установим погрешность, допущенную в результате пересчета. Катушка (см. рис. 2, а) имеет индуктивность:

Новая катушка на каркасе с увеличенным диаметром:

Ошибка при пересчете составляет 0,25 мкГн, что вполне допустимо для расчетов в радиолюбительской практике.

Ток в катушке индуктивности калькулятор



Расчет катушки индуктивности

Онлайн расчет многослойной катушки. Калькулятор считает по алгоритму с применением эллиптических интегралов Максвелла.
Катушка индуктивности — винтовая, спиральная или винтоспиральная катушка из свёрнутого изолированного проводника, обладающая значительной индуктивностью при относительно малой ёмкости и малом активном сопротивлении. Индуктивность катушки зависит от ее геометрических размеров, числа витков и способа намотки катушки. Чем больше диаметр, длина намотки и число витков катушки, тем больше ее индуктивность.

Смотрите также

Очень странный результат получается. На 3,4 мГ d20 L35 провод 1/1,2 получается один слой и расход провода менее одного метра. Как это??

Попробуйте поменять микрогенри на милигенри

Может попутали милигенри и микрогенри?

Тут расчет явно без сердечника, иначе были бы другие данные, например проницаемость сердечника.

А как же сердечник?
С сердечником или без него?

Ингвар, да чтож вам так нужны букввы НННН?
Длина! Дарю.

Длинна намотки это длинна катушки от точки начала намотки до конча рассчитанного проводника(метры), длинна проводника рассчитывается из нужного вам сопротивления. Например для магнитной системы вам надо не менее 1мм и не более 3 (2слоя намотки), а из-за длинны проводника у вас получается 6мм, придется увеличивать число слоев (до 4х) сделать катушку толще, но короче.

Главное индуктивность и сопртивение. Чем длиннее провод, тем больше его сопротивление!

Длина намотки никак не влияет на результаты. Так и должно быть?

Источник

All-Calc.com

Архивы

Свойства катушки

Онлайн калькулятор для вычисления свойств катушки.

Как пользоваться калькулятором

Введите следующие значения: диаметр проволоки, число витков, длина и диаметр катушки, сила тока. Нажмите на красную кнопку «Рассчитать». Программа автоматически произведет вычисления. Результаты появятся в поле снизу.

Теория

Катушка — полый внутри цилиндр, стержень с кружками на концах для наматывания на него проволоки.

Катушка индуктивности — катушка из провода, витки которого заизолированы. Применяется в электронике и электротехнике.

Формула

Расчет количества витков:

• T = витков в обмотке;
• bl = длина катушки;
• d = диаметр проволоки;

Расчет количества витков:

n = Витки / T

• n = количество витков;

Расчет наружного диаметра катушки:

cd = (2 x n x d) + bd

• cd = наружный диаметр катушки;
• bd = диаметр катушки;

Радиус середины катушки:

r = (n x d + bd) / 2

• bd = диаметр катушки;

Площадь поперечного сечения:

a = PI x r x r

• r = радиус середины катушки;
• a = площадь поперечного сечения;

Источник

Онлайн помощник домашнего мастера

Онлайн-расчет катушки индуктивности

Катушки индуктивности являются неотъемлемым элементом различных радиоэлектронных схем. Основным её свойством является наличие большой индуктивности при малой емкости и низком активном сопротивлении. В этом обзоре описано, как выполнить самостоятельный расчет катушки индуктивности, какими внешними параметрами она должна обладать, что бы были достигнуты требуемые рабочие параметры.

Калькулятор расчета катушки индуктивности

Индуктивность можно рассчитать самостоятельно или выполнить онлайн расчет с помощью специального калькулятора. Для автоматического расчета наиболее часто используется программа Coil32. Её можно бесплатно скопировать с одноименного сайта либо воспользоваться онлайн калькулятором. Пользоваться этой программой достаточно просто.

При работе с ней сначала нужно выбрать тип изделия (однослойная или многослойная, с ферритовым сердечником или без него, возможны другие варианты). Задав в калькуляторе расчет геометрических параметров, диаметр провода, число витков, свойства сердечника можно с помощью программы получить ожидаемую индуктивность изделия. Для получения необходимой величины можно в расчетах изменять число витков и диаметр провода.

Собранное изделие по рассчитанным параметрам можно проверить с помощью тестера на соответствие необходимым параметрам. Такой прибор называется LC тестер. Он измеряет индуктивность катушек и ёмкость конденсаторов. При отклонении полученных параметров от заданной величины можно увеличить либо уменьшить количество витков проволоки на изделии.

При желании можно выполнить самостоятельно расчет индуктивности катушки без сердечника или с ним. Единой формулы нет, они строго индивидуальны для каждого случая. В общем случае они прямо пропорциональны количеству витков и диаметру витков. Например, расчет однослойной цилиндрической обмотки выполняют по формуле:

L = (D/10)2*n2/(4.5*D+10*l)

Где L – индуктивность в микро Генри, D – её диаметр в мм, L – длина в мм, n – число витков. Эта эмпирическая формула очень проста, она не учитывает диаметр проволоки, рабочую частоту на которой планируется применять изделие.

Расчет индуктивности катушки с сердечником более сложен. С его добавлением значение индуктивность сильно возрастает. В расчетах в формулу добавляются параметры магнитных свойств сердечника. Ещё более сложными являются формулы расчёта многослойных катушек или катушек тороидальной формы. При редком или первичном использовании лучше всего воспользоваться специальными калькуляторами. Полученные расчеты можно проверить по формулам вручную. В любом случае после изготовления можно проверить параметры собранного изделия и при необходимости их изменить.

Источник

All-Calc.com

Архивы

Свойства катушки

Онлайн калькулятор для вычисления свойств катушки.

Как пользоваться калькулятором

Введите следующие значения: диаметр проволоки, число витков, длина и диаметр катушки, сила тока. Нажмите на красную кнопку «Рассчитать». Программа автоматически произведет вычисления. Результаты появятся в поле снизу.

Теория

Катушка — полый внутри цилиндр, стержень с кружками на концах для наматывания на него проволоки.

Катушка индуктивности — катушка из провода, витки которого заизолированы. Применяется в электронике и электротехнике.

Формула

Расчет количества витков:

• T = витков в обмотке;
• bl = длина катушки;
• d = диаметр проволоки;

Расчет количества витков:

n = Витки / T

• n = количество витков;

Расчет наружного диаметра катушки:

cd = (2 x n x d) + bd

• cd = наружный диаметр катушки;
• bd = диаметр катушки;

Радиус середины катушки:

r = (n x d + bd) / 2

• bd = диаметр катушки;

Площадь поперечного сечения:

a = PI x r x r

• r = радиус середины катушки;
• a = площадь поперечного сечения;

Источник

Бесплатная программа расчёта катушек индуктивности Coil32 — Софт для радиолюбителя — Программы

 

Катушки индуктивности практически используются почти в любой радио-аппаратуре, и довольно часто перед радиолюбителями возникает вопрос:
Как рассчитать индуктивность той, или иной катушки? Конечно можно рассчитать индуктивность по определённым формулам, но это требует времени, которого радиолюбителям всегда не хватает.
Бесплатная программа Coil32, автором которой является Кустарев Валерий, позволяет быстро рассчитать индуктивность практически любой катушки.

В программе учитываются наиболее распространенные варианты каркасов катушек. Можно рассчитать бескаркасную катушку в виде одиночного витка, на каркасах различной формы, на ферритовых кольцах и в броневых сердечниках, а также плоскую печатную катушку с круглой и квадратной формой витков. Для рассчитанной катушки, так же можно сразу рассчитать и ёмкость конденсатора в колебательном контуре.

Программа бесплатна и свободна для использования и распространения. В последней версии Coil32 v11.6.1.890 доступны расчёты:

• Одиночный круглый виток
• Однослойная виток к витку
  В качестве начальных параметров при расчете катушки можно выбрать два варианта:
  1. Известны диаметр каркаса и диаметр провода, длина намотки вычисляется.
  2. Известны диаметр каркаса и длина намотки, диаметр провода вычисляется
• Однослойная катушка с шагом
• Катушка с не круглой формой витков
• Многослойная катушка
  В качестве начальных параметров при расчете катушки можно выбрать два варианта:
  1. Известны диаметр каркаса, длина намотки и диаметр провода. Вычисляется число витков, попутно определяется толщина катушки, ее омическое сопротивление постоянному току и приблизительная длина провода для намотки («сколько надо отрезать»).
  2. Известны диаметр каркаса, длина намотки и предельное омическое сопротивление катушки. Вычисляется число витков, попутно определяется толщина катушки, нужный минимальный диаметр провода  и приблизительная длина провода для намотки.
• Тороидальная однослойная катушка
• Катушка на ферритовом кольце
• Катушка в броневом сердечнике
  (Ферритовом и карбонильном)
• Тонкопленочная катушка
  (Плоская катушка на печатной плате с круглой и квадратной формой витков и в виде одиночного прямого проводника)

Для расчета дополнительных видов индуктивности, которых нет в общем списке программы под заголовком «Выберите форму катушки» — имеется набор дополнительных плагинов «Plugins». Список плагинов и их краткое описание отображены на рисунке ниже.

 

 

В чем преимущества данной программы перед аналогами?

• Программа рассчитывает индуктивность различных типов катушек под имеющийся каркас.
• Результаты расчетов выводятся в текстовое поле справа, откуда их можно сохранить в файл. Можно открыть этот файл в «MS Word» и распечатать.
• Есть возможность рассчитать добротность для радиочастотных однослойных катушек индуктивности.
• Можно рассчитать основные параметры колебательного контура для однослойной катушки
• Можно рассчитать длину провода для намотки однослойной, многослойной катушки и катушки на ферритовом кольце.
• Для расчёта катушек в броневых сердечниках, есть возможность выбора одного из нескольких стандартных сердечников, что позволяет рассчитать катушку в несколько кликов.
• Для плоских катушек на печатной плате программа подскажет оптимальные размеры для достижения наивысшей добротности.
• Программа имеет мультиязычный интерфейс (20 языков) и дополнительные наборы скинов, которые можно скачать и установить из меню «Настройки».

Программа распространяется бесплатно в стиле «Portable» и не имеет установщика. Для работы с программой — скачайте архив, распакуйте его в любое удобное для Вас место и запустите файл Coil32.exe. При постоянной работе с программой, желательно создать для нее специальную папку и вынести ярлык Coil32.exe на рабочий стол.

Скачать Coil32.
 

 

 

 

Расчет катушки на цилиндрическом сердечнике: pkuz — LiveJournal

Раз уж сегодня день космонавтики, то и тема космическая…….а именно расчет катушки на цилиндрическом сердечнике, если быть точным то разомкнутый сердечник (не думал что такая сложная тематика J).

Расчетные данные не точны, желающие могут проверить, других методик мне неизвестно.

Расчетные величины буду просчитывать для контура ПЧ от ЧБ телевизоров (мне больше нравятся  с круглым экраном).

Справочные данные на них мне не попадались, однако известно, что подстроичные сердечники из карбонильного железа, назывались СЦР.

В литературе, пятилеток и прочего, нашей промышленности, очень много рассказывалось о достижениях,  в качестве материала сердечника используют карбонильное железо марок Р-10, Р-20, Р-100.

Однако в справочной литературе лишь мельком проскакивал материал и якобы проницаемость 10,но тогда не понятно их широкое использование  в ТВ, где частоты ПЧ около 30-20мГц.

В пользу большей проницаемости говорит  частота измерений-15мГц. Марку сто встретить мне не удавалось и где она применялась неизвестно.

Порывшись в предложениях сегодняшнего дня, было сделано открытие, что теперь сердечники СЦР-1(М6*0,75*10) называются ПР6х0.75х10 . Самое интересное, в подтверждение предположения о проницаемости, мы их делаем, можем сделать на заказ из стандартного материала Р-20.Однако в размерах явно путаница с диаметром тела (или мы их штампуем с такой глубиной резьбы?).

С материалом все выбрано, данные есть, можно начинать расчет.

Многослойная нас не интересует.
Мои данные: Диаметр каркаса-8,2мм,экрана 24мм,Проницаемость 20, сердечник 4,5мм*10мм,поэтому приведу расчет для длин от 1-12мм.
В таблице последние две строки- результат расчета в Coil32,для индуктивности со штрихом(расчетная с учетом действия экрана,а начальная была 2мкгн и емкости 110пф,провод ПЭТВ-2 0,2мм).Во второй таблице просчет для проницаемости 10.


Намотанный контур с 9 витками……очень мало,резонанс где-то 12мГц,оптимальный результат 14 витков.Если кто сможет измерить индуктивность….то буду благодарен.

Как произвести расчет катушек индуктивности (однослойных, цилиндрических без сердечника)

Как произвести расчет катушек индуктивности (однослойных, цилиндрических без сердечника)

Индуктивность катушки зависит от ее геометрических размеров, числа витков и способа намотки катушки. Чем больше диаметр, длина намотки и число витков катушки, тем больше ее индуктивность.

Если катушка наматывается плотно виток к витку, то индуктивность ее будет больше по сравнению с катушкой, намотанной неплотно, с промежутками между витками. Когда требуется намотать катушку по заданным размерам и нет провода нужного диаметра, то при намотке ее более толстым проводом надо несколько увеличить, а тонким — уменьшить число витков катушки, чтобы получить необходимую индуктивность.

Все приведенные выше соображения справедливы при намотке катушек без ферритовых сердечников.

Расчет однослойных цилиндрических катушек производится по формуле

где L — индуктивность катушки, мкГн; D — диаметр катушки, см; l — длина намотки катушки, см; n—число витков катушки.

При расчете катушки могут встретиться два случая:

а) по заданным геометрическим размерам необходимо определить индуктивность катушки;

б) при известной индуктивности определить число витков и диаметр провода катушки.

В первом случае все исходные данные, входящие в формулу, известны, и расчет не представляет затруднений.

Пример. Определим индуктивность катушки, изображенной на рис. 97; для этого подставим в формулу все необходимые величины:

Во втором случае известны диаметр катушки и длина намотки, которая, в свою очередь, зависит от числа витков и диаметра провода. Поэтому расчет рекомендуется вести в следующей последовательности. Исходя из конструктивных соображений определяют размеры катушки, диаметр и

длину намотки, а затем рассчитывают число витков по формуле

После того как будет найдено число витков, определяют диаметр провода с изоляцией по формуле

где d— диаметр провода, мм, l — длина обмотки, мм, п — число витков.

Пример. Нужно изготовить катушку диаметром 1 см при длине намотки 2 см, имеющую индуктивность 0,8 мкГн. Намотка рядовая виток к витку.

Подставив в последнюю формулу заданные величины,

получим:

Диаметр провода

Если эту катушку наматывать проводом меньшего диаметра, то нужно полученные расчетным путем 14 витков разместить по всей длине катушки (20 мм) с равными промежутками между витками, т. е. с шагом намотки. Индуктивность данной катушки будет на 1—2% меньше номинальной, что следует учитывать при изготовлении таких катушек. При намотке в случае необходимости более толстым проводом, чем 1,43 мм, следует сделать новый расчет, увеличив диаметр или длину намотки катушки. Возможно, также придется увеличить и то и другое одновременно, пока не будут получены необходимые габариты катушки, соответствующие заданной индуктивности.

Следует заметить, что по приведенным выше формулам рекомендуется рассчитывать такие катушки, у которых длина намотки l равна или больше половины диаметра. Если же длина намотки меньше половины диаметра D/2 , то более точные результаты можно получить по формулам

В.Г.Бастанов, «300 практических советов»

Как сделать индуктор с воздушным сердечником-Formula

S Иногда вы не можете найти конкретный индуктор на рынке. На самом деле с этой проблемой сталкивается большинство любителей электроники, и проблема становится более серьезной, если ваш проект связан с радиочастотами. Катушки индуктивности, необходимые для РЧ-цепей (антенна, тюнер, усилитель и т. Д.), Практически невозможно найти на рынке, и единственное решение — не что иное, как их приготовление в домашних условиях.

Приложив немного практики и терпения, вы сможете сконструировать почти все индукторы с воздушным сердечником в домашних условиях.Индуктивность индуктора с воздушным сердечником может быть представлена ​​с помощью упрощенной формулы, показанной ниже, и для расчета индуктивности индуктора с воздушным сердечником можно использовать то же уравнение.

L = [d ² n ² ] / [18d + 40l]

• Где ‘L’ — индуктивность в Micro Henries [мкГн]
• ‘d’ — диаметр катушки от одного центра провода до другого центра провода. Следует указывать в дюймах.
• ‘l’ — длина катушки в дюймах.
• ‘n’ — количество витков.

Примечания:

• Длина катушки, используемой в индукторе, должна быть равна или 0,4 диаметра катушки.
• Как показано в уравнении, индуктивность индуктора с воздушным сердечником изменяется как квадрат числа витков. Таким образом, значение «l» умножается в четыре раза, если значение «n» удваивается. Значение «l» умножается на два, если значение «n» увеличивается до 40%.

Намотка катушки.

• Катушка должна быть сначала намотана на пластмассовый каркас соответствующего диаметра (равного требуемому диаметру сердечника).
• Обмотка должна быть плотной, а соседние витки должны располагаться как можно ближе.
• После завершения намотки медленно извлеките сердечник, не трогая катушку.
• Теперь нанесите тонкий слой эпоксидной смолы на поверхность змеевика для механической поддержки.
• Снимите изоляцию с концов катушки.

Пример

Предположим, вы хотите сделать катушку индуктивности с индуктивностью 10 мкГн.Диаметр катушки составляет 1 дюйм, а длина катушки — 1,25 дюйма. Вам нужно будет найти количество витков катушки.

Таким образом подставляя значения в уравнение выше

L = 10 дюймов

d = 1 дюйм

l = 1,25 дюйма

n = √ {L [18d * 40l]} / d = 26

Таким образом, количество витков катушки будет 26.

Число витков на дюйм = 20,8

Похожие сообщения

Индуктивность, импеданс и потери — Блог о пассивных компонентах

л.1,7 Индуктивность L

Не только магнитные материалы обладают магнитным полем, каждый проводник с током сам создает магнитное поле.

Рис. 1.23: Магнитные поля токоведущих проводов

Энергия может временно храниться в магнитном поле. Этот эффект технически используется в катушках, состоящих из одной или нескольких проволочных обмоток. Синонимичный термин «индуктор» утвердился.

Существуют различные типы индукторов или катушек:

• Воздушные змеевики (без феррита)
• Дроссельные катушки с сердечником из железного порошка или ферритовым сердечником
• Катушка с тороидальным сердечником
• Катушка стержневого сердечника
Типы
• SMD становятся все более важными из-за своего небольшого размера.Помимо индукторов SMD с намоткой, все большее распространение получают индукторы для многопользовательской игры.

Все катушки имеют особое поведение, более подробно описанное в следующих определениях.

1.7.1 Определение индуктивности L

Элемент схемы, который реагирует на изменение тока противодавлением, проявляет индуктивные свойства. Катушка индуктивности — это пассивный компонент, который, как сопротивление переменному току, создает противодействующее напряжение — напряжение самоиндукции.

Напряжение самоиндукции (U _ind ) на выводах индуктора зависит от скорости изменения тока (di / dt) и константы пропорциональности, индуктивности (L):

Индуктивность (L ) катушки зависит от материала сердечника, геометрии материала сердечника, витков обмотки и типа обмоток. Следующее уравнение обычно применяется для расчета индуктивности (L):

Единицей измерения индуктивности (L) является Генри (H) = Vs / A .

Индуктивность сердечников со вставленным воздушным зазором можно рассчитать по следующей формуле:

l _{среднее значение} = средняя длина магнитного пути в сердечнике (без воздушного зазора)
l _зазор = длина пути воздушный зазор (а)
мкм _r = относительная проницаемость

Эта формула, вставленная в формулу для расчета общей индуктивности, дает:

Это также позволяет определить ширину воздушного зазора, если известны требуемая индуктивность L и другие параметры.Здесь необходимо иметь в виду, что приведенная выше формула применима только в том случае, если μ _r велико, а длина воздушного зазора намного меньше средней длины в сердечнике.

Чтобы учесть паразитные эффекты и их влияние на индуктивность, Маклайман предлагает следующую форму расчета паразитных эффектов F:

w _h = высота обмотки
l _зазор = длина пути воздушного зазора ( s)
A _зазор = площадь поперечного сечения воздушного зазора
F = коэффициент рассеяния

В результате индуктивность L _F изменяется на расчетное значение L _{зазора в} раз больше, чем коэффициент рассеяния F:

Положительное влияние воздушного зазора заключается в увеличении тока насыщения для сердечника того же размера.Недостатком является то, что для достижения заданного значения L количество витков теперь должно быть увеличено, и поэтому, если нет места для обмотки, для более толстого или более одного провода в бифилярной или трехзаходной обмотке сопротивление постоянному току обмотки также увеличивается.

Ни при каких обстоятельствах не следует уменьшать количество витков для компенсации паразитного эффекта — это дополнительно увеличивает индукцию и может привести к преждевременному насыщению.

Требуемая ширина воздушного зазора для данной индуктивности L с учетом паразитного фактора F может быть рассчитана в первом приближении следующим образом:

1.7.2 Определение значения A _L

Чтобы избавить пользователя от расчета эффективной магнитной длины (l _eff ) и площади (A _eff ), для тороидальных сердечников и гильз указано соответствующее значение A _L . Он представляет собой эффективную индуктивность для одной обмотки и должен быть умножен на квадрат витков обмотки (N), чтобы получить фактическую индуктивность (L).

Величина (A _L ) представляет собой индуктивность (L) при условии N = 1 витков обмотки.Таким образом, при заданном значении A _L необходимое количество обмоток катушки может быть найдено без необходимости проделывать долгий путь с учетом геометрических данных сердечника:

Пример:
Требуемая индуктивность 100 мкГн; сердечник имеет значение A _L , равное 250 нГн / Н ²

Результат:
Сердечник должен иметь 20 обмоток для создания индуктивности 100 мкГн.

1.7.3 Импеданс Z

Если катушка индуктивности работает от переменного напряжения, очевидно, что она имеет другое сопротивление, чем при работе на постоянном токе.

Сопротивление переменного напряжения, приложенного к клеммам катушки, называется импедансом (Z) .

Рис. 1.24: Взаимосвязь между импедансом, реактивным сопротивлением и сопротивлением

Импеданс (Z) зависит от частоты и складывается из геометрической суммы сопротивления потерь (R) и реактивного сопротивления (X _L ) идеальной катушки (L).

Реактивное сопротивление X _L определяется следующим образом:

Наблюдение:

Импеданс растет с увеличением частоты.

Эта линейная зависимость продолжается до бесконечно высоких частот для идеальной катушки.

Рис. 1.25: Кривая импеданса для реальных катушек индуктивности

Однако из-за частотной зависимости проницаемости и конструкции катушки и паразитной емкости применимость катушек на высоких частотах ограничена.

Импеданс быстро уменьшается от собственной резонансной частоты; индуктивный характер катушки исчезает.

1.7.4 Собственная резонансная частота (SFR)

Рис. 1.26: Эквивалентная схема реальной индуктивности

Каждая катушка индуктивности также имеет емкостную связь, возникающую из ее обмоток или многослойных элементов. Эти паразитные емкости обозначены конденсатором (C) в эквивалентной схеме. Этот конденсатор в катушке образует параллельный резонансный контур с индуктивностью.

На собственной резонансной частоте входная энергия колеблется между элементами индуктивности и емкости.Внешняя энергия больше не поглощается (идеальная катушка).

Если катушка работает выше своего резонанса, она становится все более емкостной. На практике катушки должны работать намного ниже их резонансной частоты.

1,7,5 R потери

Активная мощность (тепловые потери) не рассеивается на реактивном сопротивлении X _L из-за сдвига фаз на 90 ° между напряжением и током. Общие потери в катушке можно объединить в сопротивление потерь (R), которое последовательно соединено с идеальной индуктивностью (L).В результате получается эквивалентная схема реальной индуктивности (см. Рисунок 1.26).

Поскольку потери в R зависят от частоты, сопротивление постоянному току (DCR) также всегда определяется в технических характеристиках. Это зависит от материала используемого провода или типа конструкции индукторов SMD и определяется при комнатной температуре путем простого измерения сопротивления.

Размер сопротивления DCR напрямую влияет на повышение температуры катушки. Поэтому следует избегать длительного превышения текущего номинального значения.Общие потери в катушке состоят как из потерь в сопротивлении постоянному току DCR, так и из следующих частотно-зависимых компонентов:

• Потери в материале сердечника (потери на магнитный гистерезис, вихретоковые потери)
• Дополнительные потери в проводнике от скин-эффекта (смещение тока на высоких частотах)
• Потери магнитного поля соседних обмоток (эффект близости)
• Радиационные потери
• Потери от дополнительной магнитной защиты (WE-MI)

Все эти компоненты потерь можно объединить в сопротивление потерь (R).Это сопротивление потерь в первую очередь отвечает за определение качества катушки индуктивности. К сожалению, математическое определение сопротивления потерь R невозможно.

Поэтому индукторы обычно измеряются во всем частотном диапазоне с помощью анализатора импеданса. Это измерение обеспечивает отдельные компоненты X _L (f), R (f) и Z (f). Добротность определяется как характеристика качества индуктора.

1.7.6 Потери меди

Потери в меди для индуктивных компонентов состоят из потерь на постоянный ток и потерь на вихревые токи.Потери постоянного тока рассчитываются по закону Ома:

P _В = потеря мощности
R = сопротивление постоянному току
I _RMS = эффективный ток

На более высоких частотах также есть потери из-за скин-эффекта и эффекта близости. Эти потери от вихревых токов можно напрямую объяснить законом Фарадея. Ток, протекающий по проводнику, создает вокруг него магнитное поле.

Это магнитное поле быстро изменяется из-за высокой частоты, так что в проводнике и в соседних проводниках индуцируется напряжение.Это напряжение генерирует ток, противодействующий исходному току. Таким образом, в проводнике, а также в соседних проводниках возникают дополнительные токи.

Рассматривая одиночный проводник, говорят о скин-эффекте. Для проводников, по которым протекают токи высокой частоты, ток течет только по внешней обшивке проводника (рисунок 1.27). Глубина проникновения, при которой плотность тока упала до значения 1 / e, определяется по формуле:

δ = глубина проникновения
ρ = удельное сопротивление
ω = угловая частота 2 πf
μ = проницаемость проводника (для меди μ ₀ )

Глубина проникновения при 50 Гц равна 9.38 мм, при 10 кГц — 0,66 мм.

Рис. 1.27: Распределение тока в проводнике на высокой частоте. В качестве примера приведен диаметр проволоки, в 7 раз превышающий глубину проплавления.

Эффект близости играет гораздо большую роль для трансформаторов, когда соседние проводники генерируют поля, смещенные током. Возможность расчета потерь на вихревые токи для простой геометрии описана Доуэллом. Теория была развита Карстеном. Математическое описание выходит далеко за рамки этой книги.

Здесь гораздо важнее описать имеющиеся варианты ограничения потерь на вихревые токи. Потери на вихревые токи зависят от величины магнитного поля. Таким образом, способ ограничения потерь на вихревые токи заключается в ограничении напряженности магнитного поля.

Это может быть достигнуто, например, путем чередования обмоток, т.е. наматывается половина первичной обмотки, затем вторичная обмотка и затем вторая половина первичной обмотки. Это снижает абсолютную величину магнитного поля и, следовательно, потери на вихревые токи.На рисунке 1.28 показан профиль поля H в обмотке из медной фольги со структурой обмотки первичная — вторичная и половина первичной вторичной обмоток — половина первичной обмотки.

Напряженность магнитного поля внутри обмотки возрастает изнутри наружу, потому что все больше витков (все большие токи) ограничиваются силовыми линиями. Магнитное поле вторичной обмотки противоположно исходному полю. Это снова служит для уменьшения магнитного поля. Уменьшение величины поля H очевидно.

Рис. 1.28: Профиль магнитного поля в трансформаторе с различными конфигурациями обмоток.

Тонкие плоские проводники, например медная фольга, также может использоваться для намотки. Толщина должна быть порядка глубины проникновения. Это следует использовать только для небольшого числа витков, потому что при большем количестве обмоток большое количество слоев вызывает более высокие потери на вихревые токи.

Еще одним вариантом уменьшения вихревых токов является намотка более тонкими изолированными проводами, а не толстыми.Здесь необходимо следить за тем, чтобы отдельные провода, подключенные параллельно, имели одинаковое распределение тока. Здесь можно использовать высокочастотные литц-провода, при которых отдельные провода скручиваются друг с другом, так что в среднем каждый провод имеет одинаковое положение в магнитном поле. С этим вариантом также нужно следить, чтобы количество слоев не было слишком большим.

1.7.7 Определение добротности Q

Компонент входящей извне энергии, преобразованной в тепло в сопротивлении потерь R, не вносит вклад в энергию, запасенную в магнитном поле.Чем больше эти потери, тем хуже индуктор действует как буфер.

Это определяет качество как фактор качества Q следующим образом:

Практические значения:

• Воздушный змеевик Q до 400
• Ферритовый дроссель Q до 150
• Многопользовательские индукторы SMD Q до 60

График качества-частоты помогает выбрать лучшую конструкцию индуктора для конкретного применения.

Фиг.1.29: График добротности — частота

Наблюдения:

• Качество повышается до максимального значения, а затем снижается.
• Допускаются постоянные малые потери в сопротивлении R индуктора вплоть до пикового значения качества.
• За пределами пикового значения становятся очевидными значительные потери, а также изменяется индуктивность из-за нелинейности ферритового материала.
• Рабочий диапазон с наименьшими потерями может быть определен до критической точки качества.Если катушка индуктивности используется на более высоких частотах, потери быстро увеличиваются.

1.7.8 Температурный режим

Рис. 1.30: Температурный дрейф многослойного индуктора

Катушки с ферромагнитным сердечником демонстрируют переменную индуктивность в зависимости от температуры окружающей среды. Если к стабильности цепей фильтров, построенных с использованием катушек индуктивности
, предъявляются высокие требования (например, в измерительной технике), целесообразно выбрать катушку с почти линейной температурной кривой.В этом случае изменение индуктивности ΔL относительно номинальной индуктивности L катушки является наименьшим. На рисунке 1.30 показан этот график для многослойной катушки индуктивности.

1.7.9 Номинальный ток

Номинальный ток, который может выдерживать индуктор, более точно определен в главе о компонентах для различных продуктов.

Номинальный ток обычно связан с заявлением о самонагреве компонента. Если компонент работает при номинальном токе, он нагревается выше температуры окружающей среды на температуру, указанную в техническом паспорте.

Затем необходимо выяснить, подходит ли полученная температура компонента для данного применения. В противном случае необходимо выбрать компонент с более высокой допустимой нагрузочной способностью по номинальному току. Необходимо убедиться, что при работе при номинальном токе деталь не превышает рабочую температуру (в противном случае необходимо снижение номинальных характеристик).

Пример:
Многослойный экранированный индуктор (WE-MI) Максимальное значение номинального тока достигается, если повышение температуры компонента превышает 20 ° C для выбранного испытательного тока.

1.7.10 Ток насыщения

Ток насыщения катушки индуктивности — это ток, при котором значение индуктивности упало на процент, указанный в таблице данных.

Пример:
Дроссели накопителя серии WE-PD

Здесь ток насыщения определяет ток, при котором индуктивность упала на 10%.

Примечание!
Специально для приложений с коммутационным контроллером или приложений с высокими емкостными нагрузками или высокими пусковыми токами, пиковый ток, протекающий через катушку индуктивности, может быть значительно выше в момент включения, чем при нормальной работе.Это может привести к полному насыщению компонента и, следовательно, к возможным последующим неисправностям электроники. Желательно понимать и ограничивать ток или активировать функции плавного пуска.

Рис. 1.31: График индуктивности-ток

---

ABC CLR: Глава L Индукторы

Индуктивность, импеданс и потери

Лицензионный контент EPCI: Würth Elektronik eiSos, Trilogy of Magnetics, распечатки справочника можно заказать здесь.

Содержание этой страницы находится под международной лицензией Creative Commons Attribution-ShareAlike 4.0.

Формулы и калькулятор для тороидальных индукторов

Тороидальные индукторы часто используются в приложениях для импульсной подачи энергии и регулирования мощности, поскольку магнитные поля в значительной степени ограничены объемом формы. Все формулы на этой странице показаны для тороидального индуктора с воздушным сердечником. Если использовать магнитный сердечник в качестве формы для намотки тороида, индуктивность тороида можно найти, вычислив значение по соответствующей формуле, показанной ниже для индуктора с воздушным сердечником, а затем умножив это значение на относительную проницаемость магнитного сердечника. основной материал.

Тороиды могут быть намотаны круглой формы, как показано на рисунке ниже:

Схема тороидального индуктора круглого сечения

Индуктивность такого тороида можно рассчитать по следующей формуле:

Уравнение для тороидального индуктора круглого сечения

, где N — количество витков, R — средний радиус формы, показанной на рисунке (в см), а a — радиус обмоток формы, как показано на рисунке (в см).

Другая формула индуктивности тороида круглого сечения показана ниже:

Альтернативная формула для тороидального индуктора круглого сечения

, где N — количество витков, D — средний диаметр формы, показанной на рисунке (в дюймах), а d — диаметр обмоток, как показано на рисунке (в дюймах).

Они также могут иметь прямоугольную форму, как показано на рисунке ниже:

Схема тороидального индуктора квадратного сечения

Индуктивность тороида прямоугольного сечения может быть найдена из следующего уравнения (Terman, Frederick E., Radio Engineers Handbook , McGraw-Hill, New York, 1943, p58.):

Уравнение для тороидального индуктора с квадратным поперечным сечением

, где N — количество витков, h — высота обмотки (в дюймах), d ₁ — внутренний диаметр (в дюймах), а d ₂ — внешний диаметр (в дюймах).

Вторая формула для тороида прямоугольной формы показана ниже:

Альтернативное уравнение для тороидального индуктора с квадратным поперечным сечением

, где N — количество витков, h — высота обмотки (в см), r ₁ — внутренний радиус (в см), а r ₂ — это внешний радиус (в см).

Калькуляторы, представленные ниже, могут использоваться для определения правильных параметров тороидального индуктора круглого или квадратного сечения. Кредит за исходный код Javascript, используемый в калькуляторе, дан Рэю Аллену, у которого есть несколько подобных полезных калькуляторов на своем веб-сайте Pulsed Power Portal.

---

Консультации, комментарии и предложения направляйте по адресу [email protected]

Ссылки для намотки рулонов Страница

Сделай сам К4ЗАД Калькулятор намотки катушки Ссылки

Радио домашние пивовары легко справляются с работой с резисторами и конденсаторами; они поставляются в аккуратных маленьких упаковках, и их ценность легко решительно, но работать с индукторами не так просто. Чтобы получить индуктивность и другие желаемые характеристики, катушки часто не могут быть куплены и должны быть намотаны на заказ.Катушка дизайн / создание включает выбор правильной формы катушки, размера провода и материал сердечника (если не воздух), все составляющие процесс немного сложный. к счастью несколько авторы / веб-программисты взяли основные формулы для конструкции индуктора и создали онлайн-калькуляторы, которые помогают определить физический параметры, необходимые для катушки с желаемой электрической характеристики. Ниже приведены ссылки на онлайн-калькуляторы. полезен при разработке катушек для радиоприложений.Смотреть на этих сайтах, так как некоторые из них перечисляют другие полезные калькуляторы.

Кому насколько мне известно во время создание этой страницы все ссылки к бесплатным калькуляторам без регистрации, необходимой для использования. Как и я использовал только некоторые из них я не давать никаких рекомендаций, и порядок листинга не указывает предпочтение. Информация о каждом может помочь вам выбрать лучшие удовлетворяя ваши потребности. Стоит отметить, что авторы некоторых критично относятся к точности используемых формул другими.

Многие благодаря авторам за их работу в создание этого браузерного дизайна вспомогательные средства доступны.

### Указывает на калькуляторы которые выходят за рамки простого решения уравнения для одного заявленного отсутствующее значение, найдя недостающее значение при условии, что другие значения введены.

Несколько Расчеты или конфигурации катушек:

Три Калькуляторы индуктивности — Единицы: nHenrys, uHenrys & mHenrys — вычисляет количество витков катушки AL и L
Индуктивность и многое другое — Несколько вариантов единиц измерения — Выход — индуктивность — Калькуляторы для доступны несколько форм без катушки.
Калькулятор индуктивности катушки — Несколько выбор единиц — вычисляет индуктивность для однослойных / многослойных соленоидов и плоские спиральные катушки
Найти L для катушек и других форм — Несколько вариантов юнитов + Проницаемость — Выходная индуктивность
Калькулятор индуктивности с двумя катушками — Входы в дюймах — Делает однослойные и многорядные многослойные катушки.Вычисляет L
Пять Калькуляторы катушки / индуктивности — Несколько калькуляторов индуктивности использование различных знаний для входных данных — Размеры в мм
Три калькулятора катушек / индуктивности — Вводятся в см или дюймах — Делает однослойный и многорядные многослойные катушки. Вычисляет L
Три калькулятора катушек / индуктивностей — Выбор единиц для входов — 2 выхода — индуктивность — другое — реактивность

Одноместный Катушки с воздушным сердечником слоя:

Калькулятор индуктивности с воздушным сердечником — Широкий выбор единиц размера катушки — Вычисляет индуктивность с выбором единицы
Воздух Конструктор сердечника индуктивности — Калькулятор — Ввод в миллигенах и дюймах — расширенный вывод на новую страницу Калькулятор индуктора с воздушным сердечником
— включает Q — Размеры в мм — Вычисляет Индуктивность, добротность и длина провода
AL Калькулятор индуктивности ### — Введите два значения и получите третье — Единицы индуктивности: mHenrys, uHenrys, nHenrys Калькулятор индуктивности катушки
— Размеры в дюймах -Вычисляет индуктивность в uHenrys и длина провода в дюймах и футах
Калькулятор с двумя катушками — Входные размеры в миллиметрах или дюймах и количество оборотов — Вычисляет индуктивность и количество витков
Helical Coil Calculator — Input размер в мм или дюймах — вычисляет индуктивность и провод длина — включает собственная емкость
Многоступенчатая конструкция катушки -Входной размер в мм — Расчеты для несколько свойств змеевика — с примерами
LF Калькулятор индуктивности — Размеры в мМетрах и МГц (для Q) — Результат в microHenrys и Q
Одноместный Слой, воздушный сердечник, калькулятор индуктивности — размеры указаны в мм МГц (для Q) — Вычисляет L в нескольких единицах измерения и длине провода Калькулятор индуктивности воздушного сердечника
— Размеры в дюймах — Выход в uHenrys
Индуктивность однослойных катушек на цилиндрические формы — введите радиус, длину, проницаемость и количество витков — вычисляет калькуляторы индуктивности uH
LC — Входные витки, диаметры катушек и проводов в дюймах — Вычисляет uHenrys и провод и катушку длина Калькулятор индуктивности катушки с воздушным сердечником
— Входные обороты, диаметр и длина рулона в дюймах — Расчет L в uHenrys
Однослойный Калькулятор воздушной катушки — Широкий выбор единиц — Входная длина, диаметры катушек и проводов — Вычисления Обороты и длина рулона
Одноместный Калькулятор слоев воздушного змеевика — ### — Поля ввода: обороты, диаметр, длина и L — введите 3, получите 4-е.- С примерами
Еще одна однослойная воздушная катушка Калькулятор — Выбор единиц — Входная длина, диаметры катушки и проволоки — Вычисление оборотов и длина рулона
Калькулятор цилиндрической катушки профессора Койла — Закрывает ли катушки намотки и намотки пространства — Прочтите инструкции первый
Два Калькуляторы катушек — выбор единиц — один рассчитывает L, другой витков и длину намотки

Одноместный Слой катушек поверх магнитного материала:

Универсальный однослойный калькулятор — ### — Ввод: 4 параметра и 5-й — банка использоваться для поиска неизвестного ядра Проницаемость
Комплексный Калькулятор катушки — Слишком обширно, чтобы резюмировать — Взгляните на это — Включает в себя собственная емкость Конструкция катушки
и калькулятор индуктивности — Ввод: размеры в метрических единицах или дюймах — Вычисляет индуктивность в uHenrys
Индуктивность однослойных катушек — вход: Обороты, размеры в мметрах и перм.- Рассчитывает L на новой странице
Расчет индуктивности круговой петли — Ввод: витки, размеры в миллиметрах и перми. — Рассчитывает L в Генри
находит индуктивность однооборотного соленоида — Выбор единиц измерения — Ввод: число оборотов, радиус длины и допустимость. — Выход L в нескольких единицах
Цилиндрическая катушка индуктивности Калькулятор дизайна — ### — с помощью 4 калькулятора — выбор единиц — Вычисляет L, повороты, допуск, площадь и длину

Тороид Катушки:

Калькулятор тороида амидона (железный порошок) — Введите желаемый размер ядра uHenrys и Amidon и цвет в найти L, повороты и т. д.
Калькулятор тороида Amidon (феррит) — Введите желаемый размер ядра uHenrys и Amidon и цвет в найти L, повороты и т. д. Калькулятор индуктивности с ферритовым сердечником
— Введите количество витков и AL, чтобы найти индуктивность катушки.
Индуктивность тороида — вход размеры сердечника в см, количество витков и проницаемость для поиска катушки Индуктивность Калькулятор индуктивности тороида
— Вход размеры сердечника в мм или мил, количество витков и проницаемость, чтобы найти катушку Индуктивность
Калькулятор индуктивности тороида на оборот — Широкий выбор единиц ввода и количества оборотов — Выходы L и другие характеристики
Калькулятор индуктивности с двумя тороидами — Широкий выбор устройств ввода / вывода & количество витков — Выходы L и другие характеристики
Калькулятор намотки тороида — Находит количество витков для питаемых железных и ферритовых сердечников. известный размер и состав материала
Некоторые Справка по работе с тороидами: (См. Также последний раздел Дополнительные Катушка Информация ниже)

Тороид Таблица спецификаций — для тороидов 88 — с гибким калькулятор
Toroid Графики характеристик — Восемь диаграмм данных по тороидам
G-QRP Информация о клубном тороиде — для обычных тороидов — включает AL данные Таблица индуктивности тороида
G-QRP Club — PDF-файл значений mHenrys для много цветов тороиды с 1-50 оборотами
Что это за материал? — Мой PDF Сборник (Скачать) методов идентификации материала тороида
Калькулятор индуктивности тороидального сердечника Ferrte — Мощный автономный калькулятор Excel с числовыми и графические результаты.
Тороиды — некоторые практические соображения — Подробная статья — с номинальной мощностью (Ватт) для многих общие тороиды
Собственная емкость Тороида Индукторы — возможно, больше, чем вам нужно знать. собственная емкость в конструкции катушки

Спираль (Плоские) Катушки

Плоские спиральные индукторы с воздушным сердечником — Большой выбор единиц измерения — Находит индуктивность — Пять других Калькуляторы катушек здесь
Калькулятор плоских спиральных катушек — Принимает вводимые размеры в дюймах или мм — вывод в uHenrys
Плоская спиральная катушка Калькулятор индуктивности — Размеры в мкм — Имеет несколько плоских форм — Другое калькулятор ссылки здесь
Однослойный Калькулятор плоской воздушной катушки — принимает вводимые размеры в дюймах или мм — вывод в uHenrys или nHenrys
Спираль Калькулятор индуктивности — Размеры в мметрах — Девять выходы, для различных форм и формул, рассчитываются Калькулятор спиральной катушки
— Габаритные размеры в мм и количество оборотов — Выход в uHenrys — Использует формулу Уиллера
Калькулятор спирали профессора Койла из паутины — Красиво — Включает в себя таблицу проводов и калькулятор резонанса — Прочтите инструкции ниже

Соленоид — Многослойные катушки:

Многослойный Калькулятор индуктивности с воздушным сердечником — Выбор единиц — Входы: L, Катушка диаметр и длина, калибр провода — несколько выходов
Многослойный Калькулятор индуктивности воздушного сердечника — Выбор единиц — Сложные входы из-за слоев — Только полезные ниже 3 МГц Калькулятор индуктивности многослойной катушки
— Air Core — мм или дюймы — сложные входы из-за слоев — Несколько выходов
Калькулятор физических свойств катушки — Для катушек соленоидов реле — Не для RF

Проницаемость — Найди Проходимость неизвестного ядра

Определите проницаемость тороида — Вводятся в mHenrys к nHenrys и мм или см размеры жилы — Выпуск Пермь.& AL
Как определить проницаемость неизвестного Ядра — Входы в uHenrys & размеры в мм — Также калькулятор индуктивности
Видеть также: Универсальный однослойный калькулятор ###

Реактивное сопротивление:

Калькулятор индуктивного реактивного сопротивления

— Принимает входные данные в герцах до ГГц и от нГенри до Генри. Калькулятор импеданса индуктора
— Принимает входные сигналы в герцах до МГц и Калькулятор реактивного сопротивления от pHenrys до Henrys
R L C ### — Единицы исправлены: uFarads, mHenrys & Hertz — Ссылки на емкостной Калькулятор реактивного сопротивления
Реактивное сопротивление Калькулятор для аккредитива и аккредитива -& Единицы фиксированы: pFarads, uHenrys и MHz

Другой Калькуляторы:

Калькулятор взаимной индуктивности — Вычисляет взаимную индуктивность с учетом индуктивности 2 катушек (в mHenrys) и их коэффициент связи.
Другой калькулятор взаимной индуктивности — То же, что и выше, но предлагает выбор единиц. Сайт разработки радиочастотных фильтров
WA4DSY — Есть несколько типов фильтров с выходными графиками — Действительно полезный; a keeper
Калькулятор коэффициента поворотов — Возводит ли отношение поворотов в квадрат. Калькулятор глубины кожи
RF Cafe — Нечасто требуется, но с отличного сайта для радиотехников и радиолюбителей. Калькулятор самоиндукции провода
— Выбор входных единиц — вычисляет L в нГенри длина провода
Комплексная конструкция катушки Тесла — Нет полезно для РФ?
Подробнее Калькуляторы катушки Тесла — Не подходит для РФ

Дополнительно Информация о катушке:

Балун и выбор сердечника трансформатора — много полезной информации и ссылки из W8JI
Проволока, Тороиды и трансформаторы — Много полезного информация — Включает таблицу сечения проводов и многое другое.
PDF — Измерение свойств мягкого ферритового сердечника — Четырехстраничный PDF-файл с информацией об измерениях.
Все о феррите из гаек & Volts Magazine — Хорошее образование со ссылками в конце

### калькуляторы которые выходят за рамки простого решения уравнения для одного заявленного отсутствующее значение, найдя недостающее значение при условии, что другие значения введены.

Пожалуйста контакт мне о других приложениях этого типа и о любые исправления информации на этой странице.

Назад на страницу указателя

Главный Сайт — Архив истории морского радио

Создано 11.11.2018 — Редакция 19.07.2021

Конструкция индуктора

с сердечниками из магнитного порошка

Чтобы получить помощь в выборе сердечника (сердечников) Magnetics для использования в конкретных конструкциях индукторов, загрузите наш инструмент для проектирования индукторов или обратитесь в Magnetics с запросом на проектирование нестандартных индукторов.

Для выбора сердечника индуктора с ограничением по току необходимо знать только два параметра проектного приложения; индуктивность требуется при постоянном смещении и постоянном токе.Используйте следующую процедуру, чтобы определить размер сердечника и количество витков.

1. Вычислить произведение LI ² где:

L = требуемая индуктивность при смещении постоянного тока (мГн)
I = постоянный ток (A)
l _e = длина магнитного пути сердечника (мм)
N = количество витков
H = напряженность магнитного поля (А • Тл / см)

2. Найдите значение LI ² на диаграмме выбора сердечника.Следуйте по этой координате до пересечения с первым размером керна, который лежит выше диагональной линии проницаемости. Это наименьший размер сердечника, который можно использовать.

3. Линия проницаемости разделена на стандартные доступные значения проницаемости керна. Выбор указанной проницаемости будет лучшим компромиссом между A _L и смещением постоянного тока.

4. Теперь известны индуктивность, размер сердечника и проницаемость. Рассчитайте количество оборотов, используя следующую процедуру:

(a) Коэффициент индуктивности (A _L в нГн / Т ² ) для сердечника определяется из его технических характеристик.Определите минимальное значение A _L , используя отрицательный допуск наихудшего случая (обычно -8%). Используя эту информацию, рассчитайте количество витков, необходимое для получения требуемой индуктивности:

Где требуется L, индуктивность (мкГн)

(b) Рассчитайте смещение в A • T / см из:

(c) Из кривых зависимости проницаемости от смещения постоянного тока определите спад на единицу начальной проницаемости для ранее рассчитанного уровня смещения.Уравнения подбора кривой, представленные в каталоге, могут упростить этот шаг.

(d) Умножьте требуемую индуктивность на спад на единицу, чтобы найти индуктивность с приложенным током смещения.

(e) Увеличьте количество витков, разделив начальное число витков (из шага 4 (a)) на начальное значение проницаемости на единицу. Это даст индуктивность, близкую к требуемому значению, после повторения шагов 4 (b), (c) и (d).

(f) Повторите шаги 4 (b), (c) и (d), если необходимо, чтобы отрегулировать смещенную индуктивность вверх или вниз, пока она не станет достаточно близко к цели.

5. Выберите правильный размер провода с помощью таблицы проводов. Продолжительность включения ниже 100% допускает меньшие размеры проводов и меньшие коэффициенты намотки, но не допускает меньших размеров сердечников.

6. Чтобы рассчитать коэффициент намотки, умножьте количество витков на площадь провода, указанную в таблице проводов, чтобы найти общую площадь провода. Разделите общую площадь провода на площадь окна сердечника, чтобы получить коэффициент намотки конструкции. Убедитесь, что коэффициент намотки приемлем, обратившись к различным подходам к намотке, описанным здесь.(Область ядра и область окна можно найти в таблице данных ядра или на странице каталога.)

7. Если будет присутствовать значительная пульсация тока, оцените потери в сердечнике, используя процедуру расчета потерь в сердечнике. Если потери в сердечнике переменного тока приведут к слишком большому нагреву или к КПД ниже требуемого, тогда индуктор может быть ограничен потерями, а не насыщением. Варианты конструкции для этого сердечника должны учитывать более крупный сердечник, материал с более низкой проницаемостью, материал с меньшими потерями или некоторую комбинацию этих трех.

Пример выбора сердечника

Определите размер сердечника и количество витков для удовлетворения следующего требования:

(a) Минимальная индуктивность при смещении постоянного тока 0,6 мГн (600 мкГн)

(б) Постоянный ток 5,0 А

1. LI ² = 0,6 X 5,0 ² = 15,0 мГн • A ²

2. Используя диаграмму Kool Mμ Toroids LI ² , найдите 15 мГн • A ² на нижней оси.Следование этой координате по вертикали приводит к выбору 0077083A7 в качестве соответствующего ядра для вышеуказанных требований.

3. Из данных сердечника 0077083A7 коэффициент индуктивности (A _L ) этого сердечника составляет 81 нГн / Тл ² ± 8%. Минимальное значение A _L этого ядра составляет 74,6 нГн / т ² .

4. Количество витков, необходимое для получения 600 мкГн без нагрузки, составляет 90 витков. Чтобы рассчитать количество оборотов, необходимых при полной нагрузке, определите уровень смещения постоянного тока: H = N • I / l _e = A • T / см, где l _e — длина пути в см.Смещение постоянного тока составляет 45,7 А • Тл / см, что дает 71% начальной проницаемости по кривой смещения постоянного тока 60 мкм Kool Mµ. Скорректированные обороты составляют 90 / 0,71 = 127 оборотов.

5. Пересчитайте уровень смещения постоянного тока в А • Тл / см: кривая зависимости проницаемости от смещения постоянного тока показывает 57% начальной проницаемости при 64,5 А • Т / см.

6. Умножьте минимальное значение A _L 74,6 нГн / т ² на 0,57, чтобы получить эффективное значение A _L = 42,5 нГн / т ² . Индуктивность этого сердечника 127 витков и 64.5 А • Тл / см будет минимум 685 мкГн. Требование индуктивности соблюдено.

7. Таблица проводов показывает, что для передачи 5,0 А при плотности тока 500 А / см требуется 17 AWG. ² . 127 витков 17 AWG (площадь провода = 1,177 мм ² ) равняется общей площади провода 149,5 мм ² . Площадь окна 0077083A7 составляет 427 мм ² . Расчет заполнения окна, 149,5 мм ² /427 мм ² соответствует приблизительному коэффициенту намотки 35%.0077083A7 со 127 витками 17 AWG представляет собой конструкцию, которую можно изготовить.

Загрузить программу проектирования индукторовContact Magnetics

Катушки индуктивности и формулы для расчета индуктивности Уравнения

Стили корпуса индуктора

Катушки индуктивности — это пассивные устройства, используемые в электронных схемах для хранения энергии в виде магнитного поля. Они дополняют конденсаторы, накапливающие энергию в виде электрического поля.An идеальная катушка индуктивности эквивалентна короткому замыканию (0 Ом) для постоянного тока (DC), и представляет собой противодействующую силу (реактивное сопротивление) переменным токам (AC), которая зависит от от частоты тока. Реактивное сопротивление (сопротивление протеканию тока) катушки индуктивности пропорциональна частоте тока, протекающего через него. Индукторы иногда называемые «катушками», потому что большинство индукторов физически построено из секций, скрученных в спираль. проволоки.

Свойство индуктивности, препятствующее изменению тока, используется для цель предотвращения прохождения сигналов с более высокочастотной составляющей во время пропускание сигналов низкочастотных компонентов.Вот почему индукторы иногда называемые «дросселями», поскольку они эффективно подавляют более высокие частоты. Обычный применение дросселя в цепи смещения радиоусилителя, где коллектор транзистор должен быть запитан постоянным напряжением, не позволяя RF (радиочастота) сигнал от проводки обратно в источник постоянного тока.

При использовании в серия (левый рисунок) или параллельно (правый рисунок) со своей схемой комплимент, конденсатор, комбинация индуктора-конденсатора образует цепь, которая резонирует с определенной частотой, которая зависит от значений каждого компонента.В сериале В цепи сопротивление току на резонансной частоте равно нулю при идеальных компонентах. В параллельной цепи (справа) сопротивление протеканию тока бесконечно с идеальными компонентами.

Реальные индукторы из физических компонентов демонстрируют больше, чем просто чистую индуктивность, когда присутствуют в цепи переменного тока. Общая схема Слева показана модель симулятора. Он включает в себя фактический идеальный индуктор с параллельным резистивный компонент, реагирующий на переменный ток.Резистивная составляющая постоянного тока соединен последовательно с идеальной катушкой индуктивности, а конденсатор подключен через всю сборки и представляет собой емкость, имеющуюся из-за близости обмоток катушки. Симуляторы типа SPICE используют эту или даже более сложную модель для облегчения большего точные расчеты в широком диапазоне частот.

Связанные страницы на RF Cafe
— Индукторы и Расчет индуктивности
— Преобразование индуктивности
— Стандартные значения индуктивности
— Продавцы индукторов

HamWaves.ком на сайте есть очень сложный калькулятор индуктивности катушки, позволяющий ввести диаметр проводника.

Уравнения (формулы) для объединения катушек индуктивности последовательно и параллельно приведены ниже. Приведены дополнительные уравнения для катушек индуктивности различной конфигурации.

Катушки индуктивности с последовательным соединением

Общая индуктивность последовательно соединенных катушек индуктивности равна сумме индивидуальных индуктивности. Держите единицы постоянными.

Тороид с закрытой намоткой

Прямоугольное сечение

Индуктивность коаксиального кабеля

Индуктивность прямого провода

Эти уравнения применимы, когда длина проволоки намного больше диаметра проволоки (см. диаметр проволоки здесь). Справочник ARRL представляет уравнение для единиц дюймов и мкФ:

Для низких частот — примерно до VHF, используйте эту формулу:

Выше VHF скин-эффект приводит к тому, что в верхнем уравнении приближается к единице (1), поэтому используйте это уравнение:

Прямой провод, параллельный плоскости заземления с заземленным одним концом

Справочник ARRL представляет это уравнение для прямого провода, подвешенного над землей. плоскость, заземленная одним концом на плоскость:

a = радиус проволоки, l = длина провода параллельно плоскости заземления
h = высота провода над пластиной заземления до конца провода

Индуктивность параллельной линии

Многослойная индуктивность с воздушным сердечником

Уиллера Формула:

Катушки индуктивности с параллельным соединением

Общая индуктивность параллельно соединенных катушек индуктивности равна обратной величине индуктивности. сумма обратных величин индивидуальных индуктивностей.Держите единицы постоянными.

Константы и переменные формулы индуктивности

Следующие физические константы и механические размерные переменные применимы к уравнениям на этой странице. Единицы для уравнений показаны в скобках в конце уравнений; например, означает, что длина в дюймах, а индуктивность — в Генри. Если единицы не указаны, то можно использовать любые. при условии, что они согласованы для всех сущностей; т.е. все счетчики, все мкГн и т. д.

C = емкость
L = индуктивность
N = количество витков
W = энергия
ε _r = Относительная диэлектрическая проницаемость (безразмерная)
ε ₀ = 8.85 x 10 ^-12 Ф / м (диэлектрическая проницаемость свободного пространства)
µ _r = Относительная проницаемость (безразмерная)
µ ₀ = 4π x 10 ^-7 H / м (проницаемость свободного пространства)

1 метр = 3,2808 фута <—> 1 фут = 0,3048 метра
1 мм = 0,03937 дюйма <—> 1 дюйм = 25,4 мм

Также точки (не путать с десятичными точками) используются для обозначения умножения во избежание двусмысленности.

Индуктивное реактивное сопротивление

Индуктивное реактивное сопротивление (X _L , в Ом) пропорционально частоте (ω, в радианах / сек или f в Гц) и индуктивности (L в единицах Генри).Чистая индуктивность имеет фазу угол 90 ° (напряжение отводит ток с фазовым углом 90 °).

Энергия, запасенная в индукторе

Энергия (Вт, в Джоулях), запасенная в катушке индуктивности, равна половине произведения индуктивности. (L, в Генрие) и ток (I, в амперах) через устройство.

Напряжение на индукторе

Свойство индуктора противодействовать изменению потока тока вызывает противодействие ЭДС. (напряжение) на его выводах, полярность противоположная приложенному напряжению.

Коэффициент качества индуктора

Добротность — это безразмерное отношение реактивного сопротивления к сопротивлению в катушке индуктивности.

Однослойная круглая катушка индуктивности

Уиллера Формула для d >> a:

Обычно для a = радиус проволоки:

Примечание. Если длина выводов значительна, используйте расчет прямого провода, чтобы добавить это индуктивность.

Поиск эквивалента «R

_Q »

Поскольку «Q» индуктора — это отношение реактивной составляющей к резистивной составляющей, эквивалентная схема может быть определена с резистором, включенным параллельно катушке индуктивности. Этот уравнение действительно только для одной частоты «f» и должно вычисляться для каждой частоты. представляет интерес.

(PDF) Самоиндуктивность цилиндрической катушки с воздушным сердечником в воздухе / Калькулятор катушек

18.08.2015

Мы предоставляем калькулятор катушек как бесплатную версию.

Калькулятор катушек Пожалуйста, не стесняйтесь обращаться к нам, если вы хотите отправить вам программное обеспечение.

Самоиндуктивность цилиндрической катушки с воздушным сердечником

в воздушном / катушечном калькуляторе

John Martinos

[email protected]

http://ioannismartinos.wix.com/imartinos

http: // www. researchgate.net/profile/J_Martinos

Themis Martinos

themismartinos @ gmail.com

http://www.researchgate.net/profile/Themis_Martinos

LinkedIn: Themis Martinos

LinkedIn: John Martinos

Используя последовательную интеграцию, мы вычисляем самоиндукцию по соответствующей формуле для цилиндрических катушек с воздушным сердечником. в воздухе. Мы использовали программное обеспечение Matlab для расчета формулы и разработали приложение (названное: Coil Calculator / бесплатная версия) с инструментом

Matlab-GUI (графический интерфейс пользователя).Экспериментальные измерения от 7 катушек используются для сравнения измеренной индуктивности собственной

в воздухе с теоретическими значениями из Coil Calculator. Кроме того, мы использовали бесплатное ПО TEDDY для сравнения теоретических значений

из Coil Calculator с таковыми из TEDDY. Результаты очень интересны, так как теоретические значения, полученные с помощью Coil Calculator и

TEDDY, отлично согласуются.

I. ВВЕДЕНИЕ

Круглые катушки с необработанным сердечником и прямоугольным поперечным сечением

используются во многих промышленных приложениях, таких как датчики в вихретоковом неразрушающем контроле

или компоненты схем.

точное знание самоиндукции в воздухе является важной частью

при проектировании катушек. В этой работе мы разработали программное приложение

(названное: Coil Calculator) для расчета собственной индуктивности

по соответствующей формуле для цилиндрических катушек

с воздушным сердечником в воздухе.

II. ТЕОРИЯ / РАСЧЕТНАЯ ФОРМУЛА

Импеданс цилиндрической катушки с воздушным сердечником в воздухе

определяется по формуле [1]:

 

   

2

2

025 20

,

21

= d, 1

кН

на выходе

на воздухе

на выходе

I kR kR

iN e

ZH k

k

















где,

ω = 2πf, угловая частота в (рад / с)

f, — рабочая частота в (Гц)

μo = 4π10-7, — магнитная постоянная в (N / A2)

Rin, — внутренний радиус катушки в (мм)

Rout, — внешний радиус катушки в (мм)

H, — высота катушки в (мм)

Н, — количество витков

Далее,

   

1

I, = d,

b

a

ab xJ xx



(2)

где J1 (x) — функция Бесселя первого порядка первого рода.

Воздушное сопротивление Zair имеет форму Zair = R + iXair, где R

(сопротивление катушки) является действительной частью, а Xair (реактивное сопротивление

катушки) является частью изображения. Цилиндрическая катушка в воздухе

моделируется как идеальный индуктор [1], и также предполагается, что сопротивление катушки

незначительно [2]. Следовательно, резистивные члены

не появляются в уравнении (1). Индуктивность катушки связана с величиной сопротивления воздуха

величиной

 

2 2 2 2

0 3

воздух воздух воздух воздух воздух

LZRXXXX



    

Из уравнений (1) и (3)

 

   

2

2

025

20

,

21

= d, 40002 = d, 40002

на входе

на выходе

на выходе

I kR kR

Ne

LH k

k

k

HRR





000

000





III.