Расчет параллельного включения резисторов: Онлайн-калькулятор расчета последовательного и параллельного соединения резисторов — Мир Антенн

Содержание

Расчет параллельного включения резисторов — Яхт клуб Ост-Вест

Из закона Ома и первого и второго правил Кирхгофа следует:

При параллельном соединении величина обратная полному сопротивлению, равна сумме величин, обратных сопротивлений ветвей.

При параллельном соединении полное сопротивление цепи меньше самого малого из сопротивлений ветвей.

Поскольку 1/R = G, т.е. проводимость, то
при параллельном соединении электрические проводимости отдельных ветвей складываются

Параллельное соединение двух сопротивлений

При параллельном соединении двух сопротивлений формула (1) упрощается

Параллельное соединение двух сопротивлений

При параллельном соединении двух сопротивлений формула (1) упрощается

Калькулятор параллельных сопротивлений

Калькулятор определяет сопротивление нескольких параллельно соединенных резисторов.

Пример. Рассчитать эквивалентное сопротивление двух резисторов 20 Ом and 30 Ом, соединенных параллельно.

Введите величины сопротивлений в поля R₁

, R₂ и т.д., добавляя при необходимости нужное количество полей для ввода, выберите единицы сопротивления в миллиомах (мОм), омах (Ом), килоомах (кОм) или мегаомах (МОм) и нажмите кнопку Рассчитать.

1 мОм = 0,001 Ом. 1 кОм = 1 000 = 10³ Ом. 1 МОм = 1 000 000 = 10⁶ Ом.

Эквивалентное сопротивление R_eq группы параллельно соединенных резисторов является величиной, обратной сумме величин, обратно пропорциональных сопротивлениям этих резисторов.

Иными словами, проводимость G параллельно соединенных резисторов равна сумме проводимостей этих резисторов:

Эта формула для R_eq и используется в данном калькуляторе для расчетов. Например, общее сопротивление трех резисторов 10, 15 и 20 ом, соединенных параллельно, равно 4.62 Ом:

Если параллельно соединены только два резистора, формула упрощается:

Если имеется n соединенных параллельно одинаковых резисторов

R, то их эквивалентное сопротивление будет равно

Отметим, что общее сопротивление группы из любого количества соединенных параллельно резисторов всегда будет меньше, чем наименьшее сопротивление резистора в группе и добавление нового резистора всегда приведет к уменьшению эквивалентного сопротивления.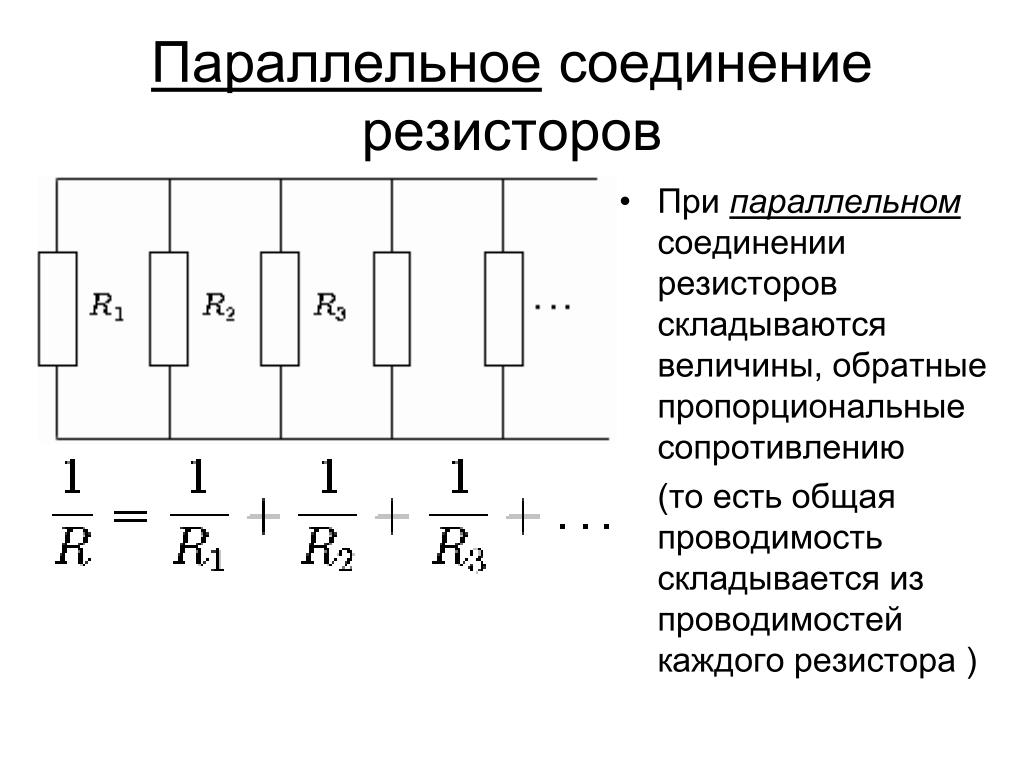

Отметим также, что все резисторы, соединенные параллельно находятся под одним и тем же напряжением. Однако токи, протекающие через отдельные резисторы, отличаются и зависят от их сопротивления. Общий ток через группу резисторов равен сумме токов в отдельных резисторах.

При соединении нескольких резисторов параллельно всегда нужно учитывать их допуски и рассеиваемую мощность.

Примеры применения параллельного соединения резисторов

Одним из примеров параллельного соединения резисторов является шунт в приборе для измерения токов, которые слишком велики для того, чтобы быть напрямую измеренными прибором, предназначенным для измерения небольших токов или напряжений. Для измерения тока параллельно гальванометру или электронному прибору, измеряющему напряжение, подключается резистор с очень маленьким точно известным сопротивлением, изготовленный из материала со стабильными характеристиками. Этот резистор называется шунтом. Измеряемый ток протекает через шунт.

В результате на нем падает небольшое напряжение, которое и измеряется вольтметром. Поскольку падение напряжения пропорционально току, протекающему через шунт с известным и точным сопротивлением, вольтметр, подключенный параллельно шунту, можно проградуировать непосредственно в единицах тока (амперах).

Параллельные и последовательные схемы часто используются для получения точного сопротивления или если резистора с требуемым сопротивлением нет или он слишком дорог, если его приобретать в небольших количествах для массового производства

. Например, если устройство содержит много резисторов по 20 кОм и необходим только один резистор 10 кОм. Конечно, несложно найти резистор на 10 кОм. Однако для массового производства иногда бывает лучше поставить два резистора на 20 кОм параллельно, чтобы получить необходимые 10 кОм. Это приведет к снижению себестоимости печатной платы, так как будет снижена оптовая цена компонентов, а также стоимость монтажа, так как будет уменьшено количество типоразмеров элементов, которые должен установить на плату автомат установки компонентов.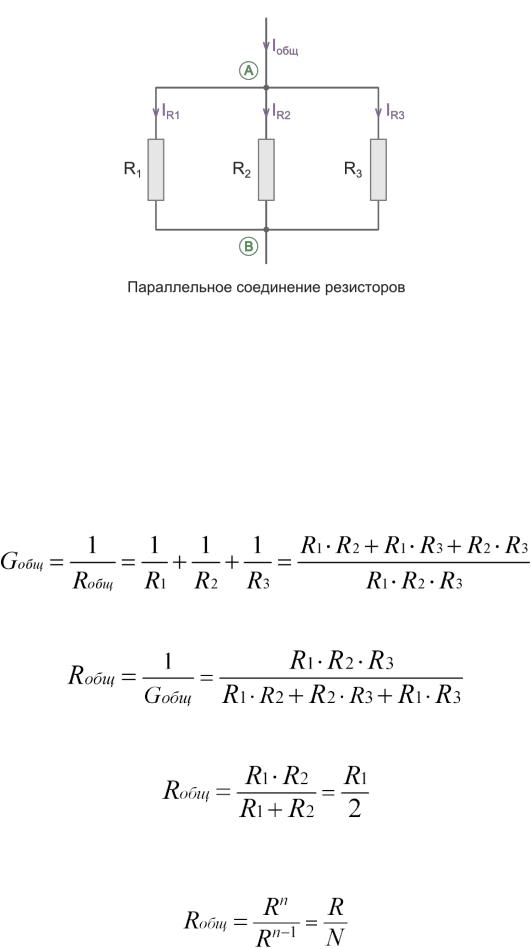

Примеры расчетов

Электротехнические и радиотехнические калькуляторы

Электроника — область физики и электротехники, изучающая методы конструирования и использования электронной аппаратуры и электронных схем, содержащих активные электронные элементы (диоды, транзисторы и интегральные микросхемы) и пассивные электронные элементы (резисторы, катушки индуктивности и конденсаторы), а также соединения между ними.

Радиотехника — инженерная дисциплина, изучающая проектирование и изготовление устройств, которые передают и принимают радиоволны в радиочастотной области спектра (от 3 кГц до 300 ГГц), также обрабатывают принимаемые и передаваемые сигналы. Примерами таких устройств являются радио- и телевизионные приемники, мобильные телефоны, маршрутизаторы, радиостанции, кредитные карточки, спутниковые приемники, компьютеры и другое оборудование, которое передает и принимает радиосигналы.
В этой части Конвертера физических единиц TranslatorsCafe.

com представлена группа калькуляторов, выполняющих расчеты в различных областях электротехники, радиотехники и электроники.

На этих страницах размещены конвертеры единиц измерения, позволяющие быстро и точно перевести значения из одних единиц в другие, а также из одной системы единиц в другую. Конвертеры пригодятся инженерам, переводчикам и всем, кто работает с разными единицами измерения.

Мы работаем над обеспечением точности конвертеров и калькуляторов TranslatorsCafe.com, однако мы не можем гарантировать, что они не содержат ошибок и неточностей. Вся информация предоставляется «как есть», без каких-либо гарантий. Условия.

Если вы заметили неточность в расчётах или ошибку в тексте, или вам необходим другой конвертер для перевода из одной единицы измерения в другую, которого нет на нашем сайте — напишите нам!

Последовательное соединение резисторов

Последовательное соединение – это соединение двух или более резисторов в форме цепи, в которой каждый отдельный резистор соединяется с другим отдельным резистором только в одной точке.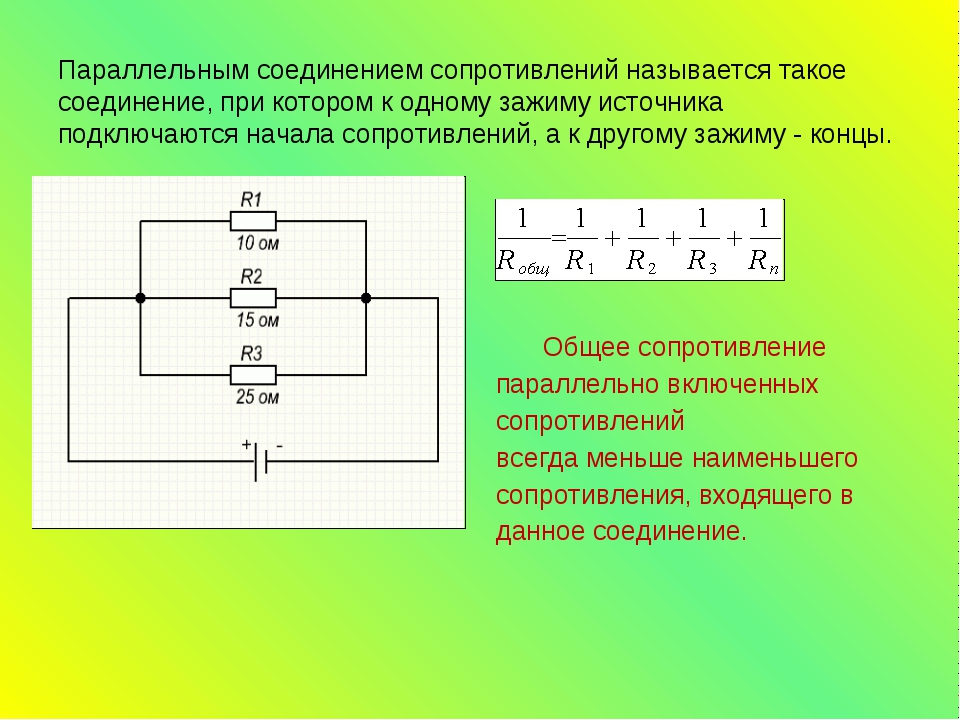

Общее сопротивление R

_общ

При таком соединении, через все резисторы проходит один и тот же электрический ток. Чем больше элементов на данном участке электрической цепи, тем «труднее» току протекать через него. Следовательно, при последовательном соединении резисторов их общее сопротивление увеличивается, и оно равно сумме всех сопротивлений.

Напряжение при последовательном соединении

Напряжение при последовательном соединении распределяется на каждый резистор согласно закону Ома:

Т.е чем большее сопротивление резистора, тем большее напряжение на него падает.

Параллельное соединение резисторов

Параллельное соединение – это соединение, при котором резисторы соединяются между собой обоими контактами. В результате к одной точке (электрическому узлу) может быть присоединено несколько резисторов.

Общее сопротивление R

_общ

При таком соединении, через каждый резистор потечет отдельный ток.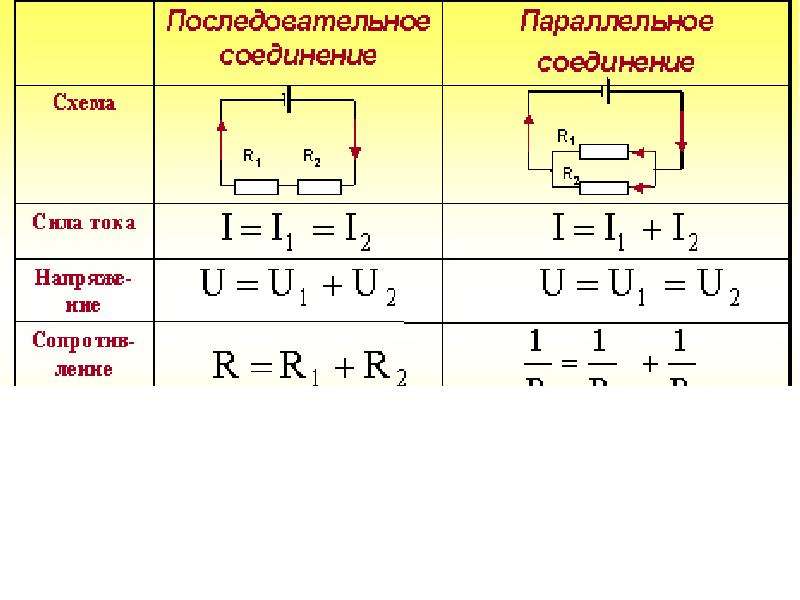 Сила данного тока будет обратно пропорциональна сопротивлению резистора. В результате общая проводимость такого участка электрической цепи увеличивается, а общее сопротивление в свою очередь уменьшается.

Таким образом, при параллельном подсоединении резисторов с разным сопротивлением, общее сопротивление будет всегда меньше значения самого маленького отдельного резистора.

Формула общей проводимости при параллельном соединении резисторов:

Формула эквивалентного общего сопротивления при параллельном соединении резисторов:

Для двух одинаковых резисторов общее сопротивление будет равно половине одного отдельного резистора:

Соответственно, для n одинаковых резисторов общее сопротивление будет равно значению одного резистора, разделенного на n.

Напряжение при параллельном соединении

Напряжение между точками A и B является как общим напряжением для всего участка цепи, так и напряжением, падающим на каждый резистор в отдельности.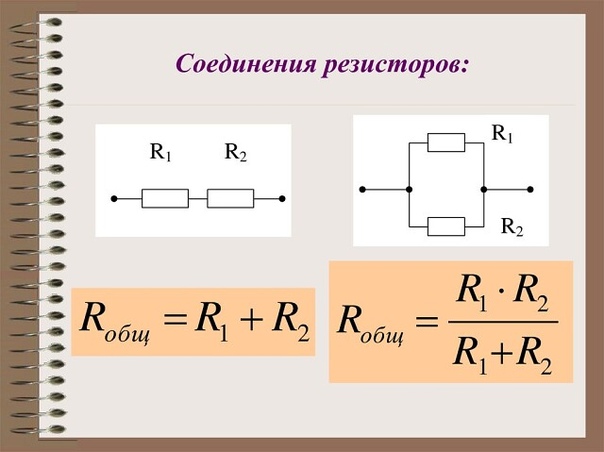 Поэтому при параллельном соединении на все резисторы упадет одинаковое напряжение.

Электрический ток при параллельном соединении

Через каждый резистор течет ток, сила которого обратно пропорциональна сопротивлению резистора. Для того чтобы узнать какой ток течет через определенный резистор, можно воспользоваться законом Ома:

Смешанное соединение резисторов

Смешанным соединением называют участок цепи, где часть резисторов соединяются между собой последовательно, а часть параллельно. В свою очередь, смешанное соединение бывает последовательного и параллельного типов.

Общее сопротивление R

_общ

Для того чтобы посчитать общее сопротивление смешанного соединения:

Цепь разбивают на участки с только пареллельным или только последовательным соединением.
Вычисляют общее сопротивление для каждого отдельного участка.
Вычисляют общее сопротивление для всей цепи смешанного соединения.

Так это будет выглядеть для схемы 1:

Также существует более быстрый способ расчета общего сопротивления для смешанного соединения.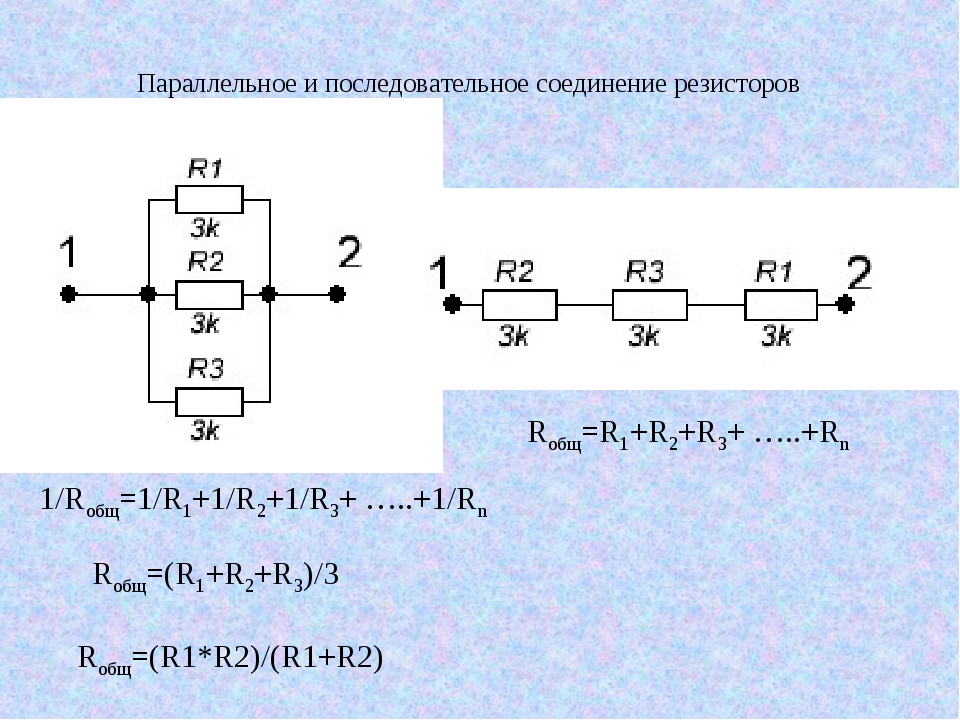

Можно, в соответствии схеме, сразу записывать формулу следующим образом:

Если резисторы соединяются последоватеьно — складывать.
Если резисторы соединяются параллельно — использовать условное обозначение «||».
Подставлять формулу для параллельного соединения где стоит символ «||».

Так это будет выглядеть для схемы 1:

После подстановки формулы параллельного соединения вместо «||»:

О параллельном соединении резисторов: расчет подключения, определение мощности

Достаточно большое количество радиолюбителей занимается сборкой, модернизацией и ремонтом разнообразных схем; для кого-то это работа, а для кого-то просто увлечение или хобби. В любом случае необходимо иметь представление о процессах, происходящих в схеме, физических свойствах самих элементов цепи и особенностях взаимодействия элементов между собой.

Диагностика электронных схем

Компоненты электронных схем

Все множество компонентов и элементов делится на две основные группы:

Активные элементы, особенностью которых является возможность усиливать проходящий по ним сигнал. К такой группе, в первую очередь, относятся транзисторы и построенные на их основе схемы;
Пассивные элементы, которые не предназначены для усиления сигнала. Элементами, которые относятся к этой группе, являются резисторы, конденсаторы, катушки индуктивности, диоды и остальные аналоги данных компонентов.

Наиболее простым элементом по своим характеристикам и свойствам является резистор. Основное назначение резисторов заключается в ограничении величины тока, проходящего по нему. Все существующие резисторы подразделяются на два вида:

Постоянные – шунты, имеющие постоянное значение электрического сопротивления;
Переменные – шунты, сопротивление между контактами которого меняется механическим путем;

Центральными характеристиками резисторов являются:

Сила рассеивания, которая представляет собой максимальную мощность тока, выдерживаемую шунтом долгое время и рассеиваемую в виде тепла при постоянных характеристиках самого шунта;
Параметр точности представляет собой максимальное отступление от величины реального сопротивления в течение эксплуатации шунта;
Умение компонента противодействовать прохождению электротока в электрической цепи называется сопротивлением. Соответственно, с повышением сопротивления нарастает противостояние прохождению электротока.

Соединение резисторов

В радиотехнике встречается ряд конфигураций по состыковке компонентов в целом и шунтов в частности. Совмещение шунтов подразделяется на такие виды:

Набор параллельных резисторов;
Последовательное подключение шунтов;
Смешанное соединение резисторов.

Сопряжение резисторов

Последовательное соединение резисторов

Последовательным сопряжением компонентов называют такое сплочение нескольких шунтов, при котором каждый одиночный шунт подключается к следующему единичному шунту только в одной точке. Поскольку при последовательном включении по шунтам протекает одинаковый электрический ток, сталкивающийся постоянно с новой преградой в виде последующего сопротивления, то суммарное противодействие возрастает и равно сложению сопротивлений. Согласно картинке выше, при последовательном соединении суммарное последовательное сопротивление равно:

Rобщ=R1+R2, где:

Rобщ – суммарное противостояние цепи;
R1 – противодействие первого шунта;
R2 – противодействие второго шунта

Последовательное сопряжение шунтов

Напряжение при последовательном соединении компонентов понижается на любом отдельном элементе, опираясь на закон Ома, суммарное напряжение такого участка необходимо складывать. Соответственно, результирующий показатель напряжения возможно найти по выражению:

Uобщ=UR1+UR2, где:

Uобщ – суммарное напряжение участка;
UR1 – разность потенциалов на первом шунте;
UR2 – разность потенциалов на втором шунте.

Поскольку проходящий по компонентам электроток неизменный, то справедливо равенство:

Iобщ=IR1=IR2, где:

Iобщ – суммарная сила тока;
IR1 – электроток первого шунта;
IR2 – электроток второго шунта.

Дополнительная информация. При последовательной состыковке компонентов варьирование сопротивления любого элемента из этого участка влечет за собой как изменение сопротивления всего участка, так и изменение силы электротока этого участка.

Параллельное сопряжение резисторов

Параллельное соединение резисторов представляет собой такое соединение элементов, при котором резисторы подключаются друг к другу обоими выводами.

Дополнительная информация. В радиоэлектронике параллельные резисторы могут использоваться с целью снижения суммарного противодействия электротоку. Также мощность при параллельном стыковании компонентов возрастает сравнительно с каждым отдельным элементом.

При параллельном соединении шунтов через каждый единичный элемент потечет свой ток, и значение силы электротока будет обратно пропорционально сопротивлению компонента. Поскольку суммарная проводимость параллельного соединения возрастает, а общая сопротивляемость электротоку убывает, то, согласно закону Ома, общее сопротивление при параллельном соединении равняется:

Gобщ =1/Rобщ =1/R1+1/R2+1/R3;
Rобщ =1/Gобщ =R1R2R3/R1R2+R2R3+R1R3, где Gобщ – общая проводимость цепи.

Напряжение при параллельном соединении компонентов равняется разности потенциалов на каждом из компонентов:

Uобщ=UR1=UR2=UR3.

Направление токов в параллельной цепи

Калькулятор поможет определить суммарную силу тока цепи при параллельном совмещении, соответствующую сумме токов через каждый шунт:

Iобщ=IR1+IR2+IR3.

Смешанное соединение резисторов

Смешанное соединение резисторов представляет собой последовательное и параллельное соединение резисторов одновременно. Для определения суммарного противодействия цепи с разнотипной состыковкой шунтов требуется придерживаться последовательного алгоритма:

Схематически разделить цепь на отдельные участки, включающие в себя последовательное и параллельное соединение сопротивлений;
Рассчитать суммарный импеданс всех разделенных областей;
Представить первоначальную схему в виде сопротивлений, имеющих некоторую величину эквивалентного сопротивления;
Находите суммарное противодействие упрощенной схемы.

Понимание, что такое последовательное и параллельное соединение проводников, и поведения электрических характеристик при таком соединении позволит без особого труда проводить расчет, конструировать устройства различных конфигураций с требуемыми значениями параметров. Появится возможность упрощать и модернизировать схемы, вносить дополнительно какие-либо новшества в цепь.

Видео

Оцените статью:

Последовательное и параллельное соединение резисторов

Последовательное и параллельное соединение резисторов в схемах являются самыми распространенными, также – это база для расчета более сложных схем.

Последовательное подключение

Начнем с последовательного соединения. По этой схеме каждый резистор подключается с другим только в одной точке, их может быть в цепи 2, 3 и больше.

Рис. Последовательное подключение.

Обозначение:

Обозначим сопротивления: R1, R2, R3 и напряжение источника в цепи Uц. При подключении источника питания в ней начнет протекать ток Iц. В цепи с последовательным соединением ток протекает по всем резисторам один за другим. Поскольку ток течет через все резисторы их сопротивления и ток суммируется, Iц = I1+I2+I3, Rц = R1 +R2 + R3, чем больше отдельно взятое сопротивление, тем тяжелее электронам преодолевать участок цепи.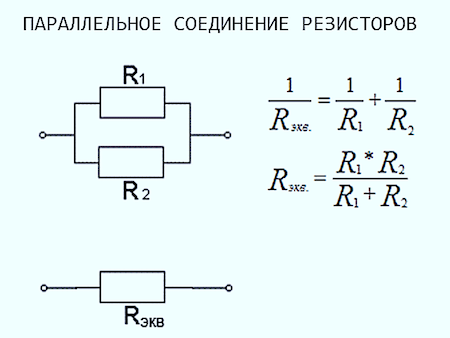 Мощность резисторов при последовательном и параллельном соединении рассчитывается по разным формулам. В последовательных цепях – складываем, в параллельных – это обратно пропорциональная величина.

Параллельное соединение

Рис. Параллельное подключение.

Данный вид подключения характерен тем, что все элементы цепи соединяется выводами в одной точке друг другу, т.е. точка входа и выхода всех нагрузок сходятся в одну точку (или еще одно обозначение на схемах – //). Электроток, двигаясь по проводнику, дойдя до общего соединения делится на количество имеющихся веток. Если представить движение воды в трубе, то можно сказать, что вода двигающиеся по одной трубе, равномерно перетекает в несколько отводов, подсоединенных к ней. В нашем случае заряженные электроны, двигающиеся по проводнику, также растекаются на количества предложенных веток в узле.
Более наглядно это можно представить в виде формул:
1. Каждый вид соединения находится под одинаковым напряжением:
U = U1 = U2;
2.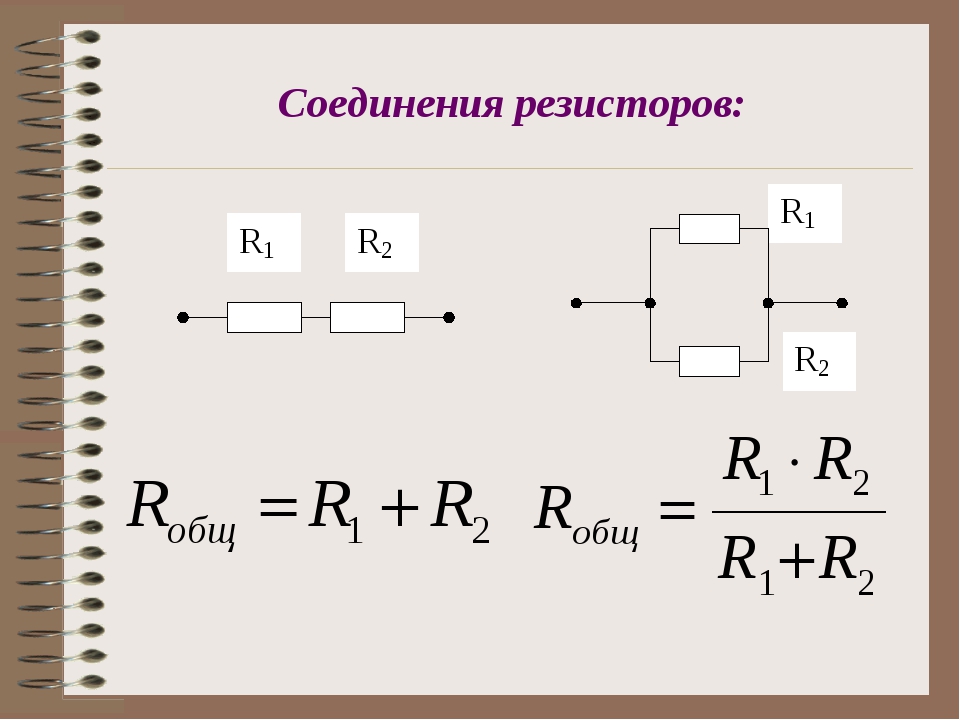 Суммарная сила тока равняется суммарному значению тока каждого участка
I = I1 + I2;
3. Сопротивление цепи равно сумме величина обратных сопротивлению участка:
1/R = 1/R1 + 17R2 + . . . + 1/Rn;
4. Сила тока пропорциональна сопротивлению каждого участка
I1/I2=R2/R1.
Далее рассмотрим схему как работает не только последовательное параллельное, но и смешанное соединение резисторов.

Смешанное подключение

Рис. Смешанное подключение резисторов

В электрических схемах используются не только типовые схемы, но и смешанное, созданное из критерий определенных требований. Чаще всего в схемах встречается третий вариант, представляющий набор из элементарных типов схем. В смешанных участках учитываются не только элементы, но и направления движения тока.
При вычислении мощности резисторов смешанного подключения используются формулы для параллельного и последовательного соединения резисторов, формула также является составной.

Основные законы электротехники, наиболее часто используемые для расчетов

Рассмотрим основные законы электротехники и свойства последовательного и параллельного соединения резисторов для участка цепи

Закон Ома

Напряжение находится по закону Ома по формуле I=U/R – чем больше сопротивление, тем меньше ток. Напряжение можно найти из этой же формулы. U=R*I, ток умножается на сопротивление. Запишем эту формулу для каждого участка U1=R1· I1, Un=Rn · In.

Законы Кирхгофа

Первый закон

Ещё один очень важный закон — это закон Кирхгофа. Для участка цепи постоянного тока их два.

Рис. иллюстрация к пояснению действия первого закона Кирхгофа.

Первый закон имеет формулировку: Сумма всех токов, входящих в узел и выходящих из него равна нулю.
Если посмотреть на схему, I1 – это ток, который заходит в узел, I2 и I3 – это электроны, которые вытекают из него.
Применяя формулировку первого закона можно записать формулу по-другому:
I1-I2+I3=0. В этой формуле знаки плюс имеют значения, которые прибывают в узел, минус, который отходит от него.

Второй закон Кирхгофа.

Рис. иллюстрация к пояснению действия второго закона Кирхгофа.

Если к цепи с включенными сопротивлениями подключен один источник ЭДС (батарея питания) тогда всё понятно, можно обойтись законом Ома. А, если, источников несколько и схема с различным схемным расположением элементов, тогда вступает в силу второй закон, который гласит: сумма токов всех источников питания для замкнутого контура, равна сумме падений напряжения на всех сопротивлениях участка в этом контуре.
E1- Е2 = – UR1 – UR2 или E1 = Е2 – UR1 – UR2.

Параллельное и последовательное соединение резисторов, решение задач

Алгоритм расчёта смешанных подключений находится в тех же правилах, что и в элементарных схемах расчета последовательного и параллельного соединения резисторов. Ничего нового нет: нужно правильно разбить предложенную схему на пригодные для расчета участки. Участки, с элементами, подключены поочередно либо параллельно.

Рис. Порядок замещения при расчете сложных позиций более простыми.

Для решения задачи на последовательное и параллельное соединение резисторов необходимо правильно оценить цепи элементов. Рассмотрим схему №1 на рис.
На схеме присутствует параллельная и последовательная часть соединения элементов. Для расчета очень важно аккуратно, шаг за шагом упрощать цепи и не брать сразу всю схему (рис.1). Как же правильно определить параллельное и последовательное соединение резисторов?

Для примера расчета возьмем резисторы R3, R4, которые подключены параллельно. Эквивалентный резистор этих элементов, будет равенRэ. = 1/R34 =1/R3 + 1/R4, после преобразования формулы и приведения к одному знаменателю получим R34 = R3 · R4 / (R3 + R4). Э. = 1/3+1/4 /(3+4) =1,7 Ом.

Далее видно, что приведённая эквивалентное R эк и R6 соединены последовательно, чтобы узнать сопротивление их необходимо сложить, тогда общее сопротивление будет равно R346 = R34 + R6, тогда Rэк346 = 1,7 + 6 = 7, 7 Ом.
Заменяем на схеме одним общим элементом, теперь, позиция упрощается еще больше (рис 3).

Теперь образовалась ситуация – включение трех элементов в //. Как вычисляется такое соединение нам уже известно, 1/ R23465 = 1/ R2 +1/R346 + 1/R5 после вычисления правой части получаем 0,82 Ом. После окончательного вычисления получаем R23465 = 2,1 Ом. Здесь следует обратить внимание, что общее сопротивление получилось меньше самого меньшего из трех.

Заменяем эти сопротивление одним эквивалентным R23465. В конечном итоге все выглядит уже намного проще. Rц = Rэк + R1+ R2. R об. = R ц = 1,21 +7+1 =9,21 Ом.
Из приведенного алгоритма расчёта видно, как из сложной схемы путем простого математического вычисления и применения правил сокращения резисторов участок становится простой и понятной.

Схема с подключением сопротивлений «треугольником»

Рис. Расчетная схема соединения резисторов в треугольник.

Иногда некоторые затруднения возникают при разборе схемы соединения в треугольник.

Рассмотрим на примере рисунка расчет резисторов по этому подключению.
Из схемы видно, что R1 и R2 соединены последовательно Rэ12 будет соединяться R3 последовательно.

Затем Rэ123 соединяется с сопротивлением R4, R5 в последовательную цепь. Затем все это объединяется с Rэ в //.

Проведем несложные вычисления учитывая, что
R1, R2, R4, R5 равняется 1 Ом. R3, R7 – 2 Ом.
RЭ1,2 = R1+R2 = 1+1=2 Ом.

Вычисляем параллельное подключение: Rэ 12 с R3. Rэ1,3 = (Rэ12*R3) /(Rэ12+R3) = (2*2) /(2+2) = 1Ом.

Далее мы видим последовательное: RЭ123 + R4 + R5 = 1+1+1 = 3 Ом.
И последнее – Rэ123 4 5 с R6 – параллельное.

Общее сопротивление цепи Rц = Rоб = (RЭ1,2,3,4,5 *R6) /(RЭ1,2,3,4,5+R6) = (3 * 2) / (3+2) = 1,2 Ом. Как видно, что расчет подобного варианта также не сложный.

Расчет последовательного и параллельного подключения резисторов онлайн

Подсчитать значение мощность и сопротивлений подставляя их в формулы можно только в учебных целях, или, когда объемы не очень большие. Наиболее практичный вариант расчета является онлайн калькуляторы, которые расположены на многочисленных интернет ресурсах. Для расчёта любой сложности нужно правильно определить тип соединения резисторов последовательное или параллельное и внести данные для расчета в поля калькулятора.

Также такая форма расчета подойдет и для проверки результатов решения учебных задач.

Последовательное и параллельное соединение резисторов и конденсаторов

Электрические цепи состоят не только из резисторов, в них применяется большое количество различных деталей, например, конденсатор, которые подключаются в последовательное, // и смешанное соединение.

Рис. Замещения последовательно включенных элементов.

Определение этому элементу можно дать следующее: Конденсатор – это совокупность проводящих тел служащий для накопления электрического заряда.
Элементарный конденсатор имеет две пластины, форма этих пластин может быть различной: сферической, круглой, цилиндрической, прямоугольной – по форме пластин разделяется и тип конденсатора.

Важное свойство. Одно из важных свойств конденсатора: если заряжается одна пластина конденсатора, то благодаря явлению электростатической индукции заряжается и вторая половина, но с противоположным знаком.

Устройство конденсатора

Плоский конденсатор состоит из двух плоских пластин отстоящих друг от друга на маленькое расстояние. У конденсатора к двум пластинам припаивается вывод всего их получается два.

Типовые схемы подключения конденсаторов

Рассмотрим различные виды подключения конденсатора.

Последовательное

Первый вид — это последовательное соединение.
Предположим, что емкость этих конденсаторов будут равны. Тогда заряды также будут равны: q1=q2=q3, как и в примере с резисторами, сложный тип позиций с конденсатором можно упростить, заменив несколько элементов одним. У элементов соединенных друг за другом, общая емкость будет обратно пропорциональная всем имеющимся элементам. То есть: Rэк будет равняться 1/С1 + 1/С2 +…. 1/Сn/
Напряжение складывается, U эк = U1 + U2+ … Un.

Параллельное

Второй тип подключения конденсаторов – это соединение в паралель

Рис. Схема замещения элементов, включенных в параллель.

Соответственно эти конденсаторов обозначены C1, C2, … Cn заряды: Q1, Q2, … Qn и напряжение: U1, U2, … Un.

У элементов в // емкость складывается Сэ = C1 + C2 + … C n.
Напряжение Un на каждом конденсаторе будет равно напряжению на эквивалентном
Uэ = U1 = U2 =… = Un – это особенность параллельного подсоединения всех элементов цепи.

Емкость будет складываться из суммы отдельных элементов Сэ =С1 + С2 + … Сп.

Рис. Расчетные позиции элементов при различном включении.

Простая позиция, которая не требует преобразования №1 – последовательное подключение. По известной формуле для этих поз. запишем 1/Сэ = 1/С1 +1/С2 +1/С3, подставив формулу значения, которые даны в условии задачи, получим 1/Сэ = 1/С1 +1/С2 +1/С3 = 59 мФ.

Не требует преобразования и 2 схема: емкость общего конденсатора будет равняться сумме конденсаторов которые включены в параллельной цепи: Сэ =С1 +С2 +С3
Сэ = 100 + 200 + 500 = 800 мФ.

Рассмотрев рис. №3 видно, что пара конденсаторов включена параллельно и один последовательно. Алгоритм преобразования таких цепей мы уже рассматривали, поэтому: сразу же находим емкость конденсатора Сэ соединения: Сэ = С1+С2 = 200+500 = 700 мФ.

Теперь находим общие эквивалентную емкость элементов с последовательным подключением 1/Сэ = 1/С2,3 +1/ С1 = 89 мф.
Практическая задача решена.

Внимание покупателей подшипников

Уважаемые покупатели, отправляйте ваши вопросы и заявки по приобретению подшипников и комплектующих на почту или звоните сейчас:

+7(499)403 39 91

Доставка подшипников по РФ и зарубежью.

Каталог подшипников на сайте themechanic.ru

Внимание покупателей подшипников

Уважаемые покупатели, отправляйте ваши вопросы и заявки по приобретению подшипников и комплектующих на почту или звоните сейчас:
tel:+7 (495) 128 22 34
[email protected]
Доставка подшипников по РФ и зарубежью.
Каталог подшипников на сайте

Внимание покупателей подшипников

Уважаемые покупатели, отправляйте ваши вопросы и заявки по приобретению подшипников и комплектующих на почту или звоните сейчас:
tel:+7 (495) 646 00 12
[email protected]
Доставка подшипников по РФ и зарубежью.
Каталог подшипников на сайте

§ 11. Последовательное, параллельное и смешанное соединения резисторов (приемников электрической энергии)

Последовательное, параллельное и смешанное соединения резисторов.

Значительное число приемников, включенных в электрическую цепь (электрические лампы, электронагревательные приборы и др.), можно рассматривать как некоторые элементы, имеющие определенное сопротивление.

Это обстоятельство дает нам возможность при составлении и изучении электрических схем заменять конкретные приемники резисторами с определенными сопротивлениями. Различают следующие способы соединения резисторов (приемников электрической энергии): последовательное, параллельное и смешанное.

Последовательное соединение резисторов.

Рис. 25. Схемы последовательного соединения приемников

При последовательном соединении нескольких резисторов конец первого резистора соединяют с началом второго, конец второго — с началом третьего и т. д. При таком соединении по всем элементам последовательной цепи проходит один и тот же ток I.

Заменяя лампы резисторами с сопротивлениями R1, R2 и R3, получим схему, показанную на рис. 25. Если принять, что в источнике Ro = 0, то для трех последовательно соединенных резисторов согласно второму закону Кирхгофа можно написать:

E = IR₁ + IR₂ + IR₃ = I(R₁ + R₂ + R₃) = IR_эк (19)

где R_эк = R₁ + R₂ + R₃.

Следовательно, эквивалентное сопротивление последовательной цепи равно сумме сопротивлений всех последовательно соединенных резисторов. Так как напряжения на отдельных участках цепи согласно закону Ома: U₁=IR₁; U₂ = IR₂, U₃ = IR_з и в данном случае E = U, то для рассматриваемой цепи:

U = U₁ + U₂ +U₃ (20)

Следовательно, напряжение U на зажимах источника равно сумме напряжений на каждом из последовательно включенных резисторов.
Из указанных формул следует также, что напряжения распределяются между последовательно соединенными резисторами пропорционально их сопротивлениям:

U₁ : U₂ : U₃ = R₁ : R₂ : R₃ (21)

т. е. чем больше сопротивление какого-либо приемника в последовательной цепи, тем больше приложенное к нему напряжение.

В случае если последовательно соединяются несколько, например п, резисторов с одинаковым сопротивлением R1, эквивалентное сопротивление цепи Rэк будет в п раз больше сопротивления R1, т. е. Rэк = nR1. Напряжение U1 на каждом резисторе в этом случае в п раз меньше общего напряжения U:

U1 = U/n. (22)

При последовательном соединении приемников изменение сопротивления одного из них тотчас же влечет за собой изменение напряжения на других связанных с ним приемниках. При выключении или обрыве электрической цепи в одном из приемников и в остальных приемниках прекращается ток.

Поэтому последовательное соединение приемников применяют редко — только в том случае, когда напряжение источника электрической энергии больше номинального напряжения, на которое рассчитан потребитель. Например, напряжение в электрической сети, от которой питаются вагоны метрополитена, составляет 825 В, номинальное же напряжение электрических ламп, применяемых в этих вагонах, 55 В. Поэтому в вагонах метрополитена электрические лампы включают последовательно по 15 ламп в каждой цепи.

Параллельное соединение резисторов.

При параллельном соединении нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви (рис. 26, а).

Рис. 26. Схемы параллельного соединения приемников

Заменяя лампы резисторами с сопротивлениями R1, R2, R3, получим схему, показанную на рис. 26, б.
При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Поэтому согласно закону Ома:

I₁=U/R₁; I₂=U/R₂; I₃=U/R₃.

Ток в неразветвленной части цепи согласно первому закону Кирхгофа I = I₁+I₂+I₃, или:

I = U / R₁ + U / R₂ + U / R₃ = U (1/R₁ + 1/R₂ + 1/R₃) = U / R_эк (23)

Следовательно, эквивалентное сопротивление рассматриваемой цепи при параллельном соединении трех резисторов определяется формулой:

1/R_эк = 1/R₁ + 1/R₂ + 1/R₃ (24)

Вводя в формулу (24) вместо значений 1/R_эк, 1/R₁, 1/R₂ и 1/R₃ соответствующие проводимости G_эк, G₁, G₂ и G₃, получим: эквивалентная проводимость параллельной цепи равна сумме проводимостей параллельно соединенных резисторов:

G_эк = G₁+ G₂ +G₃ (25)

Таким образом, при увеличении числа параллельно включаемых резисторов результирующая проводимость электрической цепи увеличивается, а результирующее сопротивление уменьшается.

Из приведенных формул следует, что токи распределяются между параллельными ветвями обратно пропорционально их электрическим сопротивлениям или прямо пропорционально их проводимостям. Например, при трех ветвях:

I₁ : I₂ : I₃ = 1/R₁ : 1/R₂ : 1/R₃ = G₁ + G₂ + G₃ (26)

В этом отношении имеет место полная аналогия между распределением токов по отдельным ветвям и распределением потоков воды по трубам.

Приведенные формулы дают возможность определить эквивалентное сопротивление цепи для различных конкретных случаев. Например, при двух параллельно включенных резисторах результирующее сопротивление цепи:

R_эк=R₁R₂/(R₁+R₂)

при трех параллельно включенных резисторах:

R_эк=R₁R₂R₃/(R₁R₂+R₂R₃+R₁R₃)

При параллельном соединении нескольких, например n, резисторов с одинаковым сопротивлением R1 результирующее сопротивление цепи Rэк будет в n раз меньше сопротивления R1, т.е.:

R_эк = R1 / n (27)

Проходящий по каждой ветви ток I1, в этом случае будет в п раз меньше общего тока:

I1 = I / n (28)

При параллельном соединении приемников, все они находятся под одним и тем же напряжением, и режим работы каждого из них не зависит от остальных. Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются включенными.

Поэтому параллельное соединение имеет существенные преимущества перед последовательным, вследствие чего оно получило наиболее широкое распространение. В частности, электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, всегда включают параллельно.

На электровозах постоянного тока и некоторых тепловозах тяговые двигатели в процессе регулирования скорости движения нужно включать под различные напряжения, поэтому они в процессе разгона переключаются с последовательного соединения на параллельное.

Смешанное соединение резисторов.

Смешанным соединением называется такое соединение, при котором часть резисторов включается последовательно, а часть — параллельно.

Например, в схеме рис. 27, а имеются два последовательно включенных резистора сопротивлениями R1 и R2, параллельно им включен резистор сопротивлением Rз, а резистор сопротивлением R4 включен последовательно с группой резисторов сопротивлениями R1, R2 и R3.

Рис. 27. Схемы смешанного соединения приемников

Эквивалентное сопротивление цепи при смешанном соединении обычно определяют методом преобразования, при котором сложную цепь последовательными этапами преобразовывают в простейшую.

Например, для схемы рис. 27, а вначале определяют эквивалентное сопротивление R12 последовательно включенных резисторов с сопротивлениями R1 и R2: R12 = R1 + R2. При этом схема рис. 27, а заменяется эквивалентной схемой рис. 27, б. Затем определяют эквивалентное сопротивление R123 параллельно включенных сопротивлений и R3 по формуле:

R₁₂₃=R₁₂R₃/(R₁₂+R₃)=(R₁+R₂)R₃/(R₁+R₂+R₃).

При этом схема рис. 27, б заменяется эквивалентной схемой рис. 27, в. После этого находят эквивалентное сопротивление всей цепи суммированием сопротивления R123 и последовательно включенного с ним сопротивления R4:

R_эк = R₁₂₃ + R₄ = (R₁ + R₂) R₃ / (R₁ + R₂ + R₃) + R₄

Последовательное, параллельное и смешанное соединения широко применяют для изменения сопротивления пусковых реостатов при пуске э. п. с. постоянного тока.

Расчет сопротивления и интервала его абсолютной погрешности при параллельном включении резисторов и при последовательном включении этих же резисторов

Министерство образования и науки Российской Федерации

Новосибирский Государственный Технический Университет

Кафедра ТОР

Расчётно-графическая работа №1

По метрологии

Вариант №22

Факультет: РЭФ

Группа: РТС9-41

Студент: Подрезов Р.В.

Преподаватель: Абрамович В.И.

Новосибирск — 2007 г.

Задача 1.1Б:

При измерении частоты сигнала получены следующие результаты наблюдений :

18,305; 18,308; 18,312; 18,309; 18,304; 18,306; 18,309; 18,310; 18,303; 18,308.

Считать, что генеральная совокупность отклонений результатов наблюдений распределена по нормальному закону.

Определить: результат измерения частоты ; значения среднего квадратического отклонения результатов наблюдений (исключить, если имеются промахи), значения среднеквадратичной погрешности результата измерения , указать его доверительную вероятность ; интервал случайных погрешностей с доверительной вероятностью .

Решение:

Результат измерения вычисляется как среднее арифметическое значений полученных при наблюдениях.

Случайное отклонение определяется как разность полученного значения при наблюдении и результата измерения.

Таблица 1. Таблица результатов наблюдений

По данным таблицы 1 можно провести оценку среднего квадратического отклонения результатов наблюдений:

Зададимся уровнем значимости .Из таблицы наибольшего приведённого отклонения для соответствующих и находится величина допустимых значений . Наиболее сомнительный результат — , для которого . Проверим, выполняется ли неравенство:

Отсюда делаем вывод об отсутствии промахов.

Значение среднеквадратичной погрешности результата измерений рассчитывается из соотношения:

Интервал погрешности измерения с заданной доверительной вероятностью определяется по формуле:

где — коэффициент Стьюдента (обратное распределение Стьюдента)

Результат измерения: , ,

Задача 1.15

Сопротивление составлено из двух резисторов с и .

1. Чему равно и интервал его абсолютной погрешности при параллельном включении резисторов.

2. Чему равно и интервал его абсолютной погрешности при последовательном включении этих же резисторов.

Решение:

; — абсолютная погрешность сопротивления первого резистора;

; — абсолютная погрешность сопротивления второго резистора;

При параллельном включении:

Ответ: ,

При последовательном включении:

Ответ: ,

Задача 2.2

Электрическая схема устройства сведена к эквивалентной, состоящей из последовательно включённых: источника постоянного напряжения, сопротивлений и . На измеряется падение напряжения вольтметром В2-27 с входным сопротивлением .

Определите, в какой цепи из трёх указанных ниже относительная погрешность измерения напряжения будет наибольшей, рассчитайте её величину, сформулируйте условия на соотношения ; при которых она будет мала.

1 цепь :

2 цепь

3 цепь

Решение:

Рисунок 2. Эквивалентная схема для расчёта истинного значения напряжения

Рисунок 2. Эквивалентная схема для расчёта измеренного значения напряжения

Выразим погрешность через сопротивления совершив некоторые математические выкладки:

1 цепь

2 цепь

3 цепь

Задача 3.6а

Какой минимальной верхней частотой полосы пропускания канала должен обладать осциллограф для измерения длительности фронта импульса порядка с погрешностью ?

Решение:

Измеренное значение длительности фронта импульса:

Отсюда время нарастания будет равным:

Согласно определению относительная погрешность:

Следовательно, измеренное значение длительности фронта можно выразить как:

Время нарастания при подстановке примет вид:

К тому же:

В итоге выражение для минимальной верхней частоты будет выглядеть так:

Расчет величин сопротивлений уравнительных резисторов

Параллельное включение транзисторов используется не только для уменьшения размеров теплоотвода, но и в случае, когда заданный ток нагрузки I_н_max не может быть обеспечен имеющимися в распоряжении типами транзисторов. При этом ток через каждый из параллельно соединенных транзисторов не превышает допустимого значения.

Схема включения уравнительных резисторов показана на рис. 2.7.

Рис. 2.7

Нужно иметь в виду, что при параллельном соединении транзисторов неизбежный разброс их характеристик может привести к существенно не одинаковому нагреву переходов транзисторов. В то же время очевидно, что параллельное соединение транзисторов выходного каскада эффективно лишь тогда, когда ток нагрузки распределяется между параллельно включенными приборами достаточно равномерно. Поскольку разбраковка партии транзисторов на группы с одинаковыми характеристиками, как правило, не проводится, то основным способом обеспечения равномерного распределения токов (а значит, и рассеиваемых мощностей) является включение в эмиттерные цепи транзисторов небольших одинаковых сопротивлений R_э1 = R_э2 = R_э3 = … = R_э_n = R_э.ур. Величина уравнительных сопротивлений находится по формуле

где S_max – максимальное значение крутизны переходной характеристики транзистора выбранного типа по постоянному току, которую удобно находить через статический коэффициент усиления тока b и входное сопротивление транзистора

здесь i_б – ток базы, соответствующий значению U_бэ.нас, которое приведено в справочных данных, для выбранного типа транзистора; – разброс характеристик транзистора по току силовой цепи; здесь I_к_min и I_к_max – значения минимального и максимального токов коллектора, взятые из справочных данных, для выбранного типа транзистора. При отсутствии в справочнике необходимой информации l_i задается в пределах 1,5–2,0; l_i_доп. – допустимая величина отношения токов параллельно соединенных транзисторов.

Для определения l_i_доп. следует задаться допустимым повышением температуры перехода = 5ºС…20ºС и определить относительное приращение мощности рассеяния

здесь коэффициент запаса по температуре K_з = 0,75…0,85; ΔP_к – потери мощности на уравнительных резисторах.

При работе каскада усилителя в режимах классов A и B δI_к.доп. = δP_к.доп., следовательно

Мощность уравнительных резисторов определяется следующим образом

При расчетах уравнительных резисторов необходимо учитывать, что значение P_э.ур. при использовании непроволочных резисторов не должно превышать 2 Вт. В противном случае необходимо применять проволочные резисторы, у которых при больших рассеиваемых мощностях резко возрастают массогабаритные показатели.

Для удобства дальнейших расчетов параллельно включенные транзисторы целесообразно заменить одним эквивалентным с параметрами:

Уравнительные резисторы, включенные в эмиттерные цепи, образуют последовательную отрицательную обратную связь по току, увеличивая тем самым температурную стабильность каскада и его входное сопротивление. Вместе с тем на этих резисторах рассеивается дополнительная мощность, что снижает коэффициент полезного действия каскада. Поэтому, чтобы избежать дополнительных потерь мощность, в отдельных случаях, применяют параллельное включение транзисторов без уравнительных сопротивлений. В этом случае расчетный ток через каждый транзистор составляет 50 – 60 % от номинального, т.е. транзисторы работают с недогрузкой по току. При этом через отдельные транзисторы может идти ток, составляющий 70 – 90%, а через другие – 20 – 40% от номинального значения, но в целом такая схема будет работать достаточно надежно.

Пример. Проведем расчет величин уравнительных резисторов для схемы, представленной на рис. 2.8, в которой в параллель включены два транзистора КТ816А (КТ817А), обеспечивающие I_н= 3 А. Примем допустимую разницу температур коллекторов транзисторов = 10ºС; K_з = 0,75; l_i = 1,5.

Рис. 2.8

Из соотношения (2.16)

Входное сопротивление транзистора КТ816А (КТ817А) при I_к= 3А

Примем величину β_max = 2β_min = 2·20 = 40, поскольку данные о максимальном значении коэффициента усиления в справочнике отсутствуют. Из (2.15) определяем максимальное значение крутизны переходной характеристики транзистора по постоянному току

а затем из (2.14) значение

Округлим полученное значение в соответствии с рядом номинальных величин (ряд Е24) R_э.ур.= 2,0 Ом. Мощность резистора определяется по (2.17) и составляет

Полученное значение мощности превышает 2 Вт, поэтому либо надо применять проволочные резисторы, номинальная мощность которых превышает рассчитанное значение (в рассматриваемом случае можно, например, использовать резистор С5-37В мощностью 5 Вт), либо для уменьшения величины P_э.ур. можно вместо одного резистора номиналом 2 Ом включить несколько резисторов параллельно, общее сопротивление которых будет обеспечивать значение R_э.ур.близкое к расчетному. Это даст возможность применять непроволочные резисторы, массогабаритные показатели которых, как правило, существенно лучше, чем проволочных.

Например, из ряда Е24 выбираем резисторы номиналом 6,2 Ом, которые при параллельном включении будут обеспечивать R_э.ур.= 2,067 Ом. При таком инженерном решении мощность полученного резистора будет определяться соотношением

где n – число резисторов, включенных параллельно и обеспечивающих необходимое значение R_э.ур.. В рассматриваемом примере n = 2. Из (2.18) получаем

что дает возможность применять непроволочные резисторы, например марок МЛТ; С2-33 и т. д.

Замена одного проволочного резистора на несколько непроволочных резисторов меньшей мощности должна быть обоснована сравнением массо-габаритных показателей. В рассматриваемом примере резистор марки С5-37В номиналом 2 Ом, мощностью 5 Вт имеет массу 7 г, диаметр и длину корпуса 11 мм и 26,2 мм, соответственно (объем составляет » 2,5 см³). Резистор марки МЛТ номиналом 6,2 Ом, мощностью 2 Вт имеет массу 3,5 г, диаметр и длину корпуса 8,6 мм и 18,5 мм, соответственно (объем составляет » 1,07 см³). С учетом того, что резисторов МЛТ в одном плече каскада должно быть шесть, общая масса составит 21 г, а объем 6,42 см³. Очевидно, что в данном случае предпочтительнее применять проволочные резисторы.

Параллельное соединение резисторов

Господа, в прошлый раз мы с вами говорили про последовательное сопротивление резисторов. Сегодня я бы хотел вам рассказать про другой возможный вид соединения – параллельное.

Чем различается последовательное и параллельное соединение я уже писал в предыдущей статье. Но все-таки вытащу сюда картинку из той прошлой статьи, я ж знаю, что вам будет лень ходить по ссылкам .

А) – Последовательное соединение

В) – Параллельное соединение

Рисунок 1 – Последовательное и параллельное соединение

Как мы видим из рисунка 1, параллельное соединение – это такое соединение, при котором одни концы всех резисторов соединены в один узел, а другие концы – в другой узел.

Сейчас наша задача будет разобраться, как ведут себя токи, напряжения, сопротивления и мощности при таком подключении. Для этого прошу вас взглянуть на рисунок 2, где подробно разрисован расклад дел для параллельного соединения. Будем полагать, что мы знаем величины R1, R2 и R3, а также величину приложенного к схеме напряжения U. Про токи же мы ничего не знаем.

Рисунок 2 – Параллельное соединения

Что мы видим на рисунке 2? Ну, в первую очередь – два узла А и B. В узел А сходятся одни концы всех резисторов, а в узел В – другие концы. Пусть узел А имеет потенциал φ₁, а узел В – потенциал φ₂. Из рисунка 2 видно, что для всех резисторов R1, R2 и R3 у нас одна и та же разность потенциалов U.

Как следует из статьи про потенциалы, это означает, что напряжение на всех резисторах у нас одинаково и равно приложенному напряжению U. Это важный вывод, его следует хорошо запомнить.

С токами дело обстоит по-другому. Проанализируем рисунок 2 слева направо. Пусть у нас в цепи течет ток I. Течет он себе, течет, никого не трогает и тут вдруг натыкается на узел А. Что в этом случае говорит полюбившаяся вам статья про первый закон Кирхгофа? А то, что ток I в узле А разделится на три тока I₁, I₂, I₃. При этом будет выполняться равенство

То есть через резистор R1 будет протекать ток I₁, через резистор R2 – ток I₂, а через резистор R3 – ток I₃.

Итак, у нас в системе уже тихо-мирно текут себе три тока. И все хорошо, пока они не наткнуться на узел В. Тут снова вступает в силу первый закон Кирхгофа. Эти три тока I₁, I₂, I₃ вновь соединятся в один ток I. Причем после узла В ток будет иметь такую же величину I, какой он был до узла А.

То есть если все вышесказанное воплотить в лаконичный язык наскальной живописи, положение дел можно представить себе вот так

Как же найти эти самые токи I₁, I₂, I₃? Господа, полагаю, вы уже догадались, что на помощь нам придет горячо нами всеми любимый закон Ома. Действительно, мы знаем сопротивления резисторов и, кроме того, нам известно, что на всех них падает одно и тоже напряжение U. Поэтому легко находим токи

Отлично, мы разобрались с напряжениями и с токами в такой схеме. А помните в статье про последовательное сопротивление мы ловко преобразовали три резистора в один с эквивалентным им сопротивлением? Нельзя ли и здесь сделать что-то подобное? Оказывается, вполне себе можно. Как мы помним, токи в схеме распределены таким вот образом

Обзовем эквивалентное сопротивление буковкой R. И подставим в это выражение только что найденные нами токи I₁, I₂, I₃

Видим, что здесь без проблем можно сократить левую и правую части на U. Получаем

Господа, важный вывод: при параллельном соединении резисторов обратное эквивалентное сопротивление равно сумме обратных сопротивлений отдельных резисторов.

То есть для упрощения различных расчетов электрических схем такую вот цепочку параллельно соединенных резисторов можно заменить одним резистором с соответствующим сопротивлением, как показано на рисунке 3.

Рисунок 3 – Преобразование параллельного соединение

Весьма частый случай на практике, когда соединены параллельно не много резисторов, а всего два. Поэтому полезно знать наизусть итоговое сопротивление такой схемы. Давайте посмотрим, чему оно равно:

То есть, если у вас два сопротивления соединены параллельно, то по этой формуле вы легко высчитаете общее сопротивление. Рассмотрим пример. Пусть у нас параллельно соединены два резистора 10 кОм и 15 кОм. Чему равно их общее сопротивление?

Заметьте, господа, итоговое сопротивление у нас получилось 6 кОм, что меньше 10 кОм и 15 кОм. То есть при параллельном соединении общее сопротивление меньше любого из составляющих. Это всегда верно для любого количества резисторов, а не только для двух. Итоговое сопротивление всегда уменьшается (в отличии от последовательного сопротивления, где итоговое сопротивление всегда растет). Этот факт полезно запомнить.

Еще один часто встречающийся на практике случай – когда параллельно соединены несколько резисторов с одинаковым сопротивлением. Допустим, каждый из них обладает сопротивлением R1 и всего их N штук. Тогда по нашей общей формуле для эквивалентного сопротивления

То есть при параллельном соединении N одинаковых резисторов с сопротивлением R1 итоговое сопротивление будет в N раз меньше этого самого сопротивления R1.

Так-с, с током разобрались, с напряжением разобрались, с эквивалентным сопротивлением вроде тоже…осталась мощность. Для этого воспользуемся вот этим выражением, которое мы писали чуть выше в статье

Умножим левую и правую части на напряжение U.

Как мы помним из статьи про мощность произведение тока на напряжение есть мощность. То есть мы можем записать

где Р – мощность, выдаваемая источником;

P₁ – мощность, рассеиваемая на резисторе R1;

P₂ – мощность, рассеиваемая на резисторе R2;

P₃ – мощность, рассеиваемая на резисторе R3.

Заметьте, господа, формула в точности такая же, как и для случая последовательного соединения резисторов. И там и там мощность, выдаваемая источником, равна сумме мощностей, рассеиваемых на резисторах цепи.

Итак, господа, мы рассмотрели основные соотношения при параллельном соединении резисторов. Теперь осталось поговорить, где это параллельное соединение можно использовать и для чего.

1) Ну, во-первых, параллельное соединение применяют во всех случаях, когда хотят запитать несколько нагрузок от одного источника напряжения. При этом пользуются тем свойством, что при параллельном соединении напряжения на всех нагрузках одинаково. То есть, допустим, вы берете источник напряжения, выставляете на нем напряжение 5 В и цепляете к этому источнику сразу несколько своих устройств. Узлами А и В в этом случае будут клеммы источника. На каждое из устройств в этом случае придет напряжение 5 В. Да и все устройства в вашей квартире (лампочки, компьютеры, телевизоры и все прочее) соединены между собой параллельно.

2) Второе возможное применение встречается не так часто, но, думаю, о нем тоже следует рассказать. Допустим, вы делаете какую-то схему, где необходим очень точный подгон сопротивления. Скажем, надо получить сопротивление 6 кОм. Такое сопротивление найти нелегко, их просто не продают. Зато у вас есть два сопротивления 10 кОм и 15 кОм. Вы их соединяете параллельно и получаете требуемые 6 кОм. Как показывает практика, 3 параллельных резисторов достаточно для получения итогового результирующего сопротивления требуемого номинала с весьма хорошей точностью. Конечно, таких вещей лучше избегать и, если есть возможность, всегда стараться применять стандартные сопротивления. Но бывают случаи, когда это невозможно, и тогда приходит на помощь этот метод.

3) Третий пункт будет немного похож на первый. Его суть заключается в следующим. Допустим, нам надо снять с источника питания 10 Вт мощности. А у нас в наличии только резисторы, которые позволяют рассеивать на себе 1 Вт. Что делать? Можно соединить 10 резисторов параллельно и с каждого снимать по 1 Вт. Мы же помним нашу формулу

Конечно, лучше брать не 10 резисторов, а хотя бы 15 и рассеивать на них меньше, чем 1 Вт. Работать на пределе никогда не следует.

Кстати, тут очень вовремя к моменту написания статьи пришли платы с производства! Господа, прошу вас взглянуть на рисунок 4.

Рисунок 4 – Плата нагревателя

На нем изображена плата нагревателя (флешка для масштаба). В чем суть? Имеется весьма сложное устройство, предназначенное для работы в арктических условиях. Найти же компоненты, которые надежно функционировать при температурах минус 55 градусов и при этом стоят адекватных денег и обладают адекватными размерами бывает непросто. Обычно элементная база в лучшем случае рассчитана на минус 40 градусов. И было принято решение разработать вот такой вот нагреватель для прогрева чувствительных к холоду аналоговых узлов устройства. Он управляется с микроконтроллера и автоматически включается при температурах меньше минус 40 градусов. Как вы можете видеть из рисунка 4, этот нагреватель представляет собой 30 параллельно соединенных резисторов с сопротивлениями 150 Ом. Каждый резистор, согласно документации, способен рассеивать до 1 Вт мощности. Используя изученные формулки, мы можем посчитать, что в сумме такая система обладает сопротивлением

и теоретически может рассеивать мощность

Ну, с сопротивлением вопросов нет, оно действительно равно 5 Ом. Ну, плюс-минус 5 % на допуск резисторов, что в данном случае вообще не критично. А вот с мощностью тут не так все однозначно. Помните про закон Джоуля-Ленца, который мы рассматривали? Резисторы будут греться, причем не слабо. Как показывает практика, если нагружать резисторы по полной, то есть рассеивать на каждом по 1 Вт, то в течении нескольких секунд их температура улетит за 150 градусов. Такая высокая температура критична для резистора и может привести к его разрушению. Я был готов к такому развитию событий, поэтому заложил для платы нагревателя максимальное напряжение 9 вольт. Это значит, что на каждом резисторе будет выделяться

что почти в два раза меньше максимально допустимой мощности в 1 Вт. В сумме на всей плате выделялось, соответственно

Эксперимент показал, что резисторы достигли температуры с комнатных 25 градусов до критичных 120 градусов приблизительно за 10 секунд работы и температура продолжала уверенно расти. Очевидно, если оставить на длительное время включенным такой нагреватель при комнатной температуре, он неминуемо выйдет из строя. Возможно, при работе на минус 55 градусах перегрев бы не был столь критичным, однако хотелось исключить вариант спалить плату на столе, поэтому я понизил напряжение, подаваемое на плату на 3 вольта: стал подавать 6 вольт. Теперь на каждом резисторе рассеивалось

а на всей плате

Теперь температура поднималась до 100-110 градусов примерно за 30-40 секунд работы и оставалась на этом уровне (выходила в точку термодинамического равновесия). Эта температура вполне подходит для нагревателя. Однако пока это были лишь эксперименты на столе при комнатной температуре, главный эксперимент – в термокамере на минус 55 градусах – впереди. Возможно, по его результатам потребуется чуть увеличить рассеиваемую мощность. А может все останется как есть и этой мощности будет достаточно для вывода девайса на режим за адекватное время, время покажет .

На сегодня все, господа. Удачи вам и до новых встреч!

Вступайте в нашу группу Вконтакте

Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it.

Как рассчитать падение напряжения на резисторе в параллельной цепи

Обновлено 28 декабря 2020 г.

Автор: S. Hussain Ather

••• Syed Hussain Ather

TL; DR (слишком долго; не читал)

На приведенной выше схеме параллельной цепи падение напряжения можно найти, суммируя сопротивления каждого резистора и определяя, какое напряжение получается из тока в этой конфигурации. Эти примеры параллельных цепей иллюстрируют концепции тока и напряжения в разных ветвях.

На схеме параллельной цепи, падение напряжения на резисторе в параллельной цепи одинаково для всех резисторов в каждой ветви параллельной цепи. Напряжение, выраженное в вольтах, измеряет электродвижущую силу или разность потенциалов в цепи.

Когда у вас есть цепь с известной величиной тока , потока электрического заряда, вы можете рассчитать падение напряжения в схемах параллельной цепи следующим образом:

Определите объединенное сопротивление или сопротивление к потоку заряда параллельных резисторов.Суммируйте их как 1 / R _всего = 1 / R ₁ + 1 / R ₂ … для каждого резистора. Для приведенной выше параллельной цепи полное сопротивление можно найти как:
1. 1 / R _всего = 1/5 Ом + 1/6 Ом + 1/10 Ом
2. 1 / R _всего = 6/30 Ом + 5/30 Ом + 3/30 Ом
3. 1 / R _всего = 14/30 Ом
4. R _всего = 30/14 Ом = 15/7 Ом
Умножьте ток на общее сопротивление, чтобы получить падение напряжения в соответствии с законом Ома В = IR .Это равно падению напряжения во всей параллельной цепи и на каждом резисторе в параллельной цепи. В этом примере падение напряжения составляет В = 5 А x 15/7 Ом = 75/7 В.

Этот метод решения уравнений работает, потому что ток, входящий в любую точку параллельной цепи, должен быть равен текущий уход. Это происходит из-за текущего закона Кирхгофа, который гласит: «алгебраическая сумма токов в сети проводников, встречающихся в одной точке, равна нулю.»Калькулятор параллельной цепи мог бы использовать этот закон в ветвях параллельной цепи.

Если мы сравним ток, входящий в три ветви параллельной цепи, он должен равняться общему току, выходящему из ветвей. Поскольку падение напряжения остается постоянная на каждом параллельном резисторе, это падение напряжения, вы можете суммировать сопротивление каждого резистора, чтобы получить общее сопротивление и определить напряжение по этому значению. Примеры параллельных цепей показывают это.

Падение напряжения в последовательной цепи

•• • Syed Hussain Ather

В последовательной цепи, с другой стороны, вы можете рассчитать падение напряжения на каждом резисторе, зная, что в последовательной цепи ток постоянен на всем протяжении.Это означает, что падение напряжения на каждом резисторе разное и зависит от сопротивления в соответствии с законом Ома В = IR . В приведенном выше примере падение напряжения на каждом резисторе составляет:

V_1 = R_1I = 3 \ times 3 = 9 \ text {V} \\ V_2 = R_2I = 10 \ times 3 = 30 \ text {V} \\ V_3 = R_3I = 5 \ times 3 = 15 \ text {V}

Сумма каждого падения напряжения должна быть равна напряжению батареи в последовательной цепи. Это означает, что наша батарея имеет напряжение 54 В.

Этот метод решения уравнений работает, потому что падение напряжения на всех резисторах, установленных последовательно, должно в сумме составлять общее напряжение последовательной цепи.Это происходит из-за закона напряжения Кирхгофа, который гласит, что «направленная сумма разностей потенциалов (напряжений) вокруг любого замкнутого контура равна нулю». Это означает, что в любой точке замкнутой последовательной цепи падение напряжения на каждом резисторе должно равняться общему напряжению цепи. Поскольку ток в последовательной цепи постоянный, падение напряжения должно различаться на каждом резисторе.

Параллельные и последовательные схемы

В параллельной схеме все компоненты схемы подключаются между одними и теми же точками на схеме.Это дает им их разветвленную структуру, в которой ток разделяется между каждой ветвью, но падение напряжения на каждой ветви остается неизменным. Сумма каждого резистора дает общее сопротивление, обратное каждому сопротивлению ( 1 / R _всего = 1 / R ₁ + 1 / R ₂ … для каждого резистора).

В последовательной цепи, напротив, есть только один путь для прохождения тока. Это означает, что ток остается постоянным на всем протяжении, а падение напряжения на каждом резисторе отличается.Сумма каждого резистора дает общее сопротивление при линейном суммировании ( R _всего = R ₁ + R ₂ … для каждого резистора).

Последовательно-параллельные схемы

Вы можете использовать оба закона Кирхгофа для любой точки или петли в любой цепи и применять их для определения напряжения и тока. Законы Кирхгофа дают вам метод определения тока и напряжения в ситуациях, когда природа цепи как последовательной и параллельной может быть не такой простой.

Как правило, для цепей, которые имеют как последовательные, так и параллельные компоненты, вы можете рассматривать отдельные части схемы как последовательные или параллельные и соответственно комбинировать их.

Эти сложные последовательно-параллельные схемы можно решить несколькими способами. Один из методов — рассматривать их части как параллельные или последовательные. Другой метод — использование законов Кирхгофа для определения обобщенных решений, использующих систему уравнений. Калькулятор последовательно-параллельных цепей учитывает различную природу цепей.

••• Syed Hussain Ather

В приведенном выше примере текущая точка выхода A должна равняться текущей точке выхода A. Это означает, что вы можете написать:

(1). I_1 = I_2 + I_3 \ text {или} I_1-I_2-I_3 = 0

Если рассматривать верхний контур как замкнутую последовательную цепь и рассматривать падение напряжения на каждом резисторе, используя закон Ома с соответствующим сопротивлением, вы можете написать:

(2). V_1-R_1I_1-R_2I_2 = 0

и, проделав то же самое для нижнего контура, вы можете обрабатывать каждое падение напряжения в направлении тока в зависимости от тока и сопротивления, чтобы записать:

(3).V_1 + V_2 + R_3I_3-R_2I_2 = 0

Это дает вам три уравнения, которые можно решить несколькими способами. Вы можете переписать каждое из уравнений (1) — (3) так, чтобы напряжение было с одной стороны, а ток и сопротивление — с другой. Таким образом, вы можете рассматривать три уравнения как зависимые от трех переменных I ₁, I ₂ и I ₃ с коэффициентами комбинаций R ₁, R ₂ и R ₃.

\ begin {align} & (1).I_1-I_2-I_3 = 0 \\ & (2). R_1I_1 + R_2I_2 + 0 \ times I_3 = V_1 \\ & (3). 0 \ times I_1 + R_2I_2-R_3I_3 = V_1 + V_2 \ end {выровнено}

Эти три уравнения демонстрируют, как напряжение в каждой точке цепи каким-то образом зависит от тока и сопротивления. Если вы помните законы Кирхгофа, вы можете создать эти обобщенные решения схемных задач и использовать матричную нотацию для их решения. Таким образом, вы можете подставить значения для двух величин (среди которых напряжение, ток, сопротивление), чтобы найти третью.

Резисторы при параллельном расчете

Описание как рассчитать резисторы параллельно

Резисторы параллельно

Если ток в цепи распределяется по нескольким резисторам, мы называем это параллельной цепью резисторов. На всех резисторах одинаковое напряжение.

Если общие ток и напряжение известны, мы можем вычислить общий сопротивление по закону Ома по следующей формуле.

\ (\ Displaystyle R_ {ges} = \ гидроразрыва {U} {I} \)

Если значения тока или напряжения неизвестны, мы можем сложить проводимости отдельных резисторов.

\ (\ Displaystyle G_ {ges} = G_1 + G_2 + G_3 \) das entspricht \ (\ displaystyle \ frac {1} {R_ {ges}} = \ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3} \)

Пример с тремя резисторами \ (220 \), \ (330 \) и \ (470 \) Ом

\ (\ displaystyle \ frac {1} {R_ {ges}} = \ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3} = \ frac {1} {220} + \ frac {1} {330} + \ frac {1} {470} = 0.0097 \)

\ (\ Displaystyle R_ {ges} = \ гидроразрыва {1} {0,0097} = 103 Ом \)

Для схемы, в которой два резистора включены параллельно, мы можем перейти к более простой формуле, добавив две дроби

\ (\ displaystyle \ frac {1} {R_ {ges}} = \ frac {1} {R_1} + \ frac {1} {R_2} = \ frac {R_1 + R_2} {R_1 · R_2} \)

Это приводит к

\ (\ Displaystyle R_ {ges} = \ гидроразрыва {R_1 · R_2} {R_1 + R_2} \)

Пример

\ (\ Displaystyle R_ {ges} = \ гидроразрыва {220 · 330} {220 + 330} = 132 \)

Как рассчитать полное сопротивление параллельной цепи?

Эффективное сопротивление резисторов, подключенных параллельно

Параллельная цепь имеет три важных характеристики :
(a) Разность потенциалов одинакова на каждом резисторе.
(b) Ток, который проходит через каждый резистор, обратно пропорционален сопротивлению резистора.
(c) Полный ток в цепи равен сумме токов, проходящих через резисторы в ее параллельных ветвях.
Когда два или более сопротивления подключены между двумя общими точками так, что к каждой из них приложена одинаковая разность потенциалов, они считаются подключенными параллельно.
Когда такая комбинация сопротивлений подключена к батарее, все сопротивления имеют одинаковую разность потенциалов на концах.
Вывод математического выражения для параллельной комбинации:
Пусть, V будет разностью потенциалов между двумя общими точками A и B. Тогда из закона Ома
Ток, проходящий через R ₁, I ₁ = V / R ₁… (i)
Ток, проходящий через R ₂, I ₂ = V / R ₂… (ii)
Ток, проходящий через R ₃, I ₃ = V / R ₃… (iii)
Если R — эквивалентное сопротивление, то по закону Ома полный ток, протекающий по цепи, определяется выражением
I = V / R… (iv)
и I = I ₁ + I ₂ + I ₃… (v)
Подставляя значения I, I ₁, I ₂ и I ₃ в уравнение.(v),
\ (\ frac {\ text {V}} {\ text {R}} = \ frac {\ text {V}} {{{\ text {R}} _ {\ text {1}} }} + \ frac {\ text {V}} {{{\ text {R}} _ {\ text {2}}}} + \ frac {\ text {V}} {{{\ text {R}} _ {\ text {3}}}} \ text {} …… .. \ text {(vi)} \)
Отменяя общий термин V, получаем
\ (\ frac {\ text {1}} {\ text {R}} = \ frac {\ text {1}} {{{\ text {R}} _ {\ текст {1}}}} + \ frac {\ text {1}} {{{\ text {R}} _ {2}}} + \ frac {\ text {1}} {{{\ text {R} } _ {3}}} \)
Эквивалентное сопротивление параллельной комбинации сопротивлений меньше, чем каждое из всех отдельных сопротивлений.
Эквивалентная схема показана на рисунке.

Важные результаты о параллельной комбинации:

Полный ток в цепи равен сумме протекающих по ней токов.
В параллельной комбинации резисторов напряжение (или разность потенциалов) на каждом резисторе одинаково и равно приложенному напряжению, то есть В ₁ = В ₂ = В ₃ = В.
Ток, протекающий через каждый резистор, обратно пропорционален его сопротивлению, поэтому чем выше сопротивление резистора, тем меньше ток, протекающий через него.

Люди тоже спрашивают

Проблемы параллельной цепи и их решение

Три резистора, R ₁, R ₂ и R ₃, подключены параллельно к батарее, как показано на рисунке.

Рассчитайте
(a) разность потенциалов на каждом резисторе,
(b) эффективное сопротивление R цепи,
(c) ток, I, в цепи,
(d) токи, I ₁, I ₂ и I ₃, проходящие через каждый резистор.
Решение:
(a) Поскольку это параллельная схема, разность потенциалов на каждом резисторе составляет 6 В, то же самое, что и разность потенциалов на батарее, которая составляет 6 В.

резисторов последовательно и параллельно

резисторов последовательно и параллельно
Далее: Правила Кирхгофа Up: Электрический ток Предыдущее: ЭДС и внутреннее сопротивление Резисторы, вероятно, встречаются чаще всего. компоненты в электронных схемах.Практические схемы часто содержат очень сложные комбинации резисторов. Поэтому полезно иметь набор правил для поиска эквивалентных сопротивление некоторой общей схемы резисторов. Оказывается, мы можем всегда находите эквивалентное сопротивление повторным применением два простых правила . Эти правила относятся к резисторам, включенным последовательно, и в параллели.

**Рисунок 18:** *Два резистора соединены последовательно.*

Рассмотрим два резистора, включенных в серию , как показано на рис.18. Понятно, что через оба резистора протекает одинаковый ток. Ибо, если бы это было не так, заряд накапливался бы в одном или другом резисторов, которые не соответствовали бы установившаяся ситуация (таким образом нарушая основное предположение этого раздела). Предположим, что падение потенциала от точки к точке есть. Это падение представляет собой сумму потенциальных падает и на двух резисторах и соответственно. Таким образом,

(135)

Согласно закону Ома, эквивалентное сопротивление между и — отношение падения потенциала в этих точках и ток, протекающий между ними.Таким образом,

(136)

давая

(137)

Здесь мы использовали тот факт, что ток является общим для все три резистора. Следовательно, правило

Эквивалентное сопротивление двух последовательно соединенных резисторов равно сумма отдельных сопротивлений.

Для резисторов, соединенных последовательно, уравнение.(137) обобщает к .

**Рисунок 19:** *Два резистора подключены параллельно.*

Рассмотрим два резистора, соединенных по параллельно , как показано на рис. 19. Это Из рисунка видно, что падение потенциала на двух резисторах равно тем же. В общем, однако, токи и которые протекают через резисторы и соответственно разные. По закону Ома эквивалентное сопротивление между и — отношение падения потенциала через эти точки и текущий которая течет между ними.Этот ток должен равняться сумме токи и протекающие через два резистора, в противном случае заряд будет накапливаться на одном или обоих переходах в цепи. Таким образом,

(138)

Следует, что

(139)

давая

(140)

Здесь мы использовали тот факт, что падение потенциала является общим для всех трех резисторов.Ясно, что правило

Обратное эквивалентное сопротивление двух сопротивлений. подключенных параллельно — это сумма обратных величин индивидуальные сопротивления.

Для резисторов, соединенных параллельно, уравнение. (140) обобщает на .

Далее: Правила Кирхгофа Up: Электрический ток Предыдущее: ЭДС и внутреннее сопротивление

Ричард Фицпатрик 2007-07-14

17.5 параллельных резисторов | Электрические схемы

17,5 Резисторы параллельные (ЭСАФК)

Когда мы добавляем резисторы параллельно цепи:

Есть больше путей для прохождения тока, что обеспечивает разделение тока на разные Дорожки .
Напряжение на резисторах то же . Напряжение на АКБ в цепи равно напряжению на каждом из параллельных резисторов:
\ [{V} _ {\ text {battery}} = {V} _ {1} = {V} _ {2} = {V} _ {3} \ ldots \]
Сопротивление току уменьшается .Полное сопротивление \ ({R} _ {P} \) дается по:
\ [\ frac {1} {{R} _ {P}} = \ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2}} + \ ldots \ ]

При параллельном подключении резисторов начальная и конечная точки для всех резисторов одинаковы. Эти точки имеют одинаковую потенциальную энергию, поэтому разность потенциалов между ними одинакова, независимо от того, что вставьте между ними. У вас может быть один, два или несколько резисторов между двумя точками, разность потенциалов будет не изменить.Вы можете игнорировать любые компоненты, находящиеся между двумя точками в цепи, при вычислении разницы. между двумя точками.

Посмотрите на следующие принципиальные схемы. Аккумулятор во всех корпусах одинаковый, меняет только резисторы добавляются между точками, отмеченными черными точками. Если бы мы измерили разность потенциалов между две точки в этих схемах, мы получим одинаковый ответ для всех трех случаев.

Давайте посмотрим на два параллельно подключенных резистора более внимательно.Когда вы создаете схему, вы используете провода, и вы можете думаю, что измерение напряжения в разных местах на проводах будет иметь значение. Это неправда. В Измерение разности потенциалов или напряжения будет отличаться только в том случае, если вы измеряете другой набор компонентов. Все точки на проводах, между которыми нет компонентов схемы, дадут вам одинаковые измерения.

Все три измерения, показанные на рисунке ниже (т. Е. A – B, C – D и E – F), дадут вам такое же напряжение.Различные точки измерения слева не имеют компонентов между собой, поэтому нет изменение потенциальной энергии. То же самое относится и к разным точкам справа. Когда вы измеряете разность потенциалов между точками слева и справа вы получите одинаковый ответ.

Рабочий пример 7: Напряжения I

Рассмотрим принципиальную схему:

Какое напряжение на резисторе в показанной цепи?

Проверьте, что у вас есть и единицы

У нас есть схема с батареей и одним резистором.Нам известно напряжение на батарее. Мы хотим найти это напряжение на резисторе.

\ [{V} _ {\ text {battery}} = \ text {2} \ text {V} \]

Применимые принципы

Мы знаем, что напряжение на батарее должно быть равно общему напряжению на всех остальных цепях. компоненты.

\ [{V} _ {\ text {battery}} = {V} _ {\ text {total}} \]

Есть только один другой компонент схемы — резистор.

\ [{V} _ {\ text {total}} = {V} _ {1} \]

Это означает, что напряжение на батарее равно напряжению на резисторе.

\ begin {align *} {V} _ {\ text {battery}} & = {V} _ {\ text {total}} = {V} _ {1} \\ {V} _ {1} & = \ text {2} \ text {V} \ end {выровнять *}

Рабочий пример 8: Напряжения II

Рассмотрим эту схему:

Какое напряжение на неизвестном резисторе в показанной цепи?

Проверьте, что у вас есть и единицы

У нас есть схема с батареей и двумя резисторами.Мы знаем напряжение на батарее и один из резисторы. Мы хотим найти это напряжение на резисторе.

\ begin {align *} {V} _ {\ text {battery}} & = \ text {2} \ text {V} \\ {V} _ {B} & = \ text {1} \ text {V} \ end {выровнять *}

Применимые принципы

Мы знаем, что напряжение на батарее должно быть равно общему напряжению на всех остальных цепях. компоненты, которые находятся последовательно.

\ [{V} _ {\ text {battery}} = {V} _ {\ text {total}} \]

Общее напряжение в цепи — это сумма напряжений на отдельных резисторах

\ [{V} _ {\ text {total}} = {V} _ {A} + {V} _ {B} \]

Использование зависимости между напряжением на батарее и общим напряжением на резисторах

\ begin {align *} {V} _ {\ text {battery}} & = {V} _ {\ text {total}} \\\\ {V} _ {\ text {battery}} & = {V} _ {1} + {V} _ {\ text {resistor}} \\ \ text {2} \ text {V} & = {V} _ {1} + \ text {1} \ text {V} \\ {V} _ {1} & = \ text {1} \ text {V} \ end {выровнять *}

Рабочий пример 9: Напряжения III

Рассмотрим принципиальную схему:

Какое напряжение на неизвестном резисторе в показанной цепи?

Проверьте, что у вас есть и единицы

У нас есть схема с батареей и тремя резисторами.Мы знаем напряжение на батарее и двух резисторы. Мы хотим найти это напряжение на неизвестном резисторе.

\ begin {align *} {V} _ {\ text {battery}} & = \ text {7} \ text {V} \\ {V} _ {\ text {известное}} & = {V} _ {A} + {V} _ {C} \\ & = \ текст {1} \ текст {V} + \ текст {4} \ текст {V} \ end {выровнять *}

Применимые принципы

\ [{V} _ {\ text {battery}} = {V} _ {\ text {total}} \]

Общее напряжение в цепи — это сумма напряжений на отдельных резисторах

\ [{V} _ {\ text {total}} = {V} _ {B} + {V} _ {\ text {known}} \]

Использование зависимости между напряжением на батарее и общим напряжением на резисторах

\ begin {align *} {V} _ {\ text {battery}} & = {V} _ {\ text {total}} \\ {V} _ {\ text {battery}} & = {V} _ {B} + {V} _ {\ text {known}} \\ \ text {7} \ text {V} & = {V} _ {B} + \ text {5} \ text {V} \\ {V} _ {B} & = \ text {2} \ text {V} \ end {выровнять *}

Рабочий пример 10: Напряжения IV

Рассмотрим принципиальную схему:

Какое напряжение на параллельной комбинации резисторов в показанной цепи? Подсказка: остальная часть Схема такая же, как и в предыдущей задаче.

Быстрый ответ

Схема такая же, как в предыдущем примере, и мы знаем, что разница напряжений между двумя точками в цепь не зависит от того, что находится между ними, поэтому ответ такой же, как указано выше \ ({V} _ {\ text {parallel}} = \ text {2} \ text {V} \).

Проверьте, что у вас есть и единицы — длинный ответ

У нас есть схема с батареей и пятью резисторами (два последовательно и три параллельно).Мы знаем напряжение на батарее и двух резисторах. Мы хотим найти это напряжение на параллельном резисторы, \ ({V} _ {\ text {parallel}} \).

\ begin {align *} {V} _ {\ text {battery}} = \ text {7} \ text {V} \\ {V} _ {\ text {известное}} = \ text {1} \ text {V} + \ text {4} \ text {V} \ end {выровнять *}

Применимые принципы

Мы знаем, что напряжение на батарее должно быть равно общему напряжению на всех остальных цепях. компоненты.

\ [{V} _ {\ text {battery}} = {V} _ {\ text {total}} \]

Напряжения складываются только алгебраически для последовательно соединенных компонентов. Параллельно подключенные резисторы можно рассматривать как один компонент, который включен последовательно с другими компонентами, а затем могут быть добавлены напряжения.

\ [{V} _ {\ text {total}} = {V} _ {\ text {parallel}} + {V} _ {\ text {известное}} \]

Использование зависимости между напряжением на батарее и общим напряжением на резисторах

\ begin {align *} {V} _ {\ text {battery}} & = {V} _ {\ text {total}} \\ {V} _ {\ text {battery}} & = {V} _ {\ text {parallel}} + {V} _ {\ text {known}} \\ \ text {7} \ text {V} & = {V} _ {\ text {parallel}} + \ text {5} \ text {V} \\ {V} _ {\ text {parallel}} & = \ text {2} \ text {V} \ end {выровнять *} temp text

В отличие от последовательного случая, когда мы добавляем резисторы параллельно, мы создаем еще путей, вдоль какой ток может течь.Таким образом, мы уменьшаем на общее сопротивление цепи на !

Взгляните на диаграмму ниже. Слева у нас такая же схема, что и в предыдущем разделе с аккумулятором и резистор. Амперметр показывает ток \ (\ text {1} \) \ (\ text {A} \). Справа мы добавили второй резистор параллельно первому резистору. Это увеличило количество путей (ответвлений), по которым может пройти заряд. по цепи — общее сопротивление уменьшилось.Вы можете видеть, что ток в цепи имеет повысился. Также обратите внимание, что ток в разных ветвях может быть разным.

Общее сопротивление ряда параллельных резисторов НЕ является суммой отдельных сопротивлений, как общее сопротивление уменьшается с увеличением количества путей для тока. Дано полное сопротивление для параллельных резисторов. по:

\ [\ frac {1} {{R} _ {P}} = \ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2}} + \ ldots \ ]

Давайте рассмотрим случай, когда у нас есть два резистора, включенных параллельно, и выясним, каким будет конечное сопротивление.Эта ситуация показана на диаграмме ниже:

Применяя формулу для общего сопротивления, получаем:

\ begin {align *} \ frac {1} {{R} _ {P}} & = \ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2}} + \ ldots \\ & \ text {Резисторов всего два} \\ \ frac {1} {{R} _ {P}} & = \ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2}} \\ & \ text {Добавить дроби} \\ \ frac {1} {{R} _ {P}} & = \ frac {1} {{R} _ {1}} \ times \ frac {{R} _ {2}} {{R} _ {2 }} + \ frac {1} {{R} _ {2}} \ times \ frac {{R} _ {1}} {{R} _ {1}} \\ \ frac {1} {{R} _ {P}} & = \ frac {{R} _ {2}} {{R} _ {1} {R} _ {2}} + \ frac {{R} _ {1}} {{R} _ {1} {R} _ {2}} \\ & \ text {Переставить} \\ \ frac {1} {{R} _ {P}} & = \ frac {{R} _ {2} + {R} _ {1}} {{R} _ {1} {R} _ {2} } \\ \ frac {1} {{R} _ {P}} & = \ frac {{R} _ {1} + {R} _ {2}} {{R} _ {1} {R} _ {2} } \\ {R} _ {P} & = \ frac {{R} _ {1} {R} _ {2}} {{R} _ {1} + {R} _ {2}} \ end {выровнять *}

Для любых двух параллельно включенных резисторов мы теперь знаем, что

\ [{R} _ {P} = \ frac {\ text {произведение сопротивлений}} {\ text {сумма сопротивлений}} = \ frac {{R} _ {1} {R} _ {2}} { {R} _ {1} + {R} _ {2}} \]

Делители тока

Цель

Проверьте, что происходит с током и напряжением в последовательных цепях при добавлении дополнительных резисторов.

Аппарат

Аккумулятор
Вольтметр
Амперметр
Провода
Резисторы

Метод

Подключите каждую цепь, показанную ниже
Измерьте напряжение на каждом резисторе в цепи.
Измерьте ток до и после каждого резистора в цепи, а также до и после параллельного ветви.

Результаты и выводы

Сравните токи через отдельные резисторы между собой.
Сравните сумму токов через отдельные резисторы с током до параллельного ветви.
Сравните различные измерения напряжения на параллельных резисторах.

Рабочий пример 11: Параллельные резисторы I

Цепь содержит два параллельно включенных резистора. Резисторы имеют значения сопротивления \ (\ text {15} \) \ (\ text {Ω} \) и \ (\ text {7} \) \ (\ text {Ω} \).

Какое полное сопротивление в цепи?

Проанализировать вопрос

Нам говорят, что резисторы в цепи включены в параллельную цепь и что нам нужно рассчитать общую сопротивление.Значения двух резисторов указаны в правильных единицах, Ом.

Применять соответствующие принципы

Было показано, что полное сопротивление резисторов, включенных параллельно, является произведением сопротивлений, деленных на сумма. Мы можем использовать

\ [{R} _ {P} = \ frac {{R} _ {1} {R} _ {2}} {{R} _ {1} + {R} _ {2}} \]

У нас всего два резистора, и теперь мы резисторы. {2}} {\ text {22} \ text {Ω}} \\ & = \ текст {4,77} \ текст {Ω} \ end {выровнять *}

Цитировать окончательный результат

Полное сопротивление параллельно включенных резисторов \ (\ text {4,77} \) \ (\ text {Ω} \)

Рабочий пример 12: Параллельные резисторы II

Мы добавляем третий параллельный резистор в конфигурацию (настройку) в предыдущем примере.Дополнительные резистор имеет сопротивление \ (\ text {3} \) \ (\ text {Ω} \).

Какое полное сопротивление в цепи?

Проанализировать вопрос

Нам говорят, что резисторы в цепи включены в параллельную цепь и что нам нужно рассчитать общую сопротивление. Значение дополнительного резистора указано в правильных единицах, Ом.

Применять соответствующие принципы

Общее сопротивление резисторов, включенных параллельно, составляет

. \ [\ frac {1} {{R} _ {P}} = \ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2}} + \ ldots \ ]

У нас есть три резистора, и теперь мы резисторы.В данном случае это:

\ begin {align *} \ frac {1} {{R} _ {P}} & = \ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2}} + \ ldots \\ & \ text {есть три резистора} \\ \ frac {1} {{R} _ {P}} & = \ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2}} + \ frac {1 } {{R} _ {3}} \\ & \ text {добавить дроби} \\ \ frac {1} {{R} _ {P}} & = \ frac {1} {{R} _ {1}} \ times \ frac {{R} _ {2} {R} _ {3}} {{R} _ {2} {R} _ {3}} + \ frac {1} {{R} _ {2}} \ times \ frac {{R} _ {1} {R} _ {3}} {{R} _ {1} {R} _ {3}} + \ frac {1} {{R} _ {3} } \ times \ frac {{R} _ {1} {R} _ {2}} {{R} _ {1} {R} _ {2}} \\ \ frac {1} {{R} _ {P}} & = \ frac {{R} _ {2} {R} _ {3}} {{R} _ {1} {R} _ {2} { R} _ {3}} + \ frac {{R} _ {1} {R} _ {3}} {{R} _ {1} {R} _ {2} {R} _ {3}} + \ frac {{R} _ { 1} {R} _ {2}} {{R} _ {1} {R} _ {2} {R} _ {3}} \\ & \ text {переставить} \\ \ frac {1} {{R} _ {P}} & = \ frac {{R} _ {2} {R} _ {3} + {R} _ {1} {R} _ {3} + { R} _ {2} {R} _ {3}} {{R} _ {1} {R} _ {2} {R} _ {3}} \\ {R} _ {P} & = \ frac {{R} _ {1} {R} _ {2} {R} _ {3}} {{R} _ {2} {R} _ {3} + {R} _ {1} {R} _ {3} + {R} _ {2} {R} _ {3}} \\ {R} _ {P} & = \ frac {\ left (\ text {15} \ text {Ω} \ right) \ left (\ text {7} \ text {Ω} \ right) \ left (\ text {3} \ text {Ω} \ right)} {\ left (\ text {7} \ text {Ω} \ right) \ left (\ text {3} \ text {Ω} \ right) + \ left (\ text {15} \ text {Ω} \ right) \ left (\ text {3} \ text {Ω} \ right) + \ left (\ text {7} \ text { Ω} \ right) \ left (\ text {15} \ text {Ω} \ right)} \\ {R} _ {P} & = \ frac {315 {\ Omega} ^ {3}} {21 {\ Omega} ^ {2} + 45 {\ Omega} ^ {2} + 105 {\ Omega} ^ { 2}} \\ {R} _ {P} & = \ frac {315 {\ Omega} ^ {3}} {171 {\ Omega} ^ {2}} \\ {R} _ {P} & = \ text {1,84} \ text {Ω} \ end {выровнять *}

Цитировать окончательный результат

Полное сопротивление параллельно включенных резисторов \ (\ text {1,84} \) \ (\ text {Ω} \)

При расчете сопротивления для сложных конфигураций резисторов вы можете начать с любой комбинации двух резисторы (последовательно или параллельно) и рассчитайте их полное сопротивление.Затем вы можете заменить их одним резистор с рассчитанным вами полным сопротивлением. Теперь используйте этот новый резистор в сочетании с любым другим. резистор и повторяйте процесс, пока не останется только один резистор. В приведенном выше примере мы могли бы просто иметь использовали ответ из первого примера параллельно с новым резистором, и мы получили бы тот же ответ.

Рабочий пример 13: Параллельные резисторы III

Мы добавляем третий параллельный резистор к первой конфигурации (настройке), работающей параллельно.Дополнительные резистор имеет сопротивление \ (\ text {3} \) \ (\ text {Ω} \)

Какое полное сопротивление в цепи?

Проанализировать вопрос

Применять соответствующие принципы

Мы можем поменять местами резисторы, не меняя схему:

Мы уже рассчитали, что полное сопротивление двух резисторов в пунктирной рамке равно \ (\ text {4,77} \) \ (\ текст {Ω} \). {2}} {\ text {11,77} \ Omega} \\ & = \ текст {1,84} \ текст {Ω} \ end {выровнять *}

Цитировать окончательный результат

Полное сопротивление параллельно включенных резисторов равно \ (\ text {1,84} \) \ (\ text {Ω} \).Это тоже самое Результат как когда мы сложили сразу все три резистора.

Сопротивление

Учебное упражнение 17.1

Как называется единица сопротивления и каков ее символ?

Решение пока недоступно

Объясните, что происходит с общим сопротивлением цепи, когда резисторы добавляются последовательно?

Решение пока недоступно

Объясните, что происходит с общим сопротивлением цепи, когда резисторы добавляются параллельно?

Решение пока недоступно

Почему батарейки разряжаются?

Решение пока недоступно

Резисторы

в схемах — Практика — Физический гипертекст

Давайте начнем процесс с комбинирования резисторов.В этой схеме четыре последовательных пары.

слева
R _с = 3 Ом + 1 Ом R _с = 4 Ом R _с = 4 Ом + 2 Ом R _с = 6 Ом

правый
R _с = 2 Ом + 3 Ом R _с = 5 Ом R _с = 1 Ом + 4 Ом R _с = 5 Ом

Эти пары образуют две параллельные цепи, одну слева и одну справа.

слева

1	=	1	+	1
R _p	=	4 Ом	+	6 Ом

R _p =	12 Ом	= 2,4 Ом
	5

правый

1	=	1	+	1
R _p	=	5 Ом	+	5 Ом

R _p =	5 Ом	= 2.5 Ом
	2

Каждый набор из четырех резисторов включен последовательно с другим.

слева
R _с = 2,4 Ом + 0,6 Ом R _с = 3 Ом

правый
R _с = 2,5 Ом + 0,5 Ом R _с = 3 Ом

Левая и правая половины цепи параллельны друг другу и батарее.

1	=	1	+	1	=	2
R _p	=	3 Ом	+	3 Ом	=	3 Ом

R _p =	3 Ом	= 1,5 Ом
	2

Теперь, когда у нас есть эффективное сопротивление всей цепи, давайте определим ток от источника питания, используя закон Ома.

I _итого =	В _всего	+	24 В	= 16 А
	R _всего		1,5 Ом

Теперь пройдемся по цепи (не буквально, конечно). На каждом соединении ток будет делиться: больше по пути с меньшим сопротивлением и меньше по пути с большим сопротивлением. Поскольку заряд не протекает нигде в полной цепи, ток будет одинаковым для всех элементов, последовательно соединенных друг с другом.

Левая и правая половины схемы идентичны по общему сопротивлению, что означает, что ток будет равномерно делиться между ними.

8 A для резистора 0,6 Ом
на слева .

8 A для резистора 0,5 Ом
справа .

С каждой стороны ток снова делится на две параллельные ветви.

Ветви на слева имеют сопротивления в соотношении…

R _{1 и 3}	=	4 Ом	+	2
R _{2 и 4}	=	6 Ом	+	3

что означает, что токи разделятся в соотношении…

для резисторов 1 Ом и 3 Ом
на слева .

для резисторов 2 Ом и 4 Ом
на слева .

Ветви на правом идентичны, поэтому ток разделяется на две равные половины.

☟

для резисторов 2 Ом и 3 Ом
на справа .

для резисторов 1 Ом и 4 Ом
на справа .

Резисторы, включенные параллельно | Прядильные номера

Компоненты находятся в параллельных , если они совместно используют два узла, например,

Мы раскрываем свойства параллельного соединения, рассматривая схемы резисторов. Определить параллельные резисторы немного сложнее, чем последовательные резисторы.

Автор Вилли Макаллистер.

Содержание

Параллельное соединение

Компоненты работают параллельно, если их два терминала подключены к одним и тем же узлам.

На следующем изображении $ \ text R1 $, $ \ text R2 $ и $ \ text R3 $ расположены параллельно. Две горизонтальные линии представляют два узла, общие для всех трех резисторов.

Просмотрите определение узла

Просмотрите определения узла и распределенного узла в этой статье о терминологии схемы.Еще один хороший ресурс, который поможет вам разобраться в параллельных схемах, — это статья о схематической эквивалентности.

Поскольку резисторы подключены к одним и тем же узлам, на каждом параллельном резисторе появляется одинаковое напряжение.

Резисторы на следующем изображении — это , а не , подключенные параллельно. Есть дополнительные компоненты (оранжевые прямоугольники), разделяющие общие узлы между резисторами. Эта схема имеет четыре отдельных узла, поэтому $ \ text R1 $, $ \ text R2 $ и $ \ text R3 $ не имеют одного и того же напряжения.

Резисторы параллельно

Вот схема с параллельными резисторами. В этой схеме есть источник тока. Мы не используем их очень часто, так что это должно быть весело.

Текущий источник $ \ text I_ \ text s $ направляет текущий $ i $ к $ \ text R1 $, $ \ text R2 $ и $ \ text R3 $. Текущий $ i $ возвращается на нижний терминал текущего источника. но мы еще не знаем, какое напряжение $ v $ или как $ i $ распадается на токи трех резисторов.

То, что мы знаем,

Текущее значение $ i $ — некоторое заданное постоянное значение.
Сумма токов трех резисторов должна составлять $ i $.
Напряжение $ v $ появляется на всех трех резисторах.

С помощью этого небольшого количества знаний и закона Ома мы можем найти то, чего не знаем,

Нам пока неизвестно напряжение $ v $, появляющееся на резисторах и источнике тока.
Мы не знаем, как $ i $ распадается на токи трех резисторов.

Используя то, что мы знаем, мы можем записать эти выражения,

$ i = i _ {\ text R1} + i _ {\ text R2} + i _ {\ text R3}

$
$ v = i _ {\ text R1} \, \ text R1 \ qquad v = i _ {\ text R2} \, \ text R2 \ qquad v = i _ {\ text R3} \, \ text R3 $
Переставьте три выражения закона Ома, чтобы найти ток,
$ i _ {\ text R1} = \ dfrac {v} {\ text R1} \ qquad i _ {\ text R2} = \ dfrac {v} {\ text R2} \ qquad i _ {\ text R3} = \ dfrac { v} {\ text R3}
долл. США
Подставим эти выражения в сумму токов,
$ i = \ dfrac {v} {\ text R1} + \ dfrac {v} {\ text R2} + \ dfrac {v} {\ text R3}
$
Выносим за скобки общий термин $ v $,
$ i = v \ left (\ dfrac {1} {\ text R1} + \ dfrac {1} {\ text R2} + \ dfrac {1} {\ text R3} \ right) $
Помните, что мы уже знаем $ i $ (он установлен в текущем источнике), поэтому мы можем решить для $ v $,
$ v = i \, \ dfrac {1} {\ left (\ dfrac {1} {\ text R1} + \ dfrac {1} {\ text R2} + \ dfrac {1} {\ text R3} \ right )} $
Взгляните на это уравнение.Это похоже на закон Ома, $ v = i \, \ text R $, но с резисторами, представленными в виде большого двойного обратного выражения, где обычно появляется $ \ text R $.
Заключаем,
Для резисторов, включенных параллельно, общее сопротивление обратно пропорционально сумме обратных величин отдельных резисторов.
(Это набитый ртом. Легче понять уравнение, чем произносить его вслух.)
Эквивалентный параллельный резистор
Предыдущее уравнение предлагает способ определения нового резистора , эквивалентного трем параллельным резисторам.
$ \ text R _ {\ text {parallel}} = \ dfrac {1} {\ left (\ dfrac {1} {\ text R1} + \ dfrac {1} {\ text R2} + \ dfrac {1} { \ text R3} \ right)}
долл. США
Новый резистор является величиной, обратной сумме обратных величин. Это эквивалентно в том смысле, что для данного $ i $, вытекающего из источника тока, появляется такое же напряжение $ v $.
Мы можем записать это немного меньше, перевернув гигантскую обратную величину,
$ \ dfrac {1} {\ text R _ {\ text {parallel}}} = \ dfrac {1} {\ text R1} + \ dfrac {1} {\ text R2} + \ dfrac {1} {\ text R3}
долл. США
Вы можете заменить три параллельных резистора одним эквивалентным резистором, и $ i $ и $ v $ останутся неизменными.
С «точки зрения» источника тока невозможно отличить эквивалентный резистор от трех параллельных резисторов.
$ \ text N $ резисторы параллельно
Мы можем обобщить уравнение параллельного резистора для любого количества резисторов, включенных параллельно. Вывод этой формулы для резисторов $ \ text N $, включенных параллельно, следует точно таким же шагам, которые мы проделали выше для трех резисторов, включенных параллельно.
$ \ dfrac {1} {\ text R _ {\ text {parallel}}} = \ dfrac {1} {\ text R1} + \ dfrac {1} {\ text R2} + \ ldots + \ dfrac {1} {\ text {R} _ \ text N}
долл. США
$ \ qquad \ quad $
Ток распределяется между резисторами, включенными параллельно
Давайте выясним, как основной ток $ i $ разделяется и течет через каждый резистор.Мы ищем $ i _ {\ text R1} $, $ i _ {\ text R2} $ и $ i _ {\ text R3} $.
Примените закон Ома к отдельным резисторам. $ v $ одинаково во всех уравнениях,
$ i _ {\ text R1} = v / \ text R_1 \ qquad i _ {\ text R2} = v / \ text R_2 \ qquad i _ {\ text R3} = v / \ text R_3 $
Основной ток $ i $ разделяется на три отдельных тока. Эти токи соединяются и возвращаются к источнику тока. Это означает, что токи отдельных резисторов должны суммироваться с основным током.
Величина тока в каждом резисторе составляет , обратно пропорционально номиналу резистора.
Это будет лучше, если мы сделаем пример с действительными числами.
Проверка концепции
ПРОБЛЕМА 1
а. Найдите напряжение $ v $.
г. Найдите токи в трех резисторах.
г. Покажите, как в сумме токи отдельных резисторов составляют $ i $.
Шаги к решению:
Найдите эквивалентное параллельное сопротивление $ \ text R _ {\ text {parallel}} $.
Найдите напряжение $ v $, используя закон Ома.
Найдите отдельные токи, снова используя закон Ома.
Убедитесь, что токи резистора в сумме соответствуют требуемым.
Показать ответ
Часть а. Эквивалент $ \ text R _ {\ text {parallel}} $ равен обратной обратной сумме трех резисторов.
$ \ text R _ {\ text {parallel}} = \ dfrac {1} {\ left (\ dfrac {1} {50 \, \ Omega} + \ dfrac {1} {100 \, \ Omega} + \ dfrac {1} {500 \, \ Omega} \ right)}
долл. США
$ \ text R _ {\ text {parallel}} = \ dfrac {1} {(0.02 + 0,01 + 0,002)} = \ dfrac {1} {0,032} = 31,25 \, \ Omega $
Теперь мы знаем ток и эквивалентное сопротивление. Мы можем найти напряжение $ v $ на всех резисторах, используя закон Ома
.
$ v = i \, \ text R _ {\ text {parallel}}
$
$ v = 100 \, \ text {mA} \ cdot 31.25 \, \ Omega = 3.125 \, \ text V $
Часть б. Зная $ v $, мы можем вернуться и вычислить токи отдельных резисторов,
$ i _ {\ text R1} = \ dfrac {v} {\ text R1} = \ dfrac {3.125 \, \ text V} {\ text {50}} = 62,5 \, \ text {mA}
долл. США
$ i _ {\ text R2} = \ dfrac {v} {\ text R2} = \ dfrac {3.125 \, \ text V} {\ text {100}} = 31.25 \, \ text {mA} $
$ i _ {\ text R3} = \ dfrac {v} {\ text R3} = \ dfrac {3.125 \, \ text V} {\ text {500}} = \ phantom {0} 6.25 \, \ text {mA } $
Вот как выглядит решение,
Часть c. Проверка: Суммируются ли токи резистора с током источника?
$ 62.5 \, \ text {mA} + 31.25 \, \ text {mA} + 6.25 \, \ text {mA} = 100 \, \ text {mA} \ qquad \ checkmark $ Да!
Как электроны «знают», через какой резистор пройти?
Распространенный вопрос о параллельных цепях: «Когда ток достигает первого резистора, как электроны« выбирают »или« знают », через какой резистор проходить?» Или «Как электроны« решают », куда идти? ”
Как известно, электроны — не люди, у них нет маленьких электронных мозгов (насколько нам известно).Здесь нет выбора или принятия решения. Они не выбирают и не решают, через какой резистор протекать, точно так же, как молекула воды «решает» или «выбирает», через какую сторону камня она будет проходить в потоке. В любой цепи, включая параллельные цепи, каждый электрон реагирует только на электрические силы, исходящие от напряжения и от отталкивающего роя окружающих электронов.
На основе только что найденных токов резисторов,
ПРОБЛЕМА 2
Через какой резистор проходит наибольшая доля тока?
Выберите один: $ \ quad $ наименьший $ \ quad $ средний $ \ quad $ наибольший
показать ответ
Самый маленький резистор несет наибольшую долю тока.
ПРОБЛЕМА 3
Через какой резистор проходит наименьшая доля тока?
Выберите один: $ \ quad $ наименьший $ \ quad $ средний $ \ quad $ наибольший
показать ответ
Самый большой резистор проводит наименьшую долю тока.
ПРОБЛЕМА 4
Каков относительный размер эквивалентного резистора по сравнению с параллельными резисторами?
$ \ text {R} _ \ text {parallel} $ больше, чем самый большой резистор.
$ \ text {R} _ \ text {parallel} $ находится между самым большим и самым маленьким резистором.
$ \ text {R} _ \ text {parallel} $ меньше самого маленького резистора.
показать ответ
Эквивалентный параллельный резистор меньше самого маленького параллельного резистора. Всегда.
Проблема 5
Какой резистор имеет наибольшее напряжение?
Выберите один: $ \ quad $ наименьший $ \ quad $ средний $ \ quad $ наибольший
показать ответ
Вопрос с подвохом.Все три резистора имеют одинаковое напряжение. Вот что значит быть параллельным. Все они имеют одинаковое напряжение.
Особый случай — резисторы 2 доллара параллельно
Из общего уравнения два резистора, включенных параллельно, имеют эквивалентное сопротивление
.
$ \ text R _ {\ text {parallel}} = \ dfrac {1} {\ left (\ dfrac {1} {\ text R1} + \ dfrac {1} {\ text R2} \ right)} $
Мы можем немного поработать алгеброй, чтобы придумать альтернативное выражение с одной дробью.Вместо того, чтобы просто сказать вам ответ, это обряд посвящения в самостоятельную работу с алгеброй в первый раз. Ответ спрятан, так что вы можете попробовать это самостоятельно, прежде чем посмотреть. Посмотрим, сможете ли вы получить выражение для $ \ text R _ {\ text {parallel}} $ в виде одной дроби.
Два резистора параллельно
$ \ text R _ {\ text {parallel}} = \ dfrac {1} {\ left (\ dfrac {1} {\ text R1} + \ dfrac {1} {\ text R2} \ right)} $
Обработайте знаменатель, чтобы очистить дроби. Общий знаменатель — $ \ text R1 \, \ text R2 $.
$ \ text R _ {\ text {parallel}} = \ dfrac {1} {\ left (\ dfrac {1} {\ text R1} \, \ dfrac {\ text R2} {\ text R2} \ right) + \ left (\ dfrac {1} {\ text R2} \, \ dfrac {\ text R1} {\ text R1} \ right)} $
$ \ text R _ {\ text {parallel}} = \ dfrac {1} {\ left (\ dfrac {\ text R2} {\ text R1 \, \ text R2} \ right) + \ left (\ dfrac {\ текст R1} {\ text R1 \, \ text R2} \ right)} $
$ \ text R _ {\ text {parallel}} = \ dfrac {1} {\ left (\ dfrac {\ text R1 + \ text R2} {\ text R1 \, \ text R2} \ right)} $
Переверните большую дробь, чтобы получить уравнение для двух параллельных резисторов,
$ \ text R _ {\ text {parallel}} = {\ dfrac {\ text R1 \, \ text R2} {\ text R1 + \ text R2}} $
Произведение на сумму.Это стоит запомнить.
Особый случай — резисторы 2 $, подключенные параллельно
Что делать, если два параллельно включенных резистора имеют одинаковое значение. Что эквивалентно $ \ text R _ {\ text {parallel}} $?
Пусть $ \ text R1 = \ text R2 $. Мы назовем его просто $ \ text R $.
$ \ text R _ {\ text {parallel}} = \ dfrac {\ text R \, \ text R} {\ text R + \ text R} = \ dfrac {\ text R \, \ text R} {2 \ , \ text R}
долл. США
$ \ text R _ {\ text {parallel}} = \ dfrac {1} {2} \, \ text
R $
Два идентичных резистора, включенных параллельно, имеют эквивалентное сопротивление, равное половине значения любого резистора.Ток распределяется между ними поровну.
Сводка
Параллельно подключенные компоненты имеют одинаковое напряжение.
Общая форма резисторов, включенных параллельно,
$ \ dfrac {1} {\ text R _ {\ text {parallel}}} = \ dfrac {1} {\ text R1} + \ dfrac {1} {\ text R2} + \ ldots + \ dfrac {1} {\ text {R} _ \ text N}
долл. США
Используйте это уравнение, если у вас параллельно подключено три или более резистора.
Если у вас есть два параллельных резистора, вы можете использовать общую форму или объединить их как произведение на сумму,
$ \ text R _ {\ text {parallel}} = \ dfrac {\ text R1 \, \ text R2} {\ text R1 + \ text R2} $
Эквивалентный резистор $ \ text R _ {\ text {parallel}} $ всегда меньше наименьшего параллельного резистора.
Самый большой ток протекает через наименьший резистор.
.