Калькулятор индуктивности однослойной катушки • Электротехнические и радиотехнические калькуляторы • Онлайн-конвертеры единиц измерения
Однослойная катушка индуктивности: D — диаметр оправки или каркаса катушки, Dc — диаметр катушки, p — шаг намотки катушки, d — диаметр провода без изоляции и di — диаметр провода с изоляцией.
Калькулятор определяет индуктивность однослойной катушки.
Пример: рассчитать индуктивность однослойной катушки без сердечника, состоящей из 10 витков на цилиндрическом каркасе диаметром 2 см; длина катушки 1 см.
Входные данные
Диаметр каркаса или оправки катушки
Dмиллиметр (мм)сантиметр (см)дюйм
Количество витков
N
Длина катушки
lмиллиметр (мм)сантиметр (см)дюйм
Выходные данные
Индуктивность катушки
L мГн
Введите диаметр каркаса катушки, число витков и длину катушки, выберите единицы и нажмите кнопку Рассчитать.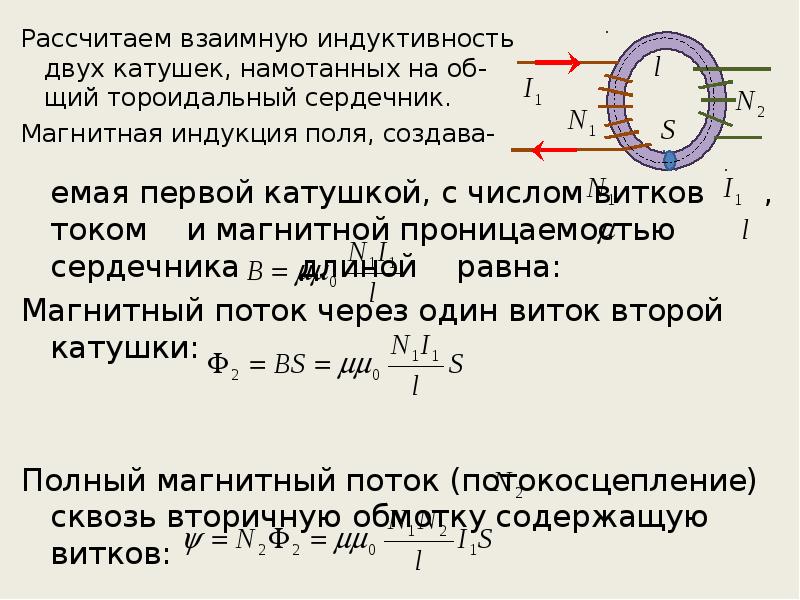
Пример: рассчитать число витков и длину намотки катушки 10 мкГн, намотанной эмалированным проводом 0,65 мм (диаметр с изоляцией 0,7 мм) на оправке 2 см.
Входные данные
Требуемая индуктивность
Lгенри (Гн)миллигенри (мГн)микрогенри (мкГн)наногенри (нГн)пикогенри (пГн)
Диаметр каркаса или оправки катушки
Dмиллиметр (мм)сантиметр (см)метр (м)дюйм
Диаметр провода без изоляции
dмиллиметр (мм)сантиметр (см)метр (м)дюймАмериканский калибр проводов
Диаметр изолированного провода
diмиллиметр (мм)сантиметр (см)метр (м)дюйм
Выходные данные
Длина намотки
l мм
Количество витков
L
На рисунке выше показана однослойная катушка индуктивности: Dc — диаметр катушки, D — диаметр оправки или каркаса катушки, p — шаг намотки катушки, d — диаметр провода без изоляции и di — диаметр провода с изоляцией
Для расчета индуктивности LS применяется приведенная ниже формула из статьи Р. Уивера (R. Weaver) Численные методы расчета индуктивности:
Уивера (R. Weaver) Численные методы расчета индуктивности:
Здесь
D — диаметр оправки или каркаса катушки в см,
l — длина катушки в см,
N — число витков и
L — индуктивность в мкГн.
Эта формула справедлива только для соленоида, намотанного плоским проводом. Это означает, что катушка намотана очень тонкой лентой без зазора между соседними витками. Она является хорошим приближением для катушек с большим количеством витков, намотанных проводом круглого сечения с минимальным зазором между витками. Американский физик Эдвард Беннетт Роса (Edward Bennett Rosa, 1873–1921) работавший в Национального бюро стандартов США (NBS, сейчас называется Национальное бюро стандартов и технологий (NIST) разработал так называемые корректирующие коэффициенты для приведенной выше формулы в форме (см. формула 10.1 в статье Дэвида Найта, David W. Knight):
Здесь LS — индуктивность плоской спирали, описанная выше, и
где ks — безразмерный корректирующий коэффициент, учитывающий разницу между самоиндукцией витка из круглого провода и витка из плоской ленты; km — безразмерный корректирующий коэффициент, учитывающий разницу в полной взаимоиндукции витков из круглого провода по сравнению с витками из плоской ленты; Dc — диаметр катушки в см, измеренный между центрами проводов и N — число витков.
Величина коэффициента Роса km определяется по формуле 10.18 в упомянутой выше статье Дэвида Найта:
Коэффициент Роса ks, учитывающий различие в самоиндукции, определяется по формуле 10.4 в статье Д. Найта:
Здесь p — шаг намотки (расстояние между витками, измеренное по центрам проводов) и d — диаметр провода. Отметим, что отношение p/d всегда больше единицы, так как толщина изоляции провода конечна, а минимально возможное расстояние между двумя соседними витками с очень тонкой изоляцией, расположенными без зазора, равна диаметру провода d.
Факторы, влияющие на индуктивность катушки
На индуктивность катушки влияют несколько факторов.
- Количество витков. Катушка с большим количеством витков имеет бóльшую индуктивность по сравнению с катушкой с меньшим количеством витков.
- Длина намотки. Две катушки с одинаковым количеством витков, но разной длиной намотки имеют разную индуктивность.
 Более длинная катушка имеет меньшую индуктивность. Это связано с тем, что магнитное поле менее компактной катушки более слабое и оно не может хорошо концентрироваться в растянутой катушке.
Более длинная катушка имеет меньшую индуктивность. Это связано с тем, что магнитное поле менее компактной катушки более слабое и оно не может хорошо концентрироваться в растянутой катушке. - Диаметр катушки. Две плотно намотанные катушки с одинаковым количеством витков и разными диаметрами имеют разную индуктивность. Катушка с бóльшим диаметром имеет бóльшую индуктивность.
- Сердечник. Для увеличения индуктивности в катушку часто вставляется сердечник из материала с высокой магнитной проницаемостью. Сердечники с более высокой магнитной проницаемостью позволяют получить более высокую индуктивность. Сердечники, изготовленные из магнитной керамики — феррита, часто используются в катушках и трансформаторах различных электронных устройств, так как у них очень низкие потери на вихревые токи.
Упрощенная эквивалентная схема реальной катушки индуктивности: Rw — сопротивление обмотки и ее выводов; L — индуктивность идеальной катушки; Rl — сопротивление вследствие потерь в сердечнике; и Cw — паразитная емкость катушки и ее выводов.
Эквивалентная схема реальной катушки индуктивности
В этом калькуляторе мы рассматривали идеальную катушку индуктивности. В то же время, в реальной жизни таких катушке не бывает. Катушки обычно конструируются с минимальными размерами таким образом, чтобы они помещались в миниатюрное устройство. Любую реальную катушку индуктивности можно представить в виде идеальной индуктивности, к которой параллельно подключены емкость и сопротивление, а еще одно сопротивление подключено последовательно. Параллельное сопротивление учитывает потери на гистерезис и вихревые токи в магнитном сердечнике. Это параллельное сопротивление зависит от материала сердечника, рабочей частоты и магнитного потока в сердечнике.
Паразитная емкость появляется в связи с тем, что витки катушки находятся близко друг к другу. Любые два витка провода можно рассмотреть как две обкладки маленького конденсатора. Витки разделяются изолятором, таким как воздух, изоляционный лак, лента или иной изоляционный материал. Относительная диэлектрическая проницаемость материалов, используемых для изоляции, увеличивает емкость обмотки. Чем выше эта проницаемость, тем выше емкость. В некоторых случаях дополнительная емкость может появиться также между катушкой и противовесом, если катушка расположена над ним. На высоких частотах реактивное сопротивление паразитной емкости может быть весьма высоким и игнорировать его нельзя. Для уменьшения паразитной емкости используются различные методы намотки катушек.
Относительная диэлектрическая проницаемость материалов, используемых для изоляции, увеличивает емкость обмотки. Чем выше эта проницаемость, тем выше емкость. В некоторых случаях дополнительная емкость может появиться также между катушкой и противовесом, если катушка расположена над ним. На высоких частотах реактивное сопротивление паразитной емкости может быть весьма высоким и игнорировать его нельзя. Для уменьшения паразитной емкости используются различные методы намотки катушек.
Для уменьшения паразитной емкости катушки с высокой добротностью для радиопередатчиков наматывают так, чтобы было достаточно большое расстояние между витками
Если индуктивность большая, то сопротивление обмотки (Rw на схеме) игнорировать уже нельзя. Тем не менее, оно мало по сравнению с реактивным сопротивлением больших катушке на высоких частотах. Однако, на низких частотах и на постоянном токе это сопротивление необходимо учитывать, так как в этих условиях через катушку могут протекать значительные токи.
Катушки индуктивности и обмотки в различных устройствах
Калькулятор расчета индуктивности катушки с воздушным сердечником
Катушка индуктивности является неотъемлемым элементом большинства современных приборов. При этом она используется для различных целей в работе электрических цепей. В случае необходимости замены можно использовать как заводскую, так и изготовленную самостоятельно катушку. Но при этом необходимо учитывать ее основной параметр – индуктивность. Для того чтобы рассчитать индуктивность катушки без сердечника можно воспользоваться универсальной формулой:
где μ0 – магнитная проницаемость вакуума, μ – магнитная проницаемость сердечника (можно взять из таблицы 1), N – число витков, S – площадь сечения катушки, l – длина намотки. Такой способ является универсальным и может использоваться, как для полых катушек, так и для имеющих сердечник.
Таблица 1
| Материал | — µ — (Гн/м) |
| Воздух | 1. |
| Алюминий | 1.256665*10−6 |
| Аустенитная нержавеющая сталь | 1.260*10−6 — 8.8*10−6 |
| Вакуум (µ0) | 4π*10−7 |
| Вода | 1.256627*10−6 |
| Водород | 1.2566371*10−6 |
| Висмут | 1.25643*10−6 |
| Дерево | 1.25663760*10−6 |
| Железо (чистота 99.8%) | 6.3*10−3 |
| Железо (99.95% чистое Fe отожженное в водороде) | 2.5*10−1 |
| Железо-кобальтовые сплавы | 2.3*10−2 |
| Медь | 1.256629*10−6 |
| Никель-цинковый феррит — магнит | 2.0*10−5 – 8.0*10−4 |
| Мартенситная нержавеющая сталь (отожженная) | 9.42*10−4 — 1.19*10−3 |
| Мартенситная нержавеющая сталь (закаленная) | 5.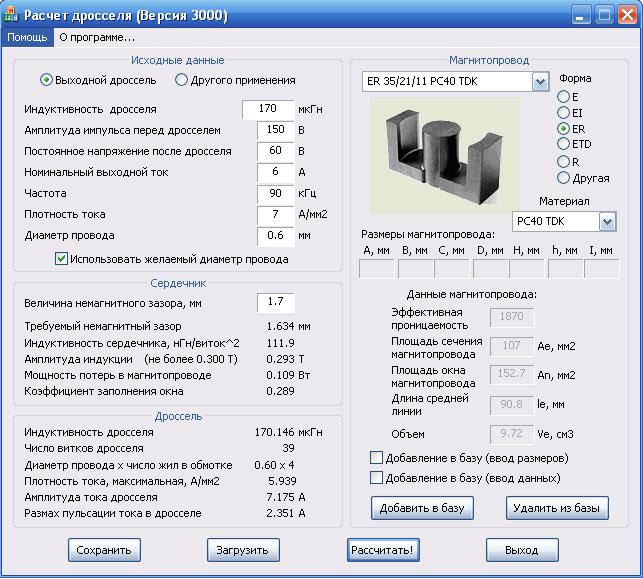 0*10−5 — 1.2*10−4 0*10−5 — 1.2*10−4 |
| NANOPERM® — магнитомягкий нанокристаллический сплав | 1.0*10−1 |
| Неодимовый магнит | 1.32*10−6 |
| Никель | 1.26*10−4 — 7.54*10−4 |
| Пермаллой (сплав 80% никеля и 20% железа) | 1.0*10−2 |
| Платина | 1.256970*10−6 |
| Сарфир | 1.2566368*10−6 |
| Сверхпроводники | 0 |
| Углеродистая сталь | 1.26*10−4 |
| Ферритная нержавеющая сталь (отожженная) | 1.26*10−3 — 2.26*10−3 |
| Фторопласт 4, Ф-4, Teflon | 1.2567*10−6 |
Если рассматривать частный вариант – катушку с воздушным сердечником, то для расчета ее индуктивности можно использовать формулу:
Где D – диаметр катушки, n – количество витков, а l – длина ее намотки.
Такой способ расчета будет справедливым для катушек, имеющих однослойную структуру, набираемых в один уровень. В случае если катушка наматывается в несколько слоев, то их толщина вносит дополнительные изменения в расчет. При этом формула расчета преобразится к виду:
Где D – диаметр катушки, n – количество витков, h – высота самой катушки, g – толщина слоя намотки.
Для упрощения процесса расчета индуктивности катушки без сердечника можно воспользоваться онлайн калькулятором. Здесь вы указываете ее основные параметры – диаметр, длину и количество витков, после чего нажать кнопку «Рассчитать» и вы получите значение индуктивности без лишних вычислений и затрат времени.
Как рассчитать сердечник и витки самодельных катушек индуктивности
Катушки индуктивности предназначены для фильтрации токов высокой частоты. Они устанавливаются в колебательных контурах и используются для других целей в электрических и электронных схемах. Готовое устройство заводского изготовления надёжнее в работе, но дороже, чем изготовленное своими руками. Кроме того, не всегда удаётся приобрести элемент с необходимыми характеристиками. В этом случае расчёт катушки индуктивности и само устройство можно сделать самостоятельно.
Кроме того, не всегда удаётся приобрести элемент с необходимыми характеристиками. В этом случае расчёт катушки индуктивности и само устройство можно сделать самостоятельно.
Устройство катушки индуктивности
Конструкция катушки
Каркас устройства изготавливается из диэлектрика. Это может быть тонкий (нефольгированный) гетинакс, текстолит, а на тороидальных сердечниках –просто обмотка из лакоткани или аналогичного материала.
Обмотка выполняется из одножильного или многожильного изолированного провода.
Внутрь обмотки вставляется сердечник. Он изготавливается из железа, трансформаторной стали, феррита и других материалов. Он может быть замкнутым, тороидальным (бублик), квадратным или незамкнутым (стержень). Выбор материала зависит от условий работы: частоты, магнитного потока и других параметров.
Кроме того, есть приборы, в которых сердечник отсутствует. Они характеризуются большой линейностью импеданса, но при намотке тороидальной формы обладают паразитной ёмкостью.
Расчет параметров катушки индуктивности
Протекающий по проводу электрический ток создаёт вокруг него электромагнитное поле. Соотношение величины поля к силе тока называется индуктивностью. Если провод свернуть кольцом или намотать на каркас, то получится катушка индуктивности. Её параметры рассчитывают по определённым формулам.
Расчёт индуктивности прямого провода
Индуктивность прямого стержня – 1-2мкГн на метр. Она зависит от его диаметра. Точнее можно рассчитать по формуле:
L=0.2l(logl/d-1), где:
- d – диаметр провода,
- l – длина провода.
Эти величины нужно измерять в метрах (м). При этом результат будет иметь размерность микрогенри (мкГн). Вместо натурального логарифма ln допустимо использовать десятичный lg, который в 2,3 раза меньше.
Предположим, что какая-то деталь подключена проводами длиной 4 см и диаметром 0,4 мм. Произведя при помощи калькулятора расчет по выше приведённой формуле, получаем, что индуктивность каждого из этих проводов составит (округлённо) 0,03 мкГн, а двух – 0,06 мкГн.
Ёмкость монтажа составляет порядка 4,5пФ. При этом резонансная частота получившегося контура составит 300 МГц. Это диапазон УКВ.
Важно! Поэтому при монтаже устройств, работающих в частотах УКВ, длину выводов деталей нужно делать минимальной.
Расчёт однослойной намотки
Для увеличения индуктивности провод сворачивается кольцом. Величина магнитного потока внутри кольца выше примерно в три раза. Рассчитать её можно при помощи следующего выражения:
L = 0,27D(ln8D/d-2), где D – диаметр кольца, измеренный в метрах.
При увеличении количества витков индуктивность продолжает расти. При этом индукция отдельных витков влияет на соседние, поэтому получившиеся параметры пропорциональны не количеству витков N, а их квадрату.
Однослойная намотка
Дроссель с сердечником
Параметры обмотки, намотанной на каркас, диаметром намного меньше длины рассчитывается по формуле:
L=*0*N2*S.
Она справедлива для устройства большой длины или большого тора.
Размерность в ней дана в метрах (м) и генри (Гн). Здесь:
- 0 = 4•10-7 Гн/м – магнитная константа,
- S = D2/4 – площадь поперечного сечения обмотки, магнитная проницаемость магнитопровода, которая меньше проницаемости самого материала и учитывает длину сердечника; в разомкнутой конструкции она намного меньше, чем у материала.
Например, если стержень антенны изготовить из феррита с проницаемостью 600 (марки 600НН), то у получившегося изделия она будет равна 150. При отсутствии магнитного сердечника = 1.
Для того чтобы использовать это выражение для расчёта обмоток, намотанных на тороидальном сердечнике, его необходимо измерять по средней линии «бублика». При расчёте обмоток, намотанных на железе Ш-образной формы без воздушного зазора, длину пути магнитного потока измеряют по средней линии сердечника.
Катушка с Ш-образным сердечником
В расчёте диаметр провода не учитывается, поэтому в низкочастотных конструкциях сечение провода выбирается по таблицам, исходя из допустимого нагрева проводника.
В высокочастотных устройствах, так же как и в остальных, стремятся свести омическое сопротивление к минимуму для достижения максимальной добротности прибора. Простое повышение сечения провода не помогает. Это приводит к необходимости наматывать обмотку в несколько слоёв. Но ток ВЧ идёт преимущественно по поверхности, что приводит к увеличению сопротивления. Добротность в высокочастотных элементах растёт вместе с увеличением всех размеров: длины и диаметров обмотки и провода.
Максимальная добротность получается в короткой обмотке большого диаметра, с соотношением диаметр/длина, равным 2,5. Параметры такого устройства вычисляются по формуле:
L=0.08D2N2/(3D+9b+10c).
В этой формуле все параметры измеряются в сантиметрах (см), а результат получается в микрогенри (мкГн).
По этой формуле рассчитывается также плоская катушка. Диаметр «D» измеряется по среднему витку, а длина «l» по ширине:
l=Dmax-Dmin.
Плоская катушка
Многослойная намотка
Многослойная намотка без сердечника вычисляется по формуле:
L=0. 08D2N2/(3D+9b+10c).
08D2N2/(3D+9b+10c).
Размеры здесь измеряются в сантиметрах (см), а результат получается в микрогенри (мкГн).
Добротность такого устройства зависит от способа намотки:
- обычная плотная намотка – самая плохая, не более 30-50;
- внавал и универсал;
- «сотовая».
Многослойная катушка
Для увеличения добротности при частоте до 10 мГц вместо обычного, одножильного провода, можно взять литцендрат или посеребренный проводник.
Справка. Литцендрат – это провод, скрученный из большого количества тонких изолированных друг от друга жил.
Литцендрат имеет большую поверхность, по сравнению с одножильным проводником того же сечения, поэтому на высоких частотах его сопротивление ниже.
Использование сердечника в высокочастотных устройствах повышает индуктивность и добротность катушки. Особенно большой эффект даёт использование замкнутых сердечников. При этом добротность дросселя зависит не от активного сопротивления провода, а от проницаемости магнитопровода. Рассчитывается такой прибор по обычным формулам для низкочастотных устройств.
Сделать катушку или дроссель можно самостоятельно. Перед тем, как её изготавливать, необходимо рассчитать индуктивность катушки по формулам или при помощи онлайн-калькулятора.
Видео
Оцените статью:Бесплатная программа расчёта катушек индуктивности Coil32 — Софт для радиолюбителя — Программы
Катушки индуктивности практически используются почти в любой радио-аппаратуре, и довольно часто перед радиолюбителями возникает вопрос:
Как рассчитать индуктивность той, или иной катушки? Конечно можно рассчитать индуктивность по определённым формулам, но это требует времени, которого радиолюбителям всегда не хватает.
Бесплатная программа Coil32, автором которой является Кустарев Валерий, позволяет быстро рассчитать индуктивность практически любой катушки.
В программе учитываются наиболее распространенные варианты каркасов катушек. Можно рассчитать бескаркасную катушку в виде одиночного витка, на каркасах различной формы, на ферритовых кольцах и в броневых сердечниках, а также плоскую печатную катушку с круглой и квадратной формой витков. Для рассчитанной катушки, так же можно сразу рассчитать и ёмкость конденсатора в колебательном контуре.
Программа бесплатна и свободна для использования и распространения. В последней версии Coil32 v11.6.1.890 доступны расчёты:
- Одиночный круглый виток
- Однослойная виток к витку
В качестве начальных параметров при расчете катушки можно выбрать два варианта:- Известны диаметр каркаса и диаметр провода, длина намотки вычисляется.
- Известны диаметр каркаса и длина намотки, диаметр провода вычисляется
- Однослойная катушка с шагом
- Катушка с не круглой формой витков
- Многослойная катушка
В качестве начальных параметров при расчете катушки можно выбрать два варианта:- Известны диаметр каркаса, длина намотки и диаметр провода. Вычисляется число витков, попутно определяется толщина катушки, ее омическое сопротивление постоянному току и приблизительная длина провода для намотки («сколько надо отрезать»).
- Известны диаметр каркаса, длина намотки и предельное омическое сопротивление катушки. Вычисляется число витков, попутно определяется толщина катушки, нужный минимальный диаметр провода и приблизительная длина провода для намотки.
- Тороидальная однослойная катушка
- Катушка на ферритовом кольце
- Катушка в броневом сердечнике
(Ферритовом и карбонильном) - Тонкопленочная катушка
(Плоская катушка на печатной плате с круглой и квадратной формой витков и в виде одиночного прямого проводника)
В чем преимущества данной программы перед аналогами?
- Программа рассчитывает индуктивность различных типов катушек под имеющийся каркас.
- Результаты расчетов выводятся в текстовое поле справа, откуда их можно сохранить в файл. Можно открыть этот файл в «MS Word» и распечатать.
- Есть возможность рассчитать добротность для радиочастотных однослойных катушек индуктивности.
- Можно рассчитать основные параметры колебательного контура для однослойной катушки
- Можно рассчитать длину провода для намотки однослойной, многослойной катушки и катушки на ферритовом кольце.
- Для расчёта катушек в броневых сердечниках, есть возможность выбора одного из нескольких стандартных сердечников, что позволяет рассчитать катушку в несколько кликов.
- Для плоских катушек на печатной плате программа подскажет оптимальные размеры для достижения наивысшей добротности.
- Программа имеет мультиязычный интерфейс (20 языков) и дополнительные наборы скинов, которые можно скачать и установить из меню «Настройки».
Программа распространяется бесплатно в стиле «Portable» и не имеет установщика. Для работы с программой — скачайте архив, распакуйте его в любое удобное для Вас место и запустите файл Coil32.exe. При постоянной работе с программой, желательно создать для нее специальную папку и вынести ярлык Coil32.exe на рабочий стол.
Скачать Coil32.
Расчет индуктивности катушек (однослойных)
Как произвести расчет катушек индуктивности (однослойных, цилиндрических без сердечника)
Индуктивность катушки зависит от ее геометрических размеров, числа витков и способа намотки катушки. Чем больше диаметр, длина намотки и число витков катушки, тем больше ее индуктивность. То что делает катушка индуктивности в колебательных контурах является очень важным и от правильного расчета зависит добротность контура.
Если катушка индуктивности наматывается плотно виток к витку, то индуктивность ее будет больше по сравнению с катушкой, намотанной неплотно, с промежутками между витками. Когда требуется намотать катушку по заданным размерам и нет провода нужного диаметра, то при намотке ее более толстым проводом надо несколько увеличить, а тонким — уменьшить число витков катушки, чтобы получить необходимую индуктивность.
Ресчет катушек индуктивности (однослойных, цилиндрических)
Рис. 1. Пример однослойной катушки индуктивности.
Все приведенные выше соображения справедливы при намотке катушек без ферритовых сердечников. Расчет однослойных цилиндрических катушек производится по формуле:
где:
- L — индуктивность катушки, мкГн;
- D — диаметр катушки, см;
- I — длина намотки катушки, см;
- n — число витков катушки.
При расчете катушки могут встретиться два случая:
- а) по заданным геометрическим размерам необходимо определить индуктивность катушки;
- б) при известной индуктивности определить число витков и диаметр провода катушки.
В первом случае все исходные данные, входящие в формулу, известны, и расчет не представляет затруднений.
Пример. Определим индуктивность катушки, изображенной на рис. 1; для этого подставим в формулу все необходимые величины:
Во втором случае известны диаметр катушки и длина намотки, которая, в свою очередь, зависит от числа витков и диаметра провода.
Поэтому расчет рекомендуется вести в следующей последовательности. Исходя из конструктивных соображений определяют размеры катушки, диаметр и длину намотки, а затем рассчитывают число витков по формуле:
После того как будет найдено число витков, определяют диаметр провода с изоляцией по формуле:
где:
- d — диаметр провода, мм,
- l — длина обмотки, мм,
- n — число витков.
Пример. Нужно изготовить катушку диаметром 1 см при длине намотки 2 см, имеющую индуктивность 0,8 мкГн. Намотка рядовая виток к витку.
Подставив в последнюю формулу заданные величины, получим:
Диаметр провода:
Если эту катушку наматывать проводом меньшего диаметра, то нужио полученные расчетным путем 14 витков разместить по всей длине катушки (20 мм) с равными промежутками между витками, т. е. с шагом намотки.
Индуктивность данной катушки будет на 1—2% меньше номинальной, что следует учитывать при изготовлении таких катушек. При намотке в случае необходимости более толстым проводом, чем 1,43 мм, следует сделать новый расчет, увеличив диаметр или длину намотки катушки.
Возможно, также придется увеличить и то и другое одновременно, пока не будут получепы необходимые габариты катушки, соответствующие заданной индуктивности.
Следует заметить, что по приведенным пыше формулам рекомендуется рассчитывать такие катушки, у которых длина намотки l равна или больше половины диаметра. Если же длина намотки меньше D половины диаметра то более точные результаты можно получить по формулам:
Как произвести пересчет катушек индуктивности (однослойных, цилиндрических)
Необходимость в пересчете катушек индуктивности возникает при отсутствии нужного диаметра провода, указанного в описании конструкции, и замене его проводом другого диаметра; при изменении диаметра каркаса катушки.
Если отсутствует провод нужного диаметра, что является наиболее частой причиной пересчета катушек, можно воспользоваться проводом другого диаметра.
Изменение диаметра провода в пределах до 25% в ту или другую сторону вполне допустимо и в большинстве конструкций не отражается на качестве их работы. Более того, увеличение диаметра провода допустимо во всех случаях, так как оно уменьшает омическое сопротивление катушки и повышает ее добротность.
Уменьшение же диаметра ухудшает добротность и увеличивает плотность тока на единицу сечения провода, которая не может быть больше определенной допустимой величины.
Пересчет числа витков однослойной цилиндрической катушки при замене провода одного диаметра другим производится по формуле:
где:
- n — повое число витков катушки;
- n1 — число витков катушки, указанное в описании;
- d— диаметр имеющеюся провода;
- d1 — диаметр провода, указанный в описании.
В качестве примера произведем пересчет числа витков катушки, изображенной на рис. 1, для провода диаметром 0,8 мм:
(длина намотки l= 18 X 0,8 = 14,4 мм, или 1,44 см).
Таким образом, число витков и длина намотки несколько уменьшились. Для проверки правильности пересчета рекомендуется выполнить новый расчет катушки с измененным диаметром провода:
При пересчете катушки, связанном с изменением ее диаметра, следует пользоваться процентной зависимостью между диаметром и числом витков катушки.
Эта зависимость заключается в следующем: при увеличении диаметра катушки на определенное число процентов количество витков ее уменьшается на столько же процентов, и, наоборот, при уменьшении диаметра увеличивается число витков на равное число процентов. Для упрощения расчетов за диаметр катушки можно принимать диаметр каркаса.
Рис. 2. Катушки индуктивности. Пример.
Так, для примера произведем пересчет числа витков катушки (рис. 2, а), имеющей диаметр 1,5 см, на диаметр, равный 1,8 см (рис. 2, б). Согласно условиям пересчета диаметр каркаса увеличивается на 3 мм, или на 20%.
Следовательно, для сохранения неизменной величины индуктивности этой катушки при намотке ее на каркасе большего диаметра нужно уменьшить число витков на 20%, или на 8 витков. Таким образом, новая катушка будет иметь 32 витка.
Проверим пересчет н установим погрешность, допущенную в результате пересчета. Катушка (см. рис. 2, а) имеет индуктивность:
Новая катушка на каркасе с увеличенным диаметром:
Ошибка при пересчете составляет 0,25 мкГн, что вполне допустимо для расчетов в радиолюбительской практике.
Рассчитать катушку индуктивности с помощью онлайн калькулятора
Катушки индуктивности являются неотъемлемым элементом различных радиоэлектронных схем. Основным её свойством является наличие большой индуктивности при малой емкости и низком активном сопротивлении. В этом обзоре описано, как выполнить самостоятельный расчет катушки индуктивности, какими внешними параметрами она должна обладать, что бы были достигнуты требуемые рабочие параметры.
Калькулятор расчета катушки индуктивности
Индуктивность можно рассчитать самостоятельно или выполнить онлайн расчет с помощью специального калькулятора. Для автоматического расчета наиболее часто используется программа Coil32. Её можно бесплатно скопировать с одноименного сайта либо воспользоваться онлайн калькулятором. Пользоваться этой программой достаточно просто.
При работе с ней сначала нужно выбрать тип изделия (однослойная или многослойная, с ферритовым сердечником или без него, возможны другие варианты). Задав в калькуляторе расчет геометрических параметров, диаметр провода, число витков, свойства сердечника можно с помощью программы получить ожидаемую индуктивность изделия. Для получения необходимой величины можно в расчетах изменять число витков и диаметр провода.
Собранное изделие по рассчитанным параметрам можно проверить с помощью тестера на соответствие необходимым параметрам. Такой прибор называется LC тестер. Он измеряет индуктивность катушек и ёмкость конденсаторов. При отклонении полученных параметров от заданной величины можно увеличить либо уменьшить количество витков проволоки на изделии.
При желании можно выполнить самостоятельно расчет индуктивности катушки без сердечника или с ним. Единой формулы нет, они строго индивидуальны для каждого случая. В общем случае они прямо пропорциональны количеству витков и диаметру витков. Например, расчет однослойной цилиндрической обмотки выполняют по формуле:
L = (D/10)2*n2/(4.5*D+10*l)
Где L – индуктивность в микро Генри, D – её диаметр в мм, L – длина в мм, n – число витков. Эта эмпирическая формула очень проста, она не учитывает диаметр проволоки, рабочую частоту на которой планируется применять изделие.
Расчет индуктивности катушки с сердечником более сложен. С его добавлением значение индуктивность сильно возрастает. В расчетах в формулу добавляются параметры магнитных свойств сердечника. Ещё более сложными являются формулы расчёта многослойных катушек или катушек тороидальной формы. При редком или первичном использовании лучше всего воспользоваться специальными калькуляторами. Полученные расчеты можно проверить по формулам вручную. В любом случае после изготовления можно проверить параметры собранного изделия и при необходимости их изменить.
Расчёт катушки индуктивности под динамик
Данный расчет является примером для определения данных катушки индуктивности на воздушном сердечнике, нагруженной динамиком. В этом примере выбрана катушка без сердечника во избежание искажений, обусловленных перемагничиванием сердечника.
На рисунке показана оптимальная катушка индуктивности в смысле отношения индуктивности катушки и ее активному сопротивлению. Конструкция получается, когда внутренний диаметр цилиндрического слоя обмотки вдвое больше его высоты, а внешний диаметр в четыре раза больше высоты и в два раза больше внутреннего диаметра.
высота 1 см; внутренний диаметр 2 см; внешний диаметр 4 см.
Пример расчета
Современные программы по расчету пассивных фильтров для акустики, дают значение катушек индуктивности в мГн, здесь нужно перевести в мкГн, т.е. умножить на 1000.
Определим данные катушки с индуктивностью 1,25 мГн (или 1250 мкГн) разделительного фильтра, нагруженного динамиком сопротивлением 4 Ом. Активное сопротивление рассчитываемой катушки должно составлять 5% сопротивления динамика. Это соотношение можно считать вполне приемлемым. Активное сопротивление катушки: R = 0,05 х 4 = 0,2 Ом.
- откуда: L/R = 1250 / 0,2 = 6250 мкГн/Ом;
- далее имеем: h = √ ((L/R) / 8,6) = √ (6250 / 8,6) = 26,96 мм;
- длинна жилы: l = 187,3 х √ (L х h) = 187,3 х √ (1250 х 26,96) = 34383 мм = 34,3 м;
- количество витков: ω = 19,88 √(L / h) = 19,88 х √ (1250 / 26,96) = 135,36 витков;
- диаметр жилы: d =0,84h / √ω = 0,84 х 26,96 / √ 135,36 = 1,95 мм;
- масса намотки: m = (h3 х 10-3) / 21,4 = (26,963 х 10-3) / 21,4 = (19595,65 х 0,001) / 21,4= 0,9 кг.
Полученные значения должны быть округлены (в первую очередь диаметр жилы) до ближайшего стандартизированного. Окончательные значения индуктивности подгоняют путем отматывания нескольких витков обмотки, намотанной с некоторым превышением числа витков сравнительно с рассчитанным.
Итак имеем данные, которые понадобятся для расчета будущей катушки:
- высота намотки h = 26,96 мм;
- значит внутренний диаметр a = 53,92 мм;
- соответственно внешний: b = 107,84 мм;
- длинна жилы: 34,3 м;
- количество витков: 135;
- диаметр жилы, соответствует стандартизированному: 1,95 мм (по меди).
Статья специально подготовлена для сайта ldsound.ru
Калькулятор индуктивности катушки— Инструменты для электротехники и электроники
Этот калькулятор помогает вычислить индуктивность катушки.
Обзор
Катушка — это самая узнаваемая форма индуктора. Этот инструмент предназначен для расчета индуктивности катушки с проволокой с учетом количества витков, диаметра петли, диаметра проволоки и проницаемости среды. Обратите внимание, что вы можете выбрать единицу измерения для диаметра петли и диаметра проволоки.{2} $$ = количество витков
$$ \ mu_ {0} $$ = проницаемость свободного пространства = 4π × 10 −7
$$ \ mu_ {r} $$ = относительная проницаемость
$$ D $$ = диаметр петли
$$ d $$ = диаметр проволоки
Приложения
Лампа для вспышки камеры
Индуктор (или катушка) играет важную роль в схеме лампы вспышки камеры. Для камеры это важный компонент, который привел к высокому всплеску напряжения на катушке запуска, которое затем усилилось действием автотрансформатора вторичной обмотки, чтобы генерировать 4000 В, необходимые для зажигания лампы-вспышки.Конденсатор, подключенный параллельно катушке триггера, заряжается до 300 В по низкоомному пути, обеспечиваемому тиристором. Однако, как только конденсатор был полностью заряжен, путь короткого замыкания на землю, обеспечиваемый SCR, был удален, и конденсатор немедленно начал разряжаться через катушку запуска. Поскольку единственным сопротивлением постоянной времени индуктивной сети является относительно низкое сопротивление самой катушки, ток через катушку нарастал очень быстро. Затем на катушке возникло значительное напряжение.Это напряжение, в свою очередь, увеличивалось под действием трансформатора на вторичную обмотку автотрансформатора, и лампа-вспышка зажигалась. Это высокое напряжение, генерируемое на триггерной катушке, также будет появляться непосредственно на конденсаторе триггерной сети. В результате он снова начнет заряжаться, пока генерируемое напряжение на катушке не упадет до нуля вольт. Однако, когда он упадет, конденсатор снова разрядится через катушку, установит другой зарядный ток через катушку и снова создаст напряжение на катушке.Высокочастотный обмен энергией между катушкой и конденсатором называется обратным ходом из-за «обратного потока» энергии от одного накопительного элемента к другому.
Диммер бытовой
Катушки индуктивностиможно найти в самых разных электронных схемах дома. В типичном бытовом диммере используется индуктор для защиты других компонентов и приложенной нагрузки от «бросковых» токов — токов, которые нарастают с очень высокой скоростью и часто до чрезмерно высоких уровней.Эта функция особенно важна для диммеров, поскольку они чаще всего используются для управления интенсивностью света лампы накаливания. При «включении» сопротивление ламп накаливания обычно очень низкое, и относительно высокие токи могут протекать в течение коротких периодов времени, пока нить накаливания лампы не нагреется. Катушка индуктивности также эффективно блокирует высокочастотный шум (RFI), создаваемый переключающим действием симистора в диммере. Конденсатор также обычно включается между линией и нейтралью, чтобы любые скачки напряжения не влияли на работу диммера и приложенной нагрузки (лампы и т. Д.).) и помочь в подавлении помех от радиопомех.
Дополнительная литература
Конструкция катушки и калькулятор индуктивности
Эта страница проведет вас через создание собственной катушки DIY / самодельной катушки. Я сделал это для изготовления катушек для хрустальные радиоприемники и Катушки Тесла, но он работает с любой катушкой цилиндрической формы. Это также полезно, если вы собираетесь использовать свою катушку в Танк LC резонансный схема.
Предусмотрен калькулятор индуктивности. ниже, чтобы упростить задачу.
Индуктивность — это часто то, чего вы пытаетесь достичь при разработке катушки. то есть вы знаете нужную индуктивность, и теперь вам нужно спроектировать катушку который будет иметь эту индуктивность.
Индуктивность
Катушки имеют свойство, называемое индуктивностью. Что такое индуктивность? Когда электрический ток изменяется при прохождении через провод катушки, он создает изменяющееся магнитное поле, которое индуцирует (производит) напряжение или ЭДС (электродвижущая сила) в проводе, который противостоит течению.Это называется индукцией и индуктивностью. — величина, определяющая способность катушки индуцировать это напряжение. Символ индуктивности — Генри, а единица измерения — H. на самом деле говорят о катушке, индуцирующей напряжение в себе, что является самоиндукцией, но мы просто скажем индукция.
Одна формула для индуктивности выглядит следующим образом:
Где:
- L = индуктивность
- u r = относительная проницаемость материала сердечника (воздух = 1)
- витка = количество витков на катушке
- площадь = площадь поперечного сечения жилы в квадратных метрах *, включая часть катушки, как показано на схеме
- длина = длина бухты в метрах *
* Калькулятор индуктивности ниже также принимает дюймы, а также сантиметры и миллиметры, и переводит их в метры за вас.
Как сказано выше, μ r — это относительный магнитный проницаемость для всего, что вы используете для сердечника катушки, цилиндр, на который вы наматываете провод. Это греческая буква мю, μ, хотя часто для удобства используется буква u, например u r . Если это полая картонная или пластиковая трубка, то картонная или пластиковая считается воздухом, и вы можете использовать 1. Такие материалы, как железо и феррит, имеют более высокие относительные проницаемости в сотнях и тысячах.Для железного сердечника приблизительное число — 100, хотя оно действительно варьируется. в зависимости от сплава. То же самое и с ферритом, который может иметь ценность где-то от 20 до 5000, но если вы не знаете, что использовать, тогда 1000 — грубый компромисс. Поскольку он умножается на остальную часть формулы, это означает использование этих материалы дадут более высокое значение индуктивности. Ядра для кристаллического радио катушки иногда бывают пластиковыми или картонными и, следовательно, представляют собой катушки с воздушным сердечником, а иногда это ферритовый сердечник.Сердечники для вторичной обмотки Тесла катушки обычно пластиковые, а меньшие могут быть картонными, и поэтому считаются катушками с воздушным сердечником.
И если вы не знакомы с обозначениями 1.26×10 -6 , это просто другой способ записи 0.00000126.
Область включает часть катушки, как показано на схеме выше. Если площадь рассчитывается с использованием радиуса, включите радиус сердцевины. плюс радиус проволоки. При расчете площади по диаметру затем включите диаметр сердечника плюс диаметр проволоки.Обратите внимание, что при выполнении расчетов для катушки с очень тонкой проволокой, как в случае кристалл радио и катушка Тесла, показанная выше (например, 24 калибра / AWG) тогда размер провода, вероятно, будет незначительным по сравнению с область жилы, и обычно можно не обращать внимания на провод.
Калькулятор индуктивности
Вот калькулятор индуктивности, который использует приведенную выше формулу. Диаграмма Вышеуказанное можно использовать в качестве руководства для некоторых параметров.
Видео — Как разработать катушку с удельной индуктивностью
В этом видео я подробно объясняю формулу индукции. а также привести пример и поговорить о других факторах, таких как емкость катушки, частота и связь.
Последовательный и параллельный калькулятор индуктивности
- Цель использования
- узнать о подключении динамиков и вычисляем импеданс, потому что 2 дня назад я потерял очень ценный винтажный усилитель KR-770 Kenwood из-за глупого подключения !!!! пора учиться логике после ай !!
[1] 2021/03/01 00:51 Мужской / 40-летний уровень / Средняя школа / Университет / аспирант / Очень /
- Цель использования
- Просто посмотреть, работает ли мой измеритель LCR. штраф😂
[2] 2020/11/29 07:28 Мужчина / Моложе 20 лет / Старшая школа / Университет / аспирант / Полезно /
- Цель использования
- Память / обучение в школе
[3] 24.06.2020 14:36 Мужчина / Уровень 20 лет / Инженер / Полезно /
- Цель использования
- просто убедиться
[4] 2020/03 / 23 00:01 Мужской / 50-летний уровень / Пенсионер / Полезный /
- Цель использования
- Хотел узнать об индукторах
[5] 11.06.2019 14:31 Мужской / 40-летний уровень / Инженер / Очень /
- Цель использования
- Расчет значений кроссовера катушки индуктивности для акустических систем.
[6] 29.11.2018 05:52 Мужчина / 60 лет и старше / Пенсионер / Очень /
- Цель использования
- прикладной резонанс
- Комментарий / Запрос
- отличный инструмент .. .Спасибо
[7] 2018/10/04 04:32 Мужской / 50-летний уровень / Учитель / Исследователь / Очень /
- Цель использования
- , чтобы получить A в прикладной электроэнергии
- Комментарий / запрос
- пожалуйста, помогите мне усердно учиться
[8] 2018/09/08 14:52 — / — / — / Very /
- Цель использования
- Разработка выбираемых полосовых фильтров.
- Комментарий / запрос
- Простота использования, очень признателен!
[9] 2018/05/17 17:32 Мужской / 50-летний уровень / Самостоятельно занятые люди / Очень /
- Цель использования
- требуется критическая индуктивность 8H @ 300ma. У меня под рукой 20H, 8H, 8H, все 150мА и такое же сопротивление.
[10] 2017/10/09 03:32 Мужской / 50-летний уровень / Самозанятые люди / Полезный /
Калькулятор индуктивности соленоида
Калькулятор индуктивности соленоида находит самоиндуктивность соленоида. Прочитав текст ниже, вы узнаете, как работает соленоид в электрических цепях и какова его индуктивность.
Как работает соленоид
Соленоиды и катушки в целом являются важными элементами электрических цепей (попробуйте RLC Circuit Calculator, чтобы увидеть индуктивный элемент в действии). Их характеристика — индуктивность L , и они действуют как инерционные элементы: катушки сопротивляются изменению тока. Изменение тока, протекающего через катушку, приводит к самоиндуцированной разности потенциалов. Индуктивность L устанавливает соотношение между потенциалом и скоростью изменения тока
В = - L * dI / dt
Минус показывает резистивный характер индуктивности; разность потенциалов препятствует изменению тока.Магнитное поле внутри соленоида вызывает такое поведение. Если мы изменим ток, мы изменим это магнитное поле. В свою очередь, это вызывает разность потенциалов в соленоиде. Чтобы узнать больше о магнитном поле внутри соленоида и явлениях индуктивности, воспользуйтесь калькулятором магнитного поля соленоида и калькулятором закона Фарадея.
Индуктивность соленоида
Соленоид — это длинная туго намотанная катушка. Мы можем описать соленоид с помощью трех параметров:
- число витков
N, - длина
л, - площадь поперечного сечения
А.-6 Т * м / А . С помощью нашего калькулятора индуктивности соленоида вы можете легко найти индуктивность соленоида для различных конфигураций. Вместо указания площади сеченияAможно задать радиусr. Затем калькулятор вычисляет площадь, принимая круглое поперечное сечение.LearnEMC — Оценка индуктивности подключения
То, что многие люди называют эквивалентной последовательной индуктивностью (ESL) конденсатора, является индуктивностью контура, образованного током, который течет по одному выводу и выходит из другого вывода.Для конденсаторов SMT правильнее называть это соединительной индуктивностью , поскольку она в гораздо большей степени зависит от геометрии соединения, чем от внутренней конструкции конденсатора. Индуктивность подключения является наиболее важным фактором, влияющим на способность развязывающего конденсатора подавать ток на высоких частотах. Оценивая индуктивность соединения, можно определить эффективную полосу пропускания стратегии развязки. Ниже описывается метод, с помощью которого можно оценить индуктивность подключения различных разделительных конденсаторов.
Шаг 1. Определите петлю
Первым шагом в оценке индуктивности развязывающего конденсатора является определение токовой петли развязки. Будут рассмотрены два случая: развязывающие конденсаторы на платах с подачей питания на дорожки и развязывающие конденсаторы на платах с силовой и обратной плоскостями.
A. Геометрия, в которой питание направляется на дорожки
Токовая петля будет состоять из пути между разделительным конденсатором и устройством, которое снимает заряд с конденсатора.На рисунке ниже текущий путь показан красным.
В. Конденсаторы развязки, подключенные к плоскостям питания
Токовая петля в этой конфигурации начинается с развязывающего конденсатора, проходит через переходное отверстие к одной из плоскостей питания, затем от одной плоскости питания к другой и, наконец, через переходное отверстие обратно к конденсатору. Импеданс пути между плоскостями питания и возврата, Zboard, обычно не считается частью индуктивности соединения. Zboard можно рассчитать независимо от индуктивности участка петли над плоскостями.Импеданс соединения с плоскостями тогда определяется выражением Z conn = jωL + Z board , где L — индуктивность пути тока над плоскостями питания. Этот путь показан красным на рисунке ниже.
Шаг 2: Определите эквивалентную геометрию
Для оценки индуктивности развязывающих конденсаторов будет использоваться индуктивность эквивалентной геометрии. Это упрощение позволит нам использовать простые выражения в замкнутой форме для расчета индуктивности.
Шаг 3: Оценка параметров расчетов индуктивности в замкнутой форме
A. Оценка ширины петли ‘w’
Ширина петли «w» — это расстояние, на котором ток проходит через конденсатор. Ниже приведены несколько примеров.
B. Оценка высоты петли ‘h’
Высота петли «h» для конденсатора, прикрепленного к силовым плоскостям, будет приблизительно равна половине высоты развязывающего конденсатора плюс расстояние между конденсатором и ближайшей силовой плоскостью.
C. Расчет радиуса провода ‘a’
Эквивалентный радиус провода развязывающего конденсатора или плоской дорожки можно оценить как 1/4 ширины корпуса конденсатора или дорожки. Конечно, большинство соединений состоит из переходных отверстий, дорожек, контактных площадок и корпусов конденсаторов, которые имеют разные эквивалентные радиусы проводов. Оценка индуктивности соединения в наихудшем случае получается при использовании наименьшего эквивалентного радиуса.
Пример 1: Печатная плата без силовых панелей
Рассчитайте индуктивность соединения для конденсатора, подключенного к устройству по дорожкам, как показано ниже.Следы имеют ширину 1 мм. Все остальные размеры показаны ниже.
Решение:
Индуктивность подключения может быть приблизительно определена с помощью уравнения прямоугольной петли (https://cecas.clemson.edu/cvel/emc/calculators/Inductance_Calculator/rectgl.html). Длина и ширина самого прямоугольника оценивается по текущему пути, показанному красной пунктирной линией на рисунке выше. Длина эквивалентной прямоугольной петли оценивается в 8 мм плюс половина длины треугольной части токовой петли (22 мм / 2 = 11 мм).Эквивалентный радиус провода a составляет 1/4 ширины дорожки.
Отв. L соед. = 29 нГн ≈ 30 нГн
Пример 2: Разделительные конденсаторы, подключенные к плоскостям питания
Рассчитайте индуктивность соединения между конденсатором и устройством, предполагая, что оба подключены к плоскости питания и возврата. Диаметр переходных отверстий составляет 2 мм, а погружной корпус и конденсатор находятся примерно на 3 мм над поверхностью пары плоскостей питания и возврата. Пренебрегайте импедансом через плоскости питания.
Решение:
Индуктивность подключения конденсатора
Для расчета индуктивности развязывающего конденсатора L cap будет использоваться формула индуктивности «прямоугольной петли над плоскостью» (https://cecas.clemson.edu/cvel/emc/calculators/Inductance_Calculator /rectgl.html). Длина и ширина эквивалентной петли для развязывающего конденсатора составляют 10 мм и 3 мм соответственно. Эквивалентный радиус петли будет радиусом переходных отверстий 1 мм.
L крышка = 3,6 нГн ≈ 4 нГн Индуктивность подключения DIP-корпуса
Индуктивность подключения корпуса DIP к плоскостям питания, LDIP, будет рассчитана по формуле «длинный прямоугольный контур над плоскостью» (https://cecas.clemson.edu/cvel/emc/calculators/Inductance_Calculator/g- wire.html). Длина петли будет 30 мм, высота петли — 3 мм, а эквивалентный радиус будет приблизительно равен 0,1 мм.
L DIP = 24.6 нГн ≈ 25 нГн
L соединитель = L крышка + L DIP = 28,2 нГн ≈ 28 нГн
Пример 3: Индуктивность контура развязывающего конденсатора
На рисунке ниже показано несколько площадок развязывающего конденсатора на печатной плате. Расстояние между верхним слоем и парой плоскостей питания / возврата составляло 0,02 дюйма; все остальные измерения показаны на рисунке. Индуктивность контактных площадок следующих конструкций была измерена с помощью анализатора цепей, и результаты суммированы ниже.
Корпус л (нГн) А 0,61 B 1,32 С 2,00 D 7,11 E 15,7 F 10,3 Индуктивность корпуса C:
Метод 1. Использование алгоритма «прямоугольная петля над плоскостью»
Вт = 0.5 дюймов, h2 = 0,02 дюйма, h = 2h2, a = 0,025 дюйма
ANS: L = 3,1 нГн ≈ 3 нГнМетод 2: Использование алгоритма «длинный прямоугольный цикл над плоскостью»
Длина = 0,5 дюйма, h = 0,02 дюйма, a = 0,025 дюйма
ANS: L = 0,75 нГн ≈ 1 нГн(Примечание: метод 2 игнорирует индуктивность из-за части магнитного потока, охватывающей переходные отверстия. Это разумная оценка индуктивности из-за потока, охватывающего только корпус конденсатора. Поток, охватывающий корпус конденсатора, преобладает в случае A.)
Индуктивность корпуса E:
Метод: использование алгоритма «длинный прямоугольный контур над плоскостью» один раз для трасс, проложенных к переходному отверстию, и еще раз для части контура с контактной площадкой и корпусом конденсатора.
Вклад в индуктивность контура от трасс:
Длина = 1,0 «, h = 0,02», a = w / 4 = 0,002 «
ANS: L t = 15,24 нГн ≈ 15 нГнВклад в индуктивность контура от колодки и блока конденсаторов:
Длина = 0,5 дюйма, h = 0,02 дюйма, a = w / 4 = 0,02 дюйма
Общая индуктивность контура: L t + L p / c ≈ 16 нГн
ANS: L p / c = 0,76 нГн ≈ 1 нГнРасчет индуктивности
В этом калькуляторе индуктивности однослойной катушки используется формула Лундина [5], для которой максимальная относительная погрешность составляет менее 3 ppm.
Значение Q вычисляется здесь по формуле из [6]; значение будет лишь приблизительной оценкой; кроме того, не учитывается влияние распределенной емкости змеевика.Большинство формул для индуктивности катушки справедливы для приближения токового слоя , где ток течет по бесконечно тонкой поверхности вокруг диаметра катушки. Это то же самое, что предположить, что катушка намотана бесконечно тонкой лентой с незначительным расстоянием между витками.Если расстояние между витками невелико, следует применить поправочный коэффициент. Более того, на высоких частотах ток течет внутрь катушки, поэтому эффективный радиус, по которому протекает ток, становится меньше. Иногда предлагается использовать в расчетах внутренний радиус катушки вместо среднего радиуса проволоки, чтобы компенсировать этот эффект. Однако разница между низко- и высокочастотной индуктивностями обычно невелика [1].
Для точного расчета индуктивности любого вида катушки (или также более сложных проводящих структур) необходимо использовать электромагнитный симулятор.Что касается формул индуктивности токового слоя для однослойных катушек, одна из наиболее широко известных — формула Уиллера [2], в которой говорится (после преобразования в метрические единицы):
L = (d 2 n 2 ) / (l + 0,45d) [мкГн]
где d — диаметр катушки в метрах, n — количество витков, l — длина катушки в метрах.
Приведенная выше формула имеет точность в пределах 1% для l> 0,4d; для более коротких катушек можно использовать хорошо известную формулу Нагаока [3] (неудобство которой состоит в том, что требуется список табличных значений для различных соотношений диаметра / длины) или другие асимптотические приближения [4].Некоторые полезные формулы, применимые для любого отношения диаметра к длине, представлены в [4] и [5];
Артикул:
[1] F.E. Terman, « Radio Engineers ‘Handbook «, Лондон, McGraw-Hill, 1-е изд., Сентябрь 1950 г. [2] Х.А. Уиллер, « Простые формулы индуктивности для радиокатушек «, Proc. I.R.E. , т. 16, pp. 1398-1400, октябрь 1928. [3] H.Нагаока, « Коэффициенты индуктивности соленоидов «, J. Coll. Sci. , т. 27, стр. 18-33, 1909. [4] Х.А. Уиллер, «Формулы индуктивности для круглых и квадратных катушек «, Proc. IEEE , т. 70, нет. 12, pp. 1449-1450, декабрь 1982 г. [5] R. Lundin, « Справочная формула для индуктивности однослойной круглой катушки «, Proc. IEEE , т. 73, нет.9, pp. 1428–1429, сентябрь 1985 г. [6] Ф. Лэнгфорд-Смит (редактор), « Справочник разработчика радиотронов «, 4-е издание, Австралия, Wireless Press, 1952 г. Пример расчета индуктивности
Индуктивность Пример расчета
Дэвид Микер
Сопутствующий файл: index1a.fem
Введение
Распространенной задачей, к которой можно применить FEMM, является расчет индуктивности индуктора с зазором.Хотя индуктивность можно оценить с помощью простого магнитного Теория схем, схемный подход обычно игнорирует утечку потока и окантовочные эффекты. Чтобы решить эти неидеальные эффекты более подробно анализ методом конечных элементов может быть заняты. Цель настоящего пример — показать, как рассчитывается индуктивность в моделировании FEMM, и сравните этот результат с приближением, полученным через магнитную цепь подход.
Пример геометрии
Примерная геометрия состоит из ламинированного EI с зазорами. сердечник с поперечным сечением, как показано на рисунке 1.Сердечник E с центральным полюсом шириной 0,5 дюйма и внешними полюсами Ширина 0,25 дюйма отделена от I-образного возвратного тракта воздушным зазором. Толщина 0,025 дюйма.
Рисунок 1: Пример геометрии
Обмотка, которая лежит в пазах E, состоит из 66 витки толстой изоляции провода 18 AWG, примерно для 66% меди заполните фракцию в окне змеевика. это Предполагается, что сердцевина расширяется на 1 дюйм в направлении страницы.В данной модели материал считается линейным ферромагнитным материалом с относительной проницаемостью из 2500.
Теория цепей Индуктивность
Для приблизительной оценки индуктивности мы можем предположить, что нет подтеков и окантовки, и что вклад железа секций на сопротивление магнитной цепи тривиально по сравнению с вклады с воздуха.Потом, поток, текущий в магнитной цепи, получается путем решения уравнения цепи:
для ф , всего поток, связанный катушкой. Модель R представляет собой сопротивление магнитной цепи, которое согласно нашим предположениям можно записать как:
, где g = 0,025 дюйма , a полюс = 0.5 в 2 и м o = 4 p (10 -7 ) H / м. Так как общий поток, связывающий катушку, тогда:
, а общая самоиндукция равна потоку, умноженному на общее количество витков:
так, чтобы самоиндукция была:
Так как в нашем случае витков 66, индуктивность работает из:
L = 1.39 мГн
Мы ожидаем, что индуктивность получена из конечных элементов. вычисления должны быть в районе 1,39 мГн.
Индуктивность конечного элемента (I)
Для создания решения методом конечных элементов индуктор помещается в центр коробки размером 2 на 2,5 дюйма. На границах области граница условие A = 0 определено. Для Для выполнения анализа методом конечных элементов ток 1 А является допустимым. несколько произвольно применяется к катушкам.Достаточно грубая плотность ячеек с ограничением размера ячейки больше 0,05 дюйма определяется везде. Сетка проблемной области изображена на рисунке 2.
Рисунок 2: Проблемная область, нарисованная в FEMM.
После выполнения анализа и запуска постпроцессора, индуктивность можно определить, нажав кнопку «Свойства схемы» в постпроцессор:
Появляется диалоговое окно с рядом свойств обмотки, если смотреть со стороны выводов обмотки.Диалоговое окно «Свойства схемы» для этого примера показано ниже на рисунке 3.Рисунок 3: Схема Диалог результатов свойств.
При отсутствии постоянных магнитов или других катушек, Результат потока / тока можно интерпретировать напрямую как собственную индуктивность:
L = 1,73 м вод. Ст.
Этот результат выше, чем 1,39 мГн, предсказанный простой подход теории цепей, потому что эффекты утечки и окантовки пренебрежение схемным подходом приводит к небольшому увеличению индуктивности.
Индуктивность конечного элемента (II)
Альтернативный подход — получение энергии через Интеграл «Энергия магнитного поля». Для этого подхода энергия получается через:
, где этот интеграл взят по всей задаче домен, а не просто над катушками. Чтобы выполнить эту интеграцию в постпроцессор, переключитесь в режим интегрального блока, нажав кнопку на панели задач.Затем выберите каждый регион в проблеме с помощью щелчки левой кнопкой мыши. Когда выделена вся проблемная область, нажмите кнопку Integral и выберите Интеграл энергии магнитного поля из выпадающего списка объемных интегралов. Если W представляет собой интегральный результат, результирующая индуктивность:
Для примера задачи результат из энергии интеграция:
Вт = 0.000865042 Джоули
Что при подстановке в формулу дает то же результат как метод (I):
L = 1,73 м вод. Ст.
Выводы
Был представлен простой пример, демонстрирующий, как FEMM можно использовать для получения индуктивности. Была рассмотрена двумерная плоская задача, и индуктивность получена из двух методы сравнивались друг с другом и с «проверкой работоспособности» оценка индуктивности по теории магнитной цепи.
Хотя результаты двух подходов конечных элементов для получения одинаковых индуктивностей в этом случае обычно лучше использовать метод (I). Причина в том, что некоторые граничные условия ( т.е. асимптотическое граничное условие, используемое для аппроксимации «открытой граничной» задачи) подразумевают, что некоторая энергия хранятся вне смоделированной проблемной области. Внутренне FEMM вычисляет поток связь с использованием метода, который учитывает эту дополнительную энергию, тогда как интегрирования B * H по всем элементам нет.
Строго говоря, один коэффициент индуктивности подразумевает линейная зависимость между приложенным током и результирующим потоком. По этой причине пример проблемы с учитывались только линейные материалы.
Если проблема связана с нелинейными материалами и есть значительная насыщенность, больше нет линейной зависимости между ток и поток. Однако есть много ситуаций, в которых применяется синусоидальный ток, и хотелось бы знать амплитуду основной гармоники потока, соответствующую приложенному Текущий.
