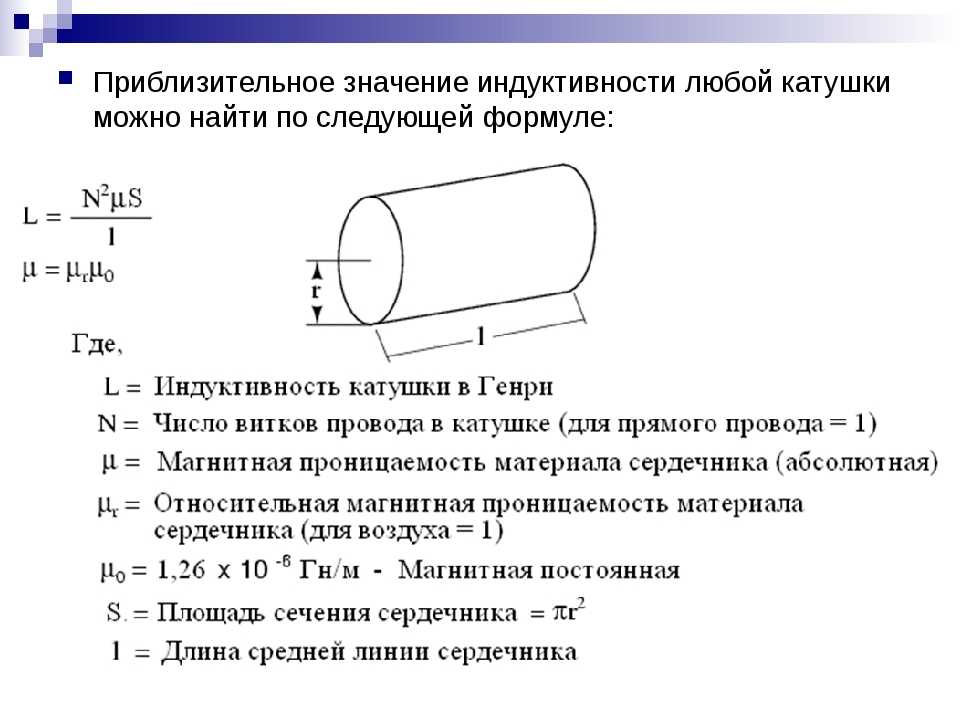
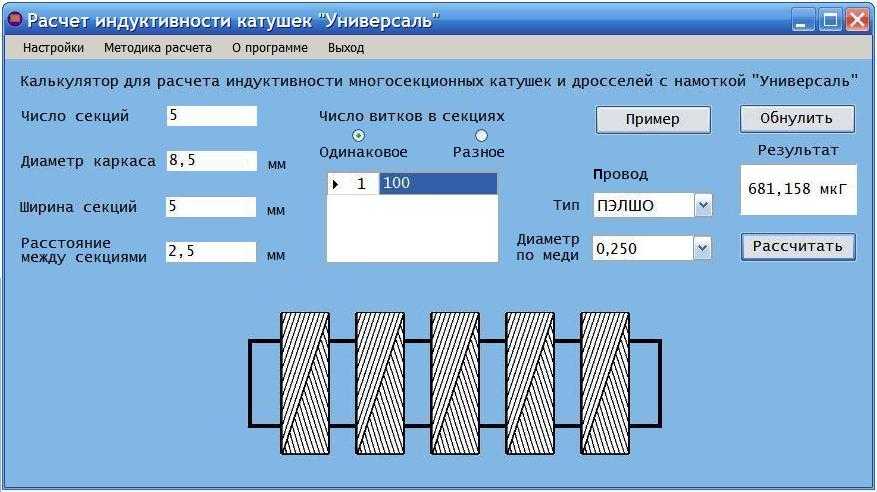
Рассчитать катушку индуктивности: On-line калькуляторы, расчет однослойной катушки индуктивности — Мир Антенн

Содержание

Онлайн калькулятор расчета многослойной катушки индуктивности

На практике нередко случаются ситуации, когда при выходе со строя катушки индуктивности, ее необходимо восстановить – намотать новую проволоку взамен старой. При этом вам уже известны геометрические параметры катушки, но требуется узнать, сколько сделать витков, слоев, их толщину и длину необходимого для этого провода. Стоит отметить, что при намотке витки должны ложиться вплотную без зазора.

Для расчета индуктивности многослойной катушки используется такая формула:

Где,

d – сумма диаметра каркаса и толщины намотки только с одной стороны;
n – количество витков;
g – толщина намотанной проволоки;
h – высота намотанной проволоки;

Из этой формулы, зная величину индуктивности, можно вывести толщину намотки:

Для определения количества витков необходимо воспользоваться формулой:

Где,

d_пр – диаметр провода
h – высота катушки;
g – толщина намотки.

Расчет количества витков

Длину одного витка можно определить следующим образом:

l_вит = π * d_вит

Где π – это константа, а d_{вит_}– это диаметр витка.

Тогда, зная общее число витков и принимая, что d – это усредненное значение диаметра для всех витков, длина всего провода будет определяться по формуле:

L_w = n * π * d

Через сопротивление провода можно определить его диаметр, для чего понадобится выразить сопротивление через геометрические параметры устройства.

R = ρ * ( L_w / S ),

где ρ – удельное сопротивление металла, из которого изготовлен проводник, а S – площадь проводника, которая определяется по формуле:

Подставив значение площади и длины провода, получим такое выражение для определения сопротивления:

Из значения сопротивления можно вывести формулу для определения диаметра провода, подставив предварительно формулу для вычисления количества витков:

После получения величины диаметра провода, можно определить количество витков, которое подставляется с остальными данными в первую формулу для расчета индуктивности.

Число слоев можно определить, разделив толщину намотки на диаметр провода:

N = g / d_пр

Посредством вышеприведенных вычислений можно определить все параметры многослойной катушки индуктивности, которые помогут вам изготовить устройство с нужными параметрами. Также, чтобы облегчить вычисления вы можете воспользоваться нашим онлайн калькулятором ниже.

Требуемая индуктивность L

мГнμГннГн

Диаметр каркаса D

ммсм

Длина намотки l

ммсм

Диаметр провода по меди d

мм

Диаметр провода по изоляции k

мм

Число витков

Число слоев N

Толщина катушки с

мм

*Длина провода Lw

**Сопротивление катушки Ω

Ом

Катушка индуктивности. Описание, характеристики, формула расчета

Главная » Справочник » Катушка индуктивности. Описание, характеристики, формула расчета

Катушка индуктивности является пассивным компонентом электронных схем, основное предназначение которой является сохранение энергии в виде магнитного поля. Свойство катушки индуктивности чем-то схоже с конденсатором, который хранит энергию в виде электрического поля.

Индуктивность (измеряется в Генри) — это эффект возникновения магнитного поля вокруг проводника с током. Ток, протекающий через катушку индуктивности, создает магнитное поле, которое имеет связь с электродвижущей силой (ЭДС) оказывающее противодействие приложенному напряжению.

Возникающая противодействующая сила (ЭДС) противостоит изменению переменного напряжения и силе тока в катушке индуктивности. Это свойство индуктивной катушки называется индуктивным сопротивлением. Следует отметить, что индуктивное сопротивление находится в противофазе к емкостному реактивному сопротивлению конденсатора в цепи переменного тока. Путем увеличения числа витков можно повысить индуктивность самой катушки.

Накопленная энергия в индуктивности

Как известно магнитное поле обладает энергией. Аналогично тому, как в полностью заряженном конденсаторе существует запас электрической энергии, в индуктивной катушке, по обмотке которой течет ток, тоже существует запас — только уже магнитной энергии.

Энергия, запасенная в катушке индуктивности равна затраченной энергии необходимой для обеспечения протекания тока I в противодействии ЭДС. Величина запасенной энергии в индуктивности можно рассчитать по следующей формуле:

где L — индуктивность, I — ток, протекающий через катушку индуктивности.

Гидравлическая модель

Работу катушки индуктивности можно сравнить с работой гидротурбины в потоке воды. Поток воды, направленный сквозь еще не раскрученную турбину, будет ощущать сопротивление до того момента, пока турбина полностью не раскрутится.

Далее турбина, имеющая определенную степень инерции, вращаясь в равномерном потоке, практически не оказывая влияния на скорость течения воды. В случае же если данный поток резко остановить, то турбина по инерции все еще будет вращаться, создавая движение воды. И чем выше инерция данной турбины, тем больше она будет оказывать сопротивление изменению потока.

Также и индуктивная катушка сопротивляется изменению электрического тока протекающего через неё.

Индуктивность в электрических цепях

В то время как конденсатор оказывает сопротивление изменению переменного напряжения, индуктивность же сопротивляется переменному тока. Идеальная индуктивность не будет оказывать сопротивление постоянному току, однако, в реальности все индуктивные катушки сами по себе обладают определенным сопротивлением.

Тестер транзисторов / ESR-метр / генератор

Многофункциональный прибор для проверки транзисторов, диодов, тиристоров…

Подробнее

В целом, отношение между изменяющимися во времени напряжением V(t) проходящим через катушку с индуктивностью L и изменяющимся во времени током I(t), проходящим через нее можно представить в виде дифференциального уравнения следующего вида:

Когда переменный синусоидальной ток (АС) протекает через катушку индуктивности, возникает синусоидальное переменное напряжение (ЭДС). Амплитуда ЭДС зависит от амплитуды тока и частоте синусоиды, которую можно выразить следующим уравнением:

где ω является угловой частотой резонансной частоты F:

Причем, фаза тока отстает от напряжения на 90 градусов. В конденсаторе же все наоборот, там ток опережает напряжение на 90 градусов. Когда индуктивная катушка соединена с конденсатором (последовательно либо параллельно), то образуется LC цепь, работающая на определенной резонансной частоте.

Индуктивное сопротивление ХL определяется по формуле:

где ХL — индуктивное сопротивление, ω — угловая частота, F — частота в герцах, и L индуктивность в генри.

Индуктивное сопротивление — это положительная составляющая импеданса. Оно измеряется в омах. Импеданс катушки индуктивности (индуктивное сопротивление) вычисляется по формуле:

Схемы соединения катушек индуктивностей

Параллельное соединение индуктивностей

Напряжение на каждой из катушек индуктивностей, соединенных параллельно, одинаково. Эквивалентную (общую) индуктивность параллельно соединенных катушек можно определить по формуле:

Последовательное соединение индуктивностей

Ток, протекающий через катушки индуктивности соединенных последовательно, одинаков, но напряжение на каждой катушке индуктивности отличается. Сумма разностей потенциалов (напряжений) равна общему напряжению. Общая индуктивность последовательно соединенных катушек можно высчитать по формуле:

Эти уравнения справедливы при условии, что магнитное поле каждой из катушек не оказывает влияние на соседние катушки.

Добротность катушки индуктивности

На практике катушка индуктивности имеет последовательное сопротивление, созданное медной обмоткой самой катушки. Это последовательное сопротивление преобразует протекающий через катушку электрический ток в тепло, что приводит к потере качества индукции, то есть добротности. Добротность является отношением индуктивности к сопротивлению.

Добротность катушки индуктивности может быть найдена через следующую формулу:

где R является собственным сопротивлением обмотки.

Катушка индуктивности. Формула индуктивности

Базовая формула индуктивности катушки:

L = индуктивность в генри
μ 0 = проницаемость свободного пространства = 4π × 10 -7 Гн / м
μ г = относительная проницаемость материала сердечника
N = число витков
A = Площадь поперечного сечения катушки в квадратных метрах (м 2 )
l = длина катушки в метрах (м)

Индуктивность прямого проводника:

L = индуктивность в нГн
l = длина проводника
d = диаметр проводника в тех же единицах, что и l

Индуктивность катушки с воздушным сердечником:

L = индуктивность в мкГн
r = внешний радиус катушки
l = длина катушки
N = число витков

Индуктивность многослойной катушки с воздушным сердечником:

L = индуктивность в мкГн
r = средний радиус катушки
l = длина катушки
N = число витков
d = глубина катушки

Индуктивность плоской катушки:

L = индуктивность в мкГн
r = средний радиус катушки
N = число витков
d = глубина катушки

Конструкция катушки индуктивности

Катушка индуктивности представляет собой обмотку из проводящего материала, как правило, медной проволоки, намотанной вокруг либо железосодержащего сердечника, либо вообще без сердечника.

Применение в качестве сердечника материалов с высокой магнитной проницаемостью, более высокой чем воздух, способствует удержанию магнитного поля вблизи катушки, тем самым увеличивая ее индуктивность. Индуктивные катушки бывают разных форм и размеров.

Большинство изготавливаются путем намотки эмалированного медного провода поверх ферритового сердечника.

Некоторые индуктивные катушки имеют регулируемый сердечник, при помощи которого обеспечивается изменение индуктивности.

Миниатюрные катушки могут быть вытравлены непосредственно на печатной плате в виде спирали. Индуктивности с малым значением могут быть расположены в микросхемах с использованием тех же технологических процессов, которые используются при создании транзисторов.

Применение катушек индуктивности

Индуктивности широко используются в аналоговых схемах и схемах обработки сигналов. Они в сочетании с конденсаторами и другими радиокомпонентами образуют специальные схемы, которые могут усилить или отфильтровать сигналы определенной частоты.

Катушки индуктивности получили широкое применение начиная от больших катушек индуктивности, таких как дроссели в источниках питания, которые в сочетании с конденсаторами фильтра устраняют остаточные помехи и другие колебания на выходе источника питания, и до столь малых индуктивностей, которые располагаются внутри интегральных микросхем.

Две (или более) катушки индуктивности, которые соединены единым магнитным потоком, образуют трансформатор, являющимся основным компонентом схем работающих с электрической сетью электроснабжения. Эффективность трансформатора возрастает с увеличением частоты напряжения.

По этой причине, в самолетах используется переменное напряжение с частотой 400 герц вместо обычных 50 или 60 герц, что в свою очередь позволяет значительно сэкономить на массе используемых трансформаторов в электроснабжении самолета.

Так же индуктивности используются в качестве устройства для хранения энергии в импульсных стабилизаторах напряжения, в высоковольтных электрических системах передачи электроэнергии для преднамеренного снижения системного напряжения или ограничения ток короткого замыкания.

Блок питания 0…30В/3A

Набор для сборки регулируемого блока питания…

Подробнее

Inductance Formula — GeeksforGeeks

Индуктивность — это термин, с которым должен быть знаком каждый студент-физик. Он имеет собственную формулу и часто комбинируется с сопротивлением и емкостью. Оливер Хевисайд впервые придумал эту фразу в 1886 году. Кроме того, мы используем букву L для обозначения катушек индуктивности на принципиальных схемах и индуктивности в уравнениях в честь выдающегося физика Генриха. Давайте узнаем о формуле индуктивности и о том, как ее использовать для определения индуктивности. любой предмет.

Индуктивность

Индуктивность — это свойство электрического проводника, которое заставляет его сопротивляться изменениям проходящего через него электрического тока. Поток электрического тока создает вокруг проводника магнитное поле. Напряженность поля пропорциональна величине тока и не зависит от колебаний тока. Согласно закону индукции Фарадея, любое изменение магнитного поля в цепи создает электродвижущую силу (ЭДС) (напряжение) в проводниках, процесс, известный как электромагнитная индукция.

Индуктивность присутствует во многих электрических и электронных системах, а также в цепях. Шестерни доступны в различных формах и размерах, а также различных названиях. Примеры включают катушки, дроссели, трансформаторы, катушки индуктивности и другие детали.

Единицей индуктивности в СИ является генри (Гн) , что может быть представлено в скорости изменения тока и напряжения.

Формула индуктивности

Ниже приведена формула индуктивности,

L = мкН ² А/л
Где,
L = индуктивность (Гн),
мк = магнитная проницаемость (Вб/ампер),
7 90 витков18
Н = катушка A = Окружность рулона,
l = Длина рулона (м).

Вывод перепишите приведенное выше уравнение,

E = -N(dϕ/dt)

Предыдущее уравнение изменено для вычисления значения индуктивности.

E = -N(dϕ/dt)

∴ E = -L(di/dt)

N = dΦ = L di

NΦ = Li

Следовательно,

Плотность потока обозначена B, площадь катушки обозначена A.

Li = NΦ = NBA

Hl = Ni

Намагничивающая сила магнитного потока обозначена H.

B = µH

Li = NBA

L = NBA / я = N ² BA/Ni

N ² BA/Hl = N ² μHA/Hl

∴ L = μN ² A/l

With an inductance of L, the voltage induced в катушке (В) равно,

В = L × (di/dt)
Где,
В = напряжение (вольт),
L = значение индуктивности (Гн),
i = Ток (А),
t = Затраченное время (с).

Реактивное сопротивление индуктивности рассчитывается следующим образом,

X = 2πfL
Где,
X = реактивное сопротивление (Ом),
f = частота (Гц),
L = индуктивность (Гн).

Если индуктивность последовательно

L = L ₁ + L ₂ + L ₃ . . . . + L _n

Если индуктивность параллельна

1/L = 1/L ₁ + 1/L _{2 10149 +0147 3} . . . . + 1/L _n

Примеры вопросов

Вопрос 1: Определение индуктивности.

Ответ :

Индуктивность — это свойство электрического проводника, которое заставляет его сопротивляться изменениям проходящего через него электрического тока. Поскольку индуктивность имеет N в формуле, это означает, что количество витков в проводнике прямо пропорционально присутствующей индуктивности. Однако интересным фактом является то, что даже прямые проводники несут индуктивность очень мало, чтобы быть значительной.

Вопрос 2: Что такое единица индуктивности в системе СИ?

Ответ:

Единицей индуктивности в системе СИ является генри (Гн). Открытие индуктивности приписывают Фарадею, однако введение собственной индуктивности для одиночной цепи было впервые введено Генри. Поэтому единица индуктивности посвящена имени ученого.

Вопрос 3: Определите самоиндукцию 210-виткового соленоида с площадью поперечного сечения 17 см ² и длиной 66,2 см.

Решение:

Дано: μ = 4π × 10 ^-7 N/A ², n = 210 поворотов, A = 17 × 100023 -4 M ², L = 66,2 × 10 ^-2 м
Т.к. -4 ))/(66,2 × 10 ^-2 )
∴ L = 0,0001422
∴ L = 14,22 × 10 ^-5 H

Вопрос 4: Каково соответствующее сопротивление при последовательном соединении катушек индуктивности 16H, 10H и 21H?

Решение :

Дано: L ₁ = 16 H, L ₂ = 10 H, L ₃ = 21 H
С.
L ₁ + L _{+ L _{+ L _{+ L _{+ L _{+ L _{+ L _{+ L _{+ L _{+ L _{+ L _{+ L _{+ L ₊}}}}}}}}}}}}
. 2 + L ₃
∴ L = 16 + 10 + 21
∴ L = 47 Гн

при условии. рассчитать реактивное сопротивление?

Решение:

Дано: F = 240 Гц, L = 61 H
,
x = 2πfl
∴ x = 2 × 3,14 × 240 × 61
∴ x = 91939 o

Вопрос 6: Каково соответствующее сопротивление при параллельном соединении катушек индуктивности 26H, 16H, 21H и 30H?

Решение:

Дано: L ₁ = 26 H, L ₂ = 16 H, L ₃ = 21 H, L ₄ = 30 H
Поскольку,
1/л = 1/л ₁ + 1/л ₂ + 1/л ₃ + 1/л 4
1/26 + 1/16 + 1/21 + 1/30
∴ 1/л = 0,03 + 0,06 + 0,04 + 0,03
∴ 1/л = 0,16 Гн
∴ Дл = 6,204 00012 Гн Уравнение i-v катушки индуктивности в действии
Катушка индуктивности является одним из идеальных элементов цепи. Мы узнаем больше о том, как ведет себя индуктор, внимательно изучив его уравнение $i$-$v$.
Автор Вилли Макаллистер.
Содержание
Уравнения индуктора $i$-$v$
Напряжение дросселя пропорционально скорости изменения тока
Катушка индуктивности и источник тока
Имитационная модель
Иногда катушка индуктивности «выглядит» короткой
Катушка индуктивности и источник напряжения
Имитационная модель
Пример
9{\,T} v\,\text dt + i_0$
Это производная и интегральная формы уравнений индуктора.
$\text L$ индуктивность , физическое свойство катушки индуктивности.
$\text L$ — масштабный коэффициент между $v$ и $di/dt$.
$\text L$ показывает, сколько $v$ генерируется для заданного количества $di/dt$.
$i_0$ — начальный ток, протекающий в катушке индуктивности, при $t=0$.
обозначение исчисления: $di/dt$
$v = \text L\,\dfrac{di}{dt}$
9{\,T} v\,\text dt + i_0$
Зацикленный символ $\int$ тоже из исчисления. Это интегральный признак. Его значение аналогично символу суммирования $\Sigma$. В уравнении индуктора знак интеграла представляет собой бегущую сумму произведения $v\,\times \,dt$, начиная с момента времени $t=0$ и заканчивая моментом времени $t=T$. Интегрирование противоположно взятию производной.
Напряжение на дросселе пропорционально
скорости изменения тока
Когда мы узнали о резисторах, закон Ома сказал нам, что напряжение на резисторе пропорционально току через резистор: $v = \text R\,i$ .
Теперь у нас есть индуктор с уравнением $i$-$v$: $v = \text L\,\dfrac{di}{dt}$.
Это говорит нам, что напряжение на катушке индуктивности пропорционально не току, а скорости изменения тока через катушку индуктивности. Вот что означает $di/dt$.

Для реальных резисторов мы должны позаботиться о том, чтобы напряжение и ток не становились слишком большими для резистора. Для реальных катушек индуктивности мы должны быть осторожны со скоростью изменения тока не слишком велик для катушки индуктивности. Это может быть непросто. Очень легко создать большое изменение тока при размыкании или замыкании переключателя. В статье об отдаче индуктора мы разрабатываем для этой ситуации.
Катушка индуктивности и источник тока
Теперь мы рассмотрим несколько различных простых схем, чтобы понять, что означают уравнения $i$-$v$ катушки индуктивности. По пути мы увидим, как уравнения учат нас некоторым простым практическим правилам относительно катушки индуктивности.
Первый пример — катушка индуктивности, подключенная к идеальному источнику тока.
Источник тока подает постоянный ток на катушку индуктивности, $i = \text I$.
Например, пусть $i = 2 \,\text{mA}$.
Какое напряжение на дросселе?
Уравнение индуктора говорит нам:
$v = \text L\,\dfrac{di}{dt}$
Источник тока обеспечивает постоянный ток $2\,\text{мА}$. Это интересно, но что нам действительно нужно знать, так это скорость изменения тока?
$\dfrac{di}{dt} = \dfrac{d2}{dt} = 0\qquad$ (все знают, что $2$ не меняется со временем)
Следовательно, напряжение на индукторе равно:
$v = \text L\cdot 0 = 0$
Если ток в индукторе постоянный, то $v = \text L\,di/dt = 0$ . На катушке индуктивности появляется ноль вольт. Это верно для любого значения тока и любого значения индуктора.
Имитационная модель
Вот имитационная модель катушки индуктивности $5\,\mu\text H$ с постоянным источником тока $2\,\text{мА}$. Откройте ссылку и нажмите TRANS в верхней строке меню, чтобы запустить переходную симуляцию. Результат довольно скучный. Напряжение на катушке индуктивности равно $0$. Измените катушку индуктивности или ток на что угодно, ответ всегда будет $0$.
Иногда индуктор «выглядит как» короткий
Очень популярно рисовать мысленные образы индуктора, говоря, что он «похож» на что-то. Вот наш первый пример.
При постоянном токе разность потенциалов между концами катушки индуктивности составляет $0\,\text V$. В этом состоянии индуктор ведет себя как идеальный провод. (Идеальный провод имеет $0\,\text V$ между концами, несмотря ни на что.)
Катушка индуктивности «выглядит» как короткое замыкание, когда ток в ней постоянный. {-3}} = 300 \,\text{ампер}/\text{сек}$
Это означает, что ток через индуктор будет иметь крутизну нарастания $300\,\text{ампер}/\text{секунда}$.
Удивительно, но именно это и предсказывает уравнение. Излишне говорить, что это не практическая схема. Мы просто хотим посмотреть, что происходит с постоянным напряжением. Если мы построим эту схему, ток будет увеличиваться до тех пор, пока наш реальный источник напряжения не сможет удовлетворить потребность в большем токе. Но в течение короткого промежутка времени именно так работают настоящие катушки индуктивности.
Имитационная модель
Вот имитационная модель катушки индуктивности со схемой источника напряжения. Откройте ссылку и нажмите TRANS в верхнем меню, чтобы запустить переходную симуляцию.
Пример
На самом деле мы можем придумать что-то более полезное, чем линейно возрастающее линейное изменение тока. Если мы изменим источник напряжения так, чтобы он время от времени менял направление, мы получим более интересную и потенциально полезную схему.
Вот вам задание: предположим, что амплитуда прямоугольного сигнала равна $\pm1\,\text V$, а частота равна $1\,\text{MHz}$ $($имеет период $1\,\mu \текст{сек})$.

Нарисуйте форму текущего сигнала и найдите пиковые значения.
Посмотрите, сможете ли вы это сделать, прежде чем смотреть на ответ или имитационную модель.
Подсказка: Рассчитайте $di/dt$ для двух различных состояний входного напряжения.
показать ответ
Форма волны тока представляет собой треугольную волну, нарастающую при положительном напряжении и убывающую при отрицательном напряжении.
Мы решим это по частям. Сначала определите ток при напряжении $+1\,\text V$, 9{+6} \,\text{ампер}/\text{сек}$
Нарастание тока составляет $200{,}000\,\text{ампер}/\text{секунда}$.
То же, что и $200\,\text{мА}/\мю\текст{сек}$.
Напряжение меняется с $+1\,\text V$ на $-1\,\text V$ каждые $0,5\,\mu\text{сек}$.
Насколько сильно возрастает ток на участке $v = +1\,\text V$ прямоугольной волны?

$i_{\text{+peak}} = 200\,\text{мА}/\mu\text{сек} \times 0,5\,\mu\text{сек} = 100\,\text{мА}$
Максимальное значение тока достигает $100\,\text{мА}$.
Когда напряжение падает, весь процесс меняется на противоположный. Для части $v = -1\,\text V$ вы можете снова выполнить математику с $-1\,\text V$ в уравнении наклона. Текущий наклон вниз с отрицательным наклоном той же величины. В конце отрицательного напряжения ток вернется к $0$.
$i_{\text{-пик}} = 0\,\text{мА}$.
Ток будет зигзагами между двумя пиками с прямыми линиями между ними. Откройте ссылку на симуляцию ниже и запустите симуляцию переходного процесса, чтобы посмотреть, что произойдет.
Имитационная модель
Имитационная модель схемы источника импульсного напряжения. Откройте ссылку и нажмите TRANS, чтобы запустить переходную симуляцию.
Катушка индуктивности «интегрирует» напряжение по времени, на что указывает значение тока в любой момент. Это точный «двойник» конденсатора, интегрирующий ток.
Исследовать
Что произойдет с током, если вы…?
Изменить значение индуктора на немного $(2\times)$ и на много $(100\times)$.
Изменить амплитуду или частоту источника напряжения.
Измените уровни напряжения, чтобы они не были симметричными.
Измените рабочий цикл напряжения с $50\%$ на другое значение, например $40\%$.
что означает «рабочий цикл»?
Рабочий цикл описывает импульсный сигнал. Это относится к проценту времени, в течение которого напряжение находится в высоком состоянии. Если рабочий цикл равен $25\%$, напряжение равно $+1\,\text V$ в течение четверти времени цикла. Если рабочий цикл составляет $50\%$, напряжение симметрично, проводя половину времени высоким и половину времени низким. Рабочий цикл может варьироваться от $0\%$ до $100\%$.
Аналогия с массой
Это самый полезный мысленный образ, который возникает при взгляде на индуктор.
Индуктивность, $\text L$, аналогична массе или инерции в механической системе. Энергия магнитного поля катушки индуктивности не позволяет току изменяться мгновенно, точно так же, как тяжелая масса автомобиля имеет тенденцию сопротивляться изменению скорости.