Размерность индуктивности: Индуктивность в системе си имеет размерность

Индуктивность в системе си имеет размерность

Эл.ток создает собственное магнитное поле. Магнитный поток через контур пропорционален индукции магнитного поля (Ф

B), индукция пропорциональна силе тока в проводнике
(B

I), следовательно магнитный поток пропорционален силе тока (Ф

ЭДС самоиндукции зависит от скорости изменения силы тока в эл.цепи, от свойств проводника
(размеров и формы) и от относительной магнитной проницаемости среды, в которой находится проводник.

Физическая величина, показывающая зависимость ЭДС самоиндукции от размеров и формы проводника и от среды, в которой находится проводник, называется коэффициентом самоиндукции или индуктивностью.

Индуктивность – физ. величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 Ампер за 1 секунду.

Также индуктивность можно рассчитать по формуле:

где Ф – магнитный поток через контур, I – сила тока в контуре.

Единицы измерения индуктивности в системе СИ:

Индуктивность катушки зависит от: числа витков, размеров и формы катушки и от относительной магнитной проницаемости среды

Индуктивность взаимная – величина, характеризующая магнитную связь двух или более электрических цепей (контуров). Если имеется два проводящих контура , то часть линий магнитной индукции, создаваемых током в первом контуре, будет пронизывать площадь, ограниченную вторым контуром (т. е. будет сцеплена с контуром 2).

Магнитный поток Ф₁₂ через контур 2, созданный током I₁ в контуре 1, прямо пропорционален току:

Коэффициент пропорциональности M₁₂ зависит от размеров и формы контуров 1 и 2, расстояния между ними, их взаимного расположения, а также от магнитной проницаемости окружающей среды и называется взаимной индуктивностью или коэффициентом взаимной индукции контуров 1 и 2. В системе СИ И.

в. измеряется в Генри.

Трансформаторная ЭДС. Принцип действия трансформатора основан на явлении электромагнитной индукции. Линии индукции магнитного поля, создаваемого переменным током в первичной обмотке, благодаря наличию сердечника практически без потерь пронизывают витки вторичной обмотки. Поскольку магнитный поток во вторичной обмотке изменяется со временем (т.к. в первичной обмотке переменный ток), то согласно закону Фарадея в ней возбуждается ЭДС индукции. Трансформатор может работать только на переменном токе, т.к. магнитный поток, созданный постоянным током, не изменяется с течением времени.

Пусть первичная обмотка трансформатора подключена к источнику тока с переменной ЭДС E₁ и с действующим значением напряжения U₁. На вторичной обмотке ЭДС E

2 и напряжение U₂.

Из законов Ома следует, что напряжение на обмотке равно

(1)

где r — сопротивление обмотки. При изготовлении трансформатора сопротивление первичной обмотки r₁ делают очень малым, поэтому часто им можно пренебречь. Тогда

Если пренебречь потерями магнитного потока в сердечнике, то в каждом витке вторичной обмотки будет индуцироваться точно такая же ЭДС индукции e₁, как и ЭДС индукции e₂ в каждом витке первичной обмотки, т.е. e₁ = e₂. Следовательно, отношение ЭДС в первичной E₁ и вторичной E₂ обмотках равно отношению числа витков в них:

(2)

Трансформаторный ток. Токи обмоток обратно пропорциональны числам витков (I

1/I₂ приблиз = w₁/w₂ = 1/n). С увеличением тока активно-индуктивного приемника вторичное напряжение несколько снижается.

Рис.1.11. К определению магнитного потока рассеяния в катушке с ферромагнитным сердечником

часть магнитного потока катушки замыкается не по сердечнику, а по воздуху. Эта часть потока носит название потока рассеивания Ф_р (рис. 1.11). Таким образом, полный поток, сцепленный с витками катушки равен

.

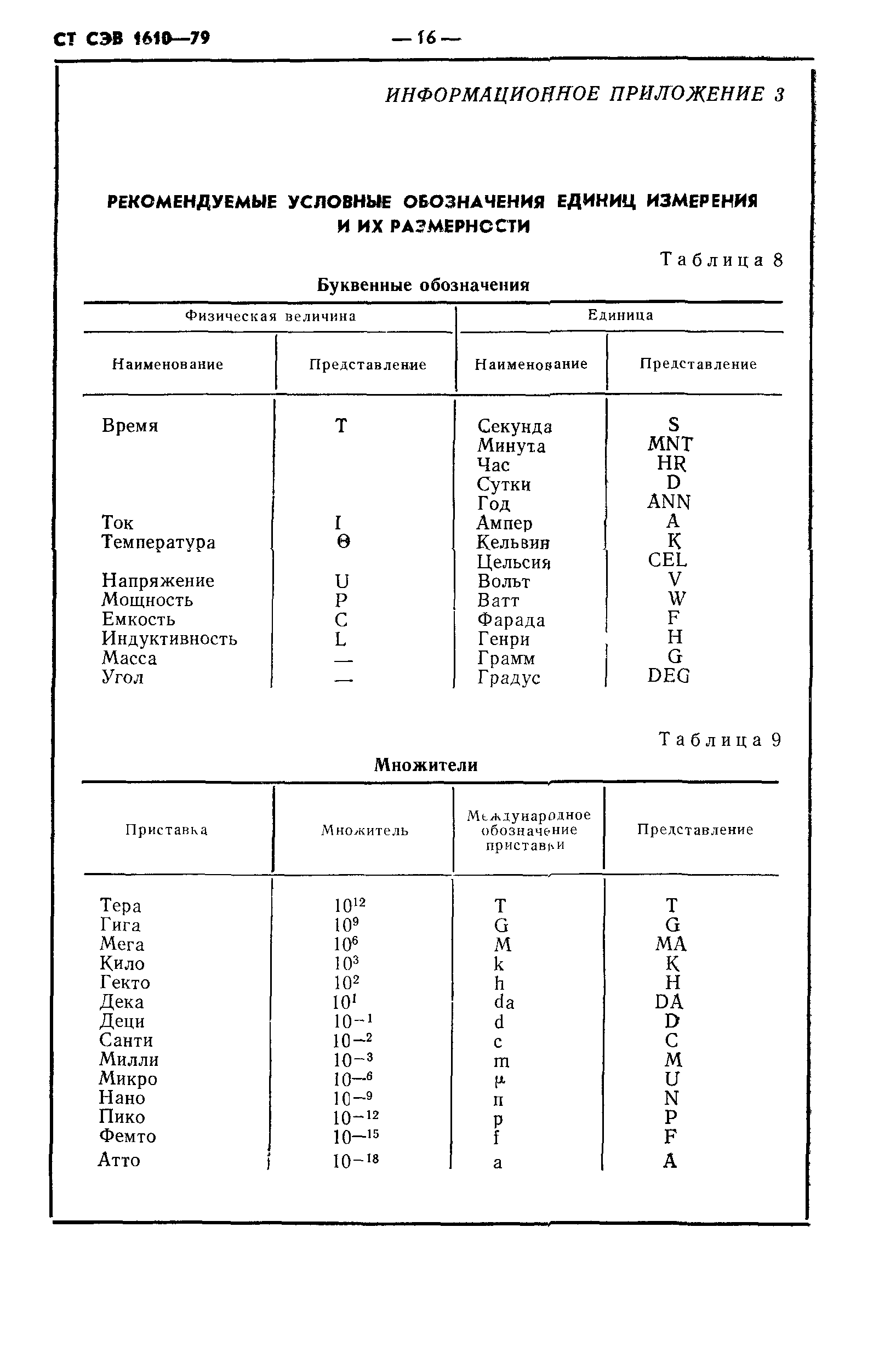(1.14)

На основании закона Ома для магнитной цепи (1.7) можно написать выражение для потока рассеяния:

.

Так как , то .То есть поток рассеяния , в отличие от потока в сердечнике, совпадает по фазе с током и связан с ним линейной зависимостью. Следовательно, на векторной диаграмме вектор потока будет совпадать с вектором тока (рис.1.12).

Рис.1.12. Векторная диаграмма магнитных потоков, ЭДС и токов катушки с ферромагнитным сердечником

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Увлечёшься девушкой-вырастут хвосты, займёшься учебой-вырастут рога 9834 – | 7695 – или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Размерность – индуктивность

Размерность индуктивности в системе CGSM равна размерности длины и поэтому CGSM-единица индуктивности получила название сантиметр. CGSM магнитный поток, пронизывающий этот контур, равен 1 мкс. [1]

Размерность индуктивности L – мкГн; емкое. [3]

Размерностью индуктивности в системе СГС является длина [ L ]; единицей измерения индуктивности в этой системе служит сантиметр. Индуктивность, равная 1 см, в 10 раз меньше 1 гн: 1 ед. [4]

Таким образом, размерность индуктивности в системе CQS-M совпадает с размерностью длины. Единицей индуктивности в системе CGS-M является сантиметр. [5]

Показать, что г 2С имеет размерность индуктивности , ] / L / C – размерность сопротивления; L / r – размерность емкости. [7]

Из (64.3) следует, что размерность цо равна размерности индуктивности , деленной на размерность длины. [8]

Из (64.3) следует, что размерность р 0 равна размерности индуктивности , деленной на размерность длины. [9]

Очевидно, что ( a – f – Ъх) имеет размерность индуктивности . Величина этой индуктивности является в данном случае линейной функцией положения якоря соленоида.

[10]

Постоянные Н, входящие в выражение сопротивлений реактивных двухполюсников, имеют размерность индуктивности для двухполюсников классов I и IV и размерность, обратную емкости, для классов II и III. Для нахождения постоянной Я надо определить характер сопротивления двухполюсника ( индуктивный или емкостный) при частоте, превышающей наибольшую резонансную. [11]

В системе СГСМ за единицу индуктивности принимается 1 сантиметр, так как размерность индуктивности контура в этой системе единиц оказывается равной размерности длины. [12]

Из сравнения (98.1) с (93.1) видно, что размерность Li та же, что и размерность индуктивности , и поэтому взаимная индуктивность измеряется в тех же единицах, что и индуктивность. [13]

Из сравнения (110.1) с (105.1) видно, что размерность L12 – та же, что и размерность индуктивности , и поэтому коэффициент взаимной индукции измеряется в тех же единицах, что и индуктивность. [15]

Индуктивность — это коэффициент пропорциональности между электрическом током, проходящим в замкнутом контуре и магнитным потоком, образуемым этим током через поверхность, у которой контур является краем.

Индуктивность обозначается символом L, принятым в честь Э.Ленца.

Ф = L I , отсюда
L = Ф / I = 1Вб / 1А = 1 Гн

Ф — величина магнитного потока, которая пронизывает контур с 1 витком;
I — величина тока;
L — индуктивность витка;
L — коэффициент пропорциональности между Ф и I.

Если катушка состоит из N витков, то полным потоком (или потокосцеплением) будет сумма магнитных потоков через все витки, тогда

Индуктивность L зависит от размеров, формы проводника, количества витков и т.п., от магнитной проницаемости среды.

Единица измерения в системе СИ названа генри (Гн) в честь Дж.Генри. В Гауссовой системе и СГС, СГСМ системах индуктивность считают в сантиметрах 1 Гн = 1000000000 см, 1 см = 1 нГн. Для сантиметров используют название абгенри.в качестве единицы. В системе СГСЭ единицу индуктивности называют статгенри, либо оставляют без названия.

1 статгенри приблизительно равен 8,987552 х 10 в 11 степени генри.
1 Гн = 1000 Миллигенри
1 Гн = 1000000 Микрогенри
1 Гн = 0,001 Килогенри
1 Гн = 0,000001 Мегагенри

Рассчитать индуктивность и осуществить быстрый перевод единиц измерения можно с помощью онлайн калькулятора.

ИНДУКТИВНОСТЬ • Большая российская энциклопедия

ИНДУКТИ́ВНОСТЬ (от лат. inductio – на­ве­де­ние, по­бу­ж­де­ние), ве­ли­чи­на, ха­рак­те­ри­зую­щая маг­нит­ные свой­ст­ва элек­трич. це­пи. И. яв­ля­ет­ся ко­ли­че­ст­вен­ной ха­рак­те­ри­сти­кой эф­фек­та са­мо­ин­дук­ции. Элек­трич. ток, те­ку­щий в про­во­дя­щем кон­ту­ре, соз­да­ёт в ок­ру­жаю­щем про­стран­ст­ве маг­нит­ное по­ле, при­чём маг­нит­ный по­ток $\text{Φ}$, про­ни­зы­ваю­щий кон­тур, пря­мо про­пор­цио­на­лен си­ле то­ка $I: \text{Φ} = LI$. Ко­эф. про­пор­цио­наль­но­сти $L$ на­зы­ва­ет­ся И. или ко­эф­фи­ци­ен­том са­мо­ин­дук­ции кон­ту­ра. И. за­ви­сит от раз­ме­ров и фор­мы кон­ту­ра, а так­же от маг­нит­ной про­ни­цае­мо­сти сре­ды. В СИ И. из­ме­ря­ет­ся в ген­ри (Гн), в сис­те­ме еди­ниц СГС име­ет раз­мер­ность дли­ны (1 Гн = 10

9 см). 2S/l$, где $μ_0$ – маг­нит­ная про­ни­цае­мость ва­куу­ма. И. це­пей, в ко­то­рые вклю­че­ны со­ле­нои­ды, в осн. оп­ре­де­ля­ет­ся их ин­дук­тив­но­стью.

Генри (единица индуктивности — Энциклопедия по машиностроению XXL

Генри (единица индуктивности) 132 136  [c.330]

Генри — единица индуктивности и взаимной индуктивности. Наименование единице дано по имени американского ученого Д. Генри (1797—1878).  

[c.53]

Эта единица получила наименование генри (Гн). Генри равен индуктивности электрической цепи, с которой при силе постоянного тока в ней 1 А сцепляется магнитный поток 1 Вб.  [c.132]

Индуктивность (Z. — коэфициент самоиндукции) — коэфициент пропорциональности между 9. д. с. самоиндукции. и скоростью изменения тока в проводнике. Единица индуктивности генри равна 1 гн=в-сек/а =ом-сек. Индуктивностью в один генри обладает цепь.  [c.515]

Уравнение (7. 119) написано в предположении постоянства индуктивности. Согласно (7.118) единица индуктивности генри (Г) определяется как индуктивность такого контура, который при протекании по нему тока 1 А оказывается сцепленным с потоком 1 Вб. Согласно (7.119) генри есть индуктивность такого контура, в котором возникает э.д. с. самоиндукции, равная 1 В при равномерном изменении протекающего по нему тока на 1 А в секунду. Оба определения дают размерность  [c.224]

Единицей взаимной индуктивности так же, как и единицей индуктивности, является генри. Исходя из понятия взаимной индуктивности, генри можно определить так генри — взаимная индуктивность двух контуров, с одним из которых сцеплен магнитный поток 1 Вб, если по другому  [c.90]

Генри (Гн) — единица индуктивности и взаимной индуктивности — производная единица СИ, а также единица магнитной проводимости.  [c.81]

Индуктивность в практической системе единиц измеряется генри (гн).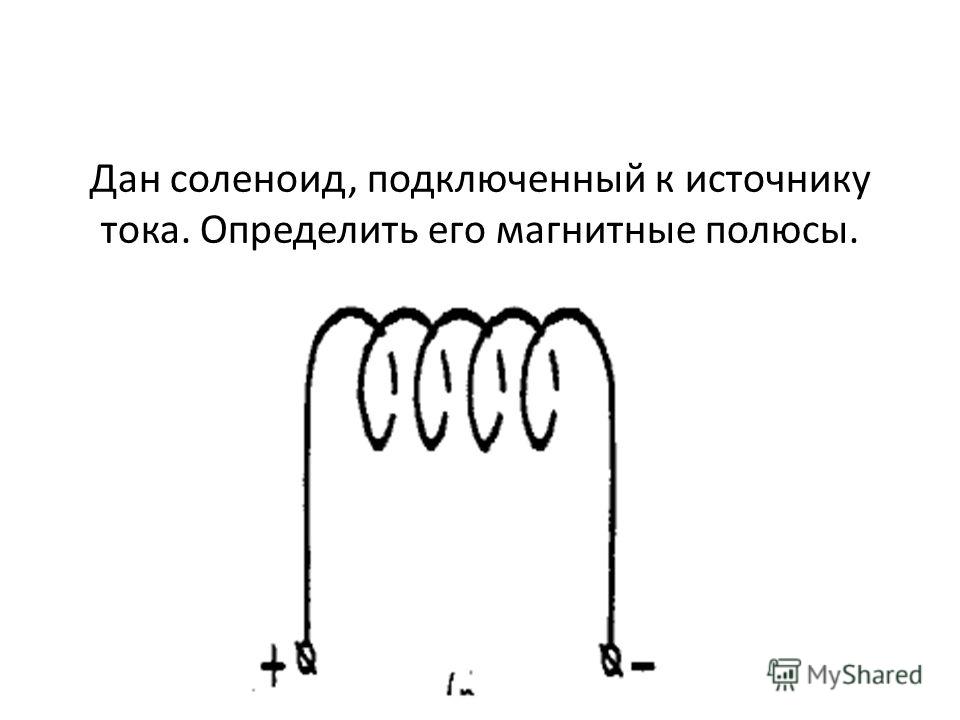 Индуктивность цепи или катушки равна I гн, когда при равномерном изменении тока на 1 а в сек. в ней наводится э. д. с., равная 1 в 1 гн равен 10 абсолютных электромагнитных единиц (сантиметров).  [c.484]

В качестве единицы индуктивности и взаимной индуктивности в системе МКСА принят генри (гн).  [c.143]

За единицу измерения индуктивности принимается генри (Г).  [c.98]

Низкочастотные трансформаторы и дроссели представляют собой катушки с индуктивностью, чаще всего в единицы — сотни генри, в конструкции которых предусмотрены замкнутые магнитные цепи (маг-нитопроводы). В зависимости от назначения трансформаторы подразделяются на силовые, входные, выходные, промежуточные и импульсные. По применению в конструкциях РЭА они делятся на трансформаторы обычного типа и микромодульные.  [c.200]

Единица измерения генри названа в честь американского учёного Джозефа Генри, который открыл явление индуктивности примерно в то же время, что и Фарадей.  [c.336]

Индуктивность — свойство проводника, которое позволяет ему аккумулировать энергию в магнитном поле, вызываемом протекающим через него током. Единица измерения — Генри.  [c.384]

В 1889 г. второй Международный конгресс электриков включил в состав системы еще три единицы джоуль — единицу энергии, равную 10 единиц энергии СГСМ ватт — единицу мощности, равную 10 единиц мощности СГСМ квадрант (впоследствии генри )—единицу индуктивности, равную 10 единиц индуктивности СГСМ.  [c.88]

Генри, единица индуктивности, равен 10 ед. СГСМ. Название генри дано лишь в 1893 г. Первоначально эту единицу назвали квадрантом, поскольку в системе СГСМ единица индуктивности есть сантиметр, а 10 см — это длина четверти земного меридиана.  [c.13]

В нерационализованной системе МКСА jio=10 Гн/м. Единицы индуктивности и емкости — генри и фарад — при рационализации не могут измениться. 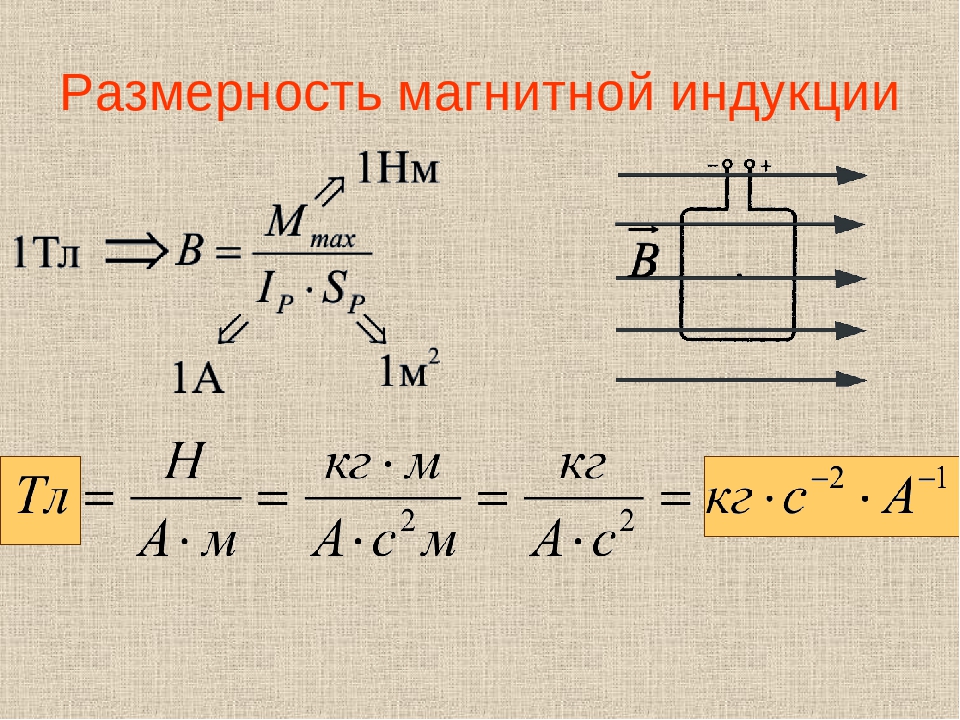Поэтому рационализуются сами понятия и во. В рационализованной системе МКСА и Международной системе абсолютная магнитная и абсолютная диэлектрическая проницаемости вакуума, называемые магнитной и электрической постоянными, равны  [c.116]

Взаимная индуктивность (М — коэфициент взаимоиндукции) двух магнитносвязанных цепей есть коэфициент пропорциональности между э. д. с., индуктирующейся в одной из цепей, и скоростью изменения тока в другой цепи. Единица взаимной индуктивности генри равна ом-сек. Две электрические цепи обладают взаимной индуктивностью, равной 1 гн, если изменение тока в одной из них со скоростью 1 а в секунду индуктирует в другой электрически несвязанной цепи э. д. с., равную 1 в. При отсутствии магнитного рассеяния поток, созданный одним контуром, сцепляется полностью с другим, и в этом случае Мх =Li L , где L и Z-2 — индуктивности соответствующих контуров. При наличии рассеяния ij.  [c.515]

ГЕНРИ (Ги, И) — единица СИ индуктивности и взаимной индуктивности, равная индуктивности электрич. контура, возбуждающего магн. поток в 1 Вб при силе тока в нём 1 А. Назв. в честь Дж. Генри (J. Henry).  [c.435]

Сантиметр [см ст 1) единица длины в СГС, СГСЭ, СГСМ и т. п. относится к числу основных ед. систем размерн. обознач. символом L. Сантиметр равен 0,01 метра. С. рекоменд. ГОСТ 8.417—81 (СТ СЭВ 1052—78) к применению в качестве дольной ед. СИ. См. метр и п. 1 табл. 15 2) ед. коэфф. трения качения в СГС (см. метр), 3) ед. емкости в СГС, СГСЭ (см. фарад), индуктивности и магн. проводимости в СГС, СГСМ (см. генри).  [c.318]

Многие инженеры, а их, по-видимому, большинство, рассчитывают динамические характеристики сравнительно сложных систем с помощью аналогий. Одной из наиболее распространенных является аналогия подвижности Файрсто-уна. В соответствии с методом Файрстоуна, который по существу является обратным так называемому методу аналогий импедансов, напряжение выбирается в качестве аналога скорости, а ток — как аналог момента или силы.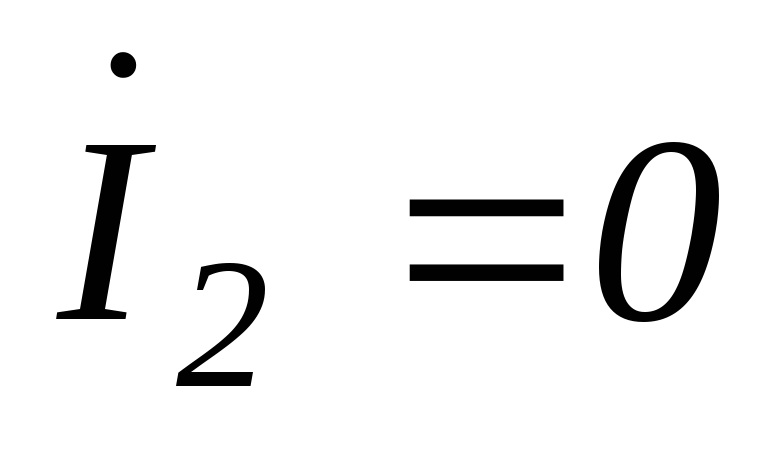 Таким образом пружина заменяется индуктивностью, а масса — емкостью. Поскольку массы относятся к инер-циальному пространству, то их аналоги — конденсаторы имеют одну обкладку заземленной. Эквивалентная схема системы соответствует схеме, приведенной на фиг. 4.14,в. Размерность индуктивностей может быть дана в рад/см-кГ вместо генри, а размерность емкостей — в см-кГ-сек вместо фарад, поскольку это позволяет перейти к любой системе единиц.  [c.146]

Аналогией электрического импеданса здесь является не удельный акустический импеданс z (который определяется как частное от деления давления на скорость), но величина г, делённая на 8. Необходимо подчеркнуть, что электрические системы являются только аналогами, помогающими нашему анализу (поскольку электрические фильтры более известны большинству из нас, чем акустические). Аналог тока измеряется в см 1сек, аналог напряжения —в дин/см . Ёмкости и индуктивности измеряются не в фарадах и генри, а в надлежащих акустических единицах наконец, передаваемая мощность измеряется не в ваттах, а в эрг сек.  [c.260]

За единицу измерения индуктивности в систе.ме МКСА принимается генри (гн), в СГСМ — см.  [c.136]

ГЁНРИ (Гн, И), единица СИ индуктивности и взаимной индуктивности. Названа в честь амер. учёного Дж. Генри (J. Henry). 1 Гн равен индуктивности электрич. контура, возбуждающего магн. поток в 1 вебер при силе пост, тока в нём 1 А. Другое эквивалентное определение 1 Гн — индуктивность электрич. цепи, в к-рой возникает эдс самоиндукции в 1 В при равномерном изменении тока в этой цепи со скоростью 1 А/с. 1 Гн=1 В-с/А=1 Вб/А= = 10 см (ед. СГСМ)=1,11-10-12 ед. СГСЭ  [c.113]

Техн. требования к И. и. стандартизованы в ГОСТе 22261—76, для мостовых И.и.— в ГОСТе 9486—79. ф Электрические измерения, 14 изд., Л., 1973 Справочник по электроизмерительным приборам, 2 изд., Л., 1977. В. П. Кузнецов. ИНДУКТИВНОСТЬ (от лат. ]п ис-tio — наведение, побуждение), величина, характеризующая магн. св-ва электрич. цепп. Ток, текущий в проводящем контуре, создаёт в окружающем пр-ве магн. поле, причём нитный поток Ф, пронизывающий контур (сцепленный с ним), прямо пропорционален току Г. Ф=L . Коэфф. пропорциональности Ь наз. И. или коэфф. самоиндукции контура. И. зависит от размеров и формы контура, а также от магнитной проницаемости окружающей среды. В СИ И. измеряется в генри, в Гаусса системе единиц она ххмеет размерность длины (1 Гн=10 см).  [c.219]

---

ТОЭ Лекции — №20 Самоиндукция. Индуктивность. Ток в индуктивности

Если в катушке, изображенной на рис. 20.1, магнитное поле создается собственным током i, то магнитный поток называется потоком самоиндукции и обозначается ФL, а индуцируемая в катушке ЭДС еL – ЭДС самоиндукции. В соответствии с формулой (20.1) она равна:

где ψ – потокосцепление самоиндукции, величина, пропорциональная протекающему по катушке току: ψ = Li.

Коэффициент пропорциональности L между потокосцеплением и током называется собственной индуктивностью или просто индуктивностью катушки (контура). Она зависит от формы и размеров катушки, а также от магнитной проницаемости сердечника. Ее размерность В x с/А=Ом x с. Эта единица измерения называется генри (Гн).

Подставляя последнее выражение в (2.15) и полагая L = const, получаем следующую формулу, определяющую ЭДС самоиндукции:

На рис. 2.18 показано изображение индуктивности на электрической схеме; uL – напряжение на зажимах катушки, обусловленное электродвижущей силой самоиндукции, или другими словами, напряжение, наведенное в катушке собственным переменным магнитным полем.

Все три стрелки на схеме (i, eL, uL) принято направлять в одну сторону. Раньше мы видели, что при одинаковых направлениях стрелок напряжения и ЭДС они имеют разные знаки. Поэтому:

Знак минус в правой части формулы (2.16) обусловлен принципом Ленца, определяющим направление индуцированной ЭДС. В рассматриваемом случае он может быть сформулирован следующим образом:

ЭДС самоиндукции направлена так, что своим действием препятствует причине, вызвавшей ее появление.

Причина появления ЭДС самоиндукции – изменение тока. Поэтому при возрастании тока она направлена ему навстречу, при уменьшении тока – в одну с ним сторону.

Препятствуя изменению тока, ЭДС самоиндукции оказывает ему сопротивление, которое называется индуктивным и обозначается хL. В соответствии с формулой (2.16) его величина определяется индуктивностью и скоростью изменения тока, т.е. частотой. Формула, определяющая индуктивное сопротивление, имеет вид:

В цепях постоянного тока такого понятия мы не встречали, так как при постоянных магнитных полях ЭДС самоиндукции не возникает. Пусть ток, протекающий по индуктивности, определяется выражением (2.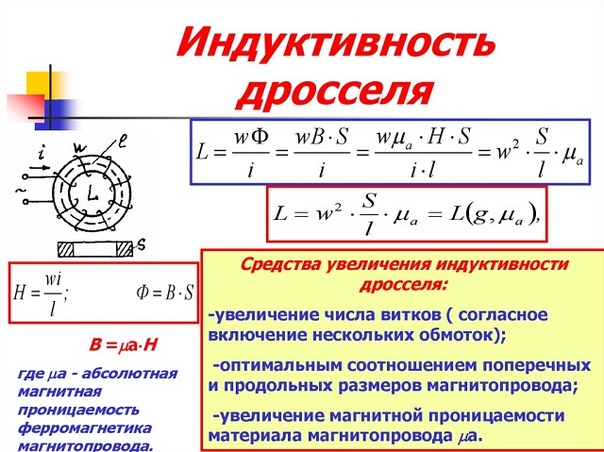 13). Тогда напряжение на ее зажимах, в соответствии с формулой (2.17), равно:

Это – мгновенное значение напряжения. Его амплитуда равна:

Аналогичное выражение получается (после деления на √2) и для действующих значений:

откуда

где Bl — индуктивная проводимость.

Запишем соответствующие формулы в символической форме:

Так как

то

Отсюда

Аналогично для действующих значений

Уравнения, связывающие напряжение и ток в индуктивности, как в вещественных, так и в комплексных числах, представляют собой закон Ома для индуктивности.

Начальная фаза напряжения больше начальной фазы тока на 90° . В индуктивности ток отстает от напряжения на четверть периода. Выражение закона Ома, записанное в символическое форме, указывает на этот сдвиг фаз.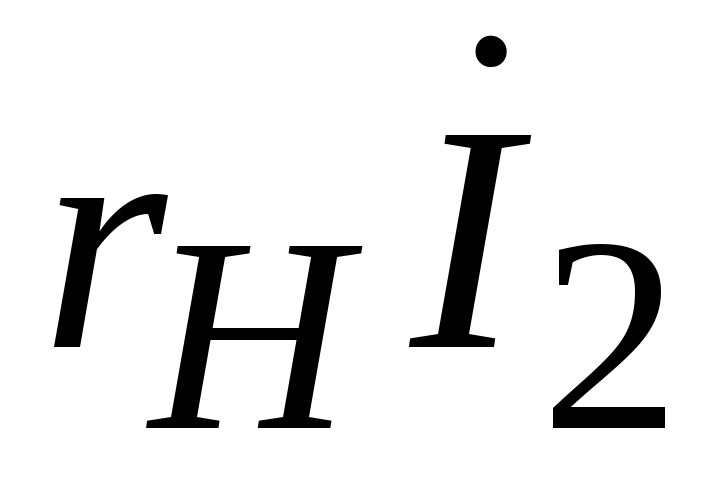 Вспомним, что умножение вектора на j приводит к его повороту на угол 90° против часовой стрелки.

Согласно уравнениям (2.18) UL получается путем умножения произведения IxL на j, в результате чего вектор UL оказывается повернутым относительно вектора I.

Пример 2.5. Мгновенное значение напряжения на индуктивности определяется выражением uL = 200 sin(ωt+60°)В. Записать выражение мгновенного значения тока, если L = 63,67 мГн, а частота питающего напряжения f = 50 Гц. Построить векторные диаграммы напряжения и тока.

Решение. При частоте f = 50 Гц циклическая частота ω = 314 с-1, и индуктивное сопротивление xL = ωL = 20 Ом. Амплитуда тока равна:

Так как в индуктивности ток отстает от напряжения на четверть периода, его начальная фаза меньше начальной фазы напряжения на 90° : ψi = ψu – 90° = 60–90–30°.

Итак, i = 10sin (ωt–30°). Векторная диаграмма показана на рис. 2.20.

ЭДС самоиндукции и индуктивность цепи

Дата публикации: 01 марта 2015.
Категория: Статьи.

При замыкании выключателя в цепи, представленной на рисунке 1, возникнет электрический ток, направление которого показано одинарными стрелками. С появлением тока возникает магнитное поле, индукционные линии которого пересекают проводник и индуктируют в нем электродвижущую силу (ЭДС). Как было указано в статье «Явление электромагнитной индукции», эта ЭДС называется ЭДС самоиндукции. Так как всякая индуктированная ЭДС по правилу Ленца направлена против причины, ее вызвавшей, а этой причиной будет ЭДС батареи элементов, то ЭДС самоиндукции катушки будет направлена против ЭДС батареи. Направление ЭДС самоиндукции на рисунке 1 показано двойными стрелками.

Таким образом, ток устанавливается в цепи не сразу. Только когда магнитный поток установится, пересечение проводника магнитными линиями прекратится и ЭДС самоиндукции исчезнет. Тогда в цепи будет протекать постоянный ток.

Рисунок 1. Электродвижущая сила самоиндукции в момент замыкания цепи направлена против ЭДС источника напряжения	Рисунок 2. График постоянного тока

На рисунке 2 дано графическое изображение постоянного тока. По горизонтальной оси отложено время, по вертикальной оси – ток. Из рисунка видно, что если в первый момент времени ток равен 6 А, то в третий, седьмой и так далее моменты времени он также и будет равен 6 А.

На рисунке 3 показано, как устанавливается ток в цепи после включения. ЭДС самоиндукции, направленная в момент включения против ЭДС батареи элементов, ослабляет ток в цепи, и поэтому в момент включения ток равен нулю. Далее в первый момент времени ток равен 2 А, во второй момент времени – 4 А, в третий – 5 А, и только спустя некоторое время в цепи устанавливается ток 6 А.

Рисунок 3. График нарастания тока в цепи с учетом ЭДС самоиндукции	Рисунок 4. ЭДС самоиндукции в момент размыкания цепи направлена одинаково с ЭДС источника напряжения

При размыкании цепи (рисунок 4) исчезающий ток, направление которого показано одинарной стрелкой, будет уменьшать свое магнитное поле. Это поле, уменьшаясь от некоторой величины до нуля, будет вновь пересекать проводник и индуктировать в нем ЭДС самоиндукции.

При выключении электрической цепи с индуктивностью ЭДС самоиндукции будет направлена в ту же сторону, что и ЭДС источника напряжения. Направление ЭДС самоиндукции показано на рисунке 4 двойной стрелкой. В результате действия ЭДС самоиндукции ток в цепи исчезает не сразу.

Таким образом, ЭДС самоиндукции всегда направлена против причины, ее вызвавшей. Отмечая это ее свойство, говорят что ЭДС самоиндукции имеет реактивный характер.

Графически изменение тока в нашей цепи с учетом ЭДС самоиндукции при замыкании ее и при последующем размыкании в восьмой момент времени показано на рисунке 5.

Рисунок 5. График нарастания и исчезновения тока в цепи с учетом ЭДС самоиндукции	Рисунок 6. Индукционные токи при размыкании цепи

При размыкании цепей, содержащих большое количество витков и массивные стальные сердечники или, как говорят, обладающих большой индуктивностью, ЭДС самоиндукции может быть во много раз больше ЭДС источника напряжения. Тогда в момент размыкания воздушный промежуток между ножом и неподвижным зажимом рубильника будет пробит и появившаяся электрическая дуга будет плавить медные части рубильника, а при отсутствии кожуха на рубильнике может ожечь руки человека (рисунок 6).

В самой цепи ЭДС самоиндукции может пробить изоляцию витков катушек, электромагнитов и так далее. Во избежание этого в некоторых выключающих приспособлениях устраивают защиту от ЭДС самоиндукции в виде специального контакта, который замыкает накоротко обмотку электромагнита при выключении.

Следует учитывать, что ЭДС самоиндукции проявляет себя не только в моменты включения и выключения цепи, но также и при всяких изменениях тока.

Величина ЭДС самоиндукции зависит от скорости изменения тока в цепи. Так, например, если для одной и той же цепи в одном случае в течение 1 секунды ток в цепи изменился с 50 до 40 А (то есть на 10 А), а в другом случае с 50 до 20 А (то есть на 30 А), то во втором случае в цепи будет индуктироваться втрое большая ЭДС самоиндукции.

Величина ЭДС самоиндукции зависит от индуктивности самой цепи. Цепями с большой индуктивностью являются обмотки генераторов, электродвигателей, трансформаторов и индукционных катушек, обладающих стальными сердечниками. Меньшей индуктивностью обладают прямолинейные проводники. Короткие прямолинейные проводники, лампы накаливания и электронагревательные приборы (печи, плитки) индуктивностью практически не обладают и появления ЭДС самоиндукции в них почти не наблюдается.

Магнитный поток, пронизывающий контур и индуктирующий в нем ЭДС самоиндукции, пропорционален току, протекающему по контуру:

Ф = L × I ,

где L – коэффициент пропорциональности. Он называется индуктивностью. Определим размерность индуктивности:

Ом × сек иначе называется генри (Гн).

1 генри = 10³; миллигенри (мГн) = 10⁶ микрогенри (мкГн).

Индуктивность, кроме генри, измеряют в сантиметрах:

1 генри = 10⁹ см.

Так, например, 1 км линии телеграфа обладает индуктивностью 0,002 Гн. Индуктивность обмоток больших электромагнитов достигает нескольких сотен генри.

Если ток в контуре изменился на Δi, то магнитный поток изменится на величину Δ Ф:

Δ Ф = L × Δ i .

Величина ЭДС самоиндукции, которая появится в контуре, будет равна (формула ЭДС самоиндукции):

При равномерном изменении тока по времени выражение

будет постоянным и его можно заменить выражением . Тогда абсолютная величина ЭДС самоиндукции, возникающая в контуре, может быть найдена так:

На основании последней формулы можно дать определение единицы индуктивности – генри:

Проводник обладает индуктивностью 1 Гн, если при равномерном изменении тока на 1 А в 1 секунду в нем индуктируется ЭДС самоиндукции 1 В.

Как мы убедились выше, ЭДС самоиндукции возникает в цепи постоянного тока только в моменты его включения, выключения и при всяком его изменении. Если же величина тока в цепи неизменна, то магнитный поток проводника постоянен и ЭДС самоиндукции возникнуть не может (так как

. В моменты изменения тока в цепи ЭДС самоиндукции мешает изменениям тока, то есть оказывает ему своеобразное сопротивление.

Рисунок 7. Бифилярная обмотка катушки

Часто на практике встречаются случаи, когда нужно изготовить катушку, не обладающую индуктивностью (добавочные сопротивления к электроизмерительным приборам, сопротивления штепсельных реостатов и тому подобные). В этом случае применяют бифилярную обмотку катушки (рисунок 7)

Как нетрудно видеть из чертежа, в соседних проводниках токи проходят в противоположных направлениях. Следовательно, магнитные поля соседних проводников взаимно уничтожаются. Общий магнитный поток и индуктивность катушки будут равны нулю. Для еще более полного уяснения понятия индуктивности приведем пример из области механики.

Как известно из физики, по второму закону Ньютона ускорение, полученное телом под действием силы, пропорционально самой силе и обратно пропорционально массе тела:

или

Сравним последнюю формулу с формулой ЭДС самоиндукции, взяв абсолютное значение ЭДС:

Если в этих формулах изменения скорости во времени

уподобить изменению тока во времени , механическую силу – электродвижущей силе самоиндукции, то масса тела будет соответствовать индуктивности цепи.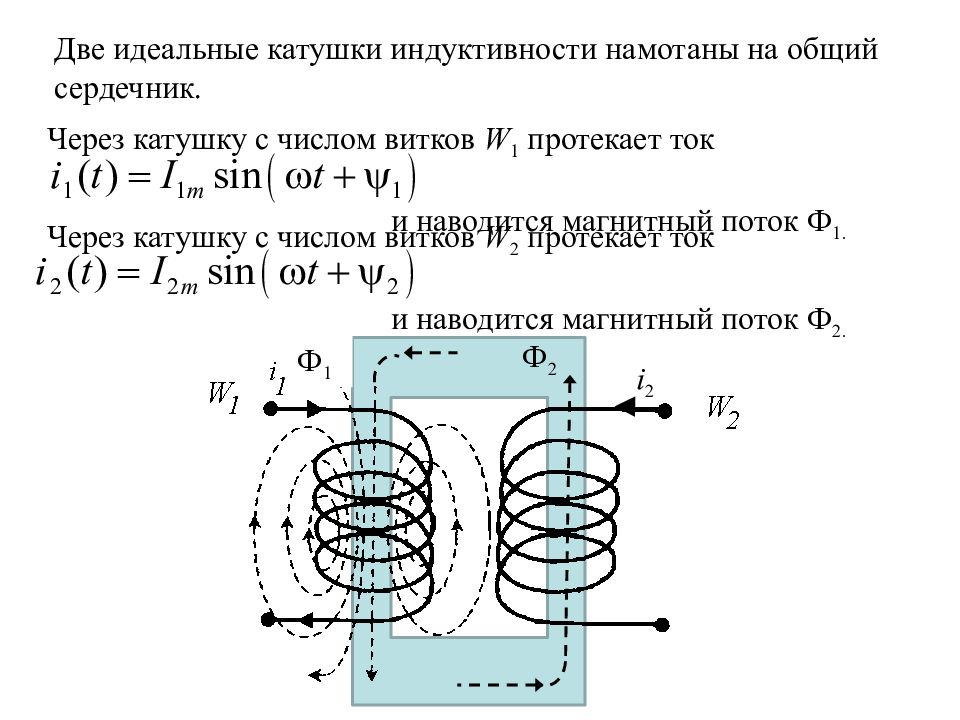

При равномерном прямолинейном движении a = 0, поэтому F = 0, то есть если на тело не действуют силы, его движение будет прямолинейным и равномерным (первый закон Ньютона).

В цепях постоянного тока величина тока не меняется

и поэтому e_L = 0.

Источник: Кузнецов М.И., «Основы электротехники» — 9-е издание, исправленное — Москва: Высшая школа, 1964 — 560с.

Примеры расчёта индуктивности.

В настоящем разделе рассмотрим типовые примеры расчёта индуктивности: индуктивность длинного соленоида, индуктивность коаксиального кабеля и индуктивность двухпроводной линии.

6.9.1. Индуктивность длинного соленоида.

Длинный соленоид представляет собой цилиндрическую поверхность, диаметр поперечного сечения которой значительно меньше её продольного размера. По рассматриваемой поверхности равномерно намотан провод, по которому может течь ток силы . Шаг намотки принимаем пренебрежимо малым. Число витков на единицу длины соленоида – конструктивный параметр соленоида – будем считать известным. По определению индуктивности необходимо оговорить систему токов, генерирующих магнитное поле в окружающем пространстве и контур, на который натянута поверхность. Через эту поверхность рассчитывается поток вектора магнитной индукции с помощью индуктивности . Принято рассчитывать индуктивность длинного соленоида как систему с постоянным вектором магнитной индукции, поток которого через совокупность поперечных сечений соленоида в пределах единицы длины определяет погонную индуктивность длинного соленоида. В условия вакуума с помощью теоремы о циркуляции убеждаемся, что величина индукции магнитного поля в произвольной точке пространства внутри соленоида равна

(1)

Поток вектора магнитной индукции через поперечное сечение соленоида (магнитный поток) определяется выражением:

(2)

Суммарный магнитный поток через поперечных сечений соленоида (учитываем единицу длины соленоида!) равен:

(3)

Из соотношения (3) следует формула, позволяющая рассчитать погонную индуктивность длинного соленоида:

(4)

В соотношении (4) значок волны над буквой призван обратить внимание читателя на то, что размерность величины отличается от размерности величины индуктивности устройства в целом.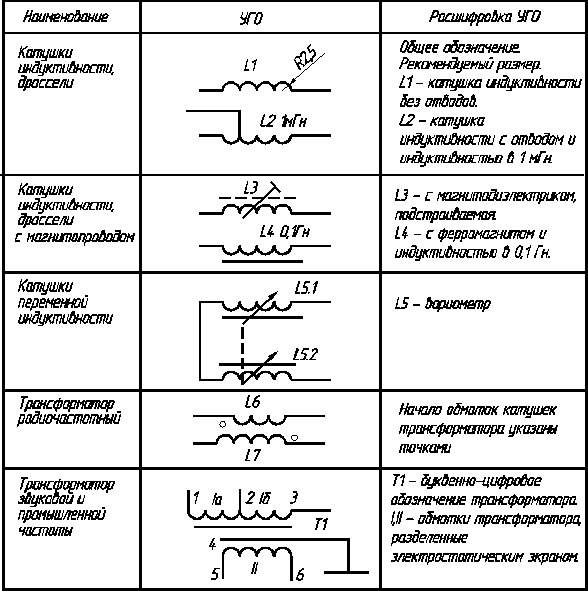

 

Узнать еще:

6.4. Сопротивление в цепи синусоидального тока

      Если напряжение подключить к сопротивлению R, то через него протекает ток

     (6.7)

     Анализ выражения (6.7) показывает, что напряжение на сопротивлении и ток, протекающий через него, совпадают по фазе.
        Формула (6.7) в комплексной форме записи имеет вид

     (6.8)

      где     и     — комплексные  амплитуды  тока и напряжения.
     Комплексному уравнению (6.8) соответствует векторная диаграмма (рис. 6.4).

     Из анализа диаграммы следует, что векторы напряжения и тока совпадают по направлению.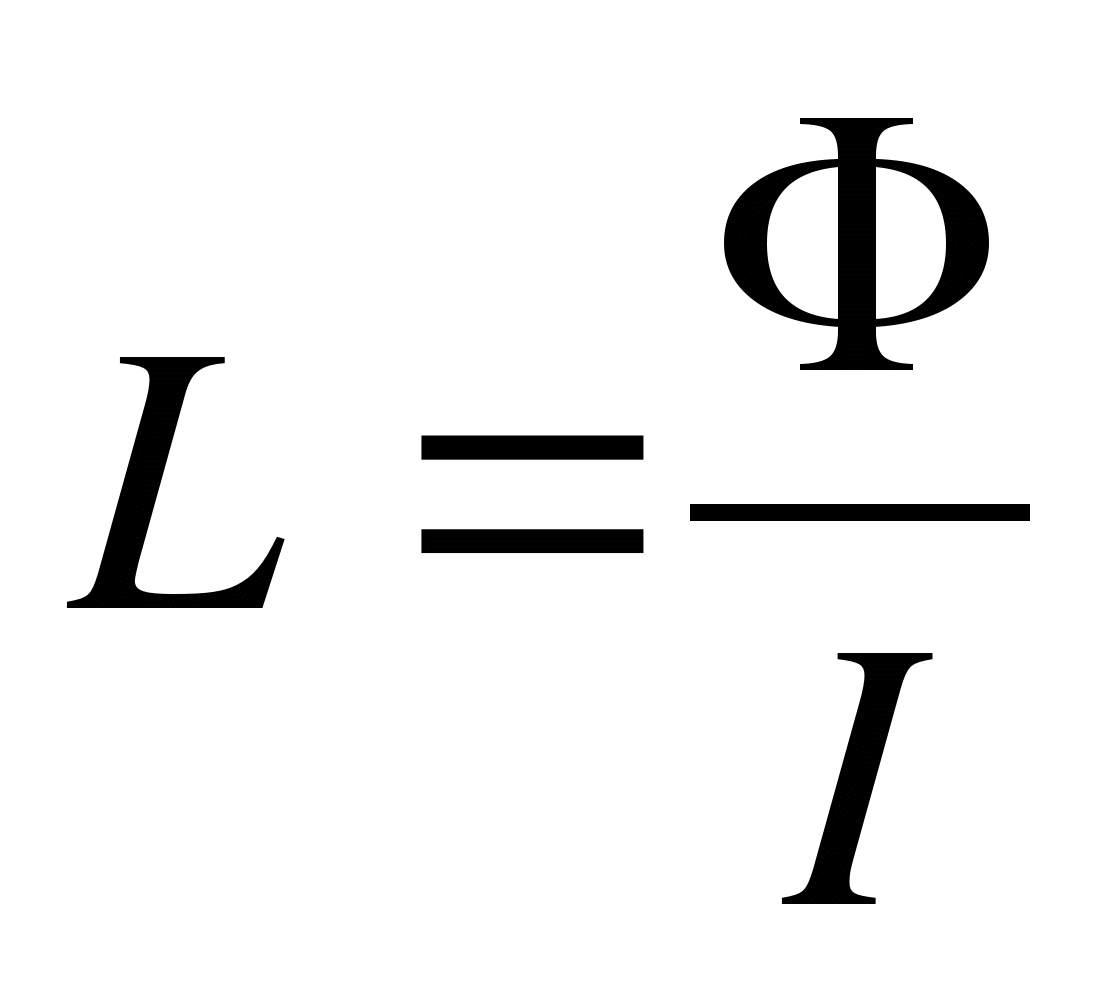

     Сопротивление участка цепи постоянному току называется омическим, а сопротивление того же участка переменному току — активным сопротивлением.

                               Рис.6.4
     Активное сопротивление больше омического из-за явления поверхностного эффекта. Поверхностный эффект заключается в том, что ток вытесняется из центральных частей к периферии сечения проводника.

6.5. Индуктивная катушка в цепи синусоидального тока

     Сначала рассмотрим идеальную индуктивную катушку, активное сопротивление которой равно нулю. Пусть по идеальной катушке с индуктивностью L протекает синусоидальный ток . Этот ток создает в индуктивной катушке переменное магнитное поле, изменение которого вызывает в катушке ЭДС самоиндукции

     (6.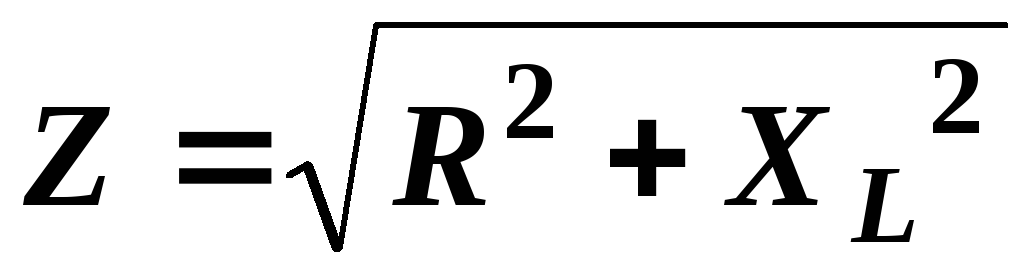 9)

     Эта ЭДС уравновешивается напряжением, подключенным к катушке: u = e_L = 0.

     (6.10)

     Таким образом, ток в индуктивности отстает по фазе от напряжения на 90^o из-за явления самоиндукции.
     Уравнение вида (6.10) для реальной катушки, имеющей активное сопротивление R, имеет следующий вид:

     (6.11)

     Анализ выражения (6.11) показывает, что ЭДС самоиндукции оказывает препятствие (сопротивление) протеканию переменного тока, из-за чего ток в реальной индуктивной катушке отстает по фазе от напряжения на некоторый угол φ (0^oo), величина которого зависит от соотношения R и L.      Выражение (6.11) в комплексной форме записи имеет вид:

     (6. 12)

      где Z_L — полное комплексное сопротивление индуктивной катушки ;
            Z_L — модуль комплексного сопротивления;
            — начальная фаза комплексного сопротивления;
          — индуктивное сопротивление (фиктивная величина, характеризующая реакцию электрической цепи на переменное магнитное поле).
      Полное сопротивление индуктивной катушки или модуль комплексного сопротивления

.

       Комплексному уравнению (6.12) соответствует векторная диаграмма (рис.6.5).

Рис. 6.5

       Из анализа диаграммы видно, что вектор напряжения на индуктивности опережает вектор тока на 90^o.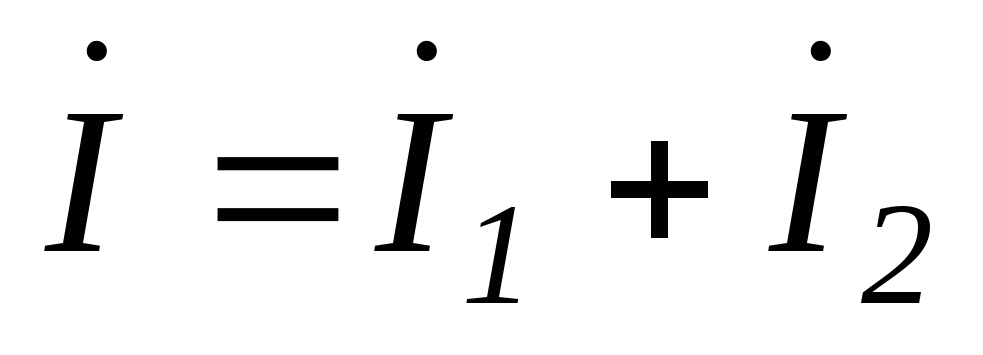
    В цепи  переменного тока напряжения на  участках цепи складываются не арифметически, а геометрически.
       Если мы поделим стороны треугольника напряжений на величину тока I_m, то перейдем к подобному треугольнику сопротивлений (рис. 6.6).

     Из треугольника сопротивлений получим несколько формул:
                     ;                     ;
    Рис. 6.6

;

;           .

6.6. Емкость в цепи синусоидального тока

     Если к конденсатору емкостью C подключить синусоидальное напряжение, то в цепи протекает синусоидальный ток

;

.     (6.13)

      Из анализа выражений 6.13 следует, что ток опережает напряжение по фазе на 90^o.

      Выражение (6.13) в комплексной форме записи имеет вид:

,    (6.14)

       где — емкостное сопротивление, фиктивная расчетная величина, имеющая размерность сопротивления.

        Если комплексное сопротивление индуктивности положительно
       , то комплексное сопротивление емкости отрицательно

        .

       На рис. 6.7 изображена векторная диаграмма цепи с емкостью.
       Вектор тока опережает вектор напряжения на 90^o.

Рис. 6.7

6.7. Последовательно соединенные реальная индуктивная

катушка и конденсатор в цепи синусоидального тока

       Катушка с активным сопротивлением   R  и индуктивностью   L  и конденсатор емкостью  С  включены последовательно (рис.6.8). В схеме протекает синусоидальный ток

.

     Определим напряжение на входе схемы.
       В соответствии со вторым законом Кирхгофа,

               (6.15)

       Подставим эти формулы в уравнение (6.15). Получим:

            (6.16)

     Из выражения (6.16) видно: напряжение в активном сопротивлении совпадает по фазе с током, напряжение на индуктивности опережает по фазе ток на 90^o, напряжение по емкости отстает по фазе от тока на 90^o.
     Запишем уравнение (6.16) в комплексной форме:

(6.17)

           Рис. 6.8

       Поделим левую и правую части уравнения (6.17) на √2.
       Получим уравнение для комплексов действующих значений токов и напряжений

       ,     (6.18)

       где — комплексное сопротивление цепи;
      — модуль комплексного сопротивления, или полное сопротивление цепи;
              — начальная фаза комплексного сопротивления.

       При построении векторных диаграмм цепи рассмотрим три случая.

1. X_L > X_C, цепь носит индуктивный характер. Векторы напряжений на индуктивности и емкости направлены в противоположные стороны, частично компенсируют друг друга. Вектор напряжения на входе схемы опережает вектор тока (рис.6.9).
2. Индуктивное сопротивление меньше емкостного. Вектор напряжения на входе схемы отстает от вектора тока. Цепь носит емкостный характер (рис.6.10).
3. Индуктивное и емкостное сопротивления одинаковы. Напряжения на индуктивности и емкости полностью компенсируют друг друга. Ток в цепи совпадает по фазе с входным напряжением. В электрической цепи наступает режим резонансного напряжения (рис.6.11).

       Ток в резонансном режиме достигает максимума, так как полное сопротивление (z) цепи имеет минимальное значение.

         Условие возникновения резонанса: , отсюда резонансная частота равна

      .

         Из формулы следует, что режима резонанса можно добиться следующими способами:

1. изменением частоты;
2. изменением индуктивности;
3. изменением емкости.

      В резонансном режиме входное напряжение равно падению напряжения в активном сопротивлении. На индуктивности и емкости схемы могут возникнуть напряжения, во много раз превышающие напряжение на входе цепи. Это объясняется тем, что каждое напряжение равно произведению тока I₀ (а он наибольший), на соответствующее индуктивное или емкостное сопротивление (а они могут быть большими).

.

Рис. 6.9                            Рис. 6.10                              Рис. 6.11

6.8. Параллельно соединенные индуктивность, емкость

и активное сопротивление в цепи синусоидального тока

       К схеме на рис. 6.12 подключено синусоидальное напряжение . Схема состоит из параллельно включенных индуктивности, емкости и активного сопротивления.
       Определим ток на входе схемы.

      В соответствии с первым законом Кирхгофа:
            ,     (6.19)
      где
            — активная проводимость.

                    Рис. 6.12                                            

        Подставим эти формулы в уравнение (6.19). Получим:

,     (6.20)

       где   — индуктивная проводимость;
                — емкостная проводимость.

      Из уравнения (6.20) видно, что ток в ветви с индуктивностью отстает по фазе от напряжения на 90^o, ток в ветви с активным сопротивлением совпадает по фазе с напряжением, ток в ветви с емкостью опережает по фазе напряжение на 90^o.
        Запишем уравнение (6.20) в комплексной форме.

,     (6.21)

        где   — комплексная проводимость;
              — полная проводимость;
              — начальная фаза комплексной проводимости.

        Построим векторные диаграммы, соответствующие комплексному уравнению (6.21).

Рис. 6.13                            Рис. 6.14                              Рис. 6.15

      В схеме на рис. 6.12 может возникнуть режим резонанса токов. Резонанс токов возникает тогда, когда индуктивная и емкостная проводимости одинаковы. При этом индуктивный и емкостный токи, направленные в противоположные стороны, полностью компенсируют друг друга. Ток в неразветвленной части схемы совпадает по фазе с напряжением.
      Из условия возникновения резонанса тока получим формулу для резонансной частоты тока

.

       В режиме резонанса тока полная проводимость цепи — минимальна, а полное сопротивление — максимально. Ток в неразветвленной части схемы в резонансном режиме имеет минимальное значение. В идеализированном случае R = 0,

      и      .

        Ток в неразветвленной части цепи I = 0. Такая схема называется фильтр — пробкой.

6.9. Резонансный режим в цепи, состоящей

из параллельно включенных реальной индуктивной
катушки и конденсатора

           Комплексная проводимость индуктивной ветви

           где   — активная проводимость индуктивной катушки;
                   — полное сопротивление индуктивной катушки;
                   — индуктивная проводимость катушки;
                   — емкостная проводимость второй ветви.

           В режиме резонансов токов справедливо уравнение:

  или  

           Из этого уравнения получим формулу для резонанса частоты

     (6.22)

           На рисунке 6.16 изображена векторная диаграмма цепи в резонансном режиме.

     Вектор тока I₂ опережает вектор напряжения на 90^o. Вектор тока I₁ отстает от вектора напряжения на угол φ,

     где             .

     Разложим вектор тока I₁ на две взаимно перпендикулярные составляющих, одна из них, совпадающая с вектором напряжения, называется активной составляющей тока I_а1, другая — реактивной составляющей тока I_р1.

                  Рис. 6.16

     В режиме резонанса тока реактивная составляющая тока I_р1 и емкостный ток I₂ , направленные в противоположные стороны, полностью компенсируют друг друга, активная составляющая тока I_а1 совпадает по фазе с напряжением (рис. 6.17). Ток I в неразветвленной части схемы совпадает по фазе с напряжением.

                  Рис. 6.17

Если L и R обозначают индуктивность и сопротивление соответственно класс 12 по физике CBSE

Подсказка : Сначала вычислите формулу размерности L и R, используя формулы V = iR и $ E = L \ dfrac {di} {dt} $ соответственно. Как только вы найдете формулу размерности L и R, разделите двумерные формулы, чтобы найти формулу размерности $ \ dfrac {L} {R} $.
Используемая формула:
V = iR
$ \ left [V \ right] = \ dfrac {\ left [W \ right]} {\ left [C \ right]} $
$ E = L \ dfrac {di} { dt} $

Полное пошаговое решение :
Чтобы вычислить размерную формулу $ \ dfrac {L} {R} $, нам сначала нужно некоторое выражение для L и R в терминах известных величин.С этим мы можем затем вычислить размерную формулу L и R и разделить их, чтобы найти размерную формулу $ \ dfrac {L} {R} $.
Чтобы найти формулу размерности R, воспользуемся законом Ома. Согласно закону Ома, разность потенциалов (V) на резисторе и ток (i), протекающий через резистор, связаны соотношением V = iR, где R — сопротивление резистора.
Отсюда получаем, что $ R = \ dfrac {V} {i} $…. (я).
Разница потенциалов V между двумя точками равна работе, совершенной над единичным зарядом, чтобы переместить его между этими двумя точками.{-2}} \ right] $… .. (ii).
Давайте теперь вычислим размерную формулу индуктивности L.
Для этого мы будем использовать закон Фарадея, который использует, что ЭДС, индуцированная в катушке, равна $ E = L \ dfrac {di} {dt} $… .. ( iii), где l — индуктивность катушки, а i — ток в катушке.
Мы можем записать уравнение (iii) как
$ L = \ dfrac {E} {\ dfrac {di} {dt}} $
Это означает, что формула размерности L имеет вид $ \ left [L \ right] = \ dfrac {\ left [E \ right]} {\ left [\ dfrac {di} {dt} \ right]} $.
Индуцированная ЭДС — это разность потенциалов, и мы уже вычислили размерную формулу разности потенциалов.{- \ dfrac {t} {\ tau}}} $…. (v).
Здесь $ \ tau $ называется постоянной времени, а его значение для схемы L-R равно $ \ dfrac {L} {R} $.
Если мы посмотрим на уравнение (v), мы увидим, что e возведено в степень $ — \ dfrac {t} {\ tau} $, а степень — это просто число без размерности. Следовательно, $ \ dfrac {t} {\ tau} $ не должно иметь размерности. Для этого $ \ tau $ должен иметь измерение времени, а это значит, что $ \ dfrac {L} {R} $ имеет измерение времени.

3 Метод решения сетки индуктивности, емкости, сопротивления (LCR) для двумерного уравнения Гельмгольца

3 Метод решения сетки индуктивности, емкости, сопротивления (LCR) для двумерного уравнения Гельмгольца

Через декартову дискретизацию дифференциального оператора в (4.13), [66] получили метод конечных разностей на прямоугольной сетке. При интерпретации по методу TLM [67], [68], метод с сосредоточенными индуктивностями, емкостями, сопротивлениями и допуски на прямоугольной сетке представлены в [65] и [69]. Значение сосредоточенного сопротивления получается из (4.11) и для сосредоточенной проводимости из (4.12). В значение сосредоточенной индуктивности вычисляется непосредственно из (4.9), а сосредоточенная емкость получается путем умножения емкости из (4.9) с помощью DxDy. Dx и Dy обозначают длины ячеек прямоугольной сетки в направлении x и y соответственно. Другой элементы схемы могут быть легко введены в любую точку сетки. Схема структура сосредоточенных элементов на сетке приводит к разреженной матрице. Однако очень Для получения достаточно хорошей точности необходимо использовать мелкую сетку. Рисунок 4.4. изображает сравнение аналитических результатов из (4.18) с результаты метода сетки LCR для импеданса Z _в порта в положении (x = 10 мм, y = 10 мм) в прямоугольной полости с размерами (L = 160 мм, W = 120 мм) и h = 7 мм.Шаг сетки Dx = Dy = 2 мм использовался для метода сетки LCR. моделирование. Даже с такой мелкой сеткой сравнение показывает небольшие отклонения Минимумы величины импеданса, которые указывают на небольшую неточность моделируемой индуктивности. Это недостаток метода, так как необходимость тонкой сетки приводит к более высокие затраты на моделирование по сравнению с методом FEM в разделе 4.4.
Прямоугольные плоскости использовались для сравнения на Рисунке 4.4 с включить сравнение с аналитическим решением.Когда метод используется для самолетов с ребрами, не параллельными одному из декартовых направлений или же , потребуется плотная сетка для получения точной дискретизации геометрия на этом краю. Хотя суб-сетка на краю — это возможность уменьшить общий размер сетки, усилие на дискретизацию геометрии намного выше по сравнению с метод конечных элементов в разделе 4.4, в котором используется треугольная сетка.

(а) Сравнение величин.

(б) Сравнение фазового угла.

Рисунок 4.4: Сравнение Z _в между аналитическими решение (4.18) и решение сеточного метода LCR. Полость размеры (Д = 160мм, Ш = 120мм, В = 7мм), положение порта для Z _в составляет (x = 10 мм, y = 10 мм), а шаг сетки равен Dx = Dy = 2 мм. К. Пощалко: Моделирование излучения печатных плат под металлической крышкой

Inductance — The Physics Hypertextbook

Обсуждение

введение

Готовы? Вот так.

Пуск с соленоидом. Пропустите через него ток, и вы получите электромагнит. Поле внутри задается формулой…

B = μ 0 nI = μ 0	N	I
	ℓ

В то же время соленоид — это еще и устройство для улавливания магнитного потока.

Φ _B = NBA

Статическая ситуация, безусловно, достаточно интересна, но когда дело доходит до потока, то, что нас действительно волнует, — это скорость изменения во времени.Это то, что дает нам электромагнитную индукцию или индуцированную электродвижущую силу, или как вы хотите это называть. Эта ситуация описывается законом Фарадея.

Давайте снова рассмотрим эти уравнения, но с изменением во времени. Соленоид с изменяющимся током, проходящим через него, будет генерировать изменяющееся магнитное поле.

дБ	= мк 0	N		dI
дт		ℓ		дт

Это изменяющееся магнитное поле затем улавливается тем самым соленоидом, который его создал.Захваченное поле называется потоком, а изменяющийся поток генерирует ЭДС — в данном случае самоиндуцированную или обратную ЭДС.

ℰ = —	d Φ B	= — N	⎛	мкм 0	N		dI	⎞	А
	дт				ℓ		дт

Немного переставив вещи, мы получаем это уравнение…

ℰ = —	мкм 0 AN 2		dI
	ℓ		дт

, что может показаться не очень большим, пока вы не поймете, что члены первой дроби в значительной степени определяются геометрией соленоида.Если бы мы выбрали другую конфигурацию проводов, произошло бы то же самое.

Самоиндуцированная ЭДС в цепи прямо пропорциональна скорости изменения тока во времени ( dI / dt ), умноженной на константу ( L ). Эта константа называется индуктивностью (или, точнее, самоиндукцией ) и определяется геометрией схемы (или, чаще, геометрией отдельных элементов схемы).Например, индуктивность соленоида (как определено выше) определяется формулой…

Символ L для обозначения индуктивности был выбран в честь Генриха Ленца (1804–1865), чьи новаторские работы в области электромагнитной индукции сыграли важную роль в развитии окончательной теории. Если вы помните, Закон Ленца гласит, что индуцированный ток в цепи всегда действует таким образом, чтобы противодействовать изменению, которое в первую очередь его вызвало. Это наблюдение является причиной того, почему во всех версиях закона Фарадея стоит знак минус.Ленц поставил нам знак минус, и мы чествуем его знаком L .

Индуктивность лучше всего определяется по ее роли в уравнении, полученном из закона индукции Фарадея. Некоторым это не нравится, и они предпочитают определения, написанные в форме простого предложения субъект-глагол-объект.

На английском языке мы бы прочитали это как «самоиндукция ( L ) — это отношение обратной ЭДС () к временной скорости изменения тока, производящего ее ( dI / dt ).«Как я уже сказал, мне не очень нравится такое определение, но оно помогает нам определить подходящие единицы измерения.

⎢	H =	В	=	Дж / К	=	(кг · м 2 / с 2 ) / (A · с)	=	кг м 2	⎤
		А / с		А / с		А / с		A 2 с 2

Единицей индуктивности является генри , названный в честь Джозефа Генри (1797–1878), американского ученого, открывшего электромагнитную индукцию независимо и примерно в то же время, что и Майкл Фарадей (1791–1867) в Англии.Первым свои открытия опубликовал Фарадей, поэтому ему заслуга в большей степени. Генри также открыл самоиндукцию и взаимную индуктивность (которые будут описаны позже в этом разделе) и изобрел электромеханическое реле (которое легло в основу телеграфа). Схема с собственной индуктивностью в один генри будет испытывать противоэдс в один вольт, когда ток изменяется со скоростью один ампер в секунду.

Индуктивность — это что-то. Индуктивность — это сопротивление элемента схемы изменениям тока.Индуктивность в цепи — это аналог массы в механической системе.

ℰ = — л	dI	⇔	причина изменения	=	сопротивление изменить	×	курс сдачи	⇔	F = м	d v
	дт									дт

индуктивный датчик петли

Движение на некоторых перекрестках контролируется с помощью индуктивных петлевых детекторов (ILD).ILD — это петля из проводящего провода, проложенная всего на несколько сантиметров ниже тротуара. Когда автомобиль проезжает через поле, он действует как проводник, изменяя индуктивность контура. Изменение индуктивности контура указывает на наличие автомобиля наверху. Затем эту информацию можно использовать для активации сигналов светофора, отслеживания транспортного потока или автоматического цитирования.

примеры

Индуктивность

зависит от геометрии

соленоид ( A площадь поперечного сечения, N количество витков, ℓ длина, n количество витков на длину)

Φ B	= N	B		А
Φ B	= N	мкм 0 NI		А
		ℓ
Φ B	=	мкм 0 AN 2		I
		ℓ
d Φ B	=	мкм 0 AN 2		dI
дт		ℓ		дт
л	=	мкм 0 AN 2		=	мкм 0 Aℓn 2
		ℓ

коаксиальных проводников ( a внутренний радиус, b внешний радиус, длина ℓ)

Φ B	=	⌠	Б	·	d A
		б						б
Φ B	=	⌠	мкм 0 I		ℓ др	=	мкм 0 Iℓ	⌠	др
			2π r				2π		р
		a						a
Φ B	=		мкм 0 ℓ		пер.	⎛	a	⎞	I
			2π				б
d Φ B	=		мкм 0 ℓ		пер.	⎛	a	⎞	dI
дт			2π				б		дт
л	=		мкм 0 ℓ		пер.	⎛	a	⎞
			2π				б

тороид ( A площадь поперечного сечения, R радиус вращения, N количество витков)

Φ B	=	N	B		А
Φ B	≈	N	мкм 0 NI		А
			2π R
Φ B	≈	N	мкм 0 NA		I
			2π R
d Φ B	≈		мкм 0 AN 2		dI
дт			2π R		дт
л	≈		мкм 0 AN 2
			2π R

прямоугольная петля ( w ширина, h высота, a радиус провода)

Φ B

=

N

Φ B

=

N

⎡ ⎢ х w х w ⎤ ⎥ мкм 0 NI ⌠ г др + ⌠ x др + ⌠ г др + ⌠ x др 2π р р р р a a a a

Φ B

=

2

мкм 0 N 2

⎡

y ln

⎛

х

⎞

+

x лин

⎛

y

⎞

⎤

I

2π

a

a

d Φ B

=

мкм 0 N 2

⎡

y ln

⎛

х

⎞

+

x лин

⎛

y

⎞

⎤

dI

дт

π

a

a

дт

л

=

мкм 0 N 2

⎡

y ln

⎛

х

⎞

+

x лин

⎛

y

⎞

⎤

π

a

a

Эта формула не совсем работает, поскольку она игнорирует краевые эффекты.Вы можете найти точную формулу (а также скрипты, которые будут рассчитывать индуктивность для вас) в Интернете на нескольких веб-сайтах по электротехнике.

Может ли кто-нибудь помочь мне с этим, — Пусть l, r, c и v обозначают индуктивность, сопротивление, емкость и напряжение соответственно. Дайм — Физика и Измерение

Knockout JEE Main May 2023 (легкая рассрочка)

Персонализированный наставник AI и адаптивное расписание, Материал для самообучения, Уроки выходного дня, Наставничество от наших экспертов, Неограниченные пробные тесты и персонализированные аналитические отчеты, Круглосуточная поддержка в чате сомнений.

5499 / —

купить сейчас

Knockout JEE Main April 2021 (один месяц)

Персонализированный наставник AI и адаптивное расписание, Материал для самообучения, Уроки выходного дня, Наставничество от наших экспертов, Неограниченные пробные тесты и персонализированные аналитические отчеты, Круглосуточная поддержка в чате сомнений.

14000 ₹ / — 4999 / —

купить сейчас

Knockout JEE Main Май 2021 г.

Персонализированный наставник AI и адаптивное расписание, Материал для самообучения, Уроки выходного дня, Наставничество от наших экспертов, Неограниченные пробные тесты и персонализированные аналитические отчеты, Круглосуточная поддержка в чате сомнений.

22999 ₹ / — 9999 ₹ / —

купить сейчас

Серия тестов JEE Main May 2021

Мудрые тесты без ограничений по главам, Неограниченные предметные мудрые тесты, Неограниченные полные пробные тесты, Получите персонализированный отчет об анализе производительности.

6999 / — 2999 / —

купить сейчас

Knockout JEE Main May 2022

Персонализированный наставник AI и адаптивное расписание, Материал для самообучения, Уроки выходного дня, Наставничество от наших экспертов, Неограниченные пробные тесты и персонализированные аналитические отчеты, Круглосуточная поддержка в чате сомнений.

34999 ₹ / — 14999 ₹ / —

купить сейчас

Теория, формулы, вывод и ее приложения

В 1831 году Майкл Фарадей научно объяснил теорию электромагнитной индукции.Термин индуктивность означает способность проводника противодействовать протекающему по нему току и индуцировать ЭДС. Согласно законам индукции Фарадея, электродвижущая сила (ЭДС) или напряжение индуцируется в проводнике из-за изменения магнитного поля в цепи. Этот процесс называется электромагнитной индукцией. Индуцированное напряжение противодействует скорости изменения тока. Это известно как закон Ленца, а индуцированное напряжение называется обратной ЭДС. Индуктивность делится на два типа. Это, самоиндукция и взаимная индуктивность.Эта статья посвящена взаимной индуктивности двух катушек или проводников.

Что такое взаимная индуктивность?

Определение: Взаимная индуктивность двух катушек определяется как ЭДС, индуцированная магнитным полем в одной катушке, противодействующая изменению тока и напряжения в другой катушке. Это означает, что две катушки магнитно связаны друг с другом из-за изменения магнитного потока. Магнитное поле или поток одной катушки связывается с другой катушкой. Это обозначено M.

Ток, протекающий в одной катушке, индуцирует напряжение в другой катушке из-за изменения магнитного потока.Величина магнитного потока, связанного с двумя катушками, прямо пропорциональна взаимной индуктивности и изменению тока.

Теория взаимной индуктивности

Ее теория очень проста, и ее можно понять, используя две или более катушек. Его описал американский ученый Джозеф Генри в 18 веке. Это называется одним из свойств катушки или проводника, используемого в цепи. Свойство индуктивности таково: если ток в одной катушке изменяется со временем, то ЭДС будет индуцировать в другой катушке.

Оливер Хевисайд ввел термин индуктивность в 1886 году. Свойство взаимной индуктивности — это принцип работы многих электрических компонентов, работающих с магнитным полем. Например, трансформатор является основным примером взаимной индуктивности.

Главный недостаток взаимной индуктивности заключается в том, что утечка индуктивности одной катушки может прервать работу другой катушки, используя электромагнитную индукцию. Для уменьшения утечки требуется электрическое экранирование.

Расположение двух катушек в цепи определяет величину взаимной индуктивности, которая соединяется между собой.

Формула взаимной индуктивности

Формула двух катушек имеет вид

M = (μ0.μr. N1. N2. A) / L

Где μ0 = проницаемость свободного пространства = 4π10- ²

μ = проницаемость сердечника из мягкого железа

N1 = витки катушки 1

N2 = витки катушки 2

A = площадь поперечного сечения в м ²

L = длина катушки в метрах

Единица взаимной индуктивности

Единица взаимной индуктивности — кг.m ² .s ^-2 .A ^-2

Величина индуктивности дает напряжение в один вольт из-за скорости изменения тока 1 ампер / секунду.

Единица измерения взаимной индуктивности СИ — Генри. Это взято у американского ученого Джозефа Генри, который объяснил явление двух катушек.

Размер взаимной индуктивности

Когда две или более катушек связаны друг с другом магнитным путем с одним и тем же магнитным потоком, тогда напряжение, индуцированное в одной катушке, пропорционально скорости изменения тока в другой катушке.Это явление называется взаимной индуктивностью.

Считайте, что общая индуктивность между двумя катушками равна L, так как M = √ (L1L2) = L

Ее размер можно определить как отношение разности потенциалов к скорости изменения тока. Он задается как

Поскольку M = √L1L2 = L

L = € / (dI / dt)

Где € = индуцированная ЭДС = выполненная работа / электрический заряд по отношению ко времени = M. L ² . T- ² / IT = M.L ² .T-3.I ^-1 или € = M. L ^-2 . Т-3. A ^-1 (Поскольку I = A)

Для индуктивности

ϕ = LI

L = ϕ / A = (B. L ² ) / A

Где B = магнитное поле = (MLT- ² ) / LT ^-1 AT = MT ^-2 A ^-1

Магнитный поток ϕ = BL ² = MT ^-2 L ² A ^-1

заменитель значение B и ϕ выше формулы L

L = MT- ² L ² .A ^-2

Размер взаимной индуктивности, когда L1 и L2 одинаковы, определяется как

M = L / (T- ² L ² .A ^-2 )

M = LT ² L ² .A ^-2

Вывод

Следуйте инструкциям, чтобы получить вывод взаимной индуктивности .

Отношение ЭДС, индуцированной в одной катушке, к скорости изменения тока в другой катушке является взаимной индуктивностью.

Рассмотрим две катушки L1 и L2, как показано на рисунке ниже.

Две катушки

Когда ток в L1 изменяется со временем, магнитное поле также изменяется со временем и изменяет магнитный поток, связанный со второй катушкой L2. Из-за этого изменения магнитного потока в первой катушке L1 индуцируется ЭДС.

Кроме того, скорость изменения тока в первой катушке индуцирует ЭДС во второй катушке. Следовательно, ЭДС индуцируется в двух катушках L1 и L2.

Это дается как

€ = M (dI1 / dt)

M = € / (dI1 / dt). … .. Уравнение 1

Если € = 1 В и dI1 / dt = 1 Ампер, то

M = 1 Генри

Кроме того,

Скорость изменения тока в одной катушке создает магнитный поток в первой катушке и ассоциируется со второй катушкой.Тогда из законов электромагнитной индукции Фарадея (индуцированное напряжение прямо пропорционально скорости изменения магнитного потока, связанного) во второй катушке, наведенная ЭДС определяется как

€ = M / (dI1 / dt) = d (MI1) / dt… .. Уравнение 2

€ = N2 (dϕ12 / dt) = d (N2ϕ12) / dt… eq 3

Приравнивая уравнение 2 и 3

MI1 = N2ϕ12

M = (N2ϕ12) / I1 Генри

Где M = взаимная индуктивность

€ = взаимная индуктивность ЭДС

N2 = количество витков в первой катушке L1

I1 = ток в первой катушке

ϕ12 = магнитный поток, связанный в двух катушках.

Взаимная индуктивность между двумя катушками зависит от количества витков на второй катушке или соседней катушке и площади поперечного сечения.

Расстояние между двумя катушками.

ЭДС, индуцированная в первой катушке из-за скорости изменения магнитного потока, дается как:

E = -M12 (dI1 / dt)

Знак минус указывает противодействие скорости изменения тока в первая катушка при наведении ЭДС.

Взаимная индуктивность двух катушек

Взаимную индуктивность двух катушек можно увеличить, поместив их на сердечник из мягкого железа или увеличив количество витков двух катушек.Единство связи существует между двумя катушками, когда они плотно намотаны на сердечник из мягкого железа. Утечка флюса будет небольшой.

Если расстояние между двумя катушками небольшое, то магнитный поток, создаваемый в первой катушке, взаимодействует со всеми витками второй катушки, что приводит к большой ЭДС и взаимной индуктивности.

Взаимная индуктивность двух катушек

Если две катушки расположены дальше и друг от друга под разными углами, то индуцированный магнитный поток в первой катушке создает слабую или небольшую ЭДС во второй катушке.Следовательно, взаимная индуктивность также будет небольшой.

Две катушки на расстоянии друг от друга

Таким образом, значение этого параметра в основном зависит от расположения и расстояния между двумя катушками на сердечнике из мягкого железа. Рассмотрим рисунок, который показывает, что две катушки туго намотаны одна поверх сердечника из мягкого железа.

Катушки плотно намотаны

Изменение тока в первой катушке создает магнитное поле и пропускает магнитные линии через вторую катушку, которая используется для расчета взаимной индуктивности.

Взаимная индуктивность двух катушек определяется как

M12 = (N2ϕ12) / I1

M21 = (N1ϕ21) / I2

Где M12 = взаимная индуктивность между первой катушкой и второй катушкой

M21 = взаимная индуктивность вторая катушка к первой катушке

N2 = витки второй катушки

N1 = витки первой катушки

I1 = ток, протекающий вокруг первой катушки

I2 = ток, протекающий вокруг второй катушки.

Если поток, связанный с L1 и L2, такой же, как ток, протекающий вокруг них, то взаимная индуктивность первой катушки ко второй катушке задается как M21

Взаимная индуктивность двух катушек может быть определена как M12 = M21 = M

Итак, две катушки в основном зависят от размера, витков, положения и расстояния между двумя катушками.

Самоиндукция первой катушки

L1 = (μ0.μr.N1 ² .A) / L

Самоиндукция второй катушки

L2 = (μ0. μr.N ² .A) / L

Перемножьте две приведенные выше формулы перекрестно

Тогда взаимная индуктивность двух катушек, которая существует между ними, дается как

M ² = L1. L2

M = √ (L1.L2) Генри

Вышеприведенное уравнение дает магнитный поток = 0

100% магнитная связь между L1 и L2

Коэффициент связи

Доля магнитного потока, связанного с двумя катушек к общему магнитному потоку между катушками называется коэффициентом связи и обозначается буквой «k».Коэффициент связи определяется как отношение разомкнутой цепи к фактическому коэффициенту напряжения и коэффициент магнитного потока, полученный в обеих катушках. Поскольку магнитный поток одной катушки соединяется с другой катушкой.

Коэффициент связи определяет индуктивность катушки индуктивности. Если коэффициент связи k = 1, то две катушки соединены вместе прочно. Итак, все линии магнитного потока одной катушки перерезают все витки другой катушки. Следовательно, взаимная индуктивность — это среднее геометрическое индивидуальных индуктивностей двух катушек.
Если индуктивности двух катушек одинаковы (L1 = L2), то взаимная индуктивность между двумя катушками равна индуктивности одной катушки. Это означает, что

M = √ (L1. L2) = L

, где L = индуктивность одиночной катушки.

Коэффициент связи между катушками

Коэффициент связи между катушками может быть представлен как 0 и 1

Если коэффициент связи равен 1, то индуктивной связи между катушками нет.

Если коэффициент связи равен 0, то между катушками существует максимальная или полная индуктивная связь.

Индуктивная связь представлена ​​в 0 и 1, но не в процентах.

Например, если k = 1, то две катушки соединены идеально.

Если k> 0,5, то две катушки связаны плотно.

Если k <0,5, то две катушки связаны слабо.

Чтобы найти коэффициент связи между двумя катушками, необходимо применить следующее уравнение:

K = M / √ (L1. L2)

M = k. √ (L1. L2)

Где L1 = индуктивность первой катушки

L2 = индуктивность второй катушки

M = взаимная индуктивность

K = коэффициент связи

Приложения

Приложения взаимной индуктивности are,

• Трансформатор
• Электродвигатели
• Генераторы
• Прочие электрические устройства, работающие с магнитным полем.
• Используется при вычислении вихревых токов
• Цифровая обработка сигналов

Таким образом, все это касается обзора взаимной индуктивности — определение, формула, единица измерения, деривация, коэффициент связи, коэффициент связи и приложения. Вот вам вопрос, в чем недостаток взаимной индуктивности между двумя катушками?

Страница не найдена | MIT

Перейти к содержанию ↓

• Образование
• Исследовать
• Инновации
• Прием + помощь
• Студенческая жизнь
• Новости
• Выпускников
• О MIT
• Подробнее ↓
  • Прием + помощь
  • Студенческая жизнь
  • Новости
  • Выпускников
  • О MIT

Меню ↓ Поиск Меню Ой, похоже, мы не смогли найти то, что вы искали!
Попробуйте поискать что-нибудь еще! Что вы ищете? Увидеть больше результатов

Предложения или отзывы?

Улучшен расчет индуктивности рассеяния в пазах для пазов различной формы

1.

Cavagnino A (2017) Алгоритмы с повышенной точностью для расчета индуктивности рассеяния двухслойных обмоток. IEEE Trans Ind Appl 53 (5): 4422–4430. https://doi.org/10.1109/TIA.2017.2712687

Артикул Google Scholar

2.

Салех К., Самнер М. (2018) Бездатчиковое управление скоростью пятифазных приводов PMSM с низкими искажениями тока. Электр Eng 100: 357. https://doi.org/10.1007/s00202-017-0511-9

Артикул Google Scholar

3.

El-Refaie AM (2010) Синхронные машины с постоянными магнитами и концентрированными обмотками с дробным пазом: возможности и проблемы. IEEE Trans Ind Electr 57 (1): 107–121. https://doi.org/10.1109/TIE.2009.2030211

Артикул Google Scholar

4.

Mecrow BC, Jack AG, Haylock JA, Coles J (1996) Отказоустойчивые приводы машин с постоянными магнитами. IEE Proc Electr Power Appl 143 (6): 437–442. https://doi.org/10.1049/ip-epa:19960796

Артикул Google Scholar

5.

Di Gerlando A, Foglia GM, Perini R et al (2007) Синхронные машины с постоянными магнитами с концентрированными обмотками якоря катушки: анализ и проверка испытаний машин с одним статором и двойным ротором, с осевым потоком. Электр Eng 90:65. https://doi.org/10.1007/s00202-006-0054-y

Артикул Google Scholar

6.

Эль-Рефай А.М., Янс Т.М. (2005) Оптимальное ослабление магнитного потока в машинах с поверхностным PM с использованием концентрированных обмоток с дробными пазами.IEEE Trans Ind Appl 41 (3): 790–800. https://doi.org/10.1109/TIA.2005.847312

Артикул Google Scholar

7.

Мисир О., Поник Б. (2017) Определение индуктивностей синхронных машин с несимметричной обмоткой статора на основе уравнения напряжения одиночной катушки в обмотке статора. Электр Eng 99: 615. https://doi.org/10.1007/s00202-016-0389-y

Артикул Google Scholar

8.

Пономарев П., Линд П., Пирхёнен Дж. (2013) Влияние комбинации пазов и полюсов на индуктивность рассеяния и производительность синхронных машин с постоянным магнитом и зубчатой ​​обмоткой. IEEE Trans Ind Electr 60 (10): 4310–4317. https://doi.org/10.1109/TIE.2012.2216246

Артикул Google Scholar

9.

Schreier L, Bendl J, Chomat M (2017) Влияние комбинированной обмотки статора на уменьшение высших пространственных гармоник в индукционной машине.Электр Eng 99: 161. https://doi.org/10.1007/s00202-016-0409-y

Артикул Google Scholar

10.

Dajaku G, Spas S, Gerling D (2019) Расширенные методы оптимизации концентрированных обмоток с дробным пазом. Electr Eng. https://doi.org/10.1007/s00202-019-00760-6

Артикул Google Scholar

11.

Schreier L, Bendl J, Chomat M (2015) Влияние высших пространственных гармоник на свойства шестифазной индукционной машины, питаемой несимметричным напряжением.Электр. Англ., 97: 155. https://doi.org/10.1007/s00202-014-0319-9

Артикул Google Scholar

12.

Pyrhönen J, Jokinen T, Hrabovcova V (2014) Проектирование вращающихся электрических машин, 2-е изд. Wiley, Chichester, стр. 229–264. ISBN 978-1-118-58157-5

Google Scholar

13.

Müller G, Vogt K, Ponick B (2007) Streuung (утечка). В кн .: Расчеты электрических машин (Berechnung elektrischer Maschinen).Wiley-Vch, Weinhein, стр. 295–343. ISBN: 978-3527405251

14.

Boldea I, Nasar SA (2002) Индуктивность и сопротивление утечки. В кн .: Справочник по индукционным машинам. CRC Press, Boca Raton, pp 133–158. ISBN: 0-8493-004-5

15.

Риггерт Дж. Х., Васке П. (1967). Streuung umlaufender Maschinen (утечка во вращающихся машинах). В: Elektrische Maschninen und Umformer, Teil 2: Berechnung elektrischer Maschinen (электрические машины и преобразователи, часть 2: расчеты электрических машин), 7-е изд.Штутгарт, Германия, стр. 50–58

16.

Копылов И.П. (1988). Наврх асинхроннич строй (индукционная конструкция машины). В кн .: Ставба электричч строй (проектирование электрических машин), 1-е изд. Прага, СНТЛ, стр. 185–340. ISBN: 04-532-88

17.

Bortolozzi M, Branz L, Tessarolo A, Bruzzese C (2015) Улучшенный аналитический расчет индуктивности рассеяния прямоугольного паза ротора в асинхронных двигателях с короткозамкнутым ротором. В: Международная конференция по приложениям устойчивой мобильности, возобновляемым источникам энергии и технологиям (SMART), 2015 г., Кувейт, стр. 1–5.https://doi.org/10.1109/SMART.2015.7399266

18.

Bortolozzi M, Branz L, Tessarolo A, Bruzzese C (2015) Улучшенное аналитическое выражение для вычисления индуктивности рассеяния круглого стержня в полузамкнутом пазу. В: Международная конференция по приложениям устойчивой мобильности, возобновляемым источникам энергии и технологиям (SMART), 2015 г., Кувейт, стр. 1–5. https://doi.org/10.1109/SMART.2015.7399265

19.

Tessarolo A (2015) Аналитическое определение щелевого поля утечки и индуктивностей электрических машин с двухслойными обмотками и полузамкнутыми пазами.IEEE Trans Energy Convers 30 (4): 1528–1536. https://doi.org/10.1109/TEC.2015.2458181

Артикул Google Scholar

20.

Прието Б., Мартинес-Итурральде М., Фонтан Л., Элосеги И. (2015) Аналитический расчет индуктивности рассеяния паза в машинах с концентрированной обмоткой с дробным пазом. IEEE Trans Ind Electr 62 (5): 2742–2752. https://doi.org/10.1109/TIE.2014.2362094

Артикул Google Scholar

21.

Рихтер Р. (1967) Elektrische Maschinen (Электрические машины). Спрингер, Базель. ISBN: 978-3-0348-4066-8

Бронировать Google Scholar

22.