Резонанс в цепи синусоидального тока: Резонансы в цепях синусоидального тока (Лекция №8)

Элементы цепи синусоидального тока. Векторные диаграммы и комплексные соотношения для них. (Лекция N 4)

1. Резистор

Идеальный резистивный элемент не обладает ни индуктивностью, ни емкостью. Если к нему приложить синусоидальное напряжение (см. рис. 1), то ток i через него будет равен

.

(1)

Соотношение (1) показывает, что ток имеет ту же начальную фазу, что и напряжение. Таким образом, если на входе двухлучевого осциллографа подать сигналы u и i, то соответствующие им синусоиды на его экране будут проходить (см. рис. 2) через нуль одновременно, т.е. на резисторе напряжение и ток совпадают по фазе.

Из (1) вытекает:

;

.

 

Переходя от синусоидальных функций напряжения и тока к соответствующим им комплексам:

;

,

— разделим первый из них на второй:

или

.

(2)

Полученный результат показывает, что отношение двух комплексов есть вещественная константа. Следовательно, соответствующие им векторы напряжения и тока (см. рис. 3) совпадают по направлению.

2. Конденсатор

Идеальный емкостный элемент не обладает ни активным сопротивлением (проводимостью), ни индуктивностью. Если к нему приложить синусоидальное напряжение (см. рис. 4), то ток i через него будет равен

.

(3)

Полученный результат показывает, что напряжение на конденсаторе отстает по фазе от тока на

/2. Таким образом, если на входы двухлучевого осциллографа подать сигналы u и i, то на его экране будет иметь место картинка, соответствующая рис. 5.

Из (3) вытекает:

;

 

.

 

Введенный параметр называют реактивным емкостным сопротивлением конденсатора. Как и резистивное сопротивление, имеет размерность Ом. Однако в отличие от R данный параметр является функцией частоты, что иллюстрирует рис. 6. Из рис. 6 вытекает, что при конденсатор представляет разрыв для тока, а при .

Переходя от синусоидальных функций напряжения и тока к соответствующим им комплексам:

;

,

— разделим первый из них на второй:

или

.

(4)

В последнем соотношении — комплексное сопротивление конденсатора. Умножение на соответствует повороту вектора на угол по часовой стрелке. Следовательно, уравнению (4) соответствует векторная диаграмма, представленная на рис. 7.

3. Катушка индуктивности

Идеальный индуктивный элемент не обладает ни активным сопротивлением, ни емкостью. Пусть протекающий через него ток (см. рис. 8) определяется выражением

. Тогда для напряжения на зажимах катушки индуктивности можно записать

.

(5)

Полученный результат показывает, что напряжение на катушке индуктивности опережает по фазе ток на /2. Таким образом, если на входы двухлучевого осциллографа подать сигналы u и i, то на его экране (идеальный индуктивный элемент) будет иметь место картинка, соответствующая рис. 9.

Из (5) вытекает:

.

Введенный параметр называют реактивным индуктивным сопротивлением катушки; его размерность – Ом. Как и у емкостного элемента этот параметр является функцией частоты. Однако в данном случае эта зависимость имеет линейный характер, что иллюстрирует рис. 10. Из рис. 10 вытекает, что при

катушка индуктивности не оказывает сопротивления протекающему через него току, и при .

Переходя от синусоидальных функций напряжения и тока к соответствующим комплексам:

;

,

разделим первый из них на второй:

или

.

(6)

В полученном соотношении — комплексное

сопротивление катушки индуктивности. Умножение на соответствует повороту вектора на угол против часовой стрелки. Следовательно, уравнению (6) соответствует векторная диаграмма, представленная на рис. 11

 

4. Последовательное соединение резистивного и индуктивного элементов

Пусть в ветви на рис. 12 . Тогда

где

, причем пределы изменения .

Уравнению (7) можно поставить в соответствие соотношение

,

которому, в свою очередь, соответствует векторная диаграмма на рис. 13. Векторы на рис. 13 образуют фигуру, называемую треугольником напряжений. Аналогично выражение

графически может быть представлено треугольником сопротивлений (см. рис. 14), который подобен треугольнику напряжений.

 

5. Последовательное соединение резистивного и емкостного элементов

Опуская промежуточные выкладки, с использованием соотношений (2) и (4) для ветви на рис. 15 можно записать

.,

(8)

где

, причем пределы изменения .

На основании уравнения (7) могут быть построены треугольники напряжений (см. рис. 16) и сопротивлений (см. рис. 17), которые являются подобными.

6. Параллельное соединение резистивного и емкостного элементов

Для цепи на рис. 18 имеют место соотношения:

;

, где [См] – активная проводимость;

, где [См] – реактивная проводимость конденсатора.

Векторная диаграмма токов для данной цепи, называемая

треугольником токов, приведена на рис. 19. Ей соответствует уравнение в комплексной форме

,

где ;

— комплексная проводимость;

.

Треугольник проводимостей, подобный треугольнику токов, приведен на рис. 20.

Для комплексного сопротивления цепи на рис. 18 можно записать

.

Необходимо отметить, что полученный результат аналогичен известному из курса физики выражению для эквивалентного сопротивления двух параллельно соединенных резисторов.

7. Параллельное соединение резистивного и индуктивного элементов

Для цепи на рис. 21 можно записать

;

, где [См] – активная проводимость;

, где

[См] – реактивная проводимость катушки индуктивности.

Векторной диаграмме токов (рис. 22) для данной цепи соответствует уравнение в комплексной форме

,

где ;

— комплексная проводимость;

.

Треугольник проводимостей, подобный треугольнику токов, приведен на рис. 23.

Выражение комплексного сопротивления цепи на рис. 21 имеет вид:

.

Литература

1.     Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.

2.     Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.

Контрольные вопросы и задачи

1.     В чем сущность реактивных сопротивлений?

2.     Какой из элементов: резистор, катушку индуктивности или конденсатор – можно использовать в качестве шунта для наблюдения за формой тока?

3.      Почему катушки индуктивности и конденсаторы не используются в цепях постоянного тока?

4.     В ветви на рис. 12 . Определить комплексное сопротивление ветви, если частота тока .
Ответ: .

5.     В ветви на рис. 15 . Определить комплексное сопротивление ветви, если частота тока .
Ответ: .

6.     В цепи на рис. 18 . Определить комплексные проводимость и сопротивление цепи для .

Ответ: ; .

7.     Протекающий через катушку индуктивности ток изменяется по закону А. Определить комплекс действующего значения напряжения на катушке.
Ответ: .

Резонансные явления в цепях несинусоидального тока (Лекция №23)

В цепях несинусоидального тока резонансные режимы возможны для различных гармонических составляющих. Как и при синусоидальных токах, резонанс на к-й гармонике соответствует режиму работы, при котором к-е гармоники напряжения и тока на входе цепи совпадают по фазе, иначе говоря входное сопротивление (входная проводимость) цепи для к-й гармоники вещественно.

Пусть имеет место цепь на рис. 1,а, питающаяся от источника несинусоидальной ЭДС, в которой емкость конденсатора может плавно изменяться от нуля до бесконечности.

Для к-й гармоники тока можно записать

,

где — действующее значение к-й гармоники ЭДС.

Таким образом, при изменении С величина к-й гармоники тока будет изменяться от нуля при С=0 до при , достигая максимума при резонансе (см. рис. 1,б), определяемом величиной емкости

.

Следует отметить, что, несмотря на то, что обычно с ростом порядка гармонической ЭДС ее амплитуда уменьшается, в режиме резонанса для к-й гармонической ее значение может превышать величину первой гармоники тока.

Резонансные явления используются для выделения гармоник одних частот и подавления других. Пусть, например, в цепи на рис. 2 необходимо усилить q-ю гармонику тока на нагрузке и подавить р-ю.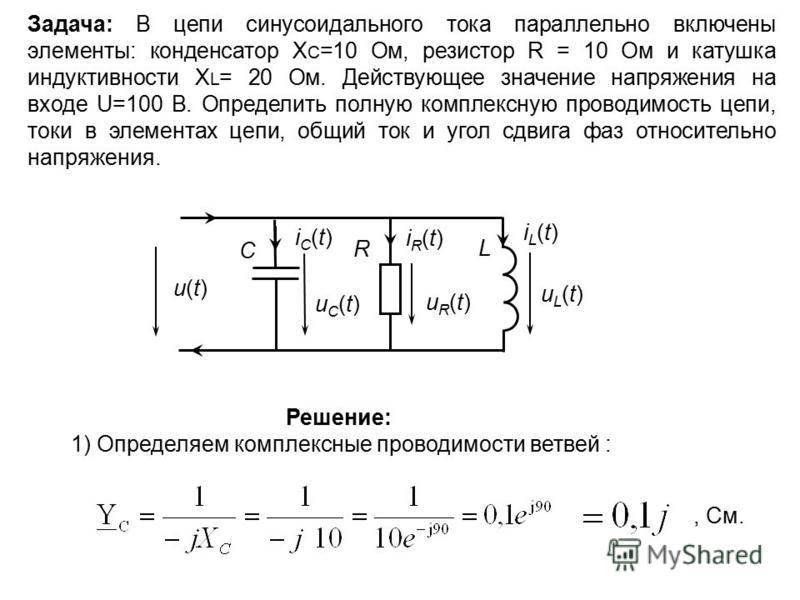

Для подавления р-й гармоники в режим резонанса токов настраивается контур :

.

Для выделения q-й гармоники вся цепь для нее настраивается в режим резонанса напряжений:

,

откуда при известных и

.

Отметим, что рассмотренные явления лежат в основе работы L-C -фильтров.

Особенности протекания несинусоидальных токов
через пассивные элементы цепи

1. Резистор.

При ток через резистор (см. рис. 3)

,

где .

Таким образом, на резистивном элементе несинусоидальные напряжение и ток совпадают по форме и подобны друг другу. Это позволяет на практике осциллографировать форму тока с помощью регистрации напряжения на шунте.

2. Конденсатор.

Пусть напряжение на конденсаторе (рис. 4) описывается гармоническим рядом .

Коэффициент искажения кривой напряжения

.

(1)

Ток через конденсатор

.

Тогда соответствующий кривой тока коэффициент искажения

.

(2)

Сравнение (1) и (2) показывает, что , т.е. конденсатор искажает форму кривой тока по сравнению с напряжением, являясь сглаживающим элементом для последнего.

Отмеченное наглядно иллюстрирует рис. 5, на котором форма кривой напряжения ближе к синусоиде, чем форма кривой тока.

3. Катушка индуктивности.

Принимая во внимание соотношение между напряжением и током для катушки индуктивности (рис. 6)

совершенно аналогично можно показать, что в случае индуктивного элемента , т. е. кривая напряжения искажена больше, чем кривая тока. Этому случаю будет соответствовать рис. 5 при взаимной замене на нем кривых напряжения и тока. Таким образом, катушка индуктивности является сглаживающим элементом для тока.

С учетом вышесказанного на практике, например в силовой полупроводниковой технике, для сглаживания выпрямленного напряжения применяют конденсаторные фильтры, а для тока – дроссели.

Высшие гармоники в трехфазных цепях

Напряжения трехфазных источников энергии часто бывают существенно несинусоидальными (строго говоря, они несинусоидальны всегда). При этом напряжения на фазах В и С повторяют несинусоидальную кривую напряжения на фазе А со сдвигом на треть периода Т основной гармоники:

.

Пусть для фазы А к-я гармоника напряжения

.

Тогда с учетом, что , для к-х гармонических напряжений фаз В и С соответственно можно записать:

Всю совокупность гармоник к от 0 до можно распределить по трем группам:

1. — гармоники данной группы образуют симметричные системы напряжений, последовательность которых соответствует последовательности фаз первой гармоники, т.е. они образуют симметричные системы напряжений прямой последовательности.

Действительно,

и

.

2. . Для этих гармоник имеют место соотношения:

т.е. гармоники данной группы образуют симметричные системы напряжений обратной последовательности.

3. . Для этих гармоник справедливо

Таким образом, векторы напряжений данной группы во всех фазах в любой момент времени имеют одинаковые модули и направления, т.е. эти гармоники образуют системы нулевой последовательности.

Рассмотрим особенности работы трехфазных систем, обусловленные наличием гармоник, кратных трем.

1. Если фазы генератора соединены в треугольник, то при несинусоидальных фазных ЭДС сумма ЭДС, действующих в контуре (см. рис. 7) не равна нулю, а определяется гармониками, кратными трем. Эти гармоники вызывают в замкнутом треугольнике генератора ток, даже когда его внешняя цепь разомкнута:

,

где , а — сопротивление фазы генератора для i-й гармоники, кратной трем.

2. Если фазы генератора соединить в открытый треугольник (см. рис. 8), то на зажимах 1-2 будет иметь место напряжение, определяемое суммой ЭДС гармоник, кратных трем:

Таким образом, показание вольтметра в цепи на рис. 8

.

3. Независимо от способа соединения – в звезду или в треугольник – линейные напряжения не содержат гармоник, кратных трем.

При соединении в звезду это объясняется тем, что гармоники, кратные трем, как указывалось, образуют нулевую последовательность, ввиду чего исчезают из линейных напряжений, равных разности фазных.

При соединении в треугольник составляющие фазных ЭДС, кратные трем, не выявляются в линейных (фазных) напряжениях, так как компенсируются падениями напряжений на собственных сопротивлениях фаз генератора.

Таким образом, при соединении в треугольник напряжение генератора

и ток

.

В свою очередь при соединении в звезду

.

4. При симметричной нагрузке ток в нейтральном проводе определяется гармоническими, кратными трем, поскольку они образуют нулевую последовательность:

.

5. При соединении в звезду и отсутствии нейтрального провода фазные токи нагрузки не содержат гармоник, кратных трем (в соответствии с первым законом Кирхгофа сумма токов равна нулю, что невозможно при наличии этих гармоник). Соответственно нет этих гармоник и в фазных напряжениях нагрузки, связанных с токами законом Ома. Таким образом, при наличии гармоник, кратных трем, в фазных напряжениях генератора напряжение смещения нейтрали в симметричном режиме определяется этими гармониками

.

Литература

1. Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
2. Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
3. Теоретические основы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.1. К.М.Поливанов. Линейные электрические цепи с сосредоточенными постоянными. –М.: Энергия- 1972. –240с.

Контрольные вопросы

1. Какой характер: монотонный или колебательный – будет иметь зависимость действующего значения тока от величины индуктивности в цепи на рис. 1 при ее изменении от нуля до бесконечности?
2. Почему на практике сигнал, пропорциональный току, получают с использованием резистивных шунтов?
3. Какие гармоники и почему определяют характерные особенности режимов работы трехфазных цепей?
4. Какие гармоники отсутствуют в линейных напряжениях и токах?
5. Почему при несинусоидальных источниках питания, соединенных в треугольник, действующее значение фазной ЭДС может быть больше действующего значения фазного напряжения?
6. При соединении трехфазного генератора и симметричной нагрузки по схеме «звезда-звезда» без нейтрального провода фазная ЭДС источника определяется выражением

Определить действующие значения линейного напряжения, фазных напряжений генератора и приемника, а также напряжение смещения нейтрали.

Ответ: .

7. В предыдущей задаче нейтральные точки генератора и приемника соединены проводом с нулевым сопротивлением.

Определить ток в нейтральном проводе, если сопротивление фазы нагрузки R=10 Ом.

Ответ: .

8. При соединении трехфазного генератора и симметричной нагрузки по схеме «треугольник-треугольник» фазная ЭДС источника содержит первую и третью гармоники с амплитудами . Сопротивление нагрузки для первой гармоники

Определить действующее значение линейного тока.

Ответ: .

2.11. Резонанс в цепях синусоидального тока » СтудИзба

2.11. Резонанс в цепях синусоидального тока.

Реактивные сопротивления и проводимость являются частотно-зависимыми величинами. Следовательно, при последовательном или параллельном соединении элементов L и C возможна на какой-то частоте полная компенсация реактивных сопротивлений или проводимостей. Режим, при котором наступает компенсация, называют резонансом. При резонансе входное сопротивление цепи становится активным, входное напряжение совпадает по фазе с входным током, а полная мощность будет активной. Угловая частота, , при которой наступает резонанс, называется резонансной или собственной угловой частотой цепи. Различают две разновидности резонанса: резонанс напряжений и резонанс токов.

2.11.1. Резонанс напряжений.

Может возникнуть в цепи с последовательным соединением L и C, рис. 2.20а.

Для этой цепи запишем:

.

Условие резонанса:

              или             ,

откуда резонансная частота .

Настройку цепи в резонанс, изменение параметров цепи при частотах , отличных от резонансной можно увидеть, если построить частотные характеристики сопротивлений, тока в цепи и напряжений на r, L, C.

На рис. 2.20б,в,г приведены частотные характеристики реактивных сопротивлений  и , суммарного реактивного сопротивления , модуля полного сопротивления , модуля входного тока , а также амплитудно-частотные характеристики напряжений:

,

,

.

По графику  определена резонансная частота , по графику  можно увидеть, что сопротивление цепи при резонансе минимально и равно активному сопротивлению, по графику  — что ток в цепи при резонансе максимален. Графики , ,  имеют ярко выраженный избирательный характер, т.е. имеют максимальные значения на резонансной частоте или вблизи нее. Можно также отметить, что напряжения  и  при резонансе могут превышать значение входного напряжения. Это хорошо иллюстрируется с помощью векторных диаграмм напряжения приведенных на рис. 2.20д,е,ж при частотах ,  и  .Обратите также внимание на значения угла  на этих частотах и сопоставьте эти значения с характером реактивных сопротивлений на соответствующих частотах. Так при частотах  , реактивное сопротивление носит емкостной характер и и т.д.

2.11.2. Резонанс токов.

Возможен в цепях с параллельным соединением L и C элементов, рис. 2.21а.

Для этой цепи запишем уравнение по первому закону Кирхгофа:

Компенсация реактивных проводимостей и реактивных токов:

                     ,

произойдет на резонансной частоте

Для анализа явления резонанса токов построим частотные характеристики реактивных проводимостей рис. 2.21б, модуля полной проводимости , рис.2.21в, модуля полного тока , рис. 2.21г. Здесь отмечена резонансная частота, полная проводимость цепи при резонансе минимальна и полный ток минимален. Векторные диаграммы токов, построенные для частот , ,, рис. 2.21д,е,ж, позволяют убедиться, что токи в катушке и конденсаторе могут значительно превышать полный ток.

Резонанс в цепи синусоидального тока

Явление резонанса возможно в цепях содержащих не менее двух энергоёмких элементов. Среди таких цепей различают последовательные цепи (рис. 3.35) и параллельные цепи (рис. 3.36).

Рис. 3.35	Рис. 3.36

Для цепи, изображенной на рис. 3.35, ;;. Тогда.

Последнее уравнение может быть записано в комплексной форме:

или после подстановок

,

где — комплекс действующего значения напряжения,- комплекс действующего значения тока,- действующее значение напряжения.

Уравнение в символической форме может быть записано для комплексов действующих значений и для комплексных амплитуд.

Используя введённые ранее обозначения и, запишем закон Ома для рассматриваемой цепиили после группировки, где- комплекс полного сопротивления цепи.

Модуль — полное сопротивление цепи определяется по формуле , а фазовый сдвиг. Их частотные зависимости приведены на рис. 3.37.

Характер изменения тока в контуре (рис. 3.38) в соответствии с законом Ома – обратный по отношению к характеру изменения реактивного сопротивления контура от частоты, поэтому на резонансной частоте модуль тока будет максимальным.
	Рис. 3.38

В последовательном -контуре на частотенаблюдается резонанс напряжений, который сопровождается существенным увеличением тока (рис. 3.38).

Основные параметры резонансного контура:

1) частота резонанса ;

2) волновое сопротивление контура на частоте резонанса ;

3) добротность контура, определяемая как отношение напряжения на индуктивности или емкости к приложенному напряжению на частоте резонанса: ;

4) резонансная цепь в процессе включения и выключения питания может обеспечивать колебательный процесс затухания. Показатель, характеризующий процесс перехода из одного состояния в другое, называется затуханием контура . Колебательный процесс в контуре затухает тем быстрее, чем меньше коэффициент.

Для параллельной резонансной цепи (рис. 3.36) следует строить треугольник токов, а не напряжений.

Примером использования явления резонанса является кварцевый резонатор, условное графическое обозначение которого приведено на рис. 3.40. Эквивалентная схема кварцевого резонатора (рис. 3.41) представляет собой колебательный контур.

Рис. 3.40	Рис. 3.41

Активная, реактивная и полная мощность

в цепи синусоидального тока

В выражении закона Ома для цепи синусоидального тока присутствует множитель , называемый комплексным сопротивлением цепи. В общем случаеимеет некоторую действительную и некоторую мнимую часть:, где- активное сопротивление,- реактивное сопротивление. Как и всякий комплекс,можно записать в показательной форме:, где- модуль комплексного сопротивления, равный.

, где — действительная часть,- мнимая часть. Как и всякий комплекс,можно записать в показательной форме:, где- модуль комплексной проводимости, равный.

Под активной мощностью понимается среднее значение мгновенной мощностиза период:. Если ток, а напряжение на участке цепи, то

,

где — коэффициент мощности.

Активная мощность физически представляет собой энергию, которая выделяется в единицу времени (за целое число периодов) в виде теплоты на участке цепи в сопротивлении . Единица активной мощности – Вт.

Под реактивной мощностью понимают произведение напряженияна участке цепи на токпо этому участку и на синус угламежду напряжениеми током:. Единица реактивной мощности – вольт-ампер реактивный (ВАр). Физический смысл реактивной мощности рассмотрим на примере участка цепи с последовательным соединением,и. Пусть по нему протекает ток. Тогда мгновенное значение суммы энергий магнитного и электрического полей цепи:

Из полученного выражения видно, что имеет постоянную составляющую, неизменную во времени, и переменную составляющую, изменяющуюся с двойной угловой частотой.

На создание постоянной составляющей была затрачена энергия в процессе установления данного периодического режима. В дальнейшем при периодическом процессе энергияостается неизменной и, следовательно, от источника питания не требуется энергии на ее создание.

Ответы на все модули (для контрольного теста) по предмету электротехника, электроника и схемотехника.

Автор admin На чтение 40 мин. Просмотров 642 Опубликовано 25.02.2013

Ответы на все модули (для контрольного теста) по предмету электротехника, электроника и схемотехника.

Ответы на модуль 1 (ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ, ТОПОЛОГИЧЕСКИЕ ПАРАМЕТРЫ И МЕТОДЫ РАСЧЕТА ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА) по предмету электротехника, электроника и схемотехника.

1) Напряжение измеряется в следующих единицах: вольт (В).

2) При применении метода параллельного преобразования резистивной схемы эквивалентная проводимость равна: алгебраической сумме проводимостей резистивных элементов.

3) Электрическая мощность связана с величиной напряжения: прямо пропорциональной зависимостью.

4) При методе расчета цепей с помощью законов Кирхгофа действует следующее правило выбора контуров для составления уравнений: каждый после­дующий контур должен включать в себя хотя бы одну новую ветвь, не охвачен­ную предыдущими уравнениями.

5) Какое сходство у идеализированных источников напряжения и тока: способны отдавать в электрическую цепь неог­раниченную мощность.

6) Величина магнитного потока измеряется в следующих единицах: вебер (Вб).

7) При наличии полной симметрии между схемами резистивных цепей звезда – треугольник величина сопротивления элемента схемы треугольник: равна двум величинам сопротивления элемента схемы звезда.

8) Ток измеряется в следующих единицах: ампер (А).

9) Электрическая проводимость обратно пропорциональна: электрическому сопротивлению.

10) Электрическое напряжение – это: энергия, расходуемая на перемещение единицы заряда.

11) По второму закону Кирхгофа в любом замкнутом контуре электрической цепи: алгебраическая сумма па­дений напряжений на элементах, входящих в контур, равна алгебраической сумме ЭДС.

12) Значение индуктивности прямо пропорционально: потокосцеплению.

13) В индуктивном элементе (реактивное сопротивление) происходит:  запасание магнитной энергии.

14) К источнику электрической энергии относится: аккумулятор.

15) По закону Ома для цепи, не содержащей ЭДС: сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению.

16) Электрический ток определяется как: произведение электрического заряда и времени.

17) При расчете цепи методом контурных токов применяются: первый и второй законы Кирхгофа.

18) В емкостном элементе (реактивное сопротивление) происходит: запасание электрической энергии.

19) К приемнику электрической энергии относится: электронагреватель.

20) Первый закон Кирхгофа гласит: сумма токов, подходящих к узлу, равна сумме токов, выходящих из узла.

21) Электрическая мощность измеряется в следующих единицах: ватт (Вт).

22) При применении метода последовательного преобразования резистивной схемы эквивалентное сопротивление равно: алгебраической сумме сопротивлений резистивных элементов.

23) В резистивном элементе происходит: не­обратимое преобразование электромагнитной энергии в тепло или другие виды энергии.

24) Какое из понятий не характеризует геометрию цепи: «элемент».

25) По принципу наложения ток в любой ветви сложной схемы, содержащей несколько источников, равен: алгебраической сумме частичных токов, возникающих в этой ветви от независи­мого действия каждого источника в от­дельности.

 

Ответы на модуль 2 (АНАЛИЗ И РАСЧЕТ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА) по предмету электротехника, электроника и схемотехника.

1) В цепи синусоидального тока с резистивным элементом: ток и напряжение совпадают по фазе.

2) На практике единицей измерения полной мощности в гармонических цепях является: вольт-ампер (ВА).

3) Электрические величины гармонических функций нельзя представить: вещественными числами.

4) При последовательном соединении элементов R, L и C при положительных значениях реактивного сопротивления и угла сдвига фаз электрическая цепь в целом носит следующий характер: активно-индуктивный.

5) Если сдвиг фаз между током и напряжением меньше нуля, то: напряжение опережает ток по фазе.

6) Проекция вращающегося вектора гармонической функции на ось ординат в любой момент времени, равна: мгновенному значению функции времени.

7) В цепи синусоидального тока с катушкой индуктивности: ток опережает напряжение на угол 90º.

8) Коэффициент отношения действующего значения синусоидального напряжения к его амплитудному значению составляет: 0.707.

9) Гармоническим электрическим током называется ток, который: изменяется во времени по своему значению и направлению через равные промежутки времени.

10) Какое из свойств не относится к гармоническому току: после многократной трансформации форма сигнала изменяется.

11) Угловая частота синусоидального тока: обратно пропорциональна периоду колебаний.

12) В цепи синусоидального тока с конденсатором: напряжение опережает ток на угол 90º.

13) По первому закону Кирхгофа в комплексной форме: сумма комплексных значений токов, подходящих к узлу, равна сумме комплексных значений токов, выходящих из узла.

14) Наиболее распространенный переменный ток изменяется в соответствии с функцией: синус.

15) По закону Ома в комплексной форме: комплексное значение тока прямо пропорционально комплексному значению напряжения и обратно пропорционально комплексному значению сопротивления.

16) В цепи синусоидального тока с конденсато­ром С происходит: обратимый процесс обмена энергией между электрическим полем конденсатора и источником.

17) Амплитудные значения гармонического тока: изменяются по синусоидальному закону.

18) Коэффициент отношения среднего значения синусоидального тока к его максимальному значению составляет: 0.637.

19) По второму закону Кирхгофа в комплексной форме в любом замкнутом контуре электрической цепи: алгебраическая сумма комплексных значений напряжений на сопротивлениях контура равна алгебраической сумме комплексных значений ЭДС.

20) Активная мощность активно-реактивной электрической цепи на переменном токе не зависит от: угловой частоты гармонических колебаний.

21) Активная мощность в цепи синусоидального тока с резистивным элементом всегда больше нуля, что означает: в цепи с резистором протекает необратимый процесс преобразования электроэнергии в другие виды энергии

22)  При последовательном соединении элементов R, L и C при отрицательных значениях реактивного сопротивления и угла сдвига фаз электрическая цепь в целом носит следующий характер: емкостный.

23) Деление комплексных чисел может выполняться: только в алгебраической форме.

24) К характеристикам гармонического тока не относится: минимальные значения тока и напряжения.

25) Комплексное число нельзя представить в следующей форме: квадратичной.

 

Ответы на модуль 3 (КОЛЕБАТЕЛЬНЫЕ КОНТУРЫ. ЯВЛЕНИЯ РЕЗОНАНСА.) по предмету электротехника, электроника и схемотехника.

1) При изменении частоты внешнего источника энергии: изменяются реактивные сопротивления элементов, ток в цепи и на­пряжения на отдельных участках.

2) Какой из параметров не характеризует свойства параллельного колебательного контура? волновое сопротивление ρ.

3) Полоса пропускания резонансного контура: обратно пропорциональна его добротности.

4) Какое из мероприятий нельзя проводить для повышения коэффициента мощности электрической цепи? для компенсации индуктивной составляющей тока последовательно с приемниками включать конденсаторы.

5) Какое свойство не относится к напряжениям U_L и U_C на реактивных элементах в цепи, находящейся в режиме резонанса напряжений? напряжения совпадают по фазе и не равны по модулю.

6) Явление резонанса напряжений наблюдается в цепи: с последовательным соединением источника энергии и реактивных элементов L и C.

7) В режиме резонанса напряжений: активное сопротивление равно реактивному сопротивлению.

8) Для параллельного колебательного контура, если сдвиг фаз между напряжением на участке цепи и током меньше нуля, то: общий ток имеет емкостной характер.

9) Активная мощность равна полной мощности в режиме резонанса, если коэффициент мощности: cosφ = 1.

10) Свободные колебания контура не зависят от: частоты вынужденных колебаний источника энергии ω.

11) В режиме резонанса в случае совпадения частоты собственных колебаний wo с частотой вынужденных колебаний источника энергии ω (ω_o = ω): амплитуда гармонических колебаний энергии в цепи увеличивается.

12) Условие возникновения резонансного режима можно определить через параметры элементов схемы следующим образом: входное сопротивление (входная проводимость) схемы со стороны выводов источника энергии должно носить реактивный характер.

13) Резонанс напряжений возникает при следующем условии: полное сопротивление цепи имеет минимальное значение и равно активному значению.

14) Для параллельного колебательного контура, если сдвиг фаз между напряжением на участке цепи и током больше нуля, то: общий ток имеет индуктивный характер.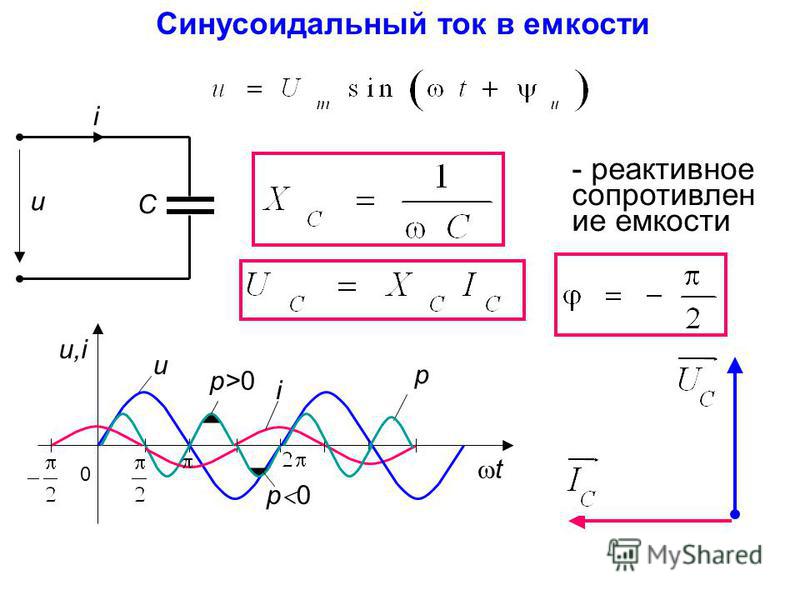

15) Резонанса токов в электрической цепи нельзя достичь следующим способом: изменением параметра активного элемента цепи R.

16) В режиме резонанса токов полная проводимость электрической схемы имеет: максимальное значение и равна значению активной проводимости.

17) Какое из свойств не относится к току источника, протекающему через цепь с элементами R, L и C в режиме резонанса токов? имеет минимальное значение.

18) При наличии в электрической цепи режима резонанса напряжений: ток максимален и совпадает по фазе с напряжением источника.

19) Основное условие возникновения резонанса токов вытекает из следующего условия: реактивная проводимость индуктивного элемента равна реактивной проводимости емкостного элемента.

20) Угол сдвига фаз между напряжением и током в электрической цепи при параллельном соединении элементов R, L и C определяется как арктангенс отношения: общей реактивной проводимости к активной проводимости.

21) Явление резонанса токов наблюдается в электрической цепи: с параллельным соединением источника энергии и реактивных элементов L и C.

22) В электрической цепи возможно появление свободных гармонических колебаний энергии, если в ней: содержатся как катушки индуктивности L, так и конденсаторы С.

23) Какой из параметров не относится к свойствам последовательного колебательного контура? волновая проводимость γ.

24) При параллельном соединении элементов R, L и C общая реактивная проводимость электрической цепи равна: полной комплексной проводимости схемы.

25) Резонанс напряжений в цепи нельзя достичь следующим способом: изменением параметра активного элемента цепи R.

26) Какое из условий не относится к токам I_L и I_C в ветвях с реактивными элементами в режиме резонанса токов? токи совпадают по фазе.

27) Если в сложной схеме электрической цепи при изменении частоты наблюдаются несколько резонансных режимов (как тока, так и напряжения) в зависимости от ее структуры, то такая схема содержит в своей структуре: более двух разнородных реактивных элементов.

 

Ответы на модуль 4 (ТРЕХФАЗНЫЕ ЦЕПИ. ТРЕХФАЗНЫЕ СИСТЕМЫ ЭДС.) по предмету электротехника, электроника и схемотехника.

1) Какое международное обозначение имеет каждая из фаз трехфазной цепи? А, В, С.

2) Линейным током в трехфазной сети называется ток, протекающий: в линейных проводах по направлению от генератора к приемнику.

3) Соединение в трехфазной сети по схеме «треугольник» образуется, когда: концы каждой из фазных обмоток соединяются с началом другой фазы, а точки соединения подключаются линейными проводами с трехфазным приемником.

4) В трехфазной системе мгновенные значения напряжения и тока каждой фазы сдвинуты друг относительно друга во времени на величину: ∆ω = 120º.

5) Величина реактивной мощности симметричной трехфазной цепи не связана прямо пропорциональной зависимостью: с синусом угла сдвига фаз между линейными напряжением и током.

6) Что не относится к достоинствам трехфазной симметричной системы? обеспечивает простоту в конструкции и надежность в работе элементов трехфазной системы.

7) Для оптимального измерения активной мощности симметричной трехфазной цепи с нулевым проводом используется: схема с одним ваттметром, который включается в одну из фаз и измеряет активную мощность только этой фазы.

8) В симметричной трехфазной сети по схеме «звезда» векторы линейного и двухфазных напряжений образуют: три равнобедренных треугольника, острые углы которых равны 30º.

9) Общий провод NN’ трехфазной симметричной системы обладает следующим свойством: мгновенное значение тока в данном проводе равно нулю в любой момент времени.

10) В трехфазной сети, соединенной по схеме «треугольник», коэффициент отношения линейного тока к фазному току, равен: √3.

11) Режим перекоса фазных напряжений в трехфазной системе приемника возникает при включении: несимметричной трехфазной нагрузки по схеме «звезда» без нулевого провода.

12) Величина активной мощности симметричной трехфазной цепи не связана прямо пропорциональной зависимостью: с синусом угла сдвига фаз между линейными напряжением и током.

13) Трехфазная система – это: совокупность трех независимых цепей переменного тока, каждая из которых называется фазой.

14) При соединении трехфазной сети по схеме «треугольник»: номинальное фазное напряжение приемника равно линейному напряжению генератора.

15) При соединении симметричной трехфазной сети по схеме «звезда» линейные токи: равны по значению и совпадают по направлению с фазными токами.

16) Трехфазное соединение по схеме «звезда» применяется в том случае, когда: номинальное напряжение приемника равно фазному напряжению генератора.

17) В соответствии с первым законом Кирхгофа ток в нулевом проводе в трехфазной сети по схеме «звезда» равен: геометрической сумме линейных (фазных) токов.

18) В каком из случаев трехфазное соединение по схеме «звезда» без нулевого провода не может применяться? при подключении к несимметричной трехфазной нагрузке.

19) В симметричной трехфазной сети, соединенной по схеме «звезда», коэффициент отношения линейного напряжения к фазному напряжению равен: √3.

20) Линейные напряжения в трехфазной схеме «звезда» определяются как: векторная сумма фазных напряжений.

21) В векторной диаграмме соединения трехфазной сети по схеме «треугольник» углы между векторами линейных напряжений составляют: 120º.

22) Линейные токи при симметричной нагрузке в трехфазной сети по схеме «треугольник» сдвинуты друг относительно друга на: 120º.

23) Трехфазное соединение по схеме «звезда» образуется, если: начала трехфазных обмоток генератора объединены в одну общую нейтральную точку.

24) Какое из условий не выполняется в трехфазной сети по схеме «треугольник»? линейные напряжения равны фазным напряжениям.

25) Нейтральным током в трехфазной сети называется ток, протекающий: в нулевом проводе по направлению от приемника к генератору.

 

Ответы на модуль 5 (ЧЕТЫРЕХПОЛЮСНИКИ) по предмету электротехника, электроника и схемотехника.

1) Входное сопротивление четырехполюсника Z_1К для А-формы записи в режиме короткого замыкания при питании со стороны первичных выводов прямо пропорционально: B и обратно пропорционально D.

2) Какое из соотношений относится к Т-образной схеме замещения пассивного четырехполюсника? C = Y₁ + Y₂ + Y₁ • Y₂ • Z_0.

3) Уравнение связи между коэффициентами: A ∙ D – B ∙ C = 1 — четырехполюсника А-формы записи показывает, что: независимыми являются только три из четырех коэффициентов четырехполюсника.

4) M-фильтрами называются электрические фильтры, в которых: произведение продольного сопротивления на соответствующее поперечное сопротивление есть величина переменная, зависящая от частоты.

5) Что не содержит внутри себя активный четырехполюсник? комбинацию R, L, C элементов без источников энергии.

6) К-фильтрами называются электрические фильтры, в которых: произведение продольного сопротивления на соответствующее поперечное сопротивление есть величина постоянная, не зависящая от частоты.

7) Границы полосы пропускания сигнала (ω₁, ω₂) определяются по частотам, на которых коэффициент передачи напряжения фильтра K(ω): увеличивается в 0,7 раза.

8) Для симметричного четырехполюсника для П-образной схемы должно выполняться следующее равенство: Z₁ = Z_2.

9) Что не содержит внутри себя пассивный четырехполюсник? набор резистивных элементов и источник тока.

10) Какие функции выполняют полосовые фильтры? фильтры пропускают сигналы в диапазоне частот от ω₁ = 0 до ω₂ и подавляют остальные сигналы.

11) Для уравнения какой формы записи четырехполюсника ток I₂ имеет противоположное направление аналогичному току I₂ уравнения Z-формы записи? Y.

12) В симметричном четырехполюснике А-форма записи принимается, что: А = D  и  соответственно: A² — B · C = 1.

13) Четырехполюсник – часть электрической цепи или схемы, которая содержит: два входных вывода для подключения источника электроэнергии и два выходных вывода для подключения нагрузки.

14) В четырехполюснике B-форма записи при входном воздействии (U₂, I₂) наблюдается отклик системы: U₁, I_2.

15) Выходное сопротивление четырехполюсника Z_2К для В-формы записи в режиме короткого замыкания при питании со стороны вторичных выводов прямо пропорционально: B и обратно пропорционально A.

16) Какое условие не выполняется в полосе прозрачности фильтра? все гармоники сигнала должны иметь время запаздывания, пропорциональное их номеру гармоники.

17) Какие функции выполняют режекторные фильтры? фильтры пропускают сигналы в диапазоне частот от 0 до ω₁ и от ω₂  до ∞, и подавляют сигналы в диапазоне частот от ω₂  до ω_2.

18) Коэффициент затухания четырехполюсника в теории измеряется в: неперах (Нп).

19) Выходное сопротивление четырехполюсника Z_2Х для В-формы записи в режиме холостого хода при питании со стороны вторичных выводов прямо пропорционально: D и обратно пропорционально C.

20) Какое из соотношений относится к П-образной схеме замещения пассивного четырехполюсника? A = 1 + Z₁ • Y_{0 .}

21) Из уравнения связи между коэффициентами: A ∙ D – B ∙ C = 1 — четырехполюсника А-форма записи следует, что его Т— или П-образная простейшие схемы замещения содержат: три независимых элемента с однозначной зависимостью между коэффициентами A, B, C, D и сопротивлениями схемы.

22) К передаточным функциям, которые являются одними из важных характеристик четырехполюсника, не относится: передаточная емкость.

23) В четырехполюснике H-форма записи при входном воздействии (U₁,I₂) наблюдается отклик системы: U₂, I_1.

24) Для симметричного четырехполюсника для Т-образной схемы должно выполняться следующее равенство: Z₁ = Z_2.

25) Входное сопротивление четырехполюсника Z_1X для А-формы записи в режиме холостого хода при питании со стороны первичных выводов прямо пропорционально: A и обратно пропорционально C.

 

Ответы на модуль 6 (ПЕРЕХОДНЫЕ ПРОЦЕССЫ) по предмету электротехника, электроника и схемотехника.

1) Индуктивность подобна разрыву электрической цепи в месте ее включения в момент коммутации, если ток в индуктивности в момент коммутации: имеет нулевое значение.

2) Какому из оригиналов функции f(t) соответствует изображение функции F(p):  

sinωt

3) По закону Ома в операторной форме для участка цепи, содержащего ЭДС, при ненулевых начальных условиях операторное изображение тока: прямо пропорционально операторному значению суммы всех источников ЭДС ветви и обратно пропорционально операторному сопротивлению всей схемы.

4) По первому закону коммутации в любой электрической ветви ток (магнитный поток), протекающий через индуктивность, в момент коммутации сохраняет значение, которое было непосредственно перед коммутацией.

5) Классическим методом расчета переходных процессов называют: определение закона изменения токов и напряжений с помощью интегрирования дифференциальных уравнений.

6) По законам коммутации переходные процессы отсутствуют в цепях, содержащих следующие элементы: только активные сопротивления.

7) Какой из этапов не относится к основным этапам расчета переходного процесса классическим методом? составление характеристического уравнения и определение его корней.

8) В схеме имеют место нулевые начальные условия, если к началу переходного процесса непосредственно перед коммутацией: все токи и все напряжения на пассивных элементах схемы равны нулю.

9) В линейных электрических цепях свободная составляющая токов (напряжений) изменяется во времени следующим образом: затухает по показательному закону.

10) Первый закон Кирхгофа в операторной форме гласит: алгебраическая сумма операторных изображений токов, сходящихся в любом узле схемы, равна нулю.

11) Следующий процесс не относится к переходному процессу: реконфигурация цепи.

12) Через какой промежуток времени t, кратный постоянной времени τ, переходный процесс считается практически завершенным? .

13)  Для описания переходных процессов используется неоднородное линейное дифференциальное уравнение с постоянными коэффициентами n-го порядка, где n — число: последовательно включенных реактивных элементов.

14) По второму закону коммутации в любой электрической ветви напряжение (заряд) на емкости: в момент коммутации сохраняет значение, которое было непосредственно перед коммутацией.

15) Второй закон Кирхгофа в операторной форме гласит: алгебраическая сумма па­дений операторных изображений напряжений на элементах, входящих в контур, равна алгебраической сумме операторных изображений ЭДС, включая внутренние источники.

16) К независимым (до

Синусоидальные функции и анализ цепей

2. Образование
3. Наука
4. Электроника
5. Синусоидальные функции и анализ цепей

Автор Джон Сантьяго

Синусоидальные функции (синус и косинус) появляются повсюду и играют важную роль в схемотехнике. Синусоидальные функции обеспечивают хорошее приближение для описания поведения входа и выхода схемы не только в электротехнике, но и во многих областях науки и техники.

Синусоидальная функция является периодической, то есть ее график содержит основную форму, которая повторяется снова и снова бесконечно. Функция продолжается вечно, колеблясь через бесконечные пики и спады как в отрицательном, так и в положительном направлениях времени. Вот некоторые ключевые части функции:

• Амплитуда В _А определяет максимальные и минимальные пики колебаний.

• Частота f ₀ описывает количество колебаний за 1 секунду.

• Период T ₀ определяет время, необходимое для завершения 1 цикла.

Период и частота являются обратными друг другу и регулируются следующей математической зависимостью:

Вот функция косинус вы можете использовать в качестве опорного сигнала:

Вы можете перемещать синусоидальные функции влево или вправо со сдвигом по времени, а также увеличивать или уменьшать амплитуду.Вы также можете описать синусоидальную функцию со сдвигом фазы в терминах линейной комбинации функций синуса и косинуса. Вот функция косинуса и функция смещенного косинуса со сдвигом фазы π / 2.

Фазовые сдвиги в синусоидальной функции

Сигнал, который находится вне фазы , сдвинут влево или вправо по сравнению с опорным сигналом:

• Сдвиг вправо : когда функция перемещается вправо, функция называется с задержкой .Пик запаздывающего косинуса находится после начала координат. Задержанный сигнал также называется сигналом запаздывания , потому что сигнал прибывает позже, чем ожидалось.

• Сдвиг влево : Когда функция косинуса смещается влево, смещенная функция называется расширенной . Пик опережающего сигнала происходит непосредственно перед началом координат. Расширенный сигнал также называется сигналом отведения , потому что сигнал отведения приходит раньше, чем ожидалось.

Вот примеры функций несмещенного, запаздывающего и опережающего косинуса.

Чтобы увидеть, как выглядит фазовый сдвиг математически, сначала взгляните на опорный сигнал:

При t = 0 положительный пик V _A служит точкой отсчета. Чтобы переместить опорную точку с помощью сдвига по времени T _S , замените t на ( t — T _S ):

где

Коэффициент ϕ — это фазовый сдвиг (или угол).Фазовый сдвиг — это угол между t = 0 и ближайшим положительным пиком. Вы можете рассматривать предыдущее уравнение как полярное представление синусоиды. Когда фазовый сдвиг равен π / 2, то смещенный косинус является синусоидальной функцией.

Выразите фазовый угол в радианах, чтобы убедиться, что он в тех же единицах, что и аргумент косинуса (2π t / T ₀ — ϕ ). Углы могут быть выражены в радианах или градусах; убедитесь, что вы используете правильные настройки на вашем калькуляторе.

Когда у вас есть фазовый сдвиг ϕ на выходе по сравнению с входом, это обычно вызвано самой схемой.

Разложите синусоидальную функцию и найдите коэффициенты Фурье.

Общая синусоида v (t) включает косинус разности углов. Во многих приложениях вы можете расширить общую синусоиду, используя следующую тригонометрическую идентичность:

Расширение общей синусоиды v (t) приводит к

Члены c и d — это просто специальные константы, называемые коэффициентами Фурье .Вы можете выразить форму волны как комбинацию синусов и косинусов следующим образом:

Функция v (t) описывает синусоидальный сигнал в прямоугольной форме.

Если вы знаете, что ваши комплексные числа переходят между полярными и прямоугольными формами, то вы можете переходить между двумя формами синусоид. Коэффициенты Фурье c и d связаны амплитудой V _A и фазой ϕ :

Если вы вернетесь, чтобы найти V _A и ϕ из коэффициентов Фурье c и d , вы получите следующие выражения:

Функция арктангенса на калькуляторе имеет положительную или отрицательную фазовую неоднозначность 180 ° (или π).Узнать фазу можно, посмотрев на знаки коэффициентов Фурье c и d . Нарисуйте точки c и d на прямоугольной системе, где c — это компонент x (или по оси абсцисс ), а d — компонент y (или по оси ординат ).

Отношение d / c может быть отрицательным в квадрантах II и IV. Использование прямоугольной системы помогает определять углы при использовании арктангенса, диапазон которого составляет от –π / 2 до π / 2.

Соедините синусоидальные функции с экспонентами с помощью формулы Эйлера

Формула Эйлера связывает триггерные функции с комплексными экспоненциальными функциями. Формула утверждает, что для любого действительного числа θ у вас есть следующие сложные экспоненциальные выражения:

Показатель степени j θ — мнимое число, где j = √-1.

Мнимое число j такое же, как число i из ваших математических классов, но все крутые люди используют j для мнимых чисел, потому что i обозначает ток.

Вы можете сложить и вычесть два предыдущих уравнения, чтобы получить следующие отношения:

В этих уравнениях говорится, что функции косинуса и синуса построены как комбинация комплексных экспонент. Сложные экспоненты играют важную роль, когда вы анализируете сложные схемы, в которых есть запоминающие устройства, такие как конденсаторы и катушки индуктивности.

Страница не найдена | MIT

Перейти к содержанию ↓

• Образование
• Исследование
• Инновации
• Прием + помощь
• Студенческая жизнь
• Новости
• Выпускников
• О MIT
• Подробнее ↓
  • Прием + помощь
  • Студенческая жизнь
  • Новости
  • Выпускников
  • О MIT

Меню ↓ Поиск Меню Ой, похоже, мы не смогли найти то, что вы искали!
Попробуйте поискать что-нибудь еще! Что вы ищете? Увидеть больше результатов

Предложения или отзывы?

ECE 291 Лаборатория 8: Резонансные схемы

ЗАДАЧИ

Демонстрация резонансных явлений в цепях RLC.Измерения резонанса характеристики и их сравнение с теорией.

ВВЕДЕНИЕ

Резонанс — одно из важнейших и общих явлений практически во всех отраслях науки и техники. Например, в механических системах часто наблюдается резонанс при колебаниях балки или пружины, поддерживающей груз. Вибрации вызваны передачей потенциальной энергии, накопленной при отклонении балки или сжатии пружины, кинетической энергии движущейся массы, вперед и назад в периодическом движении.В электрических цепях энергия, накопленная в виде электрического поля в конденсаторе, передается электрическому току в цепи, в которой индуктивность играет роль, эквивалентную инерционной массе в механической системе. Уравнения, описывающие оба резонанса, идентичны, только их коэффициенты имеют значения, связанные с механическими (масса, жесткость пружины) или электрическими (емкость, индуктивность) параметрами. Еще одна важная аналогия между двумя системами заключается в том, что вибрации можно гасить; трением в механических системах и сопротивлением электрических цепей.

Резонанс может быть очень полезен в таких устройствах, как генераторы в радиопередатчиках или электронные часы. Однако чаще они могут быть вредными, вызывая нежелательные широкие отклонения механических систем (мостов, крыльев самолетов и т. Д.) Или колебания напряжения и тока. Контроль или предотвращение нежелательного резонанса — важный аспект инженерного проектирования. Поскольку каждый электрический компонент или даже соединительный провод имеет некоторую емкость и индуктивность, в каждой цепи есть потенциал для резонанса.Как вы уже знаете, чем меньше значения индуктивности и емкости, тем выше резонансная частота. Поэтому проектирование высокочастотных цепей намного сложнее, ведь даже небольшая индуктивность и емкость соединений играют роль. В этом наборе экспериментов вы исследуете резонанс в последовательном RLC-контуре, который имеет резонанс в относительно низком и легком для обработки частотном диапазоне.

Важные взаимосвязи в электрическом резонансе:

Частота резонанса:

Пропускная способность:

Фактор качества:

PRELAB

Изобразите так называемую резонансную кривую для последовательного резонансного контура на Рис.7. По вертикальной оси отложите ток (или напряжение на резисторе R), а по горизонтальной оси отложите лог f . Укажите резонансную частоту f _o и ширину резонансной кривой (ширины полосы), которая представляет собой интервал Δf = 2πΓ между две частоты, при которых мощность, рассеиваемая в цепи, составляет ½ от максимум. Рассчитайте эти числа для определенных значений компонентов, которые вы можно использовать в лаборатории, например: R = 1k, C = 1nF, L = 50 mH.

Подсказка: Обратите внимание, что три компоненты соединены последовательно с источником напряжения, поэтому легко написать выражение для тока (с использованием комплексных чисел). Ток достигает максимума (резонанс) для определенной частоты, при которой полное сопротивление цепи равно равно R (какова фаза тока на этой частоте?). На половину мощности частот ток падает до 1 / √2.

Когда у вас есть выражение для тока, вы можете использовать его в программе для работы с электронными таблицами (например, MS Excel) или использовать какое-либо другое программное обеспечение (например, Matlab) для расчета и построения кривой резонанса (соотношение V _R / V _s как функция от log f ).Он также понадобится вам для вашего отчета.

В качестве альтернативы вы можете смоделировать работу схемы с помощью Multisim. Распечатайте кривую частотной характеристики, используя полулогарифмический график для компонентов R, L и C, указанных выше. Для лабораторного отчета измените моделирование фактическими значениями компонентов, используемых в лаборатории.

Независимо от метода создания резонансной кривой (ваши собственные расчеты или Multisim), определите количество точек данных и их местоположение (частоту) для лучшего определения резонансной частоты и ширины полосы.

ЛАБОРАТОРИЯ

Необходимое оборудование со склада: Протоборд, поводки, прицел зонды.

1. ПОСЛЕДОВАТЕЛЬНАЯ ЦЕПЬ РЕЗОНАНСА, ПРИВЕДЕННАЯ А СИНУСОИДНОЕ НАПРЯЖЕНИЕ

a) Соберите последовательный резонансный контур, показанный ниже. Используйте катушку 50 мГн из вашего набора деталей для L, выберите резистор примерно 1 кОм и конденсатор от 1 до нескольких нФ. Перед сборкой измерьте значения этих компонентов. Также измерьте сопротивление катушки с помощью цифрового омметра.Рассчитайте ожидаемую резонансную частоту.

Рис.7 Последовательный резонансный контур

b) Подключите один пробник осциллографа к источнику напряжения, другой — к R и одновременно наблюдайте за двумя сигналами на разных каналах осциллографа. Обратите внимание на амплитуды и разность фаз при изменении частоты. Если амплитуда напряжения генератора зависит от частоты, вы можете отрегулировать ее так, чтобы она оставалась постоянной, в противном случае запишите ее значения для разных частот.Получите достаточное количество точек данных для построения резонансной кривой. Постарайтесь точно определить резонансную частоту на пике кривой и частоты в точках половинной мощности по обе стороны от максимума. Измерьте также фазовый сдвиг между V _s и V _R на этих трех частотах и ​​нескольких других частотах по обе стороны от максимума. Обычно легче точно определить резонансную частоту по измерению фазы, чем по амплитуде.

c) Измерьте также напряжение на конденсаторе в резонансе, используя функцию вычитания сигнала цифрового осциллографа, которая вычитает сигналы двух каналов осциллографа. Обратите внимание, что оно больше, чем напряжение генератора. Отношение этих напряжений равно значению цепи Q .

2. РЕЗОНАНСНАЯ ЦЕПЬ ВОЗБУЖДАЕТСЯ СТУПЕНЬ НАПРЯЖЕНИЕ

Переключите генератор сигналов с синусоидальной волны на прямоугольную на резонансной частоте контура.Какова форма текущего сигнала? Вы можете объяснить это наблюдение?

Затем отрегулируйте частоту прямоугольной волны примерно до одной десятой резонансной частоты контура. Разверните изображение по горизонтали и наблюдайте за формой сигнала после шага входного сигнала. Распечатайте изображение осциллографа. Вы можете определить частоту колебаний?
Изображение показывает реакцию любой резонансной системы на внешнее возмущение, представленное здесь импульсом (прямоугольной волной).

3. МОДЕЛИРОВАНИЕ ЦЕПИ (дома).

Имитация измерений 1 и 2: частотная характеристика амплитуды и фазы и временная зависимость тока с прямоугольным сигналом на входе. Используйте те же значения R, L и C при моделировании, что и в лаборатории. Сравните результаты моделирования с измерениями.

ОТЧЕТ

• Постройте графики резонансных кривых, показывающих амплитуду (график V _R / V _S ) и фаза ( ∠ V _R — ∠ V _S ).Представьте расчетные (смоделированные) результаты в виде непрерывных кривых, а экспериментальные данные — в виде точек на одном графике.
• Сравните измеренные значения резонансной частоты и ширины резонансных кривых при максимуме половинной мощности (ширина полосы) со значениями, рассчитанными или смоделированными для компонентов схем, фактически используемых в лаборатории.
  Как изменяется фаза на резонансной кривой?
• Сравните результаты п.